アインシュタイン著「一般相対性理論の基礎」(1916年)
Einstein著,“Die Grundlage der allgemeinen Relativita¨tstheorie”, Leipzig,
Barth (1916年に出版された小冊子)
《Ann. der Phys. Ser. 4, 49 (1916年3月), p769~822 にも掲載された。》
の翻訳版である内山龍雄訳「一般相対性理論の基礎」(共立出版「アインシュタイン選集2」[A3] p59~114)の引用です。
ただし、改行や式変形の補足《矢印記号が挿入されている所》を含めてかなり改変しています。また、一つの§をさらに幾つかに分割している所もあります。それらは私どもが適当に行いました。そのため、元表現は源文献でご確認下さい。また内山先生の解説も秀逸ですので、合わせてご覧下さい。また、この論文の成り立ちについてPaisの解説p355とp359もご覧下さい。
A.相対性理論の要請についての原理的考察
(1)特殊相対性理論に関する注意
(2)相対性の要請の拡張の根拠
(3)時空.物理法則を示す方程式の一般共変性の要求
(4)時間・空間的測定と座標との関係.重力場の数式的表現
B.一般共変方程式に対する数学的準備
(5)反変および共変ベクトル
(6)2階および高階テンソル
1.反変テンソル
2.共変テンソル
3.混合テンソル
4.対称テンソル
5.反対称テンソル
(7)テンソルの積
1.テンソルの外積
2.混合テンソルの縮約
3.テンソルの内積及び混合積
4.テンソルの商法則
(8)基本テンソルgμνに関する二、三の性質
1.共変基本テンソル
2.反変基本テンソル
3.基本テンソルの行列式
4.不変体積
5.時空の特性に対する注意
6.基本テンソルによる新しいテンソルの導出
(9)測地線の方程式(質点の運動方程式)
(10)微分によるテンソルの形成
(11)二、三の重要な関係式
1.基本テンソルに関する補助定理
2.反変ベクトルのDiv
3.共変ベクトルのRot
4.6元ベクトルの反対称共変微分
5.6元ベトクルのDiv
6.2階混合テンソルのDiv
7.まとめ
(12)リーマン・クリストッフェルのテンソル
C.重力場の理論
(13)重力場内にある質点の運動方程式.重力の数式的表現
(14)物質が存在しないときの重力場の方程式
(15)重力場に対するハミルトン関数.運動量・エネルギー保存則
(16)重力場の方程式の一般形式
(17)一般の場合の保存則
(18)物質の運動量・エネルギーの法則
D.“物質”現象
(19)摩擦のない断熱的流体に対するオイラーの方程式
(20)真空中の電磁場に対するマックスウェルの方程式
1.Maxwell方程式
2.電磁場のエネルギー成分
E.理論の検証
(21)第1近似としてのニュートンの理論
1.質点の運動方程式
2.重力場の方程式
(22)静的重力場内にある物指と時計.光線の湾曲.惑星軌道の近日点移動
1.静的重力場内にある物指と時計
2.光線の湾曲
3.惑星軌道の近日点移動
参考文献
[補足説明1]
アインシュタインは特殊相対性理論から、加速度を持った系においては時計の進み方がゆっくりになり、その中の物指し棒が縮むことを知ります。さらに彼は、ニュートン以来の課題であった慣性質量と重力質量の違いについて等価原理の着想に至ります。これは加速度系と重力場は同じものであることを示すものです。そのためアインシュタインは重力場の中に存在する時計はゆっくり進み、重力場の中にある物指し棒は縮まねばならいことに気づきます。(このことは「双子のパラドックスと一般相対性理論」5.を参照)
所で、重力場を作りだすのは物質でありエネルギーです。そこで彼は物質(エネルギー)は存在するだけで時空間を歪めると推測します。
これらの着想を得たのは1907~1911年の間です。しかしそのことを論じる数学は極めて複雑なものになることが予想されます。1911~1912年夏まで彼はその数学的な手法を求めてもがき苦しみます。友人のグロースマンの助力を得て彼は最終的にテンソル解析学(絶対微分学)がその解決のための数学的手段でありその鍵はクリストッフェル記号とリーマンの曲率テンソルである事を理解します。そして、時空の歪みを表すものが計量テンソルであることを理解します。
1912年の秋の段階のアインシュタインは、以下の理解に達していました。
時空を歪めるのは物質(エネルギー)である。だからその数学的表現であるエネルギー・運動量テンソルが方程式の右辺になり、左辺は時空の歪みを表す曲率テンソルの何らかの関係式であるに違いない。ただし、その曲率テンソルに関係する量(テンソル)が何であるかはまだわからない。
その左辺に関係すると思われる曲率テンソルはクリストッフェル記号により表されている。そしてクリストッフェル記号は計量テンソルの関数である。
つまり求めるべき重力場の方程式の左辺は計量テンソルの関数形で表すことができるに違いない。それはエネルギー・運動量テンソルから計量テンソルを決めるためのテンソル方程式を構成するはずだ。さらに、その様な重力場の方程式は近似的にニュートンの古典的な重力場の方程式を拡張したものになっているはずである。
数学的手段とこれから進むべき道を理解したアインシュタインは、上記の方針に従って邁進します。実際の所、正しい重力場方程式の発見は困難を極め1912年秋の段階からさらに3年の歳月を要した。
( 「アインシュタイン一般相対性理論への道程」 と 「アインシュタインの重力場方程式」 参照)
その当たりの詳細は文献8.のPaisの説明が詳しい。しかし、本稿ではそのあたりはすべて省略されて結論だけが簡潔に提示されます。
[補足説明2]
Einstein論文の数式記法について別稿「アインシュタイン一般相対性理論への道程(1907~1914年)」1.[補足説明1]で説明しましたが、本稿について確認しておきます
1.反変・共変成分表示を指数の上・下で表示。・・・1914年10月論文からそうしている。
2.反変座標成分に関する表記・・・表記dxμや∂xμは、すべてdxμや∂xμに修正。§3.訳者注*
3..クリストッフェル記号・・・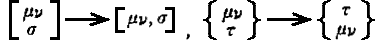 へ修正。§9.訳者注*
へ修正。§9.訳者注*
4.縮約操作に関する“アインシュタインの規約”・・・本論文から実施された。B.§5.3.
5.座標変換後の物理量の表記・・・物理量表現記号に’を付ける形。§6.1.
ただし、この点については物理量表現記号に’を付けるのでは無くて、添字指数に’を付けて表示する今日的表現法の方が優れています。各自でその様に読み替えられることを勧めます。
6.共変微分の表記・・・微分する座標の指数記号を下指数として追記する形。§10.[補足説明1]
ただし、この点については微分する座標の指数記号を下指数として追記するとき、その前に;を挿入する今日的表現法の方が優れています。各自でその様に読み替えられることを勧めます。§11.2.[補足説明1]
A.相対性の要請についての原理的考察
アインシュタインは、このA章で一般相対性理論の本質を語っています。ただし、説明文の意味を真に理解することは極めて難しい。そのため、参考文献5.の第2部 や 参考文献6.の第3回講義前半 を参考にしながら読まれると良いかもしれません。
§1.特殊相対性理論に関する注意

[補足説明1]
[光速度不変の要請]が本質である事は別稿「ローレンツ変換とは何か」や「マイケルソン・モーリーの実験の特殊相対性理論による説明」などで繰り返し説明しました。
このことが、ミンコフスキー時空の計量テンソルの特異な形と強く結びついている。それは一般相対性理論の時空の計量テンソルの形を強く拘束する。

§2.相対性の要請の拡張の根拠









[補足説明1]
ここの“光速度が一定という原理が修正されなければならない”という言い方を誤解しないで下さい。歪み曲がった時空を伝播する光の速度は一定不変です。つまり光速度をその歪んだ時空の中で測定すると一定値を保っています。そして、光はその歪んだ時空の中を、測地線に沿って真っ直ぐに進んでいます。
§3.時空、物理法則を示す方程式の一般共変性の要求










[補足説明1]
上記の“自然法則が座標変換に対して共変な等式となる任意の座標変換”について補足します。
この座標変換とは別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」3.の最初に黒二重線枠で囲った所のものです。すなわち
一般相対性理論における座標変換とは、2つの異なる世界点の間の変換を含んだものではありません。同一の世界点を座標原点とする座標軸の回転の様なものです。これはアインシュタインがミンコフスキーの業績を高く評価した一つの理由です。別稿で説明したように、ミンコフスキーは、“ローレンツ変換が四次元空間における回転にほかならないことをもしめした。”のですが、自然法則が共変でなければならない座標変換とは、その原点を空間的にずらす事も含めた座標変換では無いと言うことです。座標の原点を固定して、時間座標軸と空間座標軸の関係(つまり互いの座標軸の交叉の仕方、斜交座標の斜交の仕方を変えると言うことです。この座標変換に対して共変でなければならないと言うことです。もちろん、その様な座標変換に限っても、その中には異なった速度(加速度)で動いている座標系への座標変換を含んでいます。また、空間座標についてもその斜交角が時間的に任意の変化をする斜交座標系への座標変換を含んでいます。
もちろんこの中には、ミンコフスキー時空への座標変換やミンコフスキー時空から一般相対性理論時空への座標変換も含まれています。ただしこの言い方を誤解しないで下さい。ミンコフスキー時空は一般相対性理論のリーマン時空のある点における接空間ですから、元々同一の時空間内に取った座標系間の座標変換で移り変わると言うようなものではありません。多くの相対論の教科書の説明はこの点に於いてとても曖昧です。このことについては「基底ベクトル・双対基底ベクトルと反変成分・共変成分」1.(1)~(2)と、4.(1)~(3)をご覧下さい。いずれにしても、一般相対性理論の時空では、各世界点の微小領域においてのみ意味のある斜交座標系がとれ、その微小領域における異なった斜交座標系間の座標変換が、“自然法則が座標変換に対して共変な等式となる任意の座標変換”を意味します。
これは一般相対性理論に向かうとき、座標変換に対して必要な最重要な制約です。実際一般相対性理論の世界では4次元空間の座標原点(世界点)をずらすことも含めた座標変換などは意味が無いのですから。つまり自然法則が共変でなければならない座標変換とは4次元時空間における座標原点(世界点)を固定した回転であるようなもので無ければ成りません。もちろん一般相対性理論の世界では単なる回転ではありませんが、いずれにしてもミンコフスキーの4次元世界の座標回転をさらに一般化したようなものです。
座標変換をこのように捉えることは、4次元世界の世界距離(一般相対性理論の世界では微小である必要がありますが)が座標変換に対して不変であると言うことを理解する上でも有益です。
以下に続くEinsteinの説明を噛みしめて下さい。


§4.時間・空間的測定と座標との関係、重力場の数式的表現



[補足説明1]
上記の“(1)式の値が局所座標系の方向に無関係な、空間・時間的測定によって与えられた値を持つ”と言うことの意味は別稿「双子のバラドックスと一般相対性理論」2.(2)を復習して下さい。
ここが、特殊、一般の両相対性理論で最も解り難い所ですが、別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」2.(1)の基底ベクトルと双対基底の関係を与える計量テンソルを思い出されて下さい。その計量テンソルがミンコフスキー時空では(4)式で表されるのだった思い出されることが最も納得できる理解のしかただと思います。
物質が存在し重力場が存在する現実の時空の計量テンソルは、そのミンコフスキー時空の計量テンソルを一般化したものです。つまり(4)式の形の計量テンソルを一般化した計量テンソル(gστ)です。それは時空内の場所と共に変化しますし、別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」3.(4)で注意したように座標変換に依って変化します。


[補足説明2]
上記の(3)式については、別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」2.(5)を参照。また、(2)式と(3)式の関係については、別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」3.(1)~(6)や別項「微分幾何学3.」3.(2)2.[補足説明3]を参照して下さい。
もちろん、そこの3次元リーマン空間を4次元リーマン時・空に拡張して考える必要はあります。すなわち4次元ミンコフスキー時・空をリーマン時・空に拡張したものと考えます。なんだか禅問答の様な言い方ですが、この言い方の真意はその内わかります。お解りになったときが一般相対性理論が理解できたときです。




[補足説明3]
ここの“gστで重力場を記述できる”という説明の中には、アインシュタインがそもそもこの道に乗り出すきっかけとなったGaussの曲面論における“驚異の定理”から始まる膨大な考察の裏付けが含まれている事を忘れないで下さい。
それらを考慮しないと、アインシュタインの説明文の深遠さを読み取ることはできません。ここは一般相対性理論を理解する上で最も重要な所です。
B.一般共変方程式に対する数学的準備
訳者も指摘されているように、このB章はとても的確に解りやすく説明されています。しかし、この数学には多くの内容が含まれるため、初学者が読まれても何のことか解らないと思います。その解らない所を文中に挿入する形で補うのは大変ですから、別稿「一般相対性理論を理解するための数学的準備」を作りました。そちらを参考にされながらお読み下さい。参考文献6.と7.も有益かも知れません。



このことに付いては別稿の引用文もご覧下さい。
§5.反変及び共変ベクトル
“反変”と“共変”の概念は、おそらく一般相対性理論の数学で最も解りにくい所です。これは斜交座標で議論しなければ成らなくなった事によって必要になったのですが、斜交座標こそが一般相対性理論の本質なのです。ここは別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」1.(3)~2.(3)を参照しながらお読み下さい。
1.反変ベクトル


2.共変ベクトル


3.記号の簡易化

[補足説明1]
上記の簡易化が有名な“Einsteinの規約”ですが、このようにできることは、反変成分同士や共変成分同士では縮約できず、反変成分と共変成分でないと縮約できない事に基づきます。
そのような形で縮約した量でないと、座標変換に対して不変な物理的に意味のある量にならないのです。物理的に意味のある量を取り扱うには、その様にしなければ成らない所にリーマン幾何学の本質があります。特に、微分操作Div演算などするときにもこのことは必要です。リーマン幾何学が不変式論と言われる理由です。
そのとき、共変成分と反変成分の関係は、各時空点における時空の性質に関係する計量テンソルに依って決まります。計量テンソルを仲介にして反変成分を共変成分に変換したり、逆に共変成分を反変成分に変換することができます。
ただし、最初に定めた反変成分も元々座標の取り方に依存していますから、座標を替えると座標変換に依存して変化します。もちろん、各時空点における計量テンソルgμνも座標の取り方に依存していますので、座標変換により変化します。
Einsteinはその本質を見抜いていたと言うことです。ここはB.(11)3.[補足説明1]も参照。

§6.2階および高階テンソル
1.反変テンソル





2.共変テンソル

3.混合テンソル


4.対称テンソル


別稿「対称テンソルと反対称テンソルの独立成分の数」4.も参照されたし。
5.反対称テンソル


反対称テンソルの独立成分の数については別稿「対称テンソルと反対称テンソルの独立成分の数」2.を参照。
§7.テンソルの積
1.テンソルの外積

2.混合テンソルの縮約

ここは解りにくいところです。別稿「微分幾何学」3.(2)5.の説明をチェックされたし。
3.テンソルの内積および混合積


普通の“直交空間”ならば、いわゆる“ベクトルの内積”や“行列の積”の事を言っているのですが、“斜交リーマン空間”では“反変成分”と“共変成分”の“縮約”という形でないと意味のある量(つまり座標変換不変量)にならないと言うことです。
4.テンソルの商法則
以下ではいわゆる“テンソルの商法則”を説明しています。“テンソルの商法則”の意味は解りにくい所ですので、別稿「微分幾何学」3.(2)6.などを参照して下さい。後で繰り返しこの定理を用いますので、そこでも確認できます。




§8.基本テンソル gμν に関する二、三の性質
1.共変基本テンソル

2.反変基本テンソル
下記の“よく知られた行列式の定理”については別稿「余因子行列と逆行列の関係」、あるいは別稿「行列式と行列」2.(3)を参照されたし。



[補足説明1]
gμσが“共変基本テンソル”、gνσが“反変基本テンソル”ですが、両者を添字σで縮約(いわば内積)してできる混合型は対角成分が 1 となり、それ以外はすべて 0 となるテンソルδνμに成ると言うことです。
これが“基本テンソル”の“混合型”なのですが、この事実こそが、別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」1.(3)3.[補足説明1] や 2.(1) で述べた事に対応します。
つまり、“基底ベクトル”と“双対基底ベクトル”の互いの関係に付いての制約を表しておリーマン幾何学を展開する上で《最重要な要請・仮定》です。
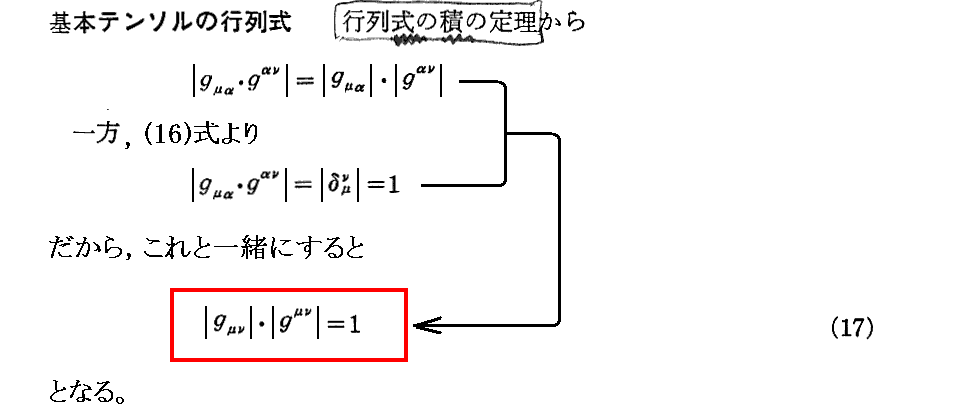
3.基本テンソルの行列式
下記の“行列式の積の定理”に付いては別稿「行列式と行列」1.(6) と 「行列式と行列」2.(1)4.[定理1] を参照されたし。
4.不変体積
以下の議論については、別稿3.(7)“体積不変量” と、 4.(6)5.“体積素片の座標変換”を参照。

下記の体積素片の変換規則である“ヤコービの定理”については別稿「重積分の変数変換とヤコビアン」をご覧下さい。



上記の“我々の時空が双曲型の連続体であるために”は解りにくい表現ですが、要するの我々が住んでいる世界はミンコフスキー時空を拡張したものであると言うことです。
5.時空の特性に対する注意


上記注意書きは 極めて重要!! です。このことが、重力場の理論(一般相対性理論)が単なるリーマン幾何学の理論ではなくて、“特殊相対性理論”を“一般化した相対性理論”と言われる理由です。ここにこの理論の本質と難しさがあります。


6.基本テンソルによる新しいテンソルの導出



§9.測地線の方程式(質点の運動方程式)
ここの“測地線方程式”の導出は明快です。



[補足説明1]
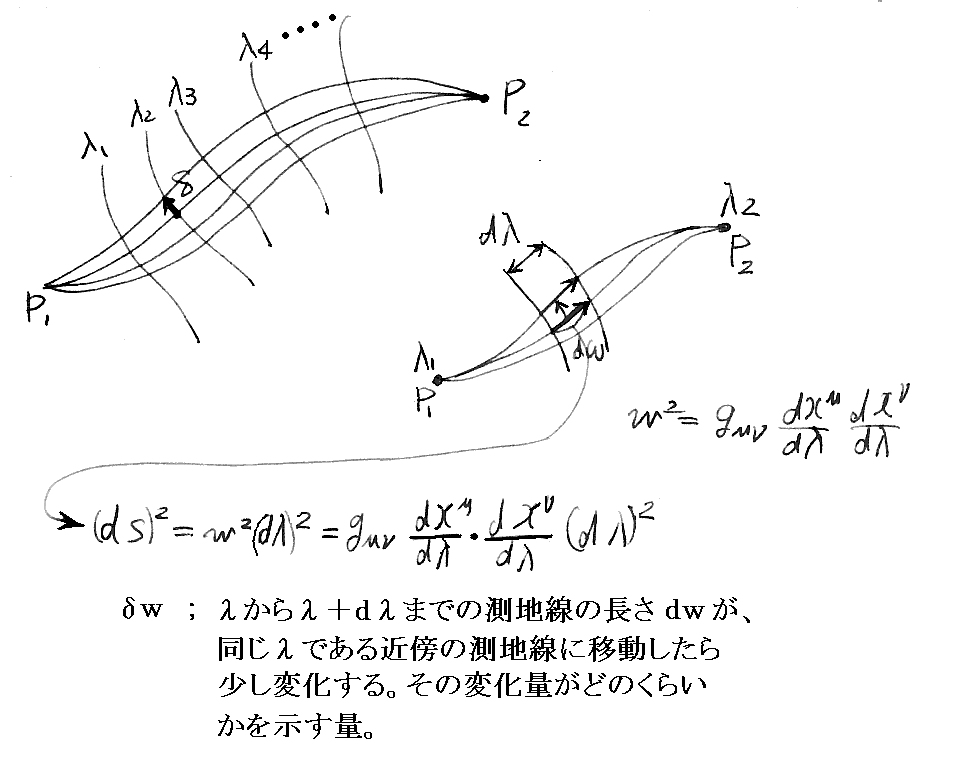


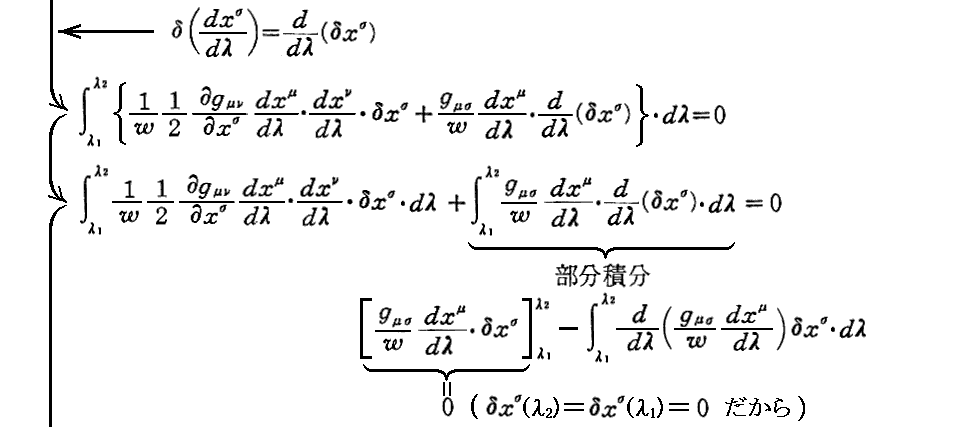



このようにして導入された“クリストッフェル記号”が何を意味するのかを理解するのは極めて難しい。
Einsteinは、この記号が別稿4.(4)で説明した意味を持つことを当然理解していたのですが、よくもまあその当たりを見極めたものだと思います。
§10.微分によるテンソルの形成


(24)式の右辺の量が共変ベクトルになることに、B§7.4.の“テンソルの商法則”を用いていることに注意。下記の“我々の定理”とは“テンソルの商法則”を指しています。




[補足説明1]
訳者注:への補足です。より正確には“共変微分”ではなくて“共変微分係数”と言うべきです。
さらに補足すると、“共変微分係数”の表示に於いて、今日では別稿6.(3)1.[補足説明1]で説明した様に、添字νの前に“カンマ ,”や“セミコロン ;”や“コロン :”などを挿入している。しかし、Einstein論文では、それらは記入されていません。特に§11の説明を読まれるときには、今日の表記を意識して読まれると良いと思います。
ここは何を言っているのか解りにくいと思います。要するに曲がった時空における座標xνに関する微分は、ただ単に
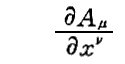
としたのでは意味のある量に成らないと言うことです。
時空自体が歪んでいる事による効果を補正した形で微分を定義しないといけない。その補正する部分が
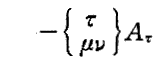
でして、この補正をしたものはテンソルの性質を持ち曲がった時空に於いても意味のある微分量となるということです。










[補足説明2]
“共変微分”の導入には様々な方法があります。Einsteinの説明と下記説明を比較検討されると、共変微分の意味が良く解ると思います。
「基底ベクトル・双対基底ベクトルと反変成分・共変成分」4.(5)
「平行移動とリーマン幾何学」4.
「微分幾何学」3.(3)
「テンソル解析学」6.(3)
共変微分は反変座標の変分に対する変化量を論じるもの(ここは別稿6.(3)1.[補足説明1-1]参照)ですから、本来反変ベクトルAμや反変テンソルAμνの共変微分係数(つまり反変成分の変化量)から話を始めたほうが解りやすい。しかし、Einsteinは共変ベクトルAμの共変微分から話を初めている。
そうしたのはおそらく、[スカラー関数の共変微分(当然共変ベクトルになる)が重要である]ことと、[リーマン時空では共変と反変のどちらがより本質であると言うことは無くて、両者が等価・対等な関係(ここは別稿1.(3)2.参照)である]こと、などを考慮してのことだろう。
§11.二、三の重要な関係式
1.基本テンソルに関する補助定理

上式の最初の=は行列式の微分の規則から下記の様にして導けます。

[補足説明1]
上記の行列式の余因数展開(A)式については別稿「行列式と行列」1.(4)3.を参照。
また(B)式は、gμνとgμνが互いに逆行列の関係になっているので、「行列式と行列」2.(3)1.の定理を用いれば成り立つことが解る。
ここは実際に3次元で計算してみた方が解りやすいかも知れません。[拡大版]
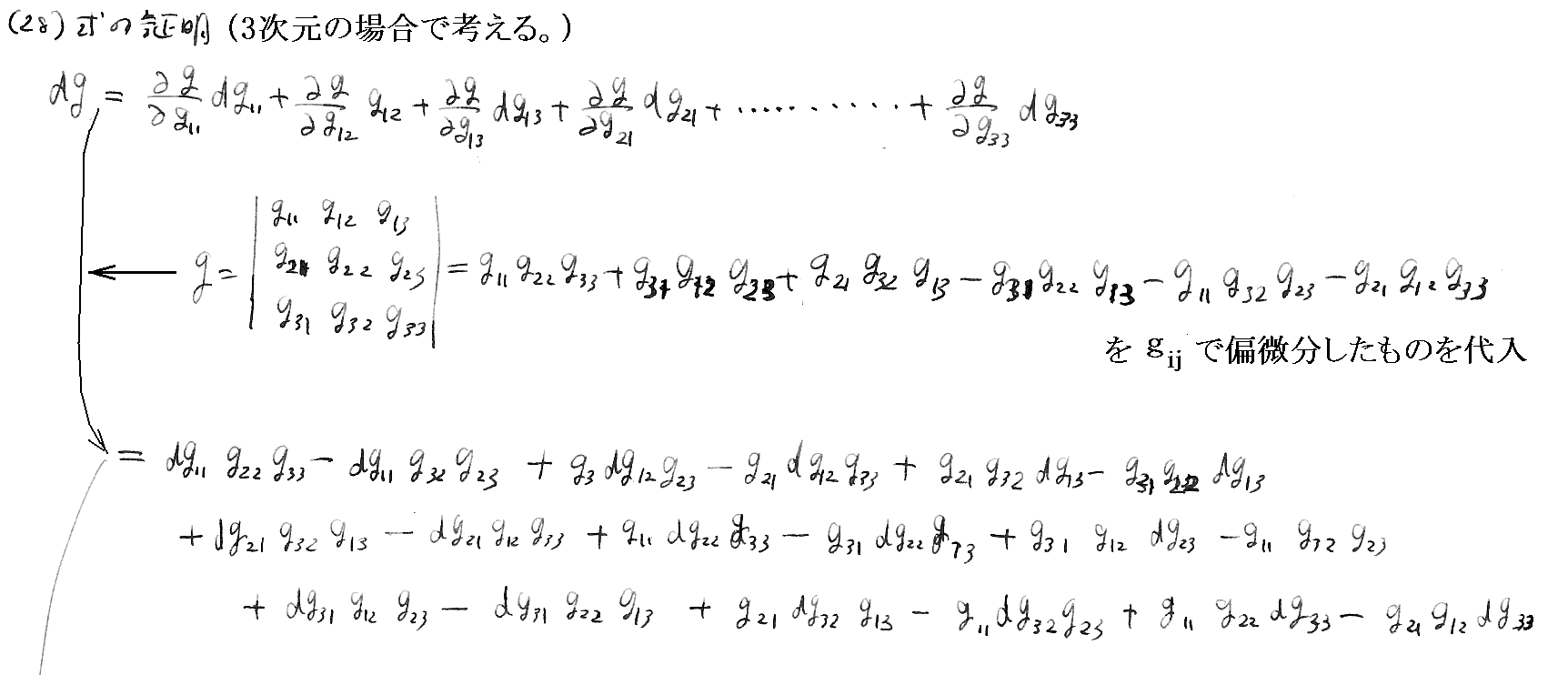
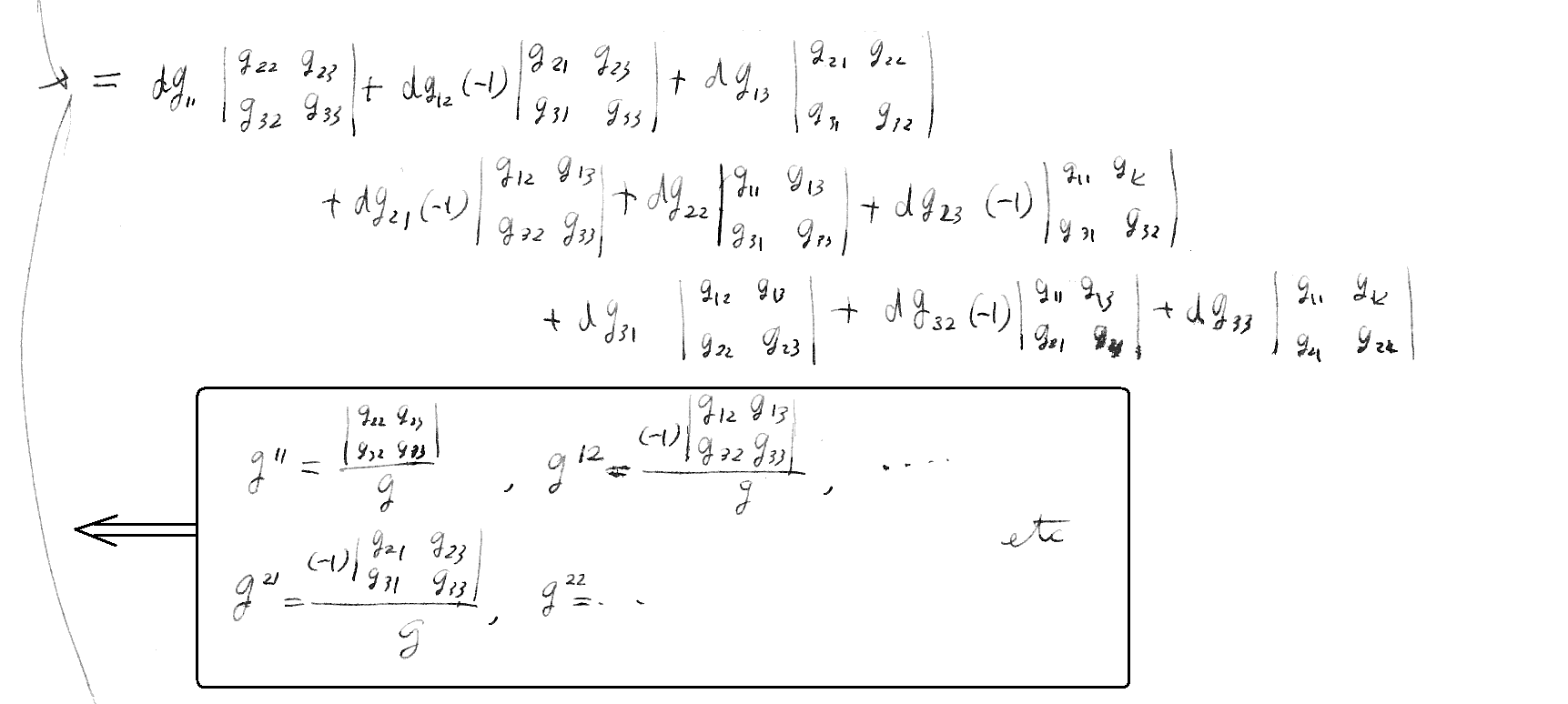
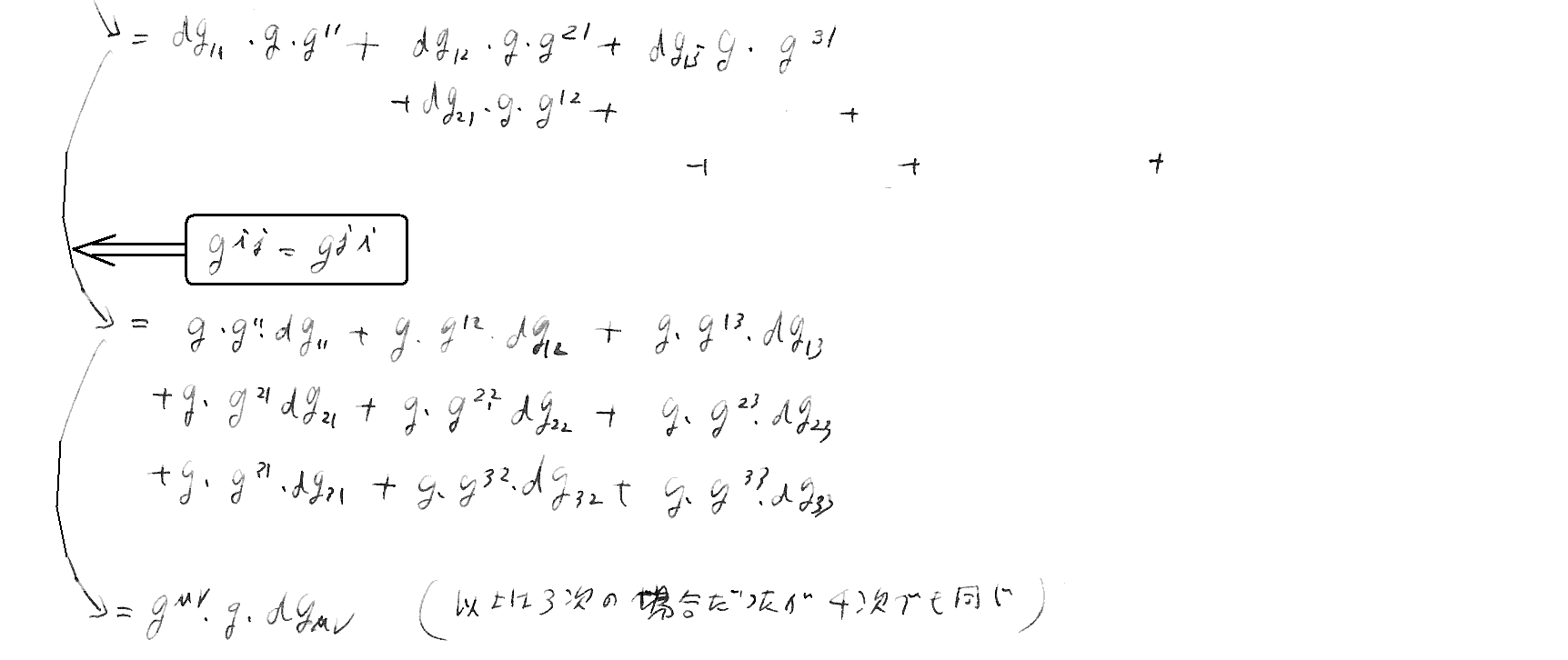

[補足説明2]
最後の式は、一般的に
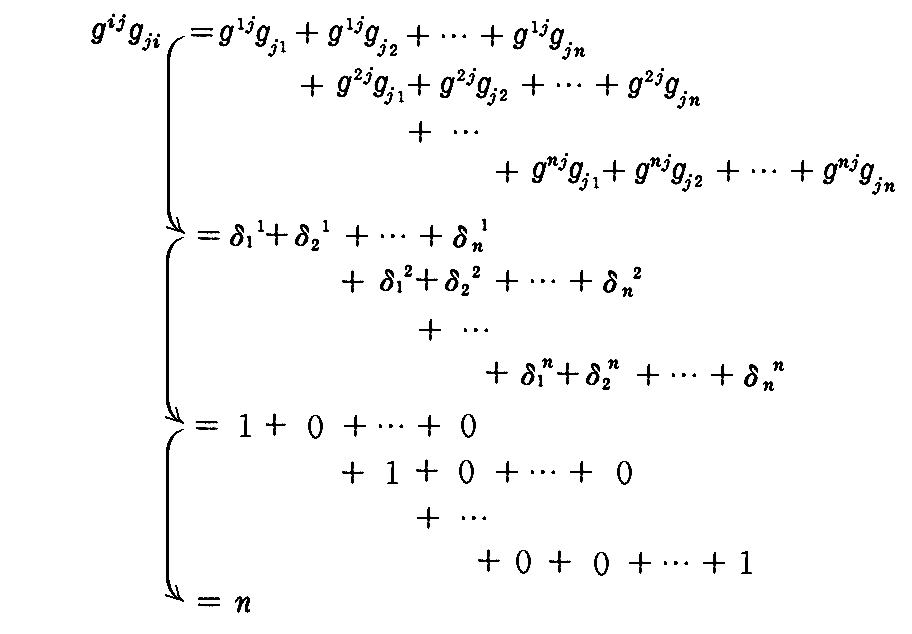
となることから明らか。

この式は重要!です。
[補足説明3]
(29)式は、実際に3次元の場合などで計算してみるとよい。[拡大版]

あるいは、(28)式から得られる式
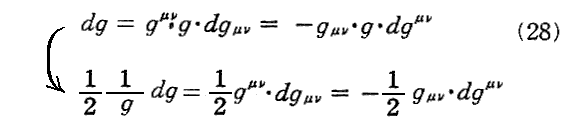
のすべての辺をxσに関する偏微分係数にすれば直ちに出てきます。


[補足説明4]
(31)、(32)式の導出計算。[拡大版]
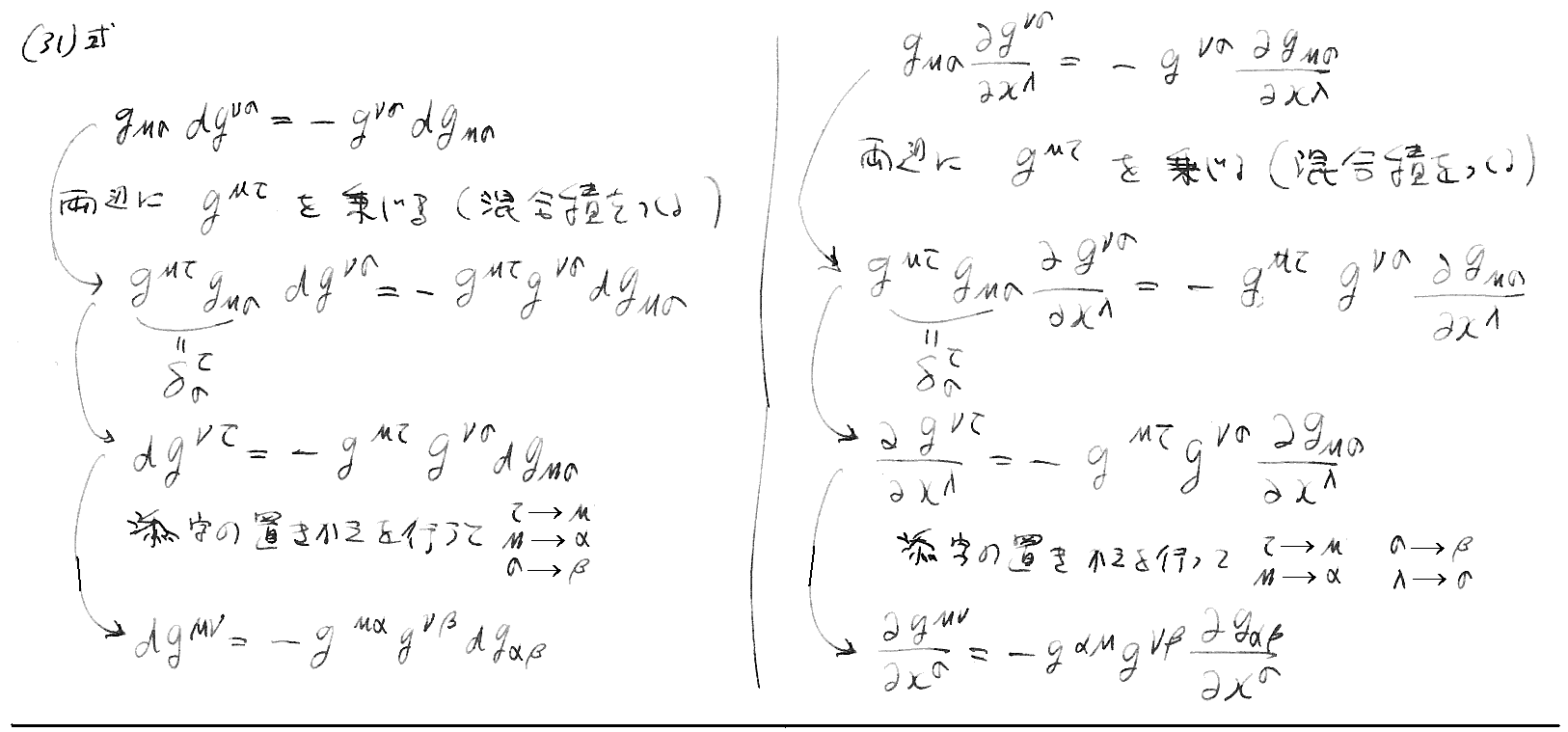

以下の(29・a)式も重要!です。

上式について補足します。左辺は∂/∂xσ(log√-g)ですからスカラーの共変微分となり、右辺のμで縮約したクリストッフェル記号は共変的4元ベクトルに成ると言うことです。
[補足説明5]
(33)、(34)、(29・a)式の導出計算。[拡大版]
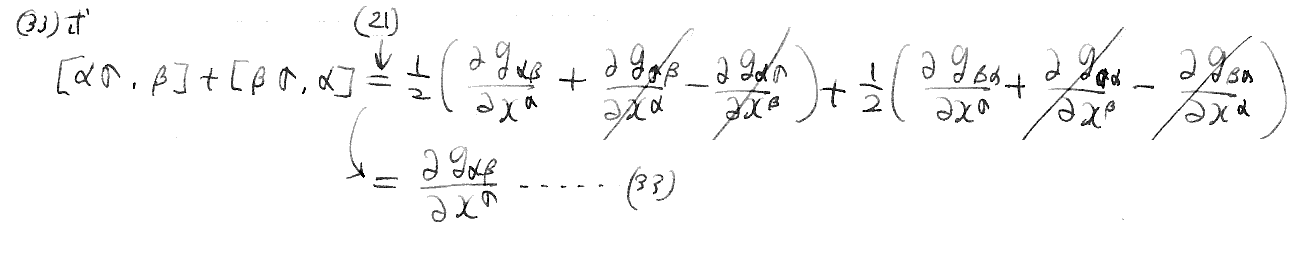
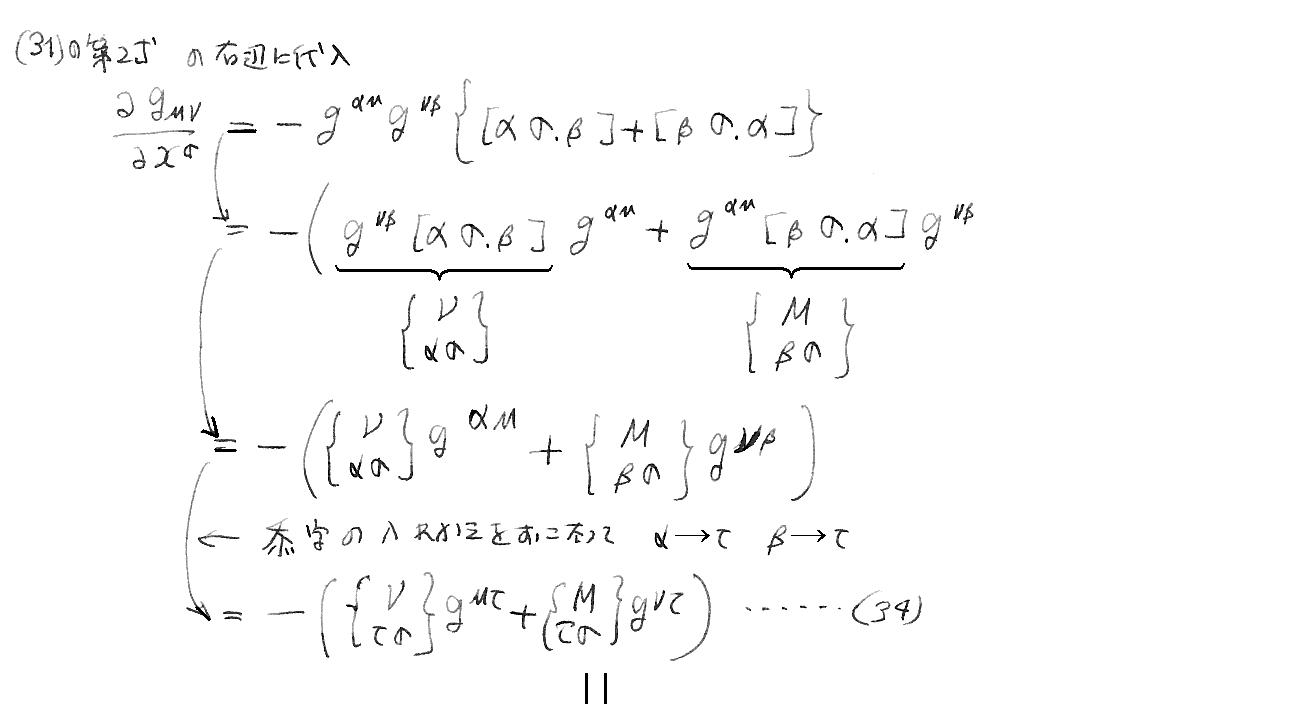
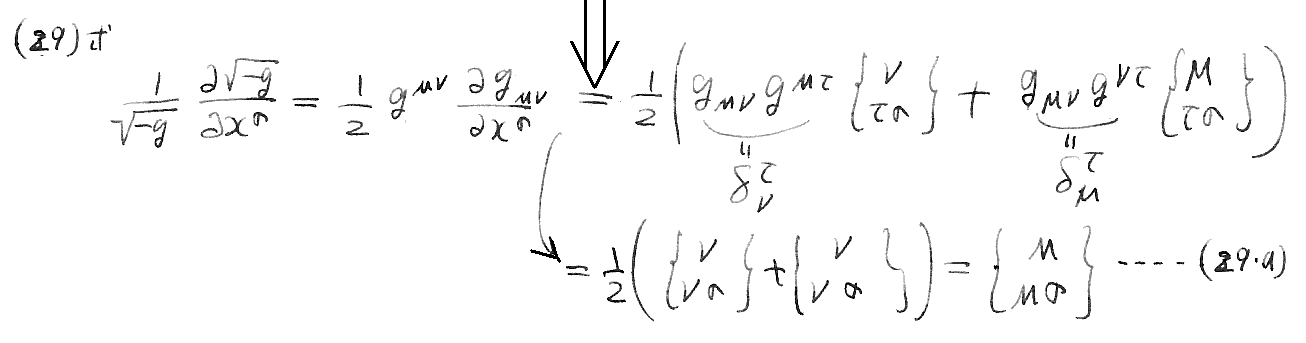
ここは、別稿「微分幾何学」3.(4)3.[補足説明]や、別稿「テンソル解析学(絶対微分学)」6.(2)4.なども参照されたし。
さらに注意すると、(33)、(34)式は以下の様に書き換えることもできる。
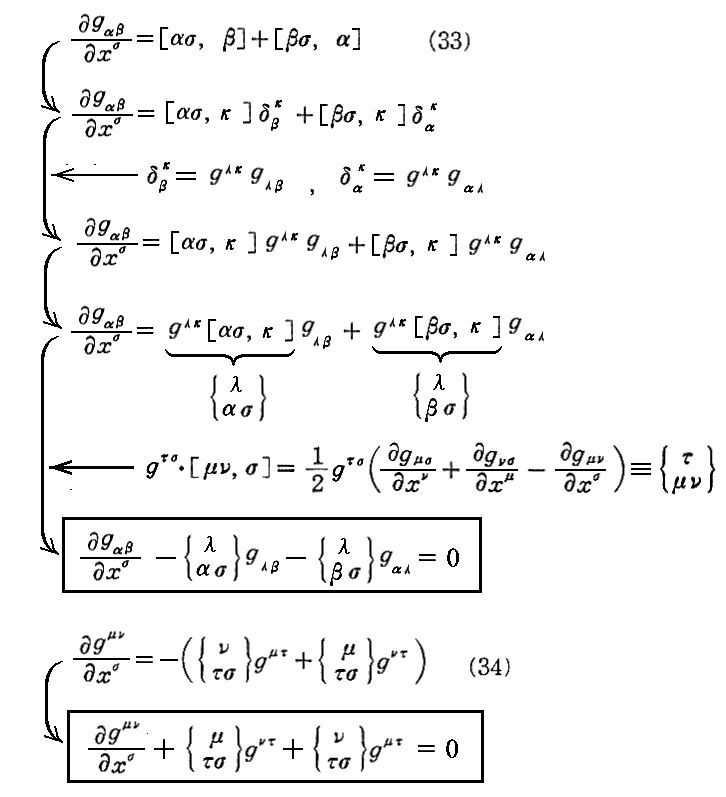
これは共変計量テンソルgijと反変計量テンソルgijの共変微分がいずれもゼロとなる事を示している。こうなることは、別稿3.(3)[例題1]や別稿6.(3)6.[gjiとgih]でも示した。これを“リッチの補助定理”という。
このことは計量テンソルが共変微分に対して定数の様に振る舞う事を示している。そのため、gij、gijを用いて行われる指標の上げ下げという操作と、共変微分という操作は互いに交換可能となる。
本項と同じ事柄の説明ですが、文献17.の附録A.1“接続整数の計算”からの引用です。
2.反変ベクトルのDiv
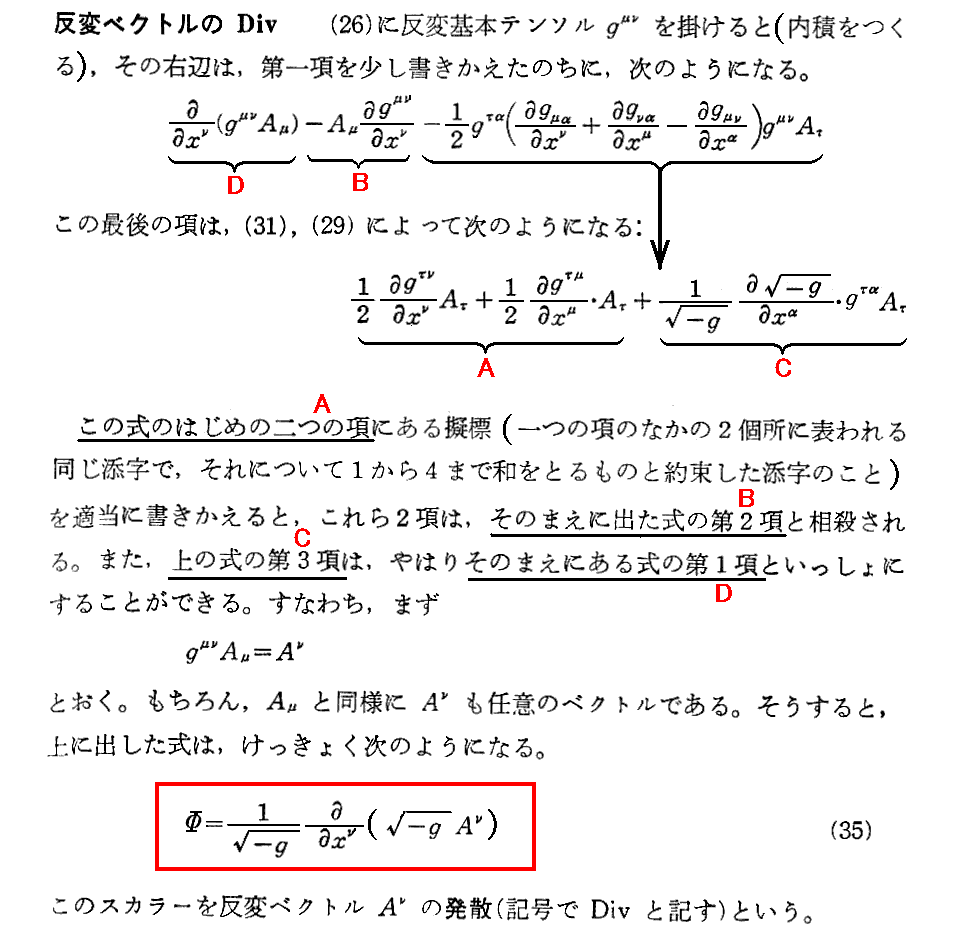
[補足説明1]
ここは説明が錯綜していて解りにくいので補足します。
まず最初の部分は別稿3.(3)[例題1]や別稿6.(3)6.[gjiとgih]で注意したように計量テンソルgijやgijの共変微分がゼロとなる(“リッチの補助定理”)を利用しています。これは計量テンソルが共変微分に対して定数の様に振る舞う事を示しており、gij、gijを用いて行われる指標の上げ下げという操作と、共変微分という操作とは互いに交換可能である事を示しています。
その当たりを、今日の共変微分表示形式“セミコロン ;”を用いて説明する。テンソルの積の共変微分に対しても“ラィプニッツの定理”が成り立つ(別稿「微分幾何学」3.(3)3.[定理])ので

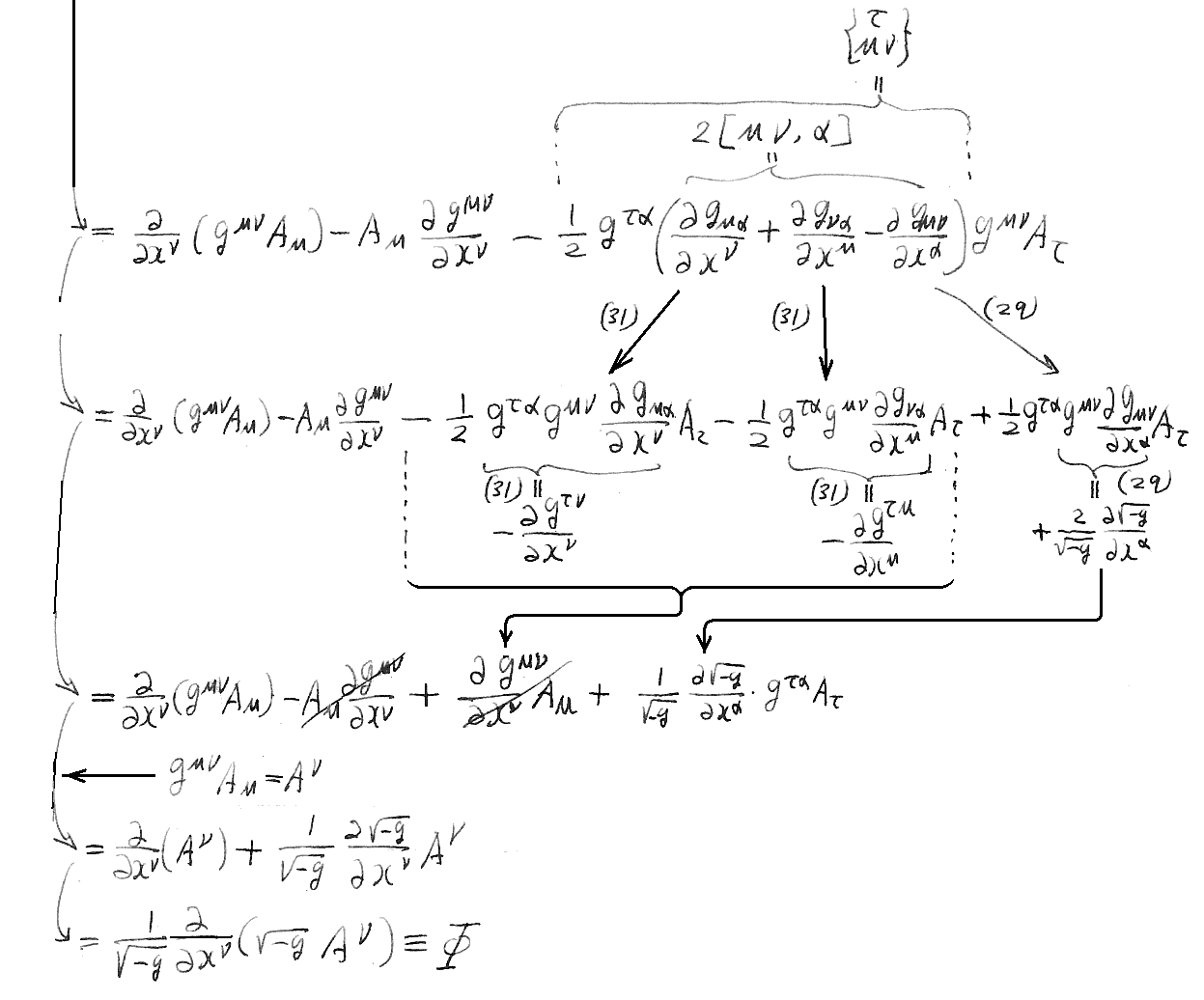
となります。
これは√-gが場所的に変化する場合も含んだ式です。後で出てくるように常に√-g=1と成る様にした、場所的に変化しない様な座標系を取れば√-gは消えて無くなります。
反変ベクトルの“発散”については別稿「微分幾何学」3.(4)3.や、別稿「テンソル解析学(絶対微分学)」6.(7)3.なども参照されたし。
[補足説明2]
ここで特に注意して欲しい事は、Div演算において共変的演算である微分操作と縮約できるのは反変成分だけです。そうして初めて座標変換に対して不変な物理的に意味のあるスカラー関数が得られる[B.(5)3.参照]。このことの意味を理解するのは極めて難しいが、とにかくそういうことです。
3.共変ベクトルのRot

ここは何を言っているのか解りにくいと思います。別稿3.(4)2.や、別稿6.(7)2.をご覧下さい。いずれにしても、上記のBμνは“2階反対称共変テンソル”となります。
[補足説明1]
この場合は、生じるものが2階共変テンソルですから、(36)式は共変成分としての意味しか持ちません。
以下の様々な微分操作で新たなベクトルや2階、3階のテンソルが生じますが、それらは最終的にそれぞれ共変成分、反変成分を持ったベクトルやテンソルです。そういったもので、物理法則が構成され、物理現象が論じられると言うことです。
それは、ある意味に於いて、現実の世界を、その中に設定された《座標系を通して見るゴースト(幽霊)の様な世界》です。リーマン時空ではそうするしか無い(別稿の《第5に重要なこと》参照)のですが、そのゴースト(幽霊)を通しても正しく論じる事ができるということだと思います。特にC.§15~16の議論などを読むとき強く感じます。
このことは、おそらく須藤文献§4.3の考察5や、C.§18[補足説明1]にも関係することだと思います。
この当たりは別稿「微分幾何学」3.(2)の[補足説明1]、[補足説明2]、[補足説明3]を復習されたし。
ここの所が、一般相対性理論を理解するのが難しい最大の理由なのでしょう。そして、一般相対性理論がリッチとレヴィ=チヴィタが作り上げた絶対微分学(テンソル解析学)に依存していると言われる理由でしょう。この当たりは、Einsteinの「グラスゴー講演」を参照。
4.6元ベクトルの反対称共変微分

ここも別稿6.(7)2.をご覧下さい。上記のBμνσが“3階(完全)反対称共変テンソル”となることは別稿3.(9)2.[補足説明1]をご覧下さい。
5.6元ベクトルのDiv

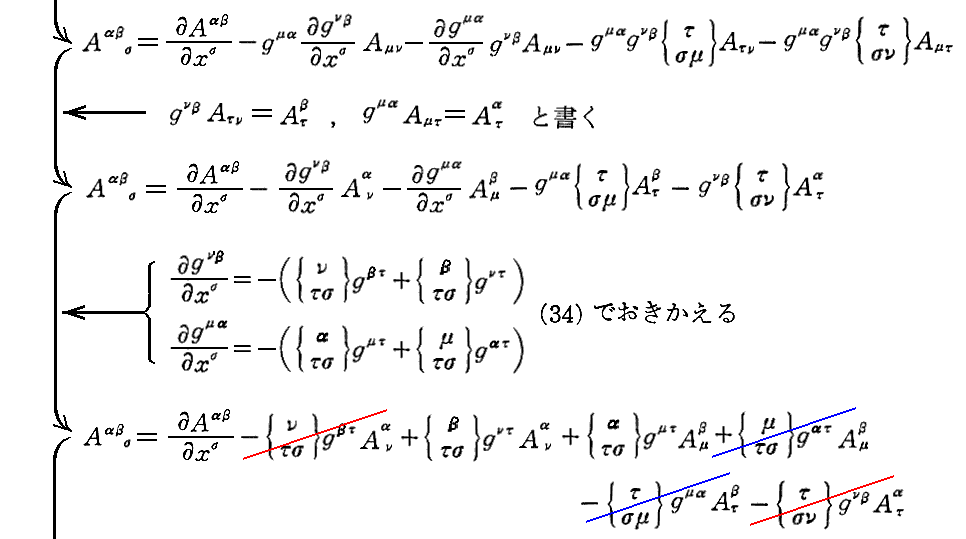

ここは、2階共変テンソルの共変微分を示す式から出発して、2階反変テンソルの共変微分を示す式を求めたと言うことです。
[補足説明1]
ここの式変形については次の事に注意して下さい。まず途中で用いた(34)式は別稿3.(3)[例題1]や別稿6.(3)6.[gjiとgih]で注意したように計量テンソルgijやgijの共変微分がゼロとなる(“リッチの補助定理”)を示している。
これは計量テンソルが共変微分に対して定数の様に振る舞う事を示しており、gij、gijを用いて行われる指標の上げ下げという操作と、共変微分という操作とは互いに交換可能である事を示しています。
その当たりを、今日の共変微分表示形式“セミコロン ;”を用いて説明すると

となる。
ここで、テンソルの積の共変微分に対しても“ラィプニッツの定理”が成り立つ事は別稿「微分幾何学」3.(3)3.[定理]などを参照されたし。


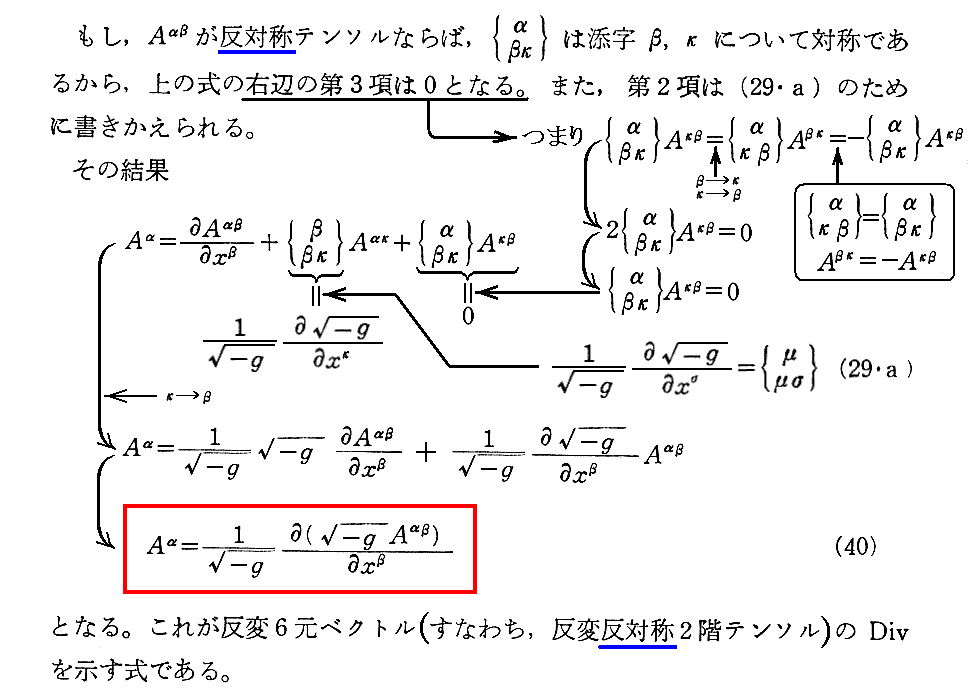
これはD.(20)1.で利用する。
6.2階混合テンソルのDiv


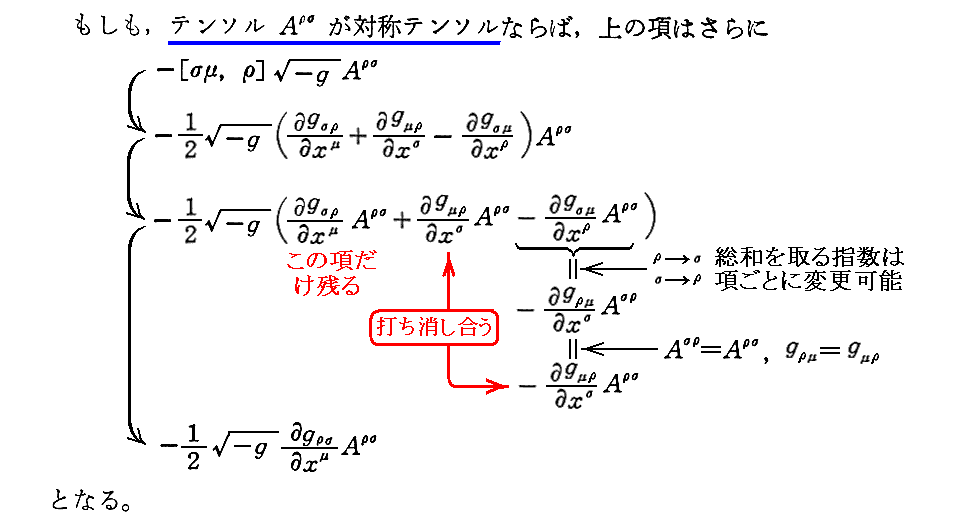


7.まとめ
[補足説明1]
この節はかなり、錯綜していますので、今日の標準的な記号を用いてまとめておきます。





§12.リーマン・クリストッフェルのテンソル
[補足説明1]
ここの“曲率テンソル”(リーマン・クリストッフェルテンソル)の導入は極めて解りにくい所です。
「一般相対性理論を理解するための数学的準備」の該当ページ
0186稿の5.
0177稿の3.(5)
0179稿の6.(5)
を十分に学習された後に、本節をお読み下さい。

ここは、共変ベクトルAμを座標変数で2回共変微分するする事を示している。その2回共変微分係数が上記の様な3階共変テンソルに成ると言うことです。その事の証明は別稿「微分幾何学」3.(3)2.[問題3]をご覧下さい。
Einsteinが以下の文節で説明している【σとτを交換したものの差を作る】と言うことは、要するに2回共変微分するときその順番を変えたものを作ってみて、その差を作ると言うことです。
これはある意味、共変ベクトルAμを(出発点と到達点を同じとして)dxσ方向→dxτ方向に平行移動した場合と、dxτ方向→dxσ方向に平行移動した場合の二つの経路についての移動結果を比較してみると言うことです。

(42)、(43)式の導出は別稿「微分幾何学」3.(5)1.を、あるいは別稿「テンソル解析学(絶対微分学)」6.(5)1.をご覧下さい。

上記の“§7の結論に従って”とは、§7で説明した“テンソルの商法則”を利用してと言うことです。
[補足説明2]
Einsteinは、共変ベクトルAμの2回共変微分の交換関係から曲率テンソルを導入していますが、2回共変微分を実施する対象としては、反変ベクトルAμを用いても良い。もちろん任意のテンソル(例えば3階(1,2)型混合テンソルTμντの場合)でも全く同様な曲率テンソルが定義できます。任意ベクトル、任意テンソルに対して同様に定義できると言うことこそ、この曲率テンソルの存在感を高めている。
Einsteinは、当初より基本計量テンソルgμνが時空の歪みを表す量であり、時空の歪みは物質(エネルギー)の存在によって生じるという考え方を持っていましたから、物質(エネルギー・運動量)テンソルと関係するものは“基本計量テンソルgμνから、微分によってつくられるテンソル”であるだろうと確信していました。そのため、その様なテンソルを探し求めていたのです。
そのとき、曲がった時空で、ベクトルやテンソルを平行移動させるとその経路による差が生じてきます。だからその差を表す量こそが求めるものだろうという思いがEinsteinにあったはずです。
曲率テンソルの導入法としては別稿ダニエル・フライシュ著「ベクトルとテンソル」6.3“リーマン曲率テンソル”で説明されている様に、
1.【共変微分の交換関係を使う方法】(5)1.で説明
2.【平行移動を使う方法】(5)2.で説明
の二通りがあります。
このとき、【1.の方法】は導出の数学的手順は単純・明快ですが、物理的意味は読み取りにくい。一方【2.の方法】は物理的意味は解りやすいが、数学的手順は込み入っています。
しかし、【1.の方法】(Einsteinが利用)と【2.の方法】は本来同じものです。実際、移動経路を微小化して小さな平行四辺形にすれば【2.の方法】は【1.の方法】に帰着します。

上記の説明については別稿「テンソル解析学(絶対微分学)」6.(5)3.もご覧下さい。
ここは何が言いたいのか解りにくいと思います。要するに時空が曲がっていない場合は人為的にその中に斜交座標や曲線座標を引いて、その座標に依って測ってみても
Bρμστ は常に 0 になると言うことです。このことは別稿4.(3)[例8]を参照されたし。
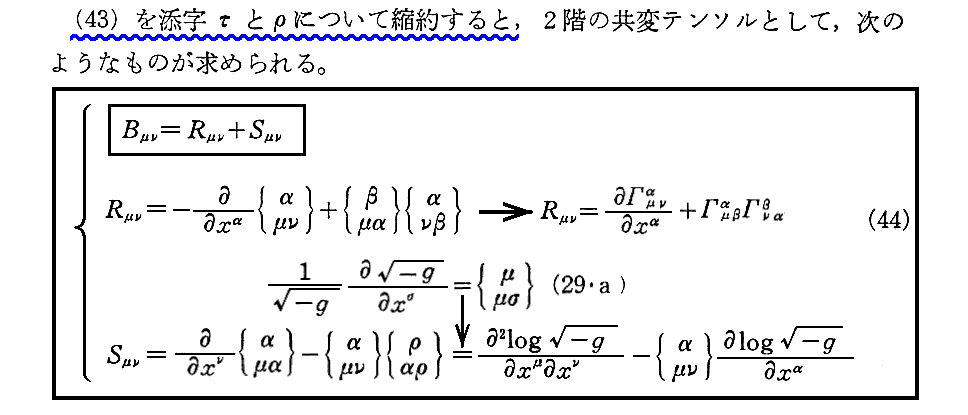
(44)式は(43)式のρとτを縮約すればすぐに導けます。特に、Sμνの最後の表現は(29・a)式を用いれば導けます。
この縮約したテンソルBμνについては、 別稿「微分幾何学」3.(5)3. と 3.(5)[問題3] や、あるいは 別稿「テンソル解析学(絶対微分学)」6.(6)2.なども参照されて下さい。

上記の§8はこちら。
上記のように座標系を選ぶと言うことは基底ベクトルのセットが形作る座標系の“単位セルの体積”が常に“=1”となるように座標曲線及びそれに沿った基底ベクトルの長さを調整すると言うことです。
利用できる座標系に対してこのような制約を課しても、一般相対性理論の展開に対して何らの不都合はありません。

C.重力場の理論
この章は参考文献6.と文献7.を参照しながら読まれると良いかも知れません。
§13.重力場内にある質点の運動方程式.重力の数式的表現


(46)式については§9“測地線の方程式”の(22)式をを参照。


§14.物質が存在しないときの重力場の方程式
本節は、私どもが[補足説明]を沢山書き加えたためにゴチャゴチャしています。そのため、最初は原文でお読みに成られた方が良いと思います。

[補足説明1]
これこそ、一般相対性理論の最重要な仮定です。このことが、重力場方程式の本質と思って良い。
このことは、電磁場が物質(エネルギー)であることを考慮すると電磁場も重力を生み出す源と見なす事を反映しています。そうして電磁場が生み出した重力場も、当然物質では無いのです。
しかし、後で解りますが、重力場もエネルギーです。しかし、そのエネルギーとしての重力場は重力場を生み出しません。上記の説明“重力場はエネルギーだが「物質」では無い”ということは、重力場自身が重力場を生み出すことは無いと言うことを言っています。
結局ここのところが重力場方程式を見つける上で、最も難しい所であり、アインシュタインが最も苦しんだ所だったのでしょう。
このことに付いては別稿「ブラックホール近傍の力学」1.(2)[補足説明1]の説明もご覧下さい。ただし、正直なところ私自身はここのところが良く理解できていません。
重力場がエネルギーであることは、重力波がエネルギー波として時空間を伝播していくことからも明らかです。明らかと言うよりも、時空の歪みが波として伝播するということが驚くべき事であり、それは重力場方程式から導けることですが、この波が現実に存在することが確認された事を持ってして、アインシュタインの重力場方程式の正しさが補強されたといった方が良いかも知れません。
なんだか禅問答みたいですが、このことの意味が以下で説明されます。

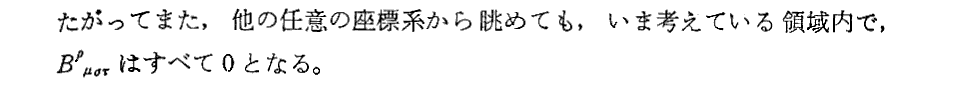
重力場が存在しない場合だからBρμστ=0は当然ですが、重力場の方程式は、この場合も含んだ形で無いといけないと言うことです。


[補足説明2]
Bμνは4次元の2階共変対称テンソルですから、独立な成分が10個あります。これは、10個の量gμνを定める方程式としては必要な性質です。
さらに、アインシュタインには、gμνこそがポアソン方程式のポテンシャルφに相当するものであり、ポアソン方程式を一般化したものが重力場方程式であるという思いがありました。
そのとき、ポアソン方程式の左辺はポテンャルの座標2階微分ですから、重力場方程式の左辺もgμνの座標2階微分を含んだものであるという確信がありました。そのときBμνは、下記(注意!!)に述べられているようにその好都合な性質を持っています。
実際のところ、Bμν=0 を満たす領域でも重力場は存在できます。だからこの方程式には重力場により歪んだ時空の場を表す計量テンソルgjiが解として含まれています。質点のまわりの重力場のみが存在し物質が存在しない場合の時空間領域の解である“シュワルツシルド解”(第1論文の解)はその様なものです。
別稿で説明する(第1論文の)シュワルツシルド解を求める手続きはとても解りにくいが、シュワルツシルドはこの“重力場の方程式”の意味を完璧に理解していたと言うことです。
補足しますと、(第2論文の)シュワルツシルド解が§16で説明する方程式の解です。ただし、√-g=1の制限を外した形の方程式を用いますが。

(注意!!)

[補足説明3]
(47)式は、物質は存在しないが重力場は存在する所の重力場の方程式です。つまり Bμν は 0 であっても Bρμστ は必ずしも 0 では無いと言うことです。もちろんBμν=0 の中には Bρμστ=0 も特別な場合として含まれます。
おそらくこのことに関して、上記で(注意!!)と追記して《黒二重線で囲った所の考察が最も重要》なのですが、Einsteinはその詳細を詳しく語ってくれていません。アインシュタインがここを簡潔に済ましたのは[補足説明4]で説明する思いがあったからでしょう。
そうは言いましても、もう少し詳しく知りたいところですので、今日の教科書のスタンダードな説明を、須藤靖著「一般相対性理論入門」§4.3から引用しておきます。この中の考察3:(ⅲ)の意味はこちらを参照あるいはこちらを参照。考察5:は後で何度も出てきます。
同様な説明ですが、平川浩正著「相対性理論」§6.1からの引用です。
今日の教科書では、このあたりは別稿で引用する下記の様な形で説明されることが多い様です。ここは
石井俊全著「一般相対性理論を一歩一歩数式で理解する」ベレ出版(2017年刊)第7章§8. と §8の末尾、さらに 杉山直著「相対性理論」講談社(2010年刊)第10章§3.や、岡部洋一著「リーマン幾何学と相対性理論」プレアデス出版(2014年刊)§7-3などを参照してください。唐木田健一著「ひとりで学べる一般相対性理論」講談社(2015年刊)第Ⅱ章§10の説明も有益です。
さらに、C.(16)[補足説明1] と、 C.(17)[補足説明1] と、C.(18)[補足説明1]もご覧下さい。


[補足説明4]
(47)式はEinsteinが大変な苦労の末に発見したものですが、それが依って立つ何か特定の前提や根拠があるわけではありません。
Einsteinは膨大な思考を積み重ねて“膨大な状況証拠”を集めて、最終的に(47)式に到達したのですが、結局の所 “その法則の正当性、妥当性はその関係式が内部矛盾を含んでおらず、自然現象を旨く説明するという審判によってのみ確立される。”と認識していた。
これは本来、物理学における法則と言われる関係式すべてについて言えることです。Einsteinはその事を十分承知していましたので、彼は上記の様に《状況証拠の説明》を簡潔にすまして、《赤線で囲ったコメント》を記したのでしょう。
[補足説明5]
後のC.§16で導かれますが、物質が存在する場所で成り立つ重力場方程式は、√-g=1の条件を課さない今日的な表現(C.(16)[補足説明2]参照)で示すと

となります。
所で、この右辺がこの方程式が成り立つ場所での物質(エネルギー)を表します。この式から行くと、本節の物質が存在しない時の重力場の方程式は
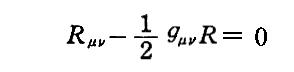
となるはずです。しかし、ここで議論されている(47)式は
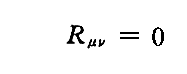
を意味します。
つまり、左辺第2項の-(1/2)gμνRの項が抜け落ちています。しかし、抜け落ちていても良いのです。なぜならRμν=0ならばgμνR=0である事は必然的に成り立つからです。上記のEinsteinの注*はこのことを意味している。
実際、アインシュタインは1915年11/18に報告(出版は11/25)した水星近日点移動を証明した論文ではRμν=0の形の方程式(より正確に言えば√-g=1の条件を課した(47)式の形)を用いており、-(1/2)gμνR項の必要性に気付いていません。それでも、水星の近日点の運動に対する場の方程式はこの修正によって影響を受けないのです。
いずれにしても、-(1/2)gμνRの項は本節§14の最初に述べた事柄あるいは[補足説明2]で述べた事柄に関係してくるのだと思います。
以上の事柄を鑑みると重力場方程式としては、11/25に報告(出版は12/2)した
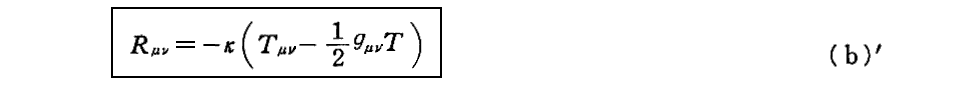
の形(これはSommerfeld宛の書簡(1915年11月28日付)で書いている形)の方がより適切かも知れません。
§15.重力場に対するハミルトン関数.運動量・エネルギー保存則

[補足説明1]
つまり、“ハミルトンの原理”の“Lagrange関数”を H=gμνΓαμβΓβνα とすると言うことです。このようにする理由は、それを“ラグランジュ方程式”(47・b)に代入すると、重力場の方程式(47)式が得られるからです。それ以外の理由はありません。
今日ではLagrange関数を“L”で、Hamilton関数“H”と書きますが、当時は逆の記号を当てていましたので混同されませんように。



[補足説明2]
《(47・a)の変分を取ってLagrange方程式(47・b)を導くこと》、すなわち《“最小作用の原理”から“オイラーの微分方程式”を導くこと》は適当な本を参照して下さい。例えばランダウ、リフシュツ著「力学}1-02、別稿「微分幾何学3(曲面幾何学)」3.(6)1.あるいは「リーマン幾何学」4.(2)[問題2]など。
いずれにしても、Lagrange関数を(47・a)の様に取れば、最小作用の原理から(47・b)を経由して重力場の方程式(47)式が導ける。ただし、[補足説明1]で指摘したように、Lagrange関数をその様に取る根拠は、そう取れば(47)が得られるということ以外にはありません。だから“ここでは、逆にそのようにしてLagrange関数を求めれば、それからエネルギー関数が導ける”と言うところに、ここの議論の本質はあります。
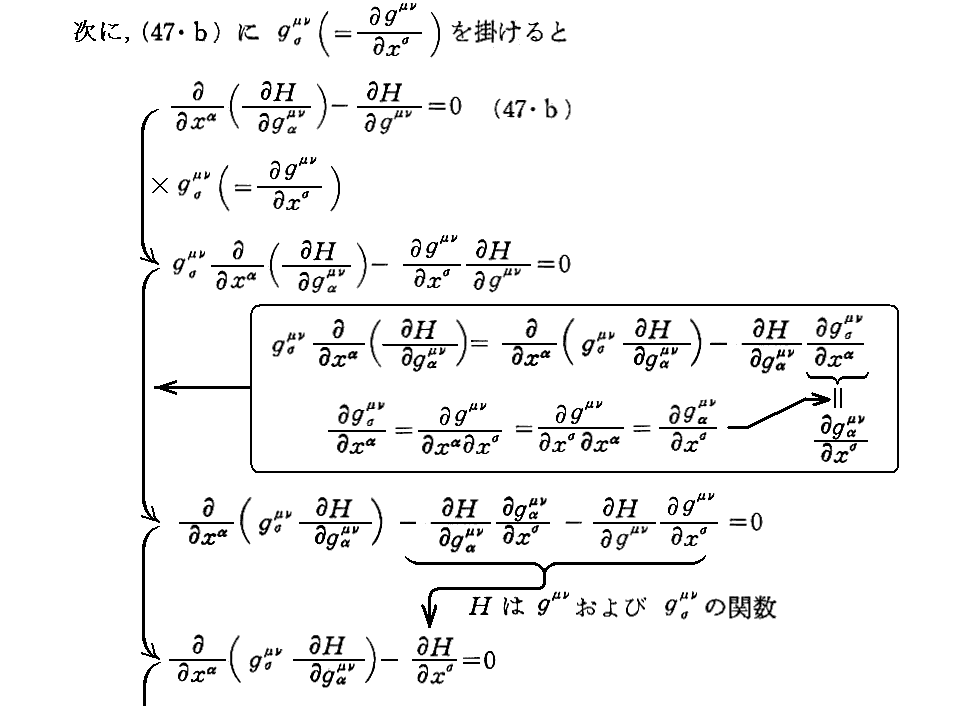
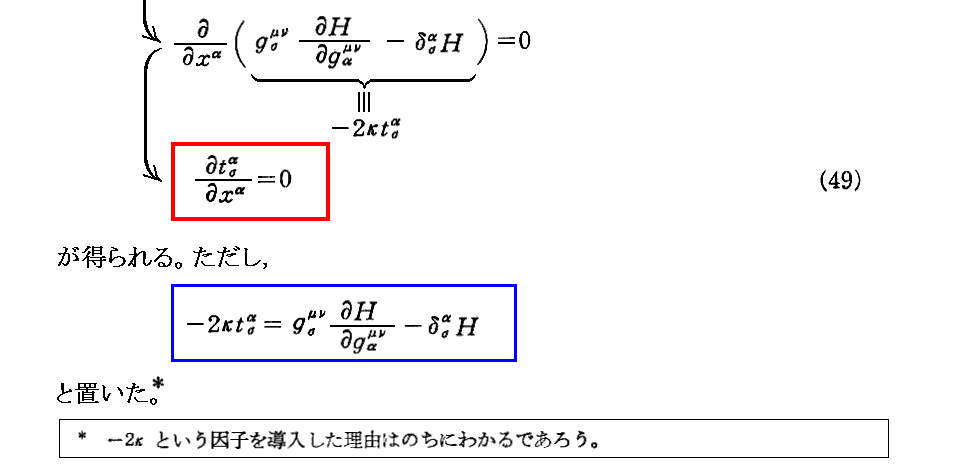
[補足説明3]
tασの意味は解りにくいが、上記定義式の右辺はまさに解析力学における“ハミルトン関数(エネルギー関数)”の定義式そのものです。だから、これは“エネルギー”を表していると解釈できるのだろう。
Einsteinが本論文を書いた当時は慣習として“ラグランジュ関数”を表すのに H の文字を当てていました。これを“ハミルトン関数(エネルギー関数)”と取り違えないで下さい。この当たりの事情は別稿プランクの論文[補足説明5]などを復習して下さい。

[補足説明4]
以下の説明でアインシュタインは、tασはテンソルでないと言っています。それはおそらく、(50)式右辺のgμνに別稿3.(3)1.の(3-14)式を、クリストッフェル記号に別稿3.(3)1.の(3-18)式を代入して計算すれば、全体としてテンソルとしての座標変換式を満たさない事が言えるからだろう。この当たりはPauliが文献9.で説明してくれているそうです。
“tασがテンソルでない”が何を意味するのか良く解らないのですが、藤井文献(1979年)§15-4などの説明を考慮すると、もし tασ がテンソルであったなら、局所的に重力場が消える様な座標変換が可能なので、等価原理により、重力場のエネルギー・運動量は常にゼロになってしまうことになるからかもしれません。だから重力場のエネルギー・運動量がテンソルでないことが必要なのでしょう。そのとき、座標系によって重力場のエネルギー・運動量が消えたり現れたりしても(49)式があらゆる座標系に対して成り立つと言うことなのでしょう。
これに対して後で出で来る重力場方程式の右辺を構成する物質のエネルギー・運動量テンソルTσμがテンソルである事は何等問題ありません。物質のエネルギー・運動量テンソルが座標変換によって消えたり現れたりする様なことはあっては成らないからです。ある座標系でゼロならあらゆる座標系でゼロであり、ある座標系で存在したらどのような座標系でも存在しなければ成らないからです。
むしろ重力場方程式が一般相対性原理を満たす(方程式の座標変換共変性)ためには、物質のエネルギー・運動量Tσμがテンソルである事は必須の条件です。ところがそのとき、テンソルではない重力場のエネルギー・運動量が“重力場の方程式”の中に現れてこないところに本質があるのでしょう。そして、ここの議論は、その様な事が起こると説明している。
しかし、そのあたりは私自身良く理解できない所です。


[補足説明5]
上記(49・a)式について補足します。


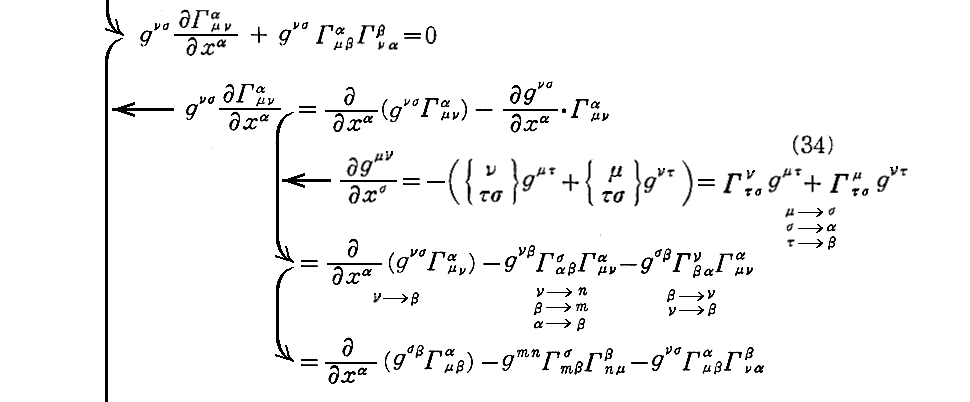
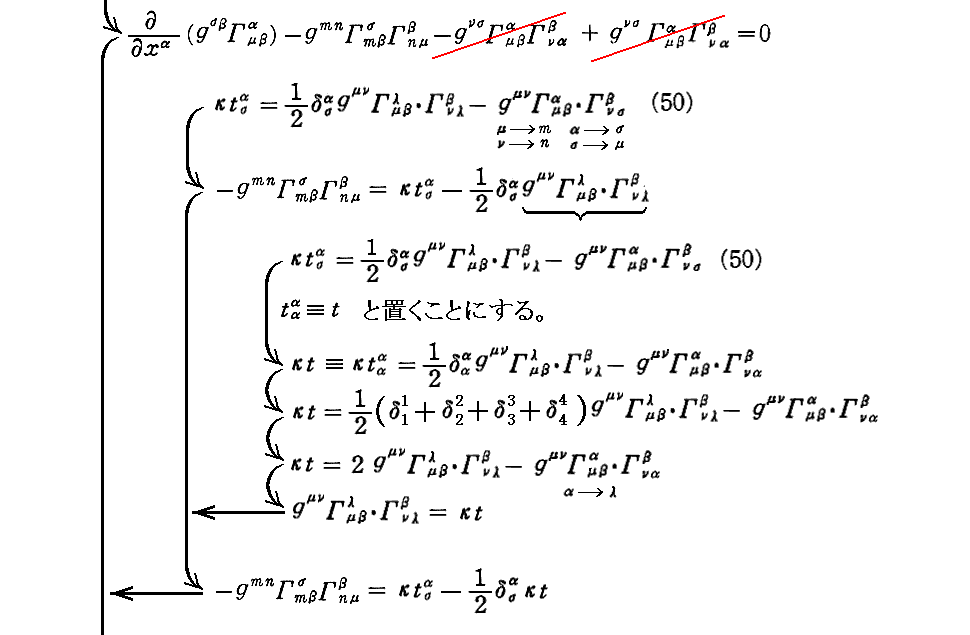
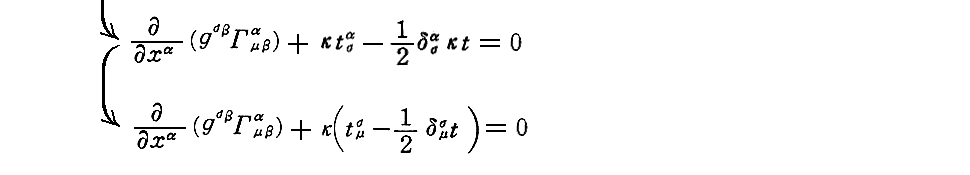
上記の式変形は錯綜していますが、元の表現はこちらをご覧下さい。
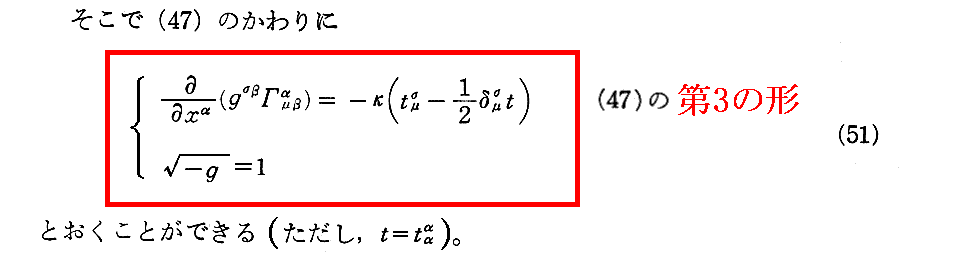
[補足説明6]
(47)式の第3の形として導いた(51)式が何を意図したものか解りにくい。
次節の説明から想像するに、物質の存在しない時空領域の重力場の方程式Bμν=0(あるいは√-g=1の条件下のRμν=0)の左辺の中に埋もれている“重力場のエネルギー”部分tσμを取り出して右辺に移項しておき、次節§16で述べる様に、この部分に“物質のエネルギー”Tσμを付け加える事で“物質が存在する時空領域で成り立つ重力場方程式”を見つけようと言うことなのだろう。
ここの発想は独創的ですが、混合型テンソルの方程式形にするとその様な考え方が適用できるという所の意味が私自身よく理解できていません。重力場のエネルギー・運動量(テンソルにあらず)は混合型表現にすると見えてくる様な性質を持つのだろうか?
実際、B.(8)2.[補足説明1] や B.(11)3.[補足説明1] などを振り返ると、混合型テンソルの中には見えなかったものを見える様にする働きがある気がしてきます。
§16.重力場の方程式の一般形式


別稿4.(2)3.[補足説明1]で説明した様に、共変テンソルや反変テンソルが対称テンソルであっても、混合テンソルの形にすると対称テンソルであるとは限りません。

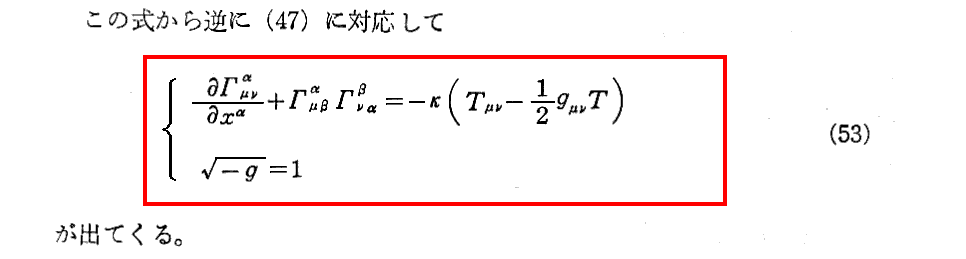
(53)式の右辺のTμνは(52)式の(tσμ+Tσμ)中のTσμの部分を意味し、重力場のエネルギー・運動量(テンソルでは無い) tσμ は含まれていない事に注意して下さい。
[補足説明1]
以下の説明文を、ここでは便宜的に三段落に分けましたが、元の説明文はこちらです。
最初の段落で“上に述べたような物質のエネルギー・テンソルの導入の仕方は単に相対性の要請だけからでは正当化されない”と言うコメントですが、これはC.(15)[補足説明4]で記した事に関係するのだと推測されます。
青二重線で囲った所がC.§14の最初のコメントと、そこの[補足説明1]で説明した事に対応します。おそらく《このコメントに Einstein の万感の思いが込められている》のだと思います。しかし、(52)、(53)式がこのコメントの要求を満たしていると言われても、私どもがその事を読み取るのは難しい。
今日の多くの教科書で取り上げられて説明されているのは、このコメントに続く赤下線部の事柄です。
このことに付いては、C.(14)[補足説明3] と、 C.(17)[補足説明1] と、C.(18)[補足説明1]もご覧下さい。



このことは§17で示される。
[補足説明2]


ここの書き換えについては別稿7.(1)2.も参照されたし。
(b)式←→(c)式の書き換えについては、あらゆる教科書で説明されているのですが、この書き換えの意味を説明してくれている教科書を知りません。
私は、Einsteinの論文を読む限りに於いては、(c)式よりも(b)式の形の方がより本質を表しているように思うのですが、今日の重力場方程式の導入法にとっては(c)式の形の方が好都合(つまりビアンキの恒等式を適用しやすい)だからなのだろう。このことについては別稿ENDをご覧下さい。
[補足説明2-1]

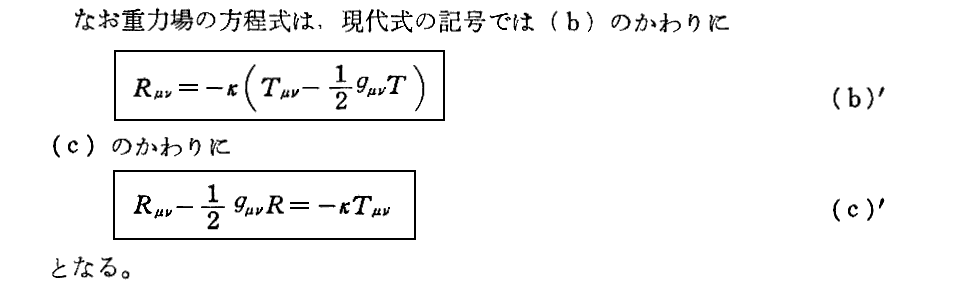
このとき、《gμνの正負》、《Rμνについての正負》、《定数κの前に付く符号の正負》に関して、別稿6.(5)1.[補足説明1-2]で内山先生が注意されている様に、本の定義によって様々な場合がありますので注意されて下さい。
[補足説明2-2] 上記訳者注を補足します。
(c)’式は共変成分で表した重力場方程式ですが、この両辺にgμαgνβを乗じて縮約して

の反変成分表示にしてもかまいません。反変成分と共変成分の関係は対等・同質ですから。
もちろん(c)’式の両辺にgμαを乗じて縮約して混合テンソル型

にしても良い。
《(c)’形》が好まれるのは、左辺がリーマンテンソルRτμσνの縮約Rσμσνとして定義されるリッチテンソルRμνがそのままの形で現れるからでしょう。
一方、C.(18)[補足説明1]の説明のようにビアンキの恒等式を適用するときなどには《(c)”形》が便利です。なぜなら別稿6.(3)1.[補足説明1-1]で説明する様に共変微分は本来反変座標に関してなされるのですが、それは共変階数が1つ増えることを意味しますので、縮約する相手は反変成分でなければならないからです。ここは別稿「微分幾何学」3.(5)[問題4]なども参照されたし。
《(d)形》は方程式中に顕(あらわ)に現れていた計量テンソルgμνあるいはgαβが単位テンソルδανに成っているので、そのことが有利になる状況では便利な形です。共変計量テンソルgβν・反変計量テンソルgαβ・単位テンソルδανの間の関係の意味はB.(8)2.[補足説明1]を復習されて下さい。
[補足説明3]
今日、重力場方程式の厳密解として有名なのはシュワルツシルド解です。しかし、この解は極座標表示の重力場方程式を用いないと導けません。
ところが、極座標表示にすると√-g=1を満足できませんので、アインシュタインが説明している重力場方程式の形にはなりません。そのためシュワルツシルド解を求めるには、ここで訳者が指摘している、より一般的な(a)’式を用いた(b)’or(c)’式の形を用いなければ成りません。
今日の教科書で√-g=1の条件を課した形で重力場方程式が提示されることが無いのは、今日の教科書の最終目標がシュワルツシルドの厳密解(ブラックホールの理解に必須)を求めることにあり、そして極座標表示のシュワルツシルド解(計量テンソル)を測地線方程式(運動方程式)に代入して三つの古典的検証(赤方偏移、屈曲、近日点移動)の説明が行われるからなのでしょう。
しかし、E.(21)で説明されているように、第1近似としてニュートン理論が出てくる事を示すには√-g=1の条件を課した直交座標系での重力場方程式から出発する方がはるかに解りやすい。
アインシュタインに取って、探し求めていた重力場方程式の正当性を確信する鍵は、それからニュートン理論が導けるかどうかということと、水星の近日点移動量が説明できるかどうか、だったのですから、彼が本論文の形(つまり√-g=1の条件を課した形の重力場方程式)で議論する必然的な理由があったのでしょう。特に、水星の近日点移動量が説明できるかどうかが重力場方程式の正当性を判定する鍵になるだろうという思いはEinsteinの脳裏に早い段階からあった(ラウエとのやり取り、1907年12月のハビヒト宛の手紙)ようですから。
おそらく彼には、(b)’or(c)’式の形の重力場方程式が、簡単に解けるとは思えなかったので、√-g=1の条件を課した形の重力場方程式にこだわったのではないでしょうか。(Sommerfeld宛の書簡(1915年11月28日付)参照)
以下の議論も√-g=1の条件の元で展開されていますので、今日の教科書と少し違った式展開となっています。そこの所を心に止めてEinsteinの説明をお読み下さい。
§17.一般の場合の保存則

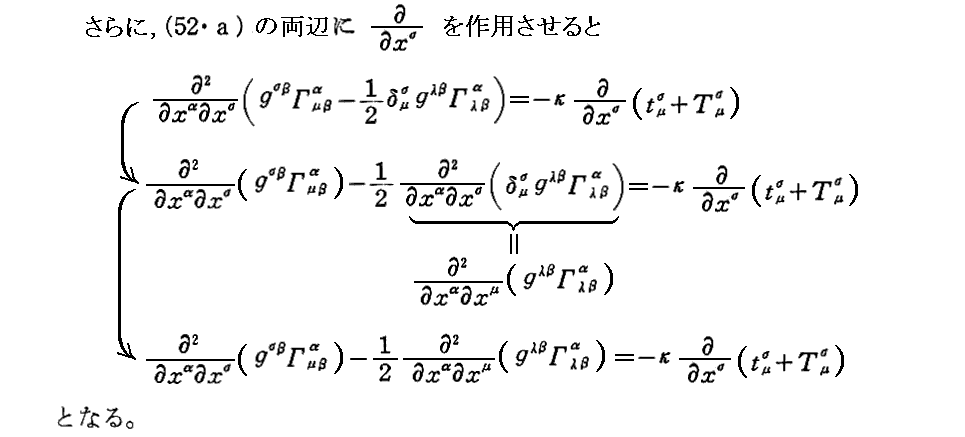
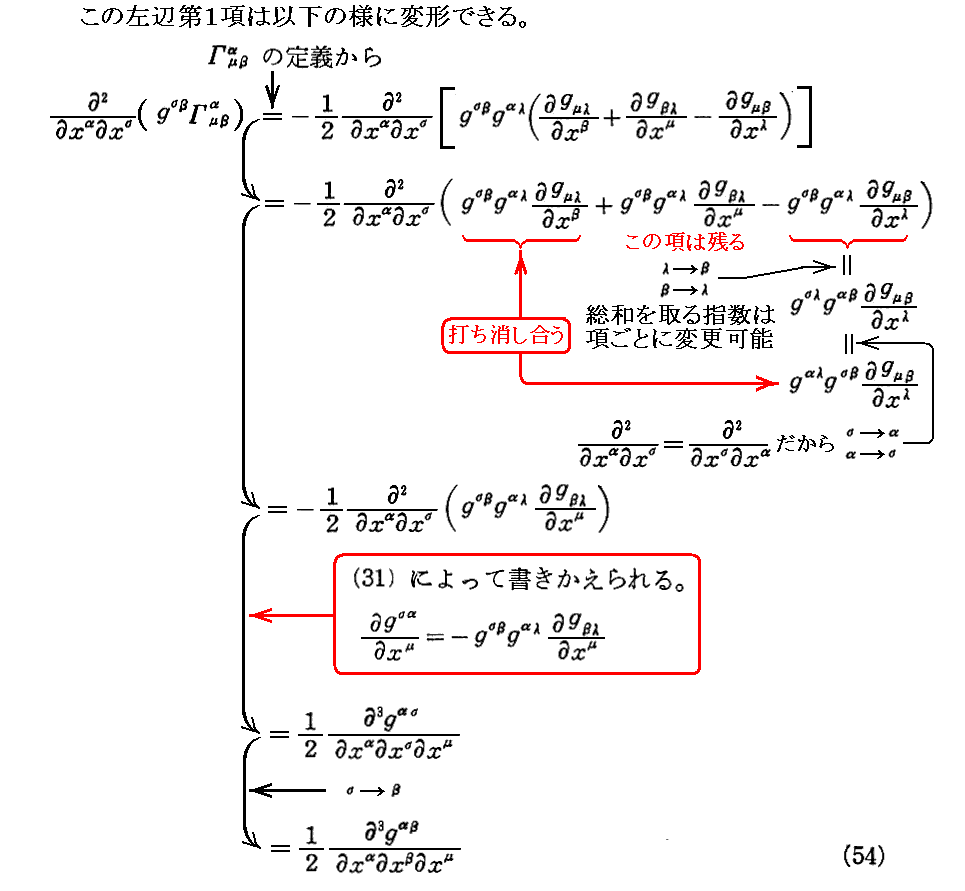
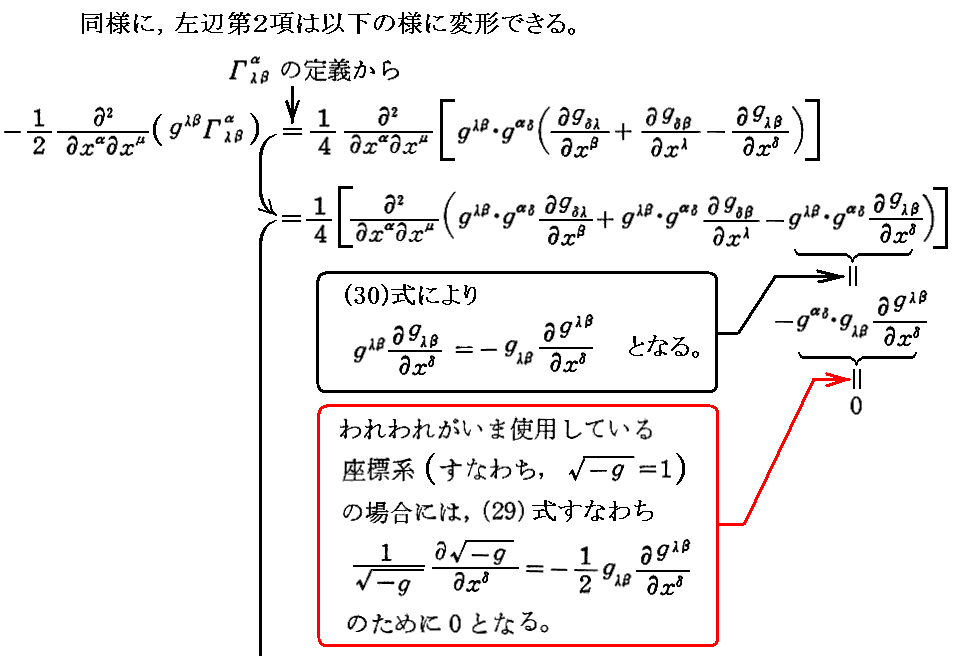
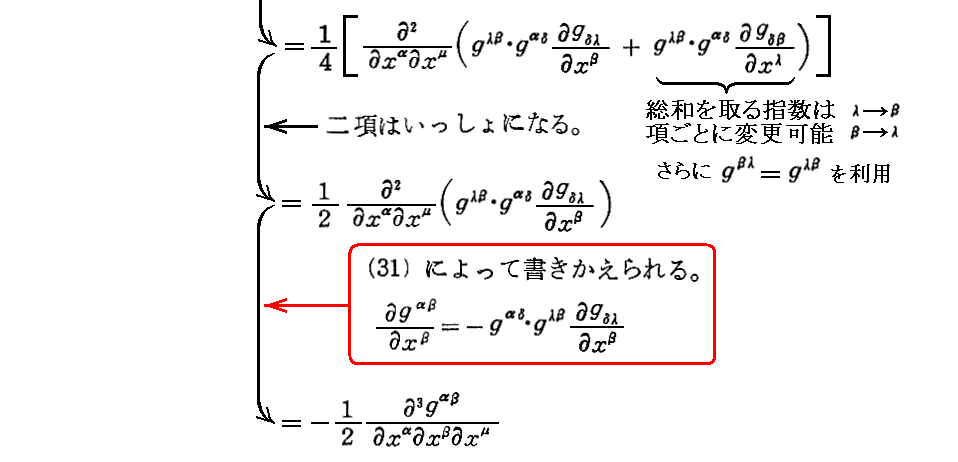
ここの式変形は錯綜していますが、元の説明文はこちらです。


[補足説明1]
《結局の所(56)式を証明することが鍵だった》のですが、Einsteinfはその証明に大変な苦労をします。しかし、ここの説明からはその当たりの事情はなかなか読み取れません。このことについては、別稿7.(1)2.[補足説明1]を参照されたし。
あるいは、石井文献第7章§7. と §8の末尾 もご覧下さい。さらに、上記の式変形は石井氏が第7章§8. で説明される中に出てくる式変形によく似ていることに注意されて下さい。
ここのところですが、Paisは、Einsteinは11月25日論文に於いて文献8.第14章のp335で説明する様にしたと言っています。
実際の所、本総説論文の説明は重力場方程式(53)式(あるいは(52)式)が正しければ(56)式が成り立つと言っているのですが、これを今日の表現C.(16)[補足説明2-1]の(c)’式
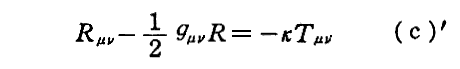
で説明すると、この左辺が正しければ、右辺のエネルギー・運動量テンソルの保存則が導かれると言っており、今日の議論のちょうど逆を行って-(1/2)gμνR項の必要性を証明していることになります。
ただし、そのとき良く解らないことがあります。本来成り立つべきエネルギー保存則は、ここでEinsteinが証明している様に、物質のエネルギー・運動量テンソルに重力場のエネルギー・運動量(テンソルではない)も含めた形のエネルギー・運動量であるべきなのに、今日の教科書の説明では(エネルギー保存則を満たさなければならないとしている式には)物質のエネルギー・運動量テンソルしか含まれていません。
実際のところ、(52)式の形では物質と重力場の両方のエネルギー・運動量が現れるから両方を含めたエネルギー保存則が証明できます。しかし、(53)式の形では物質のエネルギー・運動量テンソルしか現れないので、物質のエネルギー・運動量の保存則が成り立つことが示せれば良いのだということなのだろうか?
Einsteinは1922年に書いた文献6.『相対論の意味』(訳本のp89)で、上記(c)’式の左辺の発散が 0 になる事を証明するのに、わざわざ重力場が消える座標系に座標変換して、その事が示されるとしている。そして左辺のテンソル性から任意の座標系に於いて物質のエネルギー原理が成り立つと説明しています。本来このようにして証明すべき事なのかも知れません。これが次節§18で説明されている事の、今日的な[(c)’式を用いた]説明なのだろう。
《エネルギー・運動量の保存》と《ビアンキの恒等式》について、Paisが文献8.第15章§15c.で解説していますのでご覧下さい。Paisはこの中で、本稿の§15~§17の展開を論評しています。そこでPaisは本論文の導き方は、一つの弱点であると言っています。しかし、私はC.(16)[補足説明1]やC.(15)[補足説明4]に記しましたようにこの導き方の中に(Einsteinの本心は良く解らないのですが)より本質があるように思います。もちろんPaisは本論文の内容を(p355で)高く評価していますので、Einsteinの1916年論文(共立出版「アインシュタイン選集2」[A5]論文)に比較しての評価だと思います。[A5]論文は別稿で引用・紹介していますのでどうぞご覧下さい。
重力波はエネルギーの伝播を伴っていますから、重力場がエネルギーを持っているのは明らかです。それなのに、今日の教科書が説明するエネルギー保存則の中に、その重力場のエネルギーが含まれていないのは何故だろう。
この当たりに関係する事柄が内山龍雄「相対性理論」§31で説明されている様なのですが、そこの説明は不明瞭で私には良く解りません。
Einsteinは重力場方程式の右辺に関しては様々な機会に疑念を呈しています。例えばインフェルト文献やEinsteinの1947年文献などに於いて。このことについては、アインシュタイン、インフェルト共著(石原純訳)『物理学はいかに創られたか』(岩波書店1939年刊)Ⅲ場・相対性(2)“場と物体”(下巻のp120~125)の説明が理解のヒントになるかも知れません。昔この部分を読んだときにはまるで理解できなかったのですが、このたびこの稿を作ってから改めて読み直してみると、Einsteinの思いが少し理解できた様な気がしました。
結局のところ、この当たりの疑問はすべて別稿ENDに記した感想でつきるのかも知れません。
いずれにしましても、この当たりの事情を、EinsteinはSommerfeld宛の書簡(1915年11月28日付)に書き残しています。この書簡はEinsteinが最終的に正しい“重力場方程式”を求めた論文をベルリンの科学アカデミーに提出した11月25日の僅か3日後に書かれています。簡潔な文章ですが、彼のそれまで苦労した所を赤裸々に語っています。ただし、その内容を読み解くのは極めて難しい。
(MTW文献§17.7もごらんください)
その当たりは、C.(14)[補足説明3] と、C.(16)[補足説明1] と、C.(18)[補足説明1]もご覧下さい。
§18.物質の運動量・エネルギーの法則

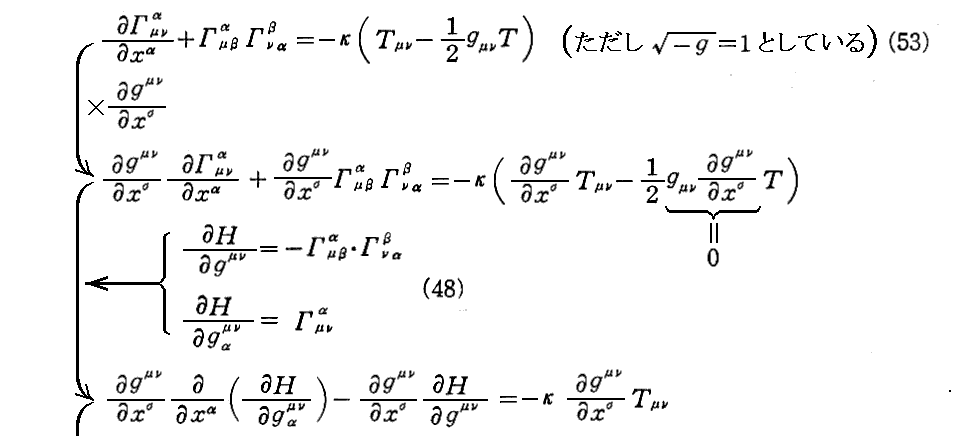
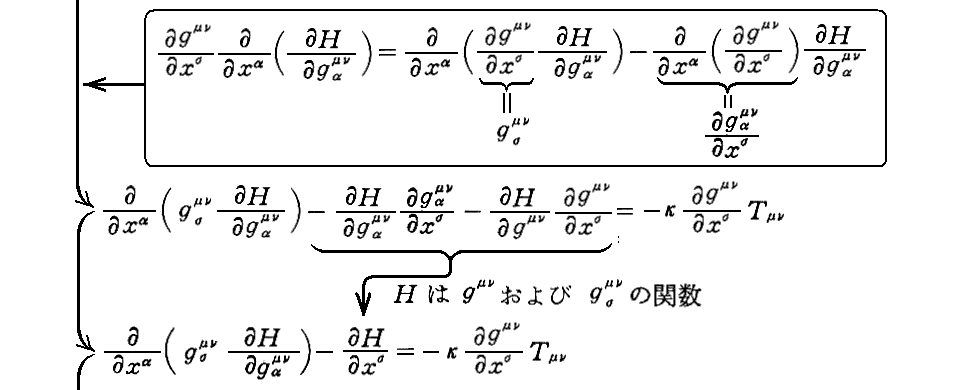
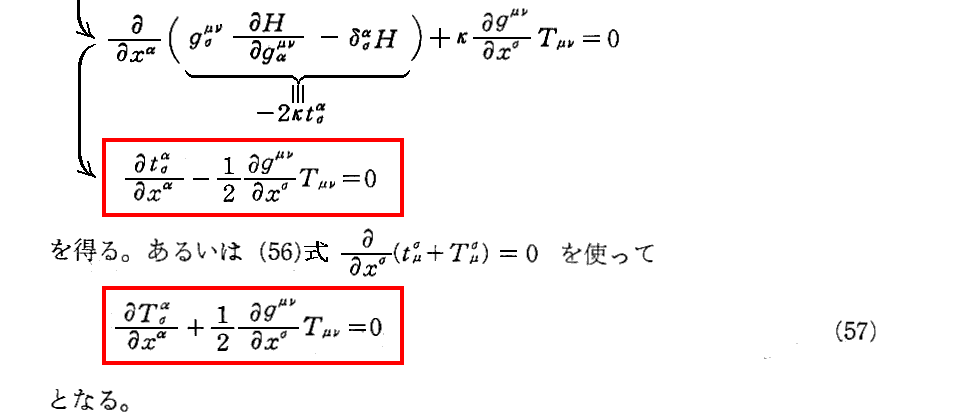
下記の(41・b)式はこちら。

B.§11.5.で(41)式を導いたとき説明した様に


[補足説明1]
ここの最後の段落の説明も解りにくい所です。
おそらく多くの教科書で指摘されている以下の事柄を説明しているのだろう。
重力場方程式(アインシュタイン方程式)にはC.§17で示された様に、もともとエネルギー・運動量の保存則(このエネルギーの中には重力場のエネルギーも含まれるから話が難しくなる)が内在している。だから重力場方程式が与える条件は10-4=6個である。
つまり、重力場の方程式
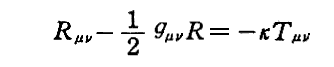
の左辺は4個のビアンキの恒等式
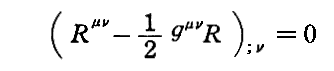
を満たしている。これらの関係式の為に重力場方程式はgμν(あるいはgμν)を一意的には決定しない。
これはちょうどマックスウェル方程式が電磁場テンソルを一意的に決定しないのと同じ様に、gμνは、任意の座標変換 xμ→xμ’ に対応する変換 gμν→gμν’ を除いて決定されることを意味する。(このことに付いては、電磁場テンソルがローレンツ変換によって変化したことや、計量テンソルがリーマン空間内の座標変換によって変化した事を思い出されたし)
すなわち、この自由度が、座標の選択は物理的内容に関係の無い約束事だと言うことを表している。
このことから、“物質現象が4個の互いに独立な微分方程式によって記述されうるならば、重力場の方程式は物質現象を記述する方程式を完全に与えることになる”と言うことなのだろう。
この当たりは内山龍雄「相対性理論」p172~173で説明されているのですが、その説明は不明瞭で私どもには良く理解できません。
いずれにしましてもこれが、Einsteintが一般座標変換に対して共変な(つまり一般相対性原理を満たす)重力場方程式を発見する過程で、最も大きな障壁であったことは確かなようです。その当たりは、内山先生の「アインシュタイン選集 第2巻」の巻頭解説p15の説明やPaisの「神は老獪にして・・・」第12章p284~291の説明 と 第14章p328 をご覧下さい。
ここは、C.(14)[補足説明3] と、C.(16)[補足説明1] と、C.(17)[補足説明1]もご覧下さい。
D.“物質”現象


§19.摩擦の無い断熱的流体に対するオイラーの方程式

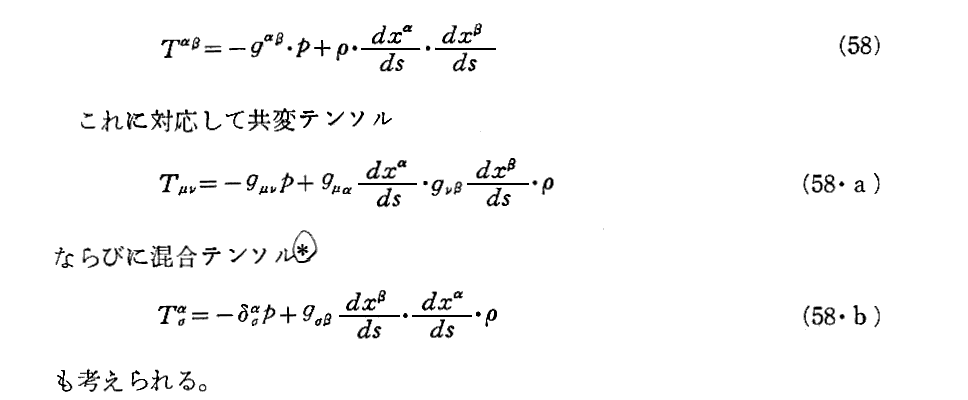




§20.真空中の電磁場に対するマックスウェルの方程式
1.Maxwell方程式

φνは(3次元世界でのベクトルポテンシャルAとスカラーポテンシャルφから構成される)“共変ベクトル”の成分である事に注意。だからそれに対してRot演算を施して得られる Fρσ は2階反対称共変テンソル(つまり共変6元ベクトル)となります。
その6元ベクトルの反対称共変微分をしたものですから、(60)式の左辺は3階共変テンソルになります。しかも完全反対称です。


Pais「神は老獪にして・・・」第12章p288に説明されている様に、EinsteinとGrossmannは1912年論文では、これをさらに双対テンソル形式表示(この場合ベクトル方程式になる)の一般共変形にしたものも示している。



上式の微分操作は、2階反対称反変テンソル(6元ベクトル)の共変微分のDivを表しています。今は√-g=1としているから(63)式の様に表されているだけです。この当たりはPais「神は老獪にして・・・」第12章p288などを参照されてください。
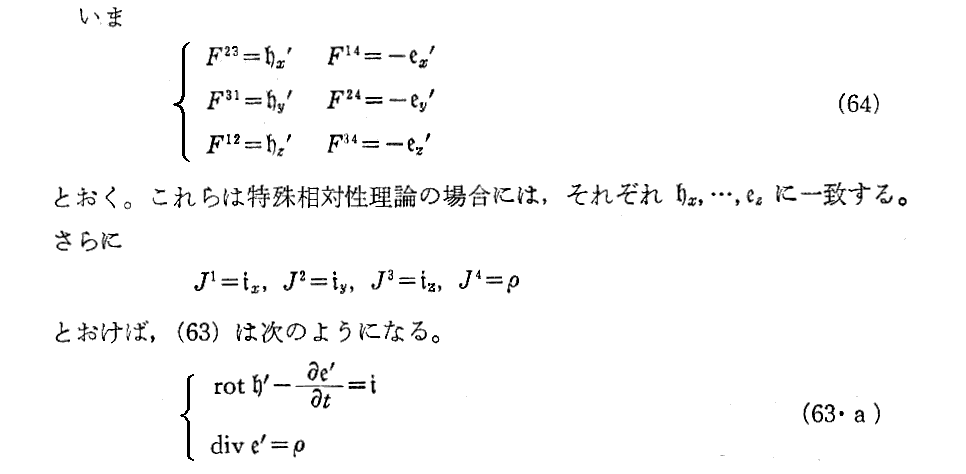
[補足説明1]
マックスウェルの式の第1の組は電磁場テンソルの反変成分(混合成分でも良い、そのときのJμは共変ベクトルJμを用いる)で構成され、マックスウェルの式の第2の組が電磁場テンソルの共変成分で構成されています。
何故その様になっているのか不思議に思われるかもしれませんが、斜交曲線座標の世界で必然的に現れる反変表示、共変表示は元々どちらが本質的で、どちらが従属的なものというものではありません。どちらも等価・同質のものです。
だから、電磁場の世界を表す自然法則が、たまたま、それぞれ反変成分あるいは共変成分を用いて表されるようになっていると言うだけです。実際のところ、別稿5.(2)[補足説明1]で説明したように、基本計量テンソルを用いれば反変表示と共変表示は自由に入れ替えることができるのですから。
この当たりは、ミンコフスキーの貢献に対するEinsteinの説明を噛みしめるべきでしょう。

[補足説明2]
Einsteinは極めて簡潔に表現しているので、ここの説明から、微分操作が普通の微分では無く共変微分に拡張されていて、方程式が一般共変性を満たすように拡張されている事がなかなか読み取れません。その事については別稿文献9.の7.(6)1.をご覧になって確認して下さい。
共変微分で生じた微分係数はテンソルですから、そういったテンソルで構成された物理法則はA.(3)[補足説明1]で説明した意味での座標変換に対する一般共変性を満たします。
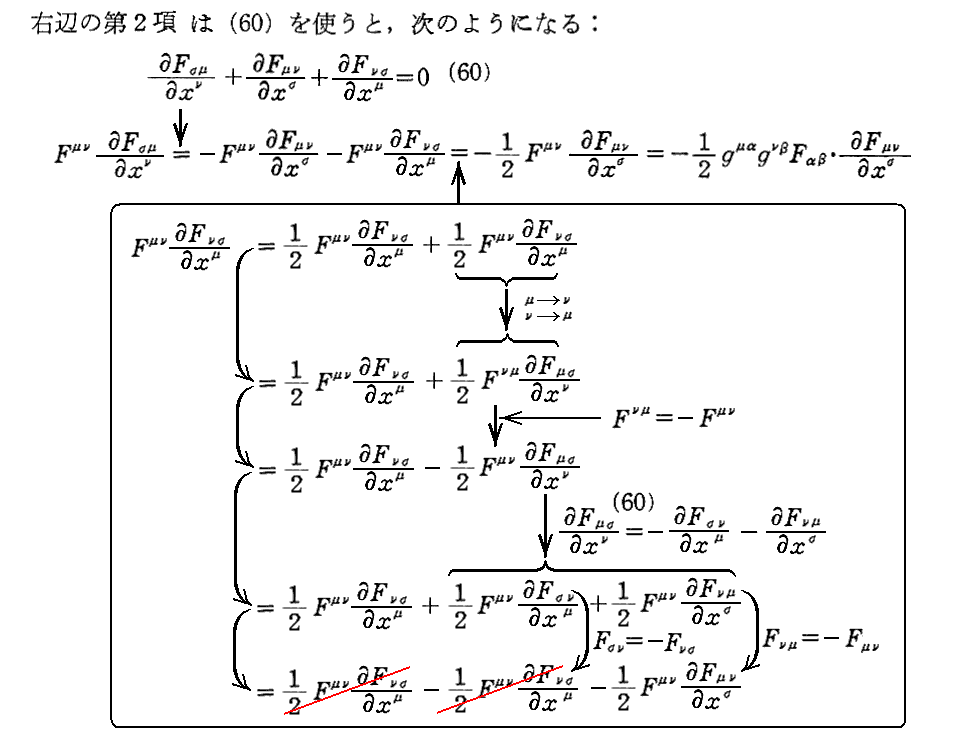
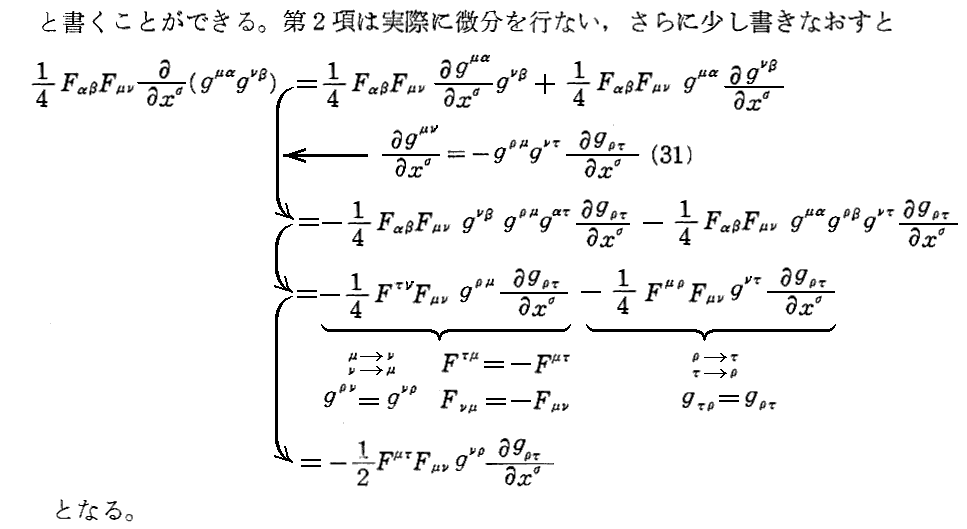
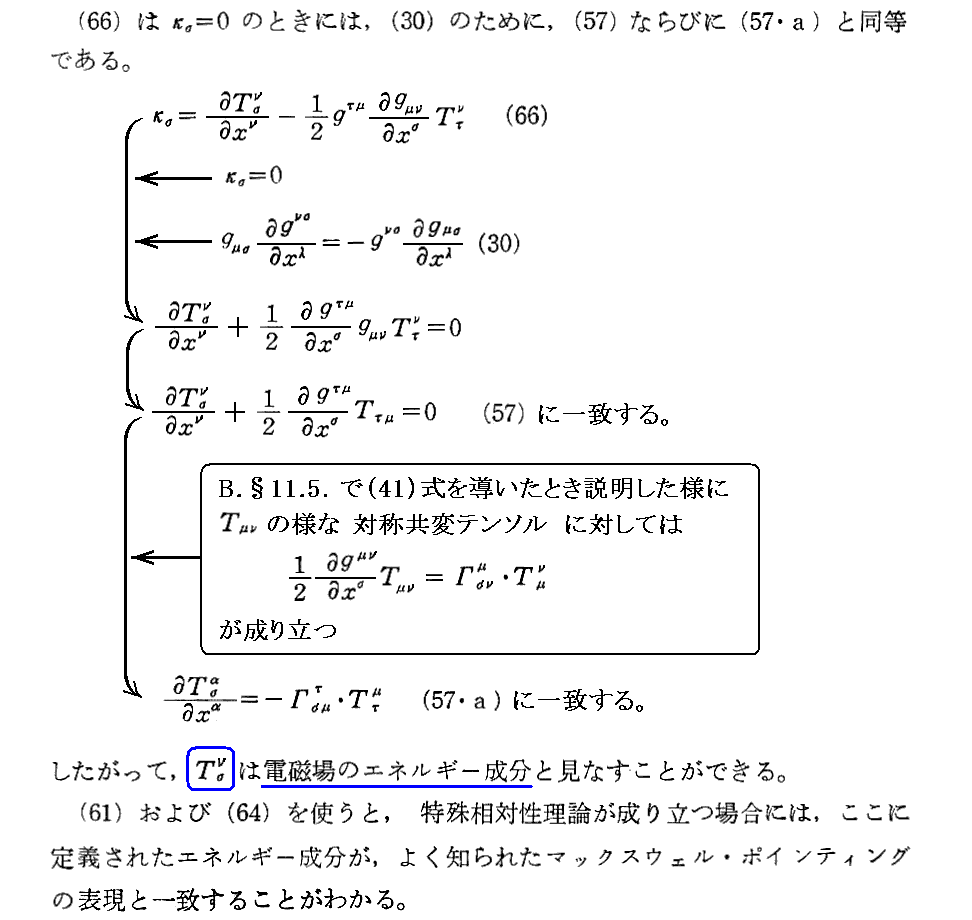
2.電磁場のエネルギー成分


上記アンダーラインを引いた文章の意味は解りにくいので、別稿「電磁場のエネルギー密度とポインティングベクトル」2.(3)[補足説明3]の説明をご覧下さい。

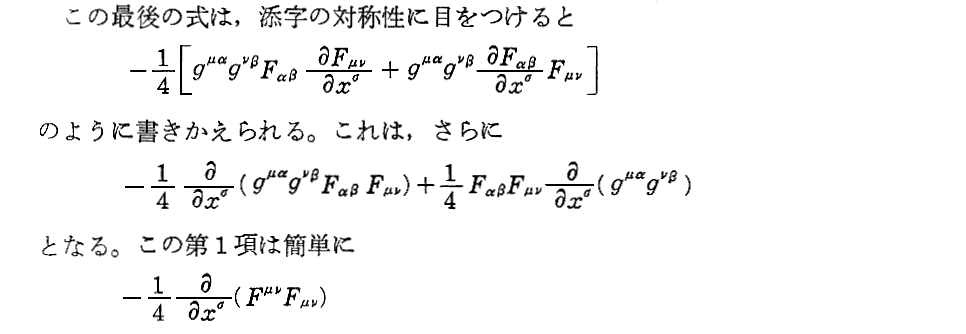



E.理論の検証
§21.第1近似としてのニュートンの理論



1.質点の運動方程式
下記の“質点の運動方程式”(46)式は§13を参照。これは§9“測地線の方程式”で導いた(22)式のことです。



ここは別稿7.(2)1.を参照。ただしそこの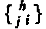 と、ここの
と、ここの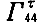 は符号を逆に定義していることに注意。また普通は
は符号を逆に定義していることに注意。また普通は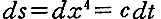 と定義するのだが、今はc=1としている。
と定義するのだが、今はc=1としている。



ここは別稿7.(2)1.や、別稿(中野董夫著)9-4.重力場中の物体の運動方程式、さらに藤井文献4.§19などもご覧下さい。補足しますと、このことが最初に示されたのは、Einsteinの超有名な論文1915年11/18§2に於いてです。
2.重力場の方程式
下記の“重力場方程式”(53)式は§16“重力場の方程式の一般形式”を参照。

そのため(53)式の右辺は
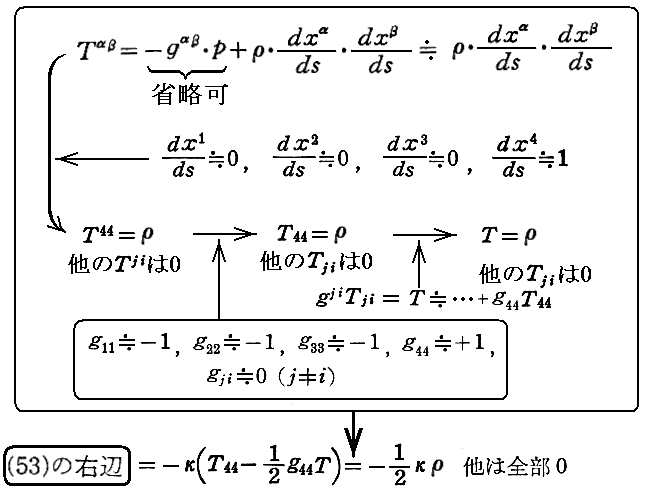
となる。
一方(53)式の左辺は
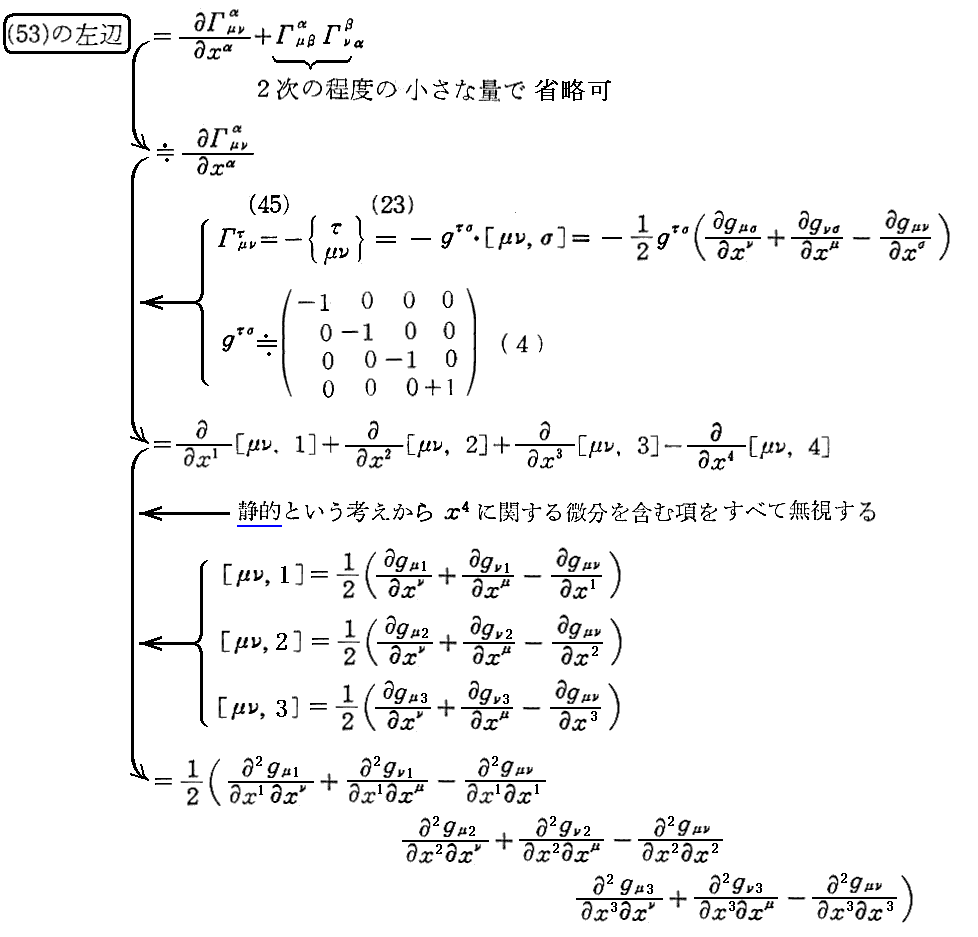
となります。


ここで補足すると、別稿「ポアソン方程式と波動方程式」1.(1)で偏微分方程式
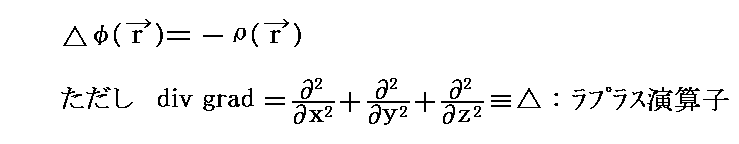
を満たす解は
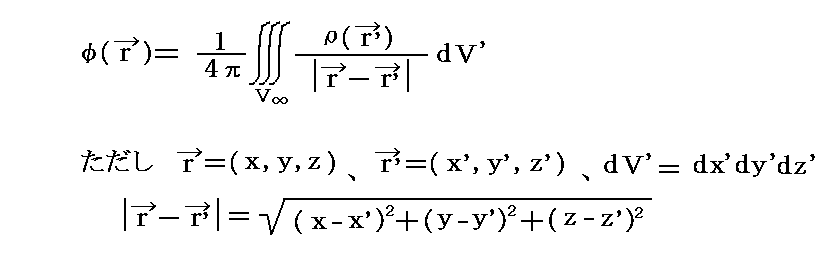
となることを証明した。
この結論を、ここでの議論に置き換えると(68)式を満足する(g44+1)の解は
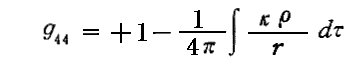
となる。右辺の+1は質点から無限縁離れた点に於いてg44→1に成ると言う境界条件から付け加えてあるだけです。上記φ(r)は無限遠(r→∞)でφ→0となるのでしたから。
次の文節の(68・a)式は、これから導かれたものです。
《重力場方程式の定数κを決定する方法》
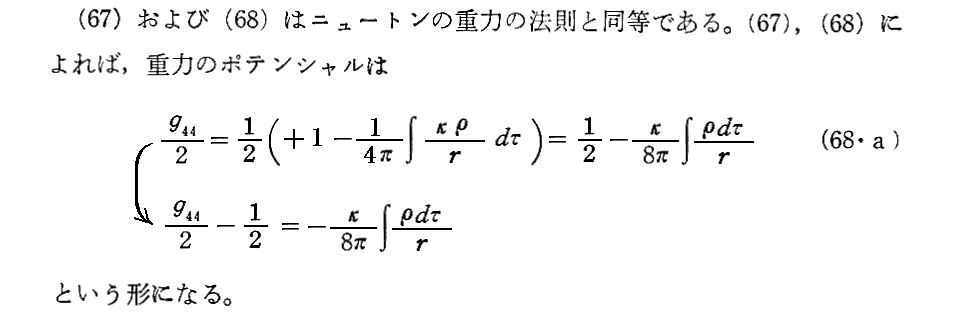


ここは別稿7.(2)2.や、別稿(中野董夫著)9-5.重力場の方程式、さらに藤井文献4.§20などもご覧下さい。
ここで展開されている議論が、今日のあらゆる教科書で踏襲されている、重力場方程式の右辺の“定数κを決定する方法”です。
§22.静的重力場内にある物指と時計,光の湾曲,惑星軌道の近日点移動
この節は別稿で紹介したSommerfeldの説明も参照されて下さい。



《重力場方程式解の定数αの決定》
補足すると、上記(70・a)式に(69)式を適用すると
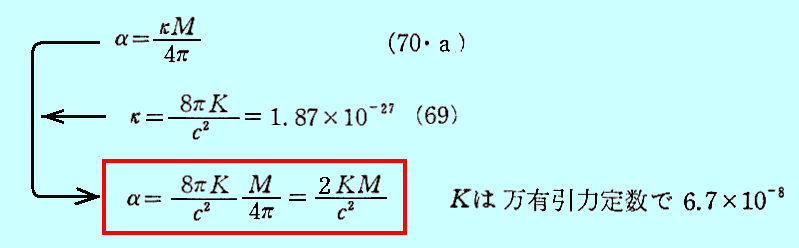
が得られる。Mは中心に存在する質量です。
これはシュワルツシルド解における“シュワルツシルド定数”(シュワルツシルド半径とも言う)に相当します。以下の議論の最終的な結論のαをこの表現にすると、お馴染みの関係式に帰着します。
[補足説明1]
Einsteinは極座標ではなく直交座標xiを用いているのでgρσの非対角成分が出てくる。Schwarzschildの様に極座標を用いればもっとスッキリするはずです。しかし、極座標にすると、この論文で仮定されている
√-g=1 が満たされませんので、重力場方程式は(47)式ではなくてC.§16.[補足説明2]で説明されている形【(c’)式で右辺=0としたもの】を用いなければなりません。もちろん、Schwarzschildは極座標を用いたのでそちらの方程式を利用した。
[補足説明2]
静的な重力場の場合には、(70)式で gρ4=g4ρ=0 (ρ=1,2,3)でなければ成らないのは、x4 → -x4 としたときでも、ds2が不変で無ければ成らないからです。
例えば事象(x1,x2,x3,x4)と(x1+dx1,x2,x3,x4+dx4)を考えたとき不変量ds2=g11(dx1)2+g14(dx1)(dx4)+g44(dx4)2である。ここで時間反転x4 → -x4 を行うと、ds2=g11(dx1)2-g14(dx1)(dx4)+g44(dx4)2となる。静的であるとは、この時間反転に対してds2が不変である事を意味するのでg14=0でなければならない。他のρ=2,3の場合も同様です。
さらに、このことが言えるため、gρσの(ρ,σ=1~3)の部分はgρσの(ρ,σ=1~3)の部分の逆行列になり、g44=(g44)-1であり、gρ4=g4ρ=0 (ρ=1,2,3)となる。

[補足説明3]
上記の“容易に証明できる”は、(70)式をC.§14.の物質の存在しないところでの重力場の方程式(47)式に代入すると独立なRμνの10個の方程式に於いて Rμν=0 となる事が証明できることを言っている。
ただし、実際に証明するには(70)式からクリストッフェル記号Γαμνを計算してリッチテンソルRμνの表現(44)式に代入しなければ成らないので、かなり面倒な計算が必要です。Einsteinには容易かも知れませんが、我々凡人にはそうではありません。その計算の様子については別稿§1[補足説明7]などをご覧下さい。実際に、その事を確認するにはかなりの計算が必要なのでここでは別の手段を取ることにします。
すなわち、上記の計量テンソルから構成される線素の表現式 ds2=gμνdxμdxν を、中心質量を原点とした“極座標”に座標変換してみます。
下記の式表現は小さくて見にくいので詳細はこちらの拡大版でご確認ください。

つまり、極座標表示の ds2 は次の様になる。
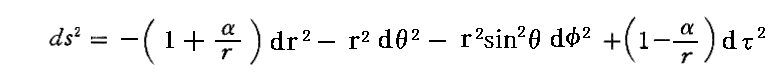
これは、1915年12月にSchwarzschildが求めた厳密解のgrrを -1/(1-α/r)≒-(1+α/r) で近似したものです。Schwarzschildの解が重力場方程式を完璧に満足することは別稿「シュヴァルツシルトの厳密解」で確認していますので、アインシュタインが直交座標で求めた解が重力場方程式を良い近似で満足することは明らかでしょう。
いずれにしても、アインシュタインが初めて求めた重力場方程式の解は厳密解に極めて近い近似の良い解([補足説明5]を参照)だったのです。
[補足説明4]
Schwarzshildの厳密解は“極座標表示”で求められたのですが、その厳密解をEinsteinがここで用いた直交座標で表示するとどうなるかを補足しておきます。
それするには、[補足説明3]で用いた座標変換
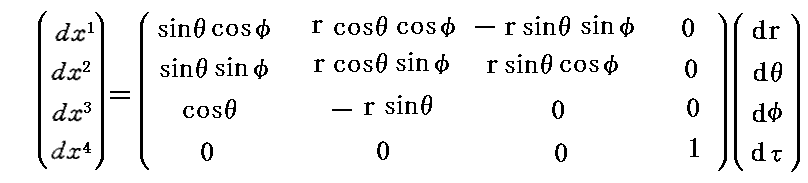
の逆変換をまず求めます。それには、別稿「行列式と行列」2.(3)(あるいは「余因子行列と逆行列の関係」)の方法を用いればよい。それに従って求めた逆変換は
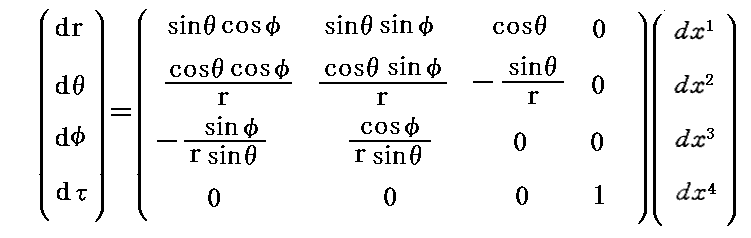
となる。
もちろん、この逆変換係数の行列は元の変換係数とは“逆行列”の関係
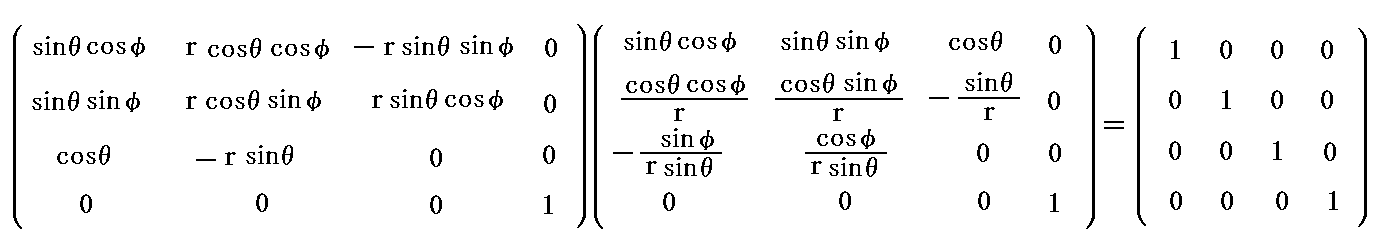
にあります。
ここで、上記逆変換の係数を
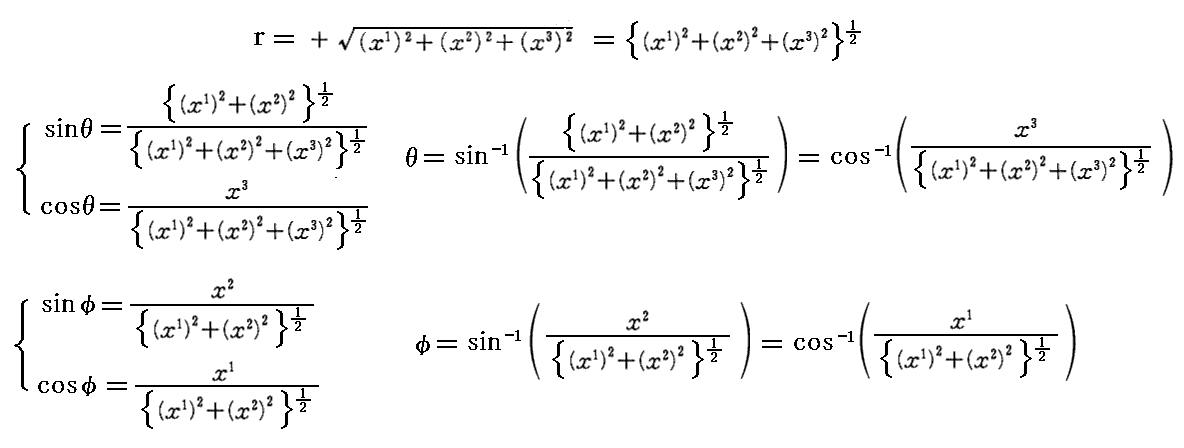
に従って、x1,~,x4の関数に変換しておけば
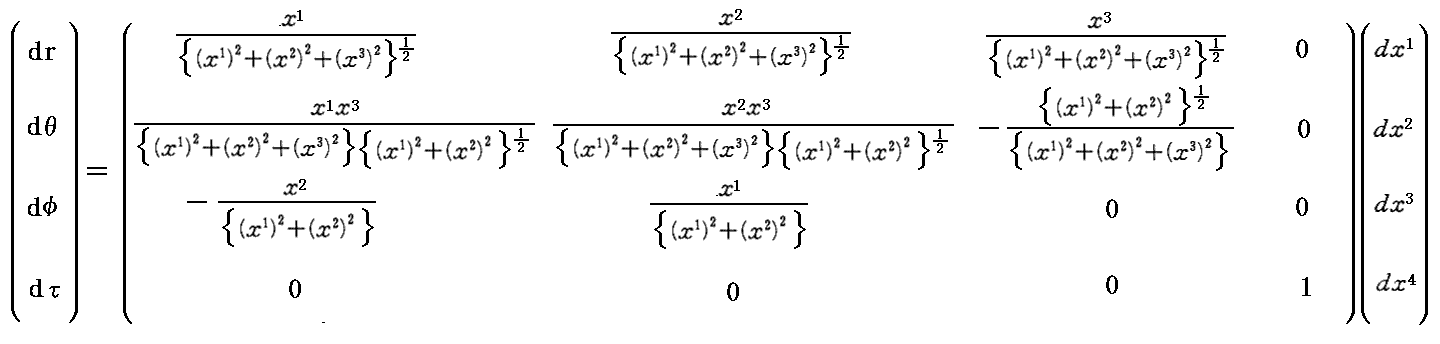
となる。
これをSchwarzshild厳密解の線素表現
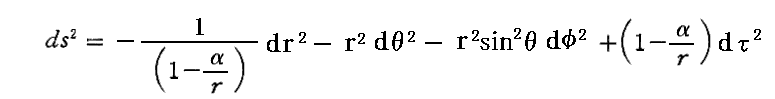
に代入すれば、(詳細はこちらの拡大版でご確認ください)
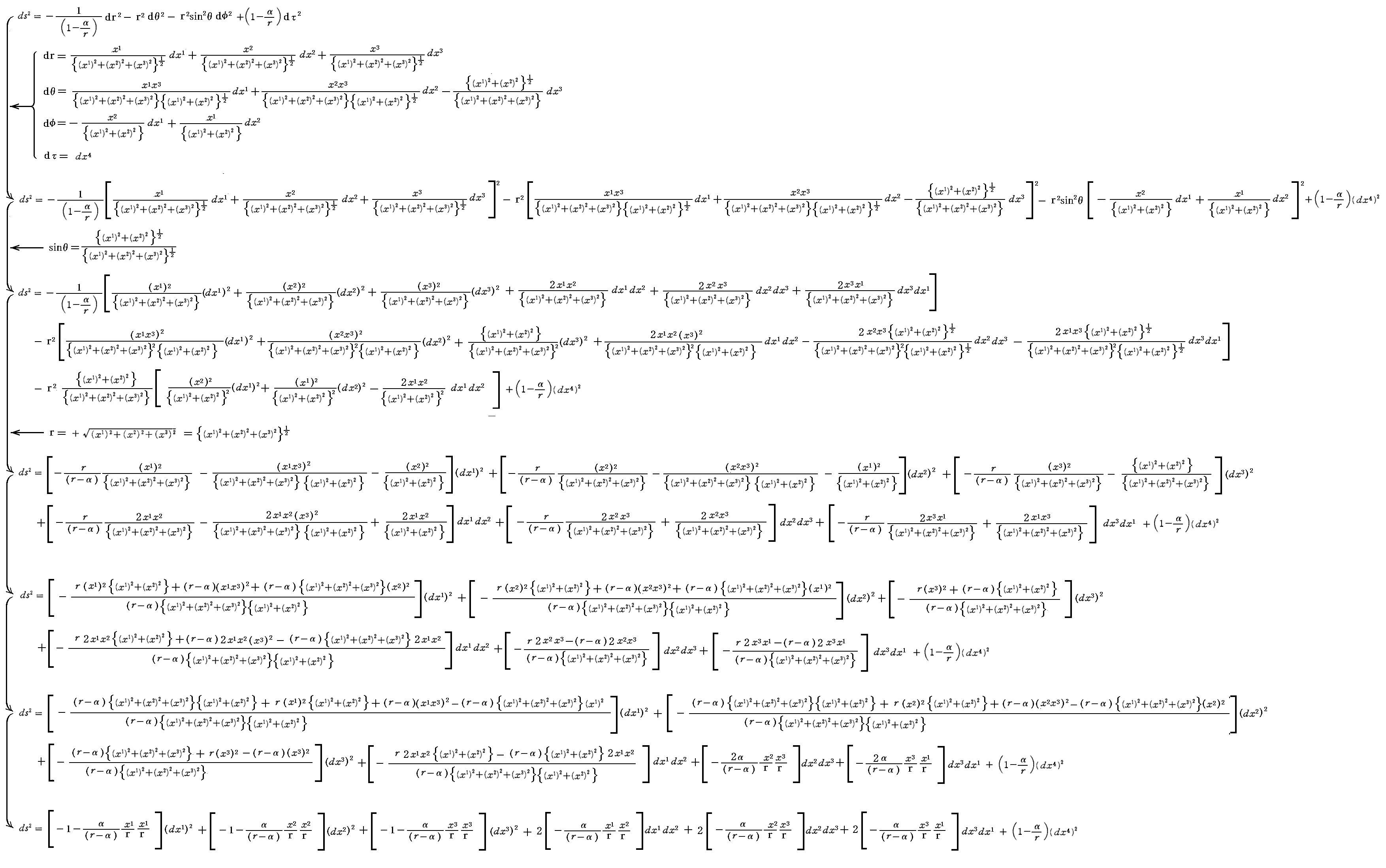
となり、厳密解の“直交座標表示”
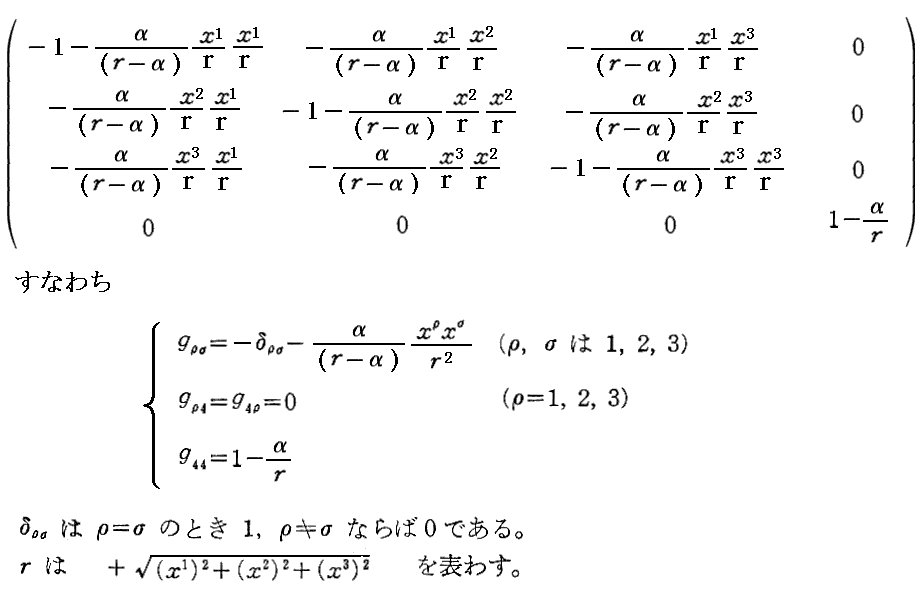
が得られる。これが、直交座標で表した《シュヴァルツシルドの厳密解》です。
ワイル著「時間・空間・物質」(1922年)§33,あるいはベルグマン著「相対性理論序説」秀潤社(1978年刊)第Ⅷ章、あるいはさらに内山龍雄著「一般相対性理論」裳華房(1978年刊)§36、等々・・・で直接この形の解が求められていますのでどうぞご覧下さい。内山先生の説明が最も後に書かれたので洗練されていて解りやすいです。
この総説論文は1916年3月に書かれています。その時点のEinsteinはSchwarzshildの厳密解(1915年12月)を当然知っていました。だから上記の手順を実行すれば“直交座標表示での厳密解”が得られたはずです。
それなのに、それを用いないで1915年11/18論文の解をそのまま用いたのは、その解がSchwarzshildの厳密解とほとんど同じである事を良く承知していた([補足説明5]を参照)ので、前節§21の展開や以下の議論には11/18論文の解のままでも適切だと考えたからでしょう。
[補足説明5]
丁度良い機会ですから、《アインシュタインの近似解》(11/18論文で提示したものです)
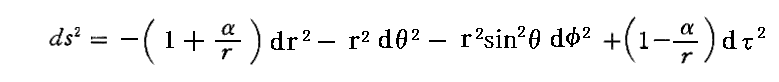
と《シュヴァルツシルドの厳密解》
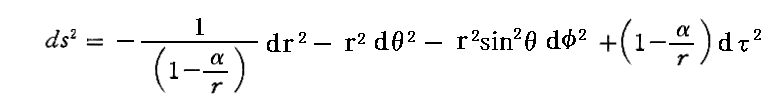
との関係をもう少し説明します。
上記の式中のαは今日“シュヴァルツシルド定数”(あるいは“シュヴァルツシルド半径”)と言われるもので

と表されます。
実際の質量について、シュヴァルツシルド半径αを計算してみると
M=太陽質量=2.0×1030kg の場合 α=2.64×103m=2.64km
M=地球質量=6.0×1024kg の場合 α=8.85×10-3m=8.85mm
程度の値になります。
そのとき、(物質が存在しなくて)重力場のみが存在する領域に対するシュウァルツシルド厳密解が成り立つのは太陽の場合は、太陽半径の外側の部分であり、地球質量の場合は地球半径より外側の領域です。
ところで、太陽半径=6.96×105km ですから、太陽半径より外側の領域に於いては、rはαよりも圧倒的に大きく(r≫α)なり (α/r)<0.00001 となります。つまり、その領域におけるgrrに対して
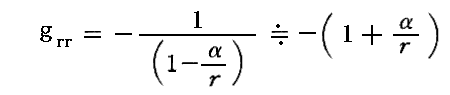
と近似することは圧倒的に正しい!! のです。実際の所一般相対性理論が作り上げられた時代には《アインシュタインの近似解》では計算精度が不十分である様な問題は存在しなかった。
逆に言えば、それ故にニュートン理論と一般相対性理論との差を実験・観測によって検出することが極めて困難だった。
所がやがて 白色矮星→中性子星→ブラックホール天体 と極めて狭い領域に質量が集中して存在する高密度天体が発見されてきます。ブラックホールとは要するにシュウァルツシルド半径より狭い領域に質量が集中しているためにその質量外領域に於いてrがαに一致するまで近付いた時空領域が問題となってくる天体のことです。
そういった領域においては、アインシュタインの近似解は成り立ちませんから、シュヴァツルシルドの厳密解解が重要になってきます。まさに《シュヴァルツシルドの厳密解》の独断場です。
[補足説明6]
さらに補足します。
上記の[補足説明4]と[補足説明5]で直交座標と極座標との間の座標変換を説明しました。そのとき座標原点はどちらも質点(質量中心)を原点として原点は動かさずに行った座標変換です。
そのとき、別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」3.(4) で説明したように、座標を変換すると計量テンソルの表現も変化します。特に3.(4)[補足説明3]で注意した様に、時空間のひずみは変化していなくても、座標系を別な座標系にすることでも計量テンソル(gij)は変化するのでした。
だから、前記の[補足説明4]と[補足説明5]の中で互いに移り変わった計量テンソルの表現は、時空の歪みは変化していないが(つまり幾何学は不変だが)そのなかに引いた座標軸を変えることによって生じた計量テンソルの変化です。
そのとき問題なのは、座標軸の引き直しは、歪んでいるリーマン空間的な時空間であるにもかかわらず、擬ユークリッド的な時空間座標として引き直していることです。だから、[補足説明4]と[補足説明5]の中で用いた引き直しの座標変換式が全時空間領域にわたって利用できるのかと言うことです。
このことを別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」4.(3)[例8]で説明した2次元平面と2次元球面の例で考えて見ます。
まず《二次元平面の場合》は空間は歪んでいませんので、[補足説明4]と[補足説明5]で説明した座標変換式の二次元版を用いれば、それを全空間領域にわたって適用することができます。
所が《二次元球面の場合》は空間が歪んでいます。そのためそこの説明の極座標の原点(地球の緯度経度の測定原点である北極点に相当する点)に於いては、そこに擬ユークリッド的な接平面を考える事ができるごく狭い領域において[補足説明4]と[補足説明5]で説明した座標変換式の二次元版を適用することができます。
そのとき、その座標変換式を、もっと緯度が下がった中緯度領域や赤道領域でも利用できるのでしょうか。おそらく、歪んだ時空であっても、それぞれの局所的な領域では接平面の様な接擬ユークリッド空間を考えることで、全領域で適用できるのでしょう。もちろんそれぞれの空間領域では、直交座標の単位目盛り棒の長さは変化しているし、極座標の単位目盛り棒のの長さも空間領域のひずみに応じて変化していくはずです。
実際、私にとってここのところが一般相対性理論で最も解らない所ですがおそらくそうなのでしょう。
1.静的重力場内にある物指と時計



“いま用いている座標系から見て” とは非常に解りにくい表現だが、おそらく“この重力場内を自由落下する人が持っている物指棒と重力場内に静止している物指棒がすれ違う瞬間に比較して”という意味だろう。
あるいは、重力場が存在しないとしたとき、その場所に引くことができる座標系から見てと言う意味だろう。重力場が存在しないと仮定して同じ場所に座標系を設定することなどできないのですが、その意味で了解するしかないと思います。次も同様。
ここは、Sommerfeldの「電磁気学」§38のLenzの説明を参照されたし。
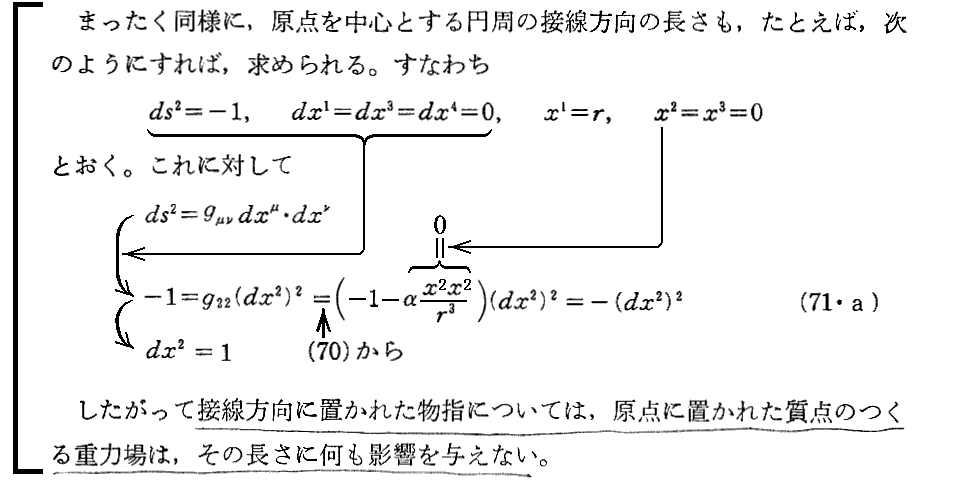

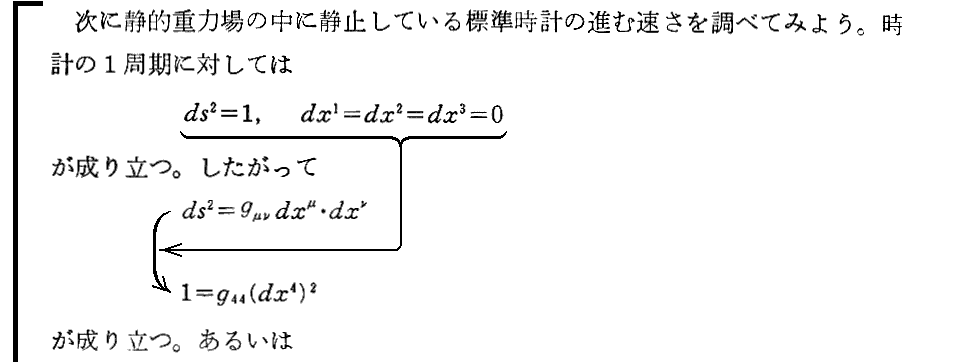
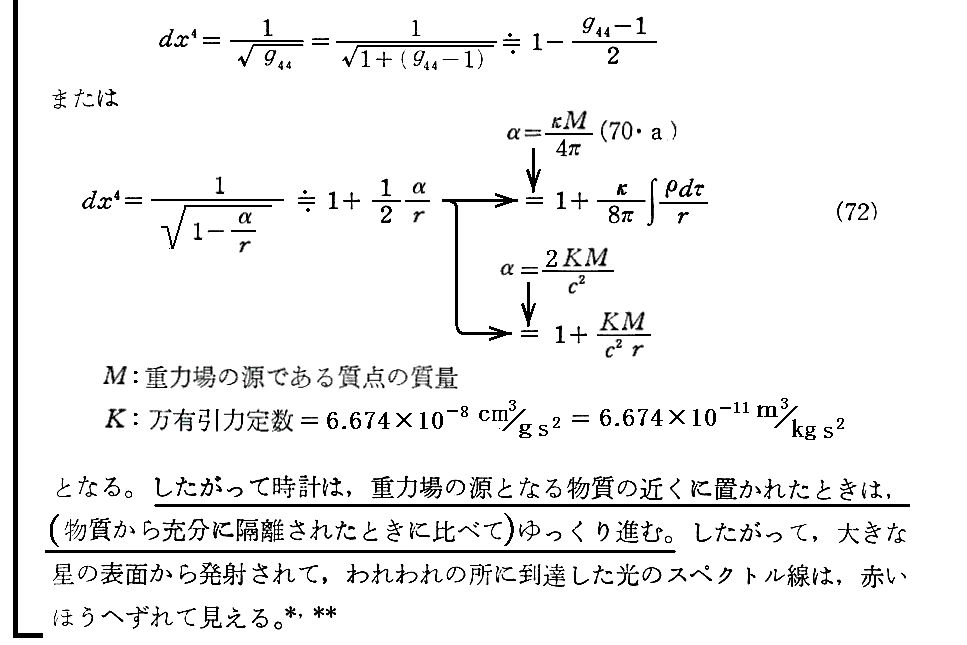

上記注 * のフロインドリッヒについてはアーミン・ヘルマン編・著「アインシュタイン/ゾンマーフェルト往復書簡」法政大学出版局(1971年刊)のp28~33と、p36~41を参照されたし。
ここは別稿7.(9)3.も参照されたし。
[補足説明1] ここは、訳者である内山先生の補足解説です。

こうなる事はE.(22)[補足説明3]で説明しました。これは、1915年12月にSchwarzschildが求めた厳密解の grr= -1/(1-α/r) を -(1+α/r) で近似したものです。
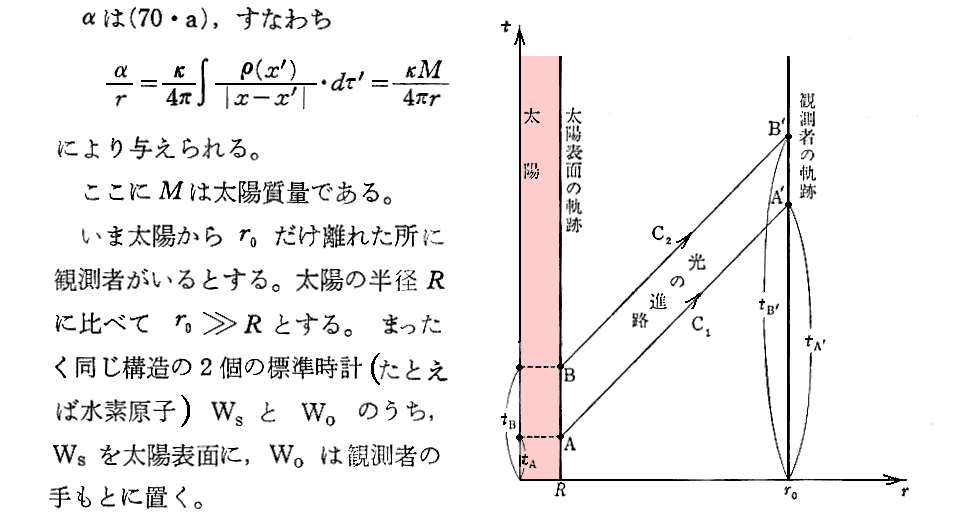





つまり、“振動周期”が 1+(α/2R) 倍になるので、次に述べる様に“振動数”は 1/{1+(α/2R)} 倍になる。

[補足説明1-1]
ここは難しい事を言っているわけではありません。恒星に近い重力場中であろうと恒星から離れた場所の重力場中であろうと《光速度は一定不変》です。光に対してds2=0が常に成り立つ事はその事を表している。だから恒星表面からやってくる光の振動数は恒星表面での振動数をそのはまま保持して地球に到達すると言うことです。
[補足説明1-2]
さらに補足すると、恒星表面で特定のスペクトルの光を放射する原子にとって、振動数の低い(つまり赤方に片寄った)光を放出しているという意識はありません。普通の振動数の光を放出しています。ただし、恒星表面の重力場の強い所では時間がゆっくり進みますから、離れた場所の人から見ると赤方に変位した光が放出された事になるだけです。
離れた場所の人から見るとその光の粒(光子)は赤方偏移した光がそのまま進んでいる様に見えますが、恒星表面が出発した光自身に取っては普通の振動数の光のままで重力場中を進んでいるつもりです。
重力場の深いところ(恒星表面)から離れた場所(惑星)へ進む光自身にとっては、自分は普通の振動数の光として出発したのだが、重力場のポテンシャルから受ける仕事のために段々エネルギーを失って仕舞うと感じているはずです。そのため-ΔE=h(ν’-ν)で定まる様に赤方に偏移した光として離れた場所の惑星へ到達することになるともいえる。つまり、光子のエネルギーが E=hν であると言う光量子理論と、重力場中で発光した光が外部に届いたときには赤方偏移しているという一般相対性理論のメカニズムと見事に調和している。
2.光線の湾曲

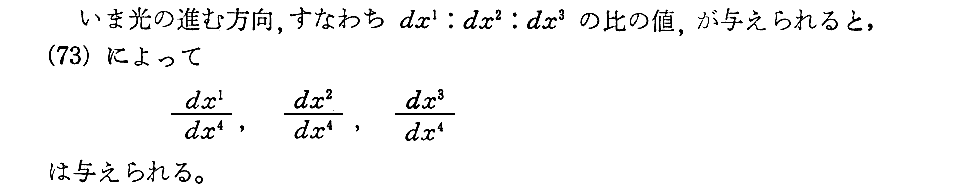
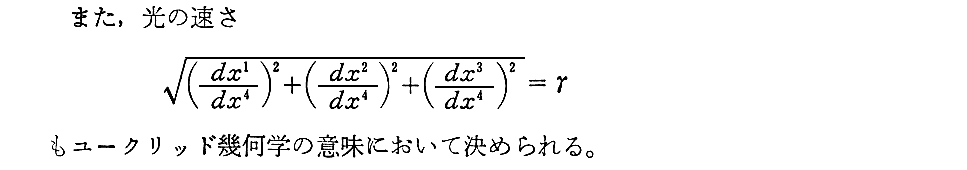


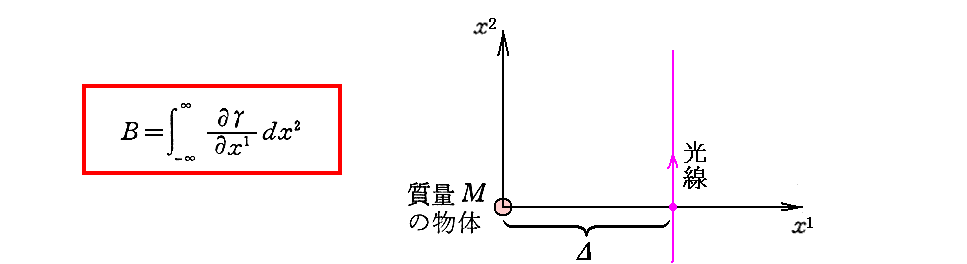
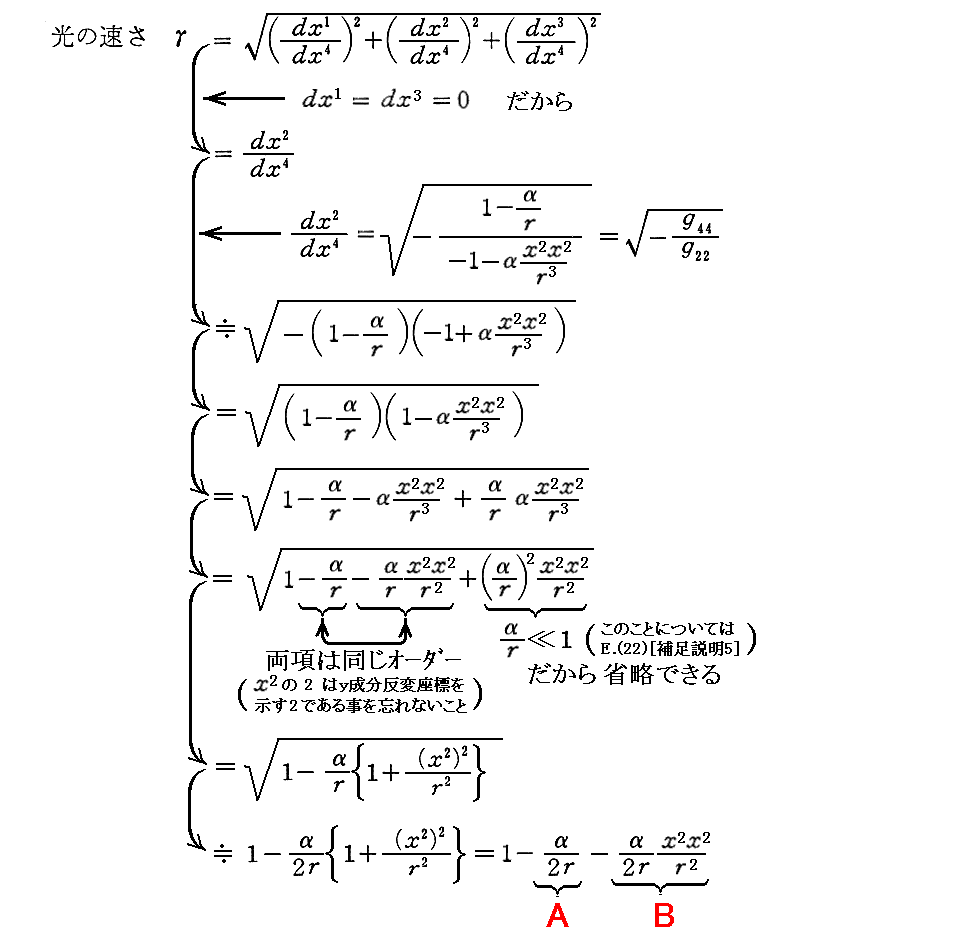
上記Bの表現式は解り難い所です。この式については「1911年プラハ論文」§4[補足説明1]を復習されて下さい。そこのcをγに、n’をx1に読み替えて下さい。
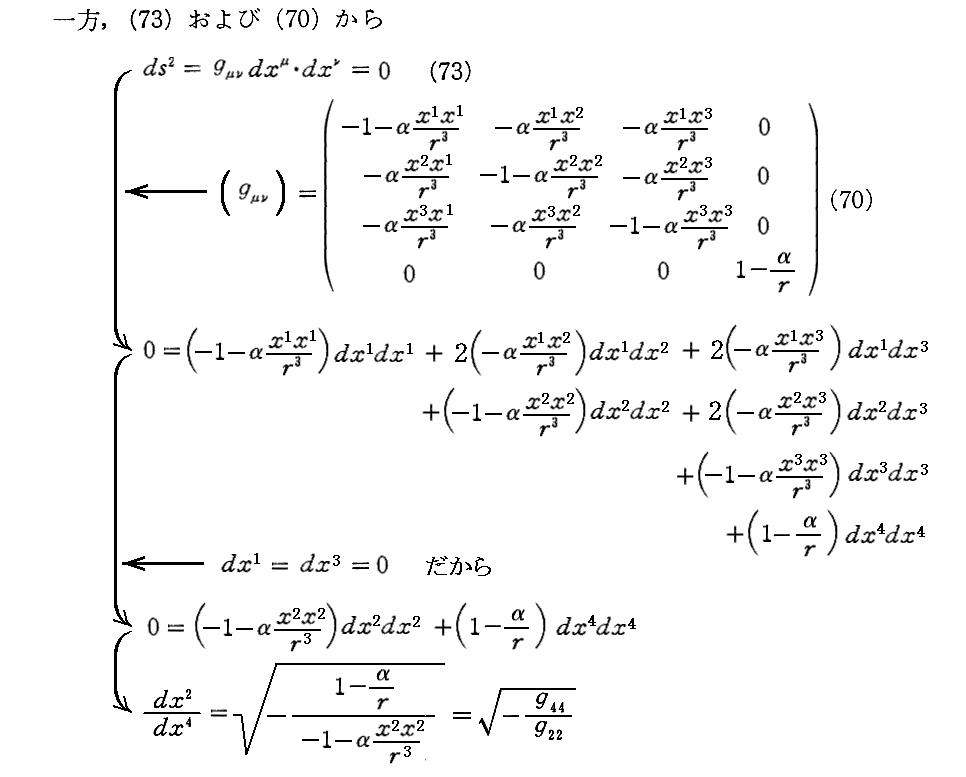
[補足説明1]
少し補足すると、上式の導き方から解る様に、Aの部分が[重力場中で時間の進みがゆっくりになる効果による光の速さの減少]を表し、Bの部分が[重力場中で空間が縮む(物差し棒が縮む)効果による光の速度の減少]を表しています。
この二つの効果で光線は湾曲するのですが、速度の変化と光線の湾曲の関係は解りにくいところです。その事の説明はEinsteinの「1911年プラハ論文」§4[補足説明1]が秀逸です。
二つの効果は一方にx2x2/r2の項がかかっているぶん少し異なるのですが、次の(∂γ/∂x1)の積分計算をご覧になれば解る様に、x2についてx2=-∞からx2=+∞まで積分すると両者の違いは無くなります。そのため空間の歪み(縮み)の効果も考慮した光の湾曲量はプラハ論文(1911年)で求めた値の“正確に”2倍です。
さらに補足しますと、重力場中では時間がゆっくり進むと同時にその点での物指し棒も縮みますから、各点での光速度は“どこで測っても”一定不変な“c”です。

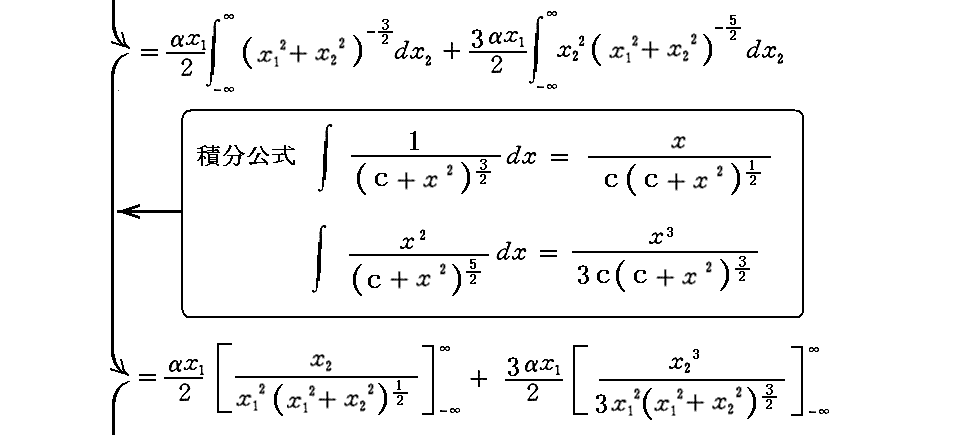
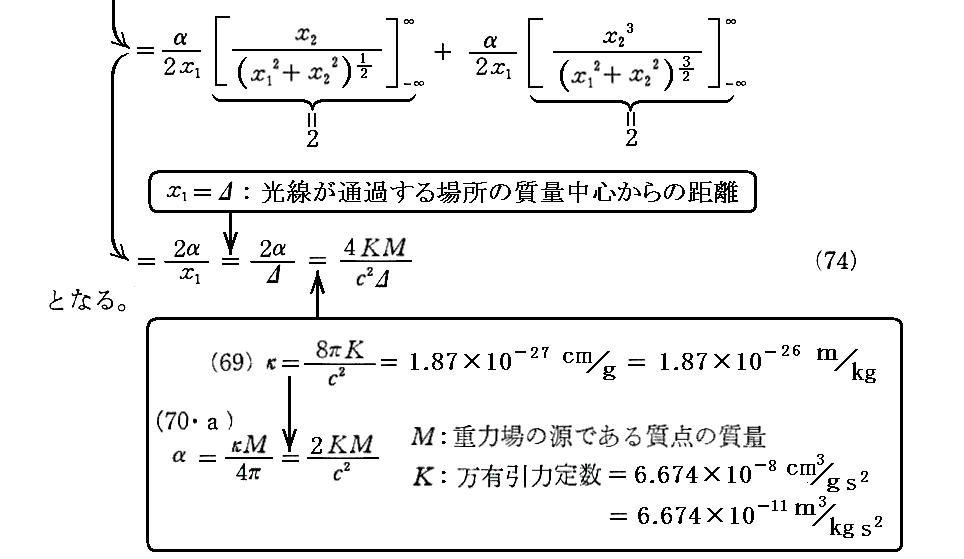

上記で訳者が比較されよと言っている論文[A1]はこちらです。その中のp.32はこちらですが、そこでの湾曲量が2KM/c2Δだったことと比較されよということです。また、(74)式の具体的計算については別稿7.(9)2.《数値計算》をご覧下さい。
3.惑星軌道の近日点移動



ここの説明は圧倒的に不足していますので、訳者が言及している論文[A4]と別稿7.(9)1.をご覧になって補われて下さい。
[補足説明1]
本冊子(論文)はシュワルツシルドの論文発表後の1916年3月に出版されました。そのため、EinsteinはSchwarzschildの仕事(1915年12月)を上記注*で引用紹介しています。Schwarzschildの厳密解を用いても惑星の軌道方程式は導出できます。そのことについては別稿7.(8)で説明しています。
《Einstein論文の解》に対する《Schwarzschildの厳密解》の位置づけに関して興味のある所ですが、その事については別稿4.§2.[補足説明6]と、本稿C.(16)[補足説明3] の説明をご覧下さい。そのとき、下記の文献情報も重要です。

Schwarzschild論文(英訳pdf版)のダウンロードサイトのURLは別稿7.(7)[補足説明6]をご覧下さい。

END.参考文献
1905年の特殊相対性理論の論文がそうであったように、この1916年論文にも参考文献は記されていません。実際、参考となるような既存の論文・論考など存在しなかったのですから、それも当然でしょう。それほど革命的・独創的な論文だったということです。
しいて参考文献をあげるなら、この論考の基礎を与えてくれた数学論文があるかも知れません。次に記すものがそれです。
- Carolus Fridericus Gaussの大論文『曲面についての一般研究』(1827年)
寺坂英孝、静間良次著「数学の歴史 19世紀の数学 幾何学Ⅱ」共立出版(1982年刊)第3章“微分幾何学”の中に日本語全訳があります。原論文はネットからダウンロードできますがラテン語なのでこの本をご覧いただくのが良いと思います。
- G.F.B.Riemannによるゲッチンゲン大学の私講師就任演説『幾何学の基礎をなす仮定について』(1854年6月10日)
矢野健太郎 訳・解説「現代数学の系譜10 リーマン幾何学とその応用」共立出版(1971年刊)の第1論文がこれの邦訳ですが、その内容は極めて難解です。その概要は別稿[補足説明1]を参照されたし。
- E.B. Christoffel, “Ueber die Transformation der homogenen Differentialausdru¨cke
zweiten Grades”,
Journal fu¨r die reine und angewandte Mathematik 70: p46~70, 1869年
“2次微分形式の変換について”
- RicciとLevi-Civita共著論文『絶対微分学の方法とその応用』(1901年)
矢野健太郎 訳・解説「現代数学の系譜10 リーマン幾何学とその応用」共立出版(1971年刊)の第2論文がこれの邦訳です。とても大部な論文で、その内容は極めて難解です。
しかし、別稿[補足説明2]や別稿[補足説明2]で説明した様に、Einsteinが必要としたものは、単なるリーマン幾何学ではなくて、4番目の次元として時間が絡んでくる時・空間です。しかも、その計量テンソルは、その特別な場合としてミンコフスキー4次元時空に帰着する特別な計量テンソルを持った時・空間です。このことは、リーマン幾何学の論理に加えてさらに難しい考察を必要とします。
そこの難しさを考慮するならば、単に上記数学論文を参考文献として掲げておけば済むものではありません。
ただし、Einsteinの下記二文献は、本論文を読む上で助けになると思います。いずれも、本論文の発表後に、その内容をより解りやすく伝えるために、Einstein自身が書いた解説書です。
- A.Einstein著,“U¨ber die spzielle und allgemeine Relativia¨tstheorie”, Braunschweig(1916年12月に完成したのですが、出版は1917年初頭です)
この翻訳版が下記のものです。
A.Einstein著(金子努訳)「わが相対性理論」白揚社(1973年刊)これは全文を別稿で引用しています。
A.Einstein著(金子努訳)「特殊および一般相対性理論について」白揚社(2004年刊)
- A.Einstein著, “Vier Vorlesungen u¨ber Relativita¨tstheorie, gehalten im Mai, 1921, an der Universita¨t Princeton.”. Braunschweig.(1922年)
A.Einstein著,“The Meaning of Relativity : Four Lectures delivered at Princeton
University”. Princeton University Press.(1921年)上記のE.P.Adams による英訳。
邦訳が下記のものです。
A.Einstein著(矢野健太郎訳)「相対論の意味」岩波書店(1958年刊)
この中の第3回講義の前半部分だけ別ページで引用。
この文献の邦訳版は石原純、他訳「アインスタイン全集 第四巻」改造社(1923年刊)の中にも77.「相対性理論についての四講義」として収録されています。矢野訳版と読み比べて見られると良いでしょう。
さらに、下記文献も本論文を読む上で有益だと思います。
- 矢野健太郎 訳・解説「現代数学の系譜10 リーマン幾何学とその応用」共立出版(1971年刊)の第3論文が本稿論文の矢野先生による邦訳版です。
内山、矢野翻訳版のどちらにも記号の誤植が結構ありますし、微妙な翻訳部分もあります。そのため両先生の翻訳を比較しながら読まれる事を勧めます。
- Abraham Pais著(西島和彦、他共訳)「神は老獪にして・・・(アインシュタインの人と学問)」産業図書(1987年刊)
第13章“重力場の理論(初めの50年)” 13b.
第14章“重力の場の方程式” 14aの後半 と 14c.“最後の歩み”
第15章“新しい動力学” 15c.
- Wolfgang Pauli著(内山龍雄訳)「相対性理論(上)(下)」筑摩書房筑摩学芸文庫(2007年刊)
原書は1921年刊です。上記訳本の元本は1974年に講談社から刊行されたものです。
- 矢野健太郎著「近代数学新書 相対性理論」至文堂(1967年刊)
この第7章“テンソル解析学の一般相対性理論への応用”を別稿で引用。
- Einstein著「自伝ノート(1947年)」東京図書(1978年刊)
この中の第5段落(p81~94)を引用。
- Einstein、Infeld共著(石原純訳)『物理学はいかに創られたか』(岩波書店1939年刊)
この中から、Ⅲ場・相対性(2)“場と物体”(下巻のp120~125)の説明を引用。
以下は、補足説明で引用した文献です。
- 須藤靖「一般相対性理論入門」日本評論社(2005年刊)
この中から2.3.座標変換・基底ベクトル、4.3.Einstein方程式を引用。さらに、別稿で
- 石井俊全著「一般相対性理論を一歩一歩数式で理解する」ベレ出版(2017年刊)
この中から第7章§7.§8.を引用。
- 杉山直著「相対性理論」講談社(2010年刊)
この中から第10章を引用。特に§3.を参照されたし。現代的な視点で明快に説明されています。しかし、ある程度理解できている方には明快かもしれませんが初めて学ぶ者には難しい。
- 平川浩正著「相対論(第2版)」共立出版社(1986年)
この中から第4章“Riemann幾何学”(p60~85)と第6章1.“Einstein方程式”を引用。
- 岡部洋一著「リーマン幾何学と相対性理論」プレアデス出版(2014年刊)
この中から§7-3“アインシュタイン方程式”、附録A.1“空間微分演算子”から引用。
内山龍雄先生は、別稿で引用している解説文に於いて
『・・・・・アインシュタインの論文は、一般的にいって、どれでも親切に、読者に解りやすいように書かれている。それにもかかわらず、冗長なところがなく、簡潔で見通しがよく、スッキリしている。論文に書かれている内容の5倍も10倍も多くのことを考えたうえで、そのなかの最も本質的な部分をとり出し、出発点から結論までを結ぶ最短コースを通って議論をすすめていくというやり方である。・・・・・』
と書かれています。
私も、確かにその通りだと思います。しかし、私には、C章、D章の説明の詳細が未だ理解できていません。数式の変形はなんとかたどれるのですが、式の意味するところが理解できていないのです。真に理解するには、Einsteinの思索過程をすべて辿ってみるしかないのかもしれません。
本稿をご覧になられて、一般相対性理論展開の梗概を承知されたと思いますので、引き続いて別稿「アインシュタインの重力場方程式」をご覧下さい。
Einsteinはグラスゴー講演(1933年)の末尾で次のように述べています。
『・・・・到達した知識の光りの中でみると、うまく当たった成果は殆ど当たり前の様に見える。そして賢い学生は誰でもあまり多くの苦労なくそれを把握できる。然し――強い欲求と共に暗中模索の年月、自信と失意の年月の交替、及び光の中への最後の出現――これを理解しうるのはただそれを経験した人たちだけである。』