時空の曲がりと測地線(測地線方程式とは何か)
一般相対性理論では、重力と相互作用する質点(物体)の運動は“測地線方程式”によって表される。これは、重力のみが働いている質点の運動は曲がった時空の測地線になる事を示している。
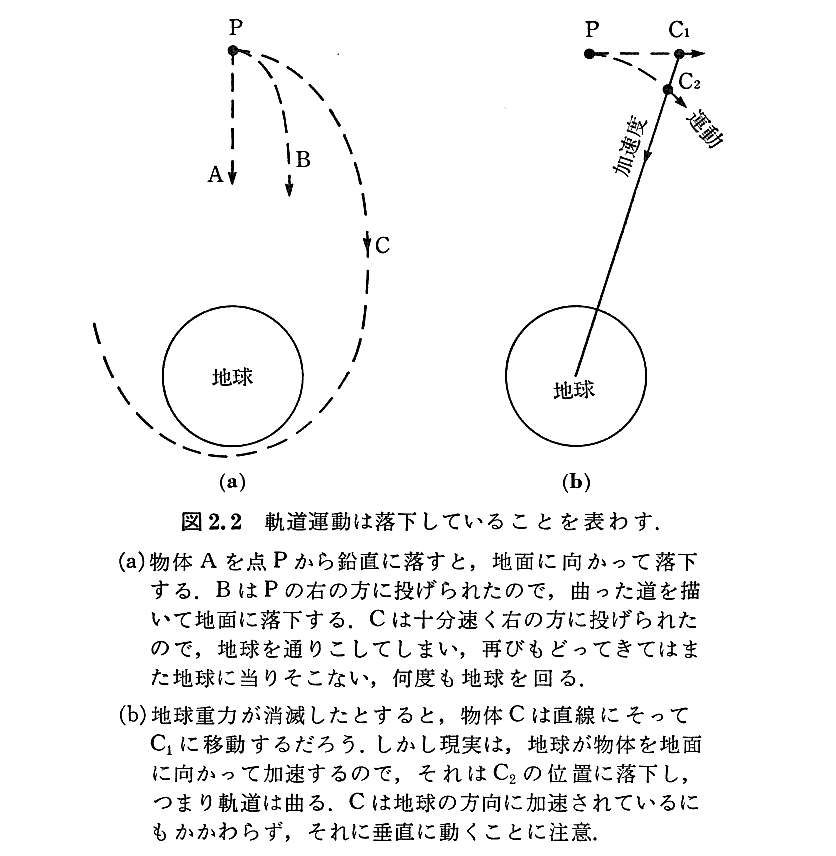
例えば、重力場の影響のもとにある地球表面で、物体を斜め上方に投射すると、手からはなれた物体は重力に依存して、放物線を描く運動をする。
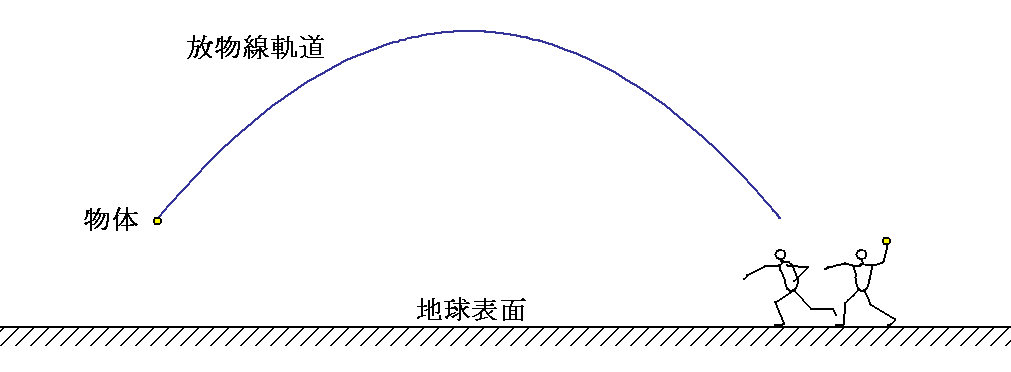
一般相対性理論は“この軌跡こそ時空の曲がりに沿った測地線(世界線)である!”と言っています。しかし、初学者にはその事の意味がなかなか理解できません。それは、空間曲率と時空曲率を混同しているからです。
このことが参考文献2.第2章p42~で説明されていますが、本稿では、ディヴィスの説明を利用して、もう少し詳しく且つ解りやすくします。以下は文献1.「重力波のなぞ」第2章“重力波とは何か”から引用した。
[補足説明]
“測地線方程式”の意味については別稿「運動方程式のローレンツ変換不変性」3.(1)2.[補足説明]をご覧下さい。測地線方程式はニュートンの運動の法則の真に正しい形(2種類の質量の等価性は空間の歪みの中に始めから組み込まれている)であり、その自然な拡張になっています。アインシュタインもその事を強調しています。
実際、重力場が無視できる場合は、ニュートンの運動の第一法則すなわち“慣性の法則”(第二法則の右辺の力の項をゼロと置いたもの)になります。ニュートンの運動の法則につきましては別稿「運動の法則」を復習して下さい。
1.電磁場と重力場の違い

2.力としての重力
(1)重力は力


(2)重力の法則






[補足説明]
以上の議論を逆にたどればケプラーの法則から重力の逆二乗法則が得られる。別稿「古典天文学」4.(8)3.を復習されたし。
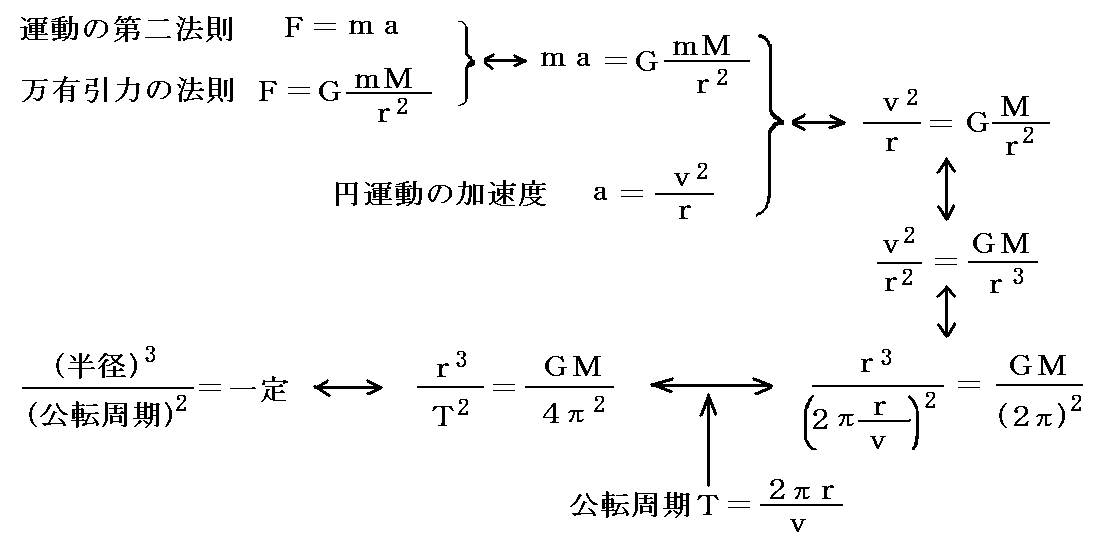
(3)重力場のエネルギー

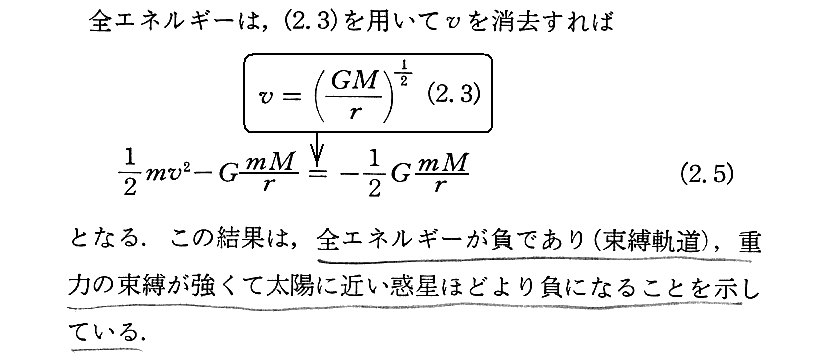

(2.6)式は何を言っているのか解りにくいが、電荷の集まりが示す静電エネルギーと同様に考えれば良い。
(4)重力と加速度

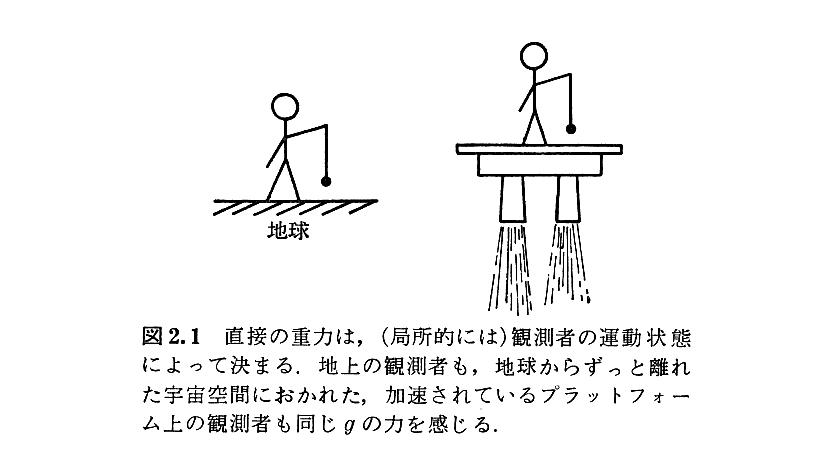


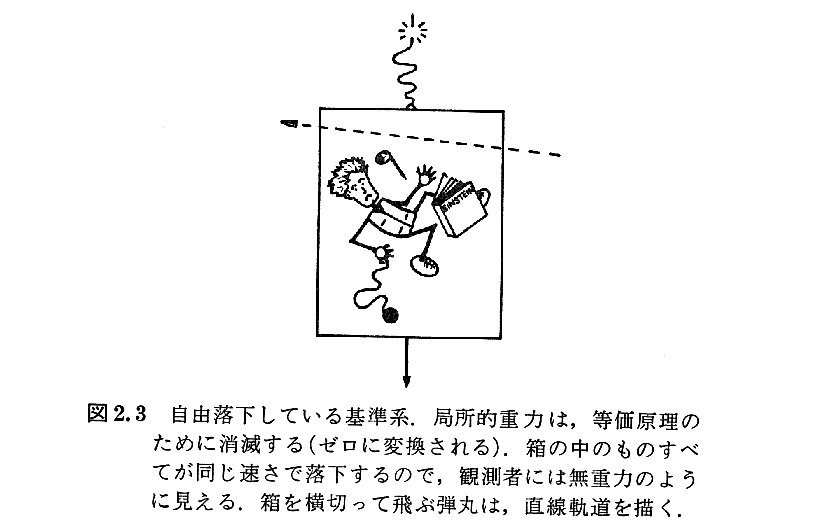
(5)等価原理



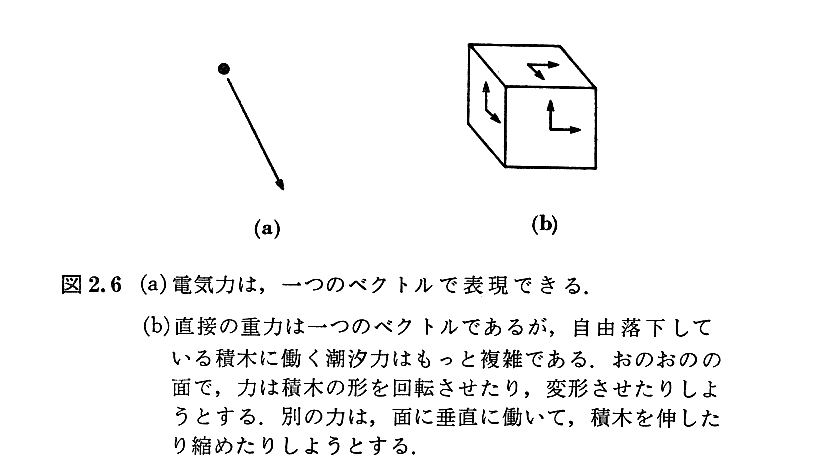
(6)重力の非局所的な影響(潮汐力)

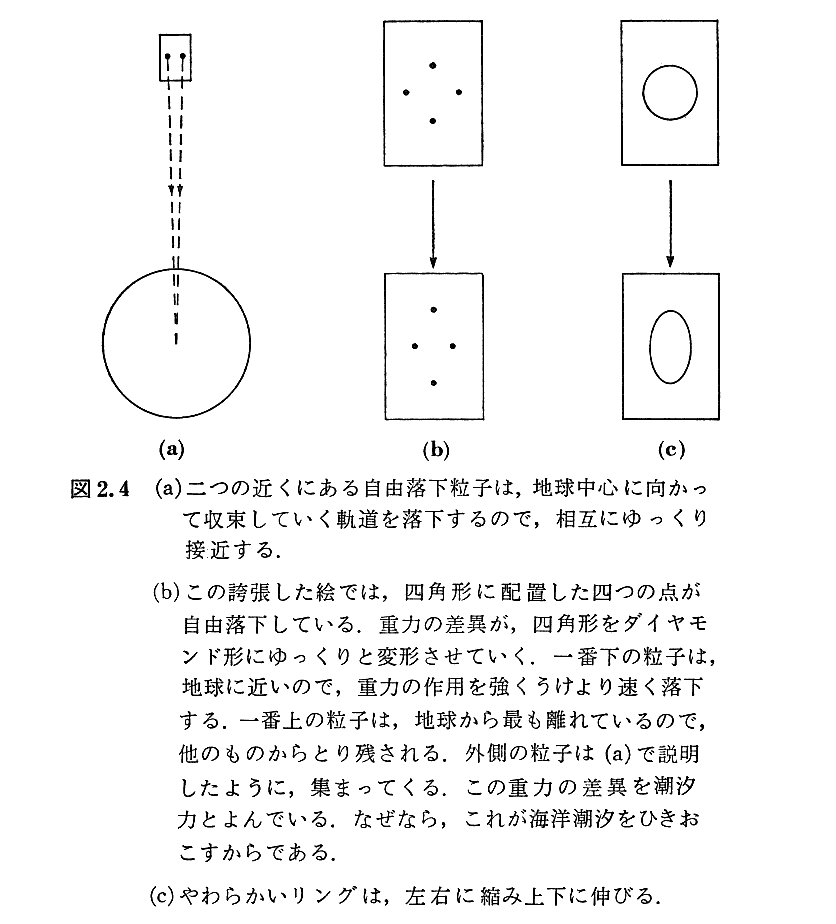





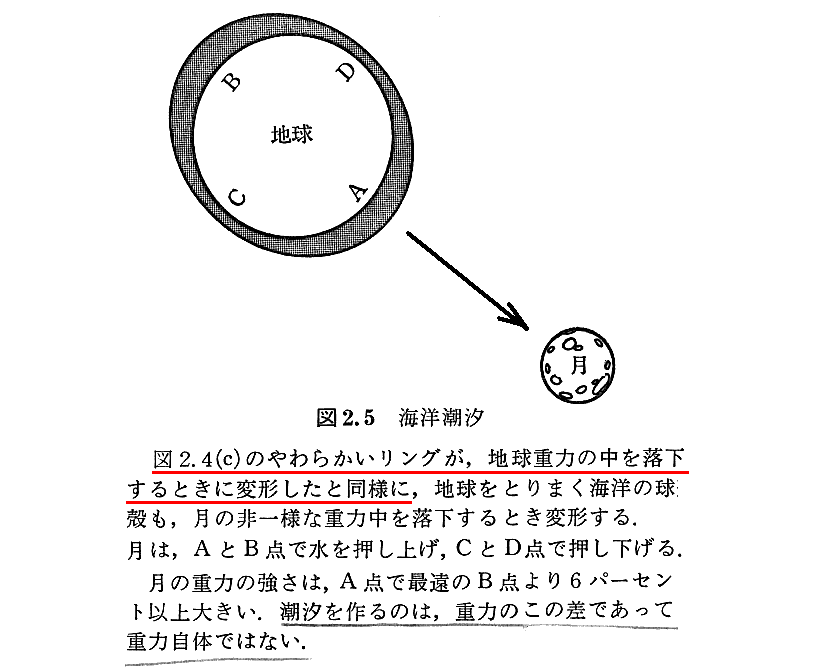
[補足説明1]
ここは別稿「潮汐力(起潮力)」4.(ロ)の計算式

を復習されたし。上式中の値から(3.32×10-2)×2≒0.06=6%が得られる。

[補足説明2]
ここは別稿「潮汐力(起潮力)」4.(ロ)の計算値

と「潮汐力(起潮力)」4.(ハ)の計算値

を比較されたし。
上記式中の値から(5.9×10-3)/(3.3×10-5)≒180倍と、(8.5×10-5)×2≒0.00017=0.017%が得られます。


3.場としての重力
(1)重力場の特徴



ここは別稿「わが相対性理論 第2部」19.[補足説明1]も参照されたし。キャベンディッシュの測定は別稿を参照されたし。




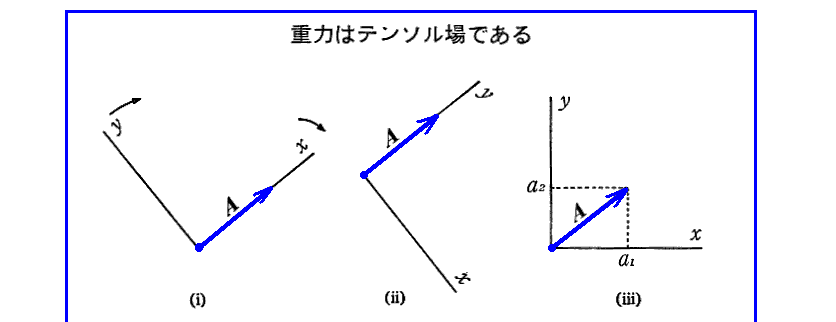
(2)重力場はテンソル場










4.曲がった時空
(1)曲がった時空





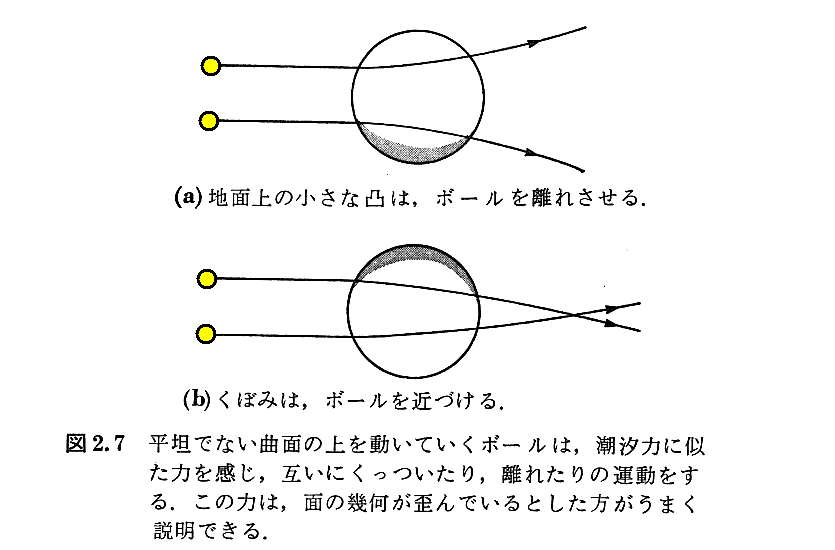
(2)測地線方程式

[補足説明]
物体が測地線に沿った運動をすることを表す物理法則が“測地線方程式”です。
ここで、測地線方程式そのものについては説明されていませんが、そのことに付いては別稿内山龍雄「相対性理論」第Ⅴ章や別稿「5.一般相対性原理と等価原理」(4)などをご覧下さい。



(3)空間曲率と時空曲率


このことは4.(4)の最後で示される。
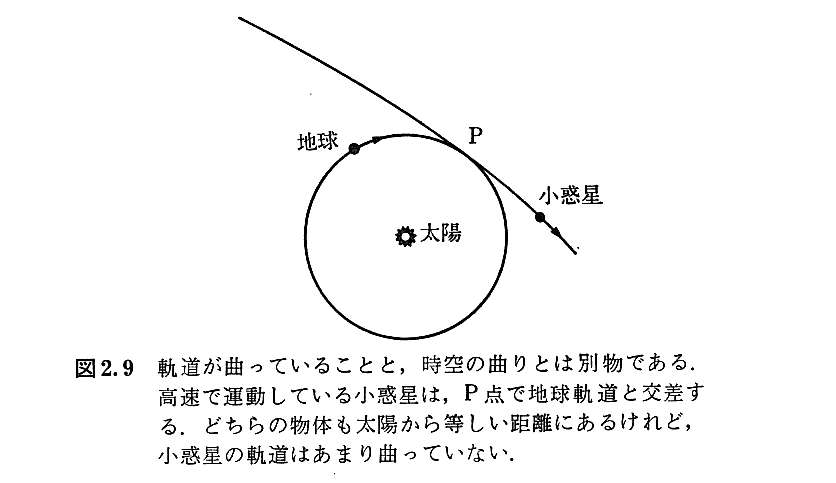

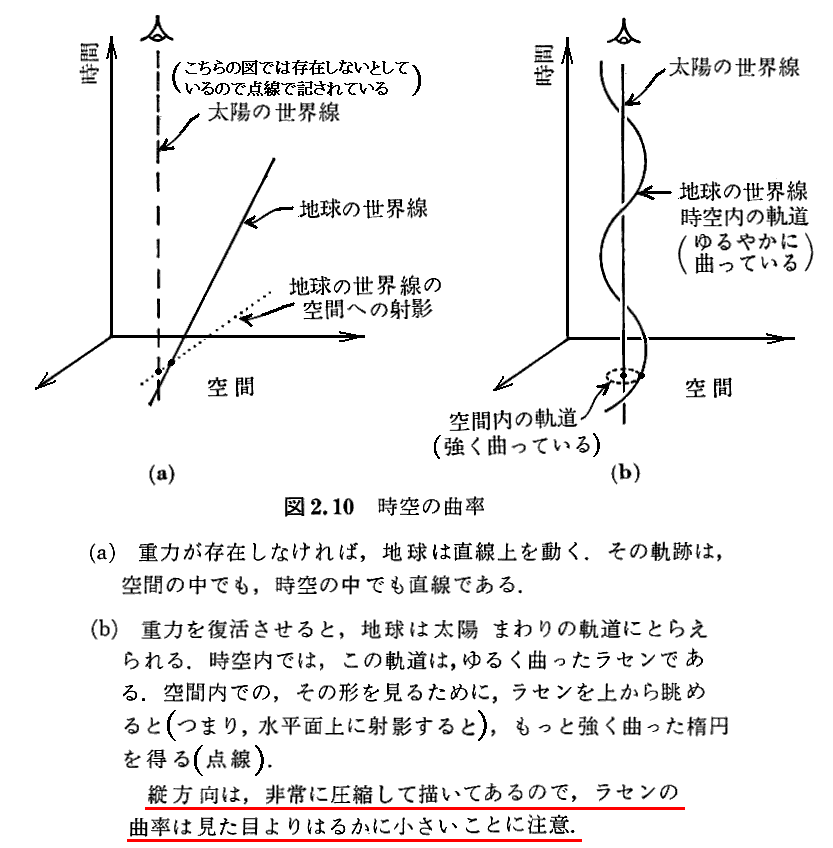



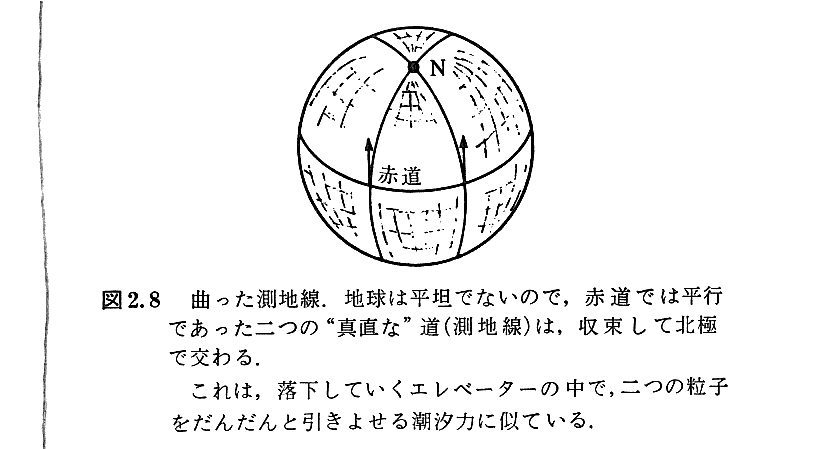
(4)世界線の曲率

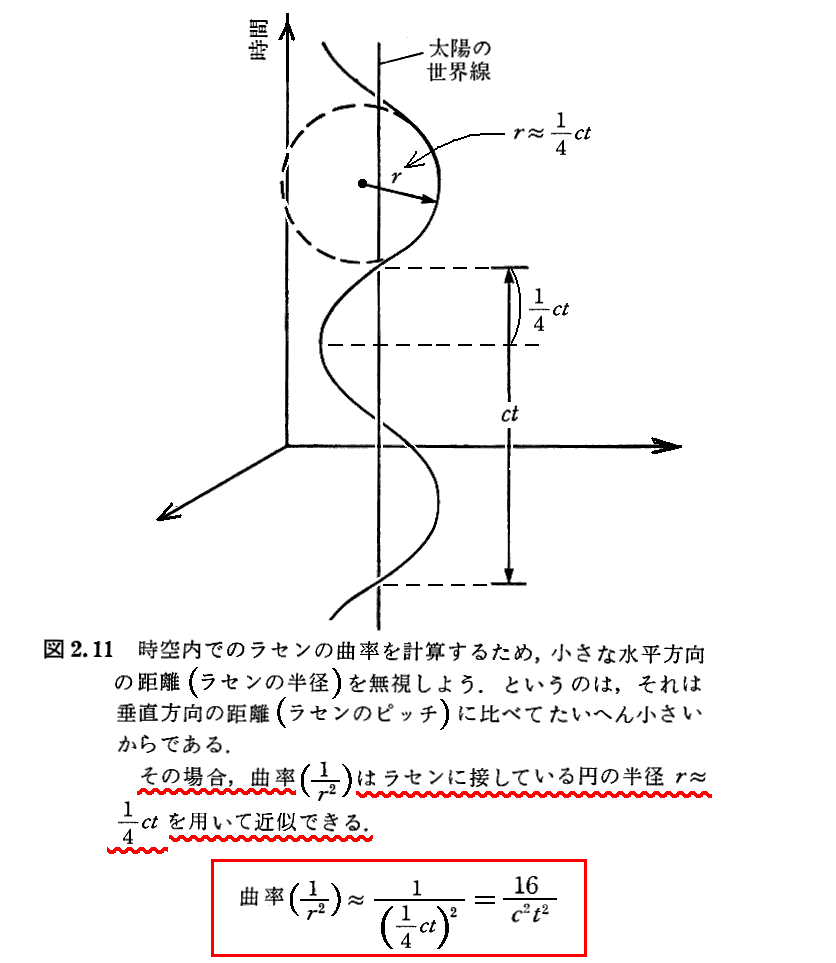
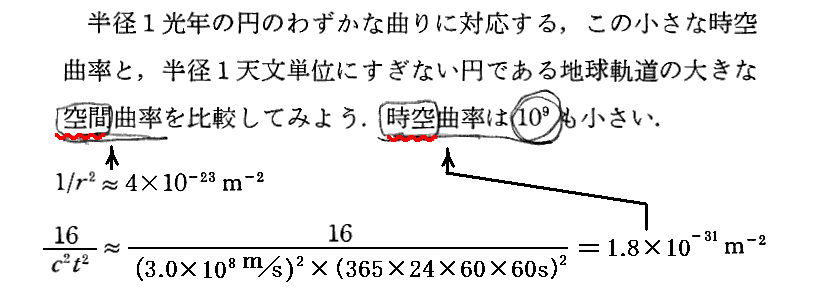
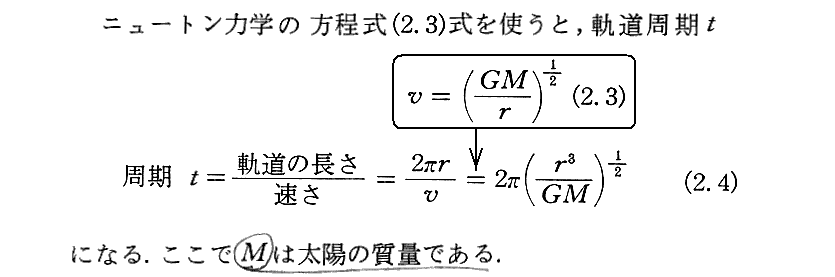
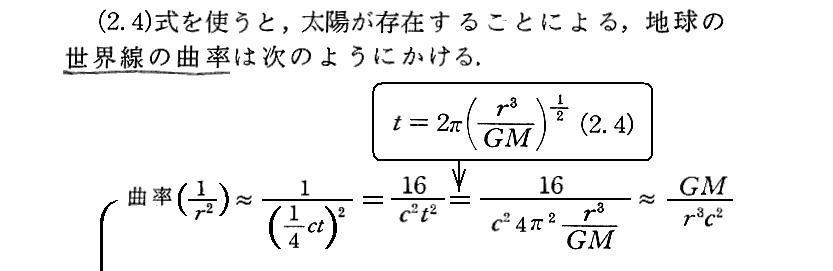

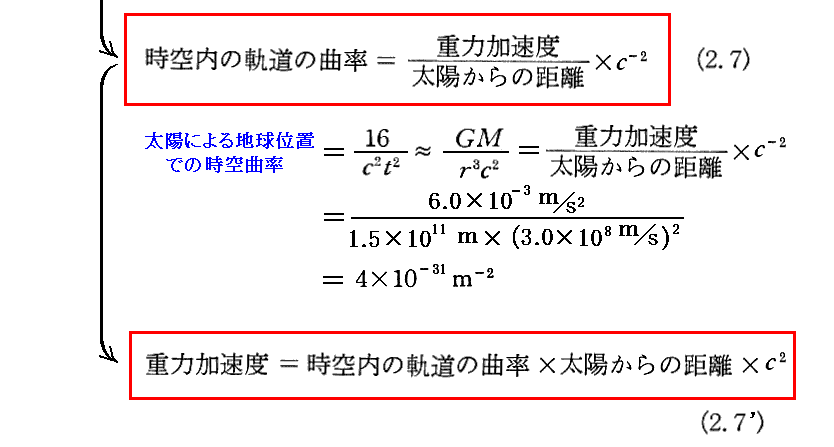

[補足説明1]
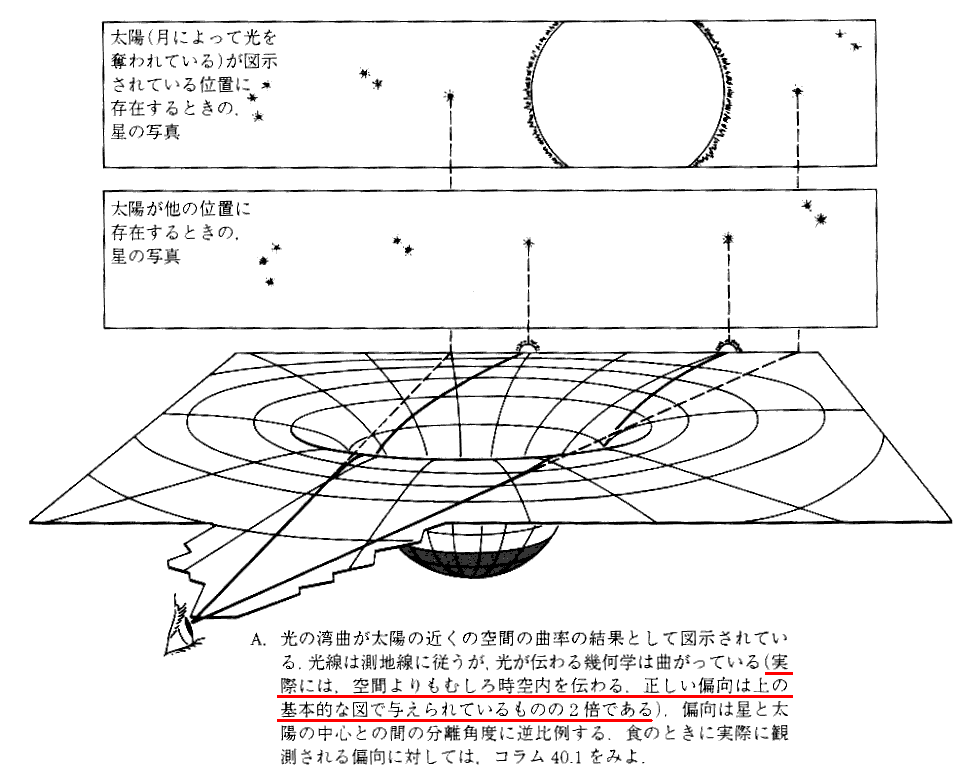
別稿「一般相対性理論の古典的検証と歪んだ時空」3-4で下記の様な説明がなされていた。

本稿での説明から明らかな様に図21は時空の曲がりではなくて、空間の曲がりしか表していない。時空図中での光の正しい測地線(世界線)を描くには本稿4.(3)で描いた様な図にしなければならない。
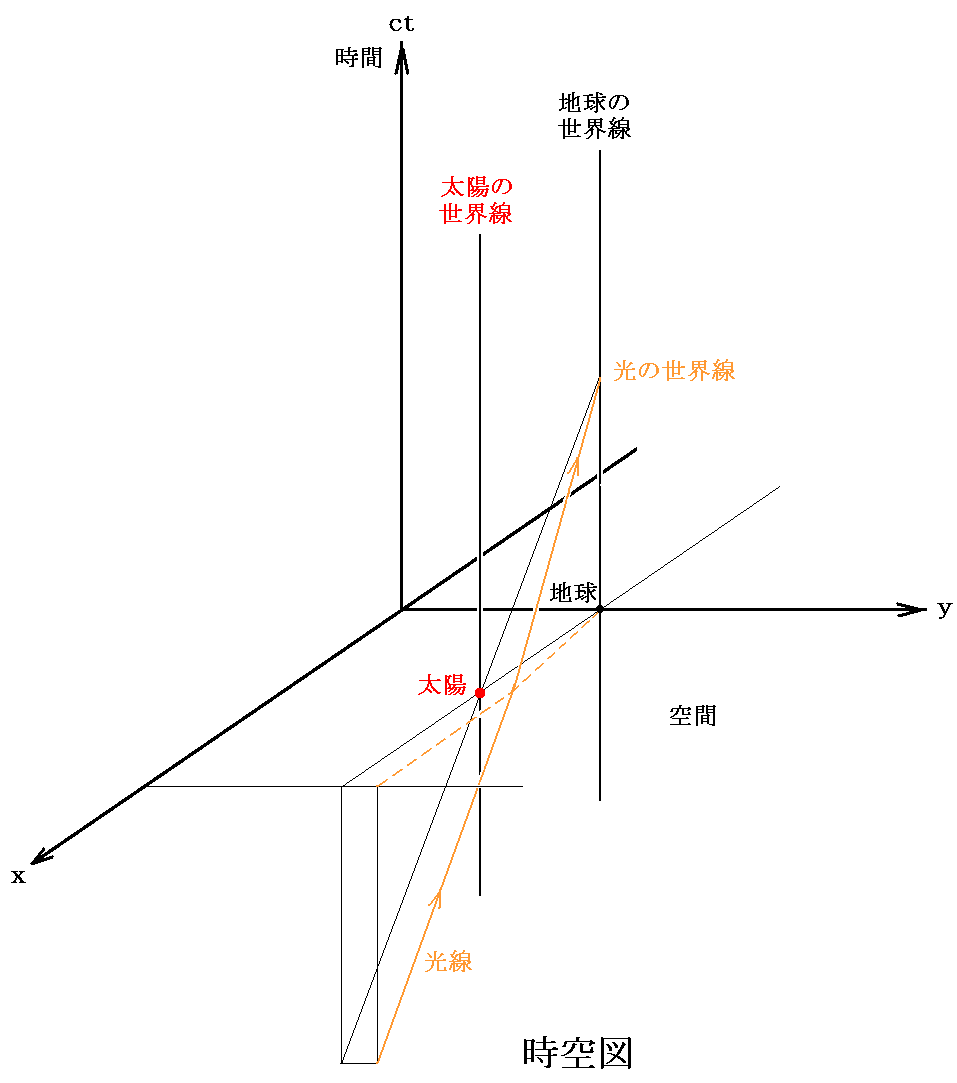
そうすれば時間と空間の曲がりを合わせた状況を反映した世界線(測地線)となる。そしてファクター2の効果が正しく反映される。ただし、世界線は旨く描けるが図から時空の曲率を読み取ることは難しくなる。
図21と上記時空図との関係はとても解りにくい所ですが、別稿「一般相対性理論の古典的検証と歪んだ時空」3-3“物差しの振る舞い”における図19のa)とb)二通りの解釈を思い出されて下さい。
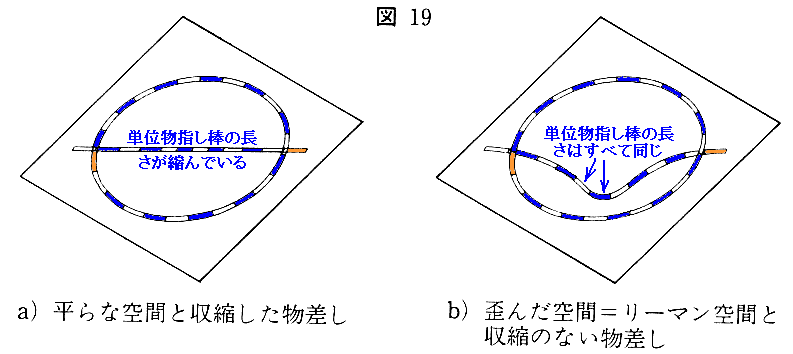
上記図21は時間軸の歪みは表せていませんが、空間の断面についてb)の立場での図だと理解すれば解りやすい。なぜなら、曲面(2次元リーマン空間)上の各点に於ける接平面に対応するものが描かれているからです。
一方上記時空図は、物差しが収縮し時計がゆっくり進むという解釈のa)の立場での図です。だから図から空間の歪みを読み取ることはできませんが、光線が時空の歪みに従って実際に進む様子は正確に表せています。
この当たりにつきましては別稿M・ウィル文献p57~58[補足説明]と、別稿2.(6)[補足説明1]もご覧下さい。
[補足説明2]
C.W.Misner,K.S.Thorne,J.A.Wheeler共著「重力理論」丸善(1972年刊)p32~33より引用。
Riemannの1854年6月10日の講演については別稿[補足説明1]を参照。リーマンの考察の限界については別稿[補足説明2]を参照。


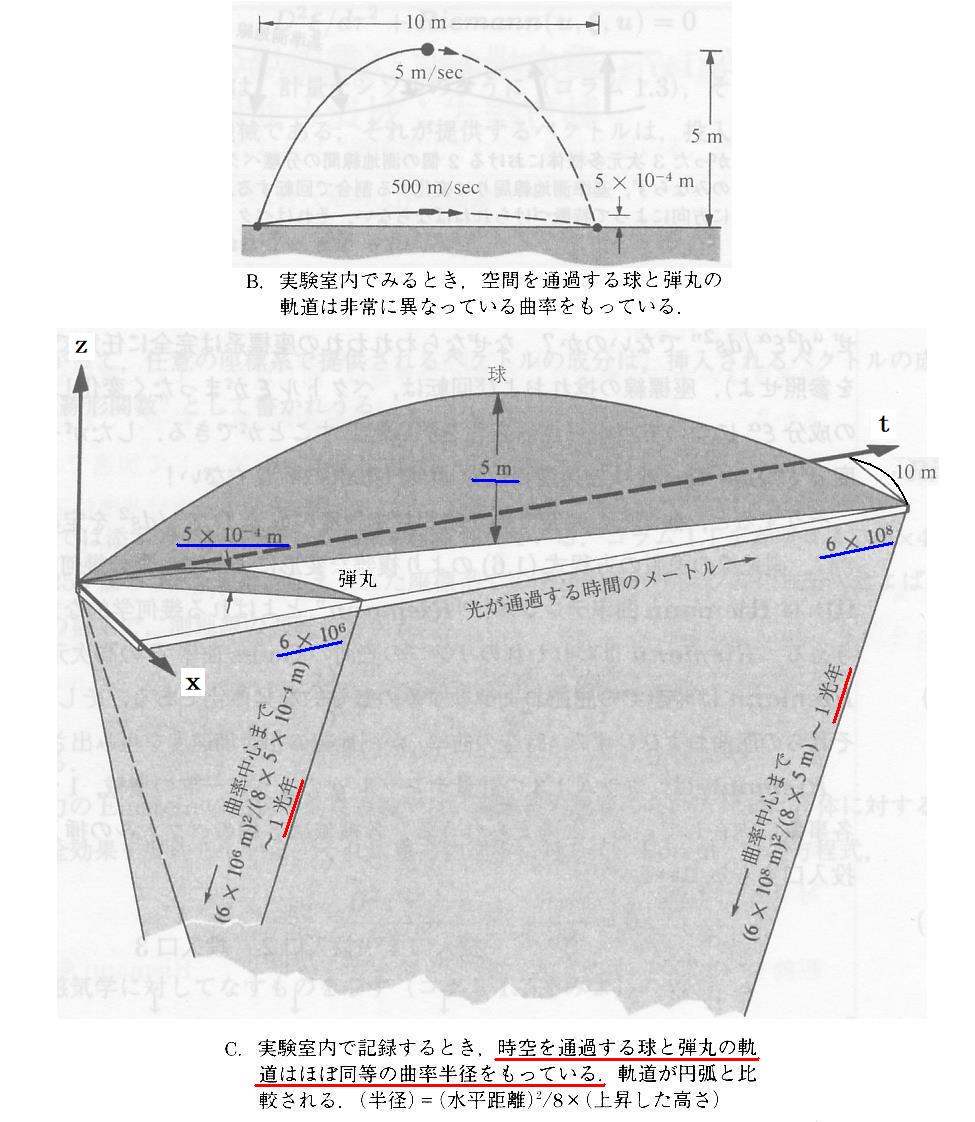

(5)潮汐加速度と時空曲率

5.一般相対性理論
(1)リーマンの曲率テンソル



(2)重力場方程式







6.参考文献
本稿は文献1.の第2章からの引用です。ただし、少し改変しています。
- P.C.W.デイヴィス著(松田卓也訳)「重力波のなぞ」岩波現代選書(1980年刊)第2章“重力波とは何か”
- クリフォード・M・ウィル著(松田卓也、二間瀬敏史訳)「アインシュタインは正しかったか?}TBSブリタニカ(1989年刊 原本は1986年刊)
この中から第2章、第3章、第4章、第5章、第6章、第10章を別稿で引用。
- 内山龍雄著「相対性理論」岩波書店(1977年刊)第Ⅴ章“一般相対性理論”
- 矢野健太郎著「近代数学新書 相対性理論」至文堂(1967年刊)郎第5章“一般相対性原理と等価原理”