基底ベクトル・双対基底ベクトルと反変成分・共変成分
(計量テンソル・クリストッフェル記号・共変微分とは何か)
一般相対性理論の難しさは、歪んだ時空の座標変換に伴うその歪んだ時空上のベクトル量、テンソル量の変化の性質を調べないといけない所にある。一般の物理法則は時間や空間座標の偏微分方程式で表されています。その時空がニュートンが仮定した様に永久不変なものであれば、それらの偏微分方程式を記述し、それらの座標変換に伴う変化を読み取ることは簡単です。しかし、その時間座標や空間座標そのものが物質(エネルギー)の存在によって歪み変化するのですから、それらの時空で物理法則を表現することはきわめて難しい。一般相対性理論の難しさの大半は、この中にある。
結局、アインシュタインはその数学的方法を発見(1912年)するのに、一般相対性理論の着想(1907年)から5年の歳月を要したのですが、その数学的難しさの大半は、歪んだ時空におけるベクトル量やテンソル量の変換法則の難しさにある。中でも反変と共変の概念の難しさが際立っている。アインシュタインは、その数学的手法を確立して3年後、ついに正しい重力場方程式を発見(1915年11月)する。
1.リーマン空間
(1)3次元リーマン空間
(2)3次元リーマン空間の微小領域
(3)《反変成分・共変成分とは何か》
2.3次元リーマン空間中の1点近傍の3次元ユークリッド空間における3次元斜交座標による表現
(1)基底ベクトルと双対基底ベクトルの関係
(2)双対基底ベクトルの図示
(3)ベクトルの成分表示
(4)リーマン計量(計量テンソル)と共変・反変の関係
(5)基本計量テンソルとベクトルの内積
(6)《基本計量テンソルとは何か》
(7)基底ベクトルが作る単位格子セルの体積Vと基本計量テンソルgijの関係
3.基底ベクトルの変換とベクトル成分・テンソル成分の座標変換
(1)基底ベクトルと双対基底ベクトルの変換
(2)微小変位ベクトルdrの座標変換
(3)任意ベクトル成分の座標変換
(4)基本計量テンソルの座標変換
(5)単位テンソル(クロネッカーのδ)の座標変換
(6)ベクトル内積の座標変換不変性の確認
(7)体積不変量
4.曲面人(2次元リーマン空間人)と3次元リーマン空間人
(1)アインシュタインの着想
(2)ガウスの曲面論
(3)3次元リーマン空間人
(4)《クリストッフェルの3添字記号とは何か》
1.クリストッフェル記号の定義
2.2.次元ユークリッド空間(平面)と2次元リーマン空間(曲面)のクリストッフェル記号
3.3次元リーマン空間のクリストッフェル記号
4.双対基底ベクトルとクリストッフェル記号
(5)《共変微分とは何か》
1.基底ベクトルの変分
2.ベクトル場wの変分
3.ベクトル場wの共変微分係数
4.反変ベクトルの共変微分係数の具体例
5.共変ベクトルの共変微分係数
6.テンソルの共変微分係数
(6)基底ベクトルの変換とベクトル成分・テンソル成分の座標変換の例
1.基底ベクトルと双対基底ベクトルの変換
2.ベクトル成分の座標変換
3.計量テンソル成分の座標変換
4.共変微分係数の座標変換
5.体積素の座標変換
5.参考文献
本稿は「一般相対性理論を理解するための数学的準備」の一部です。そのため別稿「平行移動とリーマン幾何学」、「微分幾何学3(曲面上の幾何学)」、「テンソル解析学(絶対微分学)」、「重積分の変数変換とヤコビアン」を引き続いてお読み下さい。その際、「微分幾何学」3.(1)2.[補足説明1]に留意して下さい。
1.リーマン空間
一般相対性理論の最大の難しさは、物理法則を記述するときの拠り所である時空が物質(エネルギー)の存在により歪んでしまい、その歪んだ時空で物理法則を記述し、さらにその歪んだ時空の性質を論じなければならないことです。
その歪んだ時空を記述する幾何学がリーマン幾何学なのですが、リーマン時空を表現するには、その時空間を測定する時計の進み具合が位置と共に変化し、測定棒の長さが、その向きや位置によって変化すると考えればよい。またその空間を測定する座標線(その接線方向に測定棒が向いている)の向きは場所ごとに変化し、その座標線が曲線を成し座標軸の長さが伸び縮みすと考えればよい。(詳細は4.(1)〜(3)で説明)
ところで、時間座標を距離座標と一緒に議論するのは難しいので、本稿では3次元座標が全て距離座標であるような3次元リーマン空間を考えます。
[補足説明]
多くの教科書では、共変性、反変性と基底ベクトル、双対基底ベクトルの関係を二次元平面、つまり2次元リーマン空間中の1点での接平面(2次元ユークリッド空間)上の斜交座標で論じている。例えばダニエル・フライシュ著(河辺哲次訳)「物理のためのベクトルとテンソル」岩波書店2013年刊)§4.4〜§4.6、あるいは平川浩正著「相対論(第2版)」共立出版社(1986年)§4-4など。
しかし2次元での説明は解りにくい。3次元の方が遙かに解りやすいので、本稿では“3次元リーマン空間”で考えます。
(1)3次元リーマン空間
“3次元リーマン空間”を想像するのは難しいが、ガウスが考えた3次元ユークリッド空間中の“曲面”がそれを想像する為のヒントを与えてくれる。別稿「微分幾何学」3.(2)2.[補足説明3]で説明したように、その曲面上に存在する座標曲線のみを考察することで“2次元リーマン空間”が考察できた。つまり、曲面の上に、縦横に正方形格子状の網目が引かれたゴムシートを貼り付けたと考え、その網目座標でリーマン空間の性質を論じる事ができる。そこで説明したように、それを論じる微分形式が2.(3)3.で定義された第1微分形式であり、議論を展開する為の量がそこで導入された第1基本量 E,F,G(g11,g12=g21,g22) です。
そのとき注意して欲しいことは、2次元リーマン空間の座標を決める基底ベクトルxuとxvは曲面の1点ごとに決められ、それらは曲面のその点に於ける“接平面(2次元ユークリッド空間)”の中に存在する“2次元斜交座標”でした。その接平面は接点の位置が変われば様々な傾きで変化しますが、各点の近傍に限れば平坦な平面中の斜交座標だと考えることができたのです。3次元リーマン空間においてもこのやり方を用いればよい。
3次元リーマン空間を想像することは難く、ガウスが2次元リーマン空間である曲面を高次元の3次元ユークリッド空間から眺めた様なことはできません。我々は3次元ユークリッド空間に住んでいるのですから、3次元リーマン空間を体験するために高次のユークリッド空間を利用することはできないのです。
ところで、ガウスが第1微分形式で曲面の幾何学を展開したとき、その曲面は2次元リーマン空間でありながら、その微小領域に限っては平面である2次元ユークリッド空間(接平面のこと)中の斜交座標で議論できた。ならば、3次元リーマン空間でも、その微小領域に限れば3次元ユークリッド空間中の3次元斜交座標系で議論できるだろう。
つまり、ガウスが曲面の接平面上での斜交座標(斜交基底ベクトル)で2次元リーマン空間の幾何学を論じた様に、3次元リーマン空間の中の一点の近傍に限れば、3次元ユークリッド空間中の3本の斜交座標(3つの斜めに交わる基底ベクトル)で議論できるだろう。
ここで注意して欲しいことは、“リーマン空間”の歪みを表すにはその歪んだ空間の中に存在する単位長さの測定棒の伸び縮みと、その測定棒の方向の変化で表現するしか方法は無いことです。つまり“単位測定棒の長さとその向きの場所的な変化こそが空間の歪みを体現している”。(この言い方は誤解を招きやすい。基底ベクトルが斜交したことや稜の長さが不揃いになったことがリーマン空間の歪みを直接表すわけではないからです。このことの正確な意味は4.(1)、(2)、(3)をご覧下さい。)
そして、そのような伸び縮みする単位棒を三次元的に並べた3次元空間の中の各点に、いわゆるスカラー量、ベクトル量、テンソル量が分布しているわけです。それらは一般に三次元空間の位置座標の関数であり、空間座標が異なればそれらの量は変化します。
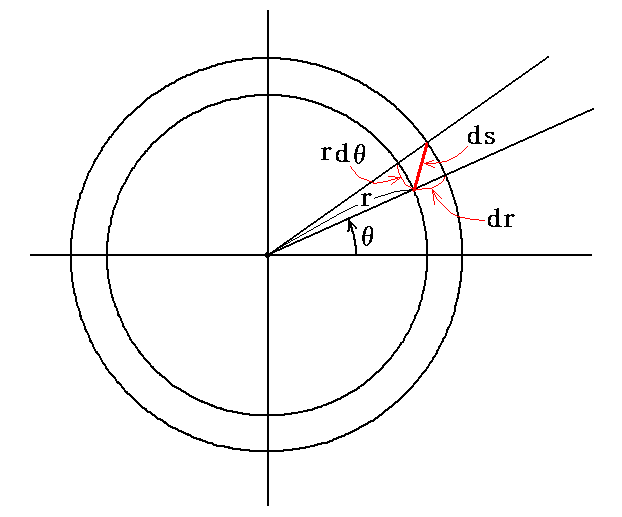
さらに、それらの量は一般に座標の変化量に関係した量です。例えば、3次元空間中の任意の1点におけるベクトル量である微小変位ベクトルdrはその地点でのベクトルの長さと方向(dr1,dr2,dr3)に関係しているのですが、そのベクトル先端の座標値までの長さに関係している、あるいは3次元空間内のスカラーの勾配ベクトルを考えると∂/∂riの様に座標の微小変化driに関係している。
そのとき、それらのスカラー量、ベクトル量、テンソル量が存在する点における座標の変化量に関係していると言われても、座標空間そのものが、場所と共に歪み変化しているのですから、そのことを、スカラー量、ベクトル量、テンソル量の表現の中に取り込んでおかねば成りません。ここが難しい。
(2)3次元リーマン空間の微小領域
座標の様子が、3次元リーマン空間中に存在するスカラー量、ベクトル量、テンソル量に関係すると言われても、座標軸の方向そのものが、あるいは座標測定の単位測定棒の長さそのものが場所的に変化しますので、それらの量の性質を調べるには、まずその内部で“座標軸の方向と、距離測定の単位測定棒の長さが一定であると見なされる微小領域をとりあげる”必要があります。
それで、取りあえずその様な微小領域を算術的に取り扱うために下図の様な“基本ベクトル”の組 a1,a2,a3 を考えます。下図の矢印は単位測定棒ですが、その測定棒の方向と長さが存在場所によって変化することが空間の歪みを表しています。(このことの正確な意味は4.(1)、(2)、(3)をご覧下さい。)
もちろん単位測定棒が接している空間の座標曲線の連なりは場所の変化と共にクネクネと曲がっていきますので、極狭い領域でのみ測定棒の接線方向の座標線は図のように直線的に延びていると近似出来るわけです。
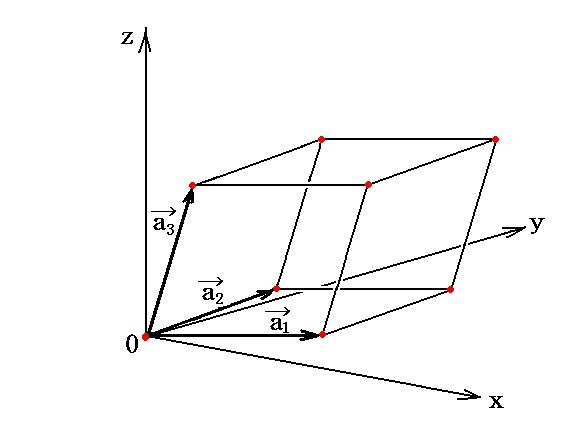
図中のxyz軸は3次元リーマン空間中の一点の近傍をあらわす3次元ユークリッド空間です。現実の時空はリーマン空間なのですが、実際の我々の生活空間のスケールに於いてはユークリッド空間との差はほとんど無いのですから、前節で説明した曲面上の1点の近傍を接平面(2次元ユークリッド空間)で近似したのと同様に3次元リーマン空間の1点の近傍領域を3次元ユークリッド空間で近似した中で考えても良いわけです。
また、格子状の網目が印刷されたゴムシートを曲面に貼り付けると、その貼り付けられた曲面の一点の近傍は接平面(2次元ユークリッド空間)で近似できると言ってもその中での網目格子はもはや正方形ではなく、平行四辺形になり、辺の長さも、平行四辺形の面積も元の貼り付ける前のゴムシード上での正方格子とは異なります。そのことが曲面がユークリッド空間ではなくリーマン空間であると言うことを表しています。
それと同様に、各点で設定された3次元ユークリッド空間中の斜交平行六面体を構成する基本単位ベクトルの方向と長さは様々に変化しているはずです。これらの平行六面体は3次元ユークリッド空間の中に作った立方体格子を3次元リーマン空間に貼り付けたときの3次元ユークリッド空間での様子を表しています。
[補足説明]
上記アンダーラインの説明は正確では在りません。なぜなら曲面上に住んでいる曲面人にとって貼り付ける前のゴムシート上の網目が正方格子だったかどうかなど知りようがないからです。それと同様に3次元リーマン空間に住む我々にとって、それに貼り付ける前の3次元ユークリッド空間に引いた格子が立方体状の格子だったかどうかなど知りようがないからです。アンダーラインの文章の正しい解釈は4.(1)、(2)、(3)をご覧下さい。
(3)反変成分・共変成分とは何か
1.単位セルの様子
ユークリッド空間とリーマン空間の関係を説明する。“ユークリッド空間”の例として“2次元平面”を考え、“リーマン空間”の例として3次元ユークリッド空間中の“2次元曲面”を考える。
そのとき、ユークリッド空間中の位置を指定するものとして、その中に縦横に密に引かれた格子状の網目を考える。
このときの網目はすべての辺の長さは同一で、すべての辺は直交して90°で互いに交わっているとして良い。そして単位網目の辺の長さがその空間の座標を定める単位長さであると考える事ができる。
次に、3次元ユークリッド空間中の2次元曲面である2次元リーマン空間中の位置を指定するものとしてその表面に縦横に密に引かれた網目を考える。これは先ほどの2次元平面に引かれた網目がゴムシートでできていてそれを2次曲面に貼り付けた様なものだと考えれば良い。
そのとき、の網目の単位セルについて以下の事が生じることに注意されたい。例えば、下図の様な4っの網目を考える。それぞれの網目は、その真ん中当たりで曲面に接した接平面上に構成されていると考える事ができる。

そのとき
- 互いに接している4つの網目について言えばそれらが交わる角度θはもはや90°では無くなる。そうなることは実際に上図の様な凸状(あるいは凹状)の曲面の上に上記の様な4つの四辺形を作ってみれば明らかです。
- 網目を構成する辺の長さはもはや1ではなくなる。つまり、座標値を数える単位棒の長さがリーマン空間の場所ごとに変化していく。このことも曲面の上に格子状のゴムシートを貼り付けてみれば明らかです。
すなわち、“平行四辺形状をした単位格子”からなる“斜交座標”を用いなければならなくなる。
2.反変成分と共変成分
前記の網目の格子の大きさを極微細に設定すればリーマン空間上の限られた領域に付いては同一の斜交平行四辺形を敷き詰めた一つの平面で近似できる。
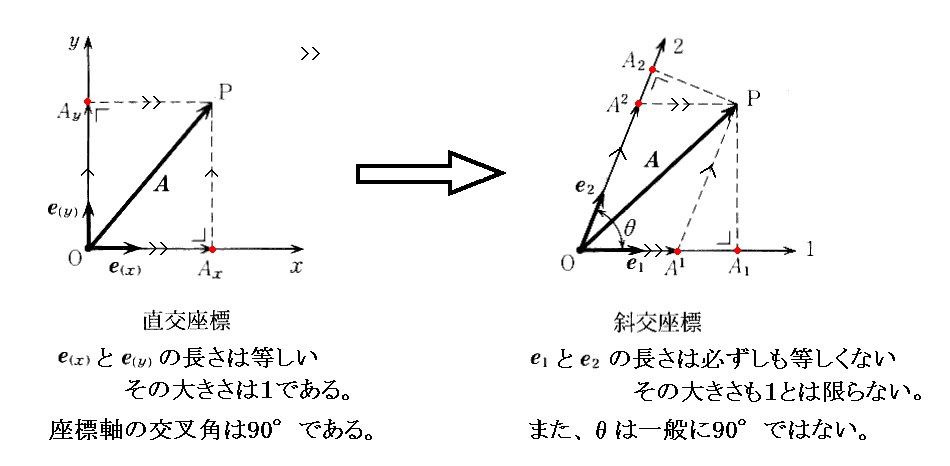
そのためリーマン空間の狭い領域に付いての位置座標、あるいはベクトルは格子の単位の長さの何倍で測定した座標成分で記述できる事になる。
このとき、P点の座標値を測る上で新たな事情が生じてくる。まず、ユークリッド空間に於ける座標値の意味を復習すると、上左図の様に単位の長さで測って何倍の長さになるかでAxとAy値が定まるのであるが、図中のAx点を定める線分は《x軸に垂直でしかもP点を通るもの》の意味でもあるし、《y軸に平行な線でP点を通るもの》の意味の二通りがある。
このとき、ユークリッド空間においては、この両者に差は無く、全く同一の座標点Axを与える。ところが、リーマン空間に於ける斜交座標では、《1軸に垂直でしかもP点を通る線分》で定めた座標点はA1となり、《2軸に平行でしかもP点を通る線分》で定めた座標点はA1となり、どちらの線分を用いるかにより、ベクトルAの成分表示が二種類に分かれてしまう事になる。
このとき、リーマン空間で必要な斜交座標で表した成分表示の内(A1,A2)を“共変成分”表示と呼び、(A1,A2)を“反変成分”表示と言う。普通添字1,2を付ける位置を上と下に変えて両者の違いを区別する。
ユークリッド空間の直交座標では、上記の二種類の成分表示がたまたま一致しているから、その様に2種類の成分表示がある事に気付かなかったのですが、本来この両者が存在する。
このとき、上右図の単位ベクトルeiの事を今後“基底ベクトル”と呼ぶことにしますが、“基底ベクトル”eiの長さは必ずしも 1 に等しいわけではありませんし、これらは互いに直交しているわけでもありません。
3.双対基底ベクトルの導入
任意のベクトルAは、反変成分を用いると
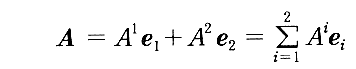
と表される。
ところが、ベクトル成分表示の意味から明らかなのですが、共変成分に対しては
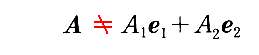
となり、“基底ベクトル”eiを用いたのでは、共変成分によってベクトルAを表す事はできません。
前節で説明したように“直交座標系”では、共変成分も反変成分もベクトルAを表示するための成分としては同等の働きをしていたのですが、“斜交座標”になると“共変成分”ではベクトルAを旨く表示できないのです。これは困ったことになりました。
そこで、共変成分を用いてベクトルAを旨く表される様にするために“双対基底ベクトル”ei というものを新たに定めます。それは、当然基底ベクトルeiが定まればそれに対応して必然的に定まる様なものでなければ成りません。実際に“双対基底ベクトル” ei は次のようにして定めます。
“方向”に関しては(e1・e2)=0、(e2・e1)=0となるように定めます。すなわち、双対基底ベクトルe1は基底ベクトルe2に垂直、かつ双対基底ベクトルe2は基底ベクトルe1に垂直に成るようにします。その“長さ(大きさ)”に関しては(取りあえず)次図の様にします。
ここで、元の“基底ベクトル”と区別するために添字 i は右上に付けています。
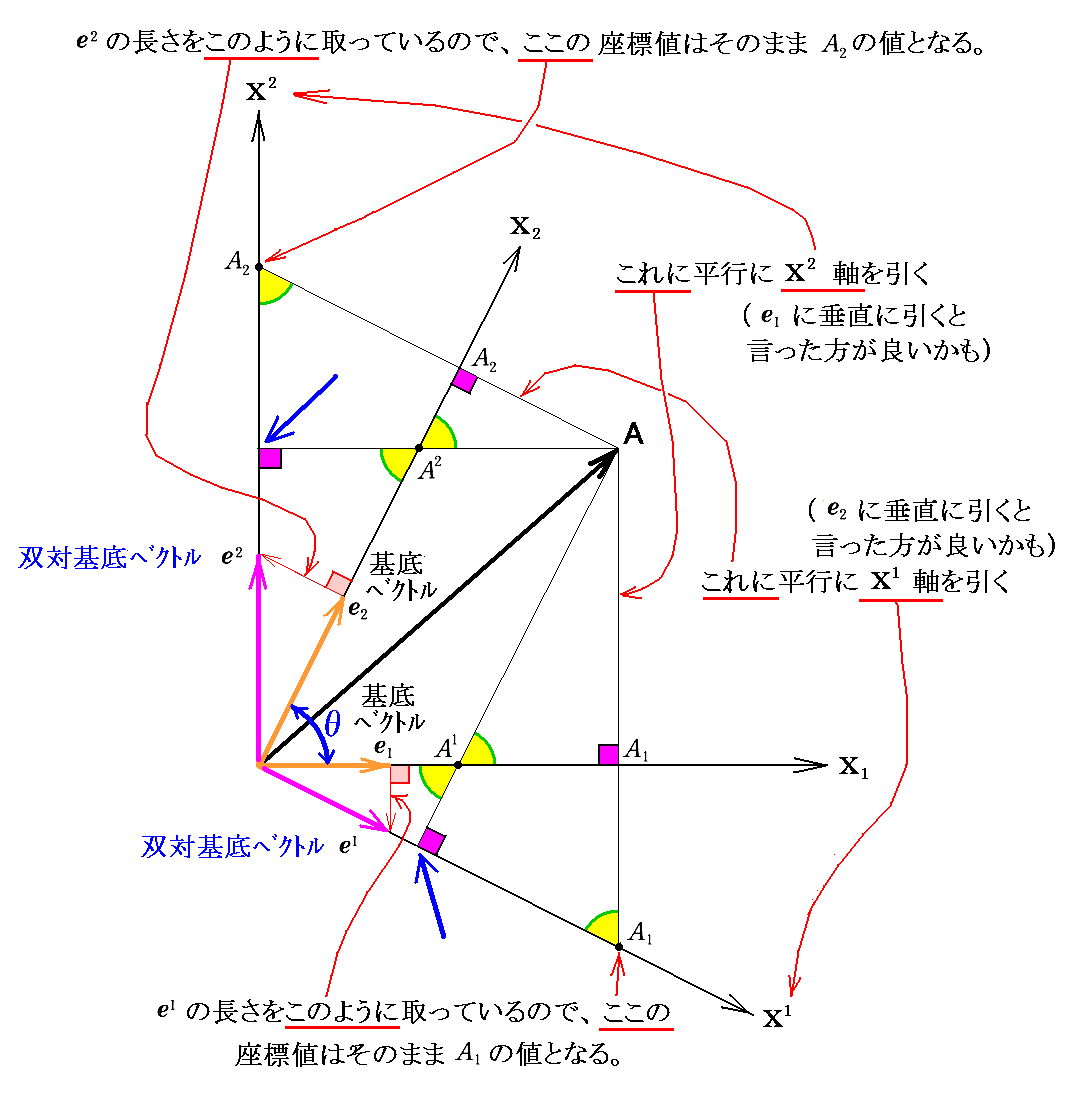
この説明はあくまで2次元リーマン空間の場合のやり方で、3次元リーマン空間の場合は2.(1)で説明します。
このようにして定まる“双対基底ベクトル”ei を用いれば、任意のベクトルA は共変成分Ai を用いて
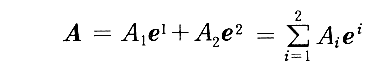
の様に表せる。
これで当初の目的は達成できたのですが、残念な事に以上の様に双対基底ベクトルの“長さ(大きさ)”を定めると、基底ベクトルの座標値と双対基底ベクトルの座標値が互いに対称的な関係になりません。つまり図中の青矢印の点の座標値がX1軸上での値であるA1に一致するわけではありません。X2軸についても同様でA2になるわけではありません。そのため実際には[補足説明1]の様にします。
2次元リーマン空間の鞍部(馬の鞍の様な場所)については、下図の様に斜交座標の交叉角θは90°よりも大きくなる。

この場合の基底ベクトルと双対基底ベクトルの関係は以下のようになる。
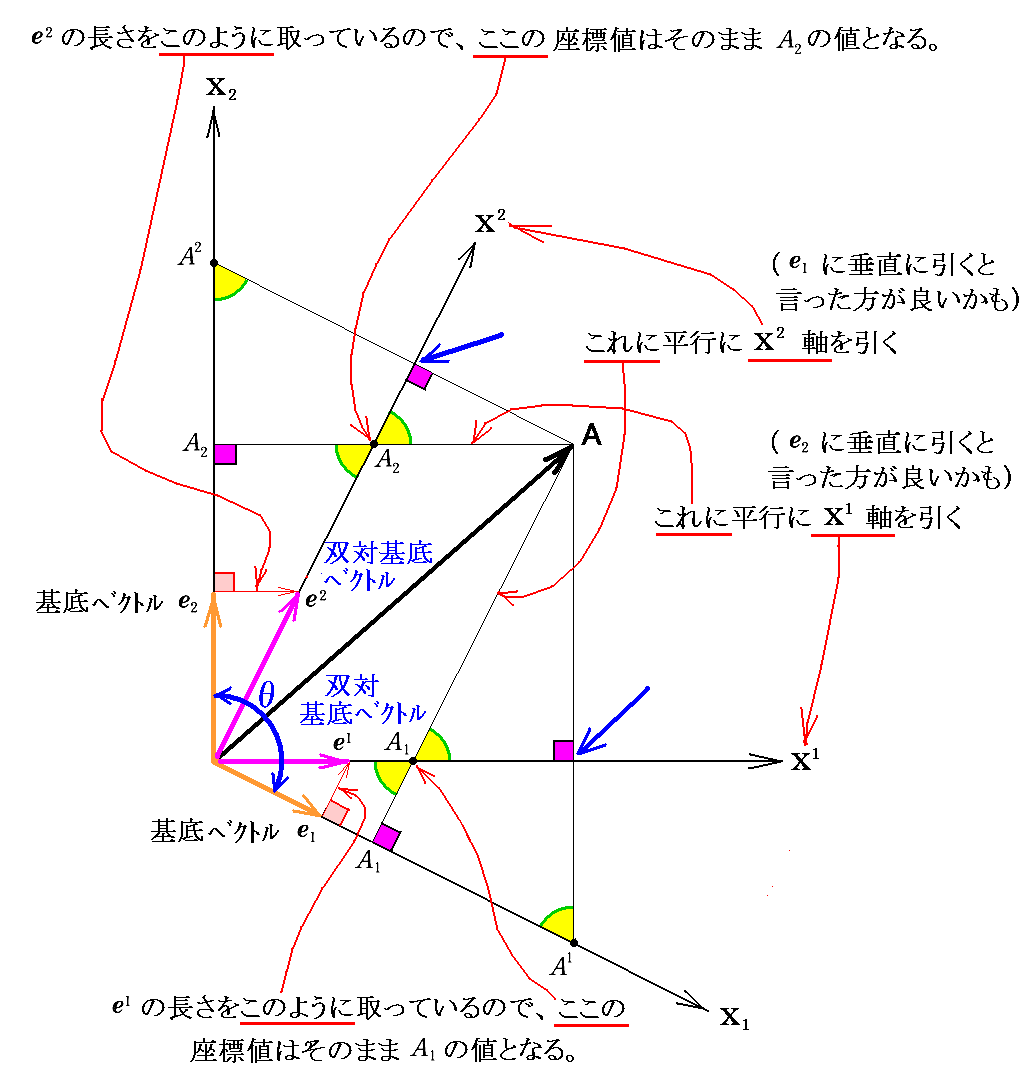
ただし、以上の様に双対基底ベクトルの“長さ(大きさ)”を定めると、基底ベクトルの座標値と双対基底ベクトルの座標値が互いに対称的になりません。つまり図中の青矢印の点の値がX1軸上でA1の値になるわけではありません。X2軸についても同様でA2になるわけではありません。そのため実際には[補足説明1]の様にします。
[補足説明1]
以上の様にして基底ベクトルe1,e2から双対基底ベクトルe1,e2を決めたのですが、一旦双対基底ベクトルe1,e2の“方向”が決まってしまえば、その“長さ(大きさ)”については、上記の様に定める必要は無い事が解る。なぜなら、双対基底ベクトルe1,e2の長さを単位として、ベクトルAのe1あるいはe2に平行な座標成分を計り直せば良いのですから。
そのため双対基底ベクトルe1,e2の“方向”に関しては上記の様に定めますが、“長さ(大きさ)”に関しては、今後の議論に便利(基底ベクトルと双対基底ベクトルの働きが互いに対称的)なように、
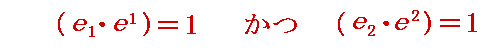
を満足するように定めることにする(正直なところ、ここが双対基底ベクトルの導入で最も重要なのですが、最も解りにくい所です)。
それでは、具体的に上記の条件を満たすように双対基底ベクトルe1,e2を決めるにはどうしたらよいのでしょうか。その為に、まず2.(2)[補足説明2]の様に第3成分e3の方向がe1,e2に垂直で大きさが常に1であると考えた3次元空間を考えます。そして、2.(1)で説明する3次元の方法で双対基底ベクトルe1,e2,e3を求める。その後で、その2次元部分のみを取り出せば良い。
4次元以上のn次元の場合は、2.(2)[補足説明3]で説明する様にn×n=n2個の線形連立代数方程式を解くことで行います。
リーマン空間であるが故に必然的に必要になった斜交座標の為に成分表示が二種類に分かれてしまったのだが、以上の様に考えれば、リーマン空間においても成分表示を用いて終始一貫した幾何学的な議論ができる事になる。
ここで注意して欲しい事は、これらの図形は2次元ユークリッド空間(平面)上の斜交座標では無くて、2次元リーマン空間に於ける斜交座標であることです。更に補足すると、それぞれの斜交座標は2次元リーマン空間のそれぞれの位置で2次元リーマン空間に接する二次元ユークリッド空間である接平面上に設定されています。
そのときリーマン空間の場所が変わればその接平面はどんどん変化していきます。その変化の様子が斜交座標を構成する斜交単位セルの中にある情報(“基底ベクトルの長さの変化”や“斜交角θの変化”)によって表現できることに注意して下さい。
2.3次元リーマン空間中の1点近傍の3次元ユークリッド空間における3次元斜交座標による表現
(1)基底ベクトルと双対基底ベクトルの関係
空間を、 a1、a2、a3 なる三つの基底ベクトルで決定される空間格子とする。この格子を今後“実格子空間”と呼ぶことにする。
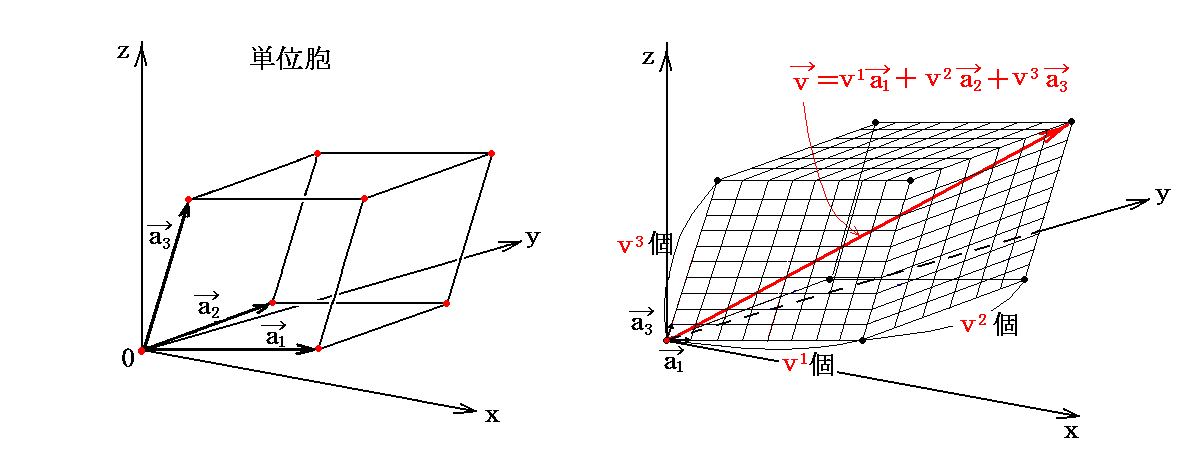
これに対して、次の定義で導入される三つのベクトル b1、b2、b3 (これを双対基底ベクトルと言う)で構成される単位格子で構成される空間格子を考える。これを“双対格子空間”と呼ぶことにする。
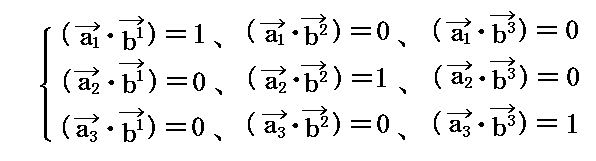
定義から明らかなようにb1はa2とa3に、b2はa3とa1に、b3はa1とa2に垂直です。またそれらの大きさは(ai・bi)=1(i=1,2,3)によって定まる。
このことの意味をもう少し説明すると、双対基底ベクトルb1は基底ベクトルa2とa3が張る平面に垂直な方向を向いており、その長さは双対基底ベクトルb1と基底ベクトルa1の内積が(a1・b1)=1となるように定められていると言うことです。
同様に、双対基底ベクトルb2は基底ベクトルa1とa3が張る平面に垂直な方向を向いており、その長さは双対基底ベクトルb2と基底ベクトルa2の内積が(a2・b2)=1となるように定められている。
同じく、双対基底ベクトルb3は基底ベクトルa1とa2が張る平面に垂直な方向を向いており、その長さは双対基底ベクトルb3と基底ベクトルa3の内積が(a3・b3)=1となるように定められている
別稿「ベクトルの内積と外積の成分表示」2.(5)2.で説明したベクトルのスカラー積(内積)とベクトル積(外積)の意味と、(a1・[a2×a3])は三つの基底ベクトルa1、a2、a3を三稜とする平行六面体の体積であることを思い出せば、それぞれの双対基底ベクトルは基底ベクトルにより

と表されることが解る。
実際、このように定義されたb1、b2、b3 の方向が前記の定義を満たしていることはベクトルの外積の定義から明らかであろう。また3つのベクトルb1、b2、b3それぞれの大きさについては、それぞれ
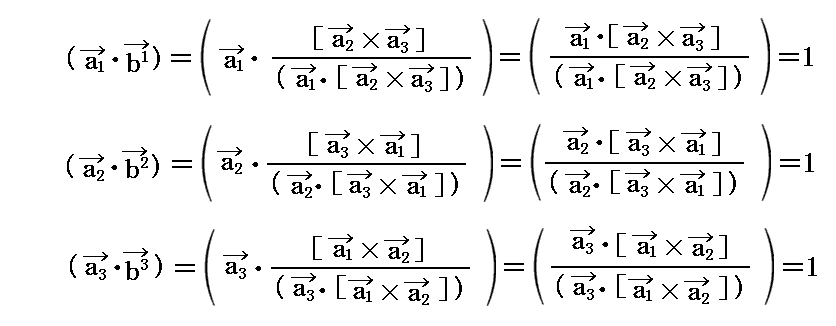
となるので、やはり定義の条件を満足している。
もちろん、元の基底ベクトルは、新たに定義した双対基底ベトクルにより
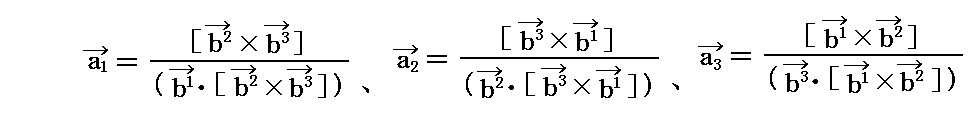
と表される。
(2)双対基底ベクトルの図示
双対基底ベクトル b1、b2、b3 を図示するには次のようにすればよい。まず基底ベクトルa1、a2、a3の3次元ユークリッド空間での座標値を定める。
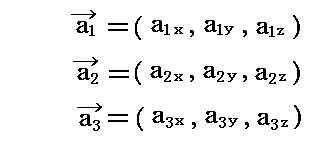
これを、上記のベクトル式に代入して成分計算して双対基底ベクトルb1、b2、b3の3次元ユークリッド空間での座標値

を得る。
その座標値に基づいて3次元ユークリッド空間内に双対基底ベクトルの矢印を図示する。双対基底ベクトル矢印の様子からその長さも明らかになる。そのように3次元ユークリッド空間を利用できることは前章1.(2)で説明した。また、そのことの深い意味は4.(1)〜(3)を参照されたし。
[例1]
具体的な値を与えて図示してみる。
例えば3本の基底ベクトルの3次元ユークリッド空間に於ける座標値を
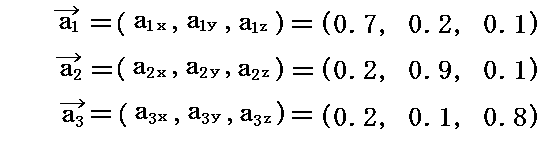
とする。
これらの値を前述のベクトル計算式に代入して双対基底ベクトルの3次元ユークリッド空間での成分値を計算すると
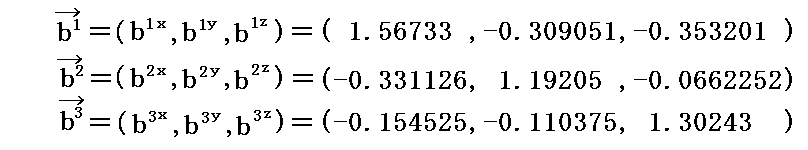
が得られる。実際の計算は面倒なのでMathematicaを利用した。
このとき、これらの成分値は最初の条件式

を満足していることが確認できる。
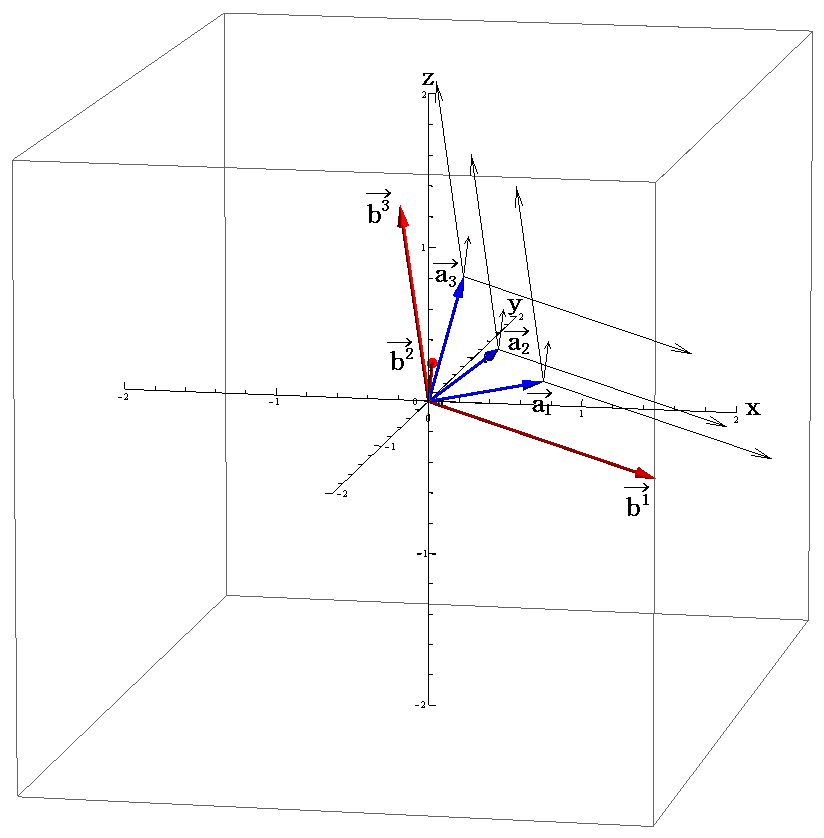
これらの3次元ユークリッド空間の成分値を用いて双対基底ベクトル b1、b2、b3 を図示すると

の様になる。[拡大図はこちら。また、視点を変えた図はこちら。]
実際の計算や図示はMathematicaなどの数式処理ソフトなど使わないと面倒だがとにかくできる。
上記の図で、例えば双対基底ベクトル
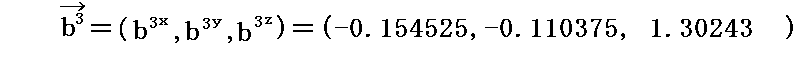
は、基底ベクトル
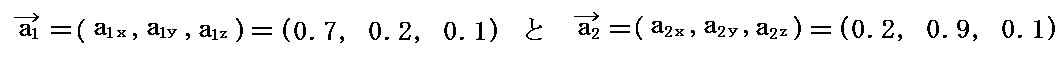
の張る平面に垂直です。
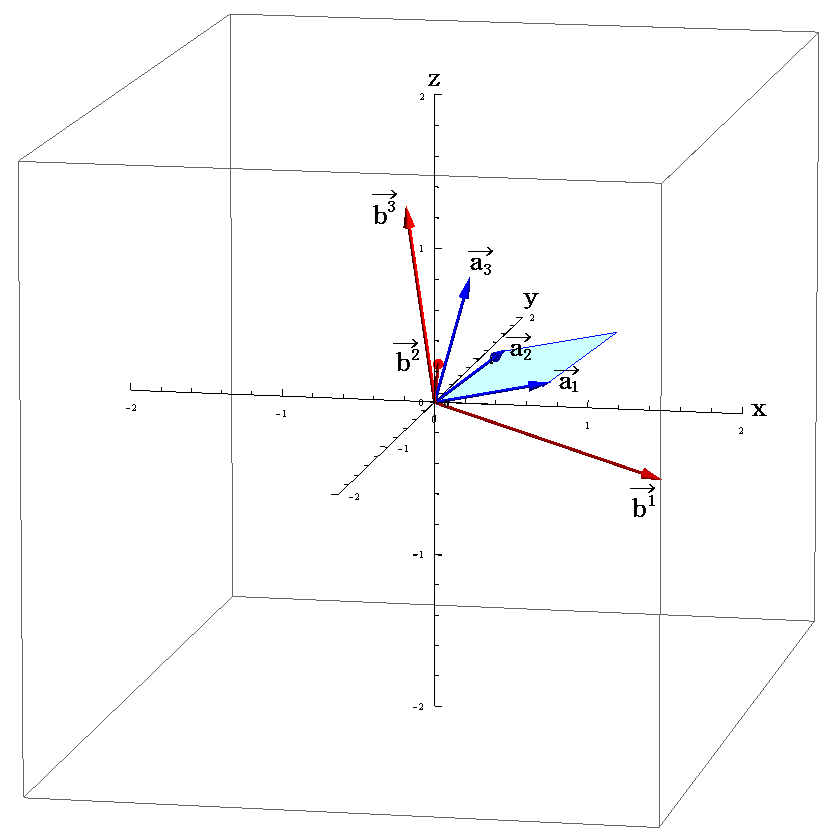
また、例えば基底ベクトル
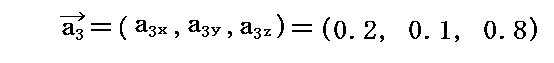
は双対基底ベクトル
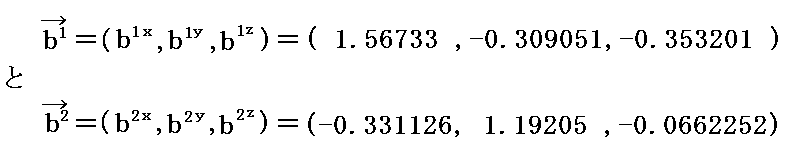
の張る平面に垂直である事を読み取って下さい。
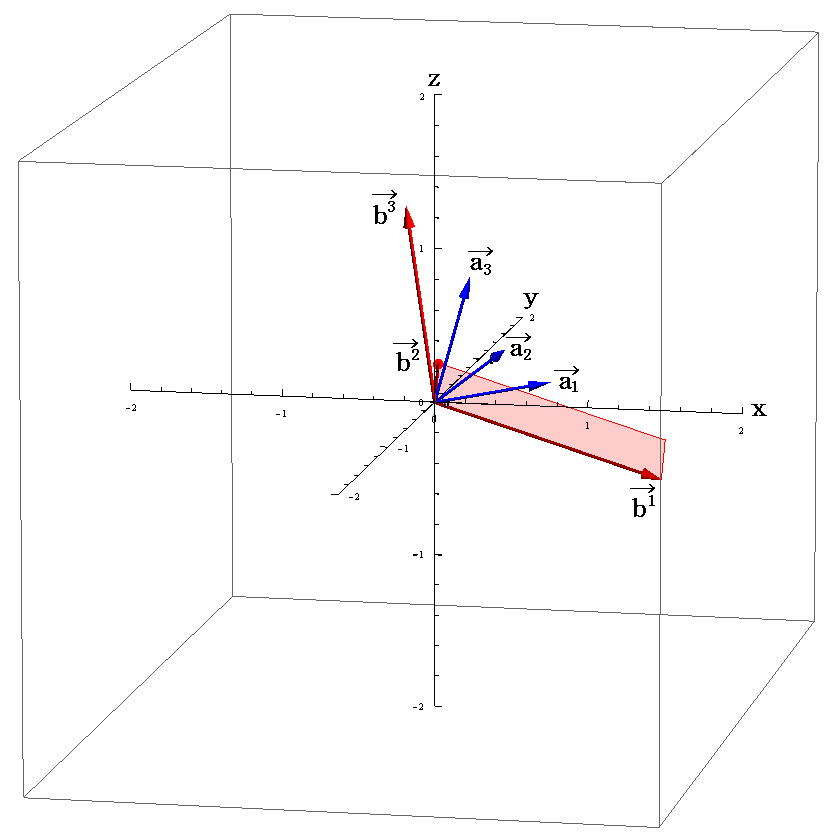
他の面もそれぞれ対応する基底ベクトル、双対基底ベクトルに垂直になっている。
[補足説明1]
上記の“基底ベクトル”と“双対基底ベクトル”の関係は、結晶解析学で習う“実格子”と“Ewaldの逆格子”の関係になっている。このことについては、別稿「X線結晶解析におけるラウエの条件式とブラッグの条件式」5.(2)2.を参照されたし。
ただし、ここで注意して欲しいことは、結晶学における“実格子”と“逆格子”は単一結晶領域内では全て同一の形状を保っているが、一般相対性理論では格子と逆格子の形状は場所の移動と共にどんどん変化していくことです。これが結晶学における“実格子・逆格子”と一般相対性理論における“基底ベクトル・双対基底ベクトル”との決定的な違いです。
一般相対性理論では、ごく近傍の隣り合った領域においてのみ“基底ベクトル・双対基底ベクトル”が同一の形状とみなすことができるだけです。この言い方には深い意味が含まれていますが、4.(1)〜(3)を読まれれば納得して頂けると思います。
[補足説明2]
ダニエル・フライシュ著(河辺哲次訳)「物理のためのベクトルとテンソル」岩波書店2013年刊)§4.4〜§4.6や平川浩正著「相対論(第2版)」共立出版社(1986年)§4-4図4.3の様に2次元の場合は、[例1]を利用して説明すると、下記の様にz座標成分を全て 1 か 0 にして、3次元のベクトル解析で計算する。そして、そのxy成分だけ取り出せば良い。
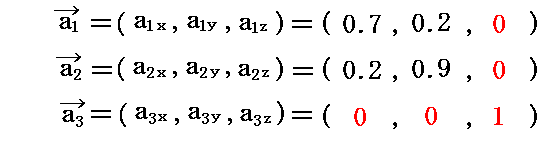
その様に取り扱えば、上記引用文献の説明も理解しやすい。
[補足説明3]
前述の様に、2次元、3次元リーマン空間の場合はベクトル解析のベクトル積・スカラー積の3次元ユークリッド空間での成分計算を実施すれば“双対基底ベクトル”を求めることができる。
4次元以上の、例えばn次元リーマン空間では次のようにする。
n×n=n2個の未知数
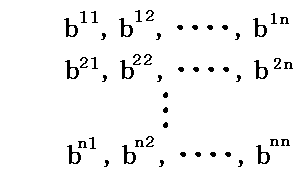
に関するn×n=n2個の線形連立代数方程式
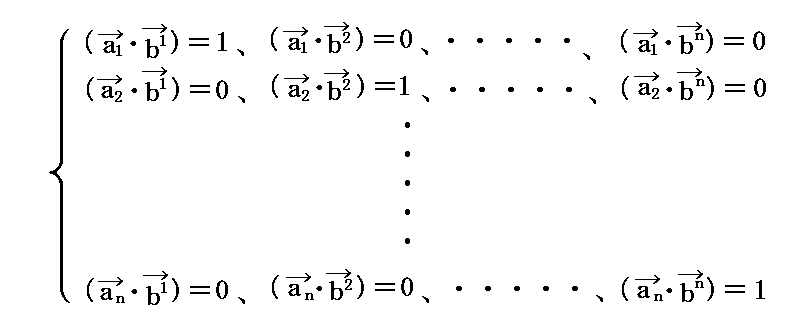
を解けば良い。これは線形連立代数方程式だから、線形代数学の授業で習うCramerの公式で解ける。この公式は『ウィキペディア(Wikipedia)』などにも解りやすく説明されているので参照されたし。
もちろん本稿で説明している3次元リーマン空間の場合もこの線形連立代数方程式を解く方法が利用できます。3次元の場合の連立方程式は
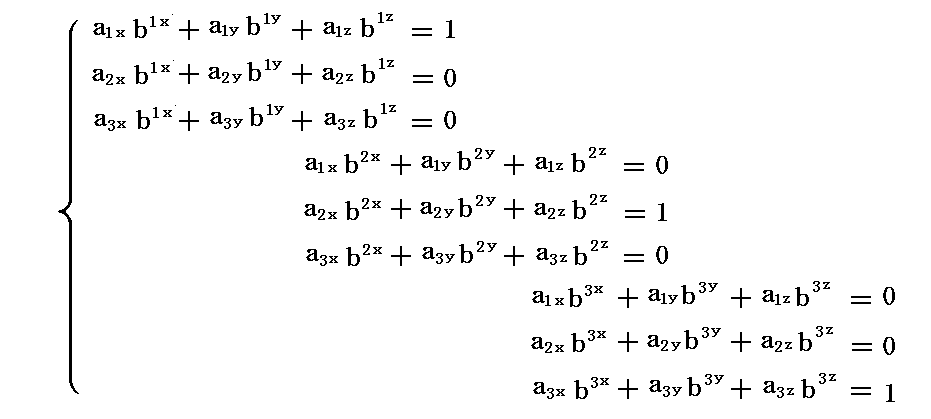
となります。
さらに、2次元リーマン空間の場合もこの線形連立代数方程式を用いる方法で解いても良い。実際、ダニエル・フライシュ著(河辺哲次訳)「物理のためのベクトルとテンソル」岩波書店2013年刊)§4.4〜§4.6ではそのようにしています。
[例2]
前述の[例1]に、[補足説明3]の3次元の場合を適用すると 3×3=9元 連立の線形代数方程式の行列表示は

となる。
この線形連立代数方程式をCramerの公式で解けば良い。手計算は大変なのでMathematicaを利用して解くと、確かに

が得られる。
[補足説明4]
ここで取り上げた例では基底ベクトルと双対基底ベクトルの違いが解りやすいように基底ベクトルの作る単位平行六面体セルとしてかなり歪んでいるものを用いました。しかし、微小領域で見た場合には3次元リーマン空間の歪みはごくわずかですからこんなに歪んでいるわけではありません。(この言い方は誤解を招きやすい。基底ベクトルが斜交したことや稜の長さが不揃いになったことがリーマン空間の歪みを直接表すわけではないからです。このことの正確な意味は4.(2)、(3)をご覧下さい。)
ところで、1.(2)で説明したように、正方格子状の網目が印刷されたゴムシートを曲面に貼り付けると、その貼り付けられた曲面の一点の近傍は2次元ユークリッド空間(つまり接平面)で近似できると言ってもその中での網目格子はもはや正方形ではなく、平行四辺形に歪みます。辺の長さも、平行四辺形の面積も元の貼り付ける前のゴムシード上での正方形格子のそれとは異なります。そのことが曲面がユークリッド空間ではなくリーマン空間であると言うことを表しています。
それと同様に、各点で設定された3次元ユークリッド空間中の斜交平行六面体を構成する基本単位ベクトルの方向と長さは様々に変化しているはずです。これらの平行六面体は3次元ユークリッド空間の中に作った立方体格子を3次元リーマン空間に貼り付けたときの3次元ユークリッド空間での様子を表しているのでしたから。
そのとき、3次元リーマン空間の歪みが小さい場合は、それに貼り付けられた3次元ユークリッド空間の立方体格子はそのままの形を保つはずです。つまり基底ベクトルは
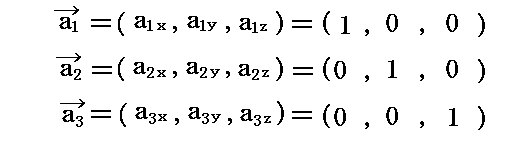
となります。
そのとき、上記と同じ手順でこれから定義計算した双対基底ベクトルは
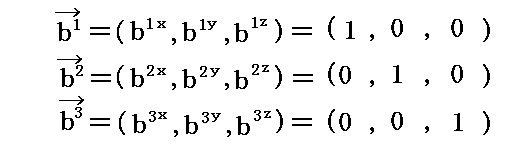
となります。
つまりリーマン空間が歪んでいない場合はユークリッド空間と同じですが、ユークリッド空間では基底ベクトルを直交関係に取りその長さを 1 とすれば、その双対基底ベクトルは元の基底ベクトルと完全に重なります。つまりb1はa1に、b2はa2に、b3はa3にそれぞれ重なります。
この場合には、2.(3)で説明する“共変成分”と“反変成分”の区別はなくなります。普通の3次元ユークリッド直交空間で習うベクトル解析、テンソル解析にはこの共変・反変という概念は表れなかったことを思い出して下さい。
(3)ベクトルの成分表現
これらの関係を用いると“実格子空間”の任意のベクトル v
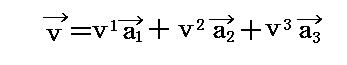
は以下の様に表せる。

ここの成分表示 (v1,v2,v3) は、基底ベクトルa1、a2、a3の長さを単位として、その長さの何個分かを表していることに注意されたし。
ただし、このように表現できるのはあくまで原点の近傍領域内のベクトルについて言えるだけであることを忘れないこと。
ここで注意して欲しいことはベクトルの大きさについては特に制限は無いのですが、“変位ベクトル”についてはその近傍領域内の位置を示す微小変位ベクトルに限るという“微小であると言う制限”がつきます。
全く同様にして、“双対格子空間”の双対基底ベクトルで同じベクトルを表すと
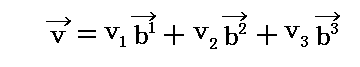
となるのですが、これについては
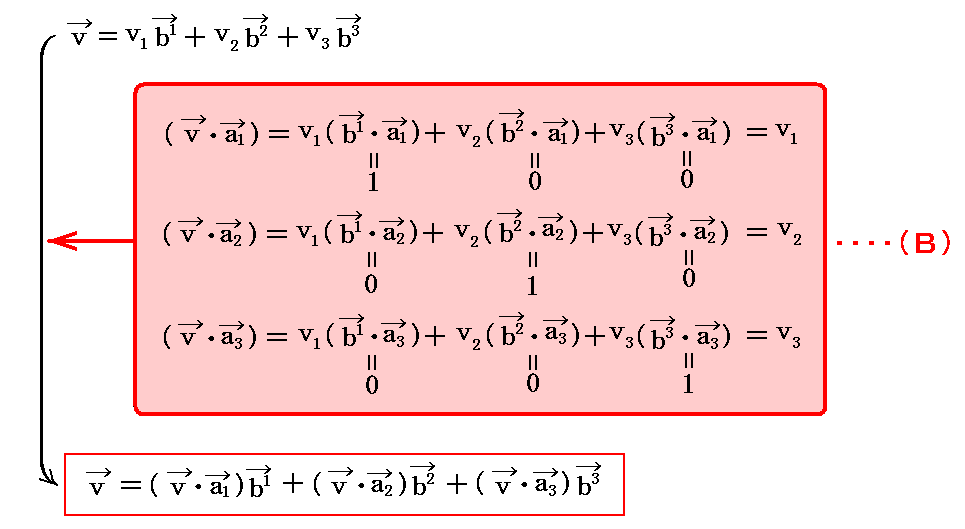
が成り立つ。ここの成分表示 (v1,v2,v3) は、双対基底ベクトルb1、b2、b3の長さを単位として、その長さの何個分かを表していることに注意されたし。
同じベクトルでも実格子空間の基底ベクトルを用いて表示するか、双対格子空間の双対基底ベクトルを用いて表示するかで、その座標値(v1,v2,v3)と(v1,v2,v3)の値は異なります。“座標値”は異なっても同じベクトルを表している事を忘れないで下さい。
(v1,v2,v3)をベクトル v の“反変成分”と言い、(v1,v2,v3)をベクトル v の共変成分”と言います。
なぜこんな名前がついているかといいますと、同じベクトル v を表示するとき、 (v1,v2,v3) は、基底ベクトルa1、a2、a3の長さが増大すると、それに反して減少するからです。
また、 (v1,v2,v3) は、基底ベクトルa1、a2、a3の長さが増大すると双対基底ベクトルb1、b2、b3の長さが減少しますので、基底ベクトルa1、a2、a3の長さと共に増大するからです。
このとき、(v1,v2,v3)が基底ベクトルの変換係数の逆変換行列で座標変換されるからこれを“反変成分”と喚び、(v1,v2,v3)が基底ベクトルの変換係数と同じ係数で座標変換を受けるからこれを“共変成分”
と呼ぶと言っている本もあります。その様に言っても良いでしょう。このことについては3.(2)と(3)を参照して下さい。
[例3]
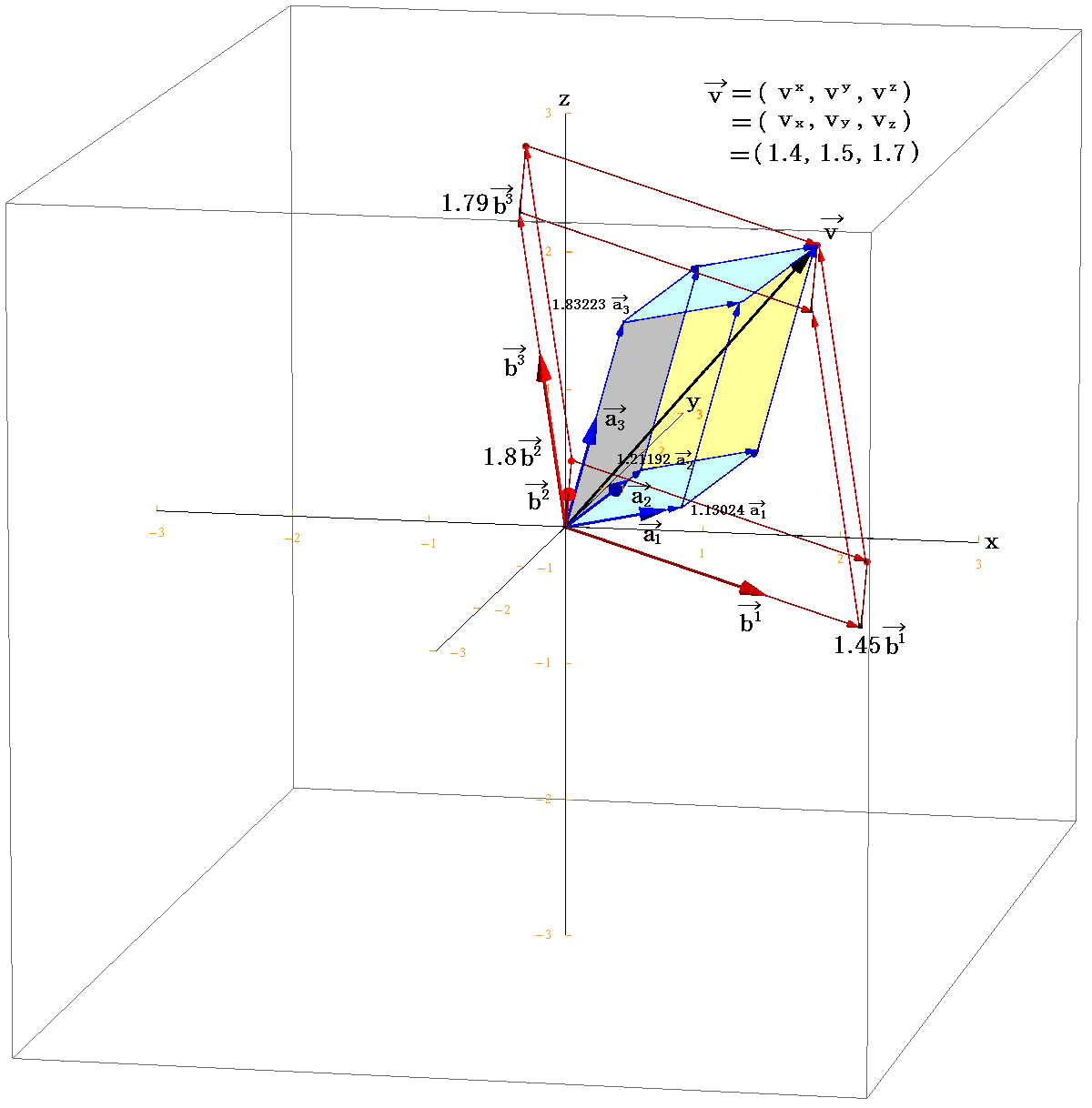
前述の[例1]の実格子空間と双対格子空間での“座標値”を計算して、上記の事情を図で示してみる。
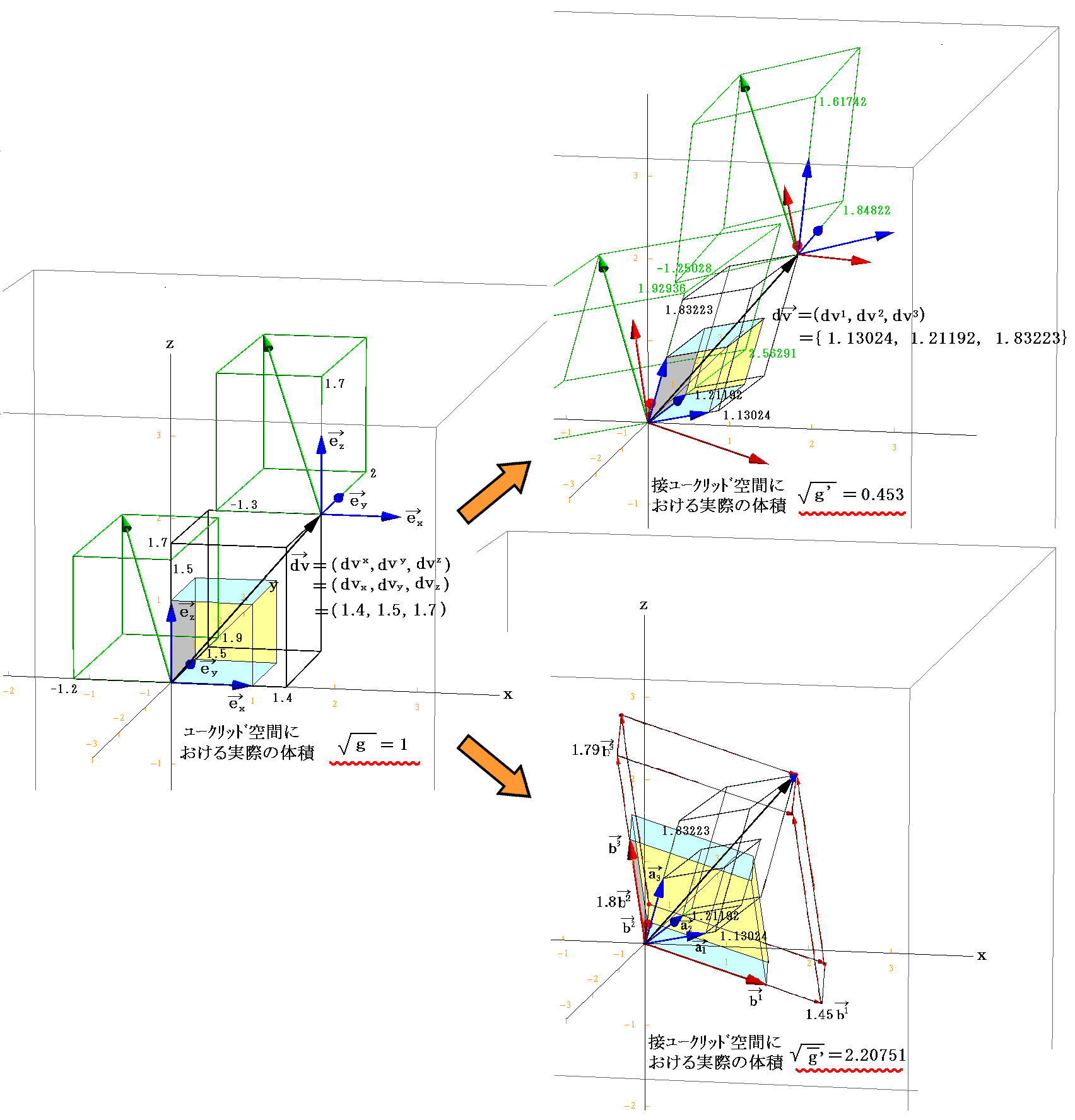
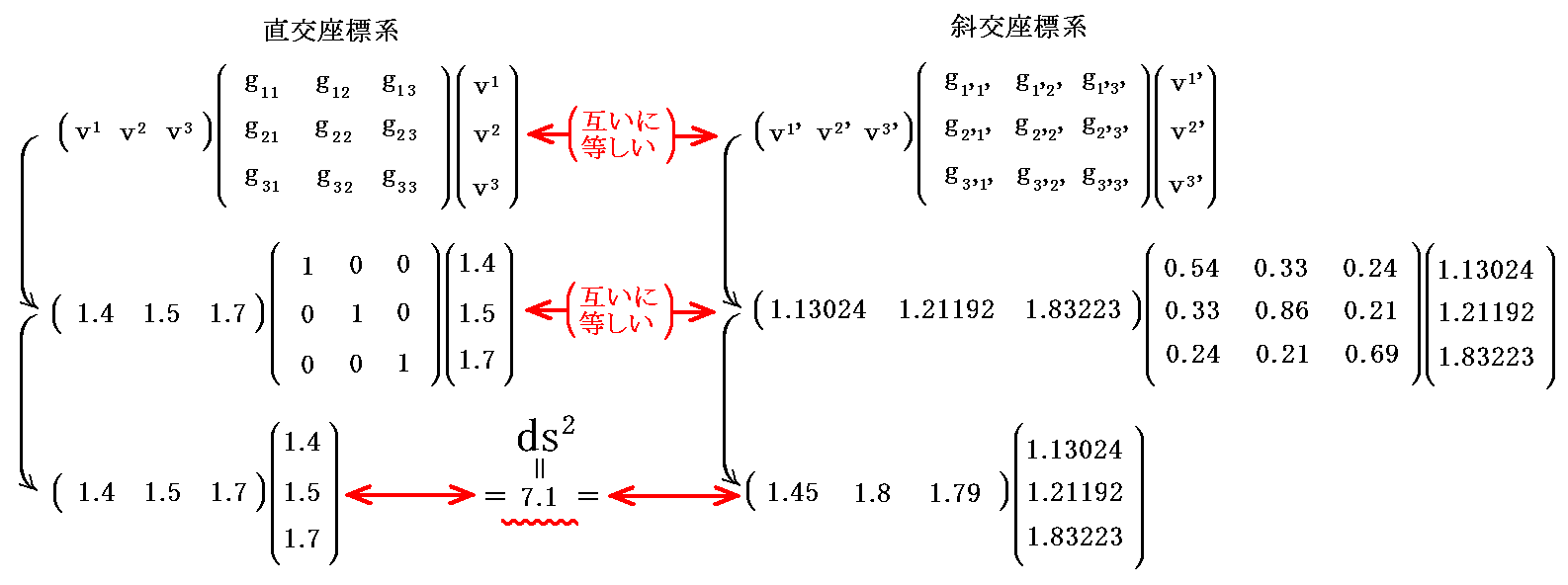
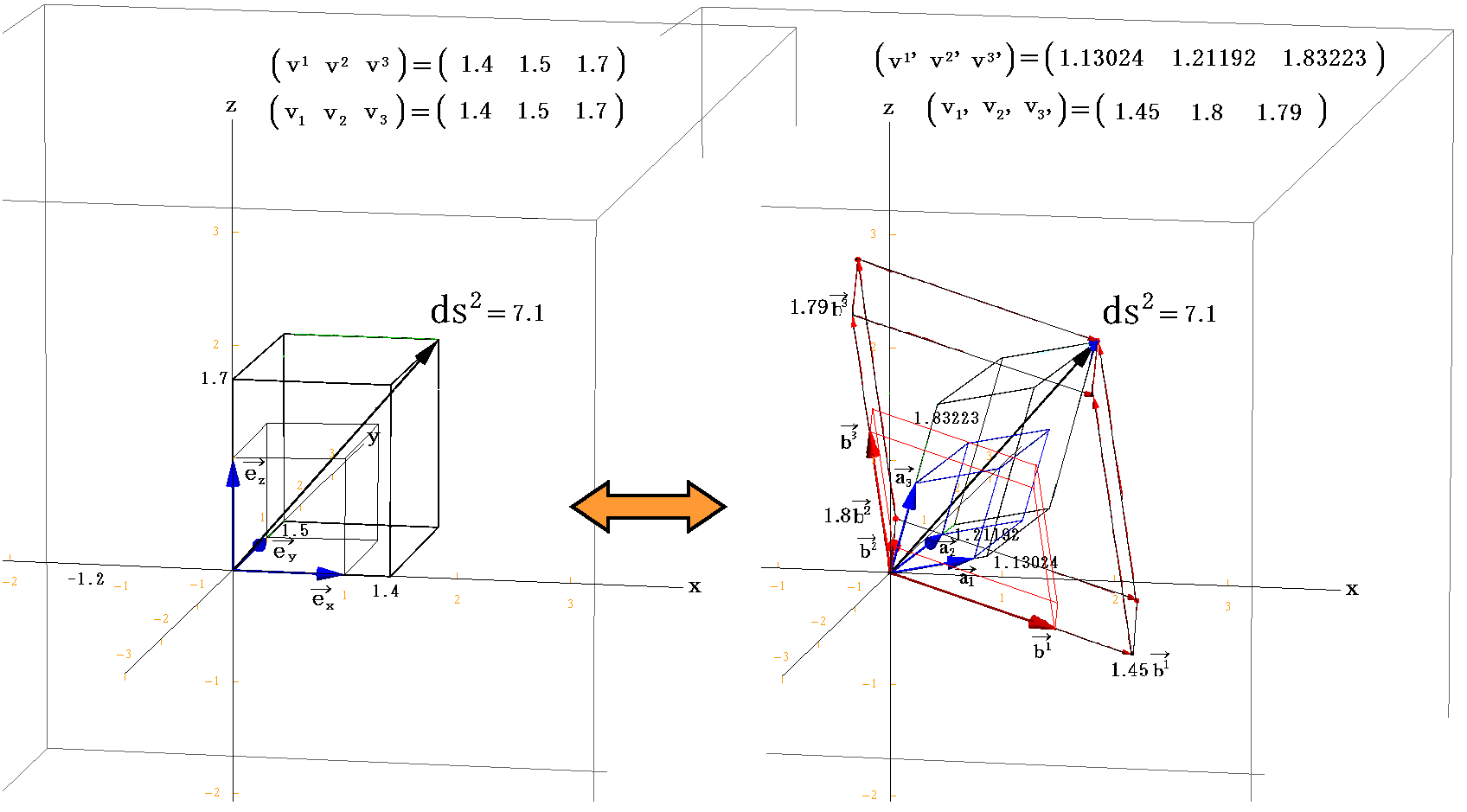
任意のベクトル v の3次元ユークリッド空間での成分座標値を v=(x,y,z)=(1.4,1.5,1.7)≡(vx,vy,vz) とする。図中の黒色矢印がそれです。
このとき反変成分(v1,v2,v3)の具体的な値は

だから次のようにして計算できる。

同様に共変成分(v1,v2,v3)は
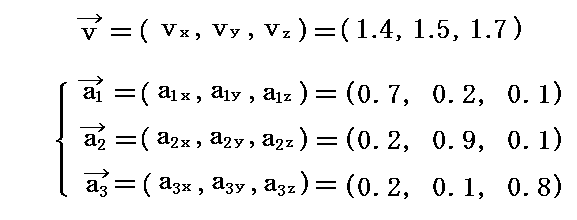
だから
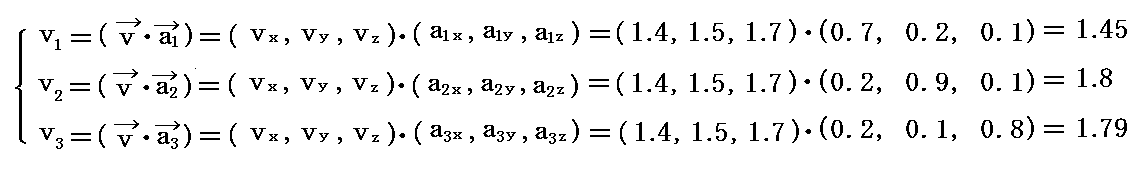
となる。
これらの値を用いて図示すると

となる。[拡大図はこちら。また、視点を変えた図はこちら。]
図から明らかなように、基底ベクトルに対して双対基底ベクトルというものを考えたのは、単位格子セルが平行六面体となった為に、ベクトル v の座標値をその単位格子セルの格子定数(つまり基底ベクトルの何倍か)で知る必要があるから。すなわち、前記の(A)式と(B)式の関係を利用したいからです。
反変成分(v1,v2,v3)、共変成分(v1,v2,v3)も図の中に全て書き込んでありますから、図でその意味を読み取って下さい。そのとき、図中平行六面体のピンク色着色面は基底ベクトル a3 に垂直であり、水色着色面は双対基底ベクトル b3 に垂直です。他の面もそれぞれ対応する基底ベクトル、双対基底ベクトルに垂直になっている事を読み取って下さい。
(4)リーマン計量(計量テンソル)と共変・反変の関係
別稿「微分幾何学」3.(2)2.[補足説明3]で説明したように、ここで考えている3次元ユークリッド空間は、曲面(2次元リーマン空間)の各点で定義された接平面(2次元ユークリッド空間)を3次元リーマン空間に拡張したものですから、上記の3個の独立なベクトル
a1、a2、a3 からできる

は“3次元リーマン空間”の原点に於けるリーマン空間の“基本計量共変テンソル成分” gij であると考えられる。
一方
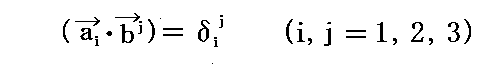
を満足するような新たな3個のベクトル bj の組を2.(1)で考えたのだが、これらのベクトルの組から

とおいた量 gij を考えることができる。
このとき任意のベクトル v を
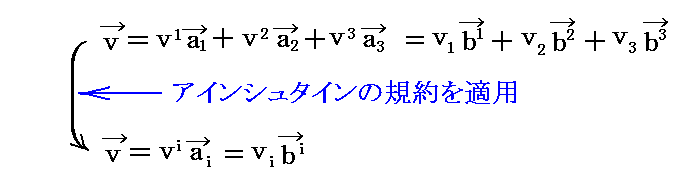
の様に表すと前節2.(3)で示したように

となる。これらは以下の事を表している。
まず、最初の式から
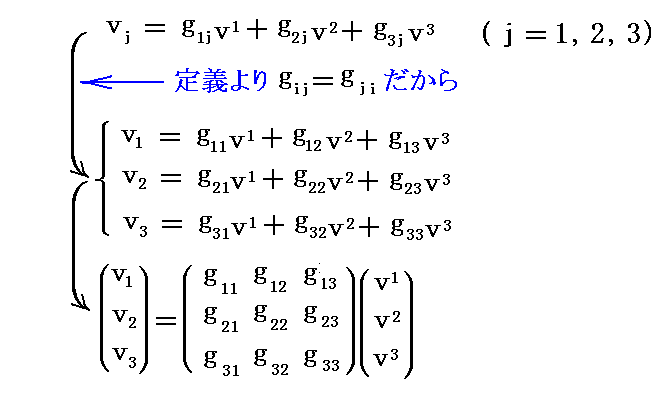
つまり、ベクトル v の基底ベクトル系での成分 (v1,v2,v3) は gij を乗じて縮約することで双対基底ベクトル系での成分 (v1,v2,v3) に変換される。このとき (v1,v2,v3) をベクトル v の“反変成分”といい、 (v1,v2,v3) ををベクトル v の“共変成分”と言うのでした。
もう一方の式から
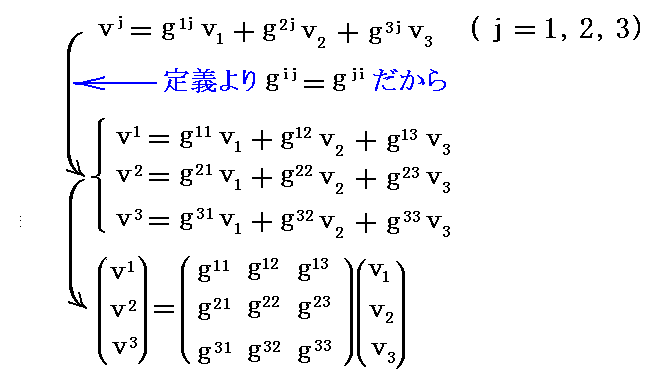
が成り立つので、ベクトル v の双対基底ベクトル系での成分 (v1,v2,v3)は gij を乗じて縮約することで基底ベクトル系での成分 (v1,v2,v3) に変換される。
すなわち gij は“反変成分”を“共変成分”に、 gij は“共変成分”を“反変成分”に変換する働きがある。
さらに、上式を用いると
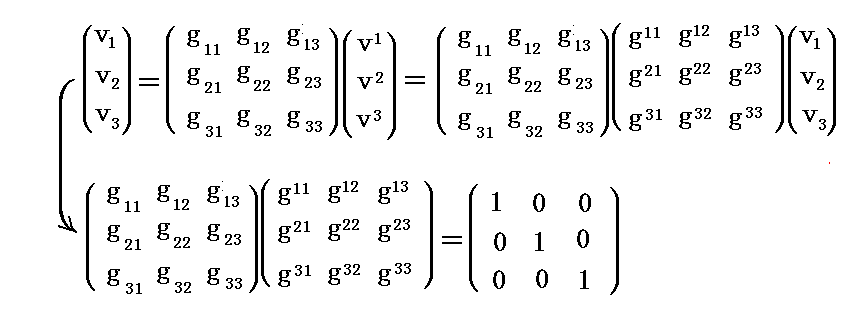
となり、gijgjk=δik が成り立つので、 gij は gij の“逆行列”である。
このようにして得られた gij と gij を”リーマン空間”の“基本計量テンソル”と言う。
いずれも“対称テンソル”になること、すなわち、gij=gjiであり、gij=gjiが常に成り立つこと、はその定義
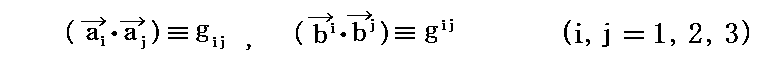
から明らかです。。
また、 gij が“共変テンソル”であることは、gijの元々の定義から解ることです。その事は別稿3.(2)3.[テンソルの例2]で説明していますのでそこをご覧下さい。
このことは、2.(5)で説明する様に gij が
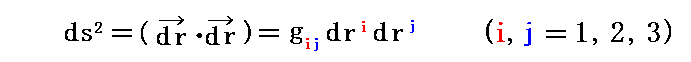
を満足することと、この式の左辺ds2がスカラーであり右辺のdriとdrjが反変ベクトルであることから、別稿3.(2)6.テンソルの商法則[補足説明2]で説明したテンソルの商法則からも証明できます。
さらに、 gij が“反変テンソル”であることは、別稿3.(2)[問題3]で証明していますのでそこをご覧下さい。もちろん上記と同様な関係式
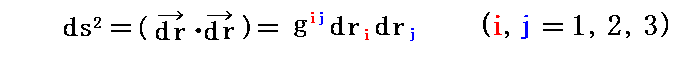
とテンソルの商法則からも証明できます。
基本計量テンソルを仲介として考えれば、基底ベクトル・双対基底ベクトルと座標値との関係や、ベクトルの反変成分・共変成分の幾何学的な意味が明らかになる。
[例4]
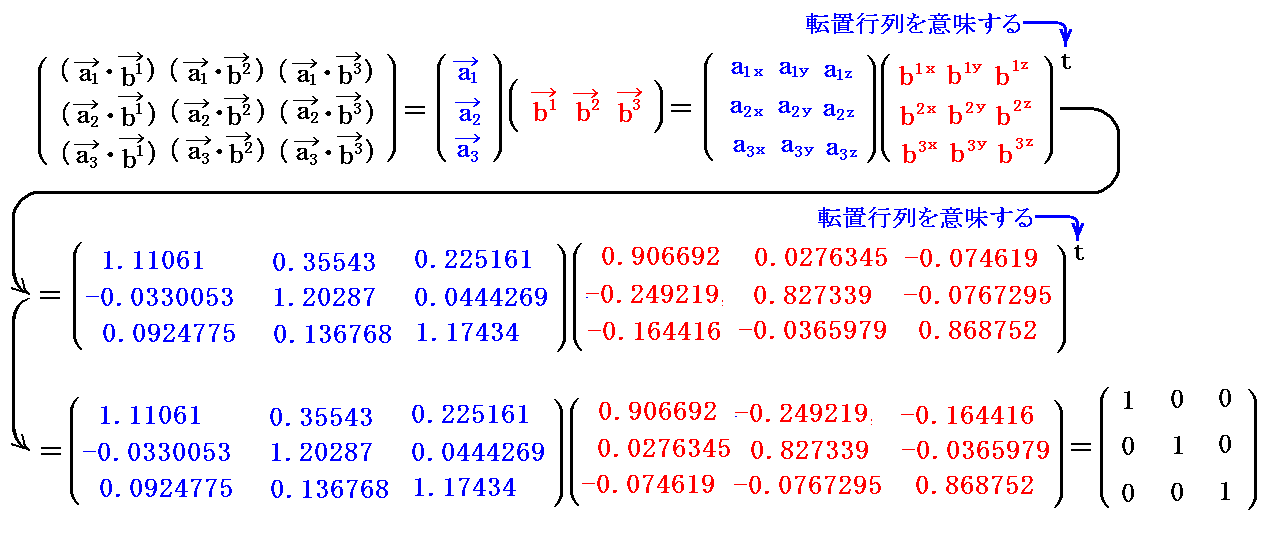
2.(2)[例1]で取り上げた基底ベクトル、双対基底ベクトルについての“基本計量共変テンソル”gijと“基本計量反変テンソル”gijを計算してみる。
基底ベクトルのユークリッド空間での座標値を用いて計算すると
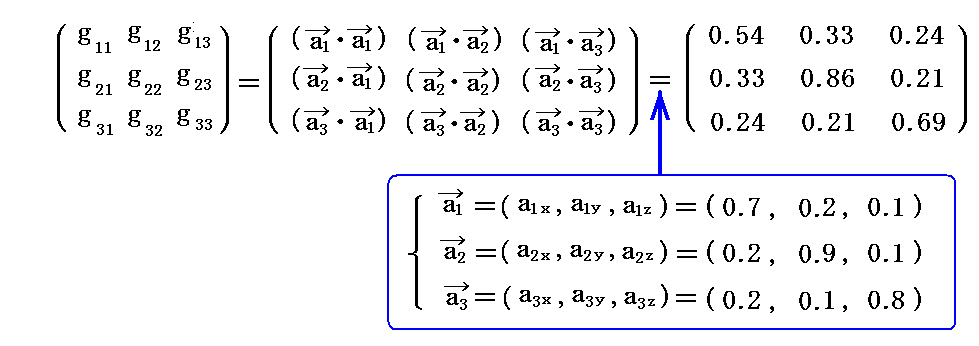
が得られる。実際の計算は面倒なのでMathematicaを利用した。このときユークリッド空間での座標値を用いて良いのは内積の結果得られるgijが“実際の長さを表すスカラー量”だからです。
同様に双対基底ベクトルの計算値を用いると
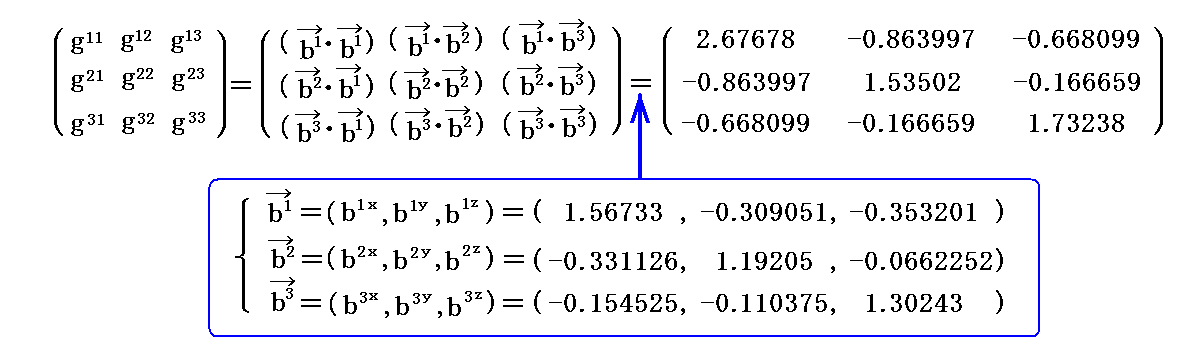
が得られる。
これら2つの行列の積を作ると確かに
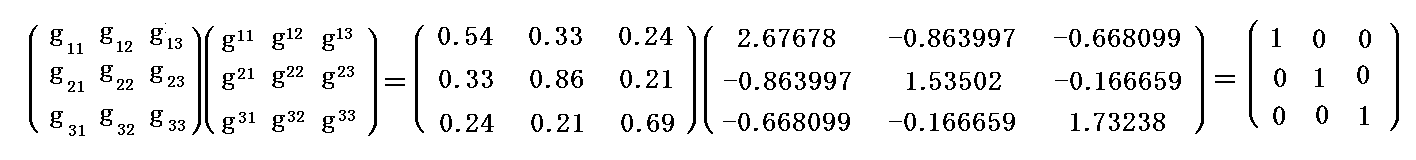
を満足している。
さらに、反変成分から共変成分への変換式

を満たしている。
これがテンソル代数学に於いて、反変ベクトル vj に基本計量共変テンソル gij を乗じて j について縮約すると共変ベクトル vi (指数を下げたベクトル)が得られると言うことの意味です。
もちろん、共変成分から反変成分への変換式
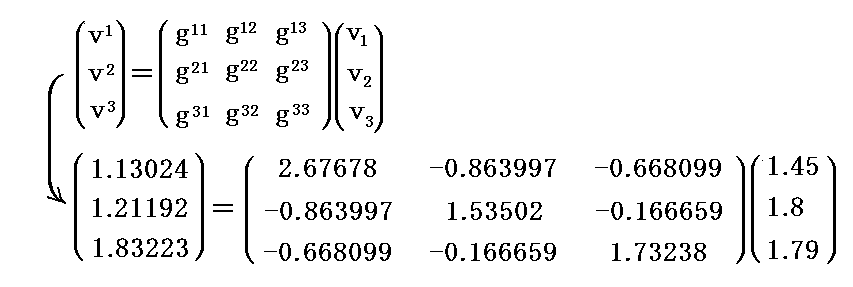
も確かに満たしている。
これがテンソル代数学に於いて、共変ベクトル vj に基本計量反変テンソル gij を乗じて j について縮約すると反変ベクトル vi (指数を上げたベクトル)が得られると言うことの意味です。
(5)[基本計量テンソル]と[ベクトルの内積]の関係
前節では3次元リーマン空間内の一つのベクトル v を考えたが、ここではもう一つ別のベクトル w を考える。このベクトルについても基底ベクトル系での成分表示 (w1,w2,w3) と双対基底ベクトル系での成分表示 (w1,w2,w3) がある。前者 (w1,w2,w3) をベクトル w の反変成分といい、後者 (w1,w2,w3)ベクトル w の共変成分という。これらについては前節でベクトル v で述べたのと同様な関係式が成り立ちます。
このとき
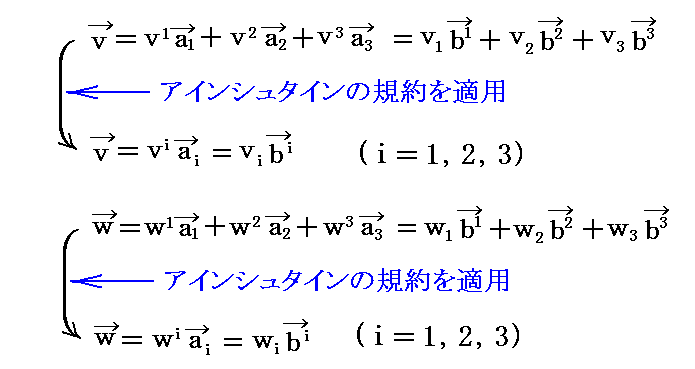
ですから、2つのベクトル v と w の“内積”は
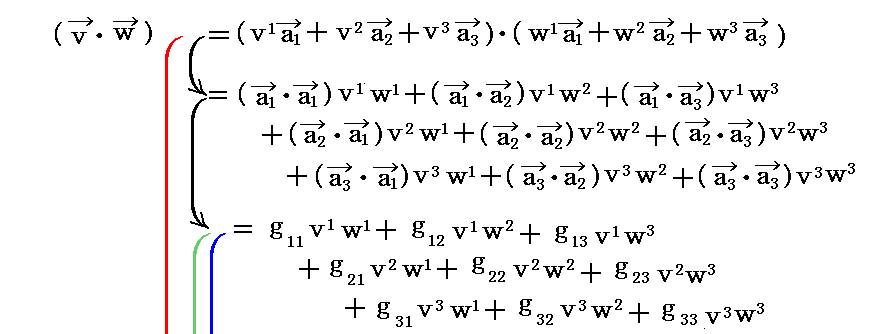
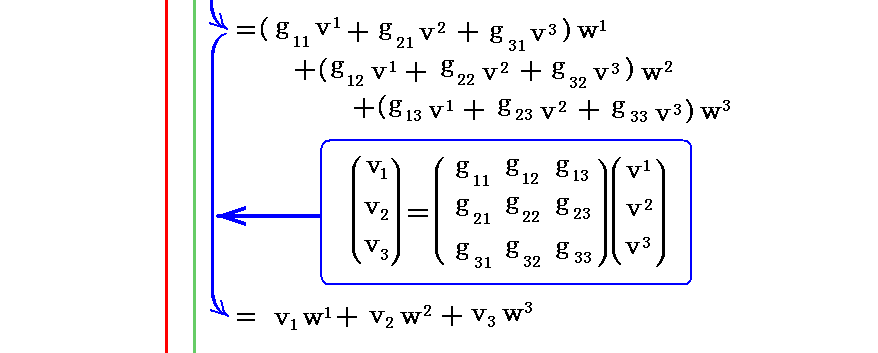

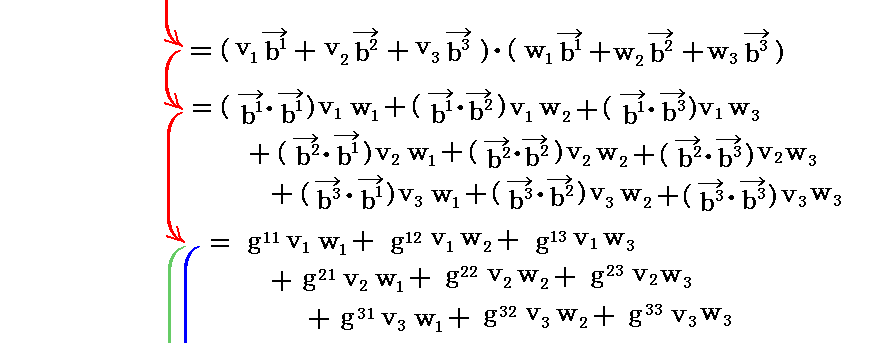
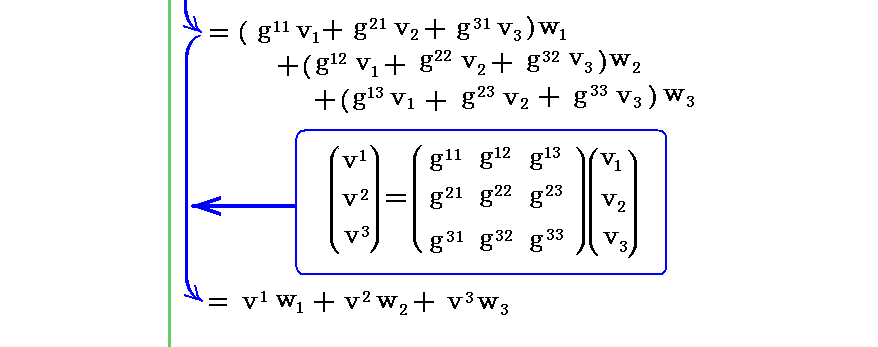
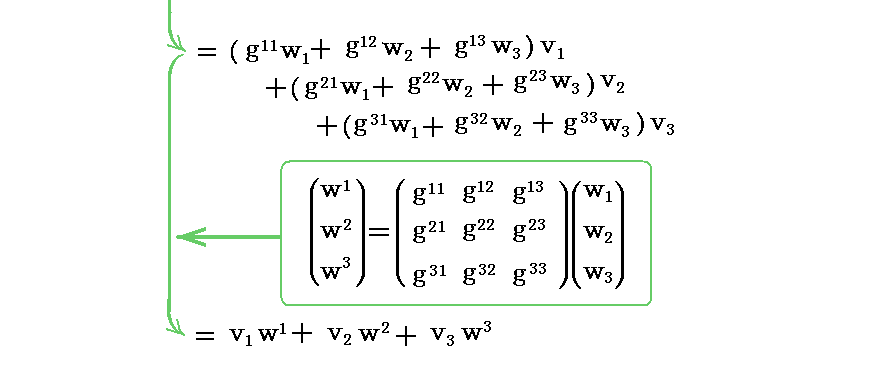
となる。
アインシュタインの規約を適用すると
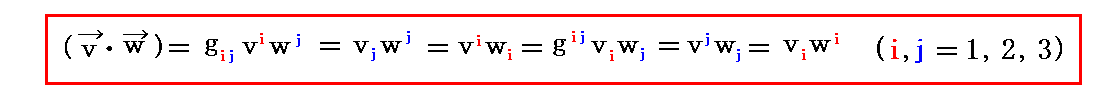
と表される。これを行列表示すると更に解りやすくなる。

[補足説明]
ここで注意して欲しいことは、計量テンソル(gij)や(gij)の役目は、反変成分や共変成分で表された“微分線要素の積”を2点間の不変な距離にすることです。これが“計量テンソル”は空間の幾何学を与えると言われる理由です。
このことは別稿の[補足説明5]でも注意しましたし、本節の最後でもう一度強調します。さらに4.(3)[例8]の最後の文節を読まれた後にもう一度この[補足説明]を振り返ってみられたし。
同様にして、微小変位ベクトルをdrとすると、この空間ベクトルの“長さds”の2乗は
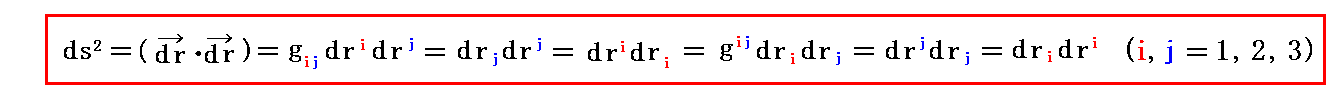
と表される。もちろん上記表現はアインシュタインの規約に従っています。
これも行列表示すると
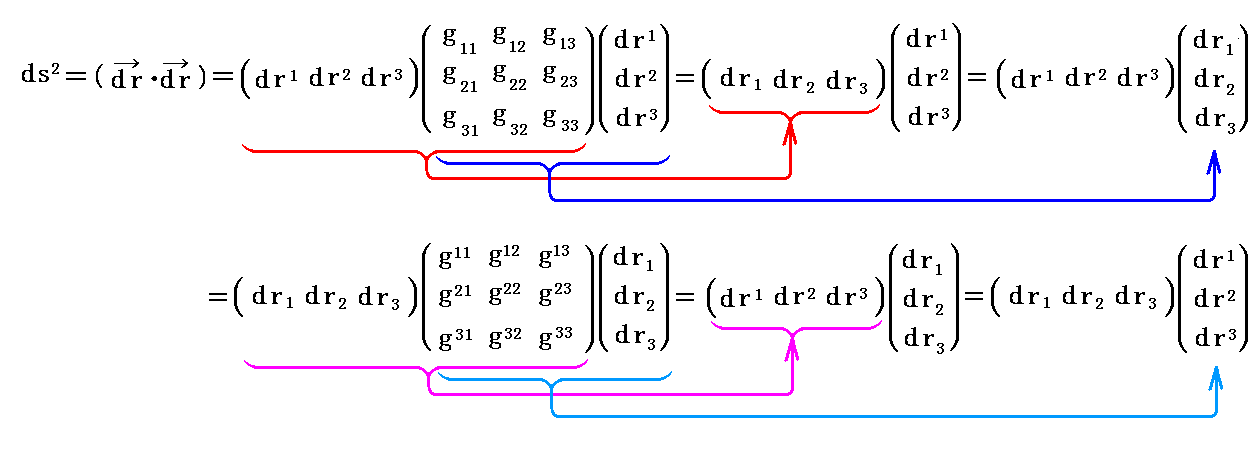
となる。4.(6)5.[補足説明2]で、上式の意味を図の上で確認していますので、御覧下さい。
さらに補足しますと、上式の右側の部分は
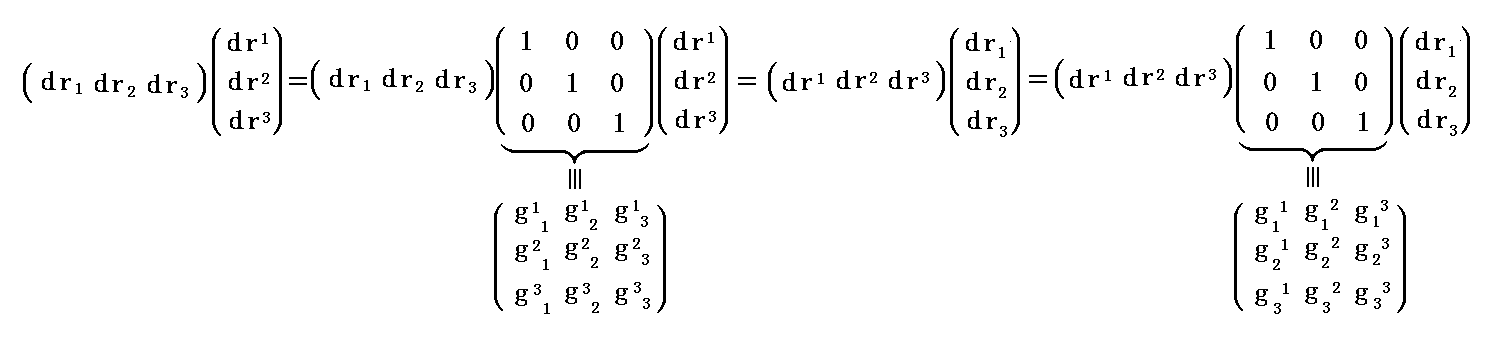
と置けます。
つまり
と言うことです。実際こうなることは、3.(5)[補足説明1]を御覧下さい。
[例5]
内積の具体例を示す。そのために新たなベクトル w を考えるが、その3次元ユークリッド空間での成分座標値を w=(x,y,z)=(-1.2,1.9,1.5)≡(wx,wy,wz) とする。図中の緑色矢印がベクトル w です。
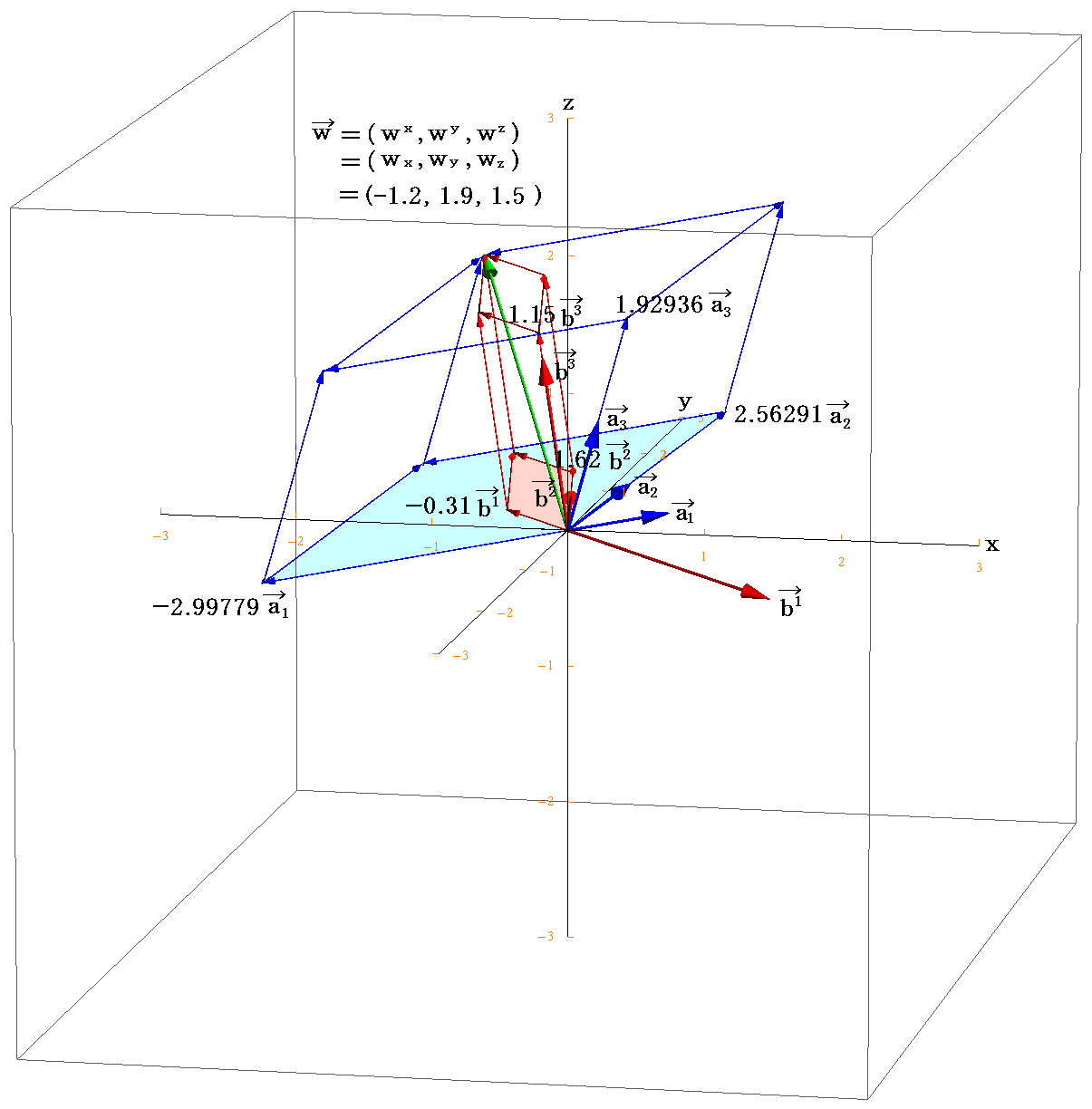
このとき、基底ベクトル系での座標値は

であり、双対基底ベクトル系での座標値は
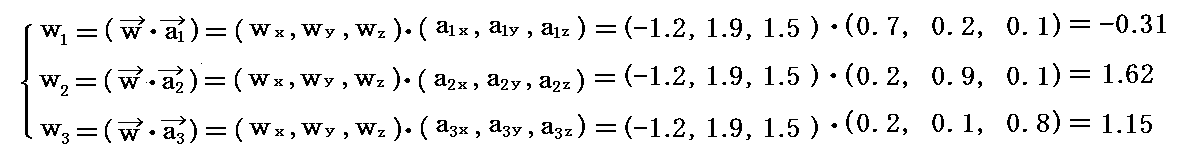
と成ります。
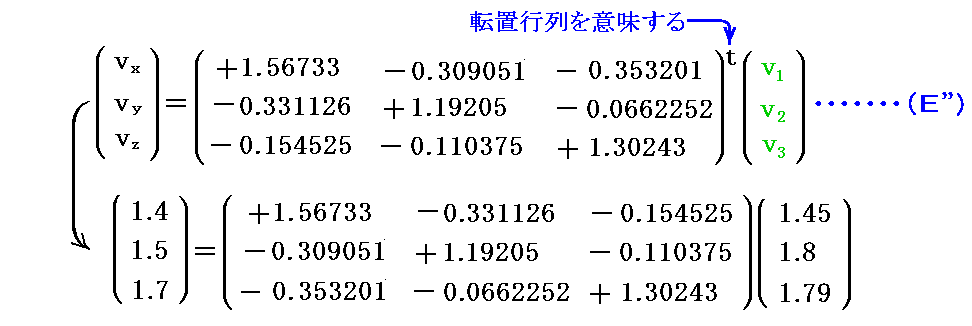
ここで、2.(3)[例3]で示したベトクル v との内積を計算してみます。

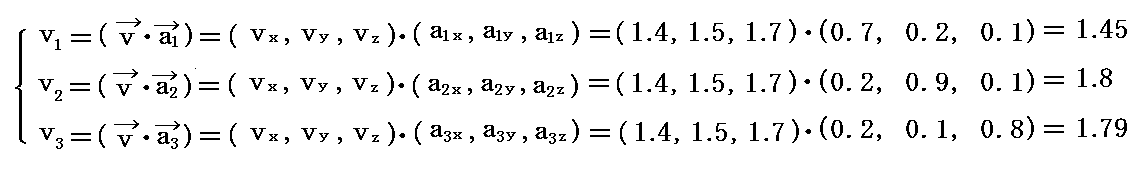
であった事と、計量テンソルの値が
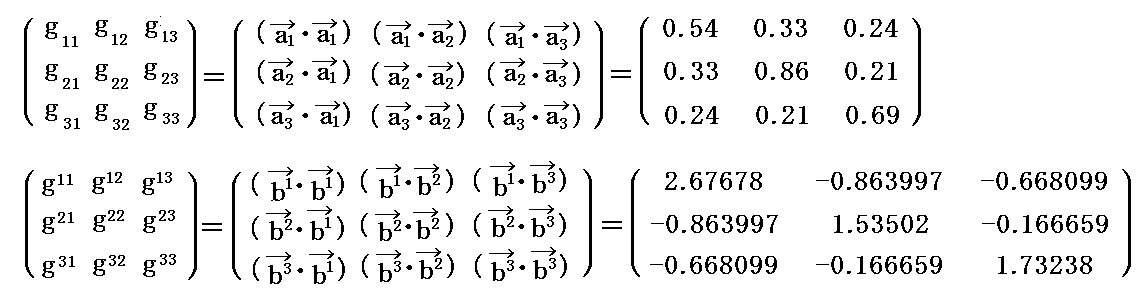
であった事を利用すると

となり、すべで同一の値が得られます。
どれとどれの座標値が掛け合わされているか下図で確認して下さい。

いずれにしても、上記の計算値は3次元ユークリッド空間での成分値を用いた計算値
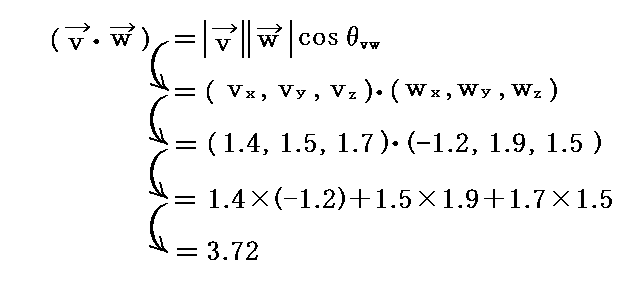
に一致します。3次元ユークリッド空間は今考えている3次元リーマン空間のその点に於ける接空間ですから、同じ値が得られるのは当然です。
ベクトル v とベクトル w の大きさと交叉角は
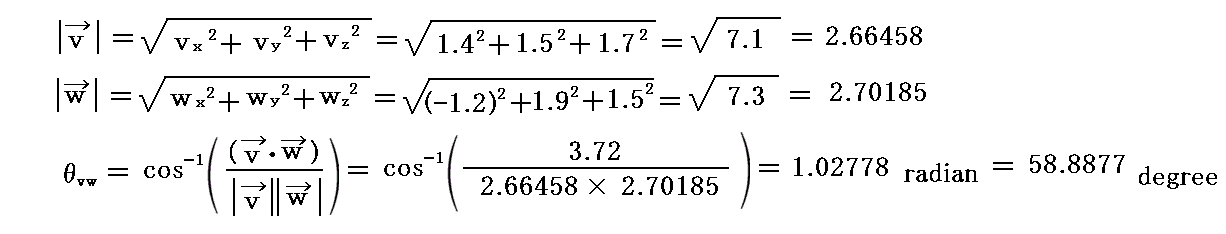
です。
接空間である3次元ユークリッド空間に設定した(x,y,z)の“直交座標系”では、普通のベクトル成分の内積公式で計算できるのに、“斜交座標系”では双対基底ベクトル系というものを考えて上記の様に面倒な計算をしなければならなくなった所をご理解下さい。
そのとき、3次元リーマン空間では、必然的に“斜交座標系”でないと隣の空間部分に接続していけないのです。
最初に、3次元空間中の1点に立方体状のセル(基底ベクトル)を設定します。次に、その各辺を周囲に伸ばしながら次々と隣り合うセルの基底ベクトル系を作り、それらを繋いでいきます。そのとき現実に“リーマン空間”に住む我々は、4.(3)で説明するように、そのように繋いで行った立方体セルが、その内に必然的に歪んできて、立方体セルを構成できなくなることに気付きます。つまりリーマン空間に住む人間は必然的に平行六面体状の基底ベクトルを用いなければならなくなるのです。そして、平行六面体状になった基底ベクトルを単位として空間中のベクトル量を測定しなければならなくなります。この当たりの事情は2次元リーマン空間である球面を正方形の格子のみで覆い尽くすことはできない事を思い浮かべれば納得していただけると思います。
そのとき具体的なベクトル量の真の長さや、二つのベクトルの内積(座標の取り方によらない不変量)などの情報が必要になった時には、上記の様な双対基底ベクトルを各点で定めて、それらの基底ベクトルを単位として測定した《反変成分》と《共変成分》の座標値を上記の様に組み合わせて利用しなければならない!のです。
このことについては別稿B.(5)3.[補足説明1]や、別稿B.(11)3.[補足説明1]も参照されたし。
そのとき、各点での《基底ベクトル》が定まっていれば、その点での《双対基底ベクトル》は2.(2)で説明した方法で定めることができます。
(6)基本計量テンソルとは何か
基本計量テンソルは、結晶解析学に於ける“格子定数”に相当します。“格子定数[lattice constant]とは、結晶格子の単位格子セルの稜の長さa,b,cと,相互の間の角度α,β,γをいう。”(岩波『理化学辞典』より)
3つの基底ベクトルが張る平行六面体の稜の長さを|a1|,|a2|,|a3|とし、ベクトルa1とベクトルa2のなす角をθ12、ベクトルa2とベクトルa3なす角をθ23、ベクトルa3とベクトルa1のなす角をθ31とすると、2.(2)[例1]での基本計量共変テンソル gij は

を意味します。
これから直ちに

を求めることができます。実際、格子定数の値がそのようになることは[例1]の図から読み取れます。
そのとき、これらの値から逆に gij は直ちに計算できます。それ故に基本計量テンソルは格子定数のようなものだと言えます。
[補足説明]
ここで重要なことは4.(3)で説明するように、“3次元リーマン空間”の各点の近傍は“3次元ユークリッド空間”で近似できるのでしたから、3次元リーマン空間の中に引かれている網目状格子の各点の格子(平行六面体)の稜の長さ|a1|,|a2|,|a3|と稜の交差角θ12、θ23、θ31は3次元ユークリッド空間の物指し棒と分度器で現実に測定することができます。だから現実のリーマン空間の各点に於ける基本計量共変テンソル gij はユークリッド空間に存在する平行六面体から測定可能です。
すなわち、基本計量共変テンソルgijの各成分値は基底ベクトルa1、a2,a3のユークリッド空間における絶対的な長さ(大きさ)を表す数値(先に“2点間の不変な距離”と表現したもの)から上記の手順にしたがって得られるものです。
上記の説明はとても解りにくい所ですが、別稿「一般相対性理論の古典的検証と歪んだ時空」3-3“物差しの振る舞い”における図19のa)とb)二通りの解釈ができる事に留意されてください。
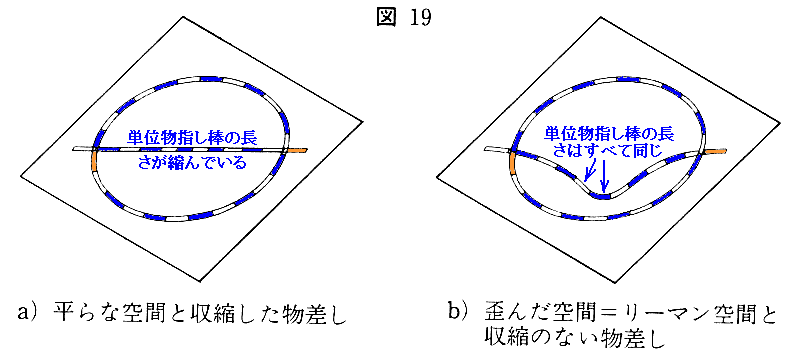
上記の“2点間の不変な距離”はb)の立場での意味だと理解すれば解りやすい。なぜなら、曲面(2次元リーマン空間)上の各点に於ける接平面に対応するものが3次元リーマン空間の各点に於ける接ユークリッド空間なのですから。その様に解釈して初めて“クリストッフェル記号”(接続係数)の意味も明瞭になります。(ここは4.(1)〜(4)で詳しく説明します)
一般相対性理論の教科書では、“接ユークリッド空間の不変的な距離”を用いるb)の立場で説明される場合と、“物差しが収縮し時計がゆっくり進む”という解釈のa)の立場で説明される場合がありますが、本来どちらの解釈も可能です。別稿「時空の曲がりと測地線(測地線方程式とは何か)」4.(4)[補足説明]をご覧下さい。
[例6]
このようにして格子定数に相当するものが与えられるから、基底ベクトルの何倍という形で与えられた座標値と組み合わせることにより、現実の位置ベクトルの長さds あるいはその2乗値であるds2 が求まる。
前節で求めたds2の計算式を2.(3)[例3]で取り上げた位置ベクトル v に適用して、その長さの2乗値を求めてみる。

となるが、これは確かに
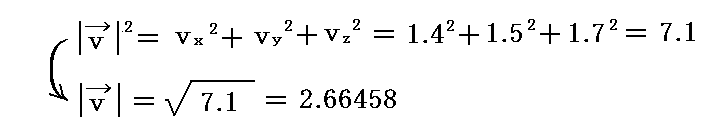
と一致している。
以上述べたことは、基本計量反変テンソル gij についても同様に成り立ちます。もちろん、そのときの計算は

に基づいて行われます。θにダッシュ’を付けたのは双対基底ベクトルの交差角である事を示すためです。
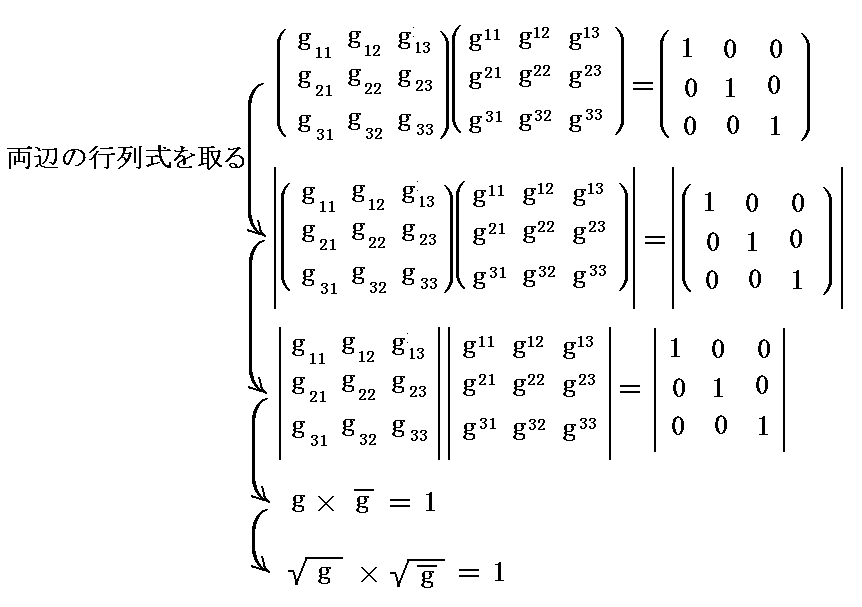
(7)基底ベクトルが作る単位格子セルの体積Vと基本計量テンソルgijの関係
基本計量テンソルの重要な性質について補足する。
3つの基底ベクトル a1,a2,a3 の張る平行六面体(単位格子セル)の体積Vは、別稿「ベクトルの内積と外積の成分表示」2.(5)2.で説明した様に
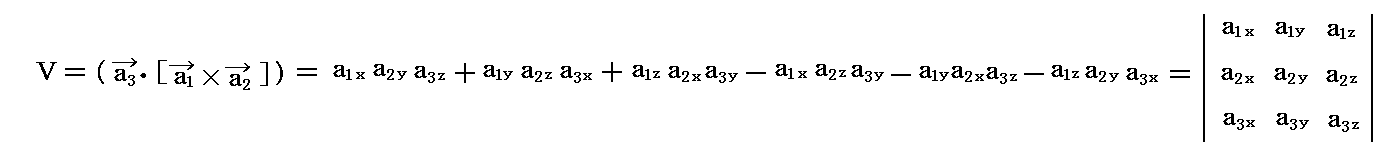
で表される。
そのため、体積Vの2乗は
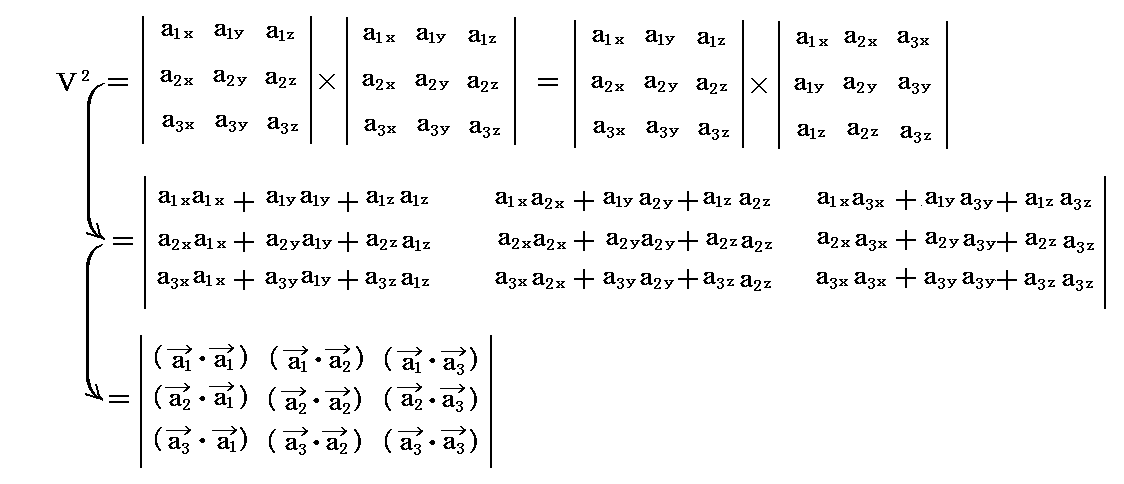
となる。式変形に行列式の性質を用いたが、詳細は別稿「ベクトルの内積と外積の成分表示」2.(5)2.[補足説明]を参照されたし。
ところで最後の行列式は、2.(4)で定義した“3次元リーマン空間”の“基本計量テンソル” gij から得られる行列式の値ですから

となる。
従って、ベクトルv=(v1,v2,v3)を対角線ベクトルとする基底ベクトル系における平行六面体の体積Vは
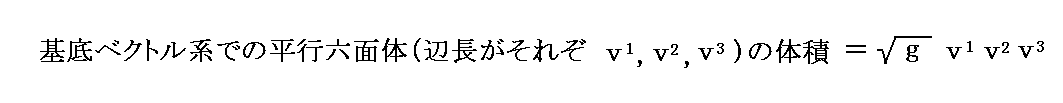
で表される。
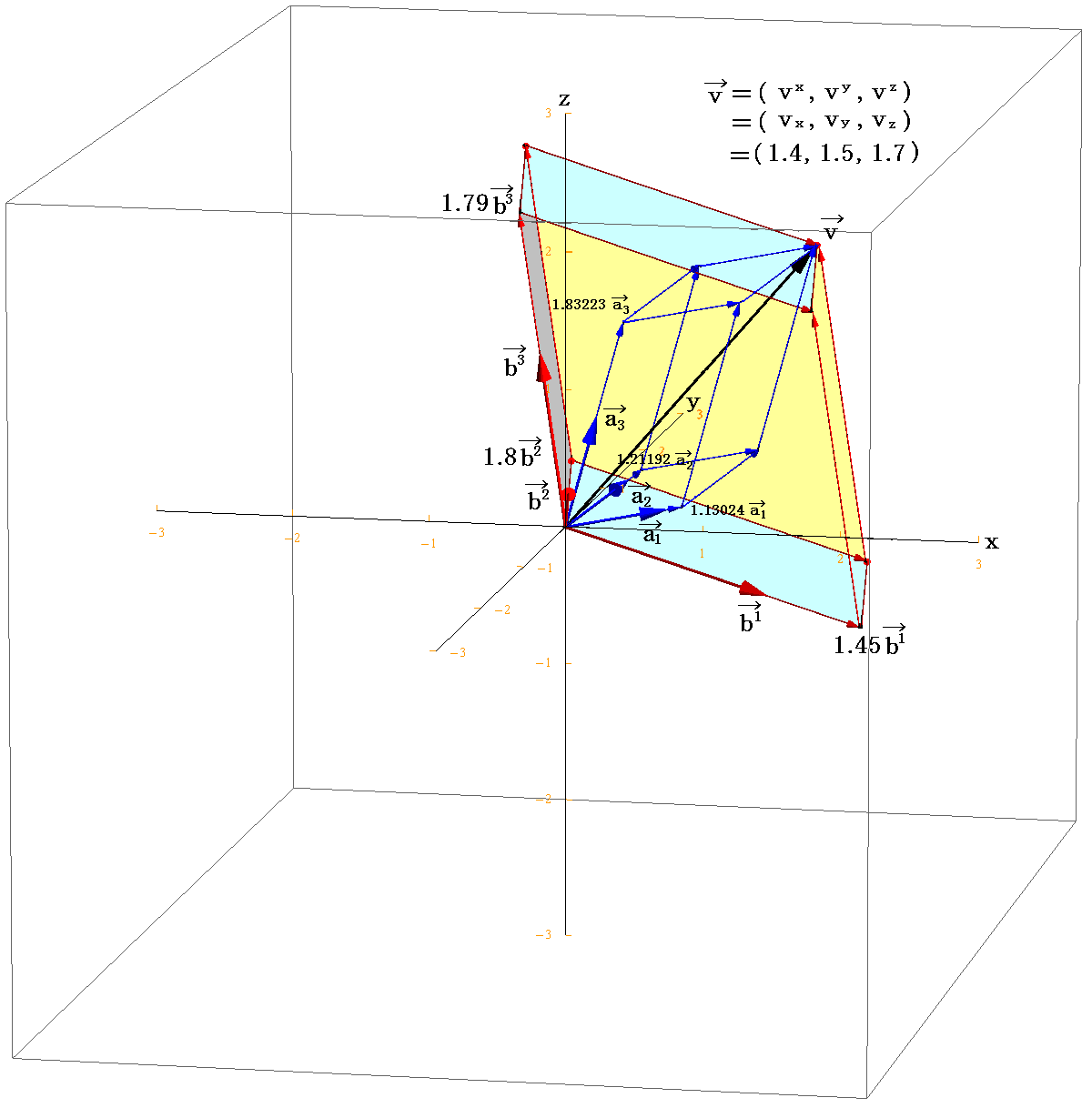
[例7]
2.(3)[例3]の平行六面体の体積
を計算してみる。
まず、3つの 基底ベクトル a1,a2,a3 の張る平行六面体(単位格子セル)の体積Vは

となる。
そのため、図の[着色した平行六面体の体積]=V×v1×v2×v3 (基底ベクトルが作る平行6面体体積Vをそれぞれの稜方向にvi倍したもの)は
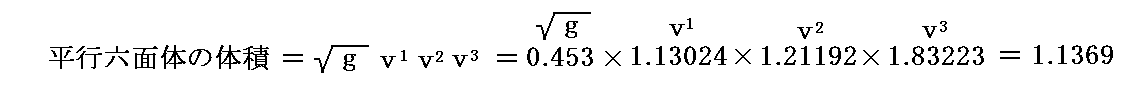
となる。たしかにその様な体積であることが図から読み取れる。
**************************************************************************
以上述べたことは、双対基底ベクトルが作る単位格子セルの体積と基本計量反変テンソル gij についても同様に成り立ちます。同様の手順ですが、その事を確認しておきましょう。
2.(3)[例3]の双対基底ベクトルが作る単位格子セル平行六面体の体積
を計算してみます。
まず、3つの 双対基底ベクトル a1,a2,a3 の張る平行六面体(単位格子セル)の体積 は
は
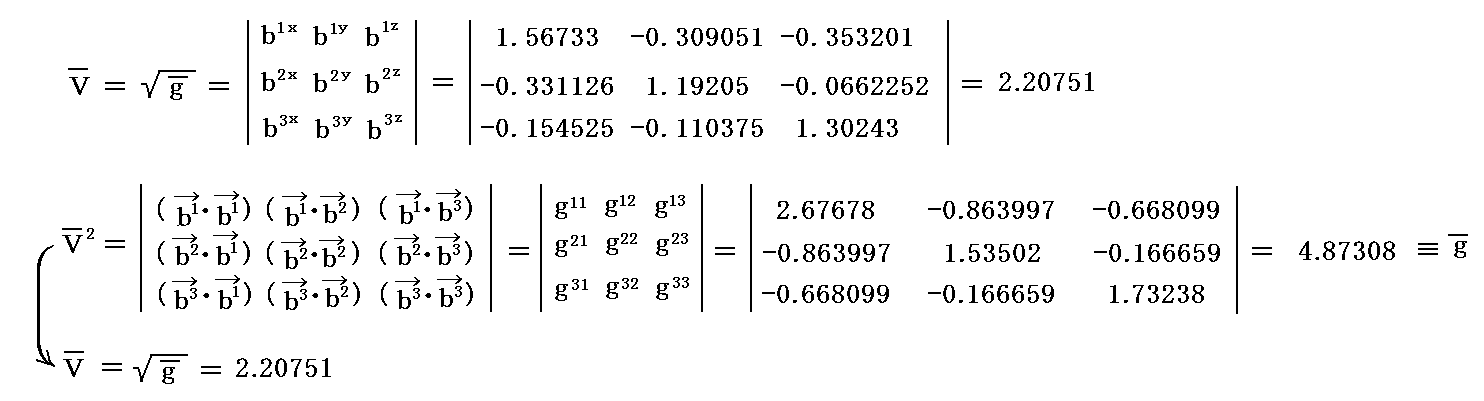
となる。ただし、双対基底ベクトルに関係した量である事をVやgの上付きバーで示している。
そのため、図の[着色した平行六面体の体積]= ×v1×v2×v3 (双対基底ベクトルが作る平行6面体体積積
×v1×v2×v3 (双対基底ベクトルが作る平行6面体体積積 をそれぞれの稜方向にvi倍したもの)は
をそれぞれの稜方向にvi倍したもの)は

となる。たしかにその様な体積であることが図から読み取れる。
**************************************************************************
このとき、
あるいは
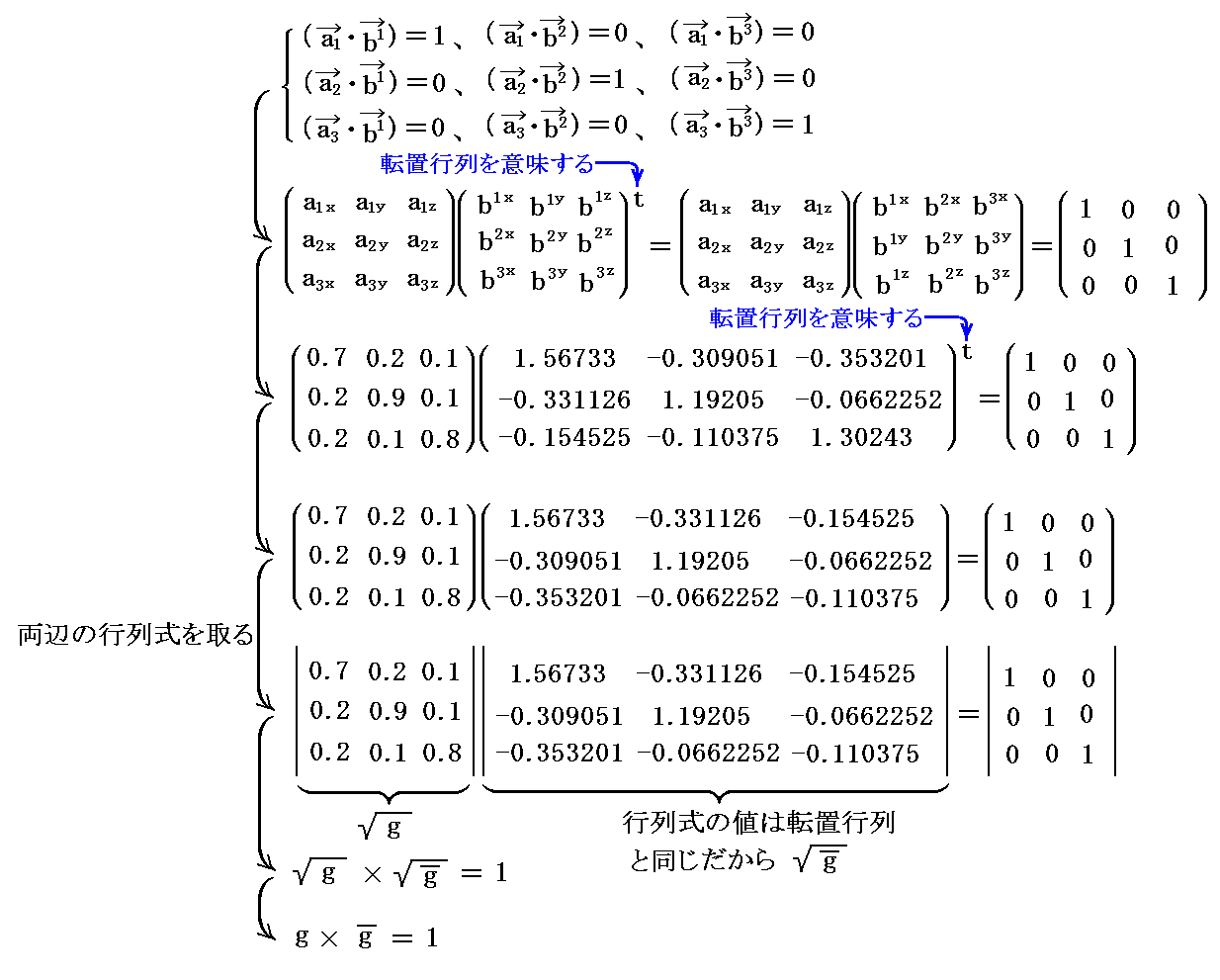
だから
このことについては4.(6)5.[補足説明1]の図を参照して下さい。
[補足説明1]
本章の話は、別稿「2.曲面論」(2)3.[補足説明2]や別稿「3.曲面上の幾何学」(2)2.[補足説明3]で説明した“2次元リーマン空間”(3次元ユークリッド空間中の曲面)での議論を、“3次元リーマン空間”に拡張したものにすぎないのですが、3次元に拡張することで“基本計量テンソル”の意味がより明確になったと思います。
また、3次元リーマン空間の各点に於ける接ユークリッド空間が、2次元リーマン空間(曲面)の各点に於ける接平面を拡張したものであると言った意味が明確なったと思います。
これらのことを踏まえて別稿「4.リーマン幾何学」(2)の“n次元リーマン空間”の議論をお読み下さい。
[補足説明2]
ここまでの説明について、Pauli著「相対性理論」の §9 と §10 の説明は秀逸ですので合わせてご覧下さい。
多くの教科書では代数的説明で済ましていますが、ここで述べた幾何学的説明と内容的には全く等価である事がPauli文献をご覧になれば納得して頂けると思います。
3.基底ベクトルの変換とベクトル成分・テンソル成分の座標変換
[補足説明1]
一般相対性理論では3階テンソルや4階テンソルの座標変換も取り扱うことになります。その場合、座標変換の行列表示が使えませんので、本来は行列表示形式の使用を避けるべきかも知れません。
しかし、1階テンソル(ベクトル)と2階テンソルの座標変換に関しては行列表示は便利で解りやすい表示形式です。そのため、ここでは行列表示も並記しています。ただし、やがて使えなくなる表示形式である事を心に留めておいて下さい。3.(1)[補足説明2]参照
さらに、補足しますと、一般相対性理論における座標変換とは、2つの異なる世界点の間の変換を含んだものではありません。同一の世界点を座標原点とする座標軸の回転の様なものです。これはアインシュタインがミンコフスキーの業績を高く評価した一つの理由です。別稿で説明したように、ミンコフスキーは、“ローレンツ変換が四次元空間における回転にほかならないことをもしめした。”のですが、自然法則が共変でなければならない座標変換とは、その原点を空間的にずらす事も含めた座標変換では無いと言うことです。座標の原点を固定して、時間座標軸と空間座標軸の関係(つまり互いの座標軸の交叉の仕方、斜交座標の斜交の仕方を変えると言うことです。この座標変換に対して共変でなければならないと言うことです。もちろん、その様な座標変換に限っても、その中には異なった速度(加速度)で動いている座標系への座標変換を含んでいます。また、空間座標についてもその斜交角が時間的に任意の変化をする斜交座標系への座標変換を含んでいます。
これは一般相対性理論に向かうとき、最大に必要な制約です。実際一般相対性理論の世界では4次元空間の座標原点(世界点)をずらすことも含めた座標変換などは意味が無いのですから。つまり自然法則が共変でなければならない座標変換とは4次元空間における座標原点(世界点)を固定した回転であるようなもので無ければ成りません。もちろん一般相対性理論の世界では単なる回転ではありませんが、いずれにしてもミンコフスキーの4次元世界の座標回転をさらに一般化したようなものです。
座標変換をこのように捉えることは、4次元世界の世界距離(一般相対性理論の世界では微小である必要がありますが)が座標変換に対して不変であると言うことを理解する上でも有益です。
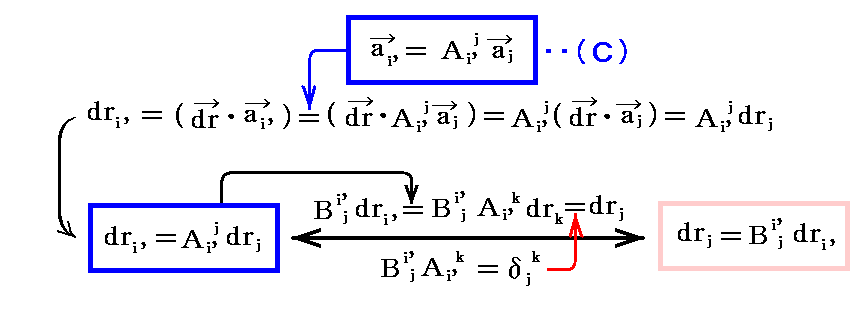
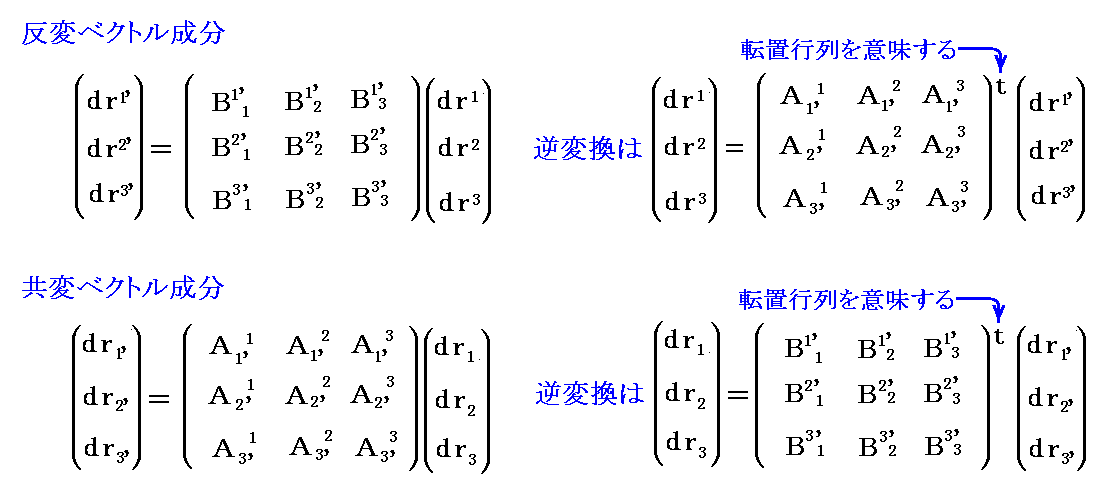
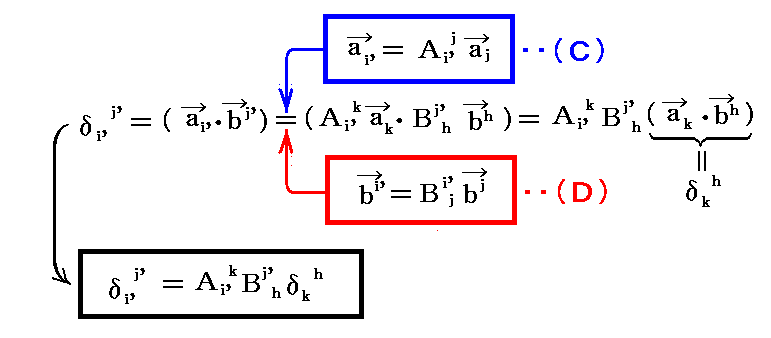
(1)基底ベクトルと双対基底ベクトルの変換
基底ベクトル a1、a2、a3 の変換を考える。今はリーマン空間の小領域を表す3次元ユークリッド空間を考えているから、その中の斜交座標の基底ベクトルの変換は一般的に次の線形変換で実行できる。変換後の新基底ベクトル は座標指数に ’ を付けて a1’、a2’、a3’ の様に表すことにする。
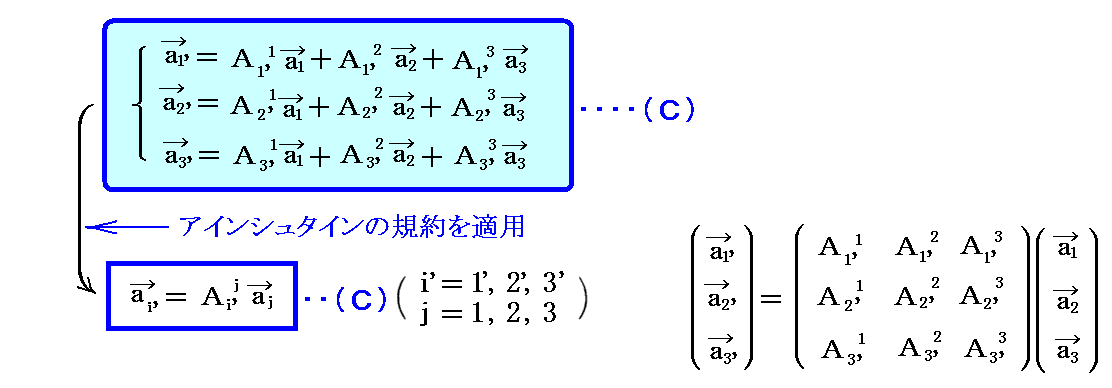
この変換式の意味は明らかであろう。新基底ベクトル ai’ が旧基底ベクトル a1、a2、a3 の線形結合 Ai'jaj で表される事を示している。これは a1’、a2’、a3’ を新基底ベクトルとする新たな座標系を定義したことを意味する。
この新たな座標系で今まで議論してきたベクトル v を表すと
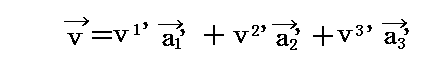
となる。
このとき、新基底ベクトル a1’、a2’、a3’ に対応する新双対基底ベクトルも在るわけで、それを b1’、b2’、b3’ としよう。そして、その新双対基底ベクトル b1’、b2’、b3’が、旧基底ベクトル a1、a2、a3 に対する旧双対基底ベクトル b1、b2、b3 から

で変換されると仮定して、その変換行列 Bi'j の性質を調べてみる。
変換後の基底ベクトル a1’、a2’、a3’ と双対基底ベクトル b1’、b2’、b3’ の間にも (ai'・bj')=δi'j' が成り立たねばならないとして、変換行列 Bi'j を計算してみる。すなわち
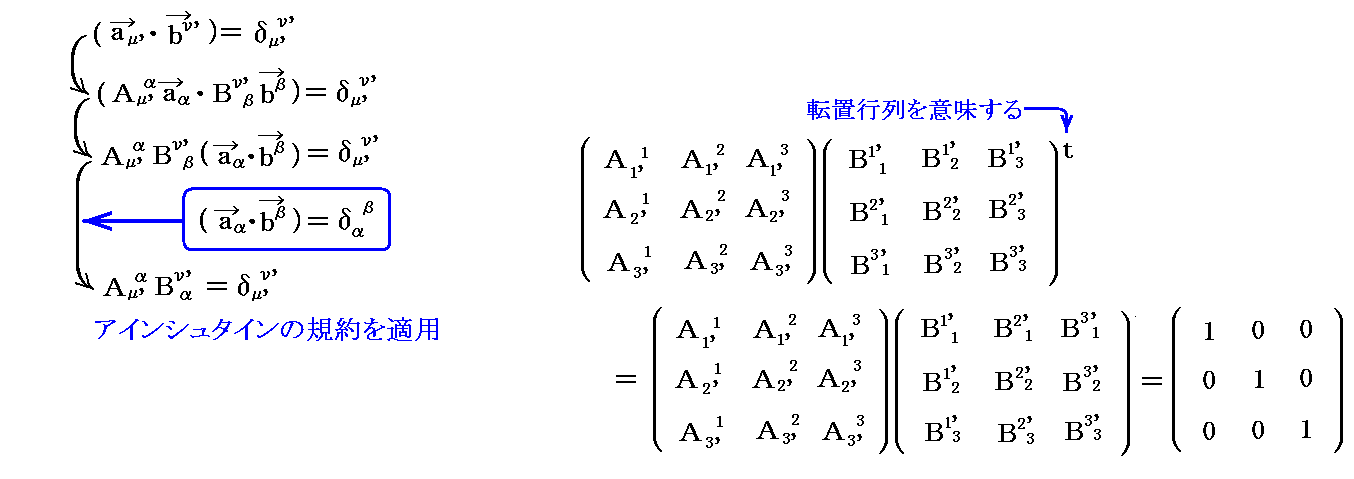
となる。
これは変換行列成分 Bi'j が変換行列成分 Ai'j の逆行列成分でなければならない事を示している。
もう少し正確に表現すると 《行列〔Ai'j〕》 と 《行列〔Bi'j〕の“転置行列”》 の積が 《単位行列〔E〕》 に成らねばならないと言うことです。
もちろんこのとき、上記のベクトル v の新双対基底ベクトル系での表現は
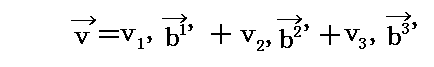
となる。
基底ベクトルの座標変換の具体的な例については4.(6)1.をご覧下さい。
[補足説明1]
Ai'j と Bi'j において添字 i と j の位置を上下のみならず左右の位置もずらしているのは、行列表示を意識してのことです。
もし Ai'j を Bi'j と同じように Ai'j と記すと、最初に設定した基底ベクトル a1、a2、a3 の座標変換係数の定義式は
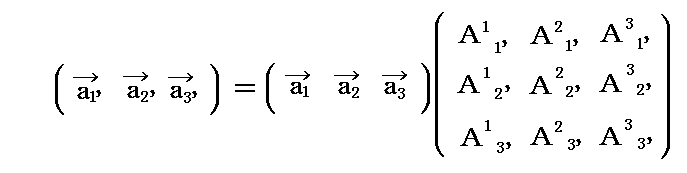
と記すことになります。
このように記すと、 Ai'j と Bi'j の関係は、行列表示で

となり、一方の行列を転置行列にする必要は無くなる。ただし、そうすると行列〔Aij'〕と行列〔Bi'j〕の積の成分計算で和をとる添字が上付き添字i と上付き添字i’の上付き添字同士に成ってしまい、次の[補足説明2]で説明する“アインシュタインの規約”が使えなくなりますので、この表示が良いかどうかは判断に迷うところです。
もちろん、このように定義すると、以後の説明の行列表示形式も少し変わってきます。どのように変わるかは、それぞれの項目で検討されればすぐに解ります。石井俊全著「一歩一歩数式で理解する一般相対性理論」第3章§3はこちらの形式で展開されていますので、参照されて下さい。
[補足説明2]
最初に注意したように、行列表示形式は高階テンソルの議論が必要になったときに破綻します。だから最初から行列表示形式を用いない方が良いのかも知れません。今後一切行列表示形式を用いないのなら、添字の左右の位置は関係なくなります。上下の位置のみが重要になり、二つのテンソルの積(縮約演算)は、必ず上と下の添字の総和を取ることさえ注意すれば良い。
アインシュタインはそのことに、早くから気付き、テンソル成分の反変成分、共変成分の本質を理解します。そうして上下の添字について和を取る縮約演算に関して、“アインシュタインの規約”を思いつきます。
アインシュタインはこのアイディアについて「私は数学における偉大な発見をなしとげた。私は、2度表れる添字について和をとらねばならないときはいつも、和の記号を削除した・・・」と冗談めかして言っていますが、“斜交座標基底”を取り扱わねばならず、反変成分と共変成分が必然的に現れる《リーマン幾何学》では、このことは本質的に重要な事だった訳です。
これらのことは、4.(3)で説明する《第5に重要なこと》に深く関係しています。
[補足説明3]
4.(1)〜(3)で説明しますが、“リーマン空間”では“斜交曲線座標”を用いざるを得なくなります。そのため基底ベクトル系に加えて双対基底ベクトル系と言うものを導入する必要があり、座標変換がとても錯綜したものになります。そのとき、ここの(C)式が表す [基底ベクトルを別な基底ベクトルへ変換] する事と、2.(1)で説明した式が表す [基底ベクトルと双対基底ベクトルの間の変換] を混同しないでください。両者は全く別の事です。
[基底ベクトルの変換]とは、別稿「微分幾何学」3.(1)2.[補足説明1]で注意した意味での変換です。その様に[基底ベクトルを変換]したら、その双対基底ベクトルは2.(1)の[基底ベクトルと双対基底ベクトル間の変換則]に従って従属的・確定的に新しい双対基底ベクトルに変換されます。だから今後は[基底ベクトルと双対基底ベクトルの間の変換]のことはあまり意識しないで下さい。
この章では、(C)式によって[基底ベクトルを変換]したら、スカラー場やベクトル場、テンソル場の成分がどのように変換されるかを考えています。“場”という言い方をしたのは、変換対象の基底ベクトル自体が場所と共に変化しており、その変換係数も場所と共に変化しているからです。そのため[基底ベクトルの変換]に伴って変換されるスカラー場・ベクトル場・テンソル場の成分も場所ごとに異なっており、その変換される様子も場所ごとに異なる。
[基底ベクトルの変換]と[スカラー場、ベクトル場、テンソル場の成分の変換]との関係は文献8.p250〜253の対応図で示されている関係になります。このとき、変換対象について文献8.p257の注意も重要です。
(2)微小変位ベクトルdrの座標変換
リーマン空間では有限の大きさの位置ベクトルは考えることはできない。なぜなら、この稿で説明してきた斜交座標を構成する基底ベクトルはリーマン空間の場所ごとで変化していくものだからです。その基底ベクトルを定義している3次元ユークリッド空間もリーマン空間の各場所の近傍領域でのみその場所のリーマン空間を近似的に表すものでしかないからです。これは、リーマン空間を議論するときいつも最初に注意される事です。
上記の様に位置ベクトルとしては微小なものしか考えることができませんしリーマン空間の微小領域に限られますが、その位置を定めるものであることは確かです。つまり空間の中の位置座標を示すものです。この“微小変位ベクトル” dr もリーマン空間(近似ユークリッド空間)でのベクトルですからその反変成分や共変成分と基底ベクトル、双対基底ベクトルとの関係は2.(3)で説明した内容になります。
微小変位ベクトルdrの“反変成分”は

となります[2.(3)の(A)式参照]。
このとき、双対基底ベクトルの変換式3.(1)(D)式を適用すると

となります。つまり“反変成分”は双対基底ベクトルと同じ変換係数 Bi'j によって変換される。
微小変位ベクトルdrの“共変成分”は
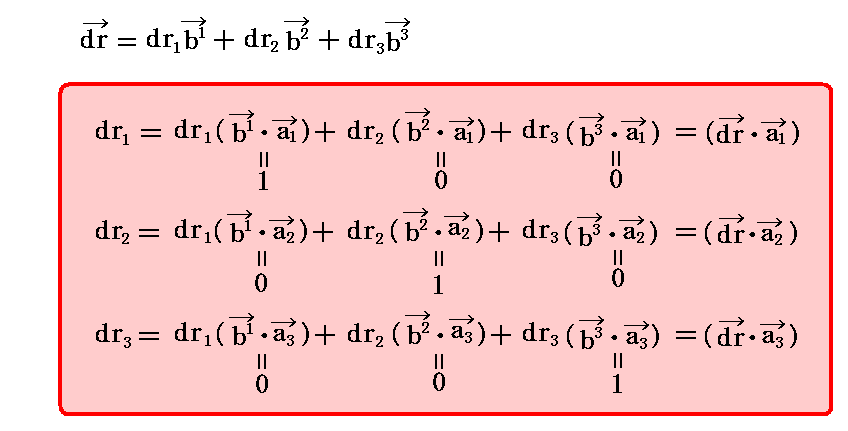
となります[2.(3)の(B)式参照]。
このとき基底ベクトルの変換式3.(1)(C)式を適用すると
となります。つまり“共変成分”は基底ベクトルと同じ変換係数 Ai'j によって変換される。
(3)任意ベクトル成分の座標変換
ここではリーマン空間のなかの各点で定義された任意のベクトル場を考える。例えば速度ベクトル場、加速度ベクトル場、運動量ベクトル場、電流密度ベクトル場などが在ります。もちろん前節の微小変位ベクトルdrもその中に含まれます。
任意のベクトルvの“反変成分”と“共変成分”の座標変換則は前節の結論を用いれば直ちに求まる。
まず、反変成分は
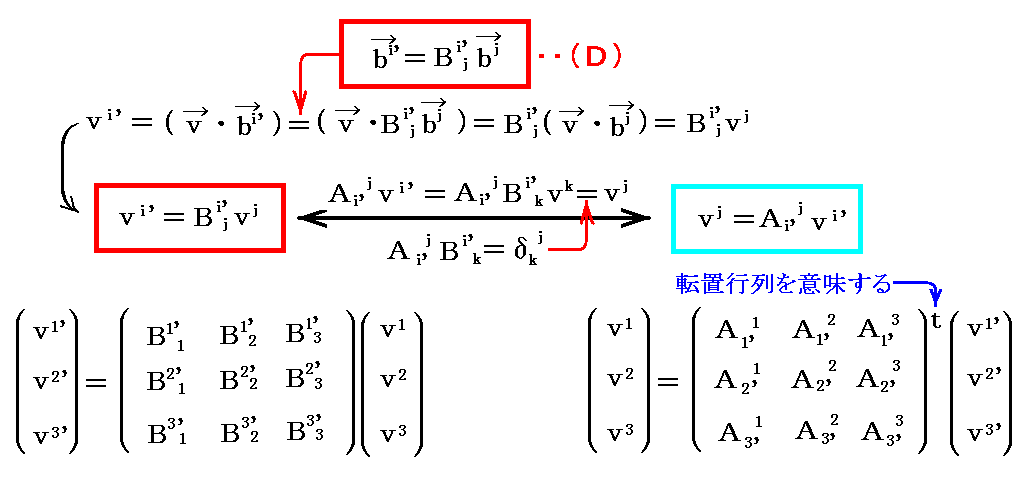
となる。つまり双対基底ベクトルと同じ変換を受ける。
すなわちベクトルの反変成分は座標位置を表す微小変位ベクトルdrの反変成分と同じ変換法則によって座標変換される。 これがテンソル代数学に於いて、微小変位ベクトルdri と同じ変換法則によって座標変換されるベクトルを反変ベクトル vi と言って指数添字を上げて表示する理由です。
同様に、共変成分は
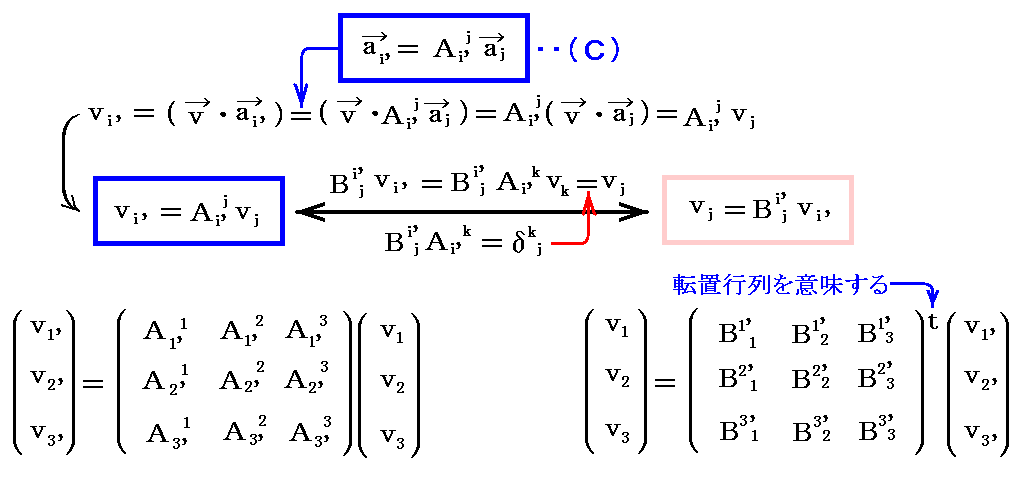
となり、基底ベクトルと同じ変換を受ける事が解る。
すなわちベクトルの共変成分は座標位置を表す微小変位ベクトルdrの共変成分と同じ変換法則によって座標変換される。これがテンソル代数学に於いて、微小変位ベクトルdri と同じ変換法則によって座標変換されるベクトルを共変ベクトル vi と言って指数添字を下げて表示する理由です。
ところで、前節3.(2)で見たように、微小変位共変ベクトルdri の変換行列は微小変位反変ベクトルdri の変換行列の逆行列でしたから、微小変位反変ベクトルdri の変換行列の“逆行列”で変換されるベクトルの事を“共変ベクトル”と言っても良いわけです。
ベクトルの座標変換の具体的な例については4.(6)2.をご覧下さい。
(4)基本計量テンソルの座標変換
テンソル成分の座標変換の例として、2.(4)で導入した基本計量テンソル gij の座標変換法則を求めてみる。
定義より、“アインシュタインの規約”を適用すると
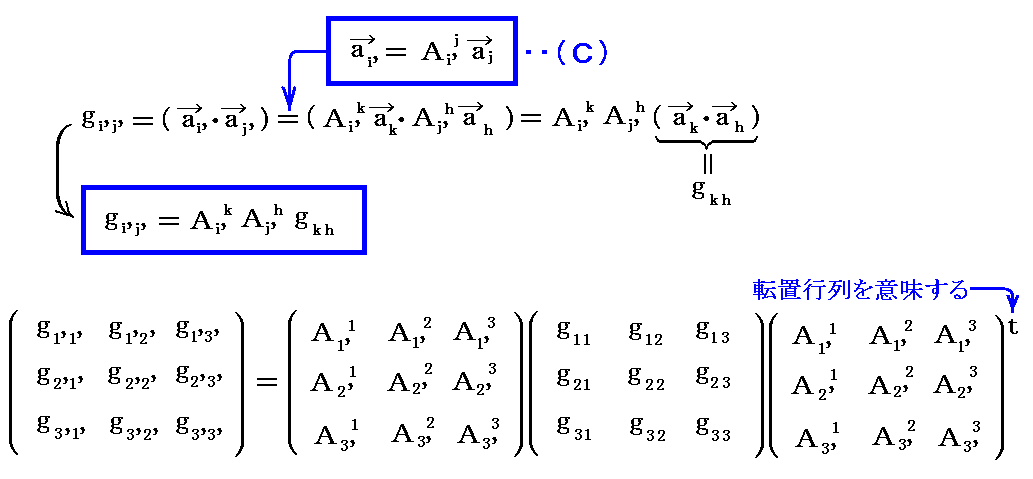
が得られる。
これは基本計量テンソル gij が2階共変テンソルで在ることを示している。
同様に基本計量テンソル gij の座標変換則を求める。
定義より、“アインシュタインの規約”を適用すると
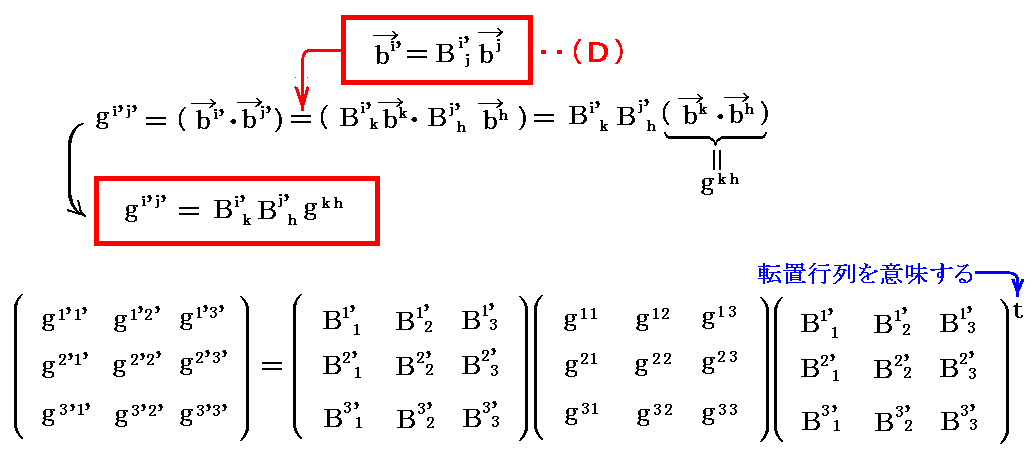
が得られる。
これは基本計量テンソル gij が2階反変テンソルであることを示している。
:基本計量テンソルの座標変換の具体的な例については4.(6)3.をご覧下さい。
[補足説明1]
基本計量テンソル gij について成り立つ上記座標変換則がリーマン空間の“線素ds2の大きさが座標変換に対して不変”であることを保証している。
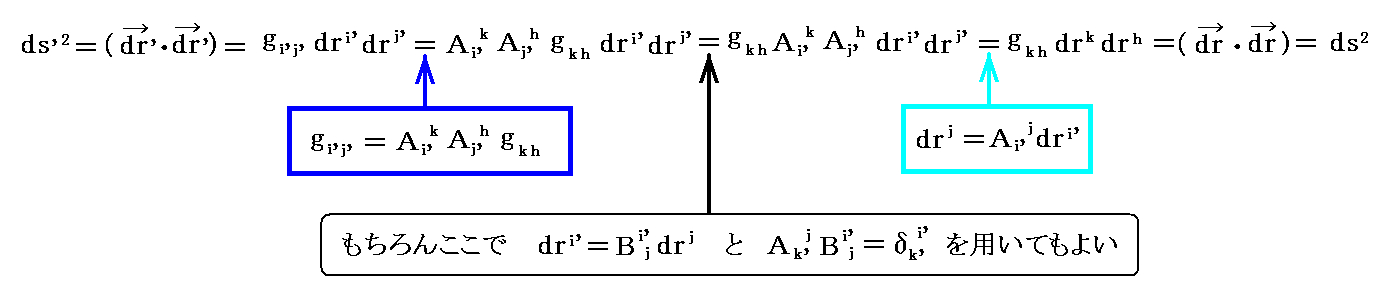
このことに関しては別稿「微分幾何学」3.(2)2.[補足説明3]の文末の説明を参照されたし。そこではここと逆に、ds2 の座標変換不変性から gij が2階共変テンソルである事を導いている。「微分幾何学」3.(1)2.[問題]も参照されたし。
[補足説明2]
3次元の場合に、基本計量テンソルによって反変成分と共変成分が互いに変換されることを2.(4)で説明した。ここで説明した基本計量テンソルの座標変換則を用いても、そのことが確認できる。
まず、基本計量共変テンソル gij を反変ベクトル vj に乗じて指数jに関して総和をとり縮約したものの座標変換則を求めると
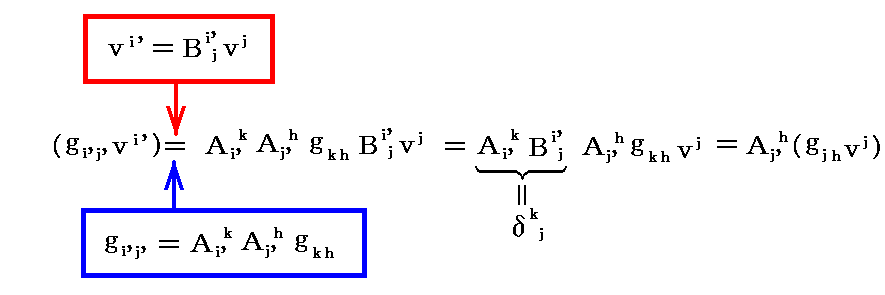
となる。つまり gijvj は“基底ベクトル”と同じ変換係数で変換されることが解る。つまり共変ベクトルとなっている。それを vj と書いているだけです。
同様に、基本計量反変テンソル gij を共変ベクトル vj に乗じて指数jに関して総和をとり縮約したものの座標変換則を求めると
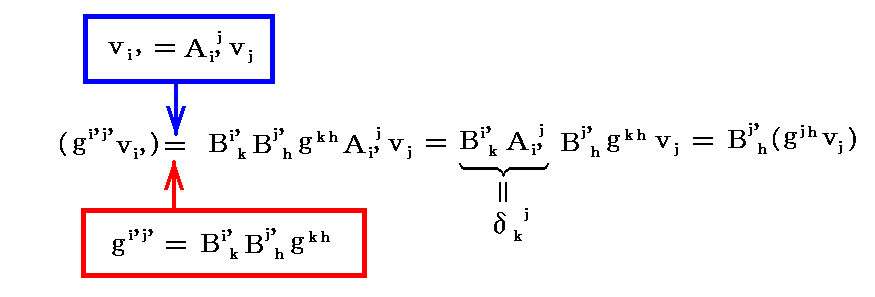
となる。つまり gijvj は“双対基底ベクトル”と同じ変換係数で変換されることが解る。つまり反変ベクトルとなっている。それを vj と書いているだけです。
ところで、 反変ベクトル vi を基本計量共変テンソル gij で共変ベクトルに変換したものをもう一度基本計量反変テンソル gij で反変ベクトルに変換すると
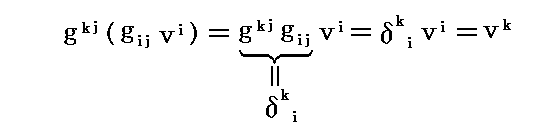
となる。つまり元に帰ります。
同様に、 共変ベクトル vi を基本計量反変テンソル gij で反変ベクトルに変換したものをもう一度基本計量共変テンソル gij で共変ベクトルに変換すると
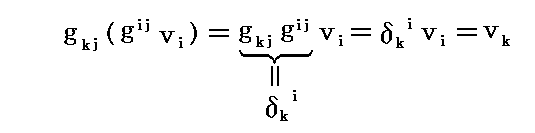
となる。つまり元に帰ります。
すなわち、もともと同じベクトル v を“基底ベクトル系”で成分表示したものを反変ベクトル vi といい、“双対基底ベクトル系”で成分表示したものを共変ベクトル vi と言うだけです。
[補足説明3]
ここで重要な補足をします。
いままで、リーマン空間(一般相対性理論の時空もその一例)の中に引かれた座標系の話をしてきました。そしてこの章で説明してきた座標の変換とは、そのリーマン空間の中に引かれた座標線(基底ベクトル・双対基底ベクトル)を別なものに引き換える事です。そうすれば、そのリーマン空間の座標の成分によって表示されていた諸々の量(ベクトル、テンソル)はその成分も変わってきます。その変わり方は座標系の変換(座標軸の引き方の変化)とリンクして変化するわけです。
これは別に難しい事を言っているわけではなくて、特殊相対性理論における擬ユークリッド空間(ミンコフスキー時空間)内の座標を別の座標に変換したとき(これがローレンツ変換に相当)に、その時空間内の任意の4元ベクトルやテンソルの成分が変換されたのと同じ事情です。
さらに、今まで説明してきた“基本計量テ共変ンソル”(基本計量反変テンソル)は、それぞれの座標系における成分表現量で表現されてきましたが、これはもともと座標が引かれているリーマン空間の“ひずみ・ゆがみ”の様子そのものを表現する量でした。
先ほど述べた座標系の変換とは、リーマン空間の“ひずみ・ゆがみ”は変わらない(幾何学は不変)ままで、その中に引く座標線を変えることですが、問題なのは、先ほど述べた時空間の“ひずみ・ゆがみ”を表す“基本計量テンソル”(双対基本計量テンソル)の成分値はその成分を測定する座標系に依存していますので、“ひずみ・ゆがみ”は変わらない(幾何学は不変な)のに座標線の引き方を変えると“基本計量共変テンソル”(双対基本計量反変テンソル)の成分値が変化してしまうことです。
さらに問題なのは、リーマン空間((一般相対性理論の時空)は、その内部の質量(エネルギー)の分布が変わればそれに応じて時空の“ひずみ・ゆがみ”の状態も変わります。そのため、“基本計量共変テンソル”(基本計量反変テンソル)の成分値も変わってしまう事です。
今から議論していく一般相対性理論とは、質量(エネルギー)の分布が時空間の“ひずみ・ゆがみ”とどの様に関係するかを示すものです。だから、“基本計量共変テンソル”(基本計量反変テンソル)の変化が、実際の時空間の“ひずみ・ゆがみ”(幾何学の変化)の変化によるのか、選んだ座標系の変化によるのかを見極めなければ成りません。ここに一般相対性理論を展開する上での最大の難しさがあります。
その事は後の議論で詳しく説明しますが、そのときにはどうぞここでの説明を思い出して下さい。
(5)単位テンソル(クロネッカーのδ)の座標変換
単位テンソル(クロネッカーのδ)は、2.(1)で説明した基底ベクトルと双対基底ベクトルの関係
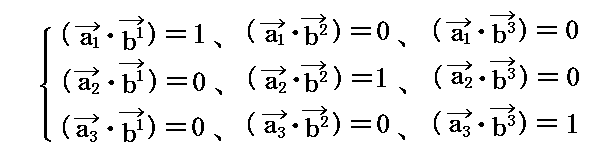
を用いると以下のように座標変換されることが解る。
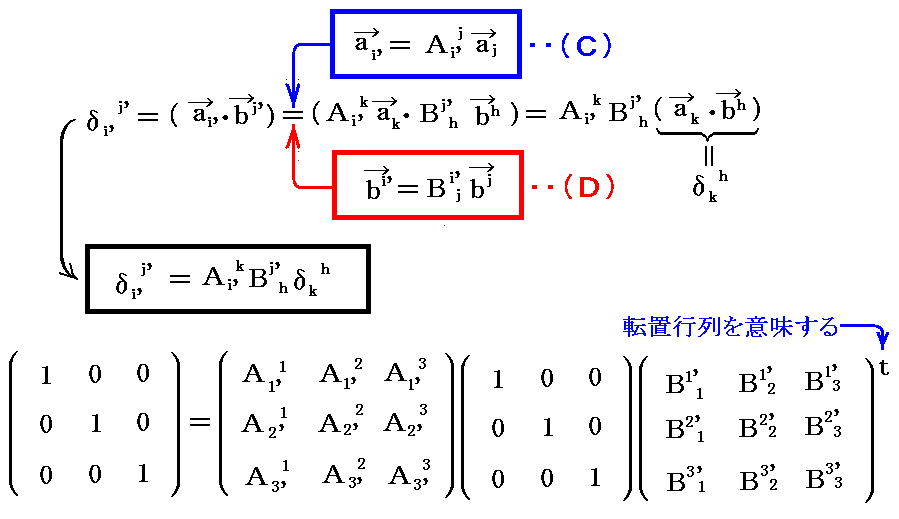
すなわち、“単位テンソル”(クロネッカーのδ)は“2階混合テンソル(1,1)テンソル”として座標変換されます。
このことは別稿「微分幾何学」3.(2)3.[テンソルの例1]も参照。
[補足説明1]
“基本計量テンソル”に 共変テンソル gij と 反変テンソル gij が有るのに、 混合テンソル gij が無いことを不思議に思われたかも知れません。それは、gij=(ai・bj)=δij となって単位テンソルになってしまうからです。単位テンソルが混合テンソルである理由もその当たりにあるのでしょう。
実際、別稿「微分幾何学」3.(2)[問題3]で説明したように、基本計量反変テンソル gij の定義の元になっている関係式は
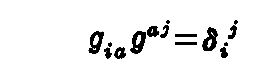
なのですが、これは基本計量共変テンソル gij と基本計量反変テンソル gji の積を添字aに関して縮約して基本計量混合テンソル gij を作る操作そのものです。
そのとき、上記の関係式は1.(3)3.[補足説明1]や、2.(1)で説明した双対基底ベクトルを導入しなければ成らなくなった理由と、導入に当たって設けた制約を具体化したものであることに注意して下さい。
つまり、上記関係式は“基底ベクトル”と“双対基底ベクトル”の互いの関係に付いての制約を表しておリーマン幾何学を展開する上で最も重要な要請であり仮定です。
(6)ベクトル内積の座標変換不変性の確認
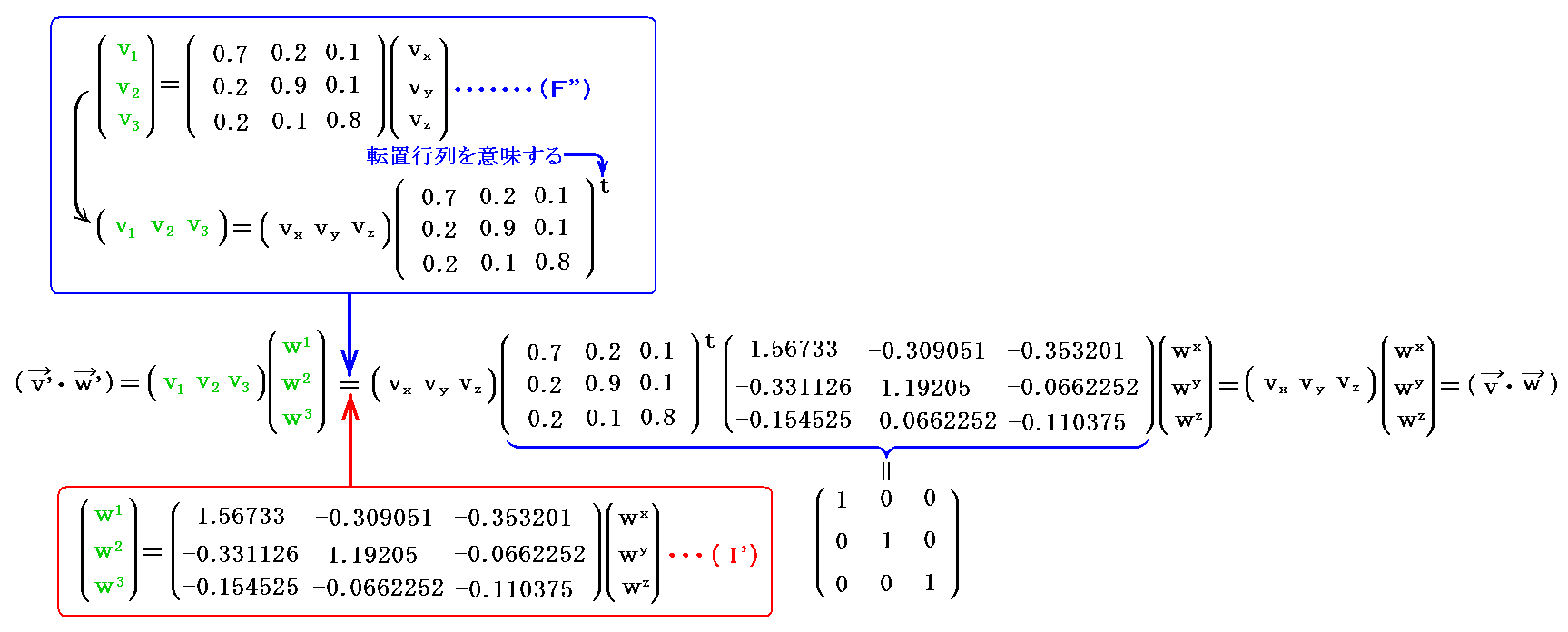
二つのベクトルの内積はスカラーだから座標変換に対して不変である事は明らかなのですが、そのことを、2.(5)で取り上げた二つのベクトル v と w の内積表現で確認しておきます。
今基底ベクトル系 a1、a2、a3 から 新基底ベクトルa1’、a2’、a3’ 系へ
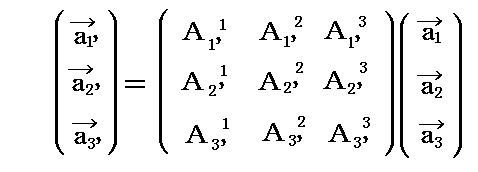
の座標変換で変換したとする。このとき、双対基底ベクトル b1、b2、b3 は新双対基底ベクトル b1’、b2’、b3’ へ

で変換されます。
また、新しい座標系でのベクトル v と w の成分を v=(v1’,v2’,v3’)=(v1’,v2’,v3’) と w=(w1’,w2’,w3’)=(w1’,w2’,w3’) とする。これらの反変成分、共変成分は、もちろん3.(3)で説明したベクトルの変換式に従って座標変換されます。
ベクトル v と w の内積が座標変換に対して不変である事は次のようにして確認できます。[拡大版]

他の内積表現式を用いても同様に証明できますので、どうぞご確認下さい。。
[補足説明1]
さらに補足すると、2.(5)[補足説明]で説明した“長さds”の2乗 ds2 は、微小位置ベクトル drの自分自身との内積ですから、座標変換に対して不変となることは明らかです。
このことは、

である事を意味します。これは簡単に
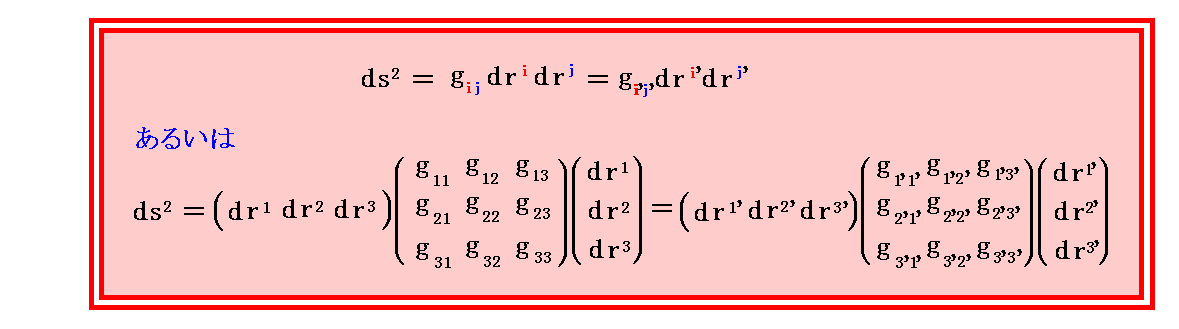
と記される場合が多い。これは一般相対性理論を論じるとき中心的な働きをする重要な式です。4.(6)5.[補足説明2]で、上式の意味を図の上で説明していますので、御覧下さい。
このとき、両座標系のベクトル成分は3.(3)で説明した座標変換式
で関係付けられています。
また、両座標系での基本計量テンソルの成分は3.(4)で説明した座標変換式

で関係づけられています。
[補足説明2]
ここでは3次元リーマン空間で説明していますが、一般相対性理論では4次元目が時間座標となった4次元リーマン時空となります。そのとき、3次元リーマン空間に於ける長さベクトルdr(ds)に相当するものが、4次元リーマン時空に於ける世界線素dsです。
そのとき4次元リーマン時空の特別な場合である“ミンコフスキー時空”では別稿「特殊ローレンツ変換から一般ローレンツ変換へ」3.(3)[補足説明1]で説明した様に
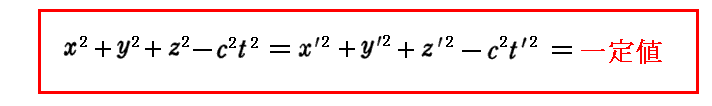
が成り立ちます。
このとき、上記の一定値=0の場合、すなわち

は“光速度不変の原理”の数式表現であり、特殊相対性理論に於ける“ローレンツ変換式”は、この“光速度不変の原理”から導かれたことを思い出して下さい(ただし、その証明のとき“相対性原理”を援用しています)。
つまり、“特殊相対性理論”とは上式がどの座標系に対しても不変的に成り立つ事を議論する不変式論に他なりません。そして、そのとき重要なのはミンコフスキーの4次元時空を表す“ミンコフスキー時空計量テンソル”
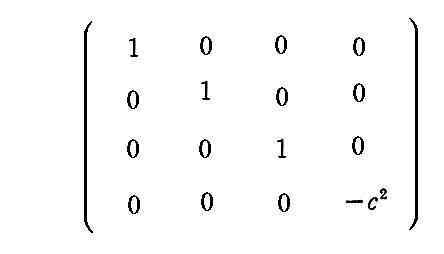
です。
それでは、もっと一般的な“4次元リーマン時空”に於ける世界線素dsはどのような式を満たすのでしょうか。
その最も簡単な例が、球対称の質量の周りのリーマン時空に対する不変式である

です(この式ついては別稿「Sommerfeld電磁気学§38」を御覧下さい)。
これは極座標を用いていますが、その計量テンソルは
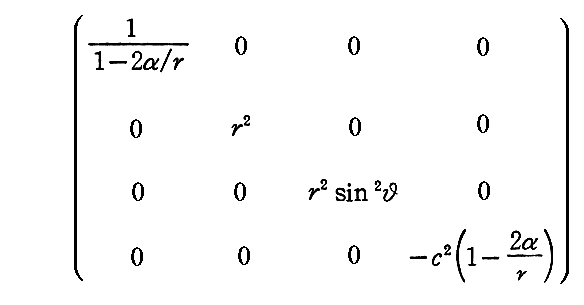
となります。この場合、計量テンソルの対角成分以外がすべて0になる特別な場合だから上記の様に簡単な形になった。
もっと一般的な時空間に対しての表現は先ほどの式を4次元時空化した
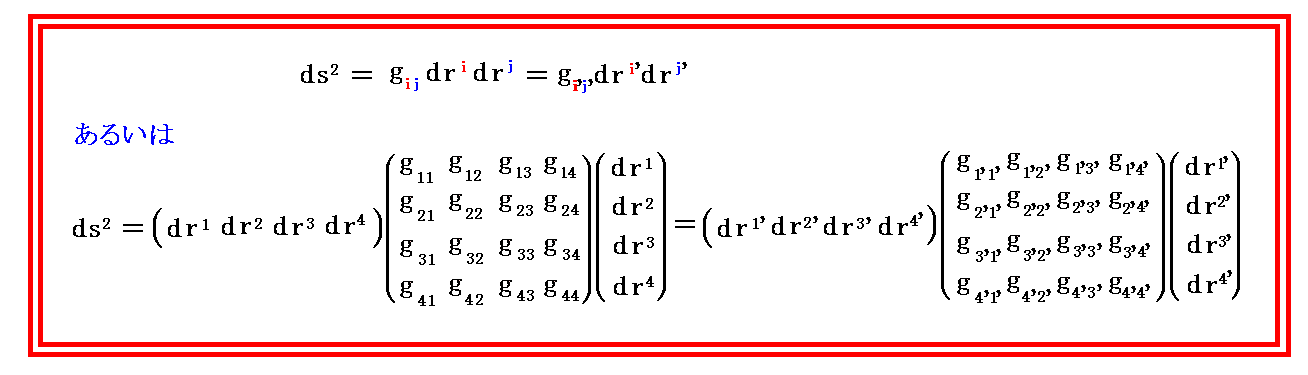
となります。“4次元リーマン時空計量テンソル”を仲介にしたこの式の不変式論であることが“一般相対性理論”の本質です。
(7)体積不変量
ユークリッド空間の直交座標系での体積素 dxdydz は、直交座標間での座標変換に対して不変量となりますが、リーマン空間で一般的な斜交座標において体積素 dv1dv2dv3 は座標変換不変量とは成りません。なぜなら“ヤコビの定理”によって、座標変換
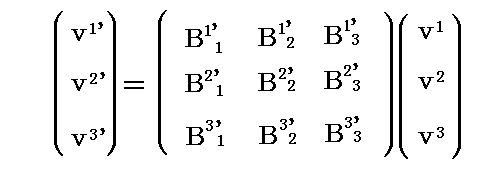
に対して体積素片 dv1dv2dv3 は
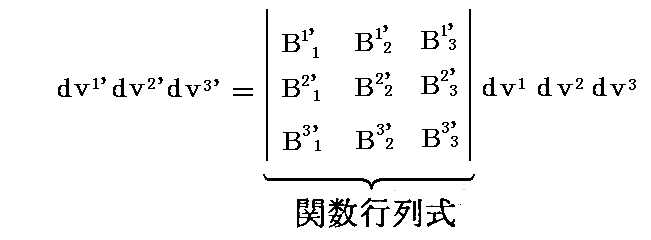
となるからです。
しかしながら、体積素片 dv1dv2dv3 が不変量となるようにこれを補正することができる。ただし、不変量になると言う意味を理解するのは極めて難しい。このことについては別稿「重積分の変数変換とヤコビアン(リーマン空間における多重積分)」を御覧下さい。
3.(4)の関係式
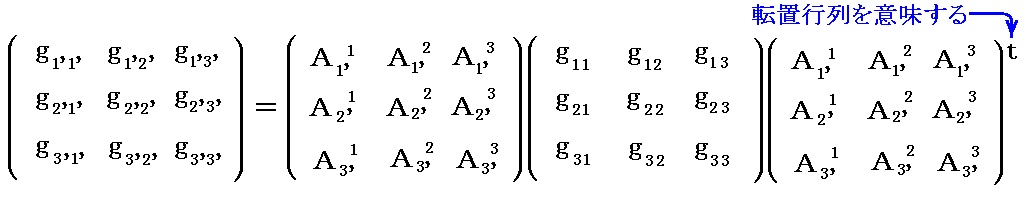
の行列式を作れば、行列式の掛け算の性質[定理3]と[定理13]を利用することによって
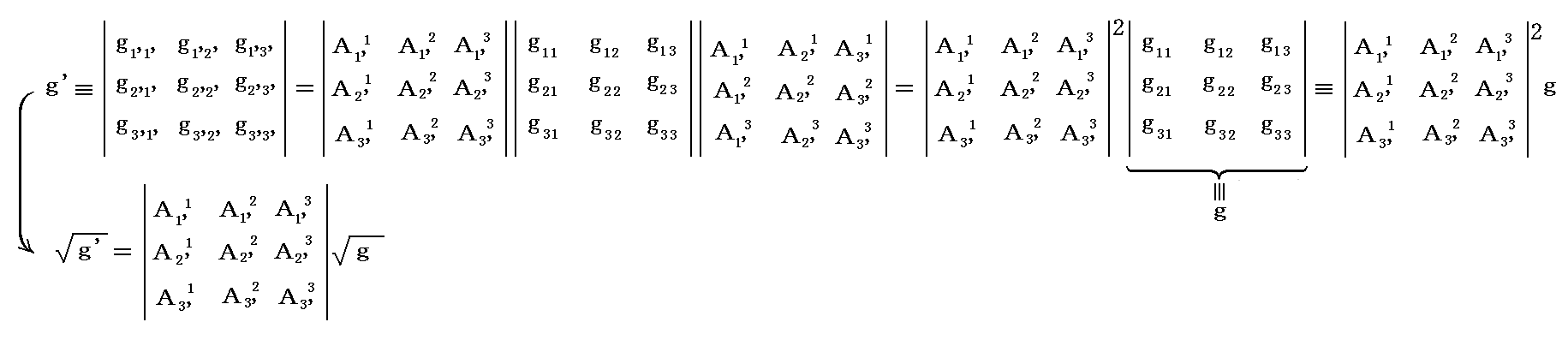
を得る。したがって、3.(5)の関係式は
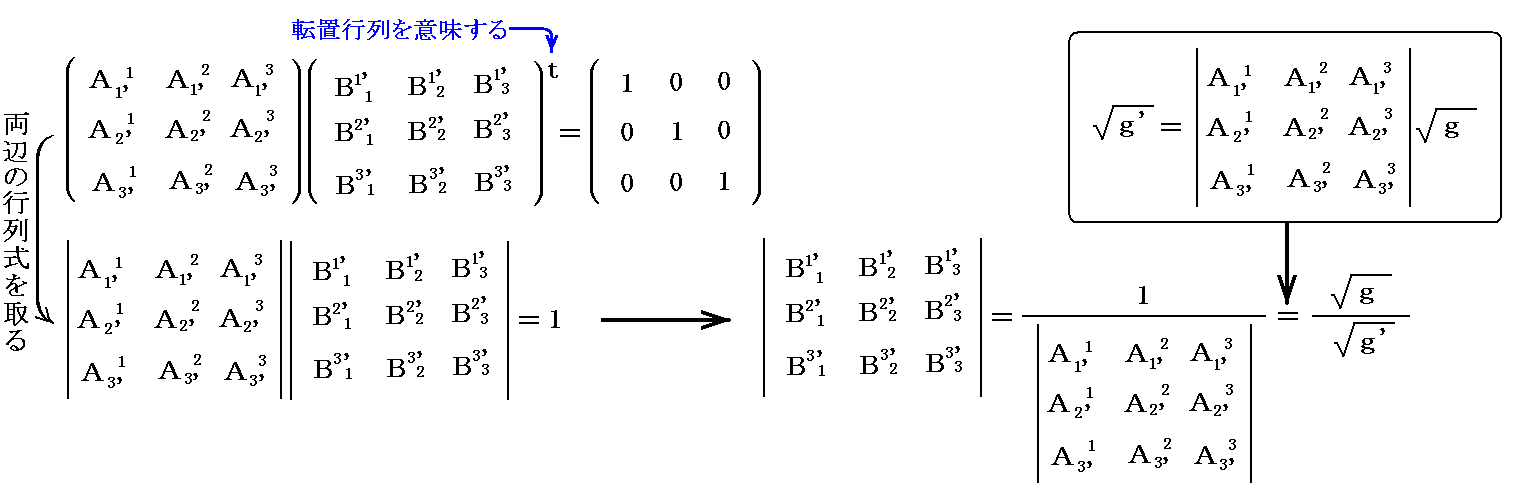
となるので
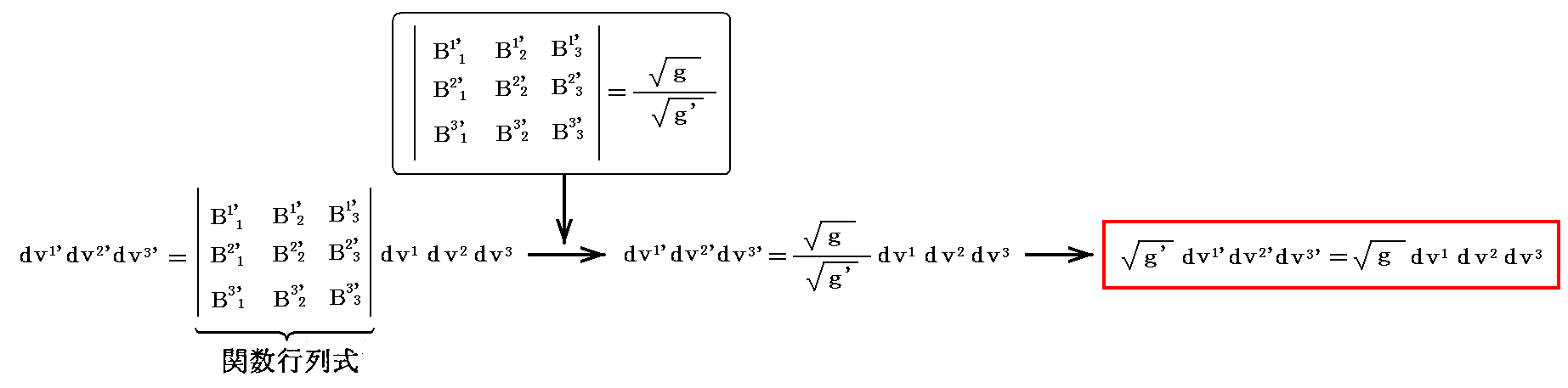
を得る。これは2.(7)での考察を鑑みると理にかなっている。このことについては別稿「微分幾何学(リーマン幾何学)」4.(2)[例題]も参照。
ここで、特に注意して欲しい事は上記の式は dv1’=1,dv2’=1,dv3’=1 とし、さらに dv1=1,dv2=1,dv3=1 と考えれば明らかな様に左辺の g’0.5dv1’dv2’dv3’と右辺の g0.5dv1dv2dv3が《等しいことを意味するのでは無く》て【積分体積素片】として左辺の g’0.5dv1’dv2’dv3’が右辺の g0.5dv1dv2dv3に《置き換えられるべき》だという対応関係を表しているにすぎないことです。
このことの意味を理解するのは極めて難しい。真に理解するためには、別稿「重積分の変数変換とヤコビアン(リーマン空間における多重積分)」4.を御覧ください。
dv1’dv2’dv3’ と dv1dv2dv3 の関係については4.(6)5.も御覧下さい。
[補足説明]
“ヤコビの定理”について補足する。座標変換式から
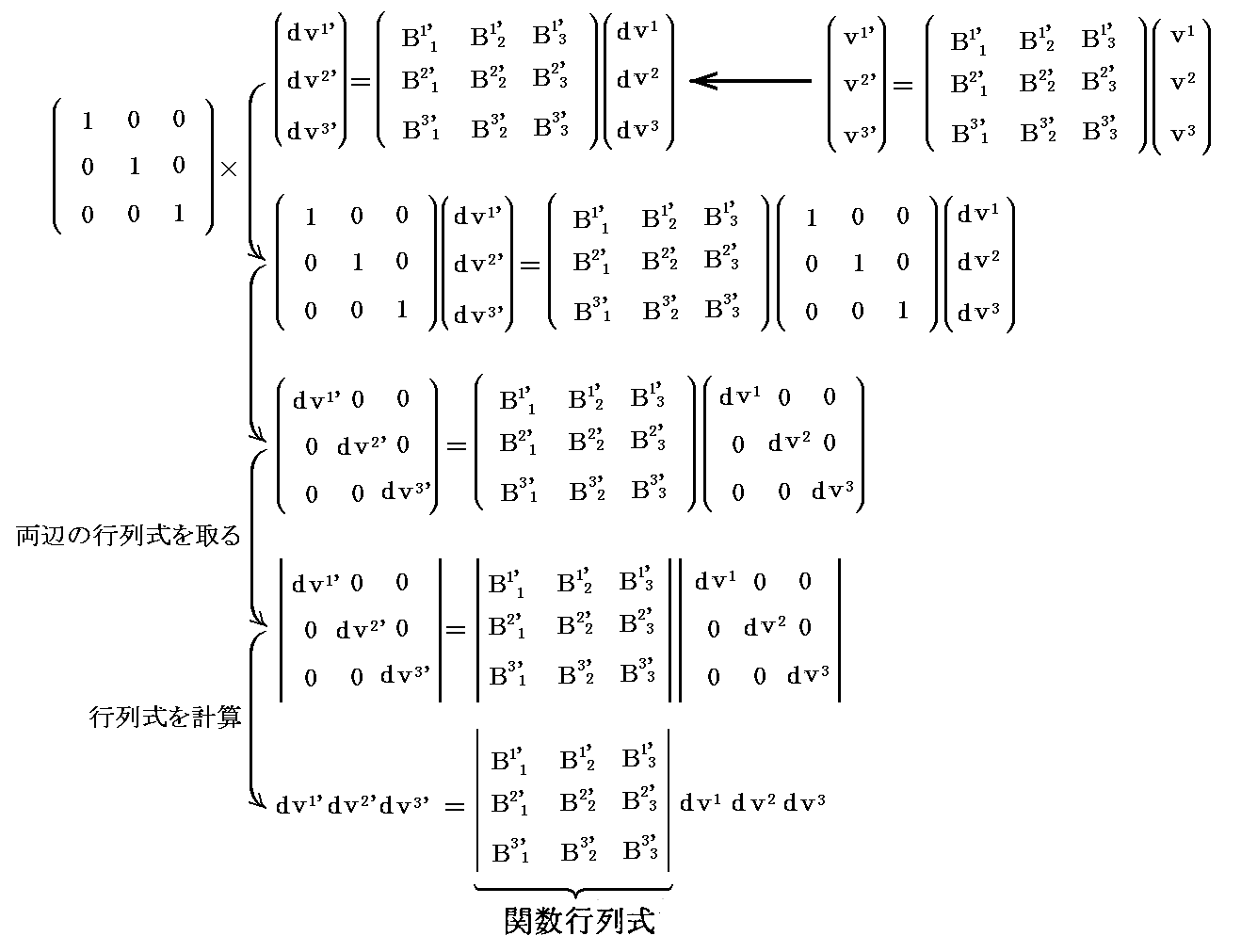
が得られる。
4.曲面人(2次元リーマン空間人)と3次元リーマン空間人
(1)アインシュタインの着想
別稿「双子のパラドックスと一般相対性理論(リンドラー座標)」5.(1)で説明したように、アインシュタインは、“等価原理”を発見した後、一般相対性理論を構築するには歪んだ時空を取り扱わねばならないことに気付きます。自伝ノートに記している様にアインシュタイン自身がそのことを理解するまでにかなりの紆余曲折が在ったのですが、最終的に、曲がり歪んだ時空の取り扱い法を見つけることが本質だと理解します。
そして、プラハ時代(1912年)に“ガウスの曲面論”がその手がかりを与えてくれることに気付きます。そのことについて1922年12月14日の京都公演で語っています。とても興味深い述懐なので以下に引用します。

アインシュタインが“ガウスの表面座標を本当に意味深いものの如くに自分に思い浮かべました。”と語っている内容を次節で説明します。
(2)ガウスの曲面論
アインシュタインが意味深いものと感じた事を理解するには、別稿 「微分幾何学2(曲面論)」 と 「微分幾何学3(曲面幾何学)」 の“中身の違い”を感じ取り、3.(2)2.[補足説明3]で説明した事柄を思い出す必要があります。
「微分幾何学2(曲面論)」では2次元ユークリッド空間のなかの曲面(2次元リーマン空間)を2.(2)3.の第1基本微分形式と2.(4)1.の第2基本微分形式の両方を用いて議論しました。ところが「微分幾何学3(曲面幾何学)」では曲面の上で観測・測定できる第1基本微分形式しか出てきません。「微分幾何学3(曲面幾何学)」では共変微分や平行移動などの新しい概念も出てきて混乱しますが、それらも含めて全てが曲面上の網目座標に関係する第1基本微分形式に関係した第1基本量 E,F,G(g11,g12=g21,g22) だけで論じられています。「微分幾何学2(曲面論)」に出てきた第2微分形式に関係した第2基本量 L,M,N(h11,h12=h21,h22)はどこにも表れません。
リーマン幾何学を理解する鍵は、そのように曲面上で定義された網目(平行四辺形)を記述する第1基本量 E,F,G(g11,g12=g21,g22) のみで論じられている事を忘れないことです。
そこで、“ガウスの曲面論”に帰るのですが、まず3次元空間中の2次元ユークリッド空間(いわゆる平面のこと)を考えます。それはゴムシートでできており、それに正方格子を単位とする網目が縦横に引かれているとします。
次にこれを3次元ユークリッド空間中の曲面(これが2次元リーマン空間です)にそのゴムシートを貼り付けます。もともと平面であったゴムシートを貼り付けるのですから、ある部分は伸ばしたり別の部分は縮めたりして貼り付けなければなりません。そうすると曲面に貼り付けられたゴムシートの網目はもはや正方格子状ではありませんが、やはり格子状(平行四辺形状)の網目を構成します。
この曲面上の網目格子については次のことが言えるでしょう。
- 曲面上の網目格子は元の平面だったときのゴムシート上の格子とは違って正方形ではありません。平行四辺形になります。そして格子の縦横の辺の長さも元のゴムシート上の格子辺長とは異なったものになります。その辺長も格子の2辺の交差角も変化しているでしょう。もちろんその変化の度合いは曲面上の位置を移動すれば場所ごとに異なるでしょう。
上記の様に曲面上の網目格子は変形しています。変形していますが、曲面の在る点の近傍に限れば、その網目格子は、曲面の各点に於ける“接平面”上に存在すると考えることができます。この接平面は平面ですから2次元ユークリッド空間です。つまり曲面上に住んでいる曲面人は、自分たちは2次元ユークリッド空間に住んでおり、自分たちが今いる点における網目状の格子は2次元ユークリッド空間(つまり平面)の上に描かれた平行四辺形だと認識していることになります。
曲面上の住人(曲面人)が曲面の別の場所に移動すると、そこに存在する網目格子はやはりその点での接平面(2次元ユークリッド空間)に描かれた平行四辺形だと感じるはずです。そのとき、新しい場所での接平面は平面(2次元ユークリッド空間)ではあるが最初の点における接平面の延長上に在るわけではありません。つまり最初の接平面と別の場所の接平面は“同一の平面ではありません”が、それぞれの場所場所では“2次元ユークリッド空間”であると考えても良いのです。そして前記の平行四辺形の格子は2次元ユークリッド空間(平面)の上に描かれているとして良い。ここはきわめて重要です。これが《第1に重要なこと》です。
- 以上の様にして、曲面人は曲面上を動き回って曲面の各点の近傍の2次元ユークリッド空間(接平面)上の網目格子の各辺の長さをユークリッド空間での物指しで測ることができます。そして各点に於ける格子辺が互いに交わる角度を2次元ユークリッド空間での分度器で測る事ができます。それらを使えば2.(6)[補足説明]で説明したように、2次元リーマン空間(曲面)の各点に於けるリーマン計量を知ることができます。
その様にして曲面人は彼が住んでいる曲面内に存在する全ての格子の辺の長さと互いの交わりの角度を測定することができます。そうすると曲面人は、その様にして互いに接続している格子の辺と交差角の情報を繋ぎ合わせてみることができます。それをした曲面人は、それは完全な平面の上に引かれた格子の辺と交差角の情報を繋ぎ合わせた場合と異なることに気付きます。つまり平面(2次元ユークリッド空間)の上に描かれていると思って測定していった格子の辺長と交差角(いわゆる“格子定数”)の各点における情報を繋ぎ合わせるだけで曲面人は自分達が曲がった曲面の上に住んでいるのだと知ることができるのです。
そのとき大事な事は、格子定数が場所とともにどの様に変化するかを読み取ることです。曲面の一箇所に於ける網目(平行四辺形状の格子)の情報が解っただけでは自分が曲面に住んでいるのか平面に住んでいるのか決して判定できません。格子定数(計量テンソル)の場所的な変化の情報を知らなければならないのです。ここが、《第2に重要なこと》です。
この情報こそ『微分幾何学』で習う“クリストッフェルの3添字記号”です。その情報はもちろん曲面の中に住んでいる曲面人でも曲面の中に引かれている格子の“格子定数(計量テンソル)”を測定し、それが場所と共に変化することから知ることができます(このことは4.(4)で説明する)。
- いままでの話は、曲面に貼り付ける前の平面状ゴムシートに引かれた網目は、縦横に直線的に引かれた正方格子であると仮定していました。それを曲面に貼り付けたためにもともと正方形の格子が平行四辺形に歪んでしまったのだと説明しました。しかし、曲面人に取って今自分が今測定している曲面上(正確に言うとその点の接平面上)の格子が貼り付ける前の2次元ゴムシート上では元々正方形状に描かれていたものであると知ることはできません。つまり曲面人に取って貼り付ける前のゴムシートが平坦な2次元ユークリッド空間であり、しかもその上の格子が正方形だったと言うことは決して知り得ないのです。
ならば、ここが大事なところですが、今まで論じてきた曲面上の網目格子は本来どの様に引かれていても良いのです。
このことは簡単な例を思い浮かべればすぐに理解できます。今曲面の例として地球表面を考えましょう。
最初は地理学で習う普通の経線と緯線がその表面上に引かれているとします。そしてそれぞれの経線と緯線の交点に於ける接平面上に、その近傍の経線・緯線で切り取られた部分の地図(5万分の1としましょう)を作ります。それらの地図の端を境界経線と境界緯線に沿って正確に切り取り、それらの地図の端を隙間が生じないようにピッタリと貼り合わせて行きます。そうすると張り合わされた地図の全体は一つの球面を構成するはずです。つまり貼り合わせる5万分の1の地図のそれぞれの辺長と辺の交差角の微妙な変化の中に地球表面が球面であることの情報が含まれている。
次に、日本の東京を北極とし、地球の裏側のアルゼンチンのリオデジャネイロを南極と考えて経線・緯線を引きます。これは前述の経線・緯線の網目とは全く異なりますが、この新たな経線・緯線で地球表面を分割して、その各点に於ける地図(5万分の1)を作ります。この地図の全体を貼り合わせると先ほどの場合と全く同じ球面ができるでしょう。つまり地球表面上に引いた網目は先ほどと全く異なりますが、それぞれの地図(格子)の辺長と辺の交差角の情報にはちゃんと地球が球面であるという情報が含まれているのです。
だから、曲面上に引かれている網目格子はどの様に引かれていても良いのです。ここが《第3に重要なこと》です。
アインシュタインはおそらく“ガウスの曲面論”から上記の事柄を読み取ったに違いない。そして、それを3次元リーマン空間に拡張します。このことは、文献6.のp64〜68のEinstein自身の説明をご覧下さい。また吉田氏の説明もご覧下さい。これらの事柄を理解するには文献1.5.“曲率テンソル例”は有益です。
[補足説明1]
上記の《3つの重要なこと》を実感するには次の例が有益です。
まず真四角で平らな天板を持つ机と、長さが全て等しい短い棒(単位棒と名付ける)を沢山準備します。この単位棒4本を互いにそれぞれの端が接して、それらの成す角が直角になるよう、前述の机の一つの隅に設置します。最初に単位棒が作った正方形の側にその一辺を共通とするもう一つの正方形を単位棒で作ります。この正方形の側にまた一つと、次々に並べていく。そうするとついに机の天板が正方形の格子で覆われる。正方形の各辺は二つの正方形に共通となり、正方形のそれぞれの隅は四つの正方形に共有される。
このとき注意して欲しいことは、すでに三つの正方形が一角につきあわされているとき、第四の正方形もすでに二辺は置かれていることになるので、残る二辺をどのように置かなければならないかは、すでに先の二辺によって完全に規定されている事です。いずれにしても、その様にして机の天板は単位棒の作る正方形で隙間無く埋め尽くされます。
次に、同じ机の天板の中央部分をバーナーで加熱します。ご存じのように温度が高くなった天板の中央部は膨張するために机の天板は盛り上がった曲面になります。この盛り上がって曲面状になった天板に先ほどと同じ事をします。机の一隅から4本の単位棒で正方形を作りながら四角形をつないでいきます。この場合には明らかに、最初の隅から机の中央に向かうにつれて、4本の単位棒で構成される四角形は正方形から歪んできます。つまり四角形の二辺のなす角は90度からずれてきます。場所が中央に近付くにつれて四角形は平行四辺形に歪んだものになりますが、いずれにしてもその様にしてつないで行った四角形で机の天板を覆い尽くすことができます。覆い尽くすことはできるが、必要とする四角形の数は最初の平坦だった机の場合よりも沢山必要になるでしょう。また、その机の反対側に到達してたとき設置される単位棒はもはや机の縁に平行(あるいは垂直)とはならないでしょう。
このとき単位棒が作る平行四辺形に対して2.(6)で説明した手順で基本計量テンソルの成分g11,g12,g21,g22を求める事ができます。今は辺の長さは全て1ですからg11=g22=1です。そして、歪んだ天板の場合はg12=g21は 0 以外のある値となります。
そのとき、微小領域に限ればその中での四角形の並びは互いに平行な線で仕切られた平行四辺形格子状になりますから、その微小領域内部の2点間の距離dsは単位棒の縦と横の並びの数duとdvとその場所の計量テンソル成分gijによって
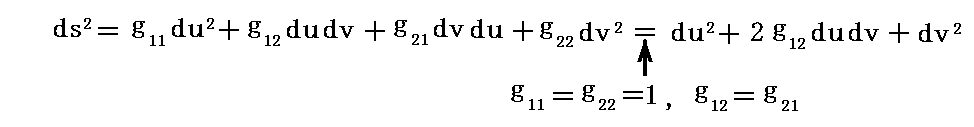
で与えられるでしょう。
もちろん、先ほどの平坦な天板の場合はg11=g22=1、g12=g21=0ですから
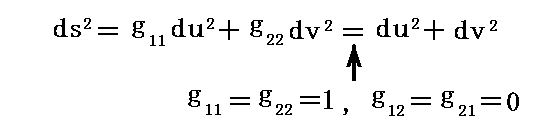
となります。
そして天板上の各点での計量テンソルgijの変化の様子から、曲面人は天板が平坦なのか曲がっているのかを知ることになる。このときただ一点の四角形の歪みからは曲面の曲がりを知ることはできないことに注意して下さい。
ここでは、長さの変化しない単位棒を連ねる事によって網目を構成したが、真ん中が盛り上がった天板の上に任意に引かれた曲線状の網目でも同じことができることに注意して下さい。それぞれの地点の網目の一辺の長さを物指し棒で測り、二辺の交差角を分度器で測って各点の計量テンソル成分gijを2.(6)に従って計算する。微小領域ではほぼ同形の微小平行四辺形で埋め尽くされているので縦横の網目の曲線の本数を数えて上記の式に代入すれば、その領域内の2点間の距離は計算できます。
[補足説明2]
アインシュシタインは1916年に書いた啓蒙書「我が相対性理論」第Ⅱ部§24で類似の例を用いています。そのとき彼が用いた例では机の天板の中央付近の単位棒は机と一緒に熱せられて机と一緒に伸びる様に説明しています。そして最初平板の上に正方格子状に存在していた網目が天板の湾曲に合わせて単位棒も伸びて曲面を構成する様に説明しています。
このような説明でも正しいです。これは今まで何度も説明してきた平板ゴムシートに描かれた正方格子を曲面に貼り付けたために格子が伸び縮みして変形した場合に相当します。またこれは上記[補足説明1]の最後で説明した真ん中が膨れ上がった天板の上に任意に引かれた曲線状の網目の場合に相当します。
この場合には、曲面上の各点に於ける計量テンソルの対角成分g11とg22はもはや 1 ではなく場所ごとに辺の長さが変化します。そのため場所ごとに(交差角と一緒に)辺の長さも物指し棒で計測しなければなりませんが、全く同様に考える事ができます。
この当たりの説明はBorn著「アインシュタインの相対性理論」第Ⅶ章§4の説明も有益ですのでご覧下さい。
(3)3次元リーマン空間人
我々は3次元リーマン空間に住んでいるとします。そのとき、どの様な事が言えるか考えてみます。
- まず言えることは、我々は3次元リーマン空間に住んでいるが、その中の各場所は3次元ユークリッド空間だと認識しても良いと言うことです。つまり、“ガウスの曲面論”における2次元リーマン空間(曲面)でもその場所ごとには接平面が存在し、ユークリッド空間だと考えて良いのでした。だから曲面上の格子も2次元ユークリッド空間である接平面に描かれているとして良かったのです。
それと同じで、3次元リーマン空間に住んでいる我々だが、その中に設定した平行六面体セルは、その点での接平面に相当する3次元ユークリッド空間の中に存在すると考えて良い。これは前節の《第1に重要なこと》ですが、これは3次元リーマン空間でも《第1に重要なこと》です。
- 次に言えることは、“ガウスの曲面論”の曲面の上に住む曲面人がその曲面を包み込む3次元ユークリッド空間の存在を知ることができなかったように、いま我々が住んでいる3次元リーマン空間の曲がり具合や歪み具合を見渡せる高次のユークリッド空間の存在を我々が知ることは決してできないことです。
我々にできるのは、3次元リーマン空間の各点に設定した平行六面体格子セルの各辺の長さと、辺の交差角の測定です。これはもちろん3次元リーマン空間の各点で定義できる3次元ユークリッド空間での測定値だと考えることができます。それは“ガウスの曲面論”で論じた曲面上の平行四辺形が、その点での接平面(2次元ユークリッド空間)上に存在していると考えたのと同じです。つまり3次元リーマン空間の各点に於いて平行六面体を設定でき、そういったユークリッド空間の平行六面体セルの集合体でもって3次元リーマン空間を埋め尽くすことができると考える。それは前節で述べた、二次元ユークリッド空間(接平面)で作られた5万分の1の地図で球形の曲面(2次元リーマン空間)を埋め尽くすことができることに相当します。
そのとき重要なことは、前節の《第3に重要なこと》で述べたように、3次元リーマン空間中の平行六面体セルの連なりを表す網目曲線はどの様に引かれていても良いのです。どの様に引かれていても、それぞれの空間点に於ける平行六面体セルの辺の長さと辺の交差角は3次元ユークリッド空間での測定棒と分度器で測定できます。つまり3次元リーマン空間でも各点に於けるリーマン計量テンソルが定義できしかも実測できる[2.(6)参照]。さらに計量テンソルを測定する網目はどの様に引かれたものでも良い。これが3次元リーマン空間で《第2に重要なこと》です。
- 次は前節の《第2に重要なこと》に関係する事柄です。3次元リーマン空間の1点に於けるリーマン計量テンソルが解っても何の意味もありません。基本計量テンソルの算出の元になる平行六面体セルはユークリッド空間中のものですからその形状でリーマン空間の歪みが表される訳ではありません。1点でのリーマン計量テンソル(平行六面体の形状)は網目の引き方に依存していかようにでも変化します。大事なのは、場所が変わったときにリーマン計量テンソルが変化していくその様子です。先に述べた地球表面を表す5万分の1の地図の例で説明すると、次々と貼り合わせていく隣り合った地図との間の辺長の変化と地図の2辺の交差角の変化の様子です。これは3次元リーマン空間でも同様で《第3に重要なこと》です。
曲がった空間の任意に定めた網目から計測できる“計量テンソルの変化の様子”をどの様にして論じたらよいのだろう。おそらく、〈アインシュタイン〉はここで行き詰まったと思われます。
プラハからチューリッヒへ帰ってきたアインシュタインは、その様な事柄を取り扱う数学が存在するかどうか調べてもらえないかと友人の数学者(グロースマン)に相談します。相談を受けた〈グロースマン〉が図書室で調べて見つけてきたのが、〈リッチとレヴィ=チヴィタ〉が1901年に作り上げていた“絶対微分学(テンソル解析学)”だった。そして彼らは、さらに〈クリストッフェル〉の仕事や〈リーマン〉の仕事にさかのぼって行きます。
おそらくアインシュタインとグロースマンはリッチとレヴィ=チヴィタの論文に引用されているクリストッフェルの論文中の“クリストッフェル記号”の意味はすぐに理解したでしょう。そしてクリストッフェルがリーマン幾何学を論じる為にこの記号を考案したことを知り、最終的に“リーマン幾何学”を知った。そして、その中の“曲率テンソル”を知ったのだと思います。このことは京都講演やグラスゴー講演から読み取れます。これが、アインシュタインが1912年の秋に行き着いた状況です[Sommerfeld宛の書簡(1912年10月29日付)と、Pais著「神は老獪にして・・・」12章参照]。
テンソル解析学そのものについては、別稿「テンソル解析学(絶対微分学)」を参照。
- 次は3章で説明した座標変換に関する注意です。
3次元リーマン空間中にスカラー、ベクトル、テンソルは存在し分布しています。それらスカラー、ベクトル、テンソルの大きさは2.(5),(6),(7)で説明したように3次元リーマン空間の格子定数である[基本計量テンソ(ルgij)]と、[格子の数を示す座標値(ガウス座標)]の積で表現されます。そのとき座標を変えるということは、格子定数の元になる基底ベクトル系を別なものに変えることです。すなわち3次元リーマン空間を分割する網目を変えることです。
網目を変えれば、その網目の個数で数えていた座標値(ガウス座標)が変わります。その座標値の変化は網目(基底ベクトル)の取り方の変更を示す変換係数に関係します。ただ、そのとき元々のスカラー、ベクトル、テンソルの成分の大きさが基底ベクトル系の網目個数(座標値)で表されていたのか、双対基底ベクトル系の網目個数(座標値)で表されていたかの違いによって反変的に変換されるか、共変的に変換されるかの違いが生じます。そのようなことが生じるのは、座標値と一緒になって長さや体積を決める元になる“格子定数(計量テンソル)”が斜交した平行六面体セルについて与えられているからです。2.(2)][補足説明4]で説明したように格子定数が常に立方体状の同じものであったら、反変と共変の違いは出てきません。歪んだ空間を表現するために平行六面体状に歪んだ単位格子セルが必要になったために“反変”と“共変”の違いが生じてきた。これが3次元リーマン空間で《第4に重要なこと》です。
- 最後は 基本計量テンソルgij と 基底ベクトル の関係についての注意です。
ユークリッド空間の様に計量テンソルを定める単位格子として立方体を全空間に渡って利用できて計量テンソルが常に単位テンソルにできる場合と、全空間に渡って一定だが単位テンソルではない場合の違いと、計量テンソルが場所的に変化すると言うことの意味の違いです。おそらくここが一番解りにくい所です。
【1】
“ユークリッド空間”でもそれを分割する網目として斜交座標を採用することはできます。さらにその座標線がグニャグニュ曲がった曲線にすることもできます。そうするとユークリッド空間に於いても計量テンソルgijは場所と共に変化しますし、その中でベクトル量を表す座標形式に反変表示と共変表示の違いが出てきます。しかし、その様にしてユークリッド空間を分割して、全空間に計量テンソルを配置してもそれらの集合からは決してユークリッド空間の歪みや曲がりを示すことはできません([例8]と[例9]を参照)。だからユークリッド空間をその様な網目で分割することは全く意味の無いことです。
ユークリッド空間の場合は全てを同じ立方体格子で埋め尽くして各点の計量テンソルは

であるとするのが得策です。そうすれば基底ベクトルと双対基底ベクトルは一致して反変・共変など面倒な性質は出てきません。
ここで次のことに注意して下さい。斜交座標やグニャグニャ曲がった曲線座標がリーマン空間を特徴づけると勘違いされているかも知れませんが、ユークリッド空間でもその様な網目で分割することはできるのですから、そこのところが本質では在りません。リーマン空間ではその様な分割しかできないことが本質なのです(4.(3)[例8]、4.(4)2.[例9]と[補足説明1]を参照)。
【2】
ところで、特殊相対性理論の“ミンコフスキー時空”では、それを分割するのに全空間に渡って基底ベクトルが互いに直交(ただし時間軸は他の空間軸に対して斜交していると考える)した同形のセルで分割することはできます。つまり、そのセルの格子定数である計量テンソルgijは全時空間に渡って同じ
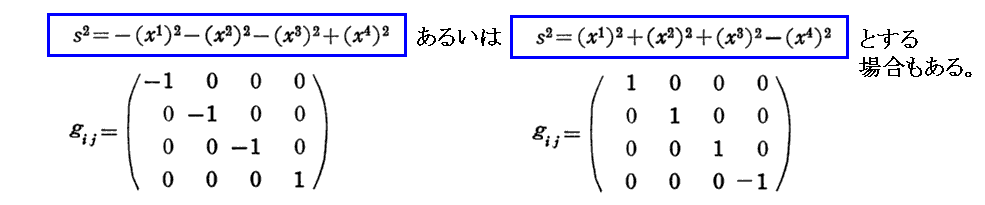
を用いる事ができます。すなわち、ミンコフスキー時空では全空間に渡って同一の計量テンソルとなる。
ただし、それはもはや単位テンソルでは在りません。対角成分しか在りませんので基底ベクトルが(時間軸を除いて)互いに直交していることは確かなのですが、対角成分が全て 1 になるようにはできなくて、+1 と−1 が入り交じっています。これは時間軸が他の空間次元の座標軸に対して直交していない(斜交している)からそうなったのです。だから基底ベクトルと双対基底ベクトルは異なったものになり反変表示と共変表示の違いが生じてきます(「ミンコフスキーの4次元世界」参照)。
時間軸だけが斜交しているのを4次元時空で想像するのは難しいが、時間1次元・空間2次元で考えると解りやすい。2.(1)で考えた図で基底ベクトルの内の2つを空間座標軸として互いに直交した単位ベクトルを取り、3っ目の基底ベクトルを時間軸を表す基底ベクトルと考え、その基底ベクトルが最初の空間座標を表す基底ベクトルが張る面に対して斜交していると考えるのです。
そのとき時間次元の基底ベクトルの長さが空間座標基底ベクトルと違っているとしても良い。その場合は軽量テンソルの時間次元成分が1(or−1)ではなくなり、(例えばこの場合の様に)gijとgijのその部分の成分値も違ってきます。
さらに補足しますと、距離不変量を表すs2の表現で空間部分と時間部分とで符号が異なる事についてですが、その様になったのは“光速度がどの座標系から見ても一定になるから”です。つまりs2が座標変換不変量であるということは光速度がどの座標系から見ても一定であるというのと表裏一体で、“そうなるように座標間の変換が規制されているから空間部分と時間部分の符号が逆になる”と言うことです。
このことは、一般相対性理論の世界でも踏襲されねば成りません。だから一般相対性理論における時空の計量テンソルは特殊相対性理論の計量テンソルを拡張したものになっています。そのため、質量(エネルギー)の存在しない時空に対する計量テンソルはミンコフスキー時空の計量テンソルに帰着します。
【3】
そして、最後は“リーマン空間”です。リーマン空間では、今まで見てきたように本質的に立方体状のセルで全空間を埋め尽くすことはできないのです。一部分なら立方体セルで埋められますが、他の場所に必ず平行六面体状のセルが生じてきます。そのため必然的に反変成分と共変成分の違いが生じてきます。全領域に渡って計量テンソルの対角成分以外を零にする様な網目格子を引くことはできません。必ずどこかで対角成分以外もある計量テンソルが生じます(4.(2)[補足説明1]の例を参照)。さらにやっかいなのは、計量テンソルの成分値gijのそれぞれが
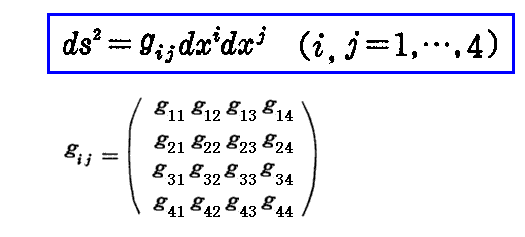
が場所的に変化する様にしか、網目を引くことはできないことです。その為に座標値(ガウス座標)と基底ヘクトルの関係も場所とともに変化してしまい、スカラー場、ベクトル場、テンソル場の微分操作を特別難しくします。
つまり、リーマン空間では計量テンソルが場所的に変化しないような網目を引くことはできないのです。これがリーマン空間で《第5に重要なこと》です。
本節で説明した《第1に重要な事》〜《第5に重要な事》については、Einstein自身がプリンストン大学講義(1921年5月)の第3回講義の前半部で語っていますので参照して下さい。
[補足説明1]
本稿の1〜3章では、3次元リーマン空間中のただ1点の格子セルを定める基底ベクトルとそれから定まるその点のリーマン計量テンソルgjiの説明。および、その点での網目の引き方を変えたとき、つまり基底ベクトルを変更したときのリーマン計量テンソルの変化(つまり座標変換)の話しかしていません。
隣り合った平行六面体のリーマン計量テンソルがどの様に変化するのか、その変化とは何を意味するのか4.(4)と4.(5)で説明します。また、そのことは2次元リーマン空間の場合には別稿「微分幾何学3(曲面幾何学)」で説明しています。一般のn次元リーマン空間については別稿「微分幾何学4(リーマン幾何学)」で説明する予定です。
[補足説明2]
上記の“一部分なら立方体セルで埋められますが、他の場所に必ず平行六面体状のセルが生じてきます。”について補足します。
4.(2)[補足説明1]で述べた中央が盛り上がった机の天板の2次元リーマン空間で説明すると、盛り上がった斜面に作られる単位棒の四辺形はもはや正方形ではなくなり変形した平行四辺形になると説明しました。
しかし、その盛り上がった斜面の部分に最初に単位棒で正方四辺形を作りそこから周囲に四角の格子を広げていっても良いのです。その様にすると、今度は最初に述べた机の隅の四角形が正方形ではなくなるでしょう。つまりリーマン空間では部分的には正方格子の座標系をとる事はできるが、その場合他の場所が必ず歪んだ四角形になってしまいます。
これは、アインシュタインが取り上げた重力場の中を自由落下する箱の実験に相当します。自由落下する箱のなかの人間にはもはや重力場は存在せず箱の中の空間も曲がってはいません。しかし自由落下する箱を大きくすると、箱の周辺ではもはや重力場は消すことができず、空間の歪みも表れてきます。つまり重力場は消すことができ、空間も歪んでいないと見なせる座標系が局所的には存在するのですが、その座標系を全空間に広げて空間全体の重力場を消し、空間全体が歪んでいないと示せる座標系は存在しないのです。
[補足説明3]
上記《第5に重要なこと》の最後の文節で述べた“その為に座標値(ガウス座標)と基底ベクトルの関係も場所とともに変化してしまい、スカラー場、ベクトル場、テンソル場の微分操作を特別難しくします。”について補足します。
今例としてリーマン空間が同一のベクトル場で埋め尽くされているとします。つまりA点と、その近くのB点でのベクトルは同じ大きさであり同じ方向を向いているとします。そのときリーマン空間では空間が歪んでいるためにA点とB点の基底ベクトルは微妙に変化しています。そのためそれぞれの基底ベクトルの長さを単位として測定されたA点のベクトルを表す座標値(ガウス座標)とB点のベクトルを表す座標値(ガウス座標)は変化してしまいます。同じベクトルなのにそのガウス座標は変化しています。これは単純に場所をAからBへ移動したときにあたかもベクトル場が変化したような微分係数を与えてしまうと言うことです。
つまり、ベクトルの成分だけをを微分しても正しいベクトル場の微分とは成らない。一定でない基底ベクトルも微分しなければならないのです。これはベクトル成分の座標微分は実際のガウス座標のA→Bへの変化と、基底ベクトルのA→Bへの変化を両方考慮した微分係数にしなければならないことを意味する。
これが曲がった空間、曲がった座標を理解する鍵です。これが“共変微分”の本質です。“共変”という言葉は、[ガウス座標値]と[基底ベクトル]の両方の変化を[共に考えないといけない]を意味します。そのとき基底ベクトルの変化はクリストッフェル記号で表されているのですから、共変微分係数には必然的にクリストッフェル記号が関係した項が含まれることになります。このことは4.(5)で説明する(あるいは「微分幾何学」3.(3)や「テンソル解析学(絶対微分学)」6.(3)など参照)。
[補足説明4]
一般相対性理論で取り扱うリーマン空間は[時間1次元]+[空間3次元]からなる4次元時空です。その時空の各点の近傍領域はミンコフスキー4次元時空で近似できます。つまり、《第1に重要なこと》で説明した2次元ガウス曲面をリーマン4次元時空に対応させると、2次元ガウス曲面の各点における接平面に相当するものが“ミンコフスキー4次元時空”です(Born著「アインシュタインの相対性理論」第Ⅶ章§7の説明参照)。
《第5に重要なこと》で説明したように、ミンコフスキー4次元時空は曲がっておらず、しかもユークリッド空間の様に座標軸が互いに直交した時空です。ただし、その時間次元と空間次元が特殊な関係になっているので、計量テンソルはユークリッド空間のそれとは異なります。異なりますが、ユークリッド空間の計量テンソルと似ていますので、“擬ユークリッド計量”と言われることがあります。
[例8]
上記《第5に重要なこと》の“ユークリッド空間”の文節で述べた“ユークリッド空間でもグニャグニャ曲がった曲線座標で分割することができ、場所ごとの分割格子セルから定まる計量テンソルが場所ごとに変化するような網目を利用することができるが、その様にしてユークリッド空間に分布させた計量テンソルの集合からは決してユークリッド空間の歪みや曲がりを示すことはできない。”の意味をもう少し具体的に説明します。
話を簡単にするために2次元ユークリッド空間(平面)で考えます。平面を曲線座標で分割するのですが、例として極座標を用います。
この平面に住む平面人は、上図の中心点から周囲に向かって物指し棒と分度器を使って空間のなかに網目を引き網目の格子定数(計量テンソル)を測定していけます。そして平面人は彼が住む全空間(2次元ユークリッド空間)を極座標の網目で覆い尽くすことができます。
この空間の“線素”は
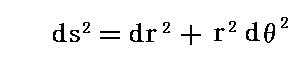
なので、各点に於ける網目の“計量テンソル”は
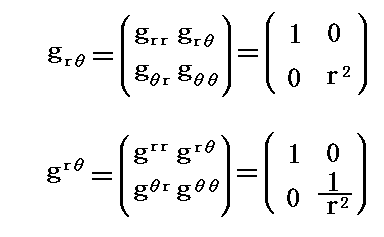
となります。この場合分割したセルの基底ベクトルは直交していますので、対角成分以外は 0 になりますが、対角成分はrの関数ですから:計量テンソルは場所ごとに変化します。もちろん曲線座標で分割した網目についての計量テンソルですからそうなったのです。
これらの計量テンソル成分の値を“クリストッフェルの記号の式
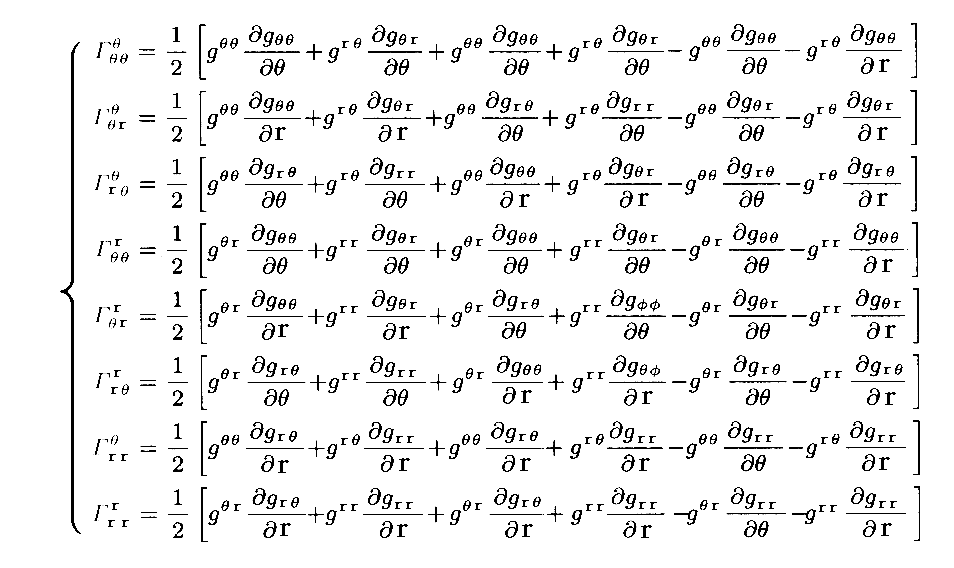
に代入します。2次元だから 2×2×2=8個 の成分を計算せねばなりませんが、ここで先ほどの計量テンソルを使うと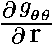 以外の偏微分は全て 0 になります。さらに grθ や gθr も全て 0 になります。そのため下記の3つの成分だけが残ります。
以外の偏微分は全て 0 になります。さらに grθ や gθr も全て 0 になります。そのため下記の3つの成分だけが残ります。
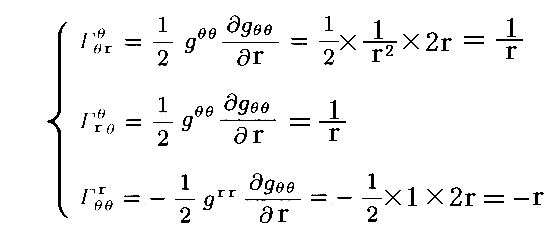
以上の様にしてガウス座標(r,θ)で与えられる平面上の全ての点のクリストッフェル記号の値が求まります。クリストッフェル記号の値は r が変われば変化しますが θ には依存しません。
これらのクリストッフェル記号を用いますと平面上の任意の(r,θ)点の“リーマン曲率テンソル”
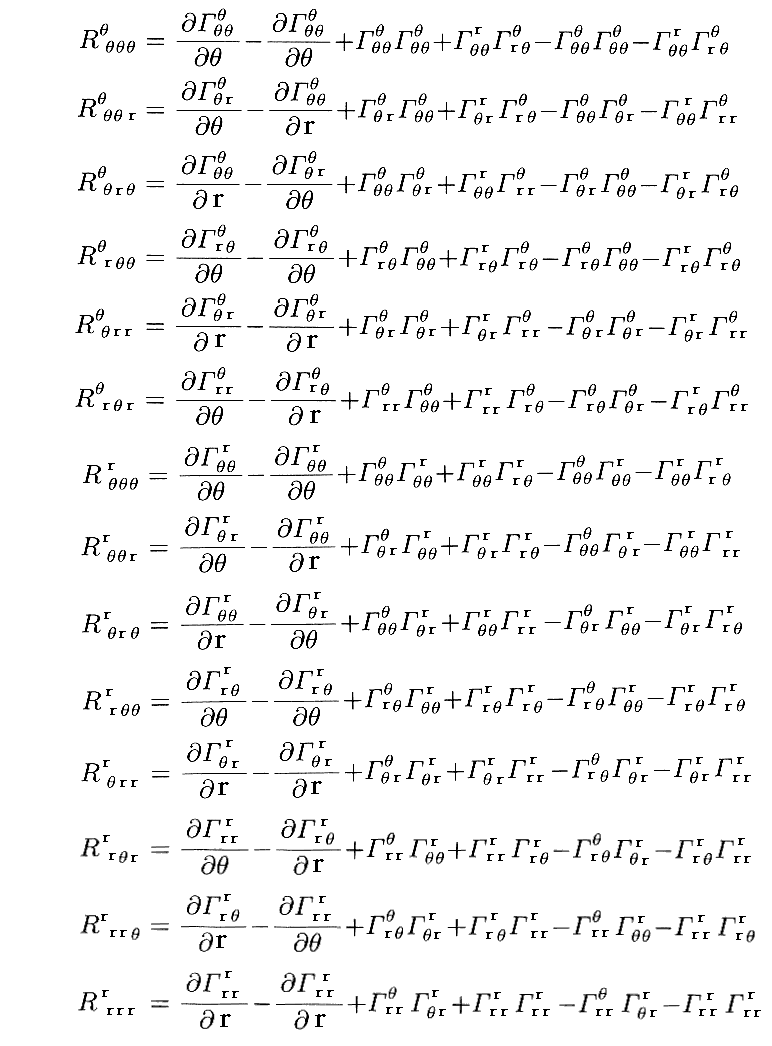
を求めることができます。2次元の場合 2×2×2×2=16成分 を計算せねば成りませんが、この中で残るのは次の6成分だけです。しかし、上で求めたクリストッフェル記号の値を代入すると全て 0 になります。

つまり極座標上の任意のガウス座標(r,θ)点においてリーマンの曲率テンソル成分は全て 0 となります。これは極座標で分割した元の2次元ユークリッド空間が全空間に渡って曲がっておらず平坦である事を示しています。
すなわち、ユークリッド空間を分割するのに斜交座標や曲線座標で分割して、各点の計量テンソルが場所とともに変化する様な状況になってもユークリッド空間が平坦であるという事実は変わりません。各点の計量テンソルから計算されるクリストッフェルの記号によって、各点のリーマンの曲率テンソルを計算すればそのことを示せます。
以上の議論を文献1の 2次元リーマン空間(球面)の場合 と比較してみられると、上記の《第5に重要なこと》の意味がお解りになると思います。
球面上に住む球面人が北極点から南極点に向かって分割線を引き、各格子の格子定数(計量テンソル)を測定しながら網目を広げて行き、球面を網目で覆い尽くすことはできます。
文献1で説明されている様に、この場合の“線素”は
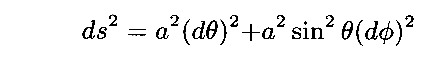
なので、各点に於ける網目の“計量テンソル”は

となります。
その網目各点の計量テンソルから計算されるクリストッフェル記号によって、各点のリーマンの曲率テンソルを計算すれば、球面人は彼の住む2次元空間が曲がっている事を知ることができます。
そのとき、リーマン空間では必然的に歪んだ四角形のセルが生じてきます(4.(4)2.[例9]の後半を参照)。
補足しますと、この球面の場合と上記[例8]の場合を比較されると別稿「微分幾何学」2.(9)3.で説明した“ガウスの驚異の定理(Theorem egregium)”の意味が良く解ります。さらに、2.(5)[補足説明]で説明した“計量テンソル”は空間の幾何学を与えるの意味も良く解ります。
[補足説明5]
3次元ユークリッド空間に設定された極座標についても上記と同様な計算をしてみると良いでしょう。
別稿「座標回転公式と球面三角法」1.(2)3.で、その場合のds2を与える式を導いていますので、それを利用すると基本計量共変テンソル(gij)は

となります。
基本計量反変デンソル(gij)は、基本計量共変テンソル(gij)と

の関係にあるので、別稿で説明する方法によって求めると
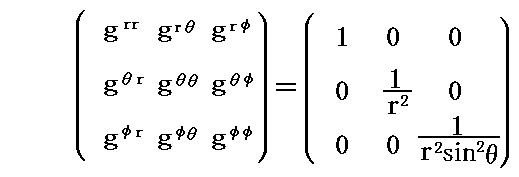
となります。
まず、これらを用いて 33=27個 の“クリストッフェル記号”を求めると

となります。
次に、この27個のクリストッフェル記号を用いて 34=81個 の“リーマン曲率テンソル”を求めます。そうすると、すべての成分値が 0 となることが解るでしょう。つまり3次元ユークリッド空間は曲がっていないのです。
これは、3次元ユークリッド空間に(x,y,z)直交座標系の網目を設定して、その計量テンソルを用いて計量テンソル→クリストッフェル記号→リーマン曲率テンソルの計算をするのであれば計算するまでもなく自明な事です。
だから、もう一度強調しますが、空間内に引いた網目が直交直線座標であるか斜交曲線座標であるかは空間の曲がりを表す上で全く関係ないのです。重要なのは、“直交直線座標で網目を引こうとしても、その網目を広げていくとやがてそれが不可能となり斜交曲線座標にならざるを得ないことが空間の曲がりを表す”と言うことです。ランダウ、リフシュツ「場の古典論」第10章§81〜82の説明はこのことを言っている。
(4)クリストッフェルの3添字記号とは何か
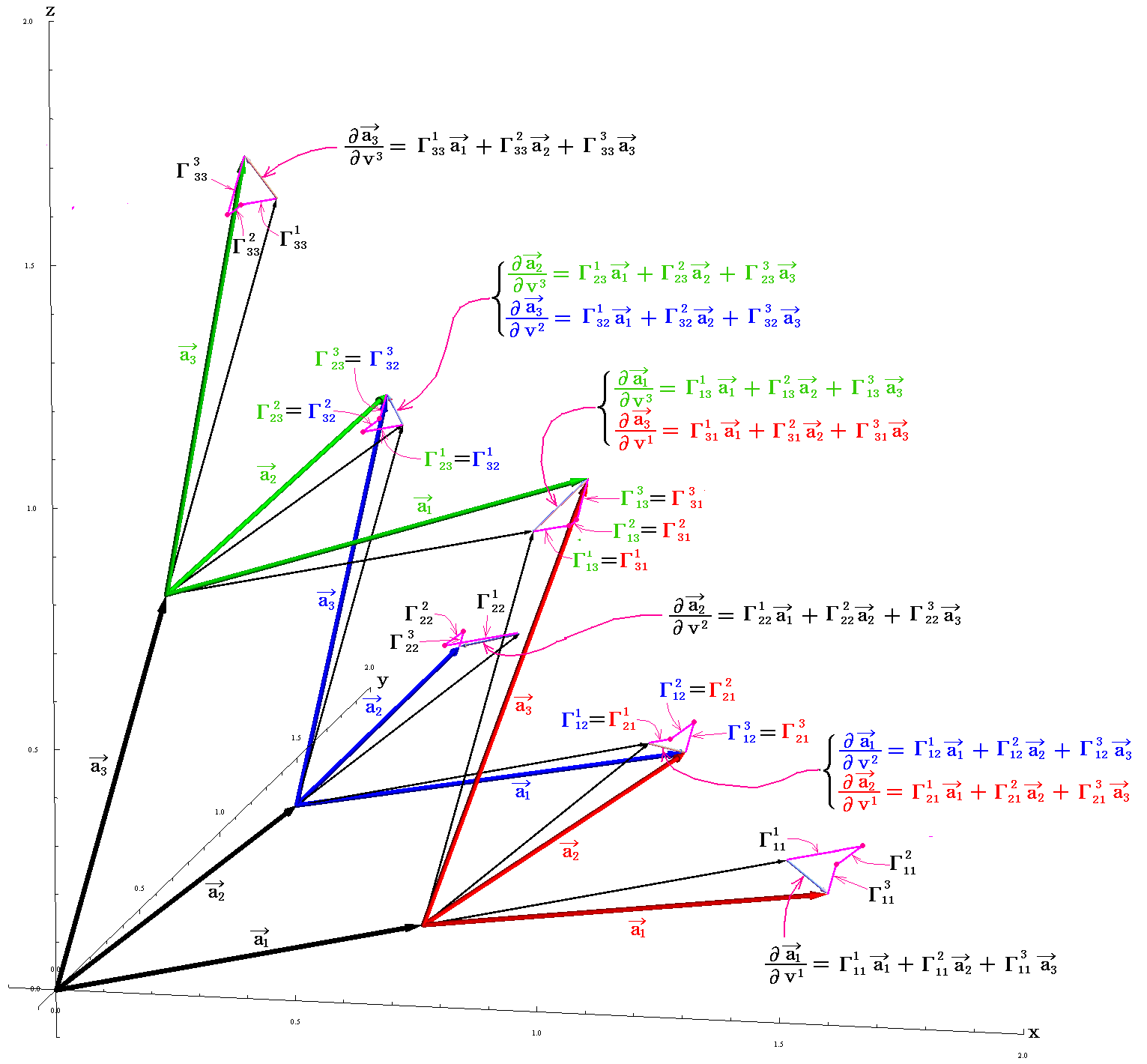
4.(3)で説明した3次元リーマン空間で《第3に重要なこと》を実現する量が“クリストッフェルの3添字記号”です。この記号の意味を説明します。
1.クリストッフェル記号の定義 [目次へ帰る]
《クリストッフェル記号の定義》
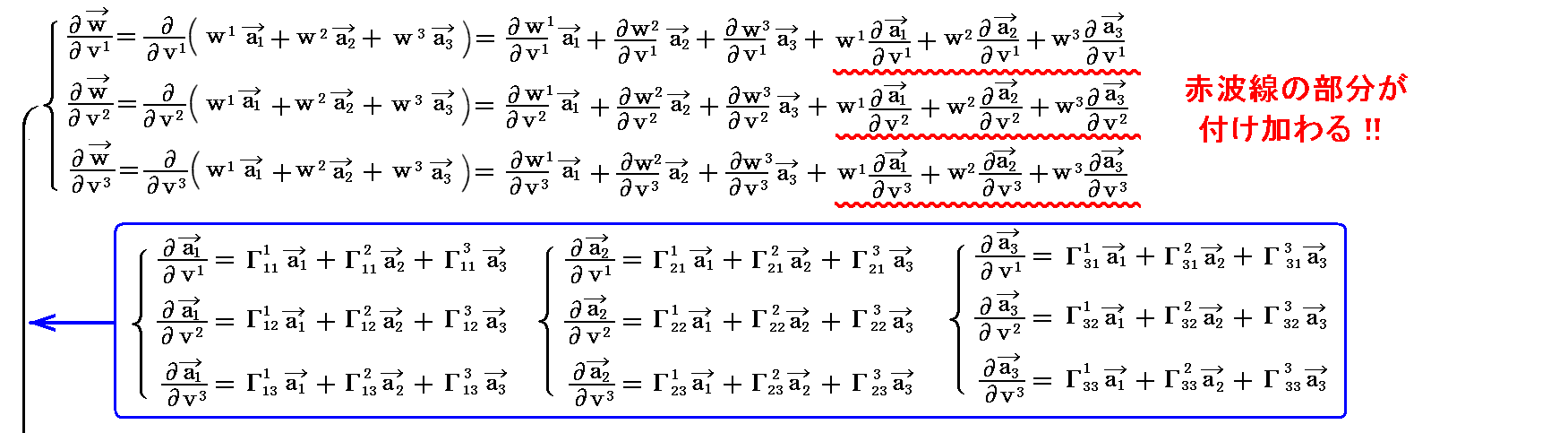
3次元リーマン空間の中を少し動いたときの基底ベクトル ai の変化を考えてみる。つまりリーマン空間中のガウス座標(v1,v2,v3)の場所から(v1+dv1,v2+dv2,v3+dv3)へ移動したときの基底ベクトル ai の変化量を求める。
その変化量は下記のような線形の形で表されるであろう。
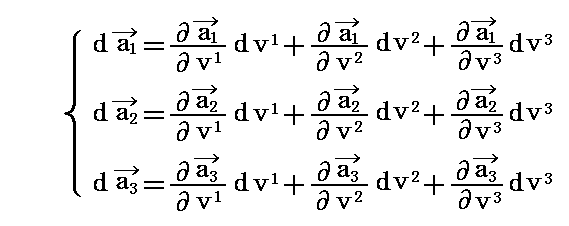
そして、上記式中の係数は下記のような基底ベクトル a1、a2、a3 の線形結合で表されると考えて良いだろう。
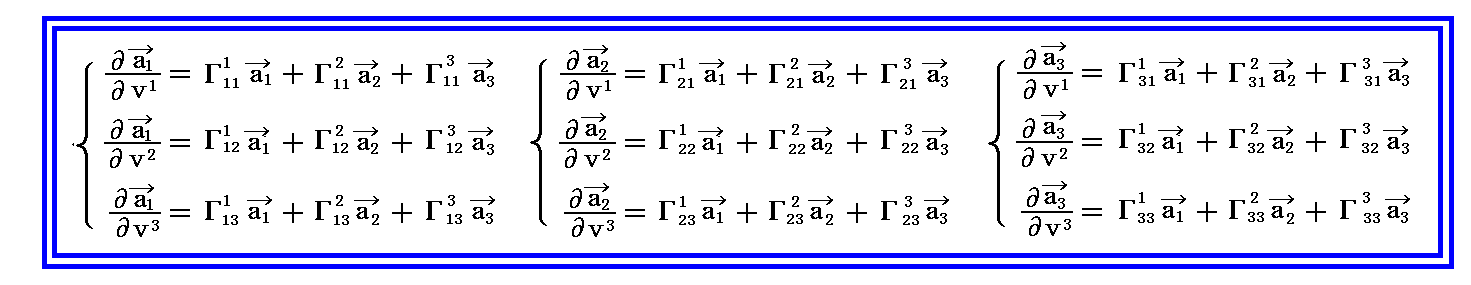
式中の係数 Γkij の添字は単にそれぞれを区別するために付けてあるだけです。当然のことですが、3次元空間の場合には 3×3×3=27個 の係数が必要になります。ただし、後で解りますが、添字ijに関する対称性から、独立なものは3×6=18個になります。
(一般相対性理論の4次元時空では、4×4×4=64個の係数が必要です。ただし、添字ijに関する対称性(後で解る)から、独立なものは4×10=40個になります。)
[補足説明1]
上式の係数だけ書き出して並べると

となるが、左端の3つはdv1=1だけ(つまり基底ベクトルa1分)変化したときの変分を示し、真ん中の3つはdv2=1だけ(つまり基底ベクトルa2分)変化したときの変分を示し、右端の3つはdv3=1だけ(つまり基底ベクトルa3分)変化したときの変分を示しています。
このことは、本節を最後まで読まれれば解ります。
[補足説明2]
上記の線形結合式の係数はちょうど3.(1)で説明した、各点に於ける基底ベクトルの変換式(そこでは同じ点での変換係数でしたが)

の係数Ai'jに相当するようなものです。今は場所を移動したときの変化の様子を表す変換式の変換係数だと考えて下さい。
上記の変換係数 Γkij は次のようにすれば求まる。
まず計量テンソル gij=(ai・aj) を vk で微分すると
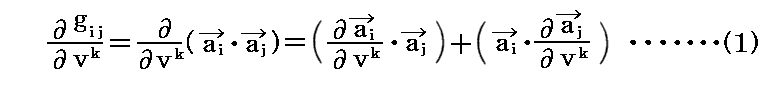
が得られる。
ここで添字ijkをijk→jki→kijとサクルリックに変えると、同様にして
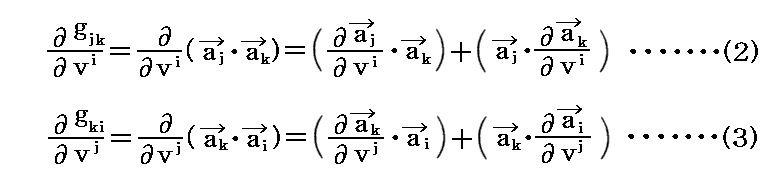
が得られる。
[注意]
このとき、ガウス座標(v1,v2,v3) の位置ベクトルを r とすれば別稿「微分幾何学」2.(1)で説明したように
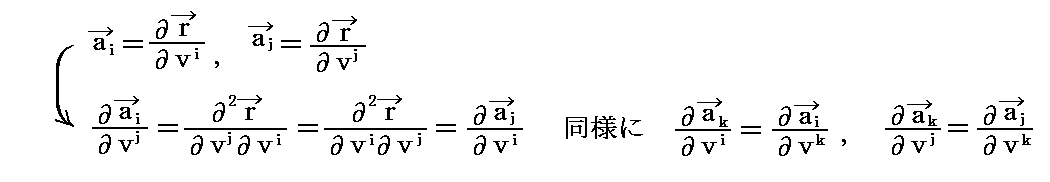
が成り立つ。
これを用いて、(2)式+(3)式−(1)式をつくれば
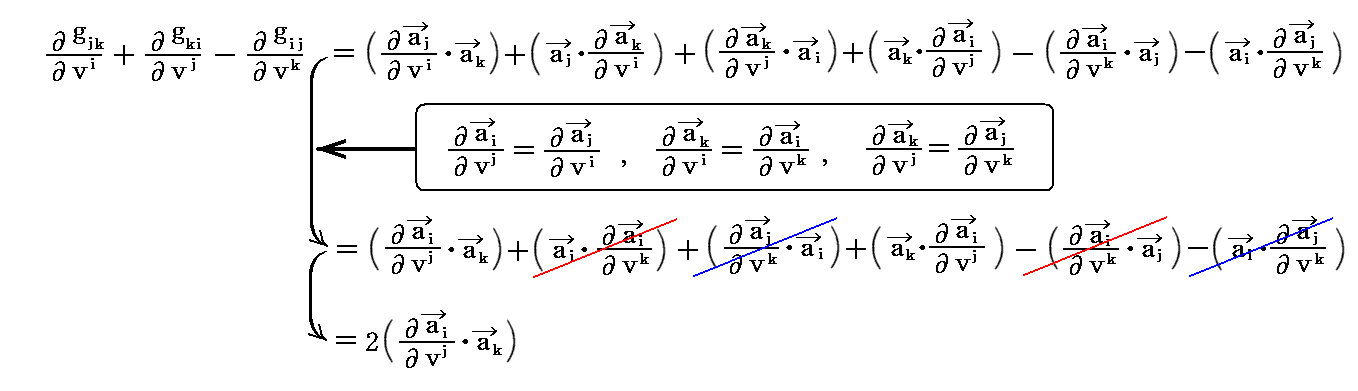
となる。
両辺に (1/2)gak (k=1,2,3) を乗じて k について総和をとる。このとき gak は“基本計量反変テンソル”
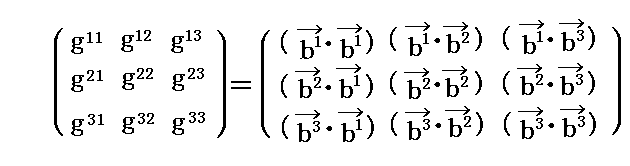
の成分である事に注意して下さい。
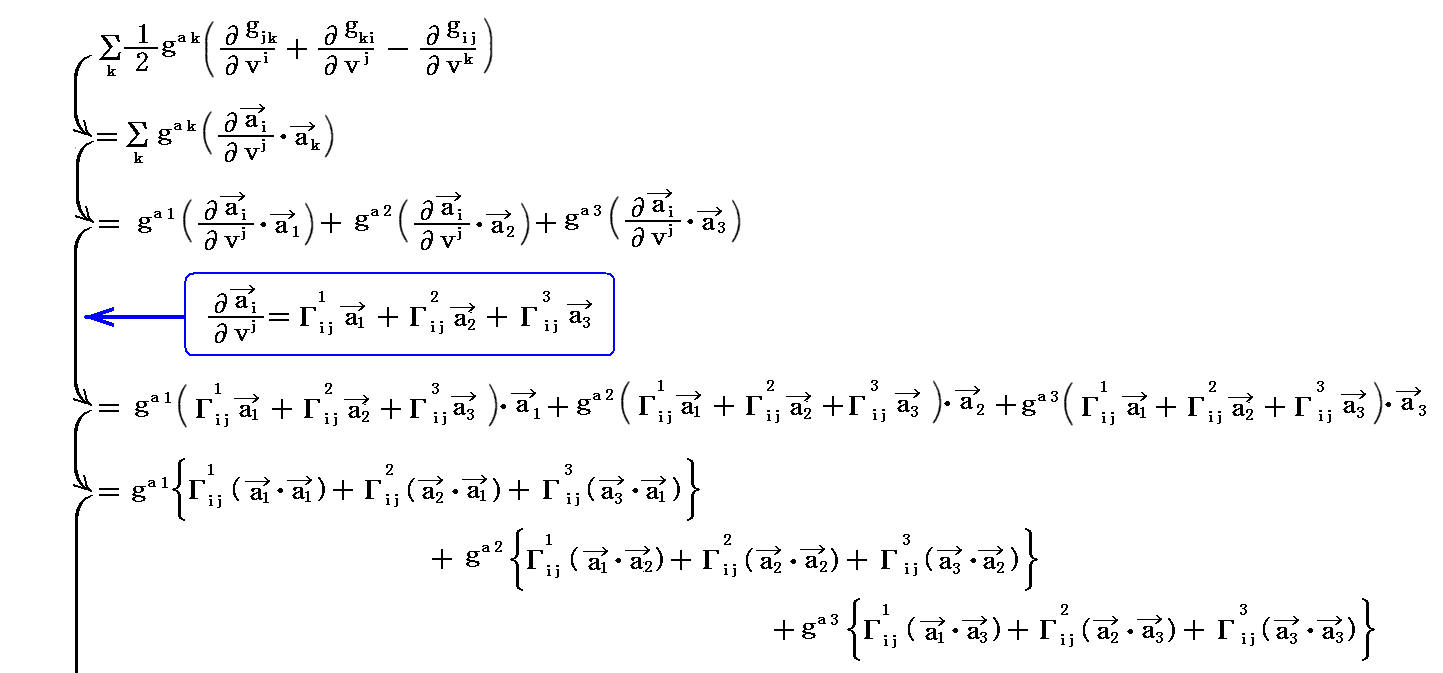
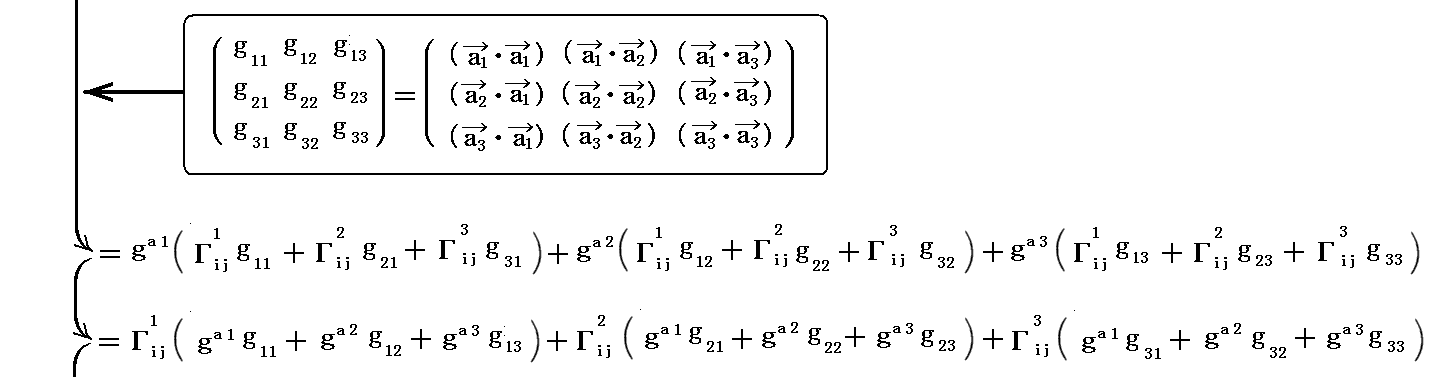

となる。“基本計量反変テンソル” gij を乗じたのは最後の赤線で囲った関係式を用いる為です。
すなわち“クリストッフェルの3添字記号”は計量テンソル成分から下記のようにして計算されるものです。
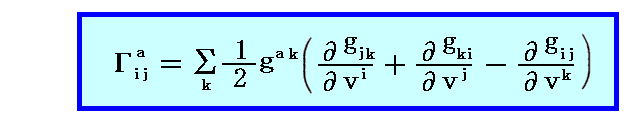
[補足説明3]
上式は重要なので、フライシュ文献1.の導き方も以下で引用しておきます。内容は同じなのですが、別の見方でも導けると言うことです。
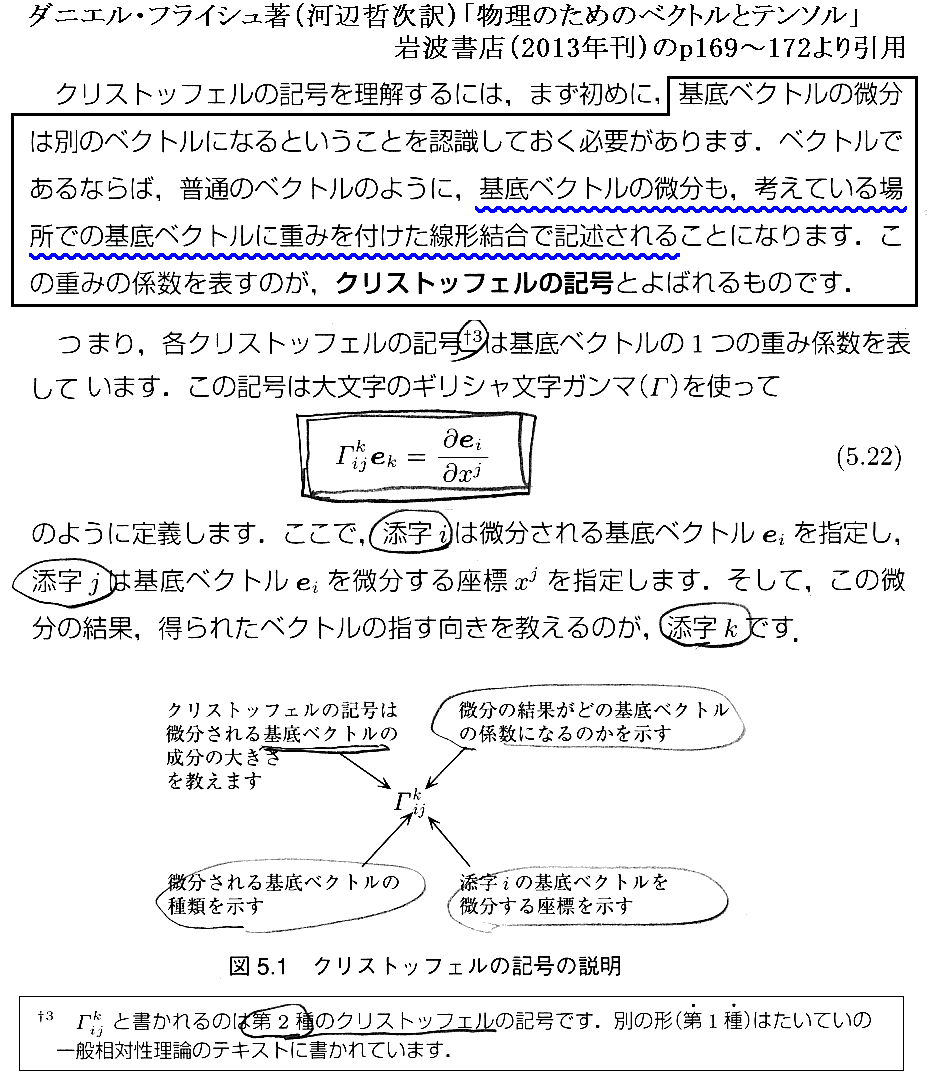


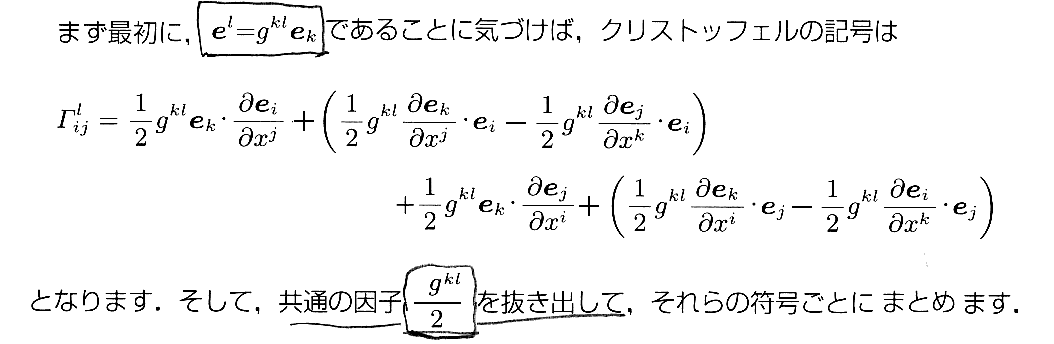
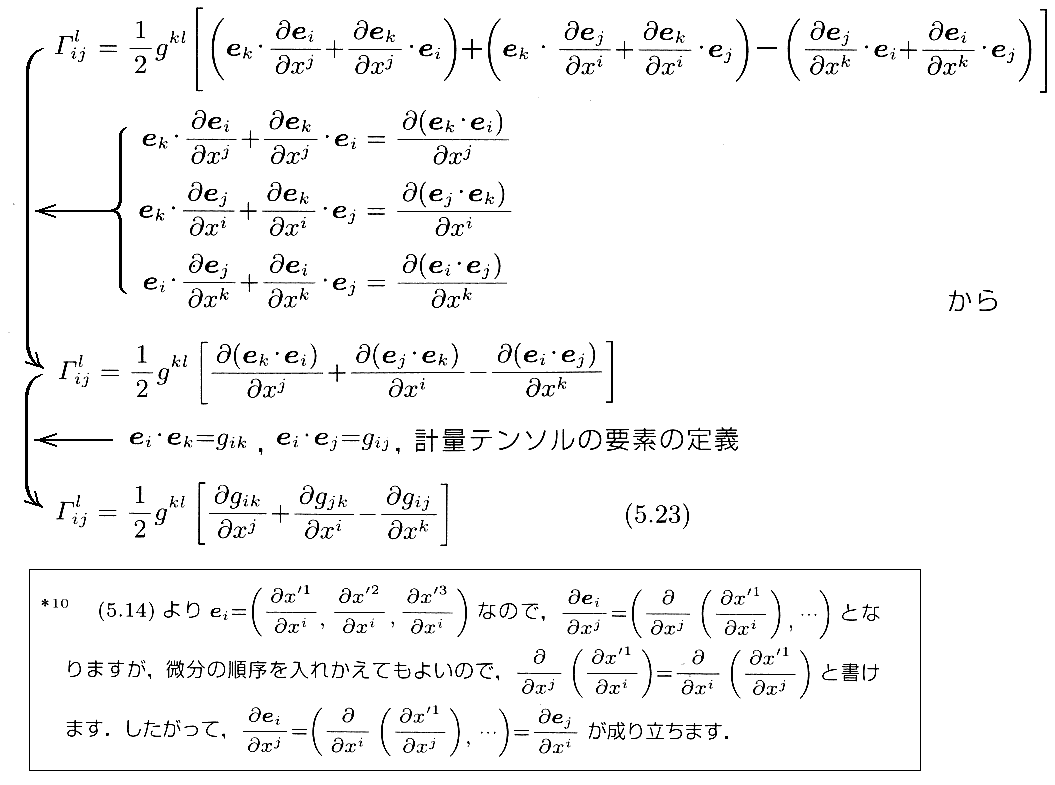
[補足説明4]
上記説明文中の(v1,v2,v3)は基底ベクトルを単位として測られた座標値“ガウス座標”である事を忘れないで下さい。
また、Γaij 定義式中の計量テンソル gij は添字 i と j の入れ替えに関して対称ですから、クリストッフェル記号は下の二つの添字 i と j の入れ替えに関して対称です。
すなわち
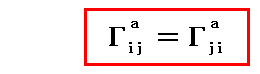
が成り立ちます。
このことの意味は[例10]の図をご覧になれば明らかです。
[補足説明5]
最も大切な事は、最初の定義式
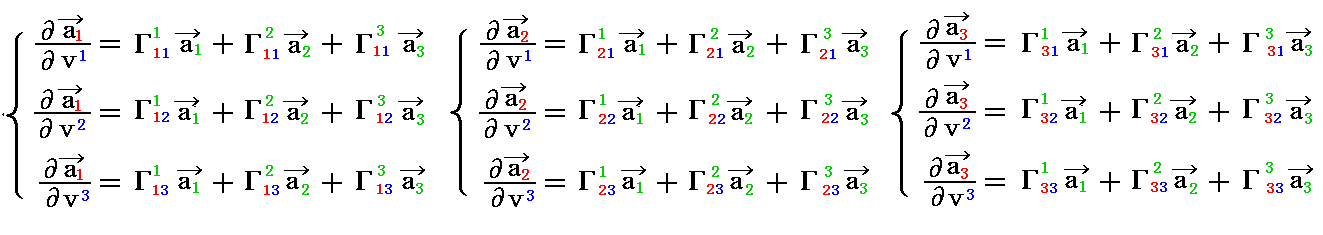
から解るように 《係数 Γkij の添字 i は基底ベクトル ai の変化の様子を表す係数であり、添字 j はその係数が基底ベクトル aj 方向の変位に関係しており、添字 k は基底ベクトル ak 方向の変位成分を表している》 ことです。
このことは頭の中に基底ベクトルの作る平行六面体セルを思い浮かべて、そのセルの稜に沿って基底ベクトルを動かしたときの変化が想像できるかにかかっています。想像できればクリストッフェル記号の意味は明らかでしょう。また、何故3×3×3=27個必要なのかも明らかでしょう。このことについては4.(4)3.を参照されたし。
クリストッフェルの3添字記号は隣り合った基底ベクトルの変化の様子を表す係数で、隣り合った基底ベクトルが作る単位セルをつなぎ合わせていくときの接続の様子を示している。その為この係数は“接続係数”と呼ばれることもある。
次項の[例9]をご覧になれば解るように、その接続の様子で空間の歪みや曲がり具合が解るわけですから、リーマン幾何学で最も大切な量です。
2次元ガウス曲面(2次元リーマン空間)の場合を別稿「微分幾何学」2.(8)で説明していますので参照して下さい。
2.2次元ユークリッド空間と2次元リーマン空間のクリストッフェル記号 [目次へ帰る] [節先頭へ]
クリストッフェルの3添字記号を理解する具体的な例として、4.(3)[例8]の2次元ユークリッド空間(平面)に於ける極座標 と、文献1.の2次元リーマン空間(球面)の球面座標 を取り上げる。
[例9]
《2次元ユークリッド空間(平面)の極座標》
下図は2次元ユークリッド空間に引かれた極座標の一部を示したものです。ガウス座標値を数えるもととなる基底ベクトルが作る単位セルの格子定数(計量テンソル)はθ方向がrで、r方向が1で与えられるのですが、(θ方向が)rでは解りにくいのでθ方向はr/20に縮めて表しています。[拡大図はこちら]
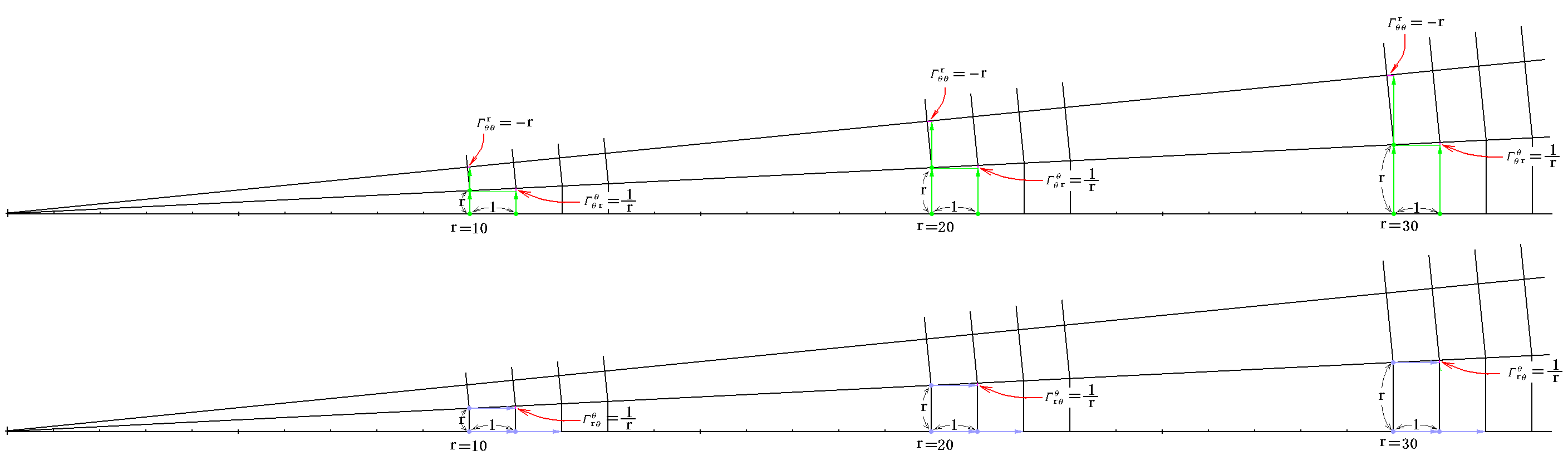
上図では細部が解りにくいのでr=10、20、30付近の格子を拡大すると
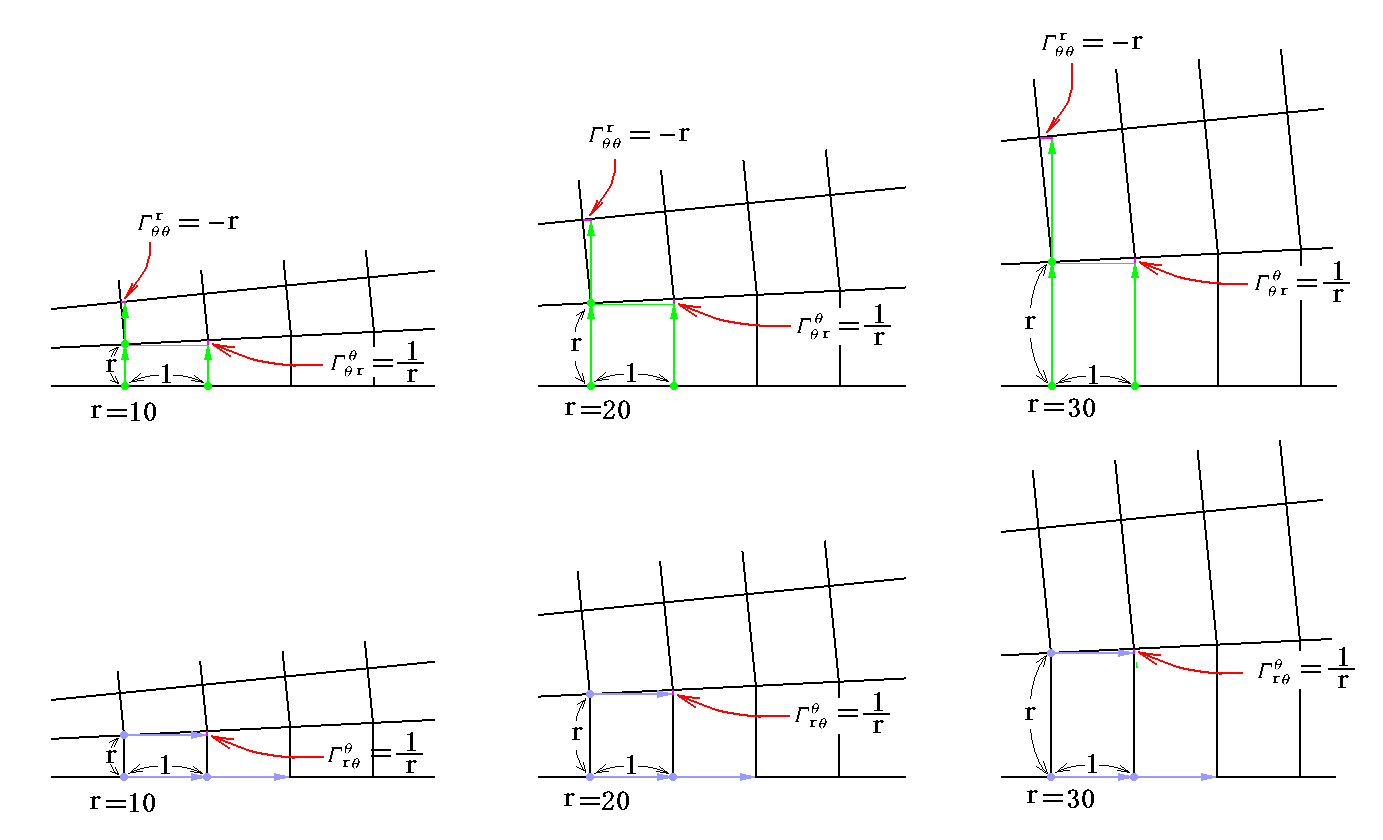
の様になります[拡大図はこちら]。
図中の基底ベクトルの変化量とクリストッフェル記号との対応は明らかでしょう。図に示されたもの以外のクリストッフェル記号成分が全て 0 に成ることも読み取れます。計量テンソルやクリストッフェル記号は場所(r,θ)と共に変わりますが、上記の様な格子を貼り合わせても平坦な空間(いまは平面)しか得られないことも明らかでしょう。
《2次元リーマン空間(球面)の球面座標》
例としてθ=π/4、π/2、3π/4付近の格子図を示します。図をご覧になれば基底ベクトルの変化の様子を示すクリストッフェル記号の意味は明らかです。下図に示されたもの以外のクリストッフェル記号成分が全て
0 に成ることも読み取れます。[拡大図はこちら]
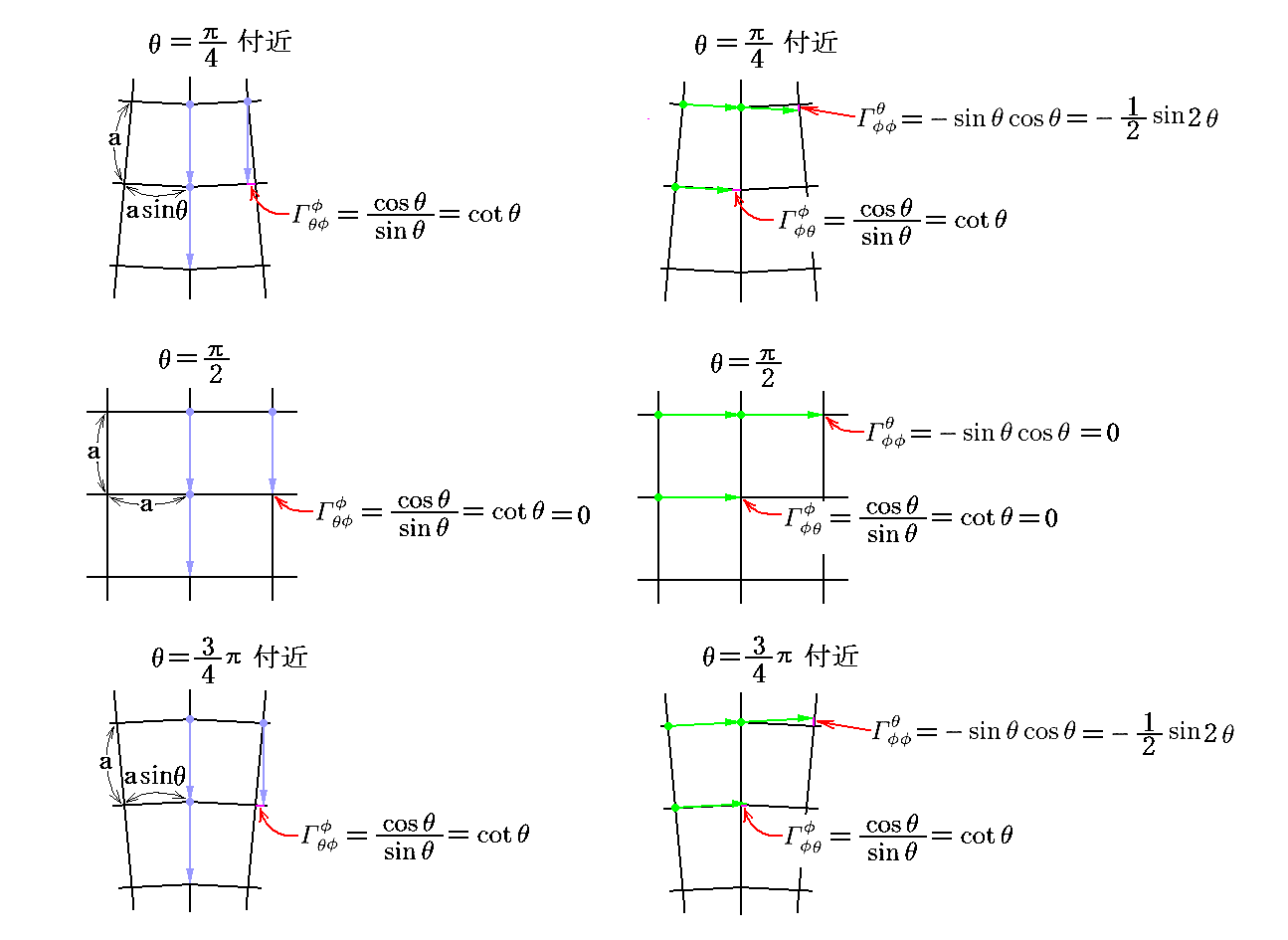
ちなみに図中の三角関数のグラフは下記の様になります。
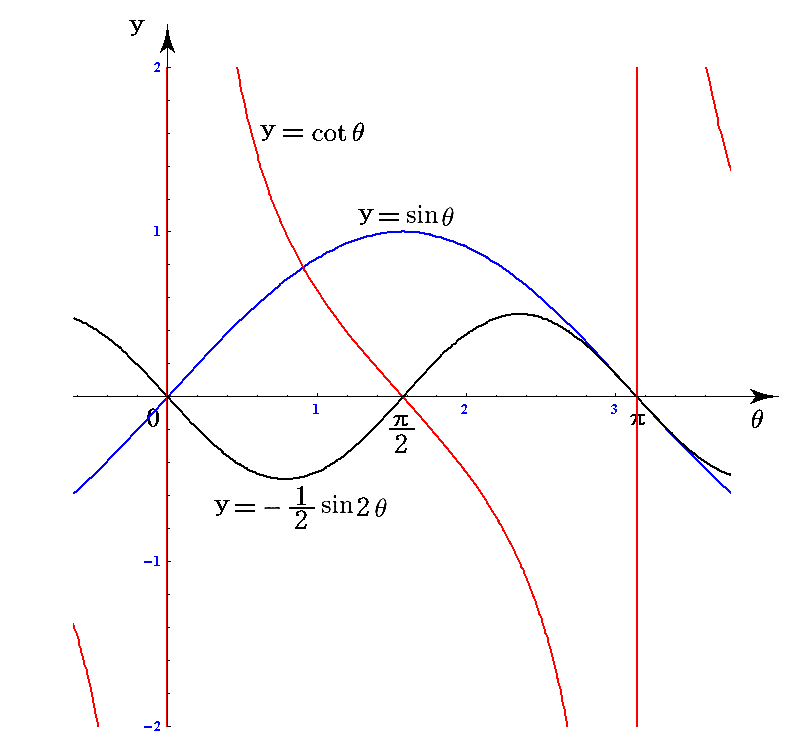
この様な格子セルを貼り合わせると曲がった空間(球面)になることは明らかです。しかも、そうなる原因はクリストッフェル記号の中に表れるθによる変化の為だということも解ります。
このとき、《第2に重要なこと》で注意したように、球面の分割線を上記の様に経線・緯線状に引く必要はありません。例えば東京に四角い測量開始の正方形を設定して、4.(2)[補足説明1]で説明した様にその四角形の一辺と同じ長さの単位棒を沢山準備して、最初に設置した四角形の四方に四辺形の網目を広げていっても良い。
もちろん網目を構成する等辺四角形はそのうち必然的に正方形では無くなりひしゃげた平行四辺形となりますが、いずれにしてもその様な四角形の網目で地球の裏側のリオデジャネイロ(ブラジル)まで地球表面を全て覆い尽くすことができます。その網目の計量テンソルを計算すれば、各地点のクリストッフェル記号と曲率テンソルは計算でき、そのことから分割した網目を繋ぎ合わせると球面となることが解ります。
[補足説明1]
くどいようですが、《第5に重要なこと》の意味をもう一度確認します。
2次元ユークリッド空間(平面)を極座標で分割した場合の計量テンソル、クリストッフェル記号、リーマン曲率テンソル(=0)を[例8]と[例9]て説明しました。
しかし、2次元ユークリッド空間(平面)ならば、極座標ではなくて正方格子状の単位セルで分割して全空間を正方形で埋め尽くすことができます。そうすれば全空間にわたって同一の計量テンソル
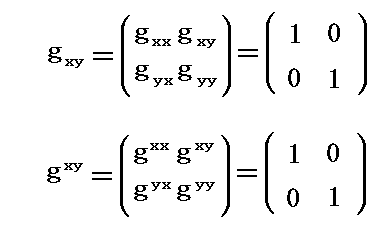
となり、クリストッフェル記号は全空間において
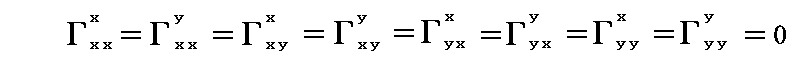
となります。そして、全ての点におけるリーマン曲率テンソルは
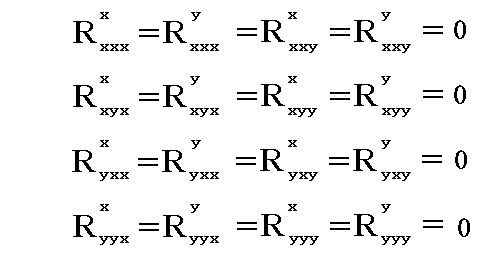
となることが直ちに解ります。
この場合全空間において基底ベクトル系と双対基底ベクトル系が一致しますので、全空間の正方格子をそのままの形を保ったまま回転させて新しい基底ベクトル系に変換しても、その空間内のベクトル成分、テンソル成分の座標値の変換に反変とか共変の様な面倒な違いは出てきません。
ところが、2次元リーマン空間(球面)では、その様な正方格子セルで全空間を埋め尽くすことはできない。局所的には正方格子セルを設定できますが、格子セルは場所の移動とともに必然的に平行四辺形セルに歪んで行きます。
歪んで行きますが、球面人は彼が住む全空間に渡って格子を設定し曲線座標を引いて分割することはできます。そして全空間の“計量テンソル”、“クリストッフェル記号”、“リーマン曲率テンソル”を測量して求めることができます。その各部分はユークリッド空間と見なせるのですから。
このことは、例えば地球の表面上のどの点に於いても、その近傍の重力を打ち消す座標変換を行うことができる事を意味します。つまり各地て、それぞれ地球の中心に向かって自由落下する座標系に乗り移れば良いのです。ただしその座標系でも端の方に行けば重力を完全に打ち消すことはできません。自由落下している系の周囲に配置した物体はやがて系の中心の方へ近付いてくるでしょうから。
つまり、局所的な無重力系はつくれても大域的な無重力系は作れないのです(。ランダウ、リフシュツ「場の古典論」第10章§81〜82参照)。このように部分的には重力は消せても他のところに必然的に重力が存在するようにならざるを得ないことは重力によって時空間が曲がっているという事を強く示唆します。
[補足説明2]
前記[補足説明1]の最後の文節について補足します。
太陽の周りの空間は太陽質量(太陽の重力場)のために歪んでいますが、宇宙空間に網目を現実に引くことはできません。もしそれができたら、2.(6)[補足説明]で説明したb)の立場を実行できたことになります。
そのため皆既日食の時に太陽の側を通過してくる光線の曲がり具合や、太陽表面や白色矮星表面からやってくる光線のスペクトル波長の赤方偏移などから間接的に時空の歪みを知ることになります。これが2.(6)[補足説明]で説明したa)の立場です。
(ここの説明はとても解り難いと思います。このことに関しては別稿「Sommerfeld著「電磁気学」§38の[補足説明]をご覧下さい。)
実際のところアインシュタインもその様にして空間の歪みを確かめたのです。アインシュタインは物質(エネルギー)の存在が空間(正確には時空)を歪める事を発見した。そして、ついに1915年11月25日、物質(エネルギー)の分布と時空の歪みを関係づける方程式(“重力場方程式”)を求めることができた[実際のところ、1912年秋の段階から更に3年の歳月を要したのですが]。アインシュタインが求めた方程式は、両者の関係を与える方程式としては最も簡明(テンソル方程式なので理解するのは難しい)なものでしたが、今のところその正しさを疑わせる実験・観測結果は存在しないので現在でも正しいと思われています。
いずれにしても、その方程式を得ることができたアインシュタインは、現実の太陽系の太陽質量や重力場の分布は解っていますから、その方程式をつかって太陽系の空間の歪みを計算できます。そして彼は、その歪んだ空間が水星軌道の近日点移動を生じさせる事を計算で示すことができたのです。それは長い間謎だった100年当たりの近日点の移動角度(43”)を数値的にも極めて正確に導き出せたので、確かに太陽近傍の空間が歪んでいることが間接的に実証されたのです。
[Paisは著書「神は老獪にして・・・」p331に“この発見(43”を導けたこと)は、アインシュタインの科学者としての生活において、いやおそらくは一生涯で、何といっても最も強く感動した経験であった、と私は思う。”と書いていますが、正にそうだったでしょう。Sommerfeld宛の書簡(1915年11月28日付)参照。アインシュタインはエーレンフェスト宛の書簡(1916年1月17日付)で、その感激の様子を具体的に伝えています。]
また、太陽近傍を通過する光線の曲がる量も特殊相対性理論(この理論は光子が質量を持つことを示している)から予想される量の2倍だったことから時空間が曲がっている事が裏付けられた。星の表面から来るスペクトル線の赤方偏移からの確認は、その観測の難しさと現実の白色矮星の質量と半径の見積の難しさからかなり年月を要しましたが現在では完全に裏付けられています。
[この当たりはSommerfeld著「電磁気学」§38の説明が秀逸ですので、是非ごらん下さい。]
さらに最近では重力波の直接観測からも裏付けられている。
3.3次元リーマン空間のクリストッフェル記号 [目次へ帰る] [節先頭へ]
ここで、3次元リーマン空間でのクリストッフェル記号の例を示す。
27個の “クリストッフェル記号” Γkij の内、下付き添字ijを入れ替えたものは互いに等しいから、定義式
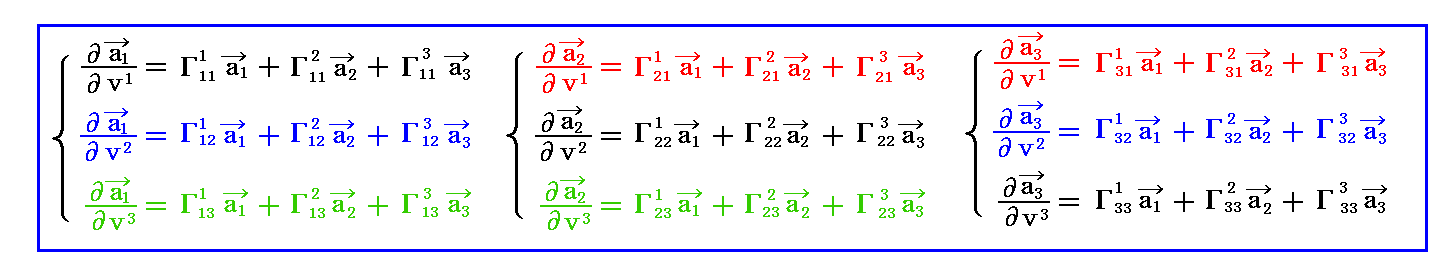
において
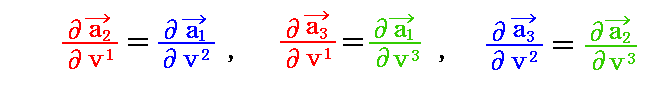
が成り立ちます(このことについては4.(4)1.[注意]参照)。
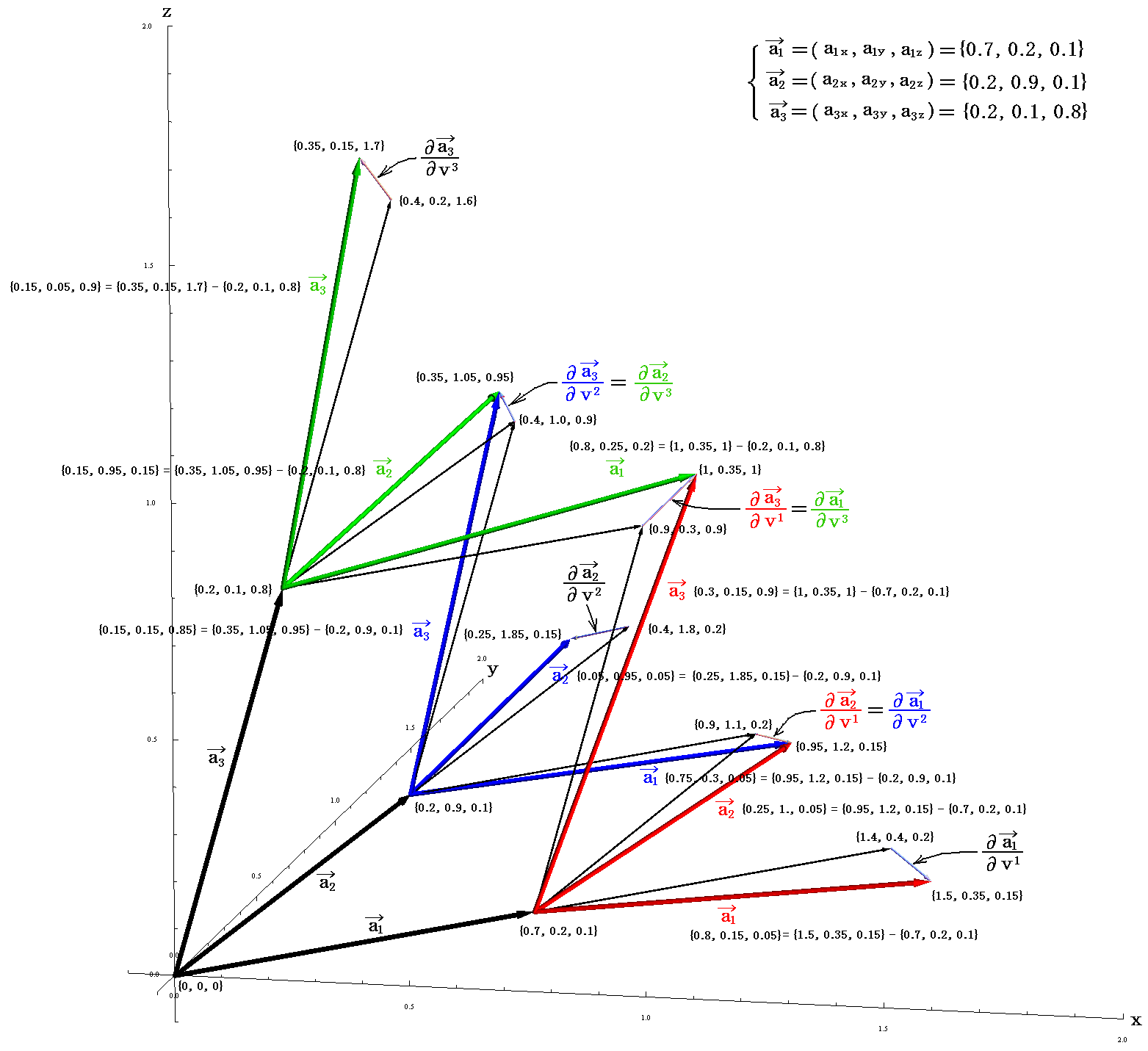
[例10]
下図は2.(2)[例1]で用いた“基底ベクトル”、 a1、a2、a3 とそれに隣接する基底ベクトル系、 a1、a2、a3 、 a1、a2、a3 、 a1、a2、a3 の状況を示している。
隣接する基底ベクトル系に添字を付け加えて区別すると図が錯綜するので、ここでは色分け(赤、青、緑)でそれぞれの基底ベクトル系を区別している。また元になるa1、a2、a3 は、2.(2)[例1]の図とは色を変えて、黒色矢印で示してある。a1、a2、a3 をそれぞれの方向に延長移行したものが、図中の黒色細矢印です。また、図では双対基底ベクトル系の矢印は省略しているが、もちろん各基底ベクトルから同様に定義できる。[拡大図]
図がかなり錯綜していて解りにくいが、図中の数値は3次元ユークリッド空間(x,y,z)の座標値です。2.(2)[例1]で用いた“基底ベクトル”、 a1、a2、a3
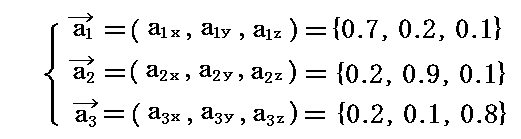
と、それに隣り合った基底ベクトル系、 a1、a2、a3

と、基底ベクトル系、 a1、a2、a3
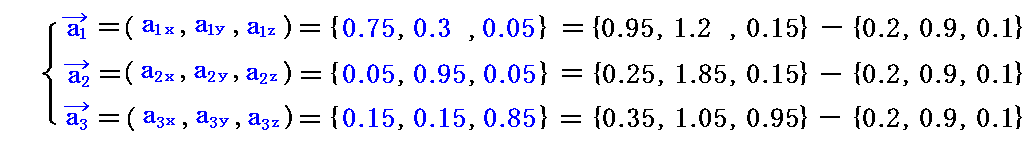
と、基底ベクトル系、 a1、a2、a3
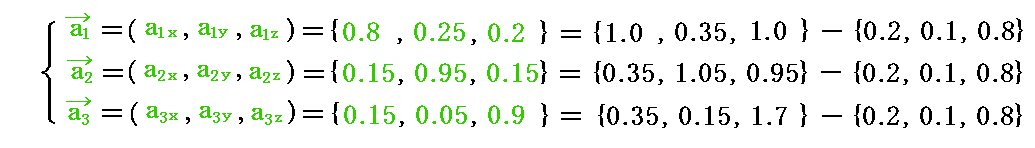
の状況を示している。
これらの隣接する基底ベクトル系の座標値の変化量は適当に仮定したもので、図中にも書き込んであります。もちろんこれらの座標値を用いるのではなくて、直接基底ベクトル、 a1、a2、a3 、 a1、a2、a3 、 a1、a2、a3 の長さとそれらの交叉角をユークリッド空間での物指しと分度器で測定したと仮定して適当に与え、それらか2.(6)の手順を逆にたどって各基底ベクトル格子の計量テンソルを求めても良い。大事なのは隣り合った基底ベクトルセルが作る格子の計量テンソルが与えられている事です。
ここで取り上げた基底ベクトルの測定値は3次元リーマン空間中に任意に引かれた分割曲線に沿って測定していることに注意して下さい。その分割線は、《第2に重要なこと》で説明したように、どのように引かれた分割曲線を採用しても良い。上図の値はたまたま採用した分割曲線に沿っての3次元ユークリッド曲線での測定値です。《第1に重要なこと》で注意したように、3次元リーマン空間の任意の点は3次元ユークリッド空間であると見なせるのでした。これこそがアインシュタインが、ガウスの曲面論から、気付いた最も重要ことです。
27個のクリストッフェル記号がどの変位に対応するか下図に示す。[拡大図]
それぞれのクリストッフェル記号が表す変位成分は元の“基底ベクトル”、 a1、a2、a3 に沿った方向であることを注意。また、4.(4)1.[補足説明1]で注意したように“基底ベクトル”、 a1、a2、a3 だけ変位したときの変位の大きさです。
さらに、変位の大きさの数値は“基底ベクトル” a1、a2、a3 の長さを単位として与えられている。このことは、実際にクリストッフェル記号の数値を計算してみれば解る。
それを実行するために基底ベクトル系、 a1、a2、a3 、 a1、a2、a3 、 a1、a2、a3 の格子セルの計量テンソルを求める。それぞれの計量テンソルは、2.(4)[例4]と同様に、その定義に従って求めれば良い。
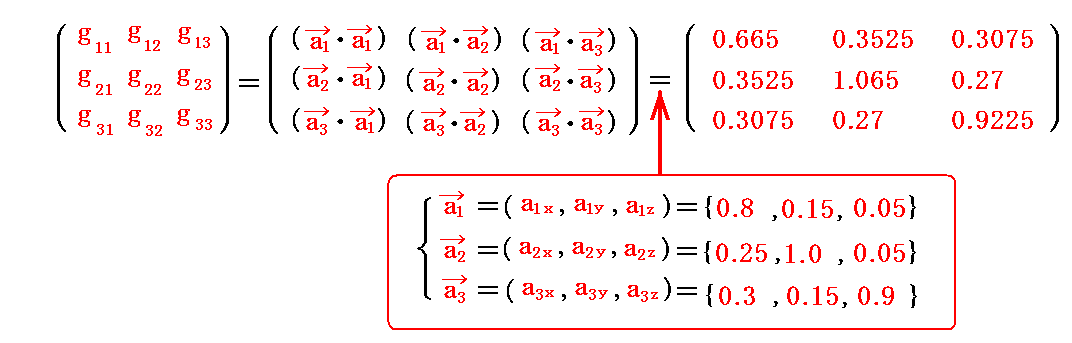
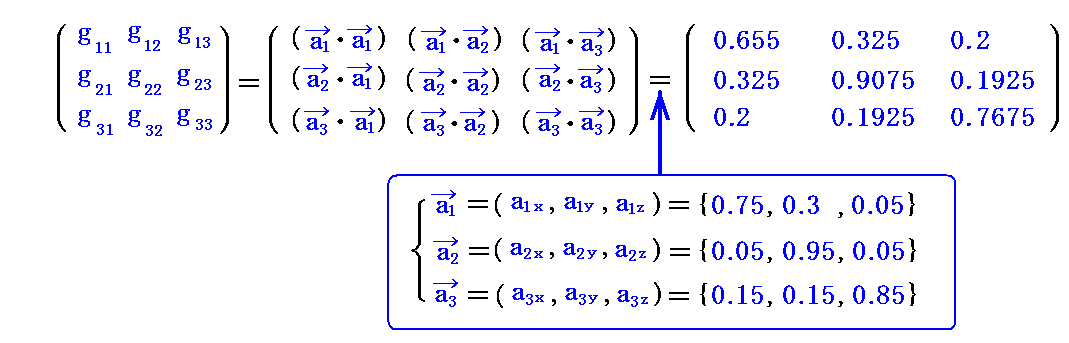
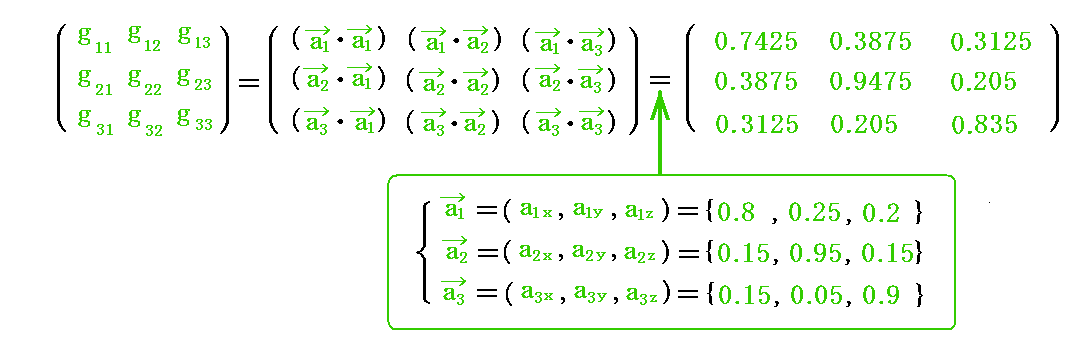
ここで求めた計量テンソル gij を用いれば2.(6)の手順により、基底ベクトル、 a1、a2、a3 、 a1、a2、a3 、 a1、a2、a3 のそれぞれの長さと互いの交叉角を計算できます。もちろんそれは、最初に与えた(x,y,z)座標値からベクトルの内積公式を用いても直接計算できます。
ここで、27個のクリストッフェル記号と計量テンソルとの関係式を全て書くと
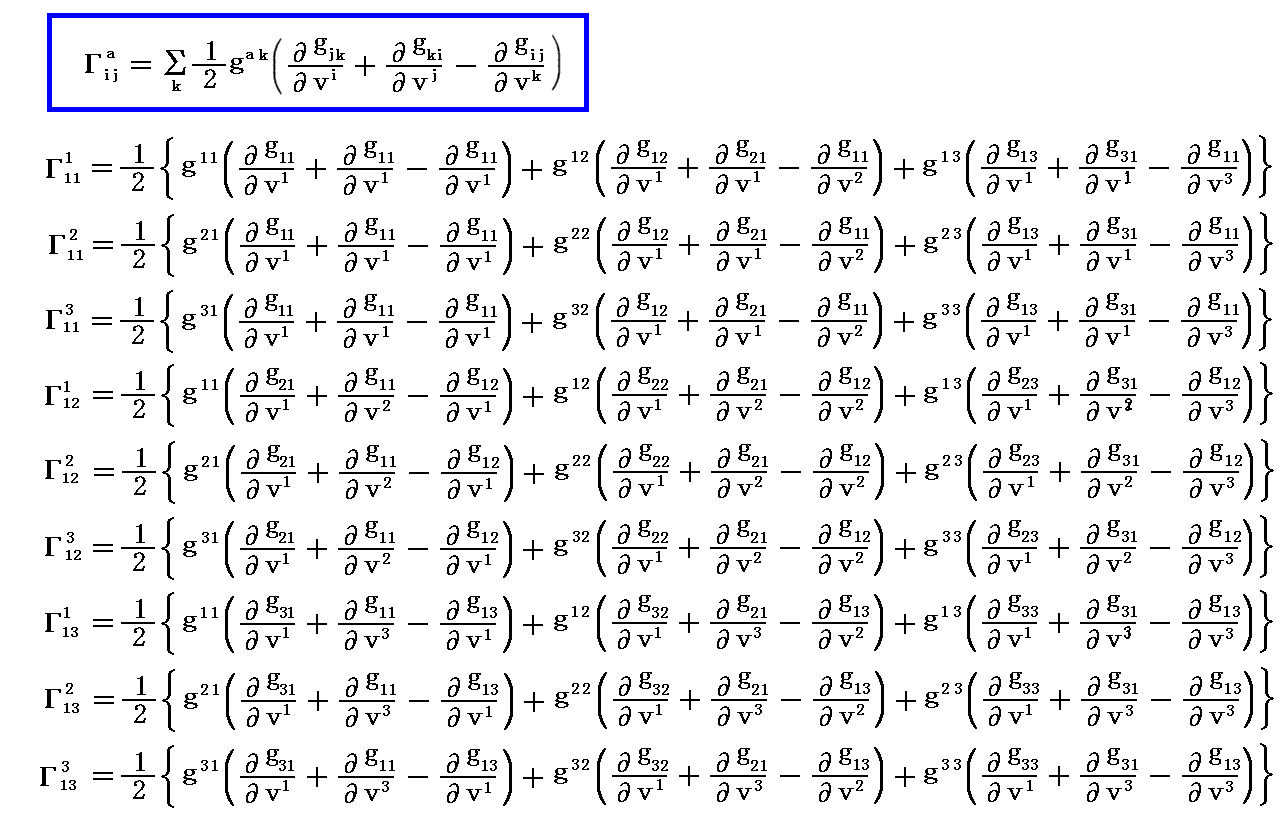
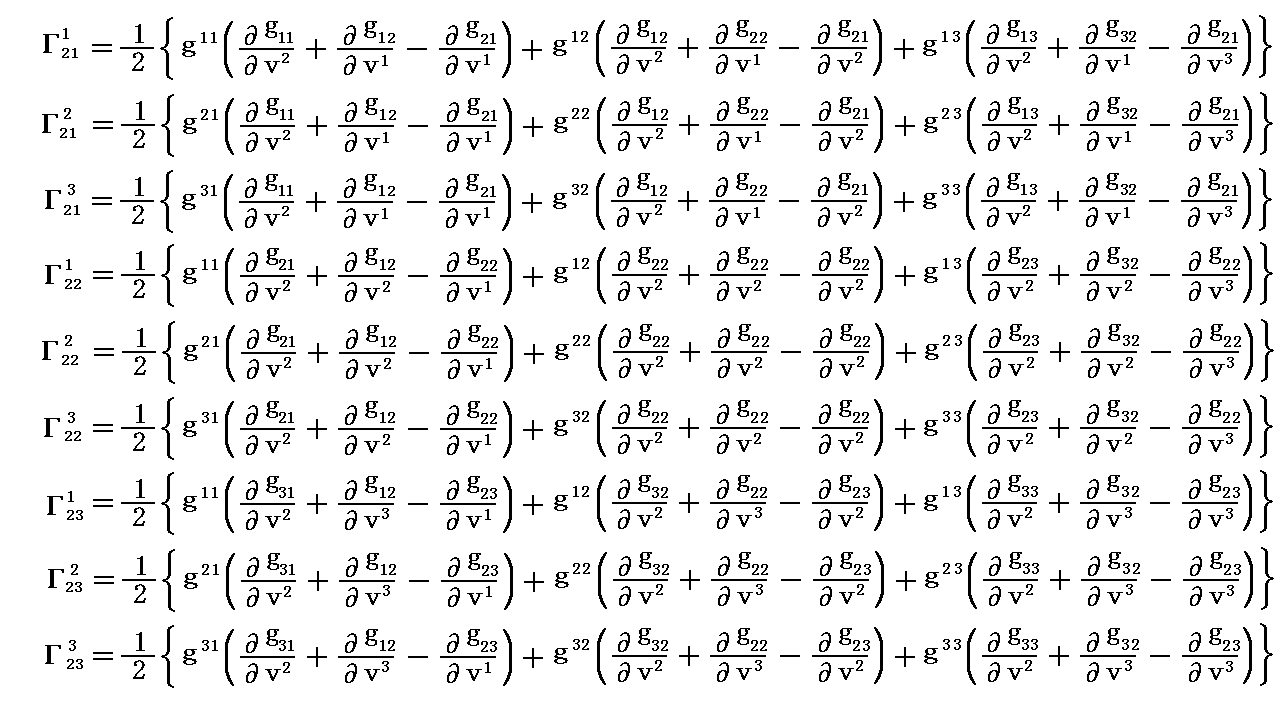
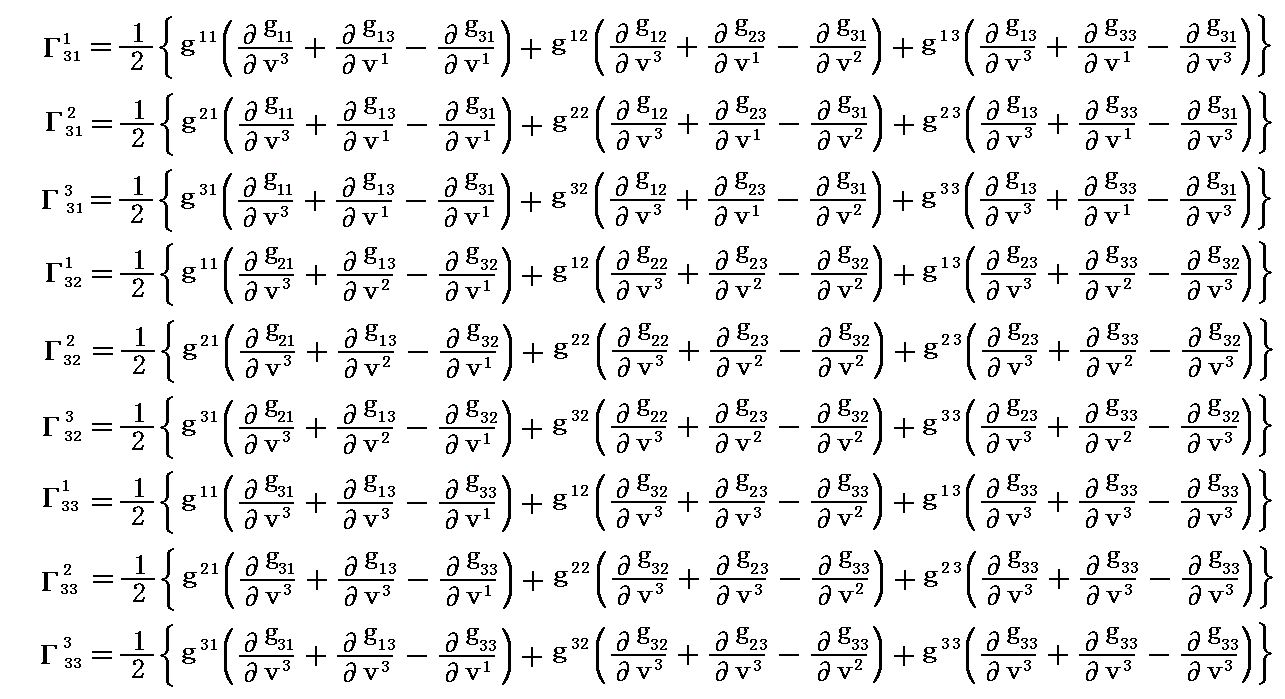
となります。
式中の基本計量共変テンソルgij は、もちろん原点における基底ベクトルから2.(4)[例4]の手順で求めた
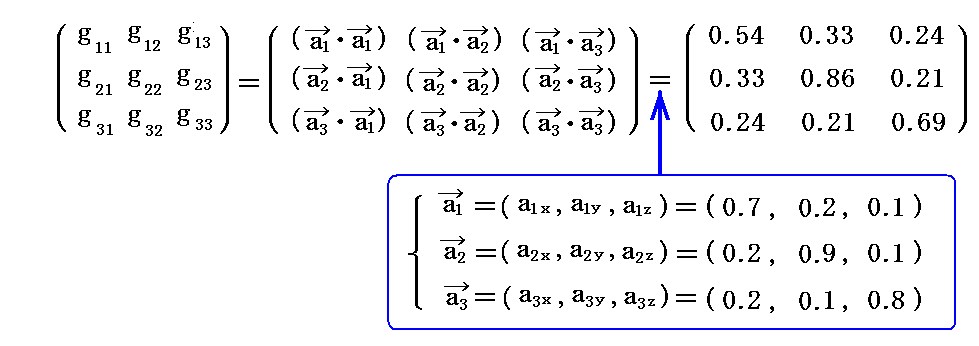
です。
また、基本計量反変テンソルgij は、2.(2)[例1]で求めた原点における双対基底ベクトルに対して2.(4)[例4]の手順を適用した
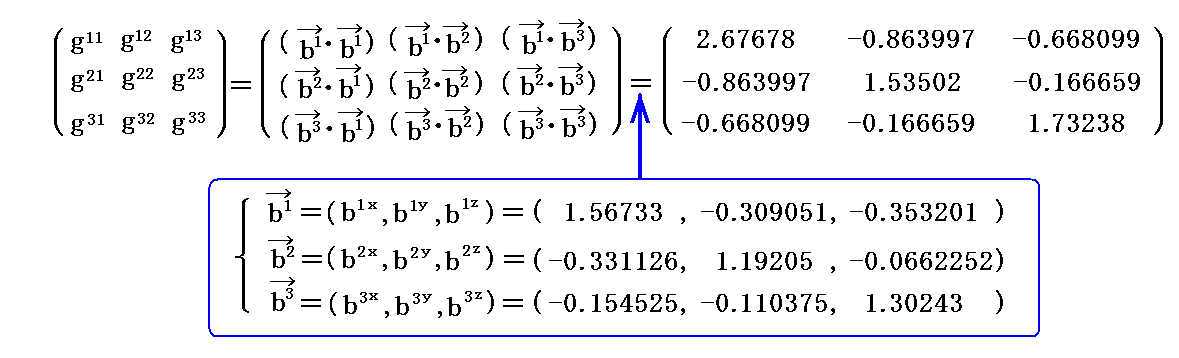
です。
また、基本計量共変テンソル gij の v1 による偏微分係数 は、v1 が基底ベクトル a1 を単位とした座標値である事を考慮すると
は、v1 が基底ベクトル a1 を単位とした座標値である事を考慮すると
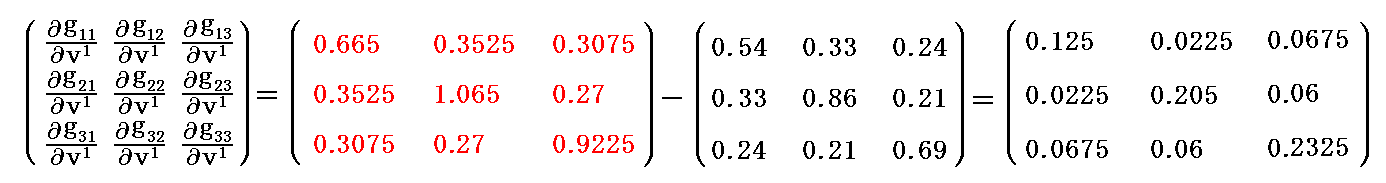
となる。同様に基本計量共変テンソル gij の v2 による偏微分係数 は、v2 が基底ベクトル a2 を単位とした座標値であるから
は、v2 が基底ベクトル a2 を単位とした座標値であるから
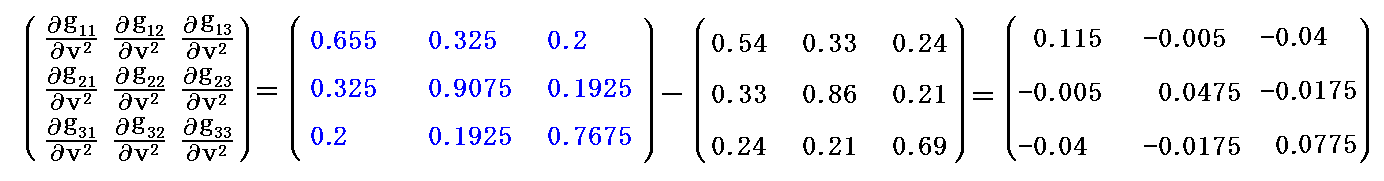
であり、基本計量共変テンソル gij の v3 による偏微分係数 は、v3 が基底ベクトル a3 を単位とした座標値であるから
は、v3 が基底ベクトル a3 を単位とした座標値であるから
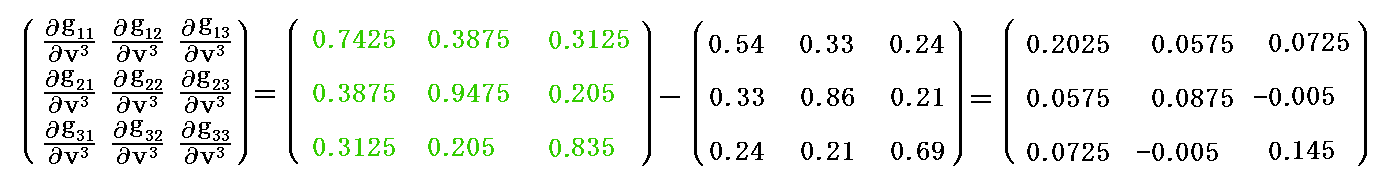
となります。
これらの値を前記のクリストッフェル記号の計算式に代入すると

が求まる。この計算はMathematicaのような数式処理ソフトを用いないと面倒ですが、とにかく前図の変位量に相当する値が得られる。
このとき、27個の “クリストッフェル記号” Γkij の内、kが同じで下付き添字ijを入れ替えたものは互いに等しくなっていることに注意されたし。だから3次元リーマン空間では独立なものは3×6=18個です。
(一般相対性理論の4次元時空では、ijの対称性からijに関して独立なものは10個ですからそれにkの取り得る4を乗じた4×10=40個となります。)
図上で比較すると変位量は基底ベクトルの大きさを単位として与えられていることが読み取れます。
4.双対基底ベクトルとクリストッフェル記号 [目次へ帰る] [節先頭へ]
4.(4)1.で説明したように、クリストッフェル記号は“基底ベクトル”の場所的な変化に伴う変分を表す係数として

で定義された。
同様な思考によって、“双対基底ベクトル”の場所的な変化に伴う変分を表す係数として
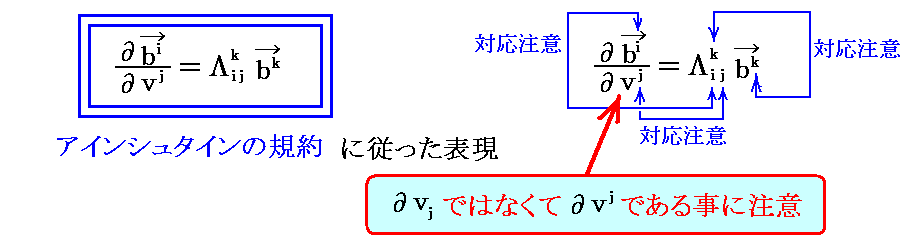
で定義されるΛkij(ラムダ)が考えられる。
ここで、変化量は座標曲線に沿った方向(すなわち “基底ベクトル”aj の接線方向)の変化で考えていることに注意されたし。“双対基底ベクトル”の接線方向は座標曲線の方向とは異なりますので、双対基底ベクトルの接線方向の変化に伴う変位を考えても意味が無いからです。
このことは、“共変微分”を考えるとき反変座標 vj の微分のみが取り上げられ、共変座標 vj に関する微分が必要とされることが無い理由でもあります。
また、このことがベクトルやテンソルの“共変微分係数”は、元のベクトルやテンソルの共変階数が一つ増えたテンソルになる理由でもあります。
いずれにしても《係数 Λkij(ラムダ) の添字 i は双対基底ベクトル bi の変化の様子を表す係数であり、添字 j はその係数が基底ベクトル aj 方向の変位に関係しており、添字 k は双対基底ベクトル bk 方向の変位成分を表している》
ところで、“基底ベクトル”ai と “双対基底ベクトル”bi には2.(1)で示した関係
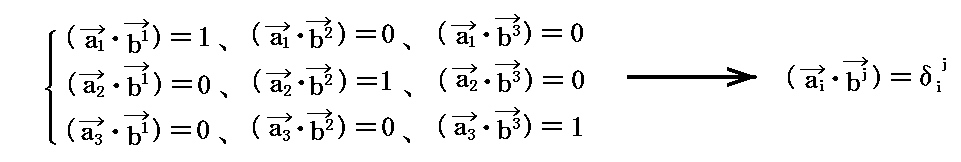
が有るのですから、Λkij は Γkij の関数として表されるはずです。その関係式は上式を用いれば簡単に判明する。
上式の両辺を vk で偏微分すると
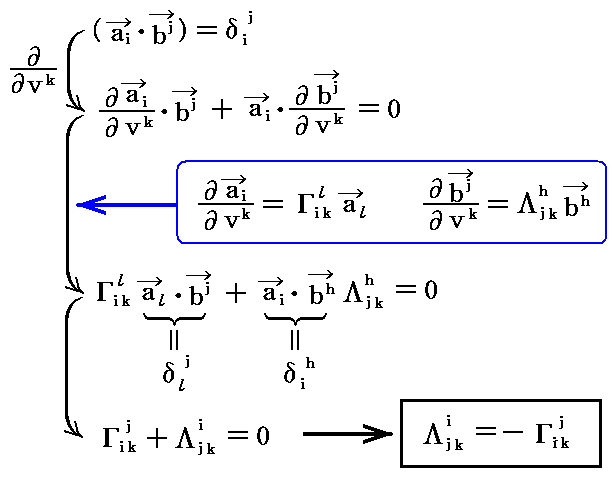
が得られる。
故に
となる。
つまり、双対基底ベクトルの変化の様子を表す係数は、基底ベクトルの変化の様子を表す係数(クリストッフェル記号)と表裏一体の関係によって決まっている。そうなることは、当然予想されることです。
上記の双対基底ベクトルに関するクリストッフェル記号の状況を[例10]の図と同様な形で確認しておくことを勧めます。
すなわち、2.(2)の[例1]の図で、まず赤矢印で示した双対基底ベクトルb1,b2,b3のセットをそれぞれ基底ベクトルa1,a2,a3の先端の位置にコピーします。
次に、4.(4)3.の[例10]で求めた[例10]の図中の基底ベクトルa1,a2,a3の先端における変化した基底ベクトルのセット、 a1、a2、a3 、 a1、a2、a3 、 a1、a2、a3 の双対基底ベクトルを2.(1)の手順によりそれぞれ求めます。
それを仮にb1、b2、b3 、 b1、b2、b3 、 b1、b2、b3 として、先ほどの図の基底ベクトルa1,a2,a3の先端に重ねて描きます。図が錯綜するので、これらの双対基底ベクトルのセットb1、b2、b3 、 b1、b2、b3 、 b1、b2、b3 は上図には記していませんが、それらは先ほどコピーした双対基底ベクトルb1,b2,b3のセットから少し変化したものになります。
そして、先ほどコピーしたb1,b2,b3のセットとb1、b2、b3 、 b1、b2、b3 、 b1、b2、b3 のベクトルとの差分が上記のクリストッフェル記号のそれぞれの指数に対応するものによって表現されるのだということを確認して下さい。
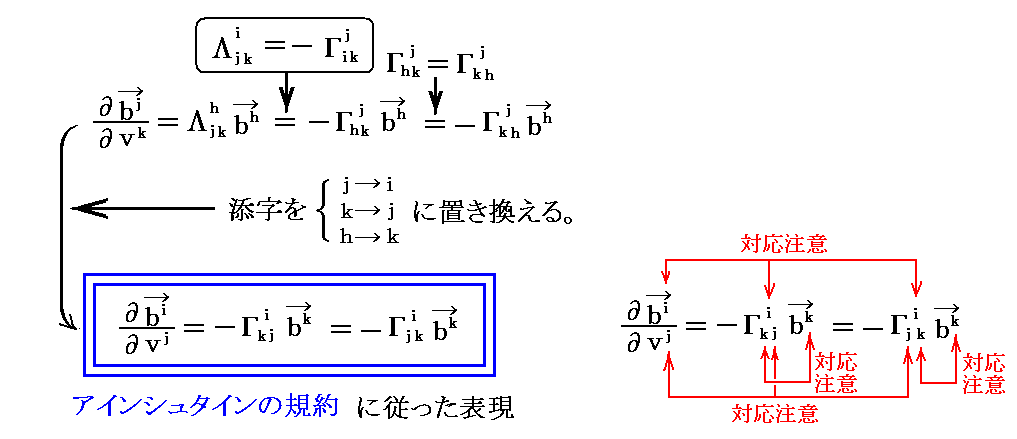
そのとき《係数 Λijk の添字 j は双対基底ベクトル bj の変化の様子を表す係数であり、添字 k はその係数が基底ベクトル ak 方向の変位に関係しており、添字 i は双対基底ベクトル bi 方向の変位成分を表している》
だから

の対応関係から解る様に、それは《係数 Γjik の添字から解る基底ベクトル ai の変化の様子を表し、その変化が基底ベクトル ak 方向の変位によるものであり、基底ベクトル aj 方向の変位成分を表している変分(Γjik)と大きさが等しく方向が反対向きの変分》 に相当します。
上記の関係式は4.(5)5.で “共変ベクトル” の “共変微分係数” を求めるときに用います。
(5)共変微分とは何か
3次元リーマン空間中に分布するベクトル場 w を例にして“共変微分”について説明します。これは4.(3)[補足説明3]で説明した内容の具体的説明です。
1.基底ベクトルの変分 [目次へ帰る]
4.(4)1.の最初に説明した基底ベクトルの変分に偏微分係数を代入して変形すると

となります。
4.(4)で説明したクリストッフェル記号は基底ベクトルの長さだけ移動したときの基底ベクトルの変化分を表すものでしたが、上記の変分ベクトル da1,da2,da3 はベクトル量 dv=(dv1,dv2,dv3) だけ移動した点の基底ベクトルの変化分を表しています。
式が複雑なのでその意味が読み取りにくい。そのため[例11]で具体的に説明します。
[例11]
2.(2)[例3]で説明したベクトル v=(dvx,dvy,dvz)=(1.4,1.5,1.7) を移動量 dv=(dv1,dv2,dv3) =(1.13024,1.21192,1.83223)と見なして、[例10]の隣接計量テンソルの変化での、基底ベクトルの変分 da1,da2,da3 を求めてみます。計算が面倒なのでMathematicaを利用します。



つまり、ベクトルdv=(dv1,dv2,dv3) だけ移動した点の基底ベクトル a1、a2、a3 は、原点に於ける基底ベクトル a1、a2、a3 に上記の変分ベクトル da1,da2,da3 をベクトル的に加算したものになります。
ただし、上記の変分ベクトルの成分は基底ベクトル a1、a2、a3 を単位として与えられているので、今後の計算をスムーズにするために(x,y,z)座標系での単位ベトクル ex,ey,ez での成分表示に直す。そうすることが可能なのは、斜交座標と言えども、3次元リーマン空間の各点での接ユークリッド空間中での座標にほかならないからです。
まず、基底ベクトル a1、a2、a3 を(x,y,z)座標系の単位ベトクル ex,ey,ez で表示すと、2.(2)[例1]の値から
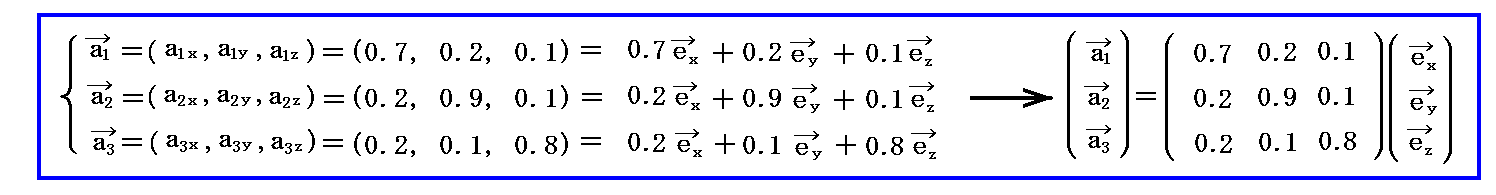
となります。
これを前記の式に代入すると

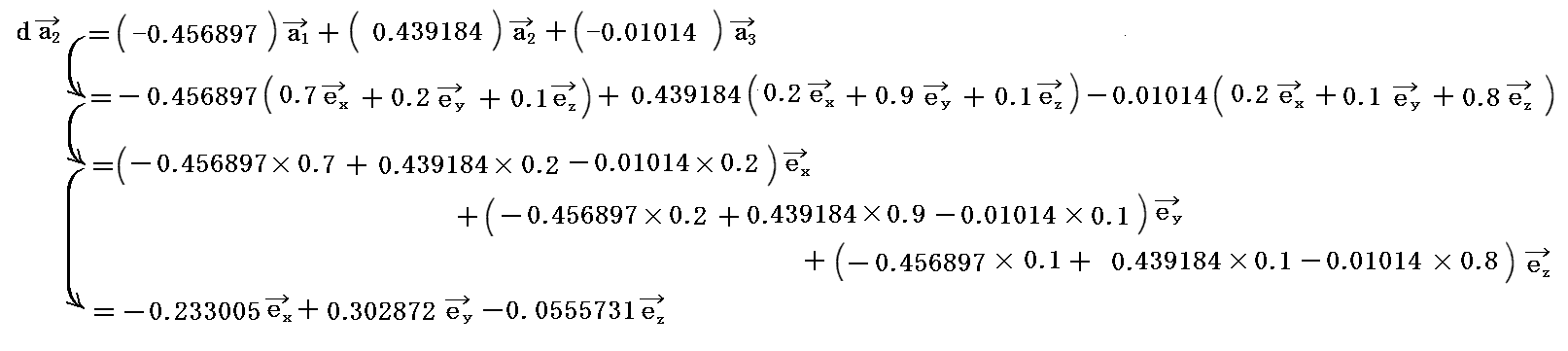
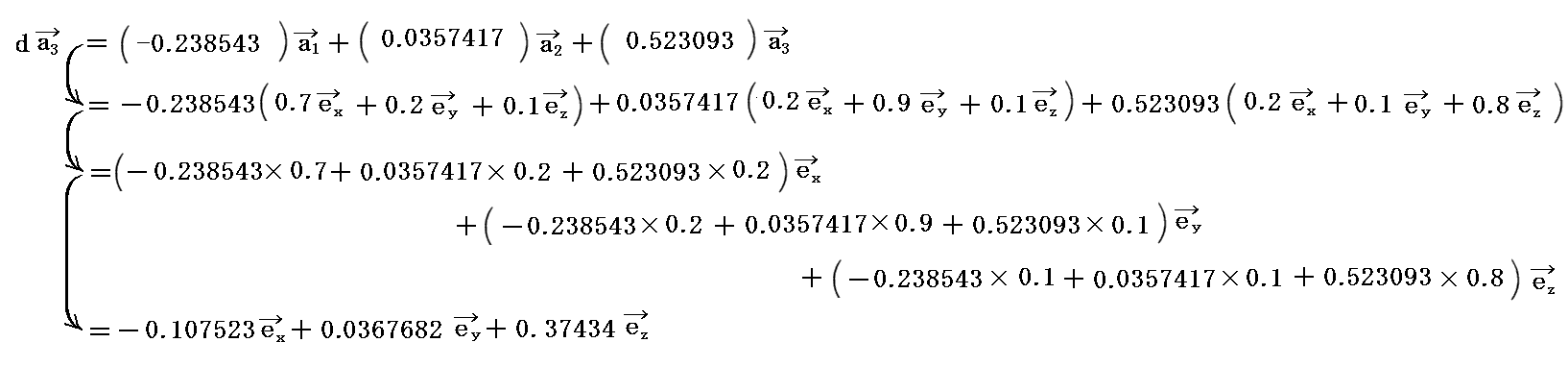
が得られる。
これの変分ベクトル da1,da2,da3 を原点に於ける基底ベクトル a1、a2、a3 に加えると、ベクトルdv=(dv1,dv2,dv3) だけ移動した点の基底ベクトル a1、a2、a3 は
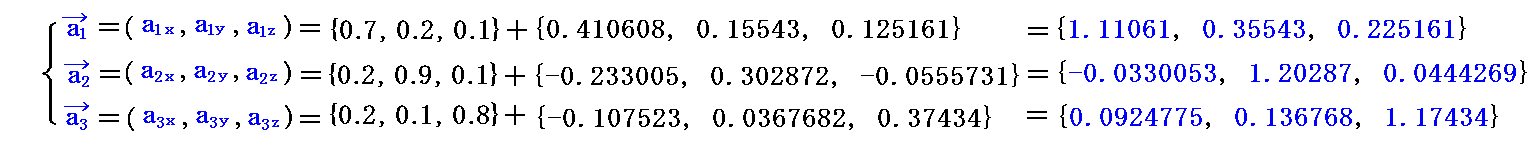
となる。
この値を用いれば、ベクトルdv=(dv1,dv2,dv3) だけ移動した点の双対基底ベクトル b1、b2、b3 は2.(1)の手順
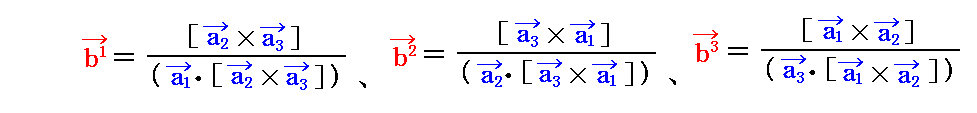
に従って直ちに求まり
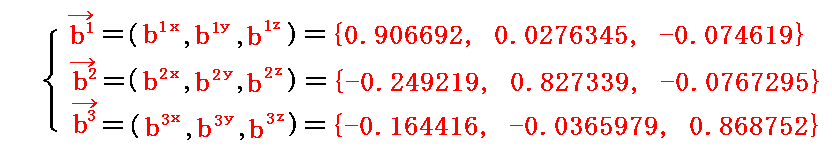
となる。
2.(2)[例1]の原点に於ける基底ベクトル a1、a2、a3 と双対基底ベクトル b1、b2、b3 の図に、dvだけ変位した点の基底ベクトル a1、a2、a3 と双対基底ベクトル b1、b2、b3 を重ねて表示すると下図のようになる。変位量dvは2.(3)[例3]の図の v を dv に変えて表示してあります。
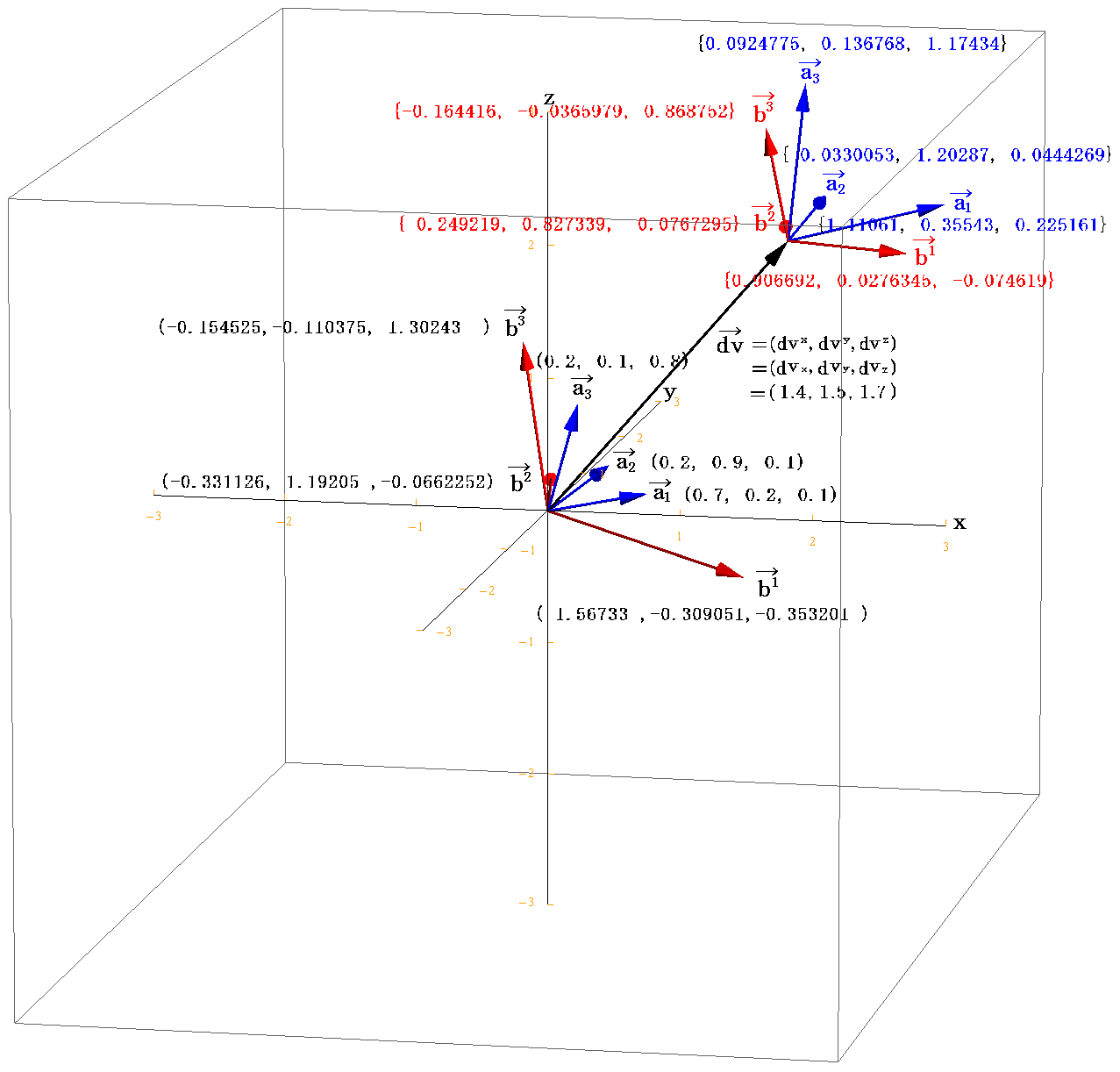
図中の座標値は3次元ユークリッド空間(x,y,z)の座標値である事に注意。
前項の図で示した3次元リーマン空間に、ベクトル場 w が分布しているとする。そのベクトル場の場所的な変化の様子を具体的な例で説明する。
[例12]
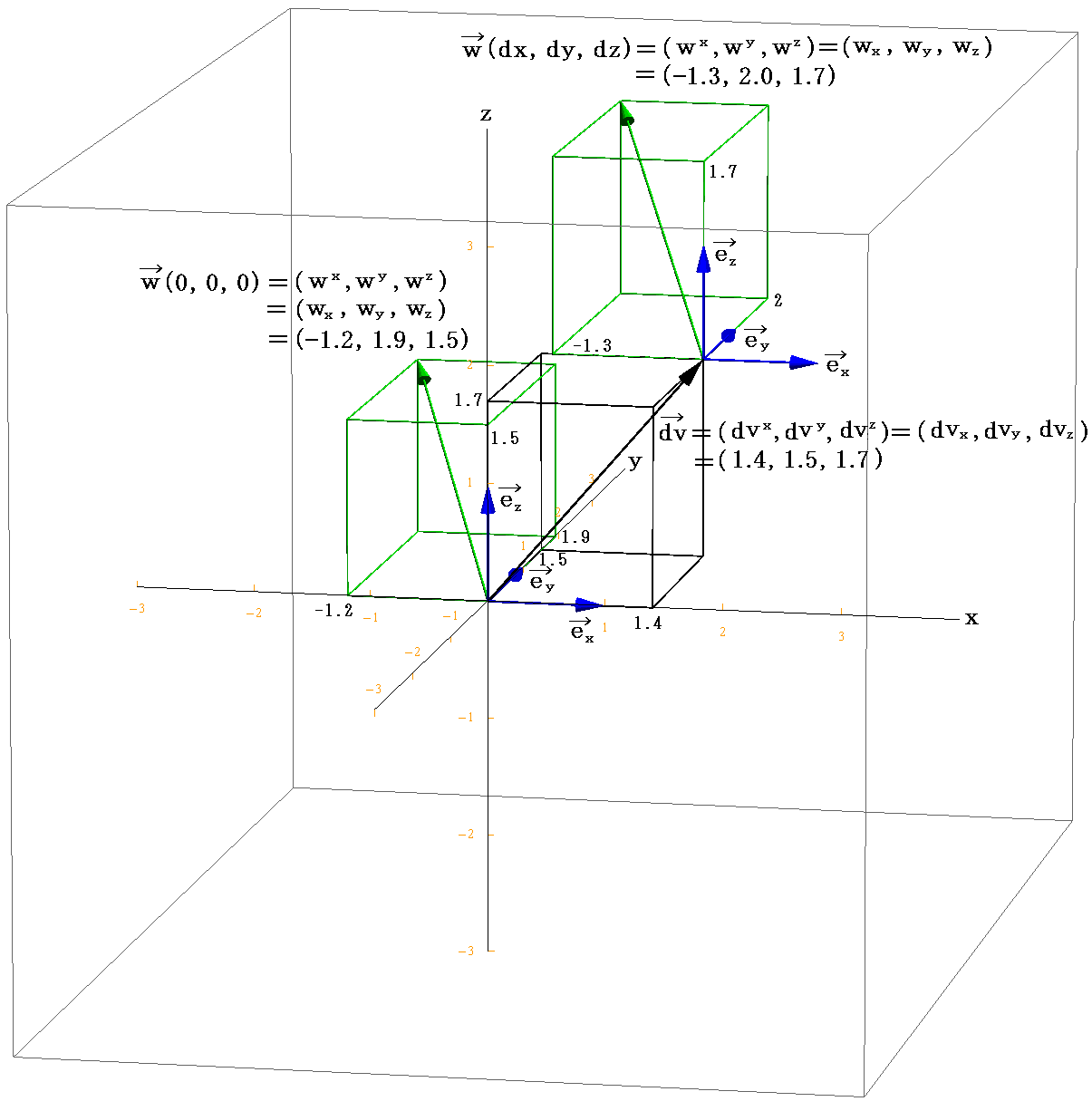
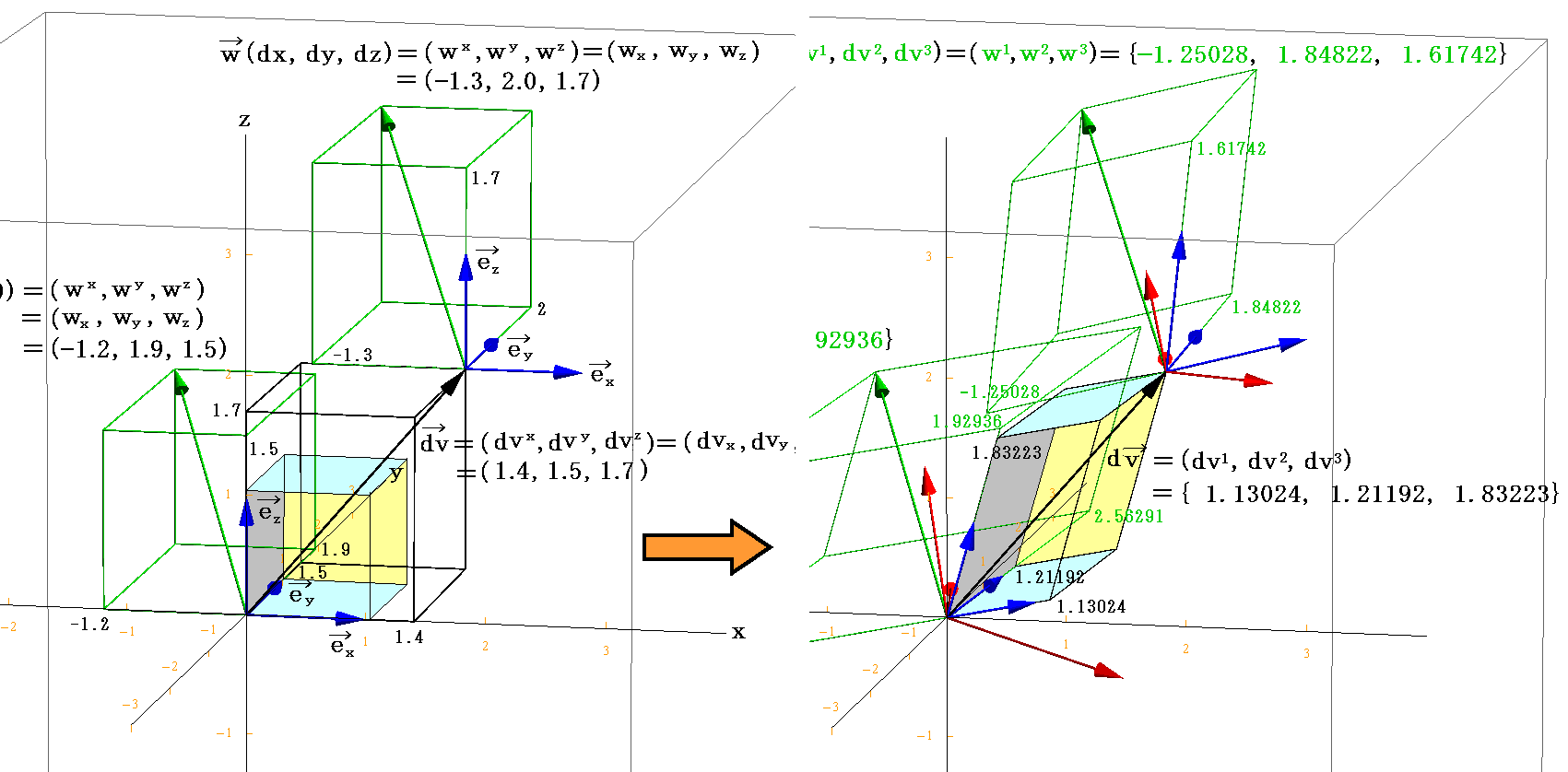
原点の w(0,0,0)を (wx,wy,wz)=(-1.2,1.9,1.5) とし、 dv だけ変位した点の w(dv1,dv2,dv3) を(wx,wy,wz)=(-1.3,2.0,1.7) と仮定する。原点の w(0,0,0) は2.(5)[例5]で取り上げた w と同じにして、dv だけ変位した点のw(dv1,dv2,dv3)をそれから少し変えてあります。
それらのベクトルをガウス座標値と一緒に図示すると

となります。図中の座標値は基底ベクトル系(a1,a2,a3)を単位とした座標値である事に注意。
図中の変位ベクトル dv のガウス座標 {1.13024, 1.21192, 1.83223} と ベクトル w(0,0,0) のガウス座標 {-2.99779, 2.56291, 1.92936} は原点における 双対基底ベクトル b1、b2、b3 から求めていますが、これは2.(5)[例5]で説明したものと同じです。また、dv だけ変位した点のベクトル w(dv1,dv2,dv3) のガウス座標 {-1.25028, 1.84822, 1.61742} は、dv だけ変位した点の 双対基底ベクトル b1、b2、b3 から2.(3)で説明した手順
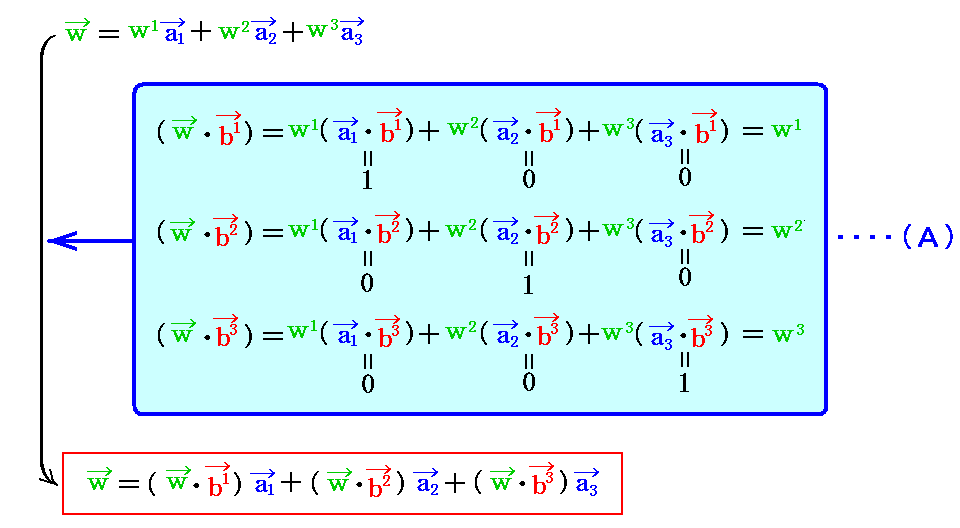
に従って求めています。そのとき、(v・bi)や(w・bi)の計算に必要なv、w、biの座標値はユークリッド座標(x,y,z)でのものです。
4.(3)で説明した《第2に重要なこと》に従うと、3次元リーマン空間を分割する網目はどのように引いても良いのでした。局所的には正方格子状に網目を引くことができます。
これは、[3次元リーマン空間]中の1点におけるユークリッド的“接空間”である[3次元ユークリッド空間]です。これを一般相対性理論の場合に当てはめると、[4次元リーマン時空]中の1点における擬ユークリッド的“接空間”である[Minkowski時空]に相当します。このことは4.(6)でもう一度説明します。
実際、上記の基底ベクトル a1、a2、a3系から

によって新しい基底ベクトルex,ey,ez系に変換すると正方格子状の座標系に変換できます。
この変換式は3.(1)で示した基底ベクトル系a1、a2、a3の変換式

の一例ですが、これは2.(2)1.[例1]で最初に仮定したex,ey,ez系からa1、a2、a3系への変換式
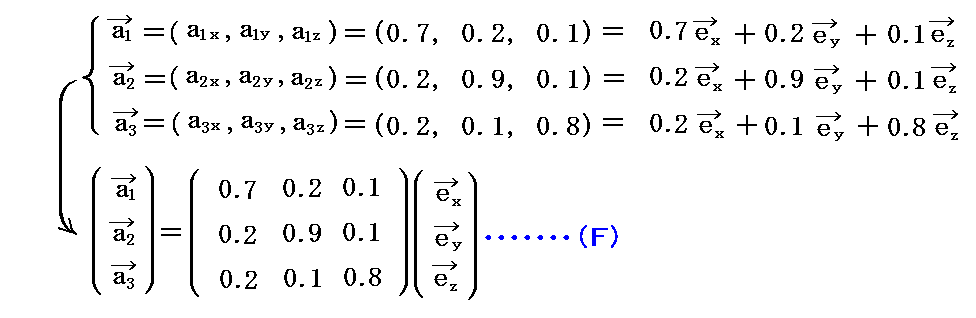
の逆変換に相当します。これは正に3.(1)で説明した“基底ベクトル”の変換式(C)式とその逆変換の関係です。
実際、(E)式と(F)式の変換係数行列を乗じると単位行列になりますので互いに逆行列の関係である事が解ります。
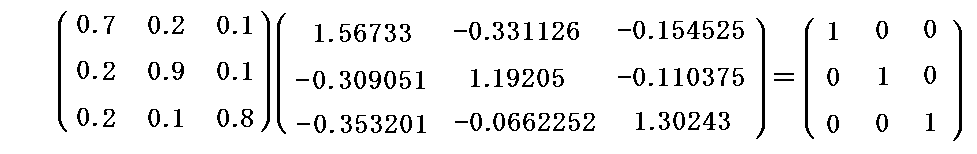
所で、(E)式の変換行列は2.(2)1.[例1]で求めた双対基底ベクトル b1、b2、b3 の(x,y,z)座標表現式
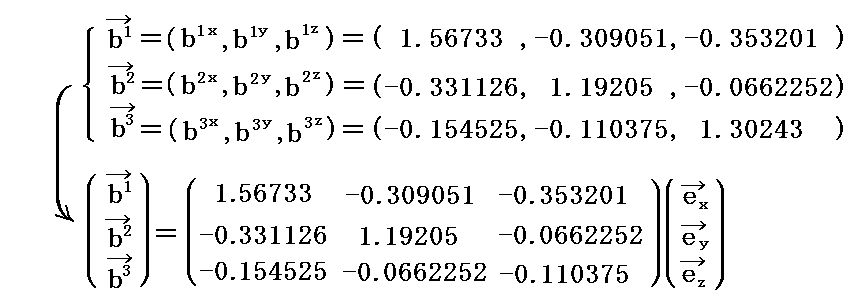
の転置行列
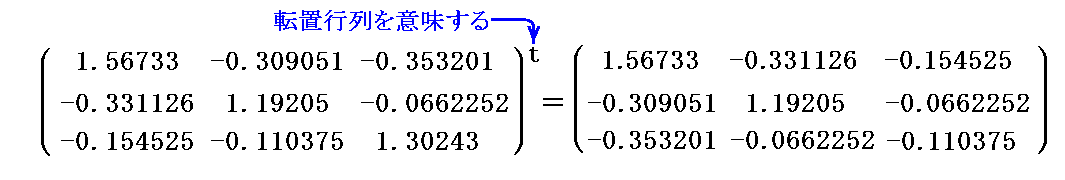
になっています。つまり“逆変換行列”は2.(2)[例1]で説明した 《双対基底ベクトル b1、b2、b3 の基底ベクトルex,ey,ez系(つまり(x,y,z)座標系)での成分表示行列》の“転置行列”になっている。
同様にdv=(dv1,dv2,dv3)離れた基底ベクトル系 a1、a2、a3もそこにおける変換式の逆変換によって正方格子の座標系に変換できます。 4.(5)1.[例11]で求めた式

から

となるが、この変換行列は変換行列
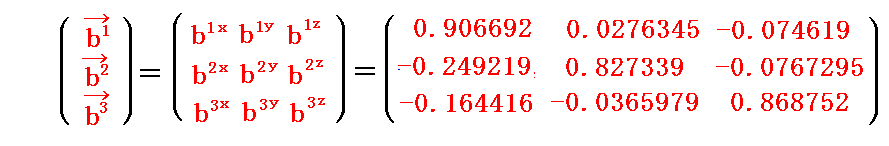
の転置行列です。だから両行列の積を作ると
となります。
当然のことですが、座標変換係数は場所に依存して変化します。だから、上記の座標変換式はある1点に於いてのみ有効な変換式です。
もちろん、3.(1)で説明した“双対基底ベクトル”の変換式(D)式とその逆変換に相当する関係式も存在します。つまり、ex,ey,ez系からb1、b2、b3系へ変換する変換式と、b1、b2、b3系からex,ey,ez系へ変換式です。そのとき、ex,ey,ez系は基底ベクトル系と双対基底ベクトル系が一致していることを忘れないで下さい。
上記の基底ベクトルの変換を実行すると下図の様になります。
このような座標系に移動すると“基底ベクトル系”と“双対基底ベクトル系”は同一となりますから、反変成分・共変成分の違いは無くなります。そのため添字の(x,y,z)も、本来は反変成分なのですが、共変成分と同じと言うことで右下に付けたものも並記しています。
[補足説明1]
このとき《第1に重要なこと》で注意したように上記二つの図[1つ目の図]と[2つ目の図]の基底ベクトル系の全てが同じユークリッド空間中に引かれた座標線に沿ってのものです。それはガウス曲面の任意の点の接平面(2次元ユークリッド空間)に正方格子を引くか、斜交格子を引くかの違いに相当します。
さらに、両方の図にはdvだけ離れた点の基底ベクトル系も描かれていますが、どちらも原点に置ける基底ベクトル系を定めたのと同じユークリッド空間に設定されています。これはちょうどガウス曲面の任意の点の接平面(2次元ユークリッド空間)に最初に設定した格子に隣り合った格子も同じ接平面に記したことに相当します。
今考えている領域が微小な場合、その様に隣り合った格子も同一3次元ユークリッド空間中で隣り合っているのだと考えることができるからです。しかしこの操作を更に次の隣り合った基底ベクトルに続けていくことはできません。なぜなら、同一のユークリッド空間中の隣り合った基底ベクトル間の変化の様子からは決して空間の歪みを表すことはできないからです。
[補足説明2]
さらに《第5に重要なこと》で説明したように3次元リーマン空間における基底ベクトル系は場所と共に必然的に変化していきます。
ガウス曲面の例で説明すると、曲面に引かれた網目を任意の点での接平面(2次元ユークリッド空間)に射影すると一般に斜交格子となり、接点における斜交格子に隣接して射影される斜交格子は接点(原点)における斜交格子から更に変形したものになります。
だから[1つ目の図]は、3次元リーマン空間中の一点(原点)付近の領域を近似している3次元ユークリッド空間(ガウス曲面の接平面に相当)の隣り合った基底ベクトル系の網目格子の変化の様子を表しています。
そのとき、[補足説明1]で注意したように、同一のユークリッド接空間に引かれた隣り合った基底ベクトルセルの変化の様子からは空間の歪みを読み取ることはできません。あくまで実際のリーマン空間の基底ベクトルの接ユークリッド空間への射影なのですから。
そのことは[例9]で説明した《2事件リーマン空間(球面)の球面座標》のθ=π/4付近の例として描いた4つの格子図

からも明らかです。
この図は実際の球面上に描かれた分割線を図中の点Aで球面に接する接平面へ射影した図です。だからこの4つの格子は同一平面上に描かれています。この4つの格子の形状は互いに変化していますが、この4つの図形の計量テンソルの変化の様子からはこの4つの格子が球面の一部であるという情報は出てきません。それは[例9]の《2次元ユークリッド空間(平面)の極座標》の例を復習されれば明らかでしょう。
だから、隣り合った格子セルの情報は本来隣り合った別の(接平面に相当する)接ユークリッド空間のものと比較しなければならないのです。このことを理解するのは難しい。アインシュタインもここの意味を理解するのに何年もの思考を要したのでしょう。そして隣り合った“接ユークリッド空間”間の格子定数の比較とは何なのかを理解する数学を探し求めていたのだと思います。
《リーマン幾何学》は正にそういった幾何学なのです。つまりリーマン幾何学はある点に隣り合った空間を議論しますが、その隣り合った空間は元の点の接ユークリッド空間とは違う別の接ユークリッド空間なのです。そう考えて初めて隣の格子定数(計量テンソル)と比較することで、空間の歪みを表すことができる。
このことは4.(2)の《第3に重要な事》で取り上げた、地球を構成する為に貼り合わせる“5万分の1の地図”が、それぞれ異なった地球表面(2次元リーマン空間)での接平面(2次元ユークリッド空間)における射影図で有り、異なった点の接平面に射影された地図だからこそ、それらを貼り合わせると球面を構成できたことに対応します。
[補足説明3]
[例11]の図や[例12]の2つ目の図には《3次元ユークリッド空間(x,y,z)の座標値》が、[例12]の1つ目の図には《基底ベクトル系(a1,a2,a3)を単位とした座標値》が書かれているので両者の関係に面食らわれるかも知れませんが、本当に重要なのは《基底ベクトル系(a1,a2,a3)を単位とした座標値》です。だから今後の議論に《3次元ユークリッド空間(x,y,z)の座標値》が用いられることはありません。
《3次元ユークリッド空間(x,y,z)の座標値》は表面に現れては来ないのですが、それと《基底ベクトル系(a1,a2,a3)を単位とした座標値》との関係はすべて空間の各点で与えられている“基本計量テンソル”gij、gijのなかに書き込まれています。つまり基本計量テンソルによって《3次元ユークリッド空間(x,y,z)》と《基底ベクトル系(a1,a2,a3)リーマン空間》の幾何学的関係はすべて定まっているのです。
【ベクトル場wの微分係数】
前項に示した[2つ目の図]は、3次元リーマン空間の一点(原点)付近を近似する3次元ユークリッド空間に正方格子座標系を設定(局所的にはいつでも可能)して、その中でdv=(dvx,dvy,dvz)=(1.4,1.5,1.7)変位したときのベクトル場 w の変化の様子を示しています。図から明らかなようにその変化量 dw は dw=(dwx,dwy,dwz)=(-1.3,2.0,1.7)− (-1.2,1.9,1.5)= (-0.1,0.1,0.2) です。
これを微分係数式で表すと、基底ベクトル ex、ey、ez は座標(x,y,z)に関係せず一定ですから
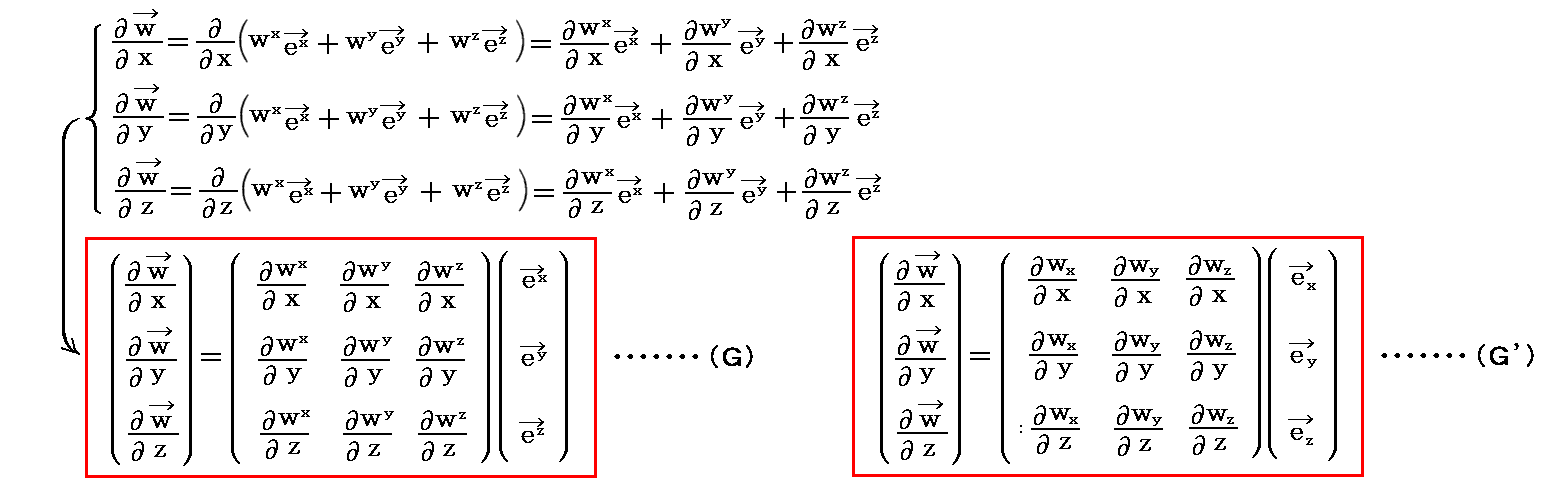
となります。
この場合、ベクトル w を反変ベクトルと見なしたときの微分係数と、共変ベクトルと見なしたときの微分係数は同じになります。そのことを明示するために(G’)式も並記しています。
【反変ベクトル場wの共変微分係数】
所が[1つ目の図]の様に、3次元リーマン空間の一点(原点)付近を近似する3次元ユークリッド空間に設置した斜交基底ベクトル系(こちらの方がリーマン空間では一般的)で dv=(dv1,dv2,dv3)=(1.13024,1.21192,1.83223) 変位したときのベクトル w の変化量 dw=(dw1,dw2,dw3) を求めようとすると難しくなります。それは原点の w を測定する 基底ベクトル a1、a2、a3 と変位点 dv における w を測定する基底ベクトル a1、a2、a3 が異なるからです。
すなわち、ガウス座標(w1,w2,w3)とガウス座標値を定める元になる基底ベクトル a1、a2、a3 系の両方がdv=(dv1,dv2,dv3)の変位に伴って共に変化するから、その両方の変化を考慮しなければ成りません。
その両方の変化を考慮した微分係数式は
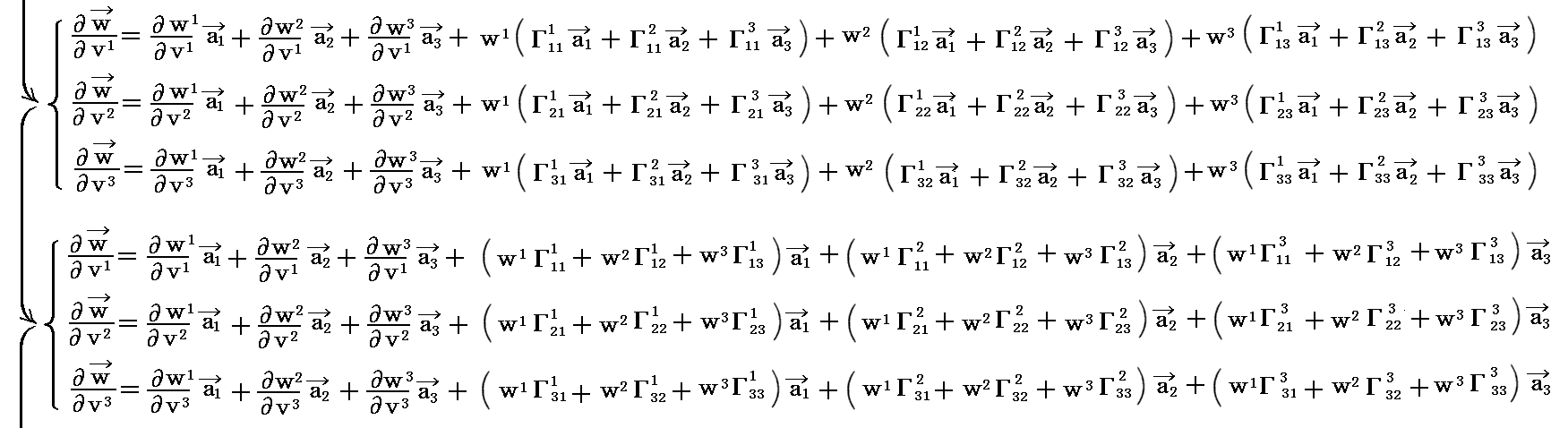

となります。
先ほどの正方格子座標系と違って斜交座標系では必然的にクリストッフェル記号が関係してきます。
最後の式の行列成分は、アインシュタインの規約を適用すると

と表されます。
これは「テンソル解析学」6.(3)2.でお馴染みの“反変ベクトル” wi の 反変座標 vj に関する“共変微分係数”そのものです。また上記の〔行列〕は(1,1)型テンソルとなることもテンソル解析学で学ぶ所です。証明は別稿「微分幾何学3」3.(2)の(3-20)式を参照。
上記の導き方は、反変ベクトルの“共変微分係数”を求める“別のやり方”です。別稿「微分幾何学」3.(3)や「テンソル解析学」6.(3)2.の導き方では、共変微分係数の物理的・幾何学的な意味がまったく読み取れませんが、ここのやり方では良く解ります。
上記(H)式が“共変微分係数”の物理的・幾何学的な意味を示しています。
そのとき、“共変微分係数テンソル成分”の表記法には様々な流儀が有ります。そのことについては別稿「テンソル解析学(絶対微分学)」6.(3)1.[補足説明]を参照されて下さい。そのとき、いずれの表記でも微分を表す指標は共変指標として必ず下側に付記されていることに注意して下さい。
ベクトル w を 共変ベクトル wi とみなしたときの 反変座標 vj に関する共変微分係数については4.(5)5.共変ベクトルの共変微分係数で説明します。
【反変ベクトル場wの共変微分】
ここで、別稿「微分幾何学3」(3)(3-22)式や別稿「テンソル解析学」6.(3)2.で出てきた“共変微分”に相当するものを導いておきます。
上記(H)式の左辺の各成分はベクトルですから
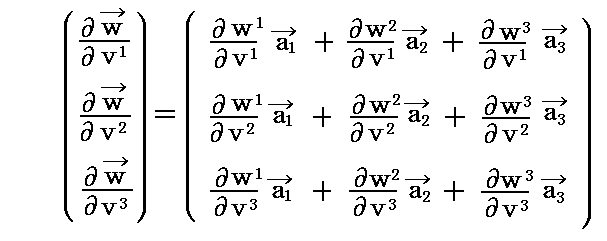
と表せます。この中のそれぞれの係数が(H)式の右辺の対応するベクトルaiの係数
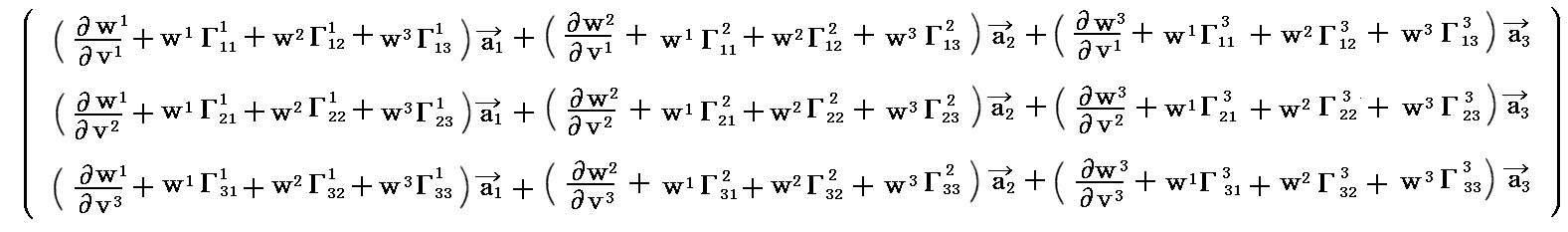
にそれぞれ対応すると考えなければならない。つまり
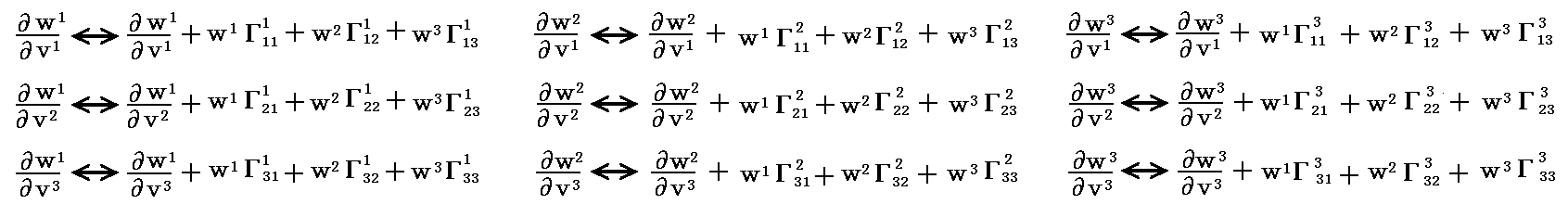
が対応する。
ここで共変微分を“δ”で表す(別稿[補足説明]参照)ことにすると

だから、この各係数を上記の対応するものに置き換える(行と列が入れ替わることに注意)と
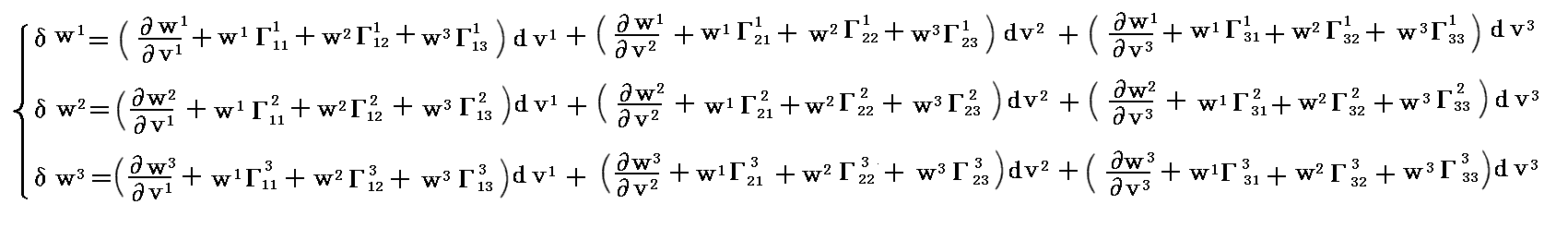
が得られる。右辺の中で、

と表せることに注意すると

となり、別稿で説明した“共変微分”の表現と一致する。
これを行列形式で表すと
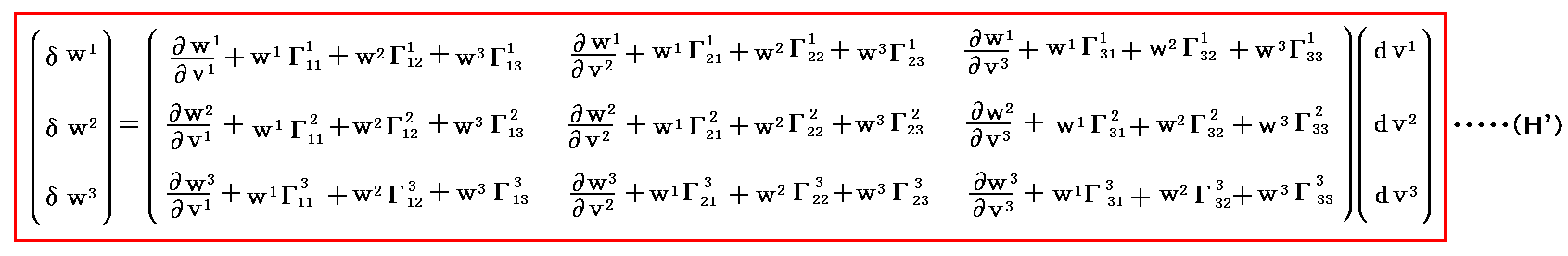
となる。
ここで、“共変微分”はその意味から言って(1,0)型テンソル(反変ベクトル)であることは明らかです。所で変分(dv1,dv2,dv3)も(1,0)型テンソル(反変ベクトル)ですから、(H’)式は“テンソルの商法則”により反変ベクトルの“共変微分係数”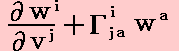 が(1,1)型テンソル(混合テンソル)であることを示している。
が(1,1)型テンソル(混合テンソル)であることを示している。
行列形式(H’)式の物理的・幾何学的意味から明らかな様に、変分ベクトルδw(“共変微分”)は、反変ベクトル場wの場所が dv1a1+dv2a2+dv3a3 だけ変化したときベクトルwがどれだけ変化するか、その変分ベトクル量を与えるものです。
[補足説明]
4.(4)3.[例10]で説明したように“クリストッフェル記号”Γijaは“基底ベクトル”が場所を移動するとどのように変化するかを表す係数でした。
そのとき、空間がユークリッド的で平坦な場合は“基底ベクトル”が全空間にわたって変化しない様な網目を引くことができます。そのため、ユークリッド的で平坦な空間ではクリストッフェル記号を全空間にわたってすべて 0 にすることができます。
前記共変微分係数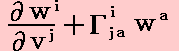 の第2項にはクリストッフェル記号が掛かっていますから、空間が平坦であれば第2項はすべて 0 とすることができます。つまり空間が平坦ならば、共変微分係数は普通の微分係数と同じにすることができます。
の第2項にはクリストッフェル記号が掛かっていますから、空間が平坦であれば第2項はすべて 0 とすることができます。つまり空間が平坦ならば、共変微分係数は普通の微分係数と同じにすることができます。
このことは、空間を記述する網目が斜交座標か直交座標かの違いでは無くて、網目がすべて同一の網目(セル)で分割できるかできないかに関係する事です。ユークリッド空間の場合には同一の網目セルで全空間を覆い尽くすことができたのでした。だからその様な網目セルを採用すれば、共変微分係数と普通の微分係数の違いを無くすることができます。
もちろん、4.(3)[例8]や4.(4)2.[例9]で見たように、ユークリッド空間でもクリストッフェル記号が 0 とならないような網目を引くことはできます。その場合には、ユークリッド空間であっても共変微分係数は普通の微分係数と異なります。
しかし、ユークリッド空間ではすべての点で網目セルが同一な(クリストッフェル記号がすべて 0 となる)網目を引くことができるのですから、《ユークリッド空間》とは適切な座標変換によってクリストッフェル記号がすべての点で 0 となる、計量テンソルの要素がすべての点で同じになる、共変微分と普通の微分の違いがなくなる様にできる空間であると言っても良い。
《歪んだ空間(リーマン空間)》では、どのように網目を引き直しても、どのように座標変換しても、そのようにすることはできません(局所的にはできますが)。
だからこそ、“共変微分”が必要になり、斜交曲線座標が必要になり、“クリストッフェル記号”が必要になり、反変成分・共変成分やその間を取り持つ“計量テンソル”(“線素”の不変性を表す二次形式に必須)が必要になったのです。これこそがアインシュタインとグロスマンが発見した《第5に重要なこと》ことです。
ここまでは、アインシュタインが1912年の秋までに理解した段階です。これが、京都講演で語っている“ただそれを含むような少々一般的の基礎はすでに幾分かその以前に私に知られました。”の内容です。ここから重力場方程式(正しい万有引力の方程式)を発見する為の苦労が始まる。
4.反変ベクトルの共変微分係数の具体例 [目次へ帰る] [節先頭へ]
上記(G)式と(H)式に4.(5)2.[例12]の数値例を代入して計算してみる。このときベクトル w の(x,y,z)系での反変成分と共変成分は同じなのですが、間違いを避けるために、(wx,wy,wz)と(wx,wy,wz)の様に区別して表示します。
[例13]
3次元ユークリッド空間でdv=(dvx,dvy,dvz)=(1.4,1.5,1.7)変位したときのベクトル w の変化量dwはdw=(dwx,dwy,dwz)=(-1.3,2.0,1.7)− (-1.2,1.9,1.5)= (-0.1,0.1,0.2)ですから共変微分係数として
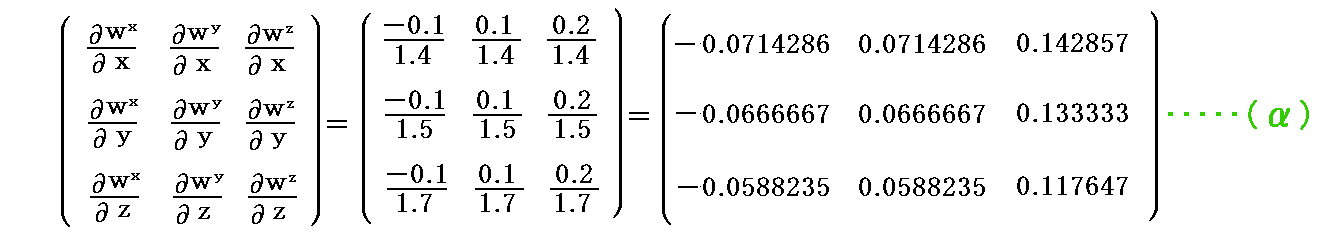
が得られる。この場合クリストッフェル記号は全て 0 ですから、クリストッフェル記号が関係する部分はすべて消えて、簡単に計算できます。
次に、3次元リーマン空間で dv=(dv1,dv2,dv3)=(1.13024,1.21192,1.83223) 変位したときのベクトル w の基底ベクトル a1、a2、a3 での変化量 dw=(dw1,dw2,dw3) は
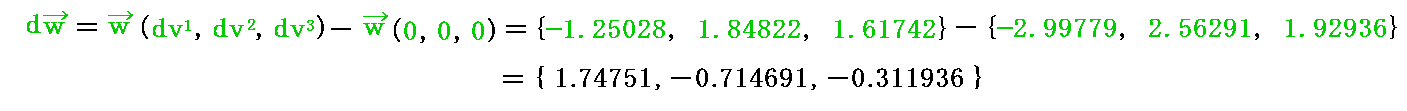
ですから
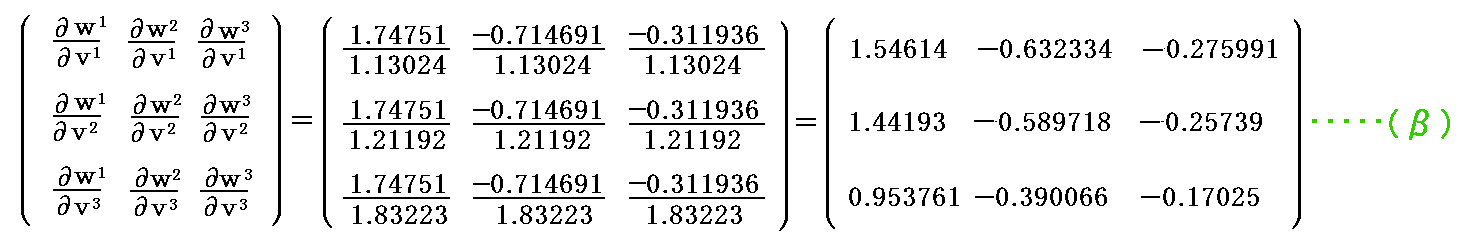
が得られる。
原点におけるクリストッフェル記号は4.(4)3.[例10]ですでに求めているように

ですから[拡大版]

となる。
これらの値を代入すると共変微分係数として

が得られる。
[補足説明1]
[例13]の数値例について以下の事に注意して下さい。
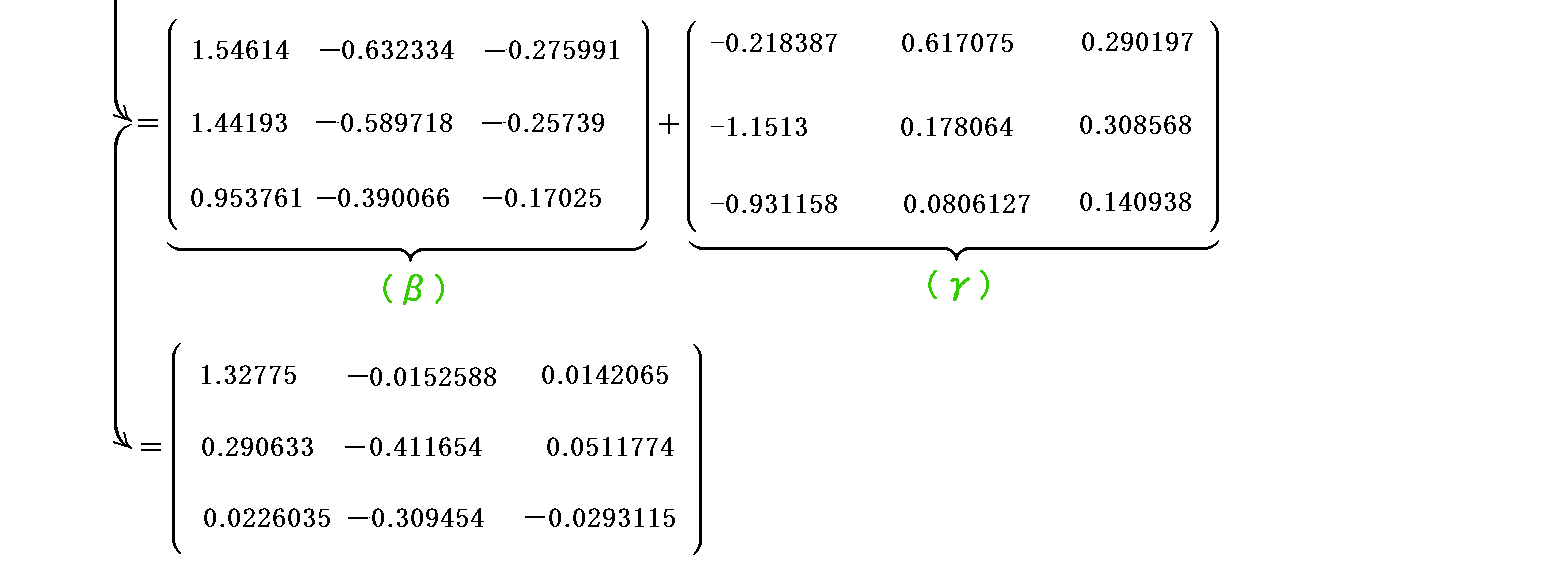
この例ではクリストッフェル記号が絡む所を強調するために、《変位dv した点の基底ベクトルの変化量》(これがクリストッフェル記号に関係する)を大き目に設定しています。そのため、上記の(β)部分と(γ)部分が同程度の大きさになってしまいました。だから共変微分係数の数値例としては適切ではありません。
本来、《変位dvでの基底ベクトルの変化量》は《ベクトル場 w の変化量》に比較して遙かに小さい。それため基底ベクトルの変化に伴うガウス座標の変化分はもっと小さくなります。つまり、(β)部分は先に求めた(x,y,z)系での微分係数(α)値と同じような傾向のテンソルとなります。それはdvの位置変化に伴う基底ベクトルの変化が無い(この場合クリストッフェル記号が絡む(γ)項は消える)として求めた値に近い。
すなわち、原点と同じ基底ベクトルの元での変位dvした点のベクトルwのガウス座標値

を用いて計算されるベクトルwの変位成分dw
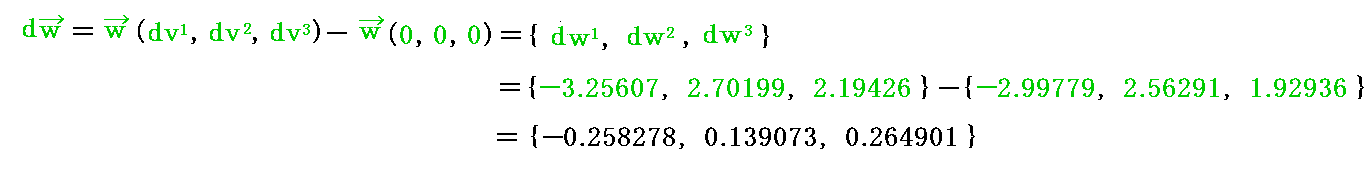
から計算した(β)値です。すなわち
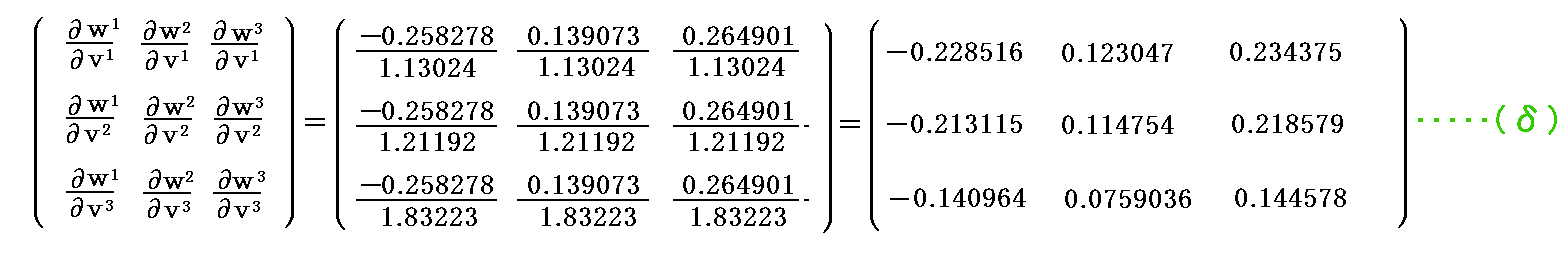
です。確かにこれは(α)値テンソル成分に近い傾向を示している。これを(δ)値としましょう。
本来の(β)部分には、変位dvに伴う基底ベクトルの変化によって生じたガウス座標測定単位の変化による(δ)値からの極わずかの変化が表れています。そして、クリストッフェル記号から導かれる(γ)部分の数値は、その(β)値を元の(δ)値に戻すための補正として表れます。実際(γ)値のその様な傾向は[例13]の(γ)値の数値例からも読み取れます。
だから、本来の(β)+(γ)値はほぼ(δ)値と同じ値になります。それだからこそ、反変ベクトルの共変微分係数は(1,1)型混合テンソルとして座標変換されるのです。
【共変ベクトル場wの共変微分係数】
4.(5)3.【反変ベクトル場wの共変微分係数】で反変ベクトル表現の共変微分係数を導きました。ここでは共変ベクトルの“共変微分係数”を導きます。4.(4)4.の結論を用いた、同様なやり方です。

すなわち、共変ベクトル w の反変座標 vj に関する“共変微分係数”は
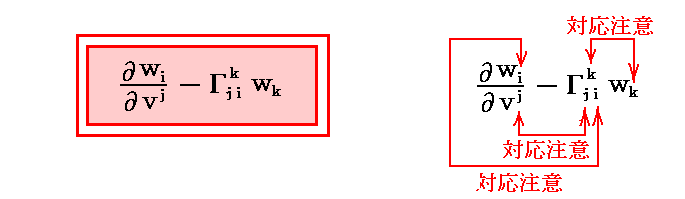
となる。これは別稿「微分幾何学3」3.(2)の(3-23)式と同じです。さらに、これは(0,2)型テンソルとなります。証明は別稿「微分幾何学3」3.(3)[問題1]を参照。上記の方法は共変ベクトルの“共変微分係数”を求める“別のやり方”です。
“さらに別なやり方”として下記の方法も有る。このやり方は、ライプニッツ公式の成立を条件として求めている点で興味深いが、4.(4)4.の結論を用いる上記方法に比べて共変ベクトルの共変微分の意味が読み取りにくい。
[補足説明1]
反変ベクトルの共変微分が定義されていれば、それから共変ベクトルの共変微分が求まる。



【共変ベクトル場wの共変微分】
共変ベクトルの“共変微分”は、4.(5)3.【反変ベクトル場wの共変微分】で説明したのと同様にすれば直ちに求まって、

となります。
共変ベクトルの“共変微分”(δw1,δw2,δw3)が((0,1)型テンソル(共変ベクトル)である事は、その物理的な意味から明らかです。そのことと変分(dv1,dv2,dv3)が(1,0)型テンソル(反変ベクトル)であることを考慮すると“テンソルの商法則”により共変ベクトルの“共変微分係数”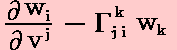 が(0,2)型テンソル(共変テンソル)であることが解ります。
が(0,2)型テンソル(共変テンソル)であることが解ります。
一般のテンソルはベクトルの直積から作る事ができます。その直積記号(○に×)を使ってテンソルを表すと、ここと同様なやり方で“共変微分係数”を導く事ができます。そのやり方は文献1.の引用ページ3.の注*7)で説明されています。
同じやり方を別の文献から引用します。式変形の途中で総和を取る添字は置き換えていることに注意されたし。


(0,3)型テンソルに成ることの証明は別稿「微分幾何学3」3.(3)[問題2]と同様にすれば良い。これはテンソルの共変微分を求める“別のやり方”でも有ります。

(1,4)型テンソルに成ることの証明は別稿「微分幾何学3」3.(3)[問題2]と同様にすれば良い。
[補足説明1]
本稿では、反変ベクトル成分 vi ・共変ベクトル成分 vj と 基底ベクトル ai ・双対基底ベクトル bj の関係を2.(3)で、また、計量共変テンソル gij ・計量反変テンソル gij ・計量混合テンソル gij(単位テンソル δij) と 基底ベクトル ai ・ 双対基底ベクトル bj の関係を2.(4)と3.(5)で説明しました。
しかし、一般のテンソルの成分については、基底ベクトル ai ・双対基底ベクトル bj とどのような関係になるのか説明していません。そのことについては文献8.第3章あるいは、須藤靖著「一般相対性理論入門」日本評論社(2005年刊)第2章や、須藤靖著「もう一つの一般相対性理論入門」日本評論社(2011年刊)第2章などをご覧下さい。
それらは2.(4)や3.(5)で説明した(ai・aj)、(bi・bj)、(ai・bj)などの内積記号による表現を拡張した直積記号(○に×)を使って表されるのですが、文献8.の第3章p250〜253を読まれれば、本稿の[共変微分係数の導出法]と別稿「微分幾何学3」3.(2)2.や「テンソル解析学(絶対微分学)」6.(3)で説明した[テンソルの“共変微分係数”導出法]との関係も明瞭になると思います。
また文献8.の、p257の注意も重要です。
下記の方法はテンソルの共変微分を求める“さらに別のやり方”です。
[補足説明2]
反変ベクトルと共変ベクトルの共変微分が定義されていれば、任意階数テンソルの共変微分が求まる。


これは、ライプニッツ公式の成立を条件として求めている点で興味深いが、4.(5)3.及び4.(5)5.を組み合わせて用いる最初の方法に比べて共変微分の物理的意味が読み取りにくい。
ちなみに、“任意テンソルの積の共変微分に関してライプニッツ公式が成り立つ”ことは直接証明できます(ただし、共変微分を表す記号の違いに注意)。
(6)基底ベクトルの変換とベクトル成分・テンソル成分の座標変換の例
ここでは[例12]で考察した二つの座標系(ex、ey、ez)と(a1、a2、a3)の間で基底ベクトル、ベクトル成分、テンソル成分がどのように変換されるか考察する。このとき行列表示形式については3.(1)[補足説明1]〜[補足説明2]に注意されたし。
ここで取り上げる例は[3次元ユークリッド空間における直交直線座標系]から[3次元リーマン空間における斜交曲線座標系]への座標変換に相当します。
これは、一般相対性理論で必要となる[擬ユークリッド空間であるMinkowski時空]から[4次元リーマン時空]への座標変換を理解する為のモデルになります。
このとき、[4次元リーマン時空]中の1点における擬ユークリッド的“接空間”が[Minkowski時空]であるように、以下で論じる[3次元リーマン空間]中の1点におけるユークリッド的“接空間”が[3次元ユークリッド空間]です。この当たりは本稿の4.(1)〜(3)で説明した所です。
上記の説明の意味は、別稿内山文献§19p119〜や中野文献§9-2p182〜などを参照されたし。
1.基底ベクトルと双対基底ベクトルの変換 [目次へ帰る]
(x,y,z)系では“基底ベクトル系”と“双対基底ベクトル系”は同一なのですが、今後は間違いを避けるために(x,y,z)座標系でも双対基底ベクトル系は添字を上げて( ex、ey、ez)と記し、今まで用いてきた (ex、ey、ez)を基底ベクトル系の表示とします。
また(x,y,z)系では、ベクトル w の反変成分と共変成分は同じなのですが、それらも(wx,wy,wz)と(wx,wy,wz)の様に区別して記します。
“双対基底ベクトル”は3.(1)で説明した変換式(D)式で( ex、ey、ez)と(b1、b2、b3)が互いに変換されます。

ところで、双対基底ベクトル ex、ey、ez を双対基底ベクトルb1、b2、b3へ変換する変換式の変換係数Bi'j は2.(2)[例1]で求めた双対基底ベクトルb1、b2、b3の(x,y,z)座標表示から直ちに求まります。すなわち

となります。これを(I)式とします。
この逆変換は、2.(2)[例1]で説明した様に

であった事を思い出すと、
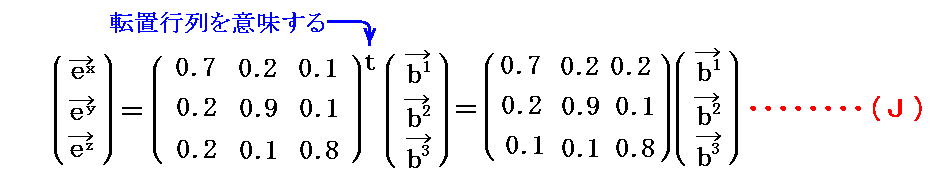
となります。これを(J)式とします。
一方、基底ベクトル ex、ey、ez から基底ベクトルa1、a2、a3へ変換する式は、4.(5)2.[例12]で説明した(F)式

です。
また、基底ベクトルa1、a2、a3から基底ベクトル ex、ey、ez へ変換する式は、4.(5)2.[例12]で説明した(E)式

です。
4.(5)2.[例12]で注意したようにこの“逆変換行列”は2.(2)[例1]で説明した 《双対基底ベクトル b1、b2、b3 の基底ベクトルex,ey,ez系(つまり(x,y,z)座標系)での成分表示行列》(Bi'j)の“転置行列”になっている。
反変ベクトル(1階反変テンソル)の変換例です。
4.(5)2.[例12]で用いたベクトル場wの反変成分は、(I)式の変換係数によって変換されるはずです。実際4.(5)2.[例12]の値に適用してみると

となり、確かに反変成分に関して前述の変換係数で変換されています。
この逆変換には(J)式の変換係数を適用すれば良い。実際4.(5)2.[例12]の値に適用してみると

となります。
同様に、2.(3)[例3]で導入した基底ベクトル a1、a2、a3 におけるベクトル v の反変成分は、4.(5)2.[例12]の基底ベクトルex,ey,ezの反変成分との間に

と、その逆変換

の関係があります。
共変ベクトル(1階共変テンソル)の変換例です。
4.(5)2.[例12]にはベクトル場wの共変成分を記していませんが、2.(5)[例5]で示したようにベクトルw場の原点(0,0,0)における双対基底ベクトル系b1、b2、b3での共変成分座標は(w1,w2,w3)=(-0.31,1.62,1.15)でした。
この共変成分座標は双対基底ベクトル系ex,ey,ezの原点における共変成分座標(wx,wy,wz)=(-1.2,1.9,1.5)と、“基底ベクトル”の変換式(F)式や(E)式の変換係数で互いに変換されます。
実際、2.(5)[例5]の値と4.(5)2.[例12]の値を代入してみると
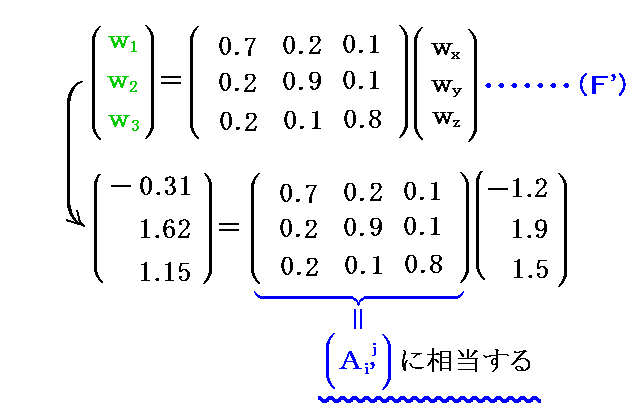
となり、確かに共変成分に関しては、(F)式の変換係数で変換されています。
この逆変換は、(E)式の変換係数で変換されて

となります。
同様に、2.(3)[例3]で導入した双対基底ベクトル系b1、b2、b3におけるベクトル v の共変成分は、4.(5)2.[例12]の双対基底ベクトル系ex,ey,ezの共変成分との間に
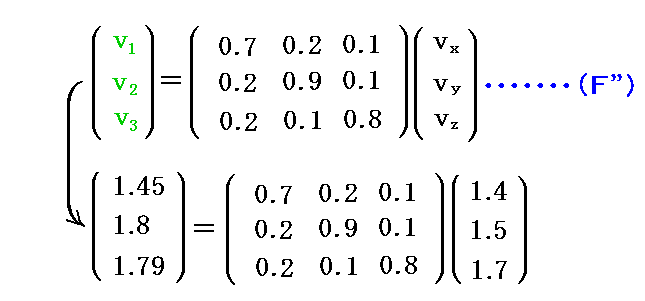
と、その逆変換
の関係があります。
これらの関係を用いれば、3.(6)で説明した“ベクトル内積の座標変換不変性”も、ベクトル v と w の内積の基底ベクトルex,ey,ez系と基底ベクトル a1、a2、a3 系間の座標変換を例として確かめることができます。
あるいは

など。他の内積表現を用いても同様に証明できます。
2階共変テンソルの座標変換例として“基本計量共変テンソル”を取り上げる。
[例12]での原点における基底ベクトル ex、ey、ezが作る格子の基本計量共変テンソルは

です。
また、原点において基底ベクトルa1、a2、a3が作る格子の基本計量共変テンソルは2.(4)[例4]で示したように
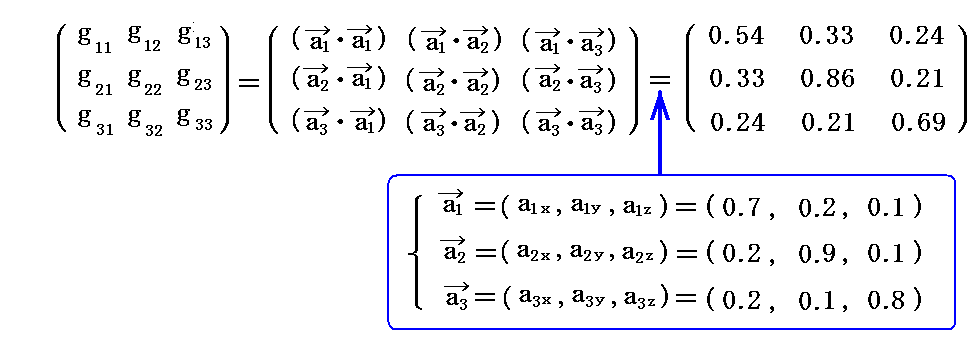
でした。
これらの成分は3.(4)で示した変換式で、確かに互いに変換されることが解る。

計量共変テンソルは対称テンソルですから、上式の両辺の転置行列を取った式も成り立ちますがこれは元の式と同じになります。
2階反変テンソルの座標変換例として“基本計量反変テンソル”を取り上げる。
[例12]での原点における双対基底ベクトル ex、ey、ez が作る格子の基本計量反変テンソルは
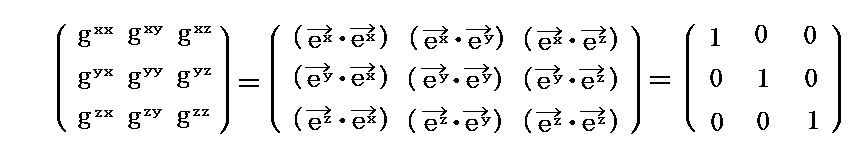
です。
また、原点において双対基底ベクトルb1、b2、b3が作る格子の基本計量反変テンソルは2.(4)[例4]で示したように

でした。
これらの成分は3.(4)で示した変換式で、確かに互いに変換されることが解る。

計量反変テンソルは対称テンソルですから上式の両辺の転置行列を取った式も成り立ちますがこれは元の式と同じになります。
2階混合テンソル(1,1)テンソルの座標変換例として“単位テンソル”(クロネッカーのδ)を取り上げる。3.(5)で説明したように“単位テンソル”は“2階混合テンソル(1,1)テンソル”として座標変換される。
ところで、2.(1)の考え方を適用すると
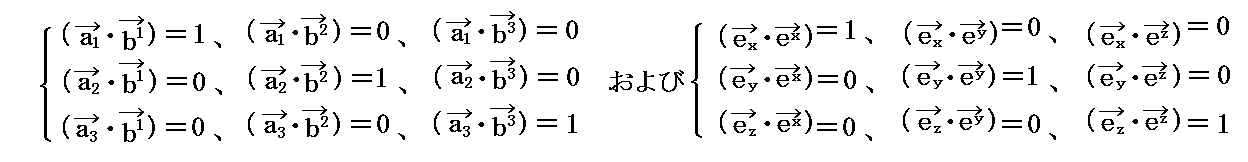
は、それぞれ基底ベクトル a1、a2、a3系 と 基底ベクトル ex、ey、ez系の座標における単位テンソルと見なせる。
ここで と見なして、3.(1)で説明した基底ベクトルの座標変換式(C)式と(D)式を用いると
と見なして、3.(1)で説明した基底ベクトルの座標変換式(C)式と(D)式を用いると
となる。実際の値を代入してみると
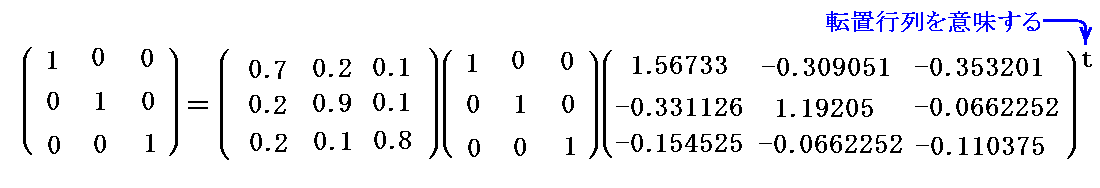
が成り立ち、単位テンソルは確かに(1,1)型混合テンソルとして座標変換されることが解る。
単位テンソルは対称テンソルですから、両辺の転置行列を取った
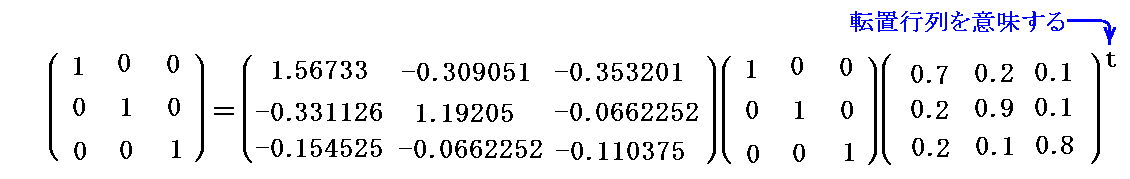
も成り立ちます。
4.(5)4.[例13]で求めた反変ベクトル場wに対する二つの共変微分係数(すなわち基底ベクトル ex、ey、ez に対するものと、基底ベクトル a1、a2、a3 に対するもの)が、(1,1)型テンソル定義の根拠となっている座標変換で互いに変換されるかどうかを確かめてみるべきですが、この計算例では誤差が大きくなり旨く示せません。その理由は4.(5)4.[補足説明1]で説明した通です。
そのため、そこで示した(α)微分係数テンソルと(δ)微分微分係数テンソルがテソンソルとしての変換式を満たしていることを示した方が良い。実際に実行してみると、この両者が(1,1)型テンソル定義の根拠となっている座標変換で互いに変換されることが近似的に確認できます。
3.(7)で体積素片の座標変換が
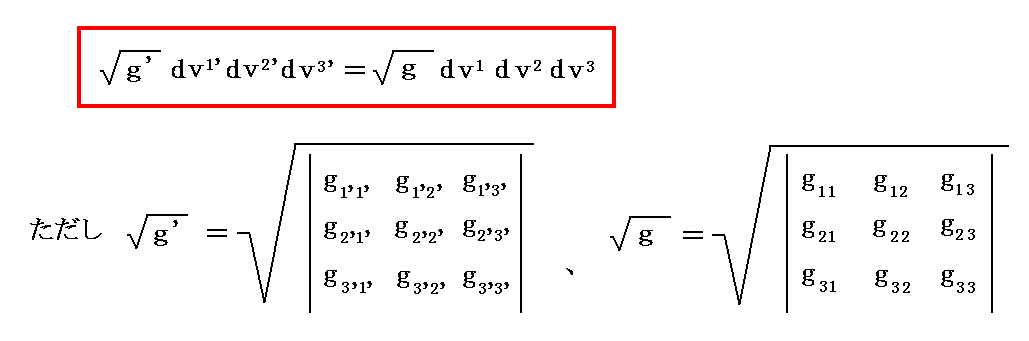
で行われなければ成らない事を説明した。
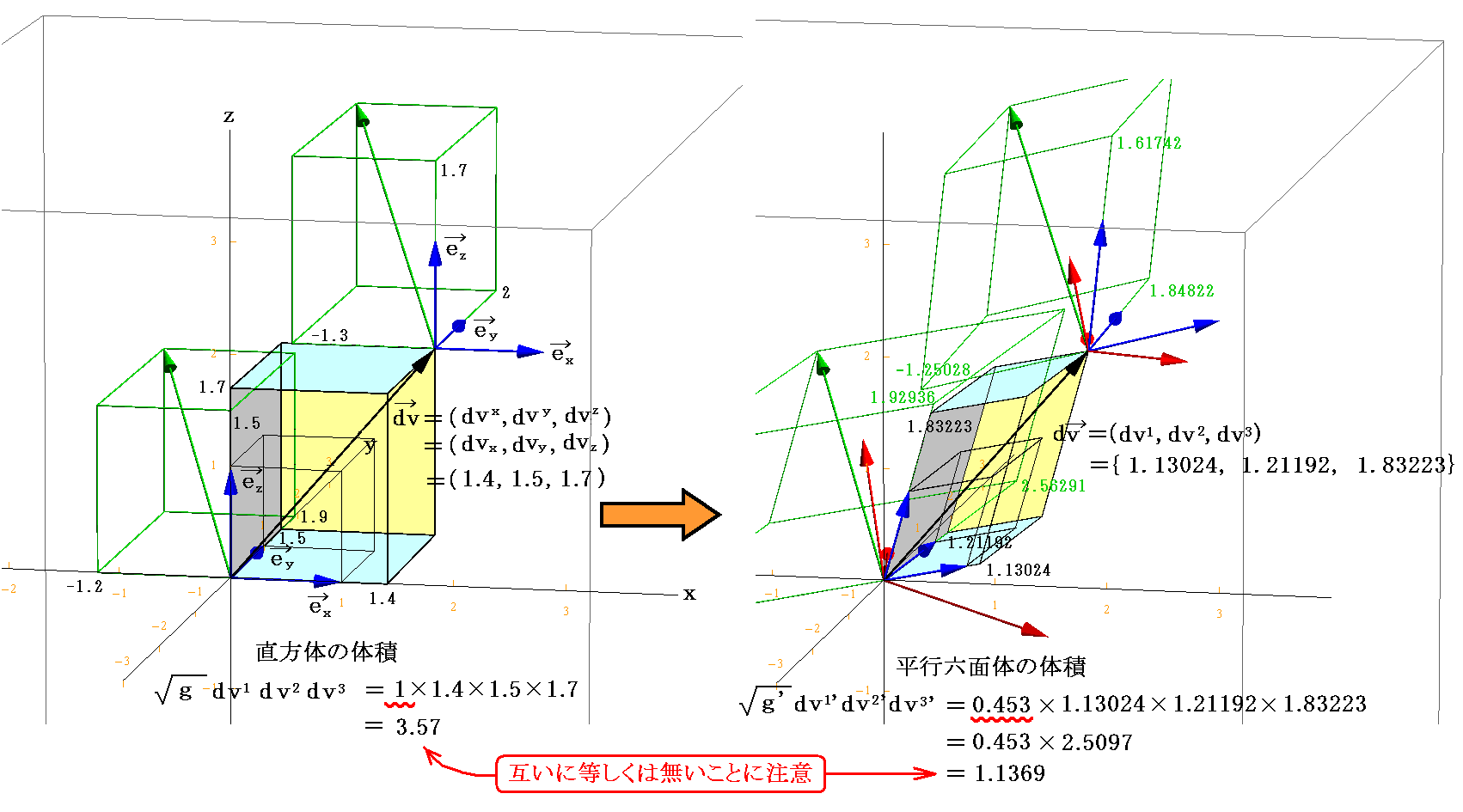
このときdv1’dv2’dv3’ とdv1dv2dv3 の関係については注意が必要です。このことを4.(5)2.[例12]で説明した[2つ目の図]から[1つ目の図]への座標変化を例にして説明する。
この座標変換において左図の立方体体積要素が右図の平行六面体の体積素に座標変換されたと考える。
そのとき右図の体積素の値は2.(7)[例7]の計算値が使えるので
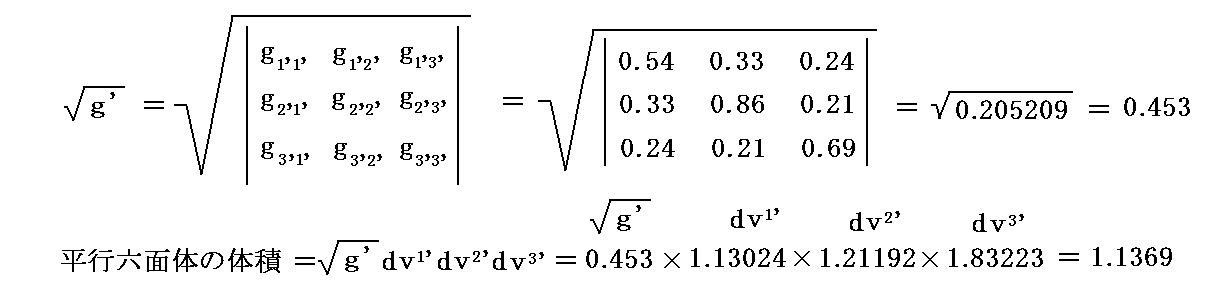
となります。
一方変換前の左図の体積素については
の関係がある。
故に、左図の体積素の一辺の長さは
でなければならないことが解る。もちろんdv1=dv2=1、dv3=1.1369 としたり、dv1=1.1369、dv2=dv3=1、・・・などなど、としても良い。
つまり、dv1’dv2’dv3’ とdv1dv2dv3 の関係は結果として決まるようなものです。だから,最初の式
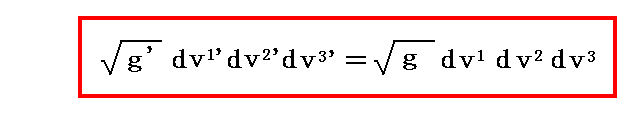
は dv1’=1,dv2’=1,dv3’=1 とし、さらに dv1=1,dv2=1,dv3=1 と考えれば明らかな様に左辺の g’0.5dv1’dv2’dv3’ と右辺の g0.5dv1dv2dv3 が《等しいことを意味するのでは無く》て【積分体積素片】として左辺の g’0.5dv1’dv2’dv3’ が右辺の g0.5dv1dv2dv3 に《置き換えられるべき》だという対応関係を表していると考えて下さい。このことに付いては別稿「重積分の変数変換とヤコビアン(リーマン空間における多重積分)」の説明を参照して下さい。
[補足説明1]
上記“単位体積素片”の実際の体積値は下図の様になります。[拡大版]
図から明らかな様に

は、[左の単位体積素片の体積値]と[右上の基底ベクトル単位体積素片の体積値]の比を表している。
このとき、左の直交座標系では反変座標と共変座標は共通ですが、右の斜交座標系では反変座標と共変座標が分かれます。そのとき、2.(7)[例7]の最後の段落で説明した様に、右側の基底ベクトル単位平行六面体の体積と双対基底ベクトル単位平行六面体の体積との間には以下の関係が有ります。
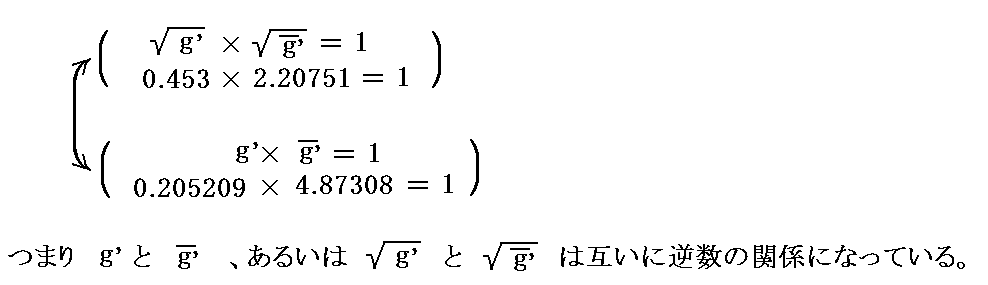
そして、2.(7)[例7]で説明した様に、左右の座標系で“共通の線素を形成する平行六面体”の体積値は下記の様になり、体積値は互いに等しくありません。[拡大版]、こちらの対応関係図も参照
[補足説明2]
しかしこのとき、3.(6)で説明した様に線素の長さの二乗ds2を表す値は座標変換しても同じになります。
このとき、下左の直交座標系では反変座標と共変座標は共通ですが、下右の斜交座標系では反変座標と共変座標が分かれることに注意して下さい。[拡大版]
5.参考文献
この稿を作るに当たって、下記文献を参考にしました。感謝!
最初は1、2章だけで簡単にすますつもりだったのですが、作っている内に説明したい事柄がどんどん増えてしまいました。それというのも1、2章の内容は3,4章と密接に関係しているからなのでしょう。
ここまでの話は、アインシュタインが1912年の秋に到達した段階ですが、彼は正しい重力場方程式を発見するまでにさらに3年の歳月を要します。そのため、この先に長い道のりが続きます。
- ダニエル・フライシュ著(河辺哲次訳)「物理のためのベクトルとテンソル」岩波書店(2013年刊)§4.4〜§4.6
この文献では、基底ベクトル・双対基底ベクトルについてとても丁寧に説明してあります。しかし、2次元での説明のために微妙に解りにくい面もあります。本稿をご覧の後にこの文献を読み直して見られると著者の意図が良く解ると思います。
この文献の§6-3(_p210〜223)を別ページで引用しています。その中の5.“曲率テンソル例”は本稿の4.(3)の説明を理解する例題として有益です。
さらに、「クリストッフェル記号と計量テンソルの関係式」の導出法を別ページで引用。
- 平川浩正著「相対論(第2版)」共立出版社(1986年)
この中から第4章“Riemann幾何学”(p60〜85)を引用。簡潔・明快な説明です。
- Bernard Schutz著(江里口良治、二間瀬敏史 共訳)「シュッツ相対論入門Ⅱ一般相対論(第2版)」丸善出版(2010年刊)
特に5章と6章を参照した。
- A. Sommerfeld著「理論物理学講座 第Ⅲ巻 電磁気学」講談社(1969年刊)の§38(p352〜369)
- EinsteinからSommerfeldへの書簡(1915年11月28日付)
- Einstein著(矢野健太郎訳)「相対論の意味」岩波書店(1958年刊)からp58〜69を引用
この中のp64〜68のEinstein本人による説明は貴重です。
- Pais著「神は老獪にして・・・」産業図書(1986年刊)12章“アインシュタイン−グロスマンの共同研究”
- 石井俊全著「一歩一歩数式で理解する一般相対性理論」ベレ出版(2017年刊)
この中の第3章をぜひお読み下さい。このp250〜253、およびp257を別ページで引用。
- ランダウ、リフシュツ共著「場の古典論」第10章§81、§82
一般相対性理論への導入としてとても秀逸だと思います。
- Wolfgang Pauli著(内山龍雄訳)「相対性理論(上)(下)」筑摩書房筑摩学芸文庫(2007年刊)
原書は1921年刊です。上記訳本の元本は1974年に講談社から刊行されたものです。この中の§9と§10を引用。