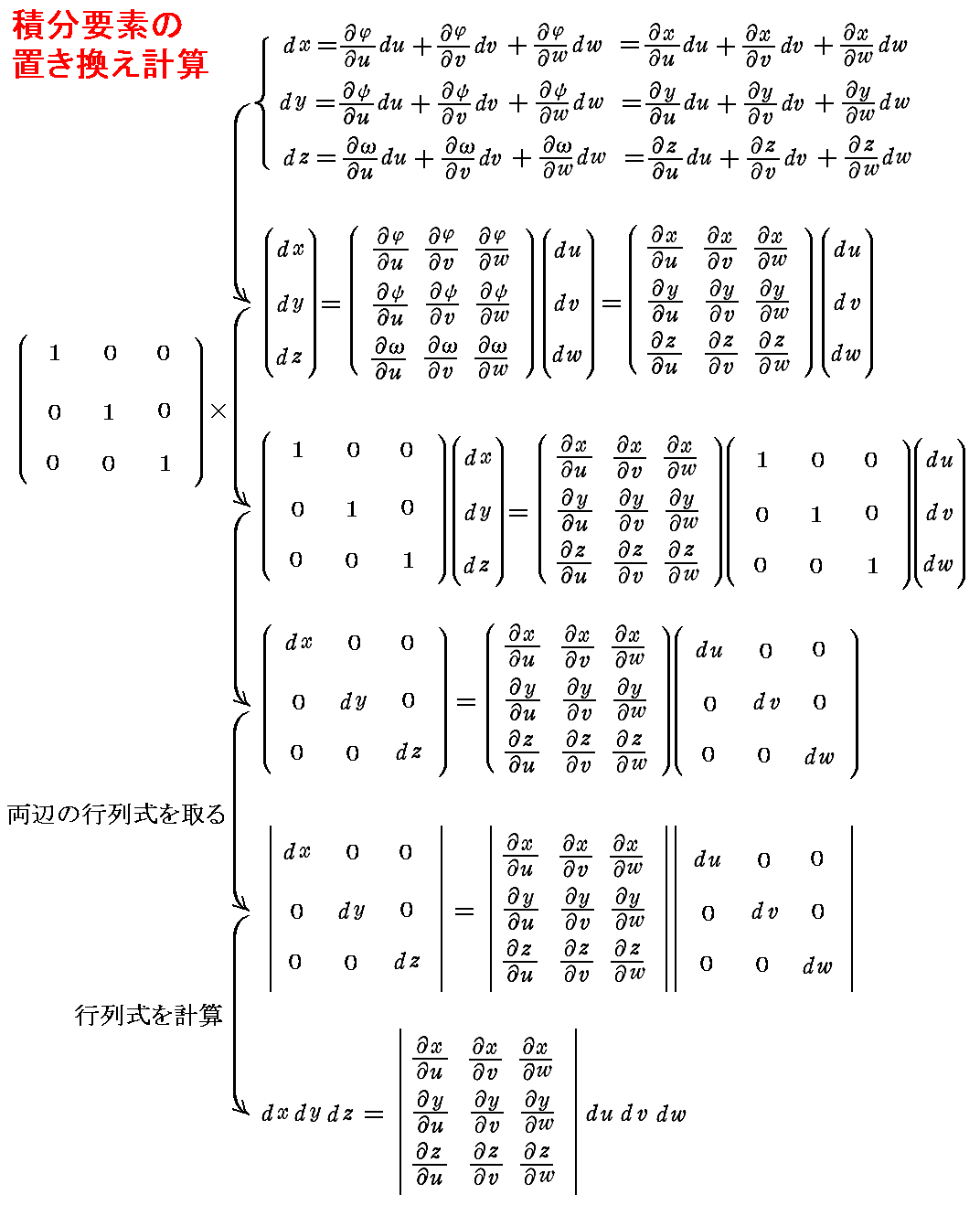
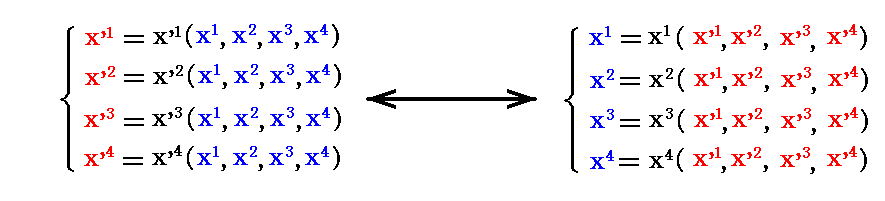
�d�ϕ��̕ϐ��ϊ��ƃ��R�r�A���i���[�}����Ԃɂ����鑽�d�ϕ��j
�@�{�e�͈�ʑ��ΐ����_�ŕK�v�ɂȂ鐔�w�e�N�j�b�N�̐����ł��B�u��ʑ��ΐ����_�𗝉����邽�߂̐��w�I�����v�̈ꕔ�ł��B
�P�D��d�ϕ��i�P�ϕ��j�̍��W�ϊ�
�@�@�i�P�j����
�@�@�i�Q�j�ȒP�ȗ�
�Q�D��d�ϕ��̍��W�ϊ�
�@�@�i�P�j��d�ϕ��̖ʐϑf��
�@�@�i�Q�j�ȒP�ȗ�
�@�@�@�@�@�@�@1�D��d�ϕ��̈Ӗ�
�@�@�@�@�@�@�@2�D�ϕ��ϐ��̕ϊ�
�@�@�@�@�@�@�@3�D���s�iJacobian�j�̈Ӗ�
�@�@�i�R�j���Ό����W
�@�@�@�@�@�@�@1�D���x�N�g���̕ϊ���
�@�@�@�@�@�@�@2�D���W�l�̕ϊ���
�@�@�@�@�@�@�@3�D���W�ϊ����̈Ӗ�
�@�@�@�@�@�@�@4�D���s�iJacobian�j�̈Ӗ�
�@�@�@�@�@�@�@5�D�V�ϐ��ł̓�d�ϕ��̎��{
�@�@�i�S�j���̂��߂ɐϕ��ϐ���ϊ�����̂�
�R�D�O�d�ϕ��̍��W�ϊ�
�@�@�i�P�j�O�d�ϕ��̑̐ϑf��
�@�@�i�Q�j�ȒP�ȗ�
�@�@�@�@�@�@�@1�D�O�d�ϕ��̈Ӗ�
�@�@�@�@�@�@�@2�D�ϕ��ϐ��̕ϊ�
�@�@�@�@�@�@�@3�D�O�d�ϕ��l
�@�@�i�R�j�O�����Ό����W
�@�@�@�@�@�@�@1�D���x�N�g���ϊ���
�@�@�@�@�@�@�@2�D���W�l�̕ϊ���
�@�@�@�@�@�@�@3�D�ϕ��̐ϑf�Ђ̕ϊ�
�@�@�@�@�@�@�@4�D�O�d�ϕ��l
�@�@�i�S�j�O�����ɍ��W
�@�@�@�@�@�@�@1�D�������W�Ƌɍ��W�Ԃ̕ϐ��ϊ���
�@�@�@�@�@�@�@2�D�ϕ��̐ϑf��
�S�D���[�}����Ԃɂ����鑽�d�ϕ�
�@�@�i�P�j���[�}����Ԃł̑��d�ϕ��ɉ�����̐ϑf��
�@�@�@�@�@�@�@1�D�l�����̊�{
�@�@�@�@�@�@�@2�D���x�N�g�������P�ʊi�q�Z���̑̐�
�@�@�i�Q�j���[�}����Ԃɂ����鑽�d�ϕ��ƎΌ��Ȑ����W����ʂ̎Ό��Ȑ����W�ւ̕ϐ��ϊ�
�@�@�@�@�@�@�@1�D���[�}����Ԃ̍��W�ϊ�
�@�@�@�@�@�@�@2�D�ϕ��̐ϑf�Ђ̕ϊ�
�@�@�@�@�@�@�@3�D�ϕ��̈�̕ϊ�
�@�@�@�@�@�@�@4�D���[�}����Ԃɂ����鑽�d�ϕ�
�@�@�i�R�j�O�������[�}����Ԃɂ�����̈�̕\�ʂɕt���Ă̐ϕ�
�T�D�Q�l����
�P�D��d�ϕ��i�P�ϕ��j�̍��W�ϊ�
�i�P�j����
�@�P�ϕ�
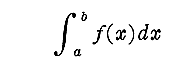
�ł����Ӂi���j�Ƃ����ϕ��ϐ��������炔�ɕϊ�����ƁA�Ӂf�i���j���A���ŃӁi���j�����A�Ӂi���j�����ł����

�ƂȂ�B����͏����I�Ȑϕ��w�ł������g�u���ϕ��h�ƌ�������̂ł��B
�@���̂Ƃ��A�^��Ɏv���͉̂��̉E�ӂɃӁf�i���j�Ȃ�����悵�Đϕ���������Ȃ���ΐ���Ȃ��̂��ƌ����Ƃ���ł��B
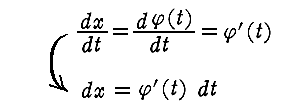
�����疾�炩�ł͂Ȃ����ƌ����邩���m��܂��A���̗l�ɂ��Ȃ���ΐ���Ȃ��̂ɂ͐[�����R������܂��B��������߂ŊȒP�ȗ��p���Đ������܂��B
�@
�i�Q�j�ȒP�ȗ�
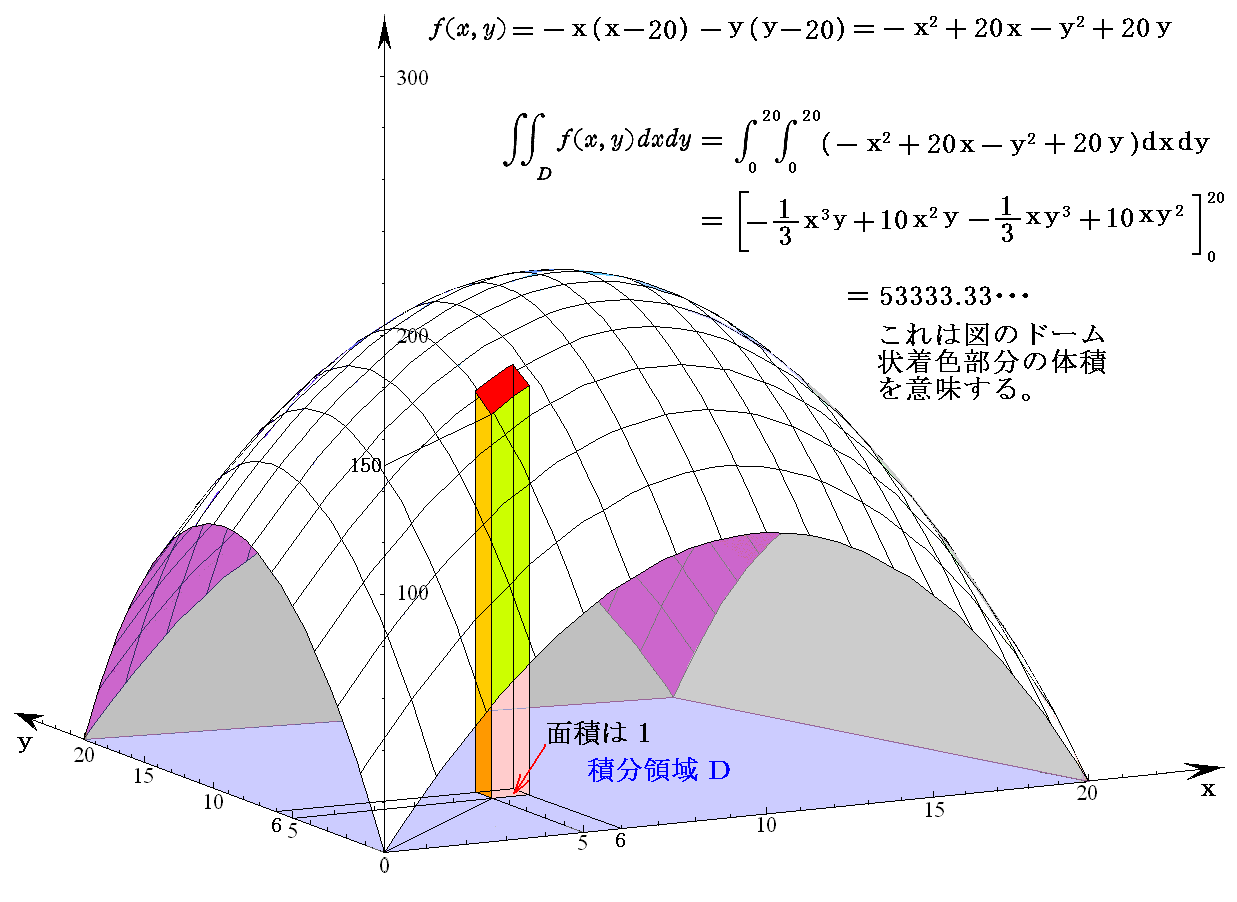
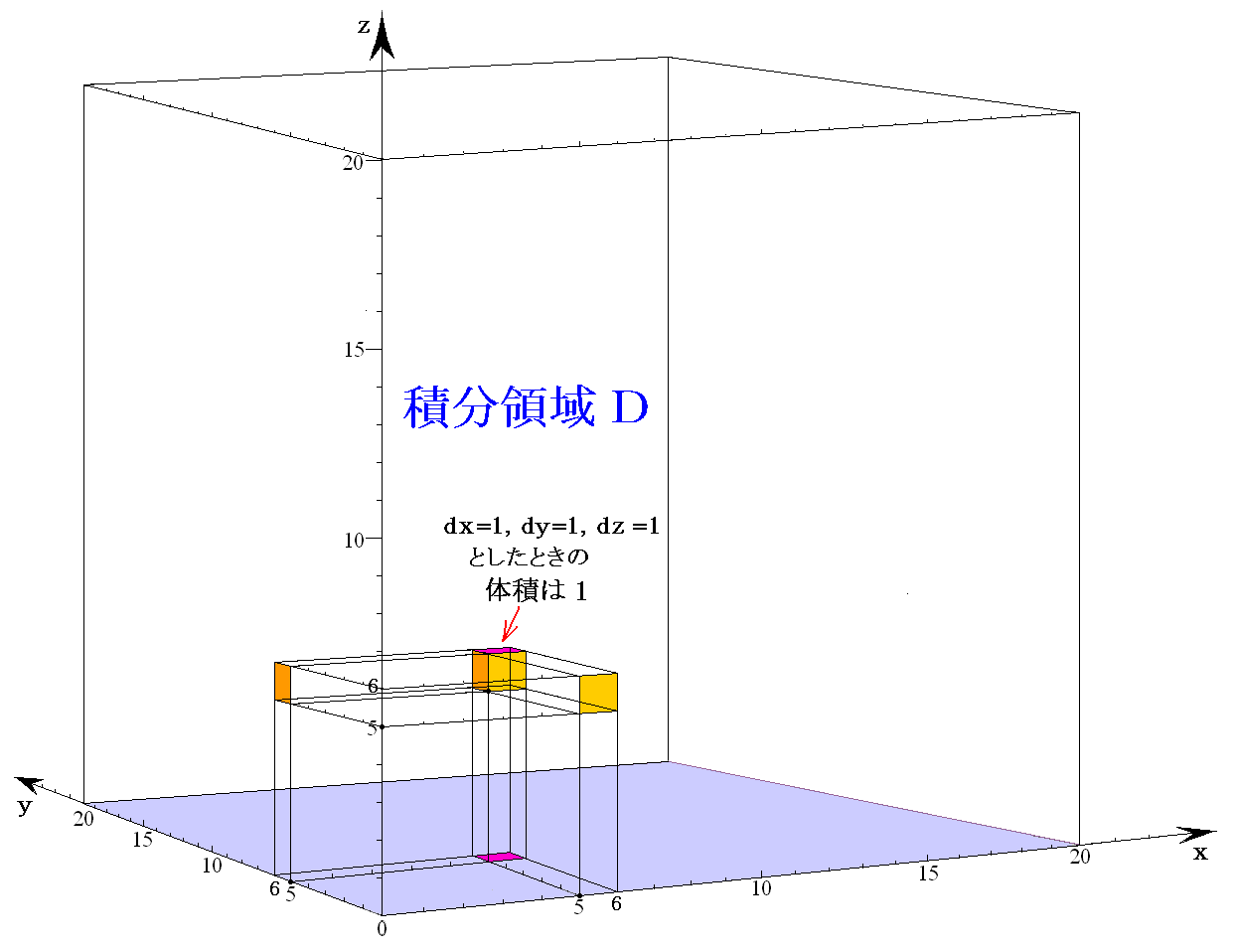
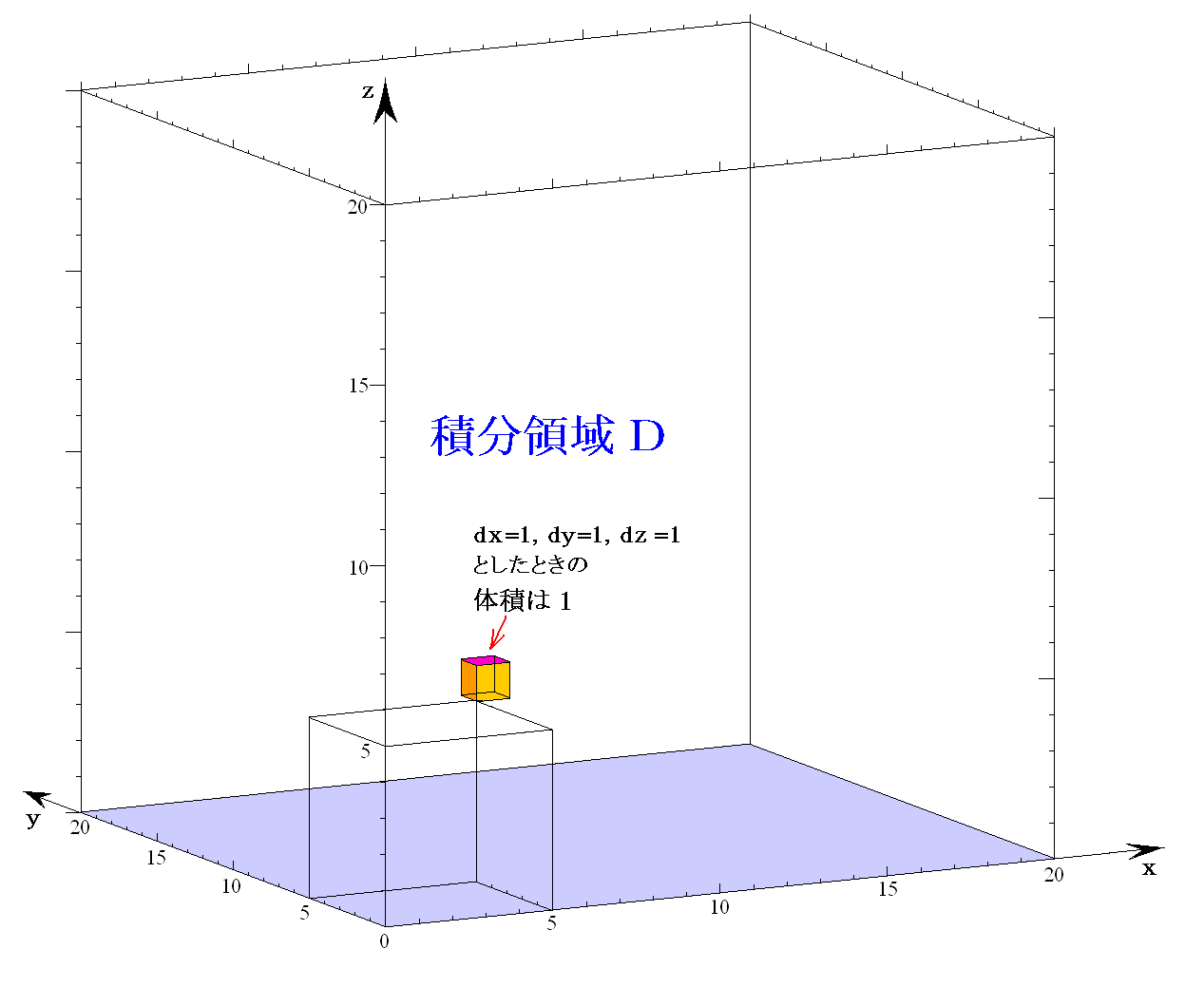
�@��Ƃ��āA��(��)���|���i���|20�j���|��2�{20���@�����グ�A����� ����0�`20 �͈̔͂Œ�ϕ�����B
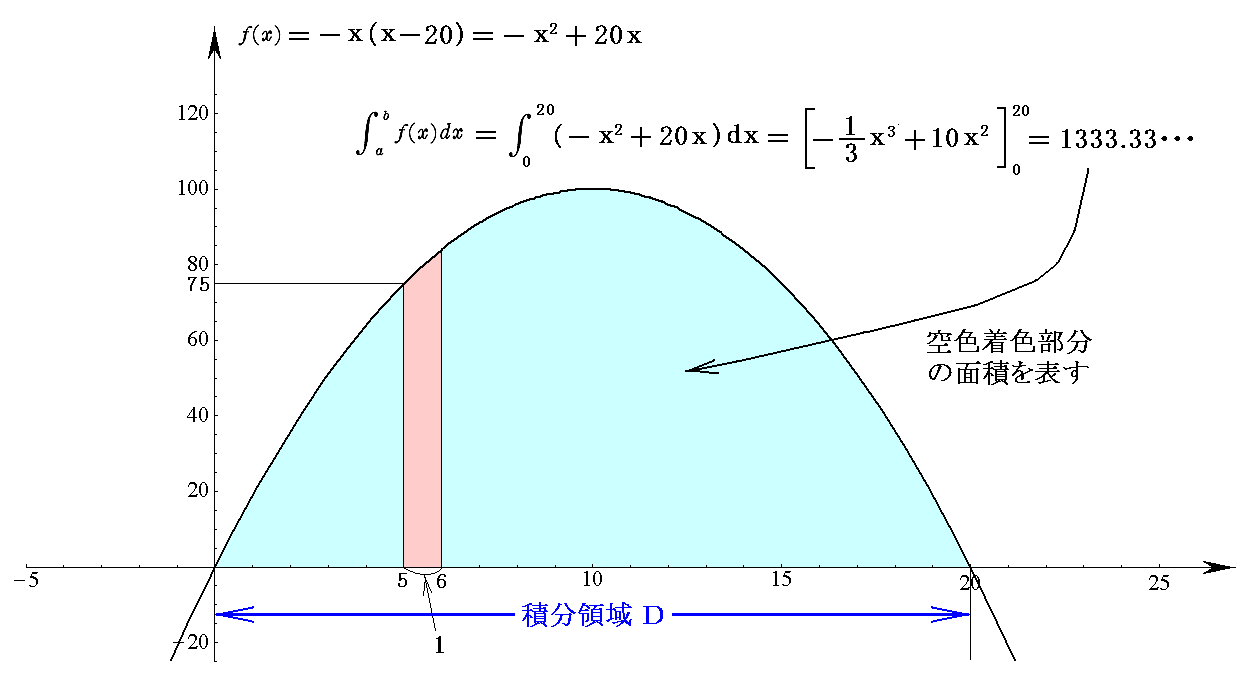
���̒�ϕ��l�͐}�̋�F���F�����̖ʐς�\���Ă��܂��B
�@���ɐϕ��ϐ�����
�̗l�ɕύX���܂��B���̂Ƃ����`��
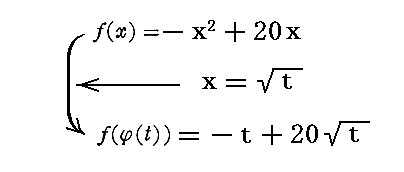
�ƂȂ�܂����A�O���t�̂��Ƃ����Ή�����ʒu�̂��i���j�l�͂��i���j�l�Ɠ����l�ɂȂ邱�Ƃɒ��ӂ��ĉ������B
�@���ۂ̏��A�Ⴆ����5�̓_�̂��i���j�����i5�j���|52�{20�~5��75�@�ł����A���̂Ƃ��̂�����2��52��25�̓_�̂��i���j�����i25�j���|25�{20�~�i25�j0.5��75�@�ł�����S�������ɂȂ�܂��B
�@�܂��A�ϕ��͈͂� ����02�`202��400 �ƂȂ�܂��B
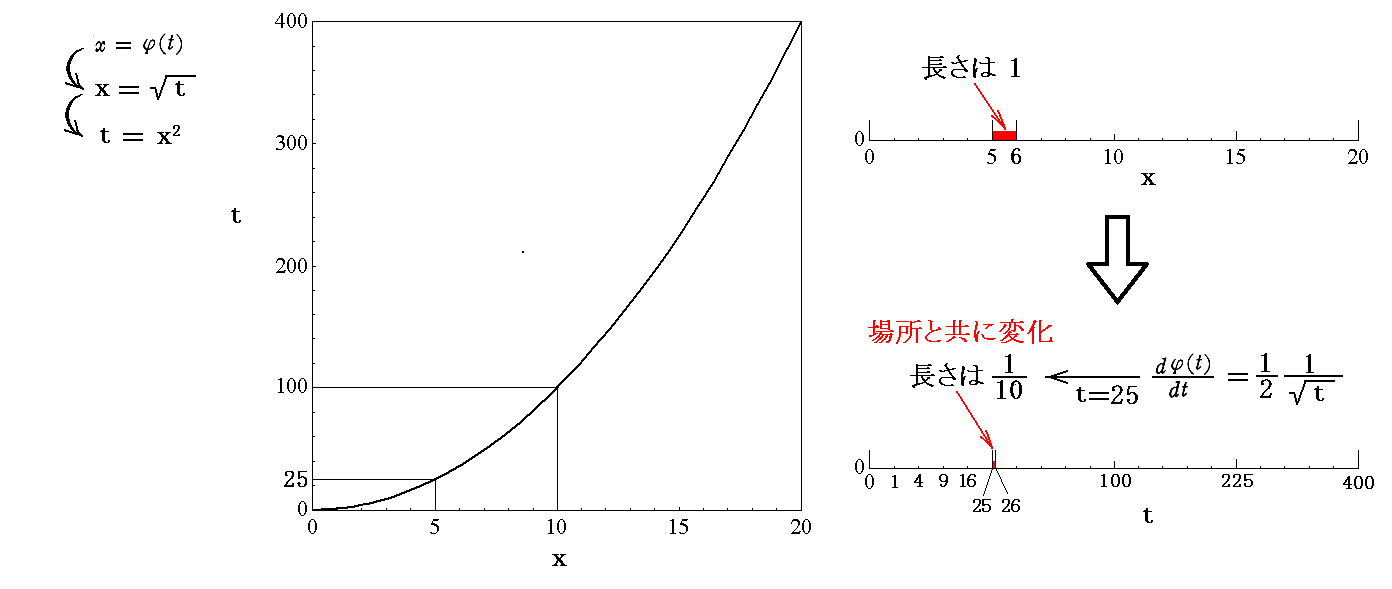
�@���̂Ƃ��A�ϐ����Ɋւ��Ă̒�ϕ��l��

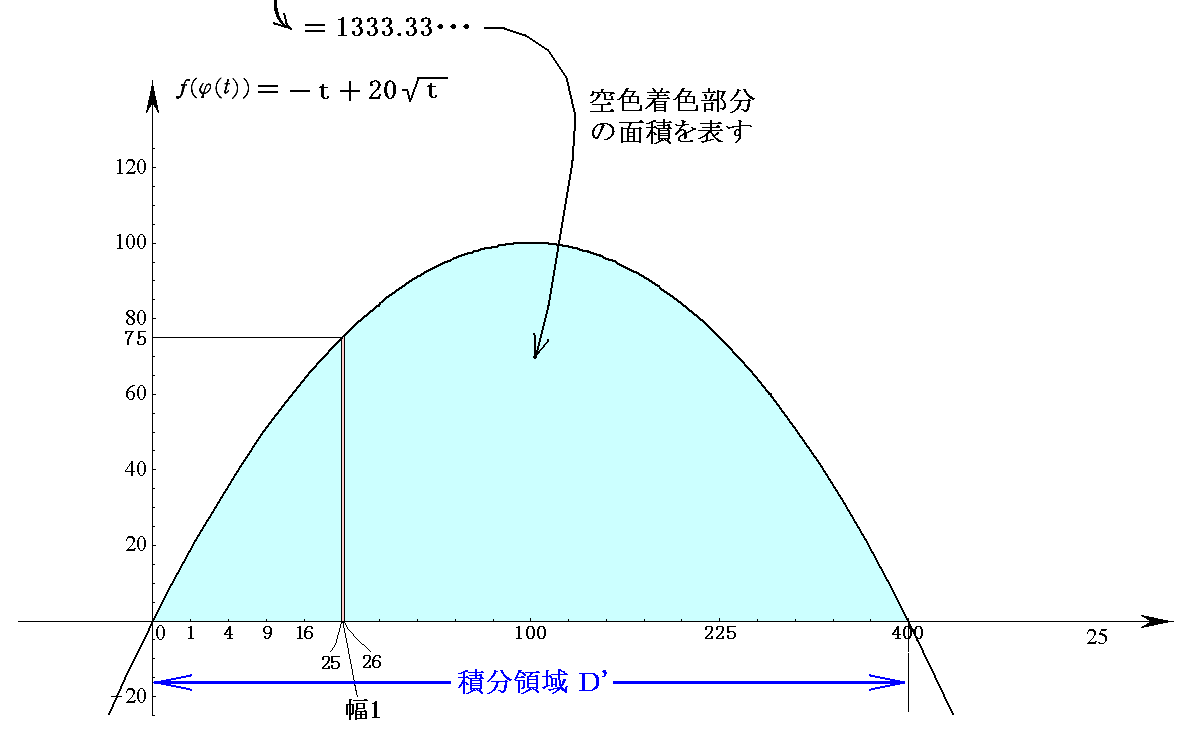
�ƂȂ�A��قǂ̒l�Ɠ����ł��B����͓����ʐϒl��\�����l�ł����瓯���ɂȂ�͓̂�����O�ł��B
�@���̂Ƃ��A�d�v�Ȃ̂̓Ӂf�i���j����������\���Ă���̂��ł��B���̎��͒�ϕ��������Ă����̃O���t���ׂĂ݂�A�����ɔ�������B
�@����͂������P�Ƃ����Ƃ��̐ϕ������A�������P�̐ϕ����̉��{�ł��邩��\���Ă���B�Ⴆ����5�̈ʒu�A�܂肔��52��25�̍��W�l�ł�
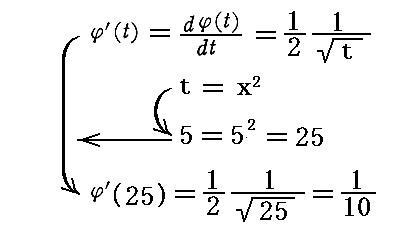
�܂�A1�^10�̒����ɏk��ł���ƌ������Ƃ������Ă���B����1�^10�͂܂��ɍ��W���̂������P�̕����g���ۂ̒����h��\���Ă���B
�@�����āA���̕ω��ʂ͂��̈ړ��Ƌ��ɕω����܂��B�܂肘���Ӂi���j�̂��_�ɉ������g���Ӂi���j�̂��Ɋւ�������W���h�ŕ\�����B
�@
�Q�D��d�ϕ��̍��W�ϊ�
�i�P�j��d�ϕ��̖ʐϑf��
�@��d�ϕ�
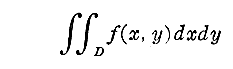
�ŁA�ϐ��ϊ�
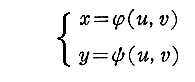
���s���ƁA�ǂ��Ȃ邩���l����B�������A�ӁA�Ղ͘A�������\�Ƃ���B
�@���̂Ƃ��s��ƍs�̊W���猾���鐫���ɂ��

�ł�����A��d�ϕ��̍��W�ϊ���
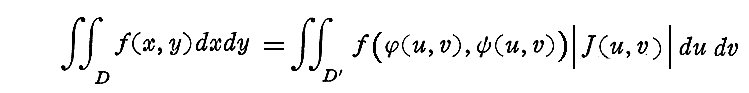
�ƂȂ邾�낤�B������
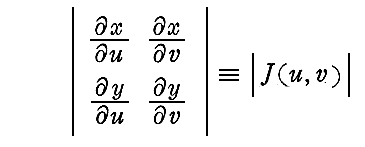
�ƒu���Ă���B���̍s�����ӁA�Ղ́@�g���s�h�@���邢�́@�gJacobian�h�@�Ƃ���
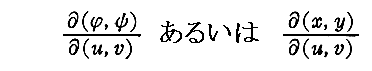
�ŕ\�����Ƃ�����B
�@���́A�@�gJacobian�h�@�������Ӗ����邩�ł��B���̎�������̗�Ő������܂��B
�m�⑫�����n
�@�����ōł�����ɂ������́A��L��
�@�@�@�i�P�j���`���W�ϊ��i���`�ʑ��j���s��\���ł���B
�@�@�@�i�Q�j�s��̐ς��s�̐ςɕϊ��ł���B
���Ƃ��Ǝv���܂��B
�@�i�P�j�ɂ��Ă͕ʍe�u�s�ƍs��v�Q�D�i�U�j�Q�D���Q�ƁB
�@�i�Q�j�ɕt���Ă͕ʍe�u�s�ƍs��v�Q�D�i�P�j�S�D�̒藝�P�ƁA���̒藝�ؖ��̌��ɂȂ����ʍe�u�s�ƍs��v�P�D�i�U�j�P�D�̒藝13���䗗�������B
�@
�i�Q�j�ȒP�ȗ�
�P�D��d�ϕ��̈Ӗ�
�@��Ƃ��āA��(���C��)���|���i���|20�j�|���i���|20�j���|��2�{20���|��2�{20���@�����グ�A����� ����0�`20�A����0�`20 �͈̔͂Œ�ϕ�����B
���̒�ϕ��l�͐}�̃h�[���F�����̑̐ς�\���Ă��܂��B
�m�⑫�����n
�@��L�̏d��ϕ��͖{�����L��̗l�ɁA�܂����̒�ϕ������{���A���ɂ��̒�ϕ������{����̂ł����A���̓�����̎菇���Ȃ��ď����Ă��܂��B
����o�Ă����ɂ��Ă����̗l�ɏȗ�����ċL����Ă���ƍl���ĉ������B
�@
�Q�D�ϕ��ϐ��̕ϊ��@�@�@�@�@�m�ڎ��ցn
�@���ɐϕ��ϐ��i���C���j��
�̗l�ɕύX���܂��B
�@���̂Ƃ���ϕ����̊��`�͕ω�����
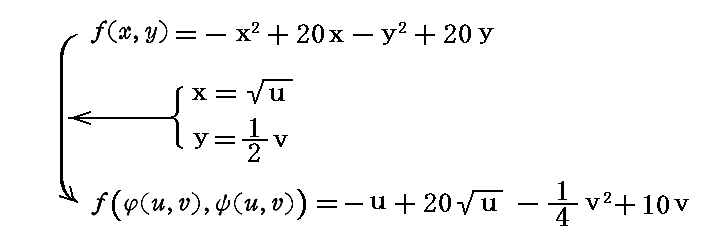
�ƂȂ�܂����A�O���t���i���C���j�Ɓi���C���j���Ή����Ă��铯��_�ł̊��l���i���C���j�͊��l���i���C���j�Ɠ����ɂȂ�܂��B
�@�Ⴆ�i���C���j���i5�C5�j�̓_�̂��i���C���j�����i5�C5�j�����|52�{20�~5�|52�{20�~5��150�@�ɑ��āA����_�ł���i���C���j���i25�C10�j�̓_�̂��i���C���j�����i25�C10�j�̒l��

�ƂȂ�A�S�������ɂȂ�܂��B
�@�������A�ϕ��͈͂͂���0�`400�Ƃ���0�`40 �͈̔͂ƂȂ�܂��B
�@���̂Ƃ��A�V�ϐ��i���C���j�Ɋւ��Ă̒�ϕ���
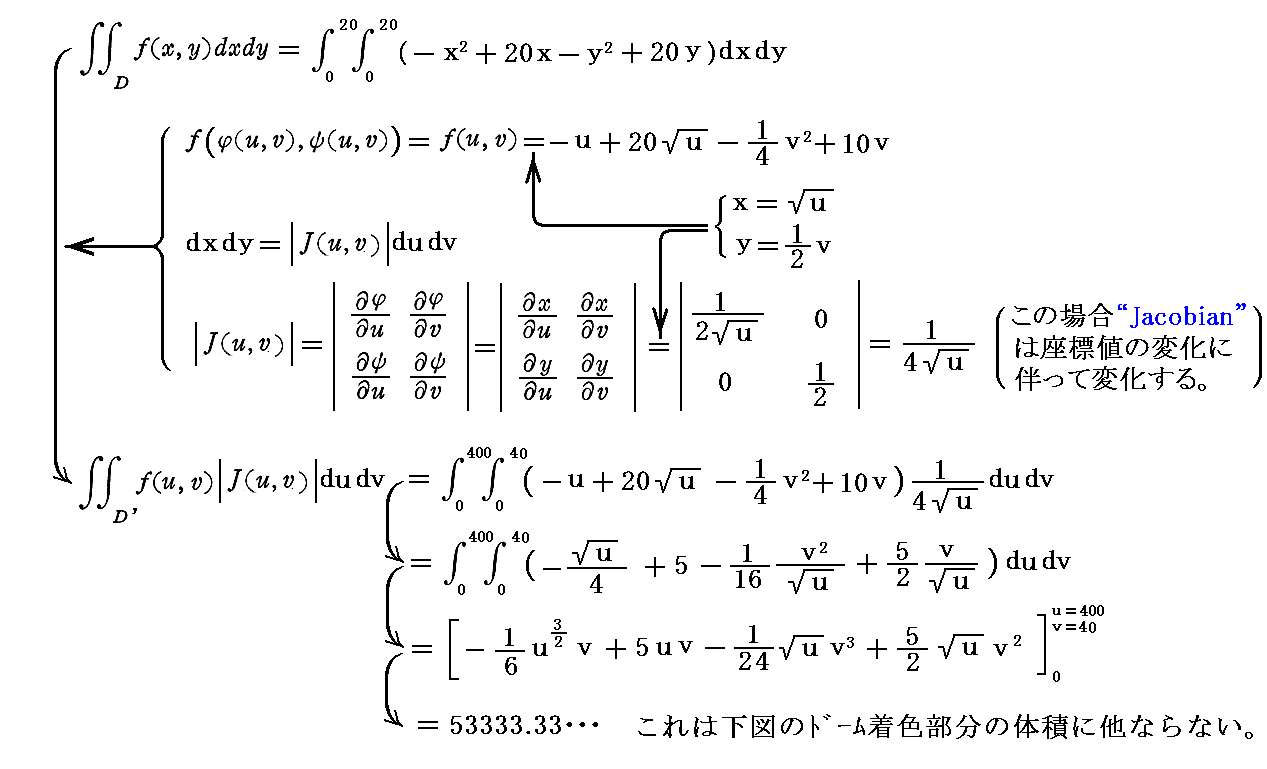

�ƂȂ�A��قǂ̒�ϕ��l�Ɠ����ł��B����͓����̐ϒl��\�����l�ł����瓯���ɂȂ�͓̂�����O�ł��B
�@
�R�D���s�iJacobian�j�̈Ӗ��@�@�@�@�@�m�ڎ��ցn
�@���̂Ƃ��d�v�Ȃ̂́@�gJacobian�h
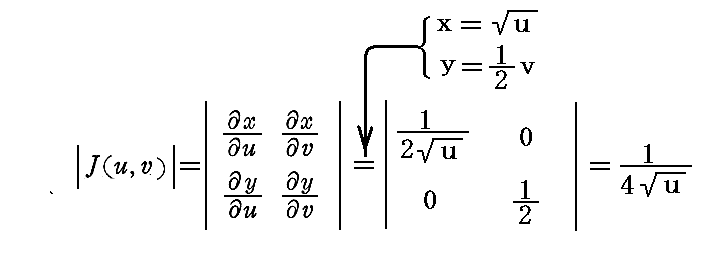
������\���Ă���̂��ł��B���̎��͒�ϕ����̗l�q�������Ă����}���ׂĂ݂�A�����ɔ�������B
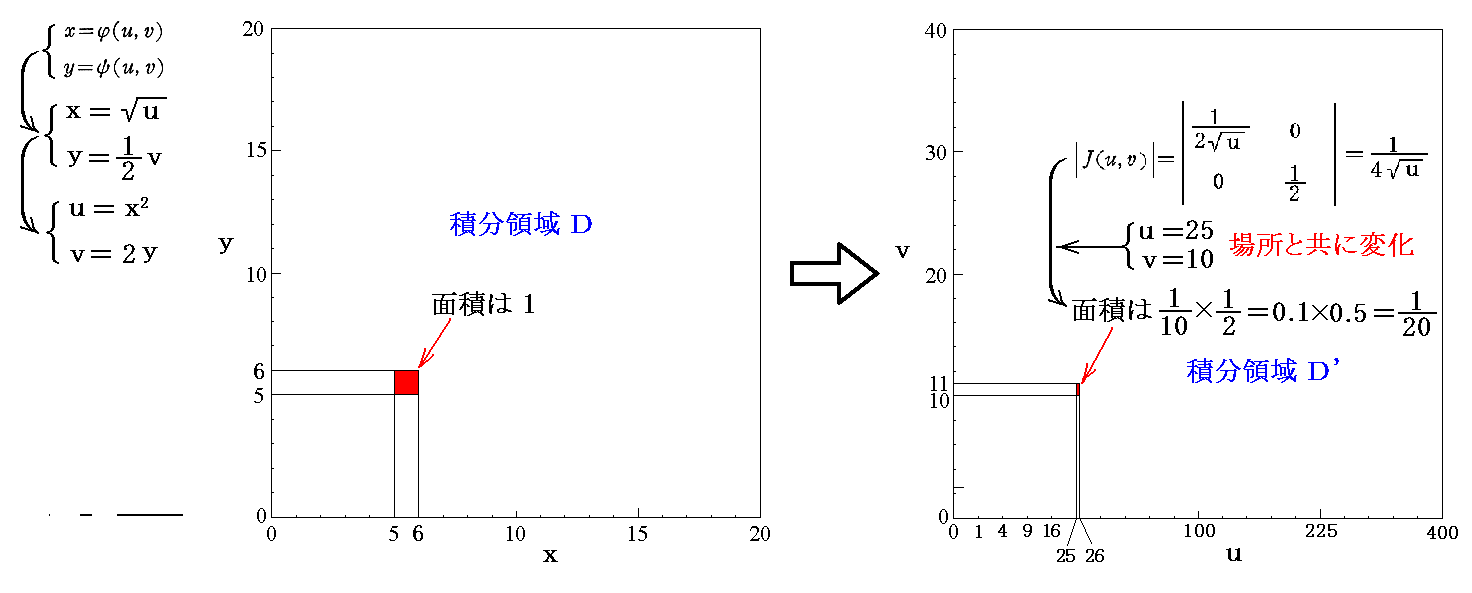
�@�Ⴆ�A�ŏ������W�ϊ��̗l�q�������}�ŕϊ��O�́i���C���j���i5�C5�j�̓_�ɉ����還�������i�������P�A�������P�Ƃ���j�ō\�������ϕ��v�f��\�������̖ʐς�1�ł��B
�@��������n�_�i���C���j���i25�C10�j�̓_�ɉ����還�������i�������P�A�������P�Ƃ���j�ō\�������ϕ��v�f��\�������̖ʐς�1�^20�ƂȂ�܂��B�܂�A���̒l���g���ۂ̖ʐρh�ł��鎖�������̂��@�gJacobian�h
�̓����ł��B������̒l�́i���C���j�̍��W�l�̕ω��Ƌ��ɕς���Ă��܂��B
�@������ɂ��Ă��A�ϕ��ʐϑf�Ђ������������ۂ̖ʐςɒ������邽�߂̗ʂ� �gJacobian�h �Ȃ̂ł��B
�@
�i�R�j���Ό����W
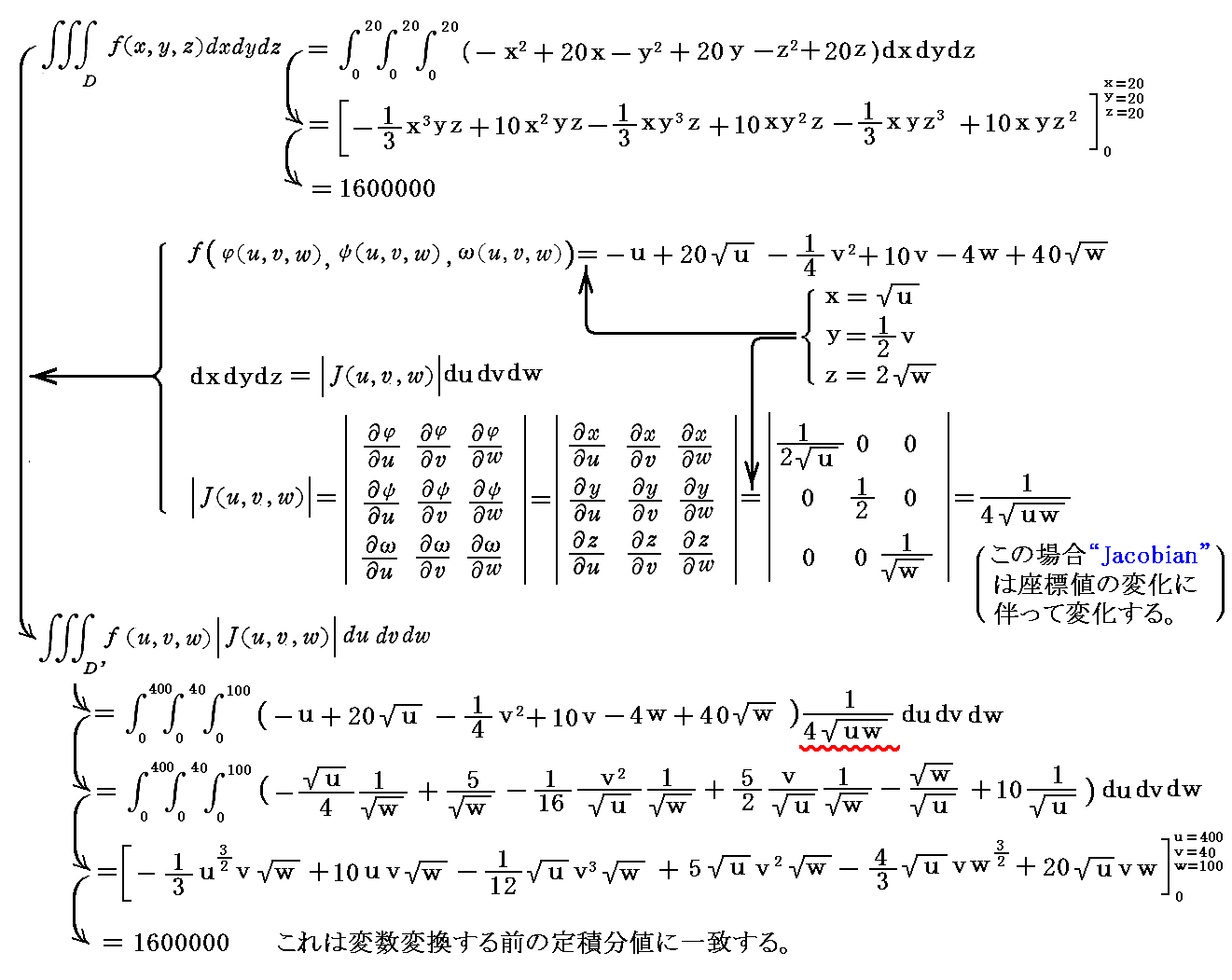
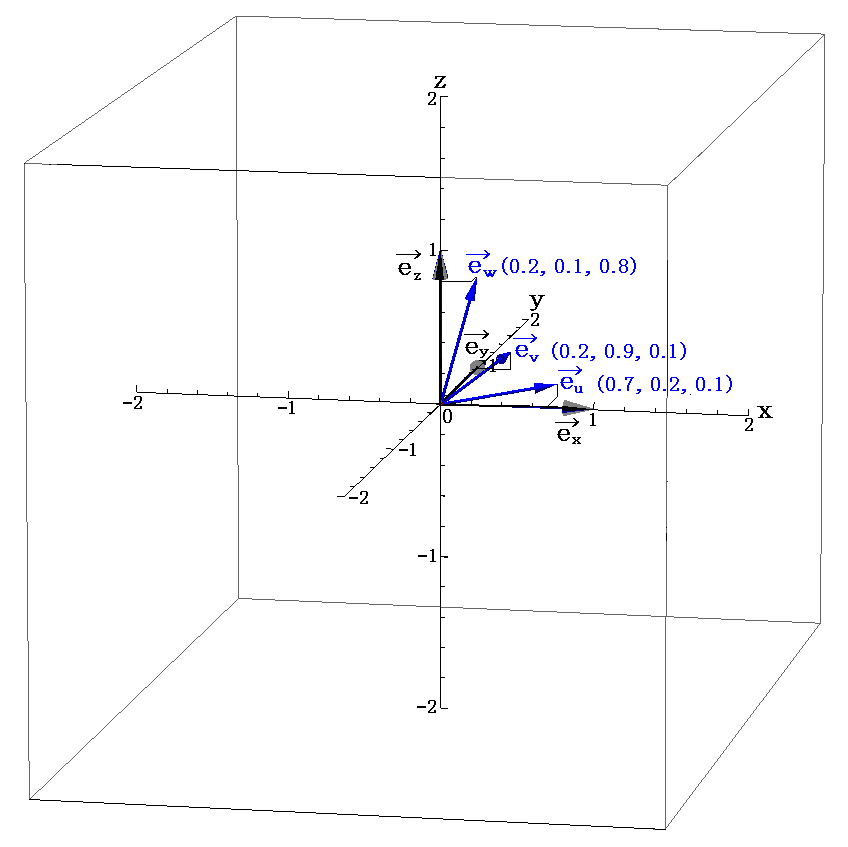
�@�O�߂̗�ł́A���W�ϊ��������Ƃ��̓��̈���݂̂ɊW���Ă����̂ŁA�gJacobian�h ���ʐς�\�����Ƃ��Ȃ��Ȃ��ǂݎ��܂���B�����ŁA���W�ϊ��������Ƃ��̗����̕ϐ��ɊW����Ό����W�����グ�Ă݂܂��B
�P�D���x�N�g���ϊ���
�@���}�̗l�ȁi���C���j���W�n�Ɓi���C���j���W�n�̊Ԃ̍��W�ϊ��������߂邽�߂ɁA�܂��g���x�N�g���h�̕ϊ��������߂�B
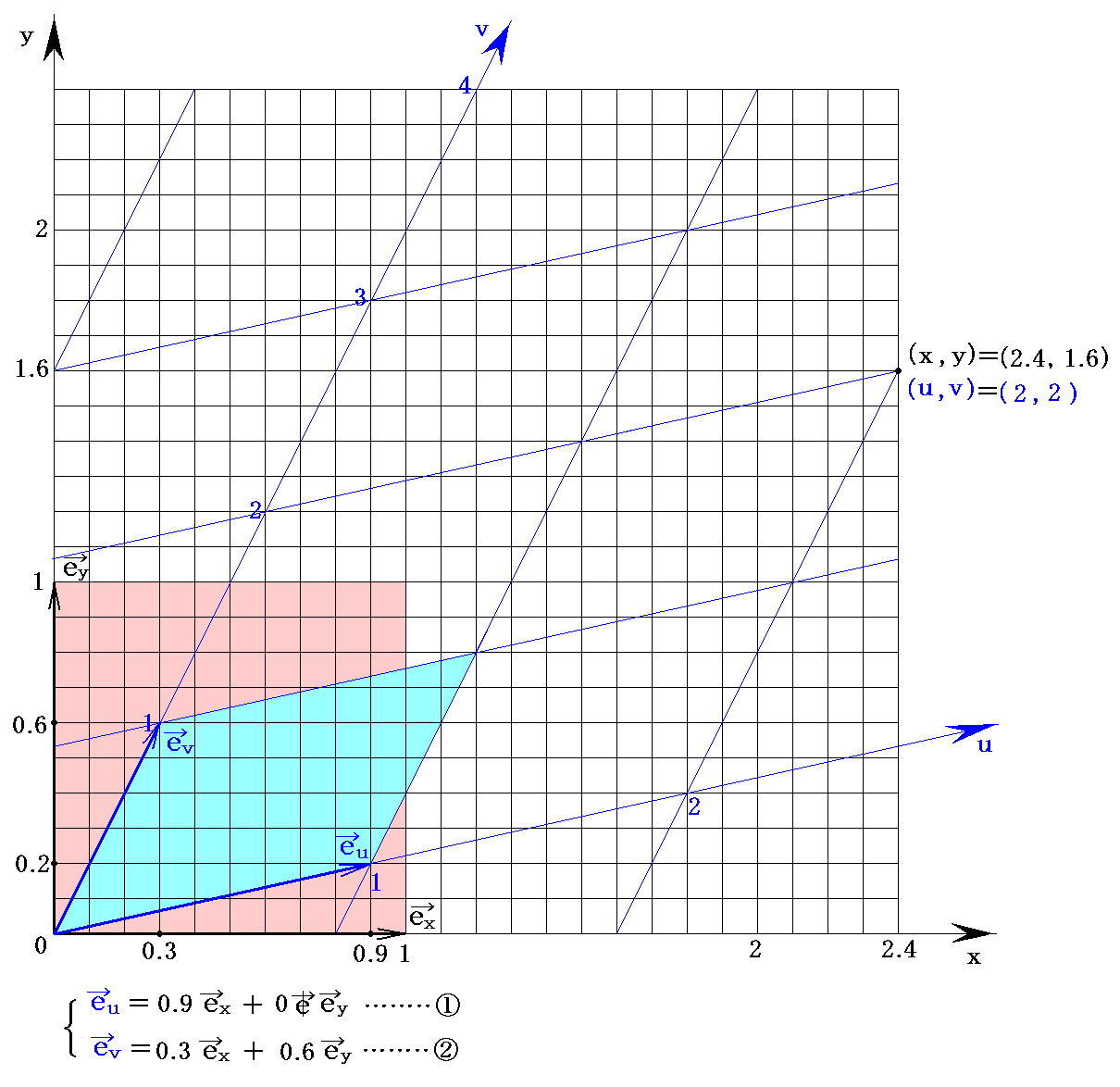
�@���ƇA���𖢒m���x�N�g����x�A��y�����߂�A���������ƌ��Ȃ��ĉ�����
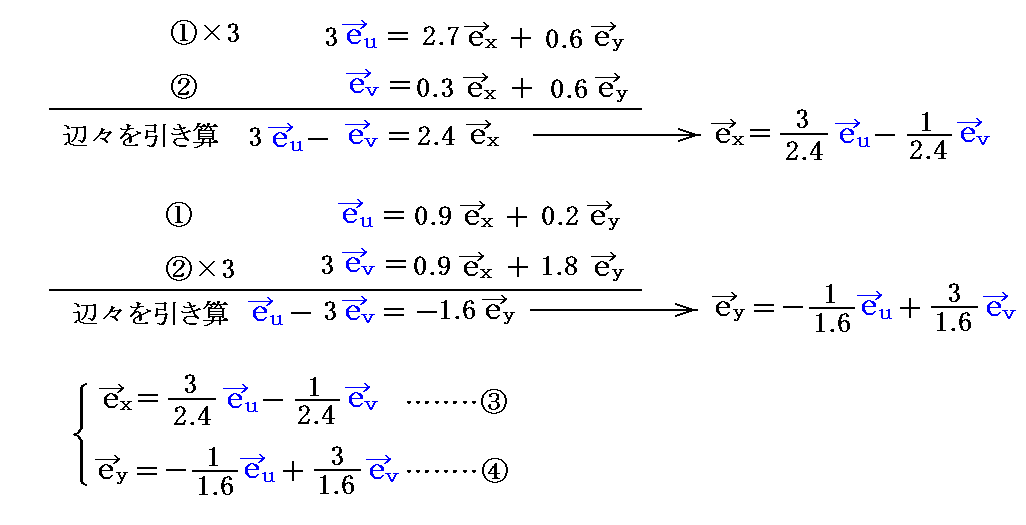
��������B���̂Ƃ�������W���̈Ӗ��͎��}��薾�炩�ł��낤�B
�@
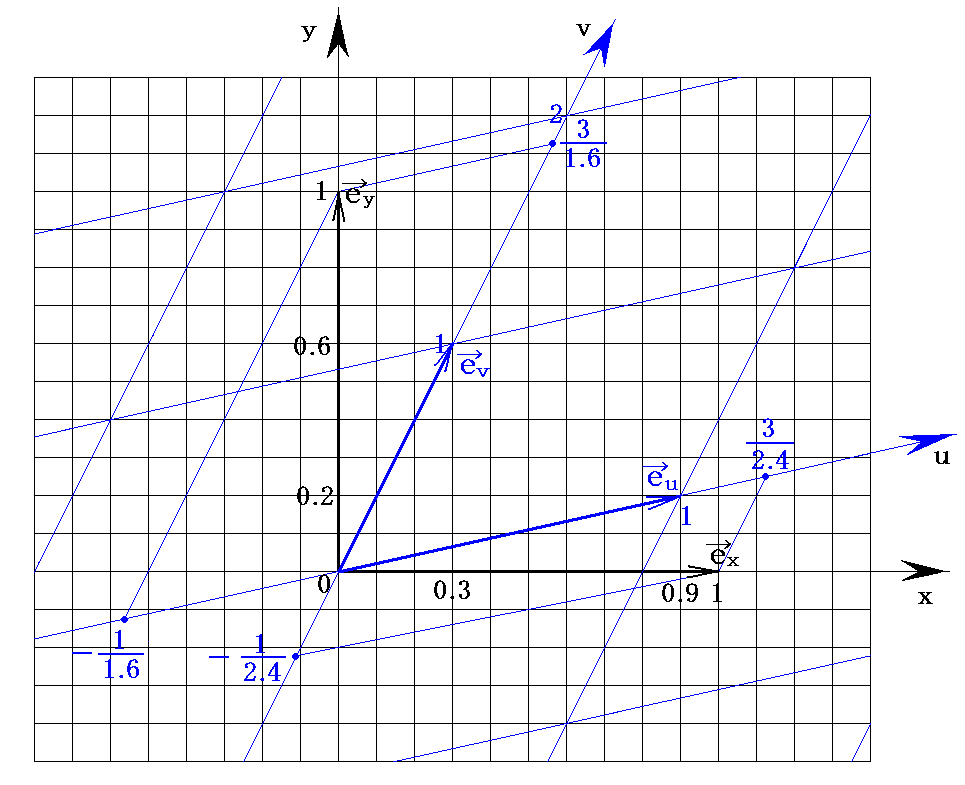
�Q�D���W�l�̕ϊ����@�@�@�@�@�m�ڎ��ցn
�@���̂Ƃ��i���C���j���W�̔C�ӂ̓_�́A�ȉ��̕ϊ����D�A�E�ɂ��i���C���j���W�Ɉڂ����B
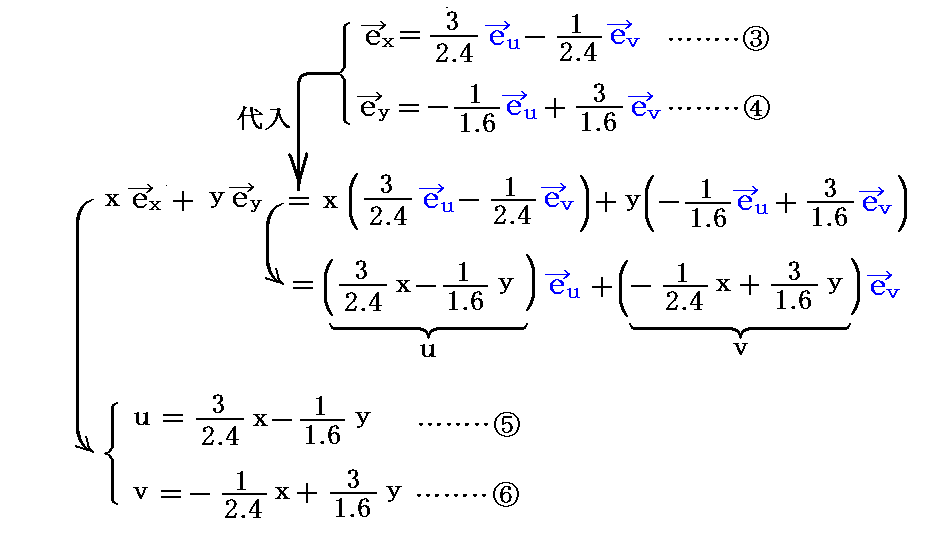
�D�A�E�����t�ɉ����i���C���j���W����i���C���j���W�ւ̕ϊ����F�A�G��������B

����͂������

�Ōv�Z����鎮�Ɠ����ł��B
�@
�R�D���W�ϊ����̈Ӗ��@�@�@�@�@�m�ڎ��ցn
�@�Ⴆ�A�i���C���j���i2.4�C1.6�j���D�A�E���ɑ���A���邢�́i���C���j���i2�C2�j���F�A�G���ɑ�������

�ƂȂ�A�m�����ŏ��̐}���̑Ή��W�����������B�܂���W�ϊ��Ƃ͓����ϕ��̈��\������_�̍��W�l�̑Ή���\���Ă���B
�@�ʂȗ�Ƃ��āA�i���C���j���i5�C5�j�ɑΉ�����i���C���j���W�̒l�����߂Ă݂�Ɖ��}�̂悤�ɂȂ�B
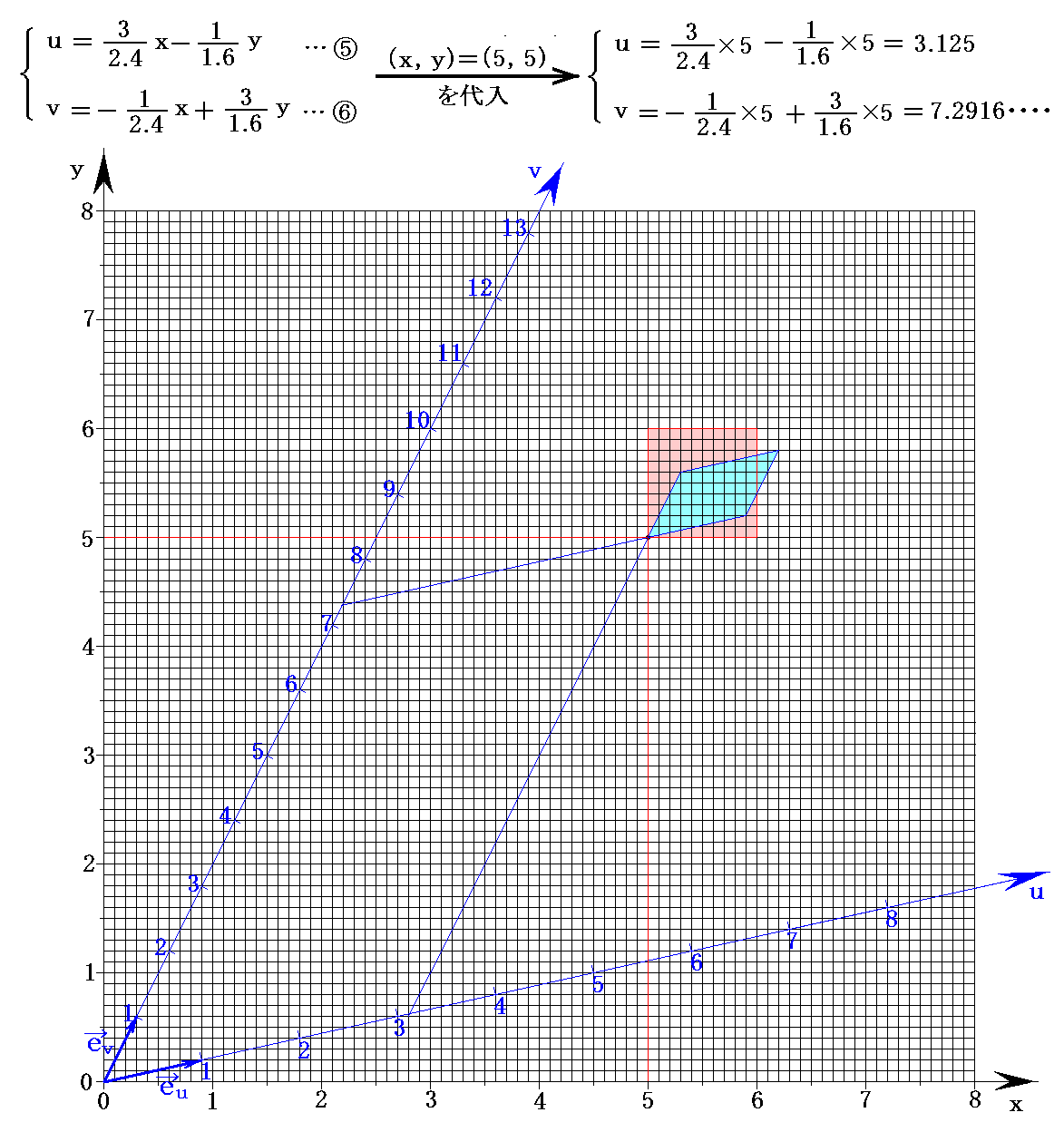
�@�i���C���j���i5�C5�j�ɑΉ�����_�ɉ�����ϕ��ʐϑf�Ђ��}������Ə�}�̃s���N�F�l�p�`�Ƌ�F���s�l�ӌ`�ƂȂ�B�����͒�ϕ��i�̐ϐϕ��ƂȂ�j������Ƃ��́i���C���j���W�n�A�i���C���j���W�n���ꂼ��ł̖ʐϑf�Ђ��Ӗ�����B
�@
�S�D���s�iJacobian�j�̈Ӗ��@�@�@�@�@�m�ڎ��ցn
�@�ϐ��ϊ������Ƃ��̓�d�ϕ��Ɍ����@�g���s�iJacobian�j�h�@���v�Z���Ă݂��
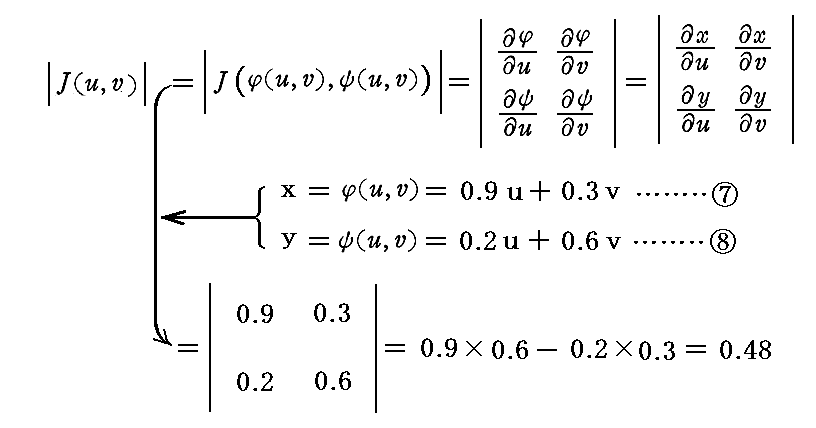
�ƂȂ�B����0.48�͑O�}�����g��F���s�l�ӌ`�̖ʐρh��\���Ă���B
�@���̂��Ƃ𗝉����邽�߂ɂ́A�O�}���̓�̂Q�������x�N�g��
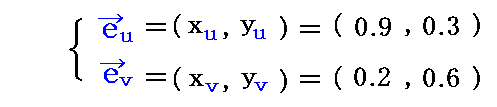
���l�����Ƃ��A��L�̍s�v�Z�l�͓�����x�N�g�����g�O�ρi�x�N�g���ρj�̐�Βl�h��\���Ă��邱�Ƃ��v���o���Ηǂ��B���ꂪ��L���s�l�ӌ`�̖ʐς�\�����Ƃɂ��Ă͕ʍe�u�x�N�g���̓��ςƊO�ς̐����\���v�Q�D�i�S�j���Q�Ƃ��ꂽ���B�����̂Q���������݂̂����o���čl����Ηǂ��B
�@���̗�Œ��ӂ��ė~�������́A���̗�̐ϕ��ϐ��̕ϊ��Ő�����V���Ȑϕ��P�ʃZ���i�ʐϑf�Ёj�̌`�͑S�ϕ��̈�ɑ��ē����`�ɂȂ邱�Ƃł��B���ׁ̈A���̗�ł��g���s�iJacobian�j�h�́A�ϐ��i���C���j�̕ω��Ɉˑ������A�S�̈�œ���̒l0.48�ƂȂ�܂��B
�@�����A�V�����ϕ��ϐ����g�Ό��Ȑ����W�h�ł̍��W�l�ƂȂ��ʓI�ȍ��W�ϊ��̏ꍇ�ɂ́A���x�N�g��
�͏ꏊ�Ƌ��ɕω����܂��B���̂��߁A���̏ꏊ���Ƃ����x�N�g����p�����g���s�iJacobian�j�h�̒l���ꏊ�Ƌ��ɕω����܂��B���̕ω�����l���d�݂Ƃ��ď悶�āA�ϕ������{����Ηǂ��̂ł��B
�@
�T�D�V�ϐ��ł̓�d�ϕ��̎��{�@�@�@�@�@�m�ڎ��ցn
�@�O�߂ŗ��p������ϕ����Ŏ��ۂɓ�d�ϕ������{����B
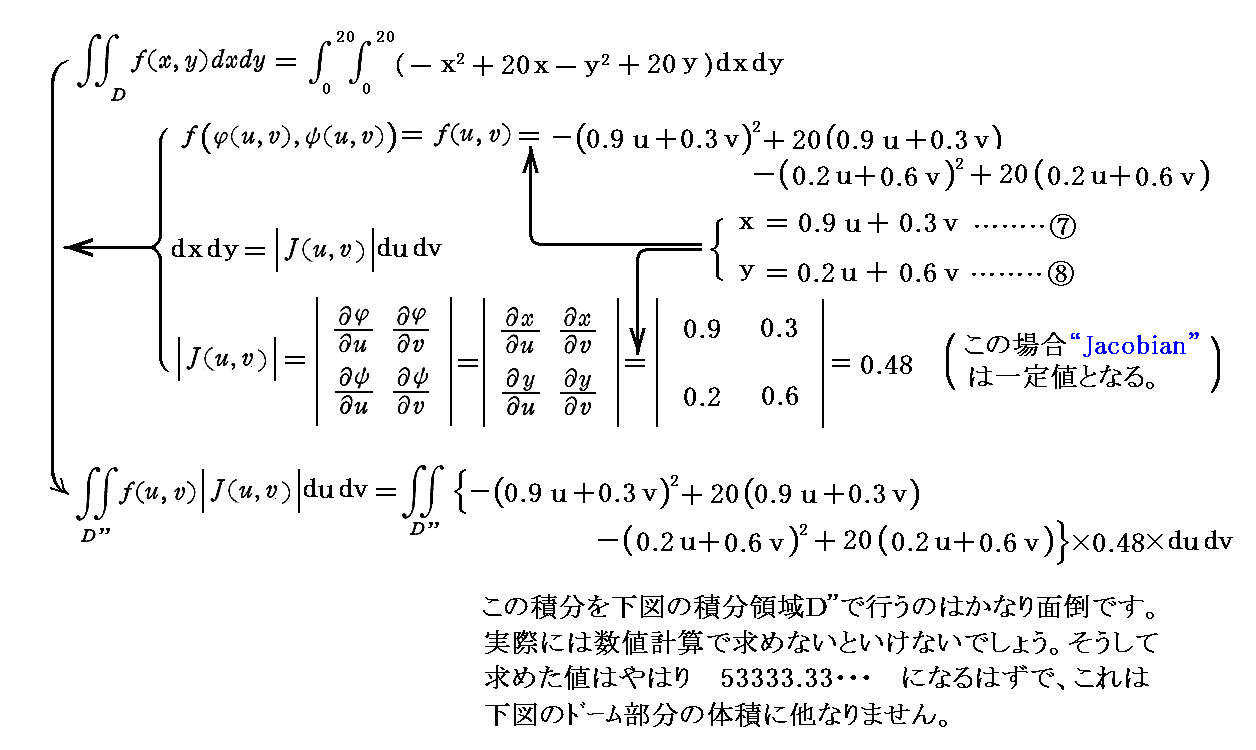
�@���̂Ƃ��}���i���C���j�Ɓi���C���j���Ή����Ă��铯��_�ł̊��l���i���C���j�͊��l���i���C���j�Ɠ����ł��邱�Ƃɒ��ӂ��ĉ������B

�@�ϐ��ϊ����Ă��A��ϕ��l�͈ȑO�ƑS�������ɂȂ邱�Ƃɒ��ӂ��ꂽ���B
�@
�i�S�j���̂��߂ɐϕ��ϐ���ϊ�����̂�
�@�d�ϕ��̕ϐ��ϊ��́A�������邱�Ƃɂ���āA��ϕ������ϕ��ł���`�ɕό`�ł���ꍇ�ɏd�v�ł��B
�@�Ⴆ��
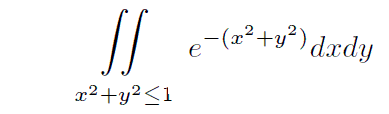
�́A���̂܂܂̊��`�ł͊ȒP�ɐϕ��ł��܂���B�������A���W���i���C���j�������W�n�����i���C�Ɓj�ɍ��W�n�ɕϊ��������ϕ������ȒP�ɐϕ��ł���`�ɂȂ��B
�@���ہA���̂Ƃ��̍��W�ϊ�����
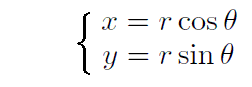
�ƂȂ�̂ŁA�g���s�iJacobian�j�h��

�ƂȂ�B���̏ꍇ�ɂ��A������ϕ��ʐϑf�Ђ̖ʐ����Ӗ����܂��B
�@�܂�A���ꂼ��̍��W�n�ł̐ϕ��ʐϑf�Ђ̖ʐς�\���Ă���B�܂�(���C���j���W�n�ł͂��������i������1�C�������P�Ƃ���j�̖ʐς��A�i���C�Ɓj���W�n�ł͂������Ɓi������1�C���Ɓ�1radian�Ƃ���j�̖ʐς�\���B
�@�����āA���̖ʐϑf�Ђ̖ʐϒl�iJacobian�j���A�i���C�Ɓj���W�n�ł����W�l�i���C�Ɓj�Ɉˑ����ĕω����܂��B���̕ω�����d�݊����悶�Ē�ϕ������{���邱�ƂɂȂ�܂��B
�@��L���g���s�iJacobian�j�h��p�����

�ƌv�Z�ł���B
�@���ɁA�ϕ��͈͂��S���ʂł���ꍇ�ɂ�

�ƂȂ邪�A���̌��ʂ�m���Ă���A
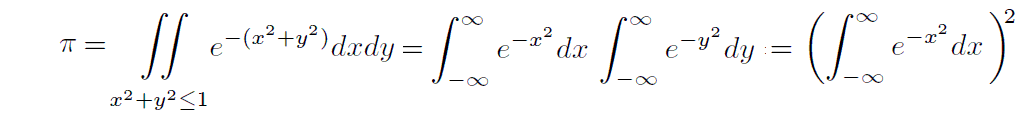
�̗l�Ȏ��ό`�����邱�Ƃ�
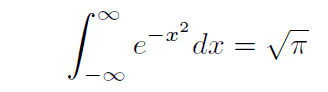
�Ȃǂ̒�ϕ��l�����߂鎖���ł���B�ϐ��ϊ��̃e�N�j�b�N��m��Ȃ��ƁA���̒�ϕ��l�����߂�̂͋ɂ߂č���ł��B
�@�����̌��_�͓��v�͊w�ɉ����ďd�v�ł��B���̓�����ɂ��Ă͕ʍe�u�}�N�X�E�F���̑��x���z���P�g�C�̂̓��͊w�I���_�̐����h�v�Q�D�i�Q�j�Ȃǂ��Q�Ƃ��ꂽ���B
�@
�R�D�O�d�ϕ��̍��W�ϊ�
�i�P�j�O�d�ϕ��̑̐ϑf��
�@�O�d�ϕ�
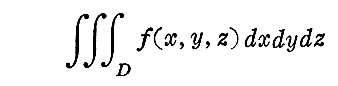
�ŁA�ϐ��ϊ�

���s���ƁA�ǂ��Ȃ邩���l����B�������A�ӁA�ՁA�ւ͘A�������\�Ƃ���B
�@���̂Ƃ��A�Q�D�i�P�j�m�⑫�����n�Ő��������l��
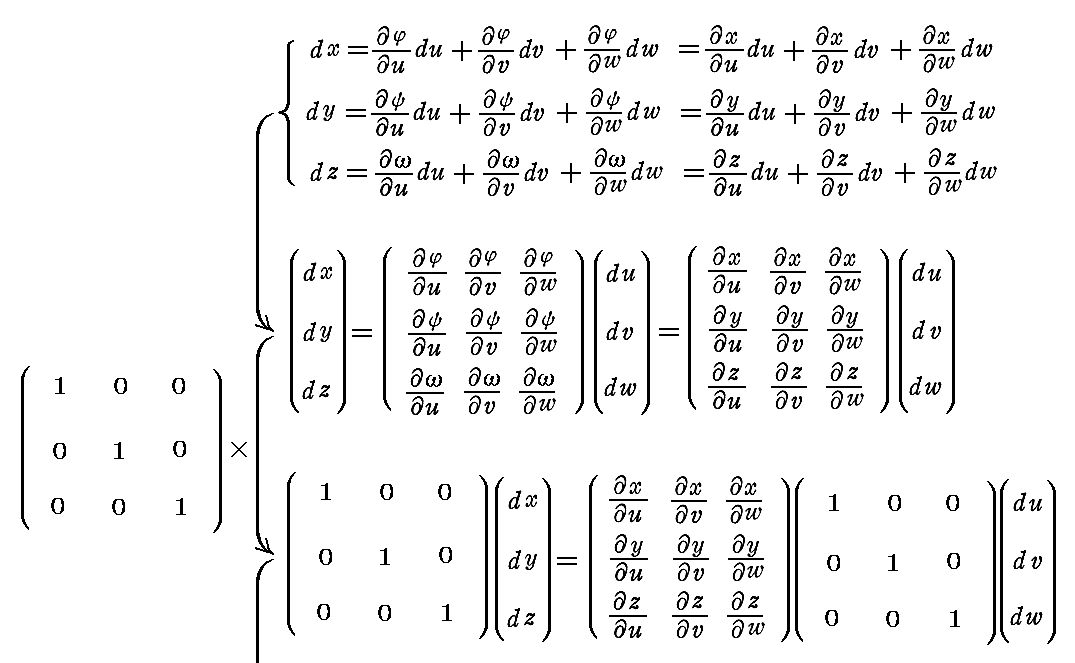

�ł�����A�O�d�ϕ��̍��W�ϊ���
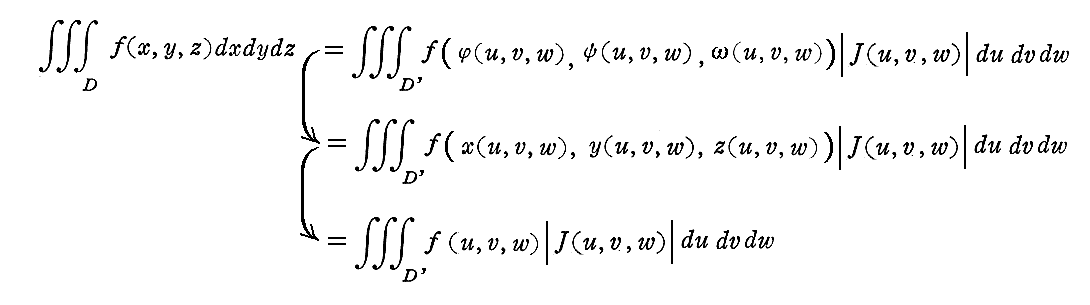
�ƂȂ�B�������A
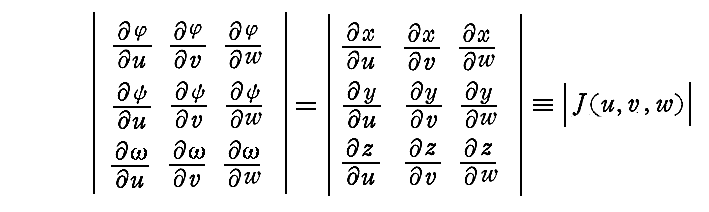
�ƒu���Ă���B���̍s�����ӁA�ՁA�ւ̂́@�g���s�h�@���邢�́@�gJacobian�h�@�Ƃ����B�܂��A�c�f�͂c�ɑΉ����邕����-��Ԃ̗L�E�̈���Ӗ�����B
�m�⑫�����n
�@���ɂ��鐔�w����ǂ�ł��ǂ�����Ȃ��̂́A�d�ϕ���ϐ��ϊ������Ƃ��ϕ��v�f���������������b�i(���C���C��)�b�������������Œu��������Ηǂ����R�ł��B����͌��Ljȉ��̗l�ɍl���邵�����@�͖����悤�Ɏv���܂��B
�@����͏�L�̕��@
�Œu�������Ă���̂ł����A���̐��������́A�ȉ��ŏq�ׂ�l���b�i(���C���C��)�b���A��������������1�~1�~1�̑̐ϑf�Ђ̎��ۂ̑̐ς�\���Ă���ƌ������Ƃ��������Ƃŕۏ����B
�@���ꂪ���ۂ̑̐ϑf�Ђ̑̐ςł���ƌ������Ƃ��������ɂ���Ă̂݁A��L���g�ϕ��v�f�̒u�������v�Z�h��������������B����ȊO���g���R�r�̒藝�h���ؖ�������@�͂���܂���B
�@
�i�Q�j�ȒP�ȗ�
1�D�O�d�ϕ��̈Ӗ�
�@���p���ĎO�d�ϕ��̈Ӗ��ƍ��W�ϊ��̈Ӗ����������B
�@�O�͂Ɠ����l�Ȋ���Ƃ��āA
���i���C���C���j���|���i���|20�j�|���i���|20�j�|���i���|20�j
�@�@�@�@�@�@�@���|��2�{20���|��2�{20���|��2�{20��
�����グ�A����� ����0�`20�A����0�`20�A����0�`20 �͈̔͂Œ�ϕ�����B
�@��d�ϕ��̏ꍇ�́A���̐ϕ��l�͕��ʏ�̐ϕ��̈�Ƃ��̏�ɒ�`���ꂽ���ň͂܂ꂽ�����̑̐ϒl���Ӗ������B����ɑ��āA�O�d�ϕ��ł́A�O������Ԃ̑̐ϑf�Ђ��ꂼ��̓_�Ɋ��蓖�Ă�ꂽ���l�ƁA�̐ϑf�Ђ̑̐ςƂ̐ς��O������Ԃ̈̕�S�̂ɂ��ĉ������킹���a���A���̈̕�ɂ��Ă̒�ϕ��l�ƂȂ�B
�@�O������ԂɏZ�މ�X�ɂ͎l�����̑̐ς�z������͓̂�����A�ϕ��l�͎l�����̑̐ς�\���Ă���B���̂Ƃ��A��d�ϕ��̏ꍇ�̐ϕ��͈͓͂��̖ʐϗ̈�ł������̂����A�O�d�ϕ��ł͐ϕ��͈͂��O�����̑̐ϋ�ԂɂȂ鎖�ɒ��ӂ��ĉ������B
�@
�Q�D�ϕ��ϐ��̕ϊ��@�@�@�@�@�m�ڎ��ցn
�@���ɁA�ϕ��ϐ����i���C���C���j����i���C���C���j�ɕύX���܂��B
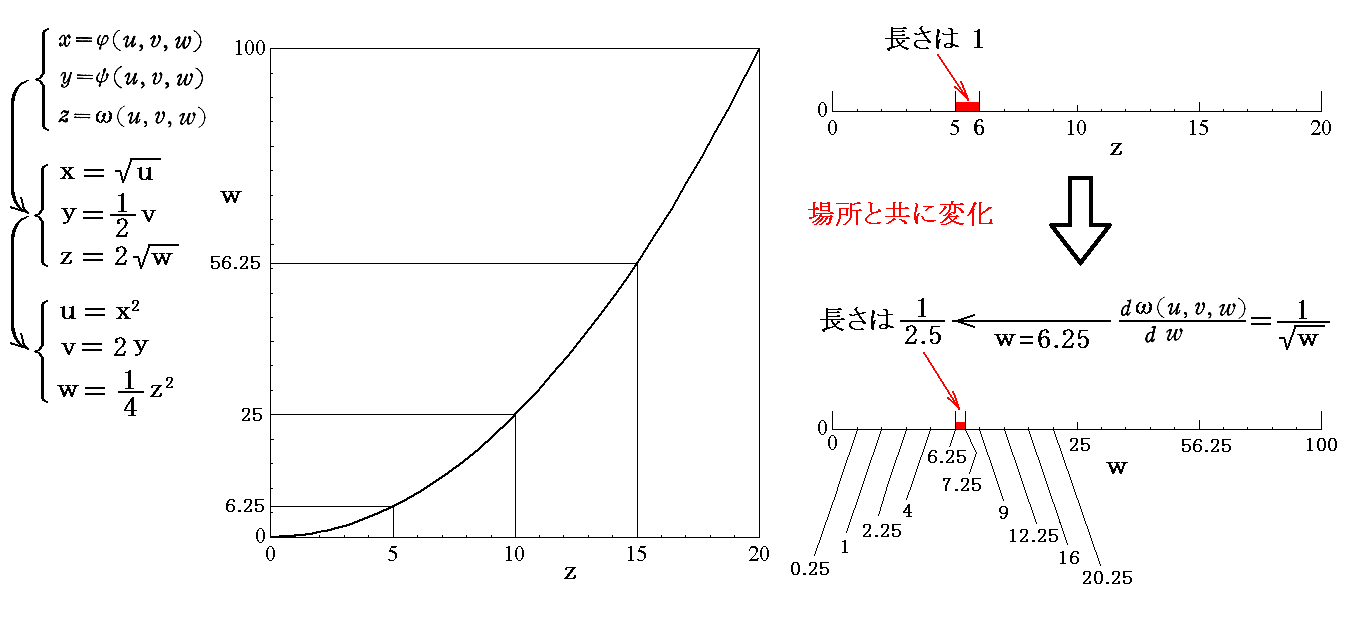
������̎��ۂ̖ڐ���̒l���A���ɉ���ɂ������A�}�̏�ŏ\���Ɍ������ꂽ���B
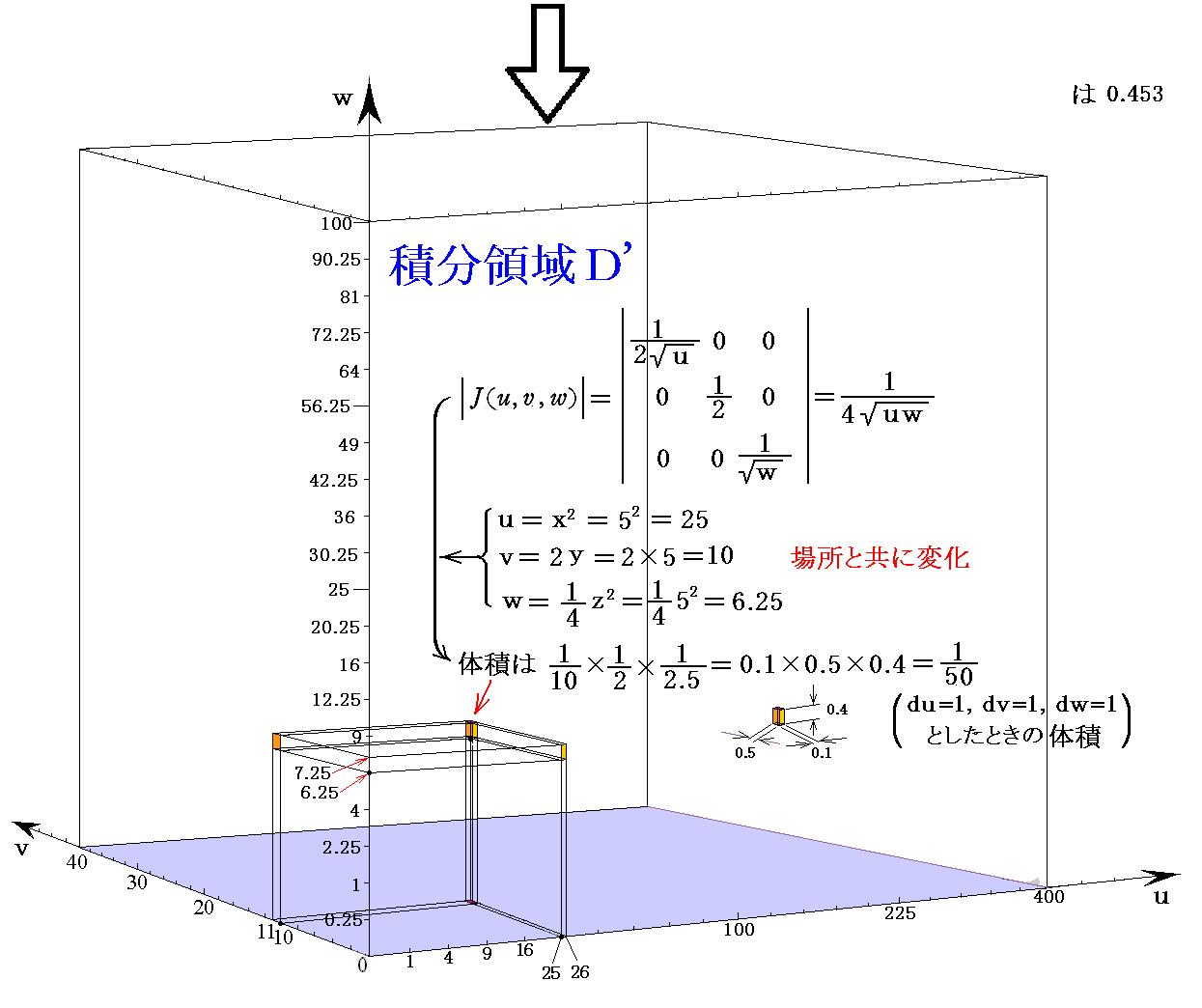
�@�����̈�ڐ���̒�������}�̗l�ɕς��̂Łi���C���C���j���i5�C5�C5�j���Ȃ킿�i���C���C���j���i25�C10�C6.25�j�_�ł̒P�ʑ̐ϑf�Ђ̎��ۂ̑̐ϊW�͎����ɏ]���Ē�܂�B
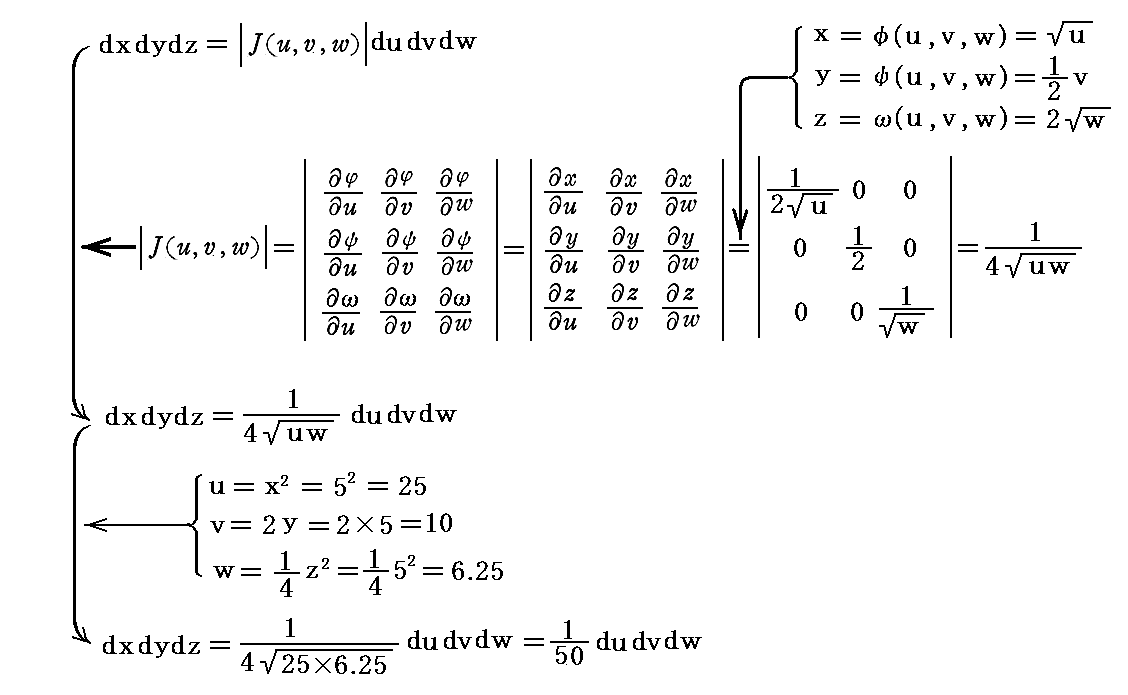
�@�܂�A�i���C���C���j���i25�C10�C6.25�j�ɉ����還������������1�~1�~1�̑̐ϑf�Ђ̎��ۂ̑̐ς�1�^50�ɂȂ�܂��B���̓���������}�̃O���t����ǂݎ���ĉ������B�O���t�̖ڐ���l�̑Ή��W���ƂĂ��������Ă��܂��̂ŋC�����ĉ������B
�@�����ŁA���ɒ��ӂ��ė~�������� �������P�C�������P�C�������P �Ƃ��A����� �������P�C�������P�C�������P �ƍl����Ζ��炩�ȗl�ɏ㎮�͍��ӂ� ������������ �ƉE�ӂ� �i1�^50�j������������ ���s���������Ƃ��Ӗ�����̂ł͖����t���y�ϕ��̐ϑf�Ёz�Ƃ��č��ӂ� ������������ ���E�ӂ� �i1�^50�j������������ ���s�u����������ׂ��t���Ƃ����Ή��W��\���Ă���ɂ����Ȃ����Ƃł��B
�@
�@����������̓I�Ɍ����܂��ƁA�gJacobian�h�� ������1�C������1�C������1 �ō\�������̐ϑf�Ђ̎��ۂ̑̐ϒl�� ������1�C������1�C������1 �ō\�������̐ϑf�Ђ̎��ۂ̑̐ϒl�Ƃ� �� ��\���Ă��܂��B���̏ꍇ�A�gJacobian�h�͂��Ƃ��̊��ł�����A���̔�͏ꏊ�Ƌ��ɕω����܂��B
��������Ɛϕ��͈� ����0�`20�A����0�`20�A����0�`20 ���A ����0�`400�A����0�`40�A����0�`100 �͈̔͂ɕς��܂��B
�@���̂Ƃ��A��ϕ����̊��`�͕ω�����
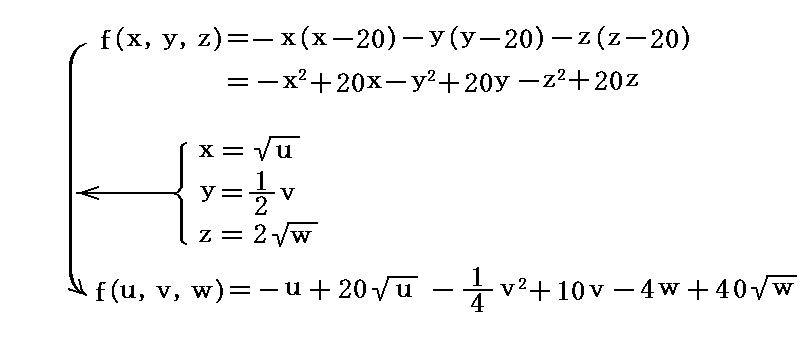
�ƂȂ�܂����A�ϕ�������i���C���C���j�Ɓi���C���C���j���Ή����Ă��铯��_�ł̔�ϕ����̊��l���i���C���C���j�͊��l���i���C���D���j�Ɠ����ɂȂ�܂��B
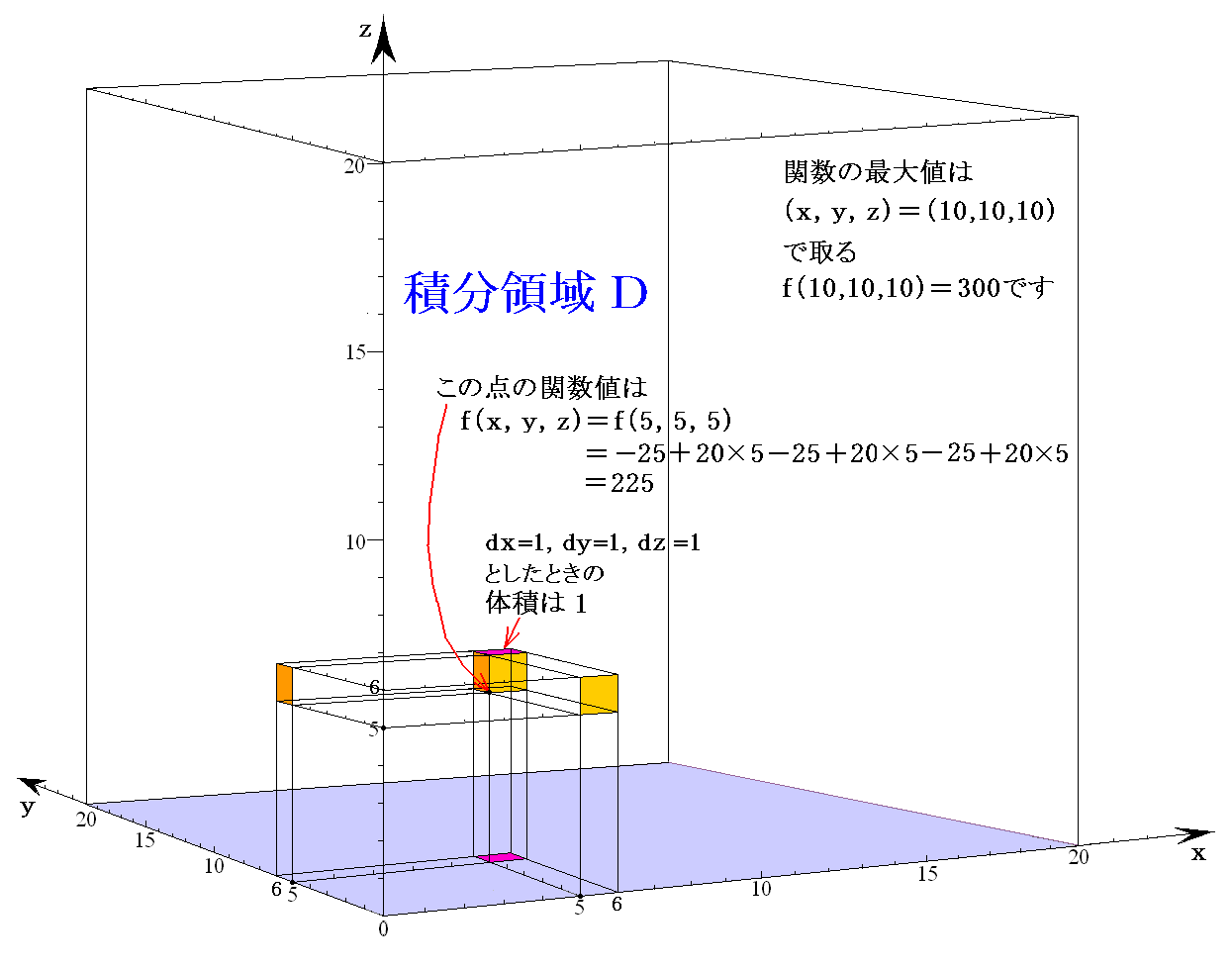
�@�Ⴆ�i���C���C���j���i5�C5�C5�j�̓_�̂��i���C���C���j�����i5�C5�C5�j���|52�{20�~5�|52�{20�~5�|52�{20�~5��225�@�ɑ��āA����_�ł���i���C���C���j���i25�C10�C6.25�j�̓_�̂��i���C���C���j�����i25�C10�C6.25�j�̊��l��
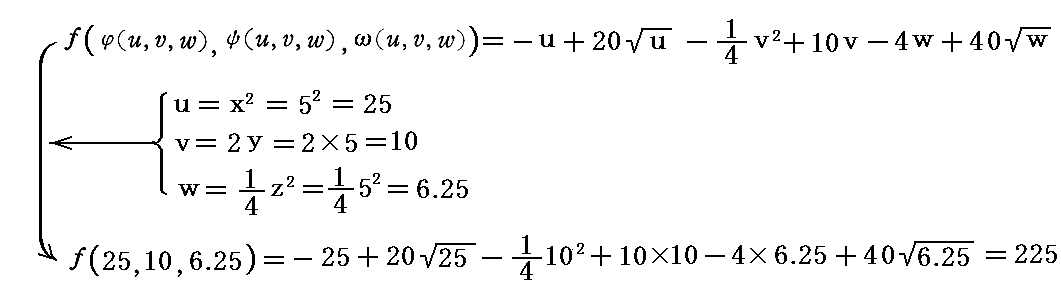
�ƂȂ�A�S�������ɂȂ�܂��B
�@����ɕ⑫����ƁA�����i���C���C���j���ő�l�́i���C���C���j���i10�C10�C10�j�̓_�Ŏ��l
���i���C���C���j�����i10�C10�C10�j���|102�{20�~10�|102�{20�~10�|102�{20�~10��300
�ƂȂ�܂��B
�@�������́A�Ή����� �i���C���C���j���i100�C20�C25�j �n�_�̊��l
���i���C���C���j�����i100�C20�C25�j��300 �Ɠ����ł��B
�@
�R�D�O�d�ϕ��l�@�@�@�@�@�m�ڎ��ցn
�@���̕ϐ��i���C���C���j�Ɋւ���ϕ��͈� ����0�`20�A����0�`20�A����0�`20 �ł̒�ϕ��l�ƐV�ϐ��i���C���C���j�Ɋւ��Ă̐ϕ��͈� ����0�`400�A����0�`40�A����0�`100 �ł̒�ϕ��l���r���Ă݂܂��B�ϕ�������i���C���C���j�Ɓi���C���C���j���Ή����Ă��铯��_�ł̔�ϕ����̊��l���i���C���C���j�͊��l���i���C���D���j�Ɠ����ł��鎖�ɒ��ӂ���ƈȉ��̗l�ɂȂ�܂��B
�@���ۂ��ϕ��̈�̑̐ς�20�~20�~20��8000�ł���A���̐ϕ��̈撆�Ŋ����i���C���C���j�����l�� �ŏ��l0�`�ő�l300 �̊Ԃ̂����ꂩ�ł�����A��ϕ��̒l����L�̗l�ɂȂ邱�Ƃ͔[���ł���B
�@���̂Ƃ��A���R�̂��Ƃł������������W�n�ł��ϕ��̈�̑̐ς�8000�ł���A�������n�̐ϕ��̈�̑̐ςƕς��܂���B�܂�A �g���s�iJacobian�j�h�Ƃ́A�����̐ςƂȂ�悤�ɒ������邽�߂̗ʂł��B
�@
�i�R�j�O�����Ό����W
�@�ʂȗ�Ƃ��āA�O�͂ōl�@�������Ό����W���O�����Ɋg�������ꍇ���l�@����B
�P�D���x�N�g���ϊ���
�@���}�̗l�ȁi���C���C���j���W�n�Ɓi���C���C���j���W�n�̊Ԃ̍��W�ϊ��������߂邽�߂ɁA�܂��g���x�N�g���h�̕ϊ��������߂�B
�@���x�N�g�� ��x�A��y�A��z �������x�N�g�������A�����A�����֕ϊ����鎮��
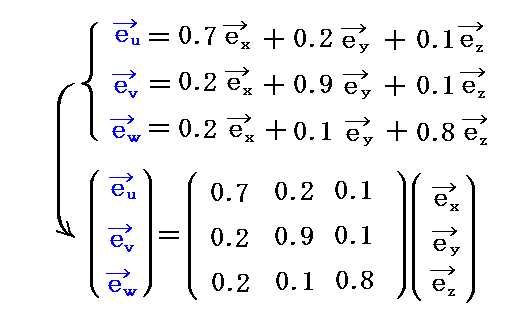
�ƂȂ�B
�@���̕ϊ�����3���A���㐔�������ƌ��Ȃ��đ㐔�I�ɉ��������x�N�g�������A�����A�����������x�N�g�� ��x�A��y�A��z �֕ϊ����鎮
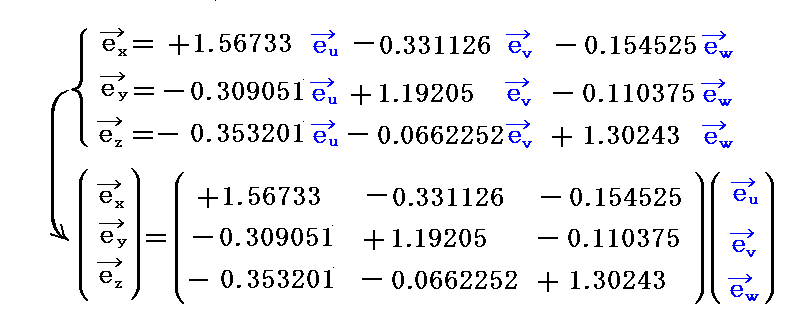
��������B���̎������߂�ɂ͍s��Cramer�̌������邢�͕ʍe�u�]���q�s��Ƌt�s��v�̕��@�𗘗p���Ă��ǂ��B
�@���̂Ƃ�������ϊ����̌W���̈Ӗ��͎��}��薾�炩�ł��낤�B
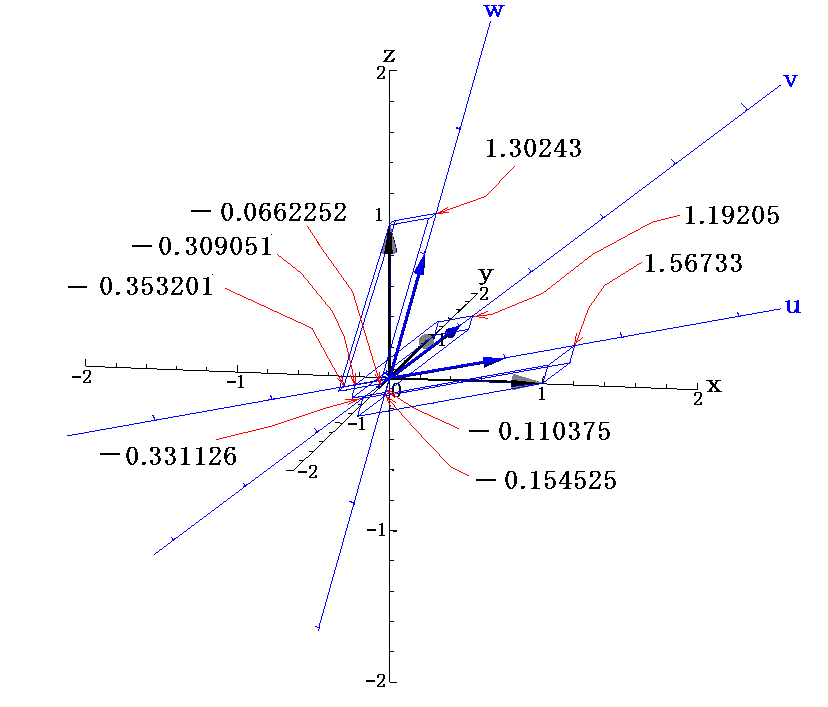
�@�܂��A��L�̓�̕ϊ��������������čs���Ό��̊��x�N�g���ɖ߂�˂Ȃ�Ȃ��̂ŁA���ϊ��W���̊Ԃɂ͈ȉ��̊W�������藧���Ƃ����炩�ł��낤

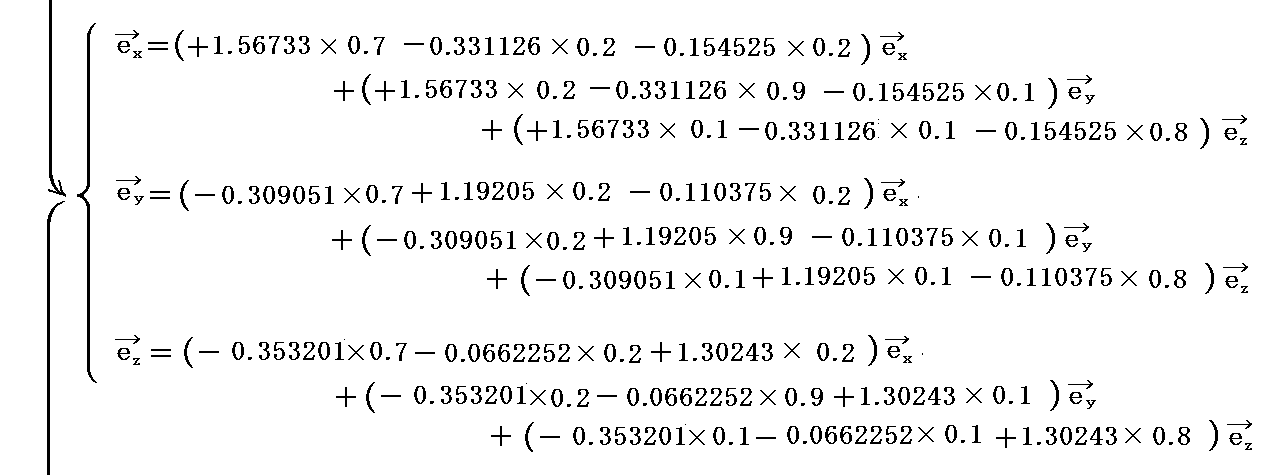
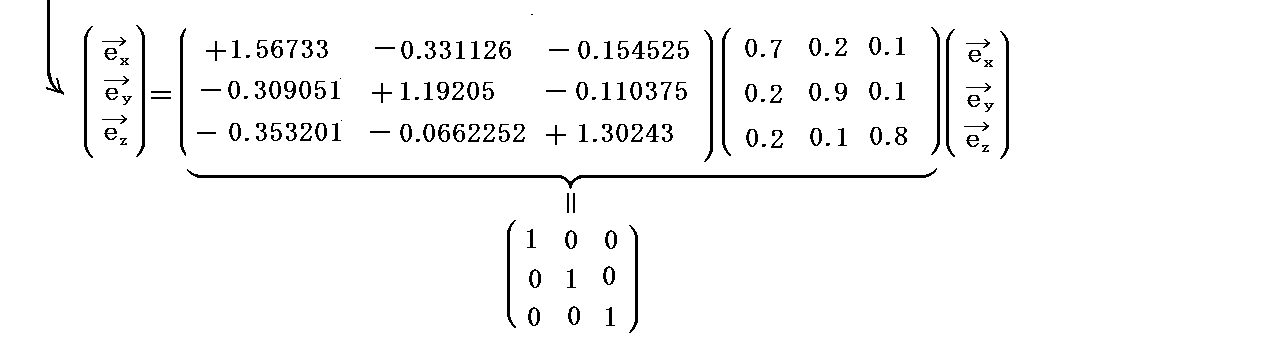
���ۂɓ�̍s��̐ς��v�Z���Ă݂�Ɗm���ɒP�ʍs��ɂȂ邱�Ƃ��m���߂���B
�@
�Q�D���W�l�̕ϊ����@�@�@�@�@�m�ڎ��ցn
�@���x�N�g���̕ϊ�����p����ƁA���W�l�̕ϊ����������ɋ��܂�B
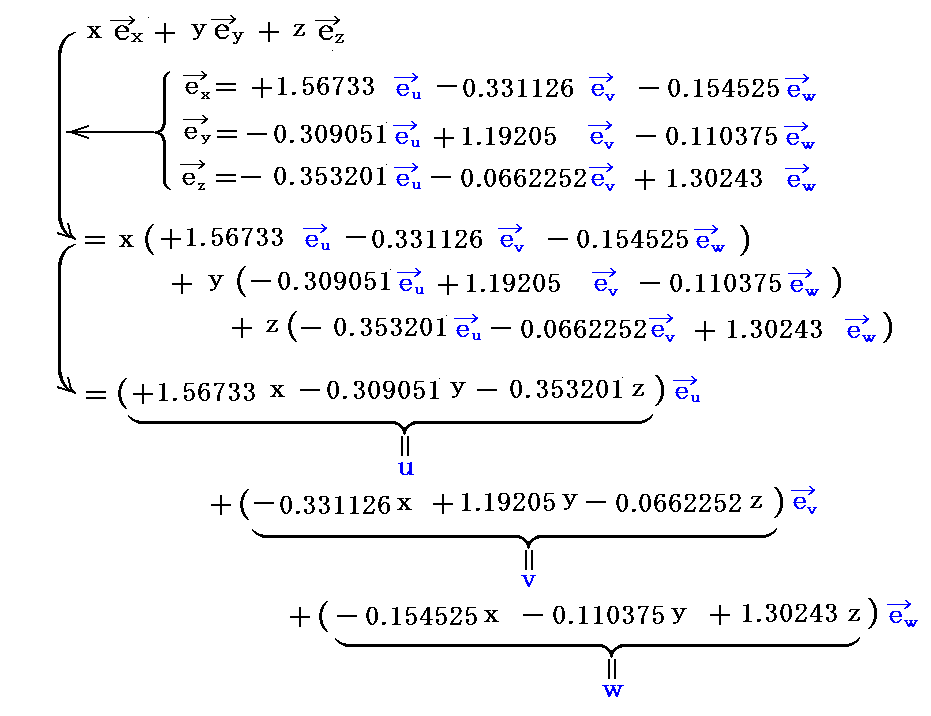
�ƂȂ�̂ŁA���̕ϊ�����������B
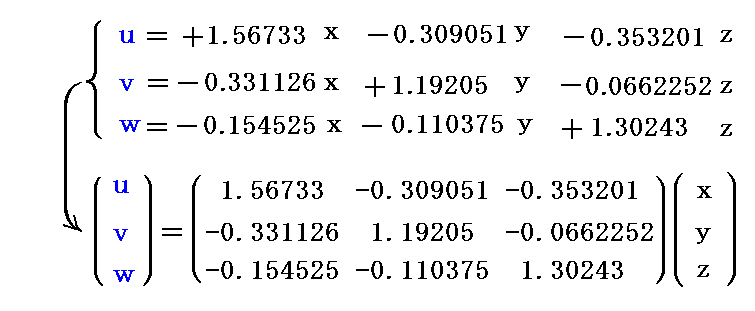
���̕ϊ����̍s������x�N�g���̕ϊ����̍s��

���g�]�u�s��h�ɂȂ��Ă��邱�Ƃɒ��ӂ��ꂽ���B
�@���l�ɂ��ď�L�Ƃ͋t�����̕ϊ�����������B
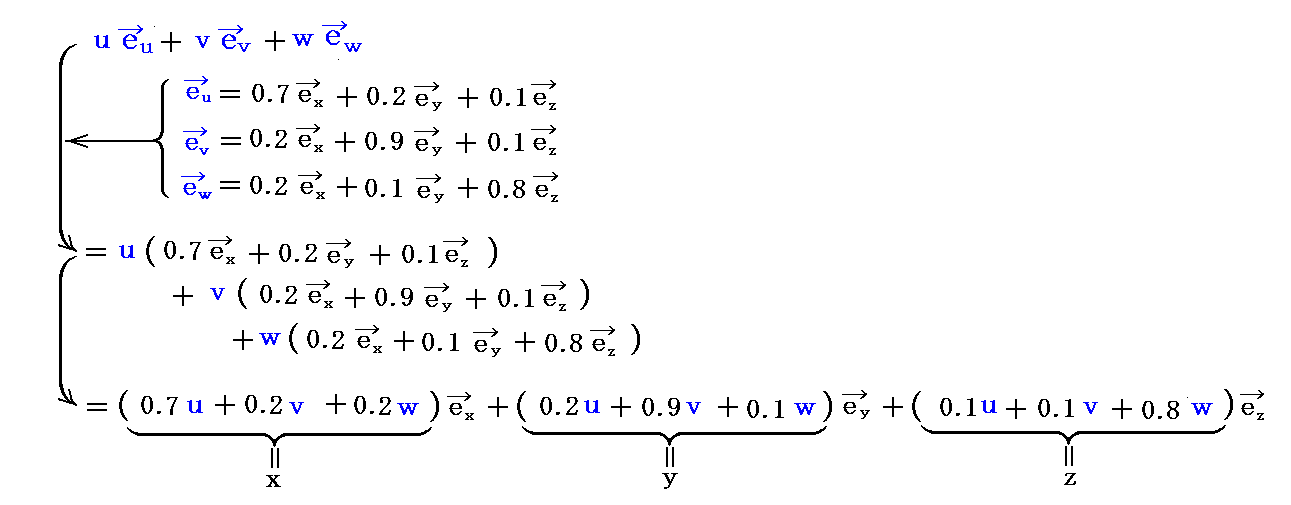
�ƂȂ�̂ŁA���̕ϊ�����������B
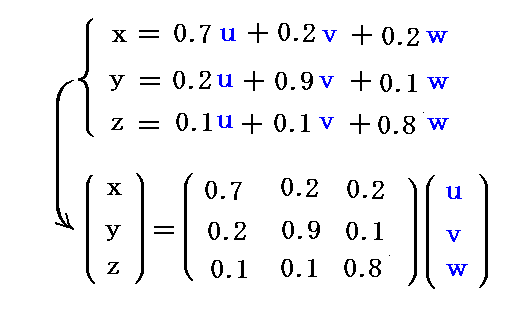
���̕ϊ����̍s������x�N�g���̕ϊ����̍s��

���g�]�u�s��h�ɂȂ��Ă��邱�Ƃɒ��ӂ��ꂽ���B
�m�⑫�����n
�@�����Ő��������l�Ȏ菇�ō��W�l�̕ϊ��������߂鎖���ł���̂́A���x�N�g���̍��P�ʃZ�����S��Ԃɂ킽���ē���ŁA���̊��x�N�g���̕ϊ��������̍��W�l�i���C���C���j�Ɉˑ����Ȃ��ꍇ�݂̂ł��B
�@��Ő�������l����ʓI�����[�}������̗l�ɁA�S��Ԃ�������P�ʎΌs�Z�ʑ̃Z���Ŗ��ߐs�������Ƃ��K�R�I�ɂł��Ȃ��Ȃ�ꍇ�ɂ́A��̎Ό��Ȑ����W�n����ʂ̎Ό��Ȑ����W�n�ւ̍��W�ϊ��������߂�̂͊ȒP�ł͂���܂���B����͕ϊ����W�l�Ɉˑ������ɂ߂ĕ��G�Ȋ��ƂȂ�܂��B
�@���̂��Ƃɕt���Ă��S�D�i�Q�j�P�D���䗗�������B�@
�@
�R�D�ϕ��̐ϑf�Ђ̕ϊ��@�@�@�@�@�m�ڎ��ցn
�@�ϕ��ϐ����i���C���C���j����i���C���C���j�ɕύX���܂��B
�@���̂Ƃ��A�����A�����Aw�������ꂼ�ꂘ��20�̕��ʁA����20�̕��ʁA����20�̕��ʂ��т����W�͈ȉ��̎菇�ŋ��܂�B
�@�܂��A����������20�̕��ʂ��т����W�́A�����̕ϊ�����(���C���C���j���i���C0�C0�j��(���C���C���j���i20�C���C���j���������A���������������Ηǂ��B
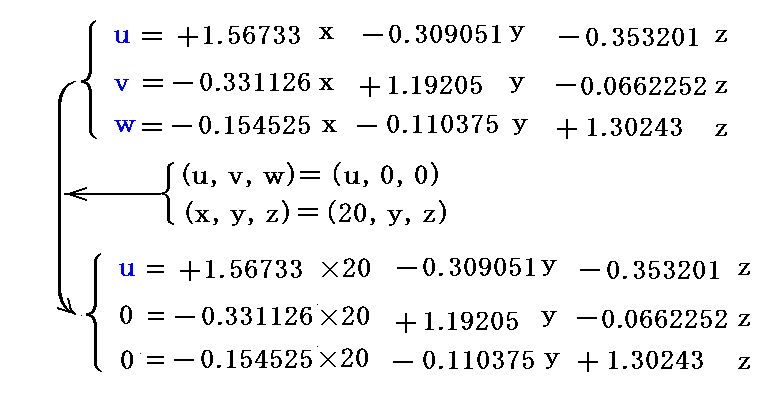
���̖��m�����C���C����3���A���������̉���(���C���C���j���i28.5714�C5.71429�C2.85714�j�ƂȂ�܂��B
�@�S�����l�ɁA����������20�̕��ʂ��т����W�́A�����̕ϊ�����(���C���C���j���i0�C���C0�j��(���C���C���j���i���C20�C���j���������A���������������Ηǂ��B
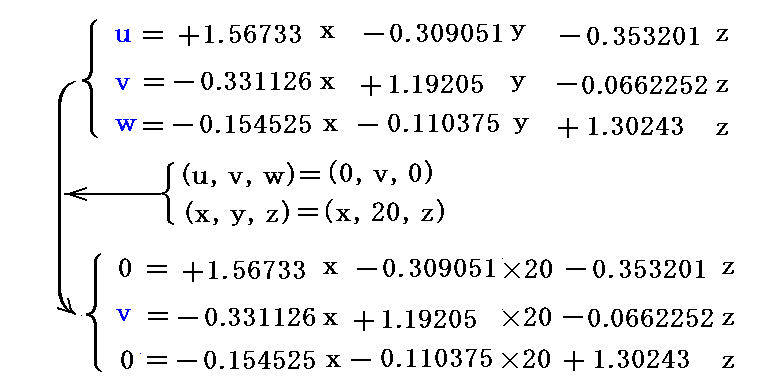
���̖��m�����C���C����3���A���������̉���(���C���C���j���i4.44444�C22.2222�C2.22222�j�ƂȂ�܂��B
�@����ɁA����������20�̕��ʂ��т����W�́A�����̕ϊ�����(���C���C���j���i0�C0�C���j��(���C���C���j���i���C���C20�j���������A���������������Ηǂ��B
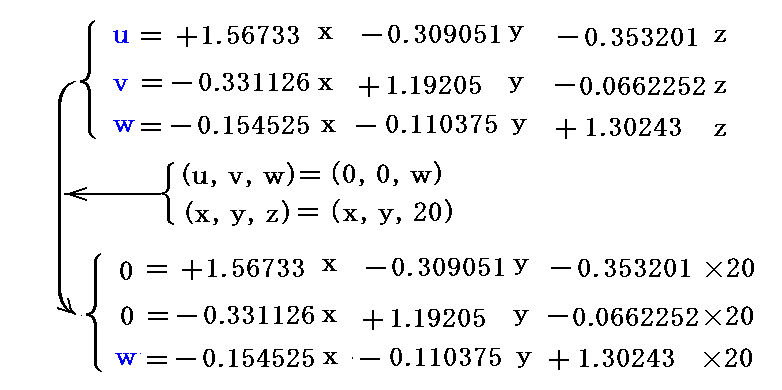
���̖��m�����C���C����3���A���������̉���(���C���C���j���i5�C2.5�C25�j�ƂȂ�܂��B

�@���W�ϊ��̗�Ƃ��āi���C���C���j���i5�C5�C5�j�̈ʒu�́i���C���C���j���W�l���v�Z�����
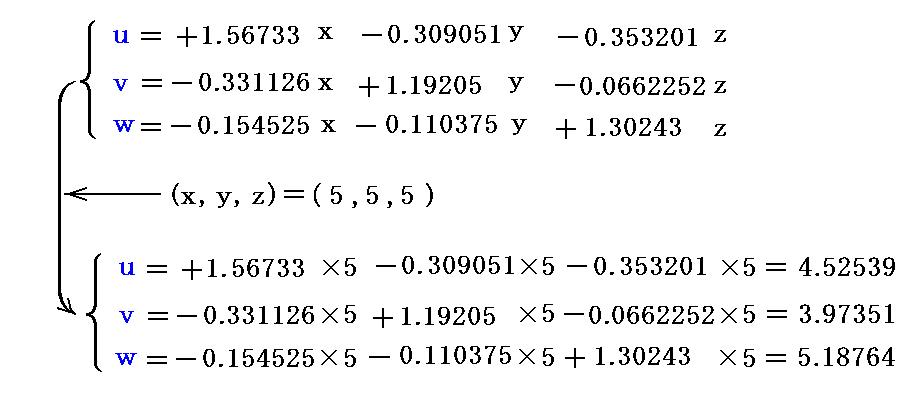
�ƂȂ�܂��B
�@���̒n�_�ł̎O�d�d�ϕ��ɕK�v�� �g���s�iJacobian�j�h ���v�Z���Ă݂��

�ƂȂ�܂��B���̏ꍇ���g���s�iJacobian�j�h �́A�i���C���C���j�̍��W�l�Ɉˑ������ɁA�S��Ԃɂ킽���ē���̒l�ɂȂ�܂��B
�m�⑫�����n
�@�����ŁA���ɒ��ӂ��ė~�������� �������P�C�������P�C�������P �Ƃ��A����� �������P�C�������P�C�������P �ƍl����Ζ��炩�ȗl�ɏ㎮�͍��ӂ� ������������ �ƉE�ӂ� 0.453�~������������ ���s���������Ƃ��Ӗ�����̂ł͖����t���y�ϕ��̐ϑf�Ёz�Ƃ��č��ӂ� ������������ ���E�ӂ� 0.453�~������������ ���s�u����������ׂ��t���Ƃ����Ή��W��\���Ă���ɂ����Ȃ����Ƃł��B
�@
�@����������̓I�Ɍ����܂��ƁA �gJacobian�h�� ������1�C������1�C������1 �ō\�������̐ϑf�Ђ̎��ۂ̑̐ϒl�� ������1�C������1�C������1 �ō\�������̐ϑf�Ђ̎��ۂ̑̐ϒl�Ƃ̔��\���Ă��܂��B���̏ꍇ�A�gJacobian�h�͂��܂��܍��W�ɊW���܂���̂ŁA���̔�͂��ׂĂ̏ꏊ�ň��ł��B
�@
�S�D�O�d�ϕ��l�@�@�@�@�@�m�ڎ��ցn
�@���́@�g���s�iJacobian�j�h�@��p���Ĥ�V�����ϐ��ł̎O�d�ϕ������{����Ɖ��L�̗l�ɂȂ�܂��B

�@
�i�S�j�O�����ɍ��W
�@���p��d�v���O�����ɍ��W�̃��R�r�A�������߂܂��B�K�v�ȗ\���m���͕ʍe�u���W��]�����Ƌ��ʎO�p�@�v�P�D�i�Q�j�R�D�Ő������Ă��܂��B
�P�D�������W�Ƌɍ��W�Ԃ̕ϐ��ϊ���
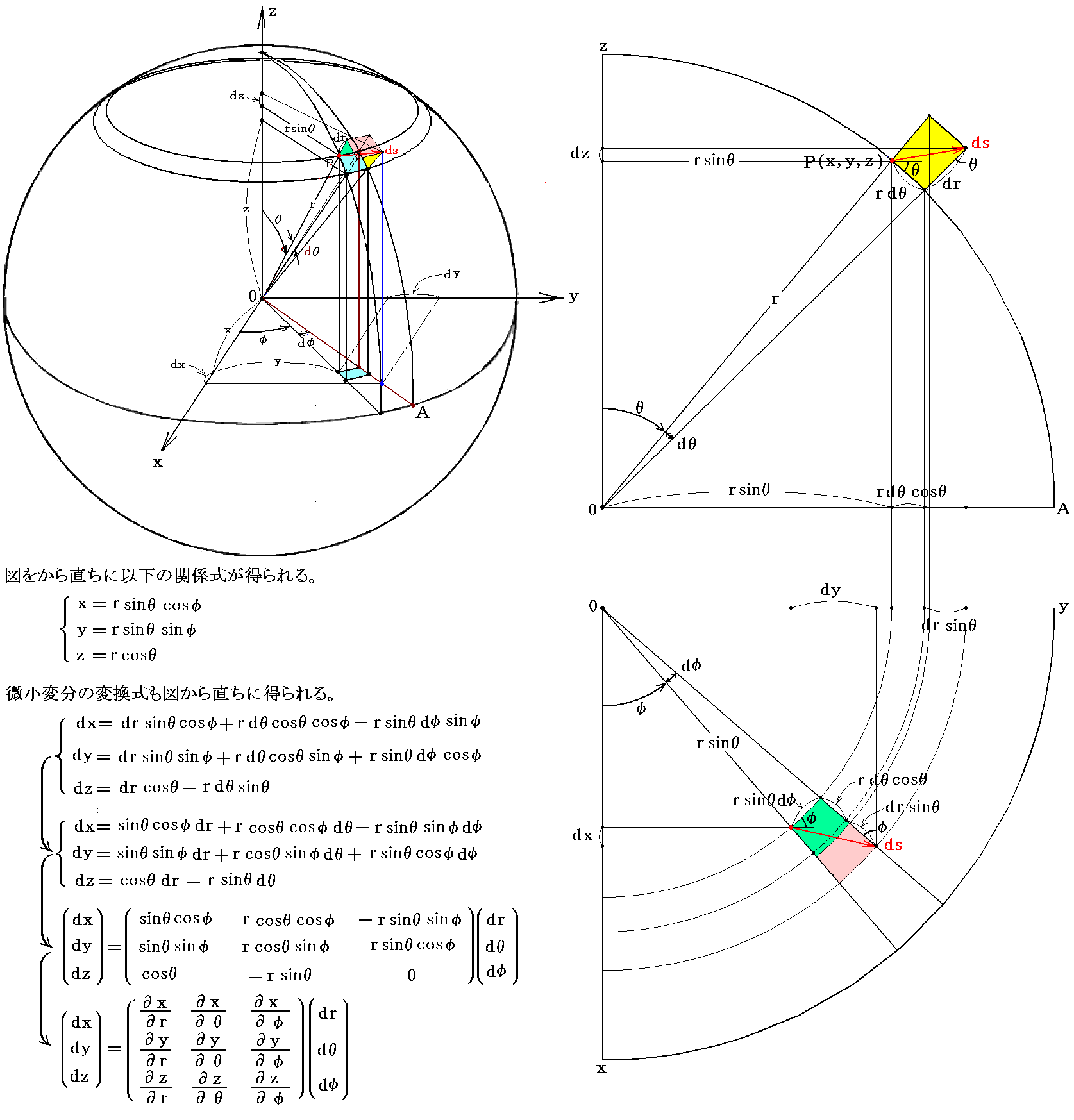
�t�ϊ����ɂ��Ă͕ʍe�u���W��]�����Ƌ��ʎO�p�@�v�P�D�i�Q�j�R�D�m�⑫�����P�n���Q�Ƃ��ĉ������B
�@
�@�O�߂ŋ��߂������ϕ��̕ϊ������A���܂Ő��������菇�ŕό`����B

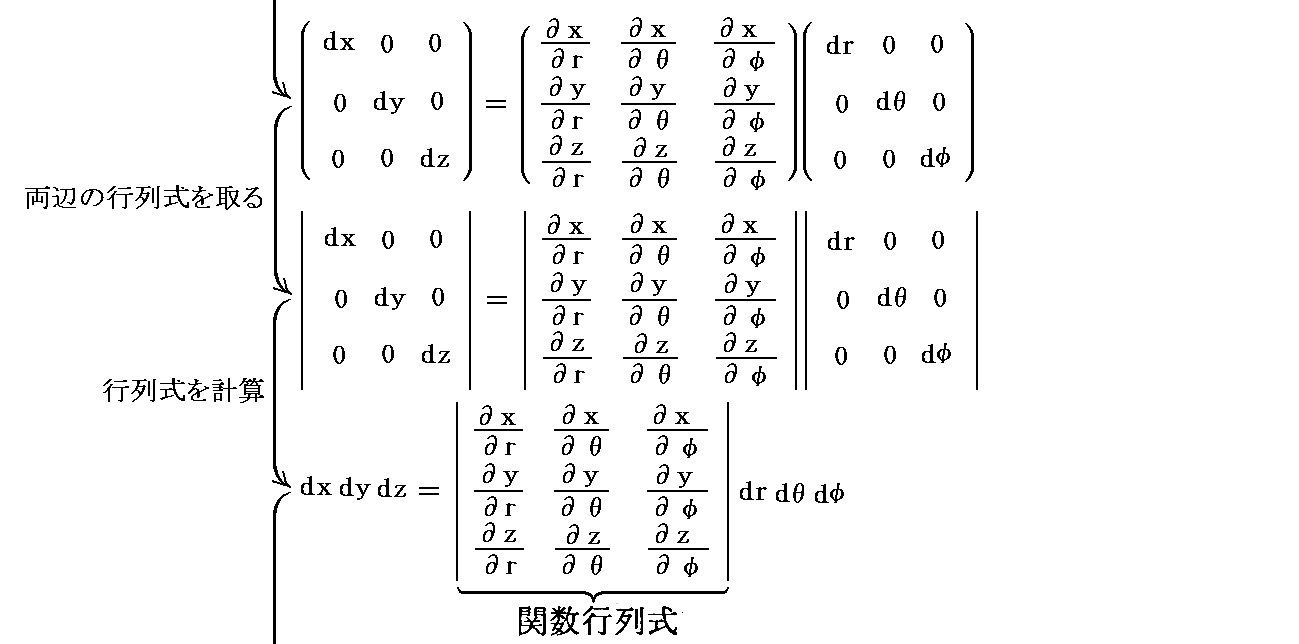
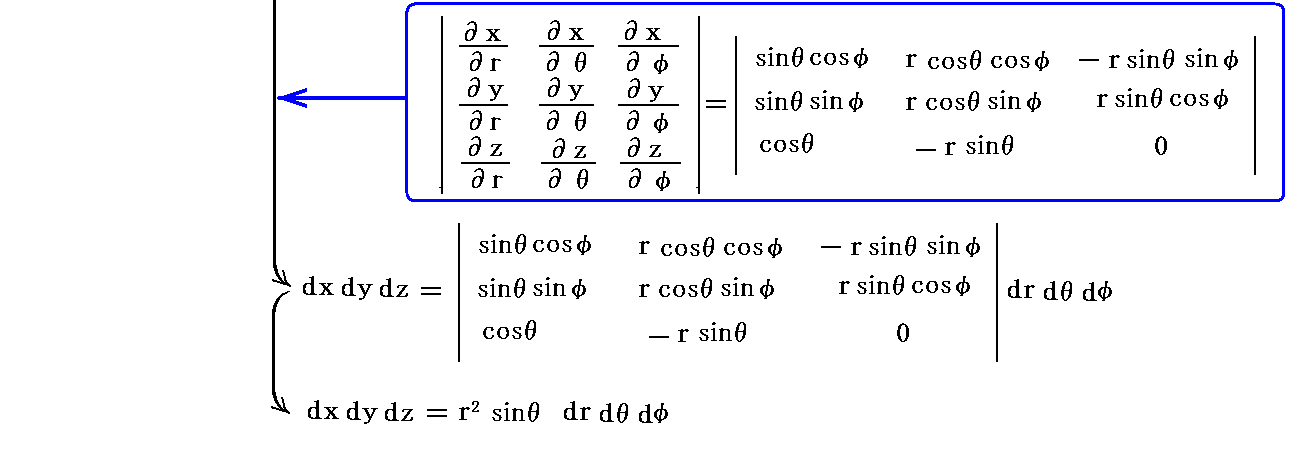
�@���̎��̈Ӗ��͔��ɉ���ɂ����B���܂܂ŁA���x�����ӂ����悤�ɁA�gJacobian�h���b��(x,y,z)�^��(��,��,��)�b����2�������� �́A ������1�C������1�C������1 �ō\�������̐ϑf�Ђ̎��ۂ̑̐ϒl�ƁA����ꏊ�� ������1�C���Ɓ�1�������������C���Ӂ�1������������ �ō\�������̐ϑf�Ђ̎��ۂ̑̐ϒl�Ƃ� �� ��\���Ă��܂��B���̏ꍇ�A�gJacobian�h�͂��ƃƂ̊��ł�����A���̔�͏ꏊ�Ƌ��ɕω����܂��B
�m�⑫�����n
�@���ꂮ�����L�̎������A���}�Ŏ�����Ă����g�����h�������`�������m�������������̔����̐ϑf�Ђ̎��ۂ̑̐ϒl�n���m������d�Ƃ��ӂō\�����������̐ϑf�Ђ̎��ۂ̑̐ϒl�n�Ƃ̔�i���}�Q�Ɓj�������Ă���Ɗ��Ⴂ���Ȃ��ʼn������B
�@��L�̊W��

����������������1�~1�~1���`�������m�������������̔����̐ϑf�Ђ̎��ۂ̑̐ϒl�n���������Ƃ��Ӂ�1�~1�~1���`�������m�������Ƃ��ӂō\�����������̐ϑf�Ђ̎��ۂ̑̐ϒl�n�Ƃ̔�������Ă��܂��B
�@���̂��Ƃ̈Ӗ��ɕt���Ă͕ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�S�D�i�U�j�T�D�Ő������Ă��܂��̂ŁA�����̐}�K���ĉ������B
�@
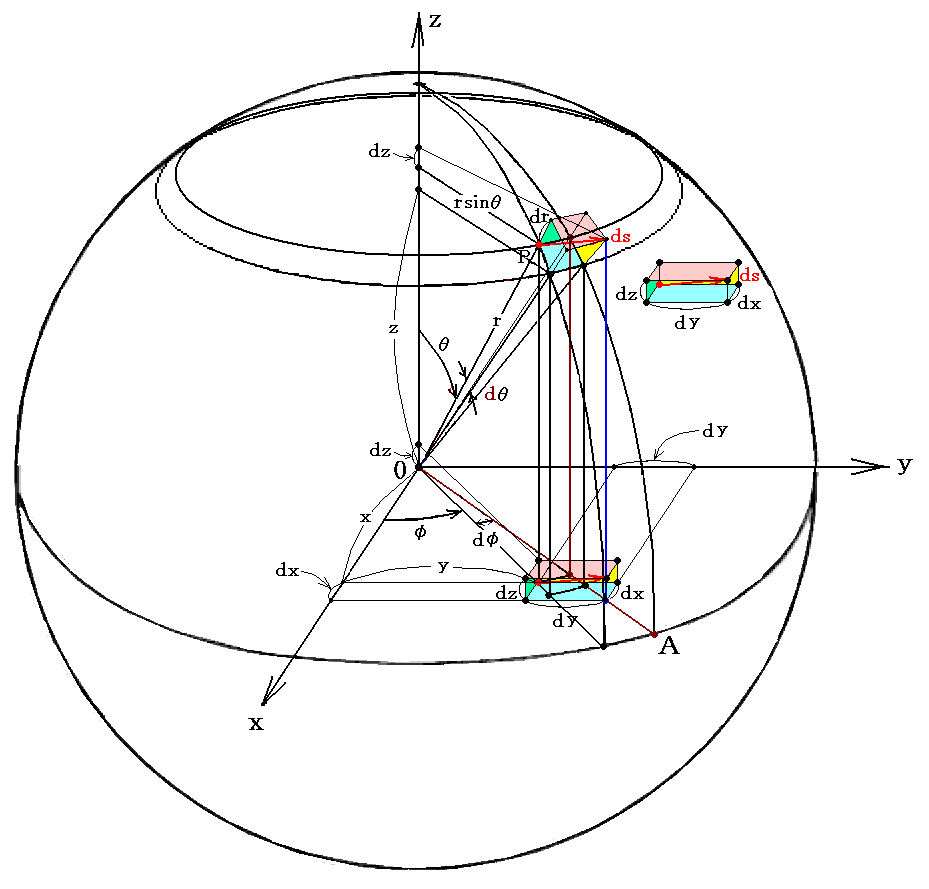
�S�D���[�}����Ԃɂ����鑽�d�ϕ�
�i1�j���[�}����Ԃł̑��d�ϕ��ɂ�����ϕ��̐ϑf��
�P�D�l�����̊�{
�@��ʑ��ΐ����_�ŕK�v�ɂȂ郊�[�}����Ԃɉ�����d�ϕ����l����B
�@���́A�ȒP�����ĂR�������[�}����Ԃ��l����B���̂Ƃ��ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�P�D�i�Q�j�Œ��ӂ����悤�ɁA�R���������̈�̕��������ł͂��ꂼ�ꂻ���ɓ\��t����ꂽ���[�N���b�h��Ԃ̒��̎Ό����W�ƍl���鎖���ł���̂ł����B�ł�����A�����̊e�ꏊ�ɂ�������x�N�g������镽�s�Z�ʑ̂̑̐ςʂ̃��[�N���b�h��Ԃɒu����Ӗ��ł̑̐ϒl�ƍl���鎖���ł��܂��B
�@���̂Ƃ��A���[�}����Ԃł͍ŏ�����Ό����W�ł�����A�ŏ�����P�ʊ��x�N�g�������P�ʕ��s�Z�ʑ̂̑̐ς��l������K�v������܂��B����͕ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�Q�D�i�V�j�g���x�N�g�������P�ʊi�q�Z���̑̐ςu�Ɗ�{�v�ʃe���\���������̊W�h�ł��łɐ������܂����B
�@�{�e�ŗp���Ă���L���ł����̐������ȉ��ŌJ��Ԃ��Ă݂܂��B
�@
�Q�D���x�N�g�������P�ʊi�q�Z���̑̐ςu�@�@�@�@�@�m�ڎ��ցn
�@�R�D�i�R�j�P�D�ŗ��p�������x�N�g���ōl����B
�@���̂Ƃ����x�N�g�� �����C�����C�����̓��[�}����Ԃł̊��x�N�g���ł����A�ڃ��[�N���b�h����i�������x�N�g���� �����C�����C�����ł��j�̒��Ɉ�����Ă���ƍl���܂��B
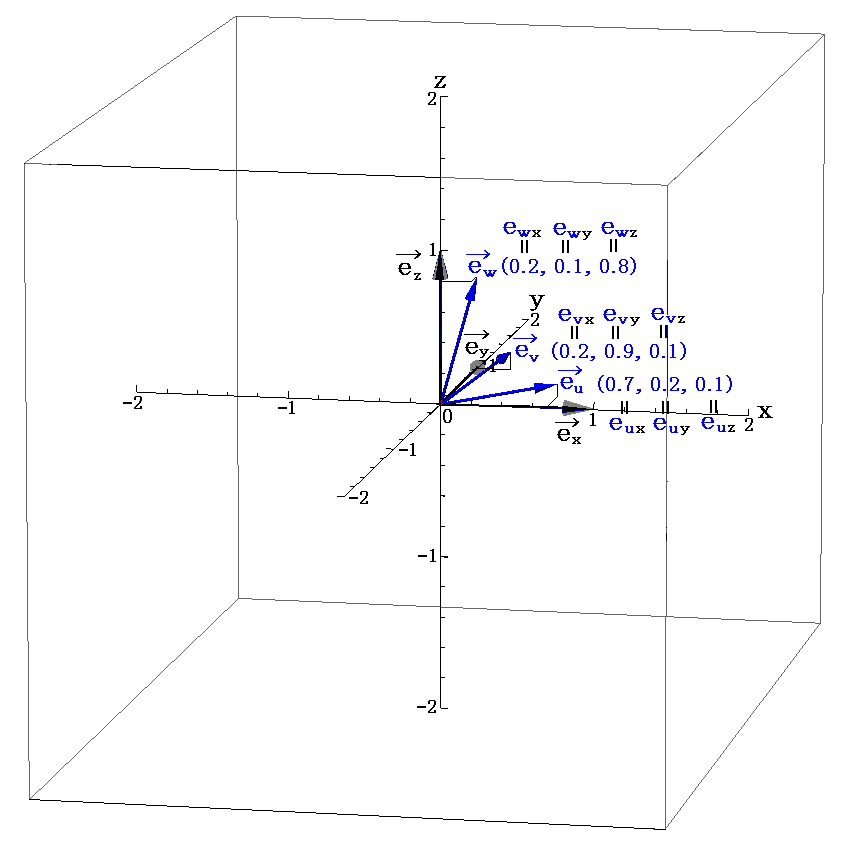
�@3�����x�N�g�� �����C�����C���� �̒��镽�s�Z�ʑ��i�P�ʊi�q�Z���j�̑̐ςu�́A�ʍe�u�x�N�g���̓��ςƊO�ς̐����\���v�Q�D�i�T�j�Q�D�Ő��������l��
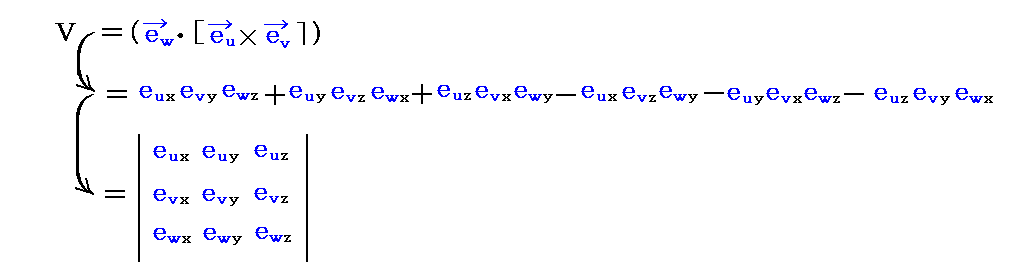
�ŕ\�����B
�@���̂��߁A�̐ςu��2���
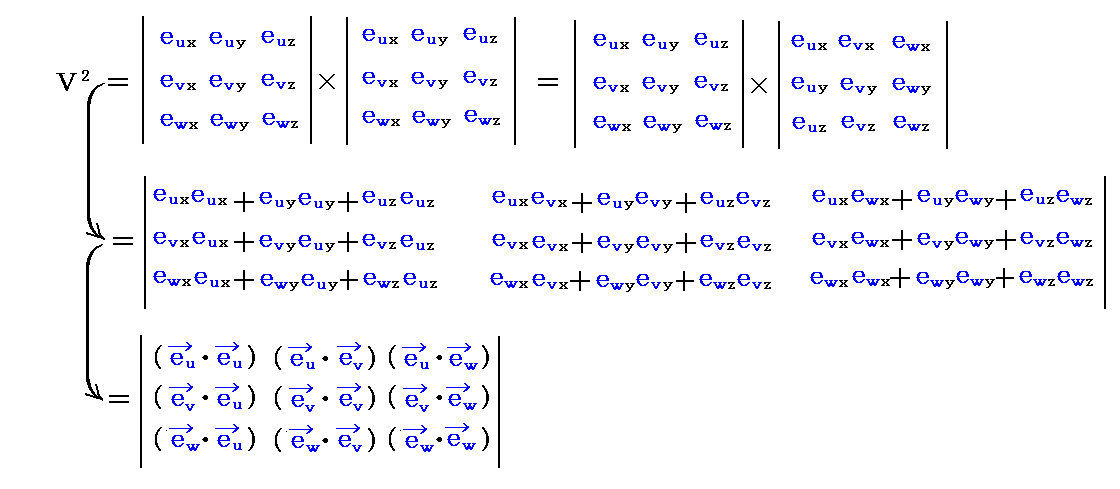
�ƂȂ�B���ό`���s�̐�����p�������A�ڍׂ͕ʍe�u�x�N�g���̓��ςƊO�ς̐����\���v�Q�D�i�T�j�Q�D�m�⑫�����n���Q�Ƃ��ꂽ���B
�@�Ƃ���ōŌ�̍s�́A�ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�Q�D�i�S�j�Œ�`�����g3�������[�}����ԁh���g��{�v�ʃe���\���h ������ ���瓾�����s�̒l�ł�����

�ƂȂ�B
�@�]���āA�x�N�g�������i�����C�����C�����j��Ίp���x�N�g���Ƃ������x�N�g���n�ɂ��������s�Z�ʑ̂̑̐ςu��
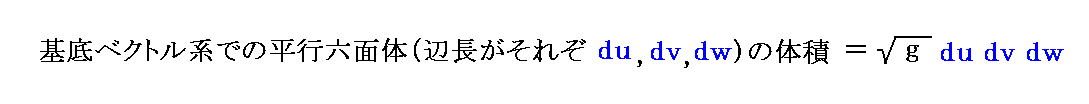
�ŕ\�����B�܂�
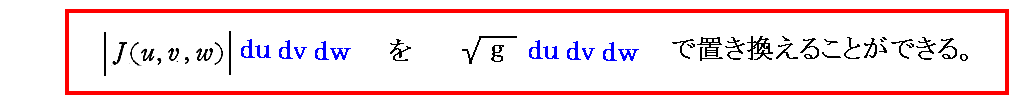
�@���̂Ƃ��A��ʓI�ɂ��g���s�iJacobian�j�h�bJ�i���C���C���j�b �����W�l�i���C���C���j�̊��ł������l���g��{�v�ʃe���\���h ������ �����W�l�i���C���C���j�̊��ł��B
�@���̂��Ƃɂ��Ă͕ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�Q�D�i�V�j���䗗�������B
�@
�i�Q�j���[�}����Ԃɂ����鑽�d�ϕ��ƎΌ��Ȑ����W����ʂ̎Ό��Ȑ����W�ւ̕ϐ��ϊ�
�P�D���[�}����Ԃ̍��W�ϊ�
�@���[�}����Ԃɂ�������W�ϊ��Ƃ́A�Ǐ��I�ȏꍇ�Ɍ�����W���K�肷���g�K��x�N�g���h�̕ϊ��������߂�ƌ������Ƃł��B����͕ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�R�D�i�P�j�ł��łɐ����������Ƃł��B���̂Ƃ��̕ϊ�����p����A�{�e�R�D�i�R�j�Q�D�Ő��������̂Ɠ��l�Ȏ菇�ɏ]���A���W�l�̕ϊ����������ɋ��܂�܂��B����ɁA���W�l�̕ϊ����̕ϊ��s��́A���x�N�g�����t�����ɕϊ�����ϊ����̍s��̓]�u�s��ɂȂ邱�Ƃ����l�ł��B
�@�������A���I�ȍ��W�ϊ��������߂�̂͊ȒP�ł͂���܂���B�Ό��Ȑ����W�̍��W�l��ʂ̎Ό��Ȑ����W�̍��W�l�ƌ��т���ϊ����ł�����A���̕ϊ����͐��`�̍s��ŕ\�����悤�Ȃ��̂ł͂���܂���B�ɂ߂ĕ��G�Ȃ���

�ɂȂ�ł��傤�B
�@�����烊�[�}����ԓ����Ǐ��I�ȍ��W�n�����̈ʒu�̋Ǐ��I�ȕʂ̍��W�n�ɕϊ�������W�ϊ������I�ȍ��W�ϊ������Ⴆ�Ȃ����Ƃ��d�v�ł��B���̂��Ƃɂ��Ă��R�D�i�R�j�Q�D�m�⑫�����n���䗗�������B
�m�⑫�����n
�@�g���[�}����ԁh�ł��g���x�N�g���h�ɑ����g�o�Ί��x�N�g���h�Ƃ������̂��l����K�v������̂ł����A���ꂮ����m���x�N�g����ʂȊ��x�N�g���֕ϊ��n ���鎖�� �m���x�N�g���Ƒo�Ί��x�N�g���̊Ԃ̕ϊ��n ���������Ȃ��ł��������B���҂͑S���ʂ̎��ł��B���̂��Ƃɕt���Ă͕ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�R�D�i�P�j�m�⑫�����R�n�Œ��ӂ����Ȃ����Ă��܂��̂ł����K���ĉ������B
�@
�Q�D�ϕ��̐ϑf�Ђ̕ϊ��@�@�@�@�@�m�ڎ��ցn
�@���[�}����Ԃɂ��������Ό��Ȑ����W�n�i���C���C���j�n���瑼���Ό��Ȑ����W�n�i���C���C���j�n�ɍ��W�ϊ������ꍇ�Ƀ��[�}����Ԃɂ����鑽�d�ϕ����ǂ̂悤�ɕϊ�����邩���l����B
�@�܂��ŏ��ɁA���W�ϊ���

�ɂ����̕ϐ����i���C���C���j����i���C���C���j�֕ϊ����܂��B
�@�����Ď��ɁA�ϕ��̐ϑf�Ђ�
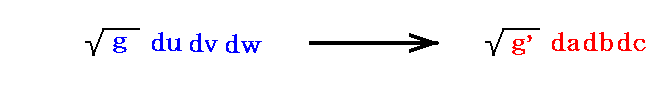
�ɕϊ�����B
�@���������f�́i���C���C���j�Ɠ���_�́i���C���C���j���W�l�ɂ����邁�����n�����x�N�g�������C�����C��������
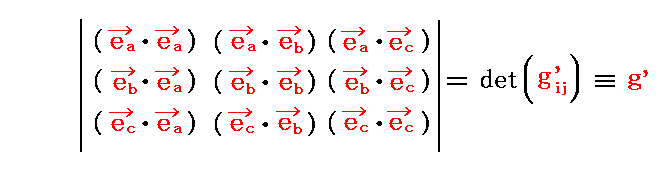
�ɂ���č\��������g��{�v�ʃe���\���h ���f���� �̍s�̒l�ł���A
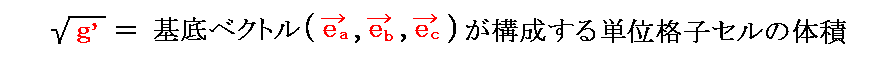
�ƂȂ���̂ł��B���̂��Ƃɂ��Ă͕ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�R�D�i�V�j �� �S�D�i�U�j�T�D �K���ꂽ���B
�m�⑫�����P�n
�@�����ŁA���ɒ��ӂ��ė~�������� �������P�C�������P�C�������P �Ƃ��A����� �������P�C�������P�C�������P �ƍl����Ζ��炩�ȗl�� ��0.5������������ �� ���f0.5������������ ���s�������̂ł͖����t���y�ϕ��̐ϑf�Ёz�Ƃ��� ��0.5������������ �� ���f0.5������������ ���s�u����������ׂ��t���Ƃ����Ή��W��\���Ă������Ƃł��B
�@
�@����������̓I�Ɍ����A�gJacobian�h�̔䁁���f0.5�^��0.5 �͓���n�_�ɂ����� ������1�C������1�C������1 �ō\�������i���s�Z�ʑ̏�́j�̐ϑf�Ђ̎��ۂ̑̐ϒl�� ������1�C������1�C������1 �ō\�������i���s�Z�ʑ̏�́j�̐ϑf�Ђ̎��ۂ̑̐ϒl�Ƃ� �� ��\���Ă��܂��B�������A�����Ō����̐ϒl�Ƃ́A�e�n�_�ɂ�����ڃ��[�N���b�h��Ԃł̕��ʂ̈Ӗ��ł̑̐ϒl�ł��B���̏ꍇ�A�gJacobian�h�͂��A���A���̊��i�܂�A���A���A���̊��ł�����j�ł�����A���̔�͏ꏊ�Ƌ��ɕω����܂��B
�m�⑫�����Q�n
�@����ɏd�v�Ȃ��Ƃ́A�����ł���0.5�����f0.5���A�����̓_�ł��ڃ��[�N���b�h����̑̐ϑf�Ђ�������������������1�A������1�A������1�ƒu���������������̑̐ϒl�ɑ���A���[�}������̑̐ϑf�Ђ�������������������1�A������1�A������1�Ƃ����������s�Z�ʑ��̑̐ϒl�ł���A���Ȃ������[�}������̑̐ϑf�Ђ�������������������1�A������1�A������1�Ƃ����������s�Z�ʑ��̑̐ϒl�ł��邱�Ƃł��B��L�g�ڃ��[�N���b�h��ԁh�̈Ӗ��ɂ��Ă͕ʍe�u���x�N�g���E�o�Ί��x�N�g���Ɣ��ϐ����E���ϐ����v�P�D�i�Q�j�K���ĉ������B
�@��������A���[�N���b�h��Ԃɂ�������ۂ̑̐ϒl���̂��̂ł��邱�Ƃ������ĖY��Ȃ��ʼn������B
�m�⑫�����R�n
�@�����܂ł��Ȃ����Ƃł����A��ʑ��ΐ����_�ōl�@����S�������[�}����Ԃ͂S�����ڂ����ԍ��W�ƂȂ�S�������[�}������ł��B
�@�����āA�O�������[�}������̊e�_�ɂ������ڃ��[�N���b�h��ԁi�R�����j�ɑ���������̂��A�S�������[�}�������̊e�_�ɂ������ڃ~���R�t�X�L�[����i��ԂR�����{���ԂP�����j�ł��B�܂���ꑊ�ΐ����_��_����S�����~���R�t�X�L�[���A�S�������[�}������̊e�_�ł���������ƂȂ�܂��B
�@���ԂƋ�Ԃ����������S�������[�}������̑̐ϑf�Ђ�z������͓̂�����A�l�������͓̂����ł��B
�@��L�̎�������ʑ��ΐ����_�ł̕\�L�ŌJ��Ԃ��Ă����܂��B
�@���łɉ��x�����������悤�ɁA��ʑ��ΐ����_�ɂ�������{�v�ʋ��σe���\�� ���ʃ� ��2�K���σe���\��������A���W�ϊ�
�ɑ���
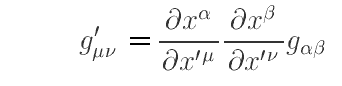
�̗l�ɕϊ�����܂��B
�@���ɗ��ӂ̍s���v�Z����̂ł����A�s��̐ς̍s��det�m�`�a�b�n�͂��ꂼ��̍s��̍s�̐�det�m�`�n�~det�m�a�n�~det�m�b�n�ɓ������̂�
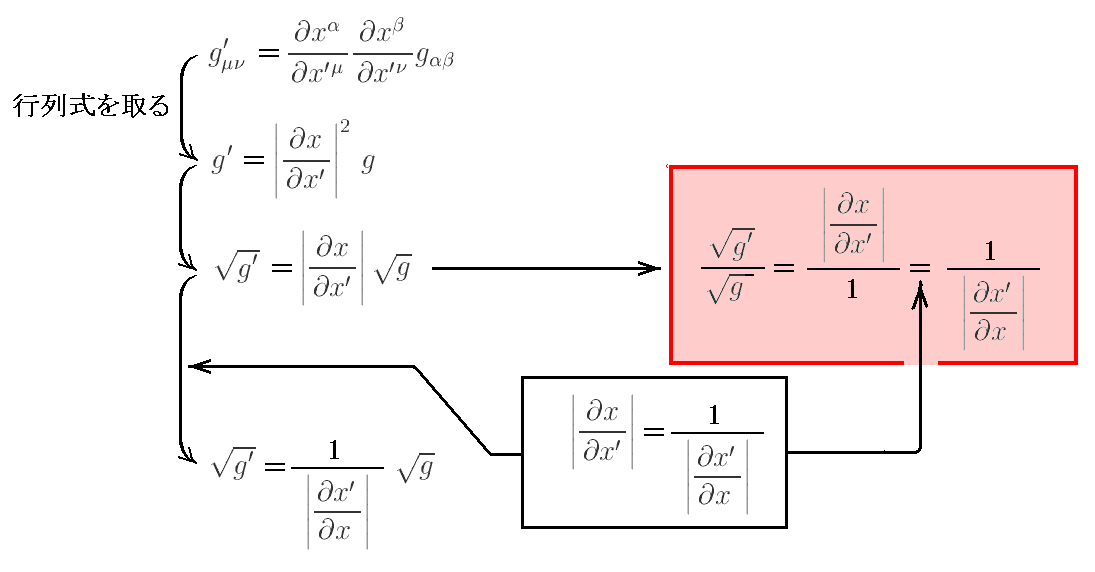
�ƂȂ�܂��B����͕ʍe�u�e���\���㐔�w�v�R�D(�T)�m��P�n�ł��łɐ������Ă��܂��B
�@�������A������
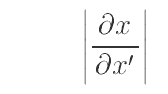
�́A�g���s�h�iJacobian�j���Ӗ����܂��B�܂�A���W�ϊ��Ƌt���W�ϊ��̊W�����狁�܂鉺�L�����R�r�A���s�����Ӗ����܂��B
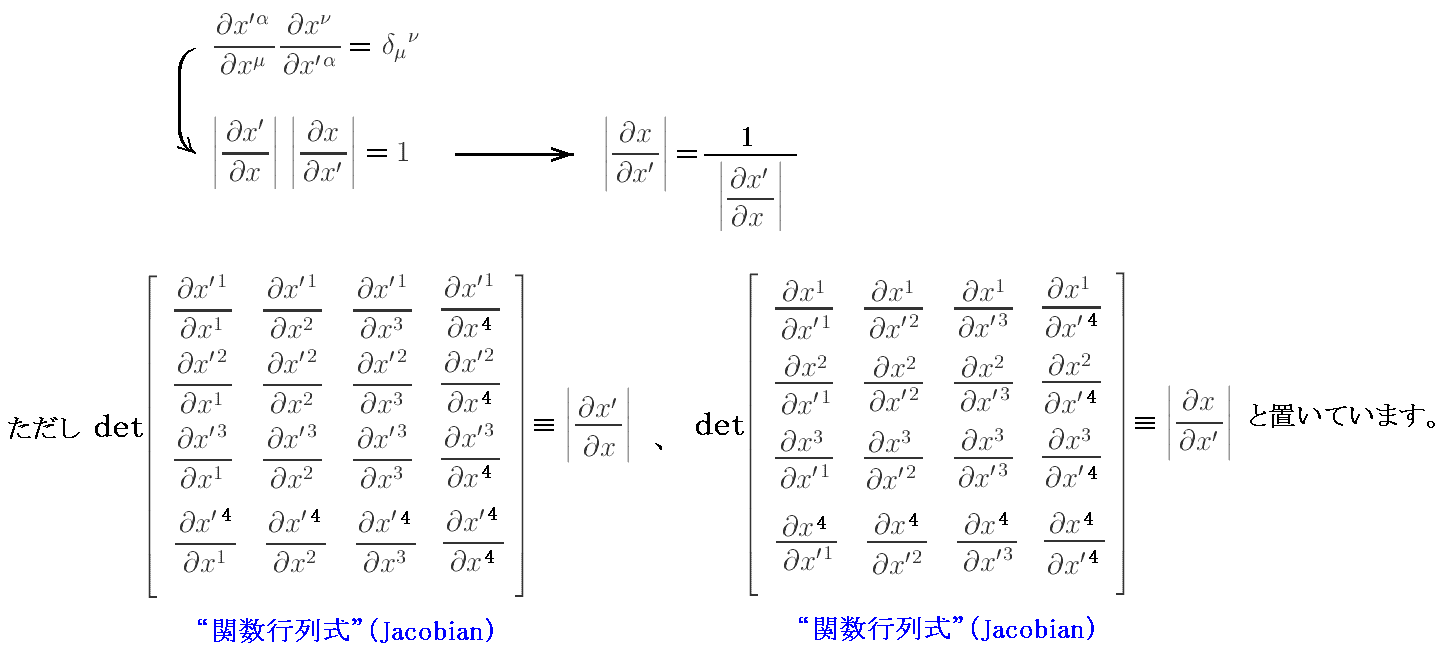
���̂Ƃ��A�s�͍s�Ɨ�����ւ����]�u�s�̒l�ƈ�v���邱�Ƃɒ��ӂ���ĉ������B
�@�s�̒�`����p���Č`���I�Ƀ��R�r�A����W�J�����
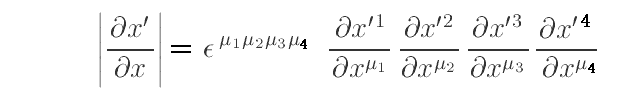
�ƂȂ�܂��B�����Ł@����1��2��3��4 �͕ʍe�u�e���\���㐔�w�v�R�D(�T)�m��Q�n�Ő��������gLevi-Civita�̃e���\�����x�h�ł��B
�@
�R�D�ϕ��̈�̕ϊ��@�@�@�@�@�m�ڎ��ցn
�@���W��ϊ���������ƌ����ė̈掩�̂��O�������[�}����Ԃ̒��ŕω�����킯�ł͂���܂���B����̐ϕ��̈��\�����W�l���ω����邾���ł��B
�@���̂��Ƃ̈Ӗ��𗝉�����̂͂Ȃ��Ȃ�����̂ł����A���܂łɐ������Ă�����K�����Δ[�����Ē�����Ǝv���܂��B
�@
�S�D���[�}����Ԃɂ����鑽�d�ϕ��l�@�@�@�@�@�m�ڎ��ցn
�@���[�}����Ԃɂ����鑽�d�ϕ��̓��[�N���b�h��Ԃɂ����鑽�d�ϕ��Ɠ��l�ɍl����Ηǂ��B���[�}����ԓ��Ɉ����ꂽ�Ό��Ȑ����W�̊e�_�Őϕ����ׂ����l���^�����Ă���Ƃ���B���[�}����ԓ��̊e�_�ł̐ϕ��̐ϑf�ЂƁA���̓_�ɂ�������l���|�����킹�����̂�ϕ��̈�i�̐ϗ̈�j�S�̂ɂ킽���ĉ������킹�Ă䂯�Ηǂ��̂ł��B
�@���ۂɂ�������s����̂͊ȒP�ł͂���܂��A�l�������̂͊ȒP���Ăł��B
�@
�i�R�j�R�������[�}����Ԃɂ�����̈�̕\�ʂɕt���Ă̐ϕ�
�@�ȏ�q�ׂ������͎O�������[�}����Ԃɂ�����̐ϗ̈�ł̐ϕ��ł������A�O�������[�N���b�h��Ԓ��̋Ȗʁi�����[�}����ԁj��ł̖ʐϕ��Ɋւ��Ă����l�ɍl����Ηǂ��B����͂܂��A�O�������[�}����Ԓ��̔C�ӂ̐ϕ��̈�̕\�ʂɕt���Ă̖ʐϕ��ɂ��Ă������邱�Ƃł��B
�@����́A���[�}����Ԃɂ������g�O���[���̒藝�h���g�X�g�[�N�X�̒藝�h�Ȃǂ̒莮���ɕK�v�ł��B���̂��Ƃɂ��Ă͕ʍe�u�S�D�gRiemann�w�h�v�́i�X�j�g�����Ɛϕ��̌����h�Ȃǂ��䗗�������B
�@
�T�D�Q�l����
�@�@���̍e�����ɓ������āA���L�������Q�l�ɂ��܂����B���ӁI
- �蕔���A���X�؉E�����u�����E�ϕ����ȏ��v�����o�ŎЁi1965�N���j
�@���̒��̑�7�́g�d�ϕ��Ƃ��̉��p�hp282�`283�Ap284�`285�Ap236�`237�Ap246�`267�Ap248�`249
- 1.6 �d�ϕ��̕ϐ��ϊ�
�@http://www2.math.kyushu-u.ac.jp/~hara/lectures/06/zoku15-060511.pdf
- ����_�����u���Θ_�i��2�Łj�v�����o�ŎЁi1986�N�j�S�D�gRiemann�w�h
�@���̒����i�X�j�g�����Ɛϕ��̌����h���䗗�������B