2.曲面論
曲面論は3次元ユークリッド空間における曲面の性質を曲線論と同様な方法で調べるものですが、テンソル解析からの記法を多少用います。
曲面に付随する量として第1基本量 gij 、第2基本量 hij を定義し、これらによって曲面の形状を表わす平均曲率 H、全曲率 Kを与える。
“ガウスとコダッツィの積分可能条件”の下に、曲線論の自然方程式に相当する、“ボネの基本定理”『関数gijとhijが与えられたとき、これらを第1基本量および第2基本量とする曲面が定まる』を導く。そして最後に、“測地線”について説明します。
ここでは、第1基本微分形式と第2基本微分形式の両方を用いた議論をしますのでリーマン幾何学との関係は曖昧です。後でわかりますがリーマン幾何学とは第1基本微分形式のみを用いて空間の幾何学的性質の全てを論じるものです[3.(2)2.[補足説明3]参照]。
(1)曲面の径数表示
(2)第1基本微分形式
(3)接線曲面
(4)第2基本微分形式
(5)曲面の曲率
(6)平均曲率と全曲率
(7)添字記法
(8)ガウスの方程式とワインガルテンの方程式
(9)積分可能条件とガウスの“驚異の定理”
(10)ボネの基本定理
(11)ガウスの球面表示と第3基本微分形式
(12)包絡面
(13)線織面
(14)測地的曲率
(15)測地的捩率
(1)曲面の径数表示
1.径数表示
空間曲線は一般に1つの径数 t に関係して変化する直交デカルト座標系内の位置ベクトル
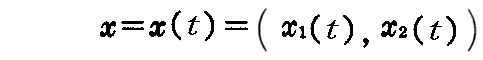
の終点の描く軌跡として表された。
その考え方を空間曲線から空間曲面に拡張すると、直交デカルト座標系内の一つの曲面を表わす位置ベクトルは、一般に2つの径数u,vに関して変化する。従って方程式は
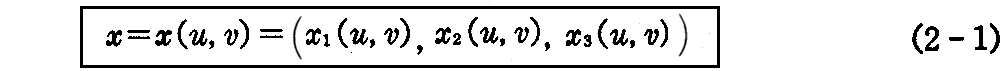
と表される。これを曲面の“径数表示”(ガウスの径数表示)といい、u,vをその“径数”という。
(2-1)式において v を一定とし、u だけを変化させれば、x(u,v) は曲面上に1つの曲線を描く。これを“u曲線”という。 u を一定とし、v だけを変化させれば、x(u,v) は曲面上に1つの曲線を描く。これを“v曲線”という。これらをまとめて、曲面の“径数曲線”と言うことにする。
2.接ベクトル
曲面上の1点x(u,v)におけるベクトル
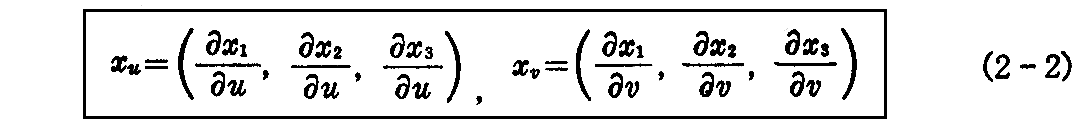
は、その点におけるそれぞれu曲線、v曲線への“接線ベクトル”です。
ここで考える曲面は u,v について何回でも微分可能で行列

の階数が2であると仮定する。このことは二つのベクトル xu と xv が一次独立であると考えることです。つまり、この二つの接線ベクトルが同じ方向に重なる事は無いとする。
[例] 原点を中心とし半径 a の球面は
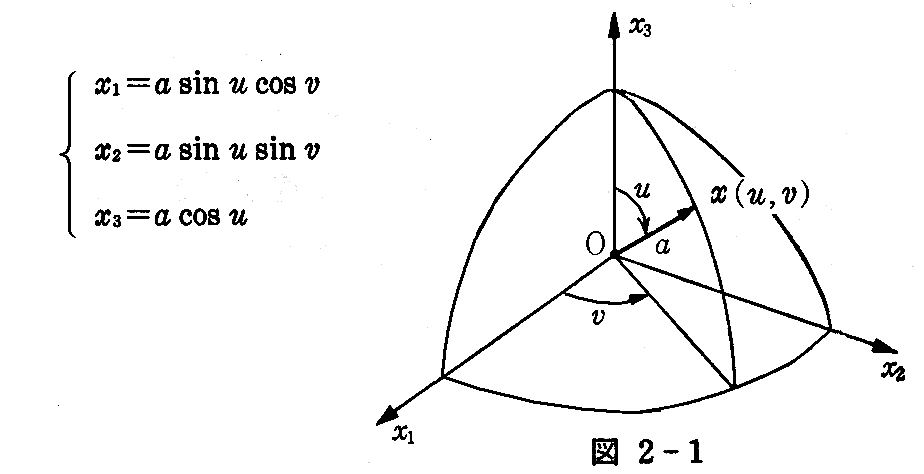
で表される。
例えば、u=π/4とすると
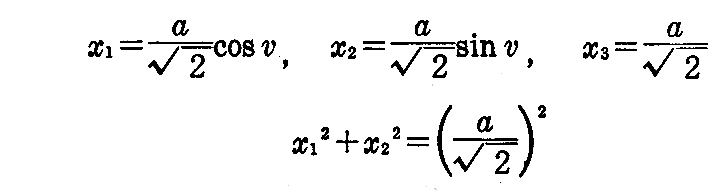
となので、u=π/4におけるv曲線はx3=acos(π/4)の平面で球面を切った切り口曲線となる。そのため一般のv曲線はx3軸に垂直な平面で切った円になる。同様にu曲線はx3軸を含む平面で球面を切った切り口である円になる。
次に

に於いてu=0と置けば
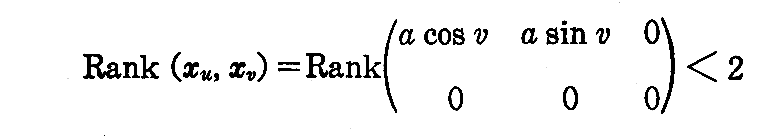
となり、u=πと置けば
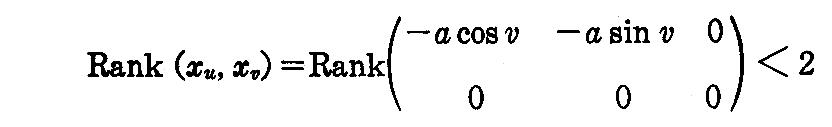
となる。そのため、北極(0,0,a)と南極(0,0,-a)の2点での階数は2ではない。このような点を径数表示の“特異点”という。特異点はこの場合のように座標軸の取り方によって生じる場合と、円錐の頂点の様に曲面そのものの性質に基づくものとがある。
[例題] “双曲的放物面”の径数表示は
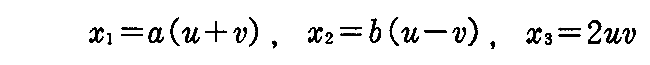
で与えられることを示し、その径数曲線はどんな曲線であるか調べよ。
[解] 双曲的放物面の標準形は
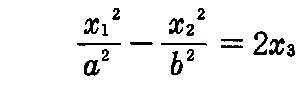
です。これを因数分解した
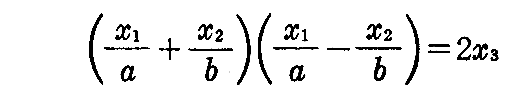
に於いて、
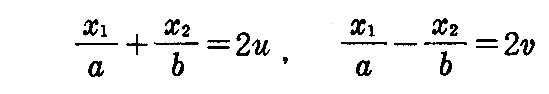
と置く。これをx1,x2について解けば

が得られる。vを一定とすればuについての1次式となるからu曲線は直線。同様にv曲線も直線となる(下左図参照)。
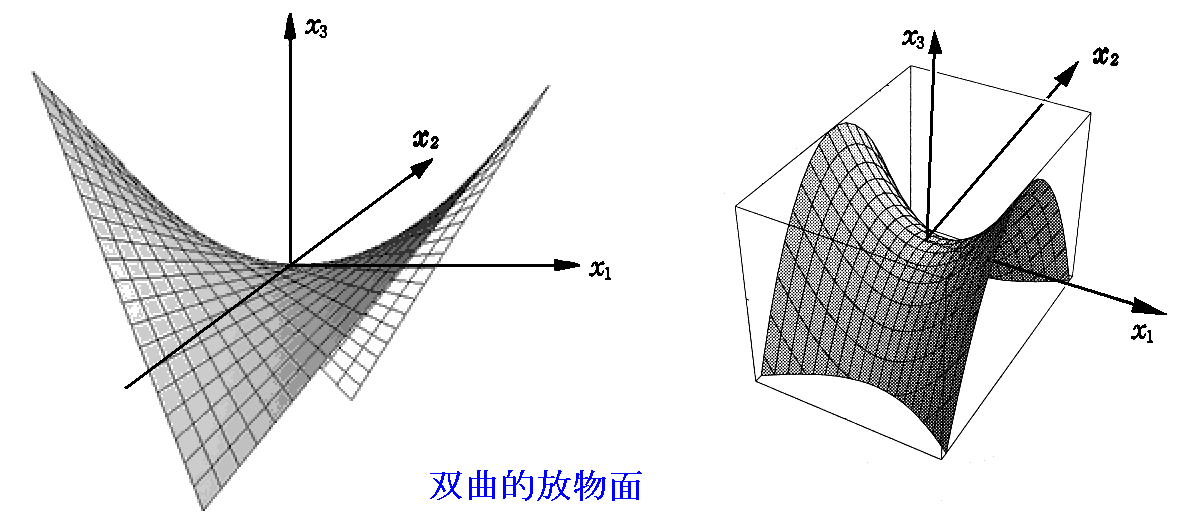
ちなみに、上右図は径数u,vとして
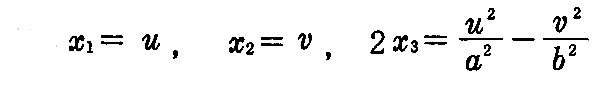
の様に取った場合です。
[問題1] 2つの空間曲線x=A(u),x=B(v)が一方のどの接線も他方の接線に平行でない2つの曲線であるとき
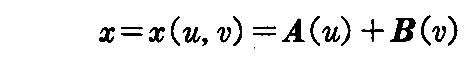
は曲面の方程式を与え、これを“移動曲面”という。
放物面
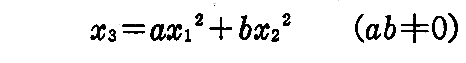
は移動曲面である事を示せ。
[証明]
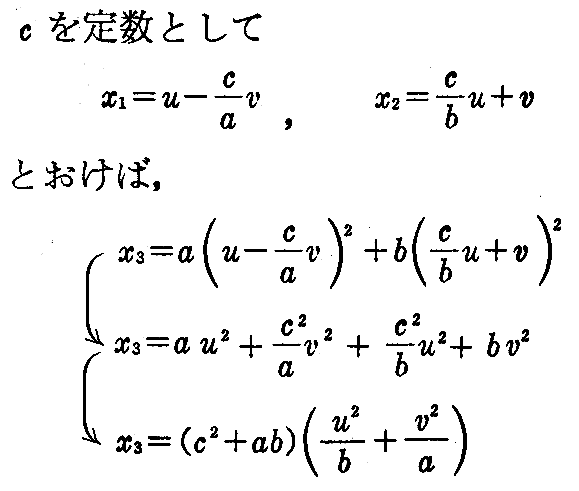
であるから
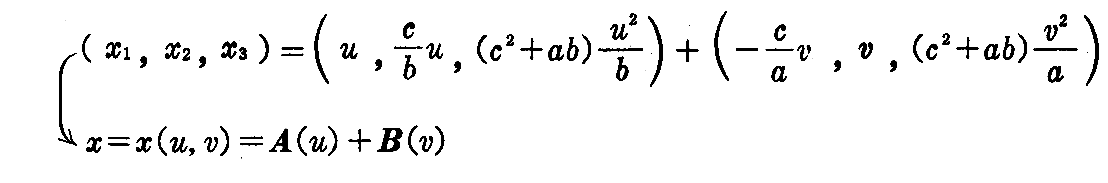
となる。
[問題2] 方程式
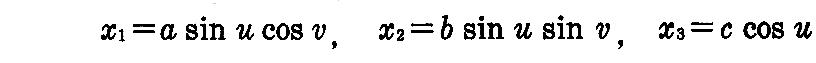
は楕円面を表わすことを示せ。
[証明]
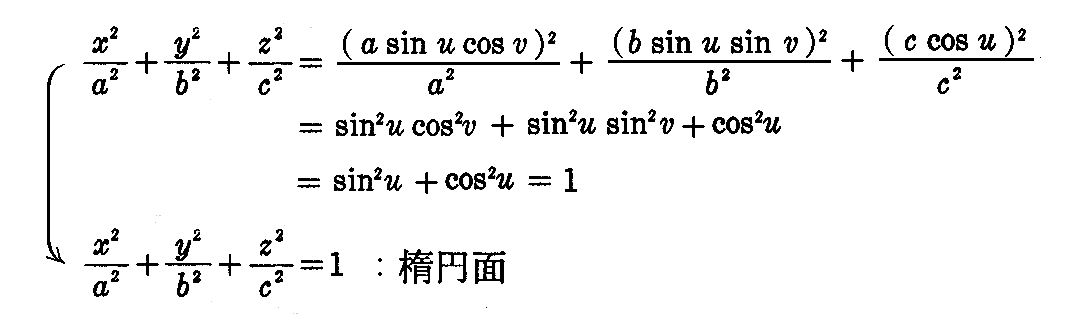
[問題3] 定直線のまわりを、一定の角速度で回転しながら、その直線の方向に一定の速度で移動する剛体の運動を“螺旋運動”という。1つの平面曲線x3=f(x1)に螺旋運動を行ってできる曲面を“螺旋面”という。その方程式は
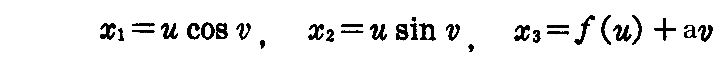
で与えられることを示せ。
[証明] 定直線x1軸、x2軸、x3軸を右手系直交座標系の座標軸とする。1点P(x1,x2,x3)を円柱座標(u,v,x3)で表せば
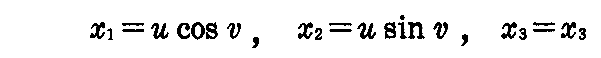
となる。
x3軸のまわりを一定の角速度で回りながら、x3軸方向に定速度で移動するから

を得る。 t を v で表わすと
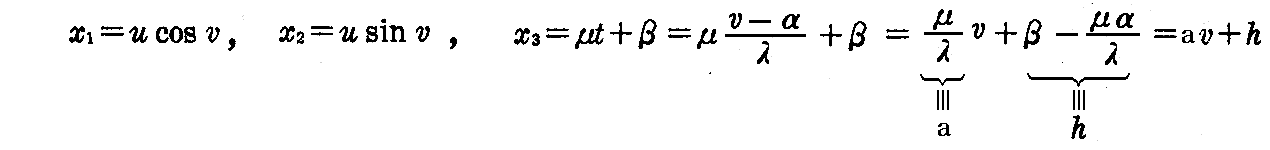
となる。いま x1x3平面上の曲線

に対して、その各点に螺旋運動を行うと、v=0 のとき
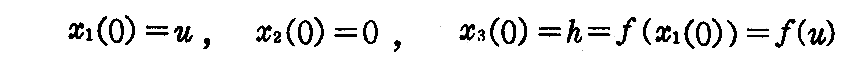
であるから、x1(0)=u を変化させれば螺旋面

を得る。
特にf(u)=定数(≡b) の場合
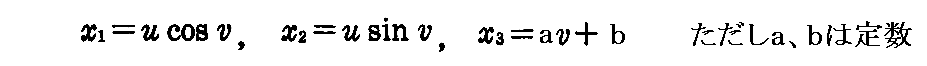
を“常螺旋面”と言い下図の様な曲面になる。

(2)第1基本微分形式
1.接平面の方程式
曲面S:x=x(u,v)の径数u,vが1つの径数 t によって
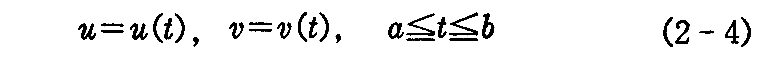
と表わされるとき、方程式
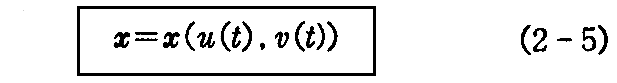
は曲面上の曲線を表し、曲線上の点x(u(t),v(t))における“接線ベクトル”は
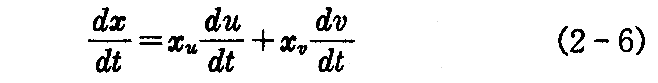
です。
このとき、duとdvをそのまま用いて
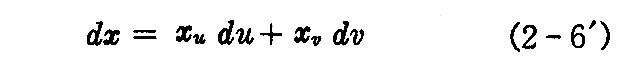
と表わす場合もある。この微少ベクトルdxは微分幾何学独特な表現で、du,dvを係数(径数)とした2つのベクトルxu、xvの一次結ベクトルを表わす。
曲線x=x(u(t),v(t))の接線ベクトル dx/dt あるいはdxは、ベクトルxu,xvの1次結合で表されているから、曲線の接線ベクトルはxuとxvの張る平面に乗っており、この平面を“接平面”と言う。“接平面の方程式”は
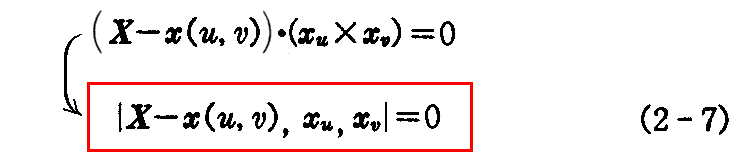
で与えられる。接平面上のベクトルを“接ベクトル”という。
接ベクトルと上記の接線ベクトルの意味を取り違えないこと。接ベクトルは接平面上にあれぱ任意の方向を向いていても良いが、接線ベクトルは曲面上の一つの曲線に沿った方向のベクトルです。。上記の接線ベクトルxuとxvは、2.(1)2.で述べた様にそれぞれu曲線、v曲線への接線ベクトルです。
[補足説明]
(2-5)式に出てきた径数 t について補足する。(2-5)式のu(t)やv(t)は曲面上に引いたu曲線やv曲線の弧長 s の関数であると考えれば、非常に理解しやすいのですが、ここの
t はそのような弧長とは限らない一般の変数を媒介変数とする曲面の位置ベクトルを表しています。
2.法線
点x(u,v) を通り“接平面”に垂直な直線を“法線”という。[xu×xv] は法線方向に向かうベクトルで、xu,xv,[xu×xv] は右手系をなす。そこでの単位ベクトル
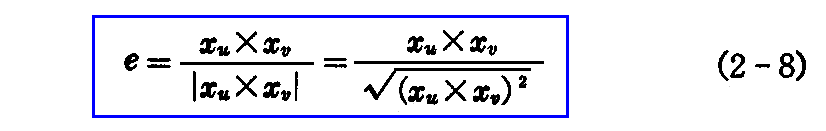
を“単位法線ベクトル”といい、正負の向きを除けば径数表示に関係せず決まる。
[補足説明]
ここで注意して欲しいことは、単位法線ベクトル e の曲面の凸凹に対する向きはu曲線とv曲線の取り方に依存することです。実際次の2つの図は同じ曲面であるがu曲線とv曲線の取り方を変えた場合に e の方向が逆転することを示している。
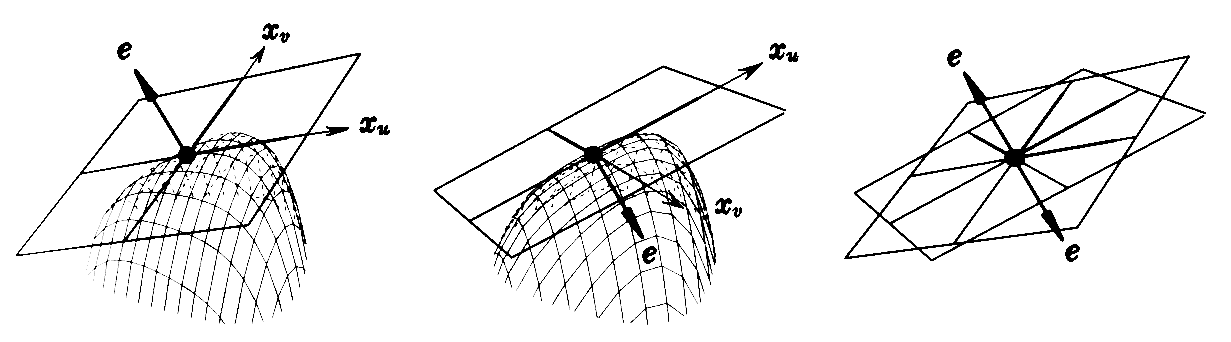
そのとき、曲面上の同一点での接平面は、たとえu曲線、v曲線の取り方が異なっていても不変です。また単位法線ベクトル e の方向はその接平面に垂直です。しかし、その向きは径数曲線の取り方に依存して、曲面の凸側に向く場合と、凹側に向く場合があります。
3.第1基本形式
曲線(2-5)式上の近接する2点間の距離を ds とすれば、(2-6)式によって
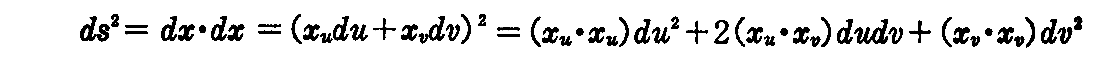
と表わせる。ここで du2,dudv,dv2 の係数を特に
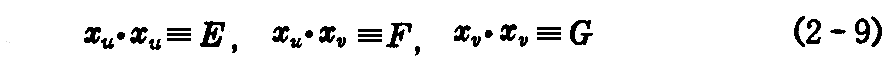
と置いて、“第1基本量”といい、 “ds” をその“線素”という。
このとき線素 ds の二乗は
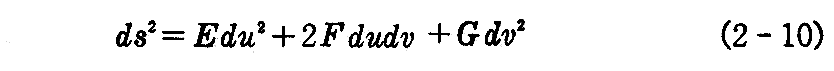
と書かれるが、この正値二次形式を曲面の“第1基本微分形式”(第1基本形式)という。
点x(u,v)から出て、曲面に接する2つのベクトル
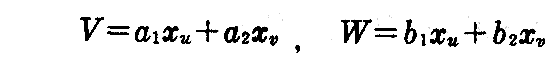
のなす角をθとすれば、(1-9)式と(2-9)式によって
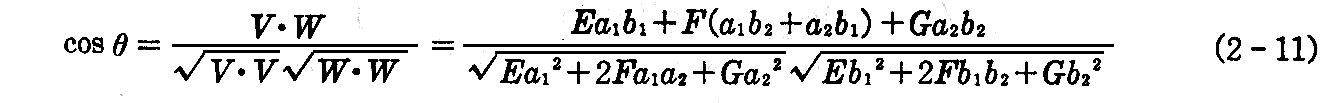
です。u曲線とv曲線のなす角 ω はそれぞれへの接ベクトル xudu と xvdv とのなす角だから、(2-11)式において、a1=1,a2=0,b1=0,b2=1 とおいて
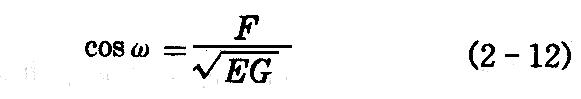
で与えられる。従って径数曲線が直交するための条件は F=0 です。
さらに(2-12)式より
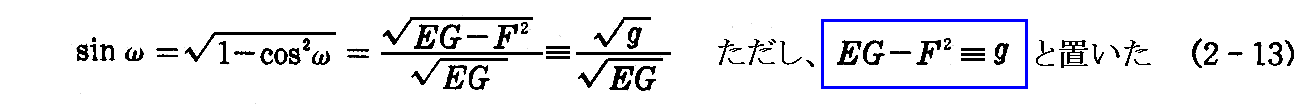
が得られる。今後は EG-F2≡g と置くことにする。
従って微少ベクトル xudu と xvdv の作る平行四辺形の面積dSは
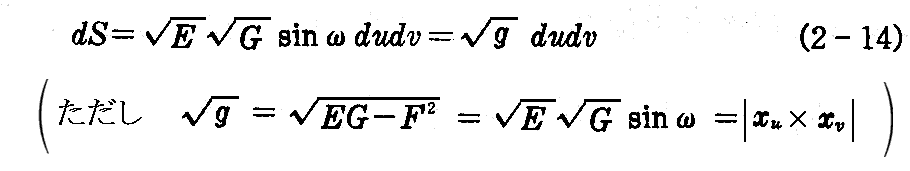
で与えられる。最後の g=(xu×xv)2 となることは、1.(1)8.の“ラグランジュの恒等式”(1-20)式を参照。
[補足説明1]
ここは、とても重要な所なのですが、ここの説明だけでは何が言いたいのか解らないので、別ページで引用する吉田伸夫著「完全独習相対性理論」の§8-1-1“ガウスの曲面論”と、§8-1-2“ガウス曲率と驚異の定理”をご覧下さい。
これに引き続く§8-2-1”リーマン幾何学の考え方〝の解説を3.(2)2.[補足説明3]でほぼそのまま引用していますので合わせてご覧下さい。
[補足説明2]
上記の説明が解りにくいのは、物理で用いる記号と少し違うからだと思います。そのため、物理でなじみの記号で (2-9)~(2-11)式 をもう一度説明します。以下はメラー著「相対性理論」みすず書房(1951年刊)のp224~227から引用。


ただしし、(11)式中のF、G、Hは本文中のE、F、Gとは何の関係もありません。単なる関数を表す記号です。

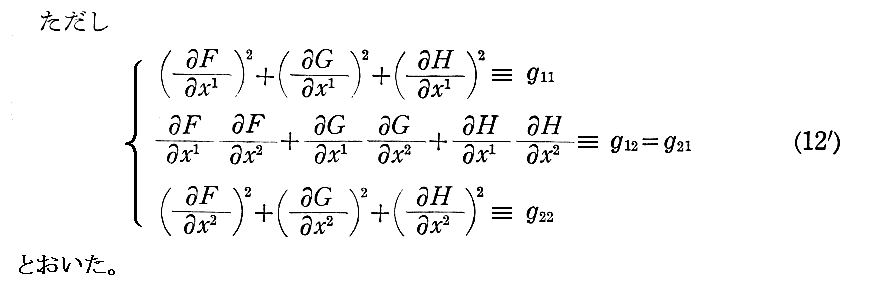
次の(13)式については別稿「ベクトルの内積と外積の成分表示」1.(5)1.を参照。


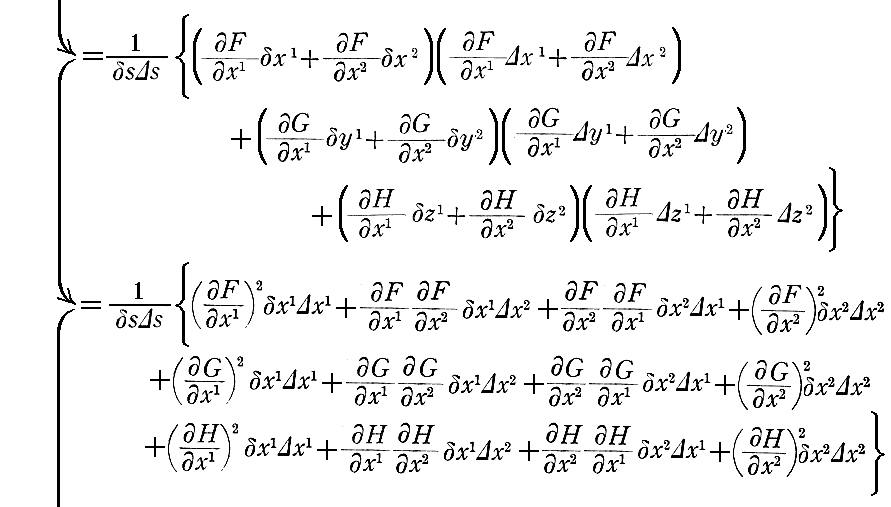
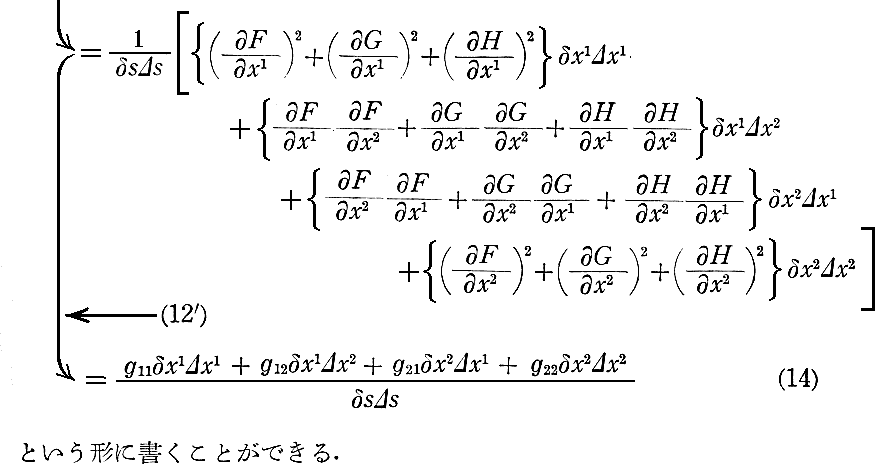




これに続く§86~§87を別ページで引用。これは、必ずしも解りやすい説明ではありませんが、参考になると思います。
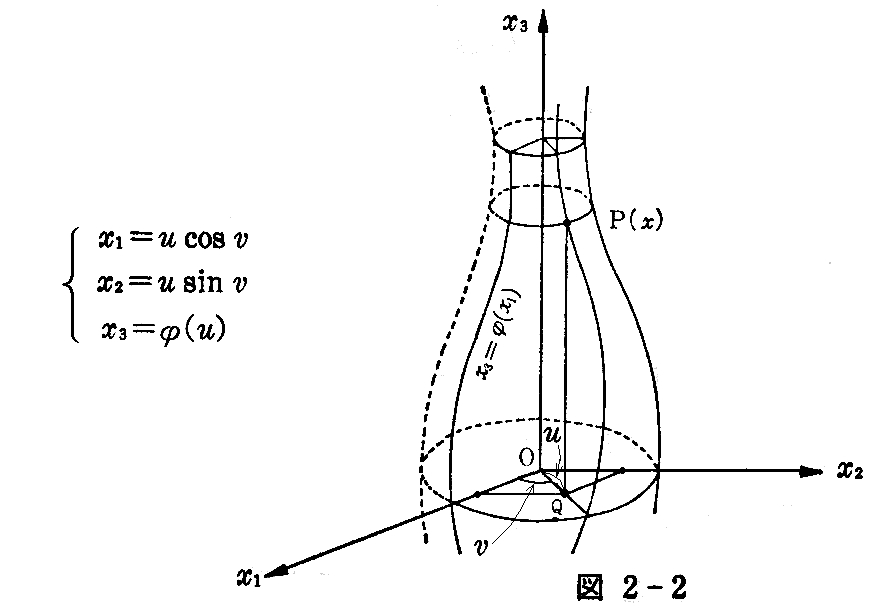
[例題] x1,x3平面上の曲線x3=φ(x1)をx3軸のまわりに回転して得られる曲面、すなわち回転曲面の第1基本式と単位法線ベクトルを求めよ。
[解] 曲面上の1点P(x1,x2,x3)からx1x2平面に下した垂線の足をQ(x1,x2,0)とする。径数 u をOからQまでの距離、径数 v をx1軸からOQまでの回転角とすれば、回転曲面の方程式は
で与えられる。したがって
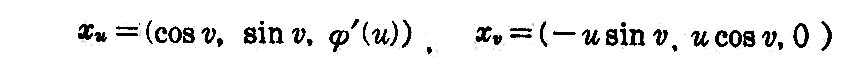
であるから、(2-9)式と(2-10)式によって

が得られる。次に(1-12)式によって
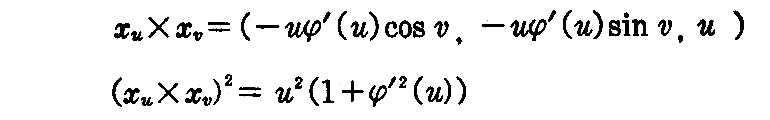
であるから、(2-8)式に代入して単位法線ベクトル
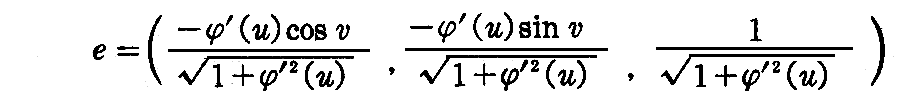
を得る。ここでu曲線は回転軸を含む平面による切り口の曲線、すなわち子午線、v曲線は軸に垂直な平面による切り口の円、すなわち平行円です。
[問題1] “正コノイド” x1=u cos v,x2=u sin v,x3=φ(v) の線素と単位法線ベクトルを求めよ。特にφ(v)=av+bの場合を“常螺旋面”という。
[解] x3が[例題]と違ってvの関数であることに注意されたし。それ以外は[例題]と同様に計算して
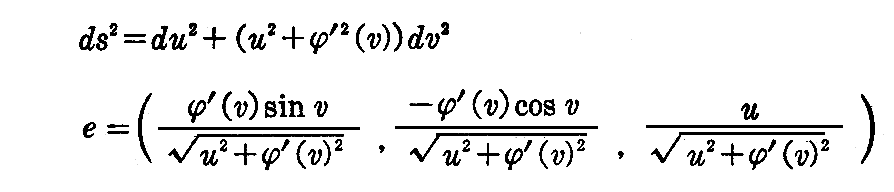
が得られる。
特に、φ(v)=av+bの場合が常螺旋面であるが、その図は2.(1)[問題3]を参照されたし。
[問題2] 曲面の方程式をz=f(x,y)とし、∂z/∂x=p,∂z/∂y=qと置けば
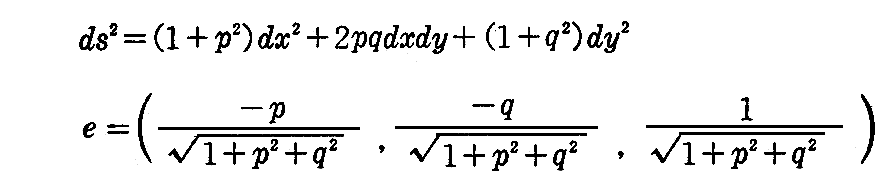
によって線素と単位法線ベクトルが与えられる事を証明せよ。ここではp,qが曲面の径数表示に於ける径数となる。
[解] x=u,y=v,z=f(u,v)と置くとdx=du,dy=dvだから、(2-9)式と(2-10)式より
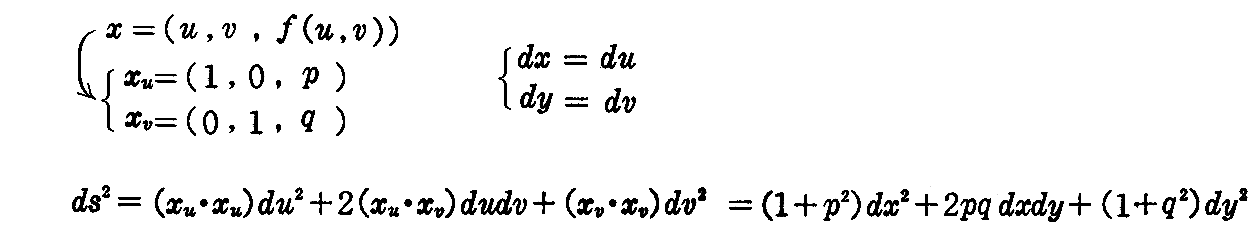
さらに
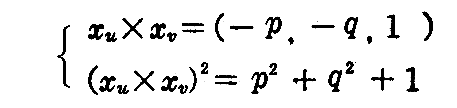
だから(2-8)式に代入して
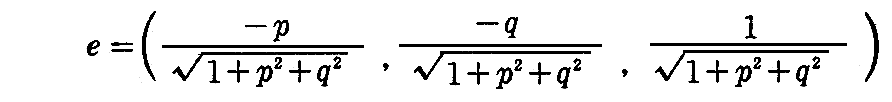
となる。
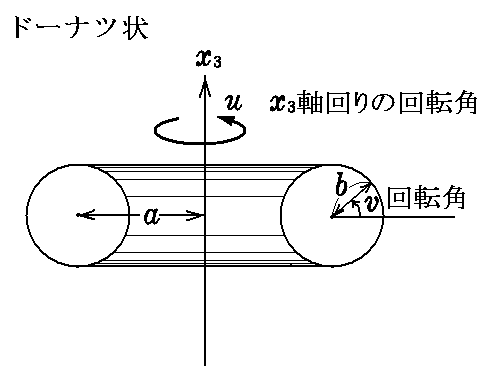
[問題3] 円をその平面内にあってそれと交わらない直線を軸として回転して生ずる曲面を“輪環面”(ドーナッ状の曲面)という。方程式
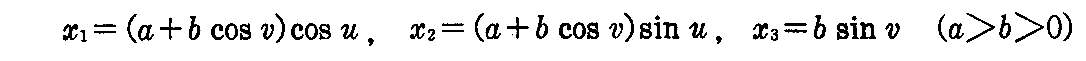
は輪環面を表わすことを示し、その第1基本形式を求めよ。
[解] aは回転軸とドーナッ部の輪環の中心までの距離、bはドーナッ輪環部の断面円の半径、vはその半径線の回転角、uはその断面位置までの回転軸まわりの回転角と解釈すれば、上記方程式が輪環面を表わすことは明らか。
第1基本形式は定義にしたがって
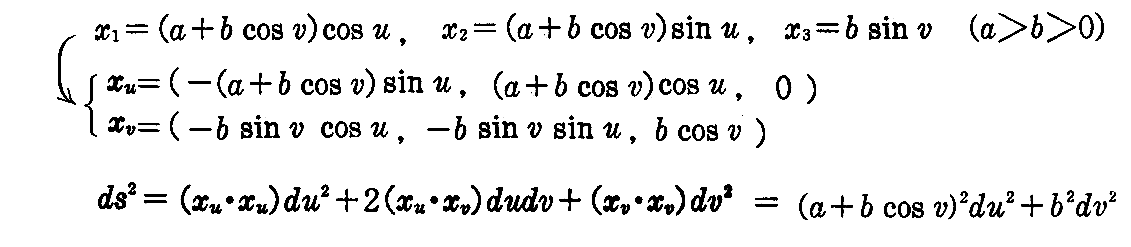
となる。
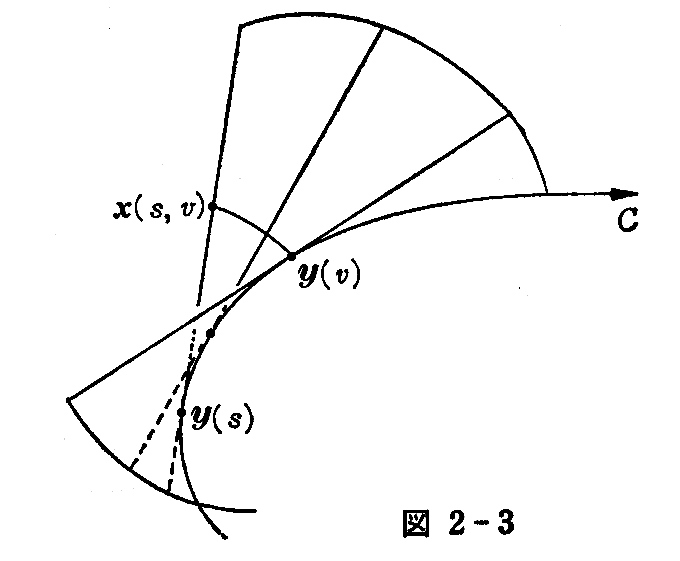
(3)接線曲面
直線でない 空間曲線y(s) の接線が作る曲面を“接線曲面”といい、各接線をその“母線”という。う。1点 y(s) における接線の方程式は接線上の任意の点x(s,v)までの距離 v を径数として用いれば
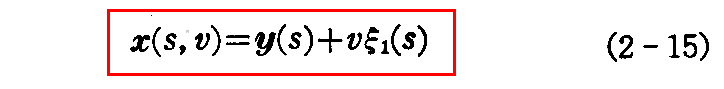
で表される。ここで s と v を独立な径数と考えれば、(2-15)式は“接線曲面の方程式”を与える。
[例題] [図の拡大版]

1.(12)2.の伸開線の方程式から、(2-15)式はまた
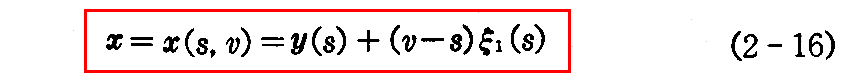
と書けるから、(v=一定の)s曲線は1.(12)2.の(1-88)式から曲線y(s)の伸開線であり、(s=一定の)v曲線は曲線y(s)の接線です。
点y(0)の近くで接線曲面の方程式を径数s,vの巾級数に展開すれば
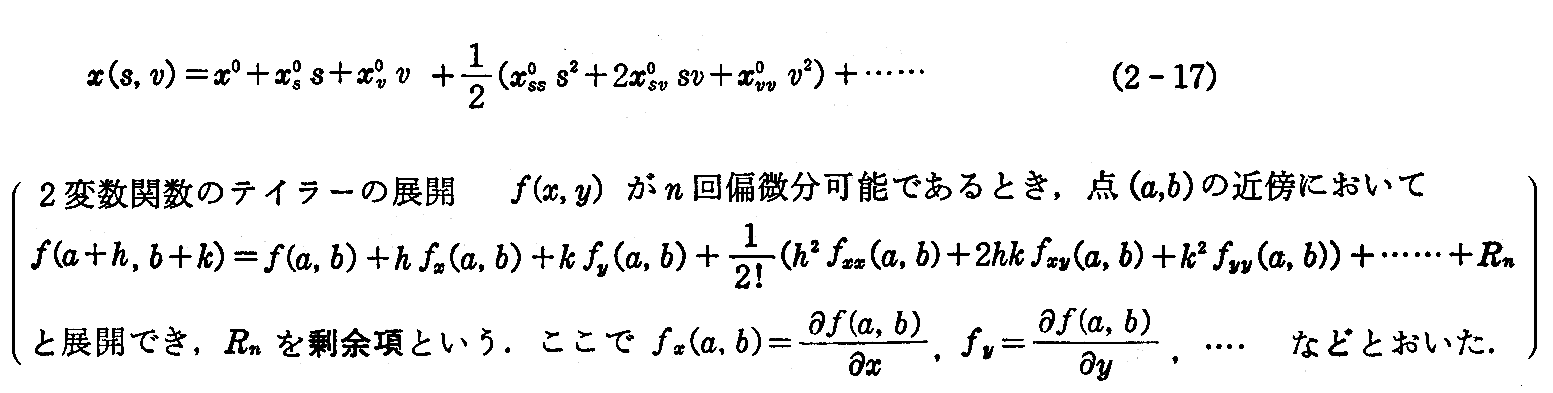
となる。ここでxs0,xv0などはxs,xvのs=v=0における値を表わす。
(2-15)式から(フルネ・セレーの公式(1-60)式を用いて)
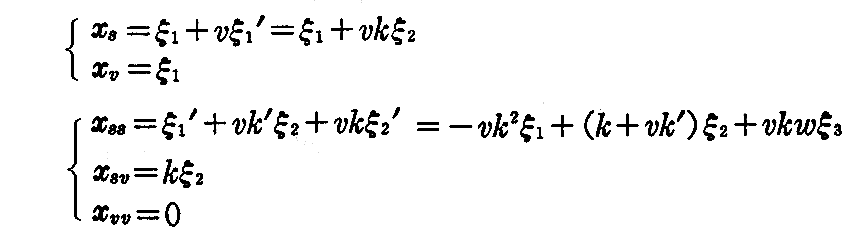
であるから、k(0),k’(0),w(0),w’(0)などをk0,k0’,w0,w0’などで表わし、さらにxsss,xssv,・・・等を(2-17)式に代入して整理すると

となる。これは曲線上の1点 y(0) における“フネル標構” y(0)ξ1ξ2ξ3 に関しての y(0) の近くの“接線曲面”の径数表示です。
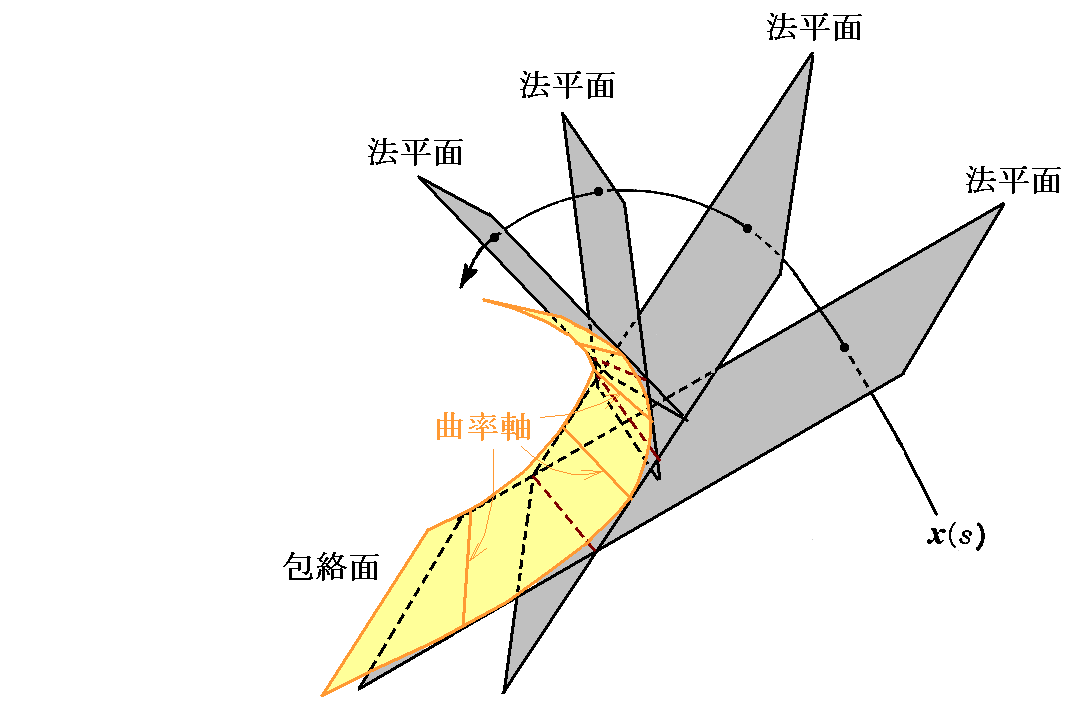
[例題1] 曲線y=y(s)の“曲率軸”[1.(9)2.参照]の描く曲面を“曲率軸曲面”という。曲率軸曲面の方程式を求め、その曲面は接触球の中心の描く曲線の接線曲面になっていることを示せ。
[解] 曲線y=y(s)の1点における“曲率軸の方程式”は v を径数として
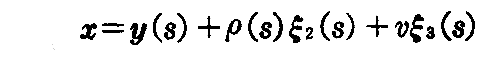
と表せる。ここでxを s と v の関数x(s,v)と考えれば、“曲率軸曲面の方程式”
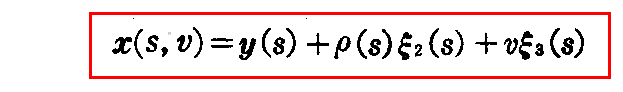
が得られる。ここのξ2,ξ3は曲線y=y(s)のy(s)点でのフルネ標構です。
いま方程式中のvをv=v(s)なるsの関数とした極曲面上の 曲線 x(s) を s について微分して(フルネ・セレーの公式(1-60)式を用いて)
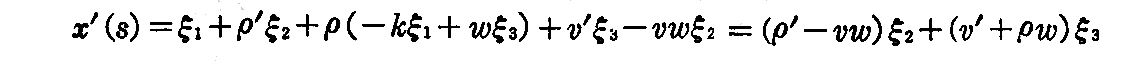
が得られる。いま、この方向(つまり曲線 x(s) の接線方向)が曲率軸の方向、すなわち ξ3 の方向と一致すれば
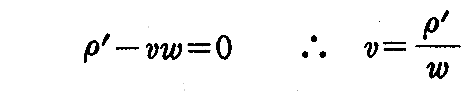
となる。従って y(s) の曲率軸曲面は
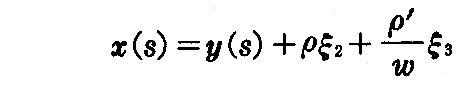
の描く曲線、すなわち接触球の中心の描く曲線の接線曲面になっている。
[例題2] 3次曲線 x1=u,x2=u2,x3=u3 の接線曲面は
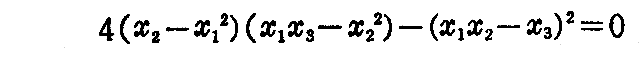
で表されることを示せ。
[解] 与曲線の接線ベクトルはx’=(1,2u,3u2)であるから接線曲面は(2-15)式により

です。ここで

であるか、これらの関係式からu,vを消去すると次の関係を得る。
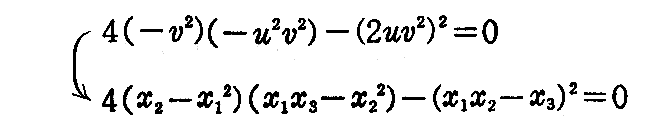
[例題3] 曲線y(s)の法平面[1.(5)2.を参照]でこの曲線の接線曲面を切った切口の曲線を“反帰(ソリカエリ)曲線”という。反帰曲線の概略図を描け。
[解] 曲線y(s)の法平面でのこの曲線の切口は(2-18)式においてy1=0だから
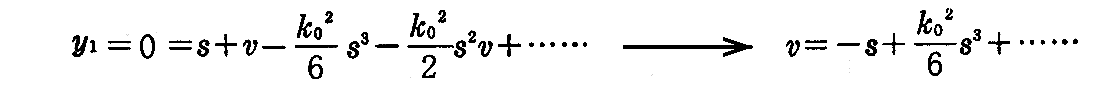
y2,y3に代入して
したがって、接線曲面の法平面による切口の曲線はy(0)の近くで
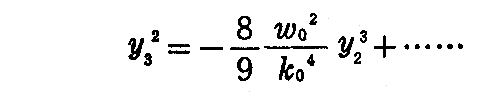
で与えられる。切口の曲線は図2-4のようにy(0)に於いて鋭くとがった稜をしている。このような点Pを通常“尖点”と呼んでいる。
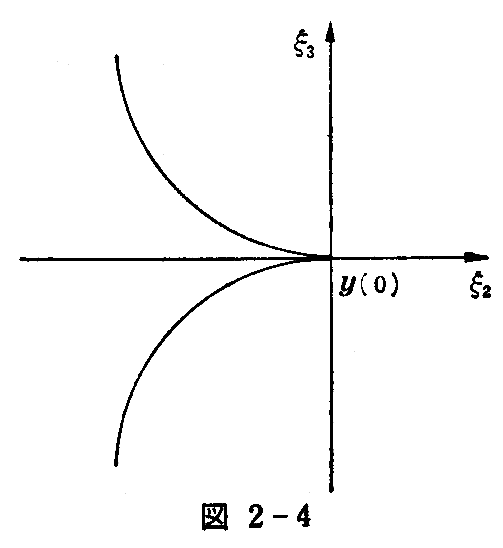
[問題1] 接線曲面の母線上の“接平面”[2.(2)1.を参照]はもとの曲線の“接触平面”[1.(6)1.を参照]と一致することを示せ。
[解] “接線曲面の方程式”(2-15)式から
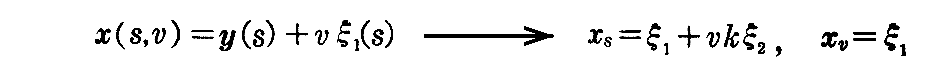
となる。もちろんここのξ1,ξ2は曲線y=y(s)のy(s)点でのフルネ標構です。
接線曲面の“接平面の方程式”(2-7)式より
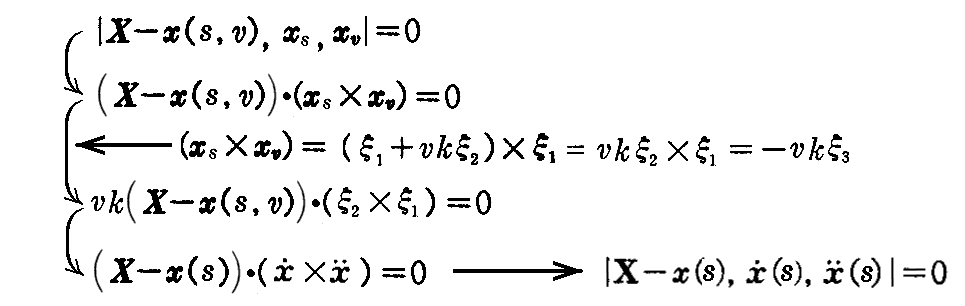
となり、もとの曲線y=y(s)の接触平面と一致する。
このとき、接線曲面の法線方向は
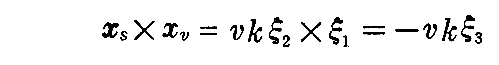
であるから、接線曲面を形成するもとの 曲線 y=y(s)の従法線方向と一致する。もちろん法線方向は v に無関係です。
[問題2] 極曲面[例題1を参照]の接平面はもとの曲線の法平面[1.(5)2.を参照]と一致することを示せ。
[解] “極曲面の方程式”を偏微分すると
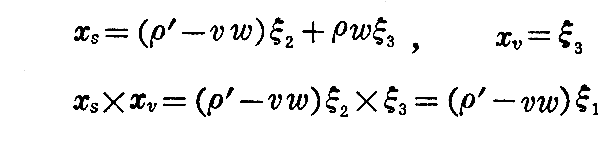
です。つまり接平面の法線はもとの曲線の接線方向と一致するから接平面はもとの曲線の法平面と一致する。そのときもちろん、接平面の方程式は v に無関係です。
(4)第2基本微分形式
1.第2基本形式
曲面S上の点x(u,v)での接平面に、この点の近くの点P x(u+Δu,v+Δv)から下した垂線の長さ p は
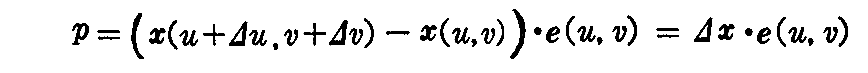
で与えられる。
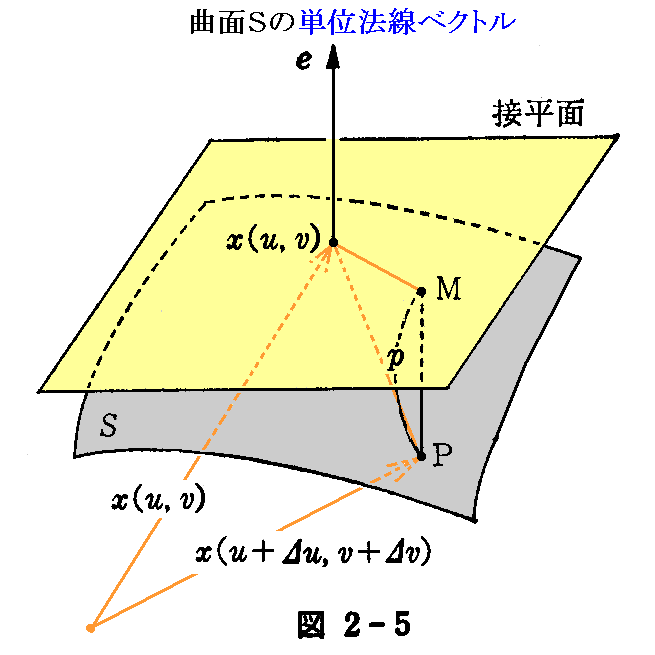
ここで、2変数関数のテイラー展開
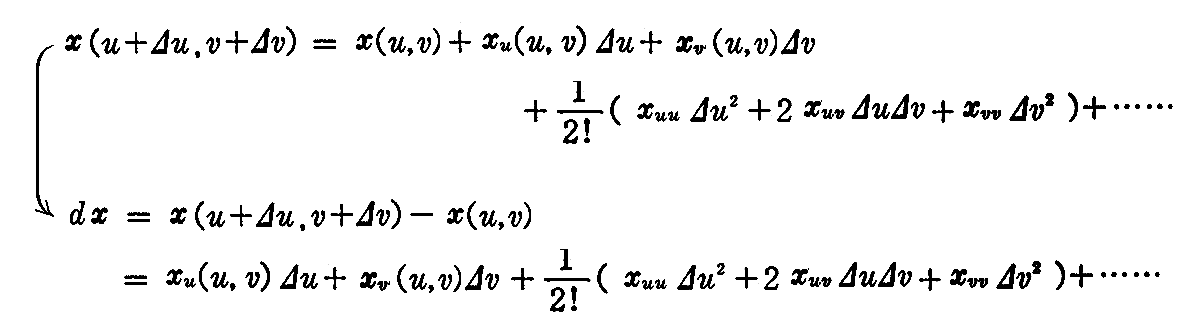
で高次の無限小を省略し、(2-8)式から

であることを考慮すると
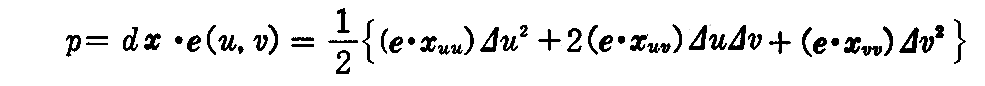
が垂線の長さの主要部として得られる。
ここで(2-19)式を用いて
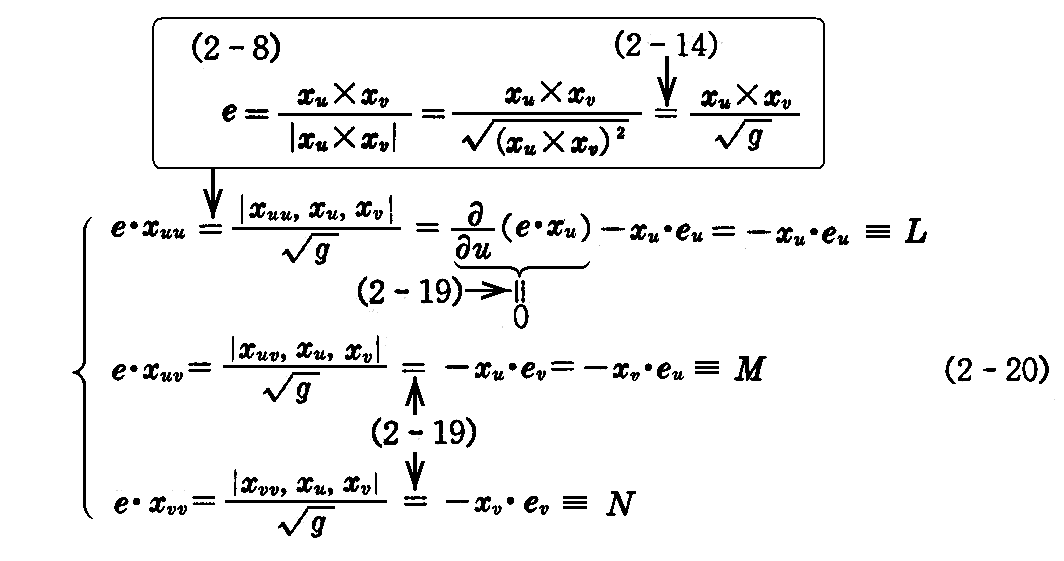
と置くことにする。これら L(u,v),M(u,v),N(u,v) を曲面Sの径数 u,v に関する“第2基本量”という。
そして2次微分形式 2p≡Π

を曲面Sの“第2基本微分形式”(第2基本形式)という。これは曲面から接平面が離れる量を表している。
2.漸近曲線 と 共役な方向
点x(u,v)で曲面Sに接する方向 du:dv が
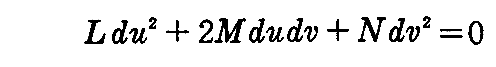
を満たすとき、この方向を“主接線方向”又は“漸近方向”という。要するにその方向線の法曲率が 0 の方向のことです。
[補足説明1]
主接線方向とは、その方向のp値が0(法曲率が0)であると言うことですから、曲面の接線が面に密着している事を意味している。つまり主接線方向とは、その方向に移動するとき曲面が2次の範囲で湾曲していない方向であると言うことです。
すなわち、主接線方向に微少量移動したとき、接線を含む接平面に下した垂線の長さpはΔsについて3次以下であると言うことです。
また、du:dv なる方向と δu:δv なる方向とが

を満たすとき、2つの方向は互いに“共役”な方向であるという。したがって、主接線方向は自分自身に共役な方向であるといえる。
[補足説明2]
共役な関係とは

であるから、2つの 微少ベクトル dx=xudu+xvdv と de=euδu+evδv が互いに直交していることを示している。
ところで、これは(2-19)式を考慮すると
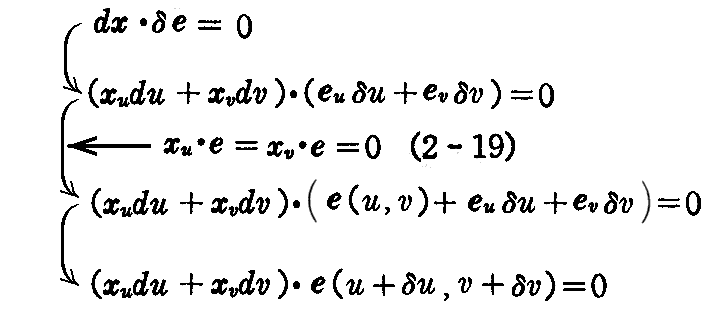
です。
つまり、まず曲面上の点x(u,v)での接平面を考える。そして、その近傍の曲面上の点x(u+δu,v+δv)に於けるもう一つの接平面を考える。その接平面の法線ベクトルがe(u+δu,v+δv)であり、これは当然点x(u+δu,v+δv)に於ける接平面に垂直です。その法線ベクトル e(u+δu,v+δv)と微少ベクトル dx=xudu+xvdvが垂直であることを言っている。
このとき、微少ベクトル dx=xudu+xvdvは点x(u,v)での接平面上にあるのですから、結局最後の式は、曲面上の2点x(u,v)とx(u+δu,v+δv)に於けるそれぞれの接平面があり、その2つの接平面が交わった線の方向が(du,dv)であることを意味している。
この時の2つの方向(du,dv)と(δu,δv)の関係を“共役”な関係と言っている。
曲面S上の曲線C の接線がつねに主接線方向を向いているとき C を“主接線曲線”または“漸近曲線”という。要するに、これは主接線方向の微少ベクトルをつないでできる曲線です。
[定理]
曲面上の曲線が“主接線曲線(漸近曲線)”であるための必要・十分条件は、その曲線上の接触平面[1.(6)1.参照]が曲面の接平面[2.(2)1.参照]と一致することです。
[証明]
曲面上の曲線 x=x(u(s),v(s))=x(s) の 接線 x’=x’(s) と 法線 e に対して
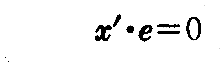
が成り立つ。
これを s について微分し、(2-20)式を用いると

となる。このときx=x(s) が主接線曲線ならば右辺は 0 だから、x”・e=0が言える。すなわち、曲線の 主法線方向 x” も曲面の法線 e に垂直となる。これは、x’ と x” の張る平面、すなわち接触平面が法線に垂直で在ることを意味する。よって接触平面が接平面に一致する。この逆も成り立つので十分条件でもある。
[証明終わり]
[補足説明3]
例えば、2.(2)[問題3]の“輪環面”(ドーナッ状の曲面)に於いて、v=π/2の曲線(ドーナッの一番標高の高い点を結んだ円)やv=-π/2の曲線(ドーナッの一番標高の低い点を結んだ円)が“主接線曲線(漸近曲線)”です。実際その円形曲線の接触平面は、その線上の点に於ける曲面の法線ベクトルに垂直となりますから、それらの円上の各点で、円の接触平面と曲面の接平面は一致します。
[例題] x3軸を回転軸とする回転面 x1=u cos v,x2=u sin v,x3=φ(u) の第2基本量L,M,Nとこの曲面上の主接線曲線を求めよ。
[解] 第2基本量L,M,Nは
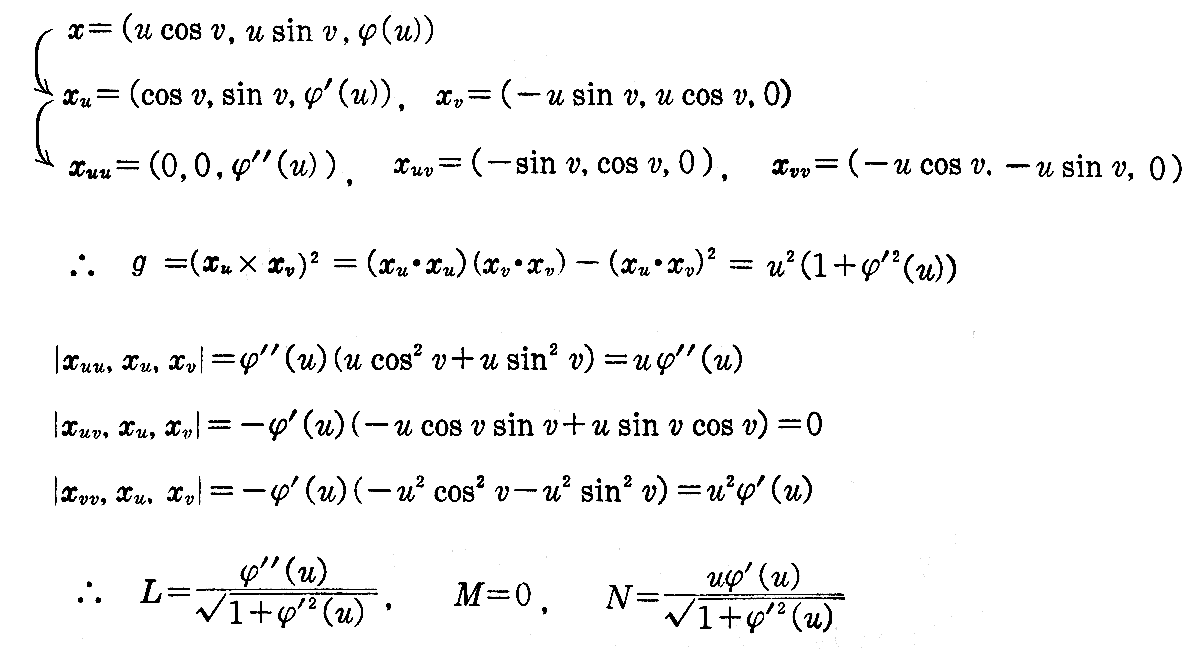
となる。また、主接線曲線の方程式は次式で与えられる。

[問題1] 次の曲面の第2基本形式を求めよ。
(1)球面 x1=a cos u cos v, x2=a sin u cos v, x3=a sin v
(2)螺旋面 x1=u cos v, x2=u sin v, x3=φ(u)+av
[解] (1)

(2)
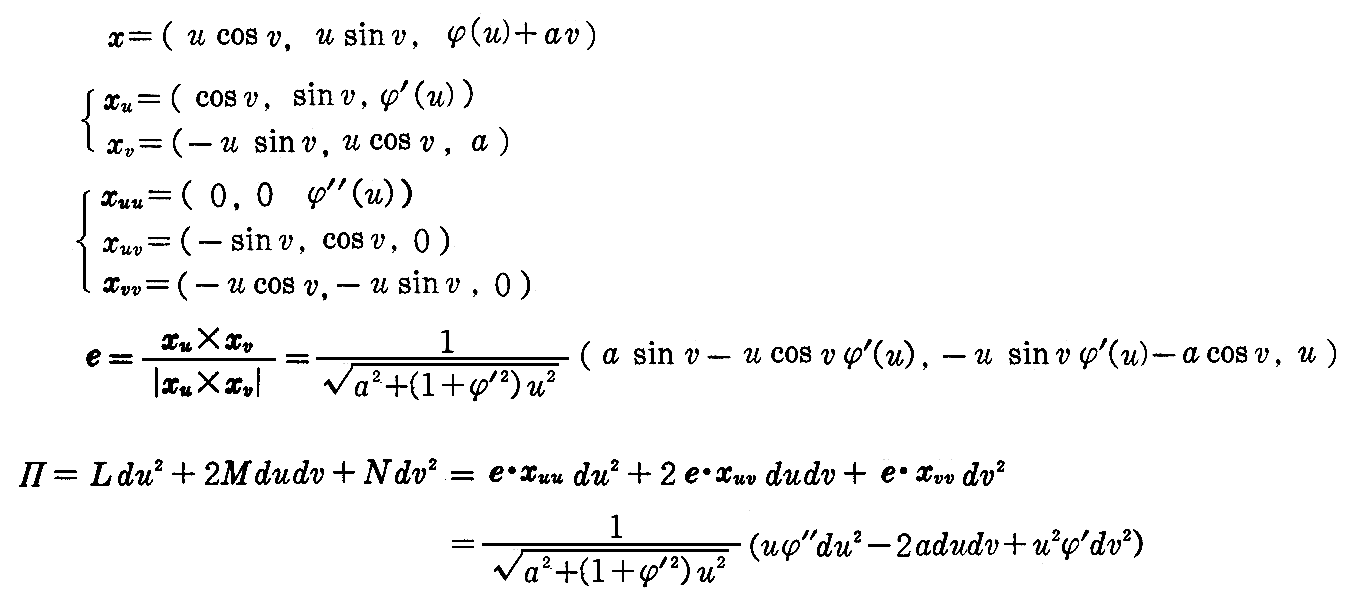
[問題2]
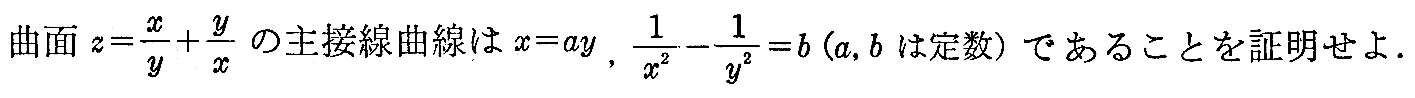
[解]
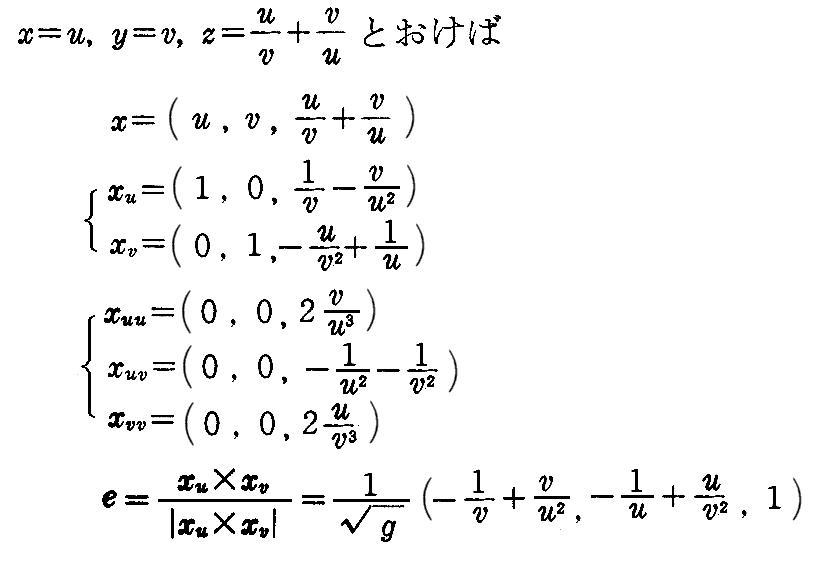
となるので、主接線曲線の方程式は
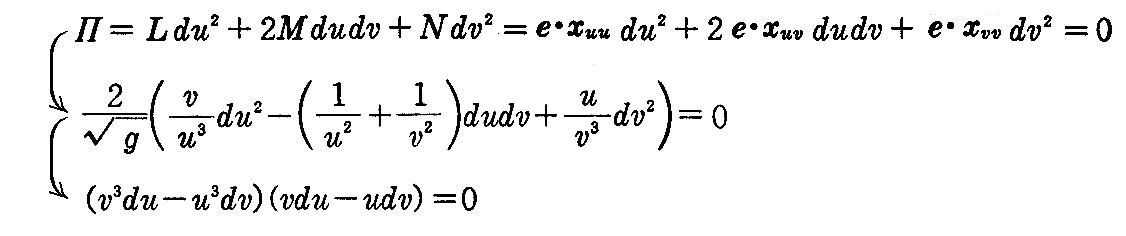
で与えられる。すなわち
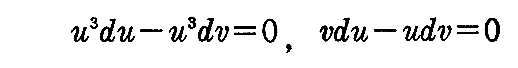
となるが、これを変数分離して積分すると
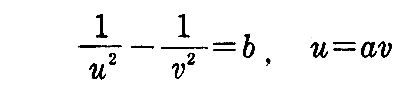
となる。
[問題3] 曲面が平面であるための必要十分条件は、L=M=N=0 であることを証明せよ。
[解]
《必要条件》
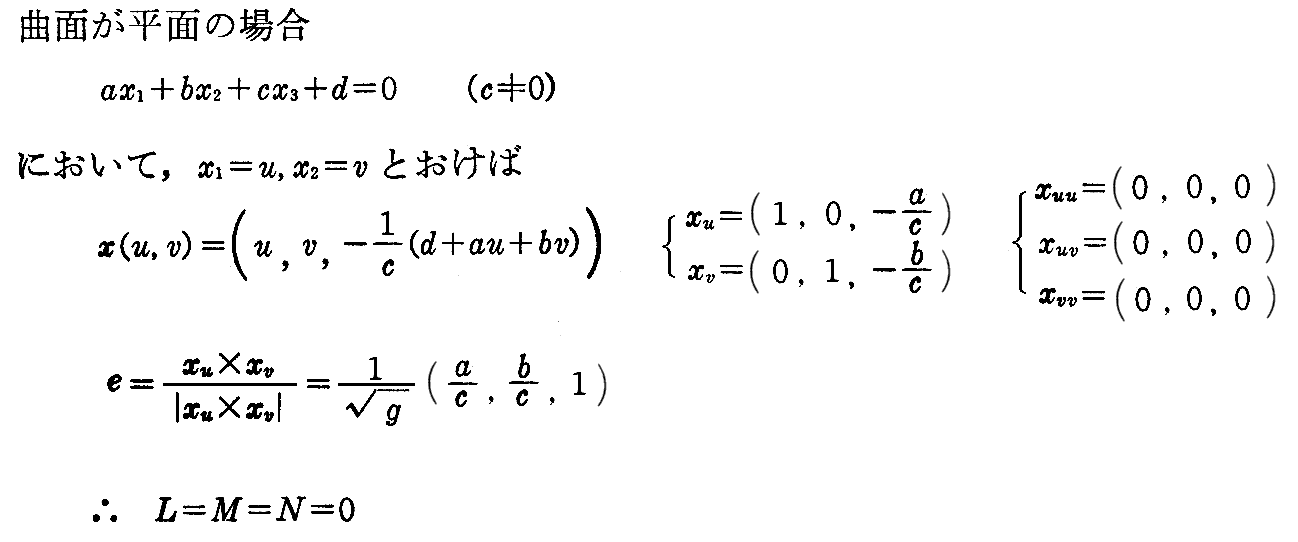
《十分条件》
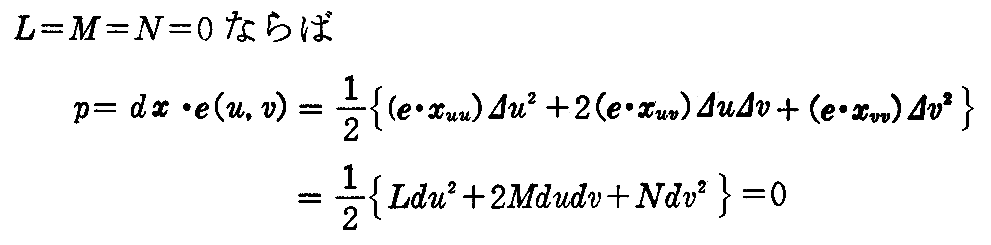
つまり、曲面上のある点x(u,v)の近傍の曲面はx(u,v)に於ける単位法線ベクトル e に対して常に垂直な面上に無ければならない。そして、x(u,v)からそれはdx移動した面上の点においても同様な条件を満たさなければならないので曲面は平面でなければならない。
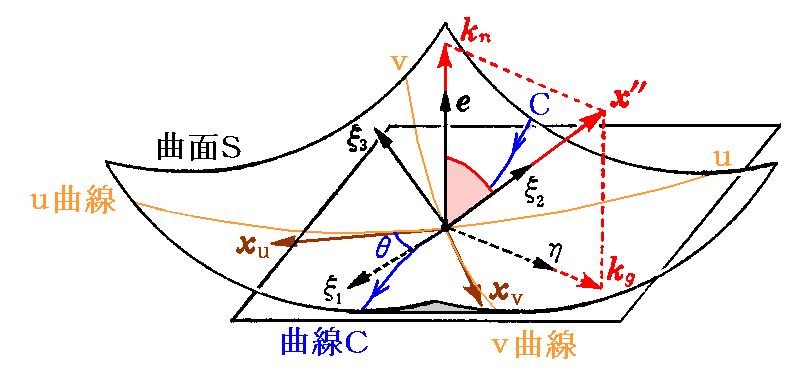
(5)曲面の曲率
1.法曲率
曲面S上の点x(u,v)を通る曲線C を x(s)=x(u(s),v(s)) とする。曲線C上の点 x(s) における単位ベクトル η を、その点に於ける曲面の法線ベクトル e と曲線の単位接線ベクトル ξ1 を用いて

となる様に定める。
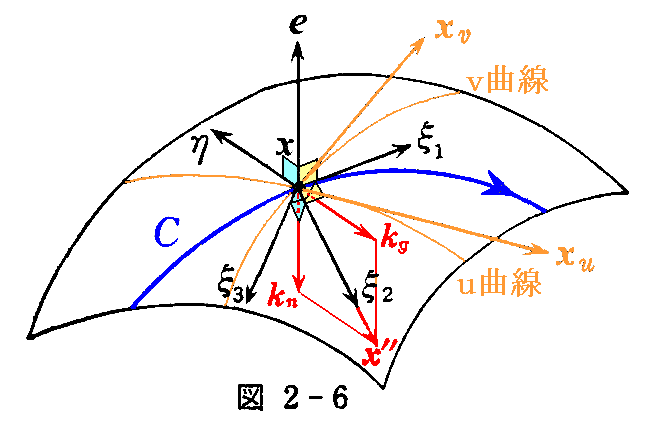
ここで曲線C の方程式を s について微分して

を得る。
x”=kξ2 を法線 e 上へ正射影したときのベクトル kn=(x”・e)e を曲線Cの“法曲率ベクトル”といい、その長さ

を“法曲率”という。
ここの図2-6は錯綜していて解りにくいのでもう一つ別な状況の図を示す。
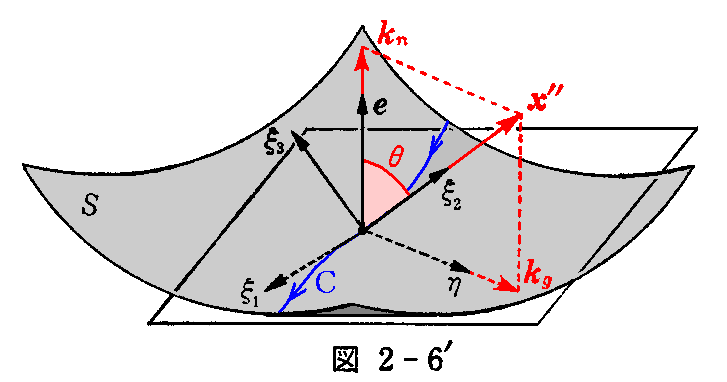
ここで、2.(2)2.[補足説明]で示したように、u曲線、v曲線の取り方とu,vを測る方向により、単位法線ベクトル e は曲面の凸側を向く場合と凹側を向く場合が在ることに注意されたし。
2.測地的曲率
x”=kξ2 を接平面上の η 方向の接ベクトルに正射影したときのベクトル kg=(x”・η)η を曲線C の“測地的曲率ベクトル”といい、その長さ

を“測地的曲率”という。
法線ベクトル e と曲線Cの 主法線ベクトル ξ2 とのなす角を θ とすれば
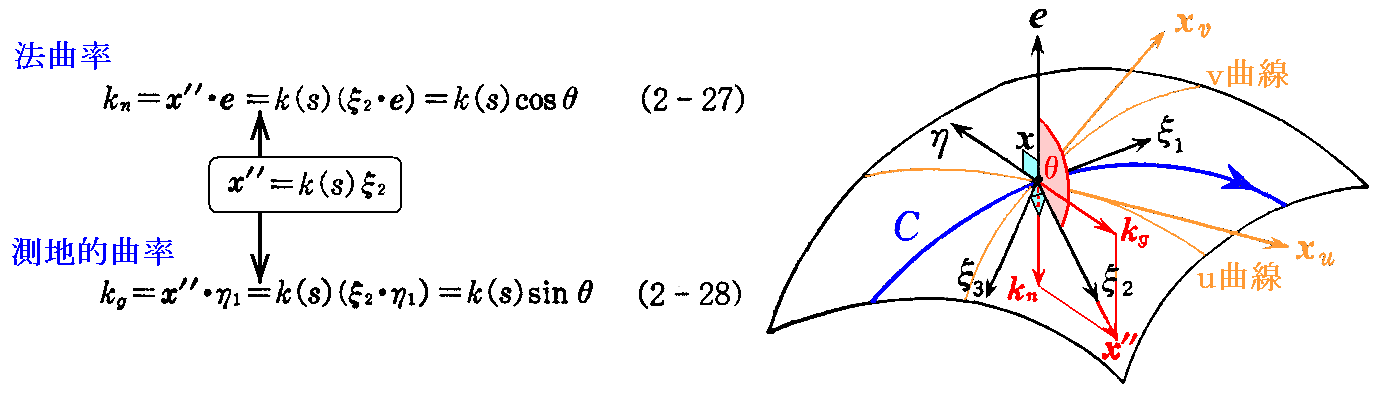
となる。
3.ムーニェ(J.B. Meusnier)の定理
前項(2-27)式に(2-24)式、(2-8)式、(2-10)式、(2-20)式を適用すると
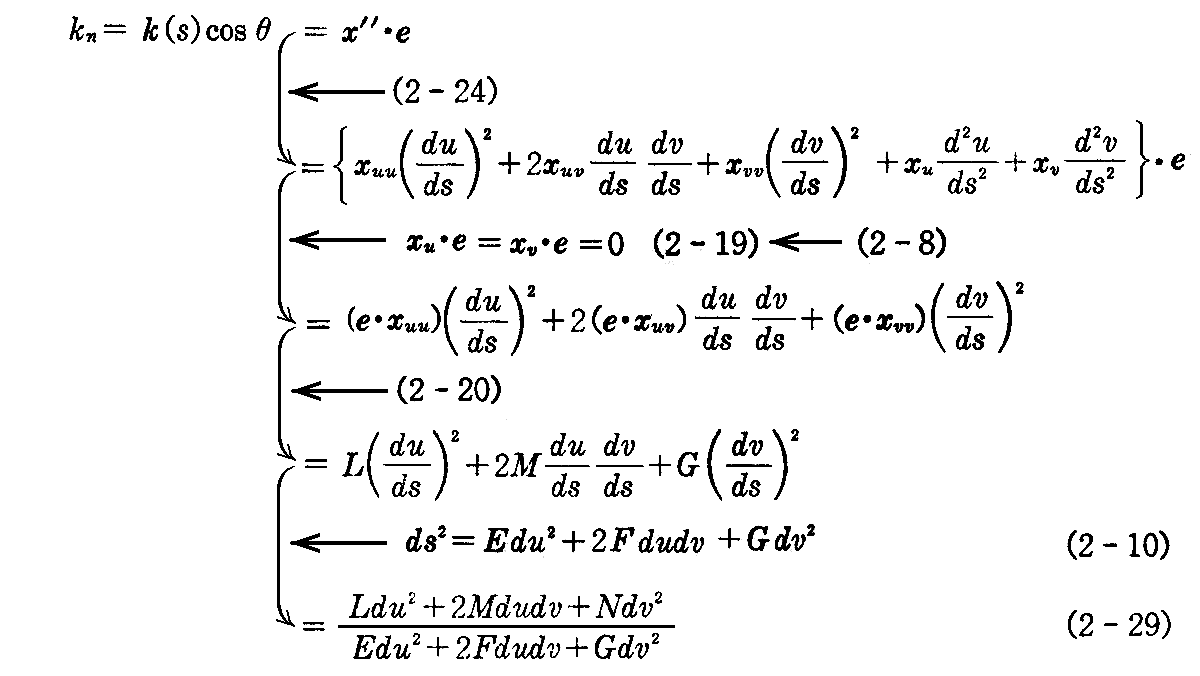
を得る。これから、曲線Cの法曲率 kn(s) は点 x(u,v) の位置と曲線Cの接線方向を定める du:dv だけに関係することが解る。したがって x(u,v) を通り、その点で互いに接するすべての曲線に対して同じ値をもつ。
すなわち同じ接線ベクトルξ1を持つ曲線群は接点に於いて(曲率k(s)は曲線ごとに異なっても)、すべて同じ法曲率kn(s)を持つ。
このことの意味はなかなか解りにくいが、もう一度繰り返すと [曲面上の各点x(u,v)ごとに、そしてその点に於ける接線方向ごとに曲面の回り具合を表わす法曲率という量が決まる] ということです。最初は曲面上の曲線を用いて曲面の曲がり具合を調べていたのですが、結局のところ [そういった曲線の取り方には依存せずに、曲面の曲がり具合を決めることができる] ということです。
下図はその当たりの状況を示している。《曲面》と《接点》と《接線ベクトルの方向》を共通にして、曲線の形を様々に変えてある。いずれにしても法曲率 knの大きさは変化していないことに注意されたし。
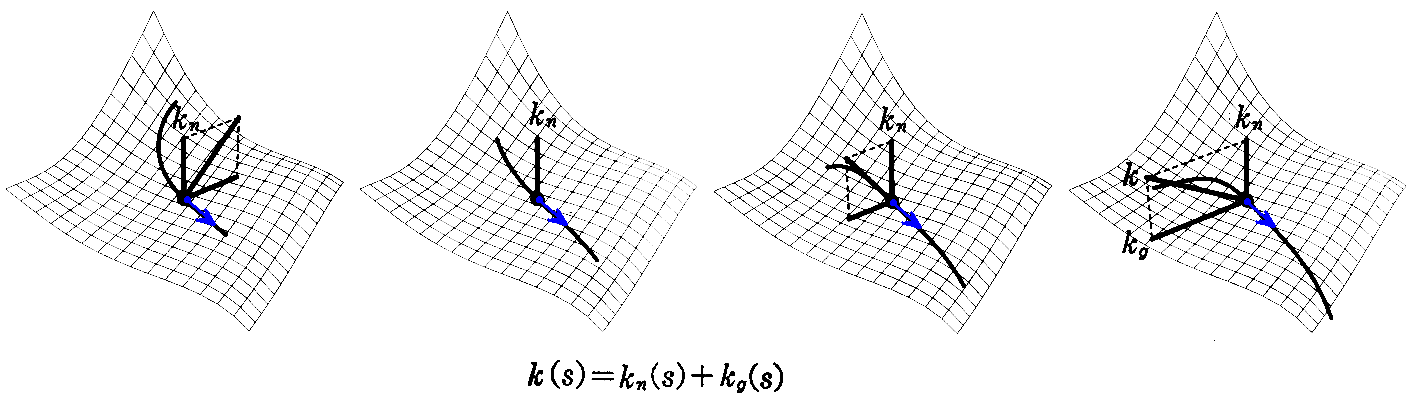
曲面S上の1点における法線を含む平面(“法平面”)による曲面の切り口の曲線C*を“直截(チョクセツ)曲線”という。そしてC*が e の正方向に曲がっているか、負の方向に曲がっているかに従って、直截曲線 C* の“曲率半径”Rに正負の符号をつけて表わすことにする(図2-7)。
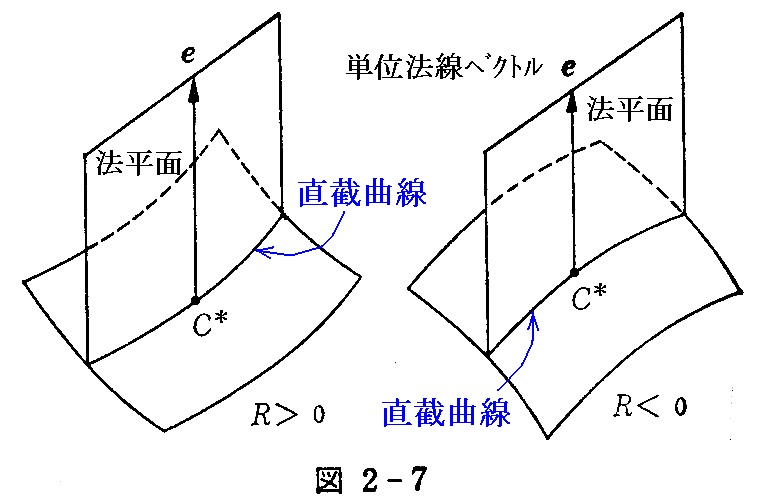
このとき2(2)2.[補足説明]で述べた様に、u曲線、v曲線の取り方とu,vを測るその方向により、単位法線ベクトル e=xu×xv/|xu×xv| は曲面の凸側を向く場合も在れば、凹側に向く場合も在ることに注意されたし。
つけ加えると、直截曲線の“曲率半径”を特にRとおいたのです。つまりRは曲率半径を定める接触平面が直截曲線と e が作る平面(“法平面”)に一致した場合の曲率半径です。
直截曲線においては 法線e と 主法線ξ2 とのなす角 θ は 0 か π であるから(2-27)式の cosθ は +1 か -1 のいずれかです。このことと R の正負の取り方(図2-7を参照)を考慮すると、直截曲線の“法曲率”(2-29)式は
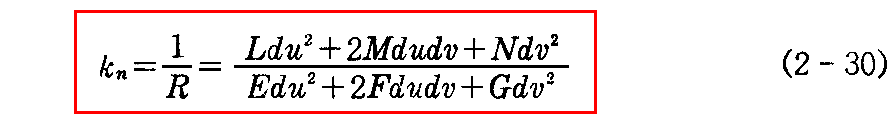
と表される。
ここでは法線の起点に於ける直截曲線 C* の接線方向と元々の曲線Cの接線方向が同じになるような直截曲線を考えている。そのため(2-30)式中のdu:dvは法線の起点に於けるC*あるいはCの接線[両接線ベクトルは一致する]を定める微少径数成分です。
このとき、直截曲線の“曲率半径”Rは、その定義から明らかな様に接触平面が直截曲線と e が作る平面に一致した場合の曲率半径です。そしてまた、同じ接線ベクトルξ1を持つ曲線群は接点に於いて(曲率k(s)は曲線ごとに異なっていても)、すべて同じ法曲率kn(s)を持つのでした。そのため法線 e の起点に於いて同じ接線ベクトルを持つ直截曲線の法曲率kn=1/Rと、元の曲線Cの法曲率kn=kcosθは同じになります。つまり
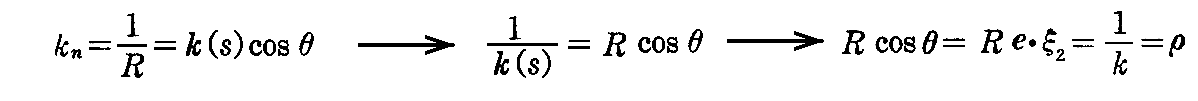
の関係が成り立つ。つまり R は 法線ベクトルe の起点における曲線Cの“法曲率半径”です。
そのため、直截曲線C* の 曲率中心 x+Re [直截曲線C*の接触円の中心]を曲線Cの接触平面に正射影すると x+ρξ2 となるから C の曲率中心に射影される(図2-8)。

空間曲線 C 上の位置x(u,v)における接触円と接触平面については1.(9)を復習されたし。上図2-8は単位法線ベクトル e がたまたま曲面の凸側を向く場合(前項図2-6の場合)を図示している事に注意。
前項に補足として示した図2-6’の様に e が曲面の凹側を向く場合は下図2-8’のようになる。ただし、これは図2-6’をη軸の回りに180度回転して上下を逆さにした状態で示していることに注意されたし。
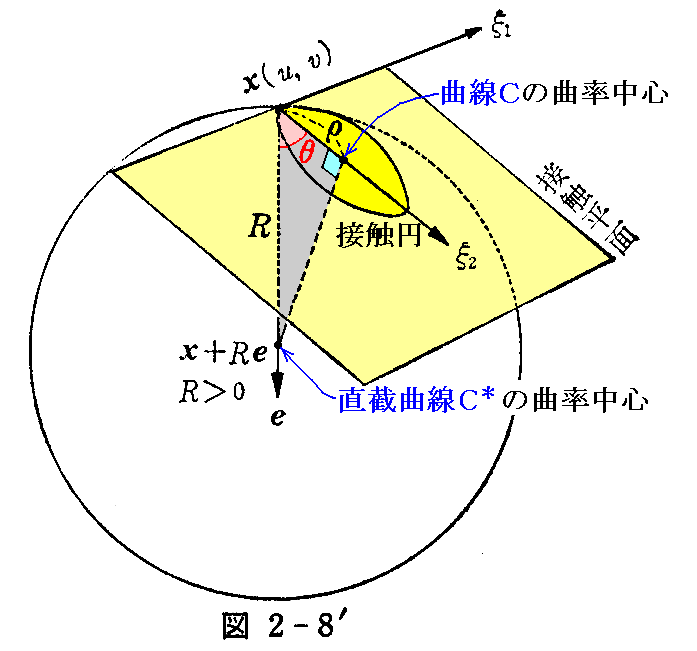
いずれの場合にも、これらの考察から次の定理が得られる。
[定理]
曲面S上の1点Pを通る曲線Cの曲率中心はその点でのCの接線を含む直截曲線の曲率中心のCの接触平面への正射影です。これを“ムーニェ(J.B. Meusnier)の定理”という。
ムーニェの定理は次のようにも言える。
直截曲線C*の曲率中心を中心とした半径|R|の球面と曲線Cの接触平面が交わった切り口が曲線Cの曲率円となる。
(2-30)式より

または

のとき、法曲率knはdu:dvの変化に対して不変です。
(2-31)式なる点を“平坦点”、(2-32)式なる点を“臍(セイ)点”という。臍点とは法線を含むどんな平面で切っても切り口の曲線の点P[法線の起点]での曲率が 0 でない一定値を取る点のことです。
[問題1] いたるところ平坦点(L=M=N=0)であるような曲面は平面であることを証明せよ。
[解] 2.(4)[問題3]ですでに証明した。
[問題2] 球面上の点は臍点である事を証明せよ。
[解] 球の半径をaとすると、2.(4)[問題1](1)の結論より
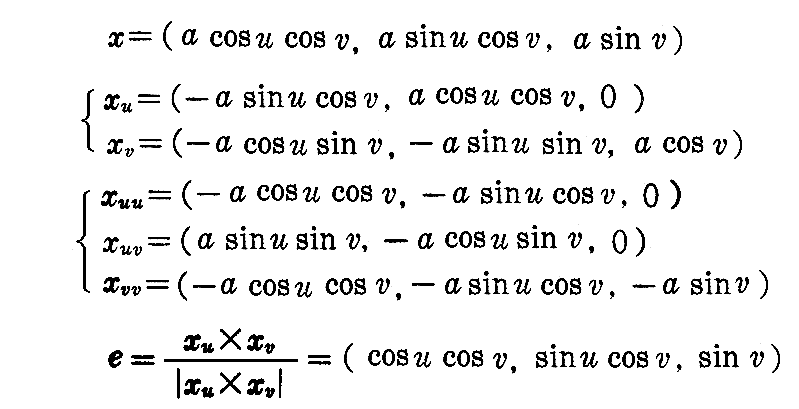
であるから
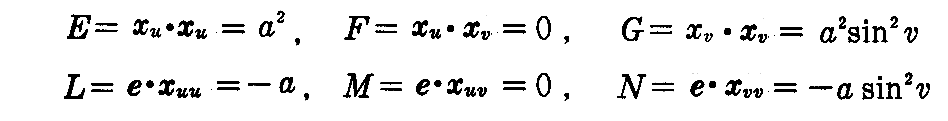
となる。よって
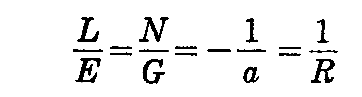
であるから臍点となる。
(6)平均曲率と全曲率
1.主曲率
曲面上の1点x(u,v) における“法曲率”が最大および最小になるような方向を求めてみよう。(2-30)式において dv/du≡λ と置けば
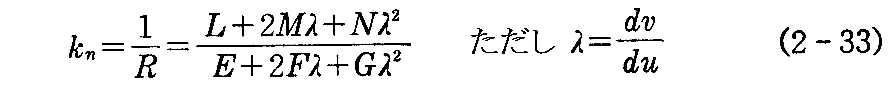
となる。
kn が極値をとるための条件は
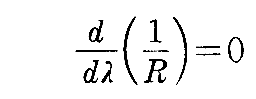
となることです。
(2-33)式を
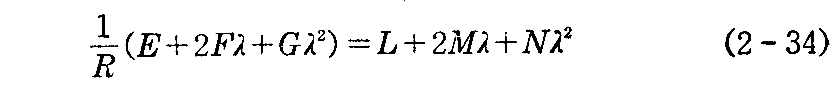
と変形して、両辺をλについて微分すると
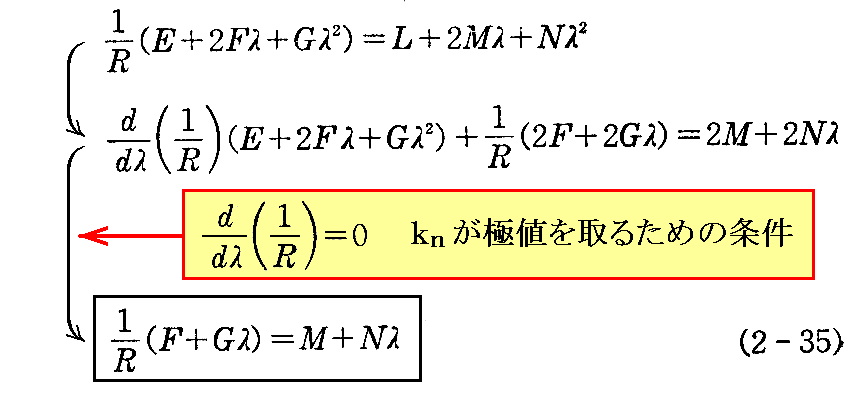
を得る。ここで、(2-35)式にλを乗じて(2-34)式から引くと

を得る。
(2-35)式と(2-36)式から 1/R を消去すると
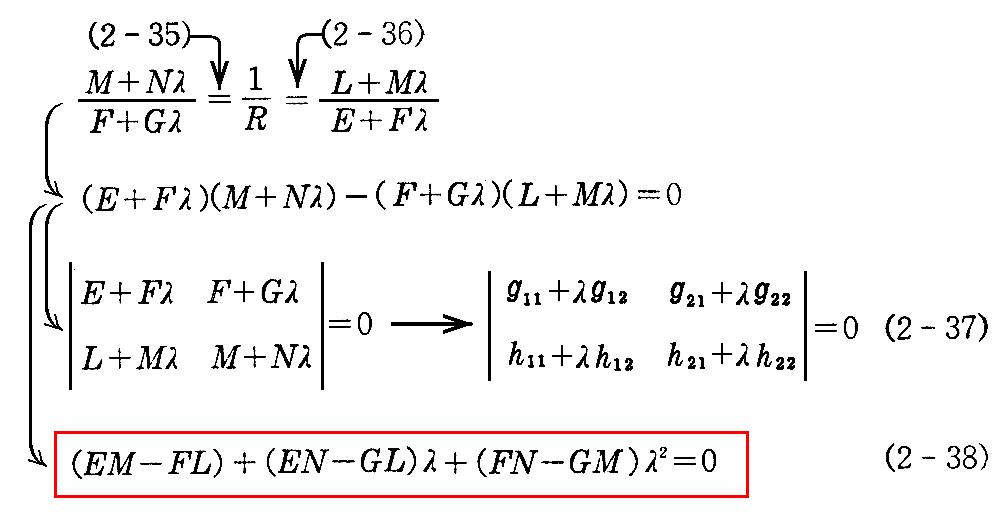
となる。(2-38)式はλについての2次方程式だから2つの根を持つ。その2つの λ=dv/du の方向に対して法曲率 1/R は極値(極大と極小)を取ることになる。
この極値を与える方向を“主曲率方向”(“主方向”)といい、この方向の法曲率を“主曲率”、その逆数を“主曲率半径”という。
曲面上の曲線の各点における接線方向が常に“主曲率方向”であるとき、その曲線を“曲率線”という。
そのため、(2-38)式は曲率線の方向(dv/du)を定める[微分方程式]と見なせる。
[補足説明]
曲率が極大値や極小値を取るような法平面の方向(“主方向”)は、常に垂直である。この事実はレオンハルト・オイラー(Leonhard Euler)が1760年に見つけた。
2.平均曲率と全曲率
次に“主曲率”求めてみよう。それは(2-35)式と(2-36)式からλを消去した方程式
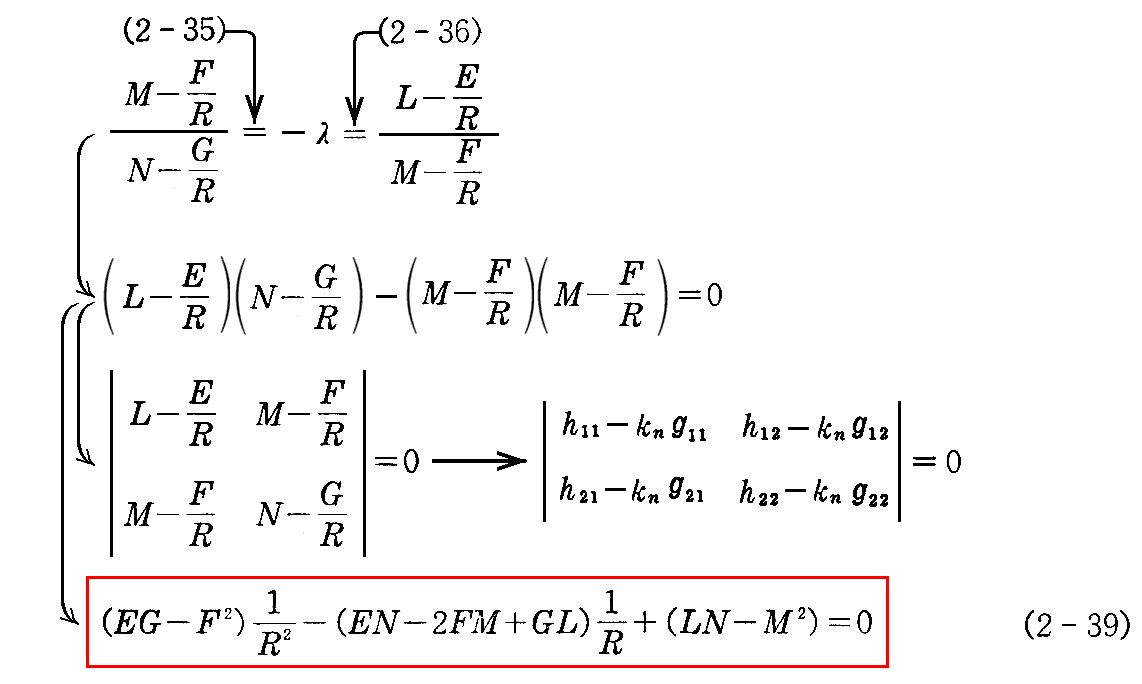
の2根として与えられる。それを 1/R1 と 1/R2 とすれば、2次方程式の根と係数の関係から

が得られる。
上記のHを“平均曲率”または“ジェルマン(Sophie Germain)曲率”、Kを“全曲率”または“ガウス(C.F. Gauss)曲率”という。

ここで“ガウスの全曲率”K は1760年にEulerが導入した“主曲率” 1/R1 と 1/R2 の積と一致し、“平均曲率”は“主曲率”の平均値であることに注意されたし。上式後半の添字記法を用いた表現については2.(7)で説明する。
考えている点が平坦点や臍点の場合でも、任意の接線方向を主曲率方向と考えることにすれば(2-38)式や(2-39)式が成り立ちます。そして上式もそのまま成り立ちます。
曲面x=x(u,v)上の各点に対して
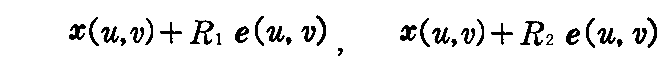
を、この点での曲面の“主曲率中心”という。ただし R1 と R2 の正負については次の[補足説明1]を参照。
さらに、点x(u,v)が平坦点でも臍点でもないとき、2つの“主曲率方向”は直交し、互いに共役です。この事は[問題1]で証明します。
[補足説明1]
[曲面の形状]と[径数曲線の取り方]により、R1 と R2 は正の場合も負の場合もあります。そして径数曲線の取り方を変えて法線ベクトルが逆転すると、R1 と R2 の正負はどちらも反転します(2.(2)2.[補足説明]を参照)。
そのとき、R1 と R2 の和に関係する平均曲率の符号は反転しますが、R1 と R2 の積に関係する全曲率(ガウス曲率)の符号は同じままです。
[補足説明2]
臍点の定義から明らかなように、曲面上のある点が“臍点”である必要十分条件は、その点で2つの主曲率が一致することです。つまり、2次方程式(2-39)式の解が重根(解の判別式がD=0)となることです。これは
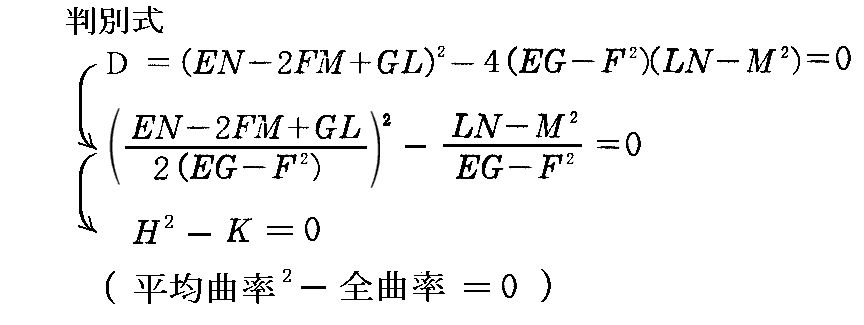
であることと同値です。
3.オイラー(L. Euler)の定理
[オイラーの定理]
曲面上の各点を通る曲率線は一般に2つあって互いに直交し、共役な接線方向をもつ。従って曲率線が径数曲線であるときは、F=M=0[[問題3]で証明]で、任意の方向du:dv と u曲線のなす角を φ とすると、du:dv 方向の直截曲線の“曲率半径” R[つまりdu:dv方向の法曲率半径]と2つの“主曲率半径”R1、R2 の間には関係式

が成り立つ。これは1760年にオイラーにより証明されたので、“オイラー(L. Euler)の定理”と言われる。この定理に関しては別ページの補足引用1と補足引用2もご覧下さい。
[証明]
径数曲線が曲率線であるときは、[問題3]により F=M=0 です。そのため、接線が任意の du:dv 方向を向く直截線の“法曲率”は2.(5)3.の(2-30)式により
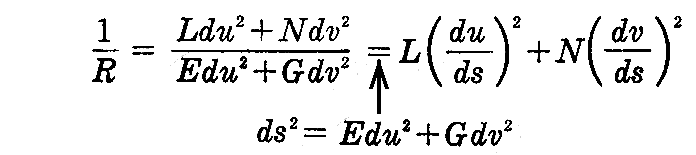
となる。
また、曲率線の法曲率を2根とする2次方程式(2-39)式は(F=M=0だから)
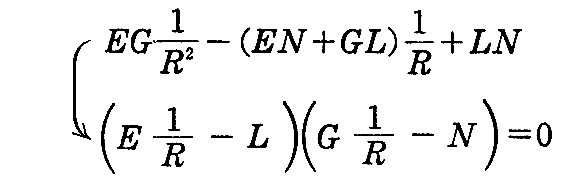
となる。それを因数分解して解いて得られる2根は
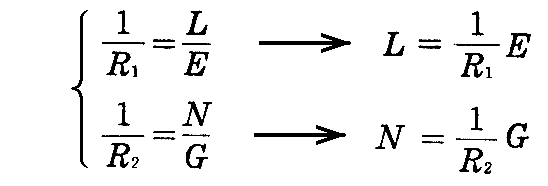
となるので、これらを最初の式に代入すると
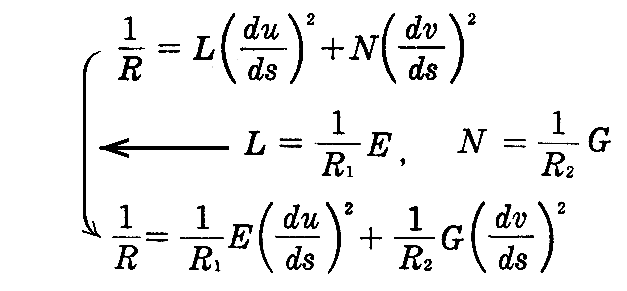
となる。
ところで、方向 du:dv が u曲線となす角を φ とすれば2.(2)3.の(2-11)式により
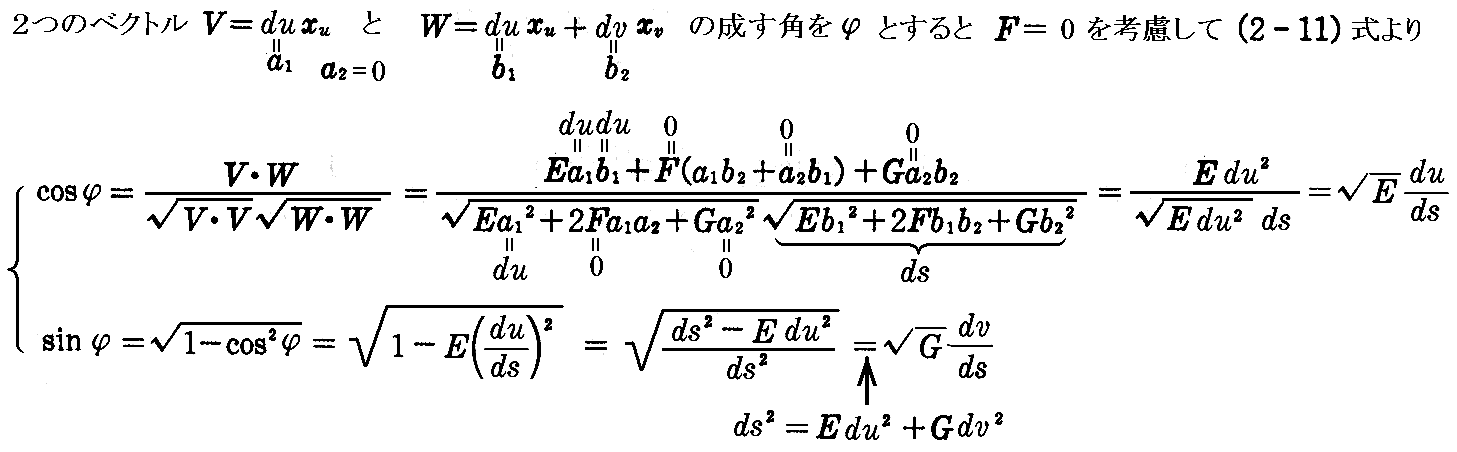
となるので、これを上式に代入すれば
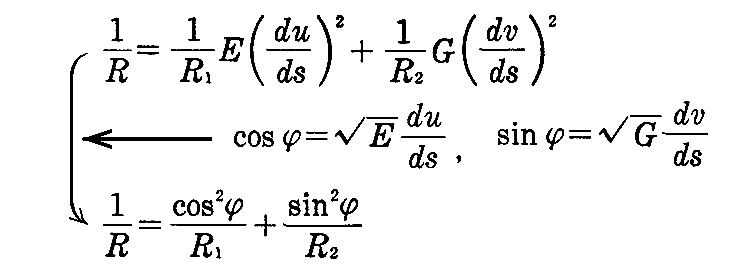
が得られる。
[証明終わり]
[補足説明1]
オイラーの定理の公式は
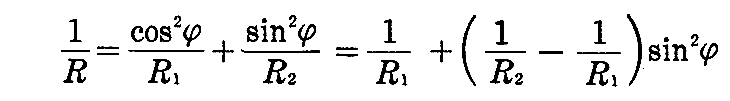
の様に変形できる。
ここで、2つの主曲率の大小関係を仮に
として sin2φ のグラフの形を考慮すると、du:dv 方向の曲率(1/R)が両極値(主曲率)の間に収まっている
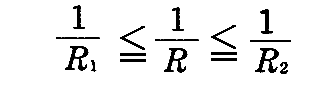
ことが解る。そして φ=0 又は φ=π/2 のときに、主曲率に一致する。
[補足説明2]
ここで説明した“オイラー(L. Euler)の定理”は、2.(5)3.で説明した“ムーニェ(J.B. Meusnier)の定理”と共に曲面上の曲線の“曲率”に関して完全な情報を提供する。
すなわち、上記の曲率半径R から定まる
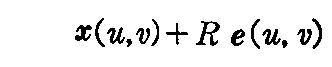
が点x=x(u,v)に於ける du:dv 方向の直截線の曲率中心を与え、それは2.(6)2.で説明した2つの主曲率中心
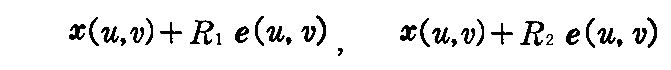
の間に存在する。
[例題] 2.(2)[問題3]で論じたを“輪環面”(ドーナッ状の曲面)
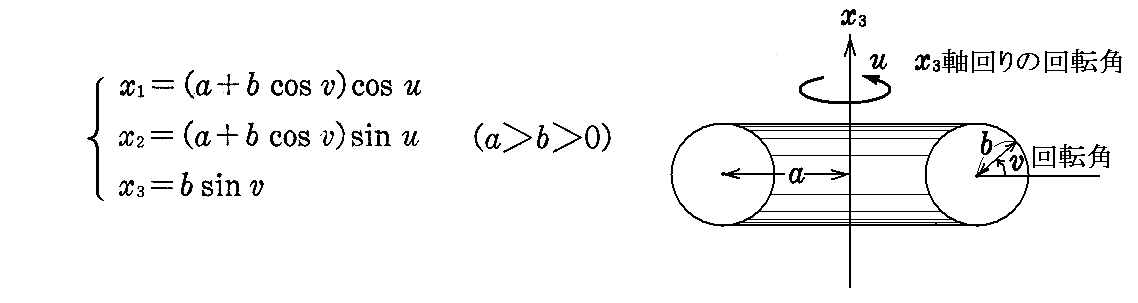
の全曲率(ガウス曲率)はその軸よりの距離がaより大ならば正、aに等しければ0、aより小ならば負であることを示せ。
[解]
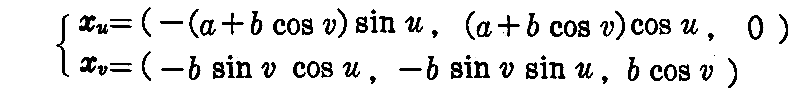
であるから、(2-9)式によって
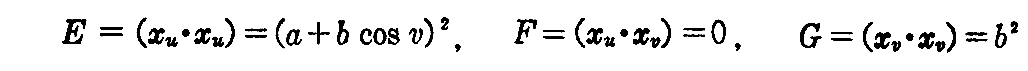
となる。次に(2-8)式によって
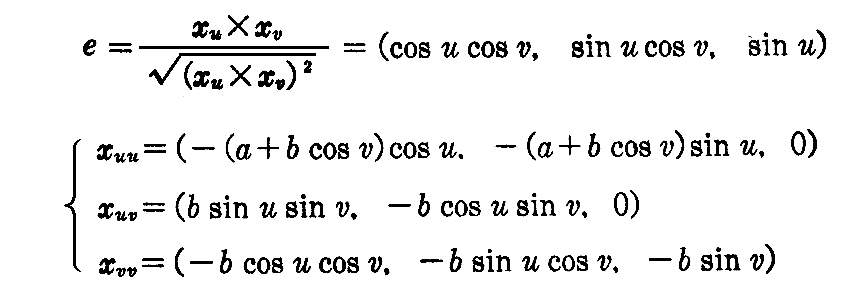
であるから

となる。従って
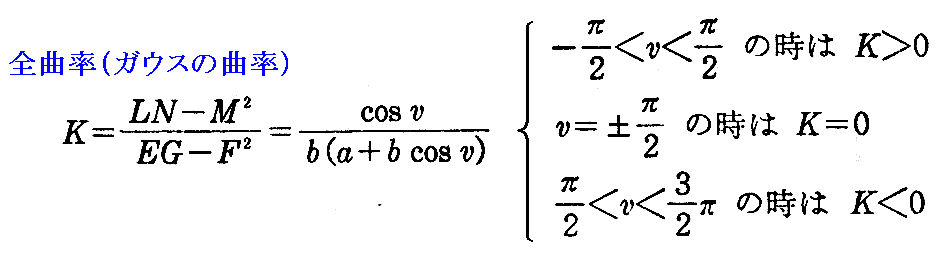
が言える。
[問題1] 曲面S上の各点に於ける2つの主曲率方向は直交し、互いに共役であることを示せ。
[証明]
まず、2つの 主曲率方向のベクトル dx1=xudu1+xvdv1 と dx2=xudu2+xvdv2 が直交することを示す。そのためには、その内積
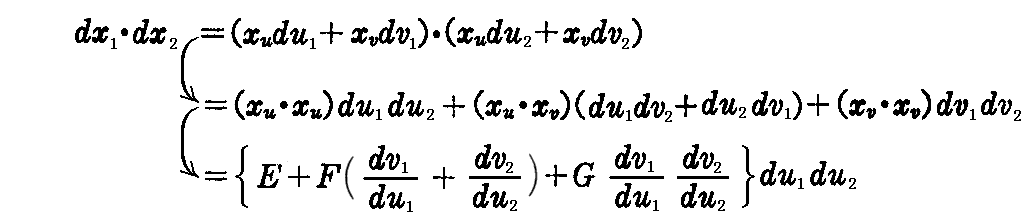
が 0 であることを示せばよい。

これらの式を前記の式に代入すると
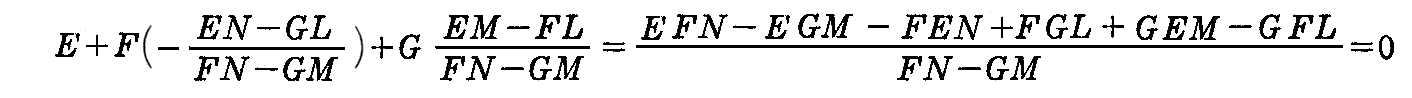
となる。確かに dx1・dx2=0 となるので、2つの主曲率方向は直交する。
次に、たがいに共役であることを示すためには、2.(4)2.[補足説明2]で述べたように、1つの主曲率方向ベクトル dx1=xudu1+xvdv1 ともう一つの方向の de=eudu2+evdv2 が直交することを示せばよい。すなわち、その内積
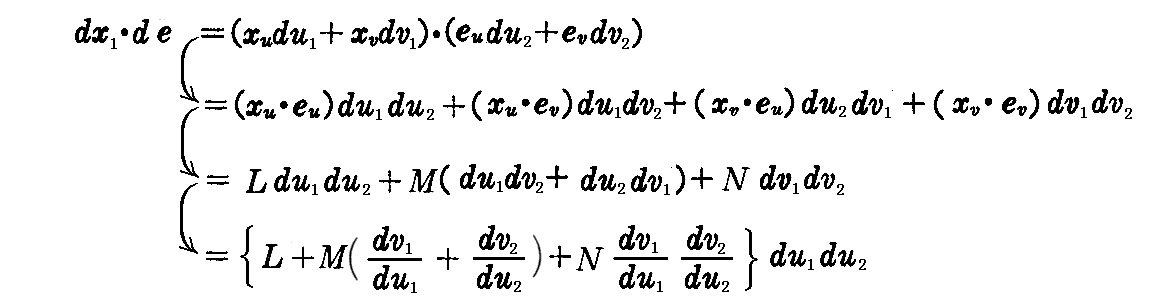
が0であることを示せばよい。

これらの式を上記の式に代入すると
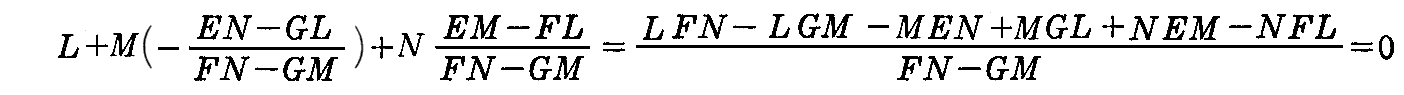
となる。確かに dx1・de=0 となるので、2つの主曲率方向は互いに共役です。
[証明終わり]
[問題2] 半径aの球面は定曲率曲面で、その平均曲率はH=-1/a、全曲率はK=1/a2であることを示せ。
[解] 2.(5)[問題2]の結論から
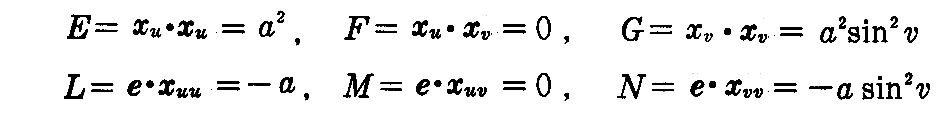
です。よってその平均曲率Hと全曲率Kは
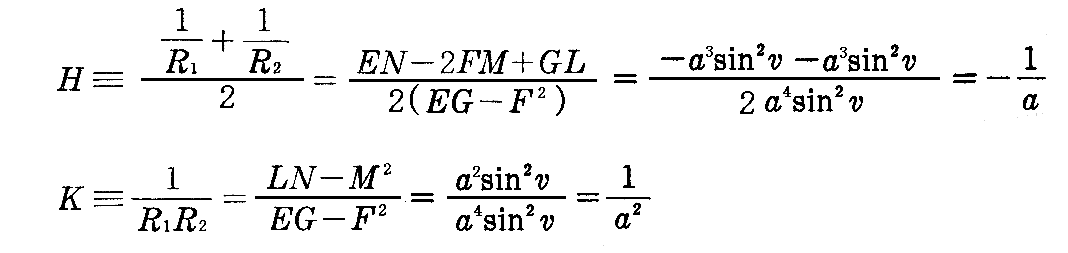
となる。これらは径数u,vに依存しないので球面が定曲率曲面であることを示している。
もちろん、これらは2.(6)2.[補足説明2]で説明したH2-K=0を満たしている。
[問題3] 至るところ臍(セイ)点でない曲面において、曲率線が径数曲線であれば、F=M=0であることを示せ。
[証明]
曲率線が径数曲線であると言うことは径数線(u曲線とv曲線)が主曲率方向であることを意味する。そのため du=0,dv≠0 および dv=0,du≠0 が主曲率方向を定める微分方程式(2-38)

の解である事を意味する。
つまりこの微分方程式(2-38)に du=0,dv≠0 を代入した式
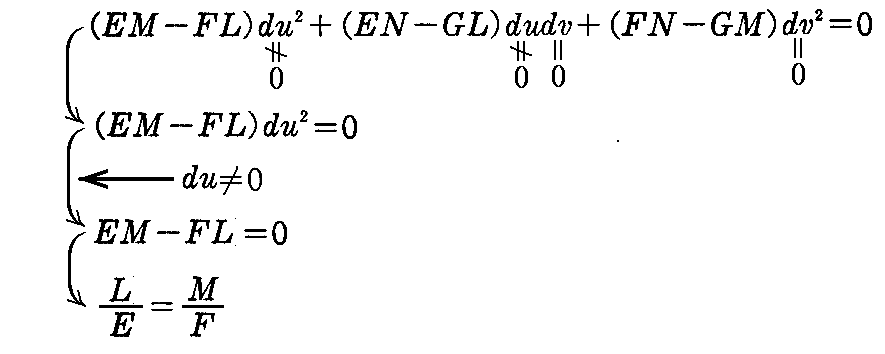
と、dv=0,du≠0 を代入した式
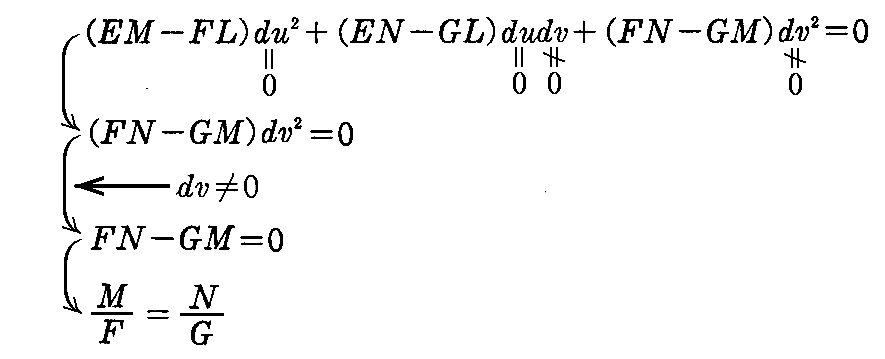
の両方が満足されねばならない。
このとき、もし F≠0 ならば
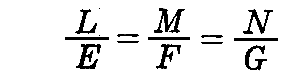
となり、曲面が至るところ臍(セイ)点でないという条件に反するのでF=0で無ければならない。
F=0が成り立つとき、1.(1)8.の“コーシー・シュワルツの不等式”により
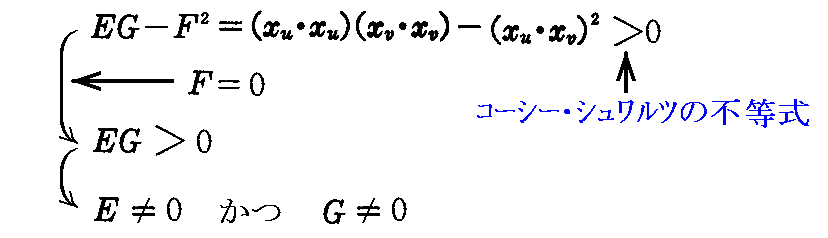
が言える。
そのため、EM-FL=0あるいはFN-GM=0のどちらからでもM=0でなければならないことが言える。すなわち、曲率線が径数曲線であれば、F=M=0となる。
[証明終わり]
[補足説明]
曲率線は主曲率方向を向いている。そのとき主曲率方向が径数曲線と一致すると仮定しているのだから、[問題1]の結論を用いるとu曲線とv曲線も直交することになる。つまりベクトルxuとベクトルxvは直交する。故にF=xu・xv=0となることが言える。これを用いれば、“コーシー・シュワルツの不等式”による後半の手順は同様に展開できる。
(7)添字記法
1.第1基本量と第1基本形式
曲面x=x(u,v)の径数 u,v を u=u1,v=u2 と置いて曲面の方程式を x=x(u1,u2) で表わせば便利なことが多い。このとき u1,u2 などをuの1乗、2乗などと混同しないように注意する必要がある。
ここで
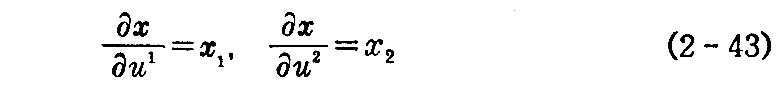
と置けば、2.(2)1.の接線ベクトル(2-6)式は
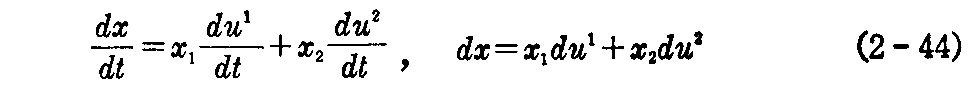
となるから、2.(2)3.で説明した曲面の第1基本形式(2-10)式は
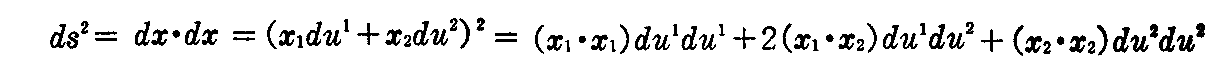
と表わすことができる。そこで第1基本量 E,F,G を

と置けば、第1基本形式は

と表せる。
ここで、a,b,c,・・・とかi,j,k,・・・などを添字として用いた場合には1,2なる値をとるものとすれば、(2-43)、(2-44)、(2-45)、(2-46)式などは

と表せる。ここで第1式は i を1,2とした場合の2個の式を表し、第3式は i,j をそれぞれ1,2とした場合の4個の式を表わす。第2式は i
についての総和を、第4式は i,j についての総和を表わす添字です。
ここで右上に記した数字は異なる成分を表し、右下に記した数字はその数字に関係する成分の何らかの偏微分成分を表すと考えて下さい。
さらに同一項内に同じ添字が上と下に同時に表れるとき(例えば第2式では xi は下に、dui は上に添字 i が表れている)には、その文字についての総和を表わすものと約束することにする。これを“アインシュタインの規約”と言う。
そうすれば和記号Σが省略できて、第2式や第4式は

と表される事になる。
この規約は様々な計算を進めるときにとても役に立つことが、やがてお解りになると思います。
第1基本量の行列表現を
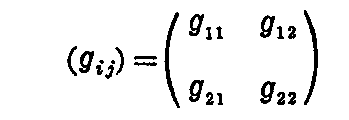
とすると、(gij)は gij=gji を満たす対称行列となる。
(gij)の行列式を
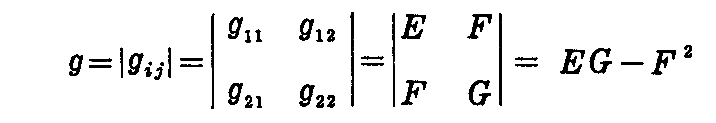
だから、(gij)の逆行列 (gij)-1≡(gij) は、(gij)の i,j要素の余因子を Gij で表して
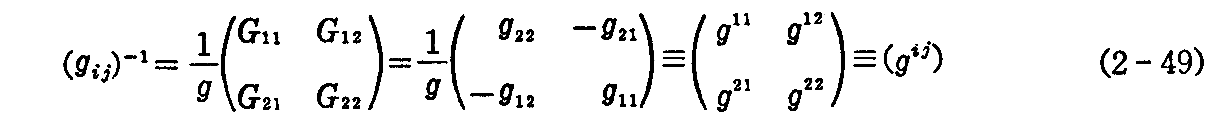
で与えられる。この逆行列も gij=gji を満たす対称行列です。
[ここは 別稿「余因子行列と逆行列の関係」 あるいは 別稿「行列式と行列]2.(3) を復習されたし。]
逆行列(gij)-1≡(gij)と行列(gij)の積は
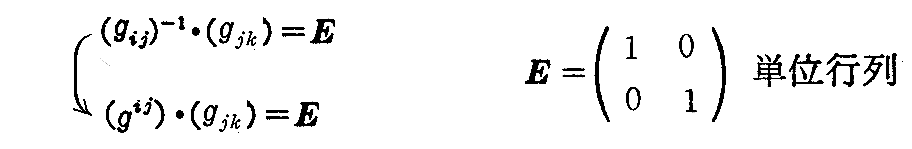
であるから
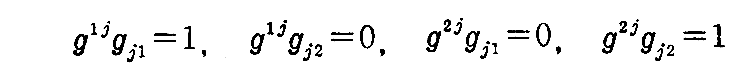
すなわち
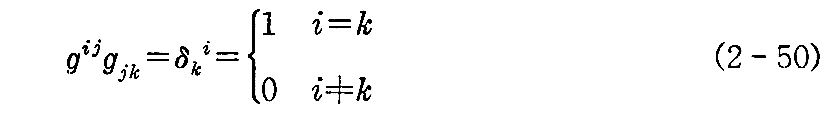
なる関係があることが解る。ここで δki を“クロネッカーのデルタ”という。
[補足説明]
逆行列(gij)-1≡(gij)と行列(gij)の積を様々な形で表してみる。
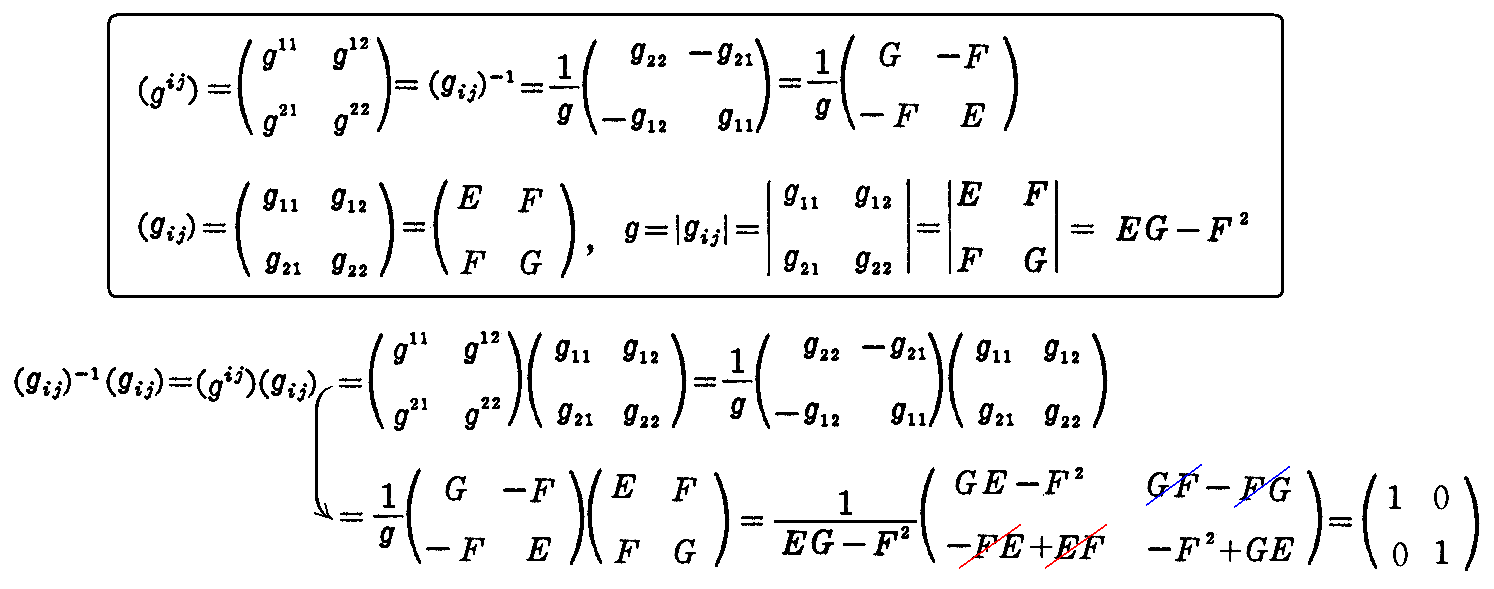
2.第2基本量と第2基本形式
第2基本量と第2基本形式に添字記法を適用すると

と表わすことができる。
[問題1] 2.(2)3.の(2-13)式を添字記号で表わせ。
[解]
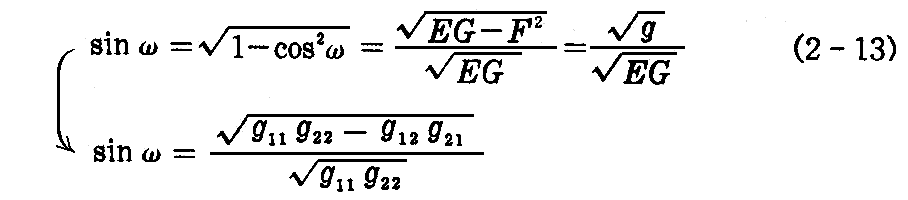
[問題2] gijgji=2 を証明せよ。
[解]
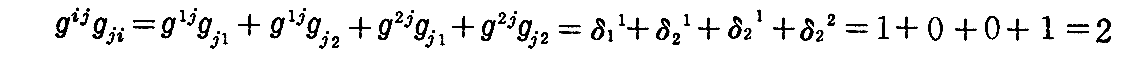
[問題3] 曲面の方程式がz=f(x,y)で与えられているとき
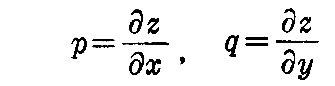
として
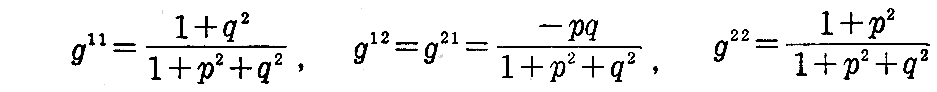
を証明せよ。
[解] 2.(2)[問題2]に倣って、x=u,y=vとおけばz=f(u,v)となる。dx=du,dy=dvだから、2.(2)3.の(2-9)式と(2-10)式より
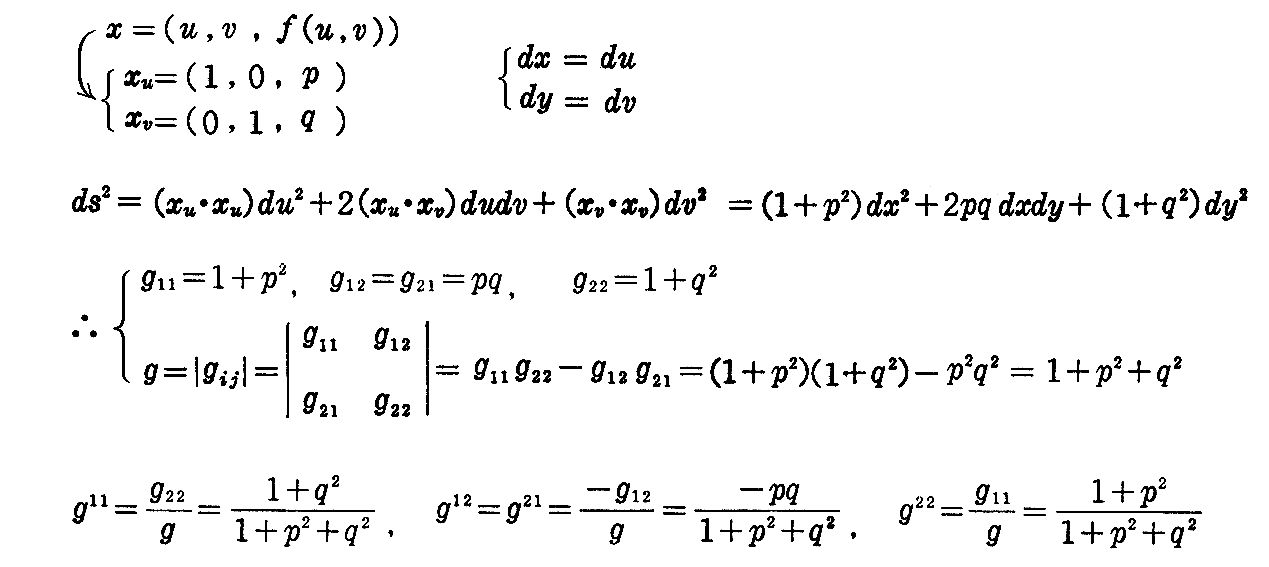
(8)ガウスの方程式とワインガルテンの方程式
1.ガウスの標構
2.(2)2.で説明した様に、曲面x=x(u,v)上の1点に於ける単位法線ベクトル e と、その点に於けるuj方向の接線ベクトル
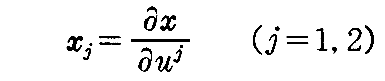
は、この曲面上の点に起点を持つ1次独立なベクトルです。これらのベクトルと、点を規定する位置ベクトルx(u1,u2)を合わせた4つのベクトルの組 x(u1,u2)x1x2e を曲面の“ガウス標構”という。
これは1.(7)2.で説明した空間曲線の“フルネ標構”を曲面に対応させたものです。そのとき、曲面上の任意のベクトルは、ガウス標構 x1,x2,e の1次結合で表される。
2.クリストッフェルの記号
最初に、曲面を表す位置ベクトル x(u1,u2)のuiとujによる二階の偏微分ベクトル
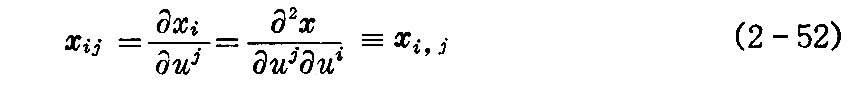
を、ガウス標構 e,x1,x2の1次結合で表すことを考える。
それが下記の様に表現できるとして、係数 Γijk,Γij がどの様なものか決定する。

各係数は、その意味から考えて i,j,k に関係するだろうと言うことで、 Γijk,Γij の様に添字を付けた記号にしてあるのですが、その詳細はまだ解りません。以下でその意味を決定します。
まず、(2-52)式から解るように xi,j=xj,i ですから
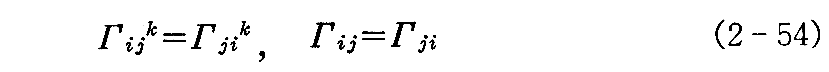
なる関係がある。すなわち添字 i , j について対称的です。
最初に係数 Γijk を調べる。
(2-8)式と(2-9)式から
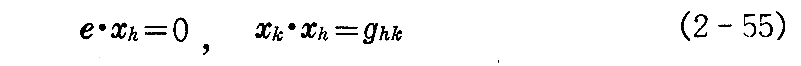
であるので、(2-52)のベクトル xi,j と ベクトル xk[(2-2)式参照] の内積を作ると
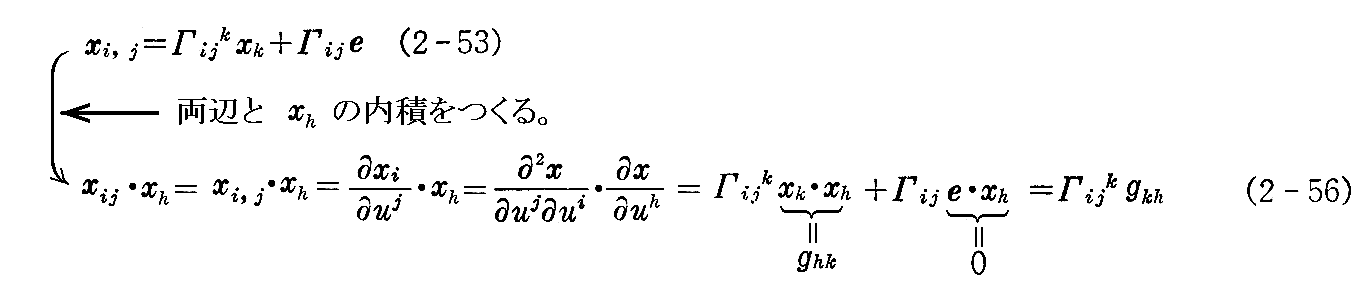
を得る。
(2-55)式の第2式を uj について微分して、再び(2-56)式を用いれば
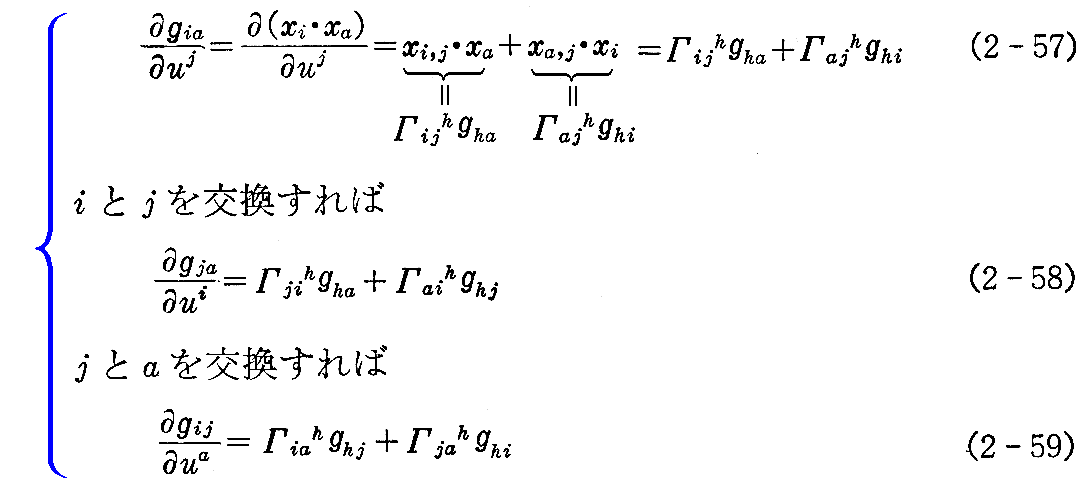
を得る。
ここで、(2-57)+(2-58)-(2-59)式をつくり、(2-54)式を用いると
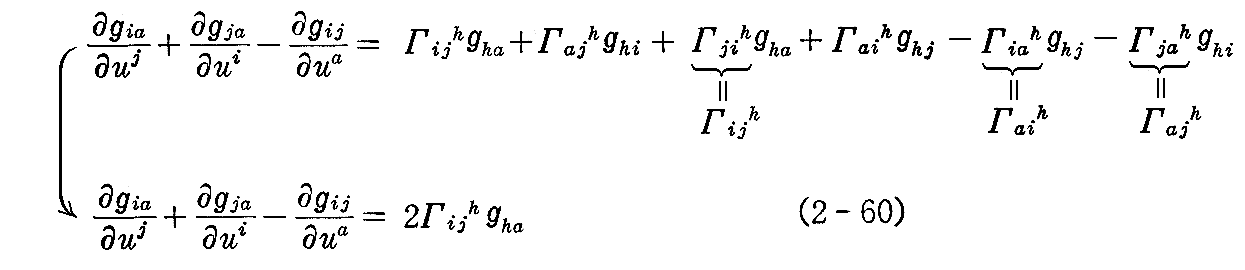
が得られる。この両辺にgkaを乗じて a について総和を取り、(2-50)式を用いると
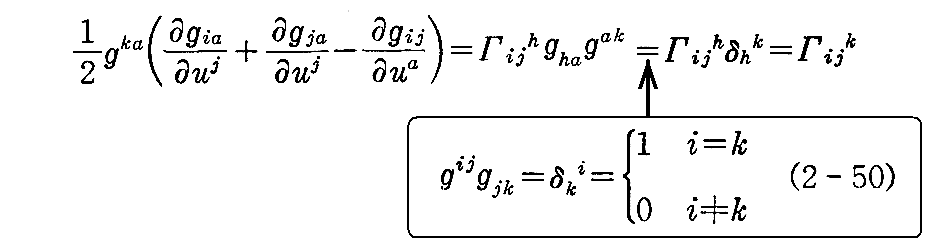
となる。
したがって、 ベクトル xi,j をガウス標構で表したときの xk の係数Γijk は gij と gij の1次の偏微分だけで表わされることが解る。つまり、(2-53)式の xk の係数 Γijk は第1基本量によって表される。
[定義]
これらを特に
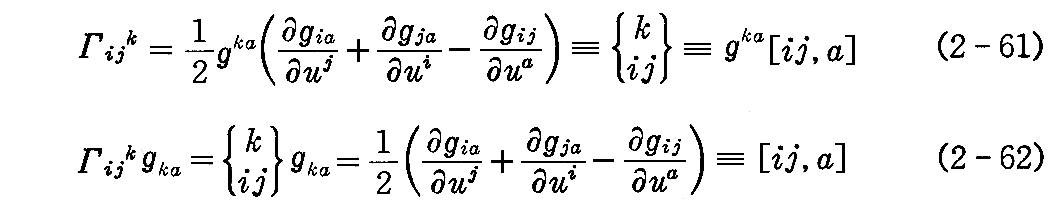
で表し、これを“クリストッフェル(Christoffel)の三添字記号”と言う。
(第1種の[ij,a]=Γija を、 Γij,a あるいは [a,ij]=Γa,ij と書く場合もあります。)
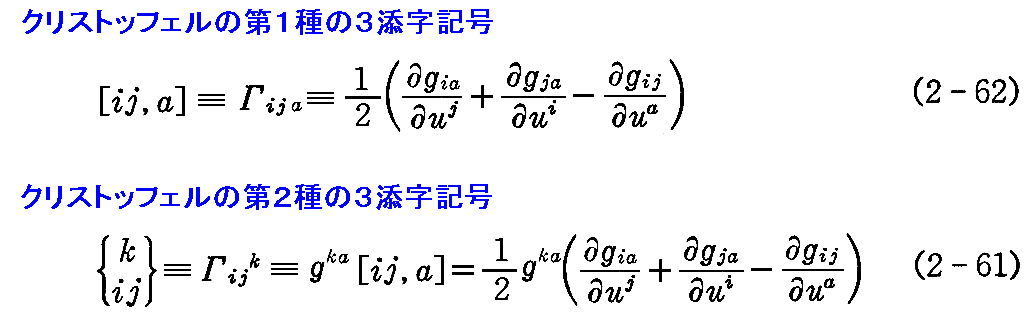
これは1868年にクリストッフェルによって導入された記号ですが、曲面論で重要です。もちろん4次元のリーマン空間(時空)を扱う一般相対性理論でも重要です。この記号の表記法については別稿6.(2)[補足説明1]を参照されたし。
ここの導入法はかなり錯綜していて解りにくいかも知れません。別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分(計量テンソル・クリストッフェル記号・共変微分とは何か)」4.(4)で説明している3次元リーマン空間の場合も参照されたし。
3.ガウスの方程式
次に(2-53)式の e の係数 Γij について調べる。
(2-53)式と e の内積を作り(2-55)式の第1式と(2-51)式を適用すると
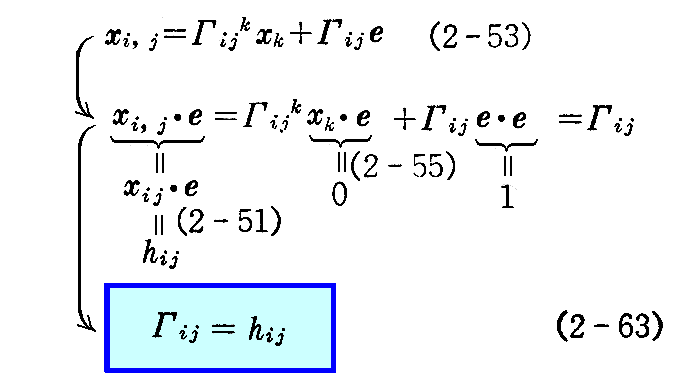
が得られる。つまり(2-53)式の e の係数 Γij は第2基本量によって表される。
結局、(2-53)式は(2-61)式、(2-63)式を用いると

となる。これを“ガウス(Gauss)の方程式”と言う。曲面論での重要な公式です。
[補足説明] 普通の記号に直すと
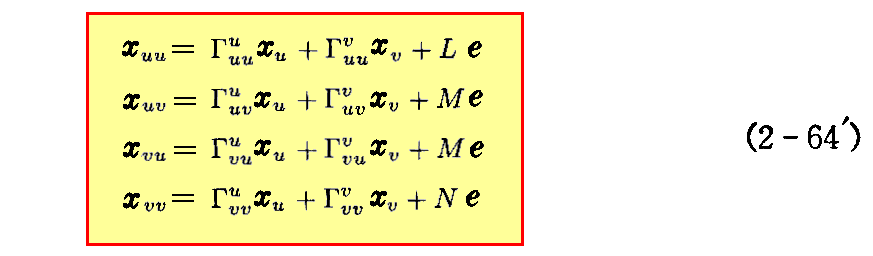
となる。([問題3]参照)
4.ワインガルテンの方程式
次に、単位法線ベクトル e の ui に関する微分 ei をガウス標構で表すことを考える。。
まず、
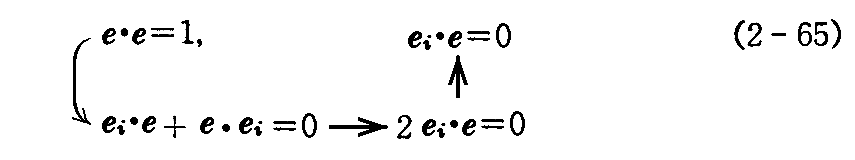
であるから、e と ei は垂直。
したがってei は xi の一次結合

で表される。この係数 Γih を以下で求める。
(2-66)式と xk の内積をつくり(2-47)式と(2-51)式を適用すれば
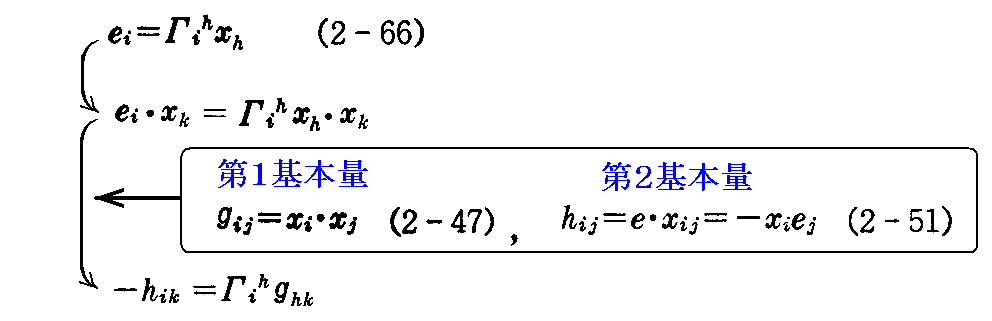
を得る。
両辺に gkj をかけ k について総和を取れば、(2-50)式が成り立つので
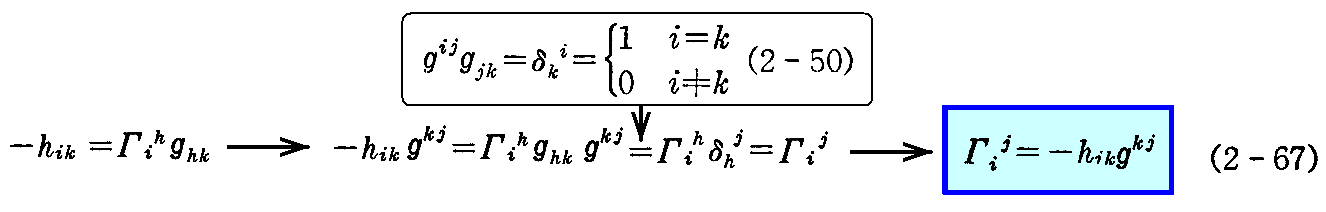
となる。:
結局(2-66)式は

となる。これを“ワインガルテン(L.G.J.J. Weingarten)の方程式”という。
[補足説明] 普通の記号に直すと
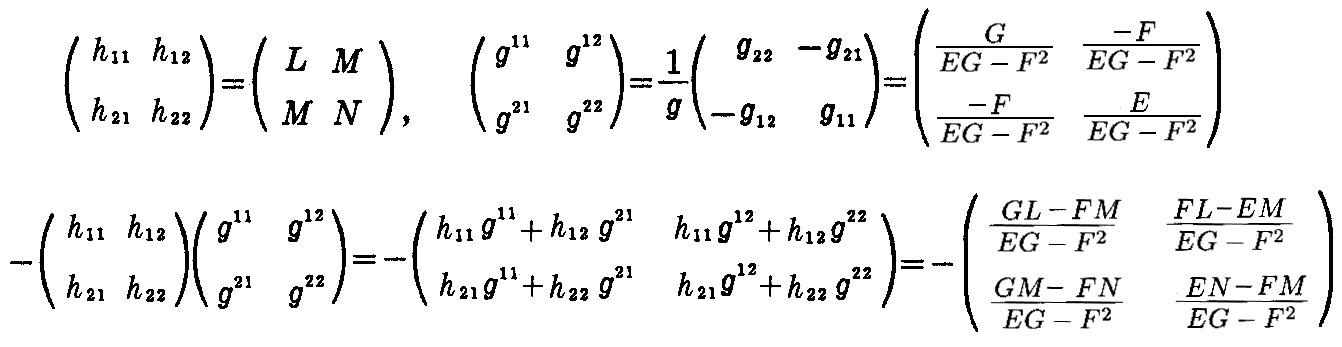
だから
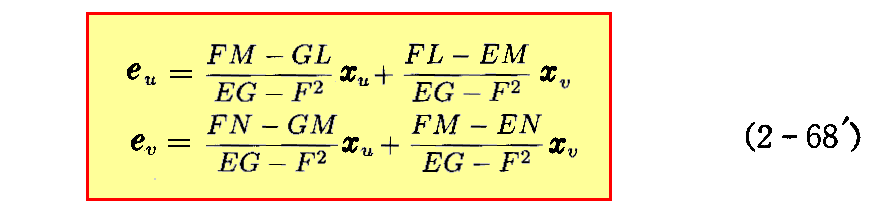
となる。([問題4]参照)
5.ガウス標構の公式
(2-47)の第1式、(2-64)式、(2-68)式をまとめると

が得られる。これは曲面の“ガウス標構”x(u1,u2)x1x2e が径数u1,u2の変化と共にどの様に変化するかを表す“重要な公式”です。
これは、1(7)3.で説明した曲線の“フルネ・セレーの公式”を曲面に拡張したものです。ただし、以下のことに注意しなければならない。
1.(11)で論じたように、曲線論ではフルネ・セレーの公式が完全な方程式を構成していた。それはフルネ標構が曲線に沿ってのただ1つの変数のみに関係していたので、フルネ・セレー公式を x,ξ1,ξ2,ξ3に関する連立の常微分方程式 と見なして解くとき、その中の2の係数曲率k(s)と捩率w(s)を全く独立な量として取り扱えたからです。
ところが、曲面論ではガウス標構が2つの径数u1,u2に関係しているので、(2-69)式を未知関数x,x1,x2,eの連立偏微分方程式とみなして解くとき、方程式中の係数第1基本量gijと第2基本量hijを互いに独立な係数と見なすことができません。そのため、第1基本量gijと第2基本量hijが満たすべき条件式をもう少し調べてみる必要があります。
それを次節で行います。
[例題] 次の式を示せ。
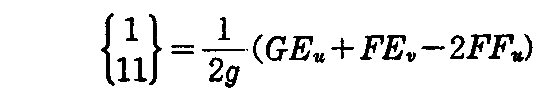
[解] (2-61)式においてi=j=k=1とおいて、aについて総和とれば
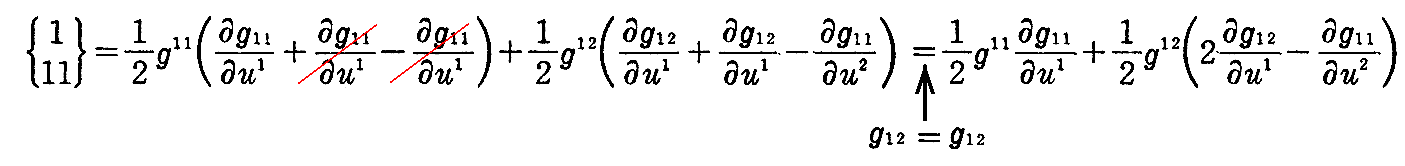
ここで、(2-49)式から
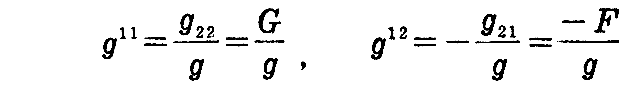
であるから
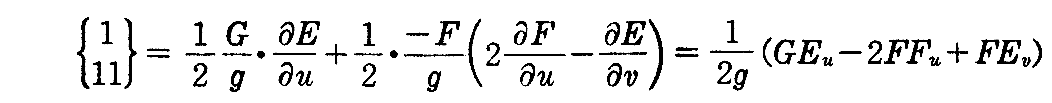
となる。
[問題1] クリストッフェルの記号は次式で表されることを証明せよ。
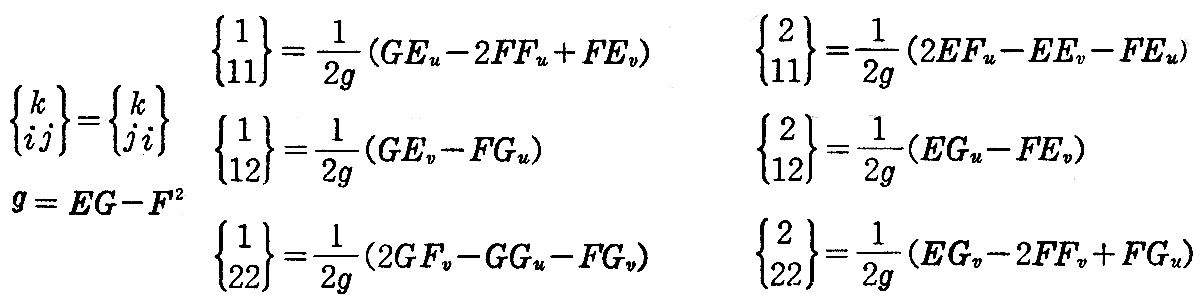

[解] [例題]と同様な手順で証明すればよい。
[問題2] 曲面が z=f(x,y) で与えられているとき、

とすると、クリストッフェルの記号は
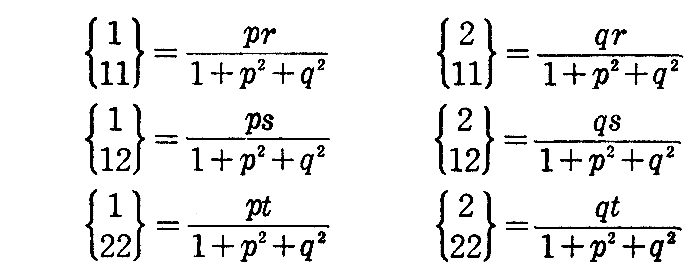
で与えられることを示せ。
[解] 2.(2)[問題2]に倣って、x=u,y=vとおけばz=f(u,v)となる。dx=du,dy=dvだから、(2-9)式と(2-10)式より
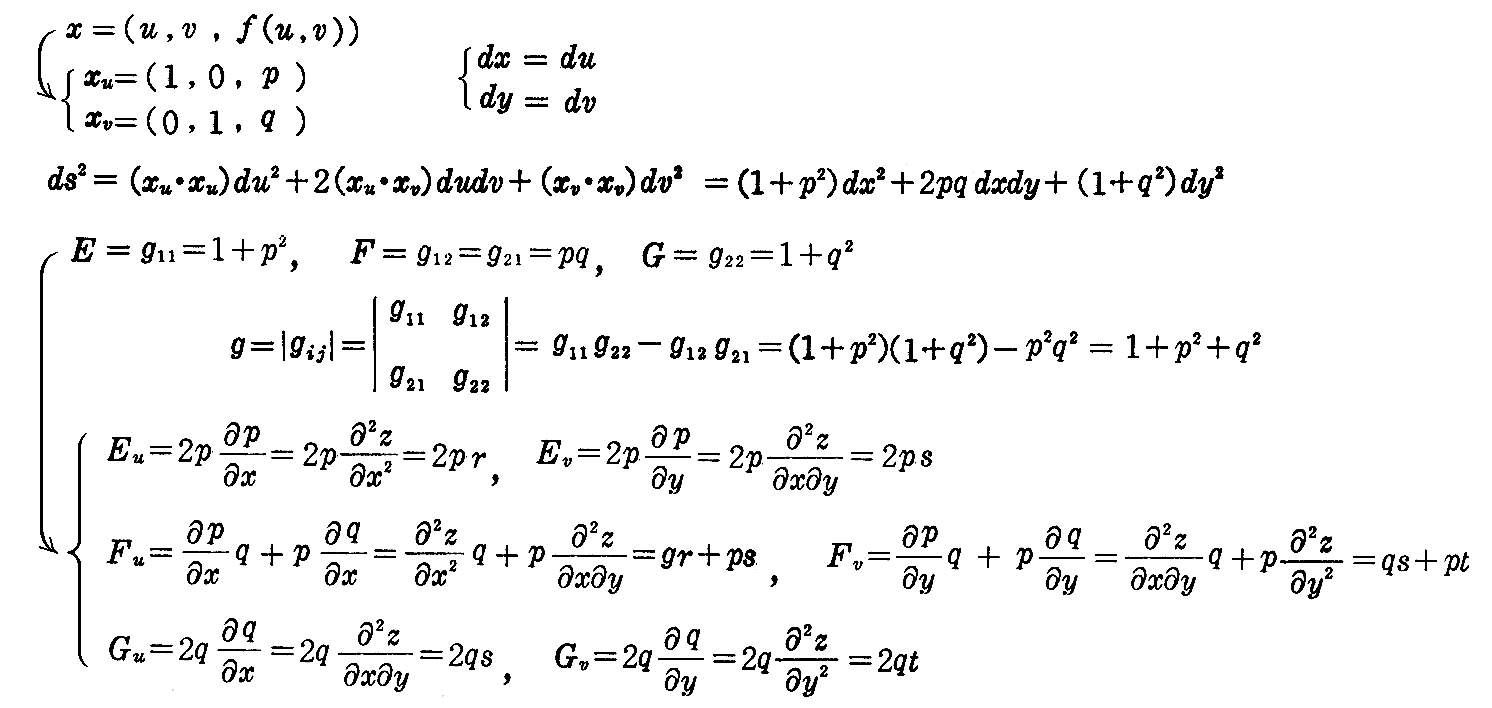
となる(2.(7)[問題3]参照)。
これを[問題1]の結論に代入すればよい。
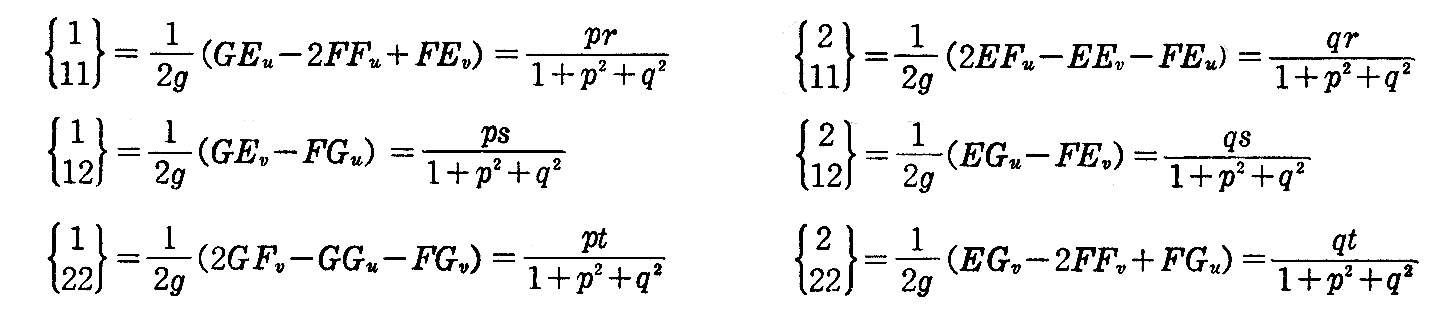
が得られる。
[問題3] “ガウスの方程式”(2-64)式を普通の記号に直して表せ。
[解] 2.(4)1.の(2-20)式

と、[問題1]の結果を(2-64)式に代入すると
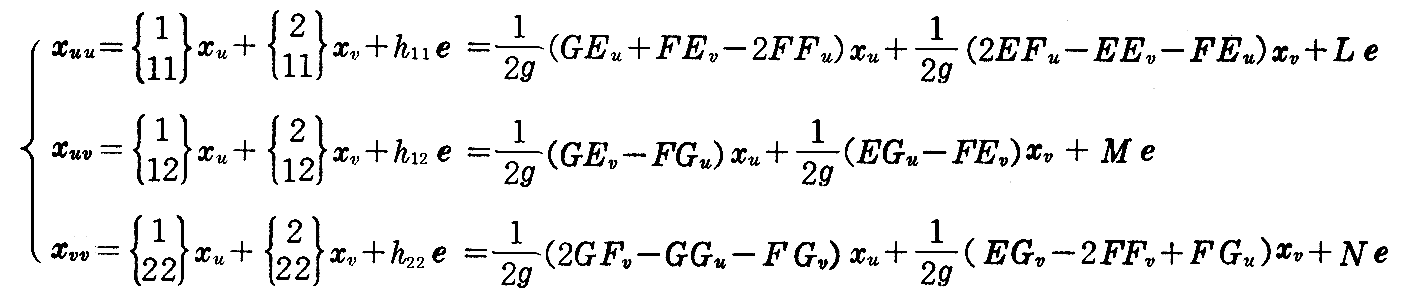
が得られる。
[問題4] “ワインガルテンの方程式”(2-68)式を普通の記号に直して表せ。
[解] 2.(7)1.の(2-49)式と2.(4)1.の(2-20)式を(2-68)式に代入すると
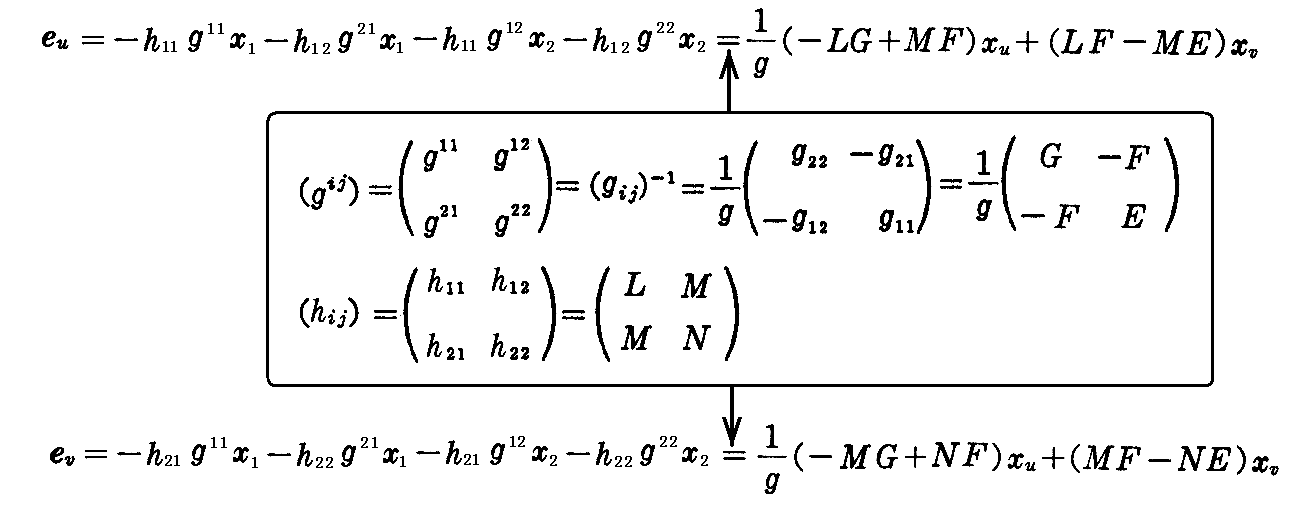
が得られる。
(9)積分可能条件とガウスの“驚異の定理”
1.ガウスの積分可能条件とコダッツィの積分可能条件
前節の最後で述べたように第1基本量gij と第2基本量hij はどちらも2つの径数u1,u2に関係しているので、お互いに独立ではありません。そのためこれらの係数間には何らかの関係があるはずです。
ところで、(2-69)の(1)(2)(3)式を x(u1,u2),x1,x2,e についての連立の偏微分方程式と見なしたとき、これらが解ける為には
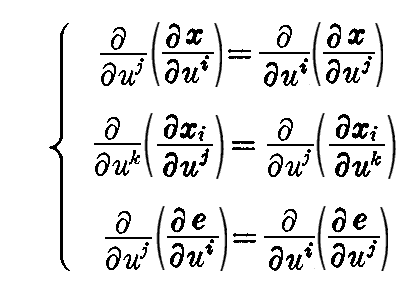
を満足しなければなりません(例えばこちら、あるいはこちらを参照)。
これらの条件式が満足されると言うことから、第1基本量gij と第2基本量hij が満たすべき条件式が得られます。
まずガウスの方程式(2-64)式を uk について偏微分したものに、さらにガウスおよびワインガルテンの方程式を適用すると
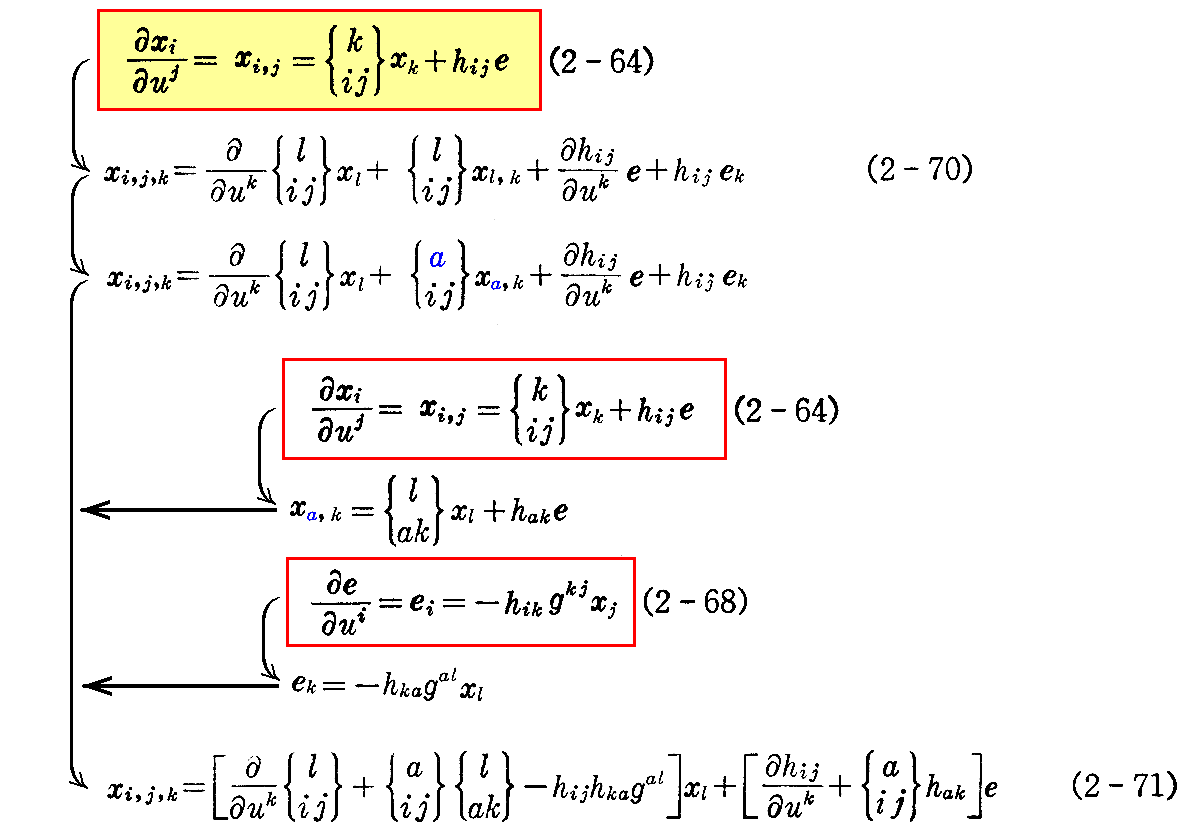
が得られる。全く同様にして i は同じだが j と k を交換した式
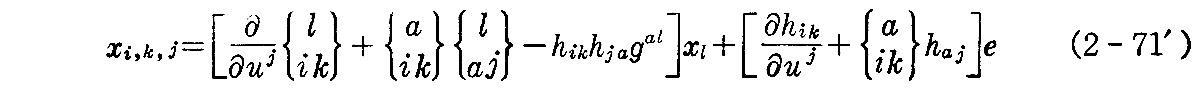
が得られる。
ここで、解xi(u1,u2)が積分の結果として得られる為には、 dxi=(∂xi/∂u1)du1+(∂xi/∂u2)du2 が完全微分(つまり積分可能)であるための必要十分条件 xi,j,k=xi,k,j を満たさねばなりません(例えばこちら、あるいはこちらを参照)。
それで、積分可能条件 xi,j,k=xi,k,j が成り立つとして(2-71)式と(2-71’)式を等値すると
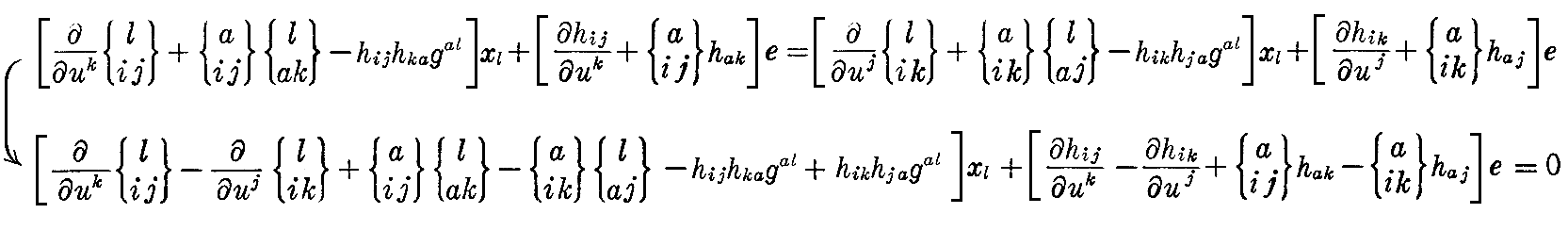
が得られる。 xl と e は一次独立だから、それぞれの係数が 0 で無ければならない。すなわち
ガウスの積分可能条件
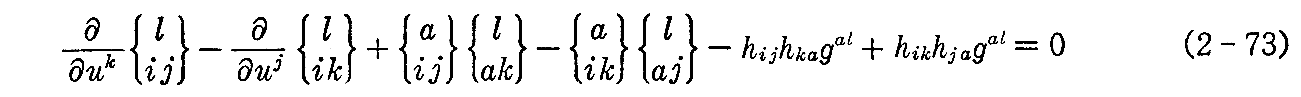
コダッツィの積分可能条件
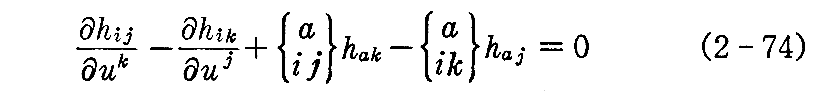
が成り立つ。要するに、前節の最後で注意したように、、(2-69)式を未知関数x,x1,x2,eの連立偏微分方程式とみなしたとき、方程式が解けるためには、方程式の係数となる第1基本量gijと第2基本量hijに対して(2-73)式と(2-74)式がさらに成り立たねばならないと言うことです。
後で(2-69)式(1)(2)(3)の連立偏微分方程式を解くのですが、解けるために(2-73)(2-74)条件が必要なので、(2-73)式を“ガウスの積分可能条件”、(2-74)式を“マイナルディ(Mainardi)・コダッツィ(Codazzi)の積分可能条件”あるいは簡単に“コダッツィの積分可能条件”と言う。
[補足説明1] ここで以下の関係に注意されたし。
[補足説明2]
本節の説明は多次元に拡張することを意識した証明の為に解りにくいが、3次元空間内の2次元曲面に限れば“ガウスの積分可能条件”と“コダッツィの積分可能条件”は以下の様にして導ける。
ガウスおよびワインガルテンの方程式が解けるためには
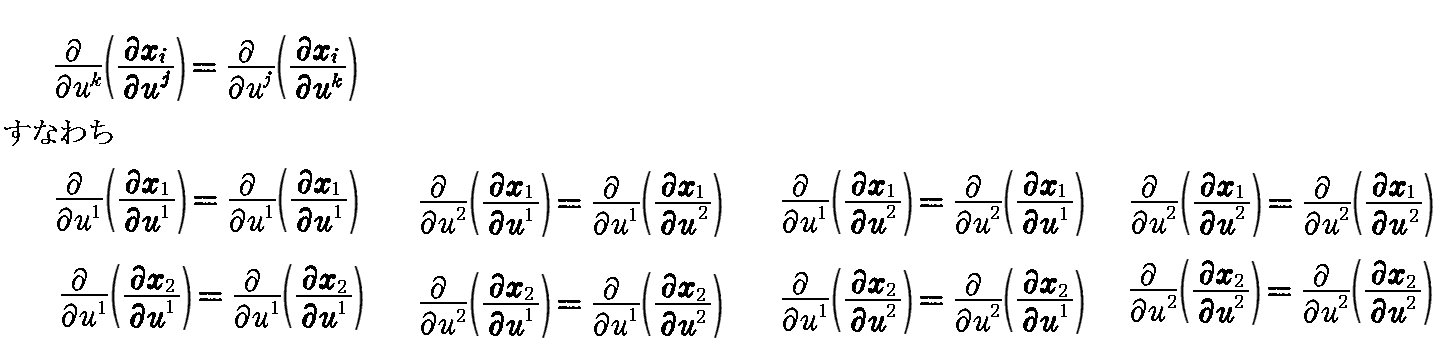
でなければならない。しかし、その内の4個は自明な恒等式ですし、残りの4個は2つずつが同じになるので、結局
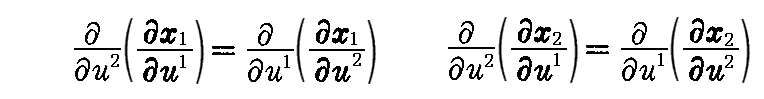
の2個が残ります。
このうちの1個
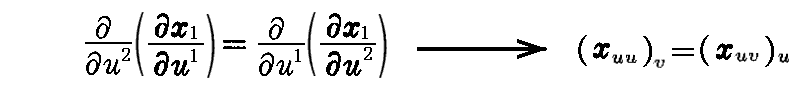
を(2-64’)式と(2-68’)式を用いて変形すると[式の拡大版]

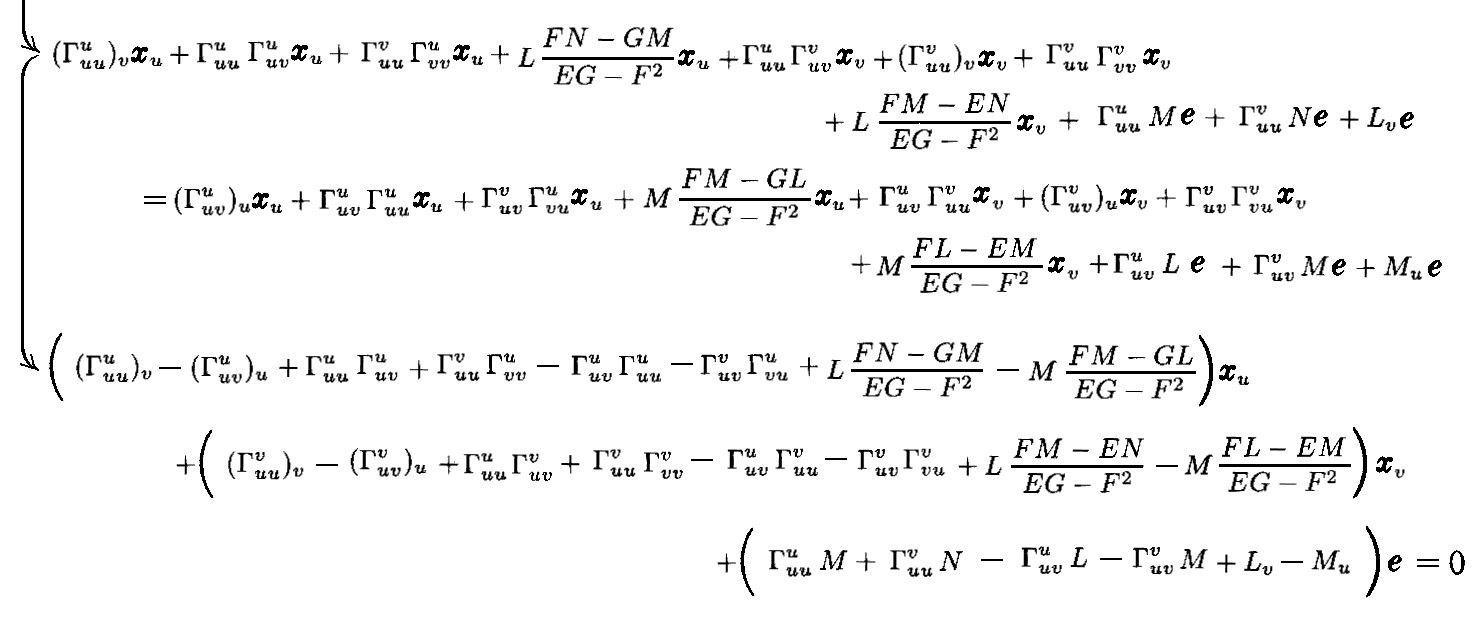
となる。この式が任意のxu,xv,e に対して成り立つためにはそれぞれの係数が 0 となることが必要です。
そのとき、 xu と xv の係数を 0 と置いたものがガウスの積分可能条件(2-73)式の2つです。また e の係数を 0 と置いたものがコダッツィの積分可能条件(2-74)式の1つです。

他のものは、 (xvu)v=(xvv)u から出てきます。
つまり、(2-73)式で j,j,k,l の組み合わ 2×2×2×2=16個 の内で独立なものは4つ、(2-74)式で i,j,k の組み合わせ 2×2×2=8個 の内で独立なものは2つです。
[補足説明3]
最初に掲げた、連立偏微分方程式(2-69)式が解けるための積分可能条件の内で、最初の
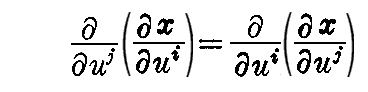
は、常に成り立っています。なぜなら(2-69)(2)式より
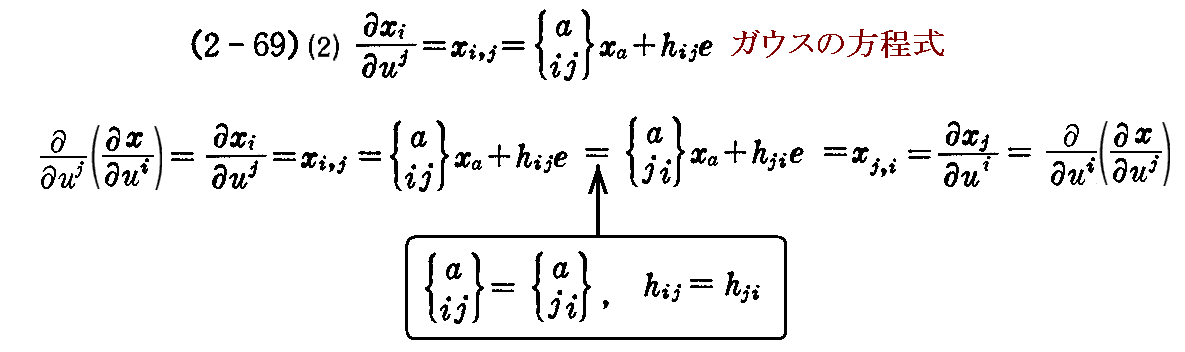
となるからです。
[補足説明4]
ワインガルテンの方程式(2-68)式から新たな条件式が出てくるかもしれませので、この方程式についても調べてみます。
ガウスの方程式にしたのと同様に、ワインガルテンの方程式(2-68)式を uj について偏微分て変形する。

全く同様にして i と j を交換した式
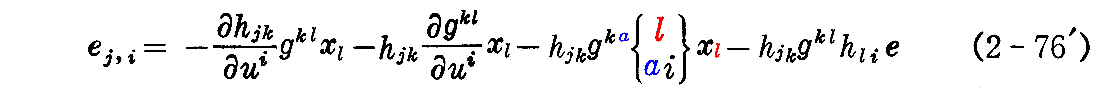
が得られる。
ここで、解e(u1,u2)が積分の結果として得られる為には de=(∂e/∂u1)du1+(∂e/∂u2)du2 が完全微分(つまり積分可能)であるための必要十分条件ei,j=ej,i を満たさねばなりません(例えばこちら、あるいはこちらを参照)。
そこで、積分可能条件ei,j=ej,i が成り立つとして(2-76)式と(2-76’)式を等値すると
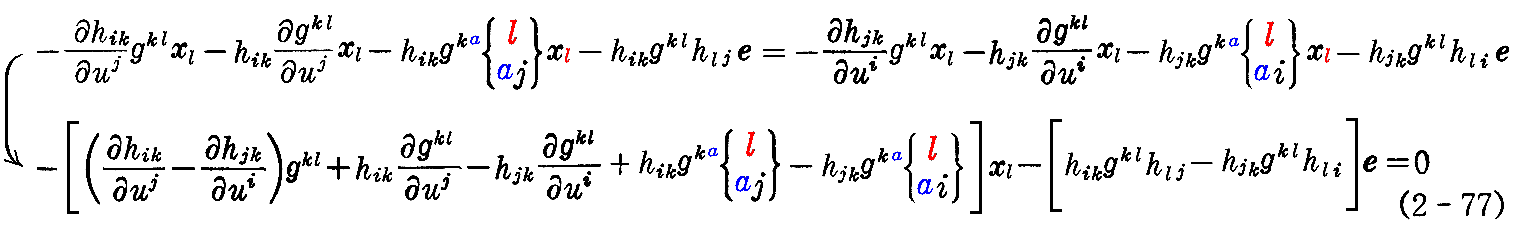
が得られる。
(2-77)式において xl と e は一次独立だから、それぞれの係数が 0 で無ければならないのですが、e の係数が0となることは自明です。なぜなら
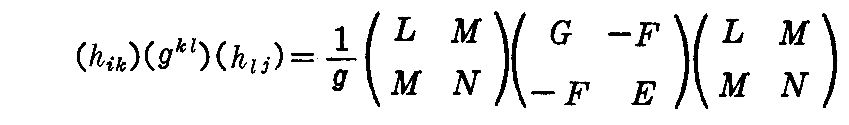
は対称行列だから
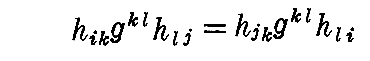
が常に成り立つからです。だから xl の係数が 0 となる事の意味を調べればよい。
ところで(2-50)式から
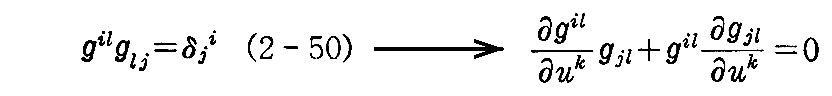
となるが、これに(2-57)式を代入すると
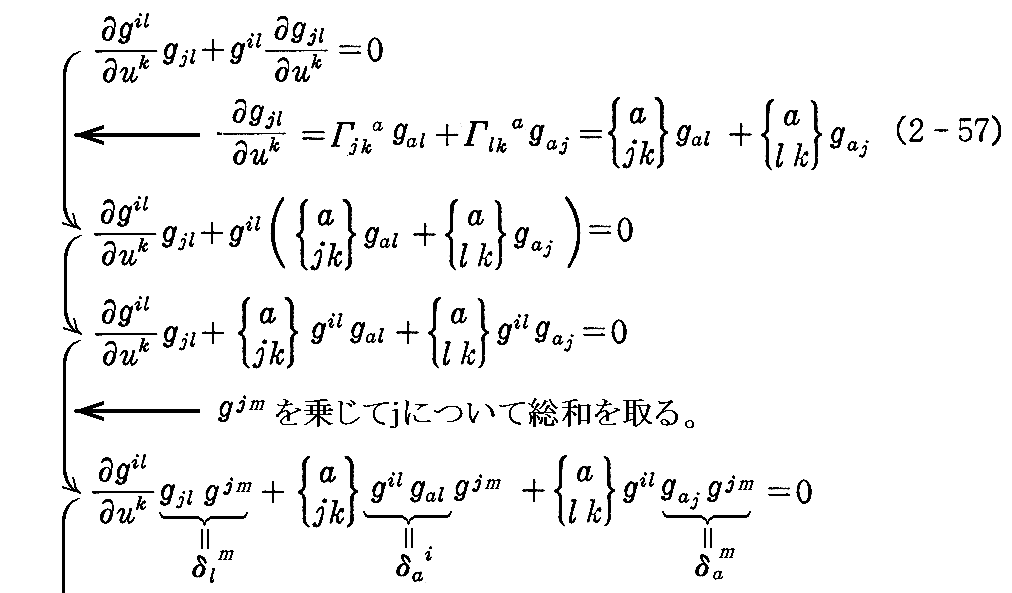
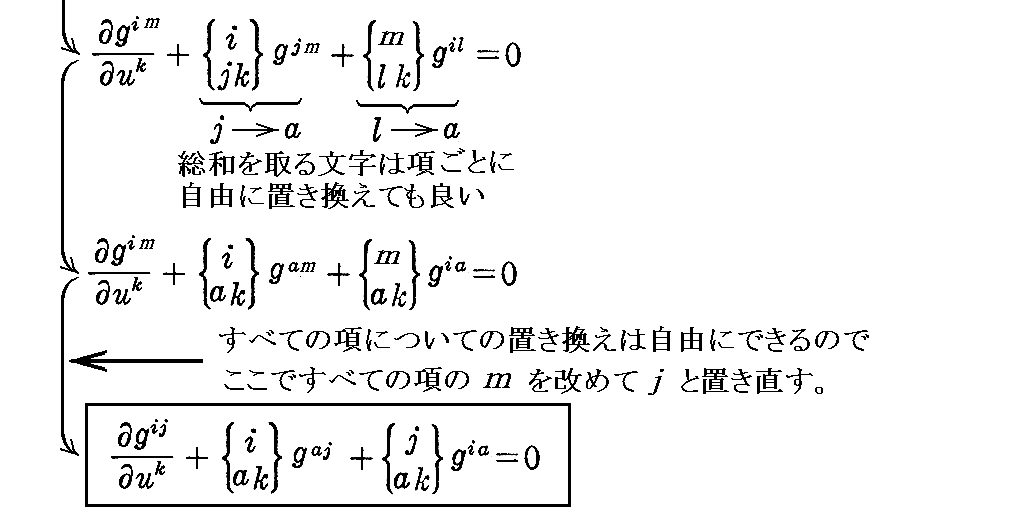
となります。
これを(2-77)式の xl の係数を 0 とした式に代入すれば
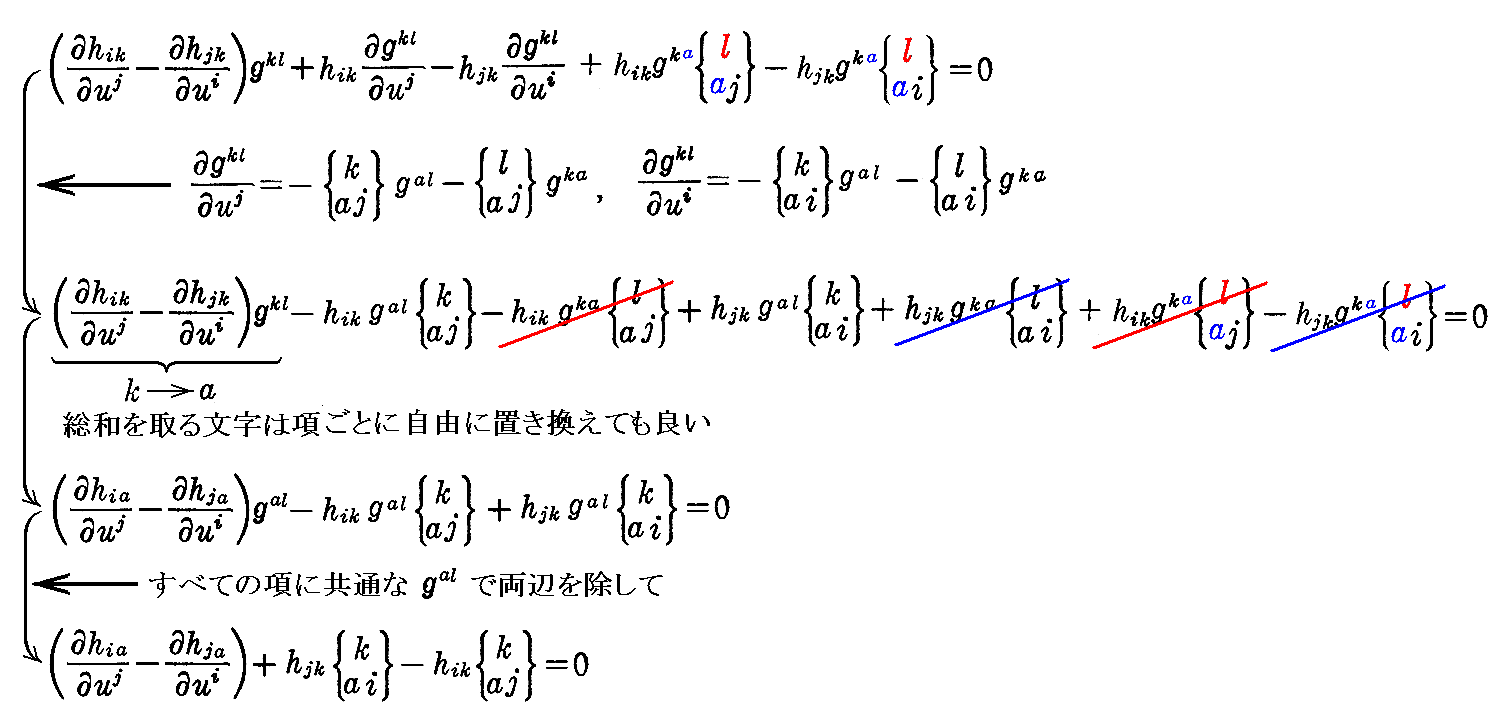
が得られる。ここで i→j,a→i,j→k,k→a の置き換えをすれば、上式はコダッツィの積分可能条件(2-74)式と完全に一致する。だからワインガルテンの方程式(2-68)式から新たな条件式は出て来ません。
この説明も多次元に拡張することを意識した証明の為に解りにくいが[補足説明2]と同様に3次元空間内の2次元曲面に限ったやり方で確認してみて下さい。
いずれにしても、 e に対する積分可能のための条件
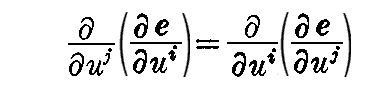
は xi に対する積分可能条件が満たされていれば、必然的に満たされています。
2.条件式の詳細
前記のガウスの積分可能条件(2-73)式についての考察を続ける。後の考察に便利な様に条件式の添字を付け直すと
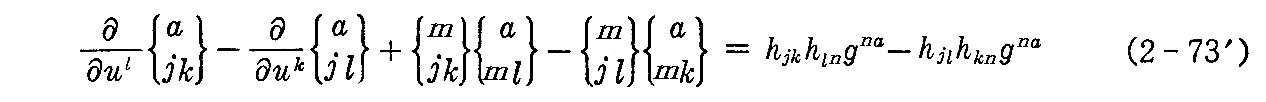
となる。ここで
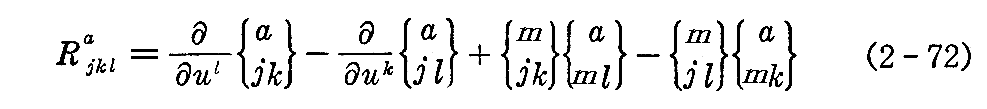
と置き、これを“第2曲率テンソル”と言うことにする。
これは、4次元のリーマン空間(時空)を扱う一般相対性理論で重要です。そこでは“リーマン・クリストッフェルの曲率テンソル”と呼ばれている。[3.(5)1.を参照]
第2曲率テンソルを用いて表すとガウスの積分可能条件(2-73’)式は
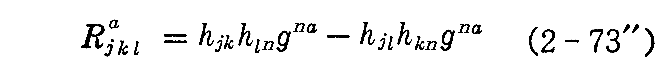
となる。
この両辺にgaiを乗じてaの総和を取る。このとき
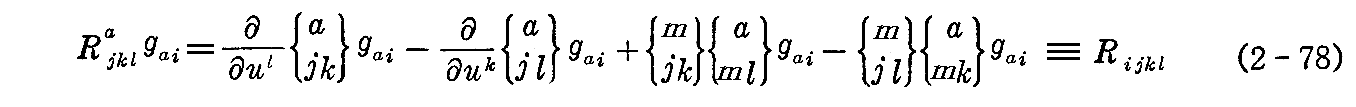
と置き、これを“第1曲率テンソル”と言うことにする。これも、4次元のリーマン空間(時空)を扱う一般相対性理論で重要です。
第1曲率テンソルを用いて表すとガウスの積分可能条件(2-73”)式は
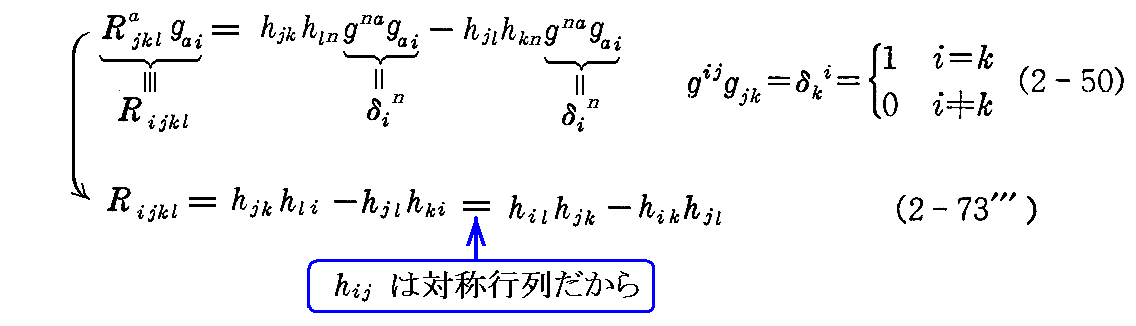
となる。
(2-73”’)式中のhijの添字交換による符号反転の性質から第1曲率テンソルRijkl は、次の代数的恒等式を満たす。
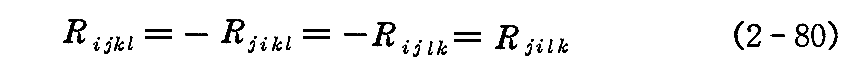
さらに4つの添字の内の1つ(例えば i )を固定して他の3つ(残りの j k l )を循環的に置き換えると
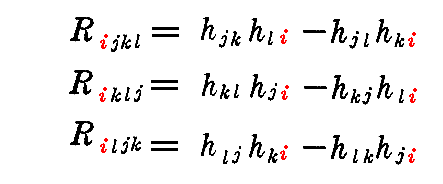
となるので、(hjk)が対称行列であることから
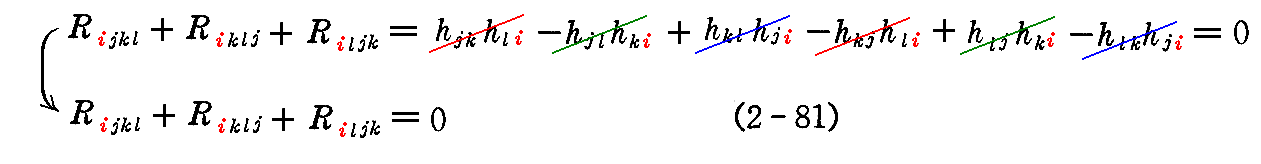
が言える。他の添字の1つを固定して残りの3つを循環的に置き換えた場合も同様です。固定する添字は4箇所あるので、(2-81)式タイプの恒等式は4個ある。
ここで添字 ijkl は 1 か 2 を取るので 2×2×2×2=16 通り Rijklが考えられる。これらすべてを具体的に書いてみる。Rijkl=hilhjk-hikhjl であることと、 hij が対称行列であることを考慮すると
R1111=h11h11-h11h11=0
R1112=h12h11-h11h12=0
R1121=h11h12-h12h11=0
R1122=h12h12-h12h12=0
R1211=h11h21-h11h21=0
R1212=h12h21-h11h22=(h12)2-h11h22=M2-LN
R1221=h11h22-h12h21=-(h12)2+h11h22=-M2+LN=-R1212
R1222=h12h22-h12h22=0
R2111=h21h11-h21h11=0
R2112=h22h11-h21h12=-(h12)2+h11h22=-M2+LN=-R1212
R2121=h21h12-h22h11=(h12)2-h11h22=M2-LN=R1212
R2122=h22h12-h22h12=0
R2211=h21h21-h21h21=0
R2212=h22h21-h21h22=0
R2221=h21h22-h22h21=0
R2222=h22h22-h22h22=0
となる。したがって R1212=R2121=-R1221=-R2112=h12h21-h11h22=(h12)2-h11h22=M2-LN であるから、 Rijkl の中で本質的なものは

の1つだけです。つまり“2次元リーマン空間”では“曲率テンソル”の独立な成分は1個だけです。
ところで、一般相対性理論で扱う“4次元リーマン空間(時空)”では各添え字が1~4(あるいは0~3)変化しますので、 Rijkl は4×4×4×4=256個あります。
しかし、添え字に対する様々な対称性と(2-81)式から、独立なものは結局のところ20個になります。このことに付いては別稿「時空と重力」§18[補足説明]あるいは別稿「対称テンソルと反対称テンソルの独立成分の数」3.をご覧下さい。
次にコダッツィの積分可能条件(2-74)式を調べる。添字 ijk は 1 か 2 を取るので 2×2×2=8 通りの条件式が考えられる。これらすべてを具体的に書いてみると
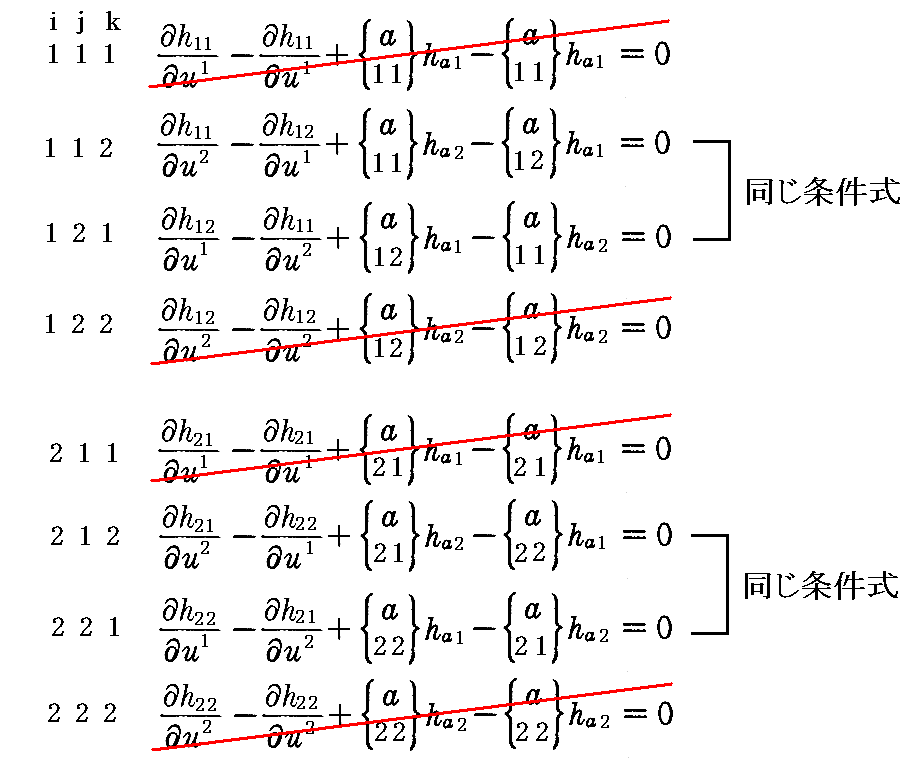
となる。そのうち4つは恒等式を表しており意味がない。残りの4つは2つずつ同じ式となる。
結局、独立な条件式は、i=1,j=1,k=2の
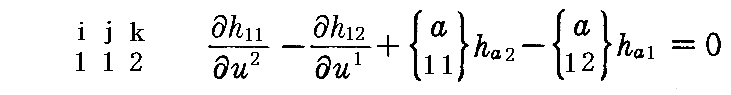
と、i=2,j=1,k=2の
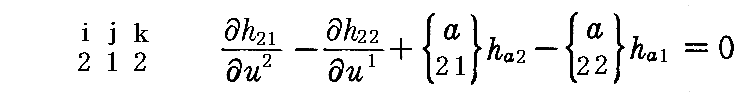
の2つだけです。
3.ガウスの“驚異の定理”
2.(6)2.で定義したガウスの全曲率Kは
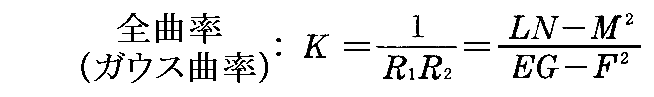
で表せたのですが、前項の(2-82)式を用いると、その分子は Rijkl で表される。ところが Rijkl は E,F,G およびそれらの導関数だけを含むものです。よって以下の定理が成り立つ。
[定理]
“ガウスの全曲率”は、第1基本量およびそれらの偏微分係数だけで表せる。
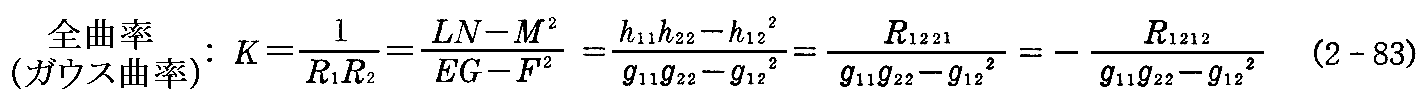
これを“ガウスの驚異の定理(Theorem egregium)”と言う。
これはガウスの大論文『曲面についての一般研究』(1827年)の§12で述べられているのですが、そこでは3.(10)1.[定理]で説明するような形で与えられています。そこの証明で述べたように、そこの[定理]の内容はここで言っていることと同じです。詳細は文献5.をご覧下さい。
これが“驚くべき定理”である理由は、全曲率(ガウス曲率)はもともと曲面に直交する法線ベクトル e(つまり曲面の湾曲に関係して曲面が接平面から離れる量を表すp値に関係した第2基本量)に関係していたのですが、p値の状態を知らなくても、曲面上の“線素”の変化の様子を与える“第1基本量”(これが一般相対性理論で中心的な役割を果たす“基本計量テンソル”gij or gij に相当する)のみで曲率が決定されると言っている所にある。
つまりガウス曲率は曲面の空間内への埋め込みの様子を示す外在の曲がり情報を必要とせず、曲面に内在する“線素”に関する情報のみで求められる(このことは別稿4.(3)[例8]と別文献2次元リーマン空間(球面) を比較すると解る)。
曲面の「曲がり具合」を表すガウス曲率が曲面の内在量のみで表されるという事実は、空間の「曲がり具合」を考察するのに「外の世界」の情報が必要でない可能性を示唆し、後の“リーマン幾何学”、そしてリーマン幾何学を数学的基礎として構築された“一般相対性理論”へ繋がる。
このことについては別稿Einstein著「我が相対性理論」§25 と Bornの説明の特にp320 を参照。さらに、3.(2)2.[補足説明3]を参照されたし。そして「基底ベクトル・双対基底ベクトルと反変成分・共変成分(計量テンソル・クリストッフェル記号・共変微分とは何か)」4.も参照されたし。
[補足説明1]
“第1曲率テンソル”(2-78)式をさらに変形する。
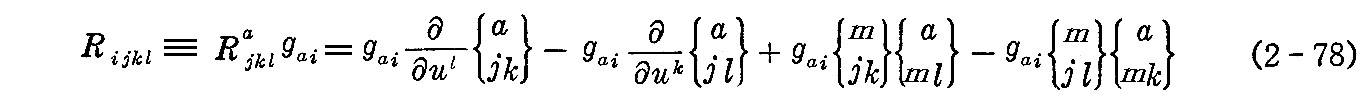
ここではgiaを左から乗じていますが、gaiを右から乗じる場合と同じです。
まず(2-78)式の《第1項》を計算する。
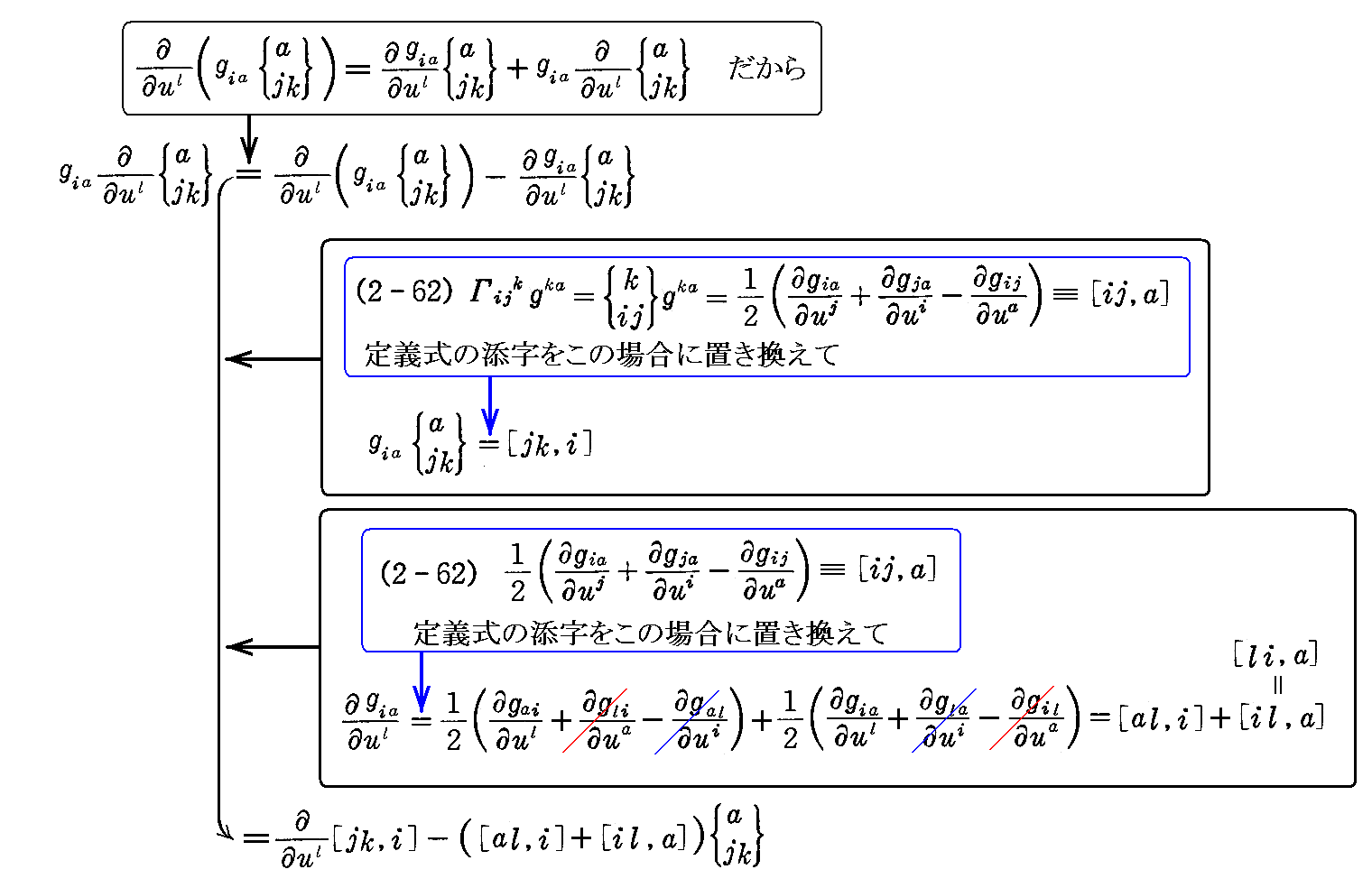
となる。
《第2項》も添字を入れ替え同様な計算をすれぱ
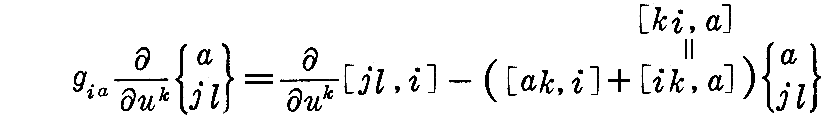
が得られる。
《第3項》と《第4項》は(2-62)式の添字をそれぞれに対応する様に入れ替えて
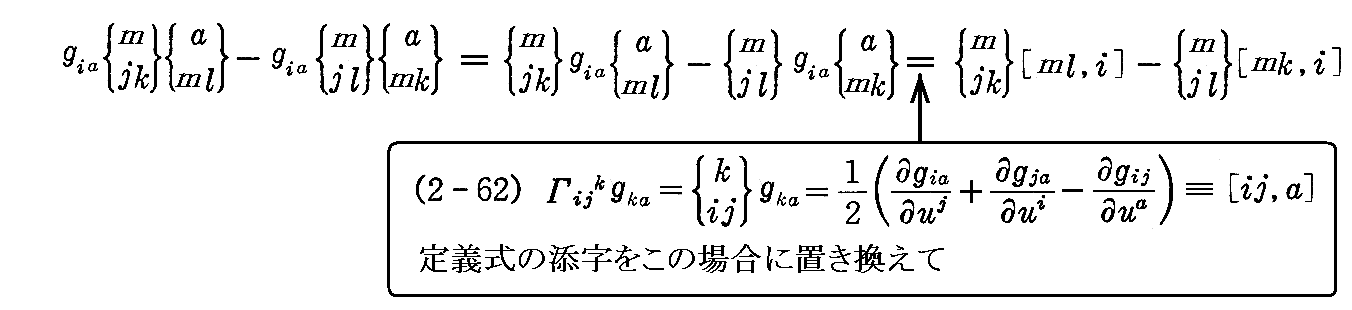
が得られる。
これらの結果を最初の(2-78)式に代入すると
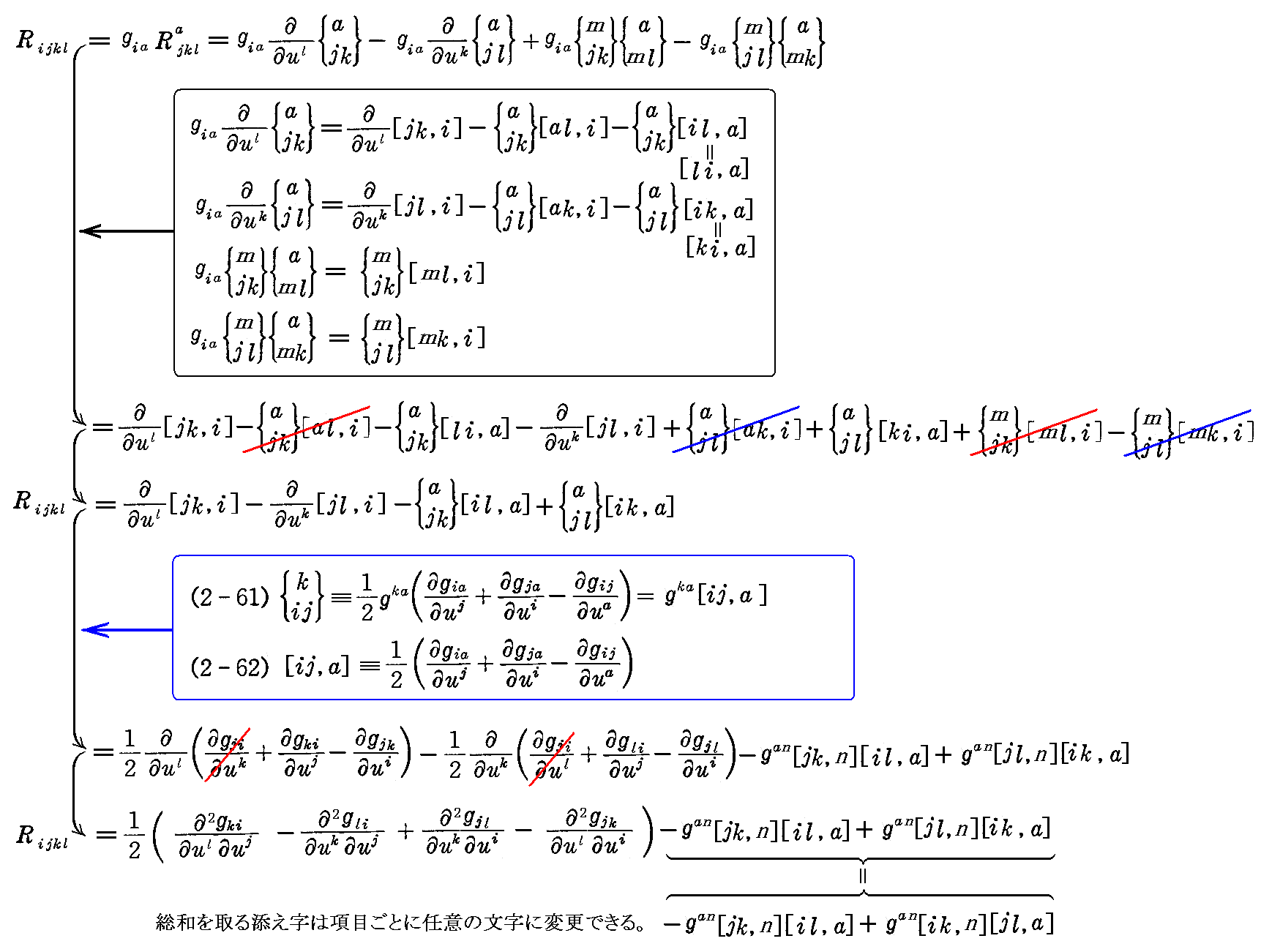
となる。この式からも、第1曲率テンソルRijkl は i と j を交換しても、 k と l を交換しても符号が変わることが確認できる。
この当たりの式変形については「微分幾何学」3.(5)[問題2]も参照されたし。
[問題1] “ガウスの積分可能条件”を普通の記号に直して表すと

となることを示せ。
[解] (2-82)式に前項[補足説明1]の結論を適用すると
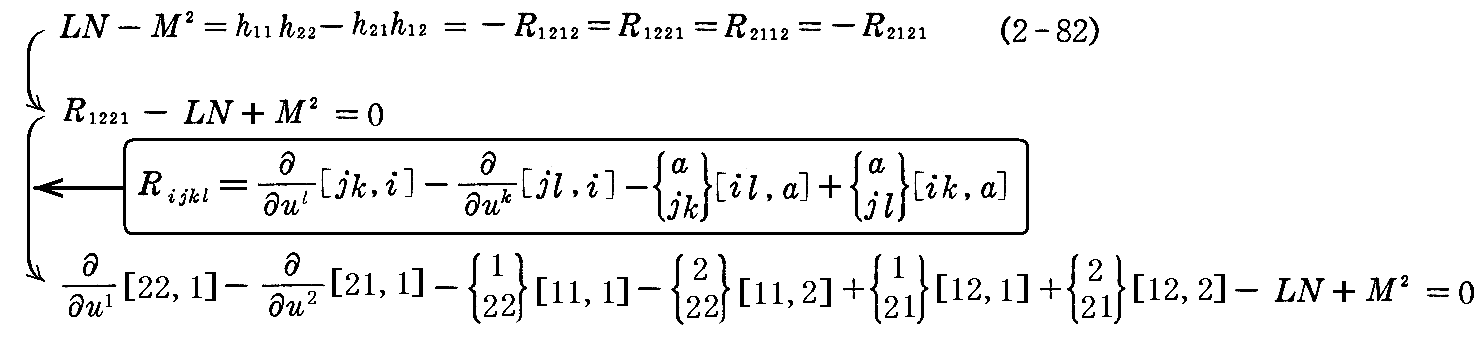
となる。ここで
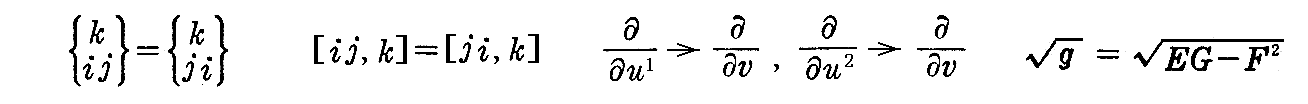
に気をつけて、2(8)[問題1]の結論
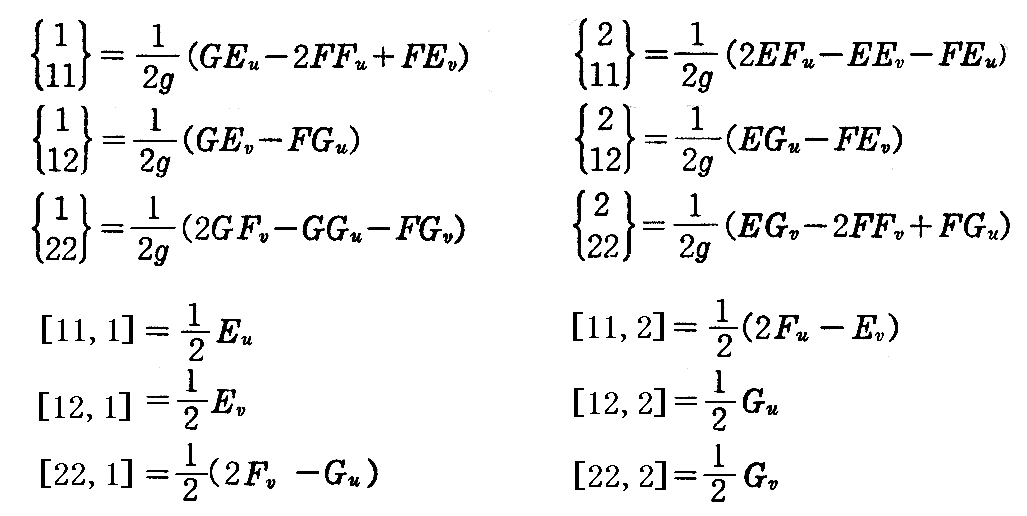
を適用してを普通の記号に直せばよい。ただし、計算はかなり面倒です。
[問題2] “ゴダッツィの積分可能条件”を普通の記号に直して表すと
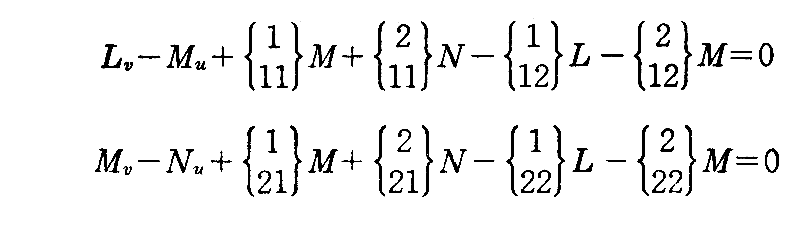
となることを示せ。
[解] 2.(9)2.で求めた関係式の記号を置き換えれば求まる。
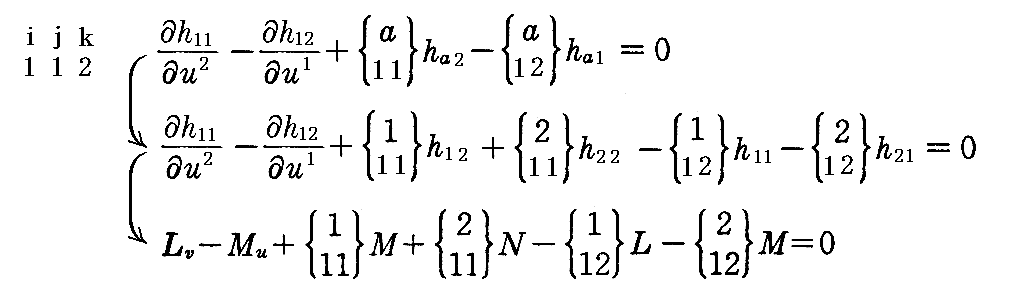
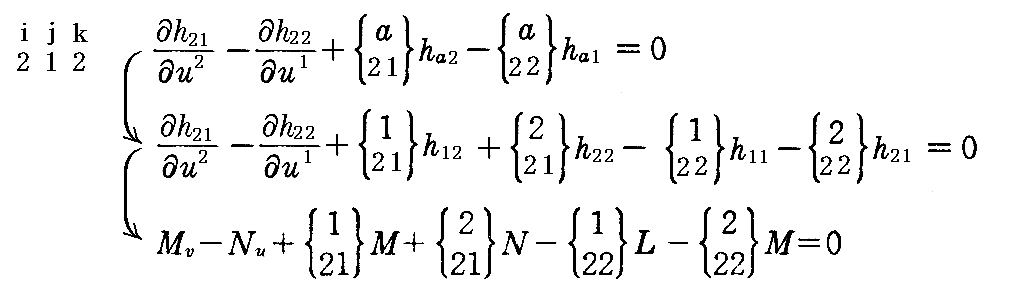
(10)ボネの基本定理
1.ボネの基本定理の証明
1つの曲面S:x=x(u1,u2)が与えられると、それから第1基本量gij、第2基本量hijを求めることができた。今度は逆に、第1基本量gijと第2基本量hijとがu1,u2の関数として与えられているとき、これらをそれぞれ第1基本量と第2基本量とする曲面x=x(u1,u2)が存在するかを問題にする。これは曲線論の自然方程式に相当する問題です。
[定理]
gij,hij が ui の関数として与えられ、至る処で gijduiduj が正値2次微分形式であるとき、これらをそれぞれ第1基本量と第2基本量とする曲面 x=x(u1,u2) が存在するための必要・十分条件は、これらが“ガウスおよびコダッツィの積分可能条件”を満たすことです。そしてその曲面は運動を除いてただ一通りに決定する。
これを“ボネ(O. Bonnet)の基本定理”と言う。
[証明]
《必要条件》
x=x(u1,u2),x1=x1(u1,u2),x2=x2(u1,u2),e(u1,u2) を未知関数とする連立偏微分方程式[2.(8)5.の(2-69)式]
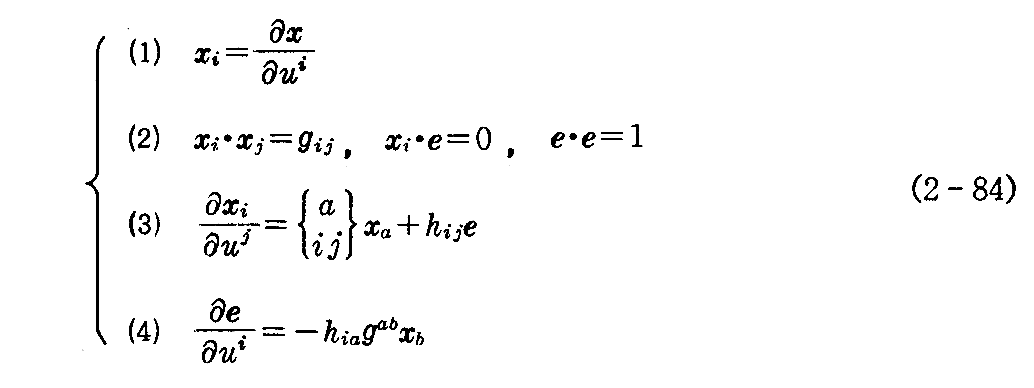
が ui=u0i のときの初期値 x=(x)0,xi=(xi)0,e=(e)0 に対して完全積分可能であるためには、前節の計算によって gij と hij が “ガウスおよびコダッツィの積分可能条件”を満たすことが必要です。
《十分条件》
gij と hij が “ガウスおよびコダッツィの積分可能条件”を満たせば、ガウスとワインガルテンの偏微分方程式は完全積分可能で初期値を満たす解 xi,e が求まることを証明する。
“ガウスおよびコダッツィの積分可能条件”を満たと言うことは、とりもなおさず
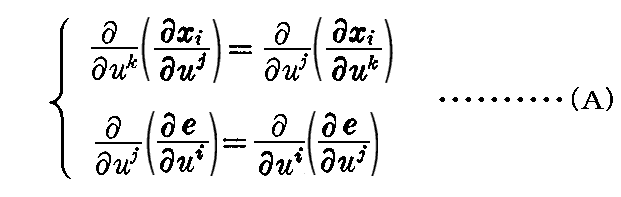
が成り立つと言うことです。
まず、
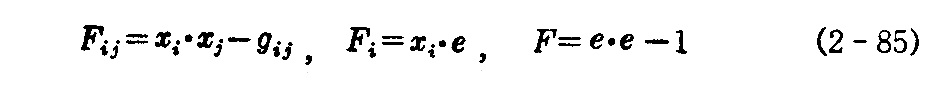
と置き、(2-85)式の《第1式》を uk について偏微分して(2-84)(3)式を用いると
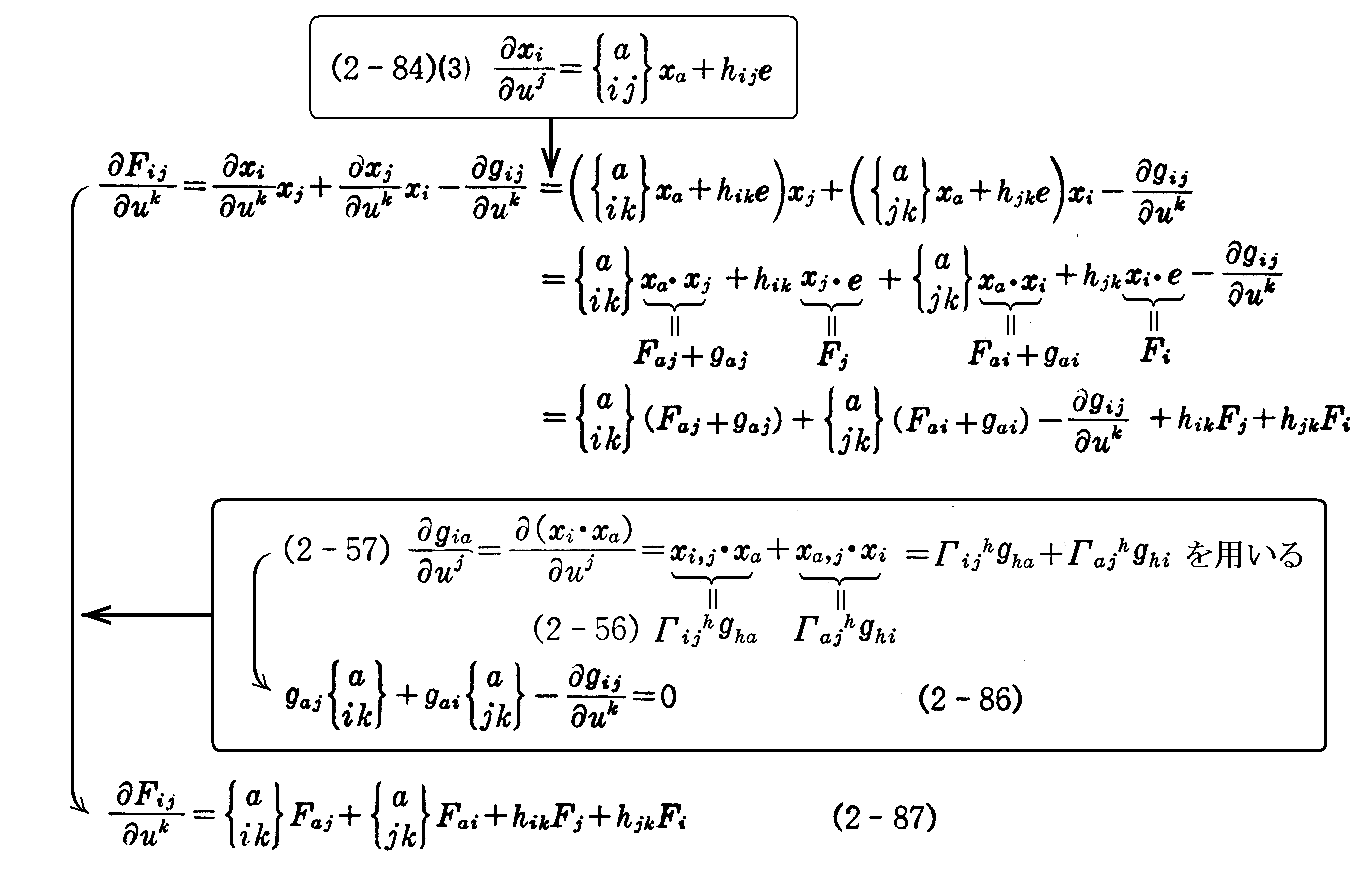
を得る。
また、(2-85)式の《第2式》を uk について偏微分し(2-84)(3)式と(2-84)(4)式を用いると
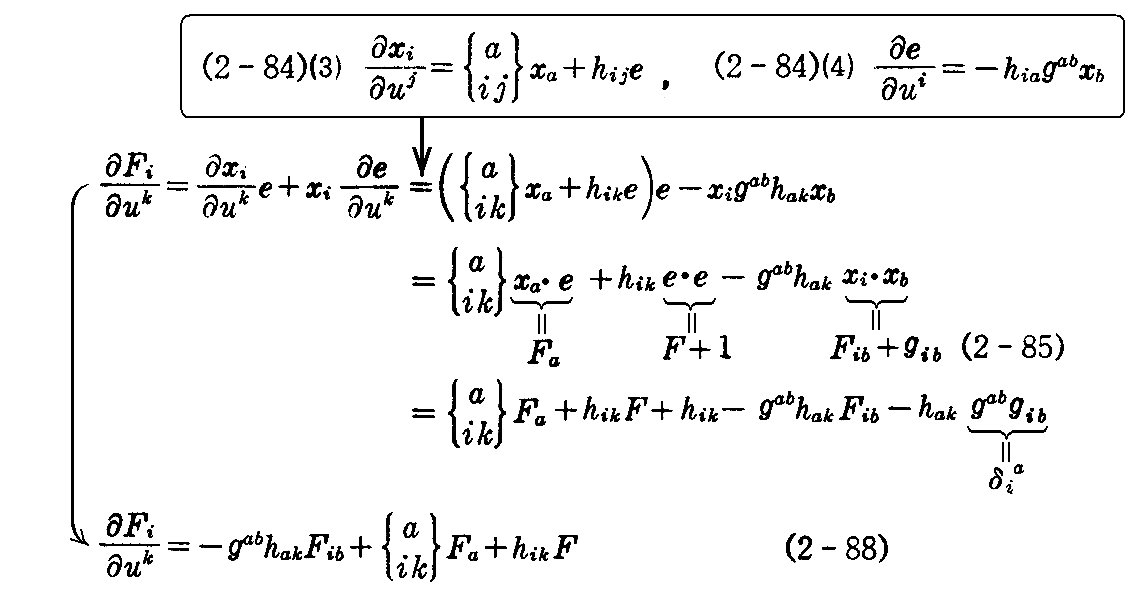
を得る。
さらに、(2-85)式の《第3式》を uk について偏微分し(2-84)(4)式を用いると
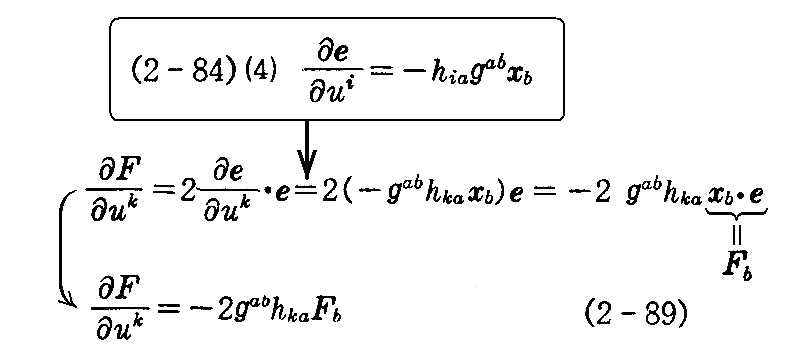
を得る。
ここで(2-87)(2-88)(2-89)式は未知関数 Fij,Fi,F についての連立偏微分方程式と考えられます。
そのとき、(2-85)式に(A)式を適用すれば
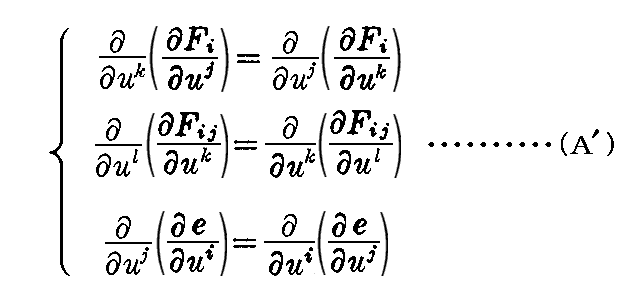
となりますから、これらの未知関数 Fij,Fi,Fは積分可能で解が求まります。
つまり、これらの uk による偏導関数はまたこれらの1次同次式( Fij,Fi,F の線型結合)であるから ui=u0i のときの初期値を
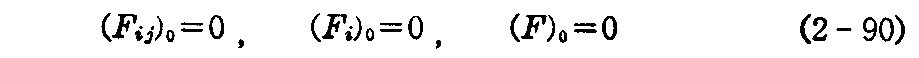
となるように定めておけば、上の連立微分方程式の uk に沿った解は至る処で常に
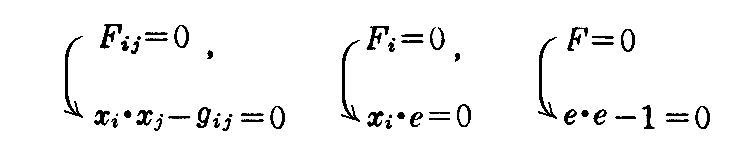
でなければならない。すなわち、曲面上の至る処で
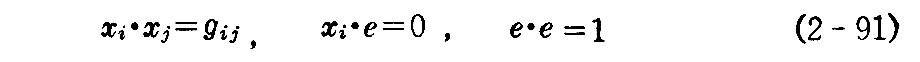
が成立する。
さらに2.(9)1.[補足説明3]で説明したように
は、常に成り立ちますから
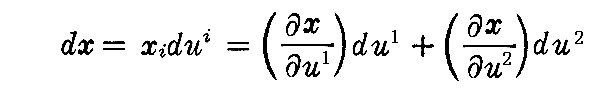
は完全微分となり
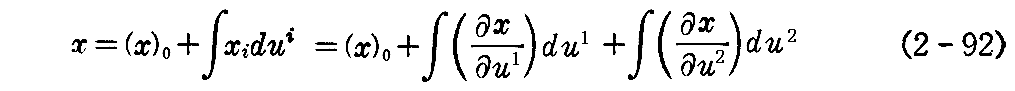
によって 曲面 x(u1,u2) が決定される(例えばこちら、あるいはこちらを参照)。
そして、xi・xj=gijであるから
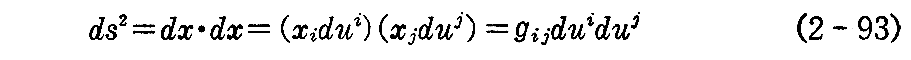
となり、
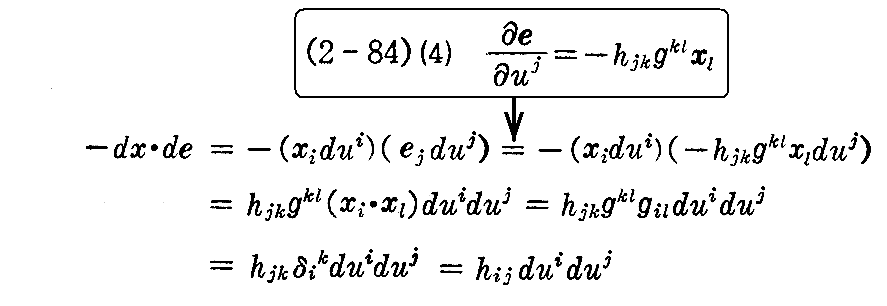
となる。したがって gij と hij は曲面(2-92)式の第1基本量と第2基本量となる。
初期値(2-90)式の与え方によっていろいろな曲面が得られるが、これらは運動によって重ね合わせることができる。つまり、剛体運動で重なり合う曲面どうしは同じ曲面と考えれば、解は一つに確定する。
[証明終わり]
[例題]
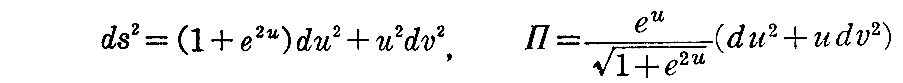
をそれぞれ第1基本形式、第2基本形式とする曲面を求めよ。
[解] 第1基本量と第2基本量は
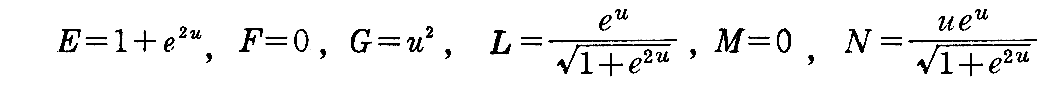
であり、クリストッフェルの記号を計算すると2.(8)[例題]と[問題1]より
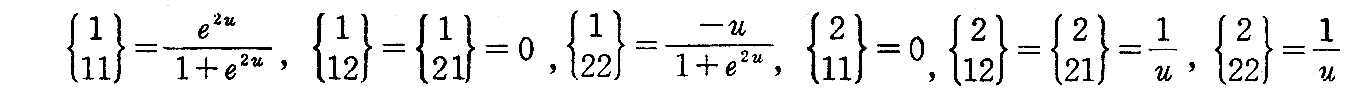
となるから、第1基本量、第2基本量はガウスとコダッツィの積分可能条件を満たす。
このとき、ガウスの方程式(2-64)式とワインガルテンの方程式(2-68)式は
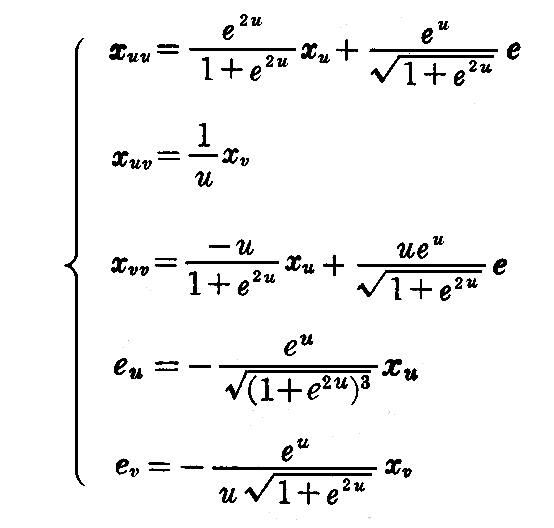
となる。ここで、法線ベクトルの e と指数の e を混同しないこと。
第3式を v について微分し、第2式と第5式を用いると

が得られる。
この微分方程式を解いて
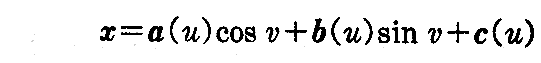
を得る。これをvで偏微分したものを第2式の右辺に、それをさらにuで偏微分したものを第2式の左辺に代入すると
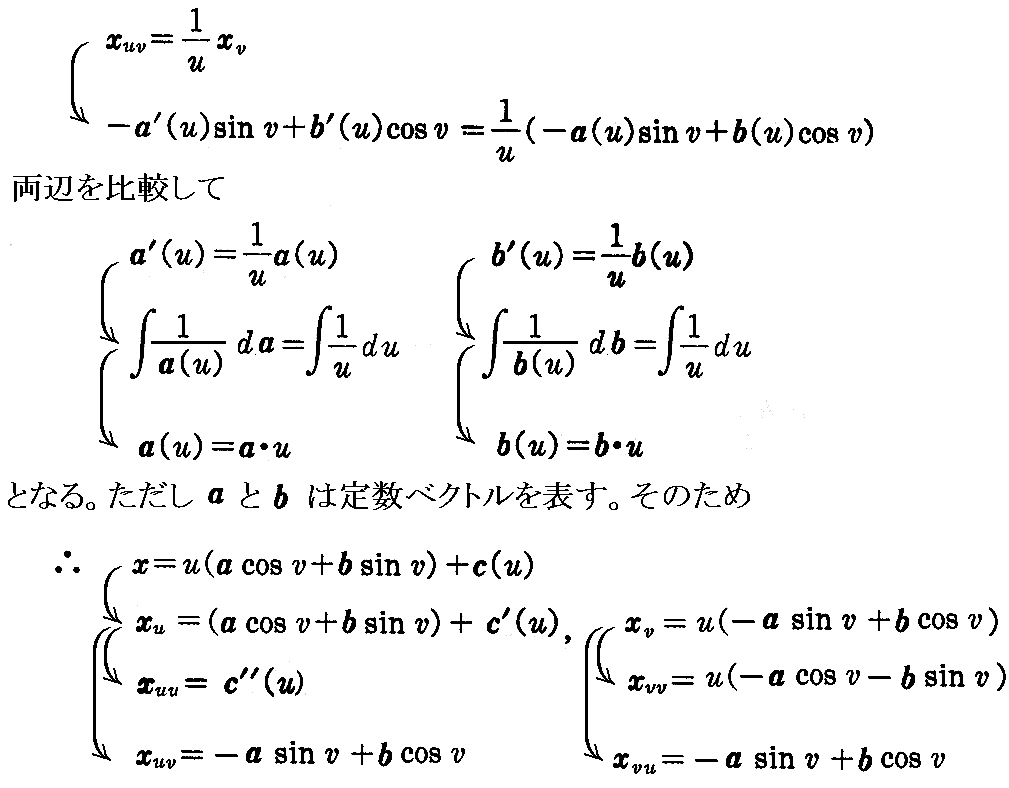
の形となる。これを第1式に代入すると

が得られる。これを第3式に代入すると
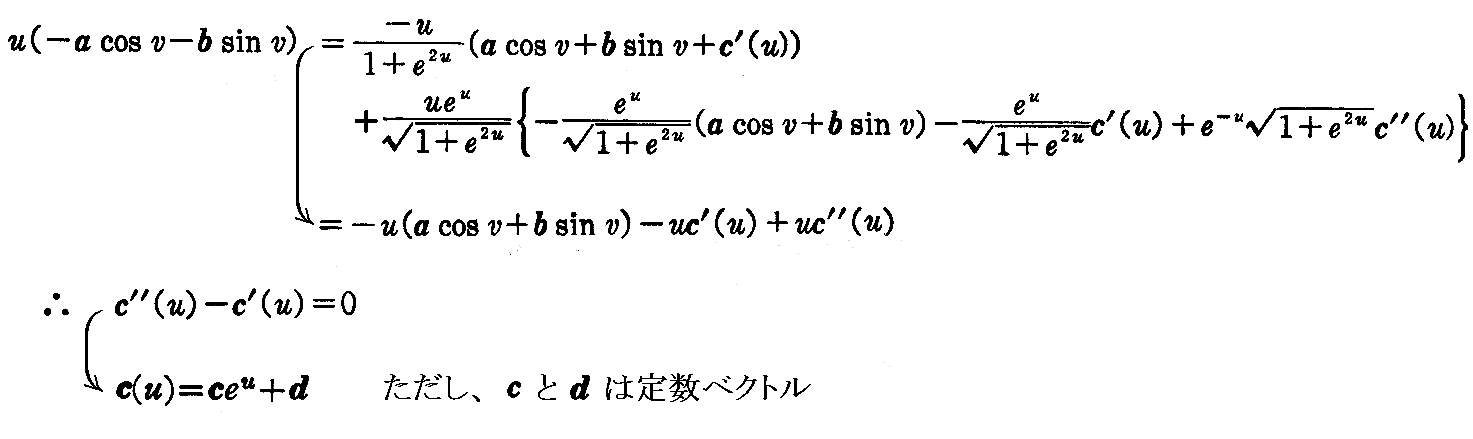
となる。
すなわち、曲面は

と表すことができる。
また前記の e の表現式に代入すると 法線 e は
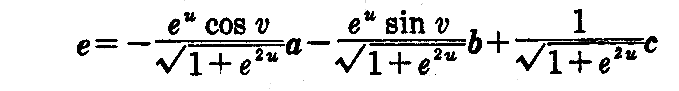
と表わせ、第4、第5式を満たすことは明らかです。
次に
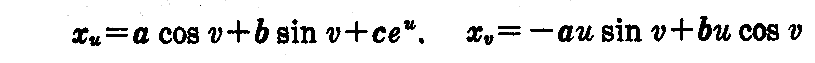
であることと、

なるべきことから
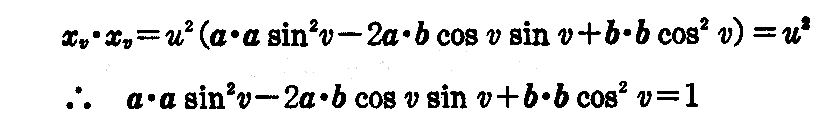
です。したがって
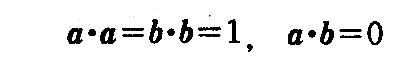
でなければならない。
これを用いて

となる。
以上の関係を用いるとxu・xu=E=1+e2n であるから

となる。
故に、a,b,cは互いに直交する単位ベクトルで、これらをそれぞれx1,x2,x3軸に取れば、問題の曲面はx3=ex1をx3軸のまわりに回転してできる放物面です。
[問題] 2次微分形式
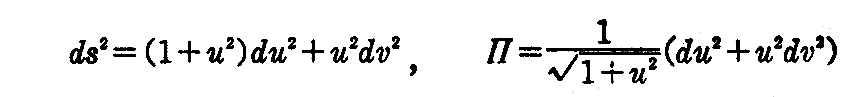
をそれぞれ第1基本量、第2基本量とする曲面を求めよ。
[解] 前[例題]と同じ手順をたどればよい。クリストッフェルの記号を計算すると2.(8)[例題]と[問題1]より
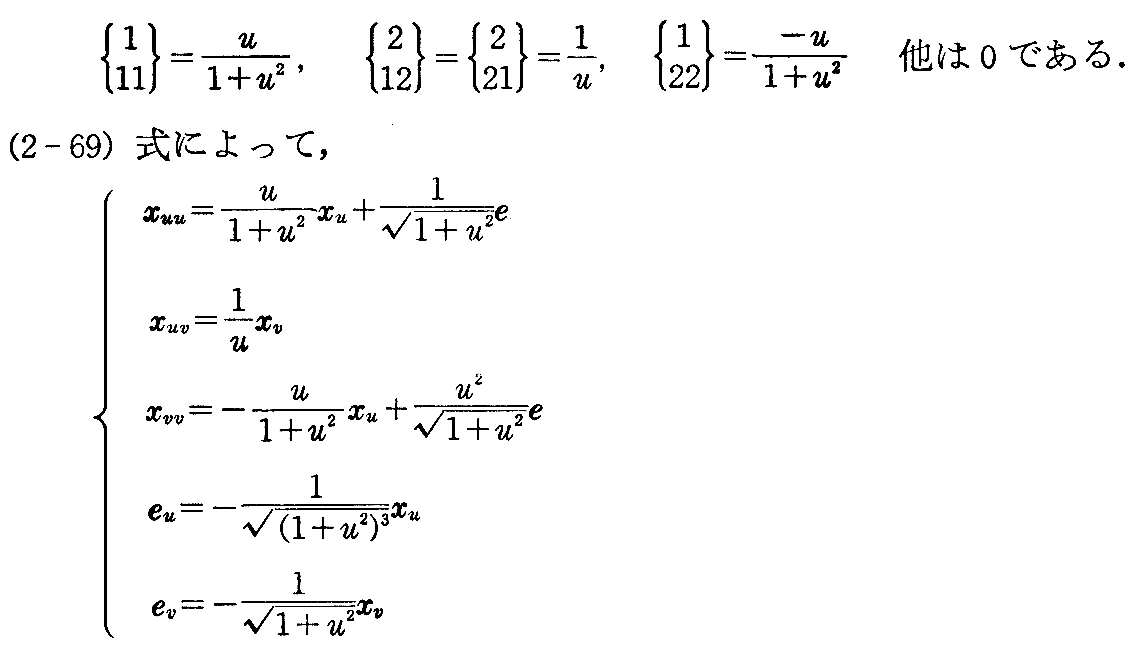
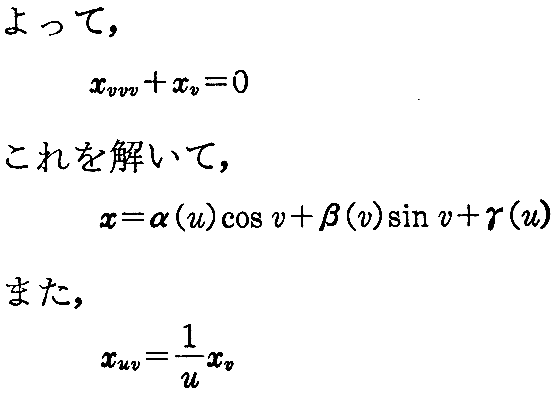



(11)ガウスの球面表示と第3基本微分形式
1.第3基本形式
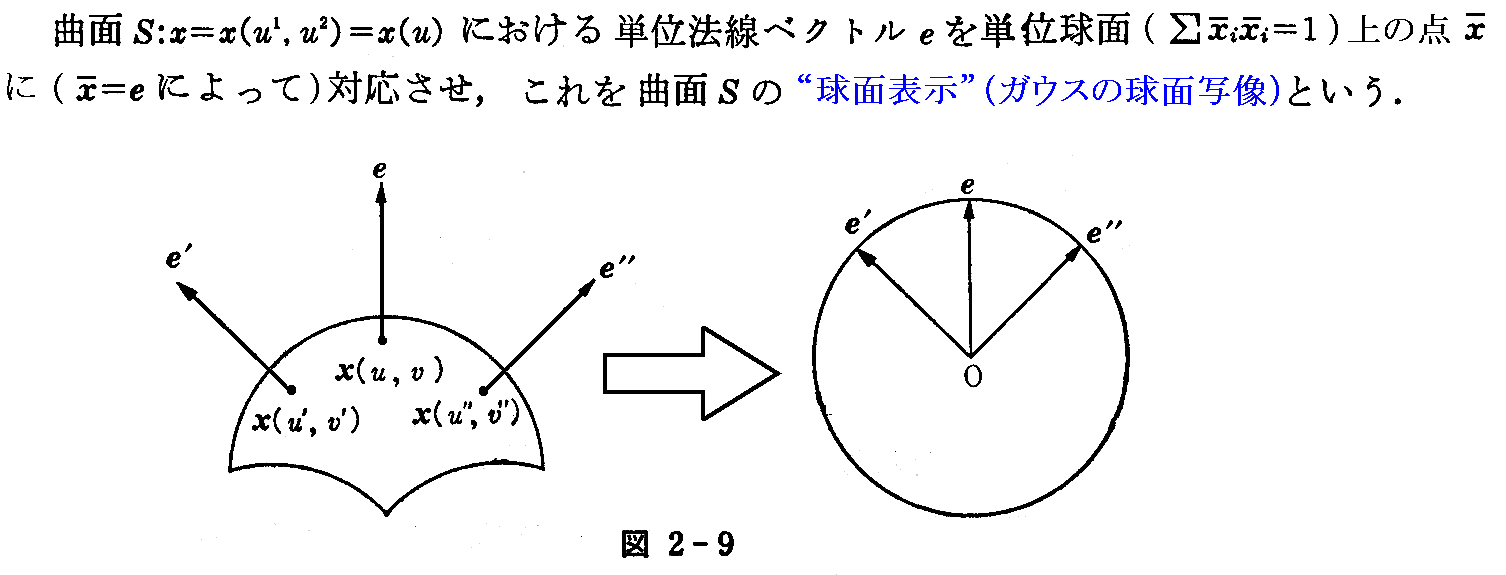
このとき、曲面S上の曲線Cを単位球面上に写像した曲線の線素dσの2乗は、“ワインガルテンの方程式”(2-68)式を考慮して

と表される。
ここで
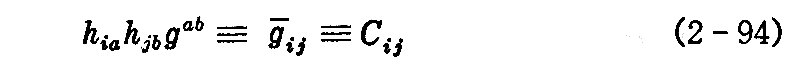
とおけば
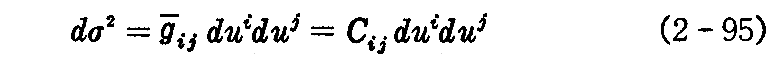
と表せる。この2次微分形式を最初に与えられた曲面Sの“第3基本微分形式”(第3基本形式)という。そしてCijを“第3基本量”という。(普通の記号で C11=e,C12=C21=f,C22=g と表すこともある。)
“ガウスの球面写像”の例
ちなみに、Gaussは1827年の大論文“曲面の研究”において、『曲面上の任意の図形の面積と、その図形を単位球面上に“ガウスの球面写像”をしたときの面積の比を考え、その図形を一点に集約した極限の面積比』として、元の曲面上の各点に於けるガウス曲率(全曲率) Kを定義した。
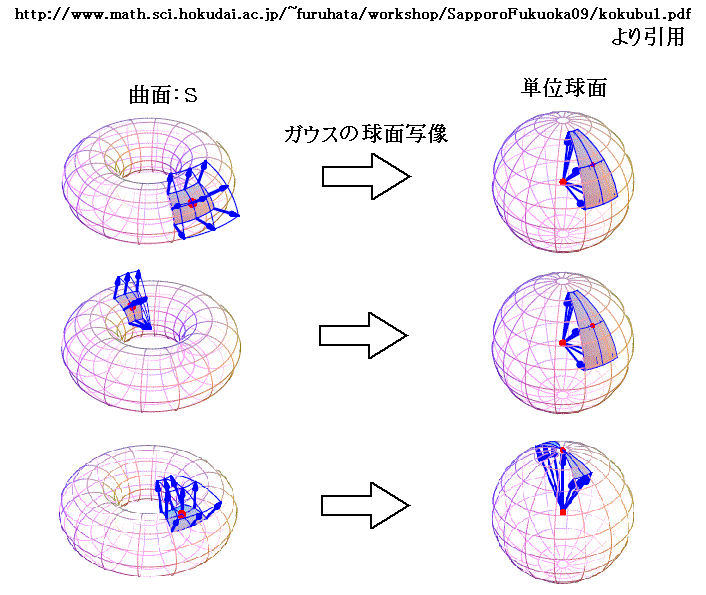
平面はどの場所でも法線ベクトル e は同じなのでガウス球面上の1点に写像される。そのためガウスの曲率(全曲率)Kは 0 となる。
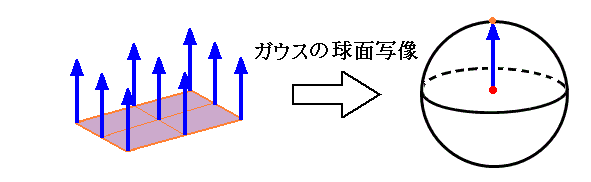
柱面はガウス球面上の曲線に写像される。曲線の面積は 0 だから、元の柱面のガウスの曲率(全曲率)Kは至る所で 0 です。これはガウスの曲率の定義(Kは2方向の主曲率の積)から考えると明らかな事ではあります。このあたりについては、以下の第3項で説明する“ガウス曲率の定理”を参照して下さい。
[補足説明]
ガウスが、ここで説明した“球面写像”なるものを考えたのは、曲面の曲率は、その曲面に法線を立て、その法線の方向の変化を調べれば解るだろうという考えがあったからです。
実際、第3項で述べるように、[曲面上の面積]と[それを球面写像したときの球面上の面積]との比はガウスの全曲率そのものだったのです。また第4項で述べるように、曲面上の測地線を球面写像で球面上に写像した曲線について興味深い定理が得られる。
2.第3基本量
第3基本量(2-94)式を、平均曲率H(2-40)式、ガウス曲率(全曲率)K(2-41)式によって表そう。
まず、C11は
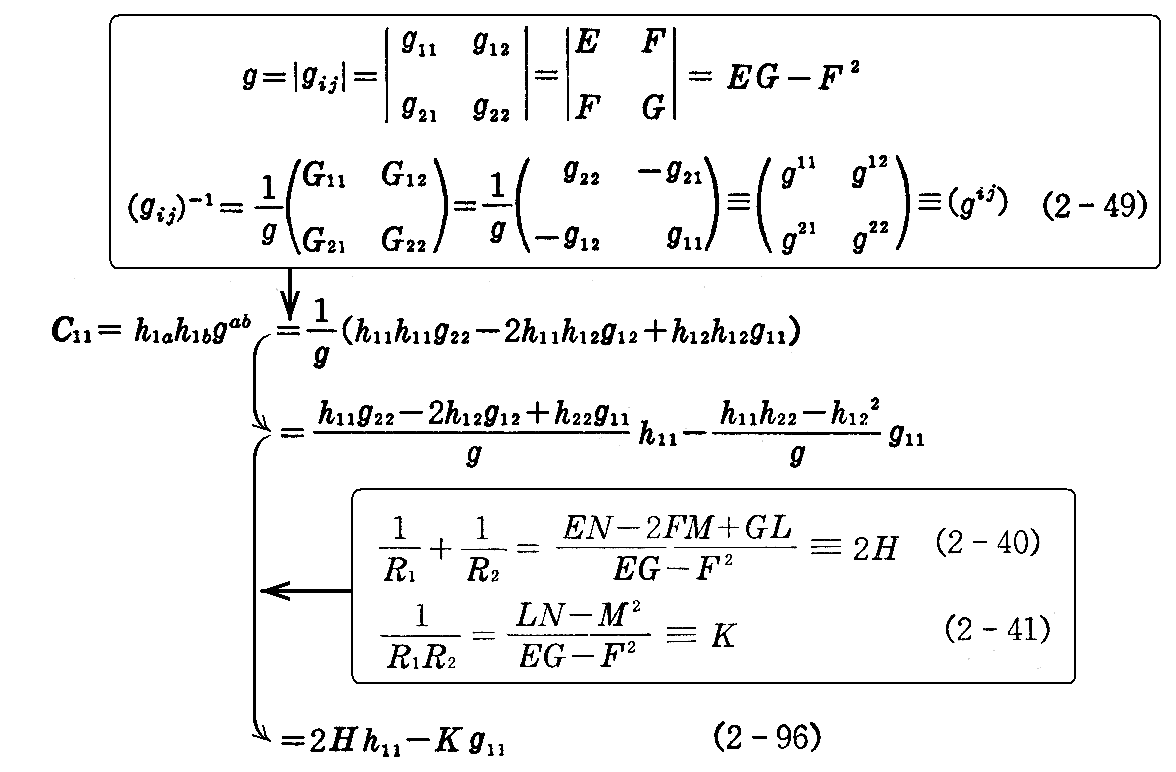
と表される。同様にして
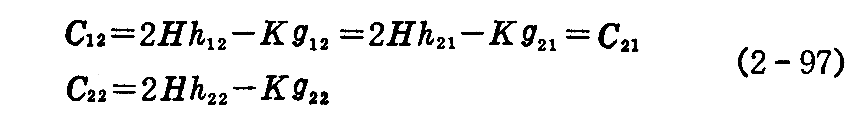
となる。
以上をまとめると

となる。つまり、“第3基本量”はもとの曲面Sの平均曲率とガウス曲率(全曲率)および第1基本量と第2基本量で表される。
したがって、(2-95)式の“第3基本微分形式”は
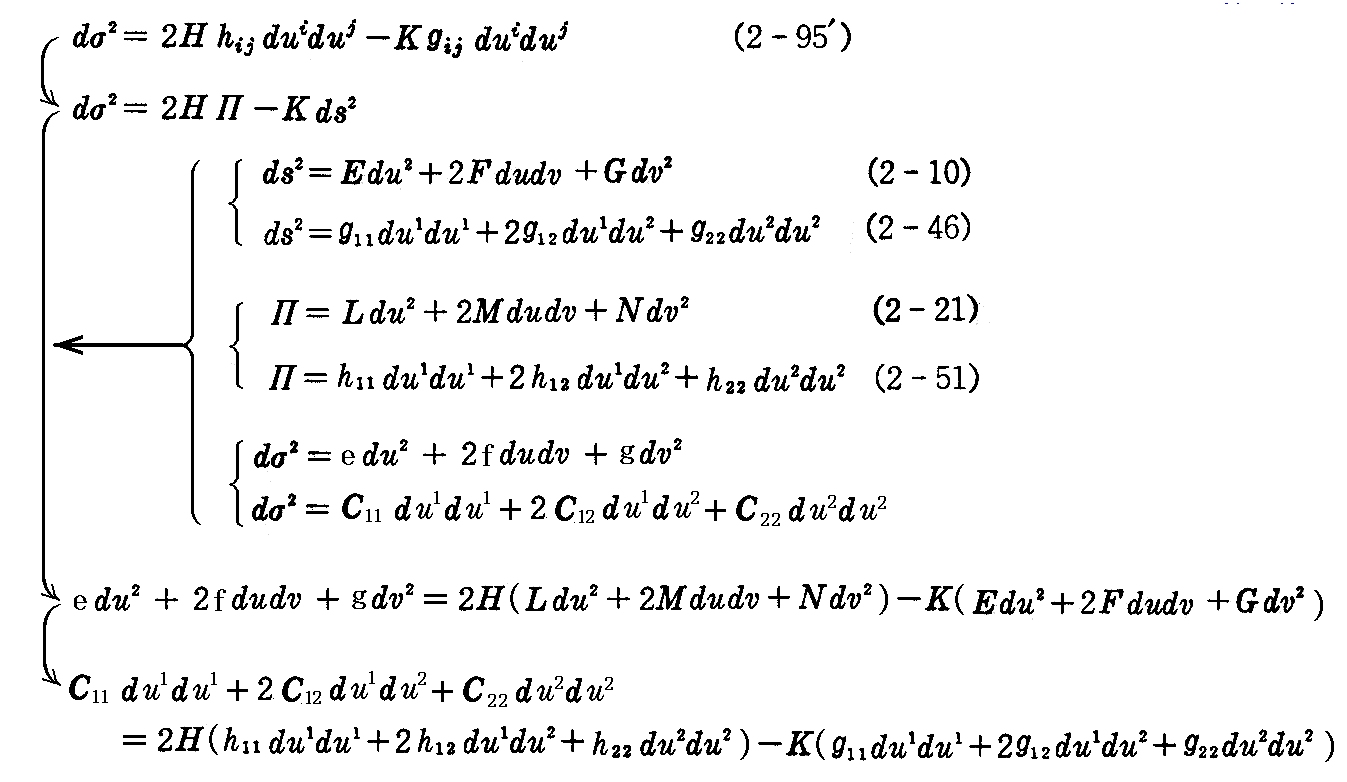
の様に、“第1基本微分形式”と“第2基本微分形式”を用いて表すことができる。
また、曲面S上の曲線Cの法曲率をkn=1/Rとすれば、2.(5)3.の(2-30)式により
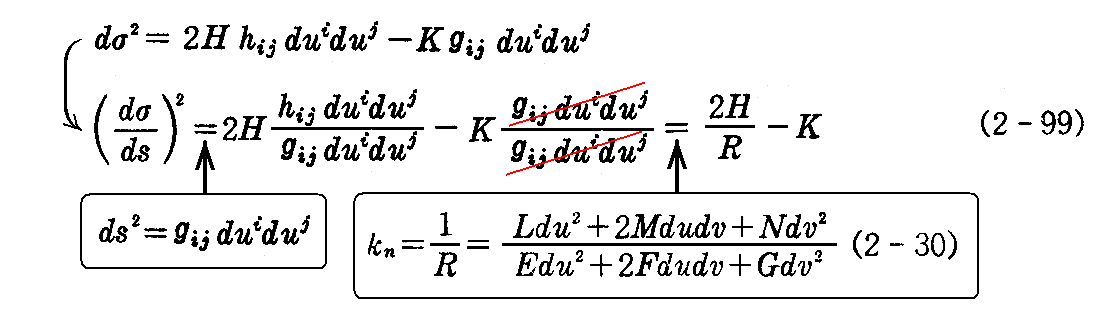
が成り立つ。
3.ガウス曲率の定理
いま(2-94)式の両辺の行列式をとれば

となる。ところで2.(2)3.の(2-14)式によって

であるから、上記の結論により次のガウス曲率の定理が得られる。
[定理]
曲面上の領域を取りその面積をAとする。その領域を球面写像により単位球面上に写像したときの写像領域面積をA’とする。そしてA’/Aの面積比を考える。次に、Aの領域を曲面上の一点に収縮(A’もそれに対応して収縮)したときの、この比A’/Aの極限値は元の曲面の領域Aの収縮点に於けるガウス曲率(全曲率)の絶対値|K|に等しい。これを“ガウス(Gauss)曲率の定理”と言うことにする。
4.曲率線の球面表示
いま曲面 x=x(u1,u2) 上の曲線 ui=ui(s) とその球面表示の曲線

とを考えれば、その接線ベクトルは

であるから、曲面上の曲線の接線
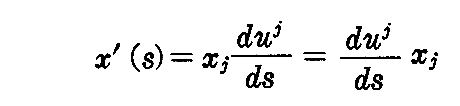
と球面表示の曲線の接線が平行になるには xa の係数を比較して
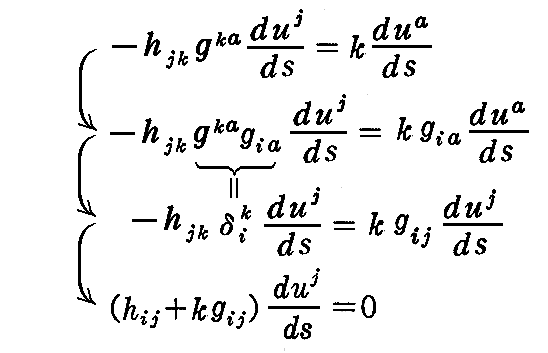
となることが必要十分条件です。ただしkは適当に仮定した比例定数ですが以下の式を満足しなければならない。
つまり、上式は
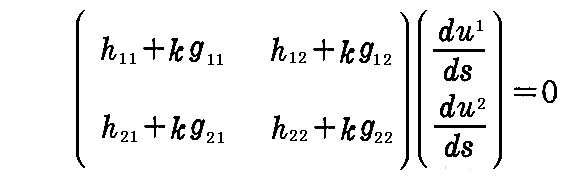
と書かれるが、このとき

だから

が成り立つことと同じです。
これは2.(6)2.の(2-39)式と同じですから、kが“主曲率”を与えることを意味する。よって次の定理が得られる。
[定理]
曲面上の曲線とその球面表示の曲線とが対応点において平行な接線を持つための必要十分条件は、この曲線が曲面上の“曲率線”であることです。曲率線とはその接線が常に“主曲率方向”(曲率が極値を取る方向)を向いた曲線のことです。
曲面上の曲率線は一般に2つあって互いに直交するから、定理の系として以下のものが言える。
[系] 曲面上の曲率線網の球面表示は球面上において直交曲線網を作る。
[問題1]
曲面の方程式をz=f(x,y)とし
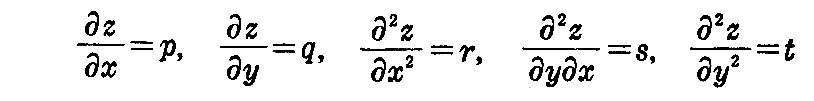
としたとき

であることを証明せよ。
[解] z=f(x,y)の第1基本量は2.(2)[問題2]により
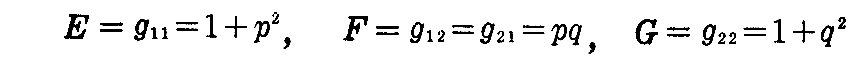
となる。
同じく2.(2)[問題2]により

だから、z=f(x,y)の第2基本量は
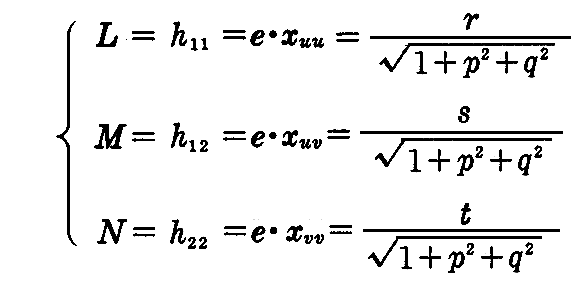
となる。
これら第1基本量と第2基本量を、2.(6)2.で説明した平均曲率Hと全曲率Kの表現式に代入すると
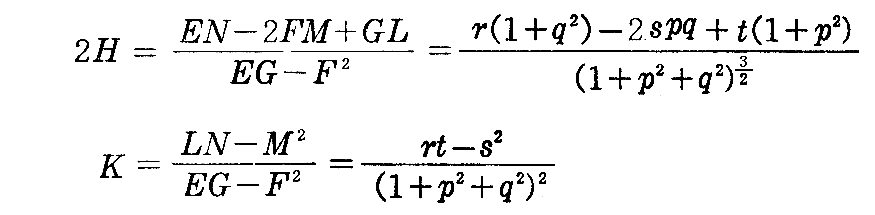
がえられる。
これら2H、Kと第1基本量、第2基本量を(2-96)、(2-97)、(2-98)式に代入すると、ただちに e=C11,f=C12,g=C22 の上記表現が得られる。
[問題2] 曲面S上の曲線の接触平面と、その曲線の球面表示像の接触平面は平行であることを証明せよ。
[解] 2.(5)[問題2]により球面上の点は臍点であるから

(12)包絡面
1.包絡面
1つの径数αに関係する曲面族 Sαが

で与えられている(図2-10)。

例えば (x-α)2+y2+z2-a2=0 はx軸上に中心をもつ半径 a の球面族を表す。
いまこの族に属さない曲面 S でその上の各点において曲面族 Sα のいずれかの曲面と接するとき、すなわち同じ接平面を持つとき S を曲面族の“包絡面”という。包絡面 S上の点P(x1,x2,x3)は定義よりいずれかの Sα 上にあるから、α の値を α(x1,x2,x3) で表わせば
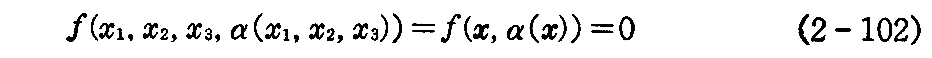
が成り立つ。
次に S と Sα とが接するための条件を求める。包絡面 S 上の曲線をP(t):x=x(t)とし

とおくと、任意の t に対して

が成立する。これを t について微分すると
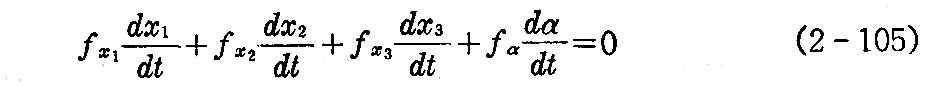
となる。t を固定すると曲面族の1つの曲面 Sα(t) と包絡面 S とは点 P(t) で接する。したがって曲線 x=x(t) の P(t) における接線は曲面 Sα(t) に接するから、曲線の接ベクトル(dx1/dt,dx2/dt,dx3/dt)は Sα(t) の法線ベクトル(fx1,fx2,fx3)に垂直です。故に
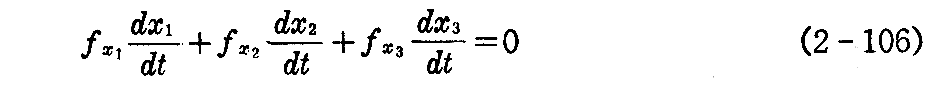
を満たす。したがって(2-105)式とから
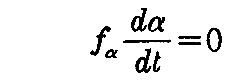
を得る。曲線の選び方は任意であるから、包絡面 Sの点P(x)に対して

となる。故に包絡面がもしあれば
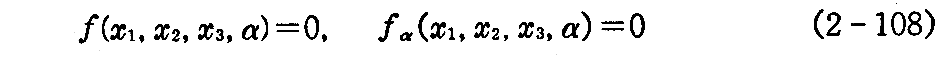
からαを消去して得られる方程式

が“包絡面の方程式”を与える。
逆に(2-108)式からαを消去した(2-109)式が常に包絡面を表すとは限らないが
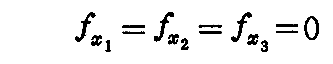
が成り立たないときは包絡面を与える。
2.特性曲線
曲面 Sα と曲面 Sα+Δα とが交わってできる曲線はそれぞれの方程式

を同時に満たす点の軌跡であるから、任意の点P(x)に対して、“平均値の定理”から
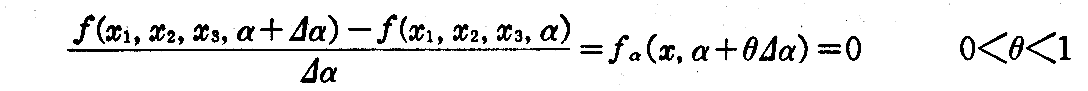
が得られる。
したがってΔα→0としたときの交線の極限の位置の曲線は
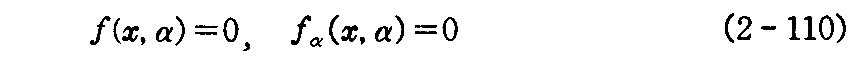
で与えられる。これを曲面族の“特性曲線”という。
特性曲線 Cαはそれに沿って曲面 Sα が包絡面に接する曲線です。そして包絡面 S 上で1径数の曲線族をなし、これらの曲線が包絡する曲線をもとの曲面族の“反帰(ソリカエリ)曲線”という。
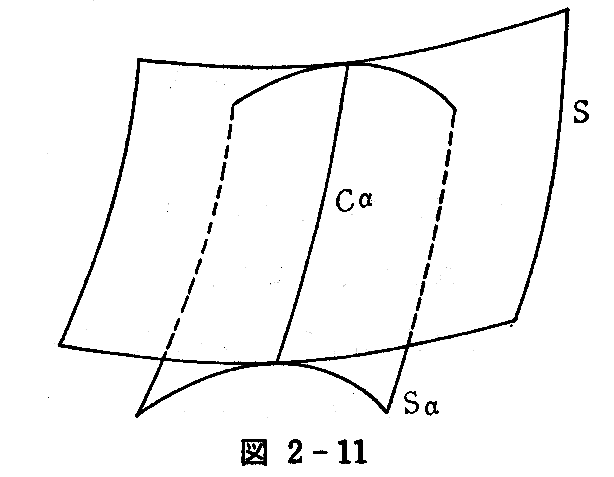
いま曲面族 Sαが反帰曲線 x=x(t) を持てば包絡面上の曲線だから(2-108)式を満たす。したがって
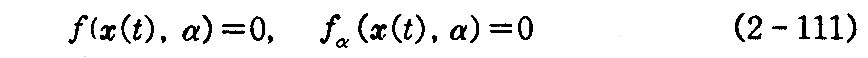
となる。
第2式を t について微分して
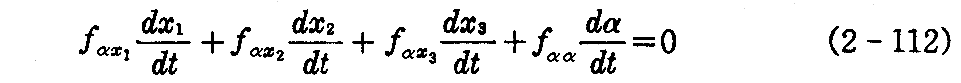
を得る。ここで1つの α に対する(2-111)式の接ベクトルと同じαに対する特性曲線 Cα の接ベクトルは一致するから(2-111)式の第2の方程式から
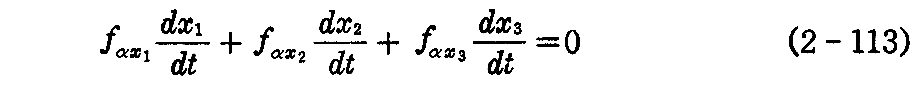
が成り立つ。故に(2-112)式とから
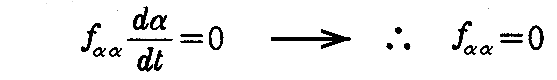
を得る。よって反帰曲線 Cαは
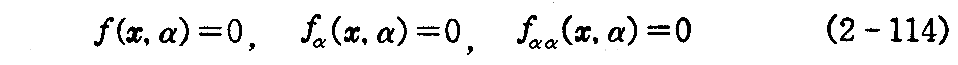
から α を消去して得られる。
[例題1] 空間曲線 x=x(s) の法平面[1.(5)2.を参照]の包絡面の方程式と、反帰曲線を求めよ。
[解]
“法平面の方程式”において s を径数と考えれば法平面族
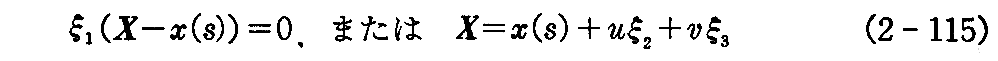
が得られる。
この平面族の包絡面の方程式を求めるために、まず s で微分すると
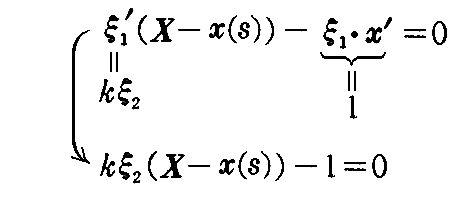
となる。 曲率 k≠0 とすれば
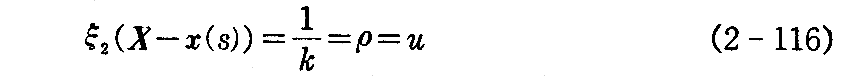
となる。よって法平面族の包絡面の方程式は

となる。
この場合の“特性曲線”は曲率中心 x(s)+ρξ2 を通り、従法線 ξ3に平行な直線すなわち曲率軸です。2.(3)[例題1]により曲率軸によって包絡される曲面は曲率軸曲面であるから法平面族の包絡面は“曲率軸曲面”であるといえる。
次に、反帰曲線を求めてみよう。(2-116)式を s について微分して

を得る。これに(2-117)式を代入すると

となる。
故に

が得られる。1.(9)2.の(1-73)式から解るように、これは曲線のx(s)における接触球面の中心を表している。よって“反帰曲線”は接触球面の中心の軌跡で、曲率軸曲面は接触球面の中心の描く曲線の接線曲面[2.(3)1.を参照]であることが解る。
[例題2] 曲面族

の包絡面を求めよ。ただし、a,rは定数、αを曲面族を規定する径数とする。
[解] 球面族の方程式
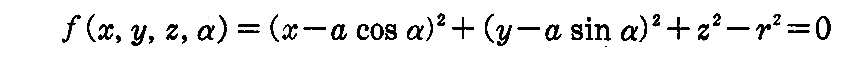
をαについて偏微分すると

となる。
これと、原方程式から α を消去するために

と置いて、原方程式に代入すると
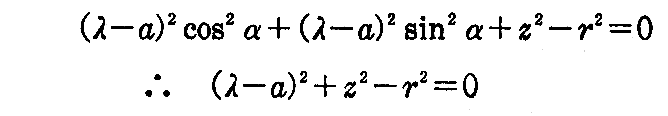
となる。これと
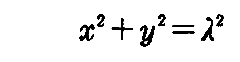
から λ を消去して
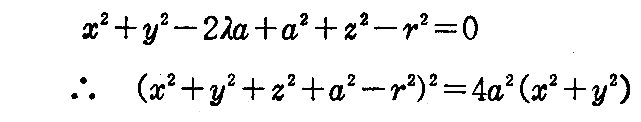
が包絡面の方程式です。
ここで
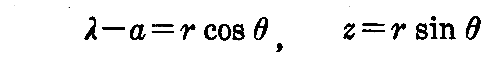
とおけば
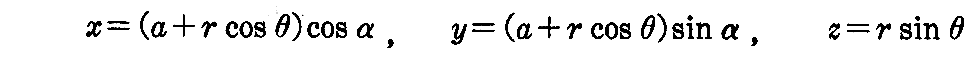
なる径数表示が得られる。これは2.(2)[問題3]により“輪環面”の方程式であることが解る。つまり包絡面は輪環面となる。
[問題1] 空間曲線の接触平面族の包絡面を求めよ。接触平面に関しては1.(6)1.を参照。
[解] ここでは s が曲面族を規定する径数 α であることに注意して

すなわち、接触平面族の包絡面は“接線曲面”[2.(3)1.参照]です。
[問題2] 空間曲線の展直平面族の包絡面とその反帰曲線を求めよ。展直平面に関しては1.(6)2.を参照。
[解] ここでは s が曲面族を規定する径数 α であることに注意して
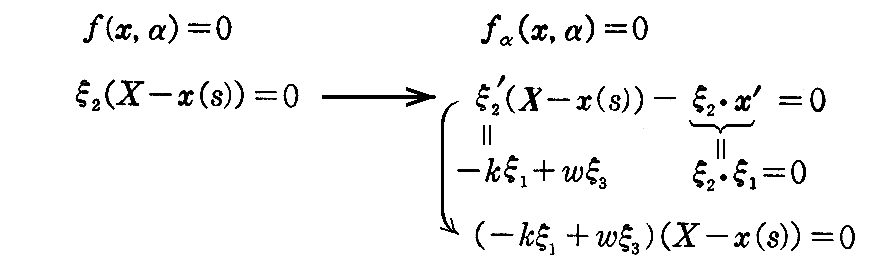
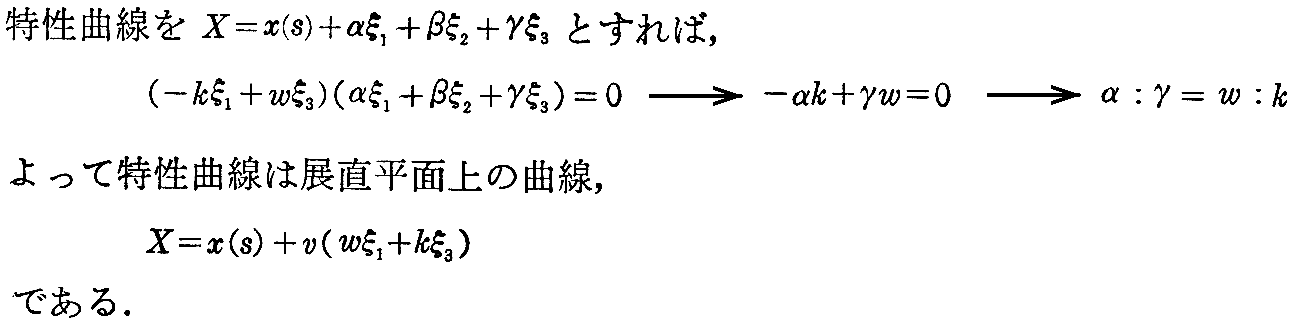
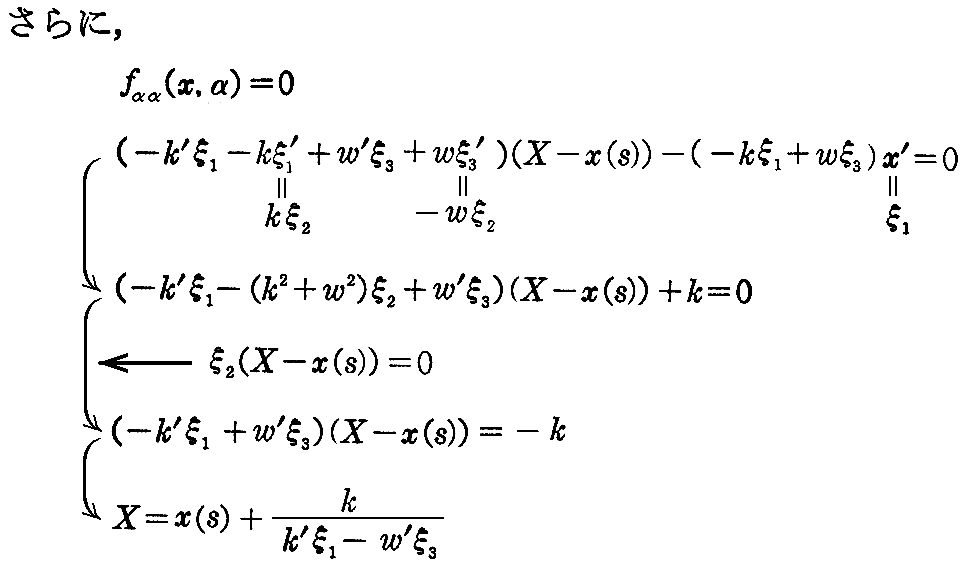
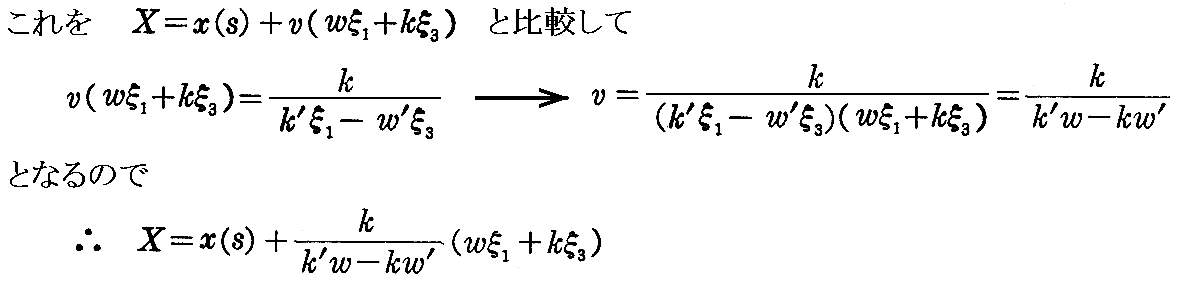
を得る。これは展直平面族の反帰曲線だから、この曲線の接線曲面が包絡面です。
(13)線織面
1.線織面
一般に空間の直線の運動によって描かれる曲面を“線織面”(センシキメン)といい、それぞれの直線を“母線”という。柱面、錐面、接線曲面[2.(3)1.参照]等はその例です。線織面は径数 s の空間曲線x=x(s)上の各点から単位ベクトル a(s) の方向へ引いた直線によって得られるものとすれば“線織面の方程式”は
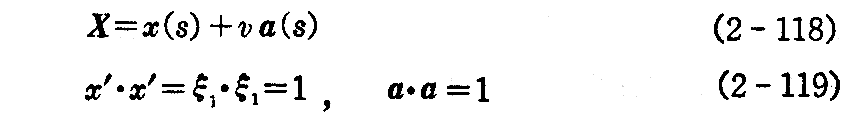
で与えられる。v,sは曲面を表す径数です。
線織面の径数 s に関する曲線x=x(s)の接線ベクトルは

となるから、その法線方向のベクトルは2.(2)2.の(2-8)式によって
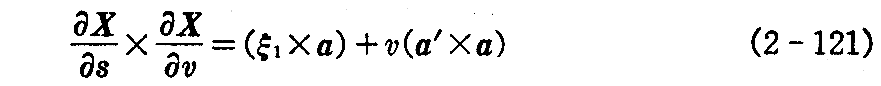
で与えられる。したがって法線方向はa’×a≠0 のときは径数 v にも関係するから、1つの母線に沿ってその上の各点で異なった方向を取る。したがって線織面の接平面も1つの母線に沿ってその上の各点で異なる。
しかし1つの母線に沿ってその上の各点で接平面が常に同一である場合には、1つの径数に関係する接平面族の包絡面と考えることができる。このような線織面は延び縮みさせることなく平面上に展開することができる。このような面を“可展面”というが、そのための条件を求めてみよう。
上記(2-121)式の法線方向のベクトルが v に関係なく同じ方向を持つこと、すなわち2つのベクトル ξ1×a と a’×a とが、1次従属
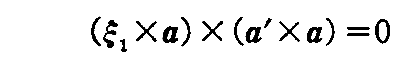
であればよい。つまり、1.(1)[問題4]によって

となればよい。
故に次の定理を得る。
[定理]
線織面(2-118)式が“可展面”であるための必要十分条件は、

なることです。ただし、ξ1=x’(s), a・a=1 です。
2.可展面
次に、可展面にはどんな曲面があるか調べてみる。まず条件(2-122)式は3つのベクトル ξ1,a’,a が一次従属であることを示しているので

を満たす(同時に 0 でない)3つの s の関数λ,μ,νが存在する(1.(1)9.参照)。
(1)λ=0 の場合
(2-123)式と a の内積をとって、a・a’=0, a・a=1 に注意すれば、ν=0が求まる。しかし条件から残りの1つのμはμ≠0でなければならない。そのため

となって線織面の母線が常に定方向を持つから λ=0 の場合は“柱面”を表す。
(2)λ≠0 の場合
(2-123)式は、
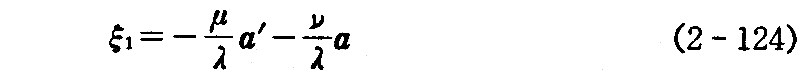
と書ける。一方において(2-118)式を
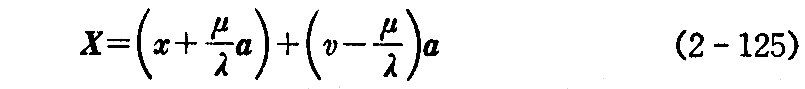
と書き直し、

とおけば“線織面の方程式”(2-125)式は、
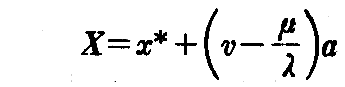
となる。
(2-126)式を s について微分して(2-124)式を用いれば
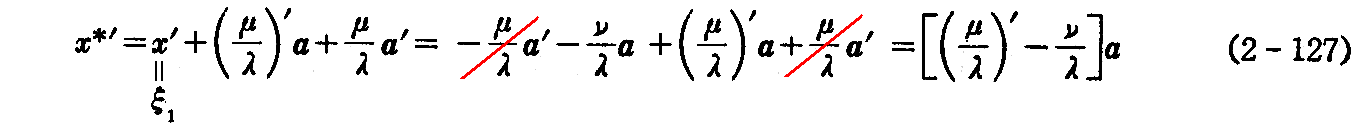
と表すことができるから次の2通りの場合が考えられる。

線織面の方程式は、v-μ/λ≡u と置いて、

の形となり、しかもx*’=0 → x*=一定 であるから線織面は x* を頂点とする“錐面”となる。
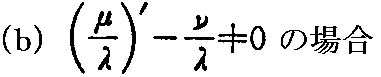
(2-127)式から、

となるから、
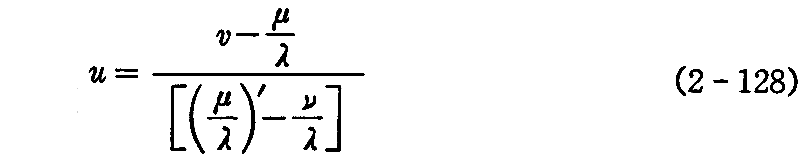
と置けば、線織面の方程式は
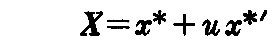
の形になる。したがってこの場合には線織面は曲線x*(s)の“接線曲面”となる。
以上をまとめると
[定理] 可展面は柱面、錐面、接線曲面のいずれかです。
最後に接線曲面は長さを変えずに平面上に展開できる事を示しておく。
2.(3)1.(2-16)式から接線曲面のs曲線はy(s)の伸開線で、v曲線はy(s)の接線です。故に
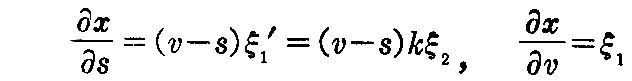
であるから接線曲面(2-16)式の線素をdσとすれば、(1-52)式によって線素は
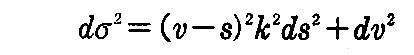
で与えられる。

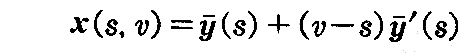
で与えられ、2つの係数 s と v とによりこの交点x(s,v)は一意に定まるからx1x2平面の曲線座標と考えられる。
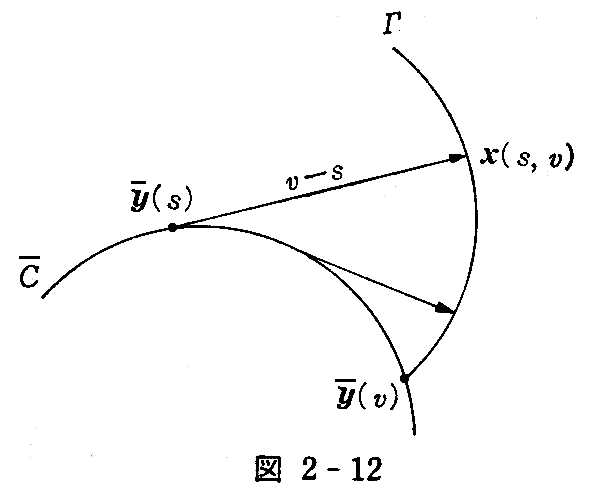
この平面上での線素をdσ1とすれば容易に
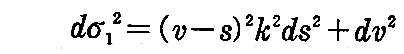
であることが示せる。
このことは接線曲面は1つの平面上に展開できるという性質を持っている。柱面、錐面についてはその作り方から以上のことは明らかです。
線織面の第2基本量は(2-20)式と(2-118)、(2-120)、(2-121)式によって

です。
v曲線、すなわち各母線は主接線曲線(2.(4)2.参照)です。しかも“ガウスの全曲率”は
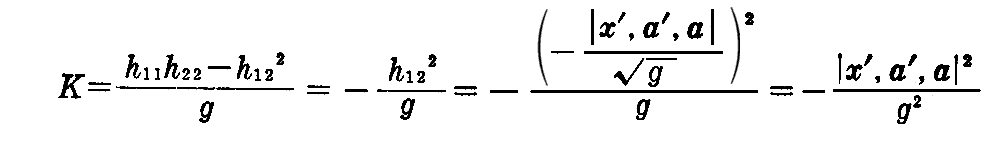
であるから、先の定理とこの式によって、次の定理を得る。
[定理] ガウス曲率(全曲率)Kが 0 の曲面は“可展面”です。
[例題] 直線

は可展面を描くことを示せ。
[解]
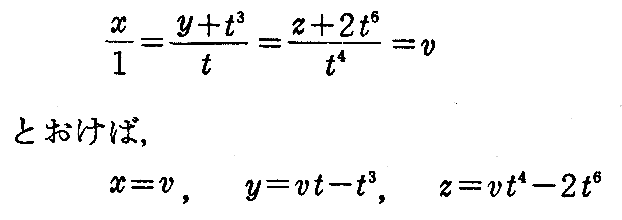
(2-118)式に於いて
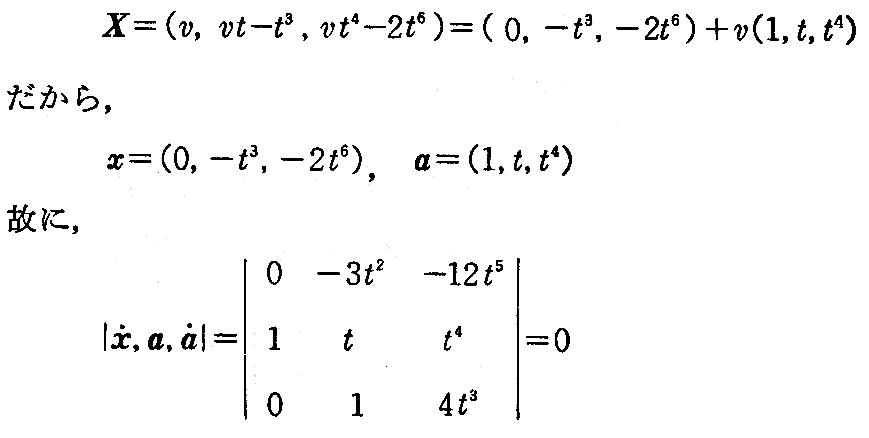
定理によって可展面を描く。
[問題1] 直線 y=tx-t3,z=t3y-t6 は可展面を描く事を示せ。
[解]

[問題2] 曲面 x=a(cos t-v sin t),y=a(sin t+v cos t),z=b(t+v) は可展面を描く事を示せ。
[解]

(14)測地的曲率
1.測地的曲率
この節では、2.(5)“曲面の曲率”で定義した“測地的曲率”kg についてさらに詳しく論じる。
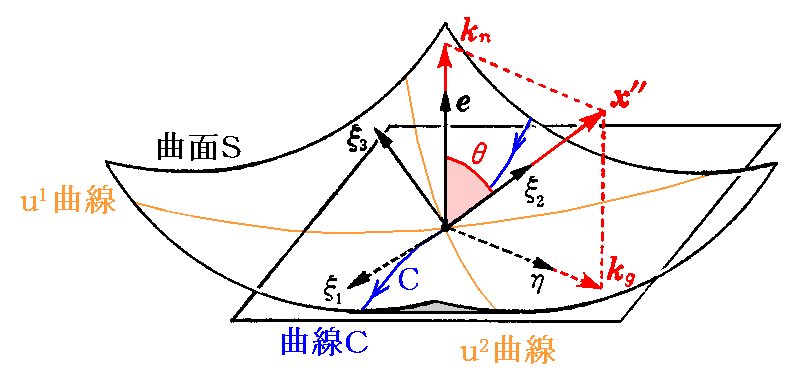
曲面S:x=x(u1,u2) 上の曲線Cを弧長 s を径数として

と表すことにする。
2.(5)における様に 曲率ベクトル x”=kξ2 は測地的曲率ベクトル kg=(x”・η)η と 法曲率ベクトル kn=(x”・e)e の直和に分解される。すなわち

です。
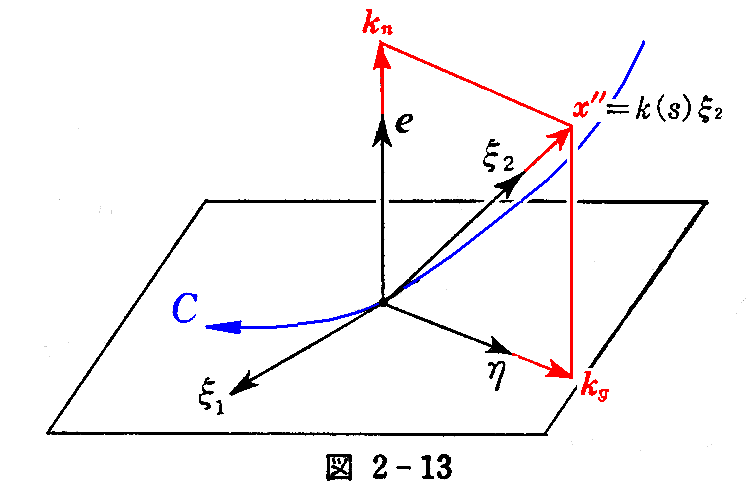
ここで“測地的曲率” kgを与える式を求める。まず(2-26)式と(2-22)式を用いて
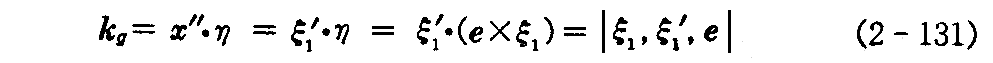
を得る。
また、曲線Cに沿って成り立つ式2.(5)1.の(2-24)式に、ガウスの方程式(2-64)式を適用すれば

が成り立つ。
ここて、x”=ξ1’であることと、曲線 C の単位接ベクトルは x’=ξ1=xidui/ds であることから、(2-131)式は(2-8)と(2-14)式を考慮して
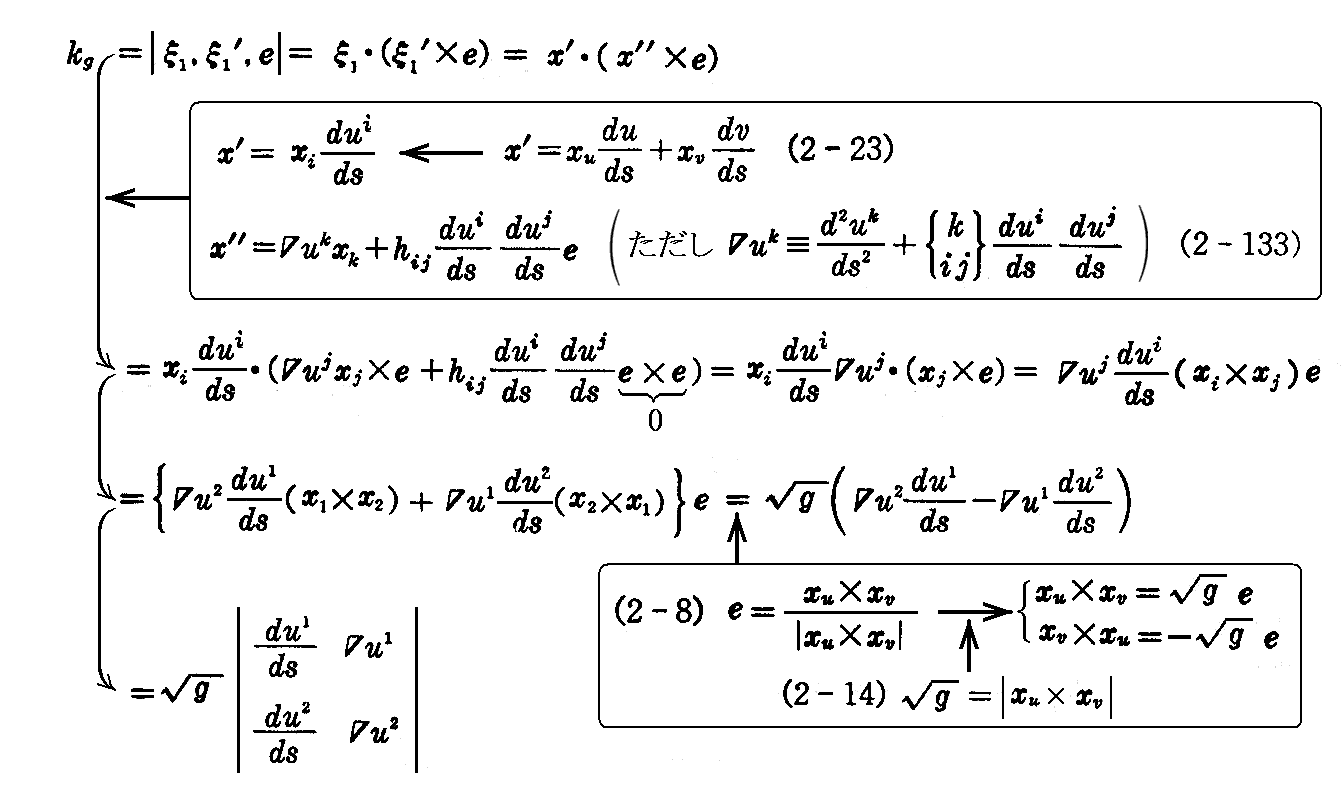
となる。
(2-134)式によって元にもどせば、“測地的曲率” kg は

で表される。
[補足説明]
“測地的曲率”kg の意味はなかなか解りにくいが、曲線Cが存在する曲面の(その点における法線ベクトル[2.(2)2.参照]に垂直な)接平面上に、その曲線Cを空間曲線と見なしたときの主法線ベクトル[1.(6)2.参照]を射影したものを見ていることになる。
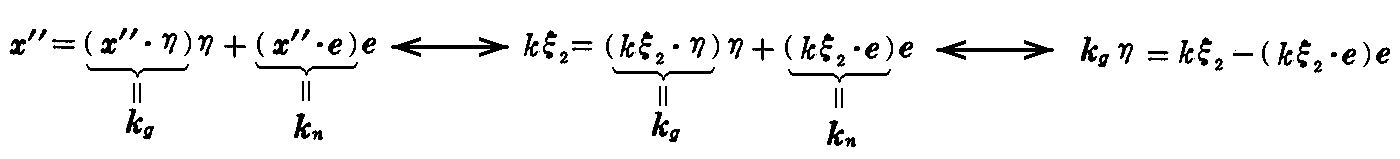
つまり曲線Cが存在する曲面自体の曲がり具合を取り除いた曲線の曲がり具合の事です。
その事が理解できれば、“測地的曲率”kg が至る処で 0 の曲線Cをその曲面の測地線と言うことも納得できる。
2.測地線
測地的曲率kgの定義から2つの曲面が1つの曲線に沿って接しているとき、この曲線の各点において、両曲面は接平面[2.(2)1.参照]を共有するから両曲面が接している曲線に沿っての測地的曲率kgは等しい。
測地的曲率 kgが 0 であるような曲面上の曲線を、その曲面の“測地線”という。
その定義から解るように、曲面上の曲線が“測地線である条件”は(2-135)式より
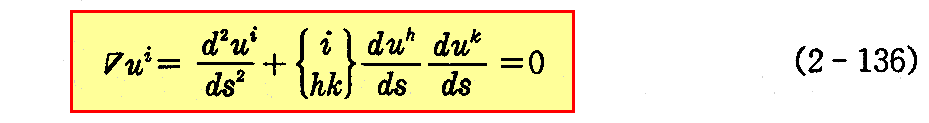
を満足することです。
このことはまた曲線 C の主法線ベクトル ξ2 が曲面の法線ベクトル e と一致する(次で証明)ことを示しているから、次の定理を得る。
[定理]
曲線上のすべての点での“主法線”[1.(6)2.を参照]の方向が、常に曲面の“法線”[2.(2)2.を参照]に一致するような曲線は、その曲面上の“測地線”である。
あるいは、曲面上の曲線Cが“測地線”であるための必要十分条件は、それが直線であるか、またはその上の各点における“接触平面”[1.(6)1.を参照]が、その点で曲面の“接平面”[2.(2)1.を参照]と垂直であると言ってもよい。
[証明]
測地線の条件式(2-136)式を(2-133)式に代入すると
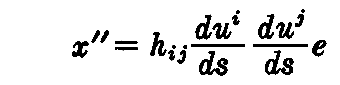
となる。
ここで
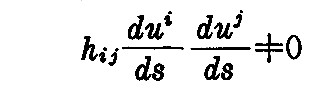
ならば、x”=kξ2であるから
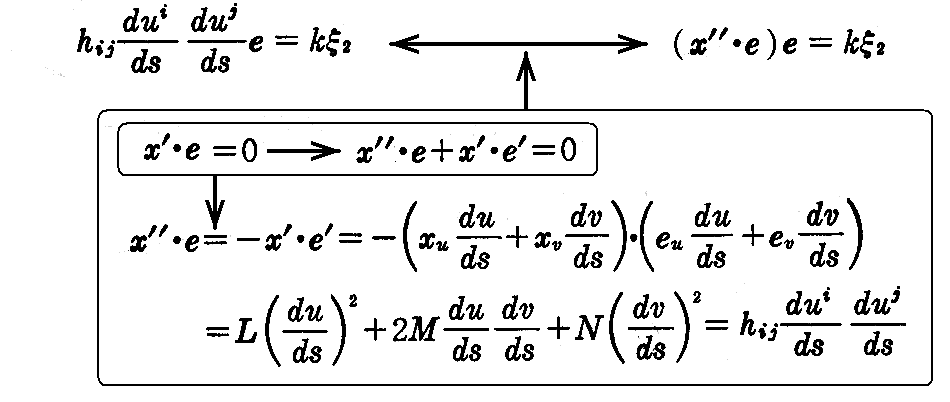
すなわち、主法線ベクトル ξ2が接平面の法線ベクトル eの方向と一致する。故に、曲線 C上の点における接触平面は接平面に垂直となる。
また、
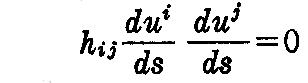
ならば
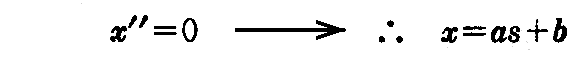
となり、Cは直線となる。
逆も明らかです。
[証明終わり]
[補足説明]
上記(2-136)式は一般相対性理論に於ける“4次元リーマン時空”においても測地線を正しく表現する式です。別稿の第5章§4参照。
[例題1] 曲面上の径数曲線が直交するとき、曲面上の曲線Cがu曲線となす角をθとすれば、その測地的曲率 kgは
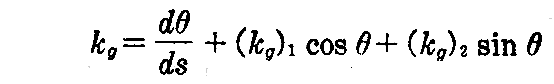
で与えられる事を示せ。ただし、(kg)1,(kg)2はu曲線、v曲線の測地的曲率を表す。
これを“モンジュの公式”という。
[解] 径数曲線が直交するから
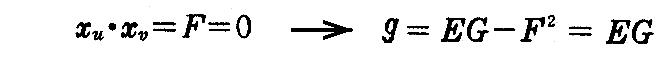
です。故に2.(8)[問題1]によって
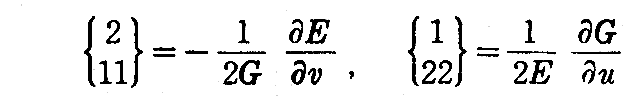
です。
次に、u曲線について s1 をその弧長とすると2.(2)3.の(2-10)式から

であるから、(2-135)式より
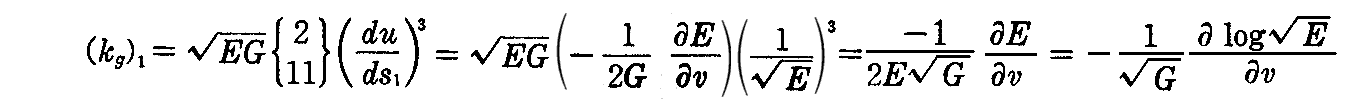
となる。
さらにv曲線については s2 をその弧長として
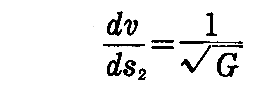
であるから、(2-135)式より
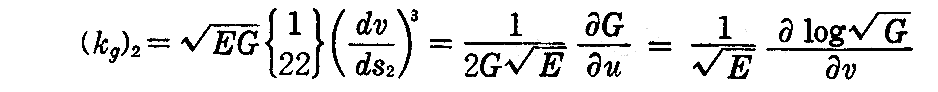
を得る。
u曲線、v曲線の単位接線ベクトルを t1,t2 とすれば
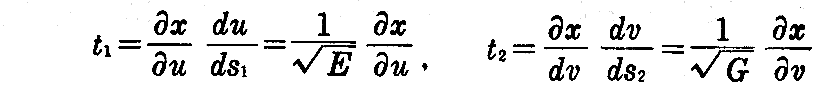
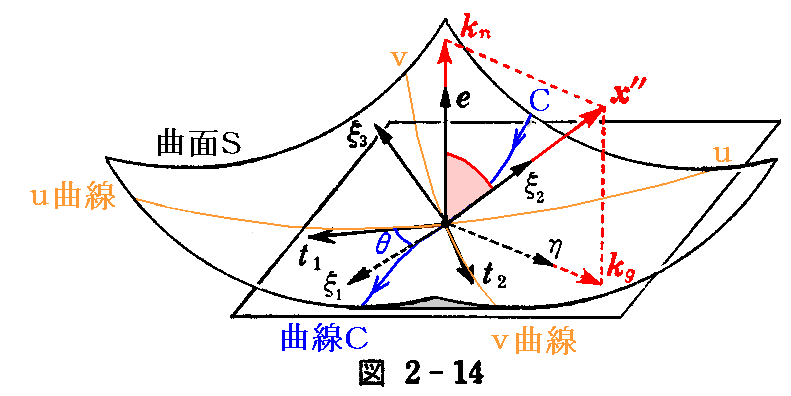
この場合、径数曲線が直交するという仮定から t1,t2,e は右手系をなすから
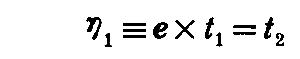
となる。よって2.(5)2.の(2-26)式から、そこのηをη1に、x”をdt1/ds1に読み替える事によって
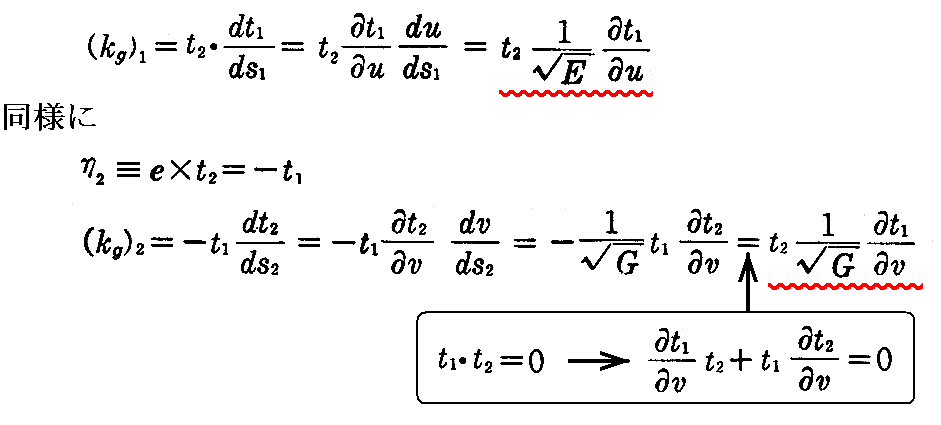
曲線Cがu曲線となす角をθとしているので
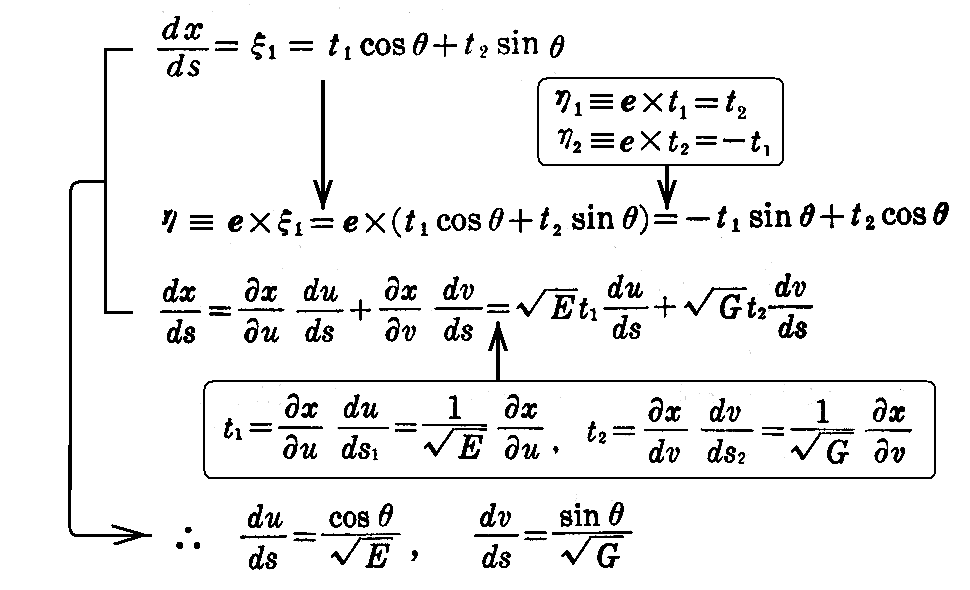
となる。これを用いると

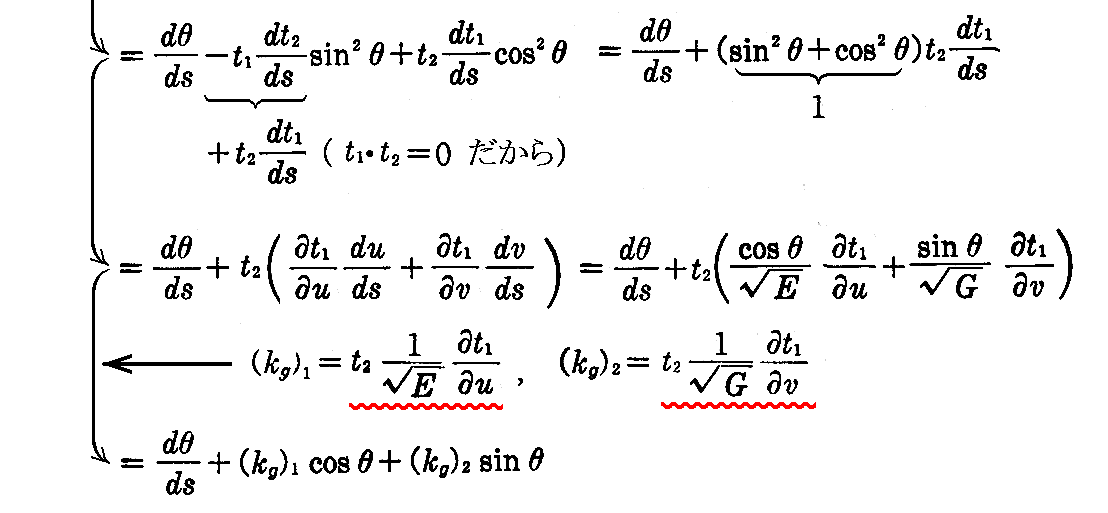
となる。
[例題2] 回転面の線素が ds2=du2+φ2(u)dv2 であたえられているとき、測地線の方程式は
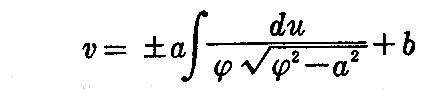
で与えられることを証明せよ。
[解]
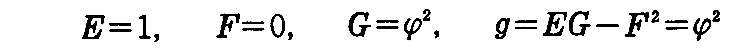
であるから、2.(8)[問題1]によって、∂φ/∂u≡φ’と書くことにすると
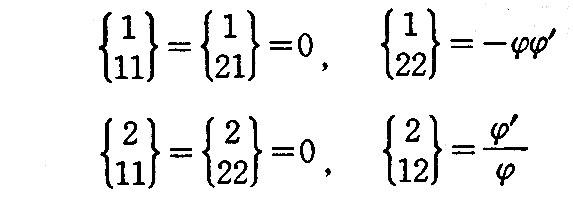
故に、(2-136)式によって測地線の微分方程式は

となる。
いま第2式において

とおけば、第2式は
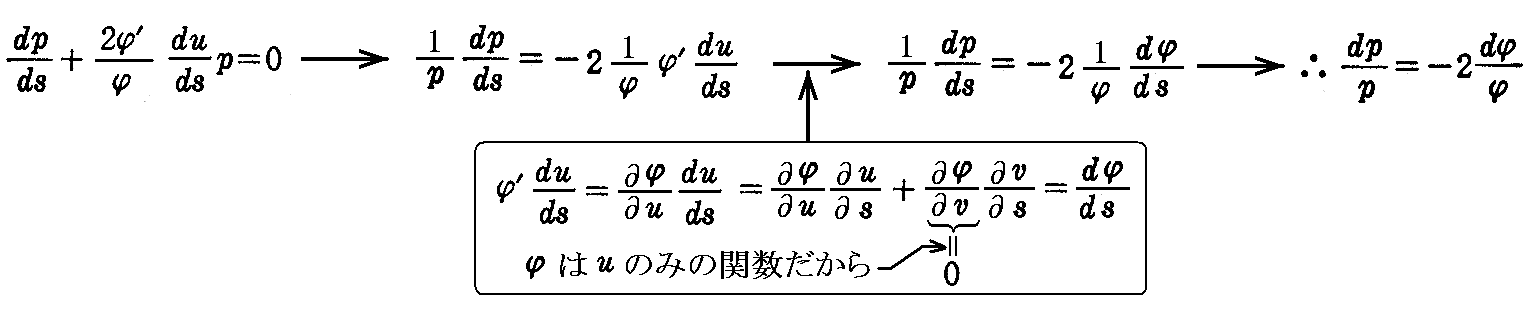
となるから
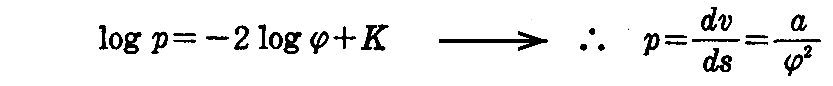
を得る。これと線素の式 ds2=du2+φ2(u)dv2 からdsを消去すると
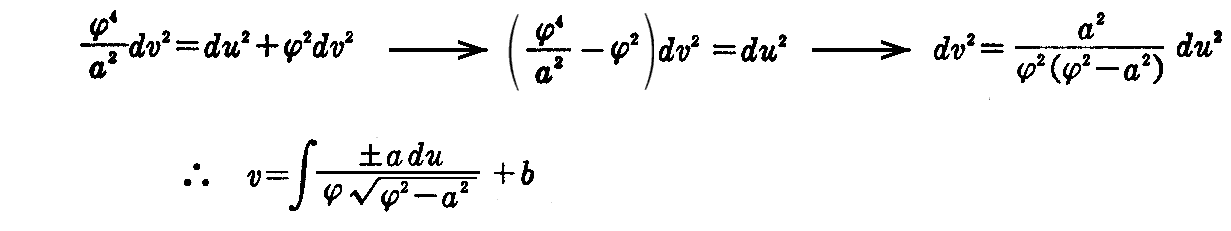
を得る。
[問題1] 球面上の大円の測地的曲率は0であることを示せ。
[解]

[問題2] 球面上の小円の測地的曲率は一定である事を示せ。
[解]
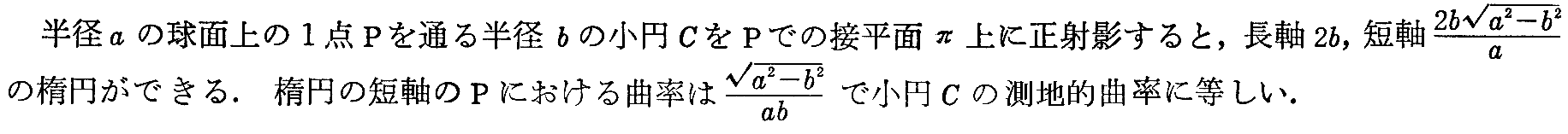
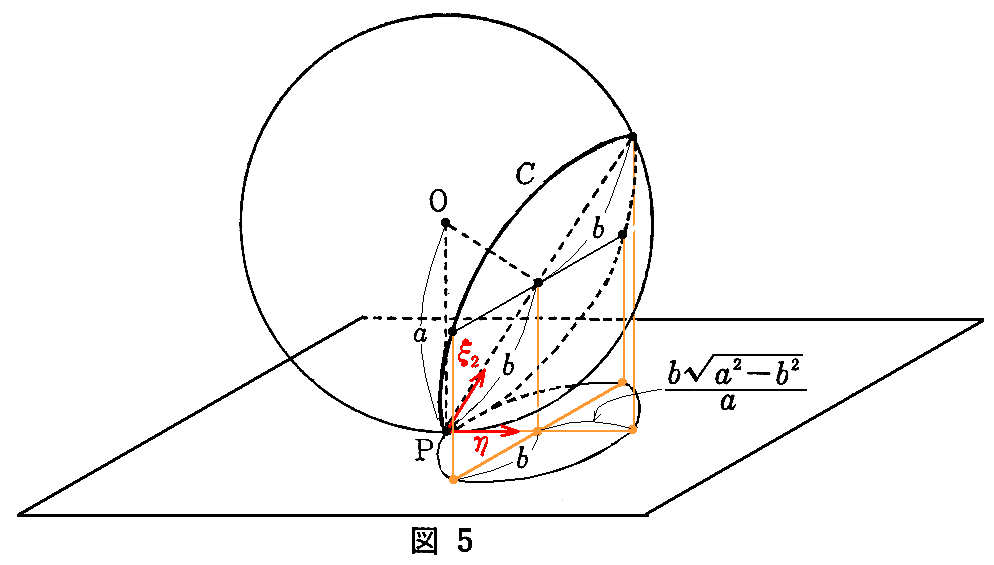
小円曲線CのPに於ける曲率半径はρ=bであるから、小円CのP点に於ける曲率はk=1/ρ=1/bとなる。
故に小円CのP点に於ける測地的曲率 kgは、ξ2とηが図中に示した方向を向く単位ベクトルであることに注意して、(2-131)式から
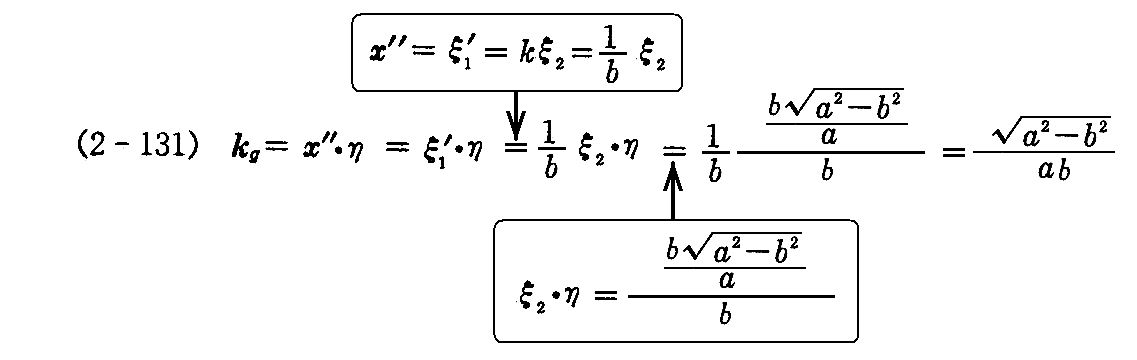
と得られる。
[補足説明]
いま下図の様な楕円のP点に於ける曲率を求めてみる。
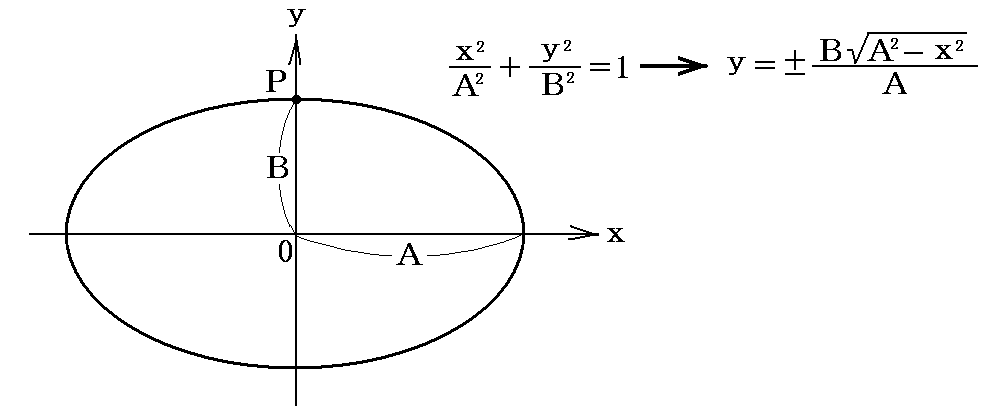
ちなみに平面曲線に於ける曲率と曲率半径はこちらで与えられます。 y’とy”を求めて公式に代入し、P点での座標値(0,B)を用いると、P点に於ける曲率は
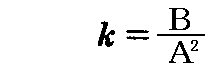
となります。所で今は
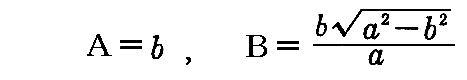
ですから、これらの置き換えをすると、最初の図の小円Cを接平面上へ射影した楕円の短軸のP点における曲率は
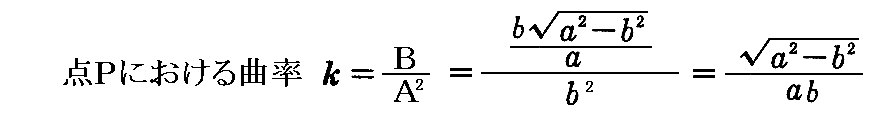
となります。つまり球面上の小円曲線Cの“測地的曲率”は、それを接平面に射影した楕円のP点における“曲率”に等しい。
[問題3] 2.(2)[例題1]で説明した回転面

の測地線を求めよ。
[解] 2.(2)[例題1]で求めたように
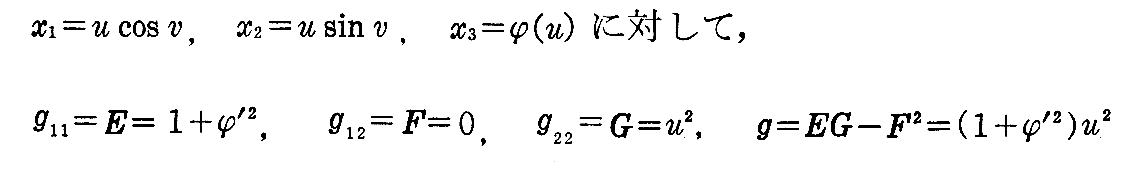
となる。ただし、ここでは∂φ/∂u≡φ’と置いている。
これらを2.(8)[問題1]の結論に適用して
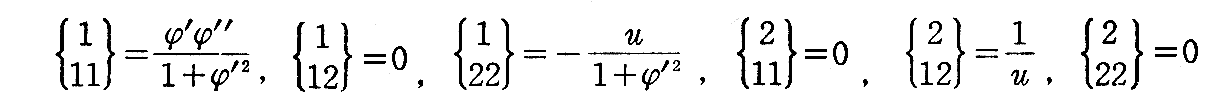
が得られる。
故に、(2-136)式によって測地線の微分方程式は
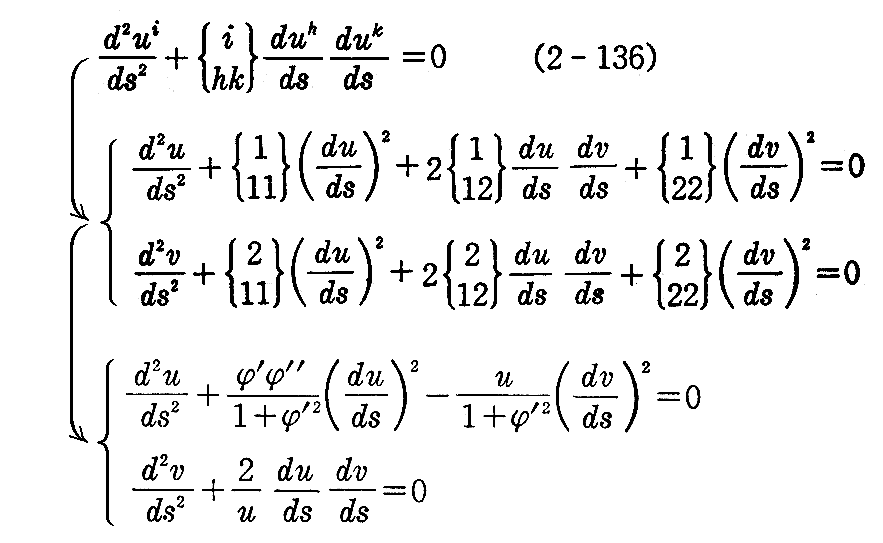
となる。この第2式に於いて
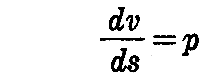
と置くと、第2式は
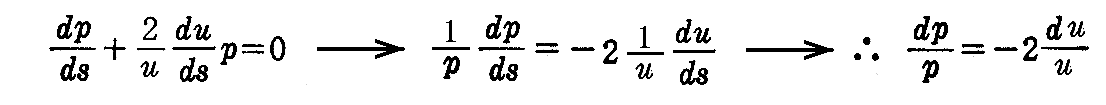
となるから
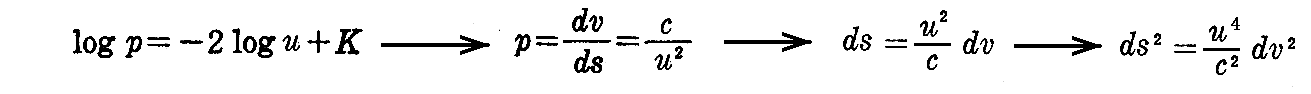
が得られる。これと線素の式 ds2=(1+φ’2)du2+u2dv2 からdsを消去すると
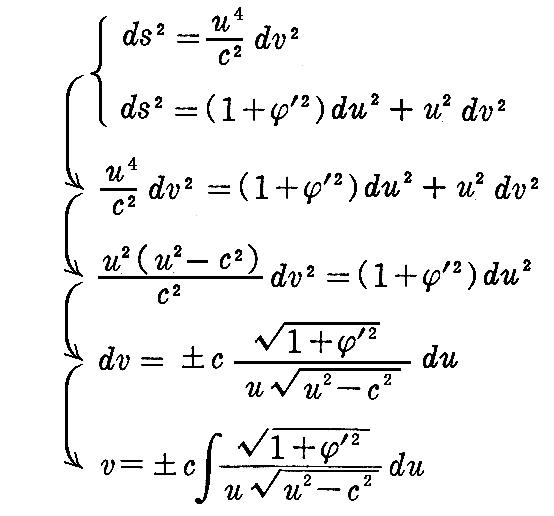
が得られる。
(15)測地的捩率
1.測地的捩率
曲線S上の曲線Cのフルネ標構を x(s)ξ1ξ2ξ3 、曲率を k(s) 、捩率を w(s) とする。
曲面上の1点x(s)における 主法線 ξ2 と曲面の 法線 e とのなす角を θ とすると
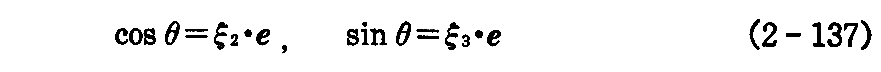
が言える。
(2.(5)1.図2-6あるいは2.(14)1.の図を参照)
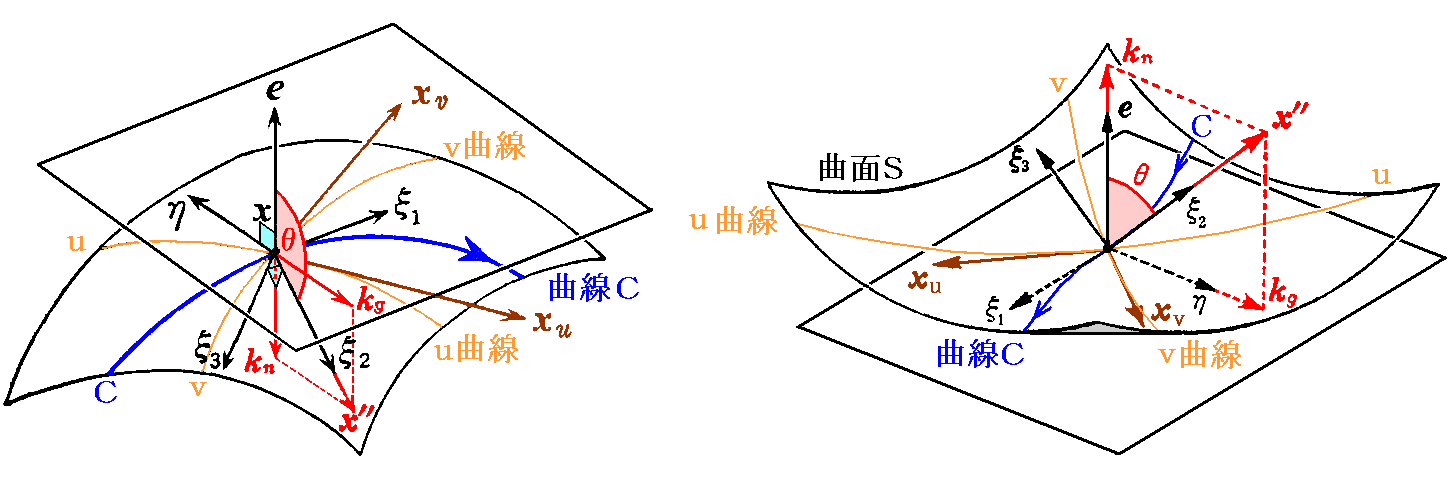
(2-137)の第2式を s について微分し、1.(7)3.のフルネ・セレーの公式を用いれば
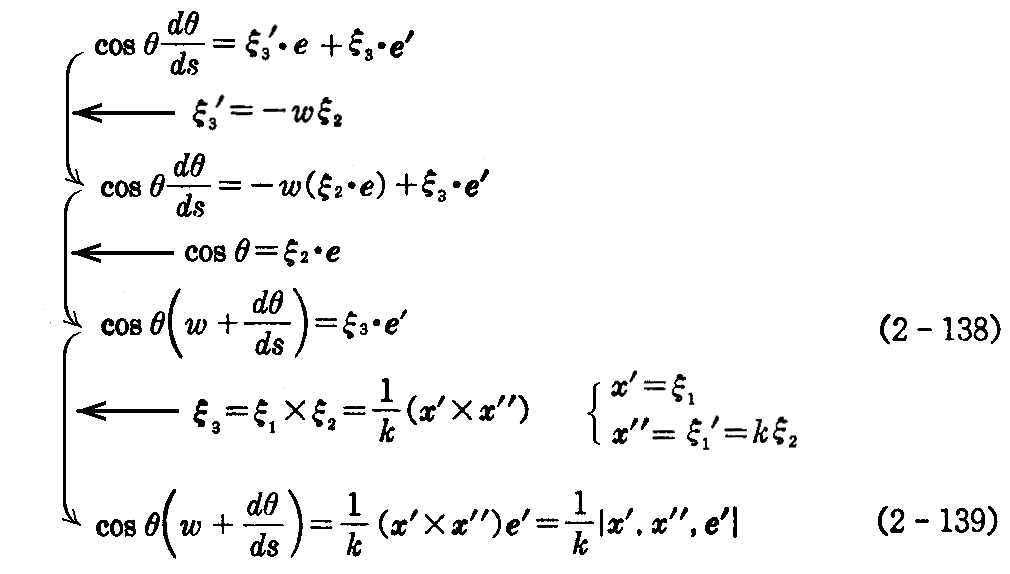
となる。
ここで、2.(5)1.の(2-24)式から
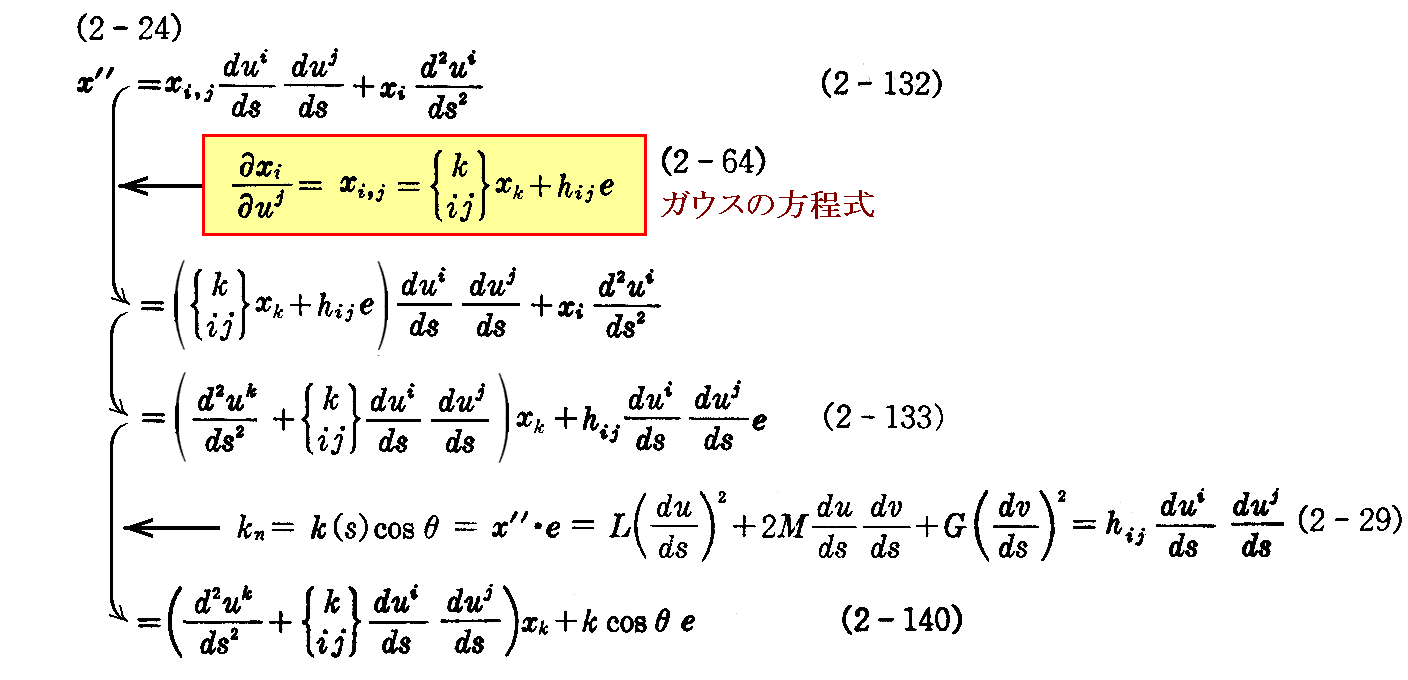
が成り立つ。
さらに、2.(8)4.の(2-68)式から
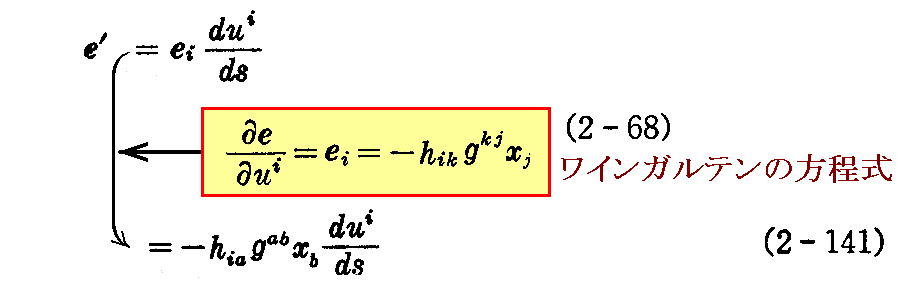
が成り立つ。
(2-140)、(2-141)式を(2-139)式に代入すれば
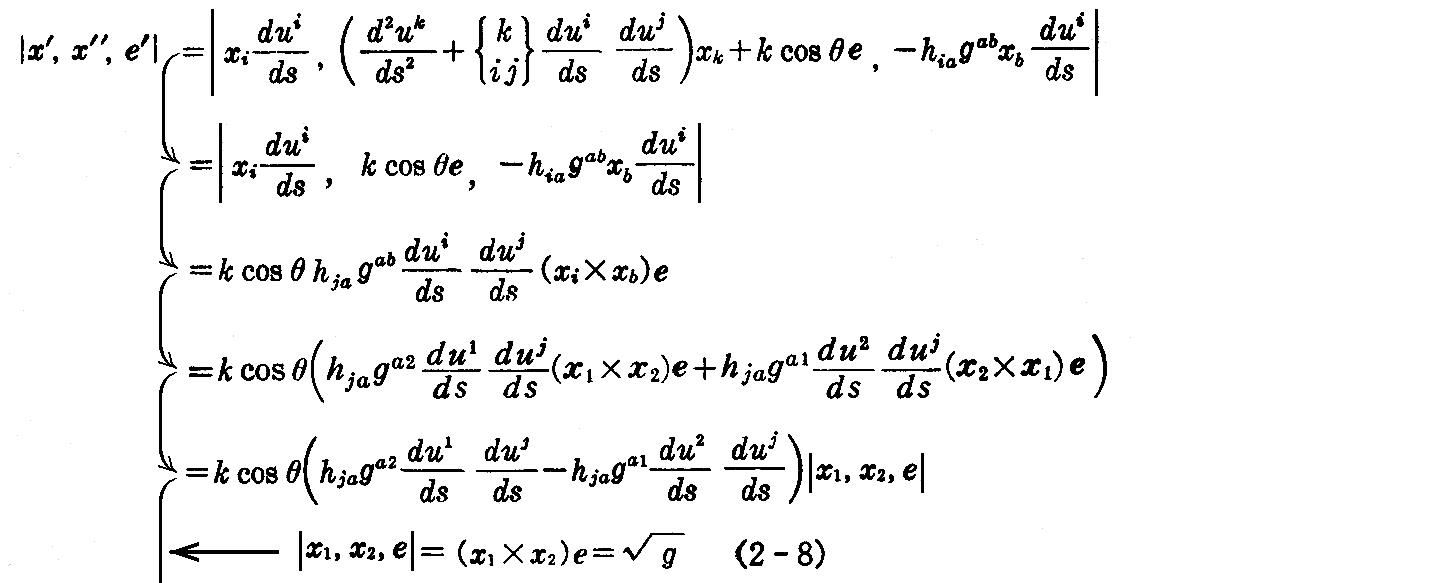
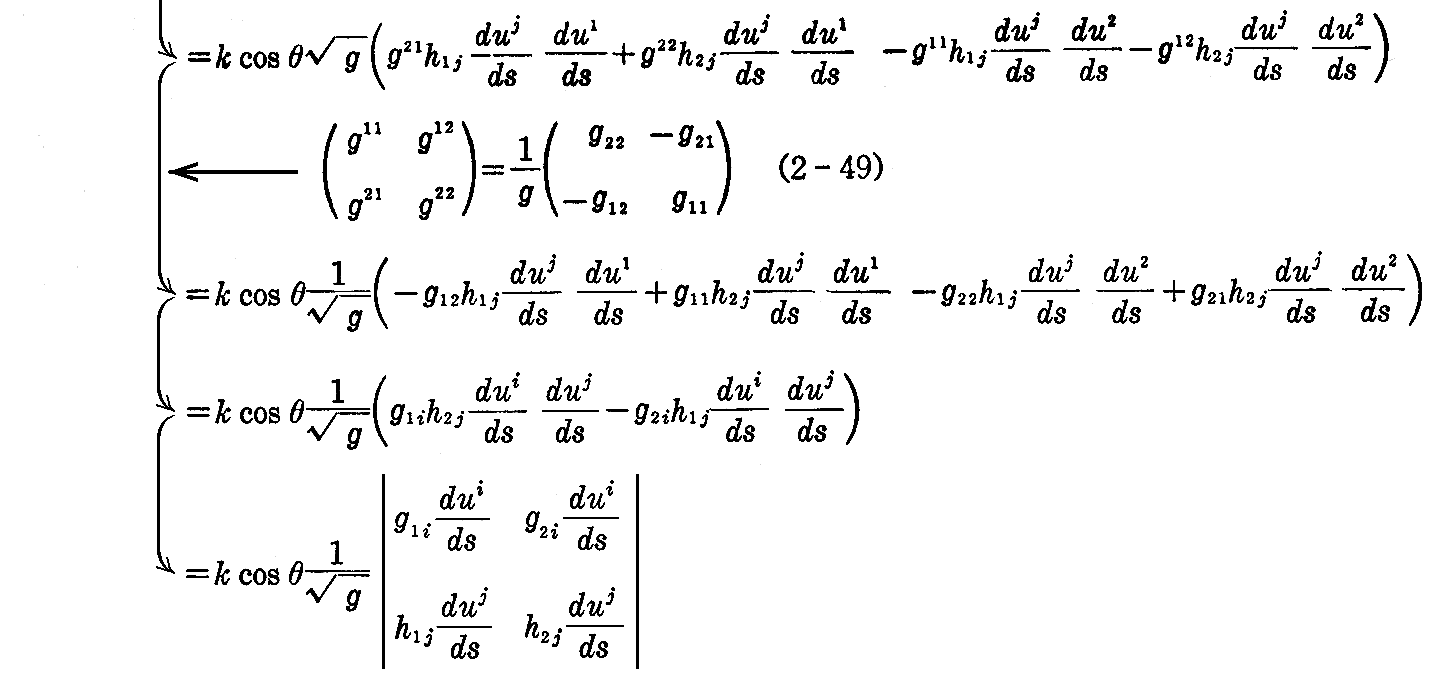
となる。
これを(2-139)式と比較して

を得る。
これを普通の記号に直して書けば
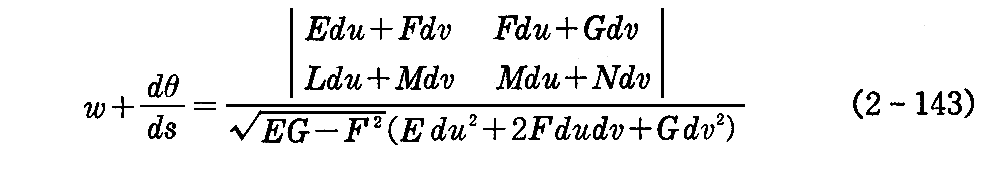
となる。(2-143)式で与えられる量を曲線Cの“測地的捩率”という。
(2-143)式から明らかなように測地的捩率は曲線Cの方向 du:dv のみで定まる量です。したがって次の定理が得られる。
[定理1] 曲面上の1点において1つの直線に接する曲線の“測地的捩率”は一定です。
さらに測地的捩率の定義の仕方から次の定理が得られる。
[定理2] 2つの曲面が定角をなして交わるとき、その交わりの曲線は両曲面上で同じ“測地的捩率”を持つ。
[例題1] 曲面上の曲率線を径数曲線にとれば、測地的捩率が0になるのは、径数曲線の方向、すなわち曲率線の方向に限ることをとを示せ。
[解] 曲率線を径数曲線にとれば、F=M=0であるから、(2-143)式は
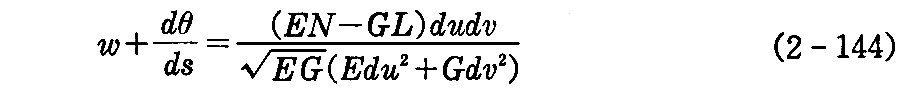
となる。したがって平坦点でも臍点でもなければ測地的捩率が 0 となるのは du=0 または dv=0 のときに限る。すなわち径数曲線がこの場合は曲率線のときです。このことを言い換えれば曲率線は測地的捩率が常に 0 である曲線であると言える。
[例題2] 曲率線を径数曲線とする曲面上において、曲線Cがu曲線となす角を φ とすれば測地的捩率が最大又は最小になるのは、φ=π/4 または φ=3/4π のときであることを証明せよ。
[解] 仮定からF=M=0であるから、2.(6)2.の(2-40)、(2-41)式は

となる。したがって
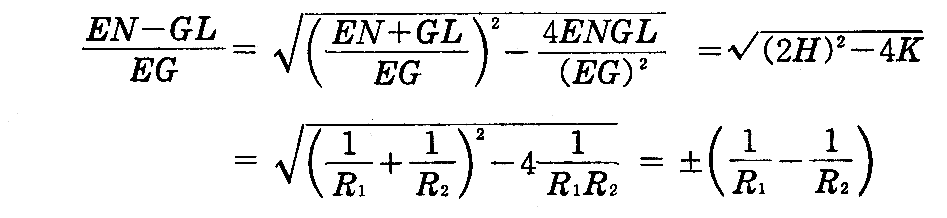
です。これを(2-144)式に代入して
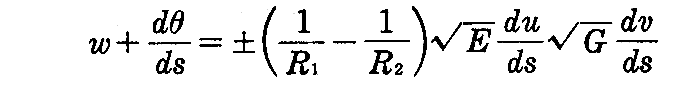
を得る。
曲線Cがu曲線となす角がφだから2.(14)[例題1]で求めたように
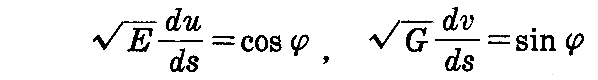
であるから
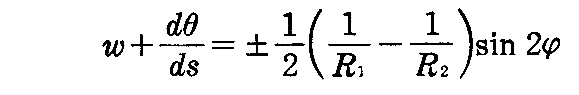
と表すことができる。故に測地的捩れ率が最大または最小となるのはφ=π/4(この場合はsin2φ=1)、またはφ=3/4π(この場合はsin2φ=-1)のときです。曲率線は互いに直交するから曲率線を2等分する場合です。この様に接線がその点での曲率線の方向を2等分するような曲線を“捩率線”という。
[問題1] 曲面上の2つの曲線が直交すれば、その交点における測地的捩率の和は0であることを証明せよ。
[解]
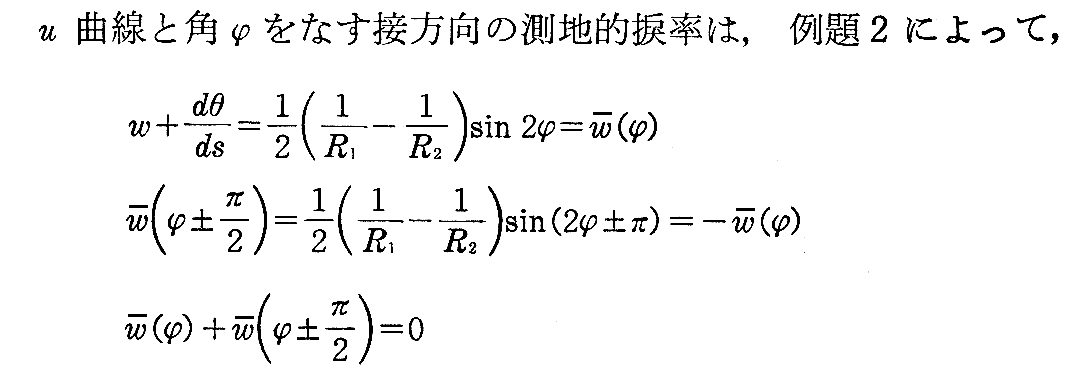
[問題2] 曲面が平面又は球面と定角で交わるとき、その交線はこの曲面の曲率線であることを証明せよ。
[解]

END(参考文献)
本稿(第2章)も文献1.を参考にしました。この章は第3章で必要となるテンソル解析の記号になれる事を考慮して書かれておりとても教育的です。本稿では、さらに解りやすくするために、文献2.、3.を参考にしてかなり改変しています。正しく改変できていれば良いのですが。
- 前田儀郎著「幾何学Ⅴ・Ⅵ(微分幾何学」玉川大学通信教育部(1969年初版刊)2章“曲線論”
これは文献2.を参考にして書かれています。解りやすくなるように工夫されていますが、省略もかなり在ります。 - 大槻富之助著「微分幾何学(朝倉数学講座15)」朝倉書店(1961年刊)
文献1.とほぼ同様な展開です。文献1.はこの本を参考にして書かれています。 - 大槻富之助著「微分幾何学演習(朝倉数学講座16)」朝倉書店(1961年刊)
文献2.と対になった演習書です。 - 田澤義彦著「曲線論・曲面論(Mathematicaで探索する古典微分幾何学)」ピアソン・エデュケーション(1999年刊)
具体的問題を数値的・図的に解くときMathematicaの威力は絶大です。
- 寺坂英孝、静間良次著「数学の歴史 19世紀の数学 幾何学Ⅱ」共立出版(1982年刊)第3章“微分幾何学”
この本にガウスの大論文『曲面についての一般研究』(1827年)の日本語全訳があります。原論文はネットからダウンロードできますがラテン語なのでこの本をご覧いただくのが良いと思います。
- 吉田伸夫「完全独習相対性理論」講談社(2016年刊)
この本より§8-1-1“ガウスの曲面論”、§8-1-2“ガウス曲率と驚異の定理”、§8-2-1“リーマン幾何学の考え方”を引用。