4.リーマン幾何学
リーマン空間を定義するために“n次元微分多様体”の抽象的な定義を与える。3次元ユークリッド空間の曲面は“2次元リーマン空間”と考えられるから、3章の曲面上で考えた種々の概念を、次元を単にnにまで拡張すればそのまま通用する。
新しくは、部分空間において曲率テンソルや共変微分などがどのようになるかを問題にし、2章におけるワインガルテンの方程式やガウス・コダッツィの方程式の拡張を述べる。
(1)n次元微分多様体
(2)n次元リーマン空間
(3)リーマン曲率
(4)標準座標と測地座標
(5)フルネ・セレーの公式
(6)リーマン空間の部分空間
(7)部分空間における共変微分・曲率テンソル
(8)測地的曲面
(9)ワインガルテンの公式
(10)ガウス・コダッツィの方程式とリッチの方程式
(1)n次元微分多様体
曲面上の幾何学においては3次元ユークリッド空間の曲面のみを考えた。リーマンは曲面論から1歩進んで、線素ds2のみに基づき、次元nが全く一般な空間すなわ“n次元微分多様体”の概念に到達し、その上での幾何学、リーマン幾何学を創設した。
この意味において[3次元ユークリッド空間内の曲面]は[2次元リーマン多様体(リーマン空間)]とも考えられる。したがって、前章における[曲面上の幾何学]は、[n次元リーマン幾何学]に拡張して考えることが出来る。
そのため、特に断らない限り“リーマン幾何学”は次元を一般的な“n次元微分多様体”の上で考えることにする。まず最初に、微分多様体を導入する前の準備をする。
1.位相空間
一般に、抽象的な集合Mがあって、その元を点という。Mを個々の点の集まりと考えないで、これらの点の間に何らかのつながりを与えるのが集合Mの“位相”である。例えば2点間に距離という概念を定義し、Mに位相を導入することもある。しかし一般には、Mの各点に近傍という概念を導入して、Mに位相が導入される。
集合Mの各点Pに、これを含むMの部分集合U(P)を考え、これをPの“近傍”という。Pの近傍は1つとは限らないから、それらの全体を{Ui(P)}で表し、Pの“近傍系”という(図4-1)。
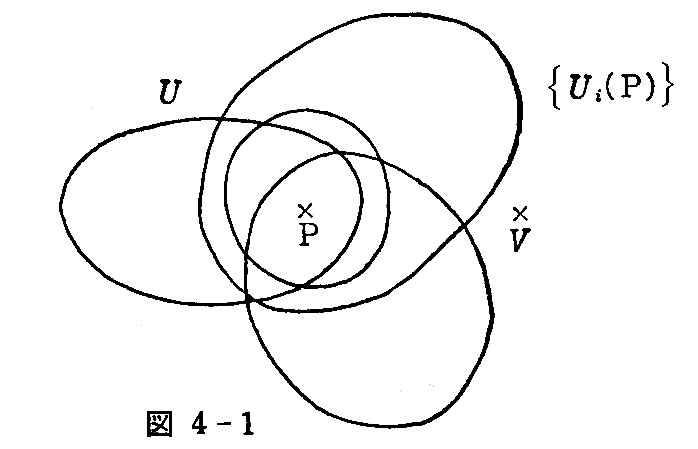
この近傍系が次の条件を満たすとき、Mを“位相空間”、または“ハウスドルフ空間(Hausdurff space)”という。この名称は位相空間理論の創始者の一人である フェリックス・ハウスドルフ にちなむ。Einstein、Levi-Civita、Hausdorff 彼らはユダヤ人故に様々な迫害を受けたが、誇り高く生きた彼らの名前は学問の世界で永遠に残るだろう。
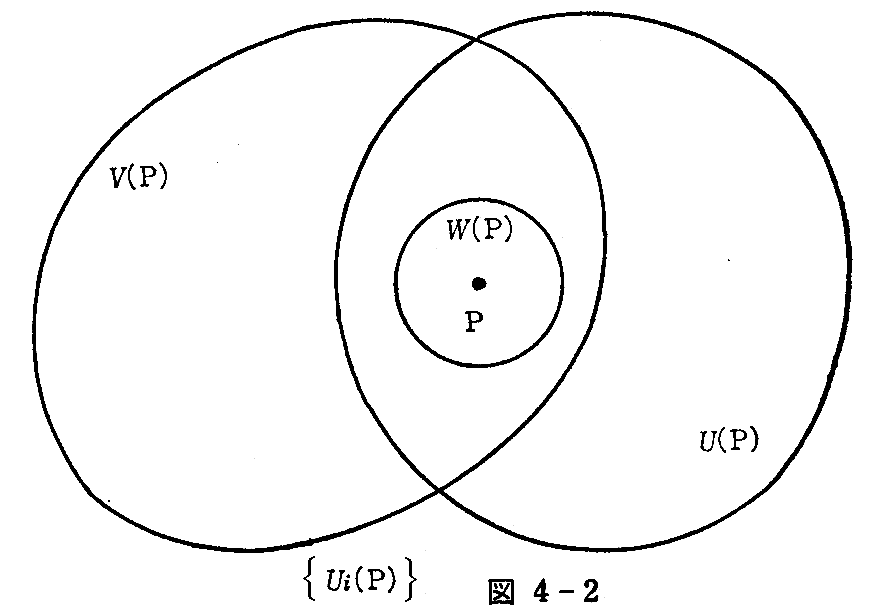
- (Ui(P))に属する2つの近傍U(P),V(P)に対して、共通部分U(P)∩V(P)に含まれるPの近傍W(P)が存在する(図4-2)。
- 近傍U(P)に属する任意の点Qに対して、V(Q)⊂U(P)なるQの近傍V(Q)が存在する(図4-3)。

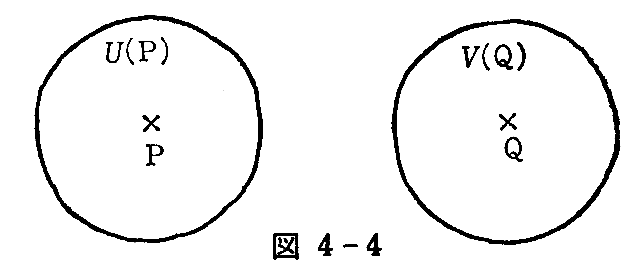
- 異なる2点P,Qに対して、U(P)∩V(Q)が空集合となるような近傍U(P),V(Q)が存在する(図4-4)。
2.開集合・閉集合
集合Oの任意の点に対して、この点の近傍でOに含まれるものがあるときOを“開集合”という。また集合Mから集合Cを除いた残りの集合M-Cが開集合であるとき、Cを“閉集合”という。集合Mを2つの共通点のない開集合に分割できないとき、この集合を“連結”であるという。
3.微分多様体
位相空間Mが、次の条件を満足するとき、“n次元微分多様体(n-dimensional differential manifold)”という。
- 位相空間Mは近傍系{Ui(P)}で覆われる。すなわち、{Ui(P)}はMの開被覆である。
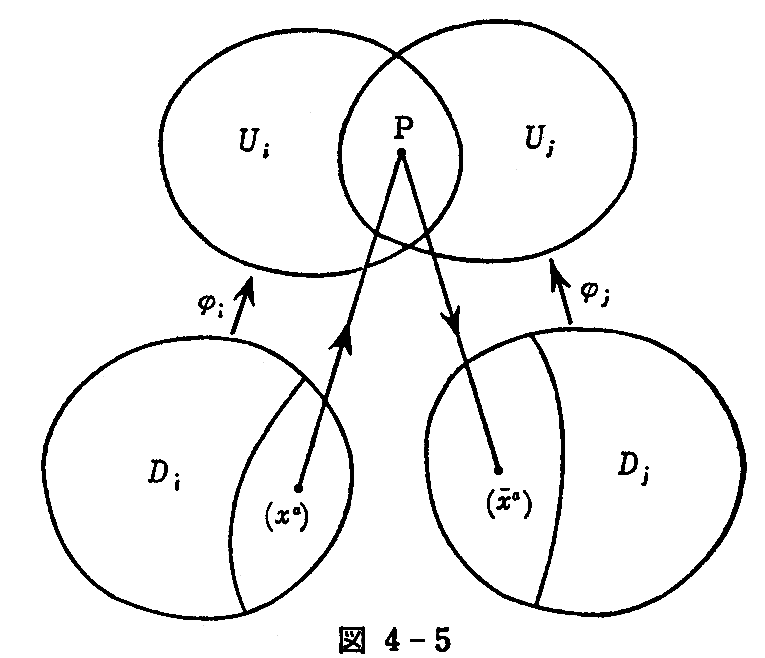
- 位相空間Mの各点の近傍Uiからn次元実数空間(x1,x2,・・・,xn)の開集合Di:|xa|<δ、δ>0(a=1,2,・・・,n)への写像φiが“同相写像”(1対1,φi,φi-1が連続)である。
同相写像φi:Di→Ui によって、Di の点(xa)=(x1,x2,・・・,xn)に Ui の点Pが対応するとき、(xa)を点Pの Ui での座標(局所座標)といい、φi と Ui を1組にしたもの (Ui,φi) を“座標近傍”という。
任意の Ui,Uj において
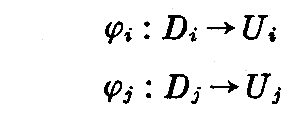
とするとき、Ui∩Uj 内の点Pに対して Ui での局所座標を (xa) 、 Uj での局所座標を とするとき
とするとき
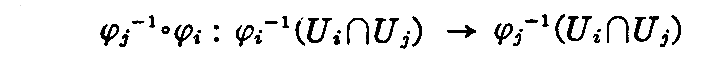
は (xa) と との1対1対応を与える(図4-5)。
との1対1対応を与える(図4-5)。
そこで、 を(xa)の関数
を(xa)の関数
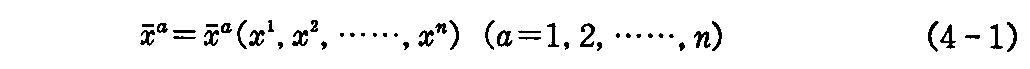
とみてCr級であるとき、MをCr級のn次元微分多様体という。
(4-1)式 は 座標(x1,x2,・・・,xn) から 座標 への座標変換を与え、逆に、
への座標変換を与え、逆に、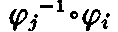 の逆の対応
の逆の対応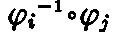 も一意に存在するから、(4-1)式 の逆の座標変換
も一意に存在するから、(4-1)式 の逆の座標変換
も存在する。したがって関数行列式は
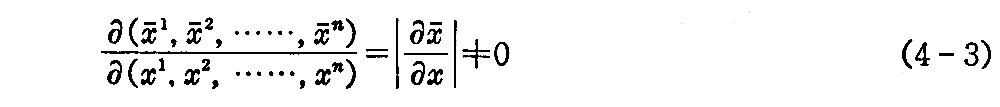
である
[例題1] n次元実数空間 Rn は微分多様体である。何となれば、開被覆として Rn 自身をとる。近傍系としてやはり Rn をとれば恒等写像 t:Rn(=U) → Rn は同相写像で、Rn の座標x1,x2,・・・,xn を Rn の局所座標と考えれば、(Rn,t) は座標近傍である。
[例題2] xy平面上の半径1の円 S1 は1次元の微分多様体(解析多様体)である。
[解] まず S1 に位相を入れる。そのために
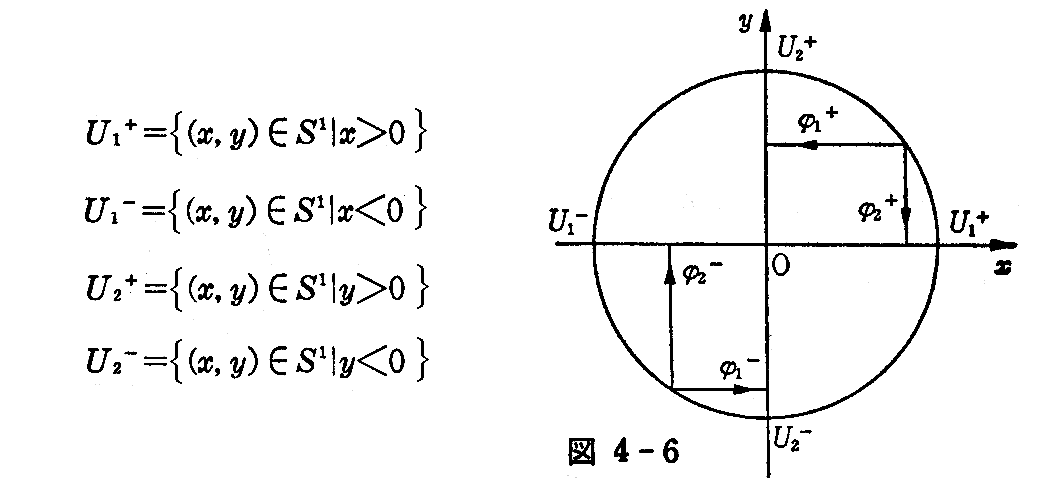
と置くと、各 Ui±(i=1,2) は S1 の開集合で {Ui±} は S1 の開被覆である(図4-6)。
次に、写像
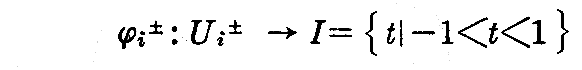
を
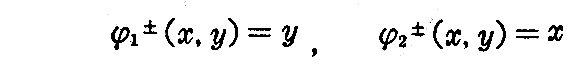
によって定めると、φ1±(i=1,2) は Ui± から I への同相写像である。故に S1 は1次元多様体で、 (Ui±,φi±) が座標近傍である。
次に、解析的であることを示そう。
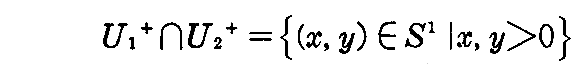
に対して、φ1+(U1+∩U2+),φ2+(U1+∩U2+) は共に開区間 I+={t|0<t<1} に等しい(図4-7)。
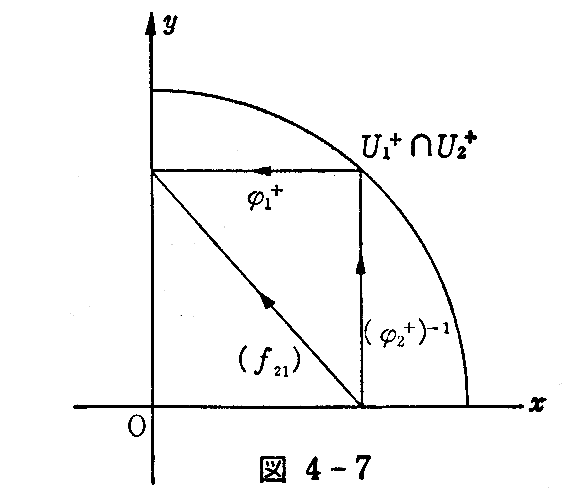
t∈I+ のとき

となり、座標変換 f21+,f12+ などは 0<t<1 では解析的である。他も同様であるから、S1は解析多様体である。
[問題] Rn+1 において (x1)2+(x2)2+・・・+(xn+1)2=r2 を満たす点(x1,x2,・・・,xn+1) の集合をn次元球面 Sn という。 Sn はn次元解析多様体であることを示せ。
[解]

(2)n次元リーマン空間
1.n次元空間の距離
3次元ユークリッド空間において、直交座標が (xi) ,(xi+dxi) であるような十分近い2点間の距離 ds は

で与えられる。
例えば、球座標
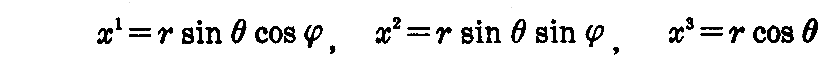
を用いれば

となる。(このことに付いては別稿1.(2)3.を参照)
また、2次元曲面 x=x(u1,u2) 上の線素は
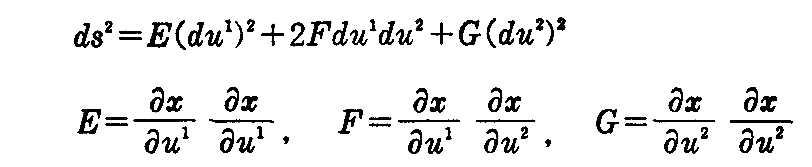
で与えられることは今まで論じてきたところです。
以上の例を鑑みれば、十分に近い2点間の距離 ds の平方を座標の微分の“2次形式”で与えられるとして良いであろう。したがって、座標がそれぞれ (xi) ,(xi+dxi) である十分近い2点間の距離 ds が座標の2次微分形式
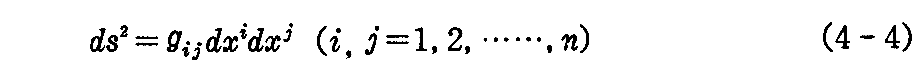
で与えられられる“n次元微分多様体”が、上の例の自然な拡張として考えられる。
[補足説明1]
ここの意味がリーマン幾何学で最も解りにくい所です。このことを説明する以下の文献は秀逸です。
佐藤文隆、R・ルフィー二共著「ブラックホール(一般相対性理論と星の終末)」中央公論社(1976年刊)第1章5節より












ただし、リーマンの考察の限界について別稿[補足説明2]と、更に別稿[補足説明2]もご覧下さい。
[曲がった空間]


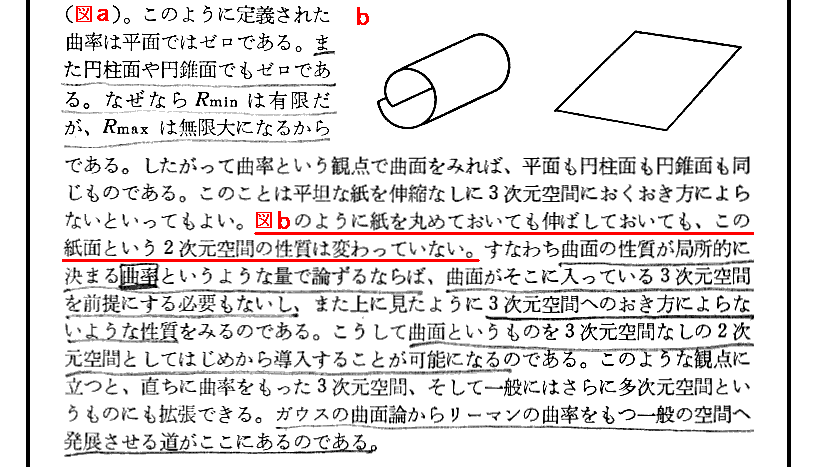
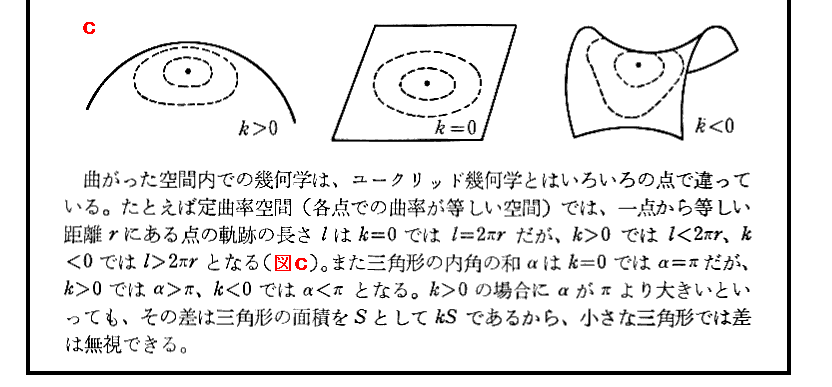
上記の“曲率という観点で曲面を見れば、平面も円柱面も円錐面も同じものである。”について補足します。
測地線で構成される閉曲線を考えて、測地線に沿ってベクトルを平行移動して1周させたとき、最初と最後のベクトルが一致していないならばその曲面はゼロでない曲率を持ち曲がっているでした。下図の(a)のばあいがそれです。
一方(b)の円錐面の場合は1周したときの最初と最後のベクトルは一致します。故に円錐面は曲がっていないのです。
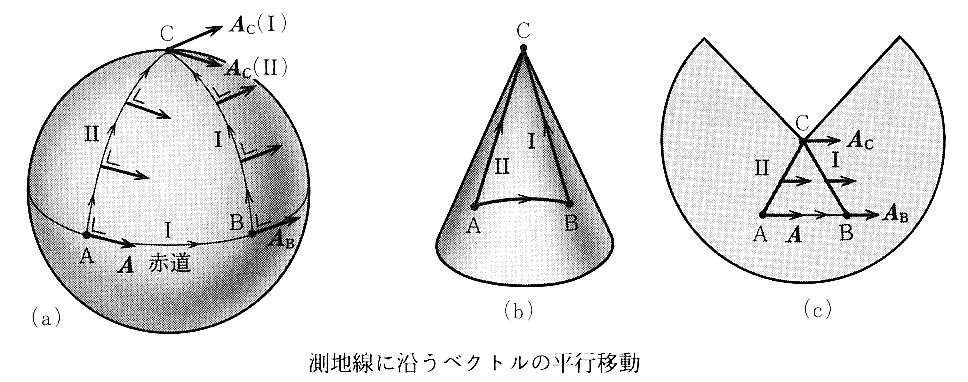
(b)の曲面は(c)の様に切り開けば、その全面を平面とピッタリと重ねることができます。だから、円錐面は見かけは曲がっていますが曲率はゼロの面です。それに対して(a)の面は決して平面に重ねることはできません。
2.n次元リーマン空間(多様体)の定義
n次元微分多様体において、近傍 U の各点Pに正定値2次微分形式

を対応させ、次の条件を満たすものとする。
(1)gij=gij(x)は(x1,x2,・・・,xn)について、微分可能な関数です。
(2)ds2は座標変換

で不変です。すなわち
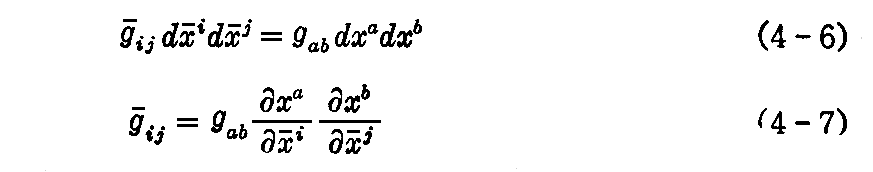
です。
このような gij の定義されたn次元微分多様体を“n次元リーマン空間”という。そして、(4-5)式で与えられるような計量を“リーマン計量”といい、 gij は i と j に関して対称なテンソルで、これを“基本計量テンソル”という。そして、 ds を隣接する2点 (xi) と (xi+dxi) の間の“距離”という。
ユークリッド空間の曲面は2次元のリーマン空間と考えられるから、3章の大部分の概念、例えば、[曲線の弧長]、[角]、[測地線の方程式]、[クリストッフェルの記号]、[共変微分]、[曲率テンソル]、・・・等々の概念は、単に次数2を一般のnにまで拡張することによって、ただちに適用できる。
第2章と第3章を振り返られると解るように、そこで提示されている定理の証明の多くが、2次元曲面にも拘わらず高次元の定理にそのまま拡張できる様な形で議論・証明されていた。これらの章を読まれるとき、何故にそのような解りにくい証明がなされているのか疑問に思われたかも知れません。それは、ここで述べた事柄を意識して、その様な証明方法にしてあったのです。
例えば、n次元リーマン空間の曲線弧 xi=xi(t)(i=1,2,・・・,n)(t0≦t≦t1) の長さ s は
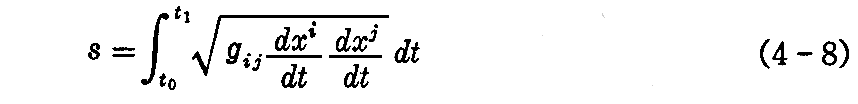
で定義される。
そして、弧長 s を曲線の方程式の係数とすれば、(4-8)式から
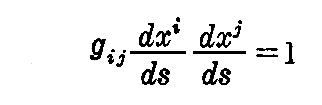
となる。
こごで
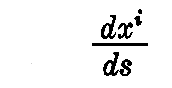
を“単位接線ベクトル”といい、反変ベクトルです。
“基本計量(共変)テンソル” gij と、3.(2)[問題3]と同様に定義される“基本計量反変テンソル” gij があれば、反変ベクトル vi から共変ベクトル vj がつくれ、逆のことも言える。
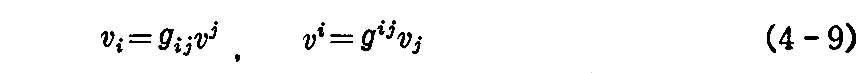
このことは、一般的なテンソルに対しても言える。例えば

これを gij を用いて共変指標を上げる、 gij を用いて反変指標を下げるという。
[例題] 曲面 x=x(u1,u2)上の面積元素dSは2.(2)3.(2-14)式を2.(7)1.の添字記法で書き直すと
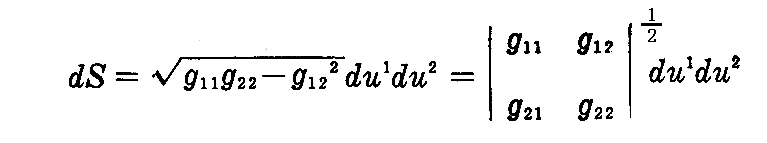
で与えられる。
これを拡張してリーマン空間における体積元素dVを
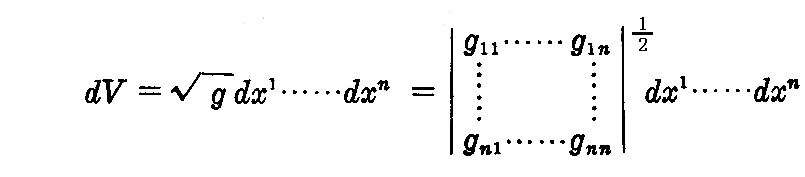
で定義したとき、dVはスカラー量であることを証明せよ。
[解] 座標変換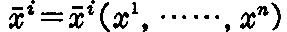 に対して微小体積
に対して微小体積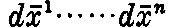 は微積分学の教えるところによって
は微積分学の教えるところによって

である。
この変数変換に対してgijは
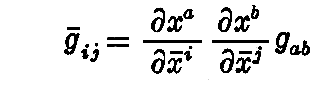
であるから、それに対応する行列式は
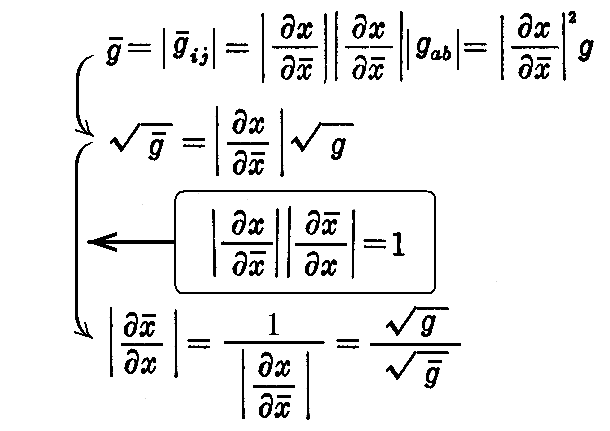
となる。
故に
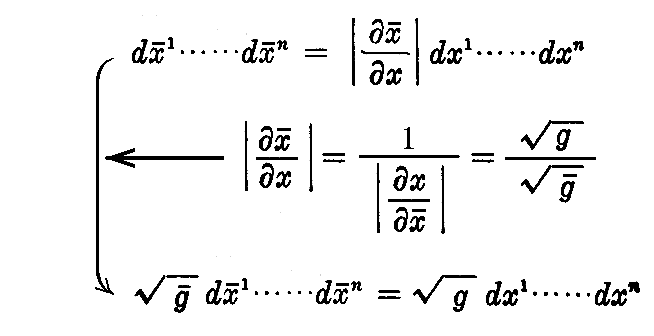
を得る。これはdVがスカラーであることを示している。
[問題1] gijgij=nを証明せよ。
[解] 2.(7)[問題2]をn次元に拡張すればよい。

[問題2] リーマン空間内の2点P,Qを通る曲線Xi(t)に沿っての積分

が極値を与えるための条件を求めよ。
[解] 3.(6)1.の議論をn次元に拡張すればよい。
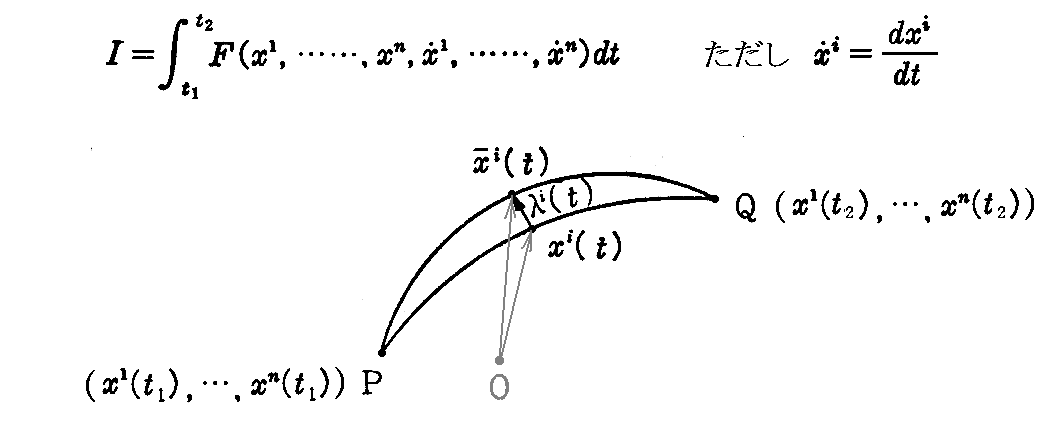
曲線の両端P,Qを固定し、曲面上を少し変化させたときの曲線を C’ とすれば、その方程式は

で与えられる。
ここで ε は絶対値が十分小さい定数で、λi(t)は径数 t についての C からの変位を表す微分可能な関数である。そして両端は変化しないから
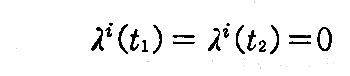
を満たす。
故に、2点P,Qを結ぶ曲線に沿っての積分値 I の変化量 I ’-I =δI は

となる。ここで、O(ε2)は、展開に於けるεの2次以上の無限小の項を表す。
元々の積分値 I が最小の極値であるためには、εの係数が0でなければならないから
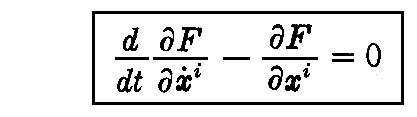
となる“オイラーの微分方程式”を満足しなければならない。
[補足説明]
ここは、何を言っているのか解りにくいので補足します。
物体はニュートンの運動方程式に従った運動をするのですが、解析力学の考察から、ニュートンの運動方程式はラグランジュの方程式と等価であることが解っている。
さらに、ラグランジュの方程式は、ラグランジアン関数Lという作用関数を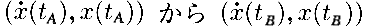 まで線積分したときの値が極値を取る条件として得られることが解っている。その極値を取るための条件がラグランジュ方程式です。ここのオイラーの微分方程式は、そのラグランジュの方程式と同じものです。
まで線積分したときの値が極値を取る条件として得られることが解っている。その極値を取るための条件がラグランジュ方程式です。ここのオイラーの微分方程式は、そのラグランジュの方程式と同じものです。
その当たりの解りやすい説明をジェームズ・B・ハートル著 『重力』 日本評論社(2002年刊)より別ページで引用していますのでご覧下さい。あるいは別稿ランダウ、リフシュツ著「力学」第1章§02でも説明されています。
さらに、別稿「5.一般相対性原理と等価原理」(4)や別稿「微分幾何学3(曲面幾何学)」3.(6)2.なども参照されたし。
[問題3] 変数変換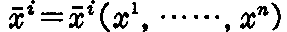 に対して、クリストッフルの記号の変換式は
に対して、クリストッフルの記号の変換式は
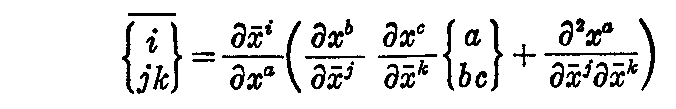
であることを示せ。
[解] 3.(3)1.(3-18)式に於いて、n次元に適用できる形で証明している。そこのuをxに変えるだけ。
[問題4]リーマン空間における測地線の微分方程式は
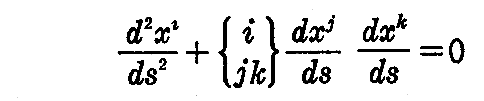
であることを示せ。
[解] 3.(6)2.(3-54)式に於いて、n次元に適用できる形で証明している。そこのuをxに変えるだけ。
[問題5] リーマン空間の“基本計量(共変)テンソル”gij 共変微分は 0 であることを証明せよ。
[解] 3.(3)[例題1]に於いて、n次元に適用できる形で証明している。そこのuをxに変えるだけ。
[問題6] リーマン空間の1つの反変ベクトルviに対して

が成り立つことを示せ。
[解] 3.(5)1.に於いて、n次元に適用できる形で証明している。そこのuをxに変えるだけ。
(3)リーマン曲率
1.リーマン曲率
リーマン空間の1点 (xi) から出る2つの1次独立なベクトル ui,vi に対して、スカラー
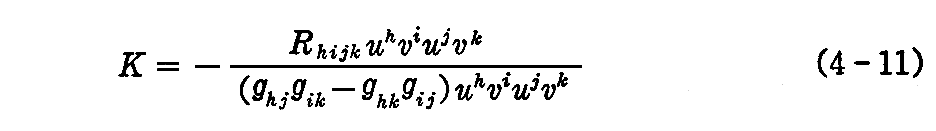
をベクトル ui,vi で定まる方向に関する“リーマン曲率”という。
これは1点 (xi) を通り、 (xi)での2次元接平面に接して全ての方向に走る測地線の集合がつくる2次元曲面の点 (xi) におけるガウスの曲率(2.(6)2.を参照)に成っている。最初に述べた2つのベクトル ui,vi は、その2次元接平面を定めるのに必要。
2.定曲率空間
いま、リーマン曲率がこれを定める2つの方向 ui,vi に無関係ならば
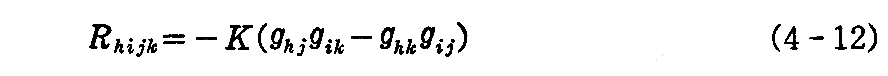
である。
ここでスカラーKを座標の関数と考えて、3.(5)[例題1](3-49)式のビアンキの恒等式と、3.(3)[例題1](3-26)式のリッチの補助定理を用いると

を得る。これに ghj を乗じて縮約すると
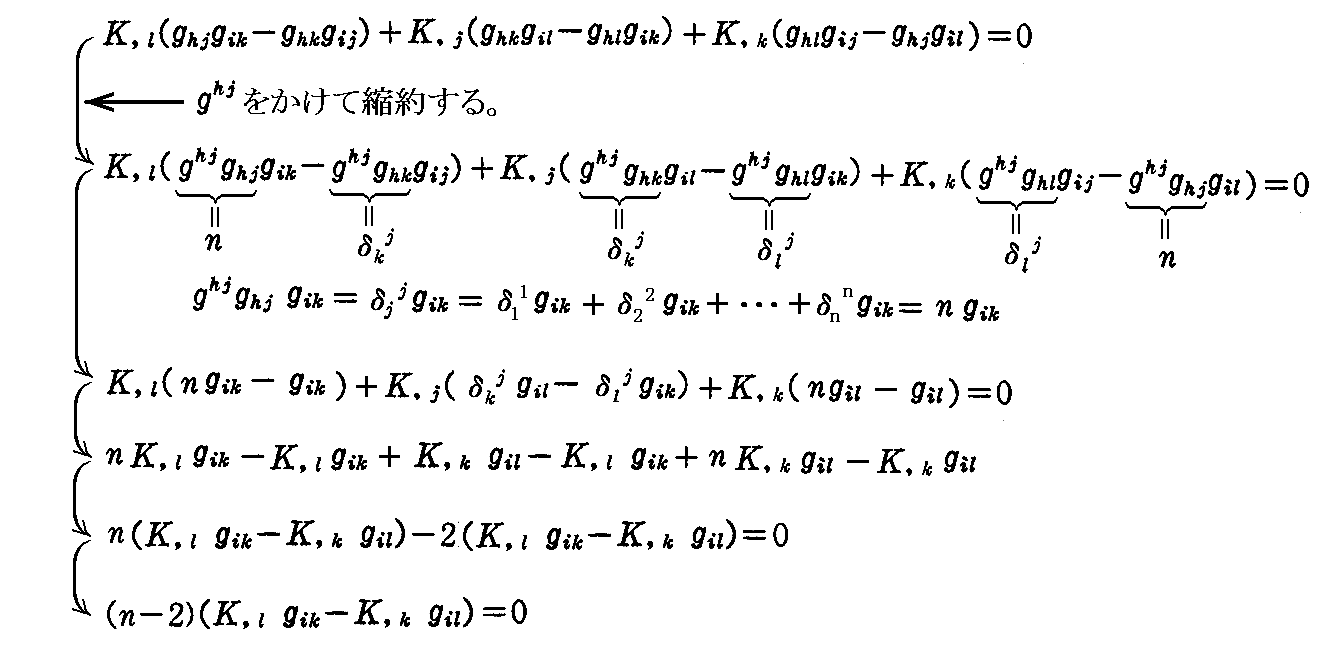
となる。さらに gik を乗じて縮約すると
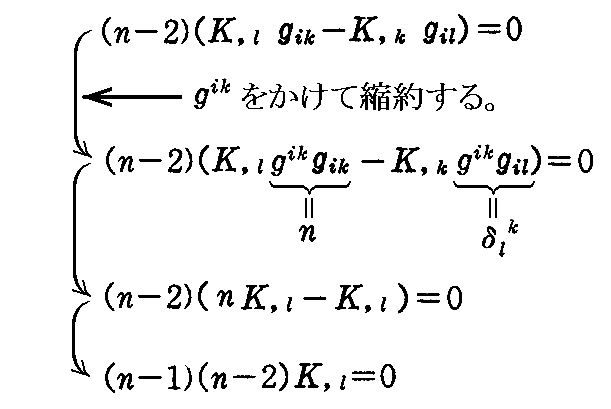
を得る。故に、n≧3 の場合には、K はスカラーであるから
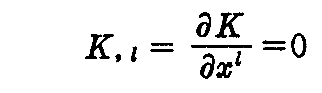
を得る。これはリーマン曲率が全ての点で定数である事を意味する。よって次の定理を得る。
[定理1] リーマン空間の各点で、リーマン曲率がこれを定める2つの方向に無関係であれば、リーマン曲率は全ての点で定数である。これを“シュアー(F. Schur)の定理”という。
このような空間を“定曲率空間”という。リーマン曲率が、ベクトル ui,vi の方向に無関係に全ての点で 0 ならば

となる。このような空間を“平坦”であるといい、平坦な空間は実はユークリッド空間であることが証明される。([例題2]で証明)
3.直交n重系
リーマン空間の1点 (xi) において、“互いに直交する”n個の単位ベクトル h(a)i (a,b=1,2,・・・,n) を考えこれを“直交n重系”という。
ここでa,bなどはベクトルの番号を、i,j,k,・・・などはベクトルの反変成分を表す指標である。したがってa,bなどの指標については総和法は通用しない。(この意味はわかりにくいので下記[補足説明]参照)
定義から

を満たす。
ここで、 h(a)i の共変成分を
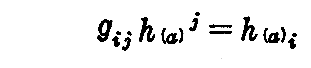
と置けば(4-13)式から
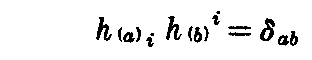
を得る。
さらに
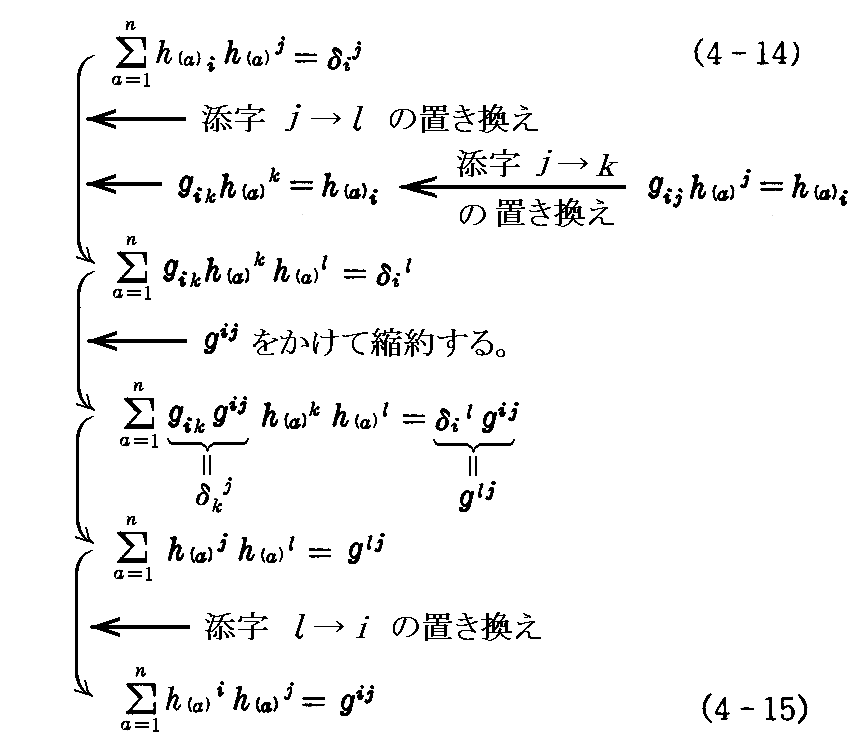
を得る。
[補足説明]
ここは何を言っているのか解りにくいが、互いに直交するように取った“n個のベクトル”の事を説明している。文中の式の意味については別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分(計量テンソル・クリストッフェル記号・共変微分とは何か)」の3次元の場合と比較すると理解しやすい。
最初の“互いに直交する”の意味は「基底ベクトル・双対基底ベクトルと反変成分・共変成分(計量テンソル・クリストッフェル記号・共変微分とは何か)」2.(1)で最初に設定した基底ベクトル

が互いに直交するように設定されている様なものだと考えればよい。もちろんそれは別稿で説明した双対基底ベクトル
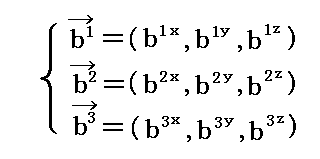
と直交するという意味ではありません。
つまり、別稿4.(5)2.[例12]の中で説明したベクトル ex,ey,ez の様なものです。本文中のaやbはこの基底ベクトルを表すのに用いたx,y,zの添字に相当します。
ここでの話は直交するように取った任意のn個の基底ベクトルについての反変成分、共変成分の話です。
文中の h(a)i は以下のように考えればよい。ここでのn個のベクトルは、前記の基底ベクトルex,ey,ez系の表記を別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分(計量テンソル・クリストッフェル記号・共変微分とは何か)」2.(2)における基底ベクトルa1、a2、a3系の表記になぞらえると
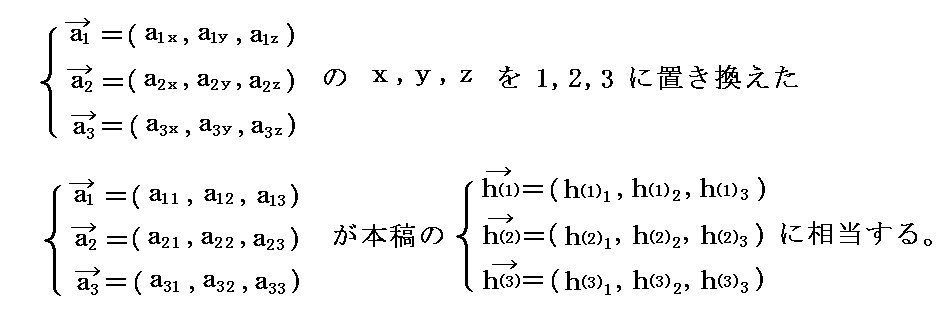
本文中のh(a) や h(b) の添字 (a) と (b) の中にはベクトル番号(1~n)のいずれかが入ります。別稿の基底ベクトルa1,a2,a3になぞらえれば、ベクトル番号(1,2,3)のいずれかが入ると言うことです。 h(a) と h(b) の違いはベクトル番号の違いを意味するのであって、別稿の基底ベクトルaiと双対基底ベクトルbiを表すとき使ったaとbの文字と勘違いしないで下さい。ここは全て基底ベクトル系の中に存在する任意のn個の直交するベクトルについての話です。
ここでは直交n重系ベクトルを、最初に反変成分で表記しているが、共変成分も反変成分も元々は同一のベクトルの別表現でしかありません。もちろん反変性分や共変成分を表す元になる基底ベクトルと双対基底ベクトルはここで言う直交n重系では互いに一致します。。その互いに一致する基底ベクトル系や双対基底ベクトル系で表した成分が直交n重系ベクトルそれぞれの反変成分、共変成分です。そして、文中の基本計量テンソルgijやgijはそれらの基底ベクトルや双対基底ベクトルから構成されたものです。
4.平均曲率
いま、n重系の2つのベクトル h(a)i と h(b)j によって定まるリーマン曲率を K(a)(b) とすれば、(4-11)式によって
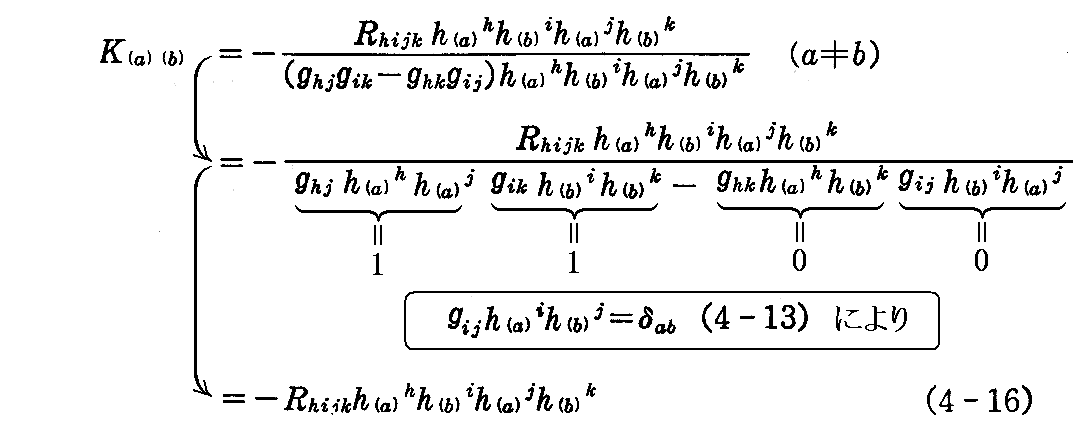
となる。
そこで、も b=1,2,・・・,n について総和をとれば
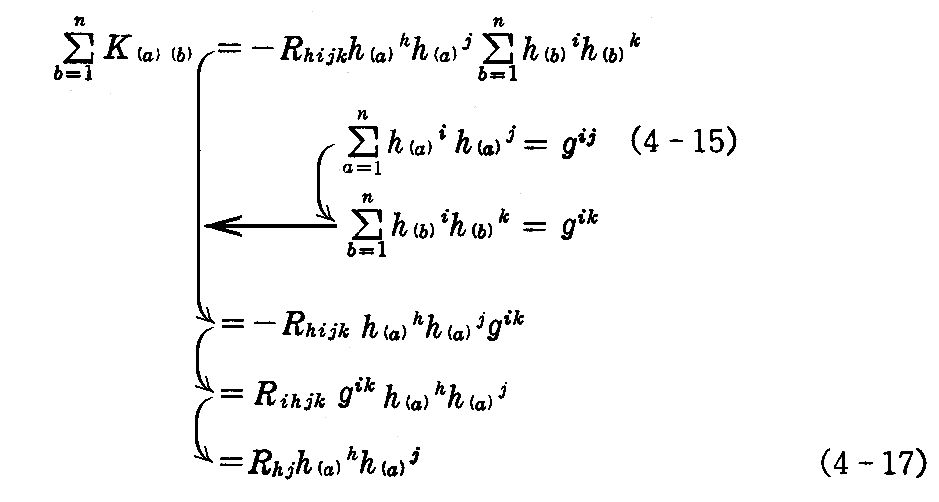
が得られる。ここで
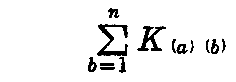
は h(a)i とこれに垂直なn-1個の互いに垂直なベクトルによって定まるリーマン曲率の和である。
(4-17)式から、n-1個のベクトルの選び方に関係しないことも明らかである。これを h(a)i に対する“平均曲率”という。
さらに
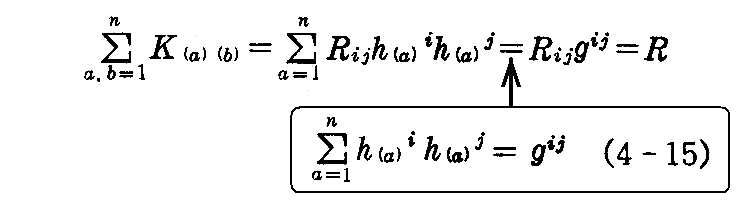
であるので、次の定理を得る。
[定理2] n個の互いに垂直な方向に対する平均曲率の和は、曲率スカラーに等しい。
[例題] vi を任意ベクトルとしたとき、この方向に対する平均曲率をMとすれば
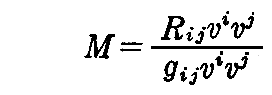
である。Mの極値を与えるような方向 vi を求めよ。
[解] まず、平均曲率Mは(4-17)式から
となる。
(4)標準座標と測地座標
(5)フルネ・セレーの公式
(6)リーマン空間の部分空間
(7)部分空間における共変微分・曲率テンソル
(8)測地的曲面
(9)ワインガルテンの公式
(10)ガウス・コダッツィの方程式とリッチの方程式
[補足説明]
[定理]
[例題]
[解]
[問題]
[解]
END(参考文献)
この稿を作るに当たって、下記文献を参考にしました。感謝!
- 前田儀郎著「幾何学Ⅴ・Ⅵ(微分幾何学」玉川大学通信教育部(1969年初版刊)4章“リーマン幾何学”
- W.Pauli著(内山龍雄訳)「相対性理論(上)(下)」筑摩学芸文庫(2007年刊)第Ⅱ編 数学的準備
原書は1921年刊です。上記訳本の元本は1974年に講談社から刊行されたもの。この第Ⅱ編は熟読する必要があるように思います。