こちらのバージョンをご利用になると鮮明に印刷されます。
絶対温度とは何か(積分因子とは何か)
熱力学に於ける絶対温度の意味を説明します。温度はとても難しい量でエントロピー(これも難しい)と表裏一体です。説明にはかなりの準備が必要ですが、なにとぞ御容赦下さい。
1.熱を記述する言葉
(1)温度temperature(T、t)
1.熱平衡
温度を定めるに当たって熱平衡という概念が導入される。これは熱学の基礎になる概念で温度(次で説明)の違う二物体を接触させると、温かいものは冷え、冷たい方は温まり、温度の変化が両方とも止まった状態になる。その場合を熱平衡にあると言う。
このとき物体Aが物体Bと物体Cのそれぞれと熱平衡にあるならば、BとCも熱平衡です。これは熱平衡の概念に附随する法則と言ってもよいし、経験的事実と言っても良い。
この事実があるからこそ、二物体BとCの温度をそれらが離れて存在しても比較することができる。つまり温度計Aを作り、まず温度計AとBと接触させて熱平衡状態を実現し、次にAとCを接触させて熱平衡状態を実現する。温度計Aを構成する物質の体積の観測によってBとCが熱平衡にあるか、あるいはそのいずれがより温かいか冷たいかを決定するのです。
2.温度の定義
温度とは何かと改めて聞かれると、これは本当に難しい量です。その当たりはおいおいに説明するが、当面は簡単に考える。
温度は、我々の涼しい・温かい、冷たい・熱いの感覚に関係している。それを量的に表すものとして温度計というものが作られた。それらは、容器に詰めた液体や気体の膨張を測ってその体積の増減でもって温度の高低を示す。通常の温度計は膨張量をより詳細に測定するために物質溜めに細管を繋いで膨張の有様を観測しやすくしている。つまり、温度の高低は物体の体積の変化量に比例していると考えられおり、それらの量の変化を引き起こすものが温度の実体です。
温度は、物質の示す二つの基準状態と熱平衡にある温度計について、それぞれの平衡時における温度計構成物体の体積を量り、二状態間の体積差を等分割する事によって目盛りを決めるような量です。つまり任意の物体の温度は、その物体と熱平衡状態にある温度計の構成物質の示す体積を量ることにより決定する。
しかし、よく考えてみると温度がどの様なメカニズムで気体や液体の膨張を引き起こすのかは何も解っていない。またその膨張によって温度を定義し、その値を知ることはできるかも知れないが、温度の実体については何も教えてくれない。
3.温度目盛り
1.ファーレンハイトの温度目盛り t
(Fahrenheit、中国語で“華倫海特”、単位は°Fまたはファーレンハイト氏が作ったと言う意味で華氏~度と言う)
1724年ファーレンハイトは前記の二つの基準状態として寒剤により達成される状態と、動物の体温を選んだ。つまり、当時人工的に造られる最低温度(氷と塩を混合した寒剤による)を0度とし人の体温を96度としてその間の温度計の体積差を12×8=96等分割して温度を定めた。これはほぼ、1気圧の元での氷りの融点を32°Fとし、沸点を212°Fとすることに相当する。
2.セルシウスの温度目盛り t
(Celsius、中国語で“摂爾修斯”、単位は℃またはセルシウス氏が作ったと言う意味で摂氏~度と言う)
1742年セルシウスは二つの基準状態として、1気圧の元での水の凝固点(氷と水が共存する状態)と、1気圧の元での水が沸騰している状態を選んだ。つまり、1気圧下での水の凝固点を0℃、沸点を100℃として、温度計の体積変化を100に等分割して温度を定めた。
これ以外にも様々の温度目盛りが考案されたが、いずれも二つの物理的状況と熱平衡にある温度計の体積を量り、二状態間の体積差を等分割して温度目盛りを定めるものです。(ダンネマン「大自然科学史」第6巻(三省堂)等参照)
ここで問題になるのは、例えばセルシウスの目盛りを例にして説明すると、二種類の温度計物質の示す温度は0℃と100℃では一致させることはできても、その間では決して一致しないと言うことです。つまり一般に0℃と100℃の間の体積変化の様子は物質によりそれぞれ異なる。つまり同じ温度の熱浴に浸けて膨張率を測定しても、例えば30℃付近では物質Aの方の膨張率が物質Bより大きいが、70℃付近では逆にBの方がAより大きいと言うようなことが起こる。
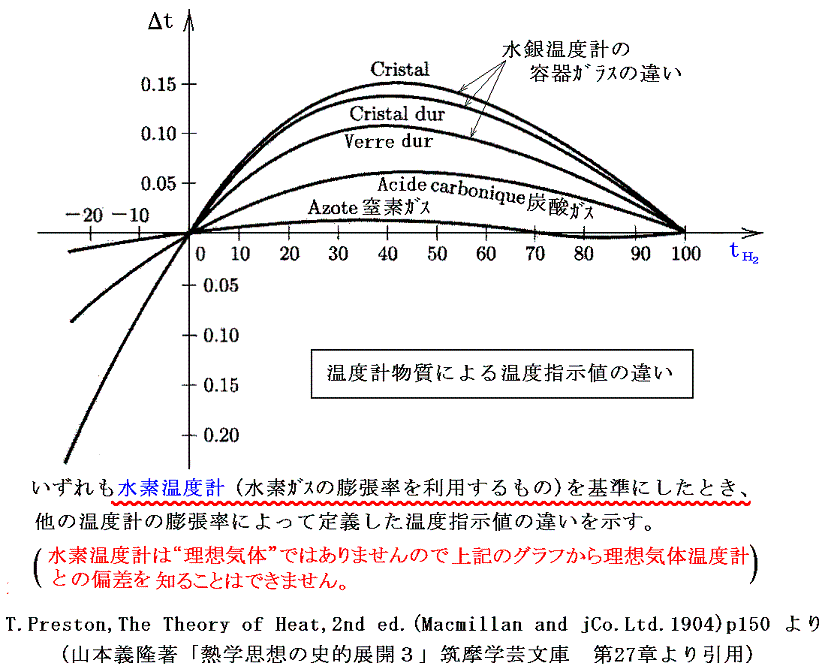
そのとき、温度計の物質によらない絶対的な温度を定めることはできないのだろうか?これは”大いなる疑問?”ですが、その解決は可能です。熱や温度についての深い考察が必要ですが、その問題は1848年のケルビンKelvin(ウィリアム・トムソンWilliam Thomson)による絶対温度の定義から始まって、最終的にクラウジウスやケルビンによって解決された。
この問題は、現実には存在しない理想気体の膨張率を基準にして上記のグラフを書くことができるかという事と同じです。つまり現実に存在する気体の熱膨張率から、現実には存在しない理想気体の熱膨張率を決めることができるかという問題です。
3.ケルビン(ウィリアム・トムソン)の絶対温度目盛り T
(単位はK(ケルビンと読む)とする。このとき”°”を付けないことに注意)
これはカルノーサイクル(ある種の熱機関)を用いて温度を定義するものです。この定義によると温度測定に用いる物質に依存しない温度目盛り(絶対温度目盛り)を打ち立てることができる。また、この定義によると必然的に温度がそれ以下に下がることがない基準点(それを0Kとする)が存在することが解る(6.(2)2.参照)。
そのため絶対温度については、温度目盛りを定める基準状態はただ一つ選べば十分で、その状態の値を定めさえすれば絶対温度目盛りを定めることができる。今日その基準点として水の三重点(水の固相、液相、気相が共存する状態、温度=0.01℃、圧力=611.73Pa=0.006気圧)をえらび、その状態の絶対温度を 273.16 [K] としている。なぜこの値を選んだかと言うと、目盛りの幅がそれまでに普及していた摂氏温度目盛りと一致するようにするためです。そのため絶対温度の1[K]はその1/273.16倍であり、 1[K]=1[℃]となる。そのため絶対温度の0Kは摂氏-273.15℃となる。以後の議論では温度の単位として実用温度には[℃]を、絶対温度には[K]を用いて説明する。
絶対温度目盛りの定義はかなり込み入っているので後で詳しく説明します。そのため、当面は1.や2.で述べたような現実の温度計の示す温度tで持って議論する。温度計構成物質の違いによる温度目盛りの違いは実際はごく僅かであるから当面の議論にはその温度定義で十分です。
1.熱量heat(Q、q)の定義
温度と同様、熱も当初は訳の解らないものでした。熱は物を燃やしたり、物体を摩擦したりしたときに現れるもので最初は様々な解釈があった。熱はある種の不滅の物質のようなものカロリック(熱素)と考えられたり、またある種の運動のようなものであると考えられたりした。前者の立場では、熱素は物質を構成する原子と結びついたり離れたりして移動する事ができる。そのさい原子と結びつくとき潜んだ形(潜熱)にもなれるし解放されて温度計で検出可能にも成るというのです。また後者の立場では熱とは物体の目に見えない程小さな各部分が極めて激しく振動することであるとするもので、摩擦熱や、我々が感じる熱いと言う感覚を旨く説明した。
このように熱の実体は当初よく解らないものでしたが、燃焼による加熱にしろ、摩擦熱による加熱にしろとにかく何らかの方法で水を熱したとき水1gの温度を1度(1℃)だけ上げるのに必要な熱量Qを1calと定める。この定義は熱量の測定法を定めているだけで熱の実体が何であるかは何も説明していない。しかし、その量を定めることはできるので当面の議論はこれで十分です。ちなみに単位のcalはラテン語calor(熱)に由来する。
2.潜熱と反応熱
物体の融点や沸点に於いて生じる現象から明らかなように、熱量が温度の上昇に用いられるのではなくて、物体の集合状態の変化に用いられる場合がある。温度が変化しないのに熱が吸収されたり放出されたりするため、温度や熱量の理解を非常に難しくするが、熱量の出入り自体は厳密に測定することができる。そのとき物質1gを一つの集合状態から他の集合状態に移すのに必要な熱量の事を潜熱という。
潜熱にはそれぞれの状態変化に応じて、固体→液体の変化に伴う物を融解熱、その逆の変化に伴う物を凝固熱、液体→気体の変化に伴う物を蒸発熱(気化熱)、その逆の変化に伴う物を凝縮熱(液化熱)、固体と気体の間の変化に伴う物を昇華熱と呼ぶ。
集合状態の変化以外に、物体の混合過程、溶解過程や化学変化などにも熱の出入りが伴う。それらを混合熱、溶解熱、反応熱、解離熱等々と言う。この中で反応熱については別稿「反応熱と熱化学方程式」で詳しく説明した。
このように温度変化を伴わない熱の移動は熱というものが何であるか考えるのをとても難しくする。しかしながら、そのことによって生じた熱量は比熱の測定に用いたのと同様な装置(例えばヘスHessが反応熱の測定に用いたような)で一定量の水の温度の上昇に置き換えることができ熱量を厳密に測定することができる。そのため潜熱や反応熱も上記の熱量の定義に含ませることができる。
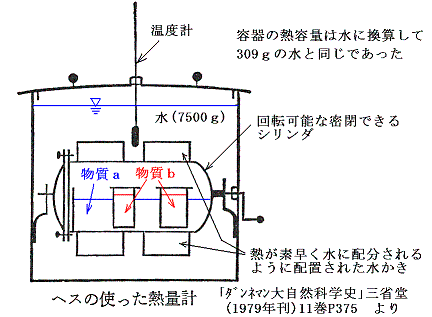
1.熱容量heat capacity(C)の定義
物体の温度を単位温度(1℃)だけ上昇させるのに要する熱量のことをその物体の熱容量Cという。
定義から明らかなように物体の得た熱量Qと、そのために起こった温度上昇t’-t=Δtの間には
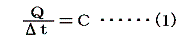
の関係が成り立つ。そのため熱容量の単位は[cal/℃]となる。
2.比熱specific heat(c)の定義
単位質量(1g)の物質の温度を単位温度(1℃)だけ上昇させるのに要する熱量をその物質の比熱cという。
比熱とは物質1g当たりの熱容量のことであるから、物質の質量をm[g]とすると前記の熱容量Cとは
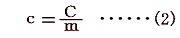
の関係にある。そのため比熱の単位は[cal/g・℃]となる。
比熱の定義と 1.(2)1.の熱量の定義から直ちに水の比熱は1.0[cal/g・℃]であることが解る。
(1)、(2)式より重要な関係式
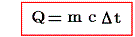
が得られる。これは熱と温度を関係づける最も重要な式です。
1.比熱の測定
種々の物質の比熱は、具体的には以下の様にして測定します。
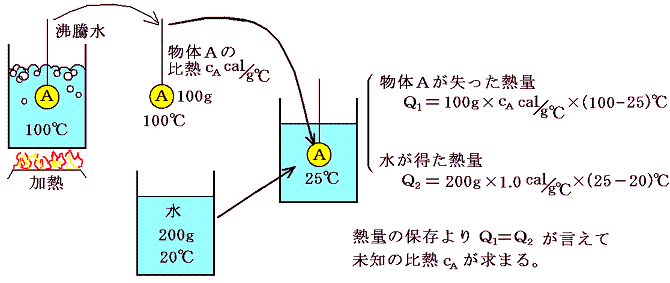
これは高校物理で習う事柄ですが、このようにして比熱を測定できることこそが熱量という量の定義を可能にする。
ここで述べた測定には、摩擦や圧縮・膨張といった機械的・力学的な仕事のやり取りはなく、熱の移動だけで実行できる。そのとき、同じ物体の比熱を、例えば上記の水を他の液体に変えたり、他の物体を仲介にして測定するなどして様々な異なった方法で測定してもいつも同一の値が得られることが経験で知られている。
そのことから熱の移動のみを伴う現象については、いわゆる熱量保存の法則がなりたち、熱というものは何も無いところから生まれたり、あるいは消えてしまったりせずいつも保存される量であることが理解できる。歴史的には、このことが上記の熱量、熱容量、比熱と言った量の有用性を保証し、それらを定義することの根拠を与えてきたのです。
しかしながら、この法則は、熱量について様々な誤った憶測(例えば熱素説のような)を呼び起こしてきた。そのため熱量について次に述べる事柄は特に肝に銘じておく必要がある。
2.一般的な熱の測定
今日熱量のみでは保存則は成り立たないことが解っており、熱は後に説明するエネルギーという量の一形態であるとされている。
一般の熱量測定は1.(2)1.における定義より明らかなように、外部から加えられた熱量、又は外部へ与えた熱量の値を与えるのみで、ある温度の物体中にいかほどの熱量が含まれているかという問いには何も答えることはできない。
つまり、ある標準状態Aにおける熱量を0と定めた後に、その状態から出発して別の状態Bに到達するまでに、その物体に供給された熱量で持って状態Bの熱量を定めてもその熱量は何の意味もないのです。
多くの経験事実から明らかな様に、状態Aと状態B定めてもAからBへ移動する方法・経路によって物体に出入りする熱量は様々に変化する。例えば0℃、1気圧の気体を100℃、10気圧にするのに、まず1気圧に保って100℃まで熱し次に温度を一定に保って10気圧に圧縮する場合と、最初に0℃の下で等温的に10気圧まで圧縮してその後定圧的に100℃まで加熱した場合で加えるべき熱量は全く異なる。
熱のこのような性質を「熱は状態量ではない」という言い方をする。この事実は重要! です。
1.比熱の温度依存性
一般に比熱は温度によって変化する。同じ1gの水の温度を1℃だけ上げるときでも、最初の温度が異なれば必要な熱量は少しではあるが変化する。そのため1.(2)1.熱量の定義も正確には水1gを14.5℃から15.5℃に温めるときの熱量を1calと決めている。
2.定圧比熱cpと定積比熱cv
熱力学的状態は温度の他に圧力とか体積の様な他の変数にも依存する。そのためそれらが規定されないと比熱も確定しない。固体や液体の場合の比熱は外圧が一定で行われるか、体積を一定で行われるかの違いによる差はその値の数%程度以下なので特にその条件を特記しないが、気体の場合はかなり異なる。
そのため気体の比熱については、測定を一定圧力のもとで行な場合を定圧比熱cp、一定体積のもとで行う場合を定積比熱cvと呼んで特に区別する。そのとき、後に述べる理想気体については cp-cv=R/M (R:気体定数、M:モル質量=分子量[g/mol])という重要な関係式(マイヤーの関係Mayer's relation)が得られる。[証明は4.(2)2.参照]
3.モル比熱C
比熱の定義は普通物質1g当たりについて定めるが、物質1mol当たりに付いて定義する場合もある。それを特にモル比熱Cといい単位は[cal/mol・℃]となる。モル比熱にすると理想気体について成り立つマイヤーの関係式は Cp-Cv=R (R:気体定数~2.0cal/mol・℃)となる。[証明は4.(2)2.参照]
なぜ、物質のモル当たり(つまり物質を構成する原子や分子の個数当たり)が重視されるかというと次に述べる興味深い事実があるからです。
気体については、定圧モル比熱Cpや定積モル比熱Cvが気体の種類によらずほぼ一定の値(単原子気体についてはCp~5.0cal/mol・℃、Cv~3.0cal/mol・℃)をしめす。気体のモル比熱が気体の種類によらないと言うことは、とても不思議な事で、それは何か一般的な自然法則に基づくことを推測させます。しかし、それをここで論じている熱力学によって説明することはできない。熱力学公理系の守備範囲外の事柄です。
固体の比熱についても、特に原子量の重い元素の固体については、特別の低温でなければ定積モル比熱Cvは元素の種類によらずほぼ一定の値(~6.0cal/mol・℃)を示す(デュロン=プティの法則 Dulong-Petit law) ことが知られています。この事実も何らかの自然法則が関係していると推察されるが、これも熱力学公理系の領域外の事柄です。
今日、これらの不思議な事実は統計力学や量子力学によって説明さている。
2.気体の性質
以下で理想気体と言われるものの性質を論じます。これは熱力学の理論を展開する仮想的な物質例としてとても大切です。ここは高校物理の授業で習う所なので、この稿では簡単に復習します。
気体の示す圧力を大気圧を例に説明する。大気の圧力はトリチェリー(伊)の指示で弟子のヴィヴィアーニが1643年行った有名な実験から計算できる。
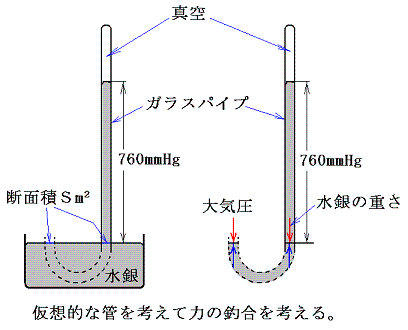
ここで水銀の密度は13.6g/cm3だから、ガラス管の断面積をSm2とすると
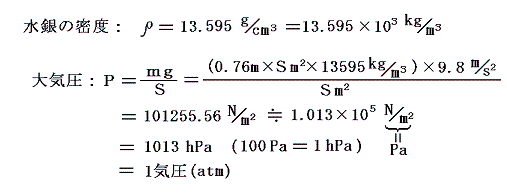
となる。
この水銀柱の高さが高度により変化する事を確かめて大気圧にその原因を帰着させたのはパスカル(仏)です。パスカルの依頼で義兄のペリエが様々な高度でトリチェリーの実験を繰り返し、高度との関係を確かめた。
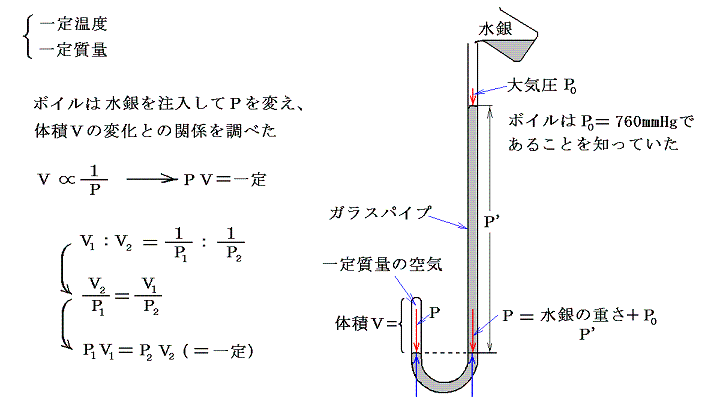
(2)ボイル=マリオットの法則(1660年)
ボイル(英)は尖端を閉じた曲がったガラス管に水銀を注ぎ込み、尖端部に閉じこめられた気体の体積と水銀柱の高さとの関係から、気体に対して成り立つボイルの法則を見つけた。温度を一定に保たねばならない事にボイルは特に気を付けていなかったが、そのことを明示したのはマリオット(仏)で1680年頃ボイルとは独立にこの法則を発見した。
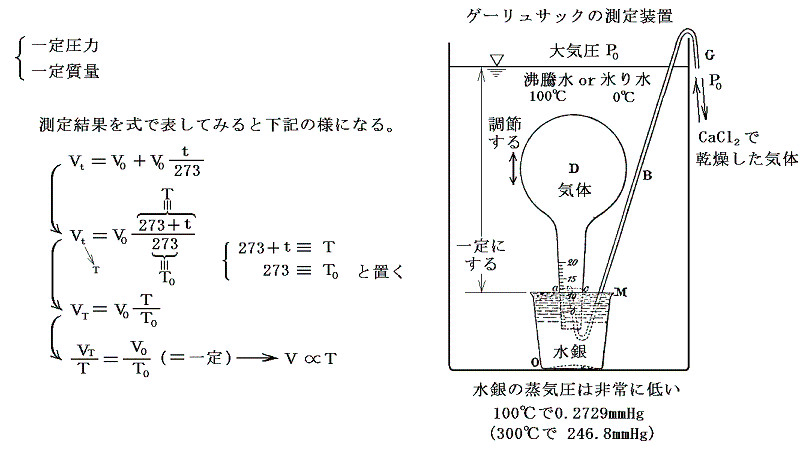
(3)シャルル=ゲーリュサックの法則(1802年)
シャルル(仏)は1787年頃にこの法則を発見していたが報告していなかったので世に知られなかった。
詳しく研究したのがゲーリュサック(仏)です。ゲー・リュサックは、水銀上に立てたフラスコDを試験しようとする気体で満たして、装置全体を水槽に浸けた。そして100℃の沸騰水と0℃の氷り水の温度間で体積変化を一定圧力の下で測定した。多くの気体(空気、O2、H2、N2、NO2、NH3、HCl、SO2、CO2、エーテル等)で調べたがいずれも0℃から100℃の間に0℃の体積の0.3749~0.3752倍膨張(膨張係数=1/266)した。気体の種類によらずほぼ一定の値を示すという驚くべき結論が得られた。
ゲー・リュサック以前に同様な測定を試みた人は多くいたが水上置換の水蒸気圧誤差の為に旨くいかなかった。ゲー・リュサックが成功した理由は、蒸気圧の小さい水銀上でおこない、しかもフラスコに詰める気体をあらかじめ塩化カルシウムを通して十分乾燥したことにある。
その後の精密な測定によると気体の膨張は、気体の種類によらず1℃当たり、0℃の体積V0の1/273倍ずつ変化するということがわかる。実はここのところは非常に微妙なところで、実用温度t(それは当然1.(1)3.に述べた何らかの物質の膨張の様子によって測る)は温度計物質に依存していてどの温度計を用いるかによって結果は微妙に変わります。だから0℃以下、100℃以上でtが1℃変化したとき体積が本当にV01/273倍ずつ変化するのか微妙な所で、この当たりが実用温度tのあやふやなところです。次の議論はその微妙な所は無視した上での話です。
以後はこの値1/273を用いて説明する。
ここで、273+tをTと置き換えると法則を表す式が特別簡単な形になることは特筆に値する。その当たりは膨張係数の意味をグラフの上で考えてみると良く解る。
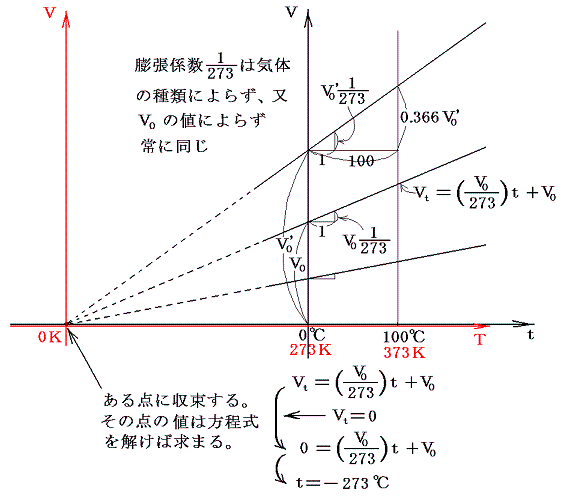
式の特性から-273℃が特別な意味を持つことが解る。気体温度計を用いる限り-273℃を温度目盛りの零点とした温度(絶対温度)がより正統性を持つことになる。つまり-273℃を0に置き換えると、y=ax+bのグラフがy=axのグラフに成り、シャルル=ゲーリュサックの法則の”体積が温度に比例する”という言い方になる。このときの温度は273+t[℃]=T[K]と置き換えたいわゆる絶対温度Tについて成り立つものであることは特に注意すべきです。ここで導入された絶対温度Tはまことにあやふやなもの[実用温度tがあやふやなので]ですが、当面はそれを絶対温度としておく。
絶対零度や絶対温度の着想自体は意外と古くからある。絶対零度の概念に思い至った最初の人はおそらくフランス人のグイヨム・アモントン(Guillaume
Amontons 1663~1705年)であろう。彼は1600年代後半の人でボイルやマリオットの晩年と同時代の人です。彼は下図の様な空気温度計を作った。
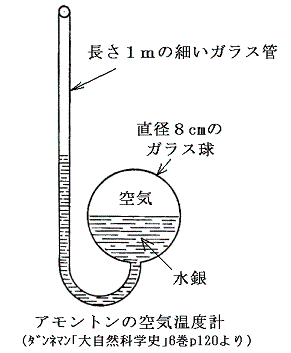
温度は容積の変化ではなくて圧力の変化で測定される。彼は気圧の効果も考慮した上で、圧力がゼロとなる様な空気の状態のときを最低温度とする考えに至った。それを基準にするとパリの最も寒いときと、暑いときの温度比は5:6であるとした。今日の摂氏温度でいくと約-240℃が最低温度と言うことになる。
空気温度計の開発当初から空気の体積がゼロになる点が-270℃付近にあり、それを絶対零度とする考え方はアンモントン以降もランベルト(728~1777年)やドールトン(1766~1844年)により1700年代から1800年代初頭に繰り返し取り上げられている。
(4)ボイル=シャルルの法則
ボイルの法則とシャルルの法則は以下の手順で統合できる。
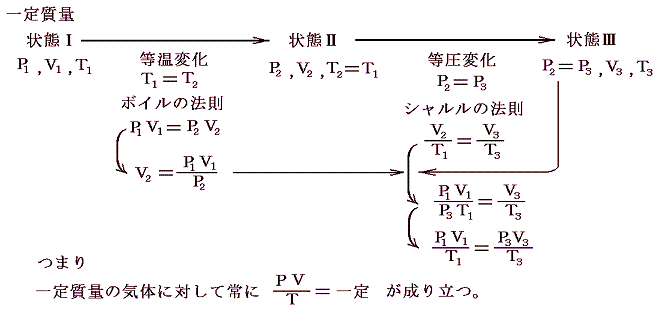
このような統合が可能なのは下図のようにボイルの法則に沿った経路ととシャルルの法則に沿った経路をつなぎ合わせればP-V座標上の任意の点を繋ぐ事ができるからです。
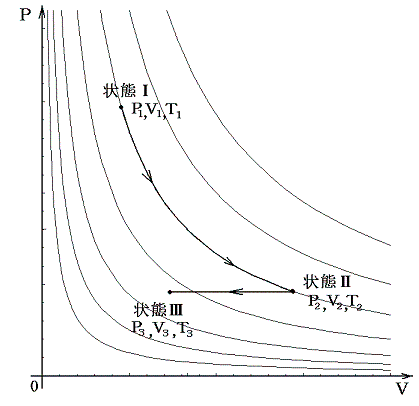
この法則は一定質量の気体を逃がさないようにしておけば、それを温めようが冷やそうが、また圧縮しようが膨張させようが、どんなことをしても良い。そのとき最初の状態のP1,V1,T1と最後の状態のP3,V3,T3を上記の式の形で組み合わせれば等号が成り立つと言っているのです。これは気体の振る舞いに関して大きな制約を課す驚くべき法則です。このとき上記の形でないとだめです。またTは絶対温度でないとだめです。
(5)理想気体の状態方程式
ボイル=シャルルの法則は気体の種類によらず普遍的に成り立つ法則ですが、厳密な測定(絶対的な温度が定まっていないのでこの言い方には語弊がある)を行うと気体ごとに法則から微少なずれ(一定値からずれる)が存在することが解る。そこで、改めてボイル=シャルルの法則が厳密に成り立つような仮想的な気体を理想気体と言うことにし、その理想気体の膨張係数でもって当面の絶対温度Tを測ることにする。理想気体そのものが仮想的なものだから、その膨張係数で定める絶対温度Tも全く仮想的なものです。今の段階では実用温度tとどの様な関係にあるのかは知ることはできません。
ここの所は、現実には定めようがない絶対温度Tに関係する性質(つまりボイル=シャルルの法則)で理想気体を定義し、その理想気体で絶対温度Tを定義している。つまり世の中に流布している理想気体の定義は循環論法の矛盾に陥っていることを心にとめておいて下さい。つまり、もし理想気体が現実に存在するのなら、それを詰めた容器を熱だめに浸してPとVを測定してPV=RTから熱だめの絶対温度Tを定めることはできますが、現実には存在しない仮想的なものだから循環論法の矛盾に陥ると言うことです。
その理想気体に対して成り立つボイル=シャルルの法則にアボガドロの法則(同数の気体は同温度、同圧力で同体積を占める)を適用するとボイル・シャルルの法則の一定値を決めることができる。アボガドロの法則によると1mol(6.02×1023個)の気体は0℃(=273K)、1気圧で22.4リットルを占める事が解っているので
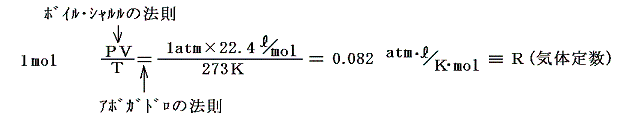
となる。そのときnmolの気体はそのn倍の体積を占めるので
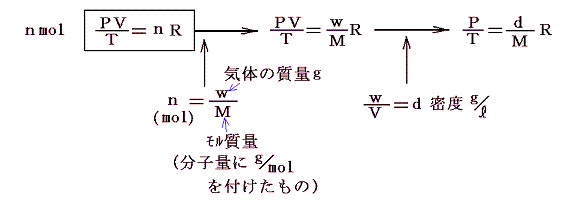
となる。上記の式を気体の状態方程式というが、モル当たりにしてこの様に表したはファント・ホッフのアイディアです。このとき、高校化学で習うように右の二式は様々な気体状物質の分子量測定に利用できる。
気体は (P,V,T,n) or (P,V,T,w) の内の三つを決めれば他は自ずと決まる。普通は n or w を定めた一定質量の気体について考察するので、その場合は二変数を定めれば残りの変数は自ずと定まり P=f(V,T)、 V=f’(P,T) や T=f”(P,V) の様な関数として表される。
気体定数Rの値は P や V の単位の取り方により変化する。このとき PV の単位が仕事(エネルギー)の単位になることに注意。
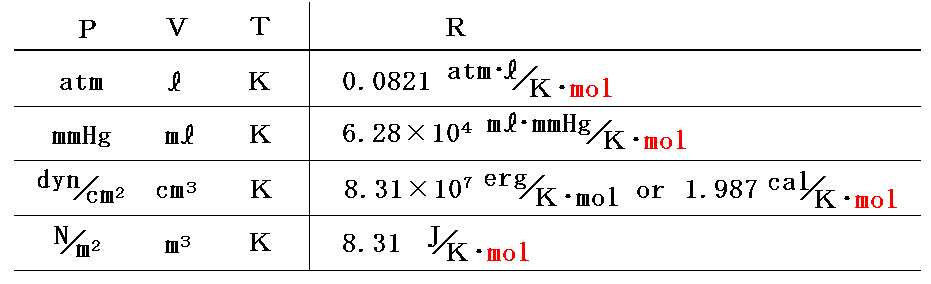
このように定めた 1mol当たりの気体定数Rは気体の種類によらずどの気体でも同じ値となる。
このHPではモル当たりではなくて単位質量についての状態方程式を用いるが、その場合には上記の値をモル質量M[g/mol]で割っておけばよい。その様に グラム単位で表した気体定数Rは気体の種類ごとに異なった値となる。
3.熱力学第一法則(エネルギー保存則)
(1)熱力学第一法則
1.第一種永久機関不可能の原理
[熱力学第一法則]
仕事は熱に、また熱は仕事に変わることができるが、そのとき一方の量は他方の量に常に比例する。つまり両者の間に当量関係がある。
熱力学第一法則は、エネルギー保存則を熱の発生や吸収を伴う現象に拡張適用したものに他ならない。このときあらゆる原理・法則について言えることであるが、法則の正しさを保証するものは、あらゆる場合に絶えず新しくその正しいことが確認されてきた長年にわたる人類の経験した事実しかない。
一つの物体系のエネルギーとは、系がそのとき存在する物理的状態によって定まる一つの量を意味する。ある状態にある物体系のエネルギー値はその物体系のある標準状態に対する値としてのみ決定できる。つまり、ある任意の状態にある物体系のエネルギーとは、その系をその状態から何らかの方法によって標準状態に移すときに、系外に持ち出されるあらゆる作用の力学的当量の総和に等しい。つまりエネルギーとは、系が外部に対して作用をおよぼすことができる能力のことに他ならない。この様にエネルギーがある物体系の内部に存在する部分を意味するとき、これを今後その物体系の内部エネルギーと言うことにする。
上記の定義を完全にするには、系が外部へ及ぼす作用の力学的当量についての考察が必要です。
外部作用として最初に考えられるのは力学的仕事です。これは多くの経験事実から外部系へ働く力と移動距離の積となることが解っている。そのとき
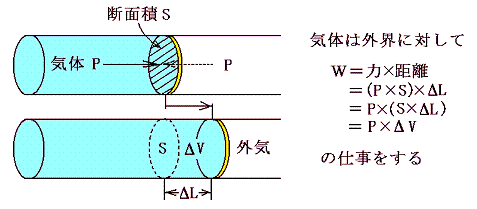
の図からあきらかなように、気体の塊のような均一系においては、その仕事量は圧力×体積変化量で表せる。
次に大切なものは熱的作用です。1.(2)で定義説明した熱量の移動によるものであるが、多くの経験事実から熱量の単位と力学的単位との間には 1[cal]=4.1868[J] の関係があることが解っている。そのため出入りする熱量にこの当量関係を適応して仕事の単位に変換することができる。
これ以外にも必要ならば、電磁気的な作用、化学的な作用等々任意の作用についても当量関係を探し出してこの議論に取り入れればよい。
このような作用の当量関係の正当性は経験事実によってのみ検証される。つまり一つの物体系を様々な道筋を通って標準状態に移行させてみる。そのとき道筋毎に作用の現れ方は異なるであろうが、それらの道筋毎に現れるあらゆる作用を力学的当量に換算して総和を取ってみる。その総和が道筋の違いによらず常に等しくなることをもって検証されるのです。Jouleが行った様々な検証実験はまさにその様なものの一例です。これらの事実の積み重ねの全体がエネルギー保存則といわれるものです。
そのとき、エネルギー保存則は、無からエネルギーを生み出すことはできないことを意味する。そのためエネルギー保存則の別表現として力学的・熱学的・化学的・その他いかなる種類の装置を用いても、それによって絶えず仕事あるいは運動エネルギーを無から生じる機関を構成することは不可能であると言ってもよい。このような機関を第一種永久機関ということにすると、エネルギー保存則は第一種永久機関不可能の原理が成り立つことと等価です。
エネルギー保存則あるいは第一種永久機関不可能の原理を今後熱力学第一法則と呼ぶことにする。
物体系の持つエネルギーは熱のやり取りや摩擦・圧縮などの仕事のやり取り、またそれ以外の諸々の物理的作用によるやり取りによってはかられる。そのとき、物体系の二つの状態が確定されていれば、その二つの状態を推移するとき外界とやり取りされる作用の総和は常に等しいのであるから、物体の持つエネルギーは物体の状態が定まれば一意に定まる量だといえる。
これこそランフォード、ゲーリュサック、マイヤー、ヘルムホルツ、ジュール等の人々によって多くの経験事実から明らかにされたエネルギーという量のもっとも重要な性質で「エネルギーは状態量である」と言われる所です。
3.(2)2.で説明するように熱d’Qも仕事d’Wも完全微分ではない。それにもかかわらず、その和d’Q+d’W=dUは完全微分であると言っているのが熱力学第一法則の内容です。(完全微分の意味は5.(2)で説明)
2.準静的可逆過程
熱力学理論で重要な状態変化は、無限にゆっくりと行われ、従って常に平衡状態にあると言われる過程で行われる。字義通りにとると、この言葉づかいは実に曖昧です。というのは、過程は必然的に変化であり、従って平衡の乱れを前提としているからです。しかしながら、変化の速さを問題とせず唯その結果のみを問題とするならば、この乱れは欲するままに幾らでも小さく採ることができる。
例えば、各瞬間において外圧を気体の圧力よりも極僅か大きくして、気体をいくらでも緩慢にその体積を任意の程度に圧縮することができる。またそのとき、一定の有限の圧縮に用いられた仕事を計算する場合に、外圧の大きさを取り扱う代わりに気体の圧力を採用しても非常に僅かの誤差を生じるに過ぎない。極限に持って行けば此の微少誤差も消失し、無限にゆっくりした圧縮に於いては、このようにして得られた結果が厳密に正しい。
ここで述べたことは、一定の圧力での圧縮・膨張にも圧力が変化する場合の圧縮・膨張についても同様に行われる。後の場合においては、小さな錘を添加したり除去したりして、外圧を常に所用の大きさに等しくしなければならない。錘を添加・除去するのに水平に押す等の無限小の力で作業できる様な配置を工夫して仕事を要しないで圧力の変化を生じせしめる様な装置を構築して作業するものとする。
熱の授受についても、外部からの仕事の場合と全く同様です。系が外部から受けるか外部へ与える値のみを取扱い、その際時間が何らの役目を勤めないならば、系が熱を受け取るか又は与えるかに従って、熱源の温度を系の温度より極めて僅かだけ高くするか、又は低くすれば十分です。この微少の差は過程の向きを決定するが過程によって最後に系に誘起される熱量の移動量には関係しない。その様にして気体の圧縮と同様に、同温度にある一物体から他物体への熱の移動を論じることができる。
これは等温過程のみならず温度の変化する過程も含まれている。そのときには、もちろんただ一つの一定温度の熱源だけでは間に合わない。例えば適当な圧縮や膨張によって自在に温めたり冷やしたりできる気体の様なものを用いたり、あるいは様々な温度を有する多数の熱源を準備して、各瞬間に於いてその瞬間の系の温度にできるだけ近い温度を有する熱源と次々に接触させる等のメカニズムを利用するものとする。
以上の様な変化を準静的過程と言う。この考え方の重要なことは、無限に緩慢な過程はすべて反対の向きにも進ませることができる点にある。これらの過程は無限小の偏差を無視すると平衡状態にあると言えるので、その過程を逆向きに進ませるためにはやはり無限小の変化を与えれば足りる。そのため準静的過程は必然的に可逆過程です。
(2)状態量と状態方程式
1.状態図
物体系のもつ状態というのは具体的にどの様に表現されるのであろうか。熱力学に於ける均質系の状態は、一般に三つの物理量、即ち圧力P、体積V、温度Tによって定まり、これらの量は一般に f(V,P,T)=0 と言う形の状態方程式を満たす。均質とはその系を構成する物体の任意の微少部分に於いて完全に同質の場合を言う。例えば理想気体の場合、2.(5)で説明したように状態方程式はPV-RT=0 となる。
このとき、均質な系に於ける温度T、圧力P、体積V等は状態が定まれば一意に定まる状態量です。このことはそれらの量の性質を考えれば明らかです。
物体の状態を表すこの三つの量の間に一つの関係式(状態方程式)が存在するので、V-T座標平面に垂直な座標軸としてPを選んだ場合、状態方程式 f(V,P,T)=0 は P=f’(V,T)なる一つの曲面をあらわすことになる。その曲面上の点でもって物体系の状態を表すことができる。そして、均質系の状態変化は曲面上の点の連なり、すなわち曲線でもって表される。そして曲線の端点が最初の状態と最後の状態を表す。
実際には三つの内の二つ、例えばTとV、を決めれば残りのPは状態方程式により必然的に定まるので、三変数の内の二つで状態変化を表すことができる。状態が変化すれば、状態を決める点(V,T)はV-T平面上で一つの曲線を描く。それらの端点を1と2として、その端点1が最初の状態、端点2が最後の状態を表す。また曲線途中の点の連なりが状態変化を表す。その様な二変数座標平面上の曲線図形を状態変化の経路図(ダイアグラム)という。
そのとき、物体系が最終的に初めの状態に戻るときには経路図(ダイアグラム)は閉じた曲線になり、循環過程(サイクル)と言われる。
この当たりの例としては別稿「気体の断熱変化」の理想気体の場合の図などを参照されたし。
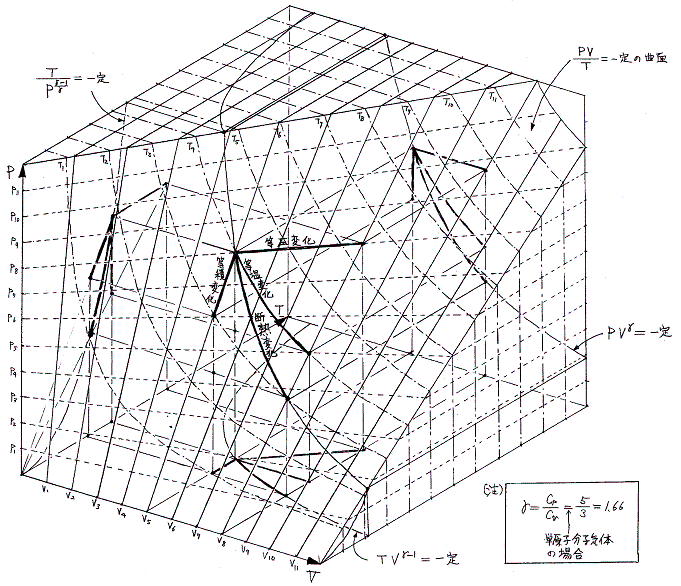
状態を表す変数として(V,T)の組み合わせ以外に(T,P)や(P,V)の組を選んでもよい。そのとき P=f(V,T)曲面上の経路図をT-P平面、P-V平面へ射影すれば、それぞれの平面上で一つの曲線が得られ、いずれも今考えている状態変化を表す経路図(ダイアグラム)となる。そのとき、状態変化を説明するのにどのダイアグラムを用いてもよい。
さらに内部エネルギーUや後で説明するエントロピーSも状態量なので(U,P)、(U,V)、(U,T)や(S,P)、(S,V)や(S,T)などの組み合わせの経路図を描くことも可能です。中でも縦軸をT、横軸をSにしたT-S経路図は極めて重要です。それは二つのS=S1とS=S1+dSの直線と経路曲線とS軸に囲まれた領域がちょうどTdS=d’Qとなり、P-V経路図の仕事PdV=d’Wと同じように、状態変化に伴って系が外界とやり取りする熱量を意味するからです。また熱機関の効率はまさに縦軸Tの作動温度に関係するからです。この当たりは後ほど6.(4)3.で詳しく説明する。
2.仕事と熱
物質系の状態1に於けるエネルギーをU1、状態2におけるエネルギーをU2とすると、熱力学第一法則はU2-U1が状態1から状態2へ推移するとき外界から物体系へ成された作用の総和に等しいことを言っている。つまり、系外から系内へ移動した熱量をQ'、系外から系へ加えられた仕事量をW'とすると
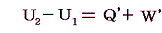
となる。[熱量や仕事量は、次で説明するように状態量ではないので、その事を明示するために’(ダッシュ)をつけます。]
前記の経路図の考え方を質量M以外に圧力Pと体積Vとによって決定される均質系に適用する。例として下図の様な状態1と状態2の内部エネルギー変化を考える。
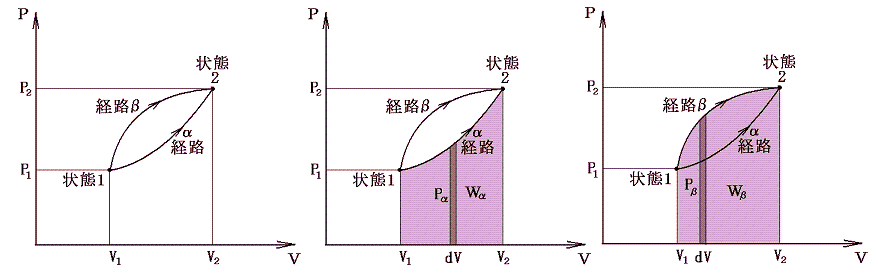
すでに述べたように内部エネルギーUが圧力Pや体積Vの変化によりどの様に変化するかを調べるには、その系を何らかの方法で最終状態(圧力や体積が異なった)に移行させ、その移行に伴う外部作用(熱の出入りや仕事のやり取り)を測定すればよい。その時、状態1から状態2へ移行するとき系に対してなされる仕事は
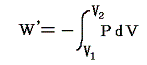
と表されるが、その積分値は経路が異なると全く異なった値(上図の灰色部分の面積×(-1)、経路αと経路βでの違いに注意)になる。このことから明らかなように
仕事は状態量ではない。経路毎に全く異なった値となる。これが仕事量の微少変分d’W=PdVが完全微分でないと言われることの意味です。
このときU1とU2は状態量だから上式の左辺U2-U1は状態1から状態2へ移行する経路にかかわらず同じ値であるが、仕事W’が経路により変化するため、移行時に出入りする熱量Q’も経路により異なることになる。つまり熱力学第一法則より
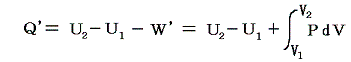
の関係があるのだから
熱は状態量ではない。経路毎に全く異なった値となる。これは1.(4)2.ですでに注意しておいた事です。これが熱量の微少変分d’Qが完全微分でないと言われることの意味です。
仕事と熱が状態量ではないということは、どんなに強調しても強調しすぎることが無いくらいに重要な事柄です。熱力学が良く理解できないのはひとえにこの事実を忘れてしまうからです。
3.循環過程(サイクル)
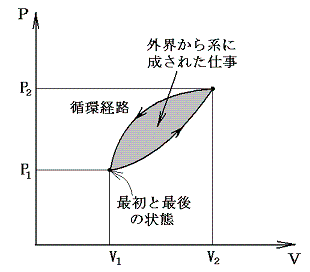
物質系がある状態から任意の変化を経て元の状態に戻るような循環過程(サイクル)をたどる場合には、上記の熱力学第一法則は
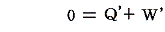
となる。つまり循環過程においては外部から系に及ぼされる作用の仕事当量の総和は零に等しい。下図のP-V図の場合循環経路で囲まれた部分の面積が1サイクルの間に系に対して成された仕事であり、それを打ち消すだけの熱が外部へ流出した事になる。
4.膨張係数、圧力係数、弾性率、圧縮率
ここで、物質変化を特徴付ける幾つかの係数を定義しておきます。
定圧膨張係数(体積膨張率):α
定圧の条件下で1℃だけ温める際の体積増加を0℃における体積V0で割ったものです。すなわち
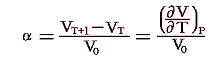
のことです。理想気体の場合は
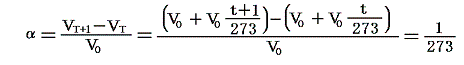
となります。こちらの説明も参照されたし。
上記と違って、膨張係数を測定する温度の体積VTで割ったもので定義すると
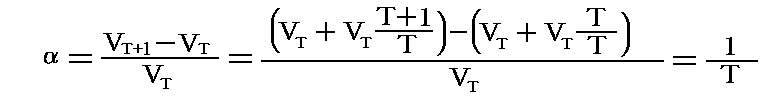
となります。つまり、この場合には理想気体の定圧膨張係数は絶対温度の逆数となります。
定積圧力係数:αP
定積の条件下で1℃だけ温める際の圧力増加を0℃における圧力P0で割ったものです。すなわち
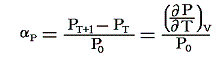
のことです。理想気体の場合は
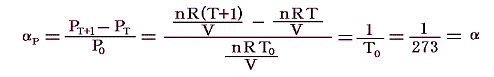
となります。
この場合についても、上記と違って圧力係数を測定する圧力PTで割ったもので定義すると
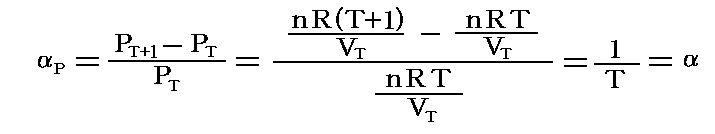
となります。つまり、この場合には理想気体の定積圧力係数は絶対温度の逆数となります。
等温体積弾性率:κ
定温の条件下での圧力の無限小増加と、それによって単位体積に生じる体積減少量との比です。すなわち
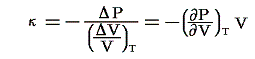
のことです。理想気体の場合には
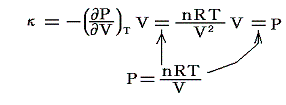
となります。
これ以外に断熱体積弾性率というのもあります。その場合はγPとなることは別稿「音速の理論」3.(2)で説明しました(ただし、γ=cp/cv)。
等温圧縮率:κ’
弾性係数の逆数、すなわち単位体積についての無限に小なる圧縮の、それに対応する圧力の増加に対する比です。すなわち
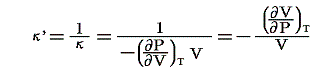
のことです。理想気体の場合には
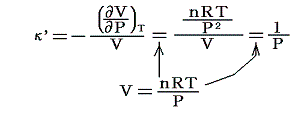
となります。これ以外に断熱圧縮率というのもあります。
[数学公式]
ここで述べた定圧、定積、等温の各変化に於ける物質の変化性状を示す三個の係数は互いに独立なものではなくて、任意の物質について一つの定まった関係式で結び付けられる。すでに述べたように、均質な物体系には、三つの状態量P、V、Tに対して状態方程式P=f(V,T)が存在する。f(V,T)を今後P(V,T)と書く事にすると、dPは完全微分なので
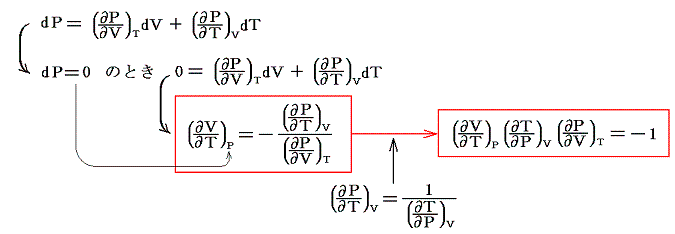
となる[完全微分の意味については5.(2)参照]。dVやdTを利用しても同様な関係式が得られる。
このことの意味を理想気体を例にして説明すると、下図のΔV,ΔT,ΔPについて
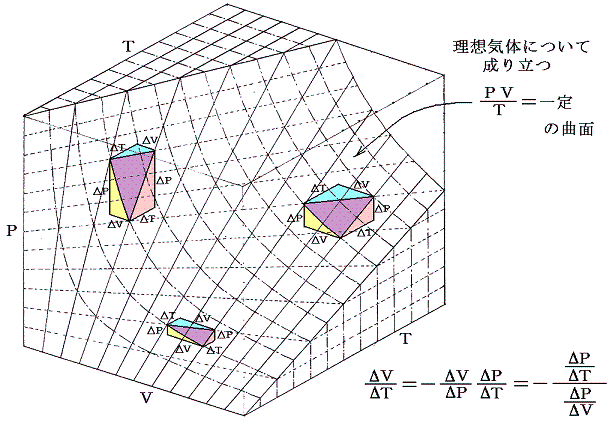
が成り立つ事です。これらの関係式は単に状態方程式曲面に対して成り立つ多変数関数の数学的な事実を表しているに過ぎない。
この関係式を用いると未知の係数を残りの二つから計算する事ができる。例えば
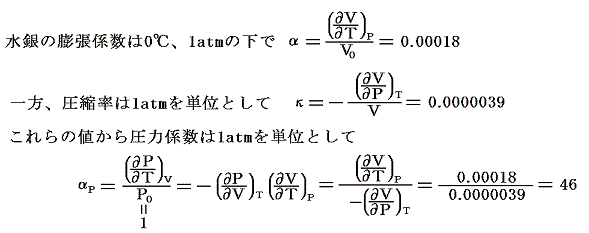
となる。すなわち0℃から1℃温める際に水銀の体積を不変に保つためには46atmの圧力増加を必要とする。
4.熱力学第一法則の応用
熱力学第一法則から多くの簡単ではあるが重要な結論が導かれる。ただし、絶対温度の厳密な導入・定義をまだしていないので、ここでの温度は1.(1)で説明した実用温度tか、又は単にt+273=Tと置いた温度だと思って下さい。このTは、2.(3)and(5)で注意したように、かなりいい加減な意味での絶対温度です。
(1)理想気体の内部エネルギー
1.ゲーリュサック=ジュールの実験
ある断熱的な容器に詰めた一様な温度にある気体に真空の容器を接続して、その接続部の活栓を開けて気体を真空中へ自由膨張させる。このとき気体は外部に対して何らの力学的な作用を及ぼさないから仕事のやり取りはしない。なぜなら真空中に噴出した気体がその容器壁へ衝突したとしても、その硬い壁は動かないのでその衝突による作用は外部に何らの力学的な仕事をしないからです。また断熱的に行っているので熱のやり取りもない。そのため熱力学第一法則(エネルギー保存則)より気体が持つ全エネルギーは最初の状態と二つの容器に拡散した最後の状態では変化しないと考えなければならない。
このような実験はゲーリュサックやジュールなどにより繰り返し行われた。そのとき彼らは気体の真空中への膨張で気体の温度がどうなるか調べたのです。具体的な手順としては高圧の気体を詰めた容器と真空の容器を活栓で接続して水槽に浸けて、熱平衡が実現されたときの水槽の水温をまず測定しておく。その後活栓を開いて暫く経ったとき水槽の温度が変化するかどうかを確かめたのです。
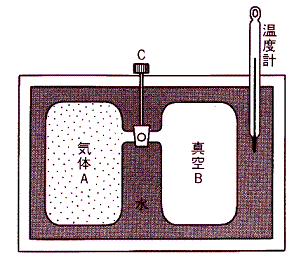
彼らはそのとき気体の体積が変化(当然圧力も変わる)したにもかかわらず温度が少しも変化しないことを見つけた。厳密に言うと極僅か変化する場合もあるが、彼らは理想的な気体については変化しないとした。つまり上記の実験で温度が変化しないような仮想的な気体を理想気体と言うことにしたのです。
この経験的な事実から「理想気体の内部エネルギーは温度のみに関係し体積や圧力には無関係です。」という重要な結論が得られる。これは最初“マイヤーの仮説”と言われていたが、今日では“ゲーリュサック=ジュールの法則”と呼ばれている。
これは状態方程式からは決して得られない、理想気体について一歩踏み込んだ性質です。状態方程式はPとVとTが互いにどの様に関係して変化するかを示しているだけで、状態が決まったとき(つまりP、V、Tが決まったとき)の内部エネルギーがどういった値になるのかは何も教えてくれない。その何も解らない内部エネルギーについて一歩踏み込んだ性質を教えてくれています。ただし内部エネルギーが温度にどの様に関係するのかは何も教えてくれない。
高校物理の教科書ではこの結論がどこから出たのか曖昧で初学者は面食らうところですが、これは単なる経験事実(ゲーリュサック=ジュールの実験や次に述べるジュール=トムソンの実験)を理想化したものでしかない。熱力学ではそれ以外の根拠は無いことに注意されたし。
[補足説明1]
高校物理でゲーリュサックの実験を教えますが、生徒はこの実験の意味をなかなか理解できません。それも宜なるかなでして、この実験の意味を正しく解釈するのは極めて難しい。最初に正しく解釈したのは、“マイヤーの関係式”を用いて“熱の仕事当量”を初めて求めたマイヤーです。
マイヤーの1845年論文に記されている上記の解釈(最初“マイヤーの仮説”と言われていた)をW.ThomsonやJ.P.Jouleは疑っていました。それで、(ゲーリュサックの実験を知らなかった)ジュールは自ら実験して見ることにしたのです。そうして、ジュールはゲーリュサックの実験結果を追認し、マイヤーの考察に納得します。
そしてさらに、ジュールとトムソンは、マイヤーの仮説は理想気体で正しいが、現実気体は水素を除き自由膨張に多少の温度変化が伴う事(次節の“ジュール=トムソン効果”)を発見します。
このあたりは山本文献18.第22章第Ⅴ節の解説が秀逸です。別ページで引用していますので御覧下さい。
なお、ゲーリュサックの実験そのものと、ゲーリュサック自身はその実験結果を正しく解釈できなかったことについては、山本文献18.第15章第Ⅲ節で説明されていますので是非ご覧下さい。この当たりを正しく説明しているのは、山本氏によるとマックス・プランクの『熱力学』と『理論熱学』だけだそうです。
2.ジュール=トムソンの実験
前項で述べたゲーリュサックやジュールの実験は気体の熱容量が器壁や水槽のそれと比較して非常に小さいので精度的には十分とは言えない。そのため精度を改良するために行われたのがW・トムソンが工夫しジュールの協力のもとで行われた、有名なジュール=トムソンの実験です。
この実験の改良点は、気体の流出を緩慢にすることにより直接に第二の平衡状態に移し第二の平衡状態の温度T2を気体の中で直接測定することです。そのため、気体の熱容量が小さいことは不利な事ではなくむしろ有利に働く。
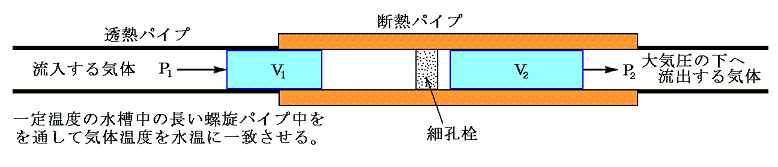
この実験では、気体が高圧P1の場所から低圧P2の場所(大気圧)へ、途中の柘植(つげ)材の管(その中に綿花もしくはほぐした絹がつめられており、気体が非常に通過しにくくしてある)を通って定常的にゆっくりと移動させられる。
実際の測定は下図に示す装置を用いて、次のように行われる。一定温度の水槽中に置かれた長い螺旋パイプの末端部に綿、絹、その他の繊維をほぐしたものを詰めて細孔栓とする。パイプは細孔栓の近くのみ断熱されており、それ以前は熱伝導性の良い金属銅パイプで構成してあり細孔栓に流入する空気の温度が厳密に水槽の水温に一致するようにしてある。細孔栓の前後の断熱された部分の管内に温度計を挿入して定常的に流れる気体の細孔栓直後の温度を測定する。測定部より下流側は大気圧(1気圧)になるように調整されいる。また上流側にポンプが設置されてあり、大気圧よりも少し高い圧力で定常的に気体を送り込むようにしてある。温度測定はポンプを連続的に働かせて定常状態になったときに行われる。
下記論文についてはこちらを参照。[図の拡大版]
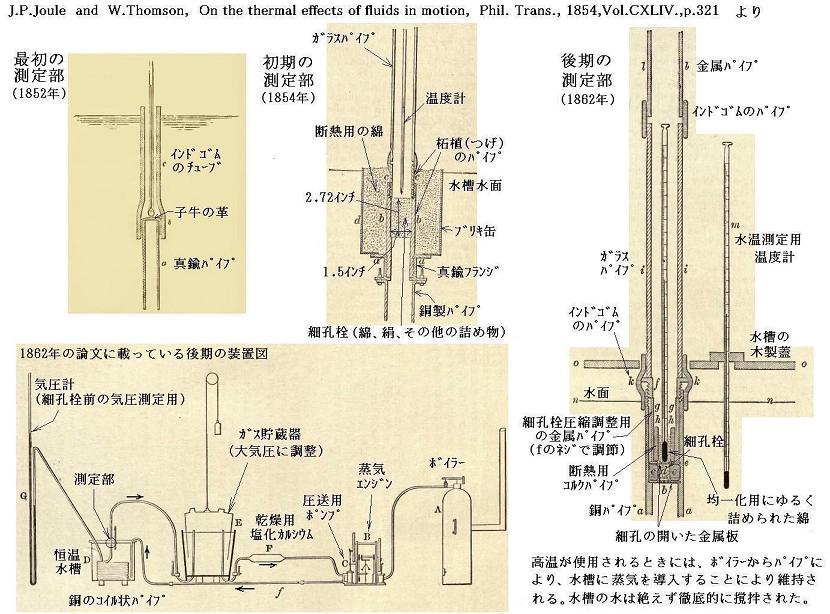
ジュール・トムソンの実験については山本文献18.第28章第Ⅱ~Ⅴ節の解説もご覧下さい。
測定の結果は、空気については非常に小さい温度変化があり、水素についてはそれが更に一層小さくほとんど測定にかからないほどであった。それゆえ理想気体に対しては温度変化が無いとして良いだろう。その様な気体を仮想的に理想気体と言うことにしたのです。
この測定は断熱的におこなわれ、しかも温度変化が少しも起こらないと見なして良いのだから理想気体に於けるボイルの法則を用いれば、細孔栓の手前での体積をV1、栓を通過した後の体積をV2とすると、P1V1=P2V2が成り立つ。
そのため、高圧側で外界から気体に対してなされた仕事P1V1は低圧側で気体が外界(大気)に対してなした仕事P2V2に常に等しくなる。それは気体に対して正味の仕事はなされず、気体の内部エネルギーが変化しないことを意味する。
これはかなり込み入った考え方です。つまり、普通の気体ならば温度変化が起こらないからと言ってP1V1=P2V2の保証などはないのだが、理想気体というものは温度が一定ならボイルの法則が成り立つようなものとしていたのだから理想気体というものを仮想的に考えるときにはP1V1=P2V2が成り立って仕事は零で、そのため内部エネルギーは変化していないと言っても良いだろうということです。
つまり、気体の体積は変わるのに、その温度は大体一定に保たれているのであるから理想気体の内部エネルギーは温度のみに関係して体積には無関係であると言える。すなわち
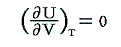
となる。
普通この実験はエンタルピーとの絡みで説明されるが、もともと理想気体というものの性質を見極めるために行われた実験であることを忘れないでほしい。この実験の一番の意義はそこにあるのだから。
理想気体ではない現実の気体に対しては温度変化を生じる。これは断熱的な変化であるにも関わらず内部エネルギーが変化する事を意味し、外部から気体になされる仕事と気体が外部に対してする仕事の間に差がある事を意味する。
例えばΔP=P1-P2=1気圧当たりで説明すると、T1=0℃のとき、空気に対してはΔT=-0.3℃、二酸化炭素ではΔT=-1.4℃であり、水素では逆に温度が上昇してΔT=+0.033℃となる。水素でも十分低温になるとΔTは負になる。温度を高くし、密度を小さくするとΔT→0となり理想気体に近づく。
このように実在気体に於いて温度が少し変化する事をジュール・トムソン効果という。これは気体分子の間に引力が働き、分子が大きさを持っているために生じるものであるが低温になるほど大きくなる。この効果は気体の液化や極低温をつくる装置に利用される。また実在気体を用いて絶対温度を定めるのに利用される[7.(2)参照]。
なお、“ジュール・トムソン効果”の詳細に付いては、別稿「ファン・デル・ワールスの状態方程式」5.をご覧下さい。
3.理想気体の性質
多くの教科書では、理想気体の性質として
- 理想気体は状態方程式 PV=RT を満足する。
- 理想気体の内部エネルギーUは(“ゲーリュサック=ジュールの実験”により)体積によらない。つまり(∂U/∂V)t=0
- 理想気体の“ジュール=トムソン効果”はゼロです。つまり(∂T/∂P)H=0
が成り立つとしています。
そして、1.が成り立てば2.や3.が証明でき、逆に2.と3.が成り立てば1.が証明できるとしている(例えば戸田盛和著「いまさら熱力学?」丸善(1997年刊)p73~82など)。
しかし、この当たりの説明は不十分なのでもう少し補足しておきます。2.(5)で述べたようにPV=RTを用いる理想気体の定義は絶対温度Tが厳密に定義されていないので循環論法の論理矛盾があり、もともとこの式は意味をなしていないのです。
だから正しくは”2.や3.は実験事実を理想化してその様な性質を持つ気体を理想気体と言うことにする”です。そのときの2.や3.で言う温度は1(1)で述べた実用温度tでかまいません。それでは2.や3.の事実と1.のPV=RTとの関係はどうなるのかと言うと、”状態方程式中のTを、熱力学第二法則を用いて定めた絶対温度(7.(1)、(2)で定めます)であると解釈するとPV=RTが2.や3.と論理矛盾が生じていないことが言える”、です。決して、”1.から2.や3.が導ける”、と言われるような関係ではありません。プランクの本を読むとこの当たりの事情がよく解る。詳しくは7.(1)2.をご覧下さい。上記の戸田盛和氏の本の説明も論理矛盾が無いことを確認しているのだと解釈されれば良いと思います。
(2)定積モル比熱Cvと定圧モル比熱Cpの関係
ここでは物質量1モル(n=1mol)の均一な一成分系を考える。
1.一般的関係
熱力学第一法則より
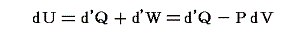
であるが、物質系の内部エネルギーUは状態量で物質系の温度Tと体積Vの連続的な関数U(T,V)と考えることができるので
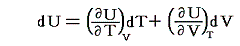
が成り立つ。そのため
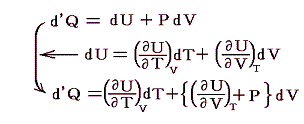
となる。
【定積の条件下】で加熱される場合、仕事は無いので、系のエネルギー変化は流れ込んだ熱に等しい。そのため定積モル比熱Cvは
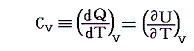
となる。
一方、【定圧条件下】で加熱される場合、定圧モル比熱Cpは
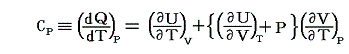
となる。上記の二式を一緒にすると
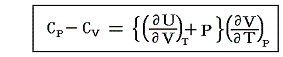
となる。この式は任意の物質について成り立つもので、右辺は定圧過程で体積膨張により消費されるエネルギーを補うために必要な余分の熱量を表す。
2.理想気体の場合
これは別稿「気体のモル比熱」で解りやすく説明しているので、ここでは簡単に記す。
4.(1)で述べたように理想気体の内部エネルギーUは温度だけの関数です。さらに、2.(5)で述べた様に1molの理想気体についてはPV=RTが成り立つ。そのためモル比熱に対して以下の関係式が成り立つ。
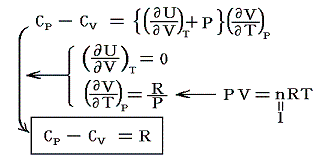
これが1.(5)2.or3.で説明したマイヤーの関係(Mayer's relation)です。
3.理想気体の比熱
理想気体では
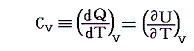
において、Uは温度のみに関係し体積には無関係であるから、Cvは温度のみに関係し体積に無関係として良いであろう。またマイヤーの関係式を援用するとCpも同様に温度のみに関係し体積に無関係として良いであろう。
この結論はH.V.Regnault(アンリ・ヴィクトル・ルニョー1810-1878)が多くの気体の測定により確認した。そのとき彼はさらに、Cpは温度のかなり広い範囲にわたって一定である事も発見した。したがって再びマイヤーの関係式を適用するとCvもまた、その範囲内で一定であるとして良いであろう。
それ故に、Cp、Cvが温度および体積に無関係であるとする事を、理想気体の条件に加えても良いであろうし、また今後そうすることにする。
ここで次のことに注意してほしい。理想気体の比熱が温度、体積によらず一定値であることは、今まで述べた理想気体の性質から理論的に証明できるような事柄ではない。実在の気体の性状から推し量って、その様に置くことにしたのです。理想気体の内部エネルギーは温度のみに関係して体積には無関係であるというのが、実験結果を理想化したものであったように、この比熱についての性質も実験事実の理想化から、そのようにしたのだということを銘記すべし。世の一般の教科書ではその当たりが実に曖昧にしか記載されていない。
[補足説明]
高校物理の初等的な計算で習うように統計力学的な考えによると理想気体の絶対温度は気体粒子の運動エネルギーに比例します。熱量を加えることはエネルギーを加えることに相当しますからどの絶対温度でもその比熱は同じになるわけです。だから統計力学的に定義された理想気体については、Cp、Cvが温度および体積に無関係であることを統計力学的に証明できます。しかし、同じことが熱力学法則から熱力学的に証明できるわけではありません。
1.理想気体の場合
これは別稿「気体の断熱変化」で解りやすく説明したので、ここでは簡単に記す。
当然のことですが可逆過程の断熱変化とする。つまり外界と可逆的に仕事をやり取りしながら膨張・収縮する。断熱変化ではd’Q=0だから

2.音速
音は圧力変化が伝播する現象ですが、変化速度が速いため音の伝播に伴う圧縮・膨張は断熱的に行われると考えて良い。さらに理想気体の状態方程式が成り立つとして良い。
力学理論によると音速は体積弾性率κ、気体密度ρと
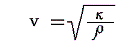
の関係にあることが解っている[別稿「音速の理論」2.参照]。この式に熱力学の成果を代入すると

となる。これは測定結果に良く一致する。
[補足説明]
ファン・デル・ワールス気体の音速は以下のように表される。
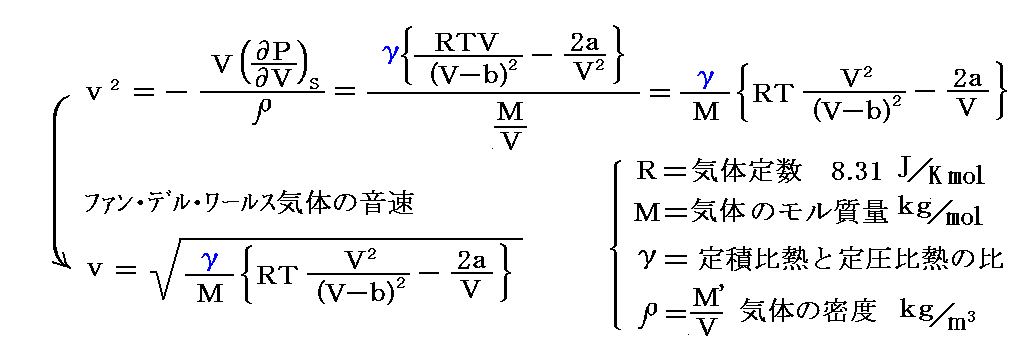
この式の導出は別稿「熱力学関数(状態方程式曲面)の性質」1.(2)4.をご覧ください。
(4)不均一系への応用
不均一系とは明確な境界面で分かたれて均質な物質が幾つか共存して成り立ってるような系や、様々な化学物質が混在して化学平衡が成り立っている様な系を意味する。
前者では液体がその蒸気と接触している場合や、固体がその融解した液体と共存している場合などが考えられる。また後者では一般の化学反応がすべて含まれる。さらに、固体がその溶媒に解ける溶解現象や、二種類の気体や液体が混合する現象などが含まれる。これらの現象の多くは後に述べる熱力学第二法則が関係するので8.まで詳細の議論は置いておく。
しかしながら、熱力学第一法則のみで説明できる事柄もある。中でも大切な応用は化学反応における反応熱と物質の性質についての議論です。化学反応熱の分野はエネルギー保存則(熱力学第一法則)だけからでも様々な重要な情報を得ることができる。
化学反応系のUは、系の内部エネルギーと呼ばれ、系を構成する粒子一つ一つの運動エネルギー(並進、回転、振動)とそれらの間の相互作用(分子間力)や各粒子を構成する原子の化学結合エネルギーの総和です。そのとき、すでに注意したように熱力学第一法則は
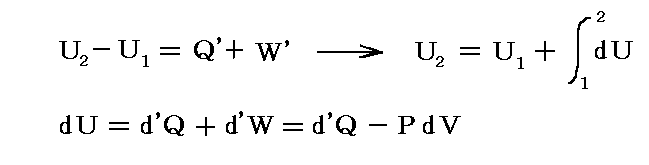
で表される。Uは状態のみの関数であり、dUは完全微分(全微分)[その詳し意味は5.(2)で説明]となる。
そのとき、“系の熱”や“系の仕事”と言ったものを単に
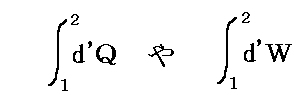
で定義することはできない。それはd’Qやd’Wは完全微分ではなくて、その積分値は状態1から状態2へ至る道筋に依存するからです。dに付けた’はその事を明示するためにつけられている。
しかし、特別な場合には、上記の積分を求めることができる。もしもd’Q=0またはd’W=0ならば、d’W=dUまたはd’Q=dUとなることは明らかです。すなわち、これらの特別な条件が成り立つときにはdUが完全微分だからd’Wやd’Qも完全微分になるのです。
化学反応に於ける内部エネルギーの変化dUを求めるのに“反応熱d’Q”を用いることができるのは、まさにこの第二の場合だからです。具体的な反応熱測定法はこちらを参照されたし。
また、前節で説明した“断熱変化”は、まさにこの第一の場合です。
もう少し補足すると、化学反応熱はd’W=0の元ではなくて、dP=0の一定圧力の元で(体積変化を許して)測定される場合が多い。その場合には
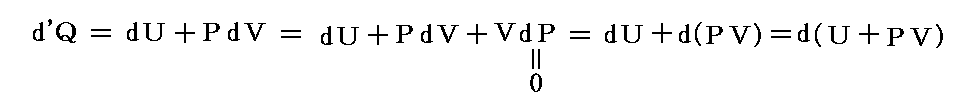
となる。この場合のPVは状態量ですから、この様な変化の場合には、反応熱は
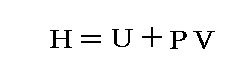
という新しい状態量(“エンタルピー”と呼ぶ)の変化と考えられる。
この状態量の変化dHに於いて、PVなる状態量の変化分d(PV)を引けば、状態量である内部エネルギーの変化dUになる。そのため、反応熱d’Qを反応に伴う内部エネルギー変化dUに結び付けることはたやすい。
ただし、その当たりは別稿「反応熱と熱化学方程式」で説明しているのでここでは議論しない。
5.完全微分方程式と積分因子
6.で説明する熱力学第二法則は極めて抽象的・数学的な法則です。使われている数学概念を理解しないと真の理解は得られないので、まずその準備から始めます。熱力学では偏微分を含む数式が沢山出てきますが、本章で述べる数学概念が理解できていないと、その意味を理解するのは難しい。
1.定義
直交座標空間の中に、定まった方向を持った曲線sが与えられているとする。(x1,y1)を曲線のはじめの点、(xn,yn)を終わりの点とし、曲線sの弧の長さをはじめの点から測るものとする。この空間の各点に連続な関数X(x,y)とY(x,y)が定義されているとする。
微少部分dsのx座標方向の成分をdx、y座標方向の成分をdyとして下記の様な(X(x,y),Y(x,y))との積を作り、その和を取る。曲線の分割の数nを限りなく大きくし、曲線要素dsを限りなく小さくした極限の値を関数(X(x,y),Y(x,y))の線積分という。
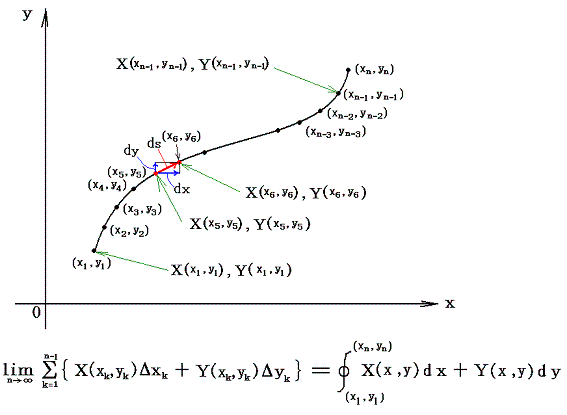
2.意味
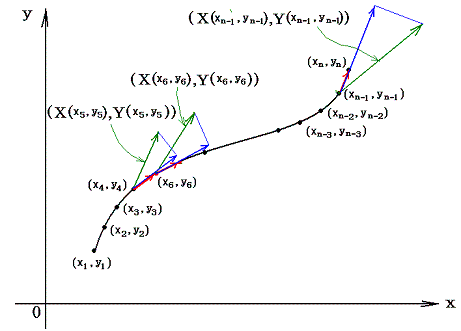
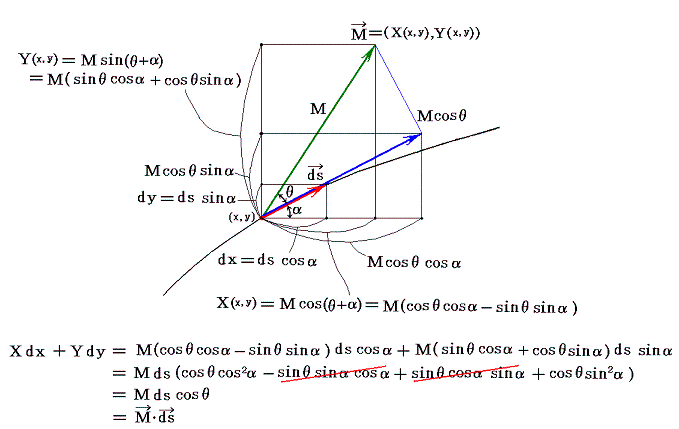
このときX(x,y)とY(x,y)を点(x,y)で定義されるベクトルのx成分、y成分と考えるとXdx+Ydyはベクトル(X,Y)とベクトル(dx,dy)の内積を意味するので、線積分とは下図のベクトル(X(x,y),Y(x,y))を経路の微少線分方向へ射影した成分にdsを乗じて経路長に沿って加え合わせて行くことを意味する。
(2)完全微分方程式
1.完全微分方程式とは
微分方程式
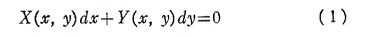
を考える。
(1)の左辺がx,yのある関数の完全微分に等しいとき、すなわち
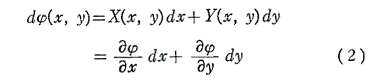
を満足する関数φ(x,y)が存在するとき、つまり
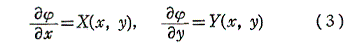
が成り立つとき、(1)は完全微分方程式という。
このような関数φ(x,y)に対して
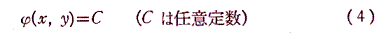
は(1)の一般解です。なんとなれば、yをxの関数と考えて(4)の両辺xで微分すれば
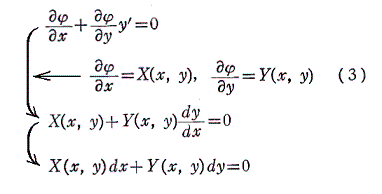
となるからです。
次に、(1)が完全微分方程式であるための必要条件を求める。X(x,y)、Y(x,y)はx,yについて連続な偏導関数を持つと仮定すれば、完全微分方程式ならば(3)式が成り立つので
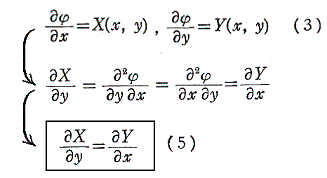
を得る。すなわち、(5)は(1)が完全微分方程式であるための必要条件です。
次に、(5)は(1)が完全微分方程式であるための十分条件でもあることを証明する。
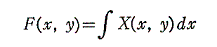
とおけば、

となる。よって
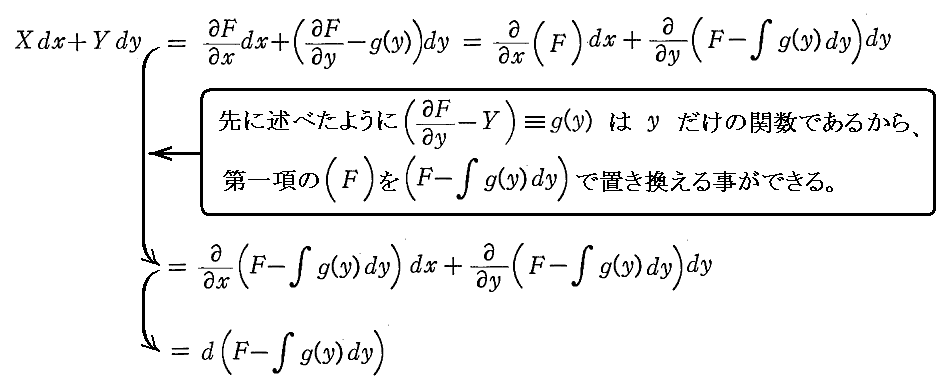
となるが、この式はXdx+Ydyが関数
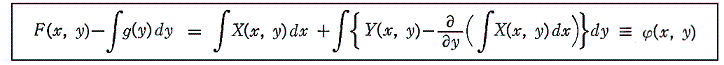
の完全微分に等しいことを示している。よって(1)は完全微分方程式です。
以上をまとめると
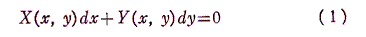
が完全微分方程式[つまり左辺がある関数φ(x,y)の完全微分dφとなる]であるためには
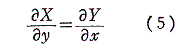
が成立する事が必要十分条件です。
そのとき(1)の解は
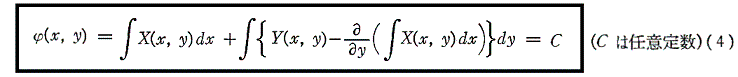
で与えられる。
[補足説明1]
実際に、上記の必要十分条件の証明法を『熱力学』に最初に適用したのはClausiusだと思います。
彼は1864年に論文集を出版する際に彼の 「熱力学第1論文(1850年)」2.(3)3.に追記した注2) に於いて上記の【必要条件の証明】を、またその論文集に付け加えた 付録B に於いて上記の【十分条件の証明】を明確な意図を持って実施しています。
Clausiusの理論展開は極めて難解ですので、そこの [補足説明6] と [補足説明7] をご覧下さい。
2.完全微分方程式の例
一般論だけでは何のことか解らないので幾つか例を説明する。
[例1]
X(x,y)がxだけの関数で、Y(x,y)がyだけの関数である場合。
この場合には、常に条件式(5)が満足される
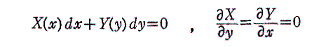
ので完全微分方程式となる。
そのとき一般解は
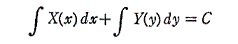
となる。
[例2]

は条件式(5)を満足するので完全微分方程式です。
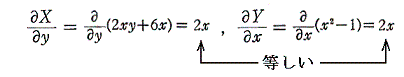
よって一般解は
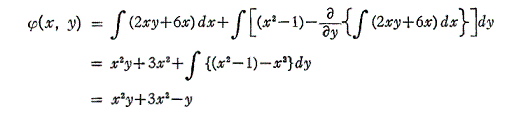
であるから、
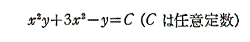
で与えられる。この結論は下記のくくり直し法でも直ちに導ける。
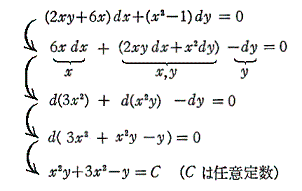
[例3]
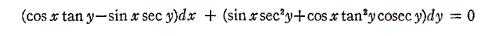
も条件式(5)を満足する。
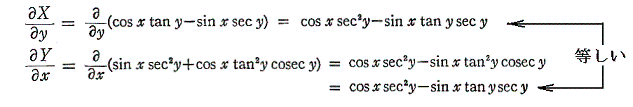
よって完全微分方程式です。ゆえに
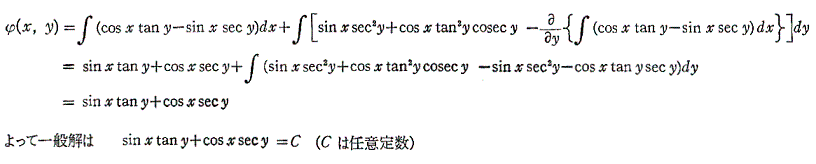
3.完全微分方程式の一般解の意味
前節[例2]を利用して完全微分方程式の意味を説明する。
完全微分方程式の
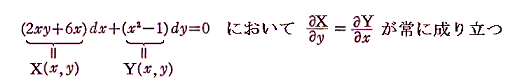
と言う条件は、一つのx,yの連続関数φ(x,y)=x2y+3x2-yが存在して
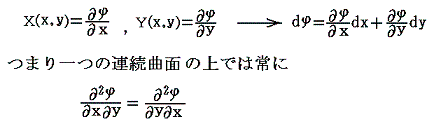
が成り立つから言えるのです。
この例の場合X(x,y)、Y(x,y)、φ(x,y)の値をxy平面に垂直にとれば、それぞれの関数は下図の三曲面を表す。そのとき(5)式が成り立つと言うことは、関数曲面X(x,y)とY(x,y)を利用して一つの関数曲面φ(x,y)を定めることができるということを意味します。このことは、下図に於いてそれぞれの関数の偏微分が関数曲面の傾きを表していることを読み取れば了解できるでしょう。
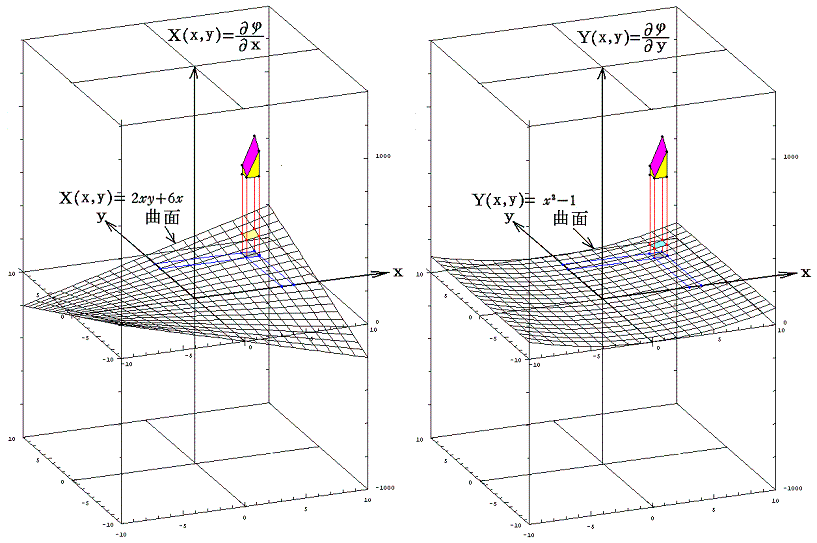
つまり完全微分方程式を解くと言うことは、ある座標点(x0,y0)のφ(x0,y0)を定めてからdxとdyを少しずつ変化させて座標点(x0+dx,y0+dy)へ移動するときの変分dφ(完全微分)を求め、それをφ(x0,y0)に積み上げながら関数曲面φ(x,y)を決めていくことです。
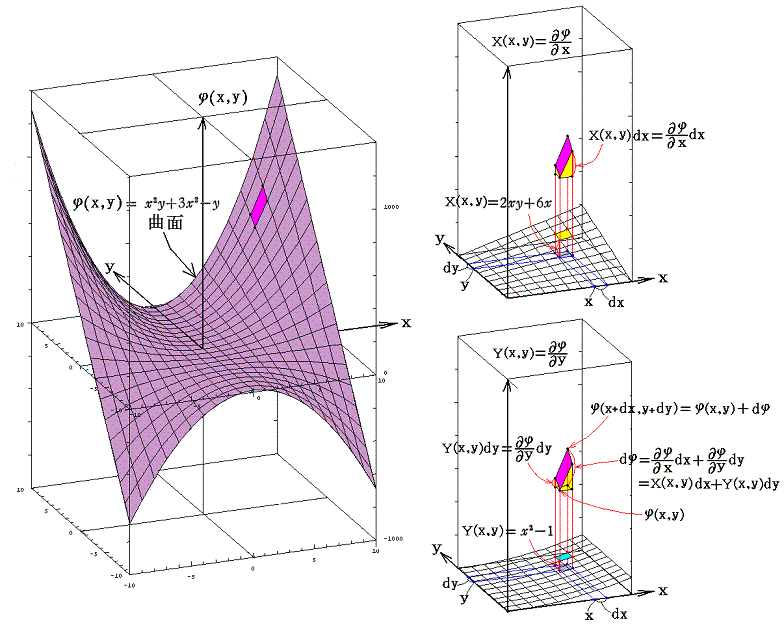
このとき φ(x,y)=C (ある定数)は 関数曲面φ(x,y) の等高線を意味する。
例えば x2y+3x2-y=100、x2y+3x2-y=0、x2y+3x2-y=-100 のグラフは下図の様になる。
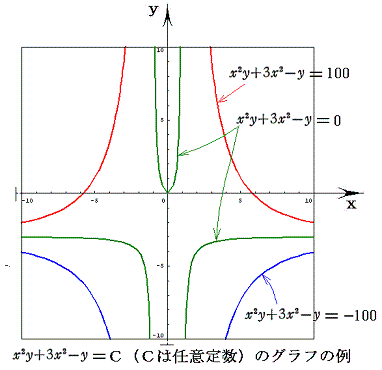
つまり完全微分方程式の (2xy+6x)dx+(x2-1)dy=0 の意味はdφが零になる方向(dx,dy)が存在し、その方向の軌跡を定めることです。解を求める操作とは等高線を少しずつ伸ばして等高線を表す曲線を求めることです。例えば上図の(x,y)=(7,7)の位置では
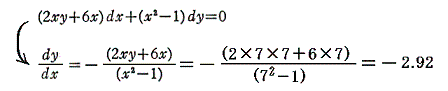
となるので、その点に於ける等高線のxy平面に於ける傾きは-2.92(下図参照)となる。
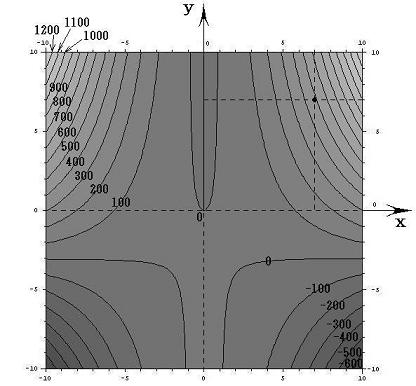
ここで、(X(x,y),Y(x,y))=(2xy+6x,x2-1)と(dx,dy)をそれぞれ2次元平面のベクトル成分だと考えるとベクトル(X,Y)とベクトル(dx,dy)の内積が零と言うことは二つのベクトル場が直交していることを意味する。つまり(dx,dy)ベクトルの方向を連ねたものが解φ(x,y)=C (ある定数)であるが、それはちょうど電場ベクトルに直交する等電位線のようなもので、どの(x,y)点に於いても上図の等高線ベクトル(dx,dy)は下図のベクトル場(X,Y)に直交していることが解る。
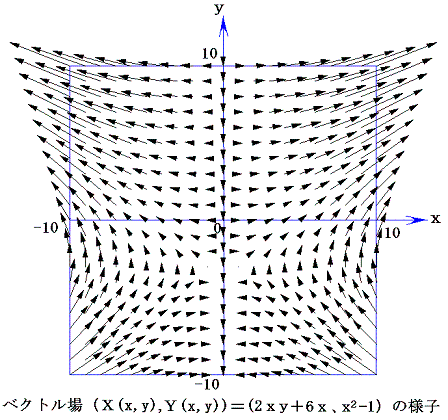
等高線の集合が関数曲面φ(x,y) に他ならないのだから、xy平面上で座標点(x,y)をあらゆる方向に移動させたときの変分 (2xy+6x)dx+(x2-1)dy=dφ を加え合わせながらプロットしていくと一つの曲面φ(x,y)ができる。そのとき、xy平面上の曲線に沿ってdφ加え合わせてゆくことは、5.(1)で説明した線積分を実施することに他ならない。
このとき最初の点と最後の点が同じならどの経路を通って線積分を実施してもそれらの値はすべて同じになる。なぜなら積分値はまさに点1と点2の標高差に他ならないのだから、経路によらないことは明らかです。
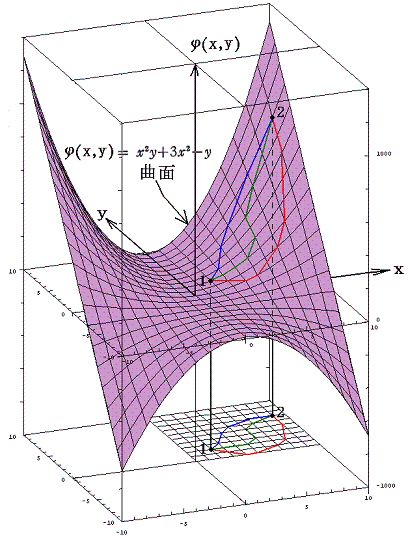
これが、完全微分方程式の左辺がある関数φ(x,y)の“完全微分”であると言うことの意味です。その完全微分成分dφをある経路に沿って線積分することは関数曲面φ(x,y)上を移動することを意味する。熱力学的な言い方をすれば、φ(x,y)は変数xとyの“状態量”であると言うことです。
これをベクトル場(X(x,y),Y(x,y))=(2xy+6x,x2-1)に付いての線積分と考えると、Xdx+Ydyはベクトル(X,Y)とベクトル(x,y)の内積を意味するので、下図のベクトル(X(x,y),Y(x,y))を経路の微少線分方向へ射影した成分を経路長に沿って加え合わせて行くことを意味する。
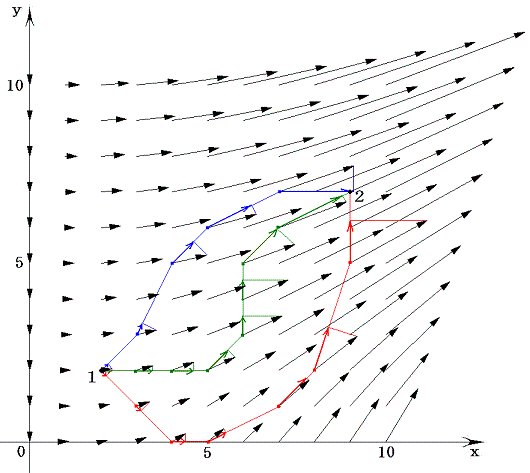
この結果が上図の三経路ですべて等しいのです。これはちょうど、保存力の場に於ける力のベクトル(ポテンシャルの勾配)と仕事の積算値との関係と同じです。
[まとめ1]
以上をまとめると以下となる。
ある関数φ(x,y)の“全微分”
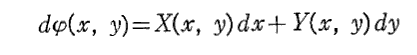
が“完全微分”であるとは、上記の全微分が
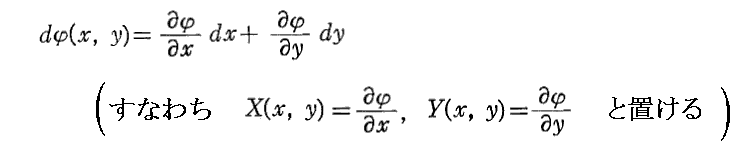
と表されて、しかも
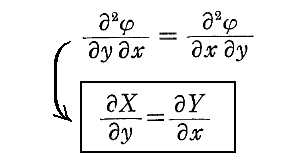
が成り立つことです。
これを幾何学的に言うと、“関数φ(x,y)が、変数x,yに関して一意に定まる値を持つ連続的な1つの曲面を表す”と言うことです。
その為あるA地点(x,y)から別なB地点(x+dx,y+dy)に移動したときの関数値φ(x,y)の変化量dφは、A地点からB地点へ移動する時の径路によらない。すなわちφ(x,y)の値は(x,y)が決まれば必ず一意に定まっているということです。
熱力学的な言い方をすれば、“φ(x,y)は変数xとyが定まれば必ず一意に定まった値を持つ“状態量”である”ということです。
1.積分因子とは
一般の微分方程式では
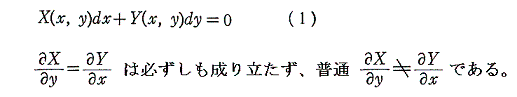
つまり“完全微分方程式”ではない。
しかしながら、この両辺にx,yのある関数 λ(x,y) を乗じて得られる微分方程式
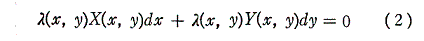
は“完全微分方程式”になることがある。
このような関数 λ(x,y) を(1)の“積分因子”という。
例えば微分方程式
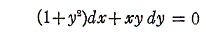
は、
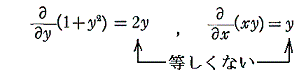
であるから、完全微分方程式ではない。しかし両辺に 2x をかけて得られる微分方程式
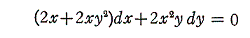
は
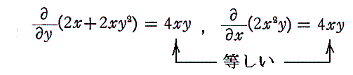
であるから、完全微分方程式です。だから λ(x,y)=2x は積分因子です。このとき当然のことですが積分因子は X(x,y)=1+y2、Y(x,y)=xy の関数形に依存する。
一般に積分因子となるものは沢山あります。例えばCを任意定数とすると λ(x,y)=C・xやλ(x,y)=C・(1+y2)-1/2、λ(x,y)=x・(1+y2)-1/2、・・・・・等々 のいずれも微分方程式 (1+y2)dx+xydy=0 の積分因子となります。積分因子であることは条件式に代入してみれば簡単に確かめることができます。
2.積分因子の効果
このとき (1+y2)dx+xydy=0 が“完全微分方程式”ではないということは、 (1+y2)dx+xydy=d’ψ なる量をxy平面上の曲線に沿って計算しながら d’ψ を積み上げていったとき、つまり線積分
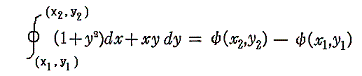
を実施したとき、最初の点(x1,y1)と最後の点(x2,y2)は同じでも、その線積分値は経路が異なれば全く違った値となることを意味する。熱力学的な言い方をすれば、”(1+y2)dx+xydy=d’ψ は(dx,dy)が決まったからと言って一意には決まらず、“状態量”ではない”、と言うことです。
d’ψがある関数ψの完全微分ではないことを示すためにdではなく’(ダッシュ)を付けたd’で表していることに注意。今後、“完全微分”では無い場合にはdに ’(ダッシュ) を付けることにする。
本によっては δψ のように δ を用いて表す場合もある。
先ほど取り上げた例 (1+y2)dx+xydy=0 に於いて X(x,y)=1+y2、Y(x,y)=xy のグラフは下図のようになる。
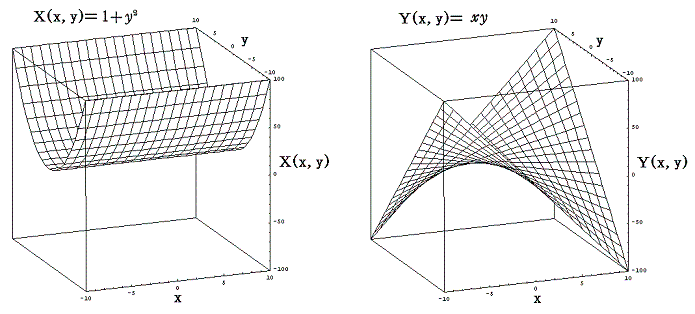
このグラフの中の領域(2≦x≦3、2≦y≦3)に着目して、 (x1,y1)=(2,2) から (x2,y2)=(3,3) までを二つの経路 (2,2)→(3,2)→(3,3) と (2,2)→(2,3)→(3,3) で移動する。そのときdx=1、dy=1を単位として移動して、各経路について (1+y2)dx+xydy=d’ψの積算値を計算してみる。
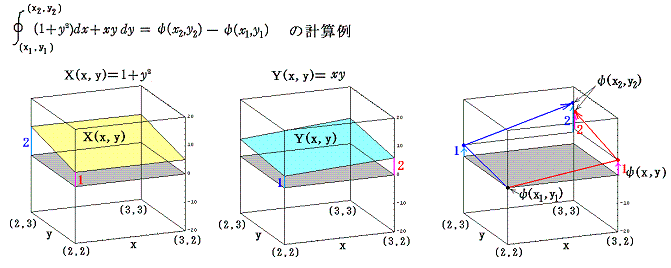
経路をもう少し拡大して (2,2)→(3,2)→(4,2)→(4,3)→(4,4) と (2,2)→(2,3)→(2,4)→(3,4)→(4,4) で積算値を比較すると
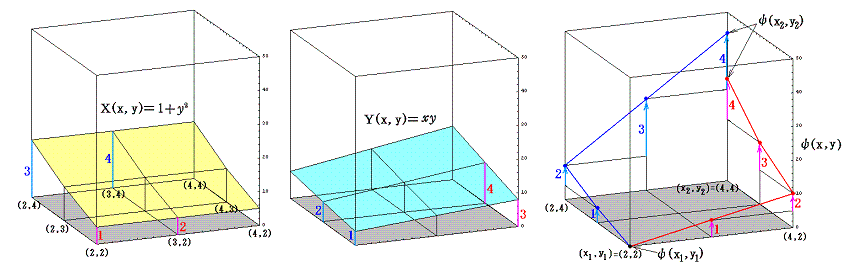
となる。図から明らかなように Σd’ψ は積算経路によって全く異なることが解る。
ところが積分因子2xを乗じた (2x+2xy2)dx+2x2ydy については、この微少成分はある連続関数φ(x,y)の完全微分dφとして表せ、xy平面上の線積分は最初と最後の点が同じなら積分経路に関係なく同一の値になることが言える。熱力学的な言い方をすれば”(2x+2xy2)dx+2x2ydy=dφは(dx,dy)が決まれば一意に決まる状態量である”。
積分因子=2x を掛けて完全微分方程式にした (2x+2xy2)dx+2x2ydy=0 に付いて同様な考察を行う。まず X(x,y)=2x+2xy2、Y(x,y)=2x2y のグラフは下図のようになる。
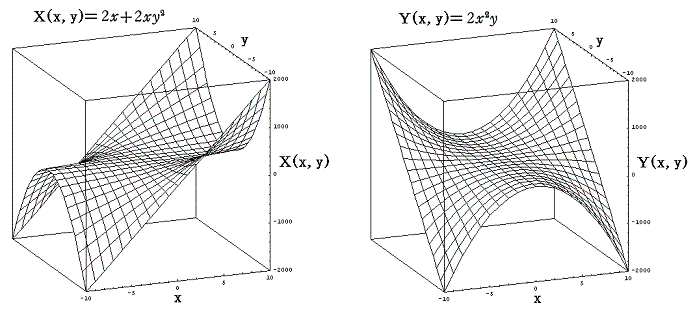
このグラフの中の領域(2≦x≦3、2≦y≦3)に着目して、 (x1,y1)=(2,2) から (x2,y2)=(3,3) までを二つの経路 (2,2)→(3,2)→(3,3) と (2,2)→(2,3)→(3,3) で移動する。そのときdx=1、dy=1を単位として移動して、各経路について (2x+2xy2)dx+2x2ydy=dφ の積算値を計算してみる。
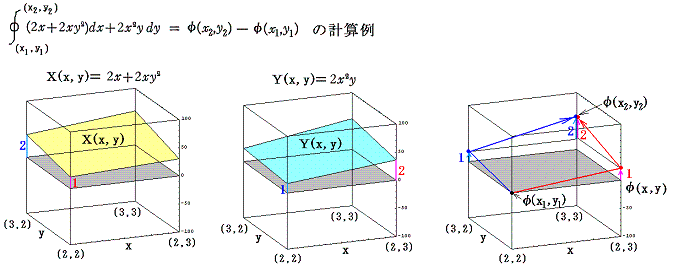
経路をもう少し拡大して (2,2)→(3,2)→(4,2)→(4,3)→(4,4) と (2,2)→(2,3)→(2,4)→(3,4)→(4,4) で積算値を比較すると
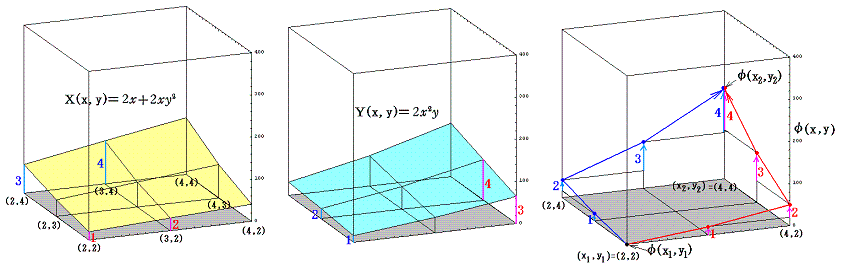
となる。
dxもdyも微少量ではなく1にしているので、有限な大きさであることによる誤差のため二つの経路の積算値は完全には一致していない。しかし、移動単位をもっと小さくしてゆけば極限に於いてΣdφが厳密に一致するであろうことは予想できる。この一致が完全微分方程式の必要十分条件、つまり任意の(x,y)点に於いて
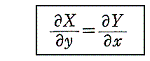
を満たすという意味です。
ここで用いた図の意味が良く理解できない方は、下図をご覧下さい。[拡大図]
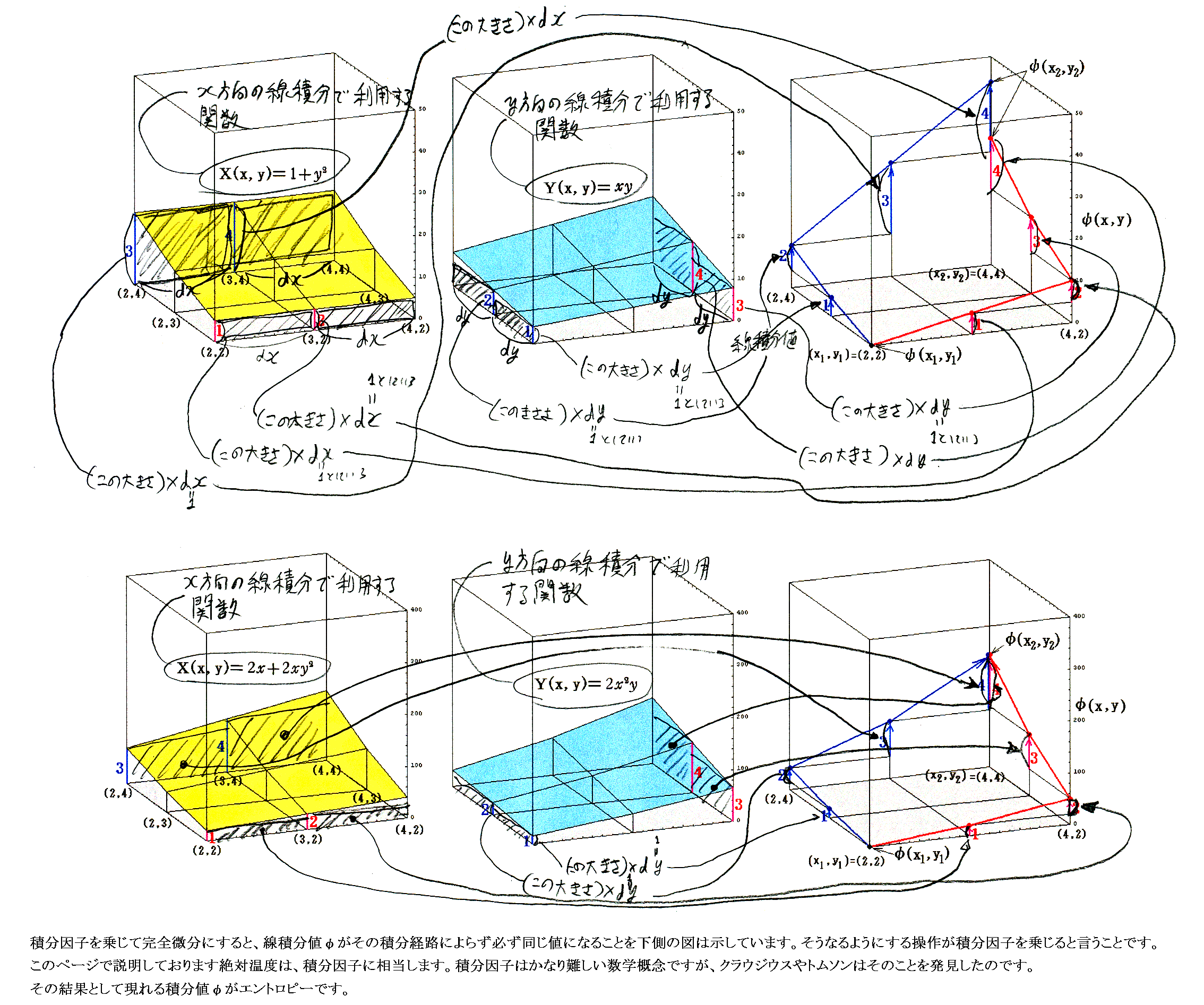
3.完全微分方程式の解φ(x,y)
ちなみにくくり直し法を用いるとφ(x,y)=x2+x2y2であることは直ちに導け、そのグラフは下図のようになる。ただし縦軸のスケールは縮小してある。
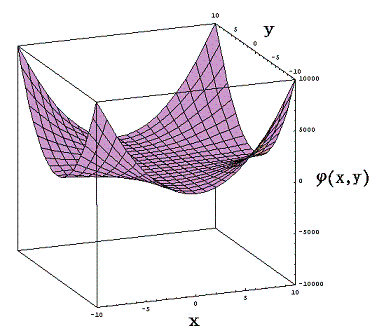
このとき等高線のグラフは下図の様になる。
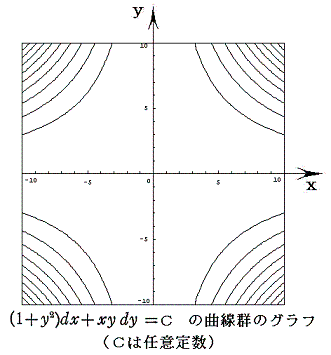
(4)“積分因子”の存在定理
1.定理の証明
ここで、完全微分方程式ではない任意の微分方程式を完全微分方程式にする積分因子は常に存在するのかが問題となるが、二変数の場合必ず存在することが数学的に証明される。つまり
X(x,y)とY(x,y)がxとyに関して連続な関数であれば、任意の二変数の微分方程式X(x,y)dx+Y(x,y)dy=0に対して、この両辺にx,yのある関数 λ(x,y) を乗じて得られる微分方程式
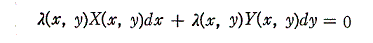
が完全微分方程式になるような関数 λ(x,y)【積分因子】は必ず存在する。
ここで”二変数の”という但し書きは重要です。三変数の場合には常に存在するとは限らないからです。三変数の場合の積分因子の存在性については参考文献(犬井文献13.、スミルノフ文献14.等々)を参照して下さい。
[証明の概略]
二変数の完全微分方程式ではない微分方程式X(x,y)dx+Y(x,y)dy=0のX(x,y)とY(x,y)を二次元ベクトルの(x,y)成分と考えると、この微分方程式の解はベクトル場(X(x,y),Y(x,y))に直交する曲線群を求めることに相当する。なぜなら微分方程式の意味はベクトル(X,Y)とベクトル(dx,dy)の内積が零であると言っており、これは二つのベクトル場(X(x,y),Y(x,y))と(dx,dy)が直交していることを意味するのだから。
例として、前項で取り上げた完全微分方程式ではない(1+y2)dx+xydy=0について説明すると、ベクトル場(X(x,y),Y(x,y))=(1+y2,xy)は下図の様(長さは1/50倍にしてある)になる。
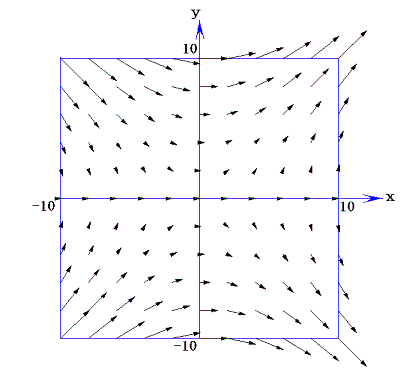
このようなベクトル場に対して常に垂直に交わる曲線群は必ず存在する。これは電場に対する等電位線の関係に似ています。実際のところ存在することを数学的に証明【スミルノフ文献14.(第3巻§75と§51)等を参照】することは結構面倒です。
しかし、存在するであろうことは了解してもらえると思いますので、その関数を F(x,y)=C(Cは任意定数) とする。数学では、これを微分方程式X(x,y)dx+Y(x,y)dy=0の“積分”と言う。
この関数 F(x,y)=C の両辺をxで微分すると、右辺は定数だから零となり、これは
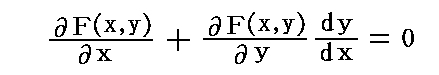
を満足する。ここで X(x,y)dx+Y(x,y)dy=0 の要請[すなわち、ベクトル場 (X(x,y),Y(x,y)) と (dx,dy) が直交している]から
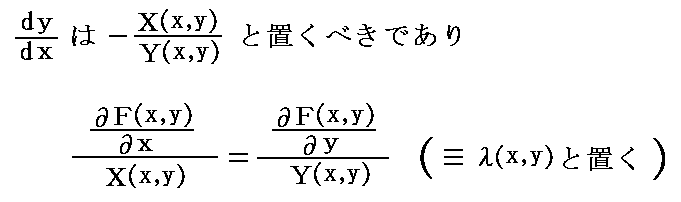
が成り立たねばならない。この相等しい両辺の商を共通の関数λ(x,y)と置けば
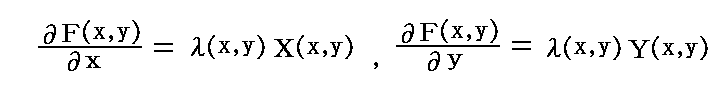
となるが、これらは先ほどの式
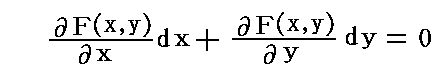
を考慮すると、完全微分である条件式
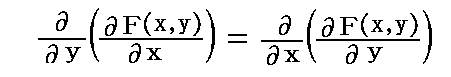
を満たしているので、これはまさしく λ(x,y)X(x,y)dx+λ(x,y)Y(x,y)dy=0 が 完全微分方程式 dF(x,y)=∂F(x,y)/∂x・dx+∂F(x,y)/∂y・dy=0 であることを意味している。故に積分因子 λ(x,y) は必ず存在して、それは
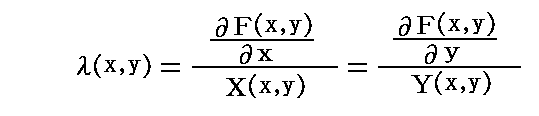
となる。
[証明終]
2.“積分”F(x,y)の意味
このとき次のことに注意されたし。この “積分”F(x,y) は λ(x,y)X(x,y)dx+λ(x,y)Y(x,y)dy=dφ(x,y) がある関数 φ(x,y) の完全微分になるというときの関数 φ(x,y) そのものです。つまり、前項の例5.(3)3.で求めた φ(x,y)=x2+x2y2=F(x,y) です。なぜなら、積分因子 λ(x,y)=2x を乗じた (2x+2xy2)dx+2x2ydy=0 についてのベクトル場 (X(x,y),Y(x,y))=(2x+2xy2,2x2y) のグラフは
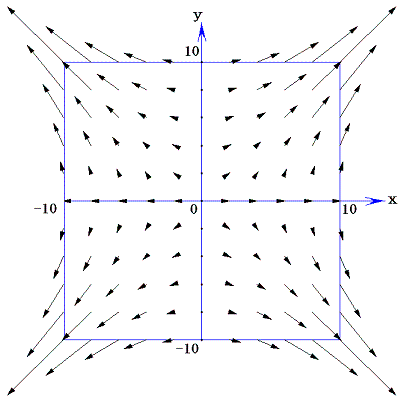
の様になる(長さは1/500倍にしてある)のだが、この図を前出の (λ(x,y)X(x,y),λ(x,y)Y(x,y))=(1+y2,xy) が表すベクトル場のグラフと比較してみと、両図の同じ(x,y)点のでベクトルは、向きが逆になる所もあり、長さの分布の様子も異なるが、その傾きは全く同一になる。
これはベクトル (λ(x,y)X(x,y),λ(x,y)Y(x,y)) はベクトル (X(x,y),Y(x,y)) を単にλ(x,y)倍したものにすぎないのだから当然です。ベクトルの傾きが全く同じなのだから、それらのベクトル場に垂直な曲線群が等しくなるのは当然です。
実際、積分 F(x,y)=x2+x2y2 と X(x,y)=1+y2、Y(x,y)=xy を
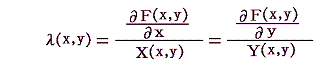
に代入すると、確かに λ(x,y)=2x が得られる。
3.“積分因子”λ(x,y)の意味
このとき、微分方程式 (1+y2)dx+xydy=0 の一般解である積分と、完全微分方程式 (2x+2xy2)dx+2x2ydy=0 の一般解である積分が、共通の積分となり、同じ解曲線 φ(x,y)=x2+x2y2=C(Cは任意定数) をもちます。
なぜなら前項で説明した様にベクトル場 ((1+y2),xy) と ((2x+2xy2),2x2) は同じ(x,y)点に於いて同じ方向を持つベクトル(大きさは異なる)ですから、各点におけるベクトルに垂直な方向の 線分ベクトル(dx.dy) をつらねた解曲線が同じになるのは当たり前だからです。
このとき、解曲線が共通だからといっても、(x1,y1)から出発して任意の微少変分(dx,dy)方向への積算値を線積分した
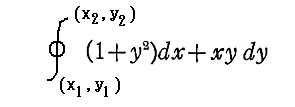
が、任意の積分終了点(x2,y2)に関して、(x1,y1)から(x2,y2)へ至る積分径路に関係無く一意に定まるわけではありません。何度も出てきたように
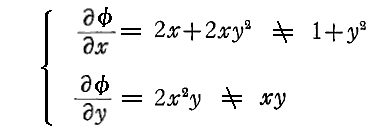
なのですから。
もちろんdΦ(x,y)=(2x+2xy2)dx+2x2ydyの積分に関しては、途中の積分径路に依存することなく
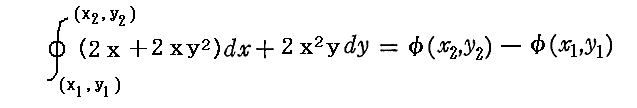
が成り立ちます。
このことは5.(3)2.で説明した通りですが、今一度、そこで述べたベクトル場について説明する。(x1,y1)=(2,2)から(x2,y2)=(4,4)までを二経路 (2,2)→(3,2)→(4,2)→(4,3)→(4,4) と (2,2)→(2,3)→(2,4)→(3,4)→(4,4) で線積分すると
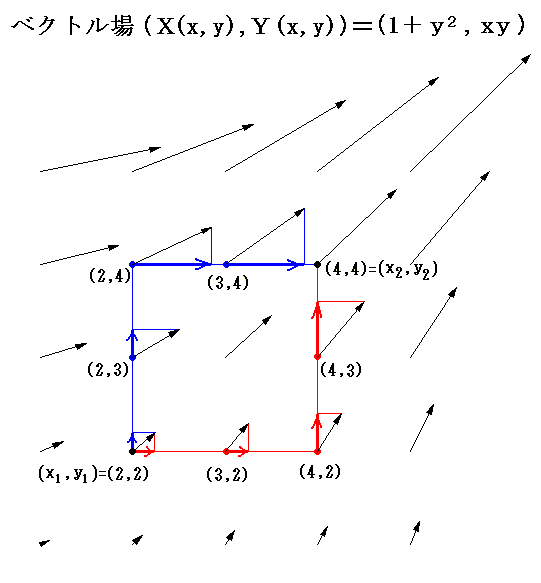
(長さは1/20倍にしてある)となり、線積分値は二経路で一致しない。
ところが、
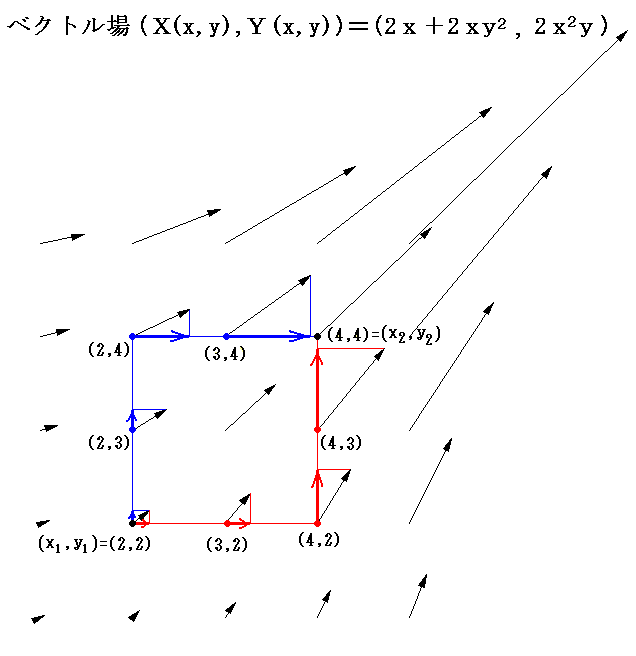
(長さは1/110倍にしてある)では、一致する。
両者の違いは、各点(x,y)に於けるベクトル(X,Y)の傾きは同じだが長さの分布が違うことから生じる。“積分因子”とは上記の線積分が経路に依存しなくなるように各点のベクトルの長さを調整する関数のことです。
どの様に調整するのかというと各点に於けるベクトルの長さがある関数φ(x,y)のgrad(勾配)になるように調整する。
つまり微分方程式X(x,y)dx+Y(x,y)dy=0の一般解F(x,y)=C(Cは任意定数)が等高線となるように調整するのです。
一般解の一つの曲線に沿って(つまり等高線に沿って)移動すると隣の解曲線との間隔が密になったりまばらになったりする。等高線が密の所は傾斜が急でまばらな所はなだらかであることを思い出して下さい。その密度の変化に対応するようにそれに垂直なベクトルの長さ(傾斜を意味する)を調整する。つまり間隔が狭いところでは長く、広い所では短くする。
実際の所、5.(3)3.の一般解の集合図(等高線図)を上記のベクトル図に重ねてみると、前者ではベクトルの長さが等高線間隔と対応していないが、後者では対応していることが解る。
このとき、一般解の曲線の一つ一つに沿ってベクトルの長さを調整していくのだが、曲線に沿って出発するとき最初に取る基準値の大きさには任意性がある。この任意性から解るように積分因子となる関数は沢山ある。実際すでに述べたようにλ(x,y)=x、λ(x,y)=3x、・・・、λ(x,y)=C・(1+y2)-1/2、λ(x,y)=x・(1+y2)-1/2、・・等々はいずれも積分因子となる。
(5)積分因子の求め方
1.積分因子は偏微分方程式の解
二変数の場合には積分因子λ(x,y)は必ず存在することは解っているのだが、それを求めるのは必ずしも簡単ではありません。積分因子λ(x,y)を決めるにはφ(x,y)=F(x,y)が解らねばなりません。完全微分方程式の場合、φ(x,y)は5.(2)1.の(4)式の様に簡単に求まりましたが、今は先ず完全微分方程式にするためのλ(x,y)を求めなければならないからです。
それは結局、λ(x,y)X(x,y)dx+λ(x,y)Y(x,y)dy=0が完全微分方程式であることの必要十分条件
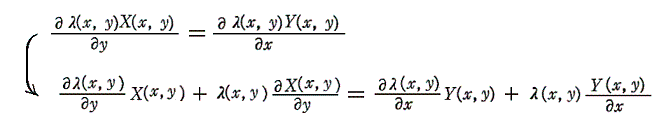
から得られる
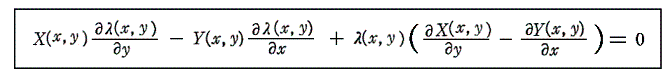
なる線形一階偏微分方程式を未知関数λ(x,y)について解くことと同じです。
当然のことですが解λ(x,y)はX(x,y)やY(x,y)の関数形に依存します。その関数の値を考慮した上であらゆる(x,y)点で上記の式を満足する関数λ(x,y)を求める。
偏微分方程式を解くのは一般に難しいのですが、ある特殊な仮定が成り立つ場合には簡単に解くことができます。そのような例を幾つかを説明します。
2.λがxだけの関数λ(x)の場合
5.(3)で出てきた (1+y2)dx+xydy=0 を例に説明します。いまこの微分方程式の積分因子がxだけの関数λ(x)であることが解っているとします。その場合上記の偏微分方程式は
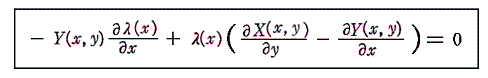
となります。
λ(x)(1+y2)dx+λ(x)xydy=0 が完全微分方程式であるための条件から
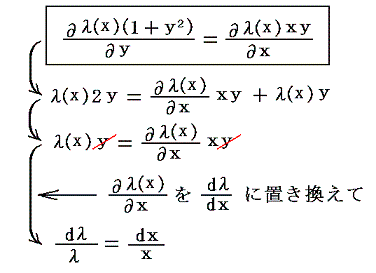
となり、唯の積分の式に簡単化できます。そのため両辺をそれぞれの変数で積分すれば
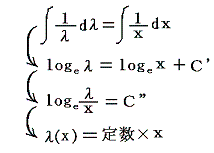
となる。これはまさに5.(3)1.で述べた“積分因子”です。この解き方が7.(1)~(3)で重要になります。
3.λがyだけの関数λ(y)の場合
同様に (1+y2)dx+xydy=0 を例にして説明します。この場合も積分因子がyだけの関数λ(y)であることが解っているとします。その場合上記の偏微分方程式は、λ(y)(1+y2)dx+λ(y)xydy=0 が完全微分方程式であるための条件から
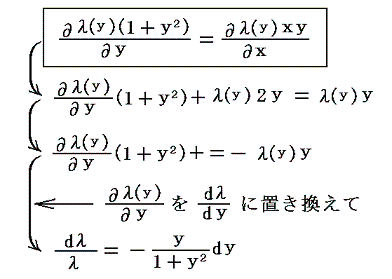
となるので、両辺を積分して
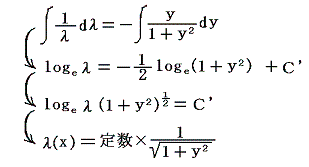
となる。これも積分因子です。実際に条件式に代入してみると
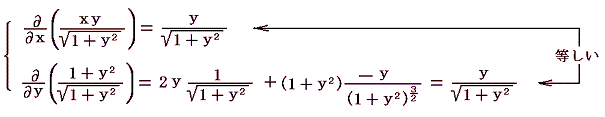
となることから了解できる。5.(4)3.と同じ範囲のベクトル図を描いてみると
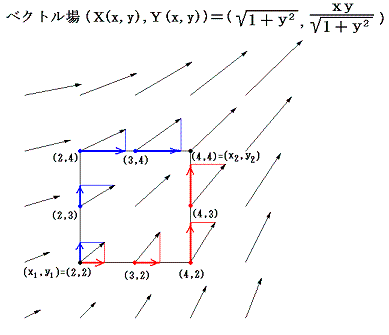
(長さは1/5倍にしてある)となり、矢印の長さの分布状況は変わっているが、線積分値は二経路で同じであることが解る。つまり、この場合も矢印に垂直な曲線群の隣同士の間隔が矢印の長さに逆比例するように矢印の長さが調整されている。
このとき5.(4)3.で説明した積分因子の意味を考えれば明らかなように前記二つの解を積の形で組み合わせた
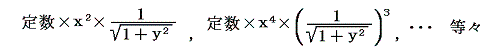
もすべて (1+y2)dx+xydy=0 の積分因子となることに注意してください。一般に積分因子は無限に存在します。ところが後で述べるように、熱力学第二法則の縛りを入れると一つに定まります。
以下の議論には積分因子λ(x,y)は必ず存在することと、λがxだけの関数λ(x)の場合の求め方が解れば十分ですので、一般的な解き方の説明は省略します。
(6)エントロピーの導入
前項までの結論を3.章で説明した事柄に当てはめてみます。
1.内部エネルギーは状態量、熱や仕事は状態量ではない
U2-U1=dUと置くと熱力学第一法則(エネルギー保存則)は
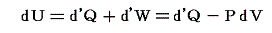
と表される。ここで内部エネルギーUが状態量であるからと言って、Q-V平面上にある連続曲面U(Q,V)が存在する訳ではありません。d’Qやd’Wは状態量ではないので物体系に出入りする熱の総量Qや仕事の総量Wを座標軸に取ることはできません。同じQやWの値(Vは共通)でもUは一つに定まらないので、QやWは状態方程式を表す変数にはなれないからです。
熱力学第一法則を
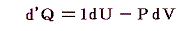
の形に書き直したとき、3.(2)2.で説明したように物質系の状態変化に伴って出入りする熱の総量は状態変化の経路ごとに異なるから熱量の変分d’Qは完全微分ではありません。
しかし、UとVは状態量なので状態方程式の変数となり得ます。このときd’Qが定まらない、つまりdUとdVの変化経路に依存すると言うことは5.(3)の議論で言うところの X(U,V)=1 と Y(U,V)=P(U,V) に関して完全微分の条件が成り立たないということです。つまり
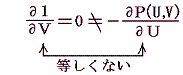
と言うことです。もちろんそのとき、着目している物質系の P(U,V) がどの様な関数になるのか何の情報もありませんが、とにかくU-V平面上の経路に沿ってd’Qを加え合わせると始点と終点が同じでもQの線積分値は経路毎に違った値になることだけは確かです。
2.変数の変換
内部エネルギーUは直接測定することは難しいので、Uが幾ら状態量だからといっても状態変数としては適当ではありません(ただし、次で説明するエントロピーSは経路図の状態変数として重要です6.(4)2.参照)。普通は変数Uを温度Tと体積Vなどに変換しておきます。
ただし温度に関しては絶対温度Tの完全な定義はまだ行われていないので、1.(1)で説明した様な任意に選んだ寒暖計(例えば水銀寒暖計や気体温度計など)の目盛りから適宜検定される実用温度tを採用します。そして絶対温度Tと区別するために小文字の t で表す。このとき圧力PはtとVの関数P(t,V)となります。
いま着目している物質系の内部エネルギーUは状態量で物質系の温度tと体積Vの連続的な関数U(t,V)と考えることができるので
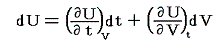
が成り立ち
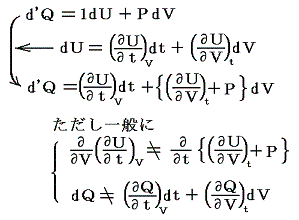
となる。これらの量は今までの議論の
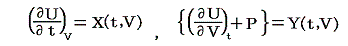
に相当する。
3.エントロピーの定義
仕事は状態量ではないので
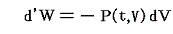
のd’Wは完全微分ではありません。だから’(ダッシュ)を付けています。ところが
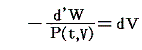
と書いてみると明らかなようにVは状態量ですから、これは完全微分dVとなります[この式の意味は3.(2)2.のグラフを思い出せば直ちに明らかになります]。
同じことがd’Qについても言えないだろうか。つまりd’Qに何かを掛けたら、それが完全微分になるような関数はないのだろうか?そのような関数はあります。
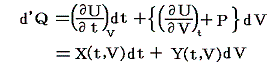
のd’Qは5.(2)で説明した意味で完全微分ではないが、二変数の場合5.(4)1.で証明したように、ある関数λ(t,V)を乗じることにより
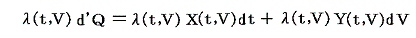
がある関数φ(t,V)の完全微分になるようにする事ができます。つまり
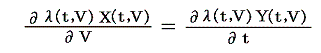
が常に成り立つようにできる。ただし、熱力学では積分因子を普通
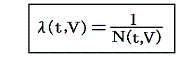
の様に書きN(t,V)を“積分分母”と呼んだりするが、単に逆数をその様に置くだけなので、今後はN(t,V)自身を“積分因子”と言うことにする。そのとき上式は
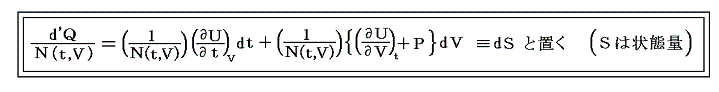
と表される。ここに出てくるd’Q/N=dSはある関数のφ(t,V)=S(t,V)の完全微分だから、それをt-V座標上の任意の経路図(ダイアフラム)に沿って線積分した値
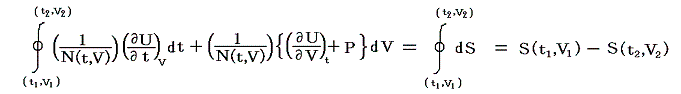
は経路によらない。つまりS(t,V)は系の状態(t,V)が定まれば一意に定まる“状態量”です。このSのことを熱力学では“エントロピー”と言う。クラウジウス(Clausius)が1865年の論文の中でその様に命名しました。これはギリシア語の”変化”を意味する言葉(τροπη)から取ったものだそうです[ギリシャ語の”中(en)”+”変転(trop)”]。
このとき“積分因子”N(t,V)は当然
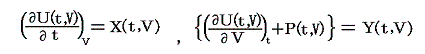
の関数形に依存するので、U(t,V)やP(t,V)が変数(t,V)のどの様な関数か解らないとN(t,V)は決まらない。
1.(1)で述べたように、実用温度tは温度を測るための温度計を構成する物質の性質に依存する。そのため同じ熱力学的現象でも、用いる温度計によってX(t,V)やY(t,V)の関数形は異なる。その為当然温度計ごとに積分因子1/N(t,V)の関数形は異なる。確かに同じ状態変化経路(もちろん座標変数の実用温度tが別の実用温度t’に変わると経路図は変わる)をたどる熱力学的現象なら、どの様な温度計を用いようとd’Qは同じはずです。また、d’Q/N(t,V)が状態量になる事情は同じです。しかし、このように温度計毎に異なる積分因子1/N(t,V)に何か意味はあるのだろうか?
これは温度計の説明のとき述べた”大いなる疑問?”と同じことで、ここで議論が行き詰まってしまう。ところが、実は思わぬ所から解決の糸口が出てくるのです。
4.着想
次に述べる熱力学第二法則を用いて定義される絶対温度をTと書くと、熱力学第二法則からd’Q/T=dSが状態量であることが保証される。そのためN(t,V)の関数形など解らなくても関数N(t,V)を“絶対温度”Tとすれば良いのです。
次章6.(2)2.で定義する絶対温度Tは、そこで説明するように物体の性質には依存しない[つまりX(t,V)やY(t,V)の関数形に依存しない]が、物体の状態がきまればその値が一意に決まる状態量です。
そして実用温度tやVで表した積分因子N(t,V)は、何度も強調するように物体の性質に依存している。しかしN(t,N)=Tと置くTは熱力学第二法則より物質の性質に依存しない。ならば、T=N(t,V)を逆に解いて実用温度tについての関数t=f(T,V)にしてみれば、この関数こそ物質の性質に依存する実用温度tを絶対温度Tで表す関数であることになる。この関数f(T,V)こそ、現実の温度tを絶対温度Tに関係づけるものです。
すでに述べたように積分因子となる関数は無限に存在します。しかし熱力学第二法則による制限を課すことにより一つに定まる事になる。
このとき異なる温度計物質を用いた温度計の温度目盛をt’で表せば X’(t’,V) や Y’(t’,V) の関数形は X(t,V) や Y(t,V)
の関数形と異なるであろうから積分因子の N’(t’,V) も N(t,V) と異なるであろう。そのため、当然のことであるが t’=f’(T,V)
の関数形は t=f(T,V) とは異なる。そのためこの関数形をそれぞれの場合に実験で求めれば絶対温度Tをそれぞれの実用温度t、t’、t”・・・・から決定できることになる。
そして、様々な物質、様々な熱力学的現象を利用して定めた実用温度計t、t’、t”、・・・・を絶対温度Tと対応付けておき、ある一つの熱浴の温度をそれらの様々な温度計で測ってみる。それらすべての温度計が同じ絶対温度を指し示せば、絶対温度の正当性、さらには熱力学第二法則の正当性が実証されることになるであろう。これは素晴らしい着想です!
実際にその関数形を求める方法は第7章で説明します。
ここで注意してほしいのは、エントロピー自体は熱力学第二法則とは無関係に導入・定義できることです。積分因子N(t,V)が存在してd’Q/N=dSを完全微分にできるということは数学的な真理なのですから。これはクラウジウスが気付いていたことです。
熱力学第二法則が関係するところは、積分因子N(t,V)を絶対温度Tにすればよいというところにあります。そのとき絶対温度Tはどこから導入・定義されたのかと言えば、まさしく熱力学第二法則によって導入されたのです。それはケルビン(W.トムソン)が1848年に気付いた事柄です。クラウジウスは、トムソンの導入した絶対温度の逆数こそ積分因子そのものだと言うことに1850年に気付きます(より正確に言いますと、Clausiusがその事を明記したのは1854年論文に於いてです)。実はケルビン(W.Thomson)もクラウジウスに僅か遅れて(1851年)独自にそのことに気付いています。
その当たりを明らかにするために、いよいよ熱力学第二法則の説明に入りましょう。
[補足説明1]
歴史的な補足をします。
Clausiusが“トムソンの導入した絶対温度の逆数こそ積分因子そのものだ”と言うことを明確に認識して、論文の中に明記したのは1854年の論文においてです。
しかし、1850年の論文の中で、その事をうかがわせる議論を展開しています。ただし、Clausiusの1850年論文をお読み頂いたら解ると思いますが、その記述からその事を読み取るのは極めて難しいです。
この論文は『熱力学』と言う学問分野を開闢(カイビャク)した大論文ですが、その中でClausiusが展開している論理の本質を読み解くのは至難です。
6.熱力学第二法則
ここはたいていの熱力学の教科書に載っているので簡単に説明します。朝永文献6.や原田文献19.なども参照されて下さい。
[2021年9月追記]
以前は上記の様に記していたのですが、熱力学展開に必須のカルノーサイクルについて秀逸な解説を最近読みましたので引用紹介します。それは、ポール・セン著「宇宙を解く唯一の科学 熱力学」河出書房新社(2021年刊)第6章“熱の流れと時間の終わり クラウジウスと熱力学第一法則・第二法則”です。また山本文献18.第19章Ⅱ~Ⅲもぜひご覧下さい。
私は今までに、カルノーサイクルを説明する文章を何十種類も読みました。しかし、どの説明もカルノーサイクルの何たるかを旨く説明できていないと感じていました。カルノーサイクルの本質的な意味を解らせてくれる説明を長い間探し求めていたのですが、上記引用文はその願いを初めて叶えてくれました。このことについては6.(1)3.[補足説明2]もご覧下さい。
(1)第二法則の発見
熱力学第二法則は、様々な熱機関に於いて高温物体だけからは動力を得られないと言う経験事実に基づく。熱機関を働かせるには必ず低温の熱の捨て場が必要なのです。これは熱が絡む動力機関の非常に奇妙な性質です。カルノーやトムソンはこのことの理由が解らず、混乱し思い悩みます。その事実がエネルギー保存則とどういった関係なのかも悩ましい事柄でした。
そういった状況の中でクラウジウスはそれこそ熱の本性であると考えて、それをそのまま受け入れることにしました。つまり、それを一つの自然法則とすればよい。そして、彼はこの新法則はエネルギー保存則と何ら矛盾するものではなくてエネルギー保存則と互いに補い合うものであることを明らかにします。この法則を用いればカルノーの考察に内在していた疑問点を解決する事ができたのです。
熱力学第一法則のところで強調しましたが、法則を保証するものは、あらゆる場合に絶えず新しくその正しいことが確認されてきた長年にわたる人類の経験した事実しかないのですから、これを一つの法則の形に昇華させても何ら不都合はありません。その表現方法は種々ありますが、普通以下のいずれかの表現を用います。
1.熱力学第二法則の定式化
1.何らかの他の変化を残さずに熱は低温の物体から高温の物体に移ることはできない。(Clausiusの原理)
2.循環的な過程によって、一つの物体から熱を取りだしそれを当量の仕事に変える様な機関はあり得ない。(Thomsonの原理)
- Clausiusの原理の”他の変化を残さずに”の但し書きは重要です。他の物体の関与(つまり他の物体の変化)によって低温物体から高温物体へ熱を移すことは可能ですから。
山本文献18.第26章Ⅰによると、Clausiusがこの部分を法則表現に付け加えたの1854年の論文でだそうです。
- Clausiusの原理の逆過程は可能です。高温の熱源から低温の熱源への熱の伝導は起こるからです。そのため、この原理は熱伝導は不可逆過程であると言っている。
- Thomsonの原理の”一つの物体から”の但し書きも重要です。これは「より低温な、もう一つの物体などなしに」と言うことであり、これがカルノーやトムソンがなぜ低温物体が必要なのかを問うて答えられなかったところです。なぜかと問うて答えられなくても、それが法則なのだとしてしまえば良い。この法則の妥当性はこの法則から導かれるあらゆる結論が正しいことによって保証されているのだから。
ここは、6.(1)3.[補足説明1]に引用した、広重氏の解説を参照されたし。
- Thomsonの原理の逆過程は可能です。内部摩擦の現象(物体をこすり合わせて摩擦熱を生じさせ一つの物体から取り出したすべての仕事をそれと当量の熱変える)がそれです。そのため、この原理は内部摩擦の現象は不可逆過程であると言っている
- Thomsonの原理で言う機関は エネルギー保存則(熱力学第一法則) は破っていませんが、もしその様な機関が可能なら周囲の大気や海洋の持つ熱から無限に仕事を取り出すことができますので、それを第二種の永久機関と言います。そのため 2.(Thomsonの原理) は第二種永久機関不可能の原理とも言われます。
もちろん、Thomsonの原理は、次の6.で述べる様にClausiusの原理と等価ですからClausiusの原理をその様に言っても良い。なぜなら、Clausiusの原理が破れて、何らかの他の変化を残さずに低温の物体から高温の物体に熱を移すことができるのなら、その余分に移した熱量の差分だけを使って可逆機関を動かして仕事を取り出せば、循環的な過程によって、一つの物体から熱をとりだしそれを当量仕事に変える機関が存在することになるからです。
- Clausiusの原理とThomsonの原理は等価です。なぜなら、次に述べるCarnotサイクル(可逆サイクル)の存在を仮定すれば、6.(1)4.で述べる様にその事が証明できるからです。
2.Carnotサイクル
Carnotサイクルは、準静的過程であって、二つの断熱過程(d’Q=0)と二つの等温過程(dt=0)とから構成されている循環過程です。準静的過程は可逆であるから、Carnotサイクルは可逆です。
Carnotサイクルを具体的に実現する可逆熱機関としては、実用温度t1の高温熱浴と実用温度t2の低温熱浴の間で働く下図の様な機構を考えればよい。ここで温度測定は1.(1)で述べたような実用温度計による温度で測られたものとする。またシリンダー内の気体は任意の実在気体でよい。
ただしシリンダーとピストン間や重りを載せるテーブルなどには摩擦は無く、ピストンやテープルの質量は無視できるように補助の滑車と重りの装置などが理想的に配置されているものとする。シリンダーは熱浴と接する部分以外は断熱的な壁でできているものとする。また重りや重りを載せる台の上下間隔は準静的過程が実現されるように無限小の大きさに分割されているものとする。
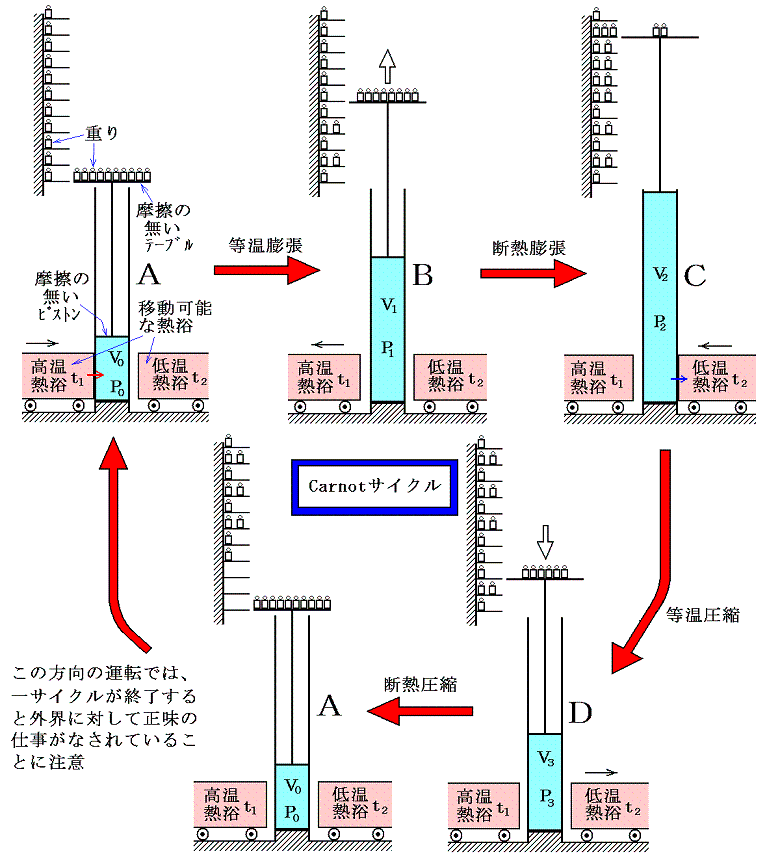
Carnotサイクルは次の手順で運行される。まず、状態の等温変化(等温線t1に沿って)によって着目している物体を状態A(V0,t1)からB(V1,t1)に移す。この途中熱量Q1が加えられたとする。次にその物体を断熱変化(断熱線に沿って)させて状態C(V2,t2)に移す。さらに続けて、等温曲線t2に沿って熱量Q2を取り去りながら状態D(V3,t2)に移す。この三番目の状態Dから、状態の断熱変化によって初めの状態A(V0,t1)にもどす。
この四つの過程の途中ではすべて仕事が行われる。熱力学第一法則によって
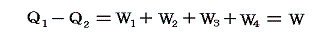
が成り立つ。
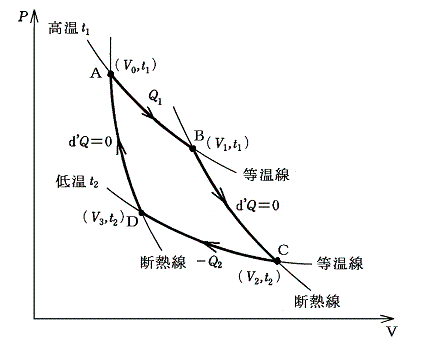
上図矢印の方向に変化させた場合(順Carnotサイクル)加えられた熱量Q1の方が取り去られた熱量Q2よりも多く、その分だけこの物体は外部に仕事を行う。したがってサイクルの途中で熱が仕事に変わり、それとともに熱量Q2が、t1からt2へ、つまり高温熱浴から低温熱浴へ運ばれることになる。
Carnotサイクルは可逆機関だから上図と逆方向に運転することもできる。その場合(逆Carnotサイクル)加えられた熱量Q2より取り去られた熱量Q1の方が多く、その差に相当する分だけ、外部から仕事がなされる。したがってサイクルの途中で仕事が熱に変えられ、それとともに熱量Q2が、t2からt1へ、つまり低温熱浴から高温熱浴へ運ばれたことになる。
ここで注意してほしいのはCarnotサイクルは具体的な熱機関を指すのではなくて、二つの温度が定まっている熱浴と温度差無しに熱量の交換を行う(準静的過程には必須の条件)ために、断熱膨張による冷却と断熱圧縮による加熱により二つの等温過程が結びつけられている可逆循環過程を指すのです。
それを実現する熱機関の機構やその作業物質は任意で良いことに注意。つまり、作業物質は実在気体で良いし、変化の途中に凝縮液化が起こっても良い。またこのときの温度は実在物質で作られた1.(1)で言う実用温度tで測ったもので全くかまわない。
このようなCarnotサイクルを行う任意の可逆熱機関に対して次の“カルノーの原理”が成り立つ。
3.カルノーの原理
二つの温度の熱浴の間で働く任意の可逆機関(Carnotサイクルはその一例)が一循環行程で吸収、排出する熱量の比は機関の構造や作業物質によらず、二つの熱浴の温度のみに関係する。つまり
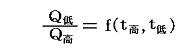
の関係式が常に成立する。これを“カルノーの原理”という。
[証明]
もし、上記の結論が正しくないとすると、二個のCarnotサイクルを組み合わせて“第二種の永久機関”が実現できる。
今物質Ⅰを用いてCarnotサイクルを運転し、他方物質Ⅱを用いて全く同一のCarnotサイクルを作り、Q高1=Q高2となるようにして正反対に運転する。この場合はⅠが温度t高の高温熱源からもらう熱量を、Ⅱがその熱源にもどすことになっているから、温度t高の熱源からの熱の出入りはゼロです。
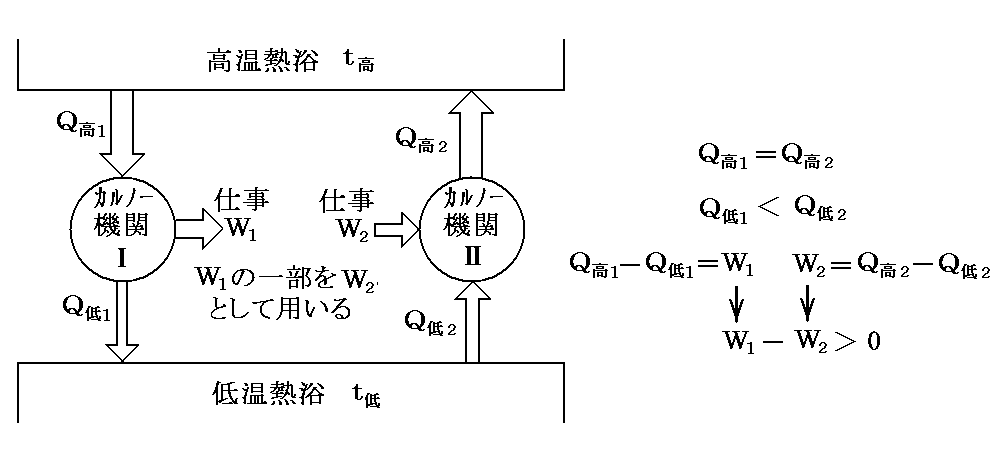
そのとき、もしQ低1<Q低2ならば、温度t低の熱源のからⅡが奪う熱量の方が、Ⅰがその熱源へもどす熱量より多いということです。熱力学第一法則からW1-W2>0となり、正の仕事が外界に対して成されることになる。従って他に何の代償も残さずに、温度t低の熱源から熱を奪って仕事にかえたことになり、(Thomsonの表現による)“熱力学第二法則”(“第二種の永久機関”が不可能の原理)に反する。
このとき、もしQ低1>Q低2ならば、ⅠとⅡの運転を逆向きにして、結局上と同じ矛盾に到達する。
結局熱力学第二法則から次の等式が成立しなければならない。そのため

が成り立つ。つまり、二つの温度の熱浴の間で働く任意の可逆機関(Carnotサイクルはその一例)に於いて高温熱源と低温熱源でやり取りされる熱量の比は、その熱源の温度にのみ依存して熱機関の構造やそれを構成する物質の性質によらない。
[証明終了]
歴史的な補足をしますと、このタイプの証明をしたのはW.Thomson(1851年論文)です。そのためThomsonは、“熱力学第二法則”の表現を前述の(Thomsonの原理)といわれる言い方にしたのです。[山本文献18.第27章Ⅲを参照]
ここで用いられている仮定は、今考えている機関が(準静的に働く)可逆機関であると言うことと熱浴の温度が定まっているということだけであることに注意。この仮定が成り立てば、“カルノーの原理”は熱力学第一法則と第二法則の当然の帰結だと言うことです。
[補足説明1]
上記の証明は Q高1=Q高2 を仮定して、しかも Q低1<Q低2 の様なことが起こるならば、熱力学第一法則により W1-W2>0 となり、正の仕事が外界に対して成されることが生じて(Thomsonの表現による)“熱力学第二法則”に反する事を導いて、“カルノーの原理”を証明しましたが、このとき(Clausiusの表現による)“熱力学第二法則”に反する事を導くやり方で証明することもできます。
その証明方法は、 Q高1<Q高2 と Q高1-Q低1=W1=W=W2=Q高2-Q低2 を仮定してこのとき成り立つ W1=W=W2 の関係式を利用してカルノー機関Ⅰが生み出す仕事W1をそのままそっくりカルノー機関Ⅱの熱の汲み上げに必要な仕事W2(=W1)に利用します。
そうすると両方のカルノー機関を1サイクル運転して元に戻すと、何らかの他の変化を残さずに熱は低温の物体から高温の物体に移る事ができたことになり、(Clausiusの表現による)“熱力学第二法則”に反することになります。だからこのような事は起こらないとして、“カルノーの原理”が証明できます。
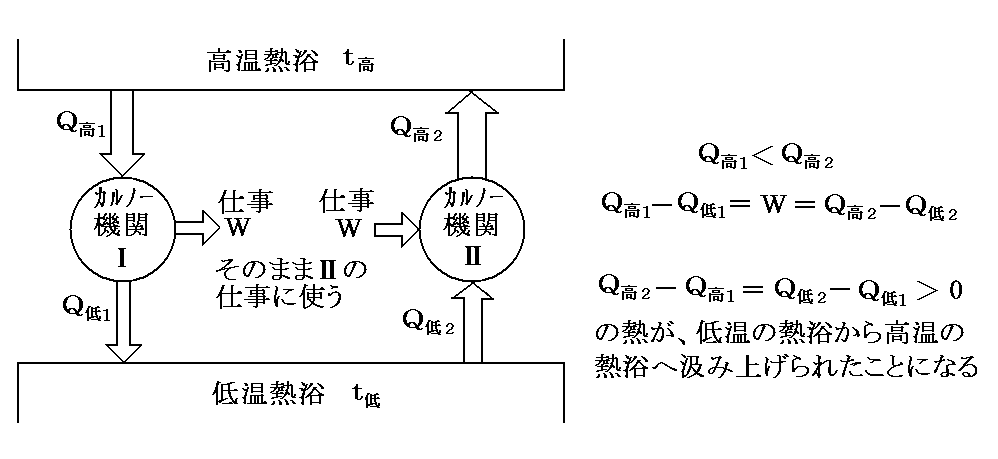
このとき、もし Q高1>Q高2ならば、ⅠとⅡの運転を逆向きにして、結局上と同じ矛盾に到達する。
次項4.で証明する様に、熱力学第二法則”の表現に於いて、Clausiusの表現 と Thomsonの表現 は全く等価ですから、どちらのやり方でも証明できるのは当たり前です。
実際のところ、Clausiusは、1850年の論文では、こちらのタイプの証明を採用しています。そのために“熱力学第二法則”の文章表現もこちらのタイプで提示することになったわけです。Clausiusは、“カルノーの原理”を承認するには、熱力学第二法則が成り立たねばならないと言うことでClausiusの表現になる熱力学第二法則を設定したということです。それを熱の性質を表す根本原理とすれば“カルノーの原理”も証明できるということです。
本質的で重要なのは“熱力学第二法則”ではなくて“カルノーの原理”の方です。そのことについての広重文献9.p35~36の解説を引用。



ここの説明は山本文献18.第26章Ⅰ~Ⅱの解説も秀逸ですからごらんください。
また広重引用文の最後の『エネルギー恒存則.にさえカルノーが到達していた』に就いての補足として、山本文献18.第21章Ⅴ“カルノーの遺稿と熱力学第1法則”を別ページで引用しておきます。
[補足説明2]
さらに補足しますと、Clausiusが1850年の論文で用いた上記の証明法を考え出したのはカルノーでして、1824年の大論文「火の動力、および、この動力を発生させるに適した機関についての考察」の中に書かれています。
ただし、カルノーは熱の本質について誤った考えを持っていました。彼は熱を高いところから流れ下って水車を回す水の流れの様なもの(彼はそれを“熱素”と言った)だと考えていました。つまり、熱は“熱素”というものが移動するのであって、水車を回す水そのものが無くならないのと同じ様に“熱素”は移動するだけで無くなることはないとしたのです。そして水車を回す水が最初高い位置にあり、水車を回した後に低い位置に移動する様に、水の存在する位置の高さの様なものが“温度”だと考えていました(広重訳の文献9.p50)。
普通、ここはカルノーの誤っていた所として強調されますが、その類似に着目したことを軽々しく批判してはならないでしょう。山本文献18.第19章Ⅱでもここは特に注目されていますが、水車から取り出せる仕事量と関係する高度差の働きが、カルノーサイクル(熱機関)が取り出せる仕事量に関係する温度差の働きに相当するという考え方自体は極めて重要な着想なのですから。誤っていたのは温度の捉え方では無くて、エネルギーである熱を作業流体(水)の様なものと見なした所ですから、温度差を高度差と見なしたのは全く正しい。
いずれにしましても、彼は上記の温度と高度の類似性から“カルノーの原理”を思いついたのでしょう。なぜなら、水車から取り出せる [仕事の量W] は [流れ下る水の量m](“熱素”の量 Q ) と [水が流れ下った高度差gh](温度差に
t高-t低 相当) の積に関係しますから、
[熱機関の効率η]=[仕事の量W]÷[流れ下った“熱素”の量 Q (流れ下る水の量m)]
∝[温度差 t高-t低 (水が流れ下った高度差gh)]
となります。これは“カルノーの原理”に他なりません。
歴史的に正確をきすと、カルノーの論文にある表現はこちらです。本項の最初に掲げた表現はClausiusによる熱力学第一法則を考慮した修正が加味されています。本来ならば以下の様に表現した方が良いかも知れません。
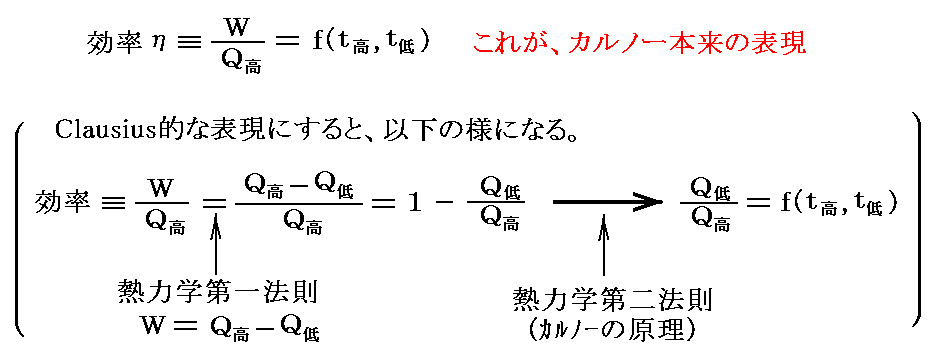
歴史的な補足をしますと、“カルノーの原理”を“熱力学第一法則”と組み合わせた形(効率=1-Q低/Q高)にしたのはW.Thomson(1854年論文)です。そのためThomsonは、1848年に提案していた絶対温度の概念を完璧なものにすることができました。[山本文献18.第29章Ⅰを参照]
カルノーは、その事(今日“カルノーの原理”と呼ばれる)を極めて巧妙な“背理法”によって証明したのです。《カルノー自身の証明法》を山本文献18.第19章Ⅳの解説で紹介しますから、まずご覧になられて下さい。
上記別稿を読まれて驚かれた方も多いと思います。上の[補足説明1]で説明したClausiusの説明と違って、熱機関が1サイクル実行する過程で熱機関に流入する熱量(“熱素”)と流出する熱量(“熱素”)が同じでも、(カルノー本来の表現の)“カルノーの原理”が厳密に証明できるのです。つまり、誤っているカルノーの“熱素”の考え方でもきちんと証明できる。これは驚くべきことです。
ただし、山本文献18.第26章Ⅱの解説の注意書きの様にカルノーの証明には不完全なところは有ります。
それでは、誤った熱素説にもかかわらず、正しく証明できた《カルノー自身の証明法》の本質はどこにあるのかということですが、山本氏は第19章引用文の末尾で

と、書かれています。確かにそこに書かれている様に
①.1サイクルが終了すると熱機関の状態が最初と全く同じ状態に復帰するサイクルを用いたこと。
②.すべての行程が準静的で逆行可能な可逆サイクルを用いたこと
は、大発明です。
しかし、私はカルノーサイクルの最重要な本質は、
③.高温熱浴からの熱機関への熱の流入がすべて一定温度の元での等温過程で行われること。
④.また、低温熱浴への熱の流出が同じく一定温度のもとでの等温過程で行われること。
⑤.そして、その両方の温度(高温と低温の状態)を繋ぐ過程では熱機関への熱の出入りのない断熱過程であること。実際カルノーはこのことを最重要な事だと考えていました(広重訳の文献9.p48)。このことの意味は解り難いかも知れませんが、熱機関の作業物質の温度変化が、不可逆過程の熱伝導の様なもので熱浴から熱をもらったり、熱浴に熱を排出して生じてはならないということです。つまり必ず断熱的過程で膨張や収縮が生じて温度が変化するものでなければ成らないということです。そして、この場合も外界と熱機関の作業物質との圧力差は無限小で可逆的に膨張や収縮がおこなわれなければ成りまません。カルノーは論文の中でこれが最大効率を実現する為には最重要な事だと述べています。(山本文献18.第19章Ⅱでもここは特に注意されています。)
の中にあると思います。
つまり、カルノーサイクルの最重要なメカニズムは熱の流入や流出の時の温度を確定しておくことができ、その確定した温度での流入や流出である事です。実際、③.④.の様に等温過程で熱の移動をさせたことが、②.の準静的で可逆な過程を可能にしたのです。 また⑤.で二つの温度状態を繋いだとき、その二つの温度状態を熱量の出入りなしに繋ぐことができ、しかもこの断熱過程が外界と熱機関の圧力差を無限小にして可逆的に実行できることが、やはり②.の準静的で可逆な過程を可能にした。
カルノーは、別稿2.で示す理想気体の状態変化を示す図 の意味を 明確に理解しており、その図上の変化曲線は、外界との熱と仕事のやり取りを無限小温度差、無限小圧力差で行うことで準静的(可逆的)に実現できることに気付いたのでしょう。カルノーが、この図が示す気体の性質から、こういった熱機関サイクルが存在するということに気付き、それを用いたことが科学史上の大発見だと思います。
すなわち、上記の③~⑤.が実行できれば、①.②.が実現できるので、カルノーが展開した議論の中に“熱素”に関する誤った理解があっても“カルノーの原理”が証明できたのです。この背理法による証明の中で必要なのは、山本氏が強調されている様に、①.の1サイクル終了すると元に戻ることと、②.の可逆であることだけですから。
上記の③~⑤.が、カルノーサイクルの性質として如何に重要であるかは、後の6.(2)に於ける“絶対温度”の導入や、6.(3)に於ける d’Q/T≡dS として状態量“エントロピー”を導入する手順を学ばれれば納得して頂けると思います。
実際、高温で熱機関に流入した熱量と低温で熱機関から流出した熱量は異なっていても、d’Q/T=dSとして“定温過程”で流入と流出を計算したエントロピーの値は1サイクル終了したら、最初のエントロピー値に復帰しているのです。
そして、このこと(1.の1サイクルが終了するとすべて元に戻る)がサイクルとして最初と最後の状態量S(エントロピー)が一致する為の条件です。つまりこの中に、“熱機関が取り込んだ熱量の一部をを外界に捨てなければならない”という“カルノーの原理”を説明する鍵があるのですから。
4.Clausiusの原理とThomsonの原理の同等性の証明
熱伝導についての“Clausiusの原理”(Clausiusの表現による“熱力学第二法則”のこと)を否定すれば熱量Q低を低温熱浴t低から高温熱浴t高へ何の代償変化も無く移動する《熱機関Ⅱ》が存在することになる。
次に別の順CarnotサイクルⅠで高温熱浴t高からQ高1(>Q低)の熱を受け取りW1=Q高1-Q低の仕事を外部に行えば、ⅠとⅡの機関を合わせて結局高温熱浴t高から熱(Q高1-Q低)をうばってすべて仕事W1に代えたことになり、“Thomsonの原理”(Thomsonの表現による“熱力学第二法則”のこと)の否定が成立する。(下図参照)
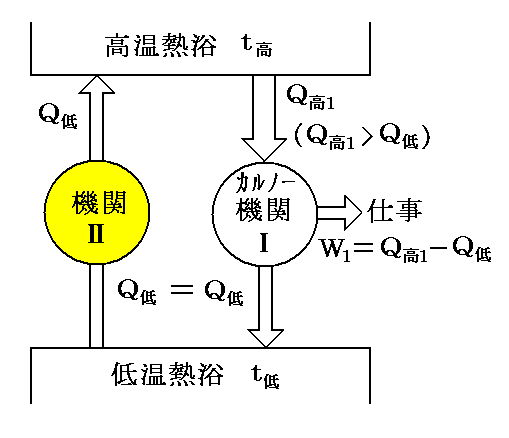
また“Thomsonの原理”が否定されれば、高温熱浴t高から熱量Q高1を奪って他に何の変化も残さずにすべて仕事W1=Q高1に変える《熱機関Ⅰ》が作れる。
その熱機関が行う仕事を、逆CarnotサイクルⅡに使用する。この機関ⅠとⅡが1行程を終えれば、熱量Q高2-Q高1=Q低2が低温側熱浴t低から高温側熱浴t高へ移り、他に何の変化も生じないことになる。すなわち“Clausiusの原理”の否定が成立する。(下図参照)
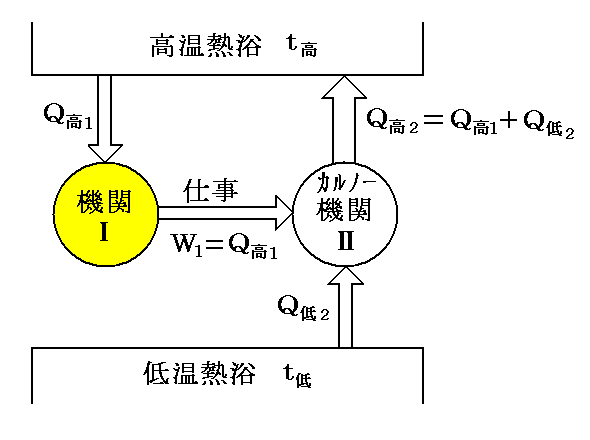
以上から、第二法則の二つの表現が同等な内容であることが示される。
(2)絶対温度の導入
ケルビン(W・トムソン)は1848年にカルノーの可逆サイクルの真の意味や意義を研究しているとき、これを使えば、温度を測るのにどういう物体を使うかに関係なく、エネルギー保存則だけに基づいて、温度の普遍的で絶対的な尺度を作ることができることに気付いた。その考え方は次のようなものです。
ただし実際に、トムソンが“絶対温度”の概念を確立するのは1854年です。その詳細は山本文献18.第27章Ⅱ、第29章を御覧下さい。
1.カルノーサイクルの効率と温度関数
カルノーサイクルを二つの温度t高とt低の間に動かします。ここで温度t高とt低は任意の熱力学的尺度で測った1.(1)で述べた実用温度です。熱力学第二法則によるとカルノー機関が高温熱浴及び低温熱浴とやり取りする熱量の比は高温熱浴と低温熱浴の温度のみに関係し、それ以外には依存しない[カルノーの原理]。
そのため、カルノー熱機関の効率は
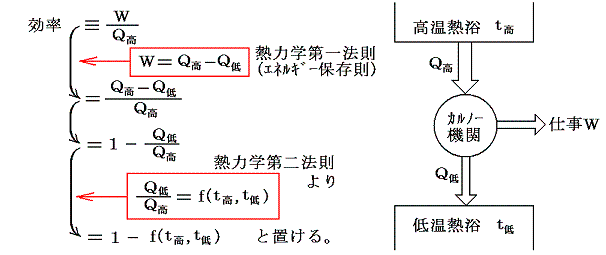
ここでf(t高,t低)がどの様な関数であるのかは熱力学第二法則からは解りません。解っているのは高温熱浴と低温熱浴の温度のみに関係することと、その温度差が大きければ効率が大きくなると言う経験事実だけです。
そのとき、この可逆機関は上記の熱浴間で働く機関としては最高の効率を実現するものです。もしそれよりも効率の良い機関(超能機関)があれば、その超能機関と上記の可逆機関を逆方向に運転させたものを同じ熱浴間で同時に働かせれば低温熱浴から熱を汲み出してそれをすべて仕事に代える第二種の永久機関ができることになり、熱力学第二法則が否定されるからです。
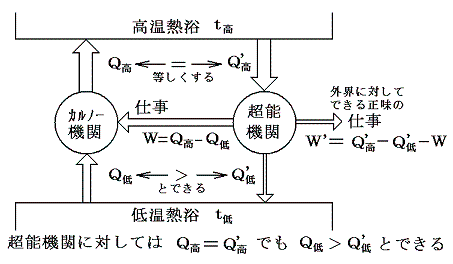
このf(t高,t低)の関数形は以下の様な三つの可逆機関を考えるともう少し限定する事ができます。
機関AとCは、温度t1の高温熱浴から同じ大きさの熱量Q1を受け取る。機関Cは温度t3の低温熱浴にQ3の熱を放出する。一方、機関Bは温度t2で機関Aから放出された熱Q2を受け取り、温度t3の熱浴にQ3の熱を放出する。
このとき機関A+Bは機関Cと同じ熱源の間で運転される一つの可逆熱機関と考えることができる。そのため組み合わされた熱機関A+Bの効率は単一機関Cと同じでなければならないので、両者が熱浴t3に排出する熱Q3は等しくなければならない。
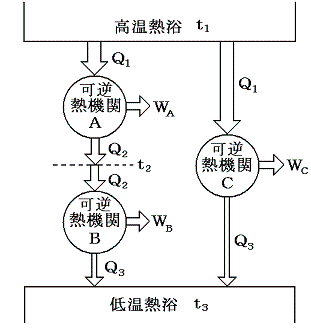
三つすべてに対して前記の式を適応すると
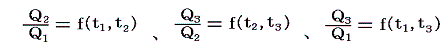
となる。これを恒等式
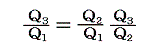
に代入すると
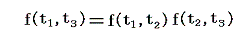
となる。つまり右辺もt1とt2のみの関数とならねばならない。このようなことが満たされるのは関数fが以下の形をしているときです。
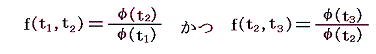
ゆえに、φ(t2)はf(t1,t2)とf(t2,t3)の積からは削除されて
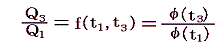
となる。そのため温度t高とt低の二つの熱源の間で作用する可逆機関に対しては
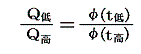
のように書くことができる。
2.絶対温度の導入
このときケルビン(W.Thomson)は次のように考えました。このφの関数形がどの様なものか、熱力学の法則からは決して定めることはできない。第一法則は温度に無関係だし、第二法則からは温度に関係していることが言えるだけですから。ならば
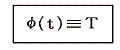
と置いて、逆に上記の関係を絶対的な温度Tを定める式だと解釈すればよい。熱力学第二法則から可逆熱機関は最高の効率を実現するものであり二つの熱源の温度が定まればその効率は一意に定まるのだから、そこに熱力学第一法則を援用すると、それは更にQ低/Q高が一意に定まることを意味する。その値を用いれば、物質に依存しない[可逆機関の効率は作業物質に依存しない]熱力学的な絶対温度を定めることができる。つまり二つの熱浴の間に可逆機関を働かせて熱の出入りを測定してその熱量でもって二つの熱浴の絶対的な温度を定めればよい。つまり
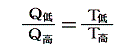
と決めればよい。これは素晴らしい着想です!実際のケルビンの推論はかなり込み入っていますが、結論としてはこのように言って良いと思います。
W.Thomson,"On an absolute thermometric scale founded on Carnot's theory of the motive power of heat, and calculated from Regnault's observations" [Cambridge Philosophical Society Proceedings for June 5, 1848; and Phil.
Mag., Oct. 1848.] あるいは [Mathematical and Physical Papers 6 Vols (Cambridge University Press),
Vol.1 p100~106] を参照。いずれもネットから無料ダウンロードできます。
- 絶対温度Tは実用温度tのある関数φ(t)であって、決してT=tと置くのではないことに注意。実用温度tを測定する温度計物質に依存してφの関数形は様々に変化する。
- この絶対温度を用いれば、可逆機関の効率は以下の様に表せます。
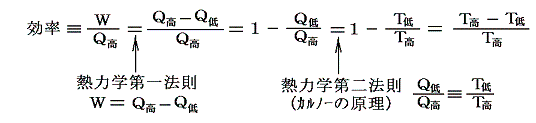
- このときT低=0なら効率は1になります。そしてT低は負になることはできません。なぜならT低<0なら効率>1となり、第一種の永久機関ができることになるからです。
- そのため温度は必ず正値であり、温度には下限(=0)があることが解る。
- 絶対温度の下限の値を定めるには適当な二つの熱源[例えば1気圧の下で沸騰している水(100℃)と、氷と平衡にある水(0℃)]を用いて、その間で可逆機関を働かせてみればよい。その時出入りする熱量が仮に測定できたとする。例えば
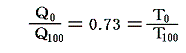
だったとする。このとき更にT0とT100の間を100等分して100Kと置くことにする[目盛り幅を摂氏温度と等しくするため]と、絶対0Kは
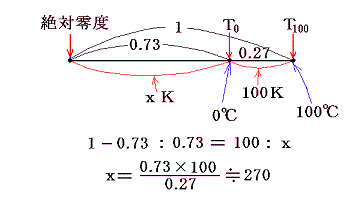
から、0K=-270℃であることが解る。また0℃=270Kとなります。
まことに素晴らしい着想なのですが、残念ながらその様な理想的な準静的・可逆な熱機関は現実には存在しません。それは、理想気体温度計が現実には存在しないのと同様です。
そのため、その2つの温度の熱源(熱浴)の間でその可逆機関を働かせて、高熱源から可逆機関に流入する熱量と、低熱源へ流出する熱量を測定して、2つの熱源(熱浴)の絶対温度を具体的に決定することはできません。残念ながら、ここで行き詰まってしまうように見えます。
ところが、ケンビンの導入した絶対温度にはとても素晴らしい性質が備わっていることをクラウジウスは発見します。
(3)Σd’Q/Tは状態量
前節で述べたように、可逆熱機関(カルノーサイクルも含まれる)を動かすとき、高温の熱源と低温の熱源の温度を一定にしておくと熱機関が受け取る熱と放出する熱との比は、常に一定の値を持つ。つまり、T高をTout、T低をTin、Q高をQout、Q低をQinと書き換えると
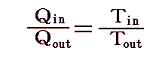
となる。クラウジウスはこの関係を次のように書き直した。

この関係式は1サイクルの間にカルノーの可逆熱機関に入る熱を、その時の絶対温度で割ったものは、同じサイクル中に放出する熱をその時の絶対温度で割ったものに等しいことを表している。その時、入るものを正、出るものを負と考えて、系に出入りする熱をその時の絶対温度(熱の出入りを測定するときの温度で、そのとき熱浴と熱機関の温度は同じです)で割ったものを集計すると、1サイクル終わるとゼロになることを示している。
クラウジウスは上記の関係式を更に一般的な可逆熱機関に適応します。任意の物体が準静的可逆的に任意の変化(図ではA点から出発してBを経過してもとの状態に戻る)をしたとする。このサイクルを多数の温度の熱源間で働くカルノーサイクルを結合したもので置き換えることができる。下図の様に、それぞれの温度圧力の状況に対応するカルノーサイクルを適当な熱源を選択しながら働かせればよい。そのとき下図の反平行で(接している)逆行する部分は互いに打ち消し合うので積算経路の中らか削除できる。
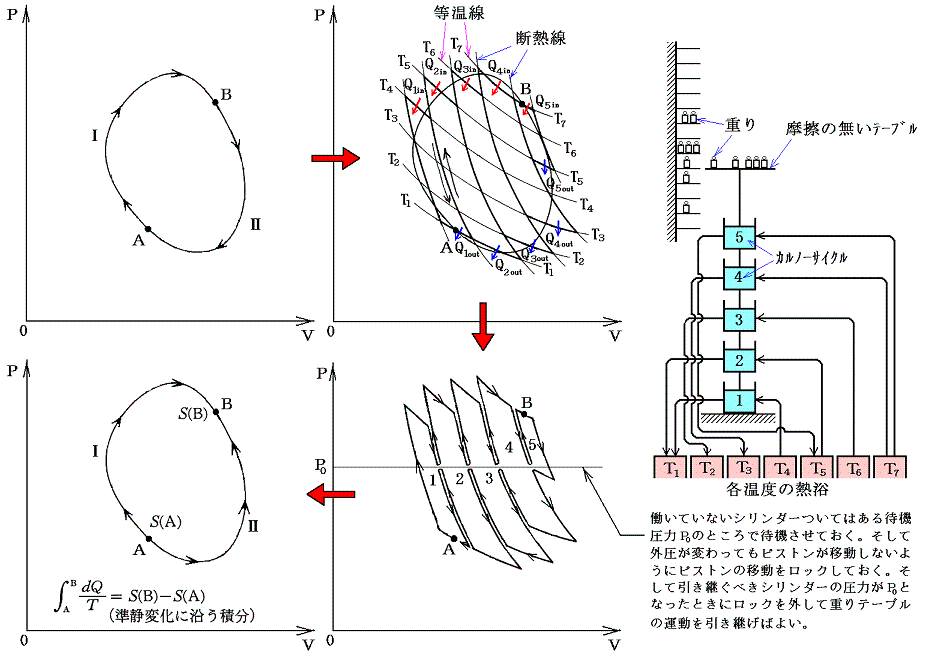
各熱源T1、T2、・・・とやり取りする熱量をQ1、Q2、・・・とする。そのとき受け取るときを正、放出するときを負として以下の和を取る。各カルノーサイクルには前記の関係式が成り立つので、全体としても
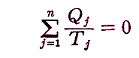
が成り立つ。無数のカルノーサイクルに分けた極限では和Σは線積分になるので
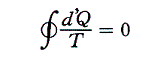
と書くことができる。すでに何度も説明したようにQは状態量ではなくdQが完全微分ではないので、それを明示するために’(ダッシュ)を付けておく。このとき積分路を図のようにB点で二つに分けてそれぞれをⅠ、Ⅱとすると
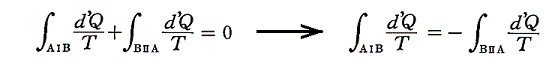
と書ける。準静的変化Ⅱを逆にたどれば熱の吸収、放出が逆になるので
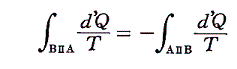
となり、従って
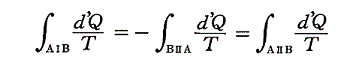
となる。このとき積分路Ⅰ、Ⅱは任意に取ることができるので、これらの積分値は途中の道によらないで、状態Aと状態Bだけで決まることを意味する。そのため

と置くことができる。
つまり、”d’Q/Tを積算した値Sは状態が決まれば一意に決まる量“状態量”である”が証明できたことになる。
つまり、“カルノーの原理”とは「可逆機関が最高の熱効率を達成するもので、その効率は熱をやり取りした熱源の温度(実用温度でよい)だけの関数である」と言うものでしたが、そのことから絶対温度が定義[ケルビンによる]できる。
そのとき、系がやり取り(もちろん可逆的に)する熱量d’Qをやり取りした熱源の絶対温度Tで割ったd’Q/Tを系の変化経路に沿って積算した値Sは、その系がたどった経路によらず系の最終的な状態のみによって決まることが言える[クラウジウスによる]わけです。
ただし、この段階では熱源の絶対温度Tを具体的にどうやって測るのかはまだ何も解っていません。それを可能にするのが次節(4)の考察です。
[補足説明1]
歴史的な補足をします。
Thomsonが上記の熱力学第二法則の数学的表現を展開したのは、彼の大論文『ジュールの熱当量とルニョーの蒸気に関する測定から導き出された数値的結果をともなう熱の力学理論について』のPart Ⅵ(1854年)においてです。この大論文は同じ題目で1851年~1854年にわたって継続的に発表されたものです。その数学的表現を得るための展開法は上記の説明とは少し違うのですが、山本文献18.第29章Ⅱで紹介されていますから、是非そちらをご覧下さい。これは、次に述べる1854年のClausiusの説明よりも数学的によほど解りやすく、今日のほとんどの教科書が採用している説明法です。
この当たりに付いてはClausiusの1876年の著書『Die Mechanische Wa¨rmetheorie』のAbschnitt Ⅲ.§8.~§9. の説明が最も洗練されていて解りやすいかも知れません。
Clausiusも1854年論文でThomsonとほぼ同じ関係式を導いています。その論理展開は山本文献18.第20章Ⅲ~Ⅴで紹介されていますが、正直なところその論理は極めて難解です。そのとき、Thomsonが早くから指摘・導入していた絶対温度に相当するものを自らの論理展開の中で導き出しています。そして、その“絶対温度”Tが数学で言うdqに対する“積分分母”になっている事を、1854年のこの論文の段階で、ハッキリと認識します。
さらに、Clausiusがこのd’Q/Tが状態量変化を示すことができる量であると明確に認識して、全微分dS=d’Q/Tを可逆変化に付いて積算することで状態量Sを決定できるとし、真の意味で“状態量”Sの存在を発見して、Sを“エントロピー”と名付けたのは1865年の論文に於いてです。
Clausiusは、1850年論文→1854年論文→1862年論文→1865年論文 と、少しずつ最終的な形に近づいて行きますが、そのときW.Thomsonが随時発表する論文と互いに刺激し・影響されながら進歩していったものと思われます。[山本文献18.第29~31章を参照]
[補足説明2]
dS=d’Q/T の T は物質系へ出入りする熱量 d’Q (状態量ではない)によって変化する物質系の状態に付随するエントロピーという量を状態量とする為の積分因子(積分分母)です。
d’Q は物質系に出入りする熱量ですがエネルギーの次元を持ちます。ところが T と言う量は、[距離]、[時間]、[質量]、[電気量]と言った次元の量の組み合わせでは表せない全く新しい次元を持つ量です。つまり全く新しい[温度]と言う次元を持ちます。だから
d’Q/T という量は[エネルギー]の次元を[温度]の次元で割った次元ですから、これも今までの物理理論には存在しなかった全く新しい次元の量です。これは乱雑さの度合いを表す量で、“エントロピー”と言われる量です。エントロピーと名付けたのはClausiusです。いずれにしても、その物質系の状態が定まれば一意に定まる状態量です。
そのとき、状態量 S は物質系が外界と熱のやり取りをすればそれに応じて物質系のエントロピー値は変化します。そのとき dS=d’Q/T の関係式は、物質系が外界から熱量を得たとき、そのときの低い温度の状態で熱量(エネルギー)を受け取ると物質系のエントロピー値の増加量は大きくなります。同じ熱量(エネルギー)を受け取るにしても、その受け取るときの物質系の温度が高かったら(外界も高い)物質系のエントロピー値の増大量は小さくなります。
つまり、物質系のエネルギーという状態量は低温で受け取ろうと、高温で受け取ろうと同じ量だけしか変化しませんが、エントロピーという状態量は、受け取るときの物質系の温度(それは渡す方の熱浴の温度でもある)に応じて、その増加量は変化します。エントロピーという状態量はその様に不思議な量です。そしてエントロピーという状態量は物質系の[温度]という状態量と密接に関係します。その様に、[温度]という全く新しい次元を持つ状態量の発見と[エントロピー]と言う状態量の発見は表裏一体だと言っても良いでしょう。
さらに補足しますと、上記の証明で用いられている微小カルノーサイクルにおいて、カルノーサイクル内部の物質系が準静的可逆の断熱過程で外界と仕事のやり取り(もちろんそのとき外界との圧力差は無限小)をする過程では、熱量のやり取りはありませんので、カルノーサイクル内の物質の温度は変化しますがエントロピーは変化しないことに注意して下さい。
ここは、別稿「Clausiusの1850年論文」3.(5)2.[補足説明2]と、3.(6)をご覧下さい。
[補足説明3]
本節で説明した関係式
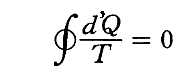
の左辺の積分はすべて準静的・可逆過程サイクルで行うものでしたが、1サイクルを行うその過程の中に不可逆な過程が含まれていた場合どうなるのだろうと疑問に思われる方も多いと思います。
上記の結論を不可逆過程を含む場合に拡張した議論は、別稿「熱力学第2法則とエントロピー」(6)で説明していますのでどうぞご覧下さい。そこの結論を紹介しますと

となります。
実は、上記[補足説明1]で説明したClausiusの1854年論文に於いて、Clausiusが求めたのはこちらの不等号のある式です【ただし、Clausiusの証明は極めて難解です】。そしてこの“Clausiusの不等式”こそ、以下(4)節で述べるエントロピー導入の着想に至る結論です。
その事に付いては、上記別稿「熱力学第2法則とエントロピー」(7)で、特にそこの[補足説明2]に於いて詳しく説明していますので、そちらをお読みになられた後で以下の説明をご覧頂くのが良いかも知れません。
(4)絶対温度と積分因子の関係
前節6.(3)で明らかになったことは、前々節6.(2)2.で定義した絶対温度Tを用いると準静的可逆変化で物質系に出入りする熱量の変分をd’Qとすると、物質系の準静的可逆変化の経路に沿ってd’Q/Tを積算した値は、その物質系の状態量となることです。
一方5.(6)3.で導入したエントロピーdS=d’Q/N(t,V)の積算値も物質系の状態量です。それならばこのN(t,V)こそ絶対温度Tそのものだと考えれば良いのではないか。そうすれば、その関数N(t,V)を使って絶対温度Tを現実の温度tで表すことができるだろう。
5.(6)4.で説明したようにまさに革命的な素晴らしい着想です。このことに最初に気付いたのはクラウジウスです。実際、このことは1850年のClausiusの大論文『熱の動力および熱の理論にたいして、導き出される諸法則について』の中でその事の試みが開始されています。ケルビンもクラウジウスに僅か遅れましたが独自に気付きました。
ここで非常に重要な仮定をします。今まで積分因子N(t,V)はtとVあるいはtとPの関数として説明してきましたが、絶対温度Tはカルノーサイクルの定義からも明らかなように物質系の状態量です。もちろん1.(1)2.で説明した現実の温度計を用いて定めた温度tも物質系の状態量です。その両者は値が違っていても同じ物理量だと考えるべきです。
そうならば、積分因子Nを絶対温度Tとするのですから積分因子は温度tのみの関数のはずです。つまりTとtは一対一の対応が付くのだから、tが定まればその時の体積や圧力とは無関係にTは一意に定まる量のはずです。だからT=N(t,V)=N’(t,P)と置くのではなくてT=N(t)と置いても良いはずです。これはプランクが「熱力学」§129で特に注意していることです。そのため今後はT=N(t)と仮定しましょう。そうすると積分因子を求めるための偏微分方程式を解く操作が劇的に簡単になります。5.(5)2.のやり方で解けばよいのですから。
実際にその事をやり遂げて、実際に用いられている実用温度計が示す実用温度tが、絶対温度Tの何度に相当するかを実験的に求めたのは Joule と Thomson です。そのことに付いては第7章で説明します。
以上のような事情で今後は6.(3)で導入したd’Q/TもdSと書いてエントロピーの完全微分、またそのその積算値Sをエントロピーと呼ぶことにしましょう。
絶対温度の測定の話(第7章)に入る前に、積算値S(エントロピー)について幾つかの補足説明をします。
1.エントロピーについて
- 物質系の状態がAからBへ状態変化するとき、その変化経路に沿って熱量の出入りd’Qを積算しても、その積算値は状態の変化経路に依存する。ところが、その出入りをするときの絶対温度で割った量d’Q/Tの積算値は状態変化の経路によらないのです。
- この状態量エントロピーは物質系の状態が定まれば任意定数を除いて一意に定まる量です。エネルギーと同じように、この量S(エントロピー)も二状態間の差のみが意味持つと言えるので、適当な基準状態を設定してそのS値をゼロとしておけば任意定数は確定できる。
- 任意状態のエントロピーの値は、基準状態(S=0としている)から、準静的可逆過程でその状態まで変化させて、その変化の過程で出入りする熱量を上記のやり方で積算すればよい。そのとき“準静的可逆過程”で推移しなければならないということは特に重要です。非可逆仮定を含む変化経路で積算したのではだめです。
- 可逆過程では、熱の移動がおこるとき熱浴と系の温度は等しいから、変化の過程で熱浴のエントロピー変化は系のエントロピー変化に反対符号を付けた値に常に等しい。
- このとき状態Aから状態Bへの変化がたとえ非可逆過程であっても、状態AのエントロピーS(A)と状態BのエントロピーS(B)の値はそれぞれにちゃんと割り振られており、それぞれの状態ごとに一意に定まっている。ただしその差を計算するには適当な準静的可逆過程をたどって状態Aから状態Bまで変化して、その過程を利用して計算する必要があるということです。
普通、熱力学の教科書では孤立系のエントロビーがその内部の不可逆性により常に増大することが強調されますが、エントロピーの最大の特徴は系の状態が定まれば、その状態に応じてエントロピーが定まると言うところにあります。つまり、一つの系のAとBの二つの状態を比較するとき、例えばAからBへ“準静的可逆過程”で移行したのか、“不可逆な過程”で移行したのかは関係なく、それぞれの状態について、その系のエントロピーが一意に決まるのです。それがエントロピーが状態量であるということの意味です。
- そのため、熱力学では、自然界で起こるあらゆる不可逆的変化は、上記の積分が適応できる可逆過程で到達可能であることを暗黙の内に仮定している。言い換えるとエントロピー変化を伴うあらゆる不可逆変化は、エントロピー変化が熱の交換だけで起こる可逆過程で正確に再現できるとしている。
- そのとき、プランクが「熱力学」§113で強調している様に「任意の二つの状態を結ぶ可逆過程が、自然の中に存在するか否かということは、先験的に自明の事でもなければ、実証できることでもない」のです。これは、熱力学の法則がなぜ正しいのか証明できないことと同じで、可逆過程の存在を前提として作り上げられているこの理論から導かれる結論が、今後どの場合にも破綻する事がないという事をもって実証されるとするしかないことです。
ここは非常に解りにくいところです。プランクは晩年に記した「過ぎし日々への個人的回想(1946年)」の中で、彼の博士論文「力学的熱理論の第二法則について(1879年)」についてキルヒホッフは“可逆過程によってのみその大きさが測定可能かつ定義可能であるエントロピーの概念を、不可逆過程に適用してはいけない。”と言って批判したことを嘆いている。熱輻射の熱力学理論で重要な貢献をしている優れた物理学者のキルヒホッフでさえもエントロピーが状態量であるということの真の意味を理解していなかったようです。
2.エントロピーの意義
可逆過程で出入りした微少熱量を絶対温度で割ったものはエントロピーの微少変化
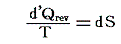
であるが、これを書き直すと
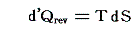
となる。これは可逆過程において出入りした熱量が絶対温度にエントロピーの変化をかけたものに等しく、熱が仕事と同じように二つの[状態量である]物理量の積となることを表している。
そのため、TとSを状態変数として経路図(ダイアグラム)を書いてみると、P-V図で面積が仕事量を表したように、T-S図では面積が状態変化に伴って系に出入りする熱量を表すことになる。
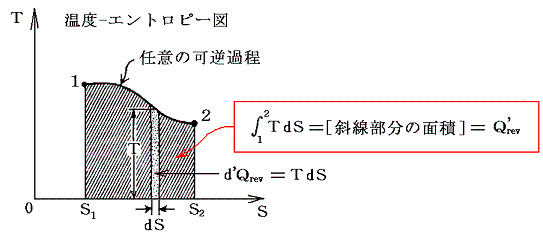
T-S図上で起こっている現象を物理的に解釈したり、エントロピーが何を意味するのかを理解するのは難しいが、系に出入りする熱量の変分d’Q=TdSの意味は極めて明瞭なので、エントロピーは状態を表す変数としてとても重要です。
この図を5.(6)3.でP-V図について注意した図と比較してみられたし。このとき、TとSは状態量だから、系の状態変化を表すグラフの独立変数に選べる。そのため、状態1と2を固定すれば、その間の状態変化の経路が異なっていてもd’Q/T=dSの1→2への積算値(S2-S1)は等しくなる。その際、経路ごとに系に出入りする熱量も仕事量も異なっていても良い。
3.状態変数としてのエントロピー
物質系の状態を示す状態変数(当然状態量)としては、普通TとS、PとVの4つの内の二つを変数に選びます。熱力学の法則は[物体系の状態変化]を[熱の出入り]や[仕事の出入り]と結びつけるもので、熱の出入りに関係する変数がTとS、仕事の出入りに関係する変数がPとVだからです。
理想気体を例にして、状態方程式のグラフを示します。3.(2)1.でPVTを状態変数とした状態方程式のグラフを示しましたが、STV、STP、SVPに関する状態方程式のグラフを描くこともできます。
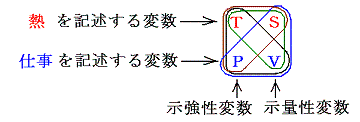
熱力学第一法則を熱力学第二法則によって書き直した

から出発します。理想気体の場合

ここで、S(T,V)=S(T,P)=S(P,V)である事に注意して下さい。いずれも同一の(P,V,T)状態のエントロピー値を表しています。二つの独立変数の関数で表されるのは、残りの変数とは理想気体の状態方程式で関係づけられているからです。
[補足説明1]
上記で求めた式に付いて補足します。
3.(2)1.でPVTを状態変数とした理想気体の状態方程式のグラフ
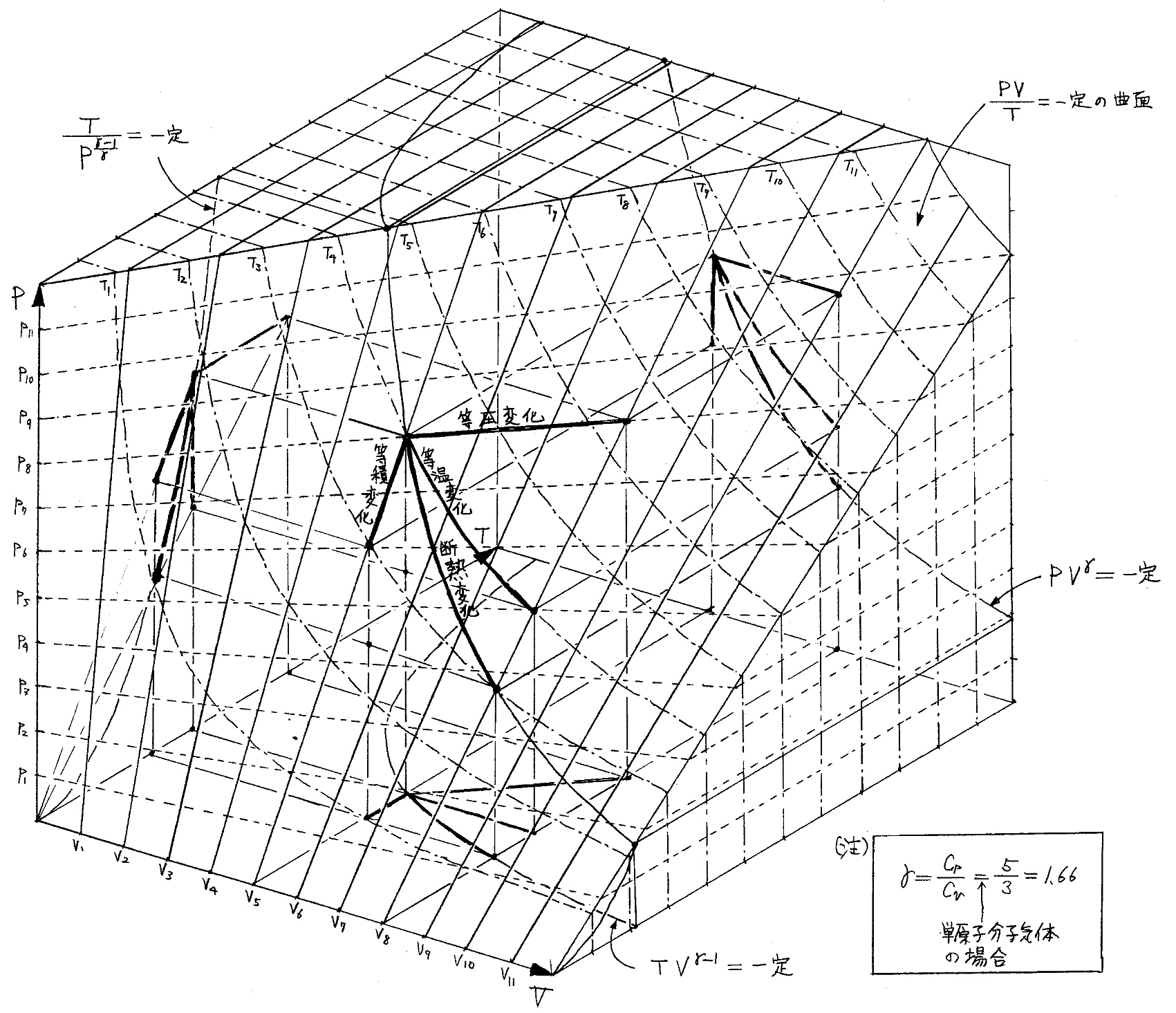
を示しました。この中に“等温変化”、“等圧変化”、“等積変化”、“断熱変化”、等々の変化曲線が記されていますが、これらはいずれも気体が封入された容器が、外界と無限小圧力差、無限小温度差で準静的可逆的に仕事と熱のやり取りをしながらたどった結果を表す曲線と見なすことができます。すなわち、
“等温変化”の場合は気体を詰めた容器は等温を実現するためにその温度の熱浴に接しており、またその容器の可動ピストン部分は外界と無限小圧力差で仕事のやり取りができるメカニズムの外界と接しています。そういった状況でピストンに働く外圧を少しずつ減らして準静的可逆的に外部に仕事を取り出しながら気体容器を膨張させて体積が増大し、圧力が下がった最終的な状態へ導くわけです。
“等圧変化”の場合は、常に同じ圧力を保てる様な機構をもつ外界と無限小圧力差で仕事のやり取りを準静的可逆的に行いながら膨張させます。そのとき気体の温度は少しずつ高くなっていきますから、その気体と準静的可逆的に熱のやり取りをする外部の熱浴の温度も少しづつ高いものに連続的に交換されていると考える必要があります。
“等積変化”の場合は気体を封入した容器は変形しないとします。その状態で、内部の気体と無限小温度差で熱のやり取りが準静的可逆的にできる外部の熱浴(温度が次々と変化できる)と接しており、最終的な圧力・温度状態へ変化していきます。
“断熱変化”の場合は、気体を封入した容器は断熱材で囲まれているとしますが、容器のピストンは外部の機構と無限小圧力差で膨張して準静的可逆的な仕事のやり取りをして、最終的な圧力・体積・温度の状態へ変化していきます。
いずれにしましても、グラフ図に描かれている変化曲線はその様に外界と準静的可逆的に熱や仕事のやり取りをしてたどる曲線だと見なせます。その様に考えれば、その変化過程に於けるd’Q/Tを積算していけばエントロピーSの変化量が計算できます。
もちろん上記の変化曲線を、外界との仕事や熱のやり取りに於いて圧力差や温度差がある、不可逆過程でたどったものであると考えてもかまいません。ただし、その場合径路過程からはエントロピー変化量を計算することができないだけです。
そのときいずれの変化でたどったものであれ、準静的可逆変化でたどったものを用いて計算すれば、状態量であるエントロピーの変化は一意に計算できて、各状態点ごとに確定されます。
そのため、最初の(P0,V0,T0)状態から、最終的な(P,V,T)状態へ変化した場合、その二つの状態に於けるエントロピーS0とSの差が上記の式で表されると言うことです。これらの式は、最初と最後の(P,V,T)状態がどの様に変化した点であっても利用できます。
[補足説明2]
本項で取り上げた例は、『熱力学』を展開するとき、必ず取り上げられる重要な例です。何故重要なのかを補足します。
まず、上で述べたように
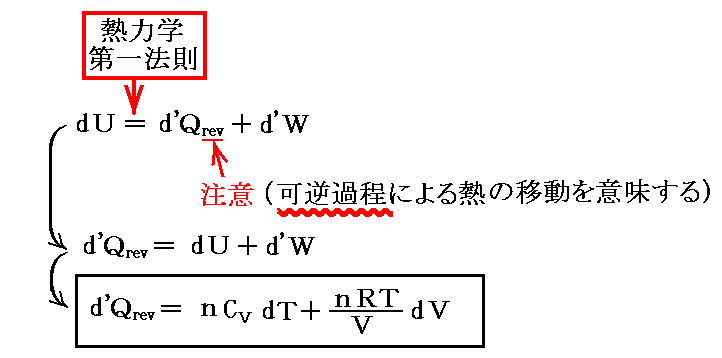
となるのですが、このときd’Qは完全微分(状態量)ではありません。実際
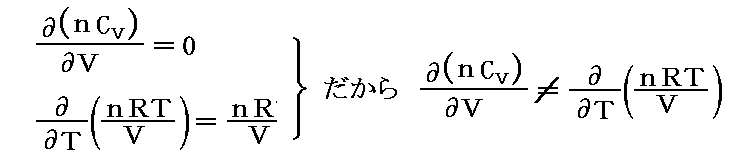
となるからです。
そのとき、5.(4)1.で説明した様に、Q(T,V)の変数が2個の場合、このQにある関数λ(T,V)を乗じる事でλ(T,V)・d’Qを完全微分(つまり状態量)にすることができます。この関数λ(T,V)を【積分因子】というのですが、今の場合それが1/Tなのです。
すなわち
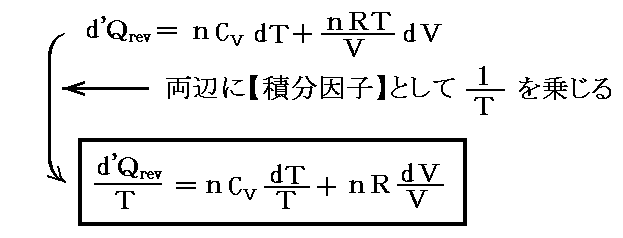
となるが、実際
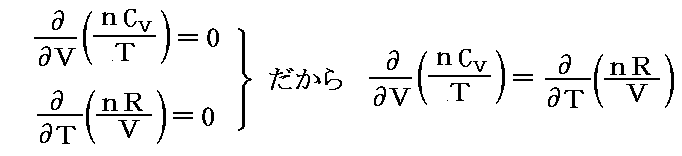
となり
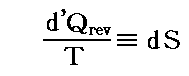
が“完全微分”(つまり“状態量”)である事を示している。
これは、5.(5)2.で述べたλがxだけの関数λ(x)の場合に相当し、“熱力学第2法則”の数学的な意味を示す大切な例です。
ここの説明が良く理解できない方は別稿「『熱力学』とは何か」7.(2)2.の〔例題 7・2〕 をご覧下さい。その例の XがTに、YがVに、dZがd’Qに、そしてdZ’=dZ/XがdS に相当します。また、そこの [補則説明2] の解説をご覧下さい。
各状態方程式をグラフにしてみる。簡単化の為にnCv=nCp=nR=1としてT、V、PはT0、V0、P0を単位としたグラフを示す。当然のことですが(T,V,P)=(T0,V0,P0)のときのSをS0=0としている。

の組み合わせの中でエントロピーSを含んでいないP=P(T,V)、V=V(T,P)、T=T(P,V)のグラフは何度も出てきた理想気体の状態方程式を表すグラフですからそれを参照して下さい。
それで最初は、エントロピーSを縦軸に選んだ三種類S=S(T,V)、S=S(T,P)、S=S(P,V)を示します。
S=S(T,V)
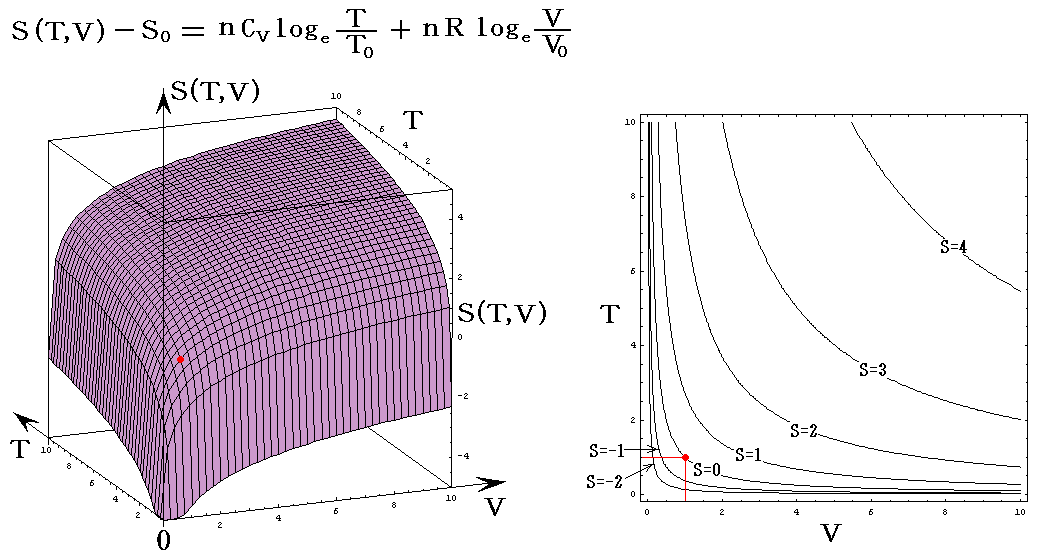
上右図は、理想気体の断熱変化(S=一定)の式 TV(γ-1)=一定 を表していることに注意されたし。
S=S(T,P)
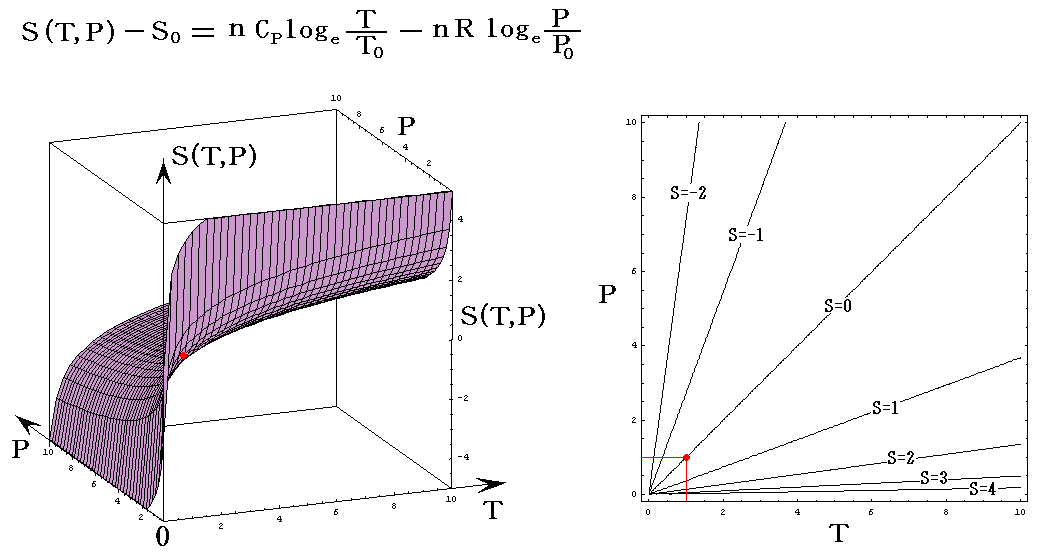
S=S(P,V)
上記の簡単化の仮定の基では、S(P,V)のグラフはS(T,V)のグラフのT軸をP軸に置き換えたものと同じになる。
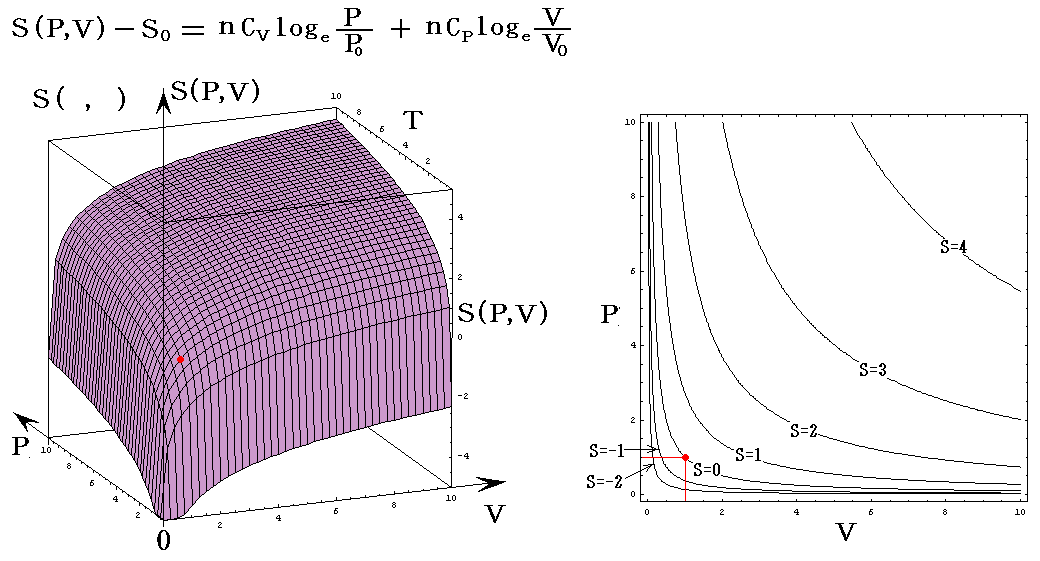
次に、上記の三種類の中でTを含んだ、S=S(T,P)の縦軸をSからPに変えたP=P(S,T)と、S=S(T,V)の縦軸をSからVに変えたV=V(S,T)を示す。
P=P(S,T)
今度も簡単化してnCv=nCp=nR=1としてT、PはT0、P0を単位としたグラフを示す。当然のことですが(T,P)=(T0,P0)のときのSをS0=0としている。このグラフはT→0、S→+∞とともにP→0に近づく。
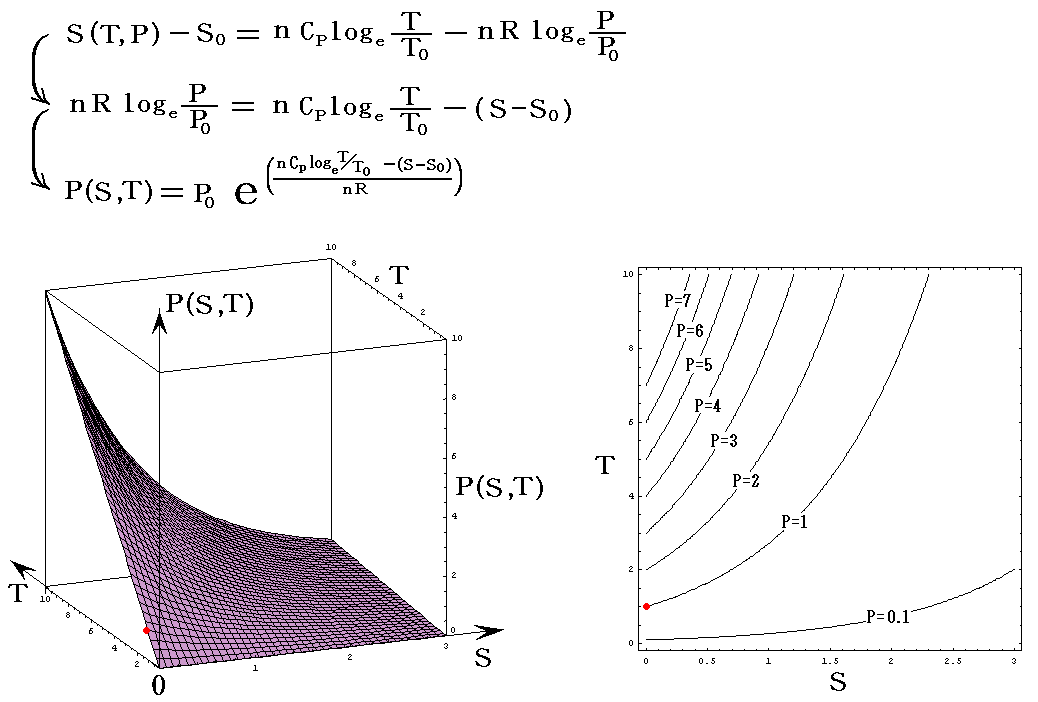
V=V(S,T)
nCv=nCp=nR=1とし、T、VはT0、V0を単位としたグラフを示す。当然のことですが(T,V)=(T0,V0)のときのSをS0=0としている。このグラフはT→+∞とともにV→0に近づく。
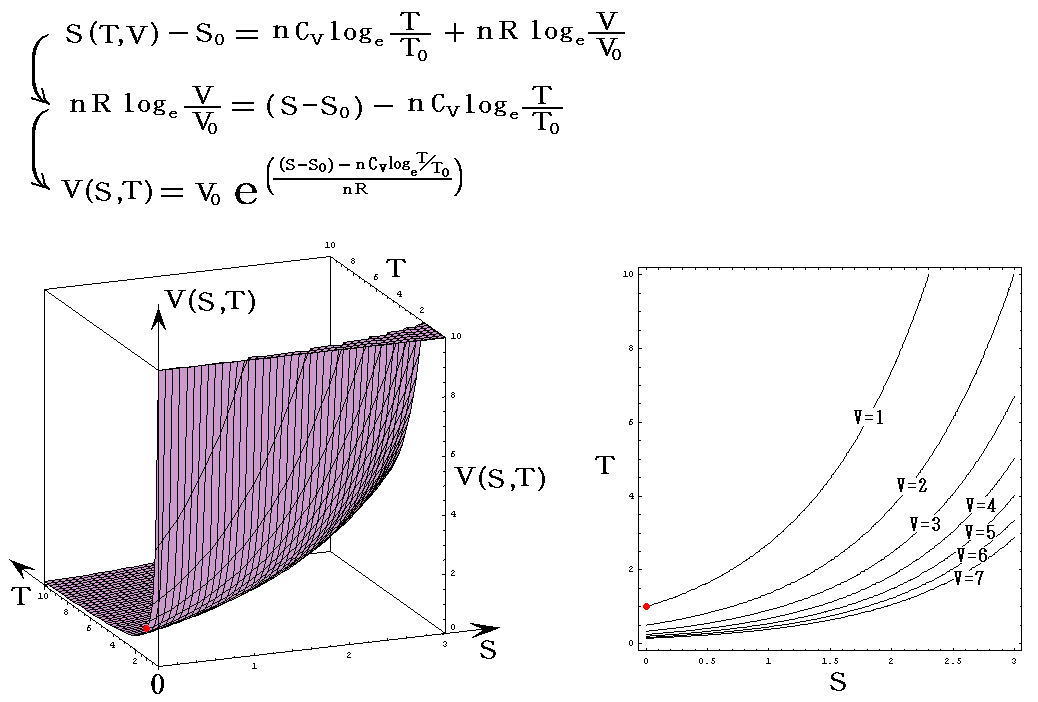
これらのグラフは工学で重宝されていますので、その様子を示しておきます。いずれも別稿「熱機関の効率(ガス動力サイクル)」中の例です。
S=S(P,V)とV=V(S,T)に付いては2.(1)2.“オットーサイクル”を参照。
S=S(P,V)とP=P(S,T)に付いては2.(6)1.“ブレイトンサイクル”を参照。
T=T(P,V)とV=V(S,T)に付いては2.(4)3.“スターリングサイクル”を参照。
T=T(P,V)とP=P(S,T)に付いては2.(5)2.“エリクソンサイクル”を参照。
(5)不可逆変化とエントロピー
“不可逆変化”のときエントロピーがどの様に変化するのか説明します。すでに述べたようにd’Q/Tの積分は、その積分が二つの状態の間で内的に可逆な経路に沿って実行されるときにのみ、エントロピー値の変化を与える。不可逆な経路に沿って実行されたd’Q/Tの積分値は状態量ではなく、可逆な経路に沿って積分が実行された値とは異なる。
1.拡散
“不可逆過程”である[拡散]の現象を、6.(1)2.で用いた機構を利用して説明します。ただし、今回はシリンダーとピストンは断熱材で作られており、状態変化の過程で外界と熱のやり取りはしないものとする。またピストンや重りを載せたテープルの質量はゼロになるように適当な滑車と重りの系が組み合わされており、それらに摩擦は無いものとする。簡単化のために実験は真空の部屋の中で行う。
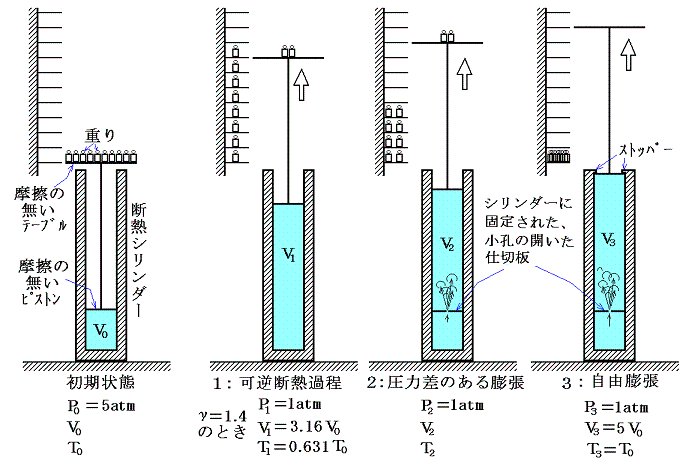
P0=5atm、V0、T0の初期状態から、次に述べる3っの方法で変化させる。
- ピストン上部のテーブルに載せた重りを無限小ずつ準静的に取り除いて、ピストンを可逆的かつ断熱的に上昇させて、最終的な圧力が1atmになるようにする。これは可逆過程なのでエントロピーの変化は
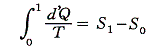
で計算されるが、断熱過程なのでd’Q=0だからS1-S0=0となる。つまりエントロピーは変化しない。このときγ=1.4の場合、“理想気体の断熱変化の公式”4.(3)を用いるとV1=3.16V0、T1=0.631T0となる。
- 図のように初期状態のピストンのすぐ下に小さな孔の開いた仕切板をいれ、最終的な圧力が1atmになるまでピストン上の重りを急速にどんどん取り除いていく。小孔の前後で気体に圧力差が生じる速度で断熱的に上昇させる。このとき小孔の前後で圧力が釣り合っていないので不可逆過程となり、外部に対してなされる仕事は1の場合より少なく、最終的な温度T2はT1よりも高い。この過程は可逆ではないので道筋はちゃんと定義できない。そのため、下図の状態0と状態2は“点線”で結んである。状態0から2への過程ではエントロピーは増加しているが、それでもなお断熱的なのです。T-S図上の面積が熱量を表すのは、その道筋が可逆過程を示しているときだけであることは注意すべきです。
- 2と同じ小孔の開いた仕切板を設置するが、今度は最初にすべての重りを取り除く。そうすると無限小の圧力で直ちに5V0の位置に取り付けられたストッパーの位置までピストンは一気に移動し、それ以後は、外部に仕事をしない断熱的な自由膨張となる。これは4.(1)1.で説明した“ゲーリュサック=ジュールの実験”と同じことで、内部エネルギーの変化は起こらず、温度変化も生じない。ただし、この場合エントロピーは最大に増加して状態3になる。この場合も正確な道筋ではないので“点線”で結んである。
状態0から状態1~3への過程をT-S座標上のP=P(S,T)グラフに記入すると下図のようになる。
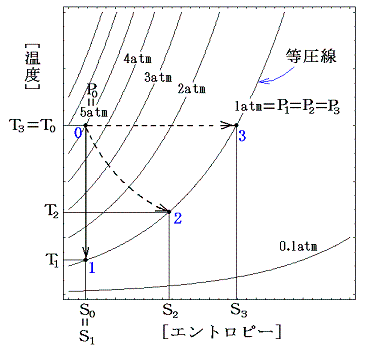
この図から、エントロピーが各過程の不可逆性の程度をはかる目安になっていることが解る。不可逆変化が起こっているときはいつでもエントロピーは増加し、同時に体系のエネルギー利用度は減少する。1の場合は棚に置いた重りをピストンのテーブルに移して圧縮して行けば元の状態0に帰れるが、2や3の状態から0の状態に帰る事はできない。つまり不可逆変化が起こると、その系から仕事を取り出すチャンスを永久に失ってしまうのです。
[補足説明1]
ここで注意してほしいことは、たとえ不可逆過程で到達した状態2や状態3に対しても状態量であるエントロピーは定まっている事です。それはもちろん前項3.で説明した準静的可逆過程を使って計算した値です。
状態3は状態0から温度T0=T3が一定になるように温度T0の熱浴から準静的に熱を加えながら、すこしづつおもりを取り除いて無限にゆっくり膨張させていく。圧力が1atmになるまでに加えられた熱量をQ03とするとS3-S0=Q03/T0で計算できる。
具体的には、6.(4)3.で求めた式
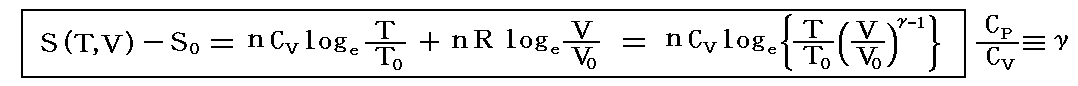
にT0=T3、T=T3と、V0=V0、V=V3=5V0を代入して求めるか、
こちらの式
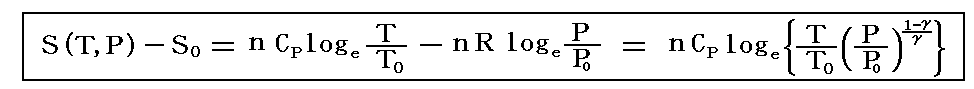
にT0=T3、T=T3と、P0=5atm、P=P3=1atmを代入して求めれば良い。
また状態2は状態0から準静的断熱変化で温度T2まで膨張させた後、温度T2の熱浴に接した状態で温度をT2に保った準静的等温変化で錘をゆっくり取り除きながら圧力1atmまで膨張させる。そのとき加えられた熱量をQ02とするとS2-S0=Q02/T2で計算できる。
このとき準静的な過程だから、図のピストンシリンダーの左側にある梯子状の錘置き場に錘のやり取りの過程が残っています。そのためその錘を再び無限にゆっくりとピストンに載せながら同じ温度の熱浴に準静的に熱を排出して圧縮して行くと元の状態0に可逆的に復帰できます。
具体的なエントロピー値の計算は、上記状態3で利用した計算式と同じものを用いて、最初の状態と最終的な状態の状態値を代入して求めればよい。
前記のように不可逆過程で状態3や2に推移させることもできますが、その場合には熱の流入は無いのにエントロピーは増大します。また、錘のやり取りの過程が梯子状の錘置き場に残っていませんから、その分の仕事を取り出すチャンスは永久に失われているわけです。
[補足説明2]
上記で準静的・可逆過程で 状態0→状態1 へ移行するときの
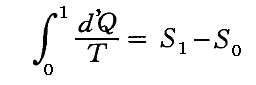
に付いて計算して求めました。
そのとき不可逆過程での遷移 状態0→状態2 や 状態0→状態3 に付いて同様の
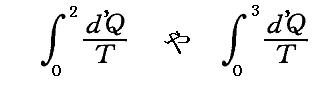
が計算できるのかどうか疑問思われる方もあるかも知れません。
それは可能でして、不可逆過程であっても計算できます。ただしそのとき不可逆過程の場合外界と系の間に温度差がある場合の熱量の移動なども含まれますので、積分するときの分母の絶対温度は、その積分を実施するときの外界の温度Teとしなければなりません。つまり
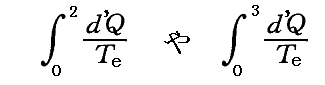
の形での積分値を計算できます。
もちろんそれは上記で説明しているエントロピー値とは全く関係ないのですが、これらの積分値は上記で説明している不可逆過程で到達した 状態2のエントロピーちS2 や 状態3のエントロピー値S3 と、どの様な関係にあるのだろうと悩まれる方もおられると思います。
そのことについて、別稿「熱力学第2法則とエントロピー」(7)2.[補足説明1]で詳しく説明していますので、どうぞご覧下さい。そこで説明される関係式は、以下で取り上げる例2.や例3.の場合も同様に成り立つものです。
2.温度差のある熱伝導
[温度差のある熱伝導]も“不可逆過程”です。例えば下図の様な、等圧での相変化を考える。その際定圧(飽和蒸気圧が同じ)だから当然等温変化(20℃)です。このとき左側1は20℃の熱源から無限小の温度差の元で、右側2は80℃の熱源から温度差がある状況で熱をもらい定圧・等温の相変化を伴った膨張が生じる。そして、シリンダーとピストンを含めた状況変化が1と2で同じように起こって、両者とも500kJの熱量を得たとする。
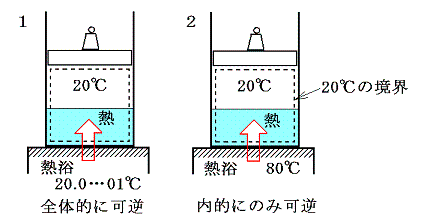
このとき、シリンダー内の水に起こるエントロピー変化ΔSwaterはどちらの場合もシリンダーの内壁に接する部分の水の温度は20℃=293Kと考えて良いので
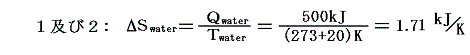
となる。一方熱浴に起こるエントロピー変化ΔSbathは熱浴の温度が異なるため異なった値となる。
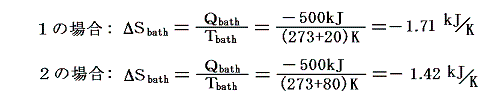
そのため、水と熱浴を合わせた全系のエントロピーは、可逆変化のみで変化する左側1の場合は変化しないが、不可逆変化を含む右側2の場合には増大する。
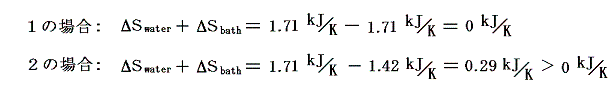
このとき、2の場合のエントロピーの増大は何処で起こるのかと言うと温度差を生じるシリンダー壁内を熱が移動する過程で生じると考えねばならない。ただしシンリンダーの質量が無視できて、その熱容量が小さい場合や、今の場合のようにシリンダー内の温度勾配が定常的だと考えられる場合は、熱の通過にともなってエントロピーの増大を生み出すが、シリンダー内に含まれるエントロピー自身の変化は無視することができる。
もちろんシンリダー内や熱浴内の撹拌が不十分でシリンダー壁面近くの温度分布が均一で無ければ、エントロピーの生成はシリンダー壁面近くの水や、熱浴の中でも生じることになる。
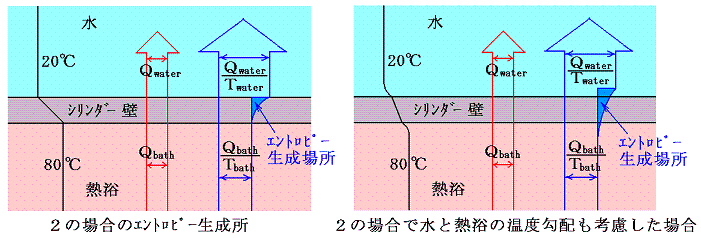
ここで、”温度差がある場合の熱伝導は不可逆過程なのにエントロピーが計算できるのはおかいしのではないか?”と思われる方がおられるかもしれませんので、具体的な例でもう少し補足します。
下図の様に断熱壁で囲まれた容器を、熱を良く通す仕切りで二等分し、それぞれに温度T1とT3(T1<T3)の同種の理想気体を1モル量ずつ入れる。この状態をAとし、エントロピーをSAとする。次に仕切りを通して高温から低温に熱が移り、やがて二つの気体が熱平衡状態を実現して同じ温度T2になったとする。この状態をBとし、そのときのエントロピーをSBとする。
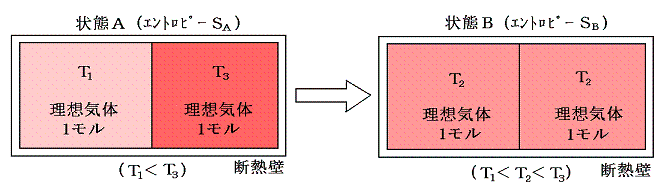
ここで、状態AからBへ変化したときのエントロピー変化を求めてみる。何度も強調したようにエントロピー変化を求めるためには、状態AからBへ準静的可逆過程で変化させて、上記の系に対して出入りする熱量を計算してdQ/Tを積算しなければならないのですが、6.(1)1.で述べたように、上記の過程は不可逆過程です。そのため可逆過程で同じ変化を実現する方法を考えます。中央の仕切りを断熱壁で置き換え、T1~T3の範囲で少しずつ温度の違う熱源をたくさん準備する。そして、高温理想気体に接する熱源を次々に切り替えながら無限小の温度差で等温的に温度T3~T2の熱源へ熱を移して自らの温度をT2とする。
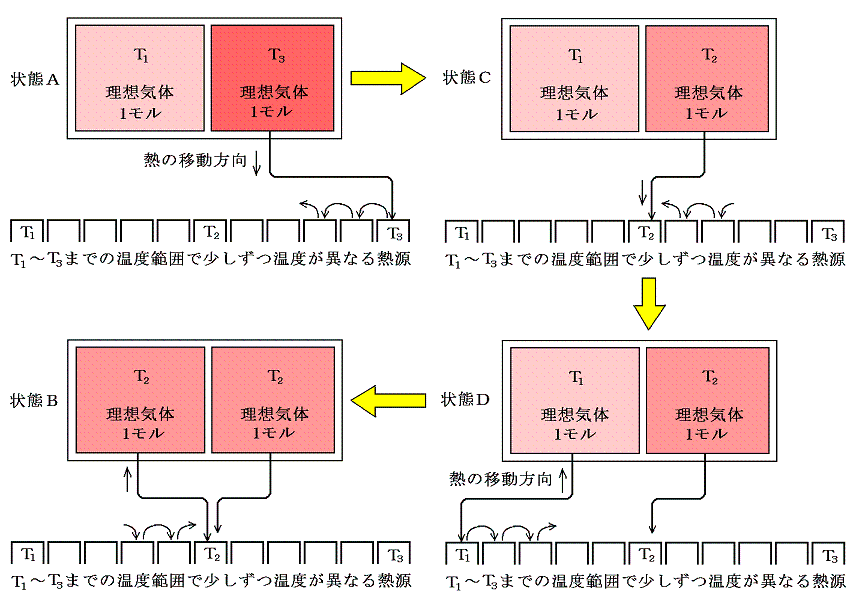
次に、低温理想気体を温度T1~T2の熱源に次々と繋ぎ替えて等温的に熱を少しずつもらって低温理想気体の温度をT2にする。このとき、外界の熱源に変化を残しながらではあるが、全ての段階の可逆性を保って着目する系の状態をAからBへ変化できたことになる。このとき外界の熱源に残っている熱量移動の痕跡をを逆向きに戻せば可逆的に元の状態に戻れるから確かに可逆過程です。
この可逆過程において系に出入りしたdQ/Tの合計値を計算するのは簡単です。その過程で体積は変化せず、理想気体の定積モル比熱Cvは一定と見なせるので
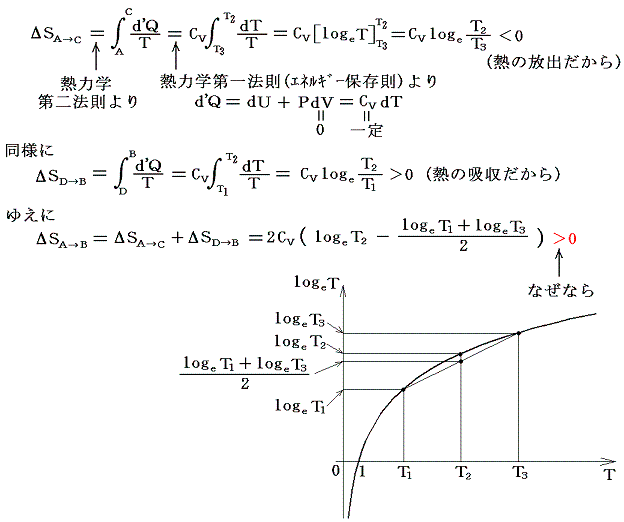
[補足説明1]
上記手順を用いれば状態Aから状態Bへ可逆的に変化させることができる。そのとき系のエントロピーは増大しているが、外界の熱源のエントロピーは同じ量だけ減少している。上記の過程をそっくり逆に行えば、外界の熱源に一時的に預けたり、それから借りたりしている熱量をすべて元に戻して最初の状態に復帰できる。つまり状態AからBへの変化が可逆的にできるのは、外界に変化の痕跡をを残しているからです。
状態AからBへの変化を外界に頼らず、直接真ん中の仕切り板を通して温度差がある状態で熱を移動させても、同じBの状態になります。そのとき、外界のエントロピーは変わらず、問題にしている系のエントロピーのみが(不可逆過程のために)増大します。その場合には外界も含めて元の状態に戻すことは二度とできないのです。
この例を考察すれば、前記の水と熱浴の温度差がある場合の熱移動において、エントロピー変化がそこでの議論の様にして計算しても良いことが理解できる。仮想的に上記例の様な外部熱源を仲介にしていると考えれば良いのです。
このことは、現実の熱機関の効率を考えるとき重要になります。別稿で述べた内的にのみ可逆な内的可逆サイクルと、内的にも外的にも可逆な過程のみからできている全体的可逆サイクルの違いです。そこで注意したように現実の熱機関は全て内的可逆サイクルと見なして、その熱効率を計算しています。
3.異種物質の混合
[異種物質の混合過程]も“不可逆変化”です。下図の様に断熱壁で囲まれた容器を仕切り板で二つの部分にわけ、一方に理想気体Ⅰを圧力P、温度T、体積V1でn1モル、他方に理想気体Ⅱを同じ圧力PとT、体積V2でn2モル詰める。この状態をAとし、エントロピーをSAとする。
次に仕切り板を取り除き二種類の気体が拡散・混合できるようにする。完全に混合して熱平衡状態になった状態をBとし、そのときのエントロピーをSBとする。
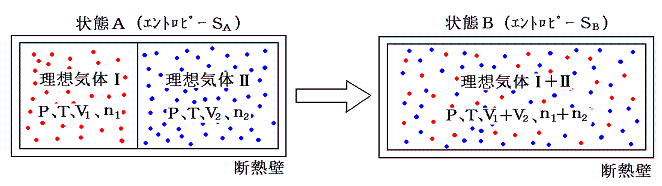
ここで、状態AからBへ変化したときのエントロピー変化を求める。エントロピー変化を求めるには、状態AからBへ準静的可逆過程で変化させて、系に対して出入りする熱量を測定しd'Q/Tを積算しなければならない。可逆変化を実現するために次のようなメカニズムを考える。二つのピストンⅠとⅡを考える。ピストンⅠは気体Ⅰは通さないが、気体Ⅱは自由に通過できるフィルターが張ってあるとする。同様にピストンⅡは気体Ⅱは通さないが、気体Ⅰは自由に通過できるものとする。このようなフィルターは現実には存在しないが、あくまで思考の上では可能であるとする。
最初に次図の様にピストンⅡを固定してピストンⅠだけが動くようにし、温度Tの熱浴に接した状態で準静的等温変化により理想気体Ⅰをゆっくりと膨張させる。このときピストンⅡに働く圧力は、ピストンⅡが気体Ⅰを自由に通過させるので、最初の圧力のままです。一方、ピストンⅠに働く圧力は、気体Ⅱを自由に通過させるため気体Ⅱの中を移動してもならん影響を受けず、通過させない気体Ⅰによる圧力だけが働く。その圧力には気体Ⅰの状態方程式にしたがった等温膨張の圧力変化が生じます。
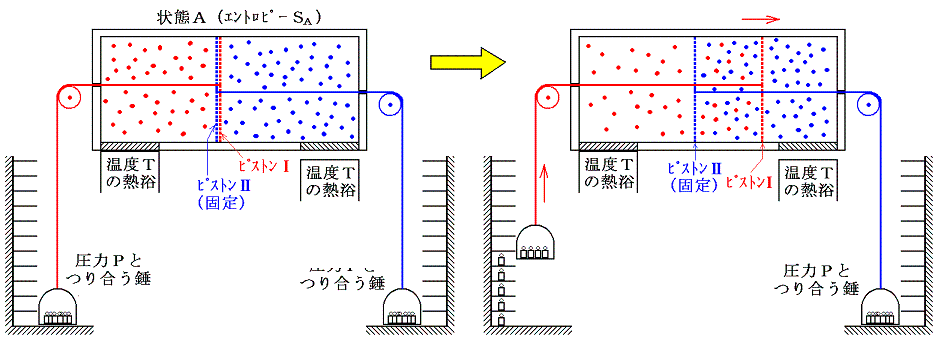
気体Ⅰが体積V1から体積V1+V2まで膨張するとき、等温変化をさせるために系に加えなければならない熱量は理想気体Ⅰが膨張に際してピストンⅠを押すことにより外部にした仕事量と同じです。理想気体の場合内部エネルギーは温度が変わらなければな同じなので、エネルギー保存則から明らかなように外にした仕事と等しいだけの熱量を加える必要があるからです。そのためこの変化によるエントロピー変化ΔSv1→v1+v2は
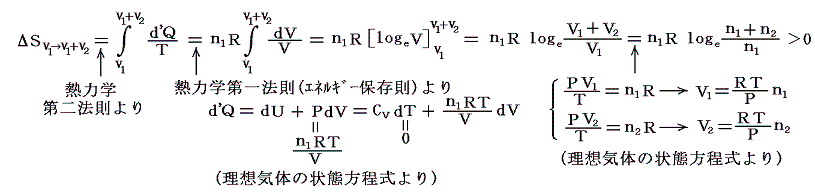
となる。
引き続いて、ピストンⅡのロックを外して自由に動くようにし、全く同様に温度Tの熱浴に接した状態で準静的等温変化により理想気体Ⅱをゆっくりと膨張させる。このときも気体Ⅰによる圧力は働きません。気体Ⅱの膨張による圧力変化だけが生じます。
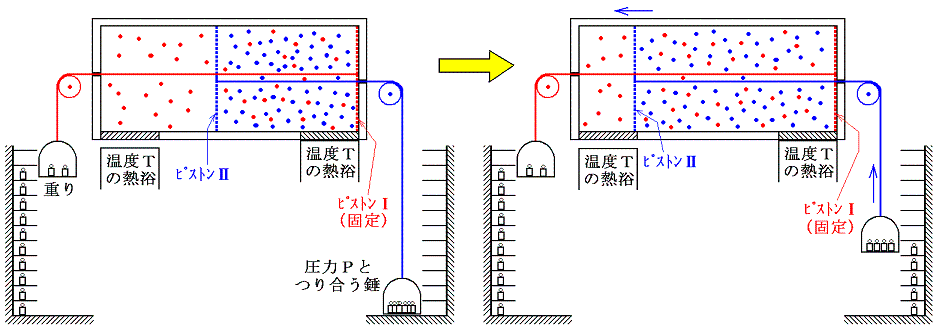
このとき気体Ⅱが体積V2から体積V1+V2まで膨張するとき等温的に変化させるために系に加えなければならない熱量は理想気体Ⅱが膨張に際してピストンⅡを押すことにより外部にする仕事と同じです。この場合も、理想気体の内部エネルギーは温度が変わらなければな同じなので、エネルギー保存則から明らかなように外にした仕事と等しいだけの熱量を加える必要があるからです。そのためこの変化によるエントロピー変化ΔSv2→v1+v2は、同様にして
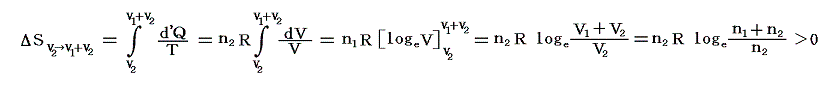
となる。
両方の変化を加えると結局状態Aから状態Bへ変化したことに伴うエントロピー変化量は
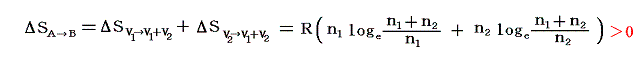
となり、エントロピーは増大する。
最初に述べた中央の仕切り板を取り除くことによる混合では、外界と仕事や熱をやり取りすることはないので、内部エネルギーは変化しません。そのため当然のことですが温度も圧力も最初のTとPがそのまま成り立ちます。
[補足説明1]
この場合も状態Aから状態Bへの可逆的な変化において系のエントロピーは増大しているが、外界の熱源のエントロピーは同じ量だけ減少している。そのとき、仕事や熱のやり取りの過程は外部の錘の位置変化や熱浴の熱量の変化として外部に残っているので、上記の過程をそっくり逆に行えば、外界の熱浴から一時的に借りた熱量や、梯子に錘を乗せることで預けた仕事の結果をすべて元に戻して最初の状態に復帰できる。つまり状態AからBへの変化が可逆的にできるのは、外界に変化の痕跡をを残しているからです。
状態AからBへの変化を外界に頼らず、直接真ん中の仕切り板を外して拡散混合させても、同じBの状態になります。しかし、その場合には外界も含めて元の状態に戻すことは二度とできないのです。
[補足説明2]
今簡単のためにV1=V2≡V、n1=n2≡nの特別場合を考察する。その場合に上式は
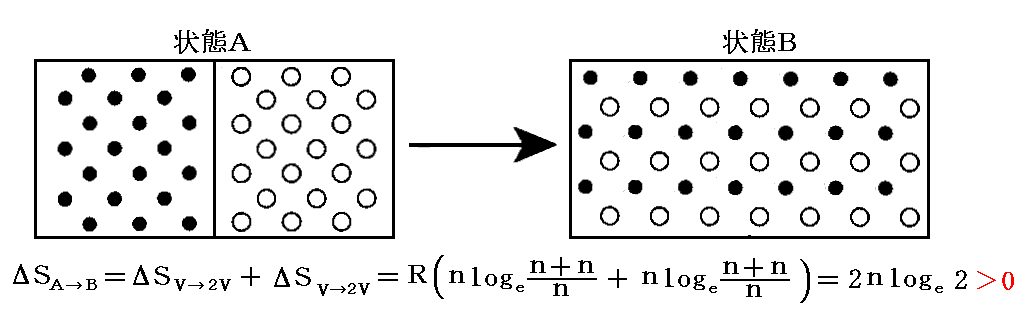
となる。
このときギブズはこの結果の奇妙な側面に注意を向けた。もし二種類の気体が同じであるならば、仕切りを取り除く前後の気体の状態は区別することができない。最初と最後の状態が同じなのだからエントロピーの変化は無い。すなわち
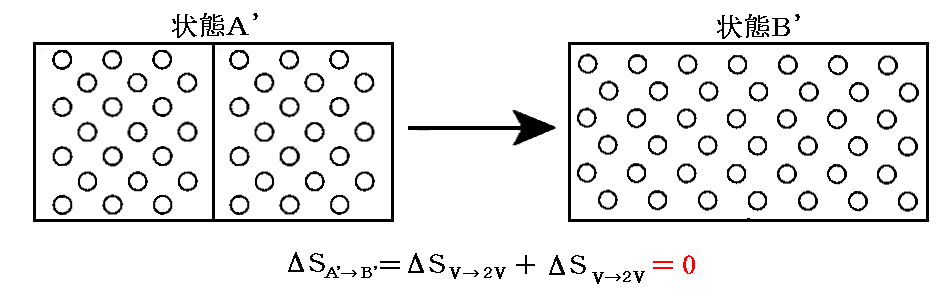
です。しかしながら、二種類の気体が異なれば、その違いがどんなに小さくても(例えば希ガスの同位体元素)エントロピーは前記のような増大を示す。一般の物理量の小さな変化は他の物理量についても小さな変化を引き起こすに過ぎない。ところが混合のエントロピーについては二種類の気体の違いがどんなに小さなものであれ、混合のエントロピーは0から突然2nloge2にジャンプするのです。この不連続的な挙動は“ギブズのバラドックス”(Gibbs paradox)と呼ばれて物理学者を困惑させた。
しかし、この疑問はやがて S=kBlogeW を用いた、エントロピーの量子理論にもとずく統計的解釈によって説明される。
このことに付いては
K.プルチブラム編集(江沢洋訳・解説)「波動力学形成史」みすす書房(1982年刊)の江沢解説文 第Ⅱ部 “シュレーディンガー小伝” の3.“粒子の統計性” をご覧下さい。このパラドックスの解消に貢献したアインシュタインやシュレーディンガーの仕事が解説されています。
さらに詳しい説明は「アインシュタイン選集1.」や「シュレーディンガー選集2.」に収録されている論文の邦訳版をご覧下さい。
不可逆な過程としては上記の[拡散]、[温度差のある熱伝導]、[異種物質の混合]以外に、[摩擦による熱の発生]、[電気抵抗によるジュール熱の発生]・・・・・・等々がありますが、いずれについても同様な事情が当てはまり、各状態に対して一意に決まるエントロピー値を定義にしたがって計算できます。その当たりは適当な教科書を参照されて下さい。
4.孤立系のエントロピー
以上の説明から明らかなように、問題の系が外界の助けを受けながら“準静的可逆過程”で、状態Aから状態Bへ変化すれば、問題の系のエントロピー増大を打ち消す様に外界のエントロピーは減少しています。そのため、問題の系と外界を含めた全体のエントロピーは変化しないのです。
ところが、問題にしている系だけで、[拡散]、[温度差のある熱伝導]、[異種物質の混合]、[摩擦による熱の発生]、[電気抵抗によるジュール熱の発生]・・・・・・等々などの“不可逆過程”によって状態Aから状態Bへ移行するようなことが起こると、そのとき外界のエントロピーは変化していないので、問題の系と外界を含めた全体のエントロピーは必ず増大することになる。
エントロピーは系の状態が決まれば、その状態に応じて定まる状態量ですが、“孤立系”のエントロピーは一定かあるいは増大していくかで、決して減少することはありません。
これがエントロピーという量に関して熱力学理論が教えてくれる驚くべき結論です。
このとき、孤立系に生じた不可逆変化を、外界の助けを借りて可逆的に生じさせると、必ず外界から熱の流入が伴っていることに注意してください。仕事に関しては(例1や例3の様に)流出していますが、熱に関しては(すべての例で)必ず流入しています。それだからこそ問題の系のエントロピーは増大しているのです。
そのとき、孤立系だけで不可逆変化させた場合には、外界とは仕事も熱もやり取りしません。そのため孤立系の内部エネルギーはエネルギー保存則から明らかなように変化しません。
だから孤立系で生じる不可逆変化というのは、可逆変化で行わせれば仕事として外に取り出せたはずのエネルギーをそのまま熱という形のエネルギーに変換してしまう変化だと考えることができます。
上記の例を検討すれば解るように、“不可逆の変化”とは[拡散]、[温度差のある熱伝導]、[異種物質の混合]・・・のように発熱が直接生じていないように見える変化も含めて、[摩擦による熱の発生]、[電気抵抗によるジュール熱の発生]・・・と同じように、仕事として取り出せる可能性を持ったエネルギーを熱という分散したばらばらで均一な形のエネルギーにしてしまう事(例2のように系内に存在した温度差を解消してしまう事を含む)だといってもよい。
そのとき、熱と言うばらばらで均一な形になってしまったエネルギーからもはや仕事を取り出すことはできないのかということですが、問題とする系よりも低い温度の外界が存在すれば取り出すことができます。しかし、それが無い孤立した系だけでは、熱というばらばらで均一な形になってしまったエネルギーから仕事を取り出すことは決してできないのです。それを法則の形で述べているのが“熱力学第二法則”(“カルノーの原理”)です。これこそが、“熱”と“温度”と“エントロピー”の関係を表すd’Q/T=dSの大発見に繋がるものでした。
さらに補足しますと、『熱力学』と言う学問分野は“温度”という物理量と“エントロピー”と言う物理量を導入することと等価です。
考えてもみて下さい、熱力学以前に展開されていたあらゆる学問分野で取り扱う物理量は、《時間》、《距離》、《質量》、それと《電気量》の次元を組み合わせて表現できるものしかなかったのです。
《温度》の次元はそれらとは全く異なるものです。温度は時間、距離、質量、電気量の組み合わせで測れるようなものでは無いことは明らかです。絶対温度は熱力学第二法則(カルノーの原理)を用いた、とても奇妙で不思議な測り方で初めて測れる様な物理量です。しかもそれは、天下り的に定義した実用温度計との対応でしか測れない様な物理量です。1.(1)2.を復習されれば解るように、絶対温度に対応させる元になった実用温度計の温度の定義こそ、温度の次元が全く新しい次元である事を示しています。
また《エントロピー》という物理量も、d’Q/Tから解るようにエネルギーの次元を温度の次元で割った次元をもちますので、それまでの物理理論の中には存在しなかった次元をもつ物理量です。これも、上で説明したように可逆変化を用いた不思議な測り方でないとその変化量が測定できない様な量です。
この二つの全く新しい次元をもつ量が必要である事は、プランクの“熱輻射公式”の導出法を思い出されればお解りでしょう。
私は、光(つまり電磁場)の理論である熱輻射公式に何故絶対温度という量が絡んでくるのかとても不思議でした。またプランクが、その公式を見つけることができたのはエントロピーの概念を輻射場に適応しての事だという事の意味が良く解らなかったのです。しかし、この二つの物理量の存在(温度とエントロピー)が発見された過程を理解したことで、その疑問も解けた様に思います。
要するに、Planckの“熱輻射公式”は、《温度》と《エントロピー》という全く新しい次元をもつ物理量の存在を発見することができなければ決して説明できない現象だったのです。だからこそ、この公式には“絶対温度”Tと“ボルツマン定数”kBが絡んでいるのです。この公式の中から量子の概念が認識されてきたというのも何か因縁めいたものを感じます。
7.絶対温度の測定
ここで、いよいよ絶対温度Tを現実の温度計で測定した実用温度tに関係付けます。
以後の議論はすべて、プランクに習って、絶対温度を測定する物体やそれと熱量をやり取りする熱機関の作業物質の単位質量当たりについて論じます。そのため示量性変数をすべて単位質量当たりに付いてのものとし、そのことを強調するために小文字で表します。また、特にそうする必要は無いのですが、間違いを防ぐために示強性変数も小文字で表すことにします。
以下の説明のなかで最も重要な事柄は、5.(5)2.で説明した積分因子を求めるための偏微分方程式
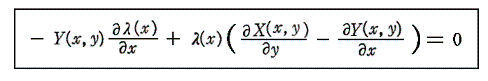
を解く操作であることに注目して下さい。
この章は別稿で引用している山本義隆著「熱学思想の史的展開」第28章も参照されながら読まれる事を勧めます[2021年11月追記]。
[補足説明1]
少しくどいのですが、ここで何をしようとしているのかを今一度説明しておきます。
まず、W.Thomsonがいみじくも指摘したように、温度というものを定義するには、2つの温度を持つ熱浴の間で可逆な熱機関を働かせて、そのとき高温熱浴と低温熱浴の間でやり取りされる熱量の比でもって2つの熱浴の温度比とするしか無いと言うことです。そのとき、温度の比が決まれば、適当な状況の熱浴(現在は水の三重点を273.16Kとしている)の温度を決めればあらゆる熱浴の温度というものは決定できます。
しかし、現実には、可逆的に働く理想的な熱機関など存在しません。それはちょうど理想気体の体積膨張の様子から絶対温度を測定しようとしても、絶対温度を体現している理想気体温度計など現実には存在しないのと同じです。
だから、(可逆では無い)現実の熱機関や(理想気体では無い)現実の実在気体を用いて測定できる量から、可逆熱機関や理想気体温度計が示すであろう真の絶対温度を求めることができるのか!という問題です。
それは、以下の様にすれば可能だと言うことです。
(1)実在物体の状態変化による方法
1.偏微分方程式の解
5.(6)3.の式から出発します。6.(4)で述べたように積分因子λ(t,V)中のN(t,V)はtだけの関数と見なせますのでN(t,V)=T(t)とおける。また単位質量当たりで考えているので
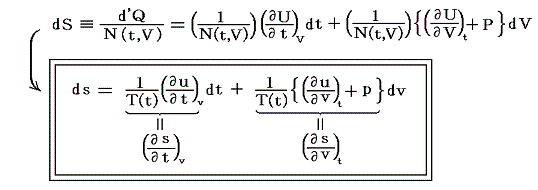
となる。ここでsは状態量ですから、dsが完全微分であることの条件式から
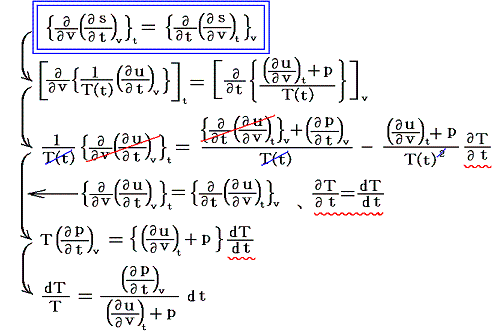
が導けます。式の変形をたどれば明らかなように偏微分が常微分に変換できる。そのため、この微分方程式は簡単に積分できて
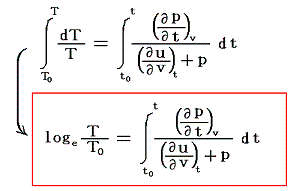
となります。これは5.(5)2.の計算過程と全く同じですからそこの例と比較してみて下さい。
これによって物質系の絶対温度Tが温度tによって完全に定められる。右辺積分記号内の分子は物質の状態方程式から積分途中の各温度tにおける値が直接得られるのでそれを用いればよい。例えば実在気体を使う温度計の場合はファン・デア・ワールスの状態方程式のような実験式を用いればよい。また分母は、熱力学第一法則(エネルギー保存則)から得られる
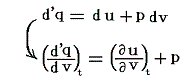
を考慮すると、物質が等温可逆膨張するときに外部から流入する熱量、あるいは等温可逆圧縮されるときに外部へ流出する熱量だから、各温度に於ける体積変化にともなう発熱or吸熱量の測定値を用いればよい。
2.理想気体温度計
ここで温度計物質として理想気体を用いる場合を説明します。現実には理想気体は存在しないのでその様な温度計はできませんが仮に存在するとしたらの話です。その温度計が示す温度tは理想気体の体積で測るとします。その温度目盛りは次のようにして定められます。単位質量の理想気体(仮に存在するとして)を1気圧の下で沸騰している水の中に浸けてそのときの体積を量ります。それをv100とする。次に同じく単位質量の理想気体を1気圧の下で氷と平衡にある水の中に浸けてその時の体積を量ります。それをv0とします。そうして単位質量の理想気体に定圧の下で(v100-v0)/100の体積変化が起これば1度の変化が生じたとします。
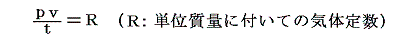
から明らかなようにp=一定の下でvが零に近づけばRは定数ですのでtも零に近づきます。体積は零以下はありませんから体積零の点が温度の零度となります。そして0℃の理想気体温度目盛りは、その時の体積v0を1度に付いての体積変化量(v100-v0)/100で割ったものに他なりません。
ところで理想気体の膨張係数αは1℃=1Kだけ温める際の体積増加分を0℃=T0Kの体積v0で割ったものです。つまり
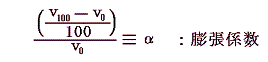
ですから、0℃の理想気体温度計による温度t0は膨張係数を用いると
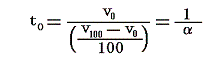
となります。
ところで、理想気体の状態方程式から
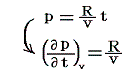
が成り立ち、また理想気体の内部エネルギーは温度のみの関数で体積に関係しませんから
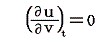
です。これらを前節の式に代入すると
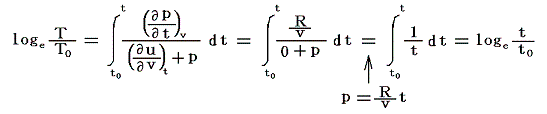
となりますから、まさに理想気体温度計が示す温度tは絶対温度Tそのものです。そのため理想気体の膨張係数αは0℃の絶対温度T0の逆数
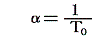
に他なりません。ただし、残念ながら理想気体は現実には存在しませんからその膨張係数を直接測定することはできません。だからこういった意味での絶対温度Tは2.(5)で注意したように定めようがありません。この当たりは7.(2)5.でもう一度詳しく説明します。
このとき次のことに注意してください。上の証明をみれば明らかなように理想気体の状態方程式p=Rt/vのtが絶対温度であると見なせるためには、“理想気体の内部エネルギーは温度のみの関数で体積には関係しない”という事が必要です。
4.(1)3.で注意したように、元々理想気体の定義には未だ定義できていない絶対温度Tを用いて状態方程式を定義し、その状態方程式でもって絶対温度Tを定義するという循環論法の論理矛盾がある。そのため、PV=RTが成り立てば理想気体の内部エネルギーUが体積によらないということが証明できるというような関係ではないのです。
正しくは、“理想気体の内部エネルギーが温度のみの関数で体積に関係しないのなら、p=Rt/vのtをケルビンが定義した意味での絶対温度であると解釈できる。”ということです。またその逆に、そのように解釈できる為には、上で見たように“理想気体の内部エネルギーが温度のみの関数で体積には関係しない。”でなければならないのです。
(2)実在気体のJoule=Thomson効果を用いる方法
測定精度を上げるには4.(1)2.で説明した実在気体のJoule-Thomson効果を用いればよい。
1.変数変換
Joule-Thomson効果を適用するために、5.(6)1.の式の状態を表す変数を(u,v)から(t,p)に変換しておく。今は単位質量あたりで考えているので
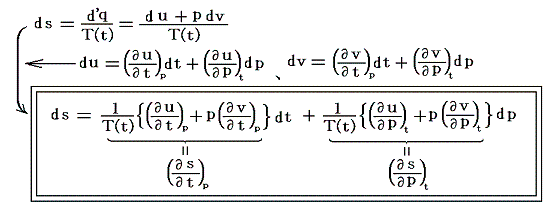
となります。uもvも状態量ですから、duもdvも完全微分となり上記の様な変換ができます。
ここでsは状態量ですから、dsが完全微分であることの条件式から

が得られる。
2.Joule=Thomson効果
4.(1)2.で説明したJoule-Thomsonの実験は、もともと理想気体の性質の決定に利用されたのですが、それよりも更に立ち入った意味を与えることができます。
すなわち、気体に、熱の授受なしに(Q=0)体積膨張V2-V1を(単位質量についてはv1-v2を)与える。そのとき気体の単位体積に及ぼされる外部仕事はp1v1-p2v2=wで表される。理想気体では、そのとき温度が一定に保たれるので内部エネルギーは変化せずw=0となる。ただし、実際の気体に対しては、熱力学第一法則(エネルギー保存則)からq=0だから
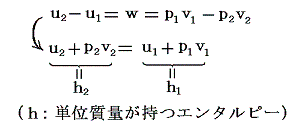
となる。つまりJoule-Thomsonの実験では状態変化の前後(つまり細孔栓の前後)でエネルギーuが一定に保たれるのではなくて、h=u+pvなる状態量(エンタルピーと呼ぶ)が単位質量について一定に保たれる。このとき実在気体ではp1v1とp2v2は等しくないので当然u1とu2は等しくない。そのため温度が変わるのです。
ここでは、簡単のために細孔栓の両側の圧力差は極めて小さくなるようにして気体を流す。両側に於ける状態を表す量の差をΔを付けて表すと
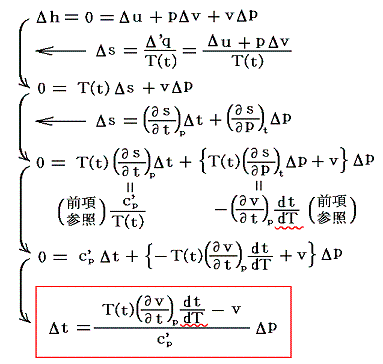
となる。これがJoule-Thomsonの実験に於いて圧力差Δpで細孔栓を押し出される気体に起こる温度変化Δtの式です。公式から解るようにその時の気体の絶対温度Tと、その温度での実用温度tと絶対温度Tの変化率dt/dTに関係している。そのためこれをdt/dTの微分方程式と見なして積分すれば
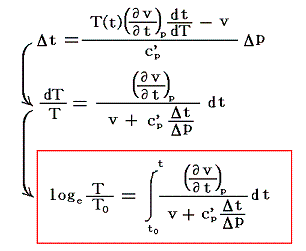
となる。右辺積分記号内の分子は物質の状態方程式から積分途中の各圧力pにおける値が直接得られるのでそれを用いればよい。また分母のvは流れている気体のその温度に於ける単位質量の体積、c’pは温度tにおける気体の定圧比熱(実在気体の定圧比熱は温度に依存する)、ΔtはJoule-Thomsonの実験の温度差、ΔpはJoule-Thomsonの実験における圧力差であるからすべて実測可能です。つまり、この実験により気体の絶対温度Tが温度tによって完全に定められる。
右辺の積分はtのみで決まり他の変数には無関係なので、最も測定がやりやすい状況で行えばよい。例えば圧力を一定(1気圧)に保った状態で温度tを変えながら微少な圧力差Δpのもとで気体を細孔栓に流し込み温度変化Δtの測定を行うのです。もちろん各温度でのvやc’pはあらかじめ測定しておく。
そのとき細孔栓の前後の気体温度をその管の中に挿入した水銀温度計で測ったとすると、tは水銀柱の体積膨張によって測られ定義されている実用温度tのことで、その温度計を用いて絶対温度Tが測定されたと言うことになる。
3.絶対温度目盛りの決定
絶対温度の目盛りを決めるために、1気圧の下で沸騰しつつある水の絶対温度をT100、1気圧の下で凍りつつある水の絶対温度をT0としてその差を

と置く。これは絶対温度の目盛り幅を摂氏温度と同じにするための措置です。さらに
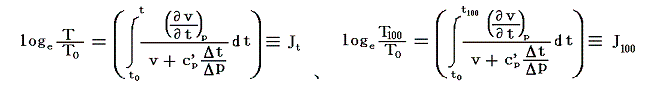
とおくと
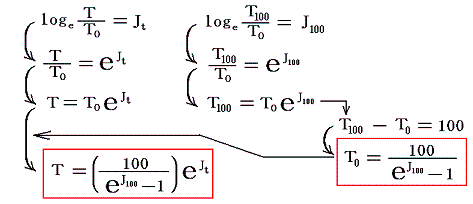
となり、実用温度tが絶対温度Tに関係付けられる。もちろんJtもJ100も任意の温度計を用いて測定した実用温度tによる、任意の気体に付いてのJoule-Thomson効果の測定値についての積分値です。
具体的な計算は以下のようにやります。すでに述べたようにJの積分はtのみで決まり他の変数には関係しないので、最も測定がやりやすい状況で行えばよい。そのため以下では一定圧力(例えば1気圧、以下の数値例では1kgw/cm2)に限定し、実用温度tの温度計物質として、細孔栓実験に用いたのと同じ気体(たとえば空気)を採用する。
このとき実用温度t0(=0℃とする)とt100(=100℃とする)は絶対温度T0とT100の熱浴[つまり1気圧の下で氷と平衡にある水と、1気圧の下で沸騰している水]と平衡にあるときの単位質量(1g)の温度計気体(空気)の体積から定める。t0のときの体積をv0、t100のときの体積をv100とし、その実在気体(空気)の膨張係数をα’(実在気体のものと言う意味で’を付けている)とする。
気体の膨張係数α’は気体の温度を1℃だけ温める際の体積増加分をt0(=0℃)の体積v0で割ったもの[3.(2)4.参照]ですから実用温度t℃のときの気体(空気)の体積(単位質量)vtは
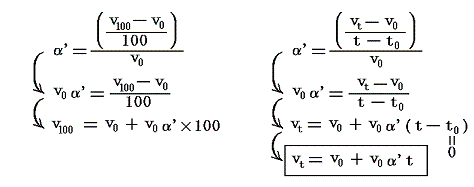
となる。これが実用温度tと実用温度目盛りの指標となる空気体積vtとの関係を表す式です。このとき
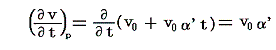
となるから、前述の式は
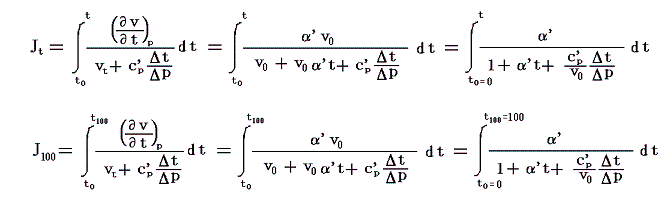
となる。それでは実際のデータを用いて0℃が絶対温度で何Kとなるか求めてみよう。
4.実際の計算例
圧力pmmHg、温度t℃における空気の密度ρtは下記の関係式で良く近似される。それを用いると0℃に於ける単位質量の体積v0と膨張係数α’は
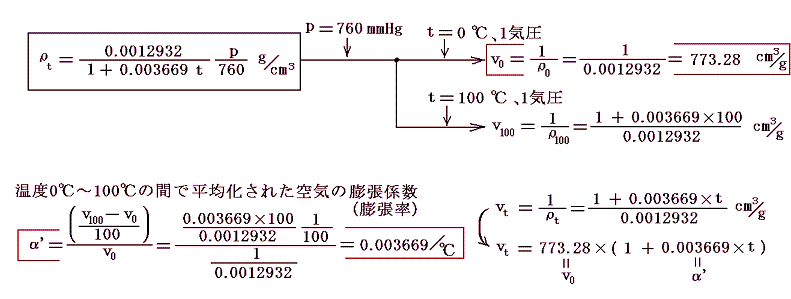
となる。
また空気の定圧比熱c’Pは圧力1[kgw/cm2]の下で0℃から100℃までの間、ほぼ一定でc’P=0.240cal/(g・℃)です。理想気体の場合は温度に依存しない[4.(2)3.参照]としましたが、実在気体の定圧比熱は温度と共に少しずつ変化します。例えば「化学便覧」(丸善)によると空気は1気圧のもとで100℃では0.24568cal/g・℃、200℃では0.24045cal/g・℃、300℃では0.24043cal/g・℃、500℃では0.24608cal/g・℃です。しかし積分の中で関与する項が他の項に比べて小さい(下表参照)ので、あまり変化しない場合には定数として計算しても差し支えない。
また空気のJoule-Thomson係数Δt/Δpは実験によると下表第二欄の様になる。これはp=1[kgw/cm2]の圧力の空気を、微少圧力差Δpの下で細孔栓を押し出したときの微少温度変化Δtを微少圧力差Δpで割ったものです。単位は[℃/(kgw/cm2)]で表してあります。工学でよく使われる力の単位[kgw]を使っているのでcgs単位系に変換したものを同じ表の第三欄に付け加えておきます。[具体的な測定法は4.(1)2.のJoule=Thomsonの実験を参照されたし。]
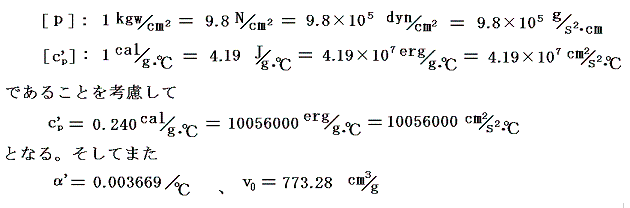
であるから下表の様に計算される。
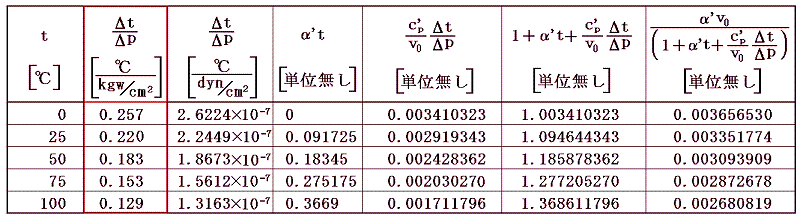
これらの値α’、v0、c’p、Δt/Δpを用いてJ100の数値積分を行う。数値積分は、台形公式では誤差が大きすぎるので、シンプソン公式を用いると
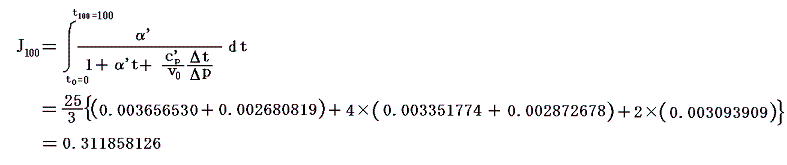
となる。このJ100の値を前項で求めた0℃の絶対温度T0を与える式に代入すると
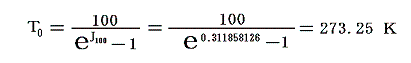
となる。実験誤差から小数点以下に0.1K程度の誤差はあるが、ここで利用したデータは、まさに-273.25℃が絶対零度0Kであることを示している。つまり、これより低い温度は無いのです。そして、もしこの温度の熱浴が準備できれば理想的な熱機関の効率を1にできる訳です。
計算に使ったExcel元ファイルはここをマウスで右クリックでダウンロード可。htmlファイルに変換していますが、もともとExcelファイルですから、Excelで読み込み再編集可。xls形式で再保存するとExcelファイルにもどります。
任意の摂氏温度t℃を絶対温度TKに直すにはすでに述べたJtを同じように測定・計算して
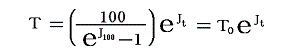
に代入すればよい。その時、当然の事ながらJt=J0=0を代入するとT=T0となり、Jt=J100を代入するとT=T100=T0+100となる。
ThomsonとJouleが1852年以降の一連の実験から得た値(マッハの本からの引用)を下記に示します。彼らの測定では0℃は絶対温度でT0=273.7Kとなります。これらは新しい目盛りでの温度(T-273.7)と0℃で760mmHgの圧力を示す定積空気温度計による温度t℃との対応関係を示している。

この表において、当然の事ながら0℃と100℃においてT-273.7とtは完全に一致しているが、それ以外の温度ではT-273.7とtは異なる事に注意。ただしその差はごく僅かです。それは、実在気体(空気)が凝縮(液化・凝固)するような温度範囲以外では、実在気体と理想気体の性質の違いはごく僅かだからです。(J.
P. Joule, and W. Thomson, "On the Thermal Effects of Fluids in Motion. Part II.", Phil. Trans. 1854, vol. cxliv. p321-364.)もとデータはこちら
マッハが強調しているように、彼らが得た結果の精度がどこまで精密であるかは、さして重要なことではない。新たに定義された目盛り[絶対温度]へ、その他の個別的な各目盛り[実用温度]を引き直すための原理はどんなものか、熱力学が明快な理論的関係を獲得するに至るための原理がどのようなものなのかがここに示されたのです。
上記の計算に用いた数値は久保亮五偏 「大学演習 熱学・統計力学」裳華房(1969年刊)P59第2章問題[C]の問[45][46]から引用しました。この問題集は若い頃かなり気合いを入れて集中して勉強しました。上記問[45][46]の解答も熟読したのですが、思考力の無い私には、なぜこの問の解答に書かれている方法で絶対温度が求まるのか幾ら考えても良く解らなかったのです。問[45][46]の解答として記載されている内容はプランクの本のそのままなのですが、私には全く意味不明でした。しかし、このHPを書いた今なら、一点の曇りもなく理解できます。理解して初めて言えるのですが、いきなりこの本を読んだのでは絶対に理解できないでしょうね。
1968年の国際度量衡総会 (CGPM) で、水の三重点 (0.01℃) を 273.16 K と定義したため、絶対温度とセルシウス温度の目盛の幅(1度の温度差)は等しく、相互の値には[絶対温度(K) = セルシウス温度(℃) + 273.15]の関係が成立する。
しかし次の事柄に注意してほしい。1.(1)3.で注意したように、摂氏温度目盛りには二つの基準点が必要でした。しかし、絶対温度目盛りの基準点は、一点だけで良いのです。そのため、水の三重点を273.16と定めた時点で目盛りの幅も同時に決定されていることになります。もともとは、セルシウス温度目盛りの幅と等しくなるように定めたのですが、今日では、そのこととは無関係に定められていると言って良いと思います。
5.理想気体との比較
前節の計算では理想気体との違いが見えてこないので上記の計算を別なやり方でやってみます。まず
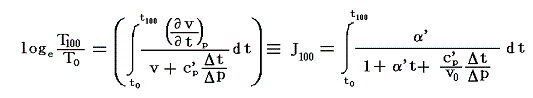
の右辺の分母に於いて
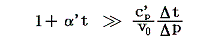
が成り立つので、Joule-Thomson係数Δt/Δpが掛かっている項がほぼゼロであると見なせる場合[理想気体ではΔt=0だから完全にゼロ]には
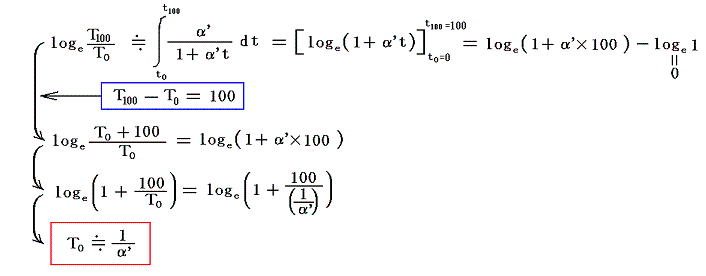
となり、0℃の絶対温度はほぼ膨張係数α’の逆数に近くなる[理想気体の膨張係数αは測定することはできないが、もし求めることができたなら、その逆数に完全に一致する]。これは2.(3)ですでに注目していた事柄です。このような事情から
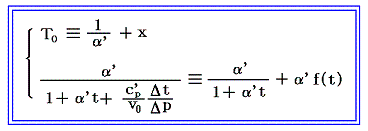
と置いて計算してみる。下段の式は
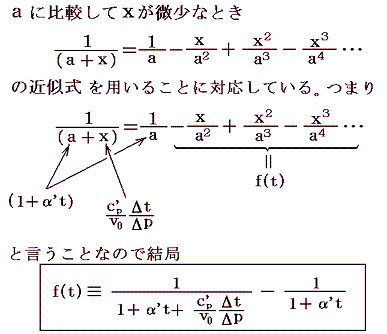
と置くことと同じです。そうすると前記の積分は
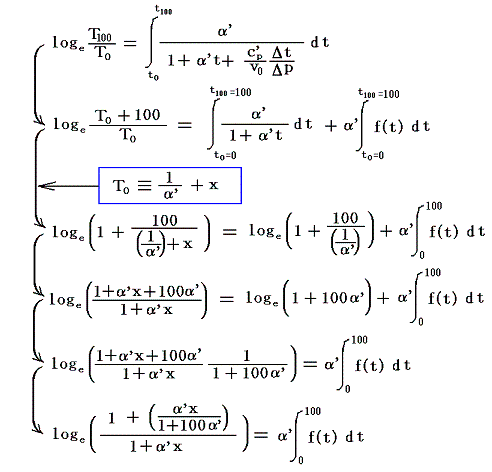
となるが、ここで
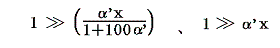
だから左辺を展開してxの1次の項だけを取ると

が得られる。前項の数表のデータを用いて数値積分を行うと
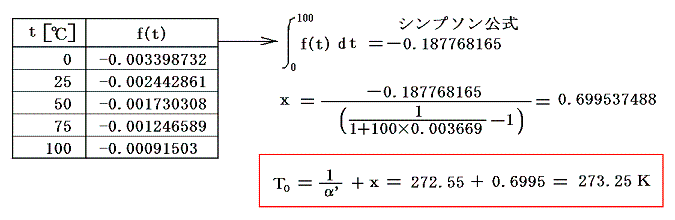
となり、前項と全く同様な結論が得られる。
この解き方から、気体が理想気体に近づけばx→0へ近づき、α’→α(理想気体の膨張係数)に近づくことが解る。
プランクは、彼の著書「熱力学」の§164で、次のように説明している。
”絶対温度の設定に対して、熱力学第二法則が原理上からみてはなはだ重要であり、また極端な温度においては欠くべからざるものであることは明らかである。
しかし、実際のところ、理想気体の膨張係数αの最も精密な数値は、熱力学第二法則とは無関係に、実在気体の膨張係数α’の測定から得られている。”
その具体的な方法は下記のようなものです。
理想気体ではその法則から明らかなように、一定圧力の下での体積V、及び一定体積のときの圧力Pは、ともに絶対温度Tに比例する。例えば100℃と0℃に於けるそれぞれの値に添え字を付けて表すと
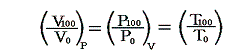
となる。
そこで、下図のような定積気体温度計や、定圧気体温度計を準備する。まず、定積気体温度計に二酸化炭素などの気体を入れ最初の圧力がPであったとする。この温度計をまず沸騰する水の中に入れてその圧力がP100に変わり、次に融解しつつある氷りの中に入れたら圧力はP0になったとする。これから(P100/P0)vの比が解り、グラフの点(1)がとれる。
次にはじめの圧力がPと同じ二酸化炭素の定圧気体温度計を使い、同じことをすれば(V100/V0)pの比がわかり、グラフの点(2)が決まる。
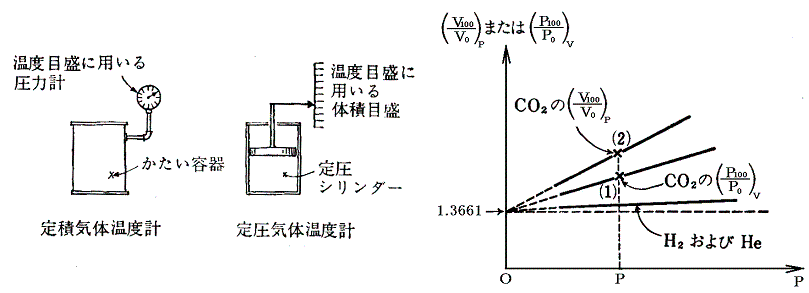
グラフの点(1)と(2)が違うのは、CO2が理想気体ではないからです。初めの圧力を変えて実験すれば、図のような曲線を描くのに十分な点を取ることができる。さらに、気体をCO2から水素やヘリウムなどに代えて同様な実験を行えば、圧力が減少するのに伴って互いに近づいていく曲線群が得られる。すべての実在気体は圧力がゼロに近づくにつれて、理想気体の性質に近くなることが解っているので、様々な種類の気体を、様々な圧力で測定して得られる曲線群を圧力P→0まで伸ばしたところが求める点です。それは1.3661へ収束しているように見える。この値から
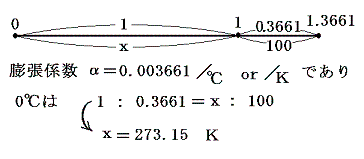
であることが解るというわけです。
この方法に原理的な裏付けがあるわけではないので何となく納得できない所があるのは偽らざる心境です。測定できない圧力の部分のグラフが直線的に伸びている保証などないわけですから。これを教えられたとき、ほんとにこのやり方しか無いのか疑問に思われたと思う。その疑問に対する答えが上に述べた熱力学第二法則を用いる方法です。それによって求めたT0の逆数こそ現実には測定できない理想気体の膨張係数αなのです。
(3)クラウジウス=クラペイロンの式を利用する方法
クラウジウス=クライペイロンの式は、最初ClapeyronによってCarnotの定理から導かれ、後にClausiusによって厳密に証明されたもので、気相と液相の熱平衡に対して成り立つ関係式です。プランクは彼の「熱力学」§177で、この関係式を用いても絶対温度Tが実用温度tの関数として決定できることを説明しています。
1.相変化とギブズの自由エネルギー
“クラウジウス=クラペイロン過程”は、一定圧力pに調整され自由に動くピストンで蓋をした円筒状容器に封入された物質の二相平衡系に生じる変化です。系に熱を加えると圧力一定・温度一定の下で相1(液体)が蒸発して相2(飽和蒸気)に変化して体積が変化する現象です。
液相(相1)にあるときの物質1gが持つ内部エネルギーをu液、気相(相2)にある物質1gが持つ内部エネルギーをu気とすると、この相変化は一定圧力、一定温度の下での準静的可逆過程だから、実用温度で測った転移温度をtとすると

となります。これは
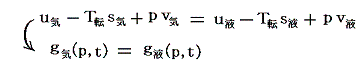
と変形してみれば明らかなように、相転移前と相転移後の1gの物質のギブズの自由エネルギー(状態量の一種)が等くなるように生じる変化です。すなわち、相転移は、相転移前と相転移後のギブズの自由エネルギーは常に等しい場合に生じる。
2.飽和蒸気圧曲線に沿ったクラウジウス=クラペイロンの式
このクラウジウス=クラペイロン過程を実用温度dtだけ異なった温度(t+dt)で行わせる事を考える。そのときの圧力は当然pからdpだけ異なった圧力(p+dp)となります。このとき(dp/dt)がp-t座標面における飽和蒸気圧曲線の傾きになります。
この飽和蒸気圧曲線に沿った状態変化では、常に両相におけるギブズの自由エネルギーは等しく保たれていますから、飽和蒸気圧曲線に沿った気相と液相のギブズの自由エネルギーの変化量は互いに等しくなります。この飽和蒸気圧曲線の傾きに対して、この事実から導かれれ成り立つ関係式がクラウジウス=クラペイロンの式です。

この式変形中に含まれている微少変分の意味は非常にわかりにくいので是非、別稿「ファン・デル・ワールスの状態方程式」4.(3)の図で確認されて下さい。このとき式中のsやvは全て実用温度tの関数ですが、変分dTだけは絶対温度Tで無ければいけないことに注意して下さい。
3.実用温度から絶対温度を求める関係式
ここで、飽和蒸気圧曲線に沿った積分を実用温度tに関して実施すると実用温度計の温度目盛 t を絶対温度 T に結びつける関係式T(t)が得られます。
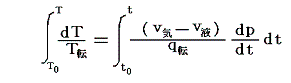
つまり、実用温度で測った各転移温度tに於ける転移熱q転と相変化に伴う体積変化(v気-v液)を用いることにより、各実用温度tが絶対温度Tで何度になるかが決定できるのです。(∂p/∂t)は転移温度tにおける飽和蒸気圧曲線の傾きであり、積分は飽和蒸気圧曲線に沿って実用温度t0からtまでおこなうと、そのときの温度差(t-t0)が絶対温度で(T-T0)に相当するということです。
その具体的な手法は別稿「ファン・デル・ワールスの状態方程式」4.(4)[補足説明2]を参照して下さい。実際の計算法は7.(2)のジュール=トムソン効果を用いる場合と全く同じですので、そこの議論を御覧下さい。
ここまでのプロセスをたどれば解るように原則的には第二法則から導かれる方程式は何れもこれを絶対温度Tの測定に利用することができる。そして、このことは5.(6)4.の□囲み枠内に書いた様に熱力学第二法則の検証に利用できる(Planck文献1.§177)。
これらはプランクが彼の著書「熱力学」の中で何度も強調していることです。
このページを読まれた方はお解りのように絶対温度とエントロピーは極めて抽象的・数学的概念です。熱力学が解らなくなる最大の原因は、ここのプロセスで出てきた式中の実用温度tを最初から絶対温度Tで置き換えてしまうところにある。本来積分因子として導入された絶対温度Tは積分因子の位置のT(t)だけで、そこに限って使っても良いものです。それ以外は絶対温度を使うべきではないのです。
ところがここで見てきたように目盛りの幅を実用温度(例えば摂氏温度)と同じにしたら(つまり100℃を373.15K、0℃を273.15Kにしたら)、その範囲外の温度でも普通の温度計による測定値と絶対温度との差は(T=t+273.15の違いを除いて)極僅かです[7.(2)4.のThomsonとJouleの測定結果参照]。
そのため多くの教科書では最初からtを絶対温度Tに置き換えて論じており、そのときdT/dt=1とした式を公式として利用している。そうしていきなり、エントロピーが状態量であるという性質を最大限利用して様々な物理量と温度Tを結びつける熱力学の有用な公式を導き出し、利用している。
絶対温度の最も重要な事柄はその値に下限があり、それは知ることができるということと、その下限から測られた絶対温度の高さが、熱機関の効率に深く関わっていると言うことです。それと絶対温度を導入する事でエントロピーという状態量を定義でき、熱の出入りが、熱の代わりにエントロピーを用いることによって、とても解析しやすくなることです。熱力学の法則から導かれる重要な公式・法則の大半は、エントロピーが状態量であるという事実を最大限活用して得られたものです。それにも拘わらず最終的に、それらの公式・法則にはエントロピーは含まれていない。
このとき、前述したように絶対温度は極僅かの誤差を無視すれば普通の温度計で簡単に測定[もちろん-273.15℃が基準ですが]することができる。ならば、現実の温度計で測定した温度tを絶対温度Tと同じと見なして、dT/dt=1として差し支えないだろう[7.(1)~(3)の式でt=T、dT/dt=1としたものが普通の教科書に出てくる式だということを確かめて下さい]。そして、後は絶対温度とエントロピーが導入された過程やその理由を忘れてしまってもかまわない。最終的な公式には現れないのだから、エントロピーという量の意味はよく解らなくてもかまわない。温度という量が測定できさえすればよい。エントロピーが状態量であるという事実を最大限活用して現実の問題に適応してゆけばよい。
熱が絡んだ現象で最も重要な概念が温度ですが、これは極めて難しい量です。熱力学第一法則のdU=dQ-PdVだけでは、その式の中の何処にも温度が入ってきていない。d’Q=TdSとしてd’QをTとdSに置き換えたとき、初めて温度が出てくるのですが、このとき状態量でないd’QをTで割ったd’Q/T=dSとして導入されるSこそ状態量エントロピーです。
熱力学第二法則はまさに温度とエントロピーを導入することと等価です。つまり熱力学第二法則は熱をエネルギーの他の形態から区別して特徴付けるものであり、熱の発生、移動の不可逆性を温度という量との関係で説明するものです。Carnotサイクルの議論を読めばその当たりの事情は了解できる。
熱力学の最大の成果はエントロピーの微分が完全微分である[エントロピーが状態量である]という事実
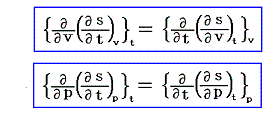
を最大限利用して、熱が絡む現象の間に成り立つ関係を導き出すことです。
そのときエントロピーの導入に伴って(積分因子として)現れた温度という物理量が、様々な物質定数、物理量を結びつける関係式に必然的に介在してきて重要な役割を果たす。
そのとき、Tとtの差は無視できるのだから、それを同等と見なせばよい。実際に知りたいのは温度という量[実用温度である摂氏温度に273.15を足せば直ちにわかるもの]と様々な物理量との関係なのですから。熱力学とはまさに熱が絡む[当然温度が絡む]現象が示す様々な法則を研究する学問なのだから。
事実世の中の大半の教科書はその立場で議論が展開されている。だからそれらの教科書を幾ら読んでも絶対温度とは何か、エントロピーとは何かがよく解らないのですが、利用する立場から行くと差し支えないわけです。その当たりは割り切って考えるべきかもしれません。しかし、そのやりかたが熱力学を難しくしており、温度やエントロピーという量の理解を困難にしている。本来ここで述べた議論をしっかりやってから上記の応用に入るべきなのだと肝に銘じたほうが良い。
最近の高校教科書ではcal(カロリー)をやめていきなりJ(ジュール)という単位で熱量や比熱を説明しています。しかし、私はそのやり方には反対です。1.(1)2.や1.(2)1.で述べたような従来の導入方法できちんと教えた方が良い。そのやり方では温度とか熱量の測定法しか定義していなくて、それらの量が何を意味するのか全く明らかではありませんが、その導入法こそ温度と熱量の本質をよく表していると思います。それであるからこそ後に明らかになった熱の仕事当量や、後に導入された絶対温度とエントロピーの概念が重要になるのですから。
8.熱力学第二法則の応用
この章は未完成です。前章7.(4)「まとめ」で説明した t=T and dT/dt=1とする普通の教科書のやり方で、熱力学第二法則から導かれる成果の幾つかを説明するもので、このHPのテーマとは関係ありません。公式集として利用するために、今後少しずつ付け加えてゆこうと思います。
(1)様々な見方
以下のように、色々な観点で見ると熱力学第二法則の特徴が浮かび上がってくる。
1.第一法則と第二法則
- 熱力学第一法則はエネルギーという状態量とその保存性について説明するものです。
- 熱力学第二法則はエントロピーという状態量と、その増大性(不可逆性)について説明するものです。
2.仕事と熱
- 孤立した物体系は外界と仕事や熱をやり取りすることにより状態変化する。そのとき外界とやり取りする仕事量W’や熱量Q’は(P,V)や(T,S)の状態変数で表された状態方程式の経路に沿った経路関数として定義されており、それらの積算値(線積分値)は、W’もQ’も積分経路が異なれば違った値になる。そのため状態変化に伴って系に出入りする仕事量も熱量も系の状態量ではない。
- 孤立系の境界を通じてやり取りされる仕事量は一般的には系の状態量PとVによりd’W=-PdVで表される。そのときやり取りされるのはエネルギーのみでエントロピーはやり取りされない。
ただし下図の様に孤立系に流入した熱以外のエネルギー(系内の抵抗Rと電流値Iによりd’W=RI2で表されたり、回転のエネルギーで表される)が不可逆な過程を引き起こせば孤立系のエントロピーは増大することになる。
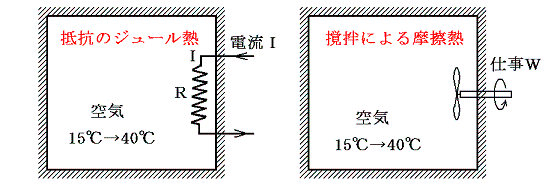
- 孤立系の境界を通じてやり取りされる熱量は系の状態量TとSによりd’Q=TdSで表される。そのとき、エネルギーとエントロピーの両方がやり取りされる。そのとき、6.(5)4.で述べたように[温度差がある熱伝導]が生じると孤立系と外界を合わせた全体系のエントロピーは増大する。
3.エネルギーとエントロピー
- 孤立した物体系のエネルギー変化は、その境界を通じてやり取りされる仕事や熱やその他諸々のエネルギー性量の移動量の総和で測定できる。
- 孤立した物体系のエントロピー変化は、その境界を通じて可逆的にやり取りされるd’Q/Tと、その系内で生じる不可逆性の変化によって決まってくる。
孤立系内で起こる現象がすべて可逆的現象のみで、境界を通じて外界とやり取りされるエネルギーの中で熱量移動が可逆的な場合には、その孤立系のエントロピーは正確にd’Q/Tの積算値で増減する。ただしそのとき熱が系内へ移動する場合をd’Q>0とし、その逆を負として計算する。また、そのとき熱量以外の形のエネルギーが境界を通じてやり取りされても良く、そのことが孤立系内に不可逆的変化を引き起こさない場合はエントロピー変化を引き起こすことはない。
孤立系が断熱されており外界と熱のやり取りをしないならば、その孤立系はエントロピーの変化が無いか、または、その系内で起こる不可逆的現象により増大し、決して減少することはない。そのとき熱量以外の形のエネルギーのやり取りが境界を通じてなされても、それが系内に不可逆な過程を引き起こすことが無ければエントロピーの変化を引き起こすことはない。
4.系と外界
熱力学の基本的な考え方の特徴は、宇宙を、その特定な(一つとは限らない)部分である“系”(system)と、宇宙のそれ以外の部分である“外界”(external world)に分けて考えることです。この様な考え方は普通の物理学では用いられません。熱力学の大きな特徴です。
熱力学とはまさに、それぞれの“系”を特徴付ける“状態量”で系の状態を記述し、“系”と“系”あるは“系”と“外界”がやりとりする“熱”や“仕事”や“物質移動”などの相互作用を通して、系の性質の変化(つまり系に付随する状態量の変化)を論じる学問です。そのとき、系内での熱の発生や境界を通じての熱の移動(すなわち系の温度とエントロピーという状態量の変化)が本質的に重要な役割をします。ここに熱力学第二法則が関係しており、熱の力学である由縁です。
このとき、系の認知と設定はそんなに簡単ではありません。なぜなら、系と系あるいは系と外界の“境界”をどのように設定するかで、熱力学の展開方法が変わってくるし、理論的に得られる結論が変わってくるからです。熱力学から有益な結論を引き出せるかどうかは、ひとえに、系と外界をどのように考え・設定するかに依存しています。
系と外界をどのような幾何学的境界で分けるかについては様々な状況があります。幾つかの例を説明します。
- 間歇燃焼ガス動力サイクルではシリンダー内が一つの系で、それ以外が外界となる。内燃機関のピストンは系と外界の境界面で、この面を通して系は外界と仕事のやりとりをする。
- 連続燃焼ガス動力サイクルではコンプレッサー→熱交換機→タービンを含んだ部分が一つの系で、それ以外が外界となる。タービンのブレード面がまさに外界との境界面で、その面を通じて外界に仕事を取り出している。そのとき物質が系内を移動する過程で物質1モルが持つ状態量が様々に変化していく。
ガス動力サイクルでは、普通吸気と排気によって気体を外界とやりとりするが、この部分を含めて閉鎖系として考えて論じる場合が多い。
- 蒸気動力サイクルでは動力伝達媒体である水が循環する閉鎖領域が系で、それ以外が外界となる。ボイラー部分で熱の注入が行われ、タービンブレード面を通じて外界へ仕事をする。系内を移動する過程で水は液体と気体の相変化を繰り返すが一つの連続する系内での変化です。
- 冷凍サイクルでは、熱を移動させるための冷媒が循環する閉鎖領域が系で、それ以外が外界となる。蒸発器や凝縮器の部分で熱を、コンプレッサーの部分で仕事を外界とやり取りしている。
- ファン・デル・ワールス気体の液体・気体共存領域では、液体領域と気体領域がそれぞれ一つの系として取り扱われる。その二つの系(相)を取り囲む容器の外側が外界となる。そして容器の側壁を通して外界と熱のやりとりがなされ、二つの相のそれぞれの状態量の変化が考察される。そのとき液体と気体の二つの系(相)の共存(あるいは相互変換)はある一定温度、一定圧力の元で実現されるが、それぞれの系(相)中の1モルが持つ状態量であるギブズの自由エネルギーgが等しくなる様な形で相転移が生じる。
この様に、系が幾つかの部分系に分かれる場合、その部分系を“相”という言い方で取り扱う場合が多い。
- 実在気体のジュール・トムソン効果に於いては、細孔栓の前後がそれぞれ一つの系として取り扱われる。そして実在気体が一方の系から他方の系へ移動したとき、系中の1モルの気体の状態量がどのように変化するかが考察の対象となる。
- 反応熱と熱化学方程式に於いては反応物と生成物をそれぞれ一つの系と見なす。反応物系と生成物系の温度を同じにするために、それらの系を取り巻く外界とやり取りしなければならない熱量が化学反応熱です。この場合には、同じ物質原子が反応前後で別々の系になると考える。
このように、系の取り方と外界との関係は千差万別です。物質を含んだ系のそれぞれに様々な“状態量”が付随しています。そのとき、状況により系そのものの認知を柔軟かつ様々に変えなければなりません。これが熱力学理論を難しいと感じる理由だと思います。
系と状態量については別稿「熱力学関数(状態方程式曲面)の性質」1.(1)で詳しく説明しておりますのでご覧ください。
(2)状態量と状態方程式
1.状態量
理想気体の状態方程式はその気体の状態を一意に定めます。その時の変数温度T、圧力P、体積Vはその状態が決まれば一意に決まる状態量です。
このときすでに出てきた
内部エネルギー: U、
エンタルピー: H=U+PV
も、その状態の物質系に附随する状態量でそのときの状態が決まれば一意に決まる量です。
さらに付け加えると
エントロピー: S、
ヘルムホルツの自由エネルギー: F=U-TS、
ギブズの自由エネルギー: G=U+PV-TS=H-TS=F+PV
も物質系の状態が定まれば一意に定まる状態量です。
これらの量が状態量であることはPVやTSなどの量も状態が定まれば一意に定まる状態量であることから明らかです。
このとき、以下の事柄に注意して下さい。
dS=d’Q/T=(dU-d’W)/T=(dU-PdV)/T や
dV=d’W/P
とおけるからと言って、決して
Q’=ST や
W’=PV
と言った置き方はできません。仕事W’や熱量Q’は状態変化の経路によって異なり状態量ではないのですから。
つまりQ’やW’は積分経路に依存し
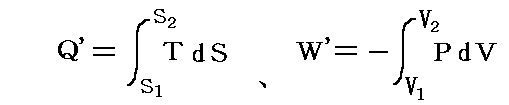
であって、決して
Q’=(T2S2-T1S1) や
W’=-(P2V2-P1V1)
ではありません。
ところがP1V1やP2V2、T1S1やT2S2は状態量であって(P1,V1)や(P2,V2)、(T1,S1)や(T2、S2)が決まれば一意に決まる量です。
PVが状態量であるということは、P-V座標平面に垂直にPV座標を取ると一つの連続な曲面になるということです。つまり
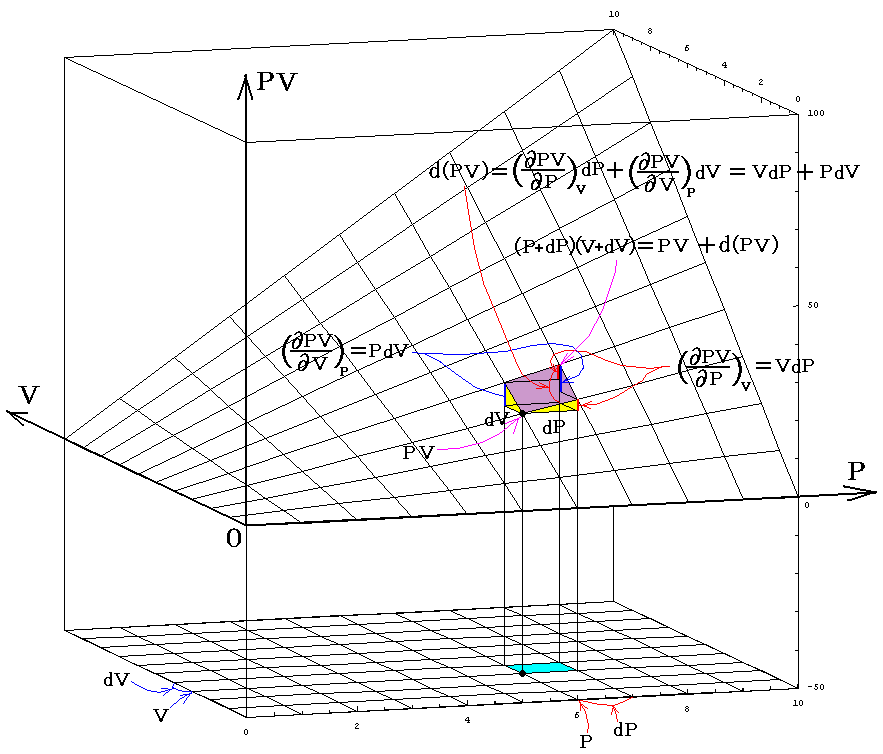
ということです。TSについても同様にT-S座標平面上にTS曲面が考えられます。
その為、d(PV)やd(TS)が完全微分である条件式
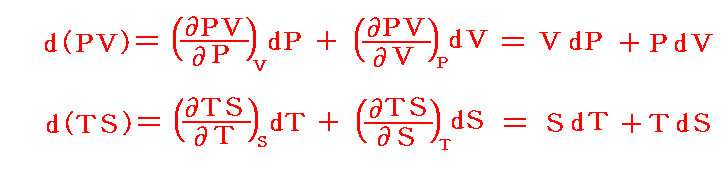
が成り立ちますので
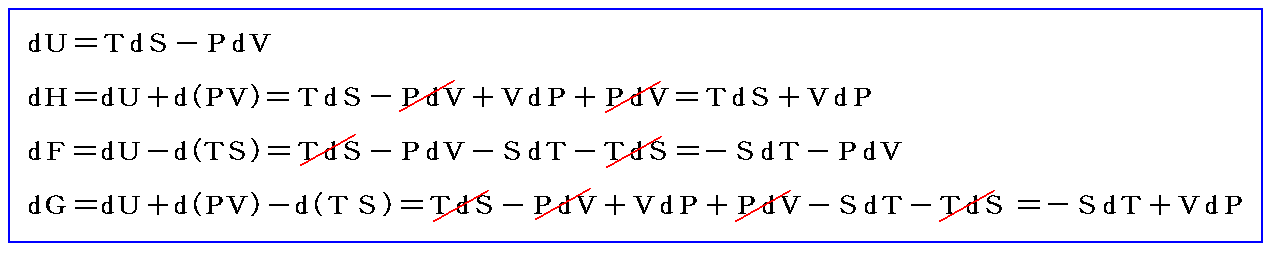
となります。
そのため、U、H、F、GはいずれもP、V、T、Sの中の二つの変数でそれぞれの微少変化量をあらわすことができます。そのとき変数の微少変分の前に掛かっているT、P、V、Sはその二つの変数の関数とみなせる。もちろんそれらの関数は完全微分の必要十分条件[5.(2)1.参照]を満たします。
このときUやH、F、Gも状態を記述する状態変数と見なすこともできますが、6.(4)3.で注意したように普通はTとS、PとVの4つの内の二つを変数に選びます。熱力学の法則は[物体系の状態変化]を[熱の出入り]や[仕事の出入り]と結びつけるものです。そのとき熱の出入りに関係する変数がTとSで、仕事の出入りに関係する変数がPとVですから。
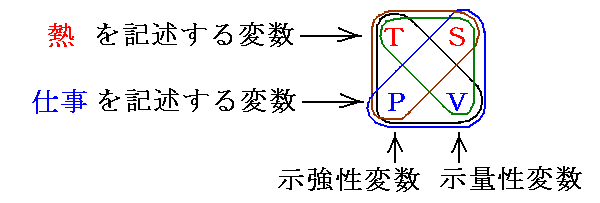
この中でS以外は直接測定することができます。dSも可逆変化の場合はd’Q/Tのように熱量の出入りd’QとTを測定すれば直接測定できますから、これらの量を状態変数とするのは妥当な選択です。
ここで導入したエンタルピー“含熱量”H、ヘルムホルツの自由エネルギーF、ギブズの自由エネルギーGは、単に状態量である内部エネルギーUに状態量であるPVやTSを足したり引いたりしたものでしかありません。それだけのものですが、物質系の状態が決まれば一意に決まる状態量(エネルギーの次元を持つ示量性変数)であることは確かです。
[補足説明1]
これらは、以下に記す様に、ある特殊な状態変化に伴う法則を解析するとき便利だから導入された。そのため“熱力学特性関数”(thermodynamic characteristic function)と呼ばれる場合がある。
エンタルピー“含熱量”Hを導入する意義については別稿「反応熱と熱化学方程式」1.(3)で説明しましたが、等圧の条件下で生じる状態変化に伴って出入りする熱量を意味する。等圧下で生じる化学変化に伴って出入りする反応熱はまさにエンタルピーそのものです。
実際

ですが、等圧変化ではVdP=0だからdH=TdS=d'Qとなるからです。つまり、この熱(エネルギー)の出入りには定圧下で生じる系の膨張や収縮に伴う仕事の変化を考慮したものになっており、状態変化に伴って出入りする熱量は系の内部エネルギーの変化分
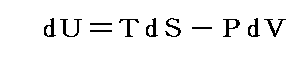
そのものではないと言うことです。
エンタルピー“含熱量”と言う名前の言われもまさにその当たりにある。
ヘルムホルツの自由エネルギーFは等温の条件下で生じる状態変化に伴って出入りする仕事の量を意味する。実際、上で導いたように
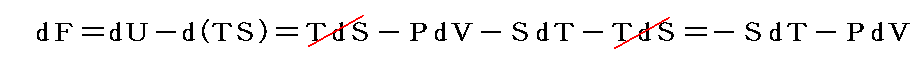
ですが、等温変化では-SdT=0となるのでdF=-PdV=d'Wとなるからです。つまり等温下の状態変化で仕事を取り出そうとしても、等温を保つために熱量が系に対して出入りする為に、系から取り出せる仕事量は系の内部エネルギーの変化分
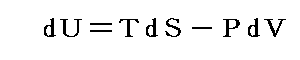
そのものではないと言うことです。
すなわち、系の内部エネルギーの変化分の一部分のみが仕事として外部に取り出せるのです。自由エネルギーという名前には、内部エネルギーの内で仕事として自由に取り出せる部分と言う意味があります。
ギブズの自由エネルギーGを導入す意義は別稿「ファン・デル・ワールスの状態方程式」3.(1)などで説明しましたが、等温・等圧の条件下で系に生じる状態変化では、常にギブズの自由エネルギーに変化が生じない様に生じるところにあります。等温・等圧の条件の下でそうなることは
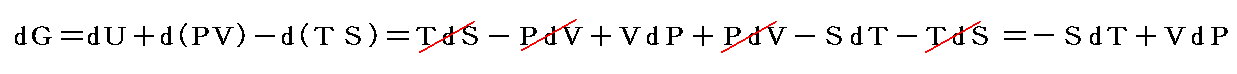
から明らかです。等温・等圧下における化学反応の平衡(多種類の物質の共存)や相平衡(気体や液体、固体の共存、あるはい混合気体、溶液、固溶体の共存)の遷移はdG=0の条件の下で生じる。つまり不均一な系の平衡を論じる時には不可欠の量です。
これは、dG=0を満足する経路(Gが極値を取る経路)に沿って化学反応や相平衡は進んでいくと言うことを意味しますが、系全体のGが変化するような現象にも使えます。例えば気相と液相が共存する系に於いて系の温度を変えると系の圧力はどのように変化するか?なども予言してくれます。それはdG気相=dG液相(つまり、dG気相-dG液相=0)を満足するように変化していくと考えればよい。この稿の7.(3)や別稿「ファン・デル・ワールスの状態方程式」4.(3)などで説明した例がそれです。このように、ギブズの自由エネルギーGは不均一系の熱力学を論じるときに絶大な威力を発揮する。
[補足説明2]
上記では、系が外界とやり取りする仕事として力学的仕事d’W=PdV しか考慮していないが、もっと異なった形の仕事をやり取りする場合も含めて一般化することができる。その場合の仕事は一般的に[示強性変数]×[示量性変数]で表される。
その様な例を幾つか挙げると、電池系が外界とやり取りする電気的な仕事は電位差Φと流れた電気量dqからΦdqとなる(他の稿ではΦの代わりにEを用いています。ここでは電場との混同を避けるためにΦにした)。誘電系では、電場Eの存在で電気双極子モーメント(誘電分極)の変化dPに伴われるエネルギー変化は-EdPとなる。磁気系では、磁場Bの存在で磁気双極子モーメント(磁化)の変化dMに伴われるエネルギー変化は-BdMとなる。表面張力γがはたらくとき、表面積の変化dAによるエネルギー変化はγdAとなる。
この様な力学的な仕事以外をすべて考慮すると、熱力学法則は
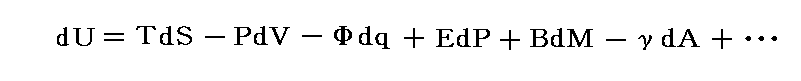
となる。
これらすべてを取り上げても複雑になるだけだから、以下では力学的な仕事以外の仕事として電気的Φdqのみを取り上げよう。そのとき系が外界と熱や仕事をやり取りして変化する場合、系の内部エネルギーの変化は
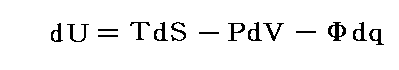
で表される。この場合には、エンタルピーH、ヘルムホルツの自由エネルギーF、ギブズの自由エネルギーGを前項と同様に定義することにすると、それぞれの微少変分の意味は下記のようになる。。
まずエンタルピーHに関しては
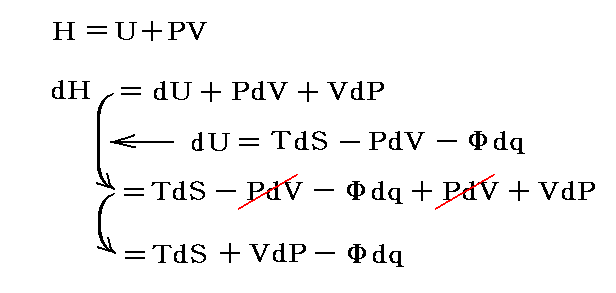
となるのだが、ここで系が等圧の元で状態変化した場合を考察すると
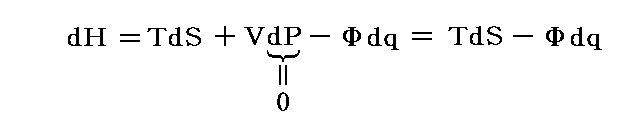
となる。この場合のエンタルピーの変化dHは状態変化に伴って出入りする熱量TdSと電気的な仕事Φdqに伴うエネルギー変化から成ることになる。
このときdP=0だからVdPの項は無くなるが、系は圧力一定の元で膨張(または収縮)に依って外界と仕事のやり取りはしています。そのとき、圧力一定の元での力学的仕事のやり取りは
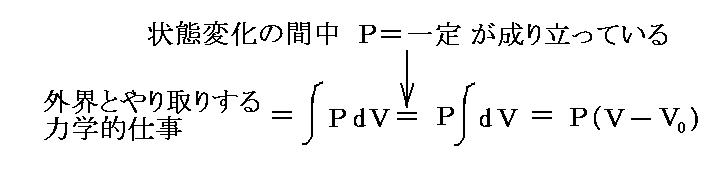
となるのですが、内部エネルギーの変化からH=U+PVによってその分の変化は差し引かれているために等圧変化でのエンタルピーの変化dHの中には含まれていないのです。
同様にヘルムホルツの自由エネルギーFに関しては
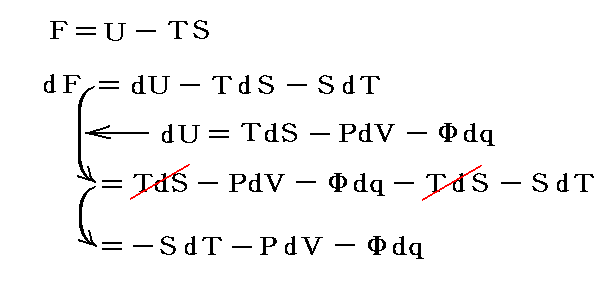
となる。ここで系が等温、等体積の元で状態変化した場合を考察すると
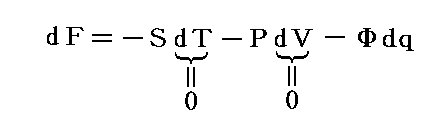
となる。体積一定だから力学的な仕事を外界とやり取りすることは無いので、この場合のヘルムホルツの自由エネルギーの変化dFは電気的な仕事Φdqに一致する。
このときdT=0だから、SdTの項は無くなるが系は温度一定の元での変化だから系は外界と熱のやり取りはしている。温度一定の元での熱のやり取りだから
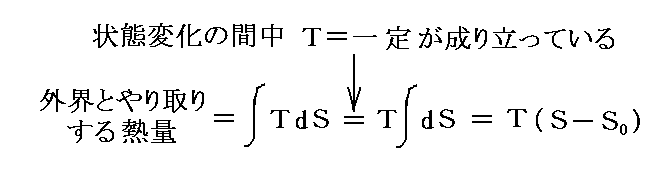
となるのですが、内部エネルギーの変化からF=U-TSによってその分の変化は差し引かれているために等温・等積変化でのヘルムホルツの自由エネルギーの変化dFの中には含まれていないのです。
ギブズの自由エネルギーGに関しては
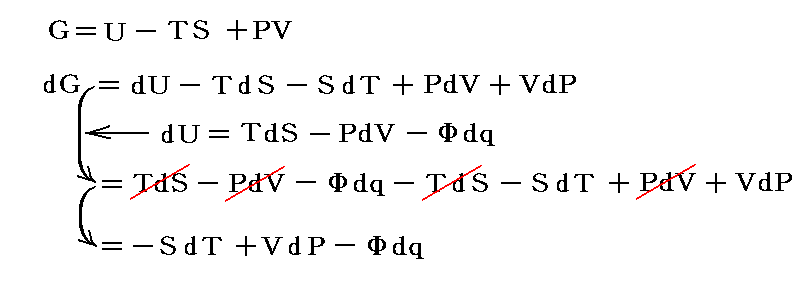
となる。ここで系が等温、等圧の元で状態変化した場合を考察すると
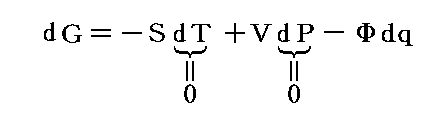
となる。この場合のギブズの自由エネルギーの変化dGは電気的な仕事Φdqに一致する。
このときdT=0かつdP=0だからSdTとVdPの項は無くなるが、温度一定、圧力一定の元での変化だから系は外界と熱や力学的な仕事のやり取りはしている。しかし内部エネルギーの変化からG=U-TS+PVによってその分の変化は差し引かれているために等温・等圧変化でのギブズの自由エネルギーの変化dGの中には含まれていないのです。
ここで、等温・等積変化に於けるヘルムホルツの自由エネルギー変化dFと等温・等圧(等積も可)変化に於けるギブズの自由エネルギー変化dGはいずれも同じ電気的な仕事Φdqによる変化を与えることに注意されたし。
2.様々な状態方程式
U(S,V)、H(S,P)、F(T,V)、G(T,P)は状態量ですから、U=f(S,V)、H=f’(S,P)、F=f”(T,V)、G=f’”(T,P)の様な関数が必ず存在します。つまりそれぞれの量に対する状態方程式が存在します。
これはちょうど理想気体のとき説明したP=f(T,V)の様なものです。理想気体のときそうしたように、それらの状態方程式を最大限利用して現実の問題を解いてゆけば良い。
ただし、状態方程式は系を構成する物質により異なりますから、それがどのような関数形になるのかは必ずしも明らかではありません。そのとき、様々な観測・実測をすることにより実験的にその形を求めることはできます。
その具体的な例を別項「ファン・デル・ワールスの状態方程式」4.(2)で紹介していますので御覧下さい。
前項で、状態方程式の状態量は
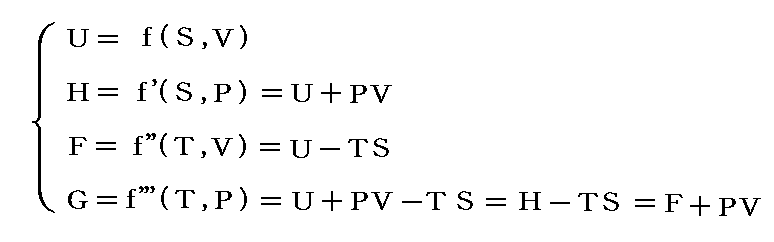
で関係づけられていることを説明しました。数学的にはこれらの変換式を“ルジャンドル変換”と言います。
ルジャンドル変換の重要な特徴は、これにより新たな状態量が定義てきると同時に、その状態量を表す独立変数を変換できる事です。以下の全微分の表現式はその当たりの事情は表しています。
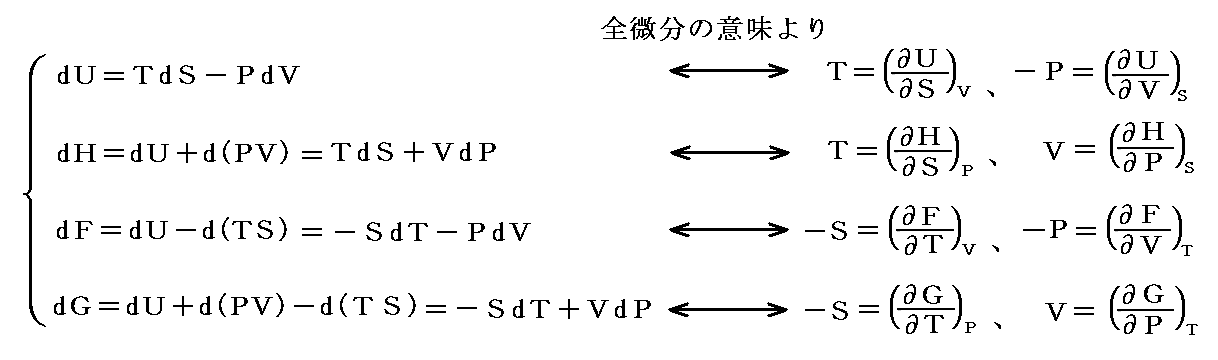
しかし、ルジャンドル変換の意味は非常に解りにくい所です。別稿「ルジャンドル変換とは何か」で解りやすく説明しておりますのでご覧ください。
様々な状態量の状態方程式曲面について、一般的に成り立つ性質を別稿「熱力学関数(状態方程式曲面)の性質」で説明しておりますのでご覧ください。これはここで説明するために作っていたのですがページ数が増えすぎたので別稿にしました。
3.Maxwellの関係式
Maxwellの関係式とは、dU、dH、dF、dGの変分がそれぞれの独立変数についての完全微分であることから成り立つ、完全微分の必要十分条件[5.(2)1.参照]そのものです。元々はエントロピーSが状態量であり、そのためdSが完全微分になることから派生してきたものです。
これらの関係式は、とても便利なものですが、安易に利用するとエントロピー導入の意義を見失ってしまい、わけがわからなくなります。熱力学が難しいのもその当たりにあるように思いますので、充分注意して利用しなければなりません。
関係式そのものは、前記dU、dH、dF、dGの定義式から、その完全微分の必要十分条件式[5.(2)1.参照]を書き記せば直ちに求まります。
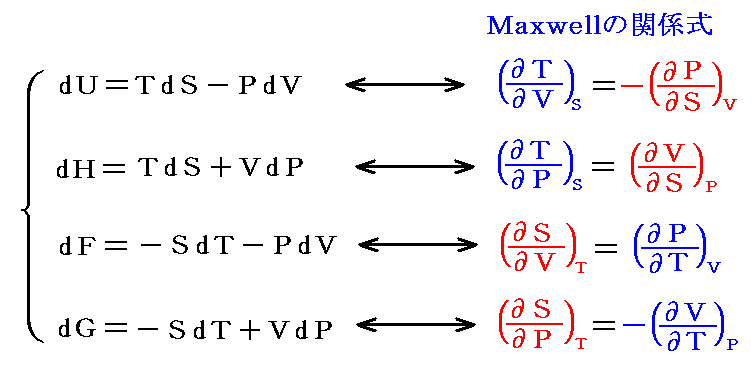
上記の赤で記した項はエントロピーを含んでいて直接実験で求めることはできない項です。一方、青で記した項は直接実験で求めることができる項です。なぜなら、S一定での偏微分は単に断熱変化であることを表しているにすぎないのですから。
Maxwellの関係式が便利で重要なのは、これらの式が直接測定できないエントロピーの変化を実測可能な量の変化に結び付けてくれるからです。実際にどんなところで使われているか調べてみると、そういったところで使われていることが解ります。
(3)化学系への応用
熱力学の起源となった“カルノーの考察”からも解るように、元々熱力学は様々な熱機関の作動原理は何か、その効率を決める原理は何なのかを研究する事から発達してきた。そして実際、そのことに関して熱力学は偉大な成果をあげてきた。その当たりは 「ガス動力サイクル」 、 「蒸気動力サイクル」 、 「冷凍サイクル」 をご覧ください。
しかし、今日その最も重要な適用・応用分野は化学の領域にあります。そのときの対象は[相の変化]と[化学反応]です。すなわち
- 様々な化学物質が相平衡や化学反応平衡にあるとき、平衡を決めている条件は何か。
- 相平衡や化学平衡が移動するとき、その変化の方向や速度を決めているはの何か。
- 相変化や化学反応変化が進行するとき、熱の移動や温度はそのメカニズムにどのように関わるのか。
です。これらの問題を解析するときに鍵になるのが、“ギブズの自由エネルギー”と“化学ポテンシャル”の概念です。その方面の研究の最大の功労者がギブズ(Josiah Willard Gibbs 1839~1903年)です。
そのことについては別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」をご覧ください。
ただし、上記別稿に進まれる前に別稿「熱力学関数(状態方程式曲面)の性質」を読まれる事を勧めます。それから、その最後4.(3)に紹介しているページに進まれて下さい。
9.参考文献
この題材は高校物理の範囲を逸脱していますが、いつか解りやすく説明するHPを作りたいと思っていたものです。
準静的可逆機関を用いて状態変化を追跡したとき出入りする熱量を測定することによってしか定義できない絶対温度をどうして知るのか?現実にはその様な理想的可逆機関などありはしないのですから、現実に存在する熱機関(熱膨張する温度計もその一種)から得られる仮の温度tから絶対温度Tを導くしかない。そのとき、どの様にして現実の温度計が示す仮の温度tからその物体の絶対温度Tを知るのだろうか?この疑問に答えてくれないと絶対温度の概念は意味を成さないし、決して理解できない。
いままで熱力学の本は沢山(専門書は10冊以上、入門書・解説書のたぐいを含めれば30冊以上)読みましたが、上記の疑問に真面目に答えてくれているのはプランクの本だけでした。
[マッハの「熱学の諸原理」にも書いてあるがプランクの本より更に解りにくい。 プランクの本を翻訳された芝亀吉氏が書かれた「熱力学」(岩波全書1967年刊)の§16、§19、 パウリの物理学講座第3巻(講談社1976年)第2章、 岩波講座現代物理学の基礎「古典物理学Ⅱ」第Ⅳ部(碓井恒丸著)(岩波書店1973年)、 等々・・・にもそれらしいことは書かれていますが、極めて難解で凡人にはとうてい理解しがたい]。
しかし、そのプランクの本も理解するのがとても難しい。良く解らない所を推察しながら解釈したのでずが、本当にここに書いたような理解でよいのか疑問が残ります。いずれにしても第二法則を理解する鍵は積分因子の数学的な考察を十分に行うことではないでしょうか。このHPを作っていて改めて感じました。
- マックス・プランク著、芝亀吉訳「熱力学」岩波書店(1941年刊)特に§153~§164、§177
原本はMax Planck著「Vorlesungen u¨ber Thermodynamik 8 Auf.(1927)(初版は1897年)
古い本ですが原理的な説明がとても丁寧です。特に絶対温度を実験的に定める方法の説明§131、§153~§164、§177については、この本に勝るものはありません。このHPの大半はこの本に依存しています。最近の本は応用の数学的な展開しか説明されておらず、本質を説明する努力を怠っているのではないでしょうか。
- マックス・プランク著、寺沢寛一、小谷正雄訳 理論物理学汎論第五巻「理論熱学」裳華房(1932年刊)
前半部が熱力学で後半が熱輻射論や統計力学の項目です。前半の部分は上記の本をほぼ踏襲していていますが、表現がより簡潔・簡略化されており明快です。しかし理解するのはさらに難しい。§49§50§61が主に関係するところです。
- エルンスト・マッハ著 物理学の古典4.「熱学の諸原理」東海大学(1978年刊)ⅩⅧ章
原本はErnst Mach著「Die Principien der Wa¨rmelehre--historisch-kritisch entwickeltの第4版(1923年)」(初版は1896年)
熱学についての大事な所はすべて書いてあるのですが、各論文のエッセンスしか書いてないので理解するのは大変です。歴史的な流れを確認するのだと思って読めば良いのだろう。
- W.Thomson,"On an absolute thermometric scale founded on Carnot's theory of the motive power of heat, and calculated from Regnault's observations"[Cambridge Philosophical Society Proceedings for June 5, 1848; and Phil.
Mag., Oct. 1848.]
絶対温度をカルノーの原理に基づいて提案した論文です。まだカルノーの原理の正確な理解に達してはいない段階の提案ですが着想自体は間違っていなかった。ネットワーク上に、これの無料ダウンロードが可能なサイトが有ります。
- J. P. Joule, and W. Thomson, "On the Thermal Effects of Fluids in
Motion.Part II.", Phil. Trans. 1854, vol. cxliv. p. .321-364.
絶対温度を実用温度に結びつける結果を報告した論文です。私自身、この論文を読んでいるわけではないのですが、ネットワーク上に無料でダウンロードできるサイトがあります。
世の中に熱力学の教科書は沢山ありますが、私の見た限りでは積分因子と偏微分方程式の積分を説明しているのは上記の本だけのようです。ただし説明はしてあるのですが、普通に読んだのではそうであるとはなかなか解りません。かなり推測を働かせるとなるほどそうなのだと解るような書き方です。いずれにしてもそこの所が説明されていないと絶対温度を真に理解するのは難しいと思います。
絶対温度の導入過程についてはどの教科書にも説明してあり、下記の本なども秀逸で解りやすい。しかし積分因子そのものを説明していないので、これらの本から絶対温度を真に理解するのは難しいと思います。
- 朝永振一郎著「物理学とは何だろうか(上)」岩波書店(1979年刊)第Ⅱ章
- エミリオ・セグレ著「古典物理学を創った人々」みすず書房(1992年刊)第5章熱をめぐって、第6章分子運動論
- W.J.Moore著 「ムーア 新物理化学(上)」東京化学同人社(1964年刊)の 第3章p71~79
- サディ・カルノー著、広重徹訳解説「カルノー・熱機関の研究」みすず書房(1973年刊)
この中に、カルノーの大論文『火の動力、および、この動力を発生させるに適した機関についての考察』(1824年)の翻訳がp39~90に収録されています。
補足しますと、この訳本にはカルノーがその後に書き溜めた『数学、物理学その他に付いての覚え書き』(p91~110)と、弟のイッポリート・カルノーが書いたサヂの伝記『サヂ・カルノーの生涯』(p111~126)も収録されています。
高校生が熱力学を勉強されるには下記の本を薦めます。これらはいずれも工学系の本ですが、とても丁寧に説明してあり解りやすい。そして、これらを読めば熱力学が実用的にいかに重要な学問であるかがよく解る。
- ジョン・F・サンドフォード著 現代の科学20「熱機関」河出書房新社(1980年刊)
古い本ですが図書館にはきっとあると思います。
- Yunus A.Cengel、Michael A.Boles共著「図説基礎熱力学」「図説応用熱力学」オーム社(1997年刊)
分厚い本ですが、とても解りやすい。
<数学参考書>完全微分方程式と積分因子はたいていの本で説明されていますが、なかなか解りづらいのでできるだけ沢山の本を読み比べて見られることを薦めます。私が参考にしたものの幾つかを記しておきます。
- 木村俊房著 新数学シリーズ12「常微分方程式の解法」倍風館(1970年刊)§8、§9
- 犬井鐵郎著 応用数学講座第9巻「偏微分方程式とその応用」コロナ社(1971年刊)第3章全微分方程式
- スミルノフ著 「スミルノフ高等数学教程 第3巻(原本Ⅱ巻第一分冊)」共立出版(1969年刊)第3章第7節
- 寺沢寛一著 「自然科学者のための 数学概論[増訂版]」岩波書店(1968年刊)§6.3、§6.4
- ネット上では次のHPが解りやすい
http://next1.cc.it-hiroshima.ac.jp/MULTIMEDIA/diffpub/node9.html
http://next1.cc.it-hiroshima.ac.jp/MULTIMEDIA/diffpub/node11.html
参考文献に上げた本が古い本ばかりで申し訳ありません。いずれも若い頃買って読んだ本です。読むには読んだのですが理解したという状況にはほど遠く、また教職についてからは教師の仕事が忙しくて振り返る暇もなく、それらの内容はほとんど忘れてしまいました。しかし、プランクの「熱力学」§160~§164に絶対温度の本質的な説明があるということは記憶の片隅にありました。記憶はしていましたが正直なところその内容は良く理解できていなかったのです。
退職して時間の余裕ができましたので、2ヶ月かけて昔に読んだ熱力学関係の本を集中的に読み直してみました。読み直してもなかなか本質が見えなかったのですが、5.(6)4.のロ囲み枠内に書いたことが見えてきて、プランクの教科書の§131、§153~§164に展開されている説明は、表現こそ違うが5.(5)2.で説明した積分因子λ(x)の偏微分方程式を解く手順そのものだと解ったときすべてが理解できました。長年の胸のつかえが下りた感じです。恥ずかしながら、やっとこの歳になって“絶対温度”と“エントロピー”のなんたるかが理解できました。
プランクの「熱力学」は今日絶版で手に入りませんが、機会がありましたら是非読んでみられることを薦めます。
[参考文献(2021年11月追記]
- 八木江里監訳「エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)
この中に「熱力学」という学問分野を開闢したClausiusの大論文(1850年)の翻訳版があります。それを更に解りやすく解説したのが別稿「Clausiusの熱力学第1論文(1850年)」です。また「Clausiusの熱力学1854年論文」と、「Clausiusの熱力学1865年論文」も別稿で引用しています。
- 山本義隆著「熱学思想の史的展開」筑摩書房(2009年刊)
第19~31章をご覧下さい。この中の 第19章Ⅱ~Ⅲ、Ⅳ、 第20章Ⅰ~Ⅱ、Ⅲ~Ⅴ、 第21章Ⅴ、 第22章Ⅴ、 第23章Ⅲ~Ⅶ、 第25章Ⅰ~Ⅴ、 第26章Ⅰ~Ⅱ 第28章Ⅰ~Ⅵ、 第29章 Ⅰ~Ⅷ、 第30章 Ⅰ~Ⅵ、 は別稿で引用しています。その際、別稿で引用している【補註・参考文献一覧】を別ウインドウで開かれて参照しながらお読み下さい。
- 原田義也著「化学熱力学(修訂版)」裳華房(1984年刊、修訂版2002年刊)
これは、熱力学の本質が解っている方が書かれた本です。その中の 第1、2,7章 と 第3章“熱力学第二法則” を別稿で引用しています。