�@���� �� �̕��� �mi �Ƃ��Ă͎��ʁA�������܂��͕��q�����g���B���x �s �A���� �� ����ё��̐����̕��ʂ����ɂ��� �g�M�u�Y���R�G�l���M�[�h�f �̕Δ����W��
�@�f�����ʕϐ��ł���̂ŁA
�@�M�͊w�����w����ɉ��p����Ƃ��A�ł�����������͉̂��w�|�e���V�����̊T�O�ł��B
�Ⴆ�A�����w���T��T�Łi��g���X)�ɂ�
�@�g���w�|�e���V�����h�Ƃ́A��ԓI�Ɉ�l�ȕ����n��1�̐����̕��ʂ��A�O�E����̏o���܂��͉��w�����Ȃǂɂ���đ�������Ƃ��A���̌n�̃M�u�Y���R�G�l���M�[�̕ω��ʂ��߂������ϐ��������B
�@���� �� �̕��� �mi �Ƃ��Ă͎��ʁA�������܂��͕��q�����g���B���x �s �A���� �� ����ё��̐����̕��ʂ����ɂ��� �g�M�u�Y���R�G�l���M�[�h�f �̕Δ����W���Ő��� �� �̉��w�|�e���V�������`����B
�@�f�����ʕϐ��ł���̂ŁA �ƂȂ�B��l�łȂ��n�ł͉��w�|�e���V�����͈�l�Ƃ݂Ȃ���镔���n�ɂ��Ē�`����B���̏ꍇ�A���w�|�e���V�����̍����l�̏ꏊ����Ⴂ�l�̏ꏊ�ֈړ������悤�Ƃ�����̗͂����̐����ɍ�p����̂ŁA���w�|�e���V�����Ƃ���B���t��Ԃł͉��w�|�e���V�����͈�l�Ȓl�����B
�Ə�����Ă��܂����A�T�ⓚ�̂悤�ʼn��̂��Ƃ������ς����Ȃ��B���܂��炱�̉�ǂ����݂܂��B
�@�{�e�͕ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v����̑����ł��B
�@�M�u�Y���A�g���w�|�e���V�����h�Ȃ�T�O���v�������̂́A�����炭�O���A���������鑊���t�̍l�@����ł��낤�B�ނ̔M�͊w���_���A���_�����o����O�_���ɂ�����o�܂�����������Ă���B
�@�ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�S�D�i�P�j�Q�D�ɉ����ĎO��������Ԃ͂t�i�r�C�u�j�Ȗʂ̏�ŕ��ʗ̈�A������Ԃ͒����̈�ƂȂ邱�Ƃ���������B�t�i�r�C�u�j�Ȗʂ̂r�����̌��z����Ή��x�s�ł���A�u�����̌��z���|�o�ł���������A�������������Ă��镽�ʗ̈�A�����̈�ł͏�ɐ�Ή��x�ƈ��͂����ł��邱�Ƃ��Ӗ�����B�s���o�����̂����݂���Ƃ��̏��K�肷�鎦�����ϐ��ł��B
�@
�@���̂Ƃ��A�M�͊w�̑�@��
�́A�n�̓����G�l���M�[�̕ω������t�͊O�E�Ƃ̔M�̂���� ���f�p���s���r �ƁA�d���̂���� ���f�v���o���u �ŕω����邱�Ƃ������Ă��邪�A�n�̓����G�l���M�[�̐�ΓI�Ȓl��������ɂȂ邩�͐������Ă��Ȃ��B��̏�Ԃ����ԕω��o�H�ɉ����āA�n���O�E�Ƃ��Ƃ肷��M��d����ώZ���邱�ƂŁA��ԕω��ɔ��������G�l���M�[�������邾���ł��B
�@���̂Ƃ��A�n�̓������m���ω��n���m���w�����n���i�s���Ă��A���̂��Ƃɂ��G�l���M�[�̕ω��́A���̎��̒��̂ǂ��ɂ����f����Ă��Ȃ��B����A�{�����f����Ă����̂����A���̕ω����ǂ��ɂ��L�q����Ă��Ȃ��̂ł��B
�@�����ŃM�u�Y�͍l�����B�n�̃G�l���M�[��Ԃ�\���ʂ̒��ɂ́A���̑��i���w��j�̏�Ԃɉ����ĕς�鉽�����t�����Ă���ɈႢ�Ȃ��B�����āA���̗ʂ͂��ꂼ��̑��i���w��j�̕����ʁi���邢�͎��ʁj�ɊW���Ă���B�܂��A���i���w��j���ƂɈقȂ�A���̂̑��ݏɂ�������ĕω�����G�l���M�[�ɊW���鎦�����ϐ��i�s�C�o�̊��j�������ł���ɈႢ�Ȃ��B������ʂƏ������B
�@�����ŁA�M�u�Y�͑��i���w��j�̑��݂Ɋւ��G�l���M�[�� ��i��i �ƕ\�����Ƃɂ����B �� �ł����đ���i���w��j������킵�A ��i �͑���i���w��) �� �̏�Ԃő��݂�����̂̕����ʁi���ʁj�ł��B
�@�܂�A ���t���s���r�|�o���u�@�̒��ɂ́A�n�S�̂ɗ�������M�ʂ�n�S�̂��O���ɑ��Ă���d���ɂ��n�̓����̃G�l���M�[�ω������\���Ă��Ȃ����A�n�̓����G�l���M�[�ω� ���t
�̒��ɂ� ����i����i �ɂ��ω����܂܂�Ă�����ׂ����ƍl�����B
�@
�@�Ƃ���ŁA�n���g�����t�h�ɂ���Ԃ́A���x��ς��邱�ƂȂ��M������肳��A���͂�ς��邱�ƂȂ��d��������肳��Ă����B�s����肾����
�ƂȂ�A�o����肾����
�ƂȂ�B
�@�r���n�ɉ�����ꂽ�M�ʂɊW���u���n������o���ꂽ�d���ɊW����̂����A�����t�i���w���t�j�����藧���Ă���Ԃ́A�����ɑ��i���w��j���ω����Ă��n�̓����G�l���M�[�̕ω���
�s�r�|�o�u �ƂȂ�B������ �t�|�s�r�{�o�u �����i���w�j���t�ő��i���w��j�̕������ω������Ƃ��̃G�l���M�[�ω��ƂȂ�B
�@���̂Ƃ����ω��ɔ����G�l���M�[�ω��������Ă�����͊O�E�Ƃ̃G�l���M�[�̂����Ƃ͂܂������W�����B�Ȃ��Ȃ��n�̓����G�l���M�[�͂s�r�|�o�u�����ω����Ă��邾���ŁA�����t�i�܂葊�ω��j�Ɋւ��G�l���M�[�� �t�|�s�r�{�o�u �̕����ł��B����̓M�u�X���������g��ԗʁh�i�����g�M�u�X�̎��R�G�l���M�[�h�ƌĂ��j�ł����A�����E�����̌��ő��i���w�j���t�����藧���Ă���Ƃ��ɂ́A�g�M�u�X�̎��R�G�l���M�[�h�͑��i���w��j�̊������ǂ̂悤�ɕω����Ă��ω����Ȃ��G�l���M�[�ł��B
�@
�@���̂Ƃ��A���ω��i���w�����j�Ɋւ�鎖��\���Ƃ��A���̑��i���w��j�ω��Ɋւ��G�l���M�[�l�͑��̕����ʁi�������A���ʁA���q���A���X�j�ɔ�Ⴕ�A�������n���̂��ׂĂ̑��Ɋւ��� �a�� ����������̂� �t�|�s�r�{�o�u �Ɉ�v����͂��ł��B���Ȃ킿�A �t�|�s�r�{�o�u������i��i �ƂȂ�͂��ł��B��i �̒l�͑� �� �̒P�ʕ����ʁi�����A���ʁA���q���A���X�j������̃M�u�X�̎��R�G�l���M�[�ł����A��i �� ������i �̐ς��G�l���M�[�ƂȂ�悤�ȗʂł��B������ �� �͌n���\�����鑊�i���w��j���� �� �ɂ��Ă̘a����邱�Ƃ��Ӗ�����B
�@
�@���i���w��j�̑��݂Ɋւ��G�l���M�[�� ��i��i ��p����ƁA�����G�l���M�[�� �t���s�r�|�o�u�{����i��i �ƕ\�����B�܂�M�u�X�̎��R�G�l���M�[���̂��̂� �t�|�s�r�{�o�u���f������i��i �ƕ\����邱�ƂɂȂ�B
�@���̂��߁A�n���O���ƔM�Ǝd��������肵�A����Ɍn���̑��̎��ʔ䂪�ω������Ƃ��̌n�̓����G�l���M�[�̕ω��� ���t���s���r�|�o���u�{����i����i �ƕ\����邱�ƂɂȂ�B���̂Ƃ� ����i����i �Ȃ�a�̕ω��ʂ͌n���O�E�Ƃ��Ƃ肵���G�l���M�[�̕ω��� �s���r�|�o���u ������G�l���M�[ ���t ����������ʂ��ȏ�ł��ȉ��ł�����܂����B
�@
�@���̂Ƃ��A�ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�S�D�i�P�j�Q�D�Ő��������悤�ɓ����E�����̌��ő��ω����N�����Ă���Ԃ͏�� ����i����i��0 �����藧���Ă���͂��ł��B
�@�����������E�����̌��������t�����藧���Ă���Ƃ��A�C�ӂ� ����i �̕ω��̑g�ݍ��킹�ɑ��� ����i����i��0 ����ɐ��藧�̂ŁA�C�ӂ� �� �� �� �̑g�ݍ��킹�ɉ����ď�� ��i����j �����藧�B
�@���ꂪ�M�u�Y���������������ł��B
�@���̂Ƃ��A�M�u�Y�������M�͊w�𑽐����n�֊g������Ƃ����̂͂ǂ������Ӗ��Ȃ̂ł��傤���B�������n�֊g�����ꂽ �g�M�u�Y�̎��R�G�l���M�[�h�f �Ƃ͉�����m��ɂ́A�M�u�Y���f�Ƌ��ɓ������� �g �� �e �̈Ӗ����l���Ă݂�Ɨǂ��B
�@
�@�{�߂�ǂ܂��O�ɁA�ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v3�D�i1�j�`�i3�j�K���Ă�����邱�Ƃ����߂܂��B
�@�g�G���^���s�[�h�g �� �g���t�{�o�u �ŕ\����邪�A�������舳���̌��ʼn��w������������Ƃ��A���̌n����o���肷�������M�ł���ƏK���B
�@�舳�̌��ł̕ω�������A�n�̕ω��ɔ����ďo���肷��d���ʂ�
�ƂȂ�B���̂��� �t�{�o�u �ŕ\������G�l���M�[�̕ω����́A�d���ȊO�ɊO�E�Ƃ���肳���G�l���M�[�ł����M���ƂȂ�B�܂艻�w�����M�ł��B�m���ہA��ŏo�Ă���}�ɂ����� �i�t�f�|�t0�j�{�o�i�u�|�u0�j���s�i�r�|�r0�j���z�M�ʂp �ƂȂ��Ă���B�n
�@���̂Ƃ��A�����M�Ƃ����̂��n�̉��x�����ɕۂ��߂��O�E�Ƃ���肵�Ȃ���Ȃ�Ȃ��M�ʂ̈Ӗ��������Ƃ�ʍe�u�����M�ƔM���w�������v�P�D�i�Q�j�Ő��������B�܂�A�����M�Ƃ͌n����舳�́A��艷�x�̌��ŏ�ԕω��i���w�ω��j����Ƃ��ɊO�E�Ƃ���肷��M���̂��Ƃł����B
�@
�@
�@���̂Ƃ��A���ɑ�Ȃ��Ƃł����A��ʓI���t�i�r�C�u�j�Ȗʏ�����x�ƈ��͂��Ɉ��ɕۂ��Ȃ���ړ����邱�Ƃ͂ł��Ȃ��̂ł��B�Ⴆ�Όn���\�����镨�̂����z�C�̂̏ꍇ���l���Č���Ɨǂ��B���z�C�̂̌n�֔M�������Ȃ���c��������ƈ��͂����ɕۂ����܂ܑ̐ς傳���邱�Ƃ͂ł��܂����A���z�C�̂̑̐ς�������Ɖ��x�����߂Ȃ����g�������͂�ۂ��Ɓh�͐�ɂł��܂���B���̂Ƃ��A�n�֏o�����ꂷ��M�ʂ��ǂ̂悤�ɒ������Ă����͈��̏�ۂ����x�������ɕۂ��Ėc�������邱�Ƃ͂ł��Ȃ��̂ł��B
�@
�@����Ȃ̂ɁA�����g���ω��h���g���w�����h���N�����Ă���n�ł͂��̗l�Ȏ����ł���̂ł��傤���H�����ɃM�u�Y�̒��z�𗝉����錮������܂��B
�@
�@
�@�Ⴆ�A�`���a�ɕω�����ł��P���Ȉꎟ�̉��w�����i���ω��ł��ǂ��j���l���悤�B
���̂Ƃ��`�Ƃa���܂e����̏�Ԃ�\����ԗʋȖʂt�i�r�C�u�j�͉��}�̂悤�ɂȂ�B
�@���̂Ƃ��A�e��������ׂĂ������`�Ŗ�������Ă���ꍇ�̂t�i�r�C�u�j�Ȗʂ����F�J�[�u�ŕ\����A�e��������ׂĂ������a�Ŗ������ꂽ�ꍇ�̂t�i�r�C�u�j�Ȗʂ��ԐF�J�[�u�ŕ\�����B�܂�A�n�̒��ʼn��w�������i�s����ƌ������Ƃ́A�قȂ��������̏�ԗʋȖʂɎ����玟�ւƑJ�ڂ��Ă������Ƃł��B��̌n�̈�̏�ԗʋȖʏ�̑J�ڂł͂Ȃ��̂ł��B�@�}�����F�����̑J�ڂ͌n�����`���a�̑��ݔ䂪�ω����Ă����ߒ��ł����A���X�ƕʂȏ�ԕ������Ȗʂ֏��ڂ��čs���̂œ����Ɠ������ɖ������Ȃ���ω����Ă������̂ł��B���̂Ƃ����C���`�a��̈ʒu�͂܂��ɕ����`�Ƃa�̑��ݔ�ɔ�Ⴕ�ĕω����Ă��܂��B�Ȃ��Ȃ�A�u�A�r�A�t�����ׂĉ��Z�I�ȗʂ������ł��B���̂��Ƃɕt���Ă͕ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�S�D�i�P�j�P�D���Q�ƁB����ɕʍe�u���C���̓T�C�N���v�R�D�i�Q�j��ʍe�u�t�@���E�f���E���[���X�̏�ԕ������v�R�D�i�Q�j�D�R�̔��v�Z���K����Ă��������B
�@������A���F�`���C�����ԐF�a���C���͖{���܂������ʂ̌n���ƍl����ׂ��ł��B��̌n�̏�ԕ������Ȗʂł͂Ȃ��ĈقȂ�n�̕ʁX�̏�ԕ������Ȗʂł��B���ꂪ���w�����ɉ����Ĕ����O�Ɣ�����͕ʂȌn�ƍl���Ȃ���Ȃ�Ȃ��ƌ������̈Ӗ��ł��B
�@
�@
�@���̗l�ɍl����A��艷�x�A��舳���̌��Ōn�ɏo���肷���g�]�ڔM�h�i���ω��j���g�����M�h�i���w�����ω��j�̈Ӗ�������܂��B���̗l�ȔM���o���肵�Ă����x���ω����Ȃ��̂͂ƂĂ��s�v�c�Ȏ��ł����A����͕ʁX�̏�ԕ������ȖʊԂ̑J�ڂɔ������̂�����ł��B��̏�ԕ������Ȗʂŕ\����n�ł́A�M��������Ή��x�͕K���オ��A�M�����o���Ή��x�͕K��������̂ł����A�قȂ��ԕ������ȖʊԂ̑J�ڂ����炻�̗l�Ȃ��Ƃ��\�Ȃ̂ł��B
�@���̂悤�ȈقȂ�n�̂t�i�r�C�u�j��ԕ������Ȗʂ��Ȃ��ł���̈���A�i�u�C�r�C�t�j��ԕ������Ȗʂł͂Ȃ��A �i�o�C�u�C�s�j��ԕ������Ȗ� �Ȃǂŕ\���ƁA�Δ����W������`�ł��Ȃ����ٓ_�E���ًȐ��̈�Ɛ���܂��B���̂��Ƃɂ��Ă͕ʍe�u�t�@���E�f���E���[���X�̏�ԕ������v�S�D�i�R�j���i�o�C�u�C�s�j�Ȗ������i���C�s�j�C���i���C�s�j�C���i���C�s�j�Ȗ��ȂǎQ�ƁB
�@���̂��ߑ��]�ڂ≻�w�����ω����N�����Ă���̈�ł��l�X�ȔM�͊w�I�����W���̑��������U���邩�[���ɂȂ��Ă��܂��B���̗l�Ȃ��Ƃ��N����̂������܂��B���ꂪ�A�M�͊w�𑽐����n�֊g������ƌ������Ƃł��B
�@
�@
�@�M�u�Y�͕������ψ�i�P���j�̂Ƃ��̔M�͊w�Ȗʂ��g���Ȗʁh�iprimitive surface�j�ƌĂсA����������Ԃ��g�U���Ȗʁh�iderived surface�j�ƌĂ�ł��܂����A���̌��t�ɂ͐[���Ӗ�������܂��B
�@�ނ����̂��̗l�ɌĂ̂��ƌ����ƁA�F���C���̕����͖{���̔M�͊w�Ȗʂł͂Ȃ��āA�M�͊w�Ȗʂ��`�̌n����a�̌n�֕ω����Ă����Ƃ��̈ړ����̉��̋Ȗʂ�����ł��B�܂����C�����ڂ��Ă���M�͊w�Ȗʂ͍��F�`���C�����ԐF�a���C�������銄���ō����i�U���j���Ăł��鉼�̋Ȗʂł��B�����������Ɠ������ɖ������Ȃ���ω��ł����̂ł��B���̂�����́A�R�{����3�D��32�͇U�Ȃǂ��Q�Ƃ��ꂽ���B
�@
�@
�@���̂Ƃ��A �g�G���^���s�[�h�g �́A���}�̗l�� �m�G���g���s�[�r���r0�i���j�̖ʁn �� �m�t0�i�r0�C�u0�j�_�ł̐ڕ��ʁn �̌�����t-�r���W���ʂƌ����_�̂t�l�ł��B���̂Ƃ��A���w�����ɔ����M�͕K�������O�Ɣ�����������E�����͂ɒ��������Ƃ��Ɍn����O�E�ɏo���肷��M�ʂ̎��ł�������A�����n�S�̂̏�Ԃ�\����ԓ_�͕K���A���}�����ʏ����ړ������_�t�f���t�h�ƂȂ�܂��B
�@
�@���ɁA���̂Ƃ��̕ω��� �̐ϕω���Ȃ��t0���t�h �̉��w�ω��Ȃ�A�w�I�ɍl����Ζ��炩�Ȃ悤�ɁA �g�|�g0 �͕K�� �t�h�|�t0 �ƈ�v���܂��B���w��͂`����a�֕ς���āA�n�̓����G�l���M�[�̕ω��������M�G�l���M�[�̕ω� �g�|�g0 �ƂȂ�܂��B�ʍe�u�����M�ƔM���w�������v�P�D�i�R�j�R�D�Ő��������悤�ɁA�����̐ϕω����N����Ȃ����w���� �i�t0���t�h�j �Ȃ�G���^���s�[�ω��i�����M�j�͌n�̓����G�l���M�[�̕ω����̂��̂�\���A����͂܂��ɉ��w�����G�l���M�[�̕ω����Ӗ�����̂ł����B�n�͔����̐i�W�ɔ����ĊO�E�ƔM��d���̂��������܂����A��L�̈Ӗ��̔����M�Ȃ�A�܂��ɉ��w�����G�l���M�[���ω��������߂ɐ������G�l���M�[�ω����ƌ�����̂ł��B
�@���}�� �t0���t�f ���舳���ő̐ϕω������w�����ɂ���ԓ_�̕ω���\���Ă��܂��B���̂��߁A�G���^���s�[�ω��������G�l���M�[�ω����̂��̂ɂȂ�킯�ł͂���܂���B�ʍe�u�����M�ƔM���w�������v�P�D�i�R�j�Q�D�̐}�Ƃ悭�悭��r�������Ă݂Ă��������B���̓�����͕ʍe�u��Ή��x�Ƃ͉����i�ϕ����q�Ƃ͉����j�v�W�D�i�Q�j�P�D�̍Ō��Œ��ӂ��܂����B
�@�Ƃ���ŁA��}�� �t0���t�h �� �t0���t�f �́A���w�����Ȃ�z�M�������A���ω��Ȃ�Ήt�́��C�̂̂悤�ȓ]�ڔM���K�v�ȋz�M���]�ڂ��A�Ӗ����Ă��܂��B���̂Ƃ��A���� �t�h �� �t�f ����L���ʏ����O��(�܂�t0�ɑ��Ĕ��Α���)�������_�Ȃ�A���M�����E���M���]�ڂɂȂ�܂��B
�@
�@
�@�ʍe�ʍe�u�����M�ƔM���w�������v�W�D�ŁA���̂���ꍇ�ɂ͔��M�����ɂȂ�ʂȏꍇ�ɂ͋z�M�����ɂȂ�̂��H�A���̓]�ڔM�������ω��┽���M�������w��������艷�x�̂��ƂŋN����̂��H�A���X�E�E�E�ɓ����邽�߂ɂ̓G���g���s�[�ω����r���l���Ȃ��Ƃ����Ȃ��Ə����܂������A���̓��������̒��Ɋ܂܂�Ă��܂��B
�@
�@���Ȃ킿�A�t�f���t�h�̂ǂꂪ��������邩�́A���ꂱ�����F�`���C���Ȗ��̌`����ԐF�a���C���Ȗ��̌`��ɂ���Č��܂����ʐڕ��ʂ̕����ɂ��܂��B�`�A�a���ȖʂƂ��������ɓʊ��ł��B���ꂪ�������w�̋��ȏ��ɏ����ꂢ�Ă�A �g�f���Œ�̏�Ԃʼn��w���t�����������h �̈Ӗ��ł��B
�@���̂Ƃ��A������w�����i���]�ځj���i��ōs���ɂ́A�O�E�ƔM�̂�����d���̂���肪�K�v�ł��B�܂��ǂ���̕����ɐi��ł������́A�O�E�Ƃ̉��x���A���͍��̐����Ɉˑ����܂��B
�@�Ⴆ�A���M�����Ƃ����̂́A�����̐i�W�ɂ��n�̉��x�������オ��ꍇ�ŁA���̂Ƃ��O�E�̉��x���n�̉��x�����������Ȃ�̂ŁA�M�͊O�E�ɗ���o���čs���A�����͂ǂ�ǂ�i��ł����܂��B�z�M�����Ƃ́A���̋t�̏ꍇ�ŁA�����ɂ��n�̉��x�����������邽�ߊO�E����M���ǂ�ǂ����Ă��Ĕ������i�W���Ă����B
�@����ɗႦ�A���ƖO�a�����C�̓��t�ɂ����āA���x�����̂܂܂ɂ��āA�O�E�̈��͂�����������Όn�͔M���ǂ�ǂ�z�����Ėc�����čs�����ׂĐ����C�ɂȂ邵�A�O�E�̈��͂��������߂�Όn�͔M���ǂ�ǂ���o���Ă��ׂĐ��ɋÏk���Ă��܂��B
�@���̂��Ƃ��n�̃G���g���s�[�ω��Ƃǂ̂悤�ɊW����̂��͕ʍe�u�Ⓚ�E�艷�Z�p�̗��j�v�Q�D�P�D�Ő������Ă���܂��̂ł������������B
�@�O�E�Ɖ��x�∳�͂��ނ荇���ƕ��t��ԂɂȂ�܂����A���̕��t�ʒu�����܂�l�q��������Ă���̂��A�g���E�V���g���G�̖@���h�ł��B
�@
�@�n�̉��x�ƈ��͂�ς���Ώo���_�̈ʒu���t0�f�֕ς��܂��B���F�`���C���Ȗʏ�̐V�����t0�f�_�ƐԐF�a���C���ȖʂƂ̋��ʐڕ��ʂ̌X�i�f�l�j���قȂ��Ă��܂����A���̋��ʐڕ��ʂ̐ԐFB���C���Ȗʏ�ł̐ړ_�̈ʒu�t*���قȂ��Ă��܂��B
�@
�@���̂Ƃ��`�����a�ւ̉��w�ω��i���ω��j���N�����Ă��A�n�� �g�M�u�Y�̎��R�G�l���M�[�h�f �͕ω����Ă��܂���B�Ȃ��Ȃ獡�̏ꍇ�͈�艷�x�A��舳�͂�ۂ��Ȃ���O�E�ƔM��d��������肵�� �t0 �_���� �t�h �� �t�f �_�֕ω������̂ł����A�M�u�Y�̎��R�G�l���M�[�f0�� �i�t�h�|�t0�j�|�s(�r�|�r0�j�{�o(�u�|�u0�j �� �i�t�f�|�t0�j�|�s(�r�|�r0�j�{�o(�u�|�u0�j �̂悤�ɁA�t�̕ω����ł�������Ă��邩��ł��B
�@
�@�ʍe�Ő��������悤�ɁA�������Ɛ������� �t�i�r�C�u�j��ԕ������Ȗ� ������A �f�i�s�C�o�j�A�g�i�r�C�o�j�A�e�i�s�C�u�j��ԕ������Ȗ� ������܂��B�����̋Ȗʂ̐����ׂ�Α��]�ڂ≻�w�����̖{�������ׂĉ𖾂ł���̂ł�����A�M�u�Y�̒��z�͂܂����唭���ł��B
�@
�@�g�w�����z���c�̎��R�G�l���M�[�h�e �� �e���t�|�s�r �ŕ\����邪�A�������艷�x�̌��Ő����鉻�w�ω��i���ω��j�ŁA���̌n����o���肷���d���ł���ƏK���B
�@���w�ω��i���ω��j�̉ߒ��Ōn�֔M���o���肷��̂ł����A��艷�x�̌��ł̔M�̏o����Ȃ̂�
�ƂȂ�B������ �t�|�s�r �ŕ\�����G�l���M�[�̕ω������O�E�Ƃ���肷���d���ƂȂ�B�m���}�ɂ����� �i�t�f�|�t0�j�|�s�i�r�|�r0�j���o�i�u�|�u0�j���d���v �ƂȂ��Ă���B�n
�@���̂Ƃ��A�O�E�Ƃ���肷��d���� �o���u �̌`�Ƃ͌���Ȃ��B�����A���̂Ƃ��n�̑̐ς��ς�炸�A�Ⴆ�Όn���痬��o��d�����O���ɑ��Ďd��������̂Ȃ�A����� �d���� �̗l�ȏ������ŕ\�����B �d �͓d�ʍ��ł���A ���� ���ړ�����d�C�ʂł��B�����āA��ԗʋȖʂ̓Ɨ��ϐ��̉����� �u ���� �� �ɕϊ�����悢�B��������ƁA�t�i�r�C���j�Ȗʂ̂������̌��z���d�ʍ��d�ɊW����B���ہA�w�����z���c���M�͊w��d�r�����ɓK�p����ۂɓ��������̂� �e �������m�ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�P�D�i�Q�j�Q�Ɓn�B�@
�@
�@���w�����i���ω��j�ɔ����Ĉ�艷�x�̌��Ŏd�������o���̂ł����A���̂Ƃ����͂o�i���邢�͓d�ʍ��d�j�����̌��Ŏ��o���ƍl���ėǂ��B
�@���̏ꍇ�A���w�����̐i�s�ɔ����ď�ԗʋȖʏ�̓_�� �t0 ���� �t�f �ֈړ�����B���}�� �e �l�̕ω��͉��w�����i���邢�͑��ω��j�̐i�s�ɔ����ĊO���Ɏ��o�����d���ʂ��Ӗ�����B�������A���̂Ƃ����w�����i���ω��j�̐i�s�ɔ����āA�����E�������ێ����邽�߂Ɍn�͊O�E�ƔM��d���̂���������̂ł����A�Ƃɂ����}�̂e�l�̕ω�
�e�|�e0 �����o�����d���ł��邱�Ƃ͊m���ł��B
�@���̂Ƃ��A���o�����d���ʂ͌n�̓����G�l���M�[�t�̕ω����̂��̂ł͂Ȃ����Ƃɒ��ӁB���̓�����́A�ʍe�u��Ή��x�Ƃ͉����i�ϕ����q�Ƃ͉����j�v�W�D�i�Q�j�P�D�̍Ō��œ��ɒ��ӂ������Ƃł����A���}����������Ζ��炩�ł��B
�@�d�r�����̏ꍇ�ɂ͉�����d�C�ʂ��ɂ��āA�t�i�r�C���j�Ȗʂ̂��������̌��z���A�d�ʍ��d���ƍl����悢�m�ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�P�D�i�Q�j�S�D�Q�Ɓn�B�i�d�ʍ��͕��ʂu��p���邪�̐ςƍ���������邽�߂ɂd��p�����B�j
�@���̏ꍇ���A�������n�̊Ԃ̏�ԗʋȖʂti(�ri�C�ui�j�Ԃ̑J�ڂ�����A��艷�x�A��舳�͂̑J�ڂ��\���������Ƃ�Y��Ă͂Ȃ�܂���B����̓G���^���s�[�ω����l�����Ƃ��̎���Ɠ����ł��B
�@���̂Ƃ��A�M�u�Y�̎��R�G�l���M�[�f�͑������n�Ԃ̑J�ڂ���莝���������Ă����B
�@
�@�ȏ�̗l�ɍl����A �g�M�u�Y�̎��R�G�l���M�[�h�f �� �f���t�|�s�r�{�o�u �ƕ\�����Ӗ�������B���łɒ��ӂ����悤�ɁA��ԕ������Ȗʂ����X�ƈقȂ����n�̂��̂֎n���ď��߂���舳���A��艷�x�̕ω��������ł����̂ł����B�܂�M�u�Y�̎��R�G�l���M�[�Ƃ���艷�x�E��舳���̌��ő��ω��i���w�ω��j���N����Ƃ��A�قȂ����n���\�����Ă���قȂ�����ԕ������Ȗʂ��q�����n�������Ă����i�܂�Ԃ���莝�j�G�l���M�[�ł��B�������̂��ꂼ��̌n���\�������ԕ������Ȗʂt�i�r�C�u�j���m���Ă�����A�ǂ��������ő��ω��i���w�ω��j�������邩�������Ă����G�l���M�[�ł��B�m���L�̗���Q�Ɓn
�@�������w�̖{�ł́A���w�����̓M�u�X�̎��R�G�l���M�[���Œ�̏�ԂŎ��������Ɛ�������Ă��܂����A�O�q�}�����C���`-�a���������ɓʂ̏�ԕ������Ȗ��`���a�̋��ʐڕ��ʂł��邱�Ƃ����̂��Ƃ�\���Ă��܂��B���w���`���a���������Ă��铙���E�����̏��ł́A�{���قȂ����n�̈قȂ�����ԕ������Ȗʂł����`���a�̏�ԕ������ȖʂƋ��ʂɐڂ��镽�ʂ��t�����t�l���f�Ȃ̂ł��B
�@��ԕ������Ȗ��`���a�̗������������ɓʊ��ł��邩�炱���A���W�����h���ϊ����\�ł���A���ʐڕ��ʂ����݂����̂ł��B���ꂪ�A�f���Œ�̃��C���ɉ����ĉ��w�����i���ω��j�͐i��ł����Ƃ������Ƃ̈Ӗ��ł��B
�@
�@
�@�Ⴆ�A�R�{�`�����u�M�w�v�z�̎j�I�W�J�R�@�M�ƃG���g���s�[�v�}���w�|���Ɂi2009�N���j��32��p267�@�ŗ�Ƃ��Ă������Ă����P�C�I�E���Ε��C�I�E���g�A�r�A�f�O���t��p���Đ�������ƁA�ȉ��̂悤�ɂȂ�B
�@�܂���L�̂t-�u-�r��ԓ����P�C�I�E�̏�ԕ������Ȗ��t�P�i�r�C�u�j���Ε��C�I�E�̏�ԕ������Ȗ��t���i�r�C�u�j�����ꂼ�ꑶ�݂���ƍl����B���҂͖{���ʂ̌n������t�P�i�r�C�u�j�Ƃt���i�r�C�u�j�͕ʂ̋Ȗʂł��B
�@�ʁX�̋Ȗʂ����A���̌`�͕ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�Q�D�i�Q�j�Ŏ�����
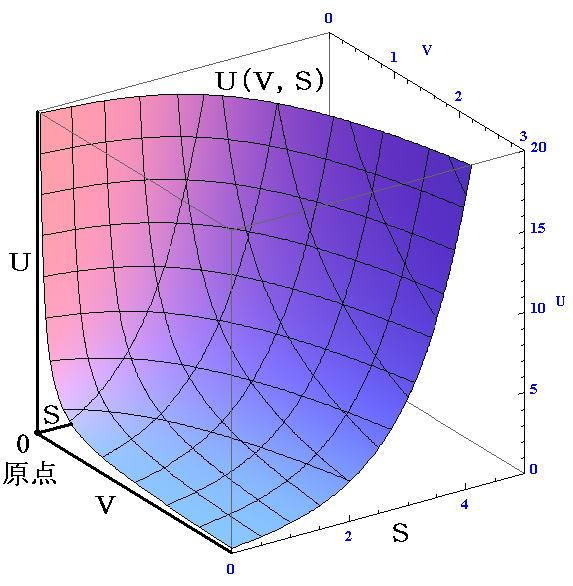
�̗l�Ȍ`�����Ă���A�݂��ɗǂ����Ă���B�������A�������ꍇ���đ��݂����B
�@���̂Ƃ��A��L���p�����̃O���t�́A���L�ɍĈ��p�����悤�ɁA���͈��i�Patm�j�̌��ł̂g�A�r�A�f�l�����x�̊��Ƃ��Ď�����Ă���B�舳��M�bp�i�s�j�̃f�[�^����A�����̃O���t�����߂��̓I�ȕ��@�͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�S�D���Q�Ƃ��ꂽ���B�܂����̍e�̂S�D�i�R�j�P�D��ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�P�D�i�R�j�P�D�Ő��������悤�ɁA���͈��̂��Ƃł́i�݂g�^�݂s�jp���bp��0�A�i�݂r�^�݂s�jp���bp�^�s��0������A�g���r�����x�Ƌ��ɒP���ɑ������܂��B
�@���͈��i1atm�j�ɉ����鉷�x�ˑ��Ȑ��Ƃ́A�O�L�̋Ȗʐ}�̂u�����̌��z�i�o�j�����̓_�ł������r�����̌��z�i�s�j������ɑ������Ă����_���q�������̂ł��B���ꂪ�u-�r���W���ʏ�łǂ̂悤�ȃJ�[�u�ƂȂ邩�́A���ۂ��t�P�i�r�C�u�j�Ȗ����t���i�r�C�u�j�Ȗ�������Ȃ��Ɖ��Ƃ������Ȃ����Ƃɂ����A���̃J�[�u�ɉ������i�r�C�u�j�_�̐^����t�P�i�r�C�u�j�Ȗ���̓_���t���i�r�C�u�j�Ȗ���̓_�̐ڕ��ʂ���ǂݎ���f�l�A�r�l�A�g�l�̃O���t�ł��B
�@���̂Ƃ��i�r�P�C�u�P�j�̃J�[�u���i�r���C�u���j�̃J�[�u�͈�v���Ă͂��Ȃ����Ƃɒ��ӂ��Ă��������B�t�P�i�r�C�u�j�Ȗ����t���i�r�C�u�j�Ȗ��͎����悤�ȋȖʂł��݂��ɈقȂ����Ȗʂł�����A�������́i�u�����̌��z���������j�̓_������łł����i�r�P�C�u�P�j�̃J�[�u���i�r���C�u���j�̃J�[�u�͏�������Ă��܂��B
�@�t�P�i�r�C�u�j�Ȗ���́A�_�i�r�P�C�u�P�j�ɉ�����ڕ��ʂ��t�����t�l���O���t�ɋL����Ă���P�C�I�E���f�P�ł��B�܂��i�r�P�C�u�P�j���W�_�̂r�l���P�C�I�E���r�P�ł��B�܂��A���̓_�ł̐ڕ��ʂƂr���r�P�i���j�ʂƂ̌�����t-�r���W���ʂƌ����t�l���P�C�I�E���g�P�ł��B
�@�����āA�t���i�r�C�u�j�Ȗ���́A�_�i�r���C�u���j�ɉ�����ڕ��ʂ��t�����t�l���O���t�ɋL����Ă���Ε��C�I�E���f���ł��B�܂��i�r���C�u���j���W�_�̂r�l���P�C�I�E���r���ł��B�܂��A���̓_�ł̐ڕ��ʂƂr���r���i���j�ʂƂ̌�����t-�r���W���ʂƌ����t�l���Ε��C�I�E���g���ł��B
�@�f�P���f���A�܂��r�P���r���A����ɁA�g�P���g���݂͌��ɈقȂ邪�A�����悤�ȃO���t�ɂȂ�̂́A���Ƃ����t�P�i�r�C�u�j�Ȗ����t���i�r�C�u�j�Ȗ��̌`�ǂ����Ă��邩��ł��B
�@
�@���̂Ƃ��A�O���t�̒l�𑪒肵�����́i�Patm�j�ł����x368.54�j���f�P���f���̃O���t���������Ă��܂����A������t�P�i�r�C�u�j�Ȗ����t���i�r�C�u�j�Ȗ��̂��ꂼ��̂u�����̌��z��1atm�ŁA�r�����̌��z��368.54�j�ƂȂ�ʒu�ŁA���ꂼ��̋Ȗʂ̐ڕ��ʂ̂t���ؕЂ̂t�l�������ɂȂ��Ă��邱�Ƃ��Ӗ�����B�܂��t�P�i�r�C�u�j�Ȗ���ŁA���́��O���t�̑��舳�͂o���Patm�A���x��368.54�j�ƂȂ�_�i�r�P�C�u�P�j�ƁA�t���i�r�C�u�j�Ȗ���ŁA���́��Patm�A���x��368.54�j�ƂȂ�_�i�r���C�u���j������̕��ʂɐڂ��Ă���Ƃ������Ƃł��B
�@�����O���t�̑��舳�́i�Patm�j�̎��ɂ����x��368.54�j��ۂ�����Ԃ��P�C�I�E�����Ε��C�I�E�̑��ω����N����B������̂Ƃ��A�n�͊O�E�ƔM�i�]�ڔM�j��d���̂��������܂����A���̏ő��ω����N���邱�Ƃ͊m���ł��B
�@
�@��L�̃O���t�ɂ��Ă��������⑫����ƁA�f���g�|�s�r�ł�������f�i�s�j�̉��x�ɑ�����z���s�r�̍��ɑ傫���e������܂��B���̂Ƃ��r�P���r���ł�����A�s�����̌��z���f�P�i�s�j�̕����f���i�s�j�̌��z��肫���Ȃ�܂��B
�@���̂��ߕ��t�_��荂�����ł��f�P�i�s�����j���f���i�s�����j�ƂȂ�G���g���s�[�̂��傫�ȑ��i�P�C�I�E�j������ɂȂ�A�ቷ���ł��f�P�i�s�ቷ�j���f���i�s�ቷ�j�ƂȂ�G���g���s�[�̏��������i�Ε��C�I�E�j������ɂȂ�܂��B�O���t�͂��̓�����̗l�q��\���Ă��܂��B
�@
�@����ɁA���͂�ς����畽�t���x�͂ǂ��ς�邩�́A���̏�ԕ������Ȗʂ̐V�������͂ł̂f�̑���l�̌�_�����߂�Β����ɒm�邱�Ƃ��ł��܂��B�����̕ω��̗l�q��\���N���E�W�E�X�E�N���y�C�����̊W���̋�̓I�Ȑ��l�������ɋ��܂�܂��B���̓�������ʍe�R�D�i�R�j�P�D�m�⑫�����T�n�Ő������Ă��܂��B
�@
�@�ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�R�D�i�Q�j�Ő��������悤�ɁA�t�i�r�C�u�j�Ȗʂ��烋�W�����h���ϊ��ɂ��f�i�r�C�u�j�Ȗʂ�f�i�s�C�o�j�Ȗʂ����߂邱�Ƃ��ł��܂��B���������̂Ƃ��A�E���̂f�i�s�C�o�j�Ȗʂ́i�݂f�^�݂s�jp��0�̗̈�́A�������m�⑫�����P����тQ�n�ŏq�ׂ��悤�ɏC�������ƍl���Ă��������B�g���
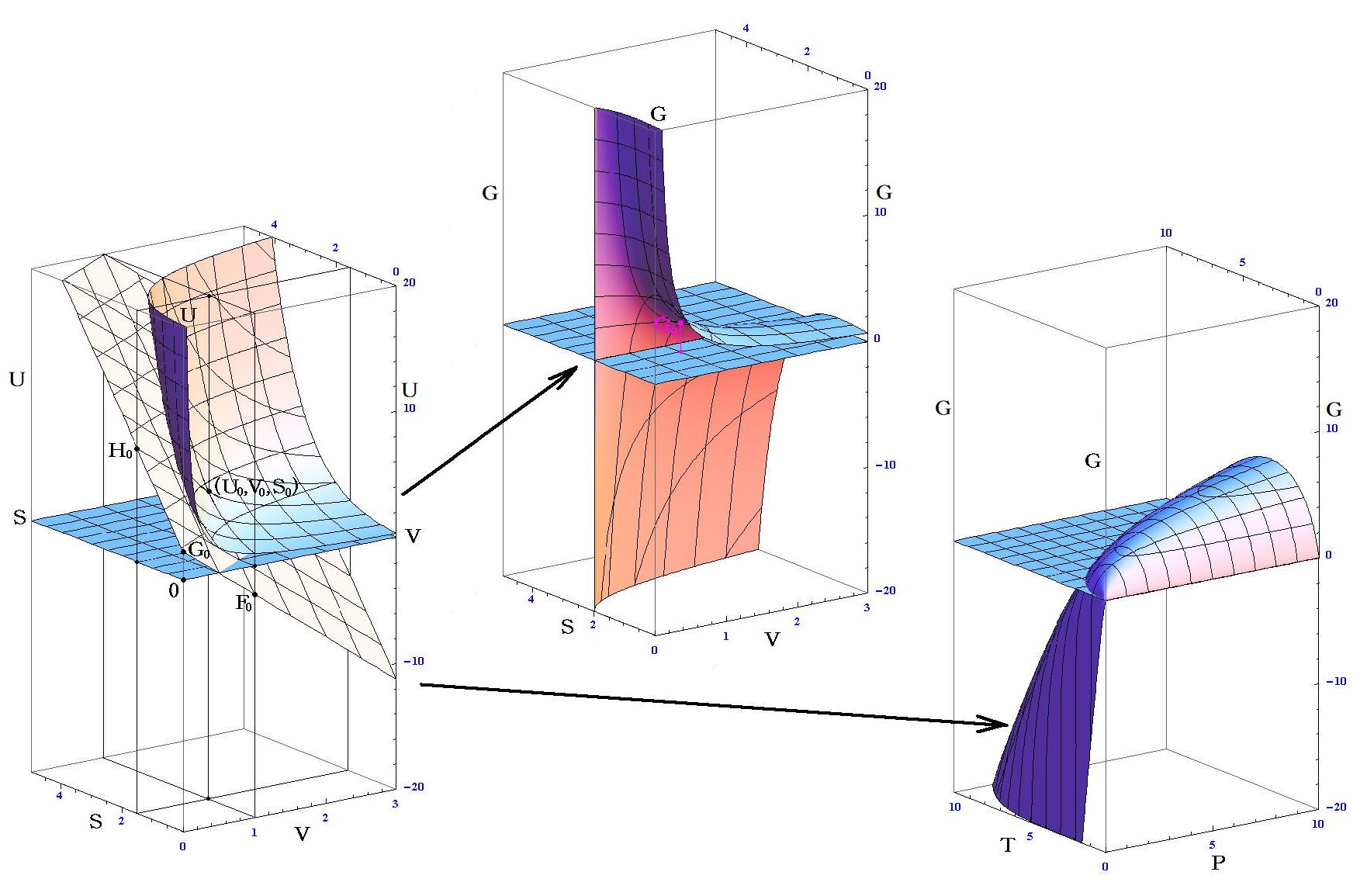
�@���̂Ƃ��A�ϐ����i�r�C�u�j����i�s�C�o�j�ɕϊ������`���f�i�s�C�o�j�Ȗ������ɏd�v�ł��B����͈ȉ��̗��R�ɂ��B
�@�܂��A���łɒ��ӂ����悤�ɂt�i�r�C�u�j�Ȗʂ͑���i���w��j���Ƃɂ��ƂȂ�A�e���̏�ԓ_�͈قȂ镽�t�Ȗ��t�P�i�r�C�u�j�Ȗ����t���i�r�C�u�j�Ȗ��̏�ɂ���B���̂Ƃ��A�����t�ł͎�������ԗʁi�s�C�o�j�͋��ʂɂȂ�̂ŁA�e���̈قȂ�����ԓ_�ɉ�����ڕ��ʂ͋��ʂƂȂ����B�܂肻�̋��ʐڕ��ʂ̂t���ؕЂ��M�u�Y�̎��R�G�l���M�[�f�������̂ł��B
�@���̂Ƃ��A��}�̂悤�ɁA���̂f�l���c���ɂ����f�i�s�C�o�j�Ȗʂ���邱�Ƃ��ł���B�܂蕽�t�Ȗ��t�P�i�r�C�u�j�Ȗ����t���i�r�C�u�j�Ȗ��̂��ꂼ��ɑ����f�P�i�s�C�o�j�Ȗ����f���i�s�C�o�j�Ȗ����ł��܂��B�����́A���ꂼ��̂t�i�r�C�u�j�Ȗʂ́i�s�C�o�j�l�ɂ�����ڕ��ʂ̂t���ؕВl�ł���f���i�s�C�o�j�̊��Ƃ��ĕ`�������̂ł��B
�@���̂��߁A�����t��Ԃł͑�������Ă��f�i�s�C�o�j�̒l�͋��ʂł��B�܂������t�ł͎�������ԗʁi���Ȃ킿�s�Ƃo�j�������Ȃ̂ŁA���t��Ԃł͓�̕��t�Ȗ��f�P�i�s�C�o�j�Ȗ����f���i�s�C�o�j�Ȗ�����������g���L�Ȑ��h��̓_�ŕ\����邱�ƂɂȂ�B���ꂪ �t���f �̃��W�����h���ϊ��ɉ����ĕϐ������ʐ���ԗʁi�r�C�u�j���玦������ԗʁi�s�C�o�j�֕ϊ����邱�Ƃ̗��R�ł��B
�@
�@�Ⴆ�C���|�t�����t�̏ꍇ�ł����A�ʍe�u�t�@���E�f���E���[���X�̏�ԕ������v�S�D�i�Q�j�̍Ō�̐}���A��̕��t�Ȗ� �f1�i�s�C�o�j �� �f2�i�s�C�o�j �Ƃ��g���L�Ȑ��h��Ō�������l�q�������Ă���B�g���
��L�̕ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v3�D�i2�j2�D���������ł��B
�@
�@���t��Ԃ́A��̕��t�Ȗ� �f�P�i�s�C�o�j�Ȗ� �� �f���i�s�C�o�j�Ȗ� ��������� �g���L�Ȑ��h ��̓_�ŕ\�����Ƃ��ł���̂����A�����g���L�Ȑ��h���i�s�C�o�j���ʂɎˉe�����������g���}�h�ƌĂԁB
�@��L��̒P�C�I�E�ƎΕ��C�I�E�̋�������̈�͉��}���ԐF�Ȑ��ƂȂ�B���}�����ۓ_�́A�O�L�̎Ε��f�O���t�ƒP�f�O���t����������_�i�s�C�o�j���i368.54�j�C1atm�j���i95.5���C1atm�j��\���B
�@��ʂɁA�C���Ɖt������������ꍇ�̋��L�Ȑ����g�O�a���C���Ȑ��h�A�t���ƌő�����������ꍇ�̋��L�Ȑ����g�Z���Ȑ��h�A�C���ƌő�����������ꍇ�̋��L�Ȑ����g���؋Ȑ��h�ƌĂ��B
�@�O�����t��Ԃ�3���̕��t�Ȗʂ̌������镔���ň�̓_�ƂȂ�B������g�O�d�_�h�itriple point�j�ƌĂ��B���̂�����̏ڂ����������R�D���ōs���B
�@
�@�����̓�̑��ɑΉ������̕��t�Ȗ��f�P�i�s�C�o�j�Ȗ����f���i�s�C�o�j�Ȗ�������������L�Ȑ��ɉ������������ω����f�P�����f�����l����B���̂Ƃ����ʂȋȏ�ł̕ω�������
�ƂȂ�B
�@�����œ]�ډ��x���s�]�Ƃ��A���̉��x�ł̓]�ڔM���p�]�Ƃ���ƁA�s�]�i�r�P�|�r���j���p�]������
�ƂȂ�A�N���E�W�E�X�E�N���y�C�����̎���������B���̎��́A���ꂼ��̏ꍇ�̓]�ڔM�i���M�j��p����������A�Z���E�����E���E�����`�]���Ȃǂ����Ȃ��ނ̏�ԕω��ɂ��K�p�ł���B
�@
�@�����́A�ʍe�u�t�@���E�f���E���[���X�̏�ԕ������v�S�D�i�R�j�ł��łɐ����������Ƃł����A���ꂼ��̑��Ɋ��蓖�Ă����قȂ��̂f�i�s�C�o�j�Ȗʂ�p���Ę_����Ƌɂ߂Č��ʂ����ǂ��Ȃ�B���̓������ �ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�R�D�i�R�j�P�D�m�⑫�����T�n �� ���e�̂S�D�i�Q�j �Ȃǂ��Q�Ƃ��ꂽ���B
�@
�@�Ƃ���ŁA��̕��t�Ȗʂf1�i�s�C�o�j�Ƃf2�i�s�C�o�j�Ƃ����L�Ȑ�����m��������ꍇ�n���m�ڂ���ꍇ�n������m�ꎟ�Ɠ̑��]���n�A�m�t�̃w���E���̑��]���n�A�m�|�������`���N��p�@�n�A�m�������w���E���n�B�ڂ���ꍇ�ɂ͂Q�����t�Ȑ���łu1���u2�A�r1���r2�ƂȂ�ꍇ�ŁA���t�Ȑ��ɉ����ω��ł��o�^���s�̒l�͕ʂ̋c�_�Œ�߂�K�v������B
�@��肭�ǂ������ɂȂ��Ă��܂��܂������A�M�u�Y�̎v�l�@�͍��x�ɒ��ۓI�ł��B���ہA�M�u�Y�̎O�̘_��(�Q�l����5�D�̍��{�|��ŎQ��)��ǂ�Ō�����Ή���l�ɁA�M�u�Y�̐����͋ɂ߂Ē��ۓI�œ���ł��B���̂��߁A�M�u�Y�̗��_�͂Ȃ��Ȃ��������ꂸ�A�M�u�Y�̍l�������y����̂Ɏ��Ԃ�v�����B�����炭�ŏ�����𗝉��ł����̂́A�����킸���̐l�������̂ł��傤�B�������A���̌�̕������w(���w�M�͊w�j�́A�M�u�Y�̔������������Ŕ��W�����B
�@�M�u�Y��1903�N��64�ŖS���Ȃ�܂����A�����������������Ă���Ίm���Ƀm�[�x���܂���������ł��傤�ˁB
�@
�@�i�P�j�œ������� �� ���g�������ϐ��h�ł����A�g���ʐ��ϐ��h�̕ϕ� ���� �ƈꏏ�ɂȂ��� �ʂ��� ���G�l���M�[�ϕ���\���B
�@�ʂ������Ӗ�����̂������ɂ߂�̂͂���߂ē�����A�ʒu�G�l���M�[�t���������ɉ����� ���� �i���̂Ƃ��̎��ʐ��ϐ����m���ʁn�͂����ł̂��ɑ����j��A�d���C�w�ɉ�����Ód�G�l���M�[�t�������ɂ�����d�� �� �i���̂Ƃ��̎��ʐ��ϐ����m�d�C�ʁn�͂����ł̂��ɑ����j�̂悤�Ȃ��̂ƍl���邱�Ƃ��ł���B���x���ʂ͂����������������ֈړ����A�d�ׂ̓��������������ֈړ������悤�ɁA���≻�w�킪�ω����Ă����X����\���Ă���ƍl������B
�@����ł������͏����͊w�ɂ�����|�e���V�����ɕ�����g���w�|�e���V�����h�ƌĂ�Ă���B���̃|�e���V�����͑��ω��ɔ������́A���w�����ω��ɔ������́A���邢�͐Z�����ɔ����u�ǂ̗����̔Z�x���ɔ������́A���X�E�E�E�ɂ��ꍇ�ɂ��ǂ̂悤�Ȃ��̂ɂł����Ă͂߂邱�Ƃ��ł���B
�@
�@�͗l�X�ɍl�����邪�A���w�|�e���V�����������Ӗ�����̂��𗝉�����̂͂���߂ē���B�����t�ɉ����Ă͕��q�ԗ͂ɔ����ʒu�G�l���M�[�ɊW���鋏�S�n�̗ǂ���\�����̂��낤���A���w�������t�̏ꍇ�ɂ́A���q�ԗ͂ɔ����ʒu�G�l���M�[�i�����鉻�w�����G�l���M�[�j�ɊW���鋏�S�n�̗ǂ���\�����̂��낤�B�܂��A�Z�������t�ł́A�n���Ɨn�}�i���j�̐��a�G�l���M�[�ɊW���鋏�S�n�̗ǂ���\�����̂��낤�B���ǂ̂Ƃ����g�G���g���s�[�h���g�G���^���s�[�h�̌��ˍ����ő����t�≻�w�������t�����܂�̂ł����A�ʂ������ȏ����S�n�̗ǂ��ŁA�ʂ���v�����ŏ��߂đ��≻�w��݂͌��ɕω�����B�O�q�̐ڕ��ʂ͂��̂��Ƃ�\���Ă����B
�@���̂Ƃ��A�ʂ͐ڕ��ʂ̂t���ؕЂł�����A�ʂ��Œ�̏�Ԃł���̂͊m���ł����A�ʂ͓����G�l���M�[�Ȗʂti�i�ri�A�ui�j�̍Œ�l�ł͂Ȃ��B�܂��ʁi�P�ʎ��ʂ�����̂f�j�͉��x�∳�͂ƂƂ��ɕω�����B�����̂��Ƃ�����ʁi�P�ʎ��ʓ�����̃M�u�Y�̎��R�G�l���M�[�j���P���ȉ��w�����E���q�Ԍ����E���a�����Ȃǂ̌����G�l���M�[�ł͂Ȃ����Ƃ͖��炩�ł��B�m���w�����G�l���M�[�ɊW������̂́A�P�D�i�Q�j�P�D�̗��Ō����l�ɁA�̐ϕω���Ȃ��������ł̔����M�g�|�g0�ŕ\�����t�h�|�t0�ł��B�n
�@�G�l���M�[�i���w�|�e���V�����~���ʁj�̎��Ԃ����������ɂ߂�̂͂���߂ē�����A�G�l���M�[�͖{��������Ԃ���̍����Ƃ��Ē�`����Ă���B������A�ǂ̂悤�ȉ��w�ω��i���ω��j�ɂ��K�p�ł��āA�����悤�ɂł����ߕύX�ł��邾�낤�B�ʂ͓K�p���錻�ۂɉ����Ă��܂��܂ɉ��߂ł��A�������n�ŕ����ʂ̕ω����ւ�錻�ۂȂ�ǂ̂悤�Ȃ��̂ɂł��K�p�ł���T�O�ł��B
�@
�@���̂Ƃ��A�����̈Ӗ����_��ɂƂ炦�Ȃ���Ȃ�Ȃ��B���ω��̏ꍇ�ɂ́A�����͈�̌n���̂��鑊����ʂȑ��֕ω����������ʂ��Ӗ�����ꍇ������A�O�E���炻�̑��V���������܂ꂽ�����ʂ��Ӗ����邱�Ƃ�����B���邢�́A���w�����̗l�Ɉ�̉��w�킪�ʂ̉��w��֕ω�����Ƃ��̉��w�����̐i�s��\���ʂ̈Ӗ��ƂȂ�ꍇ������B
�@
�@
�@�ʂ͑��i���w�����j���t��\�������ȊO�̂�����P�Ƒ��A�P�Ɖ��w��̏�ԕ����֊g�������B�ʂ͉��x�s�ƈ��͂o�̊��ł��邪�A�n�̏�Ԃ̒��̂���ɂ��ꂼ��̑��i���w��j�̏�ԁi�s�C�o�j����܂���̂Ƃ��̑���i���w��j���ƂɌ��܂�B
�@���ڑ���ł��Ȃ��n�̏�Ԃɕt����������G�l���M�[�t��G���g���s�[�r���l�X�ȕ��@�ɂ�葪��ł����悤�ɁA���w�|�e���V������i�i�s�C�o�j�͉��炩�̕��@�ő��肵���肷�鎖���ł���B
�@�t��r��p���ėl�X�ȗL�v�Ȍ��_������ꂽ�悤�ɁA���ꂼ��̑��i���w��j�̉��w�|�e���V������i���i�s�C�o�j�̊��Ƃ��Ēm���Ă����Ȃ�A���̃�i�i�s�C�o�j��p���ėl�X�ȋc�_���ł���ł��낤�B
�@����A�{���I�ȍ���̓�i�i�s�C�o�j�����߂邱�Ƃɂ���B���ꂪ�������w�̒��S���ł����Ď����Ɋ�Â��Ă̂��߂���B��������߂鏊�ɗl�X�ȔM�͊w�W�����ւ���Ă���B��̓I�ȋ��ߕ��͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�S�D���Q�Ƃ��ꂽ���B
�@
�@�e���i���w��j�̉��w�|�e���V�����͉��x�∳�͂Ƌ��ɕω�����B�ǂ̗l�ɕω����邩�͕ʍe�u�M�͊w���i��ԕ������Ȗʁj�̐����v�S�D�i�P�j�Q�D�Ő��������t�i�r�C�u�j�Ȗʂ̊e��ԓ_�ɉ������ڕ��ʂ��t�����_�̂t�l������悢�B
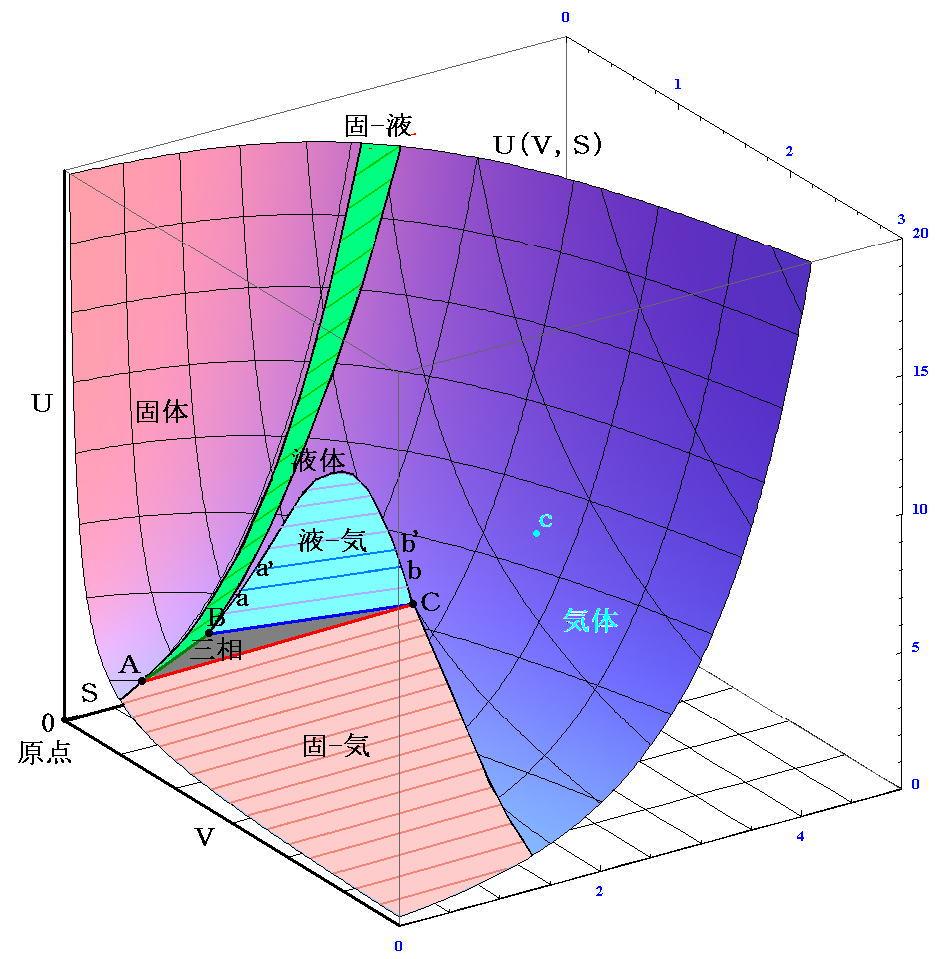
�@�Ⴆ�A�O�������̈�ł́A��L���D�F�O�p���̐ڕ��ʂ��t�����_�̒l�fslg�i�sslg�C�oslg�j����s��s�{��l��l�{��g��g�ł��邵�A�����̈�i�Ⴆ�Ήt��-�C�������̈�j�Ȃ�����F���̐ڕ��ʂ��t�����_�̒l�fslg�i�slg�C�olg�j����l��l�{��g��g�ł���B�����ĒP���ő��݂���̈�i�Ⴆ���C���̈�̂��_�j�Ȃ�����̈悃�_�ł̐ڕ��ʂ��t�����_�̒l�fg�i�sg�C�og�j����g��g�ƂȂ�B
�@
�@�����ē��R�̂��ƂȂ���A�n���̑����ʂ��l�Ƃ���ƎO�������̈�ł��l����s�{��l�{��g�ł��邵�A�t���|�C�������̈�ł��l����l�{��g�ł��邵�A�C���̈�ł��l����g�ƂȂ�B
�@
�@����ɕt��������ƁA�O�������̈�ł̉��x�s���sslg�A���͂o���oslg�Ƃ���ƁA���̗̈����s�i�sslg�C�oslg�j����l�i�sslg�C�oslg�j����g�i�sslg�C�oslg�j�ƂȂ�B���Ȃ݂Ɍn���\�����镨�������̏ꍇ�́i�sslg�C�oslg�j���i273.16K�C611.73Pa�j���i0.01���C0.006atm�j�ł��B
�@�܂��A��}�̓����̈悁�|���ł̉��x�s���slg�A���͂o���olg�Ƃ���ƁA���̗̈����l�i�slg�C�olg�j����g�i�slg�C�olg�j�ƂȂ�B�����̈悪���f�|���f�̗̈�ɑJ�ڂ���ƁA���t���x�ƈ��͉͂��x�s���s'lg�A���͂o���o'lg�ɕω����邪�A���̗̈����'l�i�s'lg�C�o'lg�j����'g�i�s'lg�C�o'lg�j�ƂȂ�B
�@���̂�����͕ʍe�u�t�@���E�f���E���[���X�̏�ԕ������v�S�D�i�R�j�Ř_�����Ƃ���ł��B�����̂��t�Ƃ��C�͂P����������̃M�u�X�̎��R�G�l���M�[�ł������B�����̋c�_�������ł͂Ȃ��P�ʎ��ʓ�����ƍl���Ă��ǂ��̂ŁA���̂悤�ɉ��߂���Ƃ���͉��w�|�e���V�������̂��̂��Ӗ�����B�܂肻���̎��ł��t�ip,T�j����l�i�slg�C�olg�j�A���C�ip,T�j����g�i�slg�C�olg�j�ƒu�������A����ɂ��t�ip+dp,T+dT�j����'l�i�s'lg�C�o'lg�j�A���C�ip+dp,T+dT�j����'g�i�s'lg�C�o'lg�j�ƒu�������Č���Γ������������Ă��邱�Ƃ�����B�����̃N���E�W�E�X�E�N���y�C�����̎��̂������o'lg�|�olg�ł���A���s���s'lg�|�slg�ł���B
�@�܂��������l�ɒP���̈悃�̉��x�s���sg�A���͂o���og�Ƃ���ƁA���̏�ԓ_����g�i�sg�C�og�j�ƂȂ�B
�@
�@�܂�A�������n�������������w�|�e���V������i�͑O�߂̍l�@���疾�炩�Ȃ悤��
�ƂȂ�B����͓����s�ƒ舳�o���ł̒�`�ł��邪�A����̓�i�����w�킉�̒P�ʕ����ʓ�����̃M�u�X�̎��R�G�l���M�[�ɑ���������̂ł��邱�Ƃ�\���Ă���ɂ����Ȃ��B
�@���w�|�e���V�����Ƃ́A���Ƃ��ƕʍe�u�t�@���E�f���E���[���X�̏�ԕ������v�S�D�i�R�j�Ř_�����P�ʕ����ʁi1����������A���邢�͒P�ʎ��ʓ�����j�̃M�u�X�̎��R�G�l���M�[�̂��Ƃł��B�������t�n�ȊO�́A�����鑽�����n�i�����t�A���w���t�A�Z�������t�A�E�E�E�j�̂����鑊��ԁA�����鐬���֊g���K�p�ł���Ƃ���̂��M�u�Y�̍l���ł��B
�@���̂Ƃ��A���̂��ꂼ��A�����̂��ꂼ�ꂪ�P�Ƃ̌n�Ƃ݂Ȃ���A��ԕ������Ȗʂti�i�ri�C�ui�j�Ȗʂ����݂��A���̍��W�i�ri�C�ui�j�̊e�Ȗʏ�̓_�ɃM�u�Y�̎��R�G�l���M�[�fi������U���Ă���B����̒P�ʕ����ʁi�P����������A�P��������A�P���q������A�E�E�E�j�̒l�����w�|�e���V������i�ł��B���̂Ƃ��A�ti�i�ri�C�ui�j�Ȗʏ�̊e�_�Ɋ���U��ꂽ�fi�i�ri�C�ui�j�l �m���邢�̓�i�i�ri�C�ui�j�l�n�́A�ti�i�ri�C�ui�j�Ȗʂ́i�ri�C�ui�j�ɉ�����ڕ��ʂ̂t���ؕЂ̂t�l�m������ʂŊ������l����i�n �ł��邱�Ƃ�Y��Ȃ��ł��������B
�@
�@���ۂ̕����ł͖����̈��͂������Ĉ��k���Ă��̐ς��[���Ƃ��邱�Ƃ͂ł��Ȃ��B������A���}���̍��W���̑̐ς́A�ǂ������Ԃ̑̐ς���̍����ł����Ȃ��B���W�l�G���g���s�[�������������Ӗ��ł����l�i���_�Ɏ������ԁj����̍����ł����Ȃ��B���W�_�i�u0�C�r0�j�ɂ�����u0���r0�����_�i�u�C�r�j���i0�C0�j�ɂ�������Ԃ���̂u��r�̍����ł��B
�@���W���Ɠ��l�ɁA�����G�l���M�[�ɂ���M�u�Y�̎��R�G�l���M�[�ɂ���i���邢�̓w�����z���c���R�G�l���M�[��G���^���s�[���j�A�����������G�l���M�[�l�͂��ׂĂ�����Ԃ��瑪���������ŕ\����Ă���B���Ȃ킿���_�ɉ�����l����̍����ł��B��}�̏�ԓ_�i�u0�C�r0�j�ɂ�����t0�����_�i�u�C�r�j���i0�C0�j�ɂ�����t�l����̍����Ƃ��Č��܂��Ă��鑊�Βl�ł��B�Ȃ��Ȃ�i�u0�C�r0�j�ɂ�����t0�́A���_�ɉ�����t�l�ɊO�E�Ƃ���肵���G�l���M�[�ʂ̕ϕ��ł��還�t���s���r�|�o���u��ώZ���Ă��Ƃ߂����̂ł�����B���ێ����I�ɂ��������Č��߂Ă���B
�@�M�u�Y�̎��R�G�l���M�[�����R�̂��ƂȂ���t���̑��݂���ʒu�i�u�C�r�j���i0�C0�j�̃M�u�Y�̎��R�G�l���M�[�l����ɂȂ��Ă���B�O�}�̍��W���_�i�u�C�r�j���i0�C0�j�ɉ�����t�i�r�C�u�j�Ȗʂ̐ڕ��ʂ̂t����_�́A�n����ԓ_�i�u�C�r�j���i0�C0�j�ɂ���Ƃ��̃M�u�Y�̎��R�G�l���M�[���̂��̂ł��B�n���O�E�ƔM��d���̂��������č��W�_�i�u0�C�r0�j�Ɉړ������Ƃ��̃M�u�Y�̎��R�G�l���M�[�͂t����s�r�|�o�u���������������̂ł����A���W�_�i�u0�C�r0�j�ɂ�����ڕ��ʂ��t����鏊�̃G�l���M�[�l�ł��B��̐}��U��Ԃ�Ή���悤�ɁA�f���t�|�s�r�{�o�u�́A��̏�Ԃɉ�����f�Ƃ̍��������߂�菇���̂��̂��ƌ�����B
�@���̂��Ƃ́A�w�����z���c�̎��R�G�l���M�[�e��G���^���s�[�g�ɂ��Ă����l�ł��B
�@���̓�����̂���ɗ��������������͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�R�D�i�S�j�m�⑫�����P�`�R�n�̂��Q�Ƃ��ꂽ���B
�@
�@���w�|�e���V�����̒�`���璼���Ɉȉ��̂��Ƃ�������B
�@�܂��A���̒�`����
�������邪�A�����
�̗��ӂ����ꂼ������Z�����
�����藧�B����͑����t�i���w���t�j�̂Ƃ��Ɍ��炸��ʓI�ɕK�����藧�W�����g�M�u�Y�E�f���G���̎��h�ƌĂ��B
�@���̂Ƃ��A���s��0�A���o��0���艷�A�舳�ω��̏ꍇ�ɂ́A����i����i��0�ƂȂ�B����́A�P�D�i�P�j�R�D�ōŏ��ɏq�ׂ�����i��i��0���l������ƁA����i����i��0��\���Ă���ɂ����Ȃ��B
�@���̂Ƃ��A���ω��̏ꍇ���u�����ui������i��i�ƕ\�����B�����łui�͑��킉�̑̐ρA��i�͑��킉�̒P�ʎ��ʓ�����̑̐ςł��B�G���g���s�[�ɂ��Ă����l���r�����ri������i��i�ƕ\�����B�����łri�͑��킉�̃G���g���s�[�A��i�͑��킉�̒P�ʎ��ʓ�����̃G���g���s�[�ł��B
�@���̏ꍇ�ɂ�
�ƂȂ�A�e�������̒P�ʎ��ʓ�����ɂ����g�M�u�Y�E�f���G���̎��h�����藧�B�܂�@����i���|��i���s�{��i���o�@�Ƃ����P�ʎ��ʂɂ��ẴM�u�X�̎��R�G�l���M�[�̕ϕ���\�����ƂȂ�B
�@����́A�������ϐ��s�C�o�C�ʂ��݂��ɏ���ɕς�邱�Ƃ��ł��Ȃ��Ƃ����ˑ��W�������Ă���B�܂��ʂ��s�C�o�̊��A���������̓�̏�ԗʂ݂̂̊��ł��鎖��\���Ă����B
�@�������O�E�Ƃ���肷��d���� �o���u �ł͖����ēd�C�I�� �d���� �Ȃ�� �o �̖����� �d �ɕϊ����Ȃ���Ȃ�Ȃ����A����͓����ł��B
�@
�@����́A���w�|�e���V�����̌��X�̓����̌o�܂Ƃ��̒�`�m�P�D�i�P�j�Q���n����o�ė�����̂ŁA����Ӗ����R�̌��_�ł��B
�@
�����́A�}�b�N�X�E�v�����N���A�ŋT�g��u�M�͊w�v��g���X�i1941�N���j�́�197�`��204���Q�Ƃ��Ă��܂��B
�@�n���P��̈�l�ȕ������琬��Ƃ��A�n�͂�����������琬���Ƃ����B�n�̒��Ɉ�l�Ȋ���̕��������݂���Ƃ��ɂ́A���̈�l�ȕ����̌��̎������̐��Ƃ����B��l�Ƃ����ƌ����Ƃ��������ł���K�v�͂Ȃ��B�n�t�̗l�Ȃ��́A�����̐�������Ȃ�ő́i�ŗn�́j�̂悤�Ȃ��́A�����C�̂̂悤�Ȃ��̂ł���l�ł���Έ�̑��ƍl������B
�@���̂Ƃ��A�ő���t���͉���ނ��̑��Ƃ��ċ��������邪�A�C���͗B��̋C���������蓾�Ȃ��B�Ȃ��Ȃ�A���̋C�̂��݂��ɗׂ荇�킹�ē�̋C�̂Ƃ��Ď�舵�����Ƃ͂ł��Ȃ�����ł��B
�@�Ⴆ�Έȉ��̂��̂͂����������Ȃ�n�̗�ł����A���ӎ���������⑫����B
�@��̑��͈�ʂɊ���̉��w�����i�������j�̍��������琬��A���̈�l���͉��w�����̑g�����ς���Ă��ێ����ꉻ�w�����̑��ΔZ�x�͕ω�������B
�@�����ŁA�����g���h�iphase�j�A�����g�Ɨ������h�icomponent�j����Ȃ�n���l����B ��ik ���� �� �ɑ��݂������� �� �̎��ʂƂ���B�e�����̊e���ւ̕��z�͉��L�̋L���ŋL�q�����B
�@�����ł́A�c�_���ȒP�ɂ��邽�߂ɓƗ������̂��̂��̂����ׂĂ̑��Ɋ܂܂�Ă���Ƃ��Ă���B�����āA���ʂ̏ꍇ�ɂ͓���̐����̗ʂ��������ɐ��蓾��ƍl����B
�@�����A���� �� ���� �� �ɑ��݂��Ȃ��ꍇ�ɂ� ��ik��0 �ł���A�Ɨ��ϐ�������邪�A�ȉ��Ő�������悤�ɏ�����������邱�ƂɂȂ�A�ȉ��̋c�_�����R�x�̐��͕ω����Ȃ��B
�@
�@�O�͂̋c�_�Ŗ��炩�ɐ������悤�ɁA�^����ꂽ���x�ƈ����̌��ŁA�����n�����t��Ԃɂ�������́g�M�u�Y�̎��R�G�l���M�[�h�f�����l�i�ŏ��j�ɐ��邱���ł����B���̏��������L�̗ʂ̊ԂɈ��̊W���ł���B�M�u�Y�̎��R�G�l���M�[�f�͊e���́g�M�u�Y�̎��R�G�l���M�[�h�fi�i�����P�`���j�̘a�ɓ������̂�
�ƂȂ�B�� �fi �� �s�C�o�C ����� �� �����̊e�����̎��� ��i1�C��i2�C�E�E�E�C��ic �Ɉˑ�����B�ϐ��Ƃ��� �s�C�o �ł͂Ȃ��� �s�C�ui �ɂ��Ă��ǂ��ɂ��ւ�炸�A�̐� �ui �ł͂Ȃ��Ĉ��� �o �ɂ����͕̂��t��Ԃɉ����� �o �͂����鑊�ɋ��ʂł���A���̂��߈�w�ȒP�ɑ���ł��邩��ł��B
�@���̂Ƃ��A�� �� �̃G���g���s�[�� �ri �A�̐ς� �ui �Ƃ����
�����藧�B���̂Ƃ��A�fi�A�ti�A�ri�A�ui �́A�s �� �o �� ��i1�`��ic �ɂ���Ċ��S���肹����B�����̏����͗� ��i1�`��ic �����{�ɐ���A���ׂĂ����{�ɐ��邾���ł��B�Ȃ��Ȃ�A�fi�A�ri�A�ti�A�ui �͂��ׂĂ����������Ӗ��̎��ʐ��̗ʂ�����ł��B
�@���̊� �fi �̌`�́A �� ���̌ŗL�̐��� ��i1�`��ic �� �s �� �o �Ɉˑ����邪�A�M�u�Y�̎��R�G�l���M�[�̌��X�̒�`�m�P�D�i�P�j�Q���n���疾�炩�Ȃ悤�� �fi �� ���� �̕ϐ� ��i1�C��i2�C�E�E�E�C��ic �̈ꎟ�������ł��B���Ȃ킿
�ƂȂ�B���̂��߁A�����C�ӂ� ��ik �ŕΔ����������̂�
�̊W�ɂ���B
�@���ׂĂ̂�ik�i����1�`���j����l�Ȕ|���ő��������Ƃ��A���ӂ̕���ƕ��q�͓��������ŕς��̂ŁA�g���w�|�e���V�����h�� �͑��̓�����ԁA�܂� ��ik�i����1�`���j �̑��ΓI�Ȕ䗦�݂̂Œ�܂�A�e���̑S���ʁi �li�f �m�Q�D�i�Q�j�P�D�Q�Ɓn�j�ɂ͖��W�ƂȂ��B�� �� �ɂ��Đ��藧�����͑��̑��ɂ��Ă����R������B
�@
�@�^����ꂽ���x�ƈ����ɉ����Čn�����t��Ԃɂ���Ƃ��ɂ́A���x�A���͈��̌��Ōn�S�̂��O�E�ƔM�Ǝd���̂��������đ��Ԃ̐����ύX�������Ă��M�u�Y�̎��R�G�l���M�[�f�͕ω����Ȃ��B���̂���
�ƂȂ�B
�@�����ŁA�����e���ʂ̕ϕ����܂������C�ӂł���Ȃ�A�ϕ��̌W���̂��Ƃ��Ƃ���0�ɓ������ꍇ�݂̂��̕����������������B�������A���ۂɂ͎���
��ik �Ɋւ���
�������̏��������݂���B
�@�����l1�`�lc���e�������S�����ŁA��܂����l�ł��B�̂ɕϕ���ik��
�Ȃ���������Ȃ���ΐ���Ȃ��B���̂��߁A�O�L�̎����[���ɂȂ邽�߂ɁA�ϕ��̌W�������Ƃ��Ƃ�0�ɐ���K�v�͖����A�ȉ��̊W�������藧���Ƃ��K�v���\���ȏ����ƂȂ�B���Ȃ킿
�Ȃ�A�S���� ��(���|1)�� �̏����������藧�Ă悢�B���̏������́A�Q�D�i�P�j�Q�D�ŏq�ׂ��悤�ɑ��̓����I�����i��i1�`��ic �̔䗦�j�݂̂ɊW���āA�e�����̑S���ʂlk�i����1�`���j�ɂ͖��W�ł��B
�@���̂Ƃ��A�����̐����Ɋւ��铯��̍s�ɂ���W���̏��Ԃ�C�ӂɕς��Ă��悢�̂ŁA���̎���������B
�@��̑�������ꐬ���Ɋւ��đ��̓ƕ��t�ɂ���A���̗��������̐����Ɋւ��Č݂��ɕ��t�ɂ���B���̂Ƃ��A�ȑO�q�ׂ��l�����t�ɂ���n�͂����������̋C�������������Ȃ��̂ŁA�����̌ő���t�����C���Ƌ������Ă���ꍇ�ɂ́A�C���̏��C�𒇉�ɂ��Čő��A�t���Ԃ̕��t��_���邱�Ƃ��ł���B
�@
�@�ȏ�̐����������悤�ɁA�����t�̏�Ԃ�
���i�����{�Q�j�̕ϐ��ɂ���ċL�q�����B
�@���̂Ƃ��A�����̕ϐ��ɑ��Đ��藧������������
���������ł��B
�@���̂��߁A�����̕������������A�i�����{2�j�̕ϐ��̓��ōŌ�܂Ō��肷�鎖�̂ł��Ȃ��ϐ���2�ƂȂ�B�܂�A���̕ϐ��͂���2�̕ϐ��̊��Ƃ��ĕ\�����i��������������j���ƂɂȂ�B����́A�gDuhem�̒藝�h�iPierre Duhem�j�ƌĂ�邱�Ƃ�����悤�ł��B
�m�⑫�����P�n
�@�Ō�܂ŕs��̕ϐ��Ƃ��ẮA��ʂ� ���x �� ���� ���I���B�Ȃ��Ȃ�A�����ōl���Ă���悤�ȑ��ω��≻�w�����̕��t�́A�O�E�ƔM��d��������肷�钆�Ō��肳��A�����̂����������ǂ�ϐ������x�ƈ��͂�����ł��B
�@���ہA���x�ƈ��͂��߂ď��߂āA�����t��Ԃ��m�肷��B
�m�⑫�����Q�n
�@��L�ȊO�ɁA�����������Ƃ��Čn�� �S�̐� �� �S�G�l���M�[ �Ȃǂ��w�肷�������������t��������ƁA��L�̕s��ϐ��̐��͂P��0�ƌ����Ă����B�s��ϐ��� 0 �ƌ������Ƃ́A�n�̕��t��Ԃ͂����܂��� ���x �� ���� �ɂ����Ă̂ݎ��������ƌ������Ƃł��B
�@
�@�O���ŏq�ׂ��n�̏�Ԃ��߂�i�����{2�j�̕ϐ��𑊂̓����I�Ȑ����ɊW��������i�����I�ȕϐ��j�ƁA���̑S���ʂ��߂�����i�O���I�ȕϐ��j�ɕ����čl�@����ƁA�O�߂̌��_��ʂȌ����ʼn��߂��鎖���ł���B
�@�܂��A�m�����t���L�q����ϐ��n �� �m�����ϐ��n �� �m�O���ϐ��n �ɕ����čl���Ă݂�B
�@�m�����ϐ��n�́A���� �̑��̊e�X�ɉ����� ���� �̓Ɨ������̊Ԃ��i���|�P�j�̔��A�܂�O�q�̔z��
�������̏c��̔��m�� �� �i����1�`���j���Ɋ܂܂�鐬�� ��i1�C��i2�C�E�E�E�C��i�� �̔�Łi���|1�j����n�� ���x�s �� ���͂o �������� {(���|1)���{2} ���ł��B
�@����A�m�O���ϐ��n���e�����Ƃ̑S������\�����L�� ���� �̕ϐ� �l1�f�`�lp�f
�ł��B���̂Ƃ��������A�����ϐ����O���ϐ������킹����o(���|1)���{2�p�{���������{2�ƂȂ�O�߂̑��ϐ��̐��Ɉ�v���܂��B
�@����A�m�����t���K�肷������������n �� �m���������������n �� �m�O�������������n �ɕ����čl���邱�Ƃ��ł���B
�@�m���������������n�Ƃ��ẮA���R�̂��Ƃł����O�q��
����(���|1)���̊W�������݂���B
�@����A�m�O�������������n�Ƃ��ẮA���x�̏ꍇ�͑O�q�� �l1�`�lc �ɂ��Đ��藧�� ���� �ł͂Ȃ��āA �l1�f�`�lp�f �ɂ��Đ��藧�� ���� �ƂȂ�B���Ȃ킿
�ł��B
�@�Ƃ���ŁA�Q�D�i�P�j�Q�D�ŏq�ׂ��悤���g���w�|�e���V�����h�� �͑��̓�����ԁA�܂� ��ik�i����1�`���j �̑��ΓI�Ȕ䗦�݂̂Œ�܂�A�e���̑S���� �l1�f�`�lp�f �ɂ͖��W�ł����B
�@�Ȃ�A�m�O���ϐ��n�ł��� ���� �� �l1�f�`�lp�f �݂̂ɊW����B�m�O�������������n�� ���� �͍l���Ȃ��Ă��ǂ��ł��낤�B
�@�܂�A�����I�ȑ��̑��ݏ�Ԃ��l����Ƃ��ɂ́A ���� �̕ϐ� �l1�f�`�lp�f ���A�n���L�q���� �m�Ɨ��ϐ��n ������A �m���������� �n����������Ă��܂����B������唭���ł��B
�@
�@���̂Ƃ��A �o(���|1)���{2�p�� �� �����ϐ� �ɑ��� ��(���|�P)�� �� ������ ��������܂���̂œ����ϐ��̓���
���s��̂܂܂ɂȂ�B�����I����l���āA������ �� �����ɐ��邱�Ƃ͂Ȃ��K�� 0 �ȏ�̐��̒l�ł��B
�@�܂�A 2�{������ �ł�����A
�@�u���݂ł����g���h�iphase�j�̐������g�Ɨ������h�icomponent�j�̐�����肽�������Q���������ł���B�v
���邢�́A
�@�u�����g�Ɨ������h�icomponent�j��L����n�͂��������i���{2�j���g���h�iphase�j���`��������B�v
�@��L�� �� �� �g���R�x�h�i��reedom�j �ƌĂшȉ��̗l�ɏ�����邱�Ƃ������B
����̓M�u�Y�ɂ���ď��߂ď�����ꂽ�W���ŁA �g�����h�iphase rule�j �ƌ�����B
�@���̖@���̓I�����_�̉��w��Hendrik Willem Bakhuis Roozeboom�ɂ��L�͂Ȏ����I�ȏؖ���L���Ă���B�����āA�t�ɂ��̑��������Ă��Ȃ���Ȃ炢���Ƃ𗘗p���ėl�X�Ȍ��_��������B�m�R�D�i�S�j�Q�D�ȂǎQ�Ɓn
�@
�@�������ǂ��̂ł����A���t�̈Ӗ���������x�m�F���܂��B
�@�g���h �mphase�́A�g�O�ρh���Ӗ�����M���V�����ɗR���n �Ƃ́A�����̏W���̂ɉ����āA���w�I�E�����I�ɋώ��ŁA���̕����Ƃ͖��Ăȋ��E�ŋ���Ă���̈敔�����Ӗ�����B��̉��w�n�̂Ȃ��Ŏ������Ă��鑊�̐���
�g�����hp �ƌ����B
�m�⑫�����P�n
�@��̑��𐬂��Ă��镔���͑��̑��̕������牽�炩�̕��@�ŕ��������o�����Ƃ��ł��܂����A�ꑱ���̘A���̂𐬂��Ă���Ƃ͌���܂���B
�@
�@�Ⴆ�Ώ�w��C�ɂ͔����ȕX���A���H�A�����C�������荇���Ă���̈悪����܂��B���̏ꍇ�͕X��������Ȃ�ő��Ɛ��H����Ȃ�t���ƁA�����C�E���f�K�X�E�_�f�K�X�̍���������Ȃ�C���̎O������Ȃ�n�ł����A�ő���t���͔����q�ƂȂ��ċC���̒��ɕ��U���Ă���B��ʓI�ȑ��̑��ݏ�Ԃ́A���̂悤�ɔ��ׂȑ��̈悪�݂��ɍ����荇���Ă���ꍇ�������B
�@�ʍe�u���C���̓T�C�N���v�R�D�i�Q�j�Ő��������g������C�h�Ȃǂ�������������ł����A�����������ł͑����������������ő��݂���ꍇ�������B
�@
�@�܂��A�R�D�i�Q�j�Q�D�̑����t �ba�b�n3�i�Łj�����ba�n�i�Łj�{�b�n2�i�C�j �悤�ɁA���ނ̌ő������ɂ߂�̂�����ꍇ������܂��B
�@
�@�������w�g���̌ő��ł������\�����ς�邱�Ƃɂ�艻�w�g���̕������ς���ĕʂ̑��ƌ��Ȃ����B �R�D�i�P�j�R�D �� �R�D�i�Q�j�R�D �������A �R�D�i�Q�j�Q�D ���bu�r�n4���a���ȂǎQ�Ƃ��ꂽ���B
�@
�@��̉��w�n�����t��Ԃɂ���Ƃ��A���݂���S�Ă̑��̉��w�g����\������̂ɕK�v�\���ȁA�Ɨ��ɕω������������w�����œ����t�����镔�����g�����h�Ƃ����B��̉��w�n�����t��Ԃɂ���Ƃ��A���݂���S�Ă̑���\������̂ɕK�v�Ȑ����̐��� �g�������h�� �Ƃ����B
�@�g�Ɨ��ɕω���������h �Ƃ����A�������͏d�v�ł��B�Ⴆ�A���ނ̋C�̂��������Ĉ�̋C�̑����Ȃ��Ă���Ƃ��A���̏�Ԃ��ς�����i�Ⴆ�Ή��x�∳�͂��ω������j����ƌ����đ����\������C�̂̔䗦���ς��Ȃ��ꍇ�́A�C�͓̂��ނł������� �P �ƂȂ�܂��B�R�D�i�Q�j�P�D���m�g4�bl�𗣕��t�ȂǎQ�Ƃ��ꂽ���B
�@�������Ƃł����A���S�ɍ����肠�������ނ̉t�̂�A��̗n�}���̓��ނ̗n���ł��A���ω��ɔ����Ă��̑g�����ς��Ȃ���A���Ƃ����ނ̉��w�����ł������� �P �ł��B
�m�⑫�����Q�n
�@�Ⴆ�A�u�t�@���E�f���E���[���X�̏�ԕ������v�R�D�i�Q�j�̐��Ɛ����C����Ȃ�g�����̈�h�ł́A���ׂĂ̑��̉��w�g���͂g2�n�ŕ\���܂�����A�����̐��� �����P�i�g2�n�j �ł��B
�@�H�����͏o���Ă���O�a�H�����ł͐H�����n�t�Ɛ͏o�H�������̓�̑�������܂����A�����͐��i�g2�n�j�Ƃma�bl�̓�� ����2 �ł��B���̂Ƃ��A�n�t���� �ma+ �� �bl- �ɓd�����Ă��邪 �ma�Ƃbl �̊����͑��ω����Ă��ς��܂���̂� �ma�bl �ň�̐����ł��B���̂��Ƃ����łɒ��ӂ��܂����B
�@�R�D�i�Q�j�Q�D�� �ba�b�n3�̉𗣕��t �̗l�ɎO��ނ̕����̓��ނ݂̂��������Ƃ��Đ������A���̓���ǂ�ɂ��Ă��ǂ��悤�ȏꍇ������܂��B
�@�����̎�ނ͂�����x�C�ӂȑI���ɂ䂾�˂��邪�A�������͗^����ꂽ�n�ɂ��ď�Ƀn�b�L�����܂�B
�@
�@��̉��w�n�̒��ŁA���݂��鑊�̏�ς��邱�Ɩ����ɁA�Ɨ��ɕς��邱�Ƃ��ł�����ԕϐ��̐��� �g���R�x�hf �ƌ����B
�m�⑫�����R�n
�@��ԕϐ��Ƃ͕����ʁi���ʁj�ɖ��W�ȕϐ������x�A���́A�����g���Ȃǂ̂��Ƃł��B
�@�C�����܂ޑ����t�ɉ����������͏d�v�ł��B���̂Ƃ��A�̐���ϐ��Ƃ��邱�Ƃ��ł��邪�A�����t���l����Ƃ��ɂ͑S�̂Ƃ��Ă̑̐ς̕ω��͈��͂̕ω��ő�\�����邱�Ƃ��ł���̂ŁA��������グ�鎖�͏��Ȃ��B
�@�C�����܂܂Ȃ��t���E�ő��̑��ω��Ɍ��������������n�t�̖��ł͈��͂��قƂ�Ǎl�����Ȃ��Ă��ǂ��Ȃ�B��������̗��_���猾���ĉe�����Ȃ��͂��͂Ȃ��̂ł����A��������قƂ�lje�����Ȃ��悤�Ɏ�舵����B���̂悤�Ȗ��ł����x���g�����l�����ׂ����R�x�ƂȂ�B���̗l�Ɉ��͎��R�x���ȗ����ċc�_���Ă��镶���i����4�D�Ȃǁj������܂��̂ŁA�����Ƃ��Ă̎��R�x���m�F����Ƃ��ɂ͒��ӂ��K�v�ł��B
�@�������A���������ɂ������̑��ω��A���������ɉ�������������A�_�C�������h�����Ȃǂ���舵���ꍇ�ɂ́A���̓�ɉ������������d�v�ɂȂ�B
�@
�@�����̗�ɂ��Ă͒��Ӑ[���l�@���K�v�ł��B�����́A�}�b�N�X�E�v�����N���A�ŋT�g��u�M�͊w�v��g���X�i1941�N���j��4�ё�3�͂́�205�`��209���Q�Ƃ��Ă��܂��B
�@�܂���̗�̑��}���g���b�q�Y���u���wOnePoint6 �����Ə�Ԑ}�v�����o�Łi1984�N���j�����p���Ă��܂��B���� ��T�����n�̌ő��|�t�����t �� ��V���O�����n�̑����t �́A���̂܂ܕʃw�[�W�ň��p���Ă��܂��̂ŎQ�Ƃ���Ă��������B
�@�ŏ��� ���R�x�� �� 0 �� �������{2 �̏ꍇ���l�@����B���̏ꍇ�ɂ� �m�����ϐ��n �͂��Ƃ��Ƃ���܂�A�����̏��ϐ��� �������{2�d�_ ���`���B
�@�O��������ς��邱�Ƃɂ���ẮA�Ⴆ�ΔM��������Ƃ����k����Ƃ��A�܂��͕�����Y������Ƃ��ɂ���Ă͊e���̑S���� �l1�f�`�lp�f�m�O���ϐ��n ���ς�����݂̂ŁA���� �m�����ϐ��n �͕ς����Ȃ��B
��P
�@��\�I�Ȃ̂��A�m���n�i����1�j�� �g�O�d�_�h �̏ꍇ�ł��B�i�s�C�o�j���i273.16�j�C611.73�oa�j���i0.01���C0.0006atm�j�ɉ������m�X�n�A�m���n�A�m�����C�n�̎O���i����3�j�������ł��邪�A���̂Ƃ��̉��x�A���͈͂�̒l�ɒ�܂莩�R�x����0�ƂȂ�B
�m�⑫�����n
�@1900�N��Gustav Tammann�͒��������ɉ����鐅�̑����t���������āA���ʂ̕X�Ƃ͌����\�����قȂ鐔��ނ̕X�����݂��鎖�������B���ʂ̕X�T�̗Z�_�͈��k�ɂ��~�����čs���A2040�C����-22.0���ƂȂ�B����Ɉ��k����ƕX�T�͕ʂ̌����\���̕X�V�ƂȂ�B�X�V�̗Z�_�͈��͂ƂƂ��ɏ㏸����B�m�����E�}�Q�Ɓn
��Q
�@�m��_���Y�f�n �݂̂�e��ɋl�߂��n�ɉ����Ă��O������������̈�͉��x�A���͂��m�肵�Ă���B
��R
�@�ő́E�t�́E�C�̂ŎO���ɕ������Ƃ͌���Ȃ��B�i�s�C�o�j���i155���C1.3�~103atm�j�ɉ������m�����n�̗l�� �m�P�C�I�E�i�ő��j�n�A�m�Ε��C�I�E�i�ő��j�n�A�m�t�̃C�I�E�n �̎O�����ڂ���l�ȏꍇ������B�C�I�E���O�d�_�����ׂĐ}������Ɖ��L�̗l�ɂȂ�B�P�C�I�E�̖��x�͎Ε��C�I�E��菬�����B���̂��ߎΕ����P�̓]�ډ��x�͈��͂̑���ƂƂ��ɏ㏸����B
�@�}�Ɏ����ŕ\���ꂽ���蕽�t�̑��ɁA����̏����蕽�t���e�ՂɊϑ������B�Ε��C�I�E���}���ɉ��M�����Ɠ_�ړ_�c��ω��Ȃ��ɑf�ʂ肵�A114���i�d�_�j�ŗZ�����ĉt�̃C�I�E�ɂȂ�B�Ȑ��n4�n3�͉ߗ�p�t�̃C�I�E�̏�������C���Ȑ��ł��B������Ε��C�I�E�̗Z�_�Ȑ��͂n4����n3�ɉ��тĂ���B�_�n4�͎Ε��C�I�E�E�t�̃C�I�E�E�C�̃C�I�E��������O�d�_�ł��B
��S
�@���E�}��1963�N��F.P.Bundy����Ă����Y�f�̑��}�ł��B�O�d�_�n�́i�s�C�o�j���i4100�j�C1.23�~105atm�j�t�߂ɂ���B
�@��������_�C�������h��l�H�I�ɍ������邱�Ƃɏ��߂Đ����i1955�N�j�����̂̓W�F�l�����E�G���N�g���b�N�ЂŁA���}�̎ΐ��̈���i�^���^����R�o���g�̋����G�}�ƂƂ��Ɂj���p������@�ł����B���}�͍������ŐG�}�ɕ���ꂽ�����_�C�������h�̎ʐ^�B
�@�Ȃ��A�G�}�Ȃ��Ń_�C�������h�����ɐ��������̂�Bundy�i1963�N�j�ŁA���x3000�`4000�j�A����1.2�~105atm�ȏ�̗̈�ɂ����Ăł������B
�@
�m�⑫�����n
�@6�~105�`7�~105atm�ȏ�̈��͂ł́A���x��15�`20�����������I�Ȍő��V�ɓ]�ڂ���Ɛ�������Ă���B���̓_�ɂ��O�d�_�b�����݂��܂��B
�@
��P
�@�m���n�A�m��_���C�I�E�n �̓��n�́A �i�s�C�o�j���i12.1���C1773mmHg�j �ɉ����� �g�l�d�_�h �ƂȂ�B���Ȃ킿 �m�ő��r�n2�7�g2�n�n�A�m�r�n2�̐��n�t�n�A�m�t�̂r�n2�n�A�m�C�̂r�n2�n �̎l������������B���̂Ƃ��Q�D�i�P�j�P�D�ŕ⑫���������悤�ɁA �r�n2 �����n�t���Ő�����������Ă��邩�ۂ��Ƃ������́A�������ɂ͂܂������W���Ȃ��B
��Q
�@�m�g2�n�n �A �m�ma�bl�n �̓��n�ɉ����āA �m�ő��H���n�A�m�X�n�A�m�H�����n�t�n�A�m�����C�n �̎l�������������l�d�_�����̈��ł��B
�@
��P
�@�m�ma2�r�n4�n�A�m�lg�r�n4�n�A�m�g2�n�n �̎O�����n�́A �i�s�C�o�j���i21.5���C��10mmHg�j �ɉ������g�d�_�h�ƂȂ�B���Ȃ킿 �m�����A�X�g���J�i�C�g�ma2�lg�i�r�n4�j2�4�g2�n�n�A�m�P�����ma2�r�n4�n�A�m�P�����lg�r�n4�n�A�m�ma2�r�n4�Ƃlg�r�n4���n�������n�t�n�A�m�����C�n �ܑ̌�����������B
�@
�m�⑫�����n
�@�O�����n�̑���Ԃ�}������ɂ͍H�v���K�v�ł��B�g���b�q�Y���u�����Ə�Ԑ}�v��V���O�����n�̑����t�V�D�P���Q�Ƃ��ꂽ���B
�@
�@���̏ꍇ�ɂ́A���̓����I�����͂�����̕ϐ��A�Ⴆ���m���x�n�܂����m���́n�ɂ���Ċ��S�Ɍ��肳���B
��P
�@��̐�������̑��Ƃ��ċ�������ꍇ�ł��B
�@��\�I�Ȃ̂��A�m���n�i����1�j���O�a���C���Ȑ��̈��i�t�̂ƋC�̂̋����j�A�Z���Ȑ��̈��i�ő̂Ɖt�̂̋����j�A���؋Ȑ��̈��i�ő̂ƋC�̂̋����j�ł��B
�@�����̏ł͓����I�����i���͂▧�x�Ȃǁj�͂�����̕ϐ��m���x�n����܂�Ό��܂�B
�@�m�O�߂̐��A�b�n2�A�����̑��}�Q�Ɓn
��Q
�@�m�����n���m�P�C�I�E�n�����m�Ε��C�I�E�n�ւ̓]�ڋȐ��̈����̌�����ԁi����2�j�����������ł��B���̏ꍇ���]�ڋ������͂��m���x�n�݂̂̊��ƂȂ�B
�@���̑��A�m�����n���O�a���C���Ȑ��̈��i�t�̂ƋC�̂̋����j�A�Z���Ȑ��̈��i�ő̂Ɖt�̂̋����j�A���؋Ȑ��̈��i�ő̂ƋC�̂̋����j�ł��]�ڋ������͂��m���x�n�݂̂̊��ƂȂ�B
��R
�@���w�I�������C�������̗�ł��B
�@�Ⴆ���m�m�g4�bl�n�m�ő̂̉����A�����j�E���n�͕������� �g�bl�i�������f�K�X�j �� �m�g3�i�A�����j�A�K�X�j ����Ȃ��m�C�̑��n�Ƌ������܂����A�ꐬ���E�n�ƍl���邱�Ƃ��ł���B
�@�e�m���x�n�ɑ��Ē�܂����𗣈� �o ���Ή�����B���̂Ƃ��A �g�bl �� �m�g3 �̑g����͑��ω����Ă��ς��܂���̂ňꐬ���ƌ��Ȃ��܂��B
�@
�m�⑫�����n
�@�z���X�g�}����1869�N�̘_���u���C���ƃ��V���i�����A�����j�E���j�̋C���M�v�ŁA���̉𗣔��������グ���B�ނ́A���̉𗣉��w�������ꐬ���E�n�̕X�|�����C�̏��ؕ��t�Ɠ����ł���ƌ��Ȃ��ĔM�͊w�̐��ʂ𗘗p�����̂ł��B���̏��ؕ��t���g�N���E�W�E�X�E�N���y�C�����̎��h��K�p���āA�𗣈� �o �̉��x�ˑ����������ؔM���v�Z���āA���̌��ʂ������Ɣ�r�����B�����ď��ؔM�̓A�����j�A�Ɖ������f�������M�ɂقړ��������Ƃ��m���߂��B����́A����܂ŔM�@�ւɂ������p�ł��Ȃ��Ǝv���Ă����M�͊w�����w�ɉ��p�����ŏ��̗�ł��B���̂��Ƃɕt���Ă��R�{����4�D��31�͇X���Q�ƁB
�@
�P�D�s���̌ő��t���s�C���t�i���C�j�̎O�����t�̏ꍇ�B
��P
�@���ނ��m�ő��`�n���m�ő��a�n���܂������n�����킸�A�m�ő��`�n���m�ő��a�n���m���҂̏��C�n�����t�W�ɂ���ꍇ�B
�@���}�̑��}���ԐF���C���̏��Y�����镽�t��Ԃł��B�m���x�n���^������A���t��������m���́n�Ɓm���C�̑g���n����܂�B����A�m���́n���^������A���t��������m���x�n�Ɓm���C�̑g���n����܂�B
���������s���̌ő��t���s�C���t�i���C�j�̏ꍇ�����A���ڂ̌ő������C�Ɣ������ē��ڂ��������ő��������ĎO�������t����ꍇ�ł��B
��Q
�@�m�ő̂ba�n�n���m�C�̂b�n2�n�́A �ba�b�n3�i�Łj�����ba�n�i�Łj�{�b�n2�i�C�j �̕��t��Ԃ� �m�ba�b�n3�����n�A�m�ba�n�����n�A�m�C�̂b�n2�n �̎O������������B
�@���̂Ƃ��̉𗣈����m���x�n�݂̂̊��ƂȂ�B�Ⴆ�b�n2��700���̂ba�n�ɉ�����ƁA�b�n2���͂�25mmHg�ɒB����܂ŋC�̂̋z���͋N����Ȃ��B���̈��͂���Ƃba�n�͂b�n2���z�����āA���S�ɂba�b�n3�ɕω�����܂ň��͈͂��ɕۂ����B�ڍׂ͕ʍe�u���t��Ԃ̔M�͊w�i�C�̂̉��w�����j�v�R�D�i�R�j�U�D���Q�Ƃ��ꂽ��
�@���Ȃ킿���R�x�� �P �ł��B�����琬������ �R �ł͂Ȃ��� �Q �Ȃ̂ł��B���̗�ł́A �ba�b�n3�A�ba�n�A�b�n2 �̓��̂ǂ̓��Ɨ������Ƃ��Ă��ǂ��B
�@�Ƃ���ŁA�O���� �����A�����j�E���m�g4�bl �̉𗣕��t�̏ꍇ�͐����� �P �ł��������Ƃɒ��ӂ��ꂽ���B
��R
�@�m�bu�r�n4�n�A�m���n�̓��n�ŁA�m���a�������bu�r�n4�5�g2�n�n�`�m�����������bu�r�n4�n�̓��̓��ނƁm�����C�n�̎O������������ꍇ�Ɏ��R�x�� �P �ƂȂ�B
�@�Ƃ��낪�A�m���a�������bu�r�n4�5�g2�n�n�`�m�����������bu�r�n4�n�̓��̈��ނƁm�����C�n���������ē𐬂��Ƃ��ɂ͎��R�x�� �Q �ƂȂ�A���x����܂��Ă������C���͂���͈͂̒l����蓾��B
�@���ۂ̑����t�̗l�q�́A����4�D�́�6.2���Q�ƁB���邢�́A���[�A�u�������w�v���Q�Ƃ��ꂽ���B
��S
�@�\���a�������ma2�r�n4�10�g2�n ����C���ɕ��u����ƁA �m�\���a�������ma2�r�n4�10�g2�n�n�A�m���������ma2�r�n4�n�A�m�����C�n �̎O��������������E�O���n�̑����t�ƂȂ�B�m�ma2�r�n4�n���m���n�������Ȃ��B���̂Ƃ����R�x�� �P �ł���A�����g���͊m�肵�Ă���̂��m���x�n����܂�m�����C���n�͊m�肷��B
�@
�m�⑫�����n
�@���̏ꍇ�A���x25���ł̏��C����19.2mmHg�ƂȂ�܂��B����͓������x�Ŏ��x80.7���̑�C�Ɋ܂܂�鐅���C�̕����ɓ������B�܂莼�x80.7���ȉ��̑�C���ł́A�\���a�������ma2�r�n4�10�g2�n�͐��a���������ĕ��Ă����B������g�����h�iefflorescence)�Ƃ����B�܂�A�n�̉𗣈�������C���̐����C�����Ⴂ�ꍇ�ɁA���a�������������A���̕\�ʂ��ᐅ�a���܂��͖������ɐ����Ă������ۂł��B
�@���Ȃ݂ɗ��_���E�ܐ��a���̐����C����25����7.85mmHg�ɉ߂��Ȃ��̂ŁA���x33���ȏ�̑�C���ɕ��u���Ă������͋N����܂���B
�@
�Q�D�s�ő��t�A�s�t���t�i�n�t�j�A�s�C���t�i���C�j�̎O�����t�̏ꍇ�B
��P
�@�m���n�A�m���n�̓��n�ɉ����āA �m�ő����n�A�m�����n�t�n�A�m�����C�n �̎O�������������ԁB���̏ꍇ�m���C���n�Ɗe���ɉ�����m���x�ƔZ�x�n���m���x�n�݂̂̊��ƂȂ�B
�@�Ⴆ�A�m�bu�r�n4�n�A�m���n�̓��n�ɉ����āA �m�ő��bu�r�n4�5�g2�n�����n�A�m�bu�r�n4���n�t�n�A�m�����C�n �̎O�������������ԁB
�@
�m�⑫�����n
�@���̂Ƃ��bu�r�n4�͐����� �bu2+ �� �r�n42- �ɓd�����Ă��܂����A���ω����Ă����̊e�����̐�����͕ς��܂���̂� �bu�r�n4 �Ƃ��Ĉ�̐����ƌ��Ȃ��܂��B
��Q
�@�����J���V�E���ba�bl2����C���ɕ��u����ƁA�ba�bl2�͋�C���̐������z�����Ă��̕\�ʂɖO�a���n�t��������B�����āA �m�ő̂ba�bl2�n�A�m�ba�bl2�̖O�a���n�t�n�A�m�����C�n �̎O��������������E�O���n�̑����t�ƂȂ�B�m�ba�bl2�n���m���n�������Ȃ��B���̂Ƃ����R�x�� �P �ł���A�����g���͊m�肵�Ă���̂��m���x�n����܂�m�����C���n�͊m�肷��B
�@
�m�⑫�����n
�@���̏ꍇ�A���x20���ł̏��C����7.5mmHg�ƂȂ�܂��B����͓������x�Ŏ��x43���̑�C�Ɋ܂܂�鐅���C�̕����ɓ������B�䂦�ɉ����J���V�E���͎��x43���ȏ�̑�C���Ő������z�����ėn�����Ă����B������g�����h�ideliquescence�j�Ƃ����B�܂�A�n�̖O�a���n�t�̏��C��������C�̐����C���̕��������ꍇ�A�����̕\�ʂ��O�a���n�t�̑w�ŕ����Ă��܂����ۂł��B
�@�����J���V�E���̏ꍇ�͔��M�����ŁA����ɐ��n�t�̋Ìœ_��Ⴍ������ʂ�����܂��B���ꂪ�A�~�G�ɘH�ʂ̓����h�~�܂Ƃ��ė��p���ꂽ��A�ċG�ɃO�����h�ɂ܂��ēy�����点�ēy����h�~����̂ɗp�����闝�R�ł��B�@
�@
�R�D�s���̉t���t���s�C���t�i�������C�j�̏ꍇ�B
��P
�@�܂������n������Ȃ���̉t�̂ƋC������������ꍇ�B
�@�Ⴆ�K�A�m�u�����x���[���n���m���n�͂قƂ�Ǘn���������Ƃ������āA���̏��C���Ɠ��E�O���n���`���ł���B �m�u�����x���[���i�t�j�n�A�m���i�t�j�n�A�m�v�����x���[���Ɛ��̍������C�n �̎O�������������Ԃ͎��R�x �P ������A�m���́n���m�肷��A����́m���x�n�ł̂݁A����́m�Z�x��n�̏��C������t���Ƌ����ł����B���邢���m���x�n���߂�Ɓm���C�̑g���n�Ɓm���́n����܂������t�n�ƂȂ�B
�@
�m�⑫�����n
�@���̗�ł́A95.3���Ńu�����x���[���̏��C����120mmHg�A���̏��C����640mmHg�ŁA���̘a��760mmHg�i��1atm�j�ƂȂ�B�܂�A�u�����x���[���ɐ����C��ʂ��ď��������95.6���ŕ������ė��o���鎖���ł���B����͕��_�̍��������i�u�����x���[���̕��_156���j���̂�����̂Ȃ�100���ȉ��ŏ����ł��邱�Ƃ������Ă���B���̂悤�ȉ��w�I��@���g�����C�����h�Ƃ����B
��Q
�@�m�G�[�e���n���m���n�̗l�ɁA�݂��ɏ����͗n�����������S�ɍ����荇�������Ƃ͂Ȃ��āA�m�ɕ������Ă���t�́n���A�����m���ʂ̏��C�n�Ƌ�������ꍇ�B���̂Ƃ��m���C���n�Ɓm�t���̔Z�x��n���m���x�n�݂̂̊��ƂȂ�B���邢���m���́n���m�肷��A����́m���x�n�œ���́m�Z�x��n�ł̂ݑ��݂ł���B
�@
�m�⑫�����n
�@���t�����ł͉���ɂ����̂ŁA�m���n�|�m�u�^�m�[���n�n�̑��}�������B
�}�����`�|�d�|�a���C�������E�O�������̈��\���Ă���B�ڂ�������������4�D�̂������������������B
�@
�S�D�s���̌ő��t���s���̉t���t���琬��ꍇ�B
�@�����ő��ł܂������n������Ȃ����A�t���ł͔C�ӂ̊����ŗn�������ꍇ�ł��B
�@�n�t�̉��x��������A�n�t�̒�������̂��ꂼ��̌��������������������͏o���n�߂��g�����_�h�i���Z�_�j�̏�Ԃł́A�m���́n�����߂�ƁA�m���x�n�Ɓm�g���n���m�肷��̂Ŏ��R�x�� �P �ƂȂ�܂��B
�@�g�߂ȗႪ�A�C���������Ȃ����i���͉��j�ł��m�g2�n�n�A�m�ma�bl�n���n�ɉ����āA�m���̐��n�t�n����A�m�X�n���m�������n�������ɐ͏o����ꍇ�ł��B
�@�ʂ̗�Ƃ��āA�m�g2�n�n�A�m�m�g4�bl�n���n�ł́A�m���̐��n�t�n����A�m�X�n���m�m�g4�bl�����n�������ɐ͏o���܂��B
�@���߂̕X�Ɖ������̊������d�_�̋��L�������g���ɑ������Ă���A�n�̉��x�͋��L�_�̉��x(��-�����A�����j�E���n�ł�-15.8���j�܂ō~��������B���̗l�ɗ�p��p�Ƃ��ė��p�ł�����̂��g���܁h(freezing mixture)�ƌ����܂����A��L�̓�̗�͐̂��犦�܂Ƃ��ėǂ����p����܂����B
�@
�@���l�ȗ�͂�����ł�����܂��B����̗���u���[�A�V�������w�v������p���Ă����܂��B
�m�⑫�����P�n
�@���̏ꍇ�A���̌����Ƃ��Đ��a���������ɐ�����ꍇ������̂ŁA�ő����m�X�n�Ɓm�������n�̓����Ȃ̂����ӂ��K�v�ł��B
�m�⑫�����Q�n
�@�ő́|�t�̂̑����t�ł́A���͂̕ω��͉��x�Ƒg���̕ω��ɂ��܂�e�����Ȃ��B���̂��߈��͂̎��R�x�����Č������㎩�R�x�� 0 �Ƃ��邱�Ƃ��ł���B�������A�������猾���ƈ��͂͏ȗ��ł����{���̎��R�x��
1 �ł��B
�m�⑫�����R�n
�@���n�̌ő��|�t�������t�͍ł�������������Ă���A�d�v�ȗႪ��������܂��B
�@�g���b�q�Y���u�����Ə�Ԑ}�v��5�����n�̌ő��|�t�����t�@��ʃy�[�W�ň��p���Ă����܂��̂ŁA���̒��̎��R�x���P�i���E�O�����t�j�̗���Q�Ƃ���Ă��������B
�@�Ȃ��A���̕����ł́A�ő��|�t�����t�ɉ����Ĉ��͂̉e���͏��Ȃ��̂ŁA���͂̎��R�x�����āA��������̎��R�x���Q���P�A�P���O�Ƃ��ċc�_���Ă��邱�Ƃɒ��ӁB
�@
�T�D�s���̉t���t���s���̌ő��t���琬��ꍇ�B
�@�C���������Ȃ����͉��ŁA�m�L����f�n���m���n�̗l�Ɍ݂��ɐڐG���Ă����m��t���n�����m�ő̒��a�n����ꍇ�B
�@
�@�C���������Ȃ����͉��ŁA��������蓾����ނ��m���`�n�A�m���a�n���m���n�����m���`�Ƃa���n�������n�t�n�A�m�`�̌����n�A�m�a�̌����n�A�m�`�Ƃa�̕��������n�̎l������������ꍇ�B
�m�⑫�����n
�@��̓I�ȗ�ɂ��ẮA�g���b�q�Y���u�����Ə�Ԑ}�v��V���O�����n�̑����t���Q�Ƃ��ꂽ���B
�@
�@���̏ꍇ�ɂ́A�����鑊�̓����I�����͂Q�̕ϐ��A�Ⴆ���m���x�n������m���́n�ɊW����B
�@�ώ��ȏ�Ԃɂ��邠���镨���B�Ⴆ�Η��z�C�̂́i�o�C�u�C�s�j��ԕ������ȖʂȂǂ��v���o���ꂽ���B
�@�m���x�n�A�m���́n�A�m�̐ρn�Ȃǂ̏�ԕϐ��̂�����i�Ⴆ�Α̐ςƉ��x�j�����߂Ă͂��߂Ďc��̕ϐ��i�Ⴆ�Έ��́j���m�肵���B���ꂪ���R�x���Q�Ƃ������Ƃ̈Ӗ��ł��B
�@�������A����������1�i��������1�j�̏ꍇ�A�O���I�ϐ��̑S�̐ςȂǂ͕ω����邪�A�����I�ϐ��̑��Ԃ̑̐ϔ��A�������̑g����Ȃǂ͑��݂��Ȃ��̂ŁA�����̗�Ƃ��Ă����Ŏ��グ�Ă��S���Ӗ����Ȃ��̂ŋc�_���Ȃ��B
�@
�P�D�������S�ɗn���������s���̌ő��t���s�C���t���琬��ꍇ�B
���ނ��m�ő��`�n���m�ő��a�n�������銄���ŗn�������ꍇ�B�m�`�Ƃa�̌ŗe�́n���m���҂̏��C�n�����t�W�ɂ���ꍇ�B���}�̑��}�̓��F���F�̈悪�Y�����镽�t��ԂŁA�m���x�n���m���́n���^������m���C�ƌŗe�̂̑g���n����܂�B
�@
�Q�D�������S�ɗn���������n�t�ł����s���̉t���t���s�C���t�i���C�j���琬��ꍇ�B
�@�m���n���m�n�}�n���琬��n�ŁA�m���̗n�t�n���m���̏��C�n���ڐG���Ă���ꍇ�B�m���x�n���m���́n�ɂ���ėn�t�Ə��C�ɉ����鉖�̔Z�x�����܂�B
�@���t�����ł͉���ɂ����̂ŗ�Ƃ��āA�m���Y�f�n�|�m�x���[���n�n�̑��}�������B
��L���}�̏ڂ�������������4�D�̂��������Q�ƁB
�m�⑫�����P�n
�@���̏��C���p�Ïk�����ė��������āA������Ăш�舳�͂̌��ŕ���������Ɨ��������n�t�̑g���ω��ɉ����ĕ��_���قȂ�ʂ̑g���̏��C����������B������p�Ïk���Ď��̏������t�Ƃ���B�ȉ����l�ȑ�����J��Ԃ��ėn�t�����̐����t�̂ɕ����鑀����g�����h�Ƃ����B
�@��̓Ɨ��ϐ��Ƃ��āA�m���x�n���m���́n�̕ς��ɁA�m���x�n���m�n�t�̔Z�x�n��I�ԏꍇ������B
�@�Ⴆ�A�m�n���n���m�n�}�n����Ȃ�n�ɉ����āA�m�C�ӂɑI�ꂽ�Z�x�n�̈�n�t���m�C�ӂɑI�ꂽ���x�n�ɉ����āA��܂����g���ƒ�܂������͂��m���C�n���o�����m�n�t�n�Ƒ����t�𐬂��B
�m�⑫�����Q�n
�@�n�t�ŁA�n�����������Ȃ��ꍇ�ɂ́A�n���Z�x�ɔ�Ⴕ�ď��C����������i���_�㏸�j���Ƃ��m���Ă���B�����1886�N��Raoult�ɂ��o���I�Ɍ�����ꂽ���̂��g���E�[���̖@���h�ƌĂ�Ă���B�������̌��van't Hoff�ɂ���ĔM�͊w�I�ɏؖ����ꂽ�B
�@
�@�܂��A�C�̗̂n���ɉ����āA�t�̂̏��C�����C���̈��͂ɔ�ׂĖ����ł���قǏ������ꍇ�ɂ́A�t�̂ɋz�������C�̗̂ʂ͉t�̏�̋C�̂̕����ɔ�Ⴗ��B���̂Ƃ����萔�͉��x�݂̂Ɉˑ�����B���ꂪ�悭�m���Ă����g�w�����[�̖@���h�i1803�N William Henry�ɂ��j�ł��B
�@
�R�D�n�t����͏o�����s���̌ő��t�ƌ��n�t���s���̉t���t���琬��ꍇ�B
�@�ł��g�߂ȗႪ�A�m�g2�n�n�A�m�ma�bl�n�̓��n�ŁA�m�H�������n���͏o���Ă����m�O�a�H�����n�ł��B�m���x�n���m���́n�����܂�ΖO�a�H�����̂m���bl�Z�x�����܂�B�m���́n���߂��Ƃ��A�m���x�n�ƂƂ��Ɂm�O�a�n�t�̔Z�x�n���ω�����l�q��\���O���t���g�n��x�Ȑ��h�ł��B
�m�⑫�����P�n
�@���n�̌ő��|�t�������t�͍ł�������������Ă���A�d�v�ȗႪ��������܂��B
�@�g���b�q�Y���u�����Ə�Ԑ}�v��5�����n�̌ő��|�t�����t�@�����p���Ă����܂��̂ŁA���̒��̎��R�x���Q�i���E���t�j�̗���Q�Ƃ���Ă��������B
�@�Ȃ��A���̕����ł́A�ő��|�t�����t�ɉ����Ĉ��͂̉e���͏��Ȃ��̂ŁA���͂̎��R�x�����āA��������̎��R�x���Q���P�A�P���O�Ƃ��ċc�_���Ă���̂Œ��ӁB
�@��̓Ɨ��ϐ��Ƃ��āA�m���x�n���m���́n�̕ς��ɁA�m���́n���m�n�t�̔Z�x�n���p�������ŁA���̑����C���ł͂Ȃ��ő��ƂȂ����ꍇ�B
�@�m�n���n���m�n�}�n����Ȃ���n�ŁA�m�C�ӂɑI�ꂽ�n���Z�x�n�̈�n�t���m�C�ӂɑI�ꂽ���́n�ɉ����āA��܂������x�̋Ìœ_��L���A���̋Ìœ_�ł͒�܂����g�����m�ő́n��͏o�����m�n�t�n�Ƒ����t���Ȃ��B
�m�⑫�����Q�n
�@�s�������n����n�������n�}�̋Ìœ_���n���Z�x�ɂ̑���Ƌ��ɉ������Ă����g�Ìœ_�~���h�����̈��ł��B����͏�ɏq�ׂ��n��x�ω��̌�����ς��������ŁA�g�Ìœ_�~���Ȑ��h���g�n��x�Ȑ��h�Ɠ������ۂ̒P�Ȃ�قȂ������̂ł��B
�@
�S�D���̉t�̂��s���̉t���t�Ƃ��ċ�������ꍇ�B�݂��ɗn����������t�ɕ������Ă���ꍇ�ł��B
�@�݂��ɗn����������w�ɕ��������m���ނ̉t�́n�́A�m��w�ɕ��������n�t���n�̂��݂��̔Z�x���m���x�n���m���́n�ɂ���Č��܂�B�܂�m���x�n�Ɓm���́n�̗��������߂Ȃ��Ƃ��ꂼ��̉t���́m�Z�x�n�͌��܂�Ȃ��B
�@��Ƃ��āA�m���n�|�m�t�F�m�[���n�n�ɂ����鑊�}�������B
��}���ڍא����͂��������Q�Ƃ��ꂽ���B
�@�X�Ȃ��Ƃ��āA�m�w�L�T���n�n�|�m���^�m�[���n�n�ɂ����鑊�}������
��}���ڍא����͂��������Q�Ƃ��ꂽ���B
�m�⑫�����n
�@��L��̗�̑��}���Q�Ƃ��ꂽ���B�}���̉����̔������̈悪���E�n����������Ă���̈�ł��B���̗̈�ł́m���x�n�A�m���́n�A�m�g����n�̓�������߂Ȃ��Ǝc�������肳��Ȃ��B���ꂪ���R�x���Q�ƌ����Ӗ��ł��B
�@���Ȃ킿�A�m���n�|�m�t�F�m�[���n�n�ɂ����鑊�}�̒ቷ�������̈��A�m�w�L�T���n�n�|�m���^�m�[���n�n�ɂ����鑊�}�̒ቷ�������̈�ł́A�m���́n�Ɓm���x�n�̗������߂ď��߂ē�t�̐������m�肷��B
�@
�@��̓I�ȗ�ɂ��ẮA�g���b�q�Y���u�����Ə�Ԑ}�v��7���O�����n�̑����t���Q�Ƃ��ꂽ���B
�@
�@���̏ꍇ�A���ׂĂ̑��̓����I�������m���x�n���m���́n�̑��ɔC�ӂɑI�ѓ����m��O�̕ϐ��i�g����Ȃǁj�n�Ɉˑ�����B���̂Ƃ��A������ �����P �̏ꍇ�͑��� ����0 �ƂȂ�̂ő��݂��Ȃ��̂� �� �� 2 �ȏ���l����Ηǂ��B�B
�@����2�A����1�ɉ����鎩�R�x3�Ƃ́A�Ⴆ���m���n�|�m�t�F�m�[���n�n�̑��}��67���ȏ�̗̈����m���x�n���m���́n���m�g���n�̎O�����R�ɕς��Ă����݂ł��邱�Ƃ�\���Ă���Ǝv����������Ȃ��B�������A���S�ɍ������Ă��āA�����I�ɂ��̑g�����ς��邱�Ƃ��ł��Ȃ��ꍇ�͗Ⴆ���̉��w�����ł����Ă��ꐬ���Ƃ��Đ�����̂ł����B������A�����Č����Έꐬ���E�ꑊ�̗̈�ł��B
�@������̑��ł͐����̔䗦�������I�ɕω������邱�Ƃ͂ł��Ȃ��̂ł�����A����͂����P�ɑ��݂ł���ƌ��������ŁA�����̗�Ƃ��Ă͖��Ӗ��ł��B
�m�⑫�����n
�@�v�����N�́A�ނ́u�M�͊w�v��262�ŁA���̗�Ƃ��ēd�����̓d�����t�i�I�X�g�����h�̊�ߗ��j��_���Ă���̂ł����A���ꂪ�{���ɑ����̂��̏ꍇ�ɑ�������̂��ǂ�����܂���B
�@
�@�m���n�ɓ��`�i���������\�������j�����m�j�bl�n3�i���f�_�J���E���j�n���m�s���bl�n3�i���f�_�^���E���j�n���n�����m���n�t�n���A�m������̑����Ȃ����������n�Ɛڂ��Ă���ꍇ�B�m��舳�́i�P�������j�n�A�m��艷�x�n�̌��ł����������̑g������ŖO�a�n�t�̔Z�x�͈قȂ������̂ƂȂ�B���̂��߂ɓ��̈��g����L����O�a�n�t�Ƃ������Ƃ������Ȃ��B�܂荬���n�t�̗n���g���䂪��O�̕ϐ����m���������̑g����n�Ɉˑ�����B
�m�⑫�����P�n
�@���̂Ƃ��A��L�̍��������ȊO�ɑ��̐�����L������̍����������͏o����ꍇ�ɏ��߂Čn�̓����I���������x�ƈ��݂͂̂ɂ���Č��肳���B���̏ꍇ�͎��R�x����2�ƂȂ�B
�@���̗l�ȏꍇ�́A��艷�x��舳�͂ɉ����鐅�n�t�̔Z�x�����S�Ɉ��ł��邩�ۂ��ɏ]���āA�͏o�����ő����ꑊ�Ȃ̂��Ȃ̂��肷�邱�Ƃ��ł���B
�m�⑫�����Q�n
�@��̓I�ȗ�ɂ��ẮA�g���b�q�Y���u�����Ə�Ԑ}�v��V���O�����n�̑����t�V�D�S���W����Ǝv���̂ł����A���ɂ͍��ЂƂǂ������ł��Ă��܂���B
�@�܂��v�����N�́u�M�͊w�v��277�ł��A���̗��_���Ă���̂ł����A���ꂪ�{���ɑ����̂��̏ꍇ�ɑ�������̂��ǂ�����܂���B
�@
�@�v�����N�́A�u�M�͊w�v��275�ɂ����āA���̗��_���Ă���̂ł����A���ꂪ�{���ɑ����̂��̏ꍇ�ɑ�������̂��ǂ�����܂���B�����̋c�_�͖{���ɉ����[�����ɂ͓���B
�@