ですから、化学反応の推進力が二つの部分、すなわちΔH項とTΔS項からなることが解る。
ΔHは、外界とやり取りする仕事PdVの効果も考慮した、系の内部エネルギーの変化に相当するもので、定圧下における反応熱に関係する。
一方TΔSは系が化学反応の進展に伴って外界とやり取りする熱量ですが、これは系のエントロピーという量の増減に関係する。
この稿では、平衡定数と熱力学第三法則の関係について解りやすく説明します。
ここの内容は、一連の稿「ルジャンドル変換とは何か」、「熱力学関数(状態方程式曲面)の性質」、「ギブズの自由エネルギー(化学ポテンシャル)とは何か」、「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」の続きです。そのため、これらのページを繰り返し引用します。
“平衡状態の熱力学”とは別稿「熱力学関数(状態方程式曲面)の性質」1.(1)2.の箇条書き4.で説明したように、系内で生じる出来事について、外界との熱と仕事のやり取りを逆転させればすべてが逆転可能で常に一意に決定できるような変化しか系内で生じない場合のことです。相変化や化学変化もそういった意味で逆転可能なものしか起こらない様な系を考察しています。
“平衡状態”という言葉の意味は非常に解りにくいのですが、それ以上の意味はありません。だから系内で機械的な摩擦によって生じる発熱や内部電流によって生じるジュール熱の発生などの現象は含まれていないと言うことです。
別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.で様々な物質のエントロピー値、エンタルピー値、ギブズの自由エネルギー値を求める方法を説明しましたが、それらはすべて系が外界とやり取りする熱量や仕事の量を通して定められた。
そのときの変化は、前節の意味での平衡状態を保った変化ですから、外界との熱や仕事のやり取りを通してそれらの相や化学種の存在の様子がどのように変化しても、それらの1モルの物質の集合が各温度や圧力に於いて持つ状態量は一意に定まった。それが、各相や化学種が示す状態方程式曲面が一意に定まると言うことですし、それらの値が外界とやり取りする熱や仕事の量を通して定まるということです。
具体的なやり方は別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.を参照。
そのようにして、相・化学種ごとに圧力や温度の関数としてギブズの自由エネルギー曲面が定まれば、多数の相や化学種からなる多成分系が互いに同一の圧力や温度の下で共存するときどのような事が言えるか調べるのが、この稿の目的です。
そのとき、相平衡や化学平衡は相種、化学種ごとが持つエネルギー値とエントロピー値に深く関係します。相平衡の状態は、それぞれの相種、化学種の持つギブズの自由エネルギー(化学ポテンシャル)の値が等しくなる状況でのみ実現される。それぞれの相種や化学種の化学ポテンシャルは温度や圧力か変われば変化しますので、相平衡や化学平衡は圧力や温度の変化によって変化します。それらの様子を調べる鍵になるのが、それぞれの相種や化学種のギブズの自由エネルギー(化学ポテンシャル)の知識です。
そのとき、多くの化学反応は平衡に達するのに時間がかかります。そのため実際に反応を行うことなく、熱的測定だけで平衡状態に達したときの平衡定数を熱力学によって論じることができることは偉大な成果です。
反応熱に関する初期の研究の大部分は19世紀の後半 Julius Thomsen と Marcellin Berthelot によって行われた。彼らは反応熱が化学反応を進める力(“化学親和力”chemical affinity)の定量的な尺度になるものと考えて、広範な熱化学的測定を行った。
そして、Berthelot は著書「Essao de Me'canique chimique (1878)」の中で次のように述べた。
“どんな化学変化でも、外部からエネルギーの干渉がなければ、大量の発熱を伴うような物体または物体系を生成する方向に進行する。”
しかし、この考えは間違っていた。この原理に従うと吸熱反応は自然には起こりえないことになる。しかし現実には反応と共に温度が下がる反応は沢山ある。また、多くの化学反応は可逆的である。
化学反応の真の推進力を理解するには、第一法則(エネルギーの変化)だけでは不十分で、第二法則(エントロピーの変化)も考慮しなければならい。このことは、19世紀後半に発達した熱力学を化学分野に適用する事によって明らかになったもので、その最大の功労者がギブズです。別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」で説明したように、ギブズの自由エネルギーこそ定温・定圧の状態変化の下で起こる化学反応の真の尺度となるものです。
定温・定圧の下で、箱の中に詰めた物質系は外界と熱や仕事のやり取りをします。そのとき、化学反応が進む(つまり化学平衡が変化する)につれて系の総内部エネルギーUは変化しますが、U-TS+PVで表されるギブズの自由エネルギーGの総量は変化しません。
化学反応に伴うギブズの自由エネルギーの変化はΔG=ΣG生成物-ΣG反応物と表せますが、ギブズの自由エネルギーの変化は零なのです。つまり、ギブズの自由エネルギーの変化ΔGが零の場合、定温・定圧下で如何なる化学反応変化が生じてもPdV以外のいわゆる“真の仕事”と言われるものは全く得ることはできません。そのとき系は平衡状態にあります。
そのとき、もしギブズの自由エネルギー変化ΔGが正の場合には、反応を起こすために“真の仕事”を系に加えてやらねば成りません。
また、ギブズの自由エネルギー変化ΔGが負の場合には、反応は自然に進行し、その際有効な“真の仕事”を系から取り出すことができます。系から取り出せる“真の仕事”の量が大きいほど最初の系状態が平衡から大きくずれていたことになる。
定温・定圧の下での反応に於いて
ですから、化学反応の推進力が二つの部分、すなわちΔH項とTΔS項からなることが解る。
ΔHは、外界とやり取りする仕事PdVの効果も考慮した、系の内部エネルギーの変化に相当するもので、定圧下における反応熱に関係する。
一方TΔSは系が化学反応の進展に伴って外界とやり取りする熱量ですが、これは系のエントロピーという量の増減に関係する。
化学反応の進行は前節で述べた二つの熱量の差に関係する。どちらも系の状態変化に伴って系から出入りする熱量なので、ここは非常に解りにくいのですが、両者が一致した状態で化学反応(相変化)は進行すると言うことです。
このことは別稿「冷凍・低温技術の歴史」2.1.で説明した水の相変化を考えてみると解りやすい。今、下図の様に100℃の熱浴に接しており、しかもピストンの上に重りを載せて1気圧の加重のもとにある水の系を考察する。
1気圧のもとでの100℃における水と水蒸気の相変化を考える。よく知られているように熱浴の温度を100℃よりもごく僅か高くするか、あるいはピストンに載せた重りをごく僅か軽くすると、外界(熱浴)から水へエネルギー(熱)が流入して水はすべて100℃の気体(水蒸気)になる。逆に、熱浴の温度を100℃よりもごく僅か低くするか、重りをごく僅か重くすとると100℃の水蒸気は外界(熱浴)へエネルギー(熱)を放出してすべて100℃の液体(水)にもどる。
ここで、100℃の水と100℃の水蒸気では水蒸気の方が熱を吸収[正確には外界との仕事のやりとり分の差はあるが]している分エネルギーが(ΔHだけ)より高い状態にある。
これだけのエネルギー差がありながら、何故この状態変化(水と水蒸気の間の相変化)が生じるのかと言うと、水の状態よりも水蒸気の状態の方が乱雑さ(エントロピー)が高い(TΔSだけ)状態だからです。
つまり前述の式に於いて
が成り立つ。
すなわち、定温・定圧の下での化学反応(相変化)は系のエンタルビー(エネルギー)変化ΔHとエントロピー変化ΔSの兼ね合いで決まる。
化学平衡が実現されている状態での化学変化(相変化)はΔG=0がいつも実現されるようにして起こる。だから、定温・定圧下に於ける化学反応熱(相転移熱)ΔHと、その過程が可逆的に行われるとき系に出入りする熱量TΔSは同じです。
もちろん、その反応に電気的な仕事など(“真の仕事”)が伴っている場合には、すでに述べたように両者に差が生じます。
[補足説明1]
ここで、上図に示した変化が右向きに進むか、左向きに進むかは外界(熱浴)のエントロピーの変化量との兼ね合いになります。最初に水と水蒸気からなる系(1気圧、100℃)が温度100℃の外界(熱浴)と平衡にあり共存しているとする。
ここで、圧力(1気圧)を一定に保ったまま外界(熱浴)の温度を100℃よりもごく僅か+Δt℃高くしてみる。そうすると、100℃で熱を吸収した水のエントロピー増加量が、(100+Δt)℃で熱を失った外界(熱浴)のエントロピー減少量よりもごく僅か多くなる。このごくわずかの温度差がトータルとしてのエントロピー増大を生み出し、水は不可逆的に外界から熱を吸収してすべて水蒸気に気化してゆく。
逆に1気圧の元で外界(熱浴)の温度を100℃よりもごく僅か-Δt℃低くすると、水蒸気は不可逆的に全て水に凝縮する。この場合100℃で熱を放出した水蒸気のエントロピー減少量よりも、(100-Δt)℃で熱を得た外界(熱浴)のエントロピー増大量がごく僅か多くなるからです。このようになることは別稿「絶対温度とは何か」6.(5)2.や、別稿「ガス動力サイクル」1.(1)4.で説明した。
上記は外圧一定の元での温度のごく僅かの変化で生じる相変化だったが、温度一定でも水と水蒸気の系にかかっている外圧をごく僅か変化させることで同様な相変化を起こすことができる。もちろんこの場合も水と水蒸気からなる部分系の体積は大きく変化する。
蒸発する場合も、凝縮する場合も、水と外界を含めた全体系のエネルギーは保存されるし、エントロピーもほとんど変化しない。しかし温度のごく僅かの違いが、相変化に伴なう系全体のエントロピーにごくわずかの増大を生じ、それがエネルギー分担の大幅な変更を促す。水と外界の温度や圧力はほとんど同じなのに、両者が担うエネルギーやエントロピーの分配の様子は大きく変化する。たとえごく僅かの温度差でもあっても、どちらの場合も高温部から低温部に熱が流れていく不可逆変化であることは確かです。
[補足説明2]
いままでは、定圧下での化学反応(相変化)の話でした。化学反応(相変化)を温度一定・体積一定の箱の中で行わせる場合には、dV=0で系と外界の仕事のやり取りはなく、熱のやり取りTdSのみとなる。
この場合の平衡条件は
となる。
すなわち、定温・定積下の化学反応(相変化)は、系の内部エネルギー変化ΔUとエントロピー変化ΔSの兼ね合いで決まる。このとき、内部エネルギーの変化分はまさに定温・定積下に於ける反応熱(相転移熱)です。
[補足説明3]
一つの反応に対する推進力が大(ΔGが大きな負の値)でも、その反応が如何なる条件下でも必ず起こる訳ではない。
例えば上記のピストン容器に1molの水素と1/2molの酸素の混合物を1atmの下で封入した場合を考えてみよう。このとき「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(2)2.で計算したように
水の標準生成ギブズの自由エネルギーはΔGf゜=-237.2[kJ/mol]である。ΔGが大きな負の値を持つにも関わらず、混合気体を永年放置しても水蒸気の生成は起こらない。
所が、一つまみの白金海綿触媒を加えると反応は瞬時に進行して水蒸気となる。反応に必要な親和力は確かに存在するのですが、低い温度では触媒が無ければこの反応の平衡状態は実現しない。
もう一つ例を挙げる。
の反応に於いて、マグネシウムが空気に曝されるとすぐに薄い酸化被膜に覆われてしまう。その後の反応は、酸素がこの被膜を通って拡散しなければ成らないので、反応速度は測定できないほど遅くなり、平衡は全く達成されない。
所が一次的にその系の一部の温度を高めてやると、その大きな親和力のために反応は瞬時に終了する。そのためΔGの大きな負値はこの化学反応の親和力を表す正しい尺度であることが解る。
以上の例から明らかなように、平衡を達成する速度は全く別の因子に依って決められる。
平衡条件を数学的に表してみる。次の化学反応を考える。
ただし、νiは化学量論的なモル数で、生成物で正、反応物で負であるように取る。
次に反応がどの程度進んだかを“反応進行度”(degree of advancement)ξで表す。ξ→ξ+dξの変化は、A1がν1dξモル、A2がν2dξモル、・・・反応して、Anがνndξモル、An+1がνn+1dξモル、・・・生成することを意味する。反応に伴う成分 i のモル数の変化は
で表される。
このとき、温度・圧力一定の元で反応物と生成物を含む系が平衡にある場合には
が成り立たねばならない。
前節の化学ポテンシャルμは1モル当たりのギブズの自由エネルギーのことです。反応物、生成物が標準状態(1atm,298K)で持つギブズの自由エネルギー値は、別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(2)2.で説明したようにして反応熱や比熱のデータから求めることができる。
ただし、これらのエネルギー値に関しては注意すべき点が多々あるので、そこでの説明をお読み下さい。いずれにしてもその様にして得られた値は数表として与えられている。
数表中のデータを用いて、標準状態に於ける任意の化学反応に伴うギブズの自由エネルギー変化ΔG゜を求めることができる。
例えば
の反応の自由エネルギー変化は数表から各物質の標準生成ギブズの自由エネルギー値Gf゜を読み取ると
となる。
平衡理論の重要な応用が、反応物や生成物が“気体の化学反応”です。この場合には、気体成分が“理想気体の法則”に従う近似が利用できる。そのため各反応物成分、生成物成分の任意の圧力、温度に於けるギブズの自由エネルギーが計算できて、化学反応平衡の平衡定数との関係を論じる事ができる。
最初は簡単のために温度は25℃(298K)に固定する。別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(3)2.、あるいは「熱力学関数(状態方程式曲面)の性質」3.(3)1.[補足説明3]で説明したように、温度を一定に保て圧力を変化させると1モルの(理想)気体のギブズの自由エネルギーは
となる。
[重要な注意]
ここでのPは単なるPではありません。G(T0,P)はG(T0,P0)からの差分を表すために、積分定数-RT0logeP0が含まれている
である事を忘れないでください。このことを忘れると以下の議論の訳が解らなくなります。
ここで理想気体の理想混合物を考える場合には、ドルトンの分圧の法則が成立する。すなわち全圧は、各気体がそれぞれ単独で全容積を占めた場合に示すであろう圧力の和になる。これらの圧力は混合気体中における各成分気体の“分圧”(partial pressure)P1,P2,・・・Pnと呼ばれ、以下の関係式を満足する。
ここでniは混合物中の成分気体 i のモル数です。
理想混合物中の個々の気体 i についても前記の式が成立すると考えると、気体反応に伴うギブズの自由エネルギー変化は
となる。
[重要な注意]
ただし、ここで
としている。この“全圧”Pは1atmである必要はなく任意の圧力でよいことに注意。。
このときさらに注意して欲しいのですが、“ギブズの自由エネルギー”は物質の状態量でした。そのため、任意の温度・圧力のギブズの自由エネルギーG(T,P)は別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(3)2.で説明したようにG(25℃,1atm)から、まず温度変化の効果のみを考慮してG(T,1atm)を求め、次に圧力変化のみの効果を考慮してG(T,P)を求めても良かった。
そのため、温度がT0=25℃(298K)でない任意の温度Tに於けるギブズの自由エネルギーの圧力変化に対しても上記の関係式はそのまま適用できます。つまり、上記の関係式はT0=25℃(298K)以外の任意の温度Tにおける反応についても正しい。そのため、以下では任意温度に拡張して説明します。
いま、各分圧Piが気体混合物における平衡圧であるとすると、平衡状態にある反応系についてはΔG(T,P)=0となるので
なる関係式が得られる。
これは、気体反応における“圧力平衡定数”KPを、この反応の温度Tに於ける“標準ギブズ自由エネルギー変化”ΔG゜に結び付ける重要な結論です。
ここでの“標準”は各成分の圧力が1atmに於ける反応変化に伴うものであることを意味しますが、反応系の全圧は1atmとは限らず任意圧力Pに於いて成り立ちます。
このとき、KPは温度の関数です。なぜならΔG(T,P0)のTは全く任意に選んだ温度ですから、ΔGは温度Tの関数です。また、RTのTもその任意に選んだ温度です。
そのとき、ΔG(T,P)は全圧Pや分圧Piに無関係ですから、KPは全圧Pには無関係ですし、個々の分圧の変化にも関係しない。
これらの分圧は最初の反応混合物中の反応物や生成物の割合を変えると変わってくる量ですが、平衡状態においてはKPが同じ値になるように互いの分圧は調整されてくると言うことです。
これは熱力学データ[標準ギブズの自由エネルギーGi(T,P0)]から平衡定数を計算できる事を示している。
また、これは最初に任意に与えられた反応気体の成分濃度(分圧)から、平衡状態に於ける生成物の濃度(分圧)を計算に依って求めることができる事を示している。
[補足説明]
圧力平衡定数KPの定義
において、Σνiは一般に零ではないのでKPが次元を持つように見える。しかし、KPは無次元量です。なぜなら3.(1)1.で注意したように、元々のPiは標準気圧1atmに対する比だからです。つまり
の様に1atmを省略して簡単に記しているのであって、次元は無いのです。
P0=1atmを用いているから、Piに具体的な値を代入するときは気圧(atm)で測った数値を代入しなければ成りません。
ここでは説明を解りやすくするために
なる反応系を考える。
体積Vの反応容器中の気体 i の“モル濃度”ci[mol/l]は
で表されるので、その分圧Piは
で表される。
そのため、平衡定数は以下の様に書き換えられる。
ここで、Δνは化学量論的な反応方程式における生成物のモル数と反応物のモル数の差です。そのため、“濃度平衡定数”Kcは圧力変化に依存しない定数(温度には依存)となる。
平衡混合気体の組成を表す“モル分率”Xiは
で表される。ここでΣniは全モル数の和である。
そのため平衡定数は以下のように書き換えられる。
ここで、KPは圧力に無関係であったが、KX=KP/PΔνなので、“モル分立平衡定数”KXはΔν=0の場合を除いて圧力の関数となる。つまり、KXは定温・定圧(P=一定)に於ける各Xiの変化に関してのみ定数となる。
幾つかの気体反応の例を文献1~3から引用する。
この反応は、Max Bodenstein[Z. physik. Chem., 22,1 (1897): 29, 295 (1899)]によって行われた古典的研究です。
彼は既知量の反応物を反応容器に密封して恒温槽中に保ち平衡に達するのを待った。平衡に達した後に反応容器を急冷して平衡を凍結した。その後、反応生成物を過剰の標準アルカリ溶液で処理して、ヨウ化水素とヨウ素を滴定に依って定量した。一方、残った水素ガスを集めてその容積を測定した。
この反応は、反応が進行する過程で全モル数が変化しない(Δν=0)。そのため
となり、KP、Kc、KXは全て一致する。
いま初めのH2のモル数をa、I2のモル数をb、HIのモル数をcとする。Δν=0であるから、反応の全ての段階で全モル数はa+b+c=一定である。またHIが2xモルできた段階では、H2は(a-x)モル、I2は(b-x)モルに減じている。
従って平衡定数は
となる。
Bodensteinによると448℃に於いて、22.13ccのH2と、16.18ccのI2を混ぜて平衡状態を実現すると25.72ccのHIが検出された。従って448℃に於ける上記の反応の平衡定数は
となる。
1900年ころW.Nernst および F.Haber は“流動法”と言われる実験的手法で工業的に重要な気体反応に関して先駆的な研究をした。
流動法では、反応気体が完全に平衡に達するように、混合気体を充分に遅い速度で、一定温度に保った加熱管中を通過させる。この流速条件は、実測反応率がそれ以上変化しなくなるまで少しずつ流速を下げてゆくことで調べられる。また、この方法では反応管中に種々の触媒を設置することで、それらの触媒の効果も計測することができる。
反応管から出てきた気体は平衡状態が変化しないように冷却され、その後に分析される。
その重要な一例が、鉄触媒を用いた場合と、用いない場合の両方について研究された“水性ガスシフト反応”です[Z. anorg. Chem., 38, 5 (1904)]。
この反応も総モル数は変化しない(Δν=0)から
が成り立つ。
初めのH2、CO2、H2O、COのモル数を、それぞれa、b、c、dとすると、平衡状態では
となる。
平衡定数を分圧で表した式(Δν=0の場合、モル数orモル分率での表現に一致)
に、温度986℃(1259K)に於ける成分気体の分析から得られた観測値を代入すると下表のようになる。
初めの濃度比が変化しても、平衡に達したときの平衡定数KP(=Kc=KX)は変化しないことが確認できる。
[補足説明1]
“水性ガスシフト反応”に対して、熱力学第三法則を適用して得た熱力学データを適用すると
が得られる。
この値は986℃に於けるKpの値に比較して圧倒的に小さいから、25℃に於ける平衡は圧倒的に左側に片寄っている。
[補足説明2]
“水性ガス”(H2とCOの混合物)は赤熱したコークスに水蒸気を通じて得られる。
この反応は、H2やCOを得る方法として、工業的に重要な地位を占めている。このとき発生するH2とCOは、当然H2OやCO2と反応するわけですから、上で説明したシフト反応の知見は重要です。
“水性ガス発生反応”について補足すると、熱力学第三法則を適用して得た熱力学データから次の値が得られる。
これは気体の分子数が増す反応ですからΔS゜>0です。常温ではΔG゜298=91.40[kJ/mol]>0ですからKP298<<1となり、平衡は圧倒的に左に片寄っている。しかし、高温になるとΔG゜=ΔH゜-TΔS゜<0となり、KPは温度とともに増大して、平衡は高温で右にずれる。
水性ガス生成反応は吸熱反応(ΔH゜>0)だから、“ル・シャトリエの原理”から言っても高温で平衡は右にずれる。
[補足説明3]
“ル・シャトリエの原理”とは、1888年に Henry Le Chatelier が唱えた原理で以下のように表現される。
“平衡にある系の状態を決定する変数のどれか一つに何らかの変化が起こると、平衡の位置はその変数の変化を減殺する方向にずれる。”
平衡定数を掛け算する事で、別の反応の平衡定数を計算できる場合がある。これは既知平衡定数が利用できる実利性の高い原理です。
例えば、[水蒸気の解離反応]と[水性ガスシフト反応]の平衡定数から、[二酸化炭素解離反応]の平衡定数が計算できる。
3.(2)2.で説明したように、平衡定数KPおよびKcは、理想気体の場合には圧力に無関係であるが、KXは圧力に依存する。すなわち
となる。
このとき、反応が系に含まれる気体の総モル数の変化をもたらさない場合(Δν=0)は、3.(3)1.で述べたように、KP、Kc、KXは全て一致する。すなわち理想気体反応ならば平衡位置は全圧に無関係です。
総モル数が変化する(Δν≠0)場合は、平衡定数KXは圧力とともに変化する。
そのとき、反応に伴って総モル数が減少するとき(Δν<0)は、圧力を高くするとKXは増加する。
一方、反応に伴って総モル数が増加するするとき(Δν>0)は、圧力を高くするとKXは減少する。
これは“ル・シャトリエの原理”の一つの現れです。
Δν≠0である反応の重要な例が“解離反応”です。中でも工業的に重要な“四酸化二窒素と二酸化窒素の解離平衡反応”(Δν=+1)は詳しく研究された。この反応は二酸化窒素から硝酸を製造する過程で非常に重要です。
最初1モル存在した四酸化二窒素が解離平衡状態にあるときの“解離度”をaとすると、N2O4が(1-a)モル、NO2が2aモルあることになる。その時の総モル数は (1-a)+2a=1+a です。従って
解離が進むにつれて、実測される圧力はN2O4の1モルに対して理想気体法則から計算される値よりも大きくなる。解離していないときの圧力Pidealとすれば、解離平衡時の圧力Pobsを測定すれば解離度aは直ちに計算できる。
実際の測定値は、318℃、1atmでa=0.38であった。従ってKX=4×0.382/(1-0.382)=0.67となる。また318℃、10atmでは、a=0.128、KX=4×0.1282/(1-0.1282)=0.067であった。
上記の解離度を平衡定数を用いた式で表すと
となる。このとき、25℃に於ける平衡定数は標準生成自由エネルギーの数表データを利用して導ける。すなわち
となるので、25℃に於ける解離度aの理論値は
となる。つまり、圧力が高いと重合が進み、低いと解離が進む。この値を前記の318℃における観測値と比較すると、温度が高まると解離が進むことが解る。
実際、この反応の熱化学方程式は、数表データから
と表されるので、この解離反応は吸熱反応です。そのため温度を上げると右側のNO2の割合が増える。NO2は赤褐色、N2O4は無色の気体なので平行移動が色の変化で解る。しかも、前述のように常温・常圧付近で平衡状態にあるので、ガラス管や注射器に詰めて下図の様な状況にすると、温度変化や圧力変化に対する“ル・シャトリエの原理”が簡単に確認できる。高校化学の演示実験として最適です。
[補足説明]
“単体気体”の解離平衡の例を下表に示す。これらのデータは高温気体反応や高層大気圏の研究で重要です。
“解離反応”は吸熱反応ですから、温度が上昇するにつれて平衡定数は増大している。つまり平衡はより右側へ片寄る。これも“ル・シャトリエの原理”の一つの現れです。
気相反応系に“不活性ガス”を添加した場合の平衡条件の変化を考察する。
まず、総モル数が変化しない反応ではΔν=0だから、不活性ガスを添加しても平衡時の混合ガス組成に変化は生じない。
しかし、Δν≠0の場合には、モル分率および全圧Pを計算する際に影響が出て来るので、平衡時の反応物の割合が影響を受ける。
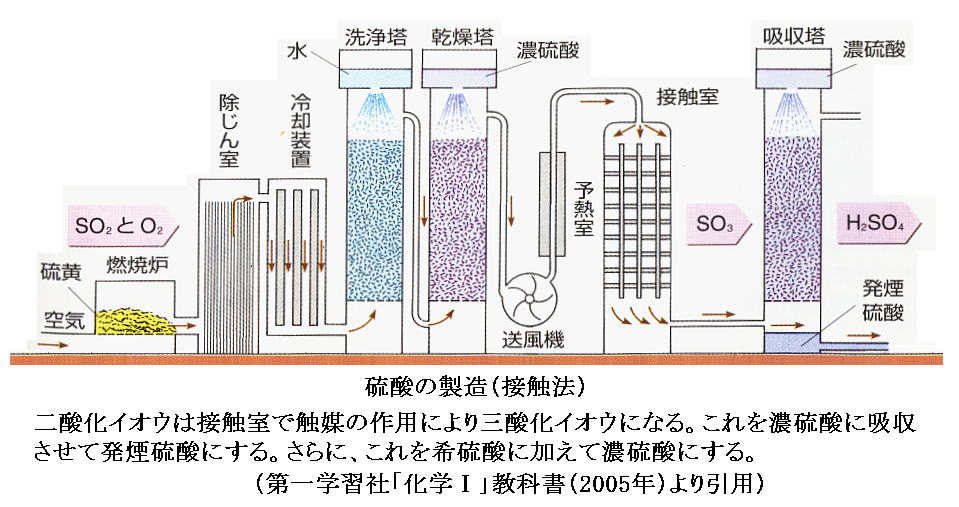
例として、“二酸化イオウの酸化反応”(Δν=-1/2)
を考察する。これは硫酸を製造する過程で必要な反応で、化学工業でとても重要です。ちなみに、SO3の1気圧下に於ける融点は16.9℃、沸点は45℃です。
初めの状態でSO2、O2、N2(不活性ガス)、SO3がそれぞれ、a、b、c、0モル存在したとする。平衡時にyモルのSO3ができているとすると、平衡時のモル分率は次のようになる。
そのため、平衡時の平衡定数は
を満足する。ここで三つの場合を考える。
例として、1atm下で総モル数1mol(20%SO2、80%O2)の場合と、同じく1atm下で総モル数1mol(2%SO2、8%O2、90%N2)の場合を比較してみる。このとき平衡時の温度を800K(527℃)とする。
平衡定数の温度依存性についての求め方は3.(3)7.で説明するが、この反応の平衡定数の温度依存性は logeKP=(22600/RT)-(21.36/R) で表される。この式から800KではKP=33.4となる。
[20%SO2と80%O2の場合]
[2%SO2と8%O2と90%N2の場合]
計算のように、窒素が多量に混入していても、SO2→SO4への転化率はそんなに変化しない。そのため、工業的には“空気”によってイオウを燃焼させた燃焼ガスがそのまま用いられる。
この反応は、発熱反応であるから、反応温度を上げると生成物のできる割合が減る。実際上は、反応が充分高速で起こり、しかも生成物の収率が落ちない温度で行う事が重要になる。工業的には500℃付近の温度が選ばれ、反応促進のために白金あるいは五酸化バナジウム触媒が用いられる。
気体のみの反応については、各気体のギブズの自由エネルギーが、その成分の分圧に依存することから任意の条件におけるギブズの自由エネルギー変化を求めその変化が0として平衡定数を求めた。
気体の他に、純粋な液体や固体が反応に関与するときには、取り扱いが少し変わってくる。なぜならば、液体や固体のギブズの自由エネルギーは圧力が変化しても、気体に比べて無視できるほどしか変化しないからです。例えば別稿の3.(3)1.[補足説明3]の酸素と水の計算例を参照。
例として“CaCO3の分解反応”を考える。
任意の条件におけるCaCO3とCaOのギブズの自由エネルギーGCaCO3とGCaOは、上に述べたように標準状態(1atm)の値としてよい。また、CO2の自由エネルギーは、CO2の分圧をPCO2とすると
で与えられる。従って任意の温度、圧力下におけるギブズの自由エネルギー変化ΔG(T,P)は次式で与えられる。
このように、純粋な成分の凝縮相(液体や固体)が反応に関与する場合には平衡定数は気体成分の分圧のみで与えられる。
CaCO3を真空にした密閉容器中で、例えば750℃(1023K)に加熱したときの様子を調べてみる。このとき、750℃に於いてCaCO3がCaOとCO2に分解するときの“標準(1atm)ギブズの自由エネルギー変化”はΔG(T,P0)=+21190J/molであることが解っているとすると、この温度に於ける平衡時の炭酸ガス分圧として
が得られる。
このことは、真空中で加熱したとき、容器内の炭酸ガス分圧が0.083atmになるまで、CaCO3の分解が続くことを意味する。完全に分解するには、CaCO3の周囲の炭酸ガス圧が常に0.083atm以下になるようにしてやらなければならない。このとき、他のガスが存在してもこの平衡関係の維持には関係しないことに注意。
これは、非常に面白い事実で、もし真空容器が、1.(2)で説明したような、重りで圧力が調整できるピストンが付いたシリンダーであったならば、水の蒸発と同じ様なことが生じる。つまり750℃ではシリンダー内の圧力が0.083atmより僅でも低ければ炭酸カルシウムは完全に分解するまで炭酸ガスの発生が続く。一方、僅かでも高ければ、炭酸ガスは全てが酸化カルシウムに吸収されて炭酸カルシウムとして固定されてしまう。
この当たりは相律の自由度と関係する事柄で、別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」3.(2)2.ですでに説明した。
このとき、容器内温度が変われば、この臨界圧力は下図の様に変化します。
次項3.(3)7.で説明するように水と水蒸気の平衡も、ここと同じ様な議論で説明できる。上図のグラフは縦軸をlogeKP=logePCO2にしているので解りにくいが、縦軸をPCO2にして温度の関数として見れば、まさに水と水蒸気の平衡に於ける蒸気圧曲線P水蒸気(T)に相当する図です。
もう一つ例として“酸化銅の還元反応”を考える。
の25℃(298K)に於ける平衡定数は、標準生成自由エネルギーの数表データが利用できるので
となる。
つまり、平衡は圧倒的に右側に片寄っている。従って、常温(25℃)では酸化銅は一酸化炭素によってどんどん還元されて金属銅に帰って行くことが解る。
前項3.(3)6.の考察を利用して液体と気体の平衡を考える。
水は大気圧(1atm)下では100℃で沸騰する。これは水の蒸気圧が100℃で1気圧になるためです。100℃では、1気圧の水と1気圧の水蒸気のギブズの自由エネルギー値は等しく、二つの状態は釣り合っています。しかし、100℃以下では水の方が安定であるから、1気圧の水蒸気よりも1気圧の水の自由エネルギーの方が小さい。100℃以上では水と水蒸気の自由エネルギーの大小関係は逆転する。この当たりは2.(2)ですでに説明した。
100℃以外の任意の温度に於ける蒸気圧はいかにして求めたら良いであろうか。それには前項3.(3)6.の考え方が利用できる。
の平衡に於いて、液体のギブズの自由エネルギーは圧力が変化してもほとんど変化しないと考えて良いので
となる。
ちなみに、数表データからT=T0=298K(25℃)に於けるΔG(T0,P0)=G水蒸気(T0,P0)-G水(T0,P0)=ΔGf゜水蒸気-ΔGf゜水=228580-(-237190)=8610J/molであるが、この値用いると
となる。実測された25℃の蒸気圧は0.03126atmですから、確かにそれなりの値が得られる。
任意温度Tに於ける蒸気圧を求めるには、(TK、1atm)に於ける水と水蒸気の標準生成ギブズの自由エネルギーの値が必要です。しかし、数表データとして与えられているのは(25℃、1atm)に於ける水と水蒸気の標準生成ギブズの自由エネルギーです。これから任意温度T、1atmに於けるデータを求めなければならない。このときやり方は二通りある。
一つは(25℃,1atm)におけるΔGf゜水蒸気とΔGf゜水から、エントロピーのデータを用いて(T,1atm)に於けるG水蒸気(T,P0)とG水(T,P0)を求める方法です。すなわち
となる。この式でT=298K(25℃)を代入すると、前記の0.031atmが確かに得られる。
もう一つは、上記の式を“ギブズ・ヘルムホルツの式”に代入して、定圧下に於ける各温度のΔH(T,P0)すなわち蒸発エンタルピーのデータを積分して求める方法です。
これは、別項「ファン・デル・ワールスの状態方程式」4.(4)で説明した“クラウジウス・クラペイロンの式”を用いて導いた式と同じです。
この二通りのやり方は
であることを考慮すると全く同じグラフを与えることが解ります。
これらのグラフは、観測値を旨く説明する。
真空容器の中で水を蒸発させて得られる水蒸気圧は25℃で0.03126atm(23.756mmHg)です。いま、この容器内に、水に溶けない不活性ガスを入れて圧力を1atm→10atm→100atmと増大させたとき、水蒸気圧がどのように変化するか調べてみる。この考え方は3.(3)5.項と同じです。
水に圧力をかけると、水のギブズの自由エネルギーが増加する(別稿の3.(3)1.[補足説明3])から、圧力をかけない(ただし水蒸気による圧力はかかっている)ときに水と平衡状態にあった水蒸気のギブズの自由エネルギーよりも、圧力をかけられた水のギブズの自由エネルギーの方が大きくなる。
従って、水蒸気が圧力をかけられた水と同じ自由エネルギーを持つ(平衡になる)ためには、水蒸気の圧力も増加しなければならない。
前節3.(4)7.では、水の自由エネルギー変化は水蒸気に比べて大きくないので、その変化を無視して議論したのだが、ここではその効果を考慮して議論してみようということです。
水(液体)と水蒸気(気体)の圧力変化に伴う自由エネルギーの変化は別稿「熱力学関数(状態方程式曲面)の性質」3.(3)1.[補足説明3]で説明したように
となる。
簡単にするために、今は温度T=25℃(298K)の場合で圧力を変える。また圧力をかける前の最初の圧力(すなわち25℃に於ける蒸気圧)をP0とする。その時は当然のことながらG水(T、P0)=G水(25℃、23.756mmHg)=G水蒸気(25℃、23.756mmHg)=G水蒸気(T、P0)が成り立っています。
P0=1atmの場合には省力していたP0ですが、今回はP0=0.03126atmですから省略せずに書いています。
ここで、不活性気体を封入して圧力を高めたときの圧力をPとする。このPは当然不活性ガスの分圧と水蒸気の分圧の和です。
圧力をかけた状態ではG水(T、P)=G水蒸気(T、P水蒸気)が成り立つので
となる。
具体的な値を計算するために、圧力をatmで表し、体積をcm3で表すことにする。そうすると気体定数Rもatm・cm3/K・molで表したものを用いる必要がある。
これらの値を代入して25℃(298K)に於ける計算値を求めると以下のようになる。
元々液体の圧力変化による自由エネルギー変化量はごく僅かだから、外圧による飽和蒸気圧の変動もごく僅かです。そのために、前節3.(3)7.の様な近似計算ができたのです。
ところで、一般のハンドブックに記載されている液体の蒸気圧表は、他の気体が存在しない場合の値です。そのため、他の気体が存在する場合に、その値を用いると上記の程度の誤差が生じることを心にとめておく必要があります。
最も簡単な反応
を例として、“反応率”αと[温度T]、[標準ギブズの自由エネルギー変化ΔG(T,P0)]との関係を考察する。反応率とは最初存在したAの内からBへ変化したものの割合のことです。最初にAが1mol存在したとすると、平衡時にはAは(1-α)mol、Bはαmol存在することになる。
いま平衡状態に於ける反応容器中の全圧をP、AとBの分圧をPAおよびPBとすると、
が成り立つ。
平衡定数KPはPB/PAであるから
が得られる。
幾つかの温度で、ΔG(T,P0)に対して反応率αをプロットしてみると
のようになる。このグラフは最初に述べた形の反応ならば、どのようなものでも一般的に成り立ちます。そのとき、ΔG(T,P0)の横軸の値は同じ反応系でも温度が異なれば変化することに注意してください。
また、これはΔν=0の反応ですから、反応率αは、反応容器の全圧Pに依存しません。そのため上記のグラフは1atmに限らず、任意の圧力Pで成り立ちます。
反応率を平衡定数KPで表すと
となる。
この“反応率”αは、3.(3)4.の四酸化二窒素の解離平衡(Δν=1)における“解離度”aに相当しますが、その時には
となって、全圧Pに関係し、しかも平方根であったことを思い出してください。
例としてノルマルブタンがイソブタンに変化する反応の反応率を計算してみる。25℃(298K)、1atmでの自由エネルギー値を数表データから拾い出して計算すると
となり、グラフ中の値が得られる。
このとき、反応容器の温度を500K→1000K→2000Kと温度を上げていくとΔG(T,P0)の値は変化していきます。その変化した値と新温度のグラフ曲線の交点からαが求まる事になります。ΔG(T,P0)の温度変化については次章4.で詳しく説明します。
もう一つ注意すると、実際には25℃に於けるノルマルブタンからイソブタンへの変化は非常に遅く、触媒がないとこの平衡に到達するのは難しい。2.(2)[補足説明3]で注意したように、平衡を達成する速度は全く別の因子が決めています。
以上の考察から解るように、色々な反応に対して標準状態(T、1atm)に於けるギブズの自由エネルギー変化ΔG(T,P0)=ΣνiGi(T,P0)が解れば平衡定数KPが計算できる。
そして、ΔG(T,P0)<0ならその反応は進行し、逆にΔG(T,P0)>0なら反応が逆に(右から左へ)進む事になるのですが、このとき注意すべきことが二つある。
一つ目は、反応物と生成物を含めた反応系の温度Tと全圧Pは常に一定でなければならないことです。
つまり反応が進むにつれて系の温度や圧力は変化してきますが、そのとき反応が進んでも系の温度や圧力は常に一定になるように外界と[熱]や[体積変化に伴う仕事]をやり取りして一定温度・一定圧力が常に保たれている。そういった状況での反応の平衡定数である事を忘れないでください。
二つ目は、平衡定数を示すときには、温度の他に必ず対応する反応式が解るように表示しておく必要がある(そのとき左右の位置関係も重要)。なぜならば、反応式の係数によって標準自由エネルギー変化も異なるからです。
3.(3)4.の例で説明すると、25℃(298K)に於いて
の様に、二つの反応式に対応して平衡定数も異なった形で与えられる。
しかし、いずれを用いてもPNO22/PN2O4は同じ値になるので、温度が同じなら反応率(解離定数a)は同じになる。
KPの温度変化を知ることは、反応に伴うギブズの自由エネルギーの変化の温度依存性を知ることです。ギブズの自由エネルギーの温度依存性は別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(3)2.で説明したように、“ギブズ・ヘルムホルツの式”により、反応のエンタルピー変化の温度依存性から求めることができる。
すなわち
を温度に関して積分すればよい。
この左側の式を“ファントホッフ(van't Hoff)の定圧平衡式”(reaction isobar)という。この式は、吸熱反応(ΔH゜>0)の場合には平衡定数が温度とともに増大し、発熱反応(ΔH゜<0)の場合には平衡定数が温度とともに減少する事を示している。これは“ル・シャトリエの原理”の一つの現れです。
また、右側の式は、logeKPを1/Tに対してプロットしたグラフの勾配は各温度に於ける-ΔH゜/Rに等しいことを示している。
例として 2HI(g)→H2(g)+I2(g) の平衡定数の温度変化を示す。[A.H.Taylor,R.H.Crist, J. Am. Chem. Soc., 63, 1377 (1941)]
この場合グラフはほぼ直線となり、実験温度範囲でこの反応のΔH゜がほぼ一定であることが解る。勾配から計算した反応エンタルピー変化は、図中の温度範囲(T=650~770K)ではΔH゜=12.33kJ(2945cal)です。ただし、この値は
2HI(g)→H2(g)+I2(g) についてのものです。この点については3.(4)の説明に留意されて下さい。
この温度領域では反応式右側の物質の方がエンタルピー値は大きいので吸熱反応です。吸熱反応(ΔH゜>0)の場合、このグラフの様に右下がりになります。もし発熱反応(ΔH゜<0)であったらグラフは右上がりになります。これは“ル・シャトリエの原理”そのままです。エンタルピー変化と発熱・吸熱の関係は解りにくいところですが、別稿1.(2)を復習されてください。
また、ここでのΔH゜値の単位に/molが付いていないことに注意してください。そうなることは、元々の3.(1)3.の議論を復習されれば納得できます。
[補足説明]
ところで、数表データから解る標準状態(25℃(298K)、1atm)における HI の“標準生成エンタルピー”はHf゜=26kJ/molです。標準生成エンタルピーを表す反応式は 1/2H2(g)+1/2I2(s)→HI(g) ですが、この式は上記の式と左右が逆で両辺を1/2倍したものです。
この反応はHf゜>0の吸熱反応ですから、25℃(298K)、1atmではHIの方がエンタルピー値が高くなります。上記の温度範囲とは逆に、25℃で HI 側のエンタルピー値が高くなるのは、25℃、1atmで安定なヨウ素の単体は固体で、それからHIを生成する反応だからです。ちなみに、ヨウ素の融点は114℃(融解熱15.5kJ/mol)、沸点は184℃(蒸発熱41.6kJ/mol)です。
ある一つの温度での平衡定数の測定値があれば、反応熱データから得られるΔH(T,P0)の温度依存性データを用いて、他の温度に於ける平衡定数を計算する事ができる。
つまり、前述の式を積分すればよいのですが、そのとき温度変化幅が小さい場合には
となる。
もし、二つの温度での平衡定数が実験的に求まっていれば、逆にその温度付近での反応にともなうエンタルピー変化ΔH(T,P0)が導ける。
例として I2(g)→2I(g) の解離反応を取り上げる。900℃(1173K)と1100℃(1373K)に於ける平衡定数は、それぞれ0.0474と0.492であることが観測から解っている。このデータから、この反応の反応熱ΔH゜を求めると
となる。もちろん、この値はT=900~1100℃付近での値であることに注意。
ちなみに、298Kに於けるヨウ素分子I-Iの結合エネルギーはΔH゜298=149kJ/mol程度です。
温度変化幅が大きい場合、積分に於いてΔH(T,P0)のデータが必要になる。これを知るには反応物と生成物の熱容量Cpが積分温度範囲で温度の関数として解っていることが必要です。
例えば、気体の熱容量が
で表され、各種の気体についてα、β、γの値が実験観測から
で与えられている場合には
となる。Δは考察している化学反応の生成物と反応物のそれぞれの和の化学量論的な差分を意味する。そして、ΔH(T0,P0)は(25℃、1atm)での反応エンタルピー変化です。
これを、前述の式に代入して積分する。
となる。
この場合ΔH(T0,P0)は化学反応熱の測定から解っているので、KPの値がどこか一つの温度で実験的に定まっていたら積分定数 I を決定することができる。そうして I が決定できれば、任意の温度に於ける平衡定数KP(T,P0)を計算する事ができる。
例として“水性ガスシフト反応”
の平衡定数KPを温度の関数として求めてみる。
1.まず実験によると標準状態(1atm,25℃)における平衡定数はKP=9.55×104が解っている。
2.つぎに、標準状態(25℃,1atm)における、この反応の標準エンタルピー変化は、数表として与えられている反応熱データから
であることが解る。
3.さらにΔCPの温度変化関数を求めるのに前記の表を用いる。ただし、ここでは[cal/K・mol]を[J/K・mol]に直して用いる。
4.エンタルピー変化式の定数決定 これらの結果を用いると
を得る。
この値が ΔH(T0,P0)=-41190 と一致しないのは奇妙に見えますが、矛盾はありません。こうなるのは、熱容量の温度変化を上記の様な式で表したために出てきた積分定数のためです。
つまり、熱容量の温度変化を表す式が仮にT→0Kまで正しいとしたときに、この値は0Kに於ける反応に伴うエンタルピー変化を表しています。ただし、もともとの熱容量の温度変化式は低温領域では成り立たないのですから、実際に0Kに於いてそうなる訳ではありません。
そうなるわけではないのですが、この様に定めておくと、最初の式のTに298Kを代入すると確かにΔH(T,P0)=-41190=ΔH(T0,P0)となりますし、熱容量の温度変化式が正しい温度範囲では正しいΔH(T,P0)を与えてくれます。
この値を用いたΔH(T,P0)のグラフは以下のようになる。
ちなみに、800KではΔH(800,1atm)=-37105[J/mol]となり、1200KではΔH(1200,1atm)=-32592[J/mol]となる。
5.積分定数 I の決定 次に、実験から求まっている標準状態(1atm,25℃)における平衡定数KP=9.55×104を用いると
となって、積分定数 I を定めることができる。
6.最終結果 従って平衡定数の温度変化の式は
となる。このとき、Tに298Kを代入してみればlogeKP=11.467、KP=95500となり、確かに初期条件をみたしている。
この式を用いれば、任意の温度の平衡定数が求まる。
例えば800KではlogeKP=1.33、KP=3.76となり、1200KではlogeKP=-0.437、KP=0.646となる。これから、温度により平衡状態が劇的に変化することが解る。
このように化学に応用された熱力学は、熱的なデータのみから平衡の位置を計算する定量的な方法を与えてくれる。これは、化学親和力に関して存在した昔の疑問に対する解答を与えており、偉大な成果です。
[補足説明1]
上記の例に於いて、実験による測定からKPを求めて、それから
の式を用いてΔG(T,P0)を求めることができる。
そうしても求まったΔG(T,P0)をΔH(T,P0)のグラフと並べて描いてみると
となる。
このとき、
の関係があるが、この式に於いて熱力学第三法則が正しい限りT→0と共にΔS→0となるので、ΔG(T,P0)とΔH(T,P0)はT→0で接する様にして一致するはずです。図の温度範囲の変化の様子からそのことは伺える。
[補足説明2]
3.(3)2.[補足説明1]で標準状態(298K,1atm)に於ける“水性ガスシフト反応”のΔHf゜、ΔS゜、ΔGf゜を計算しましたが、そこの値とここの値の正負符号が逆に成っているのは反応式の左右を逆にして考えているからです。さらにKP298の値が互いに逆数の関係に成っているのもその為です。
また、絶対値が微妙に異なるのはムーアの本とは異なる数表データを用いたからです。
[補足説明3]
ここで、以下のことに注意してください。
まず平衡定数KPの温度依存性を実験的に測定できると、それから反応に伴うギブズの自由エネルギー変化ΔG(T)が求まります。一方各温度における反応熱の測定値(あるいは一つの温度に於ける反応熱の測定値と各物質の熱容量の温度依存性データ)から反応に伴うエンタルピー変化ΔH(T)が求まります。
この両者から -{ΔG(T)-ΔH(T)}/T=ΔS(T) に依って反応に伴うエントロピー変化の温度依存性ΔS(T)を求めることができる。
一方、熱力学第三法則が成り立つならば別稿「「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」3.(4)1.で説明したように極低温域までを含めた熱容量データから任意温度での反応に伴うエントロピー変化ΔS(T)を求める事ができる。
この二つの方法で求めたΔS(T)が任意の温度で一致することを確かめることができれば、“熱力学第三法則”(ネルンストの熱定理)が検証できたことになる。このことは検証方法の例として[例証2.平衡定数&反応熱、電池起電力]ですでに紹介した。
平衡定数KPは実験によって測定できます。このとき、4.(1)の最初で述べたように、平衡定数KPは反応によるギブズの自由エネルギー変化ΔGと
の関係にありましたから、平衡定数の温度依存性KP(T)が実験的に測定できればΔG(T)=-RTlogeKP(T)によって反応に伴うギブズの自由エネルギーの温度依存性が求まります。この様にして求めたΔG(T)と、様々な温度に於ける反応熱データから得られた反応に伴うエンタルピー変化の温度依存性ΔH(T)を用いれば、反応に伴うエントロピー変化の温度依存性ΔS(T)が求まります。その様にして得られるΔS(T)=-{ΔG(T)-ΔH(T)}/Tは、4.(3)[補足説明3]で述べたように、熱力学第三法則を満たしているはずです。
この当たりは、以前述べた式変形を逆にたどってみれば明らかです。
この考え方には、熱力学の根本に関わる事柄が関係しています。
別稿「熱力学関数(状態方程式曲面)の性質」3.(4)2.で説明したように、“ギブズ・ヘルムホルツの式”は[ΔH]と[ΔGの温度偏微分係数]を結び付けるものです。その関係から明らかな様に一定圧力の元でのΔGの温度依存性が解ればエンタルピー変化ΔHの温度依存性は確定します。しかし、その逆は言えません。ΔH(T)が解ったからといって、それをTで積分して得られるΔG(T)には積分定数だけの不定性が現れるためです。そのためΔGを完全に決定することはできません。
その不定性は、別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」3.(1)で説明したように、もともと状態量Hから状態量G=H-TSを構成するときにTSという項が関わる為にS0T+定数という絶対温度の一次式が不定になることに由来しています。
ここに“熱力学第三法則”が絡んでいるのですが、もし第三法則が正しくて“T→0に於いて物体のエントロピーは全て0になる”が言えるのなら、別稿「熱力学関数(状態方程式曲面)の性質」3.(2)2.[補足説明1]に説明したグラフの関係が成り立ち、上記の積分定数 I の不定性は無くなりΔHとΔGの間の関係が確定します。
別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」3.(4)1.[補足説明1]で説明したように、熱力学第三法則が成り立てば純物質のエントロピーの絶対値を熱容量の実測に基づいて決定することができます。その具体的な方法は別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」3.(4)1.で説明しました。
任意の物質のエントロピー値が解っていれば、ギブズの自由エネルギーは、エンタルピー(反応熱)の実測値から G=H-TS に依って計算することができます。その当たりは別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(2)2.で説明しました。
そのとき、そこの[補足説明2]や[補足説明3]で説明したように、任意の化学反応変化に伴うギブズの自由エネルギー変化ΔGも同様に計算に依って求めることができます。
つまり、任意の物質のエントロピー値とエンタルピー値が実測に依って(温度や圧力の関数として)解っていれば、任意の物質の任意の温度や圧力のギブズの自由エネルギー値が計算できます。そうすると任意の温度・圧力における化学反応に伴うギブズの自由エネルギー変化ΔGも計算できますから、その反応の平衡定数も計算で求まる事になります。その当たりの関係をまとめると下図の様になる。
化学反応は平衡に到達するのに時間がかかるものが多い。また、高温や低温に於ける様子を実験で確かめるのは困難な場合が多い。その様な時に熱的な測定データから、様々な温度の平衡定数を計算によって求めることができる事は、熱力学の化学分野に於ける偉大な成果です。
[補足説明]
いまや、本質的な課題はいかにしてG(T,P)を求めるかです。
そのことを説明した文献5.のEverettの説明は興味深いので引用しておきます。
この中の統計力学的方法については文献10.プランク「理論熱学」§143~§150も参照されたし。
また、この当たりの量子力学との関係を含めた解説はK.メンデルスゾーン著「ネルンストの世界」岩波書店(1976年刊)の第4章やアブラハム・パイス著「神は老獪にして・・・」産業図書(1987年刊)のp527~531をご覧下さい。
4.(3)で取り上げた例と同様ですが、今一度“アンモニア合成反応”を取り上げる。この反応の熱力学的量の計算は別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(4)ですでに説明した。
そこでは、この反応に伴う“エントロピー変化”ΔS、“エンタルピー変化”ΔH、“ギブズの自由エネルギー変化”ΔGの温度依存性のみを求めて、圧力依存性に関しては、計算が面倒なのでやらなかった。
しかし、この稿での議論の様に気体反応に限る場合、それらの量の圧力依存性は“理想気体の状態方程式”に従うとして計算できる。それが3.(1)1.でおこなった議論です。そうして計算されるΔG(T,P)を用いて任意圧力・任意温度に於ける平衡定数を、標準圧力(1atm)の任意温度に於けるギブズの自由エネルギー変化ΔG(T,P0)に結び付けたのでした。3.(1)3.で注意したように、そこで得られる関係式
は、任意の温度に於いて正しい。
別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(4)2.で、任意温度に於ける反応のエンタルピー変化ΔH(T,P0)はすでに導かれている。
最初に、この結論を用いて任意温度の平衡定数logeKP(T)を求めてみる。
そこの結論から1モルのアンモニアが生成する反応
の任意温度(標準圧力)における反応エンタルピー変化は
でした。
ただし、そこでの計算には、ムーアの本の熱容量データではなくて原田の本の熱容量データのタイプ(B)を用いている。そのためTの関数形が4.(3)の例と少し異なっています。以下の説明に於いても同様です。
今考えている
の反応の場合、上記の生成熱を2倍した
を用いなければならない。2倍する理由は3.(4)の説明を参照。
これを4.(1)で説明した式に代入すると
となる。
ここに未定の積分定数 I が出て来ることに注意。これは元々ΔG(T)の温度偏微分がΔH(T)に結び付けられていた事から出てきたことです。ΔG(T)が決まればΔH(T)は一意に決まりますが、逆はそうなりません。ΔH(T)が与えられてもΔG(T)には積分定数だけの不定性が存在します。これが熱力学第三法則に関係するのでした。[別稿の3.(4)参照]
この式に、例えばT=298K,P=1atmにおけるKPの観測値を代入して積分定数 I を決定する。
あるいは、観測値の代わりに、標準状態(298K,1atm)に於けるアンモニア生成のギブズの自由エネルギーΔG(T0,P0)=-16.44×103J/molを2倍したものを用いて積分定数 I を決定しても良い。つまり、logeKP=-(-16.44×103×2)/(8.314×298)=13.271→KP=Exp[13.271]=5.80×105を用いても良い。
そうすると
となる。
よって
が得られる。
[補足説明1]
積分定数 I を決定するときに、標準状態(298K,1atm)に於けるアンモニア生成のギブズの自由エネルギーΔG(T0,P0)=-16.44×103J/molの2倍した値を用いて計算しても良いとしたが、このとき用いる特定温度に於けるΔG(T0,P0)を決定するとき、特定温度に於けるΔS(T0,P0)の値を用いています。そのため、そこですでに“熱力学第三法則”が用いられています。
別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(4)3.に於いて、ΔH(T,P0)とΔS(T,P0)の値からすでにΔG(T,P0)の関数形が求められている。
これを用いてもlogeKP(T)を求めることができる。
この結論を上記の式に代入してlogeKPを求めてみよう。ただし、ここでもこの値を2倍したものを用いなければならない。
これは、ΔH(T,P0)の積分と、ある特定温度のKP実験観測値から求めた前項1.の式と完全に一致する。末尾の値が微妙に異なるが、それは計算誤差による。
[補足説明2]
この稿の計算では不定の積分定数は現れず、最終的な結論が直接導ける。それはΔG(T,P0)を求めるときに用いたΔS(T,P0)の計算中に“熱力学第三法則”が用いられており、積分定数の不定性がその時点で解消されているからです。
だから、もしアンモニア生成反応のKP(T)実験観測値がこの公式から得られるKP(T)と一致すれば、それはとりもなおさず“熱力学第三法則”(ネルンストの熱定理)が検証されたことになる。
このことは、4.(3)[補足説明3]で注意したことと同じです。また、文献5.(ネルンスト)や文献6.(プランク)で熱力学第三法則の検証として繰り返し取り上げられている事柄です。
この二つの文献を正確に理解するには、文献に引用されている原論分を含めて当時の化学的知識の状況を理解しておくことが必要です。私自身、この二つの文献の内容が完全・詳細に理解できていないのですが、ここで説明した事が解ってから、彼らが展開している論理がやっと理解できました。
プランクが文献6.の最後で述べている様に、あらゆる平衡条件(相平衡、溶解度平衡、解離平衡、凝固点降下、沸点上昇、等水、・・・)に対してここと同様な取り扱いができて、それら平衡定数の実験観測結果と理論値の比較は“熱力学第三法則”の検証となる。
ここで、別稿「電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)」4.(4)3.で得られた“アンモニア生成反応”のΔG(T,P0)のグラフに立ち返って、幾つかの補足をする。
図からΔH(T,P0)がほとんど温度によらないことが解る。これは化学結合の組み替えに伴うエネルギー(ポテンシャルエネルギー)変化が、温度にほとんど影響されないためです。これは別稿「反応熱と熱化学方程式」1.(4)で注意を促した。
またΔS(T,P0)もほとんど温度によらない。もちろん反応物のΣνRSR(T,P0)も生成物のΣνPSP(T,P0)も温度上昇と供に増大するのですが、その差分ΔS(T,P0)は温度が上昇してもあまり変化しないのです。そのためT・ΔS(T,P0)は温度にほぼ比例して変化する。
故にΔG(T,P0)の温度変化はほとんどT・ΔS(T,P0)項に支配される。そのとき、アンモニア生成反応は(298K,1atm)に於ける標準生成エンタルピーがΔHf゜=-45.94[kJ/mol]<0の発熱反応ですから、T・ΔSの効果が効いてこない低温領域ではΔG<0となります。ΔG(T,P0)=0の代数方程式を解いてみれば解るように、T=456Kを境にしてΔG(T,P0)の正負は逆転する。
そのため、次のlogeKPのグラフが示しているように、456Kよりも低温側で反応は右側に、高温側で左側に片寄る。つまりより低温の法がアンモニアの生成率は高い。これも“ル・シャトリエの原理”の現れです。しかし低温では反応速度が遅いので平衡に達するのに時間が掛かる。そのため触媒の開発がとても大切になる。
また、これは生成物側で分子数の減少(Δν<0)する反応だから、圧力を高めるほど平衡はアンモニア生成側へ片寄ります。そうなる理由は3.(3)4.や5.で説明した例の場合と同じです。これも“ル・シャトリエの原理”の現れです。
[補足説明3]
ちなみに、ドイツのハーバー(Fritz Haber)が1909年7月に実験室プラントでアンモニアの合成に成功したときの状況は、175気圧、550℃下でオスミニウム触媒を使って毎時80gの液体アンモニアを生産するというものでした。その詳細は文献7.や文献8.を参照。
平衡反応
について、このΔG(T,P0)(温度Tに於ける標準生成自由エネルギー値を2倍したもの)から計算されるlogeKPのグラフを描いてみると
となる。
これから得られるKPのグラフは
となる。温度と共に急激に変化するので、高温部を拡大したものを右図に示す。
右図から1000Kに於ける理論値を読み取るとKP=3.27×10-7となる。実測値はKP=3.41×10-7であるから再現性は極めて良い。
5.(3)3.[補足説明3]で説明した、1909年のハーバーの実験室プラントにおける“反応率”αを導いてみる。前項で求めたように、任意圧力P、温度T=550℃=823Kに於ける圧力平衡定数は
となる。
最初 1 molのN2と 3 molのH2が存在し、平衡時に (1-α) molのN2と {3(1-α)} molのH2と 2α molのNH3に成ったとする。その時の全モル数は (1-α)+{3(1-α)}+2α=4-2α となり、Δν=2-(1+3)=-2 となります。
復習のために3.(2)2.の議論を繰り返すと
でしたから、前記の値を代入すると
となる。これはαの二次方程式だから簡単に解けて、α=0.194または1.806が得られる。α<1であることを考慮するとα=0.194が答となる。
もし触媒が旨く働いて化学平衡が達成されたら“反応率”α=約19%でアンモニアが得られることになり、ハーバーの得た結果が裏付けられる。
任意の温度、圧力における“反応率”αは、元の式に帰って
が得られるから、KPに
を代入して、様々な温度におけるα(T,P)のグラフを描いてみればよい。
これは、高校化学の教科書でお馴染みのグラフです。
[補足説明4]
アンモニア合成装置の模式図を示す。
高圧下で冷却するとアンモニアは液化するので、アンモニアだけを回収できる。未反応の窒素ガスと水素ガスは再び加圧・加熱して反応容器にもどす。
アンモニア合成法そのものについては文献7.や文献8.等を参照されてください。
アンモニアの語源は、古代エジプトのアメン神殿(ギリシア語でAmmon)の付近で産するロシャ(主成分はNH4Cl)をアンモンの塩(Sol ammoniacus)と呼んだことに由来する。
アンモニア自体は古くから知られていたのですが、近年このアンモニアほど人類の爆発的な増加に大きな影響を与えたものは無いだろう。
人類は農業生産を開始して以来、作物を育てるための窒素肥料の取得に苦労してきた。最初いかに肥沃な大地でも、何年か作物を育て耕作を続けると、土壌はやせてゆき生産性は急速に減少する。人類は古来、このことを防ぐために苦労してきた。
一つは作物を育てる連作の合間に何年かおきに豆類を作付けする事でした。豆科の植物の根瘤に生息するバクテリアが空中の窒素を固定してくれて地力を回復させてくれることを知った。
また、人や動物の排泄する屎尿が肥料としてたいへん有効な事を知った。実際、我々が子供の頃(1950年代)の記憶では、田舎の農業は家庭からの屎尿の回収と畑や田圃への散布を中心としてなりたっていた。
江戸時代の日本では下肥の回収と施肥が社会的なメカニズムとして広範に機能していて、自給自足のエコロジカルなリサイクル社会が形成されていた。(この当たりは 石川英輔氏が書かれた一連の書「大江戸リサイクル事情」「大江戸えねるぎー事情」「大江戸テクノロジー事情」などが面白い)
しかし、増加する人口に食料生産は追いつかなくなる。そのため農家はそれらに変わる肥料となるものを探し求めていた。そんな中で、南米ペルー沖の島々に堆積した海鳥の糞であるグアノが有力な肥料として注目される。一時は世界中からそれを求めて南米のペルーやチリへ、人々が殺到した。我々が高校時代の地理の授業ではその様に習った。しかしやがてそれはすぐに枯渇してしまう。
次に注目されたのは南米のアタカマ砂漠の硝石です。これも肥料の原料として世界中に輸出されます。しかし、そのまま採掘を続ければグアノと同様にやがて枯渇するのは時間の問題でした。
この様に肥料資源の争奪でうろたえる人類資本主義社会の状況が文献7の第Ⅰ部で生々しく説明されています。
その様な状況の中で実現したのがアンモニアの人工合成による空中窒素の固定です。そして、アンモニアから生産される窒素肥料は、屎尿・堆肥に変わって世界の農業を変えました。このことは人類社会を大きく変えます。空中窒素固定法の存在があって、現在の人類は飢えなくてすんでいる。アンモニアがこれだけの人類の増加を支えているのは確かです。
国連の推定では1900年ころの世界人口は19億人程度であった。私が高校生の頃(1965年)教えられた世界人口は36億人でした。そして現在の世界人口は70億人を超えていると推計されている。
20世紀に入ってからの、恐ろしいほどの人口爆発を支えることができたのはひとえに、アンモニアの人工合成技術のおかげです。これほど人口が増大し、現在も増大しつつある人類をいかにして養うか、それは難しい課題です。
ただ一つ言えることは、これだけ人々が増えたからこそ、科学・技術の進歩があり、我々は宇宙のこと、生命のこと、世界のことを知ることができるようになったのだと思います。そういった事の探求に携わる人々を養い、抱えていることができるようになった。少ない人々ではその様な事は難しい。人口がここまで増大して初めて、現在の文明ができあがった。
我々は、この社会の中で基本的な生活(食料を手に入れ生きて行く)をするために、何らかの仕事について社会に貢献しなければ成りません。我々は食料生産の生産性の向上に伴い食料獲得に直接かかわる仕事に就く事は少なく成りましたが、人類社会に何らかの貢献をして生きて行かねばなりません。
文献7.の第Ⅲ部ではBASF社の社長となったボッシュが、会社を発展・存続させ社員を養うために苦労する様子が描かれていますが、BASF社の様な企業の仕事もその一つです。私が就いた教師の仕事もその一つ。建築物を造る建設労働もその一つ、もちろん様々な商品を流通・販売する仕事もその一つ。
人生、食べるために生きるとは言いませんが、でも結局は子供を育て、家族が食べていけるようにするために働くのではないでしょうか。それが幸せということかどうか解りませんが。
同じ事の繰り返しですが、もう一つ例として“エタノールの合成反応”について“平衡定数”と“反応率”の関係を別稿にて説明します。この反応も化学工業で重要です。
この中で、フガシチーについてはまだ説明していませんが、理想気体における分圧をもう少し一般的な場合に拡張した概念です。
この稿は、以下の文献に依存しています。
トーマス・ヘイガーの文献(引用していない第Ⅰ部と第Ⅲ部)にも書かれている事なのですが、アンモニア合成法の発明は、“我々人類が生きて存続していく事とは何なんだろうか?”と考えさせられるテーマですね。
[物理化学関連ページを制作しての独り言]