�@��ԕ������Ȗʂ𒆐S�ɂ��ē���I�ɒ��߂�ƁA�M�͊w�̕Δ����W���̈Ӗ����ǂ�����܂��B
�@���̃y�[�W�́A�ʍe�u��Ή��x�Ƃ͉����i�ϕ����q�Ƃ͉����j�v�W�D�g�M�͊w���@���̉��p�h�̑����ł��B���̍e�̈ꕔ�Ƃ��Ă��ǂ݂��������B�܂��A�ʍe�u�t�@���E�f���E���[���X�̏�ԕ������v�����p���܂��B
�@�g�n�h�Ƃ͕����̏W�܂�̂����ŁA����ȏ�̈Ӗ��͂���܂���B�b���ȒP�ɂ��邽�߂ɁA�����ł͍ł��P���Ȍn���l����B��ԗʂ����肳��A��߂��Ă����g�n�h�Ƃ��āA���͂��C�ӂɕω��ł���s�X�g���ŊO�E�Ɛڂ��Ă���A�܂��C�ӂ̉��x�̔M���Ǝ��R�ɐڑ��E�f��ł��鑤�ǂ����V�����_�[�ɋl�߂��g�������̋ώ��ȕ����h�����グ��B
�@���̗l�Ȍn���l����Ƃ��ɂ́A�n�ƔM��d��������肷��O�E�́A���̂���肪���ÓI�i�t�I�j�ɍs����悤�ɁA���͂≷�x���A���I�ɕω������g�����̎d�����h���g�����̔M���h����ł��Ă���ƈÖق̓��ɉ��肳��Ă���B�Ȃ�����ȍl�������K�v�Ȃ̂��͎������ӏ������S�D���Q�Ƃ��ꂽ���B
�@���ÓI�i�t�I�j�ȔM�̂����ł����ď��߂ăG���g���s�[�̈ړ�������ł��A�n�̏�ԗʂł���G���g���s�[�̒l���m��ł������Ƃ�Y��Ȃ��ł��������B���̓�����̑O���Y��Ă��܂��ƁA�M�͊w���_�͖���Ȃ��Ȃ�܂��B
�@��̓I�ȏƂ��Ă��ʍe�U�D�i�P�j�Q�D�Ŏ��グ���J���m�[�T�C�N���̃V�����_�[���̕������l����悢�B���̂Ƃ��A�����ɍׂ����Ԋu�Őݒu���ꂽ�I�ɔ����ȏd�肪��R�ڂ����Ă���A���̏d��C�Ȃ��Ƀs�X�g�������̃e�[�u���ɍڂ������菜������ł��郁�J�j�Y�����������d�����ƁA�����ɏ����ȗ͂ŁA�V�����_�[�Ɛڑ��E�ؒf�ł���A���I�ȉ��x���z���������̔M������Ȃ�O�E���l����悢�B
�m�⑫�����P�n
�@�@���l�@���Ă���̂́A�V�����_�[���̂������̕����̏�Ԃ���܂�Ηl�X�ȏ�ԗʂ����̌n�ɑ��Ĉ�ӂɒ�܂�ꍇ�ł��B�ʍe�u�K�X���̓T�C�N���v�u���C���̓T�C�N���v�u�Ⓚ�T�C�N���v�������ɂȂ�Ή���܂����A�قƂ�ǂ̔M�@�ւ������Ŏ��グ���n�Ő����ł��܂��B
�@�n�̏�ԗʂ̕ω����O�E�Ƃ���肷��M��d���Ƃǂ̂悤�ɊW����̂��A�܂������̊W�ɂ��ĔM�͊w���@���i�G�l���M�[�ۑ����j�A���@���i���f�p���s���r�j����ǂ�Ȃ��Ƃ�������̂����l�@���܂��B
�m�⑫�����Q�n
�@�M�@�ւȂǂ̎��ۂ̌n�ł́A�m�O�E�Ɖ��x��������M�̈ړ��n���m�O�E�ƈ��͍��̂���d���̂����n���s���܂��B
�@����ɂ��ւ�炸�A�����ł̋c�_�����ɗ��̂́A�g���I�t���̉���h�̌��ŔM�@�ւ̐��\���c�_�ł��邩��ł��B���̂��Ƃɂ��Ă͕ʍe�u�K�X���̓T�C�N���v�P�D�i�P�j�S�D��ʍe�u��Ή��x�Ƃ͉����i�ϕ����q�Ƃ͉����j�v�U�D�i�T�j�Q�D�Ȃǂ��������������B
�@
�@�M�͊w���ł��d�v�Ȏ��͏�ԗʂƂ������t�̈Ӗ��ł��B�g��ԗʁh�Ƃ͌n���\�����镨���̏W�܂�i�O���Ő��������V�����_�[���̕����j�̏�Ԃ����܂�Έ�ӂɌ��܂镨���ʂ̎��ł��B���́A�̐ρA���x�A�����G�l���M�[�A�G���g���s�[�A�M�u�Y�̎��R�G�l���M�[�A�w�����z���c�̎��R�G�l���M�[�A�G���^���s�[�A���X�E�E�E�E�����ׂď�ԗʂƌ�������̂ł��B����Ɋւ��钍�ӎ������ӏ���������B
�@���̉ӏ������ɔM�͊w�Ɍ����d�v�Ȍ��t�����ׂČ���Ă���A���̕��͂ɂ��ׂĂ��Ïk����Ă��܂��B
�@
�@�ʍe�T�D�i�U�j�g�G���g���s�[�̓����h�Ő��������悤�ɁA�O�߂Ŏ��グ���n�ɗ�������M�ʂ̔����������f�p�͊��S�����ł͂���܂���B���̂Ƃ��A�M�ʂ̈ړ��ɂ���Đ�����n�̏�ԕω���\����ԗʂr������ɍۂ��āA���r�����S�����ɂ���ׂ̐ϕ����q����Ή��x�s�ł����B
�@�������A�Ɨ��ϐ����t���u�ł͕s�ւȂ̂ŁA�n�����p���x�����̐ςu�ɕϊ�����B
�@���ꂪ�A�M�͊w���@���̐����\���@���f�p���s���r�@�ł��B�ȉ��̐�����ǂ܂��Ή���悤�ɁA���ׂĂ̋c�_�͂��r�����S�����ł��邱�Ƃ���n�܂�܂��B
�m�⑫�����n
�@�V�k�S�Ȃ���A�r����ԗʂł��鎖�̈Ӗ��������ł�����x�������Ă����܂��B
�@���܁i�t�C�u�j�̓����s���ʍ��W��̓�_�i�t1�C�u1�j�A�i�t2�C�u2�j�ō��l�@���Ă���n�̏�Ԃ��߂܂��B���̂Ƃ��n�֔M���o�����ꂵ����A�d��������肵���肵�āA�n�̏�Ԃ��i�t1�C�u1�j���i�t2�C�u2�j�֕ω������܂��B���̂Ƃ��n�̏�Ԃ��ω����Ă����l�q�́A�i�t�C�u�j�����ʍ��W��̓_�i�t1�C�u1�j�Ɠ_�i�t2�C�u2�j�����Ԉ�̋Ȑ��ŕ\���܂��B
�@��ԓ_���A���̋Ȑ��ɉ����ĕϕ��i���t�C���u�j�����ω������Ƃ��n�ɗ�������M�ʂ����f�p�����t�{�o���u�ł��B�������o�̒l�́i�t�C�u�j�̒l�Ƌ��ɕω����Ă��܂�����A�e�_�ł̒l��p���Ȃ���Ȃ�܂���B���̂Ƃ��i�t�C�u�j�����s���ʍ��W�ɐ����ɂp�f�����Ƃ��ė��������M�ʂ�\�����Ƃɂ���B�܂�ϕ��i���t�C���u�j�ɂ���ė��������M�ʂ��f�p����ԕω��Ȑ��ɉ����Ăp�f�������ɐςݏグ�Ă����킯�ł��B���̂�����̎���͕ʍe�u�ۑ��́v�R�D�̐}���Q�Ƃ���Ă��������B���̂Ƃ������i�t1�C�u1�j���i�t2�C�u2�j�ł����Ă��A��ԕω��̌o�H���Ⴆ���f�p�̐ώZ�l�͈قȂ�B����� �|���f�v���|�o���u �Ōv�Z����d���ʂɂ��Ă����l�ł��B
�@�Ƃ��낪���f�p���A���̔M�ʂ��o���肵���Ƃ��̐�Ή��x�s�Ŋ����������r�����f�p�^�s��ώZ�����l�B�܂�i�t�C�u�j�����s���ʍ��W�ɐ����ɂr�����Ƃ��ĕ\�������n�ɗ��������G���g���s�[�̐ώZ�l�́A���̏�ԕω��̌o�H�ɂ��Ȃ��̂ł��B�܂�r�͂t�A�u�A�o�A�s�Ɠ����l�Ɍn�̏�Ԃ����܂�Έ�ӂɂ��܂��g��ԗʁh�ƂȂ�B�m�Q�D�i�R�j�̂r�i�u�C�t�j�Ȗʂ��Q�����ꂽ���B�n
�@�n���M���ǂ̂悤�Ȍo�H�ɏ]���ďo���肵�Ă��A�n�̍ŏ��i�t1�C�u1�j�ƍŌ�i�t2�C�u2�j�̏�Ԃ����܂�A��Ɉ�ӂɌ��܂���r�����݂��鎖�����������Ƃ��唭���ł����B�����炱���A�M�͊w�����҂͌n�̃G���g���s�[�l���i�s�C�u�C�o�j�̊��Ƃ��Ēm�邱�Ƃɓw�͂���B���̃G���g���s�[�l�̕ω��ׂ�A�n�̔M�̏o�����d���̏o����Ōn�̏�Ԃ͂ǂ̂悤�ɕω�����̂��A�܂��n�ւ̔M�̏o����Ǝd���̏o����͂ǂ̂悤�ɊW����̂����̏���ׂē����o����̂ł��B
�@
�@���̎���́A�O�߂Œ��ӂ����悤�ɁA�Ɨ��ϐ���ς��Ăr�i�t�C�u�j�A�r�i�s�C�o�j�A�r�i�o�C�u�j�A����Ƃ��Ă��܂��������l�ł��B�s�C�o�C�u�C�E�E�E���X�����ׂď�ԗʂł�����A�i�t�C�u�j�̂��ׂĂ̓_�ɉ����Ăs�A�o�A�u�̒l�͈�ӂɌ��܂��Ă��܂��B������ǂ̕ϐ���p���Ă��r����ԗʂł��鎖���͕ς��܂���B���̂�������P�D�i�R�j�A�P�D�i�S�j�A�Q�D�i�R�j�A�ߓ��X���������������B�������A�����̋Ȗʂ����ׂĖ��ɗ��ƌ����킯�ł͂���܂���B�t�Ƃr�����ڑ��肷�邱�Ƃ��ł��Ȃ��ʂł���Ƃ������Ƃ���A�����̋Ȗʂ̗L�p�������܂��Ă��܂��B
�@���̂Ƃ��A�ʍe�U�D�i�S�j�g��Ή��x�Ɛϕ����q�̊W�h�ŏq�ׂ��悤�ɁA�m�i���C�u�j���m�i���j�ƒu����B����ɁA�ʍe�V�D�i�S�j�g�܂Ƃ߁h�ɏq�ׂ����j�ɏ]���āA���s�^������1�Ƃ��Ă����s�Œu�������A�m�i���j���s�Ə������Ƃɂ���B
�@�Ɨ��ϐ����s���u�Ƃ���ƁA��L�̊W��
�ƂȂ�܂��B
�@����͂��f�p���s���r�ł������r�����S�����ł������Ƃ�\���Ă���B����́A�n�̏�ԗʂr���i�r�A�s�A�u�j��Ԃň�̏�ԕ������Ȗʂr�i�s�C�u�j���\�����邱�Ƃ��Ӗ�����B�Ȗʏ�̔����ϕ����r�ɑ��ĕʍe�u��Ή��x�Ƃ͉����i�ϕ����q�Ƃ͉����j�v�T�D�i�Q�j�Ő��������l�ɁA���r�����S�����ł�����������
��������B
�@���̂Ƃ��g��ϔM�e�ʁh�bv�́A���̒�`����
�ƂȂ�܂��B���̎���O�L�̎��ɓK�p�����
�ƂȂ�܂��B��������ڑ���ł��Ȃ��n�̃G���g���s�[�̒�ω��ɉ����鉷�x�ˑ������A����\�ȃf�[�^�ŕ\���d�v�Ȏ��ł��B�܂��A�����[�G���g���s�[]��[��Ή��x]��[�M��]�̊W���猾���Ă���Ӗ����R�̎��ł��B
�@����ɁA�g�舳�M�e�ʁh�bp�͂��̒�`����
�ƂȂ�܂��B
�@���̎��ɑO�L�̒�ϔM�e�ʂ�K�p����ƁA�g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���
�ƕ\���܂��B�����̗ʂ́A�M�@�ւ��O�E�ƔM��d��������肷��̂��l�@����Ƃ��d�v�ł��B
�@���̎���O�L�̎��ɓK�p�����
��������B��������ڑ���ł��Ȃ��n�̃G���g���s�[�̓������ɉ�����̐ψˑ������A����\�ȃf�[�^�ŕ\���d�v�Ȏ��ł��B����ɕ⑫���܂��ƁA��L�̊W���͎���1�D(2)2�D�ŋ��߂��gMaxwell�̊W���h�ł��B
�@�E�ӂ́i�݂u�^�݂s�jp�́A�����\���g�i�o�C�u�C�s�j��ԕ������Ȗʁh�����܂��Ă���Β����Ɍv�Z�ł���ʂł��B�Ⴆ�Η��z�C�̂u�����q�s�^�o�̏ꍇ�́i�݂u�^�݂s�jp�����q�^�o�ƂȂ�܂��B��L������
�Œ�`�����ʂ��g�舳�M�c���W���i�̐ϔM�c�����j�h���ƌ�������̂ł����A���z�C�̂ł̓���1�^�s�ƂȂ�܂��B
�@
�@�G���g���s�[�r�͌n�̏�ԗʂł��r�͕ϐ��s�Ƃu�Ɋւ��Ċ��S�����ł��B���̂����ʍe�T�D�i�Q�j�g���S�����������h�ŏq�ׂ��悤�ɁA���r�����S�����ł��邽�߂��K�v�\���������
�@
�����藧���܂��B�m�ʍe�V�D�i�P�j���Q�Ƃ��ꂽ���B�n
�@���̎��͂����
�ƕό`�ł���B���̌`���gHelmholtz�̎��h�Ƃ����L�v�ł��B�Ⴆ�Η��z�C�̂o�^�s�����q�^�u��������ƁA�g���z�C�̂̓����G�l���M�[�͉��x�����Ȃ�Α̐ςɂ��Ȃ��h����������B�m�ʍ���p99���Q�Ƃ��ꂽ���B�n
�@�O���ł��r�̊��S�����\�����瓾��ꂽ���ɏ㎮��K�p�����
��������B������gMaxwell�̊W���h�ƌ�������̂̈�ŁA���X���G���g���s�[�̊��S���������瓾��������ł��B�ʍe�T�D�i�P�j�Ȃǂ��Q�Ƃ��ꂽ���B
�@�E�ӂ́i�݂o�^�݂s�jv�́A�����\���g�i�o�C�u�C�s�j��ԕ������Ȗʁh�����܂��Ă���Β����Ɍv�Z�ł���ʂł��B�Ⴆ�Η��z�C�̂o�����q�s�^�u�̏ꍇ�͂��q�^�u�ƂȂ�܂��B��L������
�Œ�`�����ʂ��g��ψ��͌W���h��p�ƌ����邪�A���z�C�̂ł̓�p��1�^�s�ƂȂ�܂��B
�@�O�L�̎���p����ƁA�O���ŋ��߂��g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���
�ŕ\���܂��B�����G�l���M�[�̗l�ɒ��ڑ���ł��Ȃ��ʂ��܂܂Ȃ��A���̌`�̕����֗��ł��B�Ȃ��Ȃ�A���ڑ���ł���i�o�C�u�C�s�j�ŕ\���ꂽ�n�i���́j�̏�ԕ���������ʂɗǂ��m���Ă�������ł��B
�@�����̊W���͏d�v�ł��B�Ȃ��Ȃ�A���ڑ���ł��Ȃ��n�̓����G�l���M�[��G���g���s�[�̓������ł̑̐ψˑ������A���ڑ���ł���i�o�C�u�C�s�j��ԕ������ƊW�Â��Ă��������ł��B
�@���ہA�����̌��_����
��������̂ŁA�����ϕ�����
���A�K���Ȑϕ��a�H�ɉ����Đϕ�����G���g���s�[�̕ω����v�Z�ł���B��ŏq�ׂ鉞�p��ŁA���ۂɊϑ��\�ȁi�o�C�u�C�s�j��ԕ�������p���Ăt�i�u�C�s�j�Ȗʂ�r�i�u�C�s�j�Ȗʂ��܂��B
�@����ɕ⑫���܂��B��L�̂��r�̓�ʂ�̕\���ɉ����還�u�̌W���l�������̂ɁA��قNj��߂�Maxwell�̊W����p�����
�������܂����A�����ɋ��߂��bV�̊W���ƈꏏ�ɂ����
��������B����́A���ڑ��肷�鎖���s�\�ȓ����G�l���M�[�t�̕ω���m�邱�Ƃ��ł��鎖���Ӗ�����B
�@�܂�A�K���Ȑϕ��a�H�ɉ����Ă��̐ϕ������{����Γ����G�l���M�[�̕ω����v�Z�ł����B
�@���̓�����ɕt���Ă͕���5�D�u�}�����p�M�͊w�v�I�[���Ёi1997�N���j��4�́�4-4�ip155�`162�j���Q�Ƃ��ꂽ���B
�m�⑫�����P�n
�@���̂Ƃ��A�n�ւ̔M�̏o����ƊW�����g�舳�M�e�ʁh���g��ϔM�ʗʁh�̍����g�i�o�C�u�C�s�j��ԕ������Ȗʁh�̌`�ɊW����͕̂s�v�c�ȋC�����܂����A���Ƃ����g�i�o�C�u�C�s�j��ԕ������Ȗʁh�́A�n�ւ̔M�̏o����A�d���̏o�����ʂ��Ē�܂���̂ł������Ƃ��v���o���Δ[���ł��܂��B
�@�n�֔M��d�����o���肳���Ďn�߂ėl�X�ȉ��x��̐ςł̈��͂������ł����̂ł�����B���̂��Ƃ́A�g�i�o�C�u�C�s�j��ԕ������Ȗʁh�̈Ӗ����l����Ƃ��Y��Ă͂Ȃ�Ȃ����Ƃł��B
�m�⑫�����Q�n
�@���܂���A�l�X�ȕΔ����W�������炸��o�Ă��܂����A�m�M�͊w�̊�{�@�����瓾���A�C�ӂ̕����n�ɑ��Č����ɐ��藧�A�Δ����W���n�ƁA�m��̓I�ȕ����n�ŋߎ��I�ɂ������藧���Ȃ��i�o�C�u�C�s�j��ԕ������n�A�m��M�∳�k���Ȃǂ̒�`�������Ӗ������`�W���n�A�m�P�Ȃ鐔�w�������Ӗ�����W���n���������Ȃ��ł��������B��������������Ɩ���Ȃ��Ȃ�܂��B
�m�⑫�����R�n
�@�ȉ��ŁA�t���r���i�o�C�u�C�s�j��ԕ������Ȗ��̊W��_���܂����A�舳�A��ρA�����̊e�ω��ɉ����镨���̕ω�����������O�̌W���݂͌��ɓƗ��ł͂Ȃ��Ď��̊W���Ō��ѕt�����܂��B
�@�ώ��ȕ��̌n�ł́A�O�̏�ԗʂo�A�u�A�s�ɑ��ď�ԕ������Ȗ� �o�����i�s�C�u�j �� �u�����f�i�s�C�o�j �����݂���B ���i�s�C�u�j �� �o�i�u�C�s�j
�A ���f�i�s�C�o�j �� �u�i�s�C�o�j �Ə����ƁA���o�₄�u���g���S�����h�Ȃ̂�
�ƂȂ�B���s�i�o�C�u�j�̊��S�������𗘗p���Ă����l�ȊW����������B�m�g���S�����h�̈Ӗ��ɂ��Ă��ʍe�T�D�i�Q�j���Q�����ꂽ���B�n
�@�����̎��̈Ӗ��́A�Ⴆ�Η��z�C�̏�ԕ������Ȗʂ̃��u�C���s�C���o������Ζ��炩�ł��B
�@����́A���z�C�̂Ɍ��炸�C�ӂ̕����̘A���E���炩�ȏ�ԕ������Ȗ��Ő��藧�A���ϐ����̐��w�����ł��B���̂��߁A��ŏo�ė����t�i�r�C�u�j�A�f�i�s�C�o�j�A�E�E�E���X�̔C�ӂ̔M�͊w���ɂ��Ă����藧���܂��B
�@�������A�g�A���E���炩�ȏ����h���������Ȃ����ω���������悤�ȗ̈�ł͐��藧���Ȃ��̂Œ��ӂ��K�v�ł��B�m�ʍe�u�C�̂̒f�M�ω��v�R�D�Ȃǂ��Q�Ƃ��ꂽ���B�n
�m�⑫�����S�n
�@�ȉ��̊W�������w�����ł��B��ŌJ��Ԃ����p���܂��B
�@���S������\����
�ɉ����āA�]���ϐ����i���C���j����A�Ⴆ���i���C���j�ɕς����
�ƂȂ邪�A���S�����̈Ӗ�����
�����R���藧�B
�@
�@�P�D�i�Q�j�Q�D�ŋ��߂��W���ɁA�g���z�C�́h�̏�ԕ�������K�p����
�ƂȂ�A���z�C�̂̓����G�l���M�[�͑̐ςɈˑ����Ȃ����x�݂̂̊��ł��鎖���������B���������̌������ɂ́A�ʍe�V�D�i�P�j�Q�D�Ő��������悤�ɁA���ӂ��K�v�ł��B
�@
�@����ɁA���z�C�̂̏ꍇ�ɂ�
�ƂȂ�܂��B���z�C�̂̒�ϔM�e�ʂb�������x�Ɉˑ����Ȃ����l�Ƃ��Ă��邱�Ƃɕt���Ă��ʍe4�D�i2�j3�D�������������B�m�ʍe�U�D�i�S�j�R�D���Q�Ƃ��ꂽ���B�n
�@
�@�O�L���g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���\�����ɁA�g���z�C�́h�̏�ԕ�������K�p�����
�ƂȂ�A������݂��g�}�C���[�̊W���h�������܂��B�m�ʍe�S�D�i�Q�j���Q�Ƃ��ꂽ���B�n
�@
�@���z�C�̂��g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�́A���x�A�̐ςɖ��W�Ȓ萔�Ƃ��Ă����̂ŁA�f�M�ω��Ȑ���\�����́i�f�M�����炄�r��0�j
�ƂȂ�A������݂̎��������܂��B�����̎��́A���z�C�̂̏W�܂�Ɏd������������A�t�Ɏ��o�����肵���肵���Ƃ��A�n���ǂ̂悤�ɕω����邩��\���Ă��܂��B�m�ʍe�S�D�i�R�j�P�D���ʍe�u�C�̂̒f�M�ω��v���Q�Ƃ��ꂽ���B�܂��A�H�w���K�X���̓T�C�N���̌������l�@����Ƃ��Ȃǂł��d�v�ł��B�n
�@
�@�ȉ��Œ�`����� �������k���ȁf �� �f�M���k���ȁh �ɂ��āA���z�C�̂̏ꍇ�����߂Ă݂�B
�ȁf �́i�u�C�s�C�o�j�݂̂ɊW���Ă��܂��̂� �i�o�C�u�C�s�j��ԕ����� �������Ă���Β����ɋ��܂�܂��B
�ȁh �ɂ��Ă͑O�L�̒f�M�ω��Ȑ���p����悢�B
�@���̗��҂̈Ⴂ���A�o�|�u���ʂɉ����铙���Ȑ��ƒf�M�Ȑ��̌��z�̈Ⴂ��\���Ă���B�m�ʍe�u�C�̂̒f�M�ω��v�Q�D�̗��̐}���Q�Ƃ��ꂽ���B�n
�@�̐ϒe�����͈��k���̋t���ł��B������ �ȁf �� �ȁh ���t���͂��ꂼ�� �����̐ϒe���� �� �� �f�M�̐ϒe���� �ɂȂ�܂����A���ꂪ�C�̂̉����ɊW�����B���̗��҂̈Ⴂ���ʍe�u�����̗��_�v�R�D�i�P�j�j���[�g�����_���i�Q�j���v���X�̗��_�̈Ⴂ�ł��B�����Đ������̂̓��|�����f�M�̐ϒe������p���郉�v���X�̗��_�������B
�@
�@���z�C�̂͌����ɂ͑��݂��Ȃ����z�I�ȋC�̂Ȃ̂ŁA�����̎������܂��Ă����܂�Ӗ��͂Ȃ��Ǝv���邩������܂���B�Ƃ��낪�A�K�X���̓T�C�N���͗��z�C�̋ߎ��ŋc�_�ł��܂��̂ŁA�����ł͂��Ȃ���ɗ����܂��B
�@
�@���C�̂�ǂ��ߎ�����t�@���E�f���E���[���X�C�̂͂���ɏd�v�ł��B�����ł͂��ׂ������Pmol�Ƃ��ċc�_����B�t�@���E�f���E���[���X�̏�ԕ������������₂�͕��ʃ���������̒l�Ƃ��ė^�����Ă��邩���ł��B���̂����b���A�bp���P����������̒l�Ƃ����B���̂Ƃ�
�ƂȂ�܂��B�t�@���E�f���E���[���X�C�̂̓����G�l���M�[�͓������ł̑̐ϕω��i���R�A�M�͌n�ɏo���肷��j�ő̐ς̋t���ɔ�Ⴕ�ĕω����܂��B�m�ʍe�Q�D�i�Q�j���Q�Ƃ��ꂽ���B�n
�@
�@�g��ϔM�e�ʁh�bv��\��
�͈�ʓI�ɐ��藧���Ȃ̂ŁA�O�L�̎������p����ƁA�����G�l���M�[�̕ω������t��
�ƂȂ�܂��B
�@�����G�l���M�[�t�i�s�A�u�j�͏�ԗʂł�����A���t�̐��ϕ��ŋ��߂���_�Ԃ̍��t�i�s�C�u�j�|�t�i�s0�C�u0�j�͐ϕ��H�Ɉˑ����܂���B���̂��߉E�ӑ�ꍀ���u0�����̉��Łi�s0�C�u0�j����i�s�C�u0�j�܂Őϕ��������̂ɁA����s�����̉��Łi�s�C�u0�j����i�s�C�u�j�܂Őϕ��������̂������Ă����悢�B
�g��ϔM�e�ʁh�bv�i�s�C�u�j�̒�ςu0���ł̎����I�ȃf�[�^������A��L�̐ϕ������{���邱�Ƃɂ������G�l���M�[�t�i�s�C�u�j�Ȗʂ̌`�����߂邱�Ƃ��ł��܂��B
�@
�@�G���g���s�[�r�i�s�C�u�j�ɂ��Ă����l��
�ƂȂ�܂�����A�g��ϔM�e�ʁh�bv�i�s�C�u�j�̒�ςu0���ł̎����I�ȃf�[�^������A
��L�̐ϕ������s���āA�G���g���s�[�r�i�s�C�u�j�Ȗʂ̌`�����߂鎖���ł���B�m�ʍe�Q�D�i�S�j���Q�Ƃ��ꂽ���B�n
�@
�@�������t�@���E�f���E���[���X�������͋ߎ��I�Ȏ��ł��B�����炁�Ƃ��̒l�Ŏ��ۂ̋C�̗̂l�q�������ɍČ��ł���킯�ł͂���܂���B���̂��ߎ��݂̕����ɂ��Č����Ȃt�i�s�C�u�j�A�r�i�s�C�u�j�Ȗʂ�m�肽���Ƃ��́A���̍����I�ȊW���ɗ����Ԃ��āA�����Ɋւ�镨���ʂ𑪒肵�Ȃ���Ȃ�܂���B
�@�Ⴆ�Ύ��C�̂ł����C���g��ϔM�e�ʁh�bv�i�s�C�o�j��g�舳�M�e�ʁh�bp�i�s�C�o�j�̎����l�����̗l�ȋȖ��ł����A���̃f�[�^�������I�ɓ���ɂ͖c��ȘJ�͂��K�v�ł��B
�@��̓I�Ȃt�i�s�C�u�j�A�r�i�s�C�u�j�Ȗʂ̌`�́A�ʍe����}�̏��C�\�����̏��C�\�Ȃǂ��������������B
�@
�@�g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���\�����ɁA�g�t�@���E�f���E���[���X�C�́h�̏�ԕ�������K�p����
�������܂��B�m�ʍe�Q�D�i�R�j���Q�Ƃ��ꂽ���B�n
�@��L�̎��𗘗p����ƁA�t�@���E�f���E���[���X�C�̂́i�u�C�o�C�s�j�_�ɉ����� �舳�M�c���W���i�̐ϔM�c�����j�� �����܂�܂��B�m�ʍe�Q�D�i�P�j���Q�Ƃ��ꂽ���B�n
�@���l�ɁA�t�@���E�f���E���[���X�C�̂� �������k���ȁf �� �����̐ϒe������ �������ɋ��܂�B
�@�Ƃ�������� �������k���ȁf �� �f�M���k���ȁh �̊Ԃɂ��Q�D�i�Q�j�R�D�Ő�������悤�ɊȒP�ȊW�����藧�B
�����p������g�f�M�̐ϒe�����h���v�Z���邱�Ƃ��ł���B
�ƂȂ�B
�@�����ʍe�u�����̗��_�v�Q�D�́i�P�P�j���ɑ������ƃt�@���E�f���E���[���X�C�̂̉�����\������������B
�@
�@��ʂɂbv�́i�s�C�u�j�̊��ł����A�bv�����ƌ��Ȃ����̈�Ɍ�����A���z�C�̂Ɠ��l�Ƀt�@���E�f���E���[���X�C�̂̒f�M�ߒ���\�����������܂��B���Ȃ킿
�ƂȂ�A���z�C�̂̒f�M�ω��Ȑ��Ɨǂ��������ɂȂ�B
�@�������A���łɌ����悤�ɂbp�|�bv�͂��A���A�u�̕��G�Ȋ��ƂȂ�̂ŁA���z�C�̂̂悤�ɂbp�^�bv�����̊ȒP�Ȋ��ɂȂ�킯�ł��Ȃ����A�bv�ɉ����Ăbp�����ƌ��Ȃ����̈��́A���X���z�C�̋ߎ������藧�̈�ł����炱�̎��ɂ���ȂɈӖ�������킯�ł͂Ȃ��B
�@
�@���ݕ����i�t�@���E�f���E���[���X�C�̂����̈��j�̏ꍇ�ɂ��bv�A�bp�A�ȁf�A�ȁh�E�E�E���X���i�s�C�u�j�Ɉˑ����܂�����A���z�C�̂̂悤�Ɋ�b��������P���ɐϕ����Ăt�i�s�C�u�j�Ȗʂ�r�i�s�C�u�j�Ȗʂ����߂邱�Ƃ͂ł��܂���B�����ɂ���bv�A�bp�A�ȁf�A�ȁh�E�E�E���X�̒l�����߂Ă���A��ԕ������Ȗʂ����肵�Ȃ���Ȃ�܂���B
�@
�@�����悤�ȋc�_�ł����A���ɂƂ��ĉ���Ղ�����
Yunus A.Cengel�Michael A.Boles�����u�}�����p�M�͊w�v�I�[���Ёi1997�N���j
4�́�4-4�ip155�`162�j�̐���
�����p���Ă����܂��B
�@�����ŁA�����G�l���M�[�A�G���^���s�[�A�G���g���s�[�̕ω������́A��e�ρA���x�A��M�A���X�̑���\�ȗʂŕ\����ʊW����������Ă��܂��B���̊W������A�����G�l���M�[�A�G���^���s�[�A�G���g���s�[�Ȃǂ̏�ԗʂ̕ω����v�Z���邱�Ƃ��\�ɂȂ�܂��B
�@�������A���̗l�ɏ������Ƃ��r�̊��S���������炷�ׂĂ��n�܂��������ǂݎ��ɂ����Ȃ�܂��B���̓������ Maxwell�̊W���̌��߂�����܂��̂ŁA���̓_�ɒ��ӂ���Ă��ǂ݂��������B
�@
�@�ϐ����i�s�C�o�j�ɂ��Ă��A�܂��������l�Ȏ��������܂��B
�@�Ɨ��ϐ����s���o�Ɏ���
�ƂȂ�B
�@�������r�����S�����ł������Ƃ̏������璼����
��������B
�@���̂Ƃ��g��ϔM�e�ʁh�bv��
�ƂȂ�܂��B
�@����ɁA�g�舳�M�e�ʁh�bp��
�ƂȂ�܂��B���̎���O�L�̎��ɓK�p�����
��������B��������ڑ���ł��Ȃ��n�̃G���g���s�[�̒舳���ɉ����鉷�x�ˑ������A����\�ȃf�[�^�ŕ\���d�v�Ȏ��ł��B�܂��A�����[�G���g���s�[]��[��Ή��x]��[�M��]�̊W���猾���Ă���Ӗ����R�̎��ł��B�m�ʍe�T�D�i�P�j�Ȃǂ��Q�Ƃ��ꂽ���B�n
�@�����ŋ��߂�������A�g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���\����
�ƂȂ�܂����A����͂P�D�i�Q�j�Q�D�ŋ��߂��W���Ɠ������Ƃ������Ŏ����܂��B
�@���̎���O�L�̎��ɓK�p�����
��������B��������ڑ���ł��Ȃ��n�̃G���g���s�[�̓������ɉ����鈳�͈ˑ������A����\�ȃf�[�^�ŕ\���d�v�Ȏ��ł��B����ɕ⑫���܂��ƁA��L�̊W���͎���1�D(3)2�D�ŋ��߂��gMaxwell�̊W���h�ł��B
�@
�@�G���g���s�[�r�͌n�̏�ԗʂł�����A���r�����S�����ł��邱�Ƃ��K�v�\���������
�����藧���܂��B
�@���S�����\�����瓾��ꂽ�O���̎��ɁA�㎮��K�p�����
��������B������gMaxwell�̊W���h�ƌ�������̂̈�ŁA���X���G���g���s�[�̊��S���������瓾��������ł��B�ʍe�T�D�i�P�j�Ȃǂ��Q�Ƃ��ꂽ���B
�@�O�L�̎���p����ƁA�O���ŋ��߂��g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���
�ƂȂ�A�P�D�i�Q�j�Q�D�ŋ��߂��W���Ɠ������Ƃ��ؖ��ł���B
�@�������A���ڑ���ł��Ȃ��n�̓����G�l���M�[��G���g���s�[�̓������ł̈��͈ˑ������A���ڑ���ł���i�o�C�u�C�s�j�̏�ԕ������ƊW�Â��Ă�����d�v�ȊW���ł��B
�@���ہA�����̌��_����
��������̂ŁA�����ϕ�����
���A�K���Ȑϕ��a�H�ɉ����Đϕ�����G���g���s�[�̕ω����v�Z�ł���B��ŏq�ׂ鉞�p��ŁA���ۂɊϑ��\�ȁi�o�C�u�C�s�j��ԕ�������p���Ăr�i�o�C�s�j�Ȗʂ��܂��B
�@���łɕ⑫���Ă����܂��B��قNj��߂�Maxwell�̊W����p����ƁA�G���^���s�[�g(�s�C�o)�̕ω����g������\�ȕ����ʂŕ\�����Ƃ��ł��܂��B
�@�P�D�i�Q�j�`�i�S�j�ŁA�r�̕ϐ��� �r�i�s�C�u�j�A�r�i�s�C�o�j�A�r�i�o�C�u�j �Ǝ��R�ɕϊ��ł��邱�Ƃ�������Ă��܂����A����Ɠ��l�� �g�i�r�C�o�j���g�i�s�C�o�j
�֕ϊ������
�������܂��B�����ϕ�����A���ڑ��肷�鎖���s�\�ȃG���^���s�[�g�̕ω���m�邱�Ƃ��ł���B
���Ȃ킿�A�K���Ȑϕ��a�H�ɉ����ď�L�̐ϕ������{����G���^���s�[�g(�s�C�o)�̕ω��ʂ��v�Z�ł����B
�@���̓�����ɕt���Ă͕���5�D�u�}�����p�M�͊w�v�I�[���Ёi1997�N���j��4�́�4-4�ip155�`162�j���Q�Ƃ��ꂽ���B
�m���p��n
�@�Ⴆ�A�n���\�����镨�������z�C�̂̏ꍇ�ɂ́A
�ƂȂ�̂ŁA���z�C�̂̓����G�l���M�[�t�͓������ł̈��͕ω��i���̂Ƃ��O�E�Ɓg�M�h��g�d���h�͂���肳���j�ň��͂��ς���Ă����ɕۂ���鎖���킩��B
�@�t�@���E�f���E���[���X�C�̂̏ꍇ�ɂ́A���́i�o�C�u�C�s�j��ԕ��������E�ӂɓK�p���ċc�_����Ηǂ��B�t�@���E�f���E���[���X�̏�ԕ������������₂�͕��ʃ���������̒l�Ƃ��ė^�����Ă��邩�炱���ł��A���ׂ������Pmol�Ƃ��ċc�_����B
�@
�@�ϐ����i�o�C�u�j�ɂ��Ă����l�ł��B
�@�Ɨ��ϐ����o���u�Ɏ���
�ƂȂ�B
�@���̊��S�����\�����璼����
��������B
�@���̂Ƃ��g��ϔM�e�ʁh�bv��
�ƂȂ�B���̎���O�L�̎��ɓK�p�����
�ƂȂ�B��������ڑ���ł��Ȃ��n�̃G���g���s�[�̒�ω��ɉ����鈳�͈ˑ������A����\�ȃf�[�^�ŕ\���d�v�Ȏ��ł��B
�@����ɁA�g�舳�M�e�ʁh�bp��
�ƂȂ�܂��B���̎���O�L�̎��ɓK�p�����
�ƂȂ�܂��B��������ڑ���ł��Ȃ��n�̃G���g���s�[�̒舳���ɉ�����̐ψˑ������A����\�ȃf�[�^�ŕ\���d�v�Ȏ��ł��B
�@�����ŋ��߂��������g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���\����
�ƂȂ�܂����A����͂P�D�i�Q�j�Q�D�ŋ��߂��W���Ɠ������Ƃ������Ŏ����܂�
�@
�@�G���g���s�[�r�͌n�̏�ԗʂł�����A���r�����S�����ł��邱�Ƃ��K�v�\���������
�����藧���܂��B
�@���̎��ɁA�O���Ŋ��S�����\�����瓾��ꂽ����K�p�����
��������B
�@�����́A���ڑ���ł��Ȃ��n�̓����G�l���M�[��G���g���s�[�̓��ω��ł̈��͈ˑ����ⓙ�����ł̑̐ψˑ������A���ڑ���ł���i�o�C�u�C�s�j�̏�ԕ������ƊW�Â��Ă���܂��B
�@��L�̎���p����ƑO�����g�舳�M�e�ʁh�bp���g��ϔM�e�ʁh�bv�̍���
�ƂȂ�A�P�D�i�Q�j�Q�D�ŋ��߂��W���Ɠ������Ƃ��ؖ��ł����B
�@
�@�O�͂ł��t�ȖʁA�r�Ȗ����i�o�C�u�C�s�j��ԕ������Ȗ��Ƃ̊W���l�@���܂����B�����ł́A�ł������I�ŁA�ł����v����ԗʋȖ��t�i�r�C�u�j���̂��̂̐����ׂ�B�m��ԗʂt�i�r�C�u�j�Ȗʂɂ��Ă��ʍe�W�D�i�Q�j�����K���ꂽ���B�n
�@�P�D�i�Q�j�P�D�œ��������n�̓����G�l���M�[�t�i�r�C�u�j�̂t�|�u�|�r��Ԃɉ�������ԕ������Ȗ����l�@����B���l�@���Ă���n�̍ŏ��̏�ԁi���ԁj���i�t0�C�r0�C�u0�j�ł���Ƃ���B���̂Ƃ��̎����I��ԗʂs�Ƃo�̒l�͂s0�Ƃo0�Ƃ���B
�@�M�͊w���@���i�G�l���M�[�ۑ����j�̐����\�����t�����f�p�|�o���u�ɁA���@���̐����\�����f�p���s���r��K�p����
����o������B���̎����s���r�͌n���O�E�Ə��ÓI�ɂ���肷��M�ʂ��A�o���u�͊O�E�Ə��ÓI�ɂ���肷��d�����Ӗ�����B
�@��������̂���肪������ƌn�̉��x�∳�͕͂ω����Ă����̂ŁA���ÓI�Ȃ����𑱂���ׂɂ́A��Ɍn�̉��x�∳�͂Ɠ������M����d�����ɐ�ւ��Ă����K�v������B���ÓI�ȏꍇ�łȂ��Ƃs���r���n�ƊO�E������肷��M�ʂ̈Ӗ��ɂȂ�Ȃ����A�d�������ÓI�t�Ȃ����ɂ͂Ȃ�Ȃ��B�܂��A���̗l�ɊO�E�Ə��ÓI�ɂ���肷��M�ʂł����Ă̂n�̎��G���g���s�[�̕ω����v�Z���邱�Ƃ��ł��邵�A�����G�l���M�[�̕ω����v�Z�ł���B�����ɔM�͊w���A���@�����W���Ă���B
�@���̗l�ɂ��āA�n�͏�ԁi�t0�C�r0�C�u0�j����V���ȏ�ԁi�t�C�u�C�r�j�Ɉڍs���Ă����̂����A���̗l�ȊO�E�Ƃ̔M��d���̂����ɂ���Đ������ԓ_�̕ϓ��͂t�|�u�|�r��Ԃ̈�̋Ȗʂt�i�u�C�r�j���\������B
�@���A�i�t0�C�r0�C�u0�j�̏�Ԃ���u���Œ�i�܂��ϓI�Ɂj���āA�n�ɏ��ÓI�ɔM���f�p���s���r�������Ă����Ƃ���B�M��������Ƌ��Ɍn�̓����G�l���M�[�ƃG���g���s�[�͑��債�Ă����̂����A���̏�ԕω��̗l�q�͂t�i�r�C�u�j�Ȗʂ̂u�����i���u0�j�̐���Ȑ��ŕ\���ł���B
�@�M�͊w���@���ɂ��A���̐���Ȑ��t�i�r�C�u0�j�͂r�Ɋւ��ĒP���������ł���Ɠ����ɁA�K�����ɓʂ̃J�[�u�ƂȂ��i���}�Q�Ɓj�B
�@
�@�Ȃ��Ȃ�A����Ȑ��̌��z�́i�݂t�^�݂r�j���s�i��Ή��x�j������ł��B�O���Ɏd�������邱�ƂȂ��i�u�����̌��Łj�M���������āA�����G�l���M�[������i�G���g���s�[������j�����͕K�����x��������ԂƂȂ�܂��B�����n�ɔM�i�G���g���s�[�j��������Ɖ��x��������悤�ȕ��������݂�����A���ꂱ���g����i�v�@�ցh�����邱�Ƃ��ł��܂��B������A���̗l�Ȃ��Ƃ͌����ċN����܂���B
�@�n�ɔM�i�G���g���s�[�j���������ĉ��x���オ��Ƃ����ɊO�E����̔M�̗����͎~�܂��Ă��܂��܂��B�M�͕K�����x�������Ƃ��납��Ⴂ�Ƃ���ւ�������Ȃ��Ƃ����̂��M�͊w���@���ł��B���̂��ߌn�ɔM�i�G���g���s�[�j�������������邽�߂ɂ́A�O�E�̔M������艷�x���������̂ɂȂ��ւ��Ȃ���Ȃ�܂���B���̂Ƃ��A���x��������Ԃƌ������Ƃ́A����Ȑ��̌��z�i�݂t�^�݂r�jv���s�i��Ή��x�j���傫���Ȃ��Ă��邱�Ƃ��Ӗ����܂��B
�@�ȏ�̎�����A���������G�l���M�[�ω�����G���g���s�[�̗����́A���x��������Ԃł̗����قǂ�菭�Ȃ������ł��ނ̂ł��B���̂��߁i�݂t�^�݂r�j���s�͌n�̃G���g���s�[����Ƌ��ɕK�����債�Ă����܂��B
�@
�@���̓�����̎���͉��}����������Ζ��炩�ł��B���ꂪ�M�͊w���@�����t�����f�p���s���r�������Ă���邱�Ƃł��B�M�͊w���@���́A�܂������u���̂��Ƃł̓����G�l���M�[�Ȗʂ̃G���g���s�[�ˑ������������z����Ή��x�ł���ƌ����Ă��܂��B��L�̌��_�́A�M�͍������̂���ቷ���̂ɂ�������邱�Ƃ͂Ȃ��Ƃ����M�͊w���@���̕K�R�̌����ł��B�܂��A��Ή��x(������0�j�����̒l�ł������Ƃ��A�M�͊w���@���̕K�R�̌��ʂ��������Ƃ��v���o���Ă��������B
�@���t�����f�p���s���r���M�͊w���@�����̂��̂ł��邱�Ƃ́A�ʍe�u��Ή��x�Ƃ͉����i�ϕ����q�Ƃ͉����j�v��U�����邢���V�D�i�S�j�g�܂Ƃ߁h�K�����Ɖ���܂��B
�@�S�����l�ɁA�i�t0�C�r0�C�u0�j�̏�Ԃ���r���Œ�i�܂�f�M�I�Ɂj���āA�n���珀�ÓI�Ɏd���|���f�v���|�o���u�����o���Ƃ���B�d�������o���Ƌ��Ɍn�̓����G�l���M�[�͌������Ă����̂����A���̏�ԕω��̗l�q�͂t�i�r�C�u�j�Ȗʂ̂r�����i���r0�j�̐���Ȑ��ŕ\���ł���B
�@�M�͊w���@���i�G�l���M�[�ۑ����j�ɂ��A���̐���Ȑ��t�i�r0�C�u�j�͂u�Ɋւ��ĒP���������ł���Ɠ����ɁA�K�����ɓʂ̃J�[�u�ƂȂ��i���}�Q�Ɓj�B
�@
�@�Ȃ��Ȃ�A����Ȑ��̌��z�́i�݂t�^�݂u�j���|�o������ł��B�O���ƔM�̂��������邱�ƂȂ��i�r�����̌��Łj�d�����Ƃ肾����āA�����G�l���M�[������������n�̈��͕͂K��������܂��B�����A�n����d�������o�����Ƃ��A�n�̈��͂��オ��l�ȕ��������݂�����A���ꂱ���g����i�v�@�ցh����邱�Ƃ��ł��܂��B������A���̗l�Ȏ��͌����ċN����܂���B
�@�n����d�������o���ƌn�̈��͉͂������Ă��܂��̂ł����Ɍn����d�������o���Ȃ��Ȃ�܂��B�n����d�������o��������ɂ͊O�E�̎d��������舳�͂̒Ⴂ���̂Ɏ��ւ��Ȃ��Ƃ����܂���B�܂�f�M�Ōn����d�������o�������邱�Ƃ��ł���ƌ������Ƃ͌n�̈��͂͌n�̑̐ϖc���Ƌ��ɕK���������Ă����܂��B
�@���͂��Ⴂ��Ԃƌ������Ƃ́A����Ȑ��̌��z�i�݂t�^�݂u�js���|�o�̐�Βl���������Ȃ��Ă��邱�Ƃ��Ӗ����܂��B���̂Ƃ����������G�l���M�[�ω�����d���̎��o���i�̐ς̖c���j�́A���͂��Ⴂ��Ԃł̎��o���قǂ��傫�ȑ̐ϖc�����K�v�Ȃ̂ł��B���̂��߁A�i�݂t�^�݂u�j���|�o�͌n�̑̐ϑ����ƂƂ��ɕK���������Ă����܂��B
�@
�@���̓�����̎���͉��}����������Ζ��炩�ł��B���ꂪ�M�͊w���@���i�G�l���M�[�ۑ����j���t���|���f�v���|�o���u�������Ă���邱�Ƃł��B
�@���x���グ��Ək�ރS���̗l�ȕ�����A0���`4���̐��̂悤�ɉ��x���グ����̐�����������悤�ȕ���������܂����A�������̐��Ɋւ��Ă͏�L�̕s�����͕K�����藧���܂��B�����A�n����d�������o�����Ƃ��A�n�̈��͂��オ��l�ȕ��������݂�����A���ꂱ���g����i�v�@�ցh�����ăG�l���M�[�ۑ������j��܂��B
�@���ǂ̂Ƃ���ȉ��̗l�Ɍ����܂��B���L�́i�Q�j��i�R�j�����藧���Ƃ́A�i�P�j�̋Ȗʂ����W������]�����Ē��߂Ă݂�Ζ��炩�ł��B
�@�M�͊w���@���ƔM�͊w���@�����玟�̎�������ʓI�ɐ��藧�B
�@
�i�P�j��ԕ������Ȗʂt�i�u�C�r�j���u�ƂƂ��ɒP���Ɍ������Ă��������ɓ��ƂȂ�B�܂��t�i�u�C�r�j���r�Ƌ��ɒP���ɑ������Ă��������ɓ��ƂȂ�B
�@
�i�Q�j��ԕ������Ȗʂr�i�u�C�t�j���u�Ƌ��ɒP���ɑ������Ă�������ɓ��ƂȂ�B�܂��r�i�u�C�t�j���t�ƂƂ��ɒP���ɑ��債�����Ă�������ɓ��ƂȂ�B
�@
�i�R�j��ԕ������Ȗʂu�i�t�C�r�j���t�ƂƂ��ɒP���Ɍ������Ă��������ɓ��ƂȂ�B�܂��u�i�t�C�r�j���r�Ƌ��ɒP���ɑ������Ă��������ɓ��ƂȂ�B
�m�⑫�����P�n
�@���̂��Ƃ́A�g�n�h���\�����镨���������Ȃ���̂ł���ʓI�ɐ��藧���܂��B
�@�Ⴆ��0���`4���̐��̗l�ɔM�������āi�܂�����G�l���M�[�t�傳����j�Ƒ̐ς���������悤�ȏꍇ�ł����藧���܂��B�܂��A�V�����_�[�̒��ɋl�߂����������ω����N�����āA�n���ő�������������悤�ȏꍇ�ł����藧���܂��B���̂Ƃ��A0���̕X�ɔM���������0���̐��ƂȂ�̐ς���������悤�ȏꍇ�ł��A������藧���܂��B�������藧���Ȃ��������g�i�v�@�ցh����邱�Ƃ��ł��܂��B�m�ʍe�̐����Ȃǂ��Q�Ƃ��ꂽ���B�n
�@��������������ꍇ�̂t�i�u�C�r�j�Ȗʂ̌`���S�D�i�P�j�Q�D�ŏڂ����������܂��B�@
�m�⑫�����Q�n
�@�@�g�n�h���\�����镨�����g���z�C�́h�̏ꍇ�ɂ́A��L�̎������ȒP�Ɋm�F�ł��܂��B�ʍe�U�D�i�S�j�R�D�Ő��������r�i�s�C�u�j�Ȗʂ��v���o���悢�B
�@���z�C�̂̏ꍇ�ɂ͓����G�l���M�[�͐�Ή��x�݂̂̊��ł����B�M�͊w��������͂t���s�ɒP���ɔ�Ⴗ�邩�ǂ����͓����܂������A���v�͊w�����p����Ɨ��z�C�̂̓����G�l���M�[�͐�Ή��x�ɔ�Ⴗ��ʂł��邱�Ƃ������Ă��܂��B���̂����U�D�i�S�j�R�D�̋Ȗʐ}�̂s���W���t���W�ɒu��������r�i�u�C�t�j�ȖʂƂȂ�܂��B
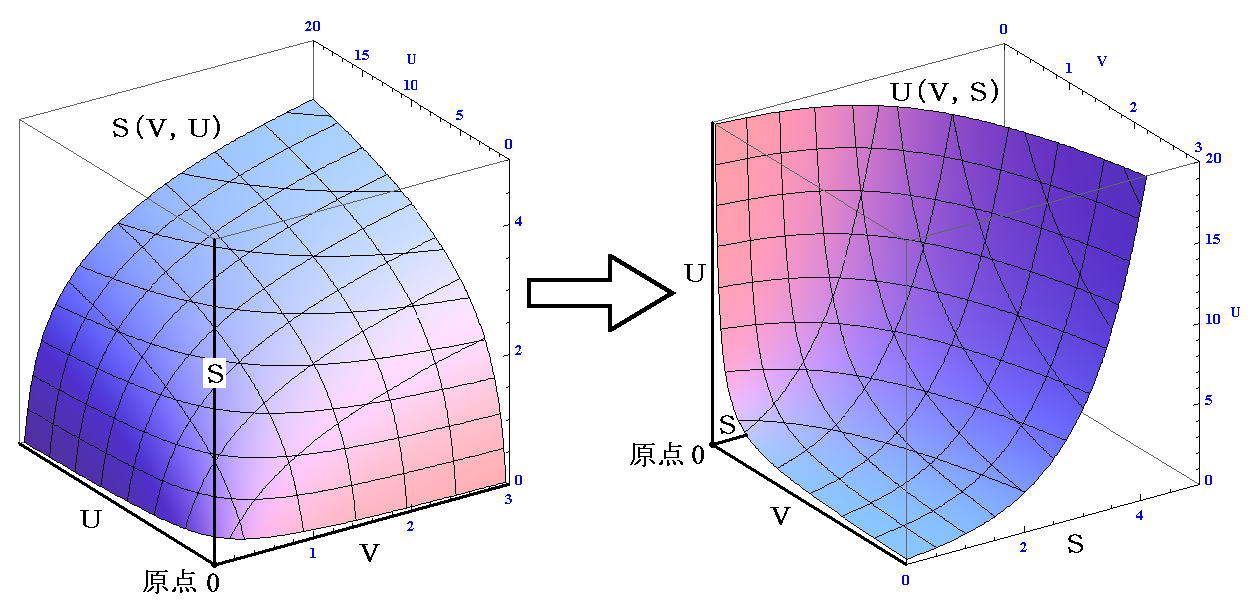
�@���̃O���t�̍��W������]���āA�ϐ����i�u�C�r�j�̋Ȗʂt�i�u�C�r�j�̃O���t�Ƃ��Č���A�O�q�̎������m���ɐ��藧���Ă���̂������ł��܂��B
�@�������A���̂Ƃ����̂��Ƃɒ��ӂ��Ă��������B�n���\�����镨�������z�C�̂̂Ƃ��A�����G�l���M�[�������Ȃ�̐ςɂ�炸�������x�i��}�̂t�����̃��C���ɉ��������ׂĂ̓_�ɉ�����r�����̋Ȗʌ��z�������j�ł������A�����̕����͓����G�l���M�[�������ł��̐ς��ς��Ή��x�i�r�����̋Ȗʌ��z�j�͕ς��܂��B������A�ȉ��Ő��������i�t�C�u�C�r�j�Ȗ��̐������A���z�C�̂̂悤�Ɂi�s�C�u�C�r�j�ȖʂɃ����N���Ă���킯�ł͂���܂���B
�@��Ή��x�s�͏�ԗʂł���G���g���s�[�r�����邽�߂̐ϕ����q���������Ƃ�Y��Ȃ��ł��������B�O�E�Ǝd���̂��������邱�ƂȂ��n�̃G���g���s�[�����債���Ƃ��̓����G�l���M�[�̕ω����z���A�n�̐�Ή��x�������̂ł��B�ϕ����q�s�ƂƂ��ɓ������ꂽ�G���g���s�[�ł������ω��ł̃G���g���s�[����i�M�̗����j�Ƌ��ɉ��x��������悤�ȕ����͂���܂���B���̂��f�p�i����ω��ł̂��t�j�Ƃs�Ƃ��r�̊W�̒��ɔM�͊w�̖{��������܂��B
�m�⑫�����R�n
�@�ȉ��łt�i�u�C�r�j�Ȗʂ̓������瓾���錋�_��������܂����A�����Ŏ����Ă���Ȗʐ}�́A���̌X���𗝉������₷���悤�Ɍn���\�����镨�̂����z�C�̂̏ꍇ��Ꭶ���Ă���̂ł����āA���ۂ̌n���\�����镨���̋Ȗʂ͂����Ƃ��тɘc��ł��܂��B
�@���p�I�ɏd�v�Ȃ̂́A�m�K�X���̓T�C�N���ɂ������C�n�A�m�Ⓚ�T�C�N���ɂ������}�C�́n�A�m���C���̓T�C�N���ɂ����鐅�i�����C�j�n�̏ꍇ�ł��B���ۂ̌`��͕ʍe����}�̏��C�\�����̏��C�\�Ȃǂ��������������B�����̕\����`�����t�i�u�C�r�j�Ȗʂ͂��Ȃ�c��ł��܂����A�O�L�̓��������Ă���̂͊m���ł��B
�@�����̕\�̓K�X���̓T�C�N���A�Ⓚ�T�C�N���A���C���̓T�C�N������͂���Ƃ��K�{�̏��ł����A�����̃f�[�^�͎����I�ɂ������܂�܂���B���̕\���쐬���邽�߂ɖc��ȘJ�͂Ɣ�p�������܂�Ă��܂��B
�m�⑫�����S�n
�@���ȏ��ɂ���ẮA��L�̌��_���n���ɐ�����s�t�ߒ��ɔ����G���g���s�[����@���ɊW����悤�Ȑ��������Ă�����̂�����܂��m�Ⴆ�A�����_�E�E���t�V�b�u���v�����w�v�㊪��21�n�B�m���ɁA�n�̕\�ʂ�ʂ��ĊO�E���痬�������M���n�S�̂ɍL����͕̂s�t�ߒ��ł����A�G���g���s�[�Ƃ��������ʂ͌n�̒��ŕs�t�ߒ���������Ƒ��傷�鐫��������܂��B�������A���̓�������P�D�i�P�j�Q�D�̉ӏ������Q�`�S�̍��Ő����������Ƃł����A��ԗʋȖʂ̌`�́A�O�E�Ƃ̔M��d���̂�����ʂ��Ă̂`�������܂���̂ł��B���̏�ԗʋȖʏ����ԓ_���ړ�����ߒ��Ōn���ɐ�����s�t�ߒ��͏�ԗʋȖʂ��̂��̂̐����Ƃ͂܂������W����܂���B
�@�M�͉��x�������Ƃ��납��Ⴂ���ւ�������Ȃ��ƌ����̂��M�͊w���@���ł��B�n�ɔM����������Ƃ₪�Čn�̉��x�͔M���̉��x�ƈ�v���M�͗��ꍞ�܂Ȃ��Ȃ�܂��B�n�ɁA���ÓI�t�ߒ��ŔM�𗬂����ݑ�����ɂ͂���ɉ��x�̍����M���ɂȂ��ւ��Ȃ���Ȃ�܂���B
�@�܂��A�d���͈��͂̒Ⴂ�O�E�ɑ��Ă����ł��܂���B�O���֎d��������ƌn�̈��͉͂������Ă����܂�����A�d�������o��������ɂ͊O���̎d���������͂̒Ⴂ���̂ɐ�ւ��Ă����Ȃ���Ȃ�܂���B
�@���ÓI�t�ߒ��ŔM���O�E����n�֗�������Ƃ��������A�d�����O���ɑ��čs����Ƃ���������M�͊w���A���@���ʼn��߂����Ƃ���������̂��A�����Ō����Ă��邱�Ƃł��B
�@�����G�l���M�[�A�G���g���s�[�A�̐ρA���x�A���͂͌n�̏�Ԃ���܂�Έ�ӂɒ�܂��ԗʂł�����A�t�i�u�C�r�j�Ȗʂ̐����͊O�E�ƔM��d���̉t�I�Ȃ�����ʂ��Ă̂ݐ����ł�����̂ł��B�i�P�D�i�P�j�Q�D�ӏ������S�j�ŏq�ׂ��Ӗ��Ōn���ł̕s�t�ߒ��̑��݂Ƃ͊W����܂���B�����͔M�͊w���_�ł����Ƃ�����ɂ������ł����璍�ӂ��Ă��������B
�m�⑫�����T�n
�@�ʍe�u���W�����h���ϊ��Ƃ͉����v�P�D�i�P�j�m�⑫�����n�Œ��ӂ����悤�ɁA�t�i�r�C�u�j�Ȗ����ʊ��ł��邱�Ƃ��g���W�����h���ϊ��h�i�R�D�i�P�j�Ő����j���K�p�ł��邽�߂̕K�v�s���ȏ����ł��B
�@
�@�t�i�u�C�r�j�Ȗ��̏�ԗʂt���r�����ڑ���ł��Ȃ��ʂȂ̂ł����A�Ȗʂ̂u�����̌��z�����͂o�ɊW���A�r�����̌��z�����x�s�ɊW���Ă���B���̂��ߍ��W���̐ςu�Ƒ��܂��āA�����\�ȏ�ԗʕϐ��u�C�s�C�o���ł��Ȗ��Ȍ`�ŋȖʂ̌`���Ɋւ���Ă����B���̂��ߔM�͊w��_����Ƃ��ɍł��d�v�ō����I�ȁg��ԕ������Ȗʁh�ł��B
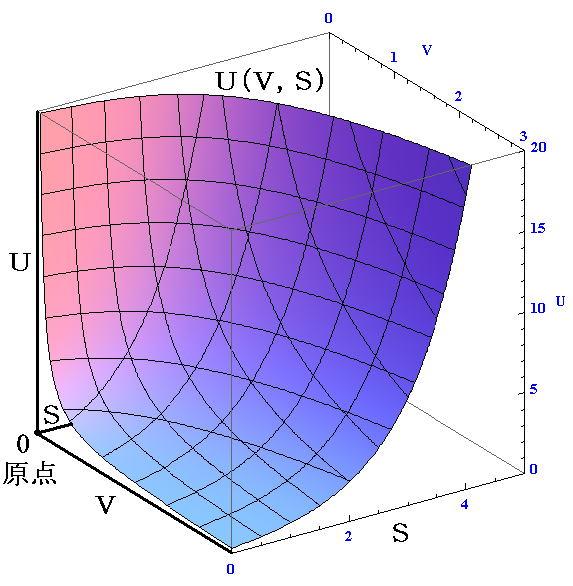
�@���t�̊��S�����̒�`����m���S�����̈Ӗ��ɂ��Ă��ʍe�Q���n
�ł���B
�@
�@����ƁA�O�߂����_�i�P�j��蒼����
��������B�������s��0�A�o��0�́A�O�߂ŏq�ׂ��悤�ɔM�͊w���A���@������̕K�R�̌��ʂł��B
�@����ɂt�̓Γ������Ȑ����z�̕ω��̗l�q��\�����Ƃ���A���������_�i�P�j���
��������B�����̌��_�͑̐ψ��ŃG���g���s�[������i�܂�n�ɔM����������j���x���オ�鎖���Ӗ�����B�܂��E���̌��_�́A�f�M�I�ɖc������i�܂�O�E�Ɏd��������j�ƈ��͂������鎖���Ӗ����Ă���B�����͈�ԍŏ��Ɏw�E�������ł��B
�@�����̊W���� ��ϔM�e�ʂbv �� �f�M���k���ȁh ����ɐ��ł��邱�Ƃ��Ӗ�����B
�����͌o�������Ƃ���v���錋�_�ł����A�M�͊w���A���@�����������Ȃ�ΕK�������łȂ���Ȃ�Ȃ��B
�@���t�������̍��܂œW�J����
�ɉ����āA���_�i�P�j�͂t�i�u�C�r�j�Ȗʂ����ɓʂɂȂ邱�Ƃ������Ă���̂�
�����藧�B���̂Ƃ��i���r�^���u�j�Ɋւ���������̔��ʎ������łȂ���Ȃ�Ȃ����Ƃ���A������
�����܂�B
�@
�@���t�����S�����ł��邽�߂̕K�v�\�������i�����Maxwell�̊W���̈�j����
�������܂��B
�@���̎����A�O���Ō�̕s�����ɓK�p�����
��������B
�@�Ƃ���ŁA�P�D�i�Q�j�Q�D�m�⑫�����R�n�Ő����������w�������A�P�D�i�Q�j���r�i�s�C�u�j�Ȗ��A���邢���P�D�i�S�j���r�i�o�C�u�j�Ȗ��ɓK�p�����
��������B
�@�������A�P�D�i�Q�j�Q�D�m�⑫�����S�n�Ő����������w�������A�o�i�u�C�r�j���o�i�u�C�s�j�A���邢���s�i�r�C�u�j���s�i�r�C�o�j�̕ϐ��ϊ��ɓK�p�����
�ƂȂ�B
�@������O�L�̕s�����ɓK�p�����
�ƂȂ�A�g�������k���h�ȁf����ɐ��ł��邱�Ƃ�������B
�@���̂��߁A���̋t���ł����g�����̐ϒe�����h������ɐ��ƂȂ�܂��B
�@����ɂ܂��A
�ƂȂ�A�g�舳�M�e�ʁh�bp����ɐ��ł��邱�Ƃ�������B
�@�����͌o�������Ƃ���v���錋�_�ł����A�M�͊w���A���@�����������Ȃ�ΕK�������łȂ���Ȃ�Ȃ��B
�@�����ŁA�M�e�ʔ�i��M��j�������k���Ƃ̊W���Ă����B�P�D�i�Q�j�Q�D�m�⑫�����R�n�m�⑫�����S�n�̐��w������p�����
�ƂȂ邪�A�����͔M�e�ʂ∳�k���̒�`�̊W��\���Ă���ɉ߂����A�M�͊w�̊�{�@���Ƃ͊W����܂���B
�@�ȏ���܂Ƃ߂�ƈȉ��̂悤�ɂȂ�܂��B�ԕs�����́A�M�͊w���A���@������C�ӂ̕����n�ɑ��Đ��藧���Ƃ������Ă���B
�@�M�e�ʂɊւ���
�ƂȂ�܂��B�P�ʎ��ʓ�����A�P�ʃ���������̔M�e�ʂł����g��M�h�ɒ����ɂ́A�����̒l�����ʂ�����Ŋ���悢�B
�@�܂��A������f�M�̌��ł̈��͂Ƒ̐ς̊W�������W���Ɋւ���
�����藧���܂��B�����W�������̕�����t���Ē�`���Ă���̂͌W���𐳂ɂ��邽�߂ł��B���͂���������Ηe�ς��������i�݂u�^�݂o�j�����ɂȂ邩��ł��B����ȏ�̈Ӗ��͂���܂��A�������߂���Ƃ��ɒ��ӂ��Ă��������B
�@
�@1�D�i�Q�j�P�D�Ő������� �舳�M�c���W���i�̐ϔM�c�����j��
�ɂ��Ă��s�������m��ł��܂����B
�@���ہA0���`4���̐���S���̗l�ɔM�������āi�܂�����G�l���M�[�t�債�āj���x���オ��Ƒ̐ς���������悤�ȕ���������܂��B
�@����ɁA�P�D�i�Q�j�Q�D�Ő������� ��ψ��͌W����p
�ɂ��Ă��s�����͒�܂�܂����B
�@���̂Ƃ� ��ψ��͌W����p �� �舳�M�c���W���i�̐ϔM�c�����j�� �̒�`�͈ȉ��̊W�ɂ���܂��B���̂��߁A�ǂ���������̕������m�肵�܂��A�݂��ɓ������Ŗ�����Ȃ�Ȃ����͌����܂��B
����͈ȉ��̂悤�ɕό`������������₷����������Ȃ��B�P�D�i�Q�j�Q�D�m�⑫�����R�n�Ő����������w������ό`�����
�ƂȂ�B�������ł�������ς���ƌ��ʂ����ǂ��Ȃ�B
�@�㎮���A�P�D�i�Q�j�Q�D���M�͊w�@���ɂ���ċ��߂� �舳�M�e�ʂbp �� ��ϔM�e�ʂbv �̍���\�����ɓK�p�����
�ƂȂ�B
�@����� �舳�M�e�ʂbp �� ��ϔM�e�ʂbv ������ɑ傫�������Ӗ�����B�܂�舳���ʼn��M����ƁA���M�ɔ����Ėc�����ĊO�E�Ɏd�������邽�ߌn�̃G�l���M�[�������B���̂��߁A�������x�㏸��B������ɂ͂���R�̔M�������Ȃ���Ȃ�Ȃ��ƌ������Ƃł��B����͂���Ӗ�������O�̗l�Ɏv����������܂��A�悭�l����ƂQ�D(�P)�Ő��������t�i�r�C�u�j�Ȗʂ̐������瓱�������̂ł��邱�Ƃ�����܂��B
�@�܂���Ή��x�s����ɋ߂Â��Ɨ��҂̍��͗�ɋ߂Â����Ƃ�����B
�@�P�D�i�S�j�P�D�ŋ��߂��W�����
�ƂȂ�B���ӂ̗ʂ̐����͉���Ȃ��� �� �� ��p �ƕ����������ł��邱�Ƃ͌�����B
�@����ɁA���t�����S�����ł��邽�߂̕K�v�\�������iMaxwell�̊W���̈�j�ƁA�P�D�i�Q�j�Q�D�m�⑫�����S�n�̐��w������p�����
��������B���̊W����O�q�̎��ɑ�������
��������B�g�M�c�����h�̐����̕����͒�܂�Ȃ����A���̑傫���ɂ͏�������邱�Ƃ������Ă���B
�@
�@�������k���ȁf �� �f�M���k���ȁh �̍��́A���̒�`�ƁA�P�D�i�Q�j�Q�D�m�⑫�����S�n�̐��w������p�����
�Ə�����B
�@����ɁA���łɋ��߂Ă����M�͊w�@���̌��_��K�p�����
�ƂȂ�B
�@����� �������k���ȁf �� �f�M���k���ȁh ������ɑ傫�������Ӗ�����B�܂�A�������ň��k����ƌn����M���O�E�֓����Ă������߂ɁA�������͑����ł���R���k�ł���ƌ������Ƃł��B����͂���Ӗ�������O�̗l�Ɏv����������܂��A�悭�l����ƂQ�D(�P)�Ő��������t�i�r�C�u�j�Ȗʂ̐������瓱�������̂ł��邱�Ƃ�����܂��B
�@�܂���Ή��x�s����ɋ߂Â��Ɨ��҂̍��͗�ɋ߂Â����Ƃ�����B
�@�܂��A �舳�M�e�ʂbp �� ��ϔM�e�ʂbv �̍���\�����Ɣ�r�����
�ƂȂ�A���łɋ��߂Ă���W�����Ăѓ�����B
�@
�t�i�r�C�u�j�Ȗʂɉ����Đ��藧��ʓI�Ȑ������܂Ƃ߂Ă����B
�@�����̊W�����M�͊w���A���@����\���B�Ƃ��ɍŌ�̎���Maxwell�̊W���ƌĂ��B�܂��A�F�M�͊w�W���Ƃ̊W����`�����瓱������B����ɁA�ԐF�s�������M�͊w���A���@�����瓱������B
�@�Ō�̎��̐����͉���Ȃ��B�ԕs�����̏��������藧�Ȗʂł��A�Ō�̎��������̂ǂ���ɂł��Ȃ�Ȗʂ����邱�Ƃ́A�Δ����̈Ӗ����l����Β����ɉ���B
�@�܂��A���̗l�ȋȖʂ��l�����Ƃ��Ƀ��̑傫���ɏ���������邱�Ƃ������ł���B����}��|��|��傫������ƁA���̐ԐF�s���������藧���Ȃ��Ȃ�B�@�@
�@
�@�t�i�u�C�r�j�Ȗ��̌�����ς����r�i�u�C�t�j�Ȗ��Ƃ��Č��Ă��Q�D�i�P�j�����_�i�Q�j���瓯�l�ȋc�_���ł���B�������A��ԗʂt�����ڑ���ł���ʂł͖������A�Ȗʌ��z���s�Ƃo�̕��G�Ȋ��ƂȂ�̂ł��܂���ɗ����܂���B
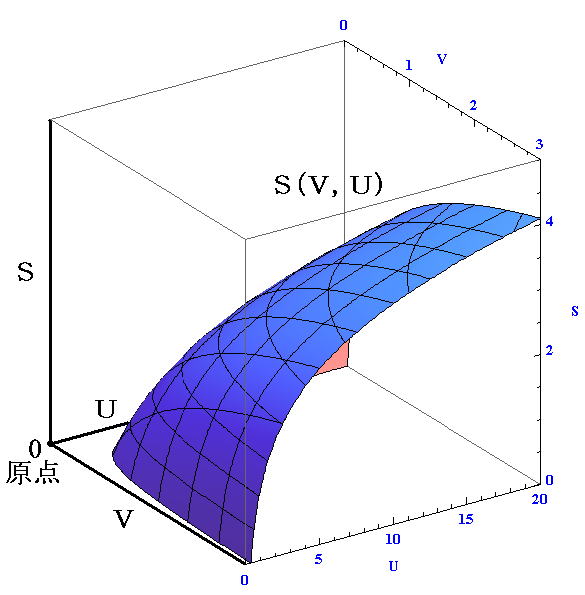
�@�r�i�u�C�t�j�Ȗʂɂ������r�̊��S�����̒�`����
�ƂȂ�B
�@
�@�Q�D�i�P�j�����_�i�Q�j��蒼����
��������B����͑O���œ���ꂽ�o��0�A�s��0�̓��R�̌��_�ł��B
�@����ɂr�̓Γ������Ȑ����z�̕ω��̗l�q��\�����Ƃ���A�Q�D�i�P�j�����_�i�Q�j���
��������B�E���̌��_�́A��ς̌��Ōn�̓����G�l���M�[���オ��Ή��x���オ�邱�Ƃ��Ӗ����Ă���B��ς̌��Ōn�̓����G�l���M�[��������ɂ͔M�������Ȃ���Ȃ�Ȃ��̂����A�M��������Ή��x���オ�邱�Ƃ��Ӗ����Ă���B
�@���r�������̍��܂œW�J����
�ɉ����āA���_�i�Q�j�͂r�i�u�C�t�j�Ȗʂ���ɓʂɂȂ邱�Ƃ������Ă���̂�
�����藧�B���̂Ƃ��i���u�^���t�j�Ɋւ���������̔��ʎ������łȂ���Ȃ�Ȃ����Ƃ���A������
�����܂�B
�@
�@���r�����S�����ł��邽�߂̕K�v�\����������
�������܂��B
�@
�@�t�i�u�C�r�j�Ȗ��̌�����ς����u�i�t�C�r�j�Ȗ��Ƃ��Č��Ă��Q�D�i�P�j�����_�i�R�j���瓯�l�ȋc�_���ł���B�������A���̋Ȗʂ͏�ԗʂt���r�����ڑ���ł���ʂł͖������A�Ȗʌ��z���s�Ƃo�̕��G�Ȋ��ƂȂ�̂łقƂ�ǖ��ɗ����܂���B
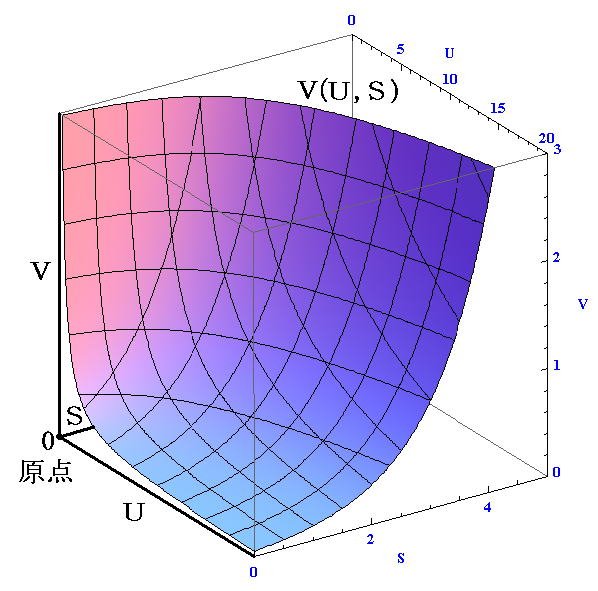
�u�i�t�C�r�j�Ȗʂɂ������u�̊��S�����̒�`����
�ł���B
�@
�@�Q�D�i�P�j�����_�i�R�j��蒼����
��������B����͑O���œ���ꂽ�o��0�A�s��0�̓��R�̌��_�ł��B
�@����ɂu�̓Γ������Ȑ����z�̕ω��̗l�q��\�����Ƃ���A�Q�D�i�P�j�����_�i�R�j���
��������B�E���̌��_�͒f�M�I�Ɍn�̈��͂��オ��Γ����G�l���M�[�����傷�鎖�������Ă���B���͂��グ�邽�߂ɂ͒f�M�I�Ɉ��k���Čn�Ɏd���������Ȃ���Ȃ�Ȃ��̂ŁA���̌��_�͓��R�ł��B
�@���r�������̍��܂œW�J����
�ɉ����āA���_�i�Q�j�͂r�i�u�C�t�j�Ȗʂ���ɓʂɂȂ邱�Ƃ������Ă���̂�
�����藧�B���̂Ƃ��i���u�^���t�j�Ɋւ���������̔��ʎ������łȂ���Ȃ�Ȃ����Ƃ���A������
�����܂�B
�@
�@���u�����S�����ł��邽�߂̕K�v�\����������
�������܂��B
�@
�@�����Ƃ��āA�l�b�g��ŏЉ��Ă���g�P���q���z�C�́h����ԕ������Ȗʂ̃O���t�\���������p�m�������A���p�����e�i�u�C�s�j�̃O���t�ɂ��Ă͂u�C�s���W���̖ڐ���ɂ��ē���Ȓu����������Ă��܂��n�B
�@�����G�l���M�[�t�i�r�C�u�j���g���W�����h���ϊ��h���{�����Ƃɂ���ĐV���ɓ���������M�͊w���f�i�s�C�o�j�A�e�i�s�C�u�j�A�g�i�r�A�o�j�̐����ɂ��Đ������܂��B�����̏�ԗʂ͂�������G�l���M�[�̎����������A�g���R�G�l���M�[�h�i�M�͊w�������j�ƌĂ��B
�@�ʍe�u���W�����h���ϊ��Ƃ͉����v�S�D�Ő��������悤�ɁA�����̔M�͊w���͈ȉ��̈Ӗ������B
�@�����̏�ԗʂ������I�ɉ����Ӗ�����̂��𗝉�����̂͗e�Ղł͂Ȃ����A�����̒l�͌n���i�t0�C�u0�C�r0�j�ŕ\������Ԃɂ���Ƃ��A�n�������̏�ԗʁi�G�l���M�[�̎����j�ł��邱�Ƃ͊m���ł��B
�@�܂��A���̏�ԓ_�i�t0�C�u0�C�r0�j�ɂ͌n�̈��͂o0���|�i�݂t�^�݂u�js���Ή��x�s0���i�݂t�^�݂r�jv�Ȃǂ̎�������ԗʂ������ɕt�����Ă��܂��B
�@
�@�O���̎������A���̍e�ŗp���Ă���t�i�u�C�r�j�O���t�Ő�������B���̂Ƃ��A�Q�D�i�P�j�Œ��ӂ����悤���t�i�u�C�r�j�Ȗʂ��������ɓʊ��ł��鎖���v���o����Ĉȉ��̐}���������������B
�@�Q�D�i�Q�j�P�D�ŗ��p�����O���t�̍��W������]�����āA�i�u0�C�r0�j���i1�C1.5�j�ɂ�����ڕ��ʂōl����ƁA�t0�C�f0�C�e0�C�g0�͐}���Ɏ������ʒu�̂t�l�ł��B
�@���Ȃ݂ɐ}���̐��l��ł͂t0��4.48�A�f0��2.24�A�e0��-2.24�A�g0��8.96�ƂȂ�B
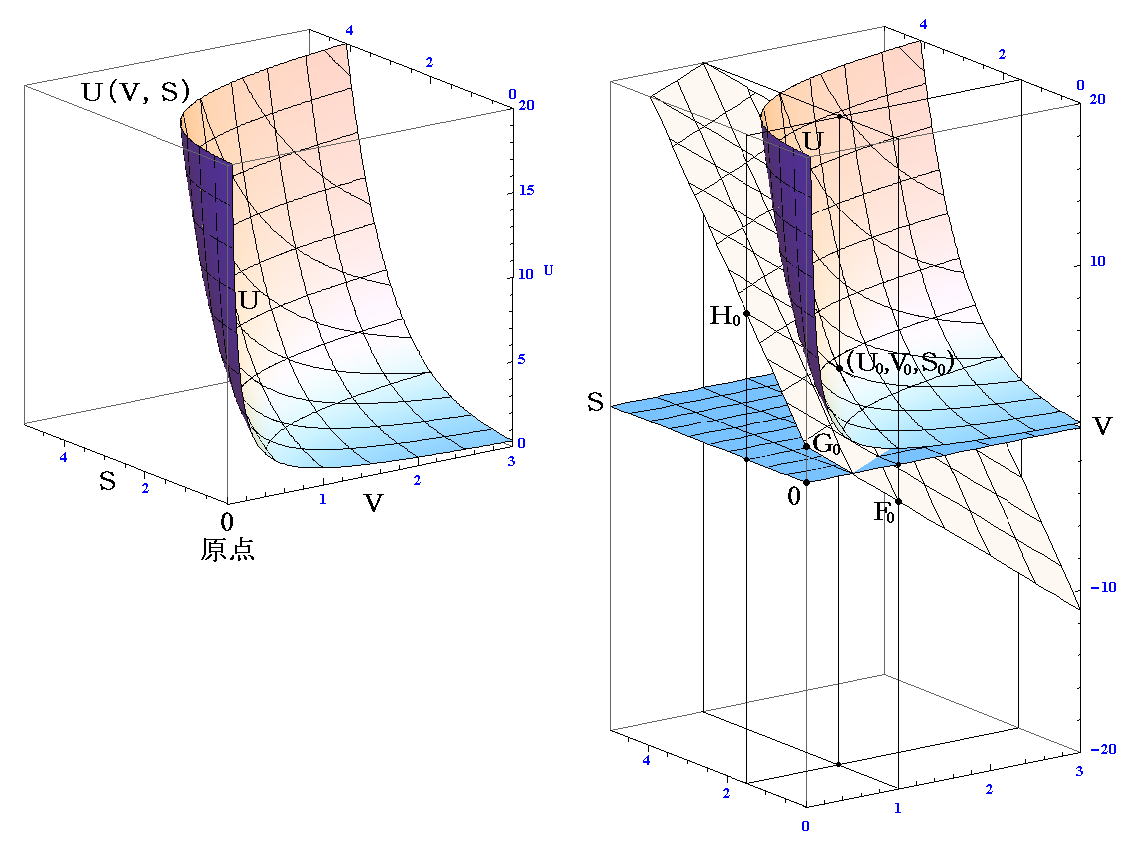
�@�ڐ��Ƃ̊W������₷�����邽�߂ɁA�u���u0�i���l�j�̕��ʂŐ�������ƁA�r���r0�i���j�̕��ʂŐ�������������Ɖ��}�̂悤�ɂȂ�B
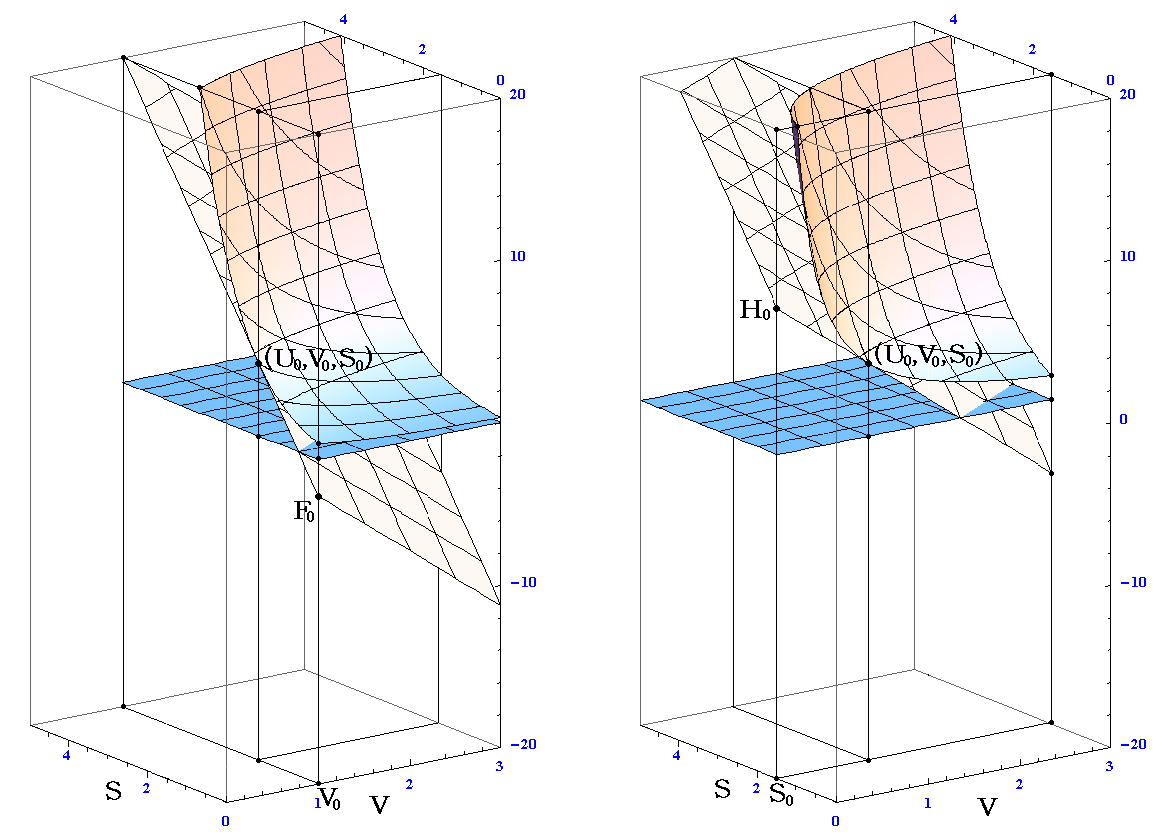
�@
�@�Q�D�i�P�j�Ő��������t�i�r�C�u�j�Ȗʂ̐����ƁA���ꂼ������R�G�l���M�[�l�̊w�I�ȈӖ�����A���L�̑召�W�����藧���Ƃ������ɉ���B
�@���̑召�W�́A�P�D�i�P�j�Q�D�̉ӏ������T�D���疾�炩�Ȃ悤�ɁA����̏�Ԃɕt�����邻���̗ʂ��ǂ̕ϐ���p���ĕ\���Ă��K�����藧�B���̂Ƃ��A�t�Ƃf�̑召�W�͏ɂ��A��ӂɒ�܂�Ȃ��B
�m�⑫�����n
�@�G���g���s�[�r�̐����͍��܂ł̋c�_����͒�܂�Ȃ��B���̂Ƃ��A�ŏ��̊�ƂȂ��Ԃ̃G���g���s�[�l��K���Ɍ��߂Ă��ׂĂ̏�Ԃł̃G���g���s�[�l�𐳂ɂ��邱�Ƃ��ł��܂��B
�@���ہA�G���g���s�[�͂��ׂĐ��̒l�ł����Ƃ��ď��߂āA��L�̕s�����͐��藧�B�Ȃ��Ȃ�O���̃O���t���̂r��0�i���j�̕��ʂ��t0�i�u0�C�r0�j�_���������ɂ���i�܂��r0��0�j�Ȃ���e���t���f���g�ƂȂ邩��ł��B
�@�����̑召�W�́A�G���g���s�[�͕K�����̒l�ł���Ƃ���ꍇ�ɂ́A�O�͂Q�D�̌��_�i�o�C�u�C�s��0�j�����R�G�l���M�[�̒�`����ȒP�ɏؖ��ł��܂��B
�@���ہA�����܂ł̒i�K�ŁA�G���g���s�[�Ƃ͉��Ȃ̂���������Ă��܂���̂ŁA��L�̐����͉��̂��Ƃ��f����Ǝv���܂��B
�@���̂����A�G���g���s�[�̈Ӗ����G���g���s�[�͕K�����̒l�łȂ���Ȃ�Ȃ�������������܂��B
�@������M�͊w��O�@���Ƃ��Ē莮������鎖���ł����A�����̎����ɕt���Ă͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�Ő������܂��B
�@
�@���R�G�l���M�[�̒l�f0�A�e0�A�g0���O�߃O���t��ł͏�ԓ_�i�t0�C�u0�C�r0�j�Ƃ͈Ⴄ�ʒu�Ŏ�����Ă��邪�A��ԁi�t0�C�u0�C�r0�j�ɕt��������̂ł������Ƃ�Y��Ȃ��ł��������B
�@�Ɨ��ϐ����i�r�C�u�j�Ƃ���@�f�i�r�C�u�j�C�e�i�r�C�u�j�C�g�i�r�C�u�j�̃O���t�@��`���Ɖ��}�̗l�ɂȂ�B
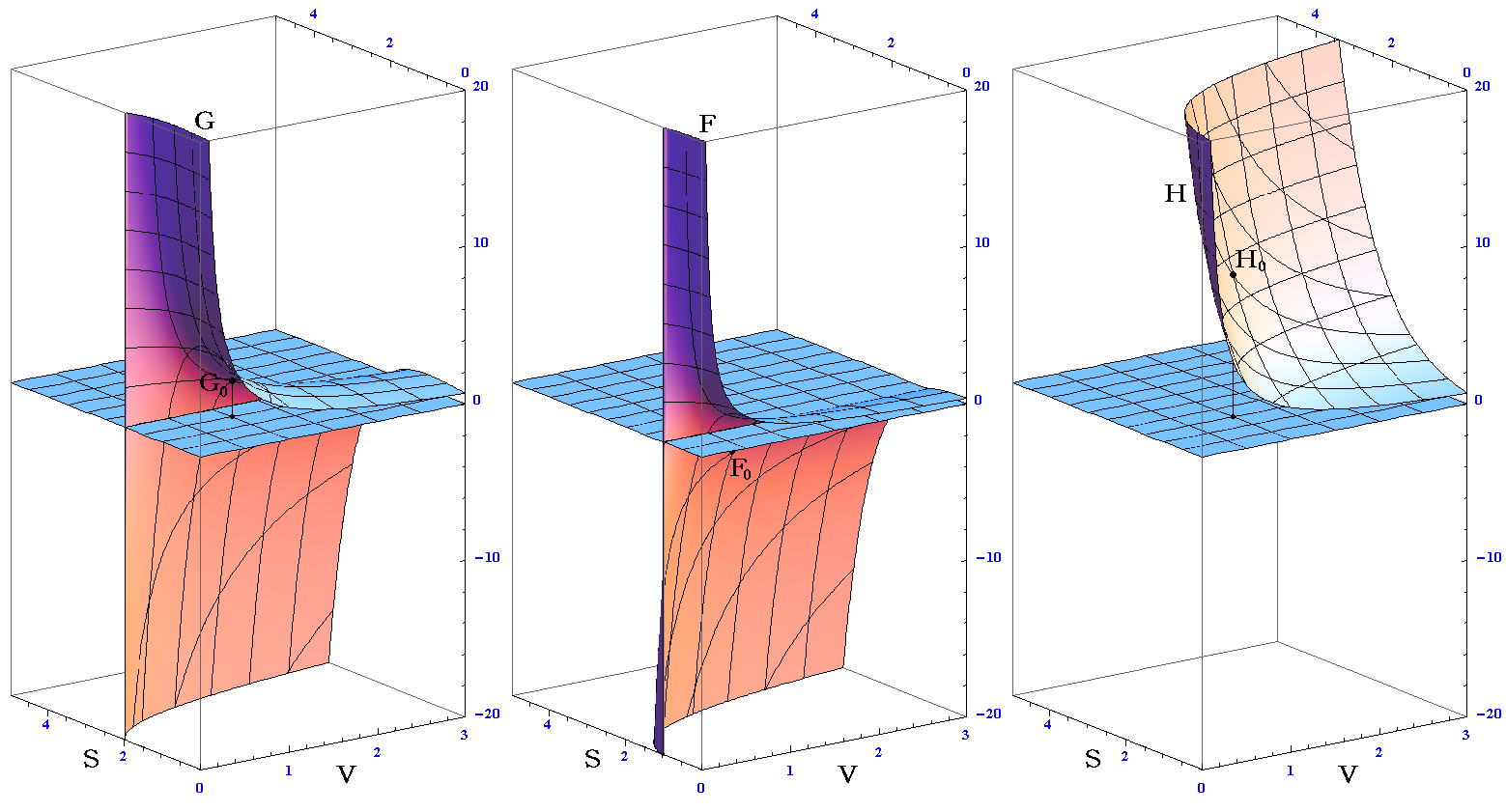
�@�_�i�u0�C�r0�j���i1.0�C1.5�j�ɂ�����l���m�F����ƁA�m���ɑO�ߐ}���̂f0��2.24�A�e0��-2.24�A�g0��8.96�ɂȂ��Ă��邱�Ƃɒ��ӂ��ꂽ���B
�@�܂��i�u�C�r�j�̂�����_�ŁA�O�߂Œ��ӂ����e���f���g���A���藧���Ă��邱�Ƃ��m�F�ł���B�������A��������ł��r��0�͈̔��ł̘b�ł��B
�@�������O���t��̌v�Z�菇�͂������ł��B
�@
�@�ʍe�u���W�����h���ϊ��Ƃ͉����v�S�D�Ő������������ŕϐ��ϊ������O���t��`���Ɖ��}�̂悤�ɂȂ�B
�@���̂Ƃ��A��}�Ɏ������u��0�`3�A�r��0�`5�͈̔͂ŁA�s��o�́A�ق�0�`���܂ŕω����邪�A�s�Ƃo�Ɋւ��Ă�0�`10�͈̔͂̃O���t�������B
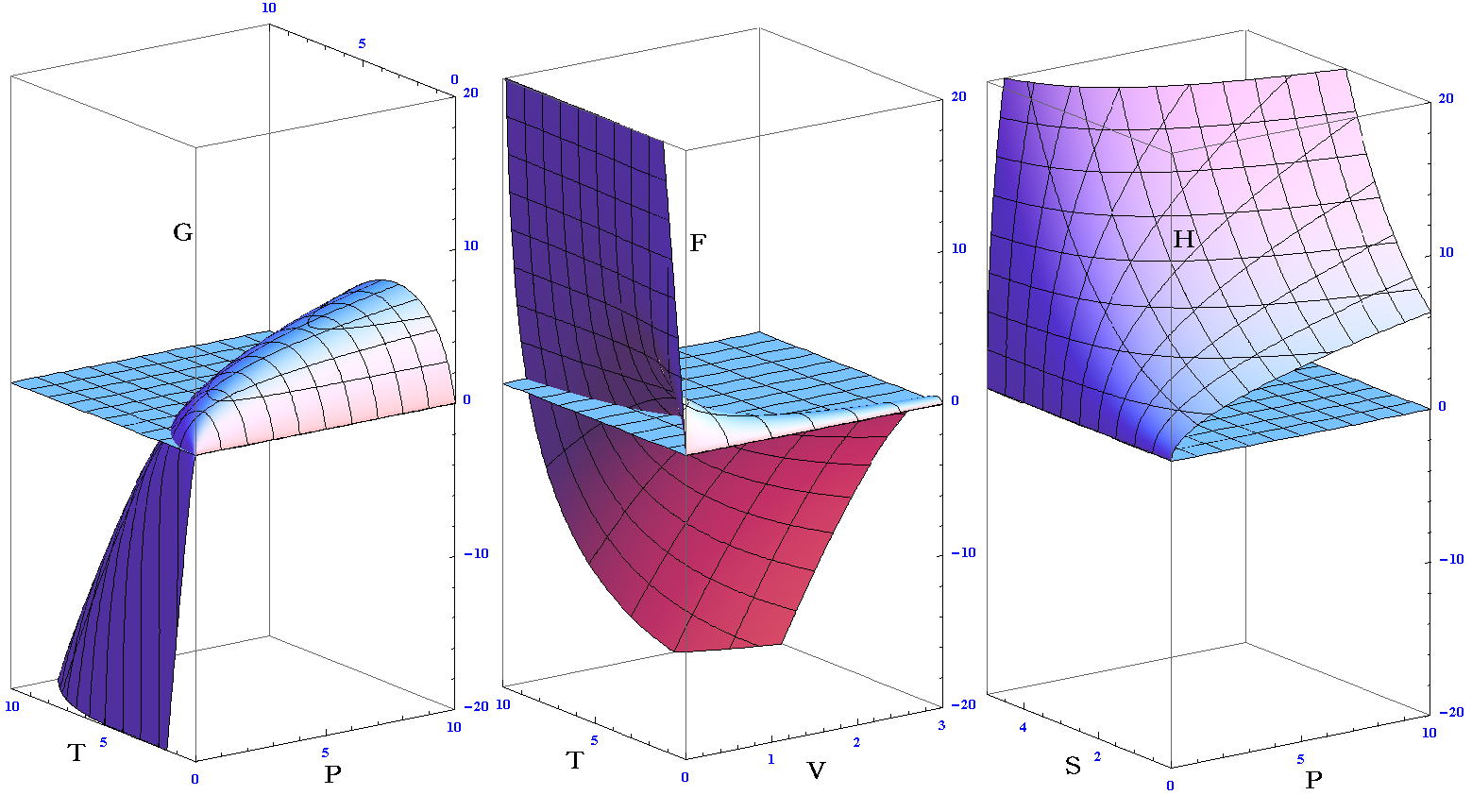
�@�O�߂́i�u0�C�r0�j���i1.0�C1.5�j�ɉ����鈳�͂o0���|�i�݂t�^�݂u�js�Ɛ�Ή��x�s0���i�݂t�^�݂r�jv�̒l�́A���ꂼ��o0��4.48�Ƃs0��4.48�ƂȂ�B
�@���̂Ƃ��A�O���t��̒l�͂f0�i�s0�C�o0�j���f0�i4.48�C4.48�j��2.24�A�e0�i�s0�C�u0�j���e0�i4.48�C1.0�j���|2.24�A�g0�i�r0�C�o0�j���g0�i1.5�C4.48�j��8.96�ƂȂ�A�O�q�̒l�ƂȂ��Ă���B
�@�������O���t��̌v�Z�菇�͂������ł��B
�m�⑫�����P�n
�@�����i�R�j�P�D�m�⑫�����P�n�A�m�⑫�����Q�n�Ő�������l�ɁA�����̃G���g���s�[�l���g�M�͊w��O�@���h�������i�܂�A�s��0�ƂƂ��ɂr��0�ƂȂ�j�ꍇ�ɂ��f�i�s�C�o�j�̃O���t�Łi�݂f�^�݂s�jp��0�̗̈�͖����Ȃ�A�s��0�ƂȂ镔���ł��������f�i�s�C�o�j�Ȗʂ͂o-�f���W�ʂɐ����Ɍ����܂��B�Ȃ��Ȃ�A�i�݂f�^�݂s�jp���|�r��0�i�s��0�j������ł��B
�@
�@����ɁA�g�i�r�C�o�j�̃O���t�ɉ����Ă��A�i�݂g�^�݂r�jp���s�ł�����A�g�M�͊w��O�@���h������������A�r��0�ƂƂ��ɂs��0�ƂȂ�A�i�݂g�^�݂r�jp��0�ƂȂ�˂ΐ���܂���B�܂�A�������g�i�r�C�s�j�̃O���t�͂g-�o���W���ʂɐ����Ɍ����܂��B�������}�̂g�i�r�C�o�j�Ȗʂ����̗l�ɏC������˂ΐ���܂����B
�@
�@���̎��A�f�i�s�C�o�j�Ȗʂ��o-�f���W�ʂ�����̌`�͏�E�}���g�i�r�C�o�j�}�̂r��0�i�܂�s��0�j�̐���Ɉ�v���܂��B�Ȃ��Ȃ� �f�i�s�C�o�j���g�i�s�C�o�j�|�s�r�i�s�C�o�j �ł����� �s��0�A�r��0 �� �f�i0�C�o�j���g�i0�C�o�j �ƂȂ邩��ł��B
�@
�@���̂Ƃ��A�����̂r�͂s�̑���Ƌ��ɑ������܂�����A�g�i�r�C�o�j�̃O���t�͂g�i�s�C�o�j�̃O���t�Ǝ����`�ɂȂ�܂��B�܂���قǂ̐}�̉E�[�}�g�i�r�C�o�j�̃O���t�͂g�i�s�C�o�j�ɒu�������āA���[�̐}�f�i�s�C�o�j�̐}�Əd�ˍ��킹�鎖���ł���B
�@���̂��߁A�g�i�s�C�o�j�Ƃf�i�s�C�o�j���d�ˍ��킹���}�̂o�����̐���ɂ�����A�������̃M�u�Y�̎��R�G�l���M�[�f�i�s�j�Ȑ��ƃG���^���s�[�g�i�s�j�Ȑ��̉��x�ɂ��ω��̗l�q�͉��}�̗l�ɂȂ�܂��B������R�D�i�S�j�Ő��������g�M�u�Y�E�w�����z���c�̎��h�̐}�I�ȕ\���ł��B
�@���̂Ƃ��A�s��0�ƂȂ�ƕ����̎��^���G�l���M�[�͂O�ƂȂ�܂����A�|�e���V�����G�l���M�[�͗�ɂ͐���܂���B���̂��߃G�l���M�[�l�̗�_�Ɋւ��Ă͔C�Ӑ����c��܂��B���̓�����͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�R�D�i�S�j1.�m�⑫�����P�`�R�n���Q�Ƃ��ꂽ���B
�@
�@���������e�i�s�C�u�j�Ȗʂ��t�i�r�C�u�j�Ȗʂɑ��Ă������܂��B�g�M�͊w��O�@���h������������e�i�s�C�u�j�Ȗʂ́i�݂e�^�݂s�jv��0�̗̈�͖����Ȃ�A�e�i�s�C�u�j�Ȗʂ͂s��0�ƂȂ�Ƃ��e-�u���W���ʂƐ����Ɍ����˂ΐ���܂���B�Ȃ��Ȃ�i�݂e�^�݂s�jv���|�r��0�i�s��0�j������ł��B
�@�t�i�r�C�u�j�Ȗʂ��s��0�ƂƂ��Ɂi�݂t�^�݂r�jv���s��0�ł�����A�t-�u���W���ʂƐ����Ɍ����܂��B
�@�����Ăe�i�s�C�u�j�Ȗʂ̂e-�u���W���ʂɂ��������Ƃt�i�r�C�u�j�Ȗʁm���邢�͂t�i�s�C�u�j�Ȗʁn�̂t-�u���W���ʂɂ��������݂͌��Ɉ�v���܂��B�Ȃ��Ȃ�e�i�s�C�u�j���t�i�s�C�u�j�|�s�r�i�s�C�u�j�ł�����s��0�A�r��0�łe�i0�C�u�j���t�i0�C�u�j�ƂȂ邩��ł��B
�@
�@�l�����X�g�́A�d�C���w�̎����I�ȍl�@����f�i�s�j�Ȑ��Ƃg�i�s�j�Ȑ��m���邢�͂e�i�s�j�Ȑ��Ƃt�i�s�j�Ȑ��n�̂s��0�ɉ�����U�镑���𐄑����āA�M�͊w��O�@���Ɍq�����g�l�����X�g�̔M�藝�h��i1906�N�j�����B���̓������ �ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�R�D �� �����R�D�̑�33�͂̐}33.1�i�p�Ƃ`����}�̂g�Ƃf���瓱�����|���g�Ɓ|���f�ɑ����j ���Q�Ƃ��ꂽ���B
�m�⑫�����Q�n
�@�O�L�m�⑫�����P�n�ɏq�ׂ��t�i�u�C�r�j�Ȗ����e�i�u�C�s�j�Ȗ��̊W�A������g�i�o�C�r�j�Ȗ����f�i�o�C�s�j�Ȗ��̊W�́A�ʍe�u���W�����h���ϊ��Ƃ͉����v�Q�D�i�Q�j�P�D�̃O���t
�ƁA�Q�D�i�Q�j�Q_�a�̃O���t
�̊W�ɑ�������B
�@���̂Ƃ��A���i���C���j�Ȗʂ̂���0�̕��ʂɉ��������Ȑ��ƁA��xu�i���C�Łj�Ȗʂ̃Ł�-1.0�̕��ʂɉ��������Ȑ�����v���Ă��邱�Ƃɒ��ӂ��ꂽ���B�����Ă��i���C���j�Ȗʂ̂������̌`��͂������債�Ă��A��xu�i���C�Łj�Ȗʂ̂������̌`��̃ł����債�����̂ֈ����p����Ă��邱�Ƃ����ӂ��ꂽ���B
�@�����ł́A�r��0�łs��0�̏����ɑ�������A����0�ŃŁ�0�̏�������������Ă��Ȃ��B���̂��߁A���i���C���j�Ȗʂƃ�xu�i���C�Łj�Ȗʂ��������鏊�̂����W�ƃō��W�l����v���Ă��Ȃ��B�܂��A�����ł����Ȗʂ͐ڂ���̂ł͂Ȃ��Č������Ă���B
�@�������i���C���j�Ȗʂ�����0�Łi�݂��^�݂��jx���Ł�0������悤�Ȃ��̂ɕς�����A�O�L�m�⑫�����P�n�ŏq�ׂ��ɂȂ�A���Ȗʂ͂����Ł�0�̈ʒu�Őڂ���悤�ɂ��Ĉ�v�����ł��낤�B
�@���̂��Ƃ́A�ȉ��ŏq�ׂ��t�i�u�C�r�j�Ȗ����e�i�u�C�s�j�Ȗ��̊W�A������g�i�o�C�r�j�Ȗ����f�i�o�C�s�j�Ȗ��̊W�ɂ��Ă����l�ł��B
�@
�@
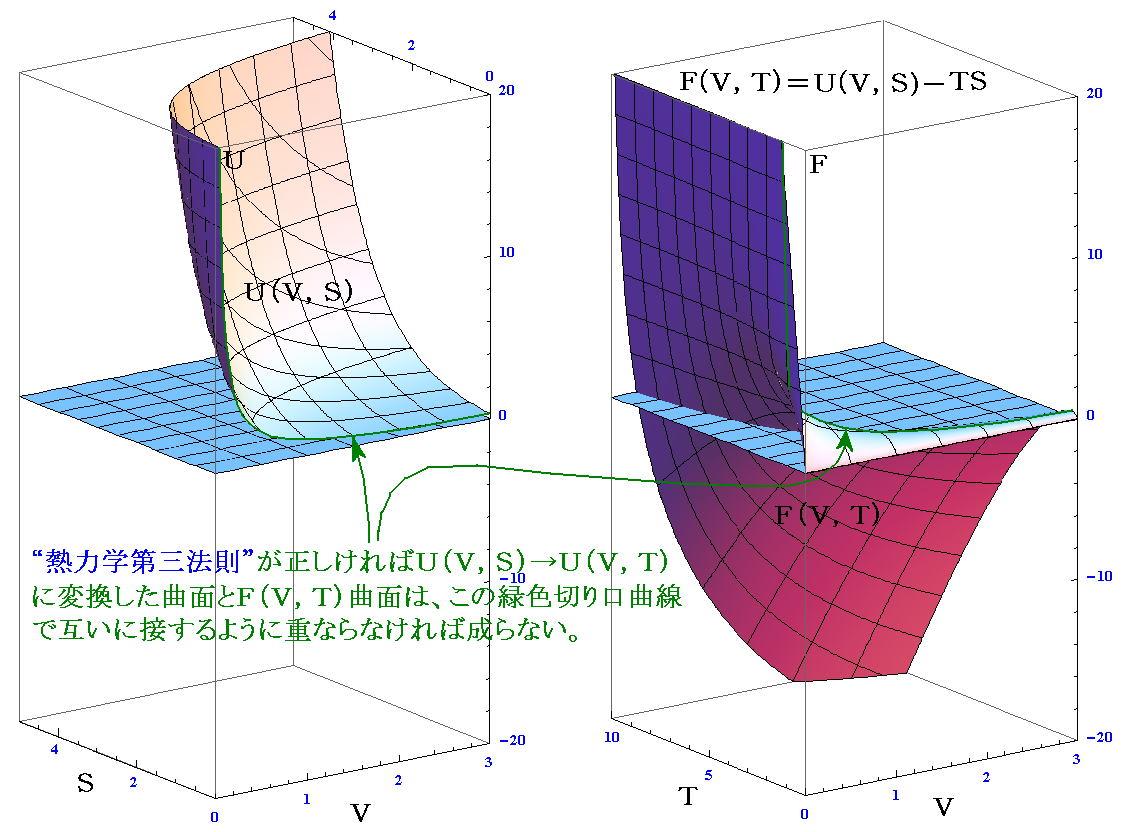
�@�t�i�u�C�r�j�Ȗ����e�i�u�C�s�j�Ȗ��̊W�ɂ��Ă�
�̒u���������������̂ɑ�������B
�@
�@
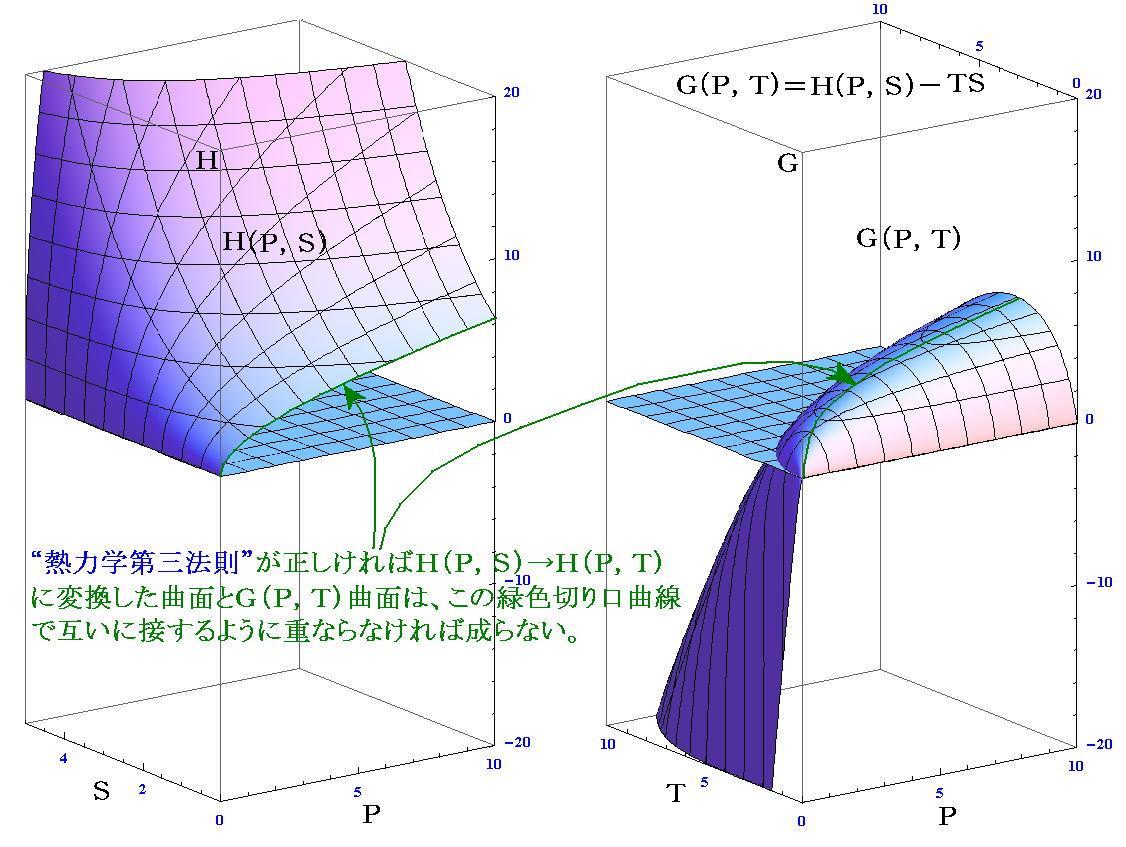
�@�g�i�o�C�r�j�Ȗ����f�i�o�C�s�j�Ȗ��̊W�ɂ��Ă�
�̒u���������������̂ɑ�������B
�@
�@
�@�ȏ�̍l�@�������悤�ɁA���߁i�R�j�Ő��������f�A�e�A�g�Ȗʂ̌��z�̐����Ɋւ��邷�ׂĂ̐����́A�Q�D�͂ŏq�ׂ��t�i�r�C�u�j�Ȗʂ̌��z�̐�������łĂ�������ł��B
�@
�@�O���̎��R�G�l���M�[�Ȗʏ�̂̔����ϕ������L�̗l�ɕ\������B
�@���̂��ƂƑ�Q�͂œ���ꂽ���_�𗘗p����ƁA�����̋Ȗʂ̐����ɂ��Ĉȉ��̌��_��������B�O�߂̔M�͊w���ȖʂɊւ��āA��0 or ��0�Ɋւ��鐫�������藧���Ă��鎖���m�F���ꂽ���B
�@���̒��Łi�݂f�^�݂s�jp���|�r�̕����͂r�̐����Ɉˑ�����B���ہA�R�D�i�Q)�Q�D�̃O���t�Łi�݂f�^�݂s�jp��0�ƂȂ��Ă���̈�ł͂r��0�ƂȂ��Ă����B���̂Ƃ��r��0�̋��ڂ͂o���s2�̃J�[�u�ƂȂ�B�r���K�����l�ƂȂ�悤�Ɋ��Ԃł̒萔������i�݂f�^�݂s�jp��0�̗̈�͖������邱�Ƃ��ł���B�������ď��߂��R�D�i�P�j�R�D�̕s���������藧���B
�@�܂��A�Ō��Maxwell�̊W���ɊW���鍀�̐����͒�܂�Ȃ��B
�@�M�u�Y�̎��R�G�l���M�[�����̋Ȑ��͂��f��0�ƒu�����Ƃɂ��
�ƂȂ�B
�m�⑫�����P�n
�@�����̐�����ǂ܂�������̂悤�ɁA�f��i���ɏq�ׂ�j�e�̋Ȗʂ̐�����_����Ƃ��ɃG���g���s�[�̐�ΓI�Ȓl���s�m���ł��邱�Ƃ́A��Ή��x�s�ɊW�����ƂĂ������������܂��B�M�͊w�������̈�ɒB�����Ǝv���Ă���20���I�����̕����w�҂≻�w�҂ɂƂ��āA�G���g���s�[�̐�ΓI�Ȓl����܂�Ȃ��Ƃ������͐V���ȔY�܂������ɂȂ��ė����̂ł��B
�@���̂Ƃ��A�l�����X�g�́A�d�C���w�I�Ȍ�����ʂ��āA�G���g���s�[�̐�Βl��]�����錮�ƂȂ�d�v�Ȓ����i1906�N�j�Ɏv������܂��B�����āA����͍ŏI�I���g�M�͊w��O�@���h�Ɍ������܂��B
�@����͎��߁i�S�j���M�u�Y�E�w�����z���c�̎��ɊW���鎖���Ȃ̂ł����A�ڍׂ͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�R�D�Ő������܂��B
�m�⑫�����Q�n
�@�ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�R�D�Ő�������M�͊w��O�@����������������A�t�i�r�C�u�j�Ȗʂ̂r��0�̋Ɍ��łs��0�łȂ���Ȃ�܂���B���̂��ߗ�Ƃ��ċ������Ȗʂ͐���������܂���B���̓�������C��(�܂�Ȗʌ��z���r��0�i�s��0�j��0�ɂȂ�悤�ɒ���)�����Ȗʂɂ���K�v������܂��B
�@
�@�܂��A�t�i�r�C�u�j�Ȗ��Ɋւ��Ă͂u�����̒f�ʂɉ�����r�����̋Ȗʌ��z���i�݂t�^�݂r�jV���s�ł�����A�s��0�ƂƂ��ɂr��0�ɐ���˂Ȃ�Ȃ����Ƃ���A�t�i�r�C�u�j�Ȗʂ��t-�u���W���ʂɐ����Ɍ�����悤�ɏC������˂Ȃ�Ȃ��B
�@
�@���ɁA�f�i�s�C�o�j�Ȗ��Ɋւ��Ă͂o�����̒f�ʂɉ�����s�����̋Ȗʌ��z���i�݂f�^�݂s�jP���|�r�ł�����A�s��0�ƂƂ��ɂr��0�ɐ���˂Ȃ�Ȃ����Ƃ���A�f�i�r�C�u�j�Ȗʂ́i�݂f�^�݂s�jP��0�̗̈悪�����Ȃ�A�������f-�o���W���ʂɐ����Ɍ�����悤�ɏC������˂Ȃ�Ȃ��B
�@
�@���ɁA�e�i�s�C�u�j�Ȗ��Ɋւ��Ă͂u�����̒f�ʂɉ�����s�����̋Ȗʌ��z���i�݂e�^�݂s�jV���|�r�ł�����A�s��0�ƂƂ��ɂr��0�ɐ���˂Ȃ�Ȃ����Ƃ���A�e�i�s�C�u�j�Ȗʂ́i�݂e�^�݂s�jV��0�̗̈悪�����Ȃ�A�������e-�u���W���ʂɐ����Ɍ�����悤�ɏC������˂Ȃ�Ȃ��B
�@
�@����ɁA�g�i�r�C�o�j�Ȗ��Ɋւ��Ă͂o�����̒f�ʂɉ�����r�����̋Ȗʌ��z���i�݂g�^�݂r�jP���s�ł�����A�s��0�ƂƂ��ɂr��0�ɐ���˂Ȃ�Ȃ����Ƃ���A�g�i�r�C�o�j�Ȗʂ��g-�o���W���ʂɐ����Ɍ�����悤�ɏC������˂Ȃ�Ȃ��B
�@
�m�⑫�����R�n
�@�ꐬ���n�����x���̏������ŏ�Ԃ��P����Q�̏�Ԃ֕ω������Ƃ��̃M�u�Y�̎��R�G�l���M�[�̕ω����f��
��p���Čv�Z�ł���B���Ȃ킿�f�i�s�C�o�j�Ȗʂ̂s�����̐���̂o�����̌��z���u�Ȃ̂ŁA�e���͂ɉ�����̐ς̑���l��p����
�Ōv�Z����悢�B�̐ς͕K�����ł��邩��A��艷�x�ł͕����̃M�u�Y�̎��R�G�l���M�[�͈��͂���������ƕK���������A�����̒��x�͑̐ςɈ˂��Ă��܂��B���̓�������O�X�߂̐}�̂t���ؕЁi�f�l�j���O�߂̃O���t�� �s�����̐� �ɉ����ď�ԓ_�����Ă݂邱�Ƃ�����ǂݎ���B
�@���̂��߁A�n���\�����镨�����C�̂̏ꍇ�ɂ́A���z�C�̂̋ߎ��u�����q�s�^�o���g����̂�
�ő�̂̏��͌v�Z�ł���B
�@�܂��A�n���\�����镨�̂��t�̂�ő̂̏ꍇ�ɂ́A�̐ς͈��͂��ω����Ă��قƂ�Ǖω������قڈ��ƌ��Ȃ���̂�
�ƂȂ�B
�@�����̊W����}������Ɖ��}�̗l�ɂȂ�B�C�̂̏ꍇ�A���͂��Ⴂ�Ƃ��ɂ͎��R�G�l���M�[�̕ω��������ɑ傫���Ȃ����Ƃɒ��ӂ��ꂽ���B
�@���̓��������̓I�ȗ�Ōv�Z���Ă݂�B
�@�Ⴆ��25���ɂ����Đ��Ǝ_�f�̂P������1�C������10�C���܂ŕω��������Ƃ��i���̂Ƃ��n�͊O�E�ƔM��d���̂��������Ă���j�̃��f��
�ƂȂ�B�܂�A�C�̂̎��R�G�l���M�[�̕ω����t�̂̂���ɔ�r���Ĉ��|�I�ɑ傫���B�����Ȃ邱�Ƃ́A�����������ł͋C�̂̑̐ς��t�́E�ő̂̑̐ς���1000�{�ȏ�傫����������[���ł���B
�@
�@������g�߂ȗ�Ƃ��āA�P�C���E0���t�߂̕X�Ɛ��̎��R�G�l���M�[�f�����͂ɂ���ĕω�����l�q�������B
�ǂ��m���Ă���悤�ɁA0���t�߂̒P�ʃ���������̑̐ς͂u�X���u�������烢�f�X�����f���ƂȂ�B�Patm�ȏ�ł͐��̕��̎��R�G�l���M�[���Ⴍ�Ȃ�B���̂��߈��͂��グ��ƕX�͗n���Đ��ƂȂ�B���͂������Ƃ��ɂ́A�̐ς���������������ƂȂ郋�E�V���g���G�̖@���ł���B
�m�⑫�����S�n
�@�Ƃ���ŁA������̎�
����́A�m�⑫�����Q�n�̎�����K�p������G���g���s�[��0�j�ȏ�ŕK�����ł��邩��A�����̎��R�G�l���M�[�́A���͈��̏������ʼn��x�Ƌ��ɕK�������������Ƃ�����B���̂�����́A�O�߂̃O���t���m�⑫�����Q�n�ɏ]���ĕ`���������Ȗʂło�����̐��ɉ����ď�ԓ_�����Ă݂�Γǂݎ���B
�@�G���g���s�[�����ڑ���ł���ʂł͂Ȃ��̂ŁA�r�̉��x�ˑ�������M�̃f�[�^�Ȃǂ��狁�܂�Ȃ��Ǝ��̂��錋�_�͓����Ȃ����A���x�ω����������Ƃ��ɂ͂r���قڈ��Ƌߎ��ł���
�̎����g����B��ʂɋC�̂̃G���g���s�[�͉t�̂�ő̂ɔ�ׂđ傫���̂ŁA���x�s�̕ω��ɑ���f�̕ω��̗l�q�͉��}�̗l�ɂȂ�B
�@���x�ω����傫���Ȃ�ƁA�R�D�i�S�j�Ő��������g�M�u�Y�E�w�����z���c�̎��h�𗘗p���Ĕ�M�̃f�[�^���狁�܂锽���M�̏���p���ă��f�̉��x�ɂ��ω������߂܂��B���̓�����͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�S�D�i�R�j�Q�D�������������B
�m�⑫�����T�n
�@�f�i�s�C�o�j�Ȗʂ̂o�����̐���̂s�����̌��z���|�r�ł���A�f�i�s�C�o�j�Ȗʂ̂s�����̐���̂o�����̌��z���u�ł��B���A��̑��`�Ƃa�i��̕����`�Ƃa�ł��悢�j�����t��Ԃɂ���i�s0�C�o0�j�_�ŁA�P����������̃G���g���s�[�ƃ����̐ς��i�rA�A�uA�j�Ɓi�rB�A�uB�j�ł���Ƃ��悤�B
�@�����āA���҂ɋɂ킸���ȈႢ���������rA���rB�A�uA���uB�ł������Ƃ��悤�B���̏ꍇ�ɂ́A�O�q�̐������疾�炩�Ȃ悤�ɁA���t�_�i�s0�C�o0�j�t�߂ɉ�����fA�i�s�C�o�j�ȖʂƂfB�i�s�C�o�j�Ȗʂ͉��}�̗l�ɂȂ�B
�@�}���璼���Ɏ��̊W��������B
����͑��`�Ƃa���������鈳�͂Ɖ��x�̊W�i�g�����Ȑ��h�j��^������̂ŁA�g�N���E�W�E�X�E�N���y�C�����̎��h���̂��̂ł��B
�@
�@�Ⴆ�A�`�Ƃ����P�C�I�E�A�a�Ƃ����Ε��C�I�E�Ă͂߂�ƁA���ۂ��r�P���r���A�u�P���u���Ɛ����Ă���B�܂�A���t�_�i�s0�C�o0�j����������ł��G���g���s�[���傫�����̑��i�P�C�I�E�j������ɂȂ�A����������ł������̐ς����������i�Ε��C�I�E�j������ɂȂ�B
�@���ۂ̂o���i1atm�j�ł̋Ȗʐ���̗l�q���ʍe�P�D�i�Q�j�R�|�P�̃O���t���A�o-�s���W���ʏ�ł̋����Ȑ��̗l�q���ʍe�P�D�i�Q�j�R�|�R�̐}���Q�Ƃ��ꂽ���B
�@
�@��̂f�i�s�C�o�j�Ȗʂ������l�Ɍ������邱�Ƃ͉t���|�C�����t�̏ꍇ�ɂ��Ă�������B��ʂɋC���̃G���g���s�[����̐ς͉t���ɔ�ׂđ傫���̂œ�������ƂȂ�B�m�t�@���E�f���E���[���X�C�̂̂f�i�s�C�o�j�Ȗ��n
�@
�@���̒��Łi�݂e�^�݂s�j�����|�r�̕����͂r�̐����Ɉˑ�����B���ہA�R�D�i�Q)�Q�D�̃O���t�Łi�݂e�^�݂s�jv��0�ƂȂ��Ă���̈�ł͂r��0�ƂȂ��Ă������̂Ƃ��r��0�̋��ڂ͂u��1�^�s�̃J�[�u�ƂȂ�B�r���K�����l�ƂȂ�悤�Ɋ��Ԃł̒萔������i�݂e�^�݂s�jv��0�̗̈�͖������邱�Ƃ��ł���B�������ď��߂��R�D�i�P�j�R�D�̕s���������藧���B
�@�܂��A�Ō��Maxwell�̊W���ɊW���鍀�̐����͒�܂�Ȃ��B
�@�w�����z���c�̎��R�G�l���M�[�����̋Ȑ��͂��e��0�ƒu�����Ƃɂ��
�ƂȂ�B
�m�⑫�����P�n
�@�ꐬ���n�����x����̂��Ƃŏ�Ԃ��P����Q�̏�Ԃ֕ω������Ƃ��̃w�����z���c�̎��R�G�l���M�[�̕ω����e��
��p���Čv�Z�ł���B���Ȃ킿�e�̐ςɉ����鈳�͂̑���l��p����
�Ōv�Z����悢�B
�@�Ⴆ�A�n���\�����镨�����C�̂̏ꍇ�ŗ��z�C�̋ߎ��o�����q�s�^�u���g�����
�ƂȂ�B
�@�Ƃ���ŁA������̎�
����́A�G���g���s�[�����ڑ���ł���ʂł͂Ȃ��̂ŊȒP�Ȏ��̂��錋�_�͓����Ȃ����A���߁i�S�j�Ő�������悤�ɂe�^�s�Ɠ����G�l���M�[�t�Ƃ̏d�v�ȊW����������B
�@
�@�Ō��Maxwell�̊W���ɊW���鍀�̐����͒�܂�Ȃ��B
�@�G���^���s�[�����̋Ȑ��͂��g��0�ƒu�����Ƃɂ��
�ƂȂ�B�G���^���s�[�g�����̏�ԕω��ł̓G���g���s�[�r�i�o�j�̕ω��͈��͂̕ω��Ƌt�ɂȂ�B�܂舳�͂Ɋւ��ĒP���������ƂȂ�B
�m�⑫�����P�n
�@�P�D�i�Q�j�`�i�S�j�ŁA�r�̕ϐ����r�i�s�C�u�j�A�r�i�s�C�o�j�A�r�i�o�C�u�j�Ǝ��R�ɕϊ��ł��邱�Ƃ���������B����Ɠ��l�ɂg�i�r�C�o�j���g�i�s�C�o�j�֕ϊ������
�ƂȂ�B
�@���ꂩ�瓾����
�̊W���́A�g�̂s��o�̕Δ����W���������I�ɑ���\�ȗʂɊW�Â��Ă���܂��B���̂��߁A���ۂ̕����̔C�ӂ̉��x�E���͂ɉ������g�i�s�C�o�j�l��W����Ԃg�i�s0�A�o0�j�l����v�Z����Ƃ��ɖ��ɗ����܂��B
�@���̗l�ɁA�g���t�{�o�u�̃��W�����h���ϊ��ɂ����ĕϐ����@�B�I�Ɂi�r�C�o�j�Ƃ���͕̂K����������ł͂���܂���B�i�s�A�o�j�̕����֗��ȏꍇ������܂��B
�@
�@�ȉ��Ő��������g�M�u�Y��w�����z���c�̎��h�ɂ��ẮA����3�D����33�͇T�g���w�e�a�͂Ǝ��R�G�l���M�[�h��Q�Ƃ���ĉ������B
�@�w�����z���c�̎��R�G�l���M�[�̒�`���
��������B����́i�e�^�s�j�����̐��̌��ł̉��x�ˑ���������Γ����G�l���M�[�t�����肳��鎖���Ӗ����Ă���B
�@�������A���̋t�͌����܂���B�t�i�s�j������������Ƃ����āA������s�Őϕ����Ăe�i�s�j�����S�Ɍ���ł���킯�ł͂���܂���B�ϕ��萔�����̕s�萫���c��܂��B���̕s�萫����菜���������g�l�����X�g�̔M�藝�h�ł��B
�@
�@���l�ɁA�M�u�Y�̎��R�G�l���M�[�̒�`���
��������B����́i�f�^�s�j����舳���̌��ł̉��x�ˑ���������G���^���s�[�g�����肳��鎖���Ӗ����Ă���B
�@�������A���̋t�͌����܂���B�g�i�s�j������������Ƃ����āA������s�Őϕ����Ăf�i�s�j�����S�Ɍ���ł���킯�ł͂���܂���B�ϕ��萔�����̕s�萫���c��܂��B���̕s�萫����菜���������g�l�����X�g�̔M�藝�h�ł��B
�@
�@�����̎����g�M�u�Y�E�w�����z���c�̎��h�Ƃ����܂����A�l�����X�g���M�藝�i�₪�ĔM�͊w��O�@���ƂȂ�j���Ƃ��ɏd�v�ȓ��������܂��B
�@�@�܂��A�����̊W���ɉ����āA���ۂɎ����i�bv��bp�̑���j�Ɉ˂��Č���ł���̂��t�i�s�C�u�j���g�i�s�C�o�j�ł��B������M�͊w��O�@�������藧���ď��߂Ăe�i�s�C�u�j��f�i�s�C�o�j���Ӗ����������ƂɂȂ�܂��B
�@�����̎����ɂ��Ă͕ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v�R�D�ƂS�D�Ő������܂��B
�@
�@���W�����h���ϊ��ɂ�蓱�������M�͊w���������I�ɉ����Ӗ�����̂��𗝉����邱�Ƃ���ł��B�M�͊w���f�i�s�C�o�j�́A�M�u�Y�̔M�͊w�Ɋւ�����_���i1873�N12���j�œ������ꂽ���̂ŁA����ɂ��M�u�Y�̎��R�G�l���M�[�ƌĂ�Ă��܂��B
�@�M�u�Y�������Ȃ闝�R�ł��̗ʂ��������́A�R�{�����R�D��32�͇U���ڂ����B�ȉ��ł��̓��e���Љ�܂��B
�@�M�u�Y�̎��R�G�l���M�[�̗����ɂ͂t�i�u�C�r�j�Ȗʂɗ����Ԃ�K�v������B
�@��̌n�̒��ő�������������Ƃ��ɁA�O�E���爳�͈��̌��ŁA�M�����������菜�����肷��Ƒ��ω����N����e���̃������i���ʁj�̊����͕ω����A�n�̑̐ς��ω�����B���̂Ƃ����x�ƈ��͈͂��̂܂ܕۂ�������Ƃ͂悭�m���Ă���B�@�M�u�Y�́A�g���ω����N�����Ă���ߒ��ɉ����ĉ��x�ƈ��͂����ł���Ƃ��������ȊO�ɔ@���Ȃ�������K�v�Ȃ̂��H�h�ƌ����^���Nj�����ߒ��ŁA�f�����ɕۂ����ʂł��邱�Ƃ������B�M�u�Y�̘_���W�J�͂��悻���̂悤�Ȃ��̂ł��B
�@�M�͊w�̍��{�@�����t���s���r�|�o���u����\�������t�i�r�C�u�j�Ȗʂɉ����āA�u�C�r�C�t�����ׂĉ��Z�I�ȗʂł������Ƃ��d�v�ł��B���Z�I�ȗʂƂ́A�n���\�����镨���ʁi���ʁj��2�{�A3�{�A�E�E�E�ɐ���A����ɉ����Ău�A�r�A�t��2�{�A3�{�A�E�E�E�ɐ���ƌ������Ƃł��B
�@���̂��߂ɁA�n�̕����ʂ������Ă��Ȗʂ̌`�͕ς��Ȃ��B�n�̕����ʂ����������ɉ����ċȖʂ̑傫���͊g��k������邪�A���̌`�݂͌��ɑ����Ȍ`��ۂB���̂Ƃ��A���̋Ȗʌ��z���炩�猈�܂鋭�x�I�ȗʂł��鈳�͂o0���|�i�݂t�^�݂u�js���Ή��x�s0���i�݂t�^�݂r�jv�͕����ʂ̑����ł��̒l��ς��邱�Ƃ͂Ȃ��B
�@���̂Ƃ��A�n�������̑����܂�ł��Č݂��ɑ��ω����Ă��t�i�r�C�u�j�Ȗʂ͌���ł���B������̋Ȗʂ�m��ɂ́A�n�ɑ��ĔM����������A�d�������o�����肵�Čn�̎��G���g���s�[�l��̐ς�ς��āA�e��Ԃɂ�����̐ρA���́A���x�A���X�̕ω���ǐՂ��Ȃ���Ȃ�Ȃ����A�Ƃɂ������̗l�ȋȖʂ͌���ł��܂��B
�@�O�������������Ԃ���A�M�̂�����d���̂��������Čn�̈��́A�̐ρA���x����ω�������ƌn���̕��������ׂČő��ɂȂ����Ƃ��̏�ԓ_�t���i�r���C�u���j�A���ׂĂ��t���ɂȂ����Ƃ��̏�ԓ_�t���i�r���C�u���j�A���ׂĂ��C���ɂȂ����Ƃ��̏�ԓ_�tg�i�rg�C�ug�j����܂�B�m���}�Q�Ɓn
�@�����ł��܁A�ő��i���ʂ�s�j�A�t���i���ʂ����j�A�C���i���ʂ�g���l�|��s�|��l�j�̋�����Ԃ��l����ƌn�̑̐ςu�ƃG���g���s�[�r�́A�����̗ʂ����ʓI�ϐ��ł��邱�Ƃ���
�ƂȂ�B
�@���̂Ƃ��́i�r�C�u�j�l�͐}���`�C�a�C�b�_�Ɏ��ʂ�s�A�����A��g���u����Ă�Ƃ��̏d�S�̈ʒu�ɂȂ�B�����āA���̏�ԓ_�ɏ�ԗʂł���n�̎��ʂl���t�����Ă���B
�@�]���ď�}�m�D�F�O�p�`�����n���ő��E�t���E�C����������������\���Ă���B�m�ΐ������n���ő��E�t����������A�m�������n���ő��E�t����������A�m�Ԑ������n���ő��E�C����������ɑ�������B
�@�Q�l�Ƃ��āA�����̏�Ԃ��i�o�C�u�C�s�j��ԓ��̏�ԕ������Ȗʏ�Ŏ����ƁA���ꂼ�ꉺ�}�����E���E���F���ɑΉ�����B
�@���Ȃ킿�A�u-�r������ŎO�����������Ԃ�\���D�F�O�p�`�̈��́A�g�i�o�C�u�C�s�j��ԕ������Ȗʁh���o-�s������ł��P�_�ɁA�u-�s���ʁA�o�|�u������ł���{�̒����ɏk�ނ��Ă���B�o�Ƃs���g��������ԗʁh�ł��邱�Ƃɒ��ӁB
�@���̗l�ɁA�i�o�C�u�C�s�j��ԕ������Ȗʏ�ł͏k�ނ������邽�߂ɁA�����������錻�ۂ���͂���ɂ͓K���ł͂Ȃ��B�t�A�r�A�u�̂��ׂĂ��g���ʐ���ԗʁh�ł����g�t�i�u�C�r�j�Ȗʁh�̕����͂邩�ɗD��Ă���B�������A�t���r�����ڑ���ł���ʂł͂Ȃ��̂����ǂ��������ł��B�m�P�����k�n�̏ꍇ�ŁA�t�Ƃr�����߂���@�͂��������Q�Ɓn
�@
�@�u-�r���ʏ�ŎO�p�`�̈�ƂȂ�O�������̈���t�i�u�C�r�j�Ȗʏ�ŕ\������Ɖ��}�m�D�F�O�p�`�̈�n�ƂȂ�B
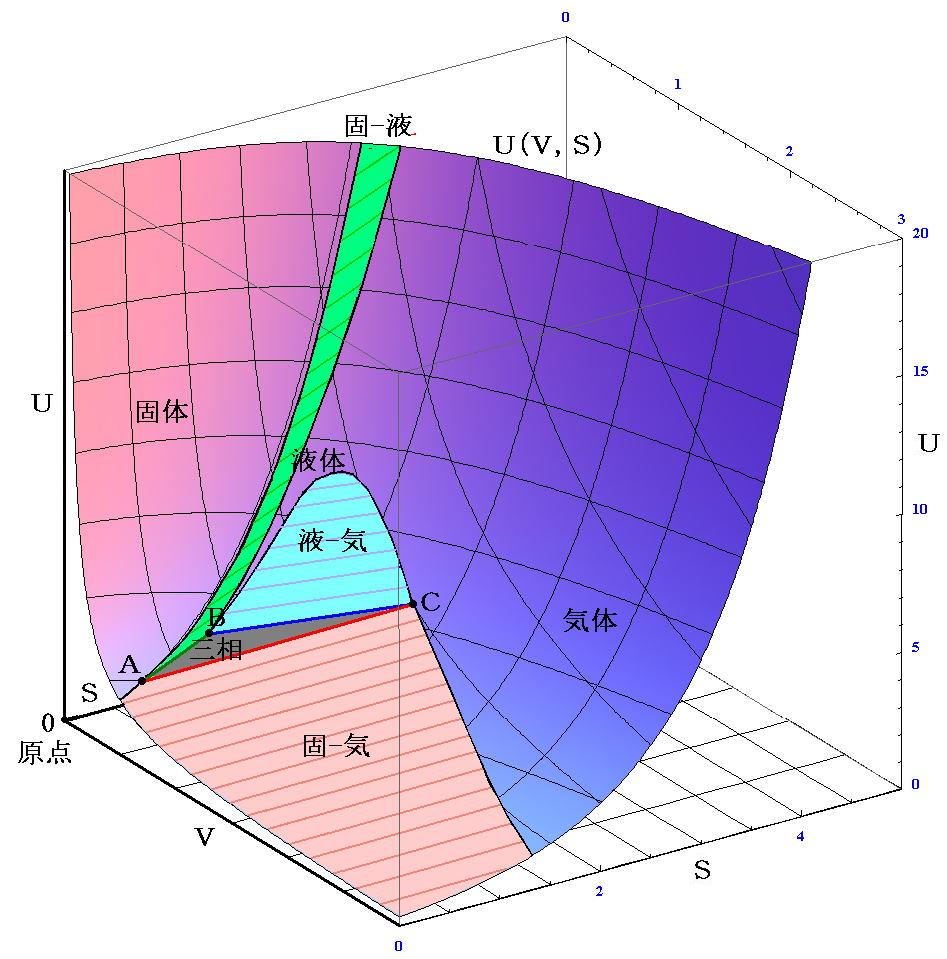
�@���̐}�Ő��藧���Ƃ��ӏ���������B
�@
�@��ԕ������Ȗʂt�i�r�C�u�j�̈З͂��������邽�߂ɁA�g�N���E�W�E�X�E�N���y�C�����̎��h���Ă݂܂��B�ȉ��̐����́AGibbs���A�ނ�1873�N�_���̒��ŁA��ԕ������Ȗʂ̊w�I�������瓱���Ă�����̂̏Љ�ł��B���_���̐����͂������ň��p���Ă��܂��B
�@�����̈�̏�ԕω��������|���ƁA����ƕ��t���x�E���͂��킸���ɈقȂ������ԕω��������f�|���f���l����B��ԕω������ƔM�͊w���ʂƂ̊W�͉��}�̂悤�ɂȂ�B
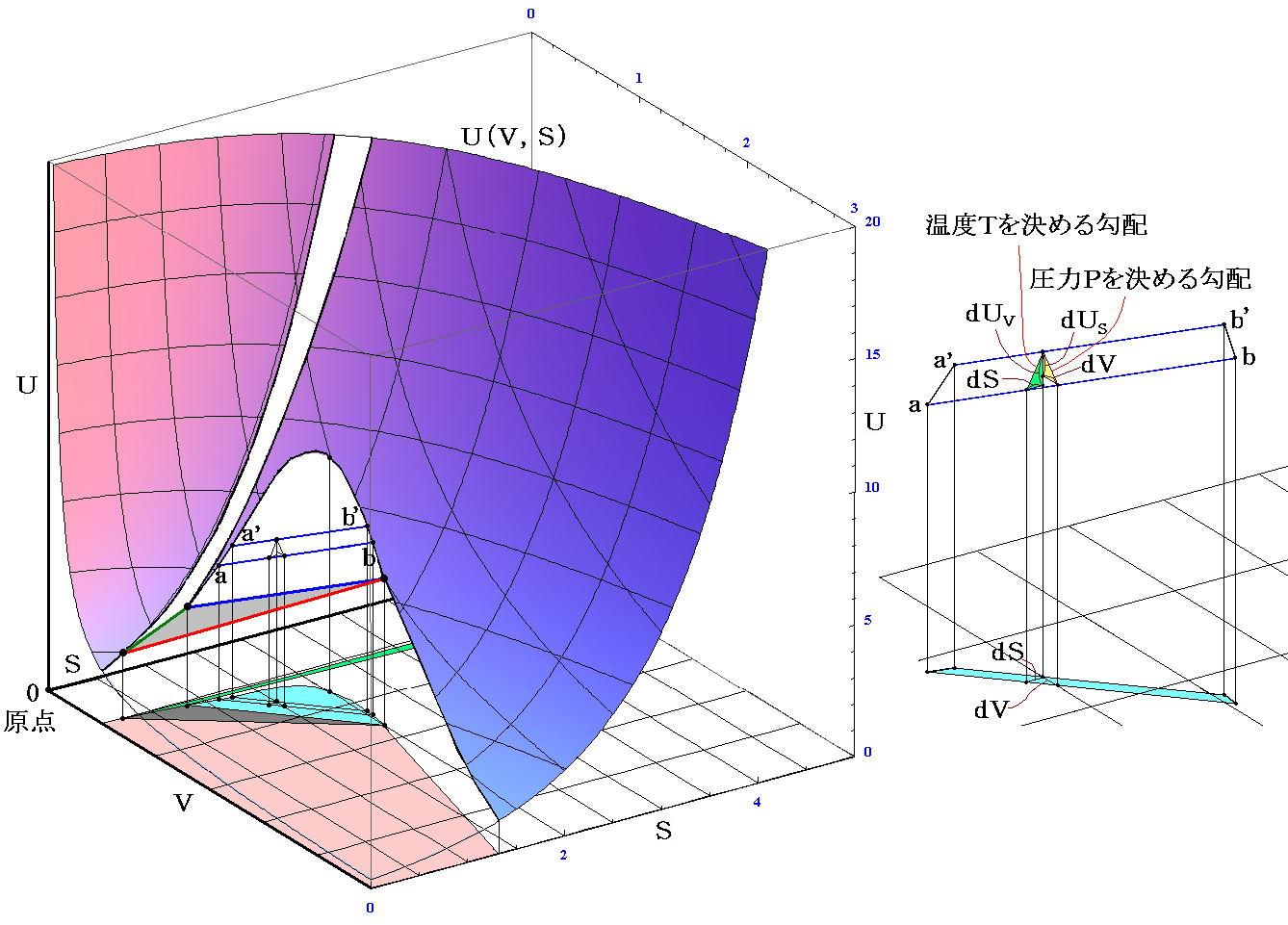
�@���̐}���́A������-���łt�i�r�C�u�j�Ȗʂɐڂ���ڕ��ʂ��`�k�u�A���t���x�ƈ��͂���-�������s�����o�����قȂ钼�����f-���f�łt�i�r�C�u�j�Ȗʂɐڂ���ڕ��ʂ��`�f�k�u�Ƃ���B��-���������f-���f�֑J�ڂ���ɂ�Đڕ��ʂ̌X�������}�̗l�ɕω�����͖̂��炩�ł��B
�@�}�̈Ӗ����璼�����g�N���E�W�E�X�E�N���y�C�����̎��h��������B
�@�}���̕����`�`�f�a�b�k�u�̓M�u�Y�̔M�͊w���_�����̋L���i���L�y�[�W�Q�Ɓj
�Ɠ����ɂ��Ă���̂ŁA��Ɉ��p�����M�u�Y�̐����Ɣ�r���Ă݂�ꂽ���B[��L�y�[�W�̓��{���͂�����ň��p]
�@�������A�M�u�Y�̓G���g���s�[�r���łŕ\���Ă��邱�Ƃɒ��ӂ��ꂽ���B
�@�܂��A�����t�i�r�C�u�j�Ȗ���ł̋c�_�ƁA�R�D�i�R�j�P�D�m�⑫�����T�n�ŏq�ׂ��f�i�s�C�o�j�Ȗ���ł̋c�_���r���Ă݂�ꂽ���B
�@
�@�M�u�X���S�D�i�P�j�Q�D�̍l�@�œ��������g�M�u�X�̎��R�G�l���M�[�h�𑽐����n�ɓK�p����ہA�g���w�|�e���V�����h�̊T�O�Ɏv���������B���ꂱ�����A�M�͊w�����w�����։��p���铹���J�����̑�Ȕ����ł��B
�@���̏ڍא�����
�@�@�@�ʍe�u�M�u�Y�̎��R�G�l���M�[�i���w�|�e���V�����j�Ƃ͉����v
�@�@�@�ʍe�u���t��Ԃ̔M�͊w�i�C�̂̉��w�����j�v
�ł��܂��B
�@����ɁA���R�G�l���M�[�̈��ł����g�G���^���s�[�h���[���W����A��舳�͂̌��ł̉��w�����ɂ��Ă�
�@�@�@�ʍe�u�����M�ƔM���w�������v
��A�g�w�����z���c�̎��R�G�l���M�[�h���[���W����A��艷�x�̌��Ő����鉻�w�ω��i���ω��j�ɂ��Ă�
�@�@�@�ʍe�u�d�C���w�|�e���V�����ƔM�͊w��O�@���i�l�����X�g�̔M�藝�j�v
�����킹�Č䗗�������B
�@
�@���̃y�[�W�͈ȉ��̕����Ɉˑ����Ă��܂��B���̓��e���ł��邾������₷�����邱�Ƃɋ߂܂����B�P�͎͂�ɕ����P�D���A�Q�A�R�͎͂�ɕ����Q�D���A�S�͎͂�ɕ����R�D���Q�Ƃ��܂����B