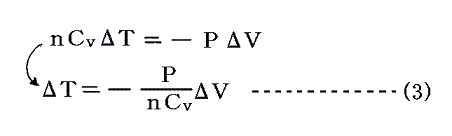このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
気体の断熱変化
昔の高校生は気体の断熱変化の公式を学んでいました。今はやりませんが、これを知らないと不便なのでここで説明します。
1.断熱変化の公式
物質量が一定の理想気体が“断熱変化”したときたどる道筋のTV面への射影は TVγ-1=一定 の曲線となる。ただし、γ=Cp/Cv=定圧比熱÷定積比熱 を意味します。
[証明]
理想気体の状態を表すPVT曲面(下図)に於いてA点からB点へ断熱膨張で変化したとしよう。そのとき気体が外部に対してする仕事は図のPV平面上の斜線部分の面積に相当する。ΔVを微少とすると体積変化ΔVでの圧力変化は無視できるので、斜線部分の面積はPΔVとなる。
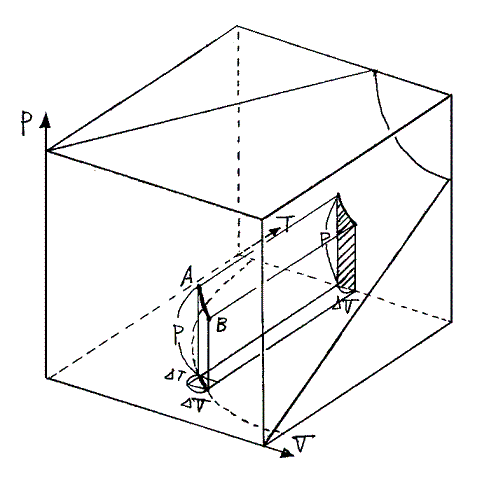
このとき気体の持つ内部エネルギーの減少分は“熱力学第一法則”(エネルギー保存則)より

となる。つまり断熱変化では気体が外部に対してした仕事が内部エネルギーの減少分になる。このことは、簡単な気体分子運動論によっても確認できます。
ところで別稿「気体のモル比熱」2.で説明する様に、“理想気体の内部エネルギーは絶対温度のみの関数”(ゲーリュサック=ジュールの法則)だから、この内部エネルギーの減少分は温度の低下となって現れる。
すなわち、理想気体の内部エネルギー変化量は

と表される。以下で、この式について補足する。
理想気体の内部エネルギーは理想気体の塊に対して出入りする“仕事”と“熱量”に依存して変化するのですが、“熱量”の出入りによる内部エネルギーの変化を見積もるには、体積が変化しない状態での熱量の出入りの計算式を利用すれば良い。そのときの熱量の出入りは[定積比熱Cv]×[温度変化ΔT]で計算できる。それが(2)式の意味です。
このとき、定積比熱Cvは温度Tに依存して変化するかも知れないが、そのときには各温度Tでの値を用いて計算すればよい。ただし、理想気体の定積比熱Cvや定圧比熱Cpは温度Tに依存しないで定数と見なせることが知られています。
[補足説明1]
高校物理Ⅱで理想気体の内部エネルギーは
U=(3/2)nRT・・・・・・・・・・(2’)
と習うがこれは単原子気体の場合にしか当てはまらない。そのかわりに上記(2)式を用いる。
(2)式は熱力学第一法則に於いて一定体積で熱を加えたときの内部エネルギー変化の式から求まる。つまりΔU=Q-Wにおいて、W=0(等積変化だから)およびQ=CvΔT(Cvは等積モル比熱)から求まる。この(2)式は二原子分子や多原子分子の気体の場合にも正しい式です。
ちなみに、上記(2’)式の係数(3/2)は二原子分子の場合に(5/2)となり、多原子分子の場合は(6/2)=3となる。何故そうなるかは高校レベルを超えるので説明は省略。
(1)、(2)式より
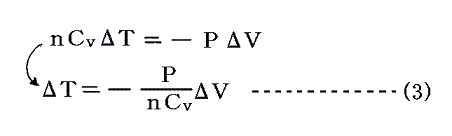
となる。
つまりA点から断熱膨張(ΔV)で到達するB点は、気体が外界に対してする仕事PΔVだけ内部エネルギーの減少した(ΔTだけ温度の降下した)点です。そのときTV面上のA→Bの軌跡を求めるには、(3)式のPを理想気体の状態方程式PV=nRTを用いてT、Vで表せばよい。なぜなら、断熱変化だろうと、その他の定圧変化、定積変化、だろうとすべて理想気体の状態方程式曲面上での変化に変わりはないのですから。
すなわち
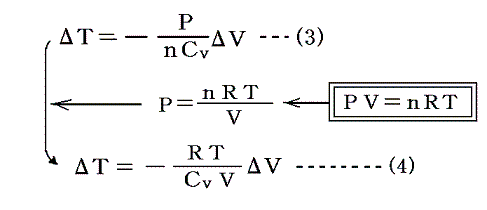
となるが、この(4)式に、別稿「気体のモル比熱」1.で証明する“マイヤーの関係式 Cp-Cv=R” を代入する。
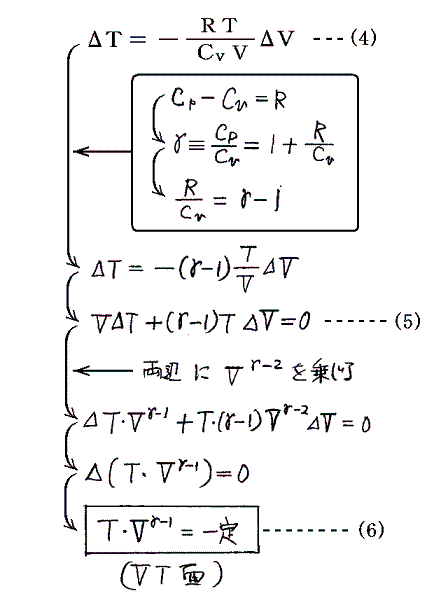
[証明終わり]
[補足説明2]
(5)式から(6)式が導けることは、(5)式がTV面上の曲線の傾きが下図の状況であることを示していることから読み取れる。
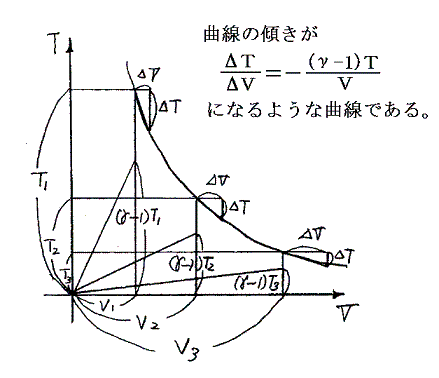
あるいは、以下の様に積分法を用いて(5)式を積分して(6)式を導いても良い。
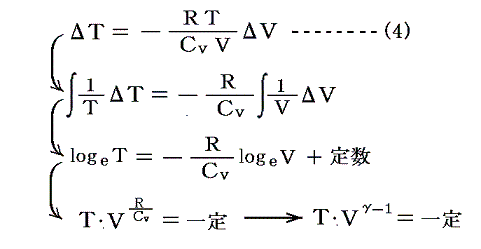
[補足説明3]
(6)式に“理想気体の状態方程式”を用いると、(VP面)や(TP面)における断熱変化曲線の方程式が得られる。
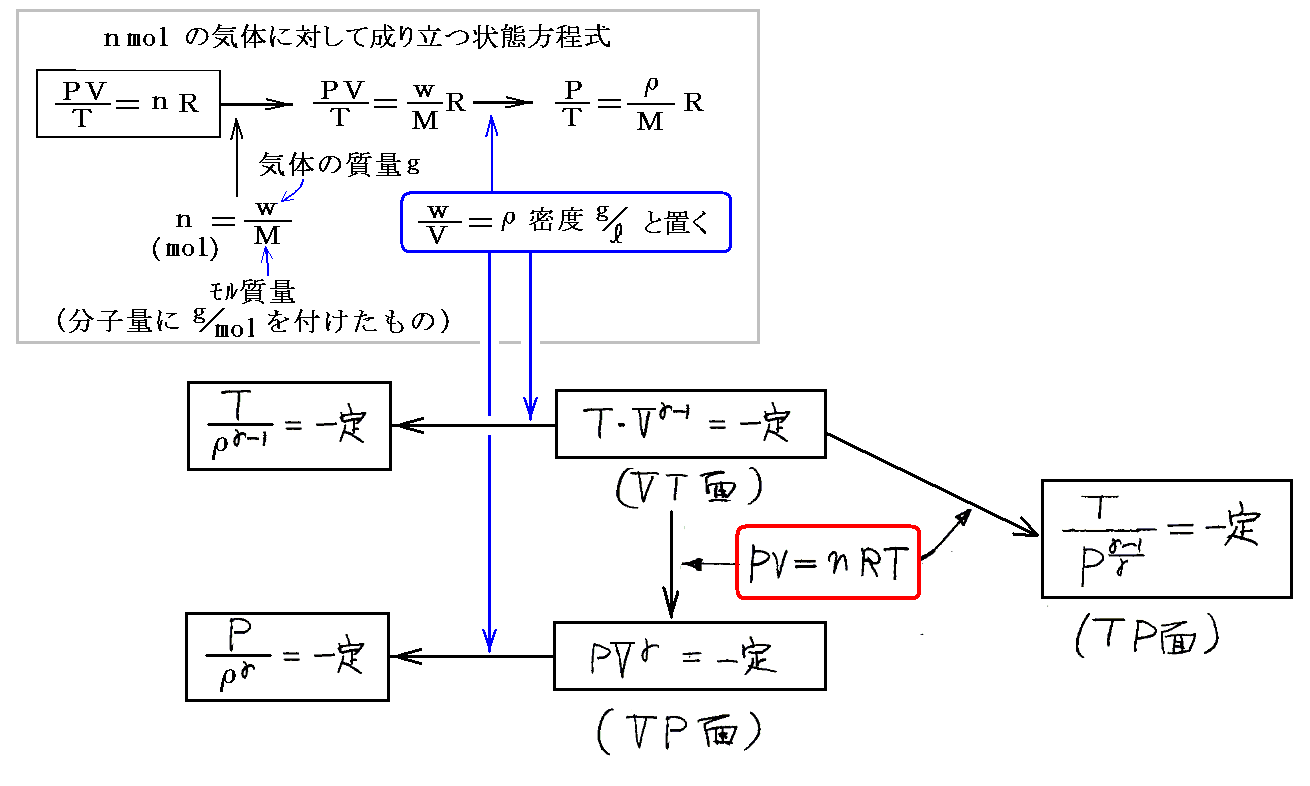
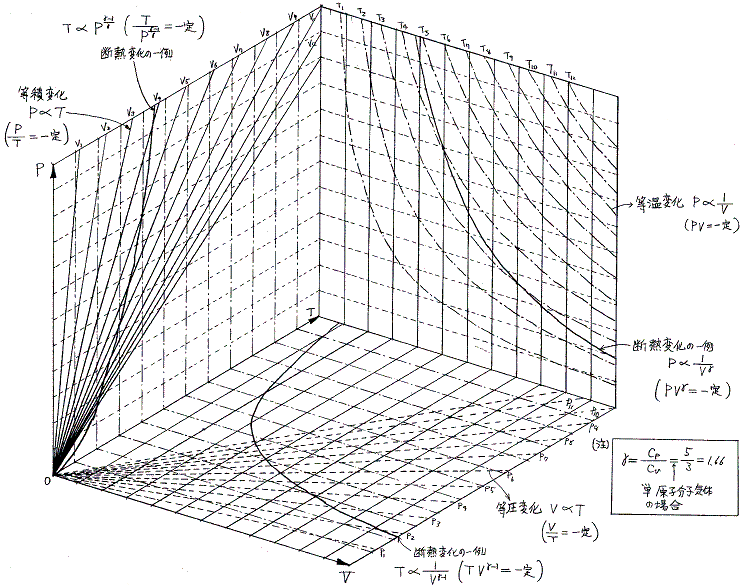
2.等温・定積・定圧・断熱変化の関係
各平面上へ射影した変化曲線は下図の様になる。
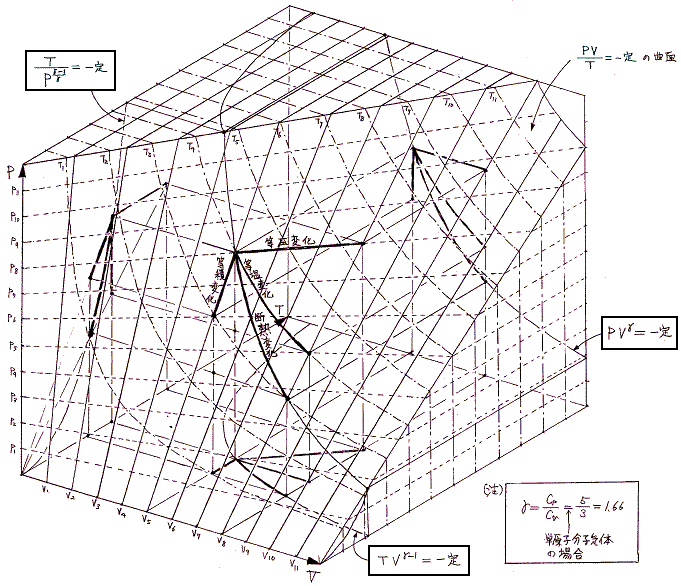
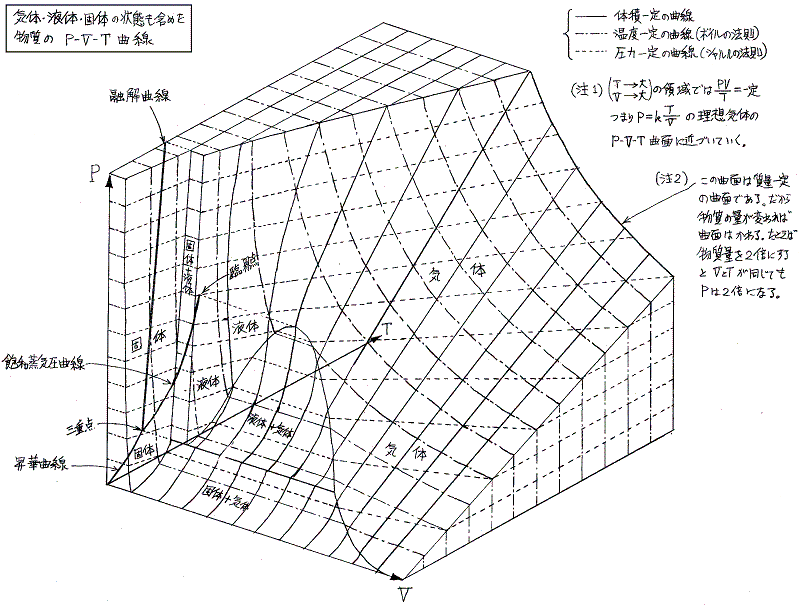
3.現実の気体の状態図
現実の気体は圧縮して低温にすると凝縮、凝固を起こして下図の様な状態図になる。
その為、現実の気体ではたとえ気体状態の領域であっても、証明に用いた理想気体の状態方程式が成り立ちませんので、1.[補足説明3]で求めた関係式は成り立ちません。
この当たりのもう少し立ち入った議論は、別稿「熱力学関数(状態方程式曲面)の性質」1.(2)4.をご覧下さい。