丂偙偺儁乕僕傪慛柧偵報嶞偝傟偨偄曽偼偙偪傜偺僶乕僕儑儞傪偛棙梡壓偝偄丅
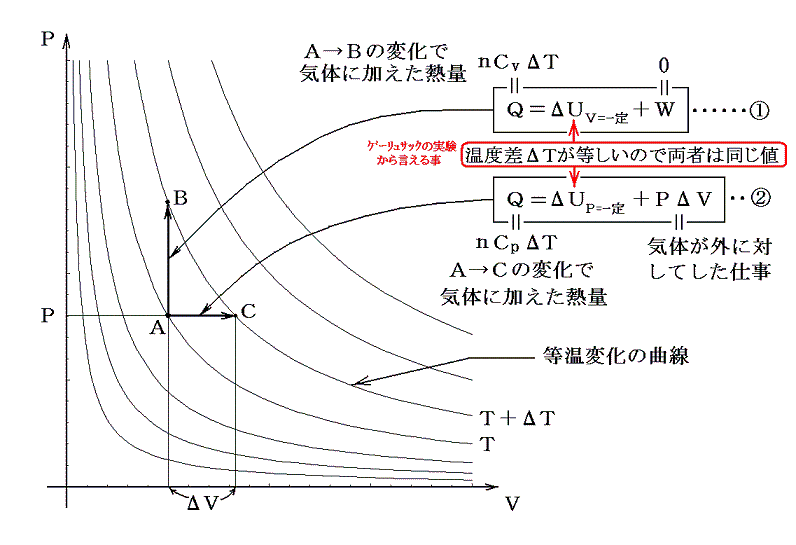
丂棟憐婥懱偵偍偄偰丄掕愊斾擬偲掕埑斾擬偺娫偵惉傝棫偮廳梫側娭學幃俠倫亅俠倴亖俼丂乮掕埑儌儖斾擬亅掕愊儌儖斾擬亖婥懱掕悢乯傪丄棟憐婥懱偺俹倁嬋慄傪棙梡偟偰徹柧偡傞丅

丂棟憐婥懱偱偼愨懳壏搙偑摍偟偄 俛 偲 俠 偵偍偗傞乬撪晹僄僱儖僊乕乭偼摍偟偄乮偙傟偼丄俀丏偱弎傋傞乬僎乕儕儏僒僢僋偺幚尡乭偐傜尵偊傞帠偱偡乯丅偩偐傜俙仺俛偺撪晹僄僱儖僊乕偺曄壔儮倀V=堦掕偲俙仺俠偺撪晹僄僱儖僊乕偺曄壔儮倀俹=堦掕偼摍偟偄丅屘偵
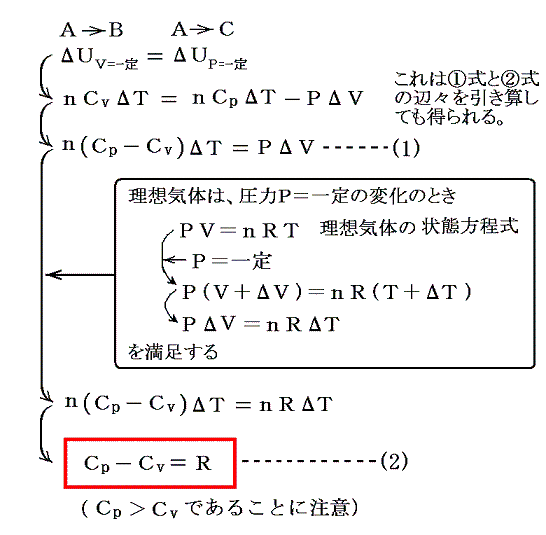
偑摼傜傟傞丅乮俀乯幃偼乬儅僀儎乕偺娭學幃乭乮Mayer's relation乯偲尵傢傟傞丅
丂乮侾乯幃偺摫偒曽傪専摙偡傟偽夝傞傛偆偵丄乮侾乯幃偺嵍曈偼亂婥懱偵壛偊偨擬検偺嵎亃傪昞偟丄塃曈偼擬検傪壛偊傜傟偨亂婥懱偑奜晹偵懳偟偰偟偨巇帠亃傪堄枴偡傞丅偦偺偲偒乻婥懱偺懱愊偼曄壔偡傞偑丄僎乕儕儏僒僢僋偺幚尡偐傜丄婥懱偺撪晹僄僱儖僊乕偼壏搙偑曄傢傜側偗傟偽曄壔偟側偄帠偑夝偭偰偄傞乼偺偱丄嵍曈偺婥懱偵壛偊傜傟偨擬検嵎偑偡傋偰塃曈偺巇帠偵曄傢偭偨偙偲偵側傞丅偦偺堊偙偺娭學幃偼乬擬偺巇帠摉検傪媮傔傞娭學幃乭偵側傞丅師復俀丏偱偦偺帠傪愢柧偡傞丅
丂
丂Julius Robert von Mayer乮撈 1814乣1878擭乯偼1842擭偵丄慜復偱媮傔偨乮侾乯幃偺娭學傪梡偄偰丄擬偺巇帠摉検傪媮傔偨丅崅峑惗偼James Prescott Joule偺丄廳傝偵傛傝塇崻幵傪傑傢偟偰悈傪偐偒傑傢偡丄擬偺巇帠摉検應掕幚尡(1847擭)傪廗偆偑丄Mayer偺曽朄偼偙傟偵愭峴偟偰偄傑偡丅
丂Mayer偼僎乕丒儕儏僒僢僋乮暓乯偑1806擭(1807擭報嶞)偵摼偰偄偨乬婥懱偺恀嬻拞傊偺暚弌乮巇帠傪偟側偄乯偱偼壏搙偑曄壔偟側偄乭偲偄偆寢榑傪弌敪揰偲偟偨丅
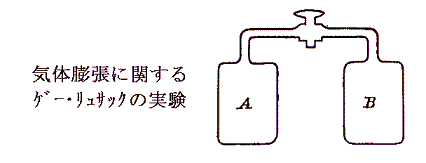
丂僎乕丒儕儏僒僢僋偺幚尡偲偼忋恾偺梕婍俙偵婥懱傪媗傔梕婍俛傪恀嬻偵偟偨忬懺偱僐僢僋傪奐偒婥懱傪俛偺拞偵奼嶶偝偣丄偦偺偲偒偺壏搙曄壔傪應掕偡傞傕偺偱偡丅偦偺寢壥偼丄壏搙曄壔偑傑偭偨偔婲偙傜側偄偲偄偆嬃偔傋偒傕偺偩偭偨丅乮偙偺幚尡偺徻嵶偵晅偄偰偼暿峞乽愨懳壏搙偲偼壗偐乿係丏乮1乯1丏傕嶲徠偝傟偨偟乯
丂偙偺幚尡寢壥偵懳偟偰丄儅僀儎乕偼丄亀恀嬻拞偱偺朿挘偱偼奜晹偵懳偟偰巇帠傪偟側偄偟丄傕偪傠傫奜晹偲偺擬偺傗傝庢傝傕偟側偄丅偩偐傜丄婥懱偺帩偮乬撪晹僄僱儖僊乕乭偼懱愊傗埑椡偑堎側偭偰偄偰傕曄壔偟側偄丅偙偺偲偒丄壏搙偑曄壔偟側偄偲尵偆偙偲偼丄偦偺帠傪昞偟偰偄傞丅亁偲峫偊偨丅
丂偙偺偙偲偐傜丄儅僀儎乕偼峏偵師偺條偵峫嶡傪恑傔偨丅
丂亀僎乕儕儏僒僢僋偺幚尡偼丄婥懱偼埑椡偵峈偟偰朿挘偡傞偲偒偩偗丄尵偄姺偊傞偲巇帠傪偡傞偲偒偩偗丄壏搙偺崀壓傪庴偗傞偙偲傪徹柧偟偰偄傞乮偙傟偼乬棟憐婥懱偺撪晹僄僱儖僊乕偼壏搙偩偗偺娭悢乭偲偄偆尵偄曽傪偝傟傞乯丅偩偐傜掕埑斾擬偲掕愊斾擬偺堘偄偼婥懱偑奜奅偵懳偟偰側偟偨巇帠偺検偦偺傕偺偩丅亁
丂偦偺偨傔丄慜復侾丏偺乮侾乯幃偼丄乬擬乭偲乬巇帠乭偺乬摉検娭學乭傪昞偟偰偄傞丅偡側傢偪
偺 俙 偑擬偺巇帠摉検傪昞偡丅
乵曗懌愢柧1乶丂丂寁嶼椺
丂崱擔夝偭偰偄傞抣傪梡偄偰乬擬偺巇帠摉検乭傪媮傔偰傒傑偡丅
丂侾m3乮侾婥埑乯偺嬻婥傪堦掕懱愊偺傕偲偱 0亷 偐傜 侾亷 抔傔傞偺偵昁梫側擬検偼 俻掕愊亖217.2cal 偱偡丅傕偪傠傫偙偺偲偒埑椡偼彮偟憹戝偟傑偡丅
丂堦曽丄侾m3乮侾婥埑乯偺嬻婥傪堦掕埑椡偺傕偲偱 0亷 偐傜 侾亷 偵抔傔傞偺偵昁梫側擬検偼 俻掕埑亖306.4cal 偱偡丅偙偺偲偒嬻婥偼 侾m3 偐傜 乮1亄1乛273乯m3 傊偲朿挘偡傞丅
偦偺偨傔
丂掕埑曄壔偲掕愊曄壔偺擬検嵎亖 俻掕埑 亅 俻掕愊 亖306.4亅217.2亖89.2乵cal乶ゥゥゥ乮俁乯
偑摼傜傟傞丅
丂
丂堦曽丄
丂掕埑曄壔偱婥懱偑奜晹偵懳偟偰偡傞巇帠亖僺僗僩儞偵摥偔椡亊僺僗僩儞偺堏摦嫍棧
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖埑椡亊僺僗僩儞偺柺愊亊僺僗僩儞偺堏摦嫍棧
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖埑椡亊朿挘偟偨懱愊
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖1.013亊105乵N乛m2乶亊乮1乛273乯乵m3乶
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖371乵J乶ゥゥゥゥゥゥゥゥゥゥゥゥゥゥ乮係乯
偲側傞丅
丂
丂偦偺偨傔丂乮俁乯亖乮係乯丂傛傝丂1乵cal乶亖4.2乵J乶丂偑摼傜傟傞丅
乵曗懌愢柧俀乶
丂楌巎揑側曗懌傪偟傑偡丅儅僀儎乕偺榑暥亀柍惗暔奅偺乻椡乼偵偮偄偰偺峫嶡亁乮1842擭乯偺塸栿斉傪暿峞偱堷梡偟偰偄傑偡丅儅僀儎乕偼偙偺榑暥偱乬掕埑斾擬偲掕愊斾擬偺堘偄偼丄巇帠偵娭學偡傞乭偲偟偰丄幚嵺偵乬擬偺巇帠摉検乭乮崱擔偺尵偄曽偱3.58J乛cal偵憡摉乯傪摫偄偰偄傑偡丅偟偐偟丄偦偺寁嶼夁掱偺徻嵶傪婰偟偰偄側偄偺偱偦偺寁嶼榑棟傪棟夝偡傞偺偼擄偟偄偱偡丅
丂杮峞偱愢柧偟偨偦偺寁嶼儊僇僯僘儉偺徻嵶乮僎乕儕儏僒僢僋偺幚尡寢壥傪娷傔偰乯傪婰偟偰偄傞偺偼1845擭榑暥亀桳婡懱偺塣摦偲暔幙戙幱偲偦偺娭學亁偵偍偄偰偱偡丅
丂偦偺偨傔丄1842擭抜奒偺儅僀儎乕偺棟夝偼傑偩晄廫暘偱濨枂側傕偺偩偭偨偺偐傕抦傟傑偣傫丅偦偺摉偨傝偼暿儁乕僕偱堷梡偟偰偄傑偡嶳杮媊棽挊亀擬妛巚憐偺巎揑揥奐亁戞22復嘪乬晛曊掕悢偲偟偰偺擬偺巇帠摉検乭偺夝愢偑偲偰傕夝傝傗偡偄偺偱惀旕偛棗壓偝偄丅