Clausiusの熱力学第1論文(1850年)
「熱の動力、および熱学へ演繹される諸法則について」
ここで紹介するものは、Rudolf Julius Emmanuel Clausius(1822〜1888)の熱力学第1論文「熱の動力、および熱学へ演繹される諸法則について」(1850年)

の翻訳版で、八木江里監訳「エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)からの引用です。
ただし、解りやすくする為に、私どもが、適当に章、節、項に分け、式変形を(矢印記入場所に)追記し、さらに(灰色囲み記事の)補足説明、等々・・・を付け加え、また文章の改行、段落分けに関してもかなり改変しています。そのため元の表現は別稿で引用している原本でご確認下さい。
ちなみに“演繹(エンエキ)”とは 『前提された命題から、経験にたよらず、論理の規則に従って必然的な結論を導きだす思考の手続』(広辞苑より) のことです。
0.FNの前書き
この論文は『熱力学』という学問分野を開闢(カイビャク)した大論文です。しかし、この中で展開されているのは混迷・混沌の中から徐々に浮かび上がってくる“光明”でして、極めて抽象的で難解です。
この論文を理解するためにはあらかじめ別稿「絶対温度とは何か(積分因子とは何か)」5.及び6.を御覧になられて、“完全微分”と“積分因子”に付いて十分理解しておくことが必要です。
また、この論文の真意を理解するにはClausiusの 1854年論文→1862年論文→1865年論文 も合わせて読む必要があります。更に、Clausiusと同時に「熱力学」の開闢に大きな貢献をしたW.Thomsonの業績も合わせて参照される必要があるかも知れません。それは、絶対温度を初めて提唱した1848年論文、カルノーの功績を世に知らしめた1849年論文、水凝固点圧力依存性の1850年論文、Clausirsの本論文(1850年)に啓発されて独自の考察を展開した
同一題目の一連の大論文『熱の力学的理論』(1851〜1854年)、絶対温度を空気温度計温度に関係付けたJouleとの一連(1852,53,54年)の共著論文、等々です。
これらについては、山本文献3.第19〜31章でその大半の主な所が紹介されていますのでそれを参照されると良いと思います。
Thomsonは、熱学を論じる時の鍵になるものがカルノーが展開したカルノーサイクルの議論の中にあると確信していたのですが、その本質を見極めることができずに悶々としていたのです。
カルノーサイクルの中に含まれる熱学の本質を明らかにしたのがClausiusが書いたこの論文(1850年)です。この中で、“カルノーの原理”が証明されることで、温度という物理量の存在が示唆され、エントロピーという状態量が存在する可能性が示されます。その事によって、カルノーサイクルの本質が解き明かされていきます。もちろん、絶対温度の概念が確立(1854年)し、エントロピーの本質が理解される(1865年)のはまだまだ先の話ですが、そこへ導くきっかけがこの論文で与えられます。
“カルノーの原理”によって温度というものを定義することができる事を最初に示唆したのはThomson(1848年)ですが、Clausiusのこの論文はその定義を更に完全なものにする事を助け、そしてカルノーサイクルの考察をさらに進めてエントロピーという状態量の存在を推測させます。このエントロピーこそ、Clausiusがこの論文で掲げた“熱力学第2法則”と密接に関係するものです。この熱力学第2法則こそ熱の本質を特徴付けるものですから、この論文は“熱力学第1法則”(エネルギー保存則)だけでは熱が関係する現象を完全に論じることはできない事を明らかにした論文だと言っても良い。
これらの考察の鍵となったのは以下の考え方です。
クラウジウスはまず、ヘルムホルツ、マイヤー、ジュールなどによって明らかにされた、熱とはエネルギー形態の一種であるという考え方を明確に採用します。そしてカルノーサイクルの様な熱機関には熱という形でエネルギーが流入あるいは流出する。それと同時に仕事という形で流入あるいは流出する。熱あるいは仕事という形で流入あるいは流出するエネルギーは一時的にカルノーサイクル内部のエネルギー(内部エネルギー)という形で保持される。そのとき内部エネルギーには熱機関の作業物質の温度変化で表す事ができる部分(自由熱)と、その様なもので表す事ができない部分(潜熱)がある事も考慮します。
いずれにしても、熱はその様にして熱機関に流入(あるいは流出)するエネルギーなのですが、カルノーサイクルの様に1サイクル作動した後で熱機関自体は最初と全く同じ状態に復帰し、熱機関の内部に含まれるエネルギーは変化していないことになる。
そのため、カルノーサイクルの様な可逆機関では、カルノー機関に流入した熱量と流出した熱量の差に相当するエネルギーが、外部に仕事として取り出せるエネルギーに一致する。
そのとき、カルノーサイクルの様な理想的可逆機関では、流入した熱量と流出した熱量の差は流入する熱浴の温度と流出した熱浴の温度の差に依存する。そのため高熱源から流入する熱エネルギーの内で仕事として外部に取り出せる割合は高熱源と低熱源の温度の差に依存する。つまり熱機関の効率(つまり流入した熱エネルギーの何割が仕事のエネルギーとして取り出せるか)は温度という物理量に極めて密接に関係していること(つまり“カルノーの原理”)を厳密、完璧に証明することができた。
この中に温度とは何かを説明する鍵が含まれており、また流入、流出する熱量をそのときの温度(絶対温度)で割った量が状態量(エントロピー)として熱の本質と深く関係していることを知るきっかけを提起した。
この論文は超難解です。そのため、山本義隆氏の文献3.第19〜31章の解説も参照されながら本稿をお読みになることを勧めます。山本氏の解説は解りやすくて秀逸です。
1.Clausiusの導入文



[原本補足説明1]

このカルノーの大論文の日本語訳が広重文献1.の中にあります。





[補足説明1]
上記赤線で囲った所は非常に大事な見解を述べています。これは原文に忠実で正確な翻訳かも知れないが、正直なところ解りにくい。文献3.の山本義隆氏の(意訳かもしれない)訳文を以下で引用しておきますの参考にされて下さい。






上記訳者註のR.Mayerの論文の英訳版はこちらです。ただし、この段階でのMayerの論理展開は不十分で明確ではありません。この当たりについては、別稿「気体のモル比熱」2.[補足説明2]をご覧下さい。



W.Thomsonの“数学・物理学論文集1”はNetからdownloadできますので、それでご確認下さい。



[補足説明2]
上記赤線で囲った所は非常に大事な見解を述べています。これは原文に忠実で正確な翻訳かも知れないが、正直なところ解りにくい。文献3.の山本義隆氏の(意訳かもしれない)訳文を以下で引用しておきますの参考にされて下さい。

2.熱と仕事の等価性に関する基本法則からの推論
(1)熱力学第1法則の提示


[補足説明1]
上記の法則がいわゆる“熱力学第1法則”(エネルギー保存則)でして、以後の説明で“基本法則”と言っているものです。ここで、上記の赤下線部の補足“熱から仕事が生ずるようなすべての場合には”には深い意味があります。その事を説明する山本文献3.の文を引用。




上記の【熱の特殊性の原理−熱力学第2法則(原理2)−】とは、本稿3.(1)[補足説明2]に続く文章の末尾に二重の赤線で四角に囲った中に記されているものです。
(2)熱と仕事は同じ(次元の)物理量だが、熱や仕事は状態量ではない















[補足説明1]
ここは何を言っているのか非常に解りにくいが、要するに、“全熱”と言うものが“状態量”である事を示唆している。“全熱”とは、今日いわゆる“内部エネルギー”Uと呼んでいるものです。
また、それと同時に別稿「絶対温度とは何か(積分因子とは何か)」3.(2)2.で説明している“仕事”と“熱”は状態量では無い事を注意している。
[補足説明2]
ここは、『熱力学』を学ぶ上で最も解りにくいところです。このことについて、後に説明する2.(3)3.[補足説明6]と、そこで引用している別稿「『熱力学』とは何か」2.(3)を、特に [補足説明1] と [補足説明2] をご覧下さい。
(3)カルノーサイクルの作業物質が永久気体(完全気体)である場合

[補足説明1]
2.(3)と2.(4)で意図しているのは、カルノーが用いた“カルノーサイクル”の詳細を詳しく検討しようと言うことです。実際、“カルノーサイクル”は、3.章で説明する“カルノーの原理”の証明には必須ですし、熱力学の展開には必要不可欠なアイテムですから。
そのとき、カルノーサイクルの作業物質として“理想気体”と(液体と共存状態にある)“飽和蒸気”を取り上げるといっています。この二つを取り上げるのは、その二つの作業物質の性質に関してすでに多くの研究がなされて、様々なデータや経験法則が知られているからです。
そして、二つを比較して取り上げたことで、もっと違った作業物質、作業環境を用いたカルノーサイクルに対する取り扱い方も解るだろうということです。
“カルノーサイクル”の本質については、別稿「絶対温度とは何か(積分因子とは何か)」6.(1)3.[補足説明2]を御覧下さい。
1.永久気体の性質


[補足説明1]
ここでいう“M.とG.の法則”とは、(Ⅰ)式を見れば解るように、今日高校物理でならう“ボイル・シャルルの法則”と“アボガドロの法則”を足し合わせた法則(理想気体の状態方程式)の事です。ドイツでは“マリオット・ゲーリュサックの法則”と呼ぶ様です。

[補足説明2]
上記は理想気体の状態方程式を説明している。このとき、1mol当たりの気体定数Rは気体の種類によらずどの気体でも同じ値となります。しかし、単位質量に付いての状態方程式ならば気体定数Rは気体の種類ごとに異なった値となります。その場合、気体についての“アボガドロの法則”から解るように、Rは比重に逆比例します。この当たりは別稿「絶対温度とは何か(積分因子とは何か)」2.(5)を復習して下さい。
また右辺の(a+t)は今日の絶対温度Tに相当する量ですが、この段階では絶対温度Tは発見されていませんので、実用温度t(摂氏温度)+a(≒273としている)のことです。このa(≒273)が何を意味するのはこの時点では全く解っていません。

[補足説明3]
上記の“ルニョーの注意深い一連の研究”とは、極論すれば別稿「絶対温度とは何か」1.(1)3.で説明したこの図の内容が解ってきたと言うことです。このことについては山本文献3.第27章Ⅰを御覧下さい。







2.カルノーの独創性は、彼が用いた熱機関を《サイクル》として働かせた事と、この機関が《可逆機関》である事にある


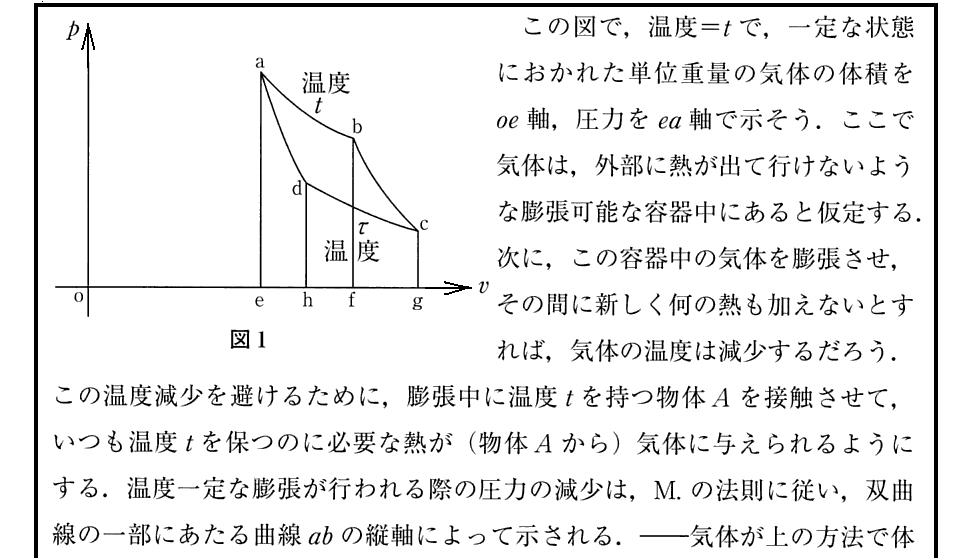







3.“基本法則”の解析的表示(数式表示)を得るために無限小サイクルを利用する

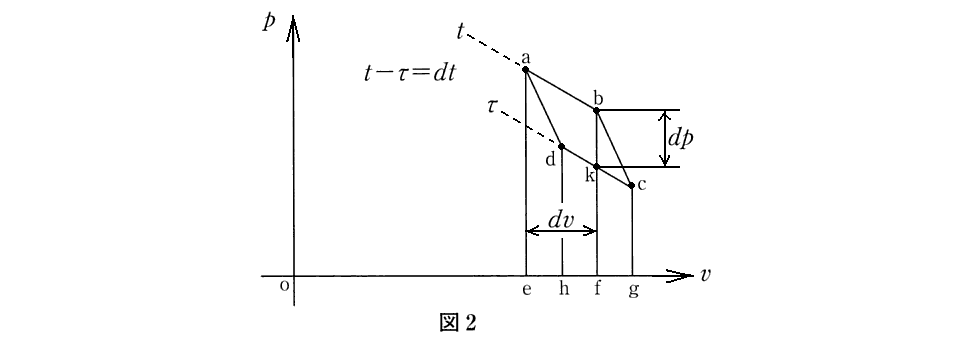


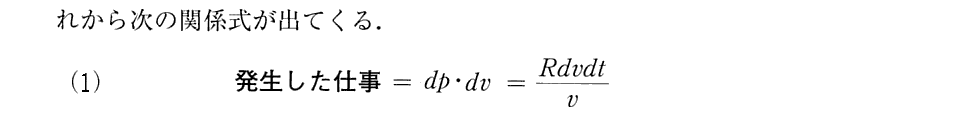
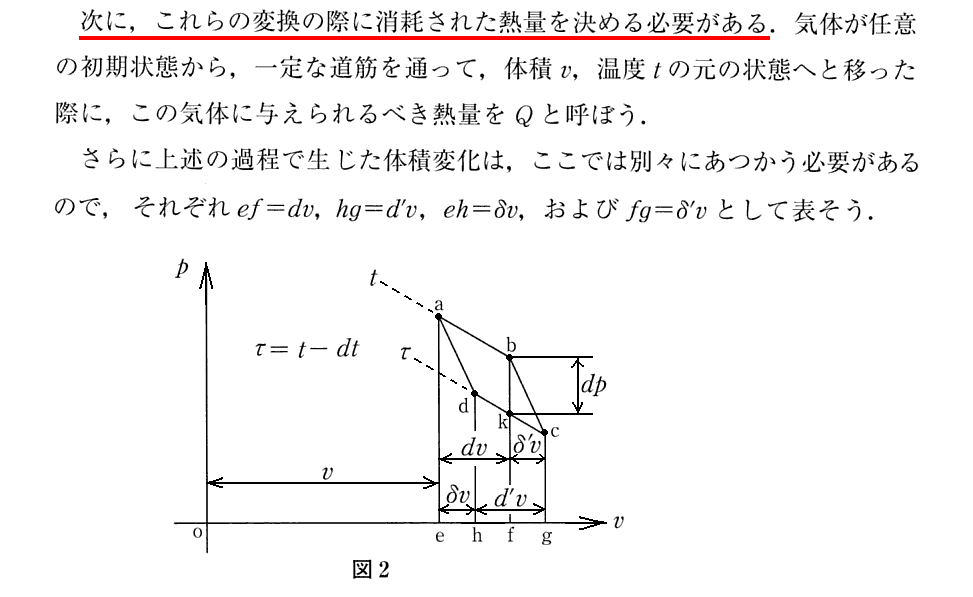




[補足説明1]
上記の補注1)は重要です。ここでクラウジウスは、最初と最後の状態は同じだが、その二つの状態間の遷移に伴って出入りする熱量dQは、その状態変化径路に依存して異なりえるので、最後の式は成り立たないことを示唆している。
つまりdQは完全微分ではないのです。




附録A はこちらで引用しています。
[補足説明2]
上記文中の“これら3つの式と(2)式とから(3)式の導出”とは下記の通りです。
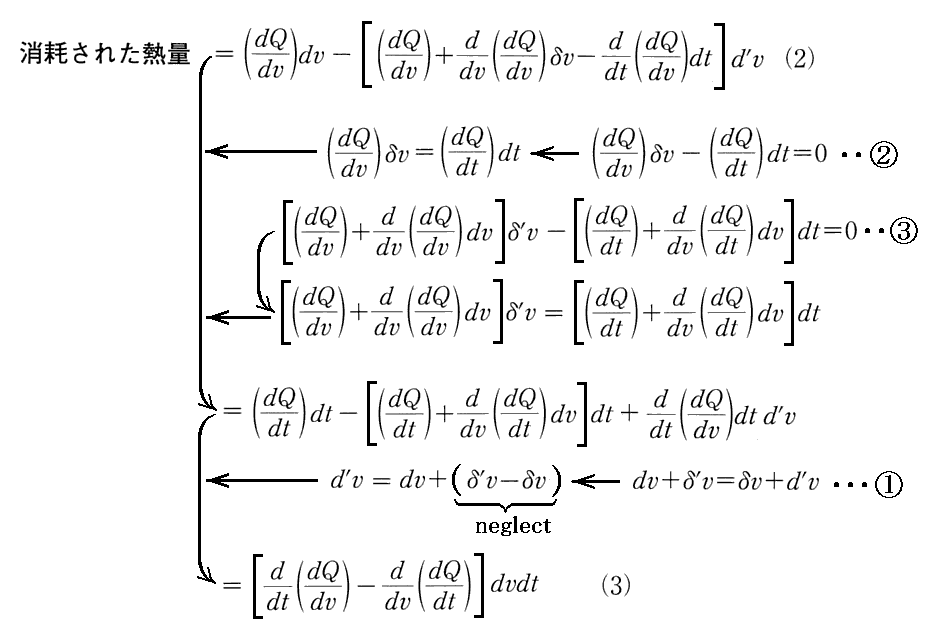
ちなみに、消耗された熱(3)式が0で無い場合は、図2の a の状態から c の状態へ遷移したとき、状態遷移の径路a→b→cなのか、a→d→cなのかに依存して、過程ごとに系に出入りする熱量が異なる事を示しています。つまり、熱量は状態量では無いことを示しています。
そしてこの違いが、 a→b→c→d→a と1サイクル終了したとき消耗された熱であるということです。


[補足説明3]
上記(4)式or(Ⅱ)式の右辺の“A”は、最初マイヤー(1842年)が、そして後にJ.P.Joule (1847年)がより正確に求めた、いわゆる“熱の仕事当量”の逆数です。この量Aは今後の議論で繰り返し出てきますので覚えておいて下さい。
Clausiustが本論文を発表した1850年という時代を考えて下さい。この時までにヘルムホルツやマイヤーのエネルギーに関する考察は発表されていましたし、1847年のJouleの有名な実験(位置エネルギーという力学的エネルギーによって容器に入れた水を攪拌して熱を発生させ、熱と仕事は相互に変換できること主張した)が発表された後です。つまりこのときまでに、熱はエネルギーの一形態であり、熱と仕事は相互に変換できるという考え方がほぼ確立された時代です。そして、その両者の変換の当量関係(上記のAの値)がマイヤーやジュールの仕事によりほぼ確定していた時代です。実際、このことは本論文の最後3.(5)で議論される。
ところで、カルノーは、“熱素”は生成も消滅もしないで、熱素の移動が仕事を生み出す(ちょうど水の流れが水車を回して仕事を生み出すが、水自体は生成も消滅もしない)。さらに、“温度”とは水の位置が高いところにあるのか、低いところに有るのかという高度の高低差に相当するようなもの(つまり高いところにある水が、高温の場所にある熱素であり低いところにある水が低温の場所に流れ下った熱素である)と考えていたのです。
トムソンはカルノーの考察の中に本質があると見抜いていたのですが、カルノーの考察の中で大きな比重を占めていた、熱を説明する“熱素”や“温度”の捉え方がトムソンの考察に混乱を来していた。そういった状況の中で、トムソンやジュールも含めた当時の人びとに取って、熱は“熱素”と言うようなものでは無くておそらくエネルギーの一種だろうということがほぼ解ってきたのが1847年ころです。しかしながら、“温度”とは何かと問われると、当時の人びとに取っても本当に分けのわからないものだったと思います。1847年の段階では温度は熱以上にその本質が解らず、それの解明はとても重要な問題だったのです。
そういった状況の中で、カルノーの原理の不完全な理解ではありましたが、トムソンは1848年にカルノーの原理を用いることで温度というものを定義することができるとして、絶対温度の概念を提出していました。
そういった時代の中で生まれたのが1850年のClausiusの本論文です。だからClausiusは上記のマイヤーやジュールの熱と仕事の等価性の考えと、トムソンによるカルノーの原理を用いた絶対温度の提案を十分に理解していたでしょう。
それらの事を理解していたからこそ、Clausiusは、熱の元である“熱素”は生成も消滅もしないというカルノーの後半の仮定こそがカルノー原理(カルノーの前半の仮定)の本質の理解を妨げている所だと見破ることができたのでしょう。
そのとき注意してほしいのですが、(Ⅱ)式 はカルノーサイクルの考察そのものの中から導かれたのです。そして、カルノーの原理の本質を理解する鍵は次の文章で述べている事柄の意味を明らかにすることだと気付いたのでしょう。

[補足説明4]
ここの文章の意味は非常に解りにくいが、Q が v と t の関数ならば、v-t座標面 に垂直に Q座標 を取れば、Q(v,t) は一つの曲面を形成しその上での Q の変分 dQ は“完全微分”となるということを言っている。そして、dQ が完全微分ならば、“完全微分で有るための条件式”[(Ⅱ)の右辺が0になること]が言えるということを記しています。
このことに付いては別稿「絶対温度とは何か(積分因子とは何か)」5.(2)3.[まとめ]を御覧下さい。
補足しますと、(Ⅱ)式は別稿「気体のモル比熱(マイヤーの関係式)」で説明している“マイヤーの関係式”cp−cv=Rとよく似た関係式である事に注意して下さい。実際、マイヤーは“マイヤーの関係式”の元になる式から“熱の仕事当量”Aを求めています。

[補足説明5]
上記の 1864年の註3)の意味も解り難いが、ここで行った議論は、カルノーサイクルの作業物質が永久気体(完全気体)では無くて実在の気体のように、サイクルの途中で液体と蒸気の平衡状態が生じる様なものでも成り立つ事を言っている。それは次の文節2.(4)で議論される。



[補足説明6]
(Ⅱ)式と(Ⅱa)式の関係は極めて解り難いので補足説明します。
まず、2.(1)でClausiusが設定した“熱力学第1法則”の表現

の解析的表現が(Ⅱ)式である事に注意して下さい。そのことは先ほどの説明

を思い出されれば了解できます。(Ⅱ)式 の導出に必要な (3)式【“消耗された熱”の表現式】 については付録Aをご覧下さい。
一方、(Ⅱa)式

は、次に述べる形で“熱力学第1法則”の設定をした場合の解析的表現です。

上記表現の意味は解りにくいかもしれませんが、その点に関しては別稿「『熱力学』とは何か」2.(3)を、特に [補足説明1] と [補足説明2] をご覧下さい。この形の表現に本質があります。
大切なのは上記の二種類の“熱力学第1法則”の設定は等価であることが証明できる事です。それには、両方の定義の解析的表現である(Ⅱ)式と(Ⅱa)式が等価である事を証明すれば良い。
すなわち、(Ⅱa)から(Ⅱ)を導く手順が、下記の注2)です。
その逆に、(Ⅱ)から(Ⅱa)を導く手順が付録Bで説明されているものです。
さらに補足します。
今日の熱力学の教科書が解りにくいのは、熱力学第1法則の表現として上記二つの表現の内の上側を採用しているにもかかわらず、その解析的表現としていきなり(Ⅱa)式が成り立つとしていることにあります。
もし、“第1法則”の表現として《上側の表現》を採用するのならば、Clausiusの様にその解析的表現として、まず (Ⅱ)式 を導き、更に上で説明した 注2) と 付録B を用いて下側の解析的表現 (Ⅱa) に変換できることを証明する必要があります。
さもなくば、別稿「『熱力学』とは何か」2.(3)のように、“第1法則”として《下側の表現》を採用し、その解析的表現は(Ⅱa)式であると展開するべきです。
このことの難しさは、後の3.(5)2.[補足説明2]で述べることに関係します。今日の熱力学教科書では、熱力学第1法則を単なるエネルギー保存則であるかのような説明をしているものが多いのですが、本稿をお読みになれば解るように、Clausiusの言う第1法則は、熱量というものが、当量のエネルギー値の仕事に変換されると言っています。つまり熱量というエネルギー形態を特別なものとして取り上げているのです。そのことを前面に出して熱力学を展開したのが別稿「『熱力学』とは何か」2.(3)で紹介した原田氏の文献です。つまり原田氏が第1法則として採用した《下側の表現》の中には、qが状態量では無いと言うことが含まれていますし、熱量の移動は熱平衡状態の元で行われことが含まれています。その“熱平衡状態”にはqの移動を完全微分にする積分因子としての絶対温度Tの概念が必須です。だから、“熱力学第1法則”は“熱力学第2法則”の成立にとって、必要不可欠の重大な影響力を持っている法則なのです。Clausiusが (Ⅱ)式 でもって熱力学第1法則を表現することから始めたのには、実に深い意味があります。そしてW.Thomsonが悩み苦しんだのもこの点にあるのでしょう。
今日の教科書でClausiusの示した“熱力学第1法則”の解析的表現である (Ⅱ)式 を取り上げている教科書が無いということは、Clausiusを正しく理解していない事を表している。
私どもが、本論文を読んだ時、最初に最も面食らったのは、(Ⅱa)式では無くて、(Ⅱ)式がこの論文で中心的な働きをしていることだったのです。
注2) 1864年に本論文を再版するときに、Clausiusが書き加えた(1864年に)補足の注意書き





[補足説明7]
上記文章の赤下線部分は、(Ⅱa)式中に現れる量 U(今日では“内部エネルギー”と呼ばれる)が“状態量”である事を注意している。
そして桃色下線部分で、(Ⅱa)の右辺の第2項の“外的な仕事”は、左辺の“流入した熱量”dQと同様に“状態量”ではないことを注意している。
ただし、ここでdUが“完全微分”になる(Uが“状態量”となることと同じ)といっている根拠が、ここの説明からは不明瞭です。
このことは山本文献3.(第25章の末尾)を始め多くの科学史研究家が指摘している所ですが、私は以下の様に捉えるべきだと思います。
すなわち、Clausiusの考え方から行くと、状態量では無い“熱”の出入りと“仕事”の出入りを加えたものが“内部エネルギー”の変化量になり、その変化量は熱と仕事を加えた径路によらないということは、熱量と仕事量が同じ“エネルギー”という量であるという考え方から行くと当然のことで、ここで“内部エネルギー”の変分を表すdUが完全微分になる(Uが状態量となる)ことは自明の事だったのでしょう。2.(2)でその事を明記しているのですから。
だから、逆にここで、今まで不明瞭であった“内部エネルギー”と言う“状態量”の存在を、熱や仕事の出入りをを通じて(Ⅱa)式によって確定しているのだと考えるべきです。2.(2)[補足説明1]も参照してください。
さらに補足します。Clausiusは本論文に続く1854年論文で、上記の意図の下に、まず(Ⅱa)式に相当するもの【1854年論文の(2)式】を掲げます。その式から、本論文の(Ⅱ)式に相当するもの【1854年論文の(3)式】を導いて、 (Ⅱa) と (Ⅱ) は等価なのだと説明しています。そのときの証明を、1864年の補足事項として上記注2)の形で本稿に追記しているのです。
更に補足しますと、上記の不明瞭さはClausiusも十分自覚していたものと思われます。それを自覚していたが故に1864年に論文集を出版する際、上記3.(3)3.[補足説明6]で説明した意味を込めて、 注2) と、更にその逆方向の証明である 付録B を書き加えたのだと思います。
いずれにしても、最後に得られた(Ⅱa)式は“熱力学第1法則”の完全・厳密な数学的表現
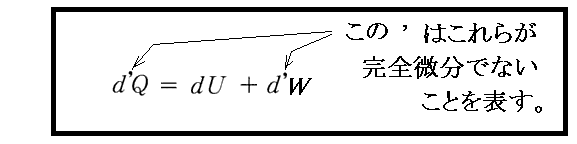
を表しています。
AR{(a+t)/v}dv=Apdv=d’Wとしていますが、Aは仕事量の測定単位を熱量の測定単位に合わせる為に乗じてあるだけです。
(4)カルノーサイクルの作業物質が液体と気体の平衡状態にある場合
(このサイクルを用いて熱の仕事当量を求める式を導く)

1.この場合のカルノーサイクルの詳細
[補足説明1]
下記の文章の意味は解り難いので補足します。
“M.とG.の法則”とは2.(3)1.で出てきた理想気体が満足する法則(Ⅰ)のことです。今日の高校生は“ボイル・シャルルの法則”と“アボガドロの法則”を一緒にしたものとして習うものです。ドイツでは“マリオット・ゲーリュサックの法則”と言うようです。
所で今からは、気体が液体状体に凝縮する領域(ファン・デル・ワールスの実在気体で言う飽和蒸気圧曲線の領域)を取り扱おうというのですから当然“理想気体”(ここ言う永久気体)でしか成り立たない“M.とG.の法則”は使えません。
しかし、カルノーサイクルの作業物質としては、そのサイクルの途中で液体状体に凝縮する様な状況が生じる実在気体(水蒸気もその一種)に対してもカルノーの原理は成り立ちます。つまり、以下ではカルノーサイクルのシリンダー内の作業環境として、液体とその飽和蒸気が常に共存している状況でカルノーサイクルを働かせようということです。
この場合でも、2.(3)2.で述べたカルノーサイクルの手順はすべて成り立ち、基本法則(前節の(Ⅱ)式や(Ⅱa)式)もそのまま成り立ちます。その事を説明しています。

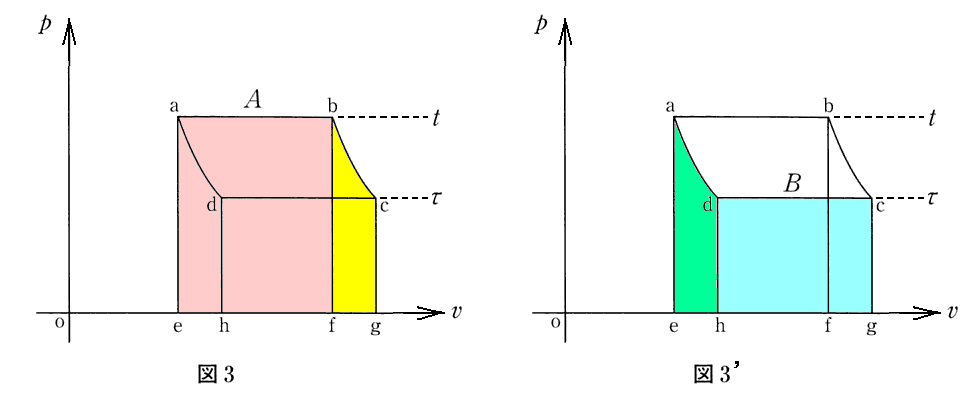

[補足説明2]
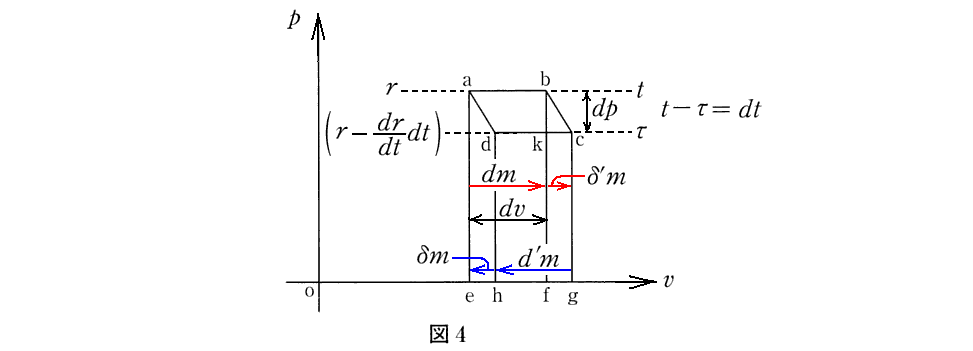
上記の過程は、作業物質が理想気体の場合の2.(3)2.の図1のa→bの等温過程による膨張に相当するのですが、今の場合の様に作業物質が実在気体で液体と蒸気が共存している領域があり、その領域をカルノーサイクルの作業環境として利用していますので、この場合は等温と同時に等圧の元でカルノー機関のシリンダー体積は増大します。
そのため、この等温過程でカルノー機関が外部になした仕事は四辺形eabfの面積(図3のピンク色着色領域)となります。

[補足説明3]
外的な仕事=fbcg とは図3の黄色着色領域の面積に相当します。


[補足説明4]
c→d の等温圧縮過程でカルノー機関に加えられる仕事が面積gcdh(図3’の水色領域)であり、d→a の断熱圧縮過程でカルノー機関に加えられる仕事が面積hdae(図3’の黄緑色領域)です。
まだ、この時代にはファン・デル・ワールスの状態方程式も、その状態方程式曲面も知られていませんが、今日知られている状態方程式曲面を利用して説明すると、ここでは下図の緑色領域内でサイクルabcdを働かせることです。

ついでに補足すると、前節(3)のカルノーサイクルは理想気体と見なせる右上の領域のサイクルabcdで働かせることです。

2.基本法則(熱力学第一法則)の数式表現

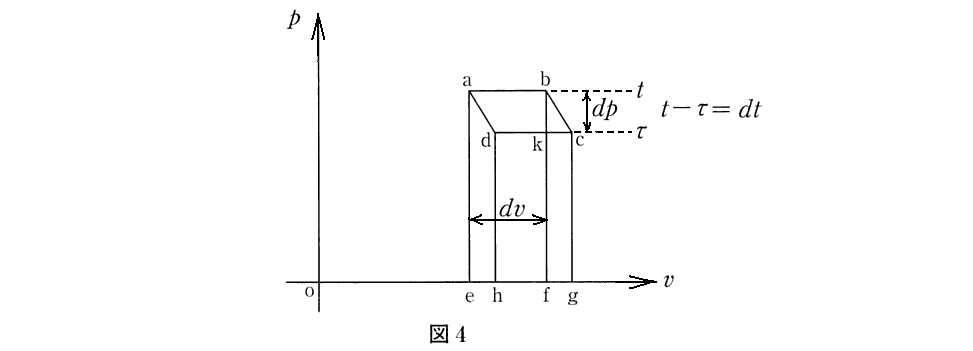

[原本補足説明]

[補足説明1]
上記の“飽和蒸気圧曲線は体積座標には無関係で温度のみの関数になる”はファン・デル・ワールス気体のp-v-T座標での状態図曲面のレリーフ図を思い出されれば諒解できます。

飽和蒸気圧曲線につきましては、別稿「ファン・デル・ワールスの状態方程式」4.(4)を参照。







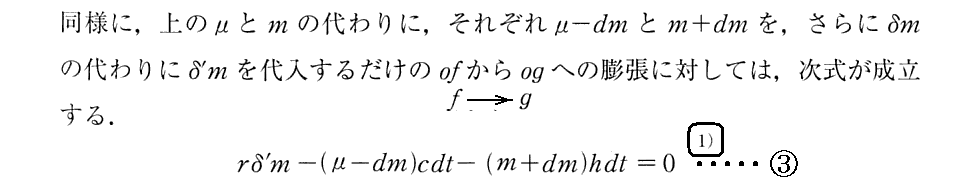


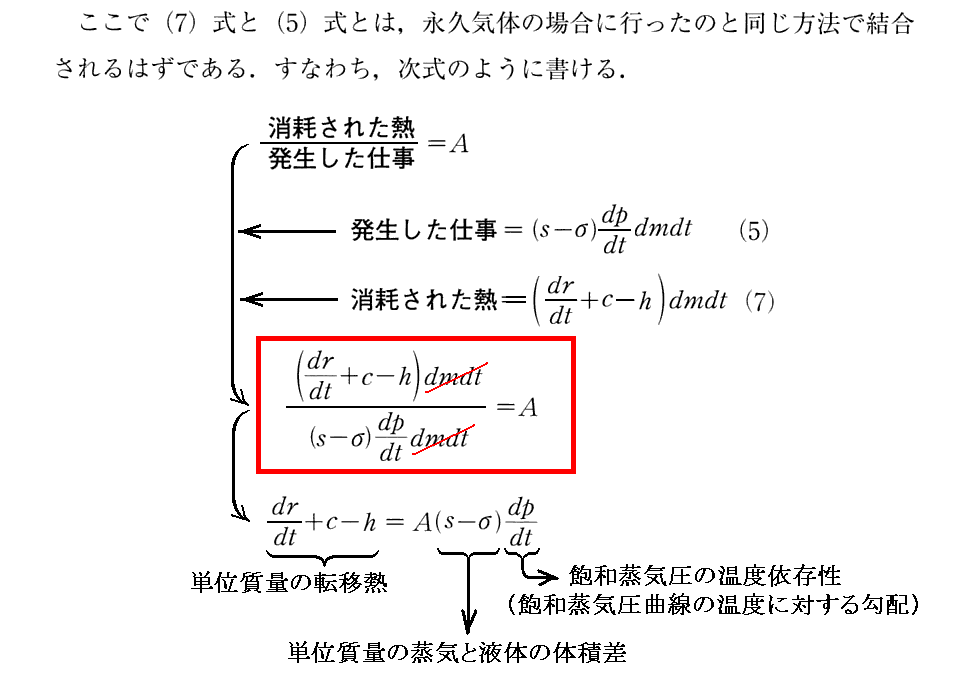

[補足説明2]
上記(Ⅲ)式の元になる式

の分子の“消耗された熱”とはカルノーサイクルに於いて高温熱源からカルノー機関に与えられた熱量とカルノー機関から低温熱源に排出された熱量との差を意味しますから、上記の式はカルノー機関によって消費された熱量とカルノー機関が生み出した仕事との比を示しています。つまり右辺のAはJouleが求めた“熱の仕事当量”の逆数を意味します。
だから、これは“熱力学第一法則”(エネルギー保存則)の別表現といってもよいもので、 [消失した熱量]+[生じた仕事]=0 であるという関係式を書き直して得られる式です。
(Ⅲ)式は、後の3.(2)2.で導く“クラウジウス=クラペイロンの式”と呼ばれている(Ⅴ)式あるいは(Ⅴa)式に似ていますが、それと混同しないで下さい。“クラウジウス=クラペイロンの式”は、“熱力学第二法則”(カルノーの原理)から導かれるもので
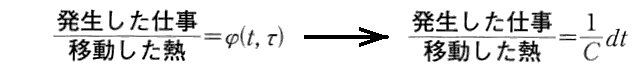
と表されます。このとき分母の“移動した熱”とは高温熱源から熱機関に与えられた熱量のみを指しており、熱機関から低温熱源に移動する熱は関与していません。
実際のところW.Thomsonが1850年以前の段階で悩み苦しんでいたのは、この二つの式のどちらが正しいのか、この式の違いは何を意味するのかという所です。(山本文献3.第29章Ⅰ参照)
ところが、Clausiusが明らかにしたのは、この両方の式は正しいのであって並立するのだということです。
上の式が“熱力学第一法則”(エネルギー保存則)の表現であり、下の式が“熱力学第二法則”(カルノーの原理)の表現なのです。
すなわち、上の式の右辺は“熱の仕事当量”の逆数を意味しており、熱と仕事のエネルギーとして等価性を表しています。
また、下の式は、その右辺が温度という量の関数であることを通して、熱機関につぎ込んだ熱がすべて仕事として取り出せるわけでは無くて必ず低熱源に熱として捨てられなければならない事を表しています。下の式は温度というものを通して熱の本質を示しています。後に、これから絶対温度が導入され、状態量エントロピーの存在が明らかになっていきます。
3.“基本法則”(エネルギー保存則)とは違うカルノーの仮定(熱量が一定=“熱素”が不変)の不合理性
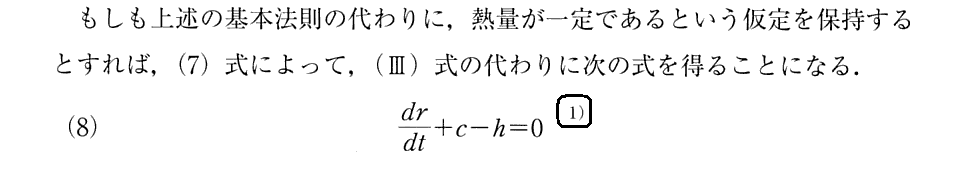






[補足説明1]
ワットの法則やルニョーの測定の詳細を知らないと、ここで何が言いたいのか良く解らないが、要するに、最新のルニョーの測定値と矛盾するのでカルノーの仮定(熱量が一定=“熱素”が不変)は間違っており、本論文の最初2.(1)で仮定した“基本法則”(エネルギー保存則)が正しい事を説明している。
すなわち、(Ⅲ)式の左辺(これは熱の仕事当量を著す式の[消耗された熱]を表す)はゼロでは無く、熱機関に流入した熱と流出した熱の差分を表し、これが発生した仕事に変わったという説明が正しいということです。






(5)永久気体の場合の“熱力学第一法則”(“基本法則”=エネルギー保存則)の数式表現




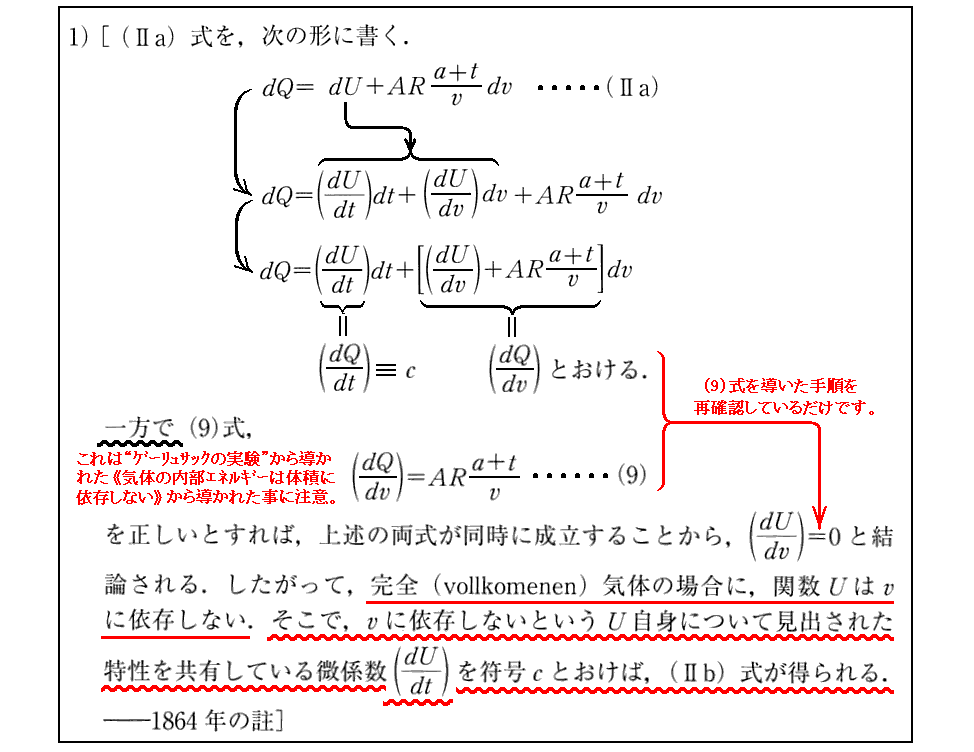
[補足説明1]
1864年の註1)を含めて、上記の説明は下記の(9)式は永久気体(理想気体)の内部エネルギーは温度が一定なら体積に依存しないことを言っています。
なぜなら上で説明されている様に永久気体に熱というエネルギーを加えても、一定温度が保たれているかぎり、それらの加えた熱はすべて膨張する為の仕事に費やされているとしているからです。そのため膨張前と膨張後では、その気体の内部エネルギーには差は無いのです。それは温度が変わらなければ内部エネルギーは変わらないという“ゲーリュサックの実験”から導びかれる結論と同じ事を主張している。


[原本補足説明1]
[原本補足説明2]

上記の付録Aと付録Bです。
(6)“熱力学第一法則”の数式表現(Ⅱb)式の応用

1.“マイヤーの関係式”


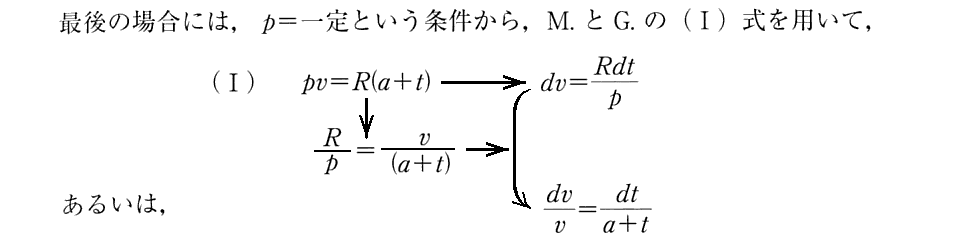


[補足説明1]
(10a)式が今日“マイヤーの関係式”と言われるもので、これはもともと、1842年にJ.R.Mayerが報告した関係式です。これはここの議論から解るように、“熱力学第一法則”(エネルギー保存則)から導けるものでして、“熱力学第二法則”は関係ありません。
Mayerはこの式からさらに“熱の仕事当量”(1/A)を求めていますが、その事はマイヤーがエネルギー保存則に通じる考え方を持っていたことを示しています。本論文では3.(6)1.で“マイヤーの関係式”から“熱の仕事当量”を求めることが説明されます。
“マイヤーの関係式”の歴史的な説明は別稿「気体のモル比熱(マイヤーの関係式)」をご覧下さい。特に、そこで引用した山本文献3.第22章Ⅴの解説を御覧下さい。マイヤーは“ゲーリュサックの実験”から『理想気体の内部エネルギーは温度のみの関数で体積や圧力に関係しない』ことを推察して、マイヤーの関係式を導くのですが、その事を導く今日的な展開が前節2.(5)[原本補足説明1]で補足されています。
いずれにしても本論文の上記展開が、“マイヤーの関係式”を導く今日の教科書的説明「絶対温度とは何か(積分因子とは何か)」4.(2)の元になっているのでしょう。そこの式変形と前節2.(5)[原本補足説明1]に説明されいる式変形を比較検討されればその事は良く解ります。
上記の説明では、マイヤーが拠り所とした、“ゲーリュサックの実験”からの“マイヤー仮説”『気体の内部エネルギーは温度だけに依存し体積には関係しない』が使われているように見えませんが、前節2.(5)[原本補足説明1]に説明されいてる中の(9)式を導くときに用いられています。だから、Clausiusの上記展開の中にすでに含まれています。
また前節2.(5)[原本補足説明2]に説明されいる事柄は、別稿「絶対温度とは何か(積分因子とは何か)」6.(4)3.[補足説明2]の今日的な説明を意味しているのでしょう。




[補足説明2]
上記Laplaceの音速に付いての考察(1816年)は別稿「音速の理論」3.(2)をご覧ください。




2.“気体の断熱変化の公式”





[補足説明1]
ここで導いた(14)、(15)、(16)式等々の公式はPoissonがすでに見出していたものですが、Clausiusはそれらの公式を熱力学的に正しく導いて見せたと言うことです。
これが、別稿「気体の断熱変化」(特にそこの[補足説明2])や、「絶対温度とは何か(積分因子とは何か)」4.(3)などで説明した、“気体の断熱変化の公式”の教科書的導出法の元になっているのでしょう。
3.“カルノーの気体定理”の導出



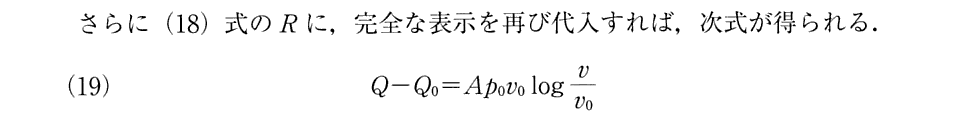

[補足説明1]
この3.項の内容も解りにくい所ですが、Clausiusはそれまでに導かれていたカルノーの結果(“カルノーの気体定理”)を確認しています。先行するカルノーの説明は山本文献3.第20章Ⅳで紹介されていますのでそこをご覧下さい。
カルノーは“カルノーの基本法則”(“熱力学第二法則”)の応用として導いているのですが、Clausirsが上記で導いているように本来これらは熱力学第一法則から導かれるものです。
カルノーが基本法則”(“熱力学第二法則”)の応用として説明をしているのは、すでにその中で温度の導入を必要としていたからです。彼にとって温度は分けのわからないものでしたが、その温度を用いないと、彼の議論は展開できなかったのですから。
Clausiustがここで何故“カルノーの気体定理”を取り上げているのか困惑するところですが、Clausiusは、これらの法則は元々“熱力学第一法則”の応用として導ける事を強調しているのでしょう。そうして“カルノー関数”が本来有るべき位置である“熱力学第二法則”導入の為の準備をしているのだと思います。
3.カルノーの基本法則と、すでに2.で記述したこととの結合から導かれる推論
(1)熱の特殊性の原理(“熱力学第二法則”の設定と、それによる“カルノーの原理”の証明)
[補足説明1]
この章の導入解説として山本文献3.第26章Ⅰの記述を引用






[補足説明2]
上記の赤四角線で囲ったClausiusの説明文の中に“カルノーの仮定の前半の部分”が何を言っていたのか書かれていないので、以下の説明の導入としてはとても解りにくい。
1.[原本補足説明1]で自ら述べている様に、1850年段階のClausiusはカルノーの論文をまだ手に入れておらず、その内容をクラペイロンとトムソンの論文から引用したと書いていますから、“カルノーの仮定の前半の部分”の本当の表現をまだ知らなかったせいもあるのでしょう。
下記本文の中で述べている様に、カルノーの仮定の前半部分とは今から証明しようとしているこちらの表現の“カルノーの定理”の事です。
実は、“カルノーの定理”はカルノー自身がすでに証明しています。そのため、以下のClausiusの証明がそれに対してどういった位置を占めるのかが解りにくく、熱力学を学ぶ初学者が最も混乱するところです。
その当たりは、先に別稿「絶対温度とは何か(積分因子とは何か)」6.(1)3.[補足説明2]を御覧頂いて確認しておかれると良いでしょう。
いずれにしましても、以下の本文が、“熱力学第二法則”に基づいて“カルノーの定理”を証明するClausiusの有名な解説です。つまり、別稿「絶対温度とは何か(積分因子とは何か)」6.(1)3.[補足説明1]で説明したものであり、別稿で引用した山本文献3.第26章Ⅱで解説されているものです。
すなわち、上記の“カルノーが述べた仮定”の前半部を“熱力学第二法則”に格上げし、それを用いた背理法によって“カルノーの原理”(熱機関の生み出しうる“仕事の最大値”は高温熱源と低温熱源の温度のみによる)を証明しています。
これが、熱力学という学問分野の出発点となった、超有名なClausiusの証明です。今日の教科書の解説も解りにくいが、そのもとになった説明も極めて抽象的でまわりくどく難解です。私は原論文を読んで見て、初めてその解りにくさを納得しました。そのわかりにくさの理由は以下の通りです。
Clausiusは、カルノーがすでに証明している、カルノーの原理を再証明するのですが、カルノーの仮定(原理)の後半部は間違っているので、その前半部のみを証明することにします。そのとき、その証明のために、カルノーの仮定の前半部をClausius表現の“熱力学第2法則”に格上げして、その“熱力学第2法則”を用いてカルノーの仮定(原理)の前半部を“カルノーの原理”として再証明しているから解り難いのです。
そのとき、「熱力学」の展開に重要なのは、Clausiusが証明し直した“カルノーの原理”そのものでして、“熱力学第2法則”はその証明の根拠としてつじつま合わせにカルノーの原理を格上げして導入したものでしか無いのです。
その様に導入したものでしかないのてすが、こちらの表現の法則の方がカルノーの原理そのものよりも“熱の本質”をより良く示しているから法則としてはこちらの方がよりふさわしいということにしたのです。
実際、カルノーは“カルノーの原理”を今日“第一種永久機関不可能の原理”といわれるものを用いて証明しているのですが、クラウジウスの掲げた“熱力学第2法則”は今日“第二種永久機関不可能の原理”といわれているものと同じです。ただしこのことを明確に指摘したのはW.Thomsonでもう少し後のことです。この当たりも、この証明手順のわかりにくさの原因かも知れません。この当たりは別稿「絶対温度とは何か(積分因子とは何か)」6.(1)1.も参照されて下さい。



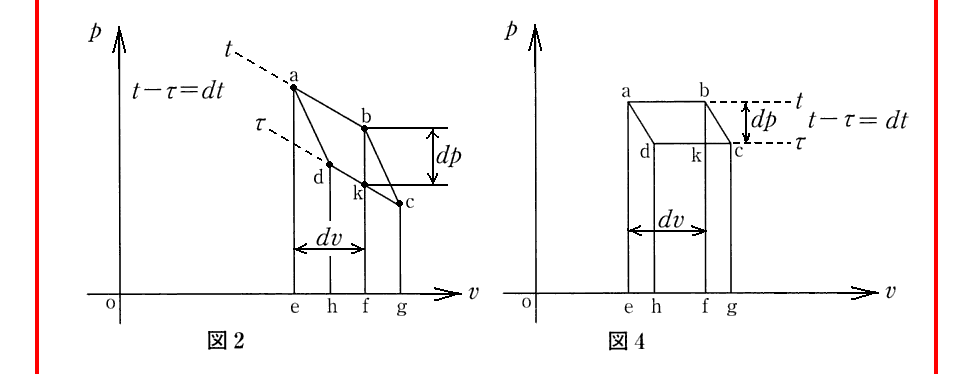






文の続きの中で、付けたり的に述べているので、これがいわゆるClausiusによる“熱力学第二法則”の表現だとはなかなか読み取れませんが、この表現がそれです。2.(1)[補足説明1]を振り替えられて下さい。
[源本補足説明]

[補足説明3]
上記の1864年の註1)が、山本文献3.第26章Ⅱの中程で紹介されている補註です。確かに、Clausiusのこの補足が無いと別稿で広重氏が説明されている事柄をこの論文だけから読み取るのは難しいかも知れません。そのことを見抜くにはClausiusが述べている続きの1854年論文も読む必要があるのでしょう。
この1854年論文の翻訳版は八木監訳文献2.の中にあります。また、その内容が山本文献3.第29章Ⅲ〜Ⅷで概説されています。



[源本補足説明]




[補足説明4]
上記の註1)で説明している(b)式は、“カルノーの原理”の数学的表現に他ならないのですが、(b)式中の C(t) こそ、Thomsonが提唱した“絶対温度”(今日では“T”と記す)です。そしてd’Qを“状態量”にする為の“積分因子”(積分分母)です。このことに付いては、2.(4)2.[補足説明2]も再読されて下さい。
上記の註1)は1864年に論文集を出版するときに書き加えられたものですから、その時点のClausiusは、その事はすでに承知していました。しかし、その事をここで書いてしまえば、この1850年論文を収録出版する意義がなくなりますから、まわりくどい説明になっています。
文中で“この論文が進展するにつれて、この関数の形を決める機会があるであろう。”と言っている機会とは3.(3)のことです。
また、“Cという表し方は、もはや不必要になるだろう。”に付いては3.(4)1.[補足説明1]を参照されて下さい。
[補足説明5]
上記の最後の表現dt/Cはとても重要な所なので、歴史的な経緯を補足しておきます。
上記の 註1)[1864年の註]の中で説明されている(b)式が“カルノーの原理”の数学的表現なのですが、これは、カルノーの1824年の大論文ですでに与えられています。ただしカルノーはCを違った表現にしていますので、その論文をご覧になられてもなかなか読み取れないのですが、全く同じ趣旨の数式です。
今日“カルノー関数”といわれている関数を“C(θ)”と表現したのはクラペイロンです。おそらくカルノーに敬意を表して文字Cを用いたのでしょう。本論文でもClausiusはクラペイロンの論文に習って同じ記号を用いています。これはまた、山本文献3.ではΘ(θ)と表されているものです。
いずれにしましても、熱力学第2法則の数式表現として
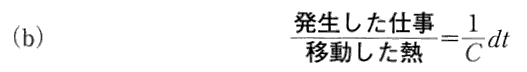
の形を最初に与えたのはカルノーの1824年の大論文です。ここは山本文献3.第20章Ⅰ〜Ⅱを参照されて下さい。
ただし、カルノーに取ってこれが熱力学第2法則の数式表現という認識はありません。それも当然です。なぜなら当時のカルノーにはエネルギー保存則である熱力学第1法則の認識も、ましてや熱力学第2法則の考えも確定していた分けではないのですから。
熱力学第2法則自体の存在を認識したのは本論文におけるClausiusが最初です。そして、その数式表現がこの式だと明確に認識していたのは、この論文を発表した時点のClausiusが最初です。
(2)“熱力学第二法則”(カルノーの原理)の数式表現
1.永久気体の場合
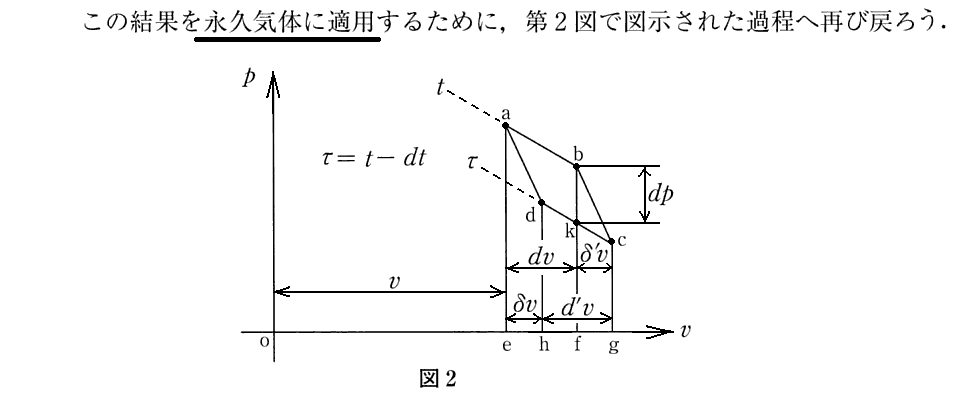


[補足説明1]
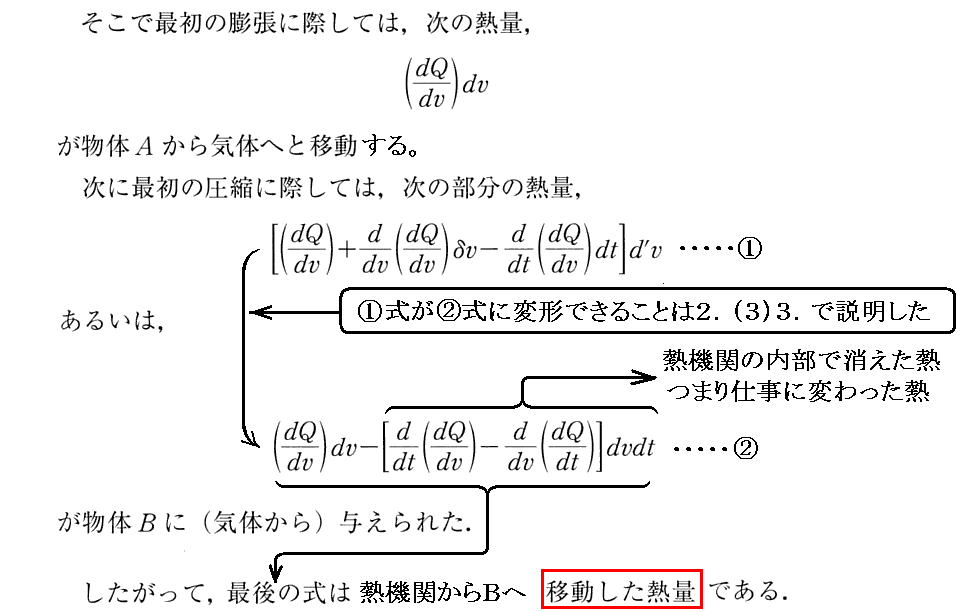
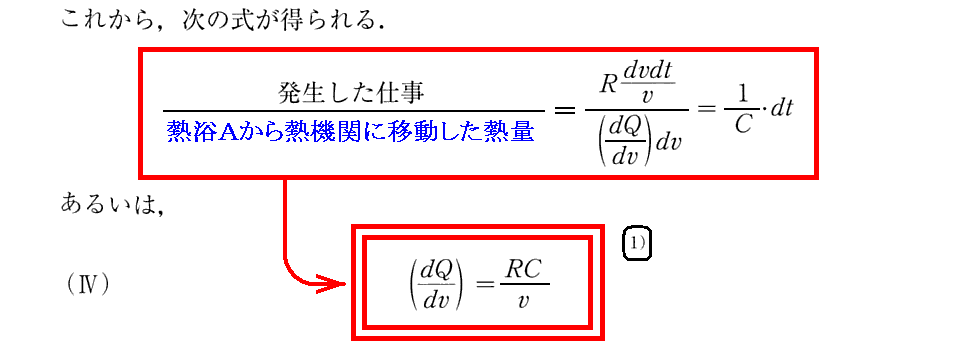
ここは、発生した仕事の部分をもっと一般の場合に適用した式にすることができる事を注意している。このことは、次項で説明されている液体と蒸気が平衡している作業環境に当てはめてみれば納得できます。
実際、R/v→(dp/dt) を R/v→dp/dT にして、Cを絶対温度Tとし、(dQ/dv)=q転/(v気−v液) と置き換えて見れば、(Ⅳ)式は今日の“クラウジウス=クラペイロンの式”そのものです。
今日の教科書では、g気(p,T)曲面とg液(p,T)曲面が交差して一致しているのが“飽和蒸気圧曲線”であるという条件から下記の様にして求めますが、そのようにして得られた関係式と全く同じです。

つまり、今日の教科書で習う“クラウジウス=クラペイロンの式”は“カルノーの原理”の数学的表現に他なりません。
そのことが次項で説明されます。そして、最終的な形が3.(4)1.[補足説明1]に続いて記されている(Ⅴa)式として求められます。
余談ですが、上記の“ギブスの自由エネルギー”を用いる今日の教科書の“クラウジウス=クラペイロンの式”の導き方を学ぶとき、面食らわれた方も多いのでは無いでしょうか。
私自身、今日の導き方がなかなか納得できなかったのですが、その理由がやっとわかりました。今日の導き方はエントロピーの存在を前提にして導いているから解りにくかったのです。
エントロピーとは何かということと、熱の移動を“状態量”にする積分因子としての絶対温度Tの意味が真に理解できていない身では理解できなかったのも当たり前だったのですね。
《相転移に於いて、相転移前と相転移後のギブズの自由エネルギーは互いに等しい》などの事柄は、ギブスにより“ギブズの自由エネルギー”が導入された熱力学が更に発展した段階で、やっと解ってくる事柄なのですから。
《上で紹介した今日の導き方》に比べて、3.(4)1.[補足説明1]の説明に従って(Ⅴa)式を導くやり方が、如何に明快か!! をぜひ感じ取られて下さい。
2.液体−飽和蒸気平衡系の場合
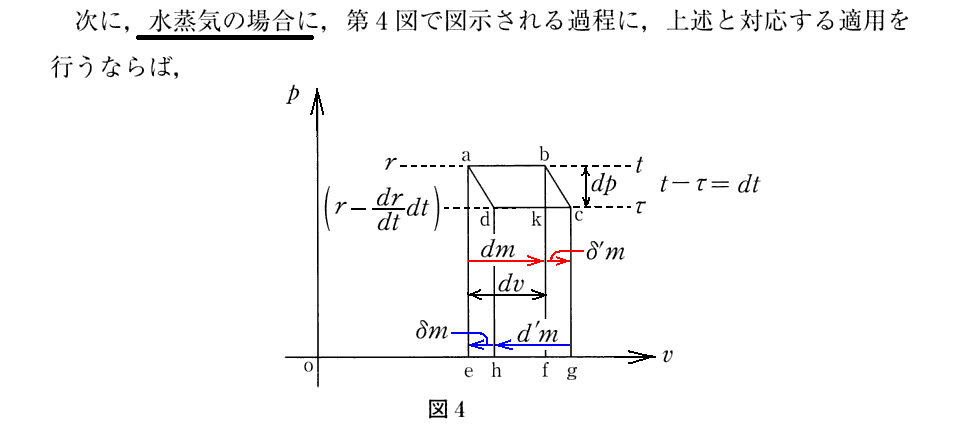

ここの説明は、2.(4)2.ですでに展開されていますのでそこを復習されて下さい。そこで定義されている様に、rは潜熱(蒸発熱=転移熱)であり、cは液体の比熱、hは飽和蒸気の比熱、sは単位質量の飽和蒸気の体積、σは単位質量の液体の体積です。


上記訳者注の 前註36-1 は 2.(4)2.の最初の註1)です。


[補足説明1]
上記の註2)の意味は解り難いが、ここでのQは単位質量当たりの状態変化の潜熱(転移熱=蒸発熱)を意味しており、これは状態(p,v)が定まれば決まる量です。その事を言っているのでしょう。この潜熱と、着目している系に外界から出入りする一般の熱量Q(状態量では無い)とを混同しないで下さい。
ちなみに、クラペイロンは別稿「ファン・デル・ワールスの状態方程式」4.(3)[補足説明1]で説明したような方法で導いたようです。もちろん、そこで説明している絶対温度Tはまだ確立していませんから、ここで言う温度tの関数C(t)となります。
いずれにしても、今日“クラウジウス=クラペイロンの式”といわれる関係式は、“カルノーの原理”(カルノーサイクルの効率表現)と等価(すなわち“原理”の数式表現)でして、それから直接導かれるものです。
さらに補足しますと、今日の“クラウジウス=クラペイロンの式”は“カルノーの原理”(カルノーサイクルの効率表現)のカルノー関数C(t)を最初から“絶対温度”Tと見なした形で“ギブスの自由エネルギー”を用いて導入されますから、この式の意味が良く解りませんが、本来は逆でして、この式[(Ⅳ)式or(Ⅴ)式]によって絶対温度Tが定義・導入されたのです。
(3)熱力学第二法則を熱力学第一法則から得られている公式に結び付ける (カルノー関数Cの決定)



[補足説明1]
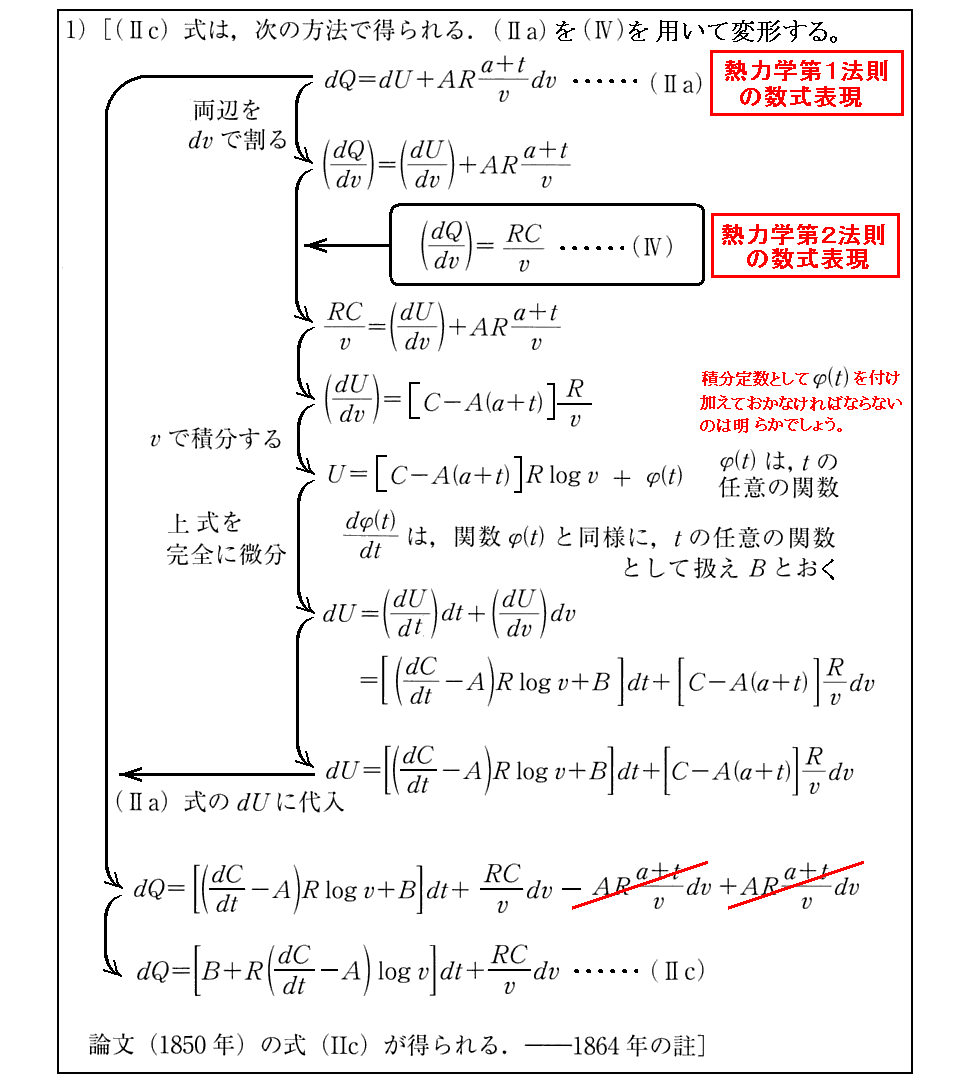
(9)式は2.(5)“熱力学第一法則”の数学的表現で導いた式です。そこで述べられているように“一定温度”で膨張する“永久気体”が満足する関係式です。
永久気体の内部エネルギーUは温度が同じならば変化しないのですから、永久気体が吸収した熱がちょうど外部に対してなされた仕事に等しい事を表している式です。つまり熱力学第1法則の数式表現の一種である

に他なりません。

[補足説明2]
上記の説明と以下に続く説明の意味は非常に解りにくい所です。
まず、上記説明で言っていることですが、(9)式と(Ⅳ)式が同じである事は、(Ⅳ)式中のカルノー関数Cは理想気体の温度関数(a+t)に熱の仕事当量(=1/A)の逆数(すなわちA)を乗じたものに等しい事を言っています。理想気体は現実には存在しませんから(a+t)は実際は実在の気体で定めた温度関数です。
そして以下に続く文章で説明していることは、カルノー関数Cはクラウジウス=クラペイロンの式に依って実験的に決定できると言って、クラペイロンとトムソンの測定値を紹介しています。
つまり、後で解るように、カルノー関数Cは絶対温度そのものに関係する量ですから、実在の気体で定めた実用温度が絶対温度で何度に相当するかを決定する道が開けることを説明している様に見える。
実際には1850年の時点で、絶対温度の概念が確立しているわけではありませんから、その事をあからさまに言っているわけではないのですが、実質的にはその事を示していると見なせます。
しかし、[補足説明4]で説明する様に、1850年段階のClausiusが本当に、上記の認識に到達していたのかどうかは解りません。
実際のカルノー、クラペイロンとトムソンの実験測定結果が山本文献3.第20章Ⅲで紹介されていますので、それを参照されながら以下の説明をお読み下さい。



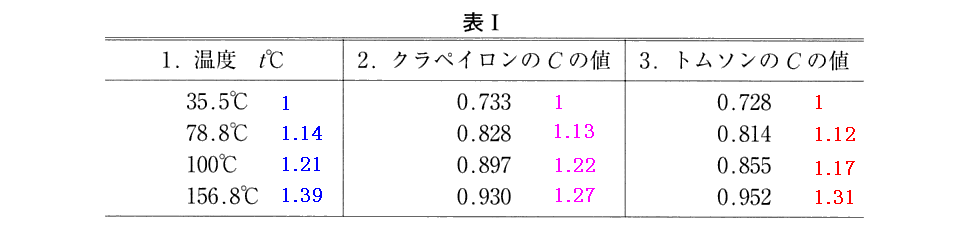


上記の“定数Aの絶対値を決定するためにも用いられる”は3.(5)2.で展開される。

[補足説明3]
ところで、
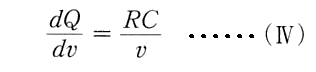
は永久気体について“カルノーの原理”を表す式でした。カルノーの原理とは熱力学第二法則を体現するものでしたから、(Ⅳ)式は“熱力学第二法則”の数式表現だと言って良い。
一方、
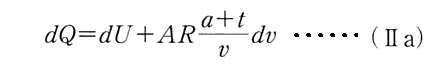
は“熱力学第一法則”(エネルギー保存則)を体現するもので、永久気体の内部エネルギーの変化は気体に加えられた熱量と仕事に等しい事を表すものでした。上記本文で説明されている様に、永久気体の場合には、これは(9)式
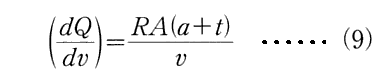
と等価であると言って良い。(9)式は2.(5)“熱力学第一法則”の数学的表現で導いた式です。そこで述べられているように“一定温度”で膨張する“永久気体”が満足する関係式です。永久気体の内部エネルギーUは温度が同じならば変化しないのですから、永久気体が吸収した熱がちょうど外部に対してなされた仕事に等しい事を表している式です。つまり、“熱力学第一法則”の数式表現です。
そのとき、後にThomsonが明確な形で導入する様に“カルノーの原理”こそ絶対温度を定義する式だといって良い。前節3.(2)の“カルノーの原理”の数式表現である(Ⅳ)式と(Ⅴ)式の中に現れてきた実用温度tの関数C(t)こそが“絶対温度”Tだったのですから。
所で、絶対温度Tとは元々永久気体(理想気体)の圧力一定のもとでの体膨張率で定めようという考え方がありましたから、(9)式の(a+t)が絶対温度と見なせるものでした。そして、(a+t)は、ほぼ“永久気体”(理想気体)と見なせる水素ガスなどによって正確に測定されていました。もちろん水素ガスは“永久気体”(理想気体)では有りませんから、その様にして定められた(a+t)はあくまで実用温度である事は変わりません。
だから、カルノーの原理と熱力学第一法則を結び付けるということは、その絶対温度を現実の実用温度tで表す関係式を導くことです。それが(Ⅱc)式です。
ただし、現実の温度tはあくまで現実の気体を理想的な気体と見なして、その温度変化に伴って生じる体積変化あるいは圧力変化で決められています。つまりマリオット・ゲーリュサックの法則(理想気体の状態方程式)によって決められた温度です。その当たりは、上記本文の説明をご覧になればおわかりになると思います。
いずれにしましても、ここは温度という物理量に対して深淵な事を論じているのですが、この議論の意味を理解するのは極めて難しい。これは後にThomsonとJouleが行った、“ジュール・トムソン効果”を用いて絶対温度を空気温度計に関係付けること(1852〜1854年)と同じ事を、“クラウジウス・クラペイロンの式”(カルノーの原理)(Ⅳ)式を用いて行っているといえます。上記本文中のクラペイロン及びトムソンの実験がそれです。これはとても重要な実験でして、山本文献3.第20章Ⅲでその詳細が説明されていますので御覧下さい。
つまり、別稿「絶対温度とは何か(積分因子とは何か)」7.(3)で説明した絶対温度の目盛りの校正法をここで展開していると言っても良い。
このことは、上記別稿7.(4)で紹介したPlanckの指摘『原則的には第二法則から導かれる方程式は何れもこれを絶対温度Tの測定に利用することができる。』の実例を示していると言えます。
このことの意味については3.(5)2.[補足説明2]で更に詳しく説明していますのでご覧下さい。
[補足説明4]
Clausiusの本節3.(3)の説明は非常に曖昧で、山本文献3.第28章第Ⅰ節で説明されているのが本当の所かも知れません。もしClausius本人が、その様に思っていたのならば、1864年にこの論文集を出版した段階のClausiusは山本文献3.第28章第Ⅱ節以降に展開されているThomsonの説明を完璧に理解していたはずですから、自分の認識が至らなかった事を[補足の註]として追記しているはずです。
それをしていないのは、おそらく、ここはClausius自身でも、1850年当時の自分が【山本文献3.第28章Ⅰで説明されているように理解していた】のか、あるいはそこの【Thomsonの疑念の様に理解していた】のかは、判然としていなかったのではないでしょうか?
実際、Thomsonが、実験・実測値から求めたカルノー関数が示す絶対温度と、実在気体の実験・観測値から決めた実用温度tとの関係を明確に理解して、ジュール・トムソン効果の実験によって両者の間の対応関係を詳細に決定して、その事に決着を付けるのは1852年にジュール・トムソン効果の測定実験をした後なのですから。おそらく、1850年に本論文を書いた時点のClausiusにはそこまで見通せてはいなかったのでしょう。
あるいは以下の様に考えるべきかも知れません。確かに、W.Thomsonがいみじくも指摘したように、温度というものを定義するには、2つの温度を持つ熱浴の間で可逆な熱機関を働かせて、そのとき高温熱浴と低温熱浴の間でやり取りされる熱量の比でもって2つの熱浴の温度比とするしか無いと言うことです。そのとき、温度の比が決まれば、適当な状況の熱浴(現在は水の三重点を273.16Kとしている)の温度を決めればあらゆる熱浴の温度というものは決定できます。
しかし、現実には、準静的・可逆的に働く理想的な熱機関など存在しません。それはちょうど理想気体の体積膨張の様子から絶対温度を測定しようとしても、絶対温度を体現している理想気体温度計など現実には存在しないのと同じです。
だから、(可逆では無い)現実の熱機関や(理想気体では無い)現実の実在気体を用いて測定できる量から、可逆熱機関や理想気体温度計が示すであろう真の絶対温度を求めることができるのか!という問題はまだ別の話で、この時点のClausiusが言っているのは現実には存在しない理想的な可逆機関のカルノー関数は、同じく現実には存在しない理想気体温度計が示す温度に等しいということだと解釈すべきなのではないでしょうか?
(4)“熱力学第二法則”の数式表現である(Ⅳ)、(Ⅴ)式の応用
1.クラウジウス=クラペイロンの式

[原本補足説明]

[補足説明1]
上記の1864年の註1)の意味は解りにくいので補足します。
まず、文中の“(すでに前註51-1)でも示されている”とはこちらの註1)の事です。その註1)に対する[補足説明4]で注意したように、上記の註を記した1864年段階のClausiusは、先ほど述べた[補足説明1]の内容をすでに理解していました。これらの事を考慮されて、上記の註1)を読まれるとその真意が理解できます。
これは3.(3)[補足説明2]における説明文中の(Ⅳ)式と(9)式を同じものだと見なして絶対温度CをC≡A(a+t)で置き換える事ができるだろうということです。ちなみにAは“熱の仕事当量”の逆数であり、aはa=273と測定されていた、理想気体の“体膨張率”(1℃上昇したときの体積の膨張する割合)1/a≡1/273 の逆数です。
実際の所、実在気体である空気を理想気体と見なして決めた実用温度は、絶対温度を極めて良い近似で体現しているのですから、カルノー関数C(t)をA(a+t)で置き換えて論じて良いだろうということです。
今日の熱力学の教科書では、別稿「絶対温度とは何か(積分因子とは何か)」7.(4)“まとめ”で指摘した様に、本来は実用温度計の温度tで表記しなければ成らない所を、最初から絶対温度Tとして論じています。
だから、今日の教科書の論理展開法の元祖がここで説明されていると言えます。
そして、CをA(a+t)に置き換えた形で、次の本文で示されている(Ⅴa)式が、今日の教科書で説明される“クラウジウス=クラペイロンの式”に他なりません。このことはすでに、3.(2)1.[補足説明1]で注意した所です。

2.飽和蒸気圧曲線を表す関数





[補足説明1]
ここは、今日の教科書では別稿「ファン・デル・ワールスの状態方程式」4.(4)“飽和蒸気厚曲線の求め方”のように説明される所です。そこを復習されればここの内容が理解できます。
一つだけ補足します。上記文中の“後者の仮定は、少なくともかなり真実に近く”の所ですが、後者の仮定とはr(蒸発熱)が一定と見なせるというところです。
この仮定は、Clausiusも注意している様に、正しくありません。このことに付いては上記別稿4.(4)[補足説明1]を復習して下さい。Clausiusは、次項3.で、水蒸気の場合にrの温度依存性を詳しく検討しています。(24)式がそれですが、これは上記[補足説明1]のグラフ
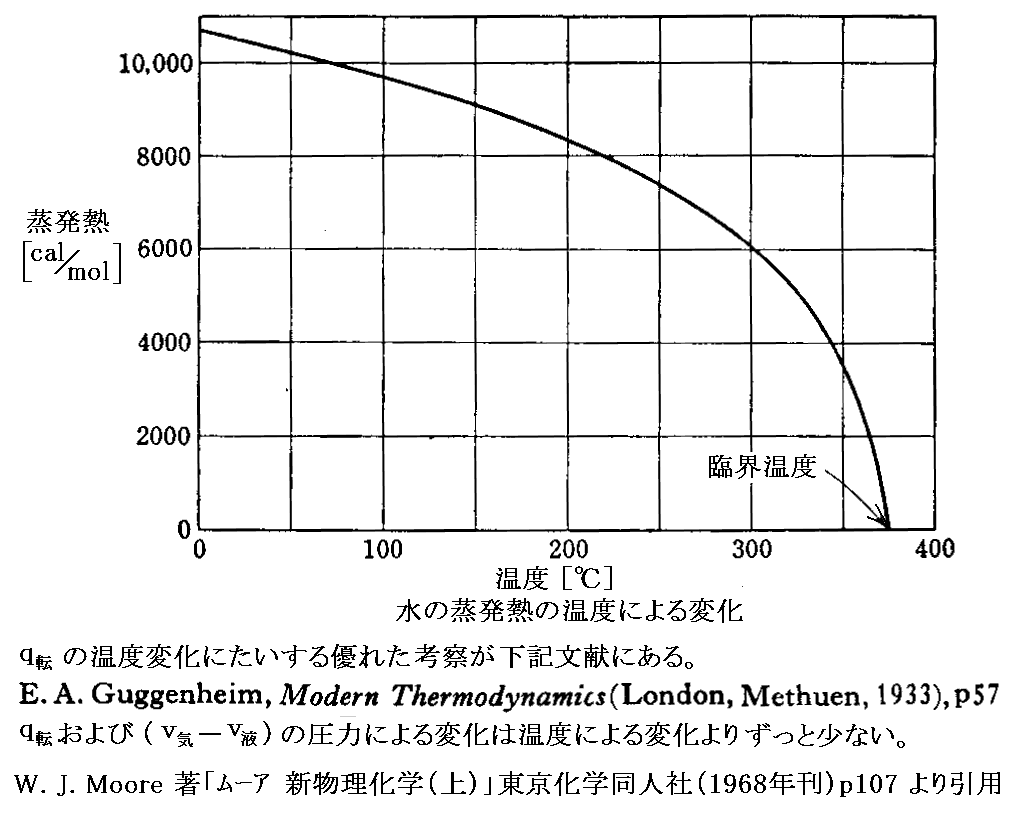
を表しています。
3.水蒸気の場合の実測値の検討
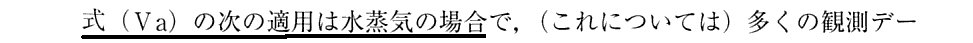



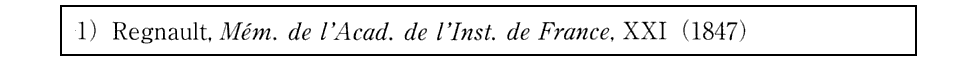



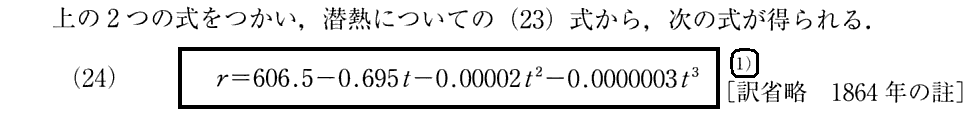
この(24)式をグラフ表示したものが前項2.の[補足説明1]で示したものです。




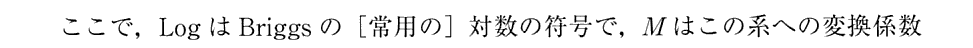










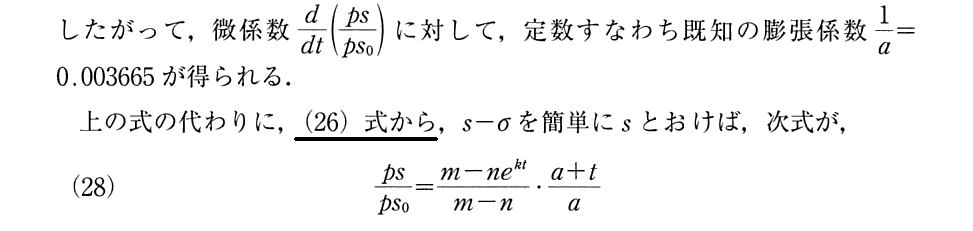






























(5)熱の仕事当量の導出

1.完全気体の利用
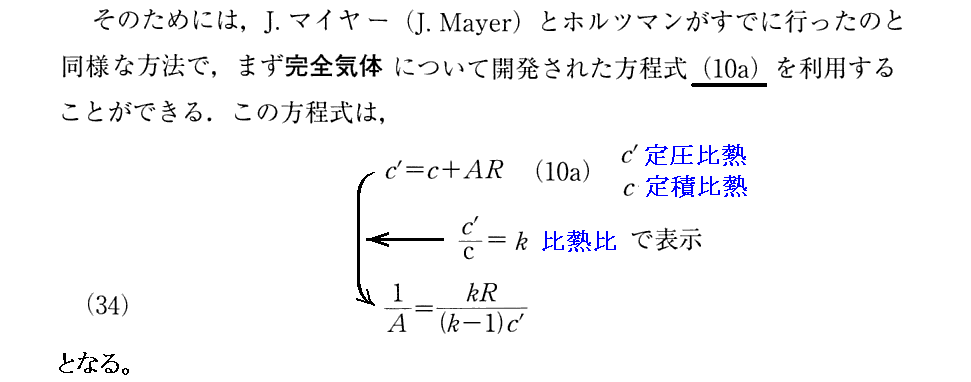
下記の(10a)式に付いては2.(6)1.を復習されたし。


[補足説明1]
“熱の仕事当量”(1/A)を求める“マイヤーの関係式”に付いては2.(6)1.ですでに説明されています。文中の(10a)式はそこで導かれたものです。
この方法による熱の仕事当量の求め方の本質は、別稿「気体のモル比熱」2.で説明した様に“定圧比熱”と“定積比熱”の差は気体の膨張に際して“外に対してする仕事の量”に関係しているという認識でした。このマイヤーの認識を明確に裏付ける理論を、Clausiusは作り上げたということです。
ちなみに、マイヤーの論文『無生物界の《力》についての考察』(1842年)の英訳版をこちらで引用しています。ただし、この論文の意図を理解するのはとても難しいです。山本文献3.第22章Ⅴの解説などを参照されながら御覧下さい。
2.水蒸気の利用
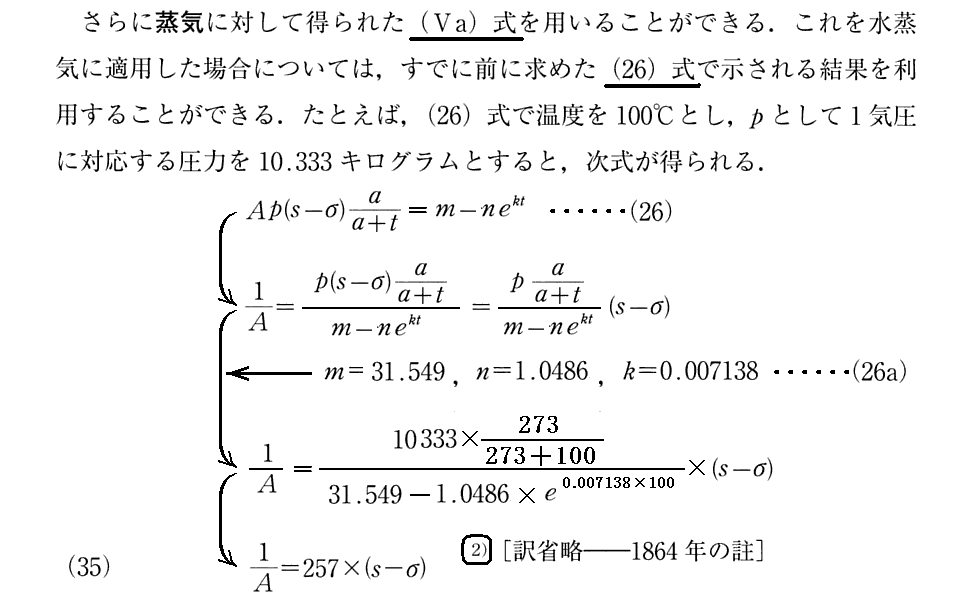
下記の(Ⅴa)式は3.(4)1.を、(26)式は3.(4)3.を復習されたし。

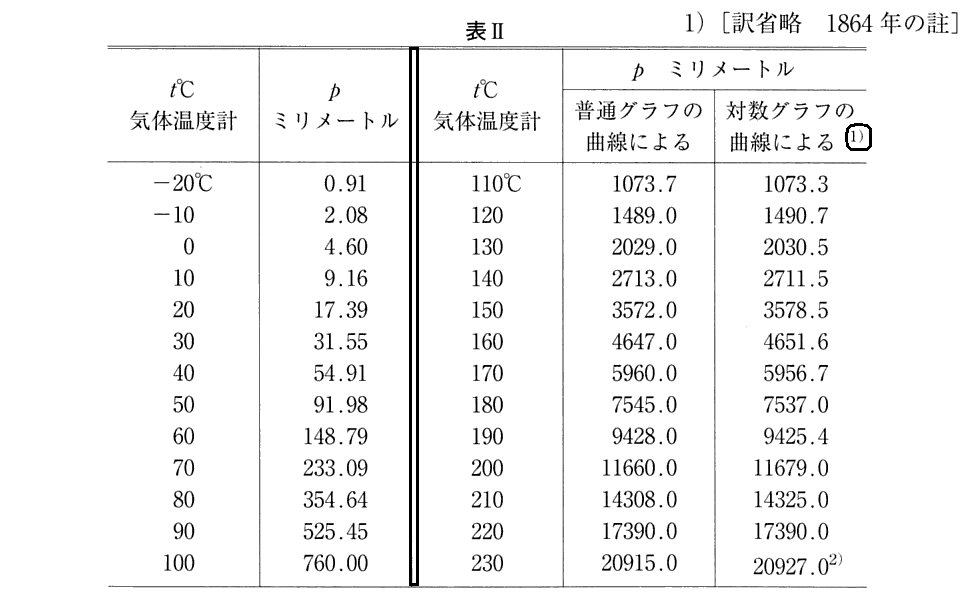
上記の“表ⅠのクラペイロンのC値 0.897”とは3.(3)で紹介されているものです。


[補足説明1]
上記でClausiusが説明しているように熱の仕事当量を求める方法としては、3.(2)2.で求めた“クラウジウス=クラペイロンの式”(Ⅴ)式を用いることもできます。
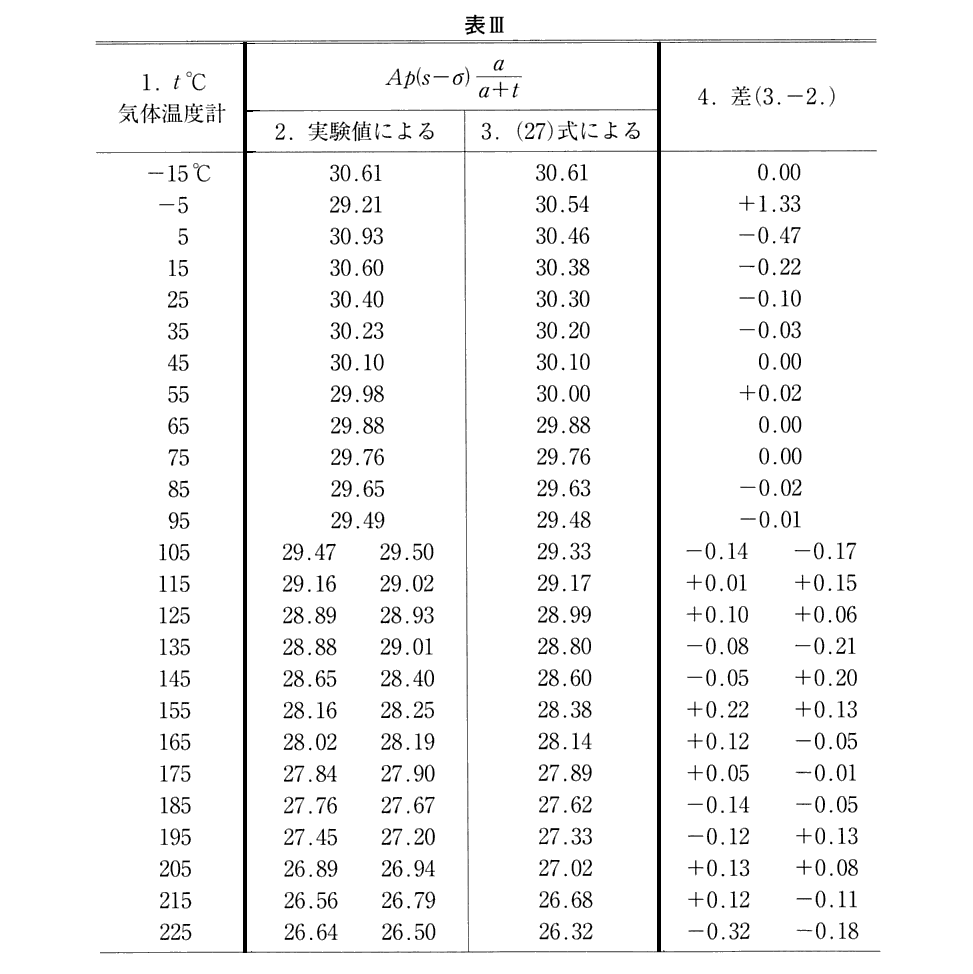
そのとき、上記の(Ⅴa)式と(26)式は以下の様にして求まる式でした。式中の、r は潜熱(蒸発熱=転移熱)であり、 c は液体の比熱、 h は飽和蒸気の比熱、 s は単位質量の飽和蒸気の体積、σ
は単位質量の液体の体積です。t は実用温度、a=273は体膨張率1/aの逆数です。
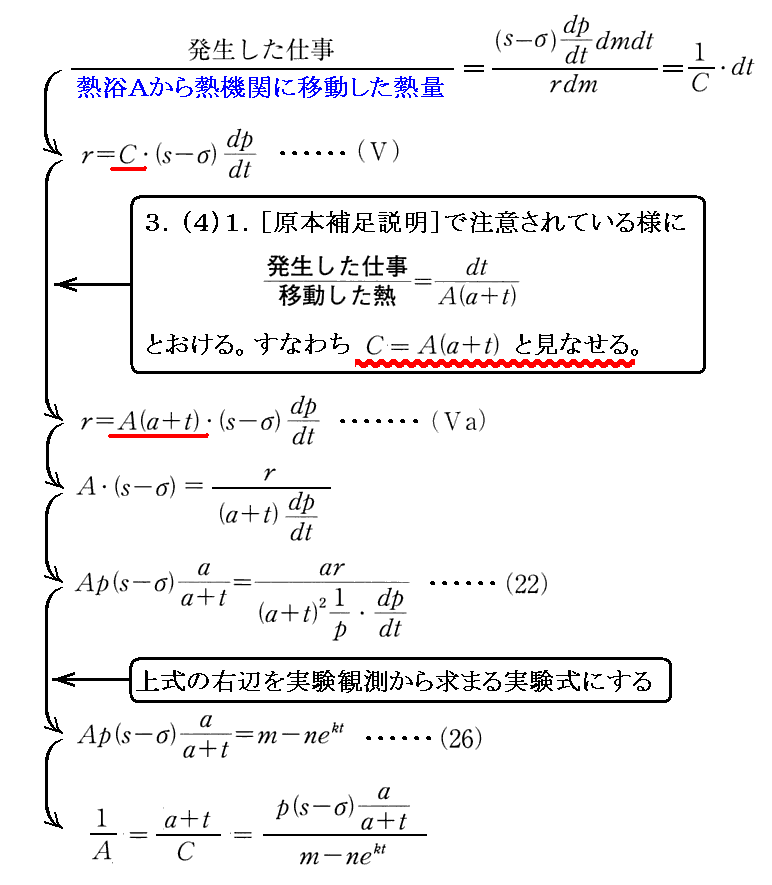
ここで、最後の(26)式は、(Ⅴa)式を水蒸気に当てはめた場合の実験観測による実験式です。(26)式の右辺は、(22)式の右辺で与えられる関数ですが、それを実測して見ると(26)式右辺の形で旨く表されるということです。
m,n,kは実験式に最も合うように観測値から決められた値で(26a)式で与えられる数値です。
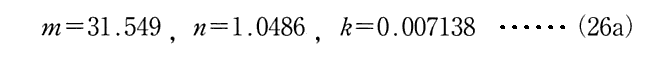
[補足説明2]
更に補足しますと、論文の最後でClausiusが“カルノーの原理”の直接の結果である“クラウジウス=クラペイロンの式”から“熱の仕事当量”を導いて見せたことは重要です。
2.(4)2.[補足説明2]でも注意したように、JouleやThomsonは、“エネルギー保存則”から導かれる
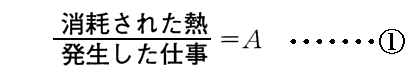
と、“カルノーの原理”から導かれる

の齟齬に苦しんでいたのですが、Clausiusは②式と同等の“クラウジウス=クラペイロンの式”から熱の仕事当量を導いて、②式が①式と全く矛盾するものでは無く並立する事を示しているのです。
要するに、すべての混乱の元は、温度の定義が不明瞭な所から生じています。①式の消耗された《熱》を《時間》、《距離》、《質量》、それと《電気量》の次元を組み合わせて得られる《エネルギー(J)》で表す事ができれば、①式は単にエネルギー保存則を表しているにすぎません。
ところが①式において熱の量を表すのにcalなる単位を用いなければ成らず、その1calとは1グラムの水の温度を1℃上昇させる熱量だと定義します。そのとき温度の単位である1℃は温度を測定する物体と熱平衡状態にある液体温度計や気体温度計の体積膨張率で定めているのです。つまり、温度という物理量はその実体が何か分けの解らないものです。
一方②式においても右辺は、①式で用いたのと同じ定義の実用温度t(℃)の関数であるカルノー関数C(t)としています。①式と②式が同じ温度の定義t(分けのわからない定義ですが)を用いてることが混乱の元なのです。
考えてもみて下さい。“エネルギー保存則”を意味する①式は

と等価でして、熱というエネルギー形態と仕事(力学的エネルギー)というエネルギー形態を加えたものは一定であるということを言っているにすぎません。だからもし、“熱”というエネルギー形態が、最初から《時間》、《距離》、《質量》、それと《電気量》を組み合わせたエネルギーの単位で表す事ができれば、上記“エネルギー保存則”を表す③式or①式の中には“温度“の概念などどこにも必要ないのです。
所が、最初に熱エネルギーを《時間》、《距離》、《質量》、それと《電気量》の次元の量でどの様に表したら良いか解らなかったので、仕方なしに、液体や気体の膨張率でもって実用温度t℃の定義をして、水1gの温度を1℃あげる熱量を1calとするという単位でエネルギーを測ることにしたのです。そして③式を①式の様に読み替えて、1calのエネルギーが何Jに相当するかを決めることにしたのです。
そのとき、②式には最初から温度の概念が本質的に絡んでいます。Thomsonが見破った様に、②式のdt/Cは“温度”の定義そのものです。
ただし、温度は《時間》、《距離》、《質量》、それと《電気量》とは全く異なる次元を持った新しい物理量ですから、それを定義する②式の左辺の分母と分子の次元が異なっていてそれを割り算した値が、《時間》、《距離》、《質量》、それと《電気量》の組み合わせでできる次元を持った量では困ります。
その為②式左辺の分母の“移動した熱量”の単位calを分子の“発生した仕事”の単位Jと同じにして、左辺の次元を消しておかなければなりません。つまり無次元の単なる数値にしなければならないのです。②式右辺のdtとCはどちらも新しい温度の次元を持つとすれば分母分子の割り算で右辺は単なる数値になるのですからです。
つまり、③式or①式の“エネルギー保存則”は②式の分母のcalをJに変換するために必要なだけです。そこに必要なだけなのですが、①式が存在しないとそもそも②式の温度の定義が成り立ちません。①式と②式が関係するはそこの所だけで、両者はもともと独立な法則で互いに並立するものです。
すなわち、『ClausiusやThomsonによる「熱力学」の【開闢】とは、カルノーの原理②式でもつて新たな物理量《温度》を定義・導入すること』です。その温度の定義とは、二つの温度の熱浴の間で可逆機関を働かせて②式で表される仕事の“効率”を求め、その値でもって、二つの熱浴の《温度という物理量》の値比を定めるというものです。値比さえ決まれば、適当な熱浴の温度を適当に決める(今日では、水の三重点の温度を273.16Kとしている)ことで、あらゆる熱浴の温度が決定できます。
絶対温度の概念がまだ確定していない1850年段階の本論文から読み取るのは難しいですが、3.(3)でClausiusが説明しようとしているのはその事です。その節の最後の表1で取り上げて説明しているクラペイロンとトムソンのC値比の実測値こそ、1列目の摂氏温度t℃が絶対温度で何度に相当するかを対応付ける絶対温度の数値比なのですから。
その祭、“効率”を定める為には②式の分子《仕事》と分母《熱》の次元を同じにして比較する必要がありますが、それをするのが①式です。そのとき①式で《消耗された熱》の cal を J に対応付ける為に用いる“実用温度”tはどの様に定めたものであってもかまいません。②式で効率を求める為に分母の《移動した熱量》の cal を J に対応付けるのに、同じものを用いておけば良いだけです。その様にして止めたdt/Cは、その過程で用いた“実用温度計”tの特性に影響される事は全くありませんので。
いずれにしても、①式によって②式の分母《熱量》の単位calを分子《仕事》の単位Jに変換すれば無次元の“効率”が確定しますので新たな次元を持つ量としての《温度》の定義も確定します。3.(5)3.末尾のClausiusの言葉はこのことを言っています。また、3.(6)末尾に引用したMaxwellの言葉もこのことを言っています。
このようにして、“《温度》という全く新しい次元を持つ物理量を厳密かつ完璧に物理学に導入することができた”のです。
3.ジュールの測定結果との比較







[補足説明1]
上記で引用されているJoule論文に対して付けられているClausiusの註)について補足します。
Jouleの測定結果の数値に付けられている註)は[1864年の補足の註]では無くて、1850年の原論文に付けられている註)です。だから、Jouleの測定値はすべて1850年以前の論文からのものです。
上記の XXXV,p.534 の論文は、その下に追記しているJuoleの1850年論文の要約です。この要約は1849年のPhil. Mag.の年度末付録号に載っているもので、おそらくClausiusは、本論文を書いた時点では、まだ正式な印刷版(Philosophical Transactions 1850年)を手に入れていなかったのでしょう。
その註)の下に、各論文の題目と、Jouleの論文集[The Scientyfic Papers of James Prescott Joule, Vol,1 (London)]に掲載されているページ数[論文集を表すSPJ,の次に記されている数字]を、私どもが追記しています。ジュールの科学論文集はNetからpdfファイルとして無料でダウンロードできますから、それでご確認下さい。
なお、山本文献3.第23章Ⅲ〜Ⅶで、Juoleの業績が解りやすく解説されています。別稿で引用しておきますのでどうぞ御覧下さい。
(6)FNの後書き
私どもが「熱力学」を学び始めたとき最も面食らったのは、《温度とは何なのか?》、《エントロピーとは何なのか?》という所です。おそらく多くの人が思い悩まれたのもこの点だと思います。
それで、この論文を読んで解ったことは、【「熱力学」と言う学問分野は《温度》という物理量と《エントロピー》と言う物理量を導入することと等価だ!! 】ということです。
このことは、 3.(1)[補足説明4]、 3.(3)[補足説明3]、 3.(4)1.[補足説明1]、 3.(5)2.[補足説明2] などを復習して頂ければ了解して頂けると思います。
Clausiusの1850年論文では、とかく 2.(3)3. や 3.(1) の部分のみが強調されますが、この論文の重要性は 2.(6) や 3.(2)、(3)、(4)、(5) の中にあると思います。この中で上記の事柄が繰り返し示唆されているのですから。ただし、その示唆を正しく見抜くのは極めて難しい。
考えてもみて下さい、「熱力学」以前に展開されていたあらゆる学問分野で取り扱う物理量は、《時間》、《距離》、《質量》、それと《電気量》の次元を組み合わせて表現できるものしかなかったのです。
《温度》の次元はそれらとは全く異なるものです。温度は時間、距離、質量、電気量の組み合わせで測れるようなものでは無いことは明らかです。絶対温度は熱力学第二法則(カルノーの原理)を用いた、とても奇妙で不思議な測り方で初めて測れる様な物理量です。しかもそれは、天下り的に定義した実用温度計との対応でしか測れない様な物理量です。本稿でも繰り返し説明されていることからも、絶対温度に対応させる元になった実用温度計の温度の定義こそ、温度の次元が全く新しい次元である事を示しています。
また、本稿ではまだ出てきていませんが《エントロピー》という物理量も、やがて解ってくる dS=d’Q/T の定義から解るようにエネルギーの次元を温度の次元で割った次元をもちますので、それまでの物理理論の中には存在しなかった次元をもつ物理量です。これも、やがて解りますが、可逆変化を用いた不思議な測り方でないとその変化量が測定できない様な量です。
要するに、「熱力学」は、《温度》と《エントロピー》という全く新しい次元をもつ物理量の存在を発見することができなければ説明できない現象・領域を取り扱う学問だったのです。おそらく、その事を明確に認識し、理解していたのはMax Planckでしょう。実際、彼だからこそ自然単位の概念を提示することができたのだと思います。
この1850年論文にはエントロピーはまだ現れていませんが、そのエントロピーと密接に関係する熱量に関係したd’Q/Tは、そこかしこに現れています。事実Clausiusは、この1850年論文に続く1854年論文でTがd’Qを完全微分にする積分因子(積分分母)である事をハッキリと認識します。これは1854年論文の最後の部分[2.(5)]に書かれています。
いずれにしましても、世の中のすべての現象を説明するには、この二つの全く新しい次元をもつ量が必要である事は、プランクの“熱輻射法則”の導出法や、ボルツマンの“シュテファン・ボルツマンの法則”の導出法を思い出されればお解りでしょう。
私は、光(つまり電磁場)の理論である熱輻射の公式に何故絶対温度という量が絡んでくるのかとても不思議でした。またプランクが、その公式を見つけることができたのはエントロピーの概念を輻射場に適応しての事だという事の意味が良く解らなかったのです。しかし、この二つの物理量《温度》と《エントロピー》の存在が発見された過程を理解したことで、その疑問も解けた様に思います。
J.C.Maxwellは1878年に次の様に言っている。
『この1850年論文によってはじめて、熱力学は確実な基礎と明確な定義と確定的な境界を有する一個の科学となったのである。』(山本文献3.第26章末尾参照)
さすが天才Maxwellですね。彼は「熱力学」の本質を完璧に理解していたようです。
4.付録(論文集 1864年の追記)
付録A. 消耗された熱に対して2.(3)3.の(3)式で与えられた表示の完全な導き方






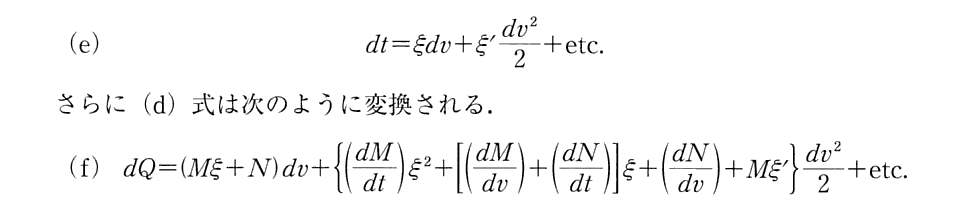
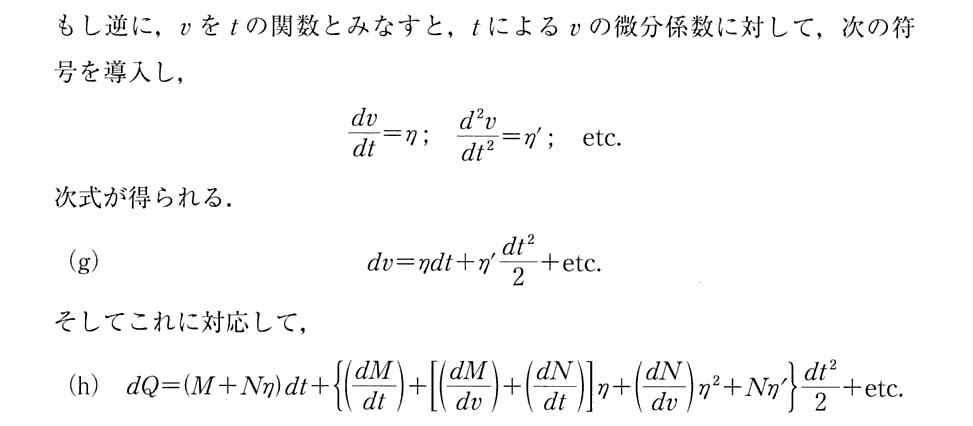











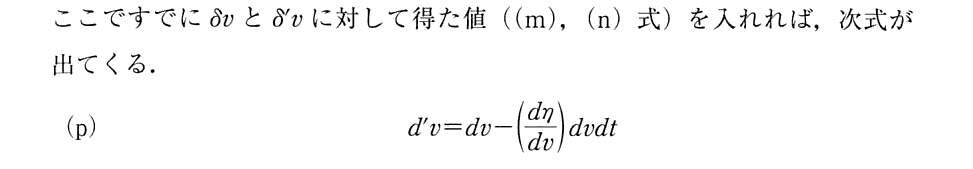


[補足説明]
ここは説明は非常に解りにくく、何が言いたいのか良く解らないかもしれません。
今日的な説明をすると、系に出入りする“熱量”は“状態量”では無いので dv と dt の変化に伴って出入りする熱量の変分dQは“完全微分”にはなり得ず、
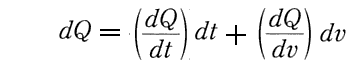
に於いて
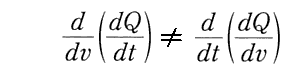
となる。つまり熱量の変分は、dv と dt の変化の順番に依存する。そのために2.(3) 3.[補足説明2]の(3)式が
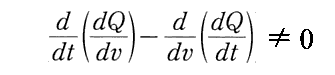
となってゼロにはならないことを言っている。
その為、熱機関が1サイクル実行されたときに、系に出入りした熱量の積算値はゼロにならず、正味の“消耗された熱量”というものが存在すると言うことです。それを表すのが(3)式です。
別稿「絶対微分とは何か(積分因子とは何か)」5.を復習されて下さい。
付録B. 2.(3)3.の(Ⅱ)式から(Ⅱa)式を導く事






上記の部分を補足すると
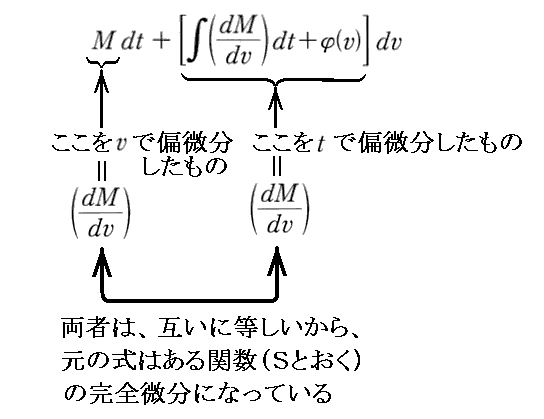
ということです。
ここで今日エントロピーの記号として用いられている S を使っているので混乱させられるが、以下で述べている様に dU の事なのだから、最初からdSでは無く dU’ とでもおいた方が良い。dSは、いずれにしても完全微分となる “内部エネルギー”の変分 dU を表している。



[補足説明1]
上記で用いた式変形の意味は解りにくいので補足説明します。
ここで用いた式変形は別稿「『熱力学』とは何か」7.(2)で証明した【定理】
の【必要条件である事の証明】に用いた式変形
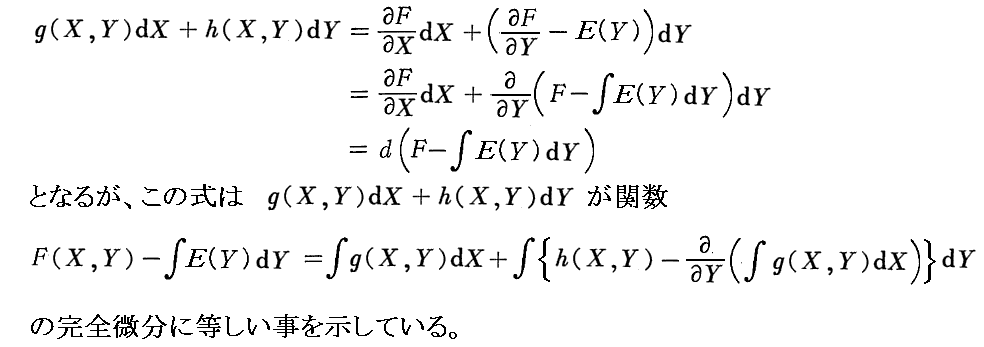
と同じです。このことは上記の引用元を復習して下さい。この式変形は、別稿「絶対温度とは何か(積分因子とは何か)」5.(2)1.でも説明したことです。Clausiusがこの数学的証明法を知っていて利用したのか、数学者が後にこの式変形を利用して証明したのかは解りませんが、この式変形には本質的な重要性があります。
いずれにしても、ここの付録Bは【上記で引用した定理】を言い換えたものと言えます。このことは、Clausiusが1864年に論文集出版する時に、わざわざ注2)と付録Bを追記することになった元々の理由である 2.(3).3.[補足説明6] と [補足説明7] の説明を振り返られて下さい。


付録C. 3.(4)3.で説明した『飽和水蒸気の密度』についての補足





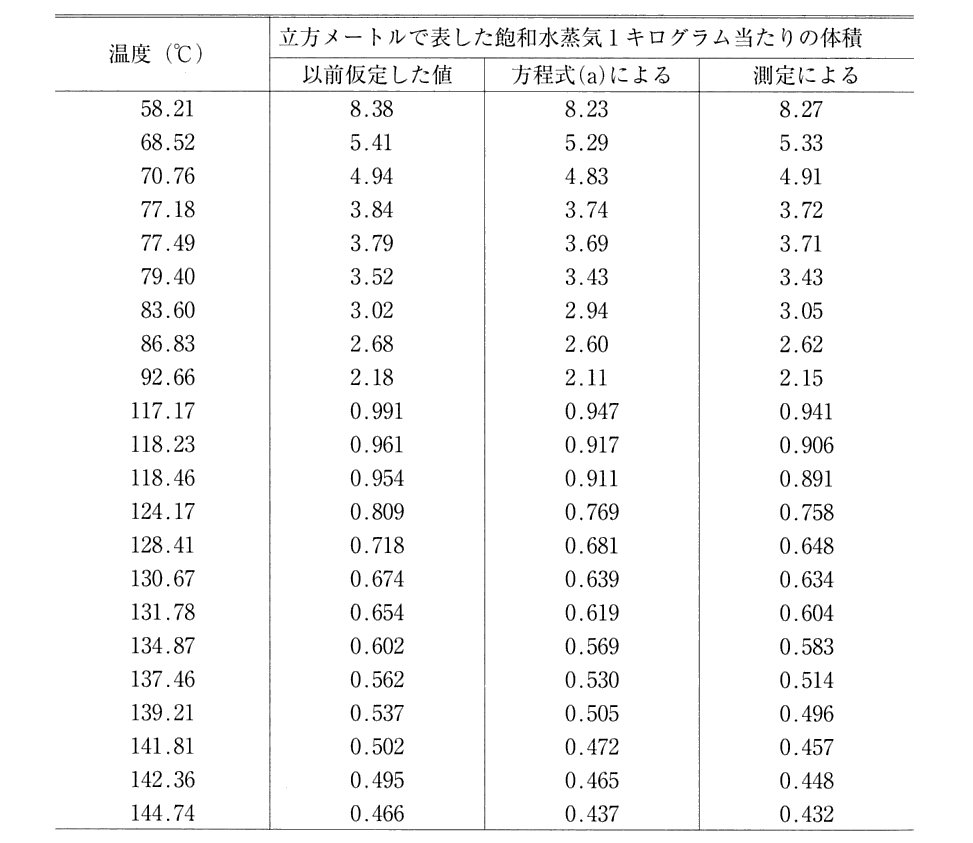



5.参考文献
- サヂ・カルノー著、広重徹訳解説「カルノー・熱機関の研究」みすず書房(1973年刊)
この中に、カルノーの大論文『火の動力、および、この動力を発生させるに適した機関についての考察』(1824年)の翻訳がp39〜90に収録されています。ただし、この論文をお読みになっても理解するのは難しいです。実際、超難解なために、当時の一流の科学者からも引用される事は無く歴史の中に埋もれてしまいます。
この論文を世に知らしめたのはクラペイロンとトムソンですが、実際のところ、天才的に頭の良かったW.Thomsonでさえも理解するのに手こずります。Thomsonは(カルノーサイクルを含めて)カルノーの理論の中に、熱の本質を解明する何かがあると感じていましたが、その何かが解らなくて悩み苦しみます。その解答を与えたのが、Clausiusの1850年の熱力学第1論文(本稿論文)です。
補足しますと、この訳本にはカルノーがその後に書き溜めた『数学、物理学その他に付いての覚え書き』(p91〜110)と、弟のイッポリート・カルノーが書いたサヂの伝記『サヂ・カルノーの生涯』(p111〜126)も収録されています。
- 八木江里監訳「エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)
本稿の訳文はこれから引用した
Clausiusの熱力学第1論文(1850年)「熱の動力、および熱学へ演繹される諸法則について」 です。これ以外に
Clausiusの熱力学1854年論文「力学的熱理論の第2主法則の修正された形について」
Clausiusの熱力学1865年論文「力学的熱理論の主法則を適用するためのさまざまな便利な形式について」
等々を別ページで引用しています。
- 山本義隆著「熱学思想の史的展開」筑摩書房(2009年刊)
第19〜31章をご覧下さい。この中の 第19章Ⅱ〜Ⅲ、Ⅳ、 第20章Ⅰ〜Ⅱ、Ⅲ〜Ⅴ、 第21章Ⅴ、 第22章Ⅴ、 第23章Ⅲ〜Ⅶ、 第25章Ⅰ〜Ⅴ、 第26章Ⅰ〜Ⅱ、Ⅲ〜Ⅴ、 第28章Ⅰ〜Ⅵ、 第29章Ⅰ〜Ⅷ、 第30章Ⅰ〜Ⅵ は別稿で引用しています。その際、別稿で引用している【補註・参考文献一覧】を別ウインドウで開かれて参照しながらお読み下さい。