このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
混合気体について“ドルトンの分圧の法則”というのがでてきます。しかし、最初に習うときにその意味が良くわかりません。そこの所を説明します。
ドルトンの法則(Dalton law)又は分圧の法則(law of partial pressure)ともいう。これはもともと、
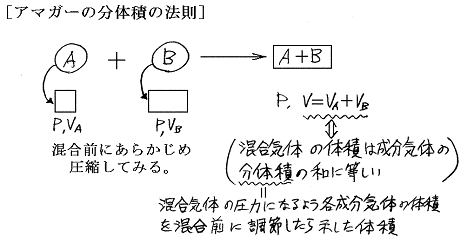
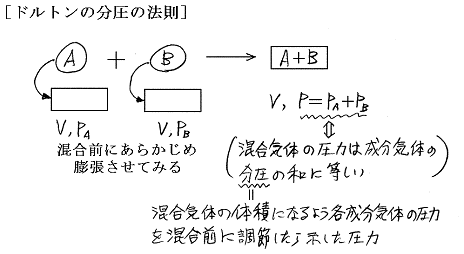
定温定圧の条件で数種の理想気体を混合して1つの混合気体をつくるとき、混合気体の占める体積は混合前に各気体が占めていた体積の和に等しく、また混合気体の圧力(全圧)は各気体の分圧の和に等しい
という関係を表わしたものであり、この関係を満たすものを“理想混合気体”という。この法則の前半部は[アマガーの分体積の法則]と言われることがある。以下、混乱を避けるために分体積と分圧に対する法則をわけて考える。
これらは経験事実から導かれた法則であり、その正しさが証明されるとかしないとか言う性質のものではない。

ここで分体積も分圧も二つの気体を混合する前に、あらかじめ測っておいたものであることに注意しなければならない。“分体積”とは、混合後の圧力になるように各成分気体の圧力を混合する前に調節してみたとき、各気体が示した体積である。気体を混合してしまったら各気体が示すそのようなものは測りようがない。
“分圧”についても同様である。混合後の体積に、混合前に各気体をふくらましてみるのである。そのとき示した圧力が各成分気体の分圧と言われるものです。
そのとき分体積の和が(圧力共通の)混合後の体積にになるとか、分圧の和が(体積共通の)混合後の圧力になるとかはまったく保証されない。例えば液体の場合、10mlの水と10mlのエチルアルコールを混合すると、混合後の体積は19.3mlとなり、決して20mlとはならない。混合した2種の物質間の相互作用のために、一般には混合前体積の和にはならない。そのどうなるか解らないところが、普通の気体が普通の状態にあるときは、ほぼ成り立つというのがこれらの法則の意味です。厳密に言えば少しずれがあるのだが、そのずれが無視できるような気体を理想気体と言う。つまり理想気体の場合、異種の気体を混合してもそれらの間には特別な相互作用は無いと言うことです。
[アマガーの分体積の法則]と[ドルトンの分圧の法則]は等価です。
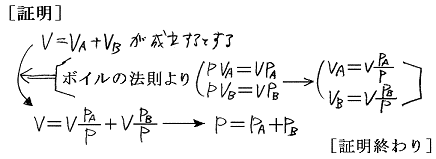
以下で分圧、分体積、モル数比に関係した重要な定理を証明する。ただし[ボイルの法則]、[ボイル・シャルルの法則]、[アボガドロの法則]、[理想気体の状態方程式]は既知であるとする。
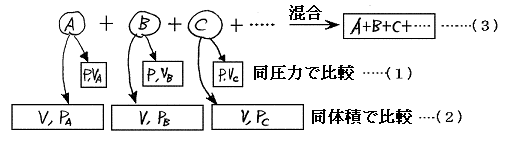
混合気体の[分圧の比]は[分体積の比]に等しく、さらに[モル数(分子数)の比]に等しい。
言うまでもないことだが[分圧の比]とは混合前の各成分気体を同温度・同体積で比較したときの圧力比であり、[分体積比]とは混合前の各成分気体を同温度・同圧力のもとで比較したときの体積比である。また[モル数の比]とは含まれる成分気体の分子数の比である。
さらに注意すべきは、この定理には[分圧]とか[分体積]という言葉が含まれているが、証明には[アマガーの分体積の法則]も[ドルトンの分圧の法則]も使われていないことです。それは[分圧]も[分体積]も以下に示す別々の独立した気体についての(1)と(2)の状態間での比較で(3)の混合状態は関係していないからです。

ところで、[ボイル・シャルルの法則]と[アボガドロの法則]は全く独立に成り立つ別の法則であり、その両者を一緒にして導かれたものが[理想気体の状態方程式]であることは高校で習う。以下はそれを用いた証明です。
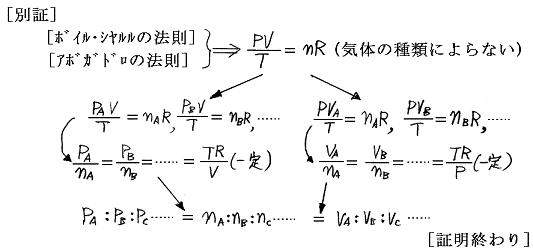
理想混合気体とは[ドルトンの分圧の法則]を満足する気体のことです。
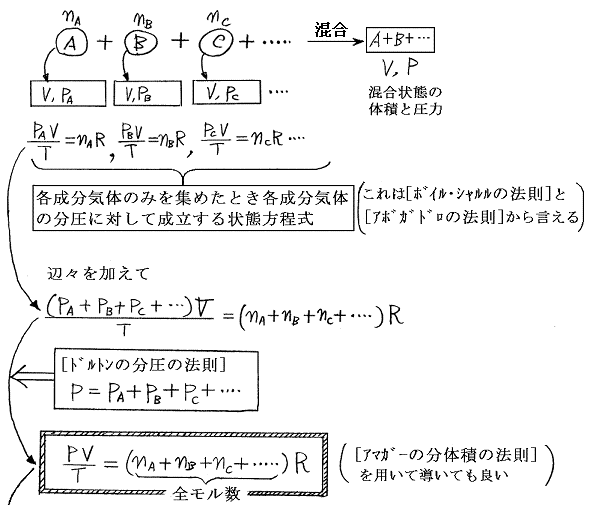
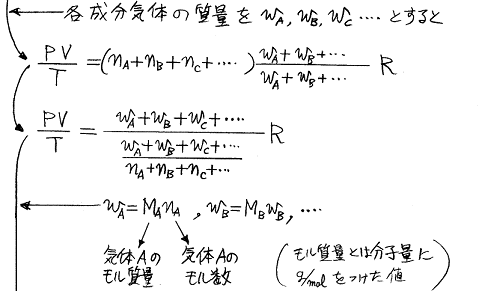
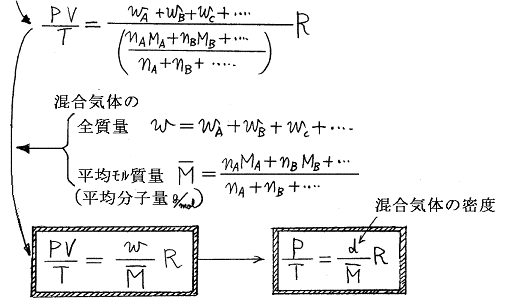
[補足説明1]
[アボガドロの法則]と[ボイル・シャルルの法則]と[ドルトンの分圧の法則]はまったく別の独立した法則です。それらの間の関係は下図のようになる。
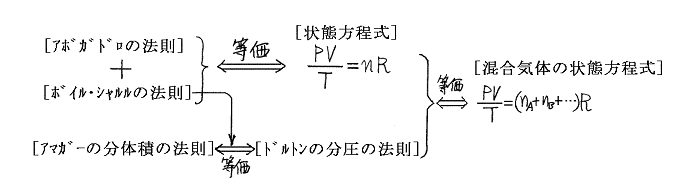
[補足説明2]
空気の“平均モル質量”(平均分子量に g/mol を付けたもの)を求めてみる。
