Clausiusの熱力学1865年論文「力学的熱理論の主法則を適用するためのさまざまな便利な形式について」
ここで紹介するものは、Rudolf Julius Emmanuel Clausius(1822~1888)著「力学的熱理論の主法則を適用するためのさまざまな便利な形式について」(1865)

の翻訳版で、八木江里監訳「エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)からの引用です。
ただし、解りやすくする為に、私どもが、適当に章、節、項に分け、式変形を(矢印記入場所に)追記し、さらに(灰色囲み記事の)補足説明、等々・・・を付け加え、また文章の改行、段落分けに関してもかなり改変しています。そのため元の表現は別稿で引用している原本でご確認下さい。
この論文は、Clausiusが最終的にエントロピーという状態量を導入・定義して、その状態量を“エントロピー”と名付けた超有名な論文なのですが、Clausiusの説明は極めて抽象的・難解で、何が言いたいのか良く解らないところも多々あります。私にとって解りやすくしようと思って当ページを作り始めたのですが、それを十分達成できたとは言えず申し訳ありません。読者の方でそれぞれ理解に努められて下さい。
補足しますと、Clausiusは熱力学に関係した考察をまとめた著書『Die Mechanische Wa¨rmetheorie』を1876年に出版しています。こちらを参照しながらご覧頂くと理解できるかも知れません。Max Planck も若い頃この著書を読むことで熱力学第二法則を正しく理解することができたと言っています。
0.導入


1.熱力学の2つの法則
(1)“熱力学第1法則”と“熱力学第2法則”








(2)“可逆変化”と“状態量”









(3)状態変数と完全微分性





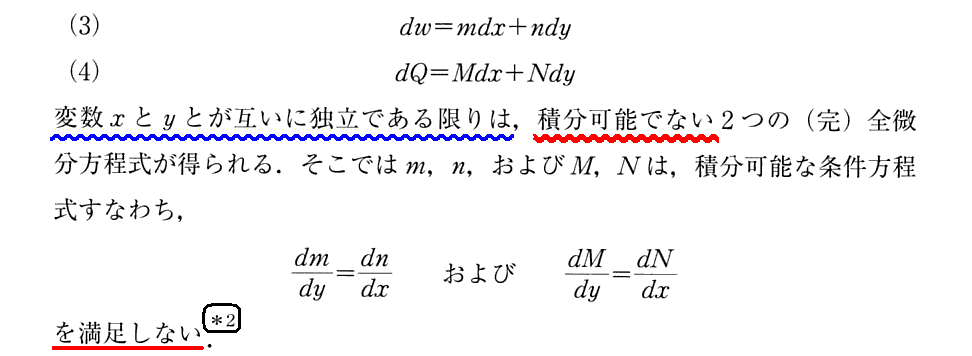

上記*2)の第Ⅰ論文の付録A,Bに付いては別稿で引用しています。

2.法則の解析的表現
(4)“第1法則”と“第2法則”の解析的表現
[補足説明]
dUの全微分表現 と (3)式dw,(4)式dQ の全微分表現が違うのは何故か解りにくい所です。Clausiusの1850年論文2.(3)3.を復習されて下さい。あるいは別稿「絶対微分とは何か(積分因子とは何か)」5.を復習されて下さい。
1.第1法則



2.第2法則



3.更なる別表現




[補足説明1]
上記(8)式は、作業物質が永久気体(理想気体)の場合で求めた1850年論文2.(3)3.の(Ⅱ)式を一般化したものです。
同じく(9)式は、作業物質が永久気体(理想気体)の場合で求めた1850年論文3.(2)1.の(Ⅳ)式を一般化したものです。実際、(9)式を以下の(5)~(7)節の手順に従って変形して(14)式あるいは(23)第3式まで簡単化すると、(9)式は上記の(Ⅳ)式に完全に一致します。その際、(Ⅳ)式中のカルノー関数CはA・T=T/Jであった事を思い出して下さい。
この当たりの展開が何を意図しているのか解り難い方は、上記の(Ⅱ)式、(Ⅳ)式における議論を思い出しながらお読み下さい。そこの議論をより一般的に行っているだけです。

(5)独立変数の1つを温度Tとする場合



(6)外力が“圧力”の場合

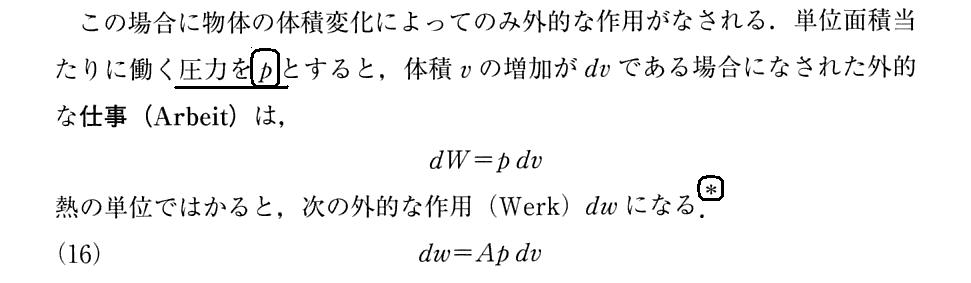

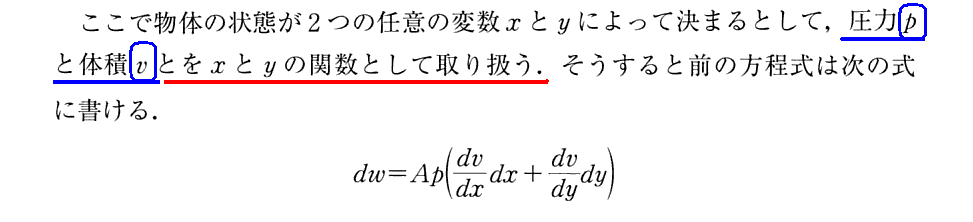

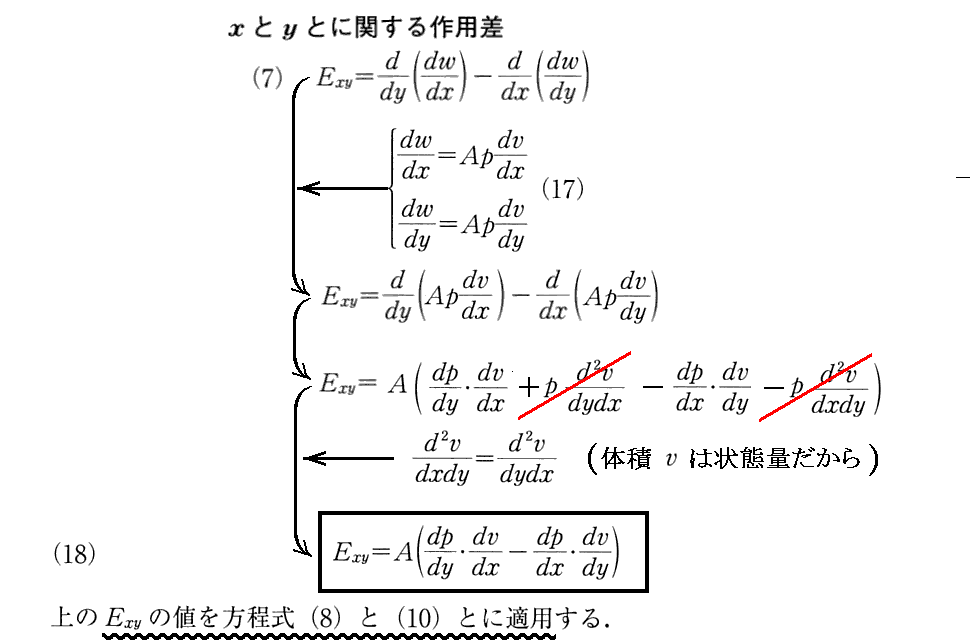
適用した結果はここには書かれていない。

適用した結果はここには書かれていない。

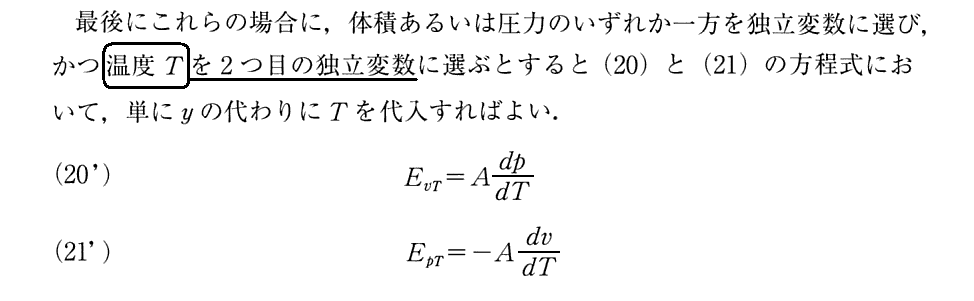
(7)外力が“圧力”で、独立変数を変更した場合


[補足説明]
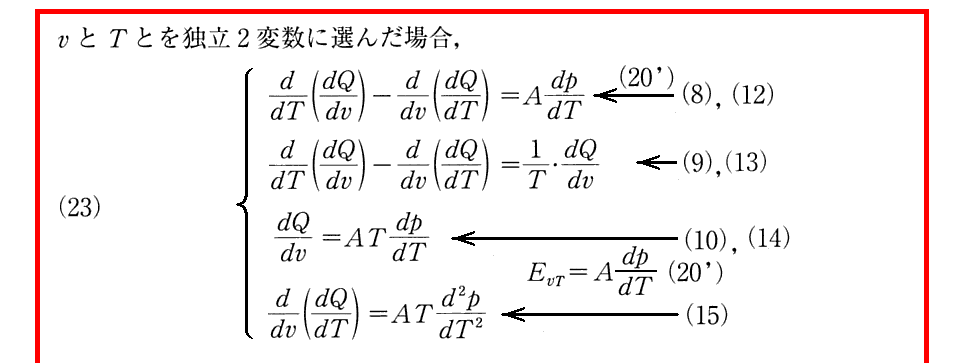
これらの式が何を意味するのは解り難いが、要するに、温度TとT+dTにおける等温的準静的可逆変化と温度TとT+dTとの間をつなぐ断熱的準静的可逆変化によって構成される閉じた微小サイクルにおいて、その微小サイクルの間に出入りする熱量と外界とやり取りされる仕事量との関係を示すものです。最初の式が、熱力学第1法則の解析的表現であり、二番目、三番目の式が熱力学第2法則の解析的表現です。
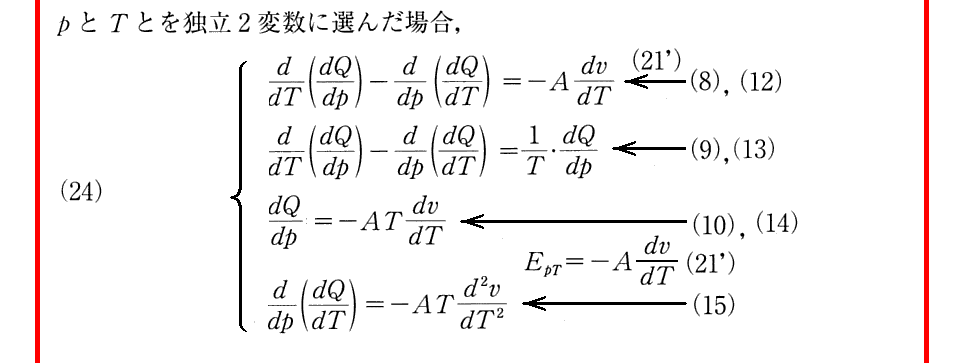
(23)の最初の式は別稿「Clausiusの熱力学第1論文(1850年)」2.(3)3.の(Ⅱ)式に他なりません。(24)、(25)の最初の式は、独立変数をpとT、あるいはvとpに変えた場合にどう表現されるかを示した式です。
同様に(23)の三番目の式は別稿「Clausiusの熱力学第1論文(1850年)」3.(2)1.の(Ⅳ)式に他なりません。
実際、(Ⅳ)式中のカルノー関数CはC=AT(A:熱の仕事当量の逆数、T:絶対温度)とおけるのでした。(24)、(25)の三番目の式は、独立変数をpとT、あるいはvとpに変えた場合にどう表現されるかを示した式です。
(23)の二番目の式の意味は解り難いが、2.(4)3.を振り返られれば解るように、熱力学第2法則を表す三番目の式は一番目と二番目の式から導かれたものでした。その二番目の式は2.(4)2.から解るように熱力学第2法則表す式でした。だから(23)の二番目の式は熱力学第2法則を表す式です。(24)、(25)の二番目の式は、独立変数をpとT、あるいはvとpに変えた場合にどう表現されるかを示した式です。
最後に(23)、(24)の四番目の式は、それぞれの一番目と三番目の式を変形すると得られる関係式ですが、いずれも熱力学第2法則を表す式と言って良いでしょう。。
3.解析的表現の更なる展開
(8)微分係数の物理的な意味と微分係数の間で成り立つ関係式








[補足説明]
これらの関係式に付いては別稿「絶対温度とは何か(積分因子とは何か)」3.(2)4.を復習されたし。
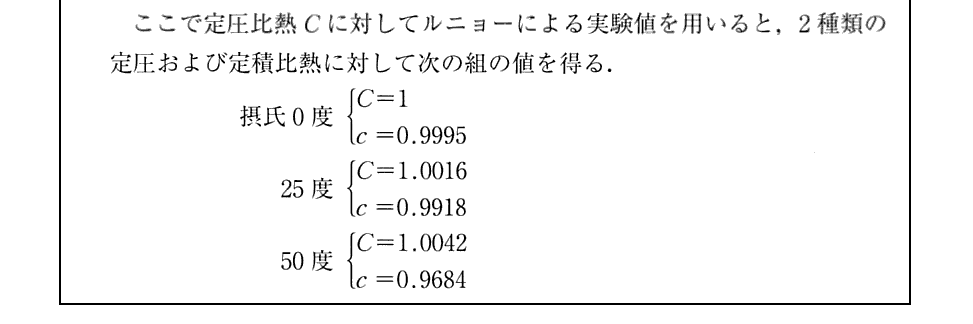
(9)定積比熱と定圧比熱

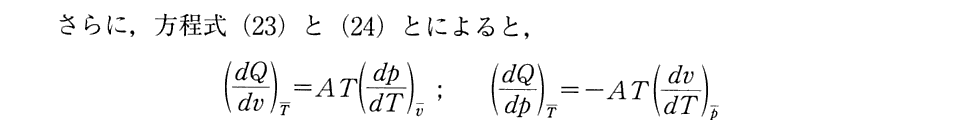







上記第1論文(1850年)のpp.43-44とは別稿「Clausiusの1850年論文}3.(5)1.の事です。





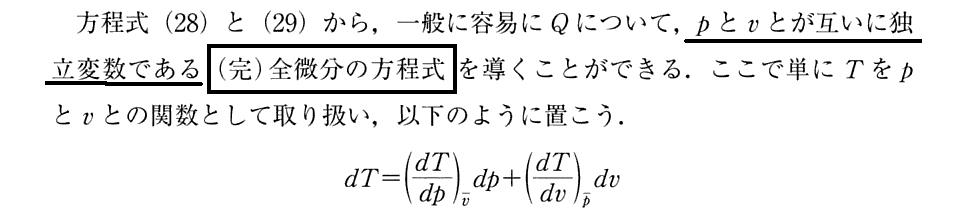

[補足説明]
これらの関係式に付いては別稿「絶対温度とは何か(積分因子とは何か)」の3.(2)4.と、4.(2)を復習されたし。もちろん、後の教科書の記述が、ここのClausiusの説明を利用しているのですが。
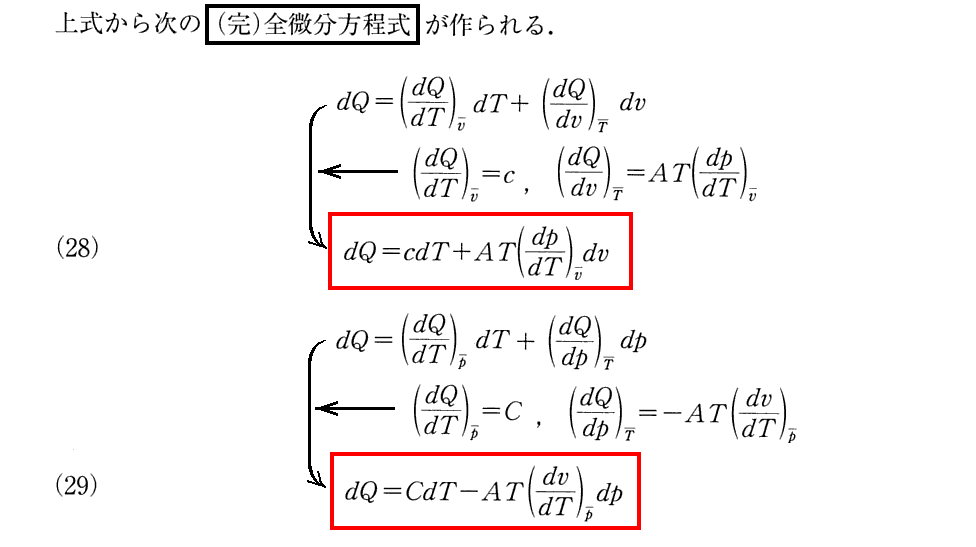
(10)dQは完全微分ではない


[補足説明]
上記(33)式の導き方がわかりません。?

となるべきであるが、先ほどの(33)式はこれらを満たしていない。よって、方程式(28)と(29)は積分可能ではない。



上記の第Ⅰ論文(1850)の導入部は別稿をご覧下さい。

要するに、“準静的可逆断熱変化”を考察すると言うこと。


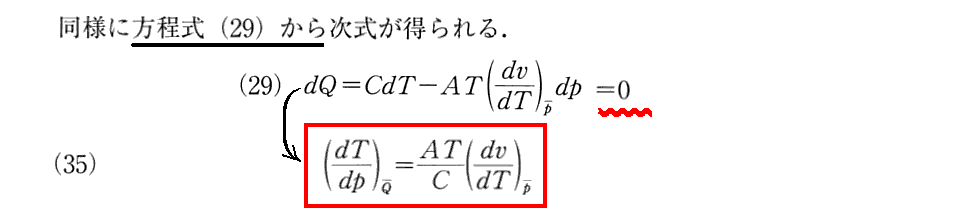
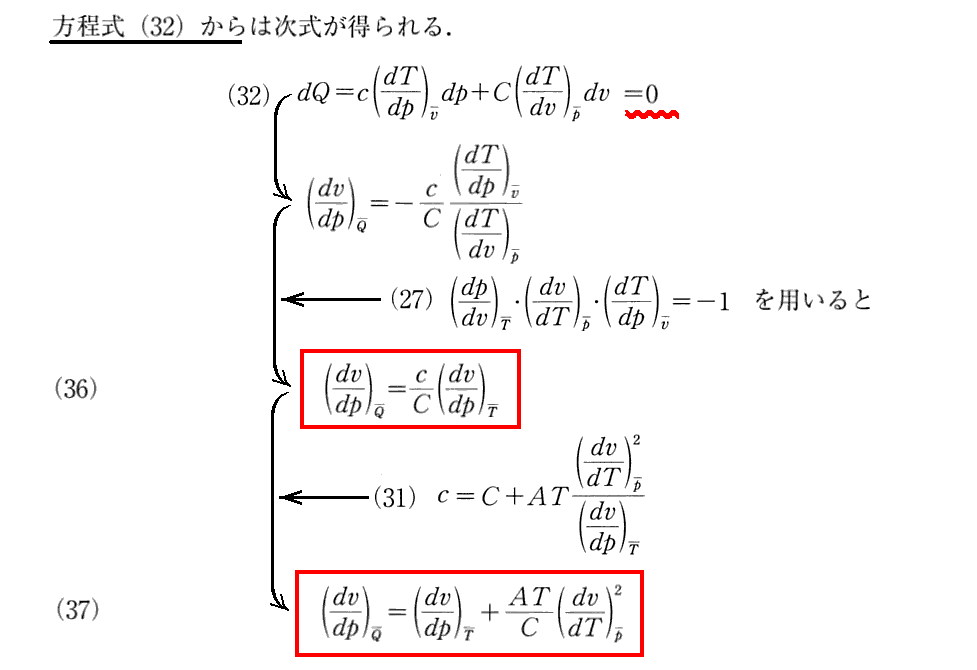
(11)完全気体の場合




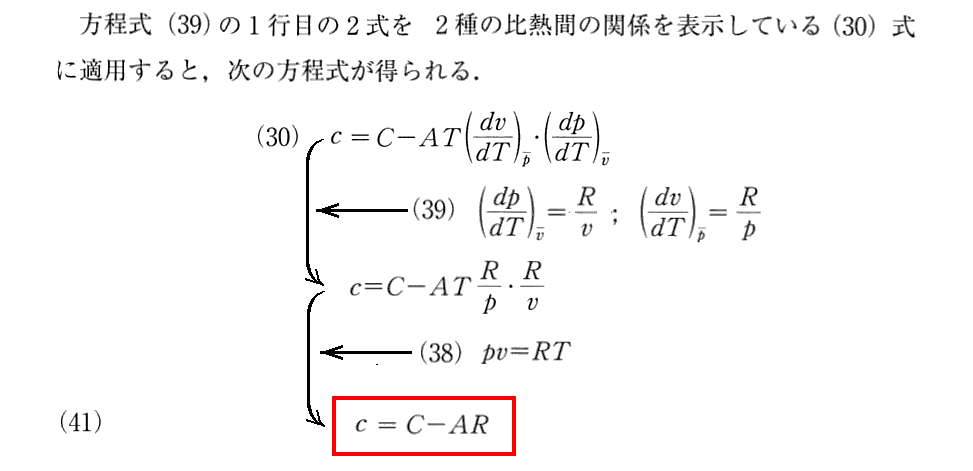


4.凝集状態を含む現象
(12)凝集状態を含む場合






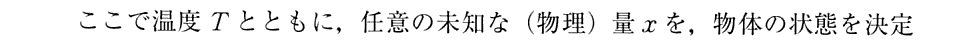
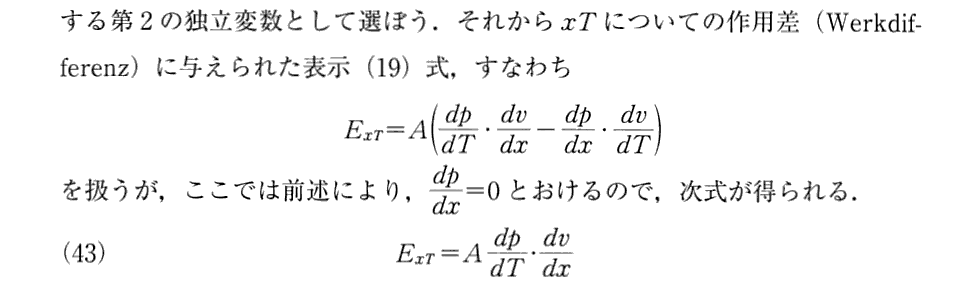
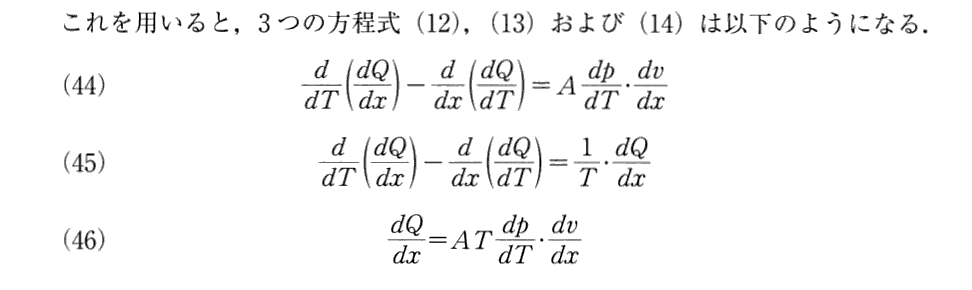
(13)方程式の導出


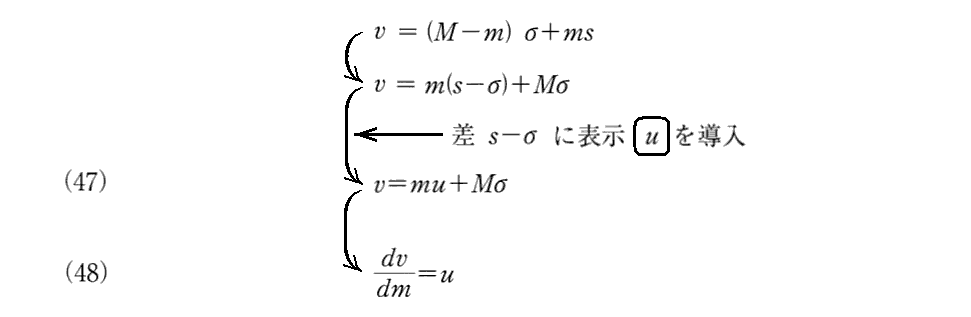



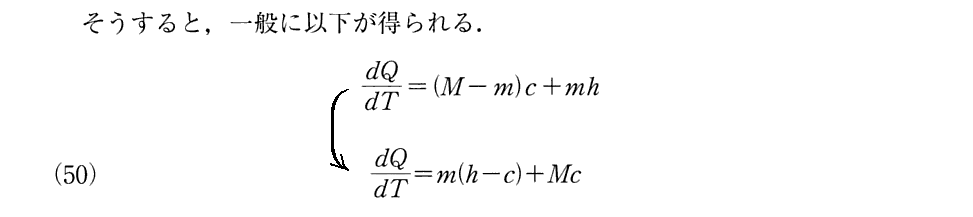

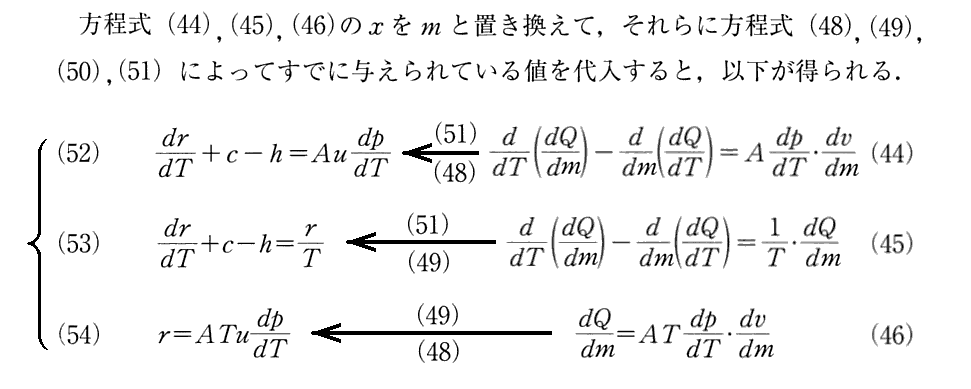

上記でClausiusが1850年論文ですでに導いていると言っている、(54)式に対応する(Ⅴ)式はこちらを参照。そこの(Ⅴ)式の カルノー関数Cが A・T であり (s-σ) が u に対応します。







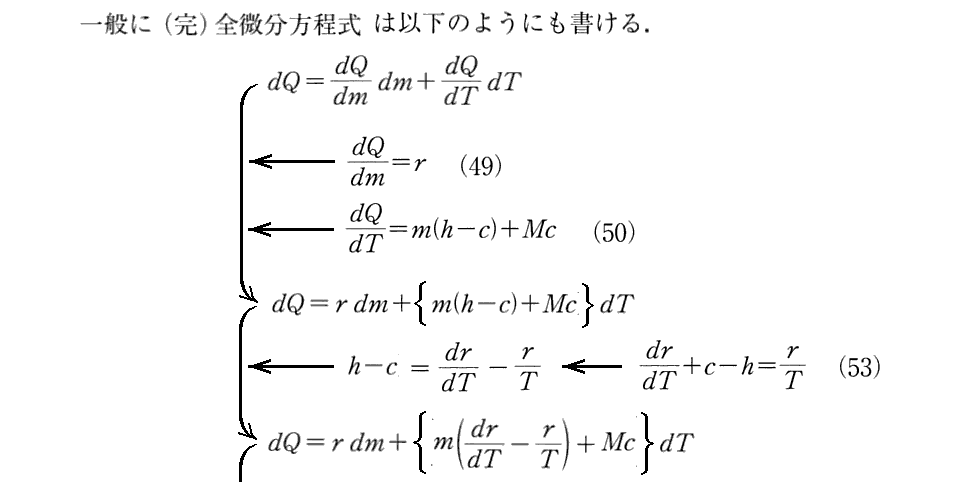
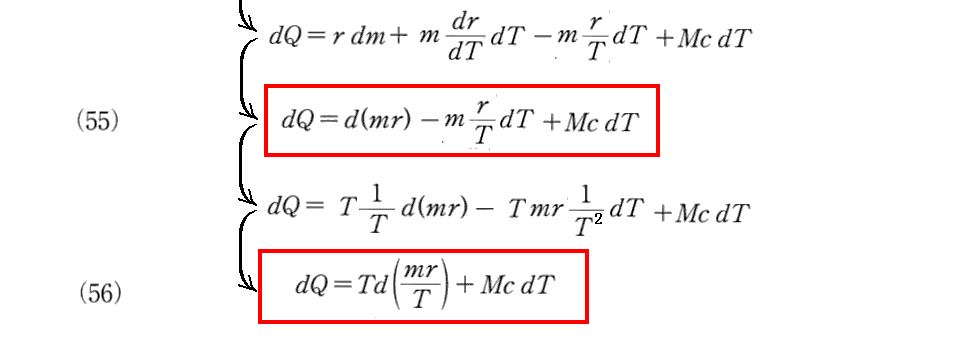

上記のClausiusの第Ⅰ論文(1850年)のpp.33-40とはこちらを参照。
5.不可逆変化
(14)エントロピーの導入・定義







上記の文節は超有名なところですので、山本氏の訳文も下記に引用しておきます。

ここの説明の意味については、別稿「『熱力学』とは何か」2.(1)をご覧下さい。すなわち、 dq/T≡dS が“状態量”となる ことを言っています。

上記のClausiusの1862年論文の山本氏による概説はこちらを参照。










ここも有名な所なので、山本氏の訳文も下記に引用しておきます。


(15)エネルギーとエントロピー決定の具体例





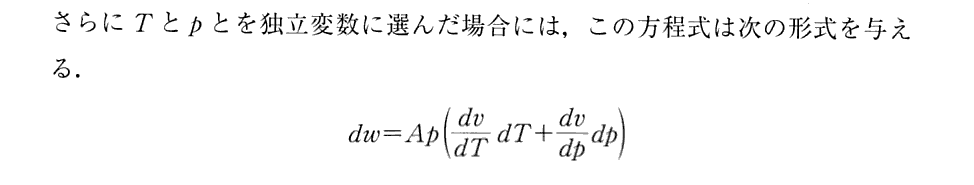
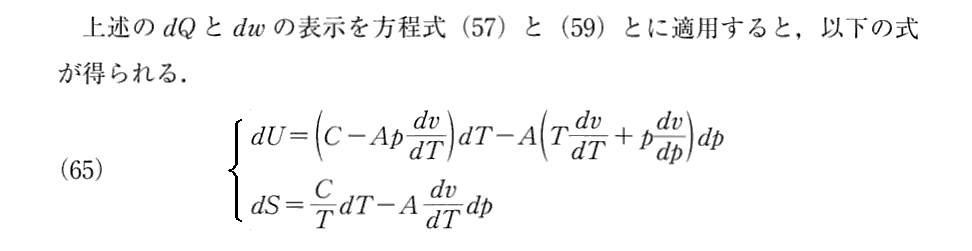


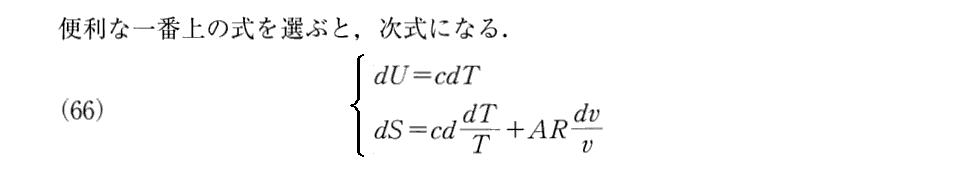






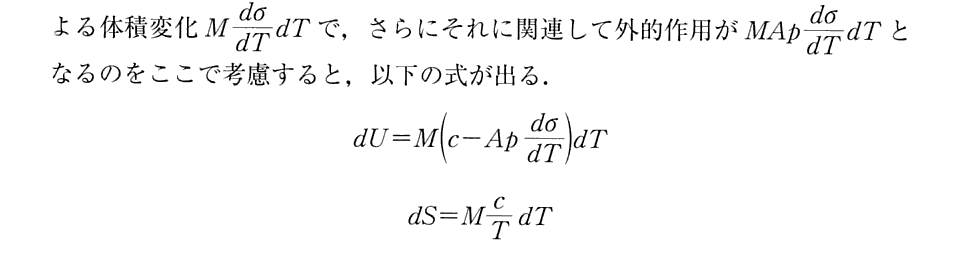


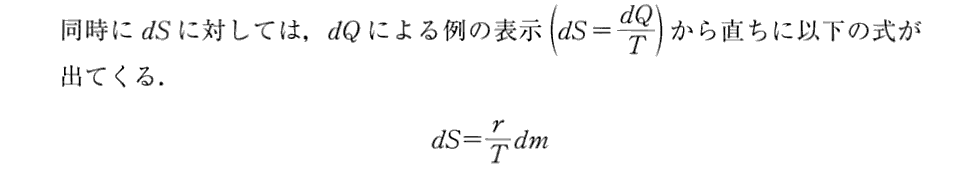


(16)非可逆過程に対する方程式

下記で用いている第1主法則(Ⅰa)と、方程式(58)。
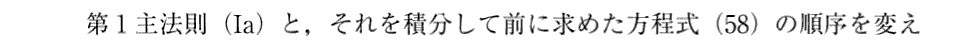
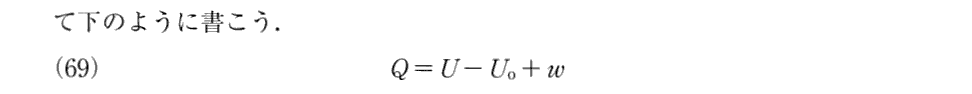




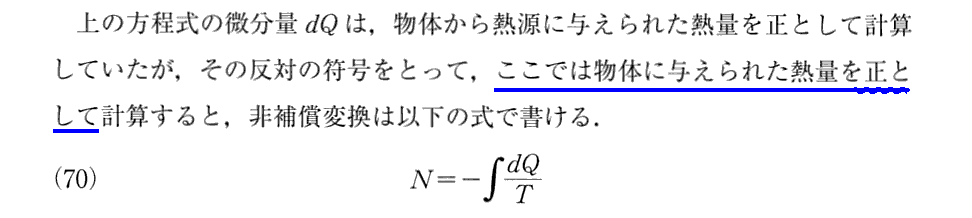



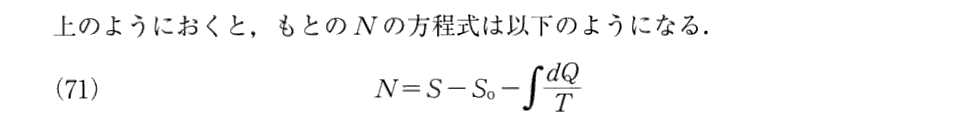

(17)宇宙のエネルギーとエントロピー






上記青下線のエントロピーを構成する2つの部分とは§14の最後の部分を参照されたし。
また上記赤波下線部分に付いては、Clausiusは熱輻射に対して、温度を定義しエントロピーを導入できる事を予言している様に見える。つまり熱輻射場も熱力学理論の守備領域だと言っている。これはやがて、ボルツマンやプランクによって発展させられる事柄ですが、上記の文がその事を予見しているのなら、恐るべき先見性と言えます。





6.参考文献
- サヂ・カルノー著、広重徹訳解説「カルノー・熱機関の研究」みすず書房(1973年刊)
この中に、カルノーの大論文『火の動力、および、この動力を発生させるに適した機関についての考察』(1824年)の翻訳がp39~90に収録されています。ただし、この論文をお読みになっても理解するのは難しいです。実際、超難解なために、当時の一流の科学者からも引用される事は無く歴史の中に埋もれてしまいます。
この論文を世に知らしめたのはクラペイロンとトムソンですが、実際のところ、天才的に頭の良かったW.Thomsonでさえも理解するのに手こずります。Thomsonは(カルノーサイクルを含めて)カルノーの理論の中に、熱の本質を解明する何かがあると感じていましたが、その何かが解らなくて悩み苦しみます。その解答を与えたのが、Clausiusの1850年の熱力学第1論文(本稿論文)です。
補足しますと、この訳本にはカルノーがその後に書き溜めた『数学、物理学その他に付いての覚え書き』(p91~110)と、弟のイッポリート・カルノーが書いたサヂの伝記『サヂ・カルノーの生涯』(p111~126)も収録されています。
- 八木江里監訳「エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)
本稿の訳文はこれから引用した
Clausiusの熱力学1865年論文「力学的熱理論の主法則を適用するためのさまざまな便利な形式について」
です。これ以外に
Clausiusの熱力学第1論文(1850年)「熱の動力、および熱学へ演繹される諸法則について」
Clausiusの熱力学1854年論文「力学的熱理論の第2主法則の修正された形について」
等々を別ページで引用しています。
- 山本義隆著「熱学思想の史的展開」筑摩書房(2009年刊)
第19~31章をご覧下さい。この中の 第19章Ⅱ~Ⅲ、Ⅳ、 第20章Ⅰ~Ⅱ、Ⅲ~Ⅴ、 第21章Ⅴ、 第22章Ⅴ、 第23章Ⅲ~Ⅶ、 第25章Ⅰ~Ⅴ、 第26章Ⅰ~Ⅱ、Ⅲ~Ⅴ、 第28章Ⅰ~Ⅵ、 第29章Ⅰ~Ⅷ、 第30章Ⅰ~Ⅵ は別稿で引用しています。その際、別稿で引用している【補註・参考文献一覧】を別ウインドウで開かれて参照しながらお読み下さい。
- Clausius著『Die Mechanische Wa¨rmetheorie』(1876年出版)
Clausius自身が最終的にまとめた書籍です。Max Planck も若い頃この著書を読むことで熱力学第二法則を正しく理解することができたと言っています。