が1.の方法による表現です。このとき“点座標”の集合は
となる。
熱力学や解析力学を学ぶとき最も解りにくいのがルジャンドル変換です。その意味についてクーラン、ヒルベルトが文献1.で明快に説明しています。以下でその内容を解りやすく紹介します。
簡単に説明するために、まず一変数の関数u(x)を取り上げます。
二次元xu空間内の一つの曲線を表すのに二つの方法がある。
上記の説明が何のことか解りにくいので、例を挙げてグラフで以下説明する。
例として u=u(x)=(1/2)(x-1)2+1/2=(1/2)x2-x+1 を考える。このグラフをそのまま描いた
が1.の方法による表現です。このとき“点座標”の集合は
となる。
次に、問題の曲線の接線とu軸切辺の集合は、接線のグラフが
の様になるので
となる。これが2.の方法による“接線座標”表現です。
[補足説明]
1.の方法の“点座標”の集合と2.の方法による“接線座標”の集合は、1対1で対応します。もちろん完全に1対1で対応するためには、関数u=u(x)の勾配がxとともに単調・連続的に変化する凹関数あるいは凸関数でなければなりません。
ルジャンドル変換を適用する熱力学関数は、実際にこの条件を満たしています。[別稿「熱力学関数(状態方程式曲面)の性質」2.を参照されたし]
2.の方法に於いて、(∂u/∂x)≡ξで表すことにする。問題にしている曲線を、(x,u(x))=(x,u)による表現から((∂u/∂x),ω)=(ξ,ω)による表現に変えてみる。
その為には、点(x,u)における接線を定める方程式を考えればよい。高校数学で習うように、点(x,u)における接線の方程式は(x,u)とu軸上の交叉点(0,ω)の二点を通る直線の方程式だから、直線の傾きを表す式により
となる。
これは、(x,u)による表現を(ξ,ω)による表現に変える変換を表しており、これを“ルジャンドル変換”という。これは“接線座標”の一方の値である切辺の値ωが、元の関数値uからξxと言う量を差し引いたものであることを表している。
このとき、変数(∂u/∂x)≡ξで表したωのグラフω(ξ)を描いてみると、それは二次元ξω空間に於ける一つの曲線を表す。
今考察している例
では、ω=u-ξx=(1/2)x2-x+1-ξx であるから、この式中の x に ξ≡(∂u/∂x)=x-1 から求まる x=ξ+1 を代入すれば、 ω=ω(ξ)=(1/2)(ξ+1)2-(ξ+1)+1-ξ(ξ+1)=-(1/2)ξ2-ξ+1/2 となる。
つまり変数がξに変換された、新しい状態量ω(ξ)を表すグラフは
となる。ωはξが決まると完全に一意に定まる関数値(状態量)です。
このグラフω(ξ)は、上記の様に u(x(ξ))=(1/2)(ξ+1)2-(ξ+1)+1 のグラフに -ξx=-ξ(ξ+1) のグラフを加えたものであることに注意。
これはxの関数である状態量uから
によって新たなる状態量ωを定めたとき、uを表していた変数xが新たな変数ξに変更されたことを意味する。
このときuとωは全く異なった状態量です。古い状態量uに状態量-ξxを付け加えることにより新たな状態量ωを作ったのですが、それを表す変数もxからξ≡(∂u/∂x)に変換されていることに注意されたし。
ルジャンドル変換の逆変換を考える。関数ω(ξ)のξに関する導関数を作る。u(x)=u(x(ξ))であることに注意すると
だから
となる。
(1)と(4)を比較すると右辺の符号が逆転しているように見えるが、(2)と(3)を比較されると以下の事情が解ります。
曲線ω=ω(ξ)のグラフの点(ξ,ω)に於ける接線の傾きが∂ω/∂ξだから、uは点(ξ,ω)における接線がω軸と交わる点の値を表している。つまりω=ω(ξ)の“点座標”から、その“接線座標”であるu=u(x)に変換されている。だから、ルジャンドル変換の逆変換もルジャンドル変換となる。
一つの対象に対し二つの等価な記述法が存在するとき、二つの記述法を取り替える操作を数学では“双対”(そうつい)と呼ぶ。ここで説明している“点座標”と“接線座標”は双対性の関係をなしている。
そのためルジャンドル変化は単に1点を他の1点に対応づけるのではなくて、接線要素(x,u,∂u/∂x)を別の接線要素(ξ,ω,∂ω/∂ξ)に対応させるものと理解することもできる。
変数を変換することの意味が一変数関数の場合には必ずしも明瞭ではないので、二変数関数で考察してみる。
三次元xyu空間内の一つの曲面を表すのに二つの方法がある。
これは自明なので、2.の方法の(A)(B)(C)に付いて更に説明する。
まず最初に、上記2.(A)による表現を求める。 曲面u=u(x,y) 上の 点(x,y,u(x,y))=(x,y,u) における接平面の方程式は、接平面上の座標点を(x’,y’,u’)とすると、高校数学で習うように
となる。今後 (∂u/∂x)≡ξ、(∂u/∂y)≡η と置いて、三つの数字の組 (ξ,η,ω) を“接平面座標”と呼ぶことにする。
曲面u(x,y)上の点(x,y,u)で接する接平面u’(x’,y’)の方程式は
であるから、接平面u’(x’,y’)がu軸を切る値u’(0,0)=ωは上式でx’=y’=0と置いた
となる。これは、まさしく(x,y,u)による表現を(ξ、η、ω)による表現に変える変換を表しており、これも“ルジャンドル変換”と言う。つまり変換後の“接平面座標”(ξ,η,ω)は
となる。
ωがξとηの関数として与えられれば、2パラメーターの接平面の群が定まり、従って考えている曲面ω(ξ,η)が決まるのは明らかです。関数ω(ξ、η)は
なる方程式からx、y、uをξ、ηの関数として定め、次の方程式
に代入することにより求めることができる。
次に、上記2.(B)による表現を求める。 曲面u=u(x,y)を x=一定の平面 で切った切り口の 点(x,y,u(x,y))=(x,y,u) における接線の方程式は、接線上の座標点を(x,y’,u’)とすると、高校数学で習うように
となる。今後 (∂u/∂y)≡η と置いて、三つの数字の組 (x,η,ωxu) を“接平面座標”と呼ぶことにする。
曲面u(x,y)上の点(x,y,u)で接する接平面のx=一定の面で切った切り口線(y方向の接線)の方程式は
であるから、接線がxu面と交わる点の値 u’(x,y’)=ωxu は上式で x’=x,y’=0 と置いた
となる。これは、まさしく(x,y,u)による表現を(x、η、ωxu)による表現に変える変換を表しており、これも“ルジャンドル変換”と言う。つまり変換後の“接平面座標”(x,η,ωyu)は
となる。
ωxuがxとηの関数として与えられれば、2パラメーターの接平面の群が定まり、従って考えている曲面ωxu(x,η)が決まるのは明らかです。関数ωxu(x,η)は
なる方程式からyとuをx、ηの関数として定め、次の方程式
に代入することにより求めることができる。
次に、上記2.(C)による表現を求める。 曲面u=u(x,y)をy=一定の平面で切った切り口の点 (x,y,u(x,y))=(x,y,u) における接線の方程式は、接線上の座標点を(x’,y,u’)とすると、高校数学で習うように
となる。今後 (∂u/∂x)≡ξ と置いて、三つの数字の組 (ξ,y,ωyu) を“接平面座標”と呼ぶことにする。
曲面u(x,y)上の点(x,y,u)で接する接平面のy=一定の面で切った切り口線(x方向の接線)の方程式は
であるから、接線がyu面と交わる点の値 u’(x’,y)=ωyu は上式で x’=0,y’=y と置いた
となる。これは、まさしく(x,y,u)による表現を(ξ、y、ωyu)による表現に変える変換を表しており、これも“ルジャンドル変換”と言う。つまり変換後の“接平面座標”(ξ,y,ωyu)は
となる。
ωyuがξとyの関数として与えられれば、2パラメーターの接平面の群が定まり、従って考えている曲面ωyu(ξ,y)が決まるのは明らかです。関数ωyu(ξ,y)は
なる方程式からxとuをξ、yの関数として定め、次の方程式
に代入することにより求めることができる。
式だけでは何のことか解らないのでグラフを用いて説明する。例として
を取り上げる。
1.の方法による表現であるu=u(x,y)のグラフは
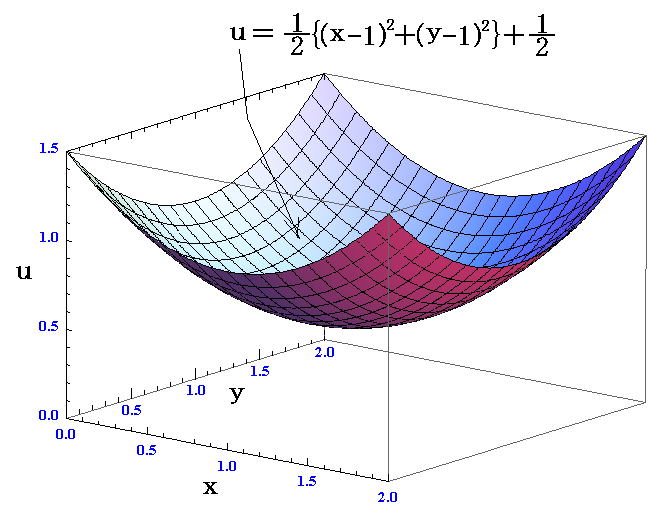
となる。これが“点座標”(x,y,u)による表現です。
このとき ξ≡(∂u/∂x)=x-1、η≡(∂u/∂y)=y-1 となる。
2.(A)の方法による“接平面座標”(ξ,η,ω)の表現の様子を見るために、幾つかの座標点に於ける接平面を描いてみる。
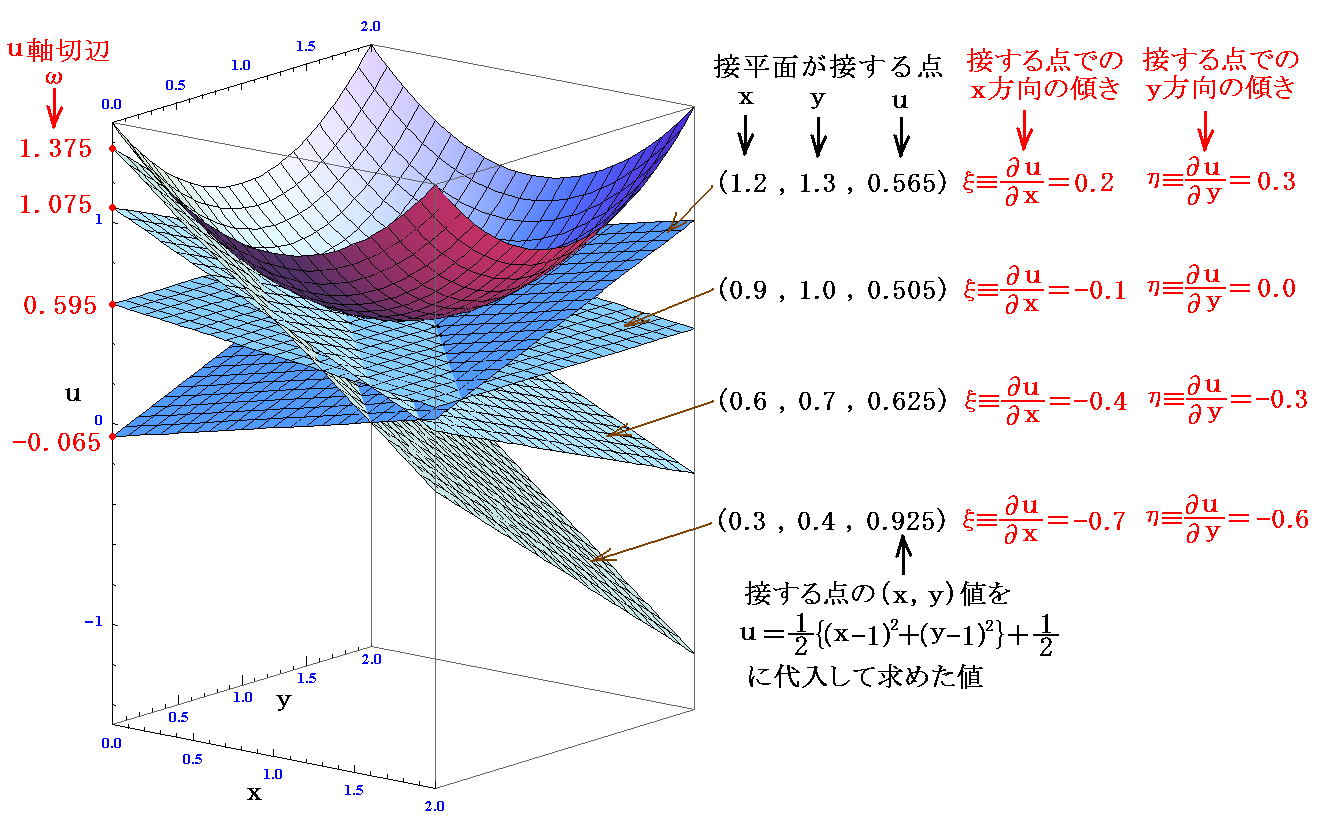
すなわち
なる点が、“ルジャンドル変換” ω(ξ,η)=u(x,y)-ξx-ηy により
なる点に変換される。
実際は、(x,y)のすべての値に対して(ξ,η)の値が存在する。そして(ξ,η)の関数として接平面がu軸を切る値ω(ξ,η)が求まる。それをするには、
によってx、y、uをξ、ηで表して、uから“ルジャンドル変換”で求めたωの式に代入すればよい。すなわち
となる。このグラフを描くと
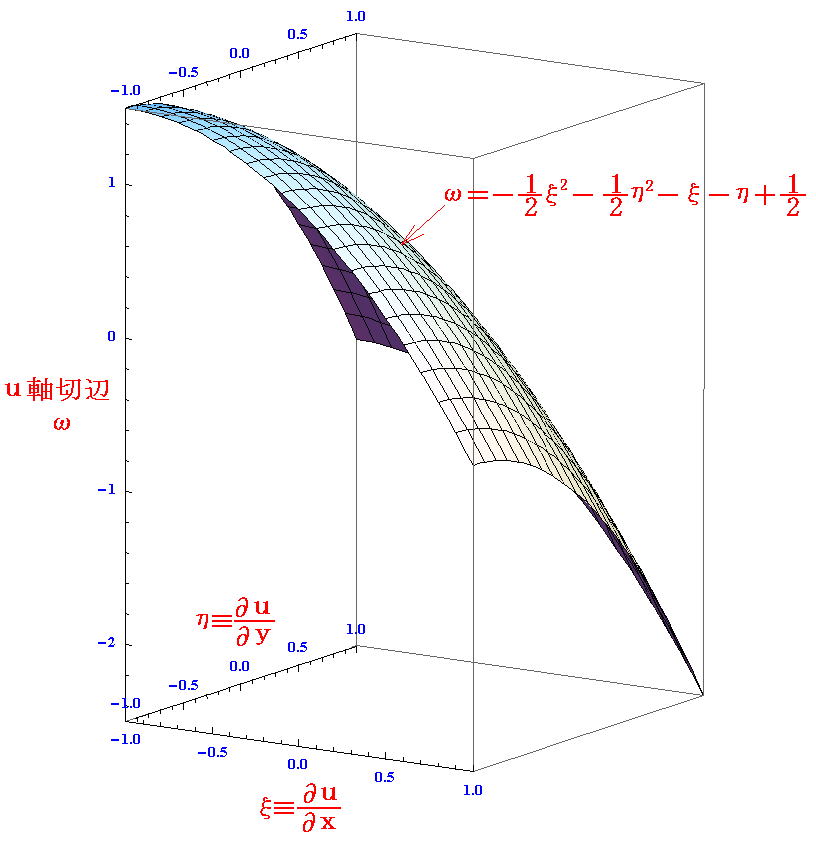
となる。
このグラフω(ξ,η)は、 u(x(ξ,η),y(ξ,η))=(1/2){ξ2+η2}+1/2 のグラフに、 -ξx-ηy=-ξ(-∂ω/∂ξ)-η(-∂ω/∂η)=-ξ(ξ+1)-η(η+1) のグラフ(下図)
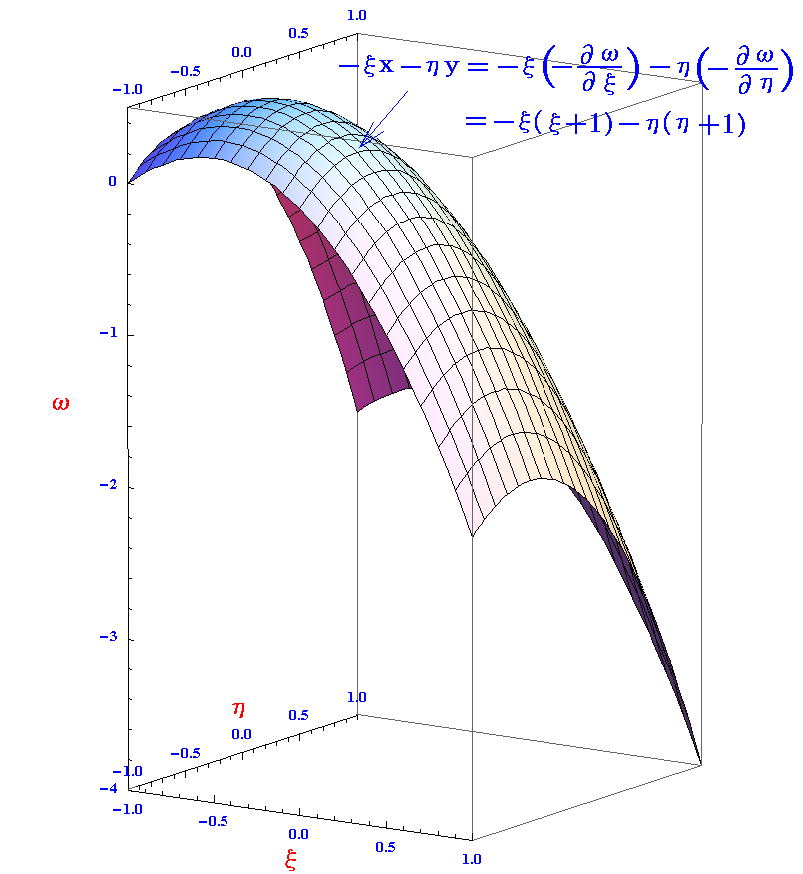
の値を加えたものであることに注意。
このときuとωは全く異なった状態量です。古い状態量uに状態量-ξxと-ηyを付け加えることにより新たな状態量ωを作ったのですが、それを表す変数も(x,y)から(∂u/∂x,∂u/∂y)≡(ξ,η)に変換されていることに注意されたし。
[補足説明1]
ルジャンドル変換に伴って変数も変換されるのだが、ωを元の変数(x,y)で表すこともできる。今の場合
だから、グラフは下図の様になる。
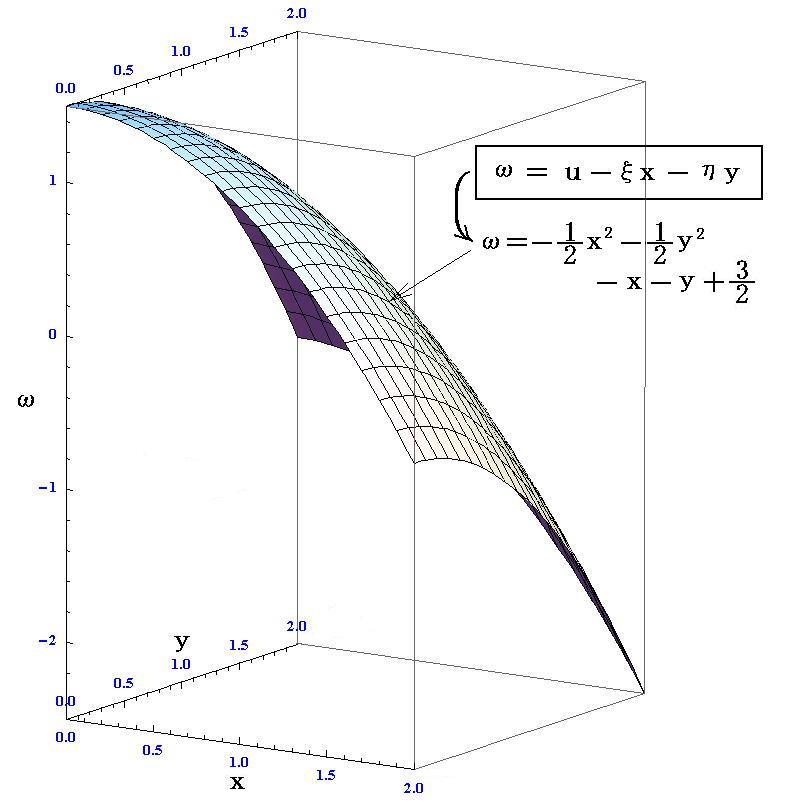
このグラフの形状は、座標原点の位置はずれるが、先ほどのグラフの形状と同じになる。
しかし、ルジャンドル変換が重要なのは独立変数を変えることができる事にあるのだから、この様にしてしまったのでは意味がない。
独立変数を元の曲面の勾配に変換する事の意味については別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」1.(2)3.2.を参照されたし。
このことは、以下の2.(B)の方法や2.(C)の方法についても同様です。
同様に、2.(B)の方法による“接平面座標”(x,η,ωxu)の表現の様子を見るために、幾つかの座標点に於ける接平面(y方向の接線)を描いてみる。
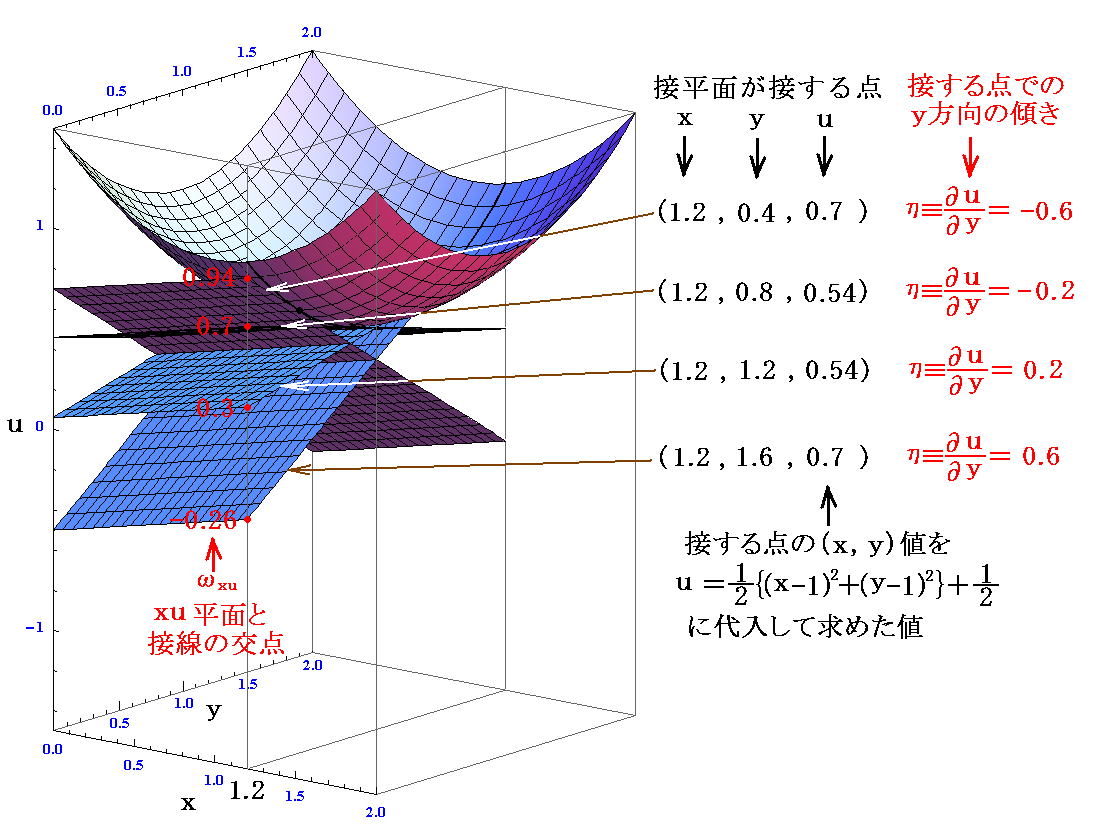
すなわち
なる点が、“ルジャンドル変換” ωxu(x,η)=u(x,y)-ηy により
なる点に変換されます。
(x,η)の関数としてのωxu(x,η)は
によってy,uをx,ηであらわして、uから“ルジャンドル変換”で求めたωxuの式に代入すればよい。すなわち
となる。このグラフを描くと
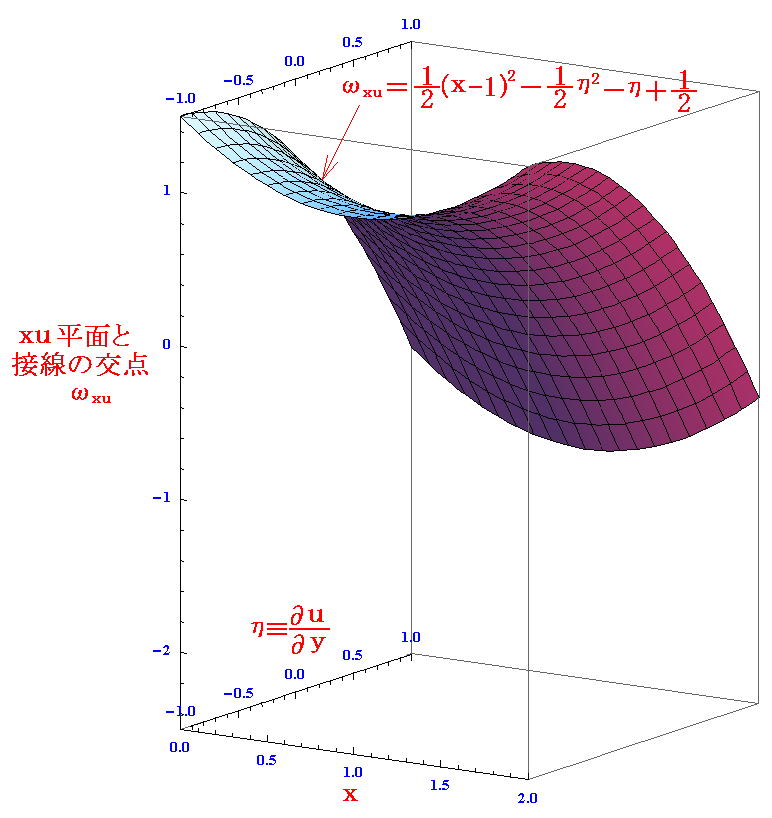
となる。
このグラフωxu(x,η)は、u(x,y(x,η))=(1/2){(x-1)2+η2}+1/2)のグラフに、-ηy=-η(-∂ω/∂η)=-η(η+1)のグラフ(下図)
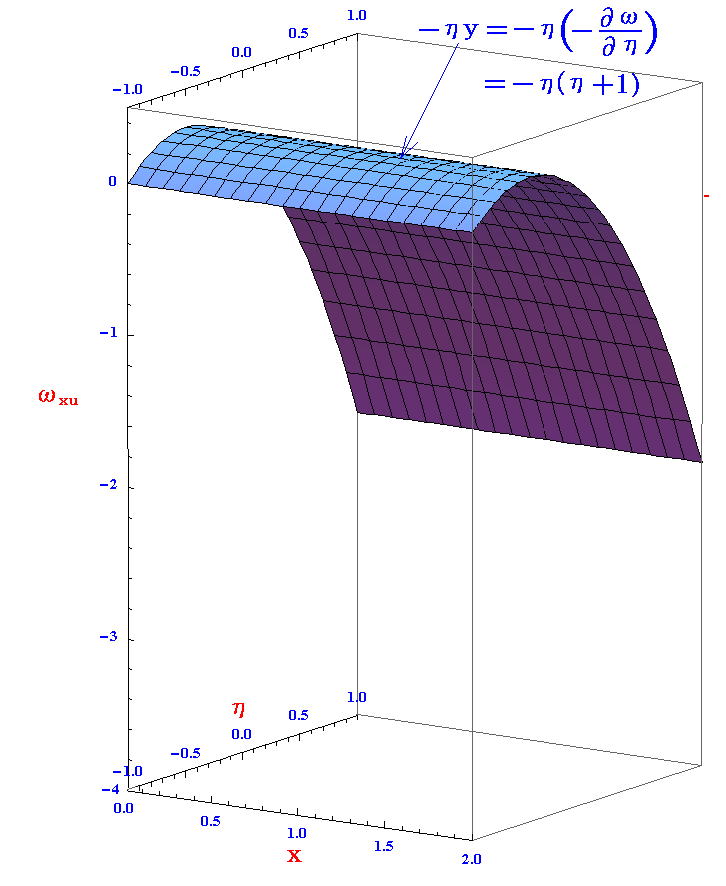
の値を加えたものであることに注意。
このときuとωxuは全く異なった状態量です。古い状態量uに状態量-ηyを付け加えることにより新たな状態量ωxuを作ったのですが、それを表す変数も(x,y)から(x,∂u/∂y)≡(x,η)に変換されていることに注意されたし。
[補足説明1]
このとき、u(x,y)とωxu(x,η)のグラフを比較してみれば明らかなように、変数ηを固定してωxu(x,η)をxで偏微分したものと、変数yを固定してu(x,y)をxで偏微分したものが同じになります。すなわち
となります。
これは次のようにして一般的に成り立つことが証明できる。
つまり、一部の変数のみを変換(今の場合y→η)するルジャンドル変換では、変換していない変数xでuとωxuを偏微分したとき、固定する変数はy→ηに変わっており、関数もu→ωxuに変換されているが、xに関する偏微分導関数は変わらない事を意味している。
このことの重要な例として熱力学に於けるU(V,S)曲面とF(V,T)曲面、およびH(P,S)曲面とG(P,T)曲面の関係がある。詳細は別稿「熱力学関数(状態方程式曲面)の性質」3.(2)2.[補足説明2]を参照されたし。
同様に、2.(C)の方法による“接平面座標”(ξ,y,ωyu)の表現の様子を見るために、幾つかの座標点に於ける接平面(x方向の接線)を描いてみる。
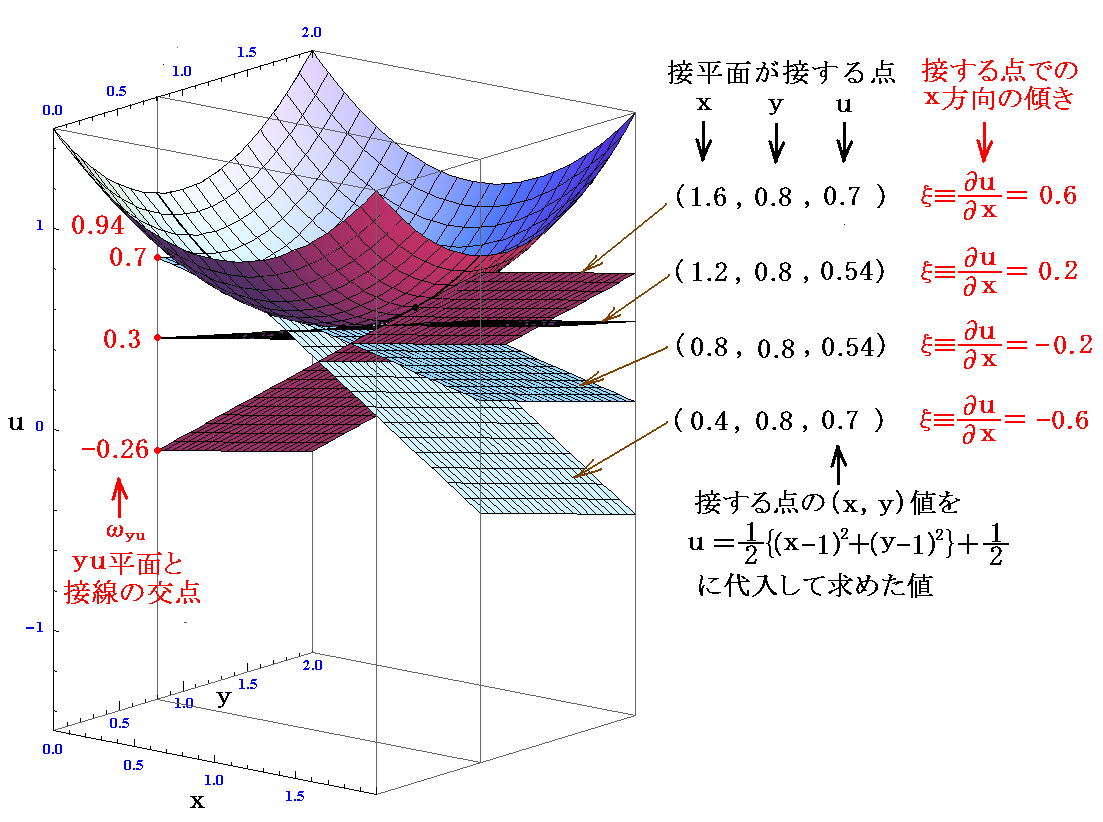
すなわち
なる点が、“ルジャンドル変換” ωyu(ξ,y)=u(x,y)-ξx により
なる点に変換されます。
(ξ,y)の関数としてのωyu(ξ,y)は
によってx,uをξ,yであらわして、uから“ルジャンドル変換”で求めたωyuの式に代入すればよい。すなわち
となる。このグラフを描くと
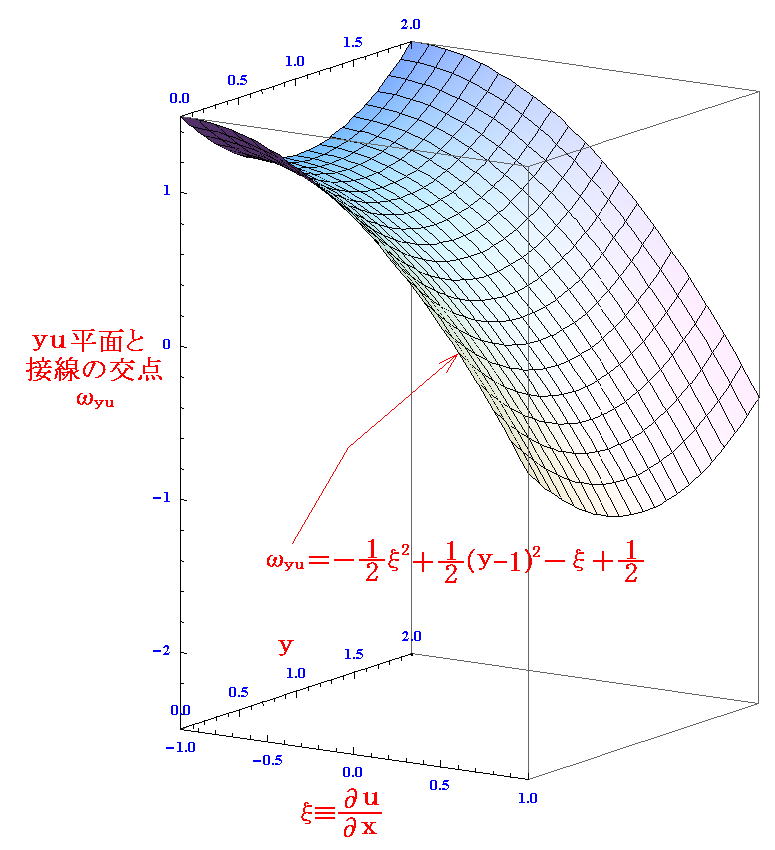
となる。
このグラフωyu(ξ,y)は、u(x(ξ,y),y)=(1/2){ξ2+(y-1)2}+1/2のグラフに、-ξx=-ξ(-∂ω/∂ξ)=-ξ(ξ+1)のグラフ(下図)
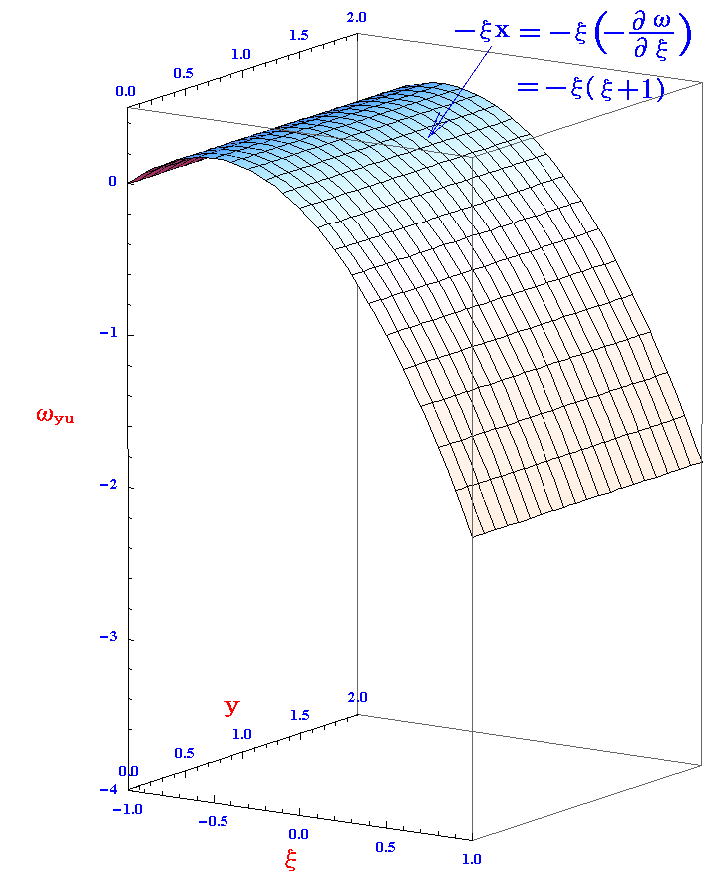
の値を加えたものであることに注意。
このときuとωyuは全く異なった状態量です。古い状態量uに状態量-ξxを付け加えることにより新たな状態量ωyuを作ったのですが、それを表す変数も(x,y)から(∂u/∂x,y)≡(ξ,y)に変換されていることに注意されたし。
[補足説明1]
このとき、u(x,y)とωyu(ξ,y)のグラフを比較してみれば明らかなように、変数ξを固定してωyu(ξ,y)をyで偏微分したものと、変数xを固定してu(x,y)をyで偏微分したものが同じになります。すなわち
となります。
これは次のようにして一般的に成り立つことが証明できる。
つまり、一部の変数のみを変換(今の場合x→ξ)するルジャンドル変換では、変換していない変数yでuとωyuを偏微分したとき、固定する変数はx→ξに変わっており、関数もu→ωyuに変換されているが、yに関する偏微分導関数は変わらない事を意味している。
二次元曲面の場合の逆ルジャンドル変換を考える。関数ω(ξ,η)のξとηの偏動関数をつくると
となるので
が言える。
(1)と(4)を比較すると右辺の符号が逆転しているように見えるが、(2)と(3)を比較されると以下の事情が解ります。
この式は、曲面ω=ω(ξ,η)の点(ξ,η,ω)に於ける接平面がω軸を切る値がuであることを表している。つまりω=ω(ξ,η)の“点座標”から、その“接平面座標”であるu=u(x,y)に変換されている。だから、ルジャンドル変換の逆変換もルジャンドル変換となる。
このように“点座標”と“接平面座標”は双対性の関係をなしている。そのためルジャンドル変化は単に1点を他の1点に対応づけるのではなくて、接平面要素(x,y,u,∂u/∂x,∂u/∂y)を別の接平面要素(ξ,ξ,ω,∂ω/∂ξ,∂ω/∂η)に対応させるものと理解することもできる。
[補足説明1]
クーラン、ヒルベルトの文献1.では、ルジャンドル変換後の関数を ω ではなくて -ω で定義しており、ルジャンドル変換を
の様に表している。
このようにすると前述の式は
となるので
となります。この定義の方がルジャンドル変換の双対性をより旨く表せます。
実際、5.で説明する様に、解析力学におけるラグランジアンLとハミルトニアンHを相互に変換するときの“ルジャンドル変換”は、この形の定義に従っています。
一方、熱力学における状態量間の“ルジャンドル変換”は、この稿で採用した定義に従っています。4.で説明するように、こちらの定義の方が幾何学的に解釈するとき便利です。
(n+1)次元空間内 の n次元曲面 を想像するのは難しいが、考え方は 二次元空間内 の 曲線 、 三次元空間内 の 曲面 と同じです。
ただし、ルジャンドル変換で新たに導入された量が、物理的に何を意味するのかを理解するのは容易ではありません。それぞれの物理学理論で解読しなければなりません。その解読の中に物理の本質があります。
熱力学に対応した定義です。この場合には
となる。
解析力学に対応した定義です。この場合には
となる。
“ルジャンドル変換”の熱力学への応用とは、第2章で説明した量をそれぞれ
u → U(内部エネルギー)、 ω → G(ギブズの自由エネルギー)、
ωxu → F(ヘルムホルツの自由エネルギー)、 ωyu → H(エンタルピー)、
x → V(体積)、 y → S(エントロピー)、
ξ → -P(圧力)=(∂U/∂V)S、 η → T(絶対温度)=(∂U/∂S)V
へ置き換えることです。
その当たりは、文献2.の第2章2.1“自由エネルギーの導入” で明快に説明されています。文献2のpdfファイルをダウンロードされてお読みください。その中に描かれている
図2.1(次図参照) を 本稿2.(2)の図 と比較されれば、すべてが了解できます。この図2.1の中にルジャドル変換の本質がすべて表されています。
図から、U,H,F,Gがすべてエネルギーの次元を持つ量であること、さらにUが(S,V)の関数、Hが(S,p)の関数、Fが(T,V)の関数、Gが(T,p)の関数であることが読み取れます。
[補足説明1]
U、H、F、G、はいずれもエネルギーの次元を持つ状態量です。
エネルギーU(S,V)からルジャンドル変換H(S,p)=U(S,V)+pVによって変数を(S,V)→(S,p)に変換したものがエンタルピー“含熱量”です。
エネルギーU(S,V)からルジャンドル変換F(T,V)=U(S,V)-TSによって変数を(S,V)→(T,V)に変換したものが“ヘルムホルツの自由エネルギー”です。
エネルギーU(S,V)からルジャンドル変換G(T,p)=U(S,V)-TS+pVによって変数を(S,V)→(T,p)に変換したものが“ギブスの自由エネルギー”です。
上記では、状態方程式曲面の縦軸をエネルギーの次元を持つ量にして表しています。ところが、状態方程式曲面の縦軸を例えばエントロピーにして表し、その状態方程式曲面に対して様々なルジャンドル変換を施した状態量(いずれもエントロピーの次元を持つ)を用いて熱力学理論を展開する事もできます。
実際、M.Planck は エントロピーの次元を持つ状態量 をルジャンドル変換によって定義しています。
すなわち S、Ψ、Φはいずれもエントロピーの次元を持つ状態量です。
エントロピーS(E,V)からルジャンドル変換Ψ=S-(E/T)に依って変数を(E,V)→(T,V)に変換したものがΨです。
エントロピーS(E,V)からルジャンドル変換Φ=S-(E/T)-(pV)/Tに依って変数を(E,V)→(T,p)に変換したものがΦです。
プランクの著書「熱力学」や「理論熱学」などを読まれるときには、ここの説明を思い出されて下さい。
別稿「絶対温度とは何か」8.(2)1.で説明したように、形式的には状態量であるUに同じく状態量であるpVやTSを足したり引いたりするのが“ルジャンドル変換”です。HはUにpVを足したものであり、FはUからTSを引いたものであり、GはFにpVを足したものあるいはHからTSを引いたものです。
そのためUに状態量であるpVやTSを加えたり、引いたりして新しい熱力学的状態量を導入しようとすると、普通の教科書では、まずHやFを導入して、最後にGを導入する事になります。
しかし、歴史的には、熱力学関数の幾何学的意味を正しく理解したギブズによって、まず“G”[2.(A)の場合]が一気に導入され、次に“F”[2.(B)の場合]が導入され、最後に“H”[2.(C)の場合]が導入された。
この当たりの詳しい説明は別稿「熱力学関数(状態方程式曲面)の性質」3.と別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」1.(2)3.2.をご覧ください。
以下の説明は文献2.からの引用です。
[補足説明2]
“G”は、ギブズ(Josiah Willard Gibbs、1839-1903年)により1873年12月に公刊された第二論文“A Method of Geometrical Representation of the Thermodynamic Properties
of Substances by Means of Surfaces”(物体の熱力学的諸性質の曲面による幾何学的表示)で導入されたので、“ギブズの自由エネルギー”と呼ばれている。論文のタイトルからも判るようにギブズはを幾何学的に導入している。
記号“G”は導入者ギブズ(Gibbs)の名前にちなむ。
“F”は、ヘルムホルツ(Hermann Ludwig Ferdinand von Helmholtz、1821-1894年)により1882年の論文で導入されたので、“ヘルムホルツの自由エネルギー”と呼ばれている。記号“F”は自由エネルギー(free energy)に由来する。
“ヘルムホルツの自由エネルギー”が導入された1882年は、“ギブズの自由エネルギー”が導入されてから9年後であり、最も有名なギブズの第三論文“On
the Equilibrium of Heterogeneous Substances”(不均質物質の熱力学について)の第2部が公刊された1878年から数えても4年後です。このことからも平衡系の熱力学についてはギブズが独走していたことが判る。
“H”には呼称が3つある。“熱含量(含熱量)”、“エンタルピー”、“カマーリング・オネスの自由エネルギー”の3つです。記号“H”で表すのは熱含量(heat content)の呼称に由来する。
エンタルピー(enthalpy)は、カマーリング・オネス(Heike Kamerlingh-Onnes、1853-1926年)が“温まる”の意味を持つギリシャ語[中に(en-)+熱(thalp)]から作った造語(1909年)です。
ちなみに、1865年にClausiusが名付けた“エントロピー”はギリシャ語[中に(en-)+変化(trope)]から作った造語です。ただし、エントロピー“S”は[エネルギー÷温度]のまったく新しい次元を持つ量(乱雑さの度合いを表す)でして、[エネルギー]の次元を持つ上記の“G”、“F”、“H”とはまったく性質の異なる物理量です。
解析力学では、普通別稿で説明したクーラン、ヒルベルトの形式の符号の定義を用いています。そのため、3.(2)のクーラン、ヒルベルト形式の定義に於いて、ω→H(ハミルトニアン)、u→L(ラクランジアン)の置き換えをして、変数を以下のように取れば良い。
このとき、ルジャンドル変換を表す式
は、ラグランジアンLからハミルトニアンHを定義する式そのものです。
[補足説明1]
n個の変数の内の変換されないm個の変数q1~qmに関する偏微分導関数に対して、2.(2)2(B)の方法[補足説明]で述べたのと同様な事情が成り立ちます。クーラン、ヒルベルト形式のルジャンドル変換のために符号が変わりますが、以下の関係式が成り立ちます。
証明は同様に行えばよい。
これを用いると、オイラー・ラグランジュ方程式は
となる。
さらに、逆ルジャンドル変換から
が導ける。
これはハミルトニアンHをpiで゛偏微分して求めても良い。すなわち
となる。
これらの方程式の組
を、ハミルトンの正準方程式(canonical equation)という。
[補足説明2]
ここの説明だけでは、ラグランジアンLとラグランジュの運動方程式(オイラー・ラグランジュ方程式)、およびハミルトニアンHとハミルトンの正準運動方程式が何を意味するのかは解りません。
この事について、最近の本では例えば村上雅人著「なるほど解析力学」海鳴社(2016年刊)などをご覧下さい。解析力学とは何かを理解するには、この本のように簡単な例を沢山当たってみるに限ります。とても解りやすく説明されています。
この本の中に出て来るラグランジュの未定乗数法については別稿で説明していますので合わせてご覧下さい。
[補足説明3]
ランダムハウス英語事典によると“canonical”(adj.)とは
【1】宗規にかなった,宗規によって定められた,教会法上の;司教座聖堂参事会員の.
【2】聖書正典に含まれている:the canonical books (of the Bible) 正経書.
【3】権威ありと認められた,正統の,規範[標準]的な;認可[容認]された:canonical works 正統の作品.
【4】〔数学〕〈方程式・座標などが〉基準の,正規の,正準の.
【5】〔音楽〕canon 形式[技法]の.
【6】〔言語学〕〈言語の形式・パターンが〉(ある言語に)特徴的な,一般的な,基本的な:
the canonical form of the past tense 過去時制の基準形式
a canonical syllable pattern 音節配置の基準パターン.(また canonic)
のこと。
[補足説明4]
村上雅人著「なるほど解析力学」海鳴社(2016年刊)p146~151 補遺2 ルジャンドル変換 を引用。
ルジャンドル変換について、文献1.に明快な説明があります。このページは、そこの記述に依存しています。その内容をできるだけ解りやすくすることに勤めました。