電気化学ポテンシャルと熱力学第三法則(ネルンストの熱定理)
電気化学ポテンシャル(electrochemical potential)について、例えば理化学事典第5版(岩波書店)には
単に化学ポテンシャルということもある。 荷電粒子(たとえばイオン)のギブズ自由エネルギーの部分モル量のことで、グッゲンハイム(E. A. Guggenheim)が提案(1929年)した熱力学的示強変数。
電気的に中性の粒子の化学ポテンシャルとの形式上のちがいは、電気的エネルギーの寄与を含んでいることで、相α中における荷電粒子iの電気化学ポテンシャルηαiは、ηαi=μαi+ziFΦαで与えられる。
ziはiの電荷数(符号を含む)、Φαはα相の内部電位。Fはファラデー定数。またμαiはα相中における荷電粒子iの化学ポテンシャルで、その内容は中性粒子の場合と同様である。
荷電粒子の運動や反応に対する駆動力は電気化学ポテンシャルの勾配できまる。
と記されている。ここでは、これをもう少し解りやすく説明します。
また、ネルンストは“ギブズ・ヘルムホルツの関係式”から“熱力学第三法則”に繋がる重要な仮説を提出した。このことについても説明します。
1.電池反応
(1)ギブズの考察
1.電化化学ポテンシャル
別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」1.(3)で説明したように、化学ポテンシャルは多成分系で物質量の変化が関わる現象ならどのようなものにでも適用できる概念でした。普通の化学変化であろうと、電気化学的な変化であろうと何にでも利用できます。
ただし、電気化学的な反応ならば、化学ポテンシャルの中に化学種の電荷に関する状況を用いて記述した方がより便利です。その為に、そういった状況を反映するように書いた化学ポテンシャルのことを電気化学ポテンシャルと言います。
今までは物質量としては質量mで議論しましたが、ここではモル数nで考えることにします。その場合の熱力学第一・第二法則は
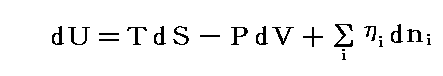
となります。ηiは化学種iの電気化学ポテンシャルです。いままでは文字μを用いて記述した化学ポテンシャルですが、電気化学的な場合に拡張したものであることを示す為に文字ηを使うことにします。
これをさらに、電気化学的な部分とそれ以外の部分に分けて考えて
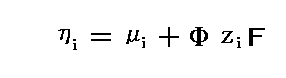
と書くことにします。電気化学的な部分がΦziFで、それ以外の部分をμiとするだけです。
別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」1.で説明したギブズの自由エネルギーの元々の導入経過を思い出せば、その様にしても良いことが解ります。
ziは化学種iの帯電価数(イオン価数)でFは“ファラデー定数”(1モルの電気量=96494クーロン)です。故に、ziFdniは化学種iの総電気量を表す。Φはその電荷ziを持つ化学種iが存在する系(相あるいは溶液)の“静電ポテンシャル”です。
これを用いると上記の熱力学法則は
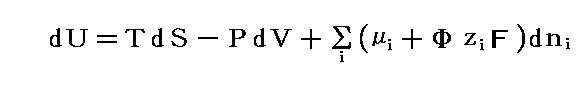
となる。
[補足説明]
ここでの電池反応も、すべて平衡状態での考察であることを忘れないでください。
系は外界と熱や仕事(PdVやEdq)をやり取りしますが、それらを準静的・逆方向に変化させることも可能で、それらの変化を逆転させると電池内部の反応はすべて逆方向の変化が実現されるとしている。つまり“可逆電池”の議論なのですが、可逆電池とは、系が外界とやり取りする熱や仕事を準静的に逆転すると、電池内の変化も逆転できるような変化しか生じないと言うことです。
単一相の電解質からなる再充電可能な二次電池では、このことが実現可能ですが、多くの一次電池は二相以上の電解質を持ちそれらの間のイオンの移動は、電池反応が進めば進むほど逆転可能ではなくなります。だからそれらの電池については、それらが準静的に逆転が可能な(わずかのdqの移動しか生じない)極狭い範囲での議論であることを忘れないでください。
だから、後で1モルの電荷が流れたときの発熱量の計算をしますが、実際に1モル流す訳ではありません。その温度・圧力において極わずか流したときに発する熱量から1モル分を計算するわけです。そのとき、もちろん電池内部電流によるジュール熱の発生などの不可逆過程も存在しないとしています。
可逆電池であるからこそ、系内の化学種に対して化学ポテンシャルが(T,P)の関数として定義できて、各(T,P)に対して一意のある値を持つことになる。
2.ダニエル電池
一般的な議論では解りにくいので“Daniell電池”(1836年)を例に取って説明する。電池は一連の相が繋がっているものであって、それぞれの相が独自の化学ポテンシャルを持ち、隣り合う二相の間ごとに平衡が成り立っている。
個々の相の境界(金属電極と溶液の境界もあれば、異なった溶液間の境界もある)はある種のイオン(電子)だけを通過させる膜で仕切られていると考えることができる。
ダニエル電池は下図の模式図で表される。個々の相はローマ数字(Ⅰ~Ⅴ)で示されている。Mは素焼きの陶器製の隔壁でSO42-イオンのみを通過させる。Zn極にCuの棒が接着してあるのは、開いた電池の起電力ΦⅠ-ΦⅤを同種の金属Cu間で測ることができるようにするためです。そうすると異種金属間の接触電位差が入らないようにできる。
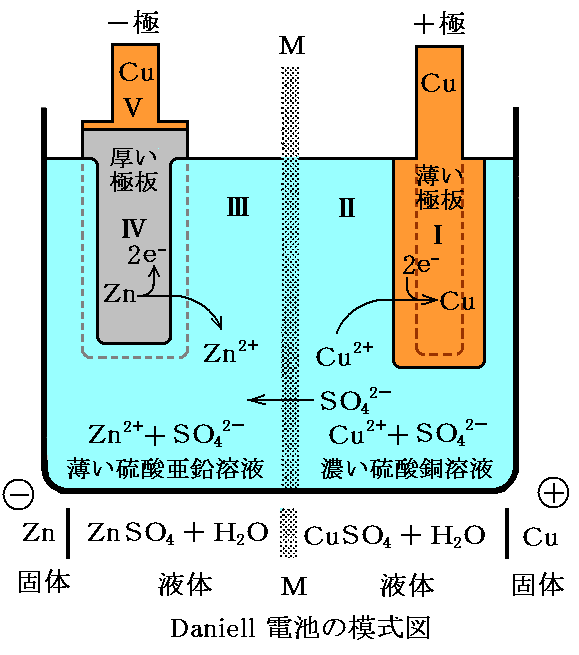
ここでは、正極と負極がきわめて大きな抵抗回路で繋がれていて無限にゆっくりと電流が流れている準静的な状況を考える。あるいは、後で説明するポテンシオメータの様なものを外界として繋いで電池起電力とほぼ同じ外部逆起電力をかけて、少しずつ電流を流すようにする。それはちょうど、系の圧力とわずか異なる外部仕事浴を準備して準静的・可逆的にPdV仕事のやり取りをするのと同じです。
そのため常に平衡状態が達成されていて、電池内部では電流によるジュール熱の発生はないものとすることができる。もちろん電池内部の化学変化は起こるので、そのことに伴う反応熱は生じます。それはちょうど、等温下で相変化が起こると潜熱が系から出入りするのと同じです。ここは解りにくい所ですが別稿「熱力学関数(状態方程式曲面)の性質」1.(1)2.の箇条書き4.を参照。
正極-負極間の電池起電力はブリッジ回路などを用いたポテンシオメーターで静電的に測定するものとする。
二溶液がイオン交換可能の半透膜で仕切られているのだが、濃度の異なる溶液が半透膜で仕切られているときにその濃度差が浸透圧の差で保たれるのと同様に、今の場合は、二溶液(二相)間のイオン濃度の差は二溶液間の静電ポテンシャルの差ΦⅡ-ΦⅢに拠って保たれている。他の境界についても同様です。
電気化学ポテンシャルηとモル数nの右下に[相の番号i(Ⅰ~Ⅴ)]と[成分の種類k(Zn2+、Cu2-、SO42-、e-)]を書き添えて表すことにする。ここで電子に対してはe-と言う記号を用いる。
電池反応に伴う相変化(化学反応)が温度T一定、圧力P一定で行われるとすると、別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」1.(1)3.あるいは2.(1)3.で述べたように、各相間において次の関係式が成り立つ。
例えば相Ⅰ-相Ⅱ間の平衡条件δG=0と、モル数一定の副条件は
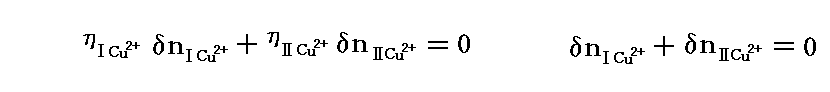
となる。この二式から、電気化学ポテンシャルの平衡関係を表す
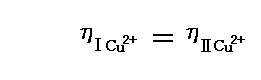
が得られる。価数z=+2であることを用いると、この式は
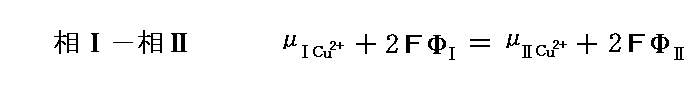
と表される。同様にして、他の相の組に対して
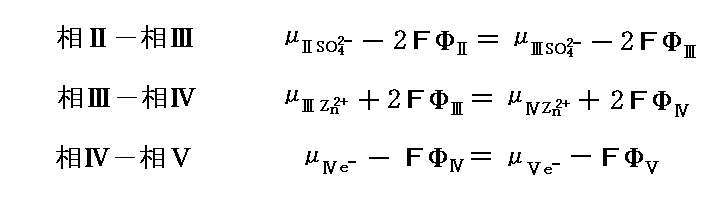
が得られる。
ところで、Cu電極とZn電極では
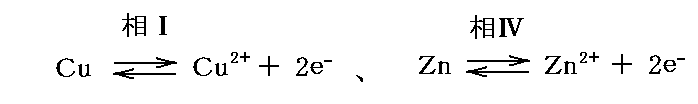
という化学反応が起こっているので、Cu電極ではCu2+イオンは2個の電子を得て中和され、Zn電極ではZn原子は2個の電子を失ってイオン化する。この平衡過程について、化学ポテンシャルを用いて表した付加条件
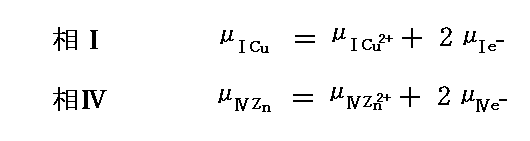
が成り立たねばならない。
最後にⅤ相とⅠ相は同じ電極物質Cuでつながれているので、そこに於ける電子の平衡過程は電子に関する化学ポテンシャルを用いて
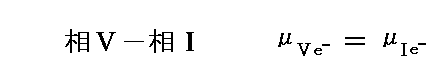
と表される。
以上で、一連の相の中で生じている“平衡状態”がすべて記述できたことになる。
3.ギブズの結論
相Ⅰ~相Ⅴの間で成り立っている化学ポテンシャルの平衡条件式に適当な定数を乗じて、左辺同士、右辺同士をすべて足し合わせる。そして、付加的な平衡条件式も考慮すると
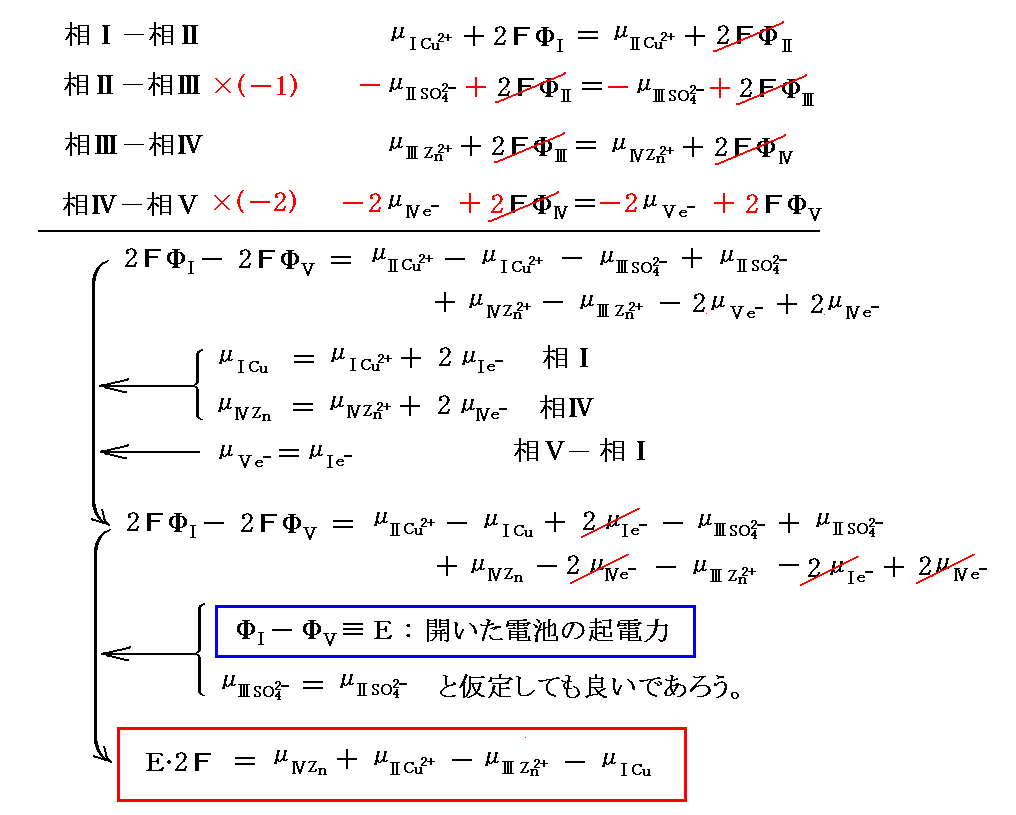
が得られる。(ふつう電位差はVを用いるが体積との混同を避けるためにここではEを用いる。)
今、電気量2FがDaniell電池の外側を通って+極(Ⅰ)から-極(Ⅴ)へ準静電的(可逆的)に移動したとする。そのとき電池内部では-極から+極へ同量の電荷が移るので、1モル分の
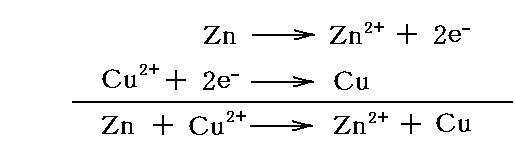
なる化学反応が圧力一定・温度一定の元で起こったことになる。もちろん、そのとき電池は外界と熱や仕事のやり取りをしている。
そのとき、前式左辺のE・2Fは電池が外部に対して行った仕事をあらわしており、右辺が上記の化学反応過程に伴うギブズの自由エネルギーの減少量を表している。すなわち
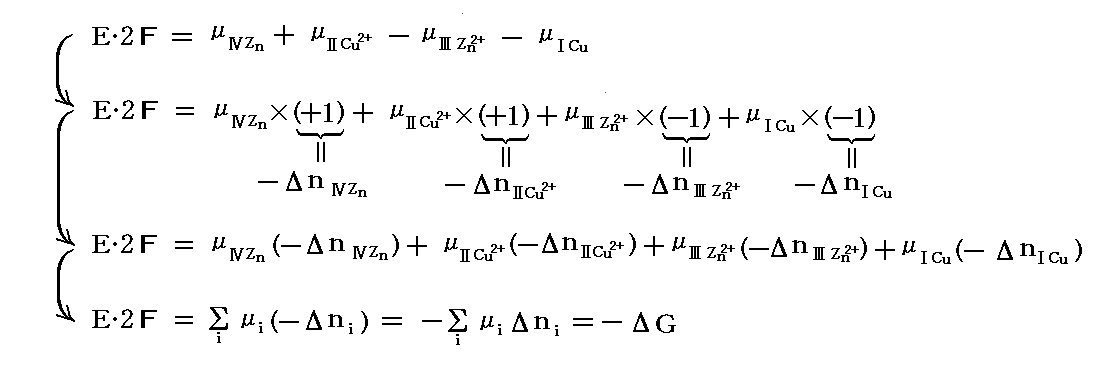
となる。上記の様にΔnを置いたのは実際に起こる反応ではΔnⅣZn=-1、ΔnⅡCu2+=-1、ΔnⅢZn2+=+1、ΔnⅠCu=+1だからです。
[補足説明]
符号の正負には注意が必要です。文献1.でSommerfeldは、ΔGやΔFは電池反応の進行にともなう自由エネルギーの減少分(>0)としてE・2F=-ΣμiΔni=ΔGとしている。しかし、ここでは、これらの量はすべて電池反応の進行にともなう自由エネルギーの変化分(<0)とすることにする。そちらの方が式の意味をを理解しやすい。
また外界とやり取りする仕事Edqは、PdVと同じ様に電池に対してされた仕事を正とし、電池が外界に対してする仕事を負とすることにする。
4.ギブズの自由エネルギー
この結論は、別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」1.(1)3.あるいは2.(1)3.で述べた法則 “圧力一定・温度一定の元で起こる相変化(化学変化)ではδG=Σμiδni=0である” に反する様に見えますが、矛盾はありません。
もともとの単位モル当たりのギブズの自由エネルギーである化学ポテンシャルは、今の場合μiではなくてηiなのです。そして実際ηiに関しては最初に説明したように
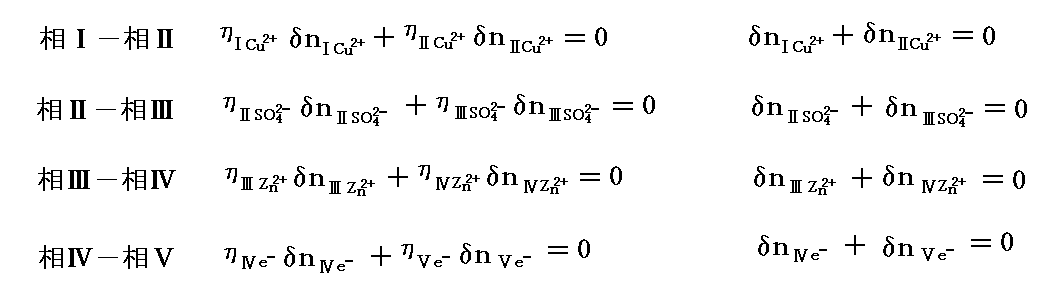
が成り立っているのですから、δG=Σηiδni=0 は確かに成り立っています。つまり、化学ポテンシャルを普通の意味での化学種の変化と電気的な変化の二つに分けたために、見かけ上、普通の意味の化学種に付随していたギブズの自由エネルギーの変化分が電気的な仕事と成って現れたわけです。
もちろん、この場合には、温度T=一定、圧力P=一定の元での変化、さらに付け加えると起電力E=一定の元での変化ですから、電池全体としては外部と熱のやり取りや機械的な仕事のやり取りをしています。電気的な仕事のやり取りが無くて機械的な仕事のやり取りだけだったら系の本来のギブズの自由エネルギーは変化しません。
別稿「絶対温度とは何か(積分因子とは何か)」8.(2)1.[補足説明2]のGの項で説明したように、温度一定・圧力一定の条件下で外界と可逆的に相互作用を行うときには、ギブズの自由エネルギー変化は“正味の仕事”にひとしい。正味の仕事とは全仕事から、系の体積変化に関する仕事PdVを差し引いたもので、今は電気的仕事Edqになります。
すなわち、1モル分の電気化学的な変化が起きて電位差EをzFの電気量が流れた場合、電池内部のギブズの自由エネルギーの変化ΔGは
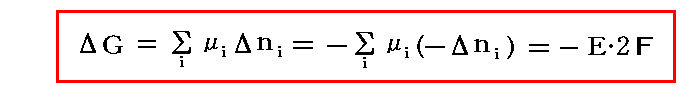
と表されることになります。このとき、電池に対してされた仕事を正とし、電池が外界に対してする仕事を負としています。
このとき、温度一定条件(電池が外界とやり取りする熱量はこの条件下におけるもの)における温度が変われば平衡状態にある各々の化学ポテンシャルの値も変わります。そのためEは温度と共に変化します。当然ΔGも温度の関数となります。
これが、電池が行う仕事に関するギブズ流の説明です。ただし現代風にアレンジしてあります。彼の熱力学に関する大論文(第三論文)を自身が要約して説明した論文がありますが、その最後でこの当たりを説明しています。要約論文のため説明が簡略化されており抽象的で難解ですが、参考に引用しておきます。
第三論文のPartⅡ(1878年)の該当部分や1887年のElectrochemical Thermodynamicsに関するLettersはネットからダウンロードできます。また、第三論文の翻訳版が最近発刊されています。それが廣政直彦・林春雄訳「ギブス 不均一物質の平衡について」東海大学出版部(2019年刊)
(2)ヘルムホルツの考察
ヘルムホルツはギブズとは独立に下記の様な考え方で今日“ヘルムホルツの自由エネルギー”といわれる概念に到達します。その思考法は、エネルギー保存則の発見・確立に関して偉大な貢献をしたヘルムホルツならではのものです。我々には前節のギブズの議論よりも物理的な意味が明解で解りやすい。
ヘルムホルツ論文(1882年)『化学過程の熱力学』を引用しておきますので参照されながらお読みください。また、山本義隆「熱力学思想の史的展開」第33章Ⅰ、Ⅱも解り易いのでご覧下さい。
1.ヘルムホルツの考察
ヘルムホルツは、起電力一定の電池の両端子が、“電位差”Eで充電されたきわめて容量の大きいコンデンサーに繋がれているとした。
いま、温度一定のもとで電池内部に電気量dqが流れる化学変化が起こり、その分だけ電池の状態が変化したとする。そのとき、コンデンサーの負極板から正極板へ電気量dqが移動する事になるのだが、コンデンサーの静電エネルギー量がE・dqだけ増大する事になる。
[補足説明]
この当たりは、コンデンサー極板に働く引力による力学的仕事で議論しても同様な結論を導くことができます。例えばフェルミ著「フェルミ熱力学」三省堂§20などを参照。
dqを流すに当たって、電池の温度一定を保つために電池へ出入りした熱量をd’Q(>0:電池への流入、<0:流出)とする。UをTとqの関数である電池の全内部エネルギーU(T,q)とすると、熱力学第一・第二法則から
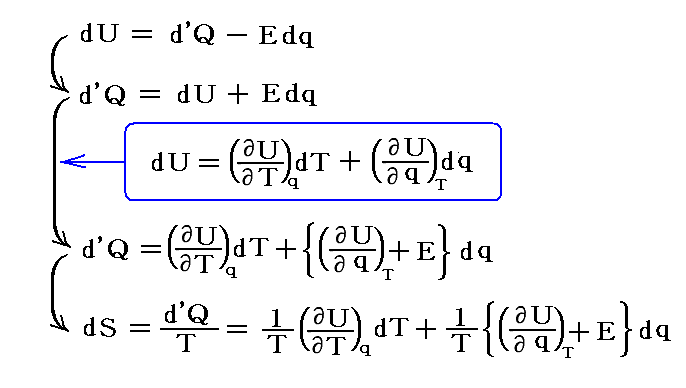
となり、絶対温度Tを積分因子として状態量であるエントロピーSを導入できる。この当たりの議論は別稿「熱力学関数(状態方程式曲面)の性質」1.(2)1.のPdVをEdqに置き換えたものと全く同じですから、そこを参照されたし。
ここで、dSの完全微分性から
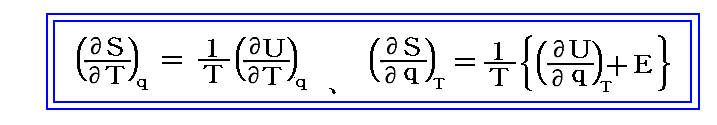
が成り立ち、さらにdSが完全微分であるための必要十分条件から
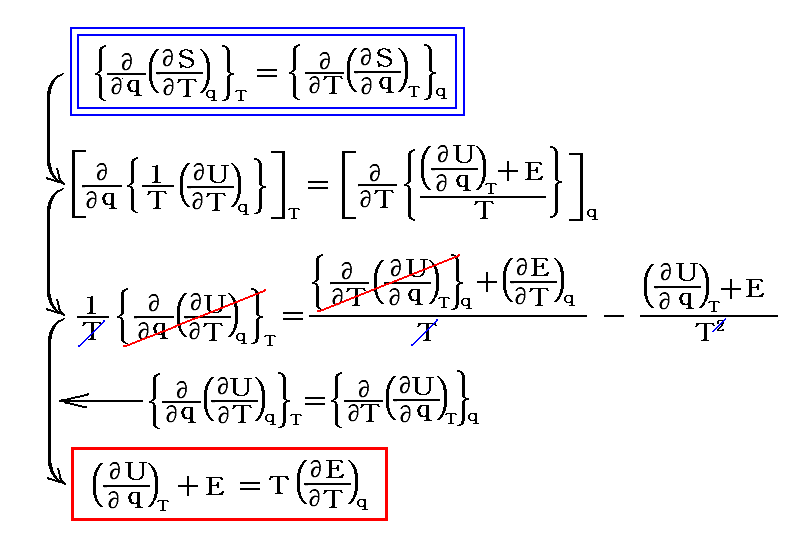
が成り立つ。これは2.(1)2.で説明する“ギブズ・ヘルムホルツの式”に相当します。
故に最初の式は
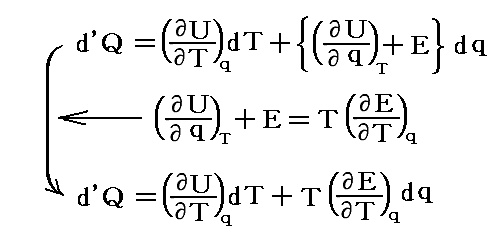
と表される。
dq=0のとき
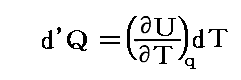
となるので、右辺第一項の (∂U/∂T)q は、dq=0および体積V=一定下に於ける電池系の定積熱容量Cvを表している。体積一定下であることは偏微分添え字に明記されていないが、元々の最初の熱力学法則を表す式に体積変化に伴う仕事の項を含んでいない事から、定積条件も成り立っている場合であると考えなければならない。
また、等温変化dT=0では
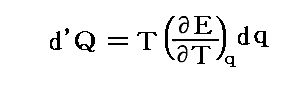
となるので、右辺第二項 T(∂E/∂T)qdq は、電気量dqの移動に際して温度一定、体積一定を保つために電池に供給しなければならない熱量を表している。
2.ヘルムホルツの自由エネルギー
ここで、ヘルムホルツは

によって、内部エネルギーUやエントロピーSと同様にTとqの関数であるF(T,q)なる量を導入する。
なぜこの様な量を導入したのかというと、前述の式が
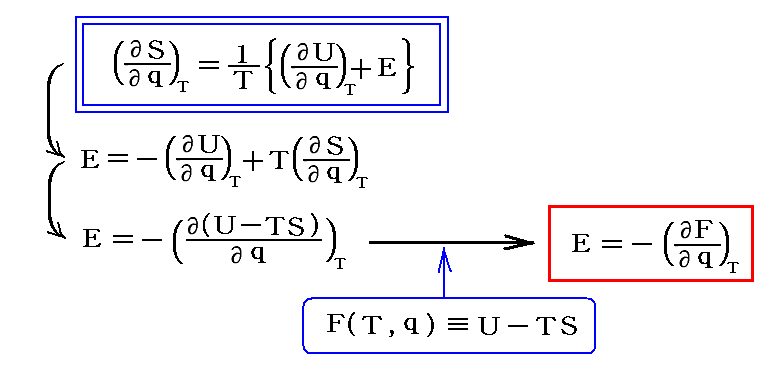
と、表されるからです。つまり、温度一定の元で生じる電気化学的な過程において関数Fはポテンシャルエネルギーの働きをすると考えることができる。今日、このFの事を“ヘルムホルツの自由エネルギー”と言う。
[補足説明]
力学に於いて、力のポテンシャルは以下の様に定義されていた事を思い出されたし。
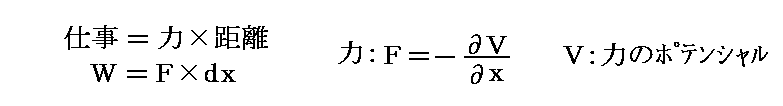
Fの定義式の両辺を絶対温度Tで偏微分すると

などの関係式が得られる。これらは、今日よく知られた関係式ですが、特に電気化学において重要な役割を果たす。
これらの考察から明らかなように状態量F(T,q)の全微分係数は以下のように表される。
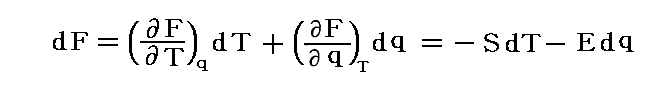
[補足説明]
Edq の代わりに PdV を用いた式は、別稿「ルジャンドル変換とは何か」4.や「熱力学関数(状態方程式曲面)の性質」3.ですでに説明している。
3.U、Sの温度依存性
1.(2)1.の最後で求めたdq=0およぴ体積一定の元での定積熱容量Cvを表す式に、前項の結論を用いると
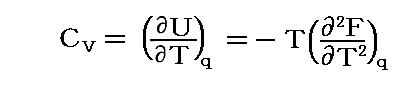
となる。
このとき、TとCvは正の量であるから、-(∂2F/∂T2)qは必ず正の値とならねばならない。そのため
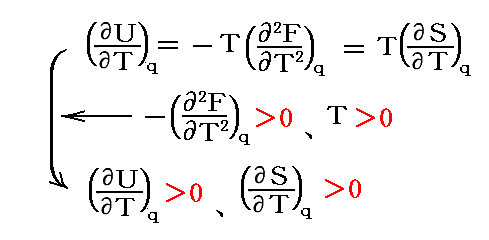
となり、q=一定(dq=0)の元では、S および U は温度Tの単調増加関数となることが解る。
[補足説明]
ここでは、電池反応を考察しているので d’W=Edq を用いて議論しているが、別稿「熱力学関数(状態方程式曲面)の性質」1.(2)1.や2.(2)3.で d’W=PdV の場合にこれらの不等号が成り立つことはすでに論じている。
ここでの不等式は、上記以外の任意のパラメーターに関する仕事 d’W=Xdy に関して成り立つことに注意されたし。
4.現代的な説明
以上の事柄は、別稿「ギブズの自由エネルギー(化学ポテンシャル)とは何か」1.(2)1.のように議論することもできる。
電池反応のように体積変化に伴う仕事は無視(V=一定)できて電気的な仕事と反応熱のみが系の記述に関係してくる場合には、熱力学法則を
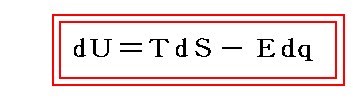
のように書き換えても良い。つまり、系の内部エネルギーの変化分 dU は外界との熱のやり取り d’Q=TdS と、電気的な仕事のやり取り d’W=Edq で変化する。ここで E は、電池の両極の電位差で、 dq は電池反応に伴って回路を流れた電気量です。 Edq の前にマイナス符号がついているのは、外に対しての仕事だから内部エネルギーがその分だけ減少するからです。このとき、 U(S,q)曲面 のq方向の勾配が E なのですから、当然 E=-(∂U/∂q)s は S と q の関数 E(S,q) です。
この様に熱力学法則を書き換えてヘルムホルツの自由エネルギーを
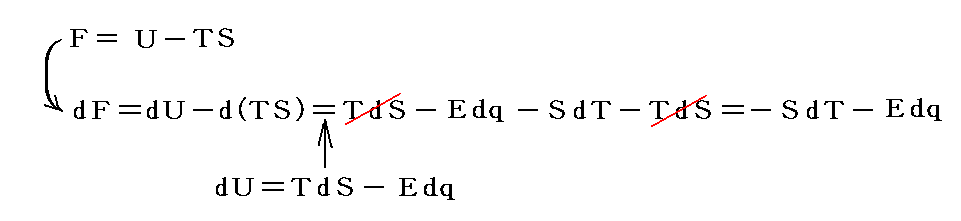
と定義する。そして、そこのグラフを下記のように書き換えると
となる。
これらは、温度T=一定、体積V=一定、そして起電力E=一定のもとで、電池が外部に対して Edq の仕事をしたときには、電池内部(それは様々な相の集合体である)の系全体としてのヘルムホルツの自由エネルギーの変化分に等しいことを表している。すなわち、今のダニエル電池の場合で1モル分の化学反応が生じたときのヘルムホルツの自由エネルギーの変化分ΔFは
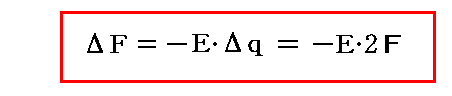
となる。このとき、 PdV の議論における P が (T,V) の関数であったように Edq の E も (T,q) の関数です。つまり E は系の温度が変われば変化します。
このとき、Δ(PV)=0 の場合には、
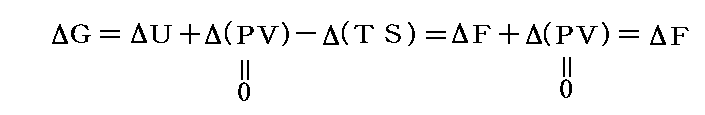
となり、ヘルムホルツの自由エネルギーの変化分ΔFはギブズの自由エネルギーの変化分ΔGと同じだから、結局ギブズの考察と同じになる。
(3)ギブズ流とヘルムホルツ流の違い
別稿「絶対温度とは何か(積分因子とは何か)」8.(2)1.[補足説明2]に於いて、熱力学第一・第二法則の数式表現
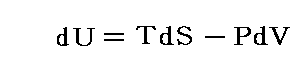
を、さらに一般化して
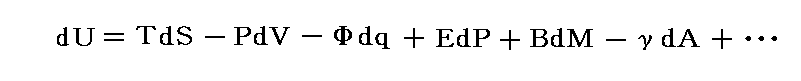
の様に表すことができることを説明しました。これを用いて外界との一般的な仕事のやり取りと系のエネルギー変化を論じる事ができます。それがヘルムホルツ流のやり方です。
そのとき、系が多成分の相や化学種から成るときには、上記の拡張表現をギブズの化学ポテンシャルの中に含ませて論じた方が便利な場合があります。3.(1)の電気化学ポテンシャルを用いた議論はそういったやり方です。ただし、そこでは結局正負の二極間の電位差と外部を流れる電気量による仕事に還元されてしまったので、多成分系に対応したメリットがあまりありませんでしたが、電池の内部構造に立ち入った議論をするときには役に立ちます。
そのように化学ポテンシャルを用いるやり方なら、多成分が関わる相変化や化学反応に対しても関わるエネルギーの種類に応じて化学ポテンシャルを上手に設定すれば、如何様にでも適用する事ができます。
2.起電力と反応熱の関係
(1)ギブズ・ヘルムホルツの関係式
前章の結論はDaniell電池に限らず一般的な電池において成り立つ。
1.温度T=一定、圧力P=一定
1.(1)4.より、T=一定、P=一定の元で1モルの電池反応が生じたときの系全体のギブズの自由エネルギーの変化分をΔG、電池反応に関わるイオンの価数をz、ファラデー定数をFとすると
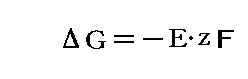
が成り立つ。
このとき、別稿「熱力学関数(状態方程式曲面)の性質」3.(4)で述べたように
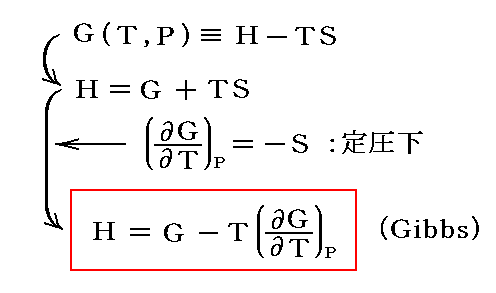
が成り立つ。
1モル当たりについての変化量をΔで表し、これらの結論を用いると
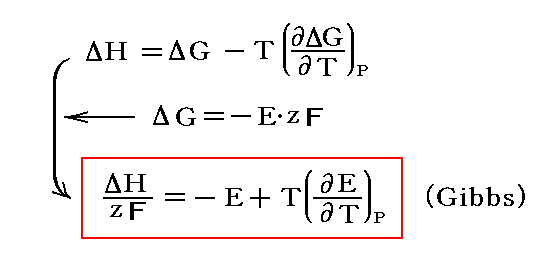
となる。このときΔHは温度T=一定、圧力T=一定の元で1モル分の電池反応が進んだときの反応熱です。
2.温度T=一定、体積V=一定
1.(2)4.から、T=一定、V=一定の元で1モルの電池反応が生じたときのヘルムホルツの自由エネルギーの変化分をΔF、電池反応に関わるイオンの価数をz、ファラデー定数をFとすると
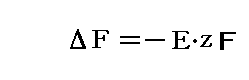
が成り立つ。
このとき、別稿「熱力学関数(状態方程式曲面)の性質」3.(4)で述べたように

が成り立つ。
1モル当たりについての変化量をΔで表し、これらの結論を用いると
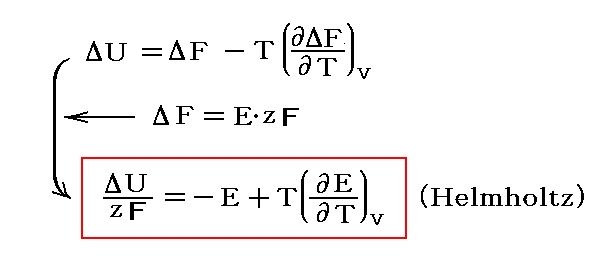
となる。このときΔUは温度T=一定、体積V=一定の元で1モル分の電池反応が進んだときの反応熱です。
ここの議論はヘルムホルツの論文に記されている手順(1.(2)2.で説明した)そのものです。それはまた、ヘルムホルツが論文の最初でエントロピーの完全微分性を用いて求めた式と同じです。1.(2)1.で説明した式の (∂U/∂q)T は、ここの ΔU/zF に他なりません。
[補足説明]
ファントホッフは上記と同じ結論をカルノーサイクルを用いて導いている(1884年)。
それは、別稿「絶対温度とは何か(積分因子とは何か)」6.(2)2.で説明した“カルノーの原理”

の仕事 dW=PdV を dW=Edq に置き換えて論じたものです。すなわち
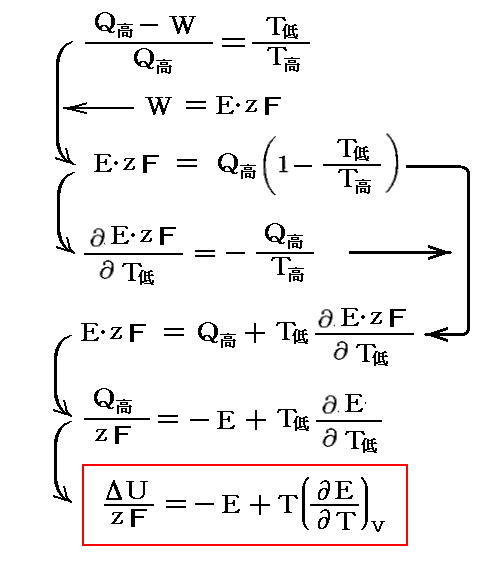
このあたりは山本文献4.p285で紹介されていますのでご覧ください。富永文献3.でも紹介されています。
3.Nernstの着想
これらの式は、ネルンストが“熱力学第三法則”を提案するとき、決定的な役割を果たした。それは、実験によるとそれほど低温でなくても“単純”な公式
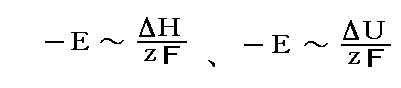
が正しいように見えたからです。
すなわち
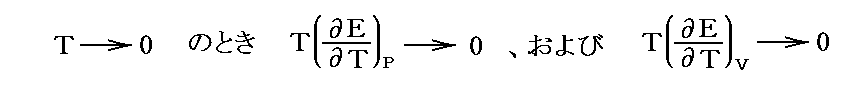
が成り立つように見えて、絶対零度では
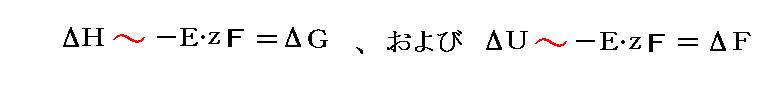
となるように見えた。
このことから、Nernstは、“ΔHとΔG (あるいは ΔUとΔF )が絶対零度で出会うばかりでなく、しかも接していなければならない”と結論した。これが熱力学第三法則になるのですが、このことに関するネルンストとプランクの考察は3.(1)~(3)で説明します。
(2)反応熱と起電力
1.Daniell電池
Daniell電池の構造からして (∂E/∂T)p と (∂E/∂T)v との間に差があるとは考えられない。実際、そのことは観測でも確かめられている。そのとき、Daniell電池の起電力とその温度変化の測定値は
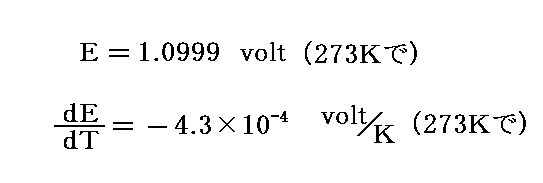
で、反応熱ΔHとΔUに差はない。その共通値を-ΔQと書くことにすると、その実測値は
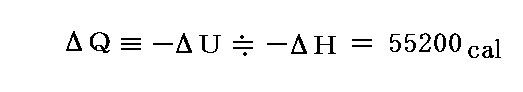
となる発熱反応です。
前述の“ギブズ・ヘルムホツの式”に 起電力E とその温度依存性 (∂E/∂T) の実測値を代入し、z=+2、T=273KとしてΔQを求めると
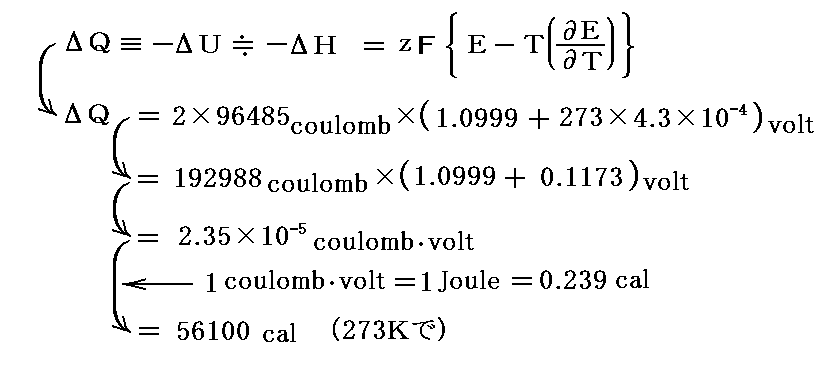
となり、実測値と良く一致する。
2.(1)3.で導いた式に、前述の反応熱の実測値を代入して電池の起電力を計算してみると
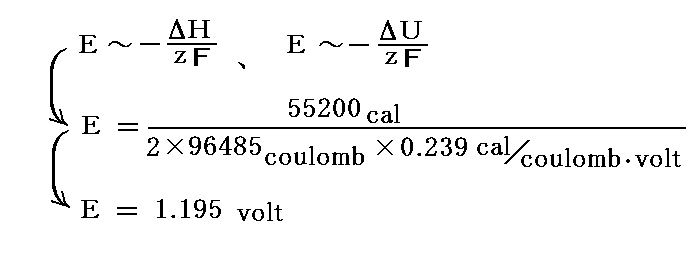
となる。これは起電力の実測値1.0999voltにかなり近い値となる。ただし、ダニエル電池の場合には、T(∂E/∂T)=0.1173とかなり小さいために言えることであって、このことが常に成り立つわけではない。その当たりはヘルムホルツも論文中で注意している。
2.カロメルHg電池
ダニエル電池起電力の温度変化は起電力の大きさに比較して小さいが、以下で述べる電池ではかなり事情がことなる。
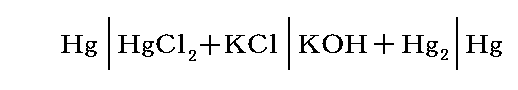
この電池の各実測値は

となる。この場合、起電力の大きさに対して、その温度変化が大きく影響してくる。
前述“ギブズ・ヘルムホツの式”に起電力E、温度依存性(∂E/∂T)の実測値を代入し、z=+2、T=273KとしてΔQを求めると
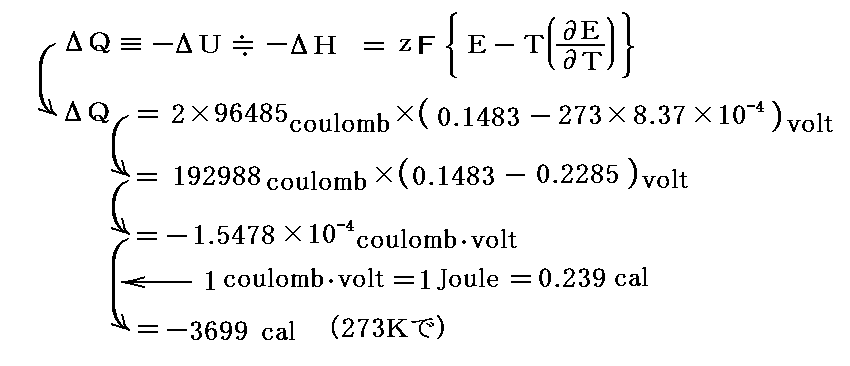
となる。確かに実測値に近い負の反応熱が得られるので、この稿で説明している熱力学的な考察の正しさが実証されていると言える。
3.Weston標準電池
1.(1)2.で述べた電池起電力測定用ポテンシオメーターの標準電池として広く利用されたのがWeston電池です。この電池の起電力Eの温度変化は小さく、また保存がよければ起電力の経年変化は1年あたり数μV以下なので,電位差測定の際に標準電池として広く使用された。特に電磁気学の実用単位を定めるとき、電圧標準原器として長い間用いられた[現在はジョセフソン効果を用いる原器が用いられている]。
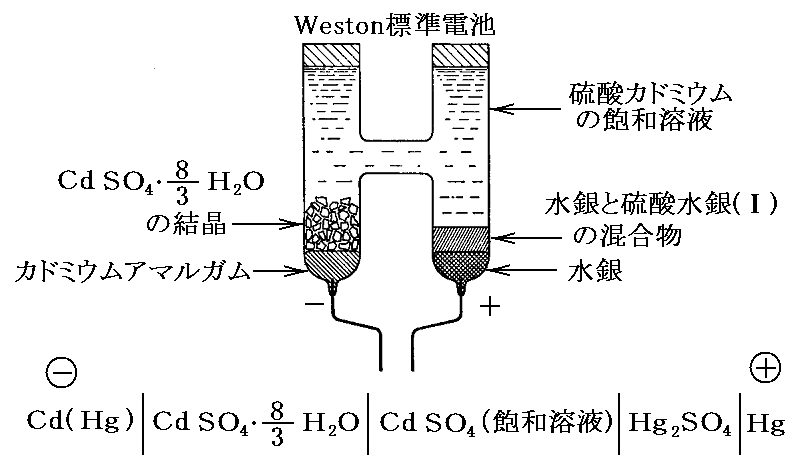
電池反応は
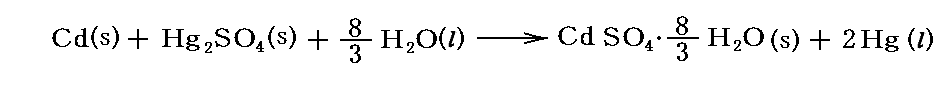
と表される。
起電力の温度依存性は以下の様に表される。ただしtは摂氏(℃)で表した温度です。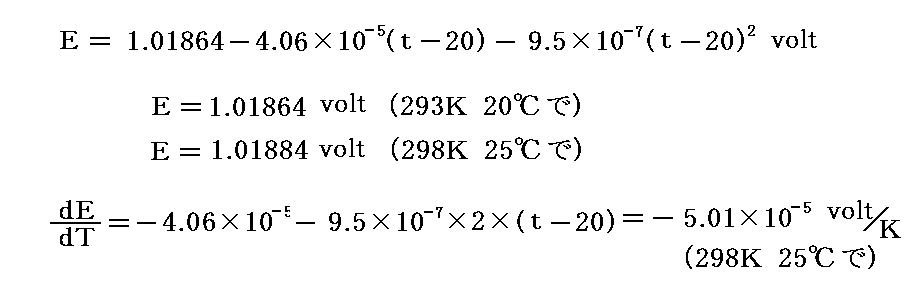
これらのデータから298K(25℃)に於けるΔG、ΔS、ΔH=ΔQを求めると

となる。
(3)基礎方程式の積分
数学的な関係式を使って、2.(1)節の式を変形すると
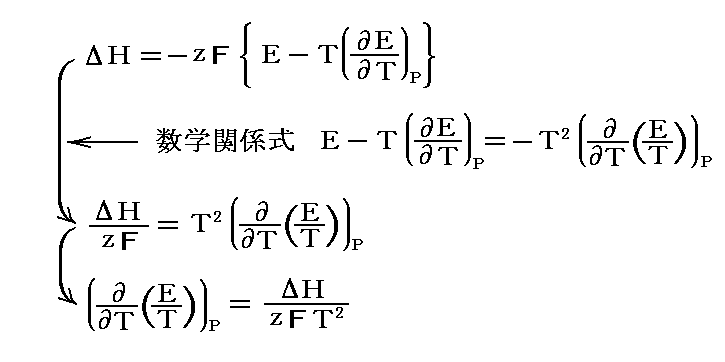
となる。
ΔHを温度によらない部分ΔH0と、温度による部分ΔHTとに分ける。後者はT→0のとき、きわめて急速に0になることが示せる。すなわち
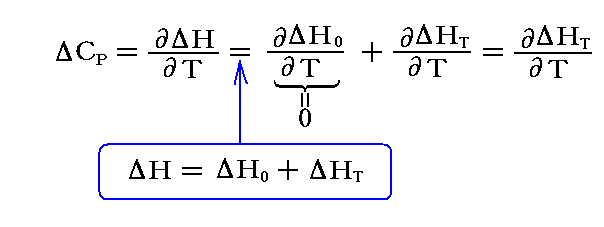
と書けるのだが、3.(3)2.で説明するように“熱力学第三法則”からT→0でΔCp→0になるからΔHTはTよりも速やかに0になる。多くの場合T4に比例する。微分のとき落ちるΔHTの定数部はもともとΔH0に含めてあるから考慮する必要はない。
前式を積分することにより直ちに
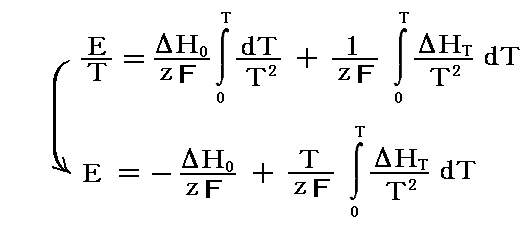
を得る。
この積分で下限を0とすることによって積分定数を正しく選んだことになる。なぜなら、“熱力学第三法則”からT→0KでTS→0であるから
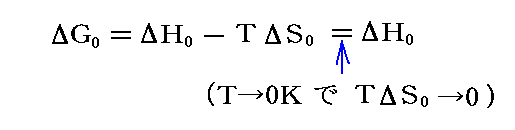
となる。そのため
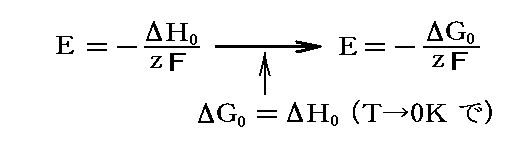
となり、元々のEの定義が成り立っていることが解る。このT→0Kで成り立つべき境界条件(つまり絶対零度での起電力がE=ΔG0/zFとなること)が上記の積分で満足されているから、積分の下限が正しく選ばれている事が解る。
反応熱が温度の関数として測定されていれば、
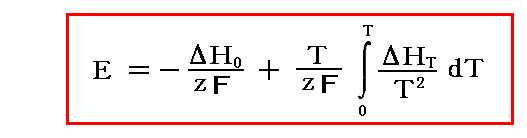
の積分計算により、起電力とその温度依存性が予言できる。
多くの電池に於いて、[反応熱測定値を用いて上記計算から求めた起電力]と[実際の起電力測定値]が様々な温度に於いて比較された。そのとき理論的な予言と実測値はきわめて良い一致を示した。これは熱力学第二および第三法則の正しさをさらに証明したことになる。
[補足説明]
上記は、文献1.§18.FにおけるSommerfeldの説明ですが、今ひとつ解りにくい。
要するに、電池反応に伴う反応熱の温度変化の様子ΔH(T)はCp(T)からも求まる。その時ネルンストの熱定理(T→0でΔS→0)が成り立てば、T→0でΔH(0)=ΔG(0)が成り立つことになり、ギブズ・ヘルムホルツの式を用いてΔH(T)からΔG(T)の温度変化の様子が求まる[別稿3.(2)2.[補足説明1]と[補足説明2]のH(P,S)曲面とG(P,T)曲面の関係を参照]。
一方、1.章で説明したようにΔG(T)は-eFEなのだから電気化学的な起電力の測定値の温度変化からからも求まる。
この両方から求まるΔG(T)を比較してみると、両者は温度が変化しても極めて良い一致が見られた。これはとりもなおさず反応熱のデータからΔG(T)を求める際に、ギブズ・ヘルムホルツの式を適用するとき必要だったネルンストの熱定理が満足されていることを示している。
同じことの説明ですが、山本文献4.第33章ⅣにNernstの著書(1918年)が紹介されています。実際の検証実験については。山本文献4.第33章Ⅳハラの実験(1908年)をご覧ください。同様な説明は文献3.の§7.2にもあります。
3.熱力学第三法則(Nernstの熱定理)
この定理は、第一・第二法則のように熱力学に新しい状態量を導入するものではないが、状態量S、F、G、・・・等を数値的に初めて決定し、実用的にするものです。
本章については、山本文献4.第33章 “ネルンストの定理と熱力学第三法則”Ⅲを最初に読まれることを勧めます。
その後で、Nernstの論文“熱測定からの化学平衡の計算について”(1906年)、およびPlanckの著書「熱力学」第4篇第6章あるいは「理論熱学」第4篇第5章を参照しながら以下の説明をお読み下さい。
(1)Nernstの熱定理の必要性
エントロピー発見・導入の過程を復習[例えは別稿「絶対温度とは何か(積分因子とは何か)」6.(3)]されれば解るように、エントロピーは元々その微分dSによって定義されています。従ってSには本来積分定数S0の不定性が必ず存在する。応用上はほとんどいつもエントロピーの差分のみが問題となるので、そのことは別に困ることではない。
またdU=TdS+PdVで定義される内部エネルギーUについても同様で、その積分定数は不定でした。しかし内部エネルギーもその差分のみが重要で、その絶対的な値が問題になることは無かった。
ところが、状態量 F=U-TS と G=U+PV-TS=H-TS に関してはTSという項が関わっている為にS0T+定数という絶対温度の一次式が不定になる。
そのため絶対温度の異なる状態を扱う場合や化学平衡の条件を立てたりする場合のように、特に状態量 F や G が関係する問題において、これらの状態量の有用性が幻想に成ってしまう。
このあたりは、別稿「熱力学関数(状態方程式曲面)の性質」3.(2)~(4)ですでに説明したところです。こうしてエントロピーの絶対値を求めることが切実な問題となってきた。
このあたりの詳細は 1906年のネルンスト論文の最初の部分 を参照されたし。また、1882年のヘルムホルツ論文のp99 や p101~102 なども参照されたし。
基本的な問題の場合いつもそうであるように、自然は考える限り最も簡単で数学的に最も満足できる答えを与える。実際、M. Planckは“Nernstの熱定理”の最終的な表現として以下のように表した。
温度が絶対零度に近づくと供にエントロピーは、相の状態や圧力やその他の変数の値にかかわらず一定値S0に近づく。S0は0に等しいと置くことができ、そのことに拠ってエントロピーはどんな物質についても絶対的に標準化できる。
こうしてエントロピーの積分形
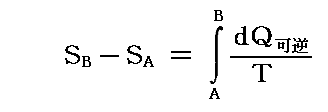
で下限をT=0に一致させS0=0とすれば、熱力学的ポテンシャルFやGの不定さを取り除くことができる。
以下で、Nernst自身が、どのような手順でこの定理を発見したのか概略を説明する。
(2)ネルンストの発見
ネルンストは、彼の電気化学の研究に他の誰よりも効果的に熱力学第二法則を使った。
彼の考察の出発点は2.(1)2.で説明した体積V=一定の過程における電気化学的な反応の反応熱に関する
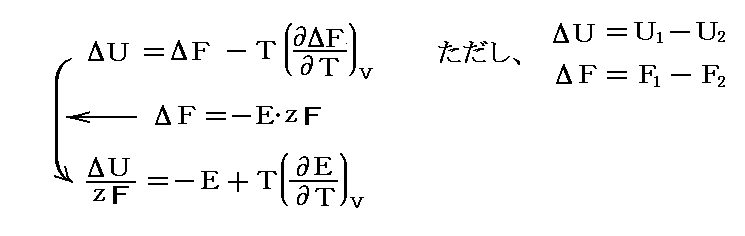
です。ΔUは体積V=一定の過程に於ける反応熱を意味する。
もちろん、たいていの場合反応熱は圧力一定のもとで測定されるので、その場合は2.(1)1.のエンタルピー差ΔHの式
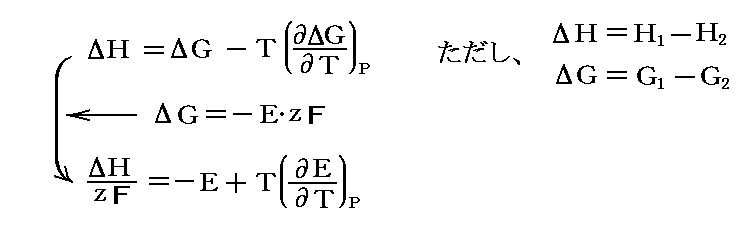
に置き換えなければならない。
ネルンストはこれらを第一法則と第二法則を結び付ける基本方程式と呼び、すべての結論をこれに帰したのですが、彼は、この関係式に関係する反応熱と電池の起電力を精力的に測定した。
その結果2.(1)3.で述べたように、それほど低温でなくても“単純”な公式
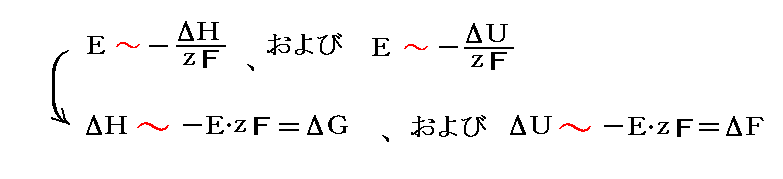
が正しいように見えたのです。そして彼は大胆にも次のように述べた。
経験によるとΔFとΔUの差はしばしばきわめて小さい。この点に関して、電流の引き起こす化学過程に対する式で、ただ固体と濃厚溶液のみが関与するような電池の組み合わせにおいては、ΔFとΔUの違いはきわだって小さい。このことはさらに、いわゆる理想濃厚溶液の挙動でも思い出される。この点は、私にとっていままで長い間注意を引かれる問題であった。
そこで、ここに極限の法則があるのではないかという推測が胸に迫ってくる。それも ΔFとΔU (あるいは ΔGとΔH )は絶対零度で互いに等しい値をとるばかりではなく漸近的にも等しいと思われる。
そうであれば
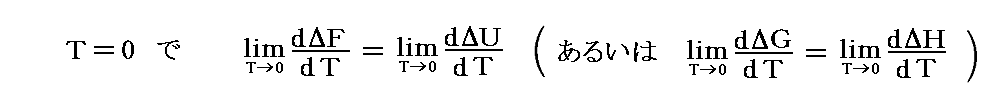
で無ければならない。
[ここはNernst文献7.のp160~161を参照。ネルンストは ΔF を A で、 ΔU を Q で表している]
上記の文章は何を言っているの非常に解りにくいが、上記事柄が T→0 で S→有限 を表していることは、久保文献「統計力学と熱力学の基本法則」5.(5)2.をご覧下さい。
ただし、松浦良平氏が解説されている様に、ネルンスト自身はエントロピーという言葉を使うのを嫌っていた様です。
当時の実験技術では十分に正確なデータも少なく、T→0に外挿できるほど十分に低温での測定は困難でもあったから、これはきわめて大胆な推論であった。ゾンマーフェルトは、“これが、今世紀(20世紀)の古典熱力学が体験した最も天才的な発展の歴史の始まりである。”と言って讃えている。
ネルンストはこの仮説を提出した後、様々な熱力学的関係式を用いて多くの実験的な検証を行った。
[補足説明1]
ネルンストの熱定理を実験的に裏付ける例については、文献2.3.4.7.に幾つか挙げられている。
ここではフェルミの「熱力学」から灰色スズと白色スズの例を引用。このとき、極低温の灰色スズと白色スズの比熱を別々に求めるのは難しくありません。それは灰色スズと白色スズの間の転移速度は低温では極めて小さくなるからです。
ムーア「物理化学」からの引用、例証1.斜方イオウと単斜イオウ,および例証2.平衡定数&反応熱、電池起電力。
例証2.の中で、[平衡定数Kの測定値から求めたΔGと反応熱のデータから求めたΔHから ΔS=-(ΔG-ΔH)/T で計算されるΔS]と[熱力学第三法則の仮説に基づいて低温域の熱容量データから計算したΔS]の比較が紹介されている。両者が一致すれば熱力学第三法則が実験的に検証されたことになる。
このことについては、別稿「平衡状態の熱力学(気体の化学反応)」4.(3)[補足説明3]、同じく5.(2)[補足説明]、同じく5.(3)2.[補足説明2]でも説明していますのでご覧ください。
ここで ΔF=ΔU-TΔS の式に戻ると
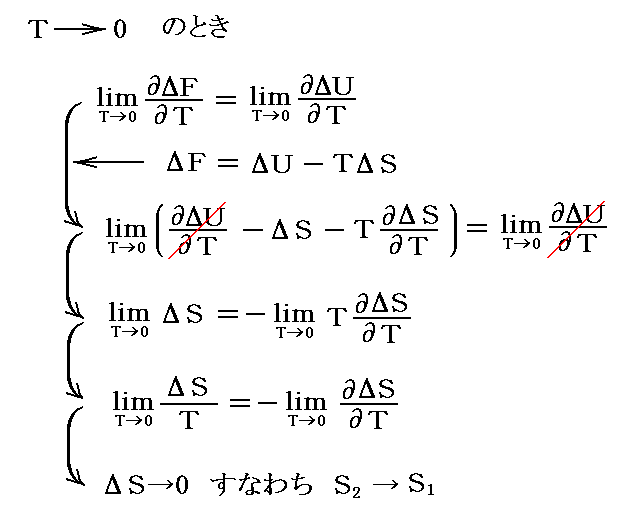
となる。こうしてPlanckの立てた式S→S0と、S0がすべての物質について0に等しい可能性がNernstの式から導かれる。
ただし、S0→0とする理論的な根拠は無くあくまでPlanckの仮説です。プランクがこの仮説を提出した1910年当時このことを支持する理論は黒体輻射のエントロピーがS∝T3からS0→0でなければ成らないことが知られていただけであり、このプランクの仮説も大きな飛躍であった。この仮説を裏付ける幾つかの実験的な事実が解ってきたのは20世紀中頃以降のようです[富永文献3.参照]。
[補足説明2]
純粋な固体状結晶間の反応のエントロピーは絶対零度で0ですが、準安定な平衡にある系(ガラス状態とか固容体)では、T→0でΔS=0が成り立たない場合もあるようです。そのような場合も含めた第三法則の拡張表現については、参考文献7.の松浦良平氏の解説文をお読みください。
いずれにしても、これらの例外は量子統計力学的に理解されるべきもので、第三法則は熱力学のみならず量子統計力学にも基礎を置くものです。この当たりについて、フェルミ「熱力学」§30の解説は興味深いので引用しておきます。また、アブラハム・パイス「神は老獪にして・・・」p527~531もご覧下さい。
[補足説明3]
このあたりの詳しい事情はNernstの1906年論文の日本語訳と、この論文を翻訳された松浦良平氏の解説文をお読みください。
また、Max Planck「熱力学」第6章を引用しておきますのでPlanckの解説をお読みください。
さらに、富永文献3.と山本文献4.に歴史的な発見の過程が解りやすく説明されています。
(3)Nernstの熱定理から導かれること
1.熱膨張係数
別稿「熱力学関数の性質」1.(3)2.で説明したように、ギブズの自由エネルギーに関するMaxwellの関係式と定圧熱膨張係数の定義から
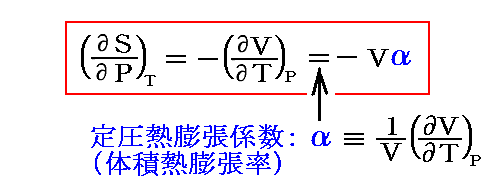
が成り立つ。
T→0に於ける極限値S0がPに拠らないから、左辺はT→0とともに0になる。従って右辺の体積変化も0であり、熱膨張係数αも0となる。
2.圧力係数
別稿「熱力学関数の性質」1.(2)2.で説明したように、ヘルムホルツの自由エネルギーに関するMaxwellの関係式と定積圧力係数の定義から

が成り立つ。
T→0に於ける極限値S0がVに拠らないから、左辺はT→0とともに0になる。従って右辺の圧力変化も0であり、圧力係数αpも0となる。
3.熱容量(比熱)
別稿「熱力学関数の性質」1.(2)1.および1.(3)1.で説明したように、定積熱容量と定圧熱容量は
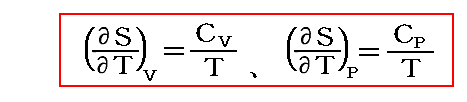
と表される。
これらを積分することにより
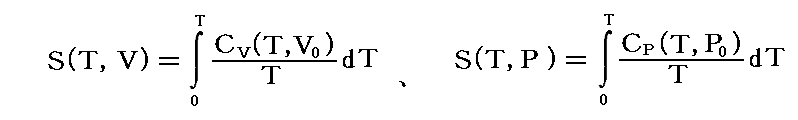
が得られる。
別稿「熱力学関数の性質」1.(2)3.および1.(2)4.の理想気体やファン・デル・ワールス気体の例で見たように、これらの積分に於ける積分定数は、ふつう第一式では体積Vだけの関数が、第二式では圧力Pだけの関数が付け加えられていた。しかし、十分に小さな温度Tの領域においては、これらの積分定数は極限値S0が漸近的にVにもPにも依らないとするNernstの熱定理に反する。そのため、Sの積分表示に於ける下限0の積分値S0は0になるべきであり、体積や圧力に依存した前記の積分定数はすべて0となるべきである。
そうすると、これらの積分から Cv と Cp はT→0で 0 に成らねばならないことが解る。なぜなら、そうでなければ下限T=0で積分が発散してしまうからです。
Nernstの指導の下にドイツの国立研究所で広範な測定が行われ、熱容量(特にCp)が絶対零度に近づくと0に近づいていくことが確かめられた。
どのような形で熱容量(比熱)が0に近づくのかは場合による。弾性体ではT3に比例することがDebyeによって示され、また電子ガスの場合はTに比例する。これらのことは理論的(量子統計力学による)にも実験的にも確かめられている。
[補足説明]
いままでの古典的議論では、理想気体の場合 Cv も Cp も常に一定であるとしたが、理想気体のこの仮定は本来正しくないことになる。
この矛盾は理想気体に対して量子力学的な取り扱いをして初めて解決される。極低温では、フェルミ・ディラック気体あるいはボーズ・アインシュタイン気体の縮退した状態の取り扱いをしなければならない。
4.絶対零度には有限な過程によっては決して到達できず、漸近的に近づけるだけである。
実在気体を冷却するには断熱膨張を用いるが、もっと低温で有効な方法は“断熱消磁法”である。これは1926年にDebyeとGiauqeが提唱し、1933年にGiauqueが実験的に初めて成功した方法です。
与えられた磁場Hによって磁化された塩の状態曲線のS-T図を示す。図中のH=const.のカーブがそれです。そのとき、真空中ならば圧力P=0であり、系の物体が固体塩の場合には体積は重要ではない。
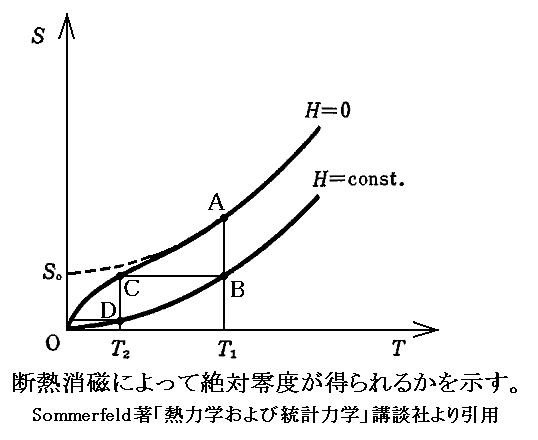
この状態曲線は原点0から出て、Tが増えるにつれ磁場によって揃えられていた磁気双極子の配向がますます乱されるために曲線は温度とともに上昇することを示している。
図には消磁された塩の状態曲線H=0も示してある。この場合は磁気的な配向秩序が全くないため、曲線はH=const.のものより上にある。しかし、これもまたNernstの熱定理によりT→0では原点Oに至る。
この原点Oに近づく曲線の婉曲した特徴的な形は、常時性物質が極めて低温で強磁性体と同じような一種の自発磁化(磁気双極子が一方向に配向する)を持つことに由来している。
いま、初期温度T1のA点に於いて外部から強力な磁場をかけて磁化された状態Bにする。この状態で断熱的に消磁するすると、S=一定の水平線に沿って物質(塩)の状態は消磁された曲線H=0上の状態Cへ移る。図から解るようにT1よりも遙かに低い温度T2に達する。しかしT=0に達することはない。
もしもNernstの熱定理が成り立たず、H=0の曲線がT=0で、0ではない極限値S0(点線で示した位置)を持っていたならば話は別である。このとき図のようにH=const.の状態の初期温度T1を適当に選べば一度の操作で温度T=0が得られてしまう。すなわちH=0状態のS=S0の点に達することができるのである。しかし、Nernstの熱定理が正しい限りその様なことは決して起こらない。
温度T2のC点に於いてさらに磁化を行い状態Dに遷移させて断熱消磁を行う二段消磁の方法でさらに絶対零度に近づくことはできる。
このあたりの詳細は別稿「冷凍・低温技術の歴史」1933年を参照されたし。
さらに、絶対零度に近づくには、“核が持つ磁気の断熱消磁冷却法”がある。この詳細については別稿「冷凍・低温技術の歴史」1956年を参照されたし。
極低温を達成する方法としては、“核磁気断熱消磁冷却法”以外に、“ポメランチュク冷却法”や“希釈冷却法”などがある。それらの詳細については、別稿「希釈冷却法、ポメランチュク冷却法、核磁気冷却法」を参照されたし。
そのとき、Nernstの熱定理が正しい限り、“どのようなテクニックを使って冷却操作を繰り返しても、決して絶対零度に到達することはできなくて、漸近的に近づくことができるだけである。”
これが“熱力学第三法則”のネルンストによる表現です。“絶対温度到達不可能の原理(1912年)”とも言われています。これは絶対零度の深い意味に基づくものです。つまり“絶対零度でゼロになるのはエネルギーでは無くてエントロピーである”ことから導かれるものです。
この法則は、物質の結晶構造の違いや、磁化状態と消磁状態の違いなどの物理的状況の違いにかかわらずT→0KとともにエントロピーSが互いに近づく“ネルンストの熱定理(1906年)”という事実と関連している。それだからこそ、どのような物理的操作を繰り返しても絶対零度に到達する事はできないのです。
これも、limΔS=0から理論的に導かれるものであって、最初に述べた“Planckの表現”(1910年)に含まれる。
(4)物質の“エントロピー”
1.純物質のエントロピー
“熱力学第三法則”に基づいて、任意の温度における純物質のエントロピーを決定する事ができる。例えば、ある物質が一定圧力下で0KからTKまで加熱された場合に次のような変化を行うとする。

この物質のP0=1気圧、T0=298.15Kにおける1モル当たりのエントロピーS(T0,P0)は以下の式に依って計算される。
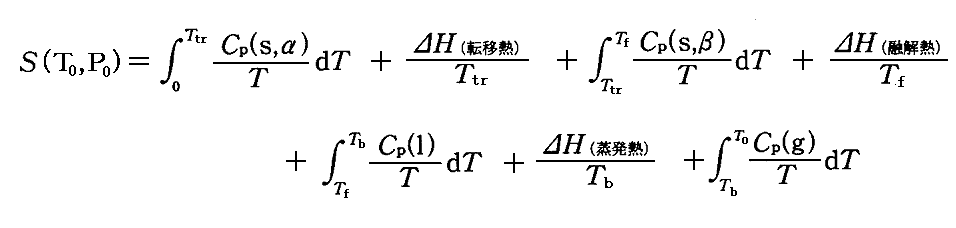
例えば塩化水素HCl(298K,1atm)の計算例についてはこちらを参照。
ここで、極低温までの1気圧下での定圧比熱の測定値が必要です。そのとき実測値の多くは15K程度までしかないが、それ以下の温度はDebye関数を用いて補外されて求められる。
20K~298.15Kの比熱の具体的データや極低温を測る温度計については「化学便覧(基礎編Ⅱ)改訂2版」(丸善刊)§8.3p865~などをご覧下さい。
次に幾つかの融解熱、蒸発熱、転移熱を示す。
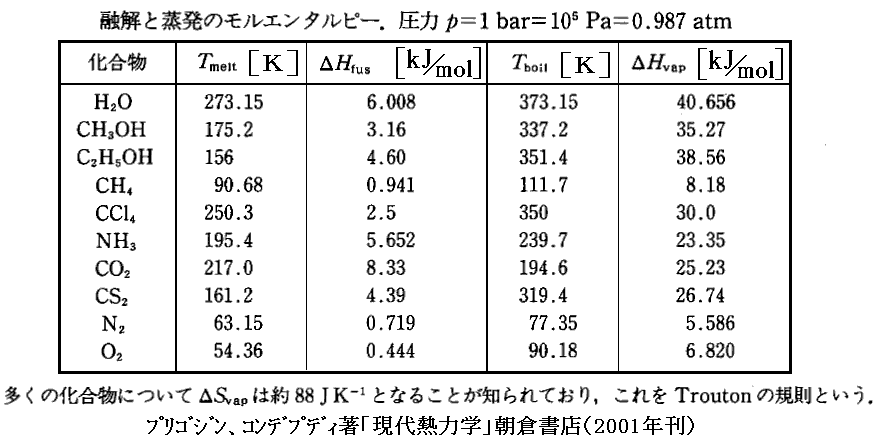
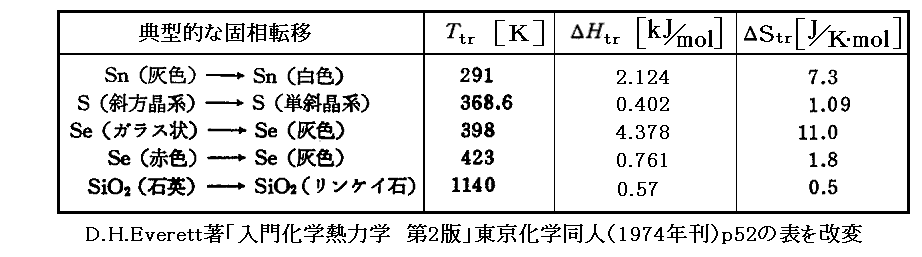
詳しくは「化学便覧(基礎編Ⅱ)改訂2版」(丸善刊)§8.5p910~などをご覧下さい。
このとき一定圧力(1気圧)下に於ける状態変化(0→TKへの温度変化)に伴って系を構成する物質は外界と熱や仕事のやり取りをしているが、エントロピーの変化はそのときの外界との熱のやり取りだけで決まることに注意されたし。なぜなら別稿「熱力学関数(状態方程式曲面)の性質」1.(3)2.で説明したように、上記の変化に伴って生じる物質のエントロピー変化は
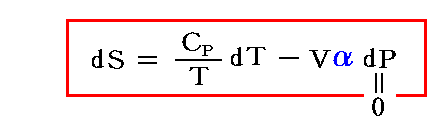
で表せますが、今はdP=0の元での変化だからです。
標準状態(1atm,25℃=298K)における各物質1モル当たりのエントロピーを“標準エントロピー”S゜と呼ぶ。上記の方法で求められた幾つかの物質の標準エントロピーを次に示す。このとき、単体も化合物も、すべての物質について前記の方法で別々にエントロピーの絶対値が求められている事に注意してください。純物質・単体のエントロピー値から計算によって化合物のエントロピー値を求めることはできません。
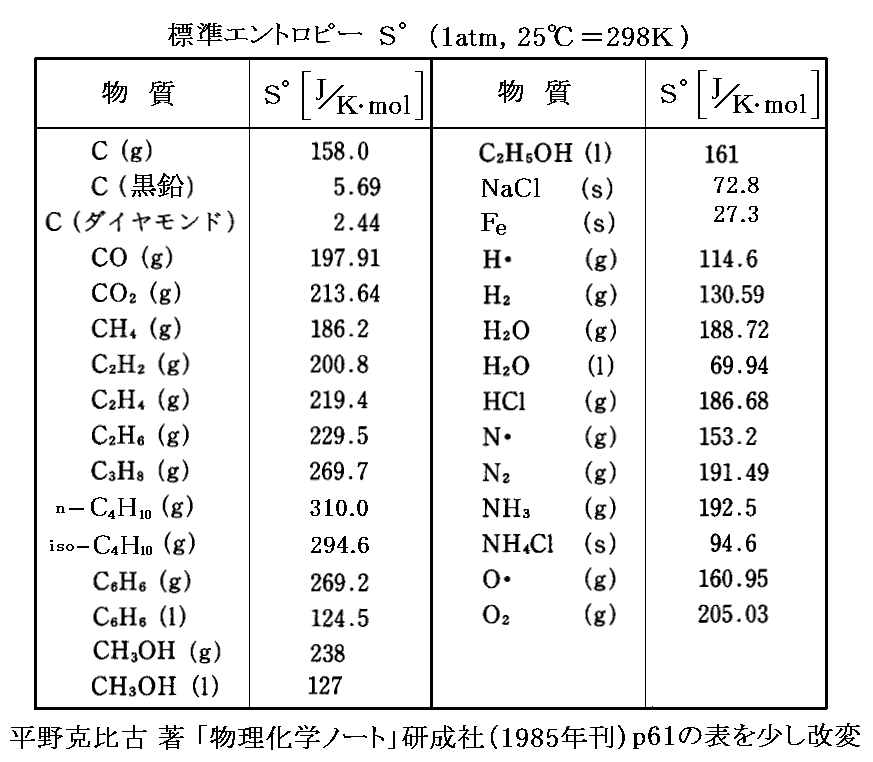
詳しくは「化学便覧(基礎編Ⅱ)改訂2版」(丸善刊)§8.3p866~などをご覧下さい。
[補足説明1]
エントロピーSの値は、“熱力学第三法則”が正しい限り、各温度に於ける比熱を測定することによって絶対的に決定できます。
しかし内部エネルギーUには[原子・分子の運動エネルギー]と供に[原子・分子間力に伴う位置エネルギー]も含まれています。運動エネルギーの部分は絶対温度T→0とともに0に成ると見なせますが、位置エネルギーを0とする絶対的な基準はありません。そのためエネルギーに関してはその絶対値を定める方法はありません。
だから、内部エネルギーUにTSやPVを引いたり加えたりして定義された量であるH、Gについても、内部エネルギーの基準の取り方に依存しますから、状態変化に伴う相対的なエネルギー差しか定めることはできません。
[補足説明2]
そのとき、化学ではどうしているかと言うと、標準状態[0℃(=298.15K)、1atm(=1.013×105Pa)]で安定な単体の1モルが持つエネルギー値[HとGの値]を“0”としている。
このとき、イオンの場合も含めるには、さらに希薄水溶液中の水素イオンH+(aq)の25℃における生成熱を“0”と置くという人為的な仮定の追加指定が必要です。
そのときG=H-TSですが、単体の純物質については、 標準エンタルピーΔHf゜ と 標準ギブズの自由エネルギーΔGf゜ はどちらも同じに“0”としています。
他の任意の圧力や温度におけるエネルギー値は、その状態変化に伴い外界とやり取りする熱や仕事の量(比熱や膨張係数などのデータ)から計算できる。
様々な化合物のエンタルピー値、自由エネルギー値というのは、上記の単体・純物質のエネルギー値“0”を基準にしたときに、化学反応によって生成した化合物の標準状態でのエネルギー値の相対的な差分でしかありません。
そのため“標準生成エンタルピー”ΔHf゜とか“標準生成自由エネルギー”ΔGf゜というふうに“生成”という言葉を付けています。さらに、生成を強調する“添え字 f”と、相対的変化量であることを強調する“Δ”を付けて表現されます。右肩の“゜”は、標準状態に於ける値であることを示している。添え字のfはformation(形成されたもの)の意味です。
化合物の“標準生成エンタルピー”ΔHf゜は単体からその化合物を生成する化学反応の反応熱データから決定できる。その具体的な方法は別稿「反応熱と熱化学方程式」5.をご覧下さい。
化合物の“標準生成自由エネルギー”ΔGf゜は、たとえ同じ標準状態でもΔHf゜とは異なった値になります。化合物を形成するときに外界と熱量のやり取りをしているのですから、両者が異なるのは当然です。
化合物の標準生成自由エネルギー値ΔGf゜は、ΔGf゜=ΔHf゜-TΔS゜により同じ化合物の標準生成エンタルピーΔHf゜からTΔS゜を引いて求めます。ΔS゜は単体から化合物を作るときの反応物と生成物の“標準(絶対)エントロピー”S゜値の加算の差ΔS゜から計算されます。そしてTに298.15K(25℃の絶対温度)を代入して計算すればよい。
この当たりを H2+1/2O2→H2O と 1/2N2+3/2H2→NH3 を例にして計算してみる。3.(2)1.で引用したデータ表を用いるとΔS゜の値は次項で計算するようにそれぞれ-0.163kJ/K・molと-0.099kJ/K・molとなる。それぞれを298.15倍した-48.6kJ/K・molと-29.5kJ/K・molをΔHf゜から差し引くと同じ欄のΔGf゜の値になることが解る。詳しくは4.(2)2.参照。
このとき、エントロピーはエネルギーとは全く異なる(次元を持つ)状態量ですから、反応物と生成物の標準状態でのエントロピー値を前記の方法でそれぞれ別々に測定して絶対的な値を求めておく必要があります。
[補足説明3]
物質のエントロピー値は必ずS>0の正値ですが、エネルギー値は正になる場合も負になる場合もあります。
幾つかの物質の標準生成自由エネルギー・絶対エントロピーのデータ表を引用しておきますので、ご覧ください。
単体の標準生成エネルギー値は、ΔHf゜もΔGf゜も“0”となっている。また、絶対エントロピーS゜は単体の標準状態でも“0でないある値”を持っていることに注意されたし。
エントロピー値は状態に付随した絶対的な値ですが、エネルギー値は状態変化に伴う相対的な変化量です。
そうであっても、3.(1)で述べたFやGに現れていた S0T+定数という絶対温度の一次式の不定性の不都合 は解決されています。
2.化学反応に伴うエントロピー変化
標準状態での化学反応に伴うエントロピー変化は生成物と反応物の標準状態での“標準(絶対)エントロピー”S゜(“絶対”という言葉と、ここでは“Δ”や“f”が付いていないことに注意)の差より求めることができる。
例えば、単体から水を生成する反応
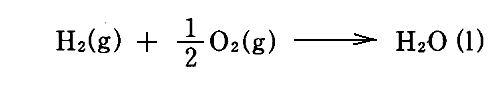
に伴う“標準エントロピー変化”ΔS゜(“変化”という言葉と“Δ”が付いている事に注意)は
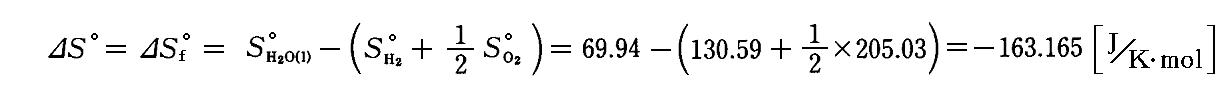
となる。ここでの場合は単体から作る生成反応での値だから、“標準生成エントロピー”ΔSf゜(“生成”という言葉と“Δ”と“f”を付ける)と言うこともある。
この値が負である事は標準状態では、生成物の方が反応物よりも秩序性がある事を示している。すなわち、水素1分子と酸素1/2分子が水1分子にまとまり、さらにそれが液体に凝縮(水は標準状態で液体)したから、分子の乱雑度が減ったのである。
もちろんこのとき、化学反応に伴って系は外界と熱や仕事のやり取りをしています。それらの変化が生じていることを含めた上での反応物と生成物を標準状態で比べたときのエントロピー変化です。
同様に1molのアンモニアが水素と窒素から25℃に於いて生成するときの“標準生成エントロピー”ΔSf゜は
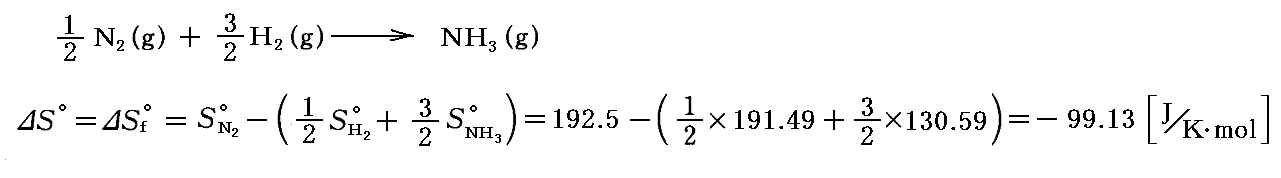
となる。この場合は気体の分子数が減少して乱雑度が減少したことに対応している。
この反応は完全に進行する事はなく平衡状態で止まりますが、完全に変化したとしてのエントロピー変化です。
[補足説明4]
前項[補足説明2]で注意したように、これらの“標準エントロピー変化”ΔS゜(反応が単体からの生成反応ならば“標準生成エントロピー”ΔSf゜と言う場合もある)を用いるとH2OとNH3の“標準生成自由エネルギー”ΔGf゜を“標準生成エンタルピー”ΔHf゜から求めることができる。
[補足説明5]
任意の化学反応に伴う“標準エントロピーの変化”ΔS゜(単体からの生成反応ならば“標準生成エントロピー”ΔSf゜と言ったもの)も同様に求める事ができる。
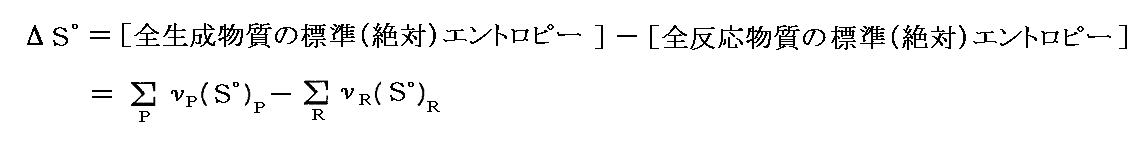
ここでνRやνPは化学反応を表す化学量論的な反応物と生成物の係数です。これは、後で説明する“標準エンタルピーの変化”ΔH゜や“標準ギブスの自由エネルギーの変化”ΔG゜を求めるのと同様な考え方です。ただし、用いるのが標準生成エントロピーΔHf゜や標準生成ギブズの自由エネルギーΔGf゜ではなくて、標準(絶対)エントロピーS゜であることに注意してください。
例として標準状態(1atm,25℃)における以下の反応で2molの一酸化炭素CO生成するときの“標準エントロピーの変化”ΔS゜を求めてみる。データ表から反応物、生成物の“標準(絶対)エントロピー”S゜の値を読み取って
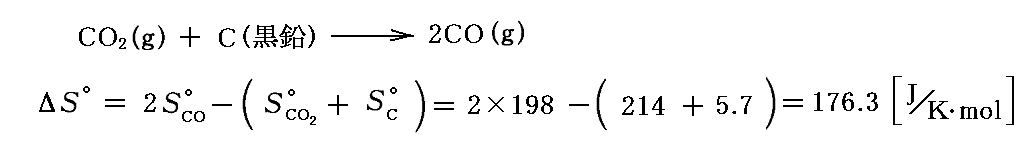
となる。この場合は気体の分子数が増えて乱雑度が増大したことに対応している。
これは上記の反応が完全に遂行されたと仮定してのエントロピー変化ですが、実際に標準状態でこの反応が実際に生じるかどうかはエントロピー値の変化だけからは解らない。あとで説明する ギブズの自由エネルギーの変化 の知識が必要です。
4.物質のエントロピー、エンタルピー、ギブズの自由エネルギー
(1)任意の温度・圧力に於ける物質の“エントロピー”
標準状態での“標準エントロピー”S゜が解っているとき、任意の温度・圧力に於ける物質のエントロピー値を求める。
1.液体・固体のエントロピー値
別稿「熱力学関数(状態方程式曲面)の性質」1.(3)2.で説明したように、上記の変化に伴って生じる物質のエントロピー変化は
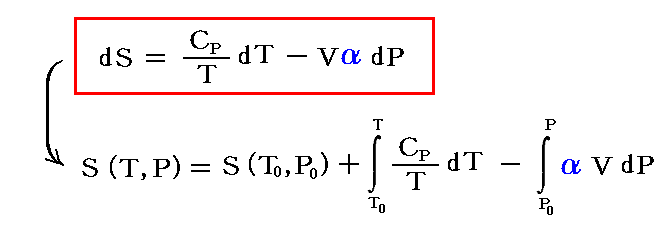
で表せます。ここでS(T0,P0)は“熱力学第三法則”から求まる標準状態に於ける“標準エントロピー”S゜です。
今1モルの物質を考えているのでCpは定圧モル比熱、Vは1モルの物質が温度T、圧力Pに於いて占める体積、αは“定圧熱膨張係数”(体積熱膨張率)α=(∂V/∂T)p/V です。一般に Cp 、 V 、α はすべて (T,P) の関数ですから、実測によって求めておく必要があります。
例えば水の場合、V=1.8×10-6m3/mol 、α=2.1×10-4/K なので、P=10×105Pa~10atm で αVP~3.6×10-3J/Kmol となります。一方 Cp=約75J/Kmol です。また、標準状態における“標準エントロピー”S゜=S(T0,P0)は約70J/Kmolです。そのため液体や固体の場合上記積分の第三項は第二項に比べると重要ではない。
一般に固体や液体のCpの圧力による変化はほとんどないので、任意の温度・圧力におけるエントロピー値は、
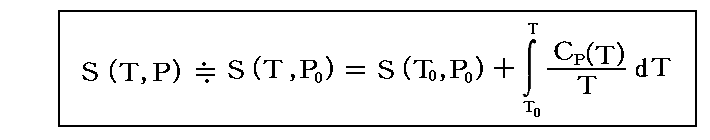
によって求めることができます。
[補足説明1]
別稿「熱力学関数(状態方程式曲面)の性質」3.(2)3.で説明した体積膨張率αや等温圧縮率κ’を用いると、体積変化の様子は次式で表される。
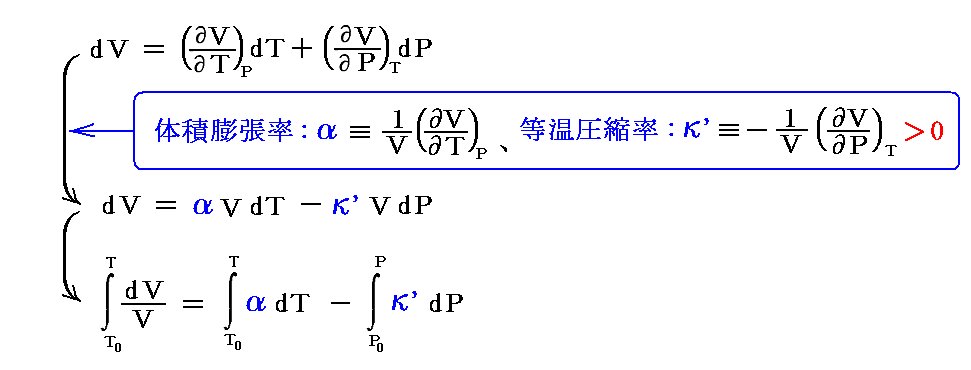
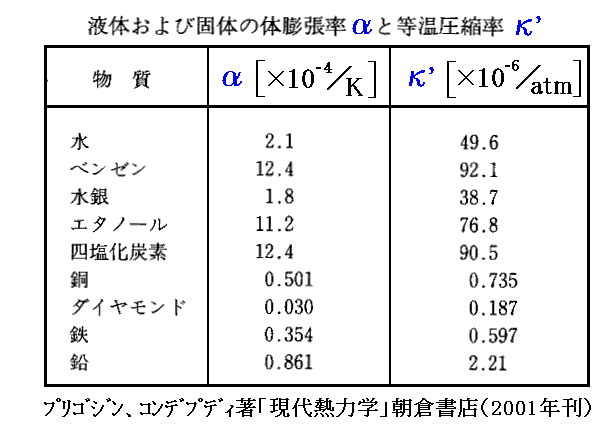
このとき、液体や固体の場合は体積は分子の大きさと分子間力できめられており、TやPが変化してもV(T,P)が大きく変化する事はなく、固体や液体のαやκ’の値は一般に小さな値です。下表に示すように、液体ではα=10-3~10-4/K 、κ’~10-5/atm 程度、固体でα=10-5~10-6/K 、κ’=10-6~10-7/atm 程度です。
そのためαやκ’の値は、100K程度の温度変化、50atm程度の圧力変化ではほとんど変化しないと見なせて積分の外に出せて
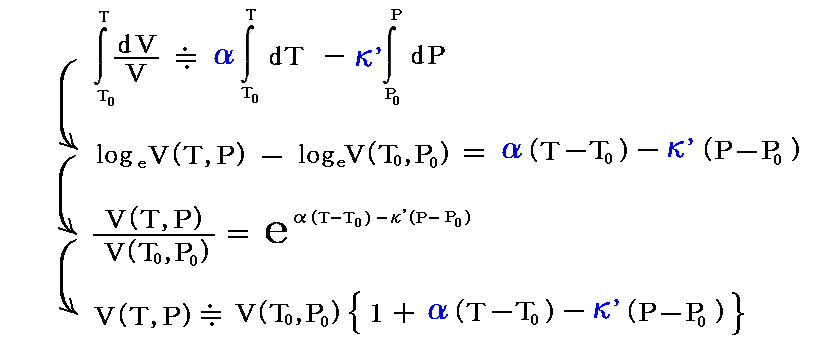
となる。上記の積分の精度を上げるにはこれらの式とα、κ’の実測値を用いて積分する。
2.気体のエントロピー値
気体の場合、別稿「熱力学関数(状態方程式曲面)の性質」1.(2)2.や1.(3)2.で説明した式を用いればよい。
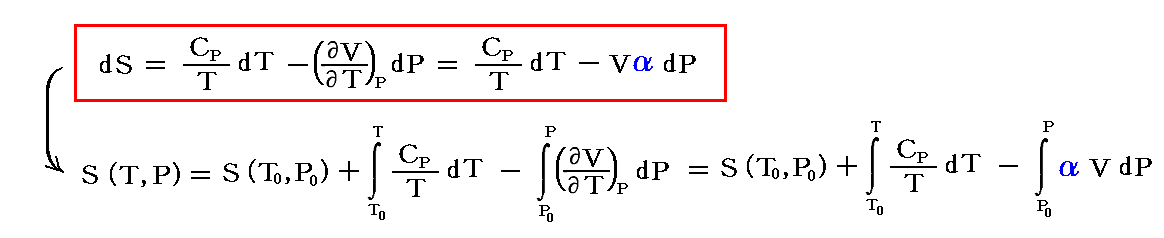
これから明らかなように、一般的に温度が高い状態はエントロピーは大きくなる。またP>P0の圧縮された状態ではエントロピーが減少します。また、
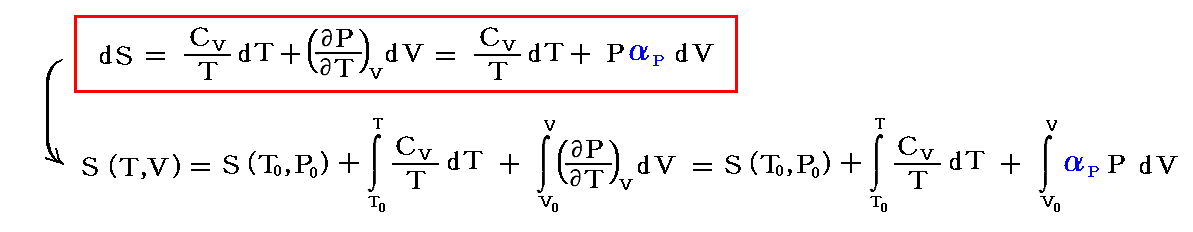
これから、V>V0の膨張した状態ではエントロピーが増大していることが解る。
今は1モルの物質を考えているのでCpは定圧モル比熱、Cvは定積モル比熱です。、α=(∂V/∂T)p/V は“定圧熱膨張係数” 、αp=(∂P/∂T)v/P は“定積圧力係数”です。これらは一般に温度と圧力(体積)の関数で実測値を用いる必要がある。この当たりは別稿4-4-3の説明も参照されたし。
“理想気体”の近似PV=nRTが使える場合には、別稿「熱力学関数(状態方程式曲面)の性質」1.(2)3.で説明した様にn=1のとき (∂V/∂T)v=R/P であり、 Cpは一定 と置けるので、積分は直ちに実施できる。
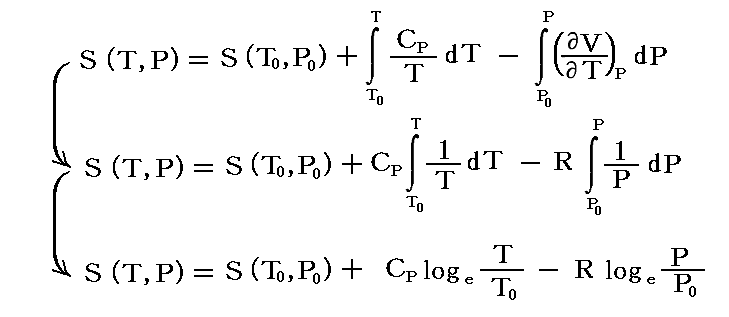
あるいは (∂P/∂T)v=R/V であり、 Cvは一定 と置けるので、
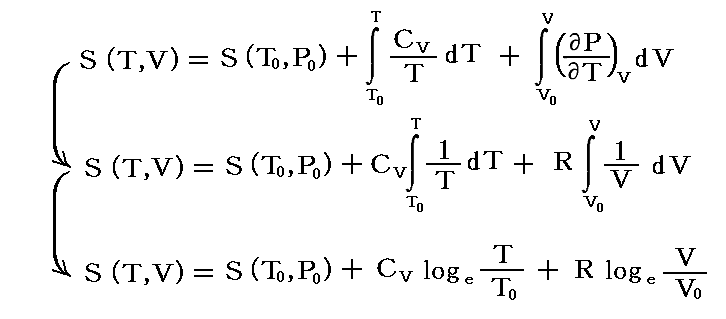
となる。これらのグラフのおよその形は別稿6.(4)3.を参照されてください。
下表は、幾つかの物質の標準状態(1atm,298.15K)に於けるモル熱容量 CP と Cv の値です。(温度,圧力)が標準状態に近い場合はこれらの値を用いた理想気体近似で計算できる。
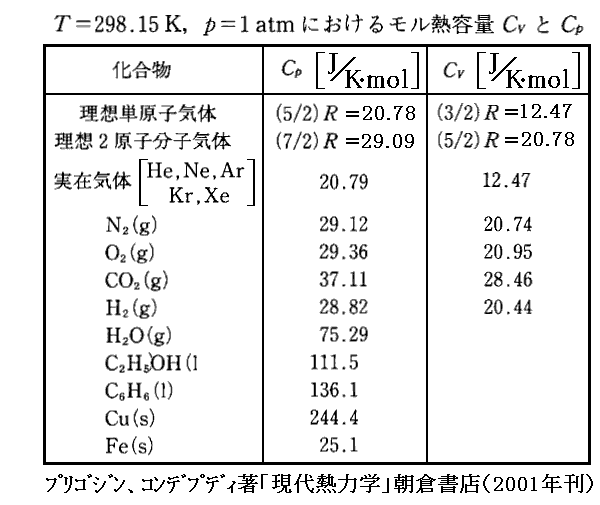
理想気体近似が使えない場合には、以下に述べる実在気体の状態方程式や、Cp(T)、Cv(T)の実測値を用いて積分を実施する。
そのとき、エントロピーは状態量だから、(T0,P0)から(T,P)へ変化したときのエントロピー差ΔS=S(T,P)-S(T0,P0)は、その積分経路に依存しない。そのため被積分関数のデータが存在する経路に沿って積分すればよい。
例えば圧力P0におけるCp(T)のデータと、温度Tに於けるV(T,P)のデータがあれば、最初にP=P0の等圧線Ⅰに沿って積分し、次にTの等温線Ⅱ’に沿って積分すればよい。データが存在するならば、等温線Ⅱ→等圧線Ⅰ’と積分しても良いし、右図のようにV-T平面上の経路に沿って積分することも可能です。
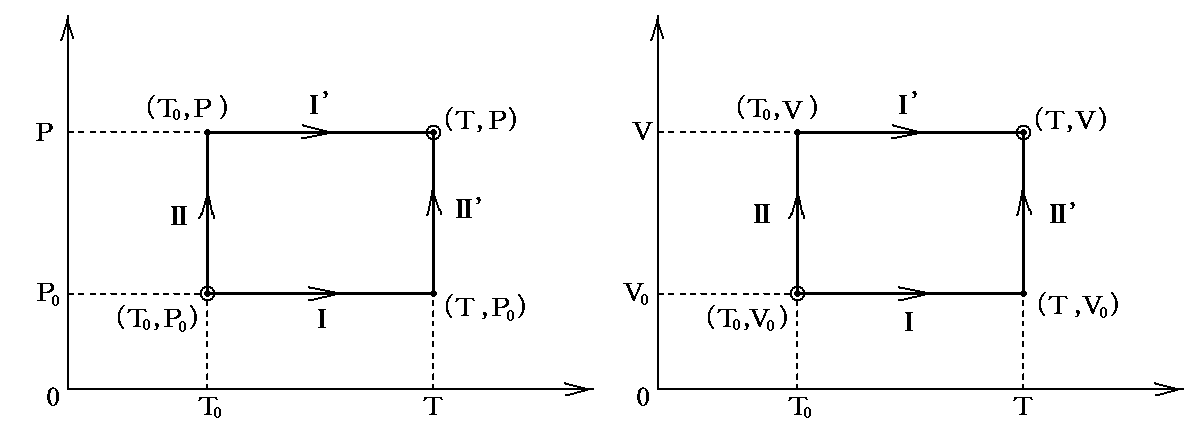
[補足説明2]
一般にCp(T,P0)の温度依存性は小さく、実験式
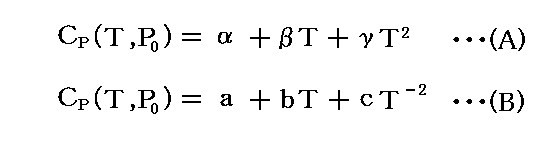
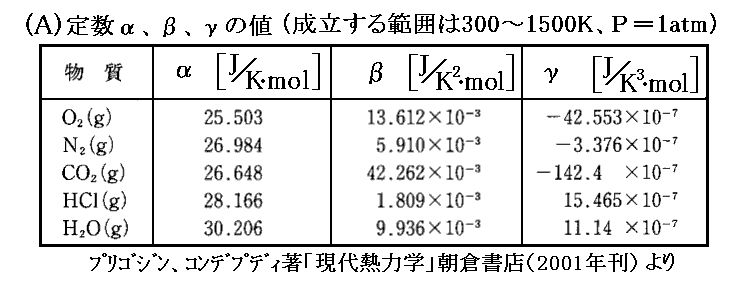
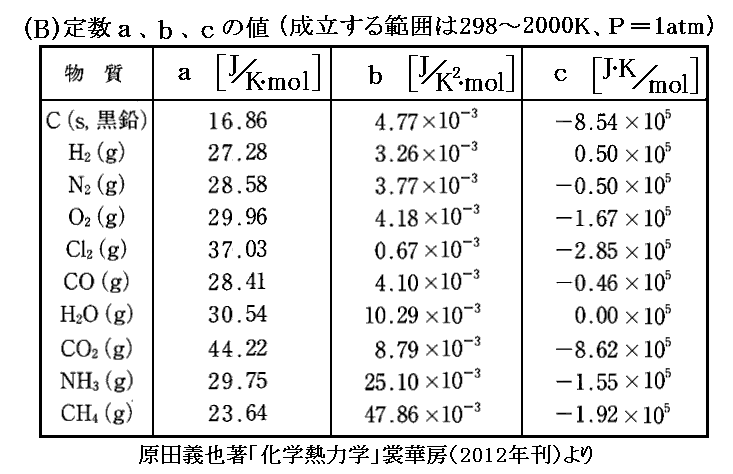
などで与えられる。これらの式のα、β、γやa、b、cは測定値に合うように調整されている。例えば1atmでのCp(T)の温度依存性は
となる。もっと詳しくは「化学便覧(基礎編Ⅱ)改訂2版」(丸善刊)§8.4p871~などをご覧下さい。
前記の積分にはこれらの値を適用したCp(T,P0)を利用すればよい。
[補足説明3]
P(T)は1モルの物質が温度Tで示す圧力ですが、ファン・デル・ワールス気体の場合には
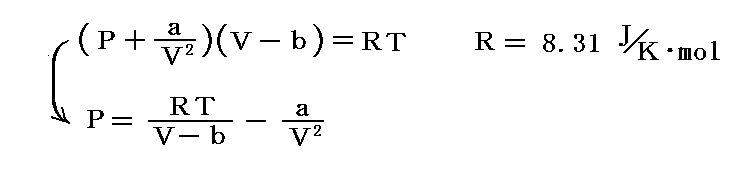
と表される。ファン・デル・ワールス係数の例はこちら。
実在気体の状態方程式は、一般的に
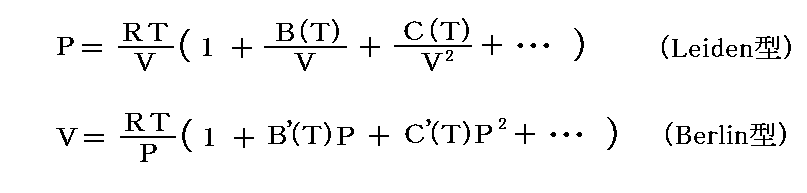
の様な級数で表すことができる。
この様な表示を“ビリアル(virial)展開”といい、 B(T)、C(T)、・・・ や B’(T)、C’(T)、・・・ は “ビリアル係数” と呼ばれている[“virial”の語源はラテン語の“vis(力 ちから)”]。
これらの係数は分子間ポテンシャルエネルギーの形に関係する温度だけの関数で、測定によって求めることができる。ビリアル係数は温度だけの関数だから、等温線ごとにB、C、・・・やB’、C’、・・・などを決定してP-V曲線を描き、それらを温度座標に沿って並べれば状態方程式曲面が得られる。
ちなみに B(T)、C(T) と B’(T)、C’(T) は以下の関係にある。
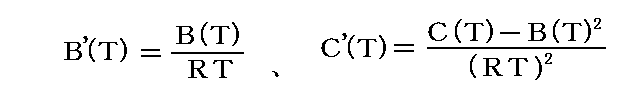
さら B(T)、C(T) と ファン・デル・ワールス係数a、b は以下の関係にある。
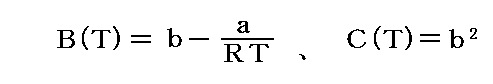
水素1molが1atm、25℃で持つ標準(絶対)エントロピー値は S゜=130.6[J/K・mol] であるが、これらから例えば100℃、100atmにおいて水素1molが持つエントロピーを計算してみる。
まず、1atmにおける定圧モル熱容量Cp=27.28+3.26×10-3T+0.5×105T-2[J/K・mol] のデータを用いて S(298,1atm)→S(398,1atm) の変化を計算をする。
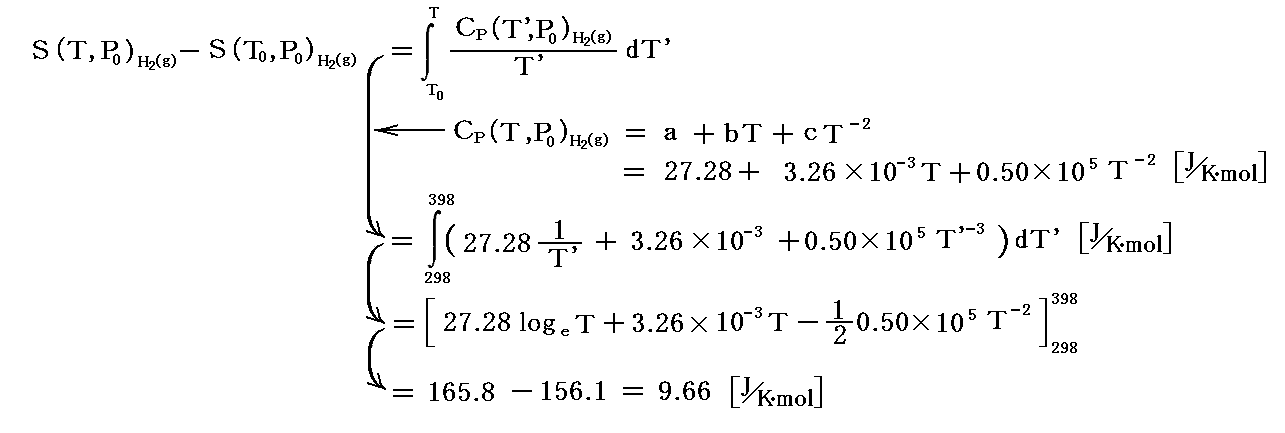
次に、100℃=398Kにおいて理想気体近似を用いて S(398,1atm)→S(398,100atm) の変化を計算する。
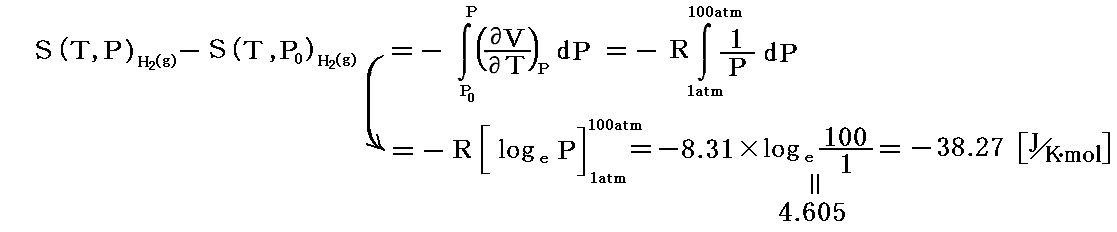
これらの値を用いると
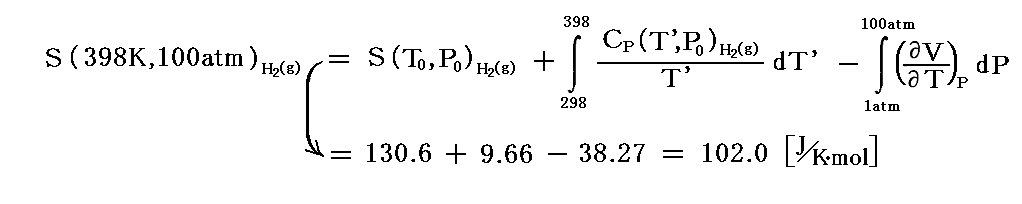
となる。
(2)標準状態に於ける物質の“エンタルピー”と“ギブズの自由エネルギー”
1.標準生成エンタルピー
エンタルピーについては3.(4)1.[補足説明2]で説明したように、絶対的な値を求めることはできません。そのため“化合物”の標準状態におけるエンタルピーΔHf゜は、標準状態[0℃(=298.15K)、1atm(=1.013×105Pa)]で安定な“単体”の1モルが持つエンタルピーを“0”として、それらの単体から、問題の化合物が作られるときの反応熱によって定める。その具体的な手順は別稿「反応熱と熱化学方程式」5.を参照されたし。
そうして計算される、化合物が標準状態で持つエンタルピーを、“標準生成エンタルピー”ΔHf゜と呼ぶ。
例えば、水の場合は直接燃焼させて、反応前と反応後を標準状態に保ったとき系から出入りする熱量を測定して
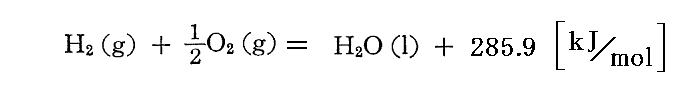
が得られる。
例えばアンモニアでは、窒素と水素から合成されるアンモニアは可逆反応だから反応熱の直接測定は出来ないが、測定可能な水素とアンモニアの燃焼熱から求まる。アンモニアは空気中で燃えないが、純粋酸素中では黄色い炎を上げて燃えて窒素と水になる。それらの反応熱は測定できるから以下のように組み合わせればよい。
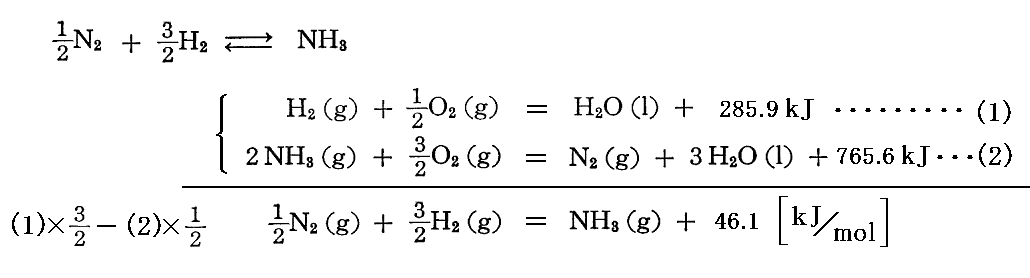
その様にして求められた “標準生成エンタルピー”ΔHf゜ 、 “標準生成自由エネルギー”ΔGf゜ 、 “標準(絶対)エントロピー”S゜ の値を幾つか示す。単体のΔHf゜やΔGf゜は“0”であるが、絶対エントロピーS゜は“0でないある値”を持つことに注意されたし。
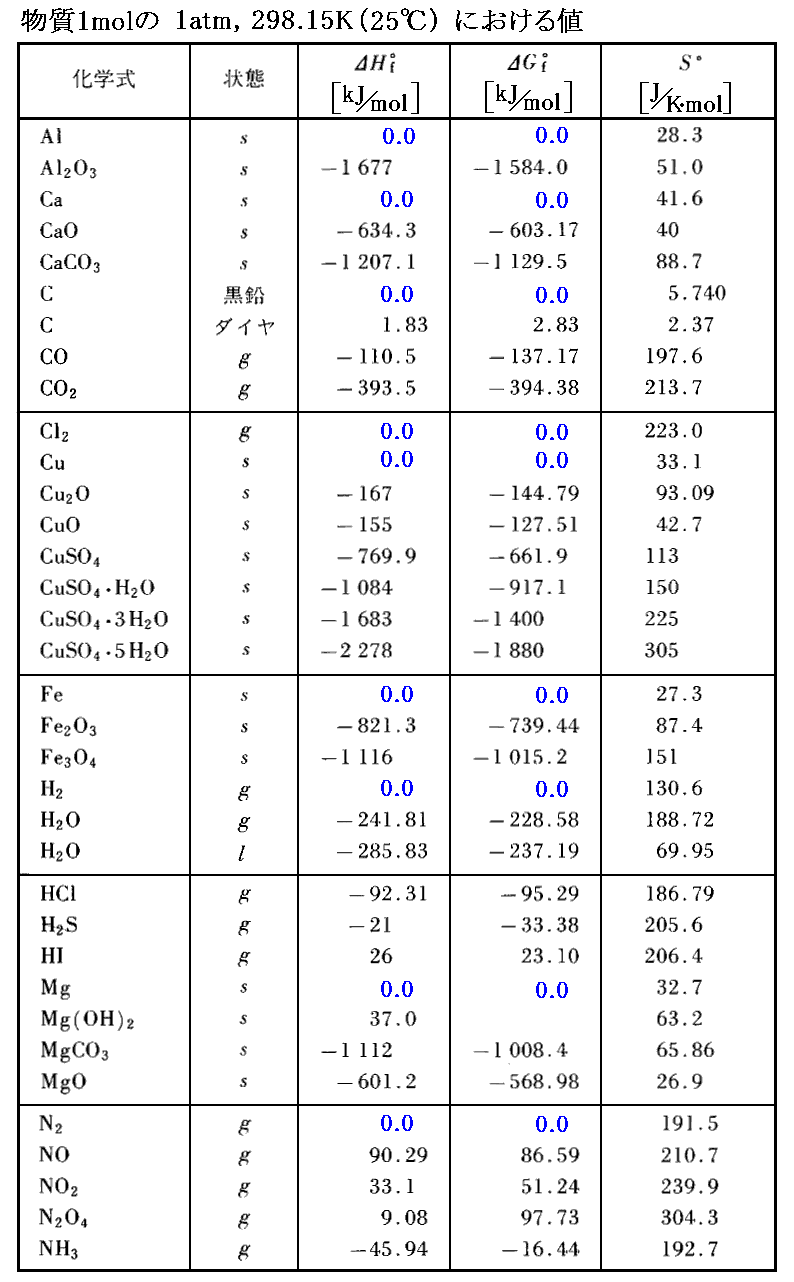
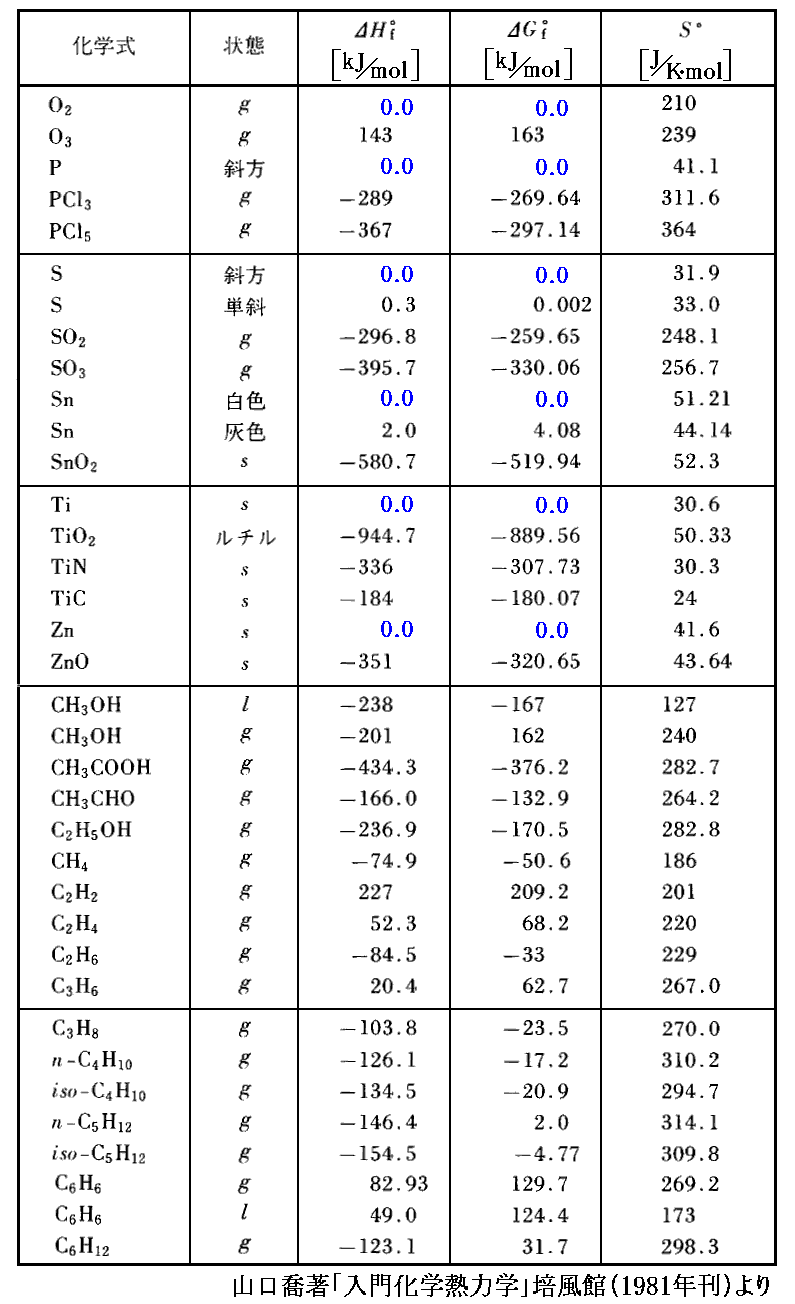
もっと詳しくは「化学便覧(基礎編Ⅱ)改訂2版」(丸善刊)§8.15p953~などをご覧下さい。
計算例の数値が引用文献とは微妙に異なりますが、ご容赦下さい。
[補足説明1]
様々な化合物の標準生成エンタルピーが解っていれば、、各種の化合物を含む反応の“標準エンタルピーの変化”ΔH゜(ここでは“生成”という言葉や添え字“f”が付いていないことに注意)は、生成物と反応物の標準生成エンタルピーΔHf゜の加算値の差から計算できる。
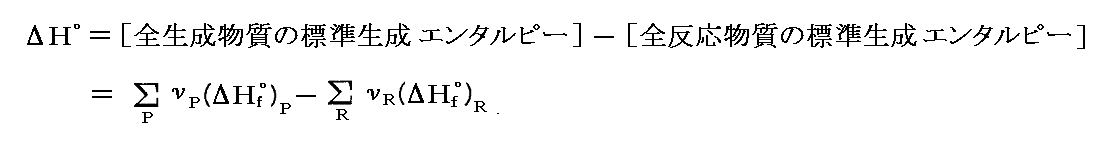
その具体的な方法は別稿「反応熱と熱化学方程式」4.(2)をご覧下さい。
例として標準状態(1atm,25℃)における以下の反応で2molの一酸化炭素CO生成するときの“標準エンタルピーの変化”ΔH゜を求めてみる。上記データ表から反応物、生成物の“標準生成エントタルピー”ΔHf゜の値を読み取ると
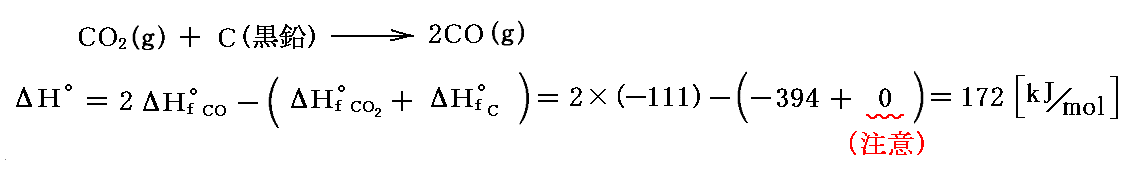
となる。この場合は吸熱反応となる。
これは上記の反応が完全に変化したと仮定してのエンタルピー変化ですが、標準状態でこの反応が実際に生じるかどうかはエントロピー値の変化だけからは解らない。あとで説明するギブズの
自由エネルギーの変化 の知識が必要です。
2.標準生成ギブズの自由エネルギー
ギブズの自由エネルギーも3.(4)1.[補足説明2]で説明したように、絶対的な値を求めることはできません。
そのため前項の方法で求まっている同じ化合物の標準生成エンタルピーΔHf゜から計算します。
まず、エンタルピーの場合と同様に標準状態[0℃(=298.15K)、1atm(=1.013×105Pa)]で安定な“単体”の1モルが持つギブズの自由エネルギーを“0”とします。
“化合物”の標準状態におけるギブズの自由エネルギーΔGf゜は、ΔGf゜=ΔHf゜-TΔS゜の式により同じ化合物の標準生成エンタルピーΔHf゜からTΔS゜を引いて求めます。
そのとき用いるΔS゜は単体から化合物を作るときの反応物と生成物の“標準(絶対)エントロピー”S゜値の加算の差ΔS゜から計算されます。そのときTに298.15K(25℃の絶対温度)を代入して計算します。
例えば水の“標準生成自由エネルギー”ΔGf゜は以下のように計算する。、まず単体から1モルの水が作られるときの“標準エントロピー変化”ΔS゜は、前項の表を利用すれば、3.(4)2.で計算したように
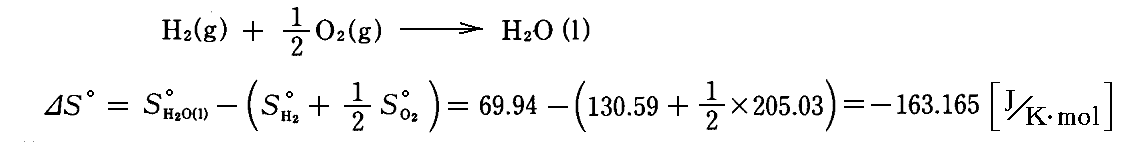
です。また水の“標準生成エンタルピー”ΔHf゜は-285.9kJ/molですから
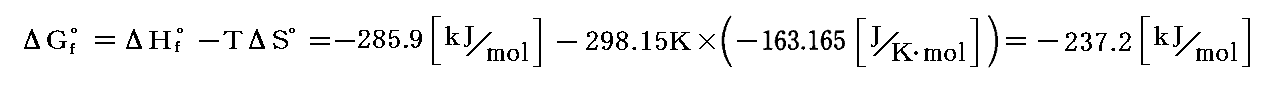
となる。
同様にして、アンモニアの“標準生成自由エネルギー”ΔGf゜は以下のようになる。
3.(4)2.で計算したように単体から1モルのアンモニアが作られるときの“標準エントロピー変化”ΔS゜は
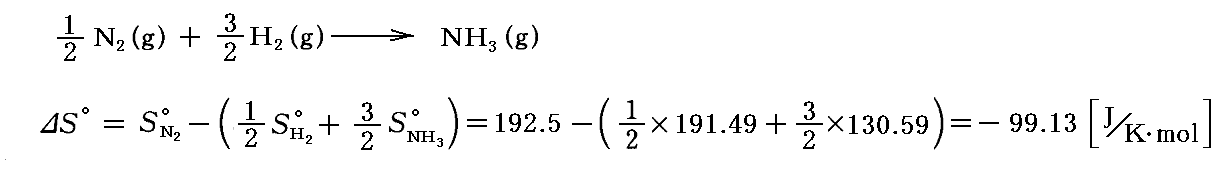
であり、またアンモニアの“標準生成エンタルピー”ΔHf゜は-46.09kJ/molですから
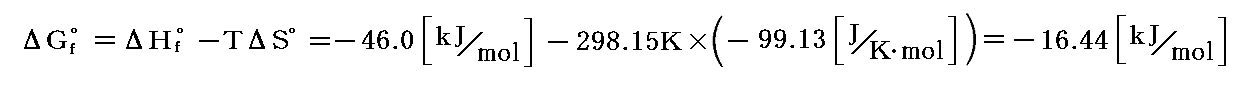
となる。
様々な物質のデータは「化学便覧(基礎編Ⅱ)改訂2版」(丸善刊)§8.15p953~などをご覧下さい。ただし、そこで示されているΔSf゜=(ΔHf゜-ΔGf゜)/Tの計算で求まるΔSf゜は“標準(絶対)エントロピー”S゜ではなくて、“標準生成エントロピー”ΔSf゜です。この両者の違いにはくれぐれも注意されたし。
[補足説明2]
各種の化合物を含む反応の“標準自由エネルギーの変化”ΔG゜(ここでも“生成”という言葉や添え字“f”が付いていないことに注意)も、標準エンタルピーの変化ΔH゜と全く同様にして生成物と反応物の標準生成自由エネルギーΔGf゜の加算値の差
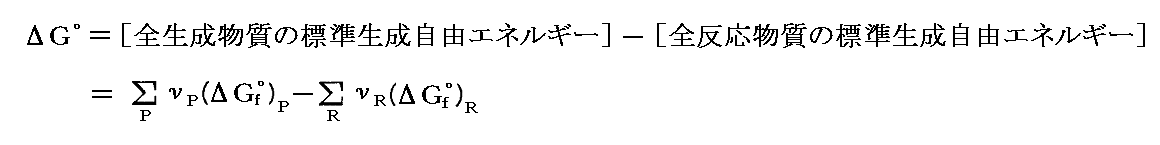
によって計算できる。
例として、エチレンが水と反応してエタノールを生成する反応の1atm、25℃における標準自由エネルギーの変化ΔG゜を求めてみる。
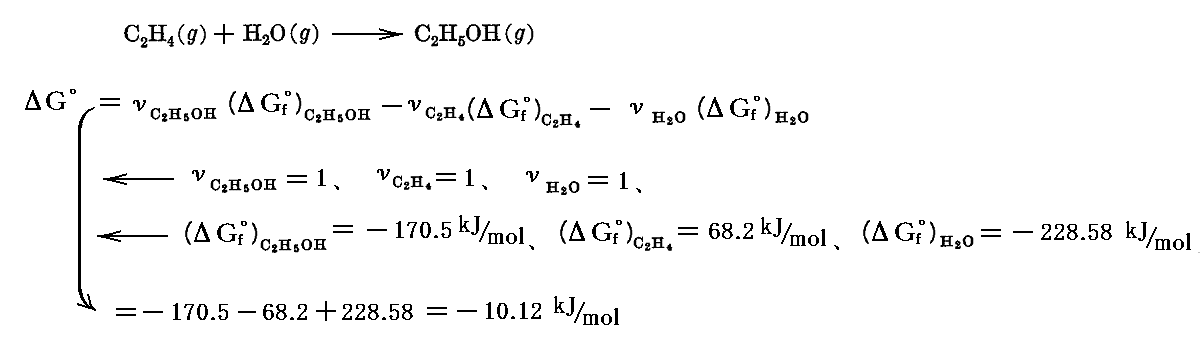
[補足説明3]
もし標準状態に於ける化学反応のエントロピー変化ΔS゜とエンタルピー変化ΔH゜がそれぞれ解っていれば
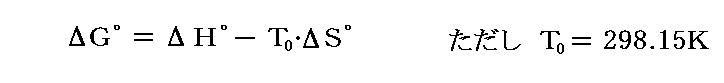
によっても、各種の化合物を含む反応の“標準ギブズの自由エネルギーの変化”ΔG゜を求めることができる。
例として標準状態(1atm,25℃)における以下の反応で2molの一酸化炭素CO生成するときの“標準ギブズの自由エネルギーの変化”ΔG゜を求めてみる。3.(4)2.で求めたΔS゜値と4.(2)1.で求めたΔH゜値を利用すると、直ちに
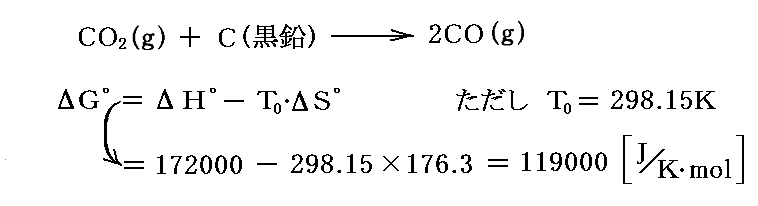
が求まる。
もちろん、前記データ表から反応物、生成物の“標準生成ギブズの自由エネルギー”ΔGf゜の値を読み取って計算しても良い。
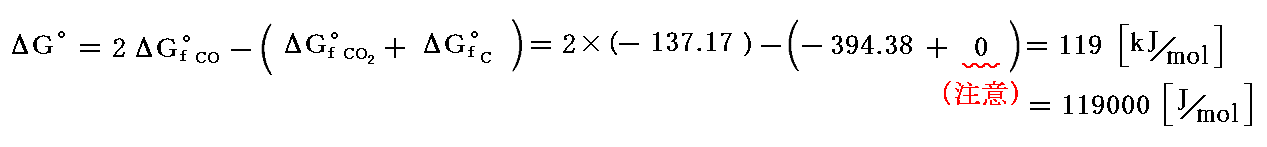
このギブズの自由エネルギーの変化値から計算される平衡定数は、上記の反応が標準状態では圧倒的に左側に寄っていることを示すのですが、その当たりは別稿で説明します。
(3)任意の温度・圧力における“エンタルピー”と“ギブズの自由エネルギー”
1.任意の温度・圧力におけるエンタルピー
別稿「熱力学関数(状態方程式曲面)の性質」1.(2)~(4)で、Sの変数をS(T,V)、S(T,P)、S(P,V)と自由に変換できることを説明した。それとまったく同様にH(S,P)→H(T,P)へ変換すると
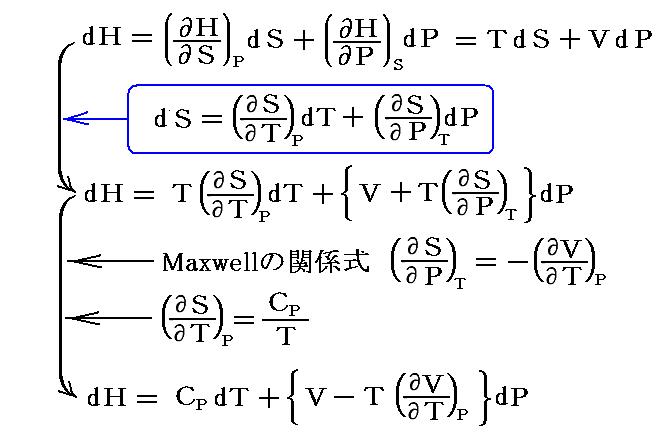
となる。
[補足説明1]
ここで、 (∂H/∂T)p=Cp となることは以下の考察からも明らかです。
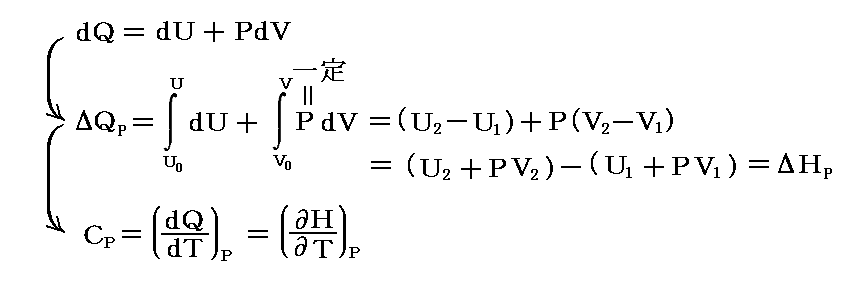
つまり、定圧条件下で状態変化が起こるときに発生する熱量ΔQpは系のエンタルピー値の変化ΔHpに等しいのです。これは別稿「絶対温度とは何か(積分因子とは何か)」8.(2)1.[補足説明1]ですでに説明した。
また、上式第二項の (∂H/∂P)T={V-T(∂V/∂T)p}={V-αTV} は物質の状態方程式が実験的に決定できれば求めることができる量です。
従って上式を積分すれば任意の温度、圧力で物質1molが持つエンタルピー値が求まる。
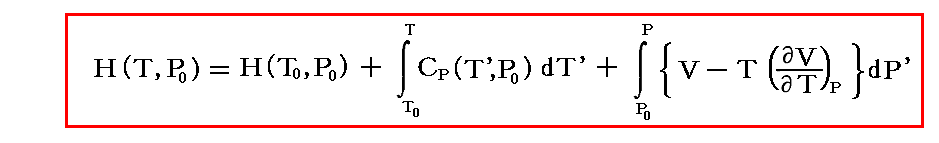
このとき、H(T,P)は状態量ですから、4.(1)で説明したエントロピーの積分と同様に、積分経路に依存しない。そのため被積分関数が実験的に求まっている経路に沿って積分を実施すればよい。この当たりは別稿4-4-2の説明も参照されたし。
例えば、一般にCp(T,P0)の温度依存性は小さいので、4.(1)2.[補足説明2]で説明した定圧下における実験式が利用できます。それを用いて、まず最初に P=P0=一定 の定圧条件下で、上式第二項の積分を実行して H(T0,P0)→H(T,P0) の変分を求める。
次に T=一定 の定温条件下で上式第三項の積分を実行して H(T,P0)→H(T,P) の変分を求める。
それらの変分を H(T0,P0) に加えれば H(T,P) が求まる。
物質が気体で、“理想気体”と見なせる場合には上記積分は簡単です。
第二項の積分において理想気体ではCp=一定と見なせるので積分の外に出せて第二項はCp(T-T0)となります。
また、PV=RTを第三項に適用すれば、 (∂H/∂P)T={V-T(∂V/∂T)p}={V-TR/P}={V-V}=0 となりますので、第三項の関与は無くなります。
[補足説明2]
定温条件下でのHの変化ΔHTは
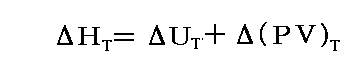
と表される。
そのとき、理想気体と見なせる気体では内部エネルギーは温度のみの関数だからΔUT=0であり、同じくPV=RTから温度が変化しなければΔ(PV)T=0となるのでΔHT=0となる。温度一定の元で圧力を変化させると、物体に対して仕事が成されるのですが、温度を一定に保つために加えた仕事分のエネルギーが熱として系外に流れ出ており、PVの積も変化しないので、熱や仕事のやり取りが生じても、系の内部エネルギーやエンタルピーは変化しないのです。
実在気体では、圧力を上げると分子間力の影響のために T(∂V/∂T)p は V と等しく成らず (∂H/∂P)T は 0 ではなくなる。そのとき、実在気体がファン・デル・ワールス気体の場合には、別稿「熱力学関数(状態方程式曲面)の性質」1.(2)4.で求めた定温条件下に於ける (∂V/∂P)T の様子を表す関係式
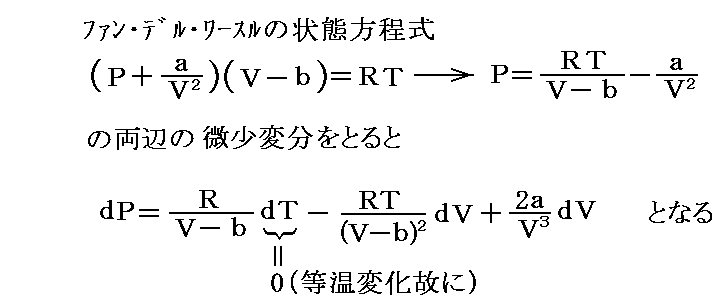
を用いて積分を実施しなければならない。
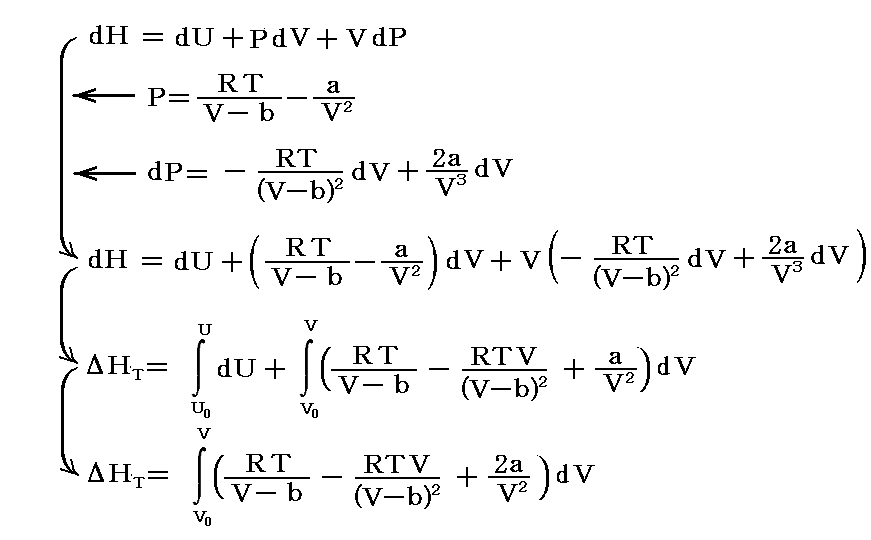
[補足説明3]
固体や液体の場合、温度が一定であれば、圧力が変わっても内部エネルギーUはほとんど変わらない。また体積変化もほとんど無く α~10-4 程度ですから、 V>>αTV となり (∂H/∂P)T={V-T(∂V/∂T)p}={V-αTV}~V で近似できる。
そのため、定温条件下での圧力変化によるエンタルピー変化は ΔHT~Δ(PV)T~VΔP~V(P-P0) の近似式で計算できる。
より正確な値が必要なときは、物質の体積膨張率αのデータを用いる。
2.任意の温度・圧力におけるギブズの自由エネルギー
別稿「熱力学関数(状態方程式曲面)の性質」3.(3)1.で説明した様に
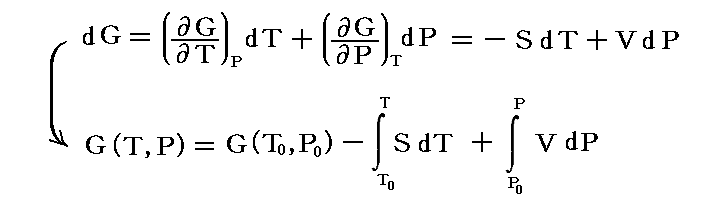
であるから、4.(1)で求められるエントロピーの温度依存性S(T)や、体積の圧力依存性V(P)を用いて積分操作を実行する。そのとき、4.(1)で述べたような近似操作が可能なら最大限利用する。
まず第二項のエントロピーSに付いての積分であるが、
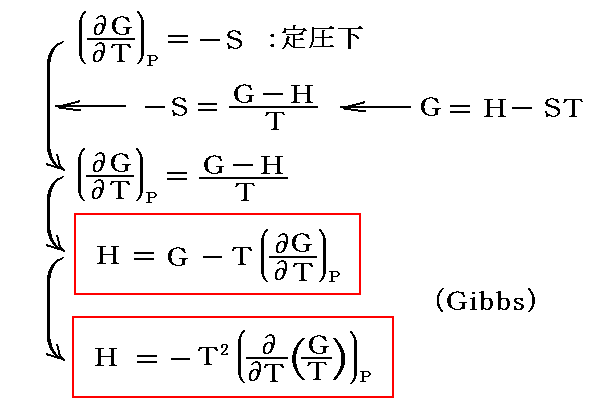
となる。これは別項「熱力学関数(状態方程式曲面)の性質」3.(4)で説明した“ギブズ・ヘルムホルツの式”ですが、これを用いれば良い。
定圧条件下(P0=一定)で次の積分を実施することにより、て任意の温度Tのギブズの自由エネルギーG(T,P0)を求めることができる。
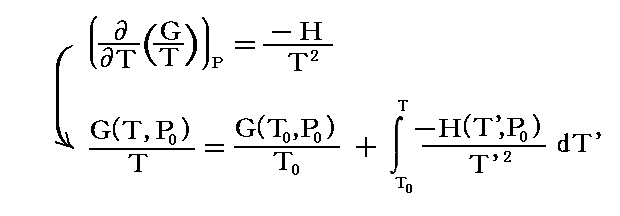
もちろんこのとき、温度T0、圧力P0に於ける標準生成自由エネルギーΔGf゜=G(T0,P0)と、圧力P0におけるエンタルピーH(T,P0)の温度依存性が知られている必要があります。
上記の値に加えて定温条件下(T=一定)の積分をすれぱ、任意の圧力Pにおけるギブズの自由エネルギーG(T,P)を求めることができる。
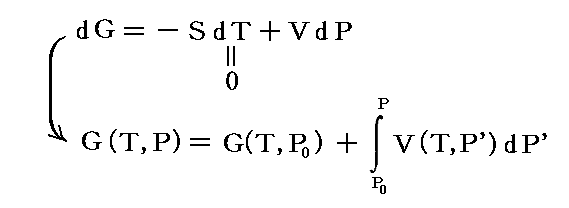
このとき、もちろん温度Tの下での体積V(T,P’)が圧力の関数として知られている必要があります。
厳密な数値を求めるのはかなり面倒ですが、ごく大まかな変化の様子を知るだけならば、「熱力学関数(状態方程式曲面)の性質」3.(3)1.[補足説明3]~[補足説明5]で説明したような計算を実行すればよい。
もし、任意温度・圧力に於けるエントロピーとエンタルピーがそれぞれ温度と圧力の関数として解っていれば
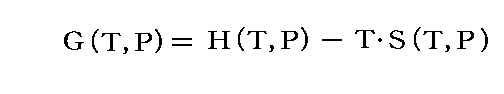
で求めることもできる。
このようにして良いことは別稿「熱力学関数(状態方程式曲面)の性質」3.(1)1.の議論を思い出してください。この当たりの式の意味が解らなくなったら各相・各化学種について成り立つ根源的な状態方程式曲面U(S,V)に帰られて、もう一度「ギブズの自由エネルギー(化学ポテンシャル)とは何か」を復習されてください。
相変化、化学反応変化に伴うものであれば、反応系と生成系の差をΔで表すと
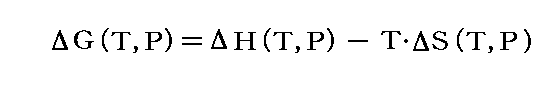
となる。
(4)化学反応に伴う“エントロピー変化”、“エンタルピー変化”、“ギブズの自由エネルギー変化”の温度依存性
前節の結論を利用すれば、任意の圧力下での化学反応に伴う“エントロピー変化”ΔS、“エンタルピー変化”ΔH、“ギブズの自由エネルギー変化”ΔGの温度依存性を求めることができます。
任意の圧力下での温度依存性を求めるには体積膨張率や等温圧縮率のデータが必要で計算が面倒になる。そのためここでは圧力一定=1atmの条件下での温度依存性のみを論じる。
例として1atmの下でのアンモニア生成について、これらの温度依存性を求めてみる。
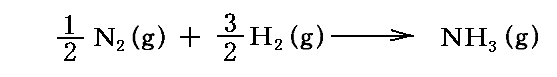
1.反応エントロピーの温度依存性
アンモニア生成の化学変化における反応物と生成物の各1molが標準状態(P0=1atm,T0=298.15K)で持つエントロピー値は3.(2)1.の一覧表から読み取れる。それらの値と4.(1)2.、および4.(1)2.[補足説明2]で説明した関係式を用いると、 (T,P0)=(TK,1atm) に於ける各物質のエントロピー値は
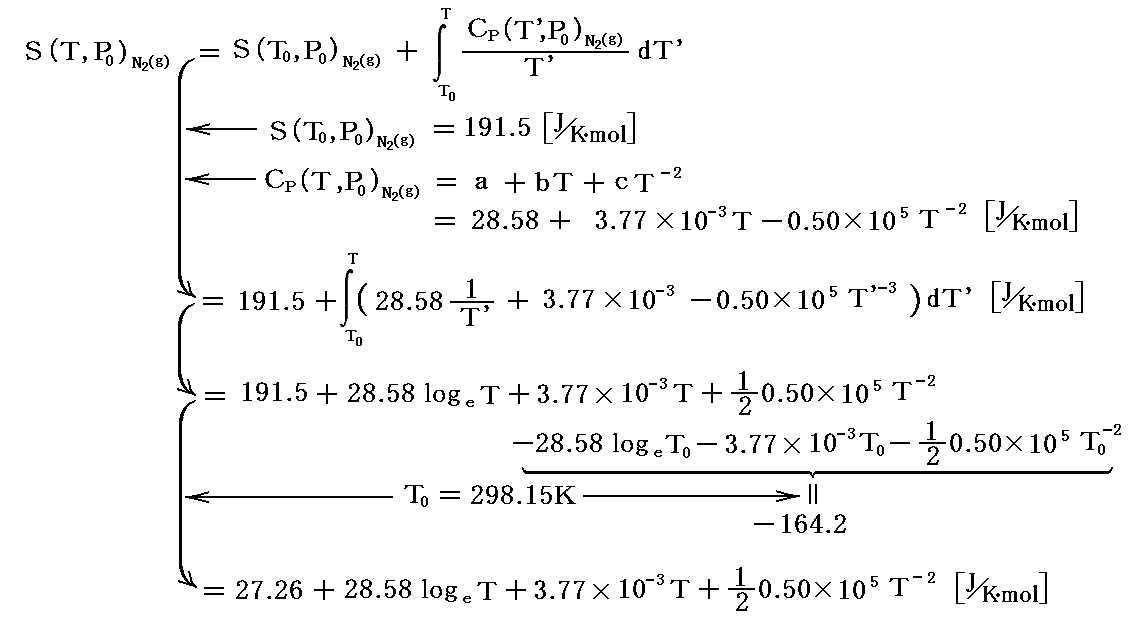
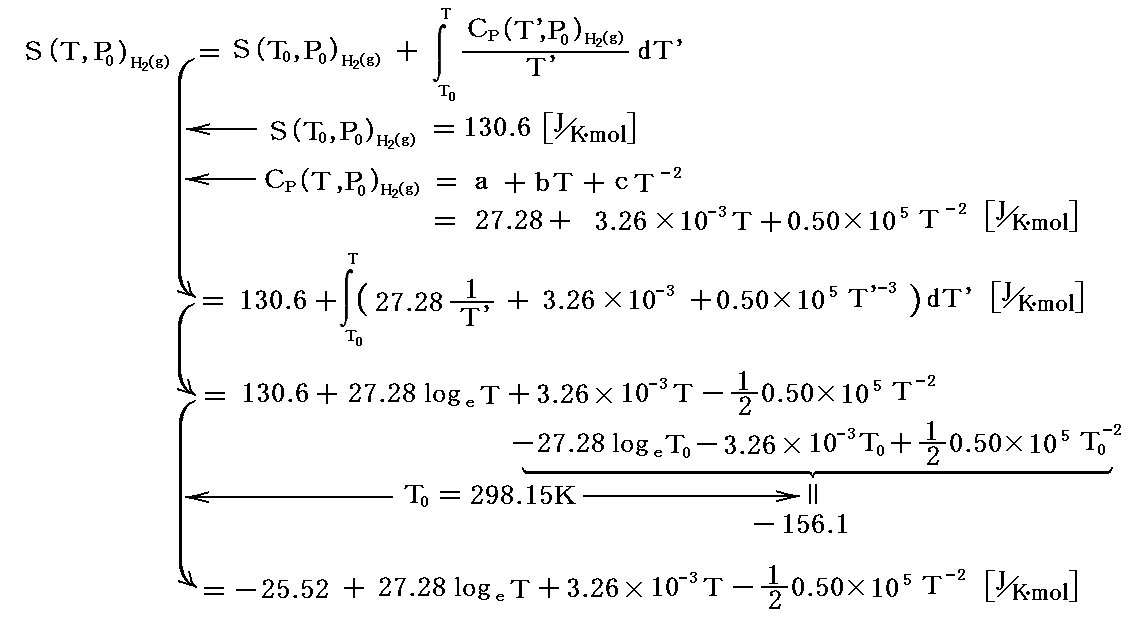
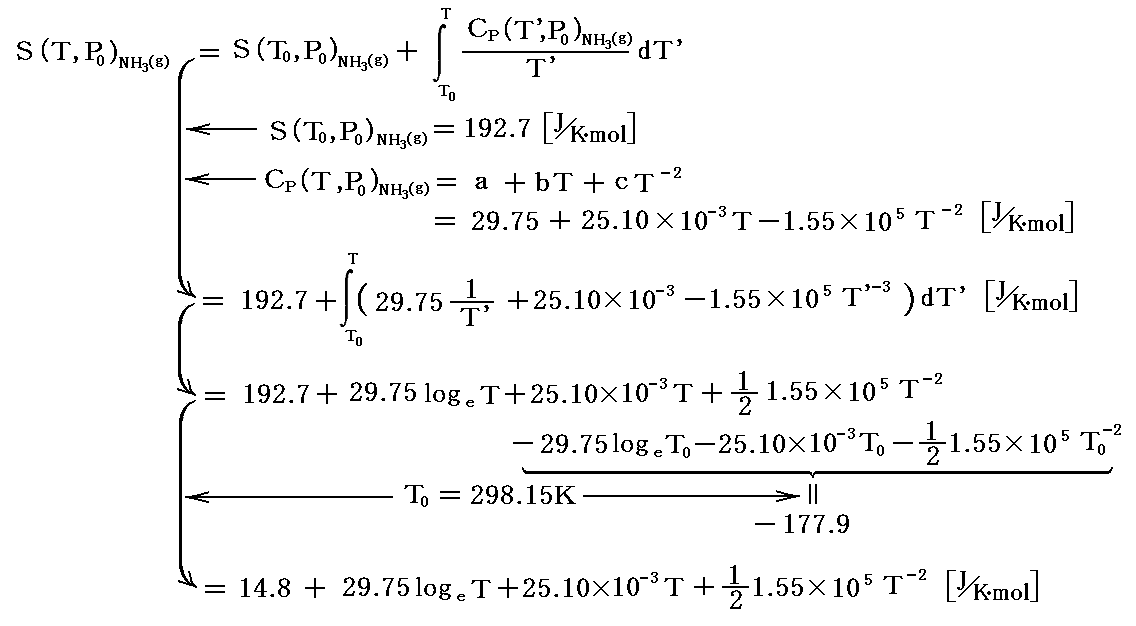
で与えられる。
これらの S(T,P0) は、すべて定圧条件下で温度Tとともに増加します。それは、 (∂S/∂T)p=Cp/T>0 であることから明らかです。
これらの値から、P0=1atm,TKにおいてアンモニア1molが生成するときの化学反応のエントロピー変化は
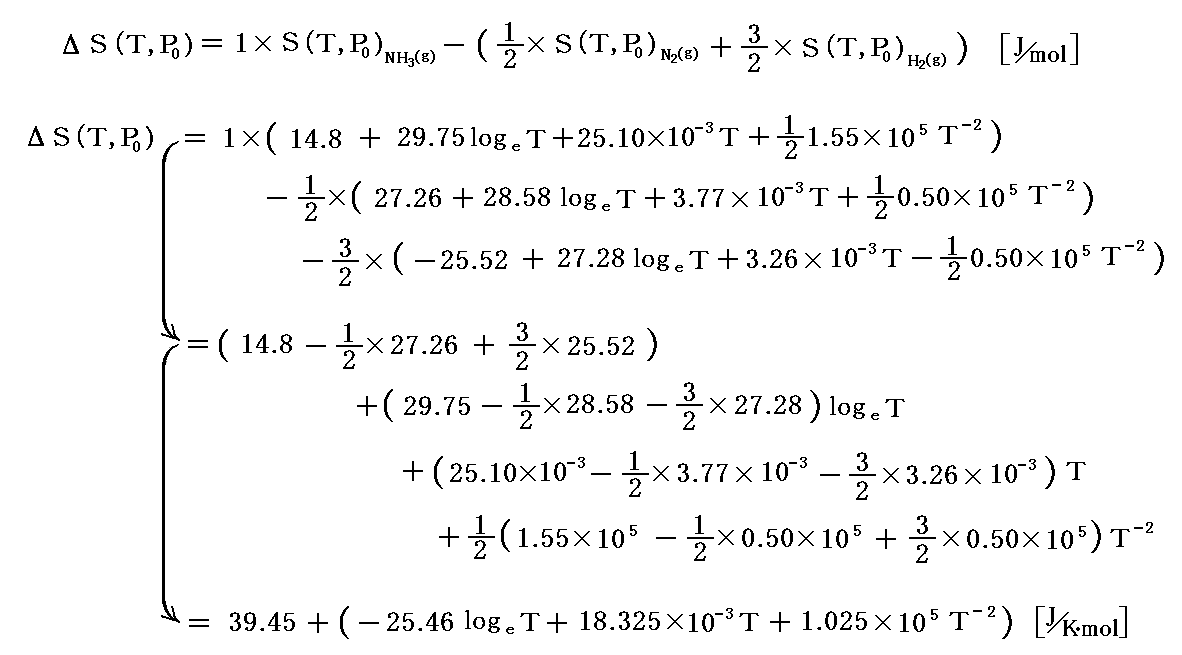
となる。
これは一般的に
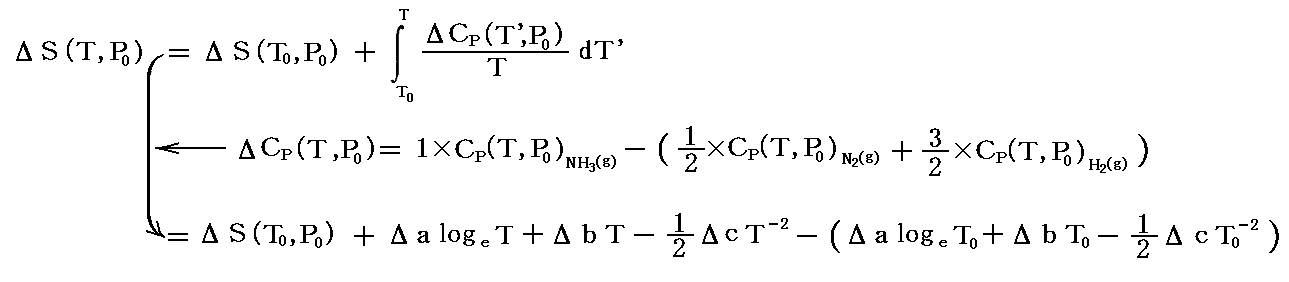
と表される。ここでのΔは上記の意味です。
前記の結論において、T=T0=298.15K(25℃)を代入するとΔS(T,P0)=ΔS(T0,P0)=-99J/K・molとなり、3.(4)2.で求めたアンモニア生成反応の“標準エントロピー変化”ΔS゜に一致するが、そうなる事は上記の式からも明らかです。
温度変化の様子をグラフ表示すると以下のようになる。ΔS(T,P0)は化学反応に伴う変化分ですから、定圧条件下での温度依存性は反応の種類によります。
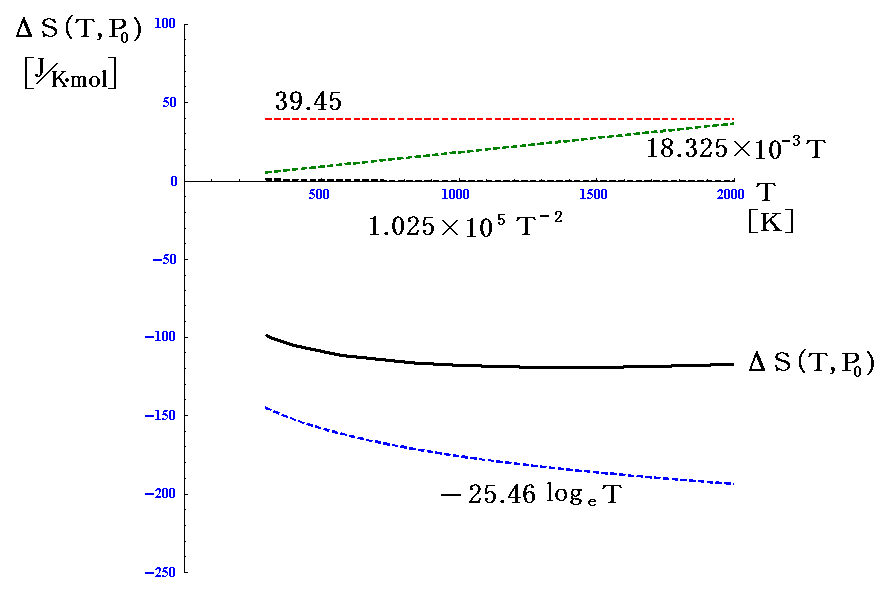
ただし、Δa、Δb、Δcに依存する様子を表すグラフに意味があるわけではありません。
[補足説明]
ここでは示していませんが、“熱力学第三法則”が正しい限り、T→0Kの領域でΔS→0となっているはずです。
2.反応エンタルピーの温度依存性
アンモニア生成の化学変化に於いて反応物、生成物の標準状態(P0=1atm,T0=298.15K)に於けるエンタルピーは一覧表で与えられている。それらの値と4.(3)1.および4.(1)2.[補足説明2]で説明した関係式を用いると、P0=1atm,TKに於ける各物質のエンタルピー値は

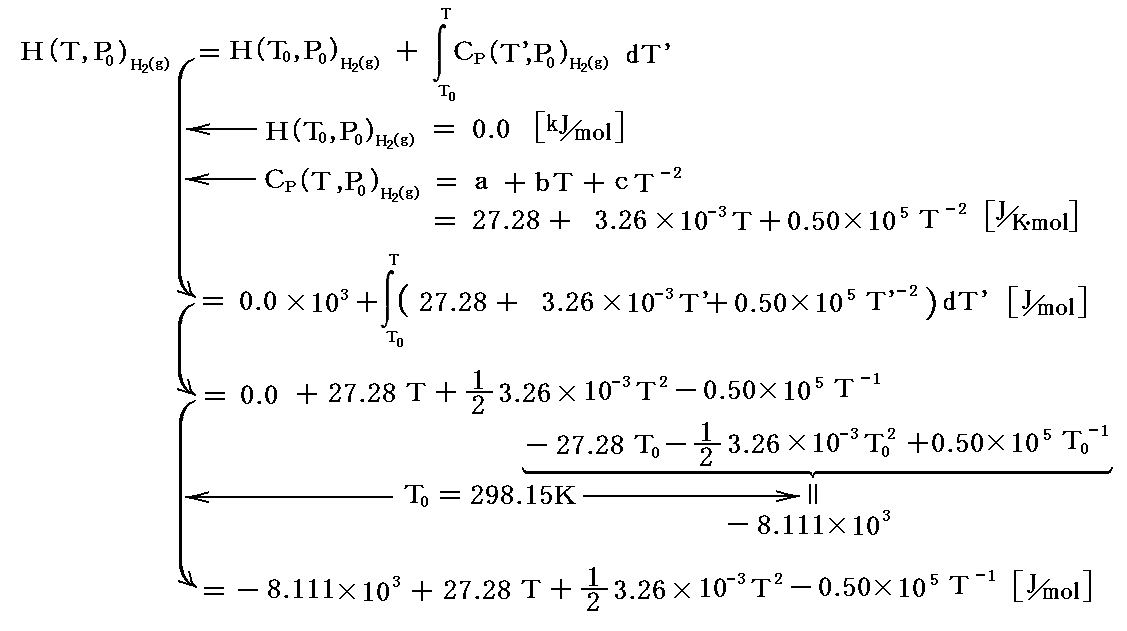
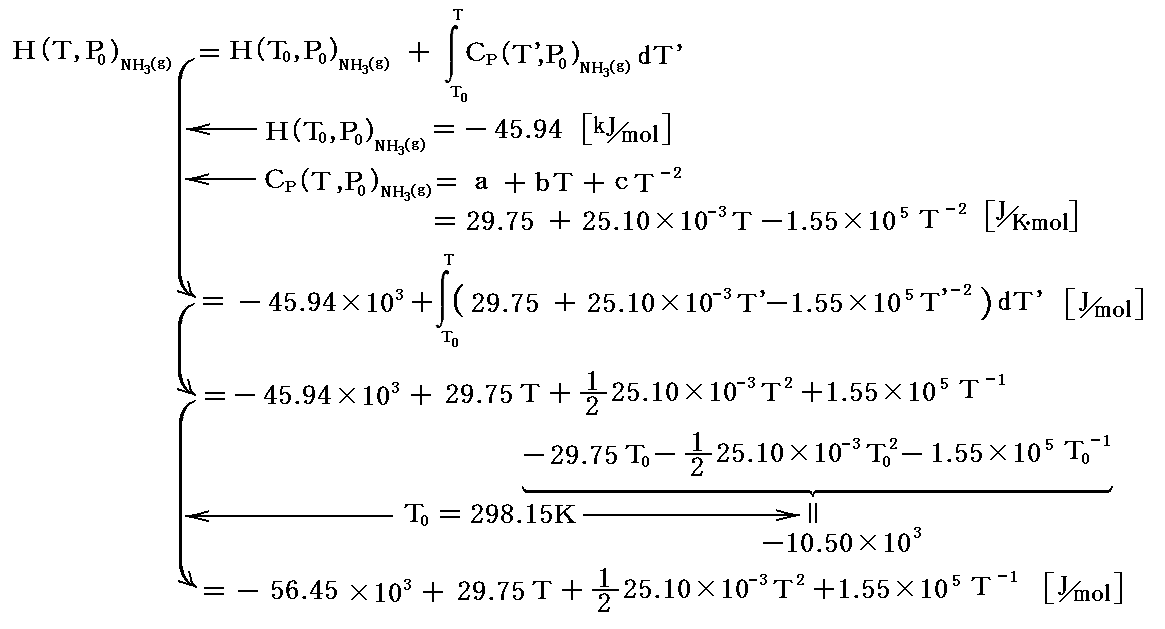
となる。
これらのH(T,P0)は、すべて定圧条件下で温度とともに増加します。それは(∂H/∂T)p=Cp>0であることから明らかです。
これらの値から、P0=1atm,TKに於けるアンモニアの生成熱は
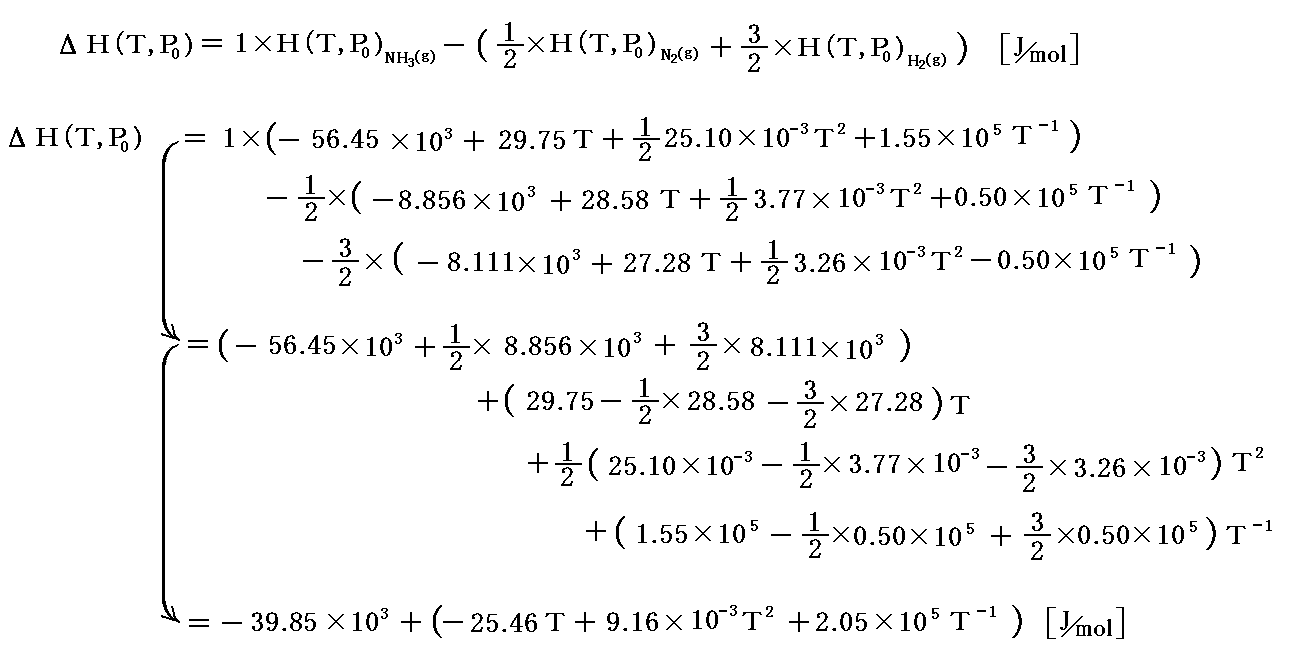
となる。
このとき、最後の式にT=T0=298.15K(25℃)を代入するとΔH(T0,P0)=-45.94kJ/molとなり、引用した数表中のアンモニア“標準生成エンタルピー”ΔHf゜の値に、確かに一致している。
これは一般的に
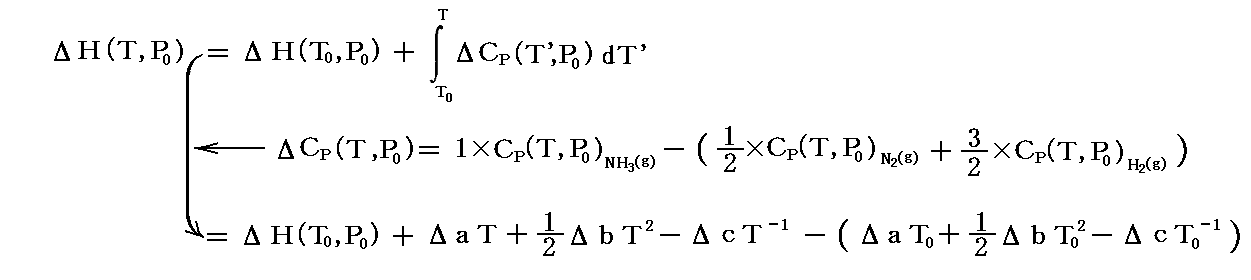
と表される。ここでのΔは上記の意味であることに忘れないこと。
前記の結論において、T=T0=298.15K(25℃) を代入すると ΔH(T,P0)=ΔH(T0,P0)=-45.94kJ/mol となり、引用した数表中のアンモニア“標準生成エンタルピー”ΔHf゜の値に一致するが、そうなる事は上記の式からも明らかです。
温度変化の様子をグラフ表示すると以下のようになる。ΔH(T,P0)は化学反応に伴う変化分ですから、定圧条件下での温度依存性は反応の種類によります。
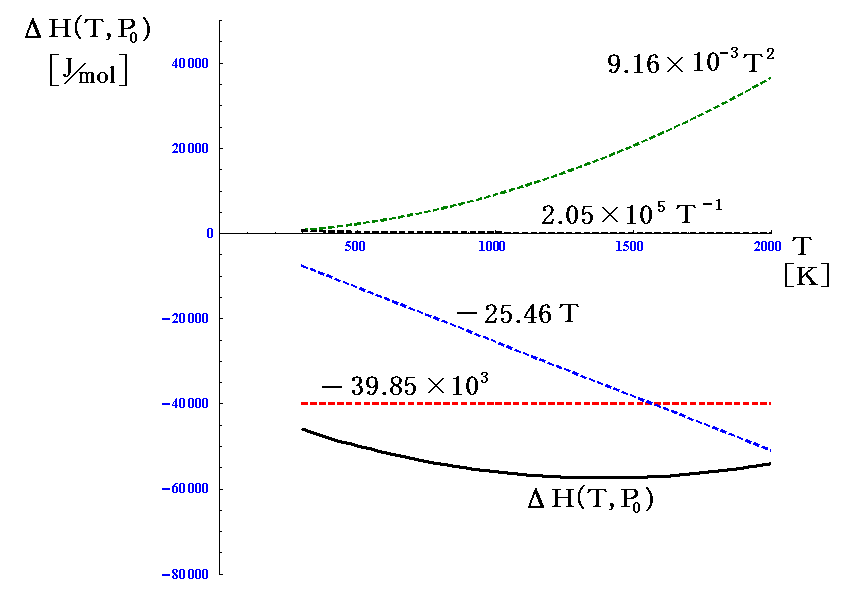
ただし、Δa、Δb、Δcに依存する様子を表すグラフに意味があるわけではない。
3.反応ギブズの自由エネルギーの温度依存性
1atmの下でのアンモニア生成におけるギブズの自由エネルギー変化の温度依存性は、4.(3)2.の最後で注意したように
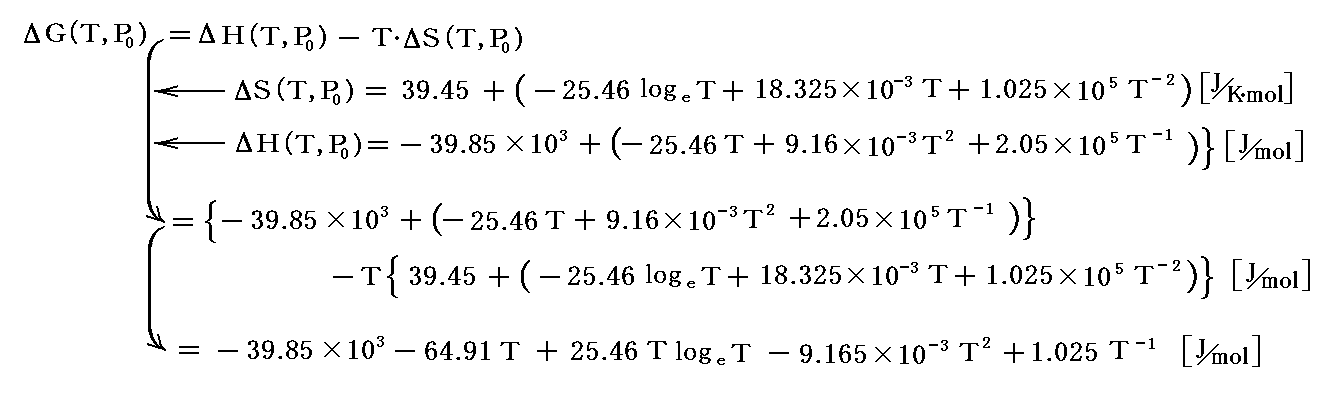
によって計算できる。
このとき、最後の式にT=T0=298.15K(25℃)を代入するとΔG(T0,P0)=-16.4kJ/molとなり、引用した数表中のアンモニアの“標準生成ギブズの自由エネルギー”ΔGf゜の値に一致している。
温度変化の様子をグラフ表示すると以下のようになる。|ΔS|<<|ΔH|ですが、エントロピー変化はT・ΔSの形でギブズの自由エネルギーに関わるのでΔG(T)の温度依存性に大きく影響します。
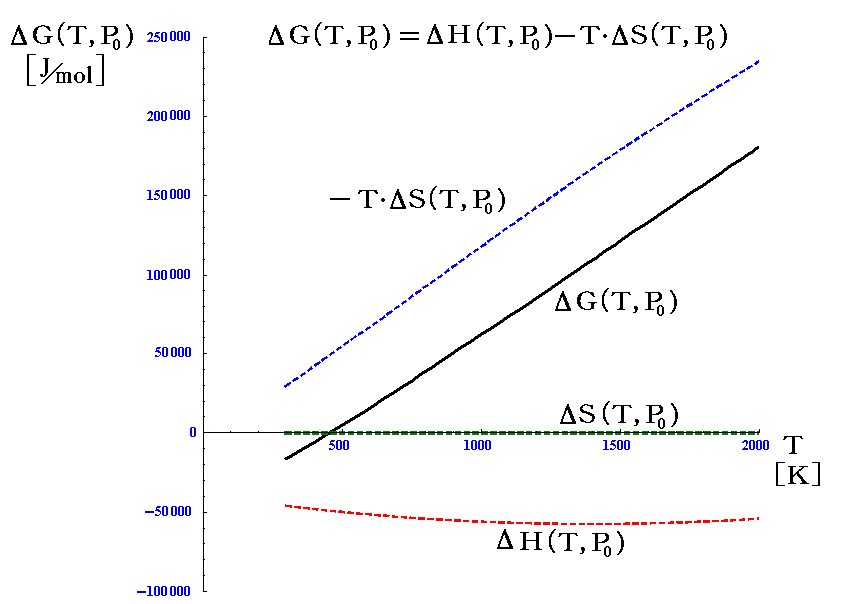
圧力P0の下では、図中のΔG(T,P0)=0となる温度Tにおいてアンモニアは窒素、水素と平衡状態を実現します。そのとき、系の圧力が変わればΔG(T,P0)=0となる温度は変化していきます。
[補足説明]
ここでは示していませんが、“熱力学第三法則”が正しい限り、T→0Kの領域でΔS→0となっているはずです。そのためT→0Kの領域でΔGとΔHは互いに接近して、T→0Kの極限点で、接する様にして一致するはずです。
ただし、そのときの値が零になるわけではありません。3.(4)1.[補足説明1]で説明したように、もともとエネルギー値についてはその絶対的な値を決める基準はありません。エネルギーの基準は標準状態(0℃、1atm)に於ける単体のエネルギーを0として恣意的に決めていたのですから。
T→0Kの領域まで拡張したときのグラフの様子は別稿「熱力学関数(状態方程式曲面)の性質」3.(2)2.[補足説明1]で説明したグラフの一例となります。ただし、ここでは化学反応に伴う変化量Δに付いての話ですから全体的な正負の状況は、そこのグラフと逆になっています。
アンモニアの合成反応について、もっと詳しい説明を別稿「平衡状態のの熱力学(気体の化学反応)」5.(3)でしておりますのでご覧下さい。そこで、アンモニアの反応率の温度と圧力依存性も論じています。
5.参考文献
この稿は、以下の文献に依存しています。
- アーノルド・ゾンマーフェルト著「理論物理学講座Ⅴ 熱力学および統計力学」講談社(1969年刊)
§12.“Nernstの熱定理”と、§18.“Galvani電池の起電力”をかなり参照しました。これは中身の濃い難しい教科書ですが、ゾンマーフェルトの説明の仕方や言い回しの端々に、熱力学や統計力学が作り上げられていった時代の状況・雰囲気を伺うことができます。
- マックス・プランク著、芝亀吉訳「熱力学」岩波書店(1941年刊)
原本はMax Planck著「Vorlesungen u¨ber Thermodynamik 8 Auf.(1927)(初版は1897年)
第6章 “エントロピーの絶対値(Nernstの定理)”§281~§296
ここで、プランクの言う熱関数Wと関数Φは、Hと-G/Tに置き換えてお読みください。
- 富永昭著「誕生と変遷にまなぶ平衡系の熱力学」第7章“熱力学第三法則”
この著作は以下のURLからダウンロードできます。
http://www.amsd.mech.tohoku.ac.jp/Thermoacoustics/Chap_7.pdf
- 山本義隆著「熱学思想の史的展開3 熱とエントロピー」筑摩学芸文庫(2009年刊)
第33章 “ネルンストの定理と熱力学第三法則”-ネルンストとプランク。
この中で、Nernstの熱定理(熱力学第三法則)の発見の歴史的な過程が、多くの文献を参考にして解説されています。
- 日本化学会編 化学の原典[第Ⅱ期]「3.化学熱力学」学会出版センター(1984年刊)
2. J. W. Gibbs,“不均一物質系の平衡について”(1878年)
ギブズの熱力学に関する大論文である第三論文(1876年第Ⅰ部、1878年第Ⅱ部)をギブズ自身が要約して、Am .J. Sci., Ser.3,
16, p441~458, 1878年に発表したものの日本語訳です。要約であるために簡略化されており、理解するのはかなり難しい。その最後の部分のみを引用しておきます。
元の第三論文と要約論文、およびギブズの論文集はネットから無料ダウンロードできます。
- 日本化学会編 化学の原典[第Ⅱ期]「3.化学熱力学」学会出版センター(1984年刊)
4. H. Helmholtz,“化学課程の熱力学”(1882年)と、この論文の訳者妹尾学氏による解説文。
- 日本化学会編 化学の原典[第Ⅱ期]「3.化学熱力学」学会出版センター(1984年刊)
6. W. Nernst,“熱測定からの化学平衡の計算について”(1906年)と、
この論文の訳者松浦良平氏による解説文。
- K.メンデルスゾーン著「ネルンストの世界-ドイツ科学の興亡」岩波書店(1976年刊)第4章p104~130
ネルンストの弟子で高名な低温物理学者であるメンデルスゾーンの解説です。注意深く読まれれば、単なる伝記ではなくて、かなり本質的に書かれていることが解ります。特に“絶対零度でゼロになるのはエネルギーでは無くてエントロピーである”は至言です。実際、絶対零度でエネルギーはゼロに成るわけではありません。
- T.Kuhn著「比熱の量子論(1974年)」p257_258以降を参照。
これは西尾成子 編 「アインシュタイン研究」 中央公論社(1977年刊)のp249~266を引用したものです。
- [参考文献の追記(2023年8月)]
山本氏が別稿で説明されているギブズの熱力学に関する第一論文(1873年4月)、第二論文(1873年12月)、第三論文(1976、1978年)を合わせて1冊にした翻訳本か2019年に発刊されました。それが
廣政直彦・林春雄訳「ギブス 不均一物質の平衡について」東海大学出版部(2019年刊)
です。どうぞ購入されてご覧下さい。