こちらのバージョンをご利用になると鮮明に印刷されます。

電磁気学の単位系が難しい理由

電磁気学の単位系が難しいのは、何種類もの単位系が並立することの中に電磁気学の本質があるからです。

１．単位系の分類

（１）単位系の種類

　歴史的に多くの単位系が提案され用いられてきたが、それらの中で理解しておかねばならないものは下記の四つです。

（１）静電単位系
（２）電磁単位系
（３）ガウス単位系
（４）MKSA単位系（いわゆる国際(SI)単位系）

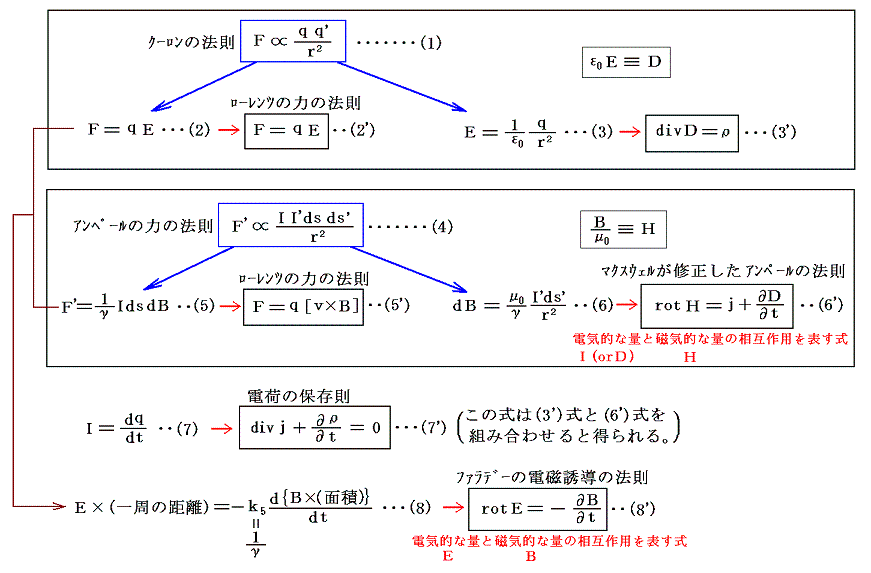
　このうち（１）〜（３）はCGS単位（cm、g、ｓ）で、（４）はＭＫＳ単位（ｍ、ｋg、ｓ）で表わされる。（１）（２）は歴史的な意味しか無いと思うかも知れないが、（１）と（２）の単位系の定義には電磁気学の根幹に関わる事柄が含まれており、また今日用いられている（４）のＭＫＳＡ単位系は（２）の電磁単位系が発展したものであるからこれらは必須の習得すべき単位系です。
　同種と考えられる量でも、単位系によって次元と数字係数が異なり、電磁気の諸法則(マクスウェル方程式等)に現われる係数も変わる。逆にこの係数の相違によって単位系の基本的特徴を示すことができる。

（２）絶対測定と絶対単位系

　電磁気学の単位の学習で最も重要な事柄は絶対単位(絶対測定)の概念である。初期の電磁気学では、電荷や磁荷の実態が何も解っていない状況の下で、電磁気現象が示す不可思議な現象を記述するために様々な物理量を導入しなければならなかった。そのとき、電荷も磁荷もその実態は知られていないのだから、新たな物理量を定義するにはそれまでに確立していた長さ・質量・時間の概念に基づいて定義するしかない。つまり電磁気学で成り立つ種々の法則というのは、新しい物理量を定義が確立している古い物理量［力やエネルギー（つまり長さ・質量・時間）］に結びつける関係式のことである。
　だから電磁気学における新物理量は、古い物理量(次元）の組み合わせで定義される。そして究極的に長さ・質量・時間に還元される。そうしてこそ、新しい物理量を絶対的に、つまり誰が・何時・何処で測っても同一の値として、測定できるわけである。そのように単位の定義が確定している長さ・質量・時間に関係づけて新物理量を定義・導入した単位系を絶対単位系といい、それらの量によって測定する事を絶対測定という。最初に導入された（１）静電単位系と（２）電磁単位系はその様な絶対単位系である。
　［絶対測定の意味については別稿「ガウスによる地磁気の絶対測定」や「絶対電位計と象限電位計の測定原理」で解りやすく説明しておりますので御覧ください。］

（３）比例係数と単位系の分類

　できるだけ簡単に解りやすくするために、真空中での電荷、電流について議論する。以下で取り上げる公式の力・距離・電流・電場・磁場等はベクトル量で、本来その方向が重要な意味をもつベクトル公式である。しかし、ここでは次元的な考察が中心なので角度や方向の関係は無視する。そして、その大きさの関係は最も簡単な配置における方向での議論（高校物理で習うもの）と思って下さい。

１．簡単な議論

　電荷の存在が最初に認識されたのは、帯電した２物体間に引力や斥力が働くことからである。いわゆる電荷に対するクーロンの法則ですが、この法則により新しい物理量である電気量ｑが定義できる。

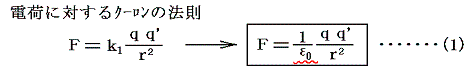
このとき比例定数をｋ₁と置いても良いのですが、今日の慣例にしたがって１／ε₀と置くことにする。
　次に、電荷と並んで磁荷というものについて電荷のクーロンの法則と類似の法則が成り立つことが解っている。この磁荷に対するクーロンの法則により、磁気的な量である磁気量ｍが定義される。磁荷は電荷とは明らかに異なった性質を示すので電気量とは異なった物理量と考えられる。そのため力の現れ方も電荷の場合と違っているので、その係数もｋ₁とは異なるはずだ。

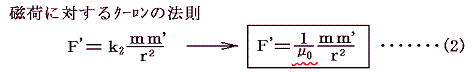
この場合も慣例にしたがって比例定数をｋ₂ではなくて、１／μ₀と置くことにする。
　次にエルステッドにより発見された、電流の磁気作用を表す式を導入する。これはやがてビオ=サバール、アンペールやマクスウェルにより洗練された形にまとめられて一つの重要な法則に昇華するが、電気的な量と磁気的な量の間にある種の関係が存在する事を示す重要な法則である。とりあえず一番簡単な表現で次のように表す。

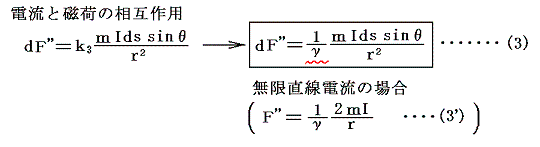
この場合も、比例定数ｋ₃を１／γと表す。ｄＦ''は電流要素による力の微少成分だが、電流が無限直線電流の場合高校物理で習うように（３'）となる。
　これにファラデーが実験的に推察したことであるが、電流とは電気量の流れである事を表す式

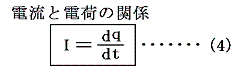
が付け加わる。（４）式は単位系の違いに影響されないので、定義式に比例定数は必要ない。
　単位系を決定づける関係式としては、これらの法則を変形したものを用いても良いし、（３）式の代わりにファラデーが発見した「電磁誘導の法則」を用いても良いが、とりあえず上記の（１）〜（４）式を用いると電気と磁気が関係した新しい物理量ｑ、ｍ、Ｉについて単位系を定めることができる。

　このとき、（１）式の電気量ｑと（２）式の磁気量ｍは全く異なった物理量と考えることができるので、それらの単位の取り方は別々に決めることができる。そのためε₀とμ₀の値は、それぞれの物理量の単位の定め方により全く独立に任意に定めることができる。
　そのとき（３）式は電気的な量（電流は電荷の流れ）と磁気的な量の相互作用による力の法則を表しているが、（１）、（２）式によりｑとｍの単位がすでに定められているので、γに関しては任意の値を取る訳にはいかず何らかの制約が存在し、ε₀とμ₀と何らかの関係で結びつけられるはずである。
　実際、４個の式（１）〜（４）に対して、未知量はｑ、ｍ、Ｉ、ε₀、μ₀、γの６個であるから６個の内の二つは任意に定めることができる。その二つを定めると他はおのずと決まってくる。
　つまり、（１）〜（４）式をｑ、ｍ、Ｉに付いて解いてそれらの未知量を消去すると、残った３個の未知量ε₀、μ₀、γに対するただ１個の式が得られる。
　今は次元的な考察なので、ｄｓもｒも同じ長さを、ｄｑもｑも同じ電気量を表すものとし、Ｆ、Ｆ'、Ｆ''がすべて同じ１［dyn］であるとして計算する。（１）×（２）÷（３'）²の計算を左辺と右辺でそれぞれ実行すると

となる。つまりこの（５）式の中の３個の未知量ε₀、μ₀、γのうち二つは任意に定めることができる。その二つの選び方と、その値の決め方で単位系の違いが生じてくる。

２．今日的な議論

今日単独の磁荷は存在しないことが解っているので、磁荷の代わりに電流要素を用いた議論をする。

　まず、電荷に関するクーロンの力の法則

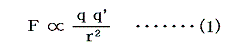
を二つの部分に分割する。

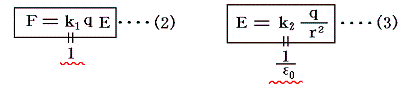
ここで、（２）式は静止している電荷に力を及ぼす場の成分［電場］の定義式であり、（３）式は電荷が電場を生じる、その作り方の法則である。それぞれに比例定数ｋ₁、ｋ₂が与えられているが、元々一つの（１）式を分割したものであるから一つにまとめることができる。普通ｋ₁＝１とおく。実際この式でｋ₁に１以外を与えても何の意味もない｡電磁気学を作り上げるときの出発点の式だから最も簡単に１と置いた方がよい。結局一つの比例定数ｋ₂だけになるが、慣例にしたがってこれを普通１／ε₀と置く。

　次に、電流要素間に働くアンペールの力の法則を用いる。この法則

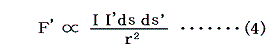
を二つの部分に分割する。

ここで（５）式は電流Ｉ＝ｎｅｓｖ＝ｎｓ×ｅ×ｖ（ｅ：電気素量、ｎ：電子の数密度、ｓ：導線の断面積、ｖ：電荷の移動速度）であることを考慮するとローレンツ力の磁束密度に関係した部分Ｆ＝ｑ［ｖ×Ｂ］を意味する。つまり動いている電荷に力を及ぼす場の成分［磁束密度］の定義である。慣例にしたがって比例係数ｋ₃を１／γと置く。一方、（６）式はビオ＝サバールの法則あるいはアンペールの法則であり、電流が磁束密度を生じる、その作り方を示す法則である。慣例にしたがって比例係数ｋ₄をμ₀／γと置く。

　以上のものに付け加えて電流が電荷の流れであることを示す式

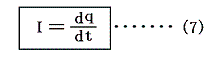
が存在する。これは単位系には影響されない定義式なので比例定数は必要ない。

ここで、本題に入る前にこれらの式について幾つかの注意をする。

• （４）式を分解した（５）式と（６）式でｋ₃とｋ₄の二つの比例定数が出てくる。このとき（５）と（６）はもともと一つの（４）式だったのだから、電場の場合と同様に一つの定数で置き換えたくなる。しかし、今度はそれはできない。
  　なぜなら、（５）、（６）式の電流 Ｉ は（７）式により、電荷ｑと結びつけられており、（１）〜（３）の電気的な法則に結びつけられている。そのとき（１）式の静電気的な力Ｆと（４）式の動電気的な力Ｆ'はもともと独立な別個の法則に由来する力である。そのため、（４）式のＦ'が（１）式のＦと独立であることを示すための比例定数を導入しておかねばならない。この比例定数が１／γであり、これは静電気的な定義（１）と動電気的な定義（４）の間を関係づける比例係数である（電気量と磁気量の次元関係を関係づける比例定数といってもよい）。
  　さらに、これに加えて（４）式をＢを仲介にして二つに分解したことに伴う比例定数μ₀をｋ₄の中に導入して置かねばならない。これは（３）式の１／ε₀に相当する比例定数である。
  　つまり、（４）式の比例定数には（１）式との関係で導入される比例定数１／γと（４）式の電流を力と結びつけて絶対定義することに伴う比例定数μ₀の両方が含まれている。普通、比例定数ｋ₃を慣例により１／γと書き、（６）式の比例定数ｋ₄は慣例によりμ₀／γと書く。
• （５）、（６）式のＢをＨに書き換えて、比例定数ｋ₃をμ₀／γと書き、比例定数ｋ₄を１／γと書いてもよい。そうするとＢではなくＨを仲介にして分解することができる。
• （６）式は磁束密度Ｂの微少成分ｄＢに関する式であるが、例えば無限直線電流では、この式はｄｓ'について積分して（６’）の様に書かれる（高校物理でならう）。
• （６）式はアンペールの法則であるが、これは電流によって磁気的な量である磁束密度Ｂ（Ｈを仲介にした場合は磁場Ｈ）が生じる事を言っており、まさしくこの法則こそ電気的な量と磁気的な量を結びつける関係式である。実際にはマックスウェルが修正して付け加えた変位電流の項をいれておかねばならないが、次元的な考察には無くても十分なのでこれで議論する。
• 電気的な量と磁気的な量を結びつける関係式として、「アンペールの法則」とは独立の法則である「ファラデーの電磁誘導の法則」
  
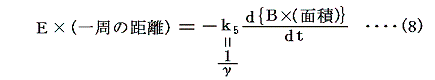
  がある。この（８）式を（２）と(５)式の代わりに用いても良い。この場合にも電気量と磁気量の次元間を関係づける未定定数１／γを導入しておく必要がある。実際、（２）式のＦと（５）式のＦ'を等しいと置くと
  
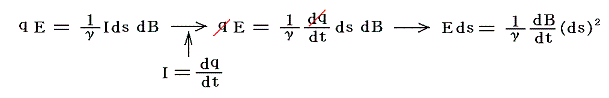
  となるので（８）式の比例定数は１／γで無ければならない。

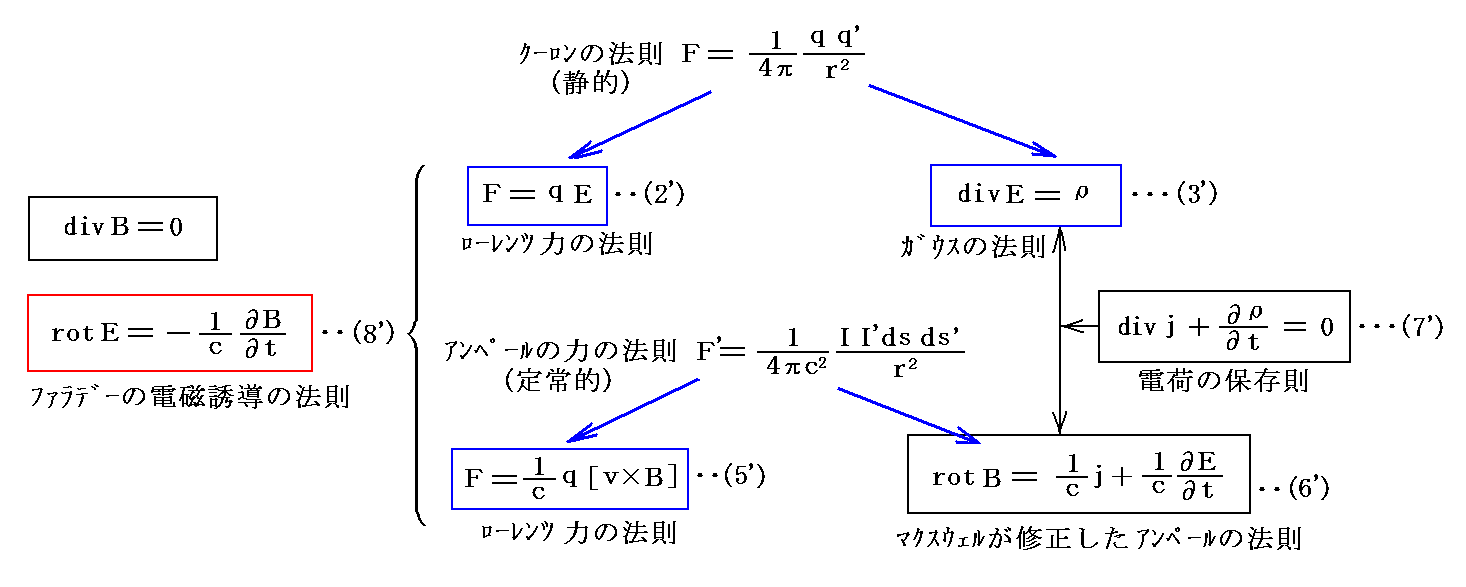
• （１）〜（８）式を今日のMKSA有理化単位系（γ＝１とする単位系）で表した［マクスウェルの方程式］、［ローレンツ力の式］と対応させると
  
  となる。５．（３）３．の一覧表を参照されて、他の単位系の［マクスウェル方程式］、［ローレンツ力公式］に対応させてみるとε₀、μ₀、γの対応が明瞭になると思います。
  　この中にdivＢ＝0が含まれていないが、これは単独の磁極が存在しない、したがって磁流が存在しない事を示しており、（８'）式と表裏一体の関係にあるので普通これを付け加えておく（別稿「マクスウェルによるアンペールの法則の拡張」参照）。これは（６'）式とともにベクトル場Ｂを規定するものであり補い合う関係にあるので、この関係式から新たな比例定数を導入する事にはならない。
• 前の対応表の中で（１）（３）式は静的な場合のみ正しい。また（４）（６）式は定常的な場合のみ正しいことに注意。しかし番号に’を付けた式は、時間的に変動する場に於いても真に正しい方程式である。　

　以上で準備は整ったので、前項の最後に導いた式と同様な式が導けることを以下で示す。５個の式（２）（３）（５）（６）（７）に対して未知量はｑ、Ｉ、Ｅ、Ｂ（orＨ）、ε₀、μ₀、γの７個である。（５）式に（６）式を代入したものを（７）式で変形する。そして、（２）、（３）式を代入して、未知量ｑ、Ｉ、Ｅ、Ｂ（orＨ）を消去すると、未知量ε₀、μ₀、γが満足すべき条件式がただ１個残る。

となり、前項と同様な関係式が得られる。

　このとき(２)と(５)式の代わりに(８)式を用いた場合、(８)式の(一周の距離)＝ｄｓ、(面積)＝ｄｓ²とすると

となり、全く同様な式が得られる。

　４．（１）３．項で説明するように(９)式中の［速度の次元を持つ定数］は実験により定めることができる。実験によるとこの値は光速度となる。単位系の違いを（９）式に集約できることは多くの本（例えば文献２、３、４、７等）で説明されているが、特に文献７が詳しくて解りやすいので参照されたし。

３．単位系を分類する基本式

　結局、電気的な量を定義する式の比例定数をε₀［真空中の誘電率(電束密度Ｄと電場Ｅの比)］、磁気的な量を定義する式の比例定数をμ₀［真空の透磁率(磁束密度Ｂと磁場Ｈの比)］、電気的な量と磁気的な量の次元を関係づける比例定数をγとし、真空中の電磁波の伝播速度をｃ（光速）とすれば、それらの間には

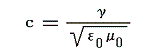
なる関係が成り立つことになる。実験によって実測（つまり絶対測定）された光速ｃは、ほぼ3×10¹⁰cm/sという値です。この式の制限のもとでγ、ε₀、μ₀のうち２つは、次元まで含めて任意に選ぶことができる。その選び方と、その次元・値の決め方により各種の単位系が区別される。
　ところで、今日光速度を表すのに文字“ｃ”を用いるのは、ラテン語のspeedを意味する“celeritas”に由来するようです。
（http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/c.html）

　真空中の光速度ｃは普遍定数ですが、測定精度の向上に伴ってｃの値が改訂されたとき、γ、ε₀、μ₀の内の最初に定めた二つは変わらないが、残りの一つの定数の値が改訂される可能性がある。以下の説明で≒で記述してある値がそれです。
　”ｃの値が改訂されたとき”という言い方には注意が必要。今日光速＝2.99792458×10⁸m/sと定められている。そして長さの単位の方が「光が1／299792458秒間に進む距離を1ｍとする」となっている。だから測定精度が向上すると長さがより正確に定められることになる。そのより正確になった１mの299792458倍が１ｓ間に光が進む距離というわけです。
　
　普通は、独立に取れる２個の係数を一番簡単な無次元量にして、数値は１とする。他の取り方も考えられるがわざわざ難しくする事はないので、その定め方は妥当である。そうするとその係数が関係する式が定義する物理量を力（長さ・質量・時間）の関数として表せ絶対測定する事ができる。
　（１）静電単位系はε₀＝１、γ＝１とする。そうするとμ₀≒１／ｃ² となりμ₀が次元を持つことになる。
　（２）電磁単位系はμ₀＝１、γ＝１とする。そうするとε₀≒１／ｃ² となりε₀が次元を持つことになる。
　（３）ガウス単位系はε₀＝１、μ₀＝１とする。そうするとγ≒ｃ となりγが次元を持つことになる。
ただし、MKSA有理化単位系はγ＝１とするが、もう一つ任意に選べるμ₀についてμ₀＝4π×10^-7N/A²としている。つまり
　（４）MKSA有理化単位系はμ₀＝4π／10⁷［N/A²_orＨ／ｍ］、γ＝１とする。そうするとε₀≒10⁷／（4πｃ²）［Ｆ／ｍ］ となりε₀も次元を持つことになる。
　なぜわざわざこのような複雑な置き方をしたのかと言うと、歴史的ないきさつがあるからです。
　まず、μ₀に次元を与えることになったのは、基本的な次元として第４番目の次元［電流Ｉ］を導入したからです。新しい次元を導入したのは電気磁気現象が全く新しい物理的現象だからそれを特徴づけるためです。
　次に、10^-7と言う小さな値にしたのは、この係数が定義（つまりそれまでに知られていた量である力に結びつけること）する電流という物理量が、実際に利用されている状況の大きさにマッチするようにするためです。
　さらに、4πをかけたのは、法則を表す公式が幾何学的状況とうまく対応するようにするためです。これらの事柄については５．章で詳しく説明する。

４．補足説明

　ここでε₀とμ₀について重要な注意をしておく。

　１．（３）２．項の（３）式の右辺の分母に現れたε₀を左辺に乗じて得られる量ε₀Ｅは普通Ｄと置き換えられて電束密度と呼ばれる。そのように置き換えれば（３）式は比例定数を含まない根元的な式になる。このとき

の二つの式は（１）式を分解したものではなくて、もともと独立な二つの法則とみなせる事でする。つまり（２）式は静止している電荷に力を及ぼす場の成分Ｅを定義する式であり、（３''）式は電荷ｑが作る場Ｄを定義する式です。電荷の実体が明らかになる前には、ＥとＤは本来まったく異なる物理量で独立に決めることができた。実際（３''）式は誘電体のような電媒質のなかでも正しい式であり、ｑがその中で作る場はＥではなくてＤなのである。
　そのような電媒質中ではＥとＤはＤ＝εＥと表されるが、この時のεは周囲の媒質に依存し、場の強度や方向にも依存し、場の時間的な変動周期にも依存する複雑なテンソル量となる。だから一般の電媒質中ではＥとＤは独立な二つの量であり、その両者を結びつける付加条件方程式がＤ＝εＥである。真空中の電荷に対してのみεはε₀という単なる定数になりＤは単にＥのε₀倍であるという意味しか持たなくなる。

　同様に１．（３）２．項の（６）式の右辺の分子に現れたμ₀を左辺に移項して得られる量Ｂ／μ₀は普通Ｈと置き換えられて磁場と呼ばれる。そのように置き換えれば（５）、（６）式は

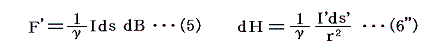
の様な二つの独立な式になる。（５）式は動いている電荷に力を及ぼす場の成分Ｂを定義する式であり、（６''）式は電流Ｉが作る場Ｈを定義する式です。磁荷の実体が明らかになる前には、ＢとＨは本来全く異なる物理量で独立に決めることができた。実際（６''）式は磁性体のような磁媒質のなかでも正しい式であり、 Ｉ がその中で作る場はＢではなくてＨなのである。
　そのような磁媒質中ではＢとＨはＨ＝Ｂ／μと表されるが、この時のμは周囲の媒質に依存し、場の強度や方向にも依存し、場の時間的な変動周期にも依存する複雑なテンソル量となる。だから一般の磁媒質中ではＢとＨは独立な二つの量であり、その両者を結びつける付加条件方程式がＨ＝Ｂ／μである。真空中の電流に対してのみμはμ₀という単なる定数になりＨは単にＢをμ₀で割ったものであるという意味しか持たなくなる。

　ここはこちらの一覧図［2013年3月追記］も参照されて下さい。この当たりはどの電磁気学の教科書にも詳しく説明してあるところですが、高校生が勉強されるには、参考文献10（下巻）の第9章「物質中の電場」、第10章「物質中の磁場」が適当だと思う。

２．静電単位系(electrostatic system of units、CGSesu系)

　γ＝1、ε₀＝1、したがって、μ₀≒1/c²＝(1/9)×10^-20s²/cm²としている。そのため真空中でＢ＝（1/c²）Ｈとなり、ＢとＨの変換係数としてc²が入ってくる。

　これは元々電気におけるクーロンの法則の比例定数を１とすることに由来する。

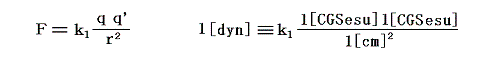
　つまり、真空中で 1 cm の距離にある等しい電荷ｑ＝ｑ’の間に働く力が 1 dyn の時、これを 1 ［CGSesu］（あるいは１ ［cm^3/2g^1/2ｓ^-1］） の電気量であると定義する。そのためクーロンの法則の比例定数ｋ₁は１になる。今日ではｋ_１＝１／ε₀とおくことが慣例であるからε₀＝1とすることに相当する。ちなみに ［dyn］（ダイン ［g¹cm¹ｓ^-2］）は CGS単位系での力の単位であり、 1 ［N］ = 10⁵［dyn］ です。このようにして新物理量である電気量ｑが導入・定義された。
　（注意）後で説明するガウス単位系との混同を避けるために、今日ではε₀にεなる次元を与えて議論している（６．（１）の表参照）。しかし、これは混同を避けるための単なる符帳のようなもので、すべての次元εの部分を無次元の１で置き換えても差し支えない。

（１）電気的な量の次元

　電気量ｑが定義できれば、ファラデーにより実験的に証明された関係式

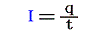
を用いて電流 Ｉ の単位［cm^3/2g^1/2ｓ^-2］と次元［Ｌ^3/2Ｍ^1/2Ｔ^-2］が決まる。
　電流が決まれば、ジュールにより実験的に証明された関係式

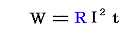
を用いて抵抗 Ｒ の単位［cm^-1s¹］と次元［Ｌ^-1Ｔ¹］がきまる。
　電流ｉと抵抗Ｒがきまればオームが導いたオームの法則により

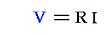
起電力（電位差） Ｖ の単位［cm^1/2g^1/2s^-1］と次元［Ｌ^1/2Ｍ^1/2Ｔ^-1］が決まる。
　電場Ｅは高校物理で習う定義式

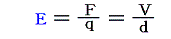
を用いれば、その単位［cm^-1/2g^1/2s^-1］と次元［Ｌ^-1/2Ｍ^1/2Ｔ^-1］が決まる。

（２）磁気的な量の次元

　電気的な量から磁気的な量の次元を求めるには、アンペールの法則か、ファラデーの電磁誘導の法則を用いればよい。たとえば１．（３）２．（６’）式のアンペールの法則を無限直線電流に適応した式

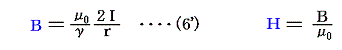
を用いて、γ＝１、μ₀＝１／ｃ²を考慮すれば、磁束密度Ｂの単位は［cm^-3/2g^1/2］、次元は［Ｌ^-3/2Ｍ^1/2］となる。また磁場Ｈの単位は［cm^1/2g^1/2s^-2］、次元は［Ｌ^1/2Ｍ^1/2Ｔ^-2］となる。μ₀に次元を与えているので、この単位系ではＢとＨの次元が異なってくることに注意。
　磁荷の次元を求めるには１．（３）１．（２）式の磁荷についてのクーロンの法則

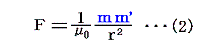
を用いればよい。μ₀＝１／ｃ²を考慮すれば、磁気量ｍの単位は［cm^1/2g^1/2］、次元は［Ｌ^1/2Ｍ^1/2］となる。この場合磁極に関するクーロンの法則には比例定数１／μ₀＝ｃ²が掛かってくることに注意。
　さらに磁気モーメント（電磁モーメント）や磁気双極子モーメントの単位や、次元はその定義式に従って求めればよい。このとき、この単位系では磁気モーメント（電磁モーメント）と磁気双極子モーメントの次元が異なることに注意（６．（１）、（２）の一覧表参照）。

３．電磁単位系(electromagnetic system of units、CGSemu系)

　γ＝1、μ₀＝1、したがってε₀≒1/c²＝(1/9)×10^-20s²/cm²としている。そのため真空中でＤ＝（1/c²）Ｅとなり、ＤとＥの変換係数としてc²が入ってくる。

　これは元々磁荷におけるクーロンの法則の比例定数を１とすることに由来する。

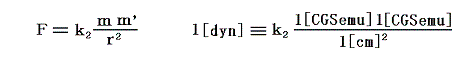
　つまり、真空中で 1 cm の距離にある等しい磁極（実際には単独の磁極をとりだすことはできない）の間に働く力が 1 dyn である時、これを 1 ［CGSemu］（あるいは１ ［cm^3/2g^1/2ｓ^-1］） の磁極の強さであると定義する。そのためクーロンの法則の比例定数ｋ₂は１になる。今日ではｋ₂＝１／μ₀と置くのが慣例であるのでμ₀＝1を意味する。このようにして新物理量である磁気量ｍが導入・定義された。
　　（注意）後で説明するガウス単位系との混同を避けるために、今日ではμ₀にμなる次元を与えて議論している（６．（１）の表参照）。しかし、これは混同を避けるための単なる符帳のようなもので、すべての次元μ₀の部分を無次元の１で置き換えても差し支えない。

（１）磁気的な量の次元

　磁気量ｍが定義できれば、磁場Ｈはその定義式

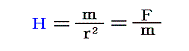
により、その単位 ［cm^-1/2g^1/2ｓ^-1］と次元 ［Ｌ^-1/2Ｍ^1/2Ｔ^-1］を求めることができる。
　磁束密度Ｂはその定義

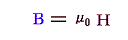
とμ₀＝１であることを考慮すると、その単位 ［cm^-1/2g^1/2ｓ^-1］と次元 ［Ｌ^-1/2Ｍ^1/2Ｔ^-1］が定まる。この単位系ではＢとＨの次元は同じになることに注意。他の磁気的な量の次元はその定義式によって求めればよい。

（２）電気的な量の次元

　磁気的な量から電気的な量の次元を求めるには１．（３）１．の（３）式ビオ=サバールの法則、１．（３）２．の（５）式ローレンツ力の公式、（６）アンペールの法則、（８）電磁誘導の法則等の何れかを用いればよい。

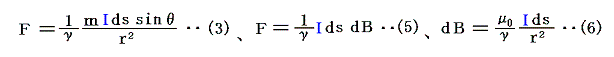
いずれを用いてもγ＝１、μ₀＝１であることに注意すれば ｍ や Ｂ の次元から、電流 Ｉ の単位 ［cm^1/2g^1/2ｓ^-1］と次元 ［Ｌ^1/2Ｍ^1/2Ｔ^-1］が定まる。
　Ｉ が求まれば電流の定義

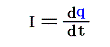
より、電気量 ｑ の単位 ［cm^1/2g^1/2］と次元 ［Ｌ^1/2Ｍ^1/2］が定まる。
　ｑ と Ｉ が定まれば

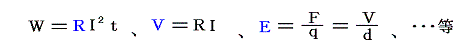
の公式を利用すれば、次々にＲ、Ｖ、Ｅ、・・・等の物理量の単位と次元が定まる（６．（１）、（２）の一覧表参照）。
　この時、電磁単位での電気量ｑを用いるとクーロンの法則に比例定数1/ε₀＝ｃ²が掛かってくることに注意。つまり電流として１単位の力を発揮する１単位の電気量は、もしその電荷が裸で存在したら静電的な力としては１単位の力のｃ²倍の巨大な力を発揮すると言うことです。ここで注意しておかねばならないのは、一単位の電荷の流れと言っても電流はそれと反対符号を持つ電荷に寄り添いながら動いているので、静電気的な正味の電気量は打ち消されて存在しない事です。

（３）磁気力による電流の定義

　実際には単独の磁極は存在しない。磁気の原因は円電流（究極的には電子スピン）に還元できる。そのため磁気的な量を定義するときの出発点として、磁荷による磁気力ではなくて、電流が生み出す電磁気力を磁気力の基本とする立場を今日では採用する。ここで電流による定義と磁荷による定義との整合性について説明する。

１．ウェーバーによる定義

　電気量を電磁単位で最初に定義したのはウェーバー（1840年）です。彼が用いた方法は導線が単位の面積の周囲を囲んでいるとき、この導線の断面を単位の時間に単位の電気量が通過する割合で電流が流れたとき、遠方に生じる磁気作用は絶対単位の単位の磁荷が及ぼす作用と同じであるという事実を利用するものです。このことは次のようにして証明できる。

　電磁単位系では磁荷に対するクーロンの法則の比例定数μ₀＝１、ビオ=サバールの法則の比例定数γ＝１とおくのですが、次節で述べるガウス単位系でも磁気的な量を電流の定義から定めていくのでμ₀、γのまま論じる。それぞれの公式は

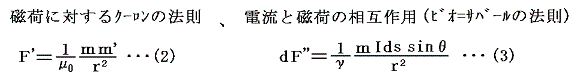
となる。
　ここで、下図の様な半径ａの円形コイルに電流 Ｉ が流れているとする。コイルの中心から距離 ｒ の位置にある磁荷ｍ' に及ぼす力を求める。（３）式のビオ=サバールの法則を用い、さらにｒ＞＞ａの場合を考えると

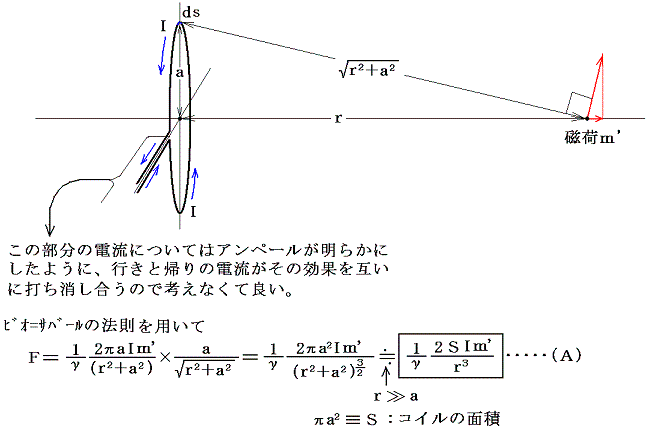
となる。
　次にコイルの中心の位置に磁気双極子モーメントｐ_m＝ｍΔＬの小磁石をコイル面に垂直に置いたとき、その小磁石から距離 ｒ の位置にある磁荷ｍ'に及ぼす力を求めると

となる。
　磁荷の実体は電流であり、電流が磁気力を生み出すと考えると（Ａ）＝（Ｂ）が成り立つと考えなければならない。

　電磁単位系では、この式からｐ_mのｍとΔＬ、そして面積Ｓが単位の大きさとすると、このとき流れる電流が単位の大きさの電流となる。電流の次元は［Ｌ^1/2Ｍ^1/2Ｔ^-1］であり、電磁単位系で測った１［CGSemuの電流］＝１［cm^1/2g^1/2ｓ^-1］の電流が定まる。単独の磁極を取り出すことができないので何とももどかしいところがある議論だが、このようにして磁荷を電流で置き換えることができる。(磁場の全空間分布の一致も確かめた一般的な証明は、例えば参考文献10の第10章3節等を参照。そこでの電気双極子を磁荷の双極子に置き換えればよい)
　ガウス単位系での関係式中のＩは静電単位で測った電荷定義による電流Ｉ_esuである。電磁単位定義の電流Ｉ_emuに置き換えるときはＩ_esu/ｃ＝Ｉ_emuとなる。（詳しくは４．ガウス単位系参照）

２．電流の絶対測定

　実際の電流を電磁単位で絶対測定するには以下のようにすればよい。ウェーバーは下図に示す正接検流計(tanθから電流値を測定するので正接という)を用いた。これは直径約20cmの銅の円環の下部を切り開いて、その両端を下方に伸びた導線に接続したものである。円環の中央部にある水平な木板の上に小さな磁針が置いてある。
　円環を地磁気子午線と平行に固定し、磁針が最初コイル面と平行になるように設置する。つぎに、円環に電流Ｉを流すと円環の中央にはコイル面に垂直（地磁気に垂直）な方向に磁場Ｈ_電流が生じる。その値はビオ=サバールの法則から求めることができる。Ｈ_電流が地磁気Ｈ_地に付け加わるため、小磁針は地磁気の北極の方向から偏向する。その偏向量θから電流値 Ｉ が測定できる。（高校物理の練習問題）

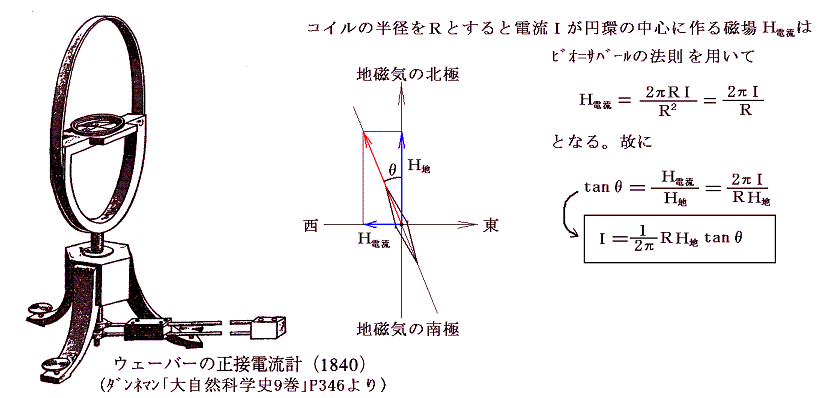
　このとき、別稿「ガウスによる地磁気の絶対測定(1832年)」で説明した方法でＨ_地は絶対測定できるので、ｔａｎθさえ測定できれば、流れた電流を電磁単位で絶対測定できることになる。後にウェーバーはもっと精度の良い検流計を開発して測定精度を改善している。

３．補足

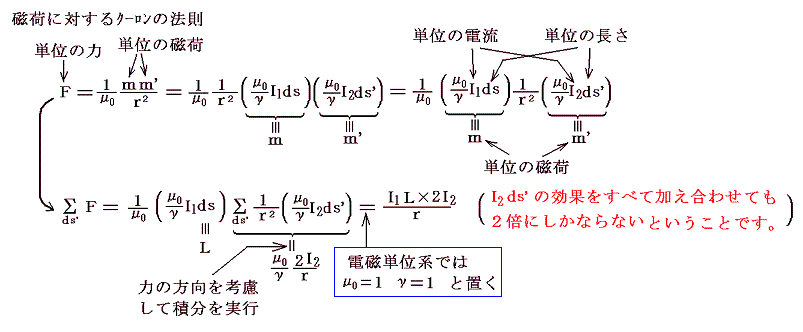
　ここは込み入っているので、もう一度見方を変えて説明する。１．（３）１．の磁荷に対するクーロンの法則と１．（３）２．のアンペールの力の法則を比較してみるとｍを（μ₀／γ）Ｉｄｓで置き換えればよいことが解る。

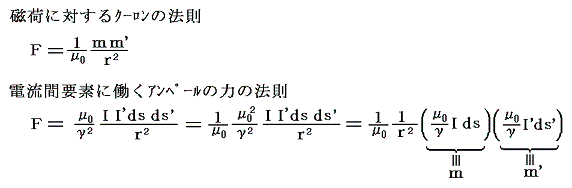
さらに、１．（３）１．のビオ=サバールの法則（θ＝90°の場合）のｍを（μ₀／γ）Ｉｄｓで置き換えてみると

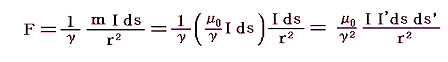
となり、すべてつじつまが合うことが解る。
　ここで、電磁単位系における電流Ｉの次元は ［Ｌ^1/2Ｍ^1/2Ｔ^-1］であることを今一度注意しておく。つまり(μ₀／γ)ＩＳ＝ｐ_m＝ｍΔＬあるいは(μ₀／γ)Ｉｄｓ＝ｍのどちらの定義を用いても、電磁単位系ではμ₀＝γ＝１(無次元)だから磁荷ｍの次元 ［Ｌ^3/2Ｍ^1/2Ｔ^-1］を距離の次元［Ｌ］で割ったものになる。　　

　電磁単位ではμ₀＝１、γ＝１、ε₀＝１／ｃ²と置くのであるから、電流要素に対するアンペールの力の法則（Ｉ＝Ｉ'、ｄｓ＝ｄｓ'とする）は

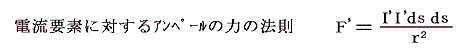
となる。上に述べたように電磁単位系ではこの式を用いて１［単位の電気量］を定める。まず、この式で距離ｒ、ｄｓ等を単位の長さ（１cm）とするとき　Ｆ'＝単位の力（１ｄｙｎ）　となる Ｉ を電磁単位で測定した１［単位の電流］とする。このときＩ＝ｄｑ'／ｄｔであることを考慮して、１［単位の電流］というのは電磁単位で測った１［単位の電気量］ｑ'が導線のある断面積を１秒間に通過するものであるから、この結果はとりも直さず電磁単位で測った１［単位の電気量］ｑ'を定めたことに相当する。
　このとき電磁単位系での電荷に対するクーロンの法則（ｑ＝ｑ'とする）は

となり、電磁単位での１［単位の電気量］ｑ'を単位の距離（１cm）離して置くと、その間に働く斥力は、静電単位で測定した１［単位の電気量］ｑが単位の距離（１cm）離れたときに働く斥力（当然定義より１ｄｙｎ）のｃ²倍の力である事を示している。
　このことは、電磁単位で測定された１［単位の電気量］ｑ'は静電単位系で定義された１［単位の電気量］ｑのｃ倍であることを意味する。４．（１）で説明するように、このｃは測定可能です。このようにして１．（３）２．の（９）式の［速度の次元を持つ定数］の値を実験によって決定することができる。

４．ガウス単位系(Gaussian system of units、CGSgauss系)

　ε₀＝1、μ₀＝1、したがってγ≒3×10¹⁰cm/sとなる。
　すでに述べたように静電単位系は電荷のクーロンの法則の係数を１、γ＝１としたためμ₀＝１／ｃ²となり、電磁単位系は磁極（磁荷）に関するクーロンの法則の係数を１、γ＝１としたためにε₀＝１／ｃ²となる。そのため、これらの単位系では電気系か磁気系の公式のどちらか一方にのみ ｃ² なる因子が表れてくる（５．（３）３．の表参照）。
　この不便を取り除くために、ガウスは電気的な量と磁気的な量を全く対等なものとし各々独立に単位を定めた。つまり電気的な量に関しては静電単位系で定義し、磁気的な量に関しては電磁単位系で定義した。
　そのため、静電的な量だけ、電磁的な量だけが絡む公式については、電気と磁気について対応する公式が同じ形になって対称性が良くなる。しかし、一つの方程式中に静電的な量と電磁的な量の両方が含まれる法則（アンペールの法則、電磁誘導の法則）の場合には、それらの量の変換係数として必然的にγ＝ｃ(光速)が入ってくる。

　この単位系の静電esu系の［ｑ］▲、［Ｅ］＝［Ｄ］●、［ε］■の次元は、それぞれ電磁emu系の［ｍ］▲、［Ｈ］＝［Ｂ］●、［μ］■の次元に等しい（６．（１）表の▲●■参照）。したがって場に関する量はすべて同じ次元を持ち電気と磁気の双対性がよいので、基礎理論はこの単位系によって記述されることが多い。

　この単位系では電気的量と磁気的量の両方が関係する公式に於いて、両者の間に変換係数ｃを入れて式中の各項の次元を整合する必要がある。そのとき一番問題になるのは、当初ｃはウェーバーとコールラウシュの実験(1856年次節参照)から光速に近い値であるという近似的な値しか解っていなかったことです。近似的な数値では基礎方程式に挿入するわけにはいかない。しかしヘルツの実験(1888年)から電磁波＝光となってからは、精度の良い光学的測定値(フィゾー1849年、フーコー1850年、マイケルソン1878年〜)を用いることができることになり、ガウス単位系の採用は精度的にも問題は無くなった。そのためヘルムホルツ、ヘルツらによって採用され普及がはかられた（プランクやランダウ・リフシュツの教科書がこの単位系）。

　ガウス単位系を有理化（５．（２）を参照）したものに、ヘビサイド及びローレンツが用いた単位系（これに付いては５．（４）２．を参照）があるが、今日では全く用いられていません。

　ガウス単位系においては、電気的な量の定義は電荷に関するクーロンの法則による電気量ｑの定義から出発する。そして、磁気的な量の定義としては今日では磁荷のクーロンの法則よりも、電流が生み出す電磁気力を磁気力の基本とする立場を取る。そのため磁気的な量も電気的な電流 Ｉ を定義することから出発する。それは３．（３）で述べた電磁単位系の電流の定義である。そのとき電流は電気量を時間微分したものだから、そのままでは電気量という物理量に対して二通りの定義が存在することになってしまう。そのことを避けるために電磁単位で測った電流密度値に光速を掛けてから速度で割って静電単位の電気密度の定義に一致させる。つまり

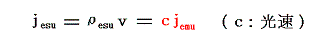
の関係式を設定する。そのため、ガウス単位系に於いて磁気的な量を定義するとき、磁荷の磁気力ではなくて、電流が生み出す電磁気力を磁気力の基本とする立場をとれば、ガウス単位系における電流や電流密度は電気的な量であるにもかかわらず電磁単位系のそれらと同じ次元と数値を持つことになる。だから、MKSA有理化単位系からガウス単位系へ電流や電流密度の数値を変換するときの変換係数も電磁単位系の対応するものと同じになる。（６．（１）、（２）の対応表のガウス単位系電流、電流密度欄の赤記載参照）
　電磁単位の１単位の量は静電単位の１単位の量のｃ倍だから、測定数値としては電磁単位で測った値の方が１／ｃ倍小さい。そのためｃ倍しておかなければいけない。この当たりはとても混乱するところであるが、ガウス単位系で実際の数値を取り扱うときには注意しなければならない。

（１）電気量の絶対測定

　静電単位系における電気量の１単位と電磁単位系における電気量の１単位は、その定義が異なるので当然違った量になる。そのとき両者の比ｃ（＝光速）は電磁気学の根幹に関わる値なのでその測定法をここで説明する。静電・電磁両単位系で１単位の電気量を絶対測定（定義が確定している長さ・質量・時間の関数として求めること）するには、原理的に以下の様にすればよい。

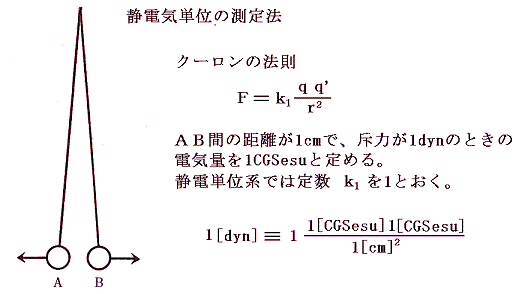
１．静電単位系の一単位の電気量（１［CGSesu］）

　二つの同じ大きさの小さな軽い導電性の球を一本の導電性の糸の両端に取り付ける。糸の真ん中を絶縁性の指示棒に結びつけて図のように吊し、摩擦電気などによって全体に電気を与える。電気は同形の球に同じように分配されるであろう。そして互いに反発して、重力の力が引き戻すのと釣り合うところまで広がるであろう。そのとき球が１［cm］離れているときに、その反発力が1［dyn］（約1000分の1グラムの重さ）となるように、与える電気量、球の重さ、糸の長さを調節する。（これは高校物理の練習問題）。そのときの電気量を 1[CGSesuの電気量]又は １［cm^3/2g^1/2ｓ^-1］ と定める。
　

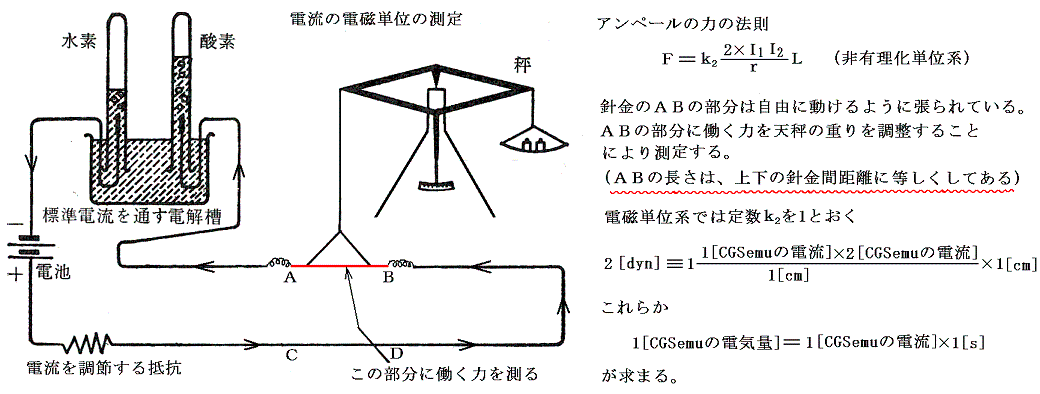
２．電磁単位系の一単位の電気量（１［CGSemu］）

　平行な直線部分を含むループ状の回路を組んで、ループ上のＡＢ辺とＣＤ辺には同じ大きさの電流が反対向きに流れるようにする。図の針金ＡＢの長さと針金の間隔ＡＣが等しくなるようにして針金ＡＢと針金ＣＤ間の斥力を天秤を利用して測定する。そのときの斥力が2［dyn］となるように電流を調整したとき 1［CGSemuの電流］が流れていると定める。
　同じ電流値を再現・維持するには、その回路の一部に酸の溶液含む電気分解槽を入れておいて、そこに毎秒発生する水素の量を目印にすればよい。その様にして測定された電流値が1秒間に運ぶ電気量を 1[CGSemu の電気量]又は１［cm^1/2g^1/2］と定める。

　ここでは電流を用いているが、この式は磁荷に対するクーロンの法則を用いた定義式そのものであることに注意。３．（３）で説明したように単位の磁気量に相当するものが単位電流が流れている単位の距離ｄｓ'に対する（μ₀／γ）Ｉｄｓ'であるが、一方の電流要素についての効果をすべて加え合わせても２倍にしかならないのである。
　
　ここでは、ＡＢの長さＬ、とＡＢとＣＤの導線間の距離 ｒ を単位の長さ、単位の距離として論じたが、これらの量は公式の分母と分子で互いに打ち消し合うので、単位の長さに取る必要は無く、両者が等しければよいことに注意。

３．二つの単位系における1単位の電気量の比較

　力の次元が［ＭＬ／Ｔ²］であることを考慮して、上記二つの定義で求められた［CGSemuの電気量の次元］＝[Ｌ^3/2Ｍ^1/2Ｔ^-1]＝[(Ｌ／Ｔ)Ｌ^1/2Ｍ^1/2] と［CGSemuの電気量の次元］＝ [Ｌ^1/2Ｍ^1/2] を比較してみると明らかなように、前者は後者に速度の次元[Ｌ／Ｔ]を乗じたものであることが解る。これは前記の電磁単位での電気量の単位［cm^1/2g^1/2ｓ^-1］×［ｓ］＝［cm^1/2g^1/2］に速度の単位［cm¹ｓ^-1］を乗じると静電単位での電気量の単位［cm^3/2g^1/2ｓ^-1］になることからも了解できる。この部分についてのMaxwellの説明をここに引用しておきます。
　両単位間の比である、この［速度の次元を持つ定数］の測定に初めて成功したのがWeberとKohlrausch(1856年)である。この測定はその後、多くの人々により繰り返し試みられた。その測定により得られた数値こそ光の真空中での伝播速度（3×10¹⁰cm／s）に相当するもので、後にMaxwellが光を電磁波と推論した裏付けの一つになったことで有名です。
　
　１[CGSesuの電気量]が 何[CGSemuの電気量]に相当するのか見つけるためにWeberとKohlrauschが用いた方法は、静電単位の電気量測定に用いた電荷をそのまますべて電磁単位を測定する回路に流して電磁単位での電流値を測定するものでした。しかし静電単位の1[CGSesuの電気量]は極めて小さいので電流として測れそうもないくらいにわずかな量であり、逆に電磁単位の1[CGSemuの電流]を上記の金属球に流し込むと、その時間をどんなに短くしても二つの球は吹っ飛んでしまうくらいに巨大である。両者の大きさがあまりにも違いすぎるので、とても難しい実験ではあるが、ウェーバーとコールラウシュは特別な工夫をしてそれを測定した。
　すなわち、上記の静電単位の測定電荷の1000000倍の電気量(彼らは既知の容量のコンデンサーに電荷をため、その電圧を測って電気量を求めた)が測定でき、上記電磁単位の測定電流の1/10000倍の大きさの電流値(彼らは衝撃検流計を用いた)が測定できればこの比例定数は測定可能である。彼らがした工夫はそれを実現するものであるが、詳細は文献4の§60、文献7の第4章、文献8のArt.771、文献9の付録6等を参照してください。
　この原論文 Ueber die Elektricitatsmenge, welche bei galvanischen Stromen durch den Querschnitt der Kette fliesst. Wilhelm Weber und R.Kohlrausch; Annalen der Physik,99(1856):10-25 は有料ですが　http://www3.interscience.wiley.com/journal/112497888/abstract　から入手可能です。しかし、この英語訳が　http://www.ifi.unicamp.br/~assis/Weber-Kohlrausch(2003).pdf　の付録に収録されているのでこちらをダウンロードされて読まれる方が良いと思う。
　
　これは、静止した電荷に力を及ぼす場の成分が電場であり、動いている電荷に力を及ぼす場の成分が磁束密度であることを示しているのだが、電荷はその両方を生み出すことができるのである。また、これは同じ符号の荷電粒子の一群が加速されていったら、反発の力は同方向の電流間の引力によって打ち消され、光の速さに近づくにしたがってその打ち消し方が完全になることを意味している(詳しくは別稿「電磁場の応力（マクスウェルの応力）」３．（４）４．参照）。マクスウェルは文献8のArt.769でこのことに注意をうながしており、Art.770でそのことを確かめるための実験を提案している。実際に実験によってこの効果を確かめたのはH.A.Rowlandです。［1876年〜1889年の一連の実験で確かめた。論文Rowland and Hutchinso, "On the Electromagnetic Effect of Convection-currnts", Phil. Mag. S.5 Vol. 27. p445, 1889年参照。これはGoogleBooksからダウロードできます］
　この当たりはまさに電磁気学の根幹に関わる事柄で、参考文献１０の第５章、６章に興味深く解説してある。また6章§8にRowlandの実験の概要が説明されている。この本は高校生が次に読むべきものとして最適だと思う。

（２）具体的な数値例（詳しくは６．（２）の換算表参照）

電気量ｑについて、電磁単位の 1[CGSemu の電気量]は静電単位の 1[CGSesu の電気量]よりもｃ倍＝3×10¹⁰倍大きい。これは電流Ｉに付いても同様である。

例えば電子の電荷ｅ（MKSA単位系で1.6×10^-19Ｃ）は静電単位系では比較的大きな 4.8×10^-10 [CGSesu]or［cm^3/2g^1/2s^-1］となり、電磁単位系では、その１／ｃ倍だけ小さな 1.6×10^-20 [CGSemu]or［cm^1/2g^1/2］（これはMKSA有理化単位系のＣoulomb単位表示の0.1倍）となる。

電位差(起電力)Ｖについては、電位差の次元が [エネルギー／電気量] であり、エネルギーの単位は両単位系で同じであることから、電磁単位の 1[CGSemu の電位差]は静電単位の 1[CGSesu の電位差]よりも １／ｃ倍＝1／3×10¹⁰倍小さい。

例えばダニエル電池の起電力Ｖ(MKSA単位系で約１ボルト)は静電単位系で １／300[CGSesu]＝10⁸／ｃ[CGSesu]or［cm^1/2g^1/2s-1］ となり、電磁単位系では、そのｃ倍だけ大きな 10⁸ [CGSemu]or［cm^3/2g^1/2s^-2］ となる。

抵抗Ｒ＝Ｖ／Ｉ［あるいは抵抗率ρ＝Ｒ(Ｓ／Ｌ)＝(Ｖ／Ｉ)(Ｓ／Ｌ)］については［起電力／電流］が関係するのでＶの１／ｃ倍と１／Ｉの１／ｃ倍の積１／ｃ²倍だけ電磁単位の１単位が、静電単位の１単位より小さい。

例えば断面積１mm²、長さ１mの水銀柱の抵抗Ｒ（MKSA単位系で約１Ω）は、静電単位系では1.1×10^-12[CGSesu]or［cm^-1s¹］となり、電磁単位系ではそのｃ²倍大きな10⁹[CGSemu]or［cm¹s^-1］となる。

コンダクタンスＧ＝１／Ｒ＝Ｉ／Ｖ［あるいは導電率(電気伝導度)σ＝１／ρ＝Ｇ(Ｌ／Ｓ)＝(Ｉ／Ｖ)(Ｌ／Ｓ)］については［電流／起電力］が関係するのでＩのｃ倍と１／Ｖのｃ倍の積ｃ²倍だけ電磁単位の１単位が、静電単位の１単位よりも大きい。

例えば水銀の0℃での導電率σ（MKSA単位系で1.063×10⁶Ω^-1ｍ^-1）は静電単位系では9.55×10¹⁵［CGSesu］or［s-1］となり、電磁単位系ではその１／ｃ²倍だけ小さな 1.063×10^-5［ CGSemu］or［cm^-2s¹］となる。

（３）静電単位系と電磁単位系の違い

　静電単位と電磁単位の数値的な違いは、その定義から明らかなように取り扱う物理現象の違い（静電気学と動電気学）に由来している。静電気学では取り扱う電気量は小さいが、電位（電界強度×距離＝エネルギー／電気量）は非常に大きな場合が問題になる。これに対して動電気学では電位（電界強度×距離＝エネルギー／電気量）はほどほどですが、大電気量の移動が取り扱われる。
　実際、高校物理の静電気学の授業で習うように、１ｍ離して置かれた１Ｃの二つの電荷が互いに反発する力は9×10⁹Ｎというとてつもなく巨大なものだから、普通の静電気の実験で取り扱う電気量は極微量であることが分かる。しかしその極微量の移動（二つの物体を摩擦すれば実現できる）で数万ポルトの電位差は簡単に作り出せる。
　一方動電気学の１Ａの電流は１Ｃという巨大な電気量が１ｓ間に通過する流れですが、それらはほんの数ボルトの電位差で生み出される。そのとき、電流は電荷がその反対符号の電荷に寄り添いながら移動する現象だから、裸の正味の電荷間に働く静電気的な力は隠されている。ボルタの電池の発見（1800年）と、それに続くエルステッドの電流の磁気作用の発見（1820年）が、動電気磁気学が形づくる驚異の世界の扉を開いた。

５．MKSA単位系（m、kg、s、A）［国際(SI)単位系の一部分］

　γ＝1、μ₀＝4π×10^-7（N/A²）＝12.566････×10^-7（H/m）、したがって

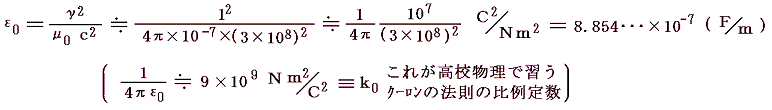
となる。この単位系ではε₀の値が改訂される可能性があるが値そのものは変わらない。光速もμ₀も定義により数値は固定されているのだから。［８．基礎定数表のε₀の誤差が0となっていることに注意されたし］

　この単位系では真空中でＤとＥの変換係数としてε₀が、ＢとＨの変換係数としてμ₀が必ず絡んでくる。しかし一つの方程式中の電気的な量と磁気的な量の変換係数として光速ｃが出てこないようにできる。光速ｃはε₀とμ₀の定義の中に含ませてしまえば良いのだから。もちろんファインマン物理学�V「電磁気学」のようにε₀と光速ｃ²を変換係数としてもよいが、そのあたりは好みの問題です。

（１）数値の調整

１．μ₀の数値調整

　MKSA単位系の定義のε₀に1/ｃ²が絡んでおり、μ₀は単なる数値であることから分かるように、元々この単位系はCGS電磁単位系に由来する。
　そのとき、なぜμ₀＝4π×10^-7N/A²（1948年の第9回国際度量衡総会）としたのかというと、電流の単位が1881年の第1回国際電気会議で定められていた実用単位系（電気工学で現実的な大きさに成るようにCGS電磁単位の数値を調整した単位系）の電流単位アンペアに一致するように×10^-7倍したのである（cm､g､sからm､kg､sに変換するとそうなる）。
　MKSA単位系の第４番目の基本単位である電流Ａ（アンペア）の単位は、1948年の第9回国際度量衡総会にて、平行導線に流れる電流 Ｉ とその間に働く力 Ｆ の関係式

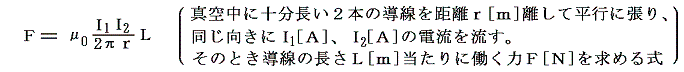
を利用して定められた。この式でＩ₁とＩ₂を等しくし、Ｌ＝1m、ｒ＝1mとしたときの力がＦ＝2×10^-7Ｎとなるような電流値を1Aと定めた。そのとき、μ₀の定義値を調節すればアンペアＡの単位の大きさを任意に調節することができる。またそのとき新しい次元の電流［Ｉ］を導入したためにμ₀は無次元量ではなくなる。つまり

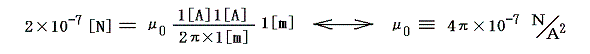
として、１アンペアが当時使われていた実用単位系の１Ａ＝0.1CGS電磁単位に一致するようにした。（ここでμ₀定義式中の4πについては次節で説明）

　４番目の基本単位として電気抵抗Ωや電気量 Ｃ ではなくて電流 Ａ を採用した理由は、「電流が電気的量と磁気的量の両方に関わりのある量であり、電流値の方が電気量そのものよりも測定しやすい」かららしい（電気量の単位 Ｃ は Ａ･ｓ から求まる）。
　このMKSA有理化単位系は、電気工学でそれまで普通に用いられていた実用単位が発展したものなので具体的な事例を取り扱うときは非常に有利になる。

２．実用単位

　実用単位系が定められたのは1881年です。当時電信技術などの電気工学が発展してきたが、そこで取り扱われる導線の抵抗はCGS電磁単位で10⁸〜10⁹のオーダー、また当時盛んに用いられたダニエル電池の起電力もCGS電磁単位で10⁸のオーダーとなりCGS電磁単位をそのまま用いたのでは非常に不便であった。そのため当時のヨーロッパで盛んに用いられていたジーメンス社製の水銀抵抗器（断面積１mm²、長さ１mの水銀柱）の0℃の抵抗を１オームと言ったり、ダニエル電池の電圧を１ボルトと呼んで慣習的にオームやボルトの単位が用いられていた。しかし、それらの定義には任意性がありバラバラであったので、CGS電磁単位の数値を調整して使いやすい単位をきちんと制定しようと言うことになった。そうして1881年の第１回国際電気会議（パリ）で定められたのが実用単位です。
　そのときの決定事項は

1. 基本単位としてcm、g、ｓを用いる。
2. 当時慣習的に用いられていたオーム（抵抗）とボルト（電圧）については、それをほぼそのまま踏襲する。
   　　　１オーム＝10⁹CGS電磁単位（ジーメンス社の水銀抵抗器の抵抗にほぼ等しい）とする。
   　　　１ボルト＝10⁸CGS電磁単位（ダニエル電池の起電力にほぼ等しい）とする。
3. 上の定義にしたがって抵抗原器に相当するものを断面積１mm²、温度0℃の水銀柱の長さで定める。正確な長さの決定は、その時にはされずに、今後の測定課題とされた｡
4. １オームの抵抗に１ボルトの電位差が掛かったとき流れる電流を１アンペアと命名する
   　それまで電流の単位にはウェバーが使われていたが国により数値が異なっていたので、混乱を避けるために新しい呼称アンペアに決まった。（Ｉ＝Ｖ/Ｒだから１アンペア＝0.1 CGS電磁単位となる。）
5. １アンペアの電流が１秒間に移動させる電気量を１クーロンと命名する。（Ｑ＝Ｉｔで秒は共通だから１クーロン＝0.1 CGS電磁単位となる。）
6. コンデンサーの電気量が１クーロンのとき、その電圧が１ボルトになる容量を１ファラッドと命名する。（Ｃ＝Ｑ／Ｖだから１ファラッド＝１／10⁹ CGS電磁単位となる。）

と言うものでした。

　以上の様に絶対単位系（電磁単位系）をもとに実用単位系が定められたのだが、定義しただけでは効果がない。役立たせるためにはその単位を簡便に実現・再現する物差しとなる物が必要である。上記3.の課題がそれである。その要請を受けて絶対単位による精密測定が実施されて
　1889年第2回国際電気会議（パリ）で１オーム＝0℃での断面1mm²、長さ106.cmの水銀柱の抵抗とする。
　1893年第3回国際電気会議（シカゴ）で１オーム＝0℃での断面1mm²、長さ106.3cmの水銀柱の抵抗とする。
　1908年第7回国際電気会議（ロンドン）で
　　　１国際オーム＝0℃で14.4521g、長さ106.300cmの均一な断面積を持つ水銀柱の定常電流に対する電気抵抗
　　　１国際アンペア＝硝酸銀水溶液を電気分解したとき、毎秒0.00111800gの銀を析出する定常電流値
　　　１国際ボルト＝１国際アンペアが１国際オームを流れるのを保持する電位差
と定められてきた。
　そして、実際にはこの定義から測定された起電力 1.0186Ｖ(20℃にて) のカドミウム(ウェストン)電池が標準電圧、また上記の水銀柱が標準抵抗として用いられた。しかし、測定技術が進歩するたびにCGS電磁単位（絶対単位）で定義値を計り直してみると国際単位の定義値に誤差があることが解ってきた。最初はその誤差を補正して利用していたが、時代と共に国際単位の定義自体が意味を持たなくなった(つまり原器はそのつど十分な制度で絶対測定できるようになった)ので1948年に廃止された。
　
　実際の工学では随時電圧・抵抗・電流の値を校正する必要がある。そのためどの時代にも標準原器となるものが、絶対単位の定義と照らし合わせて構成された。時代と共に随時、様々なものが原器として採用され且つ更新されてきたが、一般に電流標準器を構成して電流を正確に測定するのはとても難しいので、普通は抵抗と電圧の標準原器がつくられた。つまり、電流は電圧と抵抗が定まれば決められるので、実用上は電流ではなくて電圧と抵抗を基準にしているのだ。
　いろいろ変遷はあったが、今日原器として採用されているのは再現性の優れている量子ホール効果を用いる抵抗標準器とジョセフソン効果を用いる電圧標準器です。それらが示す抵抗や電圧を絶対単位で測定して原器としているわけである。実際にはそれらはプランク定数ｈと電気素量ｅの関数となるので、ｈとｅの精度を絶対測定で上げると言うことである。この当たりはネット上に沢山情報があるのでそれらを参照されたし。

　上記の実用単位を定めたとき(1881年)には、電気系の単位のみ定められたのであって、磁気系の単位は特に定められなかった。磁気的な測定と言えば、ガウスの地磁気の測定（1833年）以来、地磁気に関するものが主だったので、長い間CGS電磁単位がそのまま用いられていたからだ。
　しかし19世紀末になると電灯用電力需要の高まりと共に発電機・モーターの開発・製造が盛んになってくる。発電機・モーターなどの磁気回路の設計には磁気系の量が必須です。そのとき他の単位系との混同を避けるためにも、電磁単位系の磁気的な量の単位に固有名称を付けることが切望される状況になってきた。その当時、幾つかの磁気的な量に何人かの物理学者の名前が当てられて使われていたが国により、人によりバラバラであった。
　そこで、紆余曲折を経た後に1930年国際電気標準会議（オスロ）でようやく、CGS電磁単位の磁束の単位名を「マックスェル」、同じく磁束密度を「ガウス」、磁場の強さを「エルステッド」、起磁力を「ギルバート」とすると決められ推薦された。CGS電磁単位系については、この名称が今日に至っている。

３．MKSA有理化単位系

　しかし、1930年代に入るとMKSA単位系も国際的に注目され始め、1950年代に現在のMKSA有理化単位系が制定されることになった。この単位の電気系の単位については、前記の様にCGS電磁単位を数値的に調整したものが実用単位として使われていたので、それをそのまま使うことになった。だから電気系の量について１単位の大きさは実用単位系のそのままに等しい。ただし幾つかの量については、距離単位がcmからｍへ変わったことと、有理化したことによる数値変更はある。
　そのとき、基本単位がcm、g、sからm、kg、sに変換されたことに伴う調整がμ₀の定義に施されているため、磁気系の量は実用単位系からMKSA単位系への変換に際してかなり数値が変わる(下表参照)。そのため、実用単位における値と間違わないよう、MKSA単位系の磁気的な量については、改めて磁束（磁極の強さ）を「ウェーバー」（1946年）、磁束密度を「テスラ」（1960年）、インダクタンスを「ヘンリー」(1893年)とする固有単位名称が制定された。この中でインダクタンスの実用単位については、早い時期(1889年の第2回国際電気会議)に10⁹CGSemuを1コードライトとするとされていたが、1893年の第3回国際電気会議でヘンリーに改名されている。

４． 電磁単位系 → 実用単位系 → MKSA単位系 への数値と名称の変遷表

　下記の変換表については、Sommerfeldの文献5．の第�T章を参照されて下さい。

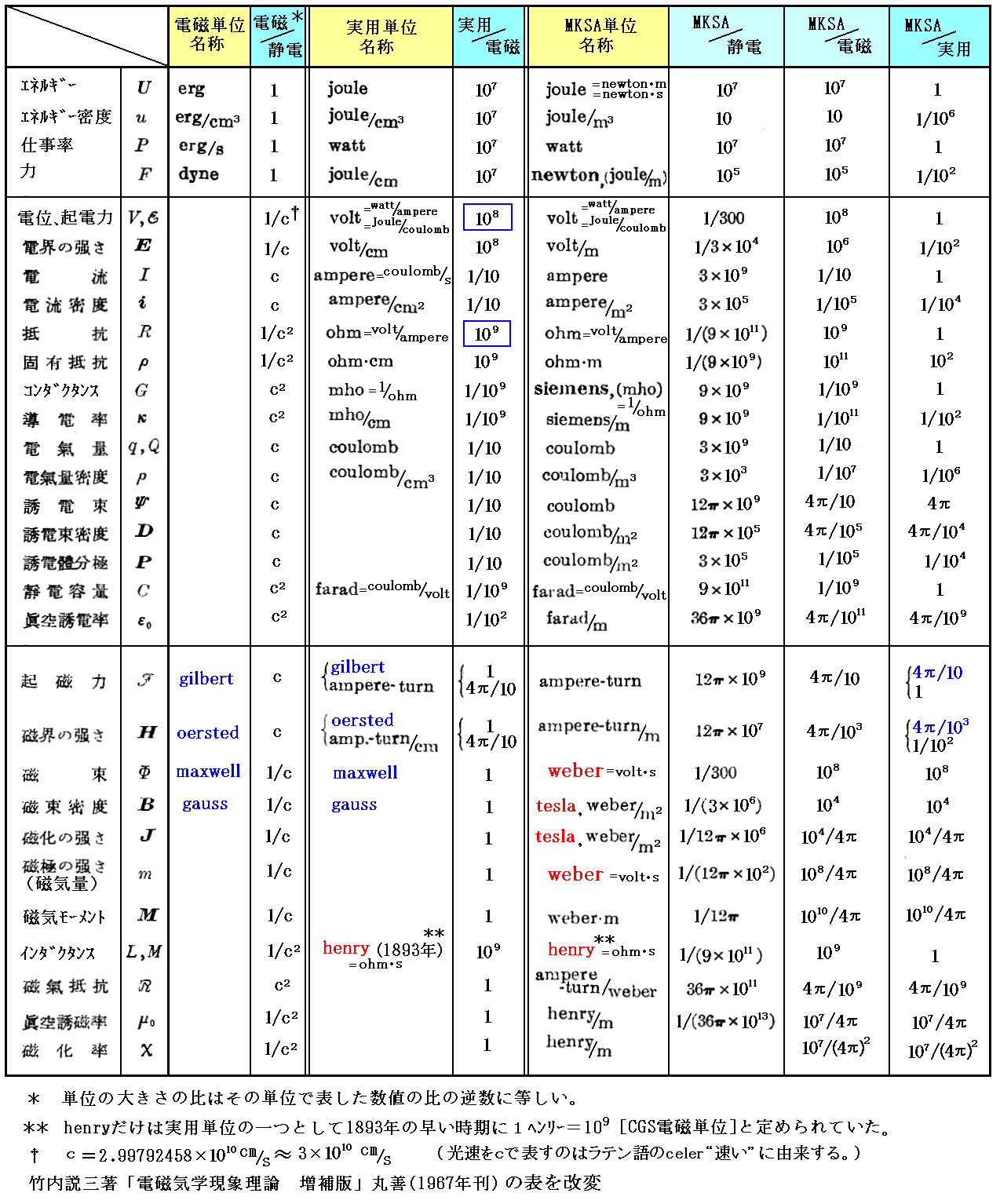
　jouleやwattは1889年第2回国際電気会議（パリ）で、もともとCGS単位系の実用単位として採用されたものです。つまりCGS単位系の１ergは実用には小さすぎるので、１×10⁷ergを１jouleと呼ぶことにして実用に便利なように導入されたものです。wattも同様で１watt＝10⁷erg/sとした。そのためMKSA単位系ではそのまま10の指数が付くことなく用いられることになった。
　またこの会議で10⁹CGS電磁単位のインダクタンスとして“コードランド”が命名されたが、これは1893年に“ヘンリー”に改名される。

　エネルギー（仕事）の単位名称にjouleが用いられたのは、いうまでもなく熱の仕事当量の測定を通じてエネルギー概念の確立に多大な功績のあったJames Prescott Jouleを記念するためです。
　また、仕事率にｗａｔｔが用いられたのは、仕事率単位である馬力を定義し普及させたJames Wattを記念するためです。なぜワットが馬力という単位を考案したのかというと、彼が改良して実用的なものとした蒸気機関の多くは当初鉱山や炭坑などで地中から水を汲み上げるポンプの動力として使われた。それまでは、その仕事を馬が行っていたのですが、彼の蒸気機関を宣伝するために、蒸気機関の水の汲み上げ能力［単位時間にどれだけの量の水をどれだけ高いところに汲み上げるか］が馬何頭分に相当するかを示す必要があったからです。

（２）有理化

１．有理化の意味

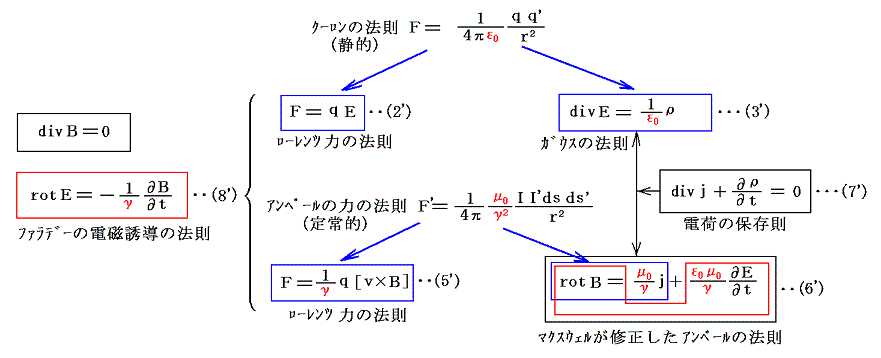
　マクスウェル方程式に4πという数字が現われるか現れないかで、非有理化単位系と有理化単位系の区別がある。力学の法則と違って、なぜπが入り込んで来たのかというと、電荷・電流などの源と、それらがつくりだす場とが、基礎法則の中で球形状・円形（サークル）状の幾何学的状況を仲介にして結びつけられているからです。
　（１）〜（３）は非有理化単位系であり、（４）は有理化単位系です。有理化単位系ではμ₀の定義のなかに4πを入れてある（つまり電流定義式に１／4πが掛かっている）。そのため、有理化単位系ではマクスウェルの方程式には4πは現れないが、高校生が最初に習うクーロンの法則やビオ＝サパールの法則には4πが現れる。
　マクスウェルの方程式や電磁場のエネルギー密度などの基礎的な式には4πの様な係数が現れない方が良いし、クーロン場のような球対称の場に4πなる係数が現れるのは自然である。有理化単位系の普及に努めたヘビサイドは、特に静電容量の表現式と蓄電器の形状とに関して有理化単位系の有利さを強調した。
　有理化（rationalized unit system）されたとは、球形がからむ式に4π（球因子 spherical factor）が、円筒形には2πが表れ、平板にはπが表れないように理屈に合うようにしたという文字通りの意味です（下表参照）。

　このとき、有理化することによってε₀とμ₀に、はっきりした物理的意味を持たせることができるようになる。つまり

• ε₀　：面積１ｍ²の極板が１ｍ離れて向かい合っているときのコンデンサーの容量（下記対応表の赤囲み式、または別稿「仕事とエネルギー」２．（４）３．参照。また、球形導体の静電容量については２．（４）１．参照）
• μ₀　：１ｍの幅をもち１ｍはなれて設置されている二枚の平行平板状送電線の長さ１ｍあたりの自己誘導係数インダクタンス（別稿「波動方程式と一般解」３．（４）参照）

２．対応表

（３）Ｅ−Ｂ対応とＥ−Ｈ対応

１．Ｅ、ＤとＢ、Ｈの次元

　ＥとＤに対して、ＨとＢのどちらをより基本的な量とするかで二通りの考え方がある。つまりＥとＨ、ＤとＢが対応すると考えるＥ−Ｈ対応系と、ＥとＢ、ＤとＨが対応すると考えるＥ−Ｂ対応系です。
　これは静電単位系やＳＩ（MKSA）単位系の様にＨとＢの次元が異なる場合に二通りの磁気モーメント・磁化の定義式の違いとなって現れてくる（電磁単位系やガウス単位系ではＨとＢの次元が同じだからこの問題は出てこない）。MKSA単位系はもともと電磁単位系由来であるにもかかわらずこのようになったのは、電流Ｉの次元を新しく導入したためにμ₀が次元を持つことになったためです。
　磁化Mを磁束密度Bと同じ次元（Ｂ＝μ₀Ｈ＋Ｍ）にとるE-H対応単位系（ＭをＪやＰ_mと書く場合もある）と、磁化Mを磁場Hと同じ次元（Ｈ＝Ｂ／μ₀−Ｍ）にとるE-B対応単位系（ゾンマーフェルトは1/μ₀をμ₀^'、−Mを＋M^'と書くべきと言っている）がある。
　これも電磁気学を難しくする要因です。古い教科書はマクスウェルの教科書以来、磁荷に対するクーロンの法則を出発点としてＥとＨを対応させて論じたE-H対応系が多かった。しかし、最近の教科書は、単独の磁極は存在しないので磁荷に対するクーロンの法則よりも、ＥとＢがそれぞれ場の中で電荷と電流に力を及ぼすベクトル成分であり、ＤとＨは源の電荷と電流が造り出す場のベクトル成分であるという考え方により電気的な量と磁気的な量を対応させるE-B対応系が主流です。その当たりをMKSA有理化単位系について、しかも静的・定常的な場合で説明すると

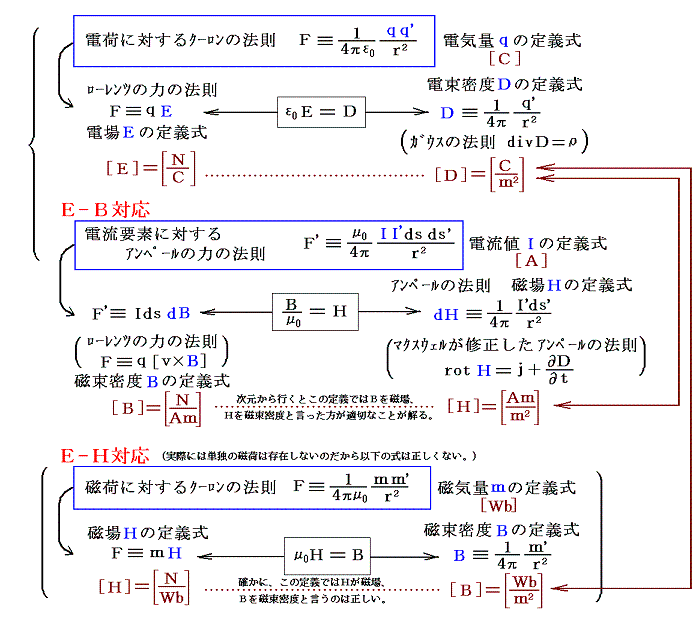
となる。次元的にはどちらもうまく対応している。つまり左側の量はいずれも力を生じる成分を表し、右側の量は力線の束の面密度を表している。微少円電流と磁気双極子は数学的には等価な磁場を生じるからＥ−Ｈ対応や磁荷は電気工学のある分野では今でも便利な見方の様です(参考文献10(下巻)10章9節参照）。
　ちなみにE-B対応系を強く主張したゾンマーフェルトを始めとして、スレーター・フランク、砂川、ファインマン等の教科書は皆E-B対応系です。我々が学生だった1970年頃は、まだCGS単位系やMKSA単位でもE-H対応系の電磁気学がまだ幅をきかしていたから、そのころ読んだゾンマーフェルトやファインマンの教科書（MKSAでE-B対応）はとても新鮮だった。しかし、今日では電媒質・磁媒質の示すあらゆる電磁気学的な性質は、つぎに述べる微視的な真に正しい電磁気学ですべて説明できると考えられているから、今日ではE-B対応かE-H対応かは余り意味を持たないように思う。ただ一つの電場ベクトルとただ一つの磁場ベクトルですべて説明できるのだから。
　下記一覧図［拡大版はこちら］も参照されて下さい。［2013年3月追記］

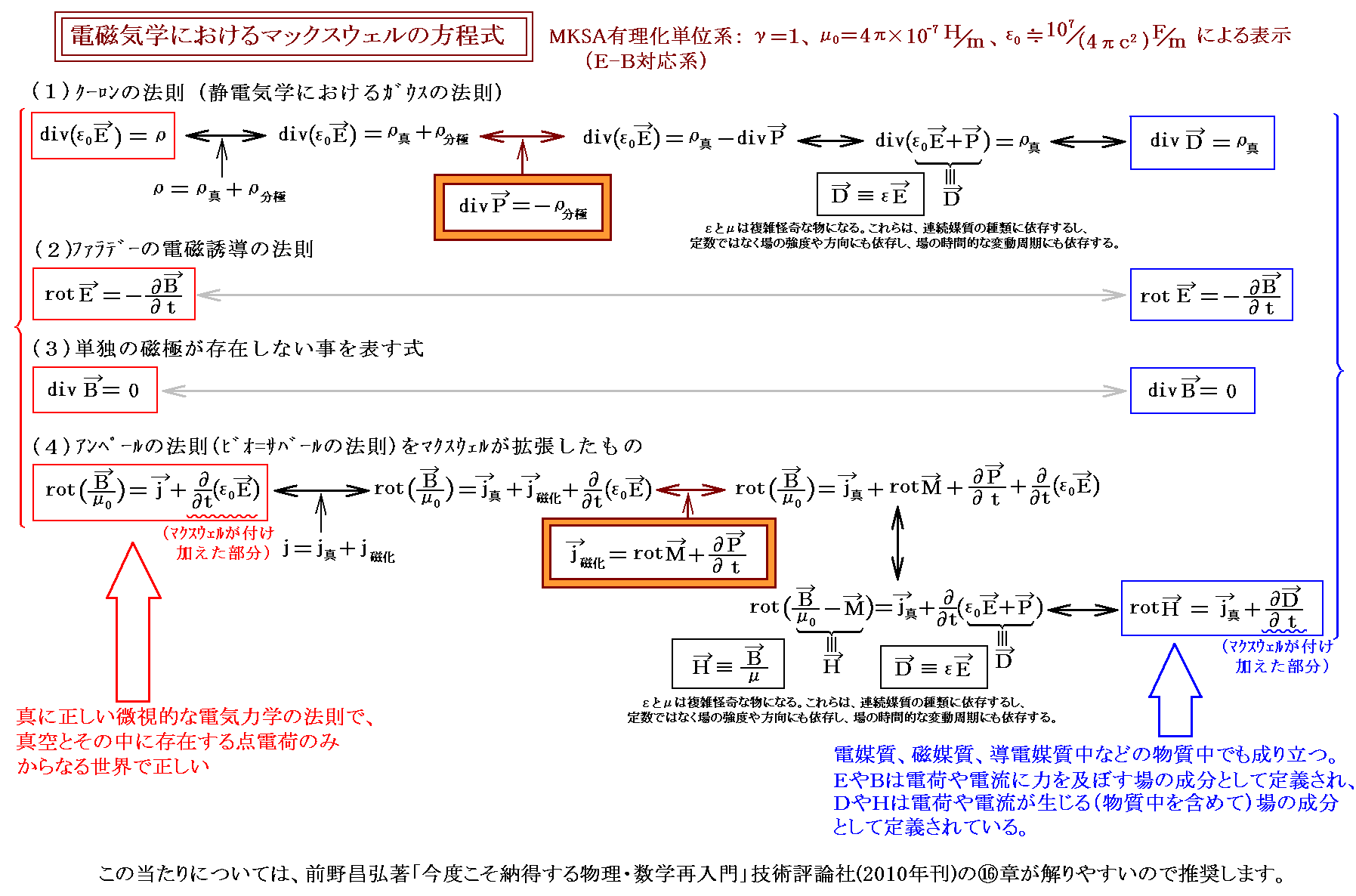
２．補足説明

　《真に正しい電気力学は［ランダウ=リフシュツ「場の古典論」（非有理化ガウス単位系）で展開されているような］微視的な電気力学で真空とその中に存在する点電荷のみからなる世界の法則であり理論です。》
　その際、誘電率ε₀も透磁率μ₀も普遍定数となる。だから本来Ｅ、Ｄ、Ｈ、Ｂの様に４つの量を導入する意味は無い。つまりＤはε₀Ｅを改めてＤと置いたに過ぎないし、Ｂはμ₀Ｈを改めてＢと置いたに過ぎない（Ｅ-Ｂ対応単位系ではＢ／μ₀を改めてＨと置き直したに過ぎない）のだから、わざわざその様に置き換えることはない。そのため（１）〜（４）の単位系の取り方により、ＥとＤ、ＨとＢは全く同じ値であったり、あるいは（真空中でも）文字通りとんでもなく異なった値になる。とんでもなく異なった値でもそのことに特に意味はない。単に単位系の取り方で値が変動しただけです。
　だからＥと、Ｂ or Ｈのどちらか一方を用いてマクスウェルの方程式を記述しておき、その二つの量のみで理論を展開していくべきです。そのときε₀、μ₀は光速ｃとの絡みで、いずれも電気的な量と磁気的な量の間の変換係数の意味を持つだけです。そして電荷が動いているとき力を生ずるベクトル成分をＢ（あるいはμ₀Ｈ）と表記したのです。
　そのとき Ｆ＝ｑ（Ｅ＋［ｖ×Ｂ］）（Ｂの替わりにμ₀Ｈでもよいが、ガウス単位系では真空中でH=Bだから Ｆ＝ｑ（Ｅ＋1/c［ｖ×Ｂ］＝ｑ（Ｅ＋1/c［ｖ×H］）となる）とニュートンの運動方程式（アインシュタインが修正したもの）を援用して議論して行けばよい。
　完全導体の場合には、その内部の電場Ｅは至る所０で、その表面にのみ電荷と電流が存在できるとすれば、いろいろな制約はあるがこちらの議論に含ませることはできる。
　
　
　ところが《連続媒質（誘電体､磁性体、導体）の電気力学［ランダウ=リフシュツ「連続媒質の電気力学」（非有理化ガウス単位系）で展開されているもの］》になるとＤやＨ（E-H対応系ではＤとＢ）は俄然重要性を増してくる。そしてＥとＤ、ＢとＨの間を結びつけるεとμ（ときにはσも含めて）は複雑怪奇な物になる。
　これらは、連続媒質の種類に依存するし、定数ではなく場の強度や方向にも依存し、場の時間的な変動周期にも依存する。そのため Ｄ＝εＥ と Ｂ＝μＨ （導体の場合はオームの法則 j ＝σＥ を含めて）を付加条件方程式と言って、理論を展開するために必須のものになり、これらも含めた上で、多くの近似的な取扱をしながら論じなければならなくなる。
　そのとき、もともとε₀、μ₀は光速ｃとの絡みで、電気的量と磁気的量の間の変換係数の意味しかないと見なすことができるのに、ＤやＢを定義するときε₀やμ₀を含めてε₀ε^*Ｅ＝Ｄ、μ₀μ^*Ｈ＝ＢとしてしまったからＥとＤ、ＨとＢが単位系によってはとんでもなく異なった値になってしまった。ガウス単位系のようにＭＫＳＡ単位系でもε₀とμ₀を外に出してε^*Ｅ＝Ｄ、μ^*Ｈ＝Ｂと定義できないのだろうか？
　
　
　ＤやＨ（E-Ｈ対応系ではB）を含んだ電磁場の理論は巨視的なものであり、必然的に多くの制約下での近似的な議論です。この立場の電磁気学と、前記の厳密な真空と点電荷の世界の電磁気学を混同しないことが重要だと思う。
　電磁気学を今日の形に集大成したマックスウェルの理論（”Treatise”の出版は1873年）が完成したのは、Ｊ・Ｊ・トムソンによる電子の発見（1897年）よりもはるか前です。だから、電磁気学の理論は、もともと電荷の実態が何か良く分かっていない時代の電媒質（誘電体）中心の後者の立場にもとづくさまざまなしがらみを内包していると考えなければいけない。実際、マクスウェル自身も「この理論によるとすべての電荷は、媒質の偏極のおつりのようなものである（"Treatise�T"p167）」と言っている。
　しかしながら、今日の電磁気学はローレンツが看破したように、真空中での電荷の概念が中心的な役割を占めている。実際ローレンツによって示された電磁気学の新しい解釈は、それまで混沌としていた多くの事柄を極めて明瞭な形で理解することを可能にした。その当たりを解説したアインシュタインの有名な文章がありますのでここに引用しておきます。
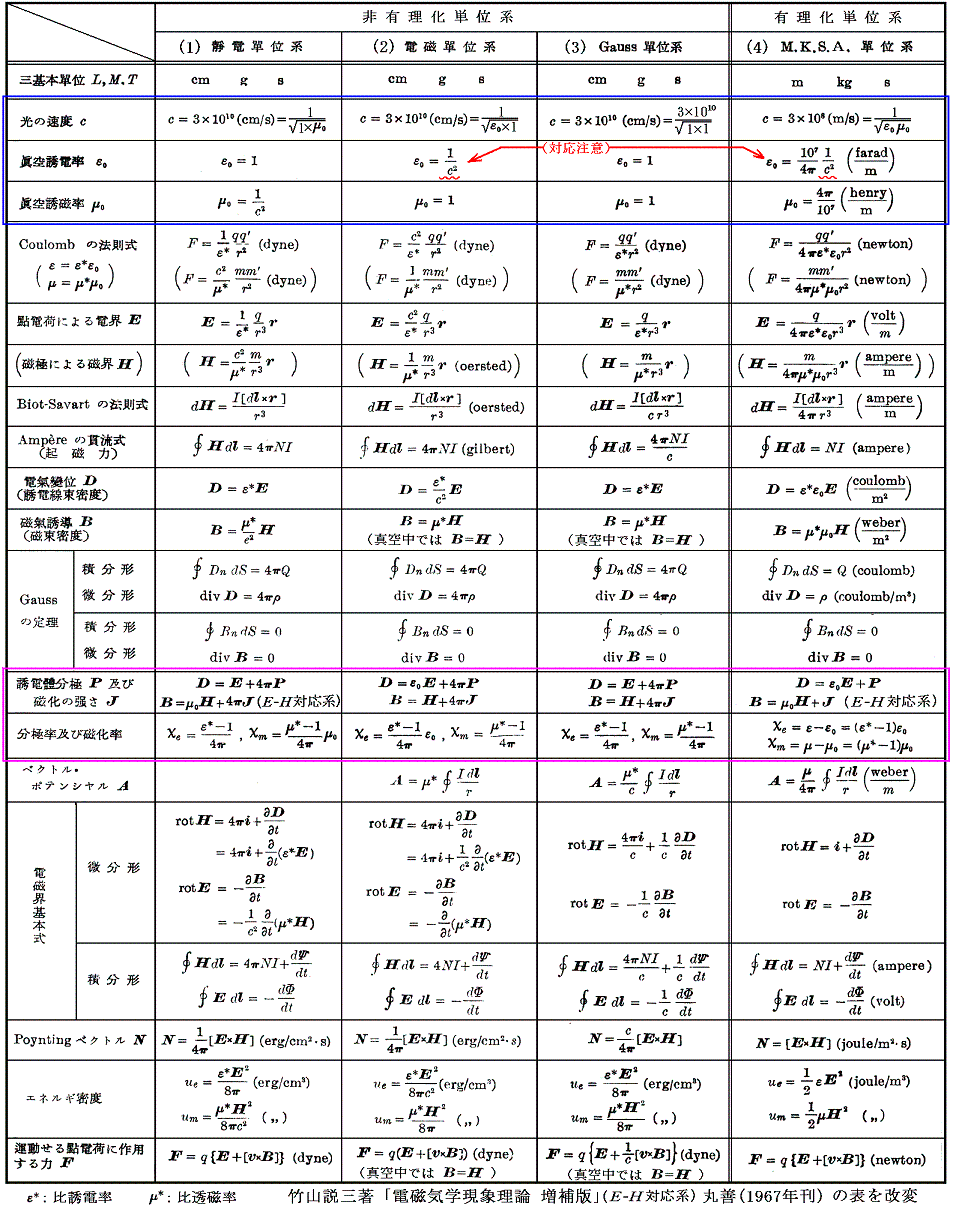
　いずれにしてもローレンツの解釈に従って、下記の対応表（E-H対応系の本から引用）で紫色で囲った公式を削除して、残りの部分において、比誘電率ε^*＝1、比透磁率μ^*＝1とおき、 ε₀μ₀＝1／ｃ² を用いて、Ｄ→Ｅと置き換え、ＨとＢに関してはどちらか一方に統一して、前者の立場に立つ厳密に成り立つ真空と点電荷のみからなる世界の電磁気学の公式で考える必要がある。

３．公式の対応表

［拡大版］

（４）まとめ

真空中での電磁気学の公式を、基本的な場としてＥとＢを採用し、まとめておく。

１．非有理化公式

　電磁気学的な現象を調べている内に、その現象を記述する物理量としてｑ、ｊ、Ｅ、Ｂが浮かび上がってきた。そして、それらの間には下記のような関係があるらしいと解ってきた。

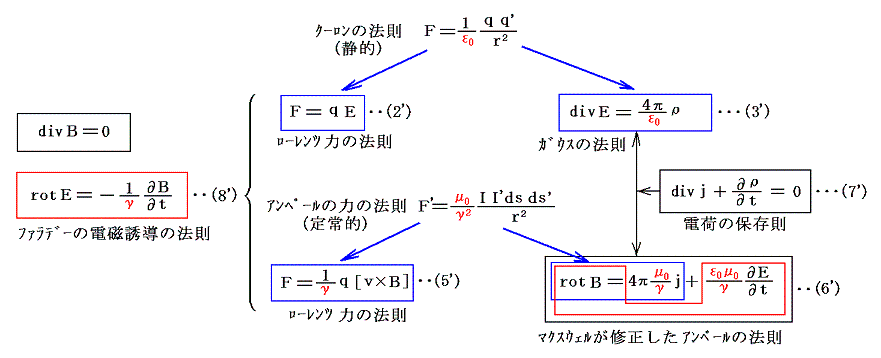
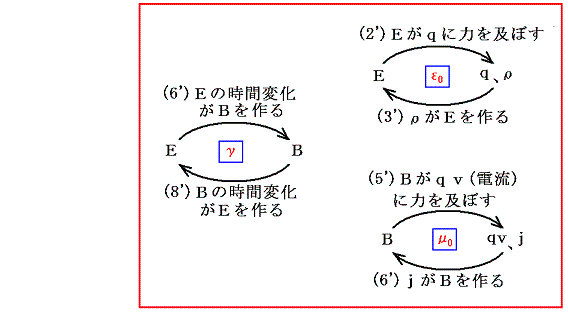
　その時、ε₀は（２'）と（３'）が本来独立と考えてｑとＥを関係づける比例定数として、μ₀は（５'）と（６'）が本来独立と考えて ｊ とＢを関係づける比例定数として、そしてγは（６'）と（８'）からＥとＢを関係づける比例定数として導入された。

［補足説明１］
　（８'）が（２'）（５'）と整合性が取れるためには、その比例定数が１／γでなければならないと１．（３)２．節で注意した。同様に、（６'）にマクスウェルが導入した∂Ｅ／∂ｔ項の係数についても（８'）式との次元的な整合性を考えれば、当然その比例定数はε₀μ₀／γと置かなければならないことが解る。
　ここでdivＥ＝4πε₀ρではなくて、divＥ＝(4π／ε₀)ρと置いたのは、もともとε₀がＤ＝εＥのＤの定義で導入されたことに由来する。μ₀についてもＢ＝μＨで導入されたからです。ただし、磁荷ｍによる定義から電流Ｉによる定義にすると、ＨではなくＢがより根元的な量となり、Ｈ＝(１／μ）ＢでＨが定義されることになる。そのためゾンマーフｪルトは（１／μ）＝μ'と置いた方が良いと言ったわけです。しかし、真に正しい真空中の点電荷の電磁気学の立場に立つと、むしろμ₀はそのままで（１／ε₀）をε₀'と置き直した方が自然だと解る。そうすると１．（３）２．の（９）式も

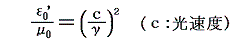
となる。ただしこの当たりは本質的な所ではないので従来通りの置き方で議論する。
　いずれにしてもこのようなわけで、ε₀は（ＥとＤではなくて）Ｅとρを関係付ける比例定数となる。同様にμ₀も（ＢとＨではなくて）Ｂとｊ（Ｉ）を関係づける比例定数と考えるべきです。そして１．（３）２．で注意したようにＦ＝ｑＥの比例定数は１で良いが、Ｆ'＝ｑ［ｖ×Ｂ］に関してはＦとＦ'が同じ力だがｑＥが生じる力とｑ［ｖ×Ｂ］が生じる力が同じである保証は無いわけだから比例定数（１／γ）を導入しておかねばならない。このγこそＥとＢを関係付ける比例定数です。
　ε₀、μ₀、γは新しく導入された物理量ｑ、Ｉ、Ｅ、Ｂの単位を定めるための係数であってそれ以上の意味は無いことを忘れてはならない。大事なことは電気磁気現象を記述するために新しい物理量が４個必要になったことと、それらが複雑に絡み合っていることです。そのために比例係数にもある関係が存在することです。

　ｑ、ｊ、Ｅ、Ｂ、ε₀、μ₀、γは、（２'）（３'）（５'）（６'）（７'）（８'）等の式で互いに関係づけられているから、当然何らかの制約があるはずです。式をやりくりしてみたら１．（３）で述べたように

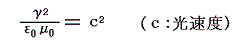
と言う関係を満たさなければならなかった。そして実験で測定してしてみると４．（１）で述べたように定数ｃは光速度だったと言うわけです。
　
　このとき、３個の比例定数ε₀、μ₀、γに対して条件式は１個だけだから２個は任意に取れる。そのためその２個を一番簡単な置き方にしよう。そして、どの２個を選ぶかで３通りの単位系が考えられる。
（１）静電単位系：ε₀＝１、γ＝１、μ₀≒１／ｃ²
（２）電磁単位系：μ₀＝１、γ＝１、ε₀≒１／ｃ²
（３）ガウス単位系：ε₀＝１、μ₀＝１、γ≒ｃ
　もともと、静電気の研究から始まったので（１）の単位系がつくられた。しかし、電流の磁気作用が発見されてからは最も重要な応用は動電気的なものとなったので、（２）の単位系が重要になった。しかし、理論的な考察には次元の対称性から（３）も捨てがたい。
　
　このように三種類の単位系が並立する事になったのは、電磁気学を展開するには４個の物理量［電荷ｑ］［電流Ｉ］［電場Ｅ］［磁場Ｂ］の導入がどうしても必要だったからです。そのとき、これらの導入には最低３個の比例定数(４個でなく３個で良いのは1.(3)2.で注意したように、そこのｋ₁に１以外を与えても何の意味もないからです)が必要なのに、条件式は１個だけだからです。つまりこれらの単位系が並立する事の中に電磁気学の本質がある。
　参考文献１０の第５章で説明されているように［電荷ｑ］と［電場Ｅ］だけを用いて電磁気学を作り上げることも可能です。しかしそれはローレンツ変換を繰り返し用いなければならない、とんでもなく複雑なものになる。そのとき［電流Ｉ］と［磁場Ｂ］を導入しさえすれば理論の展開法が劇的に簡単になる。だから３つの比例定数の導入はしかたがない。その場合３種類の単位系の並立は必然的な訳です。

［補足説明２］
　ガウス単位系では

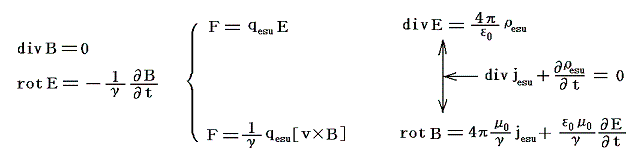
で、ε₀＝μ₀＝１、γ＝ｃと置けば良いのだが、４．で注意した様に

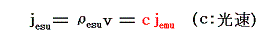
の立場に立つのなら、上記の関係は下記のようになる。

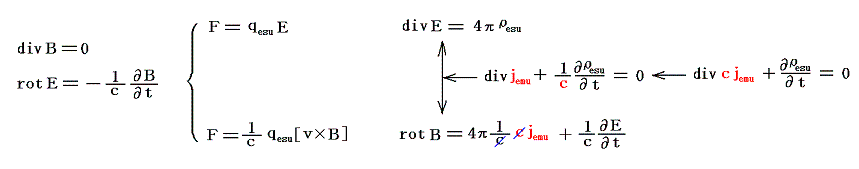
２．有理化公式

　今日の MKSA有理化単位系 は （２）電磁単位 の数値を調整し、新たな次元［Ｉ］を導入し、そして有理化したものです。
　先ず有理化ですが、下記の公式のε₀やμ₀に4πを含ませる（含ませない）で、公式に4πが現れる（現れない）が好きなように調節できることに注意。
　このとき、クーロンの法則とdivＥ＝ρ／ε₀のどちらかに4πが現れるのは別稿「ガウスの法則（静電気学）」（ただしｋ₀＝１／4πε₀でガウスの法則は（3'）式と同じ）で説明したように、両者の関係に球の表面積が絡んで来るからです。磁気的な公式についても同様です。つまり磁荷定義の場合には磁荷のクーロンの法則から電荷の場合と同じだし、電流定義では無限直線電流が作る磁場の積分で2倍が出て、その磁場を電流の周りに一周して磁力線の線積分にするとき2π倍が出るのでやはり4πが出てくる。
　有理化したために各公式は下記の様になる。

次に、新たな次元［Ｉ］を導入し、数値を調整するために
（４）MKSA有理化単位系：
　γ＝１、μ₀＝4π×10^-7［N/A²_orＨ／ｍ］、ε₀≒10⁷／（4πｃ²）［Ｆ／ｍ］
と置いた。そのため上記の一覧図は

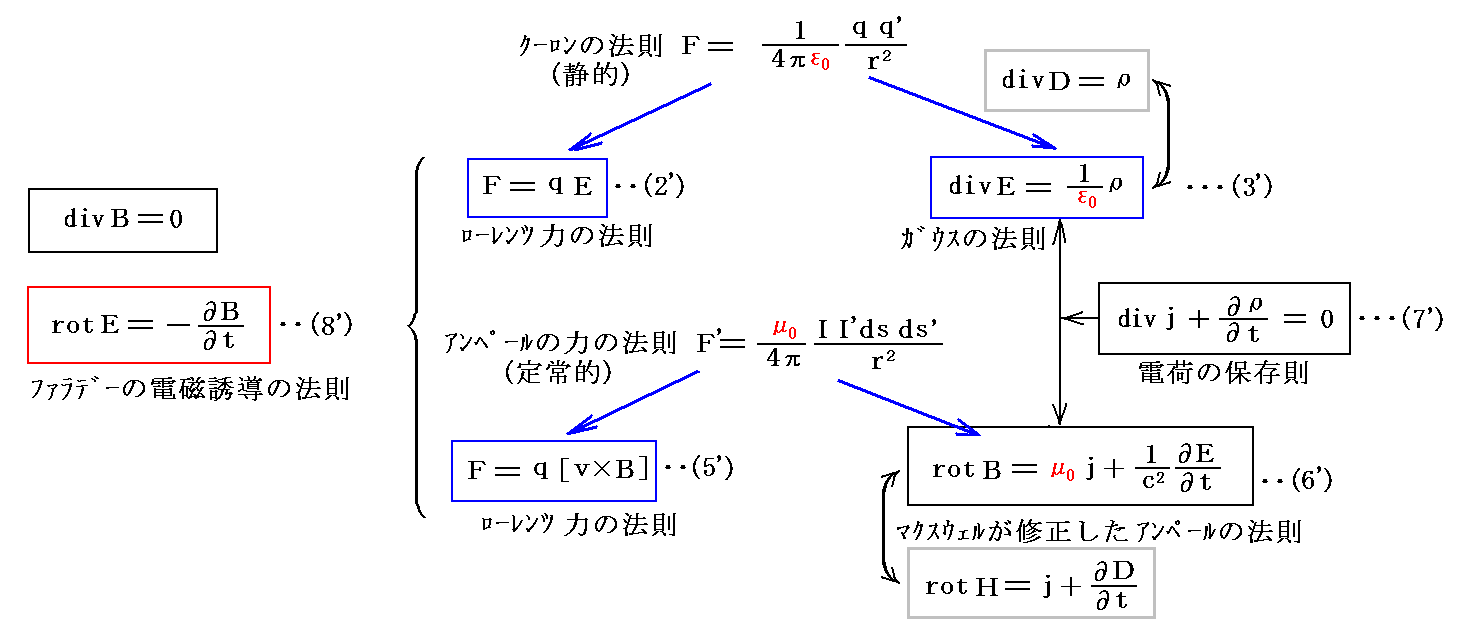
となります。

　MKSA有理化単位系は元々（２）電磁単位から派生したものなのに、新たな次元［Ｉ］を導入したために、ε₀のみならずμ₀も次元を持つことになった。
　このとき、光速ｃをε₀の中にふくませてε₀とμ₀で記述する場合もあれば、ε₀μ₀＝１／ｃ²だからμ₀＝１／（ε₀ｃ²）と置いて、ファインマン物理学�V「電磁気学」の公式のようにε₀とｃ²を用いて記述する場合もある。

　さらに補足しますと、オランダの H．A．Lorentz や英国の Oliver Heaviside は 有理化されたガウス単位系 を用いています。その場合は
（５）有理化ガウス単位系：ε₀＝１、μ₀＝１、γ≒ｃ
ですから、上記の一覧図は

となります。
　補足ですが、矢野健太郎著「近代数学新書　相対性理論」至文堂（1967年刊）も有理化Gauss（Lorentz-Heaviside)単位系（磁場H）です。この第2章§6、第3章、第4章は「ミンコフスキーの４次元世界」で、第5章はこちらで、第6章は“テンソル解析学（絶対微分学）”で、第7章は“テンソル解析学の一般相対性理論への応用”で引用。

［補足説明１］
　以上の事柄に比べて［電媒質・磁媒質中でのＤやＨの問題］、［Ｅ−Ｂ対応 or Ｅ−Ｈ対応の問題］、［電気工学のある分野で電流定義よりも磁荷定義が重用される習慣］、等々・・・はすべて上記の方程式をどの様に利用するかの発展的な事柄だと思います。
　この当たりは参考文献10（下巻）の第9章「物質中の電場」、第10章「物質中の磁場」が解りやすい。

３．数値例１［ローンツの力の法則］

　例えば、電磁場中を運動している荷電粒子に働くローレンツ力はガウス単位系で

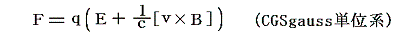
と表される。ここでＦは［dyne］＝［cm¹g¹s^-2］、ｑは［CGSesu］＝［cm^3/2g^1/2s^-1］、Ｅは［CGSesu］＝［cm^-1/2g^1/2s^-1］、ｖは［cm¹s^-1］、Ｂは［CGSemu］＝［gauss］＝［cm^-1/2g^1/2s^-1］であり、ｃ＝2.99792458×10¹⁰cm/s である。
　これを電磁(CGSemu)単位系に換算するには、ｑの代わりにｃｑ'を、ＥをＥ'／ｃとして

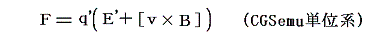
と書き換える必要がある。
　さらにこれをMKSA有理化単位系で表すためには、Ｆを10^-5Ｆ''にｑ'を10ｑ''に、Ｅ'を10^-6Ｅ''に、ｖを10^-2ｖ''に、Ｂを10^-4Ｂ''にそれぞれ置き換えて

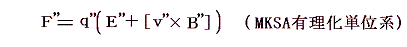
となる。ここでＦ''は［N］＝［m¹kg¹s^-2］、ｑ''は［C］＝［A¹s¹］、Ｅ''は［V/m］＝［N/C］＝［m¹kg¹s^-3A^-1］､ｖ''＝［m¹s^-1］、Ｂ''＝［Ｔ］＝［Wb/m²］＝［kg¹s^-2A^-1］で測定した値である。

４．数値例２［電気素量ｅ］

　電子１個の持つ電気量である電気素量ｅを各単位系で表してみると

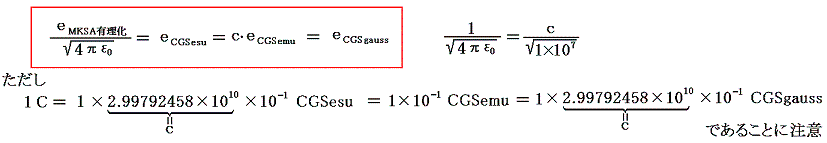
の関係がある。
　この様になるのは、元々電気量の単位はクーロンの法則に基づいており、単位の長さだけ離して置かれた等量の電気間に働く力を用いて定義されたからです。つまり

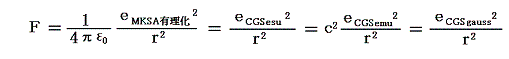
に従っている。各単位系におけるクーロンの法則の表現式がこの様になることは５．(３)３．の対応表で確認して下さい。最初の式はこの式のすべての辺にｒ²を乗じて平方根を取った式です。
　このときMKSとCGS単位系ではｒ＝1ｍ＝100cmの関係があるので、同じ電気素量ｅでも例えばMKSA有理化単位系での数値をそれぞれの単位系で表した数値に換算をするにはｃ×10^-1や10^-1を乗じなければならない。
　そのとき各単位系での電気素量の値は８．基礎定数表に示されているように

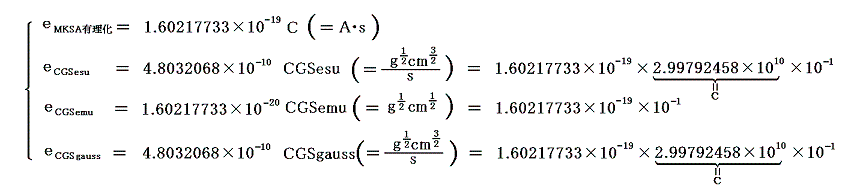
となる。
　上記の値を ｒ＝1ｍ＝100cm とした場合のクーロンの法則に代入してみる｡

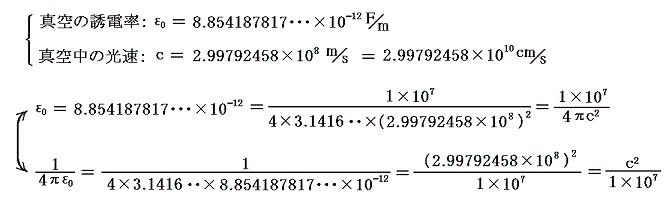
を考慮すると

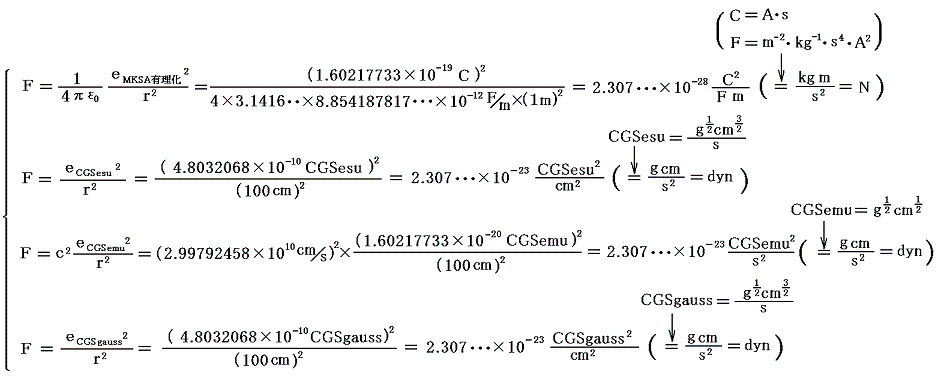
となる。ここで１Ｎ＝10⁵ｄｙｎであることを思い出せばすべて同一の力を生じていることが解る。
　このときMKSA有理化単位系ではＡ(アンペア)という新しい次元を導入して電気量の単位は C(クーロン)＝Ａ・ｓ となったが、C²／F･m は kg･m／s²＝Ｎ となり力の単位(次元)に戻っていることに注意されたし。
　上記の表現式を比較してみると、今日用いられているMKSA有理化単位系はCGS電磁単位系に由来したものであることが良く解る。そのためε₀の中に1／ｃ²がふくまれており、CGS→MKSの変換で10⁷がからみ、有理化で1／4πが生じたのです。

６．電磁気学の関係式

（１）電磁気的諸量の次元

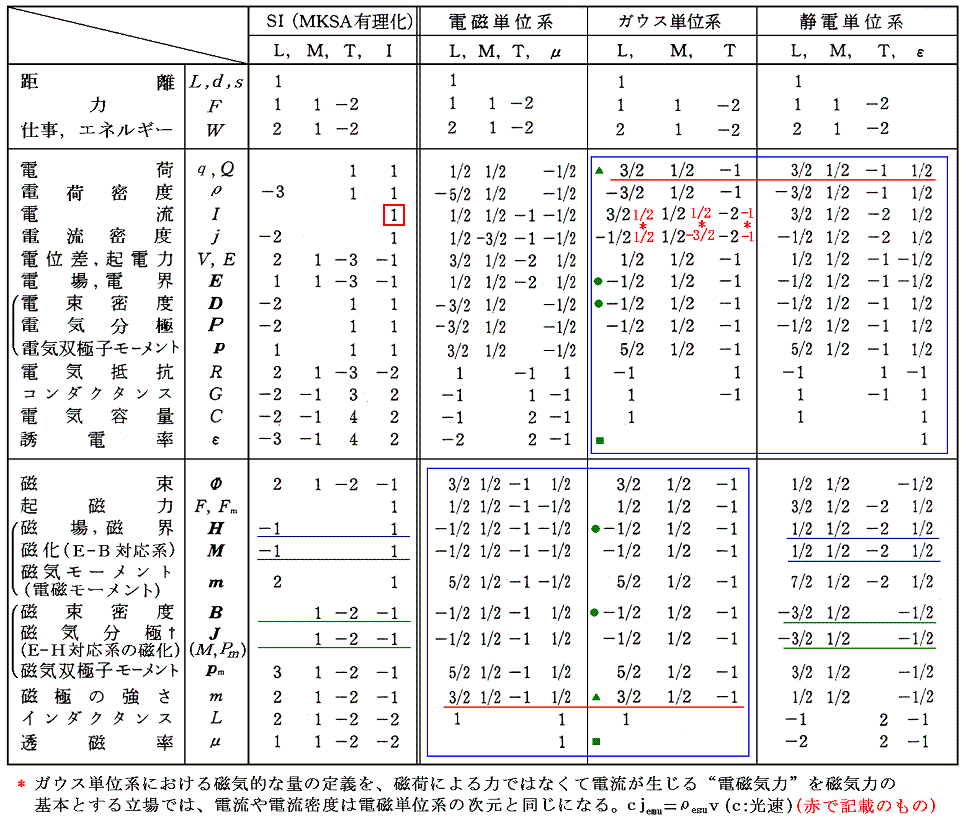
1. CGS単位系の電荷ｑと磁荷ｍの次元（赤アンダーライン）は、それらの量がクーロンの法則に基づいて定義されたことに由来する。つまり［（力×距離²）^1/2］の次元である。そのためCGS単位系では多くの物理量の次元式に1/2、3/2、・・・等の分数指数がつくことになる。
2. MKSA単位系では、新たな次元電流［Ｉ］（□で囲ったもの）を導入したために、物理量の次元式はすべて整数の指数で表せることになる。これは新しい次元を導入するメリットと言えるだろう。
3. 電磁単位系とガウス単位系ではμ₀＝１としているので磁場（磁化）と磁束密度（磁気分極）の次元は同じです。
4. 静電単位系とMKSA単位系では、磁場（磁化）と磁束密度（磁気分極）の次元が異なる。（青アンダーラインと緑アンダーライン）。その様になったのは静電単位ではμ₀＝１／ｃ²としているためであり、MKSA単位系では電磁単位系由来であるにもかかわらず電流［Ｉ］の次元を新しく導入したためにμ₀が次元を持つことになったからです。そのため二種類の磁化（E-H対応かE-B対応）が定義される事になった。
5. ガウス単位系に於いては［ｑ］▲と［ｍ］▲、［Ｅ］＝［Ｄ］●と［Ｈ］＝［Ｂ］●、［ε］■と［μ］■の次元が等しい事に注意。そのため場に関する量はすべて同じ次元を持ち電気と磁気の双対性がよくなる。
6. 各単位系の各物理量の次元はｑやｍ（又はＩ）の次元から出発して、基本的には高校物理で習う電磁気学の関係式（物理量を定義づける法則）を繰り返し適応して決めてゆけばよい。例えばＩ＝Ｑ／ｔ、Ｖ＝Ｗ／Ｑ、Ｒ＝Ｖ／Ｉ、Ｃ＝Ｑ／Ｖ、Ｅ＝Ｆ／ｑ、Ｈ＝Ｆ／ｍ、Ｂ＝γＦ／(ｑｖ)、・・・・・等々。ただし、１．（３）で説明したε₀、μ₀、γが絡む公式を適応する場合には単位系ごとに注意が必要｡
7. 電磁単位系と静電単位系を比較してみると、電荷ｑや電流Ｉの次元がちょうど[Ｌ／Ｔ]＝速度の次元だけ異なる。電位差Ｖ＝Ｗ／ｑについては仕事Ｗの次元が同じだから１／ｑの次元の差である１／速度の次元だけ異なる。また、抵抗Ｒ＝Ｖ／ＩはＶと１／Ｉの次元の差の積１／（速度の次元）²だけ異なる。

（２）電磁気的諸量の単位換算表^*

　（４）ＭＫＳＡ有理化単位系は電気工学で普通に用いられる実用単位そのものだから具体的な事例を取り扱うときは非常に有利です。これに対して、（１）〜（３）のCGS単位系は実用単位と複雑な関係にあり、具体的な事例を取り扱うときにはいちいち下記の単位換算表を使わなければならない。

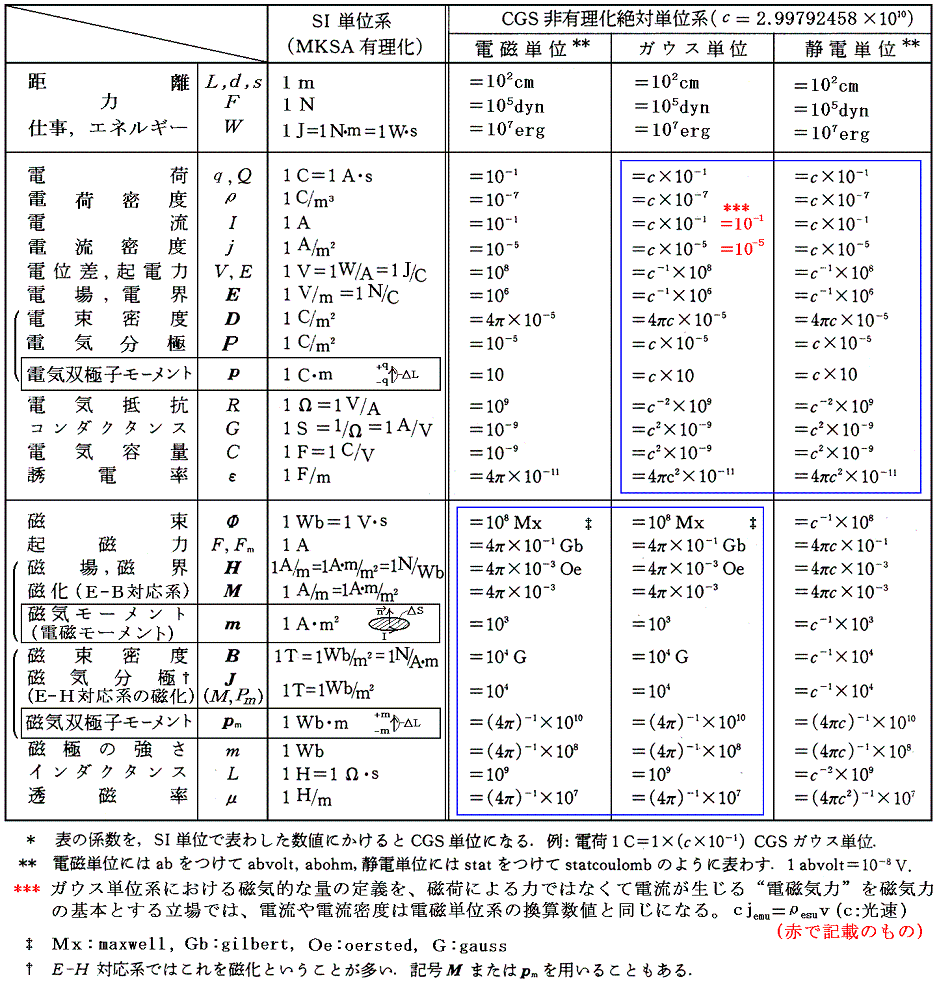
1. 電磁単位系と静電単位系を比較してみると電気量ｑや電流Ｉの数値がちょうど ｃ（真空中の光速）倍 だけ異なる。電位差Ｖ＝Ｗ／ｑの数値はＷが共通だから１／ｑの１／ｃ倍だけ異なる。また、抵抗Ｒ＝Ｖ／Ｉの数値はＶの１／ｃ倍と１／Ｉの１／ｃ倍の積１／ｃ²倍だけ異なる。他も次元の計算に対応させながら同様に考えればよい。
2. 電磁単位系の磁気的な量の１単位は、地磁気の測定単位（磁束密度の水平分力は赤道で0.4Gauss＝0.00004Ｔ）としては適当だが、それ以外の実用的な理工学には小さすぎる。１単位が電磁単位系よりも10000倍大きなMKSA有理化単位系の方が利用上便利である。
3. 実用単位の一覧表
   

（３）電磁気学の公式

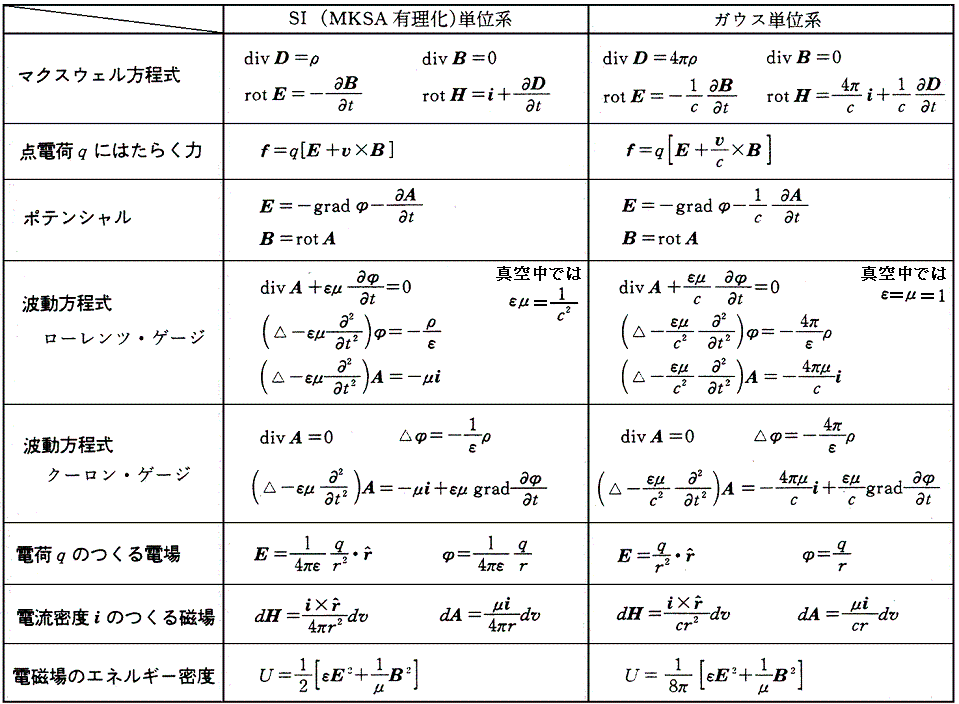
　表中のローレンツ・ゲージ（Lorenz gauge）とクーロン・ゲージ（Coulomb gauge）に付いては別稿「Maxwell方程式系の先見性と電磁ポテンシャル」２．（２）をご覧下さい。

７．ＳＩ基本単位系

８．基礎定数表

９．参考文献

　ネット上で参照できると便利なので自分用に作りました。勘違いしているところがあるかもしれませんが少しづつ充実させようと思います。電磁気の単位系は、多くの教科書の付録で説明されていますが、ここでは主に以下の書籍を参照しました。電磁気学の単位の問題には様々なしがらみがあり、式のとらえ方も時と共に変化してきたようで、我々素人は古い文献を読むとき混乱してきて訳が解らなくなる。
　最近になって一つの単位系（MKSA・有理化・E-B対応系）に世の中が統一されて来たのは嬉しいが、この単位系に過去の歴史的なしがらみが集約されており、正直なところ一番解りにくい。
　結局、どの単位系が良い悪いではなくて、ここで説明した（１）〜（４）の単位系をすべて理解するに限る。なぜなら、何種類もの単位系が並立することの中にこそ電磁気学の本質があるのだから。

１．岩波書店「理化学辞典　第5版」岩波書店（1998年刊）
　　少し古いのですが数値、数表はここから引用　

２．湯川秀樹監修、岩波講座現代物理学の基礎�T「古典物理学�T」岩波書店（1978年刊）
　　第�U部、第5章（河辺六男著）に明快に説明されている。特に§5.11

３．竹内説三著「電磁気学現象理論」丸善（1967年刊）　17章電気単位系　P451〜476
　　各単位系の対応表はここから引用

４．M.Planck著「理論物理学汎論第3巻　理論電気磁気学」裳華房(1946年刊　原本初版は1922年刊)　§1〜7、§41、§43、§45、§58〜61、§101
　かって名著と言われたシリーズの一冊です。電磁気学が完成された頃の古い教科書ですが、単位系関係の原理的な説明は、この本がとても丁寧で、且つ分かりやすい。

５．A.Sommerfeld著「理論物理学講座�V　電磁気学」講談社（1970年刊　原本は1948年刊）序文、§1〜§8、§16
　　これも有名な教科書です。ゾンマーフェルトはMKSA･E-B対応系の新しい単位系を主張しているが、どちらかというとマクスウェル、ヘルツ以来の古い電媒質の電磁気学を尊重した考え方のようです。これに対して、プランクは伝統的なガウス単位系を利用しているが、どちらかというとローレンツ、ランダウ=リフシュツのように、真空中の電荷を重視した、この意味で新しい電磁気学のようです。両者を読み比べてみると面白い。
　この本の第�T章は極めて興味深い内容なので別稿で引用しています。特に§1．歴史的回想だけでも是非ご覧下さい。

６．スレーター・フランク共著「電磁気学」丸善（1968年刊）付録�U単位P208〜215

７．木幡重雄著「電磁気の単位はこうして作られた」工学社（2003年刊）
　　ここまで解説してもらうととてもよく解る。多くの疑問が解決できました。感謝！

８．James Clerk Maxwell著「A Treatise on Electricity and Magnetism｣(1873年)
　　時間が許せば、この本をじっくり読み込むことに尽きるのかも知れない。
　　Art768〜771だけはこちらにpdfファイルで引用しておきます。
　　最近では、第1版（1873年）or第2版（1881年）ならばGoogleBooksから全文を無料ダウンロードできます。

９．エミリオ・セグレ著「古典物理学を創った人々」みすず書房（1992年刊）の第4章、特に付録5および6

１０．Edward M. Purcell著「バークレー物理学コース２　電磁気学（上）」丸善（1970年刊）の第5章「動いている電荷の場」
　　　Edward M. Purcell著「バークレー物理学コース２　電磁気学（下）」丸善（1970年刊）の第6章「磁場」
　　　この本の第9章、10章を含めて、意欲ある高校生はぜひ読まれる事を薦めます。

　もう一度強調しますが、電磁気学の難しさというのは５．(４)１．で述べたように［電荷］と［電場］に加えて［電流］と［磁場］を導入せざるをえない所にある。そのため三種類の比例定数が絡んできて、（１）〜（３）の単位系が並立する事になった。この部分の本質的な難しさに比べたら
　　１．公式の形式を整えるための有理化の操作
　　２．実用的な大きさにするための数値の調整
　　３．新しい次元の導入
　　４．電媒質・磁媒質の電磁気学
　　５．磁荷による定義から電流による定義への置き換え
等は付加的な事柄でしかない。重要さではずっと劣るのですが、これらのいずれもがε、μ、γに絡んでいるので、電磁気学をさらに難しくしている。電磁気学を理解するには、まず複雑に絡み合っている１．〜５．の事柄を一つ一つ切り分けてそれぞれが関係する部分をきちんと把握する。次に、それらの歴史的なしがらみをすべて削り落とす。そして上記の本質的な部分だけにするとすべてが見えてくる。これらの事柄は、物理量や公式の解釈のしかたが少しずつ変化してくる中で生じてきたので、切り分け把握するには、やはり歴史をさかのぼる必要がある。
　
　このページは参考文献７．を読んだことがきっかけで作りました。この本はとても面白く熟読する価値があります。今まで自分に取って曖昧模糊としていた多くの疑問点を明快に解決してくれました。この本に導かれて、若い頃読んだ色々な本を読み返してみると、今まで何となく解らなかった電磁気学が明瞭に理解できました。読み返している内に、このＨＰに書いたように説明されれば、電磁気学が本当に理解できるだろうと思ったわけです。世の中の電磁気学の本を良く読んでみれば、その多くに書いてある事柄なのですが、理解の至らない私には見れども見えず、読めども読めずだったのですね。
　電磁気学ができあがっていくそれぞれの時代で、物理量や公式の発見・解釈の変更に関わった人々（アンペール、ファラデー、ウェーバー、マクスウェル、クラウジウス、ヘルムホルツ、ヘビサイド、ヘルツ、ローレンツ、アインシュタイン等）には、この当たりの事情はよく解っていた。しかし、できあがった電磁気学をそのまま学ぶ我々には、変更理由がなかなか見えず電磁気学は難しいと感じる。私自身について言えば参考文献３．６．１０．の単位系の付録は過去に何度も何度も読み直したのですが、何時もどこかあいまいで訳の解らないものでした。しかし、このページを作った後で読み返してみると、それらのすべてが一点の曇りもなくスラスラ理解できました。
　すべてが理解できたと感じた時の気持ちは、かつて「生物の進化論」が曖昧模糊として何となくしっくり理解できなかったとき、1985年頃ですが木村資生氏の中立的突然変異浮動説を知って、すべての疑問が氷解したときの感覚です。進化論に現れていたすべてのピースが収まるべき所にピッタリと収まってすべてが明瞭に理解できた。
　今回このページを作っていて、５．(４)１．「まとめ」に書いたことが見えてきたときすべてが理解できました。電磁気学に素人の私でも本当に明瞭に理解できたので、私と同じ悩みを抱えている人も多いのではないかと思って恥ずかしながらこのページを作りました。