ガウスが地磁気の大きさを絶対測定した方法を説明します。
地磁気の偏角（水平成分の地理上の北と磁石の北の角度差）や伏角（水平成分と磁力線方向の角度）は実用上重要なので古くから観測され研究されたが、地磁気の強さの観測は18世紀後半のフンボルト（独）あたりかららしい。フンボルトは世界各地を旅行して地磁気の強さを測定して、地磁気は赤道から極へ近づくに連れて連続的に増加する事を見つけた。
彼が用いた方法は、剛性の無い糸に吊した棒状磁石を小さく振らして一定時間の振動回数を測定するものです。その場所の地磁気の水平成分の強さは振動回数の二乗に比例する。（別稿「ビオ=サバールの法則(1820年)を見つけた方法」２．（１）を参照）
これは確かに素晴らしい方法で、同一の磁石を用いれば世界各地の地磁気の強さを比較することができる。しかしその時、同じ磁石を用いなければならないと言うことは磁石の経年変化が問題になる。たとえその誤差を避けることができても、この方法では相対的な大きさしか分からない。さらに磁石が異なればこの方法による測定値は何の意味も持たないのだから何とももどかしい所である。
そのため、ガウスが模索したのは地磁気の絶対的な大きさを知る方法です。つまり、絶対測定とは、その単位が確立している質量・長さ・時間の量に還元して地磁気の大きさを表すことです。
これ以後、地磁気の水平成分の値は、他のいろいろな電磁気学的な量を絶対測定するときの基準となっていくのだから、ガウスの確立した方法は画期的なものである。別稿「回転運動の運動方程式」「電磁気学の単位系が難しい理由」等参照
単独の磁極を取り出すことはできないが、仮想的に考えられる自由磁荷については、先人が確立した逆二乗法則が成り立つものとする。これらはマイヤー、クーロン、ハーンステン等によるものだが、単独の磁極を取り出すことはできないので逆二乗法則を確かめるのは(電気力や万有引力と違ってかなり込み入った手順・推論が必要で)高校物理で習うような単純な話ではない（詳しくは文献４のエピローグ磁力法則の測定と確定を参照されたし）。ガウスはこれらの先人の功績を利用することにした。
ただし実験に用いる磁石の中に自由磁荷がどの位置にどんな大きさで分布するのかを直接知ることはできない。そこでガウスは二つの実験を組み合わせる巧妙な方法で二つの未知数［地磁気の水平分力の大きさＨ地］と［磁石の磁気双極子モーメントｐm］を決定した。以下で説明する方法がそれであるが、ここでは簡単にするために磁石を距離ΔＬだけ離れた＋ｍと－ｍの磁極からなるものとして論じる。
下図の様に偏向用磁石Ａと磁場測定用の磁針Ｂを配置する。磁石Ａは地磁気子午線と垂直かつ水平に置く。磁針Ｂはその中心に付けた剛性の無い細い糸でつりされ、水平面内で中心のまわりを自由に回転できるものとする。磁石Ａと磁針Ｂの中心間距離をｒとし、ｒは各磁石の長さに比して十分長く取る。
実際にはｍやΔＬを知ることはできないが、磁石Ａの磁気双極子モーメントｐmは ｐm＝ｍ・ΔＬ となる。ちなみにガウスが用いた磁石Ａは長さ101mm、幅17.5mm、質量142ｇであり磁針Ｂは長さ60mmであった。
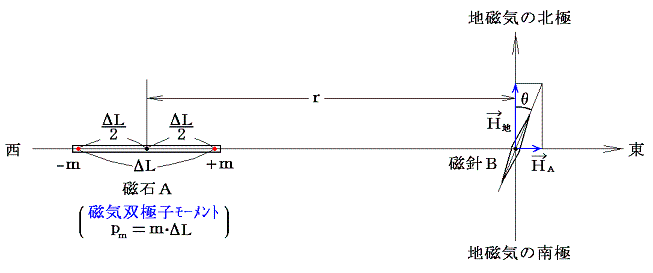
単独磁極に逆二乗法則が成り立つとすると、磁石Ａが磁針Ｂの位置に作る磁場の水平成分の強さＨAは
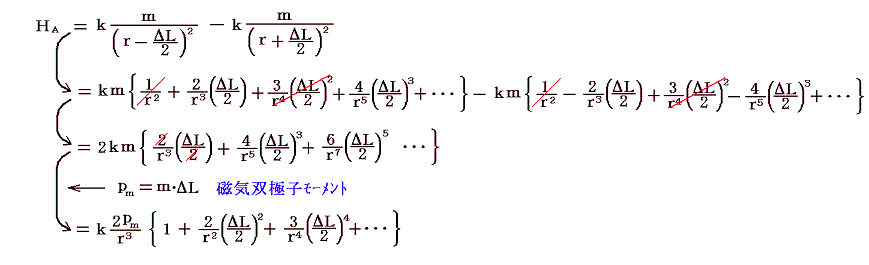
となる。ここで比例定数ｋはMKSA有理化単位系（ＳＩ単位系）では１／(4πμ0)であり、CGS電磁単位系では１となる（別稿「電磁気学の単位系」参照）。磁針Ｂは磁石Ａが無ければ地磁気子午線の方向を向くが、磁石Ａがある時は地磁気Ｈ地と磁石Ａが作る磁場ＨAの合力の方向を向く。偏向角をθとすると
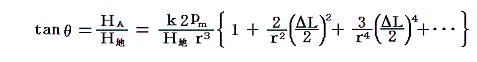
となる。ところで、ｒを大きくすると偏向角θが小さくなり測定が難しくなるのでｒはあまり大きくできない。その場合、上記の第２項の効果は無視できなくなるので第２項まで考慮する。そうすると、地磁気の水平成分の大きさＨ地は
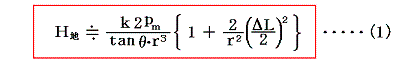
と表される。ここで実際にはｍやΔＬを知ることはできないので、磁気双極子モーメントｐmを直接計算で求めることはできないが、次に述べる実験により地磁気Ｈ地の関数として求めることができる。
偏向実験で用いた磁石Ａを剛性の無い細い糸で吊し、垂直軸のまわりを水平面内で自由に回転できるようにする。それを地磁気Ｈ地の中で小さく振らして、その振動周期Ｔを測定する。そうすると別稿「回転運動の運動方程式」２．（１）で説明したように
となって磁気双極子モーメントｐmを地磁気の水平成分Ｈ地で表すことができる。
ここで、磁石Ａの慣性モーメントＩは、その形状と質量が分かっていれば計算により厳密に求めることができる。磁石の長さａ、幅ｂ、質量Ｍとすると別稿「回転運動の運動方程式」１．(４)の例(５)のＩｚにより
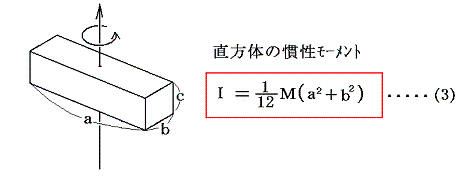
となる。
上記（２）、（３）式を（１）式に代入すれば、絶対測定された地磁気の水平成分の大きさＨ地が求まる。
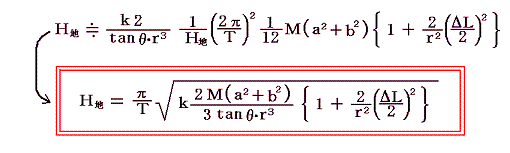
第２項まで考慮すると最終結果のΔＬに少し不確実さはあるが、とりあえず単位の定義が確定している質量・長さ・時間に還元した絶対的な数値にすることができた。これは確かに画期的な方法である。この結論を（２）式に代入すれば磁石Ａの磁気双極子モーメントｐmが絶対測定できたことになる。
ガウスは正確な値を求めるために、磁石Ａをその位置で180度回転して磁極の極性を逆にしたり、磁石Ａと磁針Ｂの東西の位置を逆にしたり、距離ｒをいろいろ変えて測定した。そして、それらのデータを統計的に解析する手段として誤差論に於いて有名なガウスの最小二乗法を用いた。
私が大学生のとき使った教科書「物理学実験」学術図書出版（1967年刊）を眺めていたら、まさにこの実験が載っていました。そのページにいろいろ書き込みがあるところを見ると、これは必修の題材だったようで学生のとき確かに実習しています。しかし当時、この実験の意味はまるで分かっていなかったのでしょうね（＾＾；）。
具体的な実験の内容は、例えば富山大学のテキスト（ http://k2.sci.u-toyama.ac.jp/expA/main061002.pdf
の実験14）等をご覧下さい。
１．木幡重雄著 「電磁気の単位はこうして作られた」工学社（2003年刊）
このページはこの本の第２章に依存しています。この本は熟読する価値あり。
２．James Clerk Maxwell著「A Treatiese on Electricity and Magnetism｣
PartⅢ ChpterⅦ Magetic Measurementsがとても詳しい。
３．Max Planck著 理論物理学汎論第三巻「理論電気磁気学」裳華房（1946年刊）
§45 に丁寧に説明されている。
４．山本義隆著「磁力と重力の発見３」みすず書房（2004年）
逆二乗法則についてはこの本の 第二十二章エピローグ磁力法則の測定と確定(p880～938)が詳しい。
５．Gaussの原論文はこちらで引用。
６．高木純一著「電気の歴史－計測を中心として－」オーム社（1967年刊）
歴史的な経過についての説明を、この本のｐ79～82より引用。