このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。

反応熱と熱化学方程式

　教科書の説明が不足しているために、始めて反応熱を習うときその意味がよく解らない所です。高校化学の教科書を補足する説明です。（取り上げた数値データは少し古いので最新の値で読みかえて下さい）

１．反応熱とは何か？

（１）物質が持つエネルギーの種類

物質は以下の４種類の形でエネルギーを持っている。そしてこれらを合わせたものを物質の持つ内部エネルギーといいＵで表す。

１．原子間力に伴う位置エネルギー（化学結合エネルギー）

　化学結合に伴うエネルギーで、化学反応により違った分子やイオン結晶や金属結晶への組み替えが起こるとエネルギーの総量は変化する。

　

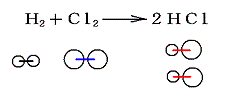
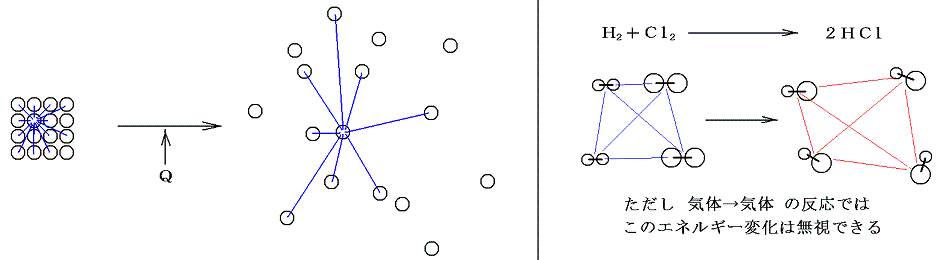
２．分子間力に伴う位置エネルギー（相変化に伴うエネルギー）

　分子間に働く力に伴うものであるが、気体分子が反応して他の分子構造の気体に変化する場合これに伴うエネルギー変化はほとんど無視できる。ただし気体から液体・固体への変化や、その逆の変化で化学変化に相変化が伴う場合はかなりのエネルギー変化が生じる。

　

３．振動・回転・並進の運動エネルギー（同温で比較する場合、この変化は無視できる）

　いわゆる温度（絶対温度）に関係する部分です。温度とは何かを論じる必要があるがここでは運動の激しさが温度に関係しているぐらいの理解でよい。そしてこの部分のエネルギーは　原子数×絶対温度　にほぼ比例すると考えることができる。そして反応の前後で物質の温度を同じにする場合は、この部分の変化は無視できる。（厳密に論じるには温度について説明しなければならないが、それをすると非常に難しくなるので、このような説明で許して下さい。ここの所を認めて頂けさえすれば熱化学方程式を非常にすっきりと理解することができる。）

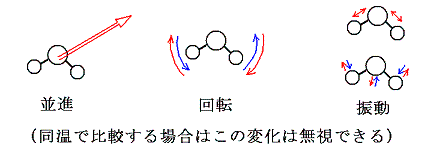
（多くの場合振動エネルギーは量子的な効果のために並進や回転に比較してエネルギーへの寄与は少なくなる。）

　高校物理�Uの理想気体の統計力学のところで（1/2）ｍｖ²＝（3/2）ｋＴと教えられますが温度はエネルギーそのものではありませんし、単純に絶対温度とエネルギーが比例するわけでもありません。それはここでの説明で、化学結合エネルギーや分子間の位置エネルギーが温度に関係していない事に表れています。また色々な物質が同じ温度でありながら熱（エネルギー）を吸収したり、放出したりして相変化をする事を思い出して下さい。“温度は物質の取りうる状態数のエネルギー変化に対する変化率に関係しています。”統計学的な取扱が必要です。しかしここでそれを論じるのは面倒なので全て省略します（詳しくは参考文献３と４を参照）。
　ただし、そのとき確実に言えることは今考えている系の並進・回転・振動等の“運動エネルギー”が増大した状態では、エネルギーの変化に対する状態数の変化率が小さくなって温度が高い状態と言われるものに成っている事です。だから大体のところ、これらの“運動エネルギー”が高い状態が絶対温度が高いと言っても良く、絶対温度に関係するいわゆる熱エネルギーと言われる物の実体だと思って良い。高校物理�Uでならう（1/2）ｍｖ²＝（3/2）ｋＴは、その最も簡単な状況に於ける表れです。
　

４．体積変化に伴う仕事のエネルギー（前記１、２の数％以下）

　このエネルギー変化は普通はほとんど無視して良い。しかし反応の前後で体積が大きく変化する場合この部分のエネルギー変化も考慮しなければならなくなる。例えば　Ｎ₂＋３Ｈ₂→２ＮＨ₃　の反応では１体積の窒素と３体積の水素が反応して２体積のアンモニアが生じるので、反応の前後の温度と圧力を同じにして比較すると４体積が２体積に縮む事になる。

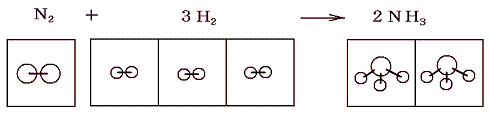
　このエネルギー変化は１．（３）で説明するように最終的には熱の出入りとなって調節される。ただし、そこで説明するようにこのことに伴うエネルギー変化（熱の出入り）は化学反応に伴うエネルギー変化の数％以下であるので、高校化学ではこの当たりは適当にごまかしている。

　

（２）エネルギーと反応熱の関係

　以下では議論を解りやすくするために物質Ａと物質Ｂが化学反応を起こして物質Ｃに成り、そのとき熱量Ｑが出入りするとする。そして文字Ａで物質Ａが持つエネルギーの総和を、同じくＢ、Ｃで物質Ｂ、Ｃが持つエネルギーの総和を表すとする。Ａは前項（１）で述べた４種類のエネルギーの総和であるが、４種類のエネルギーをそれぞれＥ１、Ｅ２、Ｅ３、Ｅ４の添え字で表すことにする。そうすると　Ａ＝Ａ_E1+Ａ_E2+Ａ_E3+Ａ_E4　となる。同様に　Ｂ＝Ｂ_E1+Ｂ_E2+Ｂ_E3+Ｂ_E4、Ｃ＝Ｃ_E1+Ｃ_E2+Ｃ_E3+Ｃ_E4　となる。
　また、最初は反応の前後で体積が変化しない反応を取り上げる。例えば溶液中の反応や、体積が変わらない容器の中で気体Ａ、Ｂが反応して気体Ｃに成るような場合である。（体積変化が生じる反応については１．（３）エンタルピーを参照）

１．発熱反応

　Ａ、Ｂ、Ｃ、Ｑがそれぞれエネルギー値を表すから、エネルギー保存則から発熱反応では当然　Ａ＋Ｂ＝Ｃ＋Ｑ　が成り立つ。ここで注意してほしいことは、物質ＡとＢが反応して物質Ｃの反応が生じた直後は　Ａ＋Ｂ＝Ｃ　となっていることである。ただし　このときの物質Ｃは最初ＡとＢが持っていた温度より高くなっている。それを最初のＡとＢが持っていた温度まで冷やすとき取り除かなければならない熱量がＱなのである。普通反応熱というのは反応前と反応後の温度を同じにする（普通25℃で比較する。）為に取り除いたり、付け加えたりしなければならない熱量の事ですが、発熱反応とは、それが取り除かねばならない場合である。図で解りやすく説明すると以下のようになる。

　このとき、エネルギーの種類も考慮すると

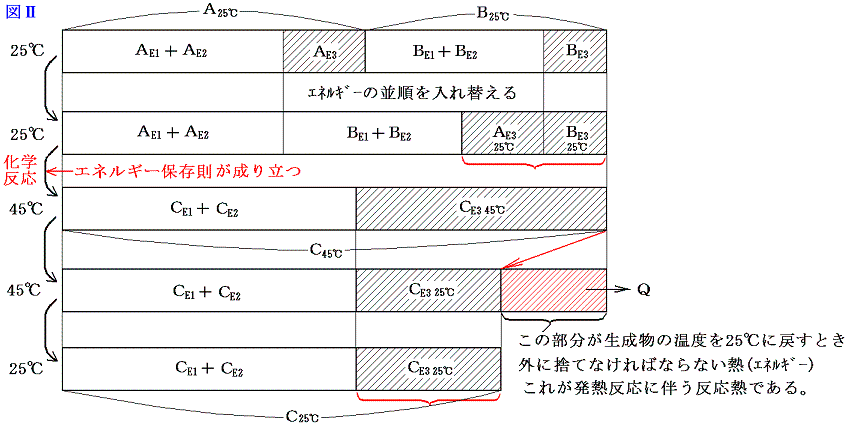
となる。ただし、普通化学結合エネルギーＥ１や分子間力に伴う位置エネルギーＥ２は、原子がバラバラに離れているときを基準点ゼロにして、結合状態（接近しているとき）のエネルギーを負で表す。（その様にする理由はこちらを参照）だから上記の図は正確ではない。正しくは以下の様に書いた方がよい。下記の正しい図と上記の図を比較してみると明らかなように、反応熱の出入りの量や、Ｅ３の大きさや、その変化量、またＥ１、Ｅ２の反応前後の差は上の図でも正しく記載されている。そのために解りやすくするために上記の図で代用したのである。正しくは以下の図で理解されたし。

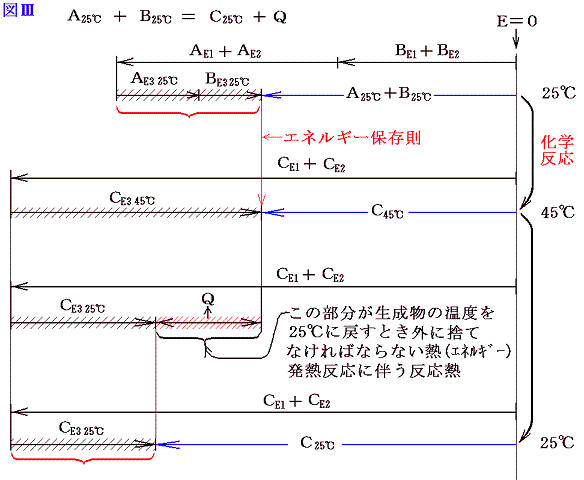
　今は体積変化を伴わない化学反応を考えているのでＥ４のエネルギー項目は省略している。ここで大切なことは物質ＡとＢが化学結合や分子間力で持っていたエネルギーと物質Ｃの化学結合や分子間力のエネルギーが異なれば、その差分を物質Ｃは分子の運動エネルギー（高温になる）として持ち、反応の前後でエネルギーは保存されると言うことです。
　そして温度を25℃に戻すとき変化するのはＣ_E3の部分であってＣ_E1とＣ_E2の部分はほとんど変化しない。
　さらに重要な事は、反応前に25℃の物質Ａ、Ｂが持っていた温度に関係する熱エネルギーの部分の和Ａ_E3＋Ｂ_E3は、反応後に25℃に戻ったとき物質Ｃが持つ温度に関係する熱エネルギーのＣ_E3とほぼ同じである事です。

２．吸熱反応

　Ａ、Ｂ、Ｃ、Ｑがそれぞれエネルギー値を表すから、エネルギー保存則から吸熱反応では当然　Ａ＋Ｂ＝Ｃ−Ｑ　が成り立つ。ここで注意してほしいことは、物質ＡとＢが反応して物質Ｃの反応が生じた直後は　Ａ＋Ｂ＝Ｃ　となっていることである。ただし　このときの物質Ｃは最初ＡとＢが持っている温度より低くなっている。それを最初のＡとＢが持っていた温度まで暖めるために加えなければならない熱量がＱなのである。普通反応熱というのは反応前と反応後の温度を同じにする（普通25℃で比較する。）為に取り除いたり、付け加えたりしなければならない熱量の事であが、吸熱反応とは、それが付け加えねばならない場合である。図で解りやすく説明すると以下のようになる。

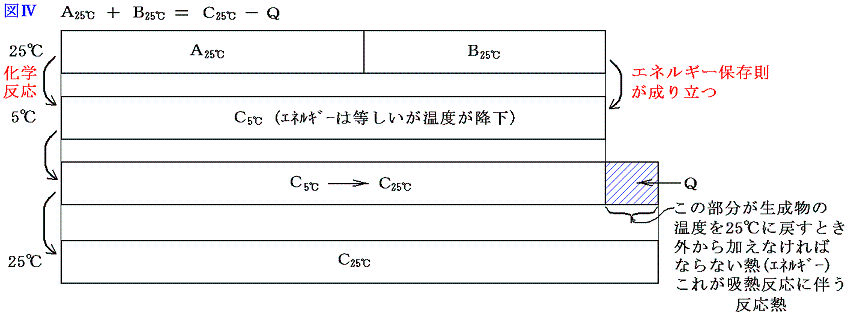
　このとき、エネルギーの種類も考慮すると

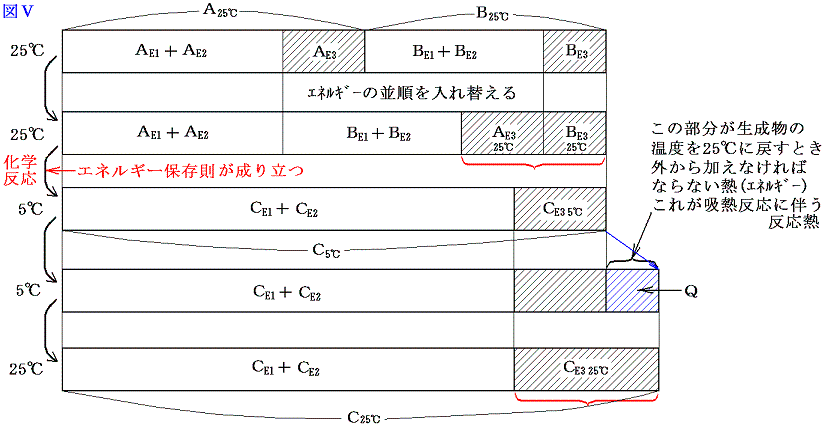
となる。吸熱反応についても、化学結合エネルギーＥ１や分子間力に伴う位置エネルギーＥ２を、原子がバラバラに離れているときを基準点ゼロにして、結合状態（接近しているとき）のエネルギーを負で表した正しい表現にすると下図の様になる。この場合も、反応熱の出入りの量や、Ｅ３の大きさや、その変化量、またＥ１、Ｅ２の反応前後の差は同じなので、解りやすくするために上記の図で代用したが、正しくは以下の図で理解されたし。

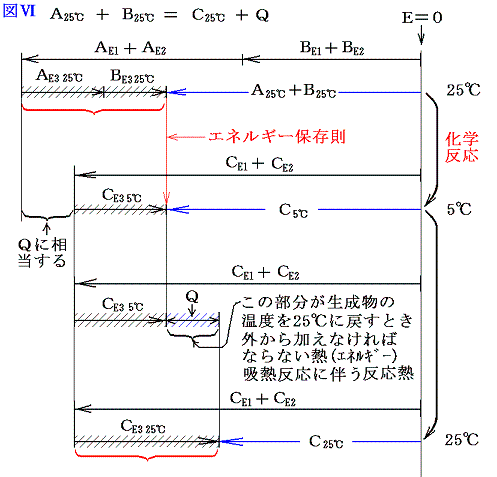
　今度も体積変化を伴わない化学反応を考えているのでＥ４のエネルギー項目は省略している。この場合も物質ＡとＢが化学結合や分子間力で持っていたエネルギーと物質Ｃの化学結合や分子間力のエネルギーが異なれば、その差分を物質Ｃの持つ原子・分子の運動エネルギー（低温になる）で調整し、反応の前後でエネルギーは保存される。
　そして温度を25℃に戻すとき変化するのはＣ_E3の部分であってＣ_E1とＣ_E2の部分はほとんど変化しない。
　さらに重要な事は、反応前に25℃の物質Ａ、Ｂが持っていた温度に関係する熱エネルギーの部分の和Ａ_E3＋Ｂ_E3は、反応後に25℃に戻ったとき物質Ｃが持つ温度に関係する熱エネルギーのＣ_E3とほぼ同じ事です。

（３）エンタルピー

１．仕事のやりとり

　今までの話は、反応の前後で体積が変わらない場合の話であった。しかし、多くの化学反応は大気圧（一定圧力)の下で行われる。そのとき多かれ少なかれ反応物の体積は変化する。そして大気との相互作用の下で、体積が膨張・収縮する事に伴って外気と仕事のやり取りをする。その場合の仕事のやり取りは、高校物理で習うように圧力Ｐに体積の変化量ΔＶを乗じたものである。

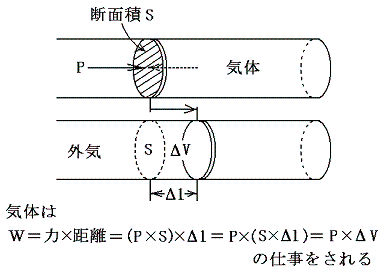
　このときＰΔＶは物質の運動エネルギーの変化を引き起こし、最終的に反応物質の内部エネルギーの変化ΔＵになる。（この当たりは別稿「断熱膨張の気体分子運動論」を参照）

２．エンタルピー（enthalpyギリシャ語”熱含量”）

　高校物理で習うように気体の内部エネルギーは温度が同じならば、体積にほとんどよらない。もちろん温度がおなじでも体積が変われば気体の密度が異なり、容器の壁への気体の衝突頻度が変化して圧力が変わる。しかし個々の気体の運動エネルギーは同じと言うことである。それならば、内部エネルギーにあらかじめＰＶ_A+Bを付け加えておく。そして反応後のエネルギーにもＰＶ_Cを付随させることにより体積変化に伴う仕事Ｗが考慮でき、それを反応熱の中に含ませることができる。つまり熱化学方程式の中に出てくる反応熱は仕事のやり取りに伴うエネルギーも含んだものにできる。
　その様にするのは、もう一度強調するが、反応熱を測定する化学変化は一定圧力（多くは大気圧）の下で行われるからである。

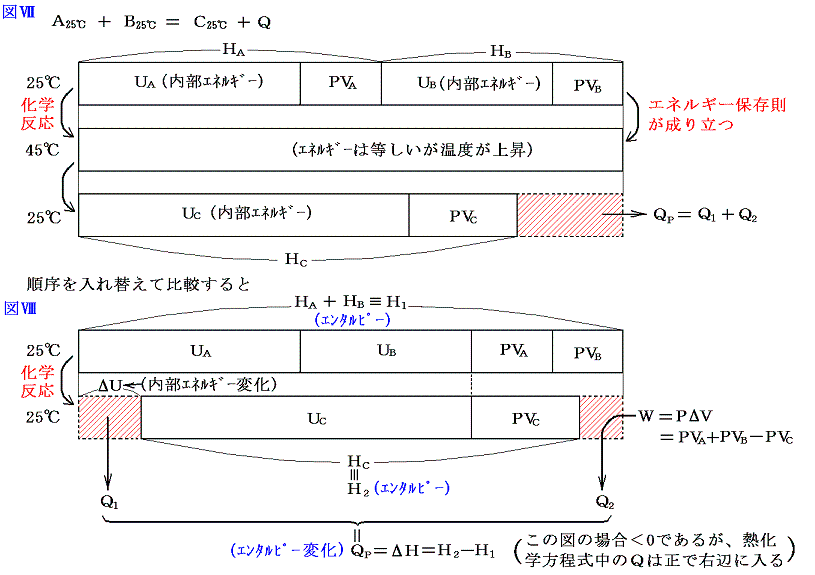
　この場合も結合エネルギーが負である事を考えると１(２)の図�Vや図�Wの形にする方がより正確かもしれない。その様にしても結論は変わらない。

一定圧力の下での化学変化に伴う内部エネルギーの変化をΔＵとすると

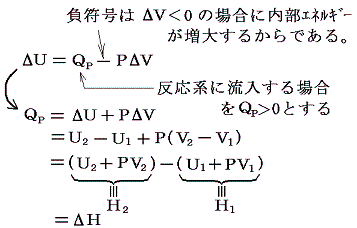
　このようにして定められた量Ｈ=U+PVをエンタルピーと言う。その変化量ΔＨは一定圧力の下での化学反応に伴って出入りする熱量Ｑ_p(１．(２)参照)になる。これに対して体積一定の密閉容器中で化学反応を行わせた場合には体積変化に伴う外界との仕事のやり取りを含まない熱のやり取りになる。これは定積の下での化学反応に伴って出入りする熱量Ｑ₁＝Ｑ_Vである。
　化学反応はほとんどが定圧の下で行われるので体積変化で生じる仕事のやり取りに伴うエネルギー変化を含んだ熱量が測定される。そのため普通、反応熱と言われるものはエンタルピーの変化ΔＨを指す。

３．仕事に伴う反応熱

　ここで、体積変化に伴う仕事で付随した熱の出入りＱ₂がどの程度であるのか見積もってみよう。高校化学で１molの気体は0℃、１気圧で22.4リットルを占めると習う。今その気体が化学反応の結果液体か固体になって体積がほとんど零になった場合に、体積変化から生じる仕事量（あるいはＱ₂）を計算してみる。１気圧＝１０１３hPa＝1.013×10⁵N/m²、　 22.4リットル＝2.24×10^-2m³ 　だから
　Ｗ＝ＰΔＶ＝1.013×10⁵N/m²×2.24×10^-2m³＝2.27×10³J 〜2.3kJ〜Ｑ₂に相当
となる。

　一般の化学反応に伴う反応熱（エンタルピーの変化ΔＨ）は数十〜数千kJであるから、上記の仕事に伴う熱量Ｑ₂は反応熱全体Ｑ_pの数％程度以下である。そのため高校化学の熱化学方程式では上記のＱ₁＝ΔＵとＱ_p＝ΔＨの区別を特に教えないで適当にごまかしているが、高校レベルではごまかした説明で良いと思う。

（４）反応熱についての注意

１．反応熱の温度による違い

　普通は反応前後の温度を25℃＝298Kにそろえて反応熱を測定するが、2000Kの下で反応熱を測定したらどのくらい違うか調べてみる。圧力はいずれも1気圧の下での反応とする。例として

の反応を考える。1気圧の下でそれぞれの気体1molを298Kから2000Kに加熱するとき必要な熱量（エンタルピー変化ΔＨ）は

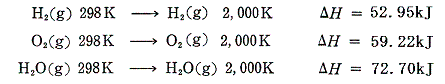
となる。これらの値は定圧比熱を温度変化で積分した値から求める事ができる。

この値を代数的に上式に結びつけると

となる。この当たりを図示すると

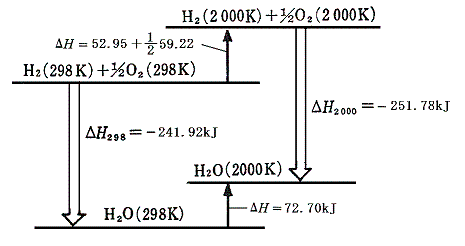
となる。

　この図は反応物の温度を298Kから2000Kまで上げるのに要するエネルギーと生成物の温度を298Kから2000Kまで上げるエネルギーにほとんど差がなく、反応前後のエンタルピー変化は測定温度による影響をほとんど受けないことをいっている。これこそ化学結合によるエネルギーと熱にともなうエネルギーを分離して１．（２）で行ったような取扱をしても良いことを正当化する根拠だと言える。

［補足説明］
　反応熱の温度変化について、ムーア「物理化学」より引用。同じく原田義也「化学熱力学」より引用｡

２．熱エネルギーは反応前後の温度が同じならばほぼ同じ

（２）１．２．の説明から明らかなように、反応熱Ｑは

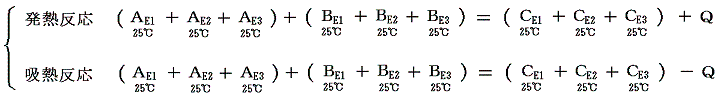
の関係を満足するが、

反応前後で温度が同じならば

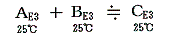
と見なせる。これは（１）３．で注意したようにＥ３のエネルギーは絶対温度と原子数が変わらなければほぼ等しいと見なせるからです。

この関係式を用いると

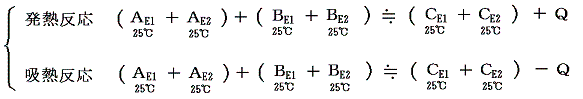
となる。この式は結合エネルギーを正として表した簡単な図でも、負とした正確な図でも、共に成り立っていることに注意。これは反応熱を測定する事によって化学結合エネルギーや分子間力に伴う位置エネルギーの変化を見積もることができることを意味する。これこそ化学者が知りたい情報である。

３．相の違いによる反応熱の違い

　反応物の相（気体gas、液体liquid、固体solid）が違えば反応熱が異なるのはＥ２のエネルギーが異なるからである。だから反応物の相を明記する必要がある。

　例えば水素と酸素が反応して１モルの水ができるときの反応熱（25℃）は生じる水の相により異なる。

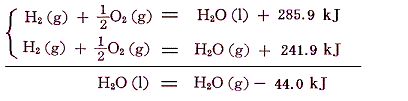
両者の差は25℃、１atmの下での、１モルの水の蒸発熱に等しい。

４．同素体の違いによる反応熱の違い

多形が存在する同素体はその形態によりエネルギー値が異なるので同素体名を明記する必要がある。

　黒鉛の燃焼熱とダイヤモンドの燃焼熱を25℃で比較するとダイヤモンドの方が大きい。これは25℃においては黒鉛の方がダイヤモンドより安定であることを意味する。(ただし超高圧・高温になると黒鉛よりダイヤモンドが安定になる)

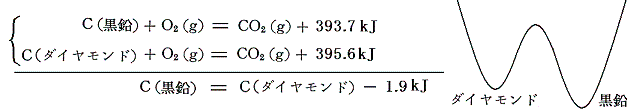
　このとき、なぜダイヤモンドが黒鉛に変化しないのかと言うと、ダイヤモンドの化学結合を黒鉛の化学結合に組み替えるとき一旦結合をゆるめたエネルギーの高い状態を経過しなければならないからです。

　液体の急冷で得られる単斜イオウから安定な斜方イオウへの転移は直接測定できる。

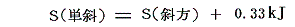
２．熱化学方程式と反応熱の種類

（１）熱化学方程式

　熱化学方程式の意味は高校化学で習うので、ここでは簡単に復習する。熱化学方程式は化学反応式とは違い代数的な方程式を表す。以下例を用いて説明する。

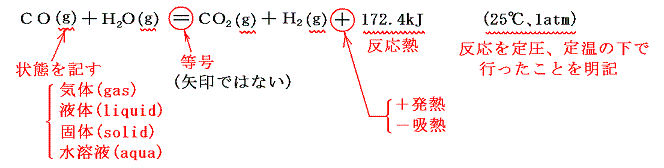
1. 熱化学方程式中の化学式は、その物質の持つエネルギーを表す。正確に言うと体積変化に伴う仕事も加えたエンタルピーを表す。
2. 左辺（反応物）と右辺（生成物）を結び付けるのが矢印→ではなくて等号＝であることが本質的に重要。［左辺のエネルギーの和］が［右辺のエネルギーの和に反応熱の出入りを加減したもの］に等しいといっている。
3. 化学式の前の係数は物質のモル数を表すが、次節で述べる着目する物質の係数を１モルとするために、他の物質のモル数が分数になることもある。
4. 代数式と同じで移項すると符号が変わり、代数計算できる。その際反応熱の前の符号の意味は１．(２)で説明した内容を意味する。
5. 物質は気体・液体・固体の相によりエネルギーが変わるので必ずどの相にあるのかを明記する。

（２）反応熱

　反応熱を何種類かに区分けし、その種類に応じて熱化学方程式を特別な書き方で表す。そして下記アンダーラインの物質１mol当たりの値で示される。
［補足説明］
　［ラボアジェとラプラスの熱量測定］、［ボンベ熱量計］、［炭化水素のエネルギー差］

１．燃焼熱

　物質１molが酸素と反応して完全燃焼するとき発生する熱量のこと。完全燃焼とはＣ→ＣＯ₂、Ｈ→Ｈ₂Ｏ、Ｓ→ＳＯ₂、等々･･･と構成元素ごとに定められた最終産物になることを意味する。

２．生成熱

　物質１molを、その成分元素の単体から作るときの反応熱を特に生成熱と言う。材料の単体に多形があるときは25℃、1atmで安定なほうを選ぶ。だからイオウならば斜法イオウ、炭素なら黒鉛、････等々となる。

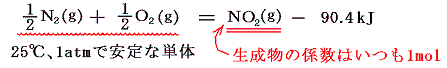
３．溶解熱

　物質1molを多量の水に溶解するときの反応熱。多量の水とは、さらに水の量を増やしても、もはや熱の発生や吸収が認められない量のこと。イオン間の距離が十分大きくて溶質イオン間の相互作用は無いと考えられる量。これは結晶格子を壊すエネルギーと水和エネルギーとの差であるが、無水結晶の溶解と、水和物の溶解では一般に無水物の方が発熱量は大きい(例　ＣaＣl₂：発熱、ＣaＣl₂･6Ｈ₂Ｏ：吸熱）

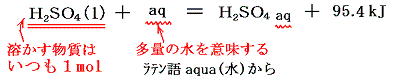
［補足説明］
　もっと一般的な溶解熱について、ムーア「物理化学」より引用。

４．中和熱

　酸と塩基（アルカリ）が中和して１molの水を生成するときの反応熱。酸・塩基が完全に電離している（強酸、強塩基の希薄溶液）ときは、その種類に関係なくほぼ56.5kJとなる。これは　Ｈ⁺＋ＯＨ^-＝Ｈ₂Ｏ＋56.5kJ　を意味する。弱酸、弱塩基の場合は、電離にエネルギーを要するので一般に56.5kJより少なくなる。

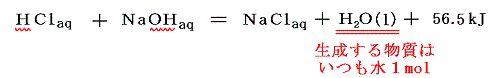
５．転移熱（融解熱、昇華熱、蒸発熱）

　一定温度下で1molの物質が相変化するときに出入りする熱量のことです。高校で習う状態図から明らかなように圧力を調節すれば、いろいろな温度で二相が共存でき、いろいろな温度で相転移ができる。一般には転移する温度によって転移熱は少し変化するが、高校レベルでは25℃、1atmですべての相を取ることが可能で、そこで転移したら反応熱はいくらになるかとしている。

３．ヘスの法則と熱化学方程式の代数計算

（１）ヘスの法則（1840年 G.H.Hess）

ヘスの法則は授業でならうので簡単に復習する。

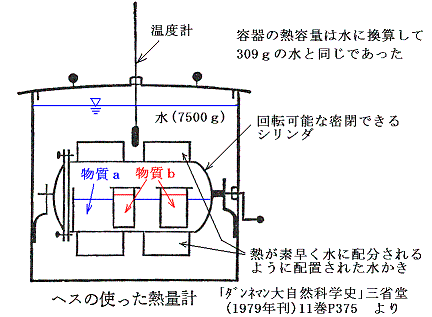
　ヘスは上図の装置で濃硫酸を種々の濃度に薄めるときの反応熱（Ａ）と、その様にして調合した種々の濃度の硫酸をアンモニア水で中和するときの反応熱（Ｂ）の和(Ａ)＋(Ｂ)は常に一定値になることを見つけた。(1840年)

　これは反応熱は反応経路によらないで反応物質と生成物質の状態だけに関係する事、および、熱化学方程式の化学式に附随させたエネルギー（定圧反応の場合はエンタルピー）は状態を規定すると一義的に定まる物理量であることを示している。そのため、熱化学方程式を代数的に組み合わせて未知の反応の反応熱を計算することができる。これをヘスの熱量加算の法則という。ヘスの法則はエネルギー保存則を言い換えた物に過ぎないが、以下述べる様に有益な情報を与えてくれる。

（２）ヘスの法則の応用例

以下の例はすべて25℃、1atmの下での反応である。

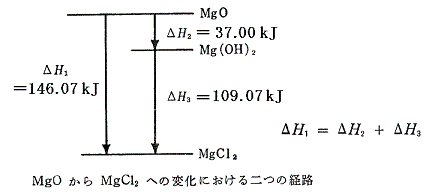
１．酸化マグネシウムと希塩酸の反応

直接反応させたときの反応熱(25℃、1atm）を熱化学方程式の形で表すと

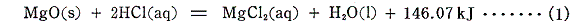
となる。この反応は、最初に酸化マグネシウムを水と反応させて一旦水酸化マグネシウムとしてから、希塩酸と反応させることもできる。この二段階の反応のそれぞれの熱化学方程式は

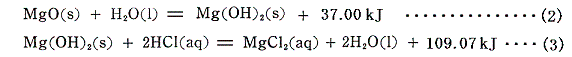
となる。（２）式と（３）式を代数的に辺々を加え合わせると、両辺のＭg(ＯＨ)₂とＨ₂Ｏが打ち消されて（１）式と一致し、まさしくヘスの法則が成り立っていることが確認できる。これらの関係を図示すると以下の様になる。

２．過酸化水素の生成熱

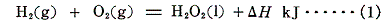
上記の熱化学方程式で表される過酸化水素の生成熱ΔＨを求めたい。しかしこの反応を直接生じさせる事はできない。そこで実現可能な二つの反応を利用する。水素は酸素中で容易に燃焼して水を生成する。また過酸化水素は水と酸素へ分解可能です。そのため、それらの反応熱は測定可能です。

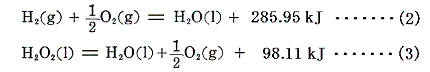
（２）式＋(-1)×（３）式で代数的に計算すると

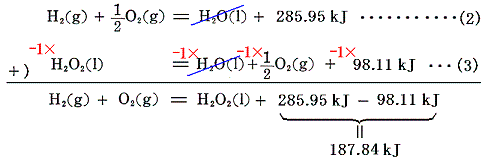
となり、（１）式の生成エンタルピーΔＨ＝188kJ　を求めることができる。

３．一酸化炭素の生成熱

　炭素の燃焼を一酸化炭素の状態で止めるのは難しい。そのため一酸化炭素の生成熱を直接求めることはできないが、炭素と一酸化炭素の燃焼熱を用いればよい。

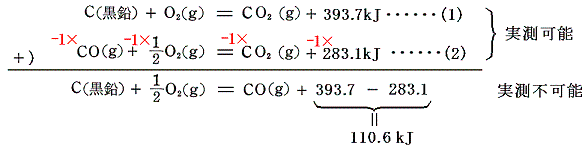
４．メタンの生成熱

　メタンの生成熱を実験によって直接求めるのは簡単ではないが、メタンを構成する単体元素Ｃ（黒鉛）、Ｈ₂の燃焼熱とメタンＣＨ₄の燃焼熱を用いればよい。

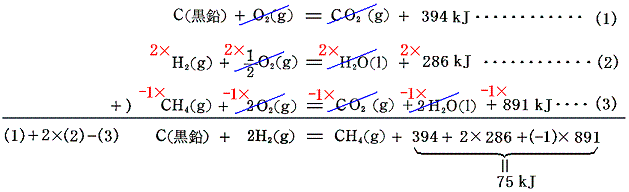
　以上の幾つかの例を見れば解るように、化合物を単体から合成する際の生成熱を直接測定することは一般に難しい。しかし、その化学式を構成するそれぞれの単体元素や生成分子の燃焼熱の測定は多くの場合簡単である。それらを組み合わせて代数計算することにより生成熱を求めることができる。

５．可逆反応

　反応が一方方向に速やかに進行するものは反応熱が測定できるが、反応が途中で止まり平衡状態になってしまう可逆反応は直接測定することができない。そのため反応熱が測定できる反応を組み合わせてヘスの法則を用いて算出する。後で説明するＮＨ₃、ＮＯ₂、ＨＩなどを参照されたし。（化学平衡の解析からも求まるが説明は省略）
　そのとき注意すべき事柄は、可逆反応の反応熱の絶対値は一般に小さい事です。（さらに言えば、反応の活性化エネルギーも低いのだか、そのことについては別稿で説明する）そういった可逆反応の例を幾つか挙げておく。

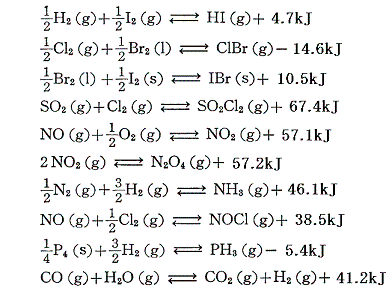
４．生成熱

（１）任意の化学反応の反応熱の求め方

化学者は物質の生成熱の値を求める事に努力するが、それはその化学反応の構成成分の生成熱の一覧表が与えられていれば

が成り立つからである。生成物から反応物を引くのは反応物を式の左辺に移動させるためである。

この関係が成り立つことを

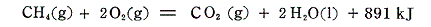
を例に使って説明する。反応物、生成物の生成熱を表す熱化学方程式を記して、　2×(1)式+(4)式−(3)式-2×(4)式　を計算してみると確かに目的の化学反応の熱化学方程式が得られる。

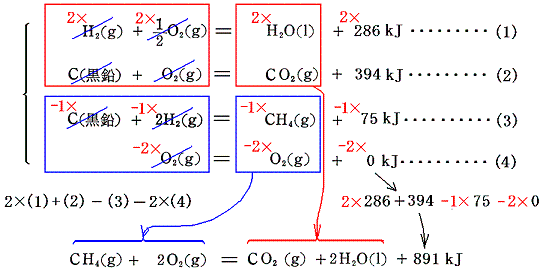
このようなことが成り立つのは、左辺がすべて単体元素で構成されており、反応の前後で原子数が保存されるために左辺の合計が常に０になるようにできるからである。

（２）標準生成エンタルピーΔＨ⁰_f（各物質の生成熱Ｑの符号を逆にしたもの）

　もともと反応熱というのは内部エネルギー（定圧の場合エンタルピー）の変化量（差分）であって、各物質が持つエネルギー値そのものではない（測定できるのはエネルギーの変化量であってエネルギー値そのものではない）。しかし前項（１）の考え方を吟味すれば明らかなように、単体の標準生成エンタルピーを０と決めることにすれば、エンタルピーの変化量が各化合物のエンタルピー値そのものであると見なしても良い。ただし、そのとき符号を逆にする必要がある。
　１．(２)の議論をもう一度復習すれば明らかなように反応熱というのは、発熱反応の場合には反応により温度が上昇した反応生成物の温度を最初と同じ25℃に戻すために取り除かねばならない熱エネルギーの事であった。だから熱化学方程式においては＋Ｑで右辺(生成物の側)に入っていた。ところが、物質の持つエネルギー(いわゆる化学結合のエネルギー）そのものについて言えば、発熱反応の場合には反応物よりも生成物のエネルギーの方が低いのである。ちょうど反応熱Ｑの符号を変えただけ低くなるのである。だから反応に伴うエネルギーの差分を反応物質そのもののエネルギー値にするには符号を逆にしておかなければならないのである。

　そのようにして求めた標準生成エンタルピーΔＨ⁰_f（Δは単体元素からの差、添え字の0は標準状態25℃、1atmでの値、ｆはenthalpy of formationのfの意味）の一例を下表に示す。

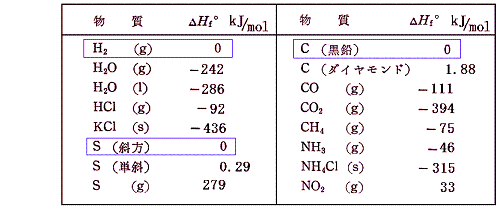
この表で25℃、1atmで安定な単体元素の値が０であることに注意。

このようにしてすべての物質の標準生成エンタルピーの一覧表が与えられれば、その値を任意の化学式のそれぞれの化合物に反応モル数に応じて割り当てさえすれば、その化学反応の反応熱を求めることができる。つまり

となる。ここで以前とは逆に反応物から生成物を引く形になっていることに注意。

標準生成エンタルピーの値を用いて以前の例を計算してみると

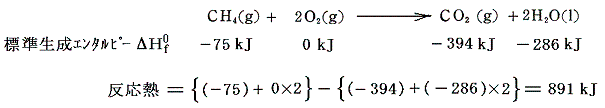
となる。つまり25℃、1atmの状態においてメタンと酸素の状態で持つエネルギーより二酸化炭素と水の形で持つエネルギーの方が少ない。その差が熱エネルギーとなって失われたのである。
　化学反応式を構成する物質の標準生成エンタルピーさえ与えられていれば、任意の化学反応の反応熱が単純な加減算をするだけで求まる。これは素晴らしい成果である。

５．生成熱測定法

　以上の話から任意の化合物の生成熱（あるいはその符号を逆にした標準生成エンタルピー）が非常に大切な量であることが解ったが、次なる問題は、あらゆる化合物の生成熱（標準生成エンタルピー）をいかにして求めるかである。

（１）物質の分類

以下は高校化学で習う分類。

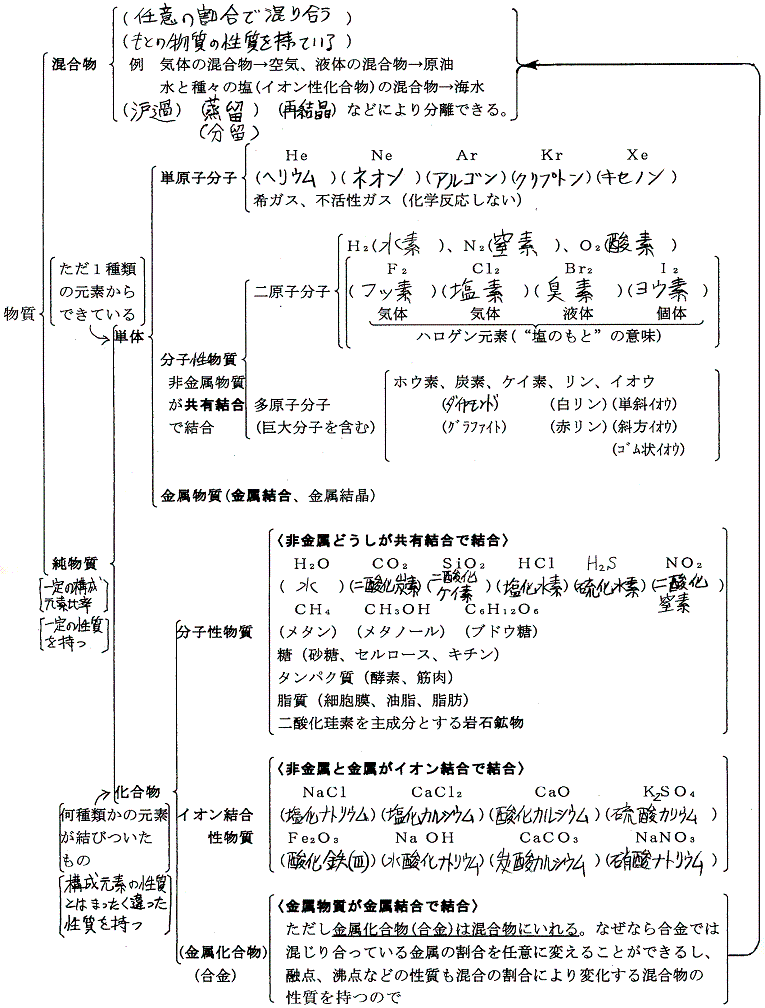
この中の分子性物質とイオン結合性物質の生成熱の求め方を説明する。

（２）無機分子性物質

　周期律表の右上に位置する元素同士の共有結合化合物である。とくに非金属元素の水素化物、酸化物、硫化物、ハロゲン化物などが主な化合物である。さらに周期律表の中程のＣ、Ｓi、Ｇe、Ｐ、Ａs、、Ｓ、Ｓe、Ｔe等が作る共有結合巨大分子。あるいはＳiとＯからなる二酸化珪素ＳiＯ₂を単位とした珪酸塩化合物(いわゆる岩石圏の主要成分)などがある。

　次の例は容易に反応が進むので簡単に生成熱が測定できる。（標準生成エンタルピーΔＨ⁰_fに読みかえるには生成熱の符号を逆にすればよい。以下同様）

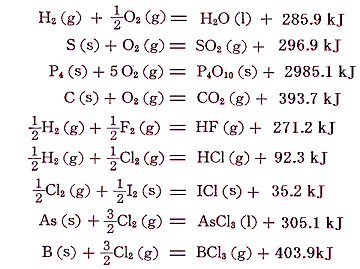
　このように直接測定できれば良いが、そうでない場合は工夫が必要。一般に、構成単体の酸化反応（燃焼反応）やハロゲン化反応、生成分子の分解反応、等々・・・の熱化学方程式を組み合わせて求める。３．（２）で説明した過酸化水素、一酸化炭素はその例であるが、以下でもう少し例を挙げる。

　窒素と水素から合成れるアンモニアは可逆反応だから反応熱の直接測定は出来ないが、測定可能な水素とアンモニアの燃焼熱から求まる。アンモニアは空気中で燃えないが、純粋酸素中では黄色い炎を上げて燃えて窒素と水になる。

　

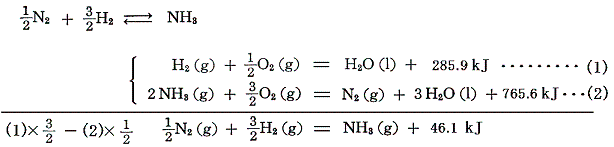
　窒素酸化物は平衡状態を形成して互いに移り変わるので、それらの生成熱を直接測定できない。

しかし、以下の様な反応を用いればよい。

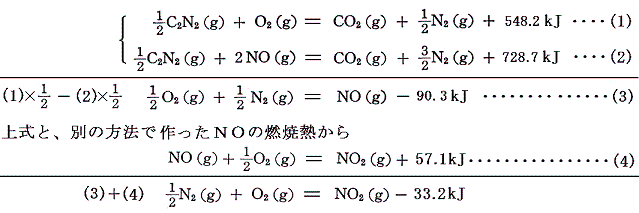
としてＮＯとＮＯ₂の生成熱が求まる。いずれも負であることに注意。
　

　水素とヨウ素の反応は可逆反応だから、ヨウ化水素の生成熱は、［塩化水素の生成熱］と［塩素とヨウ素の置換反応］から求める。

　

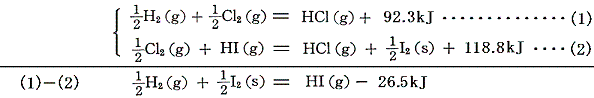
　ハロゲン間化合物の生成熱は［置換反応(3)］を用いて求める。

　

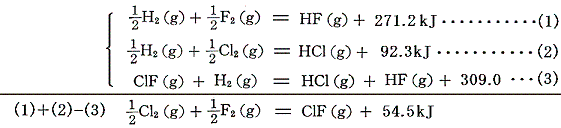
　二硫化炭素などは炭素・イオウ・二硫化炭素の［燃焼熱］から求める。

　

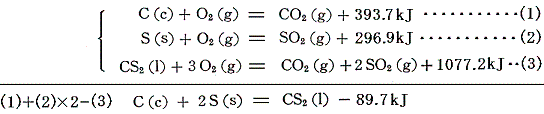
　オゾンなどの生成熱はオゾンの[分解反応]を逆に見れば求まる。

（３）イオン結合性物質

　金属陽イオンと非金属陰イオン（あるいは共有結合分子の陰イオン）のイオン結晶物質である。酸と塩基の中和でできるいわゆる塩といわれるものである。金属の酸化物、水酸化物、硫化物、ハロゲン化物・・・や、金属イオンと炭酸イオン、硫酸イオン、硝酸イオンなどのイオン結晶化合物である。

１．酸化物、炭化物、カルボニル

　下記に示す金属の酸化物やハロゲン化物は容易に生成するので直接測定できる。

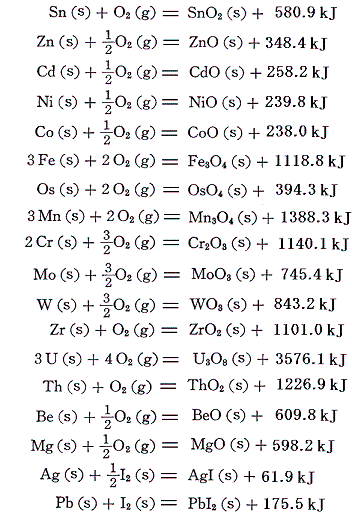
アジ化銀は［分解反応］を逆にして求める。

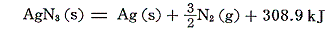
直接測定できない場合は、以下の様に反応を組み合わせて求める。
　

ＣuＯやＰbＯの生成熱は、それらの［水素による還元反応］と［水の生成熱］から求める。

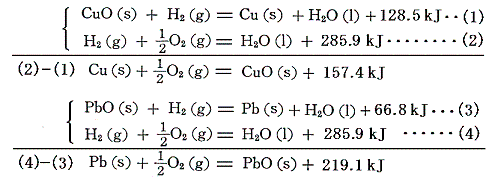
ＰbＯには黄色と赤色の同素体があるが、赤の方が安定である。
　

ＦeＯやＭnＯなどの中間酸化物の生成熱は、それらの［燃焼熱］と、前出のＦe₃Ｏ₄やＭn₃Ｏ₄の［生成熱］を組み合わせて求める。

　

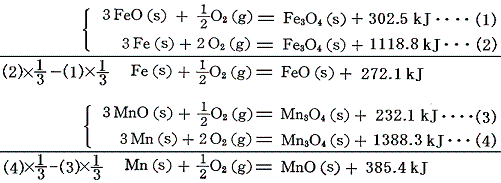
ＣrＯ₃の生成熱は、その［分解反応］と前出のＣr₂Ｏ₃の［生成熱］を用いて求める。

　

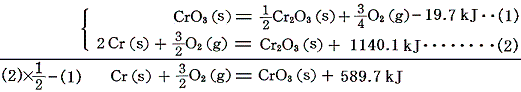
鉄やマンガンの炭化物Ｆe₃Ｃ、Ｍn₃ＣやＭnＣＯ₃の生成熱は、それらの［燃焼熱］と、Ｆe₃Ｏ₄、Ｍn₃Ｏ₄やＭn₃Ｏ₄の［生成熱］を用いて求める。

　

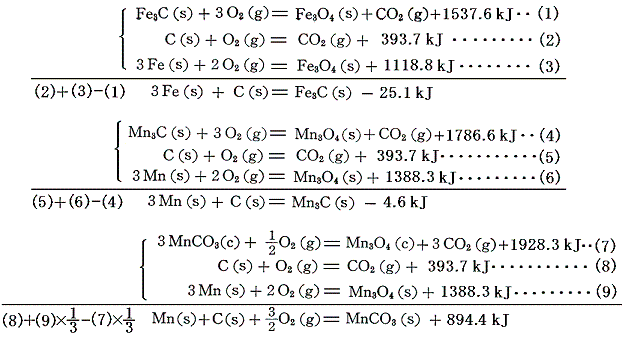
鉄カルボニルＦe(ＣＯ)₅は金属と一酸化炭素の反応でつくられ、その際の反応熱が測定されているので、すでに求めている一酸化炭素の［生成熱］を用いればよい。
　

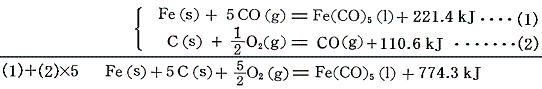
２．金属の塩酸塩

金属塩の生成熱は、［金属の酸溶液への溶解熱］と［それぞれの物質の水への溶解熱データ（表�T参照）］を用いる。

　

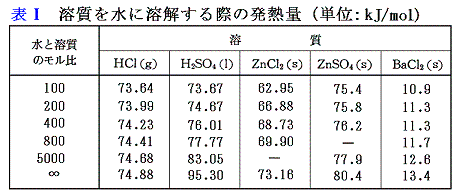
　例えば塩化亜鉛ＺnＣｌ₂は、金属亜鉛の塩酸(塩化水素の水溶液）への溶解熱を利用する。

となる。このような計算ができることは、以下のように熱化学方程式をきちんと書いてみれば分かる。

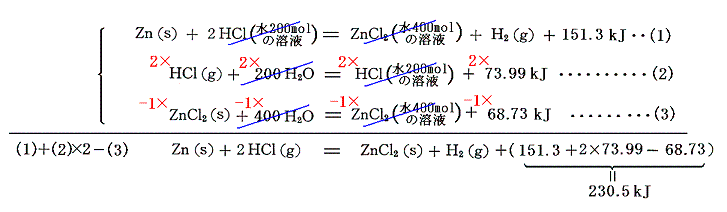
この式と、すでに求めている塩化水素ＨＣｌの［生成熱］を組み合わせれば塩化亜鉛(s)の生成熱として

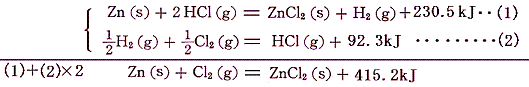
が求まる。ここで表�Tの値を加算すると各濃度の水溶液中でのＺnＣｌ₂の見かけの生成熱を得ることができる。このとき溶媒の生成熱は関係しない。
　

　ここで大切な事をもう一度注意しておく。４．（２）で説明したように、生成熱を求める物質以外の化合物の標準生成エンタルピーΔＨ⁰_f（生成熱Ｑ₀の符号を逆にした物）がすべて解っている（単体は当然0）場合は、ΔＨ⁰_fの値を化学式に代入するだけで求まる。例えば上記の例では

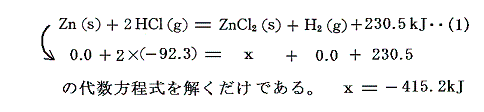
となり、これがＺnＣｌ₂の標準生成エンタルピーであり、符号を変えた+451.2kJがＺnＣｌ₂の生成熱である。非常に簡単で、熱化学方程式の代数計算など必要ない。次節以降そうやっても良いのであるが、教育的観点から熱化学方程式を並べて解くやり方で説明する。

　同様な方法で求めた金属塩化物の生成熱を記す。
　

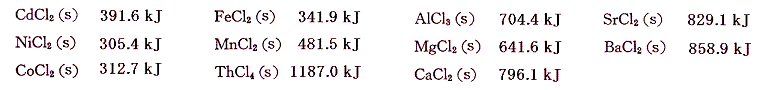
３．金属の硫酸塩

　硫酸塩の場合は、まず硫酸Ｈ₂ＳＯ₄の生成熱を求める。二酸化イオウの水溶液に塩素を反応させ、塩酸と硫酸の水溶液へ変化する際の熱量を測定する。

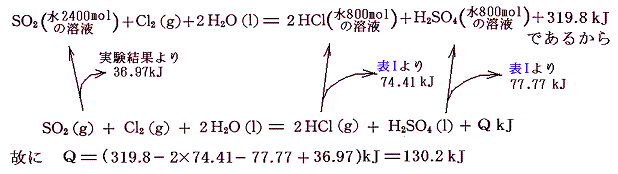
となる。この式とＨ₂Ｏ､ＳＯ₂､ＨＣｌの［生成熱］を組み合わせると硫酸の生成熱が求まる。

となるが、教育的見地から以下すべて熱化学方程式を解くやり方で説明する。　　

　上式と、三酸化イオウＳＯ₃の水への溶解熱の式を用いれば三酸化イオウの生成熱が求まる。

　

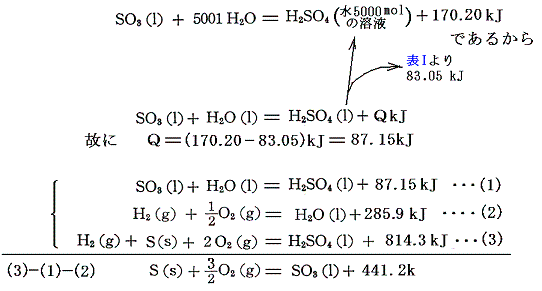
　硫酸亜鉛ＺnＳＯ₄の生成熱は［金属亜鉛を希硫酸に溶解する際の反応熱］と［硫酸の生成熱］から求まる。

　

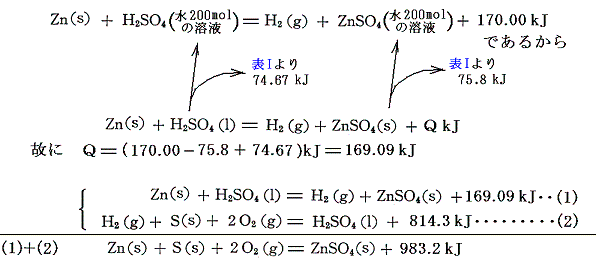
硫酸亜鉛ＺnＳＯ₄の生成熱は、次の二つのＢaＳＯ₄沈殿反応の差から仮想的化学反応を構成して求める方法もある。

この式とＺnＣl₂、Ｈ₂ＳＯ₄、ＨＣlの［生成熱］を組み合わせると硫酸亜鉛ＺnＳＯ₄の生成熱が得られる。

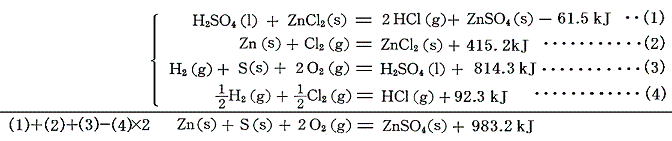
　このＢaＳＯ₄の沈殿反応を用いる方法はＺnを他の金属に置き換えれば、様々な金属硫酸塩の生成熱の算出に用いることができる。幾つかの例を記す。

　

　硫酸銅ＣuＳＯ₄の生成熱は、金属銅を硫酸溶液に溶かす方法は使えない。高校化学で習うように酸化還元反応が起こってＳＯ₂が発生するからである。そのため酸化銅ＣuＯを希硫酸に溶かす。

この式と、すでに求めたＨ_２Ｏ、ＣuＯ、Ｈ₂ＳＯ₄の［生成熱］を組み合わせると硫酸銅ＣuＳＯ₄の生成熱が得られる。、

　

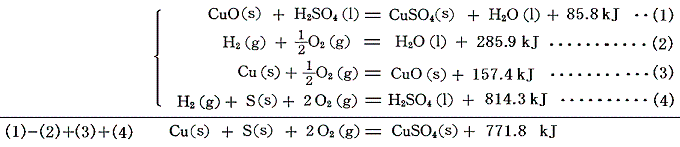
　硫酸鉄ＦeＳＯ₄の生成熱は硫酸銅溶液中での金属鉄との［置換反応(イオン化傾向はＦe方がＣuより大)］を利用する。
　

４．水和物

　水和物形成の反応熱、水和物の単体からの生成熱は一定量の水への溶解熱を無水物と水和物で比較することにより求まる。

　ＢaＣl₂･Ｈ₂Ｏの水和形成の反応熱はＢaＣl₂･Ｈ₂ＯとＢaＣl₂の［溶解熱］から求める。

　

二水和物についても全く同様である。

　

硫酸亜鉛水和物と硫酸銅水和物の生成熱を以下に示す。

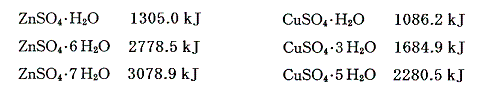
これらのデータを用いて前述の議論を逆にたどれば、無水物が水和する際の反応熱や、無水物の溶解熱と組み合わせることにより水和物の溶解熱を求めることができる。　

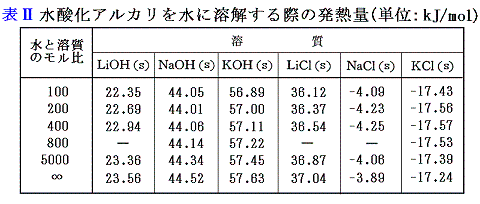
５．金属の水酸化物（水酸化アルカリ）

水酸化アルカリの生成熱は、［金属の水への溶解熱］と［水酸化アルカリの水への溶解熱］と［水の生成熱］から求まる。

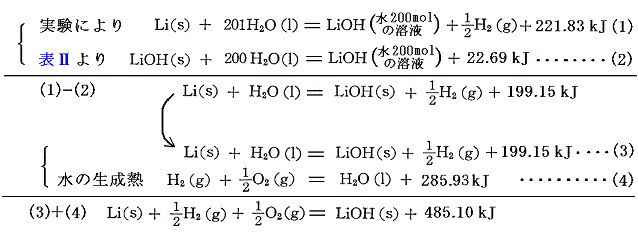
もちろん(1)-(2)+(4)でいきなり求めても良いが、金属と水の反応熱を得るため二段階で説明した。

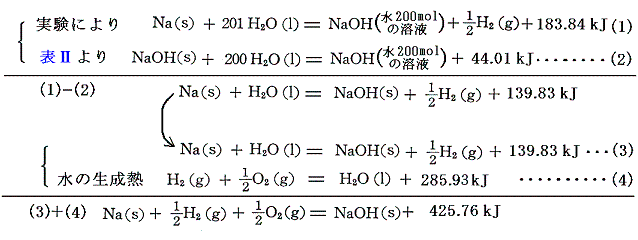
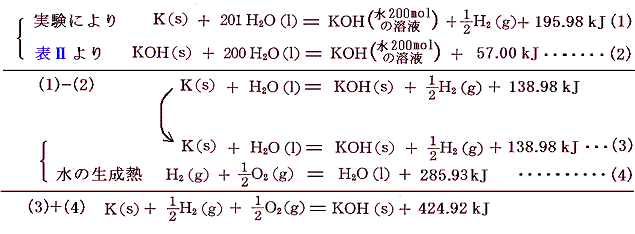
６．塩

　塩の生成熱は中和反応を利用して求める。そのため、最初に中和反応について説明する。以下の熱化学方程式は、酸と水酸化アルカリ溶液の中和熱の実測値である。

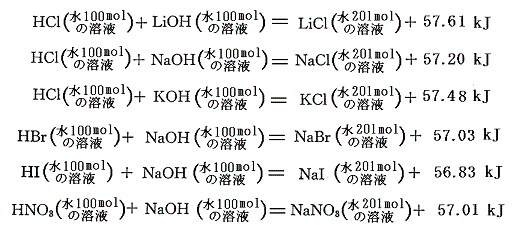
　表�Tと表�Uに記載されている各化学物質の他濃度への溶解熱のデータを用いて、他の濃度の中和熱を計算によって求めることができる。各濃度の溶解熱と水と溶質のモル比が100の場合の溶解熱との差を用いて計算すると、例えばＨＣlとＫＯＨの中和では

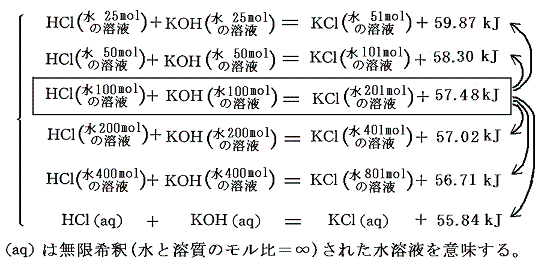
中和熱はある一定値55.8kJに近づいていく。他の例について同様な方法で濃度零への外挿計算を行えばほぼ同一の中和熱を与える。

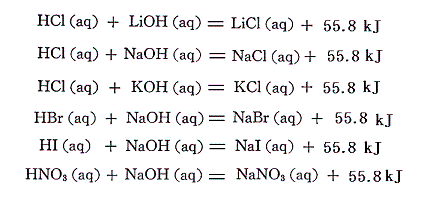
これは、電解質の完全な電離のために、酸と塩基の種類に関係なく

の反応熱が中和熱であることを意味する。　

　前出の水100molの溶液に対する中和熱の実測値に、表�Tと表�Uに記載されている各化学物質の水100molへの溶解熱データを逆に用いて、［水のない状態における中和反応の反応熱］を求めることができる。

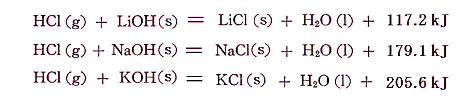
　この熱化学方程式に［ＨＣlの生成熱］と４．(３)５．で求めた［水酸化アルカリの生成熱］の熱化学方程式を組み合わせれば、ハロゲン化アルカリの生成熱が求められる。

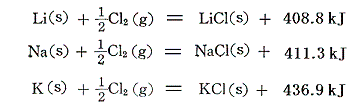
　このように、［ある濃度の酸及びアルカリ溶液の中和熱の測定値］と［その濃度への溶解熱の測定値］を利用すれば、種々の塩の生成熱を求めることができる。
　

７．イオンの生成熱

イオンの生成熱の話しに入る前に二つの例を説明する。

［例１］
　ヘスは実験によって、水溶液においては二種類の塩の陽イオンと陰イオンを交換しても反応熱に差が無いことを発見した。これは今日の言葉で言うと、例えば

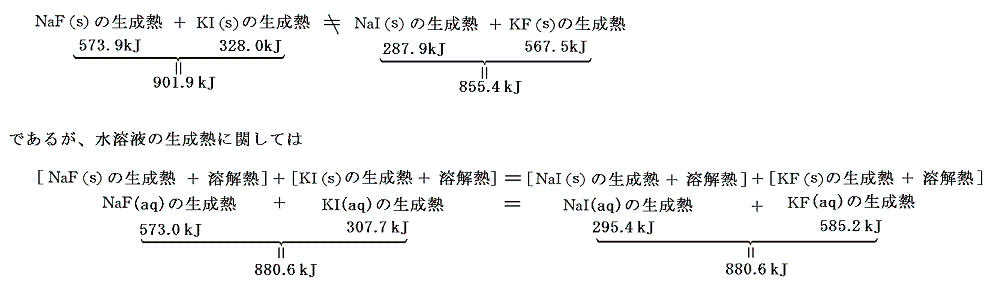
が成り立つ事である。これは、生成熱が単体から作られるものであり、水溶液を混合した後のイオン状態が同じである事を考えればある意味当然である。　

［例２］
　沈殿反応を生じるイオン結晶については、水溶液の沈殿反応を用いて、そのイオン結晶と水溶液イオンとのエネルギー差＝［格子エネルギー］＋［水和エネルギー］の値を求めることができる。
　

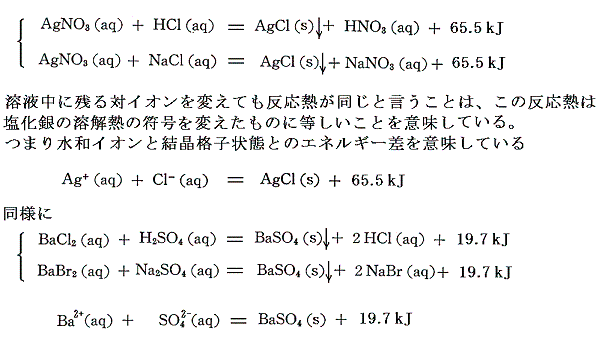
　上記の例の様に、希薄溶液に関してはイオンそのものを直接取り扱う事により化学反応を見通しよく取り扱う事ができる。そのため溶液中の各イオンの生成熱(−標準生成エンタルピー)の値を求める事ができれば便利であろう。しかし、その様な数値を手に入れることはできない。なぜならイオンの生成熱とはイオンの成分元素の単体を水に溶解してそのイオンができたときの反応熱であるが、電荷の保存則を考えれば明らかなように、必然的に他の物質との化学反応が伴い、その単体だけを水に溶かすことはできない。つまり

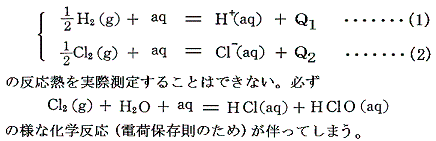
　ところが、以下の反応熱は測定できるのである。

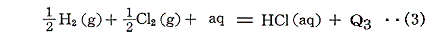
そのため、［希薄水溶液中の水素イオンＨ+(aq)の25℃における生成熱を0と置く］という新たな基準を設けさえすれば、イオンの生成熱を測定できることになる。つまり上記(１)、(３)式から(２)式のＱ₂を求めることができる。

　この167.2kJという値は絶対的な意味を持っていない。あくまで水素イオンの生成熱を基準とした相対値にすぎない。しかしそれで良いのである。
　４．(１)で行った計算例を見直して欲しい。元々人為的に単体の生成熱を0kJにして様々な物質の生成熱を求めた。その値を用いて任意の化学反応の反応熱を求めるとき、そこでの計算例から明らかなように、単体の部分は左辺ですべて打ち消しあってしまい単体の生成熱は式の中に出てこない。もともと単体の生成熱は何にしても良かったのである。本当は0kJにする必要もない。
　イオンを含む場合も単体の成分は左辺ですべて消えてしまうので、上記のような人為的な仮定を置いても良いのである。いずれにしてもＨ⁺(aq)の生成熱を定めておけば、上に述べた方法を繰り返すことにより、Ｈ⁺とペアを形成する陰イオンの生成熱を求めることができる。次にそうして求めた陰イオンとペアになる陽イオンについても同様な方法を用いれば、その生成熱も求めることができる。以下の表はその様にして求めたものである。

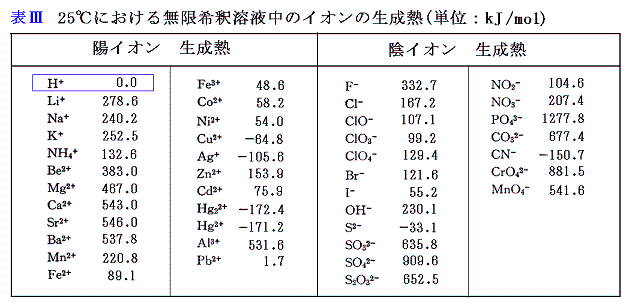
各イオンの標準生成エンタルピーΔＨ⁰_fは上記の値の符号を逆にしたものである。

　表�Vを用いれば、任意の塩の無限希釈溶液の生成熱を求めることができる。例えば上記［例１］のＮaＦ(aq)の生成熱は、Ｎa⁺とＦ^-の［イオンの生成熱］を用いて

となる。

　［例２］で説明した式をもう一度下に記す。この式の左辺はＡgＣl(aq)に等しく右辺の熱量は、まさに固体ＡgＣl(s)を無限希釈するときの溶解熱を表す。この値は［イオンの生成熱］と［固体塩の生成熱］から直ちに計算できる。

　逆にＡgＣl(s)の［溶解熱のデータ］が分かっていれば、それとＡg+とＣl-イオンの［生成熱］を用いればＡgＣl(ｓ)の生成熱を求めることができる。
　

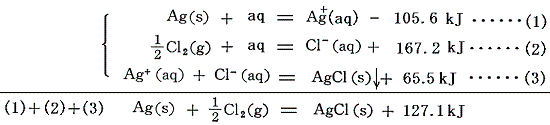
以上をまとめると

1. 表�Vのイオン生成熱を加算するだけで、塩の無限希釈溶液生成熱を求めることができる。
2. 塩の溶解熱(溶かしてイオンにすること)を実測すれば、表�Vのイオン生成熱と組み合わせて固体塩の生成熱を計算できる。
3. 固体の塩の生成熱が分かっていれば、表�Vのイオン生成熱と組み合わせることにより、塩の溶解熱を計算できる。その様にして得られ種々の塩の溶解熱を表�Wに示す。
   　

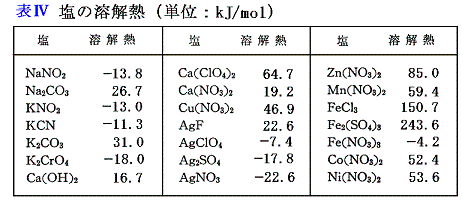
（４）有機分子性物質

　有機化合物は主に炭素Ｃの鎖に水素Ｈ、酸素Ｏ、イオウＳ、窒素Ｎ等々・・・が共有結合で繋がった分子状物質である。いわゆる生体高分子をはじめ合成樹脂、合成繊維、合成ゴムなどの工業化学製品もこの範疇に入るが、ここでは低分子量の化合物について説明する。

　有機化合物の構成元素は酸素中で容易に燃焼するので燃焼熱が測定できる。そのため各構成単体と生成物質の燃焼熱を組み合わせれば求めることができる。３．（２）４．で説明したメタンの生成熱の計算はその例である。有機化合物の生成熱の求め方は画一的で簡単だからこれ以上の説明は省略する。以下に燃焼熱と生成熱の例を挙げるにとどめる。

１．鎖状飽和炭化水素(アルカン）

アルカンの燃焼熱は以下の様になる。

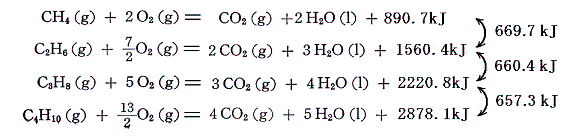
これらのアルカンの相次ぐ同族体の間の燃焼熱の差は660kJ程度である。この燃焼熱に水素と炭素の燃焼熱の熱化学方程式を組み合わせれば、各炭化水素の生成熱が求まる。

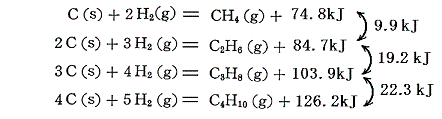
２．不飽和炭化水素

エチレンとアセチレンの燃焼熱は

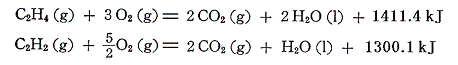
である。これから、それぞれの生成熱を求めると

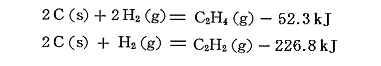
となる。不飽和結合の存在は生成熱を減少させ、負の値になる場合もある。アセチレンが加熱により容易にアセチレンブラック(不定形結晶）と水素に分解することがうなずける。
　生成熱のデータを用いてアセチレンの水素付加反応の反応熱を計算すると

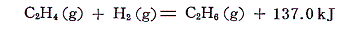
となる。

３．環状炭化水素

　いずれも25℃では液体であるが、上記例と比較のため蒸気の燃焼熱を示す。

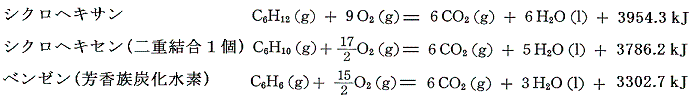
　これから求まる生成熱は

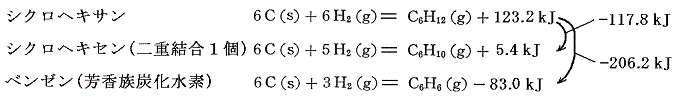
となる。
　シクロヘキサンに二重結合１個導入すると、水素原子が二個少なくなり生成熱は117.8kJ減少する。ベンゼンの生成熱は117.8×3＝353.4kJほどには減少していないことに注意。これはシクロヘキサンからシクロヘキセンへのエネルギー増大量の３倍より少なめにしか増大していないことを意味する。つまりベンゼン中の結合は３個の二重結合よりもより安定化していることを示している。
　ちなみにベンゼンに対する水素付加反応の反応熱は

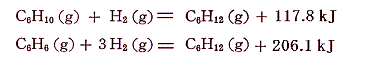
となる。またアセチレン３分子からベンゼンを合成するときの反応熱は

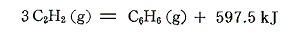
となる。

４．アルコールとエーテル

アルコールの燃焼熱は同じ炭素数のアルカンより小さい。これはアルコールの結合の方がより安定である事を意味している。

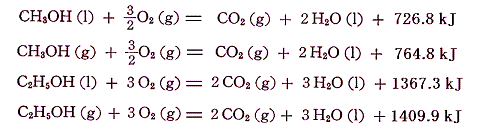
そのため、生成熱は同じ炭素数のアルカンより大きくなる。

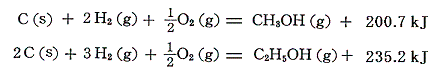
　エーテルは炭素数が同じアルコールの異性体（化学式は同じだか構造が異なる）だが、その燃焼熱はアルコールより少し大きい。すなわちアルコールよりも少し不安定な化学結合をしている。ジエチルエーテルは25℃で液体であるが、ジメチルエーテルとの比較のために蒸気の燃焼熱を示す。

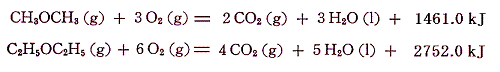
そのため、生成熱は異性体アルコールより少し小さめになる。

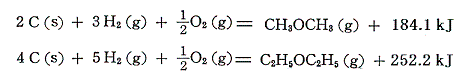
５．カルボン酸とエステル

　炭素数が同じカルボン酸とエステルは互いに異性体の関係にある。
蟻酸と酢酸の燃焼熱は

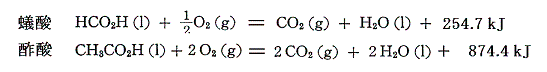
であるから、それらの生成熱を求めると

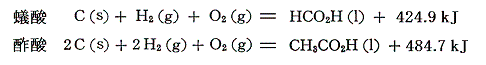
となる。同様に蟻酸メチルと酢酸メチルの燃焼熱は

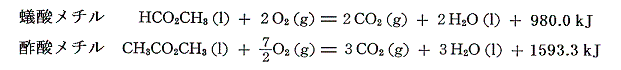
であるから、それらの生成熱を求めると

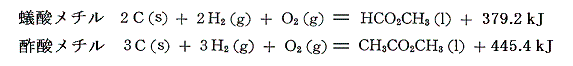
となる。
　これらの結果を用いて、カルボン酸とアルコールからエステルが生成する反応の反応熱を計算してみる。

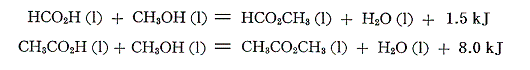
反応熱はとても小さな値になる。これはカルボン酸とアルコールが共存すれば自発的に脱水縮合してエステルとなり、同時にエステルは水によりカルボン酸とアルコールに分解してしまう事実に良く対応している。反応は平衡状態になり完結する事はない。エステルの収率を上げるには、生ずる水を何らかの方法で除去する必要がある。

（５）まとめ

　２．（２）で述べた、様々な種類の反応熱を利用して生成熱の形に集約しておけば、原理的にあらゆる化学反応の反応熱を計算によって［４．（１）、（２）参照］求めることができる。そのため生成熱はとても重要な概念である。

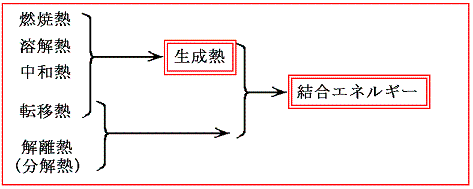
ここでさらに、転移熱や解離熱を生成熱と組み合わせると化学結合の結合エネルギーそのものを予測することができ、もう一歩階踏み込んだ議論をする事ができる。次節でその当たりを説明する。

６．結合エネルギー

　分子状の物質を原子状のバラバラの状態にする解離エネルギーが測定できれば、分子の共有結合の結合エネルギーを見積もることができる。共有結合とは、２個の原子の間で両方の核のから同時に電気的な引力を受ける電子対を仲介にして結合力が生じるものです。そのとき無限遠に離れた状態から、結合状態へ移行したときの電気的な位置エネルギーの変化量がいわゆる結合エネルギーと言われるもので、分子の組み替えに伴って出入りする反応熱の知識から、その大きさを見積もることができる。
［補足説明］ムーア「物理化学」から結合エネルギーの説明を引用。

（１）結合エネルギーの求め方

　例えば酸素と水素の共有結合エネルギーは、次の熱化学方程式を用いる。

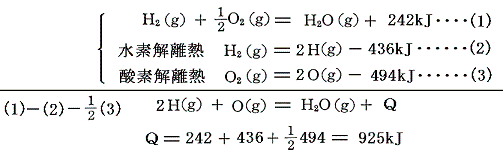
　結合エネルギーを考えるときには、反応熱より、その符号を変えたエンタルピー変化の方が理解しやすい。エンタルピー変化の関係を図示すると以下の様になる。ここで+436×(1/2)=+218kJ/molは原子気体状Ｈ(g)の１molを(1/2)molの単体Ｈ2(g)から生成するとの標準生成エンタルピーΔＨ⁰_fを、同じく+494×(1/2)=+247kJ/molは原子気体状Ｏ(g)の１molを(1/2)molの単体Ｏ2(g)から生成するとの標準生成エンタルピーΔＨ⁰_fを意味する。

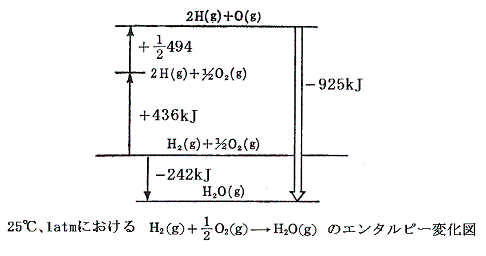
　原子状の水素と酸素が結合して水分子を形成するとき-925kJほど安定化するのであるが、水分子には２個の等価なＨ-Ｏ結合が含まれているから、水のＯ-Ｈ結合の生成エンタルピー変化は25℃において-925×(1/2)＝-463kJ/molとなる。

　メタンのＣ-Ｈ結合の場合、次の熱化学方程式を用いる。

　このことから、気体状原子からＣ-Ｈ結合が形成される際の生成エンタルピー変化は結合１本当たりに換算して-1662×(1/4)＝-415.5kJ/molとなる。ただし炭素の昇華熱を求めるのは極めて難しく、この値の信頼性はひとえにこの部分の測定値の精度に依存している。
　（３）式の黒鉛の昇華熱715kJはダイヤモンドの昇華熱とほぼ同じであるが、下表のＣ-Ｃ（ダイヤモンド）の結合エンタルピー357のほぼ二倍になるのはダイヤモンド結晶中の炭素原子１個は４本のＣ-Ｃ結合を持つが、その各結合を二つの炭素原子で分け合っていると考えなければならないので4／2＝2本分となるからである。詳しくはこちらで説明。
　上記の様にして求められた結合エンタルピーの値を表�Xに示す。

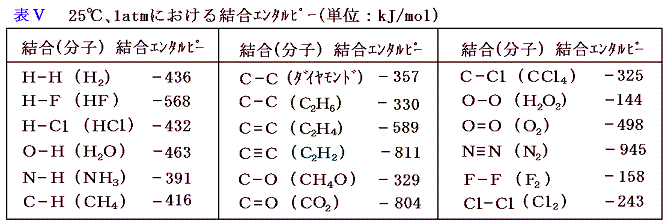
　この表中のＣ-Ｈ結合エンタルピーの-416kJ/molという値は、炭素原子に１個ずつ順番に水素原子を結合させてメタンをつくる各段階でのエンタルピー変化とは異なる。各段階のエンタルピー変化はおおよそ、-335、-519、-368、-423kJ/molであり、その平均値は-411kJ/molとなる。隣接する原子の存在いかんによって微細な違いが生じるであろうから変化するのは当然であるが、その平均値は-411となり、前記の-416ｋＪ/molに近い値になる。だから前記の値をもってしてＣ-Ｈの結合エンタルピーと行っても良いであろう。
　その際、Ｃ-Ｈの結合エンタルピー-416kJという値はメタンという特定の化合物について求めた値なので他の化合物中のＣ-Ｈ結合にそのまま適応できる保証はない。しかし、結合エンタルピーと言うのは元々色々な意味の誤差を含む物だから、その程度の信頼性と割り切って考えれば、他の化合物中のＣ-Ｈ結合に適応して様々な見積もりに利用しても良いであろう。次節はその応用例です。

（２）結合エンタルピーの総和と反応熱

　４．（１）において、生成熱を用いて任意の化学反応の反応熱を求める方法を説明したが、全く同様な考え方が結合エンタルピーを用いても成り立つ（ただし信頼性は劣る）。その当たりを

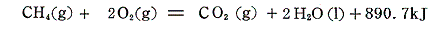
を用いて説明する。ただしこの議論は反応前後が気体状態で相変化がない場合にしか適応できないので、890.7kJから相転移熱44kJを引いて生成する水が気体状態の反応熱847kJについて議論する。

　800kJはすでに求めた反応熱847kJに比較すると6％の違いがあるが、この程度の誤差を認めれば、化学反応の反応熱を見積もるのに結合エンタルピーは十分効果的である。

　気体から気体への相変化を伴わない化学反応については

を用いて、おおよその反応熱を見積もることができる。

　５．（４）１．で説明した燃焼熱（水を気体状態にしたもの）について計算してみると

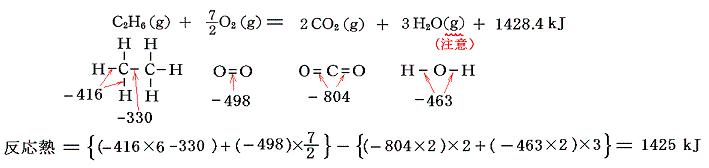
となり、ほぼ同じ値が導き出される。
　バラバラの原子状態を基準にしたエネルギー順位図を描くと以下のようになる。

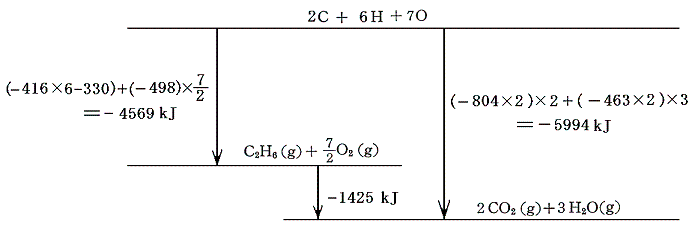
７．エネルギーサイクル

　生成エンタルピーのデータを解析するとき最も有効な方法は、全体として熱化学サイクルを構成するような一連の化学反応を利用する事である。

（１）ボルン=ハーバーサイクル

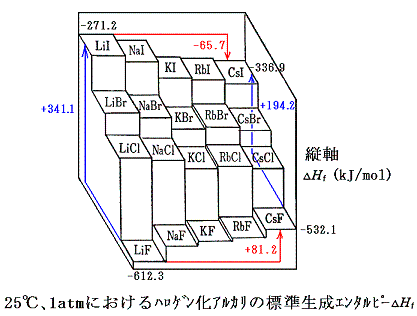
ハロゲン化アルカリの様なイオン結晶にはボルン=ハーバーサイクル（Born-Haber cycle次図参照）が有用である。

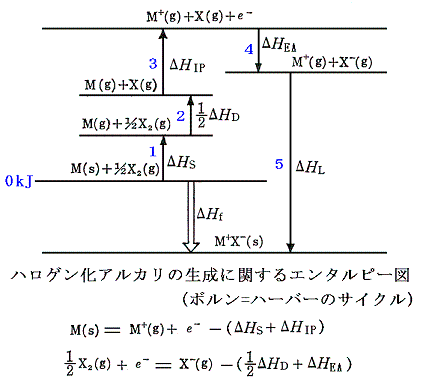
　この図でイオン結晶化合物の直接的な生成は、図の太い矢印で示されている。それに対応する生成エンタルピー変化ΔＨ_fは容易に実験から求めることができる。
　時計回りの方向をたどるもう一つの経路は次の各項から成り立っている。

1. 固体金属の昇華による気体金属原子の生成エンタルピーΔＨs
2. ハロゲン分子の解離に伴うエンタルピー変化の半分(1/2)ΔＨ_D
3. 気体金属原子を気体金属イオンにするイオン化エネルギーΔＨ_IP
4. ハロゲン原子が電子を取り込んで負イオンになるときのエネルギー変化（電子親和力）ΔＨ_EA
5. 気体状のイオンから結晶が生成するエンタルピー（格子エンタルピー）ΔＨ_L

これら二つの経路を一巡りして元に戻るとエネルギー保存則から

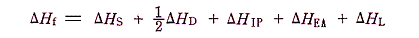
の式で表される関係が成り立つ。この中のどれかに未知の項があっても、残りの項のエネルギー値が既知なら、この式から求めることができる。エネルギーサイクルが有用な理由である。
　歴史的には、このサイクルは最初ハロゲンの電子親和力（負イオン生成エネルギー）を求める為に利用された。上記１〜５の項目の中で、１．ΔＨs、２．(1/2)ΔＨ_D、３．ΔＨ_IPは実験的に測定可能である。５．ΔＨ_Lは実験で求めるのは難しいが、結晶格子中におけるイオン間距離が解っていればクーロンの法則を用いて理論的に計算できる。それらの値を用いれば、測定が難しい４項目ΔＨ_EAを計算によって求めることができる。その様にして求めた結果を用いて、各段階のエネルギー変化量を表にすると次のようになる。

　このデータで、当然の事であるが金属イオンの生成エンタルピーはＬiＦとＬiＩ、ＣsＦとＣsＩは同じである。また陰イオンの生成エンタルピーはＬiＦとＣsＦ、ＬiＩとＣsＩは同じである。

　ＬiＦからＣsＦへの変化とＬiＩからＣsＩへの変化を比較してみると第３列目［格子格子エンタルピー変化］の変化量の違いがそれぞれのイオン結晶の生成エンタルピーの違いを生み出していることが分かる。フッ化物における格子エンタルピーの大きな増加はおそらくフッ素イオンが小型であるため正負両イオンの距離が短いため、金属イオン半径の増大に伴う格子エネルギーの増加分について、フッ化物の方が、ヨウ化物よりもより大きく影響してくるためであろう。(クーロン引力は距離の逆二乗に比例して増大する)

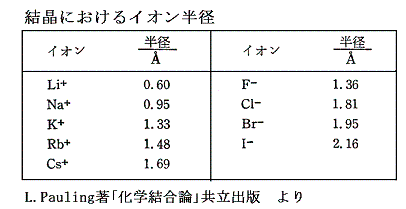
　どのアルカリ金属についても、フッ化物からヨウ化物へ向かって生成エンタルピーが増大（負値の減少）する一般的な傾向は、上記表の２列目［ハロゲンの電子親和力の増大（負値の減少）］と３列目［原子間力の増大に基づく格子エンタルピーの増大(負値の減少）］の両方の効果の反映であることが解る。この場合も、ハロゲンイオン半径の変化に伴う格子エネルギーの変化はイオン半径が最も小さいＬiが最も大きい。

　以上の結果を下図にまとめておく。エネルギー解析をしてみるとフッ化物と他のハロゲン化物の生成エンタルピーの変化の傾向が逆転している理由もそれなりに理解することができる。

（２）イオン結合

　前節のエネルギーサイクルで説明した各生成エンタルピー値を用いると、イオン結合生成の各段階の熱化学方程式を記すことができる。イオン結合は以下の三段階の変化に分解して考えることができる。

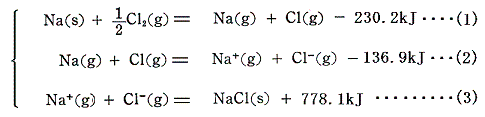
このとき（１）、（２）段階はいずれも吸熱反応だから右辺の方がエネルギーが高い（不安定）。特に（２）段階の反応で［イオン化エネルギー］の正の増大を［電子親和力］の負への減少で補うことができずに最終的に右辺の状況の方がエネルギーが高くなる。だからバラバラの正負イオンのままでは存在できない。（３）段階の正負のイオンの配列を構築した結晶格子の生成があってはじめてイオン状態でのエネルギーが低くなりイオン結合が成立する。

（３）イオンの水和エンタルピー

イオンの水和エンタルピーも測定が困難である。しかし、下図のエネルギーサイクルを用いると求めることができる。

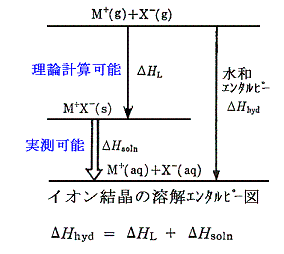
　上図の中の、ΔＨ_soln　は実験で測定できるし、ΔＨ_L　は理論的な計算で求めることができる。水和エンタルピーΔＨ_hydは測定が困難な量であるが、エネルギーサイクルを用いて計算する事ができる。下表はその様にして求めた値である。

　Ｌ_iＣlの場合水和エンタルピーは格子エンタルピーより大である（負の値の絶対値が大きい）。つまり水分子に対するイオンの引力は、結晶格子の中でのイオン相互間引力よりも大である。その結果溶媒と溶質が別々に存在するよりも溶液を作った方がエネルギー的に安定になり、Ｌ_iＣlが水に良く溶ける事実に合致している。
　ＮaＣl、ＫＣlに関しては水和エンタルピーによる安定化よりも、格子エンタルピーによる安定化の方が勝っている。その為溶解エンタルピー変化はすべて正になり、両者ともＬ_iＣlほどには解けなくなる。
　ＡgＣlは、その溶解エンタルピーはさらに正で大きくなり、極めて水に溶けにくい物質である。その格子エンタルピーが大きくなるのは、イオン間の静電的な引力以外に、銀イオンの分極率が大きいことから生じる共有結合性によるものであるとされている。

（４）電極反応

　電池の内部で進行するイオン反応

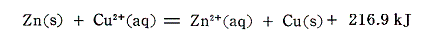
をエネルギー的に解析してみる。電子移動機構から、上記の反応は次のような段階に分けることができるであろう。

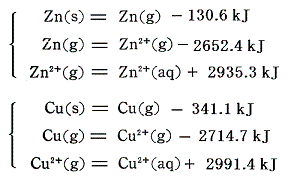
今回も反応熱その物ではなくて、その符号を変えたエンタルピー変化で見ていくことにすると、上記の変化は次のエネルギー図で表される。この図は［孤立した気体状イオン］と［２個の電子］からなる系を基準状態として、最も上部に描いてある。

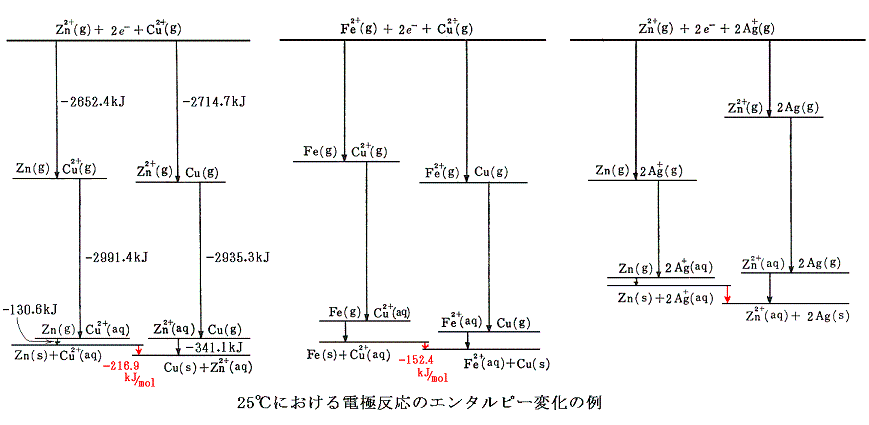
　亜鉛と銅イオンの電子交換について、左側の経路では、Ｚn²⁺が電子２個を獲得し、Ｃu²⁺は水和をする。右側の経路ではＺn²⁺は水和し、Ｃu²⁺が電子２個を獲得する。反応全体としてのエンタルピー変化は一番下の線の高さの差となる。気体イオンから［気体状金属原子］と［水和イオン］になるまでのエンタルピー変化は左右どちらの経路も差は無いので、原子間の電子の授受は２種の金属の昇華エンタルピーの差によることが解る。亜鉛と銅の金属結晶中の原子体積は亜鉛が9.16cm³/mol、銅が7.13cm³/molであるから、原子番号が隣り合っているにもかかわらず銅の方がかなりコンパクトに結合していることが解る。銅の原子核の周りの電子が亜鉛よりも緊密に詰まっているため強い金属結合を生じて、昇華エンタルピーの増加を生じているのであろう。

　鉄と銅イオンの電子交換は、図の左右の経路を比較してみれば明らかなように、鉄と銅のイオン化エンタルピーの差が生み出していることが読み取れる。

　亜鉛と銀イオンに関しては、イオン化エンタルピーの差は水和エンタルピーの差によりほぼ打ち消されており、金属亜鉛と金属銀の昇華エンタルピーの差が、その電極反応の原因であることを示唆している。

８．参考文献

　ここではエネルギー保存則（熱力学第一法則）から議論できる事柄のみを説明した。本当は、何故ある場合には発熱反応になり別な場合には吸熱反応になるのか？　何故化学反応がその方向に進むのか？　化学平衡を決定づけるメカニズムは何か？　化学反応の速度は何が決めているのか？等々･･･の疑問に答えなけばならない。それをするには、ここで説明したエンタルピー変化ΔＨに加えて、とても難しい絶対温度Ｔ、エントロピー変化ΔＳの理解が不可欠です。そのため高校ではその当たりはやりません。
　［その説明は、当ＨＰでは別稿「ギブスの自由エネルギー(化学ポテンシャル)とは何か」1.(2)1.などでしています。］
　これらの化学反応の本質を議論しなくても、ここで説明したようにエネルギー保存則だけからでも沢山の有益な情報を得ることができる。そのため高校レベルで反応熱と熱化学方程式を教えることは意義のある事だと思う。

　１．(2)の議論で化学結合のエネルギーと分子・原子の運動エネルギー（熱エネルギーとした）を分離した所などは、本当にそんな考え方が許されるのか疑問に思う所である。実際は分離できない成分もあるだろうから、どの化学の教科書も化学結合エネルギーや熱エネルギーという言い方はせず、あくまでその状態のエンタルピーと言うだけで断定を避けている。その当たりが化学理論の今ひとつしっくりこない所である。
　しかし、もともと化学の理論は物理で取り扱うものより遙かに複雑な現象に適応されるものである。だから反応熱・熱化学方程式も、酸化還元の酸化数や、化学結合の原子価と同じように、一種の便法として考えれば良いのではないだろうか。酸化数や原子価がそれなりの論理的理解と、多くの有益な情報をもたらしてくれたように反応熱も有益な概念だと思う。化学の理論とは本来その様なものであろう。　

　熱が関係する現象を学ぶとき、熱量Ｑがエネルギーに関係する量だというのは何となく理解できるが、温度Ｔという量は本当に訳が解らない。
　温度はエントロピーＳの概念と密接に結びついていて、熱力学ではΔＳ＝ΔＱ／Ｔ（定圧の下での変化なら＝ΔＨ／Ｔ）という関係式として現れる。一方統計力学では「エントロピー」＝「乱雑さ」と習いＳ＝ｋ_Bｌog_eＷ（ｋ_B：ボルツマン定数、Ｗ：系が取りうる微視的な状態の数）と表現される。しかしこの両者がなかなか繋がらない。この間のギャップの大きさが熱が絡む現象の理解が困難な理由だろう。
　このギャップを埋める関係式が　１／Ｔ＝Δ（ｋ_Bｌog_eＷ）／ΔＥ　なのですが、この式の理解が難しい。しかし、この式を理解しないと、なぜ化学変化が起こるのか、なぜ同じ温度で相変化が起こるのかが理解できない。しかし、この辺りは稿を改めて議論するつもりなのでここではしない。　

１．ストロング、ストラットン著「化学結合エネルギー」モダンケミストリー　共立出版（1980年）
　　少し古い入門書ですが、私にはとても解りやすかった本です。
　　このページを作るに当たってこの本の第2〜4章を大いに利用しました。感謝！

２．松永義夫著「化学One Point 化学反応式」共立出版(1988年)
　　このページの５．生成熱測定法は、この本の第5章をほぼそのまま引用しています。感謝！

３．F. Reif 著「バークレー物理学コース５　統計物理学（上）（下）」　丸善（1970年）
　　高校生が次に読む本としては最適。上巻の４．熱的相互作用に　１／Ｔ＝Δ（kｌog_eＷ）／ΔＥ　の関係式が導かれている。

４．　下記のＨＰで１／Ｔ＝Δ（kｌog_eＷ）／ΔＥ　の関係式が解りやすく説明してある。
　　　http://homepage3.nifty.com/iromono/PhysTips/maxtemp.html
　　　http://homepage3.nifty.com/iromono/PhysTips/maxtemp2.html