アインシュタイン一般相対性理論への道程（1907〜1914年）

１．導入

　アインシュタインは1915年に一般相対性理論を完成するのですが、ここではその完成に至るまでのアインシュタイン自身の模索過程（1907年〜1914年）をたどります。
　この歩みを始める出発点となった特殊相対性理論については別稿「アインシュタインの特殊相対性理論（1905年）」をご覧下さい。特殊相対性理論を学ぶのに1905年の原論分に勝るものはありません。
　そのとき、特殊相対性理論（1905年論文）を学ばれた後に、アインシュタインが1916年（一般相対性理論を完成した翌年）に書いた一般向け啓蒙書“U¨ber die spezielle und allgemeine Relativita¨tstheorie”邦訳名『我が相対性理論』（新版『特殊および一般相対性理論について』）の第１部を読まれることを勧めました。

　ここでは、その第１部に続きまして第２部を最初に読んでおかれることを勧めます。一般相対性理論への導入として、この啓蒙書の第２部に勝るものはありません。
　一般相対性理論は数学的に極めて込み入っており理解するのが非常に難しい。そのため、最初にこの第２部を読まれるのが良いと思います。もちろん、Born文献6の第�Z章をお読みになるのも有益ですが、これはアインシュタインの文献3．第2部を踏襲したものです。その主なところは上記文献の第２部引用稿中の（）書きの節で引用・紹介していますので、とにかく文献3．第2部をお読み下さい。
　それをお読みになられた後に以下の順番で進まれることを勧めます。

1. 　上記第2部をご覧の後に本稿の 1907年12月論文第�X章 → 1911年プラハ論文 → 別稿「一般相対性理論を理解するための数学的準備」 → 1913年の論文 → 1914年の論文 にお進み下さい。
2. 　本稿を最後まで読まれた後に、別稿「アインシュタイン著『一般相対性理論の基礎』（1916年）」をご覧ください。
3. 　上記論文を読まれて一般相対性理論展開の梗概を承知された後に、別稿「アインシュタインの重力場方程式」をご覧ください。

［補足説明１］
　改造社「アインスタイン全集」から引用した論文を読まれるときには下記のPaisの注意に留意されたし。

　上記の注意の中で、特に座標成分に関してですが、反変成分であるので ｄｘ^μ や ∂ｘ^μ と記すべきです。それにもかかわらず ｄｘ_μ や ∂ｘ_μ と記す事をかなり後の論文まで（1922年のプリンストン大学四講義録に於いてさえも）続けています。
　この点については、共立出版社「アインシュタイン選集」から引用した論文はすべて修正されています。
　
　また、Σ記号を省略する“アインシュタインの規約”による表現は1916年3月の総説論文［Ａ３］以降について言えるだけですから注意されて下さい。
　
　
　さらに補足すると、クリストッフェルは今日と違う記号を用いたのですが、アインシュタインはクリストッフェルの用いた記号を踏襲しています。すなわち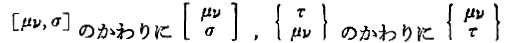の記号を用いた。
　この点についても、共立出版社「アインシュタイン選集」から引用した論文はすべて今日の記号に修正されています。

２．1907年12月4日論文の第�X章　“相対性原理と万有引力”

　アインシュタインはシュタルクの要請を受けて、彼が発見した特殊相対性理論の総説論文を1907年に書きます。
A.Einstein, “U¨ber das Rela¨tivitatsprinzip und die aus demselben gezogenen Folgerungen”, Jahrbuch der Radioaktivita¨t und Elektronik, vol.4, p411〜462, vol.5, p98〜99, 1907年12月，
（https://einsteinpapers.press.princeton.edu/vol2-doc/468）
（https://einsteinpapers.press.princeton.edu/vol2-trans/266）
この論文は改造社「アインスタイン全集」第1巻 2番目論文「相対性原理とそれから導かれる結論」として邦訳版があります。
　この論文の第�X章で、後の一般相対性理論に繋がる最初の着想を説明しています。とても興味深い内容なのでこの説明から始めます。
　この論文をお読みになるとき、Paisの解説第9章p233〜を別Windowsに表示して平行して読まれる事を勧めます。Pais文献中に青色でマークした「アインシュタインの言葉」は下記引用文でも青色でマークしてあります。

　アインシュタインは、この論文の最初に記されている着想が生まれた状況を、1922年の京都講演（別稿のp84〜）で語っています。ここは引用されることが多い有名な箇所ですが、この事の重大性はなかなか理解しがたい。文献6.の「一般相対性理論の起源についてのノート」などをご覧いただくのも良いかもしれません。
　以下の訳文は改造社「アインスタイン全集」第1巻 2番目論文より引用。

§17．加速度を有する関係系と万有引力の場

　この論文の段階では一様に加速される系に限られていることに注意されて下さい。つまり加速度が時間的に変化する分けではありません。
　ここがPais文献7のp233で言っている１．等価原理　の所です。ここは、Pais文献7のp230のモーガン原稿の説明を参照して下さい。

§18．一様に加速せる関係系に於ける空間及び時間

　ここの意味は解りにくいが、おそらく次のことを言っているのだろう。
　特殊相対性理論によると物体の変形（進行方向の収縮）は速度に依存した。だから速度が存在すれば物体の変形があるのだが、加速度が積算しないと速度の変化とならない。だから（進行方向の収縮は）各瞬間の速度には依存するだろうが、加速度そのものへの依存の影響は考えなくて良いであろう。






上記の式はおそらく別稿「双子のパラドックスと一般相対性理論」５．（４）１．と同じ様な考察で求めたのだろう。

§19．万有引力の場の時計に対する影響

注（1）は gh ではなく、ＧM／r の場と言うこと。両者の違いは別稿「仕事とエネルギー」２．（３）（５）を参照。

§20．電磁現象に対する重力の影響

３．1911年6月21日プラハ論文　“光の伝播に対する重力の影響”

A.Einstein, “U¨ber den Einfluss der Schwerkraft auf die Ausbreitung des Lichtes”, Ann. Der Phys. [4], 35, p898〜908, 1911年
　この論文をお読みになるとき、Paisの解説第11章11b．を平行して読まれる事を勧めます。また別稿で引用したインフェルトの記述を参照。さらに、1907年論文のＳ、Σ、Ｓ’系が、この論文ではＫ、Ｋ’、Ｋ₀系に記号が置き換えられていることに注意されて下さい。

https://einsteinpapers.press.princeton.edu/vol3-doc/523
https://einsteinpapers.press.princeton.edu/vol3-trans/393#,
以下の訳文は共立出版社「アインシュタイン選集」第2巻 ［Ａ１］より引用。
なお、この論文は改造社「アインスタイン全集」第2巻 14番目論文として邦訳があります。

§１．重力場の物理的性質に対する仮説

§２．エネルギーの重さ

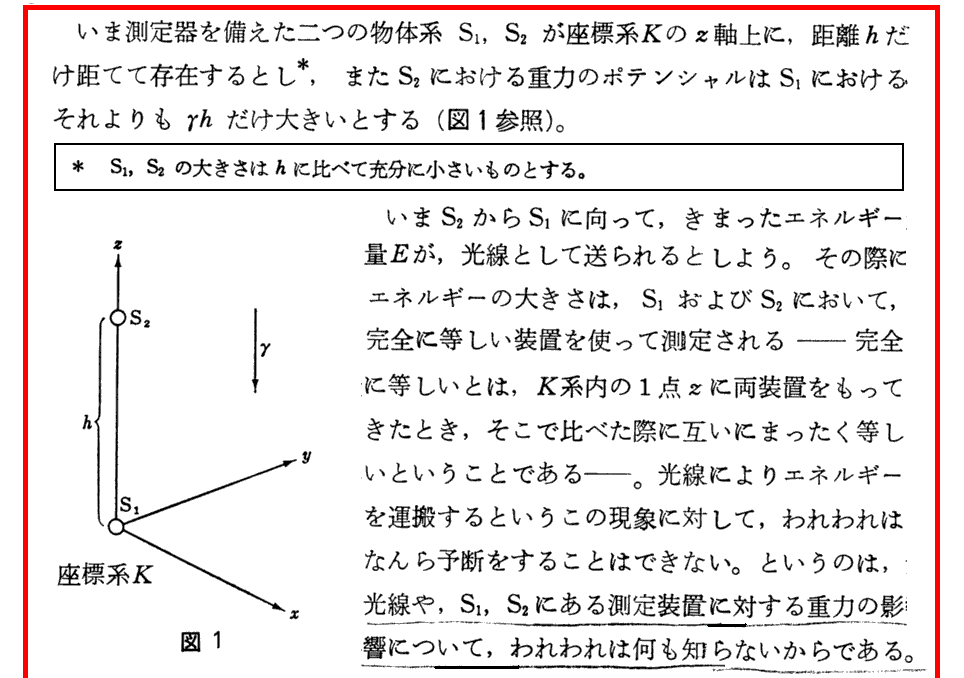
［補足説明１］
　上記の考察は独創的！です。この考察の元になった「特殊相対性理論(1905年)」§8を是非復習されて下さい。
　
　(１)式について少し補足します。この式は、地点Ｓ₂にある質量ｍ＝(Ｅ₂／ｃ²)の光子が重力場を落下する間に、重力場のポテンシャル差Φ＝γ・ｈ　(γは重力加速度ｇに相当する）によって仕事をされて、その結果　ｍｇｈ＝(Ｅ₂／ｃ²)γ・ｈ　だけ余分のエネルギーを持つようになったと考える事もできる。
　それが、「重力場の中の位置エネルギーが高い位置にいる光子はもともとその位置エネルギー分だけ余分のエネルギーを持っていた。」と言う考え方になるわけです。
　
　こういった考え方は、やがて一般相対性理論の赤方偏移の検証実験であるPoundとRebkaの実験の解釈「光子はｈν／ｃ²に等しい慣性質量を持つと同時にそれと同じ重力質量を持っている。(静止質量はもちろん 0 ですが、光子は光速度で移動する)」に通じるものです。
　
　そのとき、光子が重力場からの仕事を受けたからと言って、普通の粒子のように速度が増大するわけではありません。光子の速度は一定不変の光速です。光子の増大したエネルギーはその振動数が変化することで実現されます。すなわちプランクが発見した「光量子の持つエネルギー表現Ｅ＝ｈν」に従って振動数が変化する。
　つまり、重力場中でポテンシャルが低いところへ進む光子の振動数は増大（青方偏移）するのです。逆に、重力場の深いところから浅い所へやってく光の振動数は低く（赤方偏移）なります。そして、この現象は一般相対性理論で説明するところのメカニズムで解釈することができます。つまり別稿§22．1．［補足説明１］や、別稿７．（９）３．で説明する方法です。
　
　以上の３通りの説明はそれぞれ異なりますが、互いに論理矛盾はありません。すべて正しい解釈です。光というものはその様なものであり、一般相対性理論の世界とはその様なものなのです。

［補足説明２］
　上記の説明は錯綜していて解りにくいので図で示す。

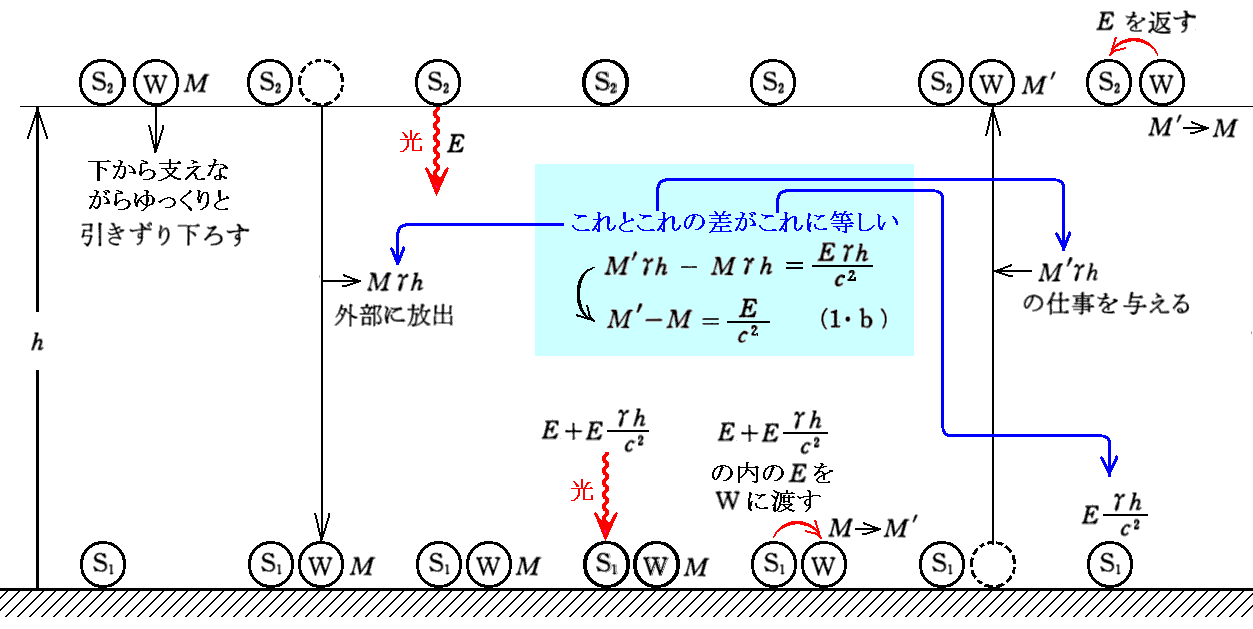
§３．重力場の中での時間および光速度

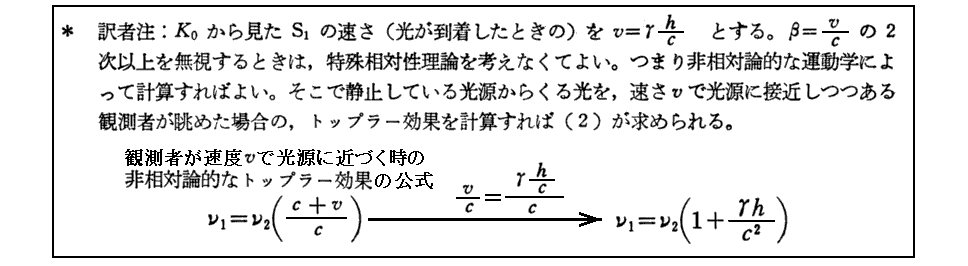
［補足説明１］
　上記*訳者注における非相対論的なドップラー効果の公式はこちら、あるいはこちらで復習されて下さい。
　もちろん相対論的ドップラー効果の公式を用いても同様に導けます。

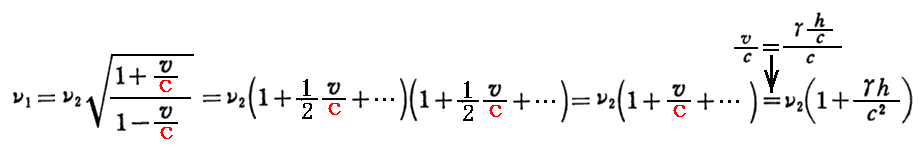
［補足説明２］
　最初に、ポテンシャルΦの次元は速度の次元の2乗に等しい事を確認する。

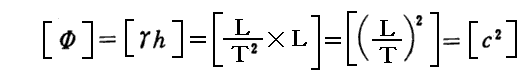
　次に、太陽表面から地球に届くスペクトルの変化分に対する上記の見積値を確認しておく。 Φ＝−ＧＭ／Ｒ に具体的な値を代入すると

となり、確かに上記でEinsteinが求めている値が得られる。

§４．重力場における光線の湾曲

＊ 訳者注： で紹介されている論文［Ａ３］p.112，（74）式はこちらです。

［補足説明１］
　§4の説明は解りにくいので補足します。
　光速度ｃはあくまで一定不変で上記の様にｃが場所によって変化するのではありません。上図の中で、ｃが場所によってｃ_１や、ｃ_２の様に変化しているのは以下で説明する意味に於いてです。
　下図のＰ₁点とＰ₂点では、太陽に近いＰ₁点の方がＰ₂点より時間がゆっくり進む。そのためＰ₁点に設置された時計の針が1秒進む間に光が進む距離がｃ₁です。同様にＰ₂点の時計（Ｐ₁の時計より早く進む）の針が1秒進む間に光が進む距離がｃ₂です。図では1秒間ではなくて、ｄｔ秒にしてあります。

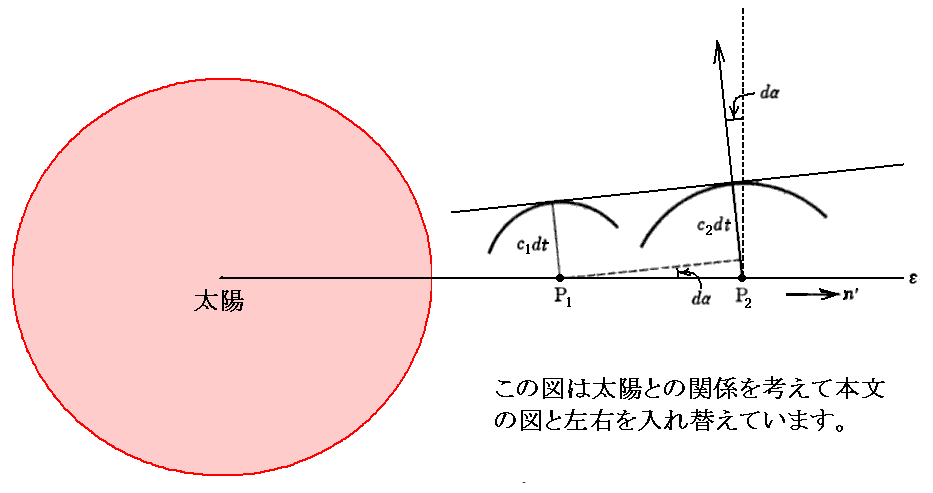
　図ではＰ₁点とＰ₂点で同じｄｔを用いていますが、これは同じではありません。例えばＰ₂点での時計の針の1．000・・・秒分の進みをｄｔで表しているとすると、その時にＰ₁点に存在する時計の針の進みでは0．999・・・・秒を示しています。つまりその分の時間の進みをＰ₁点のｄｔで表しています。それがＰ₁点の方がＰ₂点よりも時間がゆっくり進むと言うことの意味です。
　だから図中のｃ₂ｄｔはＰ₂点での時計で測った1秒分で光が進んだ距離を表しています。同様に図中のｃ₁ｄｔは、その時のＰ₁点での時計で測った0．999・・・・秒分に相当する時間で光が進んだ距離を表しています。だから図中の光が進んだ距離はｃ₁ｄｔ＜ｃ₂ｄｔとなるのです。
　さらに補足すると本当は重力場中では空間も縮みますから、Ｐ₁点のｃ₁ｄｔがＰ₂点のｃ₂ｄｔよりも短くなる割合はもっと大きくなります。ただし、本論文を発表した時点（1911年）のアインシュタインは重力場による空間の縮みについてはまだ知っていませんから、上図にはその効果は含まれていません。（この効果も考慮すると、別稿Ｅ．（22）2．［補足説明1］で説明する様に湾曲角は2倍になります。）
　
　図から明らかな様に、光線がｃｄｔ（≒ｃ₁ｄｔ≒ｃ₂ｄｔ）進むあいだに、光線が受ける湾曲角ｄαは

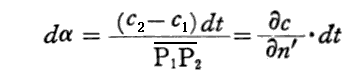
となる。ただし、光線がｎ’の増加する方向と反対側に湾曲するとき（図の場合）の湾曲を正としている。
　そこで、光が単位の長さ（ｃｄｔ＝１）だけ進む間（ｄｔ＝１／ｃ秒間）に受ける湾曲角ｄαは

となる。
　そこで結局、光が任意の道のり　ｓ　だけ進むときに、ｎ’の増加方向とは逆向きに湾曲する角αは

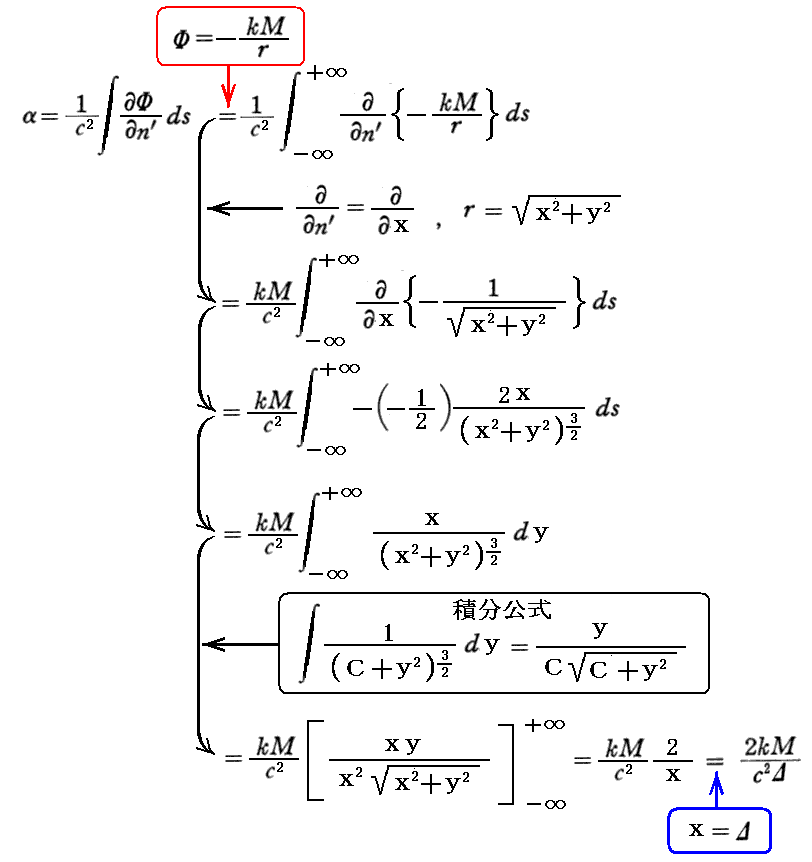
となる。
　なお、上記の積分は、次図の状況下の光線径路に沿って、ｙ＝−∞からｙ＝＋∞まで行われたものであることに注意して下さい。実際にはｙの変化と共にｘ座標も少し変化するのですが、その変動は微少なので、積分操作の中では無視できてｘはすべて一定値であると見なせます。その様に一定と見なしたときのｘの値が図中の Δ です。

　
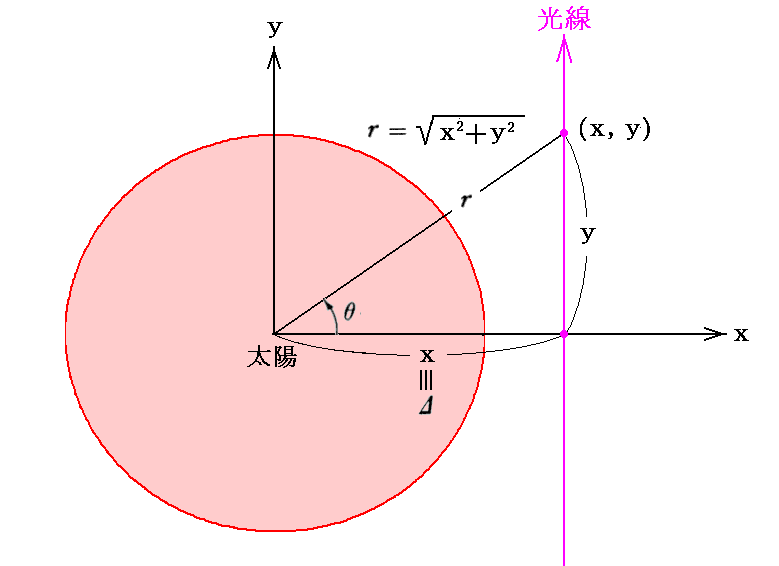
　さらに補足すると、この結論には重力場に依って空間が縮む効果はまだ考慮されていません。そのことも考慮した湾曲角の半分となっています。
　空間の縮む効果を考慮した計算がどの様になるのかは、別稿Ｅ．（22）2．でEinsteinが説明しています。そこの計算と比較して見て下さい。

［補足説明２］
　Einsteinは、本論文で、重力場の中では時間がゆっくりと進むことを証明したのですが、重力場の中では物指し棒が縮む（すなわち空間が縮む）ことにはまだ気付いていません。
　そのため本論文で導かれている重力場に依る光線の屈曲角度は、時間の遅れの効果しか考慮されていませんので、真に正しい屈曲角の半分の値しか得られていません。
　
　また、Einsteinは、本論文中で、重力場中からやってくるスペクトル線の赤方偏移も導いています。こちらは空間の歪みの効果は関係しませんので、正しい結果が得られています。
　実際、上記で求めた

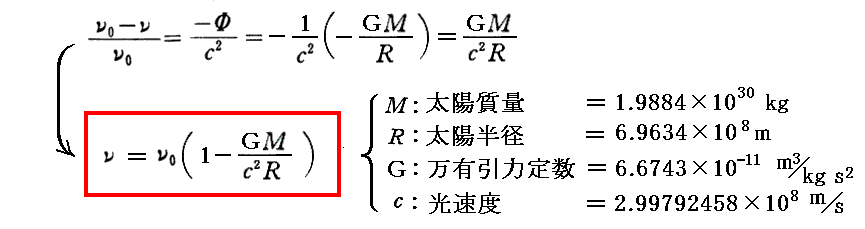
は別稿Ｅ．（22）1．でEinsteinが説明している結果と同じです。
（補足しますと、この結論は1907年12月論文§19ですでに導かれています。その導き方について、Paisの解説は秀逸です。）
　
　いずれにしても、“重力場中では時間がゆっくり進む”ことが証明できたのは大成果です。その事を導く本稿の考察は、インフェルトが賞賛している様に、独創的!!　です。

４．1913年冊子　“一般相対性理論および重力論の草案”

“Entwurf einer verallgemeinerten Relativita¨tstheorie und eine Theorie der Gravitation”
�T. Phsikalischer Teil von A. Einstein. �U. Mathematischer Teil von M. Grossmann., Leipzig, Teubner. 38pp., 1913年　この論文は草案なので、最初は小冊子として出版された、後に学術誌（1914年）にも掲載された。

　この論文をお読みになるとき、Paisの解説第12章p284〜291を平行して読まれる事を勧めます。

https://einsteinpapers.press.princeton.edu/vol4-doc/324
https://einsteinpapers.press.princeton.edu/vol4-trans/163
　以下の訳文は共立出版社「アインシュタイン選集」第2巻 ［A2］から引用しています。ただし、Einstein執筆部分の改造社「アインスタイン全集」翻訳版も別ページで引用していますので、微妙な翻訳部分は比較検討に利用されて下さい。
　また、Grossmann執筆部分の�U．数学の部は改造社「アインスタイン全集」第2巻 19番目論文より引用しています。


























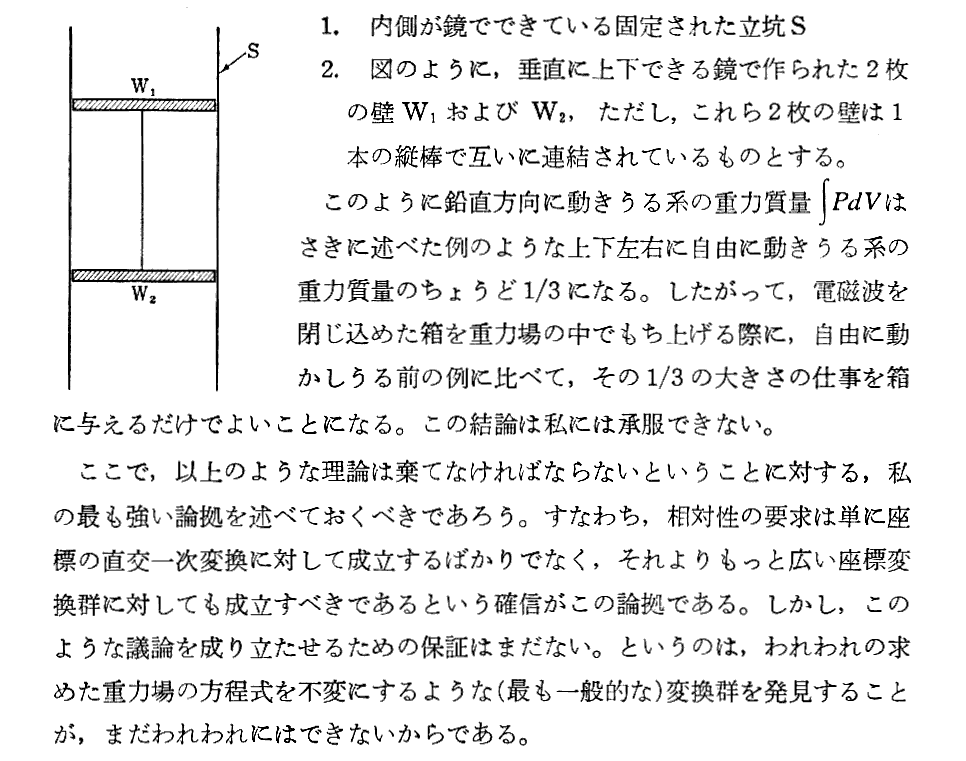
4-058-02　　１．導入　　４．1913共著 �T．物理学の部（Einstein）

　内山先生は上記の様に言われていますが、「一般相対性理論を理解するための数学的準備」を読了された方には、この論文で採用されている記法の特殊性は殆ど障害とはならないと思います。そのため改造社「アインスタイン全集」第2巻19番目論文からグロスマン担当部分を引用しておきます。なお、内山先生が推奨されている［Ａ３］のＢ．はこちらです。








































4-201-02





　補遺の末尾で述べているPhys. Zeitschrift に載せる予定の論文とは下記のものです。
Einstein , Albert (1913), "Zum gegenwartigen Stande des Gravitationsproblems." Physikalische Zeitschrift 14, 1249-1262..discussion 1262-1266（この中にBornとの議論がある）
（https://Einsteinpapers.press.princeton.edu/vol4-doc/509）
英訳版“On the Present State of the Problem of Gravitation”
（https://Einsteinpapers.press.princeton.edu/vol4-trans/210）
上記のURLからダウンロードできます。

５．1914年1月24日“一般化せられた相対性理論並びに万有引力論についての主要の問題”

https://einsteinpapers.press.princeton.edu/vol4-doc/593
https://einsteinpapers.press.princeton.edu/vol4-trans/294
以下の邦訳は、改造社「アインスタイン全集」第2巻 21番目論文から引用。

６．1914年5月29日“一般化された相対性理論に基づく万有引力理論の場の方程式の共変的性質”

https://einsteinpapers.press.princeton.edu/vol6-doc/34
https://einsteinpapers.press.princeton.edu/vol6-trans/18
以下の邦訳は、改造社「アインスタイン全集」第2巻 20番目論文から引用。

７．1914年10月29日“一般相対性理論の形式的基礎”

　この文献につきましてはPaisの解説第14章p317〜319を参照されたし。

7-254-00　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END
Ａ．理論の基礎
　　§ １．緒論
　　§ ２．万有引力の場
Ｂ．共変性の理論抄説
　　§ ３．四元ベクトル
　　§ ４．二階および高階のテンソル
　　§ ５．テンソルの乗法
　　§ ６．基本テンソルｇに関する二三の関係について
　　§ ７．最短線ならびに点運動の方程式
　　§ ８．微分によってテンソルを構成すること
Ｃ．与えられた万有引力の場における物理的現象の方程式
　　§ ９．“物質現象”に対する運動量・エネルギー定理
　　§10．連続的に分布する質量の運動方程式
　　§11．電磁的方程式
Ｄ．万有引力の場の微分法則
　　§12．座標系選択の制限の必要なことの証明
　　§13．一次的変換に関する共変性、適合せる座標系
　　§14．Ｈ-テンソル
　　§15．場の方程式の演繹
　　§16．理論の基礎についての批判的注意
Ｅ．ここで展開した一般法則の物理学的内容についての二三
　　§17．種々の見方による近似方程式を立てること
END．【訳者注】数式番号についての注意

https://einsteinpapers.press.princeton.edu/vol6-doc/100
https://einsteinpapers.press.princeton.edu/vol6-trans/42
以下の邦訳は、改造社「アインスタイン全集」第2巻 22番目論文から引用。

7-255-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-260-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END




　上記（2ｂ）式に付いての説明に関しては別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」３．［補足説明１］を参照されたし。

7-263-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

　以下のＢ．共変性の理論抄説は、1916年論文［Ａ３］「一般相対性理論の基礎」Ｂ．でも繰り返し説明しています。そちらの方が読みやすいと思います。

［補足説明１］
　反変を上付指数で表し、共変を下付指数で表す事はこの論文から実施されたことに注意されたし。
　
　このとき、座標成分は本来反変成分であるので ｄｘ^μ や ∂ｘ^μ と記すべきです。それにもかかわらず ｄｘ_μ や ∂ｘ_μ と記すとしています。この取り決めはかなり後の論文（1922年のプリンストン大学四講義録でさえも）まで続けていますので注意されて下さい。1．［補足説明1］を参照されたし。

7-266-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-274-00　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-276-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-288-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END




7-292-01

　補足しますと、（23’ｂ）式がNewtonの運動方程式を一般相対性理論に拡張したときの運動方程式に相当する“測地線方程式”です。この論文で初めて導かれた。

7-292-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END
















7-308

7-310-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

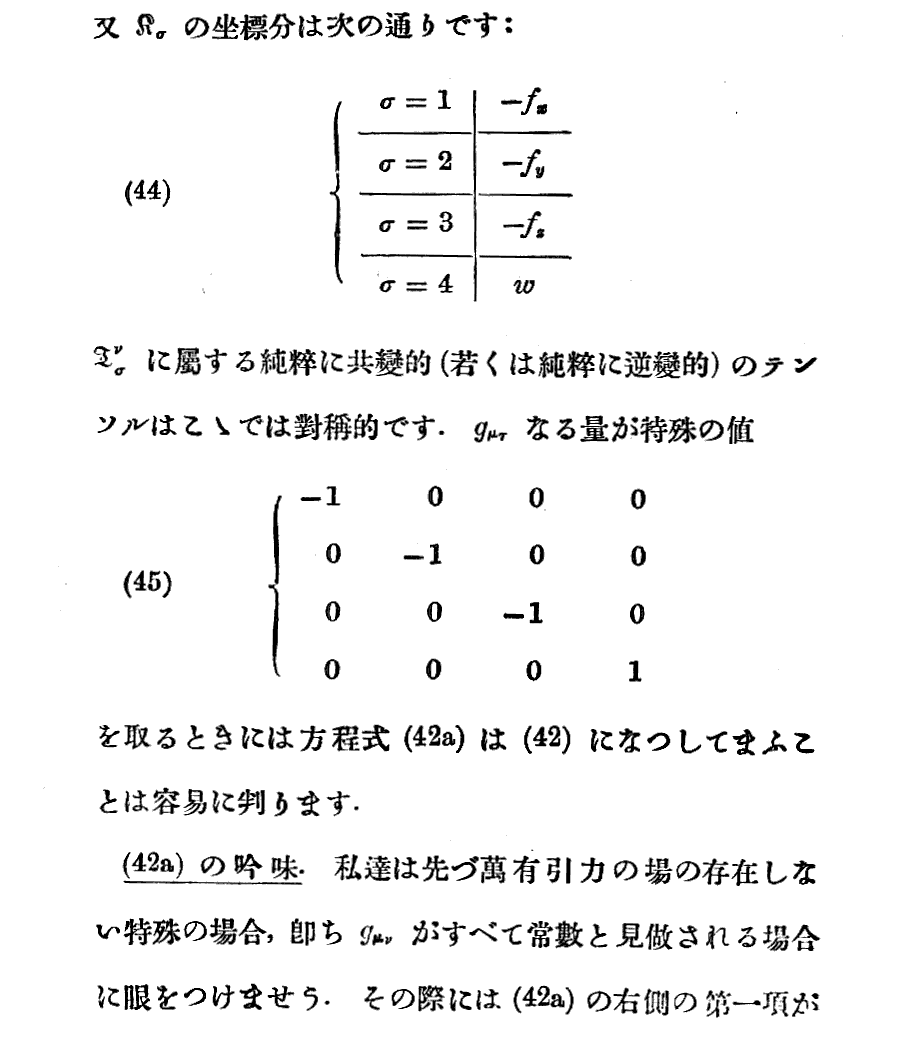
7-320-00　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-330-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

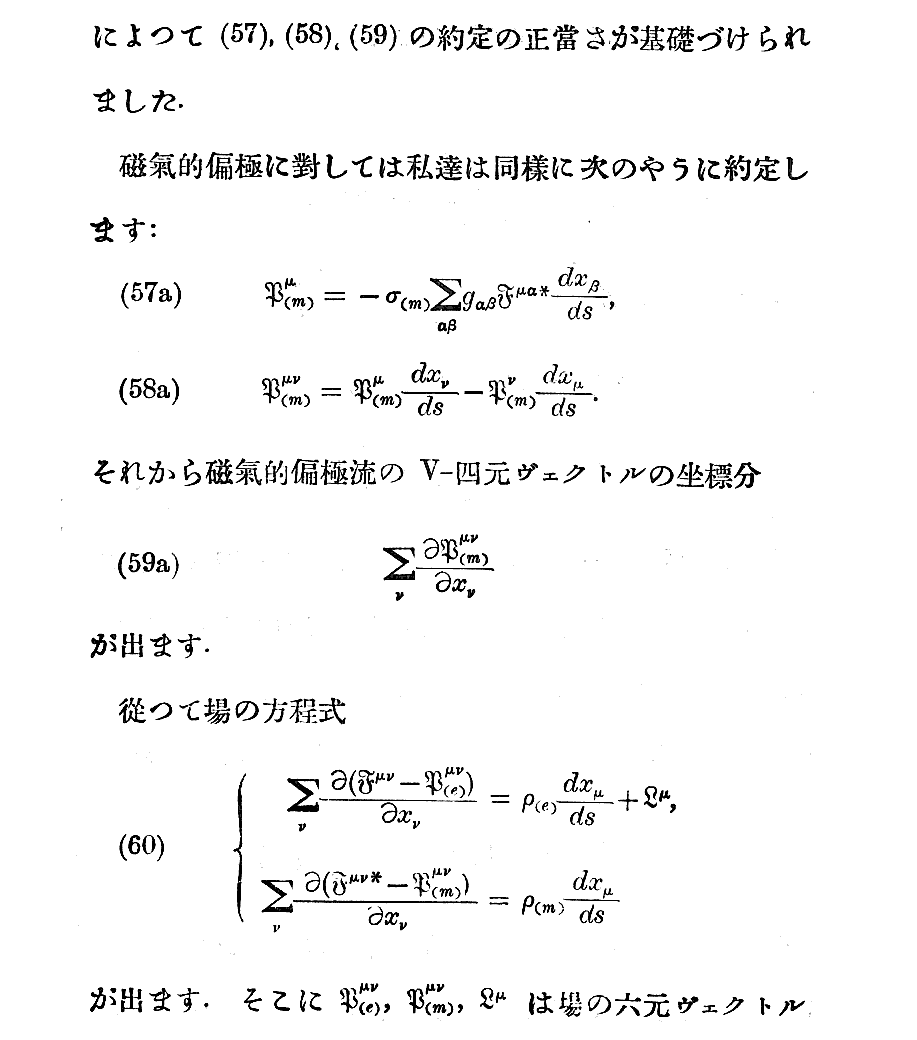
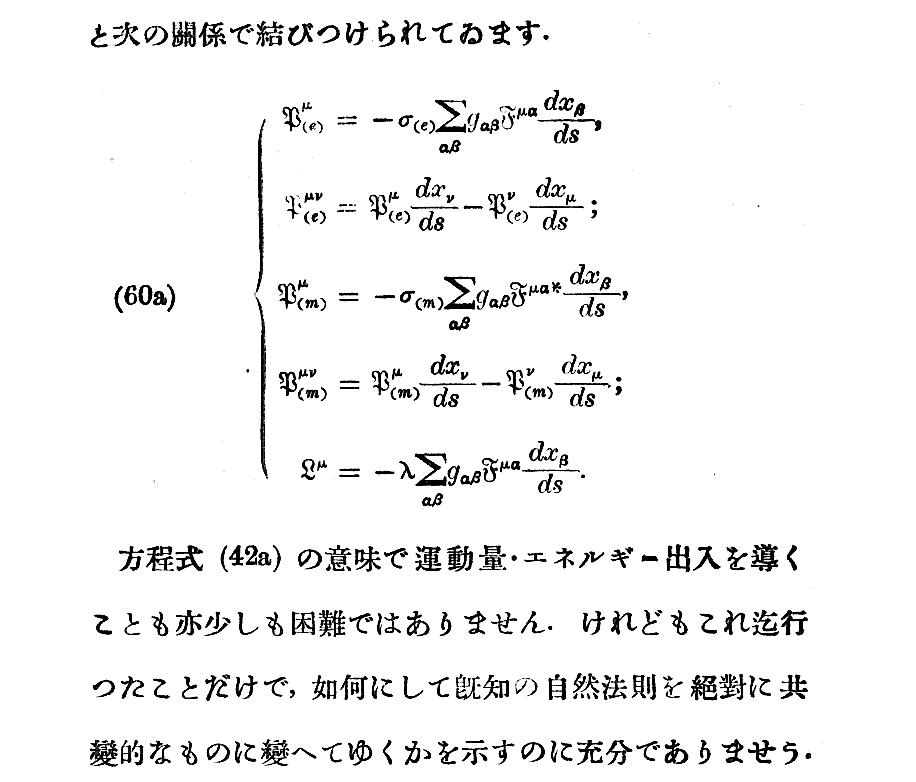
7-338-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-339-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-342-00　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-349-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-357-00　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

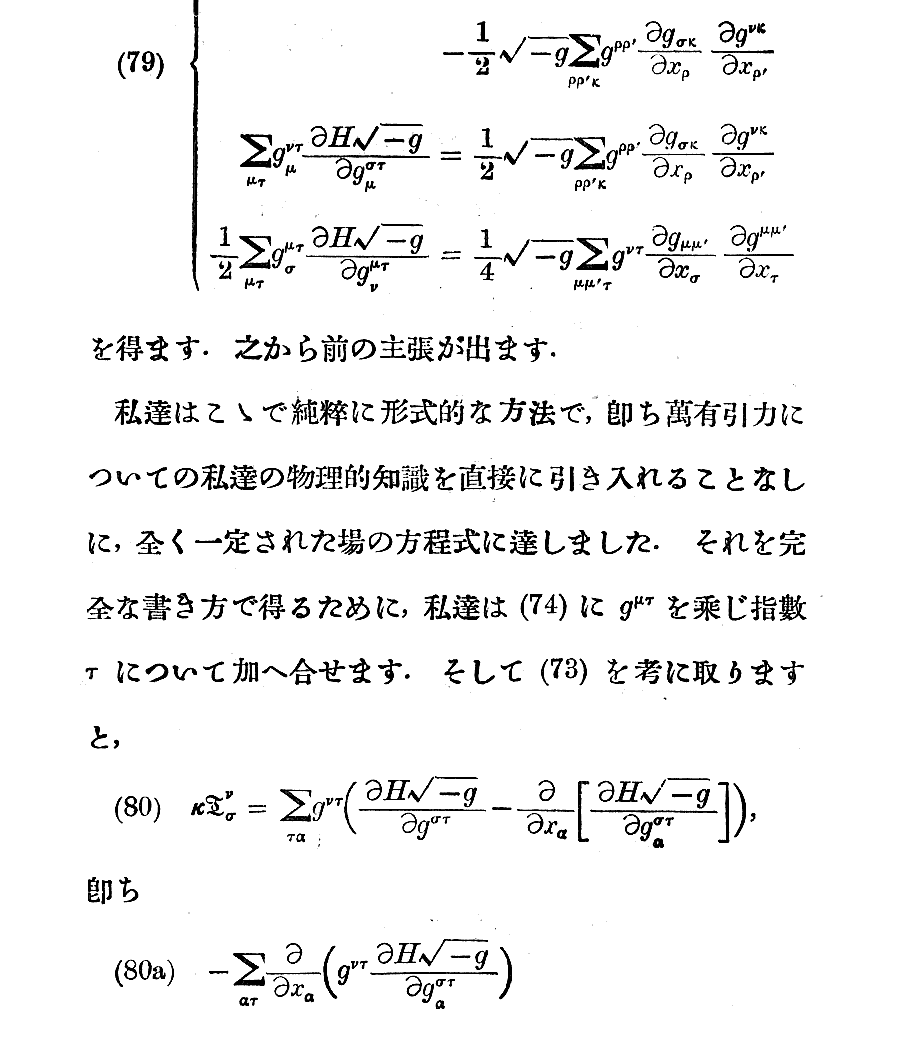
7-366-02　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END

7-374-00　TOP　Ａ１　２　Ｂ３　４　５　６　７　８　Ｃ ９　10　11　Ｄ 12　13　14　15　16　Ｅ 17　END





7-379

８．参考文献

　この稿を作るに当たって、下記文献を参照した。

1. A.Einstein著（石原純､他3名訳）「アインスタイン全集　第1〜4巻」改造社（1923年刊）
   この第１巻から1907年総説論文第�X章を、第2巻から1913年論文第2部と1914年論文のアインシュタイン・グロスマン共著論文、及び1914年1／24論文と、1914年10月論文を引用。
2. 湯川秀樹監修、内山龍雄訳編「アインシュタイン選集２《一般相対性理論および統一場理論》」共立出版（1970年刊）
   この中から、1911年プラハ論文、1913年論文第1部を引用。
3. A.Einstein著（金子務訳）「わが相対性理論」白揚社（1973年刊）第2部と第3部
   原本はU¨ber die spzielle und allgemeine Relativia¨tstheorie（1917年刊）
   　一般向けの啓蒙書ですが、極めて含蓄深い本です。アインシュタインが前書きに述べている様にこの本を読みこなすには、かなりの忍耐力と意志力が必要です。
   　ここでは第2部「一般相対性理論について」、第3部「全体としての世界の考察」と附記3、4を引用。この中の第1部「特殊相対性理論について」、附録1「ローレンツ変換の簡単な導き方」、附録2「相対性と空間の問題」は別稿で引用。
   　これは近年、「特殊および一般相対性理論について」白揚社（2004年刊）として再版されています。訳文も改良されているようです。ただしこちらは版組が縦書きなので、旧版の方が読みやすい。
4. A.Einstein著（矢野健太郎訳）「相対論の意味」岩波書店（1958年刊）
   　1921年にプリンストン大学で行った講義を出版（1922年）したものです。内容は高度で難しい。第3回講義の前半だけ別ページで引用。
   　Einsteinが1922年に来日した際に東京帝国大学で専門家向けに行った6回の特別講義は、前年に出版されたこの本と同じ内容だったと石原純は文献「アインシュタイン講演録」の中で説明してます。
   　「プリンストン四講義」の邦訳版は石原純、他訳「アインスタイン全集」改造社（1923年刊）の第4巻中にも収録されています。これには、アインシュタインの序言も掲載されていますので、その序言を考慮しつつ、矢野訳版と読み比べて見られると良いでしょう。いずれにいても内容はかなり難しいです。
5. A.Einstein著（中村誠太郎、五十嵐正敬訳）「自伝ノート（1947年）」東京図書（1978年刊）
   　アインシュタインが晩年に記した覚え書きですが極めて含蓄深く難解です。この中の特殊相対性理論（第4段落)と、一般相対性理論（第5段落）を引用。
   　これは、金子務編訳「未知への旅立ち（アインシュタイン新自伝ノート）」小学館（1991年刊）の中にもドイツ語原文からの新訳があります。この新訳もどうぞ参照されて下さい。
6. A.Einstein著（石井友幸, 稻葉明男共訳）「我が世界観」白揚社（1935年刊、1947年再販）
   　これは1922年〜1934年にいたる講演・諸寄稿を含む 。この中のp266〜274「一般相対性理論の起源についてのノート」を引用。この邦訳版は共立出版社「アインシュタイン選集」第3巻にもあります。これは特に有名な講演で、両邦訳版を読み比べて見られることを勧めます。
7. M.Born著（林一訳）「アインシュタインの相対性理論」東京図書（1968年刊）第�Z章
   　原本のドイツ語初版は1920年刊。
8. M.Born、W.Biem著（瀬谷正男訳）「アインシュタインの相対性原理」講談社（1971年刊）第�Z章
   　原本は1964年に発刊。文献7．の改訂版です。。�Y章、�Z章はかなり書き換えられています。しかし、この部分は初版の方が解りやすい。第�V章、第�W章§7〜11、第�X章、第�Y章を別稿で引用。また第�Z章の一部を引用しています。
9. Ａbraham Pais著（西島和彦、他共訳）「神は老獪にして･･･（アインシュタインの人と学問）」産業図書（1987年刊）
   　この解説は秀逸です。特殊相対性理論に関係する 6．神は老獪にして･･･、7．新しい運動学 と、一般相対性理論に関係する 9．わが生涯で最も素晴らしい考え、11．プラハの論文、12．アインシュタイン-グロスマンの共同研究、13．重力の場の理論、14．重力の場の方程式、15．新しい動力学 を引用しています。
10. W.Pauli著（内山龍雄訳）「相対性理論（上）（下）」筑摩学芸文庫（2007年刊）
    　原書は1921年刊です。上記訳本の元本は1974年に講談社から刊行されたもの。（下巻）第�W編“一般相対性理論”も熟読する価値あり。
11. https://einsteinpapers.press.princeton.edu/
    　本稿で引用したすべての論文の原版及び英訳版が上記URLにありますので、不明な点がありましたら源論文を参照されて下さい。