アインシュタインの重力場方程式(1915~1918年)
私のようなアマチュアが一般相対性理論を理解する最終目標は、Einsteinが “重力場方程式” を導いた過程を理解することだと思っています。
1.導入
Einsteinは1912年のGrossmannとの共同研究以来、3年間にわたって模索を続けていたのですが、最終的に1915年秋の4つの論文で、その事を成し遂げたと言われています。
一般には、Einsteinが1916年3月に書いた総説的論文 “Grundlage der allgemeinen Rela¨tivitatstheorie”.Annalen der Physik, ser. 4, vol. 49, pp.769-822, 1916年(これは 64ページの単行本として
Leipzig, Barth. からも出版された。)が有名です。これは共立出版社「アインシュタイン選集2」の[A3]として、あるいは共立出版社「現代数学の系譜10 リーマン幾何学とその応用」(1971年刊)の第3論文として翻訳版があります。当HPでもアインシュタイン著「一般相対性理論の基礎」(1916年)としてその詳細を紹介していますので、すでにご覧になっていると思います。
しかし、我々の様なアマチュアがこれを読んでも理解するのは極めて難しい。実際、重力場方程式を導く事ついては、その大略(梗概)しか述べられておらず極めて難解です。おそらく、上記総説論文よりも Einstein が最終的な方程式に到達したと言われている前述の4論文を学ぶ方が解りやすいのではないかと推察されます。
幸いなことに、その4論文の翻訳版が、1923年(大正12年)に発刊された改造社「アインスタイン全集 第Ⅱ巻」に収録されています。下記のものがそれです。
( )内に記されているURLはプリンストン大学のアーカイブスの原本と英訳版のURLです
- “一般相対性理論について” 11/4の集まり、11/11出版
“Zur allgemeinen Relativita¨tstheorie.” Preussische Akademie der Wissenschaften,
Sitzungsberichte, pt. 2. p778~786. 1915年
(https://einsteinpapers.press.princeton.edu/vol6-doc/243)
(https://einsteinpapers.press.princeton.edu/vol6-trans/110)
https://www.biodiversitylibrary.org/item/92536#page/870/mode/1up のp799~
- “補講” 11/11の集まり、11/18出版
“Nachtrag.” Preussische Akademie der Wissenschaften, Sitzungsberichte,
pt. 2. p799~801. 1915年
(https://einsteinpapers.press.princeton.edu/vol6-doc/254)
(https://einsteinpapers.press.princeton.edu/vol6-trans/120)
https://www.biodiversitylibrary.org/item/92536#page/871/mode/1up のp799~
- “一般相対性理論からの水星近日点運動の説明” 11/18の集まり、11/25出版
“Erklarung der Perihelbewegung des Merkur aus der allgemienen Rlativita¨tstheorie.”
Preussische Akademie der Wissenschaften, Sitzungsberichte, pt. 2. p831~839.
1915年
(共立出版社「アインシュタイン選集2」[A4]の翻訳版もあります。本稿はこちらを引用しています。)
(https://einsteinpapers.press.princeton.edu/vol6-doc/262)
(https://einsteinpapers.press.princeton.edu/vol6-trans/124)
https://www.biodiversitylibrary.org/item/92536#page/904/mode/1up のp831~
- “万有引力の場の方程式” 11/25の集まり、12/2出版
“Feldgleichungen der Gravitation.” Preussische Akademie der Wissenschaften,
Sitzungsberichte, pt. 2. p844~847. 1915年
(https://einsteinpapers.press.princeton.edu/vol6-doc/273)
(https://einsteinpapers.press.princeton.edu/vol6-trans/129)
(https://en.wikisource.org/wiki/Translation:The_Field_Equations_of_Gravitation)
https://www.biodiversitylibrary.org/item/92536#page/920/mode/1up のp844~
しかし、私のような未熟者には、これらの翻訳版を読んでも良く理解できません。それで、取りあえず、このページに翻訳版をupして紹介し、これを、Paisの解説(文献3.第14章14c.)、およびPauliの解説(文献4.)と比較しながら繰り返し読みこんで勉強してみることにしました。
上記一連の論文の簡単な紹介としては キップ・S・ソーン著「ブラックホールと時空の歪み」p104、や C.W.Misner,K.S.Thorne,J.A.Wheeler著(若野省己訳)「重力理論」丸善出版(2011年刊)17.7“アインシュタインの方程式の歴史の鑑賞” などがあります。しかし、こんな簡単な紹介で論文内容が理解できるわけがありません。
[補足説明1]
Einstein論文の数式記法について別稿「アインシュタイン一般相対性理論への道程(1907~1914年)」1.[補足説明1]で注意しましたが、本稿に関係する所を今一度確認しておきます
1.反変・共変成分表示を指数の上・下で表示は、すべての引用論文で実施。
2.反変座標成分に関する記述
改造社「アインスタイン全集」からの引用論文・・・源論文の表記dxμや∂xμをそのまま踏襲。
共立出版社「アインシュタイン選集」からの引用論文・・・すべてdxμや∂xμに修正。
3.クリストッフェル記号
改造社「アインスタイン全集」からの引用論文・・・クリストッフェルの旧表記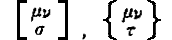 をそのまま踏襲。
をそのまま踏襲。
共立出版社「アインシュタイン選集」からの引用論文・・・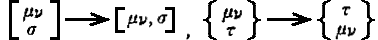 へ修正。
へ修正。
4.縮約操作に関する“アインシュタインの規約”
改造社「アインスタイン全集」からの引用論文・・・まだ実施されていない。
共立出版社「アインシュタイン選集」からの引用論文・・・規約を適用する形に修正。
5.座標変換後の物理量の表記について
物理量表現記号に’を付けるのでは無くて、添字指数に’を付けて表示するのが今日の標準的な表現法ですが、本稿の引用論文では、すべて物理量表現記号に’を付ける形が利用されています。
6.共変微分の表記・・・微分する座標の指数記号を下指数として追記する形
ただし、この点については微分する座標の指数記号を下指数として追記するとき、その前に;を挿入する今日の表現法の方が優れています。各自でその様に読み替えられることを勧めます。
2.11月4日論文
この論文をお読みになるとき、Paisの解説第14章p327~330を参照されて下さい。
https://einsteinpapers.press.princeton.edu/vol6-doc/243
https://einsteinpapers.press.princeton.edu/vol6-trans/110
以下の訳文は改造社「アインスタイン全集」第2巻 23番目論文より引用。

上記注(1)の1914年論文『一般相対性理論の形式的基礎』は、別稿で引用しています。この論文を別Windowで開いて参照されながら本論文を読まれることを薦めます。



§1 TOP §1.共変量 §2.微分法則 §3.場方程式 §4.注意 補講11/11







上記リーマン・テンソルの対称性についてはこちらをご覧下さい。

上記の私の論文の1053頁(本全集第2巻,308頁)はこちらを参照。

§2 TOP §1.共変量 §2.微分法則 §3.場方程式 §4.注意 補講11/11




§3 TOP §1.共変量 §2.微分法則 §3.場方程式 §4.注意 補講11/11


402




§4 TOP §1.共変量 §2.微分法則 §3.場方程式 §4.注意 補講11/11



3.11月11日補足論文
Paisの解説第14章p330~331を参照。
https://einsteinpapers.press.princeton.edu/vol6-doc/254
https://einsteinpapers.press.princeton.edu/vol6-trans/120
以下の訳文は改造社「アインスタイン全集」第2巻 23番目論文補講より引用。







4.11月18日論文
この論文を読まれるときPaisの解説第14章p331~334を参照されて下さい。
https://einsteinpapers.press.princeton.edu/vol6-doc/262
https://einsteinpapers.press.princeton.edu/vol6-trans/124
以下の訳文は共立出版社「アインシュタイン選集」第2巻 [A4]より引用。
邦訳としては改造社「アインスタイン全集」第2巻 24番目論文も有ります。
ここでは解り易くするために追記・[補足説明]等でかなり改変しています。元の表現は翻訳原稿でご確認下さい。


§1

(3)式の制約は必ずしも必要な制約ではありません。この条件を満たす座標系の基で議論すると言うだけです。(1)式は添字αとβに関しては和が取られていますから、結局μとνが1~4まで変化する値をとる4×4=16成分からなる方程式です。ただし、Γαμνの下の二つの添字の入れ替えたものは等価ですから、結局10個の方程式に帰着します。

上記下線部の意味は解り難いが、要するにgμνは座標変換によって変化します。だから、その座標変換に対して共変的な方程式を解いても、その解であるgμνには、その座標変換によって変化する任意性が残るかも知れないと言うことだと思います。
Einsteinは、重力場方程式(1)式を近似的に解いたのですが、(1)式の形の方程式を用いることの意味は別稿「一般相対性理論の基礎」C.(16)[補足説明3]をご覧下さい。



1.は静的な解であること、2.は球対称な解であること、3.は時間に関して対称な解であること、4.は無限遠で平坦な解(つまりミンコフスキー時空になる)であることを要求する。

[補足説明1]
上記の説明を少し補足します。
(4・b)式は行列表示すると
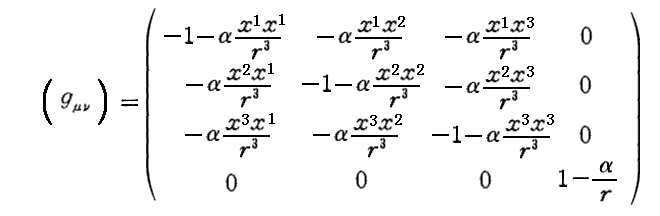
となります。
上記の“(3)が第1次の項に関して満足されている”は下記の計算から解る。拡大版はこちら。
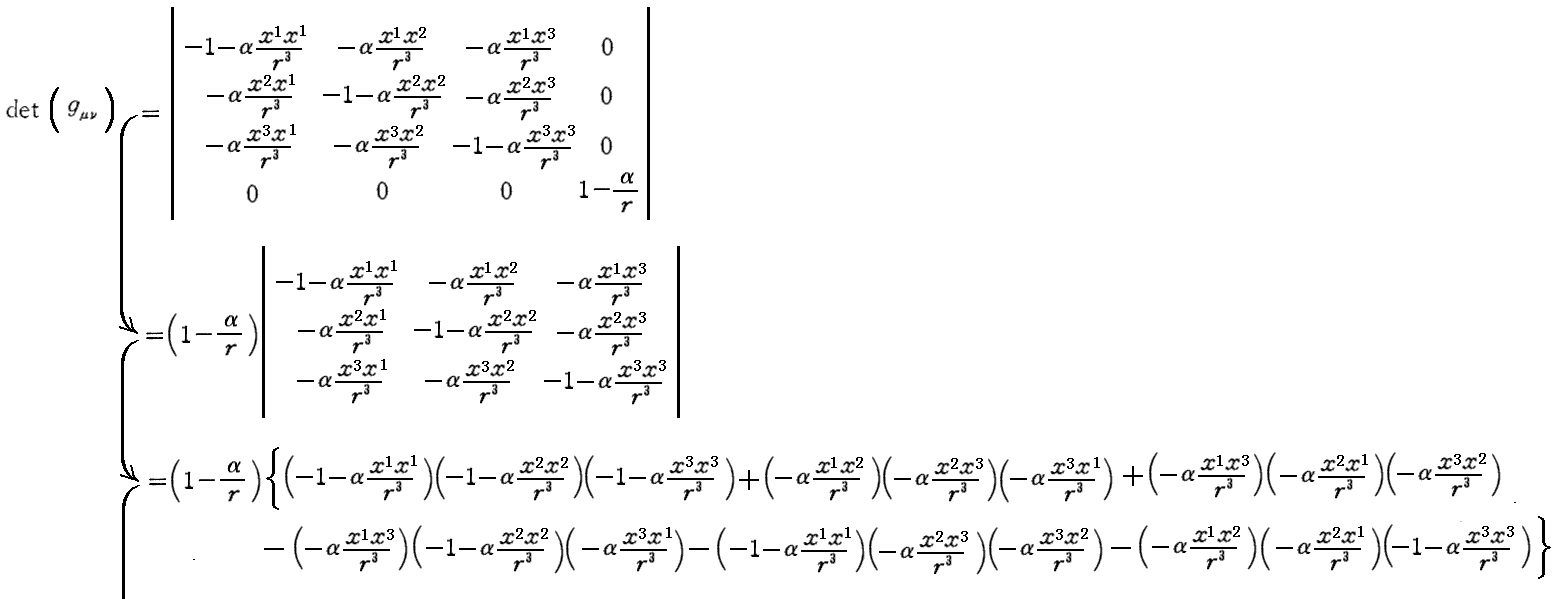

また、“次に(1)が第1近似で成立している事を最も簡単に知るのには”のところですが、要するに上記の(gμν)の表現を(1)式に代入すれば2次以上の高次の量を無視すると(1)式を満足していることが確かめられると言うことです。
近似解の正当性に付いてのEinsteinの説明は簡潔すぎて、その大変さが読み取れませんが、実際にそれを確かめるには膨大な計算が必要です(例えば[補足説明7]をご覧下さい)。
そのため、別な方法[補足説明3]によってこの解の近似度を確認します。
上記で(4・b)で仮定された近似解は、自然な仮定を元にして求められたものですが、[補足説明3]で確認するように、この近似解はシュワルツシルドが求めた厳密解に極めて近い解であることが解ります。
この当たりは別稿Sommerfeld「電磁気学」§38で紹介したW.Lenzの考察をごらんください。また、Einstein論文に対するSchwarzchild解の位置づけに関しては4.§2.[補足説明6]をご覧下さい。
[補足説明2]
論文中には明記されていませんが、Einsteinは“双対計量テンソル”(gμν)について
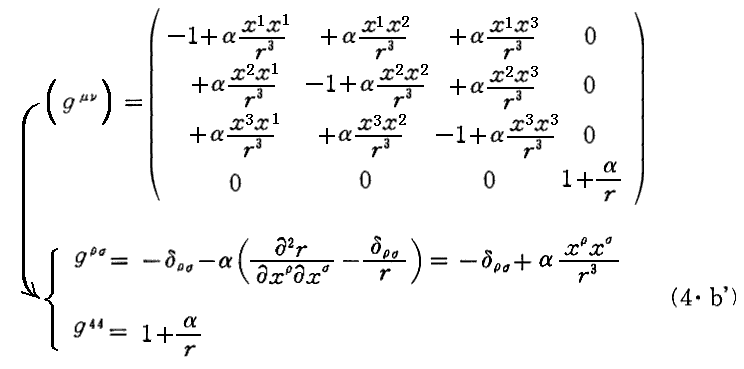
としたはずです。
実際に、こうすれば1次のオーダーにおいて確かに
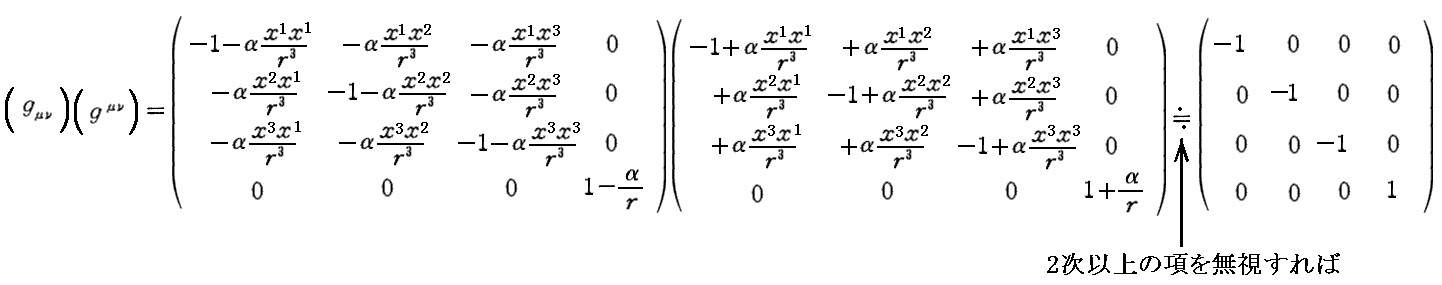
を満足します。
[補足説明3]
さらに補足します。
計量テンソル(gμν)に対する線素の表現式は ds2=gμνdxμdxν と成りますが、これに前記の式を適用して、さらに中心質量を原点とした極座標に座標変換してみます。次図の式表現は小さくて見にくいので詳細はこちらの拡大版でご確認ください。
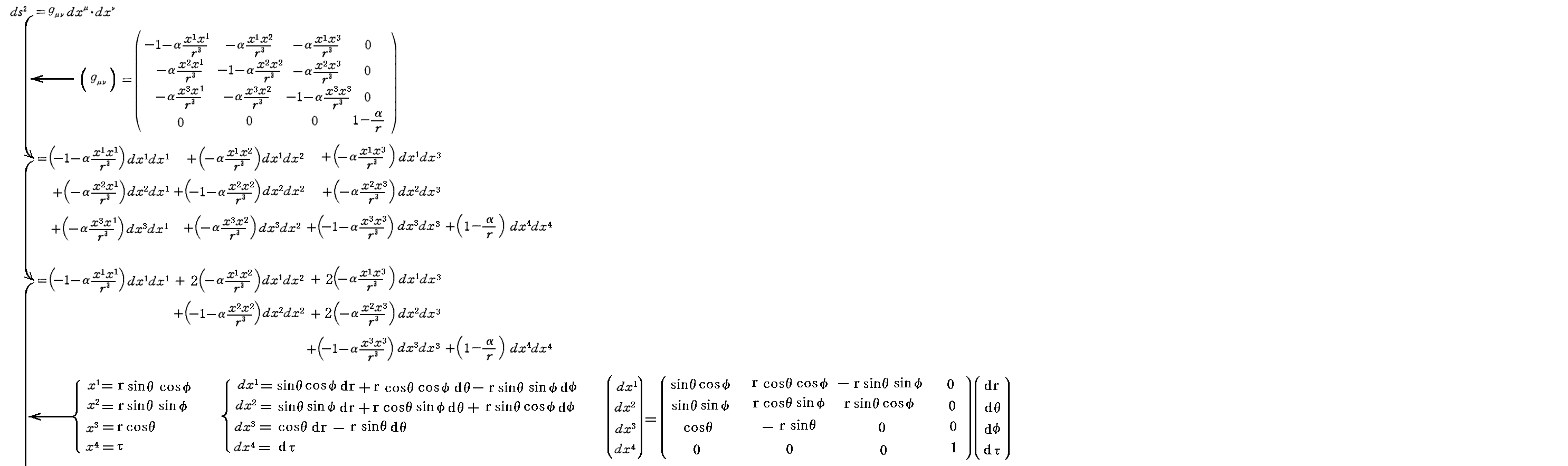

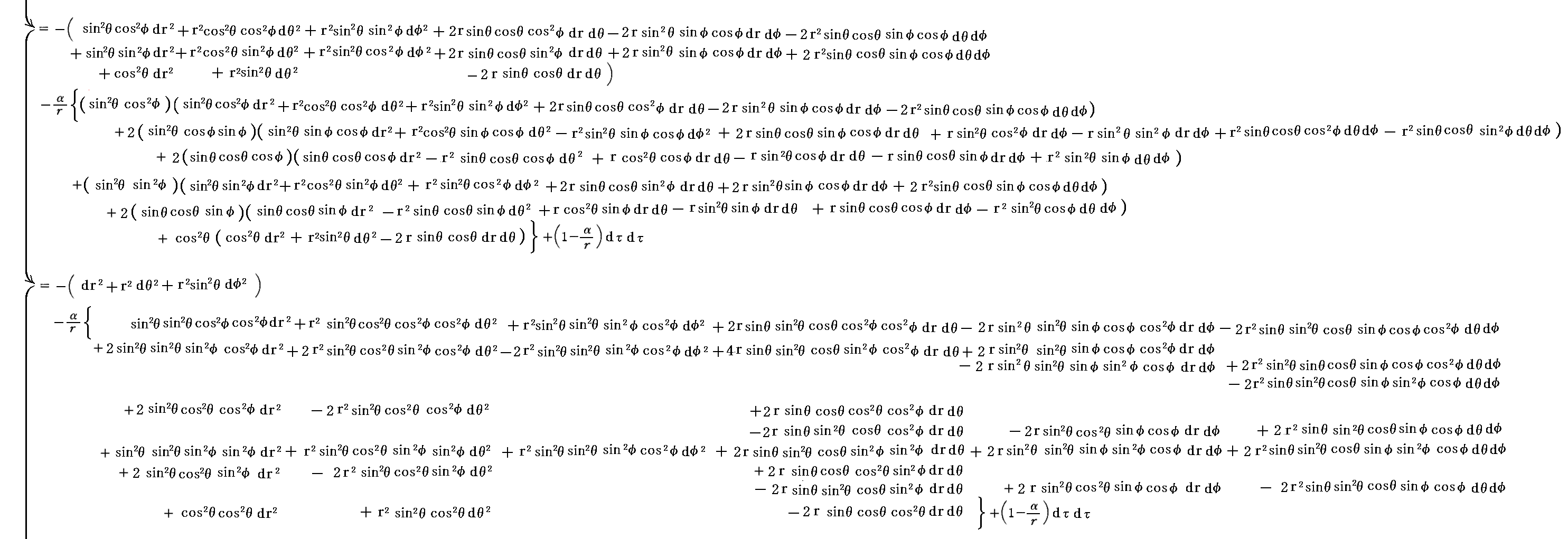

すなわち、極座標表示の ds2 は次の様になる。
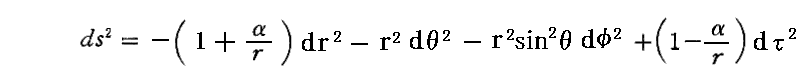
これは、1915年12月にSchwarzschildが求めた厳密解のgrrを -1/(1-α/r)≒-(1+α/r) で近似したものです。Schwarzschildの解が重力場方程式を厳密に満足することは確認されていますので、アインシュタインが直交座標で求めた解が重力場方程式を良い近似で満足することは明らかでしょう。つまり、アインシュタインが初めて求めた重力場方程式の近似解はSchwarzchildの厳密解に“極めて近い”解だった!。
このことに付いて、別稿E.§22[補足説明5]をご覧下さい。
[補足説明3-1]
上記の座標変換についてさらに補足します。
別稿「ブラックホール近傍の力学」3.(2)で強調しているように、ここの座標変換によって移ったシュワルツシルド座標系は時空間の歪みの無い擬ユークリッド空間に引かれている座標系です。もちろんEinsteinの用いている直交座標系も時空間の歪みの無い擬ユークリッド空間に引かれていた座標系です。この言い方は非常に解りにくいかも知れませんが、おそらくそうだと思います。
その様に座標変換が擬ユークリッド空間から擬ユークリッド空間であっても、ds2を構成する計量テンソルgμνは変更を受けて新しい成分表示になります。つまり基底ベクトルを別なものに変換したら基本計量テンソルも必ず変換を受けます。このことは別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」3.(4) と、そこの[補足説明3]で説明したことです。ここでは、その事を利用して、Einsteinの近似解をシュワルツシルドの厳密解と比較して見たと言うことです。

[補足説明4]
Einsteinはたった10行程度の説明ですましていますが、この部分が重力によって時空が歪む効果により光線が湾曲する現象の“正確な”解答を(学術論文で)初めて報告したものです。
その証明が、①赤アンダーライン部分でいう“簡単な計算”です。それは、別稿[A3]E.§22.2.で説明されているものですが、我々凡人には決して簡単な計算ではありません。重力場中で時間が延び、空間が縮む事をホイヘンスの原理に結びつけるやり方はとても深淵な考察です。つまり、あらゆる場所で光は一定の速度で進むのですが、重力場中では時間が延び、空間が縮むから見かけ上光はゆっくり進むのてす。ここの考察は簡単に理解できることではありません。
また“私の以前の論文”とは別稿[A1]§4の事です。そこの§4.[補足説明1]で説明したように、その時点のEinsteinは重力によって空間が縮む効果に気付いていませんでした。空間が縮む効果がなぜ抜けていたのかを説明しているのが、上記②赤アンダーラインの部分です。(ただし、その事が空間の歪みを生み出すメカニズムについて、今の私は良く理解できていません。)
補足すると、“以前の論文”で求めた光線の湾曲量が次の[補足説明5]の2.の(ニュートン力学による)湾曲量と同じになるのは、別稿E.§21.2.でEinsteinが説明している様に重力場方程式の第1近似ではg44のみが問題となり、それがニュートン力学の重力場ポテンシャルに対応するからです。つまり時間の遅れの効果のみを考慮した光線湾曲量とはg44のみを考慮した場合を意味するからです。
この事と、湾曲量が2倍になる事との関係については別稿E.§22.2.[補足説明1]をご覧下さい。
[補足説明5]
さらに補足を続けます。別稿で引用しているチャンドラセカールの解説で説明されている様に、Einsteinの本論文の内容がイギリスの科学者に(1916年、オランダのド・ジッターを通じて)伝えられた時、このことを確かめるための皆既日食観測の遠征が企てられる。そのとき、彼らは光線の湾曲量に関して三つの可能性を考えていた。
それは
1.光は重力の影響を受けることは無く、真っ直ぐに進む。
2.光は光子(粒子)として質量を持っており、ニュートンがその著書『光学』の疑問1でほのめかしたように重力によってその進路が曲がる。その曲げられる量はNewton力学に依って計算できて、それはEinsteinの予想した量の丁度半分となる(計算はこちら)。
3.Einsteinの一般相対性理論が正しく、重力場により時空が歪む(時間はゆっくりとなり、空間は縮む)効果により本論文で述べられている量ほど曲がる(計算はこちら)。
です。
つまり、Einsteinの理論が出された時には、上記“2.の可能性”は、イギリスの科学者に取って“常識となっていた”。特に1905年に特殊相対性理論が発表されて、光子が慣性質量を持つことが明らかになってからは当然のことだった。
もちろん、特殊相対性理論が知られる前から別稿で引用した様にイギリスのジョン・ミッチェルは1783年にNewtonの示唆に基づいた計算をしていますし、フランスのラプラスも似たような計算をしています。
ドイツにおける [2.の考え方] がどうだったかといいますと、別稿で引用したBorn文献第Ⅶ章p352や、をM・ウィル文献で示されている様に1801年にゾルドナーがNewton力学に基づいて計算しています。ただし、この先見的・優れた業績は、ファシストがEinsteinの業績を貶めるために1921年に利用し始めるまで、一般には知られていませんでした。ゾルドナーの業績はまだ再発見されてはいませんでしたが、当時のイギリスの科学者は当然のごとく同じ計算をした。
すなわち、Einstein理論が発表された当初から上記1.2.3.のいずれであるかを観測によって判定する事が最大の関心事であったことは確かです。
王立天文台長フランク・ワトソン・ダイソン卿は二つの観測隊を派遣した。一つはグリニッジ天文台のアンドリュー・クロンメリンが率いる隊でブラジルのソブラルへ、もう一つはケンブリッジ大学のアーサー・エディントンが率いてスペイン領赤道ギニアの海岸沖のプリンシベ島へ。
出発に先立ってエディントンは書いた『この日食観測隊は初めて光の重さ[すなわち、ニュートンの値]を立証するかも知れない。あるいは非ユークリッド空間というアインシュタインのとっぴな理論の確証を得るかもしれないし、あるいはなお一層遠大な帰結――偏向なし、という結果に到達するかも知れない。』(Observatory,42,p119,1919年の文末)。
上記文中の[ニュートンの値]とは《ゾルドナーの計算値=0.87”》のことです。

[補足説明6]
赤方偏移については1907年論文と1911年プラハ論文で、Einsteinはすでに正しい結論を得ています(そのことは別稿[A1]§4.[補足説明2]で説明すみ)。そのため、赤方偏移については僅か数行の説明で済ましています。
赤方偏移の現象は、③赤アンダーラインで簡潔に説明しているように、時間の延びのみに関係して空間の縮みには関係しません。そのため、以前に得た結論が“正しい”のです。
このことに付いてEinsteinは1916年の総説的論文の末尾で今一度説明しています。このことについては[A3]E.§22.1.をご覧下さい。。

上記の(6・a)~(6・b")式の説明文は解りにくいの改変しています。もとの文章はこちらです。
[補足説明7]
(6・a)~(6・b")式の導出は以下の通りです。
最初の、(6・a)は
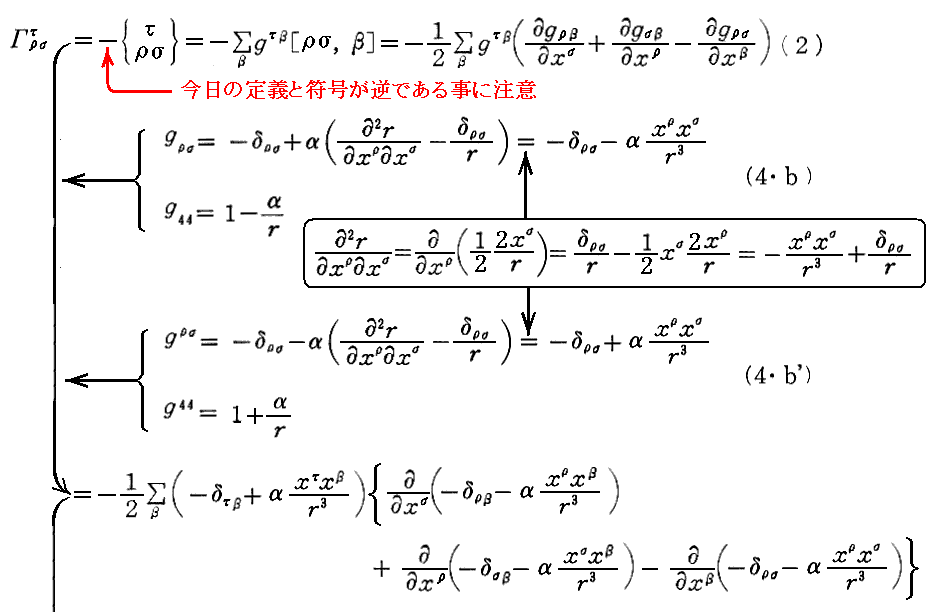
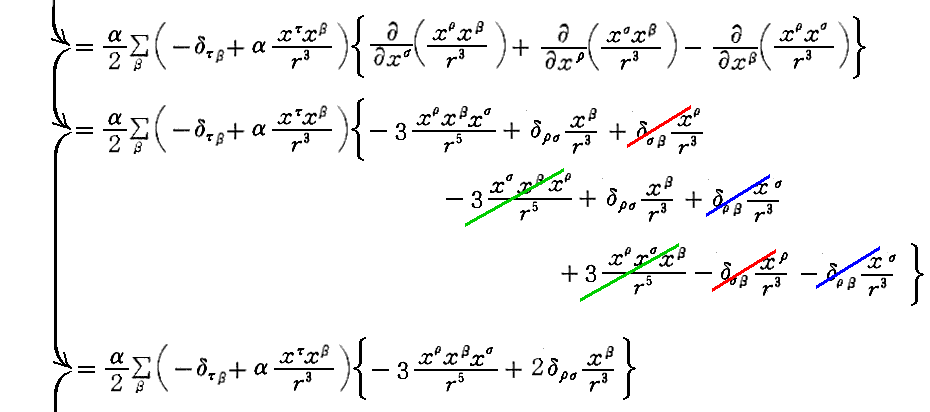
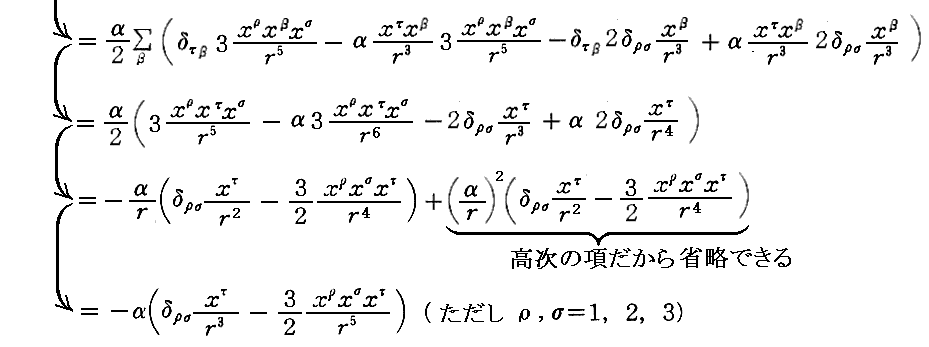
として導ける。
次の(6・b)は
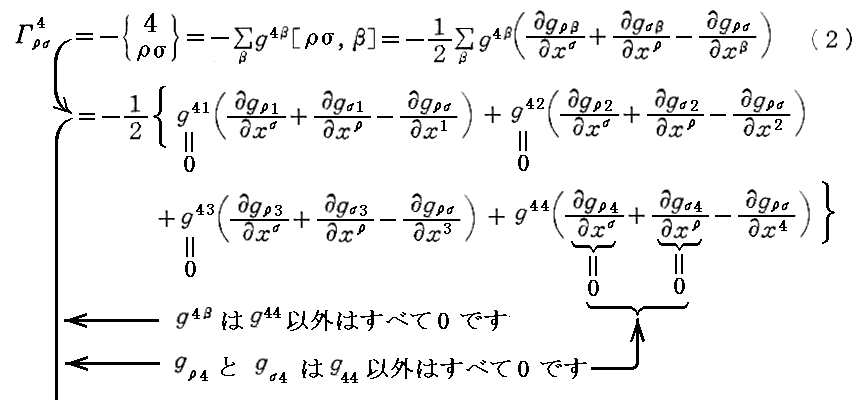
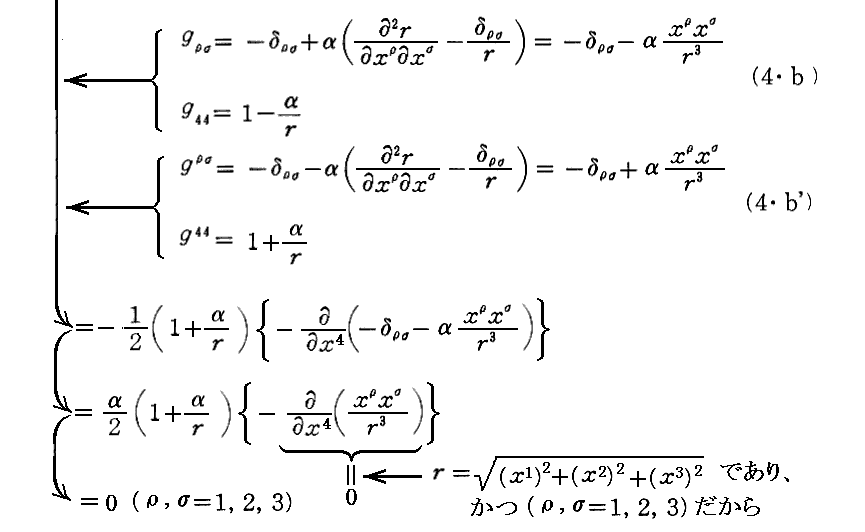
および
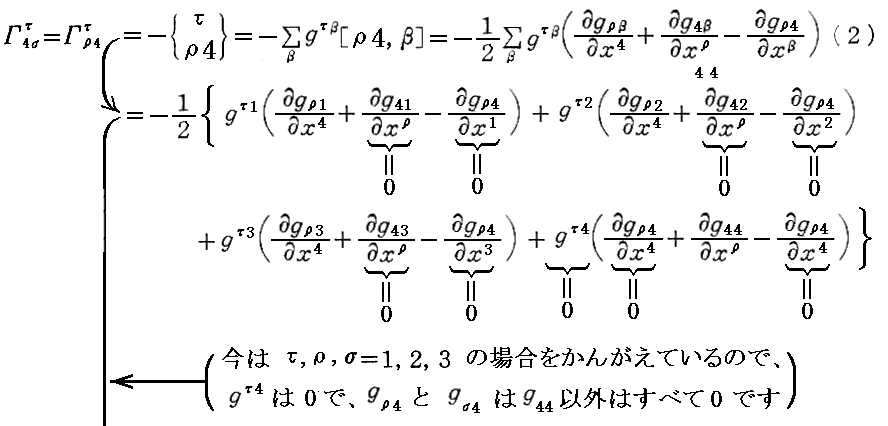
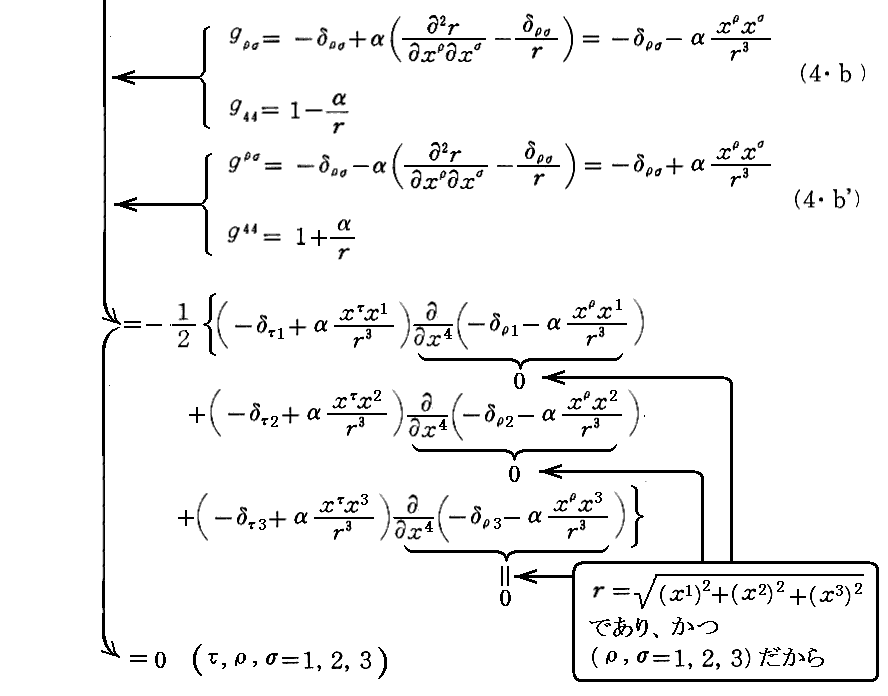
となる。
次の(6・b’)は
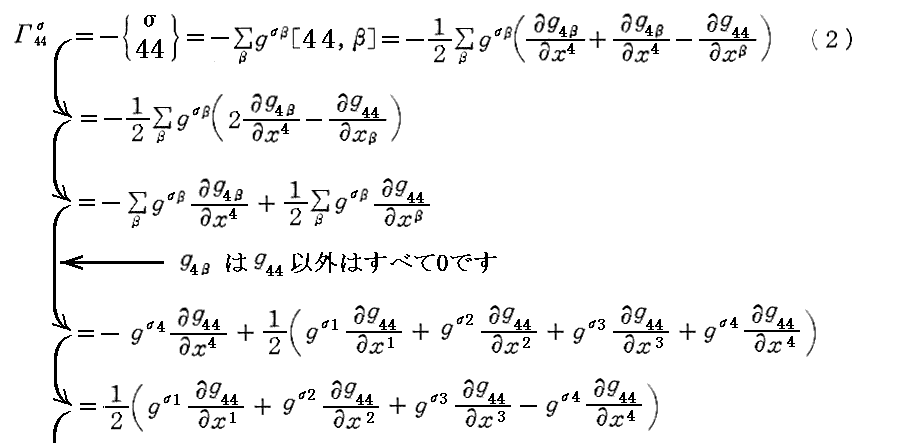
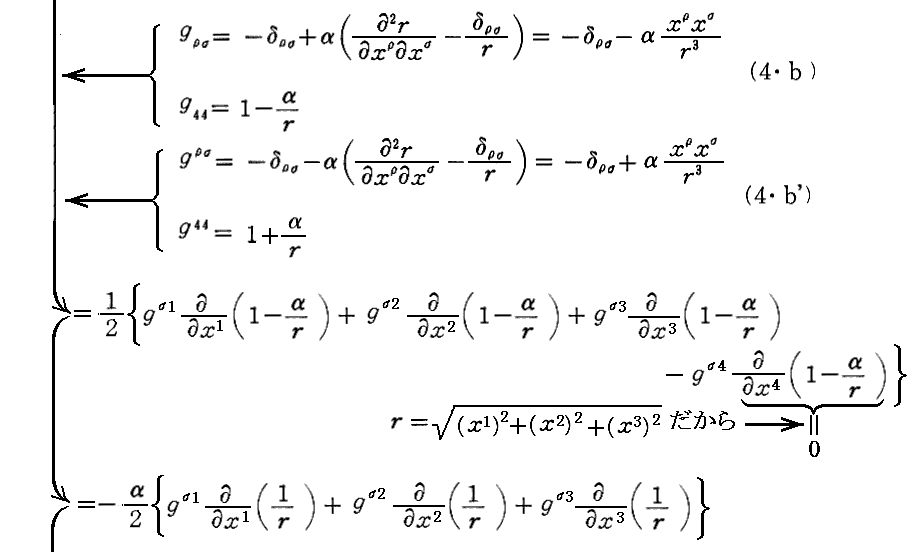
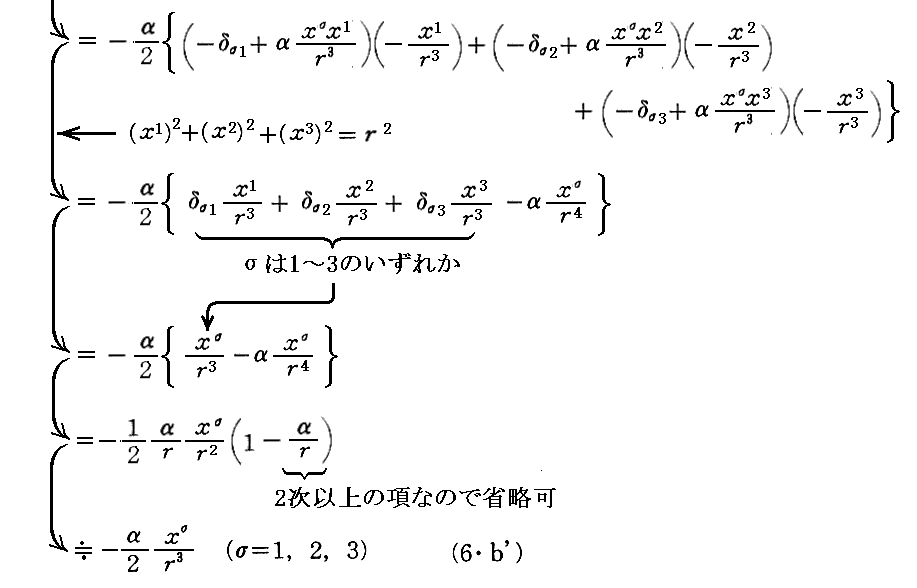
および
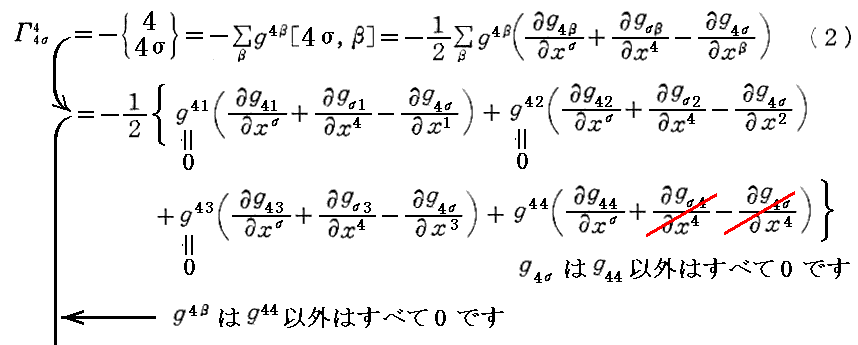
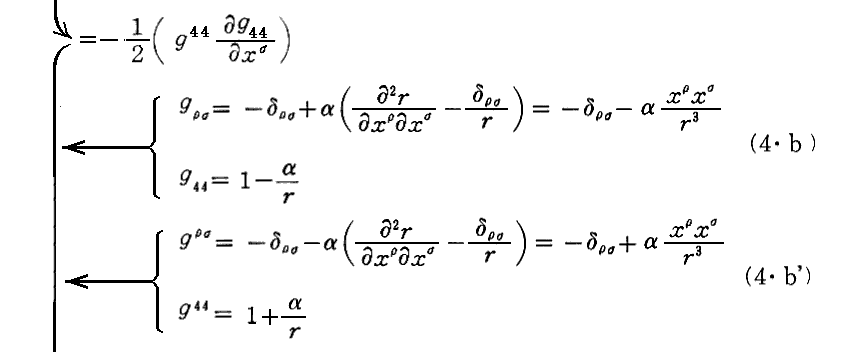
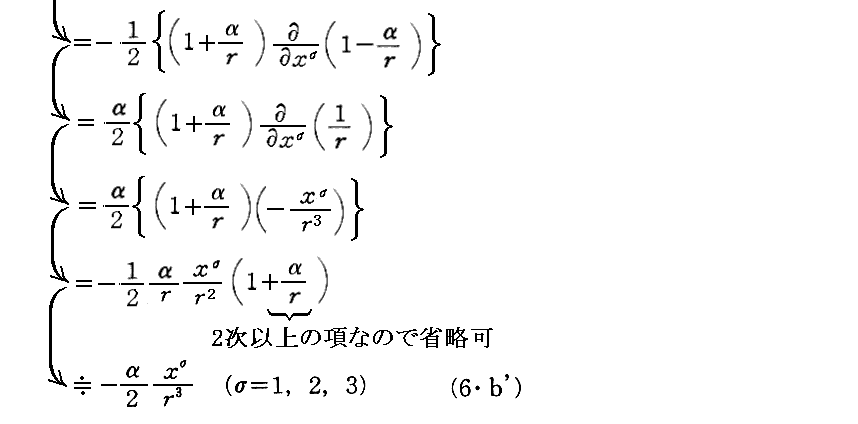
となる。
最後の、(6・b”)(4と言う添字を3個持つ場合)は

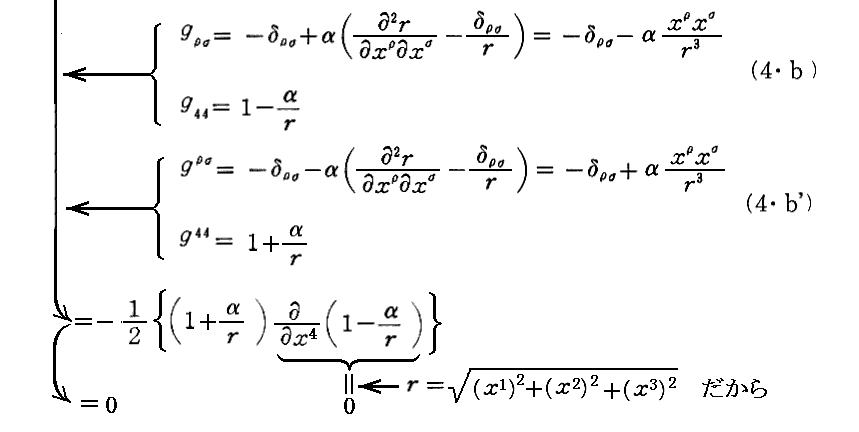
となります。
ここの確認計算から解る様に、Einsteinが仮定した近似解が実際に重力場方程式を良い精度で満たしている事を確認するには膨大な計算が必要です。シュワルツシルドが厳密解を求めるとき必要だった計算量に劣るわけではありません。

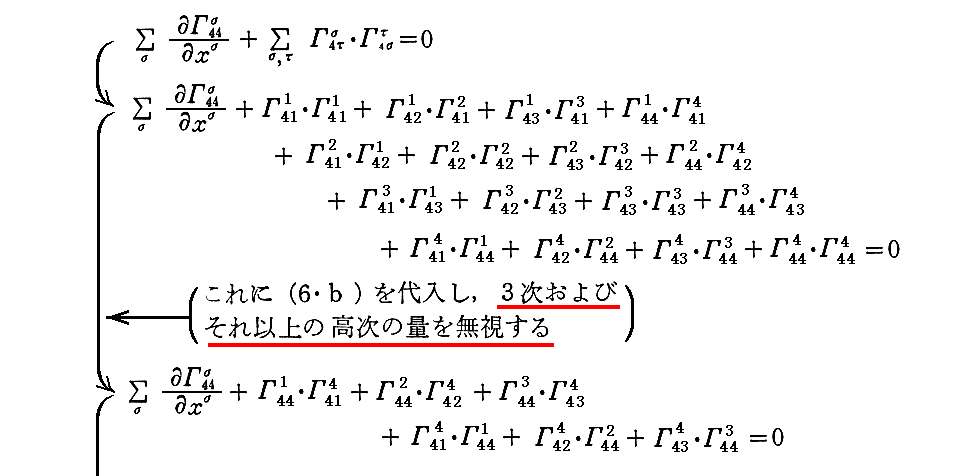

これは[補足説明7](6・b’)式を導く計算の2次の項まで考慮したものです。
[補足説明8]
実際、(6・c)が上記の偏微分方程式の解である事は以下の計算から確認できます。
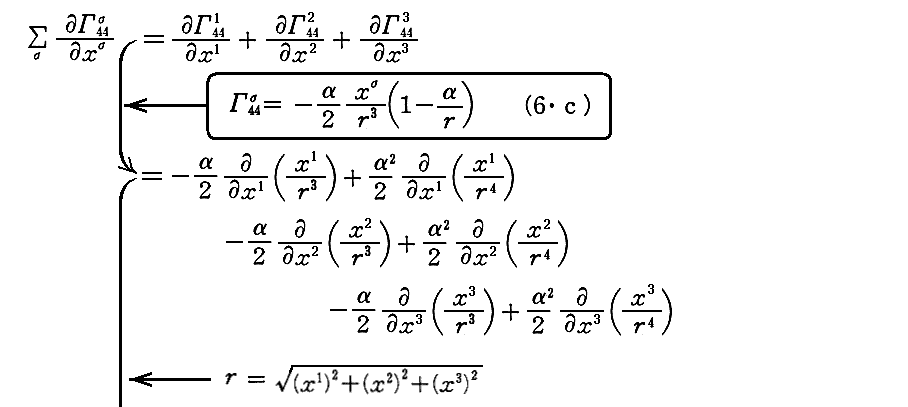
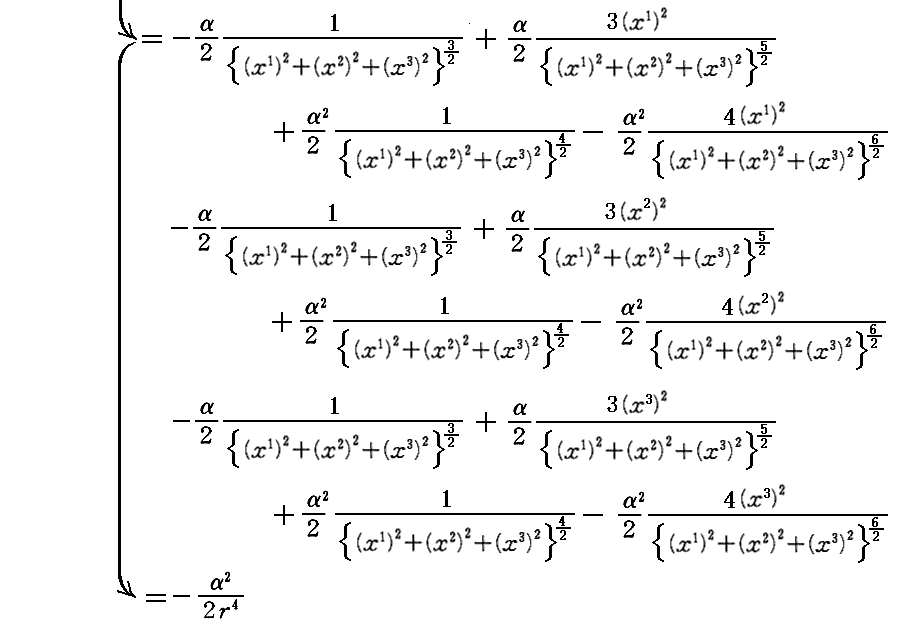
§2

“測地線方程式”の導き方について、Einsteinは何も説明してくれていませんが、それは以前の論文(1914年10月論文§7、あるいは1915年11/4論文§2)で説明しているからです。
“測地線方程式”はNewton力学における“運動方程式”に相当するものですが、(7)式ではσとτに付いては和を取っていますので、結局はνが1~4通りに変化する4個の連立方程式に帰着します。
§1の(1)式[重力場方程式]は重力場の時空の曲がり具合である計量テンソル(gμν)を決定する為の方程式でした。ここの(7)式[測地線方程式]は、(1)式を解いて求まった計量テンソル(gμν)を代入することで、曲がった時空の中での質点の運動を表す運動方程式を導くものです。
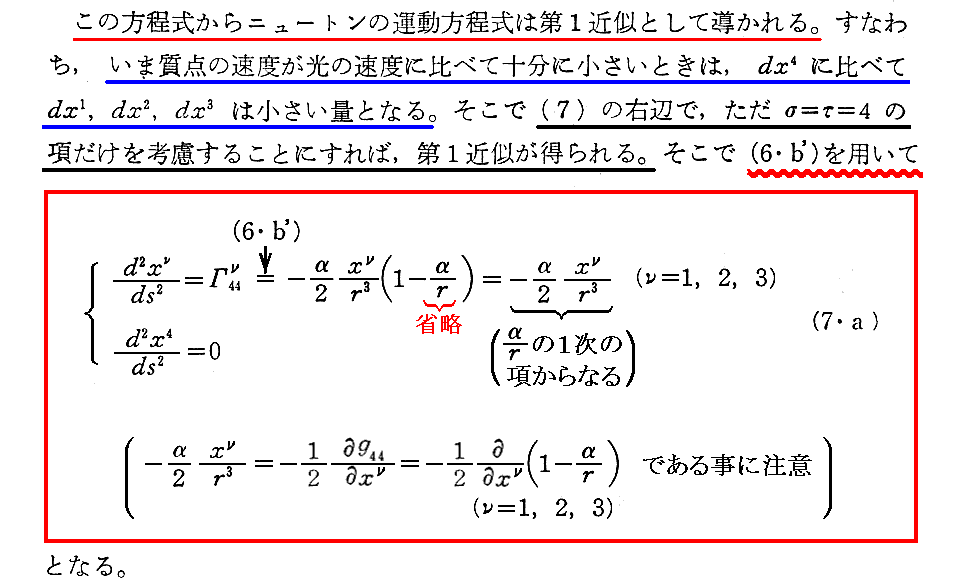
[補足説明0]
上記青アンダーラインの意味は、ds2≒-(dx1)2-(dx2)2-(dx3)2+(dx4)2=-v2dt2+c2dt2 だから v≪c を考慮すると 同じdt に対してそうなると言うことです。このことの意味は例えば別稿「時空の曲がりと測地線」4.(3)~(4)などをご覧下さい。
このことから ds≒cdt=dx4 も言えますから、下記の段落の“第1近似では s=ct=x4 とおいてよい”が言えます。つまり dx4/ds≒cdt/cdt=1 となります。だから、(7・a)の第4成分 d2x4/ds2=0 はその事を表している。
補足しますと、上記段落の考察は、Einsteintが一般相対性理論の“重力場方程式”が正当であることを確信する上で、最も重要なものでした。それが、この論文で最初になされたと言うことです。
ここはあらゆる教科書で必ず説明されている所です。たとえば、別稿7.(2)1.、別稿中野董夫文献9-4.、別稿藤井文献4.§19、別稿Weinberg文献の説明、さらに内山文献の説明 をご覧下さい。

[補足説明1]
ニュートン力学におけるエネルギー保存則と角運動量保存則(面積速度一定の法則)に相当する(8)式の導出については、別稿「楕円軌道の発見と万有引力の法則」4.(2)1.[補足説明1]の引用ページ1と、引用ページ2などを参照されると良いのですが、大事な所ですので復習をかねてここでの記号を用いて導いておきます。(θをx1x2平面からの角度とする場合は上記引用ページ1,2をご利用ください。)
まず、s=x4とおけるので(7・a)の最初の3成分は
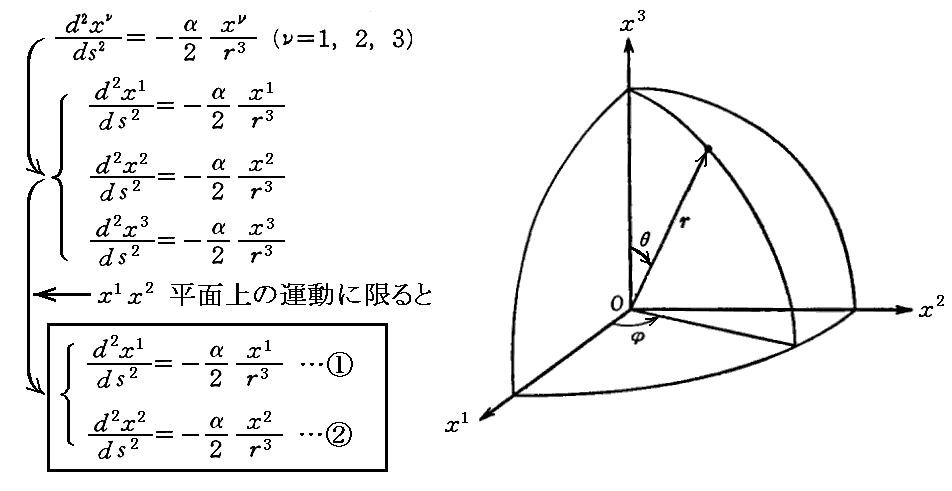
と成ります。右辺の形から、質点に働く力は距離の逆二乗法則に従う“中心力”であることが解る。
これはx1x2平面内の極座標(r,φ)で論じるたほうが解りやすい。つまり上右図でθ=π/2と固定してdθ/ds=d2θ/ds2=0、cosθ=0、sinθ=1とした場合です。
別稿2.(3)で説明した2次元極座標表示での加速度表現を用いて、上記の運動方程式を書き直すと
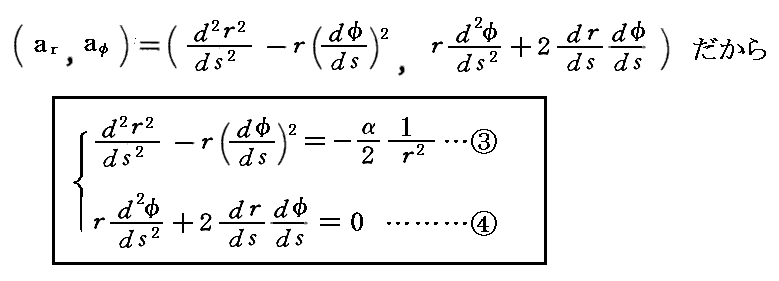
となります。
これから“エネルギー保存則”を導くには

⑤式はエネルギー保存則を意味しおり、積分定数Aは保存されるエネルギー値を示しています。
極座標表示でも同様にして

が得られます。これを本文中の(8・a)を用いて書き直すと(8)式となります。
⑤式に別稿2.(1)で説明した2次元直交座標での速度成分の極座標表示式
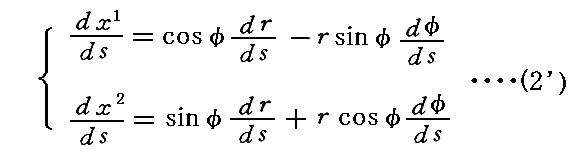
を代入すると、⑥式が得られますので、両者は同じ事を表しています。
中心力に対して成り立つ“角運動量保存則”(“面積速度一定の法則”)は、次のようにして導かれる。
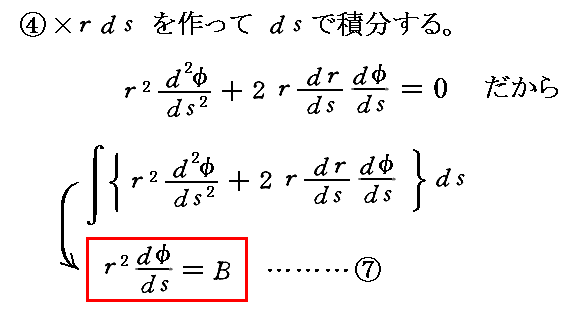
積分定数Bは、一定に保たれる角運動量値ですが、面積速度のちょうど2倍に相当します。
⑦式は直交座標表現を用いても導けます。別稿3.(3)(a)で説明した様に
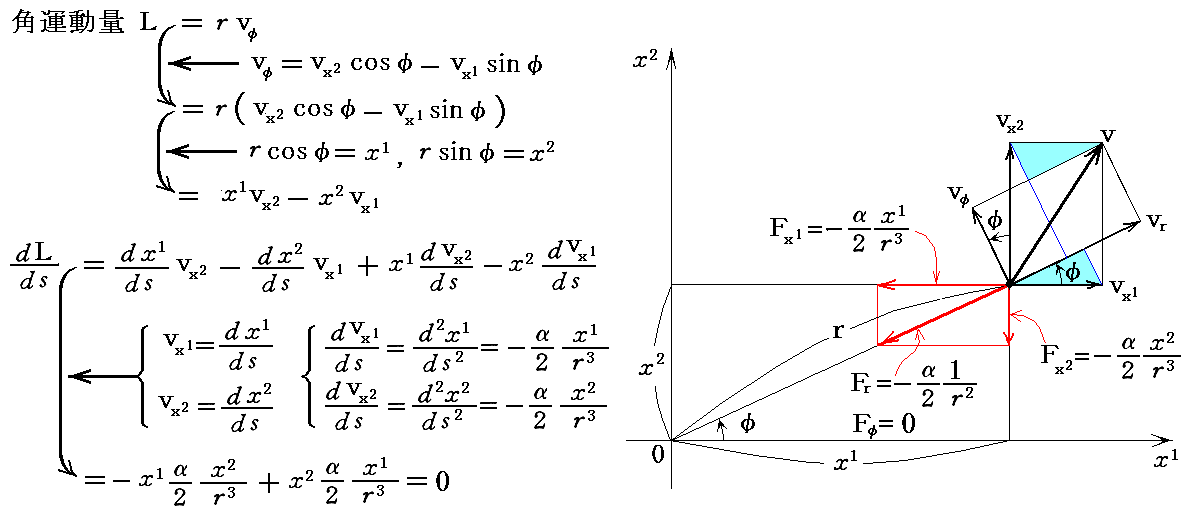
ですから、これを逆にたどれば良い。すなわち
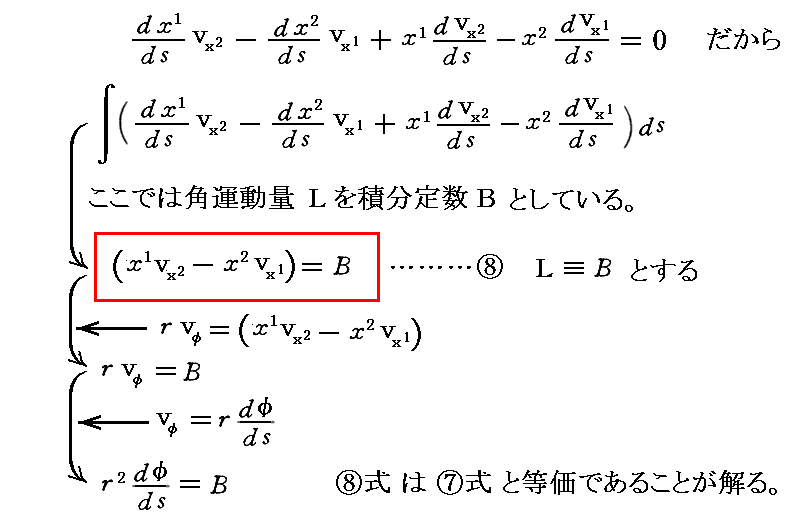 は
は
となります。
[補足説明2] 《重力場方程式の解の定数αを決定する方法》
ここでは、特に明記されていませんが、(8・a)式を考慮して(8)式をニュートン力学惑星運動におけるエネルギー保存則と比較すると、
Φ×c2=-{α/(2r)}×c2=-GM/r
となります。ここで G:万有引力定数、M:中心質量(太陽)、c:光速度 です。
上の右側の等式から、(4・b)で導入した比例定数αの値が α=2GM/c2 となる事が導けます。
もちろん、軌道方程式(運動方程式)段階で比較しても同じ値が得られます。
この定数αは、シュワルツシルドの厳密解のシュワルツシルド定数(“シュワルツシルド半径”とも言う)に相当するものです。この値は、後で近日点移動量を計算するときに必要になります。

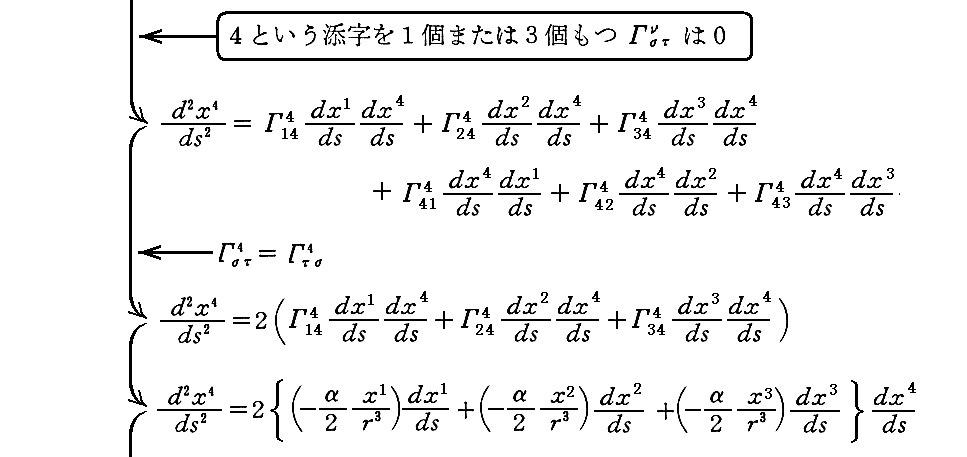
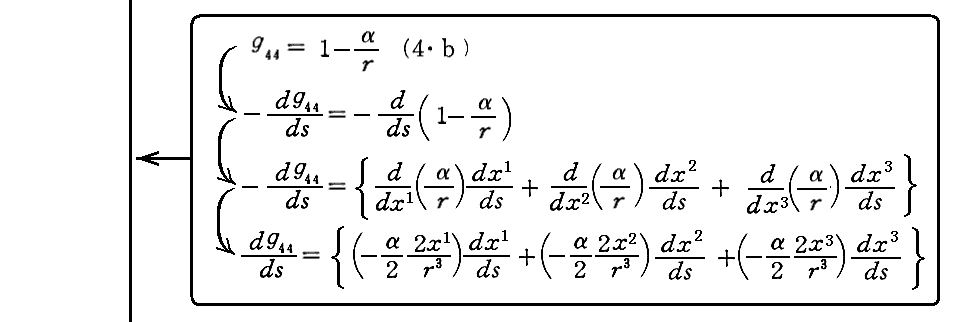

[補足説明3]
実際、(9)式が測地線方程式の解であることは以下の計算から解る。
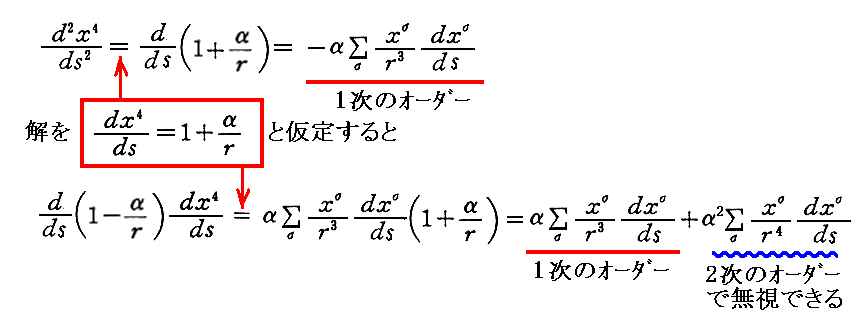
故に確かに1次のオーダーで解となっている。
ここの説明は解りにくいが、別稿の今日的な説明と比較検討してみて下さい。そこの
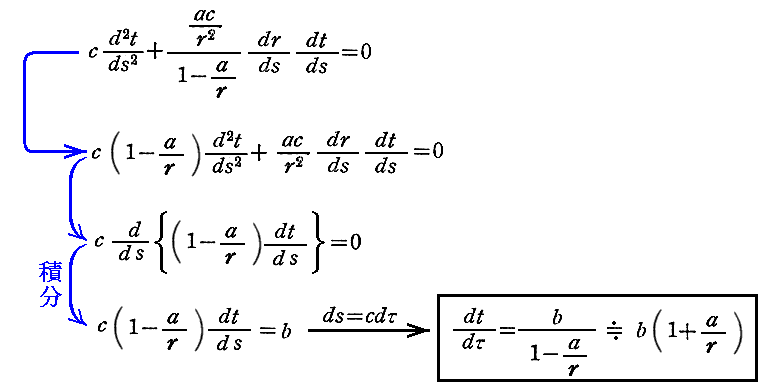
を求める手順が上記のν=4について(9)式を求める手順に対応します。
また、以下のν=1,2,3に付いての議論が、上記別稿の軌道方程式を求める手順に対応します。ただし、Einsteinは極座標ではなく直交座標を用いていますので以下の様になります。



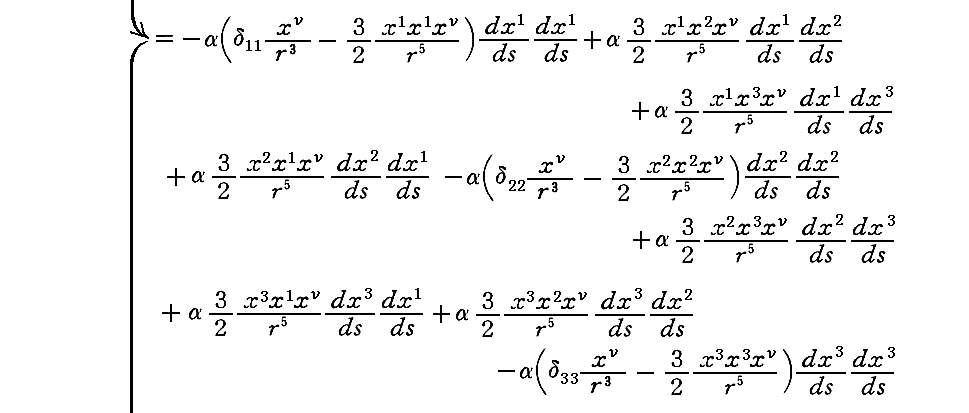
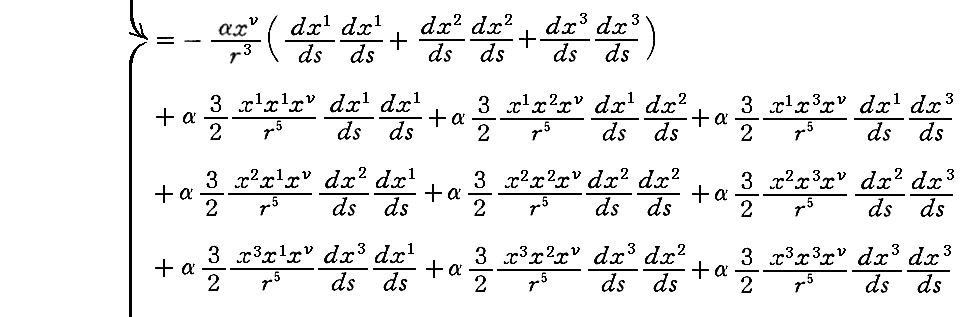
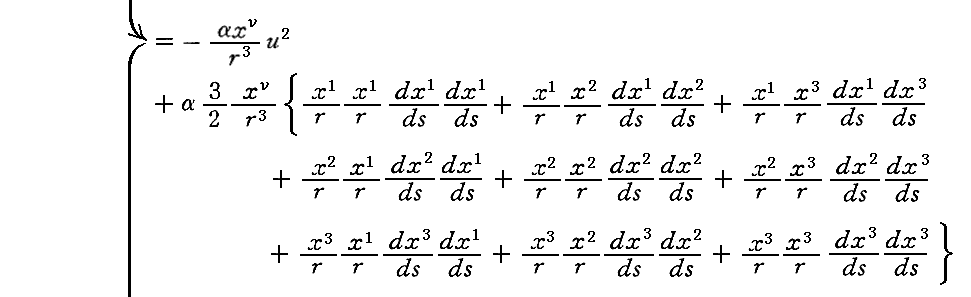




“中心力”の場合には“面積速度一定の法則”が厳密に成り立つ事は、別稿3.(3)(a)をご覧下さい。

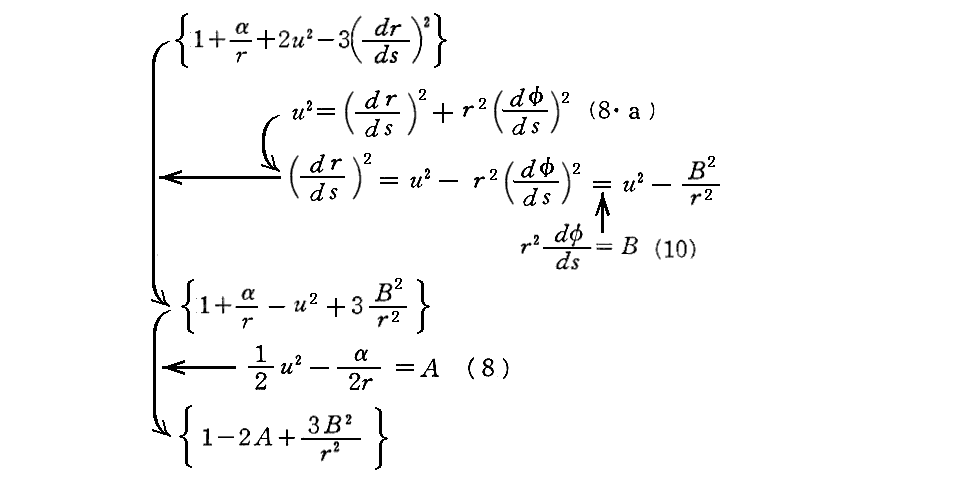
これを用いて運動方程式を変形する。
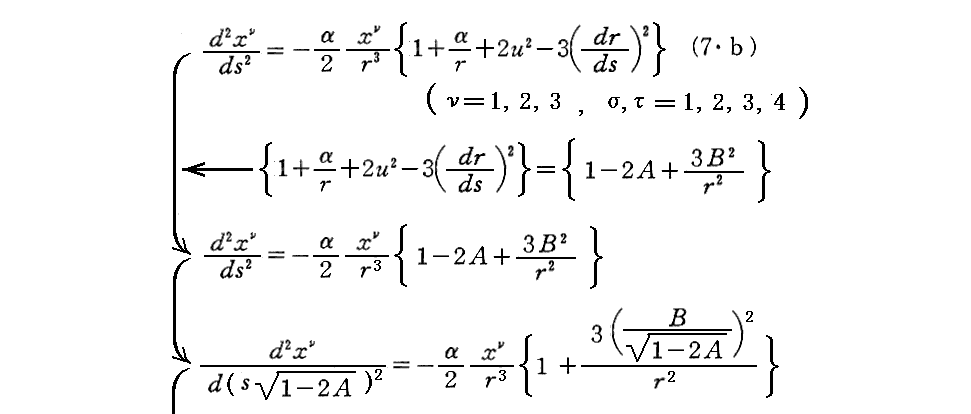

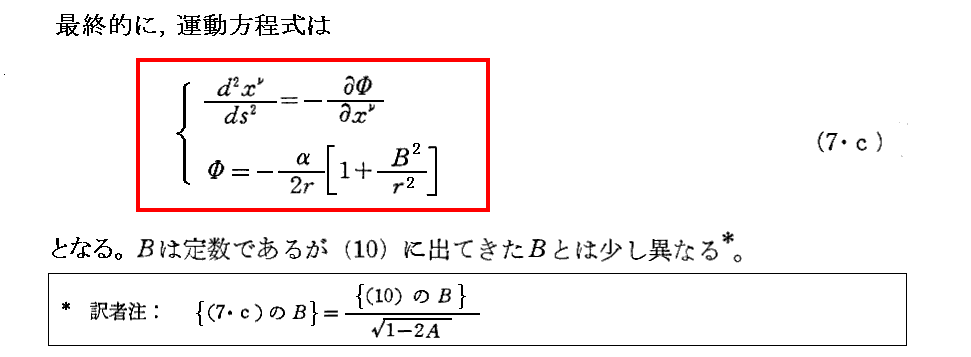
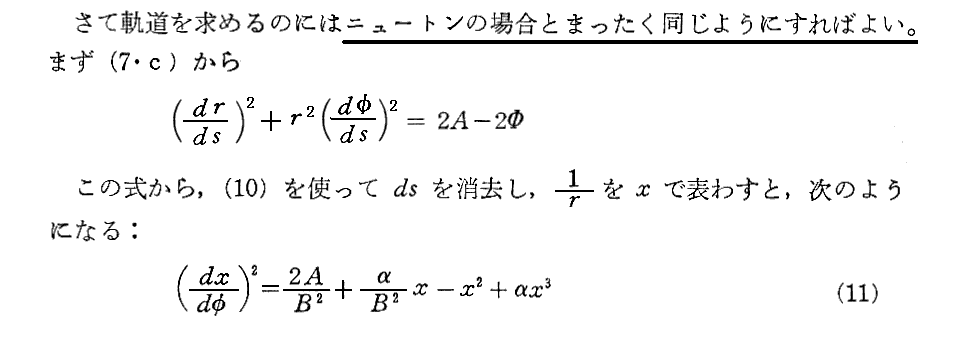
[補足説明4]
(11)式を求める手順を補足しておきます。
まず、上記の“ニュートンの場合と全く同じようにすればよい”と言っているのは別稿「楕円軌道の発見と万有引力の法則」5.(3)2.と全く同じようにすればよいと言うことです。ただしそこのθをここのφで置き換えて下さい。
(7・c)式はポテンシャル関数Φに第2項目の余分な関数が付け加わっているところがニュートン理論と異なりますが、ポテンシャル関数としての運動方程式への関わり方はニュートン理論と全く同じです。
そのため、まず(7・c)式のエネルギー積分を§2[補足説明1]に従って求める。すなわち、①,②式右辺の -(α/2)(xν/r3) を ∂Φ/∂xν で置き換えれば良い。また、そこで注意したように直交座標表示⑤式と極座標表示⑥式は等価です。そうすると、⑤式あるいは⑥式中のポテンシャル関数-α/(2r)は、ここでは Φ に置き換わります。


次に述べられているように 遠日点x=α1=1/rmax から 近日点x=α2=1/rmin まで積分すると、その間の離角φが求まる。これを2倍したものと2πとの差が、1公転したときの近日点移動角となります。
以下の“楕円積分”については数学書をご覧下さい。あるいは、別稿「ブラックホール近傍の力学」3.(4)9.をご覧頂くのが良いかも知れません。

[補足説明4-1]
上記の三次方程式は3つの根α1、α2、α3を持ちますが、三次方程式の三次の項x3の係数αが小さい場合、これらの内の2つの根、例えばα1とα2は
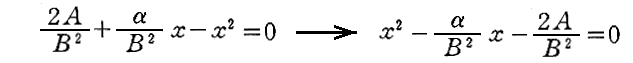
の2根に近似的に等しいはずです。そのとき二次方程式の根と係数の関係から
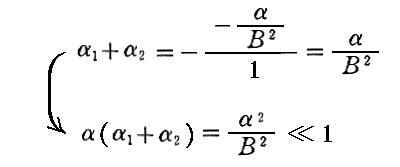
から言えます。さらにもとの三次方程式の根と係数の関係から
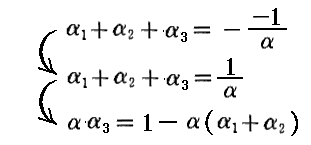
も成り立ちます。
このとき先ほどの被積分関数は因数分解形式に書き換えることができて
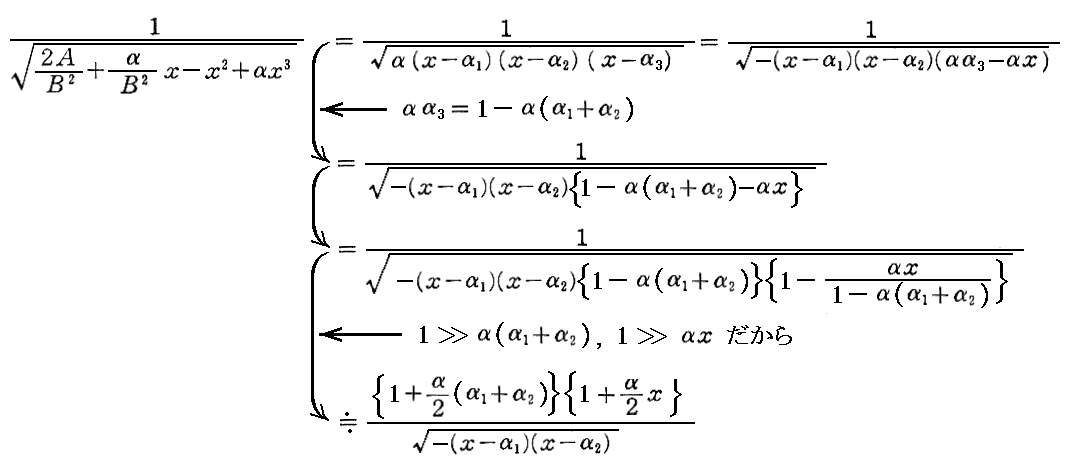
となります。

[補足説明4-2]
実際の積分計算は以下の様になります。 この当たりの説明はメラー「相対性理論」§130が丁寧です。
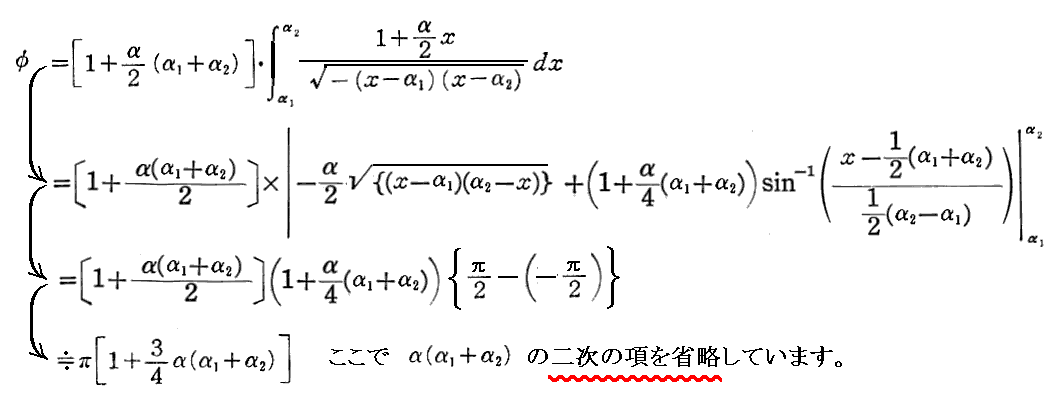 ”
”
上記の最後の2次の項を省略する近似が、Einstein が Sommerfeld宛 の書簡のなかで“こうするとニュートンの理論が第一近似で出てくるだけでなく水星の近日点移動(百年当たり43秒)も第2近似で出てきたことです。”と言っている近似です。

123-02

定数αについては§2[補足説明2]を復習されたし。実際の数値を代入した計算は別稿の《数値計算》をご覧下さい。
[補足説明5]
(12)式を導くとき、“離心率”eについての成り立つ下記の関係式を用います。
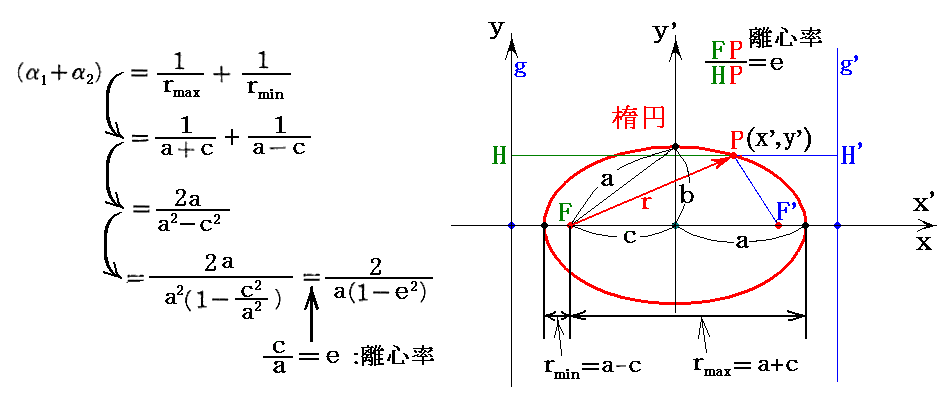
(13)式→(14)式 は“ケプラーの第三法則”を用います。
《円軌道の場合》は、高等物理で習うように
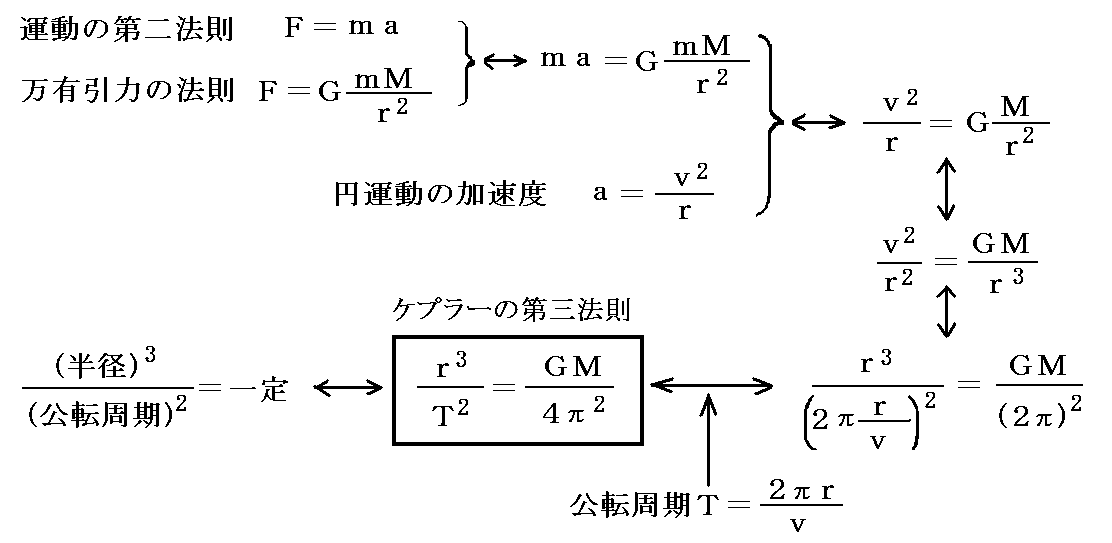
でしたが、より正確な
《楕円軌道の場合》は、別稿「質点の二次元運動」3.(3)(a),(b)で証明した関係式を用いて
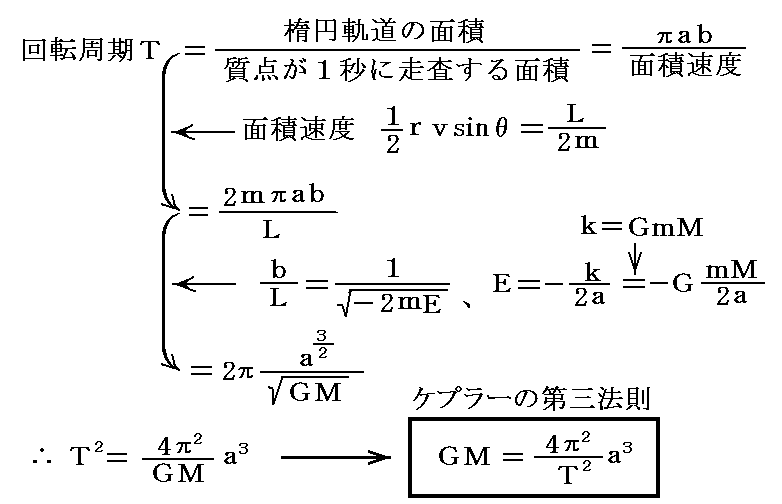
となります。
ここで注意して欲しい事は、ケプラーの第三法則は惑星に働く力が中心力でしかも距離の逆二乗法則に従う場合に成り立つ。しかし、一般相対性理論によると太陽の重力場により時空間が歪みます。その効果は見かけ上、万有引力の法則が距離の逆二乗法則から少しずれる事を意味します。近日点移動が生じるのもその現れです。そのため一般相対性理論ではケプラーの第三法則は厳密には成り立ちません。だから、ここでは近似的に成り立つとして式変形に利用しているのでしょう。
これを(13)式に代入すれば(14)式となる。このとき§2.[補足説明2]で求めた比例定数αの関係式を用いる。
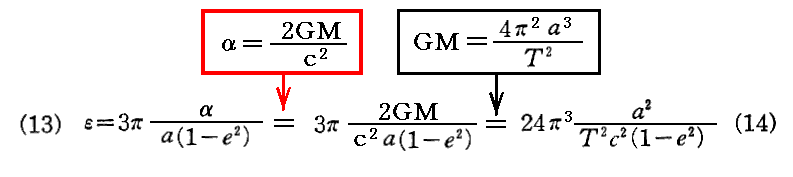

上記の歴史的顛末は別稿クリフォード・M・ウィル著「アインシュタインは正しかったか?}(1989年刊 原本は1986年刊)第 5章 水星の近日点移動(前半部のみ)をご覧下さい。


[補足説明6]
本論文は、Einsteinの一般相対性理論についての論文の中で《最も有名》なものです。
しかし、これはシュワルツシルドの厳密解が発見される前に書かれたものです。さらに言えば、11/25日の最終的な重力場方程式が提出される前に書かれています。つまり、これは、有名な-(1/2)gμνR項を見つける前に書かれています。さらに、この論文で導かれた結果に対するアインシュタインの説明“私の経験した素晴らしいことというのは、こうするとニュートンの理論が第一近似で出てくるだけでなく水星の近日点移動(百年当たり43秒)も第2近似で出てきたことです。”の第2近似でという言い方。私には、これらの事柄が前々から疑問でした。
このたび実際にこの論文を読んで、これらの疑問がすべて解決しました。
それにしても良くこの解法で、精度の良い解を得ることができたと思います。私は、逐次近似で重力場方程式を解くなんてどの様にするのだろうと思っていたのですが、読んで見てどこで近似が用いられているのか良く解りました。
結局対称性の考察を重力場方程式に適用して求めた解(計量テンソルgμν)はシュワルツシルド厳密解と殆ど同じものが得られています。もちろん厳密解と同じではありませんがそれと比較してとても近似の良い解です。このことに付いては本稿§1[補足説明3]で説明した通りです。
だから、EinsteinがSommerfeldに説明している第2近似とは重力場方程式を解くところに用いられているのではありません。対称性の仮定から求めた計量テンソル(gμν)を測地線方程式に代入して惑星の軌道方程式を求める所に用いられている近似について言っていることです。
つまり、この近似を用いる所は(シュワルツシルド厳密解を用いる)今日的な議論で近似を用いる所と同じです。これはある意味こういった方程式を解く常套手段だと言えるかも知れませんが、そのやり方での近似解ながら重要な結論を導き出せる解を得ることができたのですからさすがEinsteinです。
結局、Einsteinは√-g=1の制約を課して簡単化された直交座標表示でも逐次近似法で解くことによっても極めて正確な近日点移動量が導けたと言うことです。
この解き方は別稿7.(7)~(8)で紹介しているシュワルツシルド解を用いる解き方とほとんど同じです。私の推測ですが、シュワルツシルトはロシア戦線から休暇で帰郷したときは、ベルリン科学アカデミーの例会には努めて出席していたようですので、アインシュタインの11/18の本論文の内容も良く知っていた(別稿E.(22)3.[補足説明1]を参照)。
休暇が終わってロシヤ戦線に復帰したシュワルツシルドは、アインシュタインの11/18、11/25論文の印刷版を手に入れたとき、√-g=1の制約を外した“フルタイプのリッチテンソル”で書かれた重力場方程式に対して、“極座標”を適用して11/18論文でEinsteinが求めている解と同じ形のものが別稿[補足説明1-2]で説明した“常套手段”を用いることで導けないか試してみようと思ったに違いありません。天体物理学の専門家だったシュワルツシルトですから極座標を用いた軌道計算には習熟していたはずです。それだからこそ可能だったのでしょう。そしてそれを見事にやり遂げた。
このことに付いては別稿C.(16)[補足説明3] に記したのですが、この論文を読んでその事を確信しました。シュワルツシルドが厳密解を導いた状況については別稿7.(7)[補足説明6]をご覧下さい。
さらに、アインシュタインの逐次近似解法を知って、別稿「一般相対性理論の古典的検証と歪んだ時空」2-3のゼクスルの説明や、そこに引用したランダウの「力学」§15問題3 b)の解の説明が私自身やっと理解できました。
L・インフェルトは「アインシュタインの世界」講談社(1975年刊)の第Ⅱ部“アインシュタインの思い出”のp256で以下の様に語っています。

おそらく、インフェルトはこの論文からアインシュタインの上記の思いを強く感じたのではないでしょうか。
最後にもう一度強調しますが、この論文は膨大な思考で裏付けされた本質を語っており《大論文》です。Einsteinは極めて簡潔な文体で記していますので総ページ数が少なく、これが大論文だとなかなか解りません。しかし、本文は言葉と数式を注意深く選んで極めて簡潔・明快・的確に展開されています。水星近日点移動については1905年以来膨大な思考を続けてきた裏付けがあるからでしょう。読み直すたびにその事を思い知らされます。
5.11月25日論文
この論文を読まれるときPaisの解説第14章p334~336を参照されて下さい。
https://einsteinpapers.press.princeton.edu/vol6-doc/273
https://einsteinpapers.press.princeton.edu/vol6-trans/129
以下の訳文は改造社「アインスタイン全集」第2巻 25番目論文より引用。

上記二つのの報告 p778~はこちら です、また p799~はこちら です。





上記第2巻402頁とはこちらです。


6.万有引力の場の方程式の近似的積分
この論文を読まれるときPaisの解説第15章15d.p364~366を参照されて下さい。
https://einsteinpapers.press.princeton.edu/vol6-doc/375
https://einsteinpapers.press.princeton.edu/vol6-trans/213
以下の訳文は改造社「アインスタイン全集」第2巻 26番目論文より引用。


[補足説明]
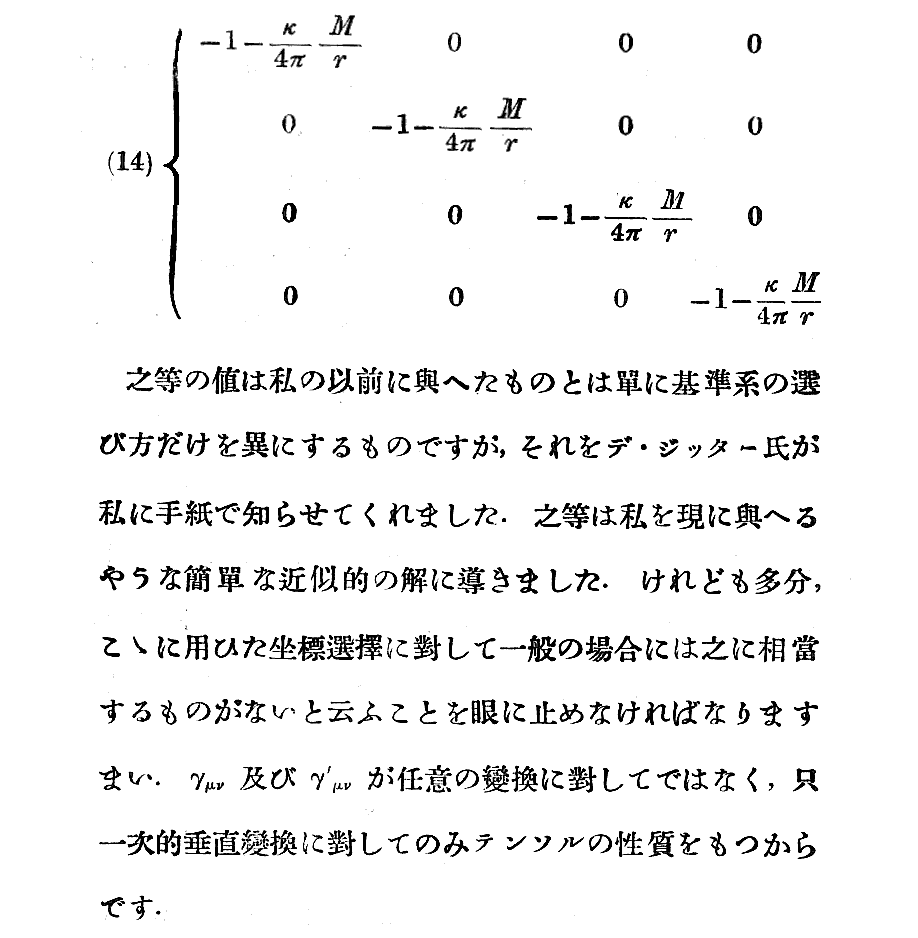
上記の記述について補足します。Einsteinは1915年11/18論文や1916年3月の総説論文「一般相対性理論の基礎」では、制限座標条件√g=-1を課した議論をし、彼の場の方程式は座標系√g=-1に対して有効でした。彼がそのようにした理由は別稿C.(16)[補足説明3]で説明した事情だからでしょう。
そこで注意した様に、シュワルツシルド解を求めるために極座標を利用しようとしたら、この制限座標条件は使えません。それと同様に弱重力場線形近似で利用する座標系は特定のゲージ条件を満たすものであって、座標条件√g=-1を満たしていません。そのため
de Sitter は、弱い場の線形化された近似で場を計算するためには、この制限座標条件を使用しないことが好ましいとEinsteinに通知したのでしょう。
実際、de Sitterは、座標条件√g=-1が放棄されたフルタイプの重力場方程式の方が適切である事を注記(1)の論文で示していたようです。それはおそらく別稿C.(16)[補足説明2-1]で説明した(b)’のタイプなのでしょう。
Einsteinが、今日普通に使われる(c)’タイプではなくて(b)’タイプにこだわったのは、最終的に求まる波動方程式の左辺と右辺の対称性
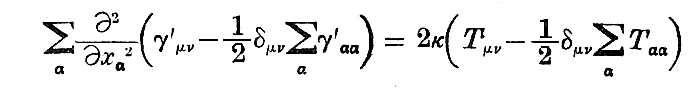
にあるのかも知れません。





[補足説明]
この論文の題目で“近似的積分”と言っているのは、重力場方程式の解であるγ’μνが遅延ポテンシャル形式の積分型の解として得られたことを意味しているのでしょう。
ここまでの内容につきましては、別稿「重力波(gravitational wave)とは何か」で解りやすく説明していますのでどうぞご覧下さい。
なお以下の記述に関しましては、Einsteinが文献8.[A8]の脚注で述べている様に、計算間違いが有るようです。そのため、その部分を修正したと言っている文献8.[A8]の§2以降をお読みになる方がよろしいのではないかと思います。
ただし、この修正の意味するところを理解するのは極めて難しい。


上記の(11)式は間違っています。[A8]論文で説明されます様に、そこの(9)式が正しい。










以下の補遺で述べていることは、後で間違っていた事が解ります。


上記【訳者注】の中の“計算上の誤り”については、Einstein自身が8.[A8]論文の脚注で説明していますのでご覧下さい。また、【訳者注】の中の後の論文“萬有引力波について”で修正したと言っているのは8.[A8]論文§2以降の事です。
実際に“重力波”の存在を確信させる事となった、連星パルサー発見の顛末については別稿「連星パルサーの発見と重力波の存在」をご覧下さい。
7.[A5]ハミルトンの原理と一般相対性理論
この論文を読まれるときPaisの解説第15章15c.p358~364を参照されて下さい。又松原隆彦氏の解説もご覧下さい。
この論文は、任意の物質ラグランジアンに対して、エネルギー・運動量テンソルTμνが重力場方程式の結果としてTμν;ν=0の保存則を満足する事を証明している。
この論文については別稿「テンソル解析学の一般相対性理論への応用」(3)~(4)も参照されながらお読み下さい。
https://einsteinpapers.press.princeton.edu/vol6-doc/437
https://einsteinpapers.press.princeton.edu/vol6-trans/252
以下の訳文は共立出版社「アインシュタイン選集」第2巻 [A5]より引用。
邦訳としては改造社「アインスタイン全集」第2巻 28番目論文も有ります。

以下の†1~†6(解説者注)は別稿で引用した松原隆彦氏の解説文からの引用です。













上記[A3]の(21),(23)式はこちらを参照。



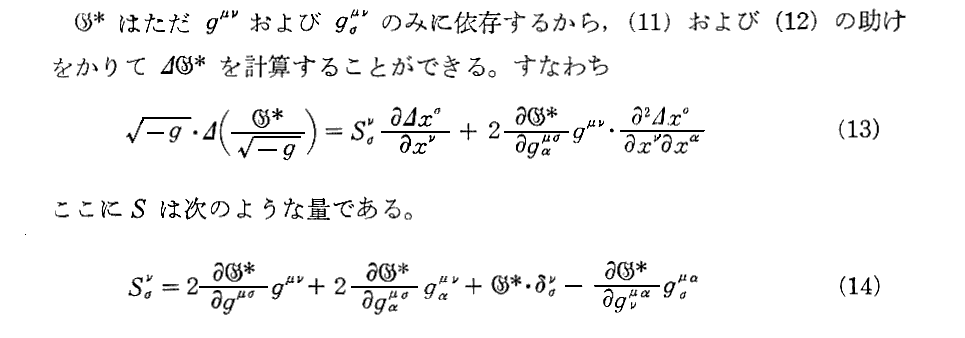





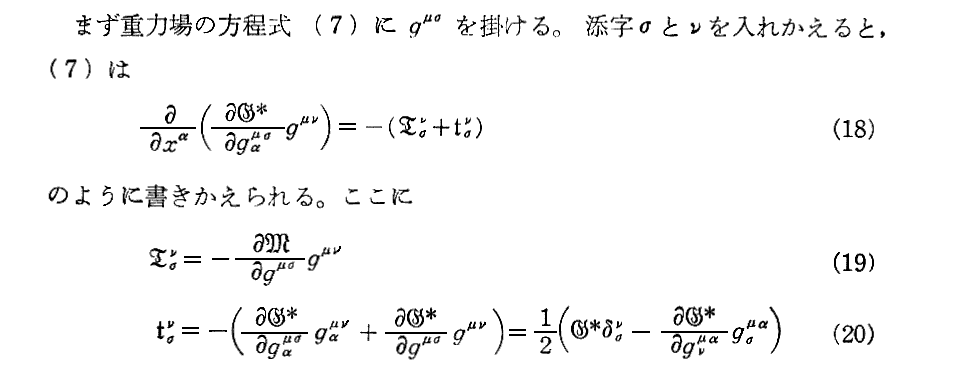





8.[A8]重力波について
この論文を読まれるときPaisの解説第15章15d.p366~367を参照されて下さい。また、Pauliの解説(文献4.§61)を参照。
https://einsteinpapers.press.princeton.edu/vol7-doc/59
https://einsteinpapers.press.princeton.edu/vol7-trans/25
以下の訳文は共立出版社「アインシュタイン選集」第2巻 [A8]より引用。
邦訳としては改造社「アインスタイン全集」第4巻 80番目論文も有ります。


8-161-01

上記§1の内容はなかなか解りにくいところです。別稿「重力波(gravitational wave)とは何か」の1、2章をご覧下さい。
8-161-02

上記[A3]の(50)式はこちらを参照。

上記の tσμ の[A3]における定義はこちらを参照。上記**訳者注は実際に計算して見れば明らか。
8-163-01

8-163-02

[補足説明]
ちなみに、上記の計算間違いをEinsteinに気付かせるきっかけとなったのは、1917年の秋にフィンランドの物理学者Gunnar Nordstro¨m(1881~1923)が√-g=1の座標条件の下で行ったある計算(それは結局誤っていたのですが)です。その結果がEinsteinの1916年論文と異なっていたので、Einsteinに何故異なるのか手紙で質問したのです。
Einsteinは、その違いが何故生じたのかを考察する過程で自分自身で1916年論文の誤りに気付いたようです。下記の文章でそのことを説明しているのですが、その説明は極めて難解です。


https://einsteinpapers.press.princeton.edu/vol7-trans/44
https://einsteinpapers.press.princeton.edu/vol7-trans/47
[補足説明]
上記の説明は極めて難解なので補足します。
このことについては以下の論文
Galina Weinstein著「Einstein's Discovery of Gravitational Waves 1916-1918」(2012/2/16)
が解りやすいのでご覧下さい。
この日本語訳はこちらです。日本語訳がつたなくて済みません。










9.[A7]一般相対性理論におけるエネルギー保存則
Pauliの解説(文献4.§61)を参照。
https://einsteinpapers.press.princeton.edu/vol7-doc/111
https://einsteinpapers.press.princeton.edu/vol7-trans/63
以下の訳文は共立出版社「アインシュタイン選集」第2巻 [A7]より引用。
邦訳としては改造社「アインスタイン全集」第4巻 82番目論文も有ります。














END.参考文献
ここまでの一連のページを作ってみて、Einsteinが“重力場方程式”を導き出した過程を説明してくれている本が、世の中に存在しない理由が良く解りました。
それは、Newtonが“運動の法則”や“万有引力の法則”を発見した過程、あるいはMaxwellが“電磁場の方程式”を発見した過程、を説明してくれている本が世の中に存在しない理由と同じです。
実はそれらの法則の発見過程は、Newtonの『プリンキピア』の中に、あるいはMaxwellの『A Treatise in Electricity ans Magnetism』の中に書かれているのですが、その中にはその法則が成り立つ事を示す膨大な状況証拠が説明されているだけです。つまりNewtonやMaxwellが発見した法則の発見過程を理解しようと思ったら、上記の本全部を読み通すしか有りません。(『プリンキピア』については、その前半のさわりの部分を別稿で、『Treatise』についても、そのごく一部分を別稿で説明していますのでどうぞご覧下さい。彼らの発見過程を理解すると言うことがどの様な事か、その雰囲気は解って頂けると思います。)
それと同様です。Einsteinが“重力場方程式”を発見した過程を理解したかったら、膨大な状況証拠を挙げて、思考を重ねていった彼の論文をすべて読んでアインシュシタインの思索過程をたどってみるしか有りません。
物理法則の発見というものは本来その様にしてしか理解できないものなのでしょう。
Einsteinは「自伝ノート」(1947年著)第5段落に以下の様に述べています。
“私は一瞬たりとも、この定式化が、一般相対性原理に予備的な閉じた表現をあたえるための、単なる応急処置である事を疑わなかった。これは本質的に、現在のところ未知の構造をもつ全体の場からやや人為的に孤立させた、重力場の理論以外の何ものでもないからです。”(この事は、1938年の文献でも述べています)
この事もその理由の一旦かもしれません。要するにアインシュタインが説明できない所を説明できる人などおりはしないと言うことです。
これらの事を理解することが、一般相対性理論を理解するということかも知れません。私自身、ここに至ってEinsteinの言っていることがなんとなく理解できたように思います。その意味に於いて一般相対性理論が理解できたと言っても良いのかも知れません。
最後に補足しますと、今日の書籍の一般相対性理論の展開は、ほとんどすべてが別稿C.(14)[補足説明3]で説明した様な形でなされています。
まあ、これが一般の教科書が取ることのできるやり方であり限界なのでしょう。そのレベルの説明しかできないということが、一般相対性理論の深遠さと難しさを表しているということかも知れません。
この稿を作るに当たって、下記文献を参考にしました。感謝!
- 石原純、他訳「アインスタイン全集 第2巻」改造社(1923年刊)
この中から 11/4全②23、 11/11全②23補講、 11/25全②25、 1916年6/22全②26 を引用。
- 湯川秀樹監修、内山龍雄編訳「アインシュタイン選集 第2巻」共立出版(1971年刊)
この中から 11/18[A4]、 1916年10/26[A5]、 1918年1/31[A8]、 1918年5/16[A7] を引用。
- Abraham Pais著(西島和彦、他共訳)「神は老獪にして・・・(アインシュタインの人と学問)」産業図書(1987年刊)
第13章“重力場の理論(初めの50年)” 13b.
第14章“重力の場の方程式” 14aの後半 と 14c.“最後の歩み”
第15章“新しい動力学” 15c.
- Wolfgang Pauli著(内山龍雄訳)「相対性理論(上)(下)」筑摩書房筑摩学芸文庫(2007年刊)
原書は1921年刊です。上記訳本の元本は1974年に講談社から刊行されたものです。熟読する価値あり。
- C.W.Misner,K.S.Thorne,J.A.Wheeler著(若野省己訳)「重力理論」丸善出版(2011年刊)
この中から、17.7“アインシュタインの方程式の歴史の鑑賞”を引用。
- The collected papers of Albert Einstein Volume 6: The Berlin Years: Writings,
1914-1917
(https://einsteinpapers.press.princeton.edu/vol6-doc/)
- L・インフェルト著(武谷三男、篠原正瑛訳)「アインシュタインの世界」講談社(1975年刊)
第Ⅱ部“アインシュタインの思い出”のp256を引用。