ブラックホール近傍の力学
1.導入
(1)Einstein解の復習
Einsteinは自らが作り上げた一般相対性理論の中心法則として「重力場方程式」を1915年11/25日に発表します。同時期に、彼はこの方程式の正しさを証明するために、今では古典となった三つの観測可能な現象の検証を提案します。その三つとは
- 水星の公転軌道の近日点移動量が説明できること。
- 太陽の側を通過してくる光線は視線角度として1.7”ほど湾曲すること。
- 恒星の表面から発出したスペクトル線は赤い方へずれて見えること。
です。
Einsteinは、1.2.3.のすべてについて文献2.の中で説明していますが、2.と3.は文献1ですでに論じているので、文献2.ではごく簡単に(ここと、ここで)済ましています。2.と3.の丁寧な説明は後の文献3.E.§22.で取り上げています。
いずれにしましても、その説明は重力場方程式
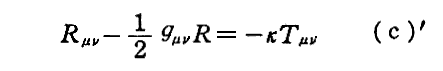
を近似的に解いた解を用いて展開されています。
ただし、この重力場方程式は極めて複雑な10元連立の非線形偏微分方程式なので簡単には解けません。そのためアインシュタインは、上記の形の方程式では無くて、√-g=1の条件を課した
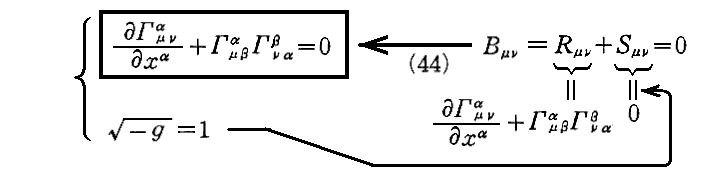
の形の重力場方程式を解いています。これは、(重力場は存在するが)物質が存在しない所での重力場方程式ですが、もちろんこの形でも完全に正しい方程式です。
そのとき、Einsteinは球状に分布する質量(彼は太陽を想定している)の外側の時空間の様子を示す解を求めました。彼の求めた近似解は、太陽半径の外側の時空間については極めて近似の良い正しい解でした。
実際、別稿「アインシュタイン著一般相対性理論の基礎」E-22[補足説明3]で説明した様に、彼の得た近似解は
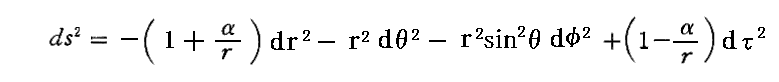
ですが、この解は、別稿[補足説明5]で説明した様に、この近似解発表のすぐ後の1916年1月に発表された《シュヴァルツシルドの厳密解》
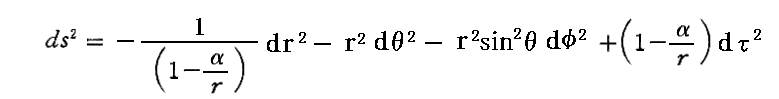
に極めて近いものでした。
つまり、《Einsteinの近似解》は
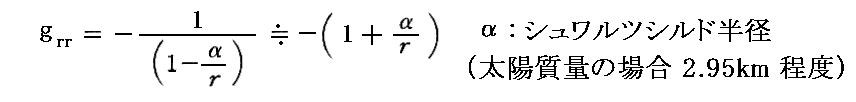
と近似するものですが、太陽半径(6.96×105km)より外側の領域に於いては、rはシュワルツシルド半径α(約3km)よりも圧倒的に大きい(r≫α)ので (α/r)<0.00001 となります。 そのため、太陽半径より外側の領域において、この近似解は極めて精度が良い!!
実際の所、一般相対性理論が作り上げられた時代には恒星半径より外側の領域で生じる現象しか取り扱えなかったのですから、《アインシュタインの近似解》で計算精度が不足する様な問題は存在しなかったのです。
その事は、裏返せばニュートン理論と一般相対性理論との差がごく僅かで、実験・観測によって一般相対性理論による効果を検証することが極めて困難だったということです。このことに付いてはPaisの解説p356をご覧下さい。
(2)シュワルツシルド解以後の厳密解の発見
ところで、重力場方程式の厳密解には、《シュヴァルツシルト解》以外に、《カー解(Kerr solution)》があります。これは、高密度天体が自転回転している場合に、その周りの時空を表す解ですが、ニュージーランドの数学者ロイ・カー(Roy Kerr)によって発見された。(R.
P. Kerr、“Gravitational Field of a Spinning Mass as an Example of Algebraically
Special Metrics”, Phys. Rev. Lett. 11, p237, 1963年)
実際、彼は、下記の様な軸対称(gijがφを含まない)の計量を持つ時空がEinstein方程式を厳密に満たす事を示した。
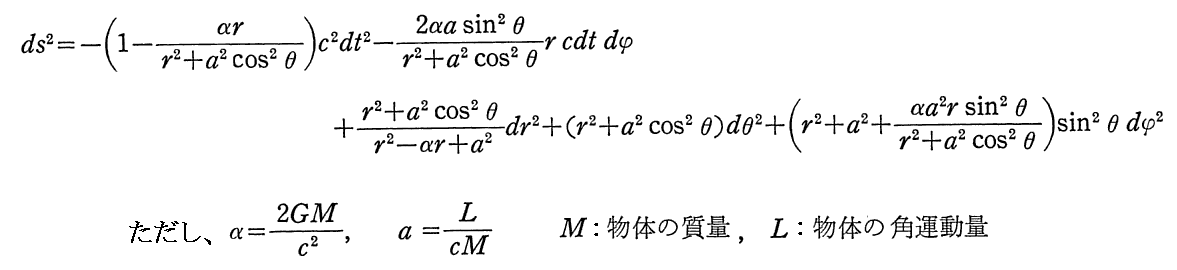
この時空解は、定常(gijが時間を含まない)であるが、cdtdφの係数g02が0でないため時間の符号の反転について対称ではない。また、これは a→0 の極限で《シュヴァルツシルト解》 に帰着します。ただし、これを導くにはかなり複雑な計算が必要です。
このとき、ブラックホールの持ち得る最大の“角運動量”Lについて
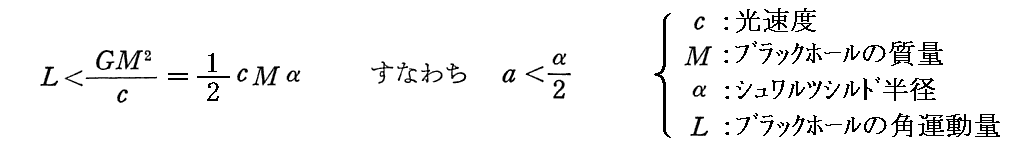
の制限があると言われています。これはシュワルツシルド半径αの付近で、質量Mの物体を光速に近い速度で回転させた場合の角運動量です。
Kerrがこの解を見つけた当時の状況については、別稿“ブラックホールって呼べば?-Kerr-”をご覧下さい。
さらに、《カー解》発見の2年後の1965年に、アメリカのエズラ・ニューマン(Ezra T. Newmann)は、高密度天体が角運動量に加えてさらに電荷を持つ場合の時空間解である《カー・ニューマン解(Kerr‐Newman solution)》を発見した。当然電荷分布も回転しています。
この解の電荷Qをゼロにする と《カー解》 に帰着、角運動量Jをゼロにすると 《ライスナー・ノルドシュトルム解(Reissner‐Nordstro¨m solution)》 に帰着する。さらに電荷Qと角運動量Jの両方をゼロにすると 《シュヴァルツシルト解》 に帰着します。
さらに補足しますと、カー・ニューマン解の計量がブラックホール外部の時空間の計量として成り立つのは
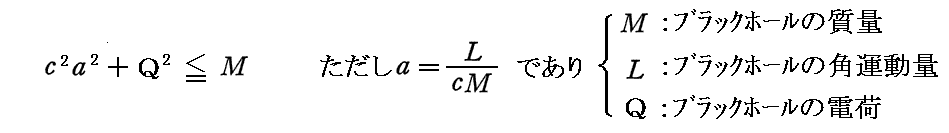
の時です。
上記の、《ライスナー・ノルドシュトルム解 (Reissner-Nordstro¨m解)》 は、一般相対性理論のアインシュタイン・マクスウェル方程式(あるいはこちらを参照の厳密解の一つで、球対称で電荷を帯びているが回転していない高密度天体の周りの時空間を表現する解です。当然電荷分布も静的なもので回転していません。
シュヴァルツシルト解の発見直後、ドイツのハンス・ライスナー (Reissner)が1916年に点状電荷の場合で、さらにフィンランドのグンナー・ノルドシュトルム
(Nordstro¨m)が 1918年に球対称帯電体の場合で場の方程式を解いて求めた。 ちなみに、このノルドシュトルムは別稿文献中に出てくる人です。
この解はWeylの「空間・時間・物質」(1922年刊の第5版)§33で説明されています。そのとき参考文献として
Reissner, H. , “U¨ber die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie”, Annalen der Physik(in German), 50 (9): 106-120, (1916)
Weyl, H. , “Zur Gravitationstheorie”, Annalen der Physik (in German),
54 (18): 117-145, (1917)
Nordstro¨m, G. , “On the Energy of the Gravitational Field in Einstein's Theory”,
Versl. d. k. Akad. v. Wetensch. Amsterdam, 20, Nr.9,10 ,1238-1245 (1918)
を挙げています。
また、内山龍雄著「一般相対性理論」§43もご覧下さい。この説明は解りやすいです。

そこに書かれているのですが《ライスナー・ワイル解(Reissner‐Weyl solution)》と言うこともあるようです。
また、Edington, “Mathematical_theory_of_Relativity”, (1923年)§78 は Nordstro¨mの論文
のみを挙げています。
幾つか補足します。
まず、《Reissner-Nordstro¨m解》はベルグマン著「相対性理論序説」(1942年刊)第13章で説明している《電荷質点の場の解》

ですが、ベルグマンは、この解を誰が求めたか特に記していませんので、おそらくこの解は《シュヴァルツシルト解》の自然な拡張として当時の研究者には、当然のごとく受け入れられていたのでしょう。
また、その続きに《回転対称性は持つが球対称ではない静的物体の周りの解》が説明されていますが、これはWeylとLevi-Civitaが解いたと明記して、その文献を引用紹介しています。こちらの解法がより複雑な考察を必要とするからでしょう。
この解についてはWeyl自身が「空間・時間・物質」(1922年刊の第5版)§35で説明しています。さらに、補足しますと佐藤・ルフィーに文献10.で説明されている様に、この“Weyl解”と“Kerr解”を組み合わせた様な解が“富松・佐藤解”のようです。
[補足説明1]
上記の《ライスナー・ノルドシュトルム解(Reissner‐Nordstro¨m solution)》 に付いて補足します。
この解は、唐木田健一著「ひとりで学べる一般相対性理論」第Ⅱ章10“アインシュタインの重力法則”の文頭に書かれている以下の説明にも関係します。


上記の“電磁場も「物質」に含まれる。”の意味は電磁場も重力の発生源になると言うことです。
《ライスナー・ノルドシュトルム解》 は、質点の持つ質量に加えて静止した電荷が生み出す位置エネルギー(つまり電磁場がさらに追加の質量の存在を意味する)が時空を歪ますと考えれば、シュヴァルツシルト解を求める手順とほぼ同様な考察で導けるのでしょう。
ここで、“「物質」とは、重力場以外の物すべてのことである。”という言い方に注意して下さい。つまり(Ⅱ.10,1)式Rμν=0は重力場が存在する場所でも成り立つと言うことです。もちろん、その重力場は重力場を生み出す「物質」そのものではありませんが、その重力場の存在が時空を歪めるのです。ここは極めて解りにくい所です。
「物質」では無いこの重力場の意味に付いては、3.(4)2.[補足説明1]で紹介したゼックスルの説明をご覧下さい。ただし、私自身は、そこのゼックスルの説明で正しいのか、本当の所は良く解りません。
上記引用文に続く説明が以下です。




(3)高密度天体の発見
1955年にEinsteinが他界した後、天文学の観測技術は急速に発達していきます。
- 屈折式望遠鏡から反射望遠鏡へ
- 目視から写真撮影による観測へ
- 反射望遠鏡のさらなる大口径化
- 電波領域の探査へ
- X線・γ線領域の探査へ
- 赤外線・紫外線領域の探査へ
- 電子技術の進歩にもとずくCCD(Charge-Coupled Device)デバイスや補償光学の発展
- 電子計算機の発展による様々なシミュレーション技術の発展
- ロケット技術の発展により人工衛星打ち上げが可能になり、大気圏外での観測へ
それらの技術革新により、新天体が次々と発見されてきます。極めて狭い領域に質量が集中して存在する高密度天体である 白色矮星、中性子星、ブラックホール、クェーサー(quasi-stellar radio source) です。そして、今日ではそれらの天体は膨大な数存在することが明らかになっています。
特に、ブラックホールは、シュウァルツシルド半径αより狭い領域に質量が集中しているために、その質量外領域の r が α に一致するまで近付いた時空領域を解析対象としなければ成らない天体です。
そういった領域においては、《アインシュタインの近似解》では役立たず、《シュヴァツシルドの厳密解解》が必要になります。
1.(2)節で述べたように高密度天体の周りの重力場方程式の厳密解には4通りあるのですが、角運動量や電荷を含めた場合の議論は難しくなるので、ここでは、高密度天体が角運動量や電荷を持っていない場合に限定して論じます。
すなわち、《シュヴァルツシルド解》を用いてシュワルツシルト半径~太陽半径程度の領域のブラックホール近傍空間に於ける粒子と光子の運動を考察します。
1.(1)節で述べた通常恒星の外部領域での議論と違って、ブラックホール近傍領域ではNewton力学理論と相対論力学理論との違いが顕著になります。
2.基本法則
ニュートン力学と相対論力学を対比しながら説明します。
(1)ニュートン力学
ニュートン力学における基本法則は、
“万有引力の法則”
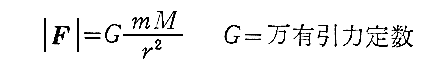
と、
“運動の第2法則”
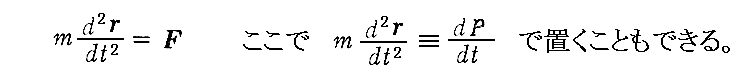
です。
いずれにしても、これらの法則は2.(2)で説明する厳密・正確な法則の近似的法則です。
後でくわしく説明しますが、質量密度が極めて大きい場所が無ければ、その近似の程度は極めて良い。しかし、質量が集中した天体の周りでは、厳密・正確な法則との差が露わになります。
1.“万有引力の法則”について補足
- 力のベクトルFの方向ですが、この法則は質量Mに対してはM→mの方向へ、質量mに対してはm→Mの方向へ働く二つの事柄を表しています。
- この法則中のFは、質量が存在することで生じる万有引力だけを想定しています。つまり電磁的な力やそれ以外の核力、弱い力、・・・などは考えてはいません。
- この法則はmとMの位置が時間的に変化する場合において、その力Fの働き方はmとMの配置の変化に応じて瞬時に調整されて新しい大きさと方向に変化する事を示しています。
つまり、ニュートン力学におけるこの基本法則には時間変数は含まれていません。空間と時間は全く独立な存在なのです。そのため、この法則からはどう考えても重力波の思想や、力は有限の速度でしか伝わらないという考え方は出てきません。
- この法則はあらゆる空間が平坦であり、あらゆる場所の時間は均等に経過していく事を前提とした上での法則です。
- この法則は質量Mに付いても、質量mに付いても等しく成り立ちます。だから本来、二体問題としての解析が可能です。
- この法則は別稿「ポアソン方程式と波動方程式」1.(1)で説明した様に、“ポアソン方程式”
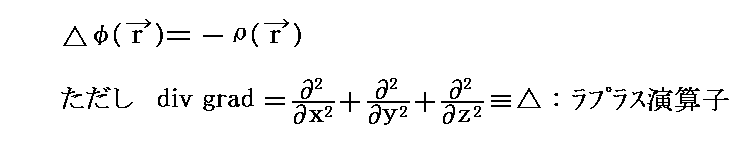
と同等です。
この形にしておくと、2.(2)相対論力学の“重力場方程式”が、この方程式の自然な拡張である事が解りやすいかも知れません。
2.“運動の第2法則”について補足
- この法則中のmについては、特殊相対性理論が示した様にvの変化に応じてその質量が変化するのですが、ニュートンの古典論では、そのことは考慮されていません。
質量はその位置や速度が変わったからと言って変化することは無いとしています。
- この法則中のFは、質量が存在することで生じる万有引力だけを想定しています。つまり電磁気力、核力、弱い力、等々・・・は考えてはいません。
(2)相対論力学
ニュートン力学における“万有引力の法則”に対応するものが、Einsteinの
“重力場方程式”
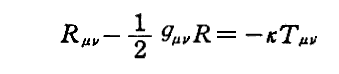
です。これはEinsteinが1915年11/25論文で発表したものです。
一見すると、上記の表現はEinstein論文中の表現と少し違う様に見えますが同じものです。このことに付いては別稿「一般相対性理論の基礎」C.(16)[補足説明2]をご覧下さい。
また、ニュートン力学における“運動の第2法則”に対応するものが
“測地線方程式”
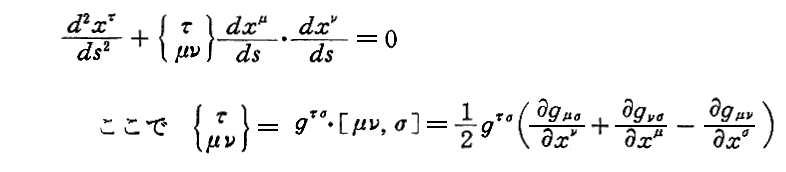
です。Einsteinは、これを1914年10月論文B.§7で初めて導いています。
この二つの法則は2.(1)で取り上げた二つの法則をより一般的、かつ厳密にしたものです。
ただし、Einstein自身は、これらの法則は、やがて発見されるであろう、電磁気力・その他の力・・・を含めた、統一的・究極的な法則の近似的な表現だろうと思っていました。実際、今日の物理学者の多くはその様に理解しています。そして究極法則の探求は続いています。
1.“重力場方程式”について補足
- この方程式の右辺は時空間の中に存在する質量(エネルギー・運動量テンソル)を意味します。左辺は時空間のひずみ具合を表しています。つまり右辺の質量の存在により右辺の時空間のゆがみを生じるのですが、両者の互いの関係を表しています。このことについては別稿前書き[補足説明1]をご覧下さい。
- この法則中には、質量(エネルギー・運動量テンソル)が存在することで生じる時空間のゆがみを表します。電磁気的なエネルギーや、その他の形のエネルギー形態も含んだ方程式ですが、本稿では質量によって生じる時空間のゆがみだけを考えることにします。
- ニュートンの万有引力との比較で考えますと、右辺が質量Mやmの存在・分布の状況を表しており、左辺がそれらの間に働く力を、質量M、mによりその回りの時空間がどの様に歪むかを持ってして表している。
- このとき、Mとmの時空間での配置が時間的に変化するとそれに応じて、その回りの時空間がどの様に変化するかも表しています。すなわち、この方程式は時間座標も含んだ方程式だと言うことです。そのため、Mやmの配置の時間的変化に応じてその回りの時空間がどの様に変化するかも表しており、時空間の変化が行き渡るのに時間がかかることも示しています。
- “重力場の方程式”は、“万有引力の法則”と違って、時間変数も含んだ時空間の状況を規定する4次元の法則です。実際、この“重力場の方程式”は、重力場が弱い場合(Mやmの密度がそんなに大きくない場合)、近似的に重力場についての“波動方程式”に書き換えることができます。

この近似的な形に書き換えてみれば、質量Mやmの配置の時間的な変化に伴って、その回りの時空間のひずみが周囲に波動となって伝播していき、Mやmの新しい空間配置に応じた時空間のひずみ状体が少し遅れて実現されることが解ります。つまり、重力は遠隔力ではなく近接力である事を表しています。
- 上記の様に、“重力場の方程式”が“波動方程式”で近似できると言うことは、“ポアソン方程式”→“重力場の方程式”への一般化が、別稿「ポアソン方程式と波動方程式」2.(4)で説明した様な意味での拡張でも有るわけです。
2.“測地線方程式”について補足
- “測地線方程式”は、ニュートンの“運動の第2法則”を一般化・厳密化したものです。その事については、ランダウ・リフシュツ「場の古典論」§87の説明が秀逸です。
- この法則の第2項は時空間のひずみに関係しますが、この時空間のひずみこそが“運動の第2法則”の右辺の力に相当するものです。
3.粒子の力学
ここでは、Mが高密度・大質量で静止しており、mはMに比較して軽量の場合を取り上げます。
(1)ニュートン力学
本来Mとmの互いの動きを考えたときmの位置が時間的に変わればそれに応じてMに働く力も変わりMも動きます。つまり、前節2.(1)で説明した基本法則を用いて問題を解くときには本来は二体問題として議論しなければ成りません。
しかし、それを実行するのは面倒なので、Mが超高密度・大質量の静止した天体の場合を考えます。そのことは、Mが作る力の場が静的で時間的に変化しない。またmの質量はMに比べて小さくそれが作る力の場は無視できるとして、mの運動を考えます。つまり、一体問題として考えます。
1.運動方程式の具体化と角運動量保存則
まず、高密度・大質量Mを原点として、質点mに働く引力Fを、質点mに対する運動方程式に適用すると

となります。
さらにベクトル演算の性質から
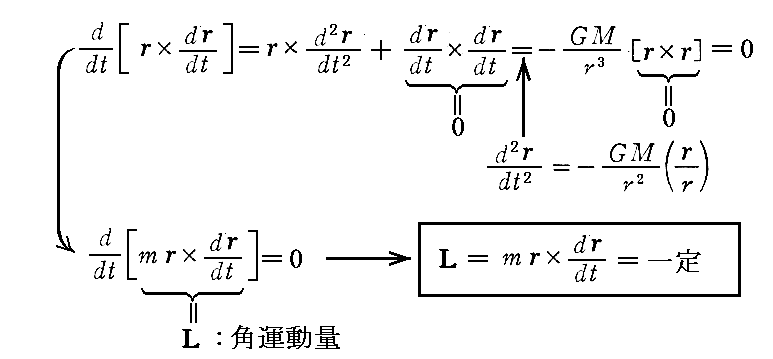
となりますので、質量Mの周りを回る質点mの持つ“角運動量”Lは常に一定であることが言えます。
このことは、質点の運動が質量Mを含んだ一つの平面内に限られることを意味します。その平面は上記の一定である“角運動量ベクトル”Lに垂直な平面です。
その為、以下の議論を最初から一つの二次元平面に限って論じる事ができる。その平面内に直交座標(x,y)と極座標(r,θ)があるとする。
2.エネルギー保存則
前項の結論を用いると

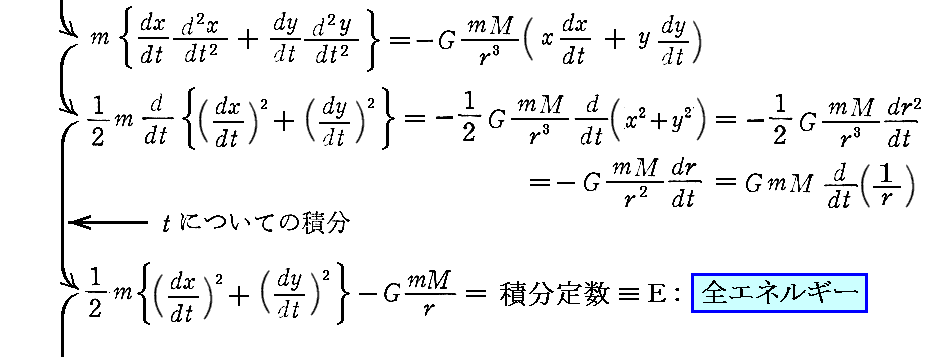

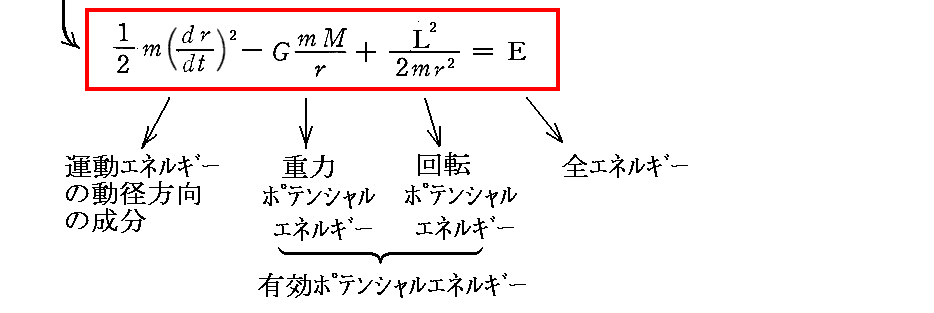
が得られる。
上記の手順は、別稿「エネルギー保存則」4.で説明した様に、エネルギー保存則を得るための常套手段です。エネルギー保存則の導出については、別稿「二体問題」1.(2)2.で、あるいは別稿[補足説明1]で引用しているエネルギー積分で説明していますので参照して下さい。
また、ここで得られたエネルギー保存則のグラフ表示については
別稿「質点の二次元運動」3.(3)(b) と、「質点の二次元運動」3.(1)~(2)をご覧下さい。このグラフは後で繰り返し参照します。
3.軌道方程式
次に軌道の形を定めます。すなわち r を θ の関数で表す事を説明しなければ成らないのですが、このことは別稿「二体問題」1.(2)1.~2.の中ですでに説明しました。
さらに、詳しい説明は別稿「楕円軌道の発見と万有引力の法則」5.(3)1.と、別稿「楕円軌道の発見と万有引力の法則」5.(3)2.でしていますので、ここでは省略します。
[補足説明1]
別稿「楕円軌道の発見と万有引力の法則」5.(3)2.で求めた軌道の形を表す解
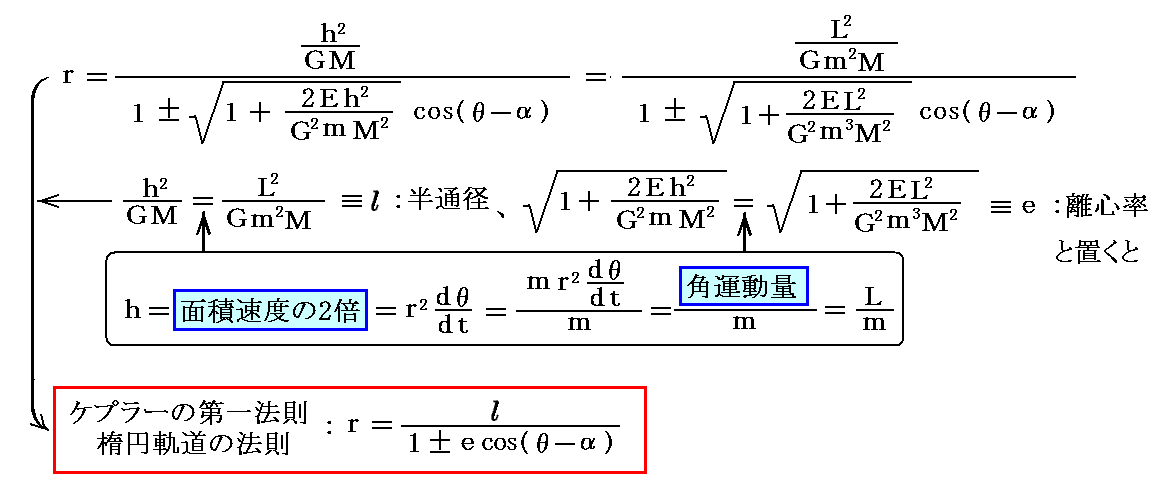
は、楕円(e<1)の場合はもちろんですが、それ以外の、放物線(e=1)や双曲線(e>1)も含めた一般の二次曲線が解となることを表してます。このことについては別稿「二次曲線の性質」5.でご確認下さい。
(2)相対論力学
Mはmに比べて大質量であり、空間の一点に静止しているとします。つまり、Mの周りの時空間のひずみ・変形は時間的に変化しない静的なものとします。またそのとき、Mに比べて軽量の質点mが作り出すその周りの時空間のひずみは無視できるとします。
これは丁度、ニュートン力学の場合の二体問題を一体問題に還元して論じる事に相当するものですが、それを“Schwarzschildの厳密解”を用いて論じます。以下は内山文献9.§36からの引用です。
質量M(ブラックホール)は空間座標系の原点に静止しているとする。いま簡単のためにMは電荷を帯びておらず、また回転していないとする。Mの周りを運動する質点m(惑星あるいは遊星)の座標を
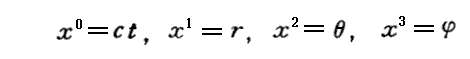
とする。またその質点mの固有時間をτとする。
[補足説明1]
この座標の意味は非常に解りにくいのですが、無限遠の観測者が、質量Mの周りの時空間のひずみが無いものとして引いた座標軸であり、座標値だと思って下さい。このことに付いては別稿「一般相対性理論の古典的検証と歪んだ時空」3-3の図20を参照されたし。今後、この座標を“シュワルツシルド座標”と言うことにします。
そうすると、mの従う運動方程式は、作用積分の作用関数(Lagrangian)L を以下の様に取った“変分法”から導かれる。
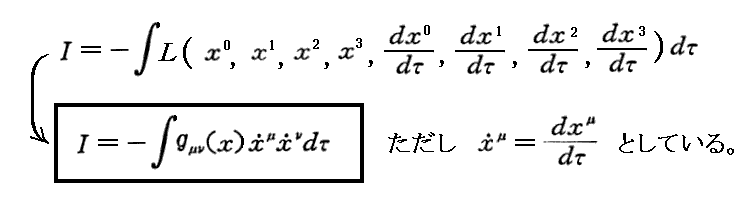
このことは別稿「等価原理」(4)などで説明しましたので、そこを復習して下さい。ただし、そこの矢野文献の添字の付け方と本稿(内山文献9.)のそれは異なります。又、そこの係数 r
はここでは固有時間τに置き換えています。以下は文献9.にしたがって展開しますが、今後そのことに対する注意は繰り返しませんので気を付けて下さい。
上記の作用積分式に“Schwarzschildの厳密解”の計量成分を代入すると、作用積分 I は
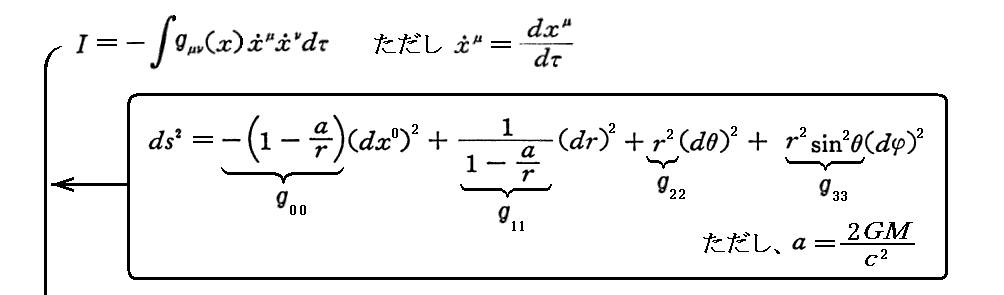
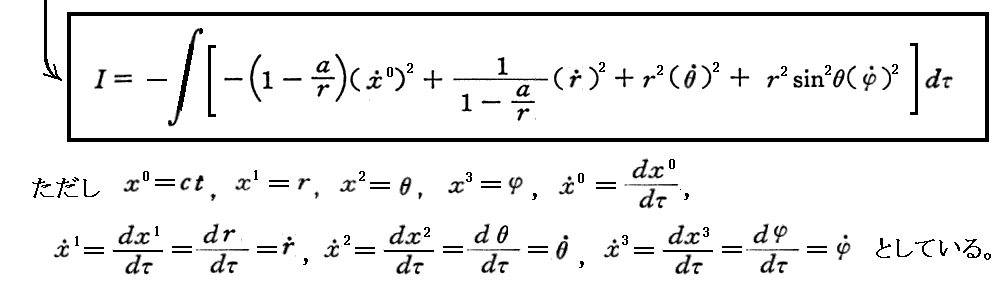
となる。ただし a は質量Mの重力半径(いわゆる“シュワルツシルド半径”)2GM/c2 です。
これより、次に記す“Lagrange方程式”(Euler方程式)が得られる。
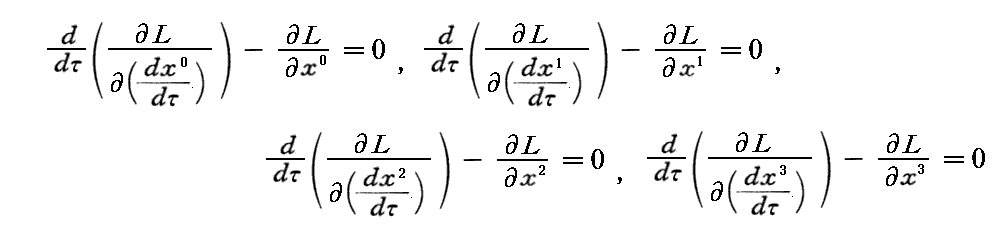
これから、質点mの運動方程式はつぎの様に定まる。すなわち
- x0 に関する変分から

x0=ctが作用関数(Lagrangian)Lの中に含まれていない循環型変数の為に、それに共役な運動量p0の時間積分が一定である事が言える。(この保存則はエネルギー保存則に関係する)
- θ に関する変分から
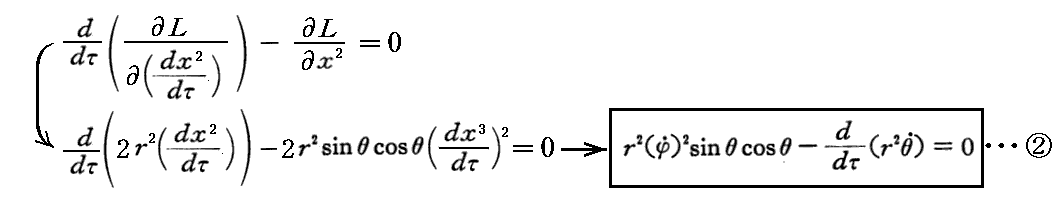
- φ に関する変分から
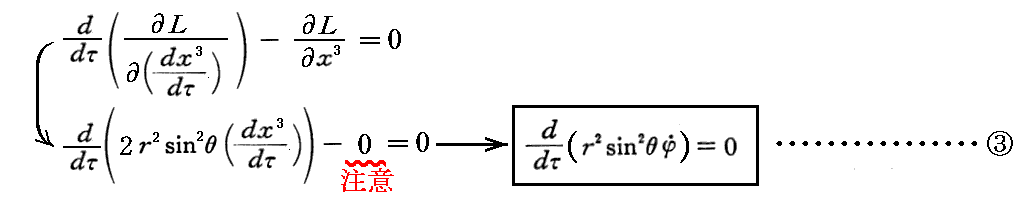
ここでも、x3=φが作用関数(Lagrangian)Lの中に含まれていない循環型変数の為に、それに共役な運動量p3の時間積分が一定である事(いわゆる角運動量保存則)が言える。
- r に関する変分から
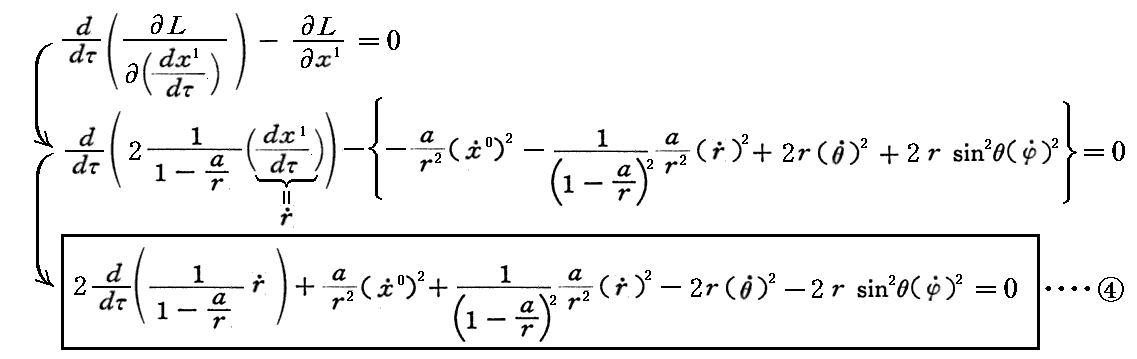
が求まる。
さらに、固有時に関する定義式
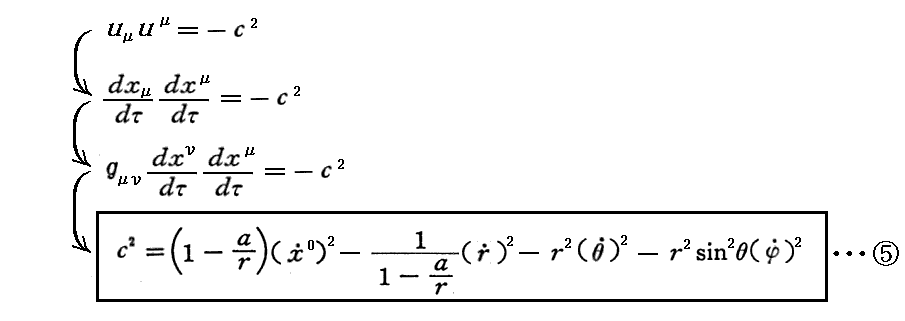
が成立する。これは、(ds)2=-c2(dτ)2ですから、シュワルツシルド解の両辺をdτで微分したものからも求まる。
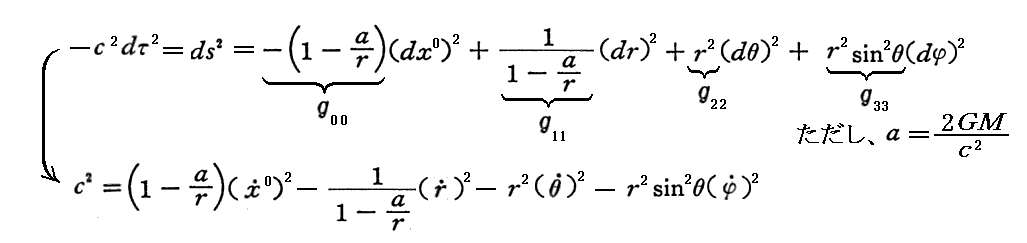
このとき、この定義式と先に得た4個の方程式は互いに独立ではない。そこで、その形が似ている r に対する“Euler方程式”④の代わりに⑤式を用いてもよい。
[補足説明2]
まず言える事は、②式をτに付いてn-1回微分すれば、 dnθ/dτn と dkθ/dτk(k=0,1,2,3,・・・,n-1)の間の関係式が導かれる。そこで、初期条件としてτ=0において θ=π/2 、dθ/dτ=0 とおけば、②をτについて順次微分することにより
θ のあらゆる階数の微分がすべて 0 となることが解る。したがって θ=π/2 は一つの解である。
今後はその解を採用することにして θ=π/2 の面内(すなわちxy平面内)の運動のみを考察することにする。
つまり、上記の方程式の解は質量M(ブラックホール)を含む一つの平面内の運動に限られると言うことです。その為、その平面としてxy平面を取り上げて今後の議論をすると言うことです。
上記の考察から③式中のθをπ/2とした場合を考えれば良い。そうすると

が得られる。 これはNewton力学における“面積速度一定の法則”に相当する。
また、①式から

が得られる。これらの関係式は次節以降で用いる。
[補足説明3]
以上で“基礎微分方程式”①~⑤と“初期積分”③’と①’を導いたのですが、ここよりも正統的な“測地線方程式”を解くやり方があります。
それに付いては別稿「テンソル解析学の一般相対性理論への応用」7.(8)をご覧下さい。
(3)二次元運動での解析(自由落下運動)
1.積分定数bの意味
“Schwarzschildの厳密解”を用いた議論をするのですが、最初は簡単のために“角運動量”L=0(つまり“面積速度の2倍”h=0)の場合を取り上げる。そのとき前節で述べた様に質点はxy面内で運動するとする。したがってθ=π/2、dθ/dτ=0、dφ/dτ=0とおける。
つまり質点がブラックホールから放射上に伸びている直線に沿ってブラックホールへ落下する運動。あるいは外向きに上昇する運動を解析する。その様な運動は当然dθ/dτ=0でありdφ/dτ=0です。
本節と次節は内山文献9.§41を参考にしていますが、かなり改変しています。
まず、前節の⑤式に①’式を代入して、dθ/dτ=0、dφ/dτ=0と置くと

が得られます。①’式を用いてさらに変形すると
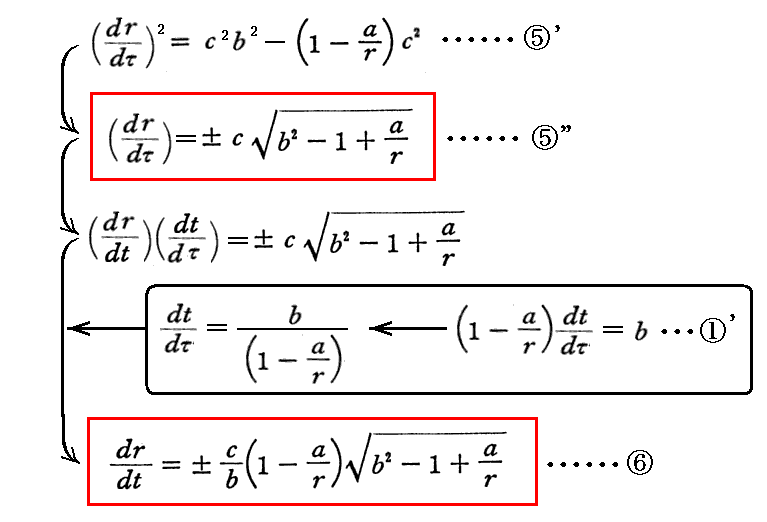
となります。
ここで、積分定数bの意味を知るために、質点mの外向きの運動を考える。ここで質点mは十分大きな運動エネルギーを持っていてポテンシャル井戸を自由上昇してr→∞まで到達できるとする。無限遠において質点mが持つ速さをv∞とすれば、⑥式より
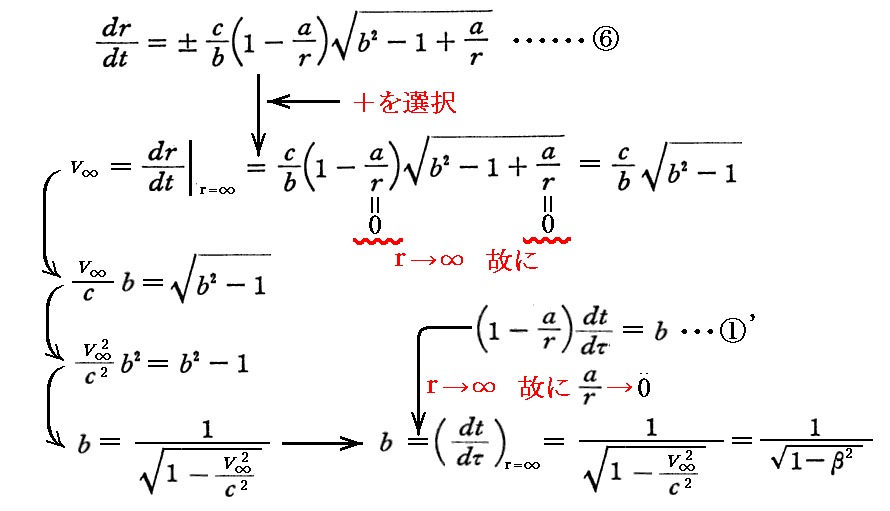
となる。ここで、無限遠における質点mが持つ速さをv∞=c・(v∞/c)≡cβと置いている。また、ここで⑤”式ではなくて、⑥式を使う事に注意して下さい。無限遠にいる観測者の距離座標、時間座標(シュワルツシルド座標)での話ですから。
いずれにしても r→∞ で v∞=0 と成る様な運動は b=1 と置くことに相当する。
後で解りますが
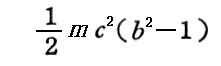
は質量mの物体が持つ全エネルギーを意味します。すなわち
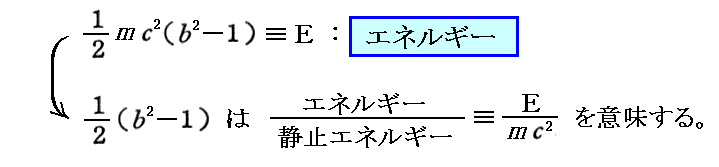
故に積分定数bを1とすることは、質量mの物体が持つ初期エネルギーがE=0であると仮定することに他なりません。
2.動径方向の自由落下現象でのエネルギー保存則
動径方向の運動に限った場合の質点mに付いてのエネルギー保存則は⑤’式より求まります。
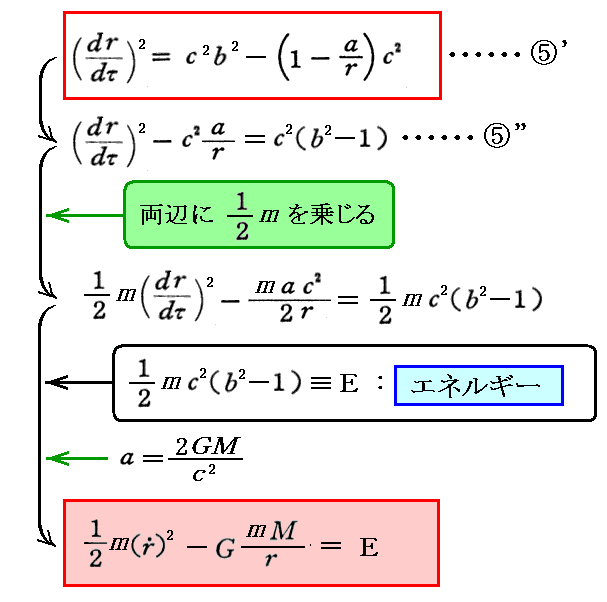
これはNewton力学のエネルギー保存則と完全に一致していることに注意して下さい。このことはとても不思議に思われるかも知れませんが、質点mが中心質量Mが作る重力場内を動径方向に自由落下あるいは自由上昇する運動に限ってたまたま言えることです。その場合にはたまたまそうなることに付いては3.(4)2.[補足説明2]で説明していますのでご覧ください。
3.自由落下運動(固有時τを用いて)
(1)落下時間 τ(r)
前節の途中で得られたエネルギー保存則⑤”式を用いれば、任意の半径r0から質量中心Mに向かって自由落下させた場合の落下位置rまでの落下時間(固有時で)を表す関数が得られる。

これをグラフで表すと以下のようになります。ただし、このグラフは r0=10a (シュワルツシルド半径の10倍)の位置から初速度0で自由落下させた場合の落下後の(固有時での)経過時間と(シュワルツシルド座標での)落下位置の関係を示しています。
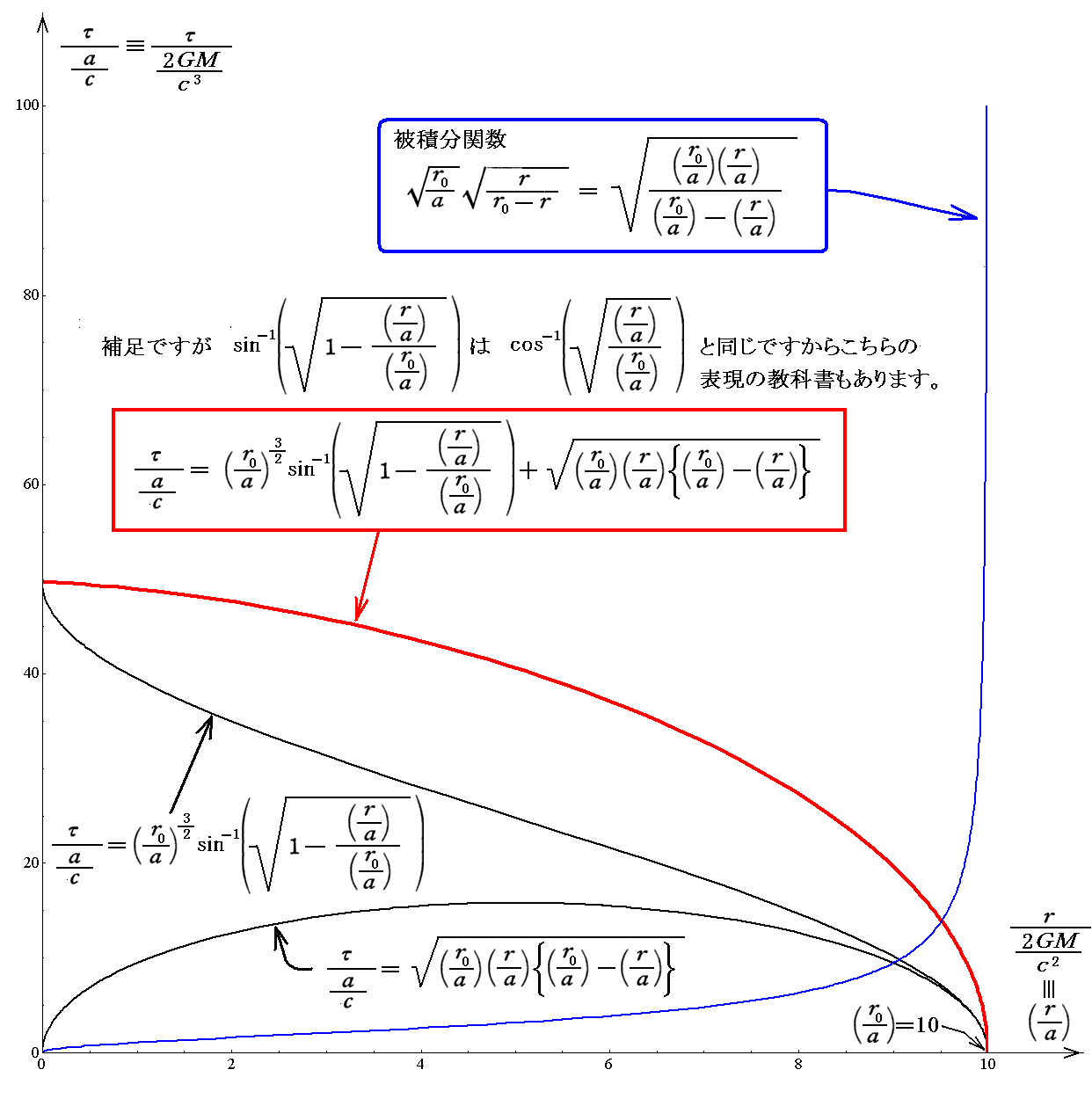
となります。
ここで注意して欲しい事は、シュウァルツシルド半径aの地点を有限の時間(固有時)で通り過ぎ、しかも質量中心Mに有限の時間(固有時)で到達することです。また、Newton力学の場合も全く同じグラフになります。ただしそのとき、縦軸は固有時τではなく、シュワルツシルド座標時間tになります。
(2)落下速度 dr/dτ
固有時を用いた、自由落下する途中の落下速度は以下の様になります。ここでも、位置エネルギー -GmM/r0 の位置から初速度0で自由落下する場合を求めます。

これをグラフで表すと以下のようになります。ただし、このグラフは r0=2a、6a、10a、∞a (シュワルツシルド半径の2倍、6倍、10倍、∞倍)の位置から初速度0で自由落下させた場合の落下後のdr/dτと(シュワルツシルド座標での)落下位置r
の関係を示しています。このときdr/dτを仮にvと記して、縦軸をv/cで、横軸をr/a(aはシュワルツシルド半径)で表しています。
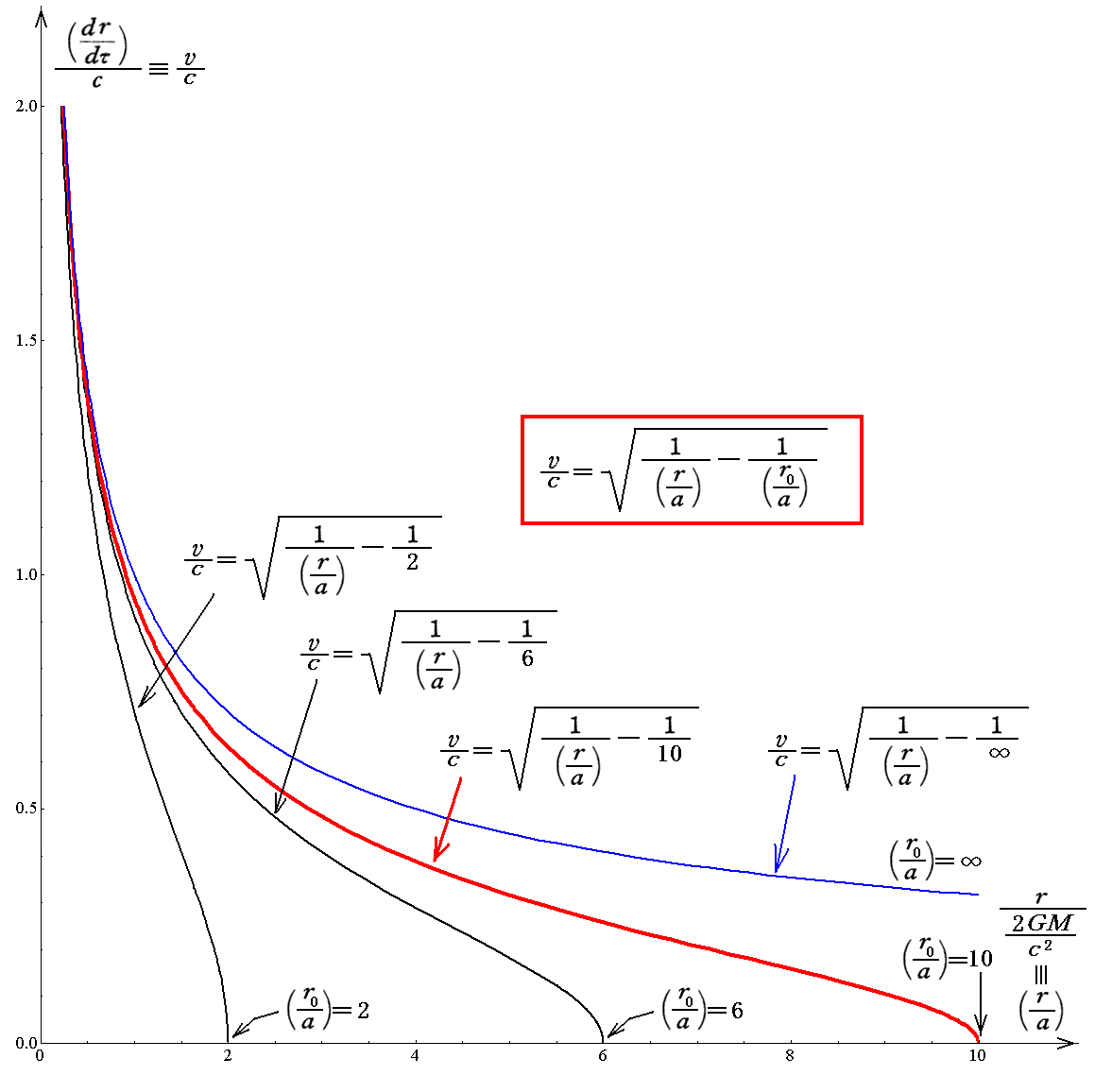
図から明らかな様に無限遠から自由落下させると(dr/dτ)はシュワルツシルド半径aで光速の値になります。それよりも中心質量Mに近い所から自由落下させた場合はシュワルツシルド半径では光速に達しません。しかし、その場合でも、シュワルツシルド半径よりも内側まで落下するとやがて光速に達し、そして光速を超えます。
(福江文献4.「ブラックホールの力学」6-1“自由落下運動”のこの部分の説明は誤っていると思います。)
現実の物体の速度が光速度を超える事はありませんので、ここで示した(dr/dτ)はいわゆる速度ではありません。ここは非常に解りにくい所なので[補足説明2]で説明します。
[補足説明1]
3.(3)2.でτをtに置き換えれば、相対論力学のエネルギー保存則はNewton力学のエネルギー保存則と完全に一致していると言いました。そのため、もしシュワルツシルド半径a以内に中心質量Mが圧縮されて存在できれば、質点mを無限遠で初速度0の状体から質量Mに向かって自由落下させたならば、Newton力学でもシュワルツシルド半径aを通過するときに、その落下速度は光速度cを超えます。Newton力学での
t は現実の時間ですから、Newton力学での dr/dt は現実の速度を意味します。だからNewton力学では光速度cを超えてシュワルツシルド半径内に落ち込んでいくわけです。
このことは多くの教科書(例えばこちらの福江文献あるいはこちらのソーン文献)でも指摘されているところです。しかし、このように重力場が強い領域ではNewton力学は正しい物理理論では有りません。そのはため実際に光速度cを超える速度となることはありません。その意味に於いても、ここで論じているdr/dτは現実の速度を表す量ではありません。
さらに補足しますと、上記のグラフを導く元になった3.(3)2.で求めたエネルギー保存則はτをtに置き換えればNewton力学と完全に一致しますので、Newton力学でいう重力場中を落下する質点mの落下速度の変化は、上記のτをtと置き換えて考えれば完全に同じになります。同じになることに付いては3.(4)2.[補足説明2]で説明していますのでご覧ください。
(福江文献4.「ブラックホールの力学」6-1“自由落下運動”の部分で、両者が異なるような説明[τかtかの違いはあります]をされていますが、それは誤りだと思います。)
[補足説明2]
何度も注意しましたが、drはシュワルツシルド座標での距離を表しています。シュワルツシルド座標に付いては3.(2)[補足説明1]で説明したように質量Mから無限遠離れた時空が歪んでいない部分の座標をそのまま質量Mの点まで適用した座標系です。一方dτはその歪んだ時空の中に存在する質点mの固有時です。だからdr/dτは現実の速度としての意味を持ち得ません。
dτで微分したものが速度としての意味を持つにはその質点mから見た空間の移動していく距離を用いなければ成りません。その距離とは無限遠で調整された物差しを質点mが落下中の重力場内に静止して設置した物差し棒で測られるものです。重力場内では物差し棒は縮みます。つまり重力場中を落下する質点mが見る物差しはその縮んだ物差し棒です。重力場内に静止している物差し棒ですが、自由落下中の質点から見るとその物差し棒は空間と共に背後に流れ去って行きます。だから質点mの内部の時計(固有時)で持って自分の側を流れ去って行く物差し棒の目盛りの変化量で質点m自身が重力場中を落下する速度を測定するわけです。重力場中の物差し棒は縮んでいますので、その物差し棒で測る自分の周りの空間が背後に流れ去って行く速度が光速度を超える事はありません。
もし仮に、我々が質量Mが作る重力場の中で静止して存在でき、上記の縮んだ測定棒を携えて、目の前を落下していく質点mの速度を我々の持つ時計で測れば、もちろん質点mの落下速度が光速度を超えることは無いでしょう。
仮に、その様にして自由落下する質点の速度の測定が可能であったとしても、シュワルツシルド座標にいる我々にとってそれをどの様に表現したら良いのでしょう。それを現実的に表現する方法はありません。
だから、上記の様にdr/dτを速度もどきのものと見なして、シュワルツシルド座標で質量中心Mからrの距離に質点mが有るときの速度と言うだけです。実際、佐藤・ルフィーニ文献10.では、その中のどこを探してもこれを速度とは言っていません。また、内山文献9.におけるこの当たりの説明には苦しい所が有ります。
以上の事柄は、今までの議論で出てきた時間微分量に関してシュワルツシルド座標tではなく固有時τに関する微分量を用いる所から生じるのですが、tでは無くτを用いる理由は、そもそもの最初に出てきたシュワルツシルド解の表現に由来します。
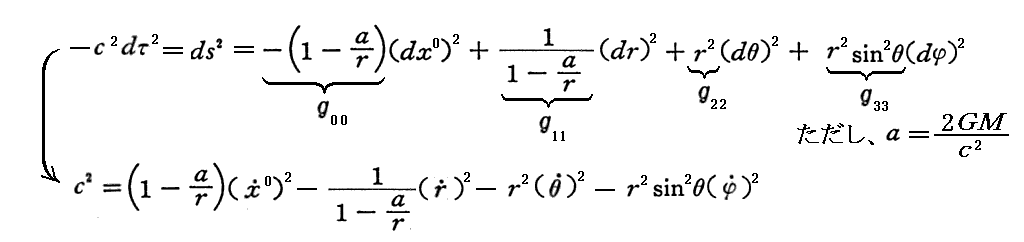
この式の左辺は質点mと共に移動する座標系の固有時cdτの二乗に相当するのでした。別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」3.(6)[補足説明2] で説明した様に、“一般相対性理論”とは“4次元リーマン時空計量テンソル”を仲介にした上式の“不変式論”なのです。
故に、この式を変形して得られる方程式は必然的にdτによる微分となります。そしてdr/dτによる現象の記述に成ります。それが実際に無限遠にいる観測者が観測できる物理的な量であるかどうかには関係ありません。先に述べた様に実際そうではありません。
おそらく、ここが一般相対性理論を理解する上で最も難しい所なのでしょう。特に質量Mがシュワルツシルド半径内に集中して存在する様な状況に於いて状況は混乱してきます。
[補足説明3]
Einsteinがブラックホールの様な質量集中状態が可能であるとは思っておらず、ブラックホールを認めていなかったのはここで説明したような一見論理矛盾としか思えないような計算結果が生じてくるからなのかも知れません。
Kip Thorne は「ブラックホールと時空の歪み」第3章p121で1939年にEinsteinが行った一つの計算を紹介しています。面白いのは、アインシュタインが示した臨界周囲(シュワルツシルド半径の1.5倍)で集団の回転速度が光速を超えると言うところです。
これは本稿の3.(4)6.(1)[補足説明1]の計算や3.(4)7.(2)で行った円軌道の回転速度はシュワルツシルド半径aの1.5倍の距離で発散すると言う計算と同じで、Einsteinは、この当たりの相対論力学の結果を正しく評価していたということだと思います。
つまり、Thorneがそこに書いているように、アインシュタインの計算は正しかったが、そのメッセージの読み方は正しくなかったのです。
4.自由落下運動(シュワルツシルド座標時tを用いて)
(1)落下時間 t(r)
シュワルツシルド座標上にいる観測者(中心質量Mから無限遠離れた点にいる観測者)から見たときの、質点mの落下の様子を補足しておきます。それは3.(3)1.で導いた⑥式から出発すれば良い。そのとき、積分定数bの取り扱いに注意して計算すると
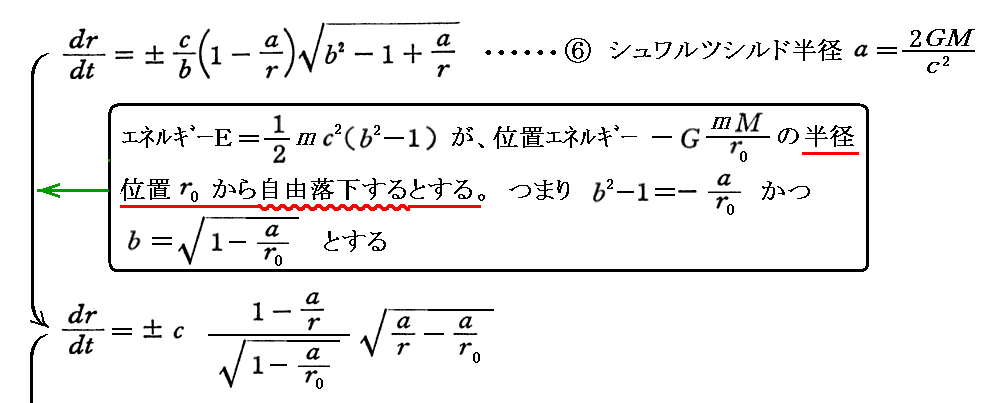
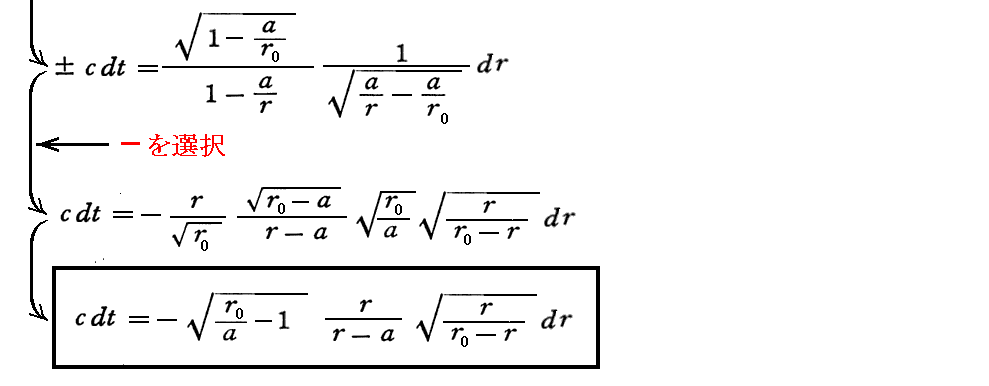
が得られる。これを自由落下位置r0から落下点rまで積分すれば、r0→rまでの(シュワルツシルド座標時表現での)落下時間が得られる。

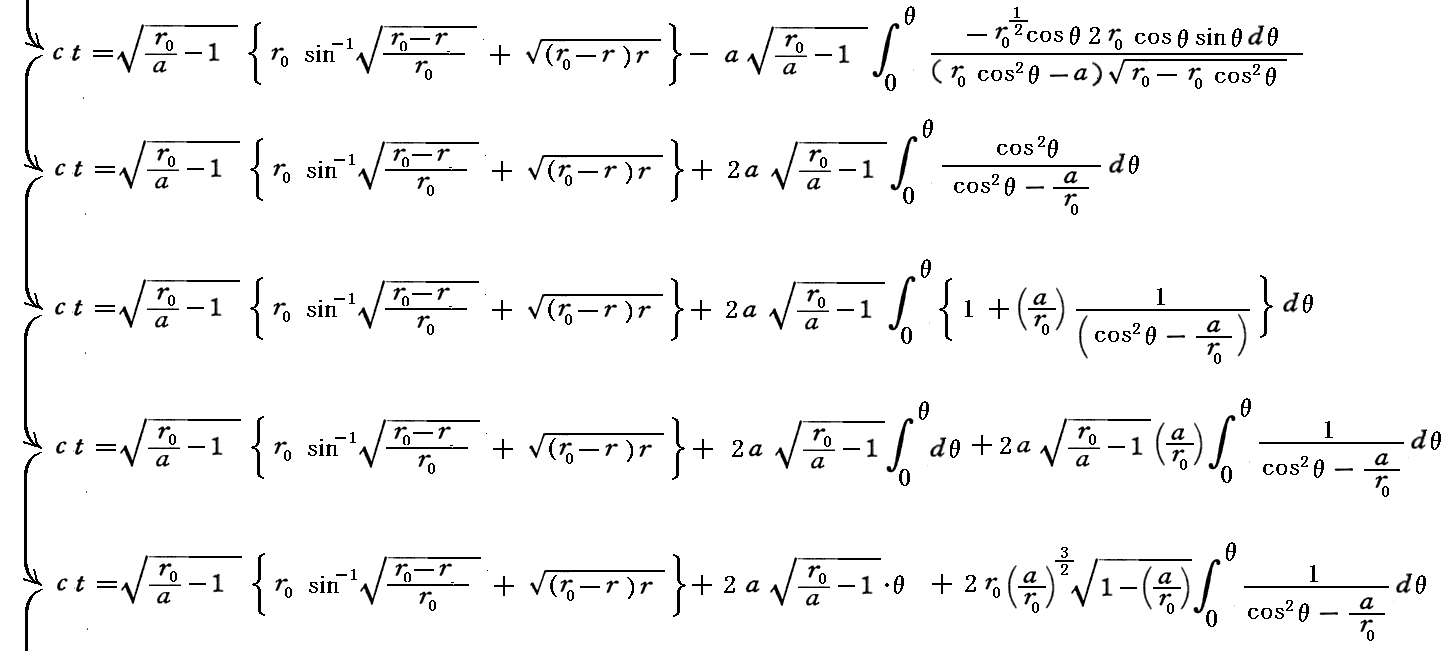
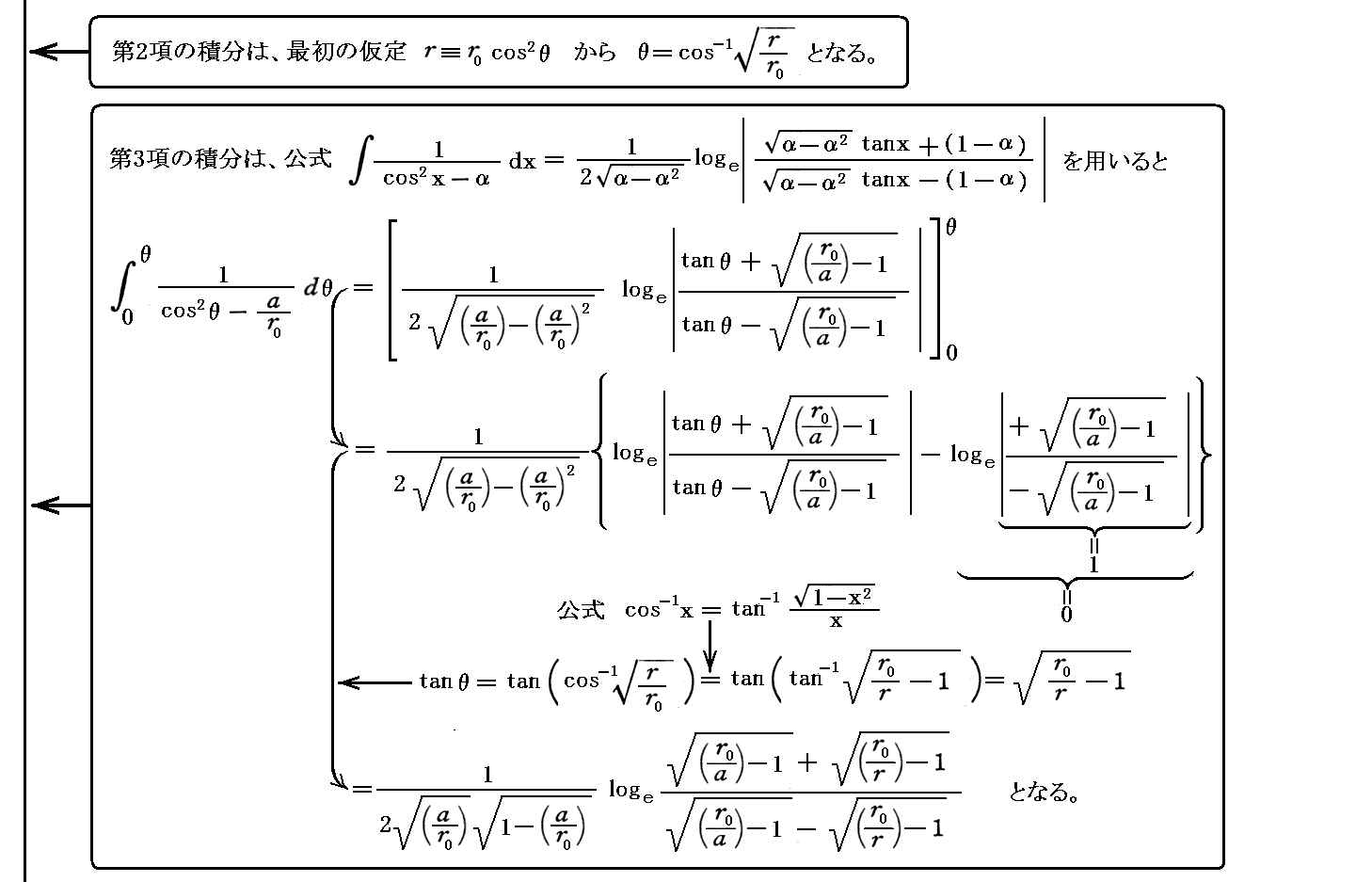

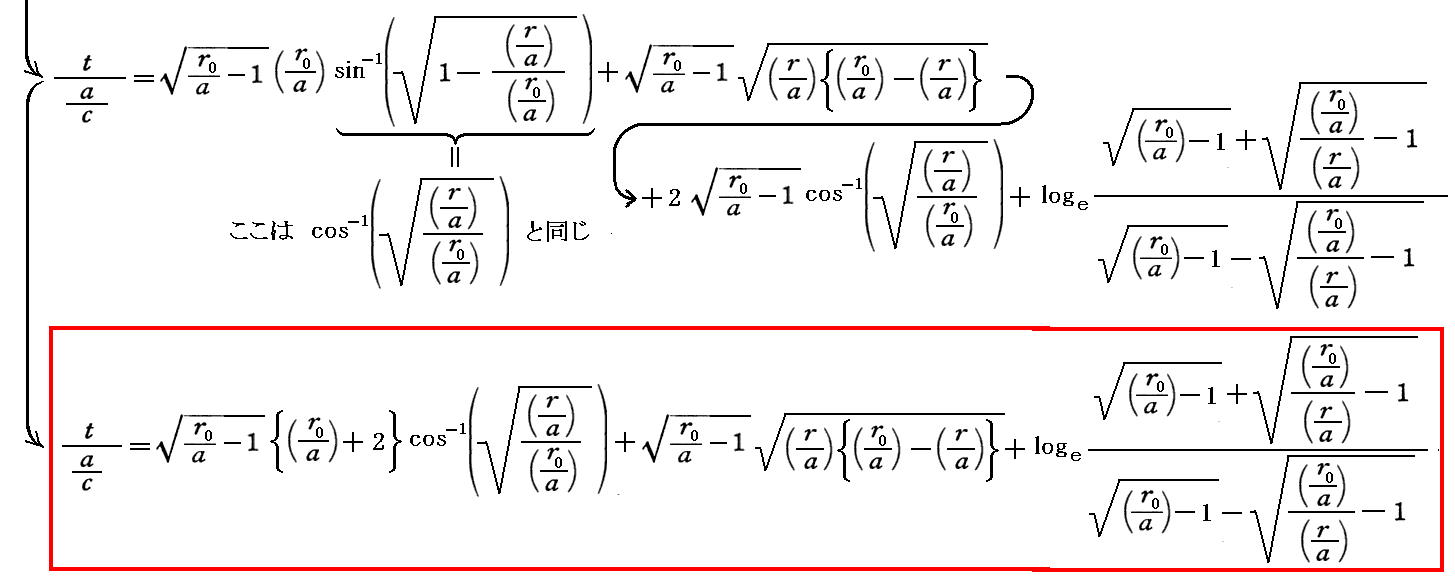
これをグラフで表すと以下のようになります。ただし、このグラフは r0=10a (シュワルツシルド半径の10倍)の位置から初速度0で自由落下させた場合の落下後の(シュワルツシルド座標時での)経過時間と(シュワルツシルド座標での)落下位置の関係を示しています。
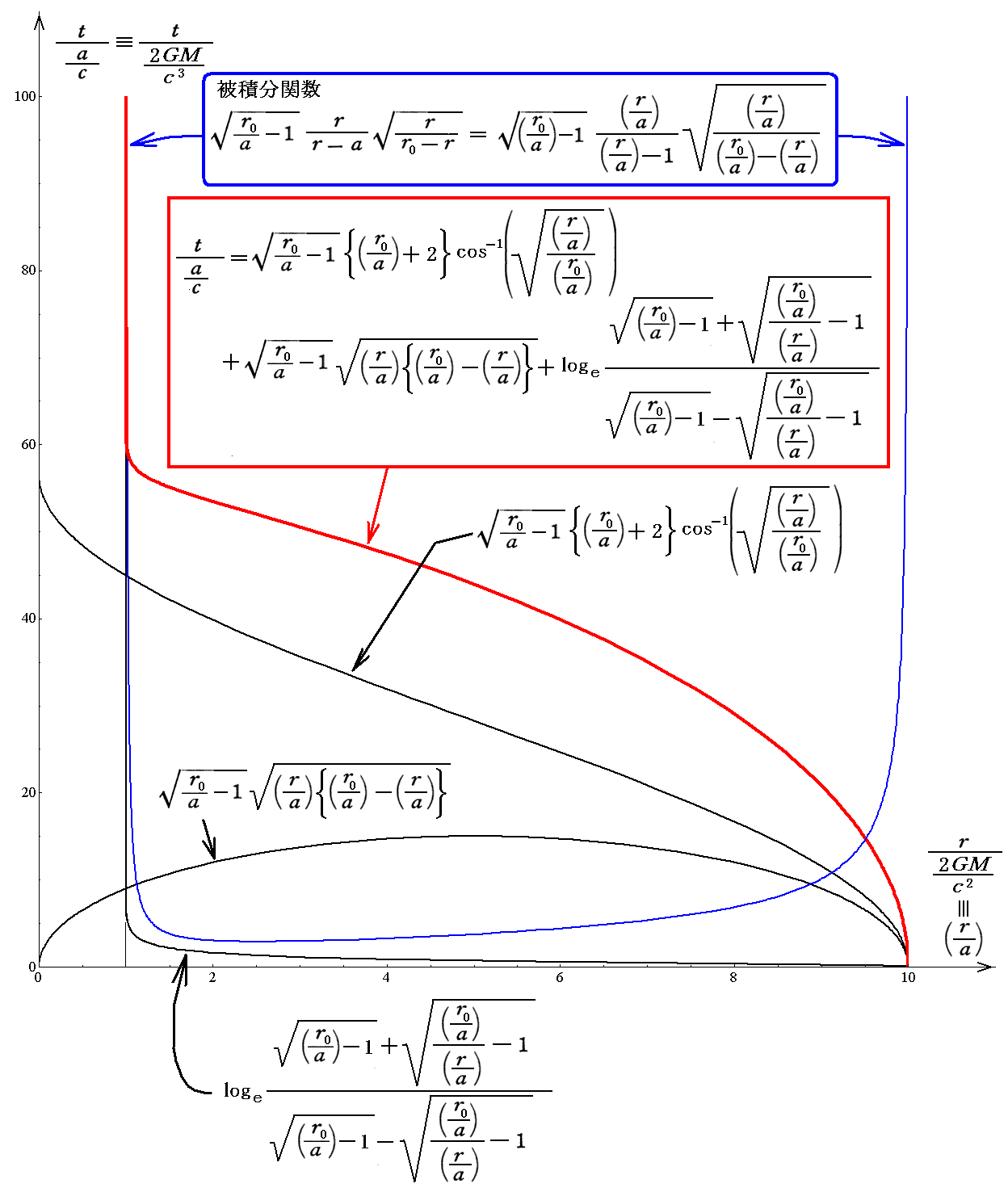
グラフから明らかな様に、質点mが質量中心Mに向かって自由落下した場合、質点mがシュワルツシルド半径aに近付くと、その地点での微小距離drを落下するのに無限の時間(シュワルツシルド座標時で)かかる様になります。
すなわち、r0からaに向かって落下するとき、シュワルツシルド半径aに近付くと落下所用時間が無限大に発散します。これは所要時間の積分を求めるための被積分関数の形からも解ります。
(2)落下速度 dr/dt
シュワルツシルド座標時をもちいた自由落下する途中の落下速度は以下の様になります。ここでも、位置エネルギー -GmM/r0 の位置から初速度0で自由落下する場合を求めます。

これをグラフで表すと以下のようになります。ただし、このグラフは r0=2a、6a、10a、∞a (シュワルツシルド半径の2倍、6倍、10倍、∞倍)の位置から初速度0で自由落下させた場合の落下後のdr/dtと(シュワルツシルド座標での)落下位置r
の関係を示しています。このときdr/dtを仮にv’と記して、縦軸をv’/cで、横軸をr/a(aはシュワルツシルド半径)で表しています。
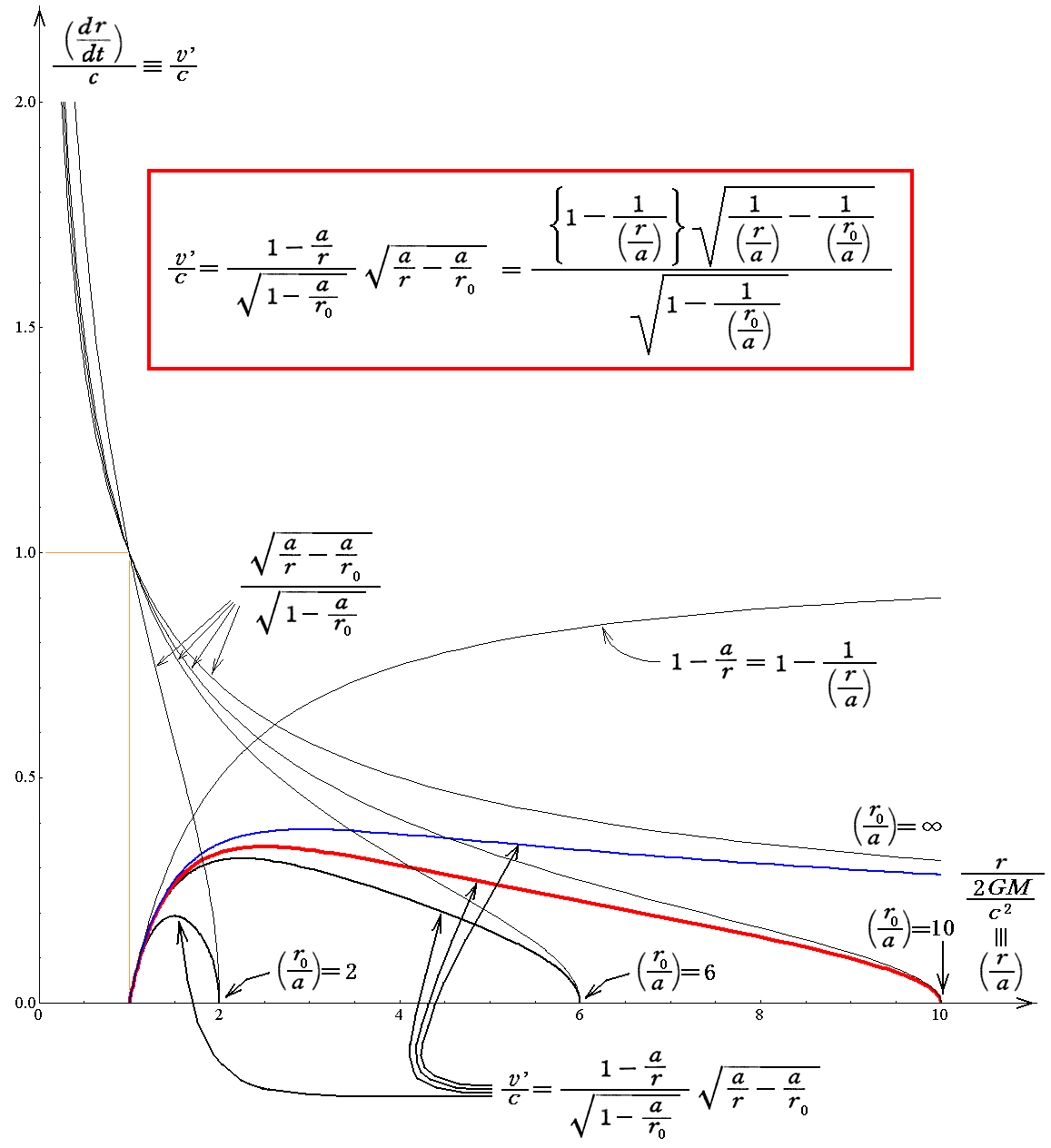
グラフから明らかな様に、r0としてどの位置から自由落下させても、シュワルツシルド半径aで必ず速度v’=0となります。このことが、前節で、シュワルツシルド半径aに近付くと落下所要時間が無限大に発散する理由です。この関数の逆数が、落下所要時間を求める為の積分の被積分関数である事に注意して下さい。
(福江文献4.「ブラックホールの力学」6-1“自由落下運動”のこの部分の説明は誤っているのでは?(1-a/r)を乗じるのを忘れられているのかもしれません。)
5.τ表現とt表現
理論を展開するとき、固有時τを用いるかそれともシュワルツシルド座標時tを用いるかで、その表現が大きく異なります。ここは一般相対性理論を理解するとき最も難しい所ですので、前節と前々節の結論グラフを重ねて表示して補足します。
(1)τ表現とt表現の違い
最初に3.(3)3.(1)の自由落下時間グラフτ(r)と、3.(3)4.(1)の自由落下時間グラフt(r)を同じr座標上で比較します。次のグラフは r0=2a、6a、10a、14a (シュワルツシルド半径の2倍、6倍、10倍、14倍)の位置から初速度0で自由落下させた場合の落下後の τ あるいは
t と(シュワルツシルド座標での)落下位置 r の関係を示しています。
その為、縦軸はτ/(c/a)とt/(c/a)が重なっています。両方のグラフ線を同じ赤色にしていますが、t(r)グラフの方をすべて破線で示すことで区別しています。
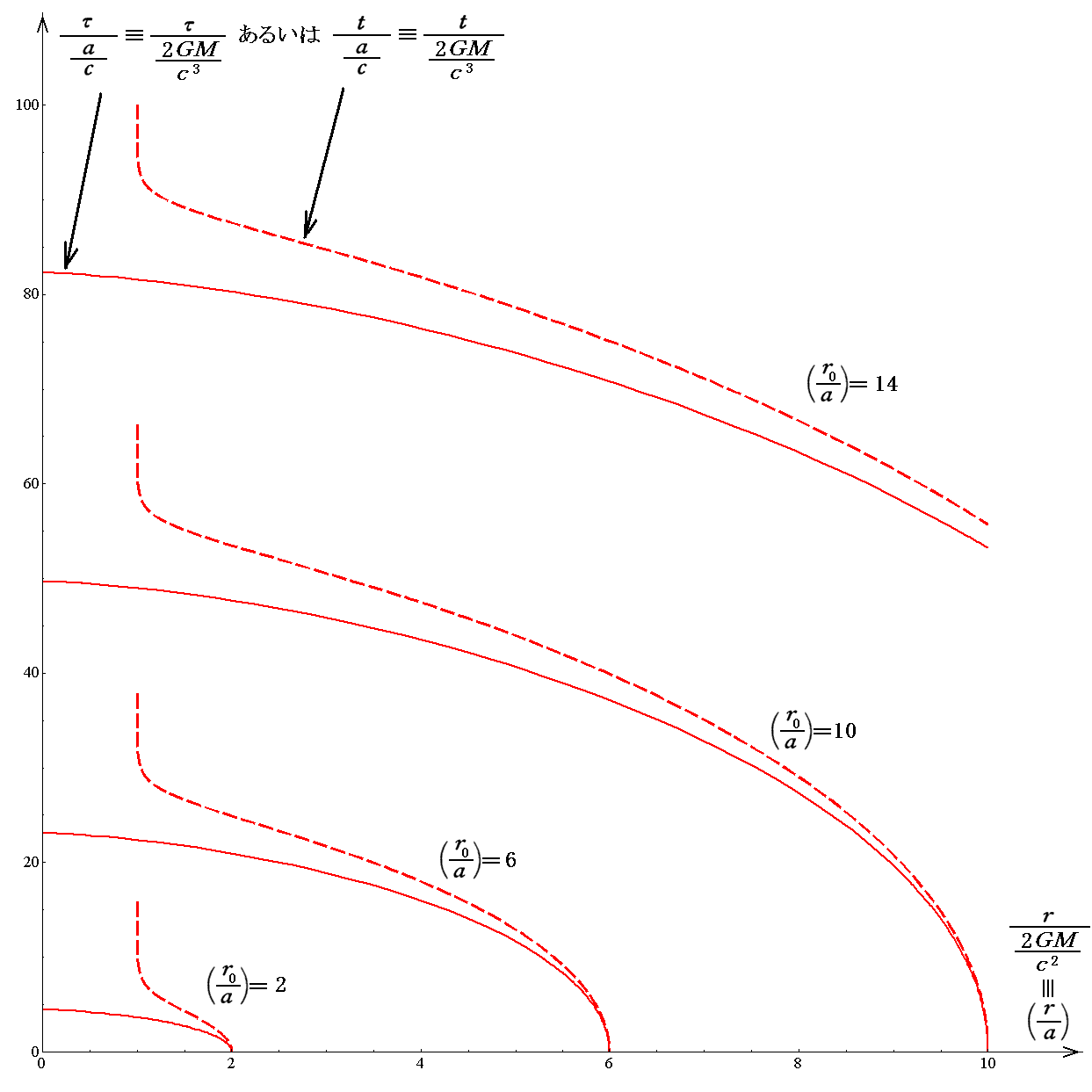
グラフから明らかな様に、t(r)はr→aで必ず発散しますが、τ(r)に関してはその様な事はありません。。
次に3.(3)3.(2)の自由落下速度グラフdr/dτ=v(r)と、3.(3)4.(2)の自由落下速度グラフdr/dt=v’(r)を同じr座標上で比較します。次のグラフは r0=2a、6a、10a、∞a (シュワルツシルド半径の2倍、6倍、10倍、無限遠)の位置から初速度0で自由落下させた場合で、落下後に(シュワルツシルド座標での)落下位置rを通過するときのdr/dτあるいはdr/dtの値のグラフです。このとき、dr/dτを仮にvとし、dr/dtを仮にv’と記していますが、現実の速度を意味するわけではないことに注意して下さい。
縦軸をv/cとv’/cを重ねて表示し、横軸をr/a(aはシュワルツシルド半径)で表しています。グラフ線の着色は以前の色分けを踏襲しています。そのためdr/dt=v’グラフの方をすべて破線で示すことで区別しています。
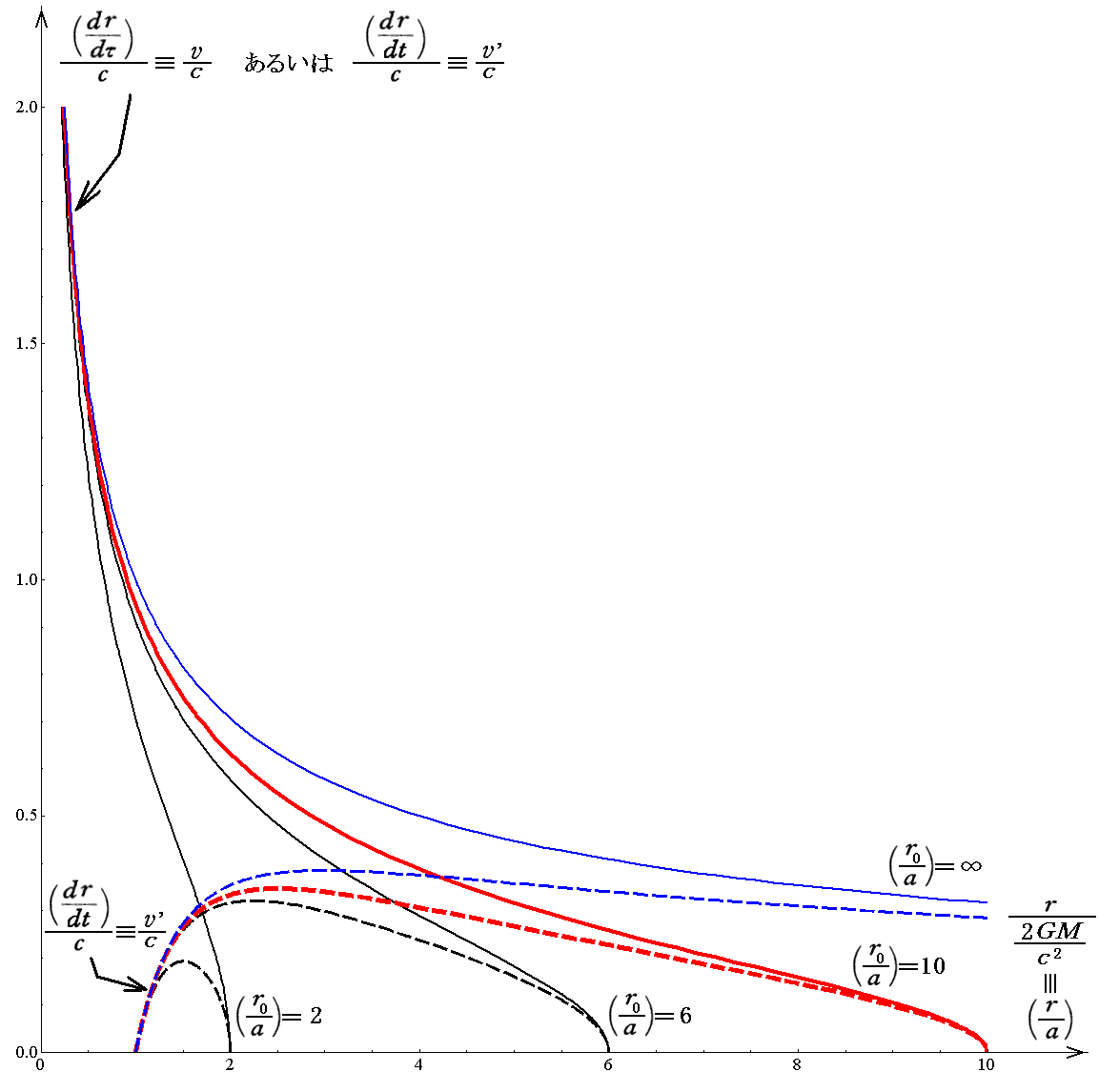
グラフから明らかな様に dr/dτ=v(r) は r→0 で無限大に発散しますが、 dr/dt=v’(r) ではその様な事はなく r→a ですべて 0 に成ります。
さらに補足します。上記二つのグラフに於いて、最初の落下開始点に近付くと v→0 となりますが、その場合には質点mの固有時τとシュワルツシルド座標時tは互いに近付いて同じになります。そのため落下開始点付近では両者のグラフ曲線は一致するはずですが、確かに一致しています。
(2)τ表現とt表現の違いの意味
前節で説明したように固有時τを用いるかシュワルツシルド座標時tを用いるかで、それぞれの表現は全く異なります。そのとき、一般相対性理論の表現としてどちらが正しいのだろうと疑問に思われる方もおられると思いますが、どちらも正しい!!。
まず、τ表現に付いてですが、3.(3)3.(2)[補足説明2]で注意したように、、“一般相対性理論”とは、そもそも“4次元リーマン時空計量テンソル”を仲介にしたds2の“不変式論”なのです。そのためシュワルツシルド解から実のある結論を導こうとすると必然的に固有時τの関数としての方程式表現にならざるを得ません。そのとき、3.(3)3.(2)[補足説明2]で注意したように、dr/dτは現実の物理的な量である速度では有りません。そのためdr/dτが見かけ上光速度を超えるような状況が生じる場合も在ります。
現実の落下速度を求めるためには中心質量Mから無限遠離れた場所で作った物指し棒を携えて、実際に質量Mが作り出す重力場の中の(シュワルツシルド座標で)rの位置に入って、その場所に静止した観測者が落下してくる質点mの速度を観測しなければ成りません。観測者の目の前を落下してゆく質点mの速度を測るわけですが、質点mの通り過ぎる速度は観測者が持つ縮んだ測定棒と観測者自身が持つ(重力場中なのでゆっくり進む)時計で測ります。その様にして測った速度はτ表現の様に無限大(r→0で)になったり、t表現の様にゼロ(r→aで)になったりすることは無いと思います。
τ表現で無限大になるのも、t表現でゼロになるのも、本来歪んだ時空間中での現象を歪んでいないと仮定した空間の座標(シュワルツシルド座標)を用いて、固有時τを適用したり、歪んでいない時間t(シュワルツシルド座標時)を適用して表現するからです。だから、表現自体の中に論理矛盾があるわけでは無いのですが奇妙な結論が生じます。
だから、現実の現象を正しく記述するには、記述する時空座標を質点mが落下した後、質点が存在する時空点での新しい時空座標に次々と取り替えながら記述しなければ成りません。そうすればより現実的な現象表現が可能になるでしょう。ただ、それをするのは難しい。
いずれにしても、表現自体は正しいのですが、t表現で行くと中心質量Mから離れた観測者が質量Mに向かって落下していく質点mを見たらその様に見えるであろうと言う状況をあらわしているにすぎません。
ただし、実際にその様に見えるかどうかはわかりません。なぜなら、この現象を無限遠の観測者が認識するには、質量Mに向かって落下中の質点が落下の各地点の位置情報を光の信号で無限遠の観測者に知らせなければ成りません。しかしご存じの様に重力場中の光速は遅くなります。もちろん重力場中の光子自身に取っては縮んだ空間中をゆっくり進む時計で自分の速度を測ると同じ光速度cで進んでいると思っています。
いずれにしても落下中の質点mが発射する光子はゆっくりと重力場中を上昇してきます。特に質点mがシュワルツシルド半径に近付くと光の速度は無限に遅くなりますので、質点mは無限にゆっくりとシュワルツシルド半径内に落下していくように見えるでしょう。ただし重力場の深い井戸の中から発する光は無限に赤方偏移していますので、光のエネルギーは無限に弱くなり、光の信号として重力場の外にいる観測者には届かなくなります。だから、無限にゆっくり落下していく質点を観測すること事態ができなくなるでしょう。
6.内山文献9.§41の説明
この当たりはとても解りにくい所ですので、内山文献9.§41の説明も紹介します。
(1)t表現
中心質量Mが作る重力場での質点mの自由落下問題を考えるのですが、最初に、質点mの外向きの自由上昇運動を考える。最初質点mは十分大きな運動エネルギーを持っていてr→∞まで到達できるとする。無限遠における質点mが持つ速さをv∞=c・(v∞/c)≡cβと置けば、r→∞におけるdt/dτ=1/√1-β2だから、①’式より
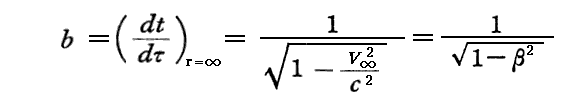
となる。今後簡単のために v∞=0 とする。これは b=1 と置くことに相当する。
そのとき、 a<r1<r2 としたとき、質点mが r2 から r1まで自由落下するのに要する時間ctは以下の様に表される。ただし、今は r1>a の範囲での積分を考えています。

ここで注意して欲しいのですが、ここではv∞=0としている為にr=∞ から r=r2 まで自由落下するのに無限大の時間がかります。しかし、それでは議論が展開できませんので、r2 まで自由落下した結果そこで持つであろう速度を r2 での初速度して与えて、それ以後の時間経過を論じています。つまりr2を通過した瞬間をt=0として時間経過を計ると言うことです。
実際に上式t/(a/c)のグラフを描いてみると以下のようになります。このとき横軸は中心星Mからの距離をシュワルツシルド半径aを単位として表した(r/a)です。また、質点mが半径
r2 の所を通過した時刻を経過時間計測の0点としているのですが、今は r2=10a としています。
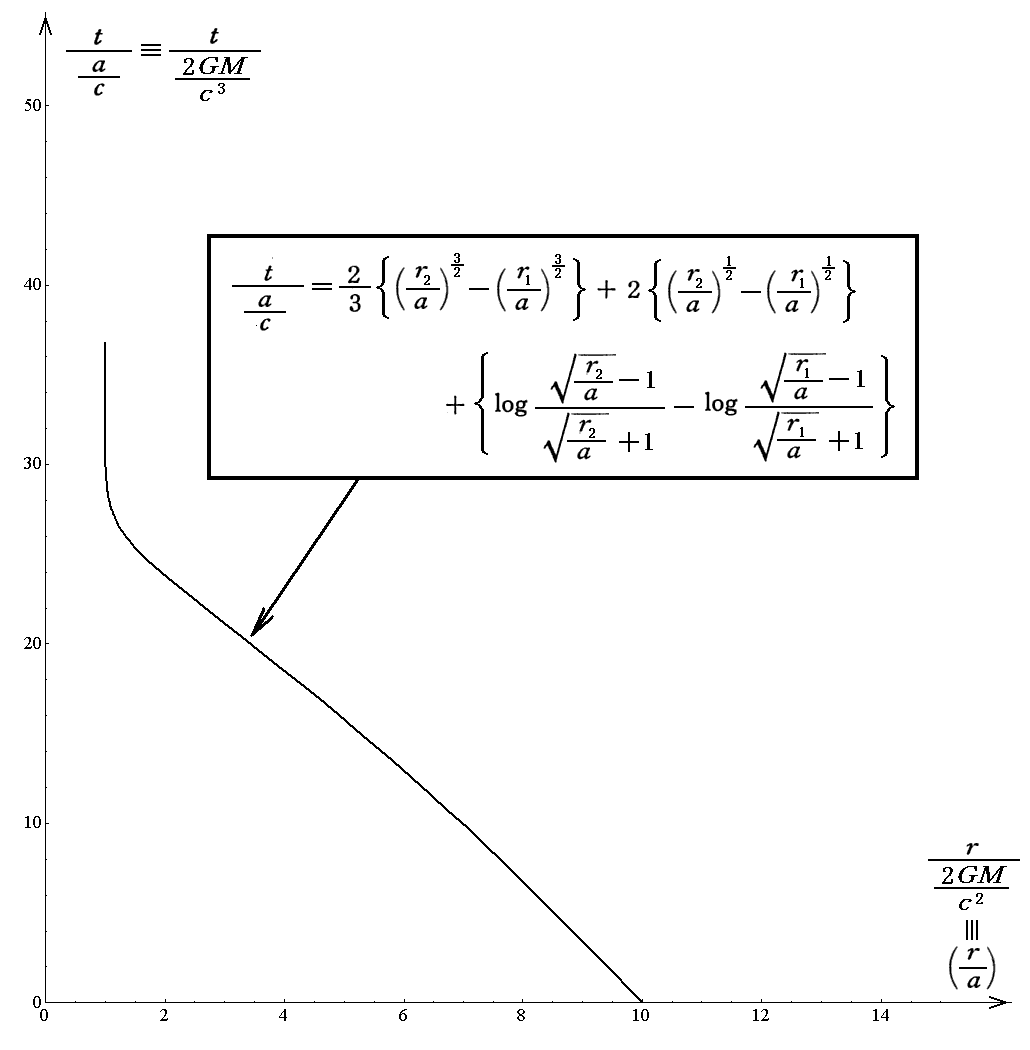
このt-rグラフは先に述べたt-rグラフと形が少し異なります。それは、先のグラフは自由落下の開始点 r2 における初速度を0としたものですが、本節では r→∞ での初速度を 0 として、自由落下させたとき、r=r2 を通過する時刻を基点にして r=r1 を通過する時刻を示しているからです。本節では、r=r2 を通過する瞬間にはすでに初速度を持っているとしています。
グラフから解る様に r1 を a(シュワルツシルド半径) に近づけたら、無限遠に静止している観測者から見たとき、r=r2 から r=r1=a に到達するのに∞の時間がかかります。そうなるのは、r1がaに近付いたとき、前述の式の右辺第三項が
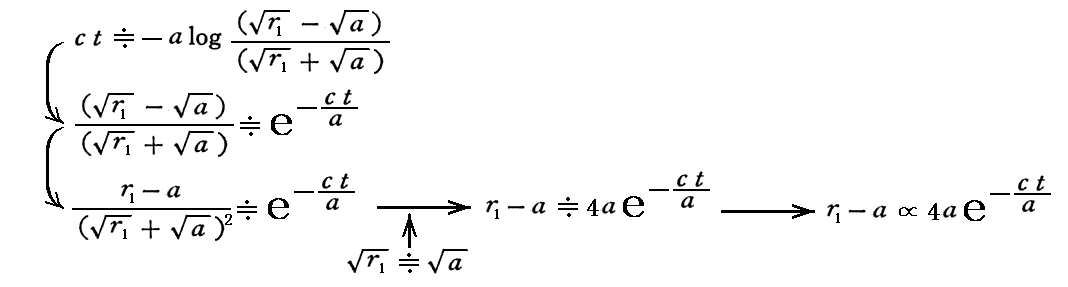
となりますから、無限の時間が経って(t→∞)、r1はaに近付いていくからです。
それは、無限遠に静止している観測者から見た質点mの落下速度dr/dtは次の様に表されるので、質点mが a(シュワルツシルド半径)に近付くにつれてその速度が0に近付くことからも解ります。
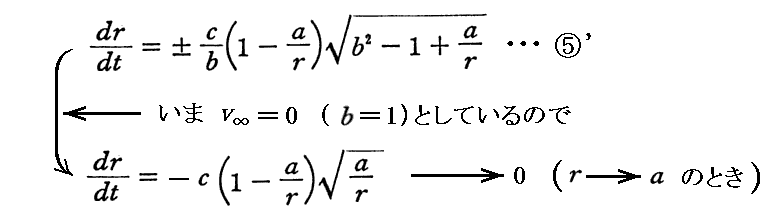
このdr/dtのグラフは3.(3)4.(2)で示したv’-rのグラフの中の“青色カーブ”に成ります。ただし、この場合には3.(3)5.(1)で示したt-rのグラフの中にはtが無限大になるために書き込めないことに注意して下さい。
(2)τ表現
以上の過程を質点mの固有時間τを用いて説明すると以下の様になる。
まず、固有時間τを用いると3.(3)2.の⑤’式から
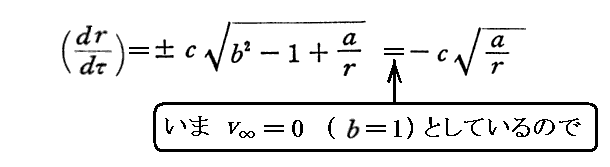
の関係式が得られる。
そのとき、r=a(シュワルツシルド半径)を通過する瞬間において、質点mにくくりつけた時計を用いて時間を計り始めるとします。
実際、v∞=0とし、r=r2通過時から固有時間経過を測り始める場合には、上式を積分して得られるr=r1の通過時刻は

ここでも先ほどと同様に、v∞=0としている為にr=∞ から r=r2 まで自由落下するのに無限大の時間がかりますが、それでは議論が進みませんので、自由落下した結果 r2 で持つであろう速度を r2 での初速度して与えて、それ以後の時間経過を論じる為に上記の様な積分にしています。つまりr2を通過した瞬間をt=0として時間経過を計ると言うことです。
上記の結果を先ほどのグラフ座標に重ねて描くと以下の様になります。ここでも、質点mが半径 r2 の所を通過した時刻を経過時間計測の0点としているのですが、今は r2=10a としています。そのためr/a=10でτ/(a/c)=0となっています。
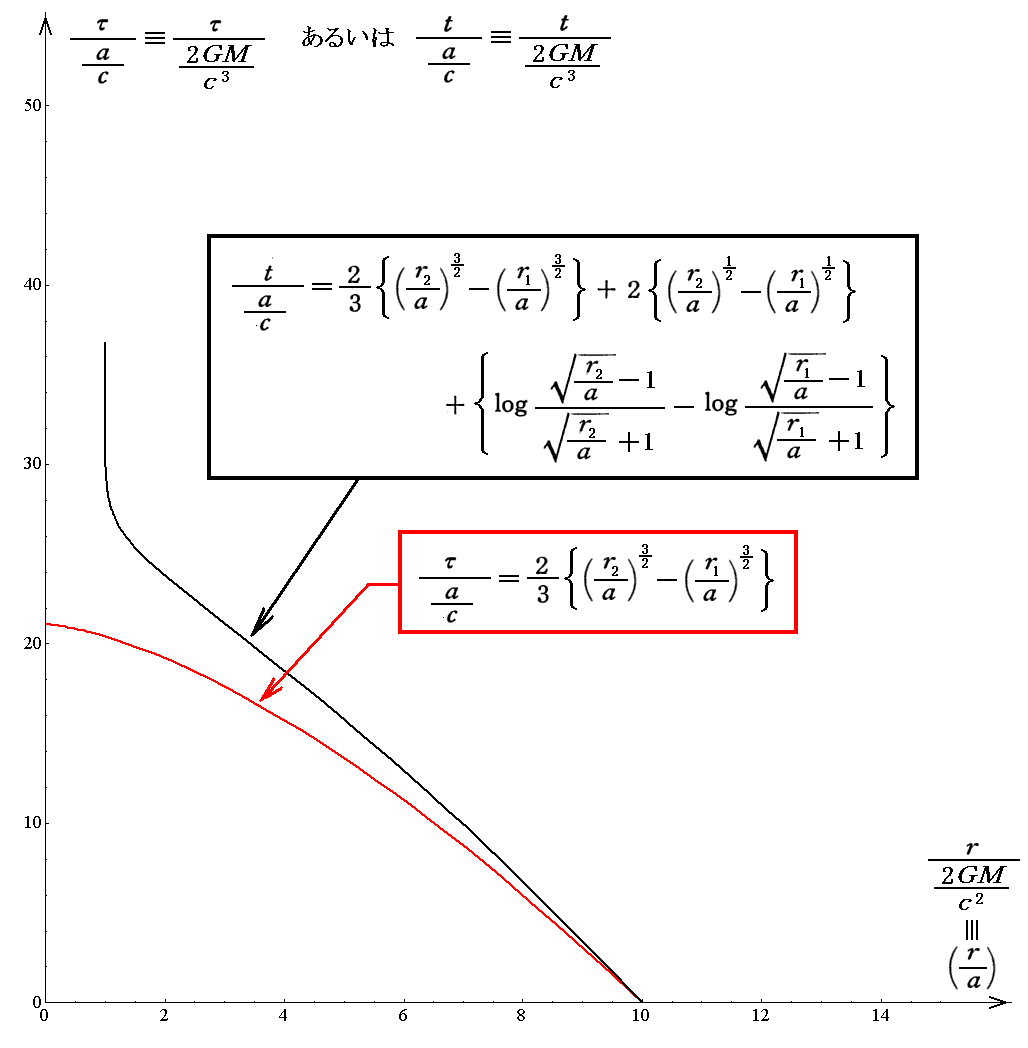
上記の式はr1<aでもr1>aでも成立しますから、これらの式から次の事が解ります。質点mに付けた時計で時間を計ると点r2に於いて初期値
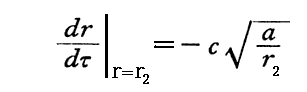
で自由落下を始めた質点は、次第にdr/dτを増大させながら有限時間
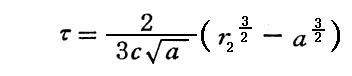
でSchwarzschild半径aに到達する。
そのときのdr/dτは
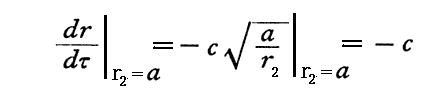
ですから、光速cとなります。ただし、これは質点mの速度を意味するわけでは無いことに注意してください。一般相対性理論での著しい特徴ですが、無限遠から自由落下させた場合はdr/dτの値はシュワルツシルド半径で光速度cになります。そして、これ以後は光速度より大きな値で
r<a の領域に侵入していきます。スタートしてから丁度
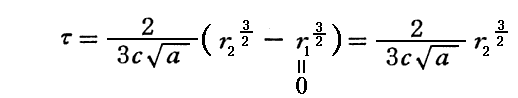
の後に原点r=0(中心星Mの存在する点)に到達する。
このとき r<a の領域でのdr/dτは上記の関数形から行くとは光速を超えてしまいますが、3.(3)3.(2)[補足説明2]や3.(3)5.(2)で説明した様に、dr/dτが質点mの速度を表すわけではありませんので、問題ありません。もし速度であるならば、光速を超える事は考えられませんので、その意味でも上記のdr/dτは速度を表す式では有りません。
[補足説明1]
以上で述べた運動の向きを逆にすれは、ブラックホール内部の点r1(<a)に於いて外向き初速度を与えて自由上昇させて、質点mを外に飛び出さすこともできる様に見えるかも知れません。実際、質点mが特異面(シュワルツシルド半径)を通り抜けて外部の点r2(>a)に到達するまでの固有時間は先ほど求めた値と同じで
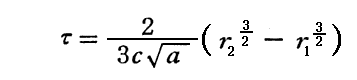
となります。ただし、シュワルツシルド半径以内に一端落下した質点mが上記の速度を獲得して重力場内を自由上昇する様な現象が起こり得るとは考えられません。そのため上記の逆向きの自由上昇が起こりえず、ブラックホール内部から物質が飛び出すことは考えられないのでしょう。
そのとき、シュワルツシルド半径以内を落下中の星(質点m)が発光して光を重力場の外向きに放射することは可能かも知れません。光子ならば上記の自由落下の逆過程としての自由上昇を実現できて、ブラックホール内部から光子が飛び出てくることは考えられます。
そのとき仮に、その様なことが起きえたとしても、これを無限遠に静止している観測者が見ると、質点mが内部の点から特異面に達するまでに無限大の時間がかかり、さらに特異面(シュワルツシルド半径)から離脱するにもまた無限大の時間がかかります。そうなることは⑤’式を検討すれば明らかです。その意味においても、光子がブラックホールの内部から地平面(シュワルツシルド半径)を突き抜けて外に飛び出すという現象は外部の観測者にとっては起こりえない事になる。
実際、光子は特異面(シュワルツシルド半径)を超えて飛び出ようとするのかもしれませんが、3.(3)5.(2)で説明したように光子は元々∞大の赤方偏移を受けた状体で出発しなければ成りませんので、有限のエネルギーを持った光子として自由上昇できないのかも知れません。振動数が低い光子のエネルギーはν→0とともにゼロとなるのですから。
原子が発光できない理由としては、シュワルツシルド半径内に落下した質点mを構成する原子は原子核レベルまで潰れてしまい、光を発生する電子の軌道運動も存在できなくなるのかも知れません。このことが最も可能性が高い理由かも知れません。
いずれの理由にしろ、光子もシュワルツシルド半径の外側に飛び出てくることはできないのでしょう。
実際ブラックホールの周りの降着円盤からの光は多く観測されていますが、それらはすべてブラックホールのシュワルツシルド半径よりも外側の領域で発光し放射されたものです。今までの観測では、ブラックホール内部からのそういった放射光は全く観測されていません。
別稿「ブラックホール質量の決定法」1.(3)で説明したように、周りを周回する星々の運動状態の観測から、Newton力学で計算すると確かに大質量が存在することは確かです。しかし、その存在を見ることができないのですから、ブラックホールは現実に存在するのでしょう。
(4)二次元運動での解析(任意の軌道運動)
1.運動方程式
次に、“角運動量”L(“面積速度の2倍”=h)が 0 でない場合を考える。ここでもθ=π/2のxy平面上での運動とする。
必要な運動方程式は3.(2)ですでに導いている。
x0 に関する変分から求まる①’式

および、φ に関する変分から求まる③’式

そして、 r に関する変分から求まる④式でdθ/dτ=0、sinθ=sin(π/2)=1 とした④’式

最後に、固有時間の定義式⑤でdθ/dτ=0、sinθ=sin(π/2)=1 とした⑤’式です。
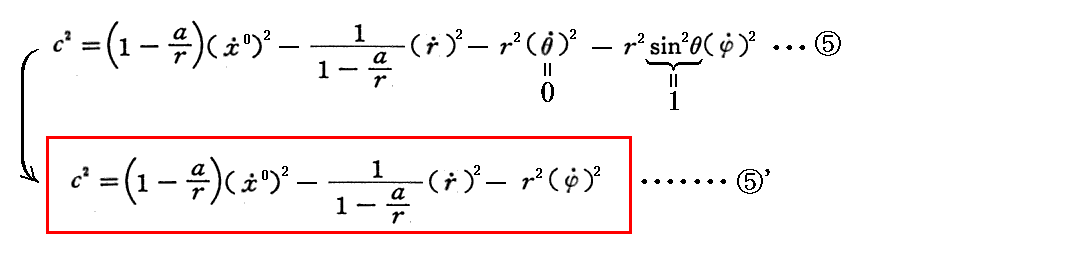
2.エネルギー保存則
⑤’式に①’式、③’式を代入して、dφ/dτ、dx0/dτを消去すると⑤”式となる。
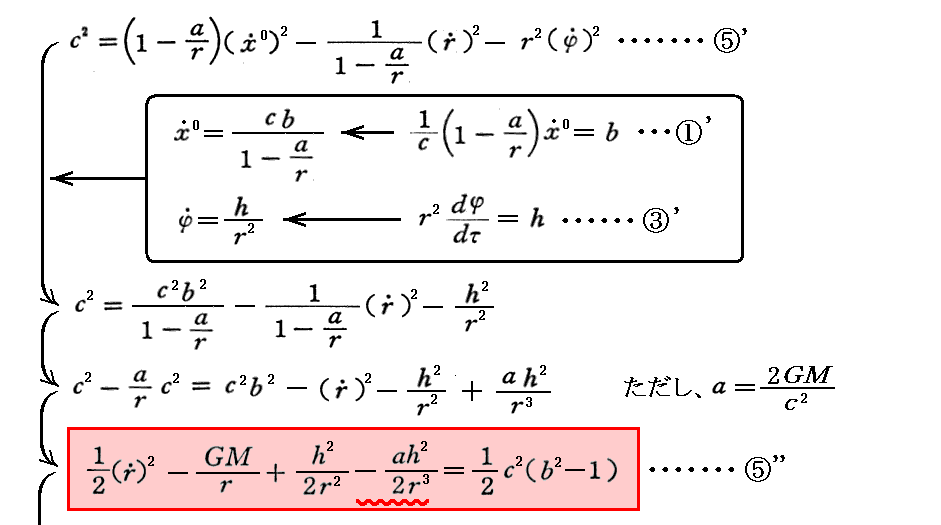
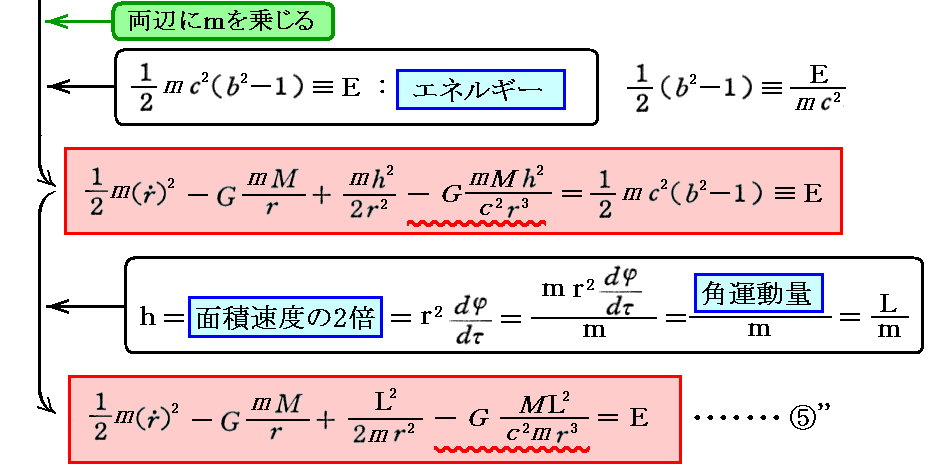
最後に示した⑤”式の表現は3.(1)2.で説明したNewton力学における“エネルギー保存則”に相当する。
このとき最後の2式は、質点mの質量mを乗じた式にしています。そのときのmは質点mの“固有質量”です。質量は観測する系に依存して変化しますが、固有質量が変化するわけではありませんので注意して下さい。このことに付いては以下に記す[補足説明1]を参照して下さい。
また、上式の第1項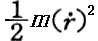 中の
中の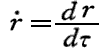 が無限遠の観測者が見た質点mの動径方向の速度を表すわけではないのですが、第1項を動径方向の運動エネルギーだと解釈できるのだろう。ここは私自身良く解りません。
が無限遠の観測者が見た質点mの動径方向の速度を表すわけではないのですが、第1項を動径方向の運動エネルギーだと解釈できるのだろう。ここは私自身良く解りません。
さらに、③’式(“面積速度一定の法則”)は質点に働く力が中心力ならば、その力が距離の逆二乗法則に従っていなくても成り立つ事に注意して下さい。このことは別稿「質点の二次元運動」3.(3)(a)で説明しました。
[補足説明1]
先ほど⑤”式に乗じるのは“固有質量”であると説明しました。ところで、特殊相対性理論によると、運動している物体(質量)はその速度に依存して質量が
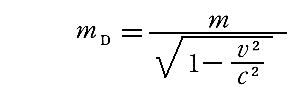
式にしたがって増大すると習います。そのとき⑤”式は運動している物体を表すのに、なぜmDを用いないでmで良いのでしょうか。疑問に思われる方もおられると思いますので補足します。
別稿「一般相対性理論の古典的検証と歪んだ時空」§3-2で“ハーフィールとキーティングの実験”を説明するとき、戸田文献の説明と、須藤文献の説明の二通りを紹介しました。そのとき、一般相対性理論の厳密解であるシュワルツシルド解の中には特殊相対性理論による[運動している時計の進みが遅くなる効果]も含まれている事を注意しました。
それと同じでして、ここで用いているシュワルツシルド解には、特殊相対性理論による[運動物体の質量が増大する効果]がすでに含まれています。だから上記の様に⑤”に乗じるのはmDでは無くて“固有質量”mでよいのです。
ここは、非常に解りにくい所ですが、別稿「一般相対性理論の古典的検証と歪んだ時空」§2-3でゼックスルが説明していますので、以下で引用しておきます。
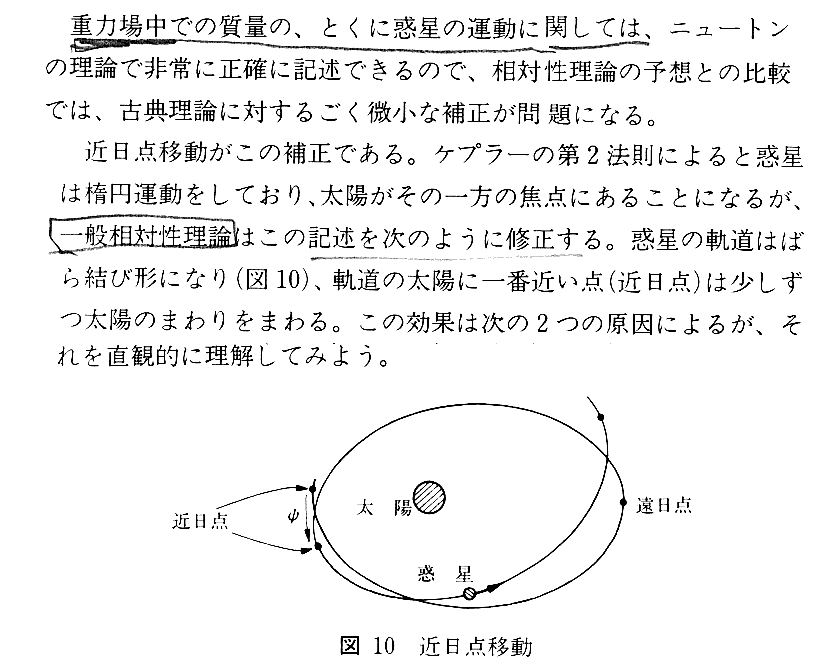





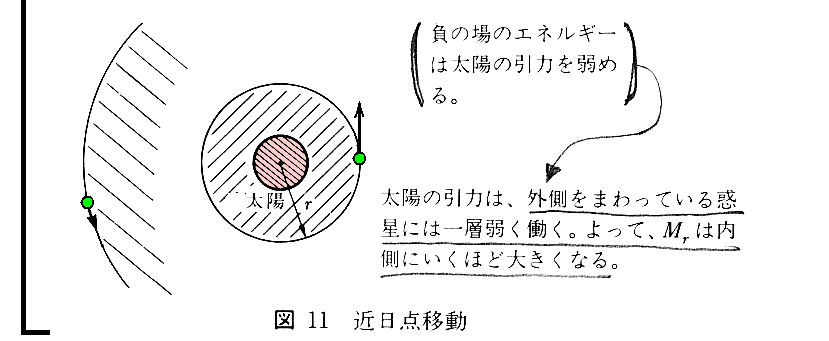
ここは非常に解りにくい所です。(2.21)式をよく吟味する必要があります。図11に記されている事柄が良く理解できない方は、別稿「万有引力の法則への補足」あるいは「化学結合(イオン化エネルギーと電子親和力)」1.をご覧下さい。

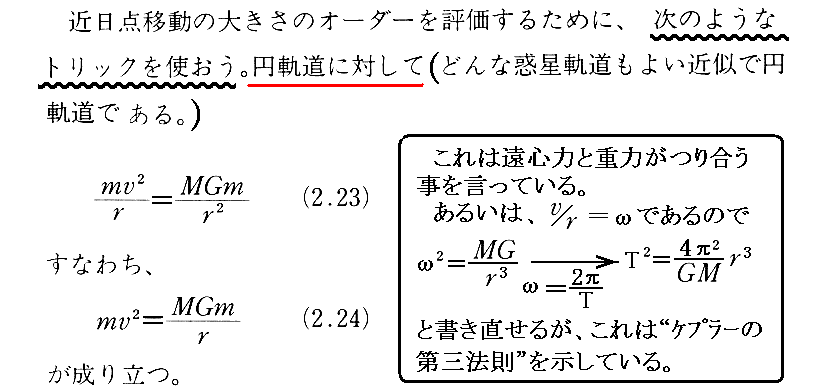



最後に得られた(2.26)式はさらに以下の様に変形できる。

様々な近似をしたために左辺第4項の数値係数が少し違うが、この式はまさに前述の⑤”式そのものである事が解る。だから、前述のように“固有質量”を乗じれば良いのです。
そうで無ければおかしな事になります。なぜなら質点mは測地線に沿って移動するわけですが、もし質点mの質量が運動と共に変化するのなら、測地線そのものが代わってしまうことになります。今は、大質量Mが作る重力場は静的であり、質点mの作る重力場の影響は無視できるとしていることを忘れないで下さい。
補足しますが、左辺第4項の数値係数が少し違うのは、様々な近似を繰り返した為もありますが、おそらくシュワルツシルド座標dtによる微分と固有時によるdτの微分の違いもあると思います。上の説明ではその違いを適当にごまかしていますので。ただし、私自身はその当たりの詳細がよく解りません。
補足しますと、Einsteinは1905年に特殊相対性理論を確立したすぐ後(1906年ころ?)に、運動物体の質量が増大するという特殊相対性理論の効果を用いて水星の近日点移動の異常値を説明できないか考えたようです。つまり、上記の(2.16)式の効果のみを考慮した議論です。そのことに付いては別稿「水星の近日点の移動」2.をご覧下さい。
[さらなる補足説明1-2]
ここの所がおそらく、シアマが「一般相対性理論(その物理的意味)」p144~145で説明している事だと思います。あるいは、別稿クリフォード・M・ウィル著「アインシュタインは正しかったか?}(1989年刊 原本は1986年刊)第
5章“水星の近日点移動(前半部のみ)”の中のこの赤線囲み部分の説明に関係するのだと思います。しかしシアマもウィルも曖昧な説明しかしていないので、その意味するところが良く解りません。
もし上記の考え方が正しいのなら、ウィルの言う第三の非線形効果は、第一と第二の効果の結果として、上述の様に第三項の非線形効果として表れると言うことのように思えるのですが? それともゼックスルの説明が間違っているのかも知れませんが?
ウィルもそこの所に、“これらの奇与の表現は非常にあいまいであり、用いる方程式の表現の仕方によって変わる。”と書いていますので、彼自身も旨く説明できないのかも知れません?
ついでに、もう少し補足します。

いままでの考察から解る様に、上記の相対論的補正(2.27)式の中に、[特殊相対性理論による運動物質の質量が増加する効果] と [一般相対性理論による重力場も質量の源(つまり重力の源)になる効果]の両方が含まれている事に注意して下さい。
もちろん、一般相対性理論は特殊相対性理論を含んでいますから、上記の両方の効果が一般相対性理論による効果であると言うべきかも知れません。

上記のランダウ「力学」p47の問3はこちらです。
[補足説明2]
本節で説明しているように、相対論力学ではエネルギー保存則の表現にNewton力学には無い新たな項があらわれます。これは[相対論力学に依る運動物体の質量はその速度に応じて増大する効果]と[重力ポテンシャルそのものが重力を生み出す質量の働きをする効果]によるのでした。
ところで、3.(3)2.で説明したように、球対称重力場では、自由落下運動および自由上昇運動のエネルギー保存則は相対論力学とNewton力学では完全に同じ形になりました。何故そうなるのかを、上記[補足説明1]に習って補足しておきます。
動径方向の運動に限る場合でも、[補足説明1]で説明した二つの効果を考慮しなければ成りません。



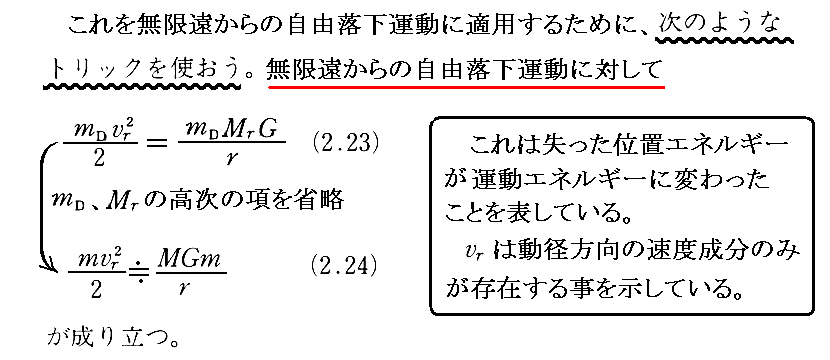


以上の議論では左辺に第3項が残るが、これは左辺の第1項、第2項に比べて高次の項で、おそらく厳密な相対論的な議論では、第3項は消えてしまうのだろう。
そのため、シュワルツシルド座標時tと固有時τの違いはあるが、3.(3)2.で説明したように、動径方向の落下運動に限れば、Newton力学のエネルギー保存則と形の上で一致するのだろう。このことは佐藤・ルフィー二文献10.第4章3.(a)の中でも強調されていますので、確かにそうなのでしょう。
3.運動の法則
④’式に、上記で求めた⑤”式と①’式、③’式を代入してdr/dτ、、dφ/dτ、dx0/dτを消去すると④”式となる。
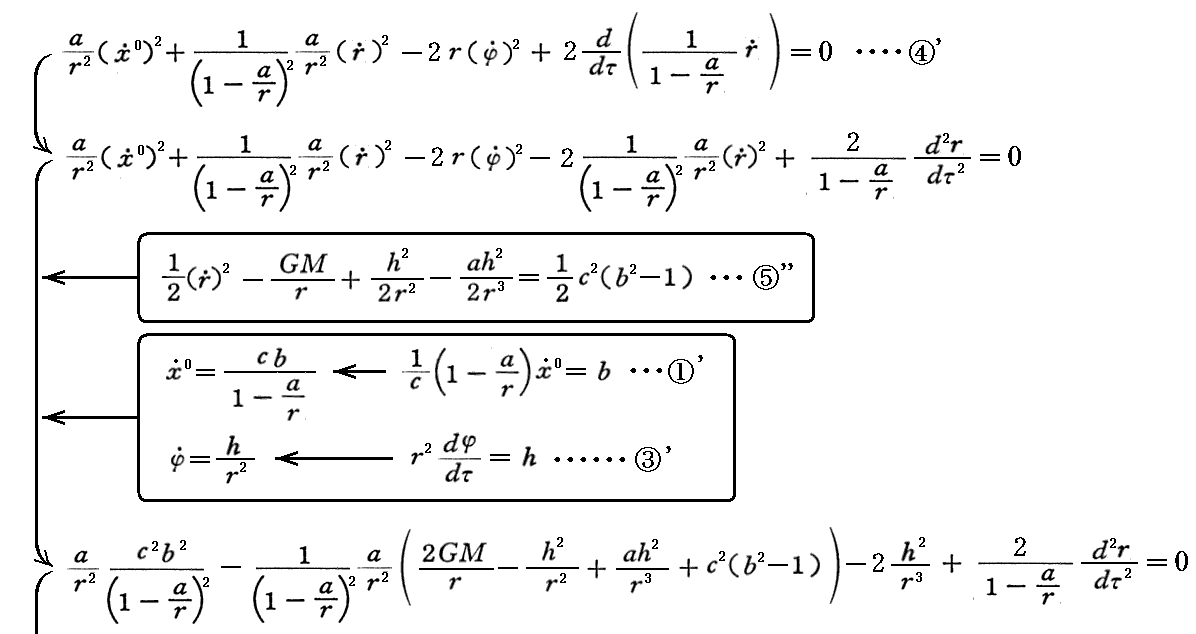
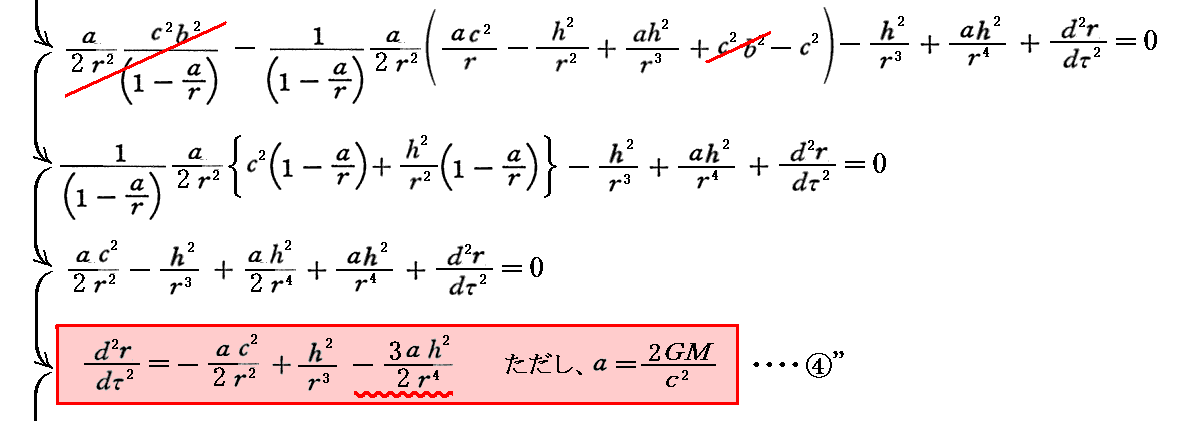
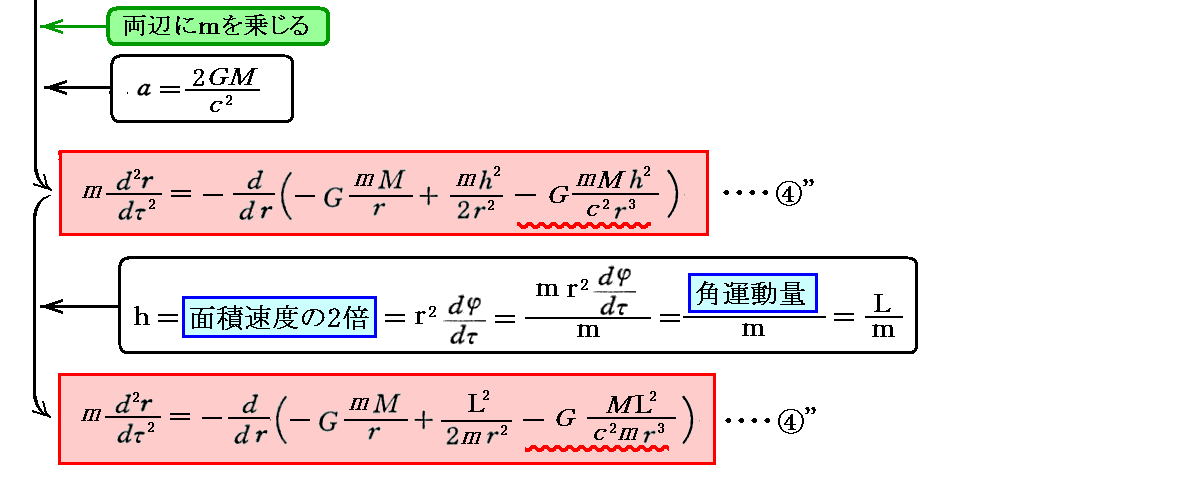
最後に示した④”式はNewton力学における“運動方程式”に相当する。また、最後の式の右辺でd/drで微分する中身は“ポテンシャルエネルギー”に相当する。このとき左辺の時間微分は“固有時間”に関してのものであることに注意して下さい。
4.軌道方程式
Newton力学で説明したのと同様に、相対論力学でも⑤”式に③’式(“角運動量保存則”)を適用して変数τを変数 φ に変換すれば、軌道の形を決定する軌道方程式が得られる。このとき用いる角運動量保存則は中心力であれば必ず成り立ちますので、相対論力学でも問題なく使用できることに注意して下さい。

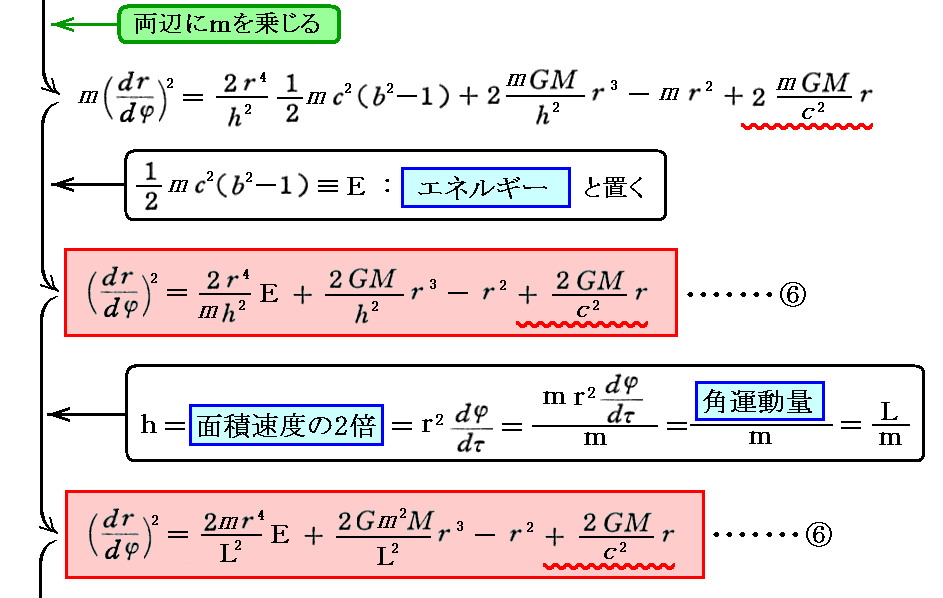
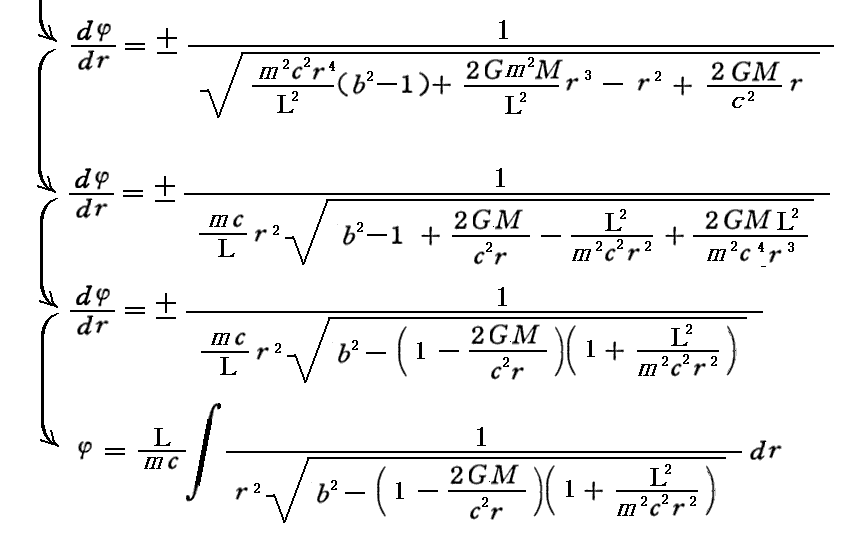
これを積分すれば r と φ の関係式を得ることができる。このとき1/r≡uの様な変数変換をすると扱いやすくなる。いずれにしても、その解は楕円関数で表される。このことに付いて3.(4)8.でもう少し詳しく説明します。あるいはハートル文献5.の説明を参照。
5.相対論力学での有効ポテンシャル曲線
④”式をNewton力学の該当する式と比較すると右辺の第2項は質点が角運動量を持っているための遠心力を表す項です。《Newton力学》では第3項が無いので、質点mが中心星Mに対して
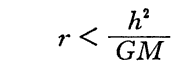
の程度に近付けば
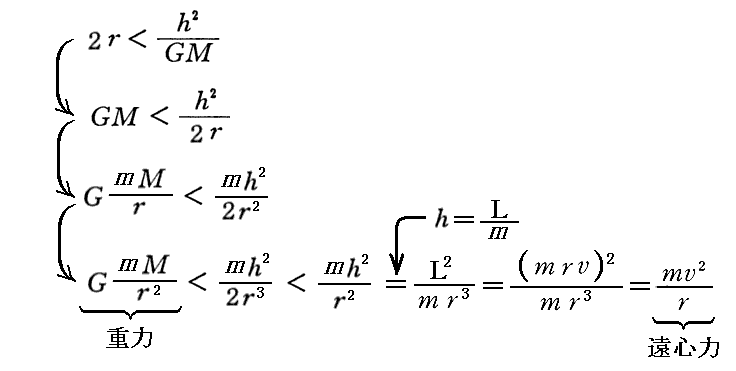
となるので、h(面積速度の2倍)が0で無い限り、遠心力項(④”の右辺第2項)が重力(④”の右辺第1項)に打ち克つ。このことに付いては別稿「質点の二次元運動」3.の逆二乗法則の力に関係したポテンシャル曲線のグラフをご覧下さい。
同じく、⑤”式のNewton力学で該当する式では左辺の第4項は存在しないので
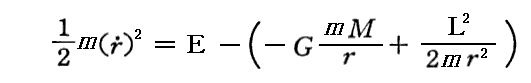
の右辺は、有限の大きさを持つある r(>0)に対して0となる。その位置で質点の速度は反転して星から遠ざかることになり、h(面積速度の2倍)が0で無い限り、質点mが星に捕獲される事は無い。つまり質点mが最初に、たとえ僅かでも角運動量L(ゼロでないh=L/m)を持っていたら決して中心星Mに落ち込む事は無い。
これに対して《相対論力学》では、角運動量L(あるいはh)にもとずく引力項
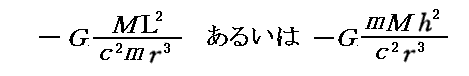
が存在する。この項は r が小さくなると遠心力項よりも必ず大きくなる。その為、相対論力学では角運動量についてある値以上でないと、質点mは必ず中心星Mに飲み込まれてしまいます。もちろん、中心星質量Mに関係しますが、ある値以上の角運動量Lを持っていれば中心星Mに飲み込まれることはありません。
このことの詳細は3.(4)6.(2)[補足説明1]で詳しく説明しますが、取りあえず、その事を議論する基礎となる有効ポテンシャルVeff(r)に付いてもう少し調べてみます。
3.(4)3.で求めた“エネルギー保存則”を表す⑤”式から始める。
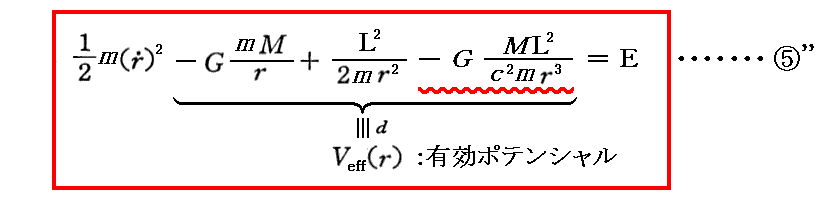
このときもちろん、c2→∞と見なすと左辺第4項が省略できるし、τに関する微分d/dτをtに関する微分d/dtで置き換えれば、先ほどのNewton力学の表現式に帰着する。
さらに補足すると、rが大きな領域では、有効ポテンシャル定義式の第3項は省略できるので、Newton力学の有効ポテンシャルと一致する。r→∞に近付くと第2項も省略できるのでV(r)→-GmM/rの曲線に近付いていく。
相対論力学の特徴が表れるのはrが小さくなり第3項重要になる領域です。
具体的に説明するために初期条件を下記の様に設定して、有効ポテンシャルVeff(r)のグラフを描いてみる。

ここで、初期角運動量L0として、地球の公転角運動量の1/1000程度を想定したのは、角運動量が大きいと一般相対性理論の効果が顕著になるブラックホール近傍に到達できる解(軌道)とならないからです。中心星Mがブラックホールであっても、中心から水星軌道半径程度以上離れるとNewton力学との違いはほとんど検知できなくなりますから、相対論力学の特徴を理解するには中心に接近しなければ成りません。
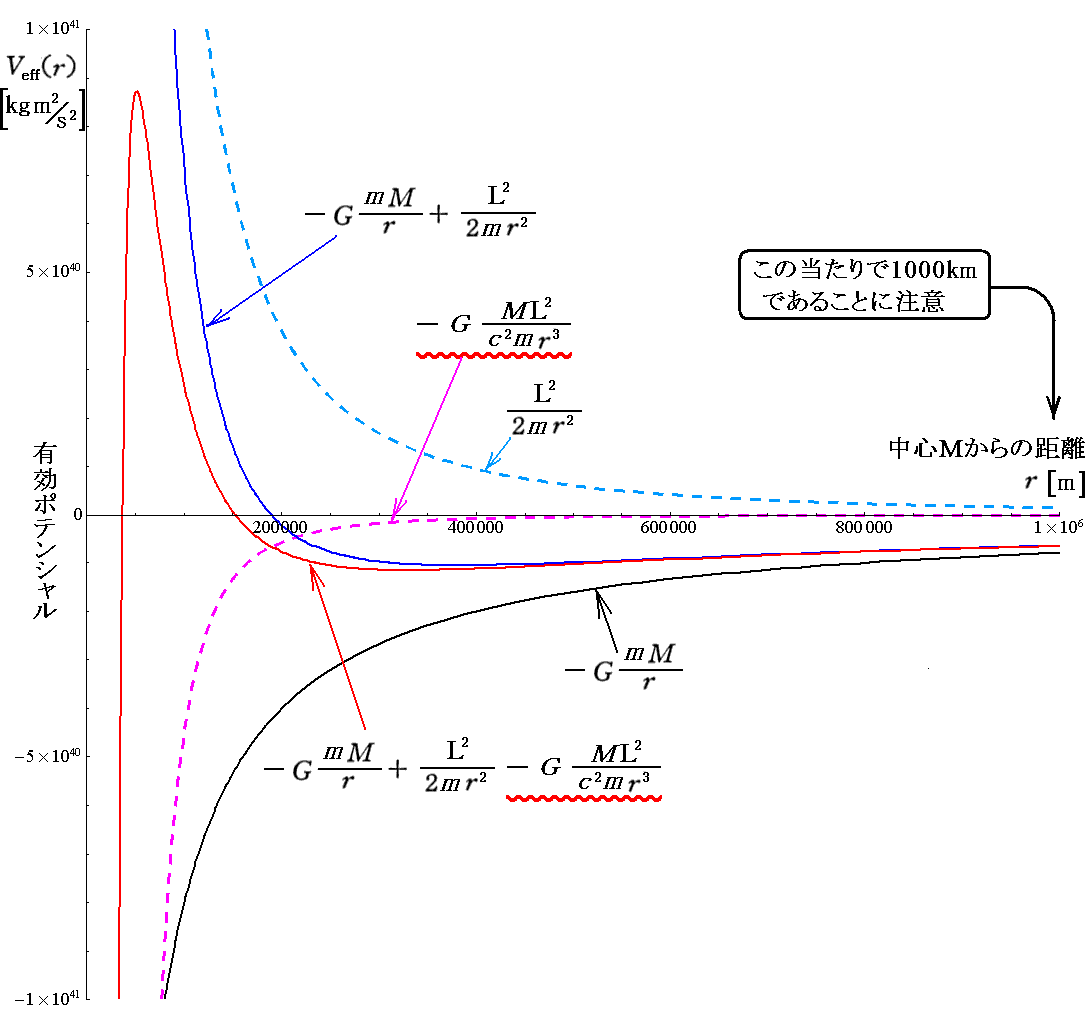
軌道運動する初期条件としての角運動量L=n・L0の n を様々変えたグラフを記すと下記の様になる。下記のグラフは L 以外は変えていないことに注意されたし。
また、ここで仮定した質量Mのブラックホールの“シュワルツシルド半径”は、a=29662.2m≒30000m≒30km です。だから、ここで取り上げた例はいずれもブラックホールM近傍での質点mの運動の様子を示すのに有効です。
[L=5×L0の場合]
[L=4×L0の場合]
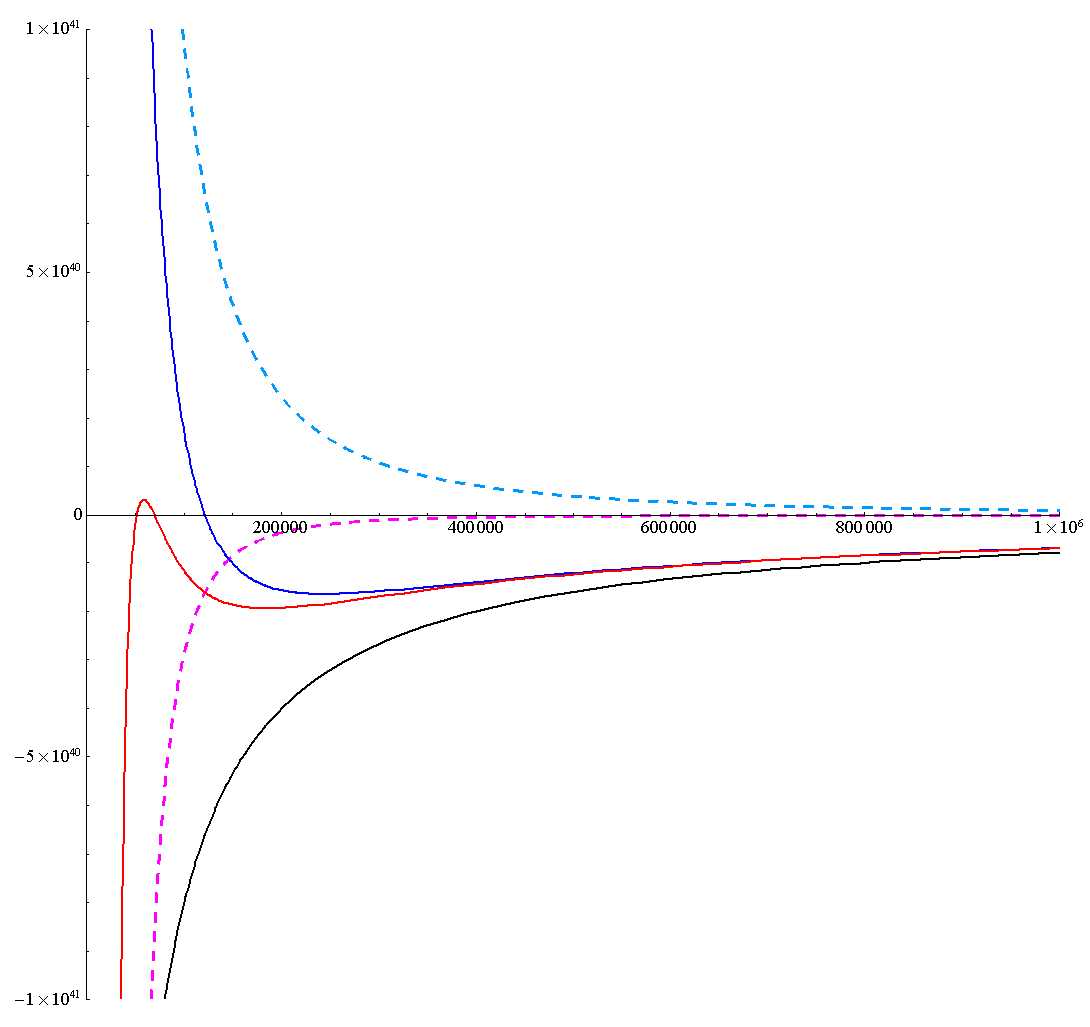
[L=3.5×L0の場合]
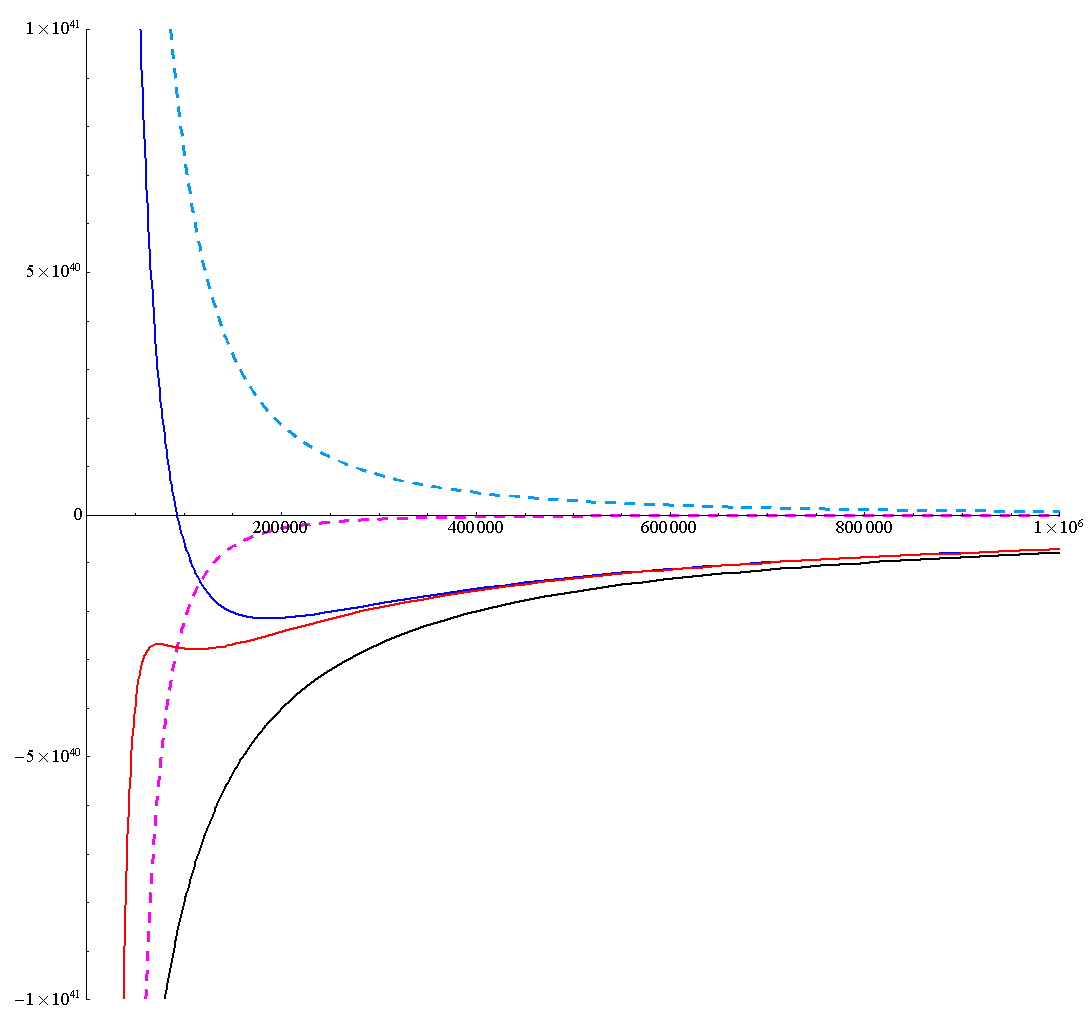
[L=3.4×L0の場合]
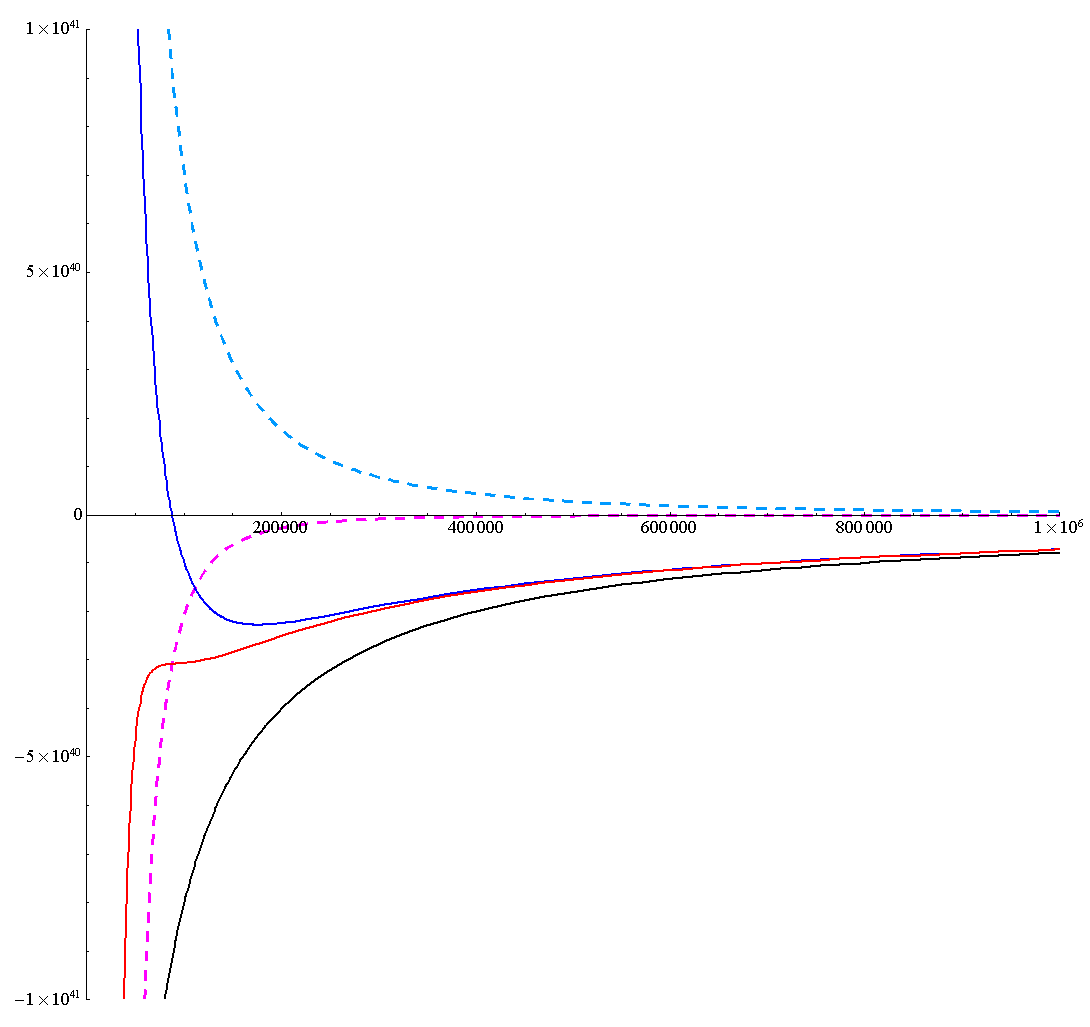
[L=3.3×L0の場合]
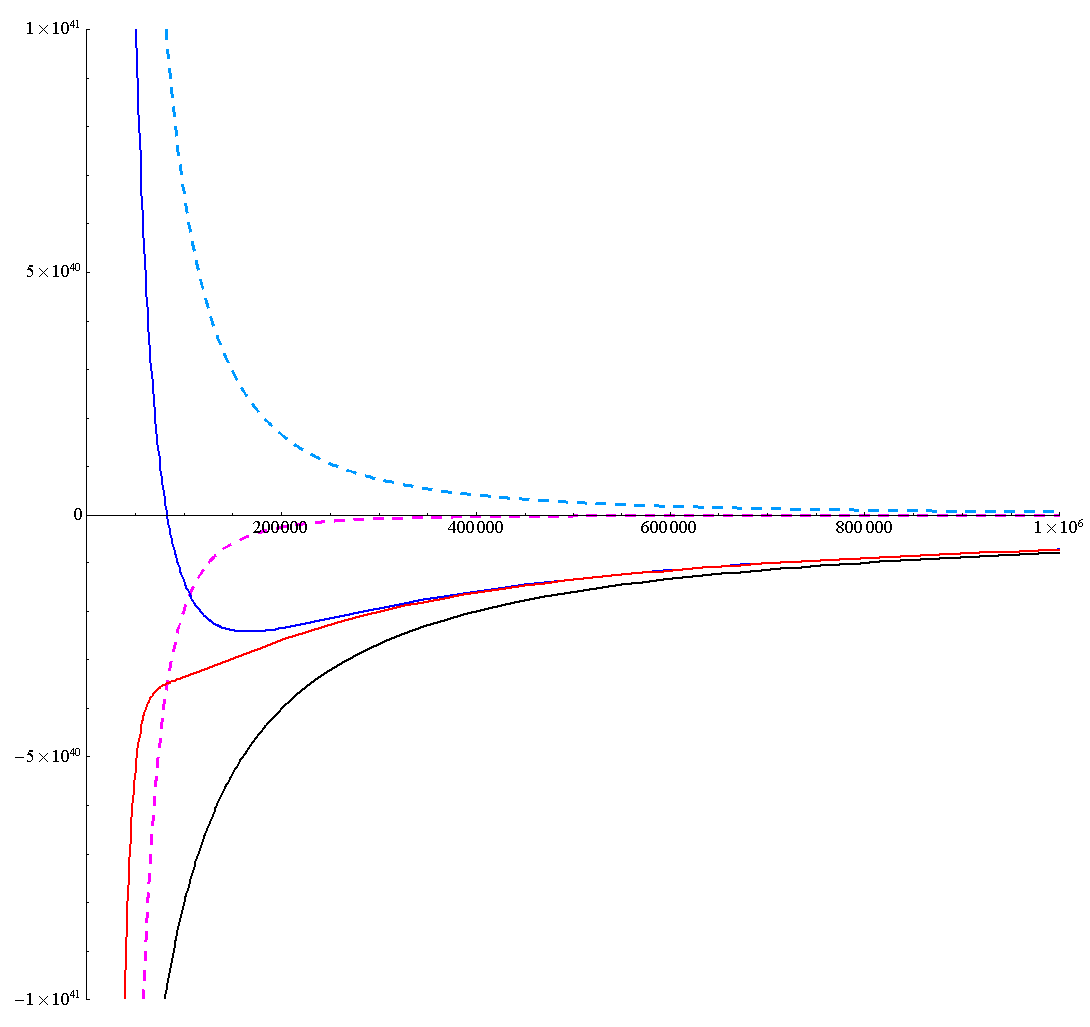
となる。
少し見にくいが、これらをすべて重ね合わせると下図になる。
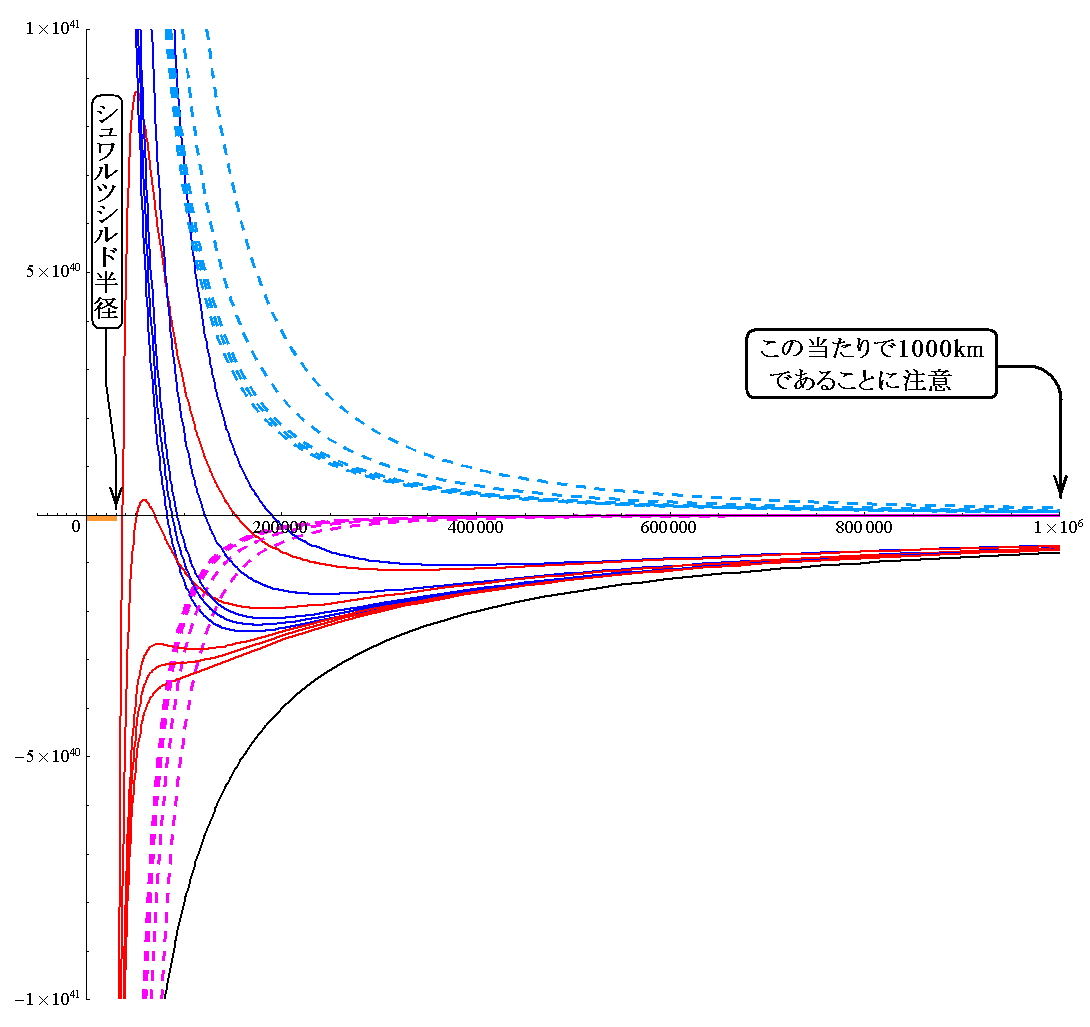
これらの有効ポテンシャルの形状を、別稿「質点の二次元運動」3.(1)~(2)に示したNewton力学の有効ポテンシャル形状と比較すると、本項の最初に述べた事柄が理解できます。
次項で、[有効ポテンシャルVeff(r)] と [質点mのエネルギー値E] との関係によって、実際の軌道がどの様に変化するかを考察します。
6.相対論力学における軌道の形
(1)有効ポテンシャルVeff(r)の極値
前項の考察から明らかな様に、相対論力学では、質点mの角運動量Lがある値以上である場合、有効ポテンシャルVeff(
r)は二つの r で極値(極大値と極小値)を取る。そのときの半径は dVeff/dr=0 の r に関する二次方程式を解くことによって得られる。
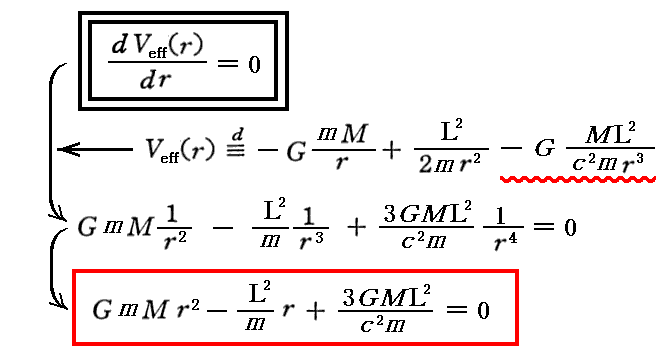
この二次方程式の解は以下となる。
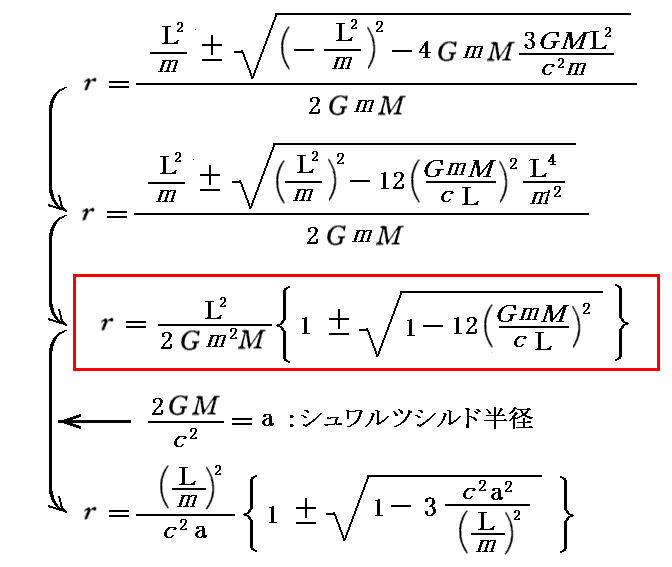
このとき得られる二つの半径(極大値を取るrmaxと極小値を取るrmin)に於いて、有効ポテンシャルが極値を取る。グラフから明らかな様に、Veff(rmax)>Veff(rmin)で、rmax<rmin です。実際、そのときの値は
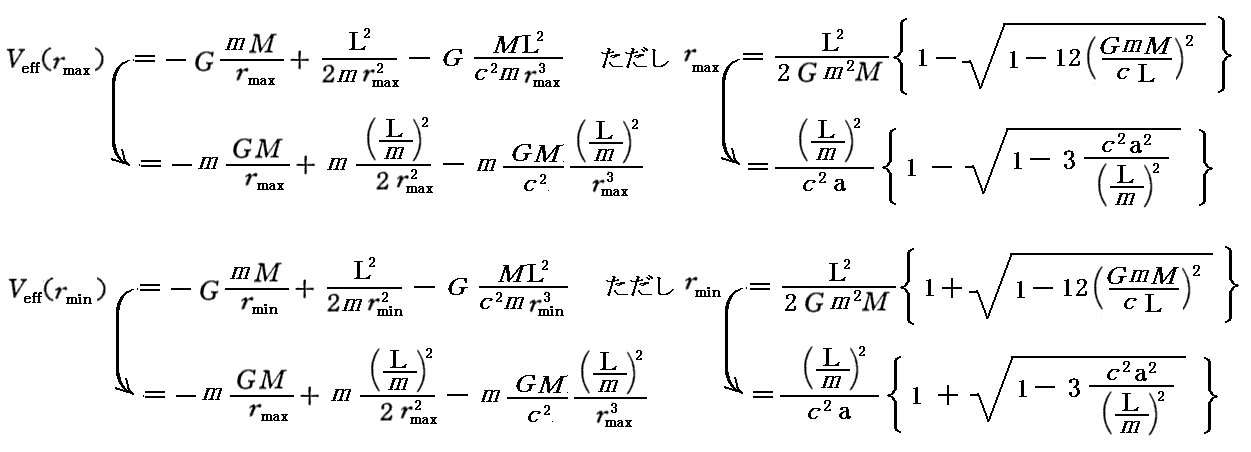
によって計算できる。
このとき、角運動量Lが、《二次方程式が二つの実数解を持つ判別式》
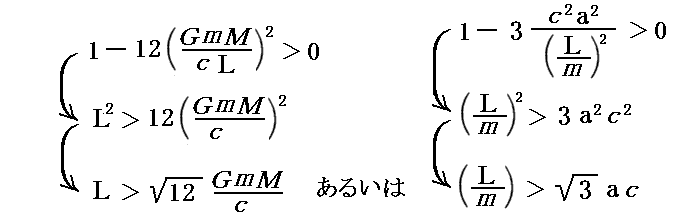
を満足する場合のみ極値が存在するのであって、角運動量が上式の右辺の値以下なら極値は存在しない。実際前項でグラフ表示した例の数値を代入すると
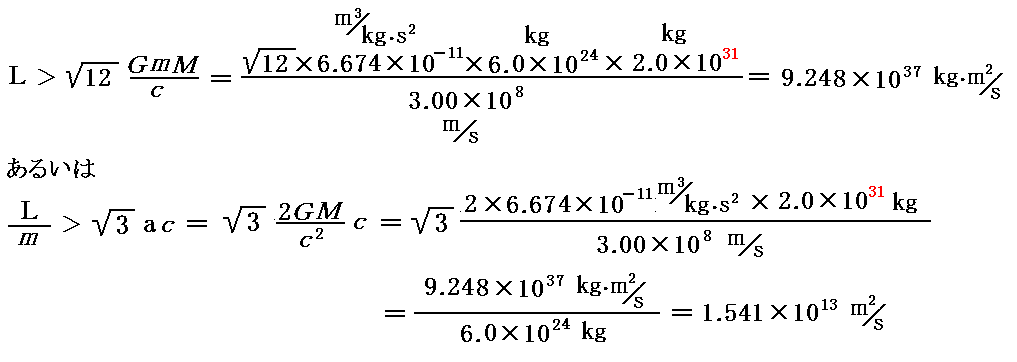
となるが、この値は最初に仮定した初期角運動量L0=2.7×1037kgm2/s の 3.42倍程度になる。
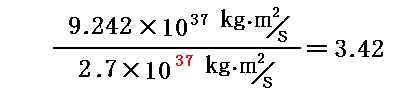
実際L=3.4×L0のグラフでは極値が無くなっている事を確認して下さい。
すなわち、
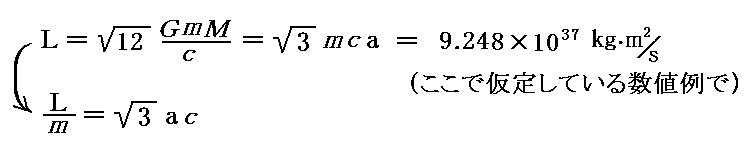
の時が極値を取れる角運動量の最低値です。つまり、そのとき
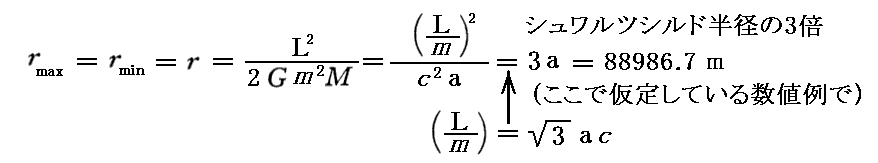
となり

となる角運動量値です。
いずれにしても、Newton力学では有効ポテンシャルの極大値が無限大の高さになるのに対して、相対論力学では最大値Veff(rmax)が存在する。そして質点mの持つ角運動量Lがある値以下になると極値を取ることなく r→0 と共に有効ポテンシャル値Veff(r)は一方的に負の無限大になっていく。
[補足説明1]
前掲の有効ポテンシャルVeff(r)が極大値をとるrmaxと極小値を取るrminが、質点mの持つ角運動量Lによってどの様に変化するのかを調べておきます。このとき具体的な数値例として、先ほどと同じ値を用います。

そして、rmaxとrminの値が質点mが持つ角運動量Lによってどの様に変化するかを調べます。そのとき、Lとして上記のL0を用いてL=n・L0と表し、横軸をnで表したグラフにしています。
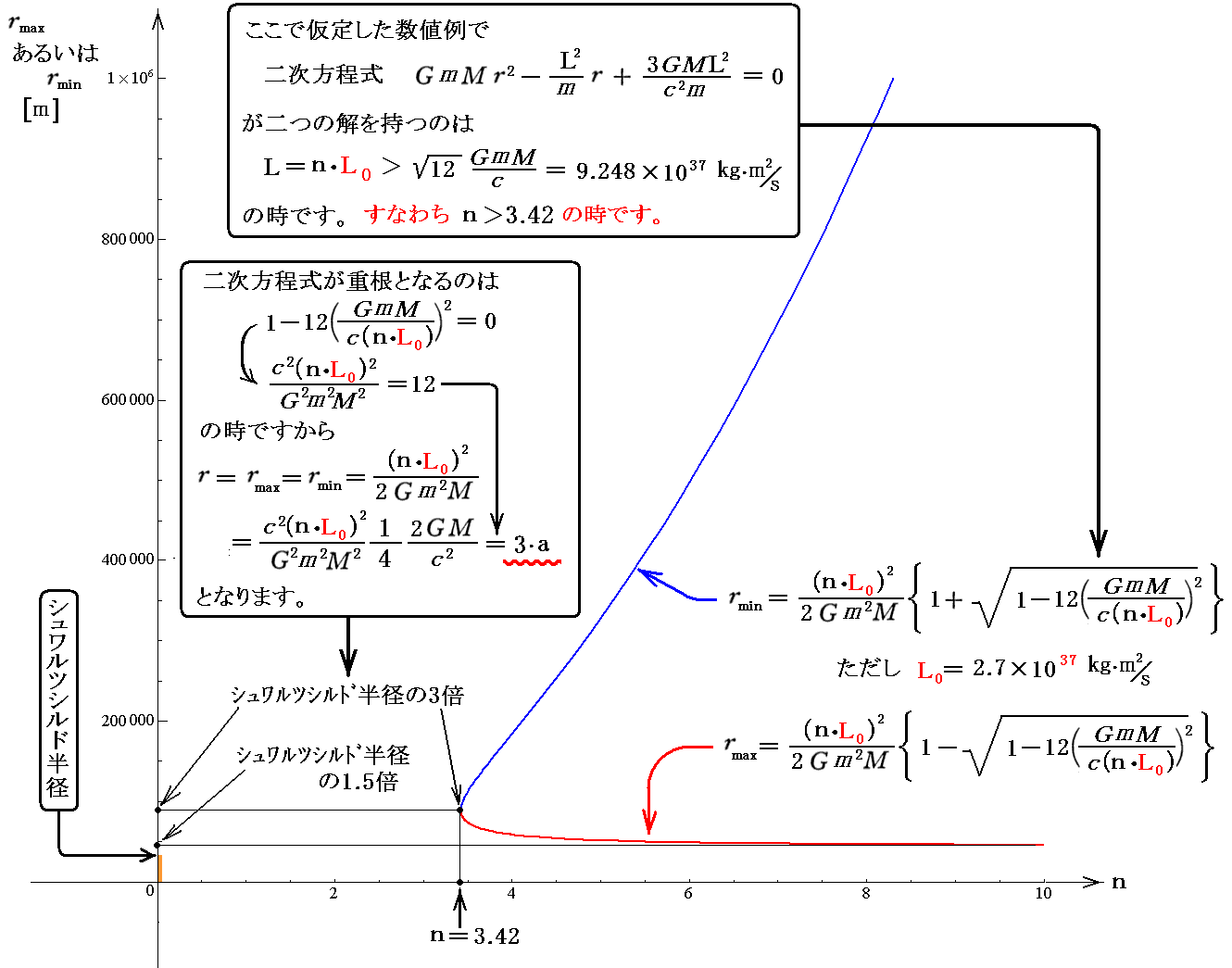
グラフから明らかな様に、先ほど求めた n=3.42 で rmax=rmin となり、そのときの r はシュワルツシルド半径の3倍になります。このことは後ほど3.(4)7.(1)でもう一度取り上げます。ここで仮定したmやMのときには、n>3.42(つまりL>9.242×1037kg・m2/s)の領域でのみ先ほどの二次方程式が二つの解を持つと言うことです。
また質点mの角運動量 L=n・L0 が増大すると rmax はシュワルツシルド半径の1.5倍に近付いていきます。これが rmax が取り得る最小値です。
このことは後ほど3.(4)8.福江文献の引用文中に出てきますので、そのときここの説明を思い出されて下さい。
[補足説明2]
Newton力学で上記のグラフがどの様になるのかを補足しておきます。Newton力学では有効ポテンシャルを示す関数の第3項がありませんので前述の式は
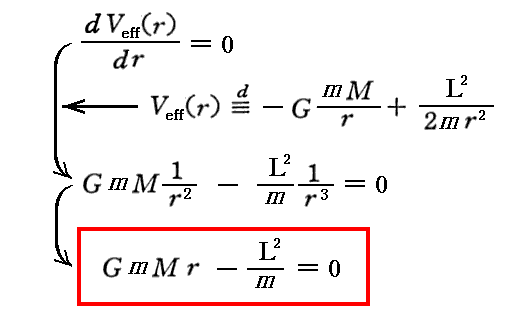
となります。
すなわち、Newton力学では rmin の一つの解が得られるだけです。しかも、その解は L の二次関数となります。
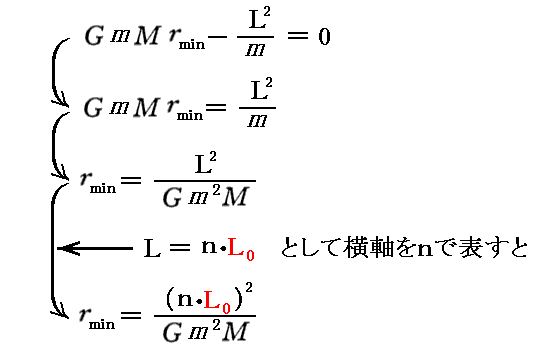
この関数を先ほどのグラフに重ねて表示すると
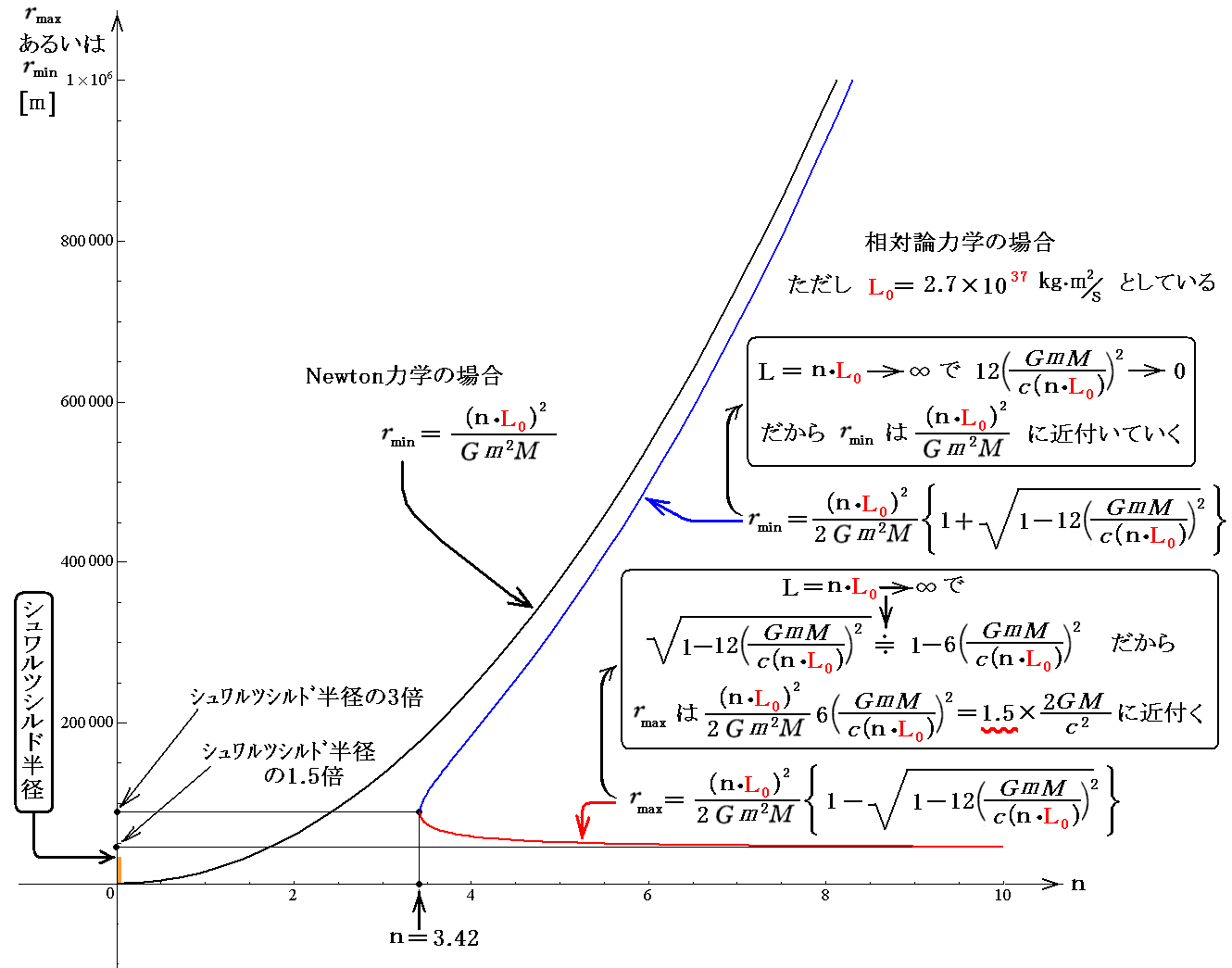
となります。
後で利用する為に、上記の縦横軸を入れ替えた(90度回転して左右を入れ替えた)グラフにしておきます。その為にまず、Lの関数である rmax あるいは rmin の式をLに付いて解きます。
r<3a の範囲では
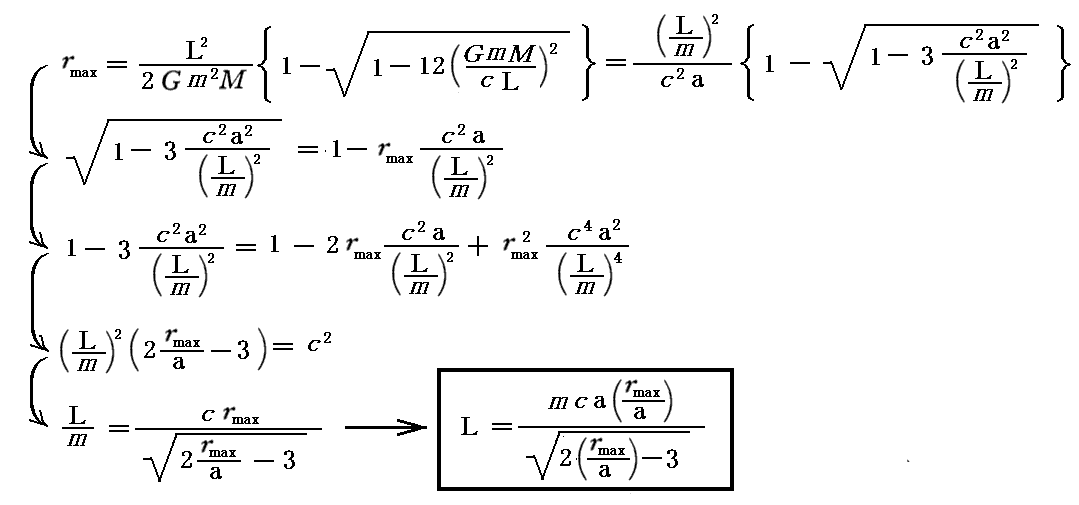
となります。
同様に r>3a の範囲では
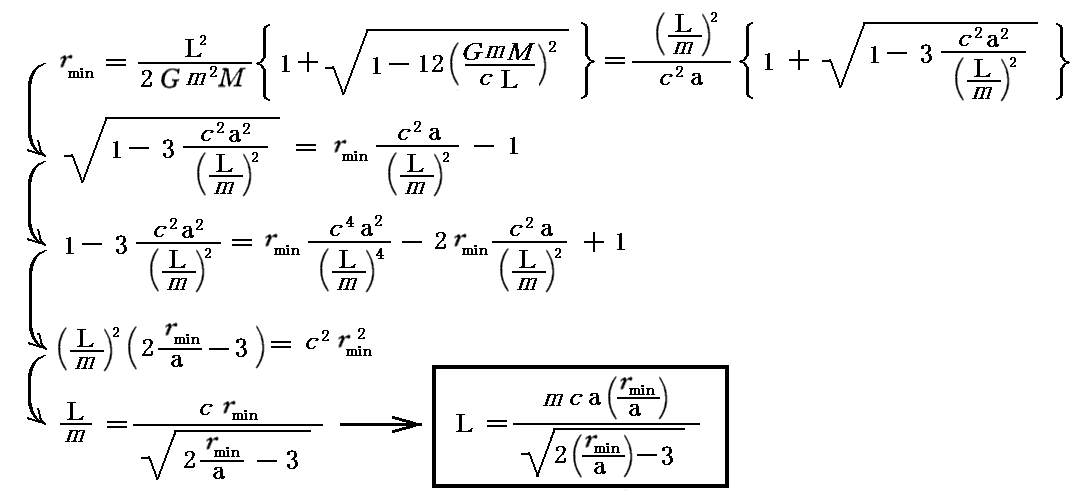
となります。これは、 rmax に付いての式と同じ形になります。
横軸として r そのものではなくシュワルツシルド半径を単位とした r/a でグラフ表示すると以下の様になります。
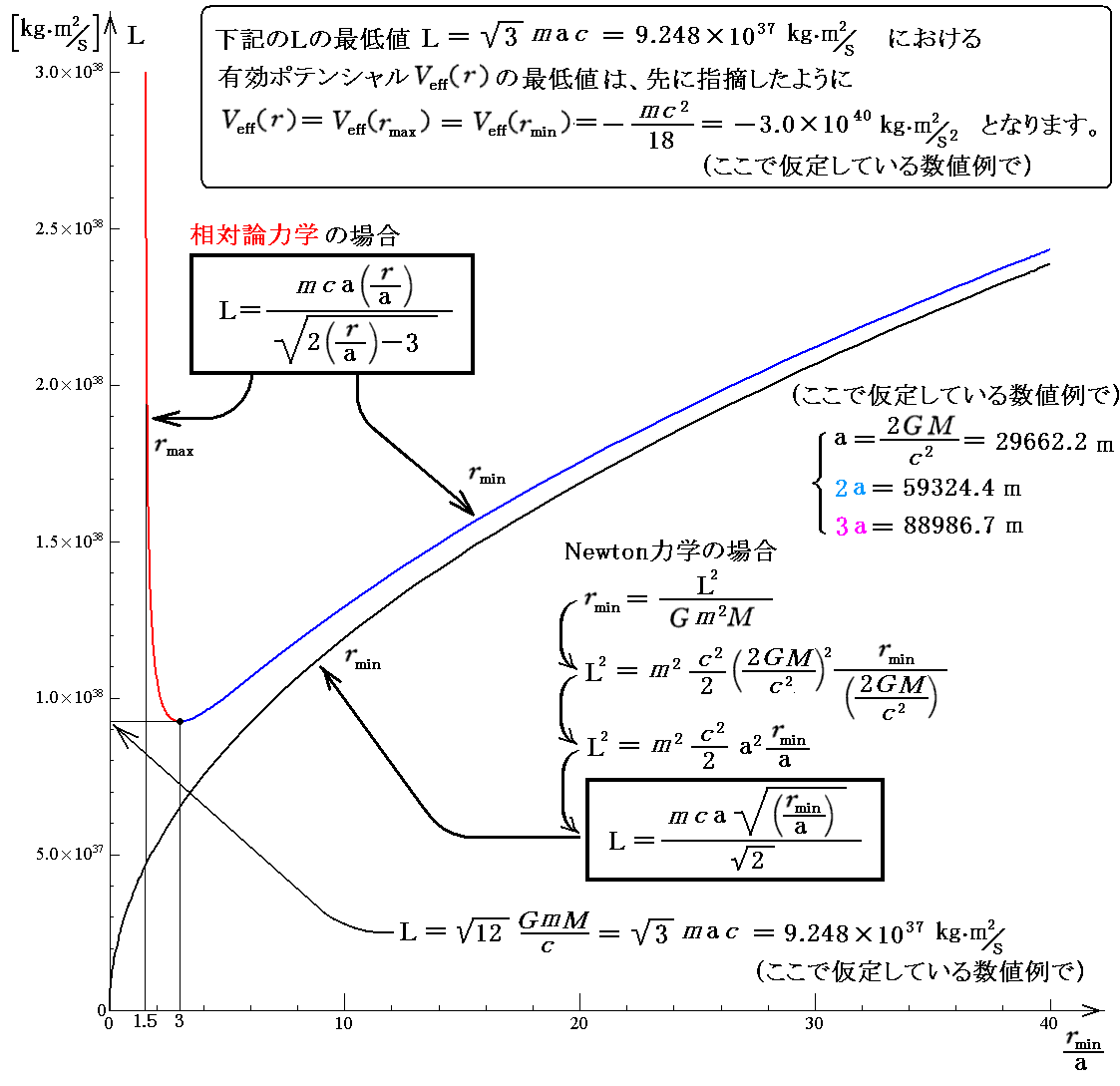
グラフの縦軸の数値はここで仮定している数値例の場合です。また、Newton力学の場合も同時に記入していますが、相対論力学の関数形は r→∞
とともにNewton力学の式に帰着することに注意して下さい。
ここで注意して欲しい事は、Newton力学に於いてもシュワルツシルド半径の概念は有効です。相対論力学で出てくるシュワルツシルド半径はシュワルツシルド座標上での値ですが、Newton力学での時空座標は、時空間のひずみが無い相対論力学のシュワルツシルド座標と同じものですから。
つまり、中心質量Mが相対論力学でブラックホールとなるほど高密度であるかと言うことは相対論力学とNewton力学の違いに全く関係しません。つまり物質がその様な高密度状体で存在できるかどうかということは両方の力学理論の預かり知らぬことです。両者の違いが関係するところは、時空間が歪んでしまうか、その様な事は生じないとするかに有るのであって、高密度で存在できるとすることはNewton力学でも当然仮定できることです。
[補足説明3]
[補足説明2]の最終グラフの縦軸を L から E or Veff に変換したグラフもついでに求めておきます。
すなわち、 3.(4)5.の最後で示したグラフでVeff(rmax)の点を繋ぎ(赤線)、Veff(rmin)の点を繋いだもの(青線)に相当する曲線のグラフです。そのとき同時に、Newton力学の場合である「質点の二次元運動」3.(1)~(2)で示したグラフの中に描かれているVeff(rmin)の点を繋いだものも示しておきます。
それを実行するには、3.(4)6.(1)で求めた、有効ポテンシャル曲線Veff(r)が極値を取るときの値Veff(rmax)あるいはVeff(rmin)中の角運動量Lを、rmaxあるいはrmin の関数で表す必要があります。そのために先ほど[補足説明2]求めた関係式を用います。すなわち
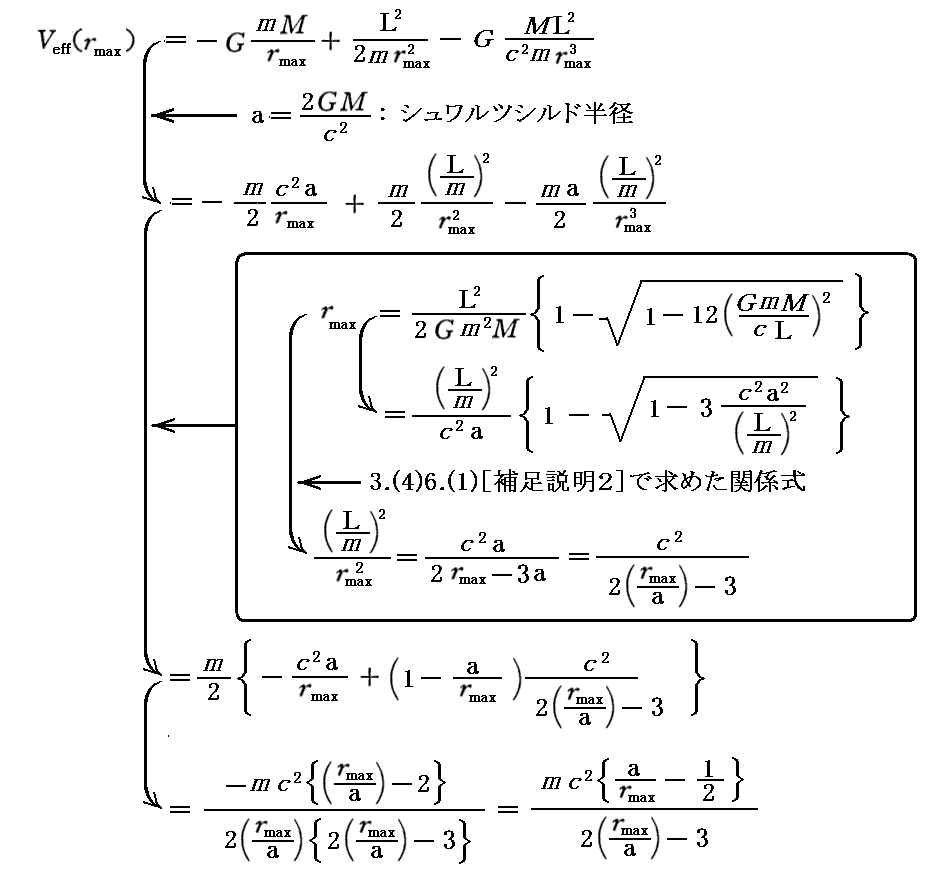
となります。Veff(rmin)に付いてのグラフ関数も同様にして
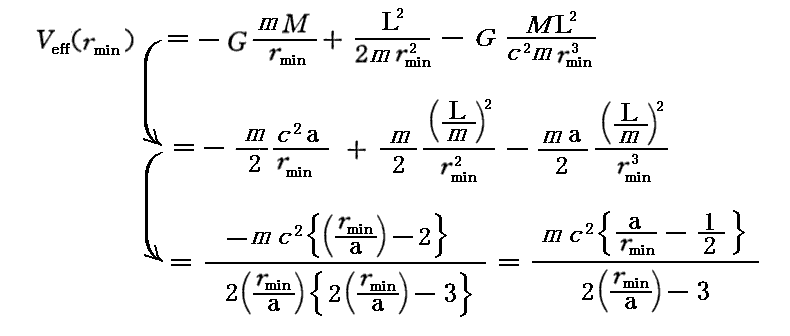
となります。これはVeff(rmax)に付いての形と同じになります。
これらの関数のグラフを3.(4)5.で求めた有効ポテンシャル曲線Veff(r)のグラフに重ねて描くと次のようになります。
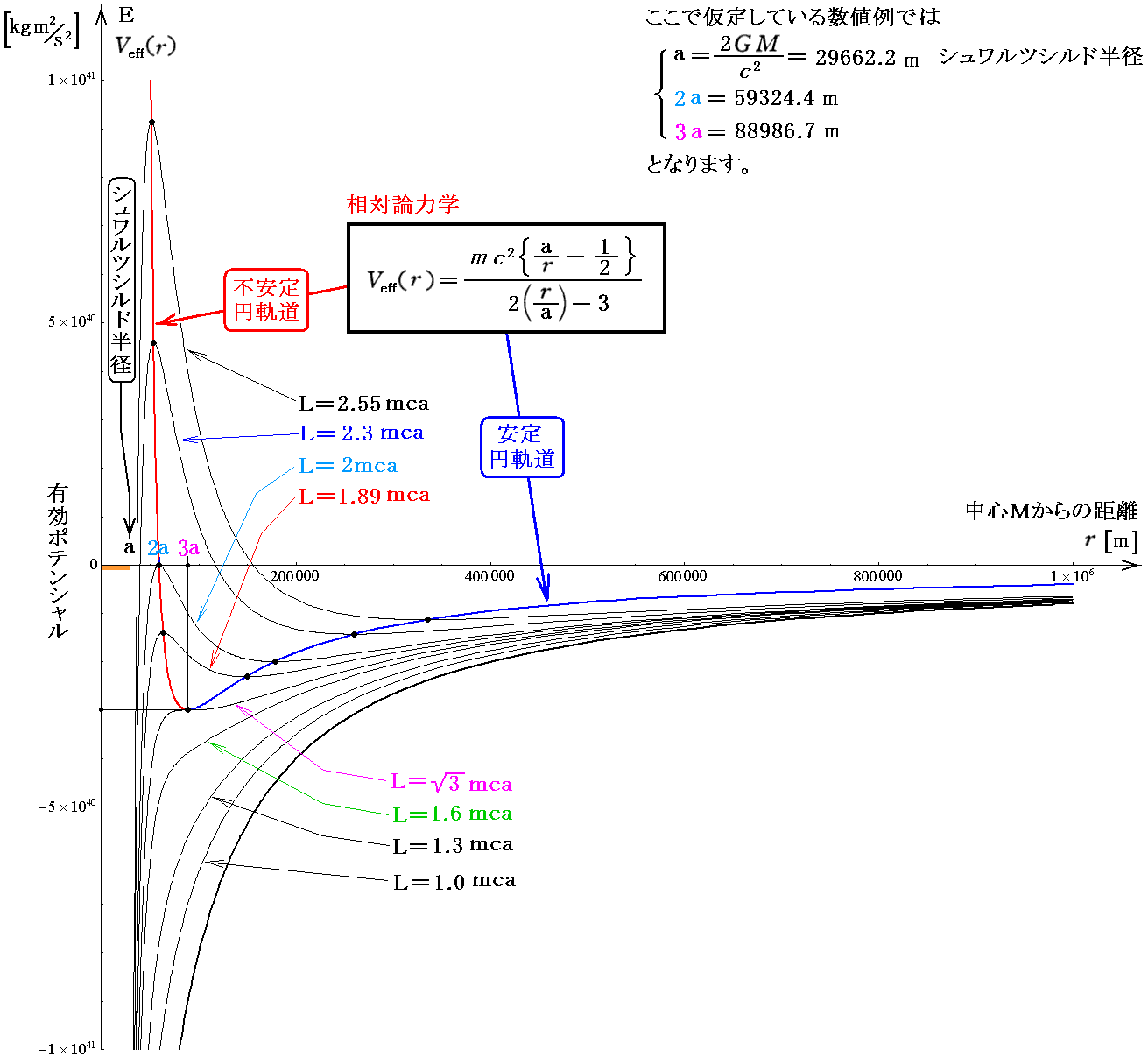
このグラフの r>3a の部分は有効ポテンシャルの極小値Veff(rmin)を繋いだものであり、3a>r>1.5a の部分は有効ポテンシャルの極大値Veff(rmax)を繋いだものであることを読み取って下さい。
そのとき有効ポテンシャルの極大値Veff(rmax)を繋いだ曲線はL→∞とともにr→1.5aの位置まで近づいていくが、決してr→0まで近付く事はないことに注意して下さい。
また、L<√3mcaでは安定円軌道は存在しなくなることに注意して下さい。そのとき、安定円軌道として可能な最小円軌道半径は3aでして、これ以下の安定円軌道は存在しません。そのため r<3a の領域に書かれているVeff(r)の赤曲線の不安定円軌道についての部分はあまり意味がありません。
さらに補足しますと、赤曲線の部分が表れてきたのは、本来ならば(つまりNewton力学では) r→0 とともに正の無限大に増大する有効ポテンシャル曲線が、第3項の
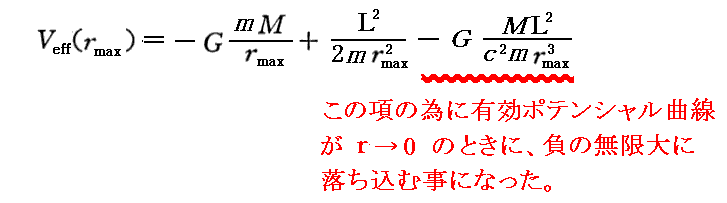
の為に負の無限大に落ち込む(r-3だからそうなる)ことに成ったためである事を忘れないで下さい。
有効ポテンシャルグラフの初期角運動量Lの値は図中に示しています。その中で、特に着色した角運動量値Lのグラフは3.(4)6.(2)[補足説明1]で用います。
丁度良い機会ですから、Newton力学の場合の同様なグラフを示しておきます。まずVeff(rmin)に付いての関数形は次のようになります。Newton力学における有効ポテンシャルについては「質点の二次元運動」3.(1)~(3)を復習して下さい。
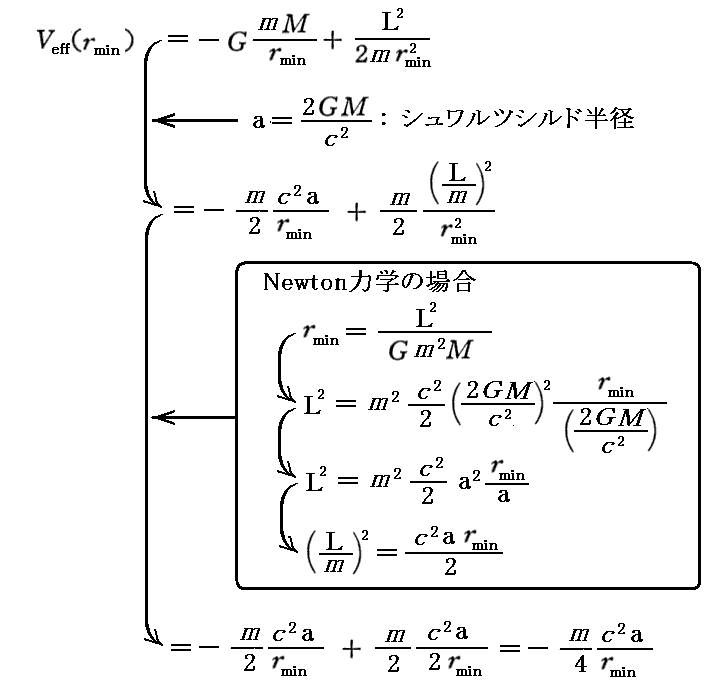
この関数のグラフは下記のようになる。
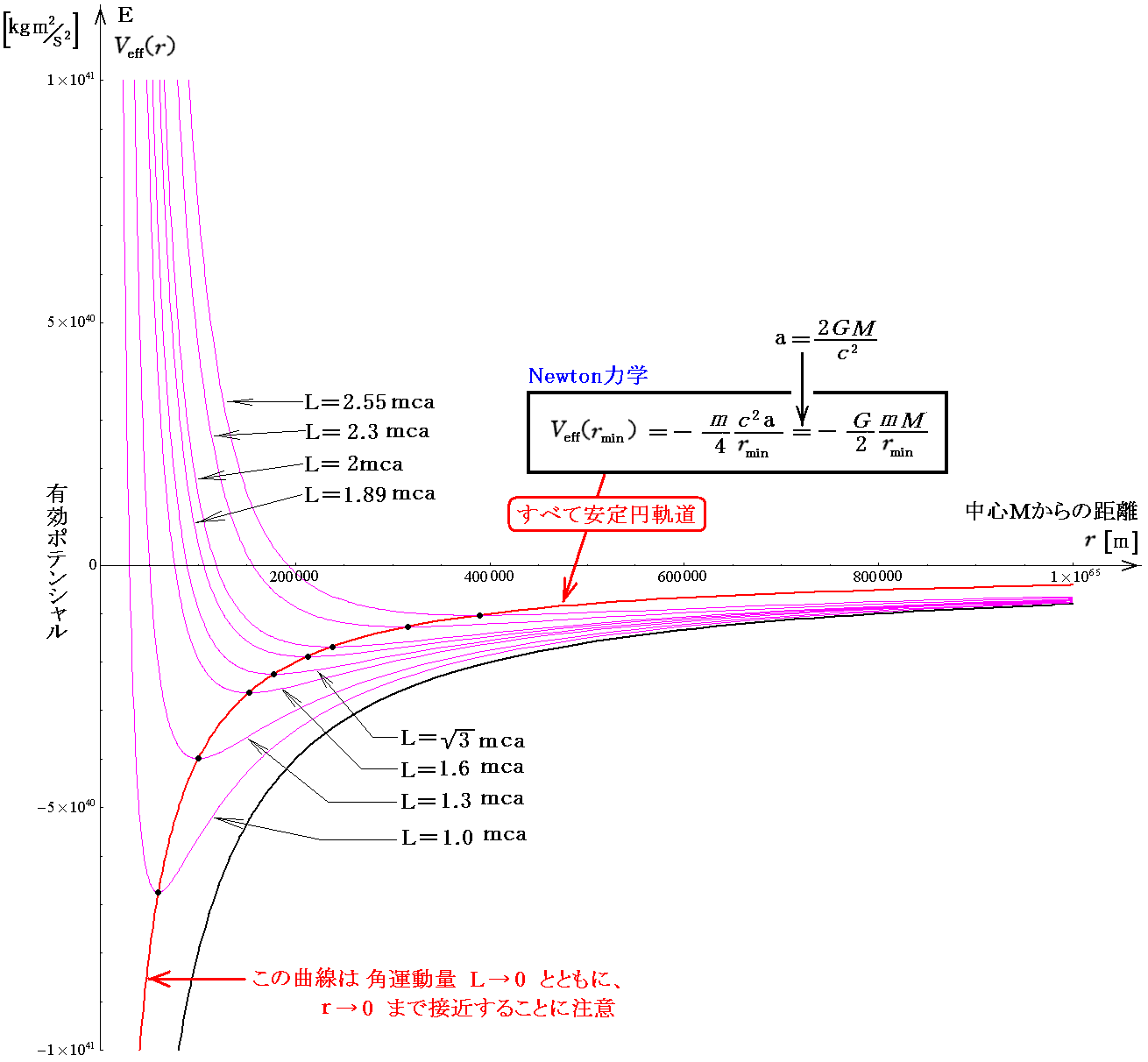
このグラフは、「質点の二次元運動」3.(1)~(2)ですでに示しています。求めた曲線が、有効ポテンシャルの極小値(最小値でもある)Veff(rmin)を繋いだものであることを読み取って下さい。そのとき、この曲線は角運動量L→0とともに、r→0の原点まで近付くことに注意して下さい。
これを、先ほどの相対論力学のグラフと重ねると以下の様になります。
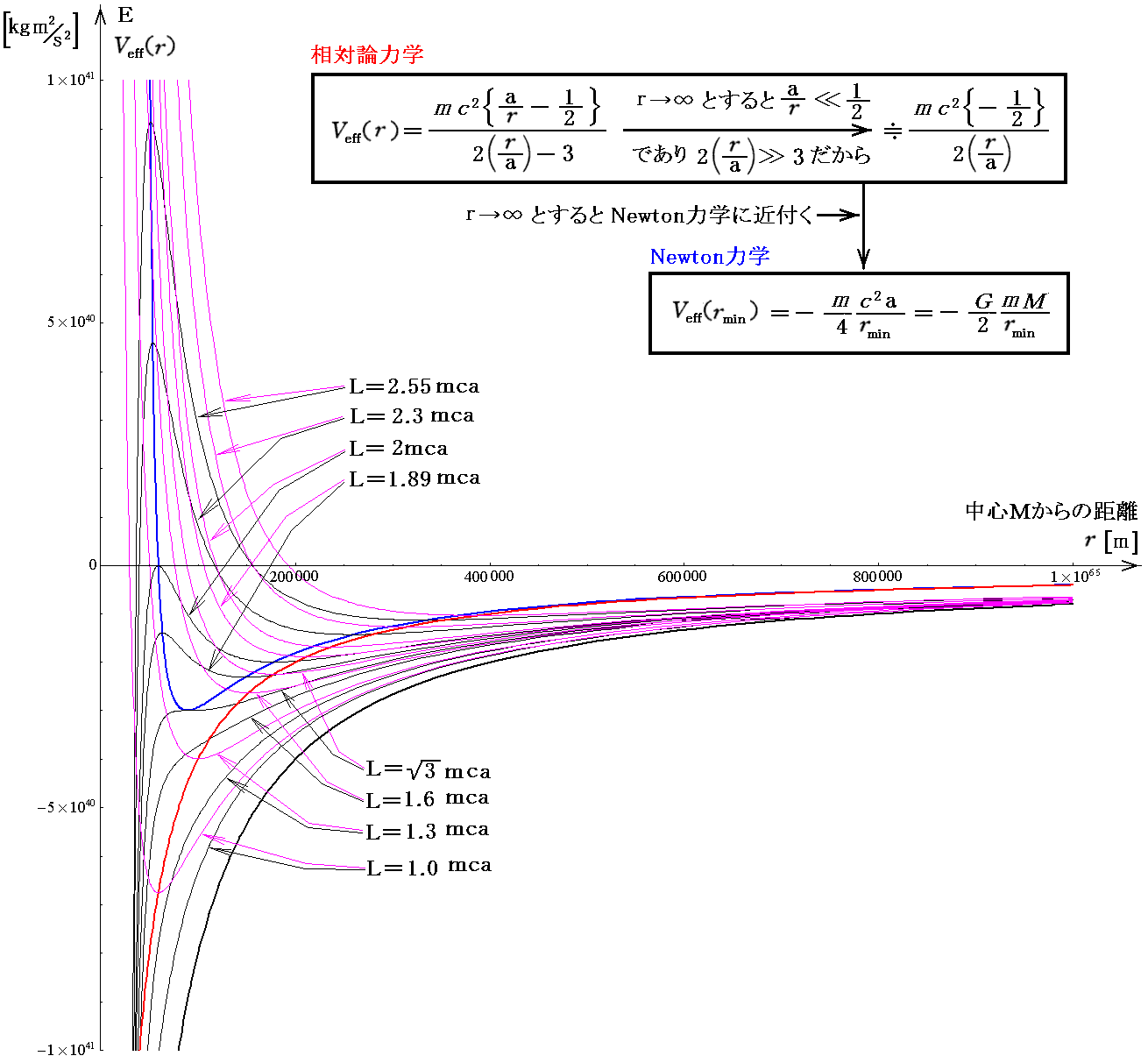
グラフがかなり錯綜していますが、初期入射角運動量Lが同一でも、Newton力学から相対論力学になると有効ポテンシャルVeff(r)の形が変化することを読み取って下さい。特にブラックホール近傍でその違いが顕著になります。
そのとき互いの関係は、縦軸を角運動量Lとした[補足説明2]の最後でしめしたグラフに似ています。ただし、r→∞としたとき、Newton力学と相対論力学の両方のグラフが横軸に接するように近付いていきます。そこが縦軸をLとしたグラフと違う所です。
また、r→∞ としたとき、相対論力学の式はNewton力学の式に近付いていきます。つまり r がシュワルツシルド半径の100倍程度以上離れると、相対論力学とNewton力学の違いはほとんど無くなり相対論的効果は検知できなくなります。
[補足説明4]
3.(4)6.(2)[補足説明1]で必要になりますので、有効ポテンシャルの最大値が 0 となるときの L の値を求めておきます。すなわち有効ポテンシャルVeff(r)の形が下図の様になるときの条件です。
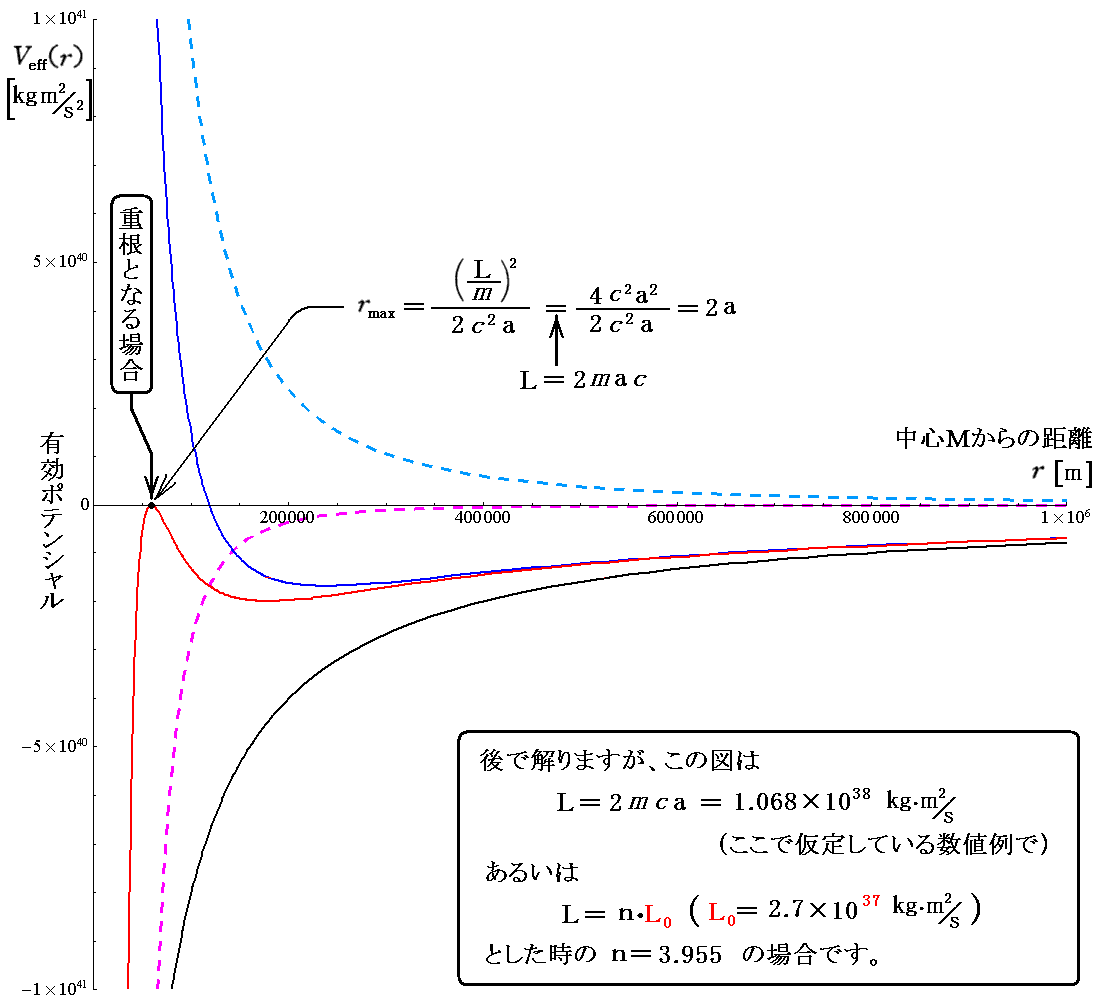
これは、有効ポテンシャルVeff(r)に対する次の二次方程式が重根をもつ場合です。
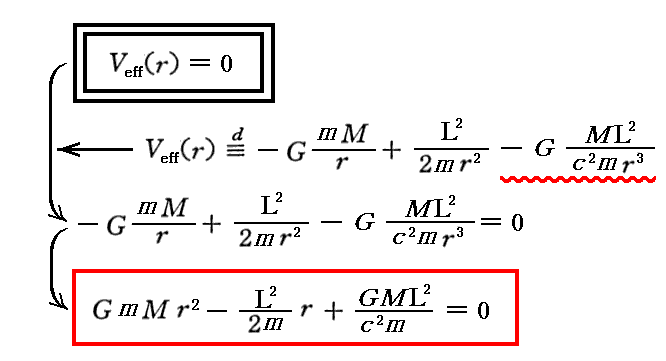
この二次方程式の解は以下となる。
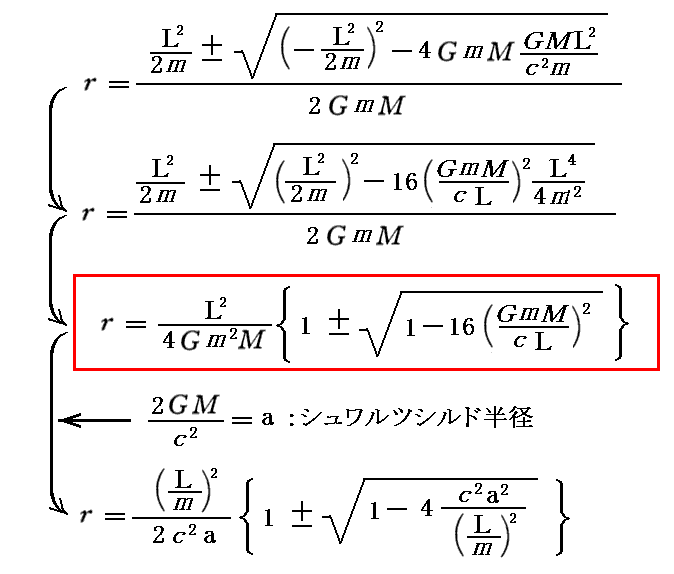
これは、有効ポテンシャルVeff(r)曲線がエネルギーE=0の線(つまりr軸)と交わる二点の座標値を表していますので、これが《重根となる条件》
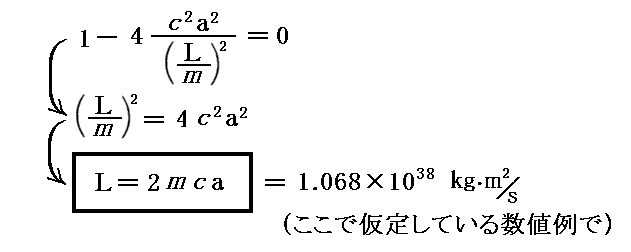
が満たされることが、有効ポテンシャルの形が最初に述べた形になる条件です。このとき、有効ポテンシャル曲線はその極大値Veff(rmax=2a)
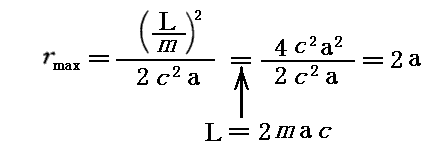
で横軸(r軸)に接する。つまり、シュワルツシルド半径aの二倍の位置で接します。
この2aが、シアマが「一般相対性理論(その物理的意味)」p147で言っている“第1の臨界距離”です。そのことの意味は3.(4)6.(2)[補足説明1]をご覧になれば解ります。また、シアマの言う“第2の臨界距離”である1.5aの意味もそこに書いてあります。
(2)角運動量一定でエネルギーを変える
質点mの実際の軌道の形は、Newton力学の中心力問題と同じ様に、質点mが持つ “エネルギー”E と “有効ポテンシャル”Veff(r) の関係に依存する。その為、“エネルギー”E の初期値を適当に仮定して3.(4)4.説明した軌道方程式を解いて求めれば良い。
実際に計算してグラフ化すれば良いのだが、面倒なのでハートル文献5.§9.3の説明を、本項での設定値に当てはめて流用します。
以下の4例の図は、 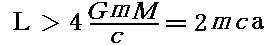 で、Veff(rmax)>0となる同一のL値 で、質点mの入射エネルギー値Eを4通りに変えたときの軌道を示している。
で、Veff(rmax)>0となる同一のL値 で、質点mの入射エネルギー値Eを4通りに変えたときの軌道を示している。
いずれも、横軸は中心からの距離rであり、縦軸は質点mについての有効ポテンシャルVeff(r) or 入射エネルギー値Eです。その具体的な座標値に関しては3.(4)6.[補足説明1]具体例のL=n・L0のnがn=4.3の場合に対応すると考えて下さい。
軌道図中央のオレンジ色の●は“シュワルツシルド半径”を示しています。また、Veff(r)グラフのピンク色着色部分は“動径方向の運動エネルギー成分値”を表している。
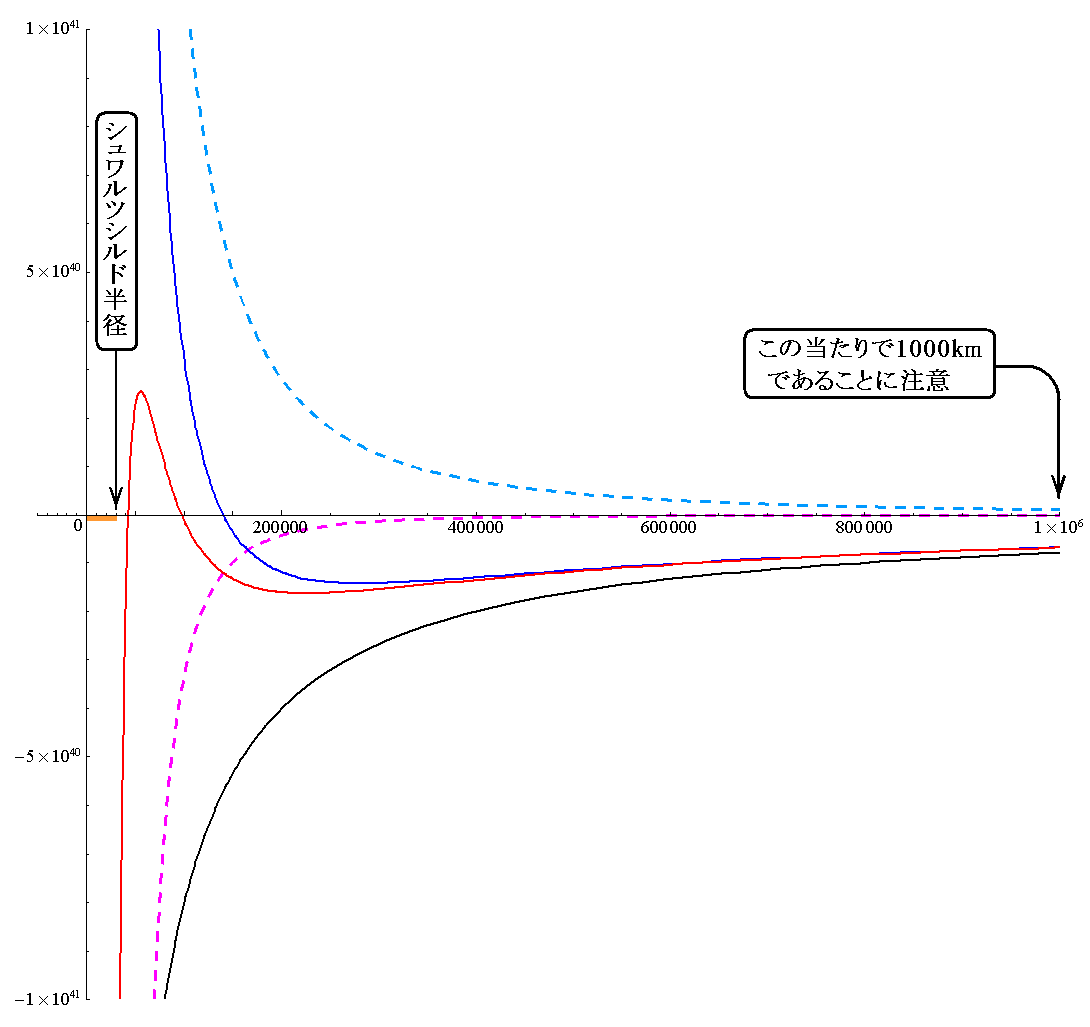
- Eが有効ポテンシャルの極値を取る場合
図の円軌道の半径は、前項で求めた有効ポテンシャルが極値を取る二つの半径です。有効ポテンシャルが極大値(いまは最大値でもある)の場所の円軌道(E’=一定)は質点mのエネルギーがEが少しでも変動すると無限円に脱出するか、あるいはr=0に落ち込むために不安定な軌道です。このことに付いては3.(4)8.でもう少し詳しく説明します。
これに対して、極小値の円軌道(E”=一定)は安定な軌道です。
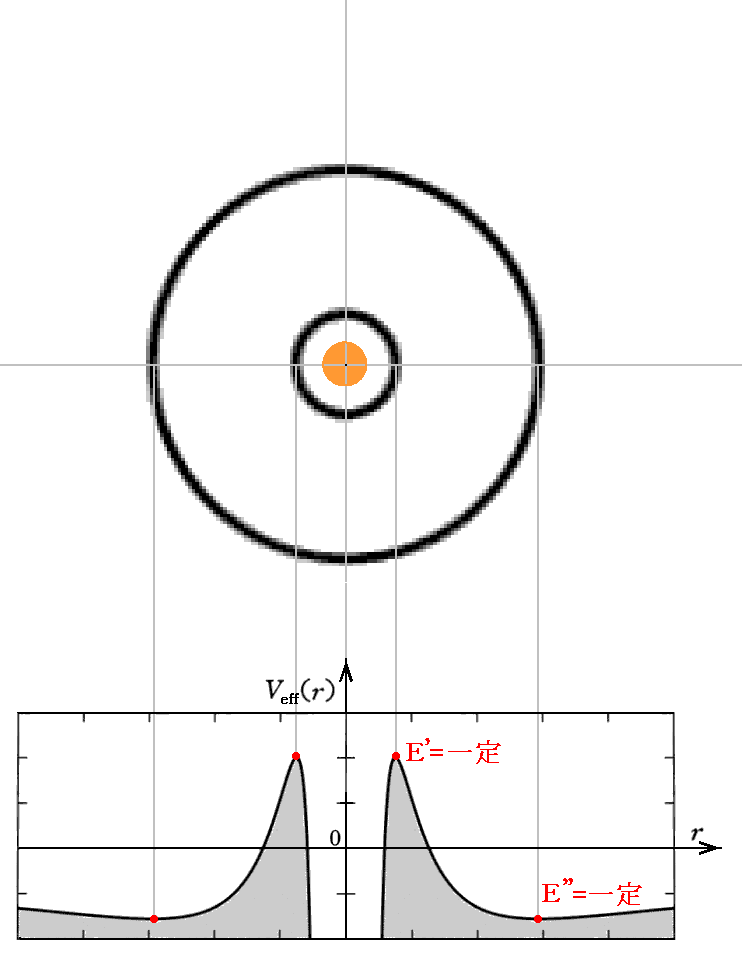
- E<0の場合
この場合は二つの転回点を回転しながら振動する軌道となる。太陽の近くを回る水星軌道などはその例です。ここの例では相対論的な効果で大きな近星点移動を行いながら公転する軌道となる。
この束縛軌道に付いては3.(4)9.でもう少し詳しく説明します。またハートル文献5.の説明を別ページで引用していますのでご覧下さい。ただし、ハートルはc、Gやmを規格化した数式で説明しているので少し解りにくいです。
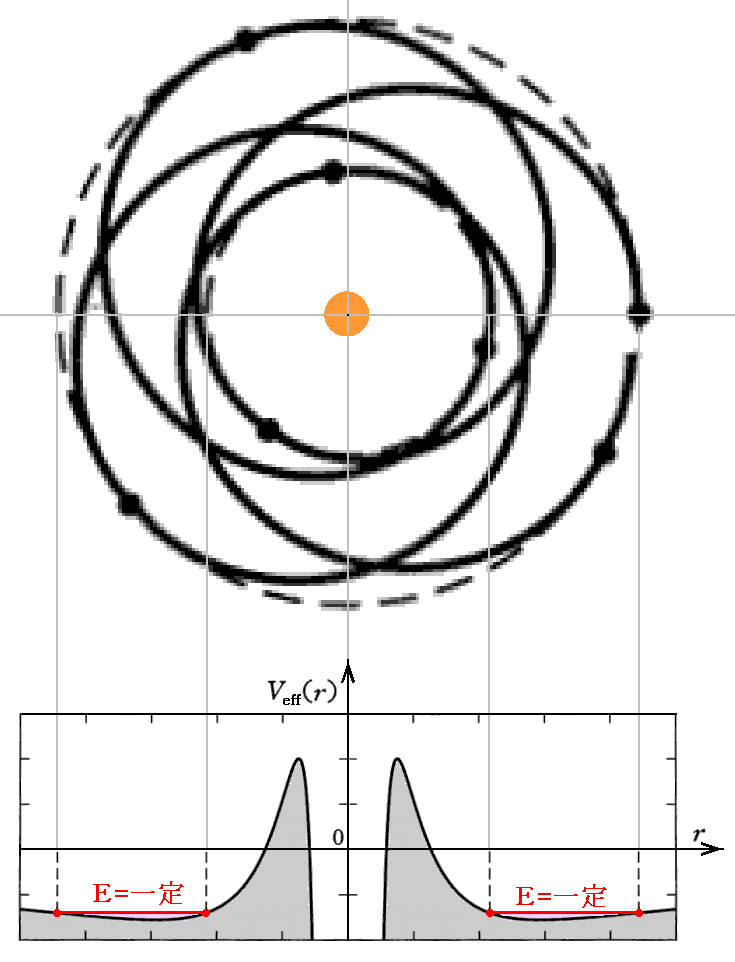
- E>0だけれど、有効ポテンシャルの最大値よりも小さい場合
無限遠からやってきて、中心付近を回転した後再び無限遠に飛び去る軌道となる。Newton力学では双曲線軌道となる場合ですが、相対論力学では双曲線とは異なる軌道になります。
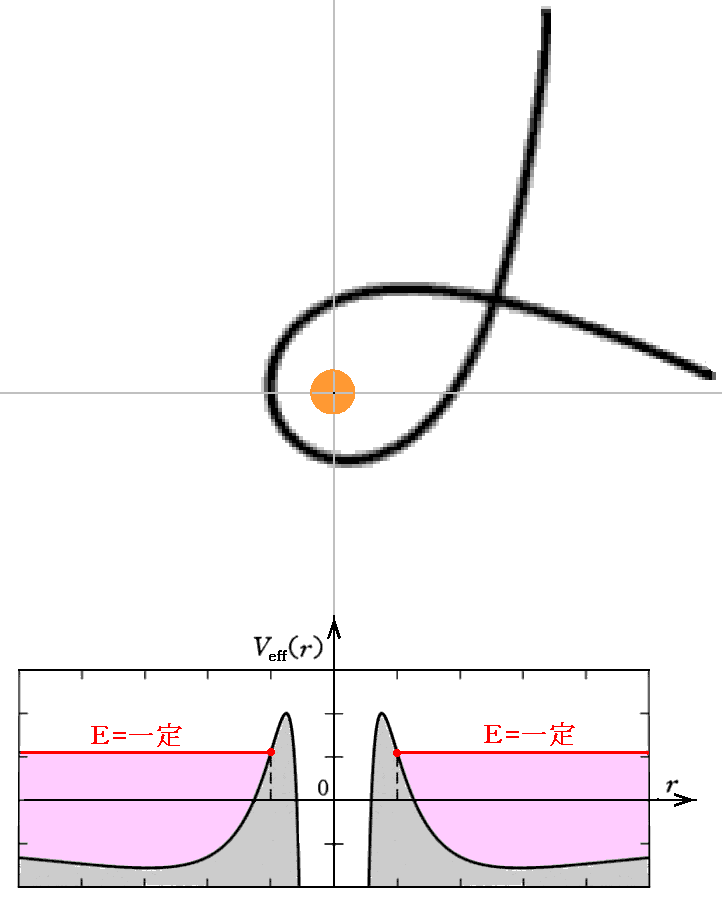
- Eの値が有効ポテンシャルの最大値よりも大きい場合
中心に落下していく。もちろん、その場合の質点mの角運動量Lは下記の有効ポテンシャルの形状から決まる値とした場合の話です。この種の軌道運動はNewton力学では起こりえないことに注意されたし。
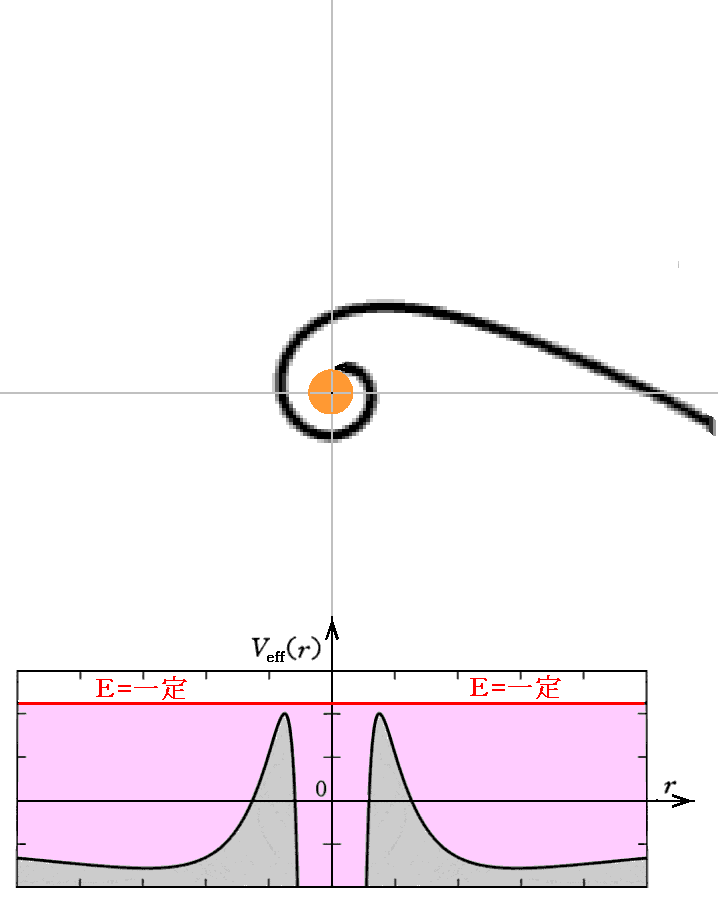
上記の4例はすべて有効ポテンシャルの形は同じですから、入射する質点mが持つ角運動量Lはすべて同じです。角運動量Lが同じになる様に初期入射速度と初期入射角度を変えることで入射エネルギーEを変えています。
すなわち、1→2→3→4と変わるにつれて入射速度を大きくし、かつ入射方向をブラックホールに対して垂直の方向からブラックホールの方へ向いた方向に変えています。
つまり、同一点から入射される時、φ方向(回転方向)速度成分をすべて同じにして、動径r方向(中心に向かう方向)の速度成分を変化させて入射させると言うことです。
[補足説明1]
入射時に持つ[初期角運動量 L]と[入射エネルギー E]の値に応じて、軌道がどの様に変化するかをまとめておきます。
軌道の形を分別するのは、3.(4)6.(1)[補足説明4]で述べた Veff(r)=0 の解が重根(rmax=2a)となるときの初期角運動量値 L=2mca と、3.(4)6.(1)の最初で説明した ∂Veff(r)/∂r=0 の解が重根(rmax=rmin=3a≡risco) となる初期角運動量値 L=√3mca です。
この二つの初期角運動量に対する有効ポテンシャル曲線を図中に示していますが、この二つで区切られる3通りの角運動量値Lで分別できます。
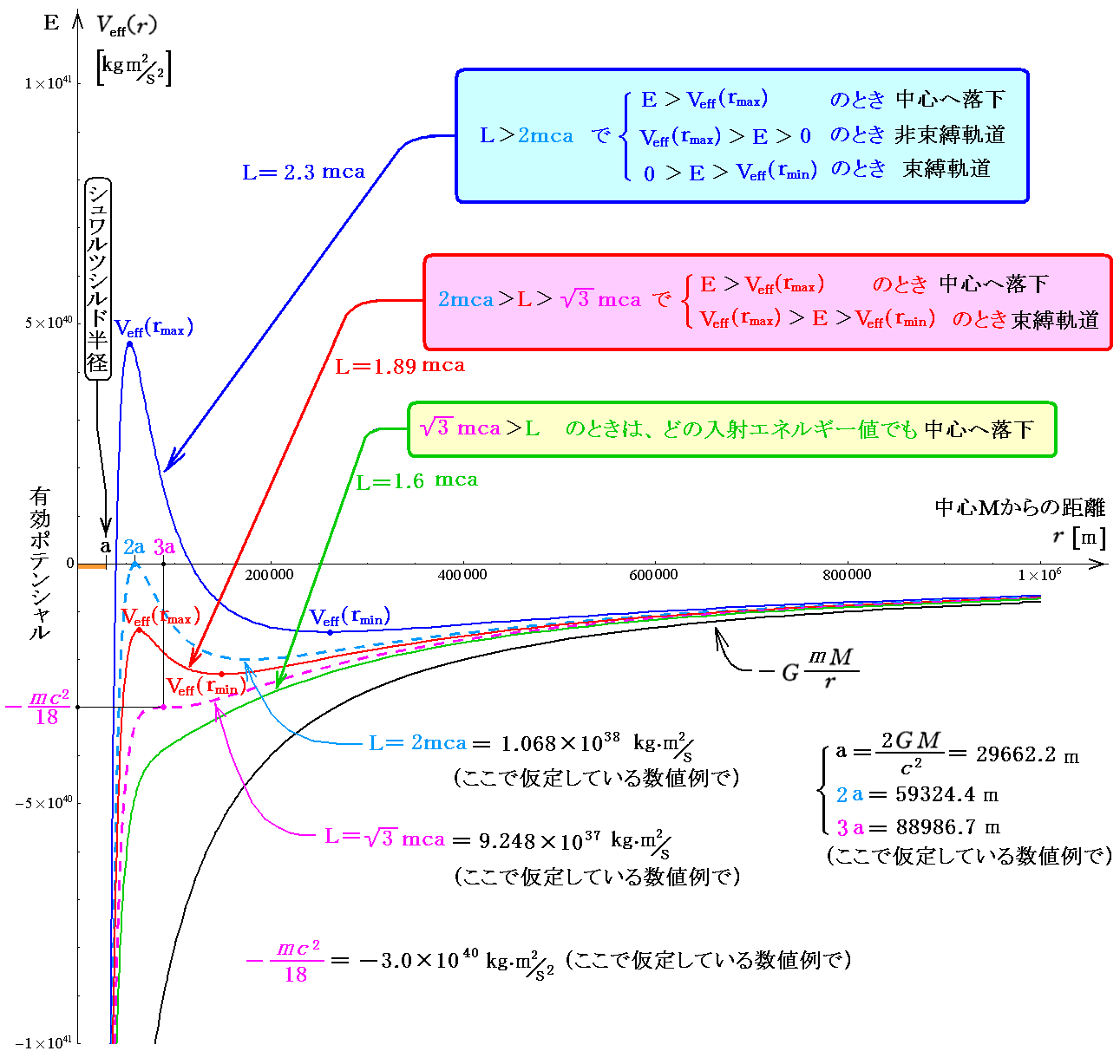
入射角運動量Lを一定の元で、入射エネルギを増大させると言うことは動径方向の入射速度を増大するということですから、より中心に向かって入射させるということです。その為に中心への落下する可能性が高くなります。
入射させる質点mの初期角運動量Lと初期エネルギーEの値が実際の軌道をどの様に変化させるのかはNewton力学で説明した状況と同じですから、別稿「質点の二次元運動」3.のグラフを参照されて下さい。
7.円軌道運動について
(1)安定最小円軌道
安定円軌道は3.(4)6.(1)で説明したように、有効ポテンシャルVeff(r)が極小となる半径r=rminにある。そこの式を見れば解るようにM/Lが大きくなると、この半径も小さくなるが、安定円軌道はいくらでも小さくなれるわけでは無い。なぜならM/Lが大きくなると言うことは角運動量Lが小さくなる事であり、Lが小さくなれば有効ポテンシャルVeff(r)の形が前掲のグラフで示したように有効ポテンシャルの極値が無くなるからです。
つまり、シュワルツシルド幾何学で“最も内側の安定軌道(innermost stable circular orbit ≡isco)の半径” risco は、先ほどのグラフで rmax と rmin が重なった時の値です。
ただし、この半径の円運動はごく僅かでも軌道が内側にぷれるとやがて中心へ落下していきますので、ギリギリの安定性である事に注意して下さい。
すなわち前掲の式から明らかな様に
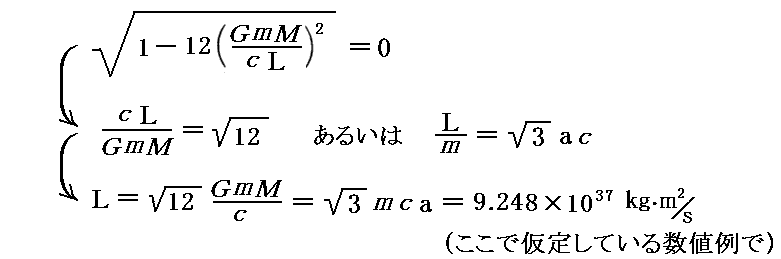
となるときの
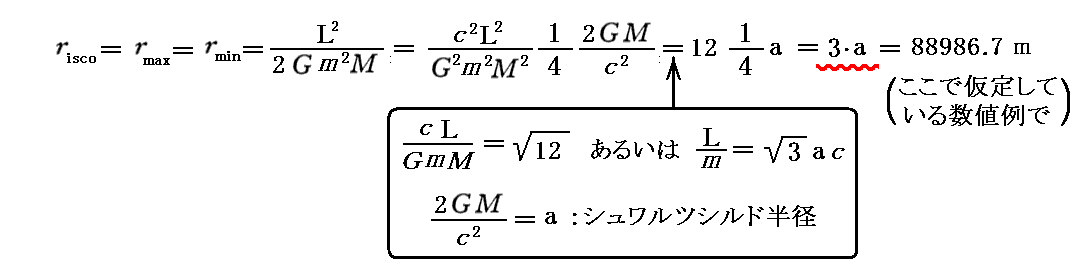
です。すなわち、riscoは、“シュワルツシルド半径”の3倍となります。実際そうなることを前掲のグラフでご確認下さい。このことは3.(4)6.(1)[補足説明1]ですでに説明しています。
このことは、ブラックホールの周りに構成される降着円盤の構造や、その事から生じるX線源の構造を論じるときに重要です。
このことは別稿「ブラックホール質量の決定法」1.(2)2.で説明していますが、“エディントン光度の見積” や “X線強度観測値によるブラックホール質量の見積”などに深く関係します。。
(2)円軌道公転速度の半径依存性
ここでの話は、3.(4)6.(2)の最初の例1.で説明した
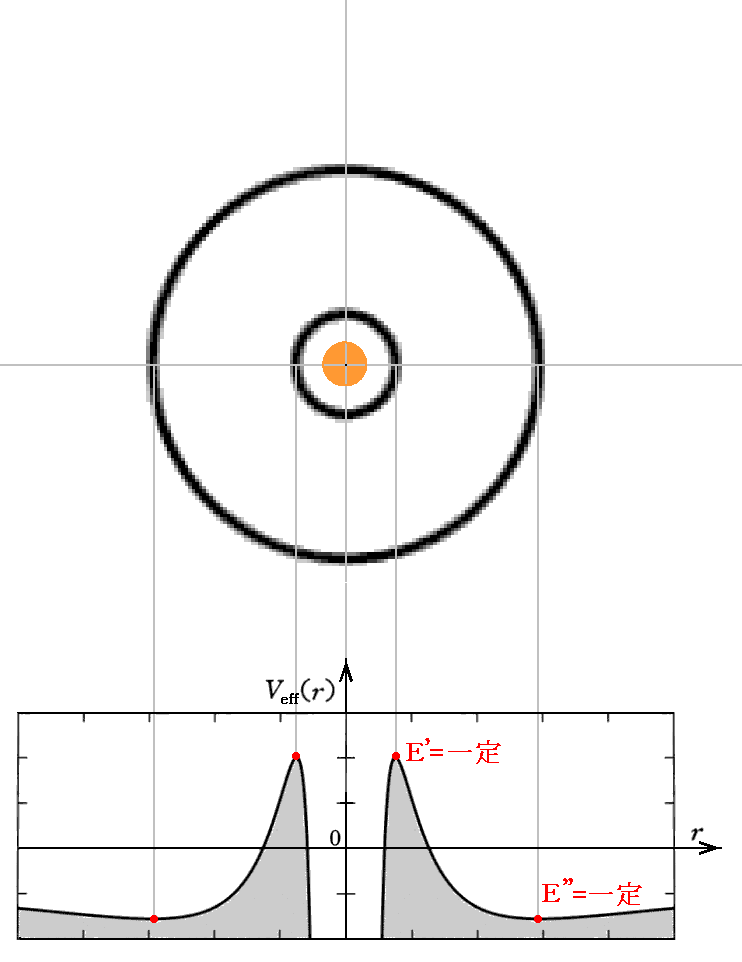
の場合の回転速度を意味します。aを中心質量がMの時のシュワルツシルド半径としたときr>3aの部分はVeff(rmin)の位置における円運動の速度vです。つまり半径rの位置で円運動をさせるためには、その半径が有効ポテンシャルの極小値に成る様な角運動量で以て半径rの位置で円周方向に打ち出すと言うことです。打ち出す初速度はその角運動量から計算される値で円周方向を向いており、動径方向の初速度はありません。
3a>rの部分も同様です。その半径の位置で打ち出す初速度はVeff(rmax)の位置における円運動の速度vです。このときも動径方向の速度成分は無しで打ち出します。ただし、この領域の円運動は前項でも説明したように不安定です。
Newton力学の場合の曲線についても同様でVeff(rmin)の位置における円運動の速度vです。
その様に、ここで想定しているのは円軌道が可能な条件での円軌道ですから、3.(4)6.(1)[補足説明2]で導いた関係式が基礎になります。そのため円軌道公転速度の半径依存性を示す式は
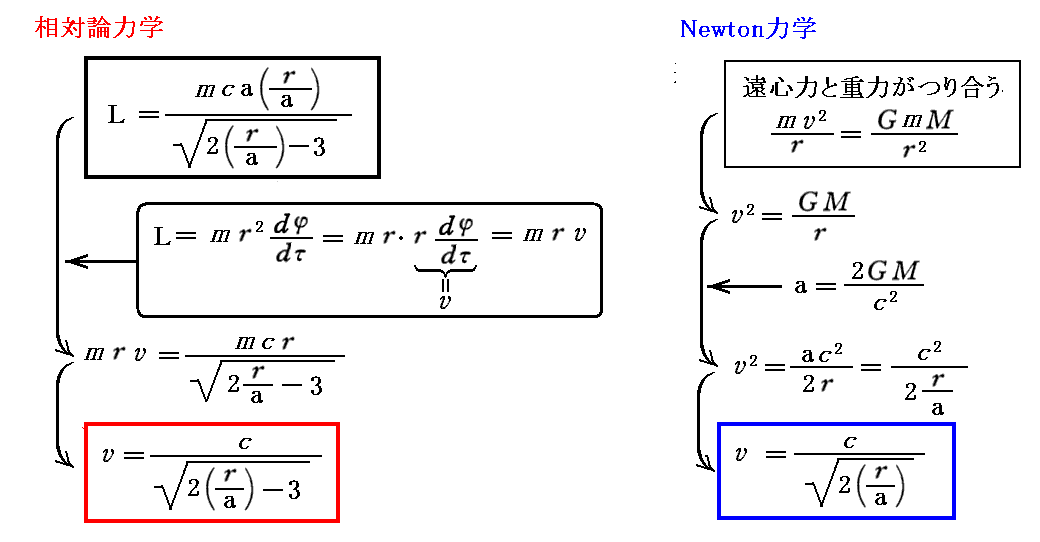
となります。すなわち、相対論力学では r→1.5a とともに円運動をする為の速度vが光速度cを遙かに超えて発散します。ただし、vを求める為のr×dφ/dτに於いて固有時τを用いていますので、ここで言うvは、いままで何度も注意したように、現実の速度ではありせんので光速度を超えて発散しても問題ありません。
比較のためにNewton力学の場合も示しています。もちろん、Newton力学でも3.(4)6.[補足説明2]で求めた関係式を用いても良い。すなわち
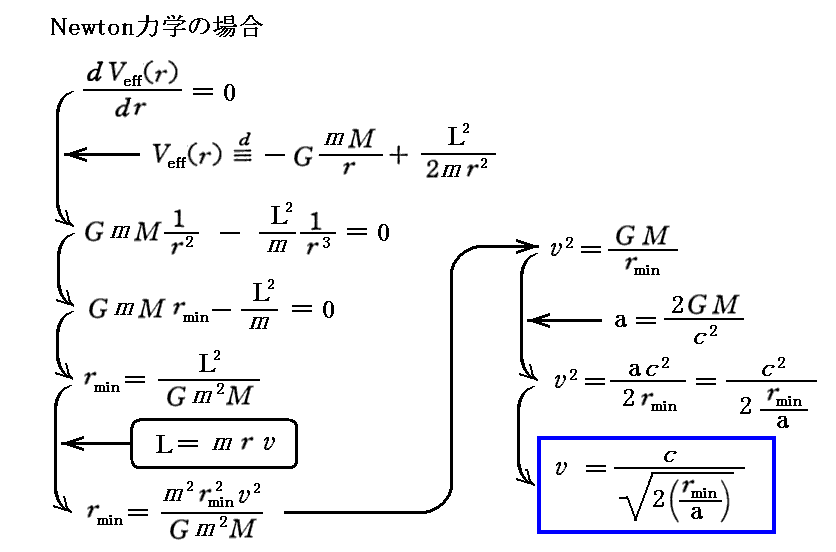
となります。いずれにしても、Newton力学では r→0 とともに回転速度は光速度cを遙かに超えて発散します。しかしNewton力学はこの領域のように重力場の強い所では成り立たない理論ですから、このような結論に惑わされる必要はありません。
上記の関係をグラフ表示すると
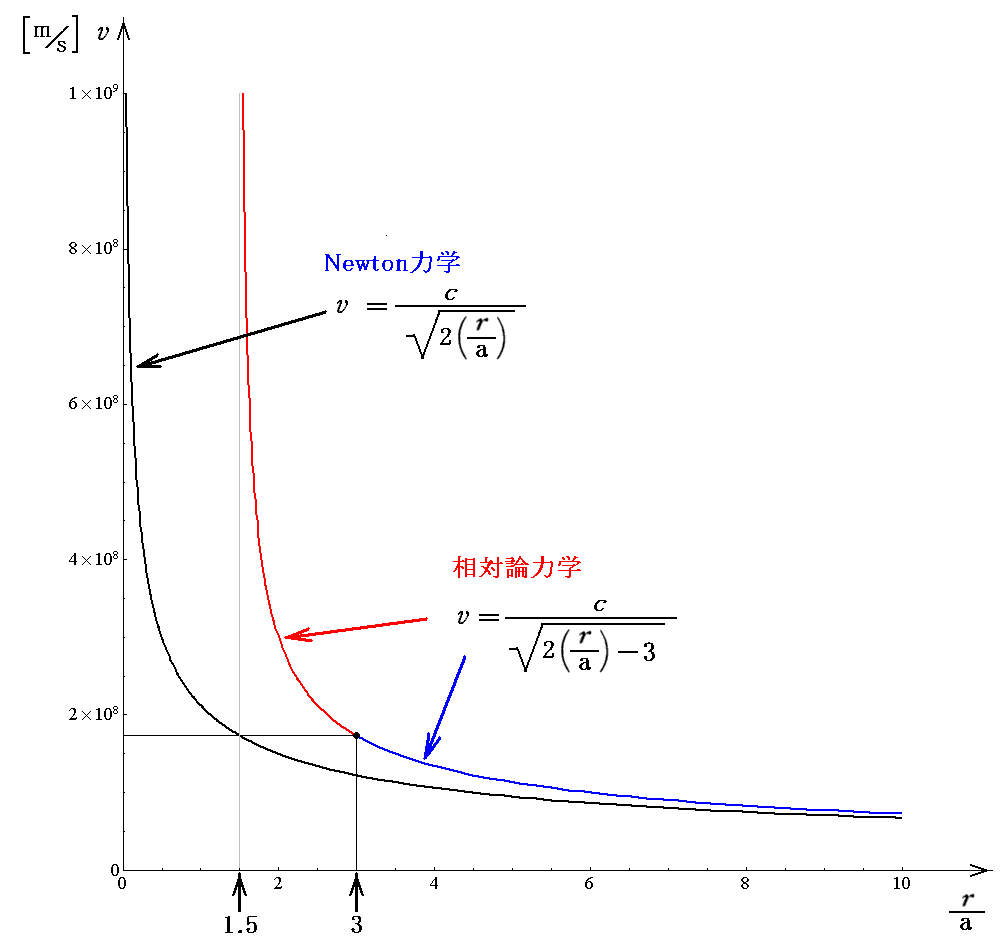
となります。横軸はシュワルツシルド半径を単位として示しています。また、縦軸の数値はここで仮定している数値例の場合での値です。
ここで注意して欲しいのですが、相対論力学で r<3a の領域は、3.(4)6.(2)の最初の例1.で説明した図のエネルギーE’の不安定領域での円運動です。その為 r=3a を境にして、グラフ線の色を変えています。
[補足説明1]
上記のグラフでNewton力学の場合 r→0 となれば、 v は光速度を超えます。もともと正しくないNewton力学ではその様な事が起こっても仕方有りませんが、今のところ正しいと思われている相対論力学に於いても
r→1.5a となれば、 v は光速度を超えます。
相対論では質点mが光速度を超えて運動することはあり得ないのに、この結果はおかしいのでは無いかと思われるかも知れません。しかし、3.(3)3.(2)[補足説明2]で説明した様に、dr/dτ≡vと置いた量である v は質点mの現実の速度を表す量では有りません。そのため v の値が光速度を超えても全く問題ありません。
(3)円軌道角速度の半径依存性
同様に角速度の半径依存性は
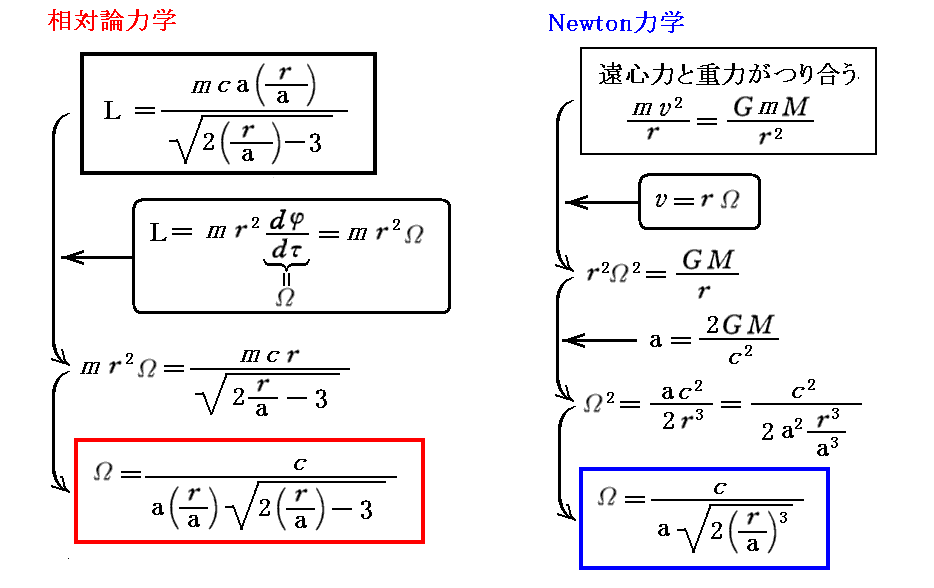
で表せます。比較のためにNewton力学の場合も示しています。
ただし、ここで注意して欲しいのですが、Newton力学での円軌道はどの半径でも安定に実現されますが、相対論力学ではr<3aの領域の円軌道は微妙なバランスの元でのみ存在できるもので、本来安定に存在できるものではありませんので、r<3aの領域の計算値にはあまり意味がありません。
上記の関係をグラフ表示すると
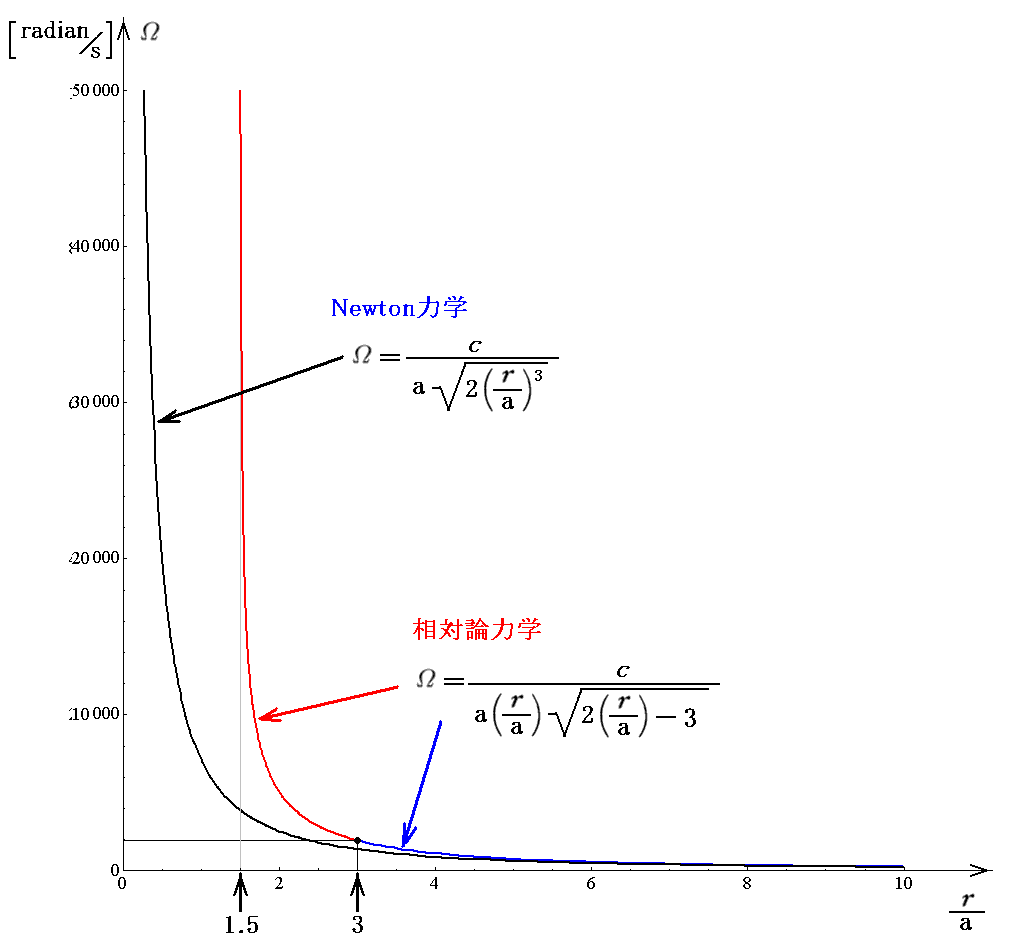
となります。横軸はシュワルツシルド半径を単位として示しています。また、縦軸の数値はここで仮定している数値例の場合での値です。
ここで注意して欲しいのですが、相対論力学の場合のr/a<3の領域は、3.(4)6.(2)の最初の例1.で説明した図のエネルギーE’の不安定領域での円運動です。その為r/a=3を境にして、グラフ線の色を変えています。
[補足説明1]
さらに補足しますと、角速度の表現をシュワルツシルド半径aをもとの表示2GM/c2にもどした式にすると
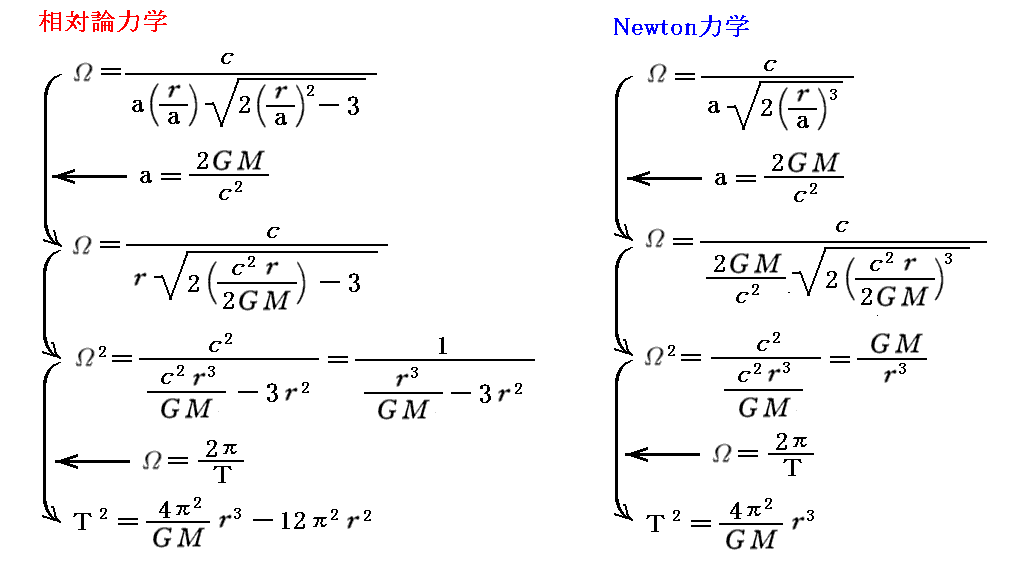
となります。
Newton力学では“ケプラーの第三法則”が得られます。また相対論力学では r が小さい領域ではNewtom力学とは異なりますが、r が大きくなるにつれてNewton力学の法則に近付きます。
相対論力学の周期は固有時τに対するものであり、Newton力学の周期は相対論力学のシュワルツシルド座標時間tに相当するものです。その違いはありますが、中心質量Mから離れた(しかも質点mの速度が0に近付く)領域ではシュワルツシルド座標時間
t と固有時τは一致すると考えて良いので、r が大きくなるにつれてNewton力学の法則(ケプラーの第三法則)に近付くと考えて良い。これは当然考えられることです。
ここのところのハートル文献9.(9.44)~(9.46)式の説明は解りにくい。話のもっていき方が良くない。ただし、訳し方が悪いのかも知れませんが?
8.不安定円軌道(rmax)について
前節の図のr=rmaxで、E=E’の場合に付いての福江文献4.「ブラックホールの力学」の説明です。この解説はわかりやすい。
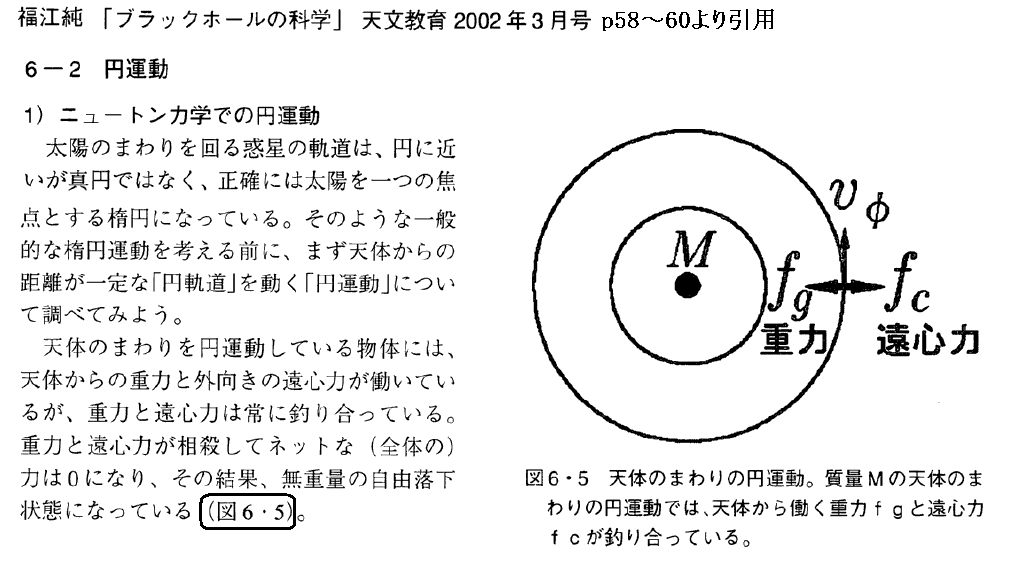
以下の文節は説明が少し不足しています。[補足説明1]を参照しながらお読み下さい。

上記の『シュバルツシルト半径の1.5倍で発散する』の意味に付いては3.(4)6.(1)[補足説明1]を参照。
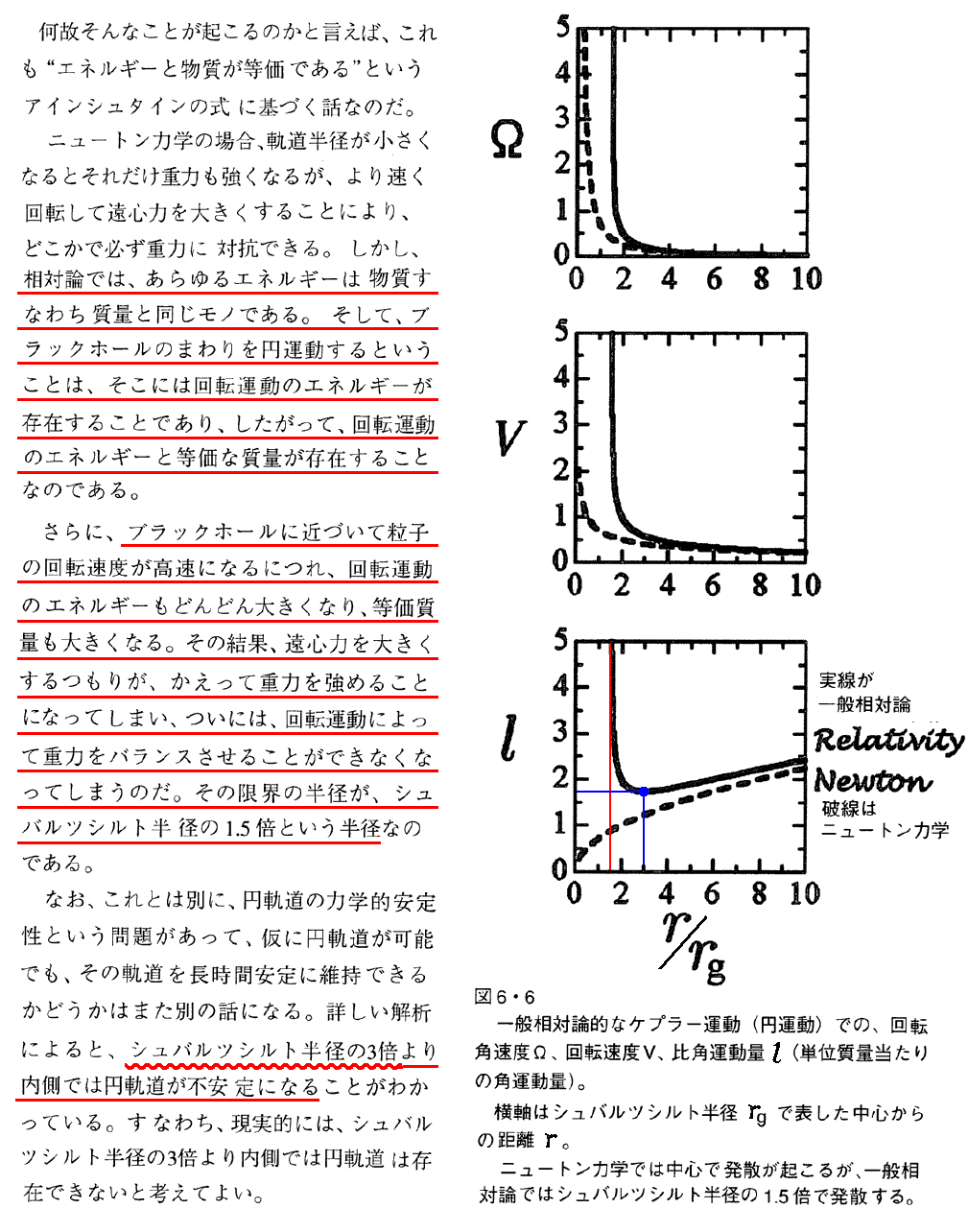
最後で述べられている『シュバルツシルト半径の3倍より内側では円軌道が不安定になる』に付いては3.(4)7.(1)を参照。
[補足説明1]
上記の説明を補足します。まず、図6・6の
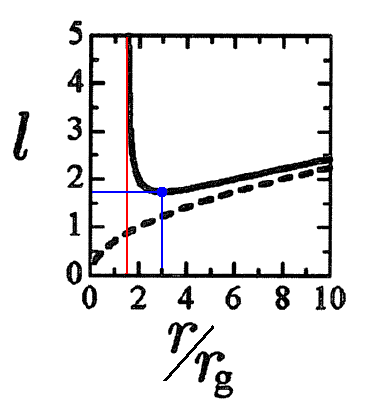
ですが、これは、3.(4)6.(1)[補足説明2]で導いた

の事です。本稿では“シュワルツシルド半径”をa で表していますが、福江文献では rg で表しています。
次に、図6・6の
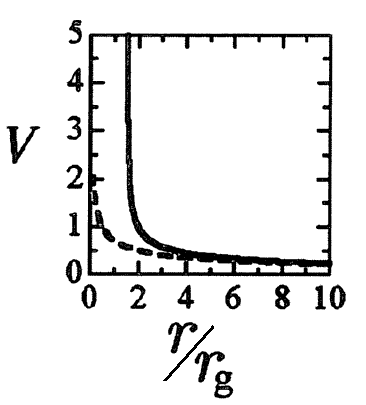
ですが、これは3.(4)7.(2)で導いた速度のグラフ

のことです。
図6・6の回転角速度Ωのグラフ
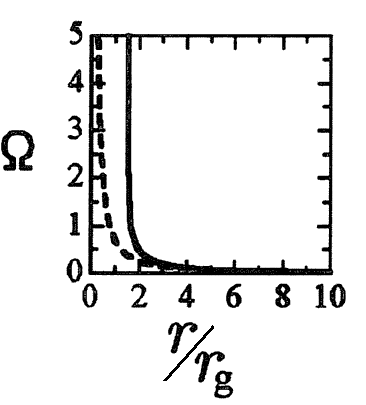
は、上述の円運動についての回転角速度ですが、3.(4)7.(3)で導いた角速度のグラフ

のことです。上文節中の円運動は、すべて rmax あるいは rmin における円運動を意味することに留意されて、上文節を再読してみて下さい。
そのとき、[円運動速度に伴う質点の質量増加]と[重力ポテンシャルの一般相対性効果]が出てきますが、そこは3.(4)2.[補足説明1]を逆にたどれば、福江文献の説明が了解できます。そこで説明した様に、上の二つの効果により相対論的なポテンシャル項が付け加わったのですから。
9.束縛軌道の形
(1)楕円関数
束縛軌道の形については3.(4)6.(2)で説明したのですが、L=4.3L0でE<0の場合の束縛軌道の形の導出に付いて、もう少し補足します。解りやすくする為に先に用いた具体的な数値を利用して説明します。

特に、質点mの角運動量Lと軌道エネルギーEを上記の値に仮定したのは束縛軌道が解となるようにするためです。この場合のポテンシャルカーブはすでに示したものに成ります。
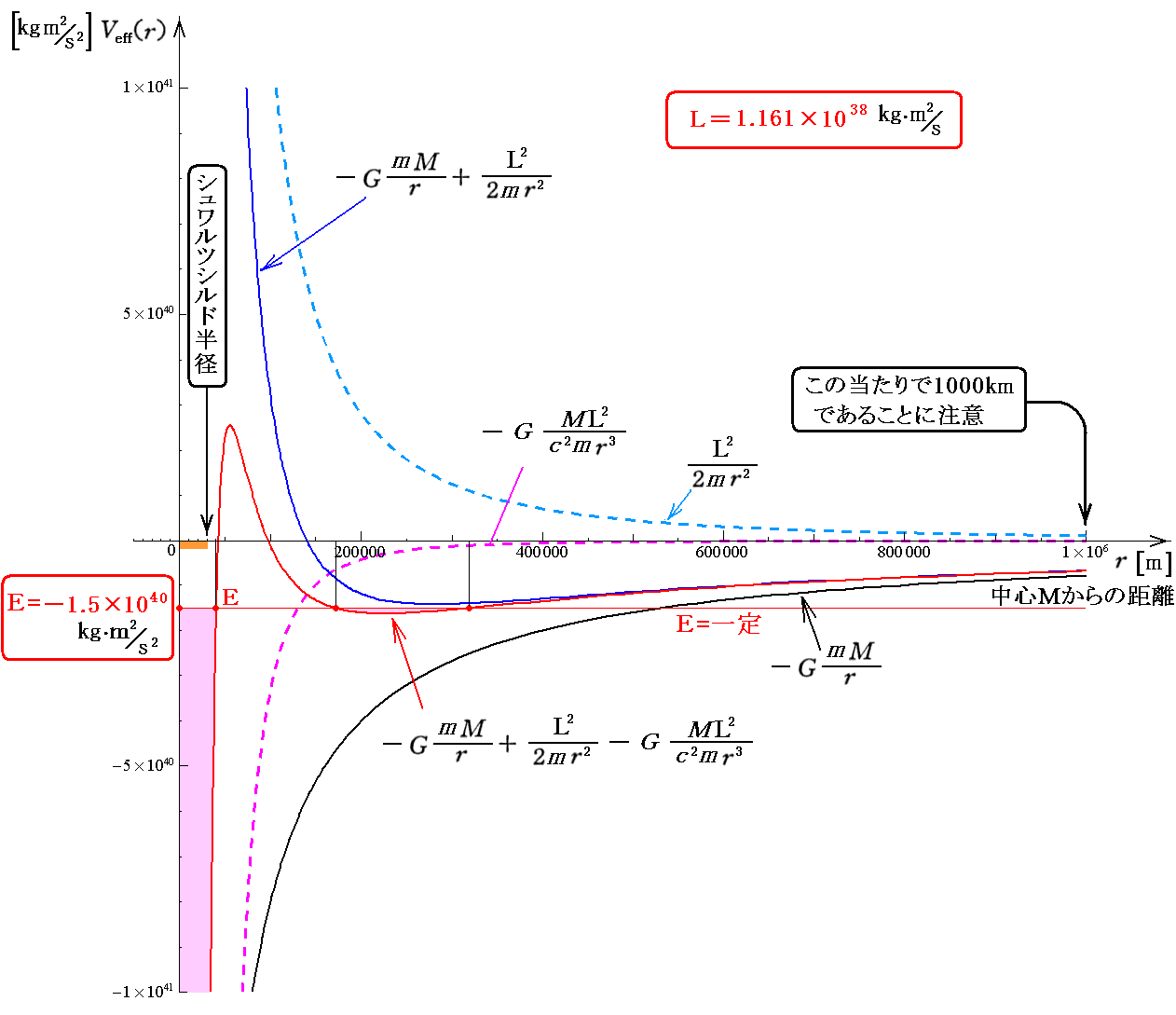
このとき、軌道の形をを決定する方程式は3.(4)4.で導いた⑥式です。
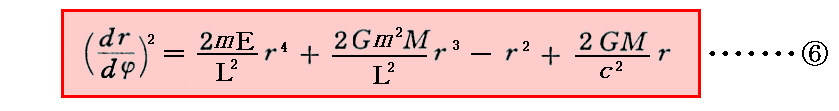
先に仮定した値を係数に適用すると
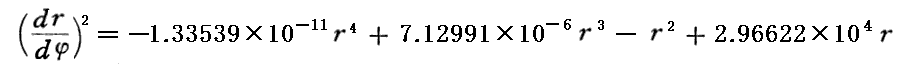
となります。これはrの4次関数でそのグラフは下図の様になります。
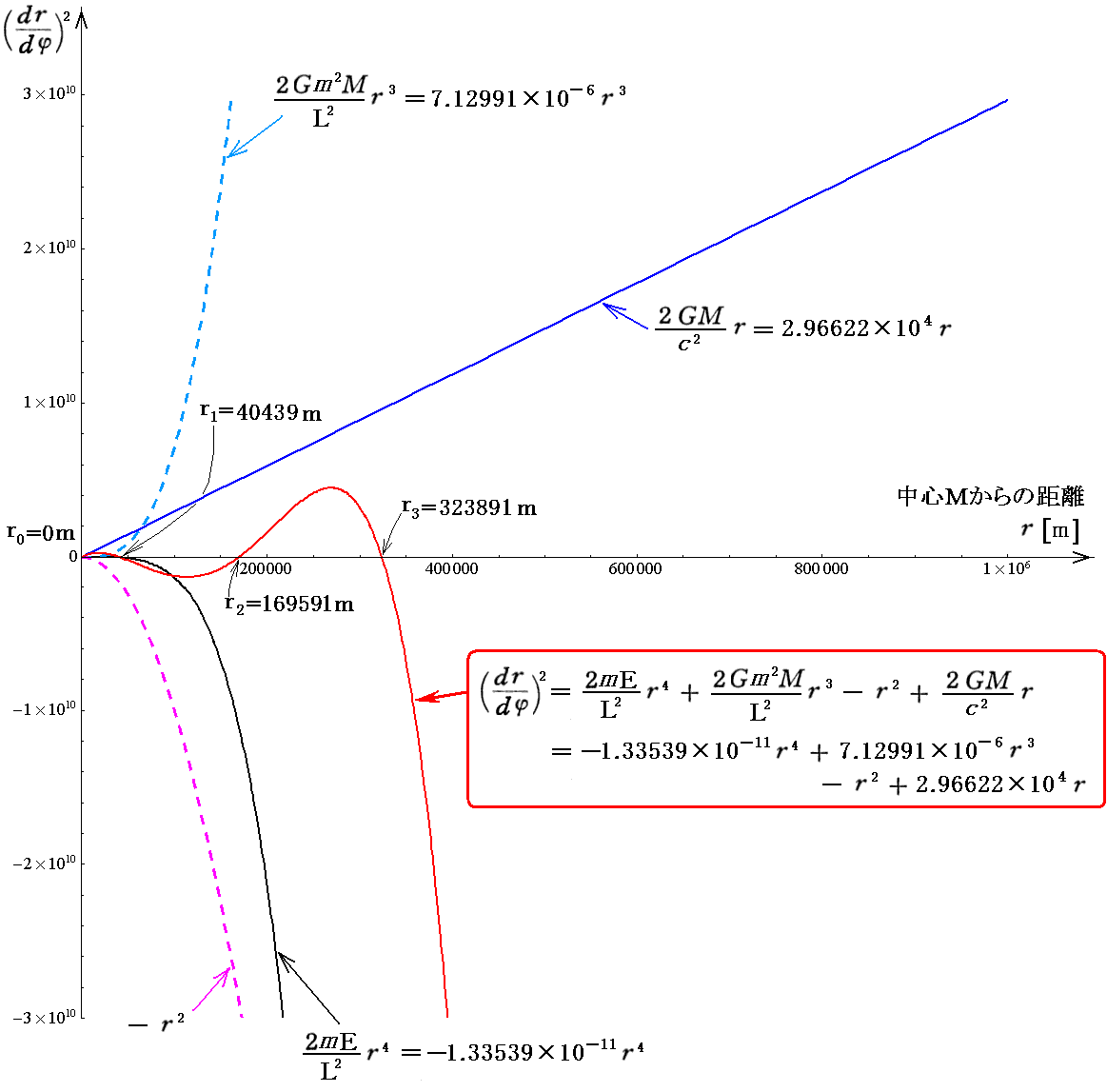
この4次曲線はr軸と4箇所で交わります。その一つは原点である事は明らかです。残りの3つの交点は次の3次代数方程式の解となります。
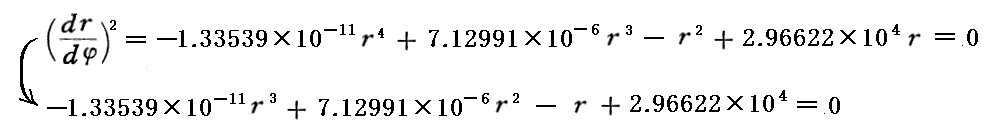
3次代数方程式の解の公式を用いて解き、4個の解を小さい方から列記すると
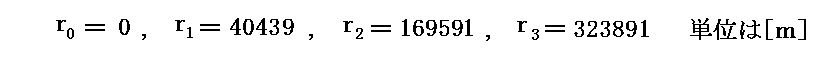
となる。ただし小数点以下は四捨五入しています。グラフからも確認できる様に、確かにr軸との交点の座標値が得られている。
この解を用いると先ほどの関数は以下の因数分解形式に書き換える事ができます。
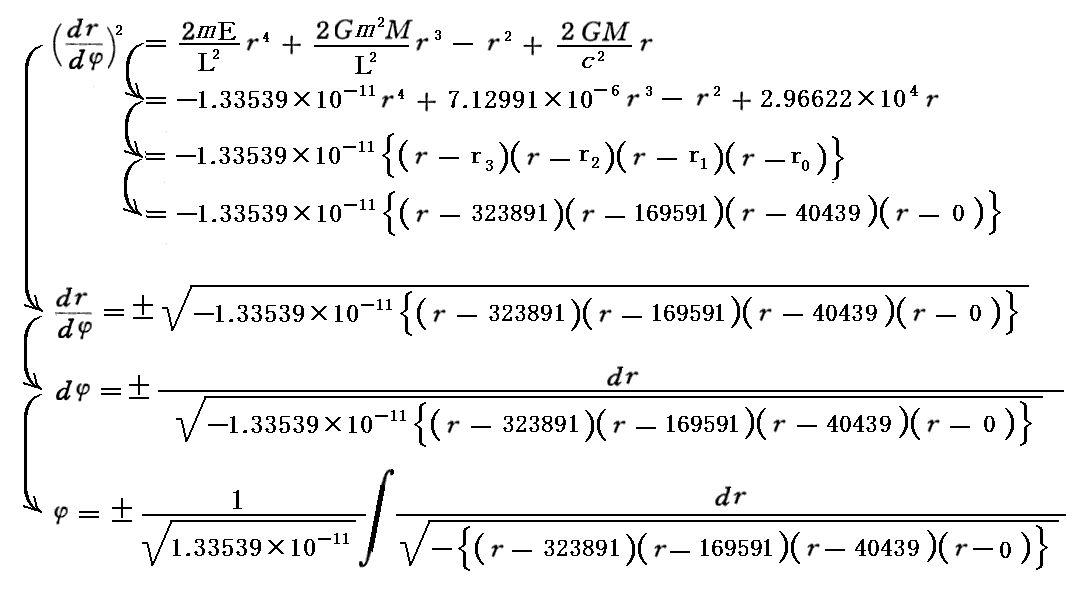
これは岩波全書「数学公式Ⅰ」p147 §31楕円積分の例 (ⅰ)4次式の平方根を含む第1種楕円積分

そのままですので、そこに書かれている解が求まります。
ただし、その公式集からはこの楕円積分がどの様なのものかは読み取れませんので、もう少し説明します。
(2)楕円積分の詳細
まず次の関数のグラフを描いてみる。
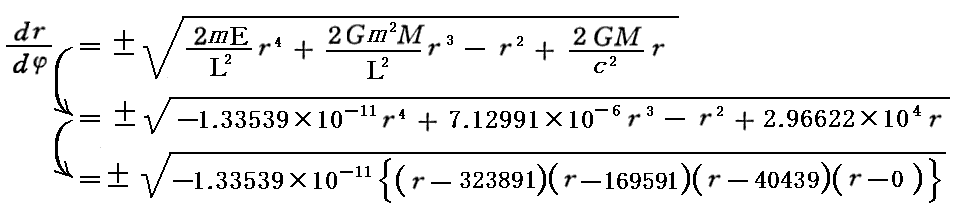
比較の為に先ほどの関数(dr/dφ)2の各係数項のグラフも同一の縦座標値で記入していますが、平方根関数にすると縦座標の大きさが指数の大きさで半分程度になる事に注意して下さい。。また、このとき、+と-の両方を示しています。さらに、(dr/dφ)2関数の負値の部分は平方根関数の中には表れていないことに注意して下さい。
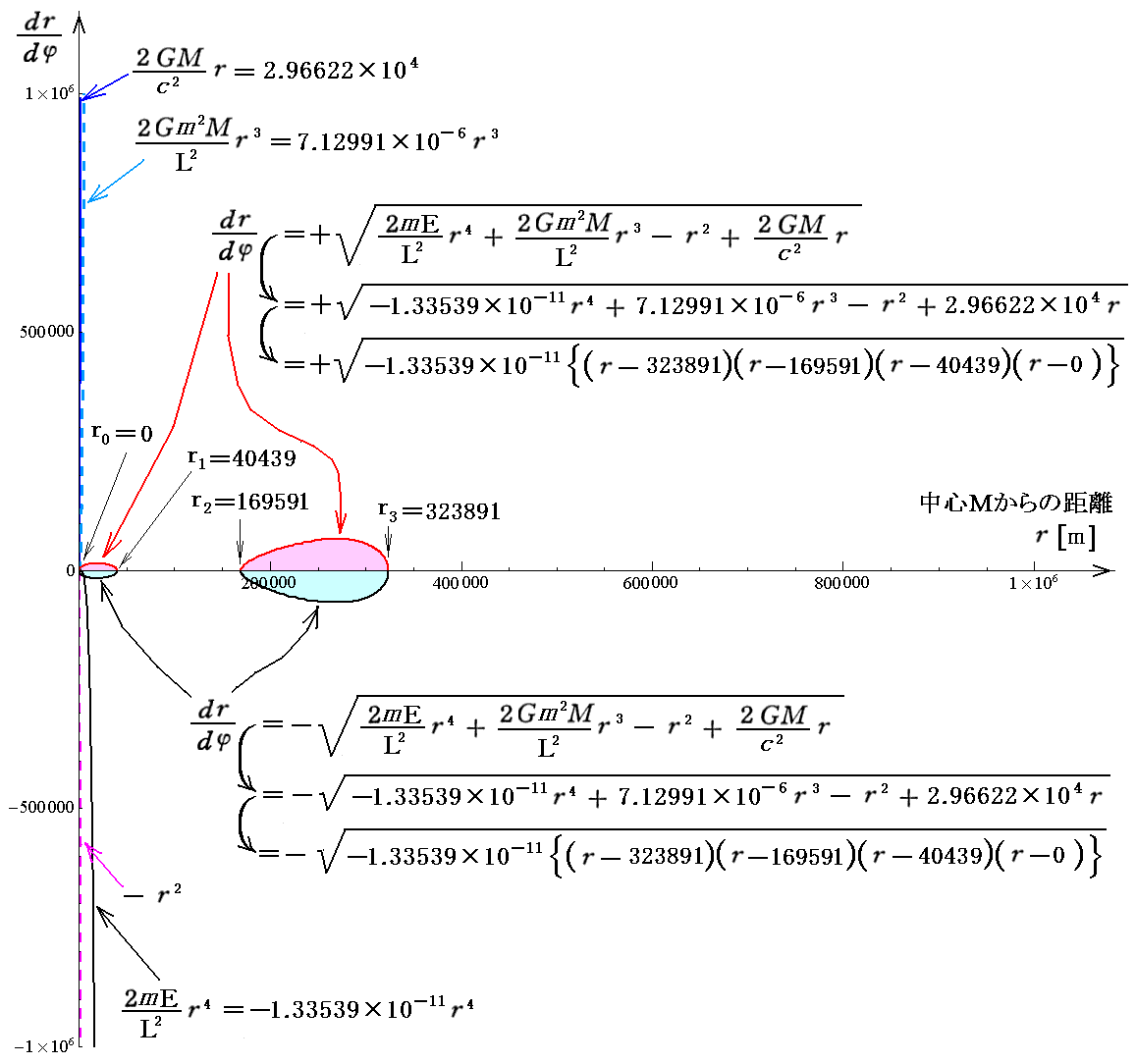
この関数をdφに付いて適切な初期条件の下で数値的に積分してゆけば3.(4)6.(2)で示した曲線を表す関数 r(φ) が得られます。被積分関数がφの関数として表されていませんが、数値的に積分してゆく場合にはその事は問題ありません。
同様に、前記の平方根関数の逆数である下記の関数を用いてもよい。
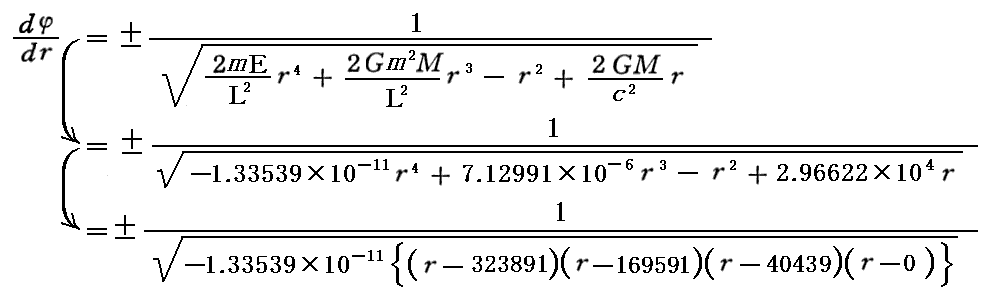
上記関数のグラフは下図の様になります
比較の為に先ほどの関数(dr/dφ)2の各係数項のグラフも同一の縦座標値で記入していますが、それらはすべて縦軸の近くに寄っています。平方根関数の逆数にすると縦座標の大きさが先ほどの平方根関数の大きさの逆数程度になる事に注意して下さい。。また、このとき、+と-の両方を示しています。そのとき、(dr/dφ)2関数の負値の部分は平方根関数の逆数には表れていないことに注意して下さい。
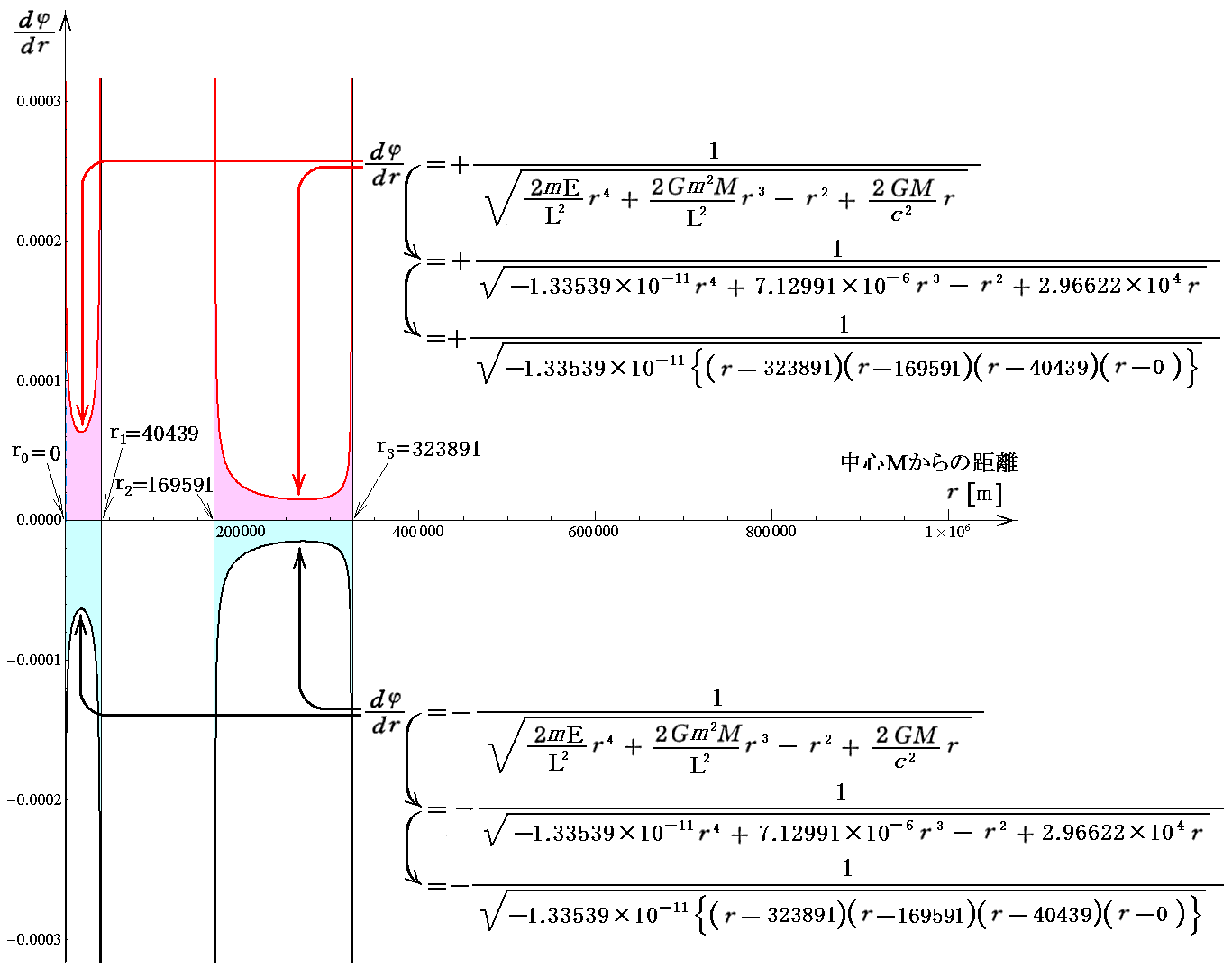
この関数をdrに付いて適切な初期条件の下で数値的に積分してゆけば3.(4)6.(2)で示した曲線を表す関数 φ(r) が得られます。このとき被積分関数は積分範囲の両端で無限大になりますが、積分が発散することはありませんので心配ありません。
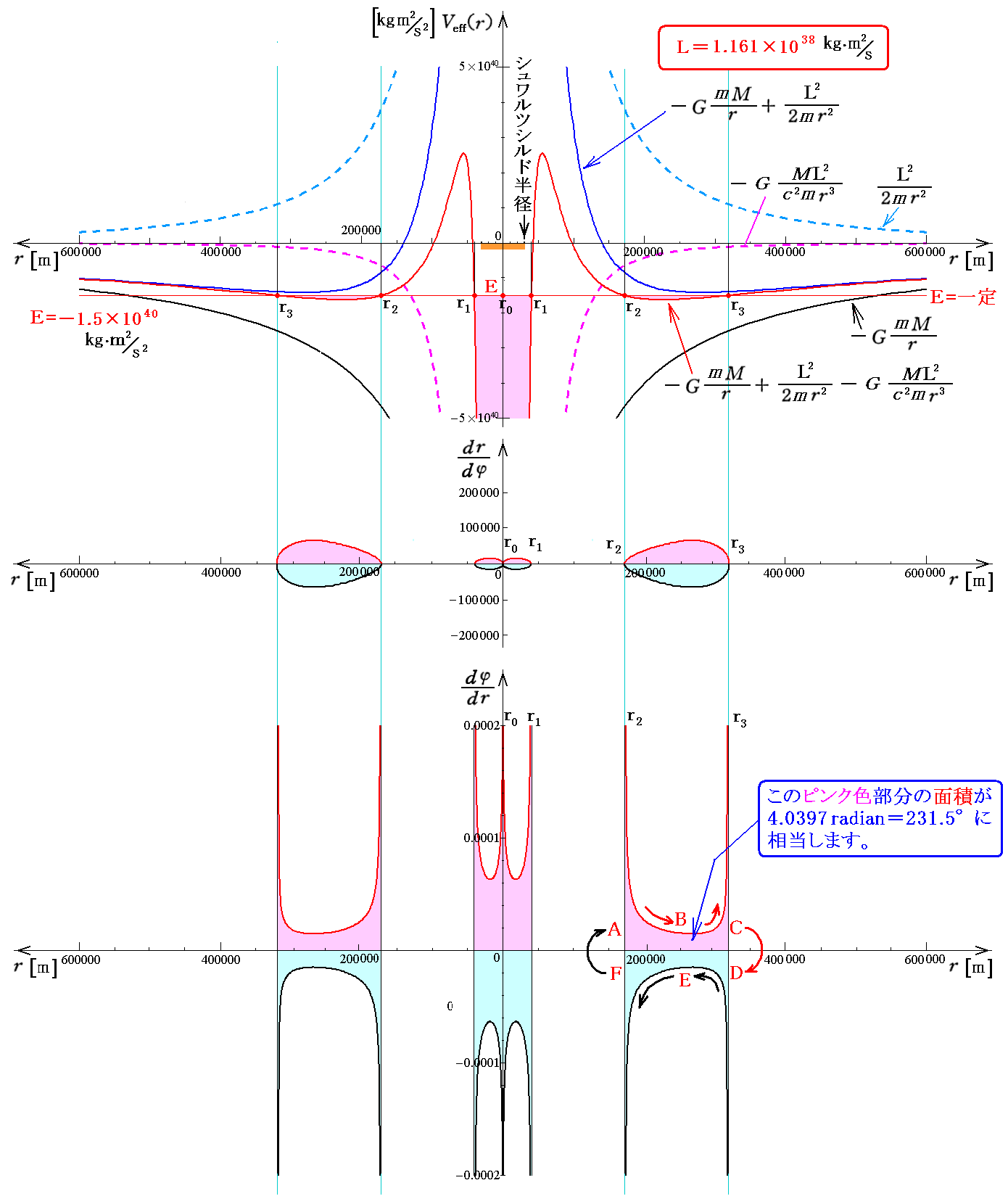
上図の最後に示した関数についてr2=169591から r までの数値積分
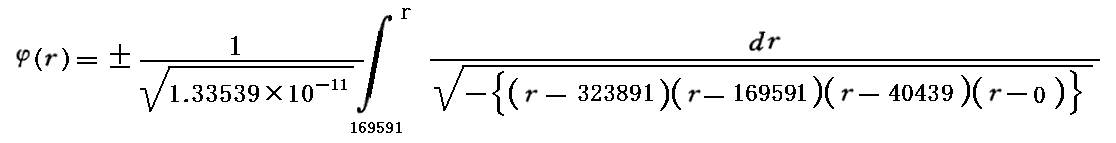
を実施してφ(r)を求める。
その様にして得られた様々な r に対するφ(r)を極座標(φ(r),r)上にプロットして、それらの点を繋いで求めた軌道の様子を表す曲線が下図です。真ん中のオレンジ色の円はシュワルツシルド半径を示しています。ここまでブラックホールに近付くと、一公転ごとにかなり大きな近星点移動が生じることが解ります。
このとき注意して欲しい事は r が r2 や r3 に近い領域では dr に対する dφ の変化量が大きいので、小刻みに積分値を計算する必要があります。
さらに注意して欲しいのですが、r2=169591での初期角運動量Lがそれ以後も保存されます。それが同一の有効ポテンシャル曲線Veff(r)の元で議論していると言うことです。そして、初期設定の動径方向の速度成分はゼロです。つまり下図のr=r2=169591の半径を持つ円周に接する方向に質点mを打ち出すと言うことです。これが、有効ポテンシャル曲線Veff(r2)上の点から出発すると言うことです。そしてr=r3=323891に到達したとき、再び有効ポテンシャル曲線Veff(r3)上の点に到達しますから、そこでの動径方向の速度成分は0となり、軌道はr=r3=323891の半径を持つ円周に接することになると言うことです。
このような関数の数値積分を実行するコンピュータープログラムは沢山ありますので適当なものを利用して下さい。次の図は、Mathematicaの“NIntegrate”と“ListPolarPlot”のコマンドを用いて描きました。
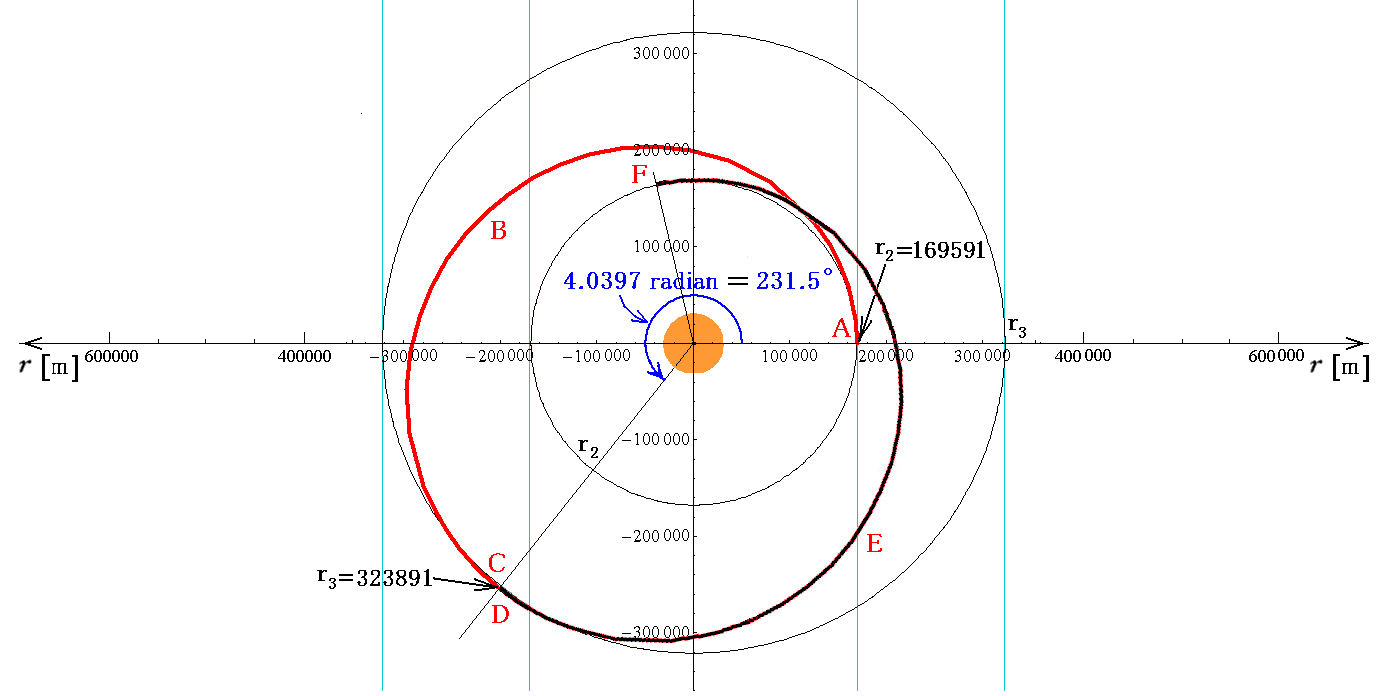
上記数値積分を r=r2=169591 から r=r3=323891 まで実施すると φ(323891)=4.0397radian=231.5°になります。これは前出グラフのピンク色部分(A→B→Cの部分)の面積に相当します。実際そうなっていることが座標値からも読み取れます。
φが4.0397radianより増大する領域の数値積分は前出グラフのD→E→Fの部分の積分を実行しなければ成りません。この部分は関数値が負ですが、積分の方向が r が大の領域から r が小さくなる方向への積分ですから、φ(r)
は r の減少と共に正の方向にさらに増大してゆきφ(169591)=(4.0397×2)radian=(231.5×2)°となります。その積分値をプロットしてゆくと、図中の黒色曲線が得られます。後は、上記二つの領域の積分操作を繰り返してゆけば良い。
図から解る様に、本稿で仮定している数値例では、一公転当たりの近星点移動角度は 231.5×2-360=103°となります。
[補足説明1]
ここでは、3.(4)6.(2)で取り上げた内の2の場合を説明しましたが、3.の場合や4.の場合も、適切なエネルギー値Eを設定して、同様な数値積分を実行すれば軌道の形を求める事ができます。
以下の部分は未完成です。今後少しずつ書き進めるつもりですが、上記の部分でも疑問に思うことが多く、自分でも本当かどうかあやふやな部分が多数有って教えを請うために取りあえずupしました。
4.光子の力学
以下をご覧になれらる前に、Einstein文献「一般相対性理論の基礎」E.(22)2.と、矢野文献「テンソル解析学の一般相対性理論への応用」7.(9)2.を復習される事を勧めます。
Einsteinは重力場方程式を近似的に解いて、その近似解(70)式を重力場内での光線の測地線方程式(73)式に適用することで光線の曲がる量を求めています。
実際Einsteintが求めた近似解(70)式は太陽半径より外側の領域を表す計量テンソルとしては極めて近似の良い解でした。その近似解を適用するところにもう一段近似を用いて偏光角を求めています。
一方矢野文献では重力場方程式の解としてシュワルツシルドの厳密解を用います。その厳密解を測地線方程式に適用して偏光角を求めているのですが、測地線方程式を解く過程でチョットした近似が用いられています。
本章ではブラックホール近傍での光線の振る舞いを調べるのですから、ここでの課題は、シュワルツシルド厳密解を用いて、それを測地線方程式に適用してできるだけ厳密・正確に解くことです。
(1)重力場内における光線の運動方程式
Schwarzschild解の応用として強い重力場(ブラックホール近傍)内での光線の振る舞いを取り上げる。
光の進路も測地線ではあるが、その接線ベクトルは常に0ベクトルであった。つまりdτ=0である。したがって光の進路を表すのに、固有時間τを使う事はできない。そこである適当なパラメーターλを用いてxμ(λ)という形で光の軌道を表す事にする。
xμ(λ)の満足すべき方程式は3.(2)と同様で、そこに①、②、③式のd/dτをd/dλに変えたものになる。すなわち
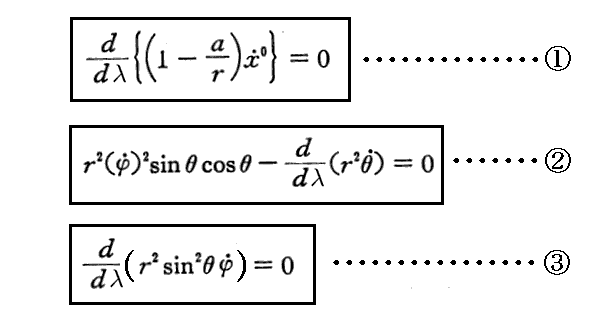
となる。ただし、

としている。
また、接線ベクトルは0ベクトルであるから、そこの⑤式の代わりに
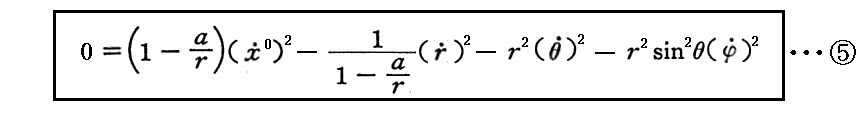
が成り立つ。
ここでも3.(2)と同様にθ=π/2とおく。つまり光の軌道はxy平面上にあるとする。また3.(2)と同様に

が成り立つ。
(2)
(3)

文献8.のラウエの本の図を紹介
Kip S. Thorne「ブラックホールと時空の歪み」“ブラックホールの発見と否認”(p110と、p118~120) のp119の説明
5.Birkhoffの定理
内山「一般相対性理論」p230の内容を追記
ハートルp218、p47を参照。
文献10.のp92の見方。
球対称の質量分布が作る重力場は、その物質(質量)分布が常に球対称性を保持しつつ動径方向に膨張や収縮をして時間的にその分布状態を変えても、物質(質量)外部の領域では必ず、シュヴァルツシルト時空になり、それは時間的に変化しない、というのがバーコフの定理です.。この定理により、重力収縮する天体の周りの時空がその天体の自転が無視できる場合、静的なシュヴァルツシルト時空になるということが言え、極めて重要な定理だと思っています。
https://ameblo.jp/metazatunen/entry-11825734989.html
これは富岡竜太「あきらめない一般相対論」第5章と同じ。
ウイキペディアの「バーコフの定理」も参照。
6.Schwarzschld座標から、クルスカル-ツェクレス(Kruskal-Szekeres)座標へ
この座標系は
M. D. Kruskal, “Maximal Extension of Schwarzschild Metric” , Phys. Rev.
119, 1743-1745 , 1960年
と
G. Szekeres, Pub. Mat. Debrecen. 7, 285, 1960年
によって独立に導入された。
ハートル上巻p314
内山龍雄「一般相対性理論」p253
ゼノンのパラドックス
7.Reissner-Weyl-Nordstro¨m解
内山龍雄著「一般相対性理論」裳華房(1978年刊) §43のReissner-Weyl解の説明を引用
8.Kerr解
クェーサーが明るく輝くメカニズムを理解する為には必須です。
9.参考文献
できるだけ多くの文献を参考にして、解り易くなることを心がけました。下記は参考にした書籍の一部です。
- A.Einstein著「光の伝播に対する重力の影響」1911年6月論文
- A.Einstein著「水星の近日点の移動にたいする一般相対性理論による説明」1915年11/18論文
- A.Einstein著「一般相対性理論の基礎」1916年3月論文
- 福江純著「ブラックホールの力学」『天文教育』2002年3月号
とても解りやすく、かつ興味深く解説されています。ただし、6-1“自由落下運動”の所には少しミスがあるように思います。
- ジェームズ・B・ハートル著(牧野伸義訳)「重力 - アインシュタインの一般相対性理論入門」日本評論社(2016年刊 原本は2002年刊) §9.3“安定円軌道”、“束縛軌道の形”
以下はこの本の付録としてのMathematicaプログラム集のwebサイトです。
http://web.physics.ucsb.edu/~gravitybook/mathematica.html
- 平川浩正著「相対論(第2版)」共立出版社(1986年)
- 小山勝二・峰重慎編「シリーズ現代の天文学8 ブラックホールと高エネルギー現象」日本評論社(2007年刊)
- マーシャ・バトゥーシャク著「ブラックホール(アイディアの誕生から観測へ)」地人書館(2016年刊)
第9章“ブラックホールって呼べば?-Kerr”を別稿で引用。第1章、第4章、第8章クェーサーも別ヘージで引用
- 内山龍雄著「一般相対性理論」裳華房(1978年刊)
第7章“Einstein方程式の厳密解”を別稿で引用。
- 佐藤文隆、R・ルフィーニ共著「ブラックホール(一般相対論と星の終末)」中央公論社自然選書(1976年刊)
少し古い文献ですが、ブラックホールの事に付いては最も丁寧に説明されている様に思います。ただし内容はかなり高度です。この中で“富松・佐藤解”も説明されています。
- 須藤靖著「一般相対性理論入門」日本評論社(2005年刊)第5章
良く書き込んであるのですが、説明が簡潔なので理解するのは大変です。本稿のページを作っていて行き詰まった時には、何度か参考にさせて頂きました。
[2021年10月追記]
- 谷口義明著「ついにみえたブラックホール」丸善出版社(2020年刊)
これは、とても解りやすくて面白い本です。高校で地学を教えていた頃(20年くらい前)に比較して、この分野は大発展を遂げているのですね。当時疑問に思っていた謎が次々に解明されていくのに感動しました。
この谷口文献で説明されているブラックホールシャドウの見え方の解明には本稿で論じている知識が必要なのですが、谷口文献では銀河系レベルの巨大ブラックホールの話が中心を占めています。
この本の中に次の萩原雄祐文献13.が紹介されていました。確かに谷口先生が言われるように、文献13.にすべてが書き込まれています。本稿のテーマを理解するには、この論文を読み込むことにつきるのかも知れません。
- 萩原雄祐著「シュバルツシルド重力場における相対論的軌道の理論」
Hagihara_Yusuke ,“Theory of the Relativistic Trajectories in a Gravitational Field of Schwarzschild”,
Japanese Journal of Astronomy and Geophysics, Vol. 8, p.67~176 , 1931年