重力波（gravitational wave）とは何か

　いままでに当ＨＰでも、重力が復元力となって生じる波動である重力波（grvity wave）すなわち海洋や大気中を伝わる長波の様な波について何度か説明してきました。
　しかし、このページで説明する重力波（gravitational wave）は重力場そのものが波として伝わるものです。すなわち電磁波のように場そのものの波動です。

１．導入

　重力波は、一般相対性理論が完成した直後の1916年6月に、Einsteinｔがその存在を予言した（文献1．）。しかし、重力場方程式の発見（1915年11月）より遙か前から、Einsteinは次の様に考えていたようです。
　ニュートンが発見した万有引力の法則については、ニュートン以来、重力源（質量）が任意の場所に及ぼす重力作用は瞬時に時空間を伝わる（遠隔作用論）と解釈されていた。しかしその後、電磁場の作用は光の速度でしか伝わらない（近接作用論）ことがMaxwellにより明らかにされていた。
　電磁場の変動が光速度でしか伝わらないということは、電磁気的な力が光速度でしか作用しない事を意味します。重力を深く考察していたEinstainは、同じ力の作用である重力が光速度でしか伝わらないのでは無いかと、当然予測していました。
　その事からEinsteinは以下の様に考えたのでしょう。、

1. 　電磁場の作用が有限の速度でしか伝わらないのと同じ様に、重力場の作用も有限の速度（光速）でしか伝わらないのではないか！　それはとりもなおさず、電磁場の波が存在する様に重力場の波が存在する事を予想させる！
2. 　そのとき、Maxwellの方程式から電磁場の波動方程式が導かれた（別稿「電磁場の非同次波動方程式」２．（２）参照）ように、重力場の方程式から波動方程式様の方程式が導けるのではないか！　
3. 　それが、導ければ重力作用の本質をより明確に理解することができるだろう！
4. 　ただし、Maxwell方程式系が（電磁場テンソルに付いて）線形の方程式系であるのに対して、重力場の方程式は場変数ｇ_ｉｊに付いて非線形である。そのため、重力場方程式から波動方程式が簡単に導けるとは思えない。
   　しかし、“弱い重力場であるという近似”を行えば波動方程式が導けるのではないか！
5. 　それを実行するには、 L.V.Lorenz が　Maxwell方程式系　から　波動方程式　を導くときに導入した“ゲージ条件”（別稿「電磁場の非同次波動方程式」３．（２）参照）と類似の手法が使えるのではないか！　

　実際のところ、Maxwell-Lorentzの電磁気学に深く精通していたEinsteinは、1913年の草案論文（Grossmanとの共著）を書き上げる過程で、すでに上記の様な考えを持っていたようです。草案論文から確かにその事は読み取れますし、実際1913年のウィーン公演後のBornとの質疑の中でその事を話しています。
　また、1914年10月29日論文§17．“種々の見方による近似方程式を立てること”でもその当たりの考察を展開しています。そして、1916年6月論文で、本稿の第２章で紹介する理論を展開した。

［補足説明１］
　上記の事柄について補足します。ローレンツ（L.V.Lorenz）は、4元電磁ポテンシャルが

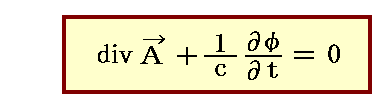
を満足するという“ゲージ条件（Lorenz gauge）”を用いて、
　Maxwell方程式

の（1）〜（6）式と波動方程式（13）、（14）式が等価である事を示して見せた。

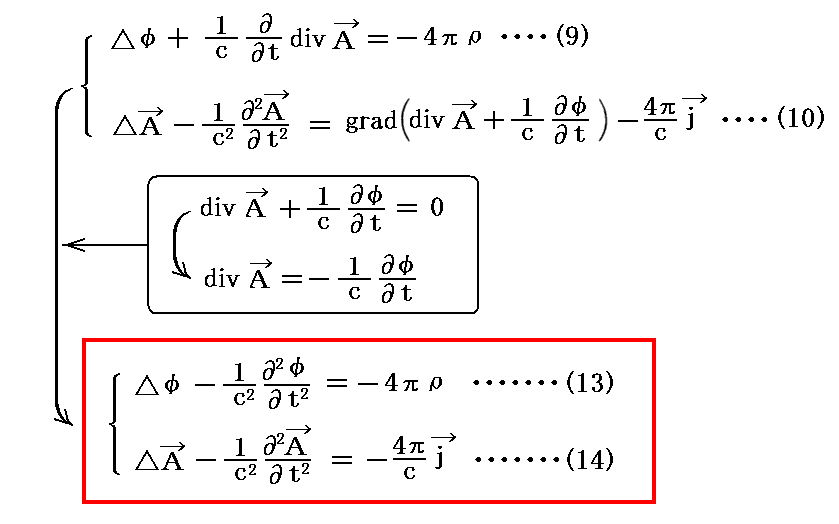
　補足しますと、（1）〜（6）式と（13）、（14）式が等価である事を示したローレンツ（L.V.Lorenz）の手順は今日の展開法とは異なっています。その事に付いては別稿「Maxwell方程式の先見性と電磁ポテンシャル」2．（2）1． のこの説明をご覧下さい。
　（1）〜（6）式から（13）、（14）式を導く今日的な手順は別稿「Maxwell方程式の先見性と電磁ポテンシャル」2．（3）1． と 2．(3)3． を復習される事を勧めます。
　
　また、この当たりの特殊相対論を用いた4元表現については別稿「ミンコフスキーの4次元世界」４．（２）と、別稿「Maxwell方程式の先見性と電磁ポテンシャル」3．を復習されて下さい。
　
　さらに、4元電磁ポテンシャルによる“4元表示波動方程式”に付いては別稿「微分幾何学」3．（4）4．や、別稿「Maxwell方程式系の先見性と電磁ポテンシャル」３．（２）［補足説明４］や［補足説明５］などを復習されて下さい。

２．重力場方程式から波動方程式の導出

　以下の展開は、Einsteinの1916年6月論文（文献1．）でなされているのですが、ここは、文献4．（Weyl第�W章§32）や、文献7．（石井文献第7章§11）を参考にして書きました。

（１）ゲージ条件

　真空中のMaxwell方程式から、電磁場には波が起こり、その波は光速で伝わっていることが導けます。
　重力場方程式も波動方程式の形に変形でき、重力場に光速の速度を持つ波が生じる事を導く事ができます。ただし、そのことが示せるのは弱重力場の条件があるときです。
　ここでは、計量テンソル場ｇ_ｉｊが、ミンコフスキー空間の計量テンソルη_ｉｊとほとんど等しく、

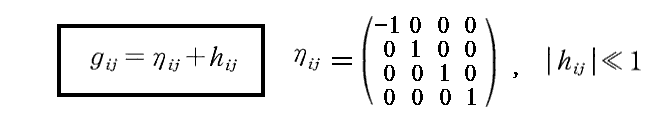
と表されると仮定します。当然ｈ_ｉｊ＝ｈ_ｊｉとしています。また、η_ijの逆をη^ｉｊとすると

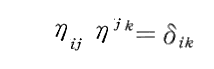
である。ｈ_ｉｊがある一つの座標系で上記の定義式で定められたときこれは弱い重力場の時に許される仮定です。
　このとき、ｇ_ｉｊの逆であるｇ^ｉｊは２次以上の項を省略すれば

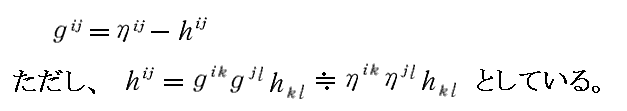
と書けます。
　さらに、ここでは、ｇ_ｉｊ の１階微分、２階微分も １ に比べて十分小さく、ｈ_ｉｊ と同じ程度の微小量であると仮定します。
　さらに、｜ｈ_ｉｊ｜≪1 である事から、ｈ_ｉｊおよびその偏微分係数に対する添字の上げ下げ(共変・反変の変換)はｇ^ｉｊの代わりにη^ｉｊで近似的に行えるものとする。
　ｈ_ｉｊなどの指数の上げ下げをｇ_ｉｊでは無くη_ｉｊで行っていますのでｈ_ｉｊは正規のテンソルでは有りません。近似的にソンソルと見なせる“擬テンソル”です。

　電磁気学を参考にしたのかどうかは解りませんが、アインシュタインは、ゲージ条件

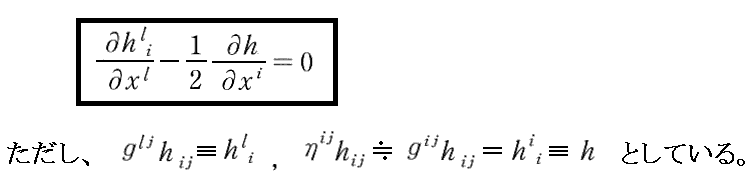
を満足する様な座標系（ｘ_ｉ）に於いて、《重力場方程式》から《波動方程式》が得られる事を示した。
　このようなゲージ条件を用いたのは、重力場方程式を弱い重力場の条件下で変形して波動方程式を導くとき、後で示す様な式が出て来るのですが、そこに現れる上記の項の左辺

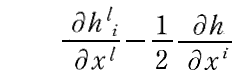
が＝0となることが必要だからです。そのため上記のゲージ条件が成り立つとしたのでしょう。しかしこの条件が成り立つ事の証明は説明してくれていません。この当たりについては、後の［補足説明１］をご覧下さい。

　上記の“ゲージ条件”が、座標を適当に変換することによって ｈ_ｉｊ の1次の量を調整して常に満たされる様にできる事を証明しよう。
　まず、

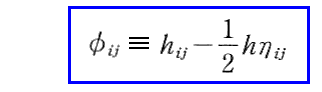
と置く。
　ここで、η^ｉｊとφ_ｉｊの縮合をφとすると、それは−ｈとなるので

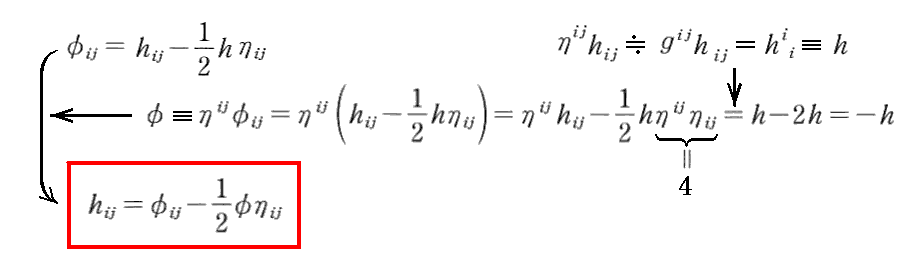
が得られる。
　これは、電磁気学におけるスカラーポテンシャルφ、ベクトルポテンシャルＡと電場Ｅ、磁場Ｂとの関係を与える関係式（別稿２．（３）３．［補足説明２］参照）の様なもので、後で導く波動方程式を解いた解 φ_ｉｊ から波動を表す計量テンソル ｈ_ｉｊ そのものを得るための式です。

　ここで、座標をｘ^ｉからｘ’^ｉへ

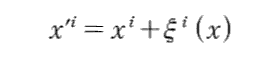
を用いて変換する。このとき、逆変換は第１近似で

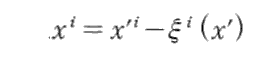
と書くことができるであろう。ただし、ξ^ｉ（ｘ）、ξ^ｉ（ｘ’）は微小量でｘ^ｉ、ｘ’^ｉの関数とする。

　このとき、別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分」3．（4） で説明したように、座標を変換すると計量テンソルの表現も変化します。そこの3．（4）［補足説明３］で特に注意した様に、時空間のひずみは変化していなくても、座標系を別な座標系にすることでも計量テンソル（今はｈ_ij）を変化させることができるのでした。そのため、取りあえず、座標系を少し変えてみたら計量テンソル ｈ_ｉｊ 、及びそれらの関数である ｈ や、φ_ｉｊ や、∂φ^ｉ_ｊ／∂ｘⁱ などが、どの様に変化するか調べてみようと言うことです。
　
　何のためにこんなことをするのかと言うと、時空間が曲がったために計量テンソルが変化したとしても、その変化の特定な部分を打ち消してしまう様な座標系を選ぶことができるのではないかと言うことです。
　その特定の部分というのが、波動方程式を導く過程でゲージ条件式で示されている部分です。

　まず、ｈ_ｉｊ の新しい座標 ｘ’^ｉ での成分表現 ｈ’_ｉｊ を求めて見る。すなわち

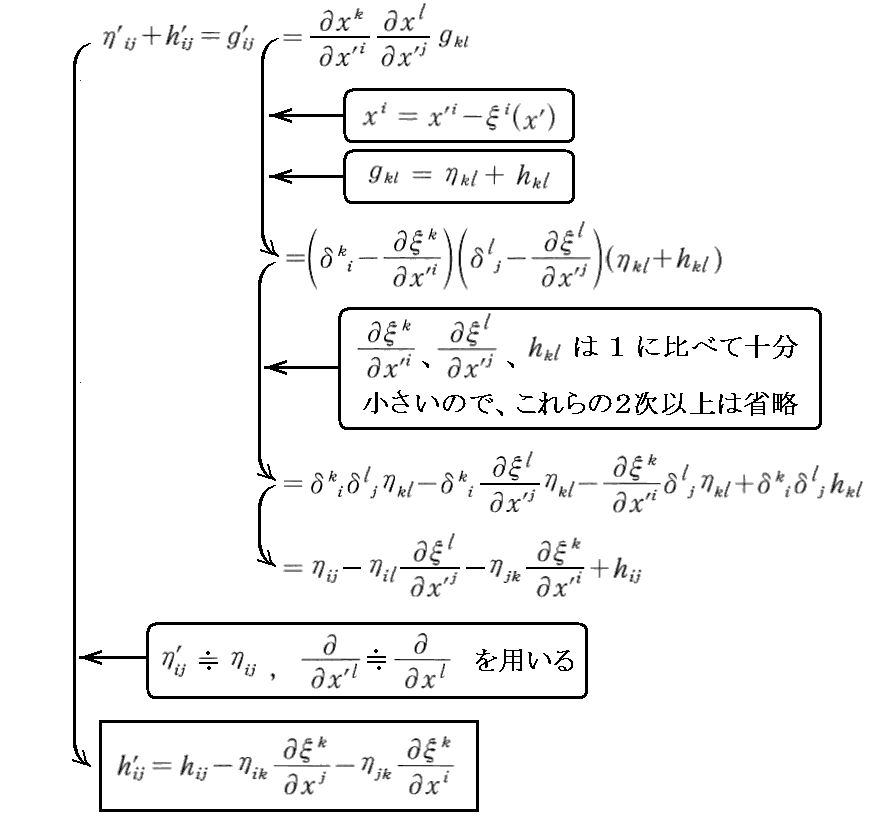
が得られる。
　ここで、新しい座標系での値 ｈ’ と φ’_ｉｊ を

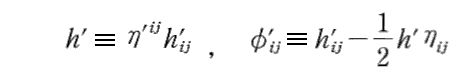
で表すと、それらはもとの座標での値と以下の関係にあることが解る。
　まず ｈ’ と ｈ の関係については

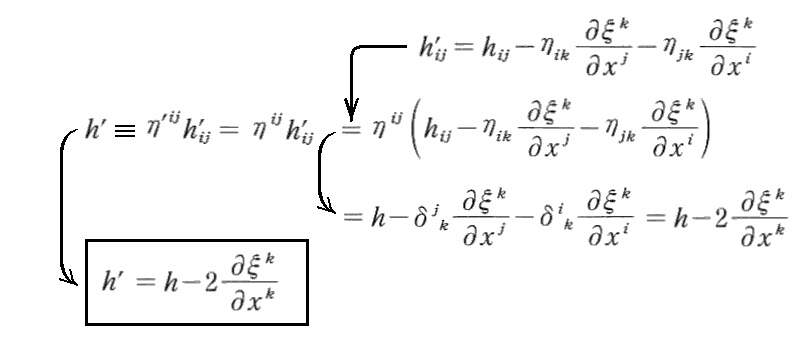
となる。
　次に φ’_ｉｊ と φ_ｉｊ の関係については

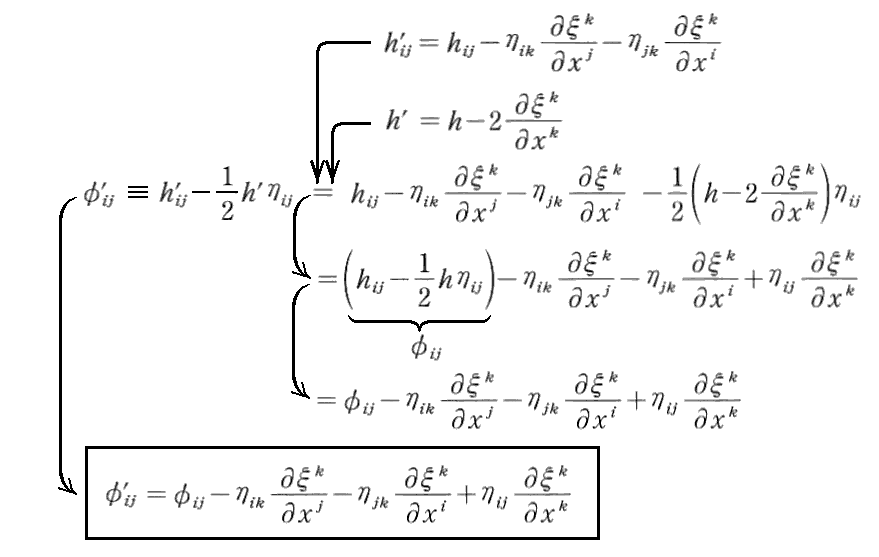
となる。
　さらに、φ^ｌ_ｉ＝η^ｌｊφ_ｉｊ　を偏微分したものについては、以下の関係式が得られる。

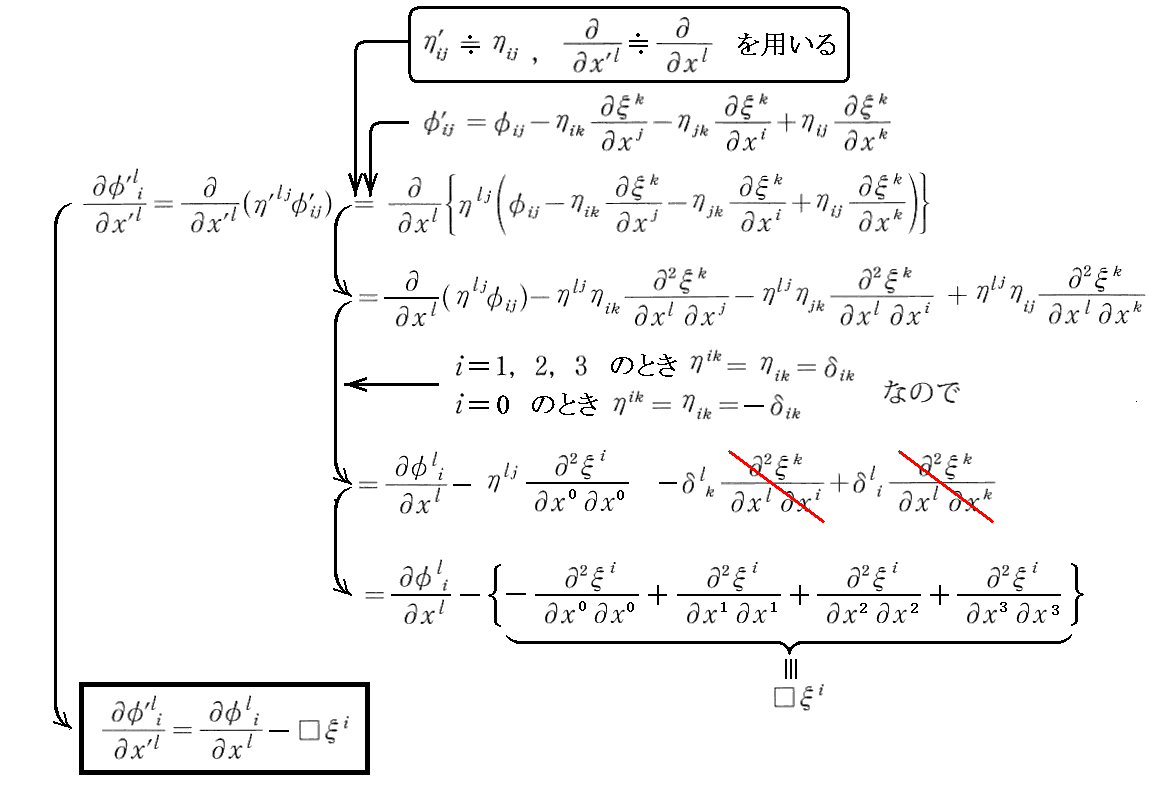
　最後の式における ξ^ｉ を、下記の非同次波動次方程式（非同次の部分が∂φ^ｌ_ｉ／∂ｘ^ｌ　である波動方程式）

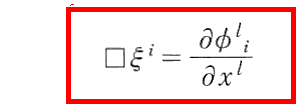
の解を採用する。具体的には ξ^ｉ（ｘ） を

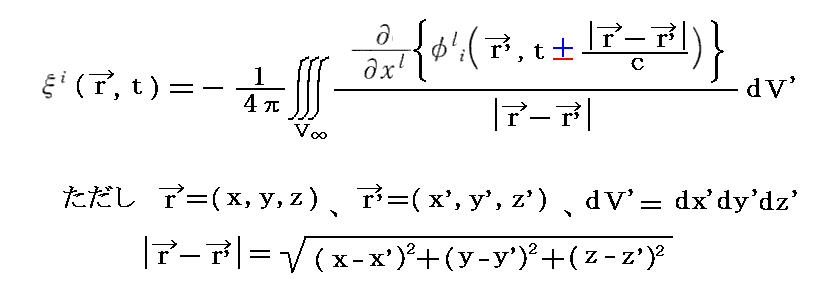
のように取るわけです（これが解である事は別稿「ポアソン方程式と波動方程式」２．を参照）。
　そうすると

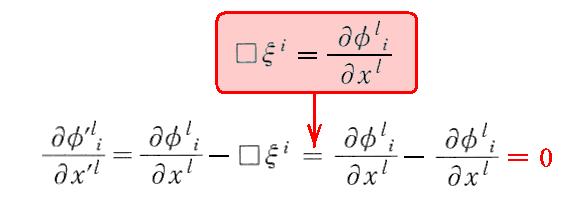
となります。
　ここで

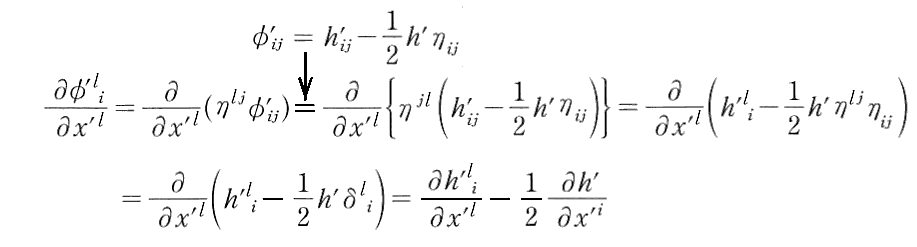
ですから、上記の様に座標系を取れば、常に ｈ’_ｉｊ は

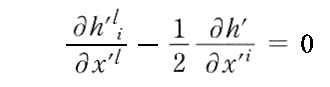
を満たすようにできる。

［補足説明１］
　ここの“ゲージ条件”の意味については、Einstein自身が別稿文献８．［Ａ８］§１の末尾で明確に説明していますのでご覧下さい。ここは別稿3．（4）［補足説明３］で注意している事に関係します。
　ただし、Einsteinは、このゲージ条件が成り立つようにするにはどの様な座標を選んだらよいのか、具体的に求める方法については説明してくれていません。
　Einsteinに取って、その様な座標が存在することは自明なことで、それを具体的に求める手順に意味があるとは思えなかったのでしょう。いずれにしても、この当たりが一般相対性理論を理解する上で最も難しい所かもしれません。
　
　ところで、文献5．§60のPauliの解説や、Paisの第15章15ｄ．の解説によると、この“ゲージ条件”が ｈ^ｌ_ｉ の１次で常に満たされる様にできる事を一般的に証明したのは D. Hilbert （ Go¨tt. Nachr., p53〜, 1917年にて）だそうです。
　この論文を持っていないので推測でしかないのですが、“どの教科書にも載っている上記の証明”はそれに由来するのかも知れません。

（２）重力場方程式から波動方程式へ

　前節の考察から解る様に、弱重力場の場合には前節のゲージ条件を加えて

のもとで重力場方程式を考察すれば良い。、
　ｇ_ｉｊ＝η_ｉｊ＋ｈ_ｉｊ　のもとで、η_ｉｊ　は定数ですから、

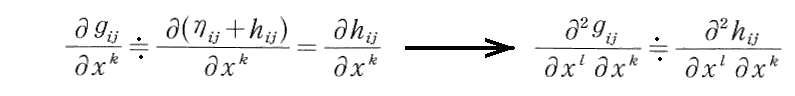
となる。これを用いて接続係数（クリストッフェル記号）を計算すると

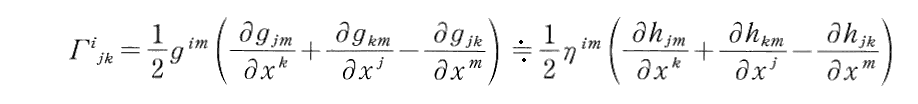
となる。
　これを用いるとリーマンの曲率テンソルは以下の様に近似できる。

　ここは、別稿1916年6月論文［補足説明］で注意した様に“フルタイプ”の曲率テンソルを用いていることに注意して下さい。
　リーマンの曲率テンソルについては別稿２（９）２．や別稿２．（９）３．［補足説明１］、あるいは別稿３．（５）１．や別稿３．（５）１．［問題２］［補足説明１］などを復習して下さい。
　ただし、これらの別稿や、Einsteinの1916年6月論文と比較検討されるときには、本稿の定義式とは少し異なっていますのでその点を注意されて下さい。

　次に、リッチの曲率テンソルは、以下の様に近似できる。

　さらに、スカラー曲率Ｒは

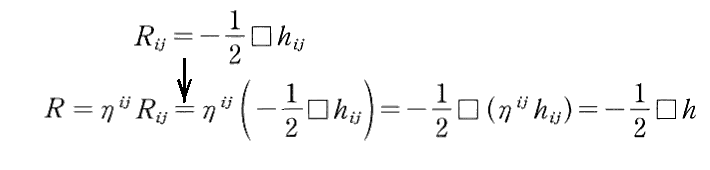
となる。
　これらの結論を用いると重力場方程式は

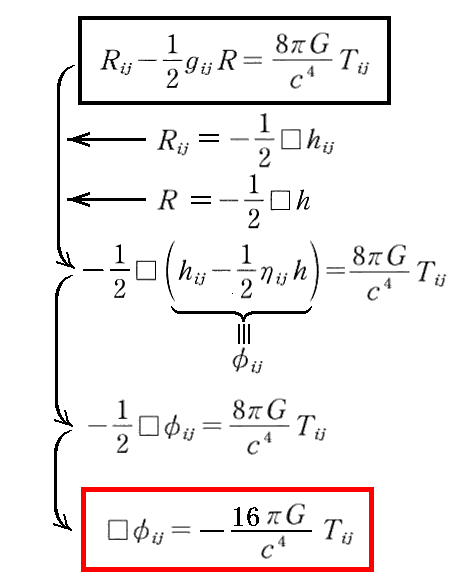
となります。ここで、φ_ｉｊは厳密な意味でテンソルでは有りませんが、近似的にはテンソルと見なせる量（擬テンソル）です。そのため、上式は一般共変性を完全に満たしてはいません。あくまで近似的に成り立つ方程式です。
　左辺は“ダランベール演算子”ですから、結局ポテンシャルφ_ｉｊに関する非同次波動方程式に帰着します。
　このとき、∂²／∂ｘ₀²＝∂²／(ｃ∂ｔ)²　ですから、ポテンシャルφ_ｉｊの波動（重力波）は“光速度”ｃで伝播することになります。
　波動方程式の二階時間微分の前にかかっている係数(1／ｃ²)の逆数の平方根（ｃ）が波の伝播速度を表している事に付いては別稿「波動方程式と一般解」３．をご覧下さい。
　さらに補足しますと、右辺のエネルギー・運動量テンソルについては近似的に

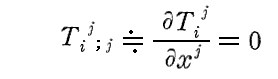
が成り立ちますが、これは φ_ｉ^ｊ に課した条件

と見合うものです。

　別稿　「ポアソン方程式と波動方程式」２．で説明したように、この非同時波動方程式の解は


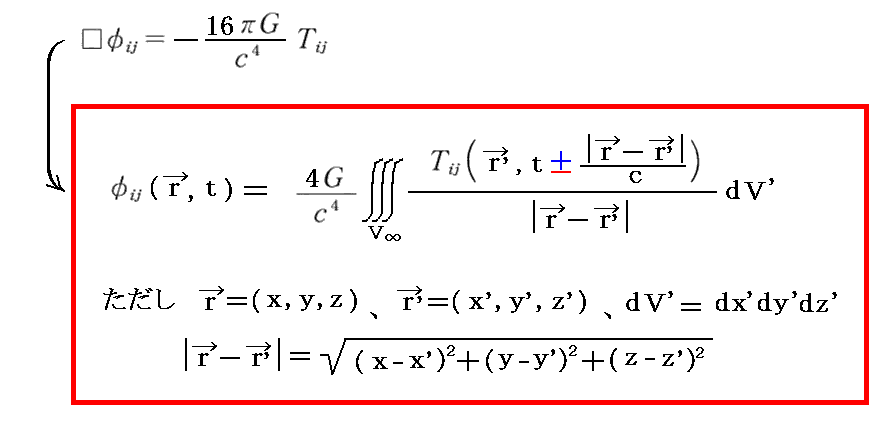
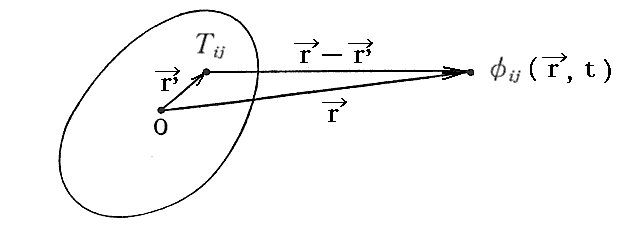
となる。
　この解に於いて、本来途中の時空間も重力源（波動方程式の右辺）により歪んでいます。その歪んだ時空を伝播して届くのですが、ここでの議論は、そういった途中の時空の歪みはすべて無視できるという弱重力場近似での説明だと言うことを忘れないで下さい。時空の波が伝わっているのですから、本来平坦な時空では無いのですが、平坦であるとしていると言うことです。

３．平面重力波

４．力学系による重力波の放出

５．重力場のエネルギー

６．参考文献

この稿を作るに当たって、下記文献を参考にしました。感謝！

1. Einstein著「万有引力の場の方程式の近似的積分」, Berlin. Berichte., p688〜696, 1916年6月
   　“近似的積分”と言っているのは、重力場方程式の解が遅延ポテンシャル形式の積分型の解として得られたことを意味している。近似的と言っているのは波動方程式が一般共変性を完全には満たしていないことを指しているのでしょう。
2. Einstein著「重力波について」, Berlin. Berichte., p154〜167, 1918年1月
   　文献1．の後半部の間違いを修正したもので、文献1．の改訂版と言って良いのですが、有名な2つのタイプの波と四重極公式が導かれています。
3. Einstein著「」
4. H.Weyl著（菅原正夫訳）「空間・時間・物質」東海大学出版会（原本の初版は1918年、第5版は1922年です。この訳本は1973年刊です）
   　特に、第�W章§32“重性波”をご覧下さい。
5. W.Pauli著「相対性理論」筑摩書房（初版は1921年刊）
   　特に、
6. J. Weber著（藤田純一訳）「一般相対論と重力波」講談社（原本1961年刊、訳本は1974年刊）
   　
7. 石井俊全著「一般相対性理論を一歩一歩数式で理解する」ベレ出版（2017年刊）
   　第7章§11“重力波の方程式”（ｐ662〜667）
8. 平川浩正著「相対論（第2版）」共立出版（初版は1971年刊、第2版は1986年刊）
   　§6.6“Einstein方程式の線形近似”、8章“重力波”
9. ジェームズ・Ｂ・ハートル著（牧野伸義訳）「重力」日本評論社（原本は2002年刊、訳本は2016年刊）
   　第21章§21．4
10. 須藤靖「もうひとつの一般相対論入門」日本評論社（2010年刊）
    　第4章“重力波”
11. 　Galina Weinstein 著「Einstein 's Discovery of Gravitational Waves 1916-1918」(2012/2/16)