このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
ニュートンが発見(1665年)した「万有引力の法則」とは、この世界のすべてのものが互いに引き合っており、その引力の大きさは下記の形で表されるというものです。比例定数Gについては別稿「H.Chavendishの実験について」参照

そのとき r は二物体間の距離を表すが大きさがある物体の場合にどのようにとればよいのか迷います。その答えは下図の様に大きさのある物体 の場合各部分(m1、m2、m3、・・・・)からの引力ベクトルをすべて求めて、それらをのベクトルの合力求めればよい。
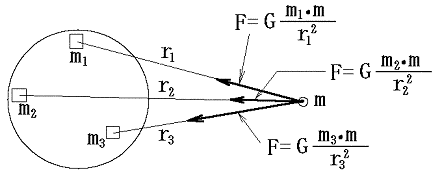
そのとき
一方の物体が完全な球体で、密度分布が球対称であり、他方が質点と見なせる場合には、その場合の合力は全質量が球の中心に存在するとして、距離は球の中心からの距離を用いればよい
これは高校物理ではしばしば出てきますが教科書ではきちんと説明されていません。以下3段階に分けて説明します。
この証明は以前「ガウスの法則(静電気学)」で用いたやり方です。円錐の底面積は高さの二乗に比例する事を利用。
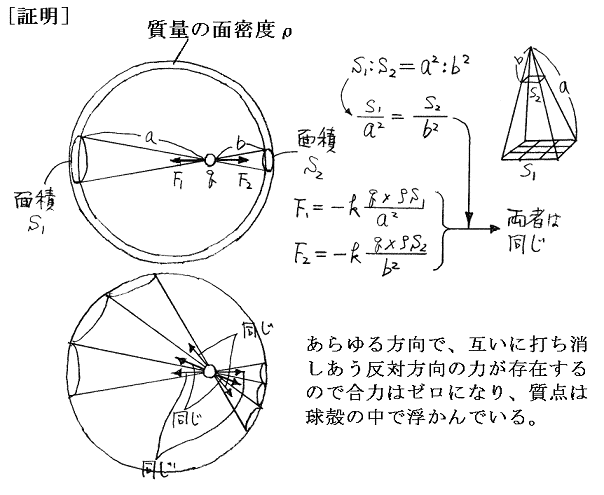
これは、「プリンキピア」第1編、第12章、命題70・定理30で証明されているものです。
この証明法はいろいろありますが、ここではニュートンが「プリンキピア(自然哲学の数学的原理)」第1編、第12章、命題71・定理31で行った幾何学を使うものを紹介します。

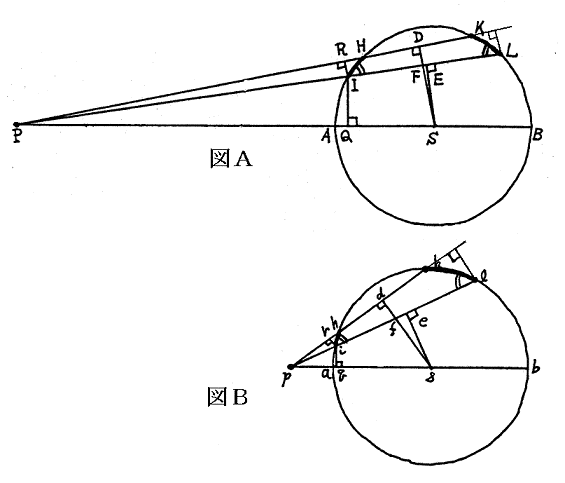

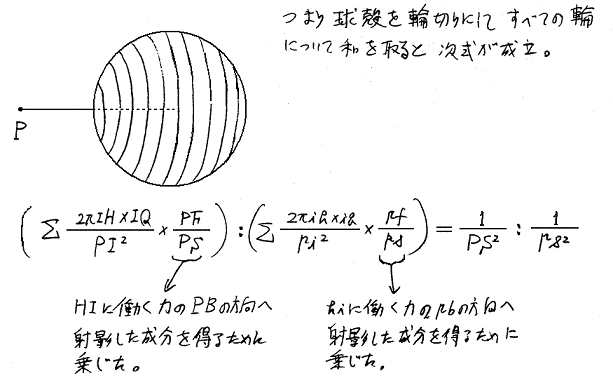
以上で球殻の外側の質点に及ぼす球殻の引力の合計は球の中心と質点との距離の逆数の二乗に比例することが言えた。つぎに球の半径を小さくした極限移行を考えると比例定数も同じGになるので結局球殻の引力は球殻の全質量が球殻の中心に存在すると考えた場合と同じである。
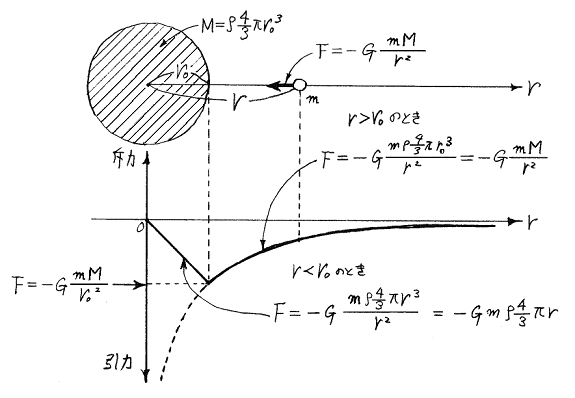
以下簡単のために密度がすべて同じ場合で計算する。球をタマネギの皮のような多くの球殻に分割して考えて(1)(2)の結論を利用する。(1)より半径rより外側の球殻は質点に引力を及ぼさない。そして(2)半径rより内側の部分は球の中心に、各部分の質量を集めたときに質点に及ぼす力と同じだけの引力を及ぼす。
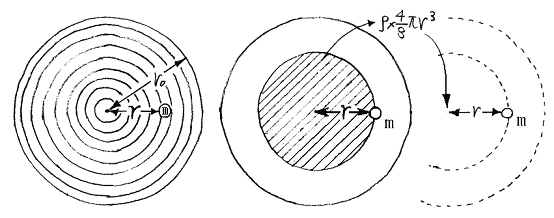
半径r0の球内全体に均等に質量(密度ρ)が分布している球に無限円から質点mを近づけるとき、各点で働く力は以下のようになる。