相対論的力学
ここでは相対論的な力学に特化して説明します。特殊相対性理論そのものについては別稿「アインシュタインの特殊相対性理論(1905年」を、また質量とエネルギーの等価性については別稿「アインシュタインの公式 E=mc2 の証明」をご覧下さい。
1.導入
(1)Planckの考察
プランクはアインシュタインの1905年論文を注意深く読み、その理論の整合性に驚嘆します。そして相対性理論に深く感銘を受け、それが本物である事を確信します。
しかし、ただ一つ不明瞭で気になる所がありました。それは第Ⅱ部§10の電子の力学における相対論的な運動方程式の表現です。
以下に引用するものは、アインシュタインの記したy成分、z成分の式中のβ項を両辺で割り算して消去した相対論的な“本来の形”に直しています。また2.章で説明するPlanckの論文の表現に合わせてμ→m、v→qに変えています。
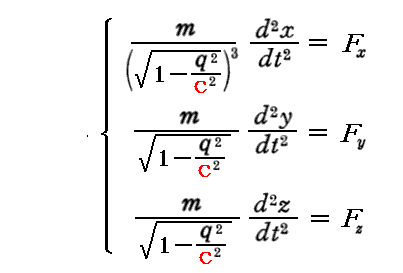
この方程式は、方向によって非対称な形になっています。
おそらくプランクはその非対称性が気になって、その原因を考えたでしょう。そして、その非対称性は、アインシュタインがローレンツ変換を適用するとき、K系に対するK’系の運動方向をx軸に沿う特別な方向とした事に因るのではないかと気づきます。
それで、以下の手順を試してみることにしました。まず静止K系(x,y,z,t)に対して(vx、vy,vz)方向に速度qで移動する座標K’系を考えます。このとき移動座標K’系のx’軸の方向をK系に対するK’系の移動速度ベクトルq=(vx、vy,vz)=(dx/dt,dy/dt,dz/dt)の方向と一致させます。そのとき、y’軸とz’軸はx’軸に垂直であり、y’軸⊥z’軸で在りさえすれば任意の方向を向いていても良いとします。(下図参照)
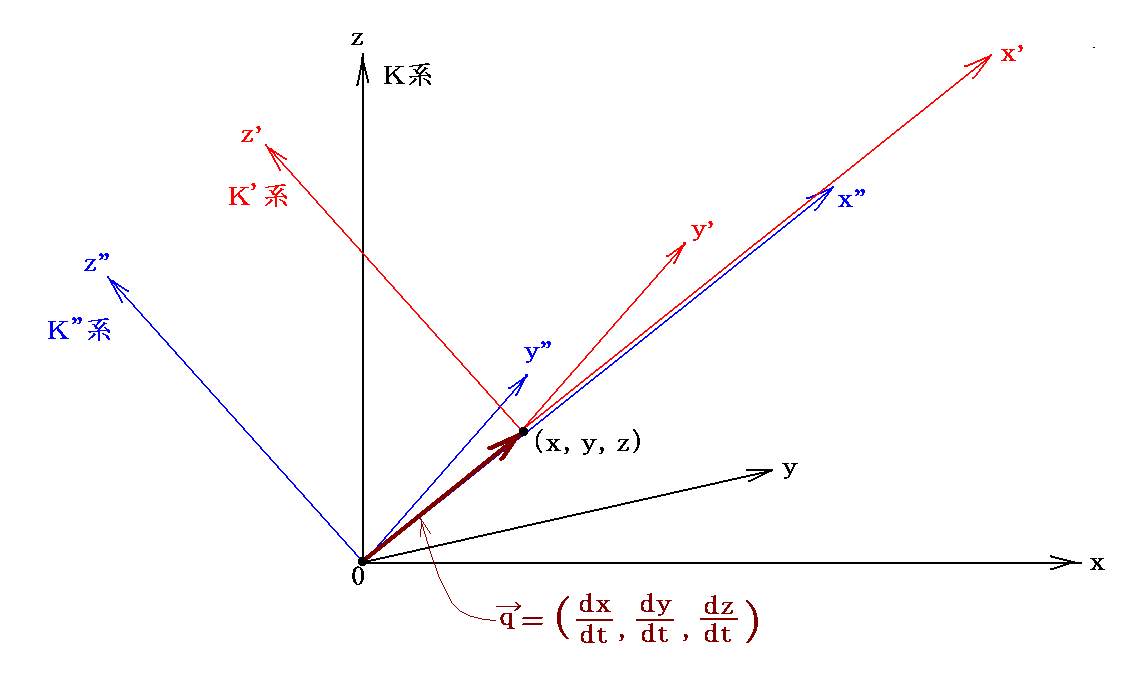
そしてK’系の原点に対して最初静止している質点(電荷e)に対してニュートンの古典的な運動方程式が成り立つとします。そう考えて良い理由は別稿の第Ⅱ部§10の電子の力学を復習されたし。ちろんそのK’系では電場ベクトル(Ex’,Ey’,Ez’)のみが存在するとします。
次にK’系のx’軸に沿って-q=(-vx、-vy,-vz)で移動するK”系を考えます。そのときx”軸に沿って(つまりx’軸に沿って)移動するときy”軸とz”軸はy’軸とz’軸に平行になるように移動するとします。このK”系の原点は当然最初のK系の原点と常に一致します。(上図参照)
このとき、K”系の原点は、最初のK系の原点と一致こそすれ、x”軸、y”軸、z”軸の方向は最初のK系のx軸、y軸、z軸とは異なっています。ここまでの作業は別稿3.(5)で説明したアインシュタインの手順とまったく同じです。
次いで、プランクはそれを最初のK系の軸に一致する三次元の座標回転をして、最初のK系での方程式に変換します。これは運動方程式の左辺はもちろん右辺の力の原因となる電場、磁場(K”系においては磁場も現れている。)もその座標回転操作に伴う値に変換します。
この最終的に元に戻った変換は最初の座標K系そのものです。だから、そうして得られる運動方程式は、K系において任意の方向に速度q=(vx、vy,vz)=(dx/dt,dy/dt,dz/dt)で運動する質点(x,y,z)に対する相対論的な運動方程式となる。
[この手順は2章で引用するPlanckの論文p138~139でPlanck自身により説明されています。]
つまりK’系からK系へのローレンツ変換によりK系で真に正しい力学方程式を見つけようというのです。これには少し面倒な計算が必要ですが、プランクはこの計算をやり遂げて真に正しい相対論的力学方程式を見つけます。それが第2章で説明するものです。
プランクのやり方を理解するには、一般的なローレンツ変換の知識が必要ですので、次節で補足します。
(2)一般的なローレンツ変換
アインシュタインの1905年論文ではK系(x,y,z,t)に対して、K’系(k系)(x’,y’z’,t’)はx’軸、y’軸、z’軸をそれぞれx軸、y軸、z軸に平行に保ったまま、x軸の正方向に速度vで移動するとしていました。この両座標系間を結ぶローレンツ変換はかなり特殊な変換なので“特殊ローレンツ変換”と呼びましたが、ほとんどの現象の相対論的な解析に充分有効で、多くの有益な予言を生み出した。
所で、前節(1)でプランクが考えた二つの座標系K’系とK系間のローレンツ変換はどのようなものになるでしょうか。その答えは、1905年論文のSommerfeldによる再編集版(1913年)にアインシュタインが追記した事柄の中にあります。すなわち
、『(光速不変の原理から言える)K系で見た光の球面波とk系で見た光の球面波の同等性から(t,x,y,z)と(t’,x’,y’,z’)の間に成り立つローレンツ変換公式を導くことができる』
です。このことは別稿2.(5)の最後の段落でも注意しました。
つまり“一般のローレンツ変換”とは一つの座標K系(x,y,z,t)に対して、任意の方向に一定速度で動いている座標K’系(x’,y’、z’,t’)を考えたとき
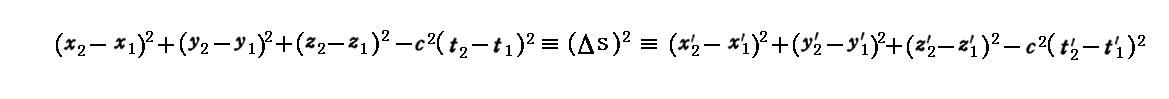
を満足する斉次線形変換の事です。そのときx’軸、y’軸、z’軸はx軸、y軸、z軸に平行である必要はなくて任意の方向を向いていて良い。
もっと簡単に言えば、時刻t=0においてK系の原点とK’系の原点が一致しているとし、K’系の時間をK系での時刻t=0から同時に測り始めるとしたとき、t=t’=0に二つの座標系の原点を出発した光の球面波がK系に於いてもK’系に於いても同じ速度cでひろがっていく様に見える様にする座標変換のことです。すなわち
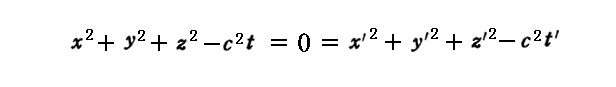
を常に満足する(x,y,z,t)→(x’,y’z’,t’)への変換形式です。
[補足説明1]
一般の座標変換には、[x軸の方向へ走る座標系への変換]はもちろん、時間的に回転角度が変化するのではない[x軸まわりの一定角度の回転]、[y軸まわりの一定角度の回転]、[z軸まわりの一定角度の回転]等を含めて、三次元座標の直交関係を保ったままの[原点のまわりの任意の一定角度三次元回転]、等々・・・も全て含まれます。それらは全てそれぞれの操作で群を成します。もちろんそれらの群を合わせたものも一つの群を成します。
そのとき、一定角度の回転操作には時間的変化は含まれていませんので、ローレンツ変換ではあるが、単なる三次元の座標回転変換となる。
2.Planckの1906年3月論文
相対論的に正しい“力学方程式”を最初に導いたプランクの論文(1906年3月)を紹介する。
原論文は、下記URLにて閲覧可。これを用いれば自動翻訳サイトの利用可。
http://wikilivres.ca/wiki/Das_Prinzip_der_Relativit%C3%A4t_und_die_Grundgleichungen_der_Mechanik
以下の訳文は文献1.より引用した。左端に記入の数字は原論文のページ数です。




上記、脚注2)のEinsteinの原論文はこちらです。




下記の青線四角囲み部分が、Planckが用いた手順の説明です。


[補足説明1]
上記の青実線四角で囲った所が1.(1)で述べたことがらです。原論文は電場、磁場の表現にドイツ文字(フラクトゥーア)を用いているが、現代の表記に書き換えて説明する。
(4)式と(5)式はそれぞれ
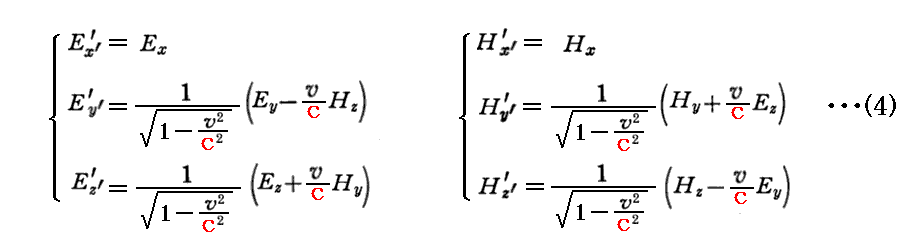
と
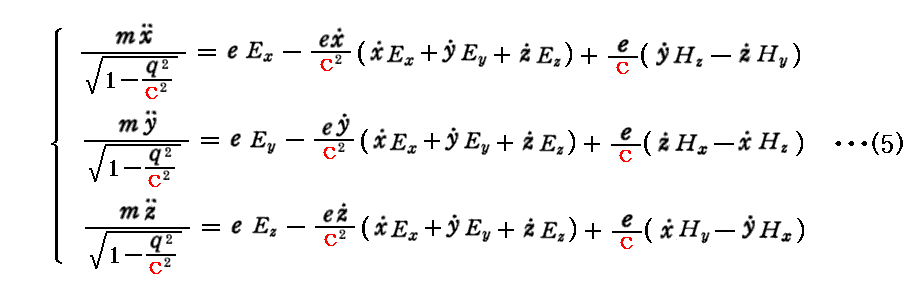
となる。
[補足説明2]
上記(5)式は以下の手順で求まる(Planckにとっては“初等的な計算”かもしれないが、私はこの式変形を見つけるのにかなり手間取りました)。
1.(1)“Planckの考察”で述べたK’系(x’,y’,z’,t’)、K”系(x”,y”,z”,t”)とK系(x,y,z,t)を考える。そこでの考察のように、K’系(x’,y’,z’,t’)に於いて最初質点(電荷e)は静止の状態から出発する。そのとき電場(Ex’,Ey’,Ez’)のみが存在するとしているので、その座標系における運動方程式はニュートンの古典的な形
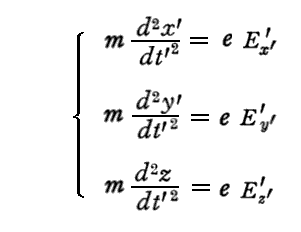
が使える。
これをローレンツ変換式と、電磁場の共変変換式
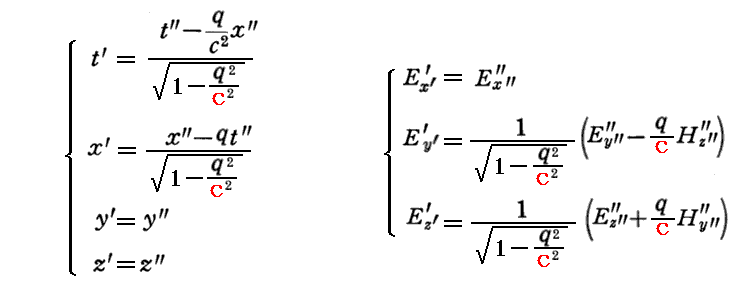
によってK”系(x”,y”,z”,t”)の運動方程式に変換すると
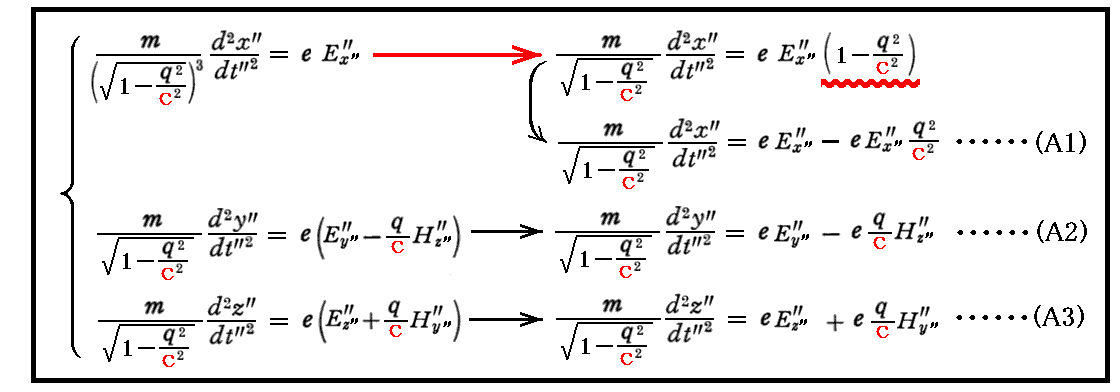
となる。ここまでの作業は別稿3.(5)で説明したアインシュタインの手順とまったく同じですからそこを復習して下さい。
次に、上記の(A1)~(A3)の運動方程式をK系(x,y,z,t)の運動方程式に変換する。このとき、時間に関してはt”=tとなることに注意すれば、K”系からK系への変換は単なる空間座標の回転となる。
ここで、x軸の(x”,y”,z”)軸に対する“方向余弦ベクトル”を(ax,bx,cx)、y軸の(x”,y”,z”)軸に対する“方向余弦ベクトル”を(ay,by,cy)、z軸の(x”,y”,z”)軸に対する“方向余弦ベクトル”を(az,bz,cz)とすると、この座標変換は以下で示す線形変換で表す事ができる。
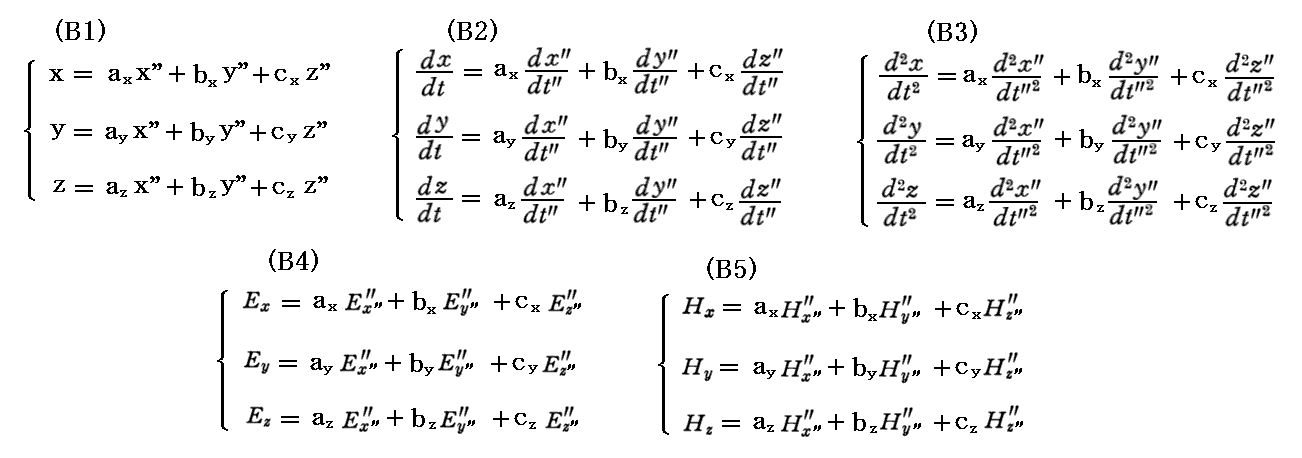
が成り立つ。
また、逆変換に関しても同じ“方向余弦ベクトル”の成分が使えて
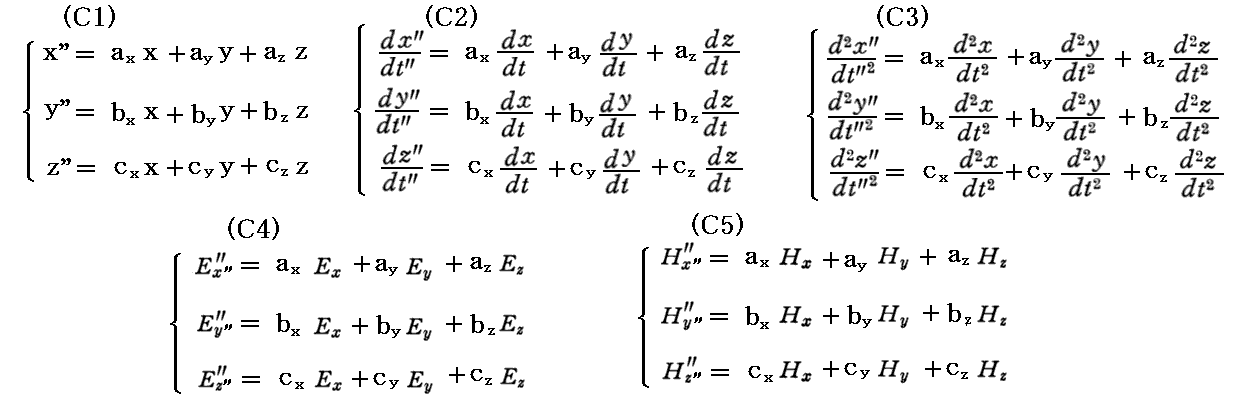
となる。
このとき、“方向余弦ベクトル”の成分に関して
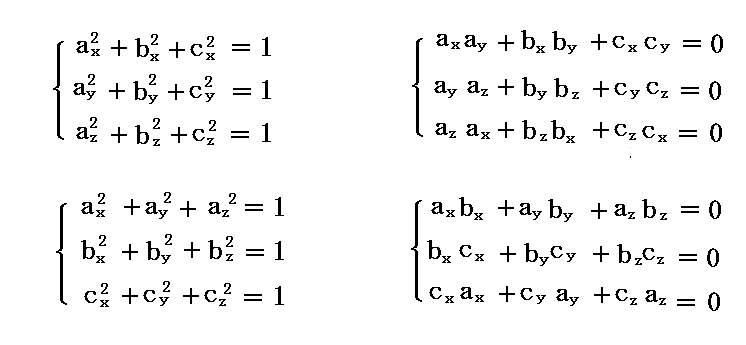
が成り立つ。このあたりは別稿「特殊ローレンツ変換から一般ローレンツ変換へ」を参照されたし。
また、速度ベクトルqの定義から明らかなように、上記の方向余弦ベクトルの中でx”軸の(x,y,z)軸に対する“方向余弦ベクトル”(ax,ay,az)は
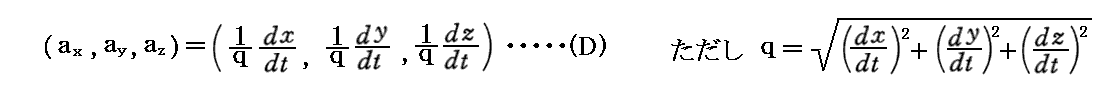
と表される。そのためEx”成分は
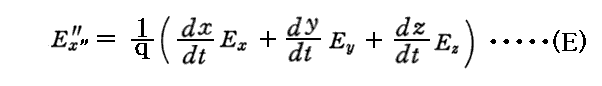
と表される。
さらに、“方向余弦ベクトル”(ax,ay,az)、(bx,by,bz)、(cx,cy,cz)が互いに直交しており、その大きさが1であることと、ベクトルの外積(ベクトル積)の定義より
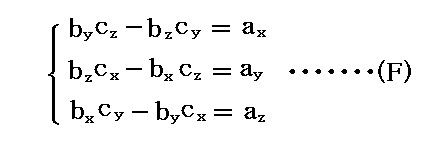
が成り立つ。“ベクトル積”については別稿を復習されたし。
ここで、先に求めた(A1)~(A3)式に対して以下の手順を実行すると(5)式が得られる。
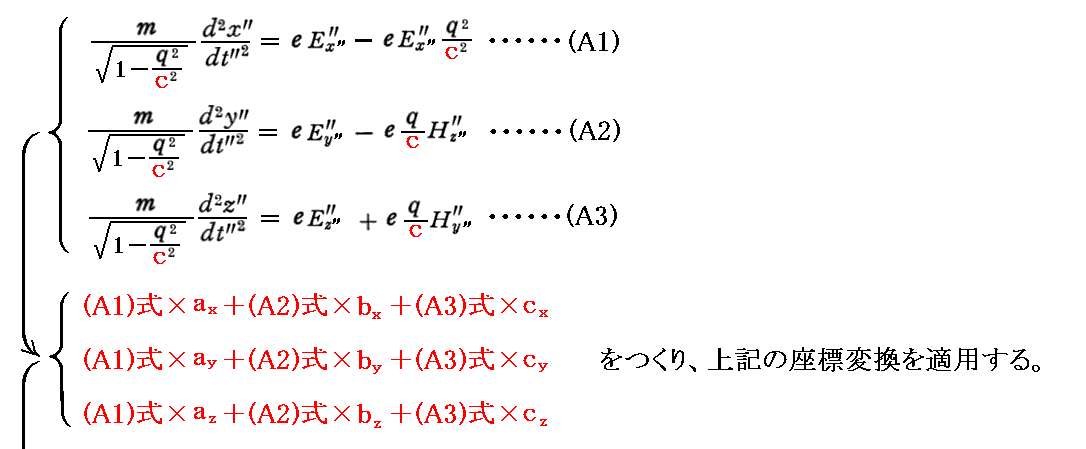
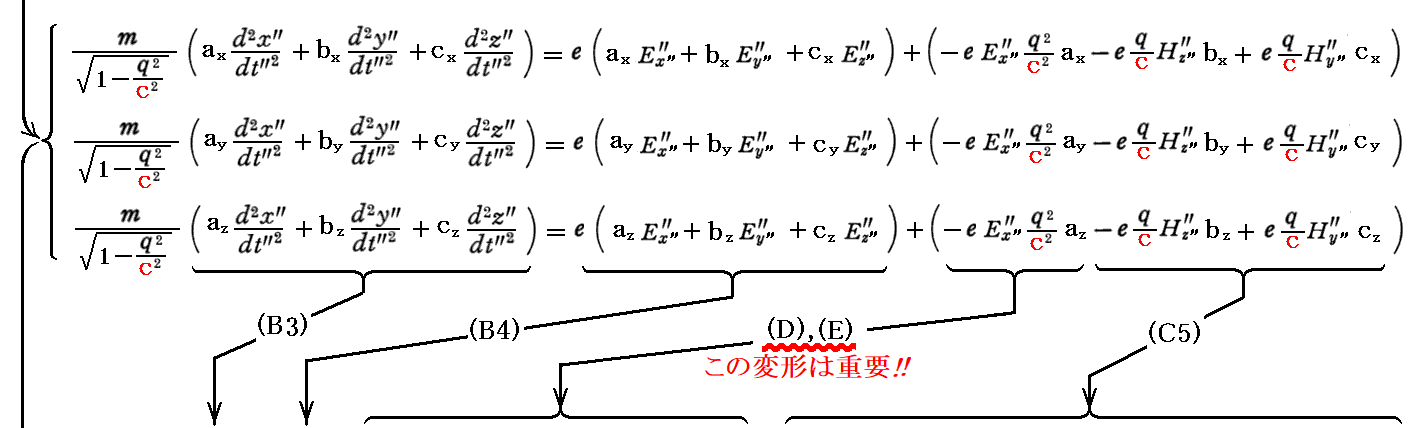
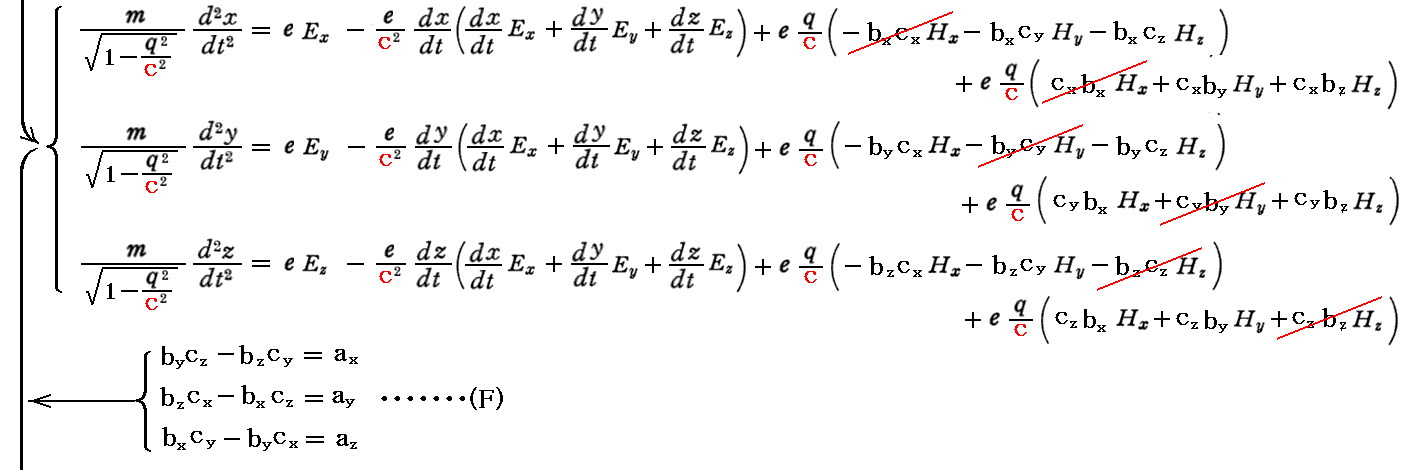

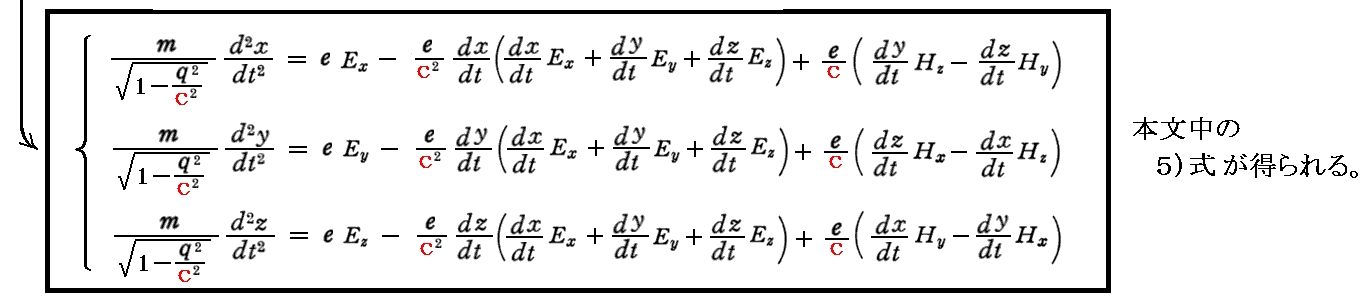



[補足説明3]
上記(6)式は、以下の手順で求まる。
まず、本文中に出てくる関係式は
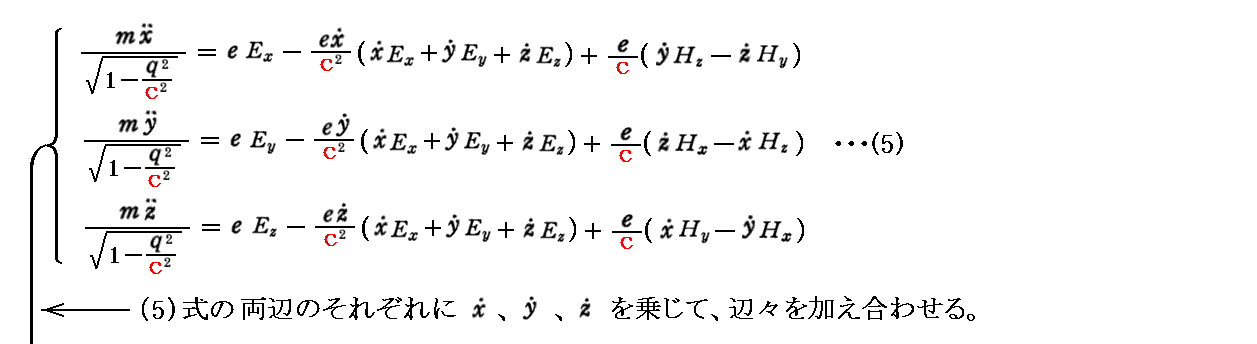

と求まる。この関係式を(5)式に代入して




これが、別稿「アインシュタインの特殊相対性理論(1905年)3.(5)[補足説明4]で説明した式です。
[補足説明4]
ここで定めた力の定義式はもともとニュートンに由来する。そのことに関しては別稿「楕円軌道の発見と万有引力の法則(「プリンキピア」の説明)」§1、§2をご覧ください。
そのとき、古典論では質量は時間的に変化しませんので時間微分の外に出せて、(2)式
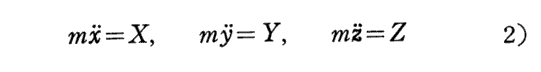
の様な表現を運動方程式(力の定義)としてきた。そして、別稿「運動の法則」3.で説明したように、この式は力を定義するものであると同時に質量(正確には慣性質量)という量を定義するものと見なせた。
しかし、相対性理論が明らかにしたように、可秤質量を観測する座標系によって“質量”という属性も変化するものと考えなければならい。そのため、力の定義としては、プランクが指摘したようにニュートンの最初の定義“運動量の時間的変化が力に比例する”に帰るべきです。そして、“運動量は慣性質量と速度の積である”とすれば、慣性質量がその運動方向によって異なる非対称的な不条理も無くなる。この形が相対論的に適切な形でしょう。
このように考えれば別稿「アインシュタインの特殊相対性理論(1905年)」3.(5)[補足説明4]で説明した様に
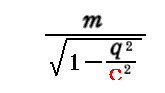
が“慣性質量”であると考えねばならない。


上式の活力Lが今日のハミルトニアン(エネルギー)Hでありmが静止質量m0の事であることに注意すれば、Planckは相対論的運動方程式から“Einsteinの公式E=mc2”をここで導いていることが解るであろう。3.(2)4.[補足説明7]参照

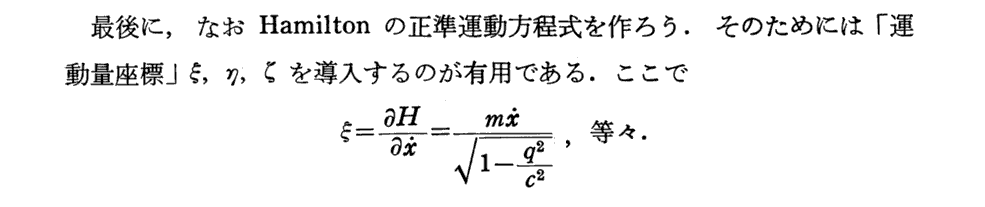


[補足説明5]
プランクは、今日の“ラグランジュ関数”Lを“運動ポテンシャル”Hと呼び、“ハミルトン関数”Hを“活力”Lと呼んでいる。
混乱しないように、現在の呼び方と表記“L”と“H”に書き直す。また、運動量座標(ξ,η,ζ)を今日的な表現の(px,py,pz)にして、ξ2+η2+ζ2=ρ2をpx2+py2+pz2=p2に置きかえる。
さらに、力(X,Y,Z)を表すポテンシャル関数U(x,y,z)が存在するとするとして、X=-∂U/∂x,Y=-∂U/∂y,Y=-∂U/∂yとする。
そうするとプランクの説明は[補足説明6]の様になる。
[補足説明6]
[補足説明3]で求めた“相対論的運動方程式”を“Lagrangeの運動方程式“
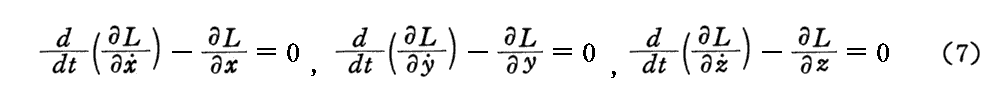
と比較すれば、“ラグランジュ関数”Lは
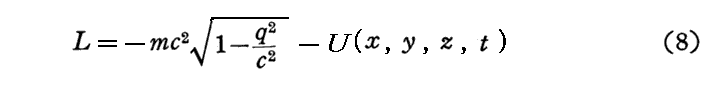
でなければならない事が解る。
実際、(8)式を(7)式に代入すると
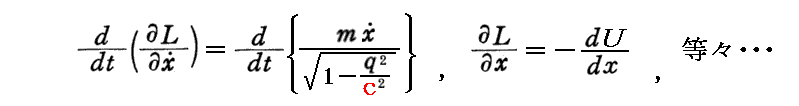
だから、確かに相対論的運動方程式
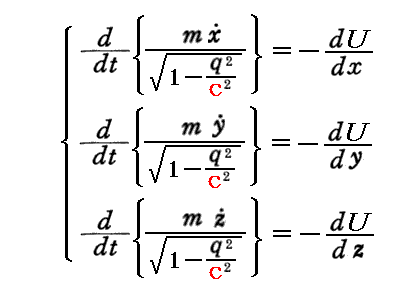
が得られる。
質点に対する“ハミルトン関数(エネルギー)”Hは
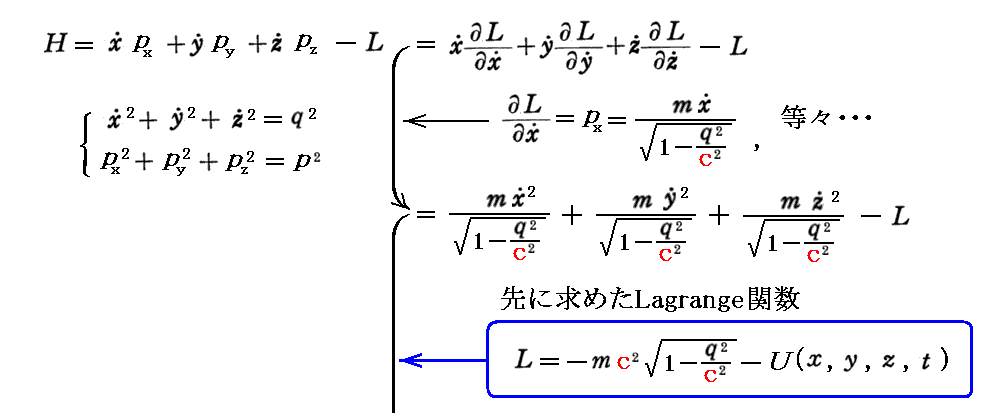
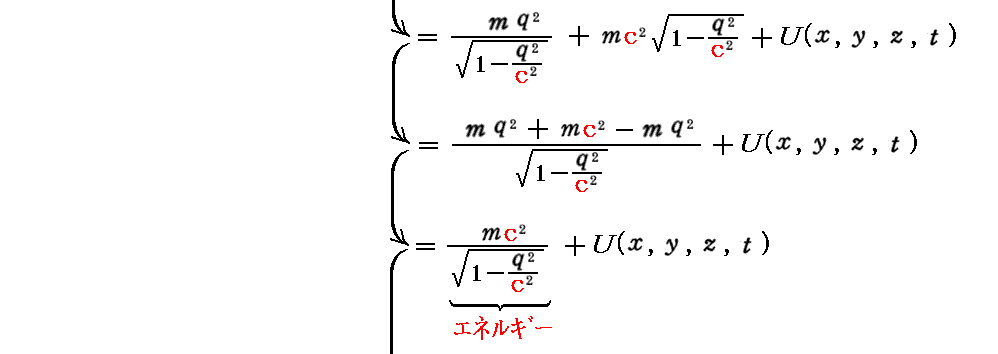
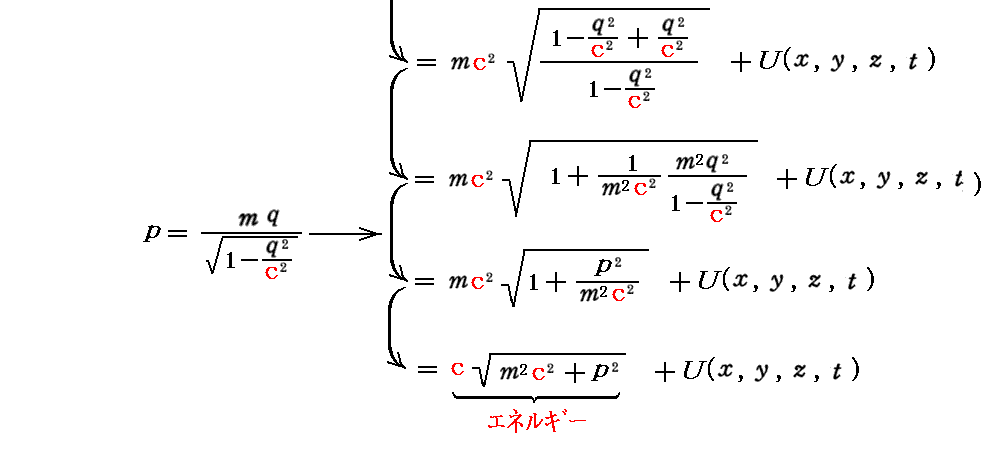
となり、Hがエネルギーを表すことが解る。
“ハミルトン関数”Hについては、別稿「ルジャンドル変換とは何か」5.をご覧下さい。
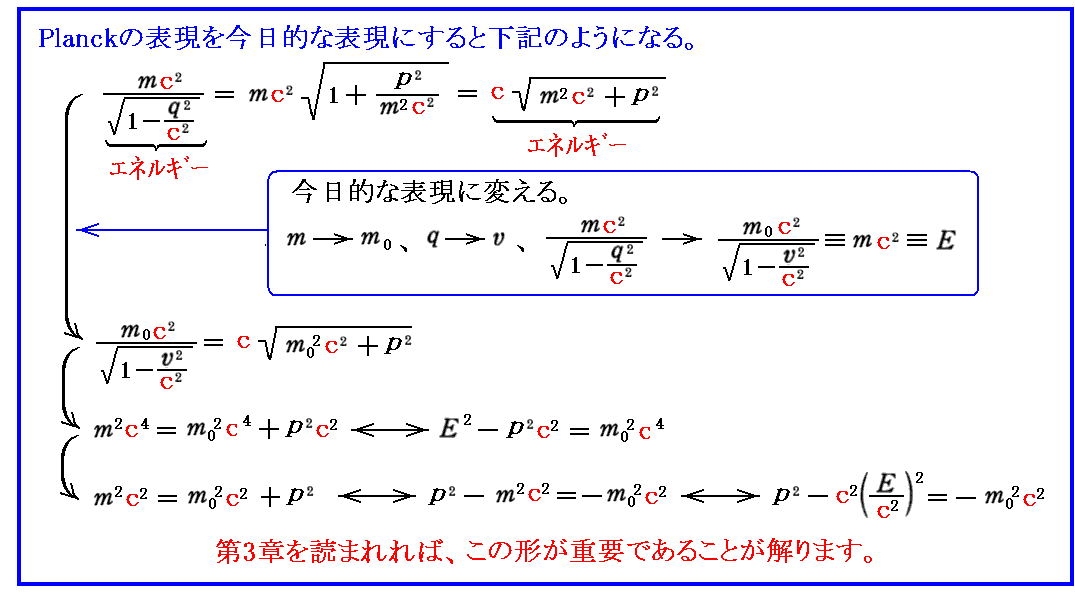
ここで
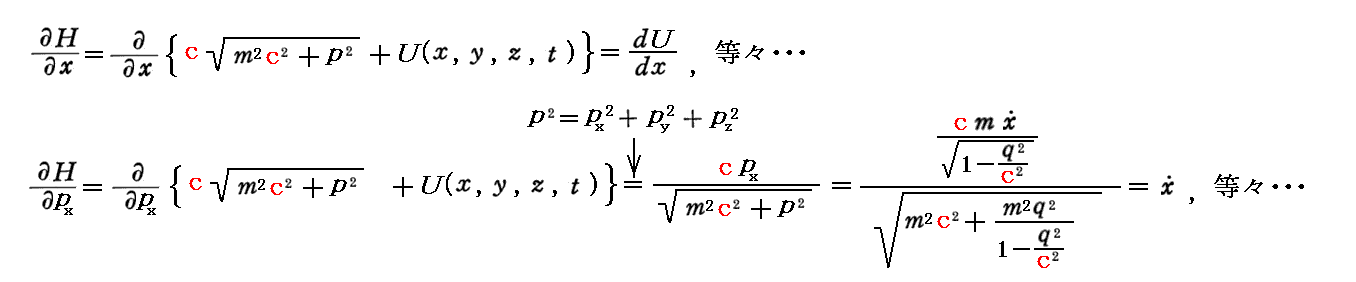
だから、“ハミルトン関数”Hが“Hamiltonの正準運動方程式”
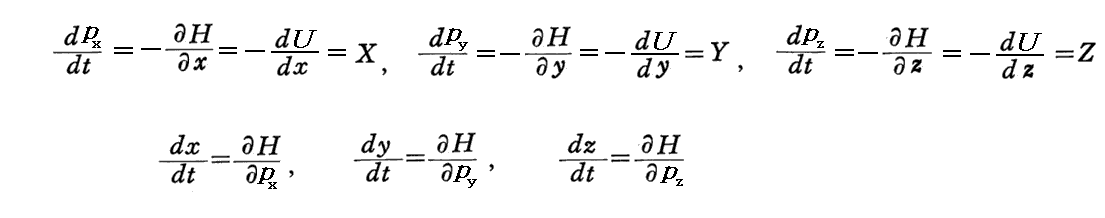
を満足することは明らかであろう。
[補足説明6-2]


ランダウ、リフシュツ「場の古典論」§87はこちら
[補足説明6-3]
電磁場中の荷電粒子の運動に対する相対論的な Lagrangian と Hamiltonian の導出は別稿「電磁場中の荷電粒子の運動(Lagranian、Hamiltonian)」をご覧下さい。
[補足説明7]
ここの説明だけでは、ラグランジアンLとラグランジュの運動方程式、およびハミルトニアンHとハミルトンの正準運動方程式が何を意味するのかは解りません。
この事について、最近の本では例えば村上雅人著「なるほど解析力学」海鳴社(2016年刊)などをご覧下さい。解析力学とは何かを理解するには、この本のように簡単な例を沢山当たってみるに限ります。とても解りやすく説明されています。
ただし、この本はラグランジュの未定乗数法とルジャンドル変換の説明が少し不足していますので、これらについては当HPの該当稿を合わせてお読み下さい。
解析力学でハミルトン-ヤコビの偏微分方程式の意味など解りにくいところですが、この本をお読みの後で、ゴールドシュタイン著「古典力学」吉岡書店(1959年刊)などに進まれるとよく理解できます。
[補足説明8]
ここのPlanckの証明は、Einsteinが1905年6月論文§10で行った証明を改良したものです。
Einsteinの考え方は、
1.[任意の速度で動いている電荷に対してローレンツの力の表現式が常に成り立つ]と仮定し、有る特殊なk系(その系では電場だけが存在し、電荷は最初その原点に静止している)で力学方程式を立てる。
2.次に、k系に対して速度-vで動いているK系から見たものに方程式の両辺をローレンツ変換する。
3.ローレンツ力を生み出す電場と磁場のローレンツ変換共変の変換式はすでに解っていますから、K系における運動方程式の右辺をローレンツの力の法則を表す形に整える。
4.右辺をその様に変形すると、それに伴って運動方程式の左辺の形が必然的に決まる。
というものでした。
つまり、EinsteinとPlanckは電気力学の助けを借りて力学の運動方程式形を導いたのです。これは、有る意味で独創的なやり方でした。
ところが、次章3.でのべるLewisとTolmanの方法は電気力学の知識を全く借用しません。二つの物体の衝突現象をk系とK系で見たとき、その両系に於いて[運動量保存則]や[エネルギー(質量)保存則]がそれぞれに成り立っていなければならないという事実だけを用いて、ローレンツ変換に対して不変な運動方程式形を導くものです。
私どもがEinsteinやPlanckの証明を読む時、ローレンツの力の法則が背後霊のようにつきまとい、何となくしっくりこない所があるのですが、LewisとTolmanの証明は電気力学の助けを借りていないことで画期的です。これは、EinsteinやPlanckの証明に数年遅れますが、重要で意義深い証明です。
この当たりはPauliが「相対性理論」§37、§38で解説していますのでどうぞご覧下さい。
[2018年5月追記]
上記の様に“ローレンツの力の法則”が相対論的な運動方程式に現れることの意味とアインシュタインの深謀遠慮に付いては別稿「運動方程式のローレンツ変換不変性」をご覧下さい。
3.相対論的力学
相対論的に正しい力学方程式は、プランクに続いてN.LewisとC.Tolmanの論文「相対性原理と非Newton力学」(1909年5月)でも示された。このp517~518に書かれている証明は、今日の多くの教科書で説明されている、“運動量保存の法則”から“相対論的運動方程式”を導くものです。LeweisとTolmanの論文は別稿で引用しておりますので参照されて下さい。
ここでは、同じやり方ですがBornの文献2.第Ⅵ章§7~§9の説明を紹介します。ただし、少し改変しています。これは教育的でとても解りやすい(Born文献2.第Ⅵ章の全体はこちらで引用)。
また、本稿には引用していませんが、文献3.バークレー物理学コース「力学」第12章も同様な方法で説明されており、教育的ですのでご覧下さい。
(1)相対論的な座標変換則と速度変換則
後に繰り返し使う“ローレンツ変換”と“相対論的速度合成則”を復習する。
1.ローレンツ変換
互いに他に対して等速度運動をする二つの座標系S、S’を考える。
S’系はS系のx軸に沿って、その正方向に速度vで動いているとする。そのときS’系のx’軸、y’軸、z’軸はS系のx軸、y軸、z軸と平行を保ったまま移動するとする。
またS系に固定された時計で計った時間をt、S’系に固定された時計で計った時間をt’とする。
そのとき、S’系のx’軸、y’軸、z’軸に固定された三本の物差し棒とS’系に固定された時計で測った、在る物体(可秤質点)の座標・時刻(x’,y’,z’,t’)と、その“同じ物体”をS系のx軸、y軸、z軸に固定された三本の物差し棒と、S系に固定された時計で測った座標・時刻(x,y,z,t)の間の関係を定めるものがローレンツ変換で以下のようになる。
ここでは、S系座標物差し棒とS’系の座標物差し棒が重なった瞬間から、それぞれの座標系に固定された時計の時間を計測するものとしている。つまり、重なった瞬間をt=t’=0とする。
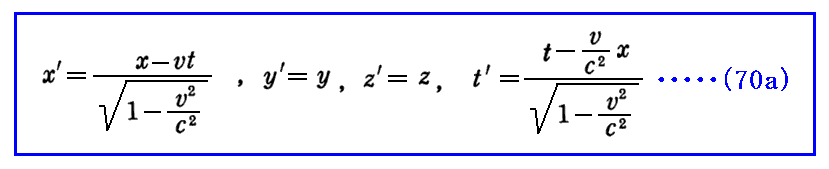
これを逆に解くと
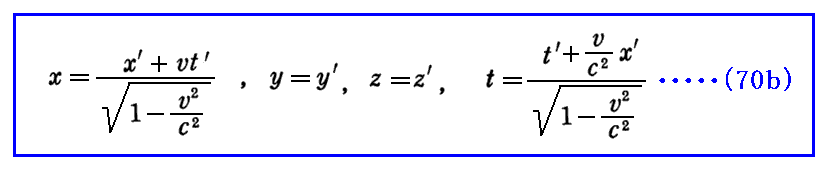
となる。
このとき(70b)は(70a)のvを-vに置きかえて、ダッシュ’のついた文字とついてない文字を入れ替えたものになっていることに注意。
逆変換の導出については別稿「アインシュタインの特殊相対性理論(1905年)」2.(5)[補足説明1]を復習されたし。
これらの公式を覚えるには、別稿Born「相対性理論」第Ⅵ章2.(1)[補足説明]や、2.(3)[補足説明]で説明する、ミンコフスキー時空図を用いた導き方を理解すると良い。
[補足説明1]
上記の変換式は(x,t)と(x’,t’)の変換式の分子が対称的な形になっていませんが、(x,y,z,ct)←→(x’,y’,z’,ct’)とするとローレンツ変換は
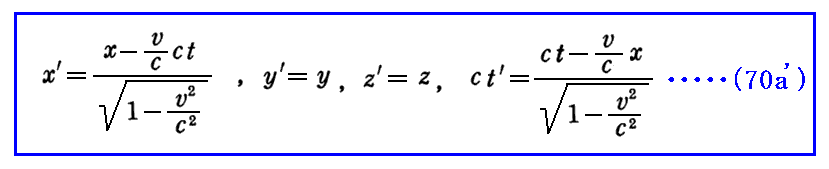
逆変換は
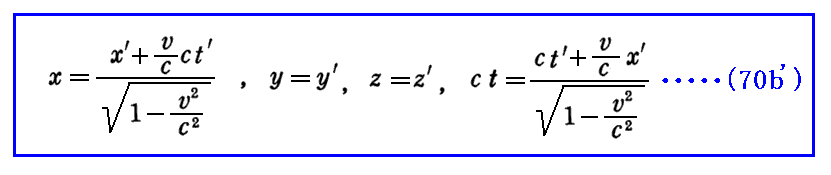
となり、対称的な形になります。
このようにすると、ctの次元は長さの次元となり(x,y,z)と一致します。そのためローレンツ変換の対称性を強調するには、こちらの形の方が見通しが良い。
しかし、“空間”と“時間”は互いに移り変わることはありませんし、本来まったく異なる物理量です。そのためローレンツ変換の物理的意味を説明するときには、空間と時間の違いを残した前記の形の方が便利で解りやすい。
そのため本稿では前述の表現を用いることにします。
2.速度の変換則(相対論的速度合成則)
前節で説明したS’系のx’軸、y’軸、z’軸に固定された三本の物差し棒とS’系に固定された時計の時刻t’で測った、在る物体(可秤質点)の速度を(ux’,uy’,uz’)とし、同じその物体をS系のx軸、y軸、z軸に固定された三本の物差し棒と、S系に固定された時計の時刻tで測った速度を(ux,uy,uz)とする。
そうすると、(ux,uy,uz)と(ux’,uy’,uz’)の間には以下の関係が成り立つ。
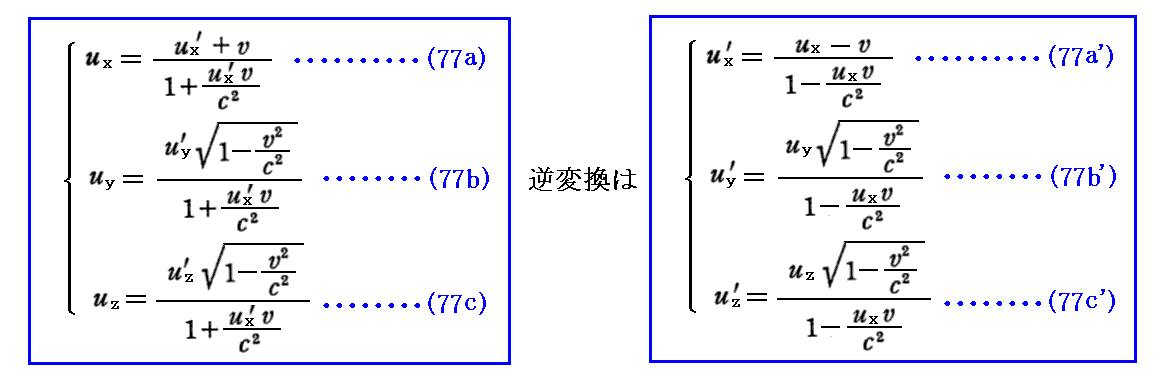
この関係式はローレンツ変換式を用いれば求められる。証明は別稿「アインシュタインの特殊相対性理論(1905年)」2.(7)あるいは2.(8)3.を復習されたし。
これらの公式を覚えるには、ミンコフスキー時空図を用いた導き方(別稿Born「相対性理論」第Ⅵ章6.(2)[補足説明]参照)を理解すると良い。
(2)相対論的力学
以下はBorn文献2.第Ⅵ章§7(p262~273)より引用。Born文献2.第Ⅵ章の全体はこちらで引用。
1.相対論的運動法則探索の指針





[補足説明1]
最後の文節で述べられている“質量は測定を行う人の基準系により、系内における物体の速度に依存する。”は別稿「アインシュタインの公式 E=mc2 の証明」1.の論述から予想される事です。
2.古典的運動量保存則の復習

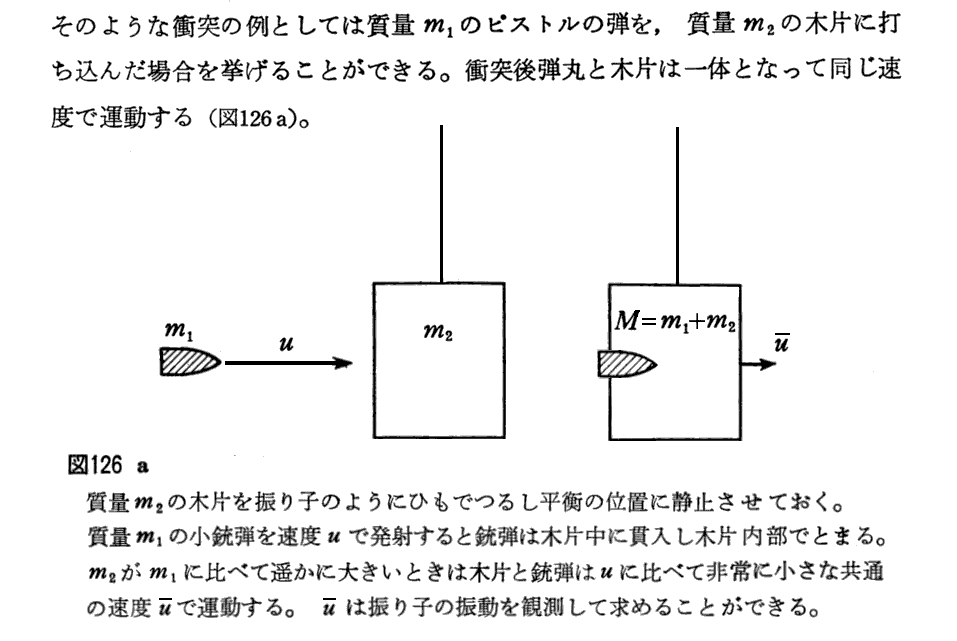


3.相対論的運動量
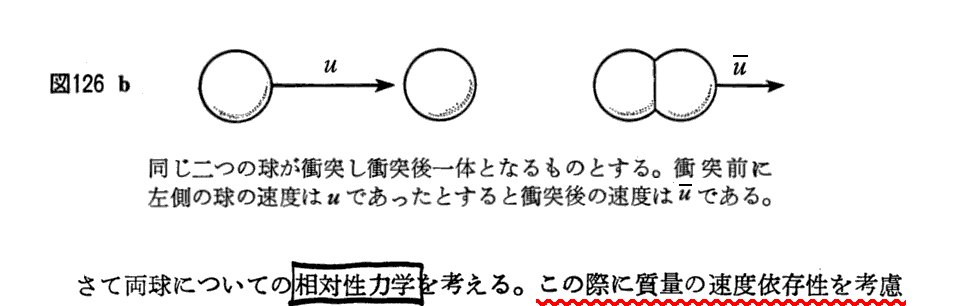

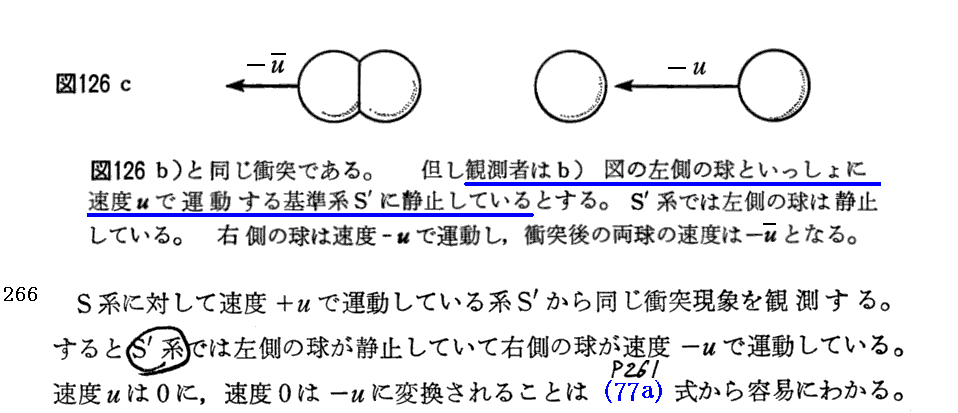
p261の(77a)、(77b)式はこちらを参照。 これらは「アインシュタインの特殊相対性理論」2.(7)と同じです。

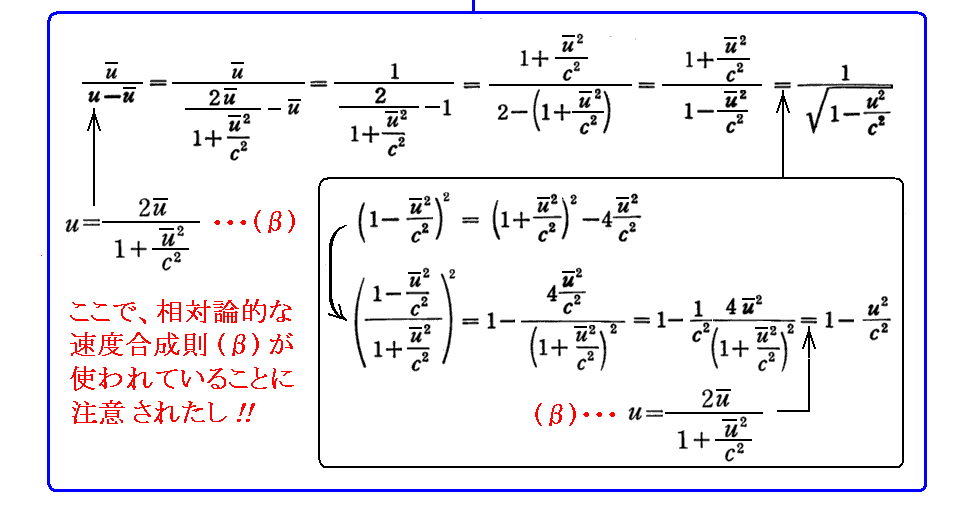
[補足説明2]
(β)式は、相対論的な“運動量保存則”(α)から導かれたものであることに注意されたし。
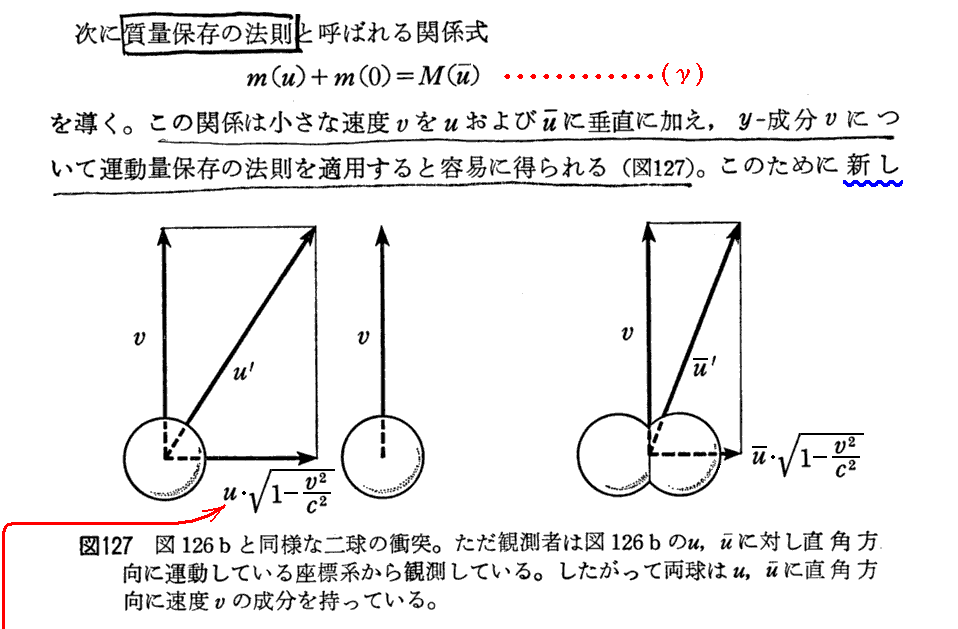

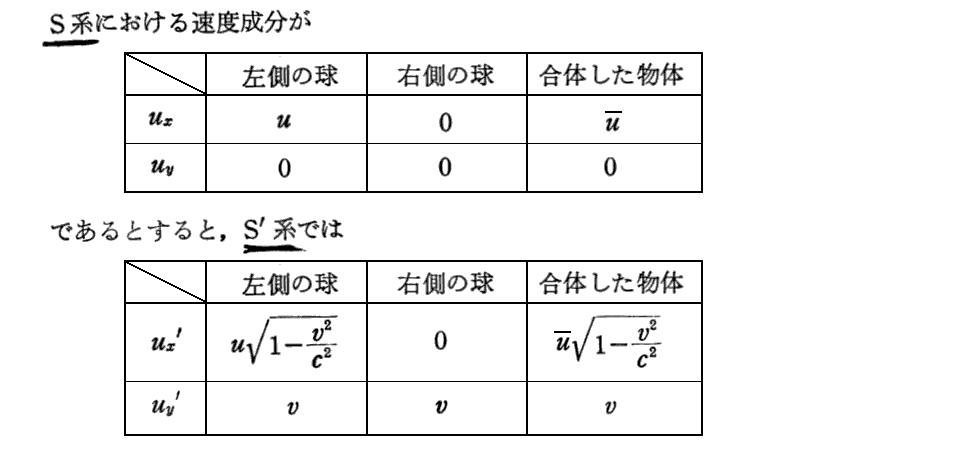
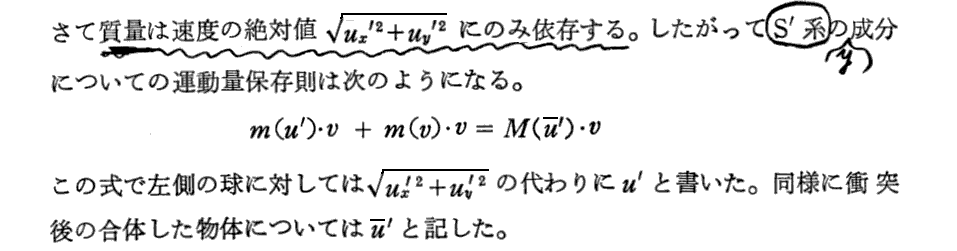

[補足説明3]
この“質量保存則”(δorγ)は、別項「アインシュタインの公式 E=mc2 の証明」で証明したことを考慮すると、“エネルギー保存則”と言っても良いものであることに注意されたし。


[補足説明4]
この“相対論的運動量”(79)式は、“運動量保存則”(α)と“質量保存則”(γorδ)(すなわち“エネルギー保存則”)がローレンツ変換しても、そのまま成り立つとして導かれた。
実際のところこのやり方で、相対論的な運動方程式を導いたのは1909年のN.LewisとC.Tolmanの論文においてです。
以上の説明を参考にされると、N.LewisとC.Tolmanの論文のp517~518に書かれている証明が理解できると思います。
4.相対論的運動方程式

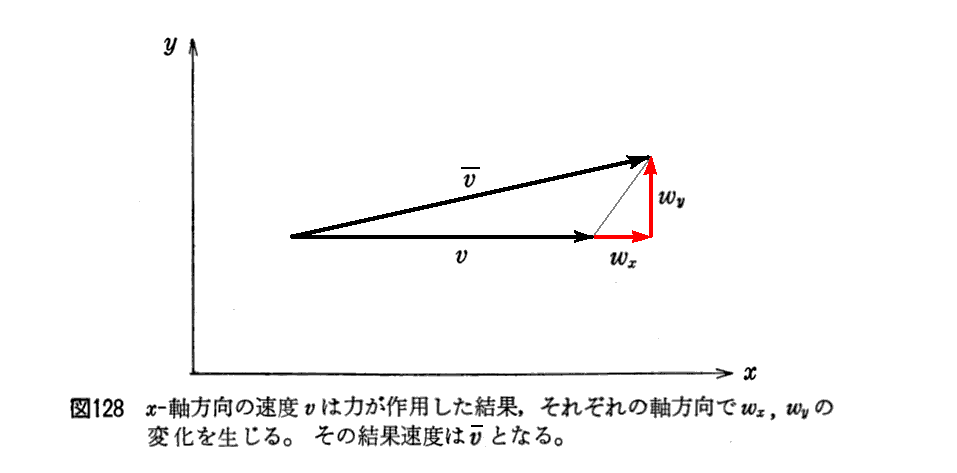
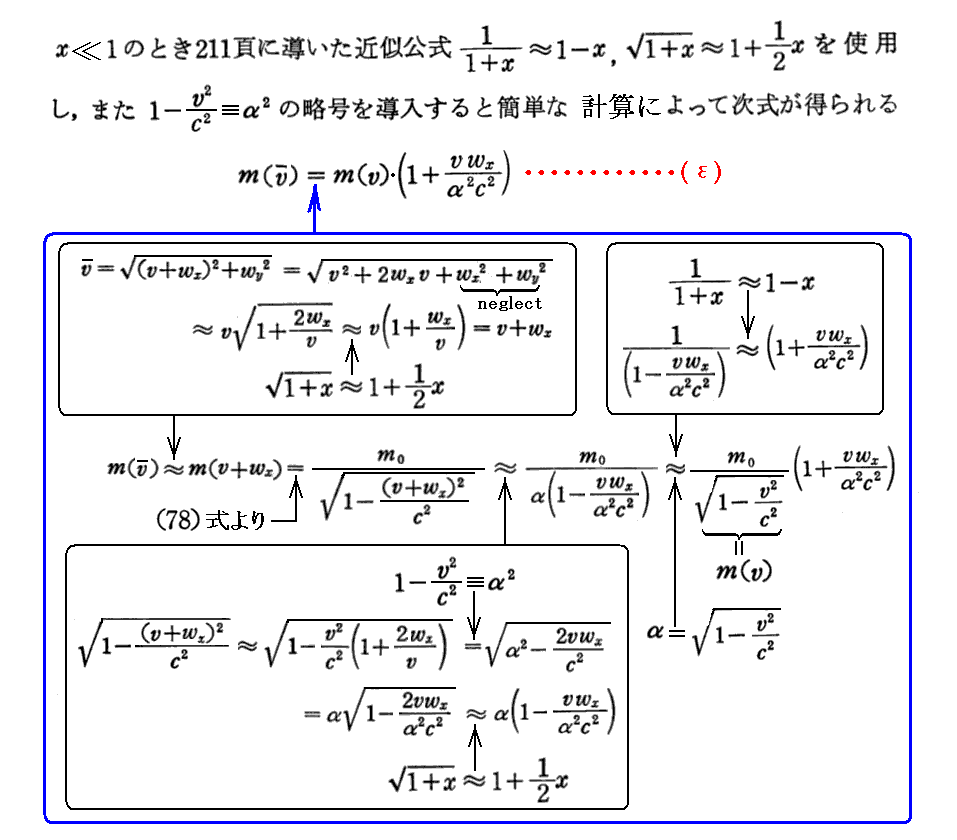
[補足説明5]
上記の説明は、前項で求めた(79)式“相対論的運動量”を上記の式“運動量の変化は力積に等しい”に適用すれば、2.“Planckの1906年3月論文”で説明した相対論的に正しい運動方程式

が得られることを言っている。
270


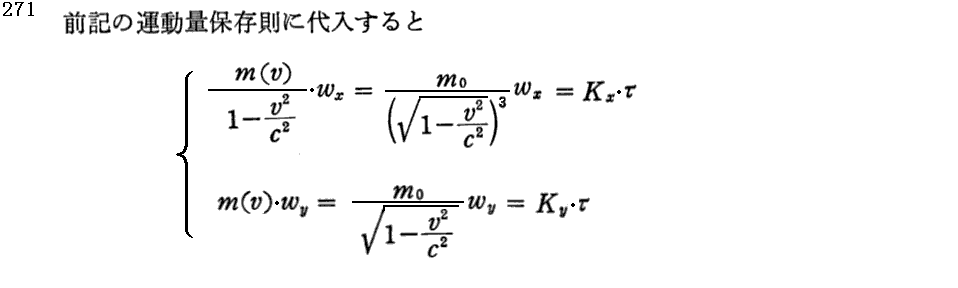


[補足説明6]
この項の後半で(80)式を求めているが、普通この式は、“相対論的な運動方程式”の時間微分を実行して求める。つまり
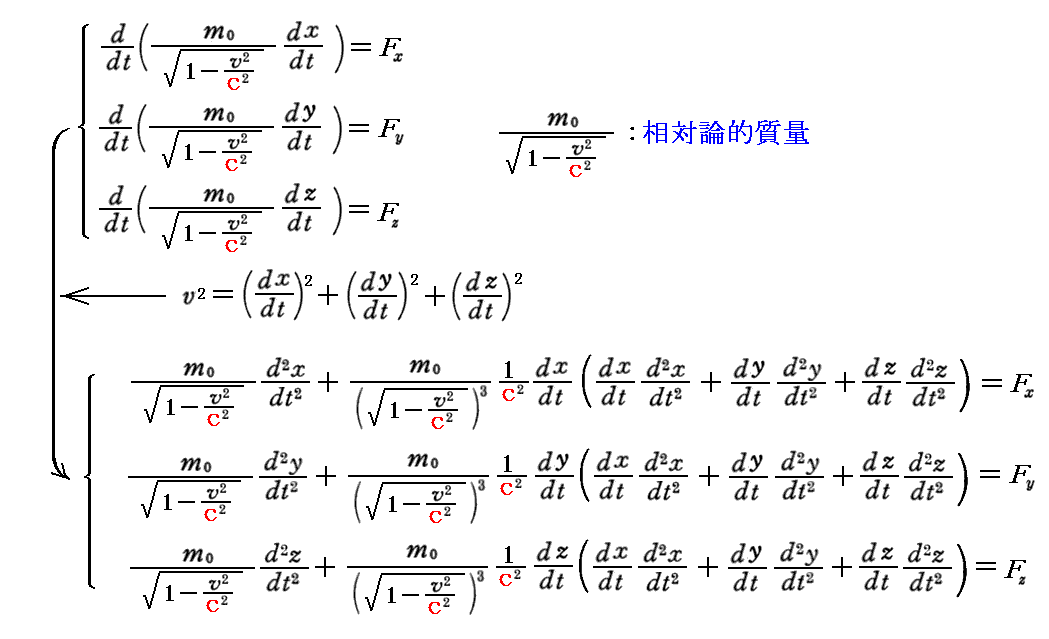
となる。
ここで、x軸を速度vの方向に取ると、vy=dy/dt=0、vz=dz/dt=0、v2=(dx/dt)2 なので、第一式が
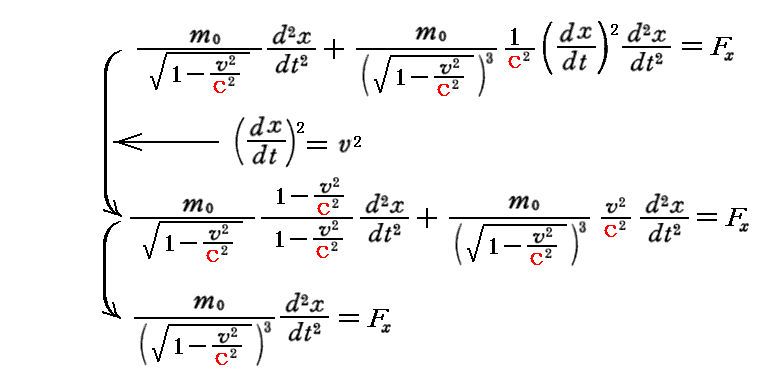
と変形でき、第二式と第三式の左辺第2項はゼロとなるので、上式は

となる。このことは、別稿「アインシュタインの特殊相対性理論(1905年)」3.(5)[補足説明4]ですでに説明した。
ただし、Bornの説明の様に、代数計算によって導くのも教育的です。ここの手順については、上記別稿[補足説明3]で引用した江沢先生の説明も参照されたし。
何度も注意したように、“相対論的な運動方程式”を無理に古典的な形(F=ma)に対応させて比較してもあまり意味はない。しかし、運動方程式を積分して実際の運動の様子を調べる時には、この形は便利です。
[補足説明7]
質点に成される[仕事]は、[力]×[距離]で表される。質点が力(Fx,Fy,Fz)を受けながら微少な距離(dx,dy,dz)だけ動いたときに質点に成される仕事dWを上記の運動方程式を用いて計算してみると

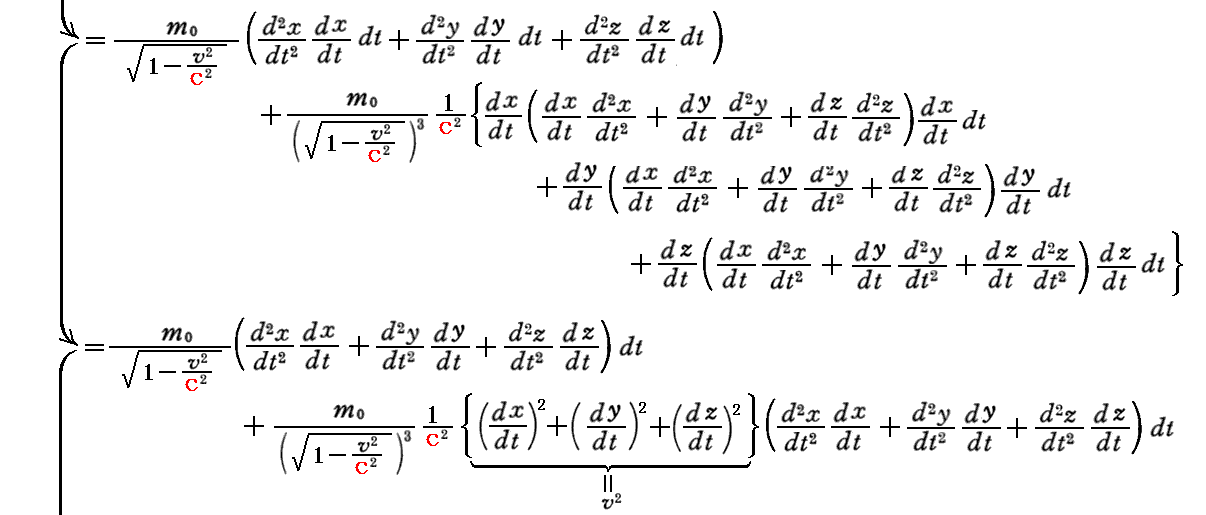
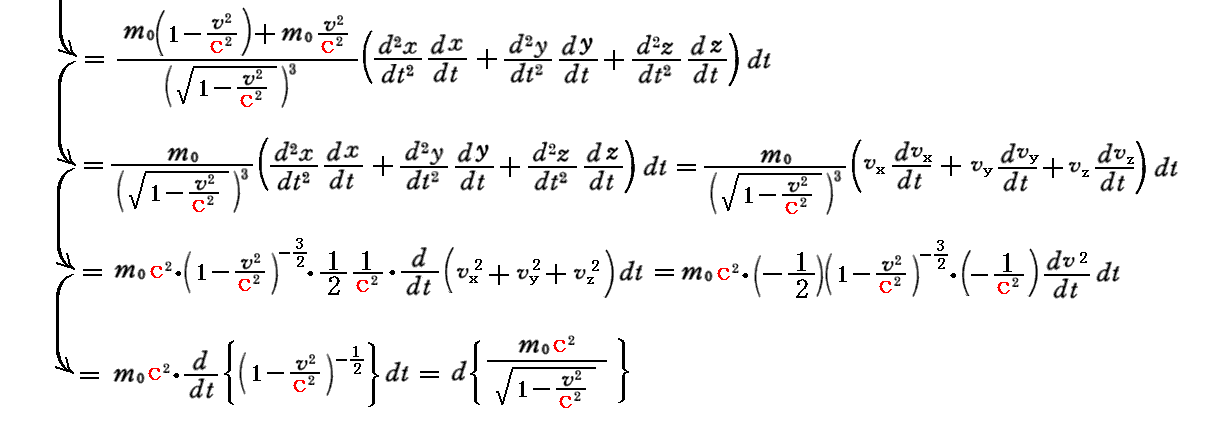
となる。従って
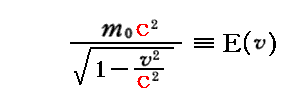
は、質点のエネルギーを意味することが解る。
このことはアインシュタインの1905年6月論文ですでに証明されていることですが、本来の相対論的な運動方程式からもスッキリと導かれる。このとき、1905年9月論文の結論を鑑みて、このエネルギー表現には深い意味が存在することを読み取らねばならない。
補足ですが、“運動方程式”と“エネルギー保存則”との関係については別稿「運動の法則、運動量保存則、エネルギー保存則の関係」をご覧下さい。
5.相対論的質量




文中のアブラハムの理論〔Ⅴ章、§13、207頁、(69)式〕については別稿引用を参照されたし。

(3)エネルギーの慣性
以下はBorn文献2.第Ⅳ章§8(p273~277)より引用。

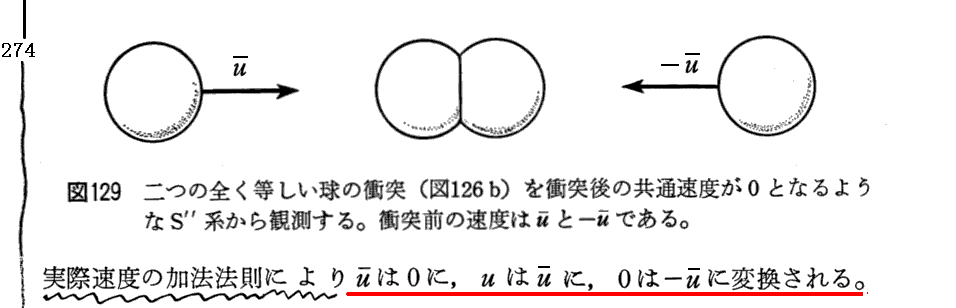
[補足説明1]
上記赤アンダーライン文章の意味することは、前出p266の式(β)を導く手順と同様に考えれば良い。
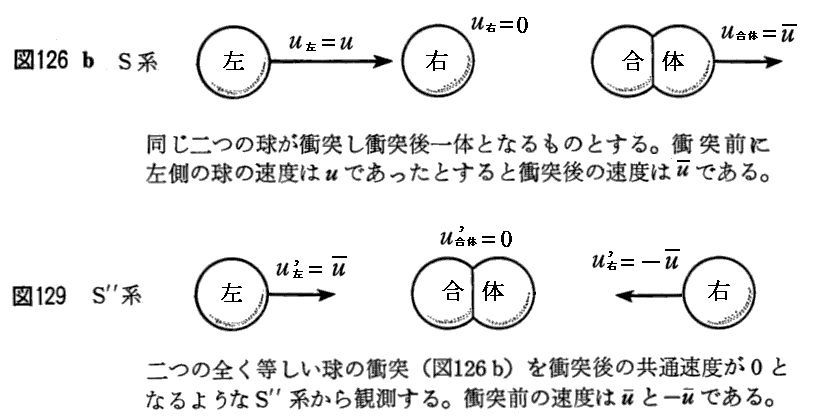
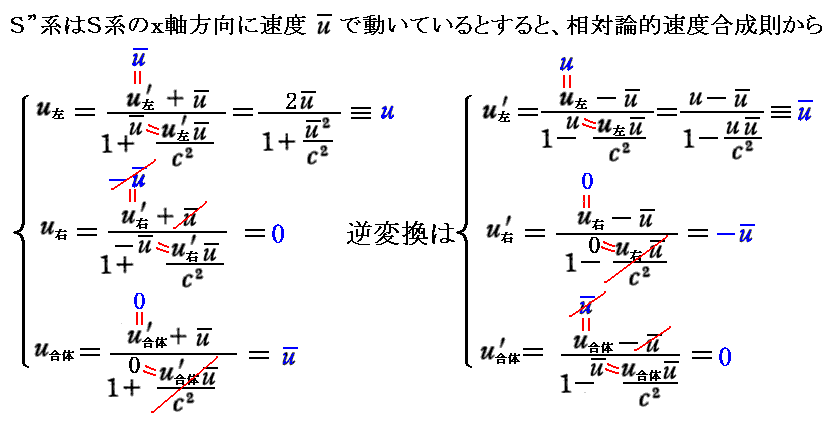
となります。従って
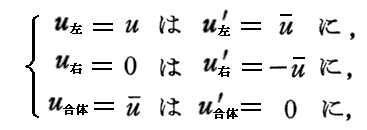
に変換されることが解る。







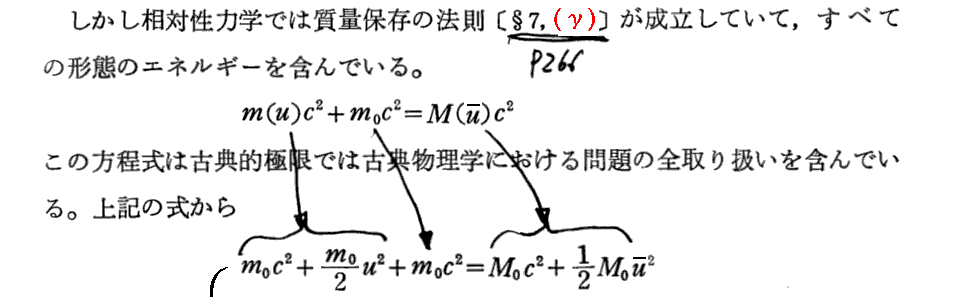
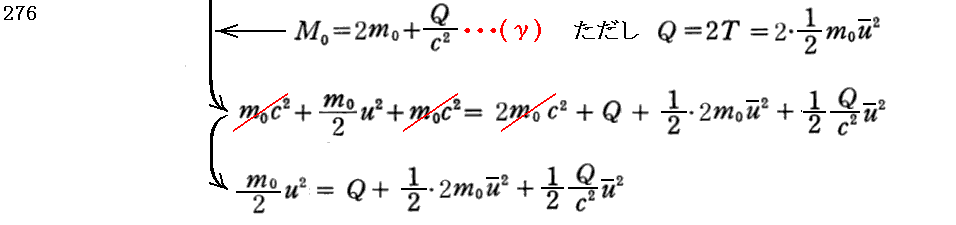

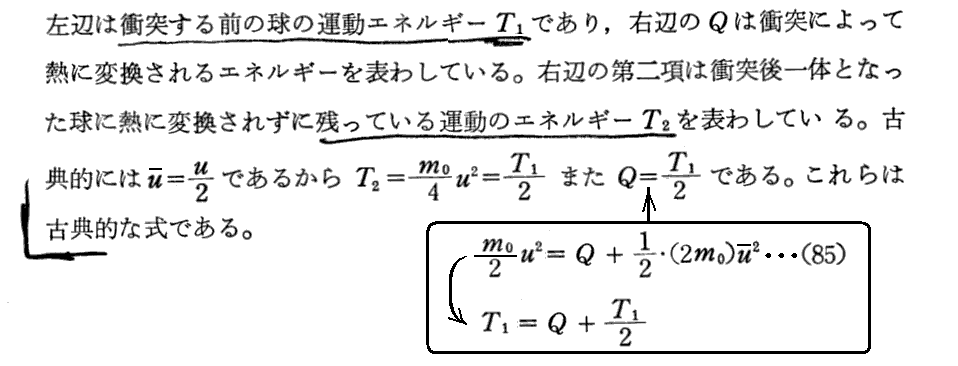

上記p270の(ε)はこちらを参照。
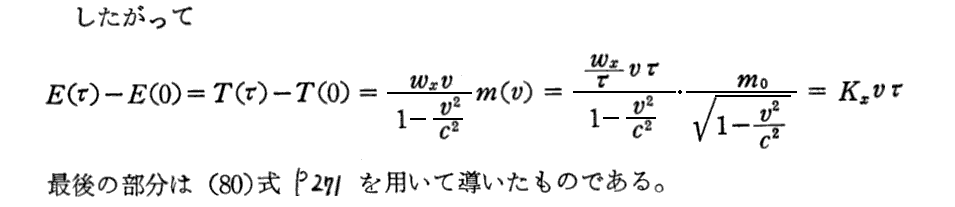
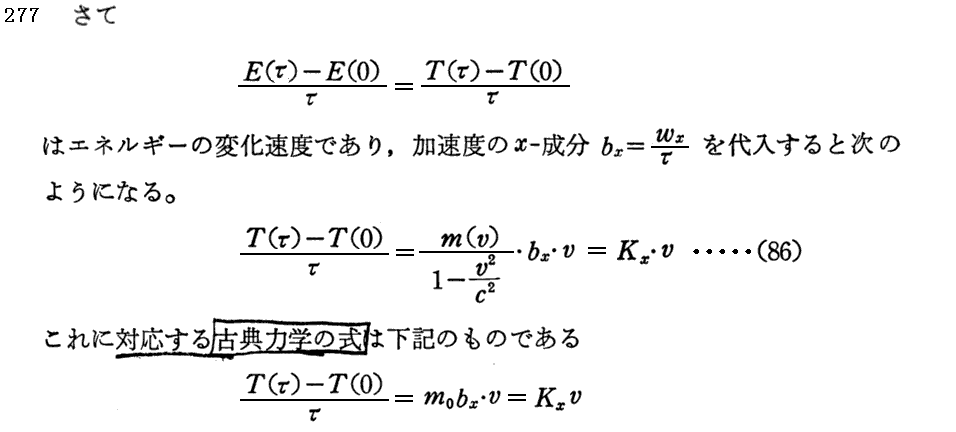


[補足説明2]
Born文献2.における続きのページ(p277~284)は別稿「アインシュタインの公式 E=mc2 の証明」の3.および5.で引用しています。ここではその部分を飛ばして、それに続くp284~を引用します。
(4)質量(エネルギー)と運動量
以下は、 Born文献2.§9.“エネルギーと運動量”(p284~288)より引用。世にある解説書で解りにくいところが、この文献では明快に説明されています。

下記“この章の第3節”は、別稿で引用している第Ⅳ章3.のことです。。

文中の“ローレンツ変換に対してx2-c2t2=Fが不変量となる”は、別稿「アインシュタインの特殊相対性理論(1905年)」で繰り返し証明(2.(4)[補足説明3] or 2.(8)4. or 1917年文献の附記1.)しましたので、そこを復習して下さい。
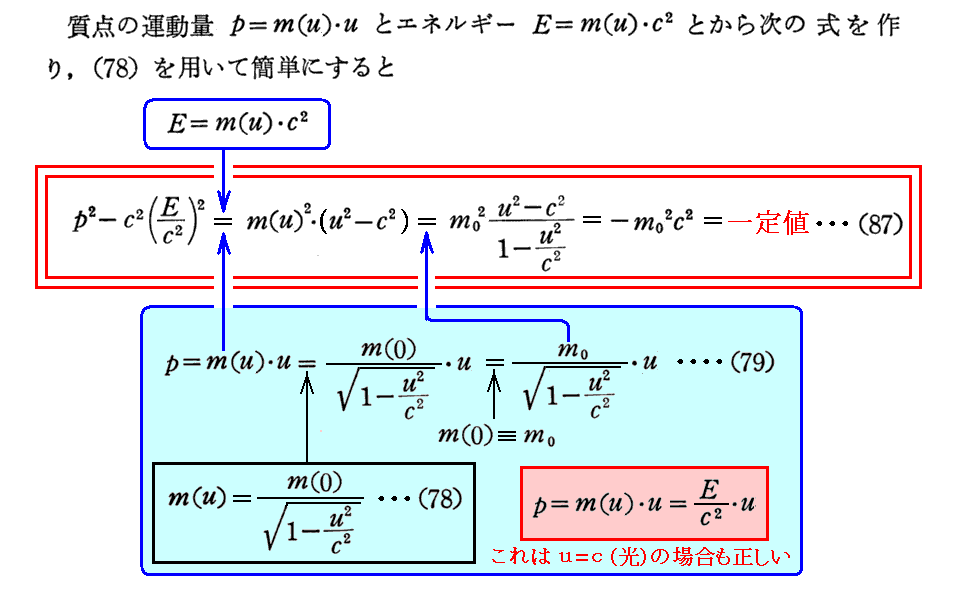
(78),(79)式はこちらで導いている。

[補足説明1]
世にある解説書で、運動量pとエネルギーEが座標xと時間tと同様なローレンツ変換に従うと説明しているものもありますが、正確には運動量pと質量m(v)が座標xと時間tと同様なローレンツ変換に従うです。
エネルギーEは定数c2の違いを気にしなければ質量m(v)と等価ですからその様に言っても良いかもしれませんが、本来時間tに対応するのは質量m(v)です。
あるいは3.(1)1.[補足説明]の形のローレンツ変換を用いると、ctに対応するのはE/cであると言うべきです。この形にすると、E/cは運動量の次元となりpの次元と一致するので、より適切かもしれません。
しかし、、“運動量”と“質量”は互いに移り変わることはありませんし、本来まったく異なる物理量です。その為ここでは、(px,py,pz,E/c)←→(px’,py’,pz’,E’/c)ではなくて、(px,py,pz,E/c2)←→(px’,py’,pz’,E’/c2)の表現を用いることにします。

(77a)式はこちらを参照。
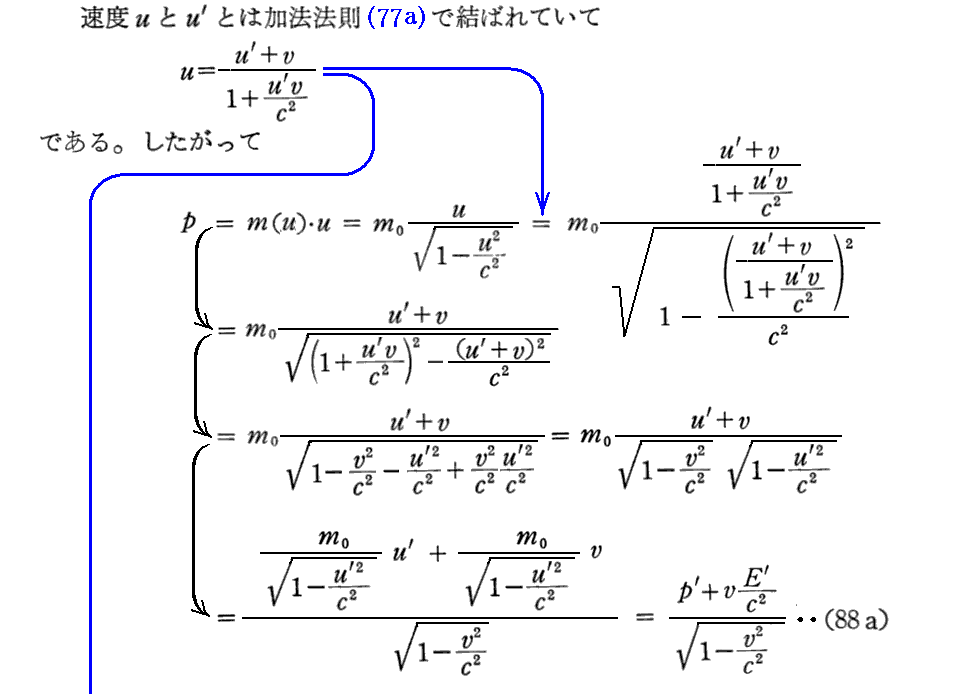
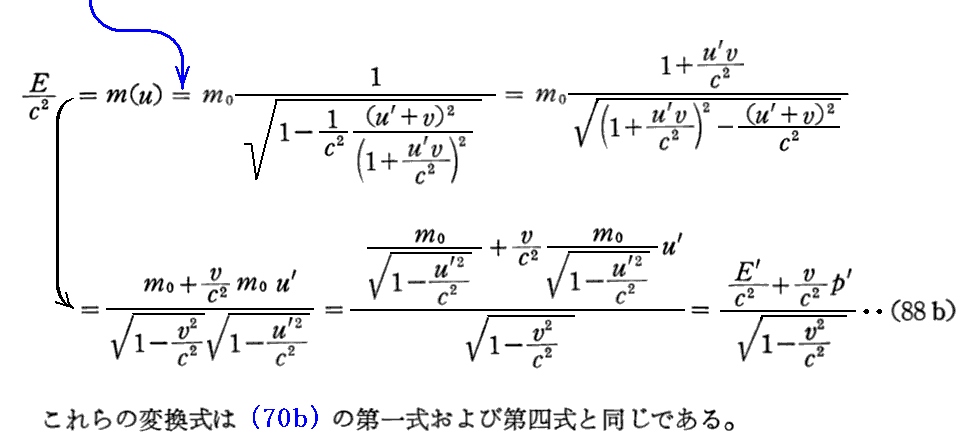
(70b)式はこちらを参照。

[補足説明2]
ここで、uy≠uy’、uz≠uz’なのに py=py’、pz=pz’が成り立つのは不思議に思われるかもしれませんが、m(u)≠m(u’) だから成り立つのです。実際、py=py’が成り立つことを証明しておきます。そのために、三次元表示で証明を最初からやり直します。
3.(1)2.で説明した様に、両座系から見た速度成分に関して
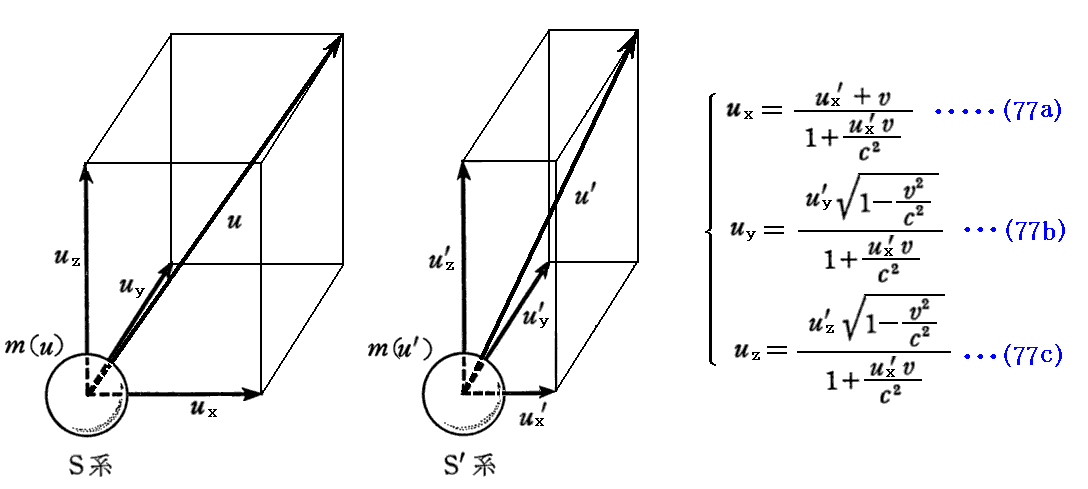
が成り立つので、
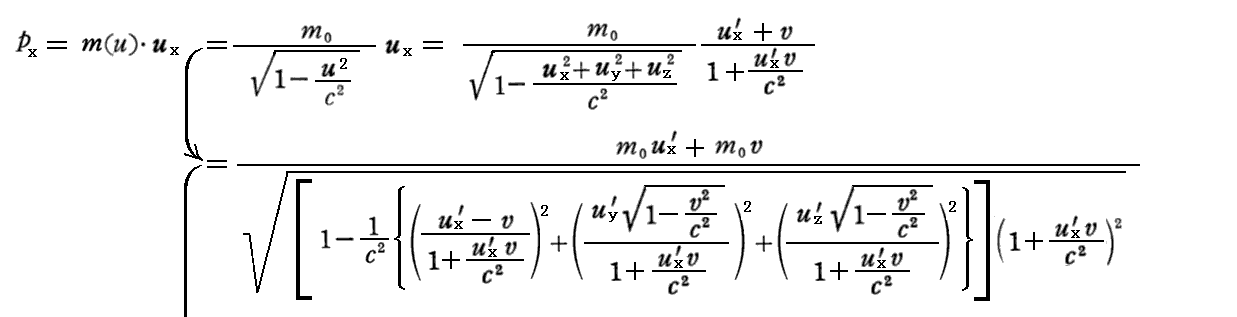
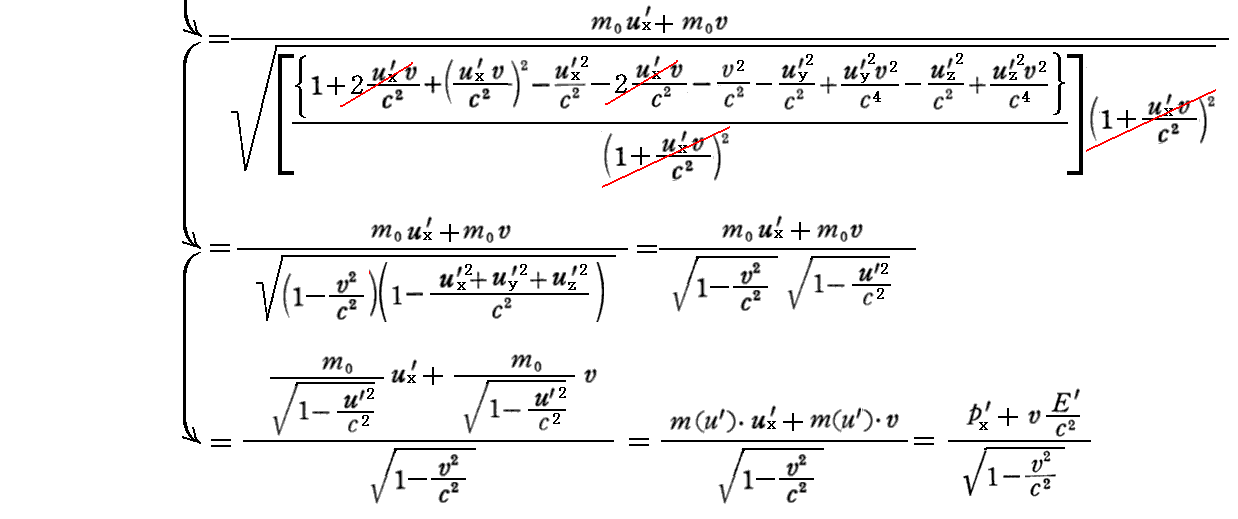
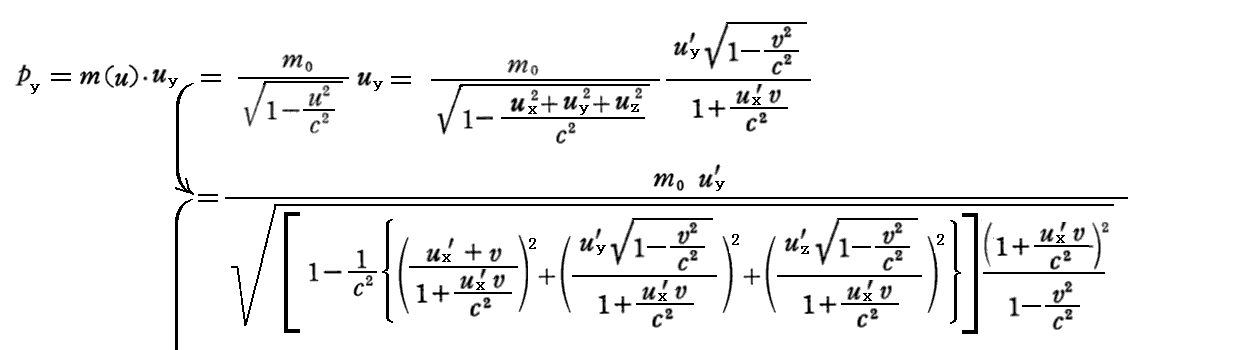
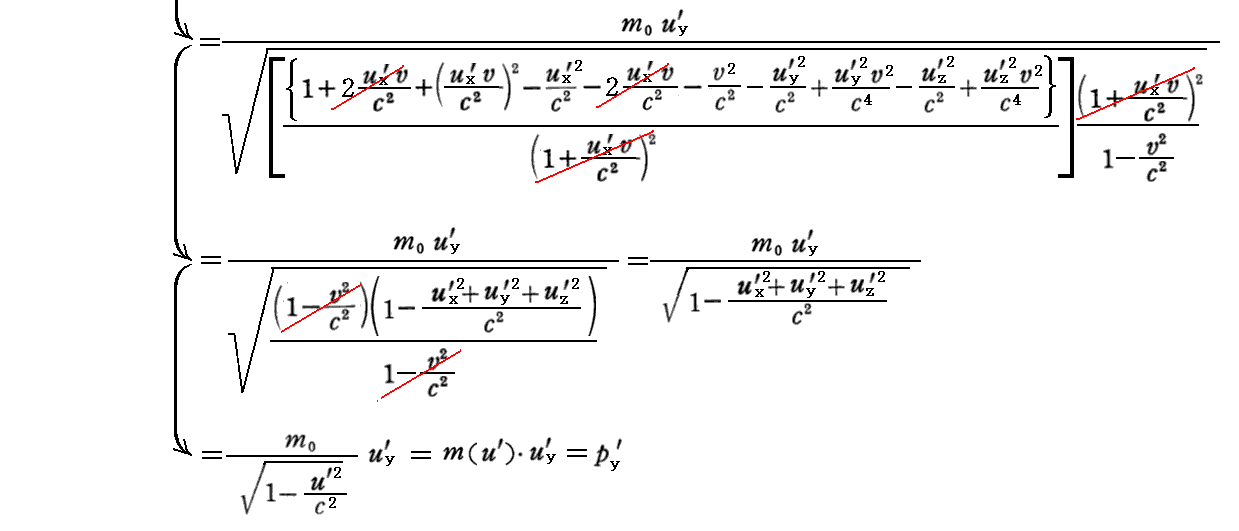
となる。pz=pz’についても同様に証明できる。
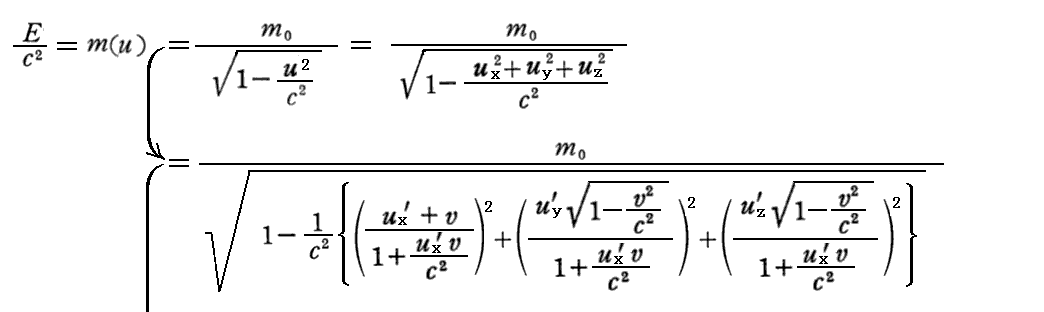
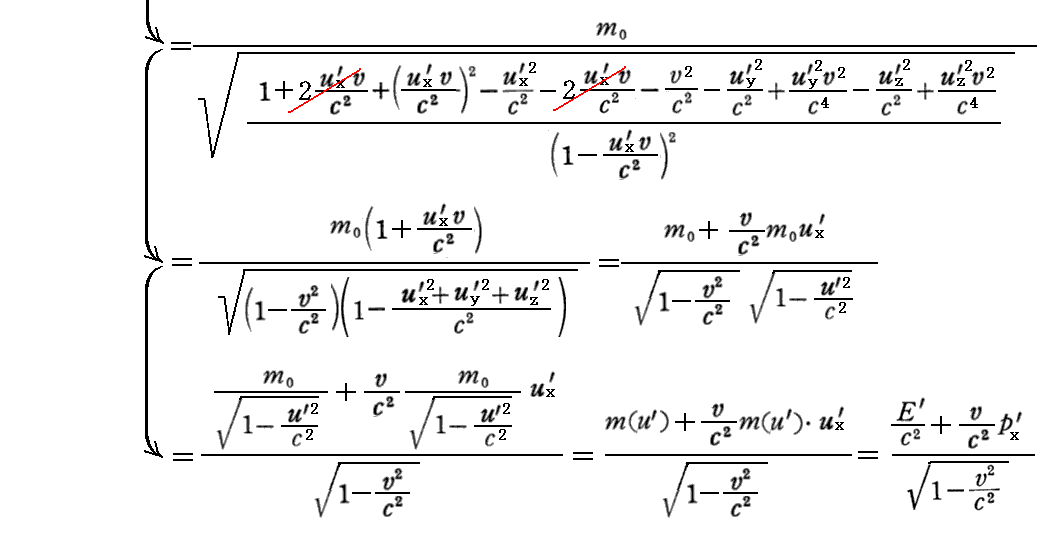
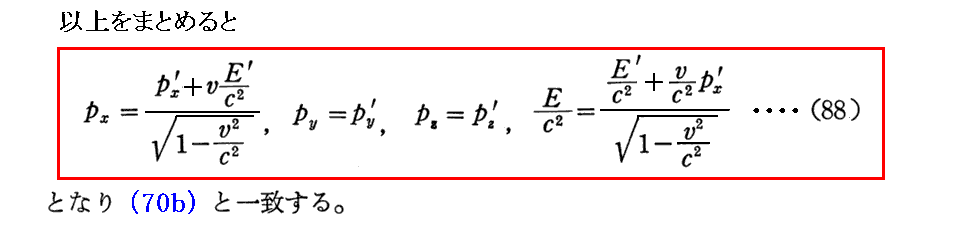
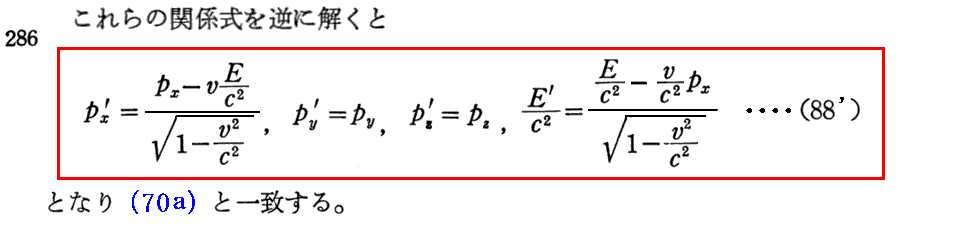
上記(70a)、(70b)式についてはこちらを参照。
[補足説明3]
逆変換(88)式と(88’)式との関係は、(x,y,z,t)←→(x’,y’,z’,t’)の逆変換(70b)式と(70a)式の関係と同じです。
(88’)式を求めるには、別稿「アインシュタインの特殊相対性理論(1905年)」2.(5)[補足説明1]と同様に、(88)を未知数px’、py’、pz’、E’/c2の四元連立方程式と見なして解けばよい。
あるいは、(88’)式のvを-vに置きかえてダッシュ’の有る無しを付け替えてもよい。
さらに補足すると、(88)式が成り立てば、これを用いて(87)式の左辺の量がローレンツ変換不変であることは直ちに言えます。それはx2+y2+z2-c2t2がローレンツ変換に対して不変であることを証明した手順と同じです。


[補足説明]
上記青波線部分については別稿「アインシュタインの公式E=mc2の証明」3.を参照されたし。
光子の運動量 p が E/c と置けるとするのは解りにくい所ですが、先の(87)式を導くとき利用した(79)式の所で注意した様に、結局のところ以下のように考えれば良いのだと思います。
まず E=hν がプランクの量子仮説から導けます。そしてアインシュタイン公式 E=mc2 が光子に対しても成り立つとします。そうすると、エネルギー E=hν の光子は hν/c2=E/c2=m の慣性質量を持つ事になります。
そのとき光子の速度はcですから運動量の一般的な定義である p=[慣性質量]×[移動速度] を適用すると、光子の運動量は
p=m×c=(E/c2)×c=E/c=(hν/c2)×c=hν/c
となります。

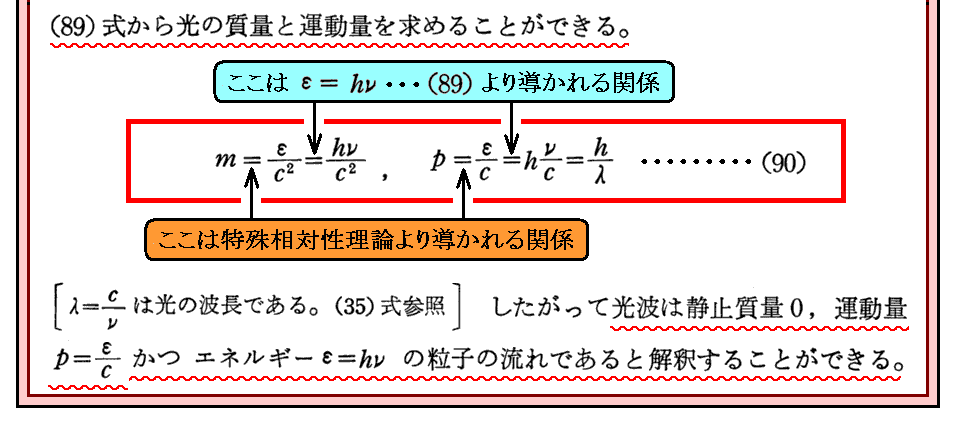
上記“特殊相対性理論より導かれる関係”については別稿「アインシュタインの公式E=mc2の証明」も参照されたし。
[補足説明4]
上記文中の(90)式は特殊相対性理論が予言する公式として極めて重要です。公式E=mc2に勝るとも劣らない深い意味を持つ。
別稿「ボーアの水素原子モデル(1913年)」5.補足(1)“ド・ブロイの仮説”で述べたように、 ド・ブロイは1924年に特殊相対性理論から導かれる【運動物体のエネルギー】を光量子とのアナロジーで【振動数】に対応させ,一般の“物質粒子”も
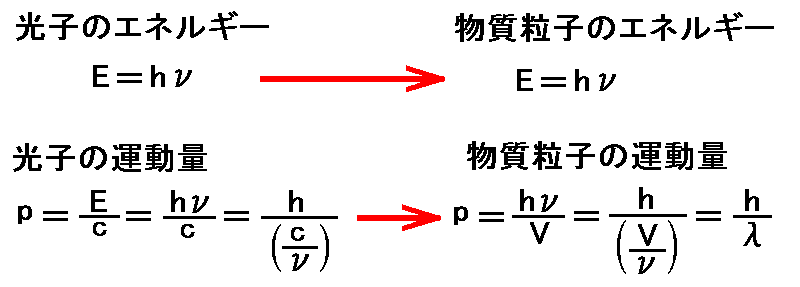
を持つとした。ここで、Vは“随伴波の位相速度”です。つまり、光子という粒子に随伴する波の位相速度はcであるが、それに相当する物質粒子に随伴する波の位相速度をVと置いています。
つまり、“物質粒子の運動速度”をv としたとき

と見なせるとしています。ここで、“随伴波の位相速度”V と “物質粒子の運動速度”v の間には
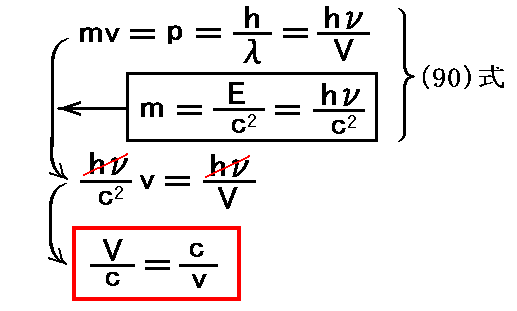
の関係があります。物質粒子の移動速度vと物質粒子に随伴する物質波の位相速度Vは異なります。しかもVは光束cよりも大きくなります。ここがド・ブロイの“物質波の仮説”で最も解りにくいところですし、この仮説の正当性を説明する上で最も難しいところです。
もう一度強調しますが、上記(90)式関係図から解る様に、ド・ブロイが“物質波の仮説”を提出する元となった(90)式は、“Einsteinの特殊相対性理論” E=mc2 と “Planckの作用量子仮説→Einsteinの光量子仮説” E=hν から導かれたものです。このことを明確に強調している解説書(高林武彦著「量子論の発展史」7章は秀逸)は少ないのですが、このことはド・ブロイもはっきり言っていることです。
この仮説は、全ての物質が波動性を持つとするもので、後にシュレーディンガーが“波動方程式”を発見して量子力学を完成(1926年)する基礎となった。
先ほどの話の続きに帰りますが、実際のところド・プロイの理論で、最も解り難くて最も飛躍する所は、
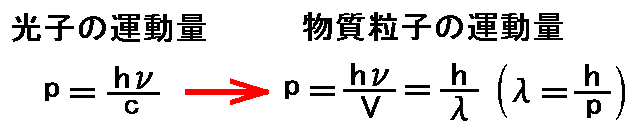
と置き換える所です。ここで、Vは“随伴波の位相速度”です。
この部分を正当化するためにド・ブロイが用いた方法を吉田伸夫著「光りの場、電子の海」のp230~231から引用。
物質波の伝わりかたとして、光学で利用される【フェルマーの原理】が使えると仮定した。一方、電子の運動は、ニュートンの運動方程式と同等の【モーペルティーの原理】によって記述される。
この2つの原理は、いずれも、「経路に沿ってある量を積分したとき、その積分値が最小になるような経路が実現される。」という形式をしている。そこで、波の伝わり方が現実の電子の運動と一致するように、2つの原理の式の間に対応関係が付けられることになる。
【フェルマーの原理の式】には《振動数》νと《波長の逆数(波数)》1/λが、【モーベルティーの原理の式】には《エネルギー》Eと《運動量》mvがペアになる形で現れているので、アインシュタインの関係式 E=hν を使って二つの式の対応を付けると、電子の運動量と波長の間の関係式 mv=h/λ が得られる。ただし λ=V/ν です。ここで v は“物質粒子の運動速度”であり、Vは“随伴波の位相速度”です。
実際のところ、ド・ブロイは別稿「アインシュタインの特殊相対性理論(1905年)」3.(2)2.[補足説明7]で説明した方法で展開した。このやり方は、ド・ブロイの学位論文(1924年)、 ノーベル賞受賞記念講演(1929年)、 ド・プロイが1930年に書いた教科書「波動力学研究序説」第3章§1.、 村上陽一著「ルイ・ド・プロイ(1892~1987)の功績」(http://www.wattandedison.com/deBroglie.pdf)、等々で説明されています。
この当たりについての解説を幾つか引用しておきます。ただし、これらの説明は解りにくいです。
ジョン・グリビン著「シュレーディンガーと量子革命」青土社(2013年刊)からp117~120、p133~134、p136~139
マンジット・クマール著「量子革命」新潮社(2013年刊)の第6章(p197~209)
K.プルチブラム編集(江沢洋訳・解説)「波動力学形成史-シュレーディンガーの書簡と小伝-」みすず書房(1982年刊)中の 江沢解説文 第Ⅱ部 “シュレーディンガー小伝” 4.波動性と粒子の統計
[補足説明5]
また、(90)式は粒子の生成・消滅がからむ素粒子・高エネルギー物理や天体物理を論じるときに、基礎となる公式です。この事については4.(4)、(5)で、もう少し詳しく説明します。



この事については4.(4)で更に詳しく説明する。
[補足説明6]
上記(91)式は別稿「アインシュタインの特殊相対性理論(1905年)」3.(3)1.ですでに求めております。そこでは光の波動説に従って求めたのですが、そこの“光束”は光量子説の“光子”と見なすこともできるからです。
このとき、さらに以下の事に注意されたし。(91)式は、S系でみた光子のエネルギーεと、同じ光子をS系に対して速度vで動くS’系から見たときのエネルギーε’の関係を表しているのですが、アインシュタインの光量子説に従ってそれぞれのエネルギー表現ε=hνとε’=hν’を適用すると
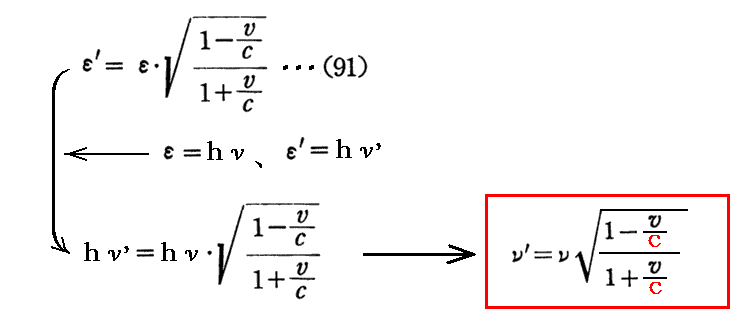
となる。これは別稿「アインシュタインの特殊相対性理論(1905年)」3.(2)2.で波動説に従って求めた“Doppler効果の公式”と同じです。
つまり、光のドップラー効果は波動説のみならず、光の粒子説でも完璧に説明できます。この事は、前記別稿2.(10)3.や3.(3)1.[補足説明6]などで何度も注意しました。
(5)電荷密度と電流密度
以下もBorn文献2.第Ⅵ章§9.“エネルギーと運動量”(p288~291)より引用。


[補足説明1]
別稿「アインシュタインの特殊相対性理論(1905年)」3.(4)[補足説明5]で説明したように電子のもつ“電荷(電気量)”はローレンツ変換に対して不変です。また電子の“数”も当然ローレン変換に対して不変です。
だから電荷密度に関してはローレンツ変換によって(92)式の様に変換することになる。
以下で(電流密度・電荷密度)を4元化するのですが、ここでも(jx,jy,jz,ρ)と定義する場合と(jx,jy,jz,cρ)と定義する場合があります。後者は第4成分の次元が他の成分と同じになりローレンツ変換係数の対称性も良くなるのですが、3.(1)[補足説明1]や3.(4)[補足説明1]で述べた理由により、この稿では前者の定義を用いることにします。
[補足説明2]
上記(92)式は、S系で静止している電荷密度ρ0を、S’系から見たらどう見えるかという式と同じです。S’系に於いて電荷密度ρはx’軸の負方向へ-vで動いている事になります。つまり

となります。
もし、電荷密度ρ0がS系において、速度ベクトル(ux,uy,uz)ですでに動いている場合、S’系から見た電荷密度ρは、S系における電荷速度の(S’座標の移動方向に沿った)成分uxにも依存して、以下のようになる。
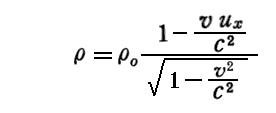
こうなることは、別稿「アインシュタインの特殊相対性理論(1905年)」3.(4)[補足説明2]で説明した。
そのため、(92)式は上式に(ux,uy,uz)=(0,0,0)を適用した式であることに注意されたし。
このとき、注目している電荷密度ρは、S’系に於いて(速度ベクトル(ux,uy,uz)をローレンツ変換した)速度ベクトル(ux’,uy’,uz’)で動いている。つまり
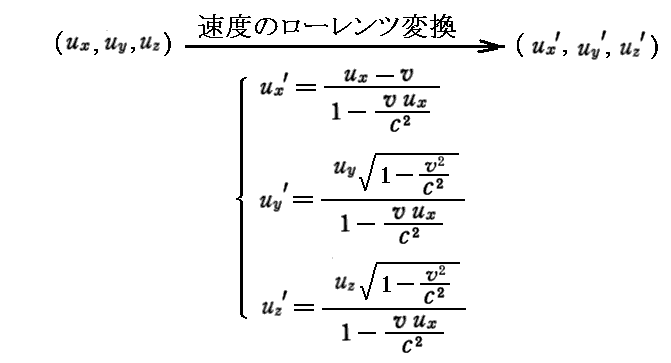
となることに注意されたし。
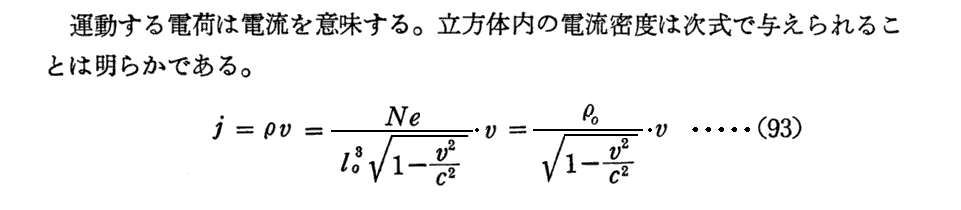
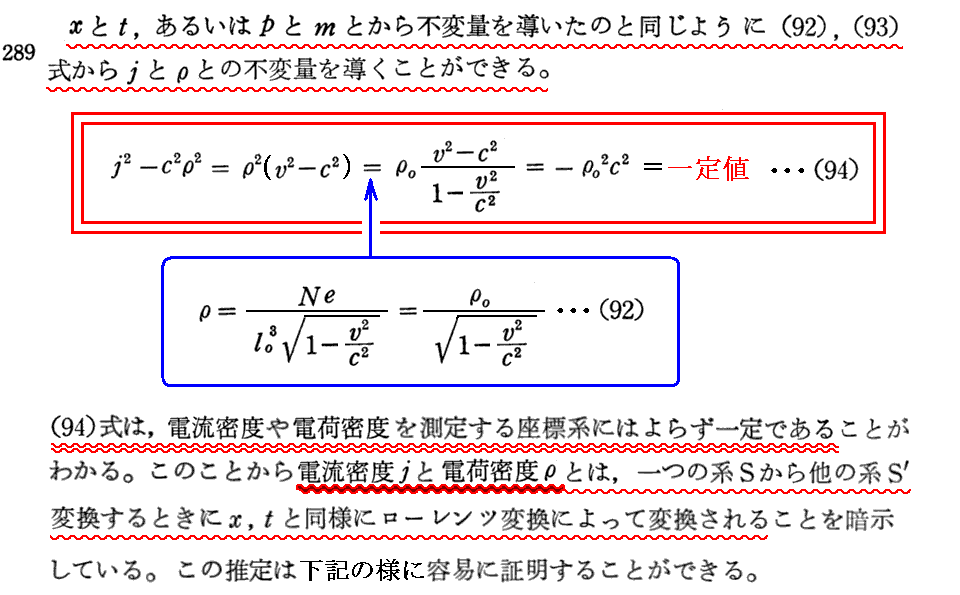
[補足説明3]
ここで、座標xと時間tと同様なローレンツ変換に従うのは、電流iと電荷eでは無くて電流密度jと電荷密度ρであることに注意して下さい。
本文中でも説明されているように、電荷(電気量)や電荷の数はローレンツ変換に対して不変です。しかし電荷密度ρはローレンツ変換とともに変化します。この事は別稿「アインシュタインの特殊相対性理論(1905年)」3.(4)[補足説明5]で注意しましたが、とても大事なことですから決して忘れないで下さい。
[電流密度]と[電荷密度]が一緒になってレーレンツ変換で変換されるということの意味を理解することは非常に難しい。なぜなら、ローレンツ変換によって変換される電流密度と電荷密度は、ある1つの時空点に存在する電流密度と電荷密度が変換される事の意味を良く考える必要があるからです。
ある1点に於ける[電流密度]を構成する電荷も[電荷密度]を構成する電荷も“同一の”電荷です。つまり、ある座標系から見るとそれは電荷密度を構成する電荷であり、それに対して動いている座標系から見るとその同じ電荷が電流密度を構成する電荷となるのです。そのとき注意して欲しいことは、電荷密度としての物理量は動いている座標系から見てもその物理的意味が失われるわけではありませんから電荷密度としても現れ続けます。ただし、動く座標系から見ると電荷が存在する場所の体積が変わりますから、動く座標系から見ると電荷密度はすこし変化して見えるわけです。その変化の度合いはローレンツ変換で的確に表されています。
上記の事情は前節(4)で説明した[運動量]と[質量]に付いても言えます。そこで説明したローレンツ変換によって一緒に変換されるある1点の時空点に於ける[運動量]と[質量]は“同一の”質量によって構成されるものです。
質量が静止している座標ではその質量に対して運動量という物理量は付随していないのですが、動いている座標系から見ると同じ質量でも運動量という物理量としての属性が現れてくるということです。そのとき、最初静止していた質量は動いて見える様になりますが、質量という属性が動いたからといって無くなるわけではなくてその属性は静止した座標系と同じ様に保持されます。もちろん、その質量は動くと少し増加して見える事になりますが。その変化の度合いはローレンツ変換で的確に表されています。
ここで注意して欲しい事は、電荷密度と違ってその質量が存在する空間が変化するから質量が変化するわけではなくで、質量自体が変化するのです。(4)節の話が運動量密度とか質量密度の様な“密度”の話では無かったことに注意して下さい。


上記(70a)、(70b)式についてはこちらを参照。
[補足説明4]
ここの説明は込み入っていて解りにくいが、“電荷密度ρ(u)”が“質量m(u)”と同様な変換法則に従うことと、[電流密度成分 jx]=[電荷密度ρ(u)]×[速度成分ux]であることに注意すれば、(px,py,pz,E/c2)←→(px’,py’,pz’,E’/c2)の変換式導出法と同じです。
以下では、速度の変換則(77a’)~(77c’)式
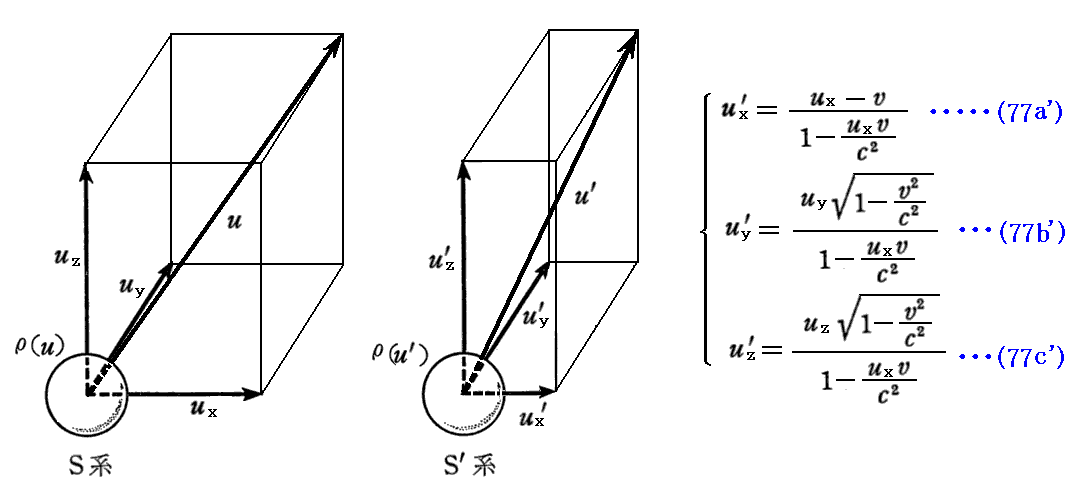
を用いて、S系→S’系の変換則を導いてみる。
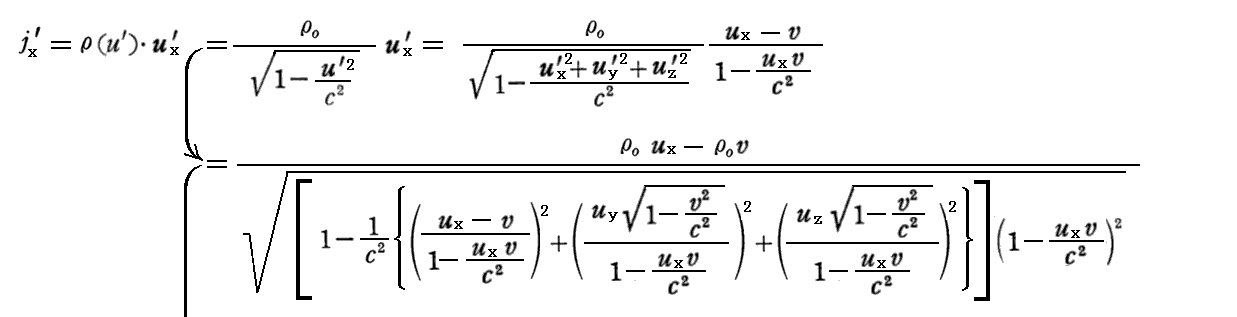
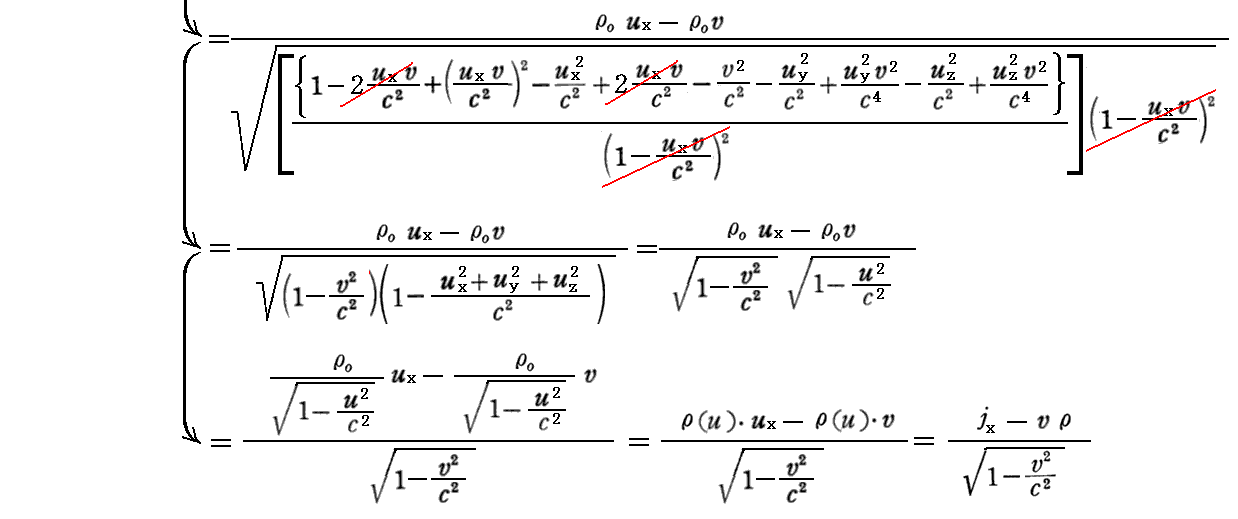
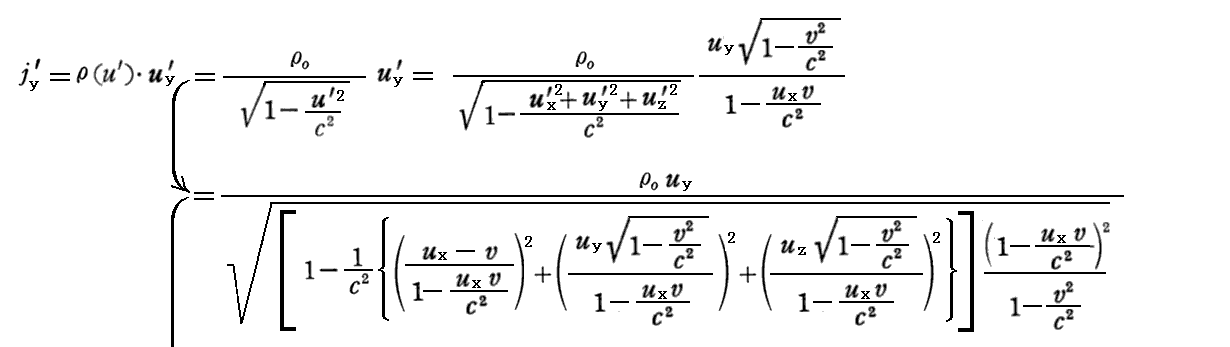
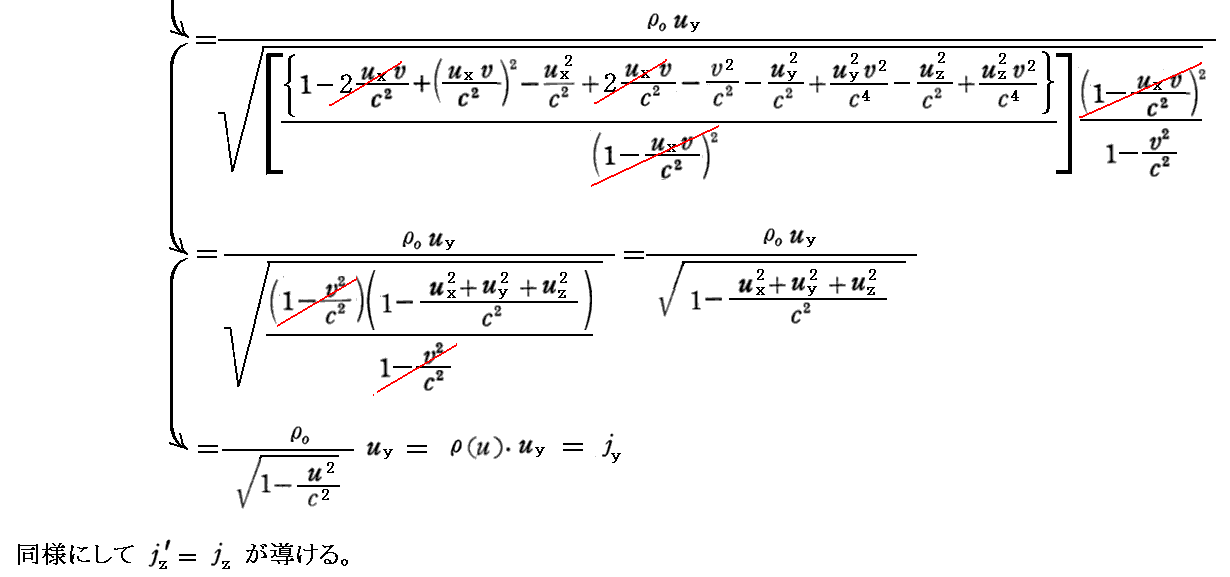
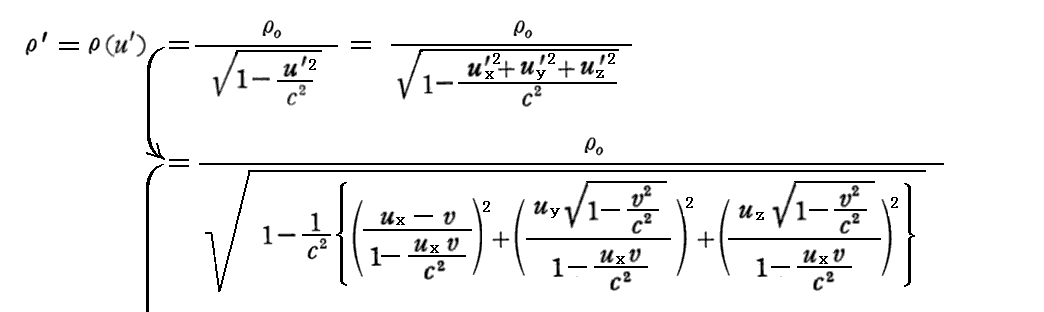
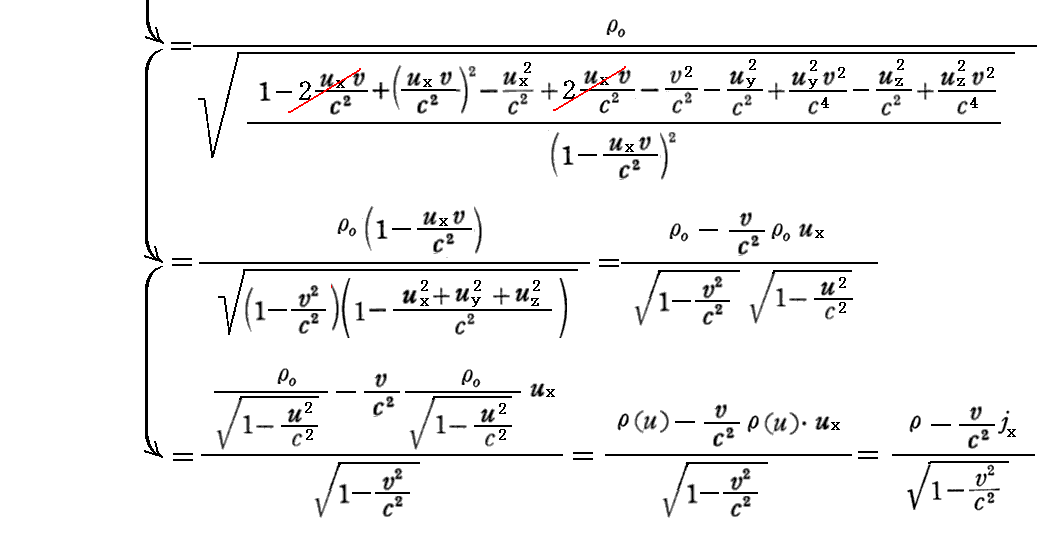
最後の電荷密度に関する変換式については、別稿「アインシュタインの特殊相対性理論(1905年)」3.(4)[補足説明2]をもう一度読み直してみられることを勧めます。
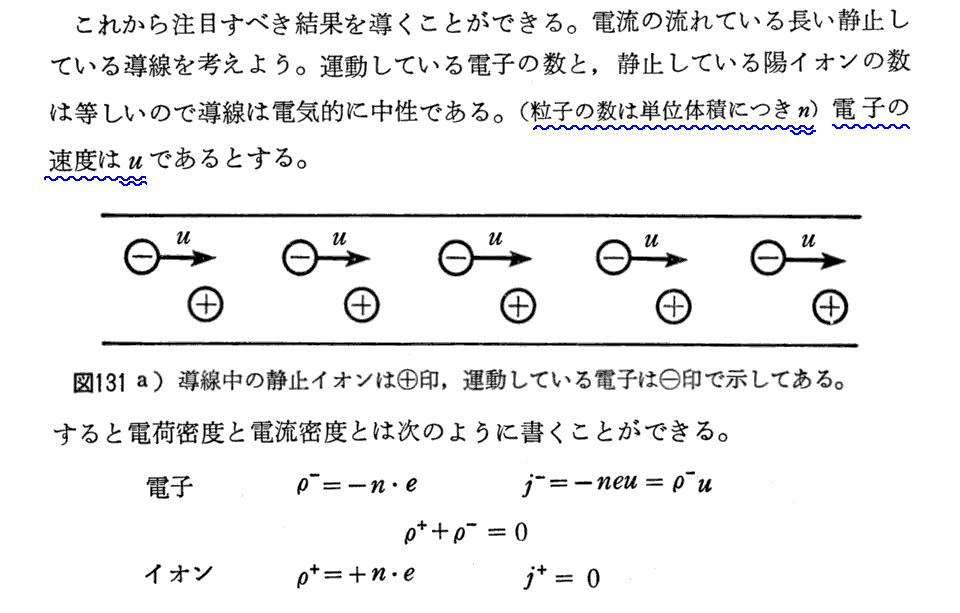


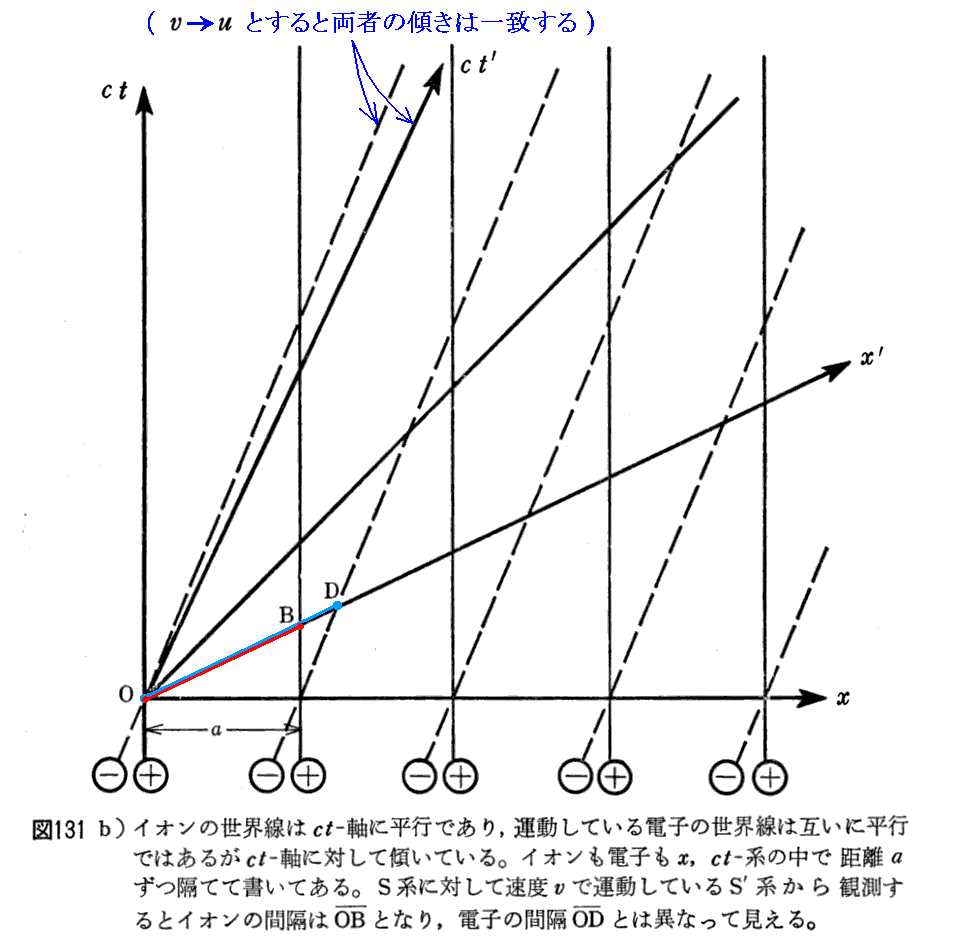
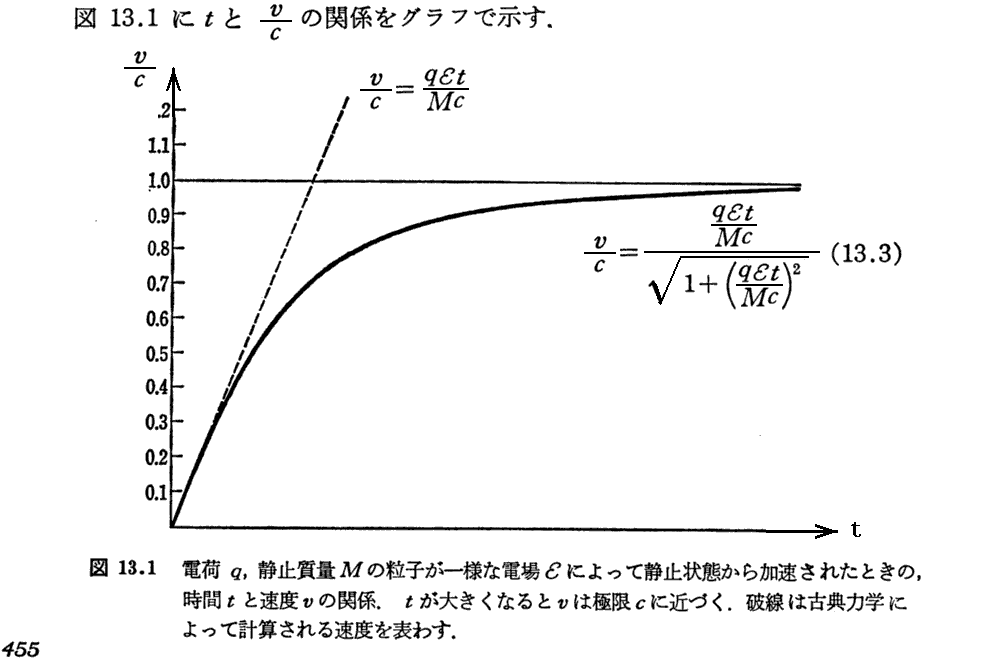
図131を正しく理解するのはかなり難しい。この図を理解する注意点を別稿「電磁場の相対性」3(3)の第3項[補足説明1]、[補足説明2]、[補足説明3],[補足説明4]に記していますので下記[補足説明5]と合わせてご覧下さい。
[補足説明5]
ここは難しい所です。図131だけでは解りにくいので、静止系(S系)から見て電流値が変化した図を幾つか示す。
(1)u1<vの場合
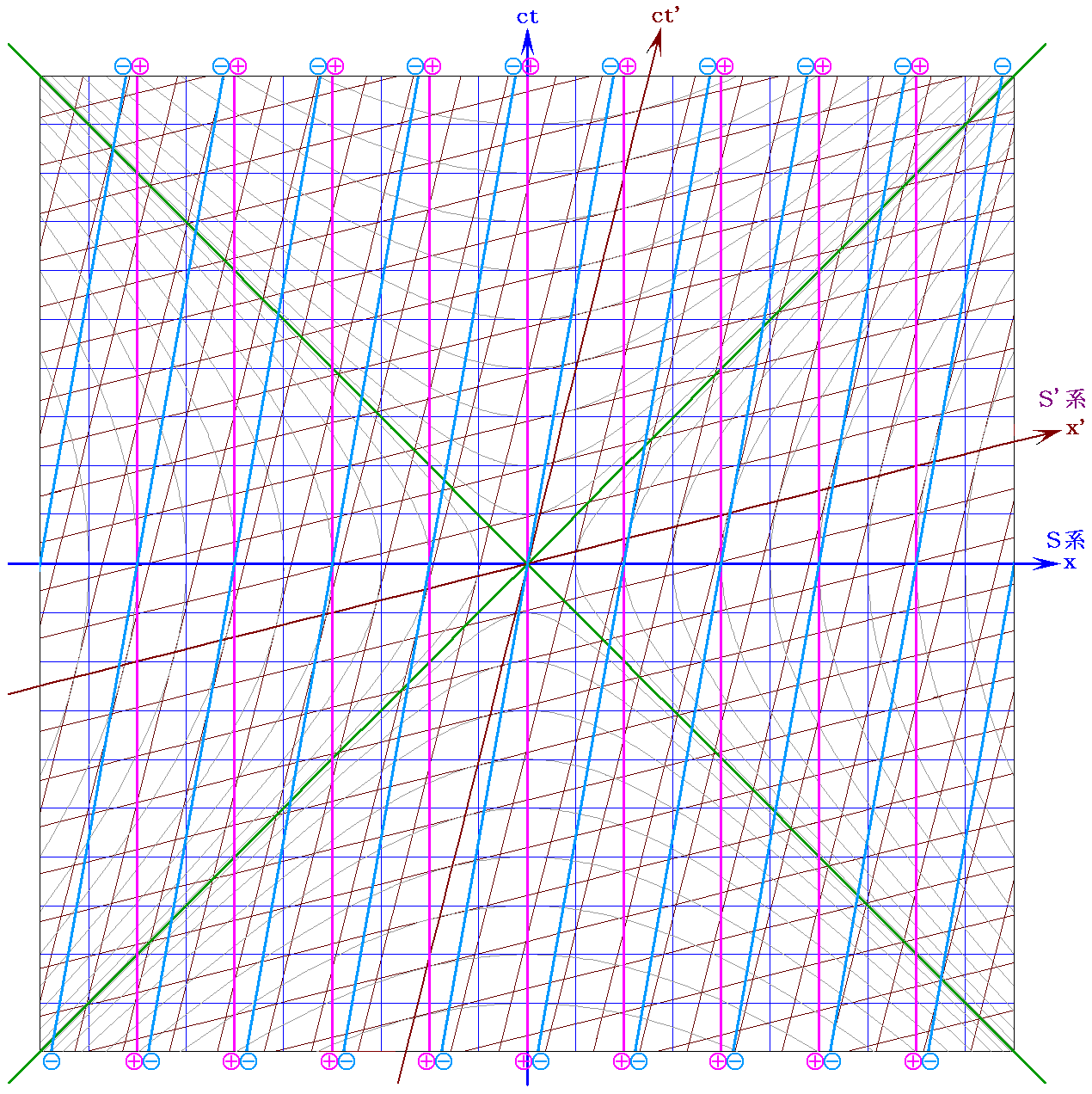
(2)u2=vの場合
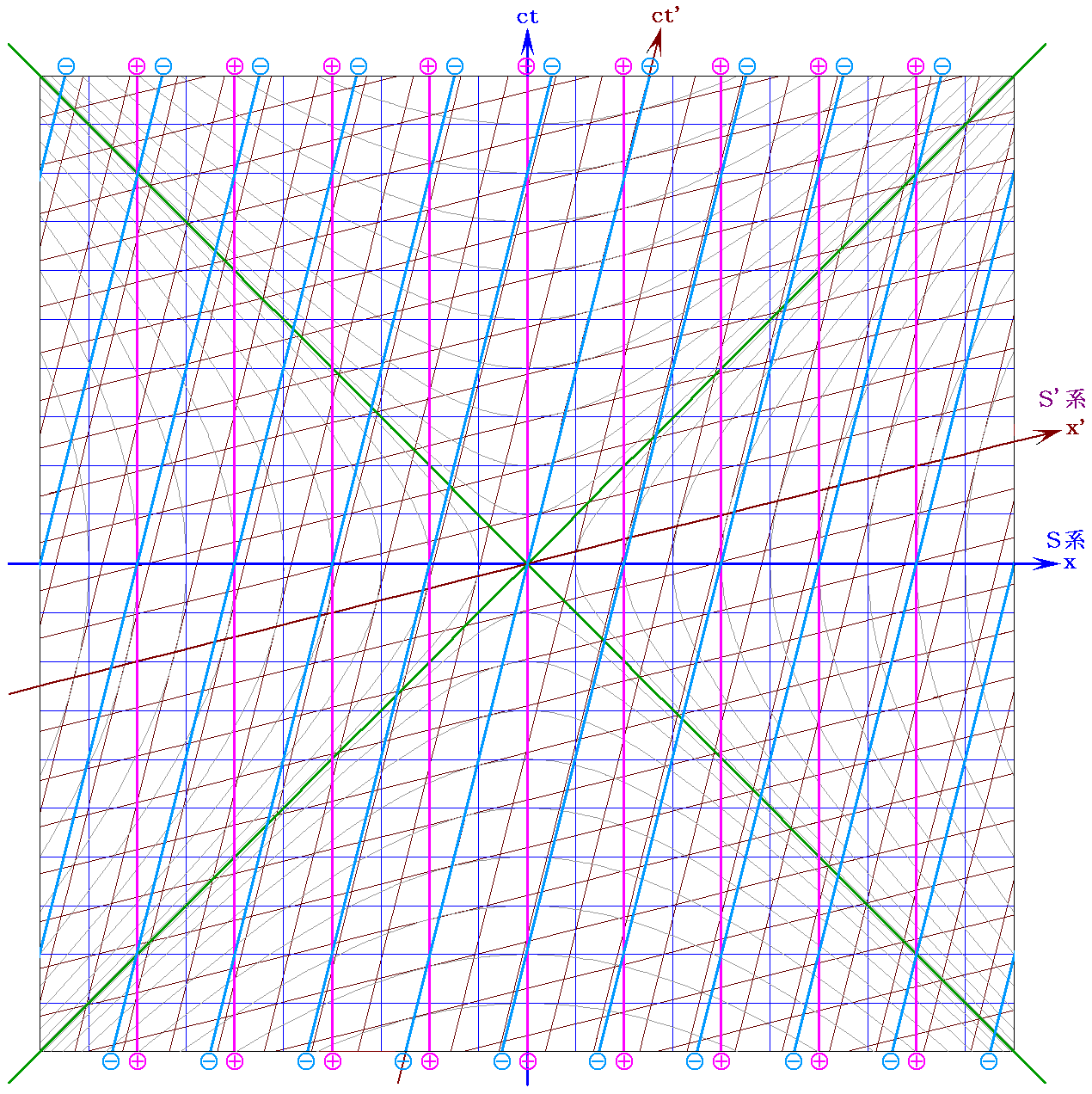
(3)u3>vの場合
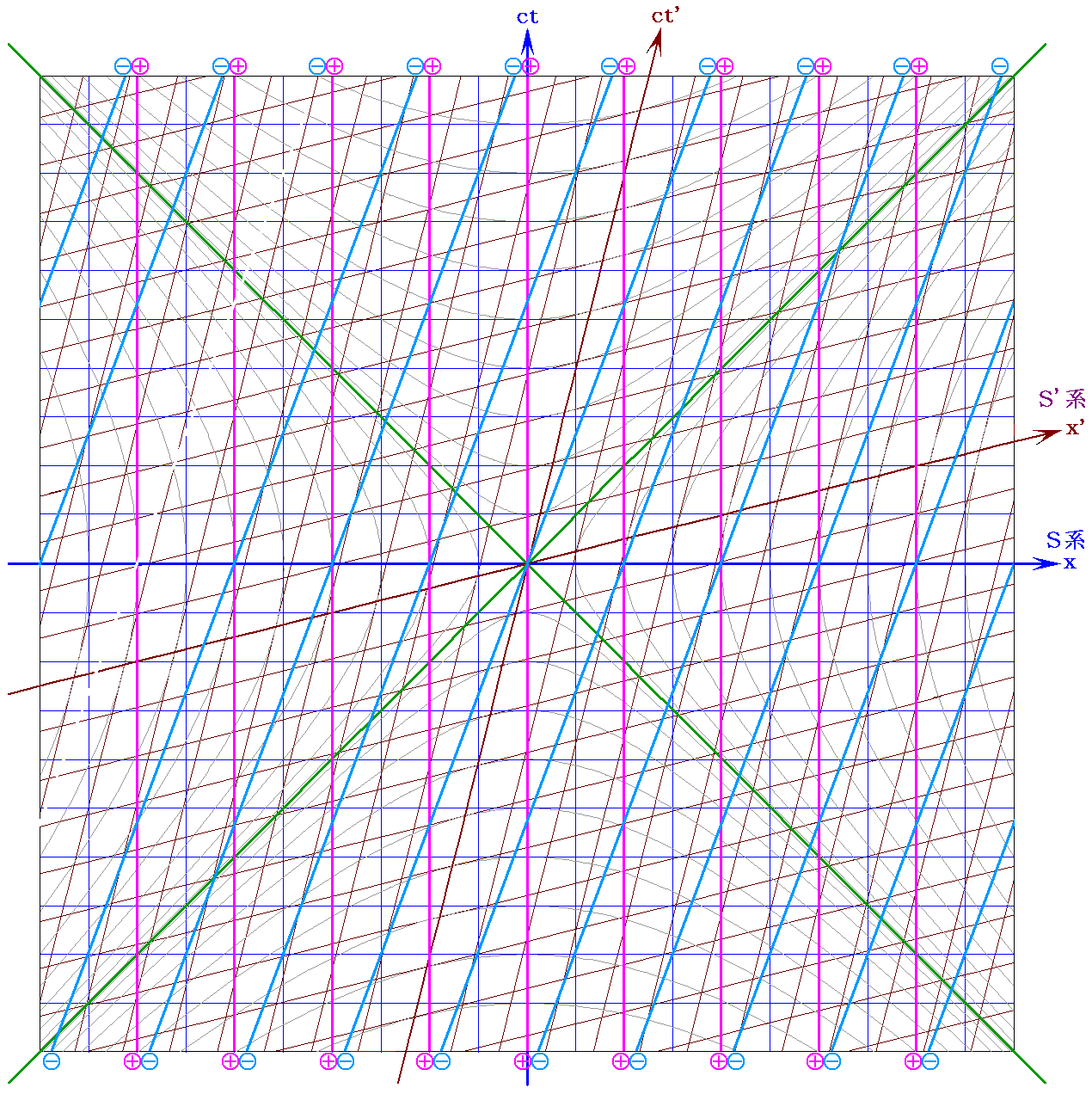
それらの図上でS’系から見たときの正・負電荷の密度変化の様子を確認されたし。
これらはいずれも静止系(S系-正電荷と共にある座標系)から見たとき電線(針金)は帯電してはいない場合を示している。
運動系(S’系-負電荷の移動方向に動いている)から見るといずれの電線(針金)も正に帯電して見える。S’系に移ると伝導電子の右向きの速度が小さくなるので、縮んでいた伝導電子間隔が元に戻って広がるからです。そのとき、運動観測系の速度vが一定でも、u1<u2<u3となるにつれて帯電量は増大することに注意。
ここで注意して欲しいことは、観測系に対して電線(針金)が動いていればその長さが縮みますが、その中を動いている伝導電子の間隔の縮みは、それとは独立に生じる事です。伝導電子の進行方向の前側の電子は過去の位置を、進行方向の後ろ側の電子は未来の位置を見ているから間隔が縮むのです。
観測する座標系に対して正・負電荷が動いていれば、それらの電荷密度(電荷間の距離)が変化しますが、正・負それぞれの電荷の動きに対して別稿「ローレンツ変換とは何か」3.(2)[補足説明4]のメカニズムがそれぞれ働くわけです。
(2)u2=vの場合でS’系から見たミンコフスキー時空図(S’系座標を直交)は下図の様になる。
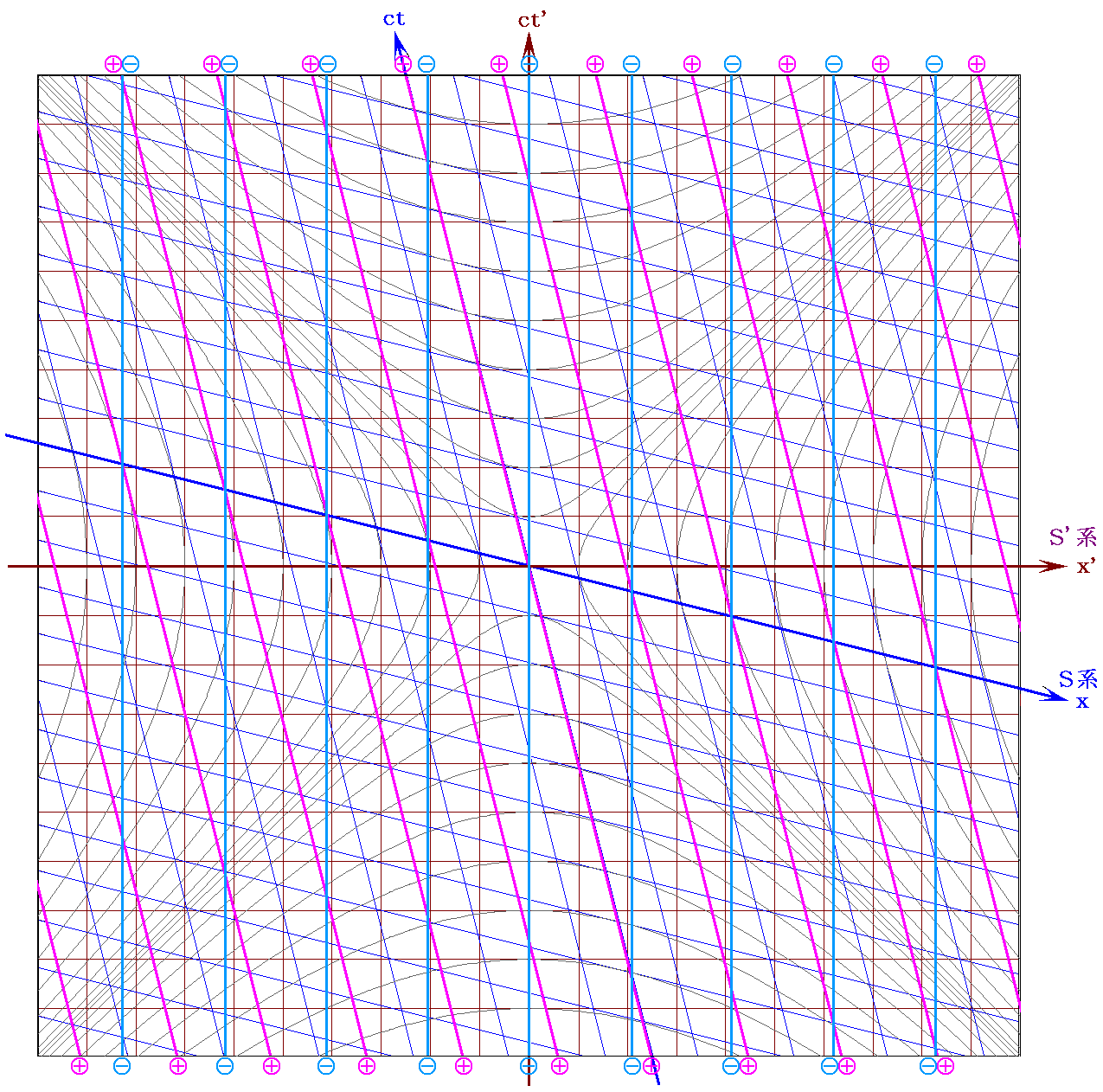
運動系(S’系)から見て電線(針金)はすでに帯電しており、かつ(正電荷による)電流も存在する。
運動系(S’系)から見て電流は流れているが帯電していない電線(針金)の場合に、図中の正・負電荷の世界線がどのようになるべきか考えてみられたし。
ここで説明されている事柄についてのさらに詳しい説明は別稿「電磁場の相対性」あるいはPurcell「電磁気学」第5章§9を参照されたし。
ミンコフスキー時空図そのものについては江沢別稿“ミンコフスキー空間”、別項「Born「相対性理論」第Ⅵ章」3.、別稿「ローレンツ変換とは何か」3.(2)[補足説明1]などを参照されたし。

文中の(Ⅴ章、§11)は別稿で引用したこちらを参照して下さい。図103、図105もそこで説明されています。また、上記の事柄については、別稿「アインシュタインの特殊相対性理論(1905年)」3.(1)と、そこの[補足説明7]も参照されたし。また、具体的な例については別稿「電磁場の相対性」を参照されたし。
[補足説明6]
この章を閉じる当たって重要な注意をします。
(4)節で説明した“運動量”と“質量(エネルギー)”や(5)節で説明した“電流密度”と“電荷密度”は、それらを観測する座標系(慣性系)に依存して変化しました。観測する座標系(慣性系)が変わればそれらの物理量がどのように変わるかを(4)節、(5)節で求めたのです。
それはそれぞれの慣性系で成り立つ“エネルギー保存則(質量保存則)”、“運動量保存則”、“電荷保存則”にそれらの事象を記述する座標成分の慣性系間の変換則(座標と時間の“ローレンツ変換”)を適用することで導きました。そのとき用いた速度の変換則は座標と時間の変換則から導いたのですし、質量(エネルギー)変換則は両慣性系で成り立つエネルギー保存則から導いたのですから。
そのとき、運動量や質量(エネルギー)、電流密度や電荷密度は観測する座標系が変われば変化しました。つまりそれらの量はローレンツ変換に対して不変ではありませんでした。つまり、ローレンツ変換に従って変換された。
この事実と、それぞれの慣性座標に於いて“エネルギー保存則(質量保存則)”や“運動量保存則”や“電荷保存則”が成り立つということの意味を混同しないでください。
(4)、(5)節で解った最も重要なことは、[運動量と質量(エネルギー)]、[電流密度と電荷密度]が、観測座標を変換するとき[時間と座標]が変換されるのと全く同じ形式で変換されることです。このことを用いれば、それらの量から作られる px2+py2+pz2-c2m2 や jx2+jy2+jz2-c2ρ2 という量が x2+y2+z2-c2t2 と同様にローレンツ変換に対して不変なことが直ちに証明できます。
つまり
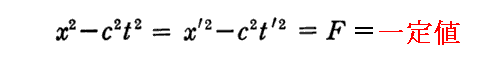
と同じように
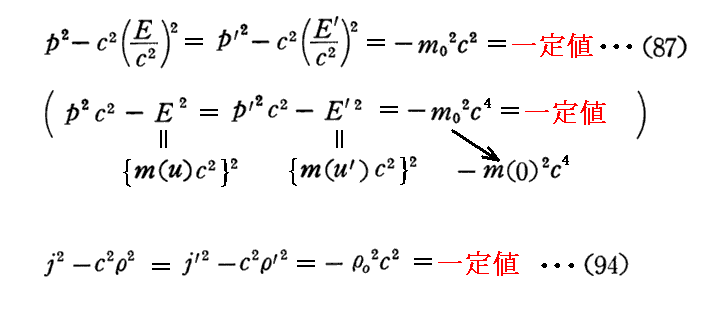
の関係式が座標系に寄らず普遍的に成り立つ。実際このことの証明は、 x2+y2+z2-c2t2 がローレンツ変換に対して不変であることを証明した手順と同様にすればよい。そのとき、ミンコフスキーはローレンツ変換をこれらの量が不変となる擬回転と同定したのです。
4次元化については、別項「4元速度、4元加速度と4元力」でもう少し詳しく説明していますのでご覧下さい。
“運動量-質量”や“電流密度-電荷密度”から構成される複合的な量 p2-c2m2 や j2-c2ρ2 は座標変換を跨いで保存されるというきわめて重要なことが解ったのですが、この性質は特殊相対性理論の段階にとどまる限りあまり重要ではありません。
しかし、一般相対性理論の様に加速度運動を含めた任意の運動をする座標系間の相対性理論を構築するとき役立ちます。実際、最初ミンコフスキーの4次元時空をあまり評価していなかったアインシュタイン(Pais文献7章p193)も、後に一般相対性理論の構築を模索する過程でミンコフスキーの考え方を高く評価するようになります。
4.相対論的力学の応用
この章で、文献3.バークレー物理学コース「力学」第13章の説明を紹介します。ただし少し改変しています。これはとても教育的で解りやすい。
文献3.では電磁気学単位としてCGSGauss単位系を用いています。さらに磁場としてHの代わりにBを用いています。Gauss単位系ではHとBは一致しますが、そのことについては別稿「電磁気学の単位系が難しい理由」5.(3)2.をご覧下さい。



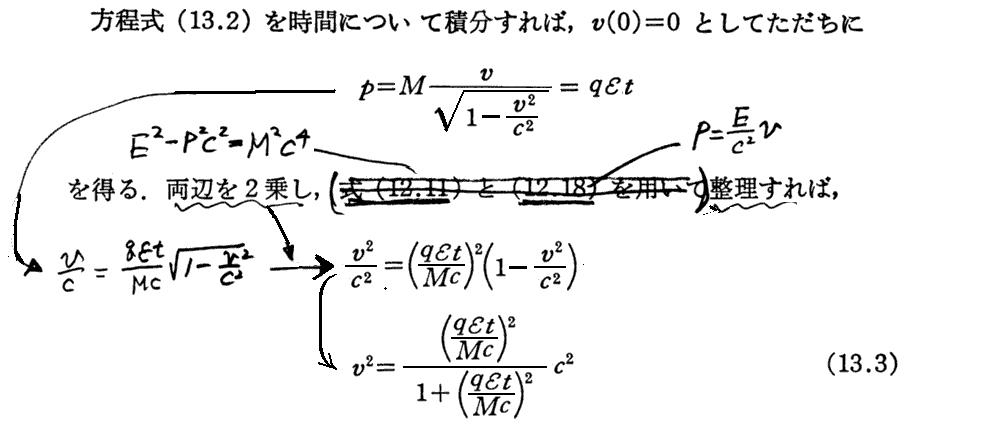
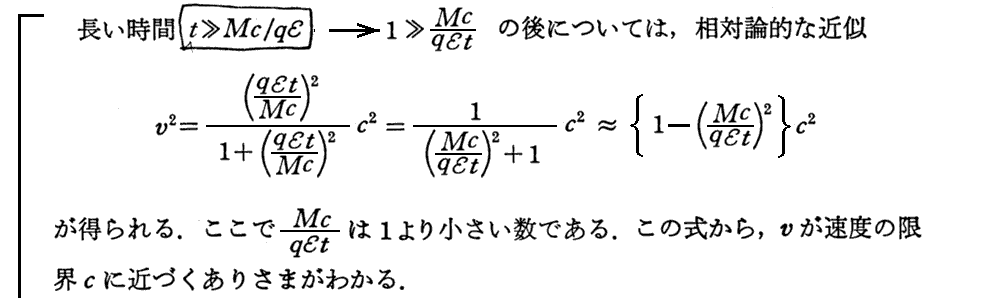
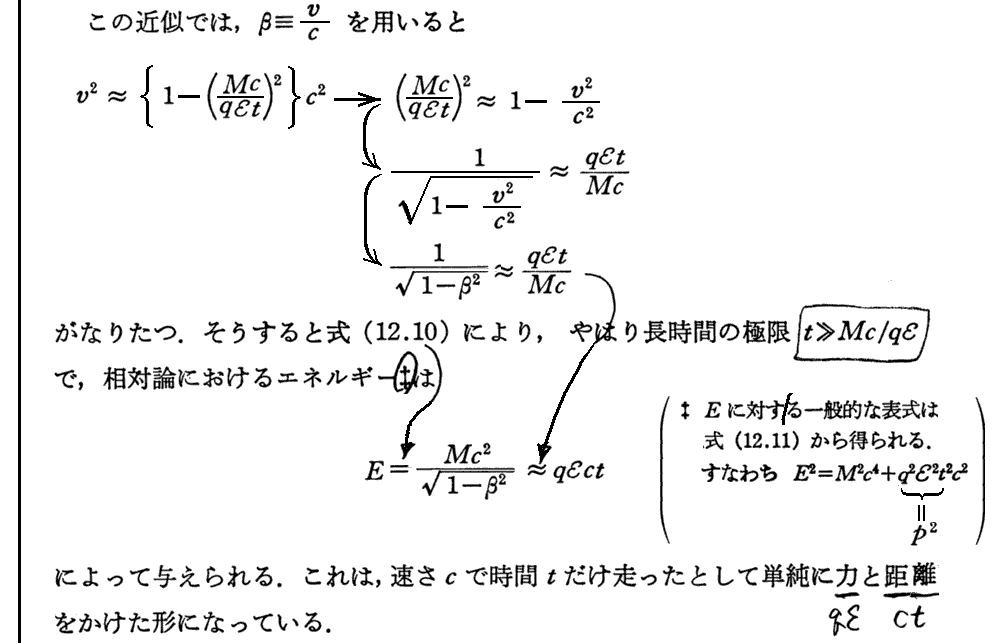
(1)運動方向にかけた一定電場による荷電粒子の加速


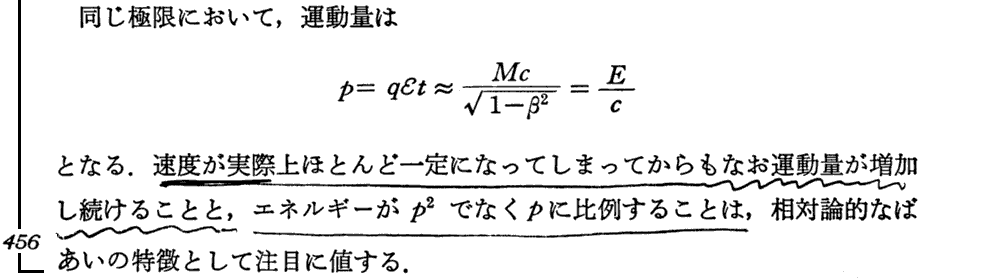



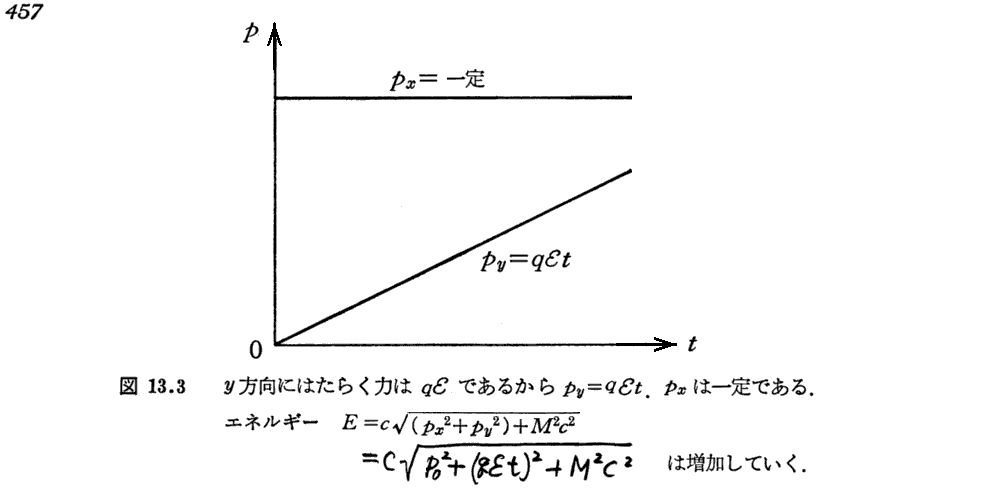
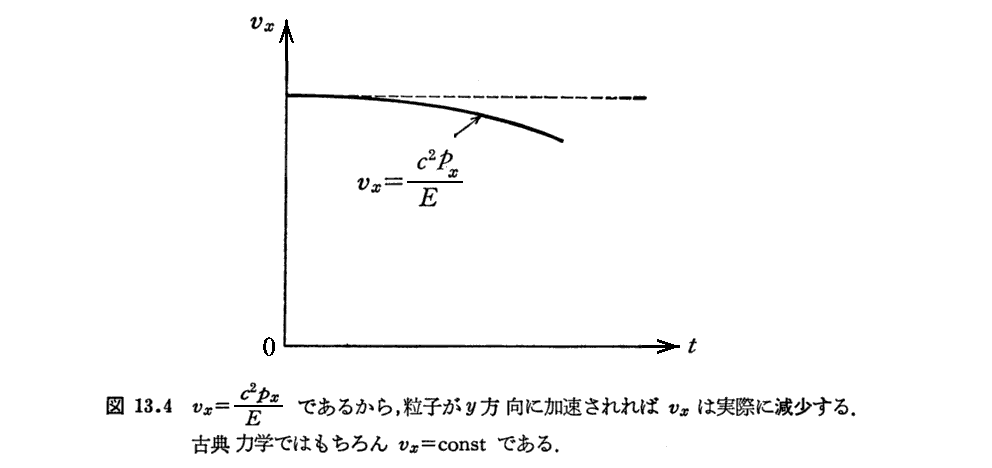
(2)横方向の電場による加速
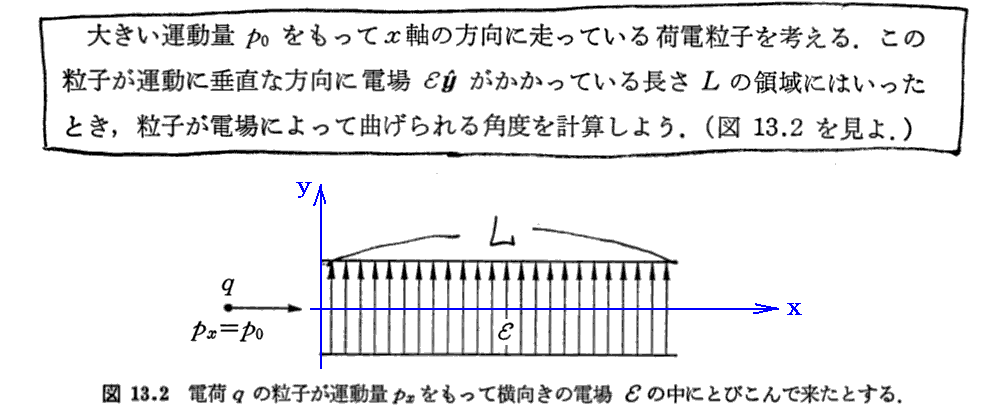
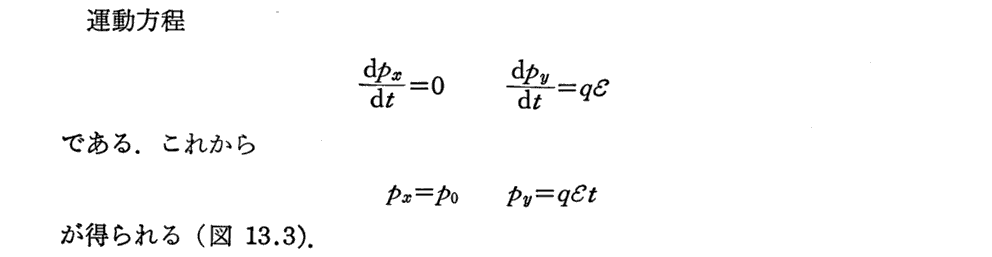
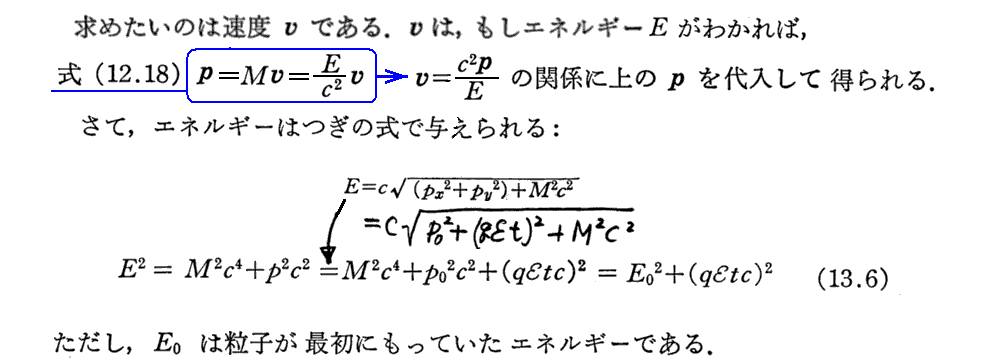

[補足説明1]
古典的なNewton力学ではこの事を説明できませんが、特殊相対性理論ではy方向に加速されて速度が増大すると粒子の慣性質量が増大します。そのため力が働いていないx方向の運動量が保存するためには速度vxは減少しなければならないのです。(もちろん、最初に持っていた速度ベクトルの方向に力のベクトルが作用する場合にはvx=0で在りつづけますので、力のベクトルの方向と加速度ベクトルの方向は一致します。)
このことは、最初の速度ベクトルの方向と、その物体(エネルギーの塊)に作用する力のベクトルの方向が一致しないときには、作用する力のベクトルの方向とその力によって生じる加速度ベクトルの方向が一致しないことを意味します。
特殊相対性理論では、力のベクトルFの方向と一致するのは運動量ベクトルの時間的変化を表すベクトルdp/dtであって、加速度ベクトル(速度ベクトルの時間的変化を表すベクトルdv/dt)ではありません。
このことは、一定の力を加えたとき、速度は光速度cに近づくが、加速度はだんだん減少していきやがてゼロになることに対応します。特殊相対性理論では一定の力Fを加えたときに増大し続けるのは運動量pであって速度vではありません。
これらは特殊相対性理論が予言する驚くべき結論ですが、もちろん v≪cの場合には古典的なNewton力学の様相に一致します。
[補足説明2]
アインシュタインは、後の講演「一般相対性理論の起源について」(1933年6月グラスゴー)で、この節の事柄に関係して興味深い事を語っている。以下はそこからの引用文(緑色括弧内の記述は私の追記)
『・・・・・・ここで道は間違いはないほど明瞭ではなかった。何故ならば物体の慣性質量は万有引力ポテンシャルに依存するかも知れないからである。事実これはエネルギーの慣性の原理(公式E=mc2のこと)によって期待せらるべきであった。
しかし、これらの研究は私の強い懐疑を生じた一つの結果に導いた。古典力学によれば、垂直な万有引力の場に於ける物体の鉛直加速度は、速度の水平成分に無関係である。従ってその様な万有引力の場においては、力学的体系あるいは重心の鉛直加速度は、その内部エネルギーに無関係に働く。しかし私の進めた理論(この節で説明したこと)では、落体の加速度は水平速度、あるいは体系の内部エネルギーに無関係でなかった。(縦方向の万有引力が横方向の運動で生じる慣性質量の増加とは無関係にいわゆる重力質量に働くと考えるととても奇妙なことが起こる。これが京都公演で「・・・ただひとり万有引力の法則にはこれ(特殊相対論)を応用することのできないのを認めて、・・・」と述べていることの内容だろう)
これはすべての物体は万有引力の場では同一加速度をもつという古い実験結果(ニュートン力学では横方向の速度が縦方向の加速度に影響することはない)と一致しなかった。また慣性的質量と重力質量の同等性の法則として公式化されることのできるこの法則(いわゆる「等価原理」のこと)は、あらゆる意義において私に接近して来た。私の記憶が正しければ---後に知る様になったにすぎなかったところのエトヴェシュの見事な実験の結果は知らなくとも、その法則の確かな有効性には何等疑問も持たなかった。・・・・・・』
アインシュタインは、同様な事柄を自伝ノート(1947年)第五段落の最初でも述べていますのでご覧下さい。
つまり、ここで説明した力学的結論は、Einsteinが一般相対性理論へ向かう一つのきっかけとなったようです。
また、アインシュタインは「等価原理」の着想を得た1907年の段階ではエトヴェシュの有名な実験を知らなかったようです。M・ウィルの本(p38)によると、彼がこの実験を知ったのは1912年だそうです。その後は、これを広範に引用した。
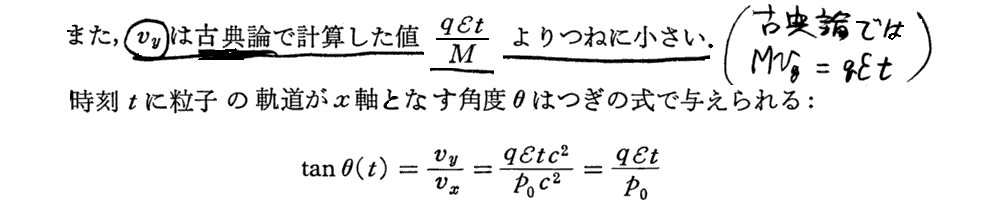

上記積分は公式集(岩波全書「数学公式Ⅰ」p110など)を参照されたし。
(3)磁場中の荷電粒子の運動

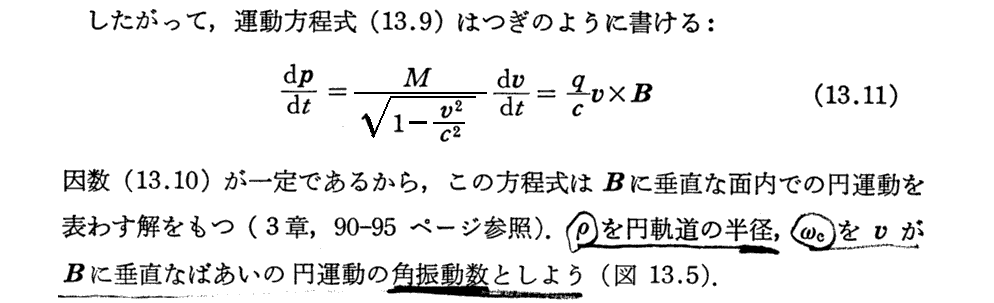
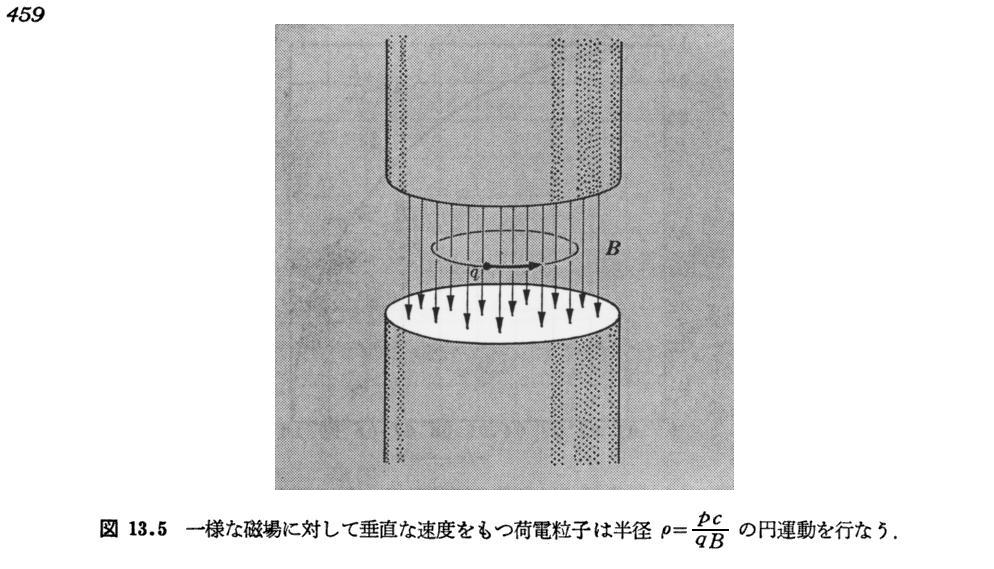

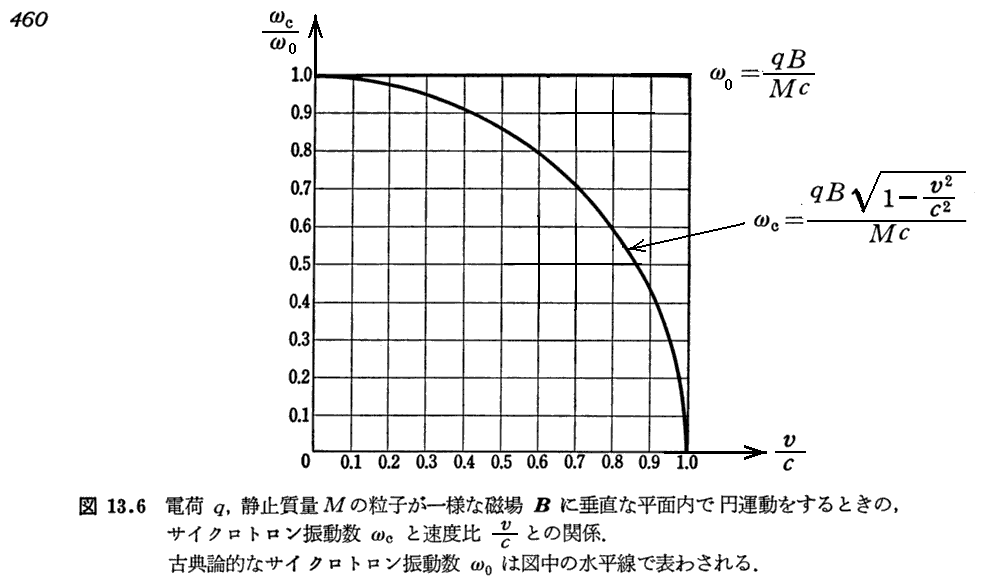

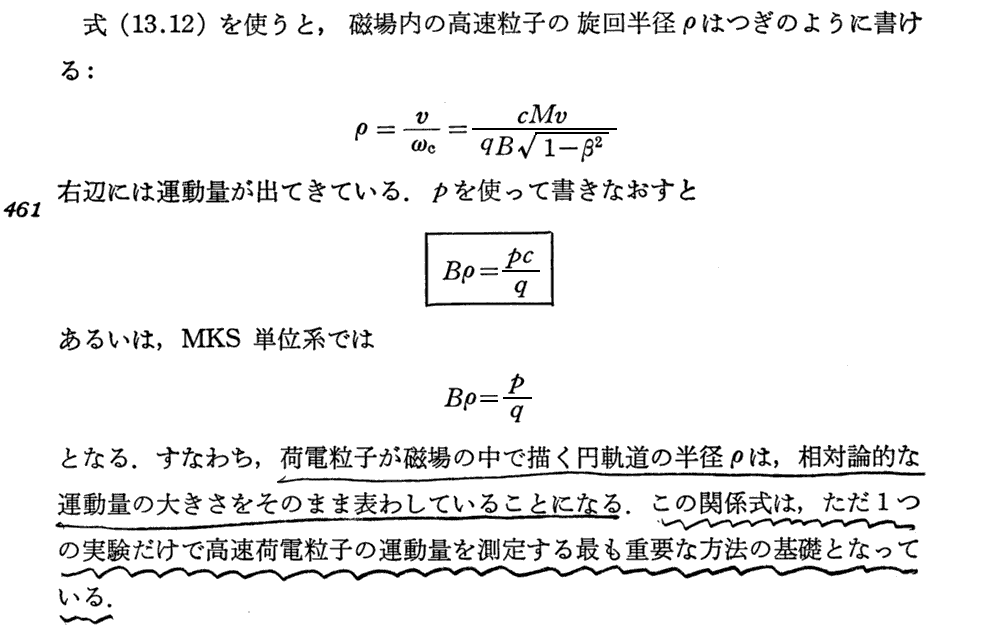
(4)重心系とエネルギー閾値
素粒子の生成と消滅に関して、エネルギー閾値が存在する。また、γ線(光子)は自由空間で可秤粒子に変化することはできない。これらは、特殊相対性理論が予言する事柄のなかでも特に重要です。





1.光子によるπ0中間子生成のエネルギー閾値

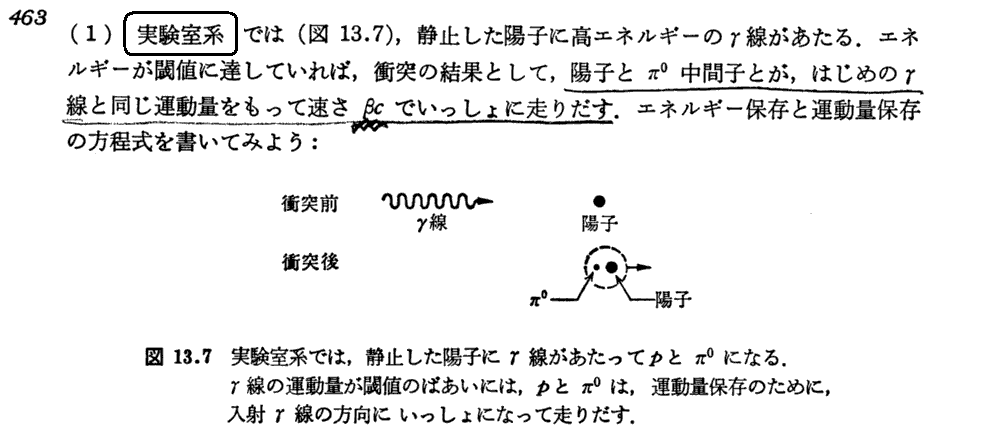
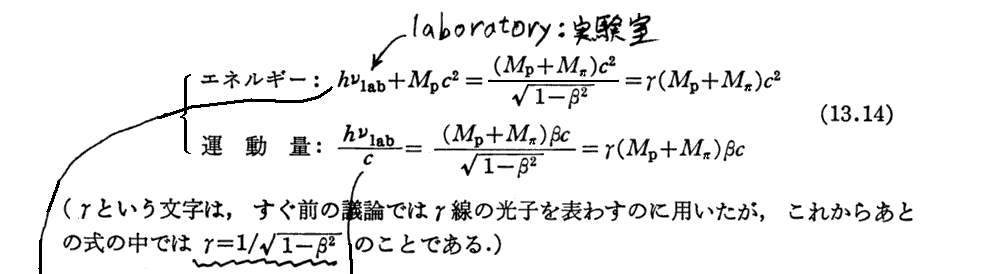
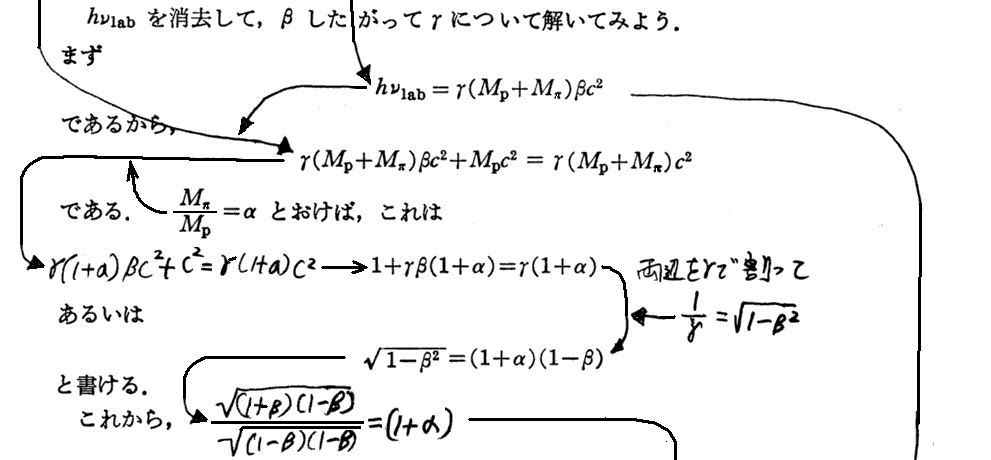
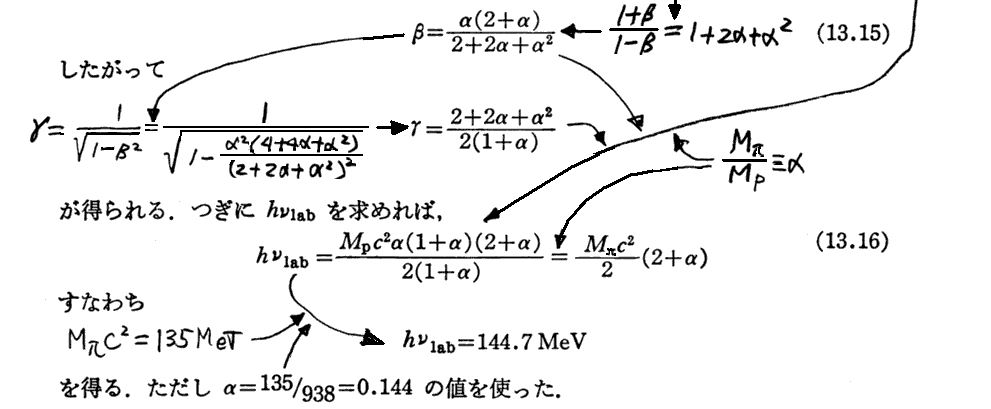
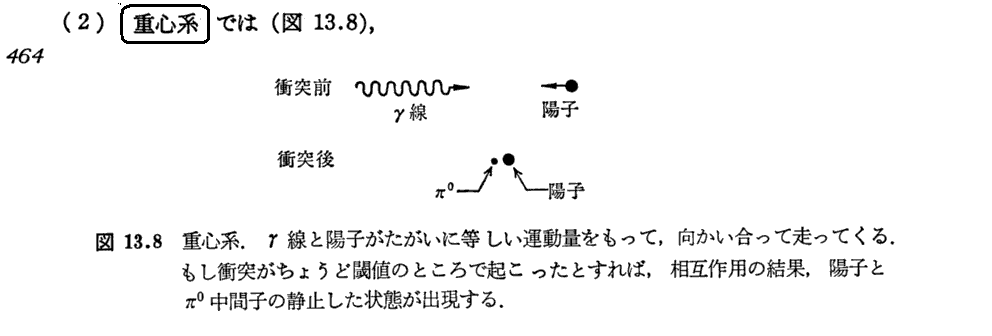
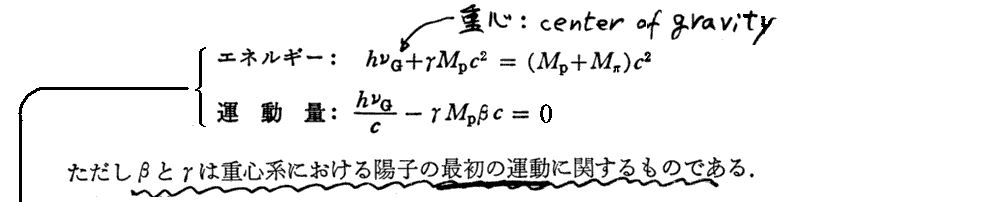
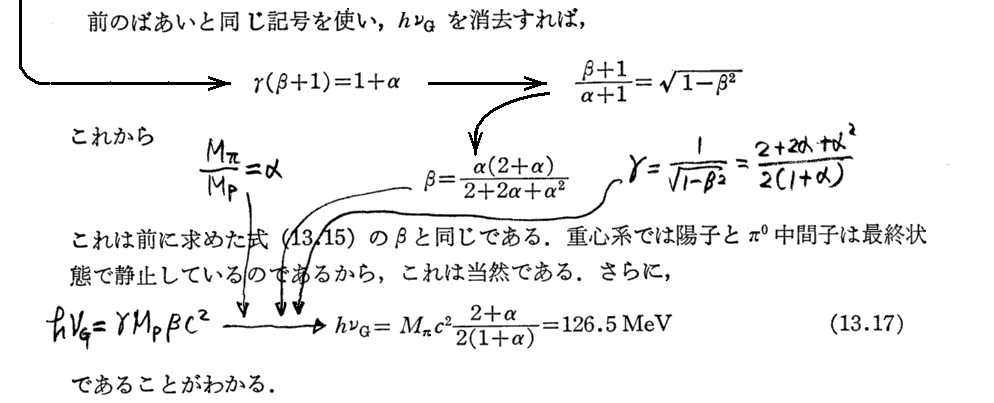
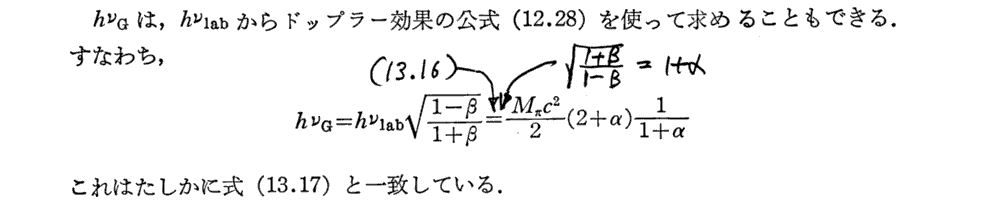
[(13.16)式導出についての補足]

[まとめ]

2.運動する粒子から取り出すことのできるエネルギー


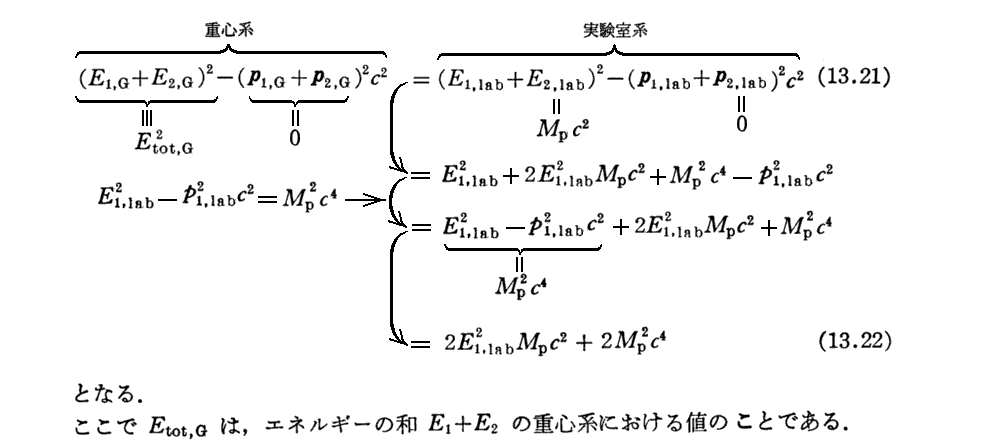
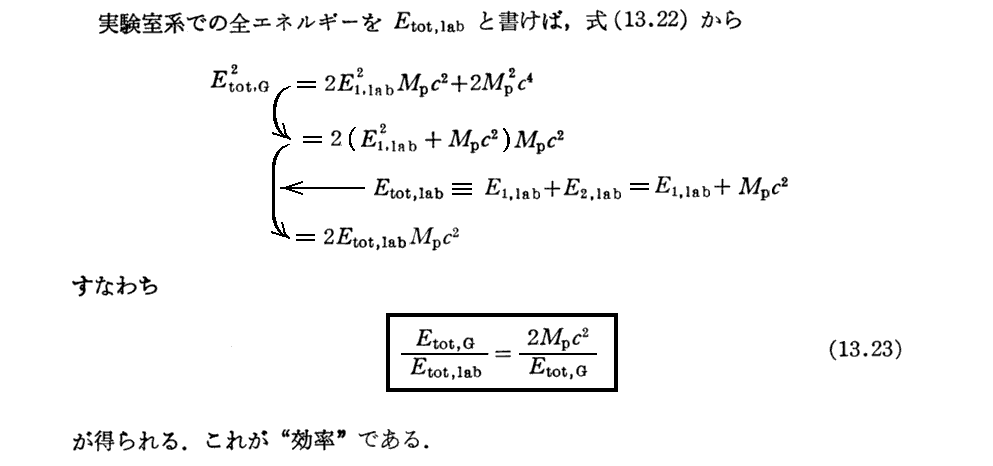

3.反陽子生成の閾値(いきち)


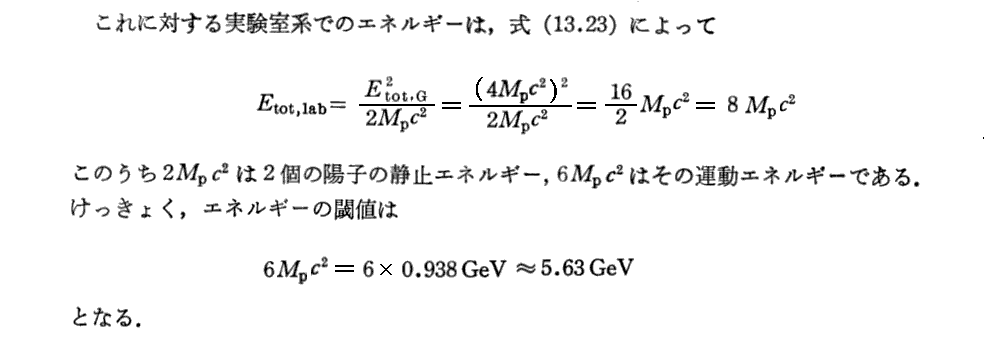

(5)光の粒子性
光の粒子性を証明したコンプトンの実験は、特殊相対性理論の検証実験としても重要です。
1.コンプトン効果

文中に記されているX線の波長(振動数)測定は、X線を結晶格子でBlagg反射させて、電離箱などを用いて行う。詳細は別稿「X線結晶解析におけるラウエの条件式とブラッグの条件式」を参照。
また、X線の散乱現象そのものについては、別稿の[補足説明2]を参照。
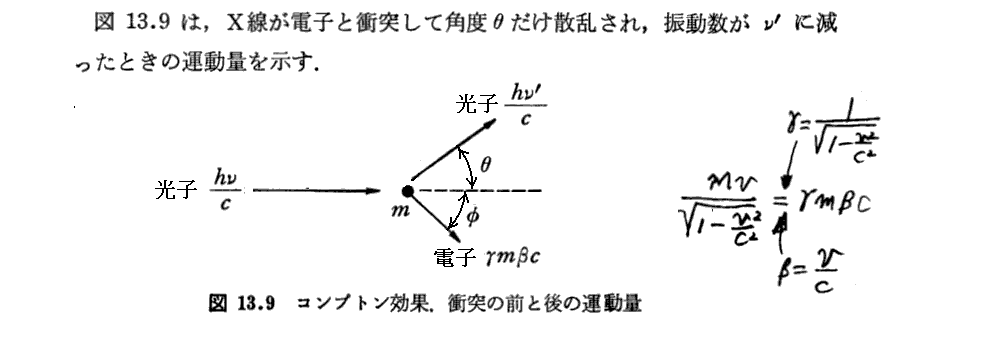
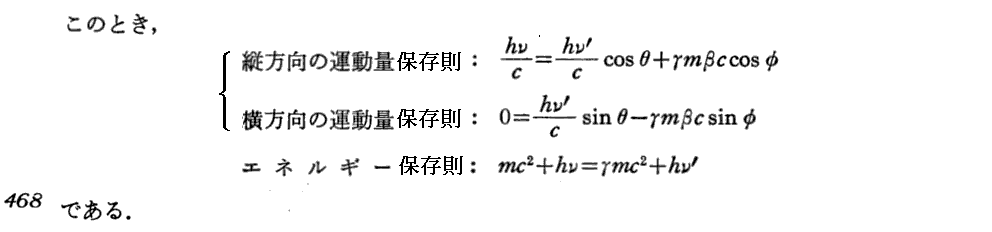

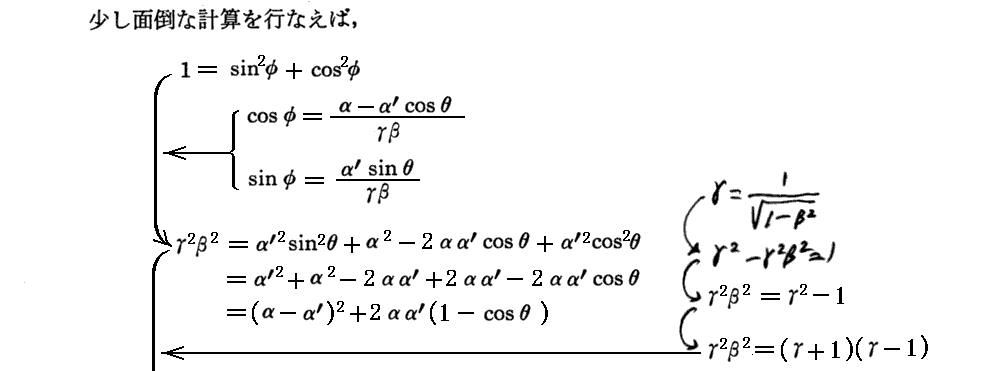
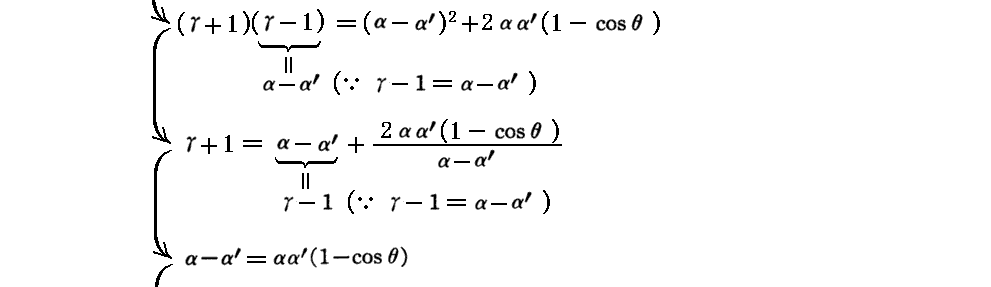
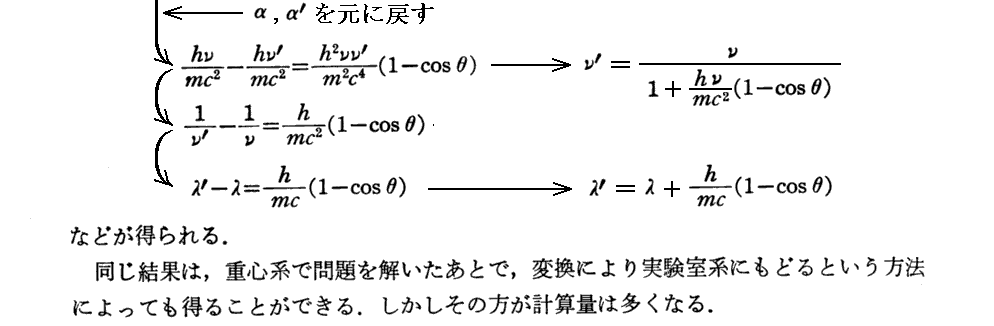
[補足説明1]
最後の式のλ’-λ≡Δλは、入射X線の波長に関係しないことに注意されたし。
ここで、h/mc(m=電子の静止質量)は“電子のコンプトン波長”と呼ばれ
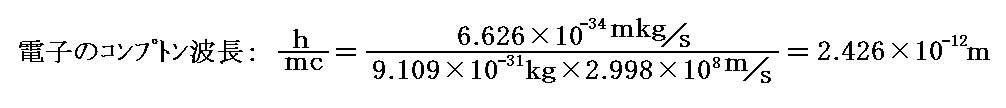
となるのだが、入射光子の波長に関係なく一定の値になる。
その為 (λ’-λ)/λ≡Δλ/λ~(コンプトン波長)/λ 程度となる。この比率は、入射光子の波長が短い(高振動数・高エネルギー)ほど大きくなり、その波長変化を明瞭に観測することができる。
[補足説明2]
コンプトン(Bulletin Nat. Res. Council., No.20, p16. 1922年)は、モリブデンMoの特性X線Kα(λ=0.708×10-8cm=70.8×10-12m)を黒鉛(炭素の結晶)に当ててθ=π/2に散乱された散乱X線波長λ’を測定した。測定値はλ’=73.0×10-12mでしたからλ’-λ=2.2×10-12mとなる。一方θ=π/2の場合の理論値はλ’-λ=h/mc×(1-cos90°)=“電子のコンプトン波長”=2.426×10-12mですから、観測値は理論値と良く一致する。
このとき、炭素原子の最外殻電子のイオン化エネルギーは11eV程度であることから、以下のことに注意されたし。
入射光量子が可視光の場合そのエネルギーは1.6~3.3eV程度です。一方、実験に用いた様なX線ではそのエネルギーはhν~17keV程度となり、最外殻電子の結合エネルギーの1000倍以上になります。そのため散乱される電子はほぼ自由電子であると見なす事ができる。
コンプトンが成功できたのは、ひとえに電子の結合エネルギーよりも遙かに高いエネルギーの(波長の短い)X線を用いたからです。実際、上記の例ではコンプトン波長は、([補足説明1]で述べたことから)入射光波長の1/30程度になりますから、波長の変化を観測できたのです。
[補足説明3]
一般的な散乱角を含めたコンプトン効果の詳細は、Comptonの論文 Phys. Rev., 21, p483~502, p715~, 1923年; 22, p409~413, 1923年、等々・・・、やComptonの著書「X-Rays and Electrons」(1926年刊)第Ⅸ章(これはnetから無料ダウンロード可)、あるいは
文献5.第4章§3 や 文献6.§124~§128 などを参照されたし。
上記論文中の Phys. Rev.,21, p483~502,1923年 は下記URLからもダウンロード可
https://www.aip.org/history/exhibits/gap/
[補足説明4]
コンプトン効果は光の粒子性を証明する実験として有名ですが、これは相対論的な力学方程式の正しさを証明する実験と見ることもできます。
散乱光子と反跳電子の方向の関係や電子が得る運動量の大きさを実験的に確かめる事ができます。そのことから、運動量保存則とエネルギー保存則は、前記の相対論的な運動量保存則とエネルギー保存則でなければならないことが確認できます。光を粒子であると見なすだけで他の部分を非相対論的な力学で計算すると、Δλ=λ’-λは相対論とは異なった式になります。
コンプトン効果が発見(1921年)された時代には、相対論的な運動方程式の正しさは、それまでに繰り返し行われた電子加速実験から、確認済みの事柄でした。そのため、コンプトン効果の説明では普通このことは強調されません。しかし、コンプトン効果による相対論的力学理論の正しさの確認も重要な事柄だと思います。
この事については別稿「コンプトン効果(1922年)と相対論的力学」で説明していますのでご覧下さい。
2.逆コンプトン効果
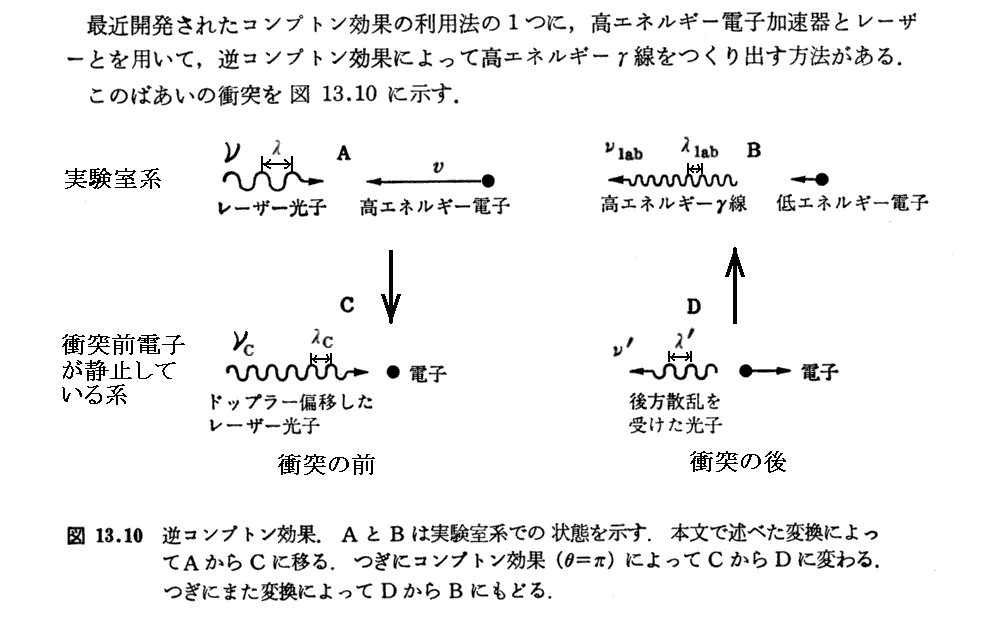

高エネルギー電子の速度で光子に近づいたときの光子のドップラー効果。導出は別稿3.(2)2.など参照。
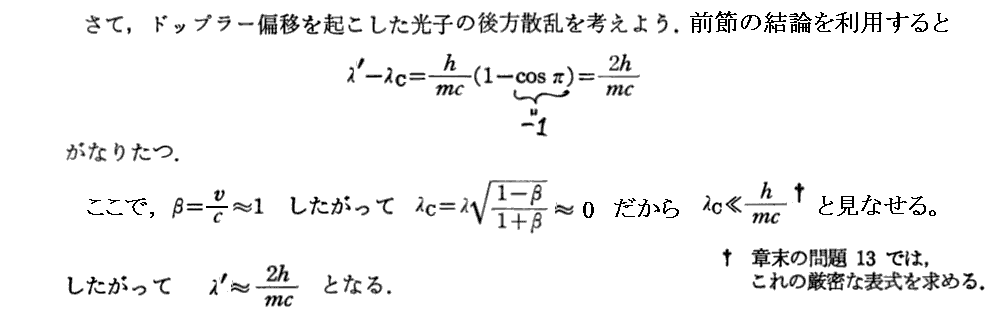


これは宇宙空間での高エネルギーγ線発生過程として重要です。
(6)文献3. 第13章末問題と解答
これらの問題を見れば、特殊相対性理論は素粒子・高エネルギー物理や天体物理で必須であることが解ります。













(7)粒子加速器

McMillanの論文はこちらで引用。


5.参考文献
- 物理学史研究会編「物理学古典論文叢書4 相対論」東海大学出版会(1969年刊)
この中の3. M.Planck著「相対性原理と力学の基本方程式」の翻訳を引用。この中の9.Lewis、Tolman著「相対性原理と非Newton力学」は別稿で引用しています。
さらに、第1論文、第2論文、第6論文、第7論文、第8論文も別稿で引用紹介しています。
- M.Born、W.Biem著(瀬谷正男訳)「アインシュタインの相対性原理」講談社(1971年刊)Gauss単位系
原本は1964年に発刊。1920年発刊の初版の改訂版です。Ⅵ章、Ⅶ章はかなり書き換えられています。本稿の第3章は、この本の第Ⅵ章§7~9に依存しています。
この本の第Ⅲ章、第Ⅳ章§7~11、第Ⅴ章、第Ⅵ章§1~6、10~11and§8の一部は別稿で引用。
- Kittel、Knight、Ruderman著「バークレー物理学コース1 力学(上巻)(下巻)」丸善(1975年刊)Gauss単位系
この中から第13章“相対論的力学の問題”と、第14章“等価原理”を引用しています。引用はしていませんが、第12章も教育的ですので、合わせてご覧下さい。
- C.メラー著「相対性理論」みすず書房(1951年刊)Gauss単位系
この本は少し難しい。本稿をご覧の後に第Ⅲ章“相対論的力学”を読まれると理解が深まります。
- 荒木源太郎著「原子物理学」倍風館(1964年刊)第4章3.コンプトン散乱
20世紀前半の原子物理学の発展を概観するには最適です。また章末の文献表は貴重です。
- E.シュポルスキー著「原子物理學Ⅰ」東京図書(1965年刊)
第9章§124~§128でコンプトン効果が説明されています。
- ジョン・グリビン著「シュレーディンガーと量子革命」青土社(2013年刊)
これからp117~120、p133~134、及びp136~139を引用。
- ランダウ、リフシッツ著「場の古典論(増訂新版)」東京図書(1964年刊) Gauss単位系
本稿をご覧の後に第1章§1~§7と第2章§8、§9をお読みになる事を勧めます。