コンプトン効果は光の粒子性を証明する実験として有名ですが、これは相対論的な力学方程式の正しさを証明する実験でもあります。この点も考慮してコンプトン効果を説明します。相対論的力学については別稿をご覧下さい。
まず最初にコンプトン効果発見以前の状況を振り返ります。
レントゲンによるＸ線の発見（1895年）以後、Ｘ線を原子の塊に当てたとき、それから新たなＸ線が生じる事が知られていました。これを“２次Ｘ線”と呼んでいたが、やがて２次Ｘ線には二種類あることがバークラ（1903年）などにより解ってきます。一つは入射Ｘ線と同じ波長のＸ線であり、他の一つは入射Ｘ線の波長とは異なり標的原子に特有なＸ線です。
もちろん当時はLaueの結晶によるＸ線回折発見（1912年）より以前ですから波長を直接測定する方法は在りません。Ｘ線の波長の見積には様々な工夫が必要でした。この当たりについて、別稿３．（３）１．［補足説明１］で引用したBarklaのノーベル賞功績説明を参照されたし。
このとき、この二種類を、別稿１．（４）で説明した1907年にバークラが見つけた二次Ｘ線中の二種類と混同しないでください。そこで言う二種類はこんにちＫ-Ｘ線とＬ-Ｘ線と呼ばれるもので、後にモーズリーによって対陰極物質から直接出て来ることが発見（1913年）される二種類の特性Ｘ線と同じものです。これも二種類の二次Ｘ線としても検出されますが、ここでの二種類の意味とは違います。
二次Ｘ線の一つの種類は、以下のメカニズムで発生する。１次Ｘ線によって標的原子のＫ，Ｌ，･･･殻から電子が光電効果によってたたき出されイオン化します。そのとき空席となった電子軌道に外殻から電子が落ち込むときBohrの理論に従って放出されるＸ線です。
これはBohr理論が説明する可視光線の場合の蛍光と同じ現象で、標的原子の種類により異なった性質（異なった硬さ、つまり物質透過性）を示し“蛍光Ｘ線”とも言われた。これは本質的には上記のモーズリーが発見したものと同じもので、次に述べる散乱Ｘ線ではありません。
もちろん、1903年当時はLaueの理論もBohrの理論も在りませんし、Ｘ線の波長を直接測定する方法も在りませんでしたから、バークラは様々な工夫をして、その特徴を特定したのです。
もう一種類が本来の“散乱Ｘ線”です。これは標的原子の外殻の電子が入射Ｘ線により揺り動かされて、新たに入射Ｘ線と同じ振動数のＸ線を二次放射線として放出するものです。この散乱Ｘ線は1903年にバークラが見つけていますが、この現象を最初に取り上げて理論的に説明したのはJ.J.Thomsonです。
そのメカニズムは別稿「線形振動子（電気双極子）による電磁波の放出」３．（２）で説明しました。これは、Bohrの原子構造論が出る前の古典的見地から論ぜられたもので以下の様なものです。
Ｘ線を電磁波とみて、これが原子に当たると原子中の電子に周期的な電場が作用して強制振動を誘起するとする。マックスウェル・ローレンツの電子論によれば、振動する電子は電磁波を放出する。この電磁波の周期は電子の振動周期、つまり入射Ｘ線の周期に一致する。これが散乱Ｘ線です。
これは、散乱Ｘ線の偏光状態や散乱強度分布などを予言します。実際、1906年に行われたバークラの実験はThomson理論が予言する散乱Ｘ線の偏光を実証し、Ｘ線が電磁波であることの証明として非常に注目されます。また、トムソンはバークラが得た散乱Ｘ線の強度から原子内電子の電子数を見積もり、それが原子番号程度であることを示します（1906年）。
これらの成果は、Laueの結晶によるＸ線回折実験（1912年）より前のＸ線の本性が何か良く解っていなかった時代のものですから、特に注目に値します。
しかし、別稿３．（３）２．［補足説明２］でも述べたように、入射Ｘ線の波長がバークラが用いた領域をはずれたり、あるいは標的原子がより重くなると、その全散乱強度も散乱強度の角度分布も単純なThomsonの散乱理論では説明できなくなります。
実測値を正しく説明するには、原子まわりの電子の分布状況も考慮した量子力学的な散乱理論が必要で、それらが達成されるのは1930年代以降です。［この当たりの詳細は文献3．の第11章をご覧ください。］
1904年にEveは、γ線を一度物質に当てて散乱させると散乱線の透過度が著しく落ちることを認めた。その後多くの人が、この問題を実験的に研究し、透過度の変化は散乱角に関係することや、その変化は物質にあまり関係しないことを確かめた。
一方、Ｘ線については、Barklaによって1904年に散乱線は１次線よりも透過度が悪いことが認められた。しかし、これはＸ線の照射をうけた物質から、その物質固有の蛍光線を出すためと考えられた。それまでの研究から、蛍光線は１次線より波長が長く、透過度が落ちることからが解っていたから、そう考えられたのです。
ところがその後、炭素のように原子番号が低くＫ、Ｌの蛍光線を出さないと考えられていた原子から出る２次Ｘ線についても同じ現象が起こることが認められるに及んで問題が紛糾してきた。
上記の現象を説明するために、BarklaはＫ準位の下にさらに他の吸収帯があるのであろうと考えて、これにＪ系列（ＪはアルファベットのＫの一つ前）の名を与え、それに対応する蛍光線が出るのであろうとの仮説を出していた。これが1917年度のノーベル賞受賞記念講演で、Barklaが述べているＪ系列です。しかし、これは、結局間違っていました。実験的にその吸収帯を確かめることも、放射線のＫ-Ｘ線よりも更に短い波長のＪ-Ｘ線を認めることもできなかったのです。
そのため、1920年のはじめ頃には、この現象は蛍光Ｘ線とはまったくことなる機構によっておこるものと考えられるようになった。
［細説明１］
上記の炭素の様に軽い元素のＫ、Ｌ蛍光線についてですが、別稿「モーズリーの法則（1914年）と周期律における原子番号」で説明した時代（1913年）まで下がると、その意味はハッキリと理解されます。そこで示したグラフをご覧になれば解るように炭素などの軽元素もＫ-Ｘ線、Ｌ-Ｘ線を放出することが予想されます。
しかし、そのグラフから予想されるように軽元素の出すそれらのＸ線は波長が10Å以上の長いもので、当時（1910年代以前）の技術では測定することができなかったのです。そのため当初、軽元素はＫ-線、Ｌ-Ｘ線を出すとは考えられていなかった。
Comptonが1927年のノーベル賞受賞記念講演で述べているように、軟Ｘ線～極紫外線（10Å～2000Å）領域の光（電磁波）の波長が全て測定できるようになるのは1920年代に入ってからです。それは別項「アボガドロ数の測定法」３．で説明したＸ線の全反射を光学的回折格子に適用して行う方法に依るもので、このことに関してComptonは大きな貢献しています。
いずれにしても、1910年代はその領域のＸ線については混沌とした状況でした。コンプトンの発見はこのような状況下で成されたものです。
コンプトンは下記の実験に先立って予備的な実験（Phys. Rev., 21, p483～502, 1923年など参照）を行っていますが、ここではPhys. Rev., 22, p409～413, 1923年に発表された決定稿の論文に従って説明します。
前項で説明したような状況の中で、1922年にComptonは下図に示すような装置を用いて２次Ｘ線を詳細に調べ２次Ｘ線の波長変化の様子を明らかにします。
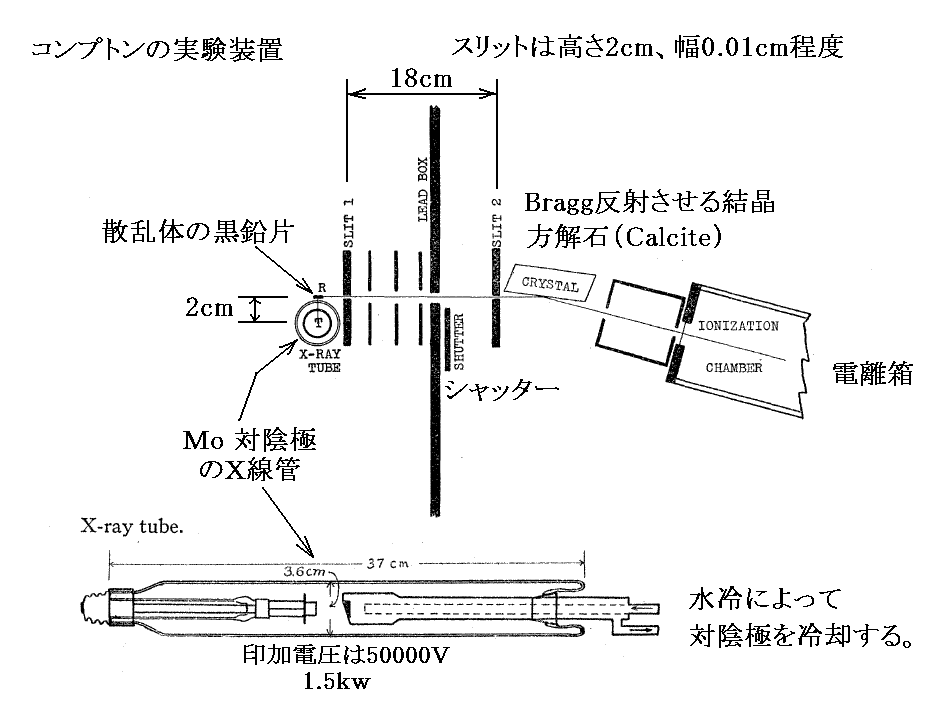
対陰極にＭo（モリブデン）を用いたＸ線管が使用された。ちなみにＭoの特性Ｋα-Ｘ線の波長は0.711Åで、１光子のエネルギーは約17400ｅＶです。これは炭素原子核を取り巻く全ての電子をはぎ取ってイオン化するエネルギーの合計値よりも大きい。
できるだけ強いＸ線を得るために、水冷管によって強力に冷却したＸ線管に50000Ｖの印加電圧で大電流（1.5ｋｗ）を流した。これは普通のクーリッジＸ線管の125倍の放射強度を持つ強力なものであった。また、強力な散乱Ｘ線を得るために、Ｘ線管のＭo極とグラファイト標的Ｒの距離をできるだけ近く（距離2ｃｍ）に設置して実験を行った。
そのとき、Ｒを中心としてＸ線管を回転移動させて、装置の他の部分を動かさないままで、散乱角を変化させることができるようにしてあった。
この様に強力なＸ線源を用いたことが、Comptonが明瞭な結果を得ることができた理由と思われる。
散乱Ｘ線の波長別の強度分布は“Braggのスベクトロメーター”で測定された。この方法については別稿「Ｘ線結晶解析におけるラウエの条件式とブラッグの条件式」４．（１）２．を参照されたし。
また、モリブデンが発する特定Ｘ線（Ｋα-Ｘ線）については別稿「モーズリーの法則と周期律における原子番号」４．（２）を参照されたし。ちなみにＭoの特性Ｋα-Ｘ線の波長は0.711Åで、１光子のエネルギーは約17400ｅＶ≒17ｋｅＶです。これは炭素原子核を取り巻く全ての電子をはぎ取ってイオン化するエネルギーの合計値よりも大きい。
コンプトンの発見は、それに先行するブラッグ親子（1912～1913年）やモーズリーの研究成果（1913～1914年）に大きく依存しています。
コンプトンの得た結果を下図に示す。
最初の源泉Ｘ線グラフの縦軸強度値とその下の三方向での２次Ｘ線グラフの縦軸強度について、同じスリット幅で観測した場合には前者が圧倒的に強くなる。そのため下図の縦軸のスケールは適当に調整して変えてある。
また左右のグラフの違いはスリット幅の違いに依る。
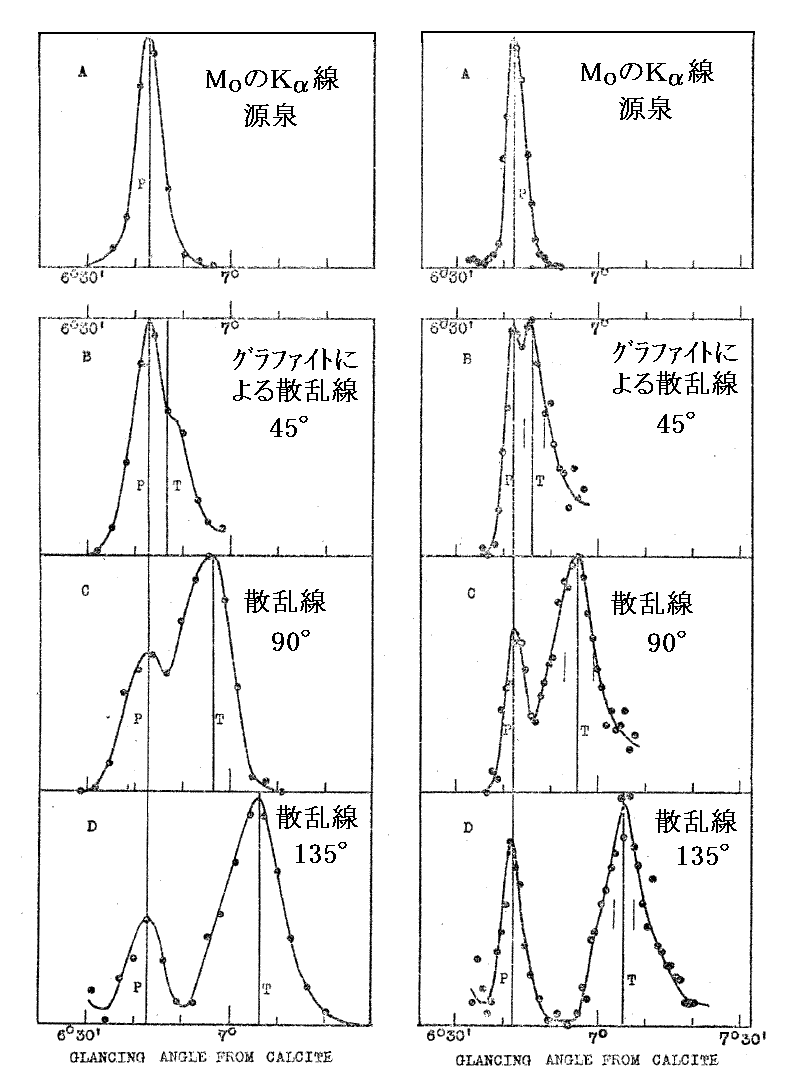
下の三つのグラフは、入射Ｘ線の方向に対してそれぞれ角度（45°、90°、135°）の方向に散乱された散乱Ｘ線の強度の波長変化の様子を表している。横軸は方解石（Calcite）結晶面と電離箱の方向が成す角を表しており散乱Ｘ線の波長に関係する。
このグラフから以下の事柄が読み取れる。
［補足説明２］
この実験が、軽い元素である炭素（グラファイト）を散乱体として行われたことに注意してください。後に解るのですが、標的原子が重い元素の場合コンプトン散乱する２次Ｘ線の強度は弱くなります。
１．（２）１．でも注意しましたが、Ｘ線を物質に当てたときに出る２次Ｘ線は、多くの人々によって研究されていました。そのとき、特に軽い元素による２次Ｘ線のなかに、蛍光Ｘ線とは違った性質のＸ線が含まれていることが解っていたのです。［J.Laub, Ann. der Phys., 46, 785, 1915年；j.A.Crowther, Phil. Mag., 42, 719, 1921年］
その２次Ｘ線は当てた１次Ｘ線よりも柔らかかったのですが、蛍光Ｘ線の様に散乱元素の種類によるようには思えなかったのです。［J.A.Gray, J.Franklin Inst. 190, 633, 1920年］
前章で得られた実験結果に対してComptonは見事な説明をした。それはアインシュタインの唱えた光量子説と相対論的力学を用いるものです。
コンプトンは前章で説明した結果を説明するために光の粒子説と相対論的力学を用いた。
光がアインシュタインの言うようにエネルギーと運動量を持った粒子であると考え、それがほぼ自由な状況にある電子に衝突して電子をはね飛ばし、自らは入射方向とは異なる方向にはじき返されると考える。
そのとき、はね飛ばされる電子は速度ｖを得るのだが、その質量ｍは相対性理論（別稿「相対論的力学」を参照）が示唆するように
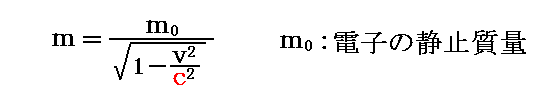
に従って変化していると考える。
その為、光子の衝突によって生じる反跳電子の運動量ベクトルは
となり、エネルギーは
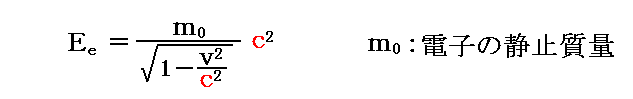
となる。
一方、光子については、ｖ＝ｃだから上記の質量公式が使えないが、特殊相対性理論に従って光は光速度で移動するため静止質量はゼロだと考える。そのとき光は光速度ｃで移動する粒子と考えて慣性質量を持つすると、特殊相対性理論（別稿「アインシュタインの公式 E=mc2 の証明を参照）が示唆するように、そのものが持つエネルギーＥをｃ2で割った値が慣性質量であるとすることができる。
そのため光子は
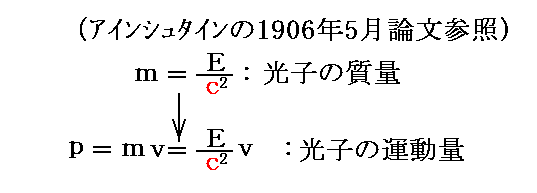
で表される運動量を持っている考えることができる。これは光に対しても正しい運動量表現です。
この式に、ｖ＝ｃを代入すると
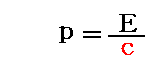
がえられる。これは元々古典的なマックスウェルの電磁気学方程式から得られるものと一致する。
ここで、光子のエネルギーは“アインシュタインの光量子説”によるとＥ＝ｈνだから
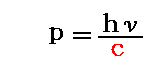
となる。これが光子の運動量を表す式です。
［補足説明１］
マックスウェルは、電場の力線に関するファラデーの直観的表象から出発して、光圧を力管の横方向の圧力の結果と考えて光の圧力を導き出していた。これはP.Lebedew（1901年）や、E.F.Nichols
と G.F.Hull（1903年）により実験的にも確認されていた。
その後、アインシュタインの光量子説と特殊相対性理論により、光が粒子としてエネルギーと運動量を持ち、光子の流れが障害物に当たると、丁度気体分子が容器の壁にぶっかる結果が重なって平均に於いて気体の圧力になるのと同様に、その障害物に対して圧力を及ぼすと考えられる様に成ってきた。
光圧の存在が、光の本姓の粒子像からも波動像からも導かれるということは、すでにたびたび強調した光の２重性の現われの１つです。
別稿「光の圧力」３．（２）［補足説明１］や別稿「アインシュタインの特殊相対性理論」２．（１０）３．［補足説明］を復習されたし。
Comptonは前節の仮定の元で相対論的力学議論を行った。
電子は衝突前に静止しているとして、衝突前の運動量はｐe＝0、エネルギーはＥe＝ｍ0ｃ2となる。光子と衝突後の電子は運動量ベクトルｍ･ｖとエネルギーｍｃ2を持つとする。ｍは前節に述べた相対論的な慣性質量で、ｖは衝突後の電子の速度ベクトルです。
一方、光子は最初ｈνのエネルギーとｈν／ｃの運動量を持ち、電子との衝突後にｈν’のエネルギーとｈν’／ｃの運動量になったとする。
この衝突現象に運動量保存則とエネルギー保存則を適用する。
まず、（１）（２）式で表される運動量保存則から、運動量ベクトルは下図の平行四辺形関係ＡＢＣＤを満たす。
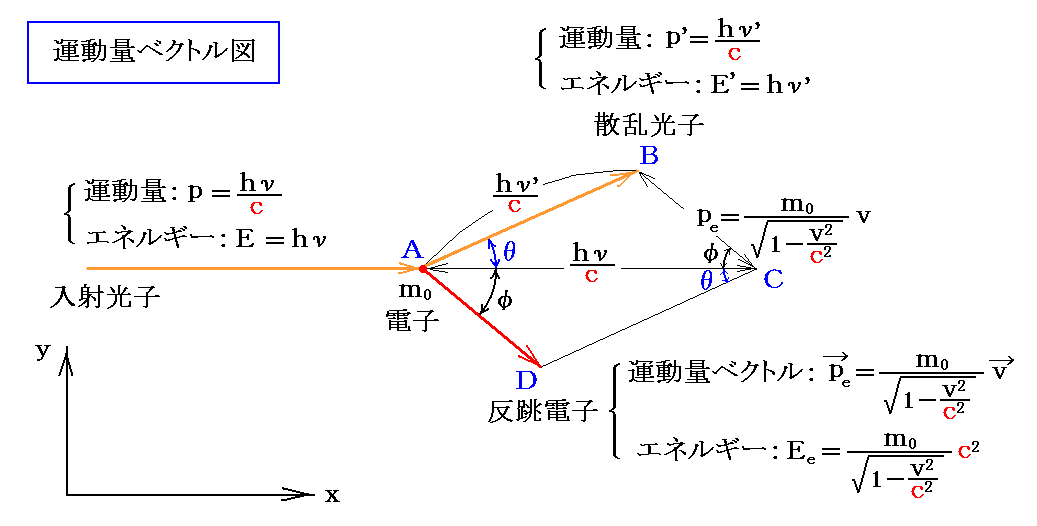
上図の三角形ＡＢＣに対して三角関数の余弦定理を適用すると
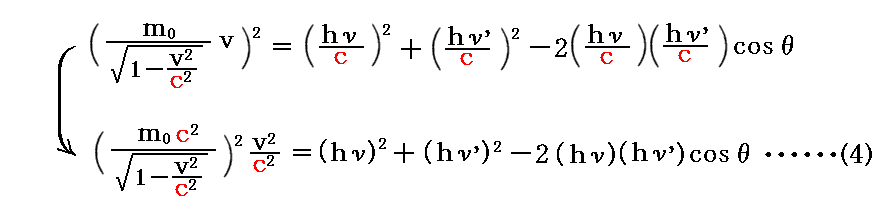
が得られる。
一方、エネルギー保存則（３）式より
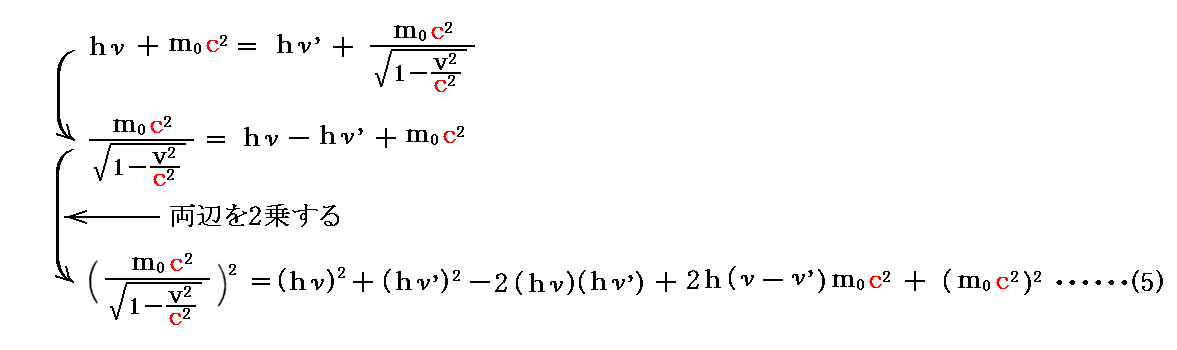
が得られる。
（５）と（４）式の片々を引き算して（５）－（４）を計算すると
が得られる。（６）、（７）式は散乱Ｘ線の振動数あるいは波長の変化量と散乱方向θの間の関係を与える。
ここで、ｈ／ｍ0ｃ （ｍ0＝電子の静止質量）は“電子のコンプトン波長”と呼ばれ
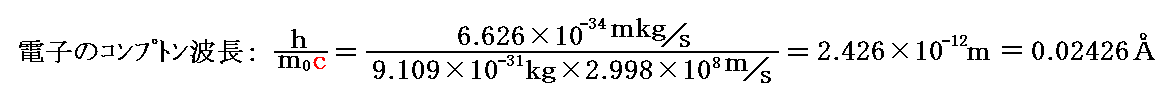
となる。
もちろん、反跳される粒子が電子ではなくて陽子などの場合には、ｍ0はその静止質量に置き変えて“陽子のコンプトン波長”と呼ばれる事になる。
（７）式を用いて、光子の散乱角度θと波長の伸びλ’－λ≡Δλの関係をグラフ表示すると
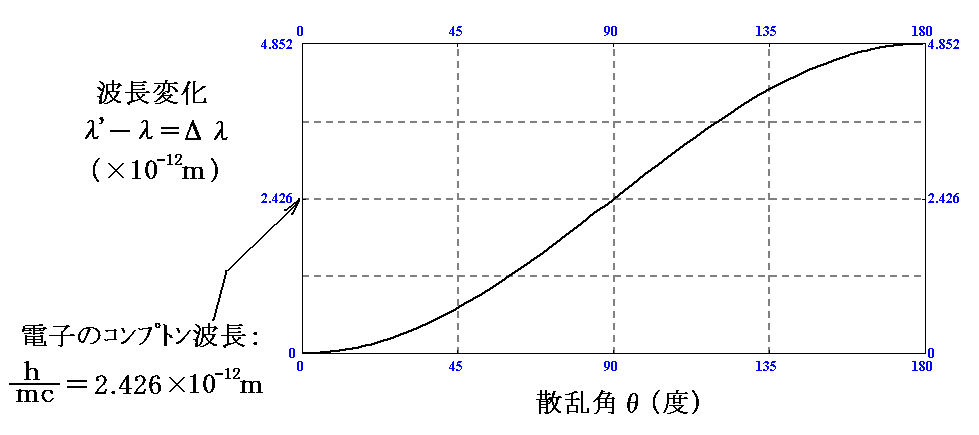
となる。
この理論値から計算される散乱角45°、90°、135°方向の散乱２次Ｘ線の波長が、前節１．（２）２．の実験観測結果のグラフピーク値と比較された。その結果は誤差0.001Å程度以下で観測値と極めて良く一致した。
（A.H.Compton, Phys. Rev., 22, p409～413, 1923年）
同様な結果は、ラジウムＣから放射されるγ線（波長λ＝0.022Å）を用いた実験観測値からも得られていた。この測定値は上記のMoのＫα線の実験ほどの精度はなかったが、それでも理論の正当性を十分に確認できた。
（A.H.Compton, Phys. Rev., 21, p483～502, 1923年）
［補足説明１］
コンプトン効果の理論では、散乱される光子は原子の外殻に存在するほとんど自由な状態にある電子によって散乱されるとしている。そのためコンプトン効果における散乱光子の波長変化量は散乱体原子の種類に依存しないはずです。
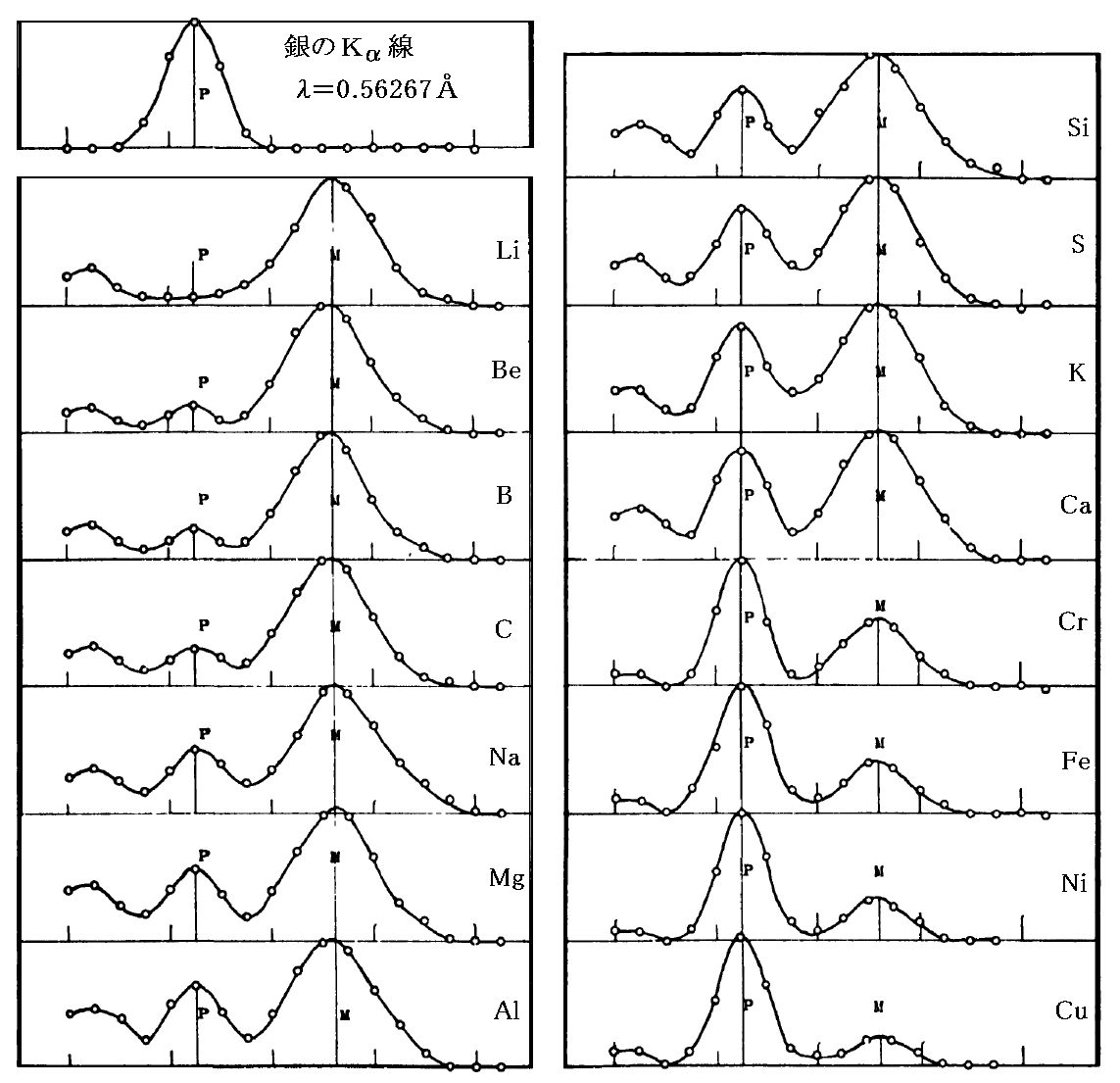
このことは、1926年にコンプトン研究室のウーによって広範囲の元素に対して確かめられた。Wooは銀の対陰極が発生するＫα-Ｘ線（λ＝0.56267Å）を15種類の標的元素（リチウム～銅）に当てて、同一の角度（θ＝120°）方向に散乱される散乱光子の波長を調べた。その結果、下図に示す様にコンプトン効果に伴う波長変化が散乱体原子の種類によらず全て同一であることが示された。
（Y.H.Woo, Phys. Rev., 27, p119, 1926年; 28, p426, 1926年）
［補足説明２］
ウーの実験は、さらに興味深い事実を示している。それは波長変化していない散乱Ｘ線強度と波長変化している散乱Ｘ線の強度について、波長変化しないものの割合が散乱体原子の原子番号と共に増大しており、波長変化するもの割合が次第に減少することである。この事は、以下の様に説明される。
Ｘ線がコンプトン効果を受けるには、ゆるく結合した電子で散乱されることが必要である。軽い元素中の電子は原子核にゆるく結合されているのでほとんどがコンプトン散乱によって散乱されることになる。ところが重い標的元素では原子核に強く結合した電子の割合が多くなる。このような電子でＸ線が散乱されると、その電子は原子核と一体となって反跳する。
光子は原子全体と衝突することになるから、（７）式中のｍ0は電子の質量ではなくて原子そのものの質量と考えなければならなくなる。そのため散乱Ｘ線の波長はほとんど変化を受けなくなる。原子核と強く結合した電子の割合が増える重い元素では当然波長変化しない散乱の割合が多くなる。上図はそのことを示している。
このことに関して１．（２）２．［補足説明２］も振り返られたし。
さらに、上記二種類の散乱Ｘ線の強度分布に広がりがあるのは、原子中の電子は完全に静止しているわけではなくて、元々いろいろな運動量を持っているためと考えられる。
［補足説明３］
（７）式の波長変化量は入射する光の波長λに依存しないことに注意されたし。つまり、λ’－λ≡Δλは光子散乱方向Θには関係するが、入射Ｘ線の波長λに無関係である。そのためより波長の短い（エネルギーの高い）光子を用いれば入射波長λと同程度以上の波長変化Δλを生じることになる。
このことは、1931年にデュモンドとカークパトリックが、対陰極元素をモリブデン（λ＝0.711Å）、銀（λ＝0.563Å）、タングステン（λ＝0.213Å）に変えて、波長の違うＫα－Ｘ線がθ＝155°の方向に散乱されるときの波長変化を調べて確認した。
（J.W.M.DuMond and H.A.Kirkpatrick, Phys. Rev., 38, p1094, 1931年）
最初は、散乱Ｘ線の波長変化量Δλと散乱角θとの関係を実験と比較することで、コンプトン効果の理論の正当性が確かめられた。その後、理論の正当性をより確かなものにするために、更に以下の検証が行われた。
ボーデとガイガーは、Ｘ線の散乱と電子の反跳が同時に起こることを巧妙な方法で確かめた。
（W.Bothe und H.Geiger, Zeits. f. Phys., 26, p44, 1924年； 32, p639, 1925年；Naturwissenschaften, 20, p440, 1925年）
下図は彼らの用いた装置で、右の模式図はその主要部分を示している。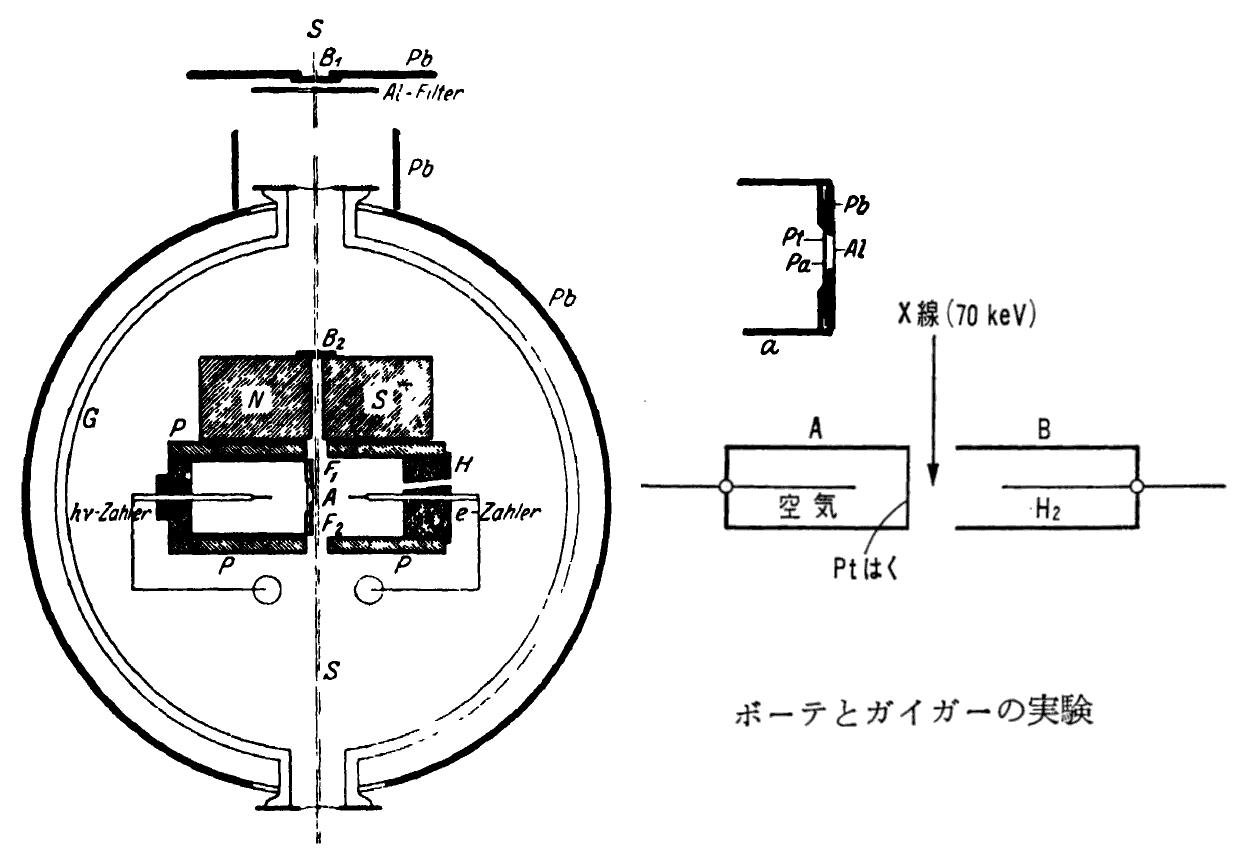
彼らはＡとＢの針頭計数管（一種のガイガーカウンター）を向かい合わせに置き、その間へＸ線を通した。Ａの計数管は薄い白金箔でふさがれ、内部に空気が満たしてある。一方Ｂの計数管は水素の中に置かれ、その入り口は開放されている。Ｘ線を水素ガス中を透過させたのは、水素はＸ線をあまり吸収しないが、散乱は充分に強く起こるからです。
Ｘ線がＡＢ間の水素で散乱されると、反跳電子は白金箔に遮られてＡの計数管に入ることができない。ところが、計数管Ａは光子（散乱Ｘ線）には感ずる。光子は箔を通り抜けて空気や計数管壁や箔自身から光電子をたたき出すからである。
一方計数管Ｂはほとんど光子（散乱Ｘ線）には感じない。なぜなら、光子は水素では極めて弱くしか吸収されないからである。しかし反跳電子には強く感じる。
当時は、真空管回路によって同時放電を記録する方法はなかったので、ＡとＢの計数管出力を直線ストリング電位計に導いて、電位変化が光学的時間目盛りとともに移動して写真看板上に記録される様にした。下図がその写真乾板の1例です。一方の曲線がＡ計数管の電位変化をもう一方がＢ計数管の電位変化を示す。乾板上の縦縞は時間間隔を示す目盛りで、その間隔は0.001秒になるようにしてある。
ＡとＢが互いに連携しないでカウントした事象もあったが、彼らはトータル5時間の観測中にＡとＢがほぼ同時にカウントする事象を66回見つけた。彼らは、統計的に考察することで、光子の散乱と電子の反跳が確かに同時に起こっている事を確認した。
［補足説明１］
Botheは、上記の実験の後で、さらに以下の実験を行った。（W.Bothe, Z. Phys., 37, p547～, 1926年）
それは蛍光Ｘ線が発生する場合に、エネルギーは波動説に従った球面波の形ではなくて、方向を持った光子の形で放出される事を下図の様な装置で確認した。
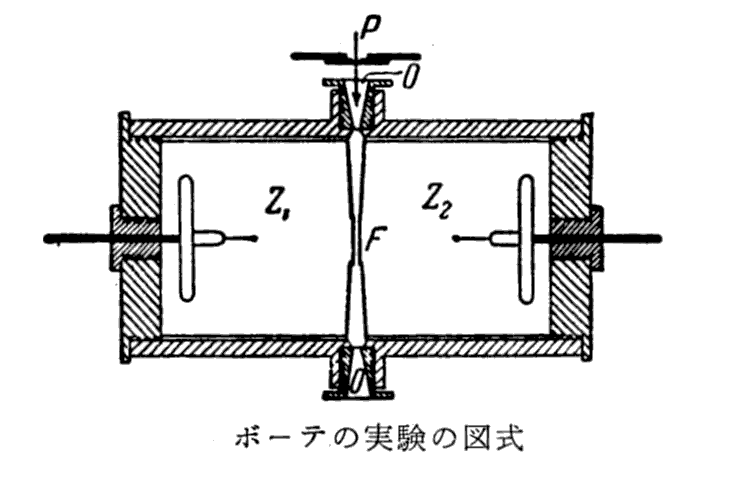
ボーデは薄い鉄または銅の箔Ｆを二つのガイガー計数機Ｚ1とＺ2の間に垂らした。十分な硬さの１次Ｘ線を上から矢印Ｐの方向に入射させ、箔を照射した。照らされた箔は蛍光Ｘ線を放出する。もしこの輻射のエネルギーが古典的な波動論のように球面波の形で伝播するのなら、両方の計数管が同時に反応するはずです。
ところが、実験結果は計数管は互いに独立にばらばらにカウントしたのである。同時にカウントする場合もあったが、それは偶然の一致として期待されるよりも多くは無かった。つまり発生する蛍光Ｘ線は方向を持った光子の形で伝播し、必ず一方の計数管でのみ捕らえられたのです。
［補足説明２］
この節で説明した、実験は1923年に提案された量子の振る舞いについてのボーア・クラマース・スレーター（BKS）理論を明確に否定したものとして有名です。BKS理論の顛末については、A.Pais著「神は老獪にして」第22章や「ニールス・ボーアの時代」第11章をご覧下さい。
ガイガーとボーテが開発した尖針係数管を複数用いた実験は同時放電法と言われ、その後の原子物理学や宇宙線物理学の実験でめざましい成果を上げることになる。
また、ボーテがベッカーと行った（後に中性子であることが判明する）ベリリウム線を発見した実験も有名ですが、同時放電法は原子核反応の研究にも重要な働きをします。
ボーテが行った一連の実験は量子論の解釈について実験的根拠を与えたということで、Botheは、Max Bornと共に1954年のノーベル物理学賞を受賞します。ボーテのノーベル賞講演は当時の実験物理学の状況を説明するものとして興味深い。しかし、このときすでにボーテは不治の病（1957年に死去）に冒されており、講演は口頭では成されなかった。
当（２）節と次（３）節に於いて、後の（４）、（５）節で述べる実験・観察結果を説明するときに拠り所となる式を導く。
２．（２）では、散乱光子のエネルギー変化（波長変化）と散乱角θとの関係を求めた。それを今一度まとめておく。
（６）式から光子が散乱によって失うエネルギーは
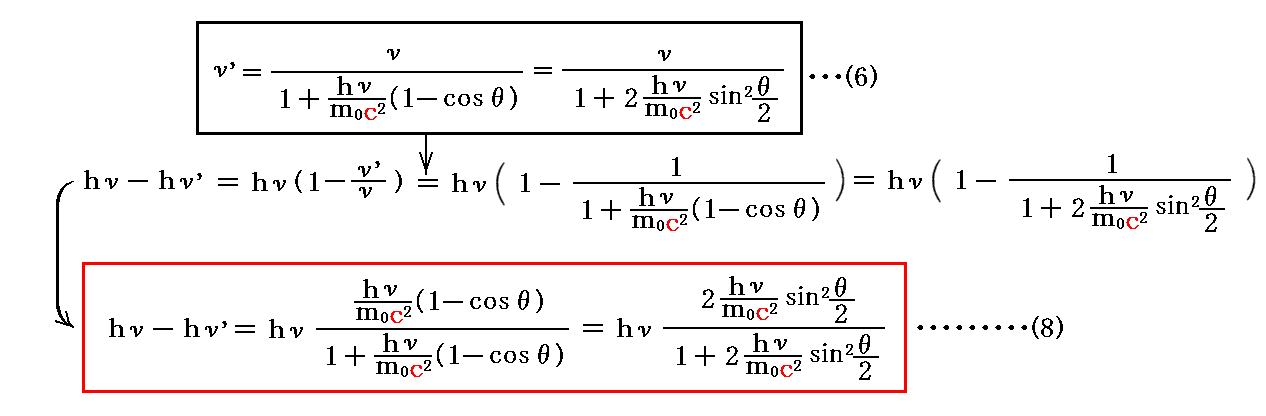
となる。
そのため散乱光子のエネルギーｈν’と散乱方向θは
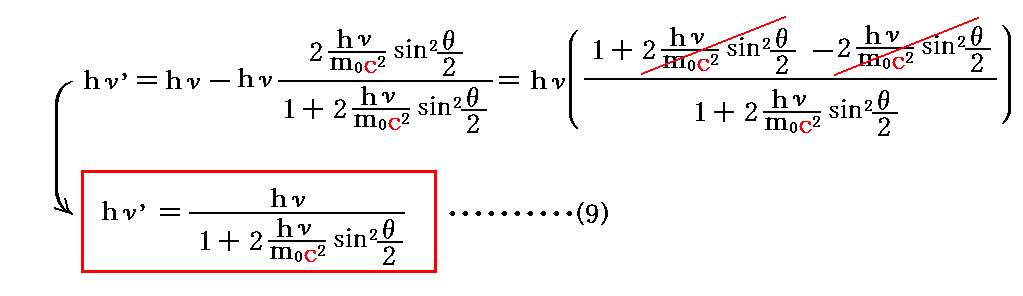
の関係で結び付けられる。ここでｈνは入射光子が持つエネルギーです。
上記の式から、光子が散乱によって失う運動量は
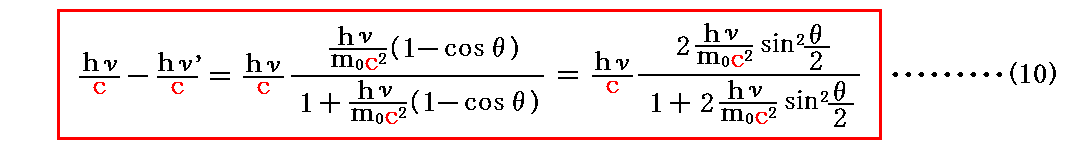
となる。
散乱光子の運動量と散乱方向θの関係は、(９)式の両辺をｃで割れば得られる。すなわち
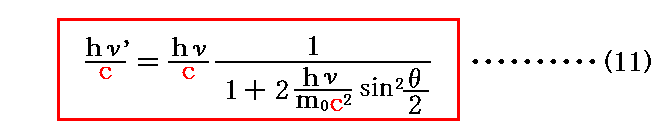
となる。ここで、ｈν／ｃは入射光子が持つ運動量です。
反跳電子が獲得する運動エネルギーおよび運動量と光子の散乱角θとの関係を求める。
最初に、反跳電子が得る運動エネルギーＥkinを２．（２）のエネルギー保存則（３）式から求める。別稿「相対論的力学」３．（３）で説明した“相対論的運動エネルギー”Ｅkinの定義を思い出すと
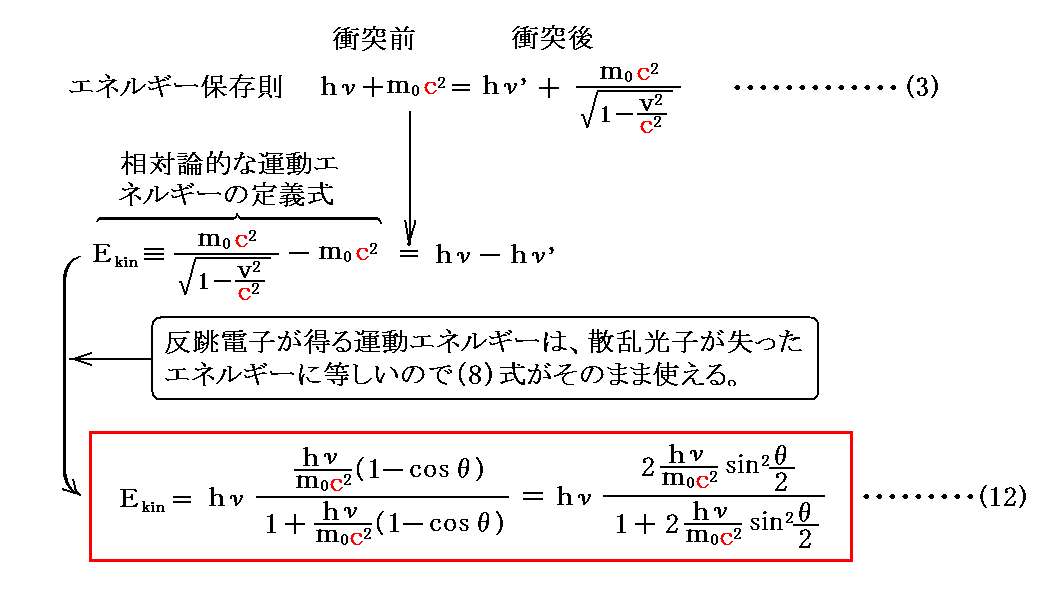
が得られる。
反跳電子が得るエネルギー（運動エネルギー）は入射光子の散乱方向θのみならず、入射光子のエネルギーｈνにも関係することに注意されたし。
次に、反跳電子が得る運動量ｐe＝ｍｖを求める。２．（２）で説明した運動量関係を示す三角形ＡＢＣに対して余弦定理を適用すると
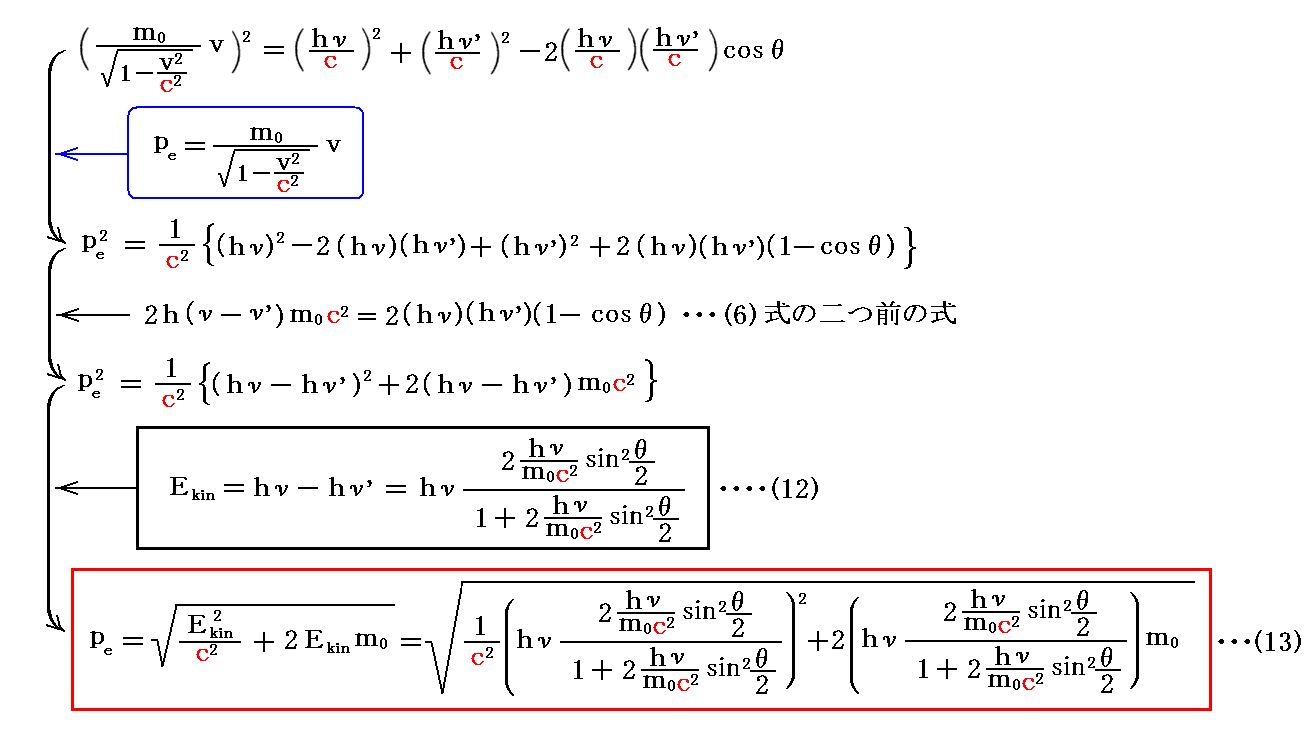
が得られる。
これが衝突前に静止（運動量ゼロ）していた電子が、光子によって反跳されたときに得る運動量ｐeです。
もちろんこれは、別稿「相対論的力学」３．（４）で求めた、電子の持つ運動量ｐeと総エネルギーＥeと静止質量ｍ0ｃ2との間に成り立つ一般的な関係
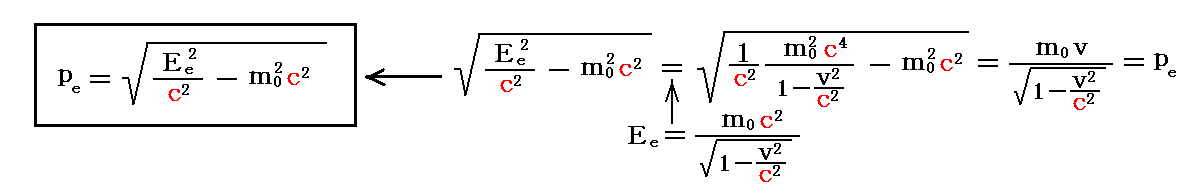
から求めることもできる。
実際、上式にＥkinの定義を代入すると
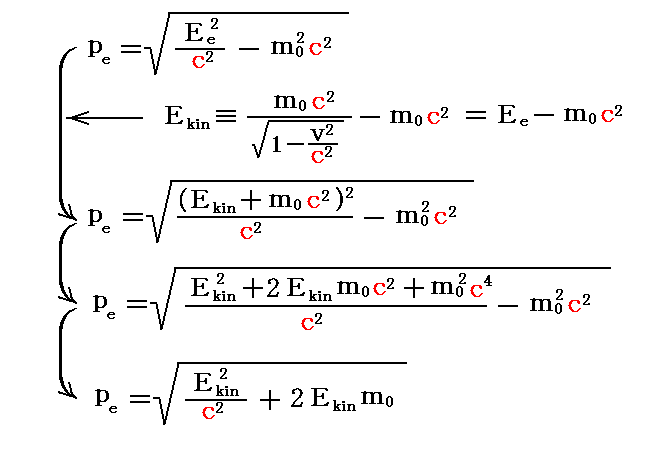
となり、直接求めることができる。
光子の散乱角θと電子の反跳角φの関係は２．（２）の運動量保存則（１）、（２）
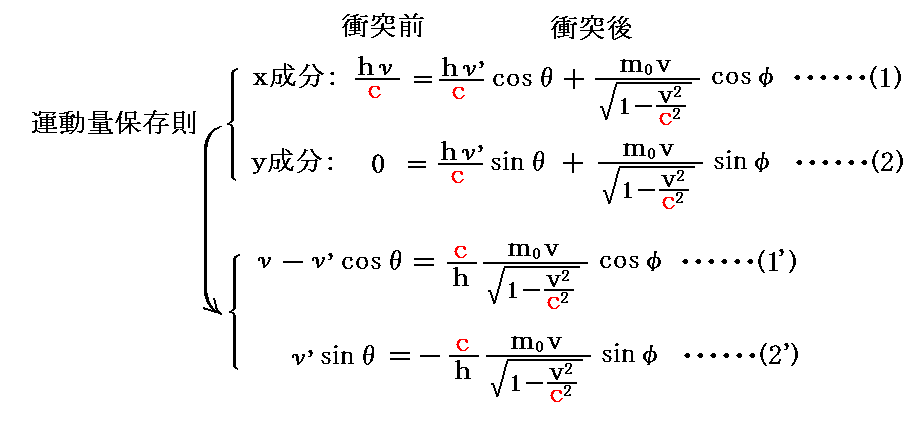
から得られる。
（１’）式の辺々を（２’）で除すると
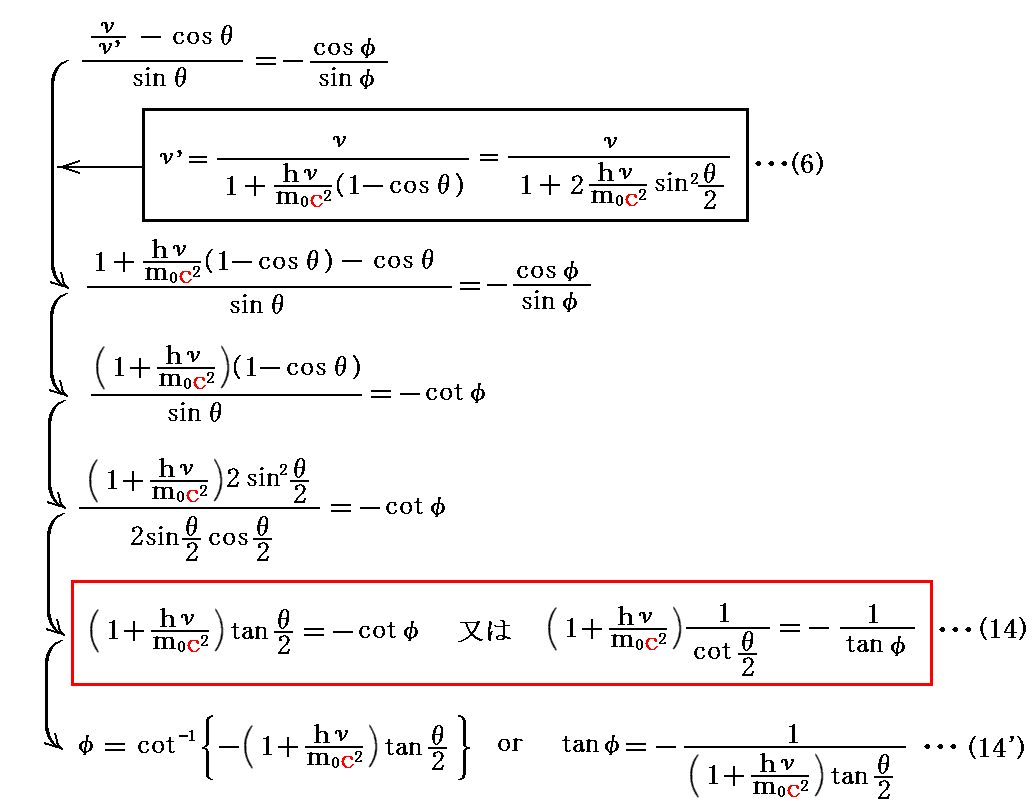
が得られる。θとφの関係式に、入射光子のエネルギーｈνが関係していることに注意されたし。
この式の実験的確認（３．（５）１．参照）に依って、３．（１）［補足説明２］で述べたボーア・クラマース・スレーター理論は明確に否定された。
前項の（１４）式を用いると、反跳電子の得る運動エネルギー（１２）式をφの関数で表せる。
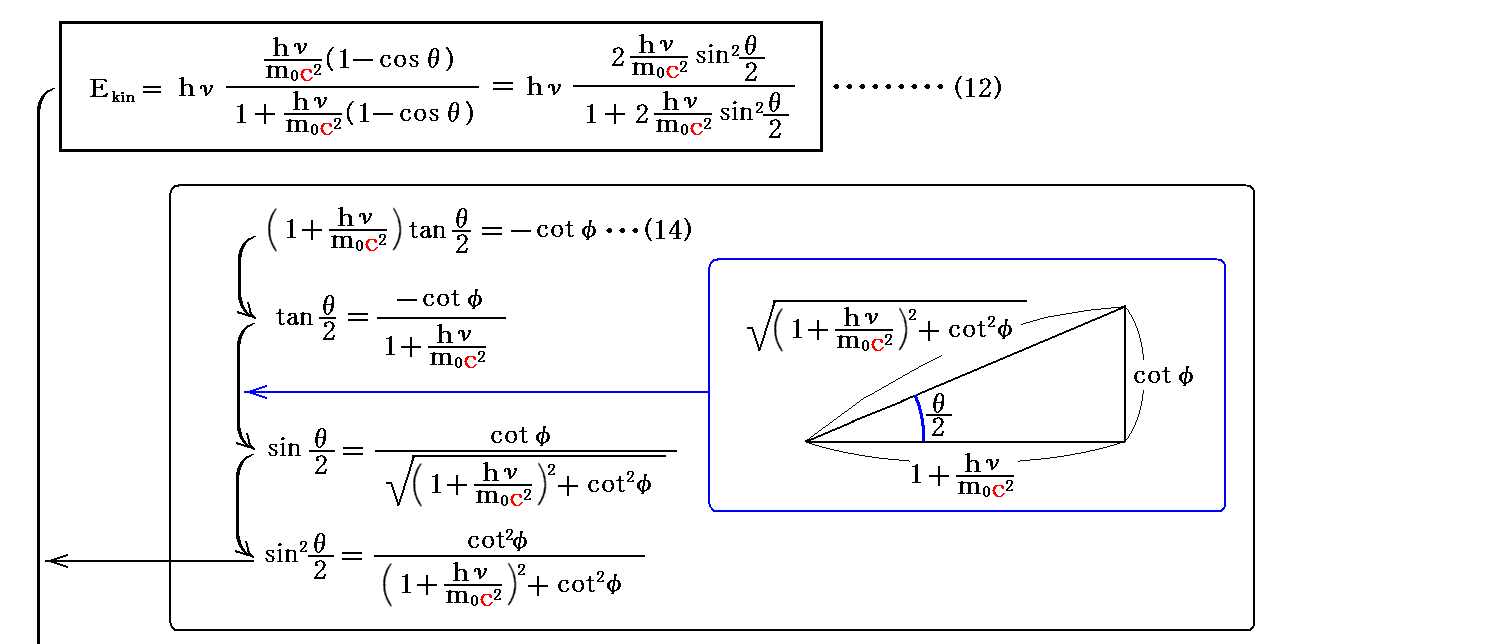
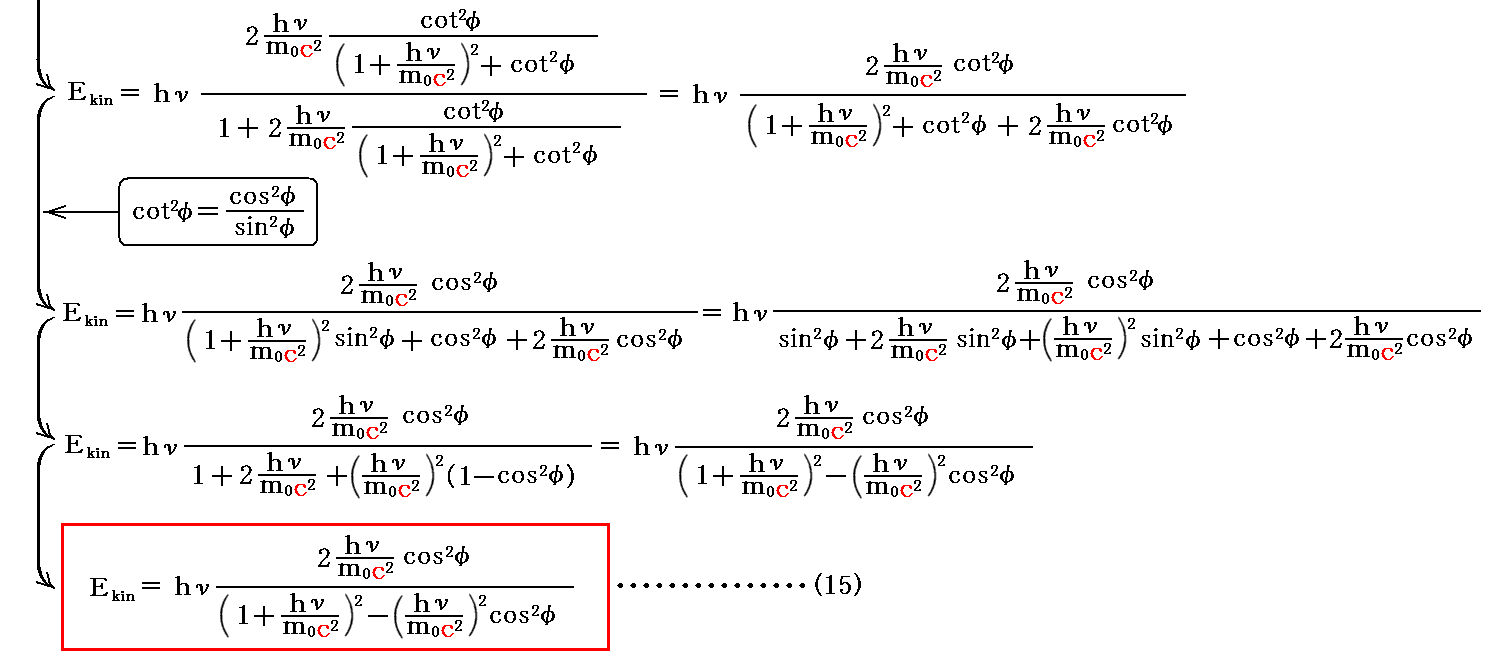
反跳電子が得るエネルギーは反跳角φと同時に、入射光子のエネルギーｈνにも依存することに注意されたし。
同様に反跳電子の得る運動量（１３）式をφの関数であらわすと
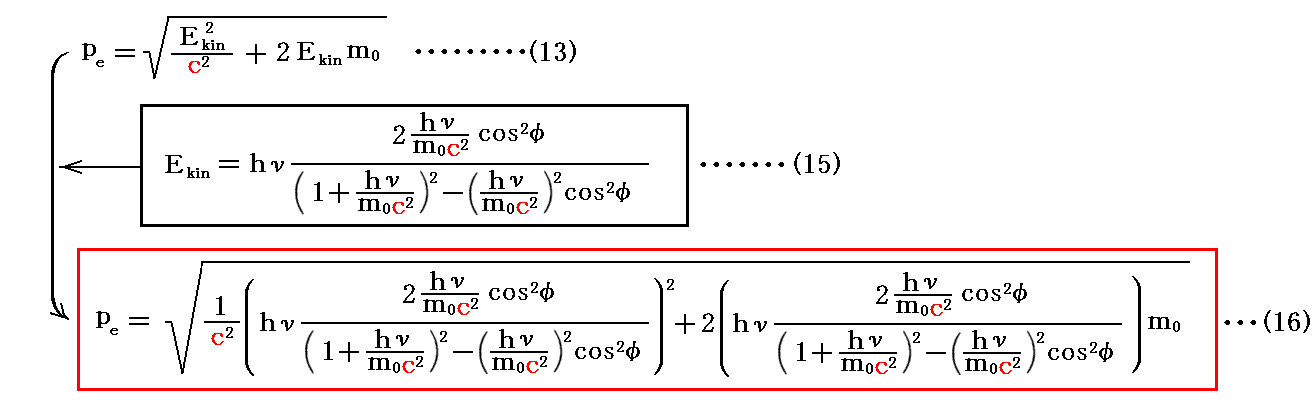
となる。
ここまでに得られた式で
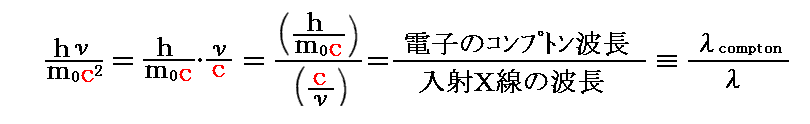
であることに注意されたし。
［補足説明１］
このとき、以下の事に注意。
反跳電子のエネルギーＥkinと反跳角φが実験で測定できると、（１５）式を逆に解くことで入射光子のエネルギーｈνが求まる。そうして求めたｈνと、反跳電子の反跳角φを（１４）式に代入すると、散乱光子の散乱角θが求まる。
つまり、反跳電子のエネルギーEkinと反跳角φが計測できれば、入射光子のエネルギーｈνと散乱角θが計算できる。
このことは３．（５）２．で説明するクレイン、ゲルトナー、トゥーリンの実験の解析で重要です。そこの［補足説明３］を参照されたし。
実例によって、前節の（８）～（１１）式と（１５）、（１６）式の関係を示す。
ComptonがPhys. Rev., 21, p483～502, 1923年で示している、ラジウムＣの出すγ線光子と電子との衝突の様子を示す。
ＲaＣ-γ線の波長はλ＝0.022Å＝2.2×10-12ｍであり、電子のコンプトン波長はλcomp＝2.426×10-12ｍだから
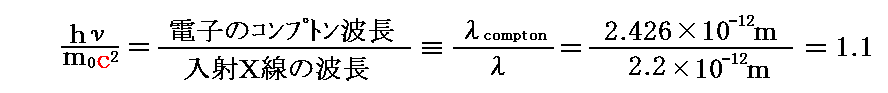
となる。
光子の散乱角θが（ 0°、20°、40°、60°、80°、100°、120°、140°、160°、180°）のときに電子が反跳される方向φは、（１４’）式を用いて計算できて、それぞれ（
-90°、-69.6811°、-52.608°、-39.5153°、-29.575°、-21.7802°、-15.3725°、-9.83278°、-4.7996､
0°）となる。
入射光子のエネルギーｈνの大きさを下図の様に設定して、散乱光子のエネルギーｈν’と反跳電子が得る運動エネルギーＥkinの大きさを図示すると
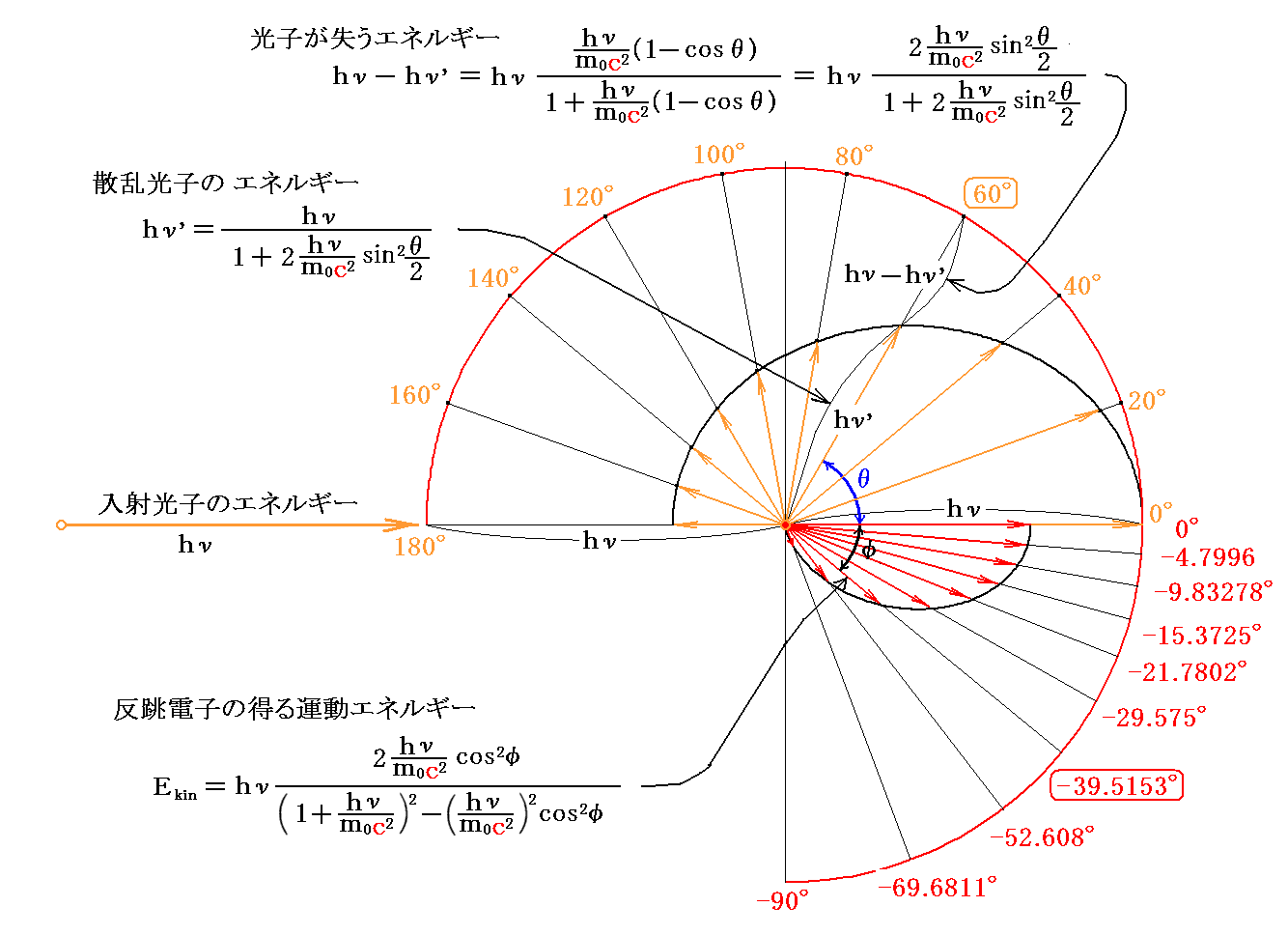
の様になる。
同様に入射光子の運動量の大きさを下図のよう設定して、散乱光子の運動量ｈν’／ｃと反跳電子が得る運動量ｐeの大きさと方向を図示すると
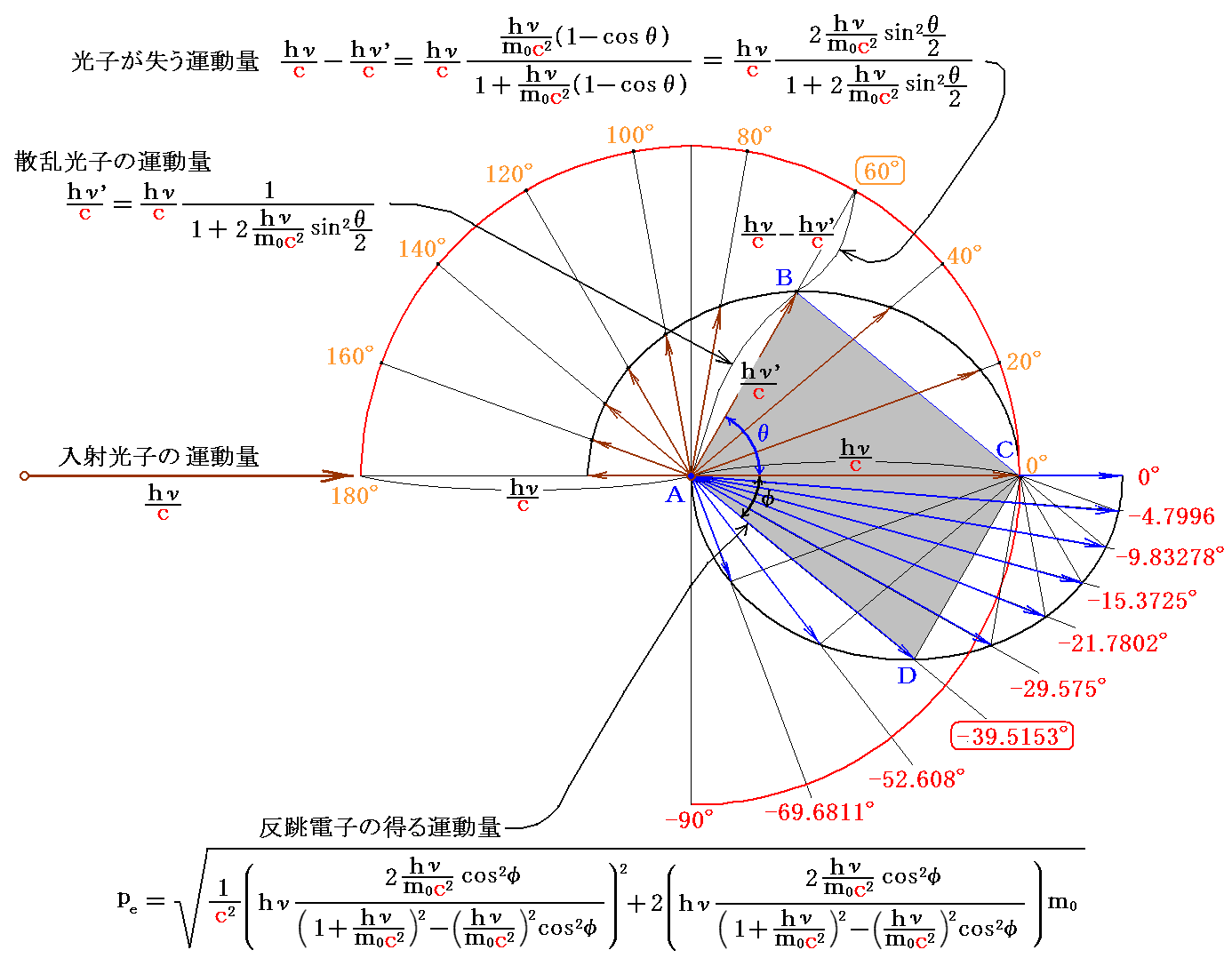
となる。
運動量図に於けるφの方向はエネルギー図のφの方向と同じですが、運動量の大きさがφとともに変化する様子はエネルギーの大きさがφとともに変化する様子と異なることに注意されたし。
また、上図の灰色平行四辺形ＡＢＣＤが２．（２）で説明した運動量ベクトルについて成り立つ平行四辺形ＡＢＣＤです。そのため、Ｃ点から反跳電子運動量ベクトルの先端点Ｄに向かう線分ＣＤは20°刻みの等角度間隔で0～－180°の間に分布することに注意されたし。そのため下側の半楕円は上側の半楕円と互いに合同です。
ComptonがPhys. Rev., 22, p409～413, 1923年で報告している、モリブデンＭoのＫα-Ｘ線光子と電子との衝突を図示する。
ＭoのＫα-Ｘ線の波長はλ＝0.711Å＝71.1×10-12ｍであり、電子のコンプトン波長はλcomp＝2.426×10-12ｍだから
となる。
この場合について、光子の散乱角θが（ 0°、20°、40°、60°、80°、100°、120°、140°、160°、180°）のときに電子が反跳される方向φを（１４’）式を用いて計算すると、それぞれ（
-90°、-79.6672°、-69.3764°、-59.1636°、-49.0541°、-39.0596°、-29.1775°、-19.3922°、-9.6775°､
0°）となる。
そのため、エネルギー図は
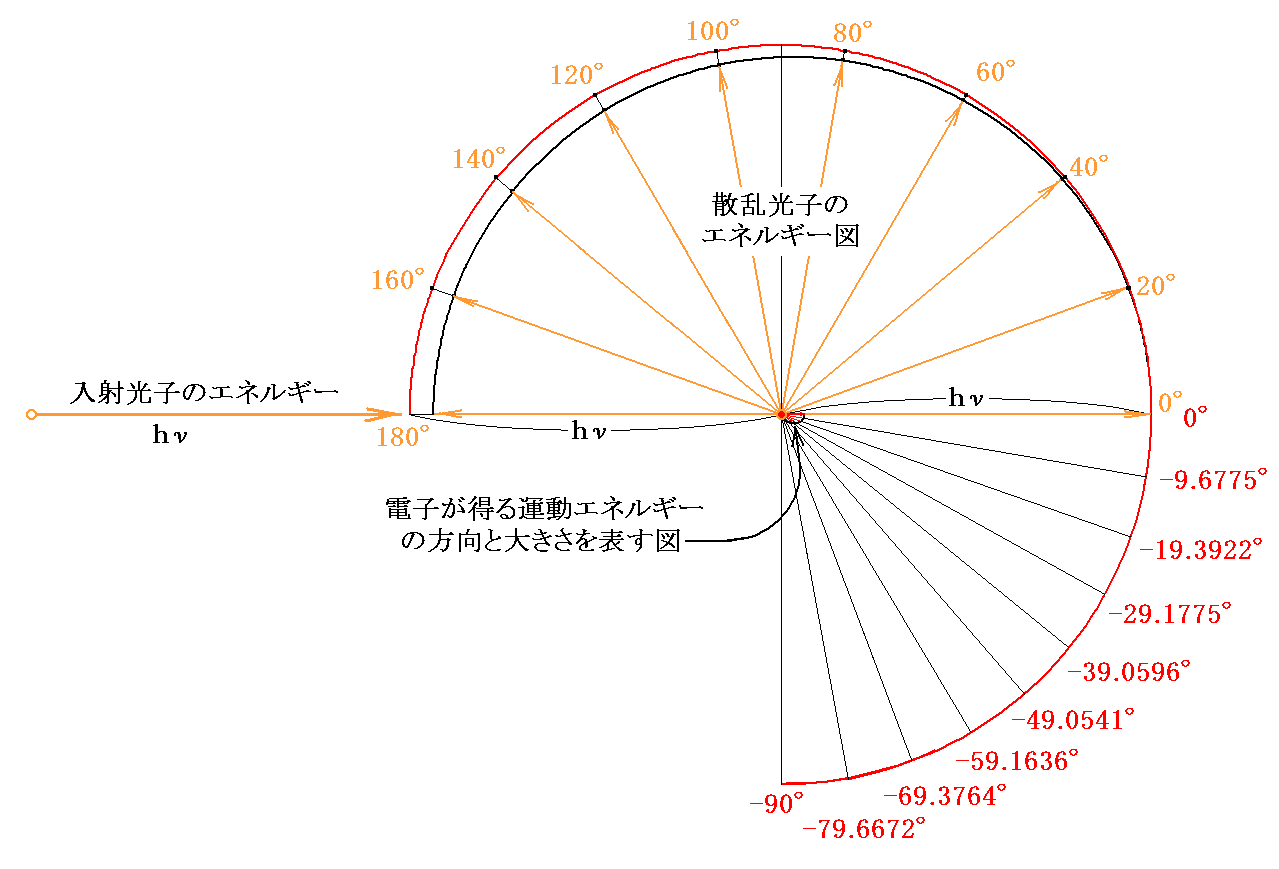
となる。前例ＲaＣ-γ線の図と比較すれば明らかなように、光子のエネルギーが低くなると電子に与えられるエネルギーの割合は少なくなる。
また、運動量図は
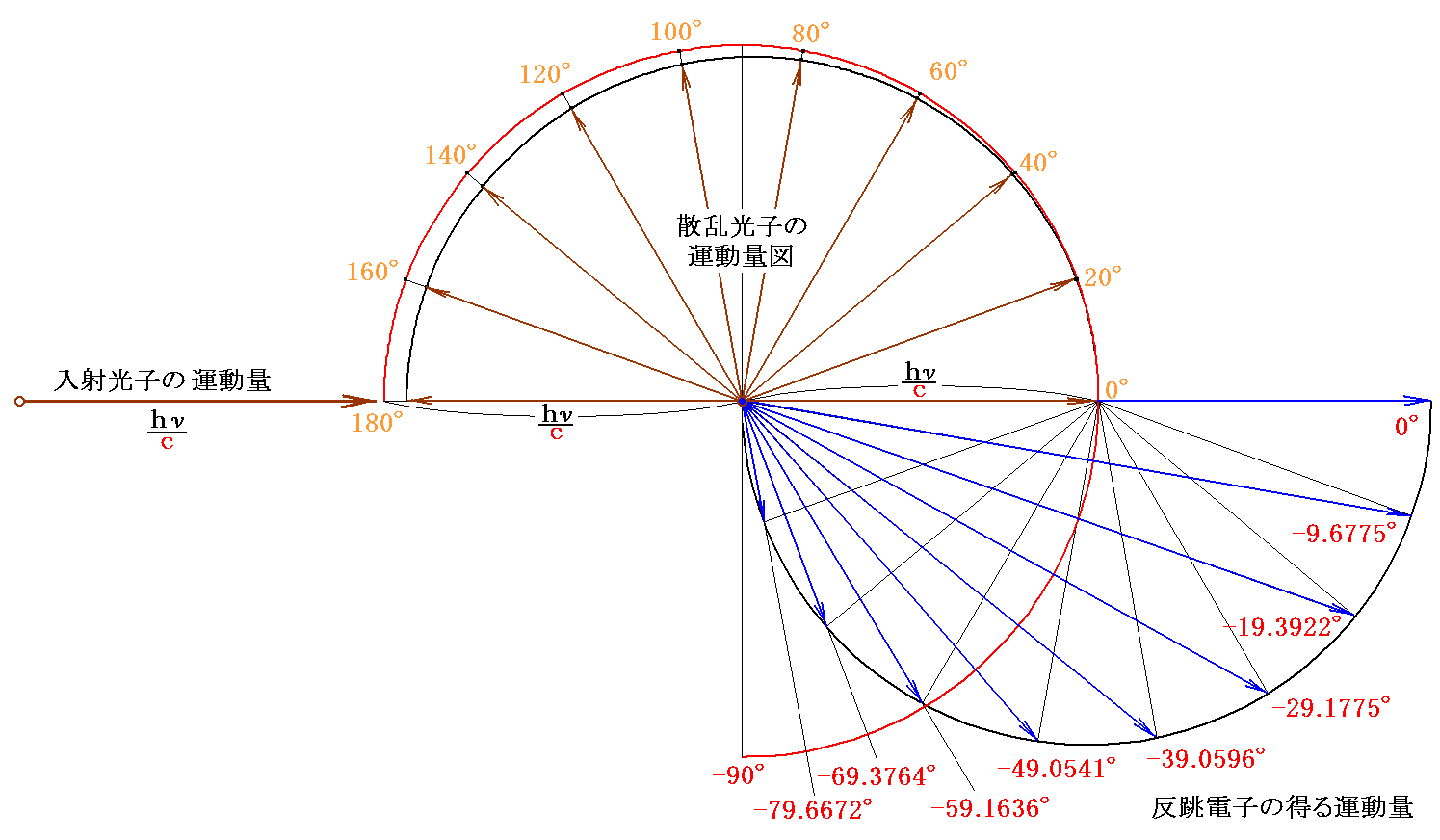
となる。
前節のγ線とＸ線の散乱と、反跳電子が受け取るエネルギーを比較してみると明らかなように、前者ではφ＝90°方向で入射エネルギーｈνの1/2程度を反跳電子が受け取るが、後者のあまり堅くないＸ線の場合にはφ＝90°の方向で入射エネルギーｈνの1／10以下の比較的わずかな部分を受け取るに過ぎないことが解る。
このために、あまり堅くないＸ線領域では、“反跳電子”は、光子が原子に完全に吸収された場合に生ずる“光電子”と区別することができる。なぜなら、“光電子”の場合は吸収された光子のエネルギーとほぼ同程度で持って飛び出て来るのに、“反跳電子”は入射光子のごく一部のエネルギーしか受け取れないからです。
また、その発生のメカニズムから予想されるように、“反跳電子”は主にはじめの光子の方向に放出されるはずです。
Ｘ線およびγ線の散乱の際に放出される反跳電子に対して、コンプトンの理論が予想する様相は、まもなくウィルソンやコンプトンによって、ウィルソン霧箱実験で確認された。
このことについて、霧箱発明者のウィルソン自身の説明をノーベル賞受賞記念講演（1927年12月12日）から引用する。
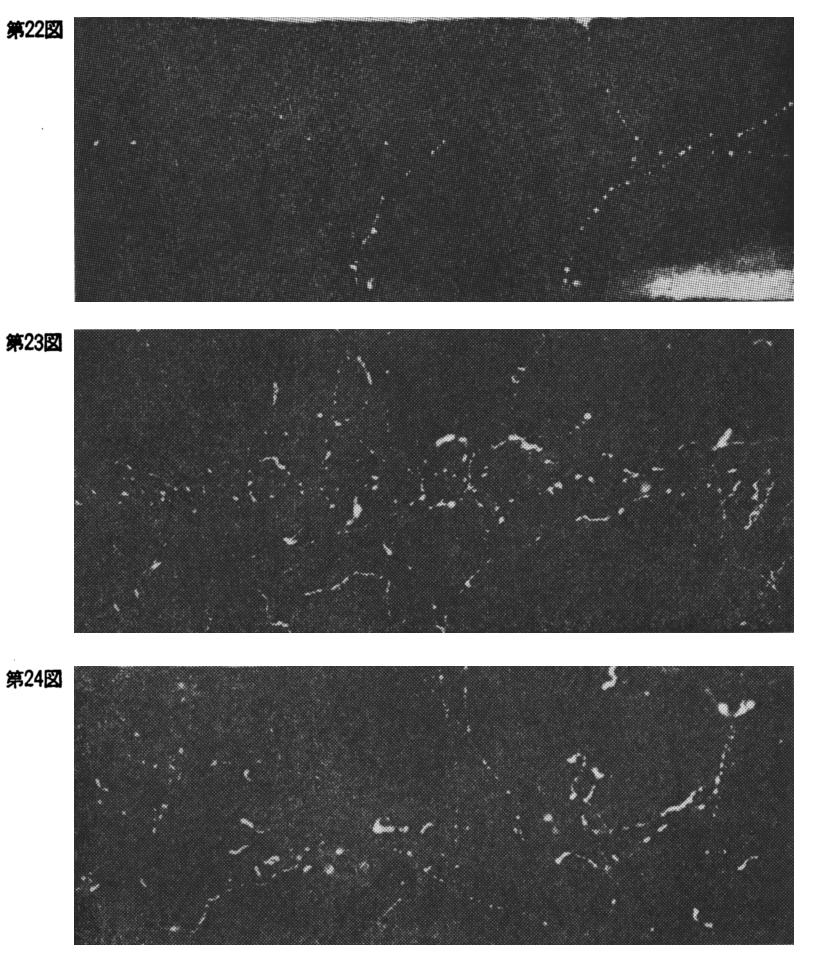
ちなみに、1927年度ノーベル物理学賞はA.H.ComptonとC.T.R.Wilsonが同時受賞して、同じ日に記念講演をしている。
［補足説明１］
ウィルソンの霧箱関連研究は主に1895～1911年に成された。そして、1911年に世界で初めてα線とβ線の個々の飛跡の写真撮影に成功した。
原子物理学研究の初期に於いて、霧箱は放射性物質から放射されるα線やβ線のエネルギーやその特性の研究に絶大な威力を発揮した。更に1921～1932年に行われたブラケットによる原子核反応の研究、1925年～1930年代に行われたコンプトン効果の検証研究、1932年に行われた中性子確認研究、1932年のアンダーソンによる陽電子の発見、等々･･･に用いられた。
霧箱実験による検証が直接的あるいは間接的に重要な貢献をして、後にノーベル賞の受賞に繋がった研究は多い。霧箱の物理学における貢献は偉大です。
［補足説明２］
ウィルソンの霧箱について補足する。それは別稿で引用したウィルソンの論文
C. T. R. Wilson, “On an Expansion Apparatus for Making Visible the Tracks
of Ionising Particles in Gases and Some Results Obtained by Its Use”, Proc. R. Soc. Lond. A 87, p277～292, 1912年
に書かれている霧箱利用上のテクニックについてです。
以下はノーベル賞受賞式でジーグバーンが行ったウィルソンの業績紹介文からの引用です。
我々は、霧箱の示す現象の解釈について詳しく知りませんが、ウィルソンのノーベル賞受賞記念講演はその紹介として極めて興味深いものです。是非お読みになることを勧めます。
前項のウィルソンの説明文中の青波線部分“コンプトンは、一定波長に対する写真にあった短い飛跡と長い飛跡の比は散乱係数と吸収係数の比に等しく、この事実だけでも自分の理論の裏付けになると指摘しました。”について補足する。
それまでの研究で光電効果に伴う入射Ｘ線orγ線の吸収係数τは、波長の減少とともにλ3に比例して減少することが解っていました。
また入射Ｘ線orγ線の電子による散乱に伴う散乱係数σは波長の減少と供に穏やかに減少することが解っていた。そのため散乱係数σと吸収係数τの比σ／τは、入射Ｘ線orγ線の入射波長の減少とともに、速やかに増大するはずです。
そのとき、上記の散乱係数と吸収係数の比は反跳電子の短い飛跡の数ＮRと光電子の長い飛跡の数ＮPの比と一致するはずです。つまり
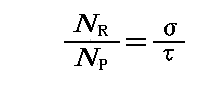
となることが期待されます。
実際、コンプトンたちは入射Ｘ線の波長を様々に変えて、霧箱中に生じる二種類の飛跡の数を数えて次表の結果を得ることができた。
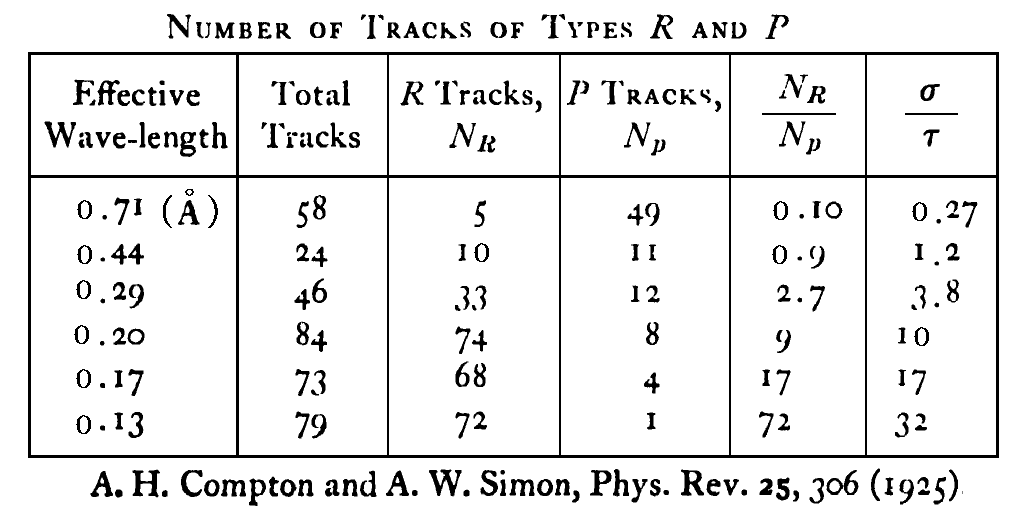
確かに、入射Ｘ線の波長が短くなるにつれて短い（球形ｏｒ魚形の）飛跡の数が、長い飛跡の数よりも圧倒的に増えてきたのです。
この結果は、堅いγ線の吸収はほとんどが反跳電子をつくるのにそのエネルギーが費やされ、光電効果は起こらなくなることを意味する。そして、短い飛跡がコンプトン効果で生じた反跳電子の飛跡であることを示している。
［補足説明３］
この短い飛跡は入射Ｘ線のエネルギーが高くなる（波長が短くなる）につれて球形→魚形→短い飛跡→長い飛跡と変化していく。
そのため、十分に堅い（エネルギーの高い、波長の短い）Ｘ線を用いれば、その短い飛跡の最初の方向から反跳電子の反跳角φを測定できる。コンプトン達はこの事を確かめる実験を実施した。この事を次節で述べる。
コンプトンはノーベル賞受賞記念講演（1927年12月12日）で、前節最後に述べた実験
A.H.Compton and A.W.Simon, Phys. Rev., 26, p289～, 1925年
の概要を述べている。
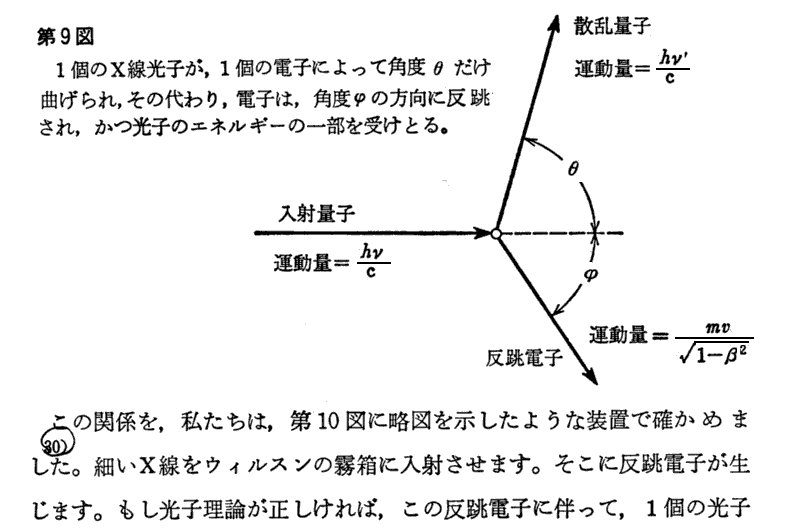
その説明文を以下に引用する。ただし、θとφはこの稿の定義に合わせて互いに入れ替えています。
［補足説明１］
上記の近似式（２）、（３）の正確な形は、３．（２）で説明した（９）式と（１４）式を参照されたし。
また、上記のウィルソンとボーデの論文は下記のものです。
28） C.T.R.Wilson, Proc. Roy. Soc. London, A 104, p1～, 1923年
29） W.Bothe, Z. Physik, 16, p319～, 1923年
［補足説明２］
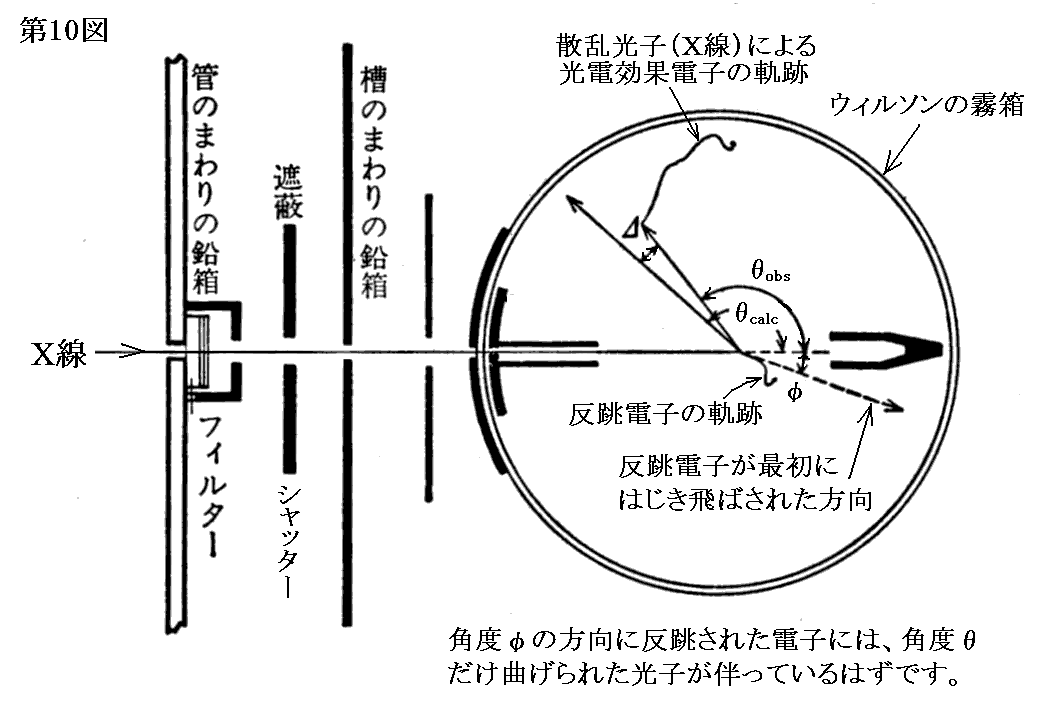
ここで、散乱される光子自身は空気を電離しないので、散乱光子の飛跡を霧箱中の飛跡で確かめることはできないことに注意されたし。
そのとき、散乱された光子が霧箱中の気体分子に吸収されると光電子を出す。そして、光電子は霧箱中に比較的長い飛跡を残す。そのため、光電子の飛跡の開始点と反跳電子の飛跡の開始点を直線で結べば光子の散乱角θを知ることができる。
前項と同様な実験が、クレイン、ゲルトナー、トゥーリンによって更に精密に繰り返された。
（H.R.Crane，E.R.Gaerttner and J.J.Turin, Phys. Rev., 50, p302～,1936年）
下図は彼らが用いた装置の模式図です。γ線源は厚い鉛の塊にあけられた細長い孔の端に置かれている。フィルターを通ったγ線の平行線束は、細長い孔を出てウィルソン霧箱に入射する。散乱体として、ウィルソン霧箱の中心に置かれた厚さ0.8ｍｍのセルロイド片が用いられた。
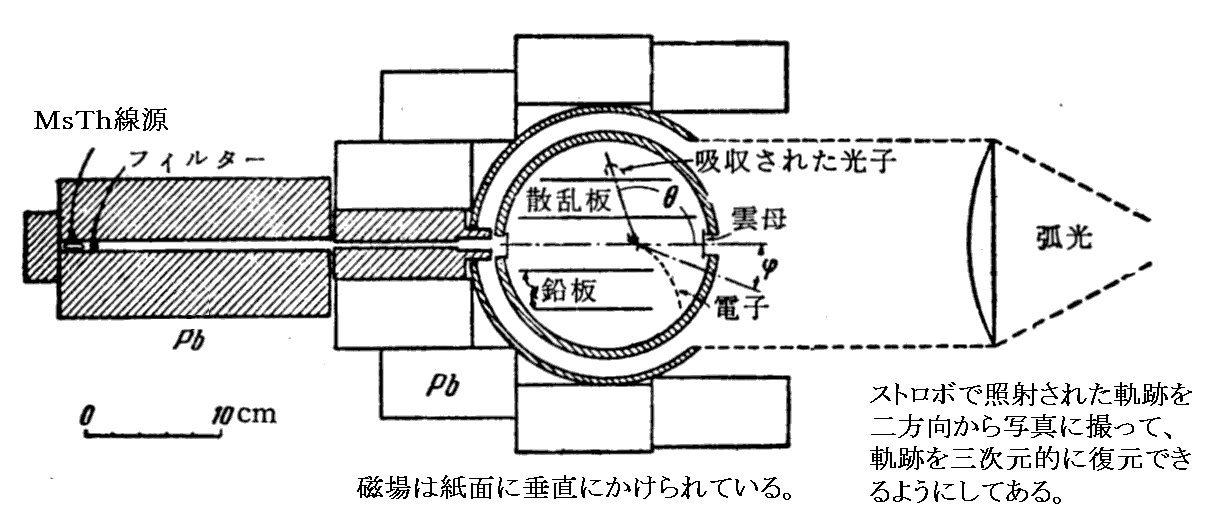
彼らは、幾つかの改善をして測定精度を上げた。
［補足説明３］
彼らの方法は次のような長所を持っている。反跳電子のエネルギーＥkinと反跳角φからコンプトンの理論によって散乱された光子の飛ぶ方向θを見いだすことができる。この事については３．（２）４．［補足説明１］を復習されたし。
その際、入射光子のエネルギーに関して何らの仮定もする必要がない。この長所は極めて大切です。なぜなら、１次γ線はフィルターを通ったといってもその純粋さはあまり確実なものではなく、入射光子が一定のエネルギーを持っているとは確信を持って言えないからです。
彼らは、θの理論的予測値と実際の観測値を比較したのです。
実際の散乱写真を３例示す。反跳電子の飛跡（箱の中央付近）と散乱光子が鉛板に吸収されて出る光電子（鉛板付近）の軌跡が見える。
上下の写真は同じ事象を、異なったカメラで二方向から撮った写真です。二方向の写真から飛跡を三次元的に再現することができる。これは元祖ウィルソンが用いて以来、常に利用された方法です。
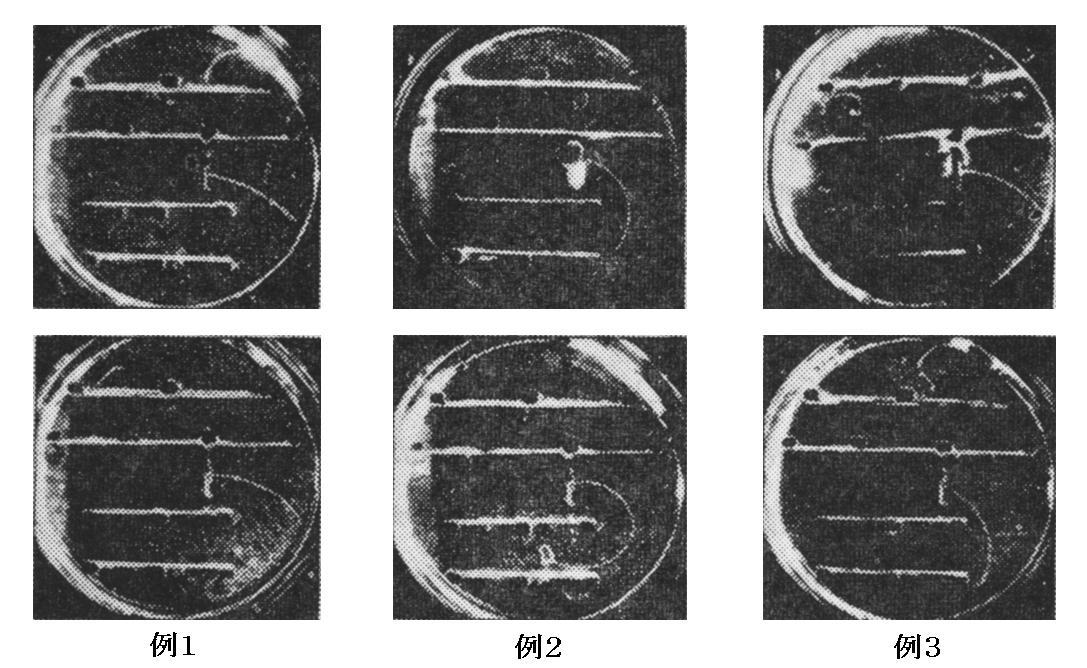
三次元的に再現された軌跡から、反跳電子の反跳角φとエネルギーＥkinが測定できる。それから計算によって散乱光子の飛ぶ方向θを求める。その理論値と、写真で見いだされる光電子の発生位置から測定されるθの観測値が比較された。
全部で10000枚の写真が撮られ、300組の電子-光子の組み合わせが見いだされた。データを整理した結果、偶然の一致の可能性を遙かに超える多数の場合において、散乱光子の実測された方向は計算値と一致した。
こうして、Ｘ線およびγ線の散乱の素過程に於いてコンプトン理論の“運動量保存則”と“エネルギー保存則”が成り立っている事が明瞭に証明された。
［補足説明４］
更にに進んだ観測装置（ガイガー・ミューラー計数管や光電子倍増管など）を用いて精度を高めた同様な実験が1930年代後半以降に多くの実験家により精力的に繰り返された。それらはいずれもコンプトンの理論を高精度で実証した。
J.C.Jacobsen, Nature, 138, p25～, 1936年
W.Bothe und H.Maier-Leibnitz, Z. Phys., 102, p143～, 1936年; Phys. Rev., 50, p187～, 1936年
R.S.Shnkland, Phys. Rev., 52, p414～, 1937年
W.G.Cross and N.F.Ramsey, Phys. Rev., 80, p929～, 1950年
光子の粒子性は、コンプトン効果の発見以前に光電効果の実験で確かめられてはいたが、それはエネルギー粒子としてたしかめらているだけでした。
コンプトン効果の実験によって、光子の粒子的性格はその運動量を含めて更に具体的かつ詳細に確かめられた。
［補足説明５］
相対論的力学運動方程式を確かめるだけなら、光の散乱を用いるよりも、電子散乱の方が適している。なぜなら散乱電子と標的電子の両方が霧箱中に飛跡を残すからです。
1932年にF.C.Champion（Proc. Roy. Soc. A, 134, 672～681, 136, p630～637, 137, p688～695, 1932年）は高速で走る電子を静止している電子に衝突させて、衝突後の二粒子の飛跡の成す角度をWilsonの霧箱で調べた。
同種粒子の衝突の場合、高校物理で習うように衝突後の二粒子の飛跡の成す角度は90°になります。しかし、衝突前の電子が高速の場合、相対論的な効果が出て来るために衝突後の飛跡の成す角度は、入射電子の速度に依存して90°よりも小さくなります。この角度変化は相対論的力学で計算できますので、入射電子の速度変化に伴う飛跡角度の変化を調べれば相対性理論が高精度で検証できます。詳細はC．メラー「相対性理論」§32の説明を参照されてください。
この稿を作るに当たって、下記文献を参照した。
