光の圧力[輻射圧]
光の圧力の概念は近代物理学でとても重要な働きをしますが、それを理解するのはなかなか難しい。できるだけ解りやすく説明します。
電磁気学の公式はどの単位系を用いるかにより係数が変化しますが、ここではすべて高校物理で使用するMKSA有理化単位系(SI単位系)で記述します。電磁気学の単位系については別稿「電磁気学の単位系が難しいわけ」を御覧下さい。
1.光の圧力の簡単な説明
音波と違って、光(電磁波)は真空中でも存在できる。しかし、物体が存在しない場所の輻射(光)の圧力を直接測定する事はできない。光の圧力とは、光が物体に当たったとき物体に働く力として初めて測定できる。[物体に働く圧力から出発して電磁波そのものが持つ応力を何もない空間まで拡張できる。マクスウェルはその様にして真空中の電磁場に応力を定義した。3.では、このマクスウェルの応力を用いて同じ事柄を証明する。]
マクスウェルの理論により光は電磁波であり、電磁波の電場と磁場は互いに垂直で、どちらも進行方向に垂直であることが解っている(別稿「電磁波の伝播」2.(2)参照、より詳しくは別稿「アインシュタインの特殊相対性理論」3.(2)1.[補足説明4]を参照)。
光が光源からやって来て、電荷に当たると、光の電場は電荷を動かす。今電荷の存在するところにやってくる光の電場はy軸に沿った方向で振動しているとすると正電荷はy軸方向に動かされる。そのとき、電場によって動かされた電荷は電場に垂直な磁場による力を受ける。磁場は電荷が動いているときだけ力(ローレンツ力 F=q[v×B]=μ0q[v×H])を及ぼし、その方向は光(電磁波)の進行方向である。
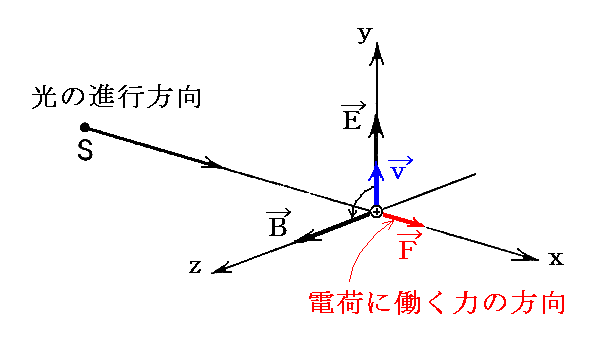
実際の電荷は中心原子の周りにバネで拘束されているような状況にある[負電荷を持つ]電子である。その電子には変位に比例する引力が働き、電子は質量m、共鳴角振動数ω0で振動する振動体の性質を持つ。ある瞬間の電場の向きがy軸の正の方向のとき、電子は負の方向の速度を持つが、ローレンツ力の方向はやはり光りの進行方向になる。いずれにしても、光が吸収されると、その物体に圧力が働くことになる。
ここは、文献1.のファインマンの説明を利用したのですが、このような考え方で光の圧力が存在する理由を最初に与えたのはMaxwellです。別稿「エーテルと電気の歴史」第8章p311~312参照。
2.光の圧力の厳密な説明
前項の議論をもう少し精密化する。以下はプランク著「熱輻射論」(物理科学の古典7)東海大学出版会P43~49の説明を参考にした。
(1)入射光
いまx’軸の正方向に進む平面波を考える。その様な平面波は別項「電磁波の伝播」2.(2)の結果を用いると(座標の取り方がそこでの場合と異なっているが)以下の様に表される。
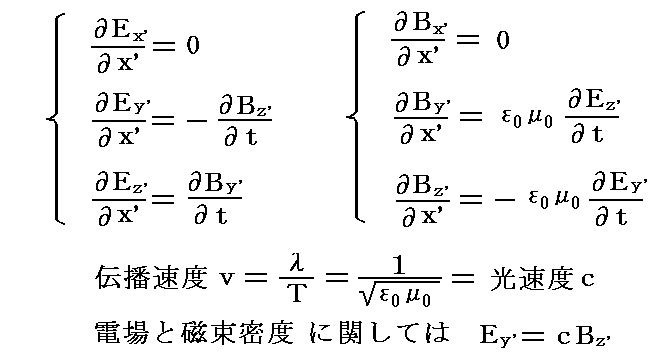
この微分方程式の一般解は
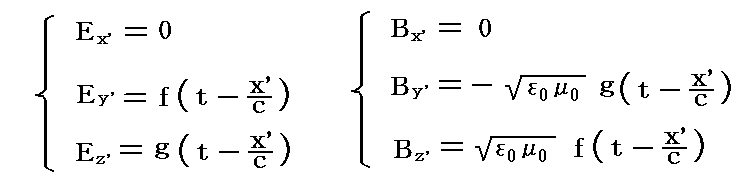
となる。これらが解となることは方程式に代入してみれば直ちに了解できる。また、これらはx'軸の正の方向へ伝播する入射波を表し、fとgは同じ一つの変数(t-x'/c)の任意の関数である。
この波が鏡のように反射する面(無限大の導電率をもつ完全導体)に当たったとする。このような導体中では無限に小さな電場でも有限の伝導電流を生み出しえる。そのときV=RIのRが零だから完全導体中の電位差は零(等電位)、そのため内部の電場はE=0となる。つまり完全導体中に電場が侵入してもその電場によって生じる電流が瞬時に電場を打ちけしてしまい完全導体中では電場は0になる。ただし、その表面に平行な振動電流は生じる可能性はある。
また、ここではこの導体は磁化されない物体とし、導体の誘電率は真空中と同じμ0とおけるとする。このとき完全導体内部の磁束密度は零である必要はないが、時間的変化は0である。なぜなら、時間的に変化する磁界が存在すると電磁誘導の法則に従って電界が作られてそれが電流を流し、その電流が磁界を作り、その作られた磁界が導体内部に最初から存在していたどんな磁界も打ち消してしまうからです。高校物理でならうレンツの法則を思い出せ。今抵抗のない完全導体だから、その打ち消しは完全に行われる。
今、導体表面からその内部に向けてx軸を、また導体表面にyz軸をとる。このとき、xy平面を前記のx'y'平面と一致させ、その面を入射面として導体に光が入射するとする。
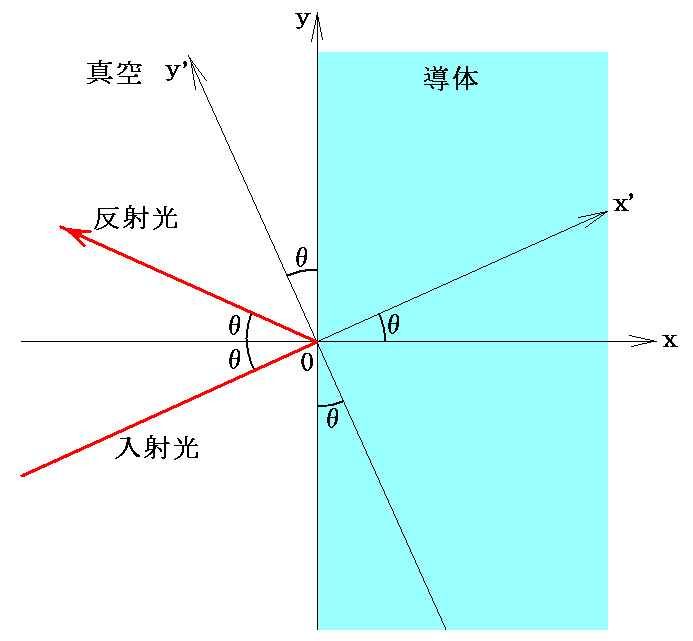
このときxyz座標系とx'y'z'座標系は以下の式で互いに関係づけられる。
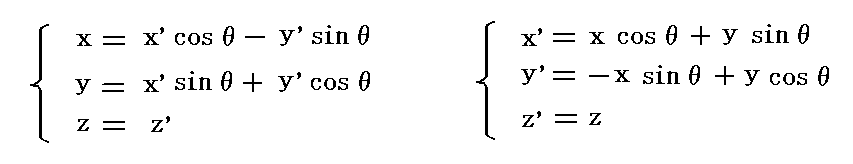
この関係は電場ベクトル成分E(Ex,Ey,Ez)と磁場ベクトル成分B(Bx,By,Bz)についても全く同様に成り立つので、前記の式を用いると
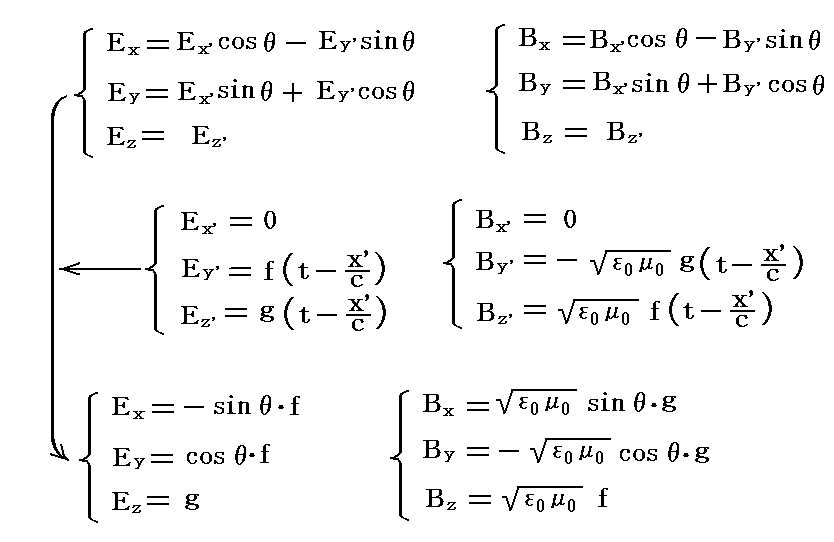
が言える。ここで関数fとgは変数
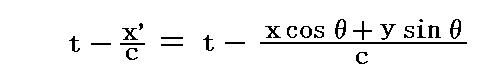
の任意の関数である。
(2)境界条件
ここで境界面において電場が満たすべき条件を求める。下図の様に境界面を挟んで一つの閉曲線を考え、その閉曲線に対してファラデーの電磁誘導の法則を適用する。
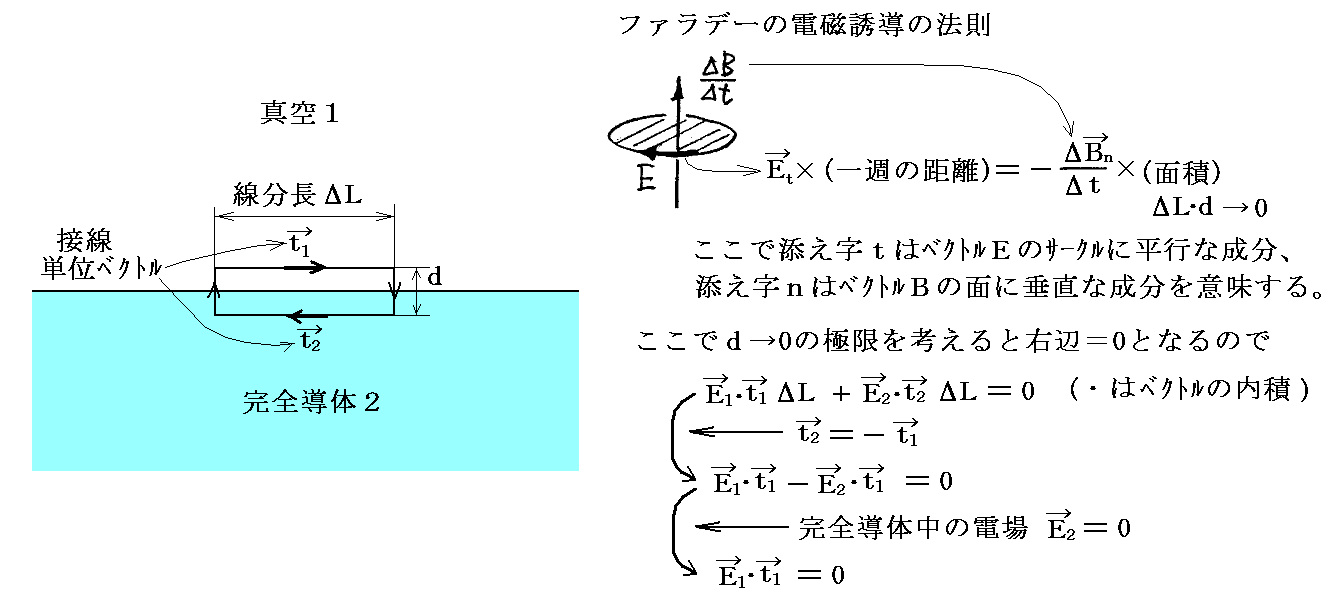
したがって、完全導体と接する真空領域の電場は、その境界面に沿った成分は0になり、法線成分のみとなる。つまりEy=Ez=0となる。
同様に磁場について下図の様な境界面を挟む高さhの平たい円筒を考える。磁力線について電気力線に関するガウスの定理と類似の法則が成り立つ。ただし単独の磁荷は存在しないので、電気の場合と違って閉曲面を横切る磁力線の面積法線成分の和は0になるという法則である。
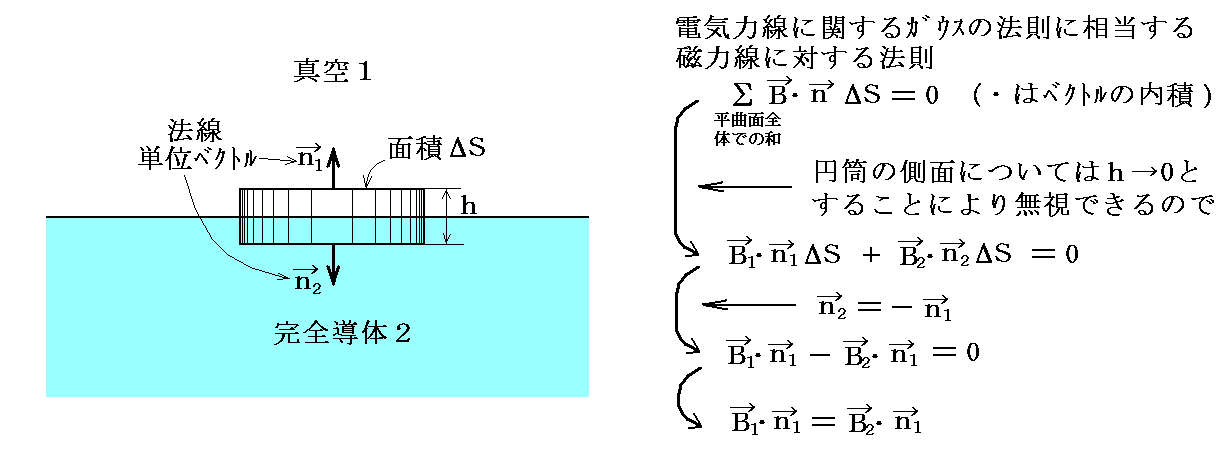
つまり境界の両側においてベクトルBの境界に垂直な成分は等しい。完全導体中に静磁場が在っても良いが、時間的に変化する磁場は許されない。なぜなら、時間的に変化する磁界が存在すると電磁誘導の法則に従って電界が作られてそれが電流を流し、その電流が磁界を作り、その作られた磁界が導体内部に最初から存在していたどんな磁界も打ち消してしまうからです。高校物理でならうレンツの法則を思い出せ。今抵抗のない完全導体だから、その打ち消しは完全に行われる。それで、今のように振動する電磁波を考えるときにはB2の境界に垂直な成分は0と考えて良いので、真空側においてもB1の境界に垂直な成分は0となる。
ところで、境界面をx=0のyz平面としているので、このyz平面の真空側に微少な面積要素ΔzΔxとΔxΔyを考えて、その周囲とその面に関してマクスウェルにより拡張されたアンペールの法則を適用する。そのとき別稿「電磁波の伝播」3.(2)で説明したように
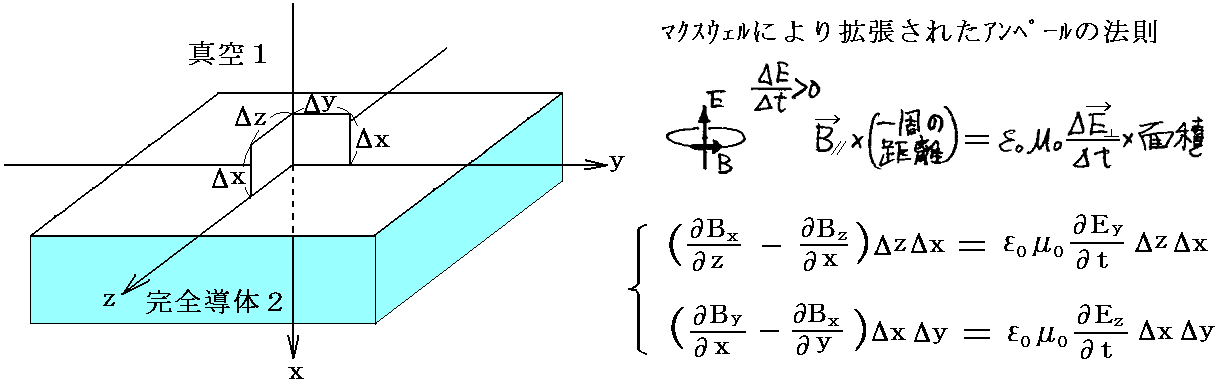
の関係式が成り立つ。ここで、EyとEzは境界面に平行な成分だから、すでに述べたように0となる。またBxは境界面に垂直な成分だから同じく0となる。そのため
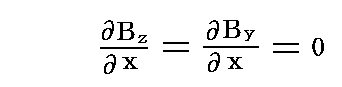
つまり、完全導体との境界面上の真空側で磁束密度Bの境界面に平行な成分の境界面に垂直な方向への偏微分は常に0になる。
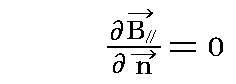
となる。
以上の結論は、電磁波の入射波と反射波が干渉して定常波ができたとき、磁場Bは常に腹になり、電場Eは節になると言っている。この当たりの具体的な状況は別稿「電磁波の伝播」3.(4)を参照されたし。ただしそこと座標の取り方が違っているので注意。
電波が導体表面にやって来たとき、電波にできることは、電荷の流れすなわち電流を流す事で、その電流は導体表面近くの極めて薄い領域に流れる。この電流がつくる電荷の分布は、マクスウェルの方程式をガウスの法則の形で満足するもので、電界を導体外部に作り、導体内部には電界は無い。導体のすぐ外側では磁界は常に表面に平行である。そして電荷が表面に平行に動くとき、その電荷はマクスウェルの方程式を満足する電流を構成して、導体の外側には表面に平行な磁界が存在するが、導体内部には打ち消されて無い。この結果は導体が電磁波を反射する事を意味する。
(3)境界付近の電磁場
結局、境界面に電磁場の法則を適応する事によって、電場の境界面に沿った成分Ey、Ezと磁場の境界面に垂直な成分Bxが境界面を挟んでその両側で互いに等しくなければならないことが言える。さらに、完全導体内の電場が零であることから、真空側の境界面に沿った電場成分EyとEzは0で無ければならない。また、Bx成分に関しては境界面の両側で0でなければならない。
これらの状況は真空中の入射波の他にそれに重ね合わされる反射波を考えて、この二つの波がyz平面のあらゆる点、あらゆる瞬間において互いに打ち消し合うように重ね合わされると仮定するときにのみ満たされる。
この仮定と反射の法則から、反射波の残りの成分は決定されて、境界面(x=0)の真空側での値は
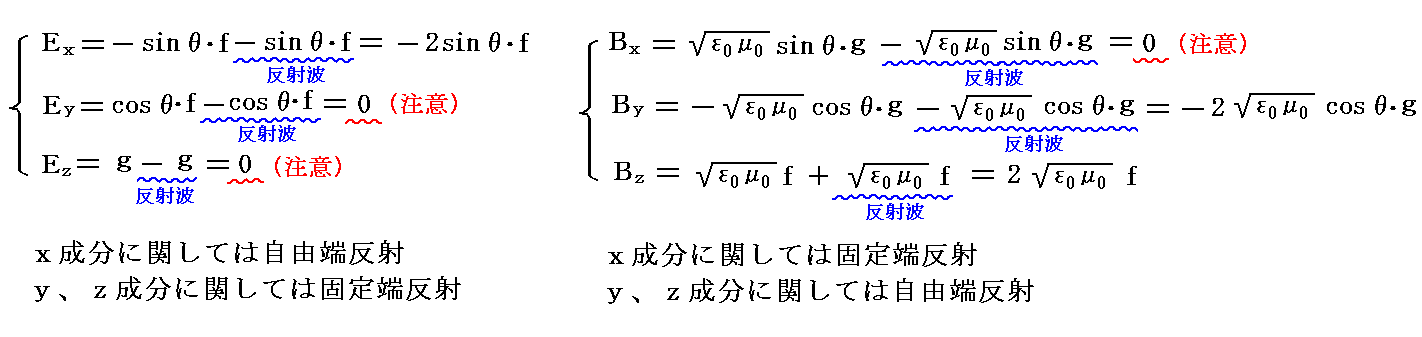
となる。ただし反射波は変数
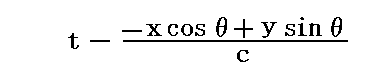
の関数であり、xの前の負符号はx軸の負の方向に進む波を表す。今はこの式でx=0とした
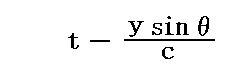
を代入すればよい。
また、境界面(x=0)の完全導体側の電場および磁場の強さは
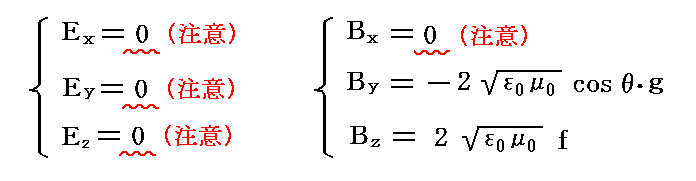
となる。ここでもまた関数fおよびgは変数
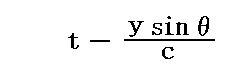
の関数である。このときEの成分は完全導体中ですべて0である。
このとき、電場の法線成分Exは境界面で不連続であるが、この不連続は境界面上に電荷があることを示す。その表面電荷密度は符号も含めて
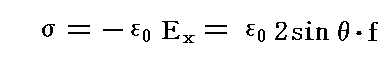
となる。導体内部では表面から有限の距離(すなわちx>0)で、6つの場の成分は全て無限に小さい。従ってx=0で有限の値を持つBy、Bzはxの増加と共に急速にゼロに近づく。
(4)導体物質に働く力
真空中に存在する電磁場によって導体物質は力学的力Feを受ける。この力の表面に垂直な成分を計算する。この力の一部は電場に、他の部分は磁場に起因する。
1.電場に起因する力
動体表面にある電荷は電場の中にあるから、電場の強さと電荷との積に比として力学的な力を受ける。このとき、場の強さは不連続で、真空側では-2sinθ・fであり導体側では0であるから、導体表面の面要素ΔyΔzに働く力学的力Feは、よく知られた静電気学の法則に従って、[前節で計算した面要素の電荷σ]と[両側の電場の強さの算術平均]とを掛けることによって得られる。
すなわち
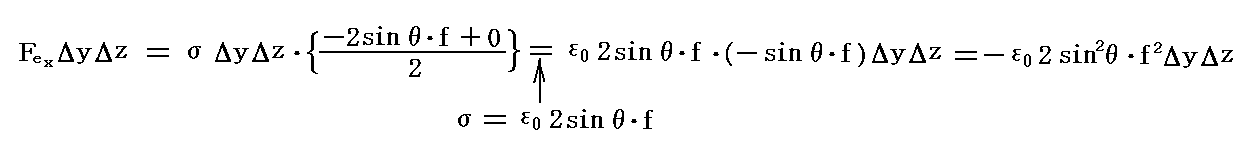
となる。この力は真空の方に向かって働き張力として現れる。
2.磁場に起因する力
磁場に起因する力学的力Fmを計算する。導体物質内部には一定の伝導電流が流れる。その強度と方向は電流密度ベクトルjは
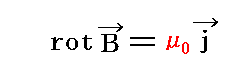
によって決められる。導体の伝導電流の流れる空間要素ΔxΔyΔzには、ベクトル積
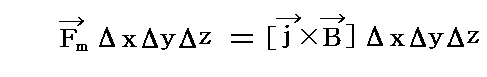
で与えられる力学的力(ローレンツ力)Fmが働く。この力の導体表面(x=0)に対して垂直な成分は
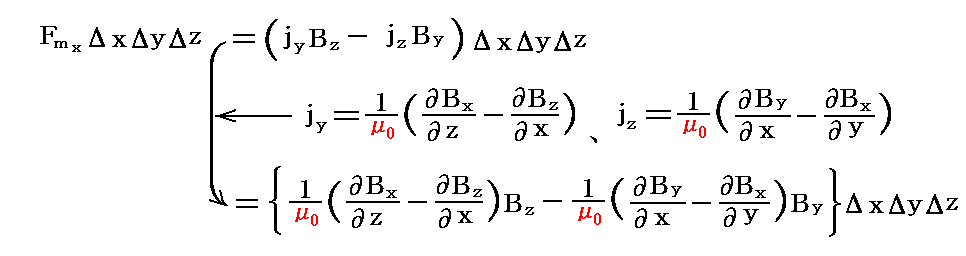
であるが、この式のyとzに付いての微係数は2.(3)の最後で述べた理由によりxについての微係数に比べて無視できるほど小さい。従ってこの式は次のように変形できる。ここでは、断面ΔyΔzをもつ導体表面に垂直のx=0からx=∞に達する柱状領域を考え、その柱状領域に働く磁場に起因する力のx成分をもとめている。x=∞でBはゼロになることを考慮して積分し、2.(3)で求めた境界面(x=0)の完全導体側の磁場の値を代入すると
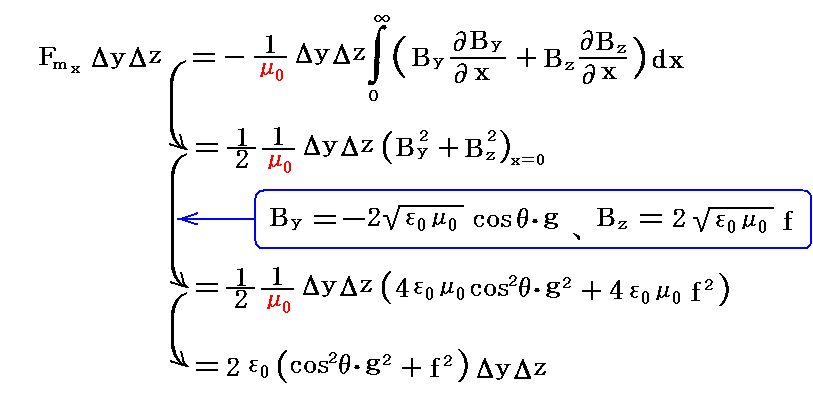
となる。
3.Maxwellの輻射圧
FeとFmを加え合わせると完全導体表面の単位面積に働くx軸方向の力は
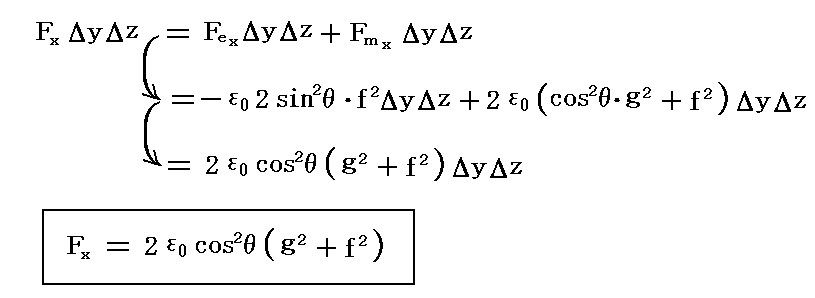
となる。これは導体表面に垂直で導体内部に向かって働く圧力として現れ、Maxwellの輻射圧と呼ばれる。
[補足説明]
上記の式は、1905年にアインシュタインによって特殊相対性理論からより完璧な形で導かれます。そこで明らかになるように上記の式はv≪c[vは光が当たる壁(鏡)の運動速度]の場合に成り立つ近似的な式ですが、ここでの議論の様にv=0の時には完全に一致します。
その導出・証明については別稿「アインシュタインの特殊相対性理論(1905年)」3.(3)2.及びそこの[補足説明3]をご覧下さい。ただし、この論文はGauss単位系(CGS非有理化単位系)で記述されていますので、ここでのMKSA有理化単位系に変換する必要があります。変換のやり方は別稿「電磁気学の単位系が難しい理由」5.(3)3.の対応表を参照して下さい。
輻射圧の存在とその大きさは最初P.Lebedewによるラジオメーター(真空中に微妙な釣り合い状態で吊した反射性金属の小円板に光を当てて力を測る装置)実験で確かめられた[P. Lebedew, Drudes Ann. 6, p433, 1901年]。
その後 E.F.Nichols と G.F.Hull がより精密に測定した[E. F. Nichols und G. F. Hull, Drudes Ann. 12, p225, 1903年]。
小山慶太著「20世紀初期における放射圧測定の考察」も参照されたし。
https://dspace.wul.waseda.ac.jp/dspace/bitstream/2065/10176/1/43137_23.pdf
(5)電磁場のエネルギー密度と輻射圧
1.電磁場のエネルギー密度
別稿「コンデンサーの持つエネルギー」、「帯電した導体球の周りの電場の持つエネルギー」や「コイルの持つエネルギー」、「磁場の持つエネルギーと電流を担う電荷が持つ運動エネルギー」で、真空中の電磁場が単位体積当たり
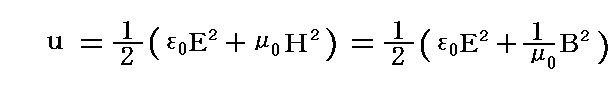
で表されるエネルギーを持つ事を示した。そこで用いた方法はとても素朴なものでしたが、ちゃんとした電磁気学の教科書で展開されている電磁場のエネルギーを導入・定義する方法も同じです。
正式には別稿「電磁気学の単位系が難しい理由」5.(4)2.で説明した電磁気学で成り立つ“Maxwellの法則”[下記参照]を用いて、力学で成り立つ仕事の定義を拡張して電磁場に於いて場自体がエネルギーを持つことを導きます。ここではやりませんが、適当な電磁気学の教科書の該当するところを御覧になって確認されて下さい。それらで展開されている数式の変形は複雑にみえますが、結局のところ前記別稿で説明している事を実施しているにすぎません。
この当たりは「ファインマン物理学 第Ⅳ巻 電磁波と物性」岩波書店(1971年刊)第6章“場のエネルギーと運動量” で解りやすく説明されていますので参照されて下さい。
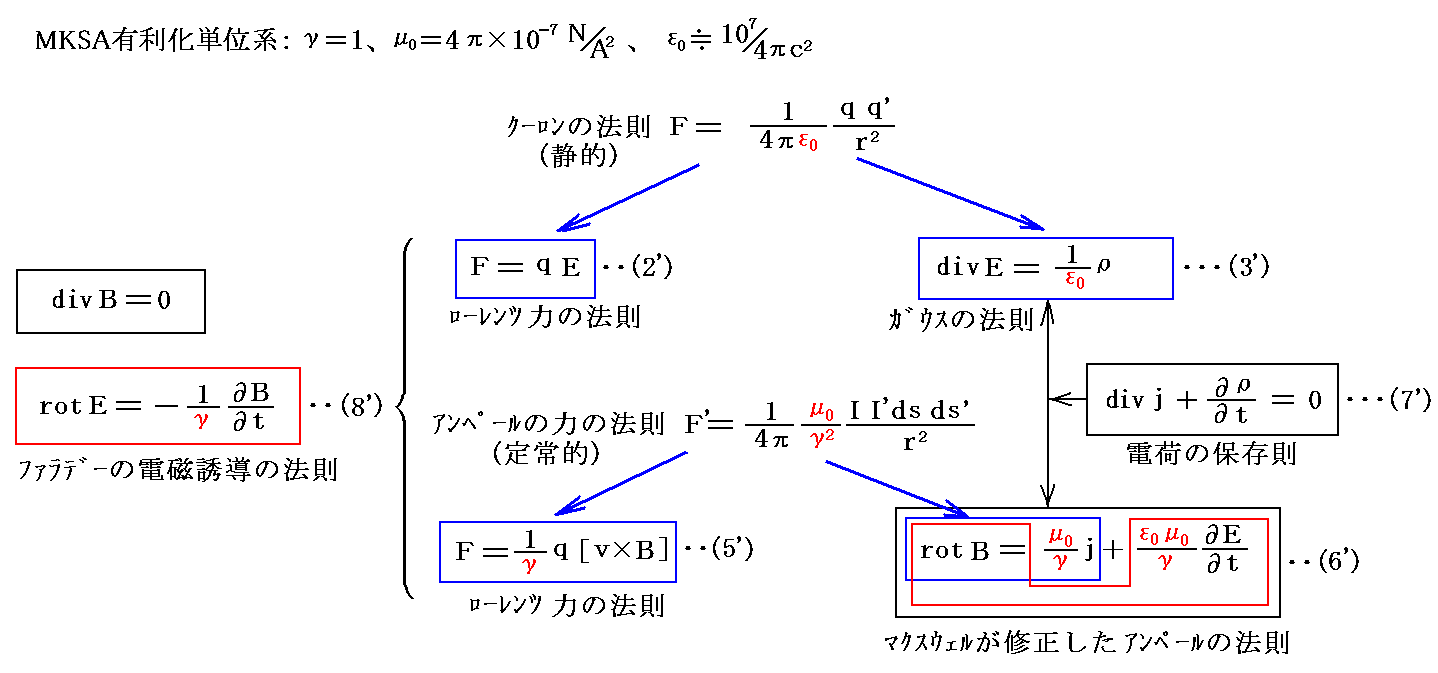
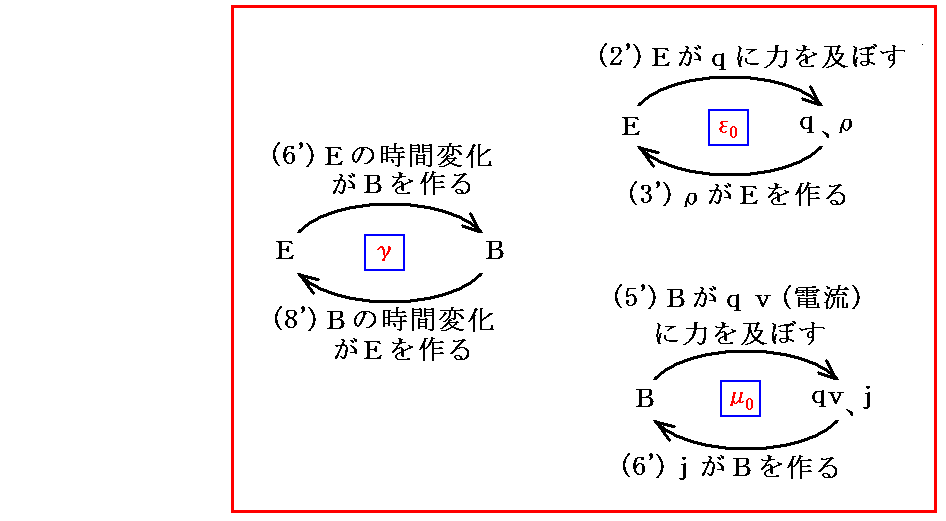
2.Poyntingの定理
1884年にポインティングはマックスウェルにより与えられた電磁場のエネルギー表現形式[前記]を“Maxwellの方程式”を用いて変形して電磁場には下記のベクトルで表されるエネルギー流が存在・定義できることを示した。
J. H. Poynting, “On the Transfer of Energy in the Electromagnetic Field”, Phil. Trans., 175, p343~361, 1884年
この内容が矢島祐利著「電磁理論の発展史」河出書房(1947年刊)に紹介されています。実際の導き方はファインマン物理 第Ⅳ巻「電磁波と物性」第6章“場のエネルギーと運動量” をご覧ください。
[Poyntingのエネルギー流の定理]
単位面積を、単位時間に流れる輻射のエネルギー流Sは
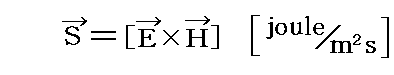
と表される。エネルギー流の方向はベクトル[E×H]の方向であり、単位面積はその方向に垂直であるとしている。
上記のエネルギー流を2.(1)で考察した入射光に当てはめる。導体の表面要素ΔyΔz≡dσにdt時間の間に当たる輻射のエネルギーIdtを考える。ここでIdσdtと書かないのはIが面積要素dσに垂直に通過する輻射エネルギー流を表すのでは無いからです。Idσは面積要素σに対して任意の角度で入射する輻射が面積σに単位時間に与える輻射のエネルギーを表します。また右辺のベクトル[E×H]は面積要素dσに垂直ではありませんので、面積要素dσ=ΔyΔzに垂直なx成分[E×H]xのみを考慮しています。
Idtは前節で求めた輻射圧と
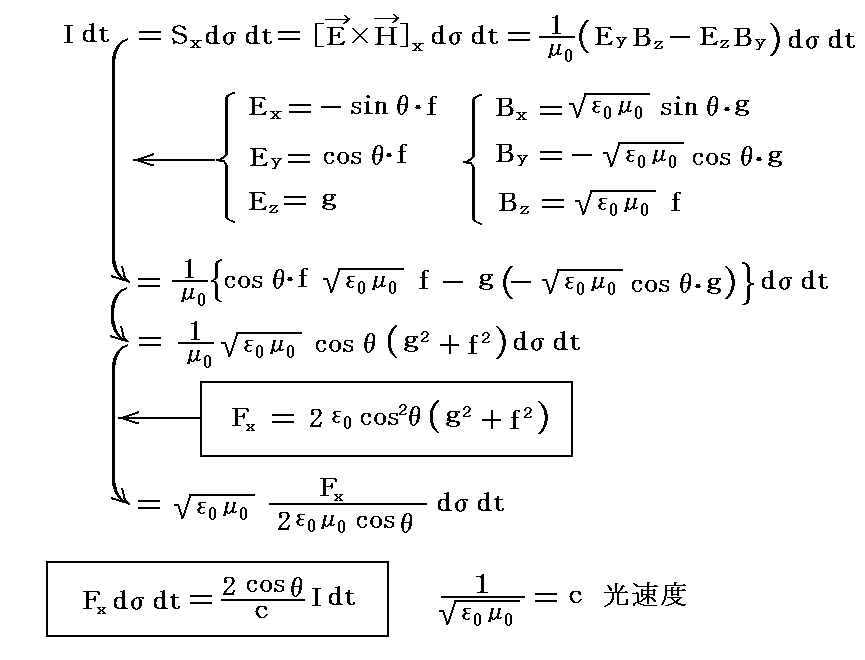
の関係で結びつけられる。
3.電磁場のエネルギー密度uと輻射圧p
前節で求めた式を用いて空洞内の輻射の全圧力pと空洞内の電磁場のエネルギー密度を結びつける。すなわち、真空中からきて導体に当たりそこで完全に反射される任意の輻射が導体に垂直に単位面積に及ぼす力学的力を計算する。
そのとき別項「キルヒホフの法則(熱的放射平衡における)」3.(1)で説明した以下の関係を用います。
空洞内部で平衡状態にある輻射を考える。空洞内部に任意の面積要素dσを考え、それを単位時間dt内に立体角dΩの方向に通過する輻射のエネルギーを求める。ここで単位面積を単位時間に単位立体角の方向へ通過していく輻射のエネルギー流をKとする。Kの事を今後輝度と呼ぶことにする。
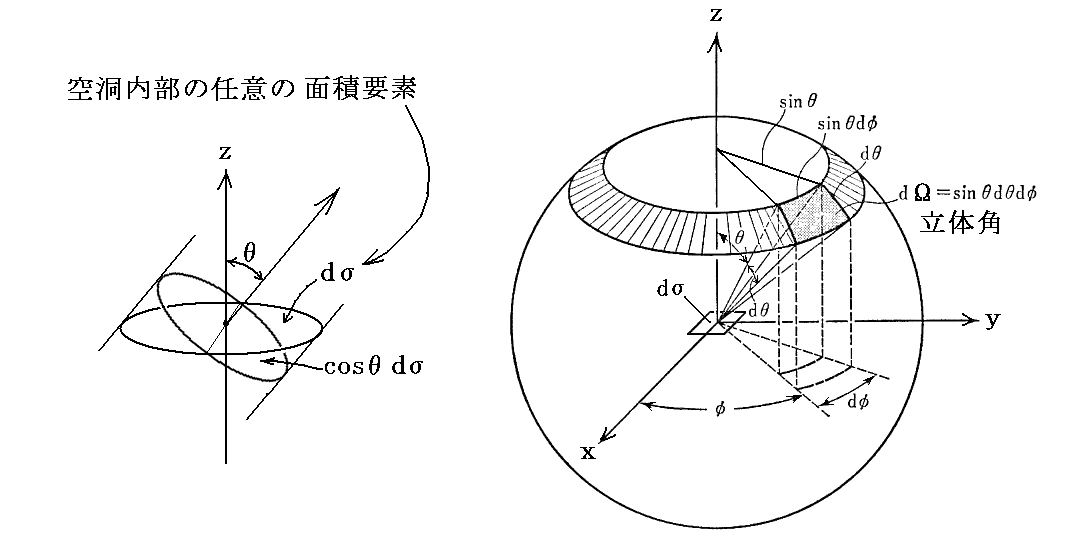
一般にKは場所と時間と方向に依存するが、ここでの議論のように平衡状態にある輻射場では、Kはすべての方向について一様と見なして良いであろう。今後その様に仮定すると問題のエネルギー流は
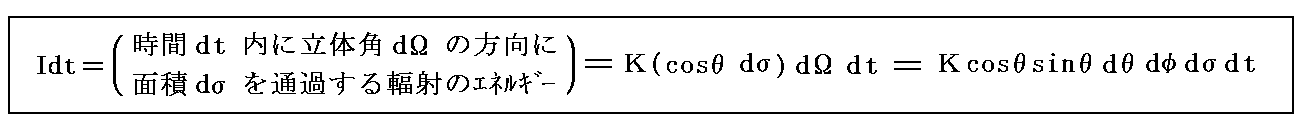
となる。IとKの意味の違いに注意。
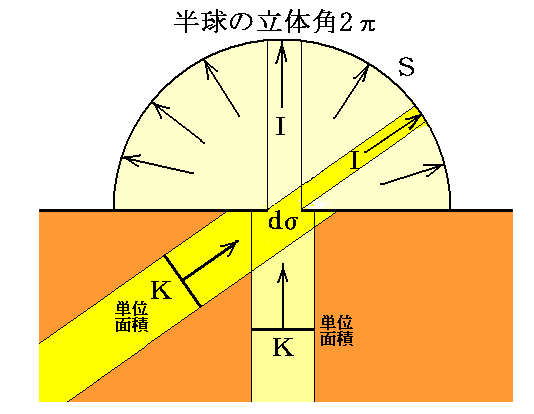
ここでKは導体表面に対してdΩの方向の輻射の輝度である。これを前記の式に代入すると
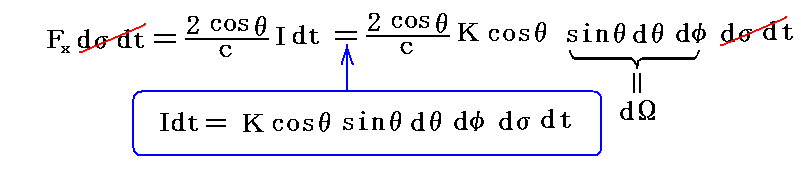
となる。導体表面の単位面積当たりに当たり、そこで反射される輻射線ビームの全圧力は上式をdΩの半球方向について積分すればよい。そのときKが、黒体輻射のように、方向に依存しないときにははKをdΩの積分の外に出せるので
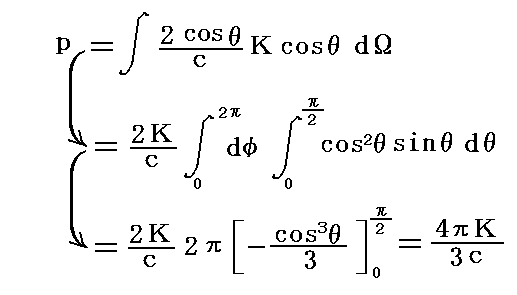
となる。
ここで、別項「キルヒホフの法則(熱的放射平衡における)」3.(1)で説明したように輝度Kは輻射の空間エネルギー密度uと

で結びつけられるので上式は
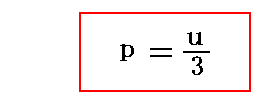
となる。これが最終的に求めたかった結論です。
[補足説明1]
高校物理の初等的な気体分子運動論に於いて、容器に詰められた単原子分子の理想気体が示す圧力pは

であると習う[高校物理Ⅱの教科書あるいはこちらを参照]。
この式と比較すると、光の圧力の場合には係数が2/3ではなくて1/3になっていることに注意されたし。
ただし、この係数1/3は2.(5)3.で議論したように、あくまで閉じた容器に閉じこめられた完全に等方的な輻射場についての、[輻射場のエネルギー密度u]と[壁に働く圧力]との関係に付いてのもであることを忘れないで下さい。
一方向のみに進行する輻射場が進行方向に垂直な壁に当たる場合には係数は1/3とは異なります。そのとき輻射が、壁に吸収されるか、あるいは反射されるかによっても異なります。
[補足説明2]
ここの議論では、輻射を完全に反射する完全導体に働く圧力として上式が導かれた。しかし、別稿「シュテファン・ボルツマンの法則」2.(5)で熱力学的考察から証明されるように、一般的な法則として、行き交う輻射の圧力は輻射場の性質のみに依存して、それを取り囲む物質の性質には依存しないと言うことができる。つまり、どの様な壁に対しても同様な圧力が働くのです。
このことから、これらの圧力は物体壁に対して働くのみならず輻射場そのものが持つものであると考えることができる。
3.マクスウェルの応力を用いた説明
(1)マクスウェルの応力
電磁場で満たされた真空中に仮想的な閉曲面を考える。別稿「電磁場の応力(マクスウェルの応力)」で何もない真空中の電磁場にも応力が定義できることを説明したが、その結論を利用して真空内の仮想的な曲面に対して働く電磁場の圧力を計算する。
マクスウェルの理論により輻射は電磁波である。電磁波の電場と磁場は互いに垂直であり、しかもどちらも進行方向に垂直である。(別稿「電磁波の伝播」参照)
今簡単のために、圧力を計算する面をx軸に垂直な平面とする。ある方向から入射してくる電磁波がx軸に垂直な単位面積に生じる応力Fは、別稿「電磁場の応力(マクスウェルの応力)」の2.(3)3.と3.(3)2.ですでに求めている。真空内の仮想面の位置に於ける電磁波の電場と磁場をE(Ex,Ey,Ez)とH(Hx,Hy,Hz)、真空中の誘電率=ε0、透磁率=μ0とすると
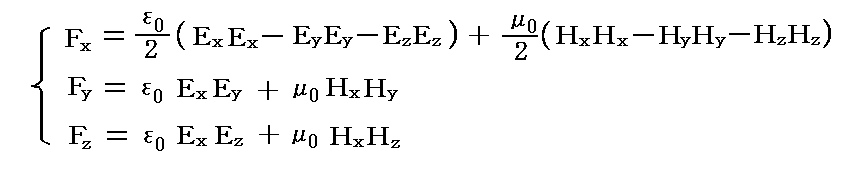
となる。ここでは前章と違ってBの代わりにHを用いているが、B=μ0Hと於けばBに変換できる。その際SI単位系(MKSA有利化単位系)ではε0もμ0も次元を持ち複雑な数値の定数となるが、その当たりについては別稿「電磁気学の単位系が難しい理由」を御覧下さい。
(2)輻射の圧力
黒体輻射の圧力を知るには、x軸に垂直な面の応力のx成分Fxだけを考えればよいので上記の式より
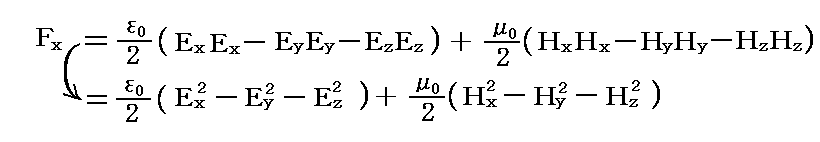
である。
輻射は電磁波であるからEとHは周期的に変化する。また、ここでは等方的な黒体輻射を考えているので、電磁波はあらゆる方向から今考えている平面にやって来る。そのため仮想平面に働く力は、それらすべての輻射の時間と方角による平均値である。<>で平均値を表す事にすると
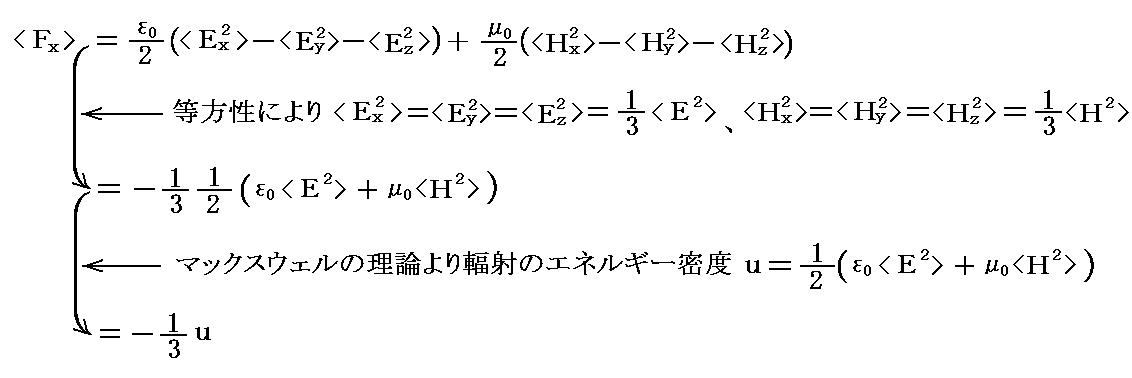
となる。
ここで等方的な輻射の場合に
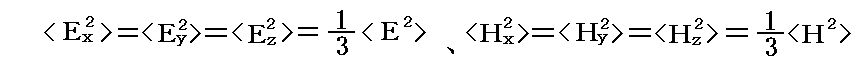
が成り立つことは以下のように考えればよい。今、進行する電磁波のEやHが時間的(例えば調和的)に変化する場合を含めて、様々な方向を行き交う電磁波の電場の二乗の平均を考える。ここで時間的変化や方向を変えたものがN通りあるとして、その電場の平均を考えることにすると
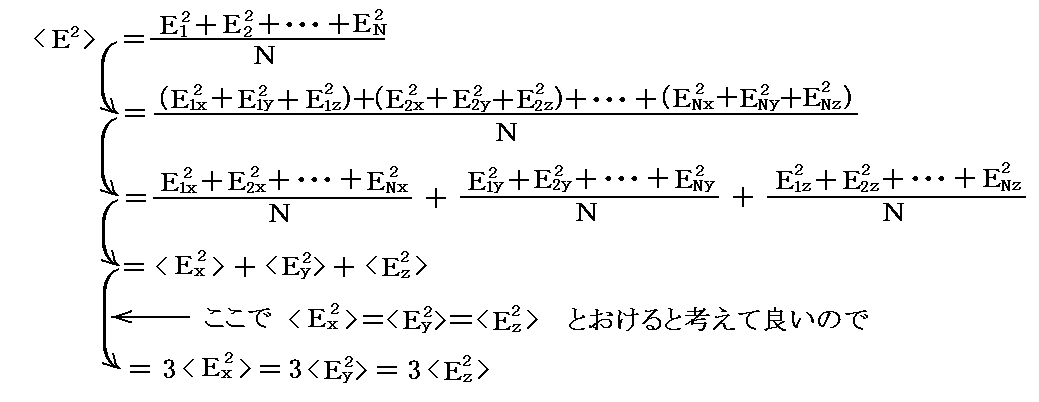
となる。<H2>に付いても同様です。
応力が負であることは、それが圧力であることを示している。そのため輻射の圧力pは
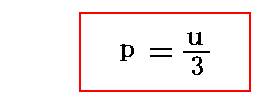
となる。結局、電磁場は圧力がかかった気体のように膨らもうとする。しかしその圧力は電磁場を物体の壁で囲まないと測定できない。壁で囲むと壁の中の電荷は移動し電流が流れ、壁のすぐ外側の電磁場はそれに応じて変化し、結局2.で述べたような事情になる。何か誤魔化された様な証明であるが、同じ結論が得られるのでおそらくこれで良いのだろう。
[補足説明1]
光の圧力の粒子説による説明です。
以下はI.E.シュポルスキー著「原子物理学Ⅰ」東京書籍(1966年刊)§125より引用

上記(125.1’)式の特殊相対性理論に基づく説明は、別稿「相対論的力学」3.(4)を参照されたし。
以下はイリヤ・プリゴジン、ディリブ・コンデプディ共著「現代熱力学」朝倉書店(2001年刊)の11章p209~210より引用。

[補足説明2]
朝永振一郎著「量子力学Ⅰ(第2版)」みすず書房(1969年刊)の第2章§13(ⅰ)に、上記[補足説明1]の議論を逆にひっくり返した説明があります。これも教訓的ですから引用しておきます。
この中で言及されている 第1章§5(ⅱ)空洞輻射の圧力 で説明されている断熱不変量の定理を用いる証明も興味深いものですから、ぜひ原本をご覧下さい。
4.参考文献
たいていの電磁気学の本で説明されていますが、このHPをつくるとき参考にした本を挙げておきます。
- ファインマン、レイトン、サンズ著「ファインマン物理学Ⅱ光、熱、波動」岩波書店(1968年)P113 9-9光の運動量 の項目に光の圧力が解りやすく説明されている。1章の証明はこの本から引用。これはもともとMaxwellが与えたものです。
- マックス・プランク著「熱輻射論」(物理科学の古典7)東海大学出版会P43~49
2章の証明はこの本から引用
- 芝亀吉著「熱力学」岩波全書P187
3章の証明はこの本から引用
- 小山慶太著「20世紀初期における放射圧測定の考察」
https://dspace.wul.waseda.ac.jp/dspace/bitstream/2065/10176/1/43137_23.pdf