音速の理論2(分子速度と比熱比)
ここでは、[音速]と[気体分子速度]の関係を導きます。
そのとき、気体中を伝わる[音速]と[気体の比熱比γ=cp/cv]の関係(別稿「音速の理論」)を利用します。そのため、音速は気体分子の内部自由度に関係する比熱比γにも関係します。
1.簡単な気体分子運動論
最初に、[気体の圧力]と[分子速度]の関係を導きます。ここは高校物理Ⅱで習う簡単な統計力学(気体分子運動論)の復習です。
(1)気体分子の運動と圧力
簡単化して以下の理想的な状況を考える。
- 気体分子の壁との衝突は完全弾性衝突。実際には壁の分子の熱運動や表面の凸凹に基づく不規則性が在るが、それらは全て無視する。
- 気体は理想気体とし分子間力は働かない。
- 理想気体のため分子の大きさはゼロと見なせる。こう仮定することで気体分子同士の衝突を無視できる。
- 単原子分子気体とする。分子の大きさが同じゼロでも、内部構造を持つ二原子分子、三原子分子・・・等々の理想気体を考えることもできます。しかしその場合には、回転や振動のエネルギーも考えねばならず複雑になるので、ここではとりあえず単原子分子の理想気体とする。
一辺Lの立方体の容器にN個の気体分子が詰められている場合を考える。
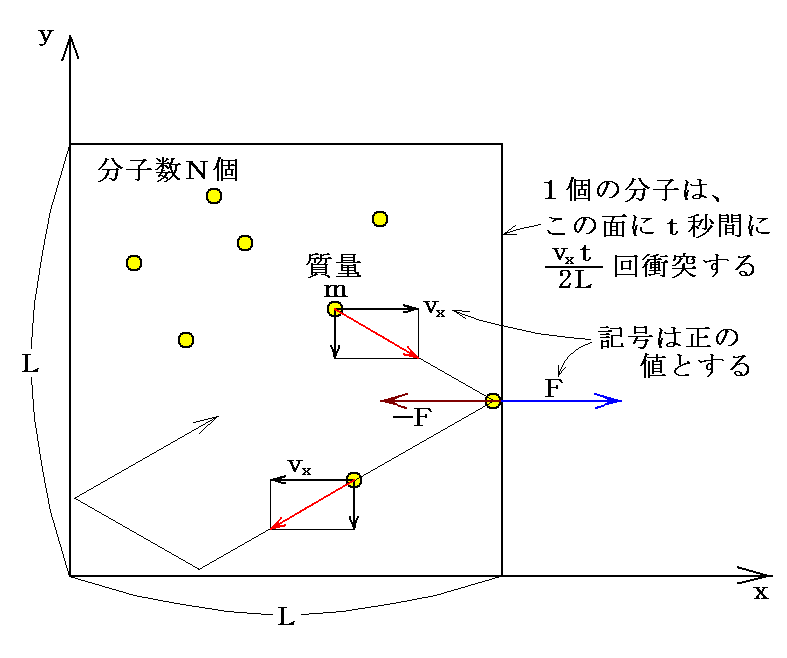
運動をxyz成分に分けて、x成分のみを考える。容器の中にN個の気体分子があり、その内の一つに着目する。
運動量の変化は力積に等しい(運動の第二法則)ので
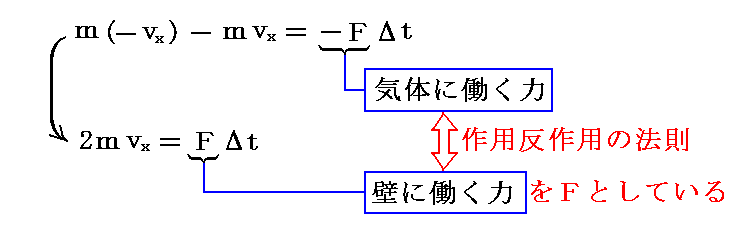
となる。
気体分子は高速なので、1個の気体分子は微小な時間間隔
t
の間に一つの壁と多数回の衝突を行う。そのため、Δt時間のみ働く瞬間的・間歇的な撃力Fの力積和を連続的に働く力F’の時間
t にわたる力積で置き換えてもよいであろう。
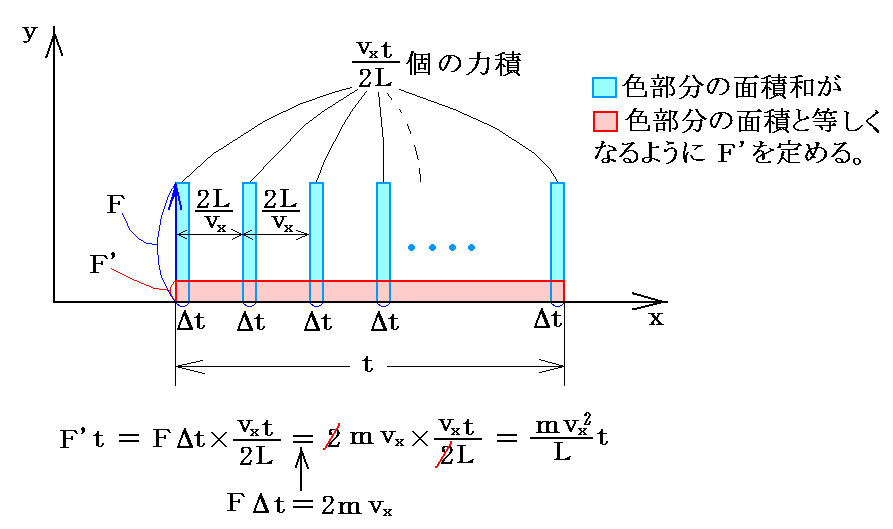
ここまでは、ただ一つ気体分子に付いての考察であるが、N個全ての気体が一つの面におよぼす力の合力をF合と記すと以下の様に変形できる。


ここで、赤四角で囲った考え方は重要です。
この式と圧力の定義より、[壁に働く圧力P]と[分子速度の二乗平均値]の関係式として
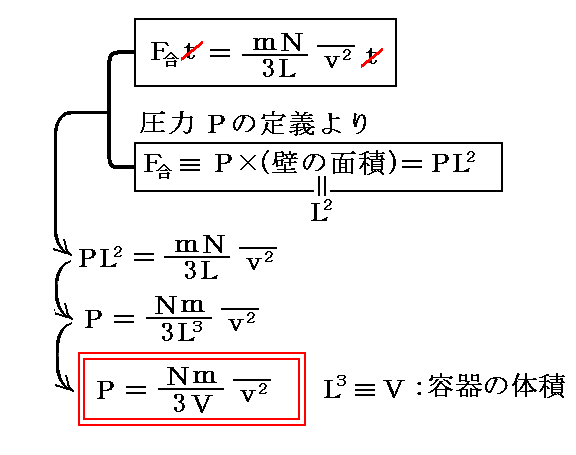
が得られる。
[補足説明1]
以上の説明に於いて[分子速度の二乗の平均]と[分子速度の平均の二乗]との違いに注意。つまり
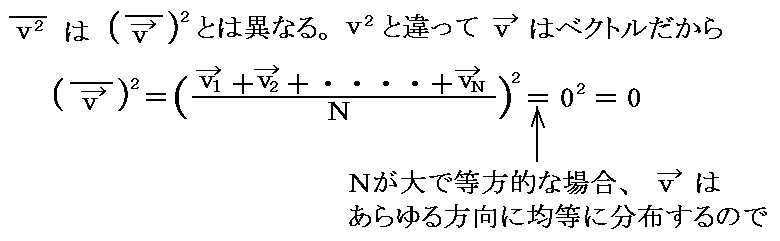
となる。
さらに[分子速度の絶対値の平均]と言う量もある。その定義は
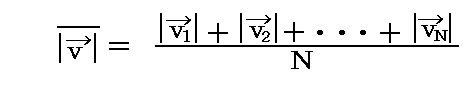
ですが、その値を求めるには速度の絶対値の分布関数(Maxwellの速度分布則)の情報が必要です。
そのことについては別稿「マクスウェルの速度分布則1“気体の動力学的理論の説明”(1860年)」3.(1)で説明していますが、特にそこで導く関係式
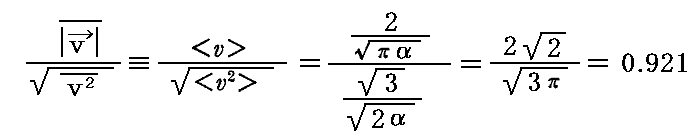
には注意して下さい。
[補足説明2]
ここで求めた関係式は
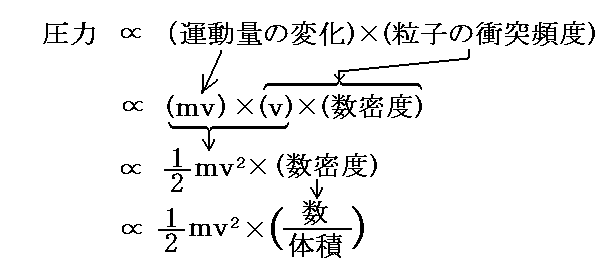
となることを意味する。
次節で説明するように、この式をボイル・ゲーリュサックの法則(高校物理ではボイル・シャルルの法則と習う)と比較すれば(1/2)mv2が気体の絶対温度Tに比例する量であることが解る。
(2)平均運動エネルギーと絶対温度
前節の結論は、“1個の気体分子の持つ並進運動の運動エネルギーの平均値”を巨視的な圧力・体積の積と結びつけるものでしたが、これを“熱力学における理想気体の状態方程式”と比較すると[気体の分子速度の二乗平均]を[絶対温度]に関係づける事ができます。

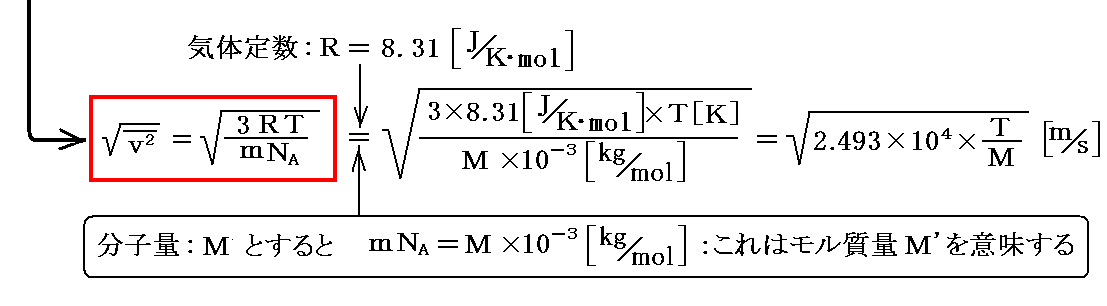
モル質量M’とは分子量Mの物質を1mol(アボガドロ数NA個)集めたときの質量のことです。
[補足説明]
上式中のmNA=Mは1モルの気体の質量ですが、これは簡単に測定できる。Tは測定できるし、Rは状態方程式を用いれば圧力Pと体積Vから測定できる。そのため気体の速度の二乗平均は計算可能です。つまり個々の分子の質量や分子の数などを知らなくても速度の二乗平均を求めることができる。
その様にして知れる分子速度vを用いれば、別稿「アボガドロ数の測定法」4.(3)で述べたη=(1/3)nmvλを用いて、粘性係数ηの実測値と単位体積当たりの気体質量(気体密度)ρ=nmの測定値から気体の平均自由行程λが求まる。そこで説明したように、平均自由行程λが求まればアボガドロ数NAや分子1個の質量mなどが求まる。
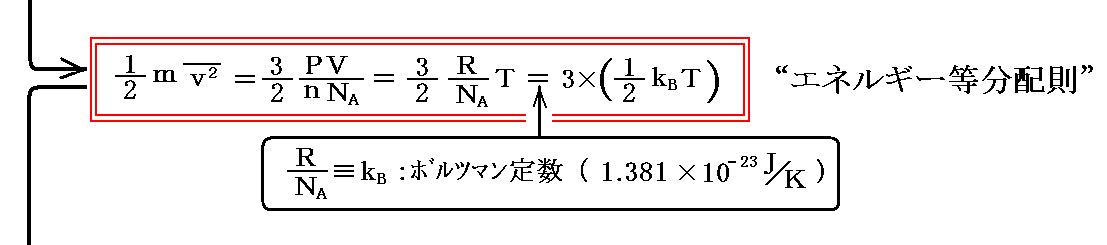
(3)エネルギー等分配則
前節に於いて気体定数Rをアボガドロ数NAで割った値をkBとおいたが、これはボルツマン定数といわれる普遍定数です。熱力学的な量である温度(ケルビンK)と、力学的な量であるエネルギー(ジュールJ)を仲立ちする換算定数でもあります。
単原子分子気体はx、y、zの三方向の速度成分を持つので自由度f=3を持つと言われる。自由度の概念を理解するのはなかなか難しいのですが、ここではそのようなものだと思ってください。
上記式の(1/2)kTの前に掛かっている3は単原子分子の運動の自由度が3であることに由来し、単原子分子が持つエネルギー(この場合運動エネルギーのみ)は、3つの自由度の各々について (1/2)kBT ずつ分配されていることを示している。
これはもう少し一般的な理論から言えることですが、粒子が温度Tの状態にあるとき、運動の1つの自由度に対して平均的に(1/2)kBTのエネルギーが分配される。このように絶対温度が決まれば運動の各自由度にエネルギーが (1/2)kBT ずつ分配されることを“エネルギーの等分配則”といいます。前節の結論はそのことが認識された、もっとも最初の例です。
[補足説明]
このとき次のことに注意されたし。
ここで求めた式は、最初に仮定した単原子分子理想気体のみならず、二原子分子、多原子分子・・・等々の内部構造を持つ理想気体についても成り立つ。
圧力はそれらの気体の回転や振動ではなく並進運動の運動エネルギーだけに関係しており、上記の式は、二原子分子、多原子分子の理想気体の並進運動のエネルギー部分だけを取り出した関係式だからです。
分子の大きさがゼロで分子間に力が働かないと見なせる場合には、この様に内部構造を持った気体でも理想気体の状態方程式(ボイル・シャルルの法則)を満たし、“理想気体”であると見なせます。
2.音速と分子速度・比熱比の関係
(1)音速と分子速度の二乗平均
二原子分子や多原子分子の場合には回転の自由度もあり、“エネルギー等分配則”が成り立つとするとそれらの自由度にもエネルギーが分配される。
そのため、多原子気体の集合体に熱(エネルギー)を与えたとき、その一部が並進運動の自由度に他の一部が回転運動の自由度に分配される。単原子気体に比べると並進運動のエネルギーの増加分は少なくなる。そのため絶対温度の上がり方も少なくなるし、圧力の増加量も少なくなる。
このことが、気体の断熱変化に伴う圧力・温度・体積変化にγが絡んでくる理由であり、断熱変化に伴う粗密波の伝播速度(音速)に比熱比γが関係してくる理由です。
前章1.(2)で求めた結論と、別稿「音速の理論」4.で求めた結論を一緒にすると

の関係式が得られる。これが、本稿で説明したかった結論です。
[補足説明1]
ここで、音速が気体分子の速度vに関係することは明らかです。なぜなら音速とは気体の疎・密の状況が次々と伝えられていくことですから。それらを伝えるのは気体分子が隣り合った気体に衝突することで次々と伝えられていく。
つまり音速は気体分子の運動速度に依存する。単純にvに比例するのではなくてv2の平均値の平方根に比例するのは、気体があらゆる方向に動いているからで、一方方向への効果に換算・平均化するとその様になる。
[補足説明2]
さらにγ=cp/cvに関係するのは、音とは有る部分の気体の固まりが次々と隣の気体を圧縮して自らは再び膨張・収縮を繰り返していく現象であることに関係する。
そのとき有る場所の気体が隣の気体によって圧縮されたとき、その圧縮という仕事に伴って受け取るエネルギーの一部が気体分子の並進速度に、他の部分は気体の回転や振動のエネルギーになる。
気体が内部構造を持った二原子分子や多原子分子では、受け取ったエネルギーの一部が回転や振動のエネルギーとなるため、並進運動の増加に寄与する部分が少なくなる。そのため速度の増加分が少なくなるので音速への寄与が少なくなる。γは自由度が大きいほど小さくなります。だからγの小さな多原子分子の場合が最も音速への寄与が小さくなる。
(2)実測値との比較
幾つかの気体について、絶対温度T=温度273K(0℃)における[分子速度の二乗平均の平方根]を上記の式に従って求め、それと[γの実測値]を用いて[音速の理論値]を求めてみる。
比較のために[音速の実測値(0℃)]も記すと下表の様になる。Ar以外では理論値と実測値は極めて良く一致する。ここで説明したような簡単な理論で求めた[分子速度の二乗平均の平方根]と[音速の実測値]が旨く結びつけられるのは驚くべき事です。
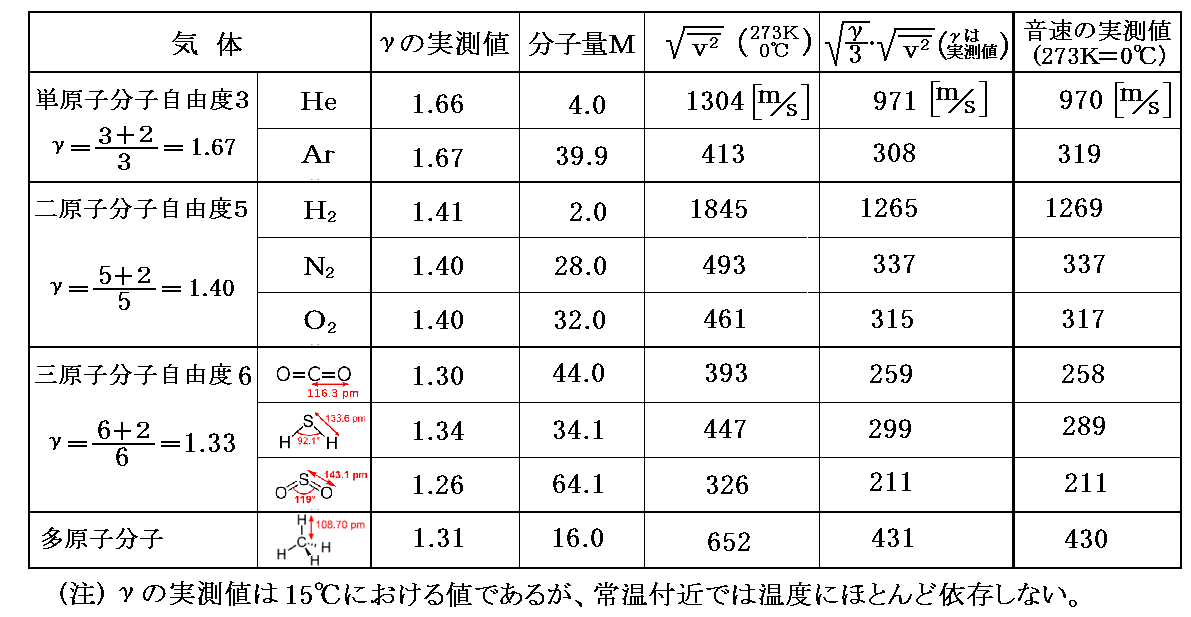
前節で注意したように気体の音速には、気体分子の内部構造が関係してきます。別稿「音速の理論」3.(2)で求めたように音速は比熱比γ=cp/cvの平方根に比例しましたが、γ(気体の定圧比熱と定積比熱の比)は気体の内部構造(単原子分子、二原子分子、三原子分子・・・等々)に依存するからです。
多原子分子の場合、気体に加えられたエネルギー(熱)は気体の並進運動のみならず回転や振動にも分配される。そのため、多原子分子では並進運動に分配されるエネルギー量が減ります。そのため断熱変化を表す公式にγの値が関係します(別稿「気体の断熱変化」参照)。
[補足説明1]
今日、γの実測値は別稿「音速の理論」4.の
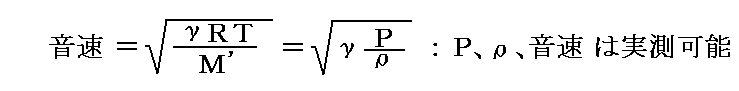
を用いて音速の実測値より求められる場合が多いので、実験値との一致は当たり前かも知れません。
ここでより重要なのは、[γの実測値]が次節で説明する気体分子の[自由度から計算される理論値]に良く一致することです。
[補足説明2]
気体の比熱比γ と気体分子の自由度 f とは

の関係があります。
[証明]
古典統計力学の“エネルギー等分配則”により、気体分子の自由度が f であるとすると1モルあたりの内部エネルギーは

と表せます。このとき、定積モル比熱cvは、体積一定の元での内部エネルギー変化dUと温度変化dTの比を意味しますので

となります。
所で、1.(3)[補足説明]で説明した様に、気体分子が内部構造を持っていて、回転や内部振動にエネルギーが分配されていても“ボイル・シャルルの法則”に従う“理想気体”と見なすことができます。
ボイル・シャルルの法則に従う理想気体に対しては“マイヤーの関係式”が成立するので、定圧モル比熱cpは

となります。
上記①、②式から、比熱比γは

と表せます。
[証明終]
(3)比熱比γと気体分子の自由度
γは気体分子の自由度と関係づける事ができます。単原子分子の自由度は 三次元空間の三方向への運動を示すもので f=3となります。
二原子分子や多原子分子の自由度は並進運動の“自由度”に回転運動の“自由度”を加えたものになります。そのとき二原子分子の場合には、その二原子を結ぶ中心軸軸の周りの回転にはエネルギーは分配されず、回転の自由度は中心軸に垂直な二方向の回転軸に関係した2になります。三原子分子の場合には三方向の回転軸に関する回転エネルギーにすべて等分配されますので回転自由度は3となります。そのため、トータルの自由度は二原子分子 f=5、三原子分子 f=6となります。
このことについては別稿「Feynman物理学Ⅱ§15-5」を参照されたし。
[補足説明0]
上記のFeynmanの説明を読まれたら解るように、“自由度”という概念はかなり曖昧でいい加減なものです。これは熱平衡状態に於いて平均的に(1/2)kTのエネルギー値を保持する可能性を持つメカニズムの“数”を意味します。
そのとき例えば、気体分子の熱平衡状態の場合、分子の並進運動、回転運動、原子振動等々・・・の運動運動エネルギーなどが(1/2)kTのエネルギー値を取り得ると考えられるから、それらのメカニズムを一つ一つを数え上げたものが自由度です。しかしそのとき、分子を構成する内部電子一つ一つも(1/2)kTのエネルギー値を取り得ることは無いのだろうか?、あるいは構成原子が調和振動するときのポテンシャルエネルギーの様なものも(1/2)kTのエネルギー値を取り得るとしなければならないのではないか?、等々・・・といくらでも疑問は出てきます。
だから、実際に、そのメカニズムが(1/2)kTのエネルギー値を取り得るのかを判定して、“自由度”を数え上げるのは難しい。特に、次に述べる量子力学的な効果が絡んで来ると簡単にそのメカニズムの数を見積もることはできません。だから、“自由度”の概念はもともとそのように曖昧なものだと割り切って理解すべきでしょう。
このとき、原子間の結合エネルギーに関係する振動運動の自由度は、常温付近では量子力学的な効果により凍結しており、この数の中に入っていません。さらに、原子や分子内の電子の運動に対応する自由度もそうです。普通の多原子気体では、常温付近での振動状態は最低のエネルギー状態にあり等分配則を満足しない。
常温付近では並進運動や回転運動に関しては多数のエネルギー状態が取れる状況にあり等分配則を満足します。しかし、温度がさらに低下すると回転運動の自由度も凍結されてきて等分配則が成り立たなくなり比熱に寄与しなくなる。
これは黒体(空洞)輻射において、エネルギー量子が大きい高振動数領域にエネルギーが分配されなくなるのと同じで、量子効果が働くためです。
この事については別稿別稿「Feynman物理学Ⅱ§15-5」と、「§15-6」を参照されたし。
2.(2)[補足説明2]で説明した様に、比熱比γと自由度fの間にはγ=cp/cv=(f+2)/fの関係が成り立ちます。ここで言う自由度fとは上に述べたもので、上記の自由度の値を代入すると、比熱比はそれぞれ、単原子分子 γ≒1.67、二原子分子 γ≒1.4、多原子分子 γ≒1.33 となる。
[補足説明1]
前節の表で、二酸化炭素が直線状分子であるにもかかわらずγが二原子分子のそれではなくて三原子分子の値になるのは興味深い。
二酸化炭素分子の形状は時間的に平均すると直線状でも瞬間的には折れ曲がった構造をとり、この折れ曲がり振動モードのエネルギー量子が他の振動モードよりも小さいので励起が起こりエネルギーが等分配されるためのようです。
[補足説明2]
ここで述べた[分子速度の二乗の平均値の平方根]と[絶対温度T]との関係式は、高校レベルの簡単な分子運動論で導くことができます。
しかし、1.(1)[補足説明1]で述べたように[分子速度の二乗の平均値の平方根]と[分子速度の絶対値の平均値]は異なります。
その時、等分配される[エネルギー(1/2)kT] を[分子速度の絶対値の平均値]と結びつけることは高校物理のレベルでは難しい。それは、[分子速度の絶対値の平均値]を求めるには気体速度の絶対値の分布[Maxwellの速度分布則]が解っていないといけないからです。
この当たりは高校レベルを越えますが、別稿「マクスウェルの速度分布則1“気体の動力学的理論の説明”(1860年)」でもう少し説明します。
3.歴史的概観
ここは参考文献2.を参照した。この章は、別稿で引用している山本義隆著「熱学思想の史的展開」第28章第Ⅵ節も参照されながらお読み下さい。 また、テル・ハール著「熱統計学」第1章の文献解説も参照されたし。
(1)ダニエル・ベルヌーイ(Daniel Bernoulli 1700~1782年) 1738年
ここで説明した初等的な分子運動論による圧力の説明はおそらくD.Bernoulliが最初であろう。彼は1738年の著書「流体力学 Hydrodynamica」の第10章で次のように説明した。
気体は激しく運動している多数の粒子からなるという仮説を用いて、気体の圧力は器壁に衝突する粒子によって生じることを説明した。ここに用いられている“分子の運動量の変化が圧力を生ずる”というのは卓抜な着想でした。
また、体積が変化すると衝突数が変化することを考察することにより、“圧力が体積に反比例する”ことも示した。
さらに、彼は“圧力が分子速度の二乗に比例する”ことも論じた。
彼の考察は時代を遙かに先んじたものだったのですが、残念なことに、そののち100年もの間この理論を引用するものはおらず、彼の考えは全く無視される。
(2)ジョン・ヘラパス(John Herapath 1790~1868年) 1821年
ヘラパスは1821年の論文で、気体は互いに衝突しながら飛び回っている粒子の集まりだという仮説を立てた。当時の一般的な考え方は、気体は斥力を及ぼしあう粒子からなる弾性流体という考え方が支配的だったから上記の仮説は革新的です。ヘラパスは上記のベルヌーイの議論を知らずにこの仮説に至ったようです。
彼は上記の仮説から“気体の圧力の成因”、“断熱変化の際の温度変化”、“溶解・蒸発・拡散”などを説明することができた。
ただし残念なことに、彼は気体の温度は粒子の平均運動量(正しくは平均運動エネルギー)によると考えたためにPV∝T2という誤った関係に導かれている。
彼はこの論文を最初ロイヤル・ソサエティに送ったが、掲載を拒否されたために別の機関誌
J. Herapath, “A Mathematical Inquiry into the Causes, Laws, and principal
Phenomena of Heat, Gases, Gravitation, etc.”, Annals of Philosophy [2],
1, p273~293, p340~351, p401~416, 1821年
に載ることになった。
この日本語訳
「熱、気体、重力などの原因、法則、およびそれらの主要な現象についての数学的探求」
は 科学の名著第Ⅱ期③「近代熱学論集」朝日出版社(1988年刊)の中に訳出されています。
ちなみに、 断熱変化の際の温度変化は、単原子分子気体に限れば、1.(1)[補足説明2]の様に(1/2)mv2が気体の絶対温度に比例する量であることが解ると、これに別稿「気体の断熱変化」で説明した気体が外に対してする仕事が気体の内部エネルギーの減少分であることを結びつけて分子運動論的に説明することができます。
多原子分子の場合には、気体分子の回転のエネルギーも変化しますので、並進運動エネルギーと回転運動エネルギーの間のエネルギー分配割合に関係する比熱比γも絡んできます。
(3)ジョン・ジェームズ・ウォーターストン(John James Waterston 1811~1883年) 1845年
ウォーターストンも衝突しながら飛びまわっている粒子の系の性質を論じた。彼は粒子の速度は様々な値を取ることを認めて、気体を閉じこめた容器の壁に当たる分子の衝突によって生じる力を計算した。それから圧力は気体の密度と分子の平均速度の二乗との積に比例することを導いた。
ウォーターストンは上記の関係式をボイル・ゲーリュサックの法則と比較して絶対温度は分子の平均速度の二乗に比例するとした。
彼はさらに、異なる分子どうしの衝突を考察して、それぞれの分子の平均二乗速度は各々の分子質量に逆比例することを見いだした。これは“エネルギー等分配則”を導いた最初の例であろう。
彼はまた、単原子分子に対するものであるが、定圧比熱と定積比熱の比を求めた。
ウォーターストンはこれらの結果を報告した論文を1845年にロイヤル・ソサエティに送ったが、掲載を拒否されたまま協会の倉庫で埋もれてしまう。この抜粋にあたるものが大英学術協会から公刊されてはいたが、その重要性は理解されなかった。
1891年に、当時王立協会の事務局長を務めていたレイリー卿は、音についてのある論文に引用されているウォーターストンの名前に目をとめて不審に思った。レイリーは協会の保管文書の中からウォーターストンの原稿を探しだして
“On the Physics of Media that are Composed of Free and Perfectly Elastic
Molecules in a State of Motion”Phil. Trans. Roy. Soc. , 183A, p1~79, 1892年
に載せて出版した。こうしてウォーターストンの業績は約半世紀後にやっと世に知られることになった。
ウォーターストンの業績に関しては、小暮智一氏の解説も参照されたし。
(4)ジェームス・ブレスコット・ジュール(James Prescott Joule 1818~1889年) 1851年
上に述べたJ.Herapath(1821年)の論文は全く当時の科学者の注意を引かなかったが、20年数年後に彼が出版した「数理物理学 Mathematical Physics; or the Mathematical Principles of Natural
Philosophy (1847年)」の中で述べた気体運動論の考えがJ.P.Jouleの注意を引いた。
彼はHerapathのアイディアを復活させ熱の運動論をいっそう具体的なものにして、1848年にマンチェスター文学科学協会で発表した。そして1851年に同協会の機関誌に発表した。
J. P. Joule, “Some Remarks on Heat, and the Constitution of Elastic Fluids”,
Mem. Lit. and Phil. Soc. Manchester, [2], 9, p107, 1851年
これは後に
Phil. Mag., 14, p211~216, 1857年 に採録されている。また彼の論文集 Scientific Papers, vol.1,p290~297 にも載っている。
ジュールは上記の論文で、気体の粒子の総数の1/3ずつが立方体の稜に平行な、大きさの等しい速度を持つと仮定して、圧力は粒子の速度の二乗に比例することを示した。つまり1.(1)で得られた式と同等なものを得た。
1.(2)[補足説明]で注意したように、式中のmNは容器の中にある気体の総質量ですが、これさえ知ることができれば圧力Pと体積Vから気体の速度の二乗平均を知ることができる。つまり個々の分子の質量や分子の数などを知らなくても速度の二乗平均が予測できる。
実際、ジュールは、この式を用いて華氏60度=15.6℃(絶対華氏温度で519度)の“水素”分子の早さを6225feet/sec=1897m/sであると求めた。これは今日知られている値にかなり近い。
彼はまた、分子速度が絶対温度の平方に比例することを用いて華氏61度(絶対華氏温度で520度)における分子速度が6225×(520/519)0.5=6230.93feet/sec=1899m/sを求めた。ちなみに0℃は華氏32度(絶対華氏温度491度)です。
これらの値を用いると、両温度での運動エネルギーの違いを計算できる。その差が温度を高めるために加えた熱量であるとして“水素”の比熱(定圧の下での単位質量当たりの熱容量)を計算した。それは水の比熱の1.506倍という値であった。
“他の気体”の比熱はその比重に反比例するはずであるから、水素の比熱から計算することができる。下表の理論値は一番上の水素の上記理論値1.506をそれぞれの気体の水素に対する分子量比で割ったものです。2列目のOxygenは1.506÷(32/2)=0.094、3列目のNitrogenは1.506÷(28/2)=0.107、4列目Carbonic
oxideは1.506÷(44/2)=0.068となる。
ジュールは、そのようにして得た幾つかの気体の比熱の理論値を実測値(定積比熱cv:下表の真ん中の値)と比較してみた。しかしその結果は

の様になり、理論値は実測値と全く合わず、実測値の方がすべて大きめの値となった。この理由がわからず物理学者を困惑させた。
さらに実測された比熱が気体分子の分子量に単純に逆比例するわけでもなかった。実際、実測された単位質量当たりの比熱に分子量を乗じてモル比熱に換算すると

となる。理論的には等しくなるはずの値が、実測値は様々にばらばらになった。特に水素は小さめ、二酸化炭素は大きめの値になることが解る。このことも大きな謎です。
このように、理論が予想する比熱は実測値と全く合わず当時の物理学者を困惑させた。
今日の知識で説明すると、実測値が理論値よりも全体的に大きくなるのは、気体分子が内部構造を持った二原子・三原子分子であるために回転の自由度にエネルギーが分配される為です。
また実測値に分子量を乗じてモル比熱に換算した値において、水素が小さめにでるのは、量子効果による回転運動の凍結が水素ではわりと高い温度から早めに起こるからです。また二酸化炭素が大きめになるのは二酸化炭素が三原子分子のために内部自由度が増えるからです。
当時の知識ではそこまで考えが及ぶはずもなく、ジュールは将来の理論と測定に望みを託してこれ以上の考察は進めなかった。
このジュールの考察は、気体の比熱を気体分子運動論で説明するという画期的なものですが、実験値とのずれを説明できなかった。それをするためには、気体分子の内部構造に起因する効果を含めた“量子論”の登場を待たねばならず、比熱は19世紀のあいだじゅう気体運動論の困難な問題であり続けた。
このことに付いては、例えば Feynman著「ファインマン物理学Ⅱ光、熱、波動」岩波書店(1968年刊)§15-5、§15-6 などをご覧下さい。
(5)アウグスト・カール・クレーニヒ(August Karl Kro¨nig 1822~1879年) 1856年
ヘラパス、ウォーターストン、ジュールはいずれも当時の学会では無名であったために、彼らの気体運動論はだれからも注目されずに放置された。
気体運動論の継続的な発展に契機を与えたのは、
1856年に出た A. K. Kro¨nigの論文 “Grundzu¨ge einer Theorie der Gase”, Poggendorff's Ann. d. Phys. [2], 99, p315~322, 1856年
であろう。
彼の研究はヘラパスやジュールとは独立になされたもので内容的に新たな進歩は無いが、発表されたのが熱の運動論が確立された後であったことや、クレーニヒが学会で権威を認められていた(彼は1851年に発刊された雑誌『諸外国の物理および物理化学』の編集や外国論文のドイツ語訳紹介などをしており、1855年からは年報「物理学の進歩」の編集者であった)ために、この論文は気体運動論の本格的な発展のきっかけとなった。
クレーニヒは気体を、三つの座標軸方向に同じ速度cをもつ完全弾性球の集まりと見なした。器壁に対する衝突によって生じる圧力を計算して、それがnmc2/vに比例することを示した。
(c:分子速度、n:粒子数、m:粒子の質量、v:気体の体積)
絶対温度をmc2に等しいとすると、これはボイル・ゲーリュサックの法則に同等であると論じた。
また、重力の影響を考慮して、容器の上部と下部とて気体の圧力は等しくない事を指摘した。しかし、その違いを表す正確な式は導かなかった。
(6)ルドルフ・クラウジウス(Rudolf Julius Emmanuel Clausius, 1822~1888年) 1857年、1858年
クレーニヒの論文が刺激となって、クラウジウスは以前から抱いていた気体運動論の着想を具体的な理論に仕上げて発表した。
1.「われわれが熱と呼ぶ運動の性質について」 1857年
R. Clausius, “Ueber die Art der Bewegung, welche wir Wa¨rme nennen”, Poggendorf's
Annalen, Bd.100, S.353~380, 1857年
以下はその英訳論文です。
“On the Nature of
the Motion which we call Heat”,Phil.
Mag. (4), Vol.14, p108~127, 1857年
日本語訳
「われわれが熱と呼ぶ運動様式について」
は 科学の名著第Ⅱ期③「近代熱学論集」朝日出版社(1988年刊)の中に訳出されています。
また、八木江里監訳「クラウジウス熱理論論文集 エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)にもあります。
この論文のはじめの2/3は、気体運動論の基礎的な考え方についての定性的な説明がなされている。その後でボイル・ゲーリュサックの法則の導出と気体の比熱が論じられる。
彼は次の三つの仮定から出発する。
- 気体の全体積に対して分子自体のしめる全体積は無視できる。
- 分子どうしの衝突や分子と壁との衝突は、衝突と衝突の間の時間に比べて無限小の時間に起こる。
- 分子間どうし、あるいは分子と壁との間の力の影響は無限小。
クラウジウスは、上記の仮定の下に分子が器壁に衝突することによって生じる力積を計算して、圧力と分子速度の関係を導いた。その導出法は1.(1)と基本的には同じですが、クラウジウスはそれをもう少し一般化した。すなわち分子の速度の大きさは一定だが、方向は任意であるとして扱った。ただし、速度の方向分布は一様と仮定されている。
いずれにしても、気体の分子運動論から気体の圧力pは
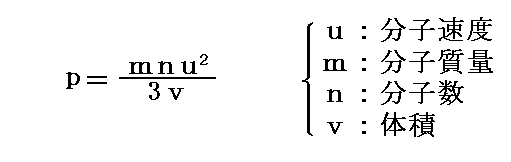
となる。
次に、彼は1.(2)と同様に、この式をボイル・ゲーリュサックの法則と比較する事により、先行者と同様に気体分子の運動エネルギーが絶対温度Tに比例すること
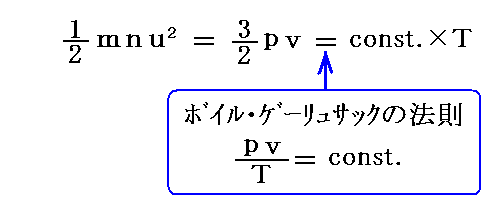
を導いた。
次に彼は、ジュールと同じように、幾つかの気体の0℃における分子速度を導いた。そのとき1kgの空気は0℃(=273K)、1気圧の下で0.7733m3の体積を占めるというフランスのルニョー(Regnault)の測定値を用いている。1気圧とは1m2の面の上に10333kgの質量が乗っているときの圧力だからp=10333kg/m2×9.80896m/s2=101355.9837N/m2となる。
これらの値を用いて、0℃、1気圧における平均の分子速度を1kgの空気について計算すると
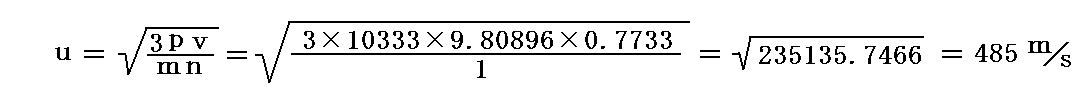
となる。
理想気体の状態方程式から明らかなように、絶対温度(273K)、圧力(1気圧)、気体の総質量(1kg)が等しいとき、様々な気体が占める体積は気体の密度(単位体積当たりの質量)に逆比例するから、他の気体の分子速度を求めるには上式中の0.7733を0.7733/ρで置き換えれば良い。ここでρは各気体の空気に対する比重を意味する。
空気の分子量28.8を用いると酸素、窒素、水素の空気に対する比重はそれぞれρ酸素=32/28.8=1.11、ρ窒素=28/28.8=0.972、ρ水素=2/28.8=0.0694となるから、これらの気体の0℃、1気圧の下での平均的な分子速度は
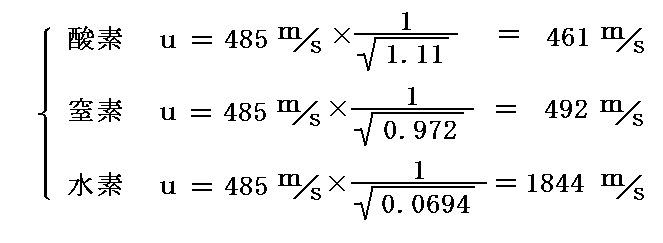
となる。
引き続いて彼は、気体分子が内部自由度を持ちうることを明らかにした。そのとき分子と器壁との衝突の際に分子の並進運動と内部運動との間に活力(運動エネルギー)の受け渡しが起こるが、平均としては分子の速度を一定とみて良いだろう。だが比熱の値にはこの内部運動が影響するはずであるとして次のような考察をした。
まず、“分子の並進運動の活力(運動エネルギー)の総和”Kは
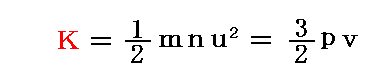
となる。
気体の定積比熱をc、定圧比熱をc’、気体の質量をq、仕事の熱当量をA(=1/4.1855J/cal=0.23892cal/J)、絶対温度をTとすると、“気体が含む熱量”Hは
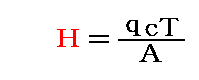
と書ける。定積比熱の値は温度にほとんど依存せずに一定値だからこの関係式が成り立つとした。
理想気体に於いて、熱力学的考察から二つの比熱の間には次の関係が成り立つ。
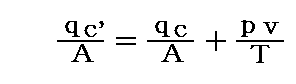
これは、別稿「気体のモル比熱」で説明したマイヤーの関係式そのものですから、導き方はそこを参照。
これを前述の式と組み合わせると
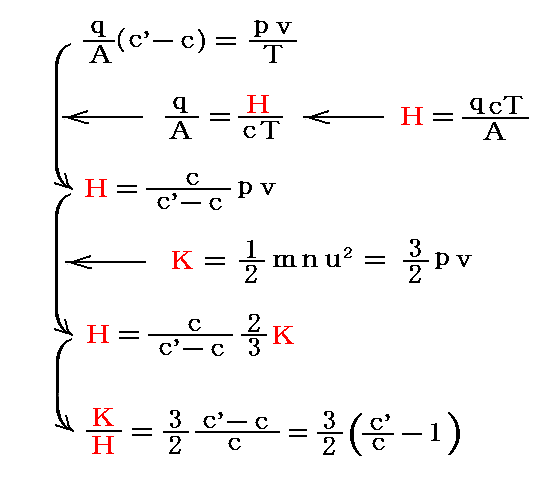
が得られる。
単体の気体に対する比熱比の測定値は
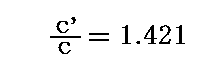
であったから、
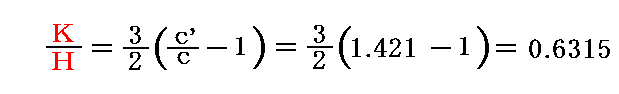
となる。これは気体の持つエネルギーの一部のみが並進運動のエネルギーを構成しており、気体分子はそれ以外の形のエネルギーを持つことを示している。これからクラウジウスは分子は“内部自由度”を持つことを結論した。
“内部自由度”はクラウジウスによって初めて考察された概念です。
2.「気体の分離した分子によって記述される平均自由行程と、熱の力学理論についての幾つかの注意」 1858年
前項の理論に対して1858年オランダの気象学者ボイス・パロット(C. H. D. Buys-Ballot 1817~1890年)は、次のような批判をした。
“気体運動論によれば気体分子は毎秒数百メートルという極めて大きな速度を持つことになるが、気体の拡散は徐々にしか生じないという経験はこの結論に矛盾する。”
クラウジウスは早速この批判を受け止め、分子間の衝突を考慮して“平均自由行程”の概念を導入した。これが次に紹介する論文で書かれており、これは画期的な内容です。
R. Clausius, “Ueber die mittlere Lo¨nge der Wege, welche bei Molecularbewegung
gasfo¨rmigen Ko¨rper von den einzelnen Molecu¨len zuru¨ckgelegt werden,
nebst einigen anderen Bemerkungen u¨ber die mechanischen Wa¨rmetheorie”,
Poggendorf's Annalen, Bd.105,p239~258, 1858年
以下はその英訳論文です。
“On the Mean Length
of the Paths described by the separate Molecules of Gaseous Bodies on the
occurrence of Molecular Motion: together with some other Remarks upon the the
Mechanical Theory of Heat”, Phil.
Mag. (4), Vol.17, p81~91, 1859年
日本語訳は、
「気体物体の分子運動による個々の分子の通過した平均距離について」八木江里監訳「クラウジウス熱理論論文集 エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)
にあります。
分子間に働く力は、遠くで引力、近くで斥力であると仮定すれば、引力から斥力に変わる距離ρがあると考えられる。分子の周りの半径ρの領域を、その分子の“作用球”と名付ける。
今着目する分子を除いて、他の分子は全部静止しているとする。それらの分子どうしの平均距離をλとすると、体積λ3に1個の割合で分子が存在すると考えることができる。
クラウジウスはまず、着目する分子がその進行方向に垂直な厚さxの層を他の分子の作用圏にぶっからずに通過する確率W(x)を計算した。
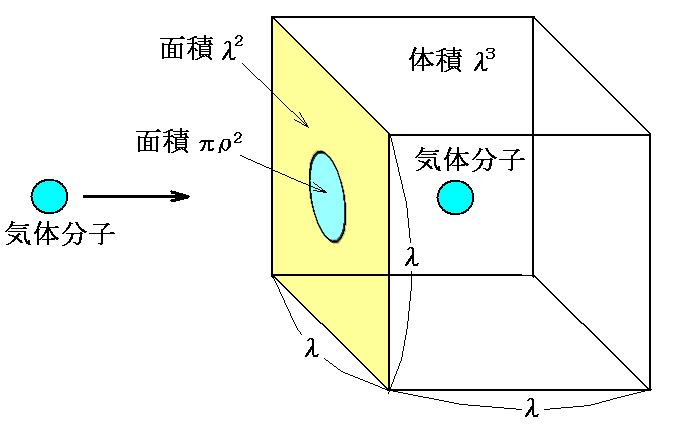
分子配置の幾何学的状況から着目する分子が厚さλの層を他の分子に衝突することなく進む確率Wλは上図の面積の比率から計算して
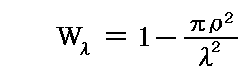
となる。分子の通過する層の厚さが2λ,3λ,・・・,nλと増加したときに、それらの厚さを層を分子に衝突することなく通り抜ける確率は、各々の厚さλをぶつからずに通過する確率の積となるので
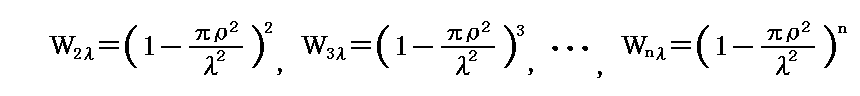
となる。この当たりの考え方は、別稿「放射性崩壊と半減期」1.で説明したのと同じです。そこの時間tを、層の重なり数nに置き換えればよい。nは層の厚さxとn=x/λの関係にあるので
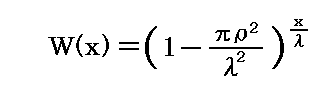
となる。ここでさらに、別稿「放射性崩壊と半減期」2.で説明したように、計算に便利な e での表現に変換すると
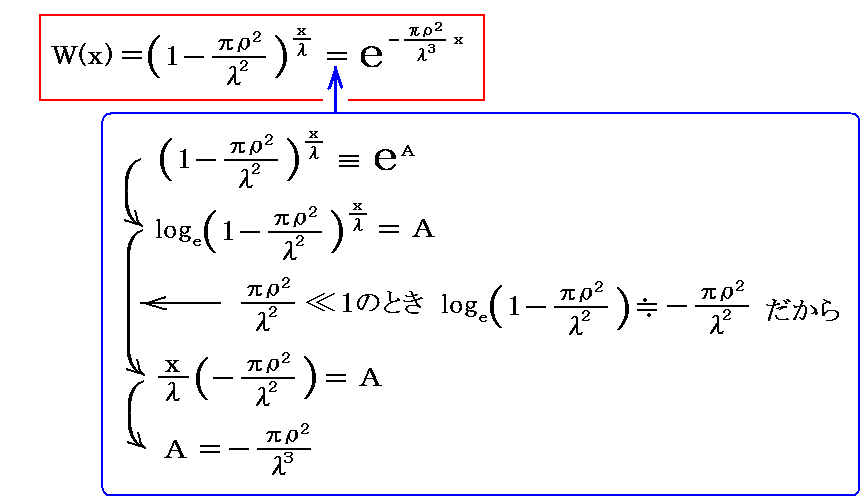
となる。
次に、同じ方向に進むN個(Nは極めて大とする)の分子を考える。xとx+dxの間の厚さdxの層中で静止分子に衝突する分子の数は
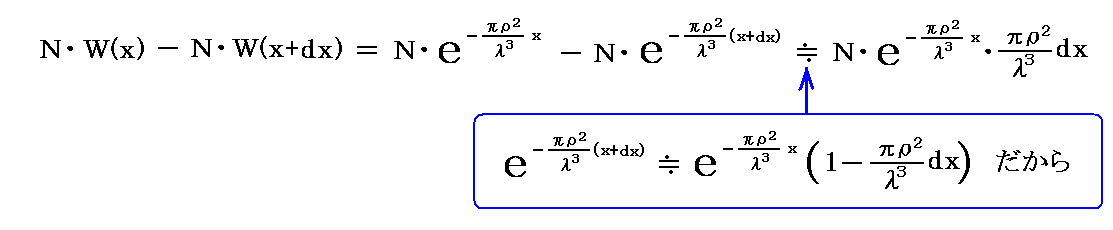
となる。これから、 分子が衝突することなく進む行程の平均値 l’は
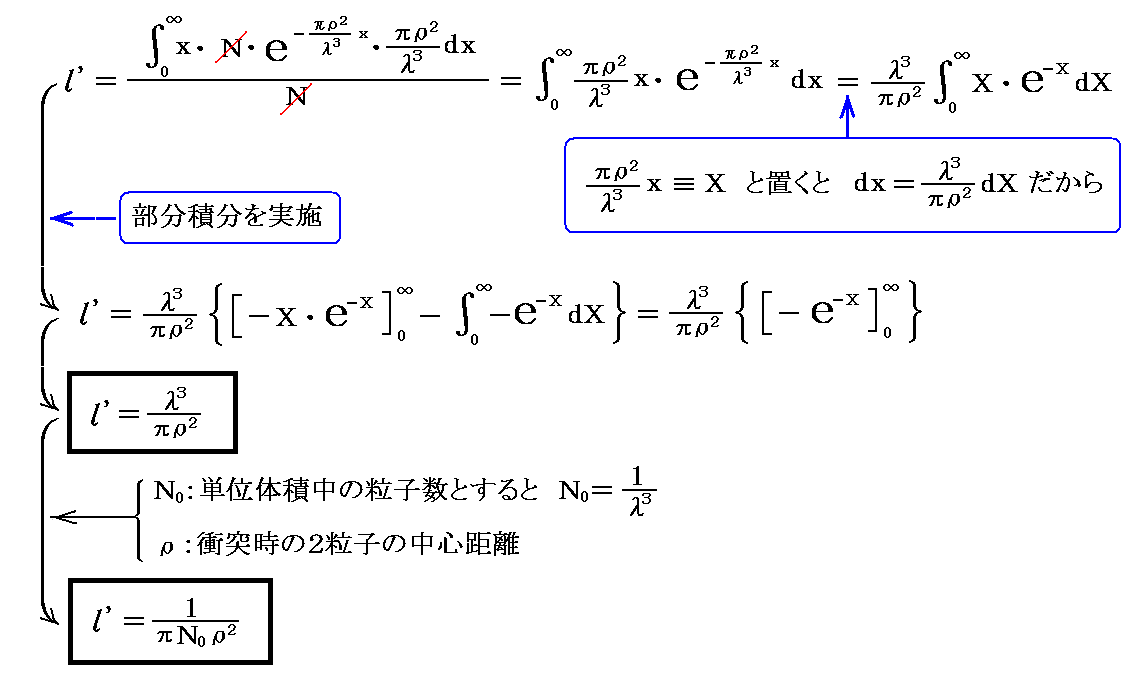
となる。これは別稿「アボガドロ数の測定法」4.ですでに説明した関係式ですが、“平均自由行程”を表すこの式を最初に求めたのはクラウジウスです。
すべての分子が運動している場合の平均自由行程は上記の3/4倍となる。ただしクラウジウスはその計算法をこの論文には記していない[R. Clausius, Phil. Mag., 19, p434~486, 1860年で説明している]。この場合の“平均自由行程”を改めて l と書くと
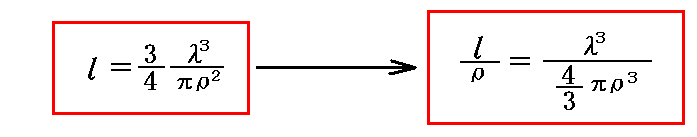
となる。
右側の式に於いて(4/3)πρ3は作用球の体積だから、 l とρの比が、[気体の全体積(nλ3)]と[分子自体の占める体積]の比に等しいことを示している。
通常の液体が気化すると体積が1000倍程度になることは当時わかっていたので、クラウジウスは上記の比が1000:1であると仮定してもう少し考察を進めている。すなわち

となる。すなわち、[平均自由行程]は[分子間距離の平均値λ]の60~80倍程度であることになる。
いずれにしても、気体分子は高速で動いているが、ごくわずかの距離動くと別の分子と衝突して跳ね返される。そのため一つの分子が短時間に長距離を移動することはない。これが気体の拡散が除々にしか生じない理由であると説明した。
“内部自由度”と“平均自由行程”の認識は、クラウジウスの画期的な業績です。
しかし、ここで以下の事に注意すべきです。すなわち当時、粒子の平均距離λも衝突時の二粒子間距離ρもその絶対的な大きさを知るすべがなかったことです。液体と気体の体積の比較からλとρのおよその比率は知ることができるが、絶対的な値は知ることができなかったのです。
もしそれが解るのならばアボガドロ数や原子・分子の大きさを知ることができる。このことに付いては別稿「アボガドロ数の測定法」4.(2)[補足説明1]参照されたし。
クラウジウスの考え方をさらに発展させ、“平均自由行程” l を気体の粘性・熱伝導・拡散と結びつけて l を求める方法を示したのがJ. C. Maxwellです。彼は1860年に、その当たりを含めた気体分子運動論の画期的な論文を発表する。
そのことについては別稿「マクスウェルの速度分布則1“気体の動力学的理論の説明”(1860年)」で説明します。
4.参考文献
ここの議論をふまえて、「気体の断熱変化」や「音速の理論」を振り返ってみられたし。そこの説明で曖昧なままになっていた幾つかの疑問が解決すると思います。
- リープマン、ロシュコ共著「気体力学」吉岡書店(1966年刊)第14章
古い本ですが、この稿の2章を書くときに参考にした。
- 広重徹著「物理学史Ⅰ」培風館(1968年刊)§9-1、p218~221
これには、原論文の引用とともに歴史的な説明が丁寧になされています。3.章の歴史的概観を書くとき、導きの糸として一番のよりどころとした。
- エミリオ・セグレ著「古典物理学を作った人々-ガリレオからマクスウェルまで-」みすず書房(1992年刊)
特に第4章、第6章、および付録10~13参照。
- 江沢洋「誰が原子を見たか」岩波書店(1976年刊) 今日これは、岩波現代文庫版で再版されています。
本稿に関係する所として、この書籍の §22 と §23 をご覧下さい。
- 八木江里監訳「クラウジウス熱理論論文集 エントロピーの起源としての力学的熱理論」東海大学出版会(2013年刊)
クラウジウス論文の翻訳版です。この中の熱力学論文の幾つかを別稿で引用しています。
