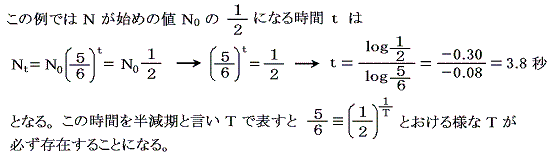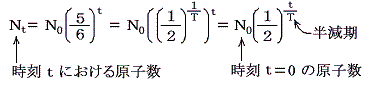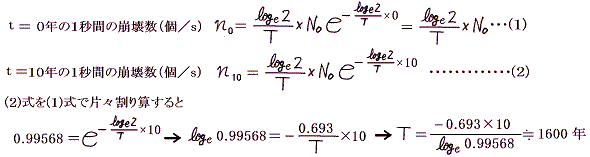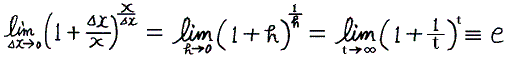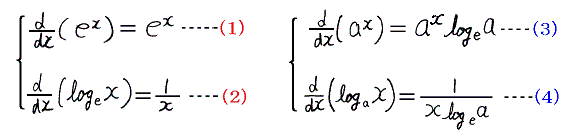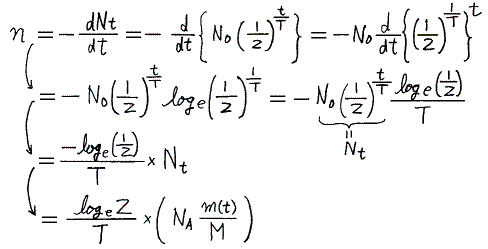このページを印刷される方はこちらのバージョンをご利用下さい。図の拡大バージョンです。

放射性崩壊と半減期

１．放射性物質の量が指数関数で表される理由

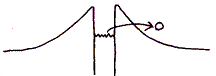　放射能というのは、井戸型のポテンシャルの中で右往左往している核子（特にヘリウムの原子核の塊が安定）が確率論的にたまたま大きなエネルギーを得て、その井戸から飛び出すのにたとえることができる。
　それは丁度、たくさんのサイコロを準備して（その数がｔ＝０で存在する放射性元素の数Ｎ_０とみなせる）、サイコロを転がす事が核子の乱雑な運動であり、それを何回も行うことが時間の経過を表すと考えることができる。すべてのサイコロを同時に、１秒に１回の割合で転がし、１の目が出たサイコロは別な元素へ崩壊したと考えて取り除くとする。そうすると

となるが、この様子をグラフにすると以下の様になる。

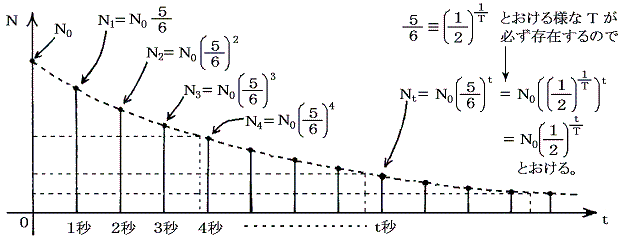
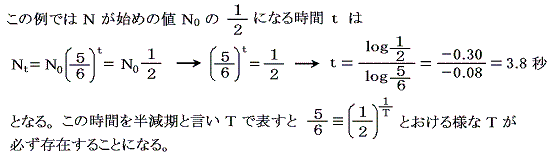
以上の議論で崩壊の確率を１／６にしたことや、サイコロを１秒間に１回の割合で振ったことは重要でない。いずれにしても必ず

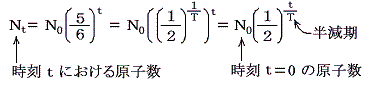
の形で表される。

２．半減期と物理量の関係

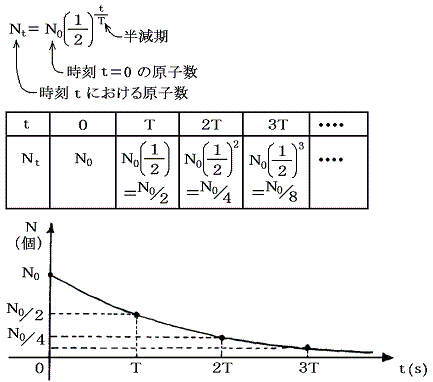
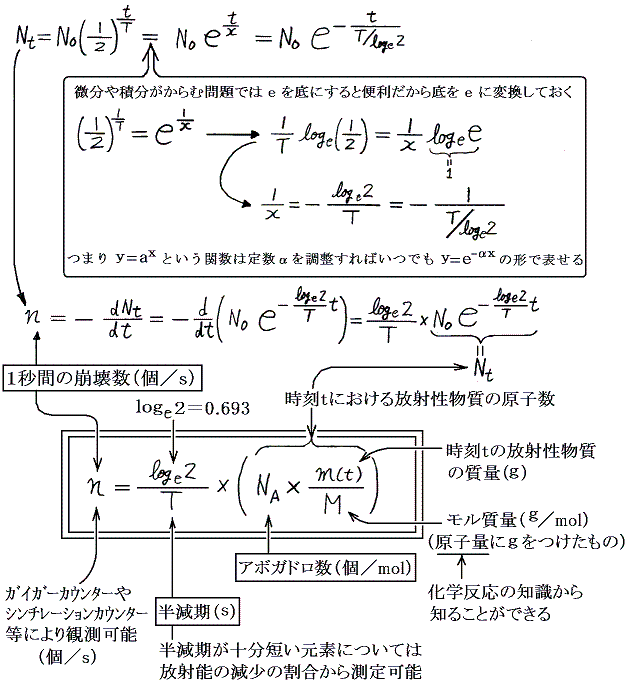
上記の公式から以下の事が読み取れる。

1. 　半減期が測定可能の放射生物質を利用するとｎ、Ｔ、Ｍ、ｍ（ｔ）の測定値からアボガドロ数Ｎ_Ａを見積もれる。
   　例えばラジウム試料からの放射線は、測定によると１０年で最初の強さの９９．５６８％に減少することが解っているので、以下のように半減期が測定できることになる。
   
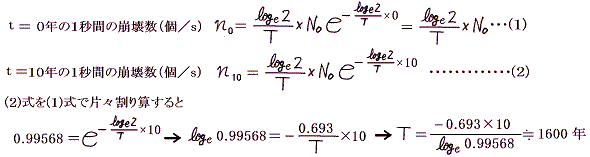
   　この半減期Ｔと実測できるｎ、Ｍ、ｍを用いれば、上記の式によりアボガドロ数Ｎ_Aが計算できる。ただし、アボガドロ数を求めるだけなら、別稿で説明する方法もある。
2. 　今日アボガドロ数Ｎ_Ａが解っているので、ｍ、Ｍが既知なら、ｎを測定することにより半減期が非常に長い放射性物質の半減期Ｔを決定できる。半減期が何億年と言った元素の半減期もこの式を利用すれば測定できる。
3. 　もしｎ、Ｔ、Ｎ_Ａ、Ｍが解れば超微量（10^-10ｇ以下）のｍの検出が可能になる。（放射化学分析や放射化分析）驚異的なごく微量分析が可能です。
   　実際、水俣病水銀中毒患者の毛髪中の水銀を放射化して、髪の毛中の分布を解析して、水俣病の原因の究明に重要な情報を提供した。
4. 　ごく微量のｍからでも放射能は測定できる。そのとき放射線の性質の違いや崩壊半減期の違いなどを導きの糸にすることにより、未知元素の存在を知ることができる。
   　実際1900年代の初頭、放射能を導きの糸として次々と新元素が発見された。

いずれもごく微量のｍでも放射能ｎが測定可能である所に、この式の威力がある。

３．指数関数の底 ｅ について

　指数関数や対数関数において、なぜ底を ｅ にするのか？
　それは微分・積分がからむ問題ではいつも

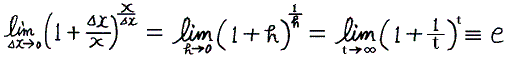
の極限操作が出でくるからです。高校数学の教科書を復習されたし。

　そのため ｅ を底とすると微分・積分の公式が（１）式や（２）式の様に非常に簡単になる。また仮に ｅ を底にしない場合でも（３）式や（４）式の様に ｅ を底にした定数 ｌｏｇ_ｅａ が微分・積分の結果の中に出てくる。

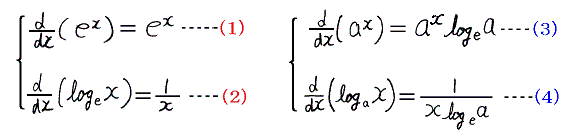
　（１）、（２）と（３）、（４）を比較すると明らかなように微分・積分がからむ問題では ｅ を底にすると確かに便利です。
　ただし、ｅ が底でなくても（３）、（４）を用いて計算すれば良いので困ることはない。実際、前述の計算を（１／２）の底のままで計算すると公式（３）を用いて

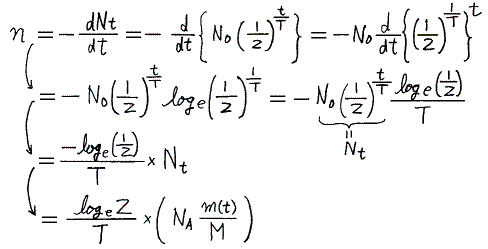
となり同じ結論が得られる。

　（１）、（２）と（３）、（４）式の関係についてもう少し補足する。
以下の議論でａは任意の値だが、ｅは2.7182818･････という値です。

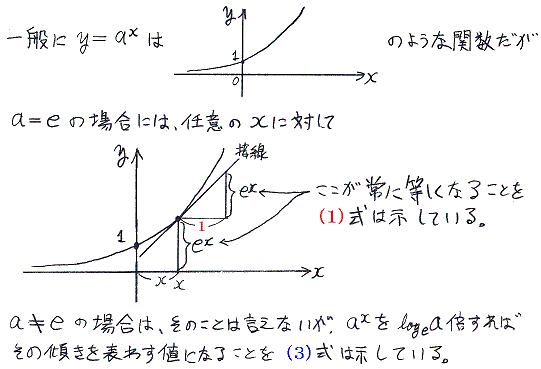
同様に

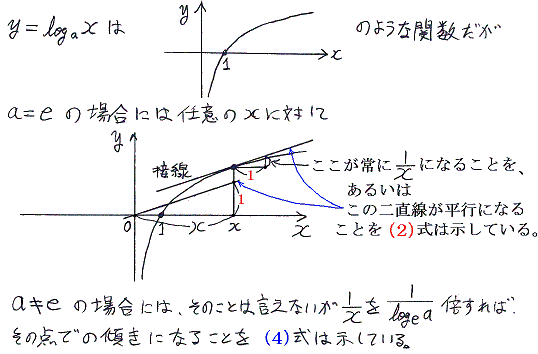
　　指数関数の底を　ａ　から　ｅ　に変換することは、統計力学に於いて極めて重要な意味を持ちます。そのことについては、別稿「統計力学」２．（５）１．〜２．などをご覧下さい。

４．自然界に於ける放射性崩壊系列

　元素は恒星内部の核融合反応と、超新星爆発時の核融合反応で作られる。その際、現存するものより大きな原子番号の元素や、原子核中の陽子と中性子の比率が現存のものと異なる元素もできる。しかし陽子の数が９２を越えるものや、中性子の数が陽子数と同じかそれよりも少し多めの原子核以外は不安定で早い時期に崩壊してなくなる。（理由の説明は省略）そのため現在の太陽系には、陽子数と中性子数の比が現在残っているものの比率から外れるものや、原子番号が９２以上のものは残っていない。

　原子番号の大きな不安定領域にある原子核の中で、²³⁸Ｕ、²³⁵Ｕ、²³²Ｔhは、その近傍の核種に比較して核構造上例外的に安定で、長い半減期を持つ。いずれは崩壊するが半減期が非常に長いので現在でも残っている。そのため、それらが今日においても少しずつ崩壊して、それらが出発点となる放射性元素の崩壊系列を形づくる。それが下図の（１）〜（３）である。

　原子番号が大きくなると陽子数と中性子数の比が、より中性子が多い方で安定になる。（理由の説明は省略）そのため横軸陽子数−縦軸中性子数の座標の上に安定同位体をプロットしてみると、原子番号が小さい安定同位体は傾きがほぼ１の直線上に載るが、原子番号が大きくなるにつれて傾きがだんだん１より大きくなる反り返った曲線上に分布するようになる。だから中性子と陽子が二個づつ減少するα崩壊を繰り返すと、中性子が多すぎる不安定領域の元素となってしまう。そのため中性子を陽子に変換するβ崩壊が起こって中性子の割合を減らし安定領域へ復帰するのである。図は、まさにα崩壊を何段階か繰り返すと、それに引き続いてβ崩壊が生じることを示している。詳しくは「核種表と放射性崩壊過程」参照

崩壊系列拡大統合図　半減期単位（ｙ：年、ｄ：日、ｈ：時間、ｍ：分、ｓ：秒、ｍｓ：ミリ秒、μｓ：マイクロ秒）

（１）ウラン・ラジウム系列（４ｎ＋２）　　　拡大図

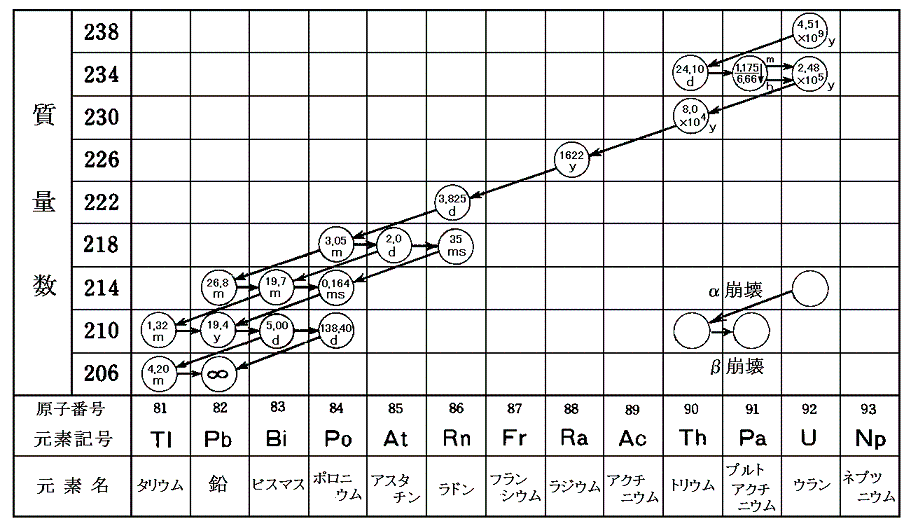
（２）アクチニウム系列（４ｎ＋３）　　　拡大図

（３）トリウム系列（４ｎ）　　　拡大図

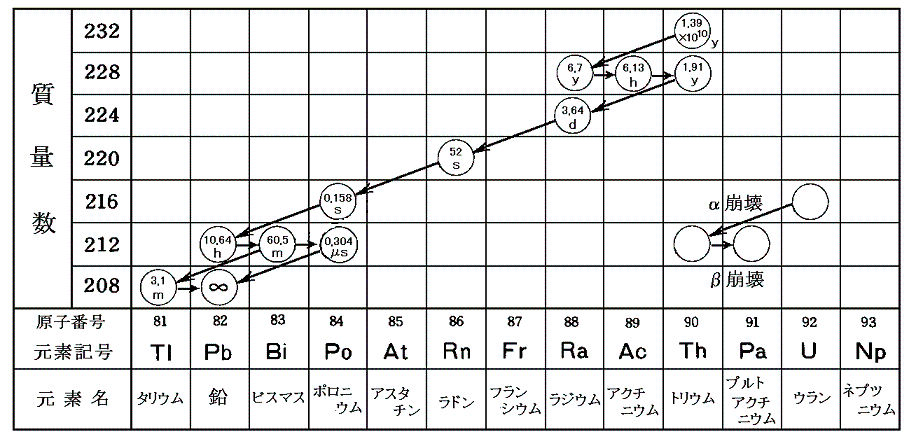
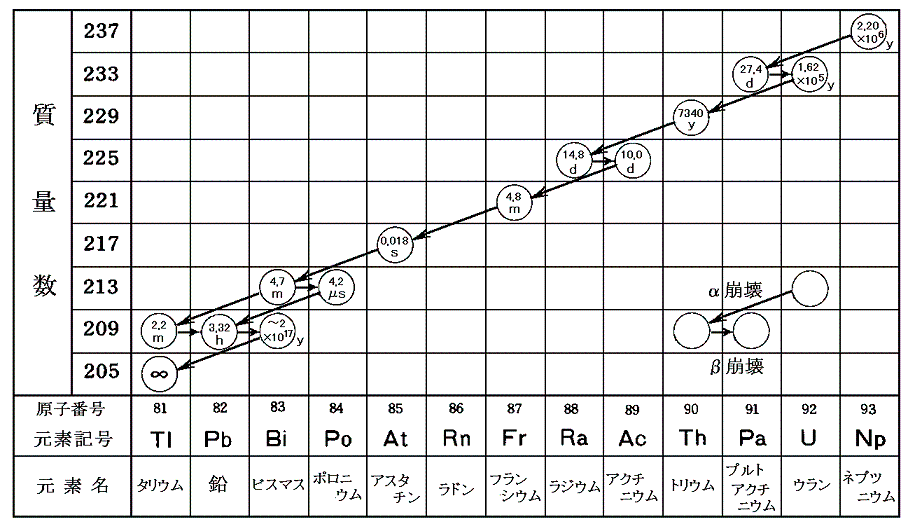
　以上の三系列が自然界に存在する。この中には（４ｎ＋１）に相当するものが無い。次に述べるネプツニウム系列（４ｎ＋１）は人工的に作られたものである。崩壊系列の出発点として考えられる質量数４ｎ＋１の重い元素で半減期の長いものを探してみると、²³⁷Ｎp₉₃が候補として上がる。これ以外はいずれもずっと短い半減期である。一番長い²³⁷Ｎp₉₃でも、その半減期はわずか220万年で他の系列の出発元素に比べると著しく短い。そのため太陽系生成時の星間物質にたとえ存在していたとしても、この崩壊系列の生成元素はすでに崩壊し尽くしている。ぜひ別稿「核種表と放射性崩壊」によって、次表の質量数に相当する同位体元素が抜け落ちており、自然界に存在しないことを確かめてください。

（４）ネプツニウム系列（４ｎ＋１）自然界に存在しない　　拡大図

（５）上記以外の天然放射性元素（詳しくは「核種表と放射性崩壊」参照）

（１）〜（３）以外で自然界に残っている放射性同位元素を質量数の小さいほうから列挙すると、

⁴⁰Ｋ₁₉：カリウム、⁵⁰Ｖ₂₃：バナジウム、³⁷Ｒb₈₇：ルビジウム、¹¹⁵Ｉn₄₉：インジウム、¹³⁸Ｌa₅₇：ランタン、¹⁴²Ｃe₅₈：セリウム、¹⁴⁴Ｎd₆₀：ネオジム、¹⁴⁷Ｓm₆₂：サマリウム、¹⁵²Ｇd₆₄：ガドリニウム、¹⁷⁴Ｈf₇₂：ハフニウム、¹⁷⁶Ｌu₇₁：ルテチウム、¹⁸⁷Ｒe₇₅：レニウム、¹⁹⁰Ｐt₇₈：白金

がある。これらの半減期は一番短い⁴⁰Ｋ₁₉でも1.26×10⁹年で、いずれも10億年〜数百億年以上の非常に長い半減期を持つために現在まで残っている。

　また、原子番号４３番のＴc₄₃：テクネチウムと６１番のＰm₆₁：プロメチウムの同位体はすべてが放射性である。半減期が一番長いものでも⁹⁷Ｔc₄₃の2.6×10⁶年、¹⁴⁵Ｐm₆₁の18年なので、この二種類の元素に関しては、たとえ星の超新星爆発時に作られたとしても、太陽系近傍で今日まで残っているものはない。