このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
電磁波とは何かを解りやすく説明します。そして、伝播速度が光の速度と一致する事を導きます。
〔ファラデーの電磁誘導の法則〕と〔マクスウェルによって拡張されたアンペールの法則〕を組み合わせれば、電磁波の存在が予見できる。
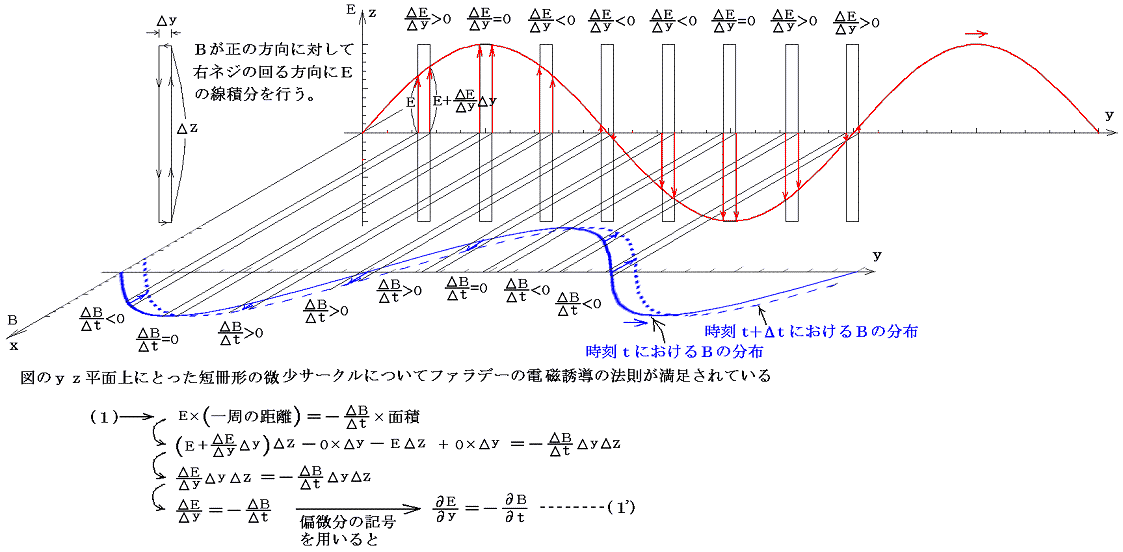
空間のある1点に於いて磁束密度Bのべクトルが下図の様な時間的変化をしているとする。このとき〔ファラデーの電磁誘導の法則〕はその点のBベクトルに垂直な微少なサークルの周りを一週する方向に足し合わせるとゼロでない電場Eが現れることを示している。その様子をグラフの下の図が表している。
Bは上向きを正、EはBの正の方向に進む右ネジを回す方向を正とする。このとき〔ファラデーの電磁誘導の法則〕とは磁束密度Bが時間的に変化しているとき、その場所付近には〔磁束密度が増加している方向〕に対して、〔左ネジの方向〕に電場は存在する事を意味する。
ここで電磁誘導の法則の起電力Vの定義を思い出せ。磁場が時間的に変化するとそのまわりに渦状の誘導電場Eができる。そこにおかれた回路に沿って電荷が動くと,誘導電場Eがローレンツ力F=qEに従って電荷に力を及ぼして仕事をする。電荷が回路を1周する間に誘導電場がする仕事を動いた電気量で割ったものが誘導起電力である。力という文字が入っているが力ではない。誘導電場 Eの回路に沿った成分を
El とすれば,誘導起電力Vは回路を1周する線積分
で表され、電圧(電位差)と同じ単位を持つ。
空間のある1点に於いて電流iのべクトルが下図の様な時間的変化をしているとする。このとき〔アンベールの法則〕はその点のiに垂直な微少なサークルの周りを一週する方向に足し合わせるとゼロでない磁則密度Bが現れることを示している。その様子を下図はあらわしている。
〔アンペールの法則〕とは電流の周りに、電流の流れる方向に対して右ネジの方向に磁束密度Bが現れることを意味する。
マクスウェルはアンペールの法則を導線の無い空間に拡張した。そのとき電流に代わるのが電場の時間的変化である。そのあたりを導線につながれたコンデンサー内におこる現象を利用して説明する。(下図参照)
図から明らかなように[電流の強さ]と[電場の時間的変化率]が対応する。だから電場が時間的変化する場所では、電流の場合と同じような磁束密度が現れると考えられる。(これは電流の定義に、電荷に対する連続の式を適応するとある意味当然の結果である)
Eは上向きを正、BはEの正の方向に進む右ネジを回す方向を正とする。このとき〔マクスウェルにより拡張されたアンペールの法則〕は電流があるとき、あるいは電場が時間的に変化しているとき、その場所付近には〔電流の方向、あるいは電場の増加している方向〕に対して〔右ネジの方向〕に磁束密度Bが存在することを意味する。
(1)、(2)式のように変形してみると図1と図2におけるE、B、ΔE/Δt、ΔB/Δt が、対称的な関係式を満たすことが解る。そのとき、BとEはお互いに影響し合い、互いに他方の変化の仕方に制約をかける。この制約が電磁場が空間を伝播していくメカニズムを決める。
ここでは、前項の(1)、(2)式を満足する解の例を示す。
xyz座標のxz平面に無限の広さで広がっている+-の帯電シートが重なって存在している。+-の電荷密度は一定かつ一様であるとする。今-の帯電シートは静止しており、+の帯電シートが時間tの正弦関数で図の様にz軸の正負の方向に沿って上下に振動しているとする。+と-の電荷密度は同じとしているので、正味の電荷は存在しない。電流のみが存在する。
その電流が1.(2)の電流 i とするとアンペールの法則により時間的に変動する磁束密度Bが現れる。磁束密度ベクトルBの方向はx軸に沿った方向であり、電流シートを取り巻く様に現れる。その磁束密度の変化に応じて1.(1)のファラデーの電磁誘導の法則よりz軸の正負の方向に沿った時間的に変化する電場Eが現れる。その電場Eは磁束密度B変化率ベクトルを取り巻くように現れる。そして、電流の変化に応じて図の様な電場Eと磁束密度場Bが現れy=0の位置からyの正負の方向へ伝播していく。
以下の①~⑧図は電磁波の伝播の時間的変化の様子を示している。zy平面上に記した電気力線で電場Eの変化の様子を、またxy平面に記した磁束密度線で磁束密度場Bの変化の様子を示している。
y軸上に記した白と黒の矢印記号で、それぞれ電場の時間的変化と磁束密度の時間的変化の大きさを表している。白矢印が1.(2’)図中の電場の矢印の時間的変化率
ΔE/Δt を、黒矢印が1.(1)図中の磁束密度の矢印の時間的変化率 ΔB/Δt
を表す。
前項の図中の電場Eと磁束密度Bが1.の(1)式を満足していることは、下図を検討すれば了解できる。
同様に下図を検討すれば電場Eと磁束密度Bが(2)式を満足していることが解る。
サークルを図中に説明した微少な幅を持った短冊形にすると積分型式の法則(1)、(2)式は微分型式の法則(1’)、(2’)に変形できる。これらはEとBに対して対称的な形をしており、別稿「波動方程式と一般解」2.(3)で行ったのと同じ取り扱いができる。
(1’)式の両辺をyで偏微分したものと、(2’)式の両辺をtで偏微分したものを一緒にすると
が得られる。
同様に(1’)式の両辺をtで偏微分したものと、(2’)式の両辺をyで偏微分したものを一緒にすると
が得られる。つまり、 EもBも同形の方程式を満足する。この形の微分方程式は波動方程式といわれるもので以下の1、2が言える。(別稿「波動方程式と一般解」3.(1)参照)
また元の(1’)(2’)式からは以下の3、4が言える。(次節3.(1)参照)
[補足説明1]
“電磁場の波動方程式”は、“電荷が存在しない場合のMaxwell方程式”から直接導けます。その導き方は別稿「アインシュタインの特殊相対性理論」3.(2)1.[補足説明1]を参照されたし。
そこの、[補足説明2]で平面波解のより一般的な表現形式を、また、[補足説明4]で上記の性質をより一般的に論じていますので併せてご覧ください。
電磁波について幾つかの注意事項を記す。
y軸の正の方向へ伝播速度v=λ/Tで移動していく正弦波(sin波)
が方程式(1’)(2’)を満たすことを示す。
つまり波を光速度cで進行させれば上記の解が方程式を満足して真空中を伝播できるということである。こうなったのもひとえにマクスウェルがアンペールの法則に付け加えたΔE/Δt項の働きによる。
別稿「波動方程式と一般解」3.(1)で述べたように、波動方程式(3)の一般的解は Ez=f(ct-y)+g(ct+y) の形にかける。ct-y=ξ、ct+y=ηとして(1”)式に代入すると
となる。ここで両辺を t で積分すると
となる。α(t)は積分定数である。これと Ez=f(ct-y)+g(ct+y) を(2”)式に代入して整理すると
となるのでα=0とおいて良い。結局 Bx=(1/c){f(ct-y)-g(ct+y)} となり Ey と同じ波形を保ちながら進行する事がわかる。そして一般解についても Ez=cBx の関係が成り立つ。
しかしここで次の事柄に注意しなければならない。 f(ct-y)はyの+方向、g(ct+y)はyの-方向に進行する波である。そしてf(ct-y)の場合は
Ey と Bx は同符号であり、g(ct+y)の場合は Ey と Bx
は異符号である。つまり電磁波はつねにEからBの方向へ右ネジをねじったときにネジの進む方向に進行することを意味する。
この当たりの、もう少しきちんとした数学的展開と証明は別稿「アインシュタインの特殊相対性理論(1905年)」3.(2)1.[補足説明4]を御覧下さい。
1.の項目で下図のような、EやBのサークル周りの積算が必要になった。
このとき、EやBがあたかもリングに沿って渦を巻くように現れ、それを積算するのだと勘違いする人がいるが、そうではない。正しくは以下の様に考える。例としてxy平面上に存在する磁束密度ベクトルBについて、微少な四角形ΔxΔyの周りでの積算をする。
同様な議論はyz平面、zx平面についても成り立つ。もちろん電場ベクトルEについても成り立つ。以下に2.項で述べた平面波について、yz平面上の微少な四角形ΔyΔzの周りの電場Eの積算値を示す。
以上述べたように、EやBの場は渦を巻く必要はない。2.(2)の項目で説明した例の様に平面波状態でも、サークルの周りの積算値はゼロでない。
進行する電磁波を示すために、多くの高校物理Ⅱの教科書は図Aのような模式図をのせている。しかしこの図は間違っている。
前項2.の図からわかるように、進行する電磁波の電場Eと磁束密度Bの大きさの比は常にc(m/s)という一定値になり、電場と磁束密度の位相はいつも一致している。そのため、正しくは図Bの様に描くべきである。このような状況でも波が進行してくれれば(1)(2)式を満足できるというのが2.(2)の議論の本質なのだ。(後藤尚久著「図説・アンテナ」電子情報通信学会より)
ところで、図Aの様に振動する電磁波はないのかということだが、反射壁で反射された電磁波と入射する電磁波が干渉してできる定常波がこの形の振動をする。その当たりを次節で説明する。
反射壁で反射された電磁波と入射する電磁波が干渉してできる定常波が前節A図の様な振動をする。下図は左から右方向に進んできた電磁波が右端の反射壁で反射されてできる定常波を表している。今簡単化のために透過波はゼロで反射率=1の完全反射をする場合を図示する。このとき後で述べる理由により電場Eは正負が入れ替わって反射されるが、磁束密度場Bはそのままで反射される。
これらの図に2.(2)と同様な線積分サークルを描いて検討すれば、このような定常波も前記の(1)、(2)式を満足するのが解る。前節に掲げた図Aは上図の時刻t=(3/8)T(磁束密度場が減少し、電場が増大している)に対応している。
図から定常波成分だけ取り出すと下図の様になる。電場と磁束密度場の同じ種類の破線が対応している。実線から破線の間隔が短くなる方向に
t=0 → t=(4/8)T となる。
上図の様に電場Eと磁束密度Bの位相がちょうど進行波の波長の半波分ずれるのは、反射面が電場Eに対しては固定端として、磁束密度Bに対しては自由端として振る舞うことに起因する。すなわち電場Eは正負が入れ替わって反射されるが、磁束密度Bはそのままで反射される。このようになったのも反射面で満たされるべき境界条件の特殊性による。
今反射壁よりも右側の部分が導体(金属)であるとする。そして反射面の位置を原点として上図の様に座標をとる。導体(金属)に電磁波が進入すると、その電場Eyに伴って電流 i が流れ電場を打ち消してしまう。導体がオームの法則を満足すると、導体内部で電磁場が満たすべき方程式は以下の様になる。
(5)(6)式より Bx を消去すると
となる。同様に(5)(6)式より Ez を消去すると
となり、EzもBxも同じ形の波動方程式を満足する。方程式に新しく現れた t
についての1次の時間微分項は波動の進行とともに減衰する効果を生じ、その解は以下の様なものになる。
ここの考察で、導体中に、経験則・実験則であるオームの法則を導入するのは、何となくしっくりこないところであるが、この当たりについては別稿「マクスウェルによるアンペールの法則の拡張」を参照されたし。
導体が導電率無限大(σ=∞)の完全導体の場合、境界条件を考慮して解析を進めると、反射面の左側(真空領域)で満たすべき解として前記の様な反射波が得られる。(詳細は高校レベルを超えるので省略)
そのようにして得られた反射波は、電磁波のBベクトルはつねにEベクトルに対して進行方向に対して右ネジをねじった方向でなければならないという電磁波の特殊性を満足する。