線形振動子（電気双極子）による電磁波の放出

　電荷が直線的に振動している電気双極子（ヘルツ双極子）からの電磁波の放出を論じます。この考え方の基礎は1889年にＨ．ヘルツによって与えられた。
　本稿の内容は別稿「調和振動子（自由振動、強制振動、減衰振動、強制減衰振動）」の議論と深く関わりますので、適宜参照されながらお読み下さい。

１．速やかに変動する場と電磁ポテンシャル

（１）電磁場の方程式

　ここでは完全なＭａｘｗｅｌｌ方程式を用いて、真空の場における議論をする。すなわち全空間にわたってε＝ε₀、μ＝μ₀とし、電荷密度ρと電流密度Ｊは全空間、及びｔ＜ｔ₀なる全時刻において与えられているものとする。ここでｔ₀は観測が行われている時刻をあらわす。
　Maxwell方程式と付加条件式

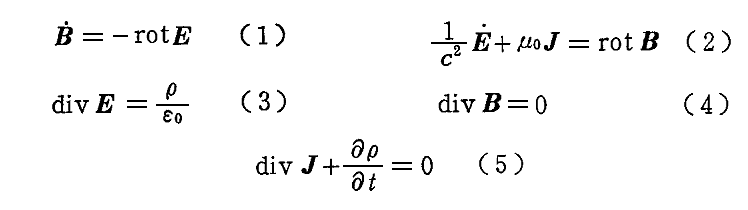
から出発する。
　ここで（４）式 divＢ＝0だから別稿で証明したようにＢはベクトルポテンシャルＡのrotで表される（ベクトル解析の公式より任意のベクトルＡに対して常にdivrotＡ＝0が成り立つ）。つまり

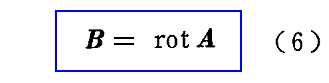
でベクトル場Ａを定義して（１）式［ファラデー（電磁誘導）の法則］に代入すると

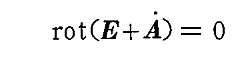
となる。別稿で証明したようにrotの後にくるベクトルがあるスカラー関数Ψの勾配で表せるので

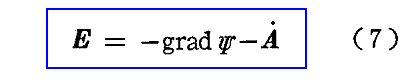
が得られる。
　ψをスカラーポテンシャル、Ａをベクトルポテンシャルと言う。（２）式［Maxwellが拡張したアンペールの法則］に（６）、（７）式を代入すれば

が得られる。ここで用いたベクトル演算rotrotＡを変形する公式はＡがデカルトの直交直線座標成分で表されている場合に限り正しいことは注意しなければならない。
　これを以下の二つの関係式に分割する。この分割は（８）式の右辺が常にゼロであることが成り立つと仮定して分解したものですが、ポテンシャル関数を適当に取れば常に可能です。

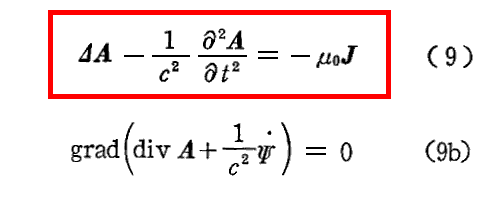
（９ｂ）式を積分すると

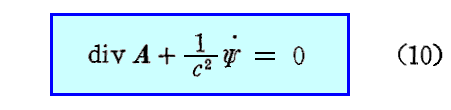
となる。これは“Lorenzゲージ”（Ludvig Valentin Lorenz）と言われる条件式です。ここで本来ならば ｔ のみの関数である積分定数が付け加わるが、ここではそれをゼロと置いている。その様にできるのはＡやΨはそれ自身では意味を持たず（６）式や（７）式を通じてのみ意味を持つからです。
　ここまでの議論は（１）、（２）、（４）式を満足するようにして導かれたものです。（３）式 divＥ＝ρ/ε₀も満足するようにするために（７）式を（３）式に代入すると

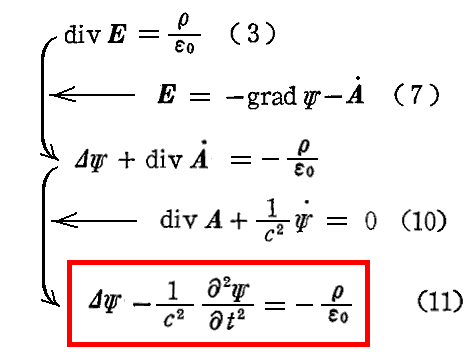
となる。
　このように、ポテンシャルＡとΨは同じ型の微分方程式（線型非同次波動方程式）を満足する。これらの式の右辺は（ｘ，ｙ，ｚ）および過去の時間 ｔ＜ｔ₀ の与えられた関数である。これらの微分方程式の解は条件式（１０）によって互いに関連している。

［補足説明１］
　式変形の中に出てきた“Lorenzゲージ”の意味はなかなかわかりにくいところです。Ludvig Valentin Lorenz がこのゲージ条件を導入したいきさつに付いては別稿「Maxwell方程式系の先見性と電磁ポテンシャル」２．（２）を、また“ゲージ条件”そのものについては別稿２．（３）をご覧下さい。

（２）方程式の解

１．遅延ポテンシャル

　前節の（９）、（１１）式は別稿「非同次波動方程式の一般解」で説明した一次の“非同次波動方程式”

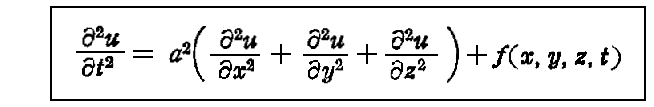
の形をしている。そのため、（９）、（１１）式の解に対してそこで説明した結論を用いることができる。
　そこの文字をここでの対応する文字に書き換える。つまり ｄｖ→ｄｖ＝ｄξｄηｄζ 、 ｕ（ｘ，ｙ，ｚ，ｔ）→Ψ（ｘ，ｙ，ｚ，ｔ） あるいは Ａ（ｘ，ｙ，ｚ，ｔ） 、 ａ²→ｃ² 、 ｆ（ξ，η、ζ、ｔ−ｒ／ａ）／ａ²→ρ（ξ，η、ζ、ｔ−ｒ／ｃ）／ε₀ あるいは μ₀Ｊ（ξ，η、ζ、ｔ−ｒ／ｃ） とすると（９）と（11）式の解として

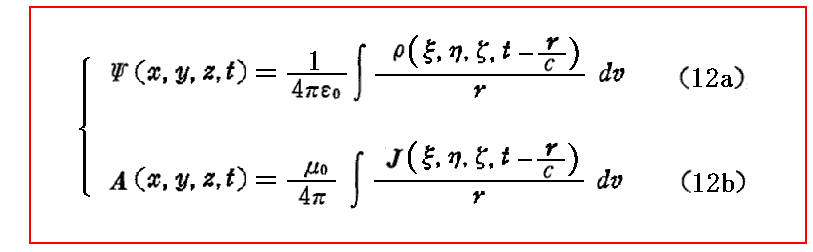
が得られる。ただし

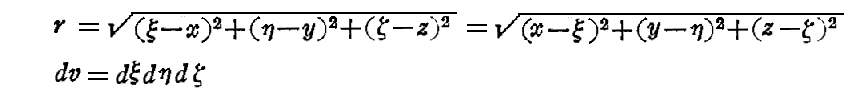
で、ｃは光速度を意味する。
　ここで （ｘ，ｙ，ｚ，ｔ） は Ψ や Ａ を求めようとする着目点の座標と時刻です。積分点 （ξ，η，ζ） で ｄτ＝ｄξｄηｄζ についての体積積分を全空間について行う。そのとき ρ や Ｊ は観測の時刻ｔでの電荷密度、電流密度ではなくて、それより以前の時刻（体積積分をする場所で異なる）

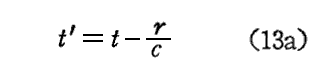
での値で行われる。 ｒ／ｃ は光が積分点から着目点まで走るのに要する時間です。（１２）式は観測の時刻より ｒ／ｃ だけ以前の電荷及び電流密度の分布から計算されることを意味するので、これらのポテンシャルを“遅延ポテンシャル”（retarde potential）と呼ぶ。
　別稿「非同次波動方程式の一般解」３．（３）で説明したように、未来の時刻

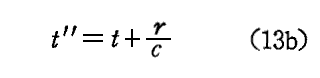
の ρ と Ｊ から計算されるポテンシャルも波動方程式の解となりうる。これは“先進ポテンシャル”（advanced potential）と言われるものですが、物理的な根拠からここでは除外する。

２．Lorenzの条件式

　前項で説明した遅延ポテンシャルが“Lorenz条件式”（10）式を満足していることを示す。
　まず、スカラーポテンシャルΨの時間微分については

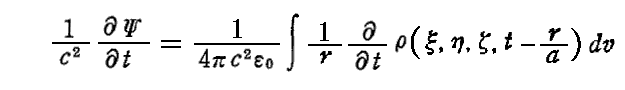
が成り立つ。

　一方 ベクトルポテンシャルＡ の空間微分については （1／ｒ） のみならず Ｊ（ξ，η，ζ，ｔ−ｒ／ｃ） の中の ｒ についての微分も考慮しなければならない。そのとき

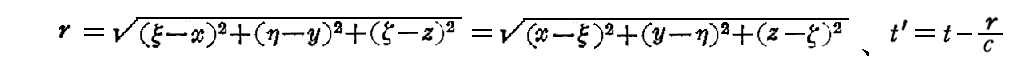
であることを考慮すると

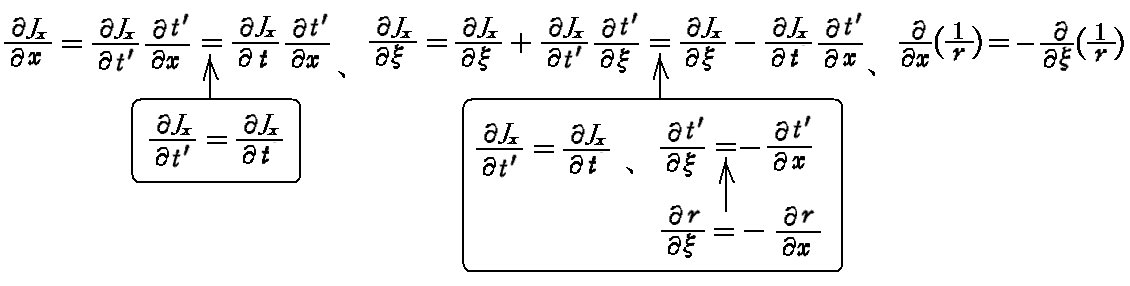
等々・・・の関係式が成り立つ。そのため

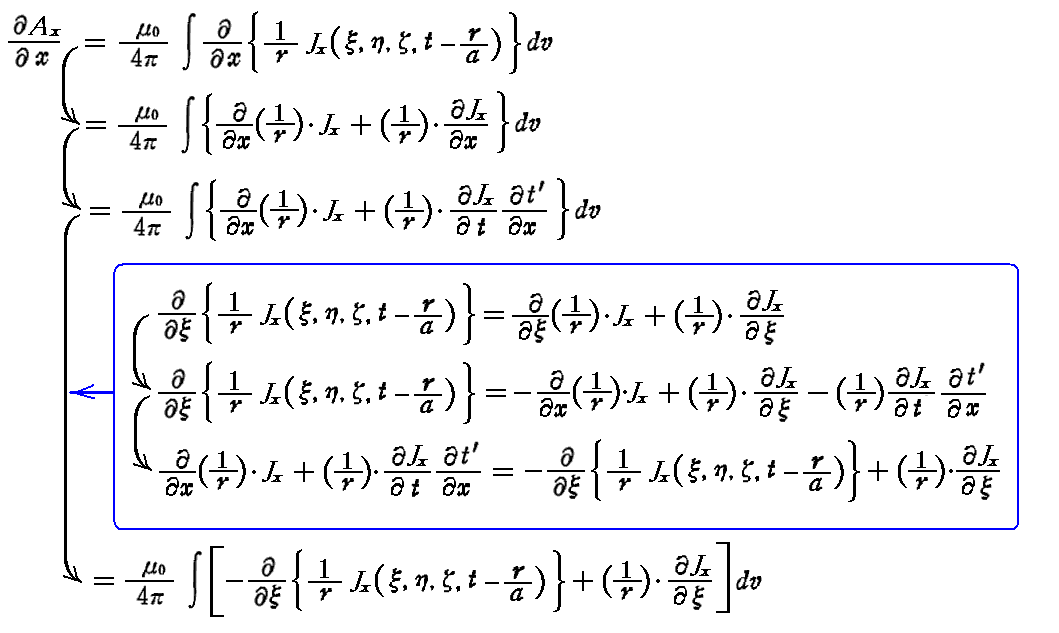
がいえる。Ａ_y、Ａ_z に付いても同様な関係が成り立つので

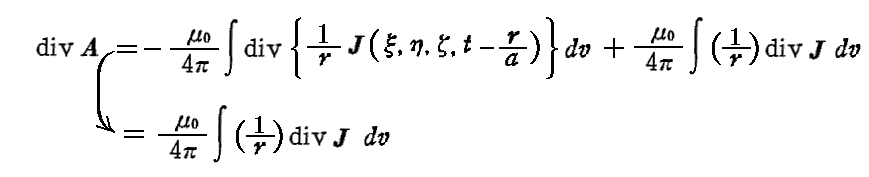
となる。右辺第１項はガウスの定理により遠方での ｛（1／ｒ）Ｊ｝ の表面積分に置き換えることができ、遠方では Ｊ＝0 だから第１項はゼロとなる。

　以上の関係式を用いると

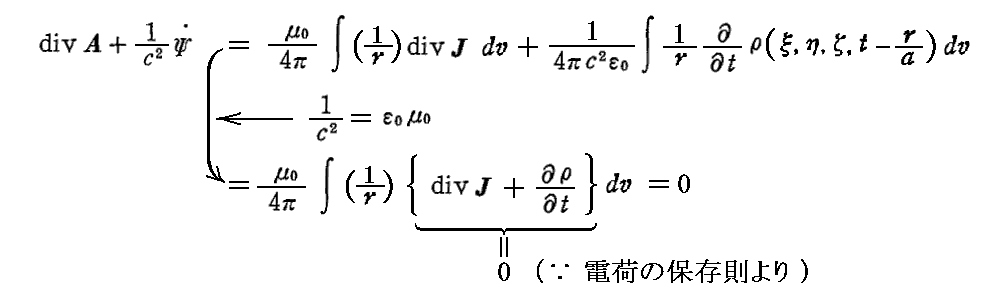
が成り立ち、前節で求めた解は確かに“Lorenzの条件式”（10）式を満たしている事が解る。

［補足説明］
　ここで用いた“電荷の保存則”は別項「マクスウェルによるアンペールの法則の拡張」（２）で説明した様に前出のMaxwell方程式（２）と（３）から得られる必然の結果であること注意されたし。
　この項の内容は、波動方程式（９）と（１１） が Lorenzの条件式（１０） と“並立できる”ことを証明していることになる。

２．電気双極子が作る電磁場

　ここの説明はH.Hertzの偉大な研究「Maxwell理論による電気的振動の力」に基づいている。
　H. Hertz, “Die Kra¨fte electrischer Schwingungen, behandelt nach der Maxwell'schen Theorie”,
　　　　　 Wiede. Ann. 36, p1〜22, 1889年　（D. E. Jones による英訳版はこちらを参照）
　
　ヘルツ論文では［直角座標・ガウス単位系］を用いて展開されていますが、本稿では［球座標・MKSA有理化単位系］を用いて説明します。

（１）Hertzベクトル

　前節で得た（１２ａ）（１２ｂ）式を Hertzの双極子 という特別な場合に適用する。これは運動する電荷ｅ が、その近くにある静止した電荷−ｅと共に、時間的に変化する電気双極子

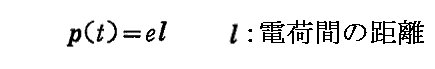
を構成している場合です。ただし、ｐ は （ξ，η，ζ）＝（0，0，0） の原点のみに存在するとする。
　（１２ｂ）に於いて

と置き積分を実行すれば、ｒ 及び ｖ は空間的には一定と見なして良いので

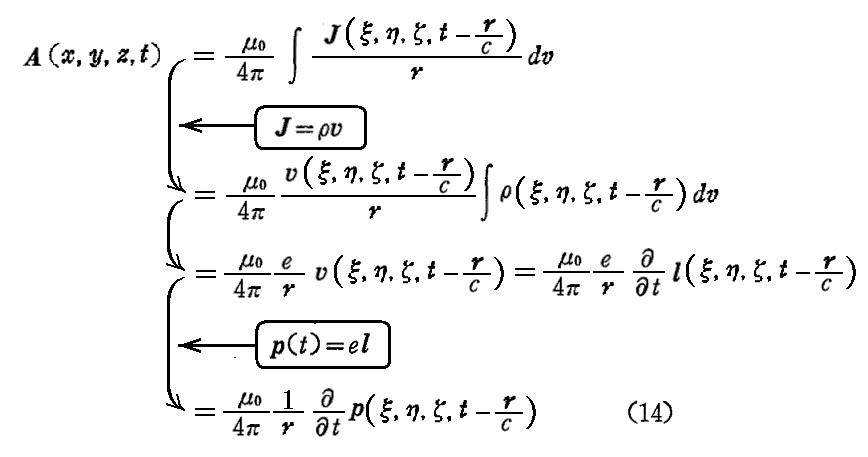
が得られる。
　ここでＨ．ヘルツに従って、ベクトルＡの代わりに“Hertzベクトル”Π

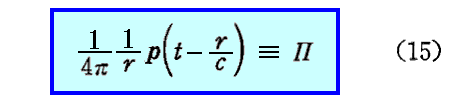
を導入するのが便利である。ｐ は （ξ，η，ζ）＝（0，0，0） の原点に存在するとしているので ｐ は ｒ と ｔ のみの関数です。
　ヘルツベクトルを用いると ベクトルポテンシャルＡ は（１４）（１５）式より

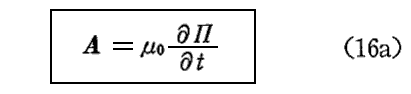
と表される。
　別稿「非同次波動方程式の一般解」２．（２）の説明、あるいは本稿１．（２）１．によると、（１５）式で表されるヘルツベクトルΠは原点のみに電気双極子ｐ（ｔ）が存在する場合の１次の非同次波動方程式

の解であり、（１４）式はまさにそのことを示している。
　上記方程式の両辺を時間で偏微分すれば

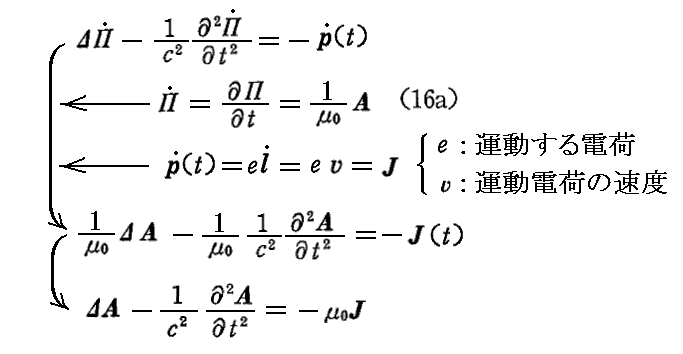
となり（９）式が得られるのでヘルツベクトルΠは今論じている現象を記述する解そのものであることが解る。
　電気双極子が座標原点のみに存在するとすると、原点以外では（９）式の右辺がゼロとなる同次波動方程式となるので、ヘルツベクトルΠ も原点を除いて以下の微分方程式

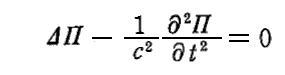
を満足する。
　（１０）式を用いれば対応する スカラーポテンシャルΨ は ヘルツベクトルΠ と

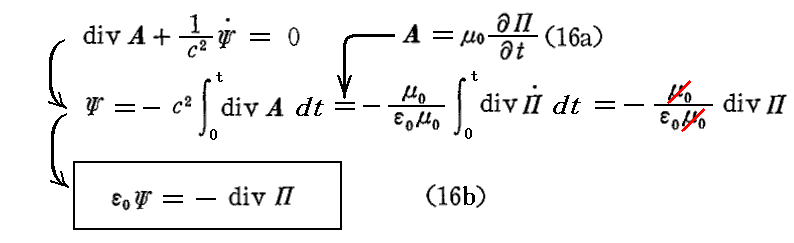
の関係があることが解る。
　（１６ａ）、（１６ｂ）式から解るようにΠ に微分演算を施すことにより スカラーポテンシャルΨ および ベクトルポテンシャルＡ が導かれるので、ヘルツベクトルΠ の事をポテンシャルのポテンシャルという意味で “超ポテンシャル” という場合もあります。

　（６）、（７）式に（１６ａ）、（１６ｂ）式を代入すれば、電磁場を表す式として

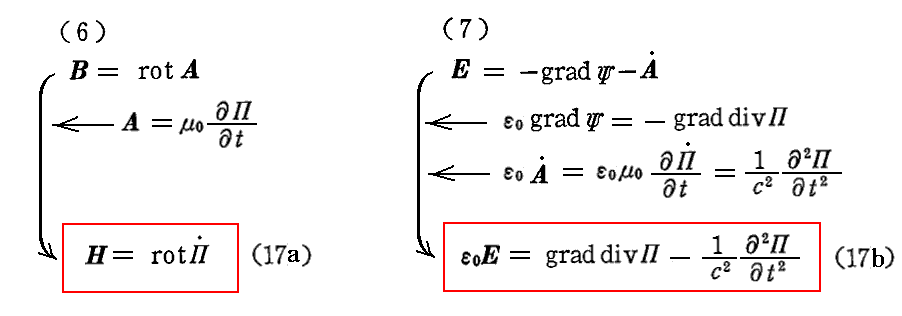
が得られる。

（２）ヘルツ双極子が作る電磁場

　双極子を構成する 運動電荷ｅ の軌道が直線であるとして、その方向（これは ヘルツベクトルΠ の方向でもある）を極座標（ｒ，θ，φ）の極軸θ＝0 に選ぶことにする。そうすればΠは

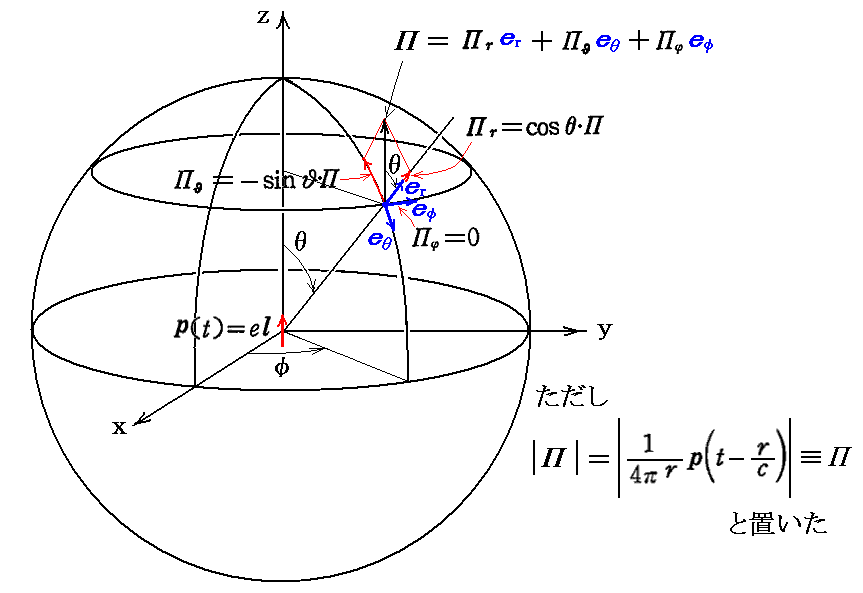
と表せます。Π は定義式（１５）式から解るように ｒ と ｔ に依存しますが θ、φ には無関係です。
　球座標表示での rot、div、graddiv演算は次の様に表せます。

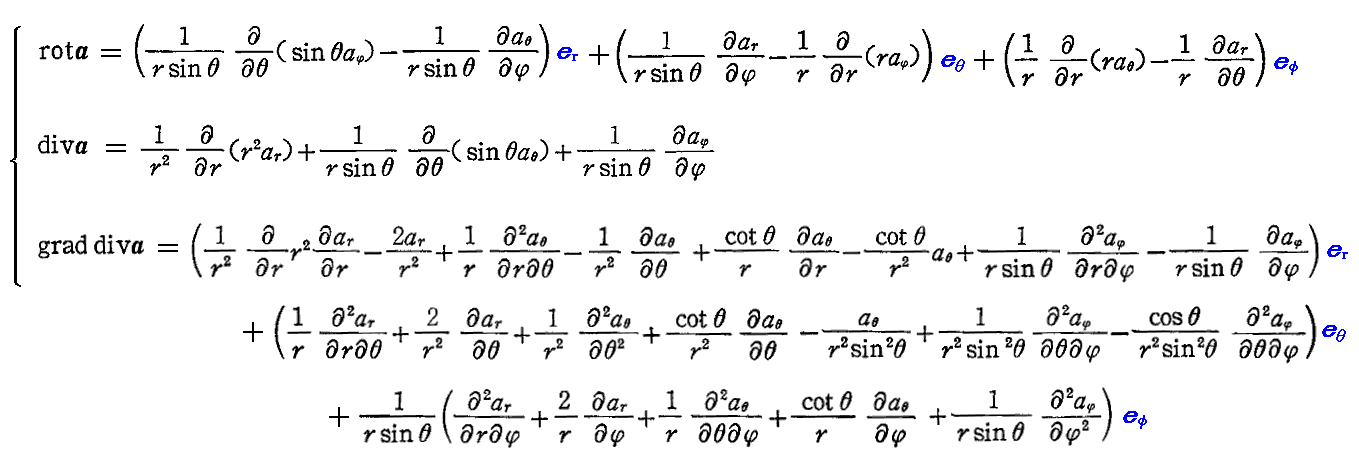
このようになることは適当な物理数学の参考書を御覧下さい。
　ここで

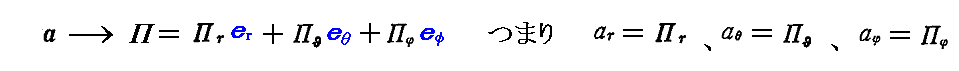
の置き換えを行い、Πは ｒ と ｔ に依存するが θ、φ には無関係であり Π_φ＝0 であることを考慮すると



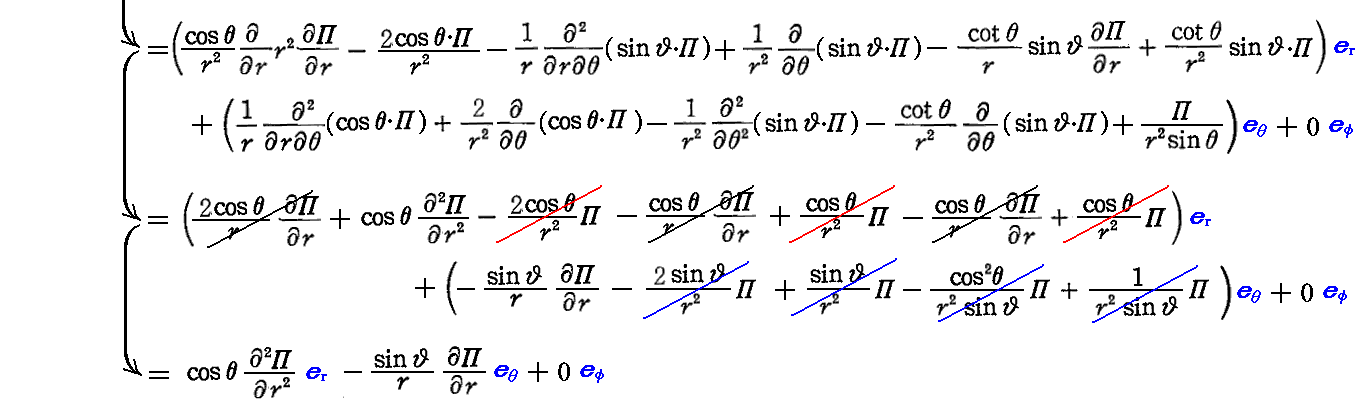
となる。

　これらの結論を（１７ａ）と（１７ｂ）に代入して電場と磁場を求める。

つまり、磁力線はｐの方向線分を中心線として、それを取りまく円であることが解る。



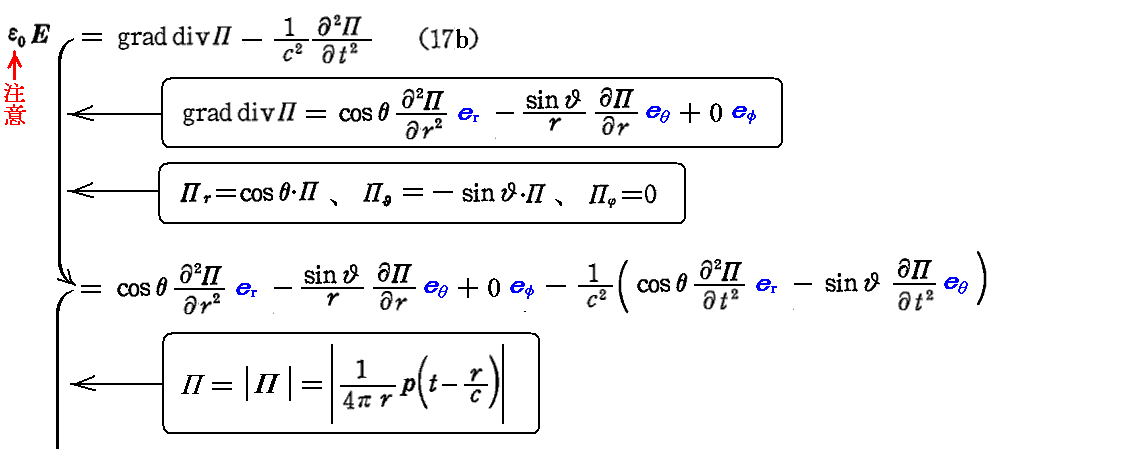
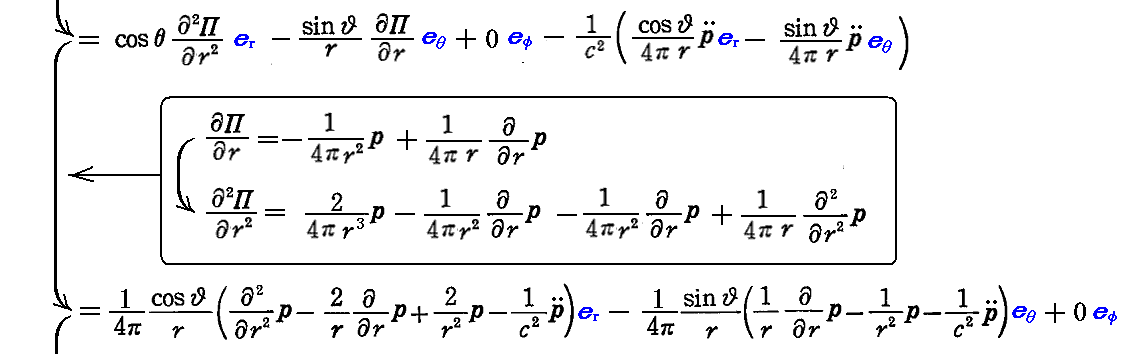
すなわち、電気力線は、ｐを含む子午線面内にあることが解る。

（３）ｒ→∞において電気双極子が作る電磁場

　電気双極子から十分離れた場所における電磁場の様子を知るには、ｒ→∞として(１８)、(１９)式で 1／ｒ について２次以上の項を省略すれば良い。すなわち

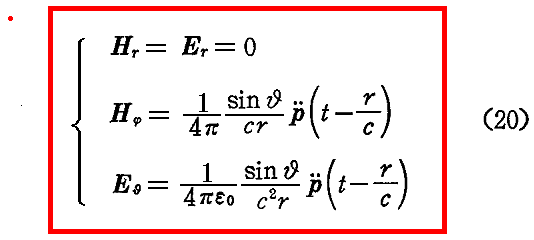
となる。ここでベクトル Ｅ と Ｈ は互いに直交し、共に動径ベクトルに垂直である。また極軸方向(θ＝0及びθ＝π）では Ｅ も Ｈ も零になり、赤道面（θ＝2／π）で Ｅ も Ｈ も最大になる。
　上式の意味することについて、ファインマン物理第�U巻の 第3章“電磁輻射” と 第4章“干渉” に教育的で解りやすい説明がありますのでご覧ください。

　さらに、（２０）式から

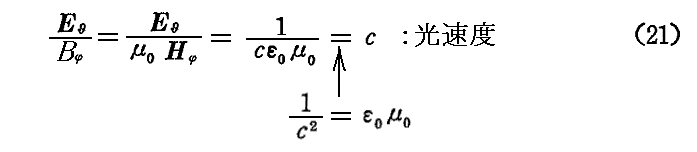
が得られる。
　これは別稿「電磁波の伝播」２．（２）で述べた平面波における Ｅ と Ｂ と光速ｃの関係及び、その伝播方向に対する方向関係と同じです。MKSA単位系ではこのように電場と磁場の次元が異なり、その比に光速度ｃが絡んでくる［ちなみにガウス単位系ではＥとＢの次元は同じになり、Ｅ_θ／Ｂ_φ＝１ となる］｡
　単位系の取り方により、その様になる理由については別稿「電磁気学の単位系が難しい理由」を御覧下さい。

　（２１）式よりMKSA有理化単位系では

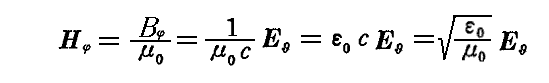
となります。
　これを用いると電磁波の進行方向に垂直な単位面積を単位時間に通過するエネルギー量である ポインティングベクトルＳ は以下のようになります。ここで、〈〉 は時間的な平均を取ることを表す。

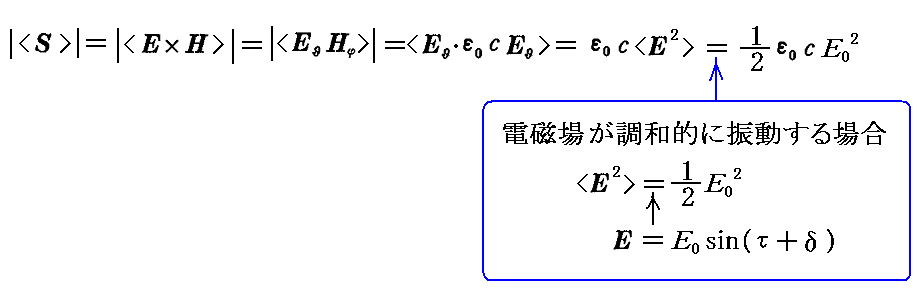
この当たりは別稿「電磁場のエネルギー密度とポインティングベクトル」２．（２）〜（３）で詳しく説明していますので、そこもご覧下さい。

　エネルギー流Ｓ はその位置における輻射の エネルギー密度ｕ と次の関係にある。

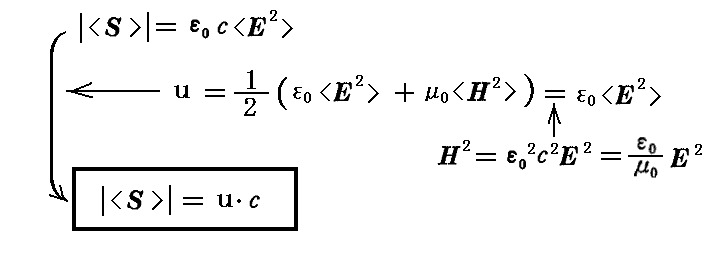
　電磁波の伝播速度が ｃ であることを考慮すると、［単位時間に単位面積を通過するエネルギー流の平均値｜〈Ｓ〉｜］＝［エネルギー密度ｕ］×［伝播速度ｃ］　となることは旨くつじつまが合っている。
　また、電磁波の形態で空間を伝わるエネルギーは、それを構成する電場と磁場が等量ずつエネルギーを受け持っていることに注意して下さい。

（４）放射エネルギー

　単位面積を通り単位時間に通過する放射エネルギーは別稿「光の圧力［輻射圧］」２．（５）２．で説明したようにポインティングのベクトルＳで表される。半径ｒ の球面位置でのポインティングベクトルの大きさは

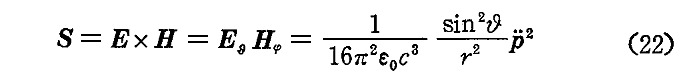
となる。ベクトルの方向は動径方向に一致しており、外向きです。
　これを、半径ｒの球面上で積分すれば、単位時間に放射される全エネルギーＳが得られる。すなわち

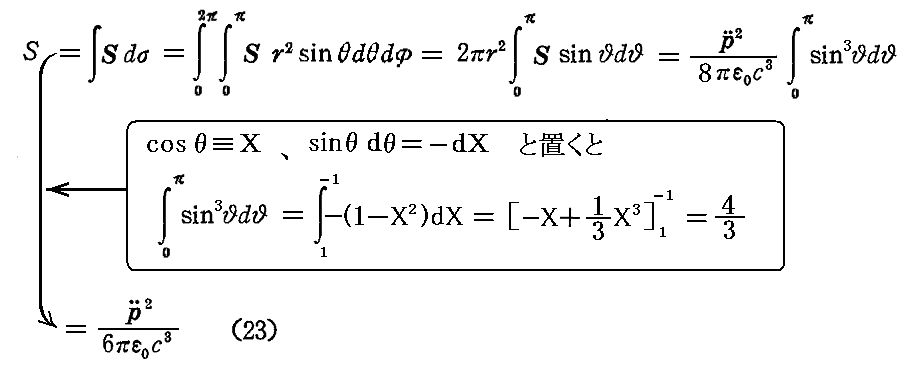
が得られる。
　ここで

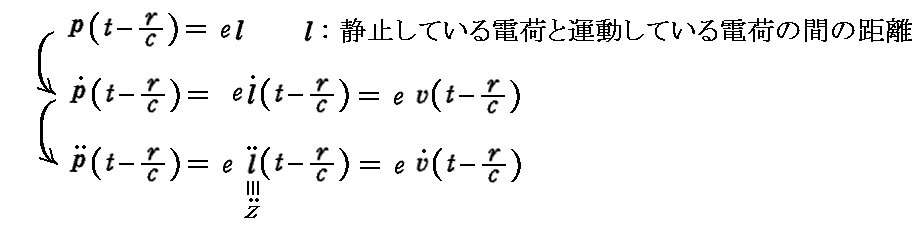
だから、双極子から単位時間に放射される全エネルギーは

となる。
　この輻射エネルギー流の基本式は、J. J. Larmor によって初めて与えられたので“ラーモアの公式”と呼ばれている。［J. Larmor, “On the Theory of the Magnetic Influence on Spectra and on the Radiation from Moving Ions”, Philosophical Magazine, 44, p503〜512, 1897年、これの日本語訳が 物理学古典論文叢書8「電子」東海大学出版会（1969年刊）4．“スペクトル線に及ぼす磁気的影響の理論について、そして運動するイオンからの放射について” です。］

　ポインティングベクトルＳ と θ の関係を図示すると下図のようになる。これは sin²θ の極図に他ならない。

　この結論は、無線通信理論で重要で、線状アンテナから放射される電波の最大輻射の方向が直線状アンテナに直角な方向であることを説明している。

　単独の双極子の代わりに、離散的あるいは連続的に配置された双極子の列が存在する場合、（１５）式は

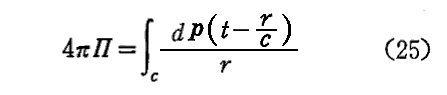
となる。ここで積分は、ｄｐの方向の変化も考慮しながら、与えられた双極子の配置曲線Ｃに沿って行われなければならない。

［補足説明１］
　“制動輻射”に付いて、シュポルスキー 著、玉木英彦他 訳 『原子物理学�T』（増訂新版）東京図書、1996年刊）の§67から引用。
　ただし、本稿の（22）式と引用文の（67．6）式の係数が（1／4π）倍だけ違いますが、本稿はMKSA有理化単位系を使用し、引用したシュポルスキーはCGS静電単位系（ε₀＝１）を用いているためです。




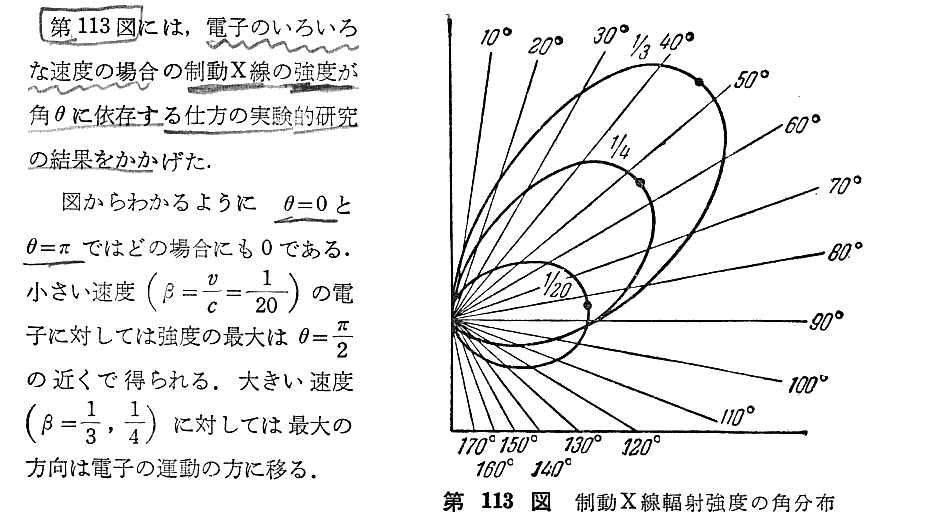
　制動Ｘ線については別稿「光電子と光子」4-2．3．も参照されたし。

３．周期的現象への応用

（１）単色光源

　電気モーメントｐ が、ある角振動数ω で単色的に振動している場合を考える。例えば

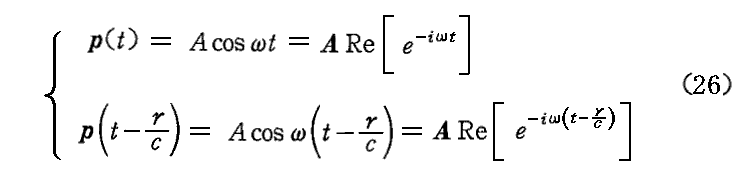
と置くことにする。ここで 波数ｋ＝ω／ｃ＝2π／λ を導入し、Ｓ や Ｓ のように場について２次の量になる場合は別として、実数部分をあらわす記号Ｒｅを省くことにする。そうすると

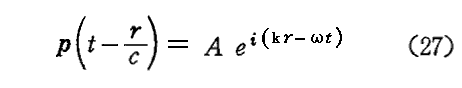
が得られる。
　（２７）式を（２０）式に代入すれば、ｒ→∞ における電磁場として

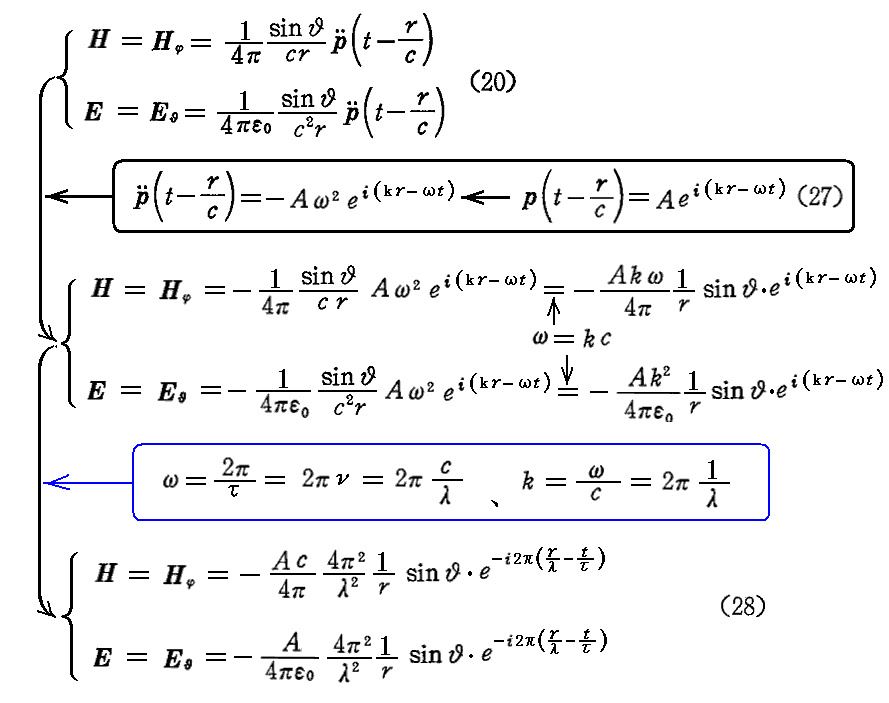
が得られる。ここで τ は振動周期、ν は振動数で ν＝1／τ の関係を満たす。これはｒが増大する方向に速度ｃ＝λ／τ で伝播していく電磁波を表している。ただしその振幅は距離ｒに反比例して小さくなる。またθの方向に関しては sinθ でその振幅が変化する。
　ところで角振動数ωには波長

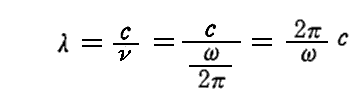
が対応するが、ｒ→∞ の領域とは

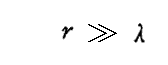
なる距離にある点の全体である。従って光源のすぐ近くが除外されるだけである。上式が成り立てば、λの値の如何にかかわらず、（１８）、（１９）式に於いて

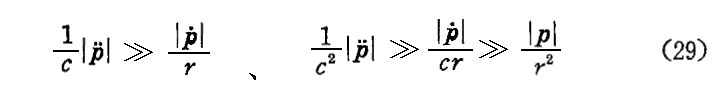
が言えるので、（１８）、（１９）式から（２０）式に移行する際に行った省略が正当化されることが解る。

　ここで説明している光源模型は単色であることと、その強度分布に於いてθ＝0及びθ＝πの方向にエネルギーを放射しない事に特徴がある。
　（２７）式から

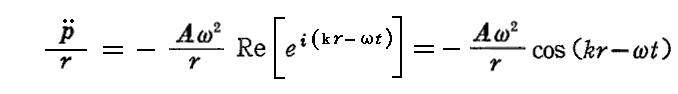
となるが、この２乗の時間平均〈〉を取れば

となる。そのため（２２）式で与えられる輻射エネルギー流は波長λの4乗に反比例（振動数νの4乗に比例）することが解る。これは極めて重要な結論です。

（２）電気双極子による散乱

　光の波長に比べて非常に小さい粒子に光を照射すると，粒子は照射光の振動数と同じ振動数で振動する電気的双極子となる。この双極子から２．（２）の（２２）式に従ってそれぞれの方向にその振動数の電磁波が放射される。これが“散乱光”となる。つまり光の散乱とは、入射した光の電場が原子中の電荷を加速振動させ、その振動電荷が周囲に電磁波を放出することに他なりません。この現象は最初にレーリーによって解析されたので、波長に比べて十分小さい粒子による光散乱を“レーリー散乱”と呼ぶ。

　ガラスや水滴中の原子や分子集団は、外部から入射する電磁波に対して規則正しく並んでいる。その様な場合には励起される二次波の位相がそろい、多数の原子（分子）集団から放射される二次波は互いに干渉し合って入射電磁波が進む方向の成分のみが残る。これは元々の電磁波に（位相の遅れを伴って）加わり電磁波の伝播速度の減少を生み出す。これが屈折の原理です。このことは別稿ファインマン物理�U「光、熱、波動」第6章“屈折率の本質”を参照されたし。

　それに対して、十分希薄な空気の様に原子（分子）がでたらめにかつ疎らに配置されている場合、任意の方向における二次波の強さは、各原子（分子）から散乱される光の強さの和になる。なぜなら、気体内の原子（分子）は互いに運動しているので、二つの原子の位相差は現在ある値をとっていても、すぐにこの位相差は変化してゆき二つの原子からの放射光の干渉効果は時間的に平均するとゼロになるからです。
　そのため十分希薄な気体によってある方向にどれだけ光を散乱されるかを知るには、ただ一つの原子（分子）による散乱の効果を調べて、それに原子数をかければよいことになる。そのとき、どの程度希薄であれば良いかは３．（２）２．［補足説明３］を参照。

１．散乱断面積

　散乱原子（分子）の最も単純なモデルは別稿「調和振動子」５．（１）で述べた様に

で与えられるであろう。
　右辺が入射してくる輻射（外部電場）による強制力を表す。その様な強制力により単振動する電荷ｅの変位を表す関数ｘ（ｔ）は２．（１）で説明したヘルツの電気双極子ｐ（ｔ）

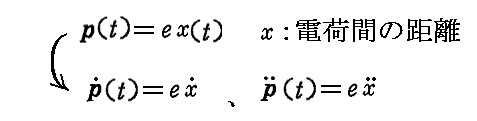
を構成する。
　このとき、左辺第２項（2ｍρが掛かっている項）は、４．輻射反作用（１）で説明するように、ヘルツの電気双極子ｐ（ｔ）が周囲に放射する二次波によって失っていくエネルギーに関係する減衰力を表す。そこの４．（２）２．の議論から解るように

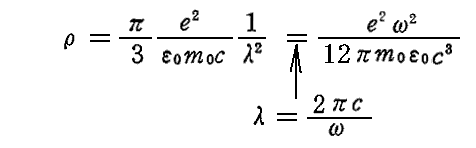
となる。
　この方程式の解はすでに別稿「調和振動子」５．（２）で求めている。そこの解の ｃ が ｅＥ₀ となることに注意すると、ヘルツの電気双極子ｐ（ｔ） の解は

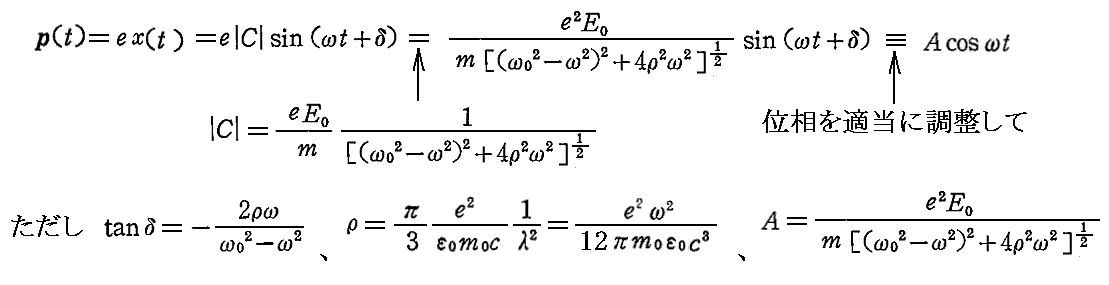
となる。
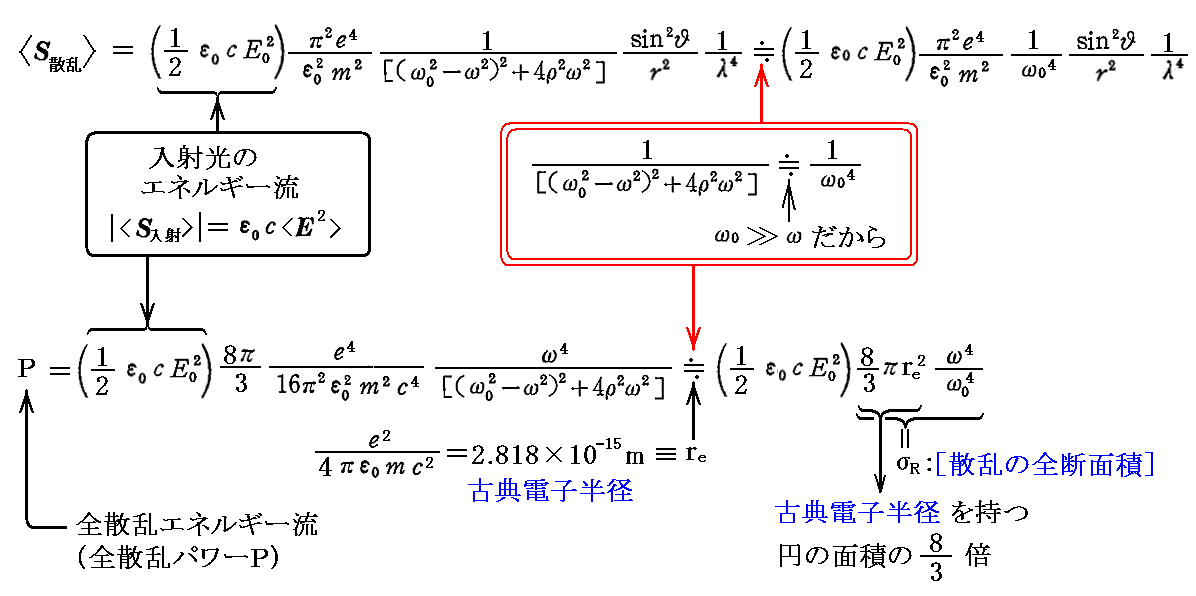
　このｐ（ｔ）を３．（１）の（３０）式に適用して２．（４）の（２２）式に代入すれば、単振動をする電気双極子ｐ（ｔ）によって放射される二次波（散乱光）のエネルギー流の時間的平均がもとまる。すなわち




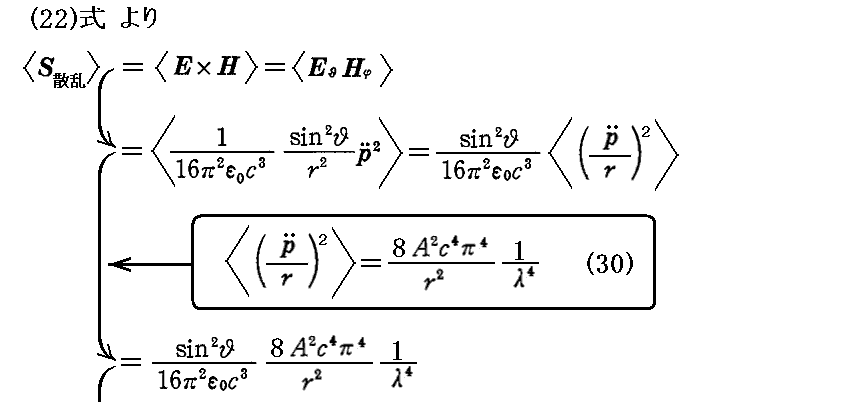
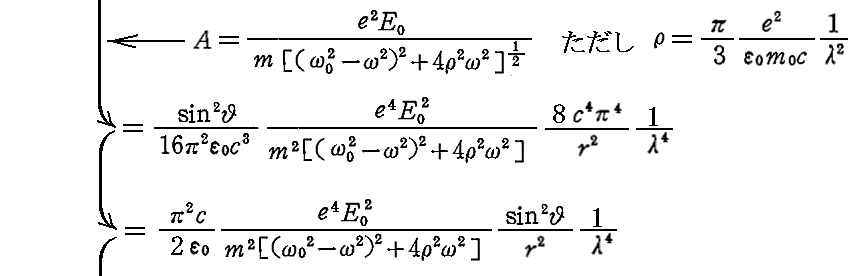
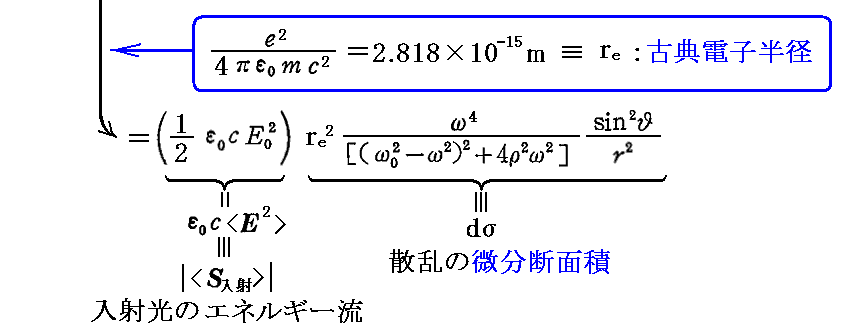
となる。これは“散乱原子”(ヘルツの電気双極子ｐ)に対して方位角θ、距離ｒ の位置の単位面積を通過する散乱光のエネルギー流を表している。
　この散乱光をあらゆる方向にわたって加え合わせた“全散乱エネルギー流”（全散乱パワーＰ）は


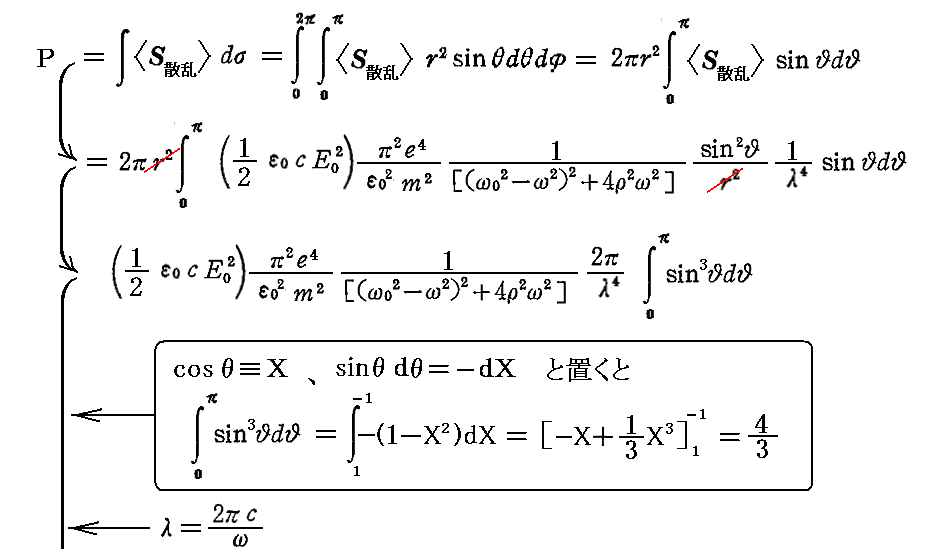
となる。
　上式の導出については、別稿ファインマン物理�U「光、熱、波動」§7-5“光の散乱”も参照されたし。

［補足説明１］
　ここで言っている“古典電子半径”とは、［電子の静止エネルギー ｍ_eｃ² ］が［半径ｒ_eの領域内に分布している電荷の静電エネルギー ｅ²／4πε₀ｒ_e ］に等しいと置いて得られるものです。
　このとき本によっては電荷の静電エネルギーとして （3／5）×（ｅ²／4πε₀ｒ₀） や （1／2）×（ｅ²／4πε₀ｒ₀） など異なる係数を与えているものもありますが、それは電荷の分布に関する仮定（球の内部まで一様に分布するか、あるいは球の表面に分布するか）の違いによるもので、その当たりの任意性があります。
　
　また実際の所、電子がこのような半径を持っているのかどうかは解りません。電子のある部分が他の部分に及ぼす力を基にして輻射抵抗を説明しようとした初期の理論で、電子が大体この程度の大きさを持つことを必要としたので、その様に名付けられただけです。［J.J.Thomson, ”On the Electric and Magneteic Effects produced by the Motion of Electrified Bodies”, Phil. Mag. S.5, Vol.11, No.6, April 1881, p229〜249、これはGoogleBooksからダウンロードできます］

［補足説明２］
　最後の式は

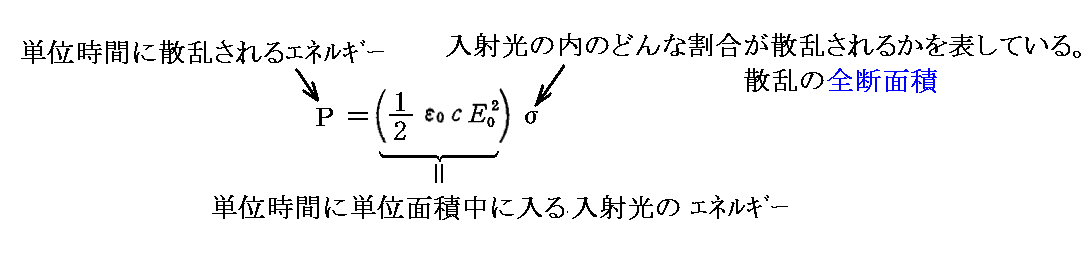
の関係を表している。
　ここで σ は面積の単位を持っており、単位時間に単位面積に入射するエネルギーの内、どの面積分に相当するものが散乱されるかという意味合いを持つので“散乱の断面積”と言われる。
　断面積という考え方はある現象がビームの強さに比例して起こる場合に使われる便利な考え方ですが、散乱体が実際にその様な面積を持っていることを意味するのではありません。ビームからある量を拾い上げるために、有効面積はどれほどでなければならないかという言い方で、現象の大きさを表すわけです。
　
　例えば、後で述べる“トムソン散乱”の場合、σは古典電子半径の円盤面積程度に成るわけですから、σ〜10^-30ｍ² のオーダーに成ります。つまり、その場合１ｍ²に入射するエネルギー流のうち10^-30ｍ² 程度の断面積に入射するエネルギー分が散乱されるという事になるわけです。

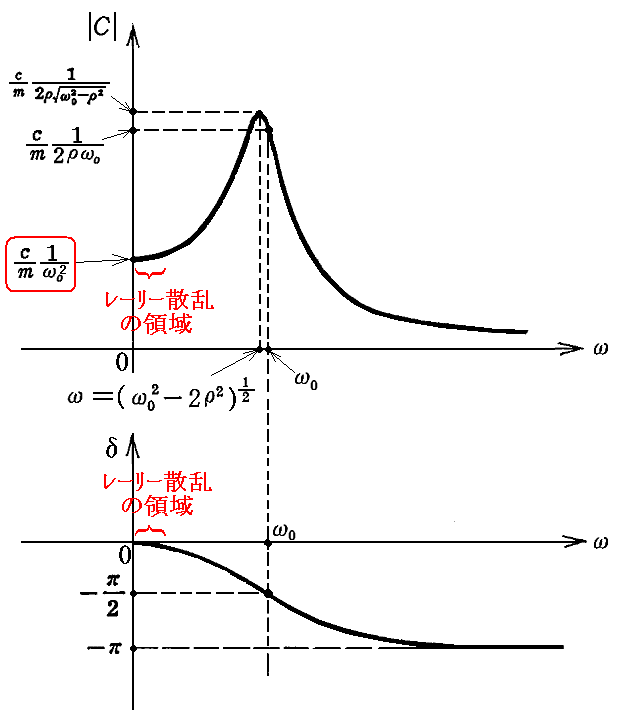
２．レーリー散乱（空が青い理由）　ω₀＞＞ω

　ここで散乱体（共鳴子）の固有角振動数ω₀が、散乱体を強制振動させる光の角振動数ωよりも、はるかに大きい場合、すわなち ω₀＞＞ω の場合を“レーリー散乱”という。
　大気中の気体分子により可視光が散乱される様な場合にはこの条件が満たされる。

　これは別稿「調和振動子」５．（２）の共鳴曲線図で下記“赤｝領域”に相当する場合です。

　このとき（直線偏光した）入射光に対して

となる｡
　ここでω₀は散乱分子に関係する性質で、入射光の角振動数ω とは関係ありません。そのため、“レーリー散乱”の強度は、入射光の強度（Ｅ₀²に関係）に比例し、入射光の角振動数の４乗に比例（波長の４乗に反比例）することになる。

• 　入射光が強いほど散乱光も強くなるので、正午頃の空が最も明るく輝くことになる。昼間の空が輝いているのは入射太陽が散乱分子によりあらゆる方向に散乱されるためです。つまり入射方向とは直角な方向ににも沢山散乱されるために太陽の方向以外の空が輝くことになる。
  　もし大気がなかったならば、月の表面で太陽を眺めたように、太陽の方向のみがぎらぎら輝いて、そのまわりの空は真っ暗であろう。
• 　光散乱は入射光の波長が短いほど著しいので、太陽からの光が空気分子によって散乱されるときには波長が短い青色の光は赤色の光よりも強く散乱される。実際 λ_赤〜2λ_青 であるから両者の比は 2⁴〜16倍程度となる。そのため、太陽の方向とは異なった方向の空からやってくる散乱光である昼間の空の色が青く見えることになる。
  　一方、明け方や夕方の様に、太陽からの光が大気層にそって入射して来るとき、厚い大気層を通ってくる間に青や紫の光は大部分が横方向に散乱され、赤い色を多く含んだ光が目に入ってくる。これが朝日や夕日が赤く見え、太陽の方向の朝焼けや夕焼けの空が赤く見える理由です。

［補足説明１］
　太陽光線が来る方向とは直角を成す空の領域をポラロイドの様な偏光板で眺めて見る。偏光板を回転すると、偏光板を透過する光の強度がわずかだが暗くなったり明るくなったりする。そのことは、本来偏らない自然光である太陽光を散乱することによって輝いている空から来る光は少し偏光していることを示している。

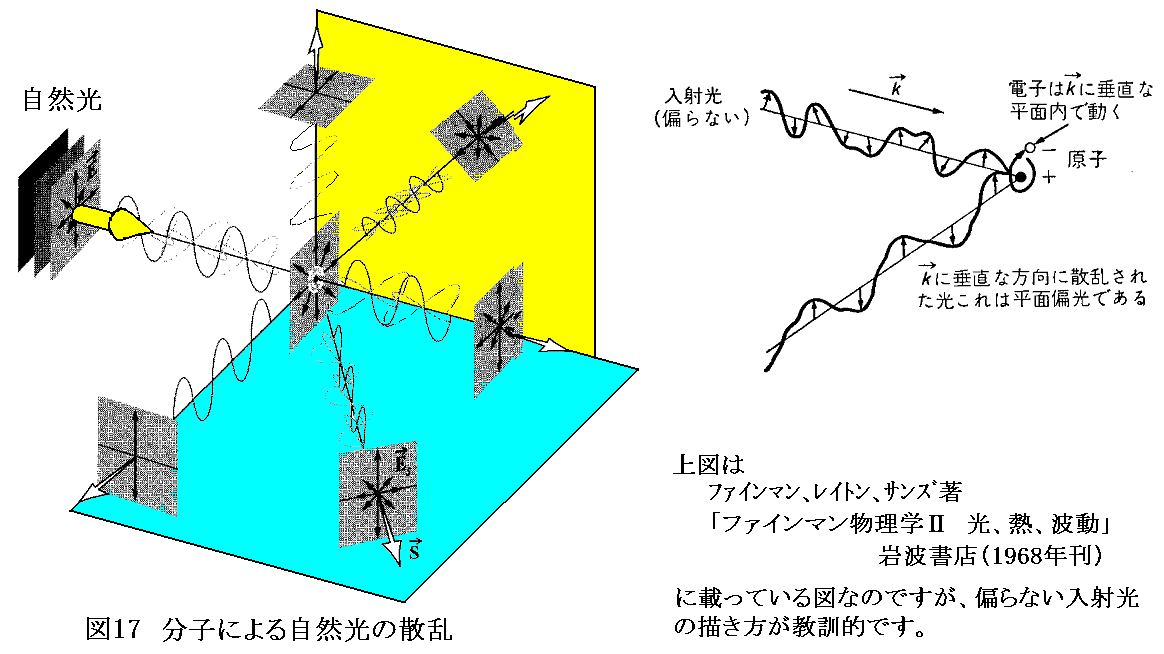
大気で散乱された太陽光が偏光していることを最初に見つけたのはアラゴ（1809年）です。またアラゴは1811年に水晶が偏光面を回転させることも発見してます。

［補足説明２］
　条件 ω₀＞＞ω を満たす分子が密に集合して固まりをなしていても、その固まりとしての散乱体の大きさが波長の1/10程度より小さく、固まりの空間分布数密度が疎らであればレイリー散乱となる。しかし、照射される粒子の大きさが光の波長と同程度になると、散乱体内の異なった場所で散乱される光同士が干渉し合うために散乱現象は複雑になる。つまり、散乱分子が密に集合して、しかもその集合体の大きさが波長程度以上になった場合、その各部分からの散乱光の位相差を考慮した干渉を考えなければならない。
　
　1908年Ｇ．ミーは均質媒質中にある任意の複素屈折率と直径をもつ球による単色平面波の散乱をマクスウェル方程式を使って計算した。それによると散乱粒子の半径を ａ とし、用いる光の波長を λ とすると、パラメター ｑ＝2πａ/λ の増大とともに前方散乱が後方散乱にくらべて急激に増大する。また ｑ＞1 の場合には散乱光強度分布に一連の極大、極小が現われる。この様な散乱を“ミー散乱”と言います。実際のところ、大気中の水滴などのエアロゾル（雲粒の半径は数〜数10μｍ程度で可視光の波長かそれより少し大きい程度）による散乱がそれです。

［補足説明３］
　“レイリー散乱”となる条件には散乱体の大きさのみならず散乱体の数密度も関わってくる。
　地上付近の１気圧大気中での酸素や窒素分子の粒子数密度は、別稿「アボガドロ数の測定法」４．（１）で見積もったように、可視光の波長（λ〜500ｎｍ〜5×10^-7ｍ）を一辺とする立方体（体積〜1.25×10^-19ｍ³程度）中に約3×10⁶個程度となる。散乱分子の大きさは波長に比べると十分小さいのだが、１気圧下の空気では極めて密な状態（間隔〜3ｎｍ〜3×10^-9ｍ程度）で存在する散乱体からの散乱となる。このような高密度媒質中での散乱波は、ホイヘンスの原理から明らかなように、前方方向において強く位相が揃った連続媒質中での光の伝播と同じになり、横方向の散乱は生じない。もし、地上付近の空気でレーリー散乱が起こるのなら、遠くの山は赤く見えるはずですがその様なことは起こらない。
　つまり、レーリー散乱であるためには、散乱体である分子は入射波の波長程度（λ〜500ｎｍ）以上互いに離れた疎な状態にあって、それらの散乱体からの横方向の散乱波の位相がバラバラであることが必要です。気体分子の間隔が可視光の波長程度以上になる為には大気の密度が地上の1／10⁶程度（つまり密度〜10^-6ｋｇ／ｍ³程度）以下になる必要がある。これは地上からの高度が100ｋｍ程度以上の高層です。つまり空が青く見える主な原因となっている散乱光は高層の希薄な大気で散乱されたものです。
　その様な高層で散乱された光が厚い大気を通して良く地上に届くものだと思われますが、我々は大気を通して何光年もの彼方からやってくる星の光を見ることができることに思いをめぐらせば、その不思議さにも納得できます。

［補足説明４］
　明るい太陽光の場合でも原子（分子）に作用する強制力の電場Ｅは約1000Ｖ／ｍ程度です。実際、太陽定数は1370Ｊ／ｍ²ｓ程度ですが、３．（３）で説明したポインティングベクトルのエネルギー流に等しいと置くと 【下記計算式は２．（３）を復習】

となります。
　これに対して原子（分子）中の電子を原子核に拘束している電場の強度は ｒ を原子（分子）の大きさ程度とすると

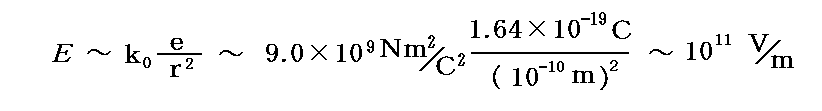
となります。
　従って原子や分子に強く拘束された電子に比較的弱い外部電場による強制力が働くことになる。そのためここで考えている振動子の電子は、その釣り合いの位置を中心に、原子（分子）の大きさに比較して微小な振幅の単純調和振動をするとして良いであろう。

［補足説明５］
　中高度の大気では、空気の熱運動が迅速に変化する局部的な密度ゆらぎをもたらしている。このような時々刻々とかなりランダムに変化するゆらぎは、分子密度の高い領域を形成し、一方向により強く散乱させる原因となる。
　スモルコフスキー（1908年）とアインシュタイン（1910年）はレーリー散乱にさらに追加する結果（つまり、空が青く、夕焼けが赤く見えることに奇与）となるゆらぎによる散乱の理論について基礎となる考えを提唱した。
　この説明にはかなりの準備が必要ですので省略します。

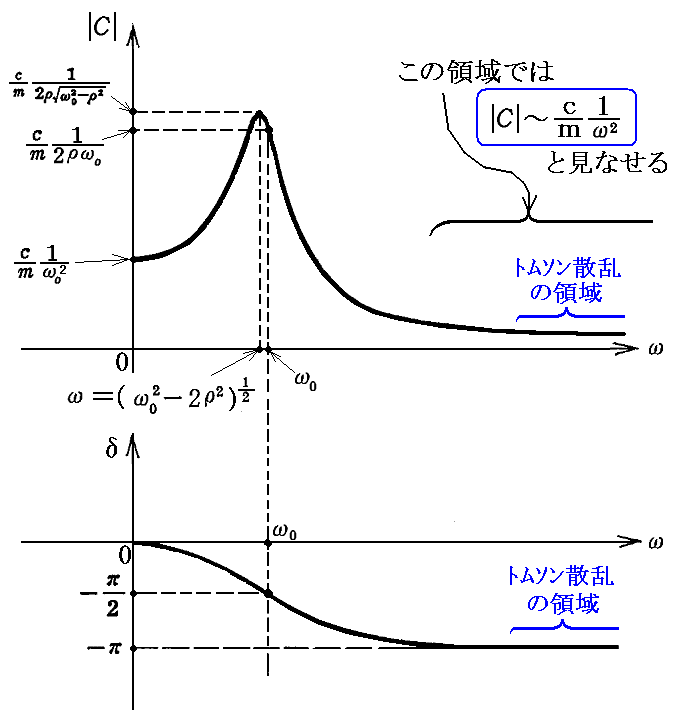
３．トムソン散乱　（ω＞＞ω₀、ω₀→0）

　散乱体（振動子）の共鳴角振動数がω₀→0の極限の場合を“トムソン散乱”という。
　自由電子による光の散乱などが相当する。

これを別稿「調和振動子」５．（２）の共鳴曲線図で説明すると、下記“青｝の領域”に相当する場合です。

　このとき（直線偏光した）入射光に対する全散乱エネルギー流（全散乱パワーＰ）は

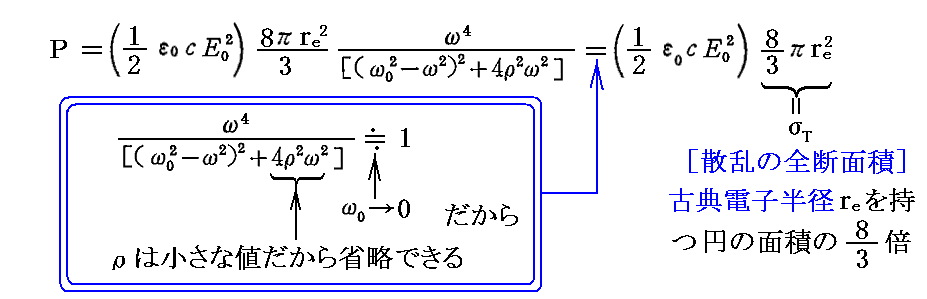
となる。つまり、電子の静止質量に比して十分小さいエネルギーの（直線偏光した）光が自由電子によって散乱される場合、散乱の全断面積は古典電子半径の円の面積の3分の8倍程度となります。
　上記の式から明らかなように、長波長の光が束縛されていない荷電粒子によって散乱される場合には以下の特徴があります。

• 　入射光の内で散乱される割合は入射光の波長（振動数）によらない一定値となる。これはレーリー散乱と大きく異なるところです。
• 　散乱体電荷の種類が変わると、
  
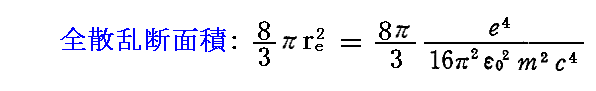
  ですから、散乱断面積（散乱される割合）は散乱体の荷電が大きいほど、また質量が小さいほど大きくなります。
  　これはレーリー散乱に付いても言えることですが、レーリー散乱の場合には散乱体分子内の荷電粒子の束縛状況（ω₀に関係する）の違いが大きく効いてきます。
  

［補足説明１］　
　光のエネルギーが大きい（硬Ｘ線などの極短波長光）場合には“コンプトン散乱”とよばれ、散乱光の波長が長くなります。“トムソン散乱”は、コンプトン散乱の低エネルギー（長波長）極限にあたり、波長の変化はありません。
　普通の電子は原子核に束縛されていますが、入射する光のエネルギーが電子の束縛エネルギーよりも十分大きくなると、たとえ原子に束縛された電子であっても自由電子と見なせてトムソン散乱の理論が適用できます。実際、波長が原子の大きさ程度までのＸ線についてはトムソン散乱と見なせます。
　
　しかし、波長が原子の大きさの１／10程度（〜10^-11ｍ）以下のさらに短い硬Ｘ線になると波としての性質より粒子としての性質が強くなり、散乱Ｘ線の波長変化が起こるコンプトン散乱になっていきます。実際波長が10^-11ｍ程度になると光子のエネルギー＝ｈν〜10⁵ｅＶ〜100ｋｅＶ程度となり、電子の静止エネルギー511ｋｅＶに近づきますからコンプトン散乱理論に従わなければ成りません。

［補足説明２］
　コンプトン散乱は、物質によって散乱されるＸ線に関してコンプトンが見いだした（1922年）もので、物質中の電子による光子の散乱として理解され、光の粒子性（光量子仮説）の実験的な証拠とされた。
　振動数ν の電磁場の量子である光子（エネルギー＝ｈν）が静止している電子に入射し、角度θ の方向に散乱されて振動数ν’（＜ν） になった場合、特殊相対性理論によるエネルギー保存則と運動量保存則を適用すると、ν’ が ν と θ の関数として与えられる。そのとき ［振動数ν］×［波長λ］＝［光速ｃ］　を用いて波長の変化量になおすと Δλ＝λ’−λ＝λ_c（１−cosθ） となり、波長の変化は散乱角度θが大きいほど顕著になります。ここで λ_ｃは電子のコンプトン波長と呼ばれ λ_c＝ｈ／ｍ_eｃ＝2.4×10^-12ｍ ［ｍ_e：電子質量］ となります。
　もともと、電子によって散乱されたＸ線の波長が長波長側（低振動数側）に変化する現象をコンプトン効果と言ったのですが、これは光子が荷電粒子によって散乱される過程ですから電子以外の荷電粒子（陽子など）でも現れます。［別稿「ガンマ線と陽子のコンプトン効果」参照］

（３）Ｘ線理論への応用

１．Ｘ線が横波であることの証明

　Ｘ線は陰極線（高速の電子の流れ）が対陰極に衝突した際に生ずる。そのとき入射電子の速度ｖ は制動されてより小さい速度になる。電子は −ｖ だけの減速を受けるのだが、その加速度の方向が陰極線の方向と同じである限り（２０）式から明らかなようにその方向への輻射は起こらない。事実そのようになることは、Kulenkampffとその弟子達が非常に薄い（ミクロン程度）対陰極を用いて、それを通過してくるＸ線を調べことで検証した。
　しかし普通のＸ線発生管の対陰極は大きな金属片を用いているので、ジグザグの制動をうけて方向による違いが平均化されてくる。そのため偏りのないＸ線が得られる。
　そのとき相対論的な速度では２．（４）の図中で注意したように輻射の極大方向は θ＝π／2 ではなくて、θ＝0 の方に傾いてくる。また、連続スペクトル（制動輻射スペクトル）には短波長側に下限があるが、これは量子論の結果である。ただしここでは、その説明は省略する。

　ここでは、1905年［これはRo¨ntgenがＸ線を発見した10年後］にBarklaが行ったＸ線が横波であることの検証実験について説明する。Barklaは前記のメカニズムで発生するＸ線放射についても（２０）式が成り立つとすればＸ線が横波であることが検証できることに気がついた。そのことを確かめるために、彼は下図のように配置された測定装置を作った。

　図の様に“１次放射”、“２次放射”、“３次放射”が互いに直角に交わるような経路を考える。経路（１）の部分を進む１次Ｘ線については、上で注意した様に偏りは無いと仮定して良いであろう。対陰極が非常に薄い場合には部分的に偏るが今は普通の対陰極を用いている故に。
　これが第一の散乱体Ｚ₁に入射し、その中に含まれる電子を振動させる。そのとき“２次放射”として経路（２）の方向に放射される２次Ｘ線は、（２０）式から解るように、図中の矢印の方向に偏っている。
　この偏った２次Ｘ線が第二の散乱体Ｚ₂に入射すると、散乱体中の電子を図の矢印の方向に振動させる。そのため第二の散乱体Ｚ₂から放射される３次Ｘ線の強度は、（２０）式より、経路（３）の方向では零になる。放射が見られるのは主に経路（１）と（２）を含む面内の方向です。３次Ｘ線のこのような振る舞いは、１次Ｘ線が横波であることを証明すると共に、２次Ｘ線が完全に偏っていることを示すものです。
　散乱体Ｚ_１、Ｚ₂にはパラフィンの球が用いられた。重い物質を使うと、特性Ｘ線が出て、これが実験結果を悪くするかも知れないからです。実際の所、特性Ｘ線は物質がＸ線に照射されたときの2次Ｘ線としても出てきますが、それは一般に偏光していません。そのとき、原子量が小さい炭素やパラフィンなどから出る特性Ｘ線は柔らかく（波長が長い）ほんの数ｃｍの空気層で吸収される。ただし、特性Ｘ線の本質が理解され、なぜそうなのかが解明されるのはモーズリーの発見以後のことです。
　これを報告したCharles G. Barklaの論文が、“Polarisation in Secondary Rontgen Radiation”, Proceedings of the Royal Society of London, Series A, March 6, vol.77, p247〜255, 1906年　です。

［補足説明１］
　バークラはイギリスの物理学者ですが、1903年に2次X線に散乱X線があることを発見した［Phil. Mag. (6)5, p685〜698, 1903年］。この散乱が原子量に比例することを観測した［Phil. Mag. (6)7,p543〜560, May, 1904年］｡これは、J．J．トムソンの原子中の電子数の推定（1906年、次項２．参照）につながった。
　さらに彼は、1904年にX線の偏りを発見し、1906年の上記実験［Proc. R. S. (A), 77( 1906年), p247］でX線が横波の電磁波であることを示した。
　さらに1907年特性X線を発見した［Phil. Mag. 11(June 1906年), p812；Phil. Mag. 14（Sept. 1907年), p408；Phil. Mag. 16（Oct. 1908年), p550］。これは後にモーズリーの発見に繋がる業績です。
　彼はこれらの貢献により1917年ノーベル物理学賞を受賞した。

２．原子内電子数の見積もり

　前項［補足説明１］のＪ．Ｊ．トムソンによる原子中の電子数推定に使われたのが、３．（２）３．で述べた“トムソン散乱”の理論です。原子中に束縛されている電子の束縛エネルギーはＸ線のエネルギーに比較して小さいので自由電子とみなされると考えたのです。そのため、トムソンはCGS電磁単位系で表されたトムソン散乱の散乱断面積

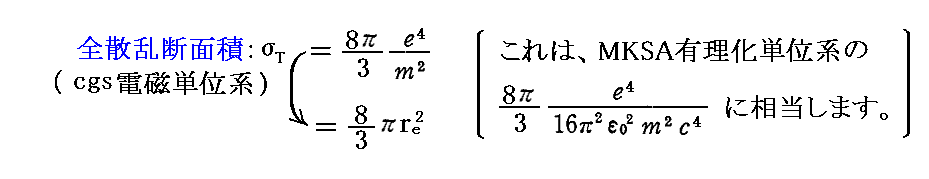
を用いました。これは、彼自身が２．（４）で説明した“ラーモアの公式”から３年前に導いていた公式です。
J.J.Thomson著“Conduction of Electricity through Gases”Cambridge Univ. Press（1903年刊）
　このときトムソンは１ｃｍ³の空気にＸ線を入射したとき散乱されるＸ線エネルギーの割合としてBarklaのデータ［Phil. Mag. (6)7,p543〜560, May, 1904年のp556］を用いました。それは、１ｃｍ³中の電子数をＮとすると

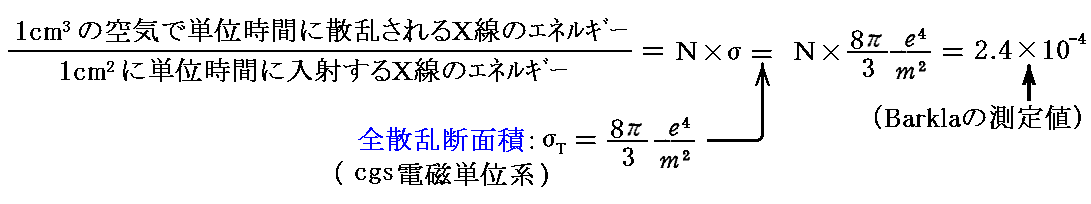
で表せます。
　このとき、バークラは、散乱量が空気の量に比例するが用いたＸ線の波長によらないことを確かめています。そのためトムソンは、彼の散乱理論の正当性が確認できると言っています。
　トムソンはこの式に当時知られていた ｅ／ｍ_e＝1.7×10⁷emu/g と ｅ＝1.1×10^-20emu ［今日の値はｅ／ｍ＝1.76×10⁷emu/gとｅ＝1.602×10^-20emu］ を適用して Ｎ の値を求めます。そして当時解っていた１ｃｍ³中の空気分子数ｎ で Ｎ を割って Ｎ／ｎ〜25 という値を求めます。これは空気分子中の窒素分子の分子量28 にとても近い値だったので、トムソンは“原子１個中には原子量（窒素は14）と同じ程度の個数の電子が含まれている”と推察する証拠の一つとしました。本当は原子量ではなくて、その約半分程度になる原子番号（窒素は7）だったのですが、その違いは彼が用いた電子の電気量が不正確だった為です。

　これを報告した論文が
J.J. Thomson,　"On the Number of Corpuscles in an Atom", Philosophical Magazine, vol. 11, June 1906, p.769-781
です。これは　http://www.chemteam.info/Chem-History/Thomson-1906/Thomson-1906.html　からダウンロードできます。
　その中の 2nd Method. Scattering of Ro¨ntgen Radiation by Gases.が該当する部分です。解りやすく書かれた短い文章ですので御覧になられて下さい。［ただし、トムソンはGCSemu(電磁)単位系を用いていることに注意。(ｅ_MKSA有理)²＝4πε₀ｃ²×(ｅ_CGSemu)² となります。］
　
　ちなみにその中に書かれている 1st Method. は光の分散理論（物質中の光の伝播速度が波長により異なること）を用いたものです。つまり光の分散の電子論を用いて原子中の電子数を見積もるものです。トムソンは彼の原子模型を使ってこの効果を計算して水素に関する観測値と比較してみた。そうすると水素はだいたい１個の電子を含むと言う結果になった。
　
　また 3rd Method. はベータ線の吸収に関するラザフォードの実験結果を用いるものです。この場合にも原子内電子の個数は化学原子量とだいたい等しいという結論になった。

　当時原子の内部構造については何も解っていなくで、原子内電子の数についても数個から数千個まで様々な考え方があったのですから、この論文の示す内容は画期的です。［別稿「ラザフォードの原子モデル」２．（１）参照］
　この当たりにつきましては、物理学古典論文叢書9「原子模型」東海大学出版会（1970年刊）2.“原子内の微粒子の数について（J.J.Thomson)”や、広重徹著「物理学史�U」倍風館14-7等も参照されたし。

［補足説明１］
　ここで散乱エネルギーを散乱電子数（Ｎ）倍で計算したのは、 Ｘ線の波長が原子の大きさ程度以下であれば同じ原子中の電子でも互いにアトランダムに分布するとして良いので、同一原子内の電子による散乱もランダムな位相を持っていると考えられるからです。そのとき、気体分子の数密度から計算される平均的な気体分子の間隔に対してはＸ線波長はさらに十分短いのですから、異なった分子からの散乱はもちろんランダムなものであると考えられる。
　しかし、原子が規則正しく密に並んだ結晶で散乱される場合には事情が変わってきます。実際、歴史的にこの後に発見されるＸ線回折現象も最外殻付近の電子によるトムソン散乱によるものですが、原子が規則正しく並んでいると原子間隔程度以下の短い波長のＸ線でも散乱波同士の干渉による回折像が生じることになります。
　ちなみに、1912年にマックス・フォン・ラウエが結晶によるＸ線回折現象を発見し、1913年にヘンリー・ブラッグとローレンス・ブラッグの父子がブラッグの法則を発表してＸ線回折による構造解析の路が開らかれた。この当たりは別稿「Ｘ線結晶解析におけるラウエの条件式とブラッグの条件式」をご覧下さい。

［補足説明２］　
　実際のところ、量子論が完成した後に振り返って見ると、Ｘ線の原子による散乱は当時トムソンが考えた以上にもっともっと込み入った複雑な現象でした。Ｘ線の波長が原子の大きさの１／10程度以下になりますとトムソン散乱ではなくてコンプトン散乱になります。また、もっと重い原子の場合には、入射Ｘ線は内核電子と量子力学的な相互作用をして、モーズリーが得たような輝線スペクトルになります。
　結局のところ、Ｘ線散乱についてトムソンの簡単な公式が成り立つのは、窒素の様に軽い原子で、しかもある狭い波長範囲のＸ線についてだけですが、幸運なことにバークラの実験はちょうどその範囲のＸ線で行われたものだったのです。　

４．加速電子の輻射によるエネルギー損失と運動に対する反作用

（１）輻射の反作用力　Ｒ

　一様な運動をする場合と異なり、加速されている電子が輻射線を放射することを２．（４）で説明した。そこの（２４）式によれば速度ｖが光速度ｃに比較して小さいときには“単位時間に放射されるエネルギー”ＳはMKSA有理化単位系で

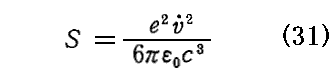
となる。
　このエネルギー損失は、電子の運動方程式にも反映するはずである。この事を考慮するために、その影響をそれと等価な力で表すことにしよう。 ｔ₁〜ｔ₂ までの加速時間が短い場合について考える。この区間の境目、及び区間の前後では運動は一様であり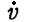は零であると見なせるものとする。この区間が短いときには速度の変化もわずかである。
　求める力を“輻射の反作用力”と呼ぶことにして、“Ｒ”で表す。この力が ｔ₁ から ｔ₂ までの間に電子に対してなす仕事は電子が輻射によって失うエネルギーの符号を逆にしたものと等しくなければならないので

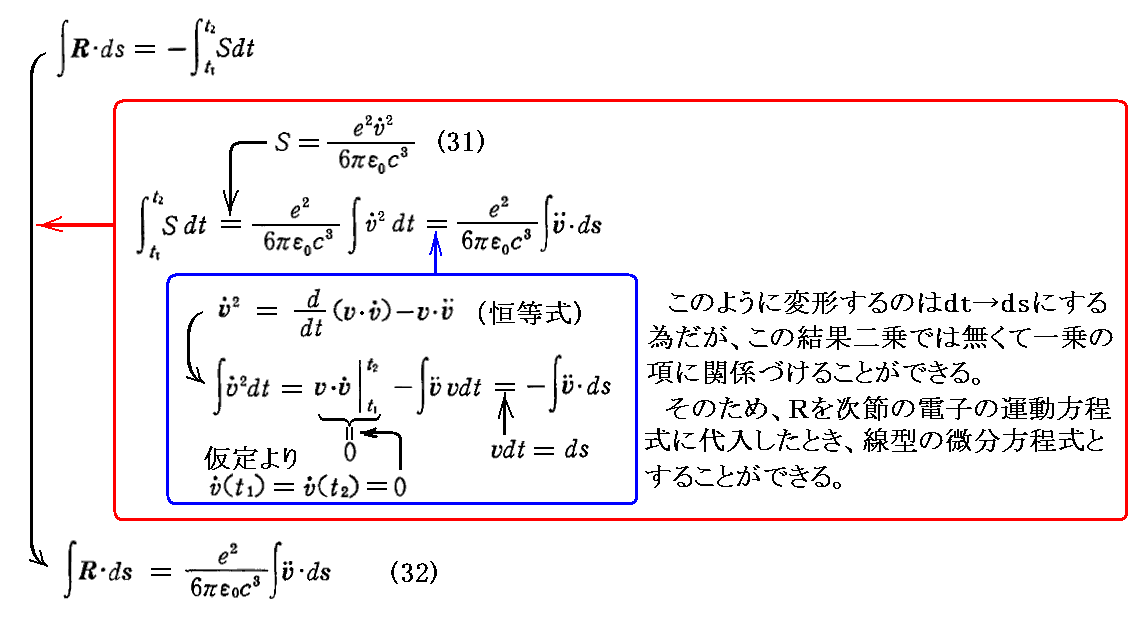
が言える。
　これを満足する“輻射の反作用力”Ｒの最も単純な式として

が得られる。(３２)式と矛盾しないような別の式があっても、それは(３３)式と大きさの程度に於いてわずかしか違わないことが示される。

（２）振動子の減衰と干渉可能距離

１．運動方程式中の減衰項

　ここで、３．（１）で光源の理想化された模型として使った平衡位置のまわりの振動という最も単純な場合について、この反作用力Ｒの効果を調べて見よう。
　振動は直線的であるとし、電子の静止位置からの距離を ξ とする。電子は原始的な結合により、その中心に束縛されているが、そのときの復元力は変位 ξ に比例するものとする。すなわち比例定数を ｋ として −ｋ・ξ で表されるとする。電子の振動は反作用力 Ｒ のために減衰するのであるが、そのときの電子の運動方程式は

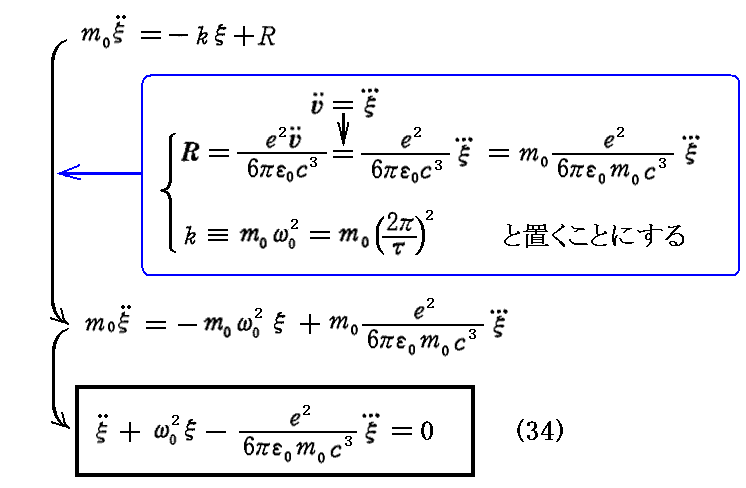
の様な“同次線型微分方程式”で表されるとして良いであろう。
　同次とは定数項が無いということです。
　また、線型とはすべての項が、 ξあるいは ξ の ｔ に関する導関数（ｄξ／ｄｔ、ｄ²ξ／ｄｔ²、ｄ³ξ／ｄｔ³、等々）の一次（一乗）項のみからなり、方程式がそれらの項の和（線形結合）で表されることです。つまり方程式の中に ξ² や ξ・（ｄξ／ｄｔ） の様な積（高次）項を含んでいない事です。
　ここで、ω₀は減衰の無い場合（Ｒ＝0）の固有角振動数です。今後、それに対応する固有振動周期をＴ₀で表すことにする。
　このような同次線型微分方程式の解としては

の形のものが考えられる。これを(３４)式に代入すると

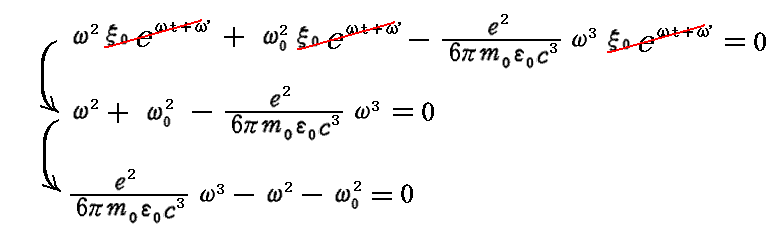
となる ω の三次方程式が得られる。

２．運動方程式の解

　前節の ω の方程式は一つの正の実根と二つの複素数根を持つ。

［補足説明１］
　このことは3次方程式　ａｘ³＋ｂｘ²＋ｃ^ｘ＋ｄ＝0　の解の判別式　Ｄ＝−4ａｃ³− 27ａ²ｄ²＋ｂ²ｃ²＋18ａｂｃｄ−4ｂ³ｄ　に於いて、
　Ｄ＝0のとき実数の三重根、
　Ｄ＞0のとき相異なる3つの実数根、
　Ｄ＜0のとき一つの実数根と一組の共役な複素数根
をもつ事が言えるからです。
　今はＤ＜0が成り立つ場合です。三次方程式の“解の判別”については、適当な代数学の教科書を復習して下さい。

　第一の正の実根は関数ξ(ｔ） が時間と共に途方もなく大きな値になるので物理的に何ら意味を満たず省略して良い。従って一組の共役複素根のみに着目して、改めて

と置いて前出の三次方程式に代入すると

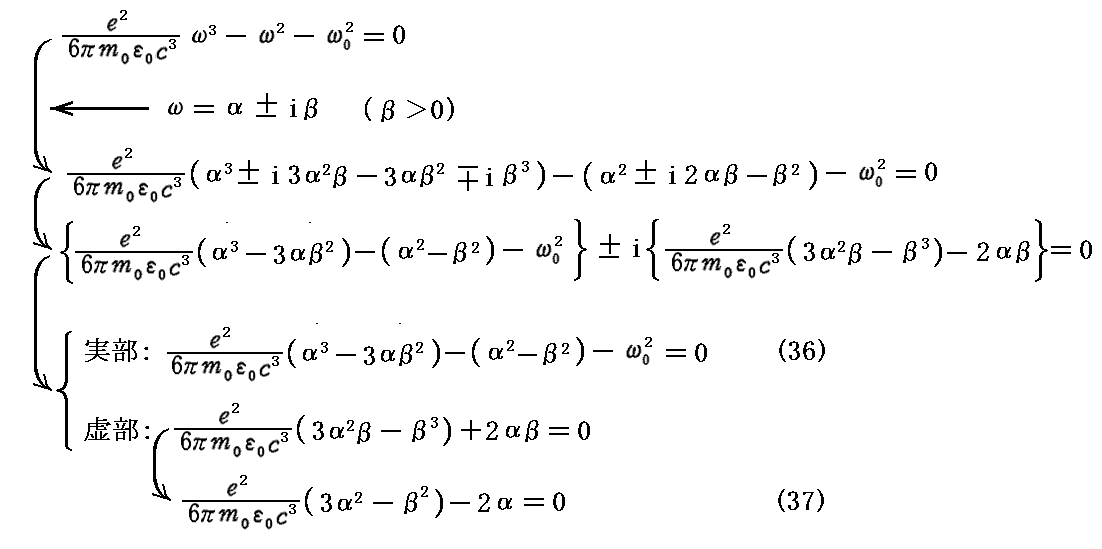
の二式が得られる。
　(３７)式より

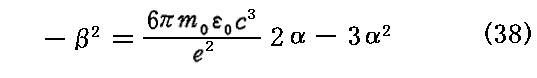
となるので、これを(３６)式に代入すると

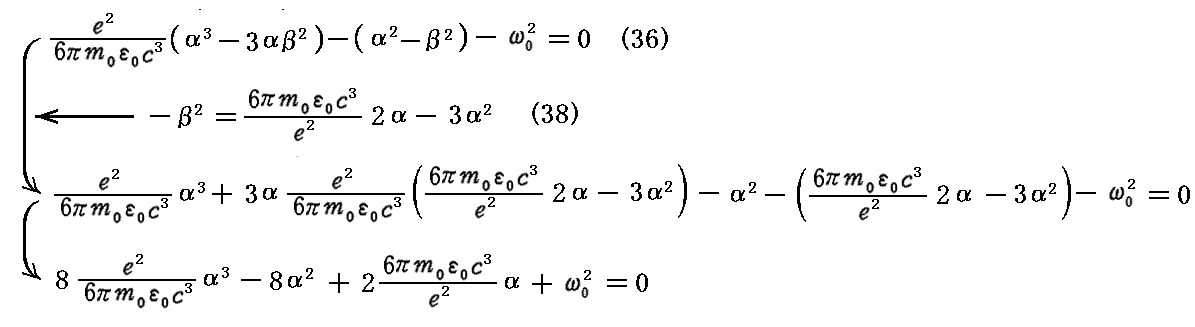
となる。
　つまり、この α に付いての三次方程式は、ただ一つの実数解を持たねばならない。このとき三次方程式の各 α の係数値を比較してみると、α の三次、二次の係数に比較して α の一次の係数と定数項が圧倒的に大きいことが解ります。実際この事は求まった α の値から ω₀²を計算してみると確認できます。
　そのため上記の実数解 α は三次方程式の高次の項を省略した

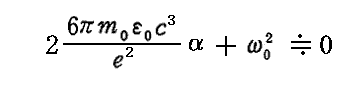
の解と考えて良い。すなわち

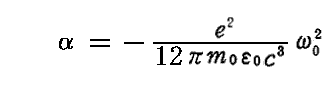
となる。ここでαは負の値であることに注意。これを(３８)式に代入すると

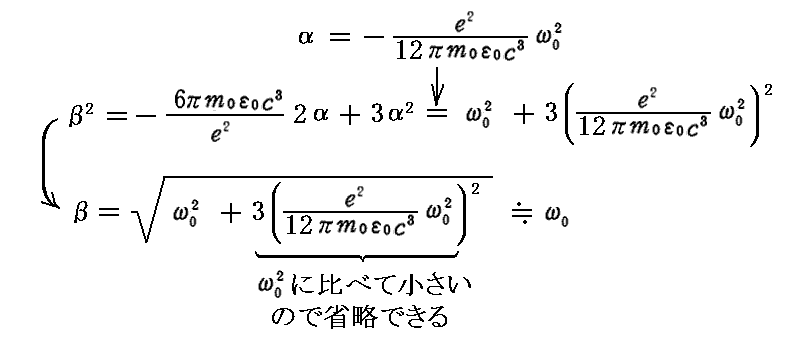
が得られるので、結局

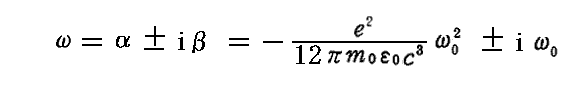
となる。
　この α と β を最初の式に代入する。定数項 ω’ を適当に調整すると

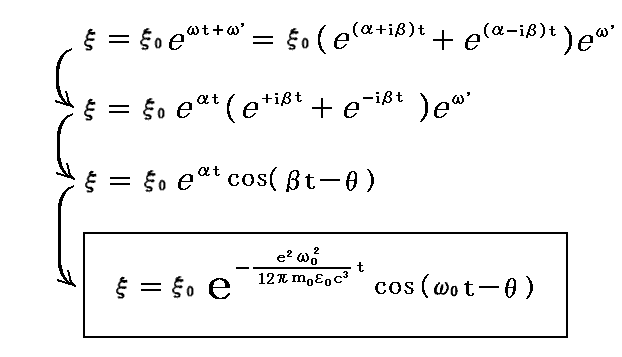
が得られる。

［補足説明２］
　この結論は別稿「調和振動子」４．で得られたものと、同じですので参照されて下さい。
　そこの運動方程式の減衰項（ ｘ の一次時間導関数）が、ここでは ξ の三次時間導関数になっています。しかし、４．（３）で説明する様に　ｄ³ξ／ｄｔ³≒−ω₀²(ｄξ／ｄｔ) とおけますので、両者は同じ運動方程式の形をしています。
　またこのことを考慮すると、そこの ρ が

に相当することが解ります。

［補足説明３］
　ここの議論は別稿「ファインマン物理�U」§7-3で展開されているのと同じです。
上記の関係式を

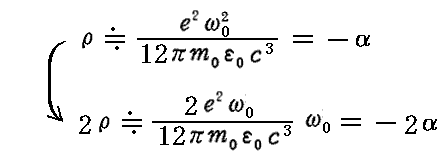
と変形して見ると、これは「ファインマン物理�U」§7-3の関係式

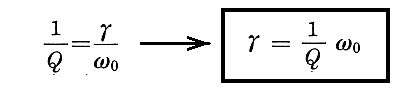
と同じです。なぜなら、そこの（7.10）式を変形すると

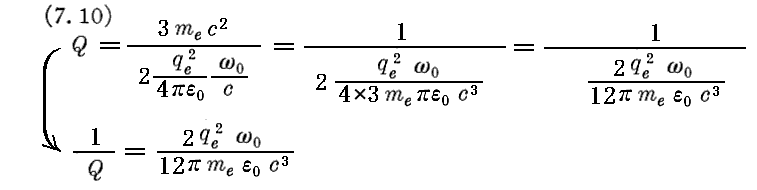
となりますが、ここの ｑ_e は本稿の ｅ であり、 ｍ_e は本稿の ｍ₀ に相当しますので両式は一致します。
　さらに、本稿の −2α （「調和振動子」の 2ρ ）がファインマン文献の γ に相当します。　

３．減衰時間と干渉可能距離

　前節の解 ξ(ｔ） は、光源として振動している電気双極子(振動子)は周囲に電磁波を放射して、時間 ｔ_e

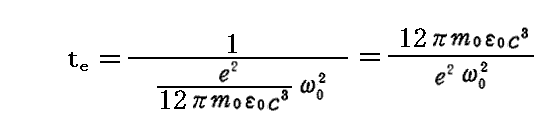
程度経過すると、振動の振幅は 1／ｅ に減少することを示している。この ｔ_e のことを“減衰時間”という。
　ここで、ω₀ は減衰の無い場合（Ｒ＝0）の固有角振動数です。今後、それに対応する固有振動数を ν₀ 、固有振動周期を Ｔ₀ 、その振動周期で伝播する放射電磁波の波長を λ₀ 、波数を ｋ₀ で表すことにすると、放射された光波の伝播速度は

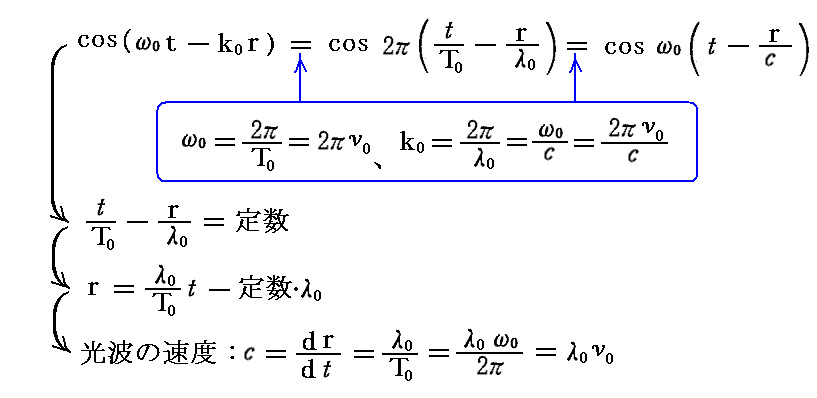
で表されるから、電気双極子(振動子)の振幅が1／ｅ倍に減少する時間 ｔ_e 間に光が進む距離 ｒ＝ｘ は

となる。
　例として、光の波長を青色可視光（λ＝4×10^-7ｍ）程度とすると

であるから

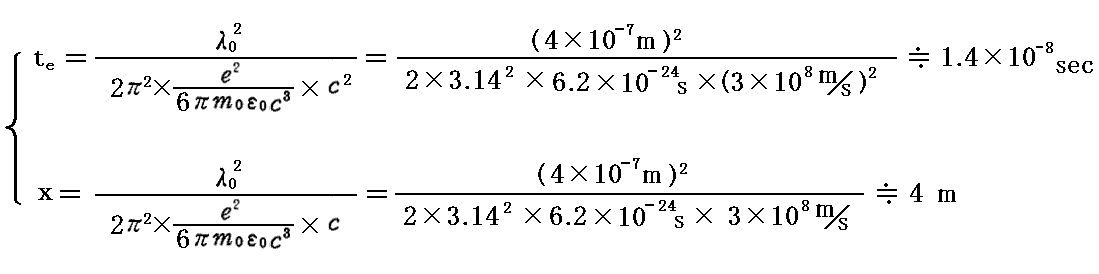
となる。つまり電気双極子の自由振動はこの程度の時間で減衰し、それから放射される光の波束の長さはこの程度になる。
　この長さは特に鋭い(特別単色度が高い)スペクトル線を選んで測った光の“干渉可能距離”(光線が自分自身と干渉できる波束の長さ）と大体同じ程度の大きさです。
　このとき青色可視光の振動周期Ｔ₀＝１／ν₀＝λ₀／ｃ＝4.0×10^-7／3×10⁸〜10^-15sec程度ですから上記の ｔ_e に比べて遙かに短い。振動が減衰するまでに電子は10⁶〜10⁷の波を送り出す。そのため光の減衰時間は振動周期よりも遙かに長く、光の波束（波連）は正弦波の連なりと見なせる。

　本節の議論はなかなか解りにくいと思います。同じ議論が別稿「ファインマン物理�U」§7-3で展開されていますので、そこと比較検討してみられると理解が深まると思います。

［補足説明１］
　ラザフォードの“有核原子モデル”が考えられたとき、中心の原子核（正電荷）と、そのクーロン引力が生み出す向心加速度によって原子核のまわりを回る電子（負電荷）の集合体からなる原子構造が予想された。
　しかし、そのような電子の円運動は、ここで述べた調和振動子の運動とよく似ている。中心電荷のまわりを加速度運動する電子からは、この稿で説明したように電磁波が放出されてエネルギーを失っていきます。そのため円運動する電子は上記の時間（〜10^-8秒）程度で原子核に落ち込んでしまい安定ではありません。これはラザフォードの原子モデルが抱える大きな困難でした。このことに付いては別稿「ラザフォード原子模型の困難」（２）もごらんください。
　
　これは原子レベルのミクロな世界では古典物理学が全く成り立たず、新しい考え方が必要であることを示しています。その様な暗中模索の中で手探りの理論として出てきたのが“ボーアの水素原子モデル”です。

（３）スペクトル線の古典的線幅

　絶対的に鋭いスペクトル線などと言うものは存在しない。切り取られたり、減衰したりする波束をフーリエ解析すれば、必ず有限なスペクトル線幅を生ずるからです。また輻射を行う粒子の熱運動によるDoppler効果によっても線幅（温度に依存する）を生じる。
　そのとき発光気体の速度分布に伴うDoppler効果や波束が有限長であることから生ずるスペクトル線幅以外に、振動子が満たす（３４）式の形に由来する本質的なぼやけが存在する。

［補足説明１］
　つまり、発光原子が（34）式で表されるよう微分方程式に従う電気双極子であると見なすことができれば、発光スペクトルの波束は必然的にｔ_eの時間程度で減衰する形をもつわけですが、その様に減衰する形をもつ波束であることに由来するスペクトル線幅のぼやけが生じると言うことです。
　ただし、この描像はあくまで古典物理学（Maxwelｌの電磁気学）に従うとそういうことが言えるというだけです。

　実際、（３４）式の解の形としてξ＝ξ₀ｅ^iβt＝ξ₀ｅ^iωtを仮定すると

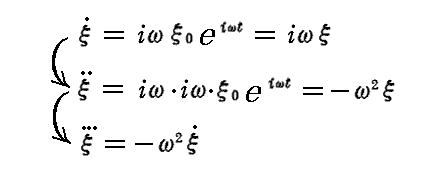
となるので、これを（３４）式に適用すると

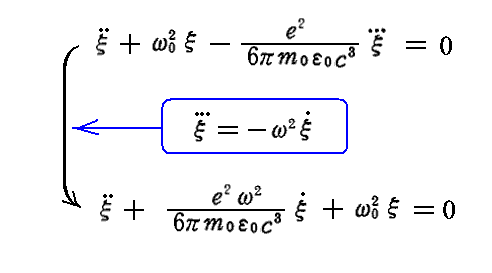
が得られる。この式を別稿「調和振動子」４．の

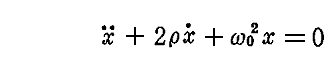
と比較すると、減衰効果を現す2ρの部分が

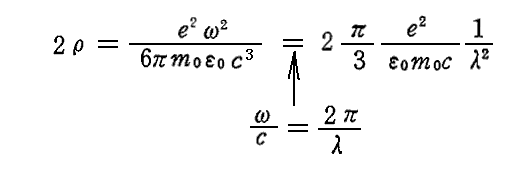
であることが解る。ρ は sec^-1 という単位を持つ量であるが、これはまさしく前項で説明した減衰時間 ｔ_e の逆数に一致している。実際、1／ｔ_e ≡Ｄと置いて、1／ｔ_e の表現式を変形すると ρ に一致することが確認できる。すなわち

となる。

［補足説明２］
　減衰時間 ｔ_e の逆数1／ｔ_e＝Ｄ を “古典的なスペクトル線の自然幅” という。それは、別稿「調和振動子」５．（３）で説明したように、Ｄ≡１／ｔ_e＝ρの２倍は（３４）式で表される調和振動子の共鳴曲線（振動数に依存する）の半値幅を与えるからです。
　
　調和振動子が外部電磁波によって共鳴するときの“共鳴曲線の半値幅”が、調和振動子が自由振動することで外部に放射する電磁波の波束のぼやけ具合を与える“スペクトル線の半値幅”に関係するというのも、不思議と言えば不思議ですが、その様にこじつけられるのは、どちらも調和振動子の微分方程式がもつ同じメカニズムによるものだからでしょう。

　例えば、光の波長を仮に青色可視光（λ＝4×10^-7ｍ）程度として “古典的なスペクトル線の自然幅” Ｄ を計算してみると

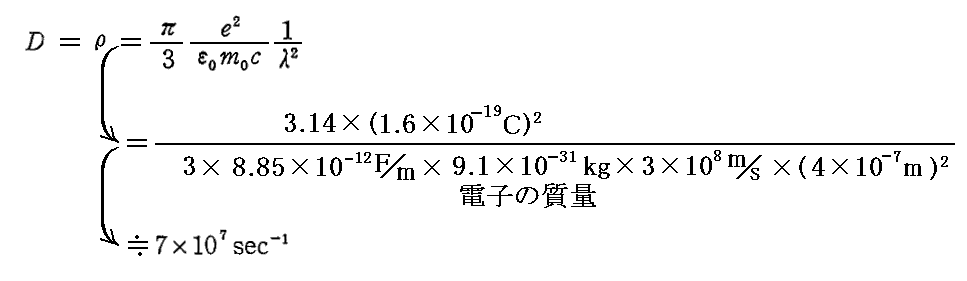
程度の値が得られる。
　これは水素の第１Balmer線の２重線の振動数間隔

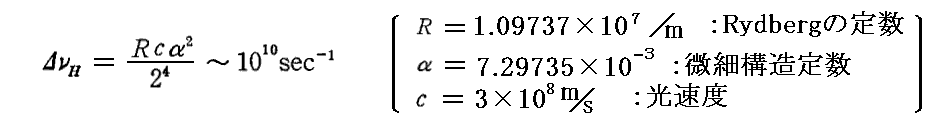
と比較してもかなり小さな値です。
　この古典的線幅は、Doppler効果を避けるために低温にして、衝突による線幅増をさけるために低圧にした極限で観測される線幅の下限を与える。
　しかしながら、個々のスペクトルの実際の線幅は、ここで計算した古典的な線幅より遙かに大きい。この幅は　放電管の温度や圧力よりも、主としてスペクトルを放射する量子状態の寿命によるものです。

［補足説明３］
　スペクトル線がぼやける原因には
　　１．ドップラー効果
　　２．他の原子・分子との衝突による遷移
　　３．シュタルク効果
　　４．オージェ効果（自己イオン効果）
などがある。　これらの説明は例えば　荒木源太郎著「原子物理学」倍風館（1964年刊）6章§20　などを参照。これには文献リストも在ります。

（４）熱輻射場と電気振動子の平衡

　Planckの黒体（空洞）輻射の理論では、“輻射の反作用力Ｒ”が重要な役割を演じる。プランクはこれを用いて、熱輻射と平衡にある振動子が光量子を放出できる状態に達したときの振幅を決めることができた。詳細は別稿「プランクの熱輻射法則（1900年）」で説明していますので御覧下さい。

５．参考文献

　このページは別稿「プランクの熱輻射法則（1900年）」で利用するために作りました。この稿の内容は以下の文献を参考にして作ったのですが大半は文献１．に依存しています。

1. アーノルド・ゾンマーフェルト著「理論物理学講座�V　電磁気学」講談社(1969年刊)§19、§36
2. マックス・プランク著「熱輻射論」（物理科学の古典7）東海大学出版会(初版の翻訳本）§104〜§115
   Vorlesungen u¨ber die Theorie der Wa¨rmestrahlung, Leipzig, Johann Ambrosius Barth,(初版は1906年刊）
3. ファインマン、レイトン、サンズ著「ファインマン物理学�U　光、熱、波動」岩波書店（1968年刊）
   　　3章“電磁輻射”、第4章干渉、5章“回折” 、6章“屈折率の本質”、
   　　7章“輻射減衰、光の散乱”、15章“統計力学の原理”、16章“ブラウン運動”
   ファインマン、レイトン、サンズ著「ファインマン物理学�V　電磁気学」岩波書店（1969年刊）第8章
   ファインマン、レイトン、サンズ著「ファインマン物理学�W　電磁波と物性」岩波書店（1971年刊）第6章
4. ジョージ・Ｐ・トムソン著「Ｊ．Ｊ．トムソン（電子の発見者）」河出書房新社（1969年刊）
   　トムソン関連の部分はこの本を参考にしました。著者はJ．J．トムソンの息子ですが、彼自身も結晶による電子線回折でノーベル物理学賞を受賞しています。この本はＪ．Ｊ．の伝記としては極めて秀逸です。ぜひ御覧になられて下さい。
5. H. Hertz, “Die Kra¨fte electrischer Schwingungen, behandelt nach der Maxwell'schen Theorie”,
   　　　　　 Wiede. Ann. 36, p1〜22, 1889年　（D. E. Jones による英語訳論文）