真空電磁場における荷電粒子の運動方程式から、荷電粒子の運動に対する Lagrangian と Hmiltonian がどのような形になるか考えます。
電磁場中の荷電粒子の運動は光速度に近い場合もあるので、特殊相対論的に正しいやり方を採用する。一般に重力は電磁気的な力に比べて極めて弱いので、重力の効果を考慮する必要はない。そのため一般相対性理論の段階まで考慮する必要はありません。
議論の出発点は、別稿Maxwell方程式系の先見性と電磁ポテンシャル」４．（２）で説明したローレンツ力を４元化したものを用いて表される電磁場中の荷電粒子の４元運動方程式
です。ここで、ｅは電荷、ｍ0はその静止質量、ｕｉは４元速度、Ｆｉｊは電磁場テンソルを表す。
上記は反変表示の４元速度を用いているので電磁場テンソルも混合テンソル表現のものを用いているが、右辺の４元速度を共変表示のものにすれば、電磁波テンソルは２階反変表示のものを用いた
となる。この当たりについては、別稿「ミンコフスキーの４次元世界」４．（２）３．［補足説明１］［補足説明２］や同ページの４．（２）５．などをご覧下さい。
ただし、特殊相対性理論の範囲での４元形式の議論は見通しが悪いので、以後は３次元形式で論じる。一般相対性理論では４元化が必須ですが、特殊相対性理論の範囲に限り、しかもある特定の慣性系ですべての現象を調べる場合には３次元形式ですべてを論じることができ、４元化は余計なプロセスです。
３次元形式でのローレンツ力が働く電荷の“相対論的な運動方程式”は
となる。相対論的な運動方程式については別稿「相対論的力学」2．と「運動方程式のローレンツ変換不変性」をご覧下さい。
これを出発点として以下の議論をする。
［補足説明］
本稿の内容は参考文献１．に依存しています。そのため電磁気学の単位系も文献１．と同じMKSA有理化単位系を用いています。
当HPの他ページや、 参考文献2．第3章§15、§16、§17、§18、§19（CGSGauss非有理化単位系-磁場H） 、 参考文献3．第13章（CGSGauss非有理化単位系-磁場H） などと比較参照されるときは注意して下さい。
まず、前述の運動方程式のローレンツ力の表現を電磁場のスカラーポテンシャルφ、ベクトルポテンシャルＡによる表現で置き換える。そうすると相対論的な運動方程式は
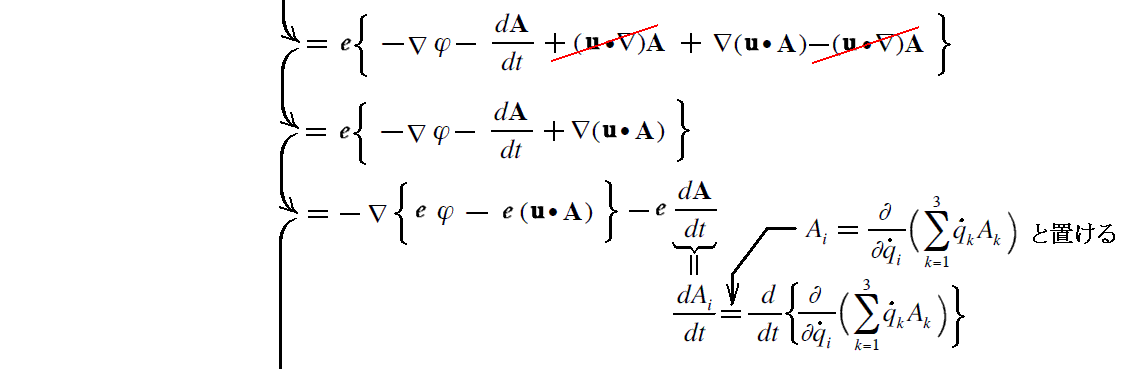
となる。
文中に記した参照すべき流体力学のページとしては例えばこちらをご覧下さい。また、ここの式変形に関しては文献2．§17も参照されて下さい。また電磁場をスカラーポテンシャルφ、及びベクトルポテンシャルＡで表す事については別稿「Maxwell方程式系の先見性と電磁ポテンシャル(ローレンツゲージ Lorenz gauge の由来)」と、文献2．§18をご覧下さい。
これを“Lagrange方程式”
と対比させると、“Lagrangian”は
とすべきことが解る。
実際、この Lagrangian を Lagrange方程式 に代入すると
となり、元のローレンツの力の法則に従った“相対論的運動方程式”が得られる。故に先ほどのLagrangianが正当化される。
［補足説明１］
ランダウは、文献2．§16で最小作用の原理の作用関数としてまず4元ポテンシャルを導入してからLagrangeianを求めています。一見するともっともらしく見えますが、何故作用関数が最初に仮定されている４元ポテンシャルになるのかの根拠は全く説明されていませんので、そういった論法は無意味です。
いままで、いろんな稿の中で何度も強調しましたが、Lagrangianを見つける方法は『Lagrnge方程式にLagrangianを代入すると既知の運動方程式が得られる様にLagrangianを構成する』です。基本的にこれ以外の方法はありません。
本稿の説明は、文献2．§17の展開を逆にたどって上記の方法を実践しているだけです。
要するに、ここで大事なことは、最終的な“相対論的運動方程式”が“変分原理”から導かれたものであることが重要なのであって、作用関数が何なのかと言うことではないのです。
変分原理から導かれたと言うことが、最終的な運動方程式が原理的に正しい法則である事を保証していると言うことです。
その様に考えれば、上記の様にして求めた作用関数は、確かに作用関数としてふさわしいと言える。
ｑｉ に共役な運動量ｐｉ は
となる。運動量ベクトルの形で書けば
となる。
［補足説明２］
特別な場合として、電磁場が存在しない“自由空間に於ける質点粒子のLagrangian”を求めると
となる。
同じく、電磁波が存在しないときの、ｑｉ に共役な運動量ｐｉ は
となる。
これらはいずれも別稿「相対論的力学」２．［補足説明６］でPlanckがすでに求めている結論に帰着する。
［補足説明３］
ｕ≪ｃと見なせる場合の“非相対論的なLagrangian”は
となります。
また、そのとき ｑｉ に共役な運動量ｐｉ は
となる。
“Lagrangian”から“Hamiltonian”を導くときの変数変換（ルジャンドル変換）
のｐには、前章２．で求めた共役運動量ｐを用いる必要がある。
そのｐから導かれる関係式
を式変形に利用する。
これらを用いると、“Hamiltonian”はルジャンドル変換によって
となります。
すなわち、電磁場中の荷電粒子の運動を表すHmiltonianとして
が得られる。
このとき、Hamiltonianが電磁場中の荷電粒子系の全エネルギーを表しているのは確かなのですが、この形からＨ＝［運動エネルギー］＋［ポテンシャルエネルギー］であること見分けるのは難しい。このことは3.［補足説明１］で説明します。
ところで、Hamiltonianは次に示す関係式を満たします。
この2つの関係式
をHamiltonの“正準方程式”と言う。
正準方程式を導いた手順から解るように、これら2式は次に述べる事柄を示しています。
この最初の方程式に先ほど求めたHmiltonianを代入すると
となるが、これは共役運動量ｐの定義式をｕについて解いたもの
に他ならない。つまり最初の方程式は“共役運動量の定義式”そのものです。
二番目の方程式は
である事を考慮すると、Lagrange方程式に一致する。
つまり、二番目の方程式はローレンツ力で表した“相対論的運動方程式”そのものです。
［補足説明１］
“共役運動量”の定義式
を、Hamiltonianの［最初の定義式］、あるいは［最後に得られた式］に適用すると
となる。
この形の表現では共役運動量ｐや磁場を表すＡが隠れてしまい役に立つとは言えないが、Hamiltonianがエネルギーを表すものであることを理解するには適している。
そのことが、ランダウの文献2．§19で説明されていますので以下で引用しておきます。これはCGSgauss単位系（非有理化、磁場H）を用いていることに注意されてお読み下さい。
上記の“前節”はこちらを参照。
上記の（16．6）はこちらを参照。また、§17 はこちらを参照。
また、ランダウは、§17の脚注1）で注意しているように、（19．2）式の第1項を静止エネルギーを含めた意味で運動エネルギーと言っている。だから（19．2）の第1項が［運動エネルギー］であり第2項が［位置エネルギー］です。
すなわち Hamiltonian＝［運動エネルギー］＋［位置エネルギー］ が成り立っている。
ランダウの言う§17の脚注1）について補足する。別稿「相対論的力学」３．（３）の（84）式でBornが言っているように、相対性理論で言う［運動エネルギー］は、もともと［運動している物体のエネルギーＥ＝ｍ(ｖ)ｃ2］と［静止物体のエネルギーＥ0＝ｍ0ｃ2］との差で定義される。
しかし、そのときＥ＝ｍ(ｖ)ｃ2の中でＥ0＝ｍ0ｃ2を分け隔てすることに特別な意味が有るわけではありません。だからランダウが言うようにＥ＝ｍ(ｖ)ｃ2を運動エネルギーと言うことにしても全く問題ないわけです。
しかし特殊相対性理論の段階だからこういった言い方ができるのであって、重力に伴うポテンシャルエネルギーが問題となる一般相対性理論の段階になると、こういった意味での［運動エネルギー］という言い方が意味を持つ訳ではありません。
そうは言いましても、Ｅ＝ｍ(ｖ)ｃ2を運動エネルギーの中に含ませることには特殊相対性理論の本質が含まれています。このことについて別ページで引用している砂川先生の説明を御覧下さい。
［補足説明２］
特別な場合として、電磁場が存在しない“自由空間に於ける質点粒子のHamiltonian”を求めると
となり、別稿「相対論的力学」２．［補足説明６］でPlanckがすでに求めている結論に帰着する。
［補足説明３］
ｕ≪ｃと見なせる場合の“非相対論的なHamiltonian”は
となる。
この稿を作るに当たって、下記文献を参考にしました。感謝！
