係尦懍搙乮4尦塣摦検丄4尦揹棳枾搙乯丄係尦壛懍搙偲係尦椡
丂係尦懍搙丒係尦壛懍搙丒係尦椡偼丄堦斒憡懳惈棟榑傊恑傓偲偒旔偗偰捠傟側偄強偱偡丅
丂杮峞偺僥乕儅偼丄暿峞乽Einstein偺摿庩憡懳惈棟榑乮1905擭乯乿丄乽Einstein偺岞幃 E=mc2 偺徹柧乿丄乽憡懳榑揑椡妛乿丄乽揹帴応偺憡懳惈乿偵懕偔傕偺偱偡偑丄偙偙偱偼帪娫丄懍搙丄壛懍搙傪昞偡婰崋偑條乆弌偰偒偰偐側傝嶖憥偟傑偡丅
丂崿棎傪旔偗傞偨傔偵丄俽宯偲俽乫宯偺帪娫傗懍搙偺昞尰丄俽宯偵懳偡傞俽乫宯偺憡懳懍搙偵偮偄偰壓婰偺傛偆偵昞婰偡傞偙偲偵偟傑偡丅偦偺偨傔丄忋婰偺峞偱愢柧偟偨帠暱傪棙梡偡傞偲偒偵偼壓婰偺怴昞婰偵彂偒姺偊偰堷梡偟傑偡偺偱屼拲堄偔偩偝偄丅
丂杮峞偱偼丄摿庩憡懳惈棟榑偵弌偰偔傞俽宯偵懳偡傞俽乫宯偺堏摦懍搙傪乮崱傑偱梡偄偨倴偺懼傢傝偵乯戝暥帤偺乬倁乭偱昞偟傑偡丅
丂
丂傑偨丄俽宯偱娤應偟偨懍搙傪
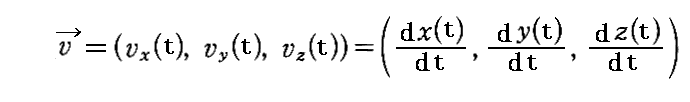
偲昞偡丅乮倶丆倷丆倸丆倲乯偼丄俽宯偵屌掕偝傟偰偄傞暔嵎偟朹偱應偭偨暔懱偺埵抲偺撉傒庢傝抣偱偁傝丄俽宯偲偲傕偵摦偄偰偄傞帪寁偱寁偭偨帪寁偺帵偡帪崗偱偡丅
丂師偵丄俽宯偺倶幉偺惓曽岦偵懍搙倁偱堏摦偟偰偄傞俽乫宯傪峫偊傑偡丅俽宯偱娤嶡偟偰偄傞摨偠暔懱偺埵抲偲帪崗傪俽乫宯偵屌掕偝傟偰偄傞暔嵎偟朹偺撉傒偲俽乫宯偲偲傕偵摦偄偰偄傞帪寁偱寁偭偨帪崗偱昞偟偨傕偺偑乮倶乫丆倷乫丆倸乫丆倲乫乯偱偡丅
丂擇偮偺宯偺帪寁偼丄俽宯偲俽乫宯偺暔嵎偟朹偺尨揰偑偡傟堘偭偨弖娫傪倲亖倲乫亖0偲偟偰丄偦傟偧傟偺帪崗傪應傝巒傔傑偡丅
丂偦偺俽乫宯偱娤應偟偨懍搙傪
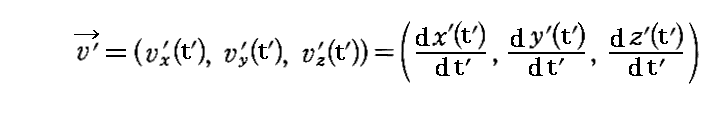
偱昞偟傑偡丅
丂
丂乽憡懳榑揑椡妛乿俁丏偱偼丄偙傟傜偺検偵 倳亖乮倳x丄倳y丄倳z乯 偲 倳乫亖乮倳x乫丄倳y乫丄倳z乫乯 傪梡偄傑偟偨丅杮峞偱偼偙傟傜偺昞婰傪暿側栚揑偱梡傞堊偵忋婰偺條偵彂偒捈偟偨丅
丂
侾丏摫擖
乮侾乯摿庩憡懳惈棟榑偵尰傟偨係尦検
侾丏係尦検
丂摿庩憡懳惈棟榑偵尰傟偨乮嵗昗丒帪娫乯係尦儀僋僩儖乮倶丆倷丆倸丆倲乯偺係惉暘偼丄娤應宯傪俽宯偐傜俽乫宯偵曄姺偡傞偵摉偨偭偰丄偙傟傜偼晄壜暘偺惉暘偲偟偰壓婰偺乬儘乕儗儞僣曄姺乭
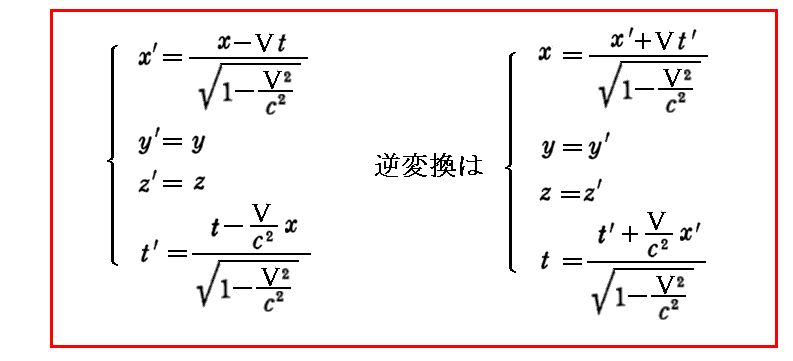
偵廬偭偰曄姺偝傟偨丅
丂偮傑傝丄屳偄偵擖傝岎偠偭偨宍偱庢傝埖傢偹偽惉傜側偄丅偙傟偼丄偁偨偐傕乮倶丆倷丆倸丆倲乯傪丄嶰師尦嬻娫乮倶丆倷丆倸乯偵戞巐偺師尦偲偟偰倲傪壛偊偨丄巐師尦嬻娫偵偍偗傞検偲偟偰庢傝埖偆帠偑偱偒丄傑偨偦偺條偵庢傝埖傢偹偽側傜側偄帠傪帵偟偰偄傞丅
丂摨條偵丄塣摦検乮倫x丆倫y丆倫倸乯偼幙検偲堦弿偵側偭偰乮塣摦検丒幙検乯係尦儀僋僩儖乮倫x丆倫y丆倫倸丆倣乯傪峔惉偡傞偲峫偊偹偽側傜側偄帠傪乽憡懳榑揑椡妛乿俁丏乮係乯偱愢柧偟偨丅
丂摨偠偔丄乮俆乯愡偱愢柧偟偨傛偆偵丄揹棳枾搙乮倞x丆倞y丆倞倸乯偼揹壸枾搙偲堦弿偵側偭偰乮揹棳枾搙丒揹壸枾搙乯係尦儀僋僩儖乮倞x丆倞y丆倞倸丆兿乯偲峫偊偹偽側傜側偄丅
丂偦偺條偵峫偊偹偽側傜側偄偺偼丄偦傟傜偺検偑乮嵗昗丒帪娫乯係尦儀僋僩儖乮倶丆倷丆倸丆倲乯偲慡偔摨偠乬儘乕儗儞僣曄姺乭偵廬偭偰俽宯偱偺抣乮娤應抣乯偐傜俽乫宯偱偺抣乮娤應抣乯偵曄姺偝傟傞偐傜偱偡丅偦偺摉偨傝偼乮俆乯愡乵曗懌愢柧俇乶偱拲堄偟偨強偱偡丅
丂
俀丏係尦検偑枮偨偡惈幙
丂乮嵗昗丒帪娫乯係尦儀僋僩儖乮倶丆倷丆倸丆倲乯偑乬儘乕儗儞僣曄姺乭偱曄姺偝傟傞側傜偽丄壓婰偺娭學幃偑惉傝棫偮帠偼捈偪偵尵偊傞丅
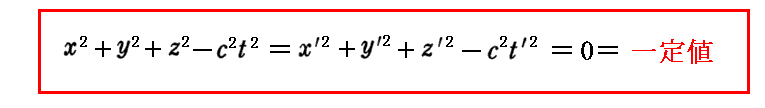
偙偺偙偲偼丄壓婰偺幃曄宍傪尒傟偽柧傜偐偱偡丅
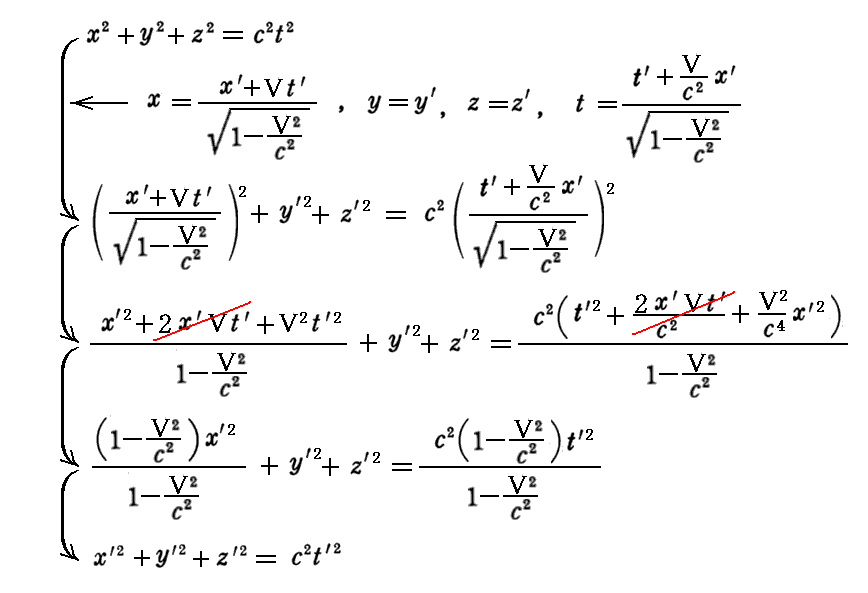
丂偙偺娭學幃偼丄Einstein偑1905擭榑暥偱巜揈偟偰偄傞傛偆偵丄倲亖倲乫亖0偵屳偄偵偡傟堘偆俽宯偲俽乫宯偺嫟捠側尨揰偐傜岝偺媴柺攇偑敪幩偝傟偨偲偡傞偲丄偙偺媴柺攇偑帪崗倲偵丄揰乮倶丆倷丆倸乯偵摓払偟偨偙偲傪帵偟偰偍傝丄偦偺摨偠揰傪俽乫宯偐傜尒傞偲帪崗倲乫偺乮倶乫丆倷乫丆倸乫乯偵摓払偟偨偙偲傪帵偟偰偄傞偺偱偁偭偨丅
丂Einstein榑暥偺俀丏乮係乯乵曗懌愢柧俁乶偱拲堄偟偨傛偆偵丄偙偺娭學幃偼憡懳惈棟榑偺崻姴偵娭傢傞傕偺偱偟偨丅
丂偝傜偵丄Einstein榑暥偺俀丏乮俉乯係丏偱愢柧偟偨傛偆偵丄偙偺偙偲傪梡偄傞偲巐師尦揑側悽奅嫍棧儮倱傪擇忔偟偨検傕乬儘乕儗儞僣曄姺乭偵懳偟偰晄曄偲側傞偙偲偑尵偊偨丅偮傑傝
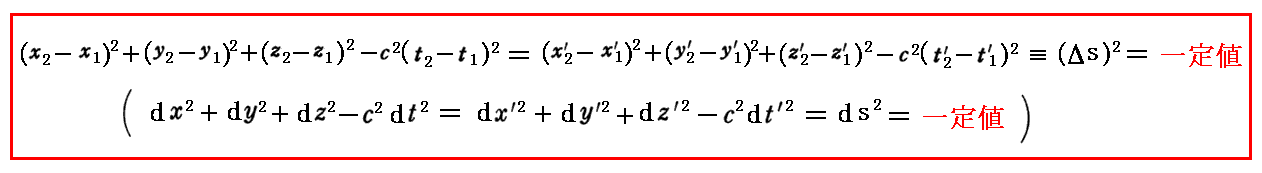
偑惉傝棫偮丅
丂摨條偵偟偰丄乮塣摦検丒幙検乯係尦儀僋僩儖乮倫x丆倫y丆倫倸丆倣乯偑乮嵗昗丒帪娫乯係尦儀僋僩儖乮倶丆倷丆倸丆倲乯偲摨偠乬儘乕儗儞僣曄姺乭偵傛偭偰曄姺偝傟傞偙偲偐傜
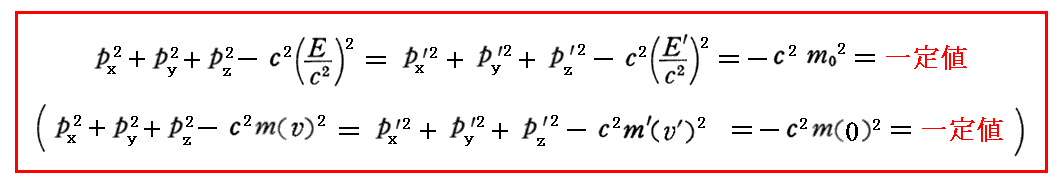
偑尵偊傞丅
丂偙偺偙偲偼乬儘乕儗儞僣曄姺乭偵傛傝娙扨偵徹柧偱偒傞丅

丂慡偔摨條偵偟偰丄乮揹棳枾搙丒揹壸枾搙乯係尦儀僋僩儖乮倞x丆倞y丆倞倸丆兿乯偐傜峔惉偝傟傞壓婰偺検偑摨條側娭學幃
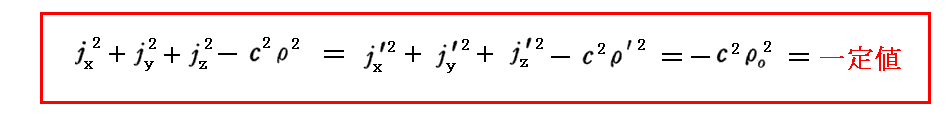
傪枮懌偡傞偙偲偑徹柧偱偒傞丅
丂偮傑傝係尦儀僋僩儖検偐傜峔惉偝傟傞偙傟傜偺検偼俽宯傗俽乫宯偺娤應嵗昗宯偵嫆傜偢晄曄揑側抣偲側傞丅
丂偙偺偙偲偼丄 倶2亄倷2亄倸2亅們2倲2 偑乬儘乕儗儞僣曄姺乭偵懳偟晄曄偱偁偭偨帠偲摨條偵偙傟傜偺検偑乬儘乕儗儞僣曄姺乭偵懳偟晄曄偱偁傞偙偲傪堄枴偡傞丅
丂
乮俀乯摿庩憡懳惈棟榑偱巊傢傟偨俁師尦懍搙偲俁師尦椡偺曄姺幃
侾丏俁師尦懍搙
丂慜愡偱弌偰偒偨乮塣摦検丒幙検乯係尦儀僋僩儖乮倫x丆倫y丆倫倸丆倣乯偲乮揹棳枾搙丒揹壸枾搙乯係尦儀僋僩儖乮倞x丆倞y丆倞倸丆兿乯偼俁師尦懍搙偺儘乕儗儞僣曄姺嫟曄偺曄姺幃傪梡偄偰媮傔偨丅
丂偡側傢偪丄俽乫宯偺倶乫幉丄倷乫幉丄倸乫幉偵屌掕偝傟偨嶰杮偺暔嵎偟朹偲俽乫宯偵屌掕偝傟偨帪寁偺帪崗 倲乫 偱應偭偨嵼傞暔懱乮壜攭幙揰乯偺懍搙乮倴x乫丆倴y乫丆倴倸乫乯偲丄摨偠暔懱傪俽宯偺倶幉丄倷幉丄倸幉偵屌掕偝傟偨嶰杮偺暔嵎偟朹偲丄俽宯偵屌掕偝傟偨帪寁偺帪崗 倲 偱應偭偨懍搙乮倴x丆倴y丆倴倸乯偺娫偵惉傝棫偮乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼
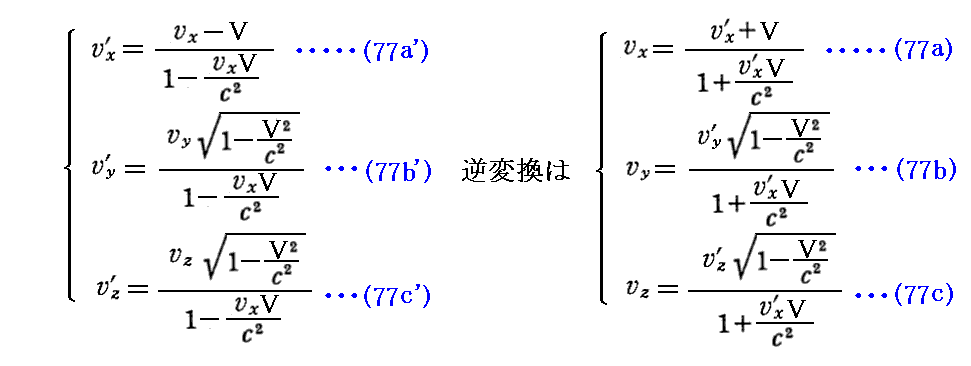
傪棙梡偟偰媮傔偨偺偱偟偨丅
丂偙傟傜俁師尦懍搙偺乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼偺媮傔曽偼暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乮1905擭乯乿俀丏乮俈乯傗俀丏乮俉乯俁丏偱愢柧偟偰偄傑偡偑丄娙扨偵暅廗偡傞偲丄儘乕儗儞僣曄姺
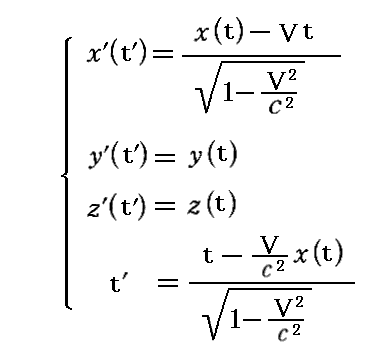
傪梡偄偰丄偦偺椉曈偺帪娫旝暘傪偟偨娭學幃傪戙擖偟偰媮傔偨丅
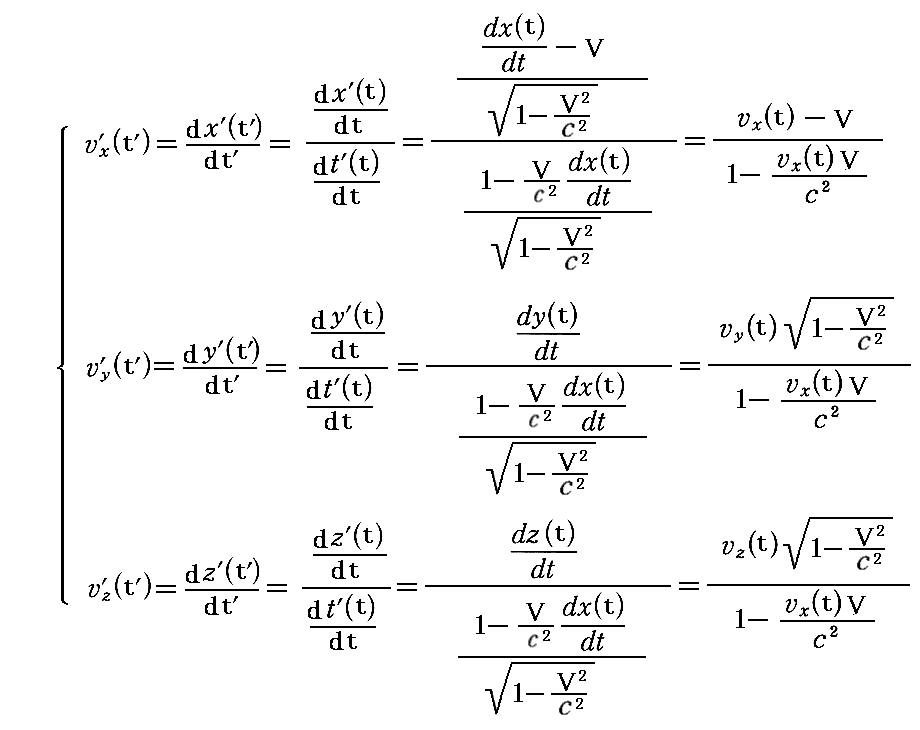
丂偙偺幃偵偮偄偰曗懌偡傞偲丄偙傟偼尦乆俽乫宯偺懍搙倁偲S宯偱偺懍搙儀僋僩儖倴偲偺亂懍搙崌惉懃亃傪昞偟偰偄傑偡丅偙偺偙偲偵偮偄偰偼暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乮1905擭乯乿俀丏乮俈乯偁傞偄偼俀丏乮俉乯俁丏傪慞偔慞偔暅廗偝傟偨偟丅
丂傕偲傕偲懍搙偼丄嵗昗抣丄塣摦検丄揹棳枾搙偲摨偠俁師尦儀僋僩儖検偱偡丅偦偺偨傔俁師尦儀僋僩儖検偺嵗昗抣丄塣摦検丄揹棳枾搙偵枾愙偵娭學偟偰偄傑偡丅側傜偽丄嵗昗抣丄塣摦検丄揹棳枾搙偑乮嵗昗丒帪娫乯丄乮塣摦検丒幙検乯丄乮揹棳枾搙丒揹壸枾搙乯偲偟偰巐師尦壔偝傟偨傛偆偵丄懍搙傕巐師尦壔偱偒側偄偺偩傠偆偐偲偄偆媈栤偑惗偠傑偡丅
丂侾丏乮侾乯偱弎傋偨巐師尦検偺摫弌乮乽憡懳榑揑椡妛乿嶲徠乯偱偼丄懍搙儀僋僩儖偼嶰師尦偺傑傑偱梡偄傑偟偨丅偦偺曄姺幃偼妋偐偵乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼側偺偱偡偑丄(嵗昗丒帪娫)係尦儀僋僩儖偑枮懌偡傞乬儘乕儗儞僣曄姺乭偲偼堎側偭偰偄傑偡丅
丂懍搙傕巐師尦壔偝傟偰乮嵗昗丒帪娫乯係尦儀僋僩儖乮倶丆倷丆倸丆倲乯偲摨偠宍偺乬儘乕儗儞僣曄姺乭偵廬偆傛偆偵偱偒側偄偺偱偟傚偆偐丅偙偺媈栤偵摎偊傞偺偑杮峞偺栚揑偱偡丅
丂
俀丏俁師尦椡
丂俁師尦懍搙倴偲摨條側帠忣偑丄暿峞乽揹帴応偺憡懳惈乿俆丏乵曗懌愢柧俁乶偱愢柧偟偨俁師尦椡俥偵偮偄偰傕尵偊傑偡丅
丂偦偙偱愢柧偟偨傛偆偵丄暔懱偑俽宯偺倶幉曽岦偵倴x偱丄俽乫宯偺倶乫幉曽岦偵倴x乫偱摦偄偰偄傞応崌偵偼
俽乫宯偺堏摦曽岦偲悅捈側曽岦偵摥偔椡偺曄姺幃偼
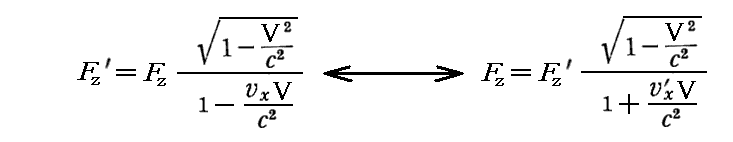
偱偁傝丂
俽乫宯偺堏摦曽岦偵暯峴側曽岦偵摥偔椡偺曄姺幃偼
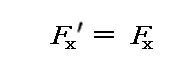
偱偟偨丅偙傟傜偺曄姺幃偼椡偺掕媊偵棷堄偟偰(嵗昗丒帪娫)係尦儀僋僩儖傗(塣摦検丄幙検)係尦儀僋僩儖偺乬儘乕儗儞僣曄姺乭傪梡偄偰摫偄偨偺偱偟偨丅
丂偙偺俁師尦椡偺曄姺幃傕乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼偱丄俁師尦懍搙偺応崌偲帡偰偄傑偡偑丄寛偟偰(嵗昗丒帪娫)係尦儀僋僩儖偺乬儘乕儗儞僣曄姺乭偲摨偠偱偼桳傝傑偣傫丅
乵曗懌愢柧侾乶
丂俁師尦懍搙傗俁師尦椡偼儘乕儗儞僣曄姺嫟曄偺曄姺幃偵偟偨偆偑丄(嵗昗丒帪娫)係尦儀僋僩儖丄(塣摦検丒幙検)係尦儀僋僩儖丄乮揹棳枾搙丒揹壸枾搙乯係尦儀僋僩儖偺條偵乬儘乕儗儞僣曄姺乭偵傛偭偰曄姺偝傟偰偄傞傢偗偱偼偁傝傑偣傫丅
丂俁師尦懍搙傗丄俁師尦椡傕乬儘乕儗儞僣曄姺乭偵傛偭偰曄姺偝傟傞傛偆偵乬係尦壔乭偱偒側偄偺偱偟傚偆偐丅偙偺媈栤偵摎偊傞偙偲偑丄杮峞偺栚揑偱偡丅
丂
俀丏係尦懍搙
丂懍搙丄壛懍搙丄椡偼尦乆嶰師尦嬻娫偺嵗昗抣丄塣摦検丄揹棳枾搙偲摨偠俁師尦儀僋僩儖検偱偡丅
丂側傜偽丄嵗昗抣丄塣摦検丄揹棳枾搙側偳偑戞係惉暘偲偟偰帪娫丄幙検丄揹壸枾搙傪晅偗壛偊偰巐師尦壔偝傟摨堦偺乬儘乕儗儞僣曄姺乭偱曄姺偝傟偨條偵丄懍搙丄壛懍搙丄椡傕巐師尦壔偝傟傞傋偒偱偡丅
丂偦偺堊偺僸儞僩偼塣摦検傗揹棳枾搙傪巐師尦壔偟偨傗傝曽偺拞偵偁傝傑偡丅
乮侾乯係尦懍搙
侾丏係尦懍搙偺掕媊
丂暿峞乽憡懳榑揑椡妛乿俁丏乮係乯乵曗懌愢柧俀乶偺曄姺幃傪拲堄怺偔専摙偡傟偽丄乬係尦懍搙乭偲偟偰
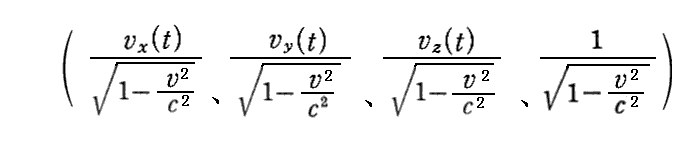
偲掕媊偡傟偽傛偄偙偲偑夝傞丅
丂偙偙偱乮倴x丄倴y丄倴倸乯偼俁師尦懍搙偱偁傝丄乮倴x亖倓倶乛倓倲丄倴y亖倓倷乛倓倲丄倴z亖倓倸乛倓倲乯 偲 倴2亖倴x2亄倴y2亄倴z2 傪堄枴偡傞丅偮傑傝丄暔懱偺懍搙傪娤應偟偰偄傞姷惈嵗昗宯偵愝抲偟偰偁傞暔嵎偟朹乮倶丆倷丆倸乯偲帪寁倲偱寁偭偨抣偱偡丅
丂幚嵺丄俁師尦懍搙儀僋僩儖偵偮偄偰惉傝棫偮乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼
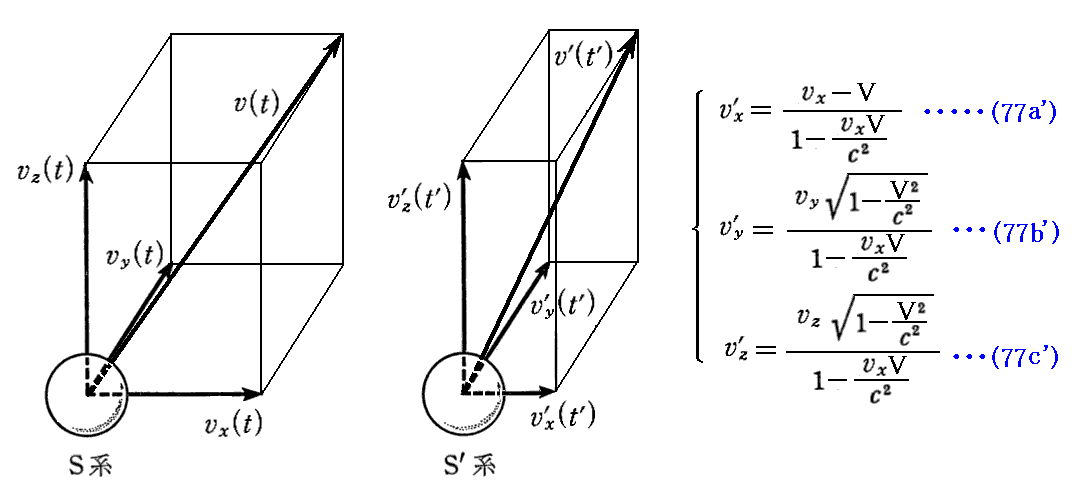
傪梡偄傟偽丄乮嵗昗丒帪娫乯係尦儀僋僩儖乮倶丆倷丆倸丆倲乯偑乬儘乕儗儞僣曄姺乭偵廬偭偰曄姺偝傟偨條偵丄忋婰偱掕媊偟偨係尦懍搙傕乬儘乕儗儞僣曄姺乭偵廬偭偰曄姺偝傟傞偙偲偑徹柧偱偒傞丅
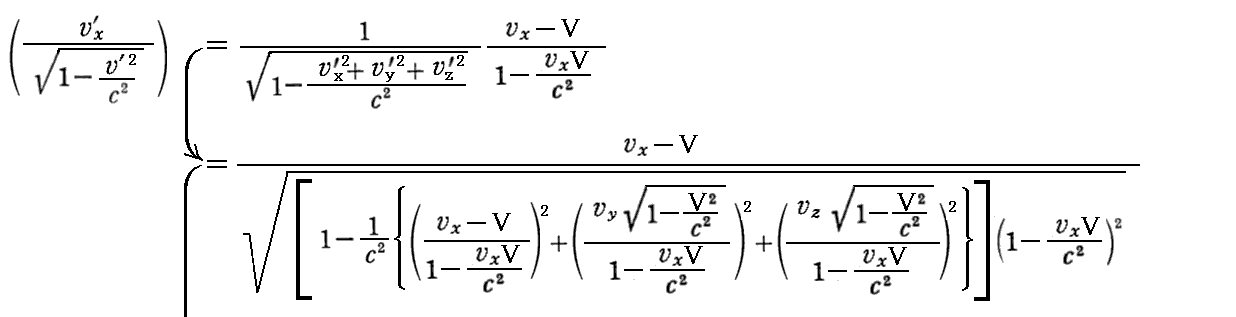
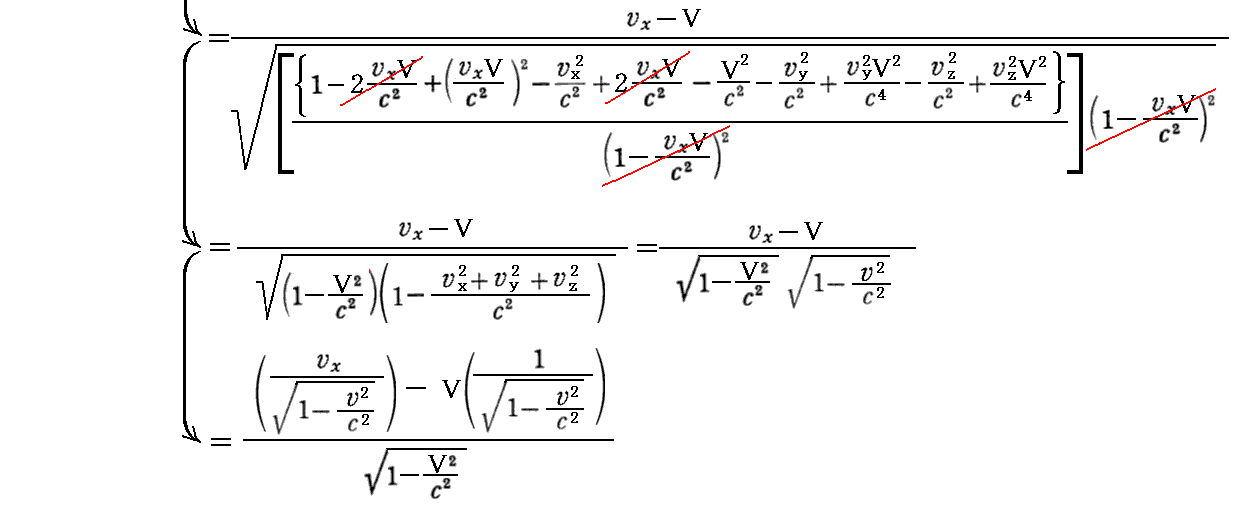
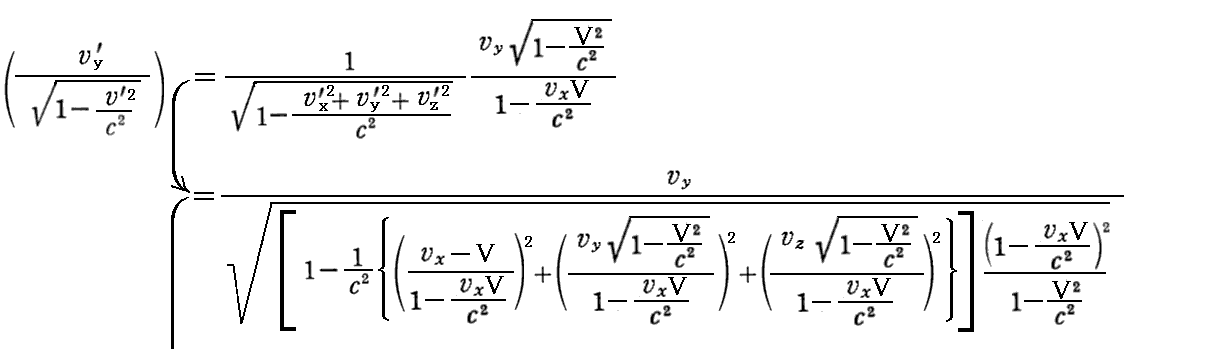
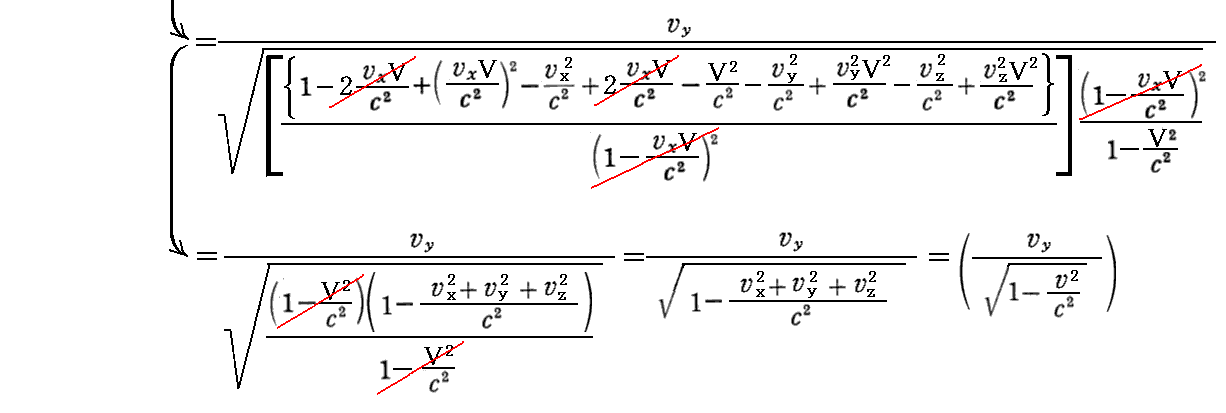
摨條偵
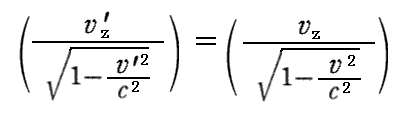
偲側傞丅
丂埲忋偺俁惉暘傪儘乕儗儞僣曄姺偲傒側偡偲丄摿偵嵟弶偺幃偺宍偐傜

戞係惉暘偼
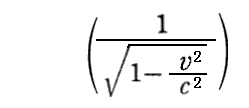
偱偁傞傋偒偙偲偑夝傞丅
丂帠幚
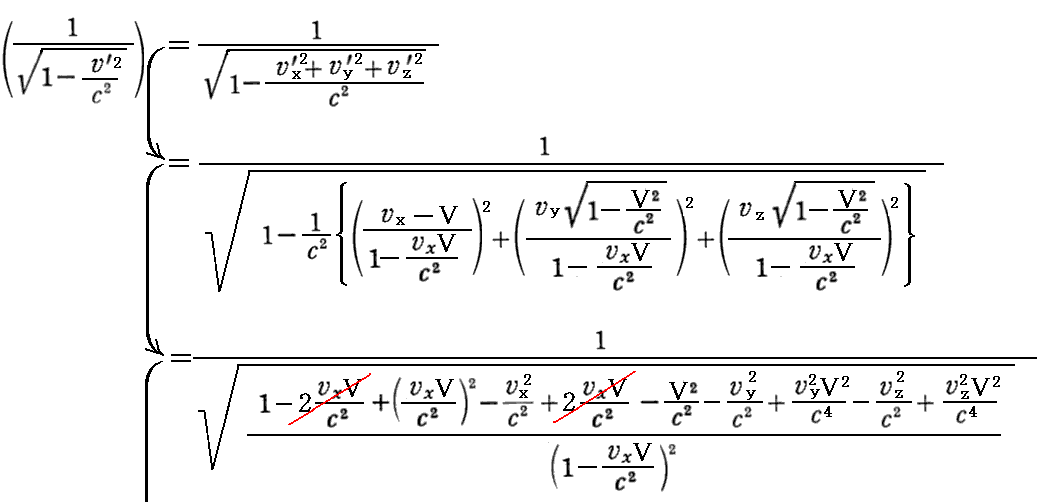
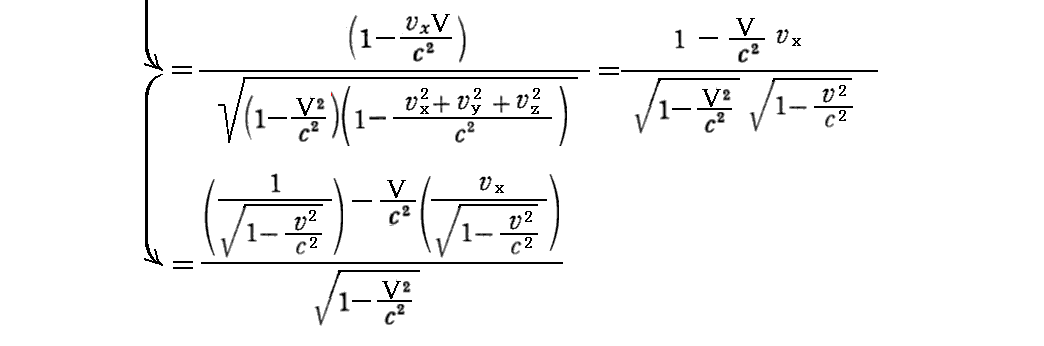
偲側傝戞係惉暘偲偟偰偺儘乕儗儞僣曄姺幃傪枮懌偡傞丅
丂埲忋傪傑偲傔傞偲俁師尦懍搙昞帵偱偺乬儘乕儗儞僣曄姺幃乭偼
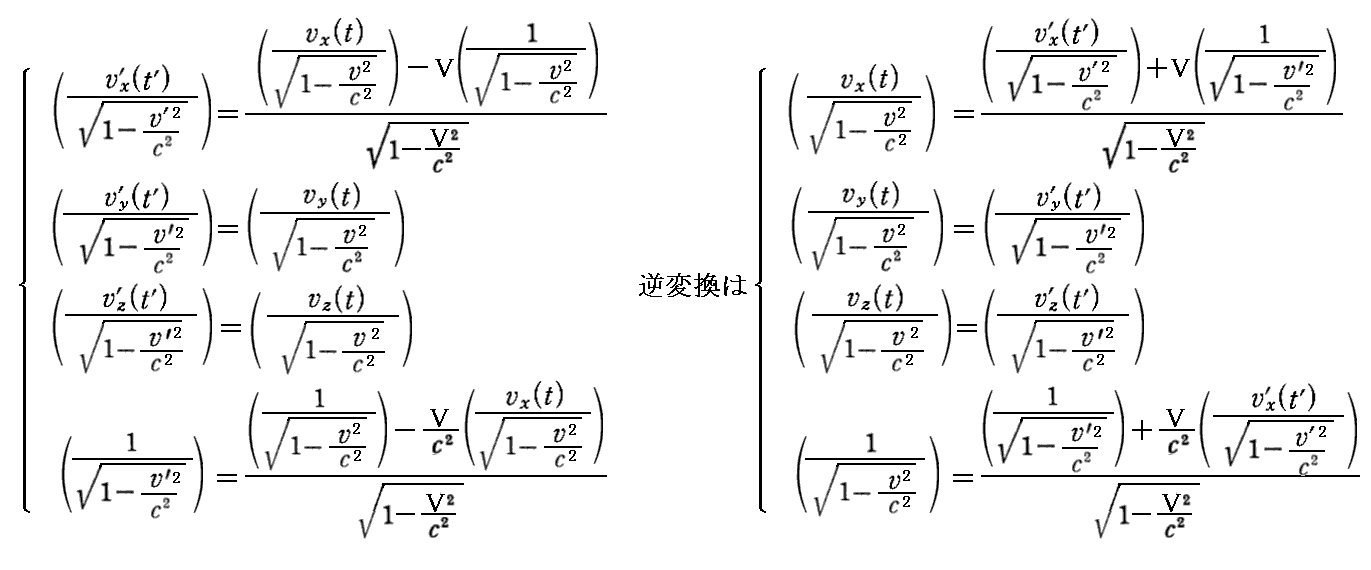
偲側傞丅偦偺偨傔嵟弶偵掕媊偟偨係尦懍搙偼妋偐偵乬儘乕儗儞僣曄姺幃乭偵廬偆偙偲偑徹柧偱偒偨丅
乵曗懌愢柧侾乶
丂忋婰偺係尦懍搙偺乬儘乕儗儞僣曄姺乭傪摫偔幃曄宍傪媡偵偨偳偭偰丄嵟弶偺幃偵婣傝
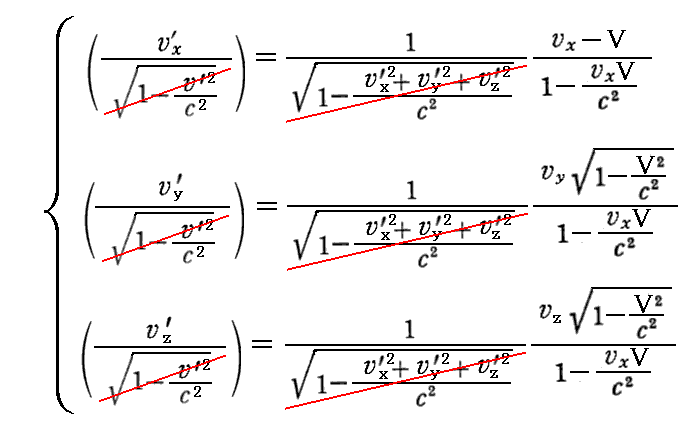
偲偡傟偽丄俽乫宯偱偺懍搙偑丄俽乫宯偱偺嵗昗抣乮倶乫丆倷乫丆倸乫乯傪俽乫嵗昗宯偺屌桳帪 倲乫 偱旝暘偟偨傕偺偱掕媊偝傟傞倴乫亖乮倓倶乫乛倓倲乫丄倓倷乫乛倓倲乫丆倓倸乫乛倓倲乫乯偵栠傝丄俽宯偱偺懍搙偑丄俽宯偱偺嵗昗抣乮倶丆倷丆倸乯傪俽嵗昗宯偺屌桳帪
倲 偱旝暘偟偨傕偺偱掕媊偝傟傞倴亖乮倓倶乛倓倲丄倓倷乛倓倲丆倓倸乛倓倲乯偵栠傝傑偡丅
丂偮傑傝丄嵟弶偺俁師尦懍搙偺儘乕儗儞僣曄姺嫟曄側曄姺幃乮77倎乫乯丄乮77倐乫乯丄乮77們乫乯偵婣拝偟傑偡丅偱偡偐傜丄偙偺係尦懍搙偺掕媊偼俁師尦懍搙偺帺慠側奼挘偵惉偭偰偄傞丅
丂
俀丏係尦懍搙偺儘乕儗儞僣曄姺
丂慜崁偱愢柧偟偨傛偆偵丄乬係尦懍搙乭傪
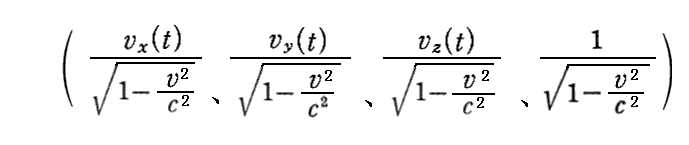
偲掕媊偡傟偽丄偙傟偼乮嵗昗丒帪娫乯係尦儀僋僩儖偲摨偠乬儘乕儗儞僣曄姺乭偵廬偆丅
丂
丂偮傑傝丄俽乫宯偺倶乫幉丄倷乫幉丄倸乫幉偵屌掕偝傟偨嶰杮偺暔嵎偟朹偲俽乫宯偵屌掕偝傟偨帪寁偱應偭偨丄嵼傞暔懱乮壜攭幙揰乯偺嵗昗丒帪崗乮倶乫丆倷乫丆倸乫丆倲乫乯偲丄偦偺摨偠暔懱傪俽宯偺倶幉丄倷幉丄倸幉偵屌掕偝傟偨嶰杮偺暔嵎偟朹偲丄俽宯偵屌掕偝傟偨帪寁偱應偭偨嵗昗丒帪崗乮倶丆倷丆倸丆倲乯偺娫偺娭學傪掕傔傞曄姺幃
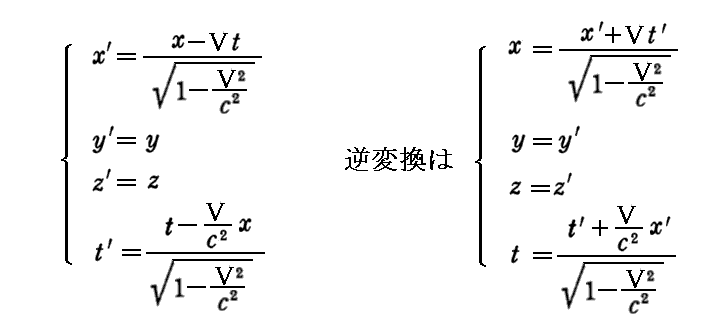
偲摨偠宍偱曄姺偝傟傞丅
丂偦傟偧傟偺嵗昗宯偵屌掕偝傟偨帪寁偺帪崗偼丄俽宯嵗昗暔嵎偟朹偲俽乫宯偺嵗昗暔嵎偟朹偺尨揰偑偡傟堘偆弖娫傪倲亖倲乫亖0偲偟偰寁帪傪奐巒偟偰偄傞帠傪朰傟側偄偱偔偩偝偄丅
乵曗懌愢柧侾乶
丂係尦懍搙偺掕媊偼丄嵟弶偵弎傋偨俁師尦懍搙偺掕媊偲偼堘偭偰偍傝丄屳偄偵堎側傞抣偲側傝傑偡丅偟偐偟丄椉幰偼屳偄偵枾愙偵娭學偟偰偄傑偡丅
丂偦偺乬戝偒偝乭偼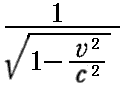 攞偩偗堎側傝傑偡偑丄嬻娫惉暘儀僋僩儖偺乬曽岦乭偼摨偠偱偡丅
攞偩偗堎側傝傑偡偑丄嬻娫惉暘儀僋僩儖偺乬曽岦乭偼摨偠偱偡丅
丂
俁丏係尦懍搙惉暘偐傜峔惉偝傟傞嵗昗曄姺晄曄検
丂乬係尦懍搙乭惉暘偑乬儘乕儗儞僣曄姺乭偵傛偭偰曄姺偝傟傞偺側傜偽丄乮嵗昗丒帪娫乯係尦儀僋僩儖偲摨條側娭學幃
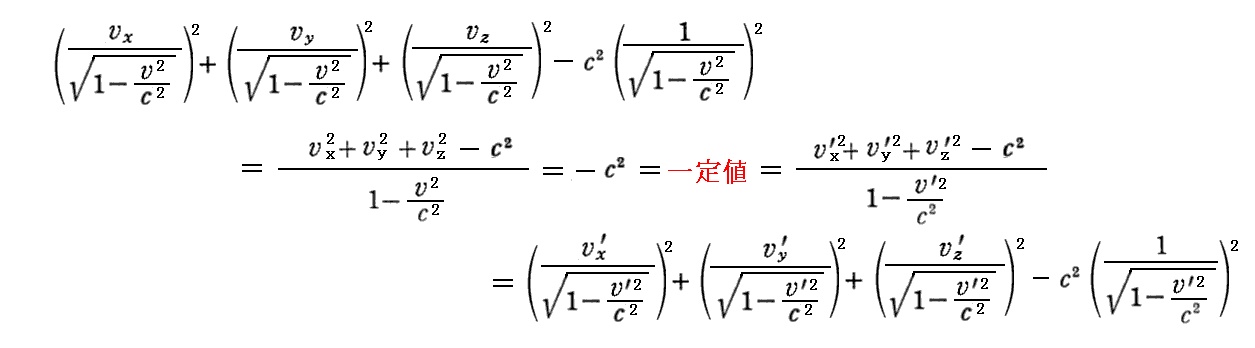
偑惉傝棫偪傑偡丅
丂偦偺偨傔
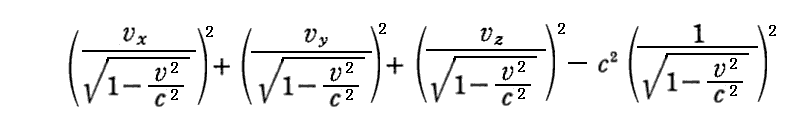
偲偄偆検偑丄嵗昗曄姺偵娭偟偰晄曄偲側傞偙偲偑夝傞丅
丂
乮俀乯係尦壔偲屌桳帪
丂係尦懍搙偺掕媊幃偵娭偟偰廳梫側拲堄傪偟傑偡丅
侾丏屌桳帪
丂乬係尦懍搙乭偺掕媊偵偍偗傞倴亖乮倴x丆倴y丆倴z乯偼丄乮倴x亖倓倶乛倓倲丄倴y亖倓倷乛倓倲丄倴z亖倓倸乛倓倲乯 偲 倴2亖倴x2亄倴y2亄倴z2 傪堄枴偟偰偄傑偟偨丅偮傑傝丄暔懱偺懍搙傪娤應偟偰偄傞姷惈嵗昗宯偺暔嵎偟朹偲帪寁偱寁偭偨抣偱偡丅
丂偙偺偲偒丄憡懳惈棟榑偱偼惷巭姷惈宯俽偵懳偟偰懍搙倴偱摦偄偰偄傞嵗昗宯俽乫偺帪娫娫妘儮冄偼丄偦偺摦偄偰偄傞嵗昗宯傪娤應偡傞傕偲偺惷巭嵗昗宯俽偺帪寁偺帪娫娫妘儮倲傛傝傕抁偔側偭偨丅偮傑傝
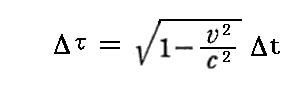
偲側傝丄摦偄偰偄傞嵗昗宯偵晅悘偡傞帪寁偺帪娫偼備偭偔傝棳傟傞丅摦偄偰偄傞暔懱偵屌桳偺帪娫偼抶傟傞偲尵偆偙偲偱偟偨丅乮暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乿俀丏乮俇乯俀丏傪暅廗乯
丂偙偺帪崗冄偺帠傪暔懱乮俽乫宯偵晅拝偟偰偄傞帪寁乯偺乬屌桳帪乭偲尵偄傑偡丅梫偡傞偵摦偄偰偄傞暔懱偺帺慠尰徾偺恑傒曽偼備偭偔傝偵側傞偲尵偭偰偄傞丅屌桳帪偺奣擮偼偦傟埲奜偺壗幰偱傕偁傝傑偣傫
丂
俀丏屌桳帪偺儘乕儗儞僣曄姺晄曄惈
丂慜崁偱愢柧偟偨姷惈宯俽偱懍搙倴亖乮倴x丄倴y丆倴倸乯傪帩偮暔懱偵屌桳偺帪娫冄偺帪娫娫妘儮冄偼乬儘乕儗儞僣曄姺乭偵懳偟偰晄曄偱偡丅側偤側傜
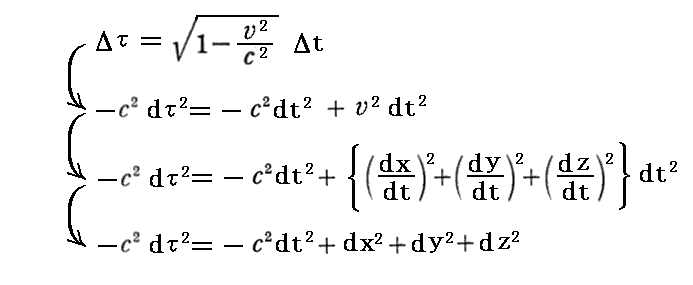
偲曄宍偱偒傞偑丄暿崁乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乿俀丏乮俉乯係丏偱徹柧偟偨傛偆偵偙偺塃曈偑乬儘乕儗儞僣曄姺乭偵懳偟偰晄曄偩偐傜偱偡丅
丂偙偺偙偲偼丄暔棟検傪巐師尦壔偡傞偲偒乬屌桳帪乭偑偒傢傔偰廳梫偱偁傞偙偲傪帵偟偰偄傞丅
丂傑偨丄亅們2倓冄2 偼侾丏乮侾乯俀丏偱掕媊偟偨乬悽奅嫍棧乭倓倱偺俀忔偦偺傕偺偱偁傞偙偲偵拲堄偝傟偨偟丅
丂
俁丏屌桳帪偺摫擖
丂屌桳帪偺摫擖偵偼條乆側愢柧偺巇曽偑偁傝傑偡丅婔偮偐偺暥專偐傜堷梡偟偰偍偒傑偡偺偱偛棗壓偝偄丅
- 摗堜曐寷挊乽帪嬻偲廳椡乿嶻嬈恾彂乮1979擭姧乯戞1復仒5乬屌桳帪偲係尦懍搙乭乮p29乣33乯
- 撪嶳棿梇挊乽憡懳惈棟榑乿娾攇彂揦乮1977擭姧乯偺戞嘩復仒14乬憡懳榑揑塣摦妛乭乮p88乣89乯
- 儔儞僟僂丄儕僼僔僢僣挊乽応偺屆揟榑乮憹掶怴斉乯乿搶嫗恾彂乮1964擭姧乯侾復仒3乬屌桳帪娫乭乮p9乣11乯
丂
乮俁乯屌桳帪昞尰偟偨係尦懍搙
侾丏係尦懍搙偺儘乕儗儞僣曄姺
丂偙偙偱丄摦偄偰偄傞嵗昗宯俽乫傪俽宯偐傜傒偰懍搙倁偱摦偄偰偄傞暔懱偵忢偵挘傝晅偄偰偄傞嵗昗宯偲偟傑偟傚偆丅
丂俽宯偐傜尒偨暔懱偺埵抲嵗昗乮倶丄倷丆倸乯偼帪崗 倲 偺曄壔偲偲傕偵帪乆崗乆偲曄壔偟偰偄偒傑偡偑丄偦偺暔懱偺懍搙傪寁嶼偡傞帪娫傪俽宯偺帪娫娫妘儮倲 偱偼側偔偰俽乫宯偱偺帪娫娫妘儮冄偱應傞偙偲偵偟偰傒傑偟傚偆丅
丂偮傑傝俽宯偐傜應偭偨暔懱偺懍搙傪 倴亖乮倓倶乛倓倲丄倓倷乛倓倲丆倓倸乛倓倲乯 偱偼側偔偰 倳亖乮倓倶乛倓冄丄倓倷乛倓冄丆倓倸乛倓冄乯 偱應傞偺偱偡丅偦偺偲偒丄
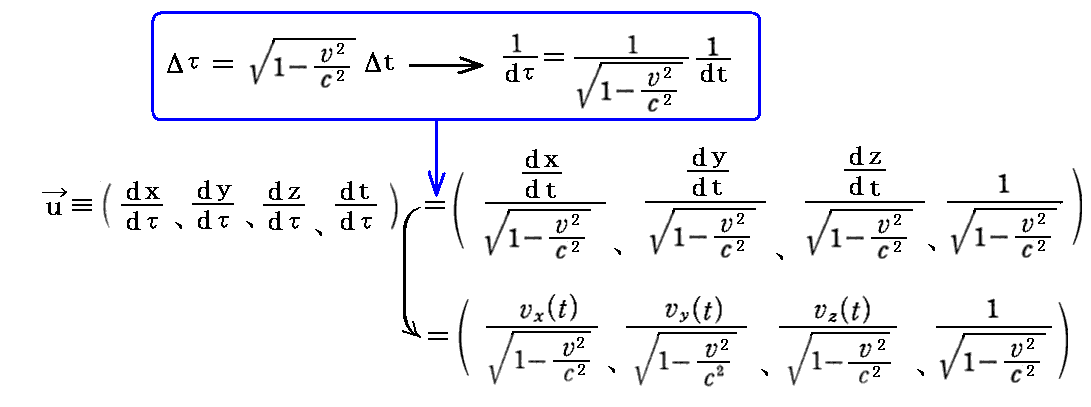
偺幃曄宍偐傜夝傞傛偆偵丄偙偺塃曈偼愭偵掕媊偟偨係尦懍搙偵堦抳偟偰偄傞丅
丂偡側傢偪丄乬係尦懍搙乭偲偼丄暔懱偑摦偄偰偄傞嵗昗宯俽偺帪寁偱應傞偺偱偼側偔偰丄偦偺摦偄偰偄傞暔懱偦偺傕偺偵晅拝偟偰偄傞帪寁偑帵偡帪崗冄乮暔懱偺乬屌桳帪乭乯偱應偭偨懍搙偺偙偲偱偡丅
丂偮傑傝係尦懍搙儀僋僩儖傪
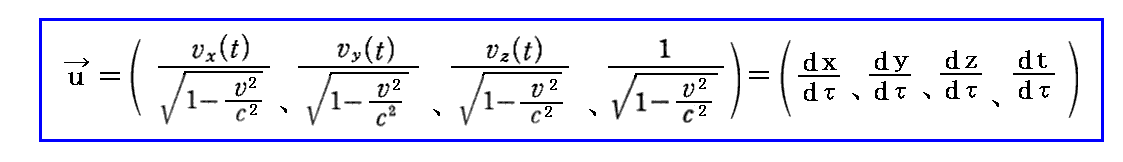
偱掕媊偟偨偲夝庍偡傟偽丄俽宯偐傜尒偨係尦懍搙儀僋僩儖偺俽乫宯偵偍偗傞抣偼
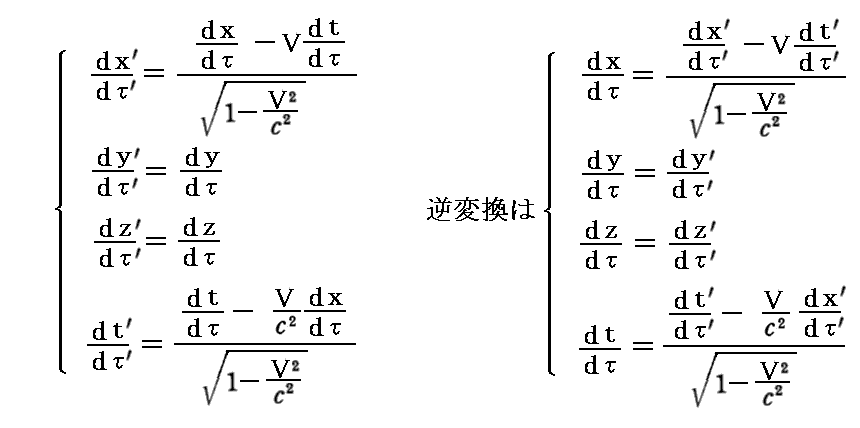
偵廬偆丅偮傑傝丄乮嵗昗丒帪娫乯係尦儀僋僩儖偲摨偠乬儘乕儗儞僣曄姺乭偱寢傃偮偗傜傟傞丅
丂偙偺乬儘乕儗儞僣曄姺乭偺堄枴偼傢偐傝偵偔偄偑丄嵍曈偼俽乫宯偐傜傒偰懍搙 倴乫乮偙傟偼彫暥帤乯偱摦偄偰偄傞暔懱偺屌桳帪冄乫偱應偭偨偦偺暔懱偺懍搙惉暘偱偡丅傕偪傠傫乮倶乫丆倷乫丆倸乫丆倲乫乯偼俽乫宯偱偺暔懱偺埵抲嵗昗偲帪崗偱偡丅
丂傑偨丄塃曈偼俽宯偐傜尒偰懍搙 倴乮偙傟偼彫暥帤乯 偱摦偄偰偄傞暔懱偺屌桳帪冄偱應偭偨偦偺暔懱偺懍搙惉暘偱偡丅傕偪傠傫乮倶丆倷丆倸丄倲乯偼俽宯偱偺暔懱偺埵抲嵗昗偲帪崗偱偡丅
丂偦偟偰丄俽宯偱偺帪崗 倲 偲俽乫宯偱偺帪崗 倲乫 偐傜峔惉偝傟傞 倓倲乛倓冄偲 倓倲乫乛倓冄乫 偑戞巐偺惉暘偲偟偰娷傑傟偰偄傞丅
丂傕偪傠傫幃拞偺 乬倁乭乮偙傟偼戝暥帤乯 偼丄俽乫宯偑俽宯偺倶幉曽岦偵懍搙倁乮偙傟偼戝暥帤乯偱摦偄偰偄傞姷惈宯偱偁傞帠傪帵偟偰偄傑偡丅
丂
俀丏係尦懍搙偺儘乕儗儞僣曄姺
丂嵗昗宯偵晅懏偡傞帪娫 倲偱旝暘偟偨 俁師尦懍搙 倴乮彫暥帤乯 偲嬫暿偡傞偨傔偵丄崱屻偼 屌桳帪 冄 偱旝暘偟偨係尦懍搙傪 乬倳乭 偱昞偡偙偲偵偡傞丅
丂偡側傢偪丄冄傪俽宯偐傜尒偰懍搙 倴乮倳偱偼側偄偙偲偵拲堄乯偱摦偄偰偄傞暔懱偺乬屌桳帪乭偲偟偨偲偒丄冄偱旝暘偟偰摼傜傟傞暔懱偺係尦懍搙傪倳乮冄乯
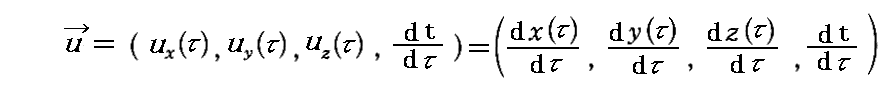
偱昞偡丅乮倶丆倷丆倸丆倲乯偼丄俽宯偵屌掕偝傟偰偄傞暔嵎偟朹偱應偭偨暔懱偺埵抲嵗昗偲丄俽宯偵屌掕偝傟偰偄傞帪寁偱寁偭偨暔懱偺帪崗偱偡丅
丂傑偨丄冄乫傪俽乫宯偐傜尒偰懍搙 倴乫乮倳乫偱偼側偄偙偲偵拲堄乯偱摦偄偰偄傞暔懱偺乬屌桳帪乭偲偟偨偲偒丄冄乫偱旝暘偟偰摼傜傟傞暔懱偺係尦懍搙傪倳乫乮冄乫乯
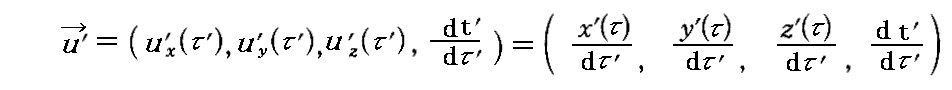
偱昞偡丅傕偪傠傫乮倶乫丆倷乫丆倸乫丆倲乫乯偼俽乫宯偵屌掕偝傟偰偄傞暔嵎偟朹偱應偭偨埵抲嵗昗偲丄俽乫宯偵屌掕偝傟偰偄傞帪寁偱寁偭偨暔懱偺帪崗偱偡丅
丂杮峞偱偼忢偵丄俽乫宯偼俽宯偺倶幉偵増偭偰倶幉偺惓曽岦偵懍搙倁偱堏摦偟偰偄傞偲偟偰偄傞丅
丂偙偺乬係尦懍搙乭偺昞尰婰崋傪梡偄傞偲丄慜崁偺乬儘乕儗儞僣曄姺乭偼

偲側傝傑偡丅
乵曗懌愢柧侾乶
丂忋婰偺係尦懍搙偺乬儘乕儗儞僣曄姺乭偺係尦懍搙傪俁師尦懍搙昞尰偵抲偒姺偊傞偲俁師尦懍搙昞尰偱偺乬儘乕儗儞僣曄姺幃乭偵側傞偺偱偡偑丄偙傟傪幃曄宍偡傞偲
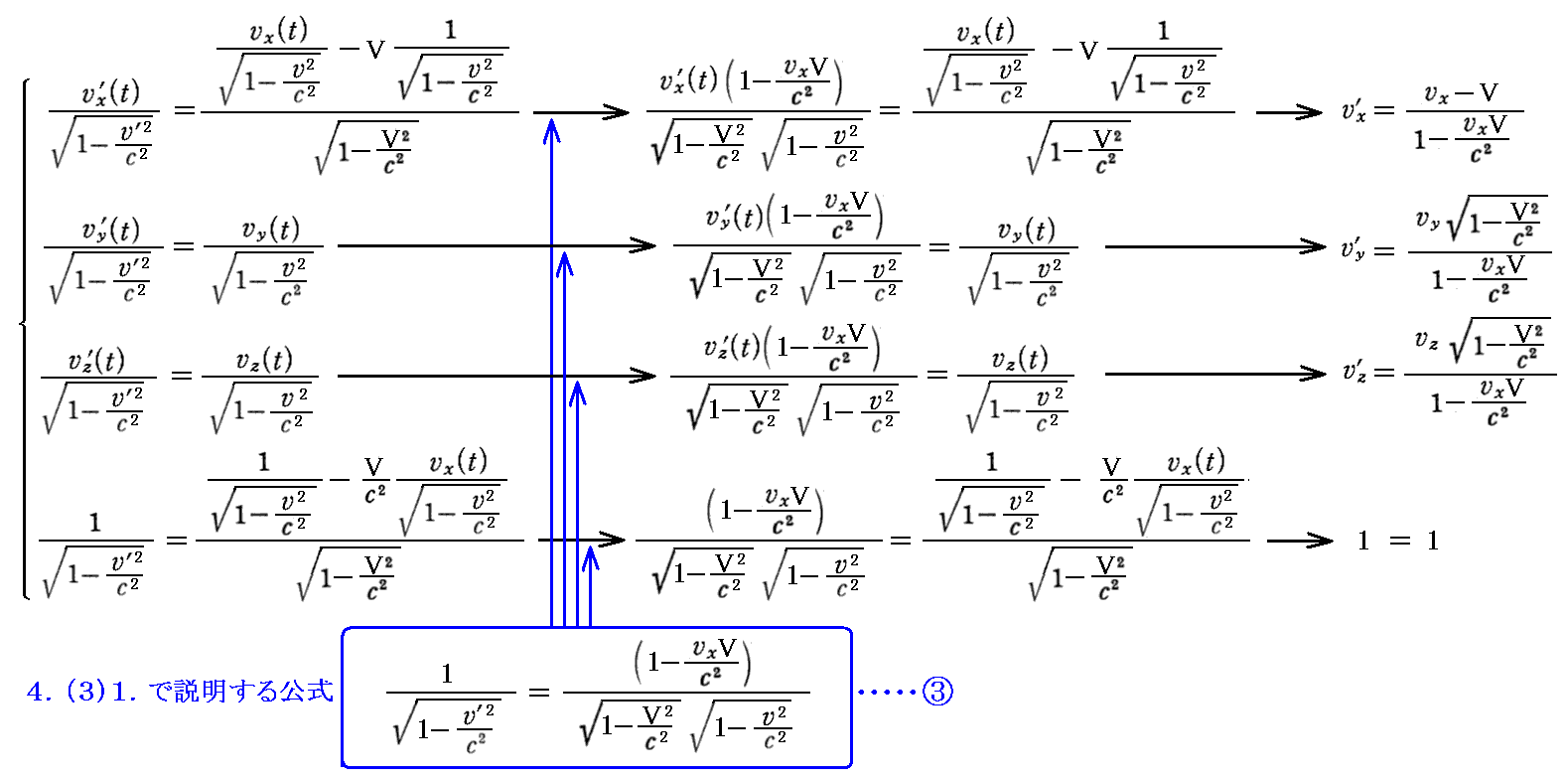
偲側傝丄俁師尦懍搙偺乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼偵婣拝偡傞丅偦偺偲偒戞係惉暘偼峆摍幃偲側傞丅
丂傕偪傠傫丄偙偺幃曄宍偼俀丏乮侾乯侾丏偱峴偭偨幃曄宍傪媡偵偨偳傞偺偲摨偠帠偱偡丅
乵曗懌愢柧俀乶
丂係尦懍搙乮倳x丆倳y丆倳z丆倓倲乛倓冄乯偼姷惈宯俽偵懳偟偰懍搙乮倴x丆倴y丆倴z乯偱摦偄偰偄傞姷惈宯俽乫偵墬偄偰惷巭偟偰偄傞幙揰偺係尦懍搙傪俽乫宯偐傜俽宯偱偺抣偵儘乕儗儞僣曄姺偟偨傕偺偲摨偠偱偡丅
丂幚嵺丄暿峞乽摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊乿俁丏乮俀乯偺寢榑傪棙梡偟偰儘乕儗儞僣媡曄姺偟偰傒傞丅傕偪傠傫偙偙偱偼懍搙乮倁x丆倁y丆倁z乯傪懍搙乮亅倴x丆亅倴y丆亅倴z乯偱抲偒姺偊偹偽側傝傑偣傫丅晧晞崋偼梡偄傞偺偑儘乕儗儞僣媡曄姺偩偐傜偱偡丅
丂俽乫宯偱偺係尦懍搙偼乮0丆0丆0丆1乯偩偐傜丄偙傟傪儘乕儗儞僣媡曄姺偡傞偲
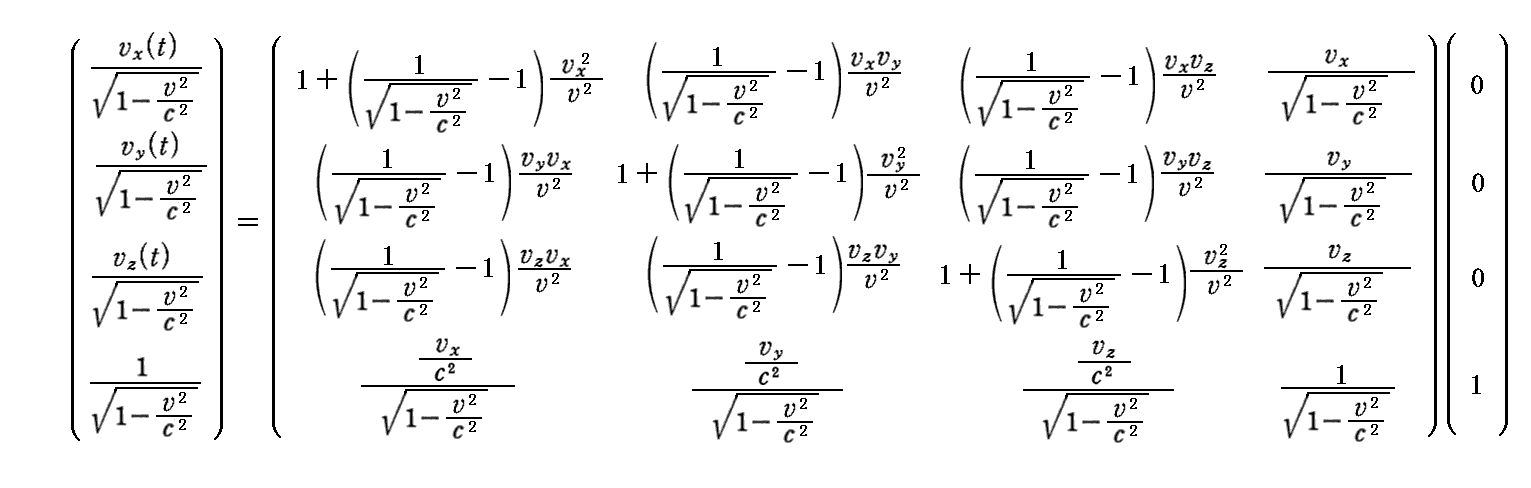
偲側傝丄俽宯偱偺係尦懍搙偺昞尰偲側傞丅
丂俽乫宯偱偺係尦懍搙偺戞4惉暘偑倓倲乛倓冄亖1偱偁傞偙偲偼丄俽乫宯偑偦偺幙揰偑惷巭偟偰偄傞姷惈宯偱偁傞帠傪丄偮傑傝偦偺幙揰偑惷巭偺忬懺偱偁傞偙偲傪昞偟偰偄傞丅
丂
丂傕偪傠傫丄俽宯偱偺係尦懍搙昞尰抣傪俽乫宯傊儘乕儗儞僣曄姺乮暿峞乽摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊乿俁丏乮俀乯偺懍搙乮倁x丆倁y丆倁z乯傪懍搙乮倴x丆倴y丆倴z乯偱抲偒姺偊偨傕偺偱乯偡傞偲丄俽乫宯偱偺娤應抣乮0丆0丆0丆1乯偵栠傝傑偡丅
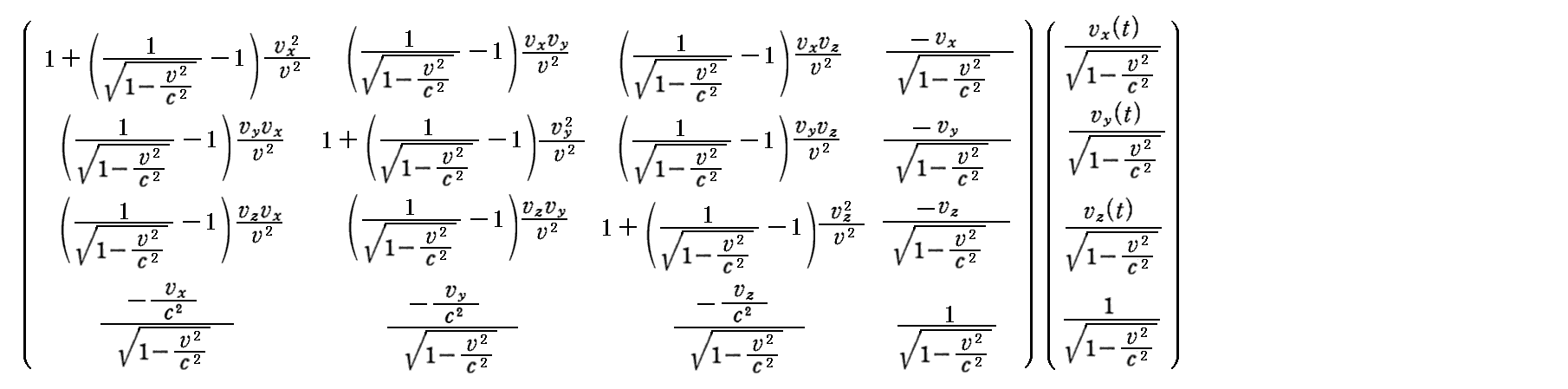
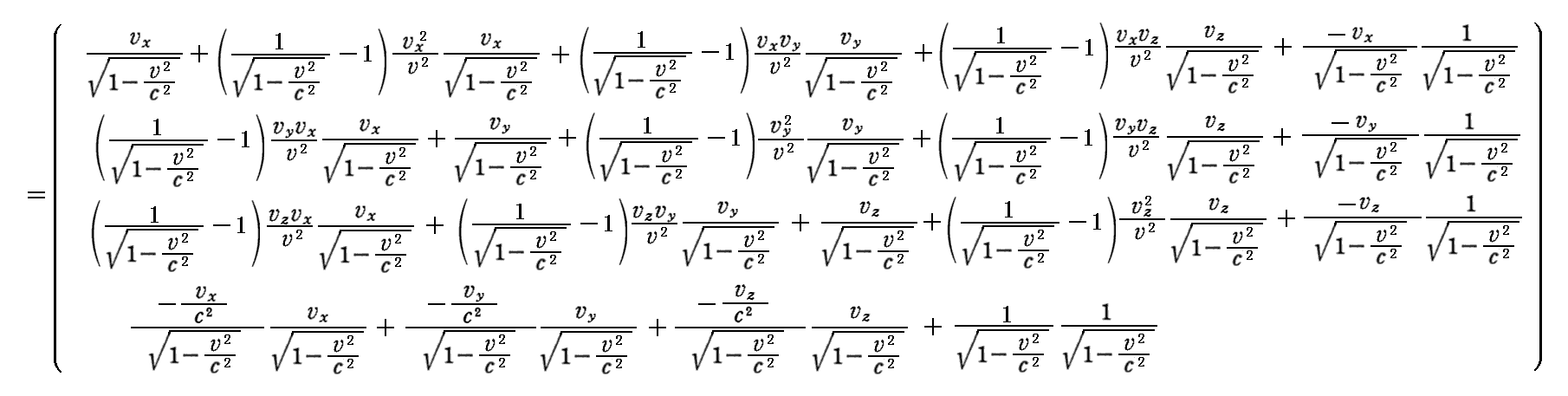
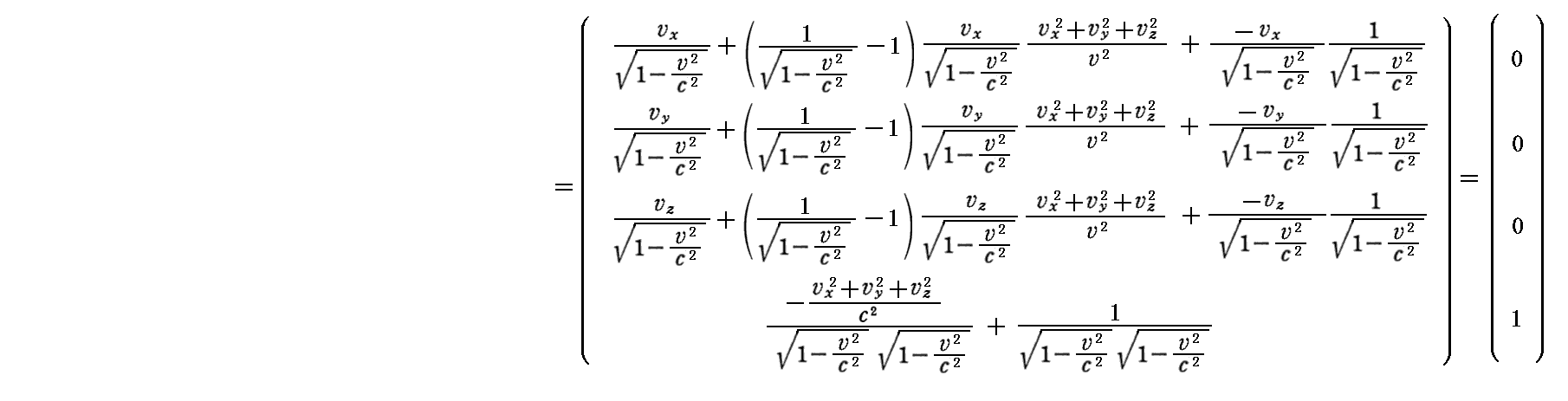
丂
俁丏係尦懍搙偺惈幙
丂係尦懍搙偼儘乕儗儞僣曄姺偵廬偆偺偱丄懠偺4尦検偲摨條偵乬係尦懍搙乭偐傜峔惉偝傟傞壓婰偺検偑
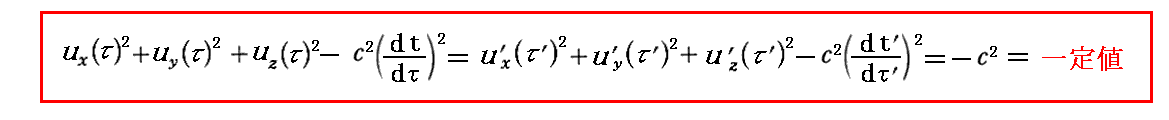
偑乬儘乕儗儞僣曄姺乭偵懳偟偰晄曄偲側傝傑偡丅
丂堦掕抣偑亅們2偵側傞偺偼慜崁乵曗懌愢柧俀乶偱愢柧偟偨傛偆偵懍搙偑僛儘偲側傞嵗昗宯傊儘乕儗儞僣曄姺偡傟偽 倓倲乛倓冄 傗 倓倲乫乛倓冄乫 偑 1 偵曄姺偝傟傞偐傜偱偡丅
丂
俁丏係尦塣摦検偲係尦揹棳枾搙偺怴夝庍
丂乽憡懳榑揑椡妛乿俁丏乮係乯偱愢柧偟偨乮塣摦検丒幙検乯係尦儀僋僩儖傗乽憡懳榑揑椡妛乿俁丏乮俆乯偱愢柧偟偨乮揹棳枾搙丒揹壸枾搙乯係尦儀僋僩儖偺掕媊幃傪乬屌桳帪乭傪梡偄偰夝庍偟捈偡偲丄偙傟傜偑乬係尦塣摦検乭偱偁傝乬係尦揹棳枾搙乭偱偁傞偙偲偑傛偔夝傝傑偡丅
乮侾乯乮塣摦検丒幙検乯係尦儀僋僩儖偺怴夝庍
丂暿峞乽憡懳榑揑椡妛乿俁丏乮係乯乵曗懌愢柧俀乶偱丄乮塣摦検丒幙検乯係尦儀僋僩儖傪師偺傛偆偵掕媊偟偨丅
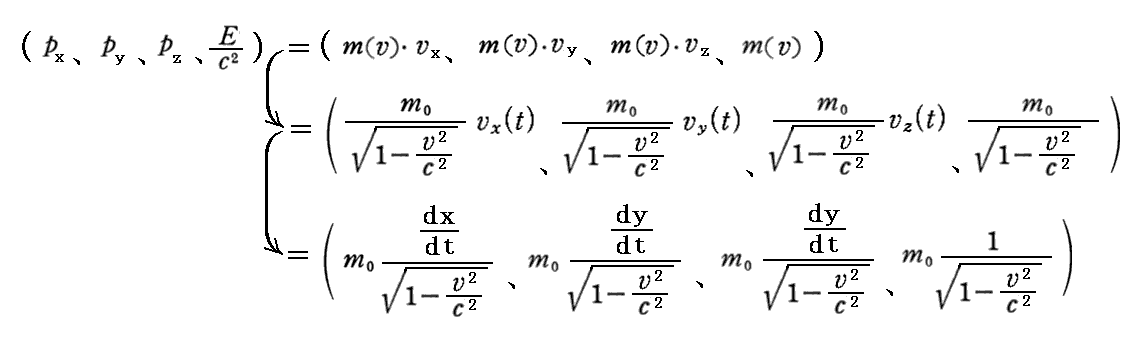
偙偙偱丄係尦懍搙偺掕媊幃偱棙梡偟偨娭學
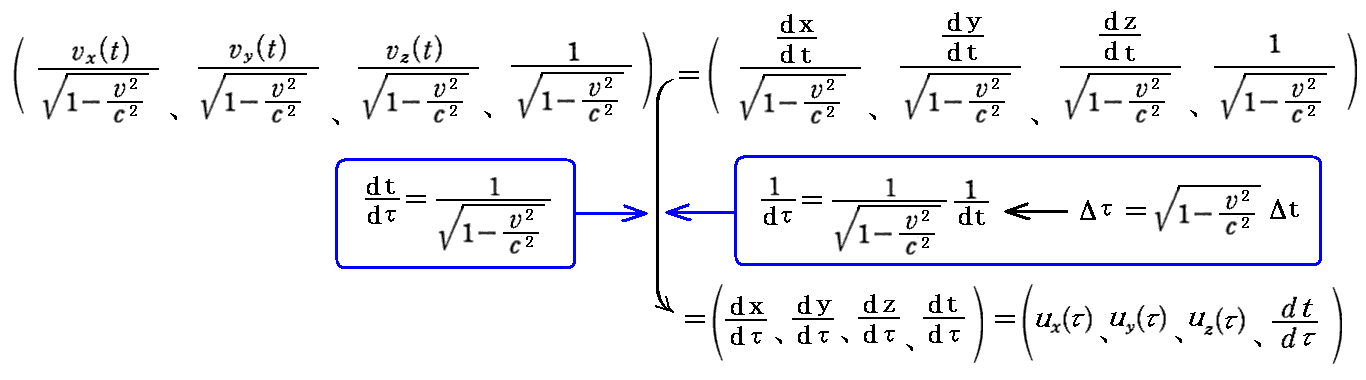
傪梡偄傞偲丄
丂乮塣摦検丒幙検乯係尦儀僋僩儖偼
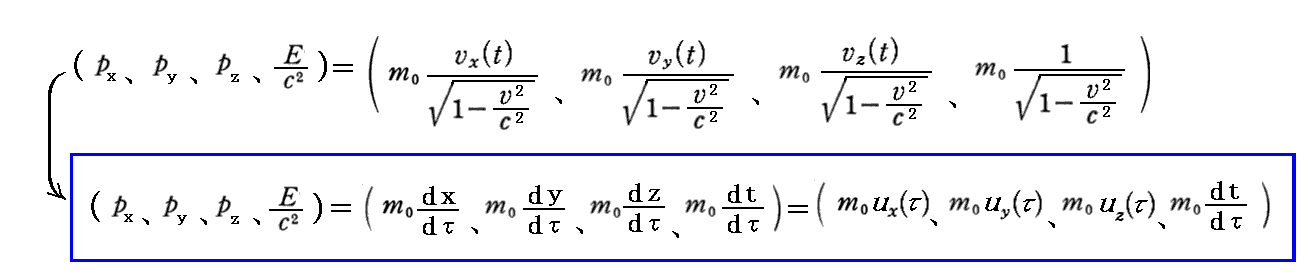
偲昞偝傟傞丅
丂偙偙偱冄偼俽嵗昗宯偱懍搙 倴乮偙傟偼彫暥帤乯 偱摦偄偰偄傞暔懱偺屌桳帪偱偁傝丄乬倣0乭偼偦偺暔懱偲偲傕偵摦偄偰偄傞嵗昗宯偐傜尒偨暔懱偺幙検偱偡丅傕偲傕偲惷巭幙検偲尵傢傟偰偄偨検偱偡偑丄帪乆崗乆曄傢傞懍搙 倴乮偙傟偼彫暥帤乯 偱摦偔暔懱偵屌掕偟偨嵗昗宯偱偺惷巭幙検偱偡偐傜丄偙傟偼偦偺暔懱偺屌桳帪偲摨偠傛偆偵丄偦偺暔懱偺乬屌桳幙検乭偲尵偆傋偒検偱偡丅
丂偮傑傝丄屌桳幙検傪梡偄傟偽擟堄偺嵗昗宯俽偵偍偄偰懍搙 倴 偱摦偄偰偄傞暔懱偺塣摦検惉暘偼丄乵屌桳幙検乶亊乵係尦懍搙乶偱昞偝傟傞偲偄偆偙偲偵側傝傑偡丅
丂偙偺乬係尦塣摦検乭偺惉暘偼丄娤應偡傞姷惈宯偑俽宯偐傜俽乫宯乮俽宯偺倶幉曽岦偵懍搙倁乮偙傟偼戝暥帤乯偱堏摦乯偵曄傢傟偽丄屌桳幙検 倣0 偼偦偺傑傑偱丄屌桳懍搙偼乮倓倶乛倓冄丄倓倷乛倓冄丄倓倸乛倓冄乯偐傜乮倓倶乫乛倓冄乫丄倓倷乫乛倓冄乫丄倓倸乫乛倓冄乫乯偵曄傢傝傑偡丅
丂偦偟偰丄忋婰偱掕媊偝傟傞乮塣摦検丒幙検乯係尦儀僋僩儖偼丄乮嵗昗丒帪娫乯係尦儀僋僩儖偲摨偠乬儘乕儗儞僣曄姺乭偵廬偭偰曄姺偝傟傑偡丅

丂偙偺偲偒傕偪傠傫丄乬係尦塣摦検乭偵偮偄偰偼侾丏乮侾乯俀丏偱弎傋偨傛偆偵
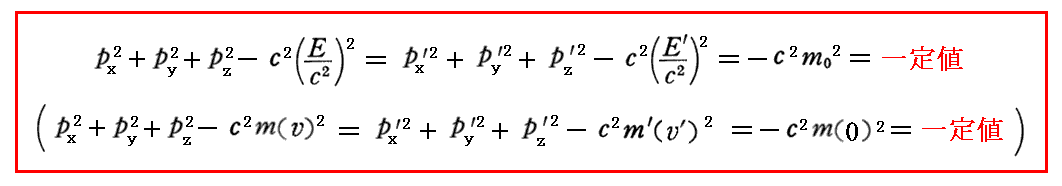
偑惉傝棫偪傑偡丅
丂堦掕抣偑亅們2倣02偲側傞偺偼丄埲壓偺乵曗懌愢柧侾乶偱愢柧偡傞傛偆偵塣摦検偑僛儘偵側傞嵗昗宯偵儘乕儗儞僣曄姺偡傞偲 俤乛們2亖倣(倴) 傗 俤乫乛們2亖倣乫(倴乫) 偑 倣0 偵曄姺偝傟傞偐傜偱偡丅
乵曗懌愢柧侾乶
丂係尦塣摦検乮倫x丆倫y丆倫z丆倣乯偼姷惈宯俽偵懳偟偰懍搙乮倴x丆倴y丆倴z乯偱摦偄偰偄傞姷惈宯俽乫偵墬偄偰惷巭偟偰偄傞幙検倣0傪俽乫宯偐傜俽宯偱偺抣偵儘乕儗儞僣曄姺偟偨傕偺偲摨偠偱偡丅
丂幚嵺丄暿峞乽摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊乿俁丏乮俀乯偺寢榑傪棙梡偟偰儘乕儗儞僣媡曄姺偟偰傒傞丅傕偪傠傫偙偙偱偼懍搙乮倁x丆倁y丆倁z乯傪懍搙乮亅倴x丆亅倴y丆亅倴z乯偱抲偒姺偊偹偽側傝傑偣傫丅晧晞崋偼梡偄傞偺偑儘乕儗儞僣媡曄姺偩偐傜偱偡丅
丂俽乫宯偱偺係尦塣摦検偼乮0丆0丆0丆倣0乯偩偐傜丄偙傟傪儘乕儗儞僣媡曄姺偡傞偲
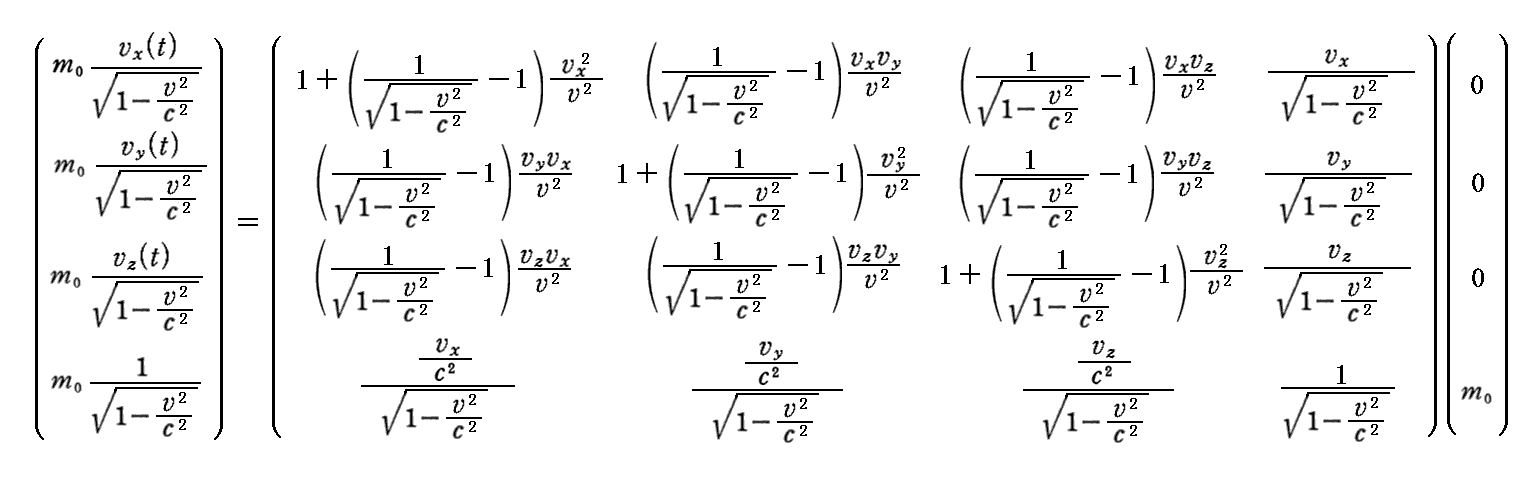
偲側傝丄俽宯偱偺係尦塣摦検偺昞尰偲側傞丅係尦塣摦検偺戞4惉暘偼暔懱偺幙検偦偺傕偺傪昞偟偰偄傞丅偮傑傝丄暔懱偺幙検偼塣摦検惉暘偲堦弿偵側偭偰帪娫揑側惉暘偲偟偰儘乕儗儞僣曄姺偝傟傞丅
丂
丂傕偪傠傫丄俽宯偱偺係尦塣摦検昞尰抣傪俽乫宯傊儘乕儗儞僣曄姺乮暿峞乽摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊乿俁丏乮俀乯偺懍搙乮倁x丆倁y丆倁z乯傪懍搙乮倴x丆倴y丆倴z乯偱抲偒姺偊偨傕偺偱乯偡傞偲丄俽乫宯偱偺娤應抣乮0丆0丆0丆倣0乯偵栠傝傑偡丅
丂
乮俀乯乮揹棳枾搙丒揹壸枾搙乯係尦儀僋僩儖偺怴夝庍
丂摨條側帠偑丄暿峞乽憡懳榑揑椡妛乿俁丏乮俆乯乵曗懌愢柧係乶偱丄掕媊偟偨乮揹棳枾搙丒揹壸枾搙乯係尦儀僋僩儖偺掕媊幃偵偮偄偰傕尵偊傞丅
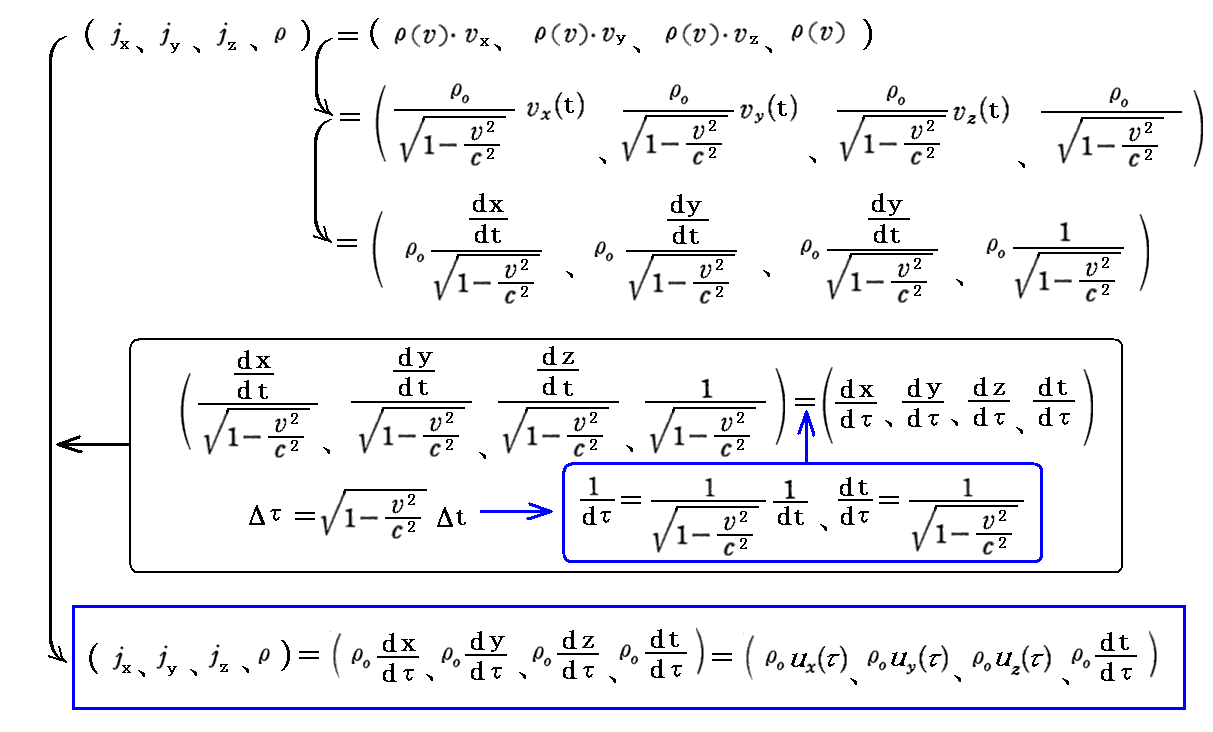
丂偙偙偱丄乬兿0乭 偼帪乆崗乆曄傢傞懍搙 倴乮偙傟偼彫暥帤乯 偱摦偔揹壸偵屌掕偟偨嵗昗宯偱尒偨揹壸枾搙偱偡偑丄偙傟偼忢偵乬儘乕儗儞僣曄姺乭偵懳偟偰晄曄側乬屌桳揹壸枾搙乭偲尵偆傋偒検偱偡丅偡側傢偪丄擟堄偺嵗昗宯偵偍偄偰暔懱偑帩偮揹棳枾搙惉暘偼丄乵屌桳揹壸枾搙乶亊乵係尦懍搙乶偲側傞丅
丂偙偺乬係尦揹棳枾搙乭偺惉暘偼丄娤應偡傞姷惈宯偑曄傢傟偽乬儘乕儗儞僣曄姺乭偵廬偭偰曄姺偝傟傑偡丅

丂偙偺偲偒傕偪傠傫丄乬係尦揹棳枾搙乭偵偮偄偰偼侾丏乮侾乯俀丏偱弎傋偨傛偆偵
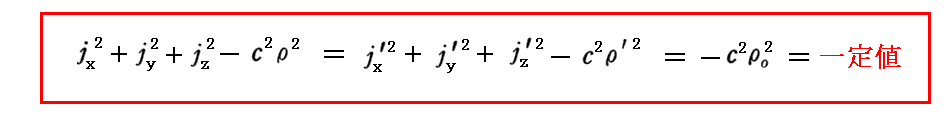
偑惉傝棫偪傑偡丅
丂堦掕抣偑亅們2兿02偲側傞偺偼丄埲壓偺乵曗懌愢柧俁乶偱愢柧偡傞傛偆偵揹棳枾搙 倞 偑僛儘偵側傞嵗昗宯偵儘乕儗儞僣曄姺偡傞偲 兿 傗 兿乫 偑 兿0 偵曄姺偝傟傞偐傜偱偡丅
乵曗懌愢柧侾乶
丂忋婰偺
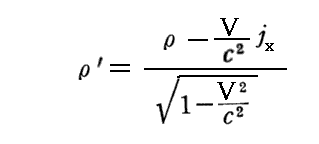
偺兿乫偼俽乫宯偐傜尒偰懍搙儀僋僩儖 倴乫亖乮倴x乫丆倴y乫丆倴倸乫乯 偱摦偄偰偄傞揹壸偺揹壸枾搙傪丄兿偼俽宯偐傜尒偰懍搙儀僋僩儖 倴亖乮倴x丆倴y丆倴z乯 偱摦偄偰偄傞揹壸偺揹壸枾搙傪堄枴偟傑偡丅傑偨 倞x亖兿乮倴乯丒倴x乮倲乯亖兿0丒倳x乮冄乯 偲 倞x乫亖兿乮倴乫乯丒倴x'乮倲乫乯亖兿0丒倳x'乮冄乫乯 堄枴偟傑偡丅偦偺偨傔忋婰偺幃偼
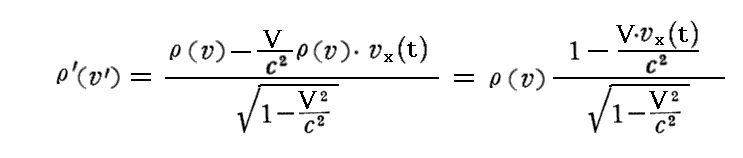
偲側傞丅
丂偙偺幃偼丄暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乮1905擭乯乿俁丏乮係乯乵曗懌愢柧俀乶偱愢柧偟偨娭學偦偺傕偺偱偡丅偦偙偺俁師尦偱偺愢柧偼側偐側偐夝傝偵偔偐偭偨偑丄偙偙偺傛偆偵係尦揹棳枾搙偺戞巐惉暘偺儘乕儗儞僣曄姺幃偱偁傞偲峫偊傞偲丄旕忢偵偡偭偒傝偲棟夝偱偒傞丅
乵曗懌愢柧俀乶
丂偙偺復偱乬屌桳幙検乭偲偐丄乬屌桳揹壸枾搙乭偲偄偆尵偄曽偑弌偰偒偨偑丄偄偢傟傕偦偺暔懱乮揹壸乯偑惷巭偟偰偄傞婎弨宯偱應偭偨偲偒偺幙検偱偁傝丄揹壸枾搙偱偡丅
丂偙偺傛偆偵峫偊傟偽丄暔懱偑惷巭偟偰偄傞婎弨宯偱應偭偨暔懱偺挿偝偑乬屌桳挿偝乭偱偁傝丄暔懱偺懱愊傪乬屌桳懱愊乭偲偄偆偙偲傕偱偒傞丅偦傟傜偺暔懱偑摦偄偰尒偊傞婎弨宯偱應傞偲丄偦傟傜偺暔懱偺挿偝偼弅傒丄懱愊偼尭彮偡傞丅
乵曗懌愢柧俁乶
丂係尦揹棳枾搙乮倞x丆倞y丆倞z丆兿乯偼姷惈宯俽偵懳偟偰懍搙乮倴x丆倴y丆倴z乯偱摦偄偰偄傞姷惈宯俽乫偵墬偄偰惷巭偟偰偄傞屌桳揹壸枾搙兿0傪俽乫宯偐傜俽宯偱偺抣偵儘乕儗儞僣曄姺偟偨傕偺偲摨偠偱偡丅
丂幚嵺丄暿峞乽摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊乿俁丏乮俀乯偺寢榑傪棙梡偟偰儘乕儗儞僣媡曄姺偟偰傒傞丅傕偪傠傫偙偙偱偼懍搙乮倁x丆倁y丆倁z乯傪懍搙乮亅倴x丆亅倴y丆亅倴z乯偱抲偒姺偊偹偽側傝傑偣傫丅晧晞崋偼梡偄傞偺偑儘乕儗儞僣媡曄姺偩偐傜偱偡丅
丂俽乫宯偱偺係尦揹棳枾搙偼乮0丆0丆0丆兿0乯偩偐傜丄偙傟傪儘乕儗儞僣媡曄姺偡傞偲
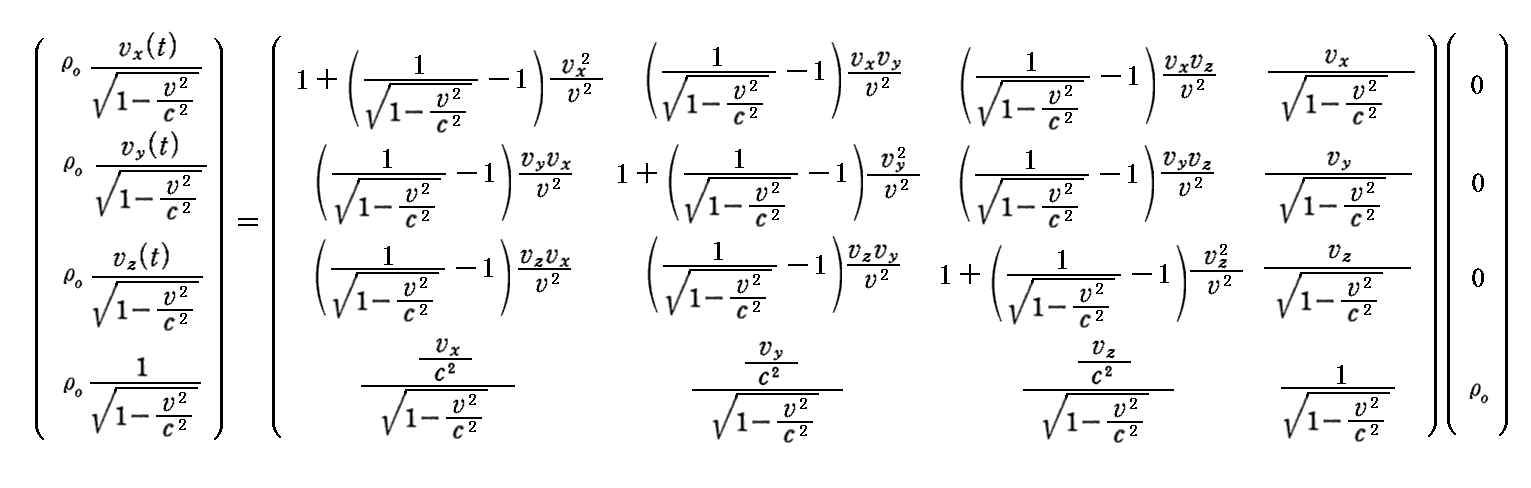
偲側傝丄俽宯偱偺係尦揹棳枾搙偺昞尰偲側傞丅
丂乬屌桳揹壸枾搙乭偑儘乕儗儞僣曄姺偵懳偟偰晄曄側偙偲偼丄揹壸枾搙傪峔惉偡傞壸揹棻巕乮揹巕側偳乯偺揹壸偑儘乕儗儞僣曄姺偵懳偟偰晄曄乮偮傑傝塣摦懍搙偵埶懚偟偰曄壔偡傞偙偲偼柍偄乯偐傜摫偐傟傞帠偱偡丅偙偺偙偲偼暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乮1905擭乯乿俁丏乮係乯乵曗懌愢柧俆乶側偳偱摿偵拲堄偟傑偟偨丅
丂揹壸枾搙偑揹棳枾搙偲偲傕偵係尦儀僋僩儖傪惉偡偲尵偆偙偲偼丄揹壸枾搙偑揹棳枾搙偲堦弿偵側偭偰帪娫揑側惉暘偲偟偰儘乕儗儞僣曄姺偝傟傞偲尵偆偩偗偱丄偦傟埲忋偺堄枴偼偁傝傑偣傫丅
丂
丂傕偪傠傫丄俽宯偱偺係尦揹棳枾搙昞尰抣傪俽乫宯傊儘乕儗儞僣曄姺乮暿峞乽摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊乿俁丏乮俀乯偺懍搙乮倁x丆倁y丆倁z乯傪懍搙乮倴x丆倴y丆倴z乯偱抲偒姺偊偨傕偺偱乯偡傞偲丄俽乫宯偱偺娤應抣乮0丆0丆0丆兿0乯偵栠傝傑偡丅
乵曗懌愢柧係乶
丂暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乮1905擭乯乿俁丏乮係乯乵曗懌愢柧係乶偱丄乬揹壸偺曐懚懃乭偑儘乕儗儞僣曄姺偵懳偟偰晄曄側傜偽揹壸枾搙偺儘乕儗儞僣曄姺嫟曄偺曄姺幃偑摫偗傞偙偲傪拲堄偟傑偟偨丅偙偙偱丄傕偭偲堦斒揑偵乬揹壸偺曐懚懃乭偑儘乕儗儞僣曄姺偵懳偟偰晄曄側傜偽丄乬係尦揹壸枾搙乭偑儘乕儗儞僣曄姺偵廬傢側偗傟偽側傜側偄偙偲傪妋擣偟偰偍偒傑偡丅
丂偙偙偱偼俽宯乮倶丆倷丆倸丆倲乯偺倶幉偺惓曽岦偵懍搙倴偱塣摦偟偰偄傞俽乫宯乮倶乫丆倷乫丆倸乫丆倲乫乯傪峫偊傞丅偦偺偲偒丄暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乮1905擭乯乿俁丏乮侾乯乵曗懌愢柧侾乶偱愢柧偟偨傛偆偵丄 倲乫偼乮倶丆倷丆倸丆倲乯偺娭悢丄倶乫丄倷乫丄倸乫傕乮倶丆倷丆倸丆倲乯偺娭悢偩偐傜丄旝暘朄偺惈幙傛傝
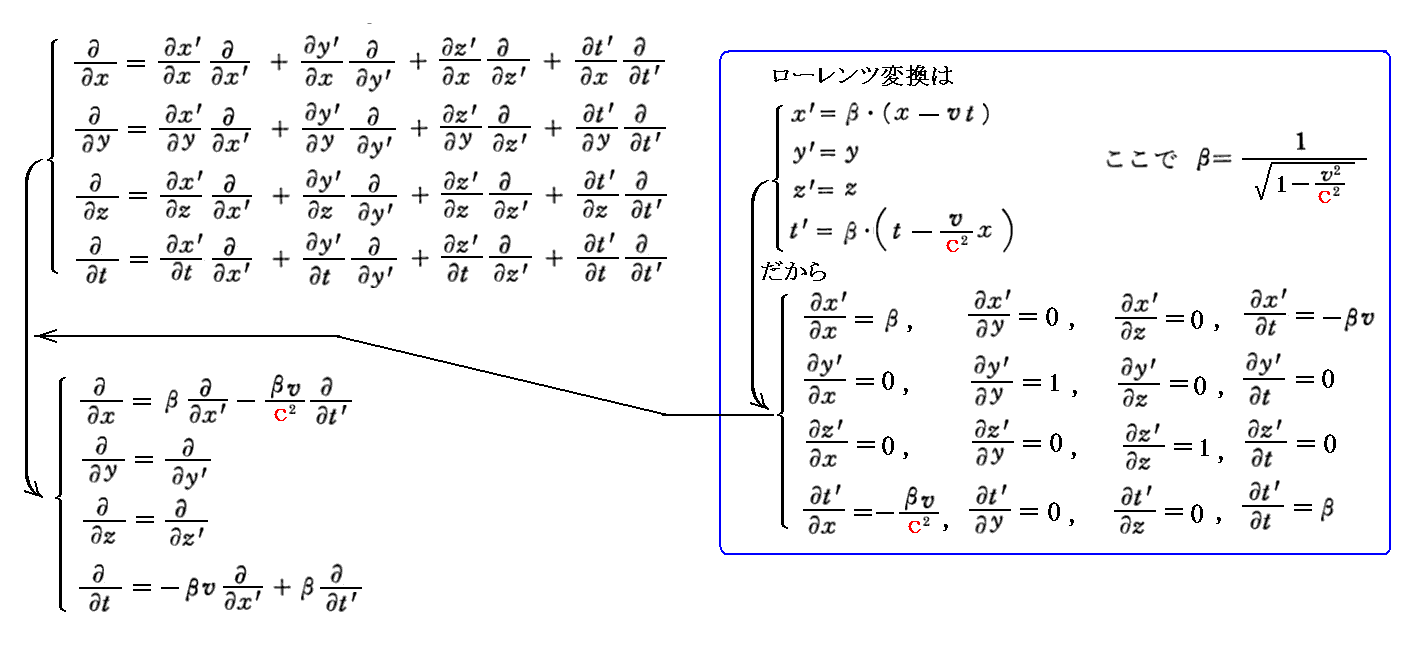
偑惉傝棫偮丅
丂偙傟傪梡偄傞偲乬揹壸曐懚懃乭偼
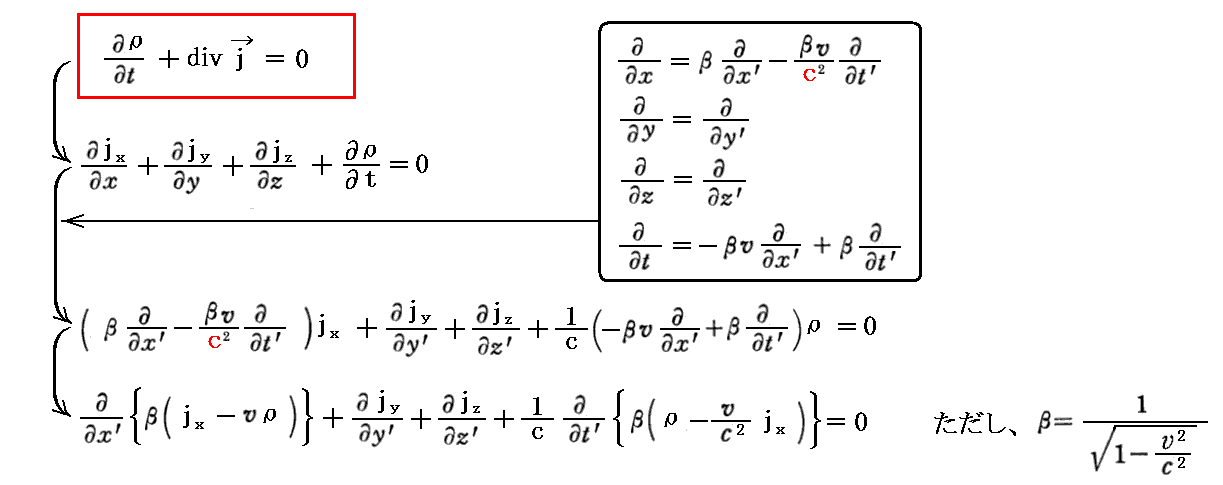
偲側傞丅
丂偙傟偼揹棳枾搙儀僋僩儖倞偲揹壸枾搙兿偑儘乕儗儞僣曄姺
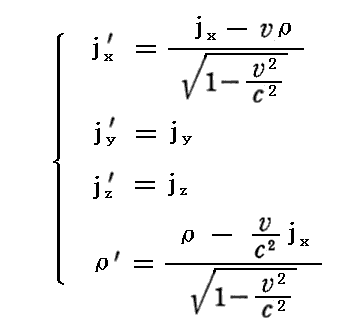
偵廬偭偰曄姺偝傟傟偽丄揹壸曐懚懃偑儘乕儗儞僣曄姺偵懳偟偰宍傪曄偊側偄

偙偲傪帵偟偰偄傞丅
丂偙偺傗傝曽偱傕乮倞x丆倞y丆倞z丆兿乯偑儘乕儗儞僣曄姺偵廬偆乬係尦揹棳枾搙乭偱偁傞偙偲偑徹柧偱偒傞丅
丂
係丏係尦壛懍搙丂
丂俁師尦懍搙傗俁師尦壛懍搙偺儘乕儗儞僣曄姺嫟曄偺曄姺幃傪尦偵偟偰丄乬儘乕儗儞僣曄姺乭偵廬偆乬係尦壛懍搙乭偺掕媊幃傪尒偮偗傑偡丅
乮侾乯俁師尦壛懍搙偺曄姺幃
丂嵟弶偵俁師尦壛懍搙偵偮偄偰愢柧偡傞丅姷惈宯俽偱偺壛懍搙惉暘傪
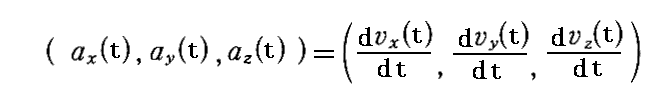
偲偟丄姷惈宯俽乫偱娤應偡傞偲偒偺壛懍搙惉暘傪
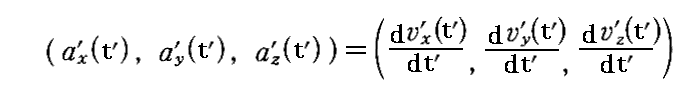
偲偡傞偲偡傞丅傕偪傠傫丄俽乫宯偼俽宯偺倶幉曽岦偵懍搙倁偱摦偄偰偄傞偲偟偰偄傞丅
丂偙傟傜偺壛懍搙惉暘偼師偺曄姺幃偱曄姺偝傟傑偡丅俁師尦壛懍搙偺曄姺幃傕俁師尦懍搙偺曄姺幃偲摨條偵峫偊傟偽傛偄丅侾丏乮俀乯侾丏偱暅廗偟偨俁師尦懍搙偺曄姺幃傪棙梡偡傟偽
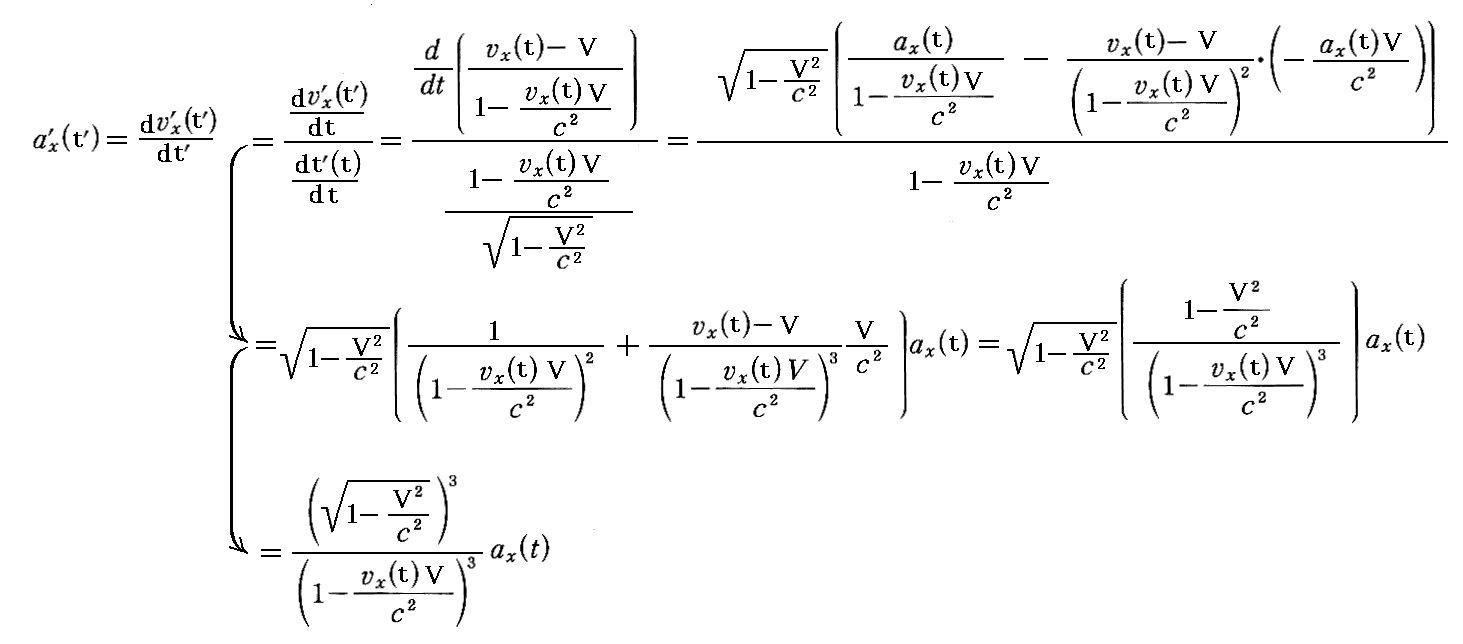
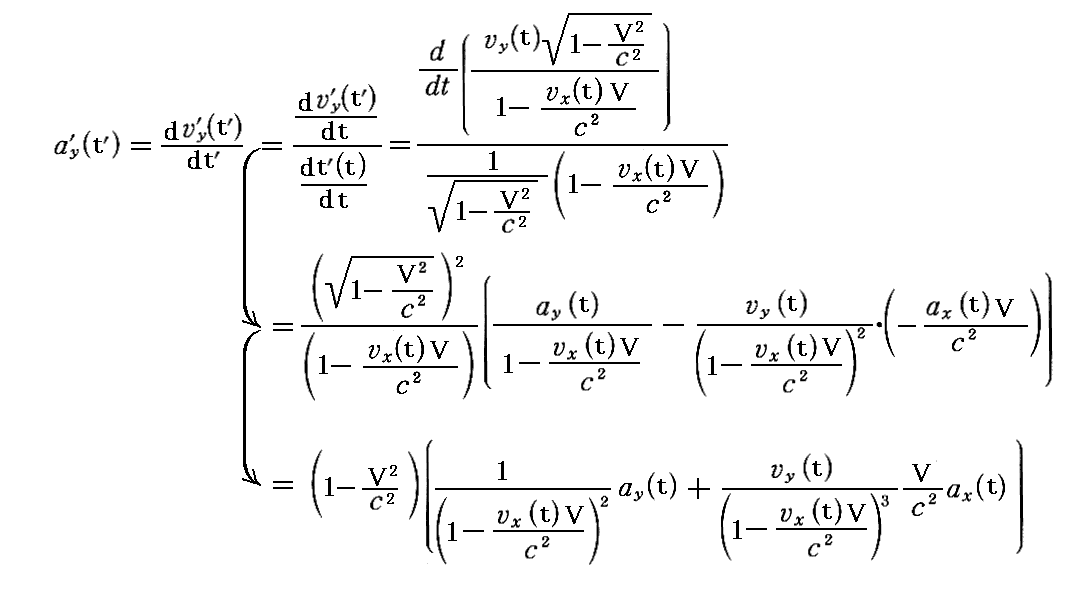
摨條偵

偲側傞丅
丂埲忋傪傑偲傔傞偲
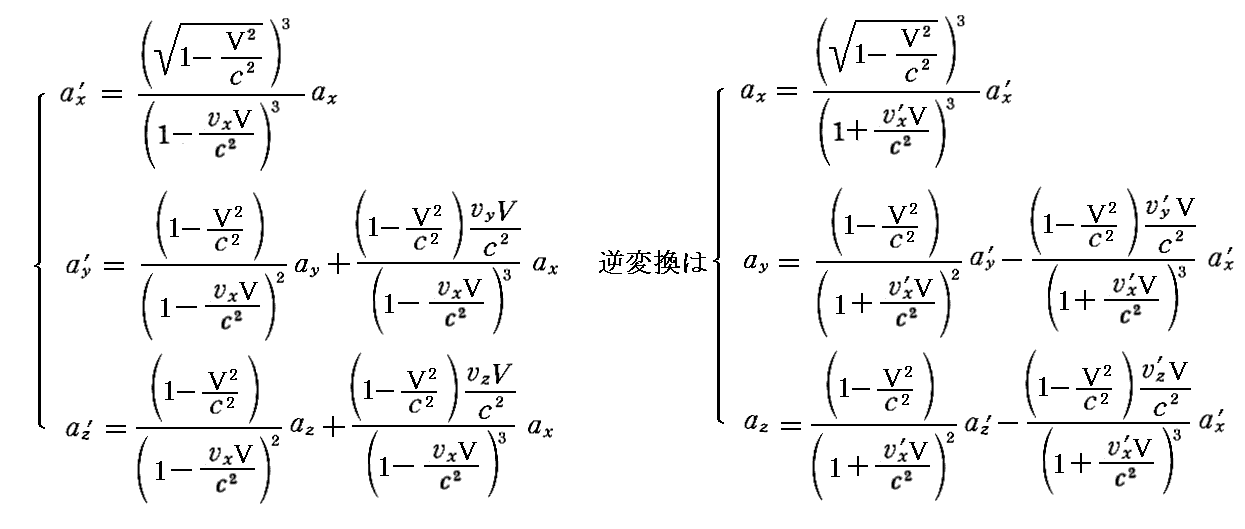
偲側傞丅媡曄姺偼憡懳惈棟榑尨棟偵傛傝丄倁傪亅倁偲偟丄乫偺晅偄偨検偲晅偄偰偄側偄検傪擖傟懼偊傟偽傛偄丅偙傟偑俁師尦壛懍搙偺乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼偱偡丅
乵曗懌愢柧侾乶
丂偙傟偼丄堦偮偺暔懱偑摦偄偰偄傞條巕傪尒偨偲偒丄俽宯偺暔嵎偟朹偲帪寁偱應掕偟偨暔懱偑帪崗 倲 偺弖娫偵帩偮壛懍搙乮倎x丄倎y丄倎z乯傪丄俽乫宯偵晅懏偺暔嵎偟朹偲帪寁偱應掕偟偨壛懍搙乮倎乫x丄倎乫y丄倎乫z乯偺帪崗 倲乫 偺弖娫偵偍偗傞應掕抣偵寢傃偮偗傞娭學幃偱偡丅傕偪傠傫丄偙傟傜偺壛懍搙偼摨偠暔懱偺摨偠帪崗乮俽宯偺帪寁偼 倲 傪俽乫宯偺帪寁偼 倲乫 傪帵偟偰偄傞偑乯偵偍偗傞偦傟偧傟偺嵗昗宯偱偺應掕抣傪寢傃偮偗偰偄傑偡丅
丂偙傟偼儘乕儗儞僣曄姺嫟曄側曄姺幃偱偼偁傝傑偡偑丄俁師尦懍搙偲摨條偵乬儘乕儗儞僣曄姺乭偦偺傕偺偱偼偁傝傑偣傫丅
丂
乮俀乯係尦壛懍搙
丂俀丏乮俁乯侾丏偱愢柧偟偨係尦懍搙儀僋僩儖偺怴夝庍傪峫椂偡傞偲乬係尦壛懍搙乭偺掕媊偼壓婰偺條偵偡傋偒偱偁傠偆丅俁師尦壛懍搙偲偺崿摨傪旔偗傞偨傔偵丄崱屻偼係尦壛懍搙傪昞偡偺偵僊儕僔儍暥帤偺乬兛乭傪梡偄傞偙偲偵偟傑偡丅
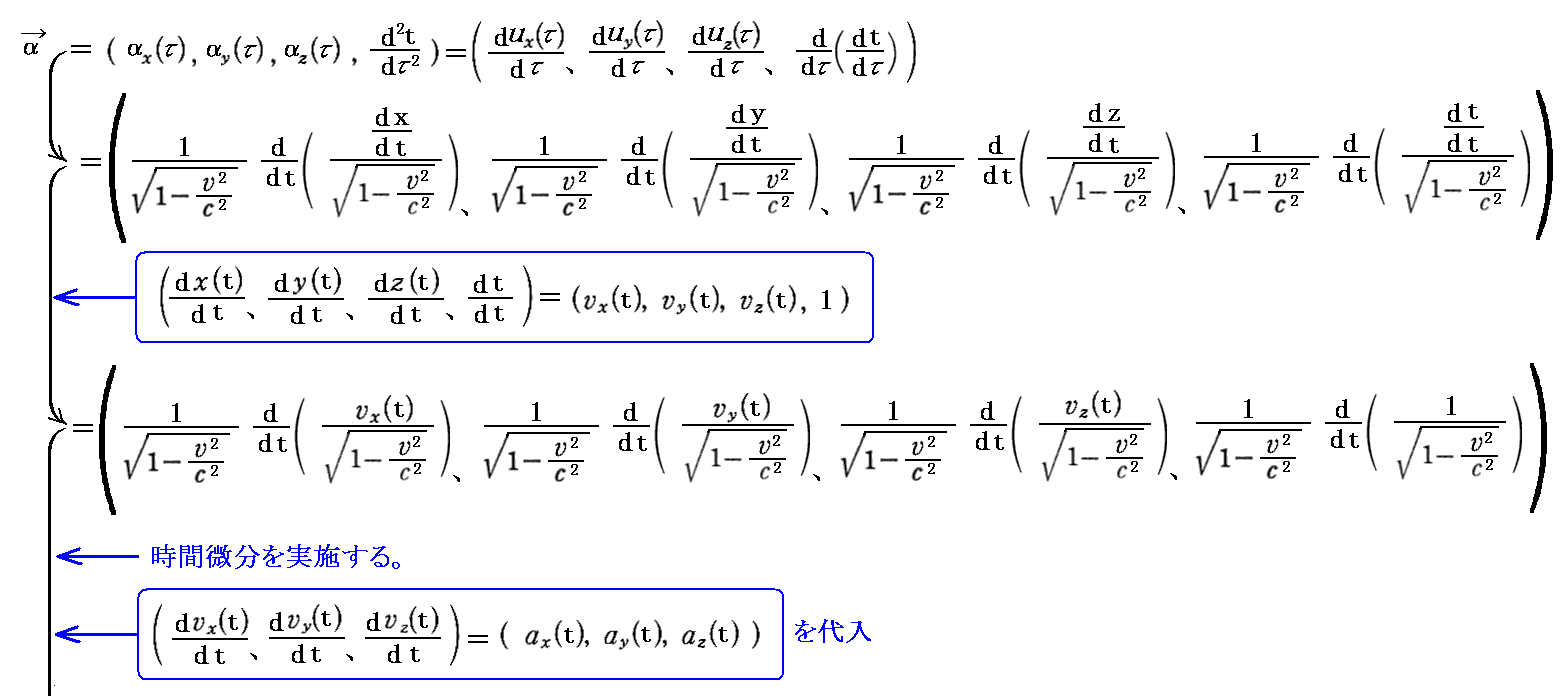
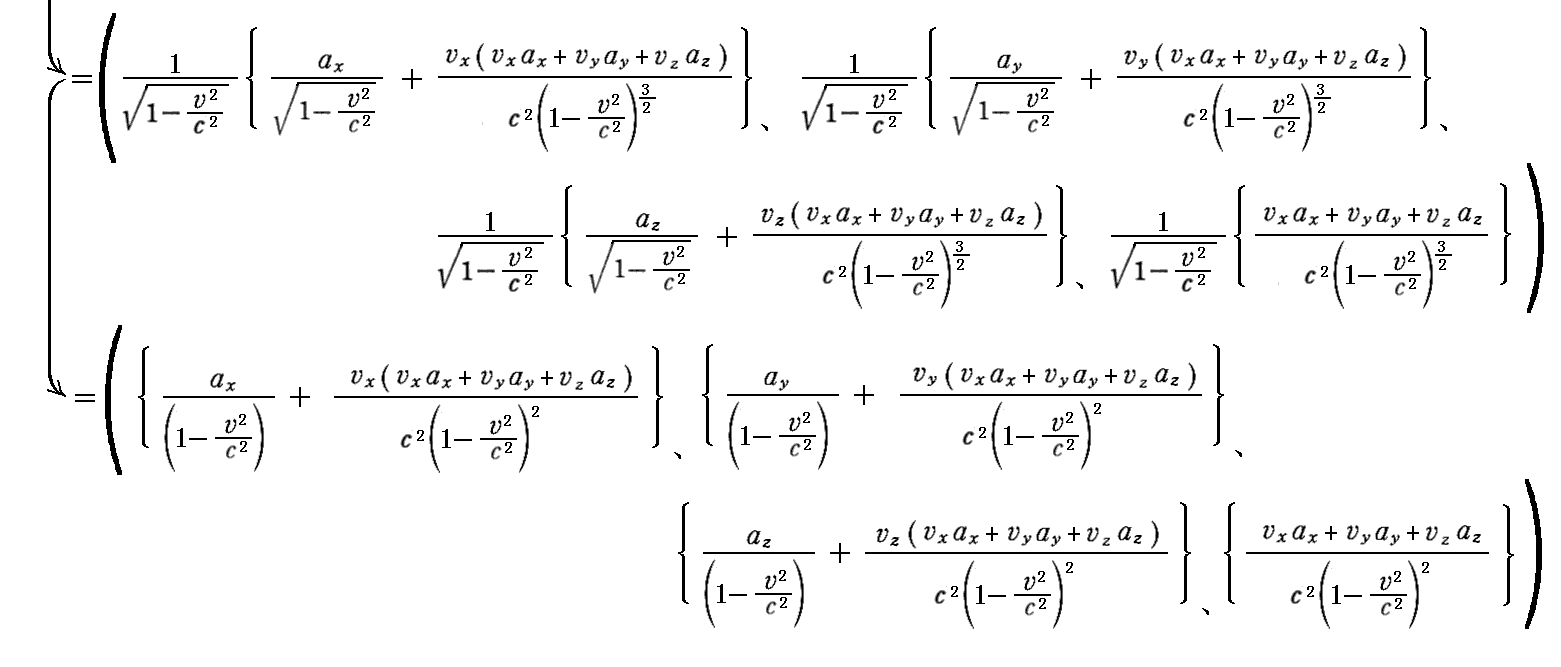
偮傑傝丄乬係尦壛懍搙乭偲偟偰
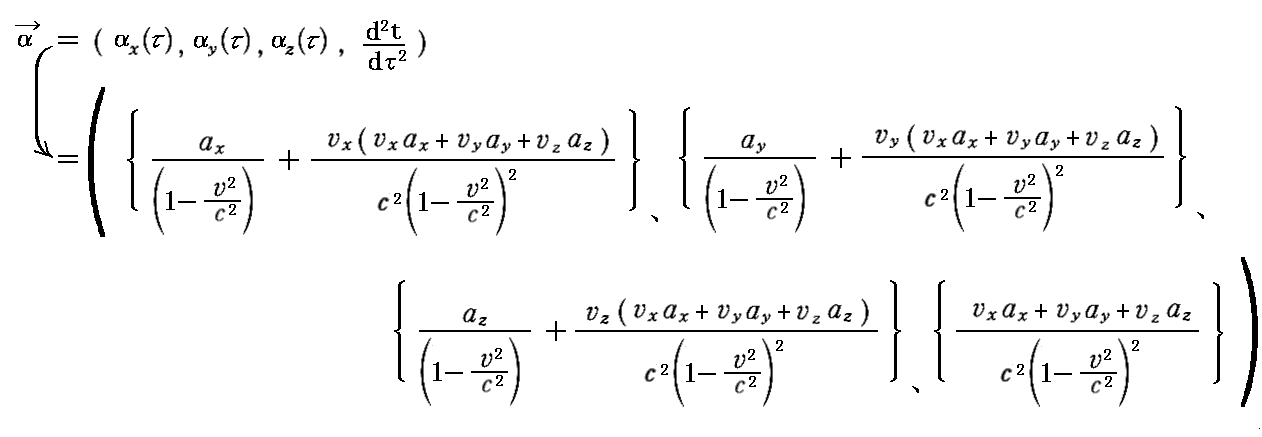
偲掕媊偡傟偽傛偄丅偙偙偱乮倴x丄倴y丄倴倸乯偼俁師尦懍搙偱偁傝乮倎x丄倎y丄倎倸乯偼俁師尦壛懍搙偱偡丅
丂偙傟偼丄摦偄偰偄傞堦偮偺暔懱傪娤嶡偟偨偲偒偵丄俽宯偺暔嵎偟朹偲暔懱偺屌桳帪冄偱應掕偟偨暔懱偑帪崗 倲 偺弖娫偵帩偮係尦壛懍搙乮兛x丄兛y丄兛z丄兛t乯偑丄俽宯偺暔嵎偟朹偲帪寁偱應偭偨俁師尦懍搙乮倴x丄倴y丄倴z乯丄俁師尦壛懍搙乮倎x丄倎y丄倎z乯偱偳偺傛偆偵昞偝傟傞偐傪帵偟偰偄傞丅
丂摨條偵丄摦偄偰偄傞堦偮偺暔懱傪俽乫宯偱娤嶡偟偨偲偒偵丄俽乫宯偺暔嵎偟朹偲暔懱偺屌桳帪冄乫偱應掕偟偨暔懱偑帪崗 倲乫 偺弖娫偵帩偮係尦壛懍搙乮兛x乫丄兛y乫丄兛z乫丄兛t乫乯偑丄俽乫宯偺暔嵎偟朹偲帪寁偱應偭偨俁師尦懍搙乮倴x乫丄倴y乫丄倴z乫乯丄俁師尦壛懍搙乮倎x乫丄倎y乫丄倎z乫乯偱偳偺傛偆偵昞偝傟傞偐傪帵偟偰偄傞丅
丂傕偪傠傫丄偙傟傜偺係尦壛懍搙偼摨偠暔懱偺摨偠帪崗乮俽宯偺帪寁偼 倲 傪俽乫宯偺帪寁偼 倲乫 傪帵偟偰偄傞乯偵偍偗傞偦傟偧傟偺嵗昗宯偱偺應掕抣偱偡丅
丂俁師尦壛懍搙偑儘乕儗儞僣曄姺嫟曄偺曄姺幃偩偭偨偺偲堘偭偰丄偙偺係尦壛懍搙偼乬儘乕儗儞僣曄姺乭偦偺傕偺傪枮偨偟偰偄傞偙偲偑徹柧偱偒傑偡乮師愡嶲徠乯丅
乵曗懌愢柧侾乶
丂係尦懍搙偺嬻娫惉暘偼俁師尦懍搙偺惉暘偺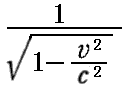 攞偱偟偨偑丄偦偺嬻娫偵偍偗傞懍搙儀僋僩儖曽岦偼堦抳偟偰偄傑偟偨丅
攞偱偟偨偑丄偦偺嬻娫偵偍偗傞懍搙儀僋僩儖曽岦偼堦抳偟偰偄傑偟偨丅
丂偟偐偟丄係尦壛懍搙偺嬻娫惉暘偼俁師尦壛懍搙偺惉暘偲丄偦偺儀僋僩儖偲偟偰偺乬戝偒偝乭傕乬曽岦乭傕堦抳偟偰偄側偄偙偲偵拲堄偟偰偔偩偝偄丅堘偭偰偄傑偡偑丄堦斒憡懳惈棟榑偱偼係尦壛懍搙偑昁梫偱偡丅
丂
乮俁乯係尦壛懍搙偼儘乕儗儞僣曄姺偵廬偆
丂係尦壛懍搙偼丄俁師尦壛懍搙偲堘偭偰丄乬儘乕儗儞僣曄姺乭偵廬偭偰俽宯偱偺娤應抣偲俽乫宯偱偺娤應抣偑寢傃偮偗傜傟傑偡丅偟偐偟丄偙偺徹柧偼偐側傝柺搢偱偡丅偦偺偨傔偁傜偐偠傔徹柧偵梡偄傞岞幃傪弨旛偟偰偍偒傑偡丅
侾丏徹柧偵梡偄傞岞幃
丂徹柧偵偼丄俁師尦懍搙偲俁師尦壛懍搙偺曄姺幃偑昁梫偱偡丅偦傟傜傪岞幃嘆偲岞幃嘇偲偟傑偡丅
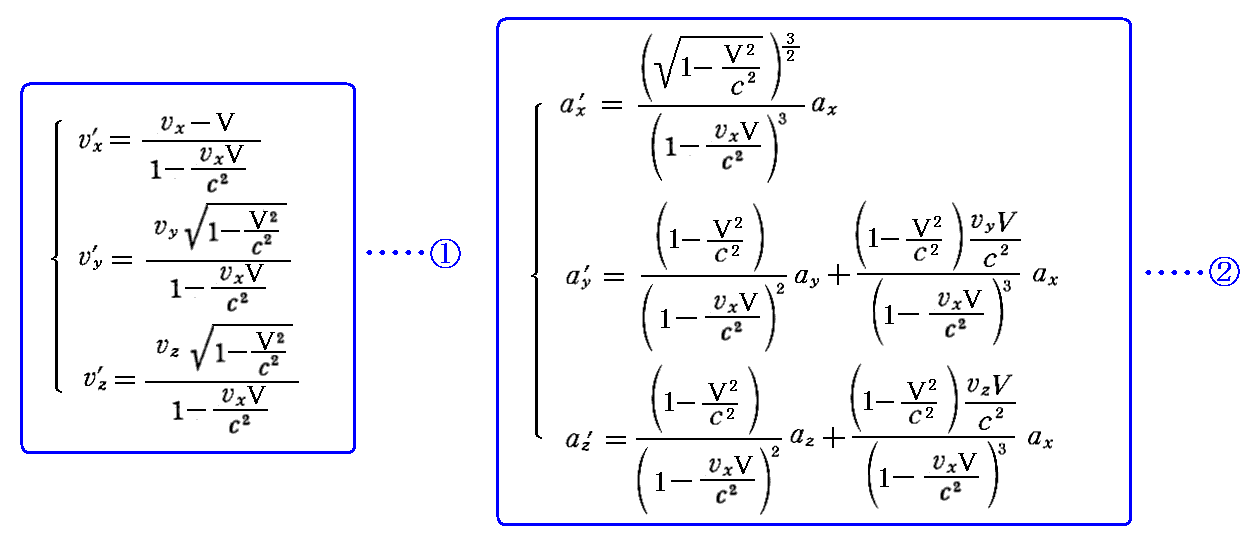
偙傟傜偼儘乕儗儞僣曄姺偱偼側偄偑丄儘乕儗儞僣曄姺嫟曄偺曄姺幃偱偟偨丅
丂偝傜偵丄係尦懍搙偺儘乕儗儞僣曄姺傪摫偄偨偲偒棙梡偟偨曄姺岞幃
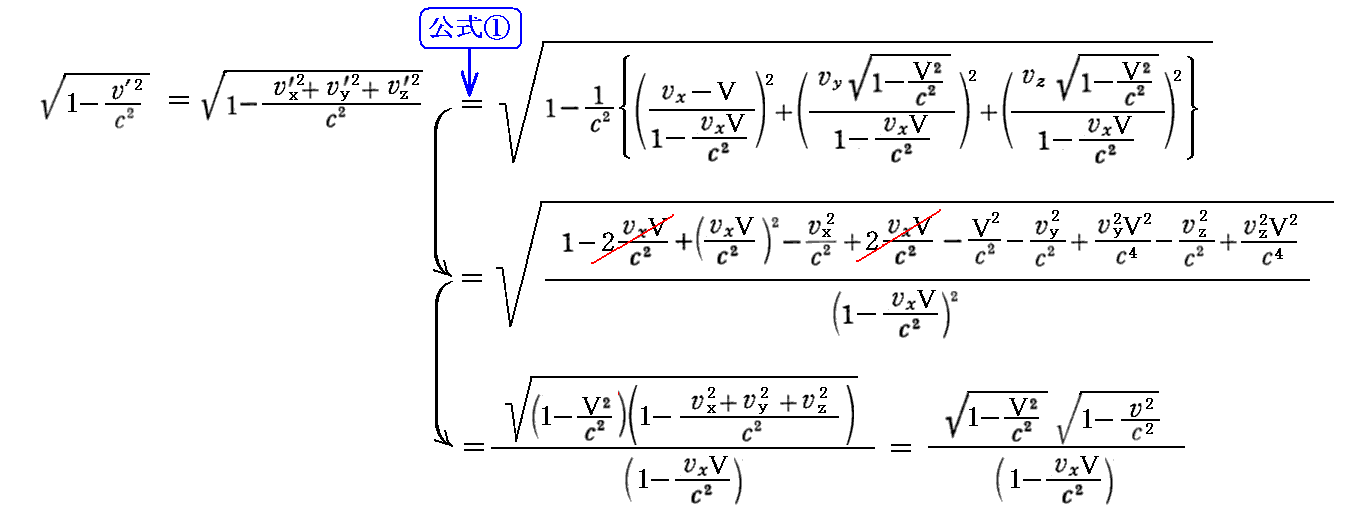
偑昁梫偱偡丅偙偺岞幃偼岞幃嘆傪梡偄偰摫偐傟傑偡丅
丂忋婰岞幃偐傜壓婰偺岞幃嘊丄岞幃嘋丄岞幃嘍偑摫偗傑偡丅
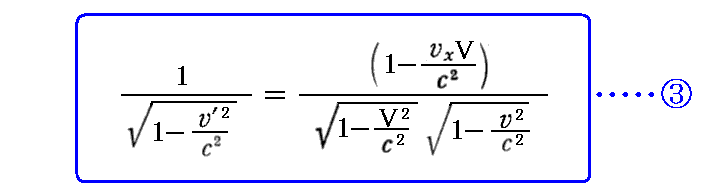
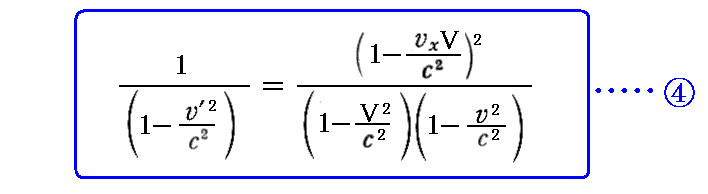
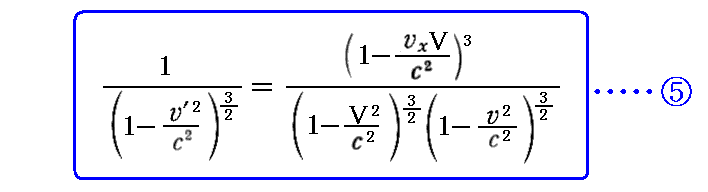
偝傜偵丄壓婰偺岞幃嘐偑摫偗傑偡丅
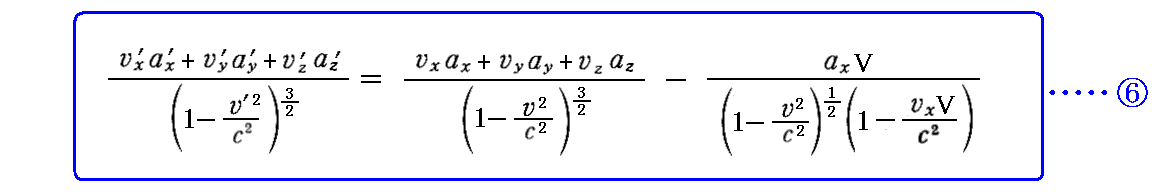
岞幃嘐偺徹柧偼丄岞幃嘆丄岞幃嘇丄岞幃嘍傪梡偄偰丄師偺傛偆偵偡傟偽傛偄丅
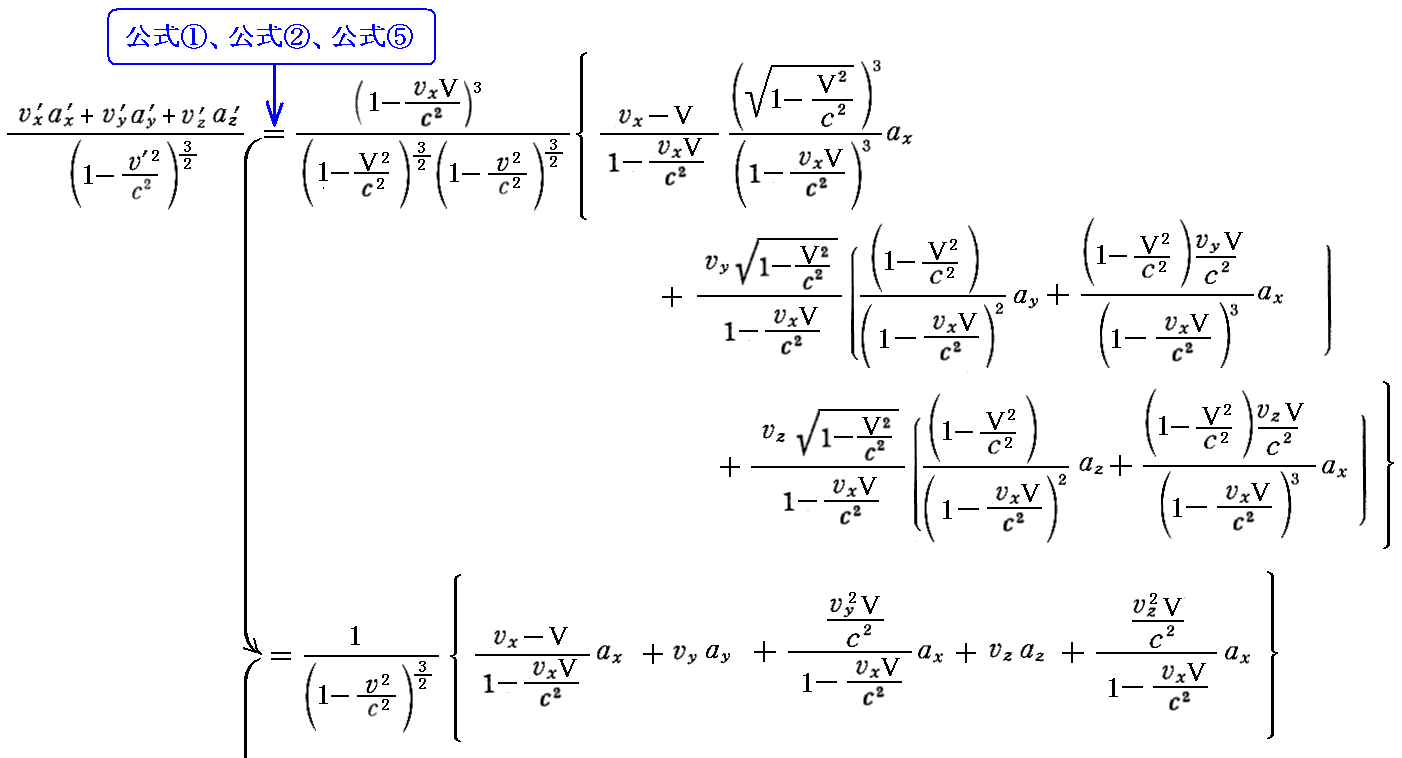
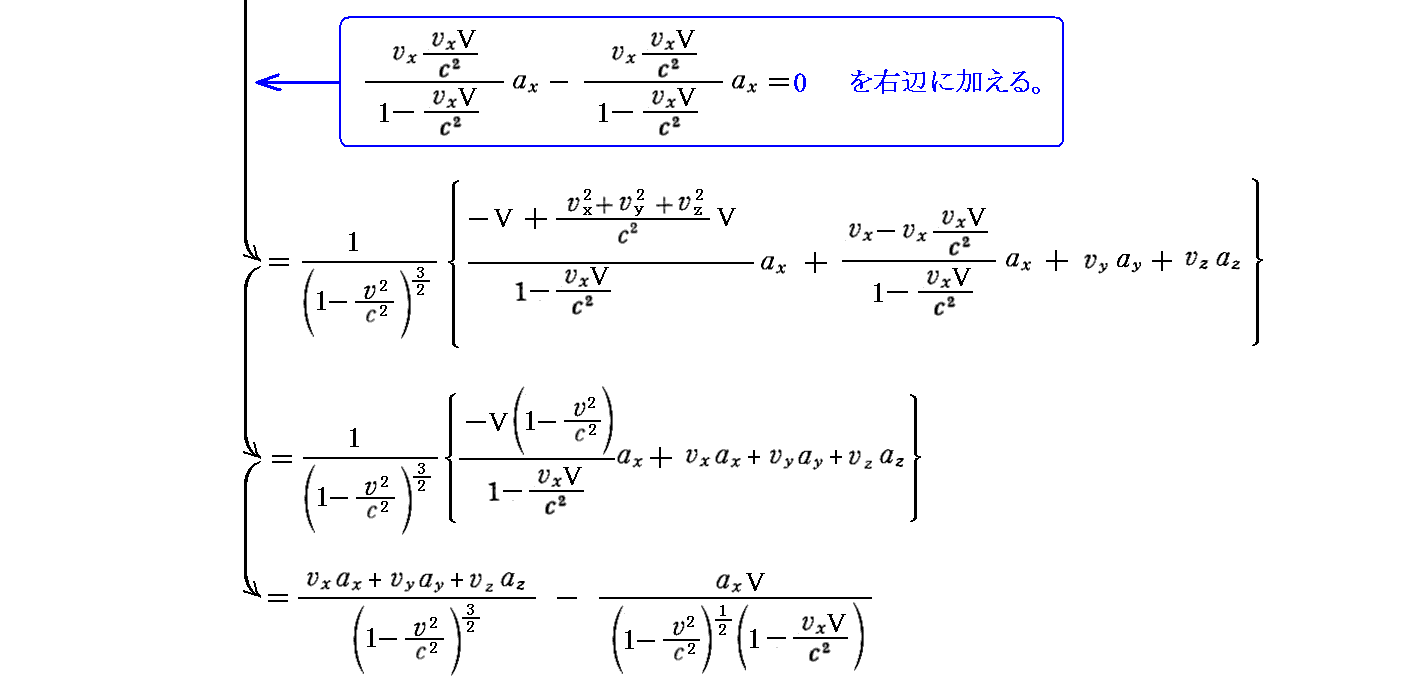
丂
俀丏係尦壛懍搙偼儘乕儗儞僣曄姺偵廬偆
丂岞幃嘆丄岞幃嘇丄岞幃嘊丄岞幃嘋偲岞幃嘐傪梡偄傟偽丄係尦壛懍搙偑乬儘乕儗儞僣曄姺乭偵廬偭偰曄姺偝傟傞偙偲偑徹柧偱偒傞丅
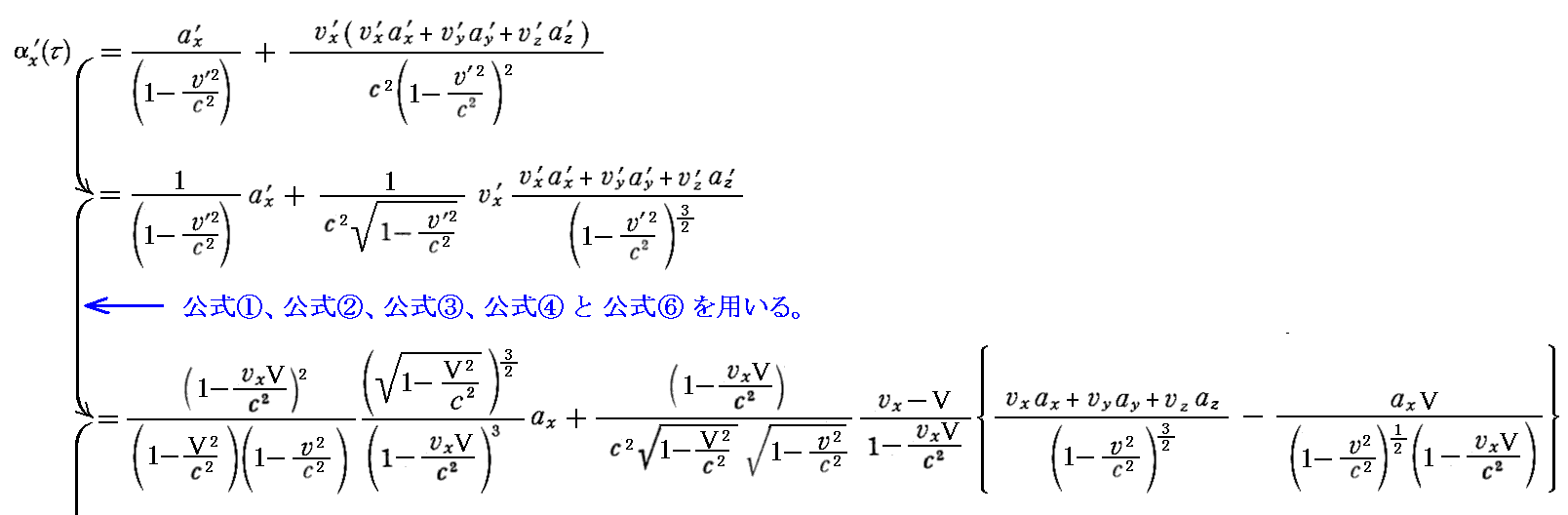
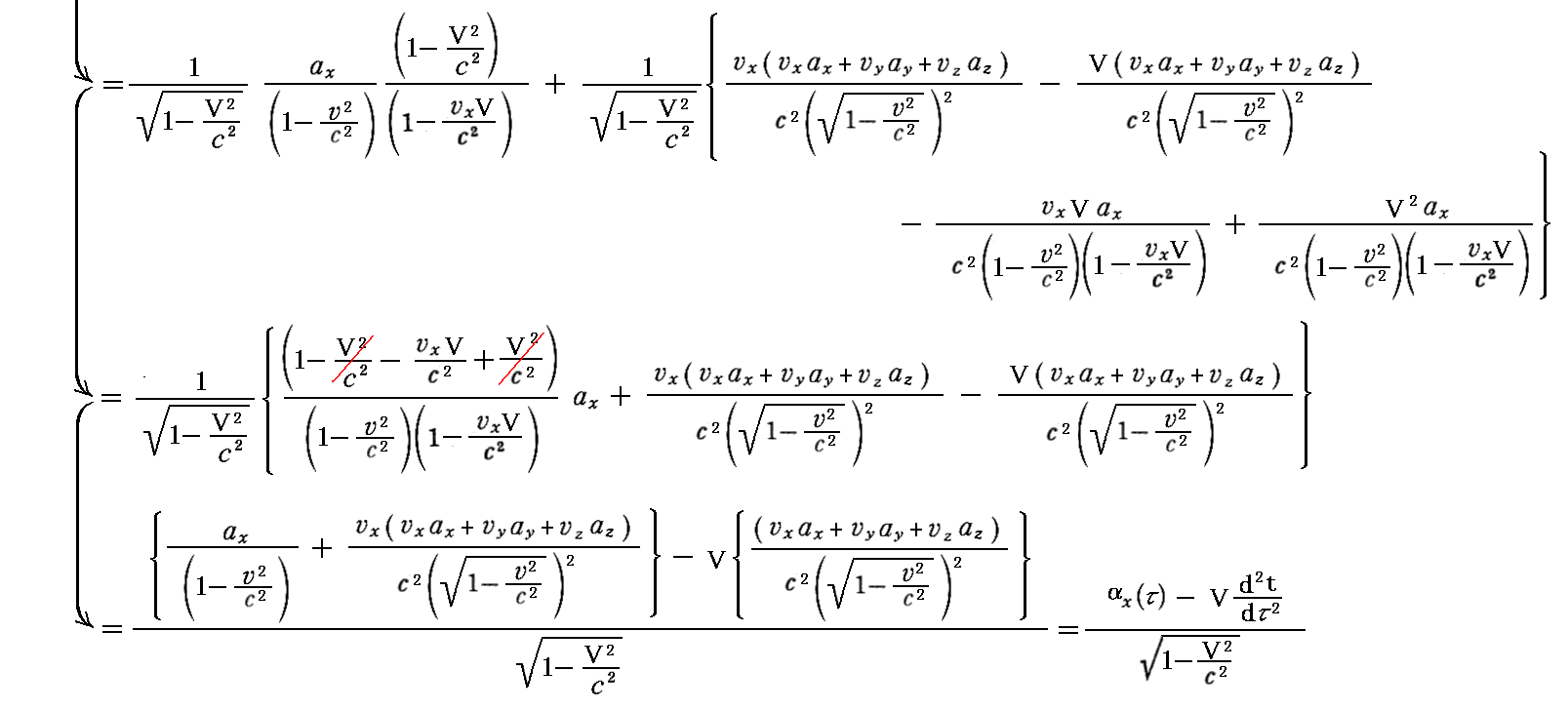

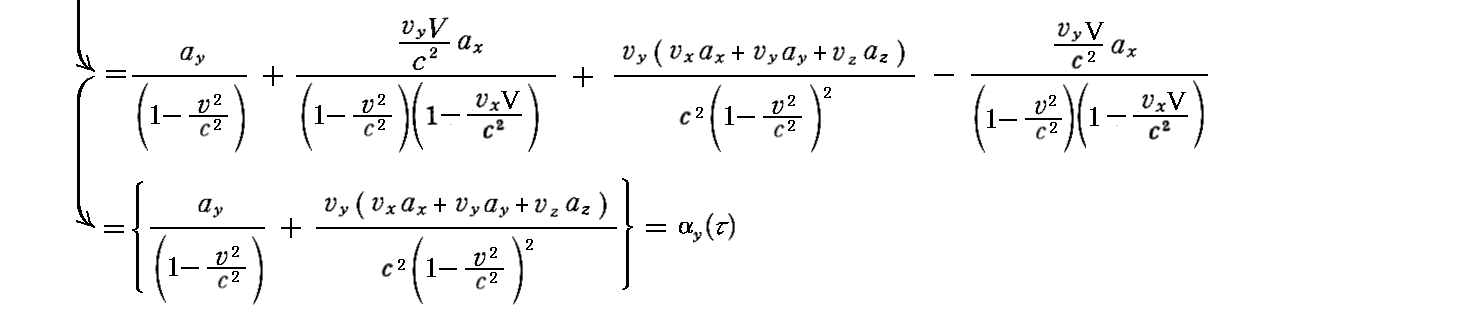
摨條偵偟偰
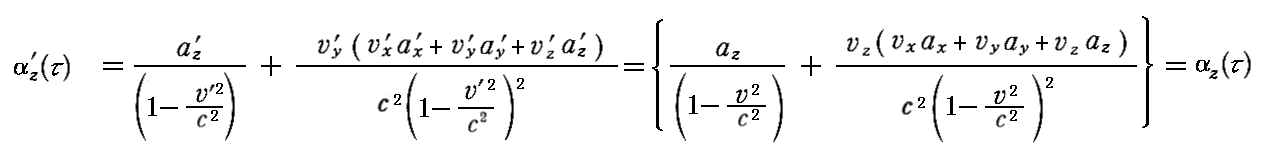
偝傜偵
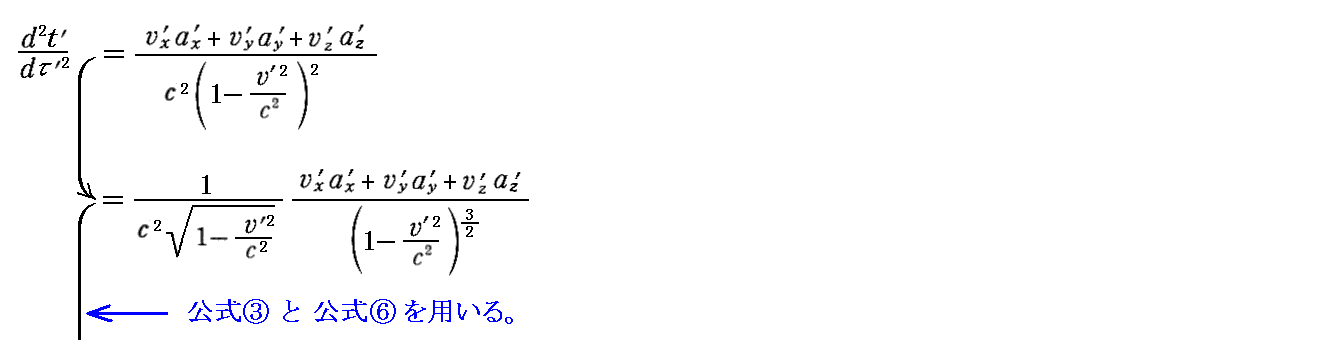
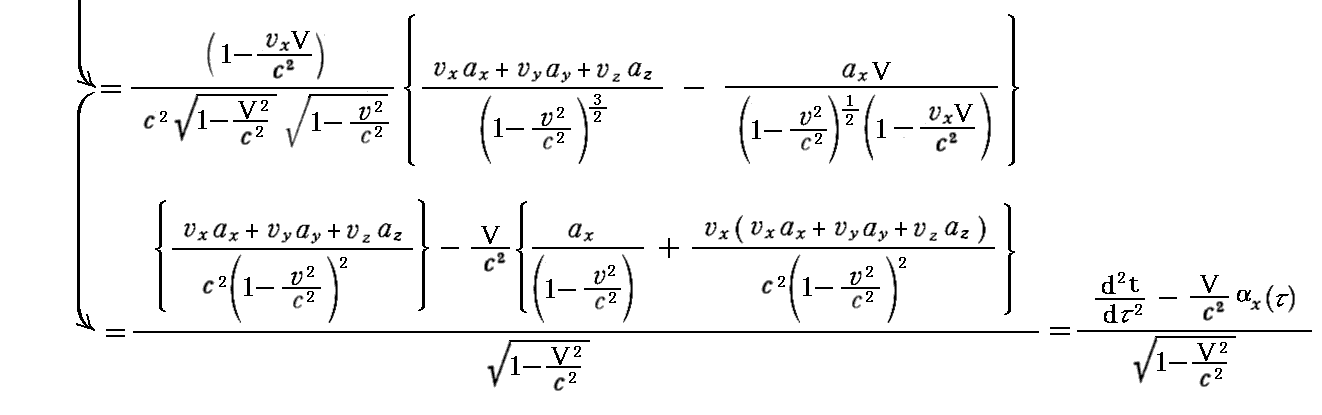
偑摼傜傟傞丅
丂偝傜偵曗懌偡傞偲丄係尦壛懍搙昞尰偵偡傞堦偮慜偺抜奒偺幃偑俁師尦壛懍搙昞尰偱偺乬儘乕儗儞僣曄姺幃乭偵惉偭偰偄傞偙偲偵拲堄偟偰壓偝偄丅
丂埲忋傪傑偲傔傞偲丄乬係尦壛懍搙乭偼俽宯偐傜俽乫宯偺抣偵埲壓偺乬儘乕儗儞僣曄姺乭偵傛偭偰曄姺偝傟傞丅

媡曄姺偼憡懳惈尨棟偐傜丄倁傪亅倁偲偟丄乫偺晅偄偨検偲晅偄偰偄側偄検傪擖傟懼偊傟偽傛偄丅
乵曗懌愢柧侾乶
丂忋婰偺係尦壛懍搙偺儘乕儗儞僣曄姺幃偵俁師尦懍搙偲俁師尦壛懍搙偵傛傞昞尰
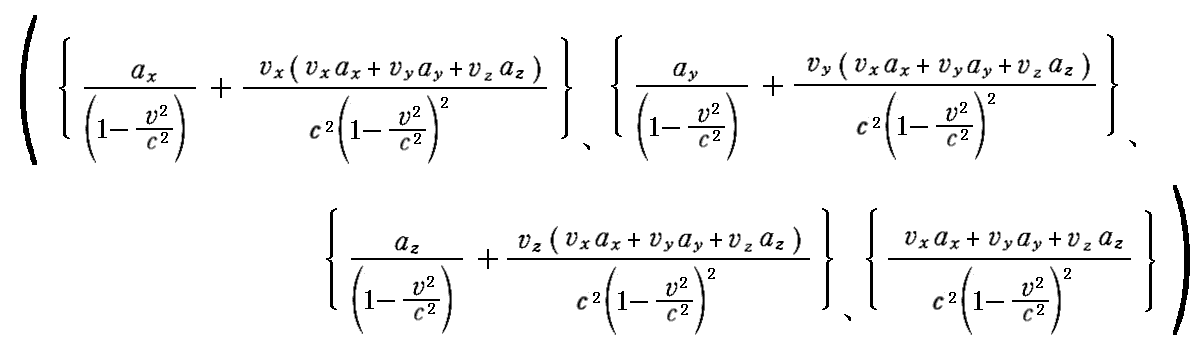
傪戙擖偡傞偲俁師尦壛懍搙昞尰偱偺乬儘乕儗儞僣曄姺幃乭
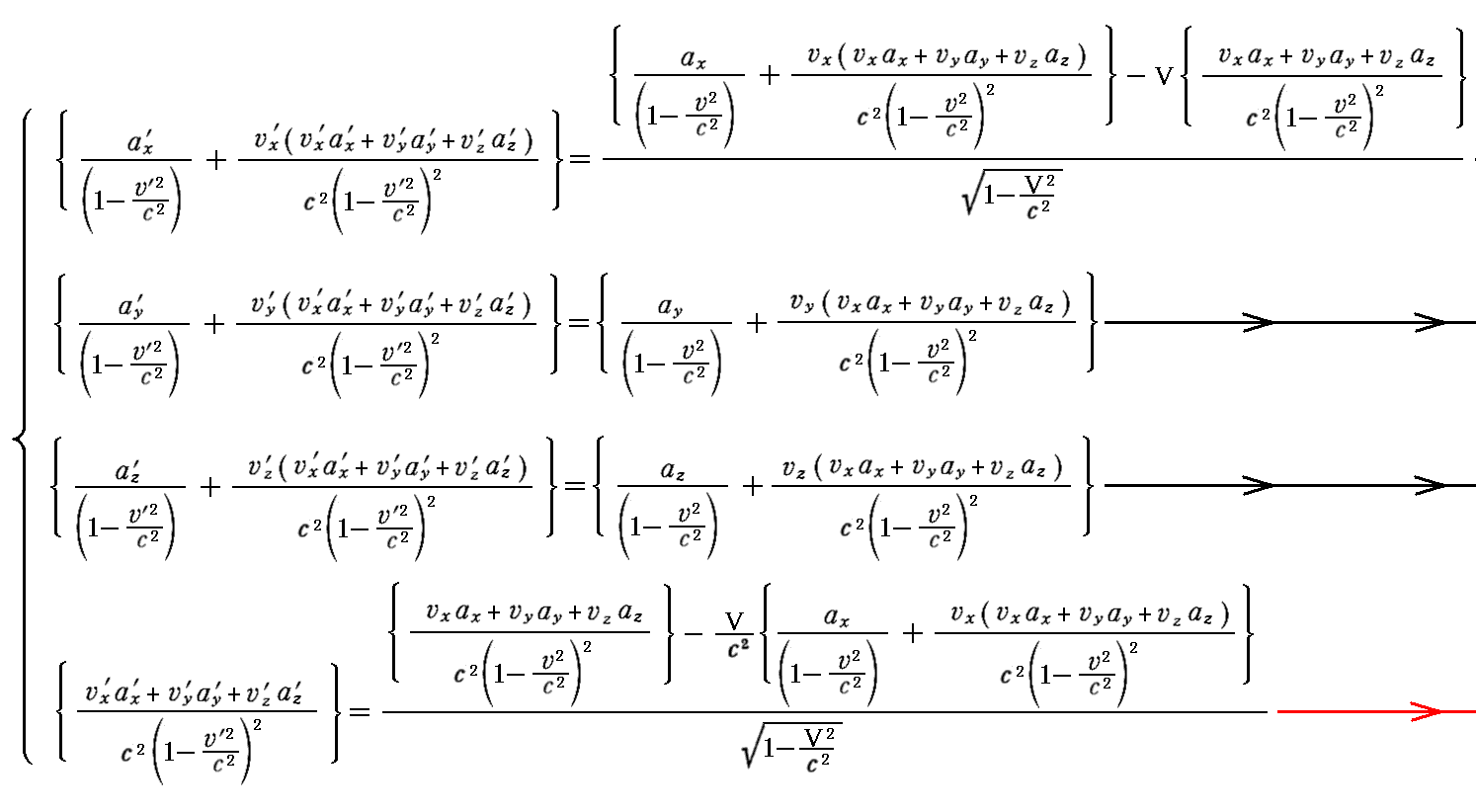
偲側傞偺偱偡偑丄偦偺嬻娫惉暘俁幃偺嵍曈戞堦崁傪係丏乮俁乯侾丏偱愢柧偟偨岞幃嘋偱曄宍偡傞丅嵍曈戞擇崁偼岞幃嘆丄岞幃嘊丄岞幃嘐偱抲偒姺偊偰塃曈偵堏崁偟偰惍棟偡傞偲丄嵟弶偺俁幃偼俁師尦壛懍搙偺乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼偮傑傝岞幃嘇偵婣拝偟傑偡丅
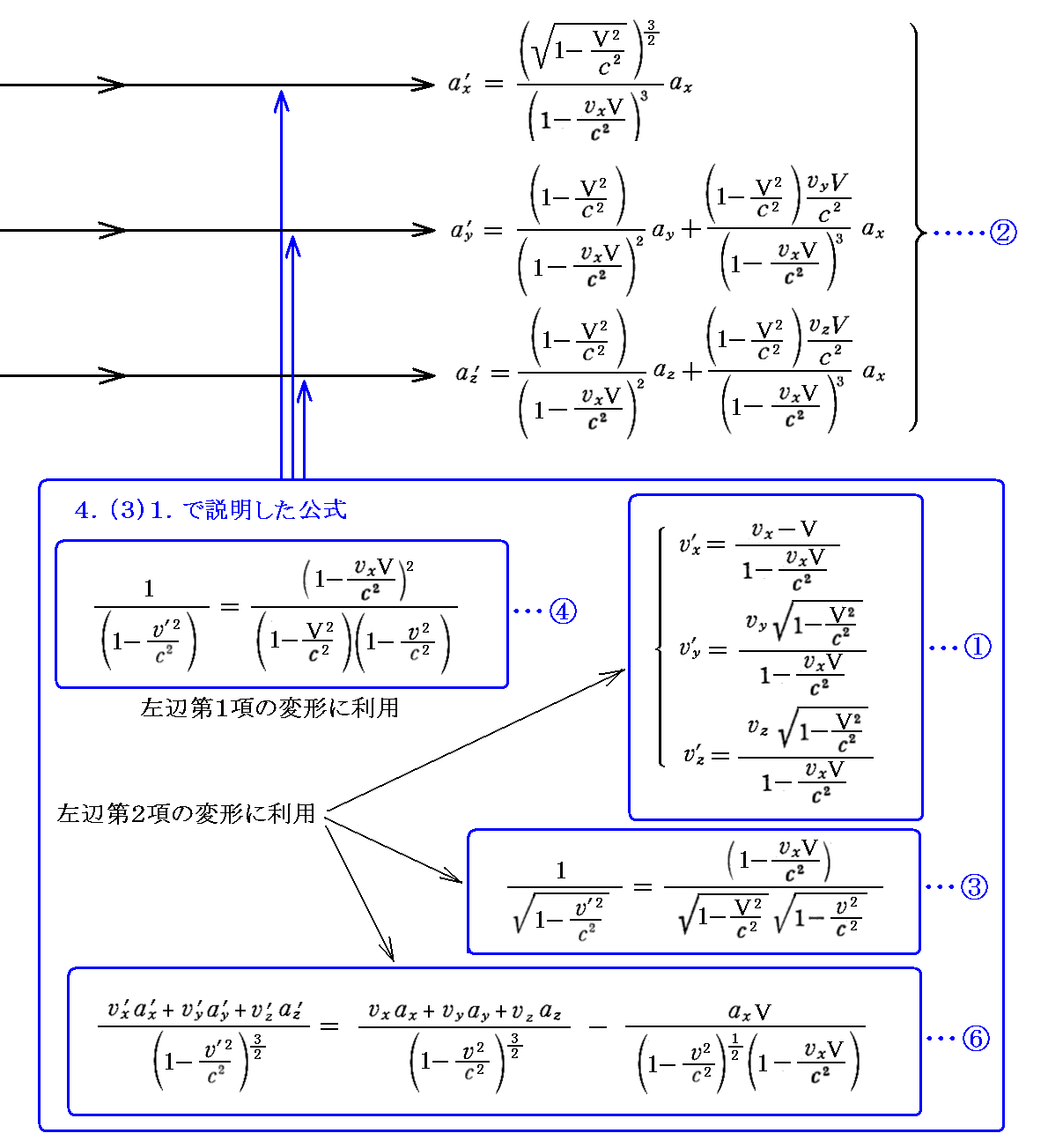
丂傑偨丄帪娫惉暘偱偁傞戞係幃偼丄嵍曈偵岞幃嘋傪揔梡偟偰曄宍丒惍棟偡傟偽
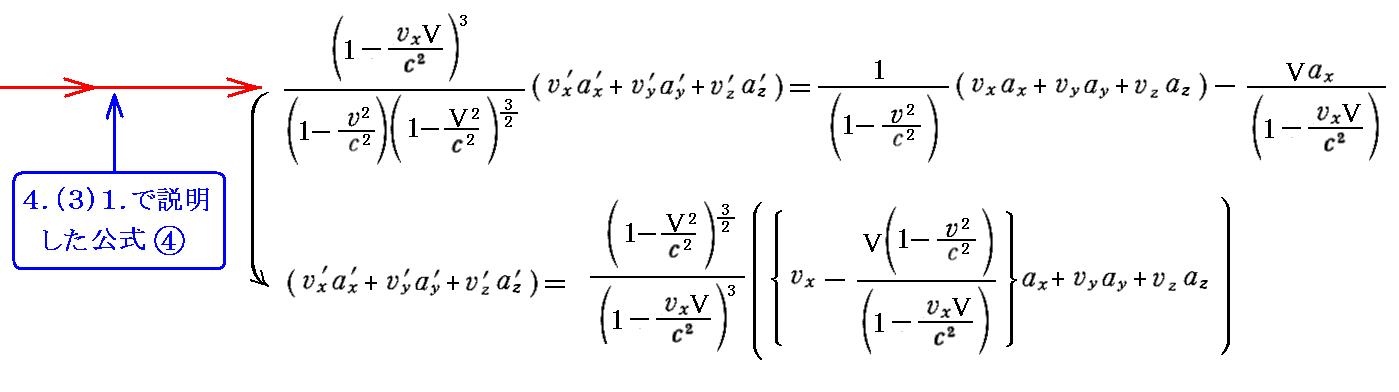
偲側傝傑偡丅偨偩偟偙傟偼偡偱偵媮傔偨岞幃嘐偲摨偠偱偡丅
丂傕偪傠傫丄偙傟傜偺幃曄宍偼係丏乮俁乯俀丏偱峴偭偨幃曄宍傪媡偵偨偳傞偺偲摨偠帠偱偡丅
丂
俁丏係尦壛懍搙偑廬偆幃
丂係尦壛懍搙偼乬儘乕儗儞僣曄姺乭偵廬偭偰曄姺偝傟傞偺偱丄懠偺係尦儀僋僩儖検偲摨偠傛偆偵
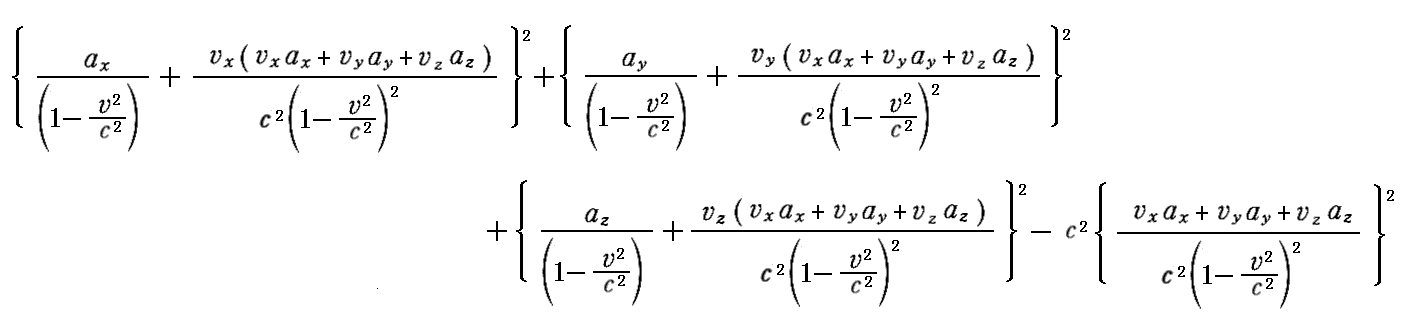
偼乬儘乕儗儞僣曄姺乭偵懳偟偰晄曄側検偲側傞丅
丂偮傑傝丄乬係尦壛懍搙乭偵晅偄偰
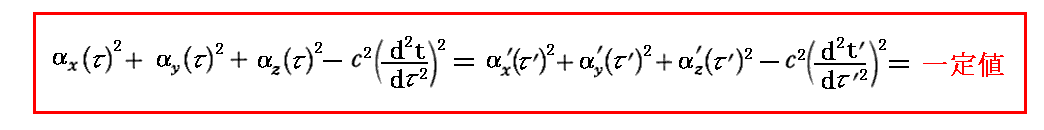
偑忢偵惉傝棫偮丅偙偺偙偲偼幚嵺偵儘乕儗儞僣曄姺幃偱曄姺偟偰傒傟偽娙扨偵妋擣偱偒傑偡丅
丂
俆丏係尦椡
丂係尦壛懍搙傪尦偵偟偰丄乬儘乕儗儞僣曄姺乭偵廬偆乬係尦椡乭偺掕媊幃傪尒偮偗傑偡丅
乮侾乯俁師尦椡偺曄姺幃
丂係尦椡傪摫偔弨旛偲偟偰丄俁師尦椡偺儘乕儗儞僣曄姺嫟曄偺曄姺幃傪暅廗偟傑偡丅
侾丏暔懱偺懍搙偑俽乫宯偺堏摦懍搙倁偲暯峴側応崌
丂俁師尦椡偺儘乕儗儞僣曄姺嫟曄偺曄姺幃偼丄暿峞乽揹帴応偺憡懳惈乿俆丏乵曗懌愢柧俁乶偱偡偱偵媮傔傑偟偨偑丄偦偺偲偒偺俽宯偐傜尒偨俽乫宯偺堏摦懍搙傪倴偱偼側偔倁偱昞偟捈偟傑偡丅
丂俽宯偺倶幉曽岦偵懍搙倁偱摦偔俽乫宯娫傊偺椡偺曄姺幃傪昞偟偰偄傞偺偩偑丄偦偙偱偼俁師尦椡偺曄姺傪峫偊偰偄傞弖娫偵偼丄椡偑摥偄偰偄傞幙揰偺俽乫宯偺懍搙偼倶乫幉曽岦偵 倴x乫 偱偁傞偲偟丄摨偠弖娫偺摨偠幙揰偺俽宯偐傜尒偨懍搙傕倶幉曽岦偵 倴x亖乮倴x乫亄倁乯乛乮侾亄倴x乫倁乛們2乯 偲偟偰偄偨丅偦偺偲偒偺恾傪杮峞偱偺婰崋偵彂偒捈偟偰嵞榐偡傞偲
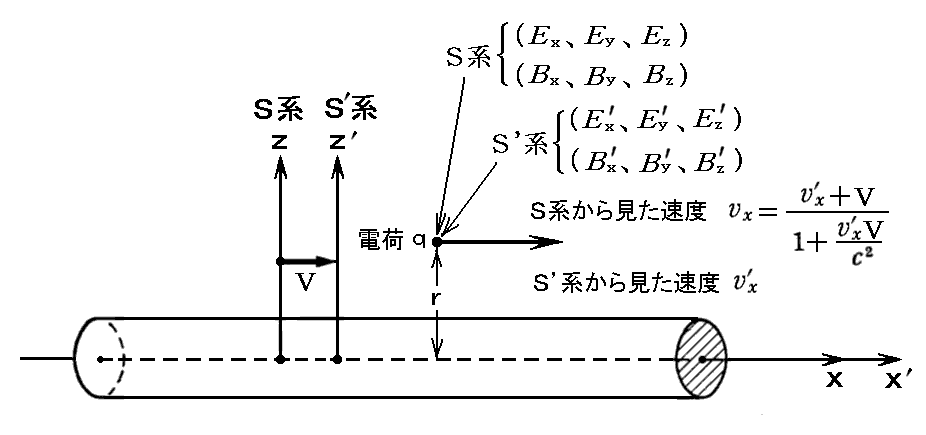
偺忬嫷偱偺曄姺幃偱偟偨丅偮傑傝幙揰乮揹壸乯偺懍搙儀僋僩儖偺曽岦偑俽乫宯偺俽宯偵懳偡傞堏摦曽岦偲暯峴側応崌偱偟偨丅
丂偙偺偲偒丄乽揹帴応偺憡懳惈乿俆丏乵曗懌愢柧俀乶偱椡偺曄姺幃傪摫偔偲偒偵偼揹帴婥妛偵偍偗傞乬儘乕儗儞僣偺椡偺朄懃乭傪棙梡偟偰偄傑偡偑丄偦偺彆偗傪庁傝偢偵媮傔偨偺偑乽揹帴応偺憡懳惈乿俆丏乵曗懌愢柧俁乶偱偡丅
丂椉幰偺堘偄偼丄偦偙偺拲堄彂偒乽揹帴応偺憡懳惈乿俆丏乵曗懌愢柧俀亅侾乶丄傑偨偼暿峞乽憡懳榑揑椡妛乿俀丏乵曗懌愢柧俉乶傪偛棗偵側傟偽夝傝傑偡丅
丂
俀丏暔懱偺懍搙偑擟堄偺曽岦傪岦偄偰偄傞応崌
丂埲壓偱俁師尦椡偺曄姺幃傪傕偆彮偟堦斒壔偟傑偡丅偮傑傝丄俽宯偲俽乫宯偐傜尒偨幙揰偺俁師尦懍搙傪
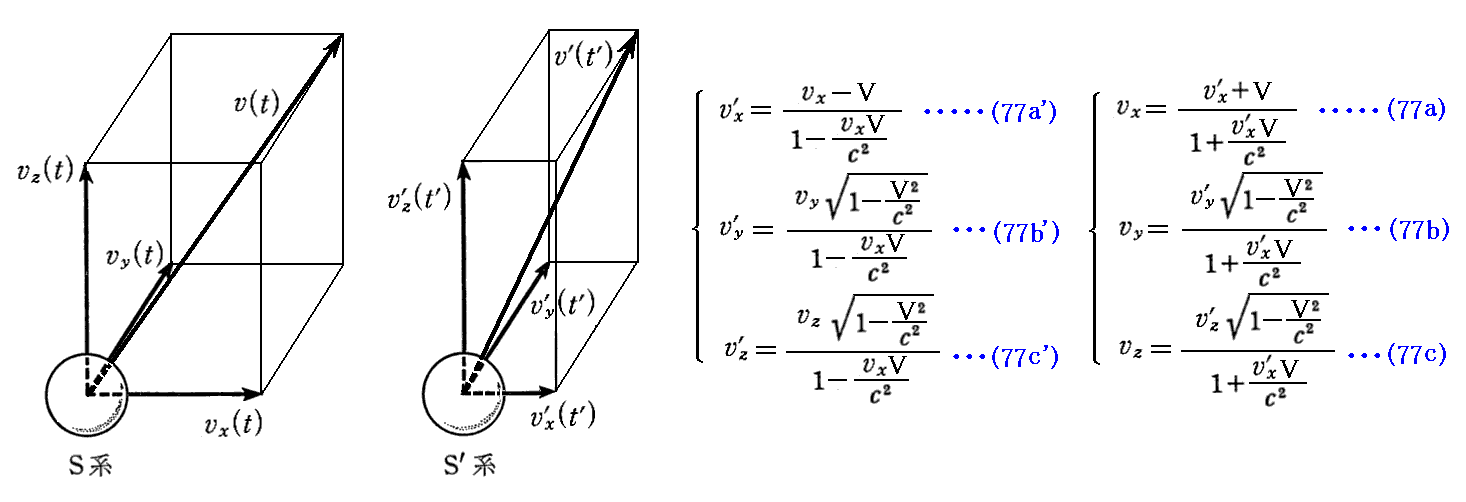
偱偁傞偲偟丄幙揰偺懍搙偑昁偢偟傕倶幉丄倶乫偵暯峴偱偼柍偄堦斒揑側応崌傪庢傝忋偘傑偡丅
丂傕偪傠傫丄偙偙偱傕俽乫宯偼俽宯偺倶幉偺惓曽岦傊懍搙 倁 偱摦偄偰偄傞偲偟偰偄傑偡丅偦偟偰椉嵗昗宯偺屌桳帪娫 倲 偲 倲乫 偼椉宯偺尨揰偑偡傟堘偭偨弖娫傪 0 偲偟偰應傝巒傔傞丅
丂暿峞乽揹帴応偺憡懳惈乿俆丏乵曗懌愢柧俁乶偺庤弴傪堦斒揑側幙揰懍搙偺応崌偵奼挘偡傞偲丄俁師尦椡偺儘乕儗儞僣曄姺嫟曄偺曄姺幃偼壓婰偺條偵偟偰媮傑傝傑偡丅
丂傑偢丄暿崁乽憡懳榑揑椡妛乿俁丏乮係乯乵曗懌愢柧俀乶偱媮傔偨傛偆偵丄(塣摦検丒幙検)係尦儀僋僩儖偺乬儘乕儗儞僣曄姺幃乭偼
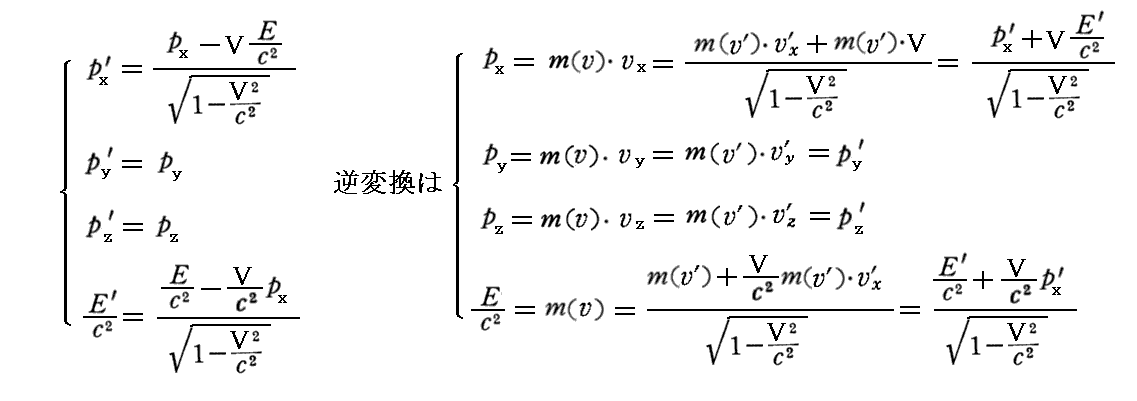
偱偟偨丅偙偺偙偲傪梡偄偰暿峞乽揹帴応偺憡懳惈乿俆丏乵曗懌愢柧俁乶偺庤弴傪孞傝懼偊偡偺偱偡偑丄摨偠孞傝曉偟傪偟偰傕擻偑側偄偺偱丄偙偙偱偼俽乫宯仺俽宯偺曄姺幃偱偼側偔偰丄俽宯仺俽乫宯偺曄姺幃傪媮傔傞帠偵偟傑偡丅
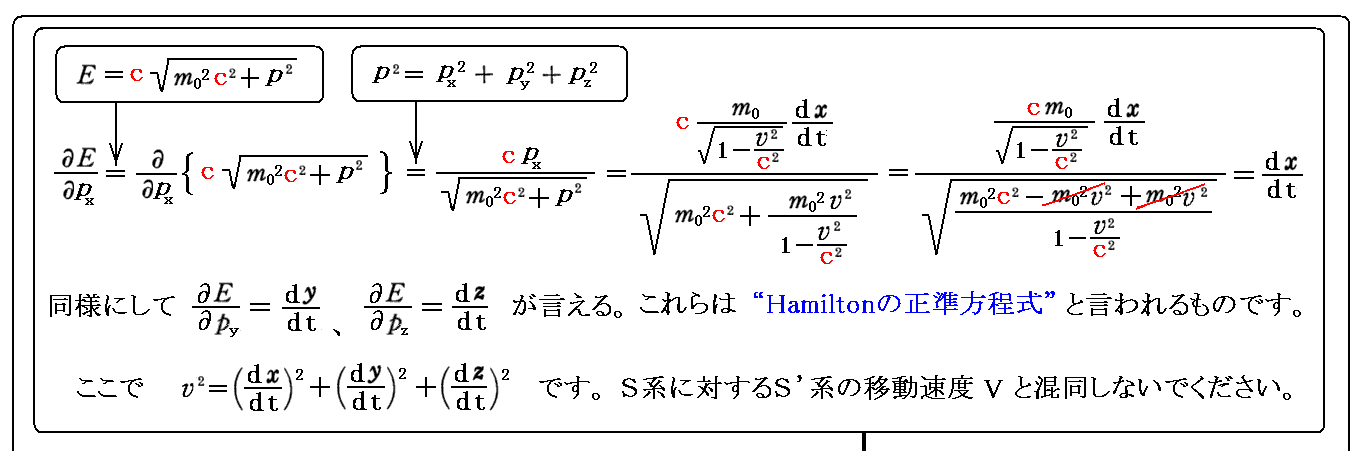
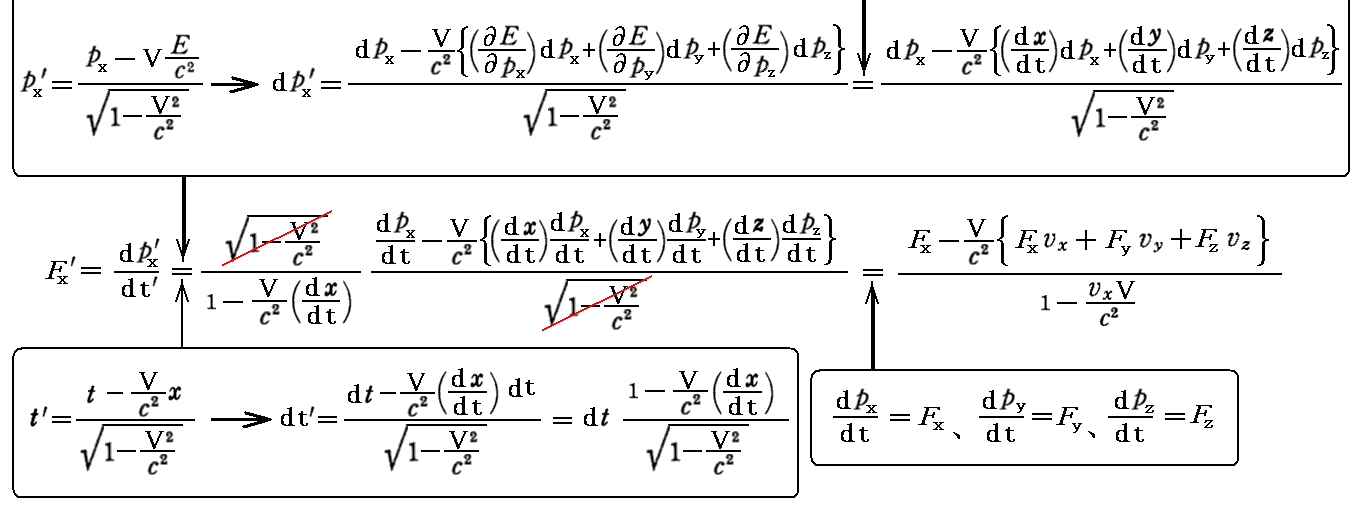
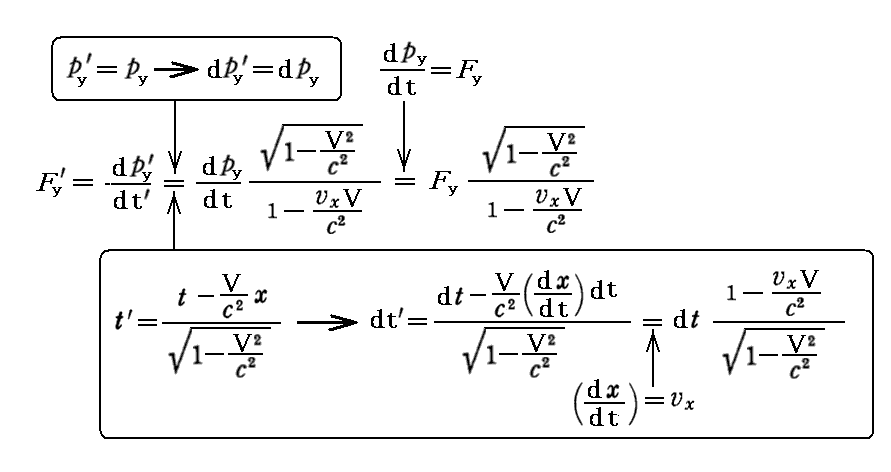
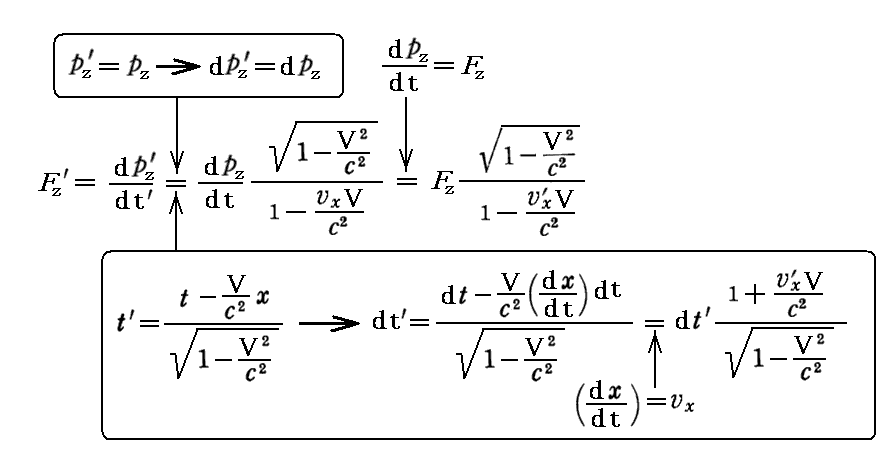
偲側傝傑偡偐傜丄寢嬊
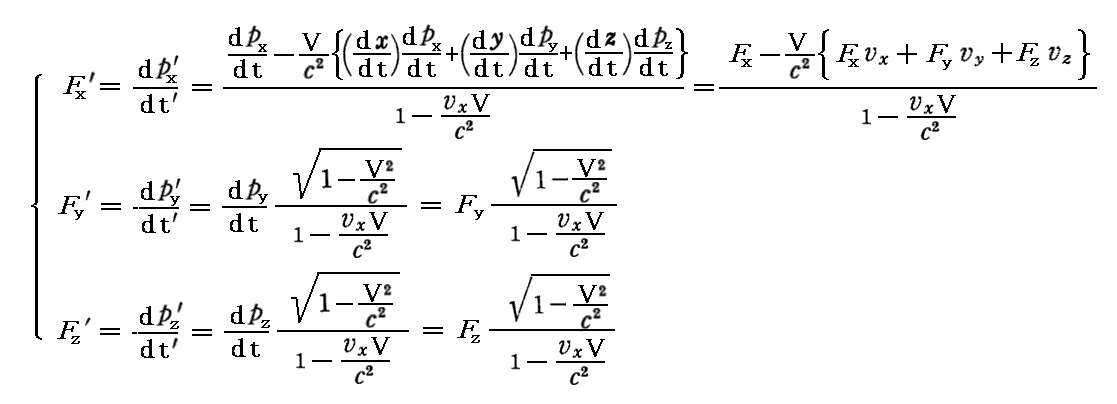
偲側傝傑偡丅
丂俽乫宯仺俽宯傊偺曄姺幃偼丄俽乫宯偱偺嶰師尦椡偐傜弌敪偟偰俽乫宯仺俽宯傊偺(嵗昗丒帪娫)儘乕儗儞僣曄姺偲丄(塣摦検丒幙検)儘乕儗儞僣曄姺傪梡偄傟偽慡偔摨條偵媮傑傝傑偡丅
丂傕偪傠傫偦傟偼丄憡懳惈尨棟偵傛傝丄忋婰偺曄姺幃偺倁傪亅倁偵曄姺偟偰丄 乫 偺晅偄偰偄側偄俥x丄俥y丄俥z丄倴x偲丄 乫 偺晅偄偨俥x乫丄俥y乫丄俥z乫丄倴x乫偲傪擖傟懼偊偨傕偺偵堦抳偟傑偡丅偙偺偲偒倴x傪俽乫宯偐傜尒偨暔懱偺堏摦懍搙偱偁傞倴x乫偵抲偒姺偊側偗傟偽側傜側偄偙偲偵拲堄偟偰壓偝偄丅
丂傑偲傔傞偲
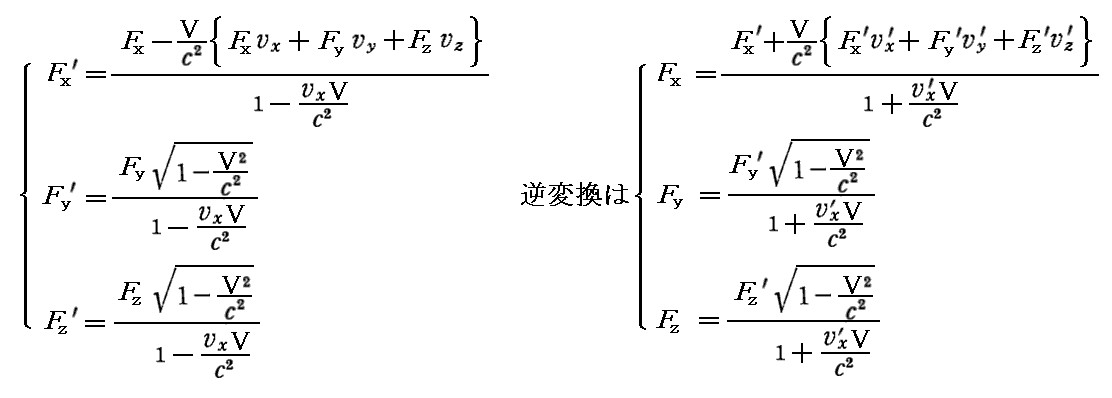
偲側傝傑偡丅偄偢傟偵偟偰傕丄偙傟偑俁師尦椡偺乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼偱偡丅
丂
乮俀乯係尦椡
侾丏係尦椡偺掕媊
丂俁丏乮侾乯偱愢柧偟偨乮塣摦検丒幙検乯係尦儀僋僩儖偺怴夝庍傗係丏乮俀乯偱愢柧偟偨係尦壛懍搙偺掕媊傪峫椂偡傞偲丄乬係尦椡乭偼壓婰偺條偵掕媊偡傟偽椙偄偱偁傠偆丅
丂偨偩偟崱屻偼丄乬俁師尦椡乭 俥 偲偺崿摨傪旔偗傞偨傔偵乬係尦椡乭偺昞尰偵偼彫暥帤偺 乬倖 乭 傪梡偄傞偙偲偵偡傞丅
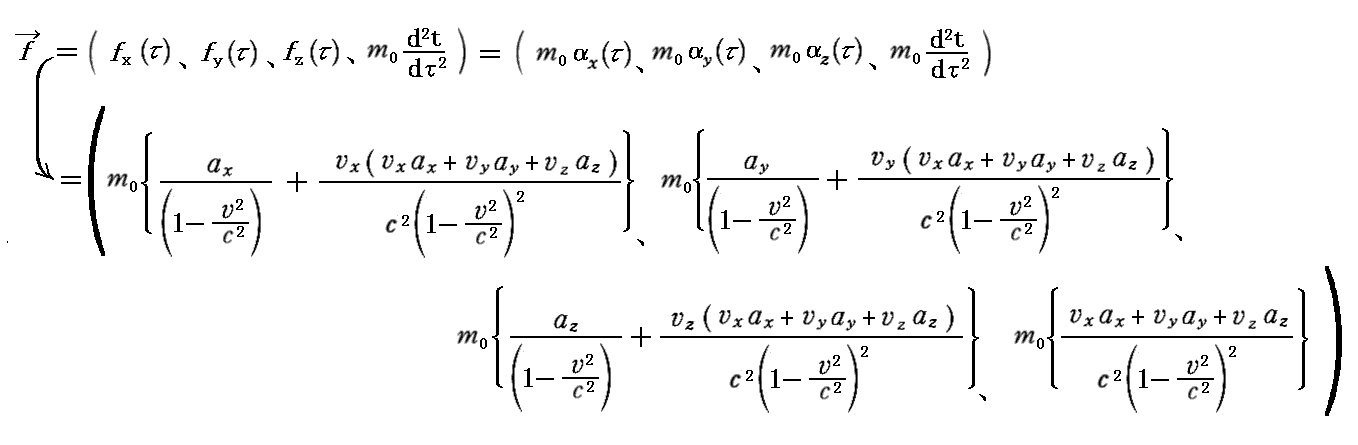
丂偙偙偱乮倴x丄倴y丄倴倸乯偼俁師尦懍搙偱偁傝乮倎x丄倎y丄倎倸乯偼俁師尦壛懍搙偱偡丅
丂偙傟偼丄摦偄偰偄傞堦偮偺暔懱傪俽宯偺暔嵎偟朹偲暔懱偺屌桳帪冄偱娤嶡偟偨偲偒偵丄帪崗 倲 偺弖娫偵暔懱偵摥偔係尦椡乮倖x丄倖y丄倖z丄倖t乯偑丄俽宯偺暔嵎偟朹偲帪寁偱應偭偨俁師尦懍搙乮倴x丄倴y丄倴z乯丄俁師尦壛懍搙乮倎x丄倎y丄倎z乯偱偳偺傛偆偵昞偝傟傞偐傪帵偟偰偄傞丅
丂摨條偵丄摦偄偰偄傞堦偮偺暔懱傪俽乫宯偺暔嵎偟朹偲暔懱偺屌桳帪冄乫偱娤嶡偟偨偲偒偵丄帪崗 倲乫 偺弖娫偵暔懱偵摥偔係尦椡乮倖x乫丄倖y乫丄倖z乫丄倖t乫乯偑丄俽乫宯偺暔嵎偟朹偲帪寁偱應偭偨俁師尦懍搙乮倴x乫丄倴y乫丄倴z乫乯丄俁師尦壛懍搙乮倎x乫丄倎y乫丄倎z乫乯偱偳偺傛偆偵昞偝傟傞偐傪帵偟偰偄傞丅
丂傕偪傠傫丄偙傟傜偺係尦椡偼摨偠暔懱偺摨偠帪崗乮俽宯偺帪寁偼 倲 傪俽乫宯偺帪寁偼 倲乫 傪帵偟偰偄傞乯偵偍偗傞偦傟偧傟偺嵗昗宯偱偺應掕抣偱偡丅
丂巐尦椡偼乬儘乕儗儞僣曄姺乭偦偺傕偺傪枮偨偟偰偄傞偙偲偑徹柧偱偒傑偡乮俆丏乮俁乯侾丏嶲徠乯丅
丂
俀丏係尦椡偺暿昞尰
丂偡偱偵愢柧偟偨丄係尦壛懍搙偺俁師尦昞尰傪梡偄傞偲丄慜崁偺掕媊傪條乆側宍偵曄宍偱偒傞丅
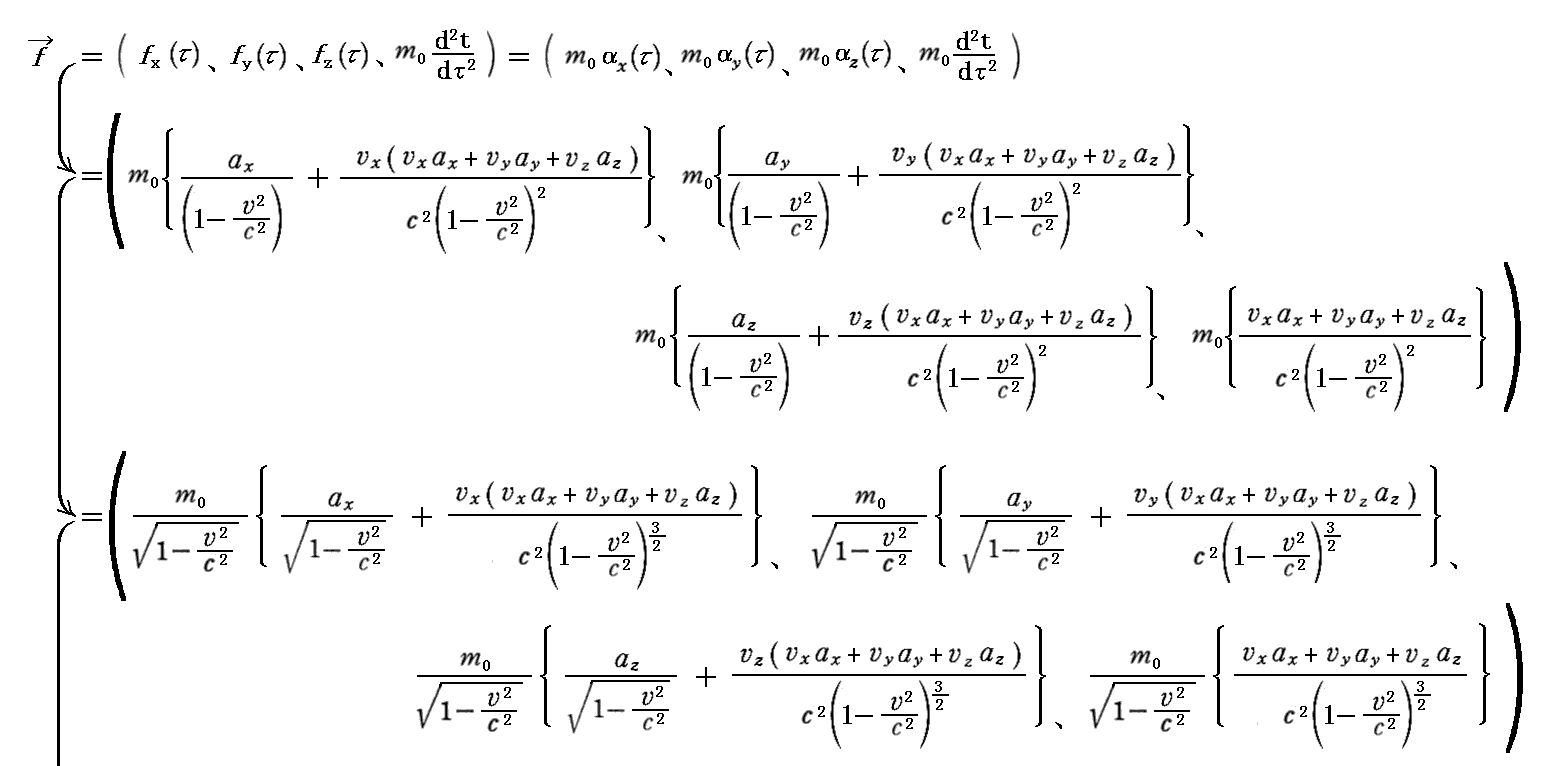
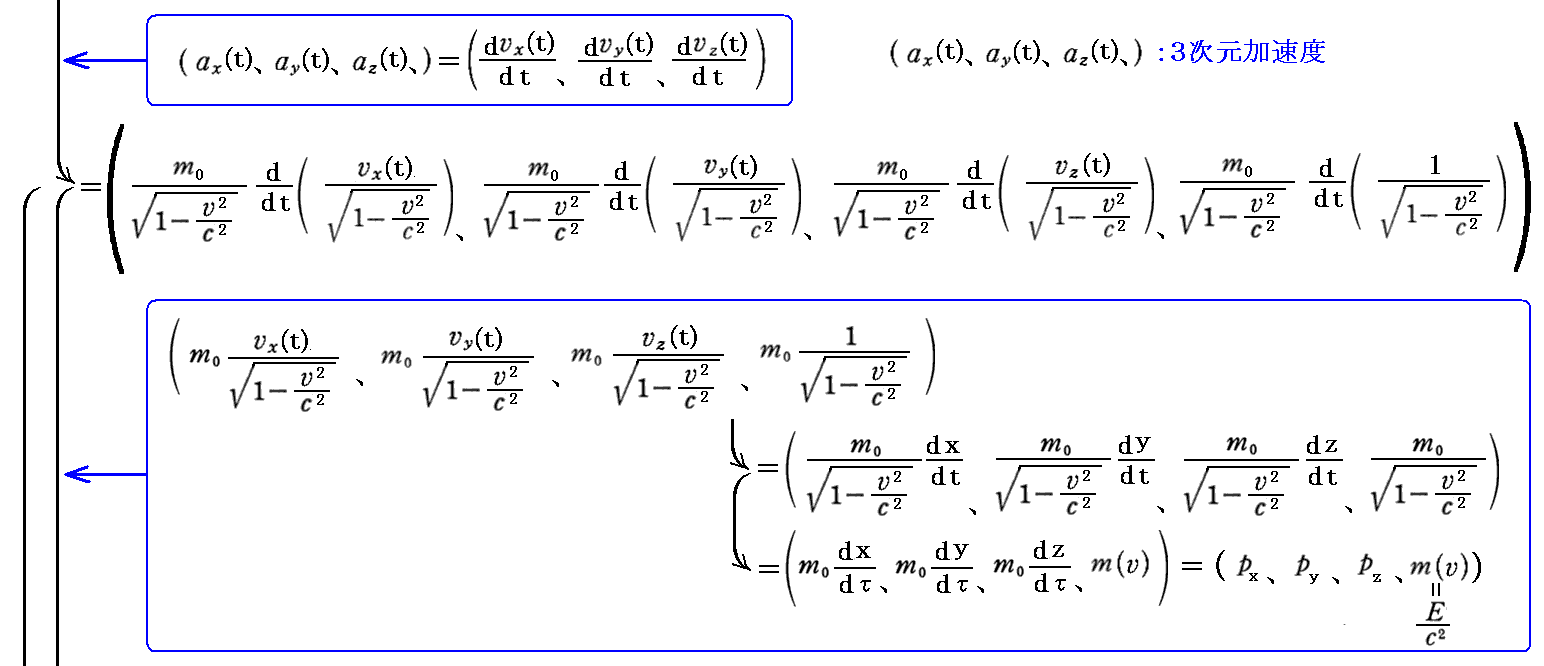
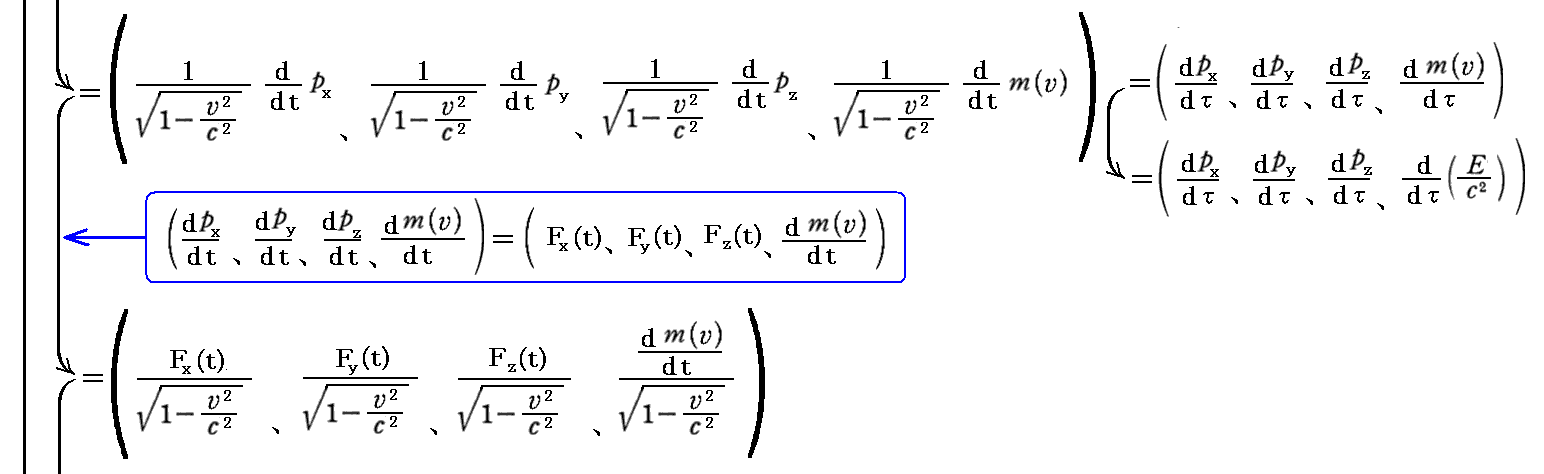
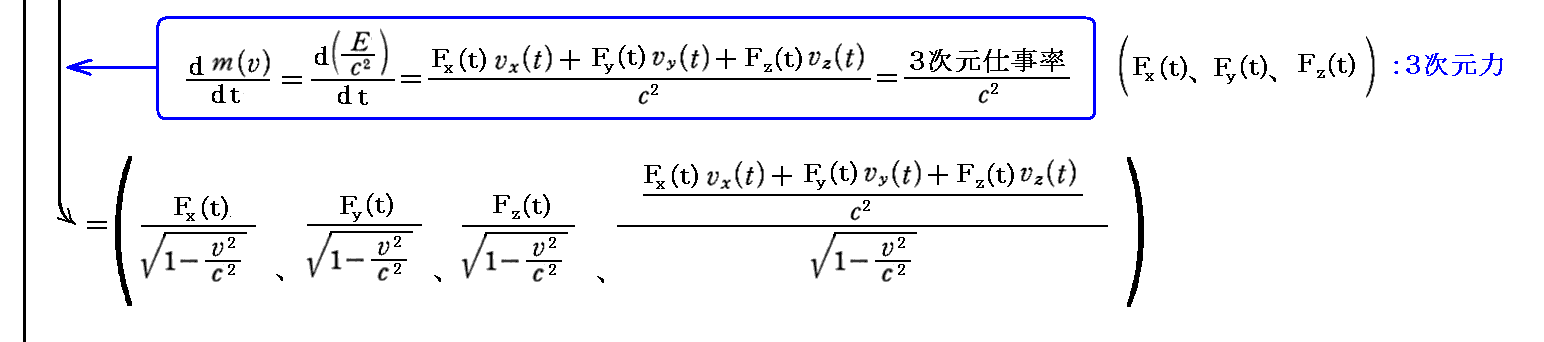
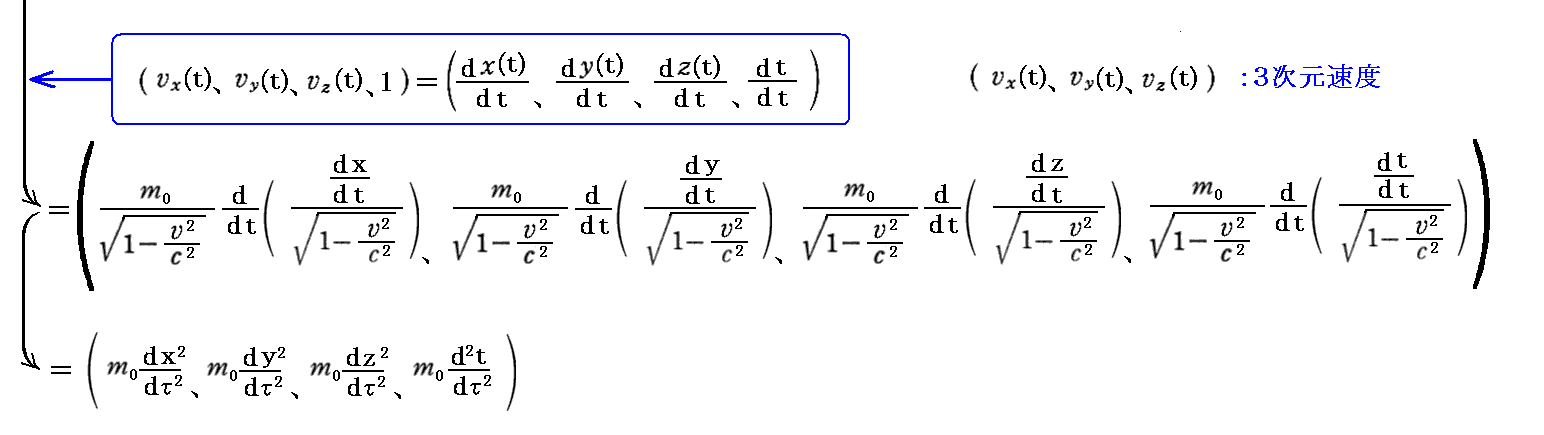
乵曗懌愢柧侾乶
丂偙偙偱乬係尦椡乭偺戞係惉暘偼丄
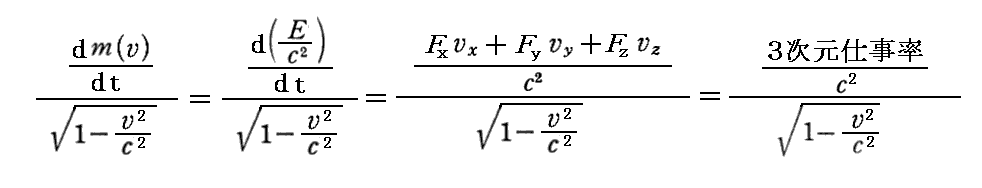
偵側傞偙偲偵拲堄偝傟偨偟丅
丂偦偺徹柧偼俆丏乮侾乯俀丏偱梡偄偨庤弴偵廬偊偽傛偄丅
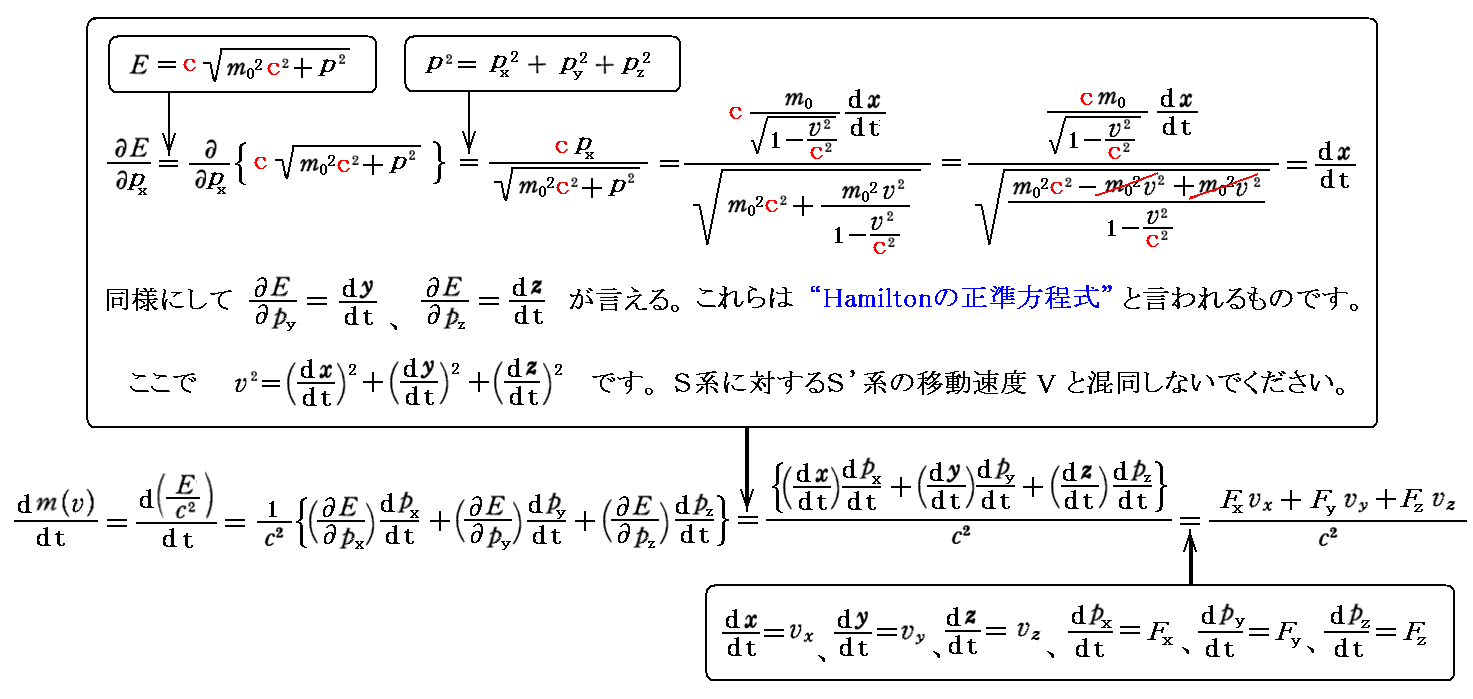
丂
************************************************************************
丂丂偁傞偄偼丄俀丏乮俁乯俁丏偱媮傔偨乬係尦懍搙乭偵偮偄偰惉傝棫偮岞幃傪梡偄偰傕椙偄丅


乬係尦椡乭偺昞尰偵偼係尦検偲俁師尦検偑崿嵼偟偰偄偰偐側傝嶖憥偟偰偄傑偡丅
丂係尦検偩偗傪梡偄偨昞尰傪庢傝弌偡偲
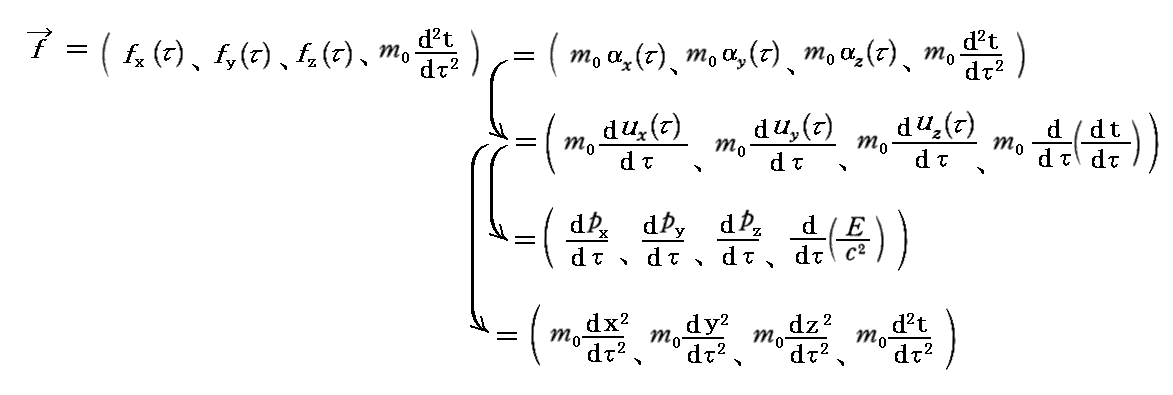
偵側傝傑偡丅
丂俁師尦検偩偗傪梡偄偨昞尰傪庢傝弌偡偲
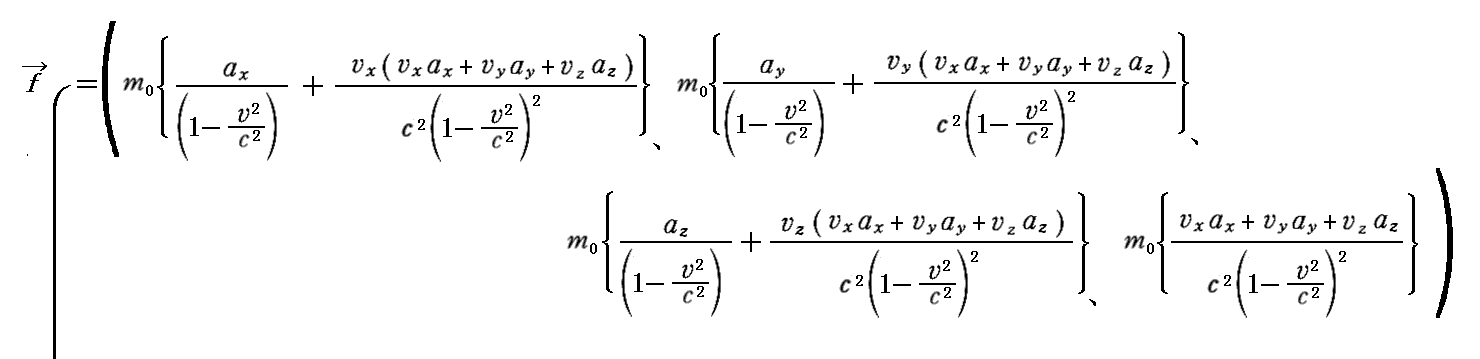
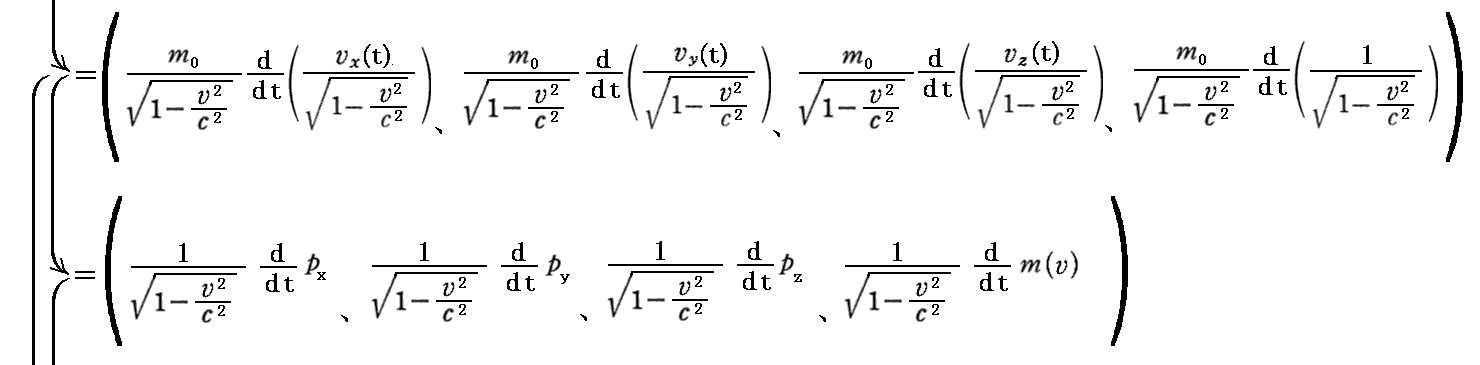
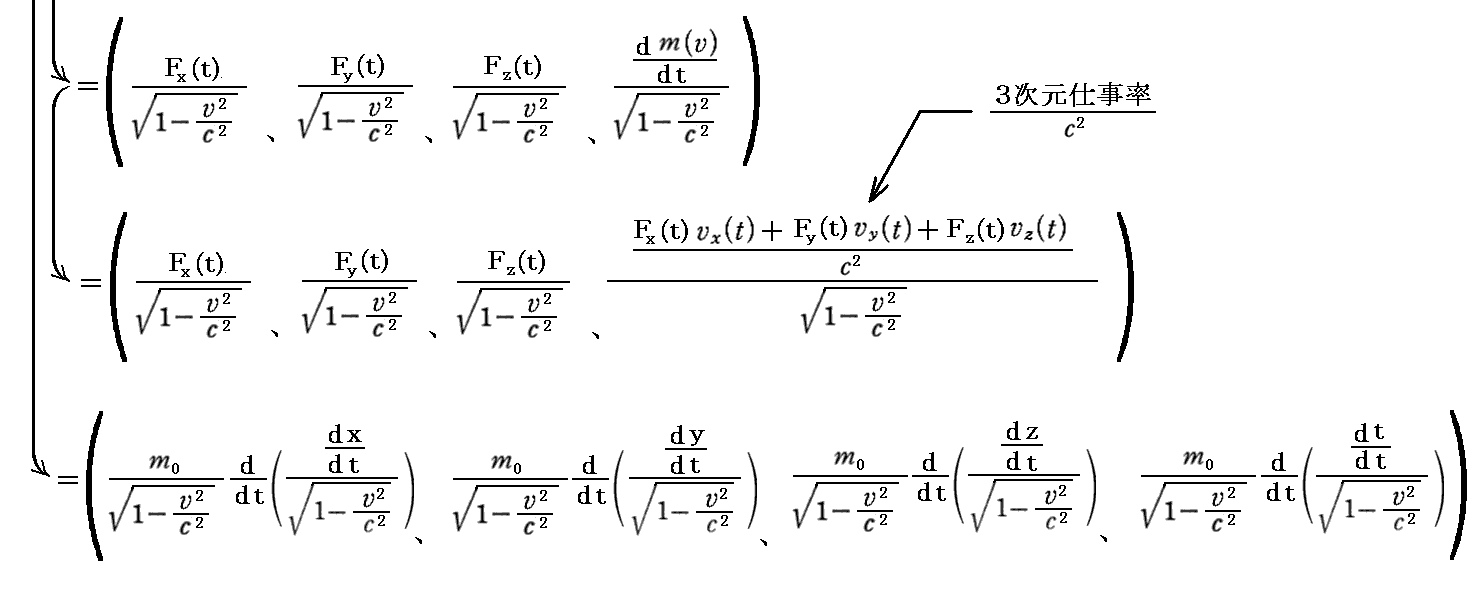
偵側傝傑偡丅
丂
乮俁乯係尦椡偼儘乕儗儞僣曄姺偵廬偆丂
侾丏係尦椡偼儘乕儗儞僣曄姺偵廬偆
丂係丏乮俀乯偱丄俁師尦懍搙偲俁師尦壛懍搙傪梡偄偰昞偟偨乬係尦椡乭傪愢柧偟傑偟偨丅
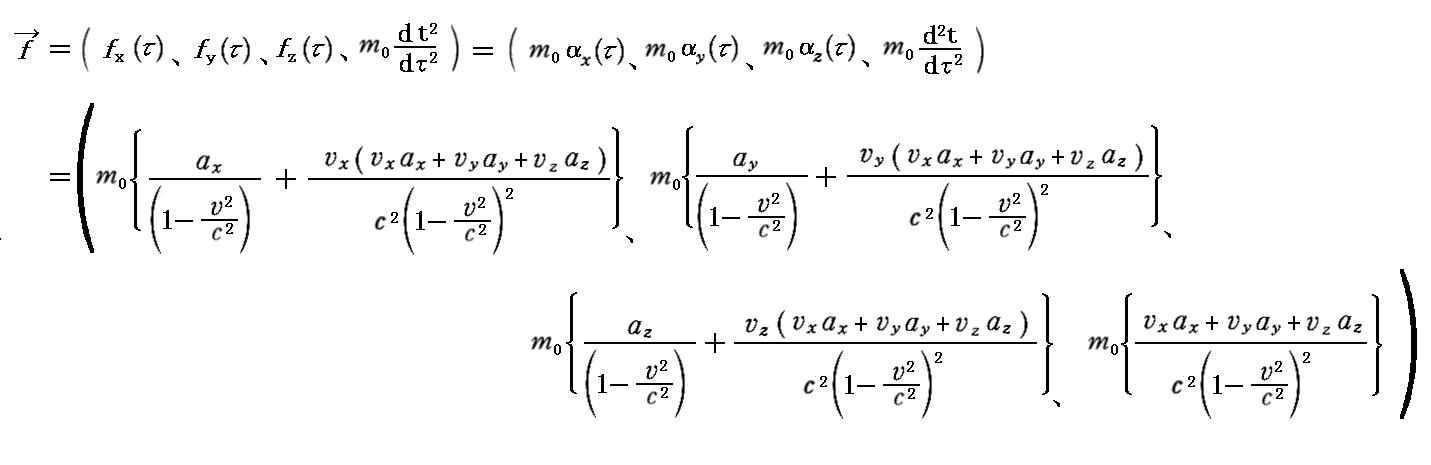
丂偙偺乬係尦椡乭掕媊幃拞偺乬係尦壛懍搙乭偺係惉暘偼乬儘乕儗儞僣曄姺乭偵廬偆偙偲傪係丏乮俁乯俀丏偱徹柧偟偨丅偦偺偨傔丄係尦壛懍搙偵倣0傪忔偠偰摼傜傟傞乬係尦椡乭傕乬儘乕儗儞僣曄姺乭偵廬偄傑偡丅偡側傢偪
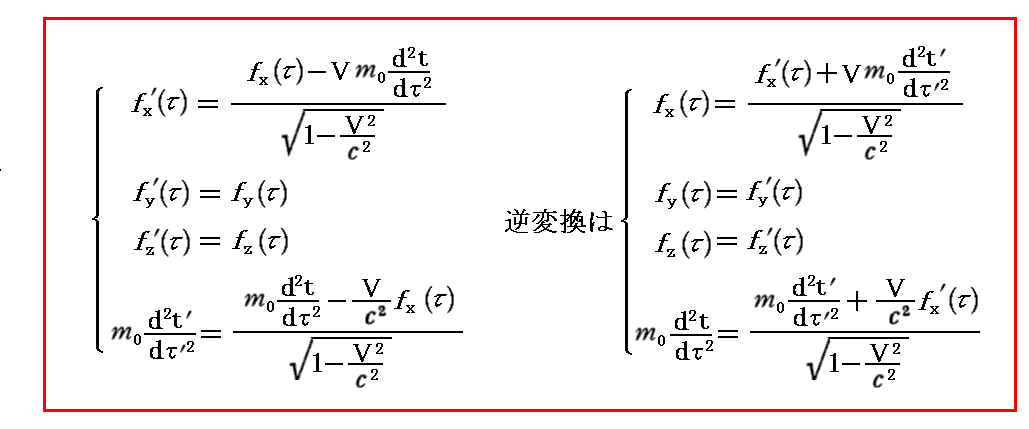
傪枮偨偡丅
乵曗懌愢柧侾乶
丂傕偪傠傫丄偙偺乬儘乕儗儞僣曄姺乭幃偼丄俽乫宯偱偺係尦椡傪俽乫宯偱偺俁師尦椡偱昞偟偨屻丄俆丏乮侾乯俀丏偱媮傔偨俁師尦椡偺曄姺幃偲係丏乮俁乯侾丏偱媮傔偨岞幃嘊傪梡偄偰曄宍偟偰傕徹柧偱偒傑偡丅徹柧偼係尦壛懍搙偺応崌傛傝娙扨偱偡丅幚嵺偵寁嶼偟偰傒傞偲
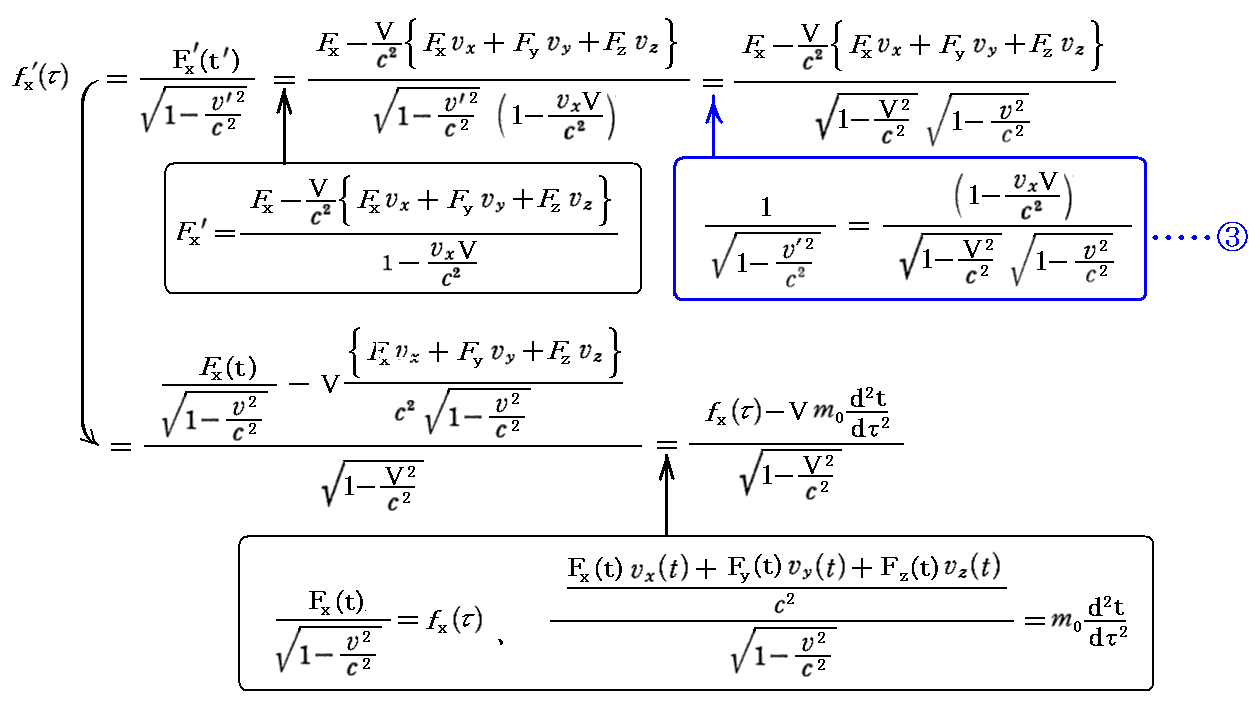
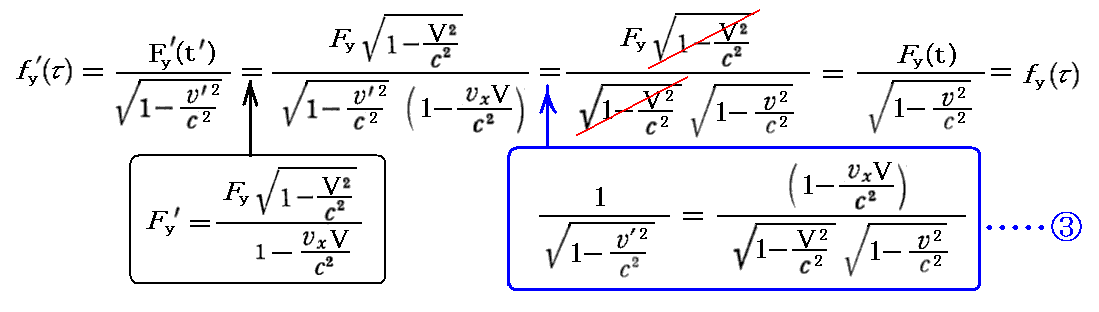
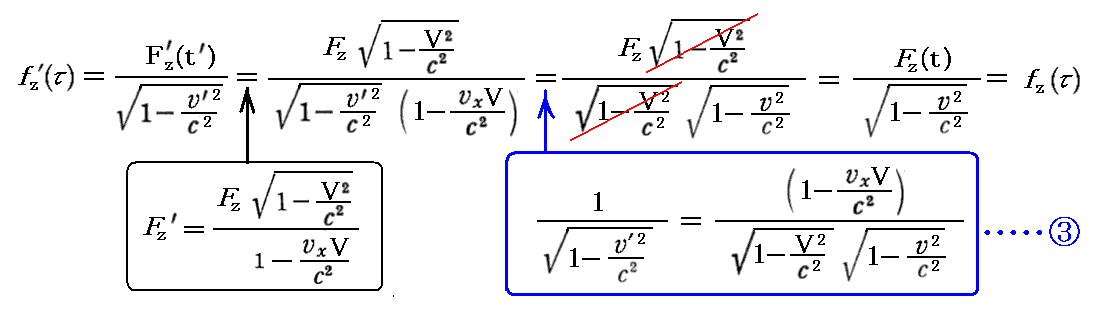
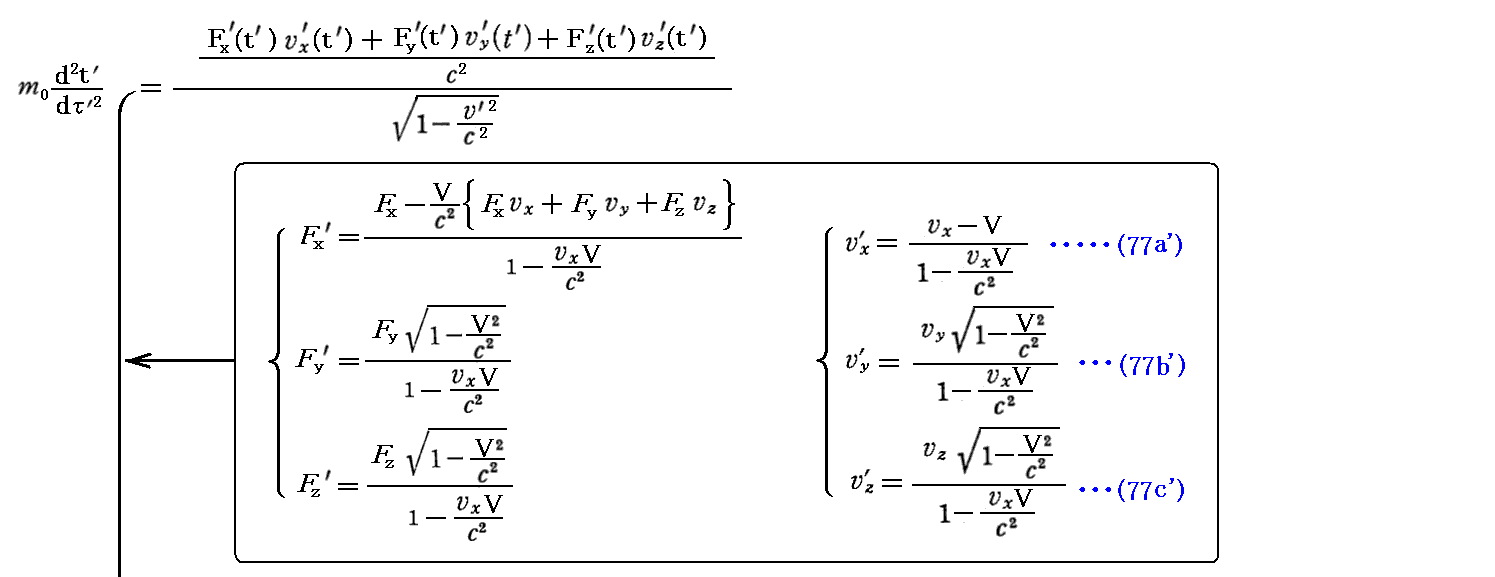
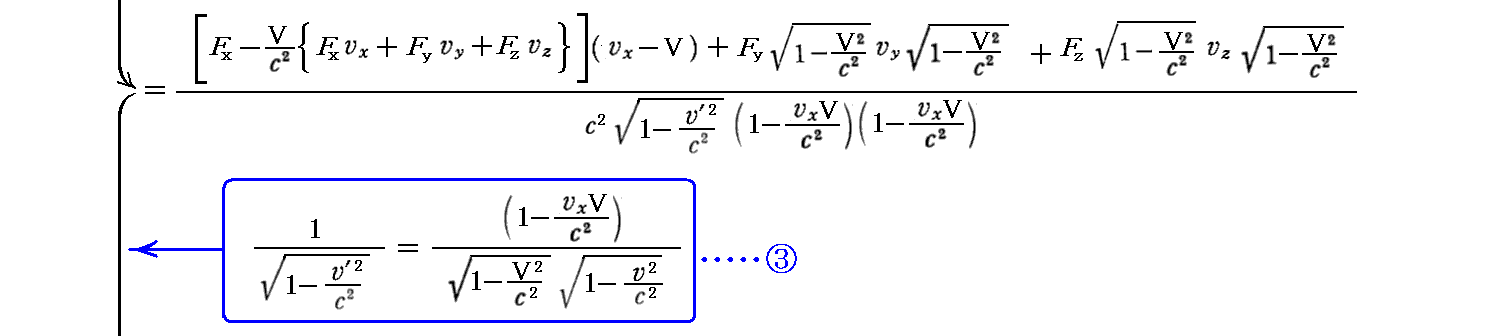
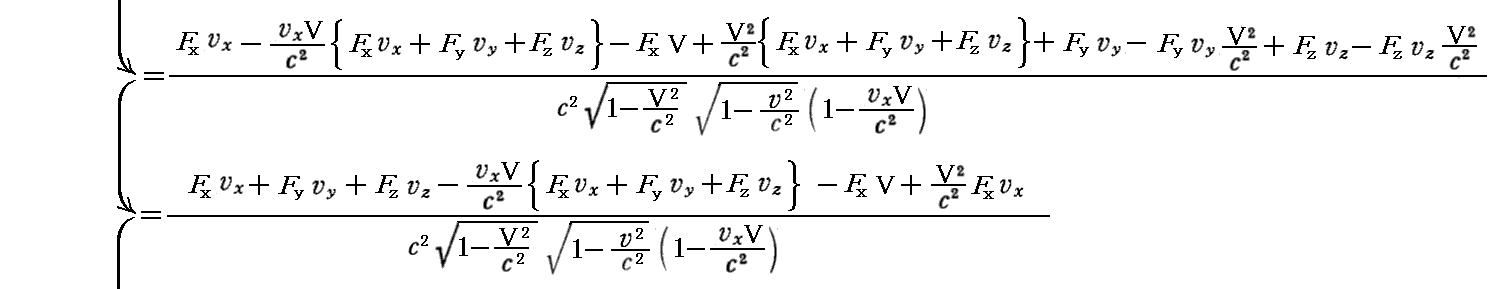
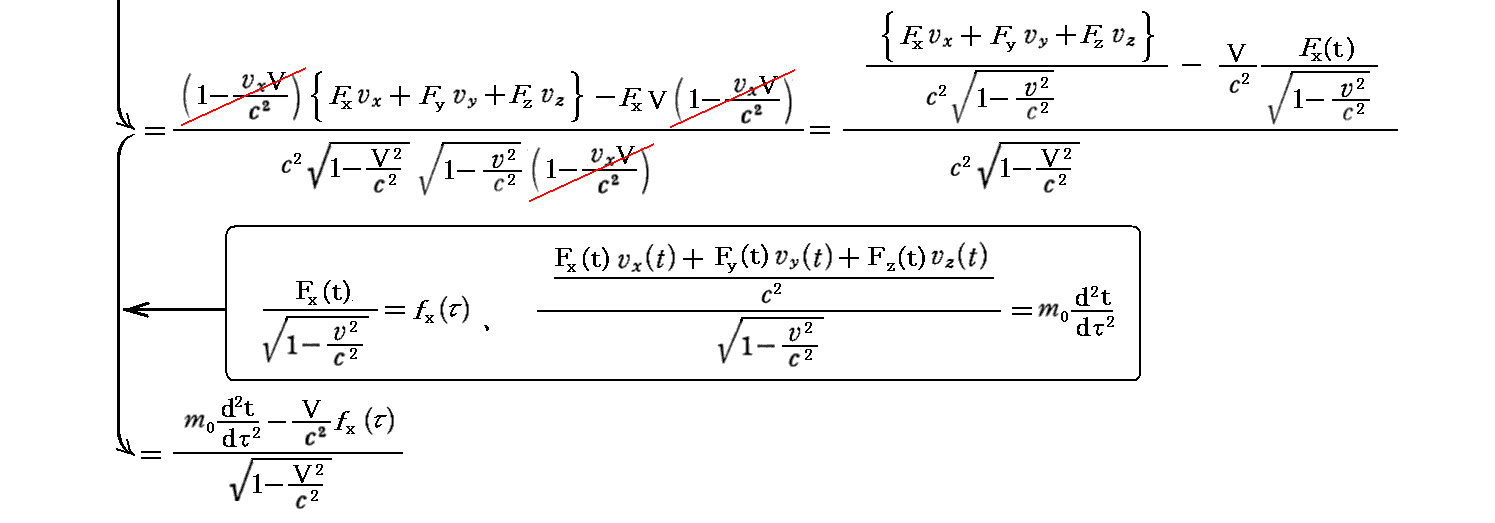
偑摼傜傟傞丅
丂彮偟曗懌偡傞偲戞係惉暘偺曄姺幃偺搑拞偺幃
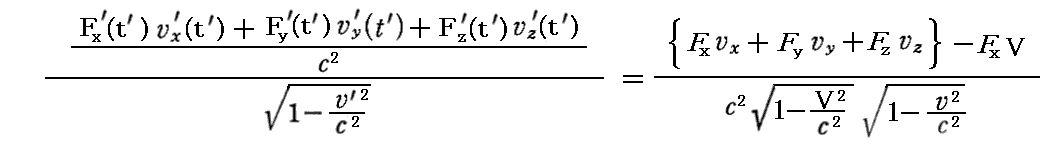
偼師偺條偵曄宍偱偒傞丅
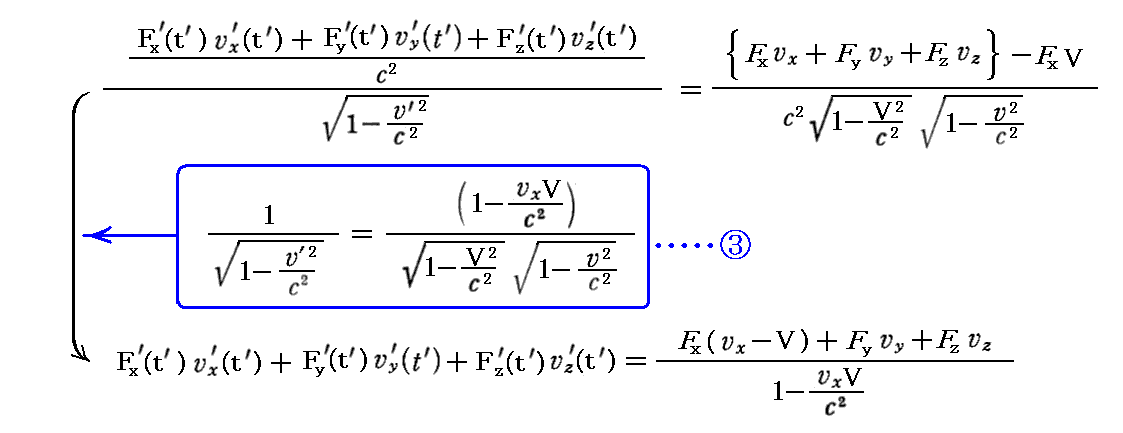
偮傑傝俁師尦巇帠棪偺曄姺幃傪昞偟偰偄傞偲傕尵偊傞丅
丂偝傜偵曗懌偡傞偲丄忋婰偺幃曄宍偱係尦椡昞尰偵偡傞堦偮慜偺抜奒偺幃偑俁師尦椡昞尰偵傛傞乬儘乕儗儞僣曄姺幃乭偱偁傞帠偵拲堄偟偰壓偝偄丅
乵曗懌愢柧俀乶
丂忋婰乬儘乕儗儞僣曄姺乭偺係尦椡偵俁師尦椡偱偺昞尰
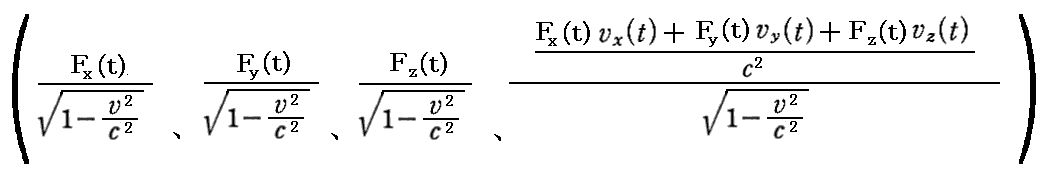
傪戙擖偡傞偲俁師尦椡昞尰偱偺乬儘乕儗儞僣曄姺幃乭偵側傝傑偡偑丄偙傟偺幃曄宍傪偡傞偲
丂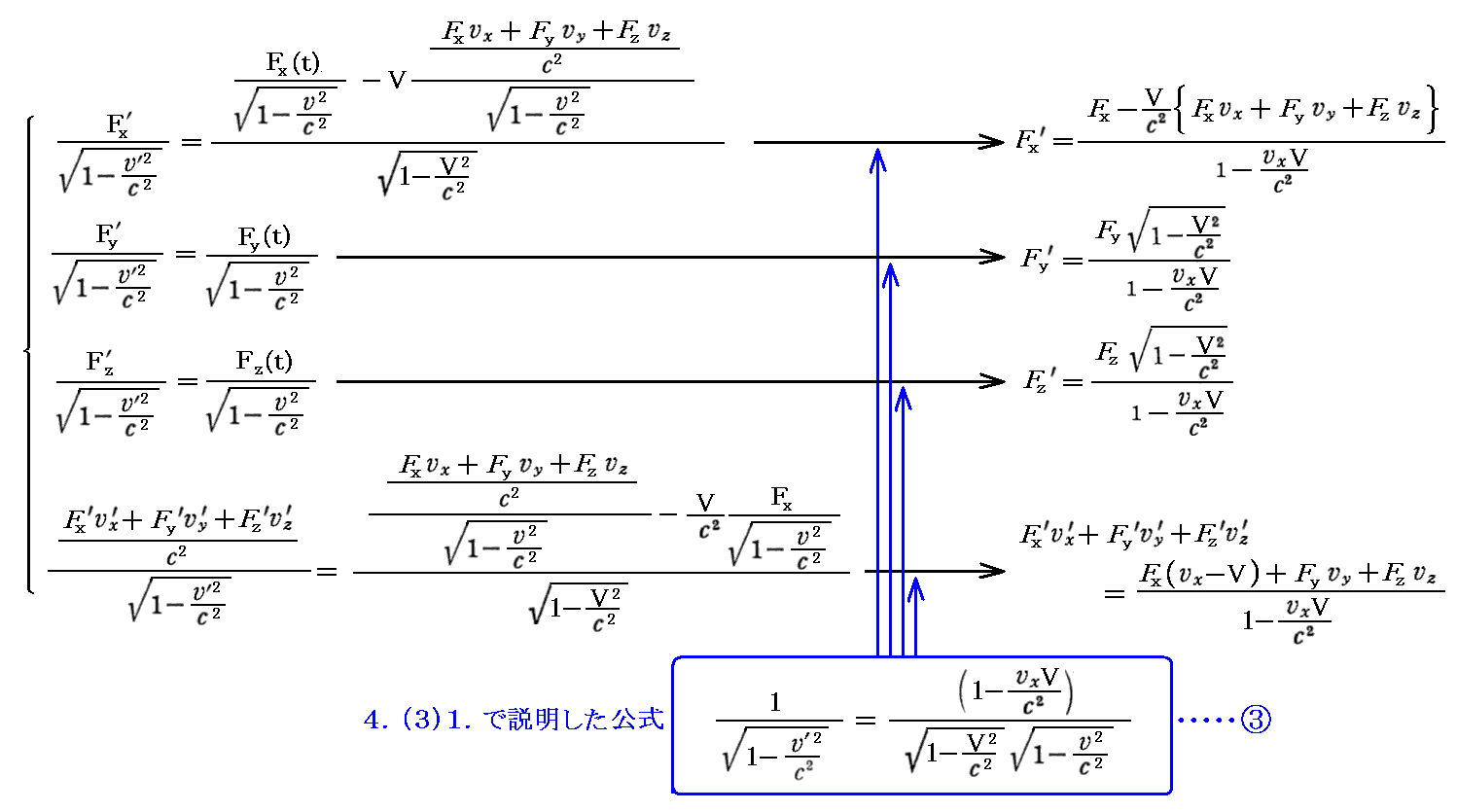
偲側傝丄嬻娫惉暘偼俁師尦椡偺乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼偵婣拝偡傞丅帪娫惉暘偺戞係幃偼俁師尦巇帠棪偺曄姺幃傪昞偟偰偄傞丅
丂傕偪傠傫丄偙偺幃曄宍偼慜婰乵曗懌愢柧侾乶偱峴偭偨幃曄宍傪媡偵偨偳傞偺偲摨偠帠偱偡丅
丂
俀丏係尦椡偺枮偨偡傋偒惈幙
丂係尦椡偼乬儘乕儗儞僣曄姺乭偵廬偭偰俽宯偺娤應抣偐傜俽乫宯偱偺娤應抣偵曄姺偝傟傑偡丅偦偺偨傔乬係尦椡乭偼丄懠偺係尦検偲摨條偵
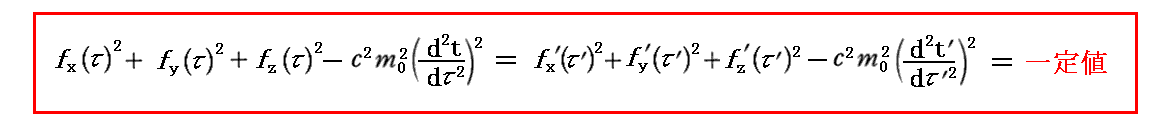
偺娭學幃傪枮偨偟傑偡丅偙偺偙偲偼幚嵺偵儘乕儗儞僣曄姺幃偱曄姺偟偰傒傟偽娙扨偵妋擣偱偒傑偡丅
丂
乮係乯係尦塣摦曽掱幃
侾丏塣摦曽掱幃
丂係尦椡偺昞尰偐傜丄乬係尦塣摦曽掱幃乭偼
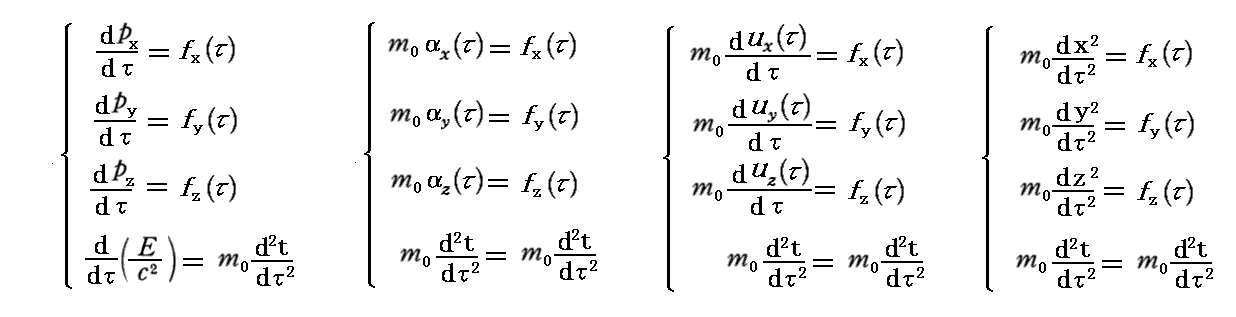
偲側傞偙偲偼柧傜偐偱偁傠偆丅
乵曗懌愢柧侾乶
丂係尦塣摦曽掱幃傪俁師尦検偱昞偡偲
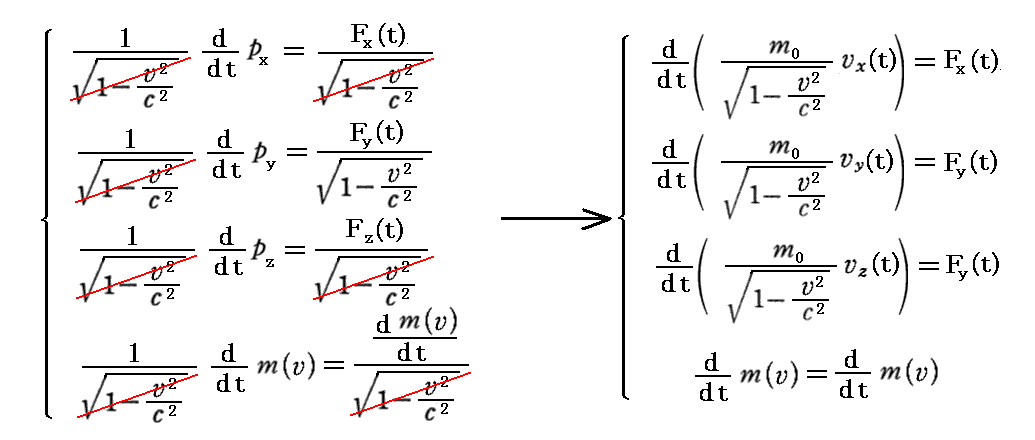
偲側傞丅嬻娫晹暘偺俁惉暘偼丄Max Planck 偑1906擭3寧榑暥偱嵟弶偵摫偄偨憡懳榑揑側乬俁師尦塣摦曽掱幃乭偵堦抳偡傞丅戞係惉暘偼峆摍幃偲側傞丅
丂
俀丏摿庩憡懳惈棟榑偵偍偗傞塣摦曽掱幃
丂懍搙倴偱摦偄偰偄傞暔懱傪娤應偟偰偄傞嵗昗宯偺屌桳帪 倲 偱偺帪娫旝暘傪丄
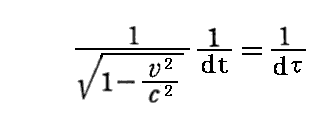
偵傛傝暔懱偺屌桳帪 冄 偵傛傞旝暘偵曄姺偡傞偲丄俁師尦塣摦曽掱幃偐傜係尦塣摦曽掱幃偑摼傜傟傑偡丅
丂偦偺摉偨傝偼暿峞乽傾僀儞僔儏僞僀儞偺摿庩憡懳惈棟榑乿俁丏乮俆乯乵曗懌愢柧俆乶偱撪嶳愭惗偺夝愢乮偦偙偱偼冄傪冃偱昞婰乯傪堷梡偟偰愢柧偟偰偍傝傑偡偺偱偛棗壓偝偄丅杮峞偺抦幆偑偁傟偽丄撪嶳愭惗偺堄恾偝傟傞偙偲偑傛偔棟夝偱偒傞偲巚偄傑偡丅偦偺拞偺悢妛揑寁嶼偼丄杮峞偱孞傝曉偟弌偰偒偨庤弴偲摨偠偱偡丅
丂乬摿庩憡懳惈棟榑乭偺抜奒偵棷傑傞尷傝丄暔懱偺乬屌桳帪乭傪梡偄偰塣摦曽掱幃傪係尦壔偡傞儊儕僢僩偼偁傝傑偣傫丅俁師尦塣摦曽掱幃偱廫暘偱偡丅
丂側偤側傜丄慺棻巕丒崅僄僱儖僊乕暔棟傗揤懱暔棟妛偵偍偗傞怓乆側暔懱偺塣摦偼丄偡傋偰偁傞摿掕偺姷惈宯忋偱榑偠傞偐傜偱偡丅偦偺姷惈宯偱偺帪娫 倲 偱昞偟偨塣摦曽掱幃傪丄偦偺姷惈宯偱偺帪娫 倲 偱愊暘偡傟偽椙偄偺偱偡偐傜丅
丂
丂偟偐偟丄偦偆偄偭偨姷惈宯娫乮摿偵屳偄偵壛懍搙塣摦偡傞乯偺暔棟妛傪榑偠傞乬堦斒憡懳惈棟榑乭偵恑傓偵偼丄杮峞偱愢柧偟偨係尦壔偺庤懕偒偼昁恵偱偡丅
丂
乮俆乯係尦懍搙偲係尦壛懍搙乮係尦椡乯
丂乬係尦懍搙乭偲乬係尦壛懍搙乭偼埲壓偺娭學幃傪枮偨偡偙偲偑徹柧偱偒傞丅
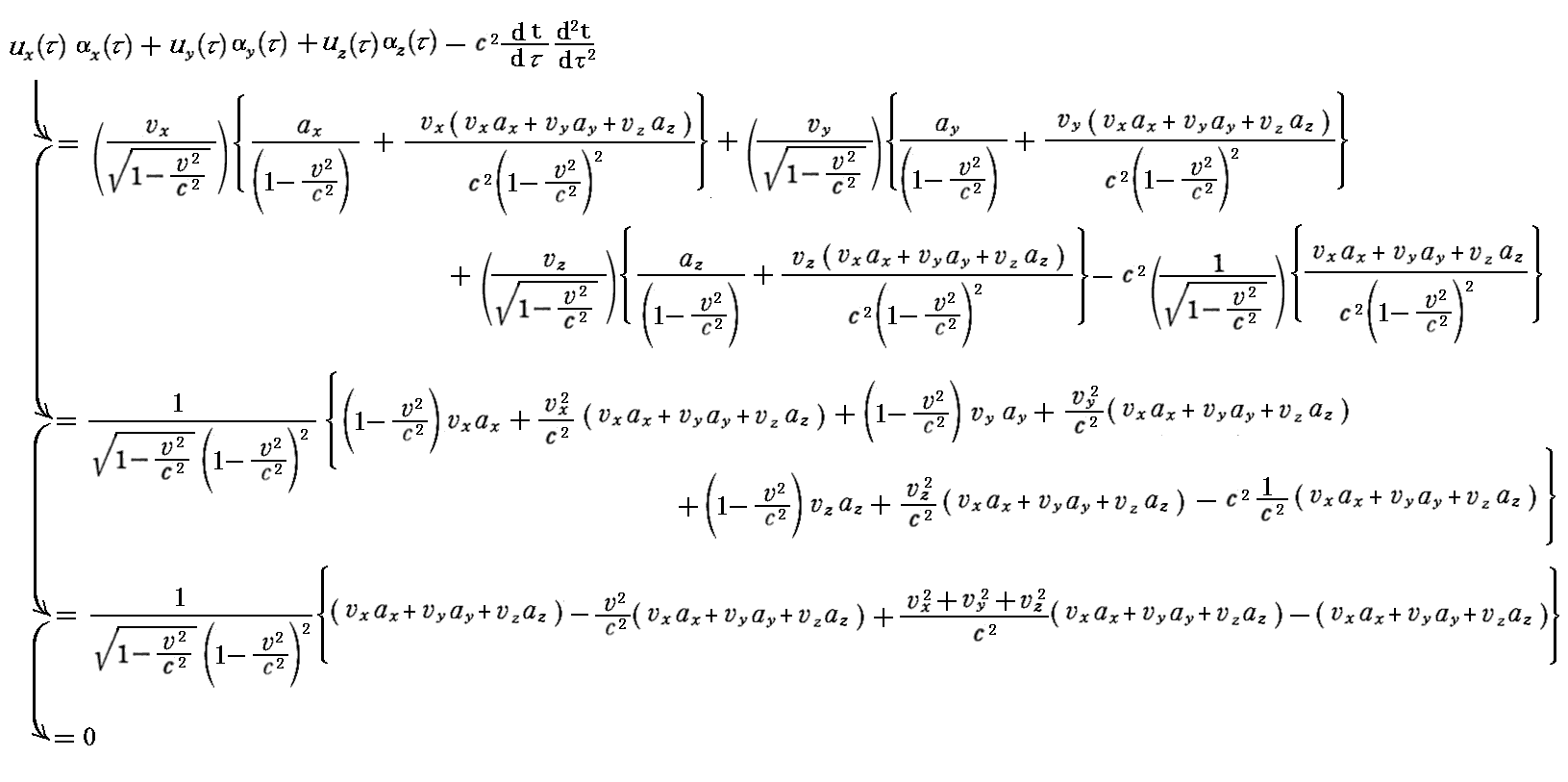
丂偙傟偼係尦懍搙儀僋僩儖偲係尦壛懍搙儀僋僩儖偺乬撪愊乭偵憡摉偡傞傕偺偑 0 偵側傞偙偲傪帵偟偰偄傞丅偦偺堄枴偱乬係尦懍搙儀僋僩儖乭偲乬係尦壛懍搙儀僋僩儖乭偼屳偄偵捈岎偟偰偄傞丅
丂傑偨丄係尦椡偼係尦壛懍搙偵晄曄検偱偁傞倣0傪忔偠偨傕偺偩偐傜丄乬係尦懍搙儀僋僩儖乭偲乬係尦椡儀僋僩儖乭偼屳偄偵捈岎偟偰偄傞偲尵偭偰傕椙偄丅
乵曗懌愢柧侾乶
丂忋婰偺帠暱偼丄俀丏乮俁乯俁丏偱媮傔偨乬係尦懍搙乭偑廬偆幃
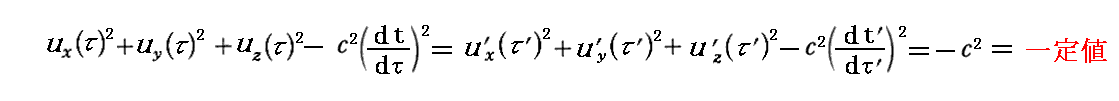
偺椉曈傪冄偱旝暘偡傞偙偲偱傕捈愙摫偔偙偲偑偱偒傞丅

丂
俇丏拲堄帠崁
丂埲忋偱丄暔棟揑側峫嶡偵昁梫側検偑偡傋偰係尦壔乮係尦嵗昗丄係尦懍搙丄係尦塣摦検丄係尦壛懍搙丄係尦椡丄係尦揹棳枾搙乯偝傟偨丅杮峞傪廔傢傞偵摉偨偭偰丄偙傟傜係尦壔偟偨検偵偮偄偰婔偮偐偺拲堄傪偟傑偡丅
(侾)係尦儀僋僩儖偺暿昞尰
丂暿峞乽憡懳榑揑椡妛乿俁丏乮侾乯乵曗懌愢柧侾乶傗俁丏乮係乯乵曗懌愢柧侾乶傗俁丏乮俆乯乵曗懌愢柧侾乶丂偱拲堄偟偨傛偆偵丄係尦壔偟偨偲偒偺戞係惉暘偲偟偰丄倲偺懼傢傝偵們倲傪丄俤乛們2偺懼傢傝偵俤乛們傪丄兿偺懼傢傝偵們兿傪梡偄傞応崌傕偁傝傑偡丅摨條側抲偒姺偊偑懠偺係尦検儀僋僩儖偺戞係惉暘偵偮偄偰傕偱偒傑偡丅
丂偡側傢偪
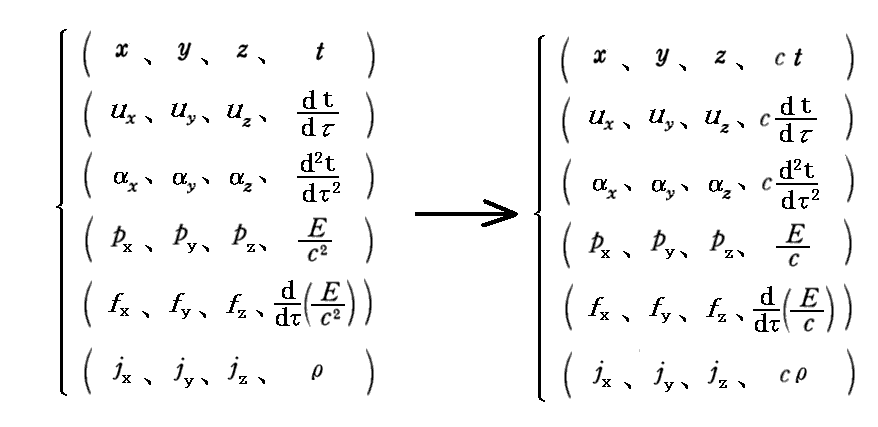
偲抲偒曄偊傞偺偱偡丅
丂偙偆偡傞偲戞係惉暘偺師尦偑戞侾乣俁惉暘偺師尦偲堦抳偡傞傛偆偵側傝傑偡丅
丂傑偨丄偦傟偧傟偺係尦検偺乬儘乕儗儞僣曄姺乭偺學悢偑戞係惉暘偲戞侾乣俁惉暘偵娭偟偰丄傛傝懳徧揑側宍偵側傝傑偡丅偨偲偊偽係尦嵗昗偵偮偄偰偼
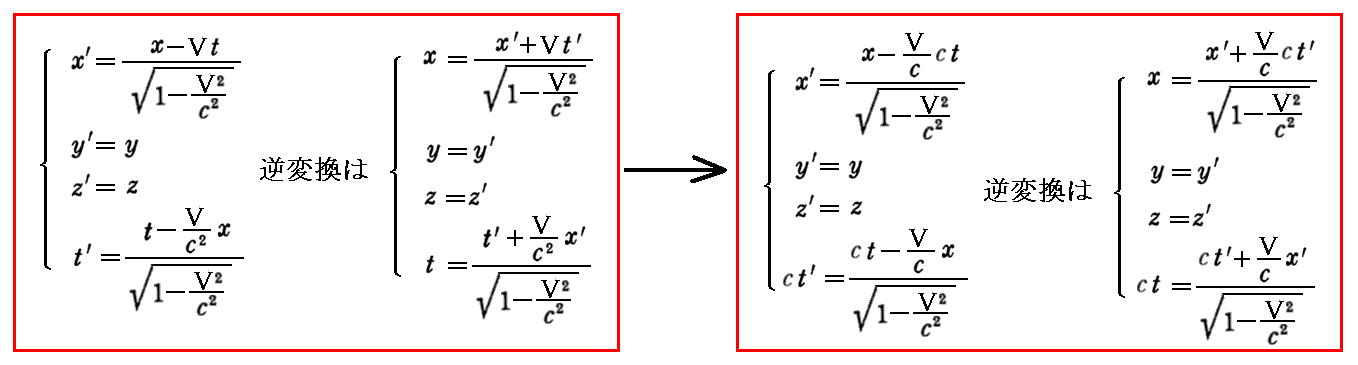
偺條偵側傞傢偗偱偡丅
丂偨偩偟丄杮峞偱偼偁偊偰嵍懁偺昞尰傪梡偄傑偟偨丅懠偺嫵壢彂偲撉傒斾傋傞偲偒偵偼拲堄偟偰壓偝偄丅
丂
(俀乯係尦儀僋僩儖偺揧偊帤偵偮偄偰
丂杮峞偱偼係尦儀僋僩儖検偺惉暘傪昞偡揧偊帤偵乮倶丆倷丆倸丆倲乯傪梡偄偰偒傑偟偨丅嫵壢彂偵嫆偭偰偼乮1丆2丆3丆4乯傪梡偄偨傝丄偁傞偄偼戞係惉暘傪戞0惉暘偲尒側偟偰乮0丆1丆2丆3乯傪梡偄傞応崌傕嵼傝傑偡丅
丂偳偺昞尰傕堦挿堦抁偱偳傟偑椙偄偲偼堦奣偵尵偊傑偣傫丅懠偺嫵壢彂偲撉傒斾傋傞偲偒偵偼拲堄偟偰壓偝偄丅
丂
乮俁乯摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊
丂偙偙偱庢傝埖偭偨儘乕儗儞僣曄姺偼丄俽乫宯偑俽宯偺倶幉偺惓曽岦傊懍搙倁偱堏摦偡傞応崌乮乬摿庩儘乕儗儞僣曄姺乭乯偱偟偨丅俽乫宯偺俽宯偵懳偡傞堏摦懍搙儀僋僩儖傪擟堄偺曽岦偵偟偨応崌偺儘乕儗儞僣曄姺乮偙傟傪乬堦斒儘乕儗儞僣曄姺乭偲屇傇丅偦偺徻嵶偼暿峞乽摿庩儘乕儗儞僣曄姺偐傜堦斒儘乕儗儞僣曄姺傊乿傪嶲徠乯傕峫偊傞偙偲偑偱偒傑偡丅
丂杮峞偱偺寢榑偼偡傋偰偦偺乬堦斒儘乕儗儞僣曄姺乭偱傕惉傝棫偪傑偡丅偟偐偟丄暔棟揑側峫嶡傪恑傔傞偵偼摿庩儘乕儗儞僣曄姺偱廫暘偱偡偺偱丄崱屻傕偟偽傜偔偼乬摿庩儘乕儗儞僣曄姺乭偱媍榑傪恑傔傑偡丅
丂
乮係乯揹帴応偺係尦壔
丂杮峞偱偼廳梫側暔棟検偱偁傞揹帴応偺係尦壔偵偮偄偰偼愢柧偟偰偄傑偣傫偑丄娙扨偵徯夘偡傞偲埲壓偺條偵側傝傑偡丅
丂揹応偲帴応傪昞偡僗僇儔乕億僥儞僔儍儖冇偲儀僋僩儖億僥儞僔儍儖俙偼堦弿偵側偭偰係尦億僥儞僔儍儖傪峔惉偟傑偡丅偦偟偰儘乕儗儞僣曄姺偵傛偭偰曄姺偝傟傑偡丅
丂偲偙傠偑丄揹応乮俤x丆俤y丆俤z乯偲帴応乮俛x丆俛y丆俛z乯偺偦傟偧傟偼係尦揑側検偱偼偁傝傑偣傫丅偙傟傜傪堦弿偵偟偰4亊4偺曽宍偵暲傋偨傕偺偑杮棃偺宍偱偡丅偮傑傝4亊4亖16惉暘偺乬係尦僥儞僜儖応乭偱偡丅偦傟屘丄揹帴応偼係尦僥儞僜儖応偲偟偰擣幆偝傟偰弶傔偰儘乕儗儞僣曄姺偵傛偭偰曄姺偝傟傑偡丅
丂偦偟偰丄偙傟偑杮峞偱愢柧偟偨乬係尦懍搙乭丄乬係尦椡乭偲堦弿偵側偭偰乬儘乕儗儞僣偺椡偺朄懃乭傪昞偟傑偡丅偦傟偼暿峞乽Maxwell曽掱幃宯偺愭尒惈偲揹帴億僥儞僔儍儖乿係丏乮俀乯偱愢柧偟偨條偵
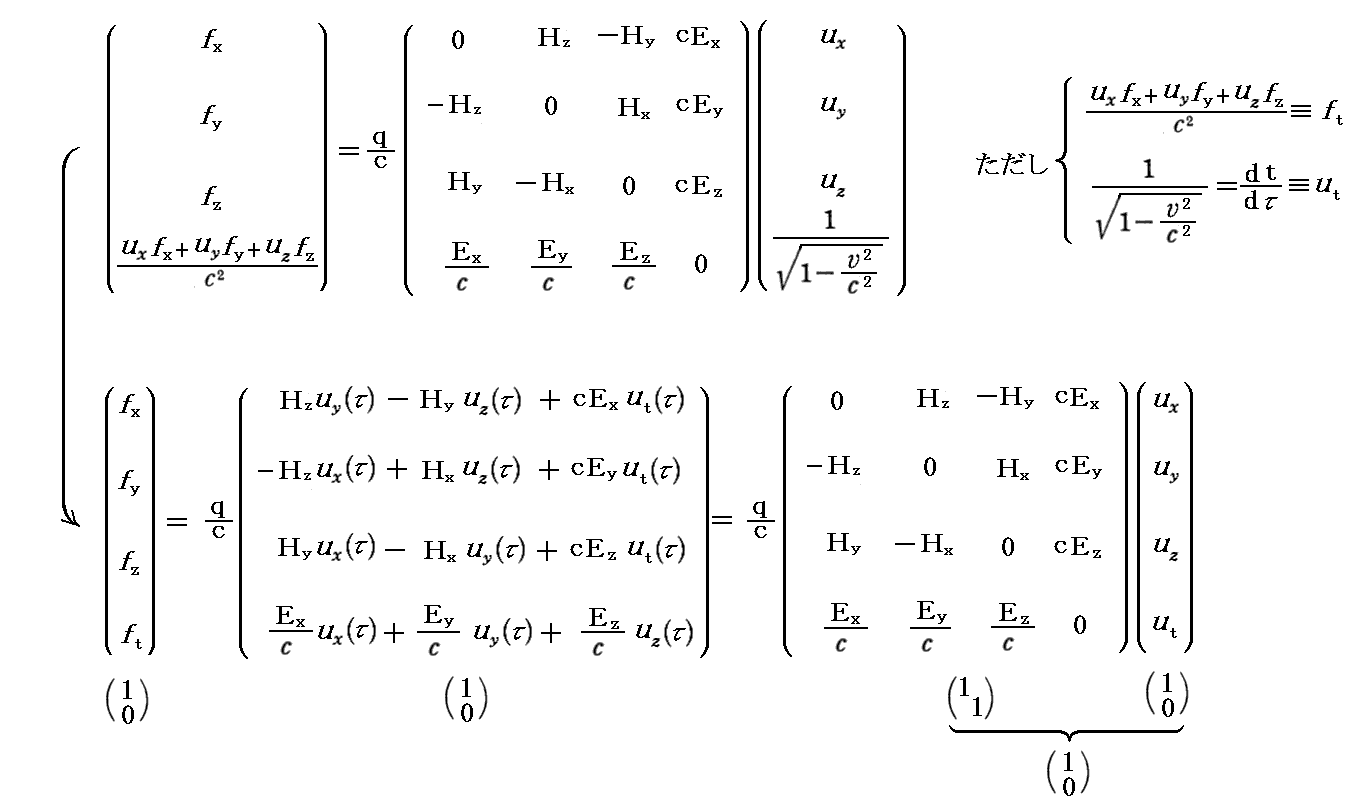
偺宍偵昞尰偝傟傑偡丅偨偩偟丄偙傟偼CGSgauss扨埵宯乮旕桳棟壔丄帴応H乯偱偺昞尰偱偡丅
丂忋婰偺揹帴応僥儞僜儖偼乮1丆侾乯宆偮傑傝崿崌僥儞僜儖昞尰偱偡偑丄俀奒嫟曄僥儞僜儖昞尰傗俀奒斀曄僥儞僜儖昞尰傕偁傝傑偡丅係尦壔偵敽偭偰嫟曄惉暘丒斀曄惉暘偺奣擮偑昁梫偵側傝丄偲偰傕擄偟偄榖偵側傝傑偡丅偙偺晹暘偺擄偟偝傪旔偗傞偨傔偵俁師尦昞尰偱変枬偟偰丄儘乕儗儞僣曄姺嫟曄偺曄姺幃傪梡偄偨曽偑椙偄偺偐傕抦傟傑偣傫丅
丂傕偪傠傫丄係尦僥儞僜儖応偲偟偰偺揹帴応偺儘乕儗儞僣曄姺幃偐傜Einstein偑1905擭榑暥仒6偱弶傔偰摫偄偨乬揹帴応傪3師尦揑側儀僋僩儖検偲尒側偟偨偲偒偺乻儘乕儗儞僣曄姺嫟曄偺曄姺幃乼乭傪摫偔偙偲偑偱偒傑偡丅偦偺偙偲偼暿峞乽Maxwell曽掱幃宯偺愭尒惈偲揹帴億僥儞僔儍儖乿係丏乮俁乯俀丏傪偛棗壓偝偄
丂偄偢傟偵偟偰傕丄偙偺摉偨傝偼暿峞乽Maxwell曽掱幃宯偺愭尒惈偲揹帴億僥儞僔儍儖乿偱愢柧偟偰偍傝傑偡偺偱偦偪傜傪偛棗壓偝偄丅
丂
俈丏嶲峫暥專
壓婰暥專傪嶲峫偵偟傑偟偨丅愢柧偺孞傝曉偟傪偄偲傢偢丄偱偒傞偩偗夝傝傗偔側傞偙偲偵搘傔傑偟偨丅
- 愇堜弐慡挊乽堦斒憡懳惈棟榑傪堦曕堦曕悢幃偱棟夝偡傞乿儀儗弌斉乮2017擭姧乯戞係復
丂偲偰傕夝傝傗偡偔愢柧偝傟偰偄傑偡丅偙偺杮偺悢幃昞尰偺婔偮偐傪棙梡偝偣偰捀偒傑偟偨丅