式中の記号の意味は下図参照。
ここで薄い(浅い)流体方程式が成り立つ前提、[波高h]≪[水深D]≪[波長λ]を忘れないでください。また、多くの参考書やHPではhの代わりにη、Dの代わりにHを用いています。それらと比較するときは読み代えてください。
この稿は、大気や大洋など有限の厚みをもった回転流体層に生じる波動の考察です。
重力波にコリオリ力が絡んだ波のことを、海洋学で“スヴェルドラップ波”(Sverdrup wave)という。大洋に生じる慣性重力波を初めて報告[考文献1.]したのが1926年のスヴェルドラップ(Harald Ulrik Sverdrup 1888~1957年)だからです。
また、地球規模の流体運動では、コリオリ力の緯度依存性のために、南北方向の運動には渦の発生・消滅が伴う。この渦運動変化が波として伝わるものを“ロスビー波”(Rossby wave)という。もともとは_偏西風の蛇行機構の説明のためにロスビー(Carl-Gustaf Arvid Rossby 1898~1957年)が1939年に提案[参考文献2.]したものですが、大陸棚に沿って伝わる陸棚波(地形性ロスピー波)、黒潮に伴う暖水渦や冷水渦、寒冷低気圧などもロスビー波とみなされている。
この稿のアニメーションは、IBMホームページビルダーに添付されているウェブアニメーター(animator.exe)で作りました。ウェブアニメーターあるいは類似のソフト(フリーソフトもあり)をお持ちなら、アニメーションファイルをダウンロードして読み込ませることで表示速度変更・コマ送り・再編集も可能です。
ロスビー波は、その平面的な広がりに比較して厚みが薄い(海の場合は浅い)流体が回転体(地球表面)の上に張り付いている場合に生じる波です。その本質はコリオリ力が緯度により異なることです。
この様な薄い(浅い)流体層の運動にコリオリ力が働くとどのような事が起こるか「吹奏流の西岸強化」や「動力学的潮汐理論におけるケルビン波」で考察してきました。ロスビー波もこれらと同様な考察なのですが、それぞれの理論のどこが同じで、どこが違うのかを見極めながら以下の説明をお読みください。
薄い(浅い)流体層に対しては、別稿「動力学的潮汐理論におけるケルビン波」1.(2)や(3)で説明したケルビンの方程式がそのまま利用できます。出発点はそこで説明した運動方程式と連続の式です。
式中の記号の意味は下図参照。
ここで薄い(浅い)流体方程式が成り立つ前提、[波高h]≪[水深D]≪[波長λ]を忘れないでください。また、多くの参考書やHPではhの代わりにη、Dの代わりにHを用いています。それらと比較するときは読み代えてください。
ケビンの理論はコリオリ力がいつも一定(ω’が一定)であるとみなせる限られた緯度の狭い領域での話でしたが、ロスビーの理論はコリオリ力の緯度変化(ω’が場所の関数)が重要になる地球規模での話です。
コリオリ力の緯度依存性を考慮した運動方程式は別稿「吹奏流の西岸強化」2.(2)ですでに出てきました。そこで説明したストンメルの運動方程式(1948年)はコリオリ力の緯度依存性が考慮されていました。さらに表面を吹く風が海水を駆動する水面の摩擦力と海流を引き留める海底の摩擦力も考慮されていました。そういった意味でストンメルの方程式の方がより複雑なのですが、ストンメルの理論は時間的な変化の無い“定常解”を見つける考察でした。その定常解に風による水面の摩擦力と海底の摩擦力が本質的な働きをしていた。
そのような項のないロスビーの運動方程式は、その意味でストンメルの運動方程式より簡単なのですが、“非定常解”の考察であることに注意してください。そのためストンメルの議論とは違った興味深い事実が出てきます。
ロスビーは、ケルビンの運動方程式中のω’を、一定ではなくて、場所の関数ω’(x,y)にします。本来は球面上での運動なので、ラプラスがしたように、球面座標で考察しなければならない。しかし、それはあまりにも複雑になり、数学的に解けないので、ロスビーは中緯度に設定したデカルト平面座標[x軸を緯線(東西線)に沿って、y軸を経線(南北線)に沿って取る]で考えた。そして、緯度とともに増大するコリオリ力の効果を近似的にβyで表した。
つまり以下のように簡略化した。
ここで、f0はデカルト平面座標の原点における2ω’=f(x,0)=2ωsinθ0の値です。βはデカルト平面座標を設定している緯度θ0でyを変化させたとき、2ω’の変化を最も忠実に表現するような比例定数です。このβyは“ロスビーのβ項”と呼ばれています。この様な近似を実施する上記のデカルト平面座標を今後β平面と呼ぶことにします。この様に置くことで方程式が解けるようになったのですから、画期的な近似・簡略化といえます。
このとき、例えばデカルト座標を緯度θ0=45°に設置した場合には、f0とβの値はそれぞれ
程度になります。正確には1太陽日(24時間)ではなくて1恒星日(23.9344696時間)で割り算すべきです。
恒星日を用いて緯度が15°変化するごとのf0とβの値を示すと下表のようになる。
| 緯度θ | f0(×10-5rad/s) | β(×10-11rad/m・s) | 備考 |
|---|---|---|---|
| 90° | 14.584 | 0.000 | 北極 |
| 75° | 14.087 | 0.593 | |
| 60° | 12.630 | 1.145 | |
| 45° | 10.313 | 1.619 | 北海道北部 |
| 30° | 7.292 | 1.983 | |
| 15° | 3.775 | 2.212 | |
| 0° | 0.000 | 2.290 | 赤道 |
f0は当然のことながら赤道で0、極で最大になります。しかしβは赤道で最大、極で0になることに注意されたし。
また、赤道から北緯15°まで移動すれば北へy~約1670000m移動したことになりますが、そのときβy~2.290×10-11×1.67×106~3.8×10-5程度となり、確かに北緯15°のf0値になります。だから、このβ平面近似はある緯度を挟んで南北30°程度の幅を持つ領域の現象に適応できる。
いずれにしても、この様に置くと前述の運動方程式は
となる。
厳密に言うと、前項で求めたものは座標空間に固定された座標値を変数とするオイラー形式の運動方程式です。そのため、左辺の時間微分∂v/∂tは本来ならばラグランジュ微分[Dv/Dt=∂v/∂t+(v・grad)v]にしなければならない。そうしなければならない理由は非常にわかりにくい所ですが、別稿「二次元・非圧縮性・完全流体の力学」1.(2)2.を復習されてください。そうすると
となる。
また、“連続の式”も、それを導いた別稿における議論を復習すれば解るように 平均水深D は本来 D+h と置くべきです。また、別稿「二次元・非圧縮性・完全流体の力学」1.(2)1.を復習されれば解るように ∂h/∂t はラグランジュ微分 Dh/Dt あるいはD(D+h)/Dt に置き換えるべきです。
ここで、ラグランジュ微分を表すDと平均水深を表すDを混同しないでください。
次節の渦位保存則の証明には、こちらのより厳密な方程式を用います。
簡略化された(1’)式の両辺をyで偏微分、(2’)式の両辺をxで偏微分すると
となる。(2”)式から(1”)式を辺々引き算すると
が得られる。
これは着目する場所(x,y)に存在する微少柱状領域の“渦度”の時間的変化を表す簡略版の“渦度方程式”です。別稿「動力学的潮汐理論におけるケルビン波」1.(2)の(3)式と比較してみられたし。
そこの[補足説明2]で注意したように(∂u/∂x+∂v/∂y)はベクトルの“発散”を表しています。そこで説明したように今考えている場所の柱状領域に周囲から流体が流入すれば渦度は増えます。
さらに、その柱状領域を横切るy方向の流れvが存在してもその場所の渦度は変化します。それは座標系の回転角速度が緯度依存性を持っているので流体が高緯度へ移動すると、渦度がより小さい低緯度の流体要素でもってその場所の柱状領域が占めなおされるからです。新たに付け加わったβvの項がそのことを表しています。
この場合も、オイラー形式の微分方程式ですから、座標空間に固定された微少柱状領域での話です。
(5)、(5’)式は、運動方程式(1’)、(2’)と連続の式(3)式以上の内容を含んでいるわけではないのですが、この様な表現にすると渦度が変化するメカニズムがよくわかります。
渦度方程式も、座標空間に固定された座標値を変数とするオイラー形式に乗っ取った厳密な形で書いてみる。そのために、左辺の時間微分∂v/∂tを厳密なラグランジュ微分[Dv/Dt=∂v/∂t+(v・grad)v]にした運動方程式を用いる。厳密な(A)式の両辺をyで偏微分、(B)式の両辺をxで偏微分すると
が得られる。(B’)式から(A’)式を辺々引き算すると
これら三つの方程式は、その形は微妙に異なりますが、いずれも(x,y)座標が固定された場所の微少柱状領域に存在する流体の渦度の変化を表す微分方程式です。すなわち厳密な“渦度方程式”です。
ここで、厳密な“連続の式”が
であることに注意して、上式を書き直してみる。
これを“渦位保存則”と言う。このとき、“渦位(potential vorticity)”と“渦度(vorticity)”ζ=(∂v/∂x-∂u/∂y)を混同しないでください。両者は全く別の量です。
このあたりの式変形に関しては、別稿「二次元・非圧縮性・完全流体の力学」の3.(3)2.ラグランジュの渦定理や5.(4)2.ヘルムホルツの渦定理の証明と比較してみられたし。そこでは[渦度ζ]÷[密度ρ]や[渦度ω]×[渦糸の断面積dσ]が保存されていたが、ここでは([渦度ζ]+[コリオリ力項f])÷[その点での流体の厚さD+h]が保存される。
このとき、(∂v/∂x+∂u/∂y)=0の非発散性(つまり波高が変化しない)流れの場合、上記の渦位保存則は
に簡単化される。
[補足説明1]
“渦位(potential vorticity)”は、もともと有限の長さの渦糸に対して、渦糸の渦度を長さで割ったものです。そのとき渦糸の長さが変化するとき渦度は変化するのですが、渦度を渦糸の長さで割ったものは変化しなかった。それは角運動量保存則が働くからです。丁度アイススケートのスピンで手を広げたり狭めたりしたとき回転の角速度は変わるが角運動量は保存されたのと同じです。渦糸の長さが長くなれば、太さは細くなります。このあたりを説明する定理が流体力学におけるラグランジュの渦定理・ヘルムホルツの渦定理・ケルビンの循環定理です。そのとき用いた運動方程式には回転を引き起こすような項は存在しなかったことを思い出してください。
しかし、ここでは回転座標系上での話なのでf0+βyの項も加わっています。そのため、1.(2)1.で説明したように、渦糸の長さが変化(太さが変化)する場合、f0+βyの項が効いてきて渦度の大きさが変化すると同時に普通の意味のポテンシャル渦度も変化します。つまり単純な角運動量保存則は成り立たないのです。そのため、ポテンシャル渦度をf0+βyの項も考慮した上記の形にしないと渦位保存則は成り立たない。
大規模な大気や海洋の流れは、ほぼ水平流なので、鉛直軸をもった渦糸の集合とみなせる。このため、その時間変化は上記のポテンシャル渦度“渦位”の保存則によってよく記述できる。
大気や海洋の厚さはせいぜい数km~数十kmであるのに対して、今から考察する波動の波長や広がりは数百km~数千kmであることは常に意識しておかねばなりません。
[補足説明2]
本によっては、(f0+βy)のことを[宇宙空間からみた地球の回転の事だから]惑星渦度、(∂v/∂x-∂u/∂y)のことを[地面に相対的な渦度だから]相対渦度と言い、(∂v/∂x-∂u/∂y)+(f0+βy)のことを絶対渦度と言っているものがあります。そして、絶対静止の宇宙空間からみて惑星渦度と相対渦度の和が保存されることを絶対渦度保存則と呼んでいる。確かに絶対静止の空間から見ればその通りなのだから誤りではないのですが、ここでの議論の様に地球表面上に設置したデカルト平面座標(β平面)上で論じている場合には、そのような言い方は誤解を招きます。
デカルト平面座標の上で論じているのは、別稿でも説明したように、仮想的な力である慣性力(コリオリ力)を導入すれば、議論がとても簡単になるからです。そうして初めて(∂v/∂x+∂u/∂y)の効果(波高の変化による渦度の変化)なども旨く取り込むことができます。[補足説明1]で説明した通りです。
偏西風の蛇行は地球規模の現象だから、絶対静止の宇宙空間から見る立場でその挙動を説明したくなるのは山々ですが、今は地球表面上に設定したデカルト平面座標(β平面)上で論じているのですから、その誘惑は押さえておかねばなりません。
渦位保存則は、流体の実質部分に付属する“渦位”が時間的に変化しない事を示している。つまり、流体の運動が運動方程式と連続の式を満足している限りに於いて、それが波の伝播のようなものであろうと、定常的な流れであろうと、任意の運動状態にある流体の実質部分[具体的には場所(x,y)の微少柱状領域を占める流体]が持つ渦位は、場所的(二次元的に考えている)にも時間的にも保存されて一定です。
これらは1.(2)1.ですでに説明した事柄です。それを保存則の形で述べているにすぎない。
議論の出発点となる連立方程式をまとめておきます。厳密な式(A)(B)(C)は非線形方程式だから解析的に解けないので、今後は最初に述べた微少変位の場合に成り立つ簡略化された方程式を用いる。
後の議論て必要になる概念を、いくつかの特別な場合で説明します。
最初に議論する特別な例は運動が時間的に変化しない定常的な場合です。つまり、方程式の時間の偏微分項が無視できる場合です。
時間的な変化が無視できる場合は、前述の方程式の∂/∂tの項がすべてゼロとおけるので
となる。ここで利用した圧力傾度と水面傾度の関係式は別稿で説明した。
(6)、(7)式は、“定常的”流れでは[水面傾度(圧力傾度)]と[コリオリ力]が常に釣り合ている事を示している。
また、この場合に実現されるのは、波高が時間的に変化しない“非発散性”の流れであることを示している。波高hは時間的には変化しないが、場所的には変化している。
これらの条件を満たす流れを“地衡流”(geostrophic currents)と言う。これは“地球回転と平衡した流れ”という意味で名付けられたようです。
“地衡流”では[水面傾度(圧力傾度)を表すベクトル]と[流速ベクトル)]は必ず直交します。実際、(6)式にuを乗じたものと、(7)式にvを乗じたものは
となる。これらの式を辺々足し算すると
が得られる。これらはベクトルの内積の定義から明らかなように
が直交することを示している。
そのとき、(6)、(7)式の符号は北半球の場合です。uとvのどちらか一方のみがゼロで無い特別な場合を考えれば解るように、北半球では水面の高い所(圧力の高い所)を右に見ながら流れる。
定常的な流れに対しては、“流線関数(streamfunction)Ψ”を導入することができて、流れの様子を視覚的・感覚的に解りやすく表現できます。流線関数については別稿「二次元・非圧縮性・完全流体の力学」2.(2)で説明しましたが、重要な概念なのでもう一度説明します。
[流線の定義]
ある瞬間に流体の微小部分がもつ速度の方向を連ねた曲線を流線と言う。だから各瞬間に於ける流体微少部分が持つ速度ベクトルはその点に於ける流線の接線方向です。つまり流線と速度ベクトルは平行で同じ方向を向いている。
ここで導入される流線こそ流体力学を特徴づける最重要な概念で、それは連続の方程式と密接に関係している。
速度ベクトルは流線に沿った線分の方向を向く。二次元流における流線の線分ベクトルを(dx、dy)とすると流線の定義より
が成り立つ。
ところで定常流(水面高の時間的変化が無い)の場合には連続の式(3)が(8)式の様に簡単化される。そのため
が成り立つ。
(8’)式は、流線の定義式における(-v)dx+udyなる微分形式(9)式がある一つの関数(-Ψ)の完全微分になる必要十分条件であることを表している。[この言葉の意味は別稿「絶対温度とは何か(積分因子とは何か)」5.(2)を参照されたし]
そのため、この-Ψ(x,y)はxy平面上の一つの連続な関数曲面z=-Ψ(x,y)を形づくり
と表現できる。ここでΨの符号を別稿「二次元・非圧縮性・完全流体の力学」2.(2)の場合と逆にしているのは、流線関数を(北半球での)水面の波高と対応させるためです。それ以上の意味は有りません。
そのとき、速度成分u、-vはある関数-Ψ(x,y)の勾配
で表すことができる。実際(10)式が成り立てば
となって(8’)式が常に満たされていることが解る。
-Ψ(x,y)を用いると流線が満たすべき(9)式は
となる。ところで、-dΨ=0を満たす線分ベクトル(dx,dy)の方向は関数曲面上のΨ=一定の曲線をxy平面に投影した等高線の方向です。そのため、(11)式は[等高線の線分ベクトル(dx,dy)]と[関数曲面Ψ(x,y)の最大勾配の方向ベクトル(∂Ψ/∂x,∂Ψ/∂y)]の内積がゼロで互いに直交していることを表している。
一方(10)式は
となるので[速度ベクトル(u,v)]と[勾配ベクトル(∂Ψ/∂x,∂Ψ/∂y)]の内積がゼロで直交している事を意味している。
そのため曲面z=Ψ(x,y)の等高線と速度ベクトル(u,v)は平行になり、曲面z=Ψ(x,y)の等高線が流線になる。そのときΨがyの正方向に高くなっていればx方向の速度成分uが負、Ψがxの正方向に高くなっていればy方向の速度成分vが正となるので、流体は常にΨの値の高い所を右に見ながら、等高線に沿って流れる。そして等高線の密集している所[つまり曲面Ψ(x,y)の勾配が大きいところ]ほど高速で流れることを示している。この関数Ψ(x,y,t)を“流れ関数(streamfunction)”あるいは“流線関数”という。
ここで、さらに以下のことに注目してほしい。コリオリ力の場所的な変化を表すβ項が小さくてf=f0+βy≒f0と近似できるときには、運動方程式(6)、(7)式と(10)式を比較してみれば明らかなように
とおける。つまり波高や圧力が、ほぼそのまま流線関数に比例する量だと見なせる。そのとき流体は、波高(圧力)の高い所を(北半球では)右側に見ながら、h(x,y)の等高線あるいはp(x,y)の等圧線にほぼ沿って流れる。
流体の運動を規制している最大の制約が“連続の式”で、これこそが流体力学を一つの学問領域として成り立たせている中心原理です。流れが非圧縮性・二次元流なら、連続の式から流線は、xy平面上のz軸方向に分布する連続でなめらかな関数曲面流線関数z=Ψ(x,y)の等高線を(x,y)平面に射影した曲線になる。
そのとき、さらに、“運動方程式”が[コリオリ力]と[圧力傾度]が釣り合うような形をしていて、時間的な変化が無視できる定常的な流れでβ項が微少なら、流線関数Ψを波高分布関数z=h(x,y)や圧力分布関数z=p(x,y)で近似的に置き換えることができる。すなわち、流体はh、pの等高線に沿って流れ、h、pの勾配が急な所ほど速く流れる。h、pの勾配が急なところは等高線[流線]が密集している所ですから、流れの幅が狭まり流速は増大する。
流れが速いほど右向き(北半球)のコリオリ力は強まる。北半球で流体が動くと、コリオリ力のために常に右向きの力を受けるが、流れが定常的になるためには、その力を打ち消す反対向きの力が常に働いていなければならない。それが進行方向の右に高く積もった水面によって生じる圧力傾度力です。圧力傾度力は水面の勾配が大きいほど強くなる。
最初に掲げた“定常流”で成り立つ(6)、(7)式では[水面傾度(圧力傾度)]と[コリオリ力]が両辺で互いに釣り合ていた。それがまさにこのことを示している。この様な条件を満たす流れを“地衡流”(geostrophic currents)と言う。地衡流は別稿「台風のメカニズム」2.などで説明したが、大規模な大気や海洋の定常的な流動運動では良い近似解となる。
β項が小さくてf=f0+βy≒f0と近似できるときには、(10)式から明らかなように等圧線に沿って吹く風の速度Vは、nを等圧線に対して直角方向の距離とすると次のように表される。
二番目の簡単化の例として運動方程式(6)、(7)式の右辺の水面高(圧力)の空間的な変化が無視できる場合を考察する。つまり流体の運動を規定する力がコリオリ力のみの場合です。
圧力項(水面高の場所的な変化)が無視できる場合には、運動方程式は次のように簡単化される。このとき空間微分項が無視できるなら、もとの浅水方程式系で連続の式の波高の時間的変化も無視できる。そのため、連続の式を考慮する必要はなくなる。そのとき、さらにコリオリ項も緯度による変化β項が無視できて f=f0+βy≒f0 と近似できる場合には
となる。
(12)式の両辺をtで偏微分したものに(13)式を代入、あるいは(13)式の両辺ををtで偏微分したものに(12)式を代入すると
となる。すなわち、角振動数がf0の振動方程式が得られる。
このとき、波高hの変化は無視しているので、“連続の式”や“渦位保存則”は意味を持たない。
前項の振動方程式は、いわゆる単振動の式だから簡単に解ける。
最初の式から
が得られるが、これを(12)式に代入して積分すると
が得られる。V0は共通です。
uとvの位相が90°異なっていることから解るように、これは流体が回転運動することを表している。実際、tを媒介変数としたuv平面上のグラフを描いてみると、速度ベクトル(u,v)の先端は時計回り(北半球)の円を描く。
速度解を時間tで積分して距離に直す。積分定数を適当に調整すると
が得られる。これらの式は、tを媒介変数としたxy平面上のグラフを描いてみれば明らかなように、時計回り(北半球)の円運動を表している。これらの式を恒等式 sin2(f0t)+cos2(f0t)=1 に代入してみると
となるので、円運動の半径=(V0/f0)であることが解る。
回転と言っても空間的に分布する流体のことですから、流体全体が同時に平行移動するように回転する運動です。コリオリ力が働く回転座標系の上で、物体がある初速度を持って動き始めると回転運動をして元の位置に戻ることを別稿「コリオリ力」3.で説明した。それと同じ事が流体全体に対して起こるのです。これらの運動については以下の事が言える。
ここで説明したような運動は慣性力の一種であるコリオリ力が原因なので“慣性振動”(inertia oscillation)と呼ばれる。
三番目の簡単化の例は運動方程式(6)、(7)式の左辺のコリオリ力項が無視できる場合です。つまり流体に働く力が水面傾度(圧力傾度)のみによって規定される場合です。
コリオリ力項が無視できる場合には、運動方程式は次のように簡単化される。このとき連続の式は前節の様に省略することはできません。つまり波高の時間偏微分項を省略することはできません。
ここで、速度成分(u,v)の波動方程式を導くだけならば、簡単化した渦度方程式(5)に於いてf=f0+βy=0と於いた式を時間積分して得られる
を用いることができる。ただし、渦位保存則としては、h→0の場合にのみ成り立つ近似的なもので正確ではありません。
正しい渦位保存則を得るには1.(2)1.で説明した渦度方程式(5)式でコリオリ力=0としたのでは簡単化しすぎています。1.(2)2.で説明した厳密な渦度方程式に於いてコリオリ力=0としなければなりません。その場合には
となり、コリオリ力が存在しないときの正確な“渦位保存則”が得られます。
“連続の式”(3)の両辺をtで偏微分した式に、“運動方程式”(14)の両辺ををxで偏微分したものと、(15)の両辺をyで偏微分したものを代入すると
が得られる。
さにら、“連続の式”(3)の両辺をxで偏微分した式に、“運動方程式”(14)の両辺をtで偏微分したものを代入し、さらに“渦度方程式”(16)をyで偏微分したものを代入すると
が得られる。
全く同様に、“連続の式”(3)の両辺をyで偏微分した式に、“運動方程式”(15)の両辺をtで偏微分したものを代入し、さらに“渦度方程式”(16)をxで偏微分したものを代入するすると
が得られる。
つまり、波高h、流速(u,v)は同じ形の線形同次波動方程式を満足します。これらは単純な長波の理論でお馴染みのものです。コリオリ力項を含んだもっと一般的な場合は3.(1)で説明します。
これらの別々の波動方程式から導かれる波高h解と流速(u,v)解は、運動方程式(14)と(15)式によって定まる関係も同時に満足しなければならない。
これらの波動方程式はお馴染みのもので、最も簡単な解を例示すると
の様になる。
速度成分(u,v)は(20)式を(14)、(15)式に代入して時間tで積分すれば求まる。もちろんこれらは速度成分に関する波動方程式(18)、(19)式を満足しています。
(20)式を(17)式に代入してみれば明らかなように
が満足されれねばならない。
位相速度が重力加速度gに関係することから解るように、これは重力を復元力とする波なので“重力波”(gravity wave)と呼ばれています。(もちろんこれは、一般相対性理論で言う時空の歪みが伝播する“重力波”とは違います。)
これらの式で kx+ly-σt=一定 という式で表される直線上では、波の位相は一定で、これを“波面(wave front)”と言う。また、kとlはそれぞれxおよびy方向の“波数(wave number)”と言い、σは振動の“角振動数(angular frequency)”あるいは“角周波数”と言う。
普通の本では平均水深をH、波高をη、角振動数をωと表しているが、この稿では平均水深をDとしており、ωは地球の自転角速度、ω’はコリオリ力項の表現に用いている。
そのため、この稿では波高をh、波高振幅をH、波数を(k,l)、角振動数をσで表している。
k、l、σでは、解りにくいので別稿「波動方程式と一般解」3.(3)で説明した波長λ、周期Tの形に書き換える。
このときそれぞれの量は下記の意味を持つ。これらの関係式は後に繰り返し利用します。
ここで、H=1、λx=6、λy=8、T=12とした波高解
の様子をアニメーション表示する。

アニメーションから明らかなようにベクトル(k,l)は“波面”に垂直なベクトルで波が伝播していく方向を示す。このベクトルを“波数ベクトル”と言う。これらはすでに別稿「偏光とは何か」2.などで説明した。波数ベクトル(k,l)と波長λの関係は下図の様になる。
図中にできる直角三角形はすべて互いに相似になる。それらの三角形について辺の比例関係を用いると
となる。
波動の規模が大きくなってくると、必然的にコリオリ力の影響が出てきます。ここではまずコリオリ力は無視できないが、緯度変化に伴う影響(β効果)は無視できる限られた緯度・領域で生じる波動を考察します。
ここで、すべての項を考慮した浅水方程式系[1.(3)参照]を考察する。ただしβ項を導入すると話は難しくなるので、ここではまずβ項が無視できてf=f0+βy≒f0=一定と置ける場合を議論します。つまり、コリオリ力と圧力傾度力の両方を考慮するが、コリオリ力の緯度依存性は無視できる場合です。
1.(3)の式(1’)(2’)(3)において f0+βy≒f0=一定と置くと
となる。
このとき(23)、(24)式から得られる渦度方程式は(5’)式に於いて、f=f0+βy≒f0=一定と置いたものになり、両辺を時間積分できます。
となり、これは波動方程式を導くときに使えます。ただし、これは渦位保存則としては近似的なものです。
正確な渦位保存則を導くには1.(2)2.で求めた正確な渦度方程式を時間積分する必要があります。それは1.(2)3.の保存則でβ=0と置いたもので、
となります。これが正確な“渦位保存則”です。このときhが小さいときには(5”)になることは簡単な計算で確かめられます。
運動方程式(23)と(24)の両辺をtで偏微分すると
となる。
ここで、波高hと流速(u,v)の間に成り立つ関係式を求めておきます。
(23’)式に“運動方程式”(24)を代入すると
となる。同じく(24’)式に“運動方程式”(23)を代入すると
となる。これらは波高解hから流速解(u,v)を導くときに用います。
(23)(24)(3)は、3つの未知関数h、u、vが互いに入り交じった連立方程式なので、一つの未知関数のみを含む単一の式に変換する。それはすでに別稿「動力学的潮汐理論におけるケルビン波」2.で求めており、そこの2ω’を現在の記号f0に置き換えればよい。繰り返しになりますが大事な所なのでもう一度説明します。
運動方程式(23)の両辺をxで偏微分すると
となる。同じく運動方程式(24)の両辺をyで偏微分すると
となる。
ここで、“連続の式”(3)の両辺をtで偏微分したものに、“運動方程式”の両辺をxやyで偏微分した(23”)と(24”)を代入し、さらに“渦運動を表す式”(5”)の積分定数をゼロと置いたものを用いると
が得られる。
“渦運動を表す式”(5”)の両辺をyで偏微分すると
となる。同じく(5”)の両辺をxで偏微分すると
となる。
ここで、“連続の式”(3)の両辺をxで偏微分したものに、“運動方程式”(23)の両辺をtで偏微分した(23’)と“運動方程式”(24)を代入し、さらに“渦運動を表す式”(5”)をyで偏微分して得られた(5*)用いると
が得られる。
同様にして、“連続の式”(3)の両辺をyで偏微分したものに、f=f0=一定と置いた“運動方程式”(2’)の両辺をtで偏微分した(2”’)とf=f0=一定と置いた“運動方程式”(1’)を代入し、さらに“渦運動を表す式”(5”)をxで偏微分して得られた(5†)用いると
が得られる。
結局、三つの量h、u、vは全て同じ形の“2階の同次波動方程式”(28)、(29)、(30)を満足する。これらは2.(3)で説明した“重力波の波動方程式”に、コリオリ力の影響を表すf0項が付け加わった形をしている。これが“慣性重力波の波動方程式”です。
[補足説明]
本来ならば、この式中に流体の運動を引き起こす力の項が導入されていてしかるべきです。例えば、月や太陽による潮汐力や、太陽輻射による南北方向の不均等加熱による温度勾配(圧力勾配)や、地球輻射による不均等冷却、更に海洋の運動に着目するのなら、その表面を吹く風の摩擦による駆動力、等々・・・・。しかし、いまは、それらの効果はすべて考えられていません。それを考えると難しくなるので、とりあえずそれをすべて省略した“自由振動・自由流動”を表す波動方程式の議論です。
前節の波動方程式(24)の解は別稿「動力学的潮汐理論におけるケルビン波」3.(1)で説明したように
と表せます。
ここでは見通しを良くするために、最も簡単な実数解
を取り上げる。
この波の様子は3.(3)で取り上げた重力波の解(20)式と同じですからそこのアニメーションを参照されてください。そのためk、l、σと波長λ、振動周期T、伝播速度μの関係も全く同じです。この波について以下の事が言える。
この波の復元力が重力と慣性力(コリオリ力)なので、この様な伝播速度を持つ波を“慣性重力波”(inertia gravity wave)と言います。
慣性重力波に伴う潮汐現象を初めて報告したのはH. U. Sverdrup(1926年 参考文献1.あるいは文献6.§133参照)なので、海洋学では大洋に生じる慣性重力波を“スヴェルドラップ波”(Sverdrup wave)と呼ぶ場合があります。
[補足説明]
コリオリ力が伝播速度に効いてくるのは、波高の高低に渦度の変化が絡んでいるからです。別稿「動力学的潮汐理論におけるケルビン波」の1.(2)[補足説明2]や1.(4)で説明したように(∂u/∂x+∂v/∂y)はベクトルの“発散”を表しており、考えている場所の柱状領域に周囲から流体が流入すれば波高の増大が生じるとともに渦度も変化します。それが波の復元力に慣性力(コリオリ力)が関わっている理由です。そのことを通じて位相速度に関係してくる。
波高変化に伴って渦度が変化することは、次節で表示する流速ベクトルのアニメーションを見れば解ります。波高の変化に伴って隣り合う流体間の速度成分がずれあうように変化するさまが読み取れます。
h(x,y,t)に対応するu(x,y,t)やv(x,y,t)の解をを求めよう。そのためには、(31)式を(26)、(27)式に適用すればよい。そうすると
や
となるので
が得られる。
この式で kx+ly=0 を満足する(x,y)座標上に存在する流体粒子は、すべて同じ位相でそろって同じ方向、同じ速度で動く。そのとき、kx+ly=0 は波数ベクトル(k,l)と位置ベクトル(x,y)の内積がゼロだから互いに直交していることを意味する。つまり、一つの波面(同一波高の点を結んだライン)上の点がすべてラインダンスをするようにそろって同じ動きをする。
(35)、(36)式はf0、σ、k、l が入り交じった複雑な形をしているが、慣性重力波の位相速度は波数ベクトル(k,l)の絶対値だけに依存して、その方向にはよらない。つまり波動方程式には元々その方向による依存性は無い。そのため波数ベクトル(k,l)=(k,0)として、波の伝播方向をx軸と一致させても解の一般性を失わない。
x軸方向に伝播する波は、(35)、(36)式でl=0と置いた式
になるが、この様に簡単化しても一般性を失わない。
このとき当然α=β=0となるが、さらに(1/k)(H/D)は、波の波長λ(=2π/k)、振幅H、水深Dが定まると、一定値と見なすことができるのでC(=定数)と置ける。さらに、理解しやすくするために(x,y)=(0,0)での(u,v)の時間的変化を考察する。
その場合、上式はさらに簡単化できて
となる。
これは時間tを媒介変数とした表示で、流速ベクトル(u,v)の先端は時間tの経過とともに半長短軸がσC と f0Cの楕円を描くことを示している。
この運動を、波数ベクトルが(k,l)となる座標系(x’,y’)から見たときの流速ベクトル(u’,v’)に変換する。(u’,v’)は、元の座標系での流速ベクトル(u,v)と以下の関係で結び付けられる。
これらの関係式を用いると
となり、(35)、(36)式と一致することが証明できる。
(35’)、(36’)式の意味するところをまとめると以下のようになる。
k、σでは解りにくいので、波長λ、周期Tで表した式
において、さらに具体的な H=1、 f0/σ=0.5(σ/f0=2)、 波長λ=40、 周期T=12、 表示幅W=20 の場合をアニメーション表示する。波高は黄色(高)青色(低)で表現し、流速ベクトルは赤矢印で示す。
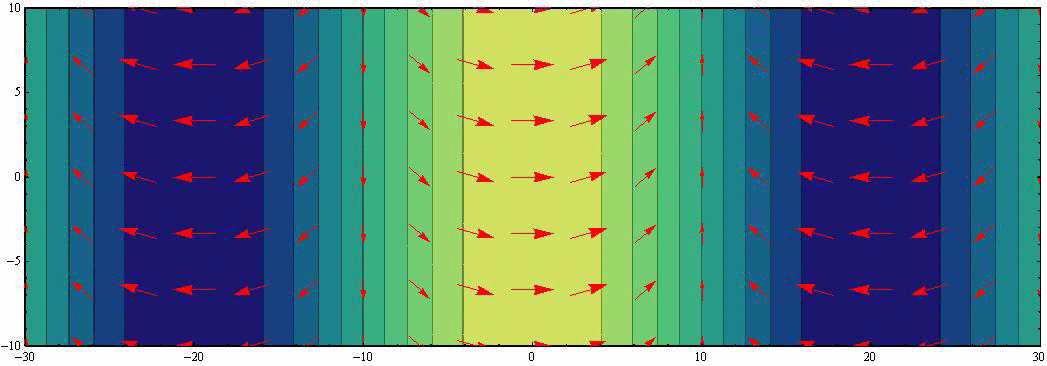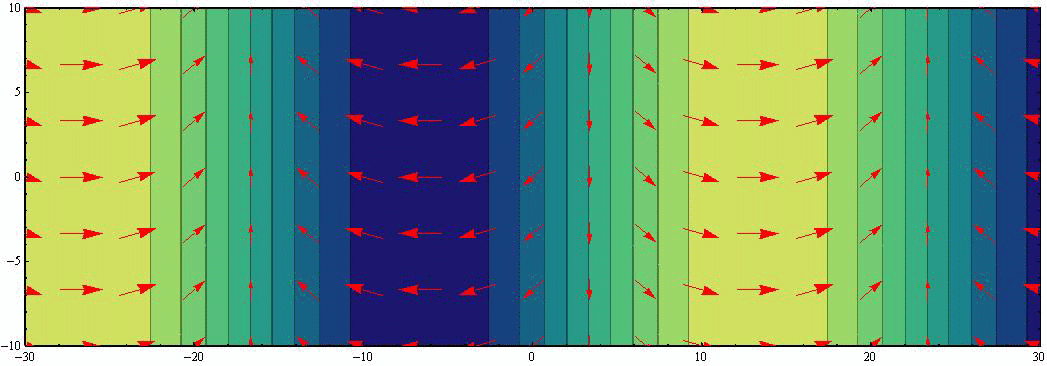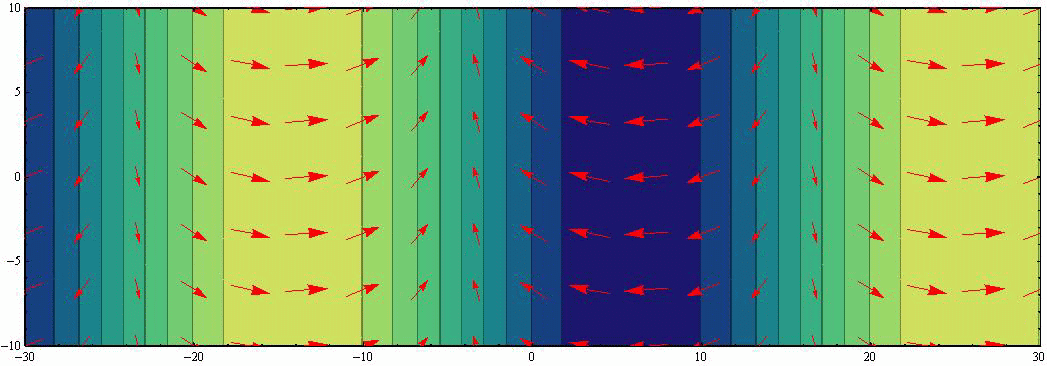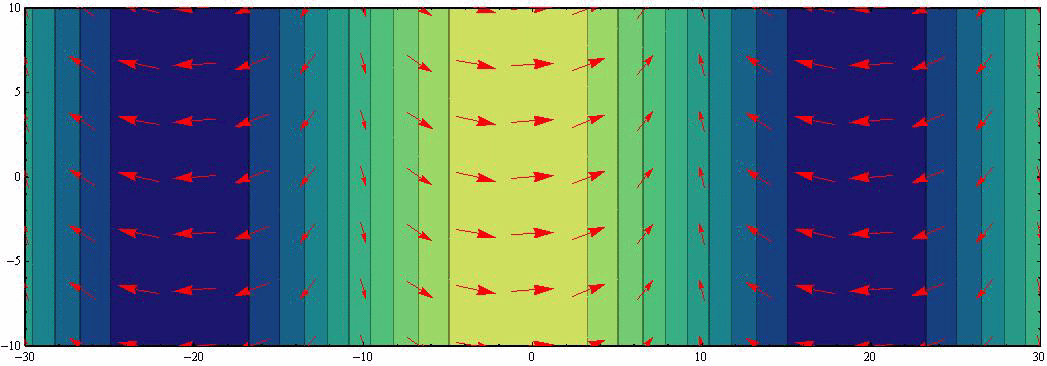
このアニメーションから以下のことが読み取れる。
f0を単位として表した角振動数を縦軸に、f0/(gD)0.5を単位として表した波数を横軸に取ったグラフで、“慣性振動”、“重力波”、“慣性重力波”の関係を示す。f0/(gD)0.5は次節で説明する“ロスビーの変形半径”の逆数です。
以下は、この図についての補足説明です。
[補足説明]
ここでは、波長や周期を定めるメカニズムについては何も議論していません。潮汐波ならば月や太陽の起潮力の周期が波の伝播速度(gD)0.5と一緒になって波長を決めました。しかし、波動方程式の中にはそういった波長や周期を決める原因になるような項はどこにもありませんから、その点に付いては議論のしようが無いからです。
仮に何らかの原因で海面や圏界面に特定の波長・周期の擾乱・攪乱が生じて波が発生したら、その波動は(30)式で与えられる位相速度を持って伝播すると言うだけです。
気象学、海洋学の理論が解りにくいのは、そういった波を生じるメカニズムを見極めるのが難しくて、ここでの話のように自由振動・自由流動の性質から入って行かざるをえないからなのでしょう。
この章で取り扱っている方程式は別稿「動力学的潮汐理論におけるケルビン波」で用いたものと全く同じです。だからケルビン波も“慣性重力波”の一種です。
慣性重力波の波動方程式は、本来その解の中に慣性振動を含んでいますから、流体粒子の運動方向は曲げられます。ところが、側壁境界面がある海洋の場合、境界が運動をブロックするために慣性振動(流体の回転運動)ができなくなる。そのような側壁境界面が有る場合の特殊な解が“ケルビン波”(Kelvin wave)です。
x軸に沿った側壁が有る特殊な境界条件のときには、f=f0+βy≒f0=一定と置いた方程式系(23)、(24)、(3)で、最初からv=0と仮定した方程式系に簡略化できる。それが別項「ケルビン波」3.(3)3.[補足説明1]に示した(A)、(B)、(C)式です。
このとき(B)式は側壁に沿った方向の流れuに関して地衡流が成立していることを示している。それは特殊な境界条件(v=0)のために出てきたものです。
また、(A)式と(C)式から側壁に沿う方向に関してはコリオリ力項を含まない単純な“波動方程式” ∂2h/∂t2=gD・∂2h/∂x2 または ∂2u/∂t2=gD・∂2u/∂x2 が導かれる。そのため、側壁方向に関しては分散性の無い“重力波”が解となる。慣性重力波は、本来その解の中に重力波も含んでいるのですから、この様な重力波と見なせる解が生じるのも頷けます。
そのときコリオリ力は慣性振動的な回転運動を生じるのではなくて、別稿「ケルビン波」3.(3)3.[補足説明2]で述べたようにy方向の波高変化を生じさせ、それとともに渦度を変化させるメカニズムとして効いている。
“慣性重力波”が湾や海峡に進入していくとき、それが側壁境界の影響を受けてどのようにして“ケルビン波”に変化していくかについて、スヴェズドラップが文献1.のp61~62で説明していますのでご覧ください。
ケルビン波は別稿で詳しく論じましたが、ここのテーマに沿ってその特徴をもう一度まとめます。
ここで丁度良い機会なので、近年注目されている“赤道ケルビン波”について説明します。それは、f=f0+βyに於いてf0=0と置けるがβ項が無視できない場合です。つまり、コリオリ力の緯度依存性と圧力傾度力の両方を考慮するのだが、コリオリ力f0は無視できる場合です。
赤道にケルビン波が存在することは、ケルビン波のメカニズムを考察すれば推測できる。別稿で説明したケルビン波はx軸(東西)方向に平行な壁がある場合の解でした。この場合にはv=0という解が得られた。地球の赤道上では、赤道を挟んでコリオリ力が働く方向が逆転するために、壁が無くても、赤道をはさんで南北両半球で対称(すなわちv=0)のケルビン波が存在できそうです。事実そのような解が存在することは次のようにして示すことができる。
ここで注意すべきは、コリオリのパラメーター f は低緯度に行くほど小さくなり赤道上では0になってしまうことです。それで赤道付近の運動を論じるには、1.(1)2.で説明したコリオリ力の緯度依存性を含んだβ平面近似を用いる必要がある。すなわち f=f0+βy で f0=0、f=βy とする必要がある。この様な近似を赤道β平面近似という。f0とβの緯度による変化の様子は1.(1)2.を復習してください。ここでは、赤道上にx軸を取る。
この近似を使い、かつ初めからv=0とおくと、赤道付近のケルビン波を表す方程式として
が得られる。
これは別項「動力学的潮汐理論におけるケルビン波」の3.(3)3.[補足説明1]、あるいは前章3.(5)1.、で示した(A)、(B)、(C)式に似ていますが、(38)式の左辺の係数がyの関数になっている所が違ってる。そのため解の様子が普通のケルビン波と異なります。
(37)式の両辺をtで偏微分した式に、(39)式の両辺をxで偏微分した式を適用すると
が得られる。これはx方向の一次元波動方程式で、x方向(赤道方向)に関しては位相速度がμ=±(gD)0.5で伝播する“重力波”となることを示している。これは普通のケルビン波と同じです。
(40)式を考慮すると、振幅がy方向でのみ変化する
の形の解が考えられる。
これらを(37)式と(38)式に代入すれば、H(y)とU(y)の具体的な形を決めることができる。
ここでH0はy=0(すなわち赤道)におけるh(x,y,t)の振幅H(0)です。y→∞でh→0となるためには、位相速度μ=σ/kは正でなければならない。すなわち
となる。つまり、赤道ケルビン波は常に東に向かって進む。これはコリオリ力と水面傾度(圧力傾度)の釣り合いを考えると当然の結果です。
この結論を用いると求める解は以下のようになる。
この様な波を“赤道ケルビン波”(equatorial Kelvin wave )と言う。
[補足説明1]
特徴的スケールはコリオリ力の効果から定まりますが、波長そのものを決める原因は別に考えねばなりません。
別稿「動力学的潮汐理論におけるケルビン波」5.(2)4.[補足説明2]で、潮汐現象に伴う赤道ケルビン波の存在の可能性を述べましたが、この場合には潮汐周期(12.42h)が水深Dと相まって波長9000kmを決めます。
赤道の成層圏大気に存在すると考えられている赤道ケルビン波(位相速度約25m/s、周期10~20日、波長約30000~40000km)については、また別のメカニズムが必要です。[J.M.Wallace
and V.E.Kousky: J.Atmos.Sci.,25,p900~907,1968年、これはAmerican Meteorological
Societyのサイトからダウンロード可]
さらに、1978年に廣田勇氏によって赤道上空40~50kmでの半年周期振動に関係するとみられる赤道ケルビン波(周期7日程度が発見された[I.Hirota,
J. Atmos. Sci.,35,p714~722,1978年、ネットからダウンロード可]。
[補足説明2]
今日エルニーニョ現象に絡んで存在の可能性が指摘されている赤道ケルビン波は、海洋表層水の温度分布変化に伴う内部密度境界層に生じるものです。そのため、gやDは内部波の理論に基づいたものに置き換える必要があります。位相速度や特徴的スケールもそれに応じた値になります。そのため伝播速度は3m/s程度となり、約3ヶ月かけて太平洋を西から東へ横断すると考えられている。
この赤道ケルビン波の伝播に引き続いて発生する赤道ロスビー波[6.(3)2.参照]の太平洋横断(東から西へ)期間は約9ヶ月と考えられています。
これと前記の3ヶ月を足し合わせたものを二倍して得られるエルニーニョ周期(遅延振動子理論)は2年程度となります。
ところが、この周期は実際のエルニーニョの2~6年周期と合わない。そのため、最近では充填放出振動子理論という新しい理論がより広い支持を受けているそうです。[参考文献11.第10章参照]
話を解りやすくするためにk、σではなくて、波長λ、周期Tに書き直した式にする。
となる。さらに具体的に H=1、 特徴スケール=10、 波長λ=40、 周期T=12、 表示幅W=20 とした
をアニメーション表示する。表示の中心線が赤道で、波は西から東へ向かって伝播する。
上図に速度ベクトル(赤矢印)を重ね合わせると下図になる。伝播速度に比べて流体速度は遙かに小さな値です。だから、柱状流体要素はほぼ同じ位置で赤道方向に沿った小さな往復運動をします。
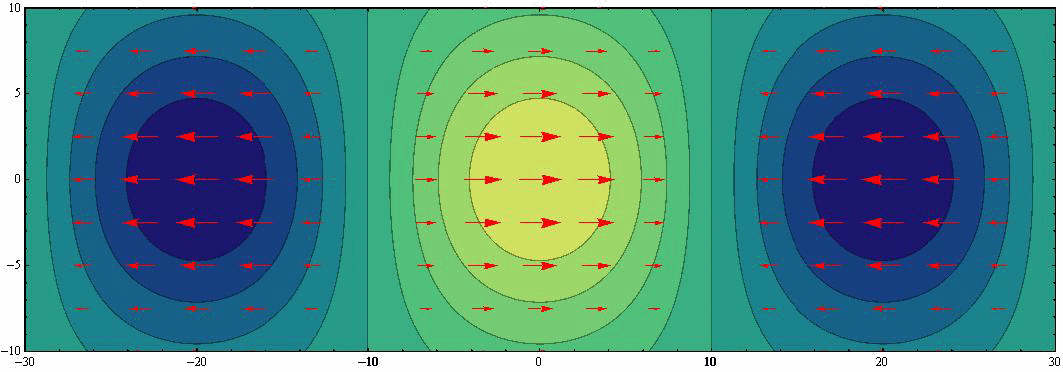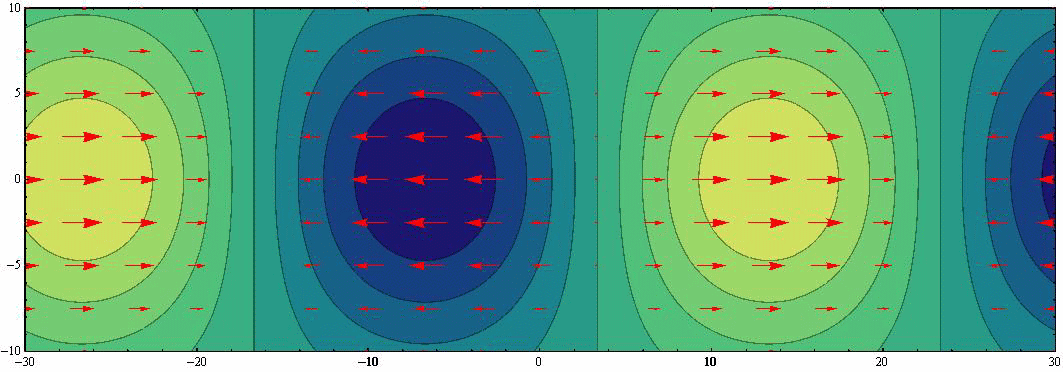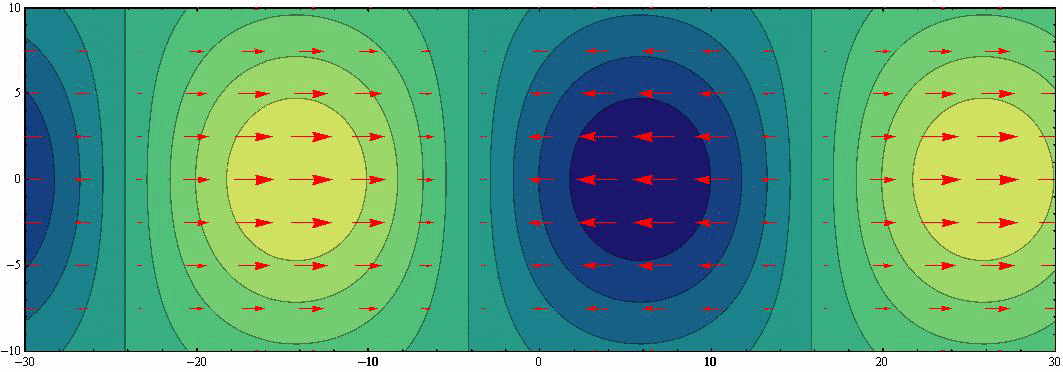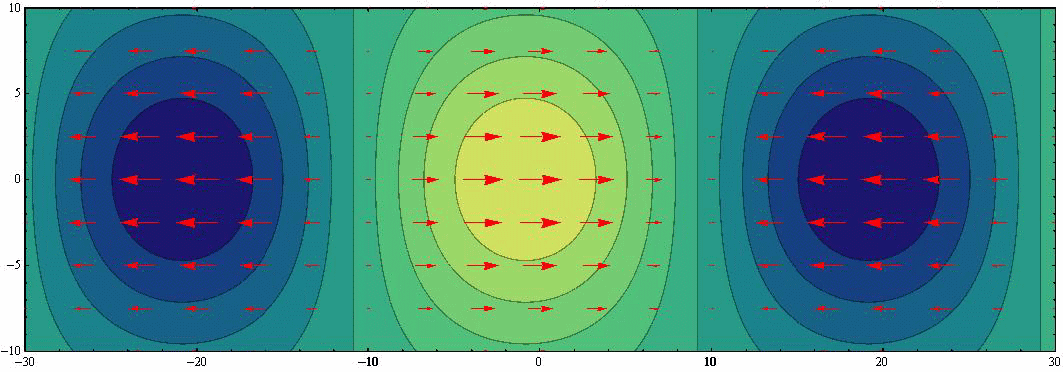
このとき、波高の変化に伴って隣り合う速度成分との間で互いの大きさが変動する。これが波高の変化に伴って渦度が変化することを示しています。また赤道に沿う方向の流れでは地衡流が実現されています。これらは普通のケルビン波と同じです。
波動の規模が地球規模になってくると、地球が球形をしていることによるコリオリ力の緯度変化(β効果)が無視できなくなります。ここで行うのはまさに地球規模の波動(プラネタリー波)の考察です。
3.章の波動はf=f0=一定の場合、4章の波動はf=βyと表される場合でした。ここでいよいよ、中緯度地帯で最も重要な“ロスビー波”について説明します。
それは、f=f0+βyに於いてf0もβ項も無視できない場合です。つまり、コリオリ力と圧力傾度力の両方を考慮し、コリオリ力の緯度依存性も考慮する場合です。
ここで取り扱う方程式系をあらためて書いておく。
前記の方程式系では、係数が変数yの関数となる項が(1’)(2’)(5’)のあちらこちらに含まれている。一般に線形偏微分方程式は、その係数がすべて定数であると解が求めやすいが、そうでない場合には容易に解けない。
そのためβ効果に関する効果として(5’)式の真ん中の項βvだけ残して、それ以外のf=f0+βyはすべてf=f0=一定で置き換える。
このとき、赤道付近ではf0とβyが同じオーダーとなるので、この近似は使えず、新たに考え直さなければならない。また、高緯度ではβ→0となるので、やはりこの近似は成り立たない。そのためここでの議論はあくまで中緯度に限定される。赤道地帯に生じる波については6.赤道波で説明します。
このように近似すると方程式の係数はすべて定数となり、解はたいへん求めやすくなる。結局のところ
が解くべき連立方程式です。
連立方程式を、一つの未知関数のみを含む、単一の式に変換する。
“連続の式”(46)の両辺をtで偏微分したものに、“運動方程式”(44)の両辺をxで、(45)の両辺をyで偏微分したものを代入する。
この両辺をtで偏微分して、“渦度方程式”(48)を代入する。そして“運動方程式”(44)式の左辺の時間微分項が無視できる地衡流近似を用いると
が得られる。この中の左辺第3項のf02の項は自由表面の渦管の伸縮の効果を現している。また第4項がβ効果に依存する項です。
“連続の式”(46)の両辺をxで偏微分したものに、“運動方程式”(44)の両辺をtで偏微分したものと、“運動方程式”(45)を代入する。
この両辺をtで偏微分したものに、“渦度方程式”(48)の両辺をyで偏微分したものを代入する。そして“連続の式”(46)式の右辺の時間微分項を無視した式を用いる。これは波高の時間的変化が無視できるとする地衡流近似です。
同様にして、“連続の式”(46)の両辺をyで偏微分したものに、“運動方程式”(45)の両辺をtで偏微分したものと、“運動方程式”(44)を代入する。
この両辺をtで偏微分したものに、“渦度方程式”(48)の両辺をxで偏微分したものを代入すると
が得られる。
このときコリオリ力項をf=f0に近似した式ではなくて、f=f0+βyをそのまま用いても上記の式変形は可能です。運動方程式のtによる偏微分や渦度方程式のxによる偏微分にはその違いは影響しません。また最後の変形に於いて地衡流近似を用いていません。つまり、vに関する方程式(52)は、[5.(1)2.で述べた近似]や[地衡流近似]を用いなくても導けます。ただし、(52)のf2の項が定数係数で無くなるので、実際に解くときには結局5.(1)2.の近似を用いなければなりません。
結局、三つの量h、u、vは全て同じ形の“定数係数の3階線形同次方程式”(50)、(51)、(52)を満足する。これらは3.(2)で説明した“慣性重力波の波動方程式”に、コリオリ力の緯度依存性を表すβ項が付け加わった形をしている。このとき(50)(51)式を導く過程で地衡流近似を用いているので、これらは“準地衡流方程式”(quasi-geostrophic equation)と呼ばれている。
ここで、波高hと流速(u,v)の間に成り立つ関係式を求めておきます。運動方程式(44)と(45)の両辺をtで偏微分すると
となる。(44’)式に“運動方程式”(45)を代入すると
となる。同じく(45’)式に“運動方程式”(44)を代入すると
となる。すなわち、今用いている近似の範囲では慣性重力波の場合と同じ関係式が使える。これらは波高解hから流速解(u,v)を導くときに使いますが、“ロスビー波”も、波の伝播に伴った楕円運動をすることが解る。
ただし、5.(5)3.で説明するように“非発散性ロスピー波”の平面波解の場合には波面に平行な往復運動になる。
最初に最も簡単な形の波高解
を考察する。これが“準地衡流方程式”(50)を満たしていることは代入してみれば直ちに確認できる。ただしそのときσは
を満足する場合に限定される。これはσに関する三次の代数方程式だから可能な解は3つある。
三つの解の様子は、例えばY(X)=-X3+20X+5のグラフの様子を考えれば解る。このグラフはY=-X3のグラフにY=20Xの一次関数のグラフを足して、それをさらにYの正方向へ5だけずらしたグラフとなる。
だから-X3+20X+5=0の解は、X=0付近に一つ[20X+5=0からほぼ求まる]、X軸の正負にほぼ同程度離れた二カ所に二つ[-X2+20=0からほぼ求まる]の合計三つの解を持つ。
今の場合に当てはめると、σ≪k(gD)0.5の場合と、σ≫β/kの場合を仮定して代数方程式を解けばよい。
これはβ項の効果が無視できる場合です。このとき(56)式のβgDkの項が省略できて
となる。これは3.(3)1.で求めた慣性重力波の角振動数の表現式(32)式と同じです。すなわち、これはコリオリ力の緯度依存性が省略できる(β→0)場合には、解は“慣性重力波”になることを表している。β→0の場合には、準地衡流方程式は3.(2)で説明した慣性重力波の波動方程式となるわけですから、この様な解が含まれているのは当然です。
ただし、今は中緯度に於ける波動を考えているので必ずしもβ→0では有りません。βが小さくなくてもkが有る程度大きければσ≫β/kを満足するσ領域がありますから、その様な状況の慣性重力波が存在するということです。そのとき、同じkに対してσ≪k(gD)0.5を満足するσ領域には次項で説明するロスビー波の解も同時に存在できます。
これら条件不等式の意味は解りにくいところですから、5.(4)5.[補足説明2]のグラフをご覧になりながら、その意味を検討してみてください。σ≪k(gD)0.5は、σ/k≪(gD)0.5と書き直してみれば明らかなように、ロスビー波は重力波の円錐曲面から離れてσ=0のk平面にごく近い所に存在すると言うことです。一方、慣性重力波はk→0となるとσは重力波から離れて原点から有る程度離れたσminに収束しますから、σ≫β/kを満足できるのです。
このとき、波面(位相が一定の場所)が進む速度(位相速度)は3.(3)1.の(34)式で求めたように
となり、重力波の位相速度(gD)0.5より常に大きくなりますが、その大きさ自体は同程度です。
例えば、緯度45°における深さ4000mの海洋の場合には、f0=10-4rad/s、程度ですから
となります。波長λが例えば潮汐波の10000kmでも、この項は0.6程度ですから、μは重力波の位相速度(gD)0.5~200m/sとそんなに違いません。
“慣性重力波”の伝播の様子や流速の様子は、3章を復習されてください。
これは位相速度が重力波のそれに比較して小さい場合です。このとき、(56)式の-σ3の項が省略できて
となる。この式で表される波を“ロスビー波”(Rossby wave)と言う。このとき必ずσ<0となるので、ロスビー波の位相は必ず西進します。ただし、波のエネルギーが常に西進するとは限りません。ここはロスビー波の議論で最も解りにくいところですから5.(4)節で詳しく説明します。
ロスビー波の位相速度は
となる。ロスビー波は位相速度が波長に依存する分散性の波です。
ここで注意すべきは慣性重力波と違ってロスビー波の位相速度を決めているのはコリオリ力の緯度変化に関係するβ項です。慣性重力波の場合は重力に関係する(gD)0.5が大半を決めていた。コリオリ力項f0と波長λはその偏差に関係しただけです。しかし、ロスビー波では、位相速度にf0や波長λは関係してはいますが、その大半を決めているのはβ項です。そのためロスピー波と慣性重力波の位相速度は全く異なります。
実際、緯度45°における深さ4000mの海洋の場合、f0=10-4rad/s、β=1.6×10-11rad/m・s、Rd~2000km程度ですから
となる。慣性重力波の200m/sに対して25m/sですから、ロスビー波の方が一桁小さい。このことから最初に用いた近似が良い精度で成り立っていることが確認できる。
もう一つ注意すべきは、ロスビー波の位相速度μは波長λが同じでも、波面の伝播する方向によって変化することです。位相速度μの表現式に掛かっている
は波面の伝播方向によって位相速度が変化することを意味する。
このようになったのはσの表現式にkが入っているためですが、それは元々コリオリ力が緯度と共に変化することに起因する。つまり、コリオリ力の緯度依存性β項のために位相速度が伝播方向によって変化する。これはロスビー波の大きな特徴です。
ここでも波を生じるメカニズムについては何も論じていませんが、中緯度ではf0とβ項は常に存在しますので、方程式の線形性から明らかなように慣性重力波とロスビー波は両方同時に重なって存在できます。
そのときσの違いから慣性重力波とロスビー波は明瞭に区別できる。例えばl=0の場合には[東進する慣性重力波]、[西進する慣性重力波]、[西進するロスビー波]の三つの波が同時に存在します。
l=0の場合について上記の関係をグラフ表示してみる。
ロスビー波の場合、波数ベクトルの大きさは同じでも方向が違えばσの値が変化しますので、3.(4)3.で示した慣性重力波の様に波数ベクトルの絶対値(k2+l2)0.5を横軸に取ることはできません。(k,l)=(k,0)の特別な場合のグラフをkを横軸に取って表示しています。
となります。このグラフのσ<0は位相速度が西向きになることをあらわしているに過ぎません。
σを常に正として、kの正負で東進・西進の方向を表すこともできます。そうすると、上記のグラフは
の様になる。これが良く見かけるグラフです。
これらのグラフから明らかなように、中緯度に於いては位相速度が(gD)0.5の重力波を境にして、速い位相速度を持つ慣性重力波と、遅い位相速度を持つロスビー波がはっきり区別できる。
このとき、流速解についても慣性重力波とロスビー波に対応するものが存在する。両者が重なって存在すると考えればよい。“慣性重力波”に伴う流速解は3章で詳しく調べました。“ロスピー波”に伴う流速解は5.(2)3.で説明したように基本的に慣性重力波と同じですが、σが異なることから流速変動の振幅と周期が異なっています。“非発散性ロスピー波”の場合は5.(5)で検討します。
ロスビー波の[位相速度が波数ベクトルの方向に依存して変化する]ことや、[位相速度の西向きの成分は波数ベクトルの絶対値が同じなら波数ベクトルの方向によらず一定になる]ことは解りにくいところなので、アニメーションで説明します。(55)式に(57)式を代入すると
となる。ここで
位相速度μや周期Tが負になっているのは、波が波数ベクトルの方向と逆向きに伝播するからで、それ以上の意味は有りません。
(A)(k,l)=(1,0) (B)(k,l)=(2/3,50.5/3) (C)(k,l)=(1/3,80.5/3)
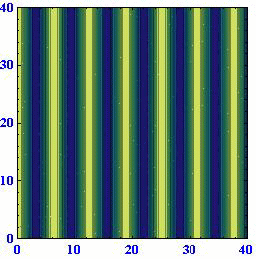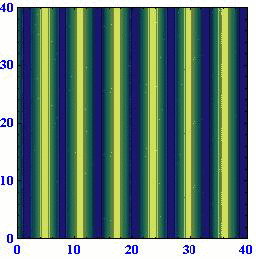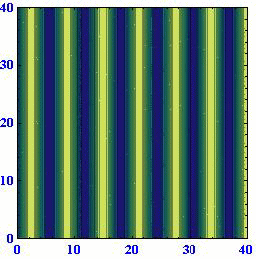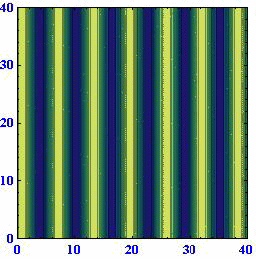
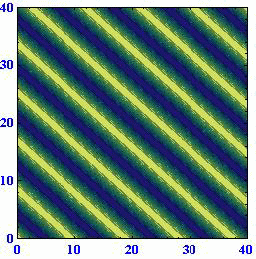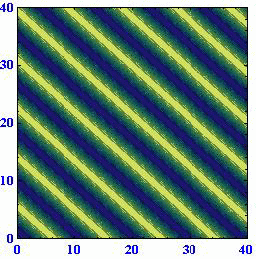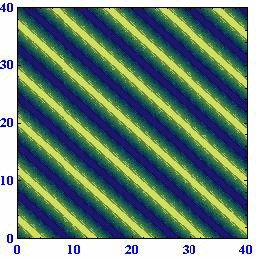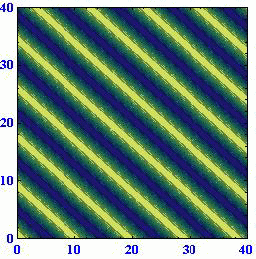
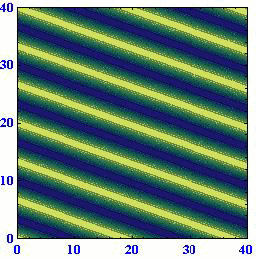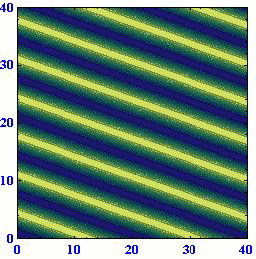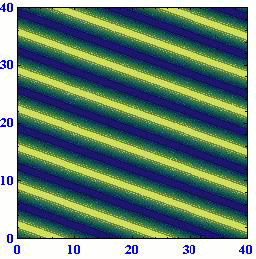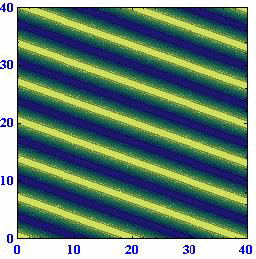
このとき波数ベクトルと波面との関係は下図の様になっている。
これらのアニメーションから、[波数ベクトルの方向が変わると位相速度がkに比例して変化する]ことと[ロスビー波は波数ベクトルの向きとは逆に進む]ことを読み取ってください。
このときさらに、波面がx軸上を西に進む速度はどの場合にも同じになります。すなわち、[ロスビー波の波面がx軸に対してどのように傾いていても波数ベクトルの絶対値が同じで有る限り西向きの速度は同じ]になります。そうなることは、上図の赤半円に内接する直角三角形のkが位相速度に比例する量であることに注意すれば明らかです。
この様な特別の性質を持つのは、ロスビー波がβ効果に伴う波だからです。
ロスビー波の理論で最も解りにくい所は、位相が常に西に向かって進むと言うことです。このことを正しく理解するには、波のエネルギーの伝播とは何かを理解する必要があります。
それは波の位相速度と群速度の違いを理解することですが、それを説明するために5.(3)4.で説明したl=0の場合についてのσとkのグラフをもう一度取り上げます。そこのグラフのロスビー波の部分だけを取り出して、σを拡大して描くと
のようになる。このとき以下の事柄が言える。
今までの議論では波を発生させるメカニズムについては何も話していませんでしたが、ここで以下のような状況でロスビー波を発生させる。β平面のx=0の位置にy軸に平行な垂直板を置いて、その板をx軸方向に角振動数σ0でゆっくりと振動させる。つまり角振動数が定まった波をx=0の位置で発生させる。
そのとき、振動板で作られた波は当然x軸の正方向と負方向にエネルギーを伝えていくはずです。ところが、今まで述べてきたように波の位相は必ず西向きにしか進みません。それではエネルギーが東と西の両方に伝わるとはどういうことなのでしょうか。その鍵は上記のグラフの中にあります。
上記のグラフでσが定まった波を発生させた場合、発生する波の波数には二つの解が存在します。図中のk1とk2です。このとき、いずれのkの値のときもσ<0ですから、今まで説明したようにこの二つの波の位相速度は負となり必ず西に進みます。
このとき、波の波数が定まっていると言っても実際に生じる波は、例えばk1の波ならばεを微少な値としてk1付近の(k1-ε)~(k1+ε)の波数の波が重ね合わされたものと考えるべきです。k2の波についても同様です。つまり
と表されます。重ね合わせる波の振幅Hは当然kの関数ですからH(k)と書かれています。つまり実際に発生する波は非常に小さな幅2εを有し、平均の波数がk1ork2の多数の波が重ね合わされたものであると考えるべきです。そのとき
と置くと、前記の式は
と
になります。
これらの式の[ ]括弧内の被積分項目は、(k-ki)、(σ-σ0)が小さな値なので、正弦・余弦関数の振幅が空間的にも時間的にも非常にゆっくり変化します。これはちょうどアナログのラジオ放送電波の“搬送波”とそれに重ね合わされた“変調波”の関係に似ています。
電波の場合は波長が変わっても伝播速度(光速)は変わらない非分散性の波なので、搬送波と変調波は同じ速度(光速)で伝わりますが、今は、波長により伝播速度が異なる分散性の波なので、“変調波”の伝播速度は“搬送波”の伝播速度とは異なってきます。そのとき、波のエネルギー輸送を担っているのは変調波の伝播速度です。その様に、搬送波の振幅の変化(変調波)が移動する速度を“群速度”といい
で表される。
一方、搬送波そのものが伝わる速度は“位相速度”といわれ
で表される。
[補足説明]
位相速度と群速度の概念は解りにくい所です。参考文献13の§26に解りやすい説明がありますが、より直観的な理解には別稿「ファインマン物理第Ⅱ巻の§6-3の説明が有益です。[光の波]と[流体を伝わる重力波]の違いはありますが本質は同じです。
流体を構成する部分要素が(光波の場合と同様に)入射してきた一次波によって二次波を生じ、それが重ね合わされたものが進行波となる。そのとき二次波の位相の遅れに関係するのがコリオリ力の効果です。その効果の関わり方の違いが“分散性”を生じ、位相速度と群速度の違いを生み出す。
波のエネルギーが位相速度ではなくて群速度で伝わるというのはなかなか解りにくいところなので、前記のグラフのk1とk2の近傍の二カ所の波を重ね合わせた合成波を用いて説明します。
k1の近傍の二カ所(k1’,σ1)と(k1,σ0)の波を重ね合わせる。
となる。
k2の近傍の二カ所(k2’,σ2)と(k2,σ0)の波を重ね合わせたものも全く同様にして
となる。
ここで具体的な数値を下記の様に取る。
これら数値を用いると、重ね合わせた波高解は以下のようになる。
k1の波は
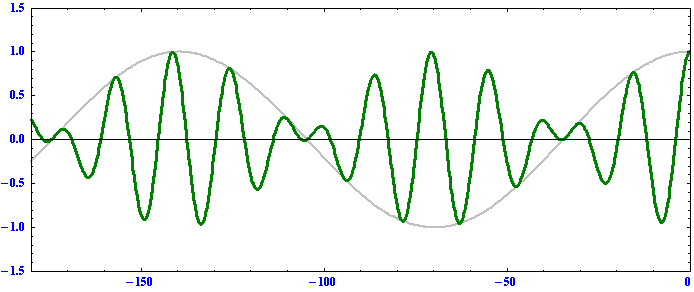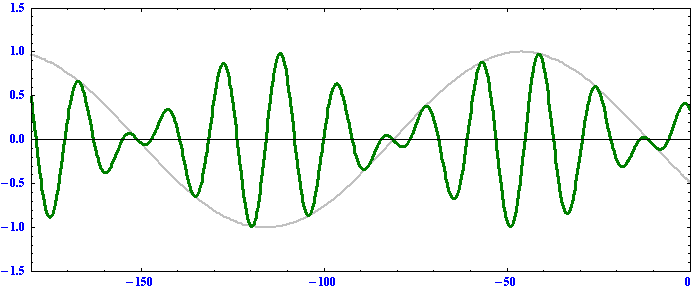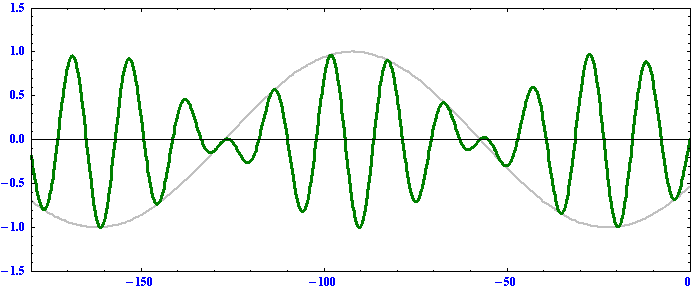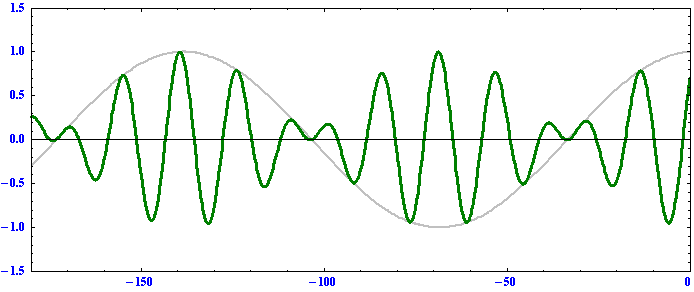
k2の波は
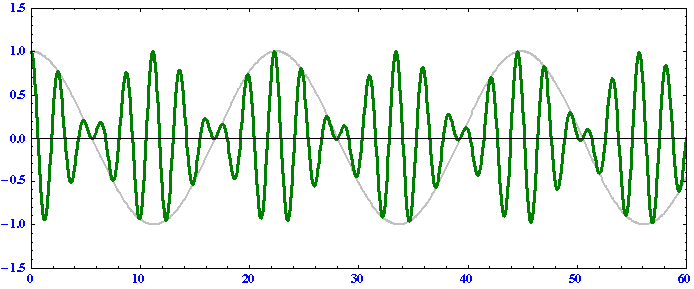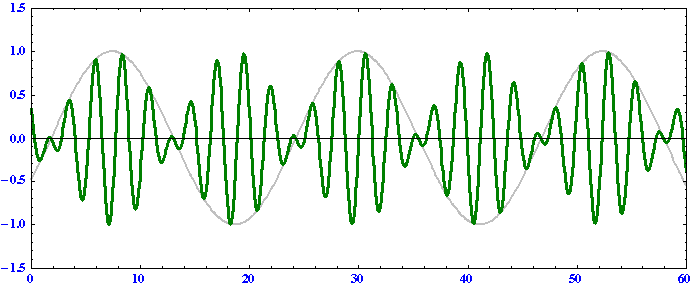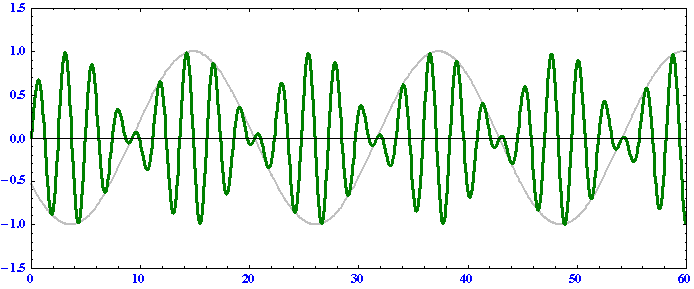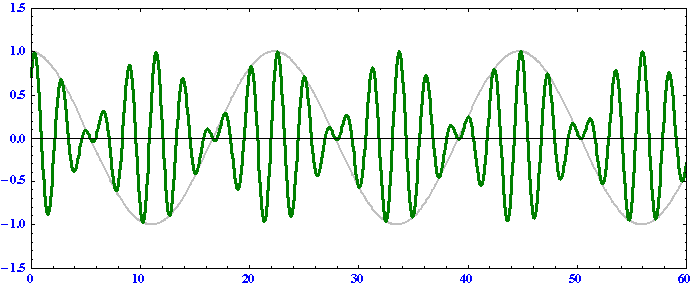
のようになる。
これらのグラフの横軸はそれぞれ原点からの距離(正が東側、負が西側)を表しますが、アニメーションが見やすいようにk1波とk2波では縮尺スケールが変えてあります。これらの例から以下のことを読み取れる。
Ibbetson と Phillipsは、この様な波が実際に生じることを巧みな実験で示した。次項でその内容を説明します。
IbbetsonとPhillips は、同一の角振動数を持つロスビー波が二種類存在し、両者の波長・位相速度・群速度がそれぞれ異なっており、それは理論の予想する通りであることを、次のような模型実験で示した[参考文献3.と4.]。
彼らは図に示す様な、同心円筒の間に流体をいれ、共通軸の回りに回転させた。このとき、容器の底は平坦ではなくて、半径が増大すると半径方向に水深が深くなるようにしてある。
このようにすると、1.(2)3.で述べた渦位保存則に於いてコリオリ力項f=f0=一定であるが、水深項DがD-β’yと変化しているために、β効果が擬似的に実現できる[詳細は5.(6)参照]。
この円形水路は直径2m程度、水路幅0.3mのかなり巨大なものです。水深は内側円筒壁部で6cm、外側円筒壁部で12cmです。この水路は4.2秒で1回転する。造波装置の板の振幅は5cm程度で、振動周期は10s~30s程度の範囲で変化させた。造波装置によって発生する波の波長や位相速度を測定するために、表面張力を押さえる薬剤を表面に滴下したのちにアルミ粉末を浮かべてある。波は水路と同期して回転するように水路上方に設置された、カメラと動画撮影用の映写機により記録された。
1965年にPhillipsが得た結論を文献3.から引用すると
の様になった。グラフ中のsが波数で、波数s=40がおよそ波長λ=11cmに対応する。
同じくIbbetsonとPhillips の1967年の論文(文献4.)から引用すると
となった。
得られた結果は、振動版の東(右)側にできる波も、西(左)側にできる波もいずれも西進(左進)した。そして、造波板の東西で波長の違う波が観測された。波長は東側(down-rotation
side)が短く、西側(up-rotation side)が長く、それらは理論的に予測されるものと一致した。
5.(4)2.や3.はl=0の一次元の波数空間kに関する議論でしたが、二次元波数空間(k,l)に拡張した場合を説明します。(k,l)座標上にσ曲面を描くと下図の様になる。
この図に置いて、三角形OCDに於ける線分ODの傾きが波速ベクトル(k,l)方向の位相速度を表す。同様に三角形BCDに於ける線分BDの傾きがx方向の位相速度、三角形ACDに於ける線分ADの傾きがy方向の位相速度を表す。
そのとき、位相を表す波面は線分ベクトルOCに垂直で、波面の進行方向は線分ベクトルOCの逆向き(線分ODの傾きは負だから)となる。
その位相波の群速度はどうなるのだろうか。前々項の議論から明らかなように、D点に於けるσ曲面の最大勾配の大きさが群速度を表す。群速度ベクトルの方向はσ曲面の最大勾配の方向です。つまり、群速度ベクトルはσ曲面のD点に於けるσの等高線(図の赤半円)に垂直です。
そのとき、エネルギーの伝播に関係する変調波の波面は群速度ベクトルの方向に垂直で、変調波の波面は群速度ベクトルの方向(D点の勾配ベクトルは正方向に向く)に進んでいく。
位相速度ベクトルと群速度ベクトルの方向が異なることは理解しにくい所なので、具体的な波の例について時間的変化を追跡してみる。今までの図は波数・角振動数空間(k,l,σ)での話だから非常に解りにくい。上図のD点の状況をxy座標・波高hの実空間(x,y,h)の値で解釈し直す。
まず、搬送波の波長λp、振動周期Tp、位相速度μpは
となる。
実空間でのエネルギー輸送速度を表す変調波の伝播速度(群速度)のx成分とy成分は、
で与えられた。これは変調波の波面の実空間での伝播速度成分を表すので、実際の群速度の大きさは
で与えられる。すなわち、実空間において、変調波の波面は搬送波の約0.065/0.058=1.1倍の速度で移動する。そのあたりはグラフ曲面の傾きからも読み取れます。
変調波の波面の移動方向は、波数・角振動数空間(k,l,σ)に於ける変調波の波数ベクトル(Δk,Δl)で表されるが、その波数と変調波の角振動数Δσは、搬送波と同様な関係式
を満たさなければならない。
このときΔσと波数ベクトルの大きさ(Δk2+Δl2)0.5は、両者の比率が上記の関係を満たせば任意に取れる。しかし、アニメーション表示したときに解りやすいのは、変調波の波長λgが搬送波の波長λpの10倍程度の場合です。その様にするにはΔσをいくらにしなければならないか見積もってみる。変調波の波長を搬送波の波長の10倍とすると、変調波の角振動数Δσは
程度にすればよいことが解る。
このときΔσを0.0234ではなくて0.021とすると、丁度この10倍が搬送波の角振動数0.21に一致する。このような整数倍にする必要性など全く無いのだが、アニメーションファイルを構成するときに整数比にしておいた方が都合が良いのでΔσを0.021として、波長の方を調整することにする。
Δσ=0.021とすると波長は
とすればよいことが解る。
ここで変調波の波面が群速度ベクトルに直交するように0.3231をΔkとΔlに分割するには
とすればよいことが解る。
搬送波の位相速度、変調波の群速度が上記の値となる波は以下の式によって表される。
この波の様子を以下でアニメーション表示する。
変調波の波長λgは19.45となりますが、アニメーション中の変調波の山と山の間隔はその半分の9.725であることに注意してください。λgx、λgyについても同様です。そうなることは5.(4)3.のアニメーションを復習すると解ります。そこの灰色カーブが変調波の波形を表しています。

アニメーションから、この例の位相速度ベクトルは波数ベクトルとは逆向きであること、群速度ベクトルが波数ベクトルの方向と異なっていることなどがわかる。また、群速度が位相速度の約1.1倍になっていることも読み取れます。
[補足説明1]
5.(4)1.で、[ロスビー波の波面がx軸に対してどのように傾いていても波数ベクトルの絶対値が同じである限り西向きの速度は同じ]になることを説明しましたが、σ曲面の上で考えるとこのことが直ちに理解できます。下図中の赤ラインの傾きがすべて同じであることが西向きの位相速度が同じになることを示しています。
[補足説明2]
5.(3)4.で説明した角振動数σと波数(k,l)の関係を三次元グラフで示す。簡単化のためにf0=gD=Rd=1、β=0.5と置いている。それぞれの波のσ曲面は下図の様になる。
これらの曲面について、ロスビー波のσ曲面と同様な考察をすると、以下のことが直ちに了解できる。
“重力波”は、波数ベクトルの大きさ・方向が変化しても位相速度ベクトルと群速度ベクトルの大きさ・方向は変化せずに常に一定値となる。そしては位相速度ベクトルと群速度ベクトルは常に同じ大きさであり両者の方向も常に一致する。
また、“慣性重力波”は、波数ベクトルがゼロのときには位相速度は無限大ですが、波数ベクトルの大きさが増大するにつれて位相速度は無限大からだんだん減少してきて重力波の位相速度(=群速度)に近づいていく。一方、群速度の大きさは波数ベクトルがゼロのときにはゼロだが、波数ベクトルの大きさが増大するにつれてやはり重力波の群速度(=位相速度)に近づいていく。そのとき、σ曲面はσ軸を中心軸として回転対称だから、これらの傾向は波数ベクトルの方向に依らない。
σ曲面を比較してみると、“ロスビー波”の特異な性質はすべてのそのσ曲面の特殊な形状に由来していることが解る。
ロスビー波が重力波や慣性重力波と根本的に違う所は、ロスビー波は完全に二次元の流体でも存在できることです。つまり海面や圏界面に蓋をしてしまって境界面の上下動を無くしてもロスビー波は存在できる。この場合には、H=0だから方程式(50)やその解(55)は意味をなさない。しかし、流速場に関する(51)、(52)式や、(50)式のhを圧力場と見なした式はそのまま成り立つ。だから流速場や圧力場がロスピー波となって伝わると考えればよいのです。
この様な波高の変化の無い場合の波を“非発散性ロスビー波”(non-divergent Rossby wave)と呼びます。このとき慣性重力波が重なって存在する事はなくてロスピー波のみが存在する。その為、ロスビー波の性質を調べるには特に適した状況です。
この場合の方程式系は5.(1)1.の(1’)、(2’)、(3)式でhが絡む項をすべて省略したものとなる。
が解くべき連立方程式です。ここでは(44’)と(45’)の右辺に圧力項を残していますが、今はこの圧力項が波高に比例するわけではありません。(u,v)の水平方向での変動を実現するために残してあるだけです。
(44’)と(45’)の右辺の圧力項をゼロで近似してしまえば、これは、2.(2)1.で説明した慣性振動を表す運動方程式にβ項が付け加わった形ですが、全体的な平行流があるとき慣性振動が重要になるのであって、慣性振動が解として注目さているわけではありません。
このとき(44’)と(45’)の両辺をyとxでクロス微分したものを片々引き算して右辺の圧力項を消去した式を得る。それに連続の式(46’)を適用すると
が得られる。
このとき得られる渦度方程式(48’)では、非発散性のためにf0に関係する項が無くなっている。つまり、慣性重力波の場合コリオリ力f0は発散性を通して運動に効いていたのですが、非発散性の場合、f0は慣性振動には効いてきますが、波動運動(渦度方程式)には見かけ上効いてこない。つまり、コリオリ力の緯度依存性(β項)のみが効いてきます。
(48’)式は二つの関数の方程式だから一つの関数のみ含む方程式にする。二次元・非発散性の連続の式(46’)が成り立つ場合、2.(1)3.で説明した“流線関数”Ψを導入する事ができます。
2.(1)3.の議論は定常流についてのもので、波高は時間的に変化しないが場所的には変化しているものでした。ここでは波高は時間的・場所的に変化しないが、流速分布は時間的に変化する非定常な場合を考察します。非定常な場合でも、非発散性(波高が変化しない)が成り立てば流線関数は定義できます。もちろん、ここでは流線関数と波高の関連性は有りません。
いずれにしても、流線関数Ψ(x,y)を用いると流速成分(u,v)は
と表される。これらを(48’)式に代入すると
が得られる。
これは5.(2)2.で求めた流速成分(u,v)が満たす準地衡流方程式の三階時間偏微分項とf0項を省略した形と同じです。だから今用いている近似の場合、元の流速成分(u,v)もこの形の方程式を満たしていると考えられる。
話を簡単にするために、平面波解を考察する。
この形の解が方程式(59)を満たすには、角振動数σは
でなければならない。これは5.(3)3.の(57)式の分母の(1/Rd2)の項が無い場合に相当します。
(61)式と(10)、(60)式を用いると流線関数Ψと流速解(u,v)は
となる。
これらの波の位相速度は波長とともに変化するので分散性の波です。これらの波は波数ベクトルとは逆方向に伝播します。また、位相速度は波数ベクトルの方向に依存して変化することや、位相速度の西向きの成分は波数ベクトルの方向によらず一定になること、また群速度ベクトルの方向は位相速度ベクトルの方向と異なることなどは5.(4)で述べた発散性ロスピー波の場合と同様です。
[補足説明1]
5.(3)3.の(57)式に於いて
ならば(61)式となりますが、“非発散性ロスピー波”の波長λが“ロスビーの変形半径Rd”に比較して特に短いわけではありません。そのあたりは5.(5)4.で示す三次元表示したσ曲面でl≠0の領域を見れば解るように波長の長いものもあります。
(1/Rd2)の項は∂h/∂tに伴う水平発散の効果(f0が関係)を現していたのであって、ここでは発散が無いのでこの項が無くなったのです。この項が無くなるとσ曲面がどのように変化するかは5.(4)5.のσ曲面と5.(5)4.のσ曲面を比較すれば解ります。
[補足説明2]
(59)式はσに関して一つの解しか持たない。これは言うまでも、なく海面に蓋をしてしまったために慣性重波波が発生できなくなったからです。
そのとき、角振動数σと波数ベクトル(k,l)の関係がどのようになるのかは、5.(5)4.で示す三次元表示したσ曲面上で検討してみてください。
前項の平面波解をアニメーション表示してみる。ここでも以下の具体的な例を示す。
ここでも
となる。
流線関数を黄色(高)青色(低)で表現し、流速ベクトルは赤矢印で示す。柱状流体要素はほぼ同じ位置で往復運動をします。
(A)(k,l)=(1,0)
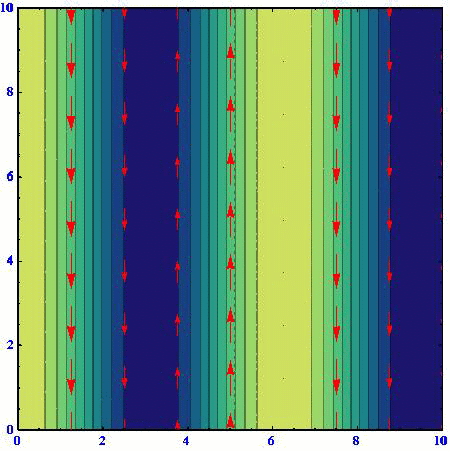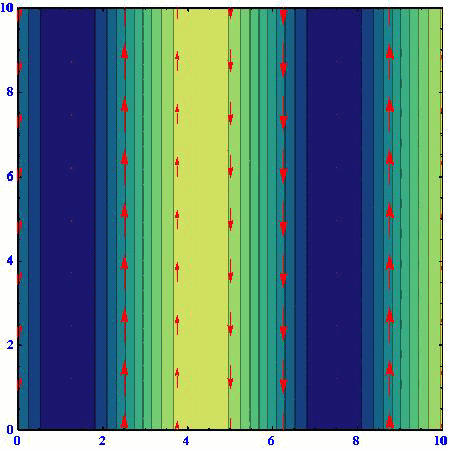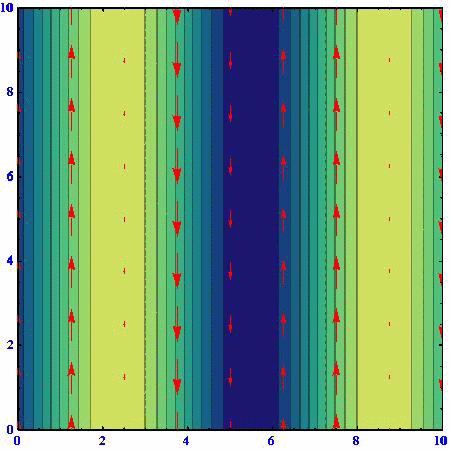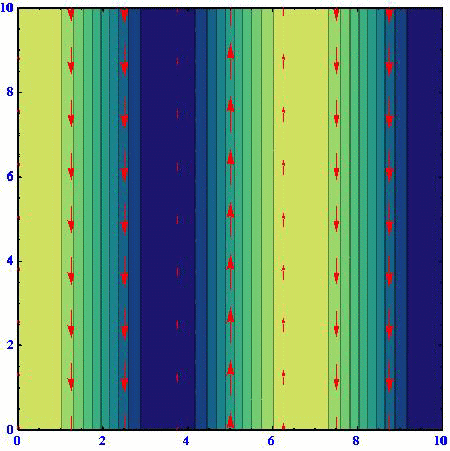
(B)(k,l)=(2/3,50.5/3)
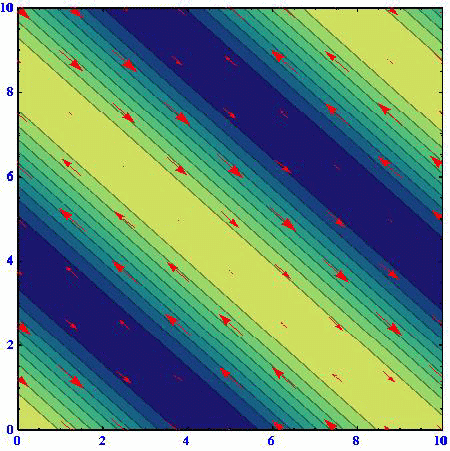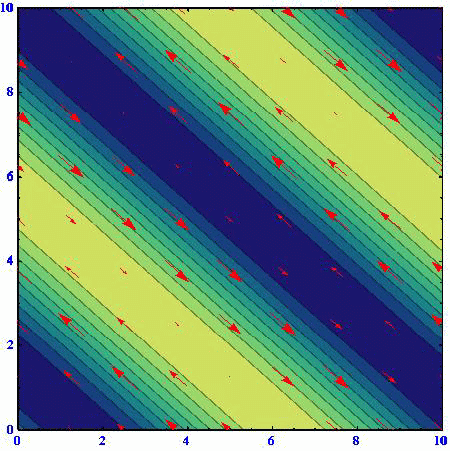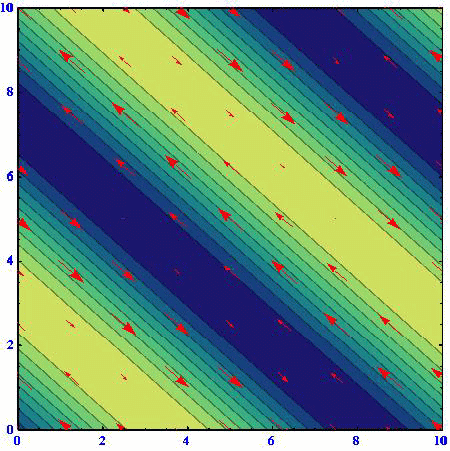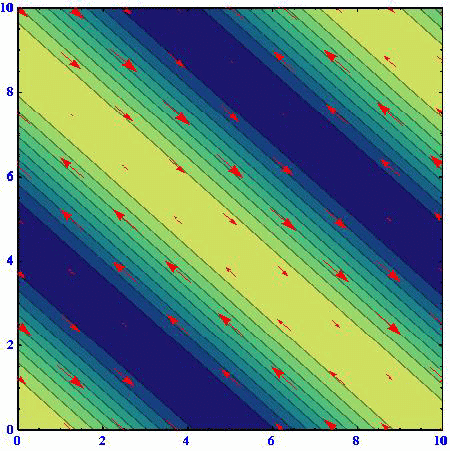
(C)(k,l)=(1/3,80.5/3)
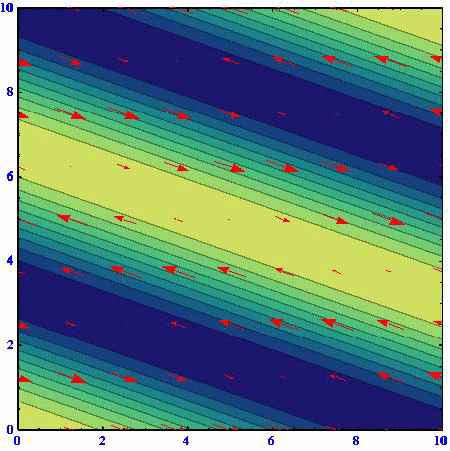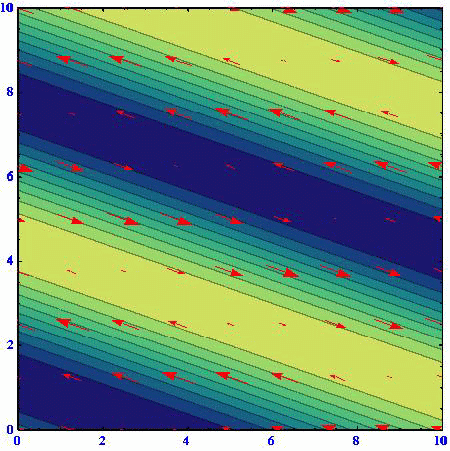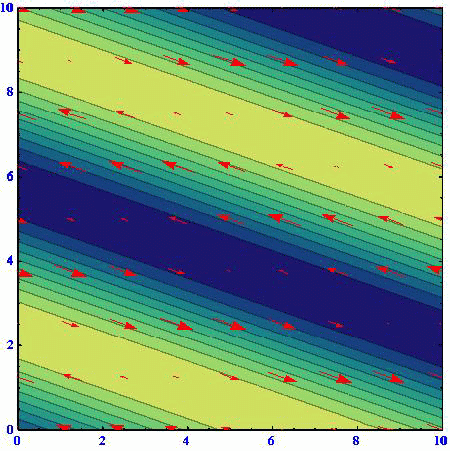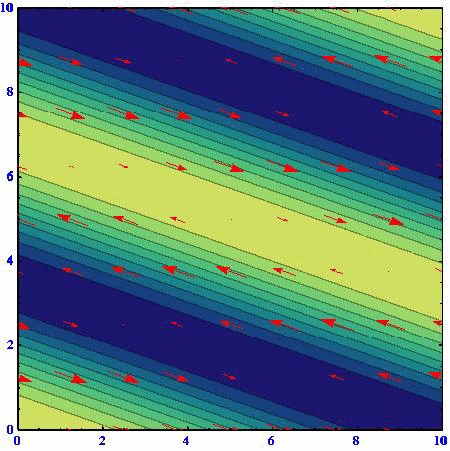
アニメーションの色の濃淡は流線関数の高低を表している。速度ベクトルは流線関数の等高線に沿っており、柱状流体要素は流線関数の高い部分を右に見る方向に動く。流線関数の等高線間隔が密なところほど速度は大きくなる。
このときk→0となると平面波の波面はx軸に平行になりますが、平面波の位相速度もゼロになりますから、それは非定常な波動ではなくなります。
流速場の変動が波となって伝わるときの復元力はβ効果です。β効果が復元力として働くメカニズムはなかなか理解しにくいところですが、(48’)式や(59)式がそのメカニズムを表しています。波動解(60)はそれらの微分方程式を満足しますから、実際にこのようなメカニズムの波が存在するはずです。その様な波の存在を指摘したのがロスビーです。
“非発散性ロスビー波”の場合、角振動数σを表す(61)式を変形すると
となりますが、これは次のような解釈ができます。
この二つのやり方の違いを図示すると
の様な関係になります。
多くの参考書では二番目のやり方で説明していますので、この稿の図と混同しないでください。ロスピー波が発生するとき、波長を決めるメカニズムが有るのか、周期を決めるメカニズムが有るのかによって両者を使い分ければ良い。
[ただし、“発散性ロスビー波”の場合は、1/Rd2の項が有るために、上記の様な簡単な関係にはなりません。]
二番目の方法で角振動数を同じになるようにして波数ベクトルの方向を変えると位相速度がどのように変化するか見てみよう。つまり、上図赤矢印の様に波数ベクトルを変化させてみるわけです。この場合には、上記のアニメーションは(x,y)を固定した位置での振動周期T(角振動数σ)はすべて同じになりますが、kA:kB:kC=3:2:1 ですから、伝播する波の波長は λA:λB:λC=1/3:1/2:1/1 となり、位相速度はμA:μB:μC=1/3:1/2:1/1 となります。
このあたりの関係は5.(4)5.と同様に、非発散性ロスビー波のσ曲面を書いてみれば直ちに了解できます。図中の青色線分OA、OB、OCの傾きが位相速度を表していますが、角振動数σが同じ場合には波数ベクトル(k,l)の大きさ(k2+l2)0.5に反比例することが見取れます。
ここで、角振動数σを一定にして波数ベクトルの大きさと方向が変われば、群速度ベクトルの大きさと方向がどのように変わるかを示す。具体的な数値例として前項で示したβ=1、σ=-0.333・・の場合を取り上げて、波数ベクトルkA、kB、kCで表される三つの波を考える。
位相速度がすべて負であることは、波数ベクトルとは逆向きに搬送波の波面が進むことを示している。東西方向に関しては、位相速度は必ず西に向かう。
群速度に関しては、波数ベクトルにより、様々な方向を向き、その大きさも変化する。東西方向に関しては西に進む場合も有れば東に進む場合もある。
このあたりは発散性ロスビー波の場合と同じです。
偏西風中に生じるロスビー波を考えるときには、一般流の効果が無視できない。ここでは非発散性で一般流中に生じるロスビー波を考える。一般流がx軸の正方向を向いており速度Uを持つとする。
この場合の運動方程式は、ラグランジュ微分D/Dtの中のu∂/∂xの項を残した形の近似式を用いる。すなわち
となる。
(63)式の両辺をxで偏微分したものから、(62)式の両辺をyで偏微分したものを引算して、さらに連続の式(46’)を適用すると
なる渦度方程式が得られる。
非発散性の二次元流では、流線関数
が導入できる。これを用いれば渦度方程式(64)は単一の関数の偏微分方程式に帰着できる。
これは(59)式にUが関係する項が付け加わった形をしている。
ここで、見通しを良くするために5.(5)2.と同じ平面波解(60)式を仮定する。これを(65)式に代入すると
が得られる。
(64)式が、ロスビーの論文[参考文献2.]中の(11)式に相当します。ロスビーはこの式を渦位保存則から導いているのですが、渦位保存則はもともと渦度方程式から得られるものですから、ここで導いたものと同じです。ロスビーはこの式に、幾つかの仮定を適用して論文中(17)式を導いていますが、これは上記(66)式の両辺をkで割って位相速度度にした式に相当します。
ロスビーはこれらの式を元にして、帯状流(偏西風)の蛇行との関係を論じています。そのとき用いられる主な考え方は、偏西風の蛇行に伴って帯状流中の流体部分が南北に移動すればβ効果により帯状流中での渦度が変化し、帯状流の蛇行が保持され、克つその蛇行が西進するであろうと言うものです[例えは文献9.p12~13、文献11.p34等を参照]。そしてロスビーは、さらに今日ロスビー波の特徴として知られている性質を論じています。
確かに、そのようなメカニズムが働いて偏西風の蛇行や西進が説明できそうです。ただし、そこで行われている仮定や実際の偏西風の蛇行との関係の説明は、かなり曖昧なところがあり、私はロスビーの論文を読んでもよく理解できません。
偏西風にロスビー波は何らかの形で関係しているのは確かですが、こんにち偏西風の形成やその蛇行そのものはもっと違う原因に依ると考えられています。[7.(2)参照]
そのため、ここではそのあたりの議論はやりません。ロスビーの考察の詳細については文献2.をお読みください。
ここでは緯度変化に伴うコリオリ力変化(β効果)が無視できるf0平面近似で考える。
このときyの正方向に向かって地面(海底)が上昇していて、yの正方向の水深がより浅くなるように D(x,y)=D0-β’y と置く(β’>0)。ここで、Dは水深を表しておりβ’は斜面の勾配ではなくて浅くなる割合を表しているのだから、yの正方向に向かって水深が浅くなるためには、β’y項の前の符号は負でなければならないことに注意。
この場合、出発点となる運動方程式は5.(1)1.の(1’)、(2’)式においてf=f0(すなわちβ=0)とおいた(44)、(45)式
です。
しかし、ここでは連続の式(46)は使えない。水深Dが場所的に変化する場合にも正しい
を用いなければならない。
(45)式の両辺をxで偏微分したものから、(44)式の両辺をyで偏微分したものを引算して、さらに連続の式(67)を適用すると
なり、5.(1)1.の渦度方程式(48)と全く同じ形の渦度方程式が得られる。つまり地面(海底)の傾斜に依って擬似的にβ効果を生み出すことができる。
(44)、(45)、(48)式は5.(1)2.で説明した方程式系と、全く同じですから、そこでの議論がそのまま成り立ちます。このような状況で生じるロスビー波を“地形性ロスビー波”(Topgraphic Rossby wave)といいます。
ただし、β効果に関係する南北(北に向かってy軸の正方向を取る)の関係を、海岸線に垂直な方向(深海から海岸・浅海に向かってy軸の正方向を取る)の関係に置き換えないといけない。
このとき、ロスビー波の位相速度ベクトルは北半球でも南半球でも西向きでした。南半球でのy軸は南極の方向を向いており、f=f0+βy<0ですから、ロスビー波はy軸の正方向に対して右向きに進むからです。これを地形性ロスビー波での疑似β効果に焼き直すと、南半球では深海から海岸(浅海)に向かうy軸の正方向に対して右向きに位相は進むことになります。
つまり、北半球では地形性ロスビー波はβ効果が増大する方向(海岸側)を右に見ながら進む。一方南半球ではβ効果が増大する方向(海岸側)を左に見ながら進む。
[補足説明]
ここで100km沖合に出ると水深が100m深くなる大陸棚について、β値を見積もってみると
程度になる。
緯度45度の深さ100m程度の大陸棚を伝播するロスビー波の位相速度は
となり、それなりの値となる。
[模型実験]
水深変化は模型実験でβ効果を出すために良く使われる手法です。実際、5.(4)4.で述べたIbbetson & Phillips の実験は、まさしくこの地形による擬似的なβ効果を利用したものです。
[陸棚波]
オーストラリア東岸の水位変化を調べていたハモン(B. V. Hammon 1962年)は、水位が周期4日と9日で規則的に上下動する事を発見した。その後の詳しい観測から波長3500km程度、位相速度4m/s程度でオーストラリア東海岸を大陸中央上空から見て反時計回りに(つまり海岸を左に見て)伝播していることが解った。
1964年にロビンソン(A. R. Robinson)は、この現象が海底地形に起因するβ効果に依って生じる地形性ロスビー波ではないかと考えて、“陸棚波”(continental shelf wave)と名付けた。この水位の変動は、低気圧の移動に伴って吹く強風によって励起されるもので、波長は数千kmになる。周期も4~5日程度で慣性振動周期(中緯度で1日程度)よりも長い。
陸棚波の特徴をまとめると下記のようになる。
赤道地帯に存在する“赤道波”(equatorial wave)の全体像は、下記の方針に従った考察から松野太郎氏によって明らかにされた。ここでは、その内容をできるだけ解りやすく説明しますが、詳細は1966年に松野太郎氏によって報告された参考文献5.をご覧ください。
前章5.(1)2.で注意したように、赤道付近では5章のロスビー波の議論で用いた近似は使えない。4章で説明した赤道β平面近似を使わなければならない。ここではx座標を赤道に沿って、y座標を北極方向を正として経線(南北線)に沿って取るとする。すなわち、f=f0+βyに於いてf0=0と置けるがβ項が無視できない場合です。4章の“赤道ケルビン波”との違いはv≠0の場合を含むもっと一般的な解を求めることです。つまり、コリオリ力の緯度依存性と圧力傾度力の両方を考慮するのだが、f0項は無視できる場合の一般的議論です。
赤道β平面近似の方程式系は4.(1)1.で説明したものと同じです。赤道をx軸を取ると
となります。
ここでは赤道ケルビン波の場合と違ってv≠0を含めたもっと一般的な解を考察しますので、vが関係する項も残されています。
ここで、(69)式の両辺をxで偏微分したものから、(68)式の両辺をyで偏微分したものを片々引き算して
が得られる。
連立方程式を、一つの未知関数のみを含む単一の式に変換する。このときyを含む項があるために、hやuに関する式に変形するのは難しいが、vに関する方程式には帰着できる。このあたりは5.(2)2.で注意したのと同じ事情があるからです。
まず、“運動方程式”(1’)、(2’)の両辺をtで偏微分し、“連続の式”(70)の両辺をxおよびyで偏微分すると
が得られる。
ここで、(68’)と(70’)からhの項を消去して、さらにβyを乗じると
となる。同様に(69’)と(70”)からhの項を消去して、更に時間tで偏微分すると
となる。
更に“渦度方程式”(71)の両辺をxで偏微分して、更にgDを乗じると
を得る。
(72)(73)(74)式を加えあわせるとv(c,y,t)に関する偏微分方程式
が得られる。
これは5.(2)2.で導いた(52)式のf02がβ2y2に置き換わった形になっている。すなわち、赤道地帯に於いては中緯度におけるf0の効果をβyが担っているのですが、この係数が変数yの関数であることが重要です。つまり、赤道地帯ではこの項のためにy方向に特異な変化が生じる。
ここで、流速成分vと波高h、流速成分uとの間に成り立つ関係式を求めておきます。
“運動方程式”(68)の両辺をtで偏微分したものと、“連続の式”(70)の両辺をxで偏微分したものから
が得られる。
同様に、“運動方程式”(68)の両辺をxで偏微分したものと、“連続の式”(70)の両辺をtで偏微分したものから
が得られる。
解v(x,y,t)が求まると、これらの式に代入する事で、波高解h(x,y,t)と流速成分解u(x,y,t)を決定する事ができます。
前節の(75)式は、第4項にyについて変化する係数が含まれているので、y方向に関する境界条件を満足する解は簡単な三角関数型とはならない。そのため、y方向に関しては未知関数Φ(y)を仮定して、次のような試行解を考察する。
これを(75)式に代入すると
が得られる。これがΦ(y)を決定するための、変数yに関する2階常微分方程式です。ここで
と置くことにすると(79)式は
となる。ここでαは長さの二乗の逆数の次元を持つ。実際そうであることはβ、g、Dの次元を考察すればすぐに確認できます。そこで変数yの変わりに次元の無い
なる変数ξに置き換えると、上式は
となる。
この2階同次常微分方程式(80)式は、量子力学の調和振動子の固有値問題(一般にはスツルム・リュービル型の固有値問題と言われる)でお馴染みのものです。ここのβ2y2は、ちょうど調和振動子のポテンシャル曲線の働きをしている。この方程式の解はよく知られており、“エルミート関数”(Hermite function)と呼ばれる特殊関数で記述できる。
境界条件から固有値が決定される所の意味は解りにくいところですが、朝永先生が参考文献14.の§41(ⅲ)および付録Ⅸで説明されています。そのまま引用しておきますので、その解説をお読みください。
朝永先生の説明から解るように、方程式(80)の解Φ(ξ)がξ→±∞でΦ→0となる境界条件を満たすたすためには、λ/αは勝手な値であることは許されず、必ず奇数の自然数でなければならない。すなわち
の条件がみたされる場合のみ解の存在が許される。
そのとき、方程式(80)の解はnの値に応じて
と表される。これはn番目の固有振動に於けるξ方向(y方向)の波動の形を表している。
ここのAnは任意の定数です。また、Hn(ξ)は“Hermiteの多項式”と言われるものでn=0,1,2,3,4・・・・・に対して
のようなn次の多項式です。この多項式は一般に
で表すことができる。この関係式の証明は前記朝永引用文献の(Ⅸ・22)式以降を参照されたし。
Φn(ξ)の具体的な形をグラフ表示すると下記のようになる。
ただしAnに関しては
としている。この様に置くと、(81’)の関数系Φn’は(-∞,+∞)において2乗可積分な関数空間で完全正規直交系をつくる。完全正規直交系の意味は朝永引用文献の(41・69)、(41・70)式を参照されたし。
ξをyに戻した(79)式を(76)式に代入すると最終的な解として
が得られる。
ただし、ここのkとσは、固有値の関係式を元のk、σで表したときの関係式
を満足しなければならない。
固有値nが0,1,2,・・・の場合の解の具体的な形を順番に見てゆこう。ここで解の性質を調べる見通しを良くするために角振動数σとx方向の波数kに関して
なる置き換えをする。要するに、σ*、K*なる無次元量で置き換える。あるいは、以下で出て来る(σ*,k*)のグラフは、角振動数σを、
を単位として、波数kを、
を単位として、測定したものと見なすわけです。
このような置き換えをすると(83)式は
となる。
(83’)、(83”)にn=0を代入した式のグラフは下図の様になる。
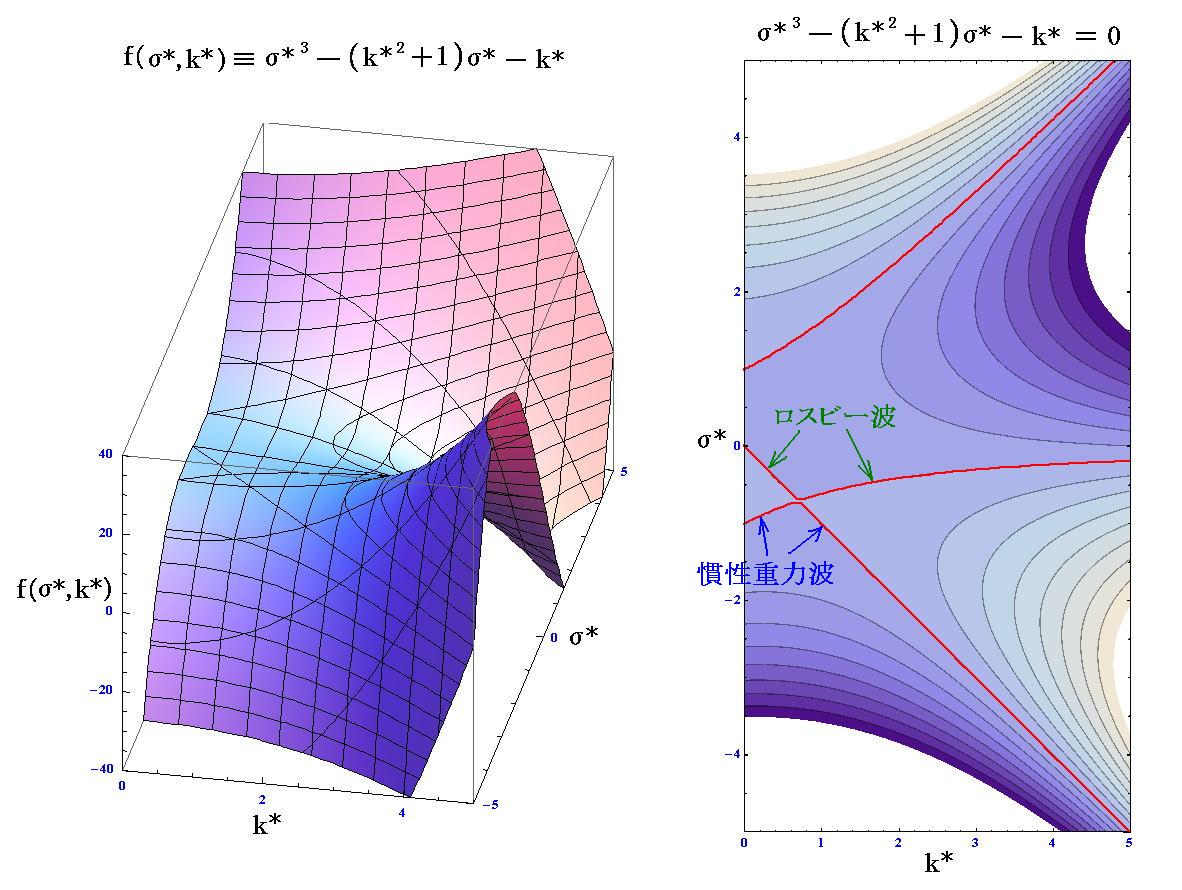
σに関する三次の代数方程式は以下のように因数分解できる。
これから、σに関する三つの解σig-*、σig+*、σR*が求まるのですが、問題は一番目の因数項から出る解σig-*と三番目の因数項から出る解σR*がk*=1/20.5 の点で交差する事です。それは上図右側のグラフから明らかです。交差する位置k*=1/20.5 は、それぞれの解を表す式でσig-*=σR*と置けば求まります。
この点を境にしてロスビー波と慣性重力波の解釈を下記のように繋ぎ替えるべきです。そのあたりの事情は上右グラフ中に記している通りです。すなわち
となる。
σ*とk*の関係式をσとkの関係式に戻して(82)式に代入すれば、n=0に対するv(x,y,t)の解が求まる。ここで、エルミート多項式 H0(ξ)=1であることを考慮すると
が得られる。vの添え字0はn=0に対する解であることを意味する。
ここで、以後の議論を簡単にするために、6.(3)でyに対して行った無次元化を、x、t、h、u、vに対しても行う。つまり
と置くことにする。前記の解v0(x,y,t)をこれらの無次元数ν、χ、ξ、t*、σ*、k*で表わすと
となる。νの添え字0はn=0に対する解であることを表している。
これらの解ν0(χ,ξ,t*)を6.(1)3.の(76)、(77)式に代入して、偏微分方程式を解けば波高解η(χ,ξ,t*)とx方向の流速成分解μ(χ,ξ,t*)が求まる。
“慣性重力波”と“ロスビー波”の違いは、σ*の所だけで、ν0の関数形そのものは両者で同じです。だから、ηとμを求める手順はすべて同様に取り扱える。
ここで、(76)、(77)式を無次元量を用いた偏微分方程式に変換しておく。無次元量に変換するとき、2階偏微分項の上側微分は1乗、下側微分は2乗で変換式を適用する。上記の変換式を用いて整理し、両辺の共通項を割り算消去すると
および
となる。
解ν0(χ,ξ,t*)を(76’)に代入すると
同じく、解ν0を(77’)に代入して
が得られる。
以上をまとめると
となる。
k*に関してはk*=1/20.5 を境にて性質が大きく変化するが、解の形から以下のことに注意しなけれはならない。
解の形から明らかなようにk*=|σ*|となる領域ではη0とμ0の解が発散してしまう。そのためk*≦1/20.5 の領域の“ロスビー波”とk*≧1/20.5 の領域の“西向き慣性重力波”は解として成り立たない。つまりその領域のそれらの解は存在しないと考えるべきです。
そのため、k*≧1/20.5 の領域の“ロスビー波”はk*=1/20.5 の点でk*≦1/20.5 の領域の“西向き慣性重力波”(群速度は東向き)に繋ぎ変わると考えなければならない。この繋ぎ替えが起こる波は、普通“混合ロスビ-重力波”(Mixed Rossby-gravity wave)と呼ばれる。
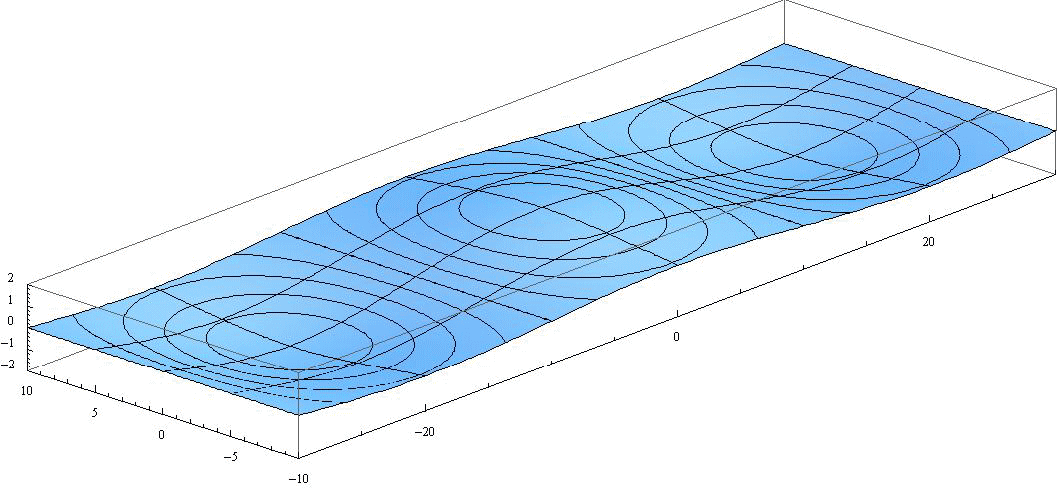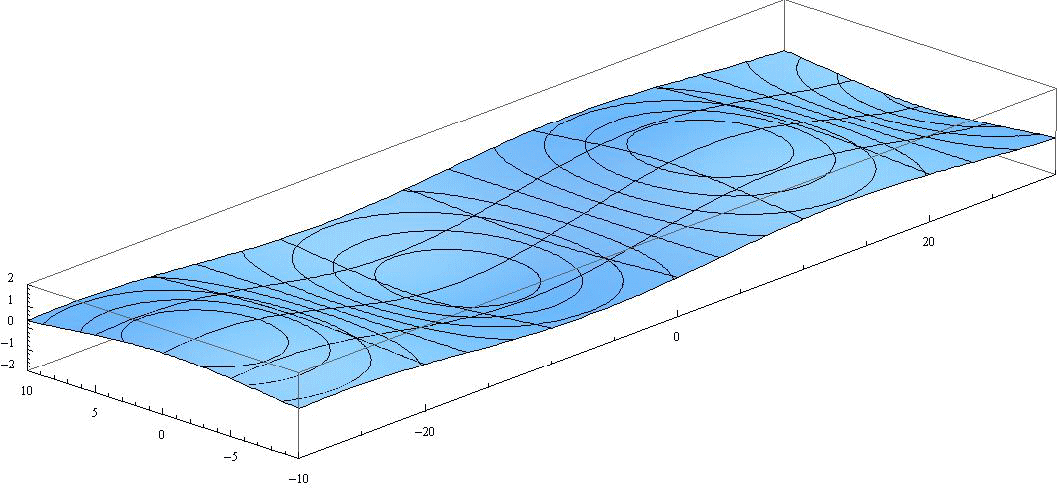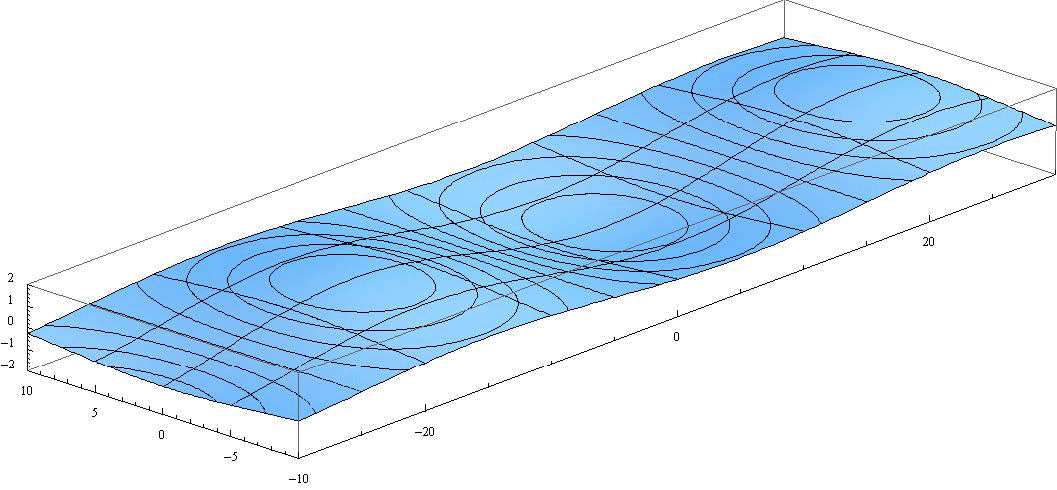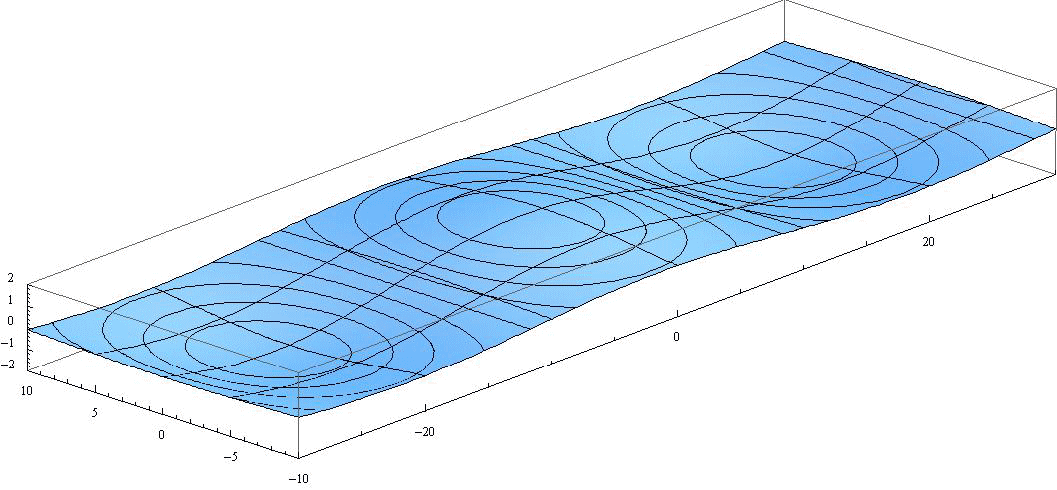
式を見ただけでは解りにくいので、グラフ表示してみる。以下のグラフでξ=0の線が赤道です。またχの正方向が東で、負方向が西です。
上記の事情により、“東向き慣性重力波”と“ロスビー波”についてはk*=1.0の場合を、“西向き慣性重力波”についてはk*=0.5の場合を表示することにする。この“ロスビー波”と“西向き慣性重力波”をあわせたものが“混合ロスビー-重力波”です。
そうすると
となる。このとき、さらにH=1、A0=0.7511・・・とする。
[東へ伝播する慣性重力波(群速度も東向き)](n=0,k*=1.0,σ*=1.618)
[西へ伝播するロスビー波(群速度は東向き)](n=0,k*=1.0,σ*=-0.618)
[西へ伝播する慣性重力波(群速度は東向き)](n=0,k*=0.5,σ*=-0.780)
今日、西へ伝播する位相速度が約23m/s、周期4~5日、波長約10000kmくらいの混合ロスビー重力波が、赤道の成層圏大気中に存在すると考えられています[M.Yanai
and T.Maruyama: J.Meteor.Soc.Japan,44,p291~294,1966年、T.Maruyama and M.
Yanai: J. Meteor. Soc. Japan, 45, p196~199,1967年、T.Maruyama: J.Meteor.Soc.Japan,45,p391~408,1967年、これらはJ.Metior.soc.Japanのサイトからダウンロード可]。
下記の解説記事なども参照されたし。
松野太郎著、“成層圏と大気波動の研究をめぐって”、「天気」1982年12月号
http://www.metsoc.jp/tenki/pdf/1982/1982_12_1167.pdf
佐藤薫著、“赤道下部成層圏準2年周期振動における大気重力波の役割”、「天気」1999年1月号
http://www.metsoc.jp/tenki/pdf/1999/1999_01_0011.pdf
河谷芳雄著、“赤道準2年振動に於けると赤道波と慣性内部重力波の役割”、「天気」2012年09月号
http://www.metsoc.jp/tenki/pdf/2012/2012_09_0807.pdf
(83’)、(83”)にn=1を代入した式のグラフは下図の様になる。
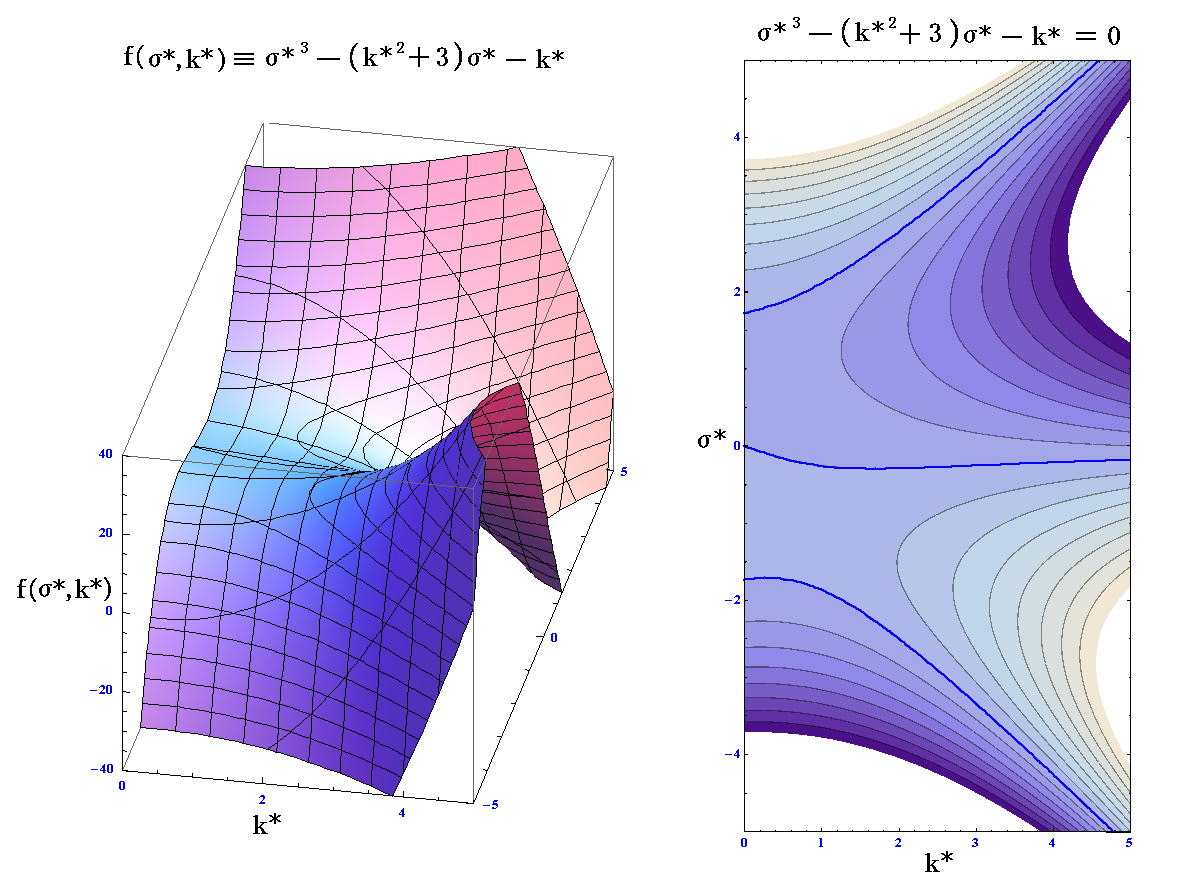
この場合も、正確なσを得るには三次方程式を解く必要がある。ただし、ここでは、5.(3)1.で採用した方法で求まる近似的な値を用いることにする。
すなわち、σ≫β/kの場合の“慣性重力波”に対する解として
が、またσ≪k(gD)0.5の場合の“ロスビー波”に対する解として
が得られる。これらをまとめると
となる。
次に、n=1の場合のエルミート多項式 H1(ξ)=2ξで表した解ν1(χ,ξ,t*)を(76’)に代入すると
同じく、解ν1を(77’)に代入して
が得られる。
以上をまとめると
が得られる。
k*=1の場合をグラフ表示してみる。その場合
となる。このとき、さらにH=1、A1=0.5311・・・とする。
[東へ伝播する慣性重力波(群速度も東向き)](n=1,k*=1.0,σ*=2.115)
[西へ伝播するロスビー波(k*=1なので群速度は西向き)](n=1,k*=1.0,σ*=-0.254)
これがエルニーニョ現象を説明する遅延振動子理論で存在の可能性が指摘されている赤道ロスビー波です。ただし、それは温度が変化する海洋の内部密度境界層に生じるものです。gやDは内部波の理論に基づいたものに置き換える必要があります。そのため伝播速度は1m/s以下となり、約9ヶ月かけて太平洋を東から西へ伝播すると考えられています。
そのとき、4.(1)で説明した赤道ケルビン波と相まって、この遅延振動子理論が予想するエルニーニョ周期はだいたい2年程度になり、実際の2~6年周期を旨く説明できないようです。そのため、最近では充填放出振動子理論という新しい理論がより広い支持を受けているそうです。[参考文献11.第10章参照]
[西へ伝播する慣性重力波(群速度も西向き)](n=1,k*=1.0,σ*=-1.861)
(83’)、(83”)にn=2を代入した式のグラフは下図の様になる。
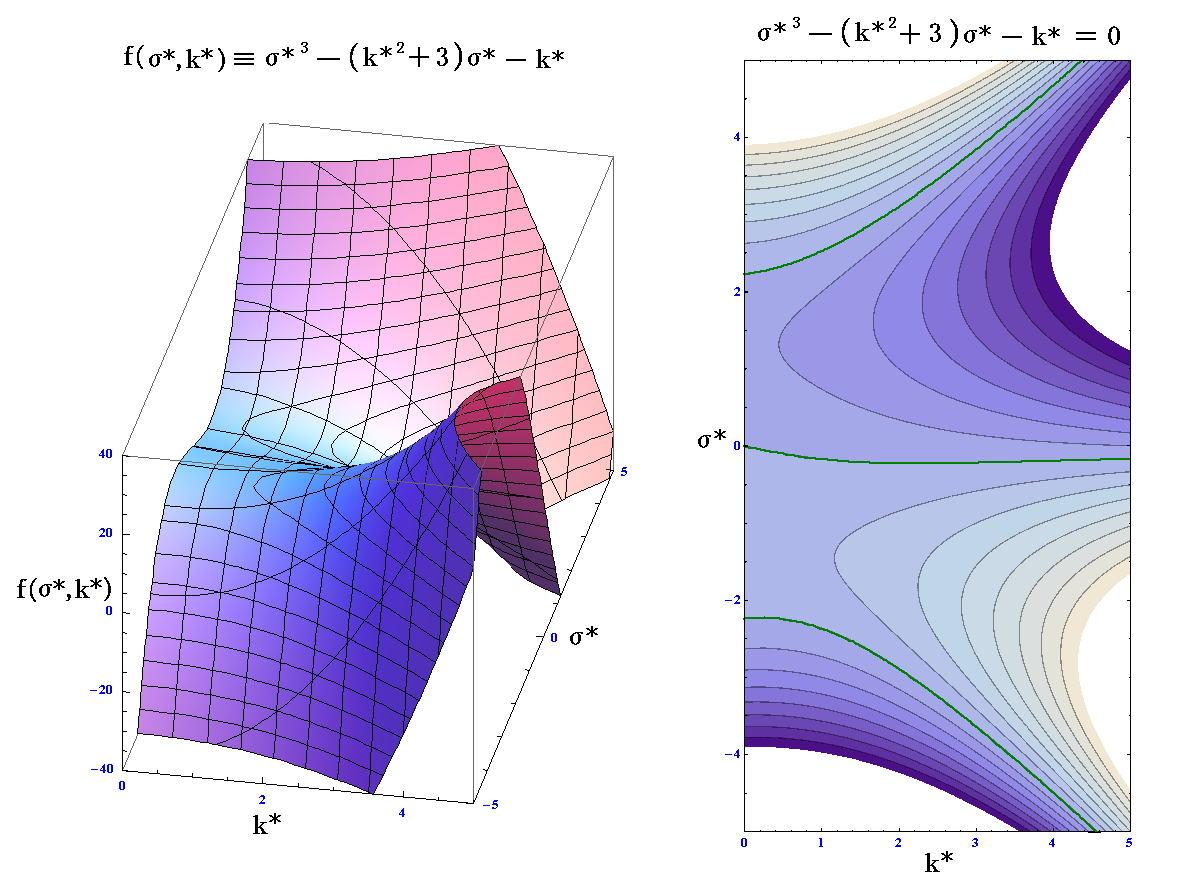
この場合も、正確なσを得るには三次方程式を解く必要がある。ただし、ここでも、5.(3)1.で採用した方法で求まる近似的な値を用いることにする。
σ≫β/kの場合の“慣性重力波”に対する解として
が、またσ≪k(gD)0.5の場合の“ロスビー波”に対する解として
が得られる。これらをまとめると
となる。
次に、n=2の場合のエルミート多項式
H2(ξ)=4ξ2-2 で表した解ν2(χ,ξ,t*)を(76’)に代入すると
同じく、解ν2を(77’)に代入して
が得られる。
以上をまとめると
が得られる。
k*=1の場合をグラフ表示してみる。その場合
となる。このとき、さらにH=1、A2=0.2655・・・とする。
[東へ伝播する慣性重力波(群速度も東向き)](n=2,k*=1.0,σ*=2.529)
[西へ伝播するロスビー波(k*=1なので群速度は西向き)](n=2,k*=1.0,σ*=-0.167)
[西へ伝播する慣性重力波(群速度も西向き)](n=1,k*=1.0,σ*=-2.361)
赤道波の全体は下図の様にまとめることができる。図には4章で考察した“赤道ケルビン波“(空色破線)も附記してある。赤道ケルビン波は、こことは別の事情のy方向境界条件を満たしていますが、見かけ上n=-1 と置いた方程式(83’)を解いた解に相当します。
実際の現象では、どういった原因で波動が生じるのかというメカニズムの問題やx方向の境界条件に依存するが、これらの波が重ね合わされた形で存在すると考えて良いであろう。
この稿は、ただ一層からなる非圧縮性流体の浅い層に生じる波の議論です。そのとき、コリオリ力(f0効果)とその緯度依存性(β効果)が波動の性質にどのように関係するかを説明するものです。
もちろん、現実の大気や大洋は、温度(塩分濃度)成層に伴う密度成層をしておりその内部境界面を伝わる波が重要になります。そのとき波の伝播速度は高度(水深)によって変化し、波動は水平方向のみならず鉛直方向にも伝播します。ここでの議論は、そういった事柄をすべて省略して単純化したものです。
コリオリ力効果、β効果に起因する複雑な性質を理解するには、上記の簡単化はやむを得ないところかもしれません。
もう一つお断りしなければならないのは、ここでは、波が発生するメカニズムについて何も説明していないことです。この稿の内容は、何らかの原因で適当な波長・振動数の波が存在したら、その波はどのような性質を持っており、どのように振る舞うのかを説明するものです。一層からなる流体表面に発生する自由振動・自由波動についての議論です。
波の波長や振動数を決めるメカニズムは有るのか、波動を励起する物理的過程は何なのか、等々・・・について何も論じていないのは申し訳ないところです。
以上の様な限定的な議論でしか有りませんが、重力波・慣性重力波・ロスビー波は大気や大洋の中に確かに存在します。この中でロスビー波は、重力波・慣性重力波に比較して位相速度はかなり遅く周期も長いために、様々なノイズの中に埋もれていて、時間的・場所的に平均化しないとその存在を認知するのは難しいようです。そのとき、理論が予想するような位相速度、角振動数、波長を持って西進するロスビー波は確かに存在して、大気や大洋の振る舞いに大きな影響を与えているようです。下記の解説記事など参照されたし。
廣岡俊彦著、“中層大気中のブラネタリー・ロスビー波”、「天気」1992年3月号
http://www.metsoc.jp/tenki/pdf/1992/1992_03_0111.pdf
廣田勇著「気象解析学」東京大学出版会(1999年刊)第7章“発見と立証(2つの研究例)”
この本は気象解析の思想書のような本でとても面白い。
ロスビーの論文(文献2.)は「大気の帯状循環流の強さの変動と作用の準恒久的中心の変位との関係」というとても長い題が付いています。これはもともと移動性高・低気圧を運ぶ偏西風帯の蛇行とその変化の特徴を明らかにするためになされたもので、“ロスビー波”の論文として知られています。
しかし、私自身この論文を注意深く読んでも偏西風との関係が今ひとつ良く理解できません。ロスビー波と偏西風との関係はロスビーが当初予想したような簡単なものではないようです。
中緯度に存在する偏西風とその波動は、太陽光輻射による加熱が低緯度と高緯度で異なることから生じる南北の温度差・密度差・圧力差に伴う循環が、コリオリ力の影響のもとに中緯度に作り出す温帯性低気圧・高気圧に深く関係しています。偏西風の存在とその蛇行の主な原因は、こんにち傾圧不安定性(J.G.Charney
1947年、E.T.Eady 1949年))によると考えられています。中緯度に発生する寒冷な高気圧、温暖な低気圧が偏西風を作り出し・強め・加速し・保持し、その蛇行を生み出すと考えられています。[別稿「大気大循環」5.中緯度における循環を参照]
そのとき、偏西風の存在と蛇行は高気圧、低気圧の発達・減衰にフィードバック的に影響を与えます。偏西風が北上すればβ効果により時計回り(北半球で)の回転が強まりますから高気圧性の渦を加速して強めます。また南下すれば同じくβ効果により反時計回り(北半球)の回転が強まりますから低気圧性の渦を加速して強めます。そして、移動性高・低気圧は偏西風によって西から東へ一日あたり約1000km流されて行きます。
このように、偏西風波動と移動性高・低気圧は互いに相互作用しており、単純に切り離して論じる事ができません。そのため偏西風の蛇行をロスビー波で単純に説明することは難しいようです。
確かに、偏西風の蛇行は複雑ですが、部分的にロスビー波で旨く説明できる現象もあるようです。特に山岳や海陸の温度差などによって励起された内部ロスビー波は鉛直上方に伝播して、成層圏・中間圏の大気循環に顕著な効果を及ぼすと考えられているようです。
ケルビン波のページを作るために浅水方程式を復習したので、ロスビー波を説明するページも作ろうと思い立ちました。私にとって気象学の論文は難しくて、ロスビー波も何のことか良く理解できていなかったのですが、今度こそ理解したくて下記の文献などを参考にして試行錯誤しながら作りました。
ここでは、ロスビー波の発生原因について何も考察していませんが、私自身この稿を作ることで浅水方程式にコリオリ力が関わる所の全体像がやっと理解できました。全体的に眺めることで、ロスビー波の性質を決めるf0効果とβ効果の働きどころも解ったような気がします。
このページを作った後で、昔読んだことがある廣田勇先生が書かれた啓蒙書、「大気大循環と気候」東京大学出版会(1981年刊)、「地球をめぐる風」中公新書(1983年刊)、「気象の遠近法」成山堂書店(1999年刊)などを倉庫から引っ張り出して読み直してみました。
廣田先生の熱い語りに導かれて、大気中の風・波動が引き起こす大気現象を研究することの面白さにあらためて引き込まれてしまいました。この中で紹介されている論文をネットで探してみると、今日その大半をpdfファイルとして無料で入手できますね。この稿で立ち入れなかったメカニズムを説明する論文も入手可能です。我々のようなアマチュアに取って面白い時代に成りました。