の様になります。ここでAは波の“振幅”(媒質が上下に振動する時の最大移動量の半分)、Tは波の“振動周期”(ある一定地点に於いて媒質が一振動する時間)、λは波の“波長”(ある固定した時刻で波を観測したとき、一つの波の山から山まで、あるいは谷から谷までの様に隣り合った同位相の場所の間の距離)です。
進行波の位相速度と群速度の概念は、ド・ブロイが可秤量物質粒子の波動力学を展開するに際して本質的な働きをします。その事はド・ブロイの1924年の「学位論文」で説明されていますが、結構難解な所ですので、本稿で基本的な所から復習しておきます。
最初に高校物理で習う進行波の表現を用いて説明します。高校物理で習う様に、典型的な進行波の数式表現は
の様になります。ここでAは波の“振幅”(媒質が上下に振動する時の最大移動量の半分)、Tは波の“振動周期”(ある一定地点に於いて媒質が一振動する時間)、λは波の“波長”(ある固定した時刻で波を観測したとき、一つの波の山から山まで、あるいは谷から谷までの様に隣り合った同位相の場所の間の距離)です。
上記の波の同位相の位置が進んでいく速度を“位相速度”と呼びますが、それは以下の様にして求まります。同位相の位置が進んでいく様子は
の様な一次関数で表されます。そのため“位相速度”は、この一次関数の傾きλ/Tとなります。
位相速度をVであらわすと
となります。
[補足説明1]
所で、(1)式に於いて
の様に置いて
の形で表して議論する場合も多い。
この場合に就いても同様で
となるので、位相速度Vは
と表せます。
前章に於いて導入した進行波と、その進行波と振動周期と波長が少し異なる進行波を重ね合わせる。ここでは話を簡単にするために、重ね合わせる二つの波動の振幅は同じとし、t=0でx=0に於ける位相が同じ場合とする。
上式の波群がどの様に伝播するのかを理解するには別稿「慣性重力波とロスビー波、そして赤道波」5.(4)3.のアニメーション図を参照されたし。
ここで赤□の部分の位相が一定である条件から、一次の直線の方程式
が得られますが、その直線の傾きが合成波の“群速度”を表しています。
群速度をUで表すと
となります。
[補足説明1]
(3)式に於いて
の様に置いた形の合成波の群速度を求める事もできます。
ここで赤□の部分の位相が一定である条件から、この場合もまったく同様な計算を実施すると、
と表されることが解ります。
[補足説明2]
群速度を求める展開は、上記とは少し違った形で進めることもできます。
ここで赤□の部分の位相が一定である条件から、一次の直線の方程式
が得られますが、その直線の傾きが合成波の“群速度”を表しています。
群速度をUで表すと
となります。
[補足説明3]
ここで説明している事は、発生させる波の振動数Tを変えたとき、伝播する波の波長λも当然変わるのですが、位相速度と群速度が異なったものになるには、振動数の変化δTと波長の変化δλは以下の様でなければ成らない事を言っている。
すなわち、ある振動数Tで波長λの波が発生して伝播していくとすると、振動数をTからT+δTに変えたとき、発生伝播する波の波長はλ+δλになるのですが、このとき
でなければ成らない。そうであって初めて位相速度と群速度が異なった値となる。
波を角振動数(角速度)ωと波数kによる表現にすると、同様に
でなければ成らない。この場合のみ位相速度と群速度が異なった値となる。
つまり、“群速度”の概念が重要なのは、普通の媒質が形成する波の位相速度は、“分散性”の性質【波の“伝播速度”が、発生・伝播する波の“振動数”(“波長”)の変化に応じて変化する】を持っているからです。
このことを上記の表現で言い換えると、λあるいはkが変化すると、当然それに応じてTやωも変わるのですが、それらを組み合わせた値である位相速度λ/T、あるいはω/kが変化して行くことを意味します。
このことについては、別稿「波動方程式と一般解」3.(3)[補足説明1]も復習されて下さい。
位相速度と群速度の関係は波の伝播速度の変化を表すグラフの上で確認できます。別稿「波動方程式と一般解」で波動の伝播速度を決めるメカニズムを説明しましたが、そこでのメカニズムは発生する波の振動数や波長には依存しませんでした。
しかし、一般には、伝播する波の位相速度は発生する波動の振動数によって変化します。振動数が変化すると言うことは波長が変化する事ですから、発生する波の波長にも位相速度は依存すると言うことです。だから別稿「波動方程式と一般解」の波動方程式中の係数cは発生する波の振動数や波長に依存して変化します。
そのとき、やっかいなのは振動数が変化したとき波の伝播速度が変化しますから、発生・伝播する波の波長との関係も変化するということです。
つまり波の伝播速度の変化の様子は振動数νと波長λの対応が一次の比例関係では無いと言うことです。だから媒質を伝わる波の伝播速度は、振動数の変化に対する発生する波の波長の変化具合のグラフから知ることができるのです。
そのグラフ上の (1/T)/(1/λ)=λ/T が、その振動数Tで振動し波長がλとなる波の伝播速度(“位相速度”)になると言うことです。
そして、そのグラフ上の任意の(T,λ)点に於ける d(1/T)/d(1/λ)=(λ/T)2×dT/dλ が“群速度”になる。
ここは非常に解りにくい所ですので別稿「慣性重力波とロスビー波、そして赤道波」5.(4)3.のグラフ図を参照して下さい。ただし、そこのグラフの座標は、 “波長”λ と “周期”T ではなく “波数”k と “角速度”(角振動数)ω に変換されています。
“位相速度”と“群速度”の違いが生じるためには、波が“分散性”である事が必須です。つまり、波の“波長”と“振動数”(同じ事ですが“波数”と“角振動”)の関係を表すグラフがカーブしていることが必要です。
この事に付いて、以下で、 もう少し説明します。
ここでは、2.[補足説明1]の形式で論じよう。ただしsin関数の代わりにcos関数を用いても同様であることを示すために、ここではあえてcos関数を用いる。更にωtとkxの順序を入れ替えても同様に議論できることを示すために、ここではあえてそうする。すなわち
を用いる。
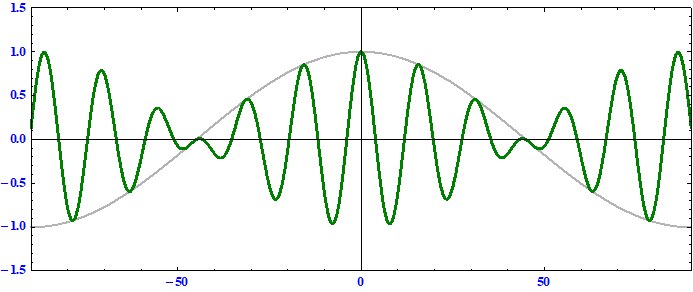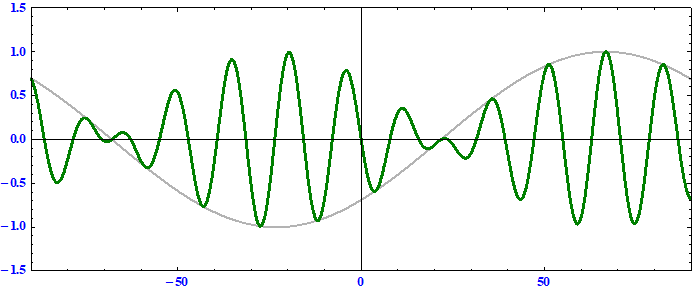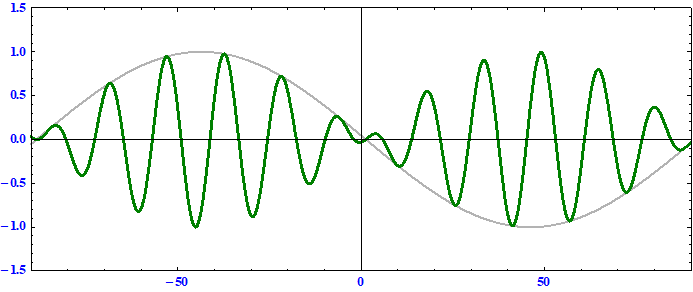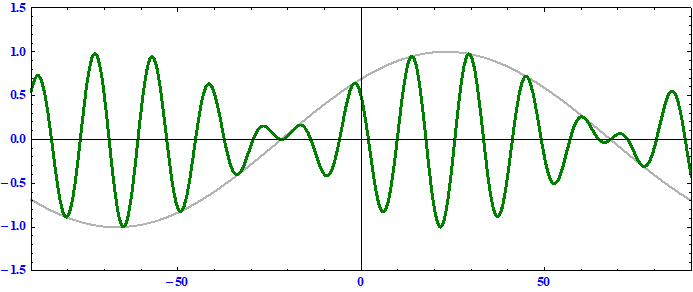
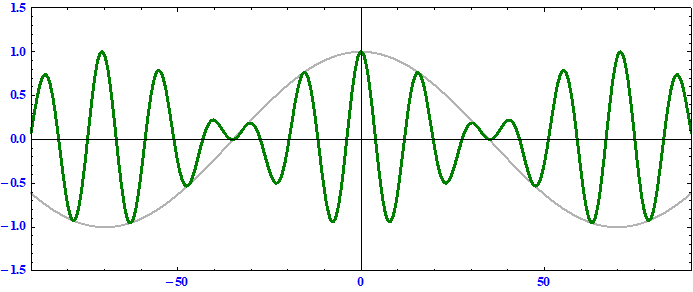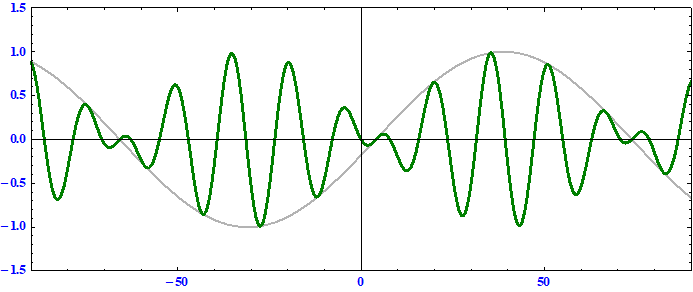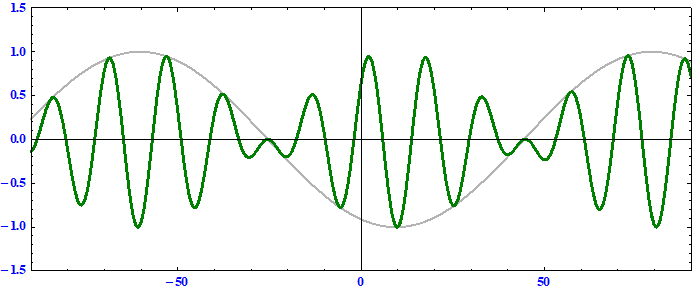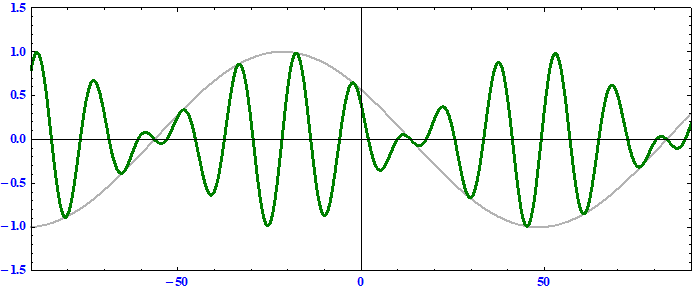
以下の三例に付いて “アニメーション表示” してみる。
ただし、(2)と(3)のケースでは10秒ごとにリセットされて t=0 の初期状態から描きなおされていますので、そこは注意してください。(1)のケースでは10秒ごとに
t=0 の初期状態の波形に復帰します。
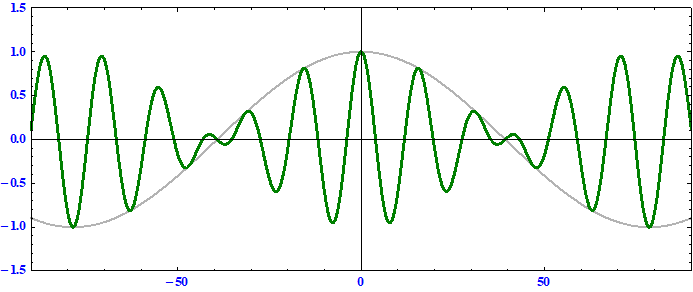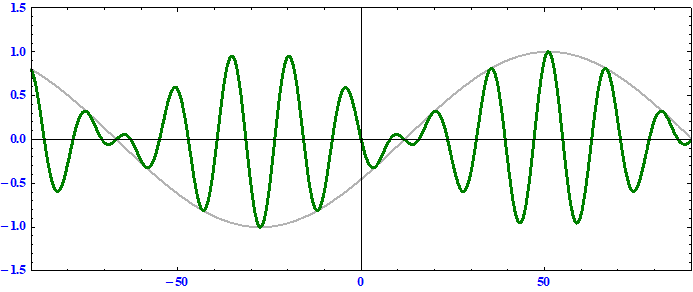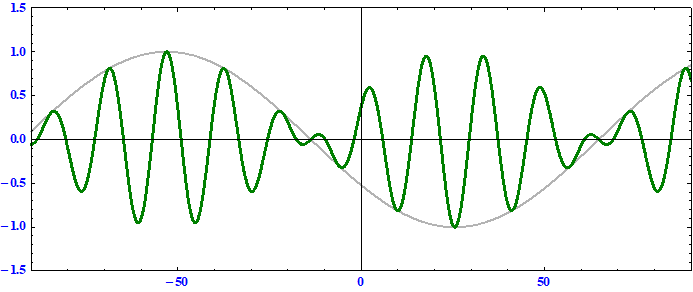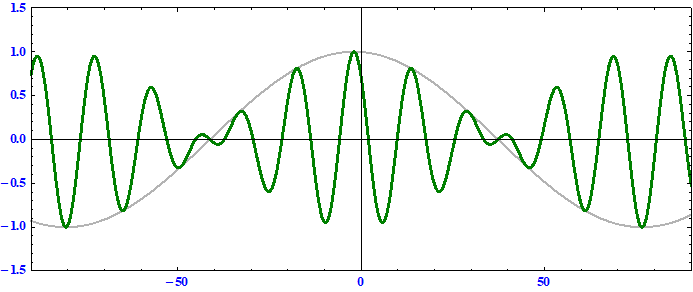
搬送波の位相速度 = 群速度 である事に注意。
搬送波の位相速度 < 群速度 である事に注意。
搬送波の位相速度 > 群速度 である事に注意。
上記三例に付いての “波数k-角振動数ωのグラフ” は以下の様になる。
(2)の “アニメーション図” と (3)の “波数k-角振動数ωのグラフ” を比較したら解る様に、“位相速度”と“群速度”の違いが生じるためには、波が“分散性”である事が必須です。つまり、波の“波長”λと“振動数”ν(同じ事ですが“波数”kと“角振動数”ω)の関係を表すグラフの傾斜が異なることが必要です。
分散性の無い波では群速度と位相速度の違いは生じませんのでくれぐれも注意して下さい。このことに関しては、次に引用するSommerfeldの本の説明が秀逸ですので参照されて下さい。
本章は Arnold Sommerfeld著 理論物理学講座Ⅱ「変形体の力学」講談社(1969年刊 原本は1944年刊)p183~208 の引用です。
ただし、Sommerfeldはできるだけ多くの事柄を説明しようとして、説明を簡潔にし、さらに講座の他巻や他節の内容をしばしば利用しています。それ故に、全巻を購入して互いに参照しながら読まないと理解するのは難しいです。
そのため、ここで省略されている事柄に関しては、別稿「水の波」や、別稿「波動」も参照されながら読まれる事を勧めます。
[補足説明]
ここは§18.§19.を学習しないと何を言っているのか解りにくいのですが、以下の事柄を説明している。
海や湖の様に重力場で液体が静止しているときには液体の自由表面は重力の等ポテンシャル面となる。このような釣り合い状態が、船の通過や風などの影響で乱されると、液体は元の釣り合い状態に戻ろうとして運動を始める。この運動は波として周囲に伝わって行く。
このとき、海や湖に起こる波のようにスケールの大きな流体の運動では、粘性の影響は極めて小さく、完全流体の理論が現実の現象を旨く説明する。容器に入れた液体の振動も復元力として表面張力も付け加えれば、基本的に同様に取り扱える。
そのため、本章の現象はすべて、《二次元・非圧縮性・完全流体(非粘性)・一様重力場》での運動として議論できる。§18.§19.ではその場合に利用できる“複素関数論”のテクニックを説明している。
およその所は、別稿「二次元・非圧縮性・完全流体の力学(ラグランジュの渦定理とは何か)」4.や、別稿「カルマン渦列(動的安定性解析)」3.(2)などを参考にされれば読み取れますので、そちらを復習されて下さい。
本節に付いては、下記(2)式の導出を含めて、別稿「水の波」§35を、あるいは別稿「波動」54.を参照されたし。ただしそこではxy座標の取り方がここと違うので、その点は注意して下さい。
上記の事柄に就いては別稿「波動方程式と一般解」2.(4)を復習されて下さい。
ここは、4.§23.3.のFig.34を復習されたし。
[補足説明1]
下記の流線を決定する“流れ関数”(“流線関数”)Ψに付いては、別稿「二次元・非圧縮性・完全流体の力学」4.(2)2.と、別稿「カルマン渦列(動的安定性解析)」3.(2)2.を復習して下さい。
[補足説明2]
補足しますと、上図Fig.38は“進行波”のある瞬間の“流線図”です。
別稿「水の波」§35.3.では、互いに逆方向に進む二つの進行波を重ね合わせた場合に生じる“定常波”の”流線図”が図35.2として示されています。これと上記Fig.38の違いに注意して下さい。くれぐれも両者を混同しないで下さい。
“進行波”に関する“複素速度ポテンシャル”f=Φ+iΨ は上で求めていますが、“定常波”に関する“複素速度ポテンシャル” がどの様な関数で表されるのかは上記別稿を参照して下さい。
【流線を示す写真】
上記の写真Fig.39aに付いては別稿「波動」55.2.[補足説明1]も参照されたし。
【流体粒子軌跡と位相伝播を示す写真】
上記の黒色アンダーラインを引いた文章が何を言っているのか解りにくいと思いますので補足します。
これは別稿「波動」54.3.[補足説明1]で説明しているように流体粒子の運動を表す楕円軌道の軌跡が、位相速度の実体と齟齬(矛盾)をきたしている事を言っています。波の振幅が小さくて、楕円軌道の軌跡が十分小さな場合のみ、その矛盾が解消されると言っています。上記別稿の説明を注意深く読まれて下さい。
[補足説明1]
(1)式に付いては(17.10)を復習する必要があるのですが、ここでは引用していません。
その為、別稿「水の波」§38.“さざなみ(表面張力波)”や、別稿「波動」57.“表面張力の波”を参照されて下さい。そちらで同じ内容が説明されています。
(2)式の証明は次項で。
上記のことは重要です。 2.[補足説明3] や 3. を復習して下さい。
以下は解りにくいところです。 §23.~§25.の解説 を復習する必要があります。
上記の記述は、ド・ブロイの1924年「学位論文」中の説明を指している。
上記の説明については、別稿「波動方程式と一般解」3.(3)[補足説明1]も参照されて下さい。
[補足説明]
Fig.41の説明は解りにくいと思います。
別稿「慣性重力波とロスビー波、そして赤道波」5.(4)3.に掲げた図fig5-4-3-03.GIFと比較して見られることを勧めます。ただし、そこの図の縦軸は角振動数ω(別稿のσ)で、横軸は波数kにしてあるため、群速度Uと位相速度Vのグラフ上での表示形式が、ここと異なる事に注意して下さい。
ここのFig.41の様に、縦軸を位相速度V、横軸を波長λにして素源波の位相速度の波長依存性のグラフ(いわゆる“分散曲線”)を描くと、上図の様に位相速度Vと群速度Uが表されると言うことです。
またこの形式の表示からも、正常分散の場合は V>U であり、異常分散の場合は V<U となる事が簡単に読み取れる。この事は本節の最初に述べた事柄です。
【位置エネルギーと運動エネルギー】
【エネルギーの伝播】
【エネルギー伝播と群速度】
[補足説明1]
ここは、解りにくいところです。別稿「波動」58.2.も参照されて下さい。
ただし、そちらでは本稿で波の振幅を表す A×(k/ω) を a と置いているので注意して下さい。上記(6)式の波高を表すη(x,t)の (k/ω)×A
を a と置いていることに相当します。
また、こちらの k=2π/λ と ω=2π/T が別稿の m と n に対応します。そして本稿では ω2=kg に相当する場合を論じています。すなわち別稿の n2/m2=(λ/2π)×g の場合です。
そのため、計算式を比較するとき注意されて下さい。本稿の(7a)式 Epot=Ekin=(1/2)ρπA2 が、別稿の(58.3)(58.6)式 V=T=(1/4)ρa2gλ に一致します。
上記(12)式と下記(13)式の導出は、別稿「水の波」§37.2.群速度の例を参照。
引用は省略。
引用は省略。
発刊の古い順に紹介しています。後刊の本は先行する本をおおいに参考にされ、その解りにくいところをより解り易くする事を心がけて書かれていますので、これらをすべて読み比べて見られる事を勧めます。そうされることで理解が進むと思います。