偏光とは何か(光の強度と偏光)
光の偏光について説明します。これは高校生に取って解りにくいものですが、光が横波であることと深く関係しています。
1.光(電磁波)の電場ベクトル
(1)電場ベクトルの方向
光の性質を決めるのが電場ベクトルである。一方向に進する光(電磁波)とは別稿「電磁波の伝播」2.(2)や「線型振動子(電気双極子)による電磁波の放出」2.(3)で説明したように進行方向に対して直角な方向を向く電場ベクトルEの変化が波となって進んでいくようなものです。
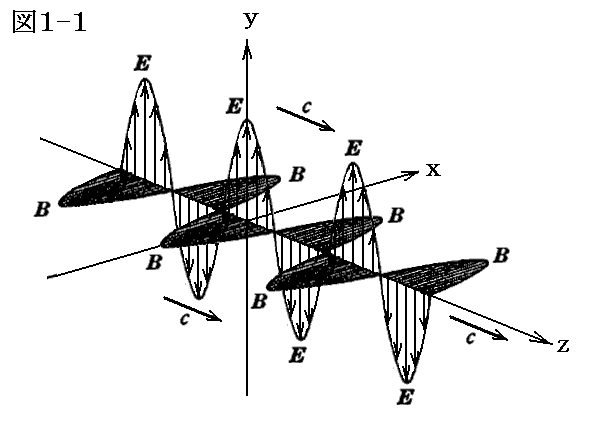
そのとき電場ベクトルに対して磁場ベクトルが存在しその方向は進行方向に垂直な面内で電場ベクトルに対して進行方向を回転軸として右90度の方向を向いている。また、別稿で説明したように電場ベクトルと磁場ベクトルの大きさの比率は常に決まった値を取る。それこそ、電磁気学におけるマクスウェル方程式が示唆する電磁場の性質についての一つの表れです。
磁場ベクトルは電場ベクトルに対して常にある定まった関係にあるので、光(電磁波)の性質を論じるときに電場ベクトルを代表させて論じることができる。今後は電場ベクトルでその性質を論じていく。
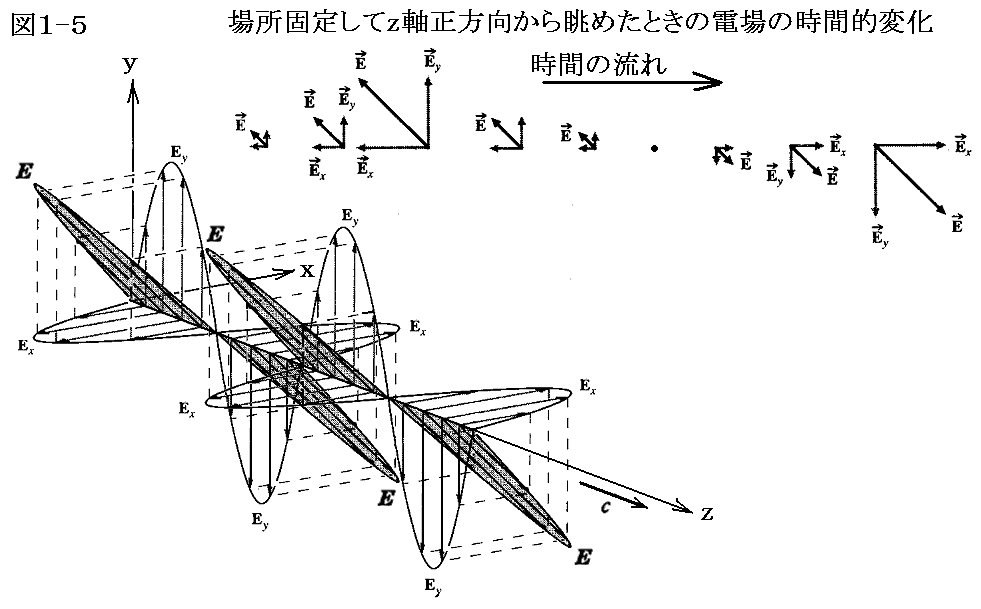
電場ベクトルはベクトルの一種ですから、進行する光(電磁波)のある瞬間のある点における電場ベクトルとして様々な方向のものが混じっていてもそれはベクトル的に合成されて、結局進行方向に対して直角な面内の一つの方向の電場ベクトルに集約される。つまり下図の中のどれかであって電場ベクトルは、時間と場所が決まれば進行方向に垂直なただ一つの方向を向いたある大きさのベクトルです。これが光は横波であると言われるところです。
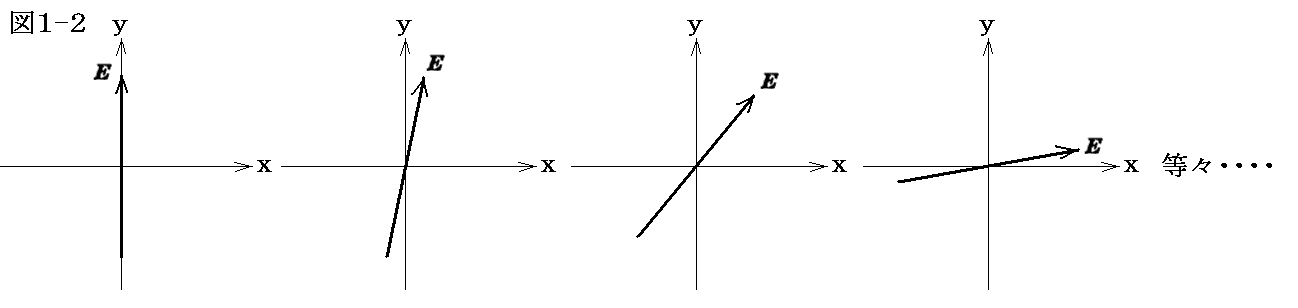
ただし、今は光はz軸の正の方向に向かっているとしており、上図はz軸の正方向から向かってくる光(電磁波)を見たときのある位置のある瞬間の電場ベクトルを示している。そのとき電場ベクトルはz軸(進行方向)に対して垂直な面内になければならないが、その面内では任意の方向を向いて良いのです。
そのとき、たとえば下図のように時間を止めて電場ベクトルの空間的な変化を観察したとき、その方向が場所的にグルグルと回転するようにその方向を変えても良い。
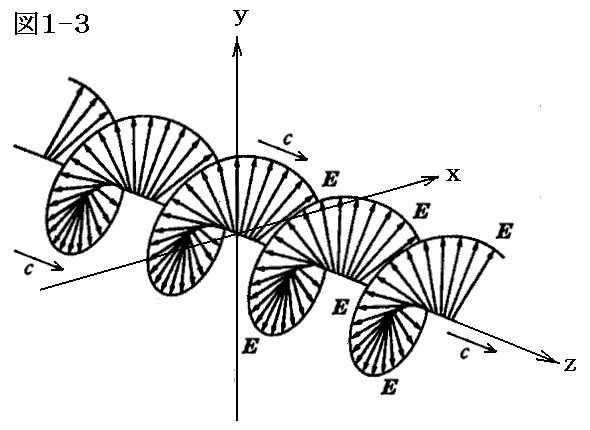
さらに、上図では電場ベクトルEの長さは皆同じように描いていますが、電場ベクトルの大きさ(振幅)が時間的、場所的にランダムに変化しても良い。また図ではある瞬間の電場ベクトルが場所的に同じピッチの螺旋を描く様に変化していますが、その螺旋のピッチが場所的・時間的にランダムに変化しても良い。もちろん螺旋の回転方向が逆向きでも良いし、場所的、時間的に途中からその向きが変わっても良い。その当たりは任意に変化して良い。いずれにしても、これらの電磁波はいずれもマックスウェルの電磁場の方程式を満足する横波です。
実際のところ、別稿「線型振動子(電気双極子)による電磁波の放出」2.(3)をお読みいただければお解りのように、電磁波を放射する電荷(電気双極子であるヘルツベクトルを構成する電荷)の運動を適当に調整すれば電場ベクトルの大きさが任意の波形で変化する電磁波を生み出せますし、ヘルツベクトルの振動方向を適当に回転変化させれば、電場の方向を進行方向に垂直な面内で任意の方向に回転変化する光(電磁波)を放射できます。
図ではz軸上におけるある瞬間の電場ベクトルしか描いていませんが、実際には同じ方向・同じ大きさのベクトルが空間的に分布しています。その様に読み取って下さい。
(2)直線偏光、円偏光、楕円偏光
前節で強調したように電場ベクトルはただ一つの方向しか向いていないのですが、ある場所でそこを通過していく電場ベクトルを観察すると、その大きさも、その方向(進行方向に直角な面内での方向)も任意に変化していくとすることができます。
しかし、その様な一般的なものは取り扱いが困難なのでここでは直進する平面波が時間的に調和的(つまりsin、cos的に)に振動する場合を論じることにしましょう。この調和振動するタイプに限っても様々な状況が考えられます。
1.直線偏光
前節の図1-1に示した様な場合です。これは光(電磁波)が向かってくる方向から見て電場ベクトルはいつも同一の方向で調和振動を繰り返しています。つまり図1-2に示したもののいずれかです。このような場合を直線偏光していると言います。ただしこの場合の電場ベクトルをx成分Exとy成分Eyに分解することもできます。そして、それぞれが位相差無しで同じ振動数で振動しながら進んでいくと考えるわけです。その様にすれば電場ベクトルの方向の違いは、そのx成分Exとy成分Eyの振幅の組み合わせの違いで表現することができます。
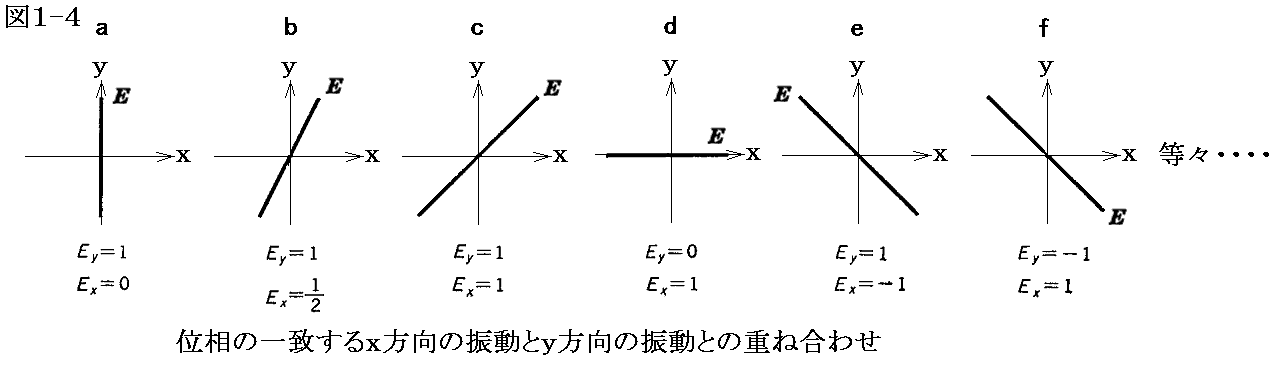
例として上図 e or f の第2象限と第4象限で振動している直線偏光の、ある時刻の電場の様子を図示すると
のようになる。他の場合も同様な分解・合成ができます。
そのときx軸y軸の方向を回転させれば最大振幅Ex0やEy0の値は変わってゆきます。しかしこの事は逆に言えば、x軸y軸の方向を調節すれば任意の直線偏光は同じ振幅の直交する二つの方向の振動成分の合成で表されることを意味します。
このとき、現実の光かx成分とy成分に分解された状態で存在するのか、それらの合成ベクトルとして存在するのかを問うことは意味のないことです。
なぜなら、x成分やy成分は4~5章で説明する偏光子や遅相子を用いた様々な実験を説明する過程で初めて確定的に推察できることであって、進行中の光がその様な成分に分かれているのかそうでないのかは誰も知ることはできないのですから。
つまり、x成分やy成分に分解するxy座標がz軸のまわりに関してどの方向を向いているのか実験をしてみるまで知りようがないので、実際どの方向に取っても良いのです。
このことは以下の円偏光や楕円偏光を成分に分解するときにも言えます。
これは、偏光を学ぶとき最も疑問に思うところですが、光(電磁場)とはその様なものだと理解するしか有りません。この当たりは3章でもう一度振り返ります。
2.円偏光と楕円偏光
前節で述べた電場の二つの成分(x成分:Exとy成分:Ey)の位相が合っていない場合、合成された電場ベクトルは一つの楕円上を動き回る。両振動の位相差の角度により様々な場合が生じる。
図1-6は、z軸の正方向に進む光(電磁波)を、場所を固定してz軸の正方向から眺めた場合の電場の時間的変化を位相差を変えて示している。
ここではx成分、y成分の振幅Ex0とEy0は同じにしているが、もちろん異なる場合も考えられる。しかし後で証明するように任意の楕円偏光は、(x,y)座標の方向を適当に調整すれば、振幅に関して必ずEx0=Ey0を満たす様なx成分:Exとy成分:Eyの合成で表せますから、その様な一般化はあまり意味がありません。
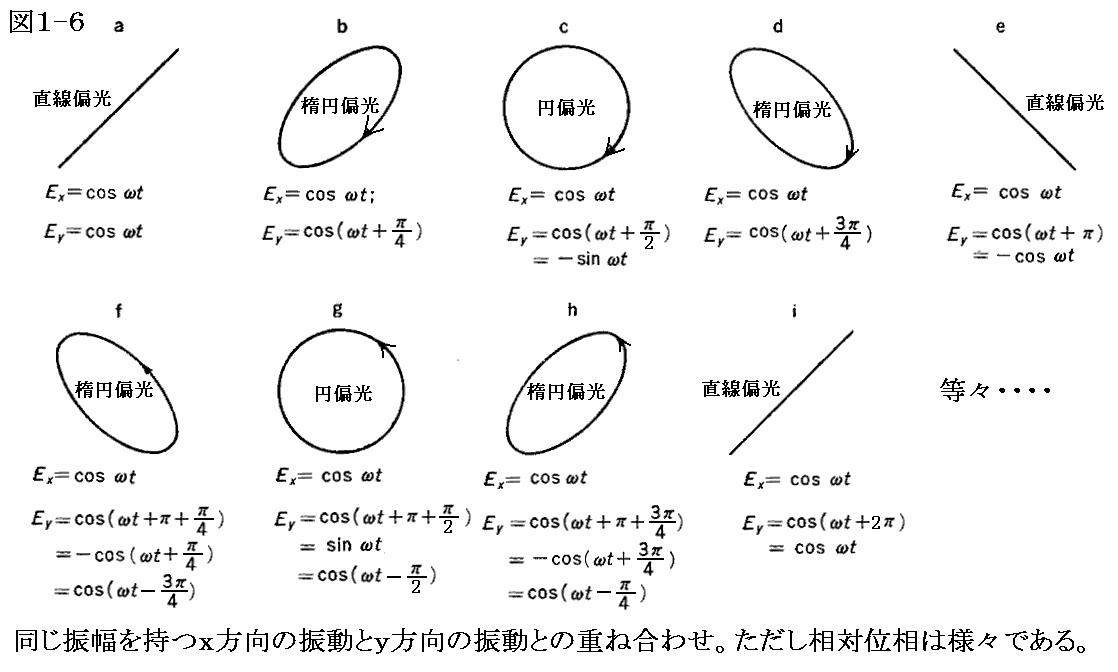
図1-6中のgの場合で、時間を止めたときの電場の空間的分布を表すと
となる。 g の光は電場がこの形の空間分布を保持しままで時間と共にz軸の正の方向へ平行移動していくものだと言えます。このとき電場ベクトル先端の回転する方向が逆の場合もあるわけで、それが図1-6中の c の場合です。
このときx座標とy座標の取り方により分解の仕方が変わってきます。座標の傾きの変化との関わりについては2.(1)節で説明します。
(3)偏光面と回転方向
1.直線偏光の偏光面
この稿ではすべて電場ベクトルが振動する方向を偏光方向、あるいは電場ベクトルと進行方向を含む面を偏光面(plane of polarizaton)と言うことにする。
場を表すベクトルの物理的な効果に注目すれば、電場こそが電荷を揺り動かす方向ですから、光を表すベクトルとしてEを採用することは妥当なことだと言える。
もちろん動いている電荷に対しては磁場ベクトルも力を及ぼしますが、その効果は電場ベクトルに比べると小さい。磁場は電荷が動いているときだけ力(ローレンツ力 F=q[v×B]=μ0q[v×H])を及ぼします。MKSA単位系でBはEの1/c倍であり、v/cは通常1に比べて小さな値なので、この影響は通常無視できます。[もちろん単位系が変わってもその当たりの事情は変わりません。別稿「光の圧力[輻射圧]」1.や「電磁気学の単位系が難しい理由」を御覧下さい。]
その意味においても、電場ベクトルの振動方向で偏光方向を規定するのが妥当だと言える。
しかし、歴史的には、磁場ベクトルの振動する方向を偏光方向(偏光面)と言ってきた経緯があります。例えばプランクの「熱輻射論」などは、こちらの定義に従っている。そのため古い文献を読むときには、偏光面がどちらの意味で用いられているのかに注意して下さい。偏光面の定義を取り違えると訳がわからなくなります。
2.円偏光・楕円偏光の右回りと左回り
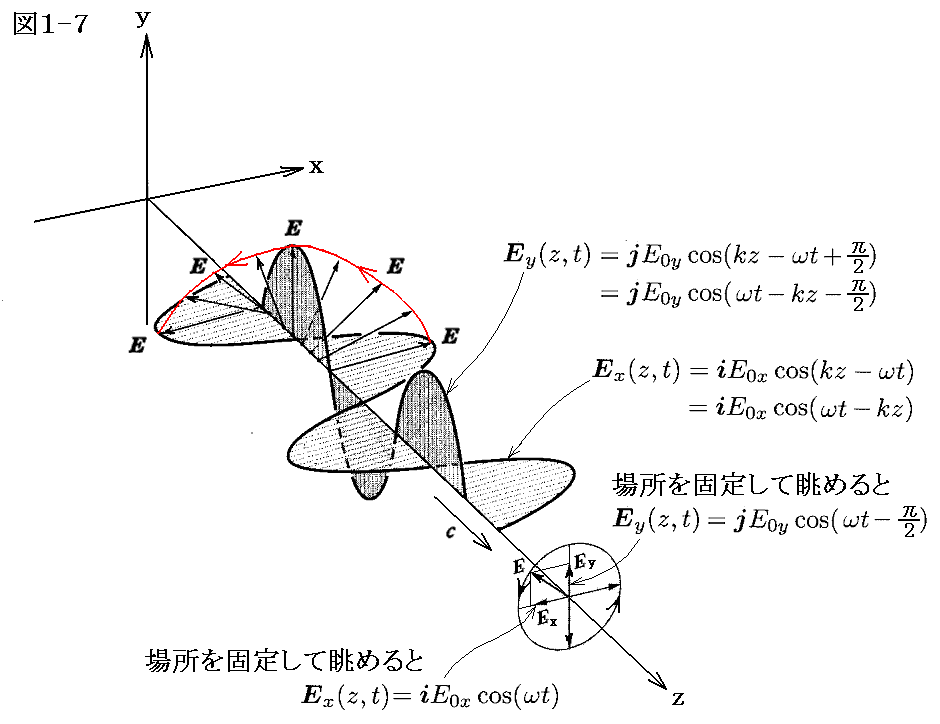
古典的な光学の本では円偏光の左右を次のように決めている。向かってくる光(電磁波)を固定された場所で見たとき、その固定点を通過する電場ベクトルが時間と共に反時計回りに回る場合を左円(楕円)偏光と言い、時計回りに回る場合を右円(楕円)偏光と言う。この定義では図1-7の光は左円偏光となります。古典的な光学では次の図1-8のように左右の円偏光を定めています。
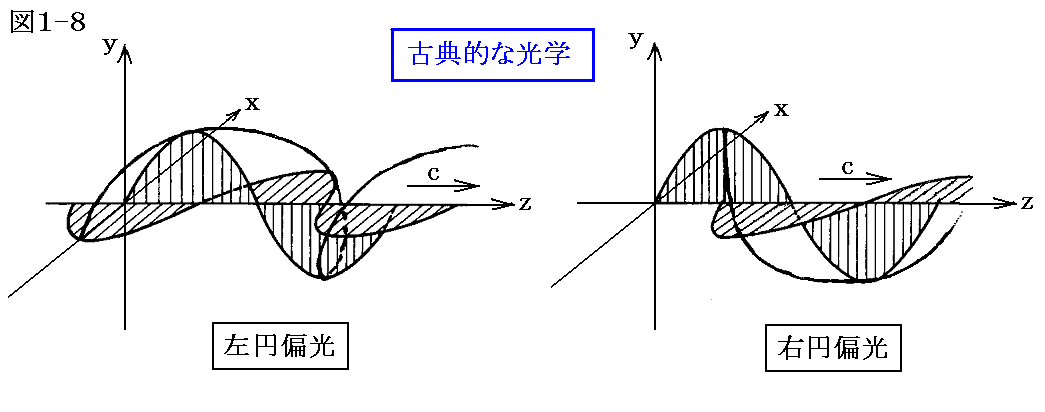
これは向かって来る光を観測する立場で見たときの電場ベクトルの回転方向に一致しています。
しかし、近代的な素粒子論(量子論)では光は光量子の集合体と考えている。そのとき光量子と共に進みながら前方に静止している電子に当たる場合を考えると、古典光学における左円偏光の光は、進行する方向に向かって見ると静止している電子に右回りの電場を加わえることになる。つまり、電子には、光の進方向に向かって見て、右回りの運動が誘起されることになる。そのため、進んで行く光子の立場で見た場合には、この場合を右円偏光と言った方が理解しやすい。すなわち、光量子論に立つ近代物理学では次の図1-9の様に右円偏光、左円偏光を決めている
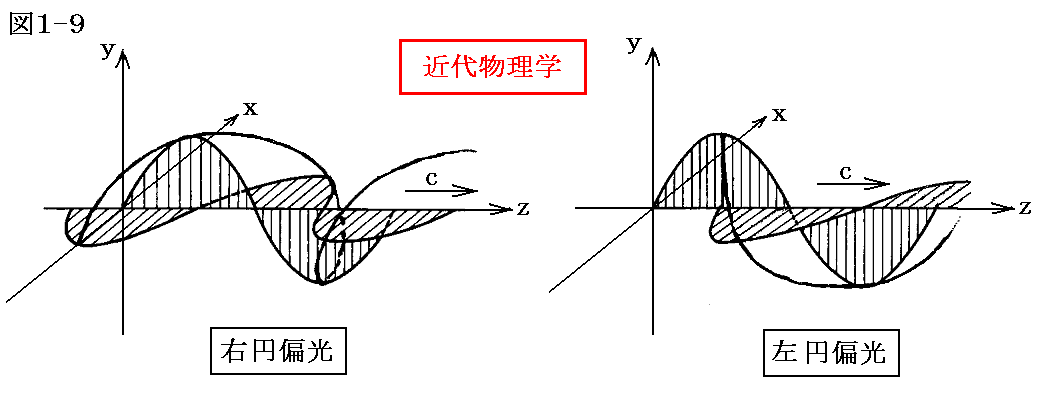
これは進んで行く光量子の立場で見たときの回転方向(スピン)に一致している。
このように右円偏光と左円偏光の定義が本によって異なっていますから、どちらの意味で用いられているのか注意して下さい。
2.調和的に振動する光(電磁波)の数式表現
ここでは直進する平面波が時間・空間に関して調和的(つまりsin、cos的に)に振動する場合を論じる。すなわちEやBの直角座標成分が
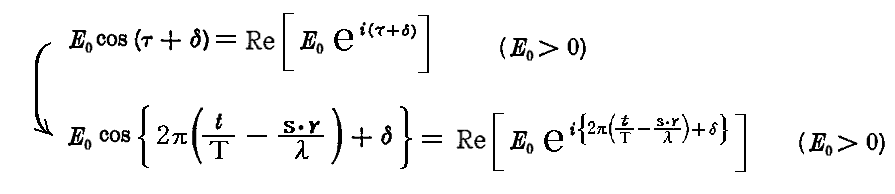
で表示されるような波を考える。
ここでτは位相項の変化部分
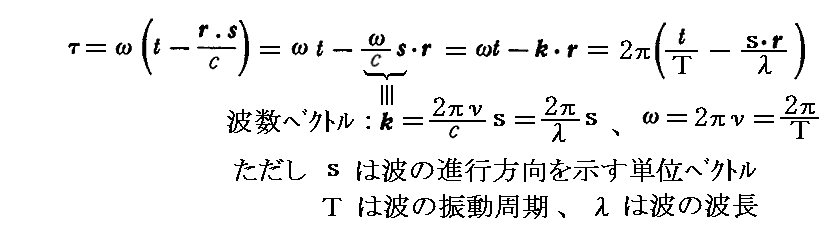
を表す。これらの式の意味についてはこちらを参照。また波動が伝播する様子を表すアニメーションはこちらを参照。
(1)楕円偏光
伝搬方向を示す単位ベクトルsの方向をz軸にとる。その場合、光(電磁波)が横波であることより電場ベクトルEはz成分は無くてx、y成分のみしか存在しない。空間の一点に於いて電場ベクトルの端点が描く曲線を調べてみる。
着目する点における電場ベクトルEは一般的に

と表せる。最初の二式よりτを消去するために、それらを変形すると
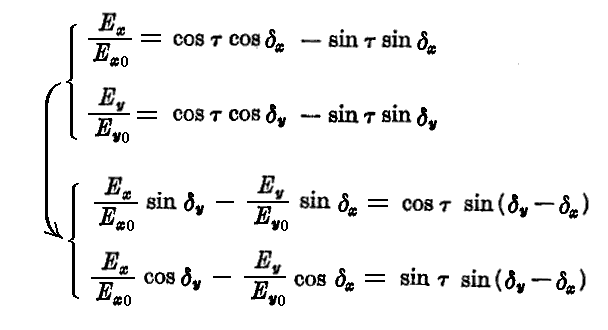
が得られる。これらの片々を二乗して加えると、δy-δx=δと置くことにして
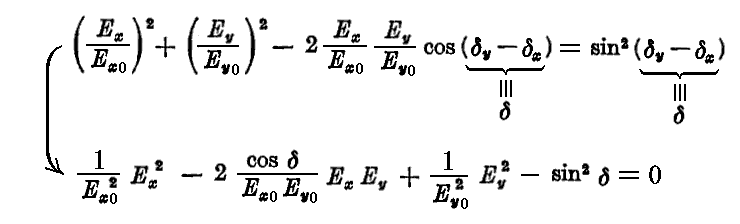
が得られる。この式は別稿「二次曲線の性質」で説明した平面上の直交座標(x、y)上の二次曲線の一般形 Ax2+2Hxy+By2+2Gx+2Fy+C=0 をしている。そこで説明したようにその係数によってその形が決まる。すなわち AB-H2>0の場合には楕円、 AB-H2<0の場合には双曲線、 AB-H2=0の場合には放物線になる。今の場合
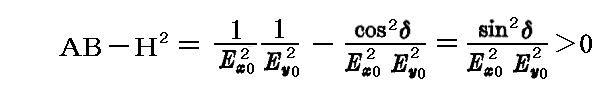
となるので楕円になる。そのためこれを楕円偏光(elliptically polarized light)と言う。
この楕円は(x,y)座標軸に平行で長さ2Ex0と2Ey0の辺を持つ矩形の内部に存在する。楕円はこの矩形と(±Ex0,±Ey0cosδ)と(±Ex0cosδ,±Ey0)なる4点で接している。この事は±Ex0または±Ey0を上記の楕円を表す式に代入してみれば直ちに確かめることができる。そのとき楕円偏光した電場ベクトルの先端が描く楕円は図2-1の様になる。
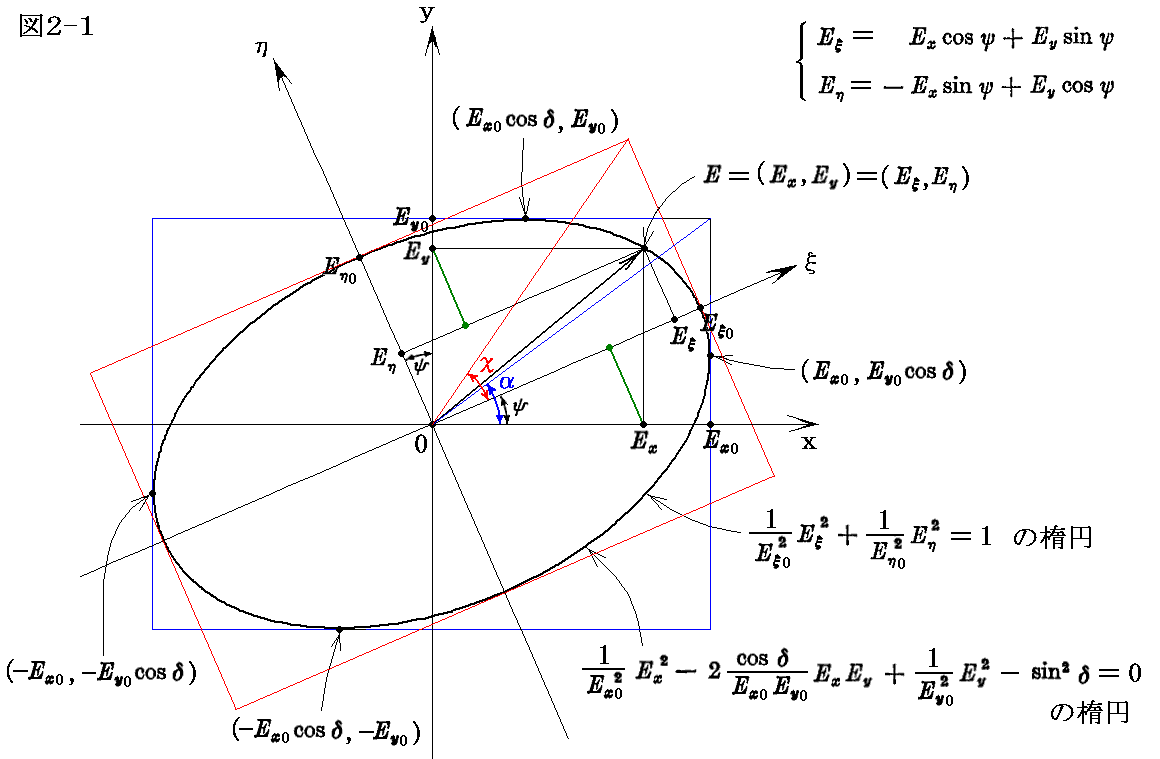
このとき適当な直交座標(ξ、η)を用いると楕円の一般形を標準形 (ξ/a)2+(η/b)2=1 に変形できる。そうするには別稿「質点の二次元運動」2.(3)(b)で説明したのと同様な手順を用いれば良い。
(x,y)座標に対して角度ψだけ回転した座標系(ξ、η)を取り、その座標系で表した電場ベクトルの成分を(Eξ,Eη)とする。(Eξ,Eη)と(Ex,Ey)は
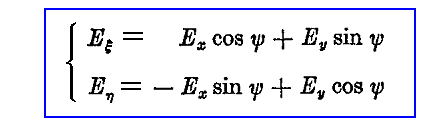
の関係を満足する。これは図2-1中の緑色の補助線を用いて考えれば直ちに了解できる。
この新しい座標系で表した楕円の式は、楕円の媒介変数表示を思い出すと
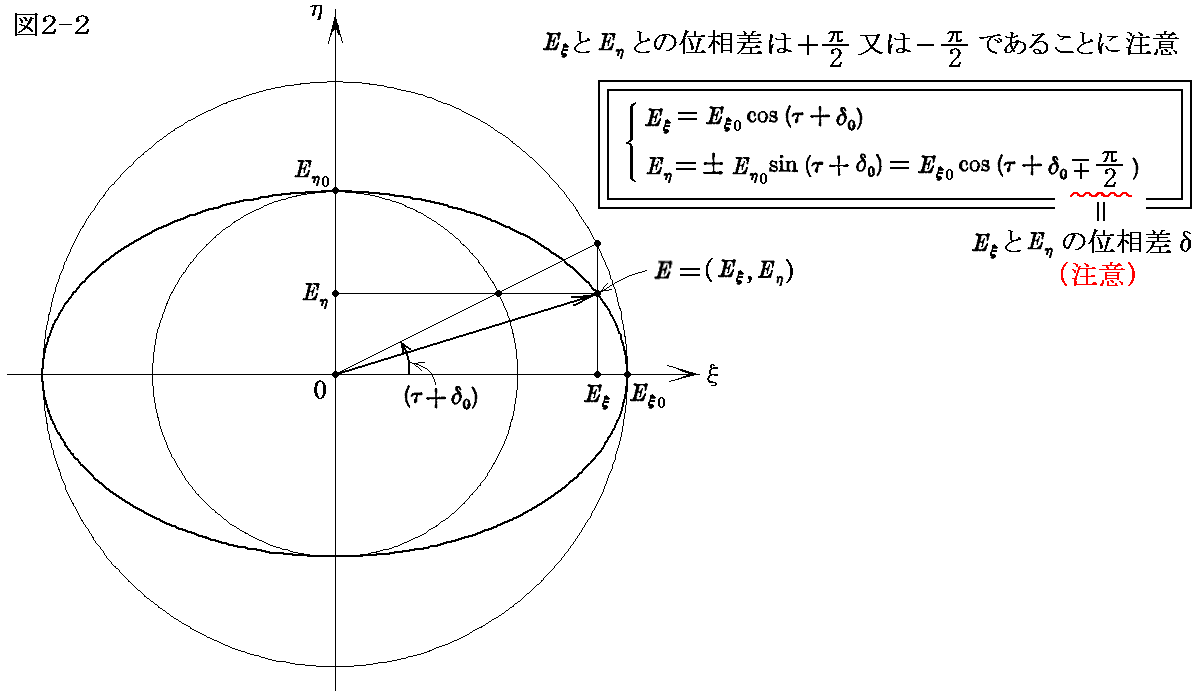
で表される。ここで電場ベクトルEを(x,y)座標成分での表示と一致させるために位相の調整値δ0を入れておかねばならないことに注意して下さい。
これらの式を用いて(Eξ0,Eη0)と(Ex0,Ey0)の関係を求める。
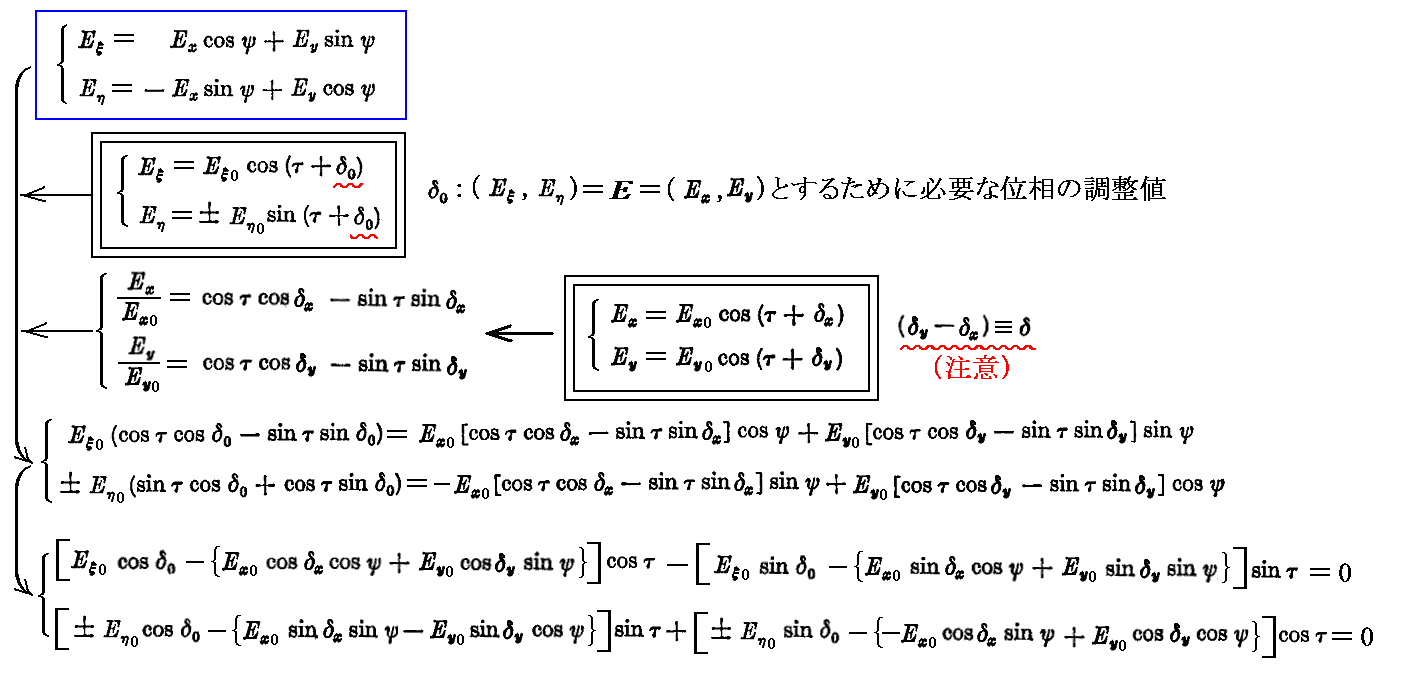
これらの式が任意のτに対して成り立つためにはcosτとsinτの係数がそれぞれゼロにならねばならないので
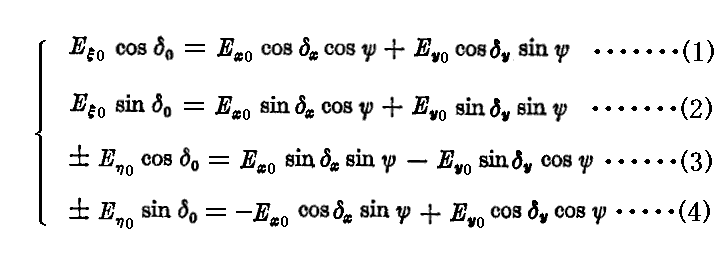
が得られる。
δ0を消去するために、(1)、(2)式の両辺を2乗して加えると
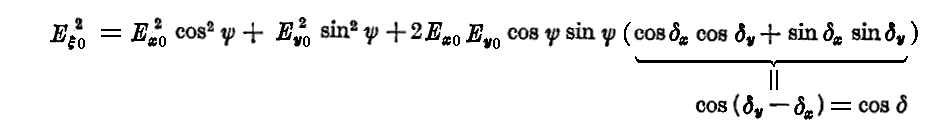
となる。
同様、(3)、(4)式の両辺を2乗して加えてδ0を消去すると
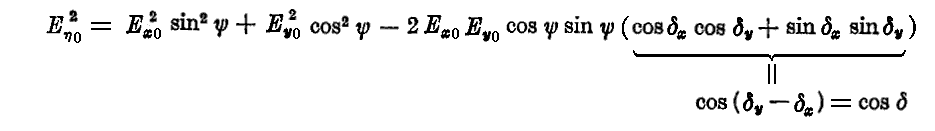
が得られる。
これらの式より
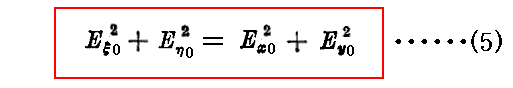
同様に、(1)式と(3)式を片々乗じたものに、(2)式と(4)式を片々乗じたものを加えるとδ0が消去できて
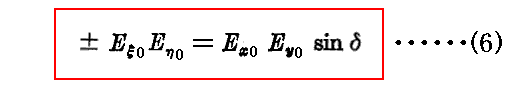
が得られる。
さらに(3)式を(1)式で、(4)式を(2)式で割り算してδ0を消去すれば

が得られる。
(6)式を(5)式で片々割り算すれば
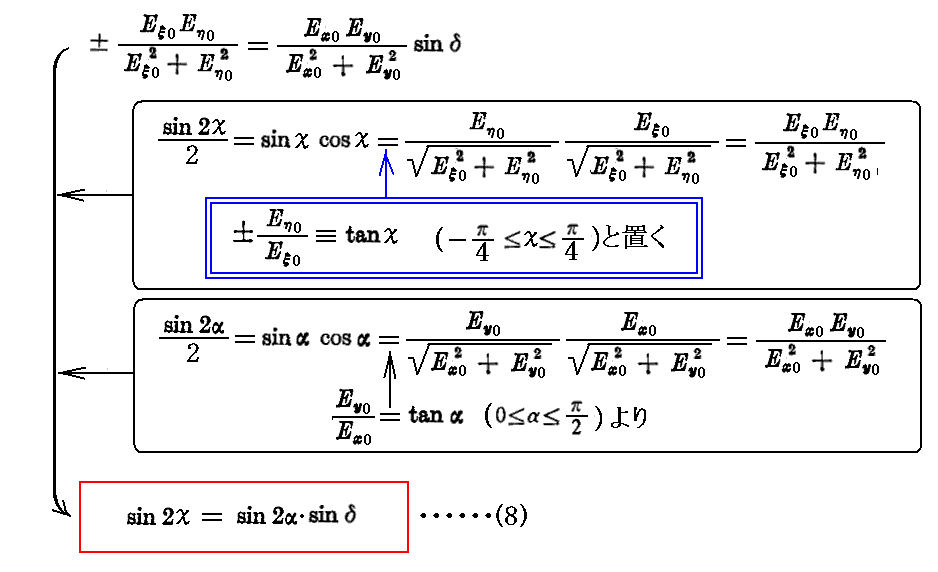
が得られる。ここでtanχ=±(Eη0/Eξ0)の値は楕円の長軸半径と短軸半径の比をあらわし、その符号は右回りか、左回りかを意味する。
振幅Ex0とEy0、及びExとEyの位相差δが解っていれば、(5)、(6)、(7)、(8)式を用いることによって、標準楕円の長軸半径Eξ0と短軸半径Eη0、及びそれらの軸の傾きψが計算できる。そのときEξとEηの位相差はきりの良い±(π/2)の内のいずれかになります。
もちろん逆に解いて(Eξ0、Eη0、ψ)→(Ex0、Ey0、δ)の変換を求めることできます。
そのとき、(ξ,η)座標に対する回転角ψを適当に調整すれば電場ベクトルの楕円に外接する矩形が正方形になる(x,y)座標の方向が必ず存在します。そのためEx0=Ey0という条件を満足するψとδを決めるために、これらの関係式(Eξ0、Eη0、Ex0=Ey0)→(ψ、δ)を使うこともできます。
ここで注意して欲しいことは電場ベクトルを(ξ,η)方向に分解したときには必ず両方向の直線偏光成分の位相差δは±(π/2)の内のいずれかになることです。そのときのEξ0、Eη0を振幅の主値と言い一般に異なった値になります。このときのξ軸とη軸を楕円偏光の主軸と言います。
一方、(ξ,η)座標に対する回転角ψを適当に調整して、電場ベクトル楕円に外接する矩形が正方形になる方向に(x,y)座標を取れば、任意の楕円偏光がEx0=Ey0となる二つの直線偏光の合成で表されます。もちろんそのときは二つの直線偏光の位相差δは切りの良い値にはなりません。
結局、光が横波であることを表現する二つの直線偏光成分への分解は、
“位相差の関係を簡単[±(π/2)の内のいずれか]にして、振幅[Eξ0とEη0]の大小にその一般性を押しつける”

または、
“振幅の関係を簡単[Ex0=Ey0]にして、位相差[δ=δx-δy]にその一般性を押しつける”
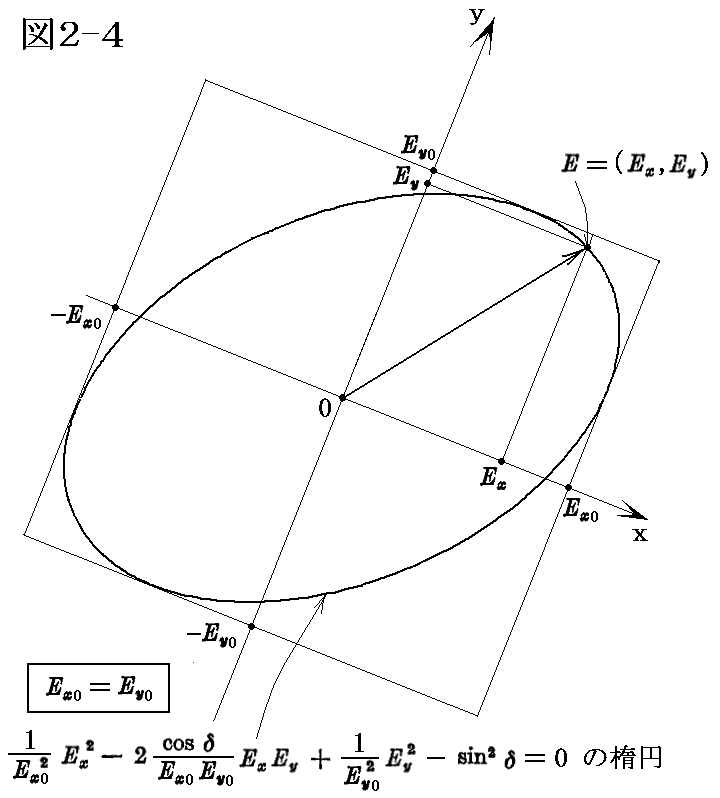
やり方、のいずれかが理解しやすい。
ただし、そのとき“どのような分解が本質的なのか?”と問うても意味が無いことに注意して下さい。古典的な光の描像での本質は“電場ベクトルの方向がグルグル回転しながら、かつその大きさが伸びたり縮んだりして変化している”ということだけなのですから。
ここで得られた結論は、最初に仮定した単色で調和的に振動する光(電磁波)に限って成り立つことに注意して下さい。そのように限られた状況でのみ正しいものですが、光の示す様々な現象を説明する上で極めて適切な描像を与えることが様々な観測結果から裏付けられています。
(2)直線偏光と円偏光
1.直線偏光
前節の議論で
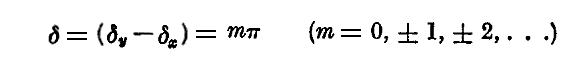
の場合、楕円は直線になり
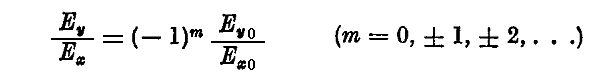
が常に成立する。このような場合を直線偏光(linearly polarized light)と言う。1.(2)1.で説明した場合に相当する。
2.円偏光
前節の楕円に外接する矩形が正方形
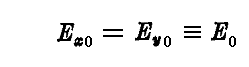
で、しかも位相差が
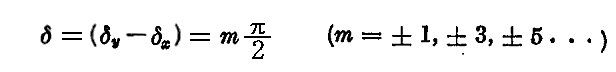
の場合には楕円は
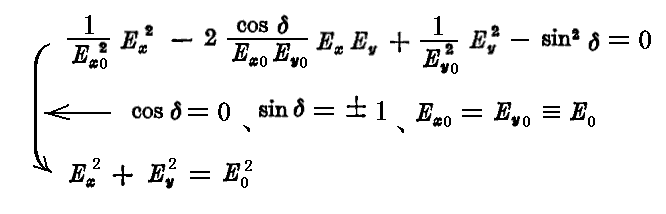
となる。これは円の方程式を表す。そのため、この場合を円偏光(circularly polarized light)と言う。
そのとき
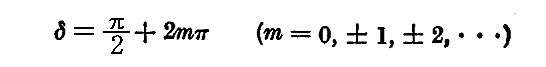
の場合は
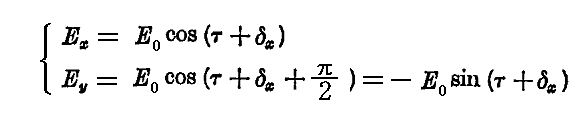
となり、向かってくる光を静止して見ると、電場ベクトルは右回り(right-handed 時計回り)に回転する。古典光学で言うところの右円偏光。
一方
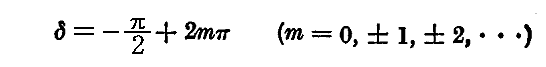
の場合は
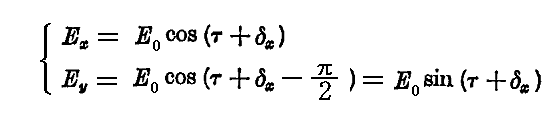
となり、向かってくる光を静止して見ると、電場ベクトルは左回り(left-handed 反時計回り)に回転する。古典光学で言うところの左円偏光。
(3)楕円偏光・直線偏光は二つの円偏光の合成で表される
任意の楕円偏光は、異なった振幅を持って反対方向に回転する二つの円偏光を合成することで表現できる。
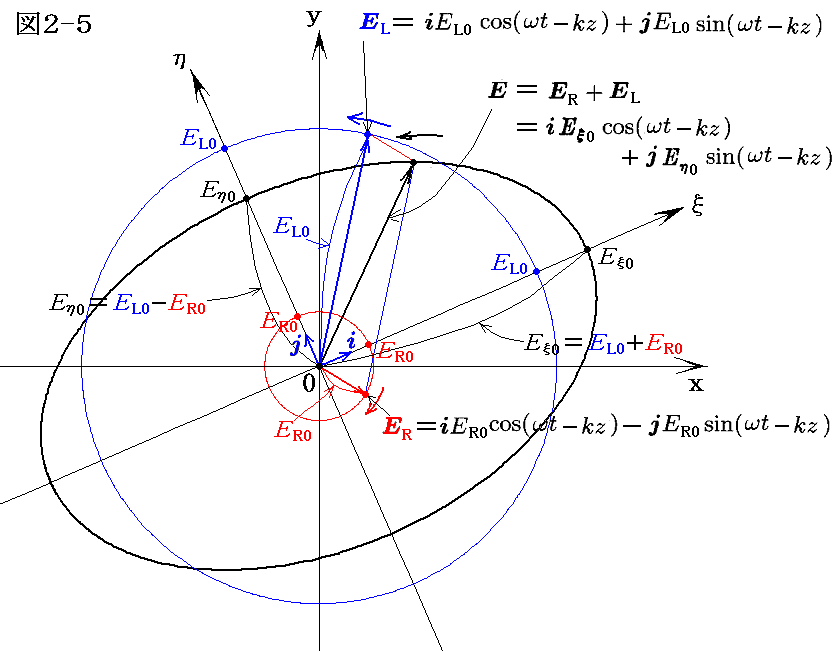
今、古典的な光学における定義で右円偏光ERと左円偏光ELを定義する。前節の結論を用いるとそれぞれ
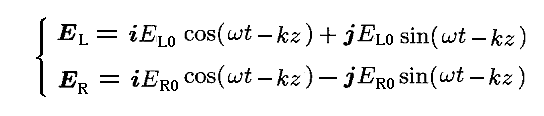
と表される。この両者を合成すると
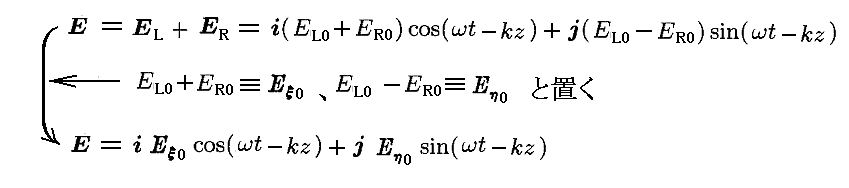
となる。これは2.(1)で説明した、(ξ,η)座標で表した場合のδ0=0、δη=δξ-(π/2) [つまりδ=δξ-δη=(π/2)]のときの楕円偏光です。図2-3の場合は、古典光学で言うところの左楕円偏光となりますが、基本的に重ね合わせた円偏光の振幅が大きい方の回転方向に一致します。
ところで、直線偏光は楕円偏光の特別な場合ですから、直線偏光も二つの円偏光の合成で表すことができる。
このように、任意の直線偏光・楕円偏光は必ず左回り、右回りの円偏光の合成で表せますから、光の状態を表すのに“左・右円偏光の方がより根源的な光波の状態である”とすることもできます。
3.光の本性
(1)自然光
通常の光源はランダムな向きの原子からなる莫大な数の放射源で構成されている。励起された各原子は偏光した波束(波連)を約10-8秒程度放射する。同じ周波数をもつすべての放射は結合して、単一の偏光した波動を形成するが、この波動は10-8秒を超えて持続することはない。[別稿「線型振動子(電気双極子)による電磁波の放出」4.(2)を参照]
新しい波束(波連)がとぎれなく放射され、全体としての偏光状態は全く予測できない変化をする。これらの変化が迅速に起こり、どんな単一の偏光状態も見極められなくなる。このような状態にある波動を自然光(natural light)と言う。
これは普通「偏光していない」光と言われるが、実際は異なる偏光状態が急速に変化しているつながりであり、「ランダムに偏光している」というのが正しい表現だろう。
そのとき、自然光は、直交している等しい振幅のインコヒーレント(非干渉的 すなわち相対的位相差が急速にかつランダムに変化している)な、任意の波形の二つの直線偏光した波動によって自然光は数学的に表現できる。
理想的な単色平面波は、無限に続く波束(波連)と見なされる。もしこの波動を伝播方向に垂直な二つの直交する成分に分解すれば、これら成分は等しい周波数をもち、無限に広がっており、したがってコヒーレント(可干渉的)である。完全に単色な平面波は必然的に偏光している。干渉して電場ベクトルが重なり合うためには波束(波連)の範囲が重なり合い、さらに光の波の位相が同期しており、偏光面が一致していることが必要です。
(2)偏った光と偏らない光
何度も強調したように電場ベクトルはただ一つの方向を向いているので、基本的にあらゆる光(電磁波)のある場所・ある瞬間における電場ベクトルは偏っています。それが光(電磁波)は横波であると言うことです。
そのとき円偏光の様な光の場合、電場ベクトルが最初ある方向で振動していても、そのうち別の方向に変わり、偏りは絶えず変化します。また別稿「線型振動子(電気双極子)による電磁波の放出」4.(2)で説明したように一つの原子は10-8秒くらい光を出し続けると考えて良い。一つの原子の出す光はある偏りを持つが、別な原子が出す光は違った偏りを示す。従って偏りは10-8秒程度以下で次々と変わっていく。
電場ベクトルの偏りが我々が検知できるよりも早く変化するならば、その場合には偏りの効果は平均化されて消えてしまうから光は偏らないと言うことになる。結局、光が偏っていることを検知できる場合に“偏っている”と言い、検知できないとき光は“偏っていない”と言うだけです。
一般の光は完全に偏光した状態や全く偏光していない状態のいずれでもない。ほとんどの場合電場ベクトルは全体として規則的でも不規則的でもない状態で変化しており、自然光と偏光した光が適当な割合で重なっていると見なせる[5.(2)5.参照]。
(3)光の角運動量
物体に入射する電磁波はエネルギーと運動量の両方を物体に与える。さらに、入射平面波が円偏光なら、物質中の電子は回転する電場Eがもたらす力に応答して円運動をさせられるであろう。そのとき、その電場は90°位相がずれた二つの直交する直線偏光した電場でできていると考えられる。それらは電子を直交する二つの方向に位相差π/2で同次に駆動する。結果として電子に生じる運動はやはり円運動となる。
実際、照射する円偏光の回転方向を逆にすると対称物に与えられるトルクの向きが反転することを、1935年にベス(Richard A. Beth)は非常に高感度な捻り振り子を用いて測定することができた。[Richard A. Beth, “Mechanical Detection and
Measurement of the Angular Momentum of light”, Phys. Rev. 50, 115 (1936)]
このようにして電磁波の波動によって角運動量が、電子が存在し束縛されている、物質に与えられることが解った。
量子力学的な記述では、電磁波は量子化されたエネルギーε=hνを持つ固まりである光子の移動と見なされる。そのとき光子は固有の角運動量+h/2πかまたは-h/2πを持つと言われる。そして荷電粒子が電磁波を放射するときや吸収するときは、エネルギーと運動量の変化と共に角運動量も変化する。[光子の持つ角運動量は光子が持つエネルギーに依存しないことに注意されたし。]
そのとき[直線偏光した光波(電磁波)]という描像と[スピンを持つ光子]という描像は、いかにしたら整合性を持って理解できるのであろうか?
純粋に円偏光した平面波は、伝播方向を向いた回転軸に関する角運動量が同じ方向に揃っている光子の集団によって構成されていると考えればよいのであろう。ところで、2.(3)で説明した様に、直線偏光(楕円偏光の特別な場合)は互いに反対方向に回転する円偏光の重ね合わせで表現できる。そのため直線偏光した光線ビームとは右回りと左回りのスピンを持つ光子が等量混合したものであると考えれば良いのだろう。また、偏光方向がランダムに変化する光とは、やってくる左スピンと右スピンの光子の混合の割合がランダムに変化しているものであると考えれば良いのだろう。
いずれにしてもその様に角運動量が揃った光子の集団が物体に吸収されることで、その角運動量が物体に与えられると考えれば良いのであろう。
その様に考えれば直線偏光の状態よりも、円偏光の状態の方がより本質的な意味を持つのかも知れない。
(4)光子
光は光子と呼ばれる“電磁気的なもの”である粒子の形で吸収されたり、放出されたりする。この描像は多くの実験事実により確認され確立されたものです。
しかし、光が本当に粒子であるかどうかという問については、今日確たる答えはない。おそらく将来にわたってその答えが得られることはないであろう。
実際のところ光が示す様々な現象を良く考えてみれば、光が空間中を進んでいく様をつぶさに観察したものではないことは直ちに了解できる。通常の物体とは異なり、我々は光子を直接見ることはできず、生成または消滅の結果を観察することで初めて粒状の光子を認識できるだけです。光子は周囲に与える影響を検出することで観察され、しかも生成か消滅するときにのみ観察可能となる。光子は荷電粒子から始まり荷電粒子でおわり、ほとんどの場合、電子から放出されまた電子によって吸収される。そして、これらの電子は通常、原子核のまわりを雲状に取りまいている電子です。結局、我々は伝播する光がつぶつぶであることを直接観測することはできないのである。
この当たりの本質を述べた文章としてマックス・ボルンが「アインシュタインの相対性理論」第Ⅴ章の最後で述べている説明に勝るものはないように思いますので引用しておきます。

光量子仮説を導入したアインシュタイン自身も“私は光子とは何であるかの問題に答えをみいだすのに一生を費やしたが、いまだにわからない。”と言っていたそうです。
しかれども今日、微視的な粒子は[静止質量]・[電荷]・[スピン]という明確で不変の物理的特性を持っており、これらの特性によりその種類が完全に特定できると考えられている。光子は静止質量・電荷ともゼロでスピンは1(h/2πを単位として)の粒子です。
また、あらゆる粒子は上記の特性とは別に[エネルギー(=c2・慣性質量)]・[運動量]・[スピンの方向]といった、ある瞬間において微視的粒子の状態を規定する特性が付随していると考えられている。cは光速度(299792458m/s)です。
この中で特に光子一つが持つエネルギーはhνであるとされている。hはプランク定数(6.626×10-34J.s)、νは光の振動数です。また光子一つが持つ運動量はhν/cです。さらに角運動量(スピン)はh/2πで一定の大きさですが、その状態は光子の進行方向に関して右回りか左回りのいずれかです。それらの量の単位(次元)は高校物理で習うものと同じです。
この当たりについては、別稿「アインシュタインの特殊相対性理論(1905年)」、「アインシュタインの公式E=mc2の証明」、「相対論的力学」、「コンプトン効果と相対論的力学」をご覧下さい。
[補足説明]
例えば、平均波長632.8nmのHe-Neレーザーが出力P=1.0mW(ミリワット)の強度で光を放射しているとすると、1秒間に P/hν=1.0×10-3W÷[6.626×10-34J.s×(3.00×108m/632.8×10-9m)]=3.2×1015個 の光子を放出していることになる。
また、降り注ぐ太陽光線の太陽定数は1370J/m2s程度ですが、可視光領域の光子のエネルギーはhν=1.6~3.2eV(1eV=1.60×10-19J)なので、太陽光線中の光子流の数密度は1021個/m2s程度となります。
今、仮に太陽が10光年彼方に存在するとすると、10光年=9.46×1016mで太陽と地球の距離は1天文単位=1.50×1011mですから、現在の位置より6.3×105倍遠くに位置することになる。その位置の太陽から地球に届く光の光子流数密度は距離の二乗に反比例して減少しますから、地球表面の1m2に1秒当たり1021÷(6.3×105)2=2.5×1010個/m2s程度届くことになります。人間の目の瞳の面積が仮に1mm2程度としても、2.5×104個程度の光子が瞳を毎秒通過することになる。
このとき、電離エネルギーがかなり大きな水素原子でもその値は13.6eV程度ですから、可視光領域の光子のエネルギーがhν=1.6~3.2eVであるということは、光子1個が目の網膜の官能基に十分作用できるエネルギーを持っていることを意味する。実際、微弱光に反応する人間の視覚の研究から、網膜の視覚細胞中の官能基は数十個、おそらく1個の光子でも検出できると考えられている。[人の光受容細胞1、受容細胞2]
そのため、上に得られた10光年彼方の太陽から来る光子流の数密度は、我々がその存在を肉眼で視認するには十分な数です。太陽がさらに10倍遠い100光年彼方に存在するとすると光子数は2.5×102個/mm2s程度と成りますから、見えるかどうかは微妙です。1000光年まで離れると2.5個/mm2s程度ですから、肉眼では見えないでしょう。
この当たりの見積計算の興味深い例を別稿「月の潮汐力が地球の自転を遅らせ月の公転を加速する。」3.(2)1.[補足説明1.2]で引用しておりますのでご覧下さい。
しかし、ここで例としてあげた太陽光線の光子数密度は非常に大きいためエネルギー伝播における量子的な性質は覆い隠されている。そのため地球に届く太陽光線は電場強度がE~1000V/m程度の電磁波として取り扱える。
今日、微視的な粒子の集団に関して個々の粒子を互いに識別することは不可能であることが判っている。さらにその識別不能の性質について、あらゆる種類の微粒子は二つのグループに分類できることが判っている。
一つは“ただ一つの粒子のみがある任意の状態を占有できる”というパウリの排他律に従う1/2の奇数倍のスピンをもつ粒子のグループ(フェルミ粒子)です。電子はフェルミ粒子グループに属している。
もう一つは“任意個の粒子が一つの状態を共有できる”というパウリの排他律に従わないスピンが0か整数の粒子のグループ(ボーズ粒子)です。光子はボーズ粒子グループに属している。
ただし、習慣上スピン(角運動量)の大きさはh/2πを単位として測る。そのためスピン1/2とはh/4πのことであり、スピン1とはh/2πの大きさの角運動量のことです。
ボーズ粒子である光子は一つの状態を共有でき、しかも現実には互いに接近して集団を形成しやすい。膨大な数の光子が同じ状態を占めると、光が本来持っている粒状的な性質は必然的に消え、電磁波という連続的な形態で電磁場が出現する。その結果、単色(単一エネルギー)の平面波を、同じ状態(つまり同じエネルギー・運動量・スピン方向)で一斉に前進する高い粒子密度の光子の流れに対応させることができる。
これに対してフェルミ粒子である電子は多数が同じ状態の緻密な集団を形成することはできない。そのため単一エネルギーの電子ビームは巨視的なスケールでも古典的な連続波となることは無い。
(5)偏光とは何か
上で述べた事を鑑みると、この稿のメインテーマである偏光という現象が実際どの様な状態を意味するのか理解することは極めて難しいことが解る。
我々は結局の所、以下の章で説明する光が示す様々な現象の観察から、1、2章で取り扱った様な数学表現を用いて光(電磁場)の描像を描いているにすぎない。
またその様な数学的表現で光(電磁場)のもつ偏光という特性を旨く表現できることから、偏光とはその様な描像で説明できるような現象であると理解しているだけなのである。
このことに付いて、A.Sommerfeld著 文献3.第Ⅱ章§16 と 第Ⅵ章§49 の説明を紹介します。

このことに付いては別稿「アインシュタインの特殊相対性理論(1905年)」2.(10)3.を参照されたし。

このことに付いては別稿「光の圧力」3.(2)[補足説明1]と、別稿「相対論的力学」3.(4)を参照されたし。








4.偏光子
(1)偏光器と検出器
ここまで述べた偏光という現象の存在とその数学的表現は、以下で述べる偏光器と検出器を用いた様々な実験的考察から発見され確立されたものです。すでに述べたように、偏光していない光の一つの数学的表現は、振幅が等しく互いに直交しているインコヒーレント(非干渉的、相対的位相差が急速にかつランダムに変化している)な二つの直線偏光の重ね合わせです。これら二つの成分の一方を阻止し、他方を通過させる素子が直線偏光器です。そういった偏光器を適当に組み合わせることにより円偏光や楕円偏光を得ることもできる。
自然光の中から特定の振動方向をもつ直線偏光を取り出す光学素子を偏光子(polarizer 偏光板)という。そして、同一素子であるが、それを回転することにより入射した直線偏光の振動方向を知る目的に使う場合にこれを検光子(analyzer)という。これらを組み合わせた装置を偏光器という。偏光子と検光子の振動方向が平行であるときを平行ニコルの状態、垂直であるときを直交(または垂直)ニコルの状態という。
偏光子(または検光子)は以下の3つの基本的な物理現象のいずれかに基づいている。
- [複屈折(二重屈折)]
2個の複屈折結晶プリズムを組み合わせ、一方の直線偏光成分を全反射により除去する素子。これにはニコルプリズム、グラン・トムソンプリズムなどがある。
- [反射あるいは散乱]
ブルースター角(材質の屈折率を n、入射角を θ として tanθ=n をみたす角)での反射を利用した素子。これにはネレンベルグの偏光器( No¨rrenberg's
Polariscope)があり、赤外用として多く使用されている。
- [二色性(選択吸収)]
一方の直線偏光成分のみを強く吸収するような媒質を利用する素子。これには電気石、ポラロイド(商品名)などがある。
そのとき、偏光器を通過した光の偏光状態を検出器で検出するわけですが、光の周波数は極めて高く、普通の検出器で測定できるのは入射強度だけです。そのとき強度は電場振幅の2乗に比例している。
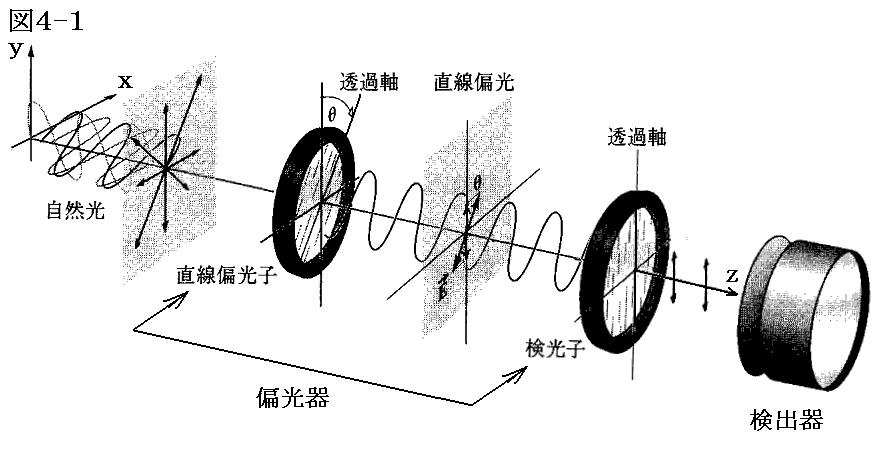
上図の様に自然光が理想的な直線偏光子に入射した場合偏光子の透過軸に平行な向きを持つ光だけが透過する。検光子が設置されていないときには、偏光子がz軸のわまりに回転しても自然光の完全な対称性から検出器からの出力は変化しない。
そのとき上で説明したように、検出器で測定できるのは入射強度です。強度は別稿「線型振動子(電気双極子)による電磁波の放出」2.(3)で説明したように電場の振幅の2乗に比例します。
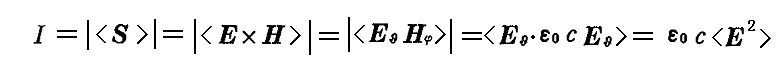
このとき図のように垂直な透過軸を持つ理想的な検光子(偏光子には違いない)を新たに導入する。図から明らかなように検光子を通過して検出器にやってくる電場は(検光子による吸収はないとすると)Ecosθで与えられる。そのため偏光子が検光子の透過軸と一致するとき検出器が測定する強度をI(0)とすると、偏光子と検光子の成す角度がθのとき検出器が測定する強度I(θ)は
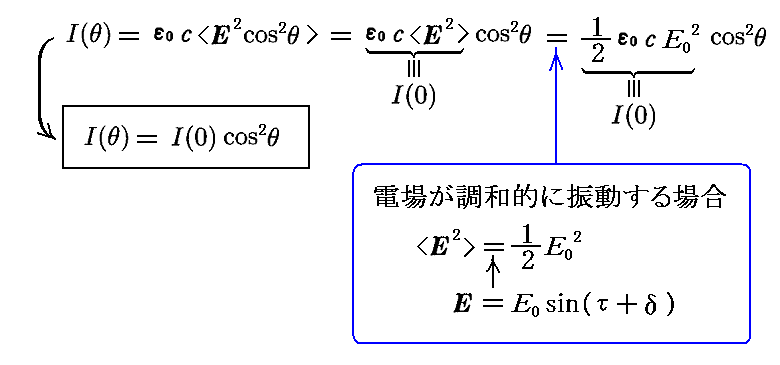
となる。今日の目でみればこの関係式が成り立つことは容易に理解できます。この関係式はナポレオン軍の技術大尉であったエティエンヌ・ルイ・マリュス(Etienne Louis Malus)によって1809年に見つけられたもので、マリュスの法則と言われています。
これは、光とは何か?、偏光とは何か?、偏光子とは何か?、等々・・・何も解っていなかった時代に見つけられたものであることに注意して下さい。歴史的には、この関係式を始めとして以下に述べる様々な実験的研究から逆に、光が横波であること、光の偏光の存在、光(偏光)の数学的モデル、光の強さの意味、偏光子の働き、反射や屈折のメカニズム、等々・・・が解ってきたのです。[この当たりは参考文献2.の4章参照]
《理想的な直線偏光子を通して測定した“自然光”のエネルギー強度》
上図ではポラロイド偏光板を用いて説明していますが、ポラロイド偏光子は吸収による減光があり厳密な測定には適していません。後で述べる複屈折を用いる偏光子の方が適しています。
そのとき、“自然光”の強度を全く偏光子を入れないで測定した場合と、吸収のない理想的な直線偏光子を通過させた後の場合で比較すると、後者の値がちょうど前者の半分になることが解ります。
これも“自然光”の数学的モデルが正しいことを示しています。
(2)複屈折偏光子
1.複屈折とは
デンマークの医師はエラスムス・バルトリヌス(Erasmus Bartholin)は『不思議な変わった屈折を明らかにするアイスランド複屈折結晶の実験(1669年)』で初めて複屈折の現象を詳しく記載した。アイスランド石(氷州石)とは今日方解石と言われる鉱物(炭酸カルシウムの結晶)ですが、この前年にデンマークの探検隊がアイスランド(氷州)から持ち帰ったのでこのように呼ばれたのです。
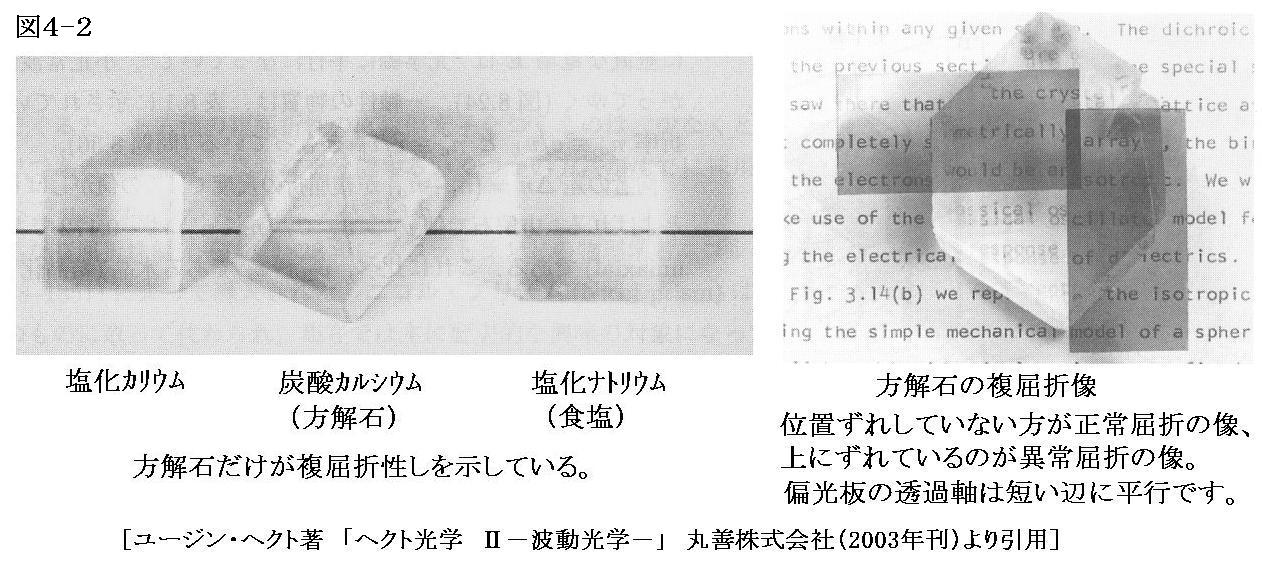
彼は結晶の境界面の作る角度が101°と79°に等しいことを見いだした。また彼は点を描いた紙の上に方解石の結晶を置き、結晶を通して点を見ると、点は一つではなく二つ見え、紙の上で結晶を回転させると二つの点の内の一つは動かず、他方は結晶の回転と共に動かない点の像のまわりを回ることを見つけた。
バルトリヌスはその現象を複屈折と呼び、方解石を通して二種類の屈折が生じる為だと考えた。動く方は「異常屈折」で、動かない方を「正常屈折」で生じるとした。かれは正常屈折の屈折率を5:3であることを知り、また像が一つしか見えなくなる方向を正確に測定した。その方向からそれるにつれて二重像の距離が変化するのを観察した。
オランダの物理学者クリスティアーノ・ホイヘンス (Christiaan Huygens 1629~1695年)はバルトリヌスの著書に刺激されて複屈折の現象を詳しく調べた。それらの結果は1690年の著作『光に関する論述』で説明されている。
方解石には二つの屈折率があり、その一つ正常光線は[入射角の正弦]の[屈折角の正弦]に対する比は常に一定(5:3)であることを見いだした。この比は入射光線のあらゆる傾きに対して一定でスネリウスの法則を満たしている。
ところが異常光線については、入射光線の傾きによってこの比が変化した。ホイヘンスは結晶の劈開面と結晶を構成する最小微小要素(今日の言い方で、結晶を構成する原子・分子を意味する)の形態との関連を推察して、最小微小要素(分子)の形態が対称的ではないために、光の伝播速度が方向により異なる(そのため波源からの素元波は半球状でなくて楕円体がつぶれたような半亜球形になる)と考えた。
ホイヘンスの原理を適用する要素波の波形が半亜球形になると、その包絡線から求まる波の進行方向について、入射角によって屈折率が異なることになる[後で説明するように、包絡線(波面)に垂直な方向には進まない]。その様な場合、方解石の面に垂直に入射しても屈折することや、斜めに入射しても屈折することなく直進する入射角度(73°20’)があることを明らかにして複屈折の現象を説明した。[ホイヘンスの説明は厳密には正しくないのですが、おおよその意味に於いては複屈折のメカニズムを旨く説明することができた。]
さらにホイヘンスは方解石の結晶を二つ重ねてみた。第一の結晶によって、元の像は二つに分かれる。第二の結晶によって、二つに分かれた像がさらに二つに分かれ、多くの場合四つになった。ところが、二個の結晶が互いにある角度を成すように配置すると第二の結晶によって光は分離せずに二本になった光線がそのまま通過した。これは後の偏光現象解明に繋がる極めて重要な発見です。
しかしながら、ホイヘンスは光の振動が音の振動と同じく縦波であると考えていたのでこの現象を旨く説明することはできなかった。縦波は進行方向に直角な方向になにも特別な方向性を持たないから、光を縦波としたのではこの現象を旨く説明できない。
4.(3)2.で説明するようにフランスの物理学者エティエンヌ・ルイ・マリュス(Etienne-Louis Malus 1775~1812年)は、窓から反射した太陽光線は、ホイヘンスが第二の方解石で観測したのと同じ性質を示すことを発見(1808年)した。マリュスは、ガラスでの反射や方解石中への入射により、光線がその側面に関してある種の整理を受けると考え、このような現象を偏光(polarization)とよんだ。ただしマリュスは光の粒子説の立場だったので、彼が言う“光の粒子に刻みつけられるある種の整理”が何を意味するのかはまったく明らかではありません。
1816年にアラゴとフレネルは共同で行った実験から、複屈折で二つに分かれた光線は再結合したとき、二つの光線の経路の長さを変えても常に同じ強さの光を与える事を見つけた。つまり二つの光線を互いに干渉させることはできなかったのです。
そのことを聞いたトマス・ヤング(Thomas Young 1773~1829年)は、ついに“光は横波である”という着想(1817年のアラゴへの手紙)に至る。
この着想を知ったオーギュスタン・ジャン・フレネル(Augustin Jean Fresnel 1788~1827年)は、方解石中の2本の屈折光が互いに直角方向に振動する横波(互いに直角に偏光した光)であると考え、これらが示す現象を定量的に説明(1821年)することができた。こうして、光は横波であるという考え方が確立してくる。
2.結晶構造と光学軸
方解石の結晶構造は下図の様になっている。炭酸イオンが“平たい三角形のおむすび型”をしているためにカルシウム正イオンと炭酸負イオンを電気的な引力で互い違いに積み重ねていくとき、立方体の相対する2頂点を指で挟んで押し潰したような形[図4-3]の結晶となる。そのとき12本の稜の長さはすべて等しくなり、6つの面を構成する菱形の形はすべて同じになる。菱形の二つの相対する角の内角は101°55’で、もう一組の角の内角は78°5’となる。そのとき、もちろんのことであるが101°55’+78°5’=180°=2直角となる。
押しつぶした対角点を結んだ線が光学軸となる。光学軸とは、その方向から入射する正常光線と異常光線の屈折率が等しい方向のことです。すなわちこの方向では、互いに直交する振動面を持つ二つの光線の屈折率は等しくなります。そのため、この光学軸に沿ってものを眺めれば像は二重には見えません。そのとき劈開面に対して入射光は傾いて入射し、また傾いた角度で結晶から出てくることになりますので、光線は境界面で屈折していますが、二重の像にはならない事に注意して下さい。
方解石の様にこの方向が一つだけのものを一軸性結晶と呼ぶ。雲母などのように、このような光学軸が二つある場合を二軸性結晶と呼ぶ。このように複屈折の起こらない軸が一つとは限らず、多くの種類の結晶では二つあることを見つけたのはブルースターです。一軸、二軸の名前の由来も文字通りその軸の本数に由来する。[参考文献2.第4章p129参照]
光学軸は内部の原子配列と関係しており、正負のイオンが均等に入り交じって現れる劈開面の方向とは必ずしも簡単な関係にありません。一般に光学軸は結晶構造の回転対称軸となります。図4-3の左図は方解石(炭酸カルシウム)の光学軸と劈開面との関係を表しています。
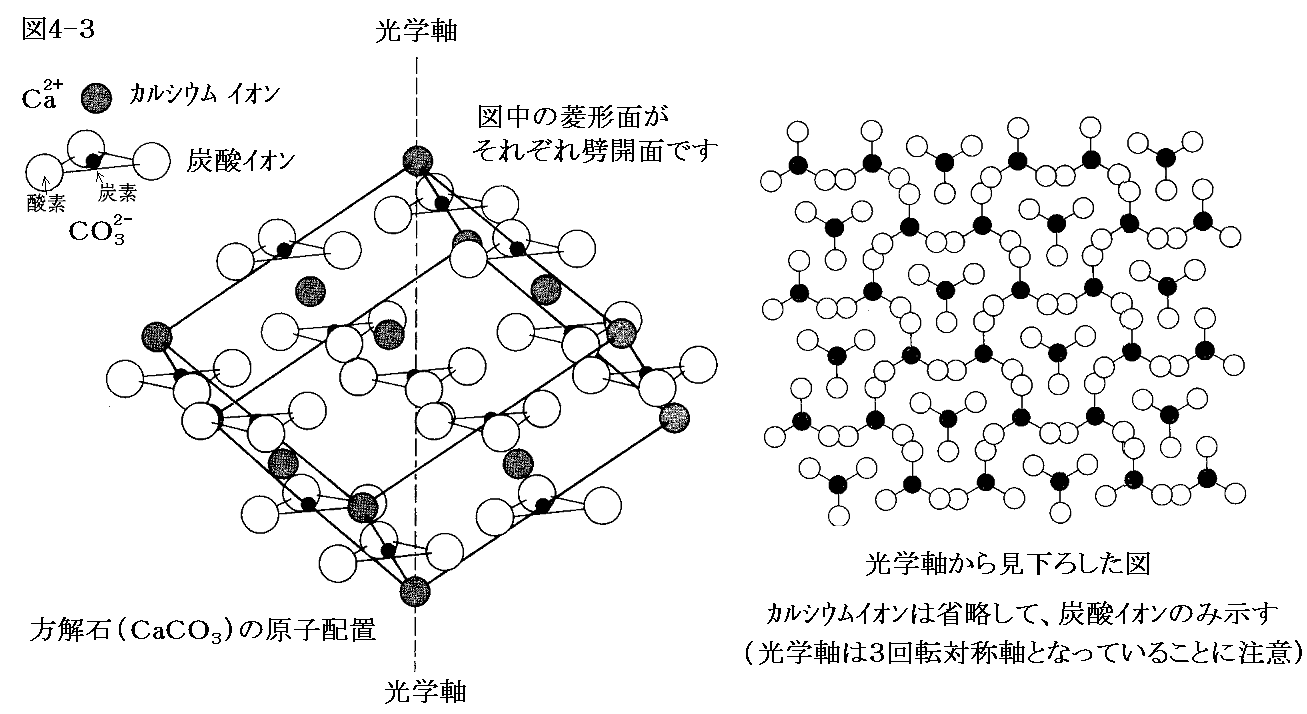
イオン結晶はある特定の面にそって割れやすく、その様に割れることで現れる面を劈開面(へきかいめん)という。劈開面上には正イオンと負イオンの両方が互い違いに並んでいる。
その様な面で割れた場合、面のエネルギーは安定なのです。正イオンのみ、あるいは負イオンのみが並ぶ様な面は安定ではありません。それは簡単な考察から了解できる。
例えば、下図の様に●正イオン、●負イオンが並んだイオン結晶を考える。そのときA-B面あるいはA’-B’面で結晶をずらす様な剪断力が働いてその面にそって原子1個分動いたとする。
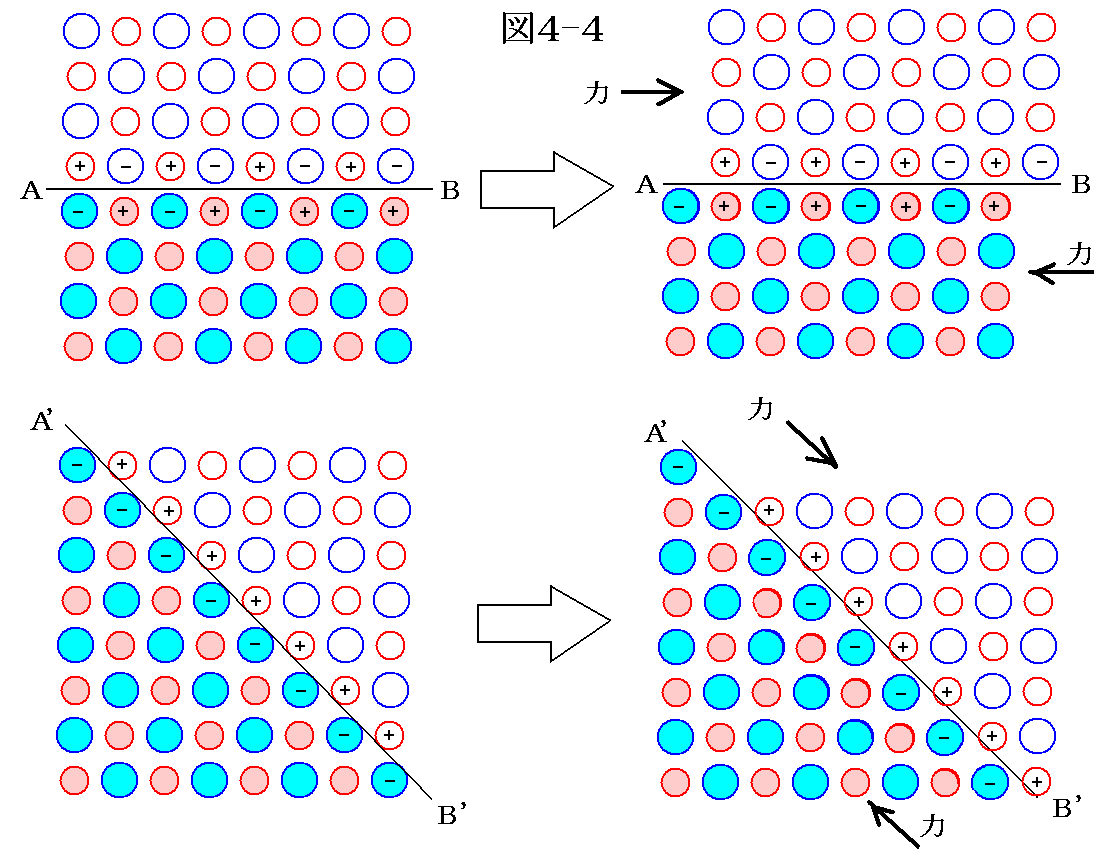
図から明らかなようにA-B面でずれた場合、面を挟んで同符号同士のイオンが相対することになり、相互の電気的反発力でA-B面で割れてしまう。そうしてできる劈開面上には正負のイオンが互い違いに並んでいるので面の上では互いに引き合い、面自体は安定となる。
一方A’-B’面でずれた場合には、面を挟んでの正負イオンとの対応状況は変化しないのでその面で割れることはない。また、たとえ割れたとしてもA’-B’面上には同符号のイオンが並ぶので、面上の同符号イオン同士の反発力によりこの面は安定ではなく、A-B面の形状に崩れ直してゆく。
イオン結晶は正と負のイオンの半径比の違いにより下左図の様な面心立方格子構造的な配置(NaCl)になったり下右図の様な体心立方格子構造的な配置(CsCl)になったり、またそれ以外の構造をとったりする。
そのとき前記の理由により下左図NaClの場合は立方形をした格子面がそのまま劈開面となりますが、下中図CsClの場合は図中に色つき線で示した四角形を含む面が劈開面となり下右図の様な結晶となる。
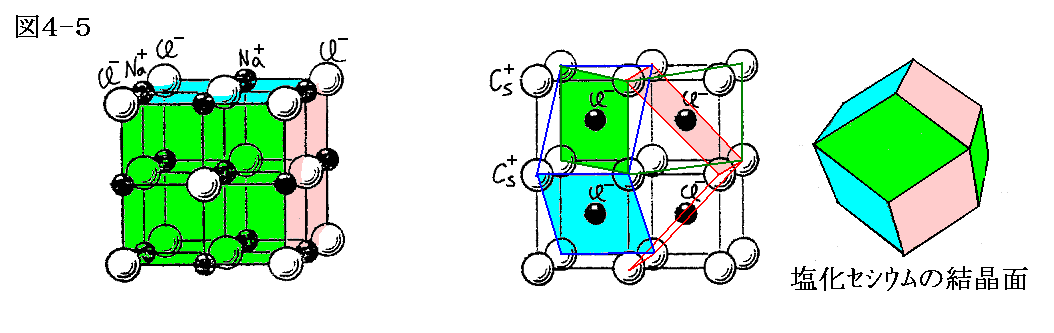
図4-3の方解石(CaCO3)の場合も、正負のイオンが互い違いに並んでいる面が劈開面上になっていることを確認してください。
光学軸と劈開面の関係はなかなか解りにくいので、方解石の場合について色々な状況を図示する。図4-6(b)(d)の紙面は図4-2や図4-7の中に示されている紙面を意味する。
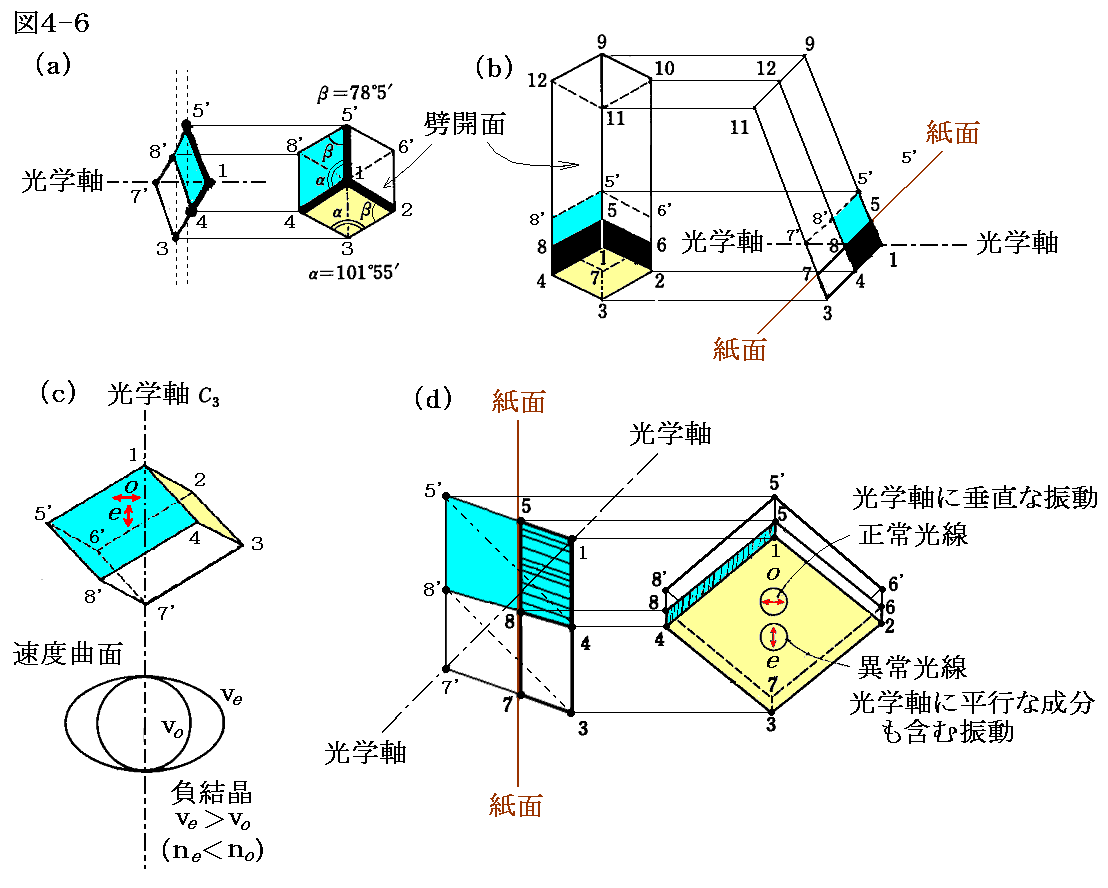
図4-6(d)の右図は方解石の薄片を紙面に密着して置いて、紙面に描いた小円を真上から見た場合を示している。紙面に描かれた小円は二重に見える(ずれの量は実際より誇張してある)。結晶を紙面の上で回転すると、 e と描いた小円は o と描いた小円のまわりを回るよう動いていく。
結晶内の1点から出る光は振動方向によって二つの光線、すなわち光学軸に垂直な電場振動方向の正常光線(ordinary ray)と光学軸に平行な振動成分を持つ異常光線(extraordinary ray)、に分かれる。それぞれの光の波は各方向に図4-6(c)の速度曲面で示される伝播速度で進行する。三次元的に各方向での伝播速度を表す速度曲面は、正常光線が球形に、異常光線が回転楕円体(一軸性結晶のとき)になる。回転楕円体の回転中心軸が光学軸に一致する。
そのとき異常光線と言えども、光線の進行方向が光学軸の方向へ近づいていくと、その光線の電場ベクトルの振動方向は光学軸に垂直になって行きます。そのため進行方向と光学軸が一致する場合には異常光線ではなくなります。そのとき異常光線の電場の振動方向は正常光線の電場の振動方向とは90°異なっていますが、光学軸に垂直であることに変わりはないので屈折率は正常光線と同じになります。そのとき光学軸が結晶の劈開面に垂直でない場合、光学軸に沿って入射する光線は、結晶境界面への入射角がゼロでない斜め入射になりますので、境界面で屈折しますが、その屈折角は正常光線と同じになります。
3.複屈折のメカニズム
図4-7は方解石の複屈折のメカニズムを説明する図です。
一般に光学軸を含む面を主平面(principal plane)と言います。さらに、その主平面が結晶の劈開面に垂直であれば、その主平面で切った結晶の切り口の事を主断面(principal section)と言います。下図は方解石の主断面を表示しています。
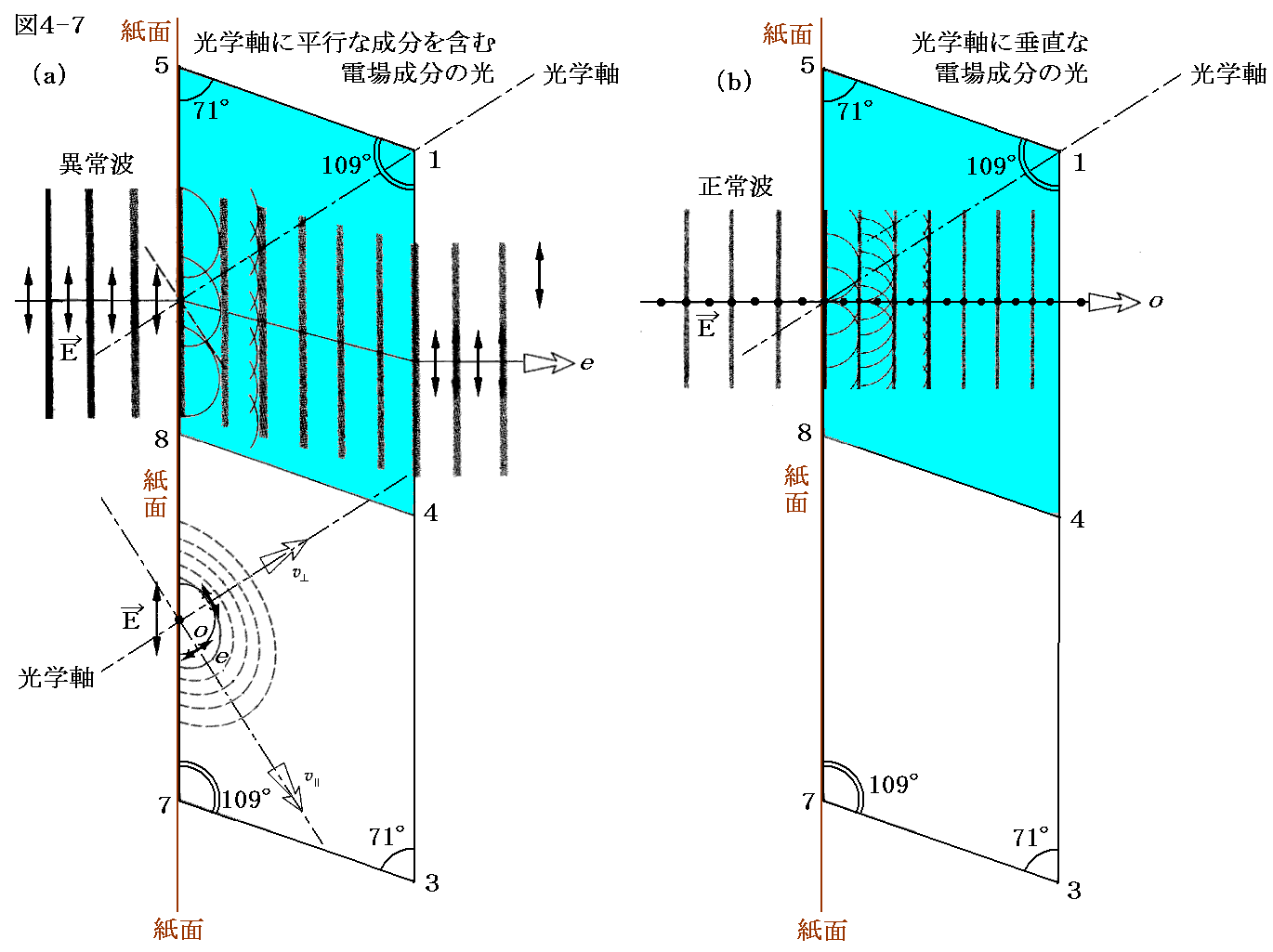
入射光の電場成分を光学軸に垂直な成分と光学軸に平行な部分を含む成分に分ける。
- 光学軸に垂直な電場成分
速度曲面は球形となるためホイヘンスの原理により入射角が変わっても屈折率は常に一定となります。図では方解石の結晶面(劈開面)に垂直に入射する場合を描いていますが斜めに入射しても事情は同じです。ホイヘンスの原理に従った屈折をします。これが正常屈折光です。結晶を通過して出てくる光は光学軸に垂直な振動方向の電場成分を持つ偏光した光です。
ホイヘンスの原理から明らかなことですが正常光線が境界面に垂直に入射した場合には、屈折は起こらずそのまま直進します。境界面に対して斜めに入射する場合のみ屈折します。
- 光学軸に平行な振動成分を持つ電場
結晶中の一点から広がっていく要素波の伝播速度は方向によって異なる。方向による速度の変化の様子を表す速度曲面は、方解石の場合光学軸を回転対称軸として光学軸方向に潰れた回転楕円体面となります。入射角を変えて屈折の様子を示すホイヘンスの原理の図を描いてみれば簡単に確認できるように、この場合入射角が変わると屈折率が変化します。
異常光線の場合、境界面に垂直に入射しても屈折することが起こります。また境界面に斜めに入射しても、そのまま直進するような入射角が存在することに注意して下さい。
図4-8は境界面に垂直に入射する異常波と正常波の波面と光線の進む方向の関係を示していますが、異方性の結晶では左図(a)の様に光線の方向(エネルギーが伝播する方向でありポインティングベクトルSの方向。当然電場はそれに垂直)は波面に垂直にはなりません。 電場ベクトルEと電束ベクトルDの方向も異なります。
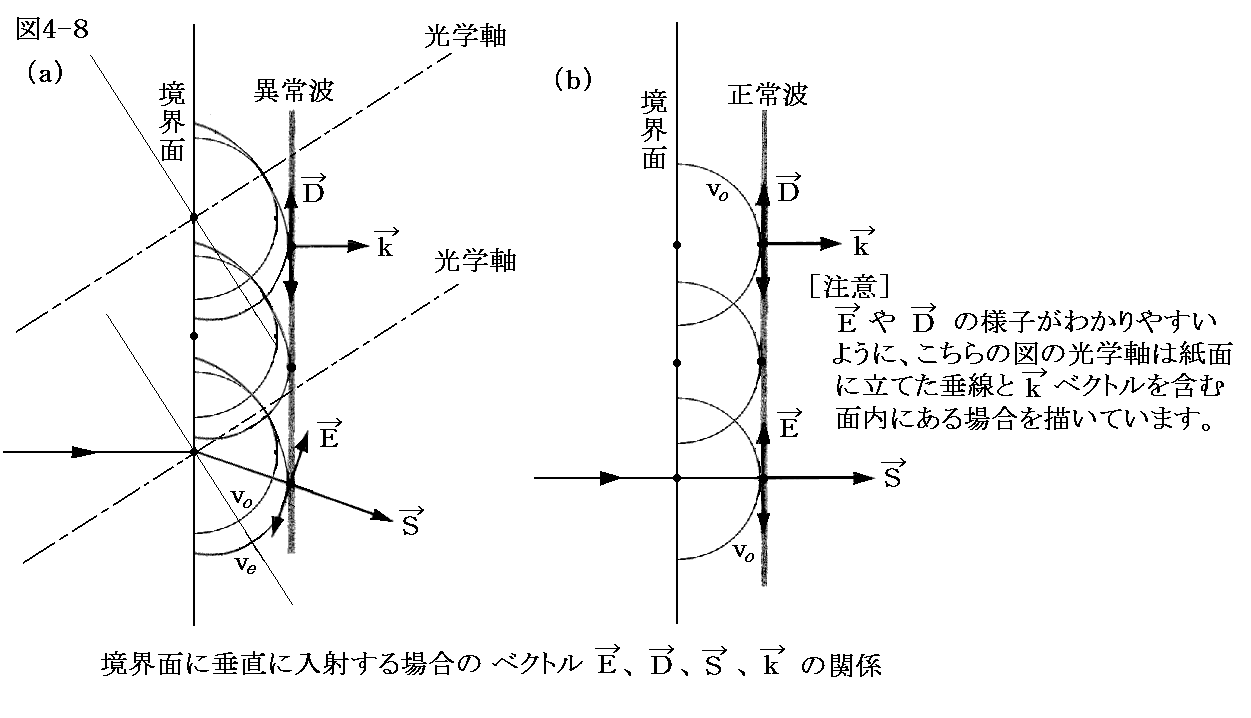
方解石の場合は上図のように、結晶内での伝播速度は異常光線の方が大きく(屈折率は小さく)なります。
正常光線の伝播速度と屈折率をそれぞれvoとnoで、異常光線のそれらをveとneで表すことにする。そのとき、方解石のようにvo<ve(すなわちno>ne)の結晶を負結晶と呼び、その反対vo>ve(no<ne)のものを正結晶と呼びます。
一軸性複屈折結晶の例を以下に示す。屈折率は波長により少し変化しますが、下表はナトリウムのD線(λ0=589.3nm)に付いてのものです。
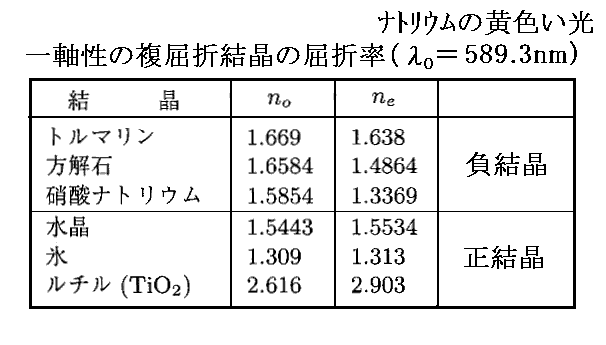
異常光線の屈折率neは入射方向により変化します。すなわち異常光線の入射方向が光学軸に近づいていくと、屈折率neは正常光線の屈折率noの値に近づいていきます。そのため上表中の異常光線の屈折率neは、正結晶の場合は最大値を、負結晶の場合は最小値を示しているのだと考えて下さい。
図4-9は負・正の一軸性結晶の速度曲面の様子を示しています。光学軸と正常・異常光線の電場ベクトルの振動方向(偏光方向)との関係に注意して下さい。また異常光線の速度曲面が楕円に変形する方向の違いに注意して下さい。
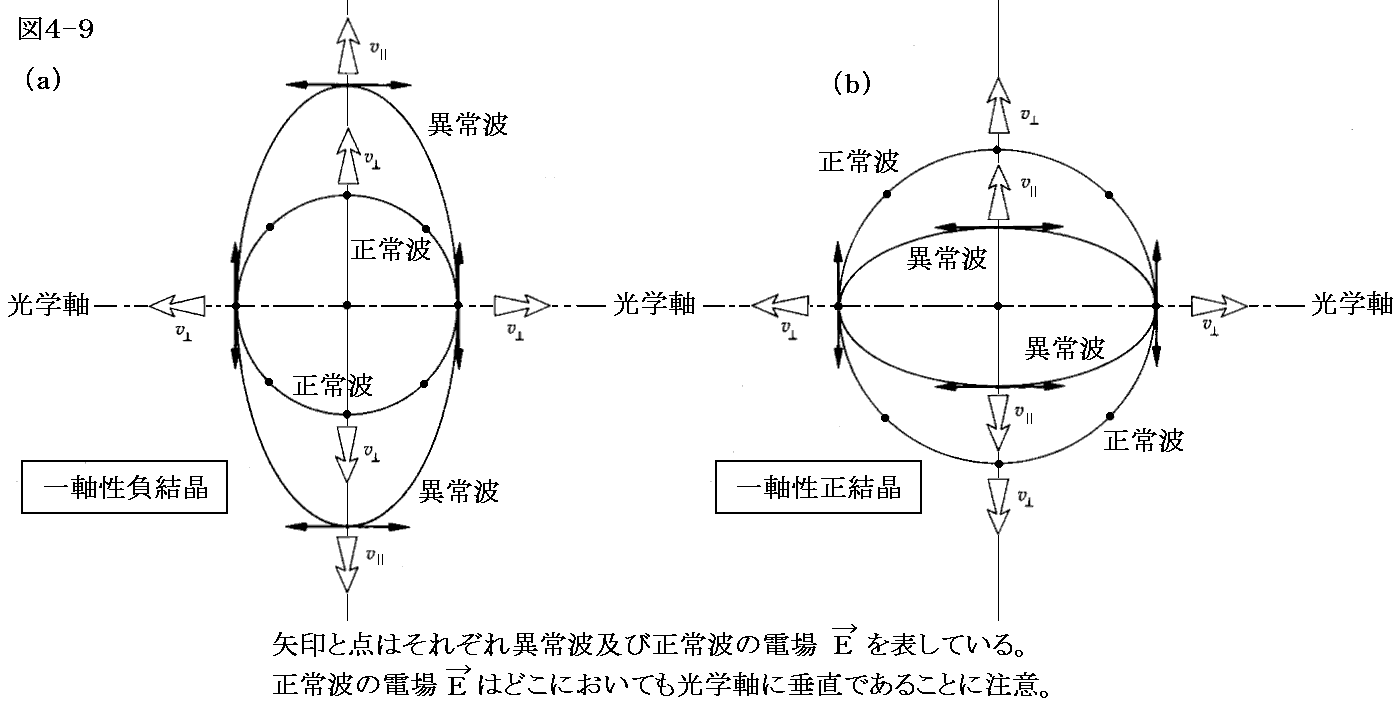
4.Rochenプリズム(1811年)とWollastonプリズム(1820年)
前節までで明らかになったように複屈折した光の異常光線と正常光線は互いに直交した偏光面を持つた偏光した光です。そのためこの事が理解された後に、直ちに複屈折結晶を偏光子として利用することが考えられた。
しかし二つの光線の屈折率の違いはわずかなので細い光束ならよいが、かなり太い光束ではどうしても二つの光の束が重なってしまい旨く分離できません。この問題を最初に解決したのは1811年のロション(Rochen)です。彼は一軸性の正結晶である水晶をプリズム状にして下図の様に組み合わせた。図中の直線(紙面に平行)と点(紙面に垂直)で光学軸の方向を示しています。右のプリズムの光学軸は紙面に垂直です。
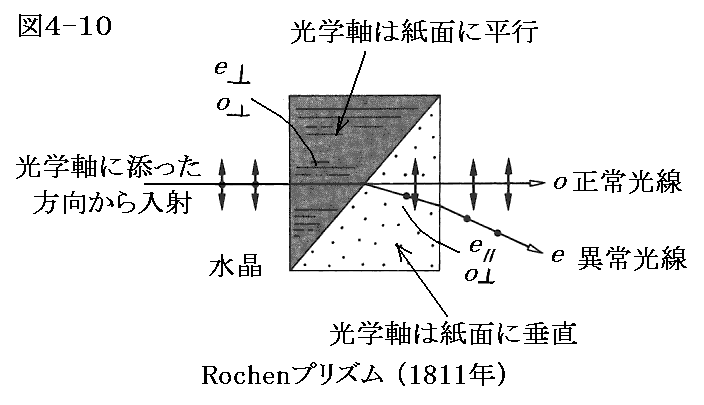
上図は水晶の場合ですが、プリズムの材質を負結晶の方解石で置き換えると異常光線の屈折方向が逆になります。[図4-11(b)]
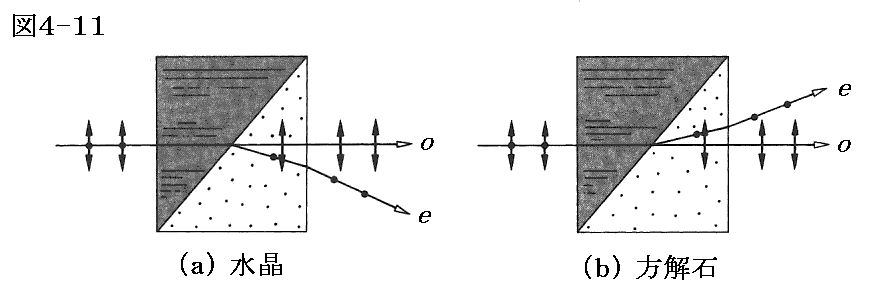
電場の振動方向が光学軸に垂直な正常光線は二つのプリズムの屈折率が同じですから接合面で屈折することなく直進する。一方、左のプリズムの光学軸に沿って入射する異常光線(ただし左のプリズム中では電場の振動方向は光学軸に垂直ですから異常光線ではない)は右側のプリズムでは光学軸に平行な方向に偏光しているために左右のプリズムで屈折率が異なることになる。そのためプリズム接合面で屈折して正常光線の方向とは異なった方向へ進む。二つに分離した光線の内の直進する光線だけを利用すれば偏光子となる。
このプリズムでは正常光線が直進するので波長による分散がない。異常光線の方は波長が異なることによる屈折率の変化があるため白色光では色が付く。
1820年にウォラストン(Wollaston)は異常光線と正常光線の分離角を大きくするために、二つのプリズムの光学軸の組み合わせを下図のようにした偏光子を考案した。図4-12は負結晶の方解石の場合を示している。
方解石ではne<noだから、最初左側部分で電場が光学軸に平行で合った異常光線が境界面越えると正常光線となり境界面の法線の方に曲がる。
左側部分に於いて電場が光学軸に垂直で合った正常光線は右側の部分では光学軸に平行な異常光線になる。このこととne<noを考慮すれば異常光線は境界面の法線から離れる方向に曲がる。
これらの事は正常光線の球形速度曲面と異常光線の回転楕円体速度曲面をホイヘンスの原理を用いた屈折の説明図に適用すれぱ了解できます。
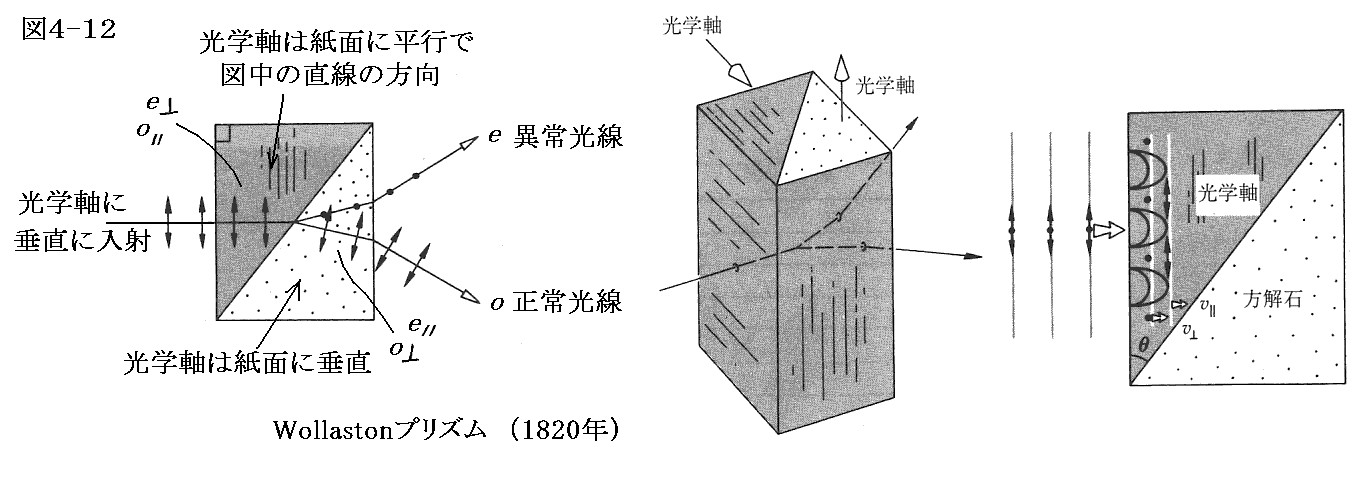
プリズムから出てくる二つの光線の間の偏角はプリズムの楔角θで決まる。普通θ=15°~45°のものが市販されている。用いる周波数と出力に応じて、プリズムの接合に接着剤(ひまし油、グリセリン、等)を使うか、使わないで接触させるだけするかが選択される。
ウォラストンプリズムには両光線の分離角度を大きくする利点はあるが、両光線とも入射光線に対して角度を持って進むから波長による分散が起こり、白色光のときには両方とも着色する。
5.Nicolプリズム(1828年)
1828年にスコットランドの物理学者ウイリアム・ニコル(William Nicol)によって導入された。効率の良い偏光子で、かっては広く用いられたが、今日では他のものに取って変わられている。
図4-6(b)の状態の長く発達した方解石の結晶を用いる。ただし角∠1-3-11 は71°ではなくて68°に研磨されている。角∠3-1-11 が90°になるように斜めに切って二つのプリズムにして、もう一度カナダバルサムで接着してある。
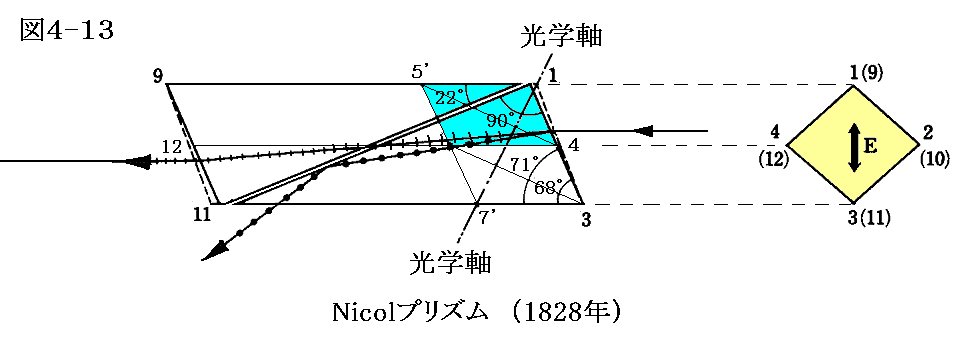
図の入射線の方向に対してno=1.658、ne=1.486であるが、カナダバルサムの屈折率はこの中間のnバルサ=1.55です。正常光線に対してはカナダバルサムの屈折率nバルサよりもnoの方が大きいので、正常光線は接着面で全反射(臨界角は約69°)をして横に逃げていく。実際そのときの臨界角は
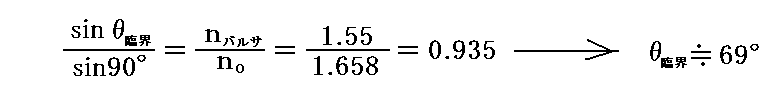
ですから全反射が確かに起こります[全反射の臨界角の求め方は別稿「光の屈折」1.(3)を参照]。角∠1-3-11 を68°に研磨したのは全反射を確実に実現するためです。
一方、異常光線に対してはバルサムは密な物質となるので全反射は起こらない。その上 ne<no であるので方解石の中に入っていくとき正常光線ほど方向を変えられることもない。
ニコルプリズムを使うと振動方向の判った直線偏光を取り出すことができる。光学軸に直角方向に振動する光は全反射により取り除かれているので偏光は完全です。紙面内で振動する異常光線のみが通過する。異常光線は横方向に少しずれるが可視光領域ではほとんど変化することなしに出てくる。
かっては、偏光子と言えばニコルプリズムを意味するぐらいおおいに用いられた。しかし、カナダバルサムは紫外線を吸収するので紫外領域での使用には適さないし、その構造から視野角が小さくて使いづらいため今日ではほとんど用いられていない。
6.Glan-Thompsonプリズム(1948年)
現在広く使用されているのは、空気層での全反射を利用したグラン・トムソンプリズム型の偏光子です。光学軸を図4-14の様に組み合わせた二つのプリズムで作ります。異常光線だけを通過させ正常光線を内部全反射させるためには、プリズムの材料として方解石を用いた場合
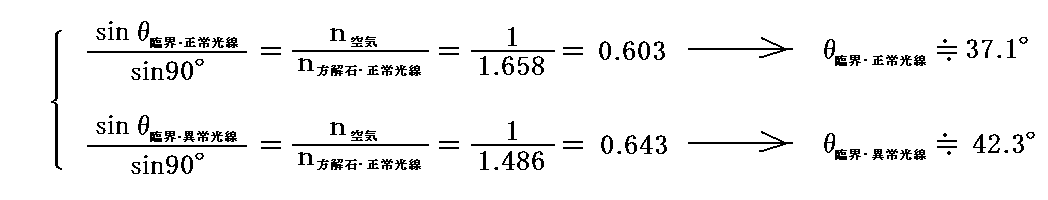
だから、プリズム角θを
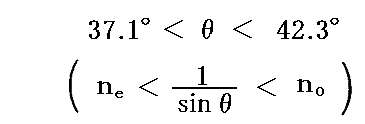
となるように決めればよい。そのときθは正常光線の臨界角よりも大きく、異常光線の臨界角よりも小さくなるため、正常光線を全反射し、異常光線を透過させる。
θ=38.5°にした場合を図示すると
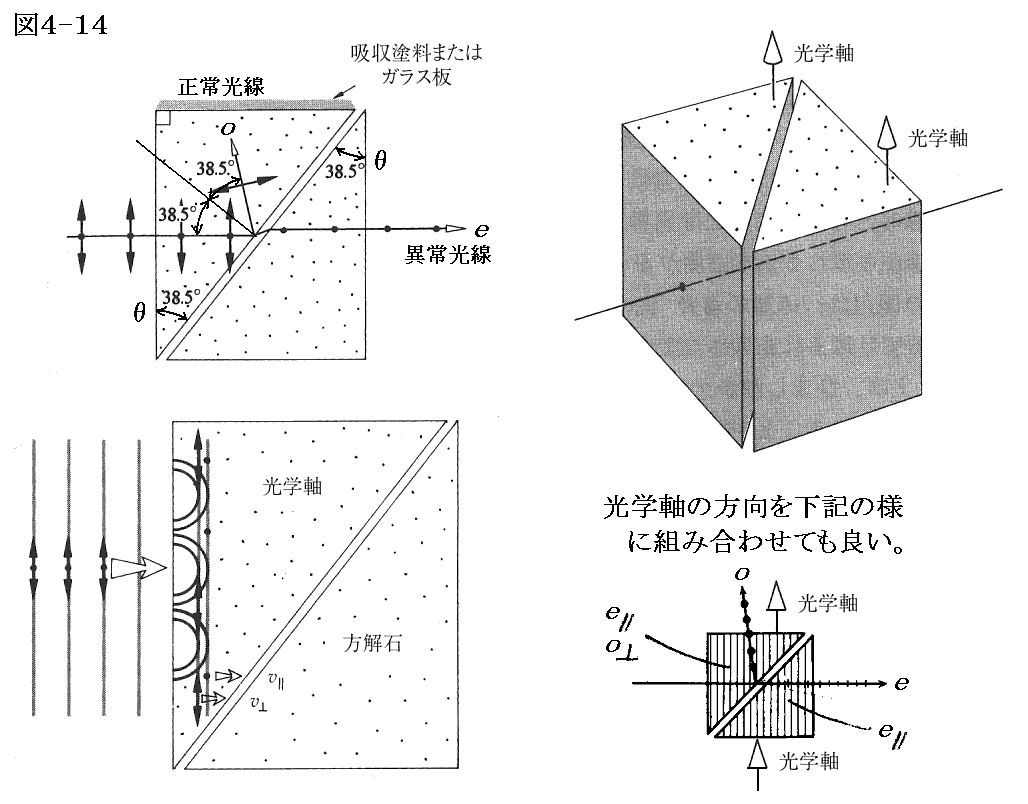
となる。
このタイプの偏光子は空気層での全反射を利用しているために、波長領域として5000nmの赤外線から220nm程度の紫外線まで利用可能です。
(3)反射(散乱)偏光子
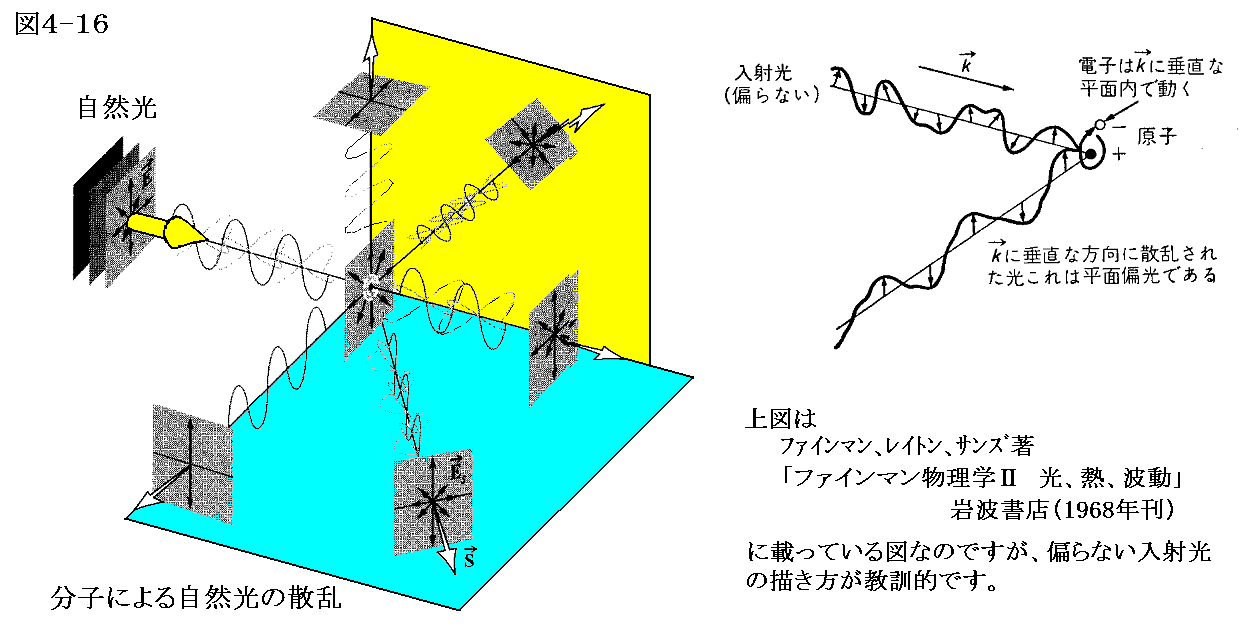
1.散乱と偏光
直線偏光あるいは自然光が空気中の分子に入射すると散乱光の電場の向きは下図の様に偏光することは別稿「線型振動子(電気双極子)による電磁波の放出」2.(3)で説明した。
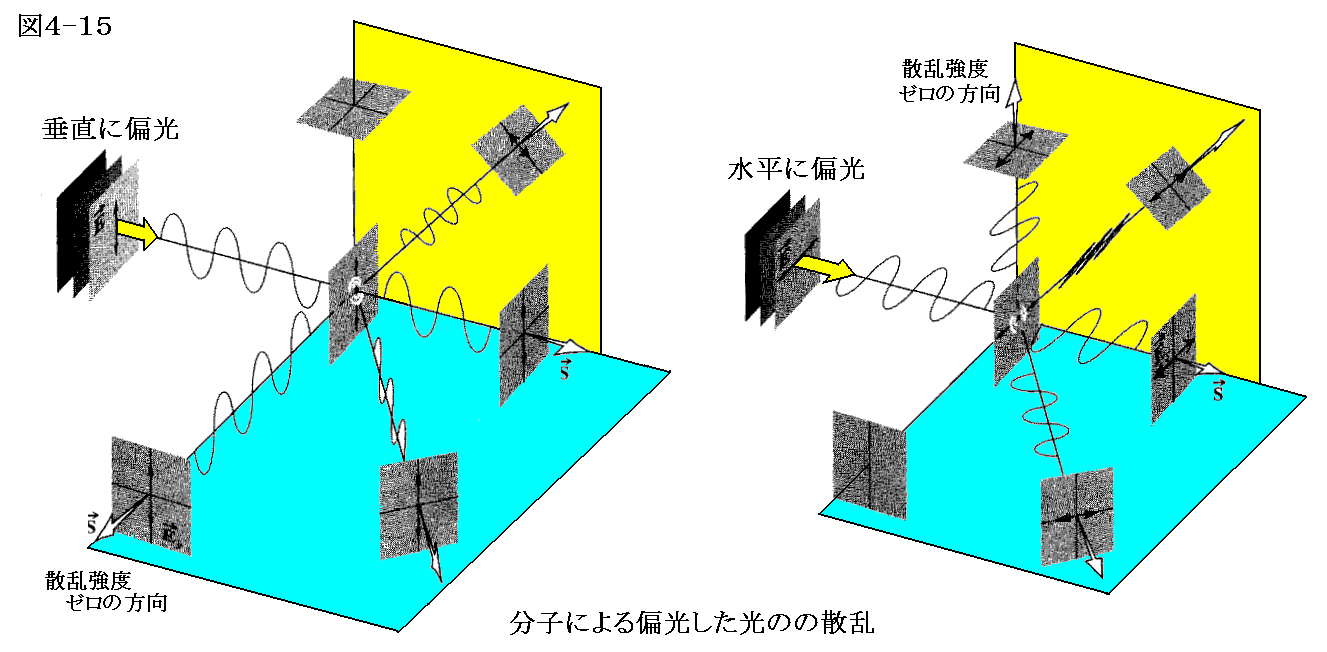
太陽光線に直角な方向の空の領域を4.(4)3.で説明するポラロイド偏光板などを通して眺めて見る。偏光板を回転すると、透過光の強度が変化して、暗くなったり明るくなったりする。そのことは、自然光である太陽光を散乱することによって輝いている空から来る光は少し偏光していることが解る。
実際に空の光の偏りを見つけたのはフランスの物理学者ドミニク・フランソワ・ジャン・アラゴ(Dominique Francois Jean Arago 1786~1853年)(1811年)です。
また、別稿「線型振動子(電気双極子)による電磁波の放出」3.(3)ですでに説明したように、バークラはこの考え方をX線に適用して、X線が横波であることを示した(1905年)ことは有名です。
2.反射と偏光
反射の現象は、入射光(電磁波)によって四方に散乱される二次的な光(電磁波)が、散乱体が規則正しく密に分布しているために、いわゆる反射角の方向の散乱光(ホイヘンスの原理で言うところの素元波)の位相が揃って強く干渉する現象です。その際ホイヘンスの原理から明らかなように特定な方向の反射光が強くなります。そのとき、反射は少なからず偏光を生じます。その様なことが生じるメカニズムについての簡単な説明は別稿「ブルースター角(偏光角)」でしました。[詳しくやるには電磁気学的な考察「フレネルの公式」が必要ですが、高校レベルを超えるので省略します]
反射による偏光の事実に最初に気づいた人はおそらく1808年のマリュスであろう。当時、パリの学術協会が方解石などの結晶が示す二重屈折の数学的理論に賞を出すことにした。マリュスは方解石の結晶を調べてこの課題に取り組んでいたのですが、ある日の夕刻、アンファル通りの自宅の窓から、沈み行く夕日の近くに位置しているルクセンブルグ宮殿のガラス窓によって彼の方に反射してくる太陽光線を、方解石の結晶を通して見ていた。そのとき彼は方解石を回転させると複屈折の為に二重に見えていた像の内の一方が消えたり現れたりするのに気付いた。彼は、さらに太陽光線に限らずロウソクの光でも水面やガラス面から反射してくる光について同様な現象が生じることを確かめた。
結局、マリュスは、窓から反射した太陽光線は、ホイヘンスが第二の方解石で観測したのと同じ性質を示すことを発見したのです。マリュスは、ガラスでの反射や方解石中への入射により、太陽光線が横振動に関してある種の整理を受けると考え、これを偏光と呼んだ。これは複屈折と偏光の真の性質を明らかにするきっかけとなった大発見で多くの科学者に影響を与えた。
1815年にデーヴィッド・ブルースター(David Brewster 1781~1868年)は反射によって起こる偏光に対して簡単な数学的法則(反射光と屈折光が互いに直角をなす)を見つけた。その条件を満たす入射角[これをブルースター角(偏光角)θBという]で物質に当たる光の反射光は完全に偏光し、それ以外の角度で入射する光の反射波は部分的に偏光していることに気付いた。そしてさらに詳しく調べてみると、この反射光が完全に偏光する入射角と反射物質の屈折率はある簡単な関係[ブルースターの法則]になることを見つけた[詳細は別稿「ブルースター角(偏光角)」参照]。 ただし残念ながら、ブルースターはニュートンによる光の粒子説の信奉者だったので、なぜその様になるのかが旨く説明できたわけではありません。
ちなみに、空中からの入射光がガラスで反射される場合ブルースターの法則のn2/n1は1.5程度となるので偏光角は56°となる。また、水面で反射する場合にはn2/n1=1.33程度だから偏光角は53°となる。ポラロイド偏光板やサングラス[普通偏光ガラスを用いている]を持っている人は、それらの偏光子を回転させながら、上記のブルースター角と等しい反射角で反射してくる光を眺めてみられることを薦める。
ちなみに、自動車のフロントガラスは偏光シートが挟み込まれたガラスが用いられています。それは路面からの反射光[路面に平行な偏光面]を遮り、そのまぶしさに幻惑されなで運転できるようにするためです。運転席に座って、フロントガラスの前で偏光板(サングラス)を回しながら外を眺めてみれば少し暗くなったり明るくなったりするので、フロントガラスが確かに偏光子の働きをしているのが解ります。
その頃の波動論には偏光について満足できる説明はなかったのですが、その後の十数年間の幾多の人々[特にヤングとフレネル]の研究を経て、光をある種の横方向の振動として表すべきであるという考え方が出てきます。これはまさしく光は横波であると言っているのですが、光の電磁波説が出てくる40年以上も前のことです。[この当たりは参考文献2.の4章参照]
3.反射偏光子
光の反射を用いることにより偏光子を作ることができる。ただし偏光角で反射された光は完全に偏光しているが強度は弱い。また、透過光の強度は強いけれど偏光の度合いは小さい。この欠点を改善するために、アラゴは下図の様な沢山のガラス板を重ねた積層板偏光器を発明(1812年)した。
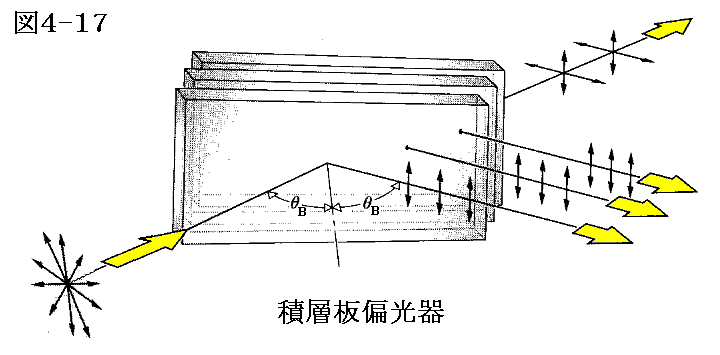
下図は積層板偏光器をさらに改良したもので、二つのプリズムの間に透明な誘電体薄膜を多層に重ねたものが挟んである。誘電体の屈折率とガラスプリズムの屈折率は、ブルースター角(偏光角)が薄膜層面に対してちょうど45°になるように調整されている。その場合境界面への入射角が45°になるので、吸収の少ない完全に偏光した光を直角方向の反射光および直進方向の透過光として取り出すことができる。
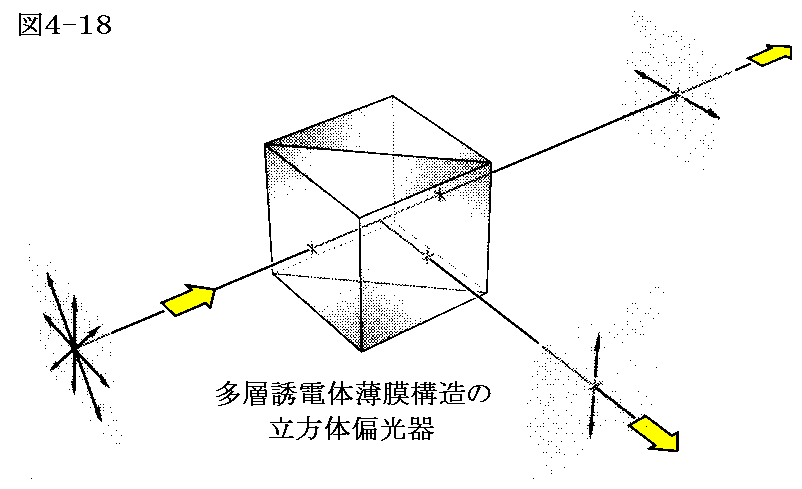
これはレーザービームを形成するときに特に有効に用いられている。
(4)二色性偏光子
二色性の偏光子は一般に異方性の物質で、ある方向の電場成分を優先的に強く吸収するが、それに直角な方向に対しては透明なものです。
1.二色性結晶
1815年にジャン・バティスト・ビオ(Jean BaptisteBiot 1774~1862年)(ビオ・サバールの法則で有名なビオです)は、トルマリン(電気石)の結晶を薄く切った板は、二本の屈折光のうち一方のみを通過させて、もう一方を吸収することを発見した。これは結晶構造の異方性から、ある方向の電場成分を優先的に強く吸収するが、それに直角な方向に対しては透明になることによります。
このよう直線偏光子を二色性偏光子と言います。二色性とは入射ビームの二つの直交する電場成分の一方を選択的に吸収することを表している。
そのような鉱物結晶は何種類かあります。例えばホウ酸塩鉱物であるトルマリン(電気石)やフェロマグネシウムケイ酸塩鉱物の紫蘇輝石(しそきせき)などです。

電気石を3mm程度の厚さに切り出すとかなり純粋な直線偏光が得られますので、昔は電気石の薄片が偏光子として結構利用されていました。
2.針金格子偏光子
下図の様な針金が縦に並んでいる金属格子は光(電磁波)を選択的に吸収して偏光子となります。
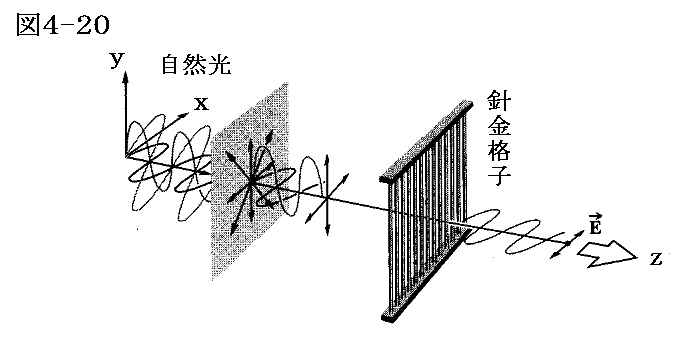
y成分に平行な電場成分は針金中の伝導電子を長さ方向に駆動して電流を発生させる。電流電子は金属結晶中の原子と衝突してそれにエネルギーを与えてジュール熱となる。こうしてエネルギーが電場から格子に伝えられてy軸に平行な電場成分は格子に吸収されてしまい格子を通過できない。
一方、x方向では電子は格子中を十分遠くまで自由に動けないため、光(電磁波)のこの方向に対応する電場成分は格子に吸収されることはない。そのためx方向の電場成分は格子を通過する。つまり格子の透過軸は針金に垂直な方向となります。
これは高校物理の電波(マイクロ波)の演示実験で習うものです。
光の様に波長が短くなっても同様の事情が成り立つのか興味あるところですが、1969年にバードとパリッシュは1mm当たり2160本の針金がある金属格子を、プラスチックの回折格子に金属を蒸着することで作り、実際に光りの波長でも上記の事情が成り立つことを確かめている。
[G. R. Bird and M. Parrish,Jr., “The Wire Grid as a Near-Infrared Polarizer”,
J. Opt. Soc. 1969年]
3.ポラロイド
1928年にハーバード・カレッジの学生であったランド(Edwin Herbert Land )は、「ポラロイドJ板」の商品名で知られている薄板状の偏光子を発明した。ヘラパイト(過ヨウ化硫酸キニーネ)と呼ばれる人造の微小な針状結晶が二色性を示すのである。ランドはヘラパタイトの結晶を極めて小さくすりつぶして、粘性の高いコロイドに混ぜて、それを細長いスリットの間を押し出すことにより薄い板を成形した。押し出すときに微小な針状結晶が機械的に押し出す方向に整列することで、偏光板となるのである。ランドは後に偏光板を発明したときのいきさつを回想しており、とても興味深い内容なのでここに引用する。
1938年にランドは更に改良した「ポラロイドH板」を発明した。それは透明な高分子性物質であるポリビニルアルコールの板を熱して一つの方向に引き延ばす。そうすると炭化水素鎖が伸長方向に整列した板ができる。その後、板を高濃度のヨード溶液に浸しヨウ素分子を浸透させる。ヨウ素分子はポリビニルアルコール板にしみこんで、その長い直鎖状分子にくっつきヨウ素分子が並んだ鎖を形成する。ヨウ素分子の並びがヨウ素の伝導電子に対して前記の針金格子の働きをして、偏光子となるのである。
その後様々に改良された「ポラロイド」は、今日最も簡便な偏光板として広範な用途で使われており、偏光板と言えばポラロイドを指すくらい普及している。しかし「ポラロイド(polaroid)」の起源は、ランドが偏光板を商品化したとき偏光(polarized light)を連想させるために付けた商品名です。
ランドは後にインスタントカメラ(撮影後に自動的にプリントするカメラ)を発明して売り出した事でも有名です。このカメラも「ポラロイド・カメラ」と名付けられていますが偏光とは関係ありません。
5.遅相子
遅相子とは、コヒーレントな二つの直線偏光成分の一方の位相を他方よりある一定量遅らせる素子です。遅相子を出ると二つの成分の相対位相は初めと異なるため、偏光状態も変化します。
(1)光路長と波数
光の干渉を考えるとき、干渉する二つの光の位相の差が重要になります。その位相差は干渉する光が進む経路の長さにと、そのとき光が通過する媒質の屈折率に関係します。
下図のような異なった屈折率の多重層の中を、SからPへ進む光線を考える。もちろん光線の進路はスネルの屈折の法則を満たすように折れ曲がっている。
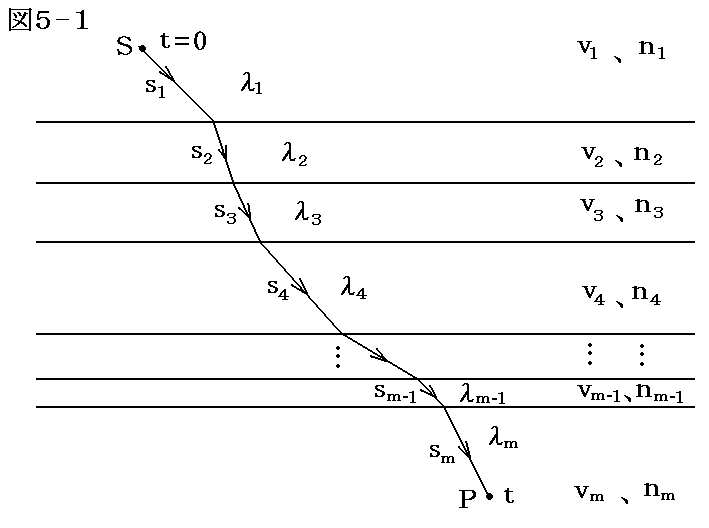
このときSからPへ光線が伝播するのに要する時間tは、それどれの媒質中での経路長をs1,s2,s3,・・・、伝播速度をv1,v2,v3,・・・とすると
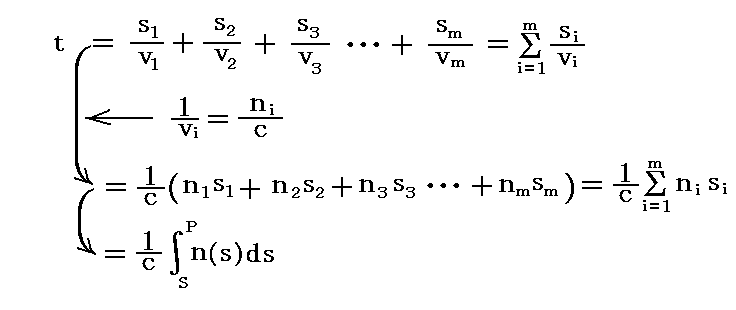
となる。
フェルマーの原理から言えるように、このときの t が極値を取る経路が実際にSから出た光線がPに到達する経路です。極値を取る場合その経路の近傍を通る光線の位相が揃うためにPまで到達できるが、他の経路を取ると、光路長が極値でないために、その近傍の光線の位相は少しずつ異なっており、光が先に進むと互いの干渉の為に途中で消えてしまうのです。[この当たりの説明は光学の本を参照してください。]
ここで
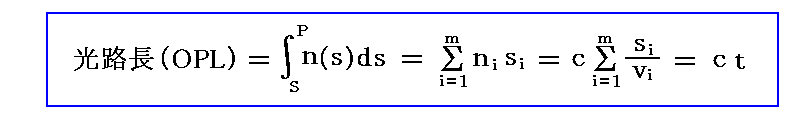
のことを、光線がたどる光路長(optical path length)という。
ところで、各媒質中の光の波長がλiである場合、各媒質中の経路長siをその媒質中での波長λiで割ったものを足し合わせたものをその光路における波数(wave number)と言うが、前記の光路長(OPL)は波数と以下の関係で結ばれる。
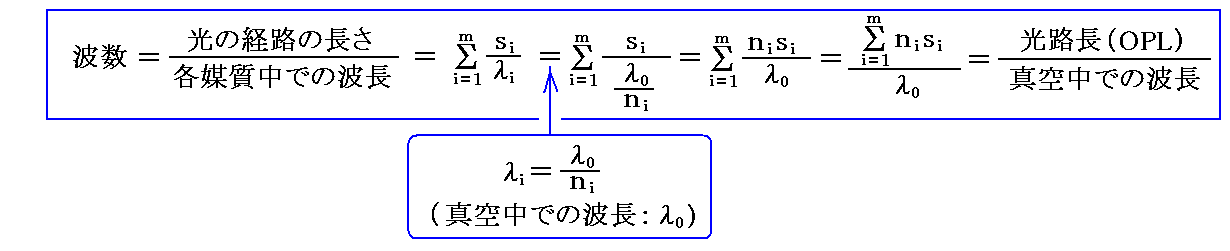
つまり、光路長とは屈折率niの媒質中の伝播距離siに等価な真空中での距離(波数×真空中での波長)を足し合わせたものに相当します。一点から出た光が様々な経路を取って進み、最終的に別な一点へ収束して互いに干渉し強め合うときには、各経路中に存在する波の数(波数)は互いに等しくなります。
周期的に振動する光が色々な媒質中を通過したときの、通過光の位相の変化量は光の通過した各媒質の長さのみならず、その各媒質中での波長(屈折率)に関係します。そのとき光路長と波数の概念は、周期的に変動する波であれば、任意の波形の波に対して適応することができます。そのため、任意の媒質を通過した光の位相がどの様に変化するかを論じるときにはとても便利な量です。
(2)遅相板
1.相対的な位相差
方解石の様な一軸性結晶を光学軸に垂直な二つの平面を持つ板に切り出す。
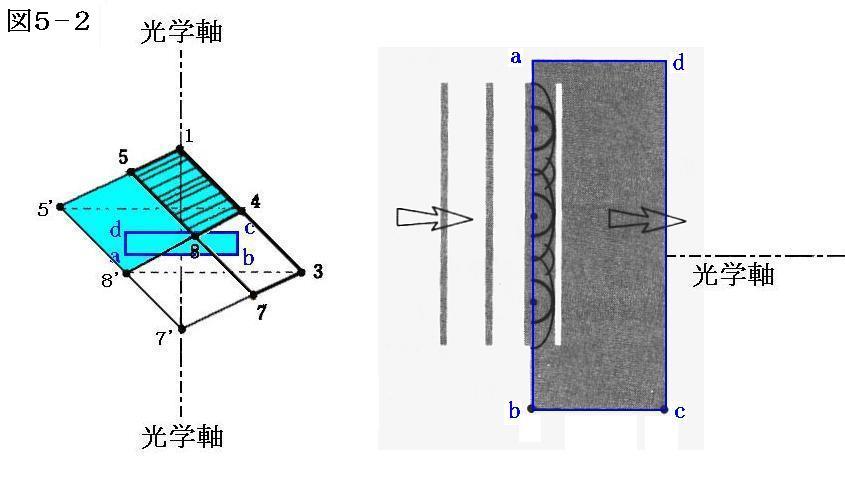
その板面に垂直に平面波を入射させる。そのとき電場Eは光学軸に垂直なります。二次波の速度曲面は正常波、異常波とも光学軸方向では互いに接しているため、これらの曲面の包絡面である正常波と異常波は一致していて、向きを変えない単一の平面波として結晶を通過する。正常波と異常波の相対位相差に変化はなく、二重像も見えない。
一方、光学軸に平行な二つの面を持つ板を切り出した場合、入射する単色平面波の電場Eが光学軸に平行な成分と垂直な成分を持っていたら、二つに分離した平面波が結晶中を伝搬する。
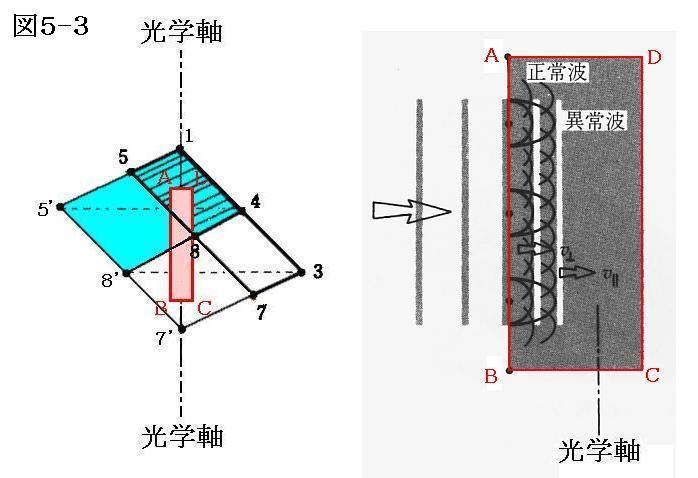
v∥>v⊥であるからno>neであり、異常波は板中を正常波より速く進む。厚さdの板を横切って出てくる電磁波は、相対的な位相差Δφを持つ異常波と正常波の重ね合わさったものになる。今後特に断らない限り、議論の対称にしている結晶板はこのように光学軸に平行な二面で切り出された結晶板(遅相子または遅相板という)であると考えて下さい。
厚さdの遅相板を横切って出てきた正常波と異常波の相対的な光路長差Λは光路長の定義より
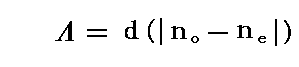
となる。ここで屈折率の差の絶対値にしているのは、正・負結晶のどちらに付いても成り立つように相対値で議論したいからです。
行路長差Λを用いると両光線の相対的な位相差Δφは

となる。ここでλ0は真空中での波長です。今後、Δφの事を遅相量(リターダンス retardance)と言うことにする。
このようにして位相変化が起こるために、上記の結晶板を出てくる光の偏光状態は直交した入射電場成分EoとEeの振幅と同時に、相対的位相差Δφにも依存することになる。
一般に|no-ne|は可視光の領域でほとんど変化しないと考えて良いが、λ0が変われば相対的な位相差Δφは変化する。そのため遅相量Δφは入射光の波長(色)λ0に依存することに注意してください[5.(6)2.も参照]。
2.全波長板
結晶板を通過した正常波と異常波の遅相量がΔφ=2πとなるような、結晶板を全波長板(全波長遅相子)と言う。この場合、正常波と異常波は同位相に戻るため入射ビームが単色の場合、偏光状態に観察できるような変化は生じません。
ただし、上に述べたように遅相量には波長(色)依存性がありますので、一つの波長(色)に関して全波長板であっても他の波長(色)に関してはそうはなりません。波長と結晶板の厚さがマッチしていなければ直線偏光を入射させても結晶板を出てくる光は楕円偏光になります。
全波長板に対して入射光がごく僅か斜めに入射すると遅相量が2πからごく僅か変化します。そのためこのような全波長板は、光学系を通過した光の偏光状態に意図せず生じる変化を除去するのに利用されます。例えば金属の表面鏡から反射される直線偏光は楕円偏光として出てくるような位相変化を受けているが、この変化はごく僅か傾けた全波長板を通すことで補正できます。
また、後ほど説明する、全波長板領域とそうでない領域が混在するバビネ補償板の様な物をつくると有益な使い方ができる。
3.1/2波長板
正常波と異常波の間にΔφ=πの相対的位相差をもたらすものを1/2波長板(1/2波長遅相子)と言います。
例えば、下左図の負結晶では、異常波は正常波に比べ速い速度と長い波長を持っているので、波動が遅相板から出るとλ0/2の光路長差Λつまり2π/2=πの相対位相差Δφが生じる。このとき振動数ν(周期τ)は遅相板を通過しても不変に保たれます。
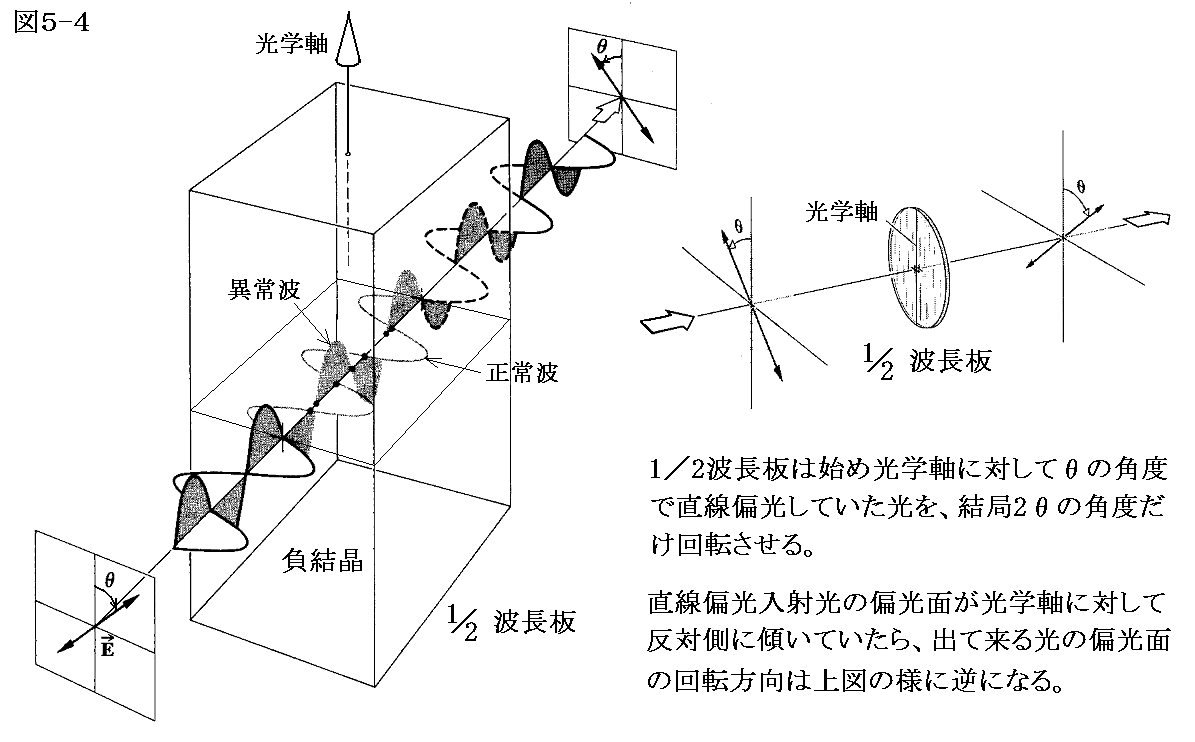
直線偏光の入射ビームの偏光面が、光学軸に対して角度θだけ傾いているとすると、1/2波長板を出た光の偏光面の方向は2θだけ回転する。そのため1/2波長板は偏光旋回子と呼ばれる事がある。
入射光が円偏光や楕円偏光の場合、1/2波長板は回転方向を右から左へ、あるいは左から右へと反転させます。
波長板が厚くなるにつれて光路長差Λ(相対位相差Δφ)は増大していく。そのとき、当然のことですが
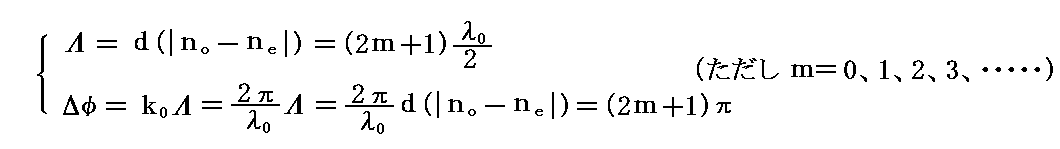
が成り立つ厚さの場合にも1/2波長板として作用する。このとき入射光の波長(色)λ0が変化すれば1/2波長板となる厚さdは変化します。
次節で述べる1/4波長板を二枚重ねて用いれば1/2波長板になります。
4.1/4波長板
正常波と異常波の間にΔφ=π/2の相対的位相差をもたらすものを1/4波長板(1/4波長遅相子)と言います。
このとき
1/4波長板の光学軸に対して角度45°の方向に偏光した直線偏光を入射すると出てくる光は円偏光に変換されます。そのとき光学軸に対する入射光偏光面の傾きを-45°にすれば円偏光の回転方向は逆転します。
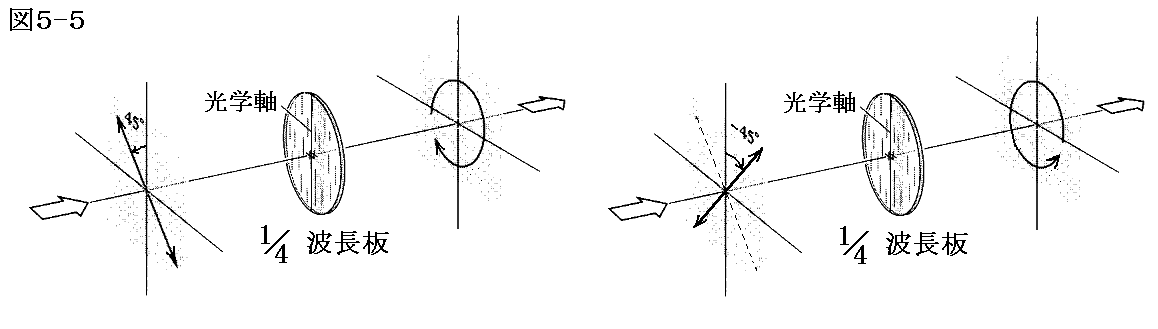
また、逆に
円偏光を1/4波長板に入射させれば出てくる光は光学軸に対して45°傾いた直線偏光になります。このとき円偏光の回転方向が逆なら-45°傾いた直線偏光となります。
《1/4波長板+偏光子で[円偏光の回転方向]を識別できる》
入射光が単色の円偏光であることが解っている場合には、1/4波長板を通過した直線線偏光が波長板の光学軸に対してどちら側に傾いているかで円偏光の回転方向がわかる。[5.(5)2.も参照]
さらに、
直線偏光を偏光面の光学軸に対する角度が45°以外で入射させた場合、出てくる光は主軸が光学軸に一致した楕円偏光になります。
また逆に、
楕円偏光を入射させるとき、楕円の長軸又は短軸が光学軸に一致するようにすれば直線偏光が取り出せます。
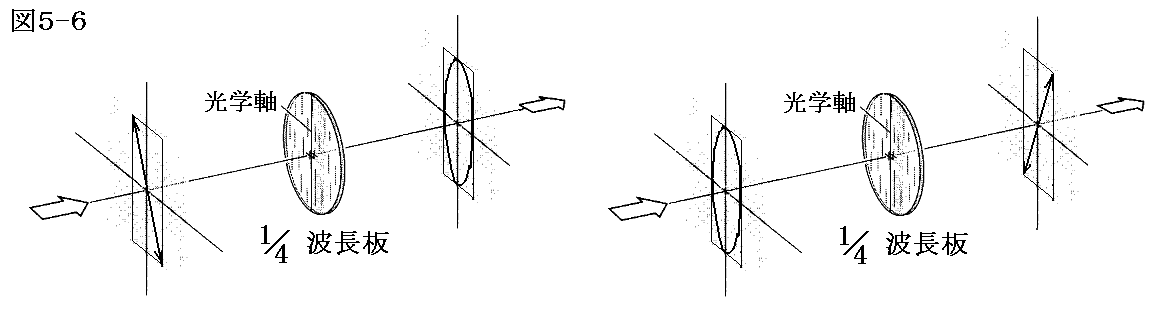
そのとき、
楕円の主軸が光学軸に一致しない場合は、楕円の形が変形した楕円偏光が出てくることになります。
これらのことは2.(1)節を復習されれば了解できます。
《1/4波長板で単色楕円偏光の[主軸の方向]と[振幅主値の比]を測定する》
入射光が単色の楕円偏光であることが解っている場合には、1/4波長板に入射してくる楕円偏光に対して遅相板の光学軸を回転させて直線偏光した出力光が取り出せるようにする。そして出力直線偏光の偏光面と遅相板の光学軸との傾きを調べれば、入射楕円偏光の主軸方向とその長さの比を知ることができる。(5.(4)1.も参照されたし)
この事は偏光板や遅相板を旨く組み合わせた実験をすれば、逆に2.(1)で展開した数学理論の正当性を確かめることができることを意味する。3.(5)で注意した様に、この様な実験の積み重ねによって、光の横波・波動説や偏光の実態が明らかになり、遅相板の働きが実証されてきたのです。
このとき
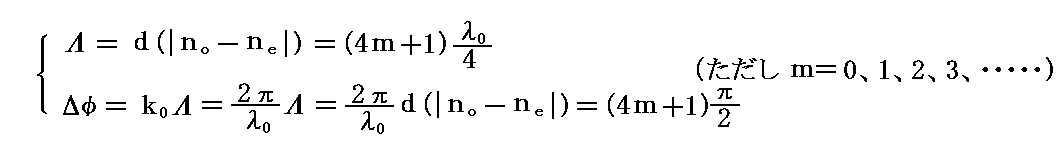
が成り立つ厚さであれば1/4波長板として作用します。
この場合も、入射光の波長(色)λ0が変化すれば1/4波長板となる厚さdは変化します。
《遅相板は“自然光”に対して顕著な効果を生じない》
光線を1/4波長板を通過させた後に、回転する検光子(偏光板)を通して見たとき、光の強度が変わらなければ元の光は“自然光”です。
遅相板に“自然光”を入射させた場合、その透過光を検光子(偏光板)で調べても何ら顕著な事は何も起こらないことに注意してください。なぜなら自然光の光学軸に平行な成分と垂直な成分はインコヒーレントで、両者の相対的位相差はランダムにかつ急激に変化している。そのため遅相子で付加的な一定位相差を与えても、位相差はやはりランダムであり、従って注目するような効果は何も生じない[3.(2)参照]。
ところで、“直線偏光”が光学軸に45°の角度で1/4波長板に入射する場合、正常光線と異常光線の成分の振幅は等しく位相は揃っているので、遅相板を出るまでに生じるπ/2の位相変化は直線偏光を円偏光に変換する働きをする。その場合は遅相板の透過光を回転する検光子(偏光板)に通して見ても光の強度は変化しない。
直線偏光の偏光面と遅相板の光学軸が45°以外の場合、透過する光は楕円偏光となるので、回転する偏光子(検光子)で見ると、透過光の強度は変動する。
この変動が無い様に(つまり完全な円偏光になるように)遅相板の光学軸の向きを調整すれば、逆に元の直線偏光の偏光方向を知ることができる。もちろん直線偏光の場合は単独の偏光子のみでその偏光方向を検知できるのですが、遅相子を挟むことによって、遅相子そのものの働きを検証できる。
このような実験事実は“自然光”と“直線偏光”の数学的モデルの正しさを実証していると言える。
5.偏光の解析
光は偏光の状態で次の7種類に分類できる。
(1)自然光
(2)楕円偏光
(3)円偏光
(4)直線偏光
(5)自然光+楕円偏光
(6)自然光+円偏光
(7)自然光+直線偏光
このとき、与えられた光が上記のどれかは、偏光子(ニコルプリズムやグラン・トムソンプリズムなど)と遅相子(1/4波長板を使う)を用いることで判別できる。以下では偏光子としてニコルプリズム、遅相子として1/4波長板を用いて論じる。
《光の偏光状態の解析》
まず、ニコルに光を通して観測し、ニコルを光の進行方向を軸として回転する。ニコルを回転したとき透過光の強度が変わる・変わらないで二つの場合が生じる。
(Ⅰ)光の強さがニコルを回転しても変わらない場合。
このとき、ニコルの前に1/4波長板を追加して置き、ニコルを回転させてみる。そのときニコルの回転と共に透過光の強度が変わる・変わらないで二つの場合が生じる。
(1)ニコルを回転しても光の強さが変わらない場合。・・・・・・・・・・・・・・・・・・・・・・・[自然光]
(2)ニコルの回転と共に光の強さが変わる場合。
ニコルの前に1/4波長板を追加した状態でニコルを回転させたとき、
光の強さがゼロになる角度が有る・無いで二つの場合が生じる。
(A)どんな角度にして透過光の強度はゼロにならない場合。・・・・・・・・[自然光+円偏光]
(B)ニコルをある角度にすると透過光の強度がゼロになる場合。・・・・・・・・[円偏光]
(Ⅱ)光の強さがニコルを回転と共に変わる場合
(1)ニコルを回転してある角度にしたとき透過光の強さが0になる場合。・・・・・[直線偏光]
(2)ニコルのどの様に回転しても透過光の強さが0になることはない場合。
このとき、ニコルの前に1/4波長板を追加して置き、それを少しずつ回転させながら、
透過光をニコルを通して見てみる。ニコルを回転させたとき変化する透過光の極大値が
最大になる方向で1/4波長板を固定する。その状態でニコルを回転させ、
透過光が0になる角度が有る・無いで二つの場合が生じる。
(A)ニコルの回転で透過光をゼロにできる回転角がある場合。・・・・・・・・・[楕円偏光]
(B)ニコルをどの様に回しても透過光をゼロにできない場合。
ここでニコルだけ回転したとき示した極大の方向と、上記の1/4波長板を挿入した後に
ニコルを回して光の極大を与えるニコルの方向が同じ・同じでないで二つの場合が生じる。
(イ)ニコルが、それだけで極大の光の強さを与えたのと同じ角度で
やはり極大の強さをを示す場合。・・・・・・・・・・・・・・・・・・・・・・・・・・[自然光+直線偏光]
(ロ)ニコルが上の位置と違った位置で光の強さが極大を示す場合。・・・[自然光+楕円偏光]
この方法のメカニズムはなかなか解りにくいのですが、“自然光”、“楕円偏光”、“円偏光”、“直線偏光”の数学的モデルが正しければ、このやりかたで判定できます。
6.遅相板の材質
- 方解石
方解石は代表的な一軸性結晶(三方晶系)の複屈折結晶ですが、あまり使われません。それは堅くてもろく、薄板状に削りだすことが難しいからです。また遅相板として使うにはnoとneの差が大きすぎて不便だからです。
- 水晶
水晶は一軸性結晶(三方晶系or六法晶系)です。複屈折の屈折率差が小さいためよく使われます。ただし自然の劈開面がなく、切って削って磨く必要があるため高価になります。
|no-ne|=|1.5443-1.5534|=0.0092 ですから、550nmの光に対する1/4波長板の最小の厚さは
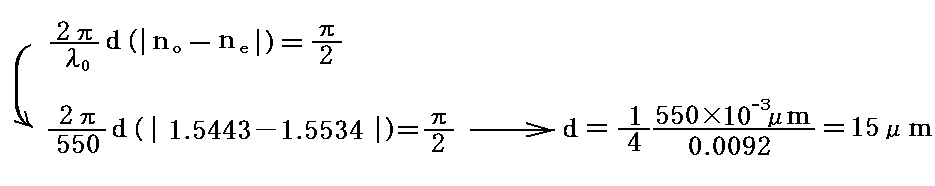
となります。このように一番薄いものをゼロ次数遅相子(zero-order retarder)と言います。これはかなり薄くて壊れやすく制作も難しいのですが、視野範囲は広くなります。
実際の波長板としては2πの整数倍を加えて所望の位相変化を生じるような厚さのものが使われます。その様なものを多重次数遅相子(multiple-order retarder)と言います。厚くなると、制作は容易になりますが、遅相子としての働きは劣ります。それは遅相量Δφが波長(色)、入射角、温度に極めて敏感になり、厚くなるほど波長による分散が強く、使用できる視野範囲も狭くなるためです。
- 雲母
雲母は二軸性結晶(単斜晶系)でフッ化金雲母、黒雲母、白雲母などがあるが、最も普通に産出するのは、うっすらと褐色がかかった白雲母[カリ雲母 KH2Al3(SiO4)3]です。これは強くて柔軟性に富んでおり、容易に大きな薄片に劈開できるのでもっとも良く使われる。
二つの光学軸は劈開面にほぼ正確に平行となる。そのため雲母の劈開面に垂直に直線偏光を入射させると電場の振動方向は二つの光学軸が存在する劈開面に平行となる。
一般に二軸性結晶は三つの屈折率で特徴づけられる[そのようにできるメカニズムの説明はかなり難しくなるので省略する]。雲母のそれらの屈折率は、ナトリウムのD線(λ0=589.3nm)に対してn1=1.5993、n2=1.5994、n3=1.5612です。
雲母を遅相板として用いるとき関係する二つの屈折率はn1=1.5993とn2=1.5994ですので、1/2波長板の最小厚は
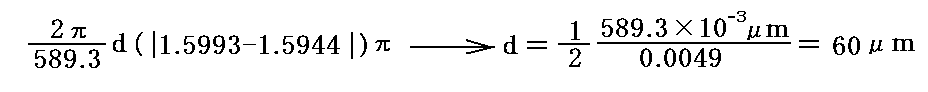
程度となります。同じく1/4波長板の最小厚は約30μmとなります。
- フッ化マグネシウム(MgF2)
波長405nmの光に対してno=1.3836、ne=1.3957 となる一軸性結晶(正方晶系)です。紫外線および3000~6000nmの赤外線領域の波長板に使われる。
- 硫化カドミウム(CdS)
ナトリウムのD線(λ0=589.3nm)に対してno=2.506、ne=2.529 となる一軸性結晶(六方晶系)です。6000~12000nmの赤外線領域の波長板に使われる。
- セロハンテープ
これはポリビニルアルコールの長い有機鎖状分子を引き延ばし整列させたものです。分子配列の異方性のために物質中の電子は分子方向とそれに垂直な方向では異なった束縛力を受けることになる。そのためこれは結晶ではないが複屈折性を持ち遅相子として利用できる。
セロハンテープを透明ガラス板の表面に貼るだけで遅相板となる。テープを何枚か重ねて貼って厚さを旨く調節できれば、1/2波長板や1/4波長板を構成できる可能性がある。[5.(6)1.参照]
(3)斜方体
1.フレネル斜方体
ここでは説明しないが「フレネルの公式」から、内部全反射は反射面に垂直な電場成分と平行な電場成分の間に相対的な位相差を生じる。例えばガラス(n=1.51)の中では、入射角51°20’で最大の相対的位相変化Δφ=45°56’を生じる。そのとき反射角が51°20’を挟んだ両側の54°37’あるいは48°37’ のとき相対的位相差はπ/4ラジアンとなる。そのため下図の様に例えば54°37’=54.6°で2回全反射させるとπ/2ラジアンの位相差が生じる。
そのため、次図のように直線偏光の偏光面が45°傾いた状態で入射させると円偏光を得ることができる。また逆に円偏光を入射させれば直線偏光を得ることができる。このような光学素子をフレネルの斜方体と言う。
さらに、斜方体の菱形角を変えたものを作ると全反射角を変えることができる。その角度を計算して調節すれば直線偏光を意図した長・短軸比の楕円偏光にすることができる。また逆に楕円偏光を直線偏光に変えることができる。
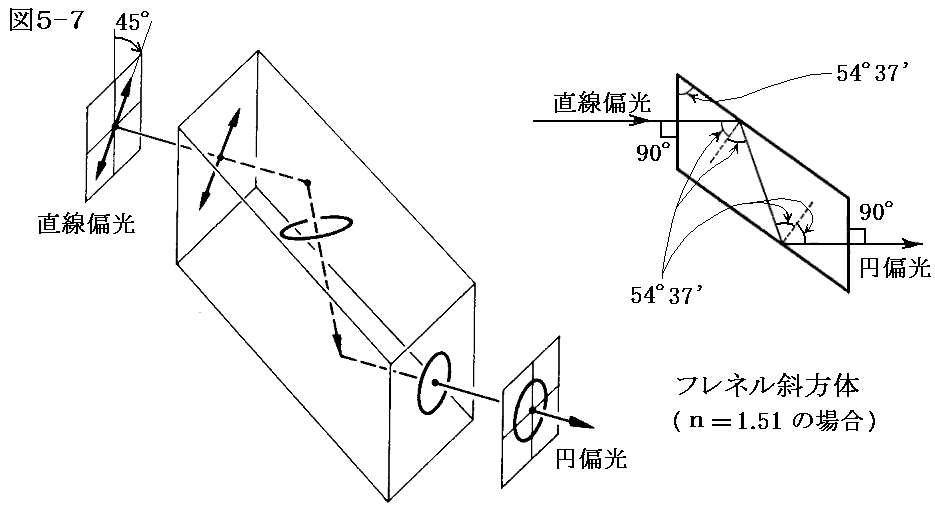
このとき、反射による遅相量Δφは波長による屈折率の変化に依存するだけで波長そのものにあらわに依存することはない。そのため遅相量Δφは波長に対して比較的ゆるやかに依存するだけで、かなり広い波長範囲(約2000nm)にわたって色依存の少ないπ/2遅相子となる。
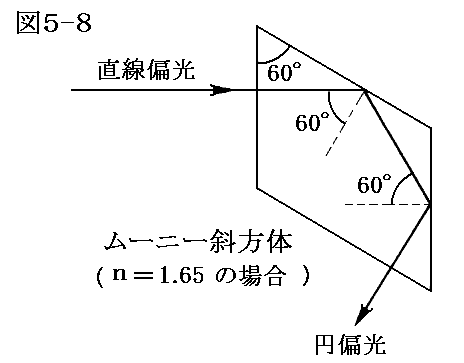
2.ムーニーの斜方体
下図も同様なメカニズムで直線偏光を円偏光に変換するもので、ムーニーの斜方体という。図は屈折率n=1.65のガラスを用いた場合を示している。
(4)補償板(可変遅相子)
遅相量Δφを任意に変えられる光学素子を補償板(可変遅相子)という。
1.バビネ補償板(Babinet compensator)
下図の様に光学軸が直交した2個のくさび形水晶(方解石を用いる場合もある)を用いる。それぞれの光学軸は線と点で図中に示してある。補償板は薄い(典型的な楔角は2.5°程度)ので光線の分離は無視できる。
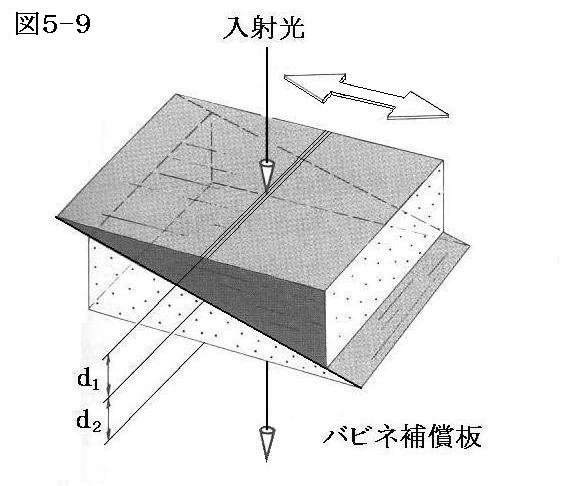
図の光線経路の位置におけるそれぞれの楔の厚さをd1とd2とするとそれぞれの楔型で生じる正常光線と異常光線の相対的位相差は 2πd1(|no-ne|)/λ0 と -2πd2(|no-ne|)/λ0 となる。上の楔中での正常光線と異常光線は下の楔ではそれぞれ異常光線と正常光線になる。符号を反転させているのはそのためで、トータルとしての遅相量は
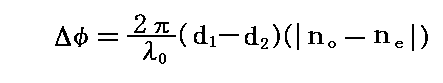
となる。遅相量Δφの符号は用いる結晶が正結晶か負結晶かで反転する。
遅相量は入射光の位置によって変わるが、両楔の厚さが変化しない補償板の幅方向に伸びる一直線上の細い領域では一定となる。そのためこの狭い領域に平行なスリットで入射光を絞って入射させ、マイクロメーターのネジでどちらかの楔を水平に動かせば遅相量を任意に調節できる遅相子となる。
直交している二枚の偏光子AとA’の間に、スリットで絞っていない状態のバビネ補償板Bを置く。バビネ補償板の光学軸は図のように両偏光子の中間角度45°に成るようにする。
検光子A’を通して“単色”の入射光を見ると、等間隔で平行な一連の暗い縞模様(下右図)が補償板の幅の方向に現れる。縞模様の左側の小さな図は出てくる光の偏光状態わ表している。これら暗い縞は、遅相量がΔφ=m×2π(m=1,2,3,・・・・)となり、補償板が全波長板として作用して部分に生じる。そこを通過する光は検光子A’の透過軸と垂直に偏光しているために検光子を通過できず暗くなるのである。
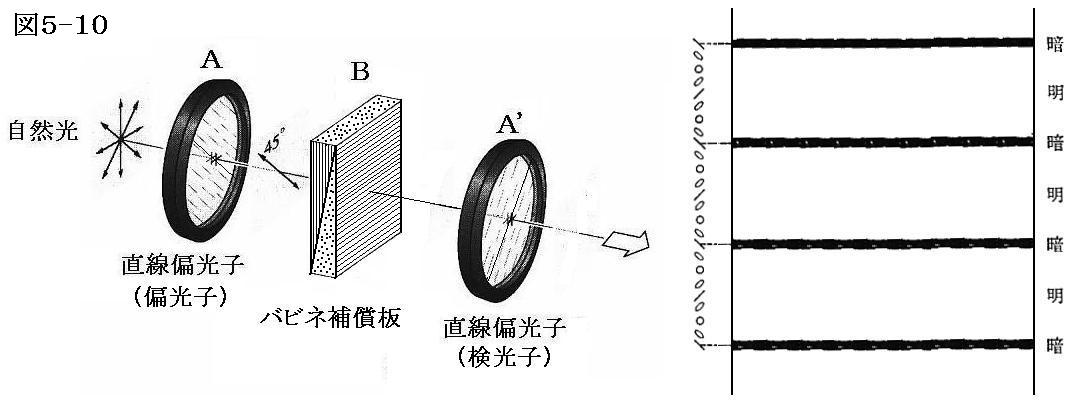
もし入射させる光線が“白色光”なら、d1=d2となる中央の部分のみ暗く(そこでは波長によらずΔφ=0)なる。そして、それ以外の縞は色づく。なぜならある波長でΔφ=m×2π(m=1,2,3,・・・・)となっても光の波長が変わると、その同じ位置でΔφ≠m×2π(m=1,2,3,・・・・)となるからである。
いずれにしても、このような配置にしたバビネ補償板を用いると以下に述べる事柄が測定できる。
《遅相量が未知の波長板の遅相量を測定する》
バビネ補償板の上に遅相量を測定したい波長板を載せると縞の位置がずれる。バビネ補償板のみ挿入した場合の縞の間隔と、バビネ補償板に未知波長板を載せて挿入したとき生じる縞のずれる量を比較すれば、未知遅相板の遅相量を測定できる。
例えば、縞の間隔の半分だけずれればπ/2ラジアンの遅相量、四分の一ずれればπ/4ラジアンの遅相量の波長板であると言えるわけです。
《単色楕円偏光の楕円の長軸・短軸の方向とその長さの比を測定する》
まず上図のA→B→A’の状態で、視野の中に見える黒い縞と縞の間の、ちょうど真ん中に位置する細いスリット状領域を確定する。その細いスリット領域がバビネ補償板で遅相量Δφが(4m+1)π/2ラジアンとなる領域です。視野の中の十字線がその位置に一致するように補償板全体の位置をマイクロメータのネジで調整しておく。
次に偏光子Aを取り去ってバビネ補償板Bと検光子A’のみにする。そして測定すべき単色楕円偏光をB→A’の方向へ通過させる。このときにも視野の中に黒い縞が並んでいるのが見えるが、バビネ補償板と検光子を互いに独立に回転させて黒い縞が最もハッキリ見えかつ、黒い縞の位置が上で調節した十字線の位置に一致するようにする。バビネ補償板の回転に伴って黒い縞の位置は移動するので、十字線の位置に合わせるのは常に可能です。このとき黒い縞が最も黒く成るように検光子の方向も回転させる。
このような状況が実現されたときには、黒い縞の部分は補償板を出た光が直線偏光に成っており、しかもその偏光面は検光子の透過軸に垂直であることを意味する。そのために透過光がゼロに成るのです。そのときバビネ補償板の光学軸と、検光子透過軸の関係は下図の様になっているはずです。
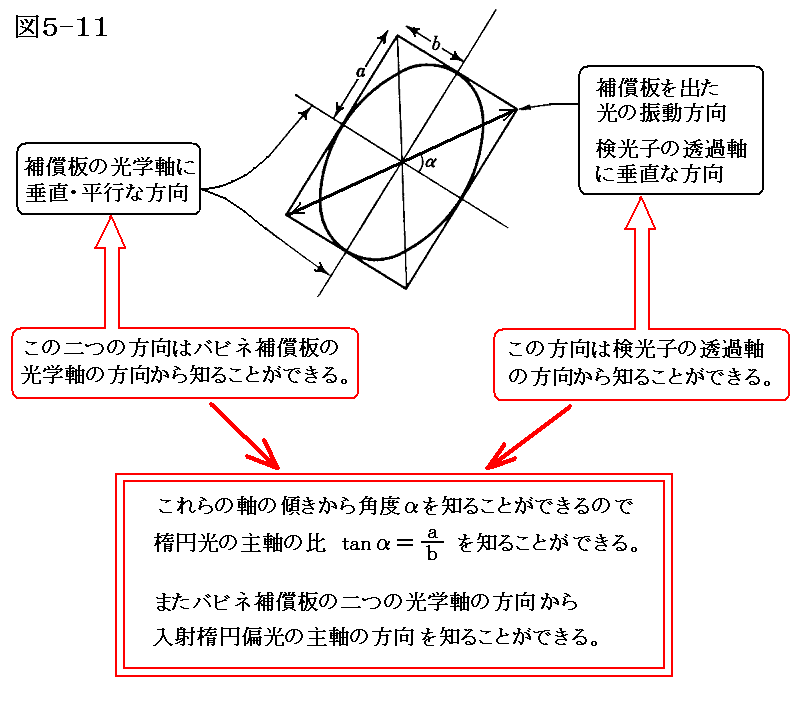
2.(1)の最後で説明したように、楕円偏光の主軸の方向では、その二つの方向に振動する電場成分の位相差がちょうどπ/2ラジアンになる。そのためにバビネ補償板の光学軸を楕円偏光の主軸の方向に一致させると十字線の位置を通過する楕円偏光は直線偏光になります。つまり、その位置の透過光は楕円偏光の二つの主軸成分に(4m+1)π/2の遅相量を生じる厚さ(d1+d2)のバビネ補償板の狭いスリット領域通過しており、補償板を出た光は完全に直線偏光している。そのため検光子透過軸を調整すれば、通過を完全に阻止できて暗い縞の領域となるわけです。
ここはなかなか解りにくいところですが2.(1)節を復習されると理解できます。
2.ソレイユ補償板(Soleil compensator)
バビネ補償板ではスリット状の狭い領域でしか望む遅相量の光線を取り出せない。この欠点を改良して全面で同一の遅相量の光線を取り出せるようにしたのがソレイユ補償板です。
一般に水晶(赤外線用にはMgF2やCdSが使われる)でつくられ、光学軸が図に示した向きに揃っている二つの楔と、これに直交する光学軸を持つ一つの直方体からできている。値d1は二つの楔の合計の厚さに相当し、二つの楔をマイクロメーターのネジでずらして調整する。そのとき入射面全体に渡ってこの値は一定となるので、広い範囲で入射する光線に対して同一の遅相量Δφを与えることができる。
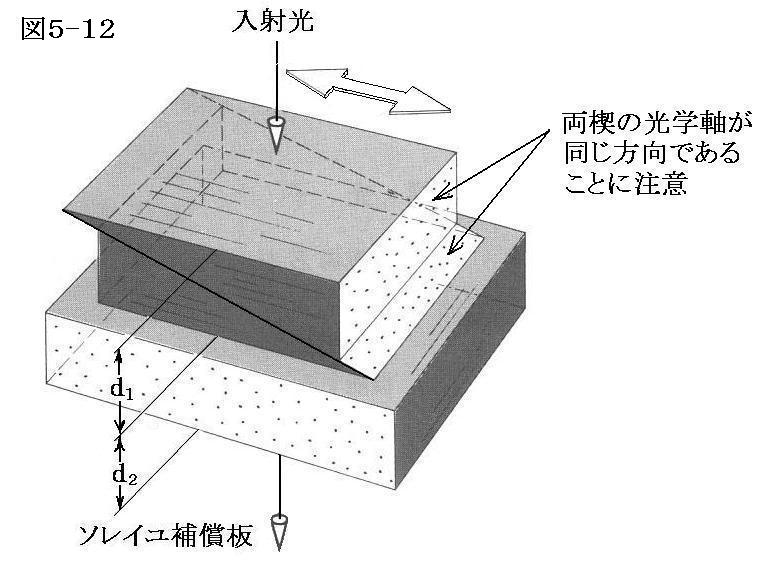
これを用いると広い視野で同一の遅相量の光線を得ることができる。
《遅相量が未知の波長板の遅相量を測定する》
図5-9に示す光学素子A→B→A’のBをバビネ補償板からソレイユ補償板に変更したものを用いても前節と同様に測定できる。
図5-9と同様な状況でソレイユ補償板の楔の一方(上側)をマイクロメータのネジで動かしていくと、視野全体が暗くなったり明るくなったりするので、遅相量の変化とマイクロメーターのネジの回転角を関係づける事ができる。未知波長板を挿入したとき生じる暗くなる位置のずれをネジの回転量で測定すればよいのです。
《単色楕円偏光の楕円の長軸・短軸の方向とその長さの比を測定する》
図5-9に示す光学素子A→B→A’のBをバビネ補償板からソレイユ補償板に変更したものを用いても、楕円偏光の長軸・短軸の方向とその長さの比を測定できる。
図5-9と同様な状況でソレイユ補償板の楔の一方(上側)をマイクロメータのネジで動かしていくと、視野全体が暗くなったり明るくなったりする。二つの暗くなるネジ位置の中間のネジ位置にすると、π/2ラジアンの遅相量が実現できていることになる。ソレイユ補償板の楔をそのネジ位置で固定しておく。
次に偏光子Aを取り除いて、未知の楕円変更をB→A’と入射させる。そしてソレイユ補償板全体を光軸のまわりに回転させて透過光が最も暗くなるように調整する。このとき、その暗さがさらに暗くなるように検光子の方向も回転調整する。両方の回転角を調整して完全に透過光がゼロにできたならば、それは図5-10に示したのと同じ状態が実現されたことになる。
以下、前節と同じ手順で計算すればよい。
(5)円偏光子
1.(直線偏光子+π/2遅相子)=円偏光子
5.(2)4.で述べたように1/4波長板(あるいはフレネル斜方体)の主要軸に対して45°傾いた偏光面を持って入射する直線偏光は円偏光となって出てくる。従って1/4波長板(フレネル斜方体)の光学軸に対して45°傾いた向きに配置した直線偏光子と1/4波長板(π/2遅相子)を組み合わせれば、“自然光”から円偏光を得ることができる。
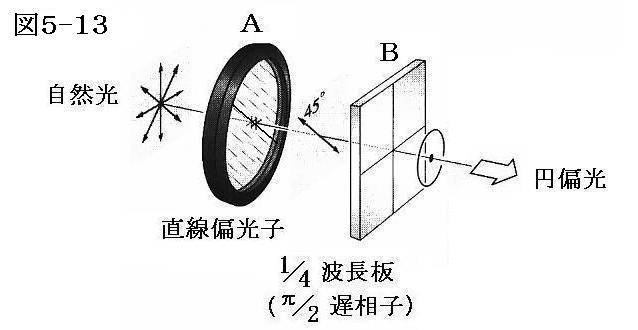
そのとき、出てくる円偏光の回転方向は、偏光子の透過軸を遅相子の光学軸に対して+45°で傾むけるか、-45°で傾けるかで逆転する。
もし直線偏光子の偏光面の軸に対して、光学軸が45°傾傾くようした1/4波長板(遅相子)を、直線偏光子の前後に貼り合わせておけば“自然光”を入射させることで両方の回転方向の円偏光を得ることができる。
なぜなら5.(2)4.の最後で述べたように直線偏光子の前(入射側)にある遅相子は“自然光”にたいしては何の効果も及ぼさないので、直線偏光子と通過側の遅相子のみが働くことになるからです。そのとき入射方向を逆にすると、直線偏光子を通過後に通り抜ける遅相子の光学軸の直線偏光子の偏光軸に対する傾きの符号が逆転するから、左右の回転方向を逆にできるのです。
2.円偏光の回転方向の検出
円偏光子は、円偏光であることがすでに解っている波動の回転方向を決定する検光子として使える。
今下図のA→Bで一つの円偏光子を形成するとする。A’→B’も全く同じように配置された円偏光子とする。この二つの円偏光子を次図のように向かい合わせに設置する。ここでは両方の円偏光子が同じ(つまり直線偏光子にたいする遅相子の光学軸の回転方向が同じ)である限り、これらの円偏光子が右回りの円偏光を生じるのか、左まりの円偏光を生じるのかは重要ではない。
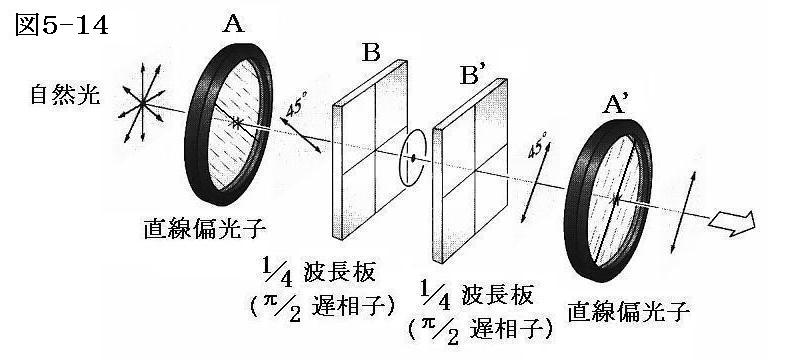
上記の素子A→B→B’→A’のA側から“自然光”を入射させる。そうするとAを通過した直線偏光はBでπ/2ラジアンの遅相量が生じて円偏光になる。そしてB’を通過するとき、さらにπ/2ラジアンの遅相量が生じる。つまりBとB’の両方でπラジアンの遅相量が生じることになる。これはBとB’あわせて5.(2)3.で述べた1/2波長板を構成することになる。そこで述べたようにBB’を通過した直線偏光は偏光面を2θだけ回転させた直線偏光になる。今の場合2θ=90°となるので、B’軸を出た直線偏光の波動はA’の透過軸に平行となりA’を通過する。
つまりA→BとA’→B’の円偏光子が両方とも“自然光”から同じ回転方向の円偏光を生じるものであれば、左右どちらの回転方向の円偏光を生じるものであっても、A→B→B’→A’と配置した光学素子は“自然光”を直線偏光にして通過させる。
《B’→A’(又はB→A)光学素子を用いると[円偏光の回転方向]が判定できる》
図5-14の中からA→B円偏光子を取り除いて、B’→A’の部分だけにする。そしてB’からA’の方向に向かって回転方向が未知の円偏光を通過させてみる。入射円偏光の回転方向が、A→B(A’→B’)の円偏光子が生じる円偏光の回転方向と同じなら通過できるが、逆の場合B’→A’の素子を通過できない。なぜなら入射円偏光の回転方向が逆ならB’を通過してできる直線偏光の偏光面はA’の透過軸に垂直になるからである。だからB’→A’の素子を通過できるか、できないかで、その回転方向が円偏光子A→B(あるいはA’→B’)の生じる円偏光の回転方向と同じか反対かが判定できることになる。
(6)多色光の偏光
1.多色光偏光の例
次の図のようにセロハンテープをポラロイド偏光板に、縦、横、斜めに何枚も貼り付けます。セロハンテープを貼る角度はランダムでかまいません。また何枚も重なった部分ができてもかまいません。
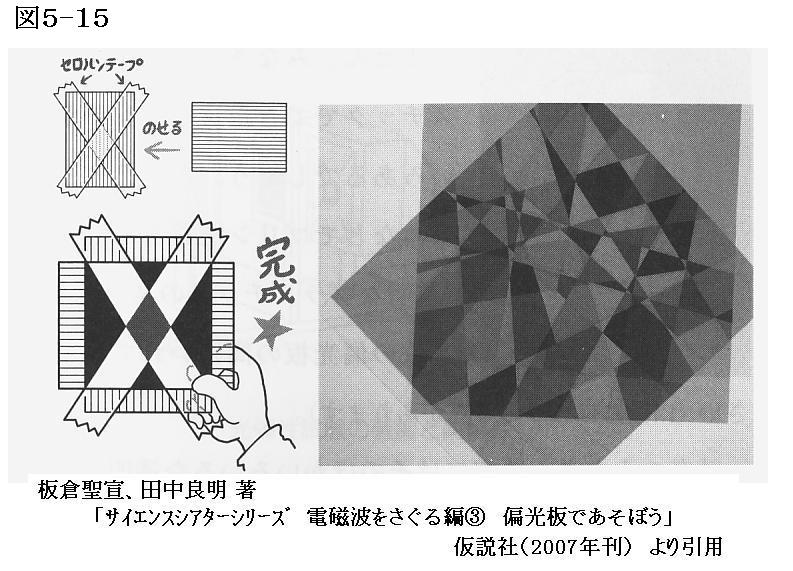
この上にもう一枚の偏光板を載せて、白色光を見てみます。そうすると下左の写真のように、貼り付けセロテープの重なり具合の違いに応じて様々な色に見えます。さらに、上に置いた偏光板を回転させると色合いが次々と変わっていきます。下右の写真はプリンなどに付属している透明なプラスチックスプーンを二枚の偏光板の間に入れて下から白色光を当てて見た物です。

さらに、透過軸が直角になるように重ねた二枚の偏光板の間にプラスチック板などを入れて、その板に力を入れて変形させます[下左図]。その様子を白色光を通して見ると、きれいな色の縞模様が見えることがあります。プラスチック板に加わる力の大きさに応じて色の模様が変わります[下右図]。これは本来等方的な透明物質が応力下にあるとき複屈折を生じるために、偏光を送ると応力に応じて偏光面が回転するために生じる現象です。縞目の数から回転角を測定して応力が測定できることになる。
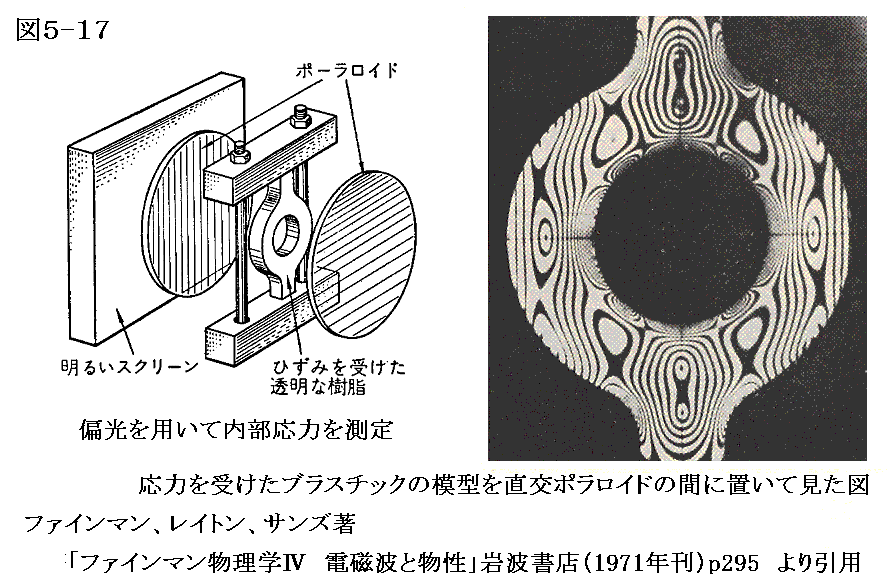
ちなみに、等方的な透明体を一方向に圧縮すると、複屈折性に成ることを最初に発見したのはブルースターです[参考文献2.p127]。このような現象は様々な物質で容易に観察されます。たとえば、多層の雲母板、氷の薄片、引っ張ったプラスチックの袋、石英(普通の白い石である花崗岩区)を細かくつぶした粒子、等々・・・・です。これらの現象もやはり、それらの物質の中を通過する光線が波長に依存する遅相量変化を受けで生じる。次節でそのメカニズムを説明する。
2.偏光と色
下図のように偏光子A→遅相子B→検光子A’を配置した光学素子を考える。
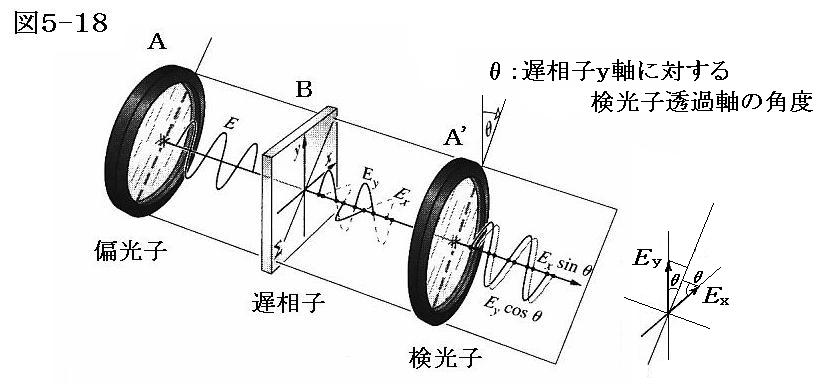
このとき、入射する直線偏光のx成分、y成分に対して、遅相子Bが生み出す遅相量Δφを考察する。
Δφ=(4m)π/2=0,2π,4π,6π,・・・・・・の場合、遅相子は全波長板として働くので、遅相子を透過しても偏光面は変化せず検光子(偏光子)A’をそのまま通過する。
Δφ=(4m+1)π/2=π,3π,5π,7π,・・・・・・の場合、遅相子は1/2波長板として働く。そのため透過光の偏光面は90°回転して検光子(偏光子)A’の透過軸に直交するため検光子を通過できなくなる。
5.(2)1.で説明したように遅相量Δφは
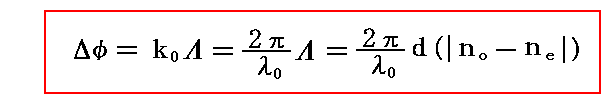
で表される。この中で厳密に言えばnoとneも波長に依存してわずかに変化するのだが、その変化量は少ないので可視光の範囲では一定として良いであろう。そのため遅相量Δφは主に分母の入射光の波長λ0に依存することになる。
例えば、青色(λ0=435nm)の光に対して全波長板として働く遅相子(遅相量Δφ=4πと仮定する)は
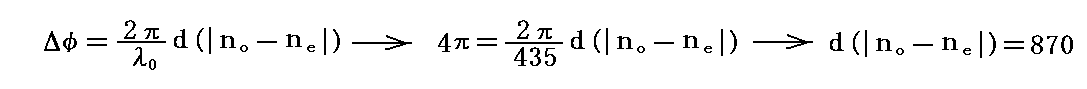
となる。
その同じ遅相子に対して、黄色(λ0=580nm)の光に対する遅相量は
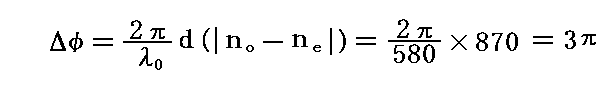
となる。故に、遅相子を出てくる光は直線偏光でかつ検光子の透過軸に垂直な偏光面を持つことになる。つまり黄色い光は検光子を通過できないのである。この遅相子を通過する435nm以外の波長の光は、一般に楕円偏光となり検光子を通過することはできるが、通過光の強度は減少する。
このとき検光子の透過軸を90°回転させると青色の光を遮り、黄色い光を通過させるようになる。別稿「光と絵の具の三原色(色とは何か)」2.で説明したように青と黄色は互いに補色の関係にあるが、検光子を90°回転させるとほぼ補色の関係にある二色を交互に透過させたり吸収したりする[もっと厳密な数学的考察は文献1.2.6.等を参照]。
他の例として、赤色(λ0=650nm)の光に対して全波長板として働く遅相子(遅相量Δφ=4πと仮定する)は
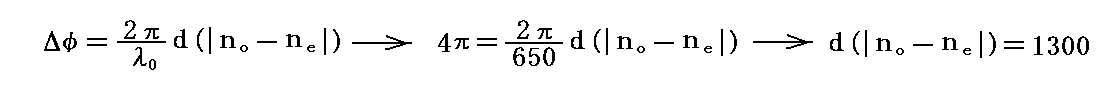
となる。
その同じ遅相子に入射する青緑色(λ0=520nm)の光に対する遅相量は
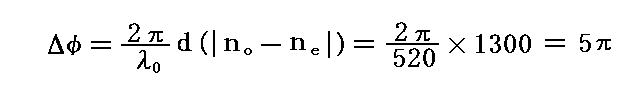
となる。つまり青緑色い光は検光子を通過できないのである。赤色と青緑色もほぼ補色の関係に近い(正確には赤の補色はシアン)ので、検光子を90°交互に回転させると上記と同じような事が起こる。
《干渉パターンによる偏光の数学的モデルの検証》
5.(6)1.の写真はこのようなメカニズムで色付いたものです。ここではやりませんが、もっと様々な状況で色の干渉パターンが生じます。今まで述べてきた偏光の数学モデルを使った計算でそれらの干渉パターンが導き出せれば、逆にモデルの正しさが実証されることになる。
実際そのことは成り立っています。
6.光の強度と偏光
光の強度(つまりある場所の単位面積を単位時間に通過するエネルギー量)は、電場ベクトルが各位置、各瞬間にどの方向を向いていようと、ある一点を通過する電磁波の電場ベクトル大きさを二乗したものを時間的に積算すればよい。
また光のエネルギー密度はある単位体積中に含まれる電場ベクトルの大きさを二乗したものを空間的に単位体積について積算すればよい。
(1)一定の方向と振動数と偏光を持つ光の強度
電磁的な輻射線に満たされている真空中では、一定時刻のある場所にある光の強度は方向・振動数(色)・偏光によって識別される。
まず、方向に注目することにして、点Oから極座標の角θ(0~π)とφ(0~2π)で決定された方向に長さrの小さな線分を引くことを考える。
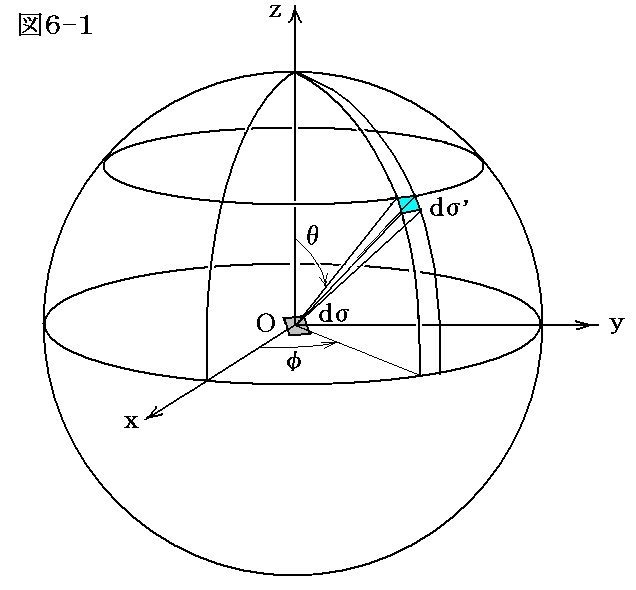
今基点Oと線分の端の点とにそれぞれ、rに垂直に置かれた面積要素dσとdσ’を考えるならば、時間dtの間にOにおかれた面dσを通して面dσ’に送られる輻射(光)の全エネルギー量は
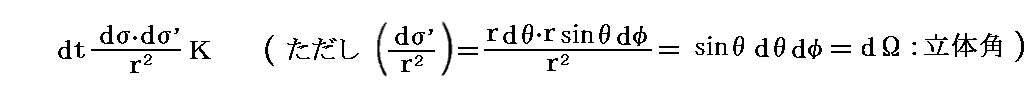
となる。ここでKは(θ、φ)方向のエネルギー輻射の強さで、位置・時間・θ・φの有限な正の関数である。ここでθ→(π-θ)、φ→(φ+π)とすると、Kに対して反対の方向の、前とは一般にまったく異なった量のエネルギー輻射の強度が得られる。
さらに輻射Kは、一連の単色的な同一方向に進む輻射線に分解できるのであるが、さらにその偏光成分に分解することができる。任意の偏光状態にあり、一方向に進む単色輻射線は、その偏光面が互いに垂直だが、その他の点は任意であるような二つの直線偏光に分解できる。両成分の強度の和が全輻射線の強度である。
そのとき強度は4.(1)で述べたように電場成分の二乗に平均値に関係するのだから、分解する方向が直交しているので、二乗成分の和は偏光面をどの方向にとるかには関係しない。そのため、今後はその二つの成分の方向を2.(1)の最後に説明した楕円偏光の主軸(ξ,η)の方向に取る。その方向の強度(振幅の二乗の平均値)をそれぞれRとR’とし、その輻射線の“強度の主値”と言うことにする。またそれに対応した偏光面を輻射線の“主偏光面”と言うことにする。RとR’はどちらも楕円の主軸方向の値であるから、一つの成分に与えうる強度の最大値と最小値を表すと言っても良い。
このとき輻射線の“強度の主値”も“主偏光面”も一般には時間とともに変化するが、ある場所・ある瞬間の輻射線の強度はこの和(R+R’)となる。
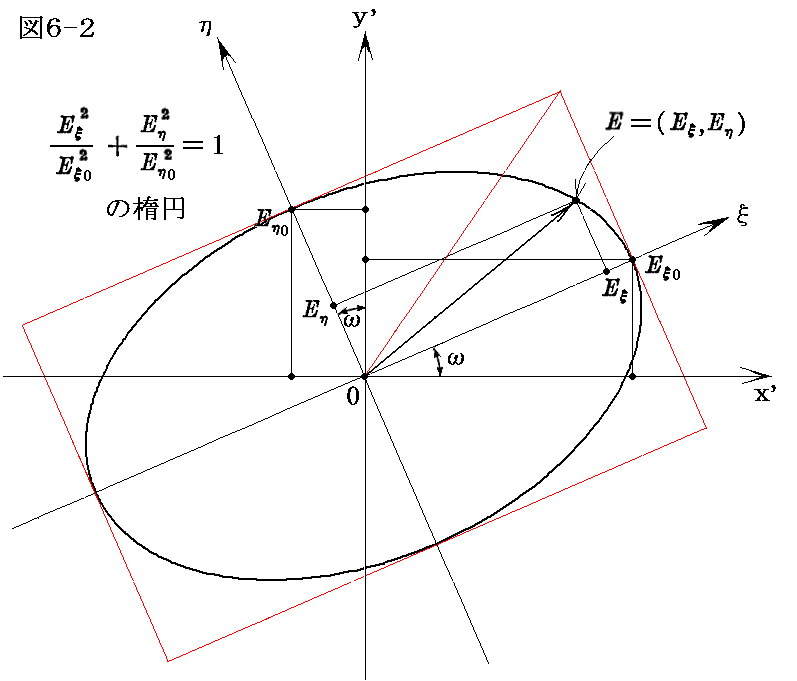
このとき主軸に対してωだけ傾いたx’軸、y’軸方向成分に分解したとき、それぞれの方向の光の強度は
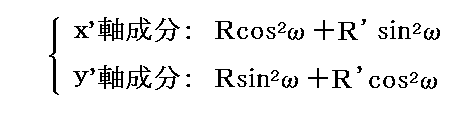
となる。
実際この両式の和は、全輻射線の強度R+R’を与え、ωには関係しなくなる。従って一般に輻射強度Kは
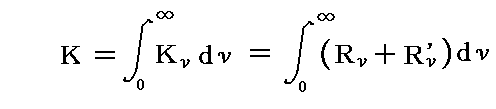
のように於いて良いであろう。ここで正の両RνとRν’は、ともに振動数νの輻射の強度の主値で、νの他に、位置、時間、θ、φに依存する。偏光していない輻射線に対してはRν=Rν’となるので
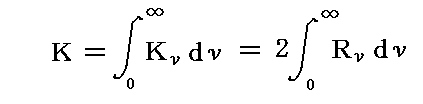
となる。
(2)輻射のエネルギーとエネルギー密度
1.一方向へ伝播する輻射のエネルギー密度
この場合は別稿「線型振動子(電気双極子)による電磁波の放出」2.(3)ですでに説明した。
そこで導いたように

だから
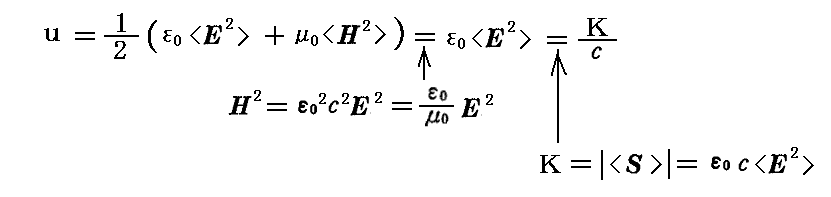
となる。
2.真空空間が、等方的な輻射で満たされている場合
等方的な輻射で満たされた真空中の一点Oの位置におけるエネルギー密度uを輻射の強度Kで表す。
これは別稿「キルヒホッフの法則(熱的放射平衡における)」3.(2)で説明したように、点Oにある微小な体積素片dτを中心とした半径rの球面を考えて、この球面を中心の体積素片dτに向かって通り抜けるすべての輻射線の強度の和を求めればよい。

このとき体積要素dτ中の円筒状体積素片s・dσ’に含まれるエネルギーは、輻射エネルギーの通過速度が光速cであることを考慮すると、上式のdtをdt=s/cとすれば良いことが解る。ここで立体角 dΩ=dσ’/r2 だから
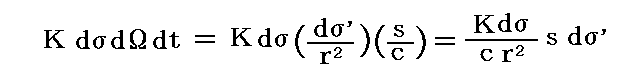
体積要素dτ全体については円筒状体積素片s・dσ’を加え合わせればよいので
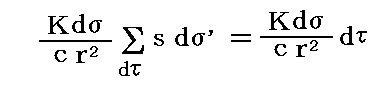
となる。
これはあくまで球面上のdσからの寄与であるので、球面全体からの寄与を足し合わせる必要がある。そのため中心点Oから見た面積要素dσの立体角をdΩ’として、これを全球面にわたって加え合わせればよい。そのとき上式のdσ/r2はまさしく、その立体角dΩ’であるから
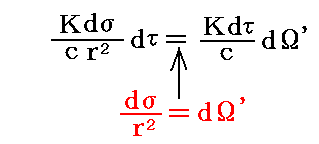
である。
一般的にKは方向(θ、φ)に依存するが、ここでは一様な輻射を考えているのでdΩ’に対する積分の外に出せて
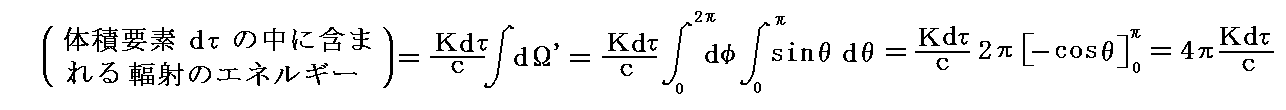
となる。
上記の値を体積dτで割れば、等方的輻射で満たされた単位体積中のエネルギー密度として
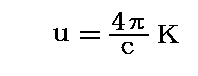
が得られる。ただし、Kはある一点をdΩの立体角方向に単位面積を通り抜ける輻射の強度(輝度)です。
次に、振動数ν~ν+dνの間のエネルギー密度は
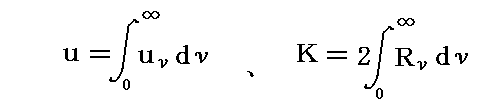
である事を考慮すると
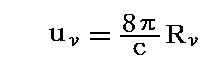
となる。これは偏光していない単色(ν~ν+dν)の輻射の単位体積中のエネルギー密度です。
7.参考文献
光学は近代物理学を理解する準備として必須の領域で、かっての物理学全集では必ずその中に重要な一分野として収録されていました。実際、ローレンツの電子論、特殊相対性理論、量子論の黎明期における多くの事柄が、光が中心的な役割を占める実験装置で観察・研究されてきました。
しかし、今日の大学の教育課程では光学について体系的に習うことはありません。私自身も教科科目として習った覚えはなく、取り立てて深く考えたこともありませんでした。そのため高校物理の授業で生徒に教えていたとき、何か今ひとつ自分自身で納得できていないし、理解できていないと感じる分野でした。偏光についても、このページを作るには作ったのですが、本当のところは良く解りません。
でも、光はこの世界に満ちあふれています。まさに世のすべての現象は光の中に存在し、我々は光を通してしか物事を認識できません。“光についてもっと学ぶ必要がある”と、日々思いを新たにしています。
以下、このページを作るに当たって参考にした本を挙げておきます。
- マックス・ボルン、エミル・ウォルフ 著 「光学の原理 Ⅰ、Ⅲ」東海大学出版会(1980年刊)
- E.T.ホイッテーカー「エーテルと電気の歴史(上)」講談社(1976年刊)第4章
- アーノルド・ゾンマーフェルト著「理論物理学講座Ⅳ 光学」講談社(1969年刊)
この本の第Ⅱ章§16の最後と、第Ⅵ章§49の最後に光の二重性について興味深い概説が有りますので引用しておきます。
- ユージン・ヘクト 著 「ヘクト光学 Ⅱ-波動光学-」丸善株式会社(2003年刊)
- 中崎昌雄 著 「旋光性理論入門」培風館(1973年刊)
- ファインマン、、レイトン、サンズ 著 「ファインマン物理学Ⅱ 光、熱、波動」岩波書店(1968年刊)
- 吉原邦夫 著 「物理光学」共立出版社(1974年刊)