このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
慣性力とは文字通り、質量が慣性をもつために現れる見かけの力のことです。慣性とは「止まっているものは止まりつづけ、等速度で動いているものは等速度で動き続けようとする性質」のことです。
慣性力は物理Ⅱで出ますが、高校生にとってわかりにくいものの一つです。しかし、以下で述べる例を吟味すれば簡単に理解できる。
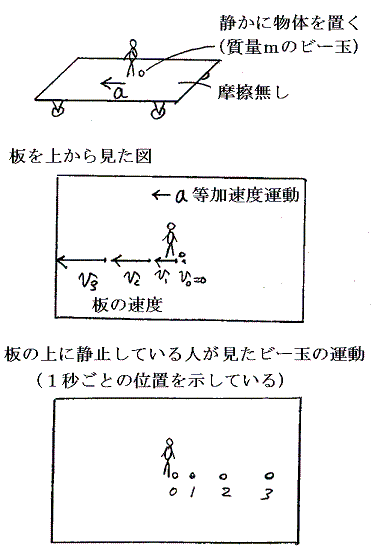
今加速度aで一方向に等加速度運動をしている板の上に乗っている人が、足下にそっと置いたビー玉を観察する場合を考える。ビー玉はその慣性のために板の上に置かれた瞬間の板の速度で等速度運動をしようとする。(慣性の法則)

質量mのビー玉の見かけの加速度は観測者の加速度ベクトルと反対の方向を向いていて、大きさは等しい。故に加速度aで等加速度運動をする平板に乗っている観測者がビー玉を見ると、ビー玉はあたかも-maの力が働いているように見える。これを慣性力という。
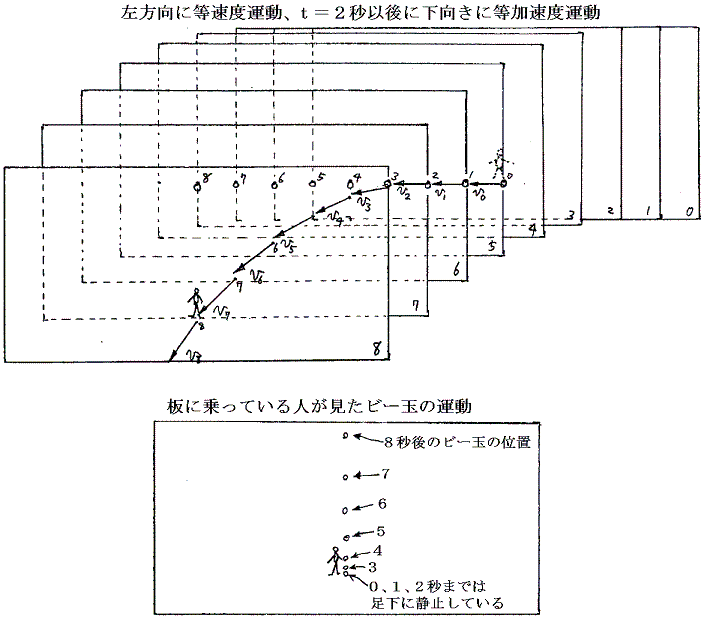
質量mのビー玉の見かけの加速度は、板が等速度運動をしている時にはあらわれず、板が加速度運動を始めると同時に現れる。だからビー玉には板が加速度運動を始めると同時に-maの力が働き始めたように見える。これはビー玉が等速度運動を続けようとする慣性のために現れる力でこれを慣性力と呼ぶ。
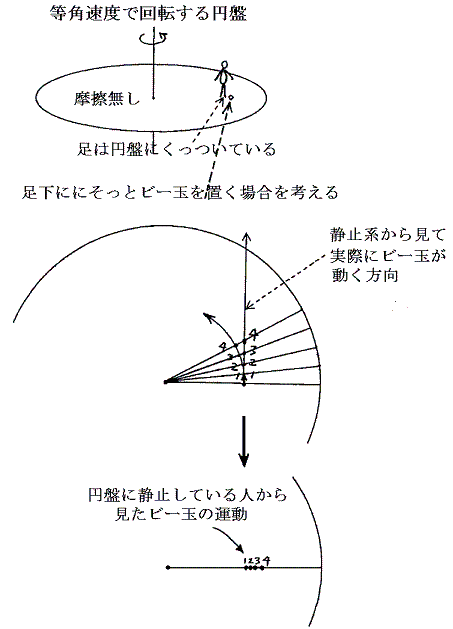
前項と同じ様な考察により、回転運動をする円盤の上に乗っている人がビー玉を見ると、ビー玉は円盤の外側に向かって加速度運動をしているように見える。その加速度を生じる見かけの力を遠心力(慣性力の一種)という。
加速度の大きさを下図の三角形に着目して求めてみる。これはホイヘンスが彼の著書「遠心力について」で展開しているものである。

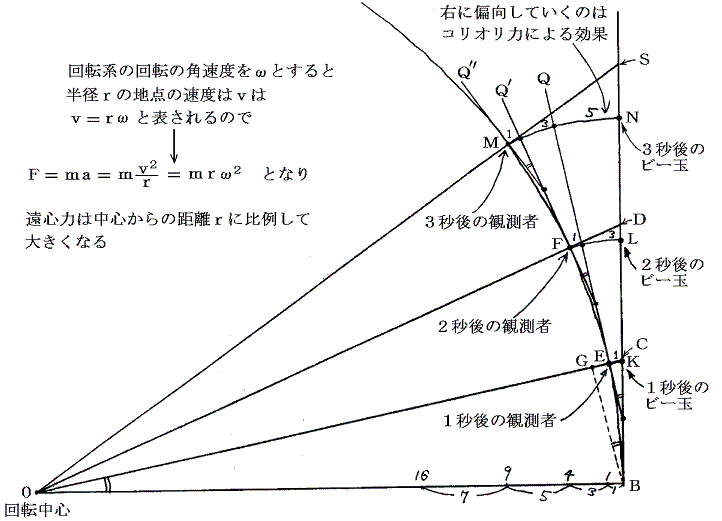
遠心力は別稿「潮汐力について」で、その説明に利用される。
この場合は観測系の加速度の大きさはビー玉の存在する場所とともに変化している(観測者の立つ位置が円盤の周辺部にいくと大きくなる。観測者はビー玉のすぐ近くで見ると考える。)のだが、その方向は回転系の円周方向に向いていて常に一定だから慣性力の大きさを求めるのは比較的簡単である。
遠心力は観測者の回転運動によって生じる様に見えるが、回転運動よりも観測者の回転中心へ向かっての並進加速度運動によって現れる慣性力で前記の例2と同じである。そのとき慣性力を表すmv2/rやmrω2のv2/rやrω2はビー玉の存在する位置の観測系座標面の慣性系に対する加速度の大きさを表しているにすぎない。
観測者の回転運動によって現れる慣性力が次ぎに述べるコリオリ力である。
今角速度ωで図のように回転している円盤の上に乗っている人が、ビー玉を円盤の縁に向かって速度v0で転がしたとする。そのとき人から見るとビー玉は進行方向に対して右向きに曲がっていく。
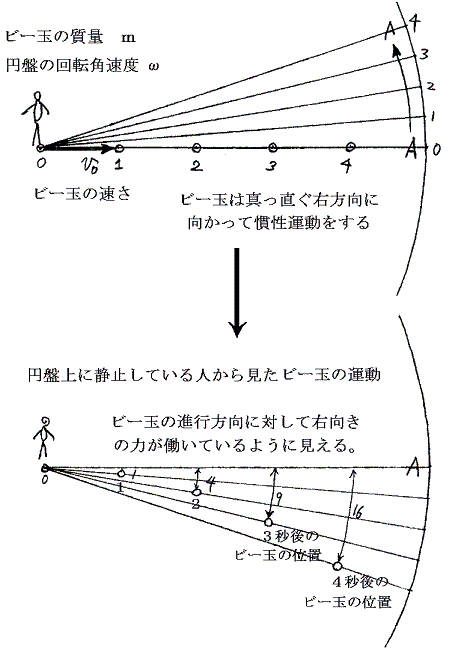
あたかも、ビー玉は進行方向に対して右向きの力を受けている様に見える。この見かけの力をコリオリ力(慣性力の一種)という。詳しい解析をすると、その力の大きさはF=2mωv0となる。(別項「コリオリ力とは」参照)
この例で現れる慣性力は、ビー玉の位置(観測者は当然ビー玉の位置でビー玉を観測する)の変化に伴って、その大きさも方向も変化していく。しかもそれはビー玉の速度ベクトルの方向と大きさにも関係する。しかしよく考えると解るように慣性力の大きさを表す2mωV0の中の2ωV0はビー玉の存在する位置の観測系座標面の慣性系に対する加速度の大きさを表しているにすぎない。観測者が立つ場所で自らが自転する回転運動に関係しているが、慣性力の一種であることに間違いない。以下でその当たりを説明する。
まず回転円盤とともに運動する人が円盤上の任意の点ABCに立っていて、そっと足下にビー玉を置いたとする。そのときビー玉は慣性系から見るとそれぞ初速度VA、VB、VCを持って投げ出されたのと同じだから、それぞれ青い矢印の方向へ移動していく。だからそれぞれのビー玉に取っては、ビー玉の近くの円盤面はそれぞれビー玉がおかれたA、B、Cを中心にして角速度ωで回転しているのと同じように感じる。だからそれぞれのビー玉が置かれた点を回転中心と見なして観測系の加速度を考えればよいのである。
次に、例えばA点において円盤上に静止している人が速度V0でビー玉を円周の方向へ投げ出しだ場合を考える。そのとき別項「コリオリ力とは」で説明したようにビー玉は下図の黒丸の様に移動していく。
このとき、ビー玉にとってビー玉の周りの観測系座標は、あたかも最初ビー玉を打ち出した位置を中心として角速度ωで回転している様に見える。しかも各時刻のビー玉から見ると、その観測系の座標(空色の短冊の部分)はビー玉の移動するV0の方向に対して直角左向きに加速度2ωV0(導出は別稿「コリオリ力とは」参照)で運動している。だから慣性力の大きさはたしかに[ビー玉の質量]×[ビー玉の位置の観測系平面の慣性系に対する加速度の大きさ]となっている。つまり1.や2.で説明した事情と全く同じである。観測系座標面の加速度を便宜的に半径rや回転の角速度ωやビー玉の速度V0を用いて表しているにすぎない。以上はたまたま半径方向の運動についての説明だが、任意の方向の運動についても全く同様になるのは別稿「コリオリ力とは」で説明したとおりである。
世の中に存在する様々な力の多くは観測者が加速度運動をしていても、それに影響されない。たとえば重力やバネによる張力等。そのとき加速度運動をしている観測者が物体の運動を調べると、それらの力と質量、加速度の関係は運動方程式F=maを満たしていない。
一般に加速度運動している系においては、運動方程式が成り立たないように見える。そのとき加速度aで運動する人から見ても、質量mに対する運動方程式が成り立つようにするために加えるべき力を慣性力という。慣性力という名称が付いているのは前記の様々な例で見たように、物体の慣性に基づいて現れる見かけの力だからだ。加えるべき慣性力は観測系の加速度をaとすると-maとすればよい。そのあたりを次の簡単な例で示す。
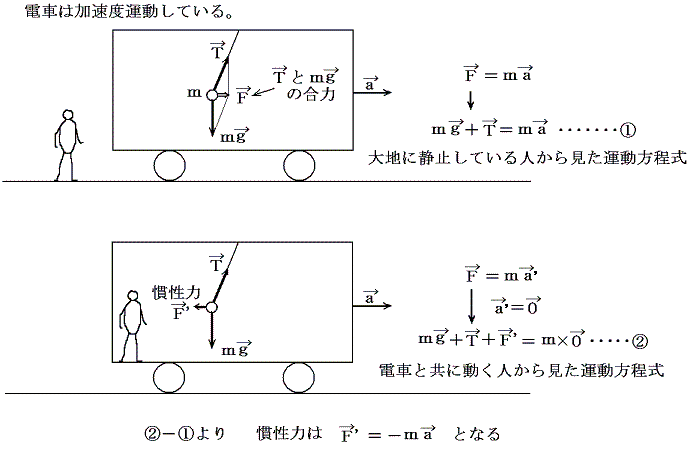
慣性力は単なる見かけの力なのに、なぜそのような力を導入するのだろうか。それは観測者や実験室系がどのような加速度運動をしているか解っている場合(もちろん解っていないと慣性力を定めようがない)には、静止系で運動方程式をたてて考えるよりも、加速度系で慣性力を導入して運動方程式を立てて解く方が劇的に簡単になる場合があるからだ。次の例はその最たるものだ。
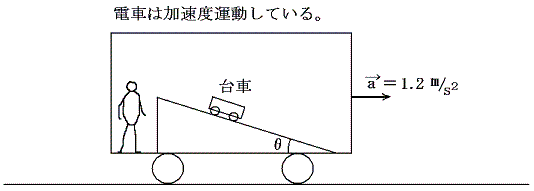
<問> 下図のように、斜面を床から角度θだけ傾けて固定し、その上に台車をのせる。電車を加速度a=1.2m/s2で走らせる。台車が電車に対して静止するためには、θを何度にすればよいか。またθ=30°にしたとき、車内の人から見た台車の加速度a’は何m/s2か。
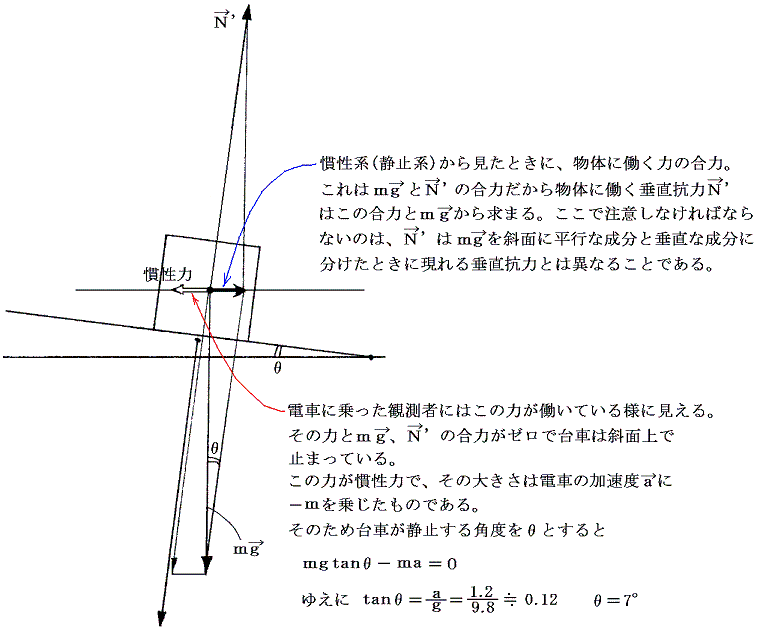
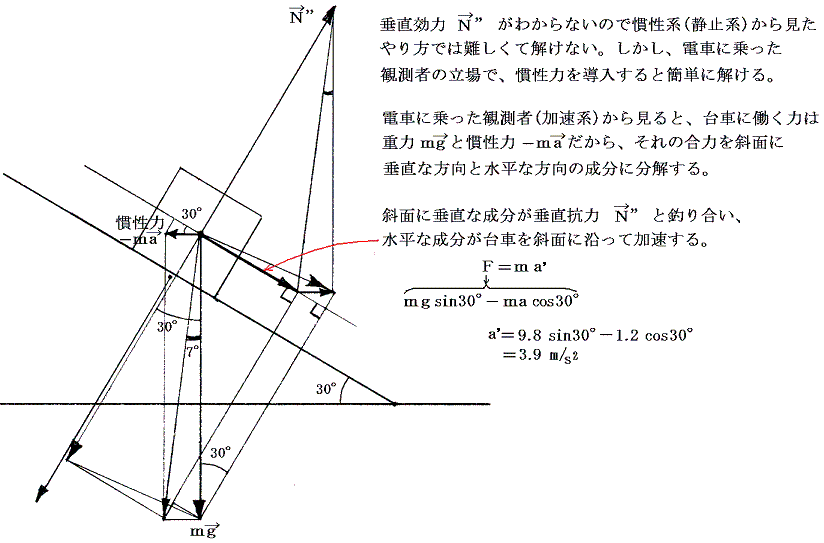
地球表面上での力学現象(落下運動やフーコー振り子)、気象学における大気大循環、海洋学における海洋大循環などでは慣性力の一種であるコリオリ力が本質的な役割を担う。いずれの場合も回転する地球表面上に住んでいる我々から見た物体、大気、海水の運動を解析したいのだから、慣性力を導入すれば運動の解析が劇的に簡単になる。
上記の様な問題の多くは、観測者のいる非慣性系(加速度運動をしている系)で物体がどのように動くかが解ればよく、慣性系(あるいは静止系)での運動を問題にしていない場合が多い。だから観測者のいる非慣性系(加速度系)で成り立つ運動方程式を知りたいのだ。
そのとき、加速度aで運動する観測者から見た質量mの運動方程式は、静止している観測者から見て成り立つ運動方程式F=ma’の左辺の力の項に-maという見かけの力をつけ加えておきさえすれば良い。そこに慣性力導入の威力がある。
