回転地球に固定された座標系における
ニール(Neil)の放物線とフーコー(Foucault)の振り子
地球表面上の任意の緯度地点に固定された座標系で成り立つ運動方程式を求める。この座標系は海洋学や気象学の理論展開で必須なのですが、微妙に解りにくいものです。その解りにくい所を説明します。
また、その応用として“ニールの放物線”と“フーコーの振り子”を取り上げます。
1.地球回転座標系
この当たりの説明は文献1.が完璧です。
(1)地球上の座標
地球の公転による回転は無視する。つまり地球中心は宇宙空間で等速直線運動をしているとする。
地球の中心に原点をおき、上記の等速直線運動をする地球に固定された座標系(ここでは静止系と考える)を(x,y,z)系とする。
次にx,y軸が赤道面内で地球に固定されて、z軸(北極を通る軸)の周りに地球の自転につれてまわる座標系(x’,y’,z’)を考える。“地球自転角速度”をωとする。
次にその座標系をy’軸を軸にしてz’軸を赤道方向にたおし、z’軸が“地心緯度”θの地表点を貫くようにする。その時の座標系を(x''、y'',z'')とする。
さらの座標原点Oを地表面O'''まで移動した座標系を(x'''、y''',z''')とする。

(2)各座標系における運動方程式
1.静止座標系(x,y,z)
静止座標系で質量mの物体が満足すべき運動方程式は
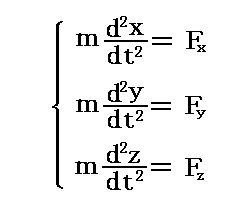
です。(Fx,Fy,Fz)は質量mの質点に働く全ての力の合力を表す。
2.座標系(x’,y’,z’)
(x’,y’,z’)系から質点mを見ると(x,y,z)座標と
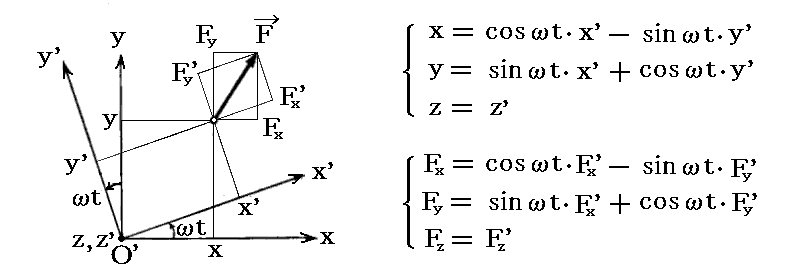
の関係で結び付けられる。
ここで
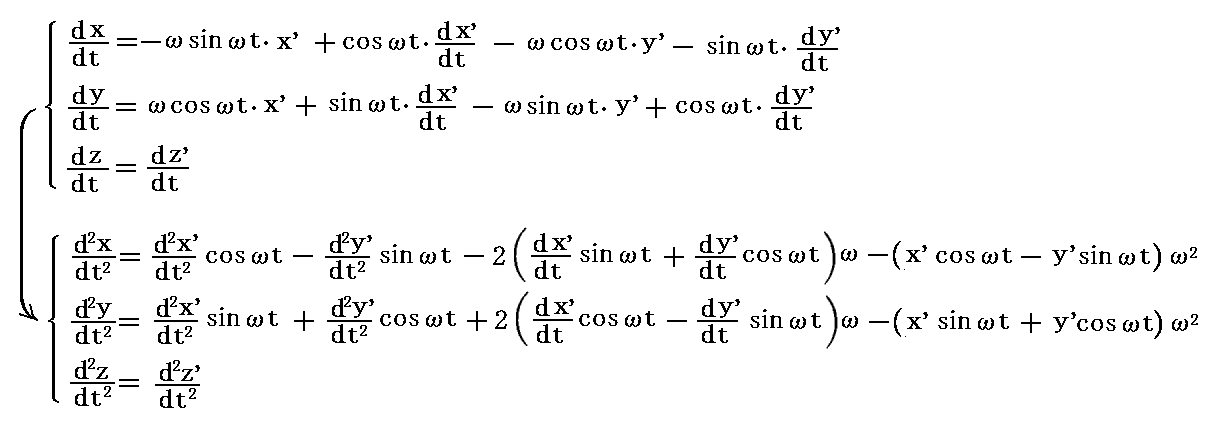
である。
これらの式を前項の方程式に代入する。このときsin2ωt+cos2ωt=1であるから
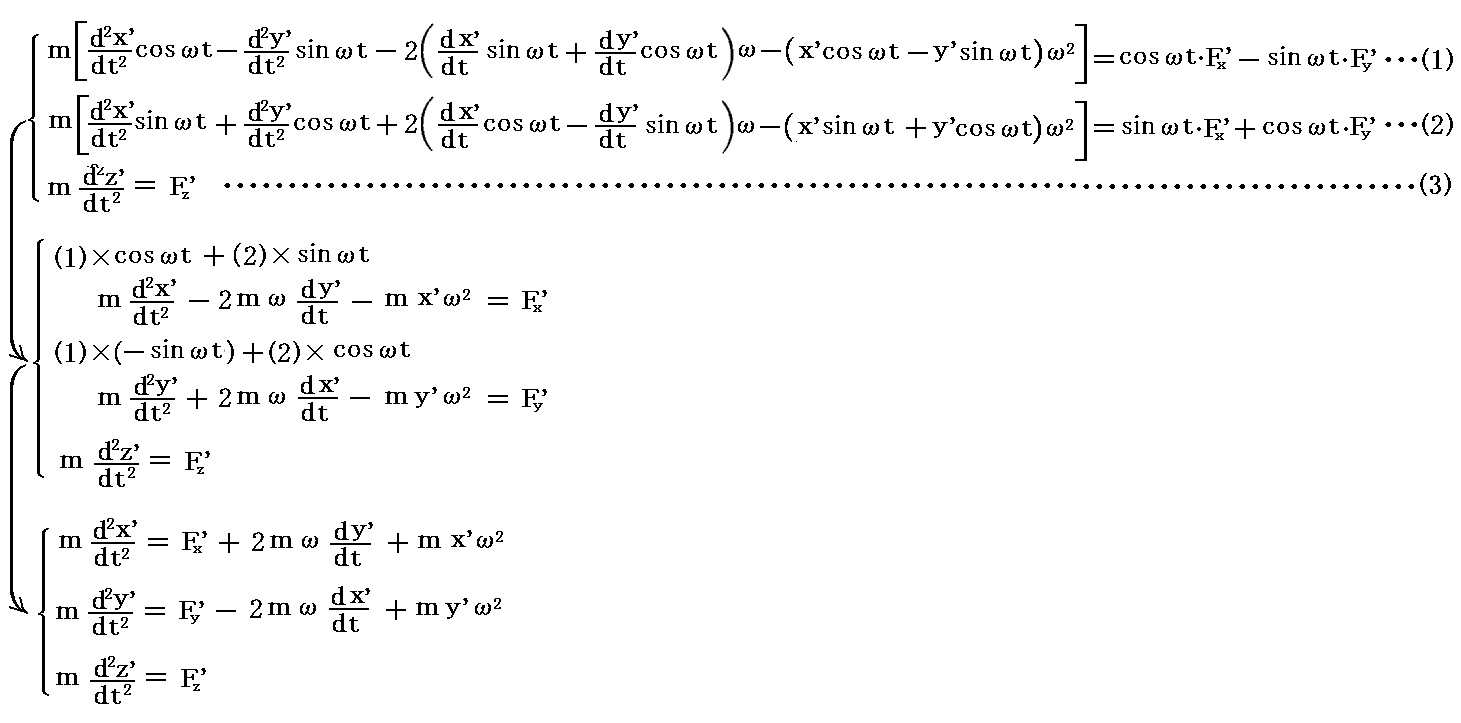
が得られる。
右辺第二項が見かけ上現れる慣性力である“コリオリ力”で、第三項が同じく慣性力である“遠心力”です。これらの項が現れることの説明は別稿「慣性力」でしております。
3.座標系(x'',y'',z'')
(x'',y'',z'')系から質点mを見ると(x’,y’,z’)座標と
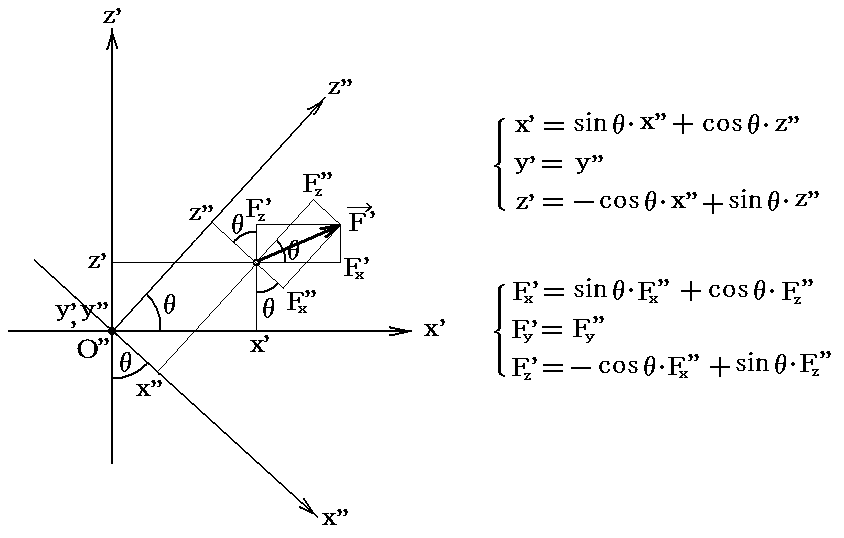
の関係で結び付けられる。
ここでθは時間的に変化しないので
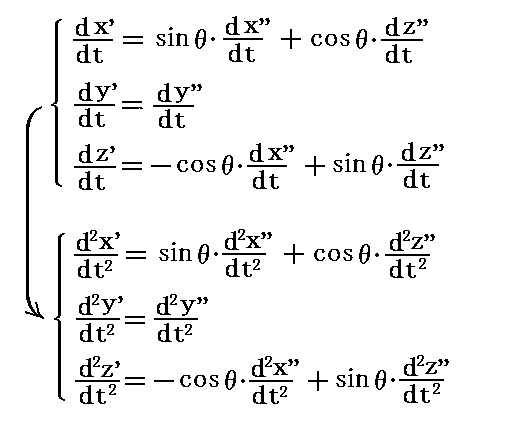
である。
これらの式を前項の方程式に代入する。このときsin2θ+cos2θ=1であるから
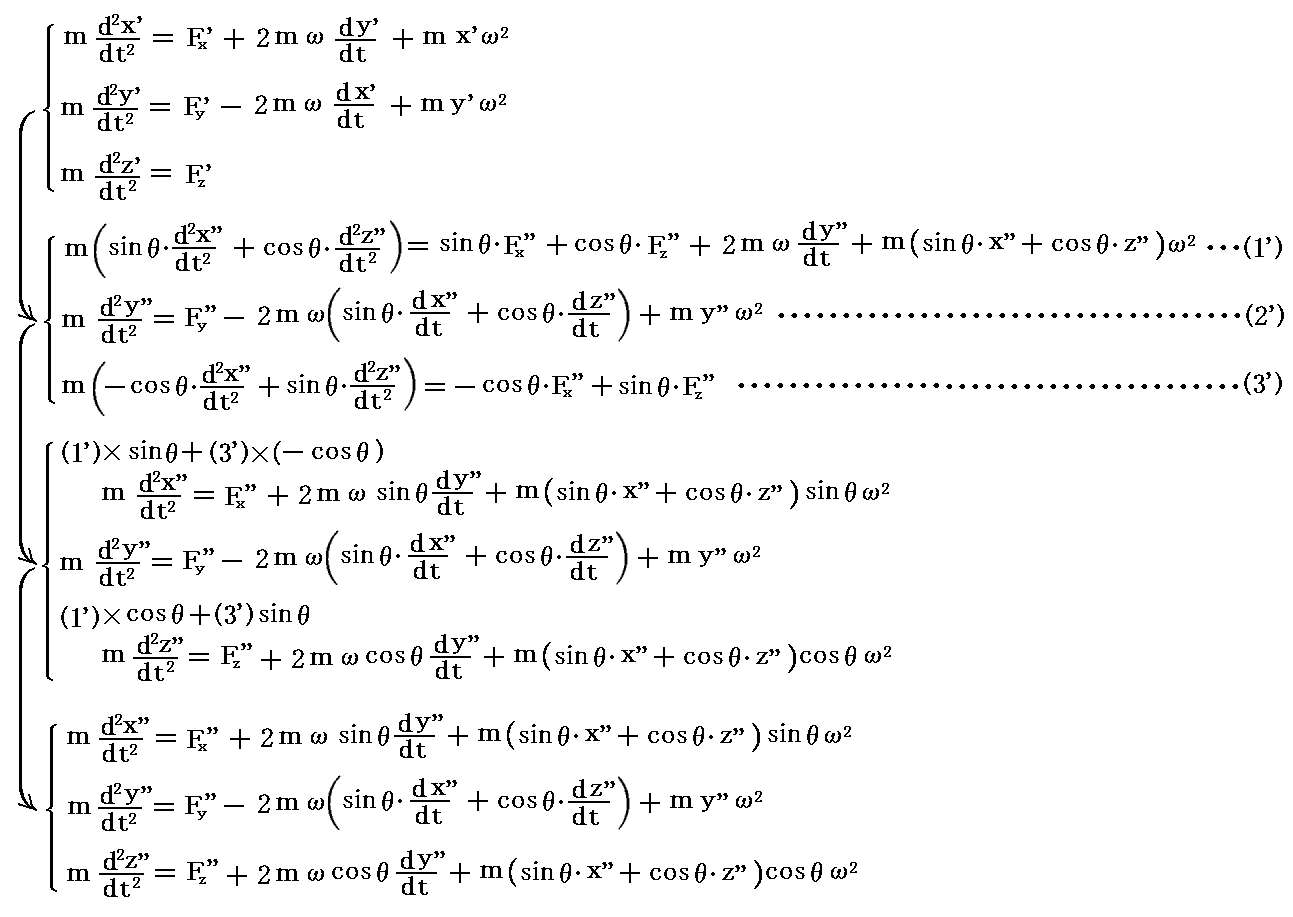
が得られる。
ωが掛かっている項が“コリオリ力”で、ω2が掛かっている項が“遠心力”です。
4.座標系(x''',y''',z''')
(x''',y''',z''')系から質点mを見ると(x'',y'',z'')座標と
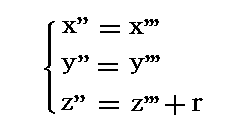
の関係にある。ここで r は“地球の半径”です。
r は時間的に変化しないので
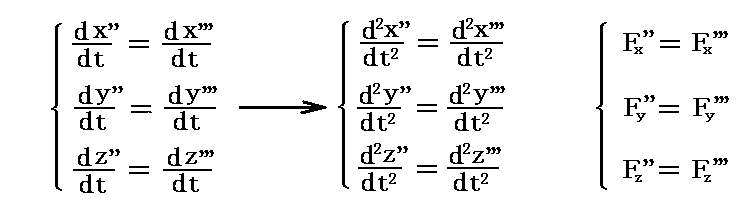
となる。
これらを前項の運動方程式に代入すると
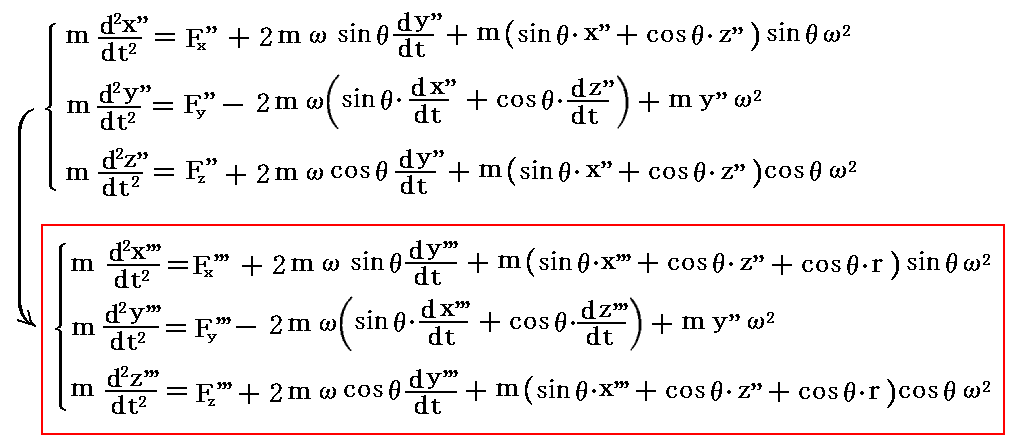
となる。
ωが掛かっている項が“コリオリ力”で、ω2が掛かっている項が“遠心力”です。
(3)地球は回転楕円体へ変形する
前節で地球表面上での運動方程式は求まっているのですが、ここからが本番で難しい所です。
前節の最後に示した運動方程式は地球が全く変形しない場合の話で、丁度下左図の状況の座標(x''',y''',z''')での話です。
この座標系での運動方程式中のωが掛かっている項は物体が動かなければ現れませんが、ω2が掛かっている項は(x''',y''',z''')座標で静止していても現れる項です。静止していてもこのような力が現れる座標系は、利用する上でとても不便です。
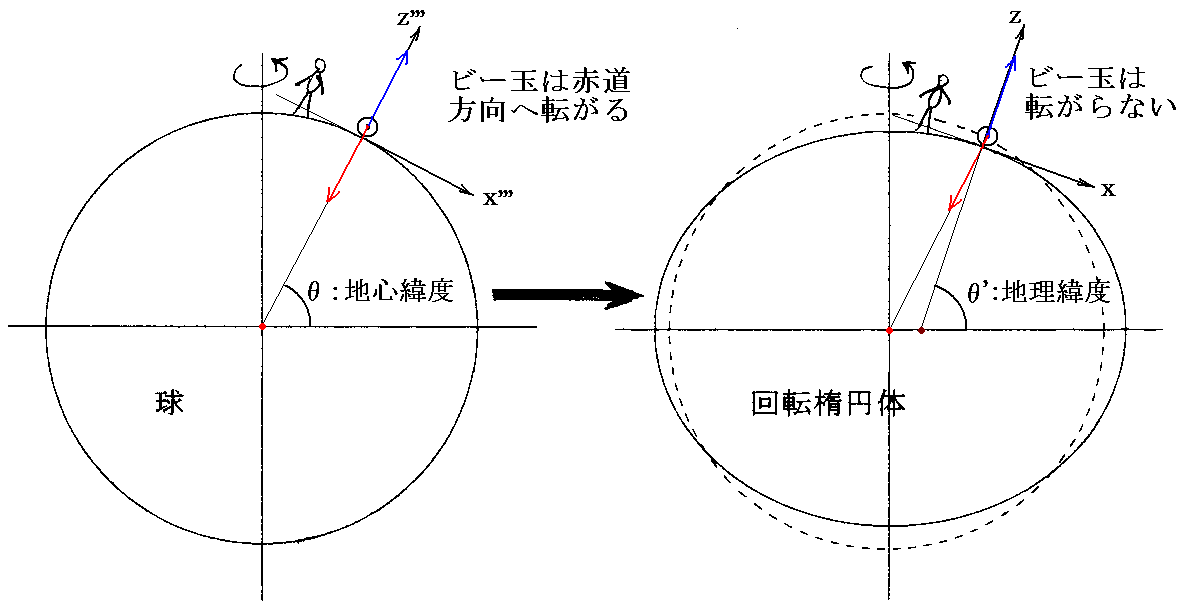
ところで、地球は自転のために現れる遠心力項を自ら取り込んで上右図の様に変形しています。つまり右図の様に座標系を取れば遠心力項が消去できるのではないかと予想されます。
我々が本当に利用したい座標系は上左図の(x''',y''',z''')座標ではなくて、上右図の(x,y,z)座標です。すなわちその座標系上では、物体に働く重力は正しくz軸の負方向を向いており、xy平面上にそっと置いたビー玉が自然には転がって行かない座標系です。
以下の図を比較すれば解るように上右図の(x,y,z)座標系を取れば、その座標系で質量mに働く重力mgは鉛直下向きとなります。その時下図の力C’こそ前記の方程式系中に現れているω2が掛かっていた項です。
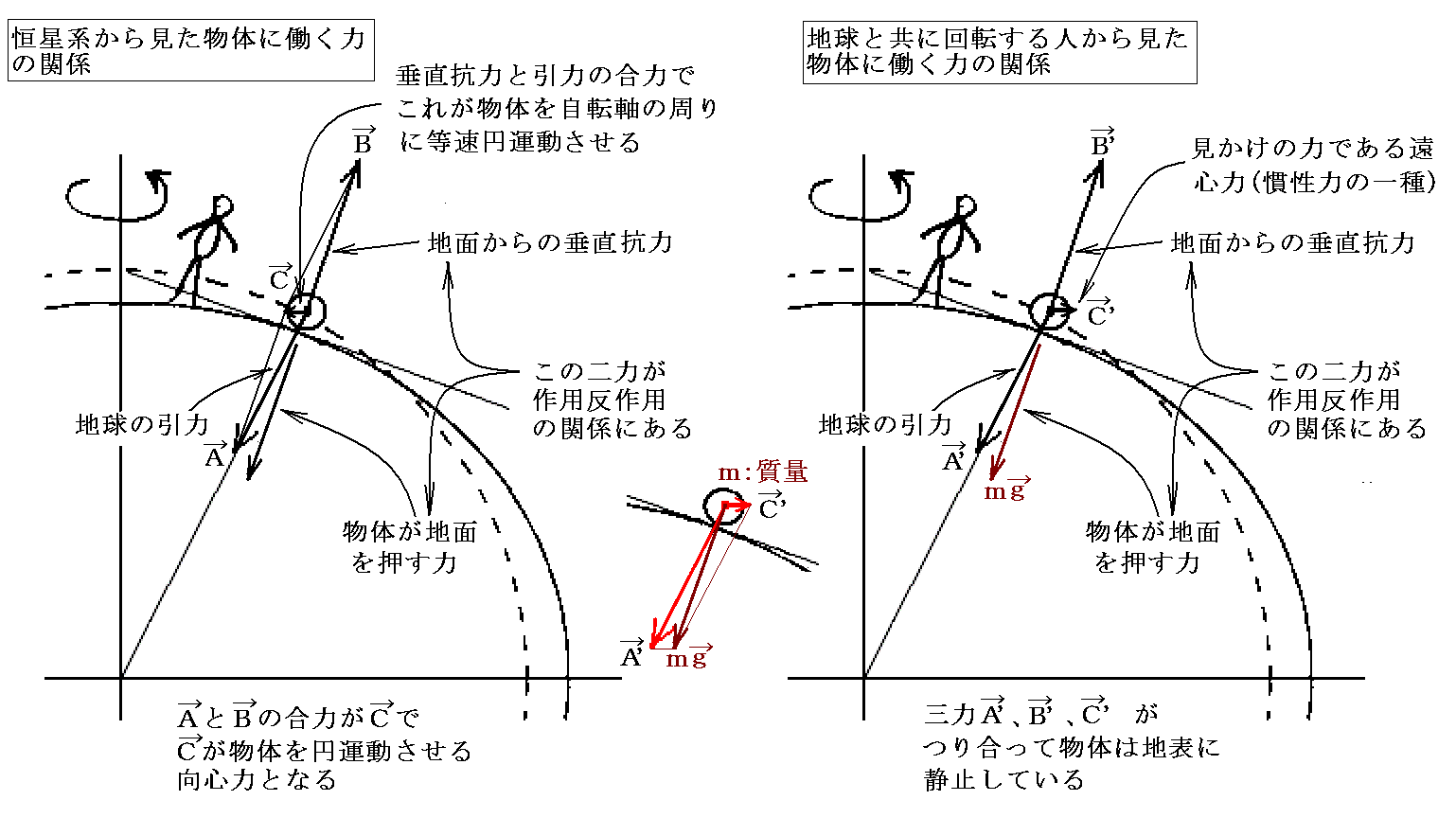
ω2が掛かっていた項が、上右図の力C’の(x''',y''',z''')成分を表します。
方程式中の成分表示式と上右図を比較して見ればすぐに解るように、成分表示の遠心力項の中でrの掛かっていない項は、x'''成分とz'''成分中のrの掛かっている項に比べて圧倒的に小さくなりますから直ちに無視することができます。実際(x''',y''',z''')座標上で様々な運動の議論をするときに x''',y''',z''≪r は常に成り立っているとして良い。
またθの変化により、rが掛かっているx'''成分とz'''成分がどのように変化するか確認してください。すなわち、θ→90°(北極)とすればx'''成分もz'''成分もゼロとなります。またθ→0°(赤道上)とすればx'''成分はゼロになりますがz'''成分は最大になります。これは、赤道上で見かけの重力が最小になることを意味します。どのくらい変化するかは高校物理の練習問題で解くところです。
上右図の様に地球重力mgが鉛直下向(-z軸方向)となり、x軸が地表面に平行で真南を向き、y軸が同じく地表面に平行で真東を向く座標系を改めて(x,y,z)座標系とすると、その座標系での質量mの質点の運動方程式は下記の様になります。
すなわち、(x''',y''',z''')系の運動方程式でω2が掛かっていた項を全て取り除き、Fz'''を重力mgとそれ以外の成分Fzに分けて記述すればよいのです。
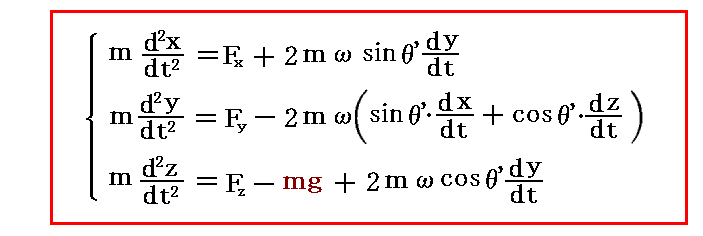
ここで(Fx,Fy,Fz)は、地球が及ぼす万有引力mg以外の力を表す。
つまり、x'''軸とz'''軸を微妙に傾けて新たなx軸とz軸にすることで、二種類の慣性力の内で遠心力の項を“重力mg”の中に含ませてしまい、見かけ上“遠心力の項”を消してしまうことができる。
これが別稿「コリオリ力」3.や「潮汐力」4.で説明したことです。
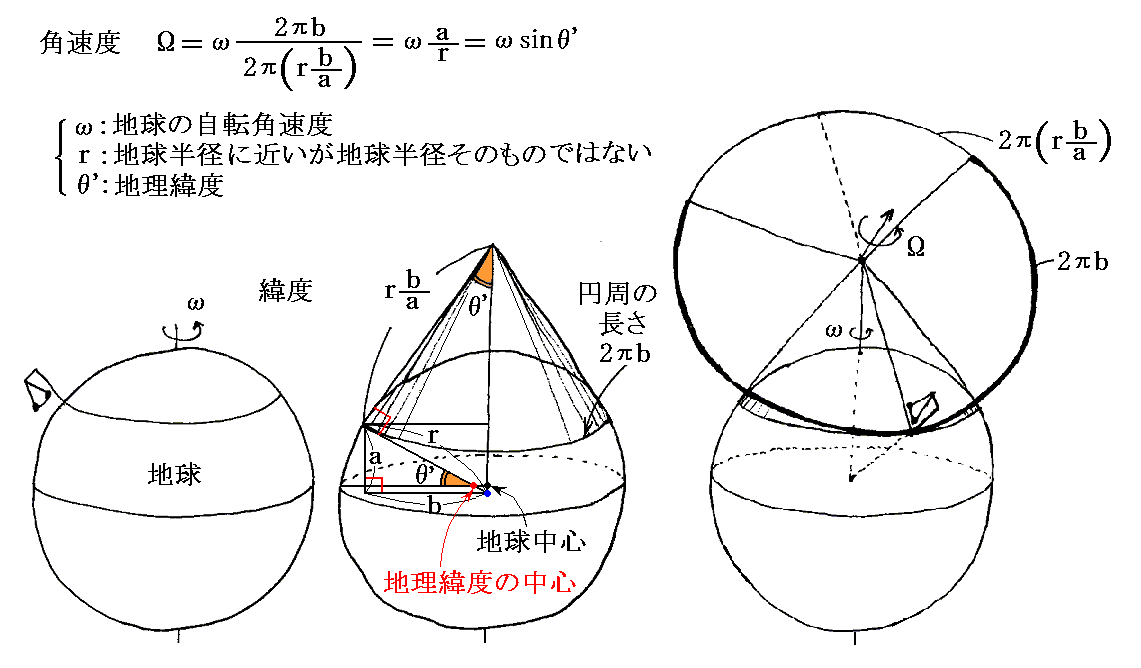
このとき、緯度は“地心緯度”θを“地理緯度”θ’に置き換えねば成りません。それは下図から明らかなように、コリオリ力に関係するのは地心緯度θではなくて地理緯度θ’だからです。
2.興味ある例題
せっかく遠心力項が消去できる座標系を導入したのですから、その座標系で成り立つ運動方程式を解いて得られる興味深い例を紹介します。
(1)ニール(Neile)の放物線
初等的な理科では、高い所から物体を静かに落としたとき、たとえ地表が地球自転のために動いていても、物体は真下に落ちると説明されます。しかし、これは間違っています。
本当は少し東側にそれて落下します。この現象は1679年にニュートンによって初めて指摘された。
1.理論計算
高さhの位置から質量mの物体を静かに落下させる問題を考える。すなわち初期条件t=0で(x,y,z)=(0、0、h)、(dx/dy、dy/dt、dz/dt)=(0,0,0)で運動方程式を解いてみる。
質点はほぼz軸に沿って落下するのでdx/dtとdy/dtは微少量となり、最初から運動方程式から省略できる。そのため、運動方程式は簡単に積分できて、解はすぐに求まります。
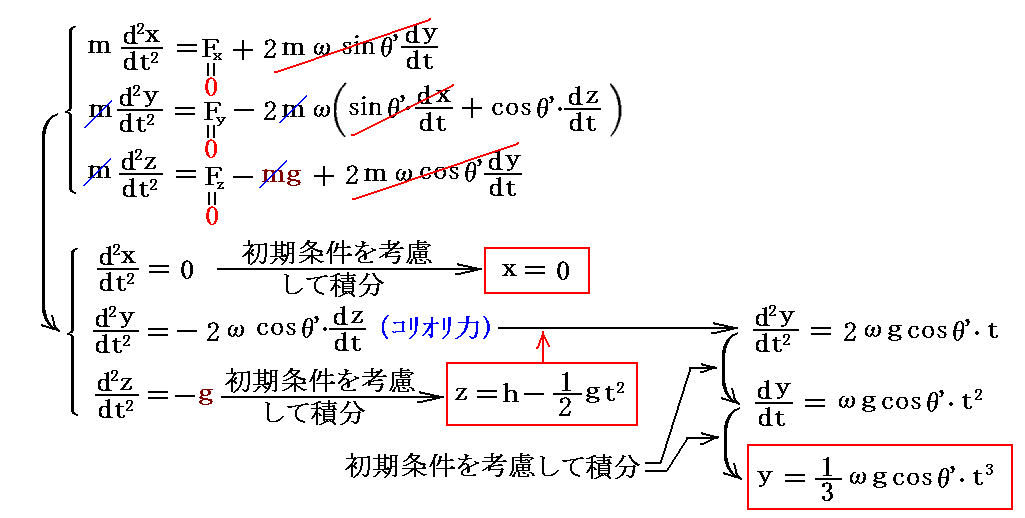
このとき、yをzの関数として表した
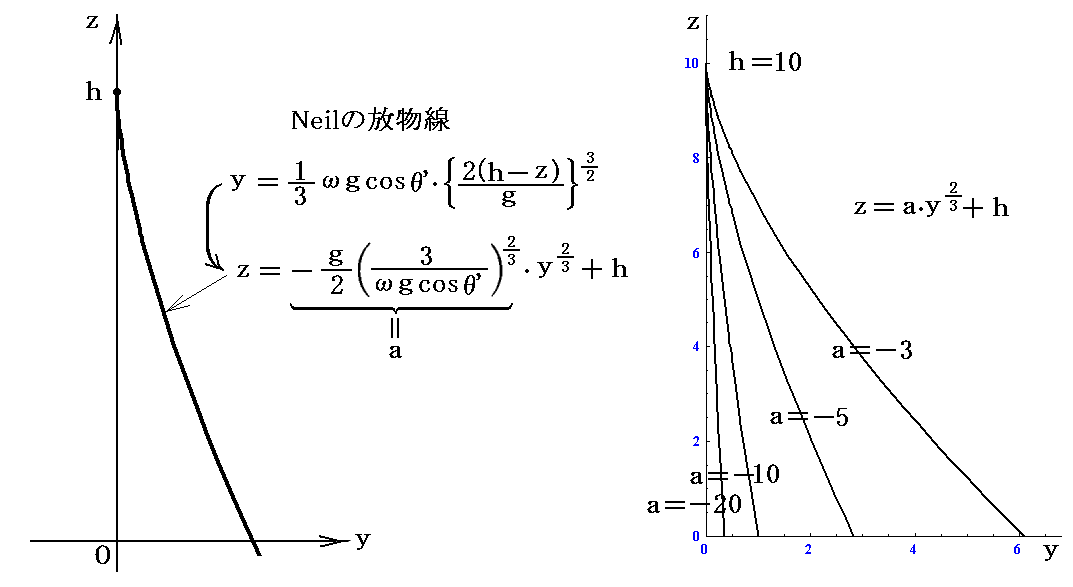
は z∝±y2/3 の形をしているが、1657年にウィリニアム・ニールがこの形の曲線の性質を調べたので、“ニール(Neil)の放物線”と呼ばれている。(https://en.wikipedia.org/wiki/Semicubical_parabola を参照)
この式で、z=0とおけば地上に到達したときの偏向量が求まり
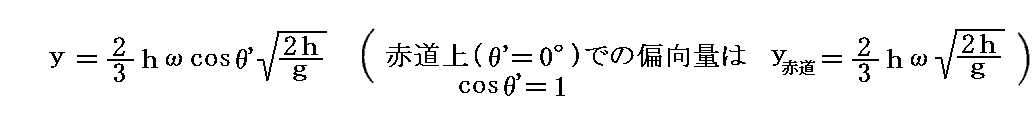
となる。すなわち、地球が回転しているために物体は真下には落ちないのです。
緯度45°の地点で高さh=100mの所から落下させると、実際に真下からどれくらい離れた位置に落ちるか計算してみる。地球自転の角速度ωは
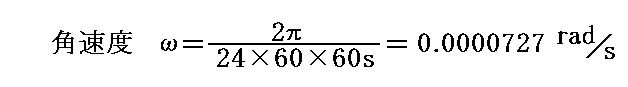
で、重力加速度g=9.8m/s2であるから、

となる。
つまり、東側に1.5cm離れた所に落ちる。h=100mで1.5cmですから、これを検出するのは極めて難しいでしょうね。
2.偏向の理由
初等的に考えると、地面は西から東へ動いていますが、高さhの点も同じ様に動いている。だから高さhから静かに落としても、静止系から見ると西から東へ地面が動く速度で水平に投げ出したのと同じです。そのめた落下中も東向きの速度を持続しますので、物体は真下に落ちるはずです。しかしこれは正しくありません。
正しくは、地面は平坦ではなくて球形をしており、地面は等速度で移動しているのではなくて回転するように移動している。そのため、その回転中心に向かって落下すると、落下速度に比例するコリオリ力 fcが働きます。つまり、別稿「コリオリ力」で説明した回転円盤の中心に向かってビー玉を転がすときと同じ現象が生じます。
下図は文献5.より引用したものですが、赤道上で落としたときの状況を示しています。
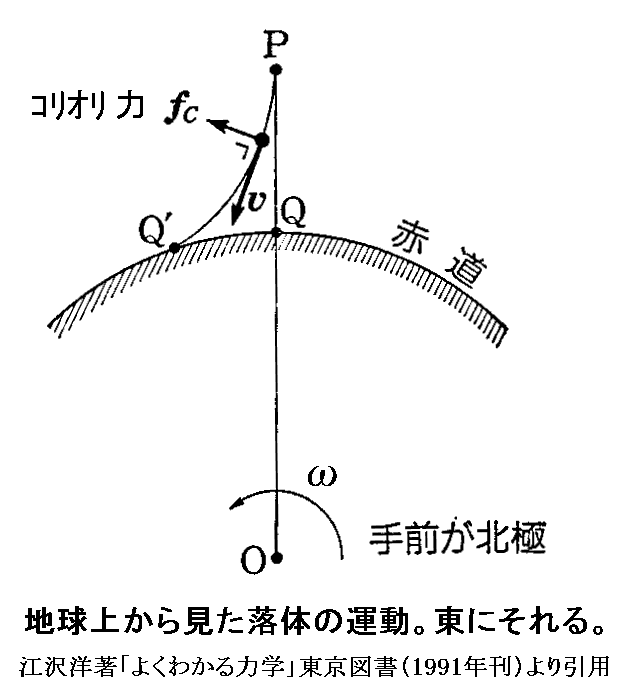
上図を右に90度回転させて、別稿「コリオリ力」の図
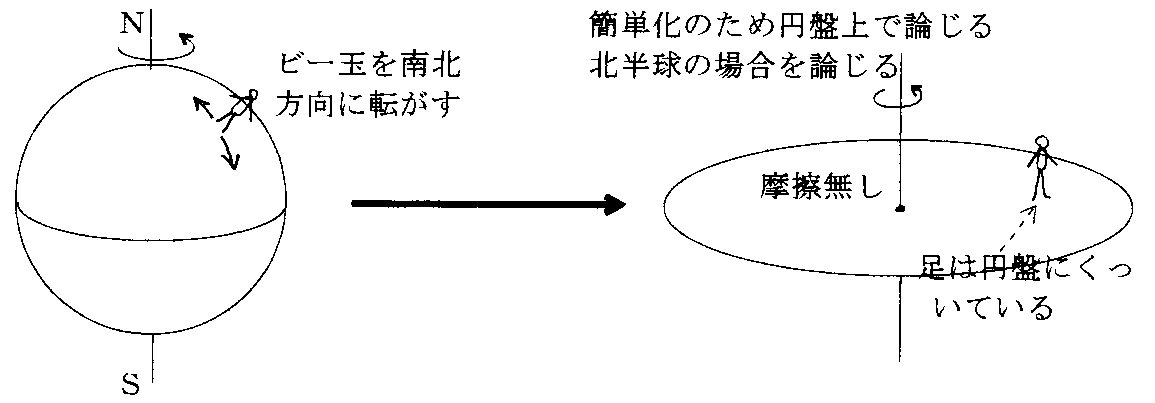
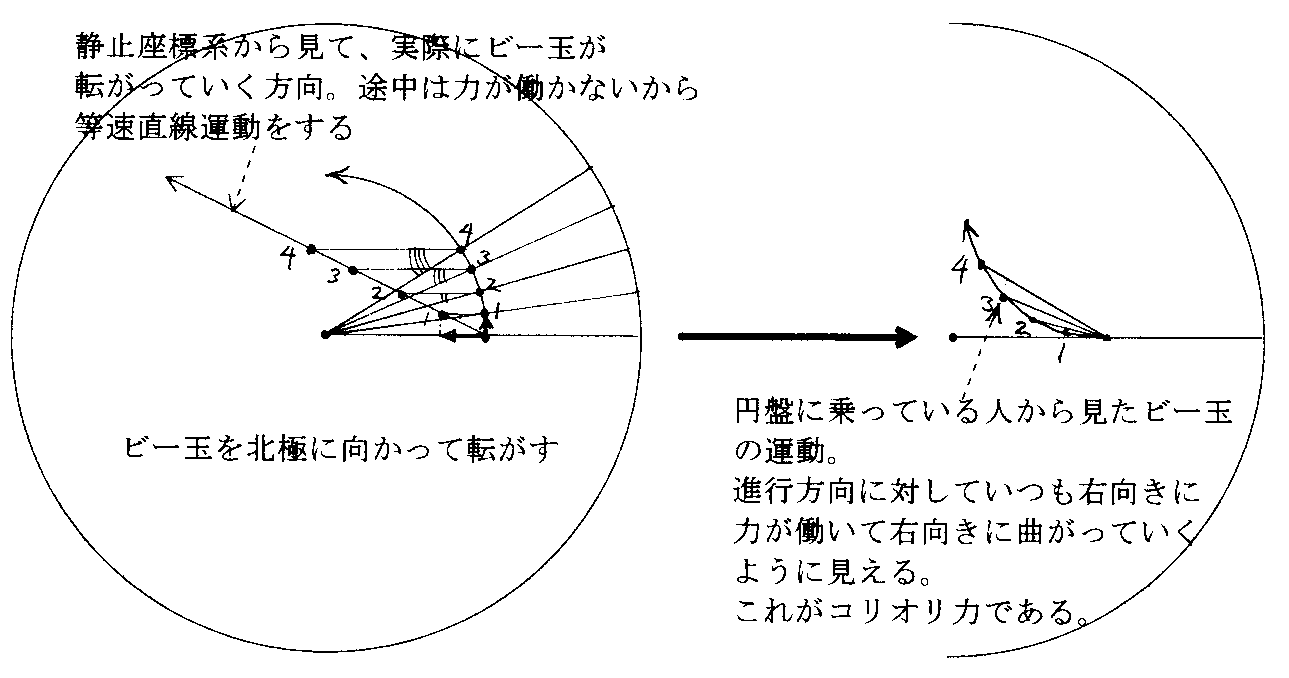
と比較してみてください。まさしくコリオリ力が原因で東側へ落ちる。
前記の理論式展開をたどれば、運動方程式中の“コリオリ力項”がその原因である事が解ります。ただし、上記の議論と異なるのは、回転中心に向かう速度が引力の為にだんだん速くなることです。そのため上図では単純な円弧でしたが、ここではニールの放物線という複雑な関数になる。
[補足説明1]
赤道に於ける偏向量y赤道を求めるだけなら、高校物理の練習問題として容易に導けます。
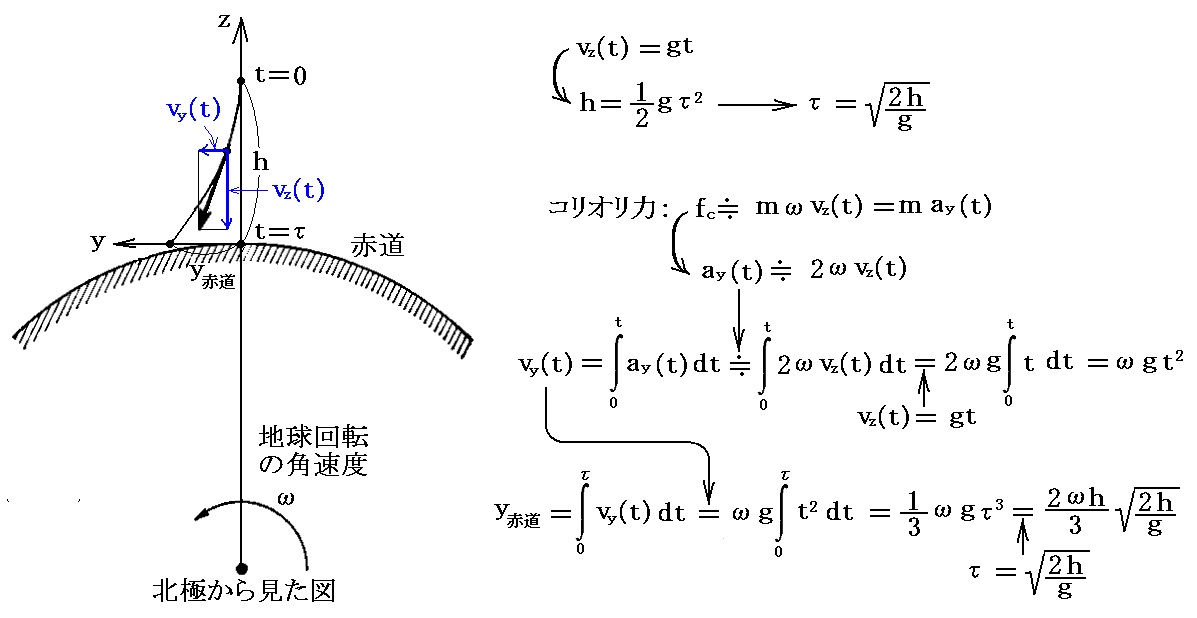
となり、赤道での公式が得られる。
[補足説明2]
落下問題がこんなに簡単に解けるのは、解くべき連立微分方程式のz方向の方程式にyの関数が含まれていないためです。そのため、まずz方向の積分をしてから、y方向の積分に取りかかれた。
後で説明するフーコー振り子の場合、連立微分方程式が互いに他方向の成分の関数を含んでいるため、落下問題で用いた方法は使えません。フーコー振り子の場合は、この稿で説明するように逆回転の座標系に移動して解くか、参考文献4.§31の様に複素数表示を用いた技巧的な方法で解くしかありません。
フーコー振り子がこの方法で解けるのは、ゾンマーフェルトが指摘しているように連立微分方程式のコリオリ力成分がジャイロ・スコピック(反対称)な性質を持っているからです。だから、もう一度逆回転する座標系に移ってコリオリ力を消してしまえばよい。
3.検証実験
文献6.7.8.によると、この現象を最初に指摘したのはニュートンのようです。ニュートンは1679年に、“自由落下においては、物体が落下運動の初めに持っている接線方向(水平方向)の速度は、地球表面の接線速度よりも(地球は回転運動をしているので)大きい。そのため慣性によって東の方へ落下するであろう。”と注意を促した。
ロイアル・ソサイエティは、ニュートンの指摘の正しさを精密な落下実験によって検証することを決議した。しかし、その振れ幅は前々項で説明した様に非常に小さいものだったので、当時の観測・測定技術では結局うまく検証できなかったようです。
このふれの検証に最初に成功するのは一世紀以上後の1791年のグリエルミーニによる実験です。その当たりの事情を記した文章を引用しておきますのでご覧ください。
[補足説明3]
ニュートンの言っていることを高校物理のレベルで確認しておきます。
地球中心からの距離が r と(r+h)の位置の水平方向の速度成分の差に、落体がhだけ落下するのに要する時間τを乗じれば、地上での偏差y赤道のおよその値を求めることができる。
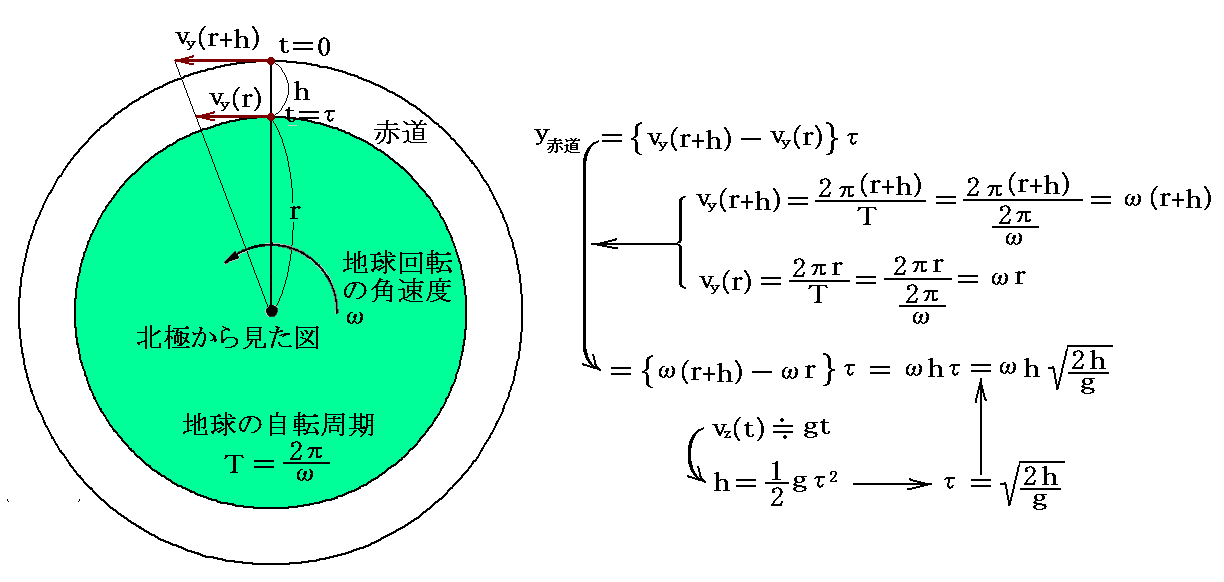
かなりおおざっぱな計算のために、正しい式と係数2/3だけの違いがあるがyの正方向にずれる理由は理解できる。
高度差h≪地球半径r なのに、たった数秒間の落下時間(h=100mでτ≒4.5s)で数cmの差がでてくるのは、地球表面の移動速度が結構大きな値だからです。
実際、赤道地面は
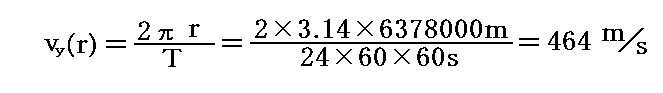
程度の速度、すなわち空気中を伝わる音速より速く移動している。そのため赤道上空100mから自由落下させると
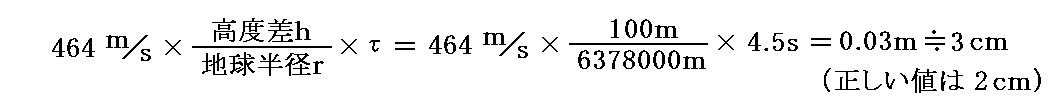
となる。
(2)フーコー(Foucault)の振り子
フーコーの振り子は有名ですが、厳密に説明するのは容易ではありません。様々な近似をして何とか理解できる現象です。だから、文献7.の第7章に記されているように当時最先端を誇っていたフランスの数学界に大騒動を引き起こした。
1.運動方程式
地球自転の影響を考慮に入れた振り子の運動を考察する。長さLの糸の端に大きさの無視できる質量mの重りをつるし、(x,y,z)=(0,0,L)の位置を支点として振らす。長さLを振り子の振幅に比べて充分長くとると、重りはほぼxy平面内を振動すると考えて良い。その際、“糸の張力”をTとすると、高校物理で習う振り子の理論より、Fx=T(x/L),Fy=T(y/L)と置けるので、質点が満足する運動方程式は1.(3)の式から
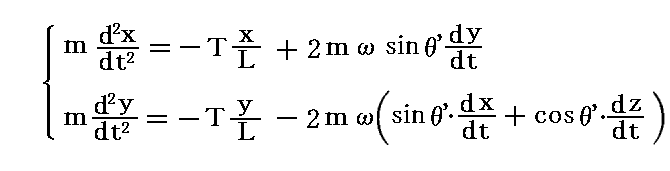
となる。z成分の運動方程式は今の近似レベルでは考えなくて良いので省略した。
ここでさらに、Lに比べて小さな振幅の場合dz/dtはほとんどゼロとして良いので省略できる。そのため解くべき運動方程式は
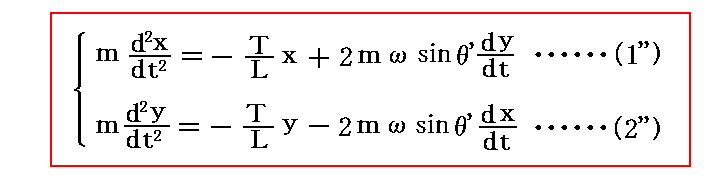
となる。これは別稿「ゼーマン効果(スペクトル線の磁場による分裂)の古典論(1896年)」2.(1)で説明した方程式と全く同じです。
そこの式で me→m 、k→T/L 、qeB→2mωsinθ’ の置き換えをすれば、そこの結論がそっくりそのまま使えます。しかし、そこの解は円運動に対するもので、フーコー振り子の理解には適していません。
そのためここでは、別なやり方で解きます。
2.方程式の変形
以下の証明は文献1.(or文献2.or文献3.)で説明されているものです。
前項の方程式の(1'')に(-y)を掛けて、(2'')にxを掛けたものを加えると

が得られる。
これは角運動量保存則が成り立たないことを表している。つまり中心からの距離の二乗に比例して変化する。
コリオリ力の項ば微少なので、運動方程式(1'')(2'')の解がどのように成るのかは、別稿「質点の二次元運動」2.(3)を復習すれば大体のところは予想できる。そこでは運動方程式中のコリオリ力項が無く、角運動量が保存される場合でしたが、中心の周りの往復運動や楕円運動に成りました。
ここではコリオリ力項が存在するために、角運動量が保存せず常に角運動量が変化していきます。これは上記の往復運動の振動線や、楕円の長軸が時間と供に回転していくことに対応します。
その回転角速度がいくらに成るかを知るには、次の変数変換をしてみればよい。
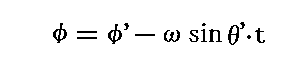
と置けば前式は
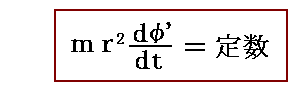
となる。
ここで、φ’は鉛直なz軸の周りを角速度-ωsinθ’で回転する座標系に於ける質点の方位角を意味しますから、上式は回転座標φ’系から見れば角運動量保存則が成り立つ事を示している。
つまり角速度-ωsinθ’で回転する座標系(質点の方位角がφ’で表される座標系)から見れば、振り子の重りは別稿「質点の二次元運動」で説明した運動をすることになる。
それを元の方位角φの座標系から見れば、φ’系で見られる往復運動や楕円運動に角速度-ωsinθ’の回転運動を重ね合わした運動となる。
3.φ’系での解
前項の方針に従って運動方程式(1'')(2'')を解いてみよう。つまり1.(3)で説明した座標系からさらに回転する座標系に移るのです。
1.(3)で説明した(x,y,z)座標のz軸を回転軸として角速度ωsinθ’(≡Ωとおく)で(z軸の正の方向から見て)時計回り(つまり北→東→南→西の順番)に回転する座標系(x’、y’、z’)を導入する。この座標系のz’軸はz軸と共通で、x’y’平面がをxy平面上を回転する。
この座標系を1.(2)2.で導入した(x’、y’、z’)座標系とくれぐれも混同しないでください。そこの(x’”,y’”,z’”)系がここでの(x,y,z)系です。そのように緯度θ’の地表面に存在する(x,y,z)座標系をz軸まわりに回転させたものがここで言う(x’,y’,z’)座標系です。その様にそこと同じではないのですが、ここでの(x,y,z)系と(x’,y’,z’)系との間にも類似の関係式が成り立ちます。
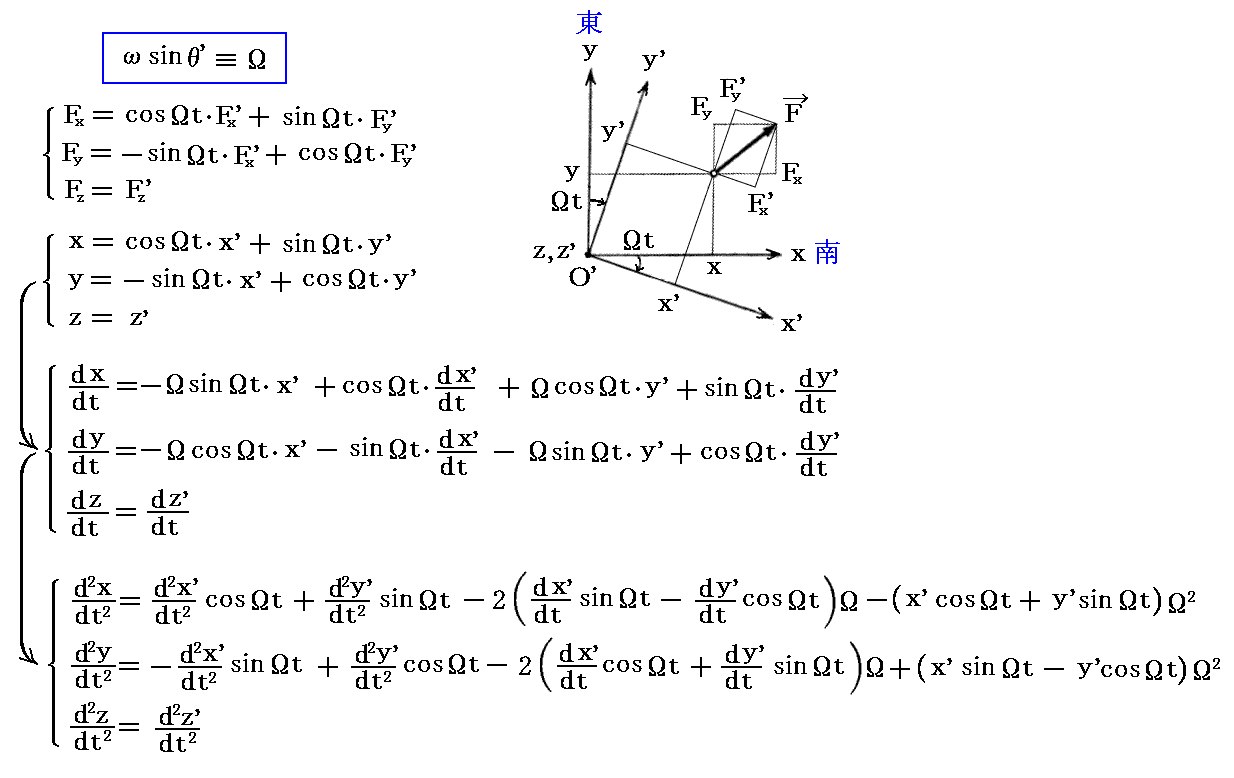
ただし、(x,y,z)系に対する(x’,y’,z’)系の回転方向が1.(2)2.の場合と逆なので、変換式の符号が少し異なっていることに注意してください。
これらの式を運動方程式(1'')(2'')に代入すると
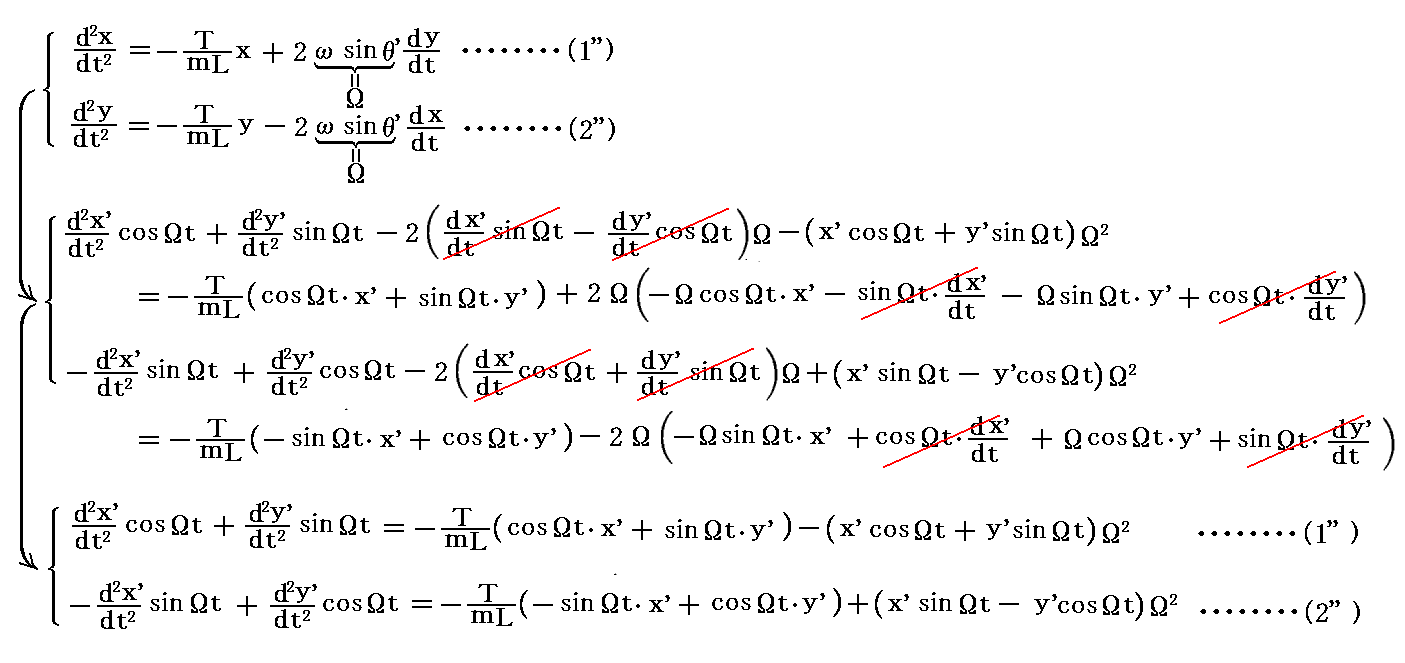
となる。
ここで (1'')×cosΩt-(2'')×sinΩt と (1'')×sinΩt+(2'')×cosΩt を求めて、さらにsin2Ωt+cos2Ωt=1であることを考慮すると
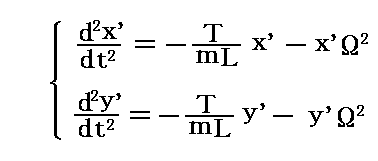
が得られる。
新たに導入した座標系(x’,y’,z’)においては、確かにΩの一次の項であるコリオリ力項は消すことができている。
そのとき、微少な遠心力項mrΩ2が残ってしまうが、Ωは非常に小さな値なのでΩ2が掛かっている項は省略できる。
ここでさらに、振り子の重りがその支点を中心とした球面上を運動するために糸の張力の変化として現れる微少な遠心力を無視すれば、重りに働く糸の張力Tは(高校物理で習うように)ほぼmgと見なすことができる。そのことを考慮すると、結局
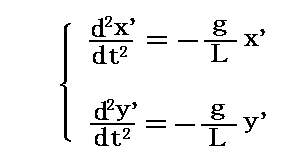
を解けばよいことになる。
様々な近似を施した結果ですが、ともかく別稿「質点の二次元運動」2.(3)で論じた微分方程式に帰着できた。次項でフーコー振り子の特質を最も良く表す解を求める。
[補足説明]
最初のφ系での方程式に現れていたコリオリ力項は元々静止系から回転系であるφ座標系に移行したために現れたものです。その時同時に現れる遠心力項は座標軸を旨く選んで重力mgの中に含ませて消してしまえたのでした。
コリオリ力項を消すためにもう一度逆回転する回転座標φ’系に移行したのですが、上記の様にφ系から回転系φ’へ移行すると新たに遠心力項mrΩ2が現れるのは致し方ないところです。
このとき別稿「質点の二次元運動」3.(3)(a)で説明したように、運動質点に働く力が中心力でありさえすれば角運動量保存則は一般的に成り立ちます。だからこの微少な遠心力項mrΩ2が新たに生じてφ’系に於ける軌道の形に影響を与えても軌道の角運動量保存則はそのまま成り立っています。
そのため、φ’系からφ系に戻ったとき生じる振り子の振動面の回転角速度Ω(歳差運動の角速度)の大きさには影響しません。だからここで微少な遠心力項mrΩ2を省略したことで軌道の形は少し変わるかもしれませんが、フーコー振り子の振動面の回転角速度に影響することはありません。
4.φ’系での解の例
t=0で(x,y)系と(x’,y’)系は一致しており、t=0に場所(x’,y’)=(A,0)で、初速度(dx’/dt,y’/dt)=(0,vy0’)で打ち出したときの運動解を求める。
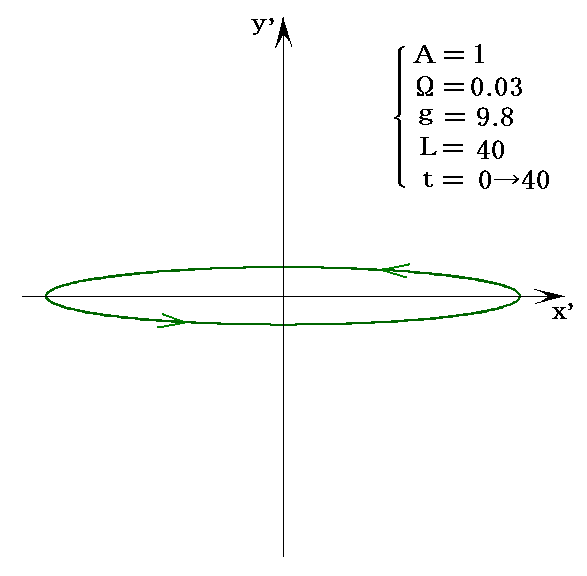
この初期条件満足する解は、別稿「質点の二次元運動」2.(3)で求めたように
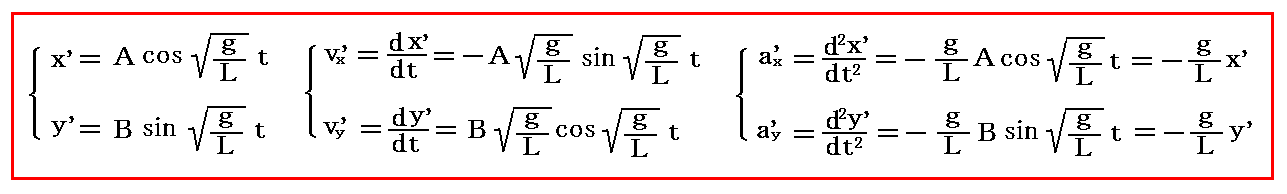
となる。この解の中で興味深い例を、さらに詳しく調べる。
1.t=0に(x’,y’)=(A,0)の位置で重りをそっと離す、すなわち初速(vx0’,vy0’)=(0,0)で離す場合
この初期条件を満たす解はB=0となる。すなわち
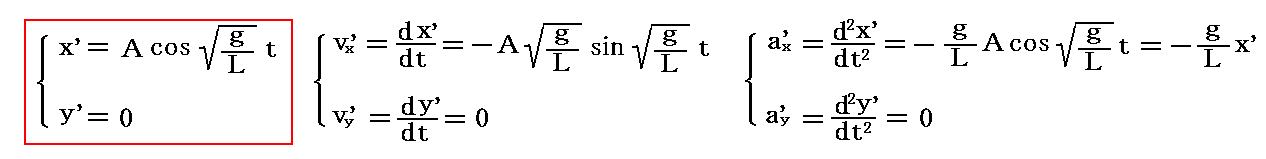
となる。
これは最大振幅Aの位置で振り子の重りをそっと離した場合に起こる運動で、常にx’軸に沿った往復振動をする。そのため常にy’=vy’=ay’=0です。
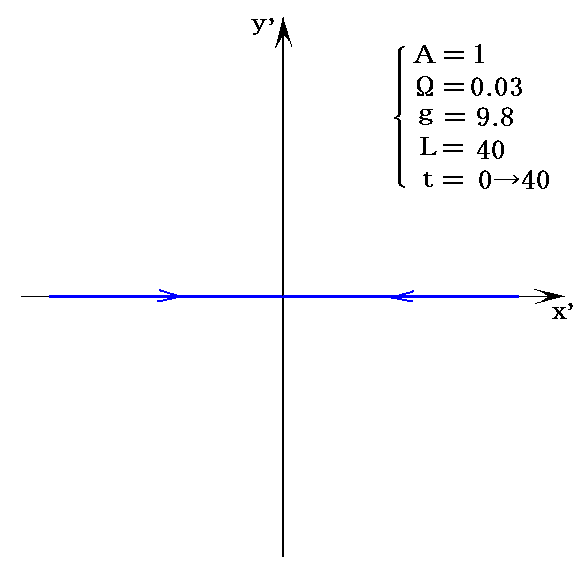
x’=±Aの位置でvx’=0となるのですが、時刻t=0でx’=Aの位置を離れた重りは、時刻
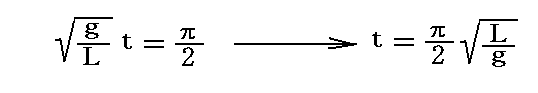
に、原点(x’,y’)=(0,0)(振り子の最下点)を通過する。そのとき速度vx’は最大値
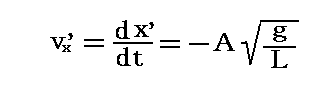
となります。
これをφ系から見ると、振り子の最下点(原点)で上記の速度を与えて振り子の振動を開始する場合に対応します。そのとき、最大振幅の位置でAΩの大きさの回転方向の速度成分を持つことになりますが、その当たりは次項で説明します。
2.t=0に(x’,y’)=(A,0)の位置で重りに北向き初速(vx0’,vy0’)=(0,AΩ)を与えて離す場合
このときt=0の初期条件より
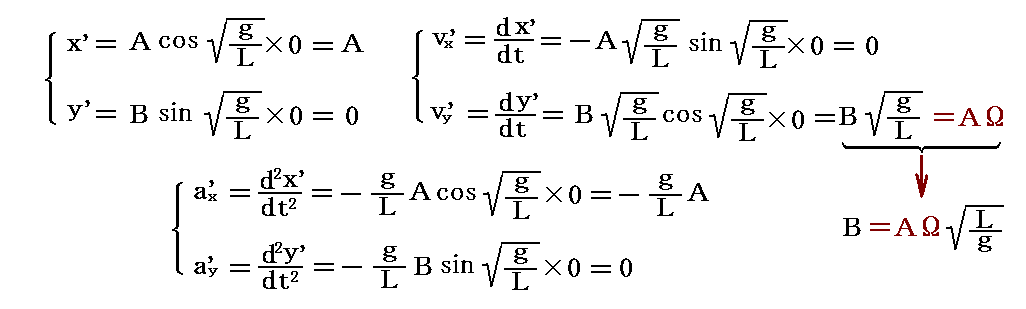
が成り立つので、y方向の振幅はB=AΩ(L/g)0.5で無ければならないことが解る。
つまりこのときの運動の軌跡を表す解は
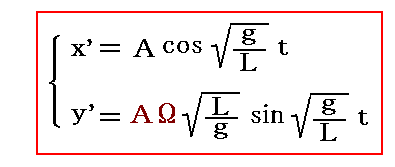
となる。
これはx’軸方向の長軸半径がA、y’軸方向の短軸半径がAΩ(L/g)0.5の楕円軌道を表している。
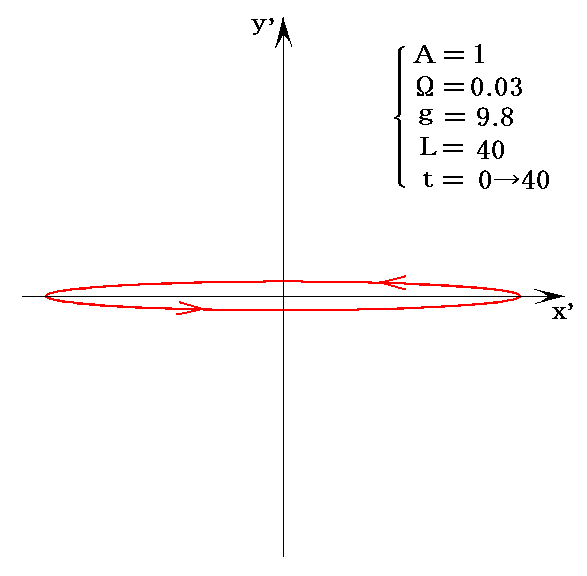
これをφ系から見ると、最大振幅位置Aで重りをそっと離したときに生じる振動に対応する。
3.t=0に(x’,y’)=(A,0)の位置で重りに北向き初速(vx0’,vy0’)=(0,2AΩ)を与えて離す場合
この場合は、x’軸方向の長軸半径がA、y’軸方向の短軸半径がB=2AΩ(L/g)0.5の楕円軌道を描く。
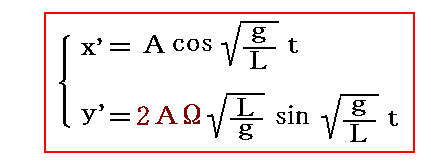
5.φ系での軌道の様子
前項の結論をφ系で見るとどうなるかを考察する。
1.φ’系でt=0に(x’,y’)=(A,0)の位置で重りをそっと離す、すなわち初速(vx0’,vy0’)=(0,0)で離す
φ系から見るとt=0に(x,y)=(A,0)の位置で重りに南向き初速(vx0,vy0)=(0,-AΩ)を与えて離すことになる。その時の軌跡は前項の解を2.(2)3.で説明した座標変換式に代入すればよい。
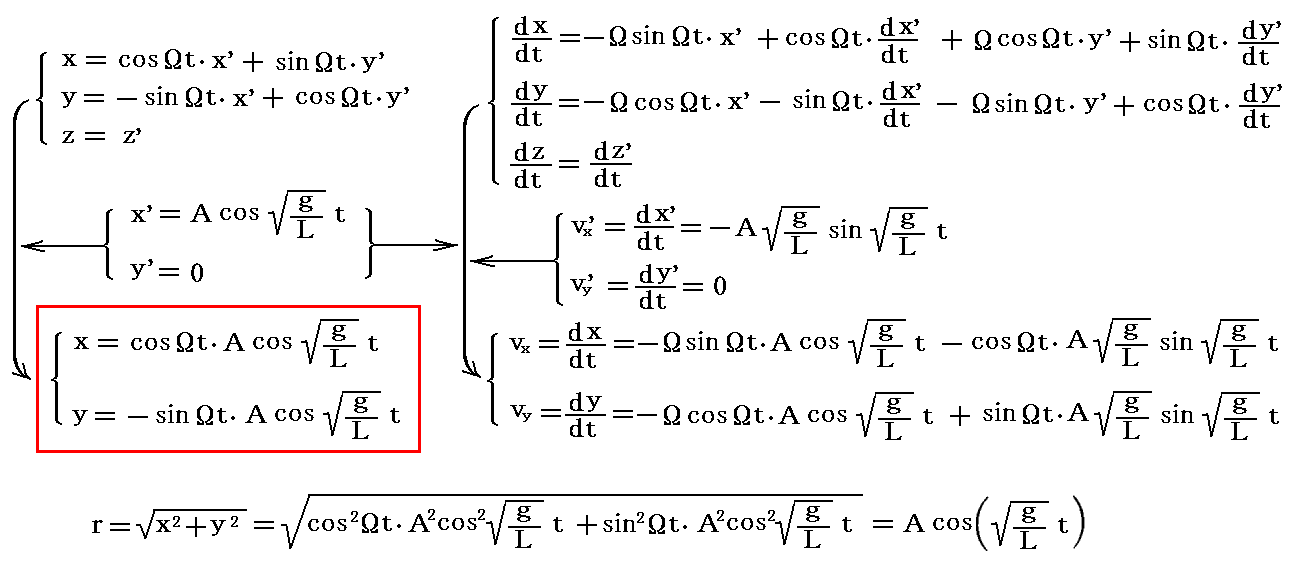
これがどのような軌跡なのかを説明するのは難しいが、rの変化の様子から周期
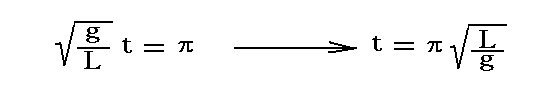
で最大振幅の位置を通過し、振り子の振動面が角速度Ωで回転していくことが解る。
また、最大振幅になる時刻の中間時刻に必ず原点を通過し、その時の速度が
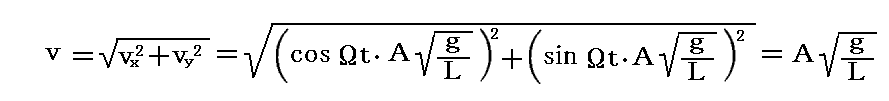
であることも解る。
数式処理ソフトMathematicaを用いて、北半球での振動回転(重りの軌跡)の様子をグラフ表示すると下図の様になる。
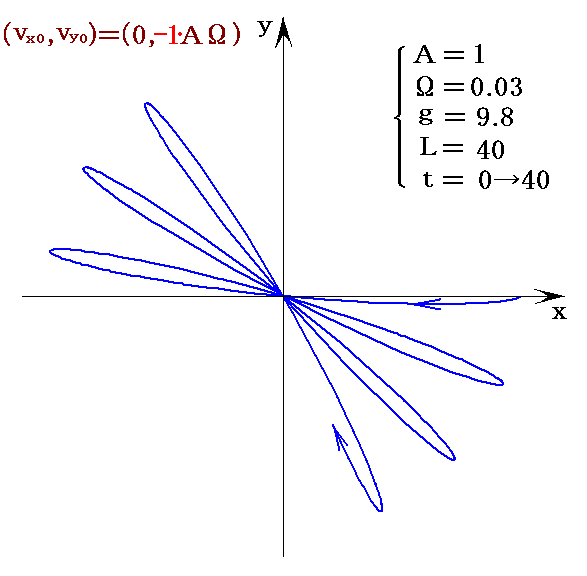
これは、振り子の運動を開始させる方法として、最下点で重りに初速v0=A(g/L)0.5を与える場合に重りが示す軌跡です。
2.φ’系でt=0に(x’,y’)=(A,0)の位置で重りに北向き初速(vx0’,vy0’)=(0,AΩ)を与えて離す
φ系から見ると、t=0に(x,y)=(A,0)の位置で重りを静かに離す、すなわち初速(vx0,vy0)=(0,0)で離すことになる。その時の軌跡は前項の解を2.(2)3.で説明した座標変換式に代入すればよい。
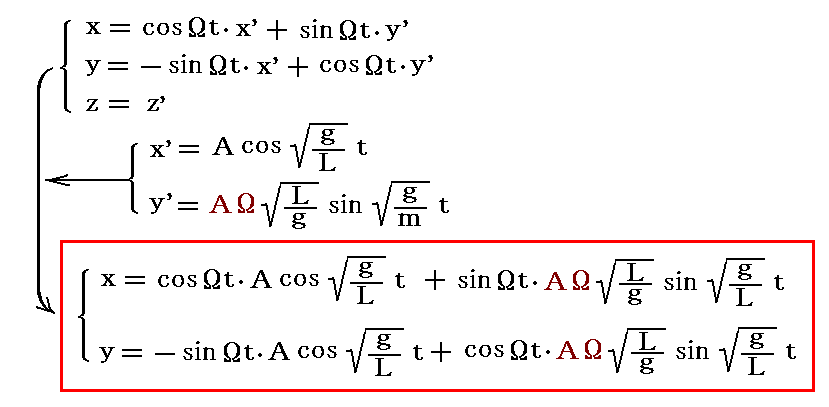
このままでは解りにくいので、原点からの距離rの時間的変化を表す式にしてみる。
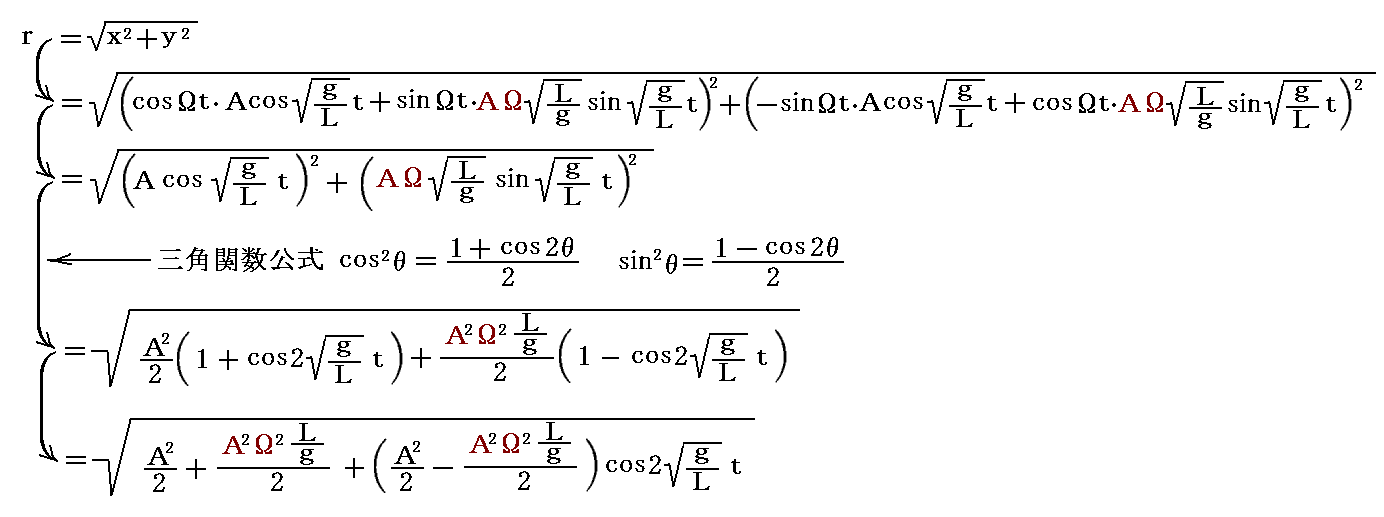
つまり、時刻t=0でr=Aだったものが、時刻
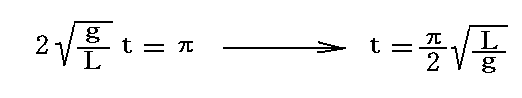
に、rの最小値
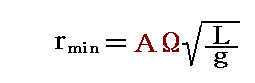
をとり、さらに同じ時間経つと再び最大値Aとなる。この場合には原点を通過することはありません。
速度についても同様です。
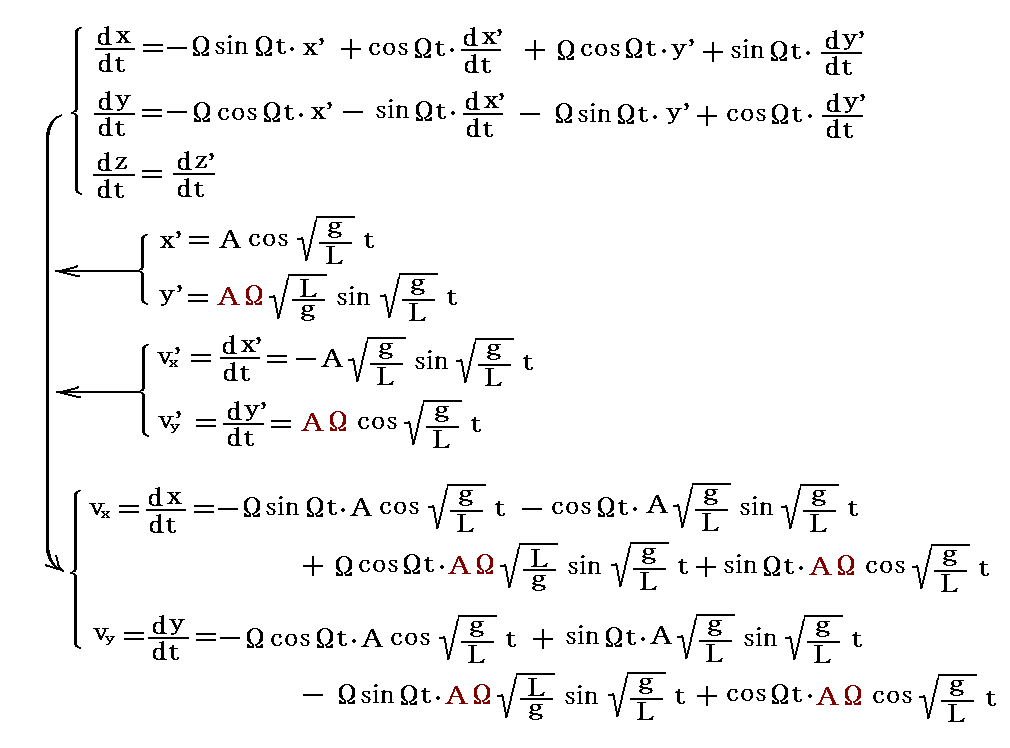
ここで注意して欲しいことはt=0で速度がゼロであることはもちろんですが、時間が
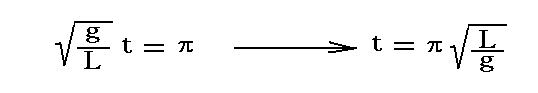
だけ経つごとに速度がゼロになることが繰り返される事です。それは最大振幅を取る時刻に一致します。つまり最大振幅に成ったとき振り子は一瞬静止してそれからまた中心(最下点)に向かって振れ始めるのです。
北半球での重りの軌跡をグラフ表示すると下図のようになる。
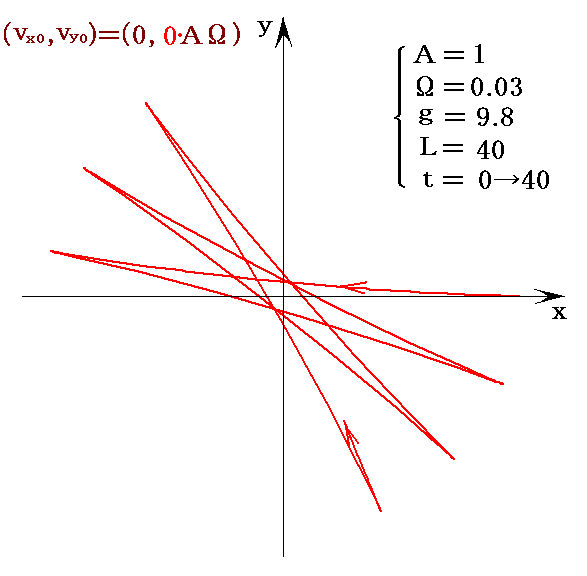
これは最大振幅の位置で、重りを静かに離して振動を開始する場合で、歴史的な実験や今日の博物館などで振り子運動を開始させるときに実際に取られている方法です。
[補足説明]
振り子の振動面が地面に対して回転していく速度は、言うまでもなく(x,y,z)座標系に対して(x’、y’、z’)座標系が回転している角速度と同じ

です。つまり地球自転の角速度に観測地点の地理緯度を乗じた値となります。
3.φ’系でt=0に(x’,y’)=(A,0)の位置で重りに北向き初速(vx0’,vy0’)=(0,2AΩ)を与えて離す
φ系から見ると、t=0に(x,y)=(A,0)の位置で重りに北向き初速(vx0,vy0)=(0,AΩ)を与えて離すことになる。 この場合の軌跡を表す式は、前項の解を座標変換式に代入して
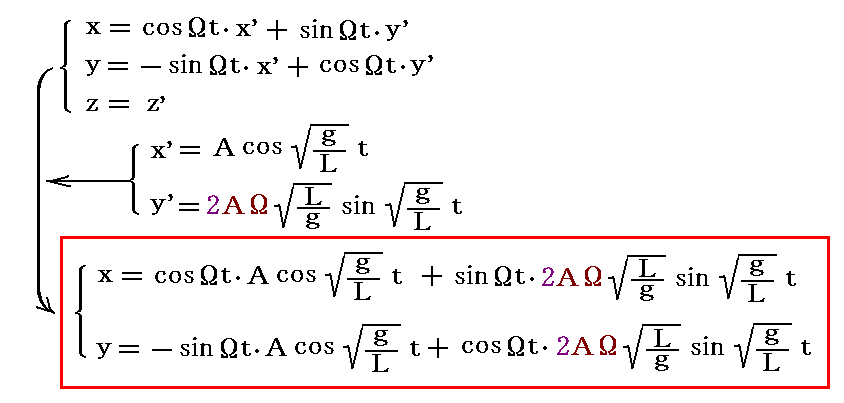
となります。
この場合は中心からの距離rが0に成ることはありません。また速度が0に成ることもありません。歳差運動で回転していく疑似楕円軌道になります。
北半球での軌跡は下図の様になります。
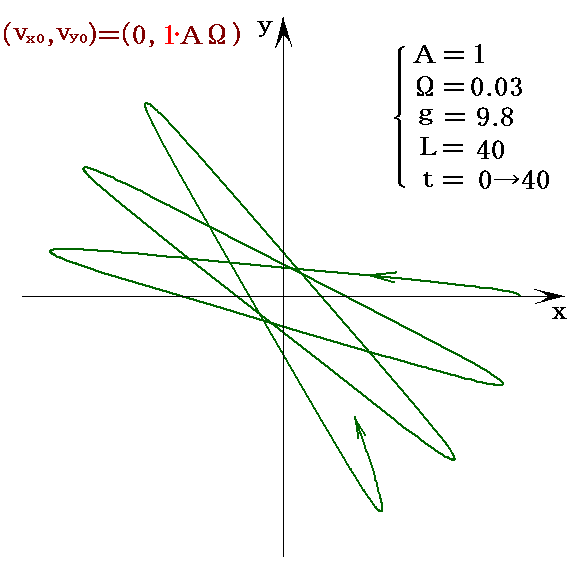
6.φ系での初速度を様々に変えた場合
前項までの議論を復習すれば解るように、φ系に於いてt=0に(x,y)=(A,0)の位置で重りに北向き初速度(vx0,vy0)=(0,nAΩ)を与えて離した場合の軌跡は
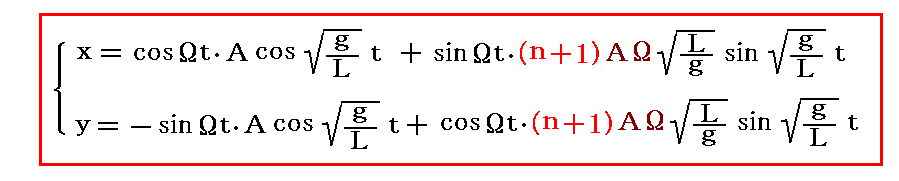
で与えられる。前項5.のそれぞれは1.n=-1、2.n=0、3.n=+1の場合でした。
ついでに、n=-0.5、n=+0.5、n=-5、n=+5の場合を図示しておきます。
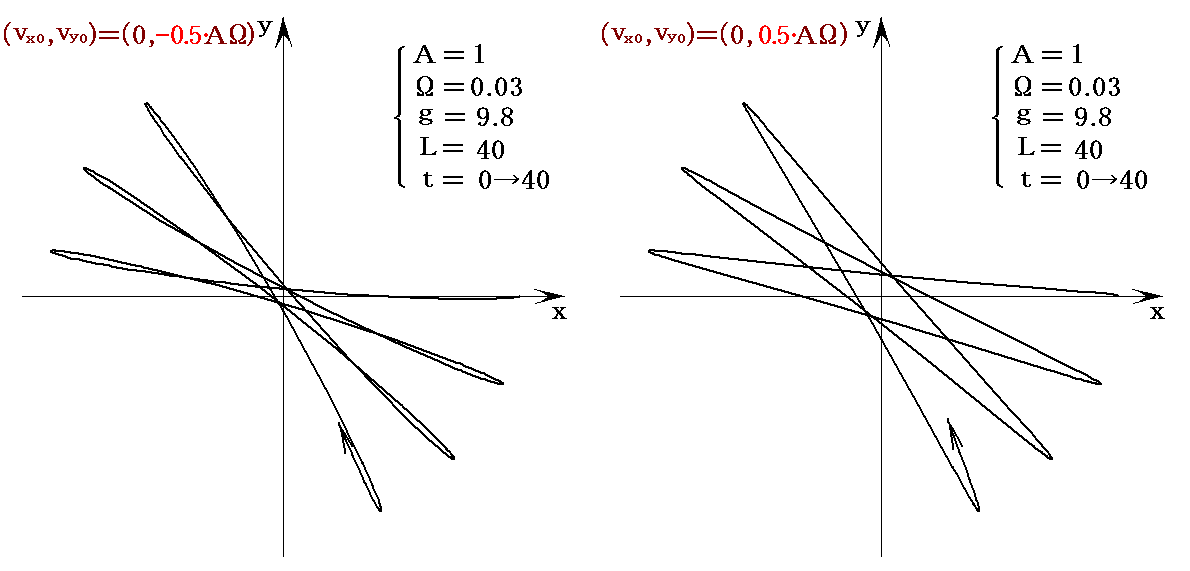
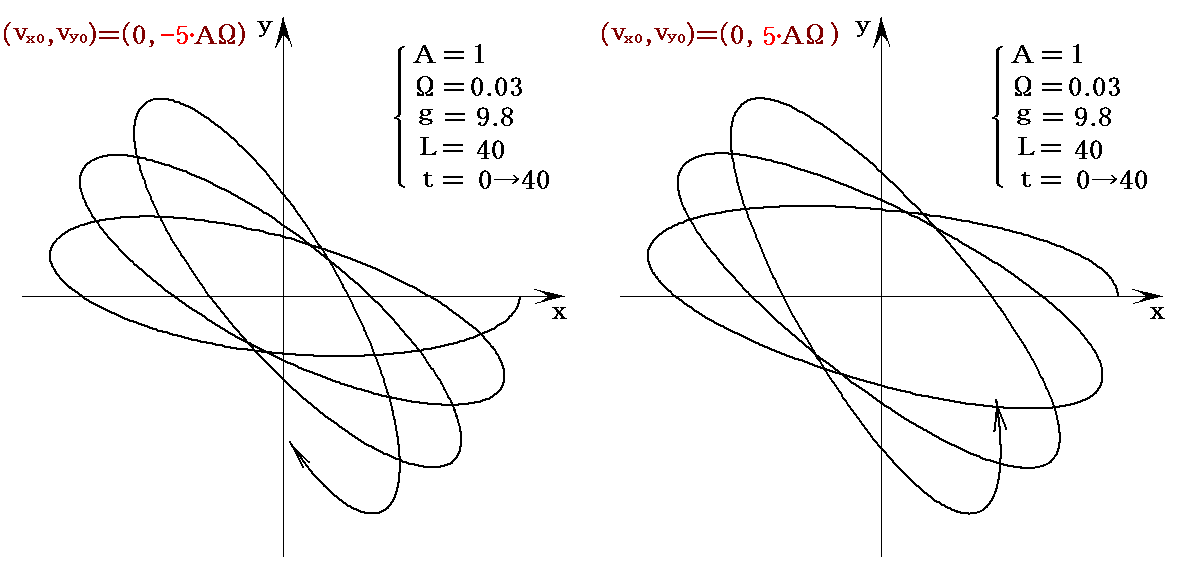
1851年にフーコー(Foucault)は、これらの実験を通じて、地球が自転している事を目に見える形でフランス科学アカデミーの学者や一般大衆に示した。
文献7によると、この実験がアカデミーの科学者に与えた衝撃はとても大きなものだったようです。
フーコーは、“いかにしてこの現象に気づいたのか”を自らアカデミーに報告している。とても興味深いところですので文献7.より引用しておきます。
3.参考文献
この稿のテーマはどんな教科書にも説明されていることなのですが、どれも微妙に解りにくい。ここでは高校生にも理解できるように徹底的にページ数をかけて途中の計算も省略せずに説明しました。
- マックス・プランク著、寺澤寛一、久末啓一郎共訳「理論物理学汎論 第一巻 一般力学(第3版)」裳華房(1928年刊 原本の初版は1916年刊です。)第Ⅰ篇、第5章
この稿の内容についての説明は、この本が完璧です。英語読みで“ニールの放物線”を“ナイルの放物線”と記している本が多いのは、おそらくこの訳本に由来するのだろう。これは昔の物理学者にはとても有名な本で大家と言われる人達は皆この本を勉強されたようですから。
- 原島鮮著「力学(改訂版)」裳華房(1966年刊)§7.4
文献1の内容が、簡略化されて解りやすく紹介されています。
- 小平吉男著「物理数学 第一巻」文献社(岩波書店・原本は1931年刊ですが文献社・復刻版は1971年刊)
この本の第一章§21に文献1.の内容が丁寧に解説されています。
- アーノルド・ゾンマーフェルト著「理論物理学講座Ⅰ 力学」講談社(1969年刊)第Ⅴ章
含蓄深い本ですが、少し難しいです。この本のp183に、低温物理で有名なカメリン・オンネスが1879年にグロニンゲン大学に提出した学位論文で、フーコー振り子の定量的考察を行った事が紹介されています。
- 江沢洋「よくわかる力学」東京図書(1991年刊)§21
解りやすく説明されています。
- ダンネマン著「大自然科学史7」三省堂(1978年刊)p333~335を引用
- アミール・D・アクゼル著「フーコーの振り子」早川書房(2005年刊)
この本を読まれれば、フーコーの振り子が、世界の最先端を担っていた当時のフランス科学界に与えた衝撃の大きさが良く解ります。この中で、第3章 落下実験の説明と第7章 フランス科学界に与えた衝撃の部分を引用。
- ヴラディーミル・イーゴレヴィッチ・アーノルド著「数理解析のパイオニアたち」シュプリンガー・フェァラーク東京(1999年刊)
原題は「ホイヘンスとバロー、ニュートンとフック」で、副題が“伸開線から準結晶まで、数理解析とカタストロフ理論のパイオニアたち”(1989年刊)です。この中の第1章“万有引力の法則”§2にNeilの放物線に関係したニュートンとフックのやりとりが説明されていますので別稿で引用。
- http://meteor.nucl.kyushu-u.ac.jp/home/ja/pendulum/dynamics1.10.pdf
上記のpdfファイルは九州大学のある研究グループのページで紹介されているものです。
この中の3章にフーコー振り子の厳密な運動方程式が、解析力学(ラグクランジアン)を用いて導かれています。解析力学を学んだ人には、解りやすく明快な説明です。
これをご覧になると、フーコー振り子の厳密な運動方程式がいかに複雑なものであるかが解ります。
ただし、いくら厳密な運動方程式が得られても、それを厳密に解くのは容易ではありません。結局近似を用いて解くことになる。