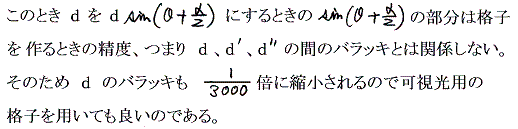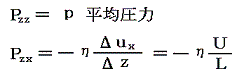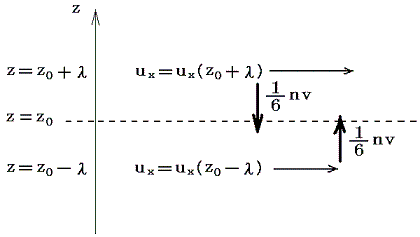このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
アボガドロ定数の測定法
導入.アボガドロ数測定の核心
高等学校で習うように、アボガドロ数が数えられるということは、目に見えないほど小さくて軽い原子や分子の一粒一粒の大きさや、質量が測定できることと同義です。だからアボガドロ数の測定法には様々ありますが、どの測定法でもその測定理論のどこかで原子レベルの大きさ、質量、電気素量また原子数を直接、または間接的に測定する事が必要です。たとえば
- 放射性崩壊を用いる場合は、崩壊していく原子を一つ一つカウントしなければならない。
- 電気素量を用いるのであれば粘性流体中の帯電微小油滴の落下の様子が電気素量一つ一つの違いで異なった動きをするところを、これまた顕微鏡で測定しなければならない(ミリカンの油滴の実験)
- X線回折を用いる方法でも原子の大きさに迫る微細な格子間隔の測定が必要である。X線回折により結晶の格子定数からアボガドロ数を求める場合はとりあえずX線の波長が解っていなければならない。しかしX線の波長を測定可能な人工的に作った回折格子(もちろんその格子幅は顕微鏡か何かで直接測定できるとして)で回折させて測定しなければならないが、そこに何らかの革新的な現象の観察がいる。X線の波長を測定できるような回折格子がどうしてできるのか?
- 粘性係数の測定から平均自由行程を求める方法では分子が飛び回る速度の測定が必要。
- ブラウン運動を用いるのであれば原子一つ一つの衝突(もちろ本当は束になって当たるのだが)の影響でふらふらする微小粒子の振る舞いを顕微鏡で直接観測しなければならない。
結局アボガドロ数を求めるには、原子がいかに小さくても一つ一つの原子が引きおこす微細な現象をどこかの段階でとらえることが必要です。しかし原子や分子はあまりにも小さく、あまりにも軽い。だから原子レベルの微少量を直接測定するのは不可能です。不可能なのに、特別な工夫をすることにより、測定可能な量で代用することができる。そこに各アボガドロ数測定法の独創性がある。以下その核心部分を考察する。
1.放射性崩壊α粒子の測定による方法(1908年)
これは数ある測定法の中で、そのメカニズムがもっとも解りやすい。その方法とは
- 放射性物質の1秒間のα崩壊数を適当な計数管を用いて測定する。
- 崩壊によって生じるα粒子すなわちヘリウムガスの発生量を測定する。
そうして、たとえばヘリウムが標準状態で22.4リットルに達するまでの時間から、その時間の間の総崩壊量を求めるとアボガドロ数NAになる。ラジウムのα(アルファ)粒子(ヘリウムイオン)の放出速度n、ヘリウムの原子量をM、一定時間t秒に得られるヘリウムの生成量mグラムとするとNA=Mnt/mとなる。
この方法の本質は、まさに放射性崩壊で生じる原子を1つ1つカウントできるところにある。初期の実験では崩壊する原子から放射されるアルファ粒子が硫化亜鉛のスクリーンに当たったときに出すシンチレーション(蛍光体に放射線が衝突する際に瞬間的に強く輝く光点が観測される現象)を暗室の中で顕微鏡を覗いて観測していた。これは非常に集中力と根気のいる大変な観測だった。またこの苦労を軽減するものとして考え出されたのがガイガー‐ミュラー計数管(1928年)だ。しかし1つ1つがカウントできる程度の崩壊量では一定量のヘリウム気体を集めるためには莫大な時間が必要になる。そのため、放射性崩壊をカウントするときの物質量とヘリウムを集めるときの物質量を変える。そして、その比が正確に測れる限りにおいて、きるだけ大きな比にした方がよい。
結局測定精度は、どこまで微量の生成ヘリウムの質量mがはかれるか、どこまで長時間のtを取りうるか、どこまでより大きな単位時間あたりの崩壊数nをカウントできるか、どこまで前述の物質量の比を正確に測れるかによって決まってくる。アボガドロ数NA=6.02×1023個/mol はあまりにも大きいので、この方法を持ってしても各部分の測定・分析には極限の技術が必要とされる。
[補足説明1]
実際に放射性物質から崩壊するα線の数をカウントして、アボガドロ数のかなり良い精度の値を得た最初の例は1908年のラザフォードとガイガーであろう。
ガイガーたちは、まず今日“ガイガーカウンター”と呼ばれる装置を開発します。
E.Rutherford and H.Geiger、“An Electrical Method of Counting the Number
of α-Particles from Radio-Active Substances”,Proc.Roy.Soc.London (A) 81 (1908), p141~161
次に、ガイガーカウンターを用いた崩壊α粒子の数と別の方法で求めた崩壊α粒子の全電気量を測定して両者を比較することで電気素量eの値を求めます。その方法はおよそ別ファイルで説明するようなものですが、下記論文で報告されています。
E.Rutherford and H.Geiger、“The Charge and Nature of the α-Particle”,Proc.Roy.Soc.London (A) 81 (1908), p162~173 [物理学史研究刊行会編「物理学古典論文叢書7 放射能」東海大学出版会(1970年刊)論文12に日本語訳あり]

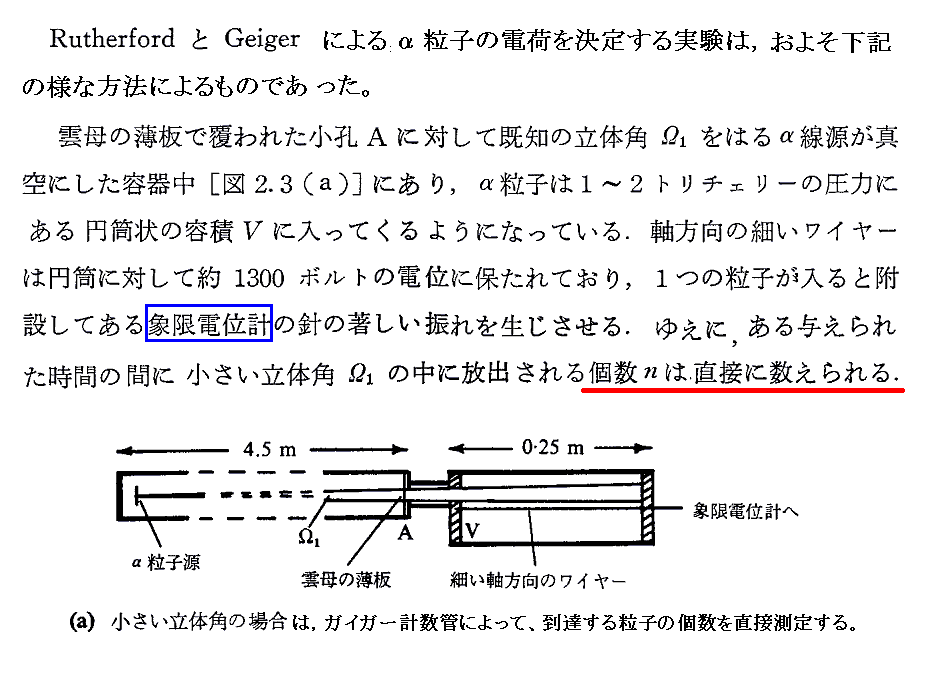
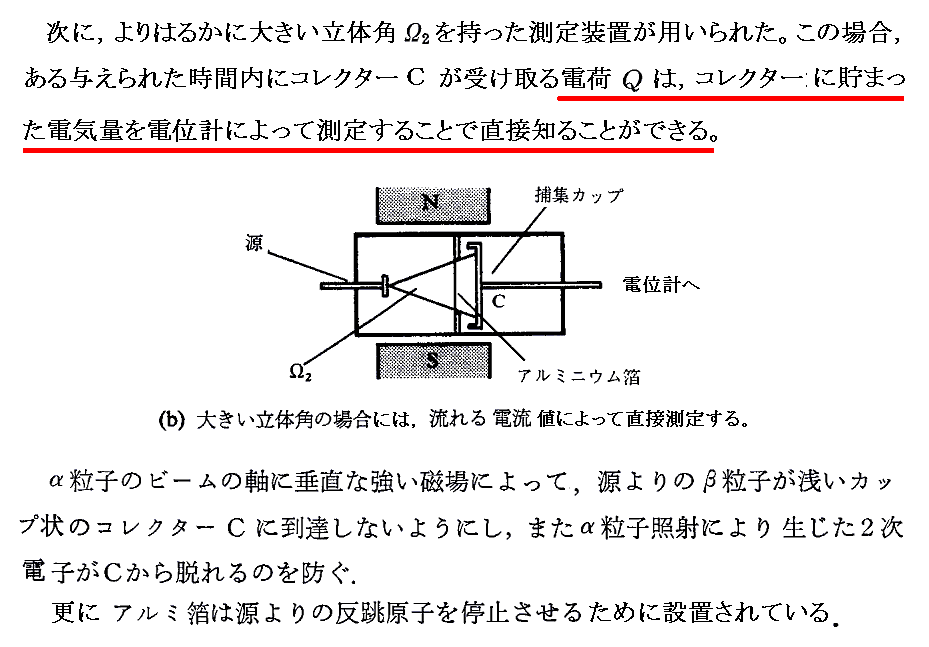
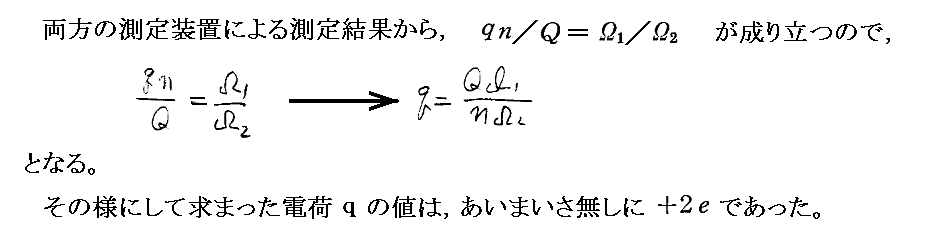
彼らが求めた電気素量e=4.65×10-10esu=1.55×10-19Cとファラデー定数から計算したアボガドロ数は今日の表現でいくとNA=6.09×1023個/molという値です。今日の正確な値はe=1.60×10-19CとNA=6.02×1023個/molですから、これらの値は当時としては驚くべき精度です。
[上記の二つの論文はRoyalSocietyの公式サイト(http://rspa.royalsocietypublishing.org/)からダウロードしたものです。]
この当たりについては、別稿「Perrinのソルヴェイ会議報告」Ⅷ.も参照されて下さい。
[補足説明2]
ちなみに上記の精度のアボガドロ数を最初に求めたのはマックス・プランク(M. Planck,“Zur Theorie des Gesetzes
der Energieverteilung im Normalspectrum”, Verhandlungen der Deutchen Physicalischen
Gesellschaft, 2, 237~245, 1900年)です。彼は自らが発見した黒体輻射の理論と、当時の黒体(空洞)輻射エネルギースペクトル分布の観測値を比較することで、プランク定数h、ボルツマン定数kBを導いて見せます。
これらの値を用いると電気素量やアポガドロ数も計算できて、今日の表現でそれぞれe=4.69×10-10esu=1.56×10-19CとNA=6.18×1023個/molとなります。これは精度に於いて他の測定法に約10年先行しており、偉大な功績です。
残念なことに黒体輻射の理論はあまりにも複雑で難解なためにアボガドロ数測定法として紹介されることはあまり無いのですが、もっと注目されても良い業績だと思います。
アブラハム・パイス著「神は老獪にして・・・(アインシュタインの人と学問)」産業図書(1982年刊)のp681に、アインシュタインが、1919年の物理学賞の候補者の推薦依頼をストックホルムから受けて、プランクを推薦したことが書かれている。
その推薦理由として、とりわけ二つの論文「正常スペクトル中のエネルギー分布法則について」と「物質と電気の素量子について」をあげた。[別稿の文献7.と8.]
そして “この仕事によって、著者(プランク)は原子の絶対的な大きさを正確に決定しただけでなく、すべての物理学に取って大変実り多いことが最近明らかになってきた量子論の基礎を、特に(彼が)築いたのです。” と述べている。
アインシュタインはプランクの上記の業績を高く評価していたようですね。
2.電気素量の測定とファラデー定数の測定から求める方法(ミリカン1910年)
これは数ある測定法の中で、もっとも有名で初期において精密な測定を可能にした。
(1)ファラデーの電気分解の法則(1833年)とファラデー定数
1833年にファラデーは以下の電気分解の法則を実験的に発見した。
Philosophical Transactions of the Royal Society, 1834年
http://www.chemteam.info/Chem-History/Faraday-electrochem.html
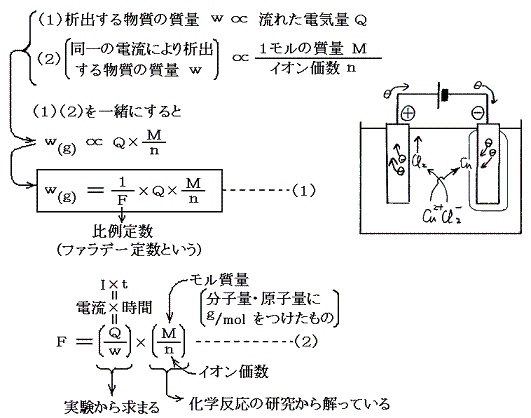
(2)式において分子量・原子量Mやイオン価数nは1800年代の初めにラボアジェ、プルースト、ドルトン、ゲイリュサック、アボガドロ等の化学反応の比較研究から解っている。目に見えないほど微細な原子や分子の相対的質量である原子量や分子量がどうして解ったのかは非常に興味あるところで、化学創生期の一大成果なのだが、その説明は稿を改めてするのでここでは省略する。
流れた電気量Qや極板に析出した物質量wは測定可能なので、ファラデー定数Fは実験によって求めることができる。その測定値はF=96500Cであった。
ファラデーの発見した事柄を原子論の立場で検討してみる。
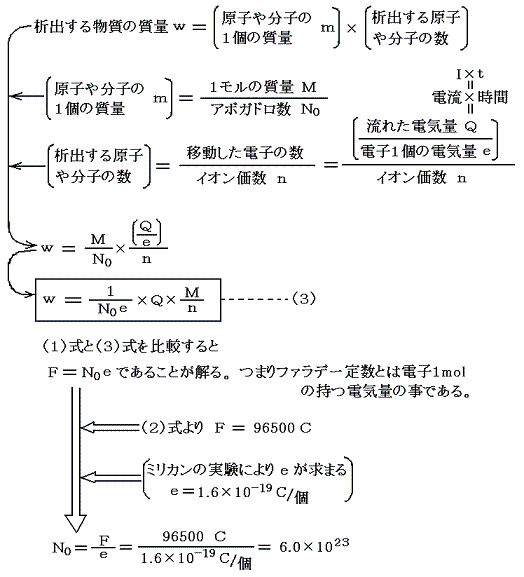
つまり電気素量eの値さえ測定できれば、アボガドロ数は測定できる。しかし電気素量の値はあまりにも小さい。それがいかにして可能になったのか?
(2)ミリカンの電気素量測定実験(1906~1917年)
ミリカンの実験は高校物理で習う所だが、その手法を簡単に復習する。電気素量はあまりにも小さいが、霧の微細な粒子を帯電させ電場の中で釣り合わせる事により電子1個が持つ電気量の違いを測定できた。
https://www.aip.org/history/gap/Millikan/Millikan.html
R. A. Millikan, “A new modification of the cloud method of determining
the elementary electrical charg and the most probable value of that charge”,
Phil. Mag., 19, p209~228, 1910年
R. A. Millikan, “The isolation of an ion, a precision measurement of its
charge, and the correction of stokes's law”, Physical Review, vol.32, p349~397, 1911年 [この論文の抄訳はこちらを参照]
R. A. Millikan, “On the elementary electrical charge and the avogadro constant”,
Physical Review, vol.Ⅱ, No.2, p109~143, 1913年
下図は1917年の実験の装置図ですが、1913年の装置も基本的にこれと同じです。
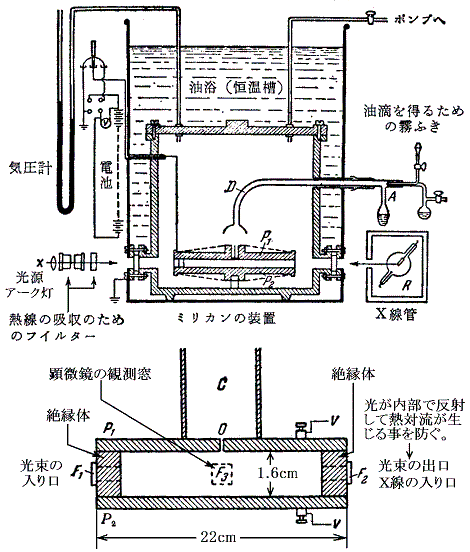
観測はF1から入射した照明光束に垂直な窓F3を通して行われるので、顕微鏡視野内の油滴は、暗い背景のなかで星のように見える。(チンダル現象を利用した限外顕微鏡の原理で非常に微細な粒子でもその存在と位置が解る)

X線用いて極板の間の空気を電離させることにより、油的の電荷を変化させることができる。そのとき電場の強さがもとのままだと、油的の速度は変化してv’Eとなる。このときの電気量q’は(7)式のようになる。
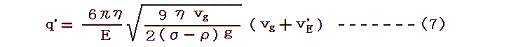
(6)式と(7)式を組み合わせると
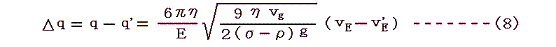
が得られる。ミリカンはX線照射により何度か電荷を変えつつ、同一の油滴を使ってたくさんの回数の測定を行いΔqがある最小値の整数倍になることを確かめた。この最小値こそが電気素量(電子1個が持つ電気量)
e だった。
この方法によるとき、電気素量はあまりにも小さいから、その違いが一つ二つと数えられる帯電状態の違いを判別するにはいかに小さくて軽い油滴を用いるかが重要である。実際ミリカンの用いた油滴は0.001mm=10-6mのオーダで当時の光学顕微鏡を用いてその大きさが測定できるようなものではない。前述の様に光の散乱でその存在とその位置が測定できるだけである。ところでqを求めるには油滴の質量が解らねばならない。油の密度は測定できるから結局油滴の半径が解らねばならない。その半径は直接測定できるほど大きくはない。半径の測定に変わるものに置き換えなければならない。それが粘性係数ηである。だからこの方法の鍵は粘性流体(空気)の中を動く球に働く抵抗力を表すストークス(Stokes)の公式にある。
ストークスの公式はもともと巨視的な流体力学の運動方程式(Navier-Stokes粘性流体運動方程式)を巨視的・数学的に解くことにより求められる。そこには微視的な考察はどこにも必要ない。Navier-Stokesの方程式は粘性流体における[変形]と[応力]の関係を記述する単なる数学的な関係(ニュートンの運動の第二法則を数学的に変形したという意味)で,粘性係数ηは[変形]と[応力]を結びつける[比例定数]として導入されるだけである。このとき粘性係数ηが測定できなければ、この運動方程式も単なる数式のもてあそびにすぎないのだが、Navier-Stokesの方程式はηを測定する方法も与えてくれる。それには、この複雑な偏微分方程式が数学的に完全に解ける希有な場合の結論を用いればよい。たとえば粘性流体が円筒パイプ中を定常的に流れているとき成り立つ関係式

において、流量Q、圧力差(p1-p2)、円筒の長さL、円筒の半径aなどを測定すれば粘性係数ηは求まる(実際にはもっと測定に便利な同心二重円筒内の流体系などが用いられる)。そしてこの式は実験結果と良くあう。そのことが、元に返ってNavier-Stokesの方程式(粘性流体における変形と応力との関係についての仮定)の正当性と固体表面では粘性流体が滑らないという境界条件の妥当性を示しているといってもよい。そのηを、同じくNavier-Stokesの方程式を数学的に解いて得られるStokesの法則に適応すれば油滴の半径aを求める事ができる。物理理論の連携のすばらしい勝利。ミリカンの油滴の実験の本質はここにある。
[補足説明1]
物理理論のすばらしい成果なのだが、問題はStokesの法則がミリカンの用いた油滴ほど小さな球体に対して正確に成り立つかというところにある。流体力学の理論はNavier-Stokesの方程式を含めすべて連続的な媒質についての議論なので、油滴があまりにも小さいと成り立たなくなる。つまり油滴の大きさ(10-6m程度)が気体分子の平均自由行程(常温、1気圧で10-7m程度)に近づくと成り立たなくなる。ミリカンの実験から電気素量、ひいてはアボガドロ数を求めるときの数値の信頼性はひとえにStokesの公式の正当性にかかっている。
そのためミリカンはStokesの公式に気体圧力P(平均自由行程は気体の圧力に逆比例する)の補正項を導入したものを用い、様々な圧力における e
の値を測定しグラフ化して圧力Pが無限大の極限値をグラフの外挿法により求めている。そのとき液滴粒子の種類や気体の種類を変えても同じ e の値が得られたことをもって補正項の正当性を評価している。
気体分子の平均自由行程の見積もりについては4.ロシュミットの測定法を参照。
補足しますとアインシュタインの“ブラウン運動理論”に於いても運動微粒子(10-6m=1μm)に対するStokesの公式の正当性が問題になりました。
ブラウン運動を確認するためにPerrinが水中に浮かべた球形微粒子の大きさも、ミリカンの用いた油滴と同じ程度の大きさでした。しかし、この場合は水中での移動ですから、液体分子の平均自由行程は気体の場合に比べてはるかに小さいために、Stokesの公式は問題なく成り立ちます。
このことに付いては別稿「Einsteinのブラウン運動理論とPerrinの検証実験」4.(2)[補足説明1]を参照。
さらに補足しますと、ペランの観察実験は顕微下での観測だったので、球形微粒子の大きさは顕微鏡によって正確に測定できました。しかしミリカンの油滴は低倍率の読み取り顕微鏡(限外顕微鏡の原理でその存在と位置が解るだけ)による移動速度の測定ですので、油滴微粒子の大きさを正確に測定することはできません。
ミリカンは油滴を重力下で自由落下させて、その落下速度を観測してStokes公式を使って逆にその大きさを求めます。その様にして半径が解った油滴にX線を照射して帯電させ、さらに電場を加えて油滴の移動速度を測定して帯電電気量を測定した。
[補足説明2]
この方法におけるもう一つの誤差の原因は粘性係数の測定値にある。事実初期の測定値の誤差はこの測定値の不確かさによることを指摘したのは日本の芝亀吉(1932年)です。
[補足説明3]
ミリカンの実験の極板間隔は1.6cm、極板間電圧は約5000Vである。ところで空気の絶縁性耐電圧は1cmあたり1万ボルト程度である。だから空気の耐電圧内にぎりぎり収まるほど高電圧をかけなければならなかったというところに注意。実際ミリカンは実験中にたびたび起こる極板間の放電破壊に悩まされます。それほど電気素量は小さいということです。だから油滴の小ささも、電圧の大きさもぎりぎりの極限での実験だった。
[補足説明4]
ミリカンの実験には先行する研究があります。それは C.T.R.ウィルソンが発見(1895~1897年)した気体を断熱膨張させると帯電粒子を凝結核として霧が発生する現象を用いるもので、J.S.E.タウンゼント(1897年)、J..J.トムソン(1898~1903年)、H.A.ウィルソン(1903年)などにより行われた。その詳細はジョージ・P・トムソン著「J.J.トムソン(電子の発見者)」第4章が詳しい。別稿で引用していますので是非ご覧下さい。この当たりの研究は後に、C.T.R.ウィルソンの 霧箱の発明(1911年) や 雷の研究(1916~1928年) にも繋がるものです。
彼らは巧妙かつ独創的な方法で霧の全質量、霧が持つ全電気量を測定し、そして霧の水滴の大きさを測定して霧粒の数を計算することで電気素量eを求めた。そのとき水滴の大きさを決めるのに“ストークスの公式”が用いられた。
この当たりについては、別稿「Perrinのソルヴェイ会議報告」Ⅶ.も参照されて下さい。
ミリカンの研究は、その“ストークスの公式”によって水滴の大きさを決定する方法を受け継いだものです。ミリカンが独創的だったのは、水滴の集合体の霧全体ではなくて、“水滴”一粒一粒に着目して、電場の中で帯電状態を変えながら一つの水滴を継続的に追跡して測定したことです。後に水滴を蒸発しにくい“油滴”に変えて更に測定精度を向上させる。
先行する研究を含めたミリカンの業績のもう少し詳しい説明は、別稿「原子物理学本論(1952年)」第1章をご覧下さい。なお、この元になったMillikan著“The Electron”(1924年)も別稿で引用していますので合わせて参照されて下さい。
3.人工の可視光学的回折格子を用いた測定で波長の解っているX線を用いて行った結晶回折像から求める方法(1923年)
高校教科書には食塩などの結晶格子を用いてX線波長を求めることが論じられているが、ここではそのような結晶格子を用いることはできない。なぜなら結晶の格子間隔を知るためにはアボガドロ数が解っていなければならないからです。だから他の方法で格子線の間隔が直接測定された回折格子を用いてX線の波長を求めなければならない。
いったんX線の波長測定できれば、後は食塩などの結晶格子を用いたX線回折の干渉縞の測定値から[食塩の結晶の格子間隔(原子と原子距離)]を求め、それに[食塩の式量(いわゆる相対質量で1800年代から化学反応の研究から解っている)]と[食塩の密度の測定値]を用いてアボガドロ数を求めることができる。(この部分は高校物理の練習問題で解くところ)
ところでX線の波長は原子レベルの大きさである。そのレベルの波長を測定するには回折格子の格子間隔は少なくとも原子の大きさの1000倍程度以内でなければならない。(これは回折格子によって干渉縞ができるメカニズムを復習すれば理解できる。回折格子によって可視光の波長を測定した生徒実験を思い出せ。)つまり10-7m=0.0001mm程度以下でなければならない。この大きさは顕微鏡を用いても測定不可能である。
ところが以下に述べるように、この1000倍程度の格子間隔(つまり0.1mm程度)を持ち光学顕微鏡でその間隔を直接測定できる様な回折格子を用いてX線の波長が測定できるのです!
事の発端はX線が空気中から結晶に入るとき屈折率が1よりもわずかに小さくなることが発見されたことにある。これはX線が空気中から固体に入るとき全反射を受けることを意味する。ただし1よりわずかに小さいだけだから全反射の起こる臨界角も大きく90度にちかい。実際λ=1.279×10-10mのX線が密度2.53のクラウンガラスに入射する場合臨界角は89度49秒(照射角は11秒)となる。この発見は臨界角より大きな反射角(非常に小さな照射角=θ)で使うならば普通の光学的な回折格子を反射格子として使って、X線スペクトルが得られることを示した。(1923年コンプトン)
この方法の本質は下図に示すように、非常に小さな照射角度θで全反射させて回折像を得るために、回折格子の格子間隔が3/1000倍程度に縮小されるのと同じ効果を得ることができるところにある。つまり格子間隔が0.1~0.01mm程度の普通の光学的回折格子を用いてX線の波長が求められる。
x線の全反射を報告した論文
Arthur H. Compton, “The total reflexion of X-rays”, Phil. Mag., 45, p1121-1131, 1923年
格子間隔が直接測定できている回折格子で初めてx線の波長を測定した論文
R. L. Doan and A. H. Compton, “X-Ray Spectra from a Ruled Reflection Grating”,
Proceedings of the National Academy of Sciences of the United States of
America, 11, 11, p598-601, 1925年
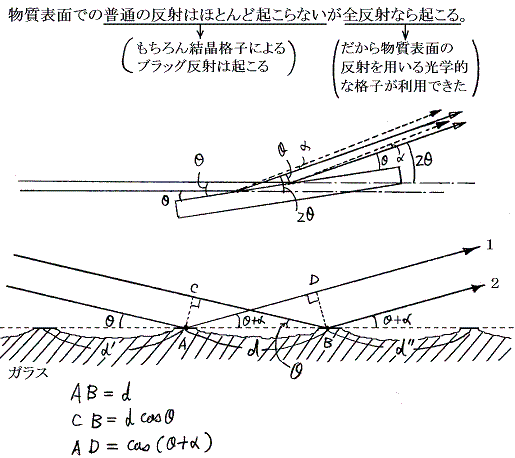
上図の経路1と2の光路差はCB-ADだから角度θ+αの方向へ反射するX線の波長をλとすると
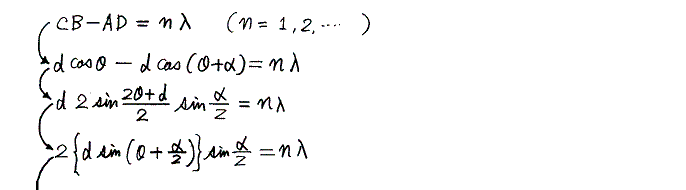


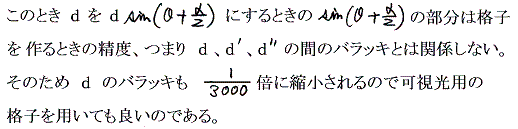
いったんX線の絶対波長が測定できれば式量と密度が解っている結晶のX線回折からアボガドロ数を求めることができる。ここは高校物理や化学で習うところなので省略する。
[補足説明]
この方法が確立してからは電気素量の測定による方法よりも、より正確なアボガドロ数値を得ることができるようになった。そのためファラデー定数をX線解析の結果得られたアボガドロ数で割る方法により、より正確な電気素量を得ることができるようになった。
しかし、1929年当時両者の測定値に【X線波長あるいは格子定数の段階で】0.2%程度の違い【ちなみにアボガドロ数あるいは電子の電気量の段階では0.66%程度の違い】があることが明らかになって大問題になったことがある。
その違いは、結局ミリカンが採用した粘性係数ηの値が小さすぎることだったのだが、それを明らかにしたのは日本人の芝亀吉(1932年)です。ちなみに【粘性係数ηの段階】では0.5%程度の違いになります。
この当たりの詳細は、菊池正士著「原子物理學本論(上)(下)」岩波書店(1952年刊)の§1.6、及び§15.13~14を参照。
4.ロシュミットの測定法(1865年)
ロシュミット(http://www.loschmidt.cz/)は以下の方法で気体の単位体積中の分子数をみつもった。
J. Loschmidt, Sitzungsberichte der K. K. Akademie der Wissenschften in
Wien, Abteilung Ⅱ, Bd.52, S.395, 1865年
上記論文の英訳が下記URLに在ります。
http://www.chemteam.info/Chem-History/Loschmidt-1865.html
(Johann Loschmidt, “On the Size of the Air Molecules”, Proceedings of the
Academy of Science of Vienna vol. 52, p395~413, 1865年)
この方法は年代的には一番最初です。しかし精度は良くない。彼が用いた手順は
- 粘性係数の測定値から、気体分子の平均自由行程を求める。
- 同じ物質の液体と気体の密度の比較から、気体の全体積中に占める分子自身の体積の割合を求める。
この二つのデータを基礎にして計算を行った。
(1)簡単な説明
まず、このような考え方で分子の大きさ、ひいてはアボガドロ数の算出が可能なことを簡単な計算で見積もってみよう。もし[アボガドロ数NA]が解っていたとすると先ず液体状態(原子は互いに密に接している)の物質1モル(Mグラム)の体積をNAで割ることから分子1個の体積、ひいては[分子の大きさ]~10-10mが解る。次に液体が蒸発して1モルの気体となったとき占める体積は、高校で習うように0℃、1atmで22.4×10-3m3であることが当時解っている。その値をアボガドロ数NAで割って1つの気体分子が占める平均の体積を求めると、[気体状態における分子間の平均的な距離]が分子直径の10倍程度になることがわかる。
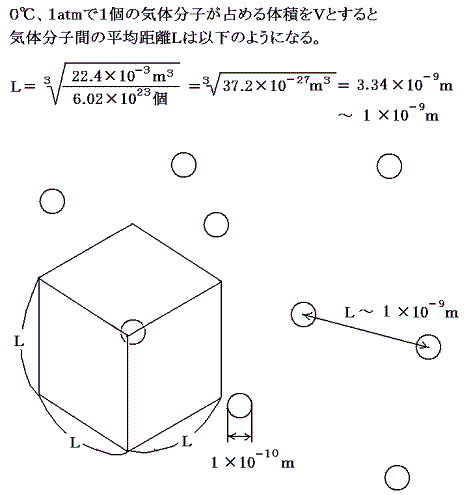
つまり気体状態の分子は、上図の様に分子直径の10倍程度の間隔でもって空間を占めていることが解る。当時、気体分子が飛び回る速度は音速と同等かそれ以上であることは解っていた。だから大きさを持った気体分子の空間占有率の幾何学的配置が解ると気体がどの程度ぶつからずに空間を直進できるか予想できる。図上で考えて分子直径の1000倍程度、分子間平均距離の100倍程度=約10-7m程度であろう。つまり衝突から次ぎの衝突までに進む空間的な距離の平均値(これを平均自由行程という)を計算できることになる。
以上の議論を逆にたどると、もし何らかの方法で[平均自由行程]と[気体が存在する体積空間中で分子が占める体積の割合]が解っていたら[アボガドロ数NA]が見積もれることになる。
(2)詳しい説明
以下で、このあたりをもう少し精密化する。

[補足説明1]
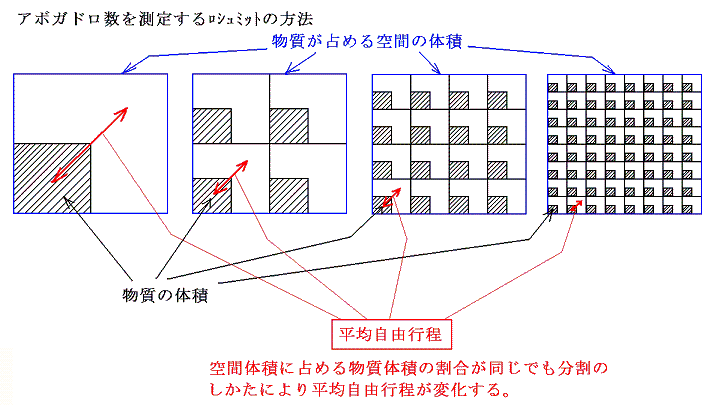
ここで次のことに注意してほしい。分子そのものの体積と分子1個が平均的にしめる空間の体積の比率はアボガドロ数がいくつであっても等い。つまり1molの気体が占める空間体積22.4×10-3m3の中で分子が占めている体積(たとえば水の場合18cm3)の相対的な大きさの比率は分子の大きさがどのようであっても、いつも等しいと言うことである。それはちょうど下図で分子のしめる部分とそれ以外の余白の部分の割合が等しいということである。
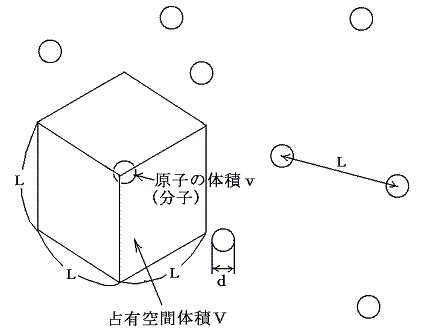
このときアボガドロ数というのは、1molの液体の体積(たとえば水の場合18cm3)を分割する数のことである。液体は分子が互いに密に接して存在する状態だから、たとえば、もしアボガドロ数NAが1個/molなら分子1個の体積がv=18cm3であり、気体になったときの分子1個が占める空間体積がV=22.4×10-3m3となることを意味する。もしNA=106個/molならv=18×10-6cm3でありV=22.4×10-9m3となる。さらにNA=1023個/molならv=18×10-23cm3でありV=22.4×10-26m3となることを言っている。
空間をしめる比率が同じだから、その様子を示す図はスケールが違うだけで余白の中で分子が占めている様子はすべて同じである。様子が同じなら分子の速度がそれらの平均間隔Lに比較して桁違いに大きいのだから平均自由行程λはそれぞれのスケールの図の様子から想像されるようにそれぞれの場合のLの100倍程度であろう。つまりNA=1個/molの場合L~0.3m程度だから平均自由行程λ~数十m程度、NA=106個/molの場合L~10-3m程度だからλ~10-1m程度、NA=1023個/molの場合L~10-9m程度だからλ~10-7m程度となる。
これは同じ1molの液体の体積(水の場合18cm3)を分子に分割する数により、平均自由行程が異なる事を言っている。だからもし、なんらかの方法で平均自由行程を知ることができたら、分割の数(アボガドロ数)が解るということです。
[補足説明2]
ちなみに、平均自由行程の概念を最初に導入したのはクラウジウスです。前記の関係式(1)は彼の1858年の論文で与えられる。
(3)平均自由行程の見積もり
故にロシュミットの議論の本質は気体分子の平均自由行程を求める方法にある。高校生には少し難しいが以下で説明する。このときの要点は平均自由行程が粘性係数に関係づけられるということと分子速度が当時予測可能になっていたことです。
粘性係数の定義
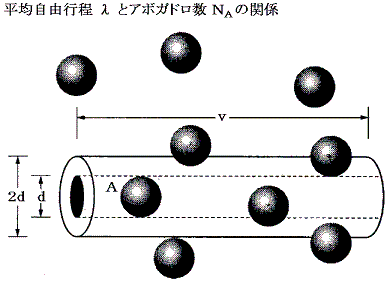
今三次元直交座標でz軸に垂直な2つの無限平面を考える。z=0の面が静止しており、z=Lの面がx軸の性の方向へuxで動いているとする。この二面の間に存在する希薄気体の流れは下図の様なものであると考えられる。
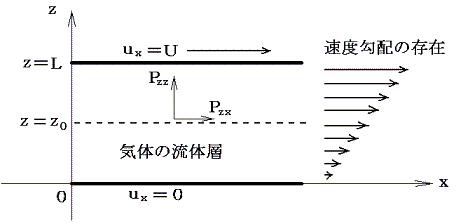
この流体のz=z0の位置にz軸に垂直な仮想的な面を考える。この面を通して上下の流体は互いに押し合っている。これが力Pzzであり、これが流体中の平均圧力pである。さらに、この面の上側の流体はこの面の下側の流体をx軸の正方向に引きずり、この面の下側の流体はこの面の上側の流体をx軸の負方向へ引きずろうとする。そのためこの面の上下で反対向きの剪断応力が生じる。両者は当然作用反作用の法則で大きさは等しい。この力の内、面の下側の流体が面の上側の流体に及ぼす、x方向の、面の単位面積当たりの平均の力をPzxとする。この力はuxのz方向の変化が存在しないと消えてしまうので、Δux/Δzが比較的小さいときにはΔux/Δzに比例するであろう。その比例定数が粘性係数ηである。
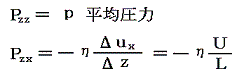
粘性係数と平均自由行程
上記流体中の流れに平行な面にそう力の源は、その面を通して上下の異なったx方向の運動量を持つ気体が交換されることにある。面の上側の部分は相対的にuxの小さい気体が入ってくることにより全体としての運動量が減少する。つまりx軸の負方向へ引き戻す力を受けたことになる。(運動量の変化は力積に等しい)。逆に面の下側の部分にはuxが大きな気体が流入してくる。そのためx方向の運動量が増大しx軸の正方向の力を受ける。
分子の質量をm、分子の平均的な熱運動の速さをv、単位体積あたりの分子数をn、平均自由行程をλとする。
いま気体分子がプラスマイナスを含めたx、y、zの6方向に同等の確率で動いているとすると、単位時間、単位面積を通してz軸に垂直な面をしたから上に超えて行く分子数はnv/6個である。そのとき平均自由行程の考え方から、z=z0の面を超えて流入してくる分子は、z=z0-λの所から、その点におけるx成分の運動量m×ux(z0-λ)を以て流入してくると考えられる。ux(z0-λ)はz=z0-λの点の速度成分であるが近似的にux(z0)-(Δux/Δz)λと考えられる。同様にz=z0の面を通して単位時間、単位面積当たり面の上から下へ流出していく粒子数と運動量はnv/6個とm×ux(z0+λ)となる。ux(z0+λ)はz=z0+λの点の速度成分であるが近似的にux(z0)+(Δux/Δz)λと考えられる。
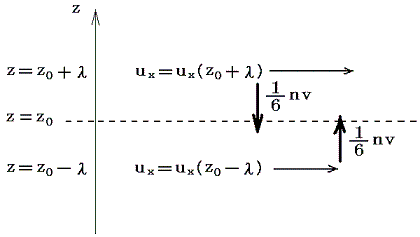
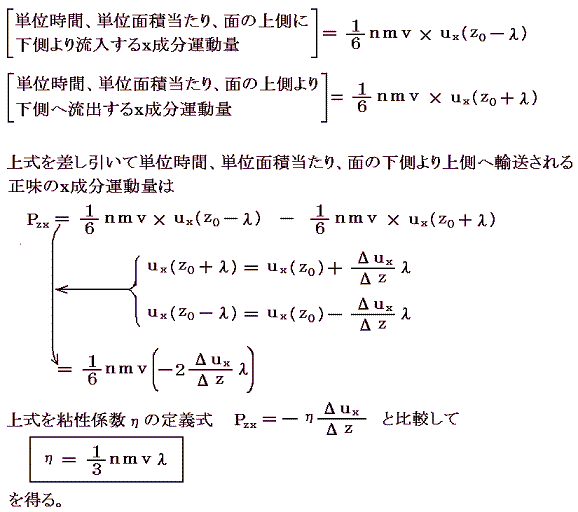
この中でnmは単位体積当たりの気体質量(気体密度)だから測定可能。“粘性係数”ηも前出の2.(3)で述べた流体力学の理論より測定可能。また気体の熱運動の“分子速度”vは気体分子運動論から当時予測可能になっていた。簡単な気体分子運動論は高校物理Ⅱで習う。そのとき分子速度を分子量・絶対温度・気体定数(いずれも測定可能)で表す式を導く。(別稿「音速の理論2(分子速度と比熱比)」1.(2)参照)
これらの値を用いて“平均自由行程”λを求めることができる。例えば気体が0℃1気圧の空気の場合η=1.7×10-5Pa・s、nm=1.3kg/m3、v=4.9×102m/s、を代入すると平均自由行程λ~10-7mが得られる。この値を上記4.(2)項の(3)式に代入すればアボガドロ数が求まる。
ロシュミットは、空気分子の大きさとして10-6mmを得た。(これは今日知られている値のほぼ4倍である)。また単位体積中の気体分子の数が分子の種類によらないことを述べたが、その数自体を論文中には与えなかった。しかしそれは彼の与えている式から算出できる。実際、その後の論文(1867)ではその値を8.66×1017個/cm3と与えている。今日、標準状態(0℃、1気圧)の気体1cm3に含まれる分子の数は「ロシュミット数(NL=2.6869×1019個/cm3)」と呼ばれている。
[補足説明1]
すでに述べたように、最初に“平均自由行程”の概念を導入して(1)式を導いたのはR. Clausiusです。このことについては別稿「音速の理論2」3.(6)2.をご覧下さい。
それを上記の様な考え方で“粘性係数”と結びつけて、“平均自由行程”の具体的な値を最初に求めたのはJ. C. Maxwellです。彼は下記論文(1860年)のPartⅠの最後で、彼の速度分布則と気体の粘性係数の測定値から気体分子の平均自由行程を算出している。
J. C. Maxwell,“Illustrations of the Dynamical Theory of Gases”, Phil.
Mag., (4)vol.19, p19~32(PartⅠ), 1860年;vol.20, p21~33(PartⅡ), p33~37(PartⅢ),
1860年 または Scientific Papers, Vol. 1, p377~409(Dover pub.) これらはネットからダウンロードできます。
また、物理学史研究刊行会編「物理学古典論文叢書5 気体分子運動論」東海大学出版会(1971年刊)に日本語訳があります。
J. Loschmidtは、上記のマクスウェルの論文を読み、平均自由行程の値を用いれば分子の具体的な大きさや数(アボガドロ数)が求まるとして、それを実行しました。
同様な算定は1860年代末から1870年代初めにかけて何人もの人々によって行われ、気体運動論の成果を広めるのに貢献した。
[補足説明2]
気体分子の運動速度が直接測定されたのは、Michelsonによる発光気体のスペクトル線のぼやけ方の測定(1892年)によるものが最初です。彼は発光気体の運動速度vによりドップラー効果が生じてスペクトル線はぼやけることを利用した。その波長の広がりΔλにスペクトル線の振動数fを乗じたものが、分子速度vにほぼ等しくなる。(ドップラー効果の公式《説明1、説明2、説明3》を思い出せば高校生でも導ける。)
原子線を用いる方法による直接の検証はOtto Sternによって1920年に初めて行なわれた。
5.コロイド粒子のブラウン運動の観察による方法(ペラン1909年)
これは1905年にアルバート・アインシュタインが求めたブラウン運動に付いての理論式に基づいて、ジャン・ペランが実験[人工的に作った微小粒子のブラウン運動を観察]して求めたものです。
アインシュタインの1905年のブラウン運動論文の日本語訳は様々出版されています。
またペランの論文
Annales de Chimie et de Physique 18, p1~114, 1909年
の英語抄訳が下記URLに在ります。
http://web.lemoyne.edu/~giunta/perrin.html
また、英語全訳版のpdfファイルはこちらに在ります。
また、ペランは第1回ソルヴェイ会議(1911年)で“分子の実在性の証明”のテーマで上記論文の内容を報告しています。その中の後半部で様々なアボガドロ数の測定法についても報告しています。この日本語訳が
物理科学の古典8「第1回ソルベイ会議報告」東海大学出版会(1983年刊)
にありますのでご覧下さい。
ちなみに、第1回ソルヴェイ会議は、“原子論の確立と量子論の幕開け”を告げる有名な会議ですが、上記ペランの報告は、原子論確立の最終章を飾るものの一つと言えます。最終章を飾る他の発見としては、この少し後に続くX線回折・電子線回折がありますが、これらは量子論の幕開けにも深く関係します(コンプトン効果、ド・ブロイの物質波の仮説)。
この方法の説明には、かなりの準備が必要で高校生には少し難しいので省略します。ただし
江沢洋著 岩波科学の本シリーズ17 「だれが原子をみたか」 岩波書店 1976年刊 p256~292
(これは岩波現代文庫で安価に再版されています)
に、高校生にも十分理解できる懇切丁寧な説明があるので興味のある人は読まれたし。
2022年2月にブラウン運動理論によるアボガドロ数測定法を説明するページ
「Einsteinのブラウン運動理論 と Perrinの検証実験」
をupしましたのでご覧下さい。
2022年12月にファインマン物理Ⅱ「光、熱、波動」第15章“統計力学の原理”、第16章“ブラウン運動”
を作りました。その中の§16-4“酔歩の問題”が解りやすいと思いますのでどうぞご覧下さい。ただし、ファインマンはEinsteinのやり方ではなくて、Langevinが創めた方法で説明していますので、そこは注意して下さい。
6.プランクの輻射公式による方法(プランク1900年)
これは年代的には他の方法に約10年先がけて、驚くべき精度を達成した方法です。
プランクの輻射公式[uν:振動数νのエネルギー密度、uλ;波長λのエネルギー密度]
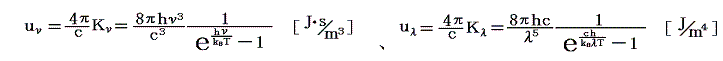
を認めてしまえば、この公式と実際の黒体(空洞)輻射のエネルギースペクトル分布を比較すればプランク定数hとボルツマン定数kBを決定できます。
kBが決定できれば、当時測定できていた気体定数Rをボルツマン定数kBで割ればアボガドロ数NAが求まります。アボガドロ数NAが解れば、その当時測定できていたファラデー定数をアボガドロ数NAで割れば電気素量eが決定できます。
そのようにしてプランクが求めた値は、その誤差3~4%程度で、当時としては驚くべき精度を達成しています。
この当たりについては、別稿「Perrinのソルヴェイ会議報告」Ⅸ.も参照されて下さい。
しかし、プランクの輻射公式がなぜ気体定数Rをアボガドロ数NAで割った量であるボルツマン定数kBで記述できるのか、またプランク定数hとは何なのかが理解できないと、この方法でアボガドロ数が測定できるメカニズムを理解することは不可能です。
プランクの熱輻射公式による“アボガドロ数”導出法を真に理解したい方は別稿「プランクの熱輻射法則(1900年)」9.(4)を御覧下さい。
実際、本稿の1.[補足説明2]で紹介した様に、Einsteinはブランク(Planck)のこの業績を極めて高く評価しています。
7.シリコン格子定数の絶対測定による方法(1965年~ )
これは現在、最も高精度な方法です。この方法は半導体技術の進化とともに、極めて高純度のシリコンを得ることができるようになり、その高純度のシリコンから結晶構造が極めて完全に近い結晶をつくることができるようになって可能になった。
結晶の格子定数(結晶の原子間隔)は結晶に当てたX線回折像の像間隔を測定すれば、X線波長との比の形でなら正確に測定できる。そのとき、X線波長の絶対測定は3.章で述べたように非常に小さな照射角度で光学的(可視光)回折格子面に入射させて、その全反射光の回折像から求める事ができた。その測定値を用いれば格子定数の絶対値も決定できる。
しかし、この方法では光学的回折格子の格子間隔の測定精度に限界があり、結晶格子定数の測定精度を高めるのは困難です。そこに登場したのが、X線干渉計と光波(可視光)干渉計を組み合わせた装置による【格子面間隔の絶対測定法】です。
この方法の要はいかにしてX線干渉縞の移動距離と移動した干渉縞数を正確に測定するかです。その内容が
藤井賢一, “キログラムの再定義をめぐる最近の動き”, 実教出版, じっきょう理科資料No.57(2005年3月4日発行)
中山貫,藤井賢一, “シリコン格子定数の絶対測定とアボガドロ定数の決定”,応用物理,
62, p245~252, 1993年
などに解説されています。詳細はこれら文献をご覧下さい。
なお、上記文献の内容を別稿「シリコン格子定数の絶対測定とアボガドロ定数」にて高校生が理解できるレベルで解りやすく説明しております。