�V���R���i�q�萔�̐�Α���ƃA�{�K�h���萔
�����_�i2013�N�j�ł͏����Â��Ȃ����������܂���
�@�P�D���䌫��, �g�L���O�����̍Ē�`���߂���ŋ߂̓����h, �����o��,
�������傤���Ȏ���No.57�i2005�N3��4�����s�j
�@�Q�D���R��,���䌫��, �g�V���R���i�q�萔�̐�Α���ƃA�{�K�h���萔�̌���h�C���p����, 62,
p245�`252,
1993�N
�ʼn������Ă�����e�����Z���������ł��郌�x���ʼn���₷���������܂��B
�@�A�{�K�h�����Ɋւ��Ă͕ʍe�u�A�{�K�h���萔�̑���@�v���Q�ƁB
�P�D���茴��
�i�P�j�A�{�K�h�����̒�`
�@���s�̂r�h�P�ʌn�ɂ����āA�����ʂ̒P�ʂł��������imol�j��
�g0.012kg(�܂�12g)�̊j��12�b�̒��ɑ��݂��錴�q�̐��Ɠ��������̗v�f���q���܂ތn�̕����ʂł���h
�ƒ�`����Ă���B���Ȃ݂ɒY�f�ɂ�12�b�A13�b�i���ݔ�@98.90�F1.10�j�̓��ʑ̂�����܂����A���̓���12�b����ɂȂ��Ă���B
�@�]���Ċj��12�b���g�������ʂl(12�b)�h��12g�^mol�͊m�肵�Ă���A���̌n�Ɋ܂܂�錴�q�̐����g�A�{�K�h�����h�mA�Ƃ������Ƃł��B12�b���q�P�̎��ʂ���(12�b)�Ə�����
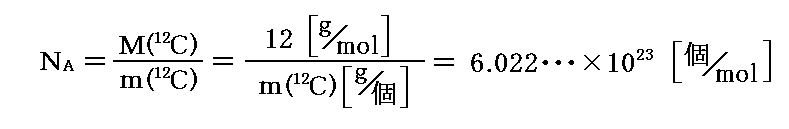
�ƂȂ�B
�m�⑫�����P�n
�@���̒�`���疾�炩�Ȃ悤�ɃA�{�K�h����������ł��邱�ƂƁA���q�P�̎��ʂ�����ł��邱�Ƃ͓������ł��B�Ȃ��Ȃ�ʍe�u�L�������i�L�������j�v�Ő��������悤�ɁA�揜�Z�����s������̐��l�̗L�������́A���Ƃ̐����̗L�������̓��ōł����Ȃ����Ɉ�v���邩��ł��B
�@������A�{�K�h�����̑��萸�x�͈��p�����Q�D�̎����10-7�̃I�[�_�[�ł����A���q�P�̎��ʂ̑��萸�x�����̃I�[�_�[�ł��B�������A�m�⑫�����R�n�Ő�������悤�ɁA���Ύ��ʁi���q�ʁj�ɂ��Ă̑��萸�x�͂����ƍ����B
�m�⑫�����Q�n
�@���ʐ��P�Q�̒Y�f���q12�b���A�{�K�h���������W�߂����ʂ��g�������ʁh�l(12�b)��12.00000������^mol�i�[���������ɑ����j�Ȃ̂ł����A�Y�f���q���o���o���̏�ԂŏW�߂����̂ƁA�_�C�������h��O���t�@�C�g�̗l�ɉ��w����������ԂŏW�߂����̂ł́A���̎��ʂ͔����ɈقȂ�B
�@�ǂ̂��炢�قȂ邩���ς����Ă݂�B�A�C���V���^�C���̓��ꑊ�ΐ����_�������Ă�����d������2�ł����ĐÎ~���ʃG�l���M�[�Ōv�Z����ƒY�f���q�P�̃G�l���M�[��
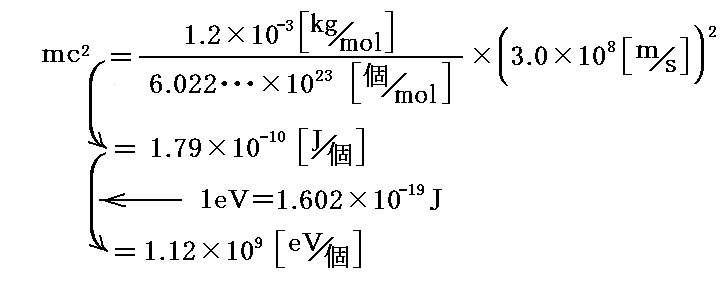
�ƂȂ�B������w�����G�l���M�[�ɔ������ʕω��ʂ́A�Ⴆ�_�C�������h���ɂƂ��ĕʍe�u�����M�ƔM���w�������v�U�D�i�P�j�\�u�̐��l�𗘗p�����
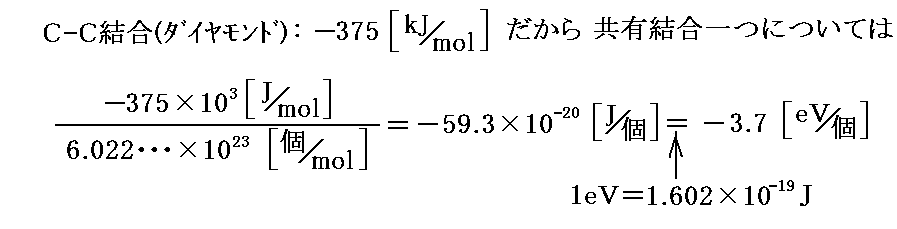
�ƂȂ�B��̒Y�f���q�͂S�̋��L�����������A�e�����G�l���M�[�̔�������̌��q�ɏ�������ƍl����ƁA���w�����i�_�C�����h�j�̂��߂ɐ�����Y�f���q�P�ɂ��Ă̎��ʃG�l���M�[�̕ω��ʂ͏�L�̒l���S�{���ĂQ�Ŋ�����
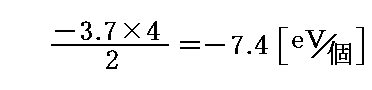
���x�ƂȂ�B
�@���̂��ߌ��q�̏W����Ԃ�10-8�`10-9�I�[�_�[�̍����o�Ă���B
�@�Ƃ���ŁA���p�����Q�D�̎���̃A�{�K�h�������萸�x��10-7�̃I�[�_�[������A�ꉞ���̓�����̌덷�͖������ėǂ��ł��낤�B�������A�����������x���オ��ƁA���̈Ⴂ�����R�l�����Ȃ���Ȃ�Ȃ��Ȃ�B�m�S�D�͎Q���n
�m�⑫�����R�n
�@���݁A�A�{�K�h�����i�P�D�i�P�j�m�⑫�����P�n�������悤�Ɍ��q�P�̎��ʂƂ����Ă��悢�j�𑪒肷��̂ɁA�Y�f�����ł͂Ȃ��āA�V���R���i�P�C�f�ri�j�������p�����܂��B
�@�Ȃ��V���R���������p�����邩�Ƃ����ƁA�����̎Y�Ƃ̔ɉh�ɔ����Z�p�̍��x���ɂ��A�������x�V���R���P�̂�p������芮�S�Ȍ���������悤�ɂȂ�������ł��B
�@���͂Ő�������e����p�̃V���R���P������́A�����̐�������ŗp���������V�ш�Z��@�i�]�[�������g�@�j�ɂ���č��ꂽ�A��̃C���S�b�g�����o�����B
�@
�@���̂Ƃ��A�d�v�Ȃ̂̓A�{�K�h�����̒�`�̌��ɂȂ��Ă����Y�f���q���P�C�f���q���g���Ό��q���ʁh�`r�irelative atomic mass�j�̑��萸�x�ł��B���Ό��q���ʂ`r(X)�Ƃ͂������g���q�ʁh�̎��ŁA12�b���q�P�̎��ʂ�12.00000����i�[���������ɑ����j�Ƃ����Ƃ��̔C�ӂ̌��f�w�̑��Ύ��ʂł��B
�@���̐��x��������Έȉ��̋c�_�͐��藧���Ȃ��̂ł����A�K���Ȃ��Ƃɂ����َ팴�q�Ԃ̑��Ύ��ʂ`r(X)�̑��萸�x�́A���q���ʂ̐�Α���l��������ɍ������x�Ŏ����ł��Ă���B����̓C�I���g���b�v�ɂ�鎿�ʕ��͊�̑��萸�x�Ɨʎq�d�C�͊w�iQED�j�ɂ���ɂ����10-10�̐��x�ɒB���Ă���B
�@�Ⴆ�ΐ��f���q���g���Ό��q���ʁh�`r�irelative atomic mass�j��
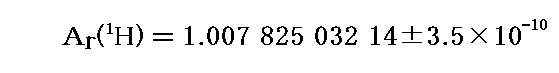
�ƂȂ�܂��B
�@
�@�َ팴�q�̎��ʂ����Z����Ƃ��̗v���g���ꌴ�q���ʒP�ʁh���iuified atomic mass unit�j�ŁA���̒�`��
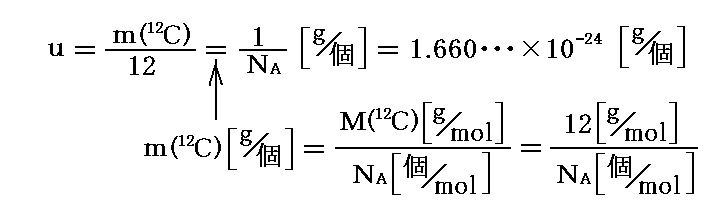
�ł��B
�@���̂Ƃ��A�ʍe�u�L�������i�L�������j�v�Ő��������悤�ɁA�揜�Z�����s������̐��l�̗L�������́A�e�����̗L�������̓��ōł����Ȃ����Ɉ�v����̂ŁA���ꌴ�q���ʒP�ʂ��̑��萸�x�i�L�������j�̓A�{�K�h������12�b���q�P�̎�����(12�b)�̑��萸�x�Ɠ����ł��B
�@
�@���̂��ߔC�ӊj��w�̂P���q������̎���
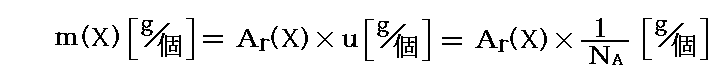
�̑��萸�x�i�L�������j���A���ǂ̂Ƃ���A�{�K�h������12�b�ior�ri�j���q�P�̎��ʂ̑��萸�x�Ɠ����ɂȂ�܂��B
�m�⑫�����S�n
�@���Z���w�ŏK���Ƃ���ł����A12�b�����q�ʑ���̊�Ɍ��܂����ߒ��͉��L�̗l�Ȏ���ɂ��B
�@���q�̑��Ύ��ʁi���q�ʁj�̊�́A���Ƃ��ƍł��y�����f�ł��鐅�f���q1��1.00000����i�[���������ɑ����j�ƌ��߂Ă����m�h���g���i�p�j1805�N�n
�@�������A���̌��q�̑��Ύ��ʂ����߂邽�߂̑��茴���́A���j�I�ɉ��w�����ɉ�����g���ʂ̒���̖@���h��g�{�����̖@���h�ł���������A�ł��邾�������̌��f�Ɖ��w�������錳�f����ɂ��������֗��ł���Ƃ������ƂŁA�_�f���q�P�̑��Ύ��ʂ�16.00000����i�[���������ɑ����j�ƌ��߂邱�ƂɂȂ����m�X�^�X�i�x���M�[�j1865�N�n�B
�@
�@�Ƃ��낪1913�N����ɂȂ�ƁA�\�f�B�i�p�j�Ȃǂɂ��A���ꌳ�f�ł����ʂ̈Ⴄ���q������Ƃ����g���ʑ́i�A�C�\�g�[�v�j�h�̊T�O���������ꂽ�BJ�DJ�D�g���\���́A�F�X�ȋC�̂̃C�I���r�[����d��Ǝ���ł܂��āA���ʑ̂̑��Ύ��ʂ����肷��̂ɏ��߂Đ�������B
�@�����āA�A�X�g���i�p�j�������i1919�N�j�������ʕ��͊��p���āA�W�I�[�N�i�āj�͎_�f���O��ނ̓��ʑ�16�n�A17�n�A18�n�̍������i���ݔ��99.762�F0.038�F0.200�j�ł��邱�Ƃ��i1929�N�j�����B
�@�܂�A����܂ł̌��q�ʂ̊16.00000�E�E�E�i�[���������ɑ����j�͂��̎O��ނ̎_�f���q�̕��ό��q�ʂł������킯�ł��B����ł́A�����ɂ��܂����ƌ������ƂɂȂ�A�ǂꂩ����̓��ʑ̌��q�����q�ʂ̊�ɂ��ׂ��ł���Ƃ������ƂɂȂ����B
�@
�@�������A����܂łɎ_�f�̕��ό��q�ʂ���l�X�Ȍ��q�̌��q�ʂ����߂��Ă���A�����ʂŗp�����Ă����̂ŁA�����̒l���ł��邾���ς��Ȃ��Ă����ނ悤�ɁA�����q�̒��ŁA���q�ʂ��ł��邾�������l�ɋ߂��Ă���̗ǂ��l�ƂȂ錳�f�E���ʑ̂��T���ꂽ�B
�@���̂Ƃ�12�b��12.000�E�E�E�ɔ��ɋ߂��l�ł������̂ŁA1960�N�̍��ۉ�c��12�b�̌��q�ʂ�12.00000�E�E�E�i�[���������ɑ����j�Ƃ��邱�Ƃɂ��܂����B
�@
�i�Q�j���茴��
�@�A�{�K�h�����̑���́A�ȉ��̌����Ɋ�Â��B�g�ő̕����̖��x�h���́A�g�������ʁh�l�i���ό��q�ʂɂ���t�������ʁj���g�����̐ρh�u�Ŋ��������̂ł���A�����̐ςu���g�������łP�̌��q����߂�̐ρh�����g�A�{�K�h�����h�mA�̐ς�����
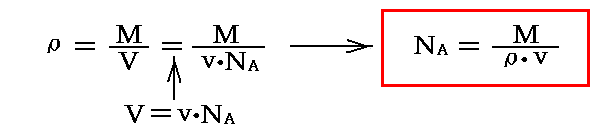
�ƂȂ�B
�@�P������������舵���ꍇ�ɂ́A�g���q�P����߂�̐ρh�����g�i�q�萔�h���i�������̒P�ʖE�̗Œ��j�����܂�Όv�Z�ł���̂ŁA�����g�P���������h���m�i�q�萔���n�A�m�������x���n�A�m���������l�n�����ꂼ�ꐳ�m�ɑ���ł���Ηǂ����ƂɂȂ�B
�m�⑫�����P�n
�@�O�߁m�⑫�����R�n�Ő����������R�ŒP���������Ƃ��ăV���R���P�������p������̂����A���ɂȂ�̂̓V���R���r�������ɂ͎��ʐ����قȂ�O��ނ̓��ʑ́@28�r���A29�r���A30�r���i���ݔ��92.23�F4.67�F3.10�j�����݂��Ă��邱�Ƃł��B
�@���̂��߁A�V���R���P�������m���������l�n�����肷��ɂ́A�e���ʑ̂��g���Ό��q���ʁh�`r�ɂ��̑��ݔ���悶�ĕ��ς��邱�Ƃ��K�v�ɂȂ�B
�@���̂Ƃ��A�P�D�i�P�j�m�⑫�����R�n�ŏq�ׂ��悤�Ɋe���ʑ̂��g���Ό��q���ʁh�`r�̑��萸�x��10-10�̃I�[�_�[���B���ł��Ă���̂ŁA�V���R���P�������m���������l�n�̑��萸�x�́A���ʑ̑��ݔ�̑��萸�x���ǂ��܂�10-10�̃I�[�_�[�ɋ߂Â��邩�ɂ������Ă���B
�m�⑫�����Q�n
�@�ʍe�u�L�������i�L�������j�v�Ő��������悤�ɁA�揜�Z�����s������̐��l�̗L�������́A�e�����̗L�������̓��ōł����Ȃ����Ɉ�v����B���̂����m�i�q�萔���̑��萸�x�n�A�m���������l�̑��萸�x�n�A�m�������x���̑��萸�x�n�̒��ōł��L�����������Ȃ����̂ŃA�{�K�h�����̑��萸�x�i�L�������j�����܂邱�ƂɂȂ�B
�@���p�����Q�D�i1993�N�j�̎���ɂ��m�i�q�萔���̑��萸�x�n���W���A�m���������l�̑��萸�x�n���V���A�m�������x���̑��萸�x�n���V���Ȃ̂ŁA�����̃A�{�K�h�����̑��萸�x�i�L�������j�͂V���ł��B���݂̑��萸�x���ǂ��܂ŒB������Ă��邩�͗ǂ�����܂���B
�@
�Q�D����@
�ȉ��ŁA�m�i�q�萔���n�A�m���������l�n�A�m�������x���n�̋�̓I�ȑ���@���������B
�i�P�j�i�q�萔�̑���
�P�D�P�ʖE�Ɗi�q�萔
�@�ŏ��ɁA�������Ō��q�P����߂�̐ςƊi�q�萔�̊W���B
�@�����\���̉�͂ɉ������g�P�ʖE(�P�ʊi�q�j�h�̊T�O���d�v�ł��B�P�ʖE�Ƃ́A�������̋�Ԋi�q�����镽�s�U�ʑ̂̂����A��Ԋi�q�̍\���P�ʂƂȂ镨�ł��B���Ȃ킿�A�����O��E���E�E�㉺�ɐςݏd�˂Ă����ƌ����\�����Č��ł��镽�s�U�ʑ̂̓��ōŏ��̂��̂��g�P�ʖE�h�ł��B
�@�V���R�������̒P�ʖE�͉��}�̂悤�ɂȂ�B
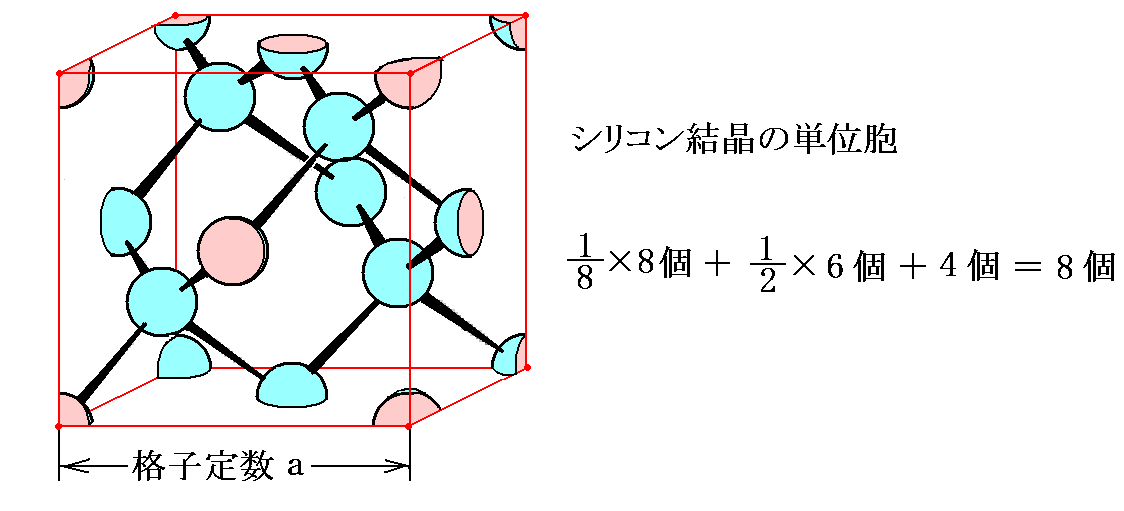
�@��}�ŗ����i�q�̒��_�ɑ��݂���W�̌��q�́A����1�^�W�݂̂��P�ʖE�ɑ����Ă���B�܂������i�q�̂U�̖ʏ�ɑ��݂���U�̌��q�͂���1�^2�݂̂��P�ʖE�ɑ����Ă���B���̂��߃V���R���P�������P�ʖE���Ɋ܂܂�錴�q�����W���ł��B
�@�V���R���P�����̏ꍇ�A�P�ʖE�͈�ӂ̒��������i�g�i�q�萔�h�Ƃ����j�̗����̂ƂȂ�̂ŁA�P�ʖE�̑̐ς���3�ł��B������V���R���P�������ŃV���R�����q�P����߂�̐��� �� ��3�^8 �ƂȂ�B
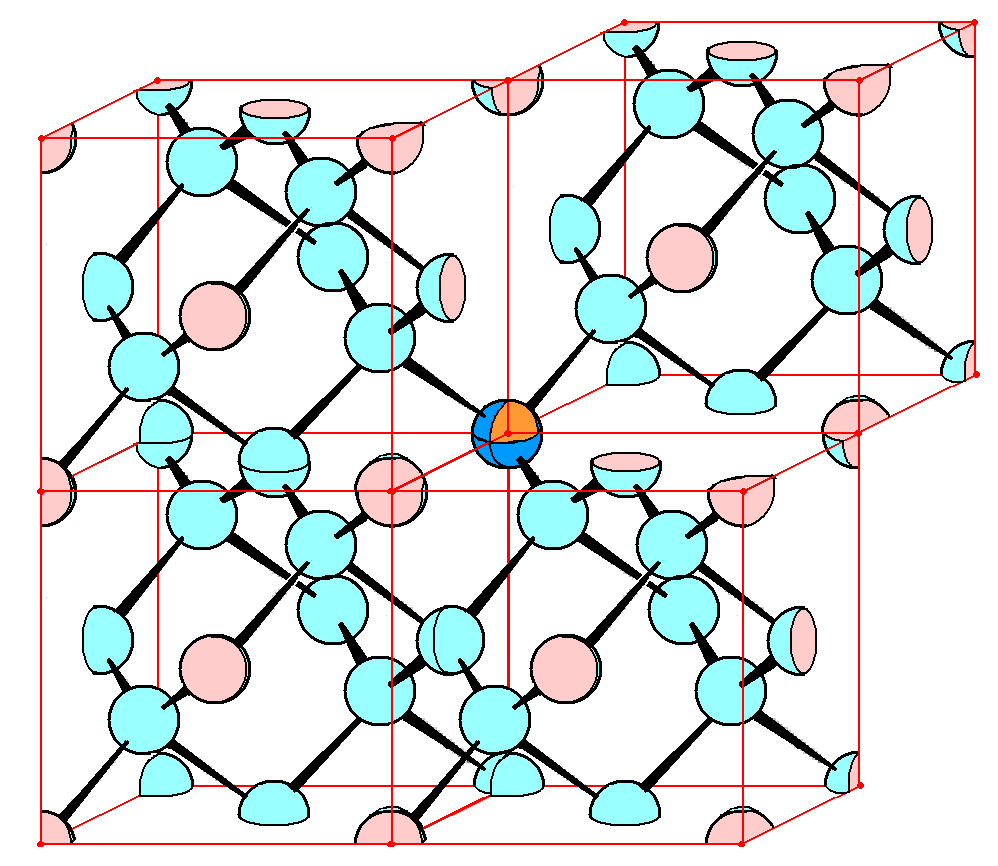
�@��}���ɋ��L������\���_���`����Ă��Ȃ����q���S���邪�A�����̌��q�̋��L�����̕����͂��̒P�ʖE�Ɋ܂܂�Ă��Ȃ��B���̓�����͉��}�̗l�ɒP�ʖE��O��E���E�E�㉺�ɐςݏd�˂Ă݂�Η����ł���B������ɂ��Ă��P�ʖE��O��E���E�E�㉺�ɐςݏd�˂Ă����ƌ����\�����Č��ł��邱�Ƃɒ��ӁB
�@
�Q�D�u���b�O�̏���
�@�w���\����͂̓����J�����A���E�G�͌������̌X�̌��q����U�����ꂽ�w���̔g���̔g�����������{�ɂȂ�������A���ɂ���ċ�����ܑ��i���E�G���_�j�����������ł���Ƃ��ė��_��W�J�i���E�G�̏����j�����i1912�N�j�B���̂Ƃ��A���E�G�́A�����t�˂Ŕ��������A���X�y�N�g���̂w����p�����B�m���̓�����́A�Ⴆ�V���|���X�L�[�u���q�����w�T�v�����}��������₷���n
�@���E�G�̘_�������\�����Ƃ������v�D�k�D�u���b�O�͂��̊ȒP�ȉ��߂�^�����B���Ȃ킿�A�����̒��ɑ��݂��錴�q�͊���̕����̖ʁi�u���b�O���ʂƌĂԁj��ɕ���ł���ƍl���A�����̊i�q�ʂɑ��Ĕ��˂̖@����K������Ή�ܑ��̕��������߂���Ƃ����̂ł���B
�@���ꂪ�u���b�O�̏����ƌ�������̂ŁA���Z�����ŏK���悤��
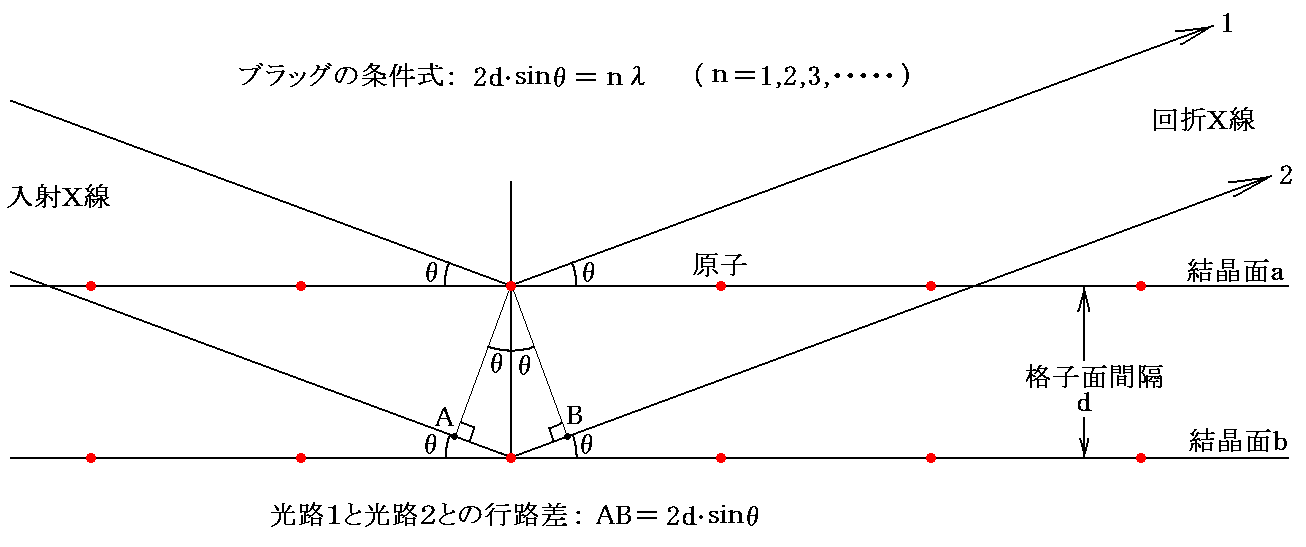
�ƂȂ�B
�@�P���̊i�q�ʂɂ�鋭�ߍ����U���́A�����I�ɂ͔��ˈȊO�̕����ɂ��N���邪���x�͏������A���ΓI�ɂ͖����ł���B������u���b�O�̏����͊i�q�ʂɑ�����ˊp�Ɣ��ˊp�����������˂ɂ��Đ��藧���ƍl���Ȃ����Ȃ��B�܂��A�P���̊i�q�ʂ�������̎U���͔���ł��葽���̊i�q�ʂɂ��Ă̏d�ˍ��킹��_���Ȃ��Ɗϑ�������܂w���͐����ł��Ȃ��B
�@�u���b�O�̕��@�ł́A�g���̒�܂����P�F�̓����w�����p�����邪�A�u���b�O�̏����͉�܂�����������łȂ����ː��̊i�q�ʂƂȂ��p�i���ˊp�Ƃ����j���K�肷���B����g���̂w���͓���̎��ˊp�łȂ��ƃu���b�O���˂͋N����Ȃ��B�u���b�O���q�́A���̍l�����Ɋ�Â�����I�Ȏ������u������Ă߂��܂������ʂ��グ���B
�@���̂Ƃ����ӂ��ׂ��́A�������̊i�q�ʂ̕����ɂ���āA�i�q�ʂ��ɑ���i�q�ʂ��̎U���̌��q����}�̂悤�ɏ㉺�ɂ�����ĕ���ł���킯�ł͂Ȃ����ł��B���̓�����͉��}�̗������Β����ɗ����ł���B
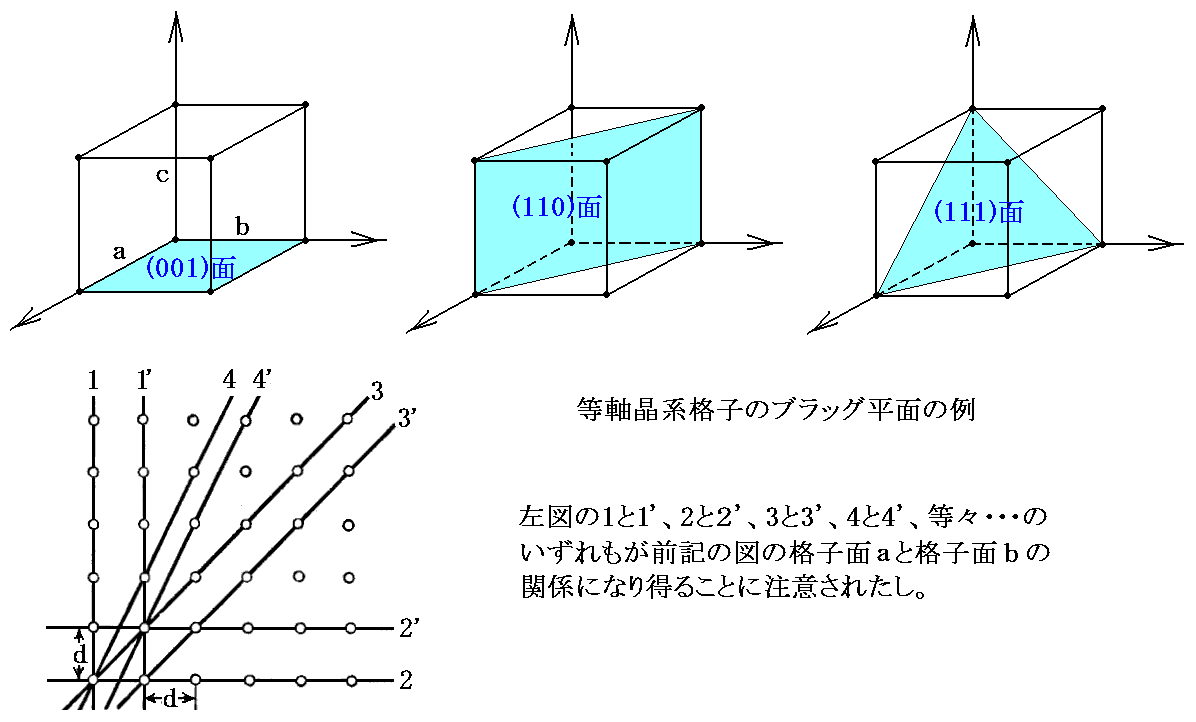
�@��ʓI�ɂ͉��}�̗l�ɁA���ʏ�̎U���̌��q�͂��ʏ�̌��q�̐^���ɂ���킯�ł͂Ȃ����A���q�ԋ��������ʂƂ��ʂł͈قȂ�B
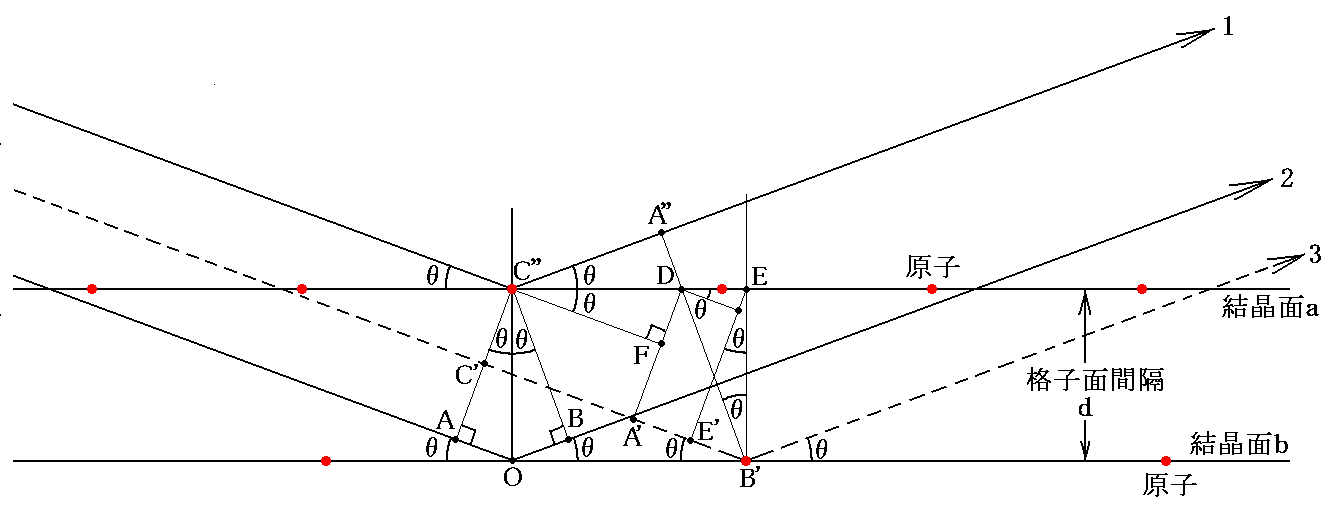
���̂Ƃ�
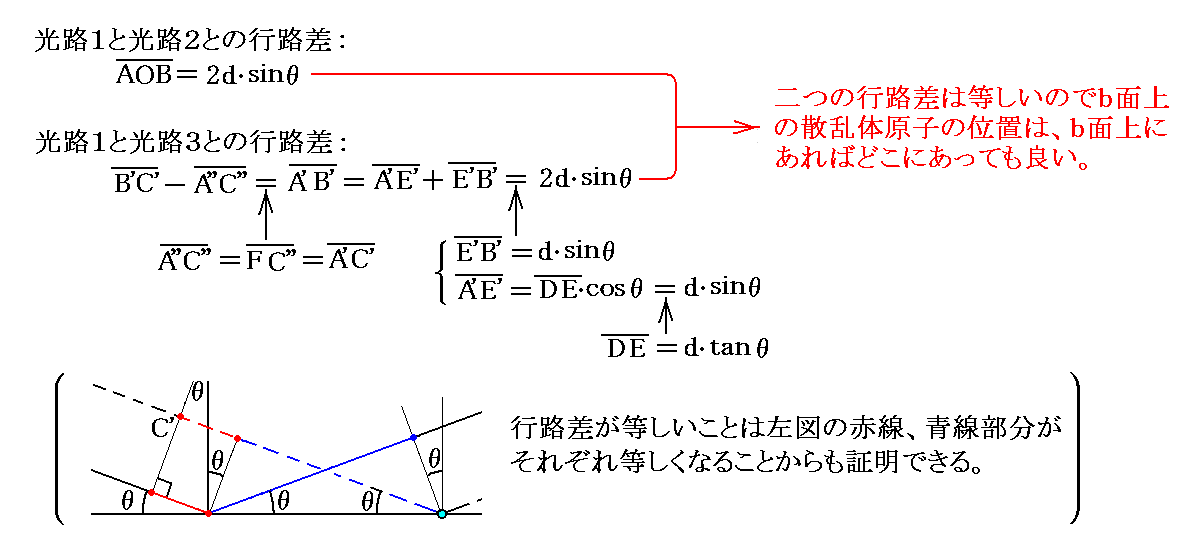
�ƂȂ�̂ŁA���ʏ�̎U���̌��q�̈ʒu�͂��ʏ�ɗL�肳������ǂ��ɂ����Ă��ǂ��̂ł���B�܂��i�q�ʏ�̌��q�Ԋu�����ʏ�̊Ԋu�ƈقȂ��Ă��Ă��悢�B���̂��Ƃ������邩�炱���u���b�O���˂͊i�q�ʂ���̔��˂ƌ��Ȃ����B�����āA�Q�D�i�P�j�S�D�Ő�������悤�ȊW��������B
�@�ŏ��ɏq�ׂ����E�G�̎����ł͗l�X�Ȕg�����܂��A���w���������ɓ��Ă�̂����A�������̊e�X�̊i�q�ʂ́A���̖ʂ̃u���b�O������������g���̂w����I�����Ĕ��˂������̂��ƍl���邱�Ƃ��ł���B
�@���E�G�̍l�����i���E�G�̏����j�ƃu���b�O�̍l�����i�u���b�O�̏����j�͌��Ǔ������Ƃ������Ă���̂ł����A���E�G�̏��������u���b�O�̏����̕�����蒼���I�ŗ������₷���B
�@�w����܂̏ڍׂɂ��Ă͕ʍe�u�w��������͂ɂ����郉�E�G�̏������ƃu���b�O�̏������v�������������B
�@
�R�D���q�P����߂�̐ςƊi�q�ʊԊu
�@�Q�D�i�P�j�P�D�Ő��������悤�ɁA�V���R���P���������g�V���R�����q�P����߂�̐ρh�� �����߂�ɂ́A�V���R���P�������g�i�q�萔�h��������Ηǂ������i������3�^�W�j�B
�@�Ƃ���ŁA�g�i�q�萔�h�����g�i�q�ʁi�u���b�O�ʁj�Ԋu�h��������Ίw�I�Ɍv�Z�ł�������A�����g�V���R�����q�P����߂�̐ρh�� �����߂�ɂ́A�V���R���P�������̓K�����g�i�q�ʁi�u���b�O�ʁj�Ԋu�h��������ł���悢���ƂɂȂ�B
�@���ۂɗp����ꂽ�̂��ʎw���i�~���[�w���j�i220�j�̊i�q�ʁm���}�n�ł��B

�@�ʎw���i�~���[�w���j�il mn�j�̊i�q�ʂƂ́A�P�ʖE�̎O�̗ŕӂ����ꂼ���� �����A�������A�����������_�ŁA���_����ł��߂��O�_�����O�p�`�����ʂ̂��Ƃł��B�P�ʖE�̎O�̕Ӓ������C���C���̏ꍇ�A�O�̎������^���C���^���C���^���̒����ɐ�_�����ʂł��B
�@���Ƃ��Ή��}�̖ʂ́B�ʎw���i�~���[�w���j�i342�j�̊i�q�ʂł��B

�@���̂Ƃ��A��̎��ɕ��s�Ȋi�q�ʂ̏ꍇ�́A���̎��Ɩʂ̌����_�͖������ɍ݂邱�ƂɂȂ�̂ŁA����ɑΉ�����w����0�ƂȂ�܂��B�܂����̕������ꍇ�͎w���̏�����o�[���L���܂��m������̗�Q���n�B
�@�V���R�������̗l���������`�i�������`�j�m�O�̗ŕӒ����S�ē������A���݂��ɒ������Ă���n�̏ꍇ�ɂ́A�ȒP�Ȋw�I�l�@
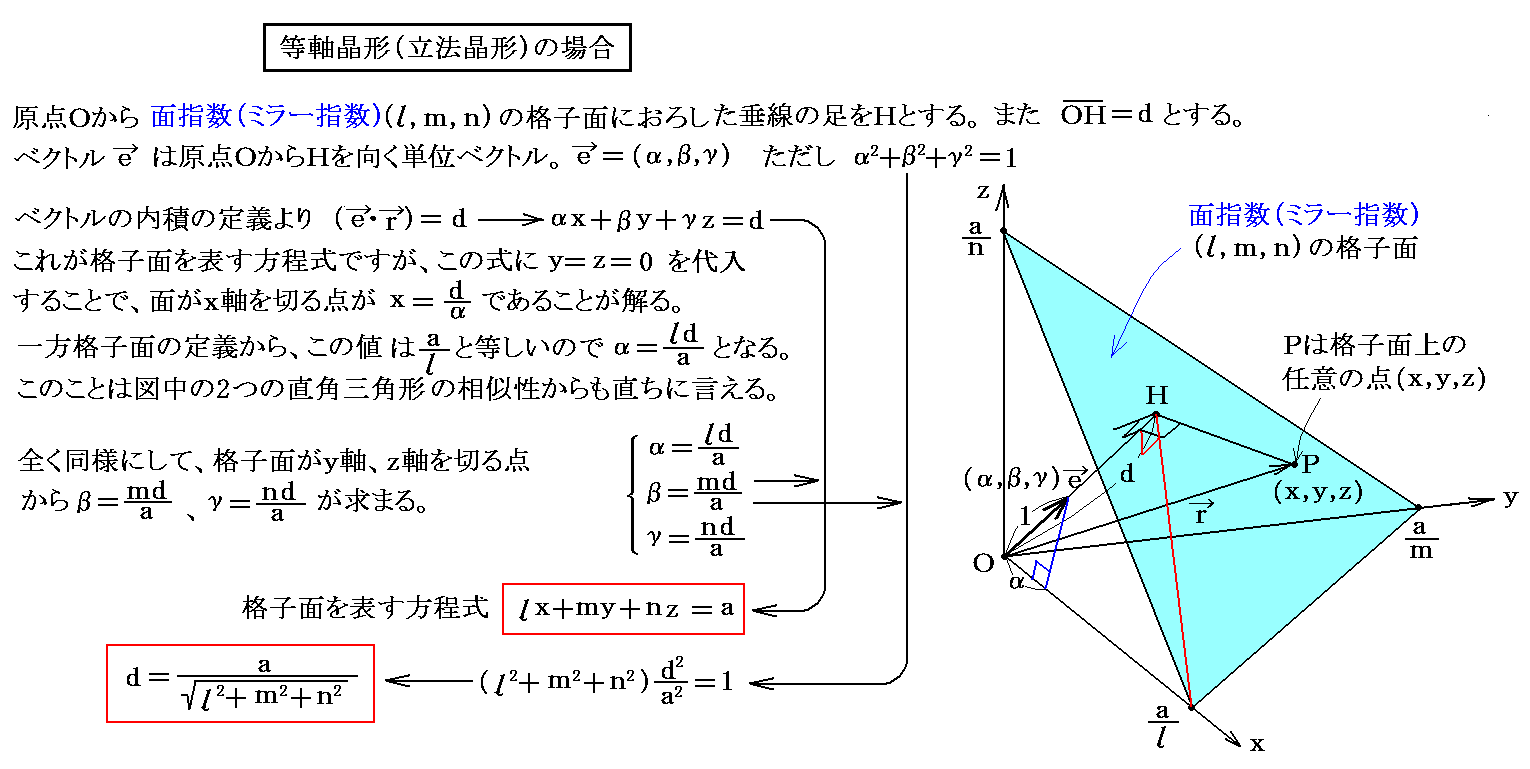
�������悤�ɁA�i�q�萔���Ɩʎw���ilmn�j�̊i�q�ʊԊu��lmn�Ƃ̊Ԃɂ�
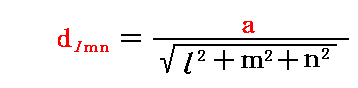
�̊W�����藧�B
�@�ʎw���i220�j�̏ꍇ�ɂ�
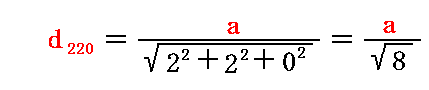
�ƂȂ�B
�@�g�i�q�ʁi�u���b�O�ʁj�Ԋu�h���̐�Α���́A�g�}�b�n�c�F���_�[�^�w�����v�h���g���čs����B�V���R���P�����̃u���b�N�����̉������O���̕��s������肾���i�����ʐ^�j�B�u���b�O���˖ʂ͌����ʂɐ����ƂȂ�悤�ɍ�肾����Ă����B���ꂼ��̌������r�A�l�A�`�ƋL���B���ɂr�Ƃl�͈�̂Ƃ��`�̕���������藣���Č����ʂɉ����������ɕ��s�ړ��ł���悤�ɂ���i�����}�j�B
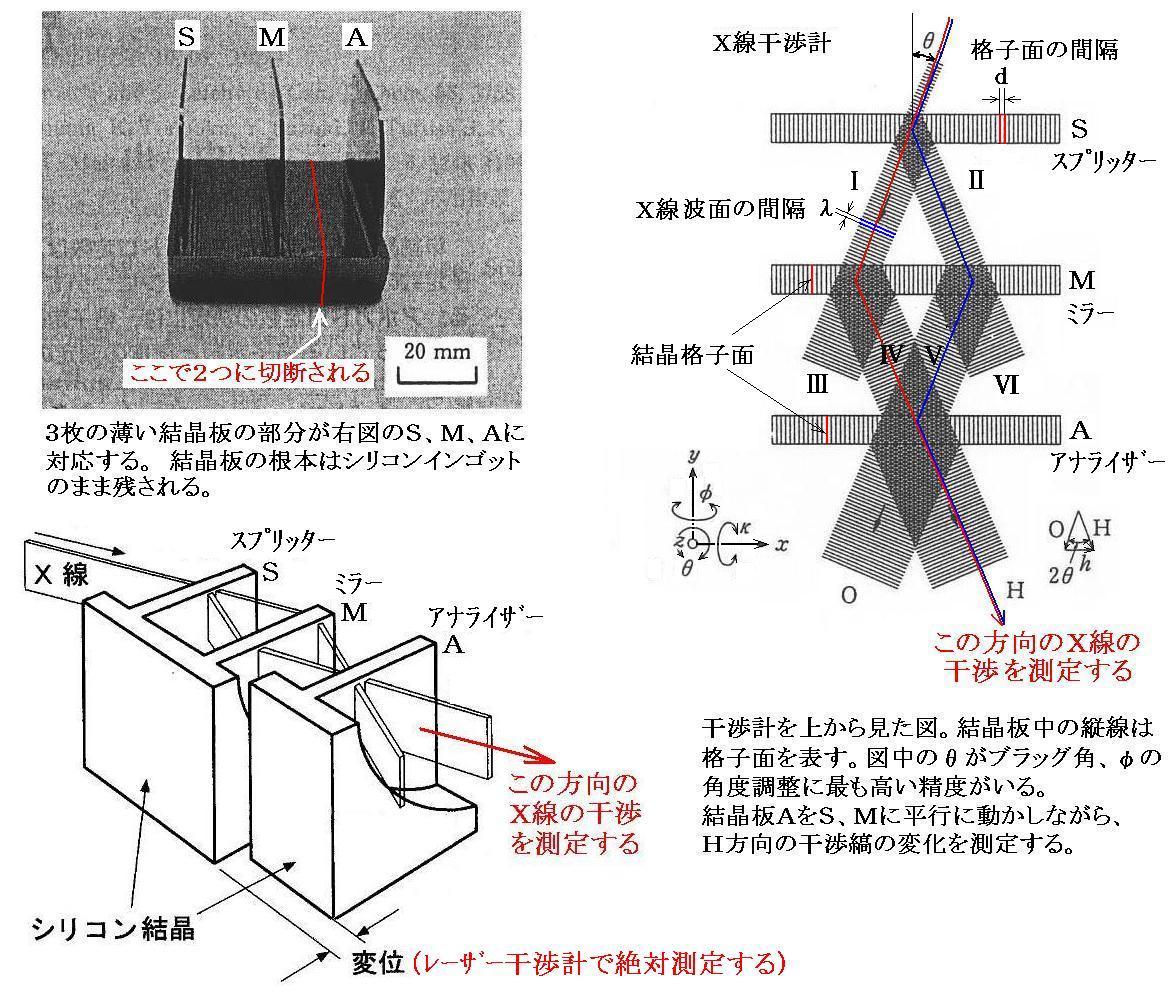
�@�w���͏�E�}�̗l�ɍŏ��Ɍ������r�ɓ��˂��āA���̂܂ܓ��߂����T�ƁA�u���b�O���˂����U�̓�ɕ�������B������A����ɓ�Ԗڂ̌������l�ŁA���ꂼ��m���߂w���n�Ɓm�u���b�O���˂w���n�̓�ɕ������V�A�W�A�X�A�Y�Ƃ���B���̓����W���X�̂w�����p������B
�@�O���ڂ̌������`�ɓ��˂���w���W�̓����g�̕��������߂���w���ƁA�������������`�ɓ��˂���w���X�̓����g�̕������u���b�O���˂���w�����p������B
�@�܂�g�����������W�́m���߂w���n���X�́m�u���b�O���˂w���n�̊����ϑ�����̂ł���B�������`�ƌ������r�E�l�̔ʂɕ��s�ȑ��ΓI�Ȃ���̗ʁi�ψʁj����������ɂ�āA�g�����Ɏˏo����銱�w���̋��オ�����I�ɕω�����B���̋���̕ω��̉ƕψʗʂ̐�Α���l���猋���̊i�q�ʊԊu���𑪒肷��B
�@
�S�D�i�q�ʊԊu�̑���
�@�����r�E�l�Ƃ`�̑��ΓI�ȕψʂ͉��}�̑��u�Ŏ��������B
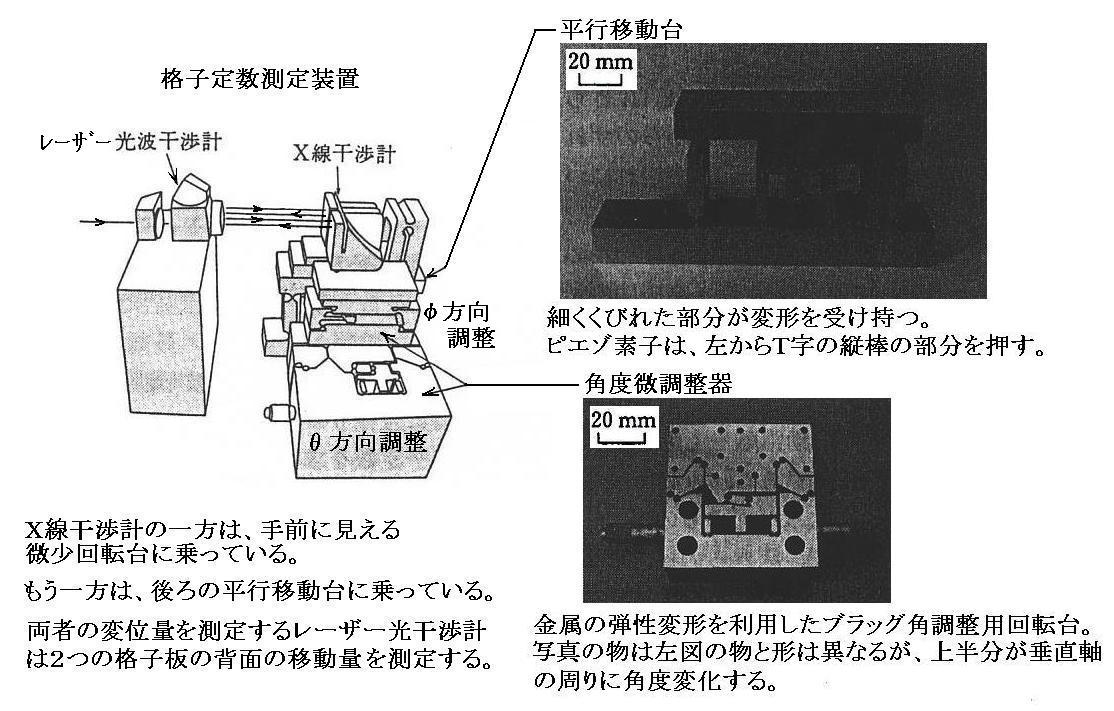
�@�O���}�����g�����������m�w���W�̓��߂w���n���m�w���X�̃u���b�O���˂w���n�̈ʑ����l����B���ȒP�̂��߂ɍs�H�������P�Ńu���b�O���ˊp��30���̏ꍇ���l����B���̂Ƃ��u���b�O�̏������@2���E������30�����P�~���@���A�m�i�q�ʂ̊Ԋu���n���m���˂w���̔g���Ɂn�Ɉ�v����B
�@�����r�E�l�ƌ����`�̊Ԃɕψʂ������ꍇ�̂���u�Ԃ̈ʑ��W��}������Ɖ��}�̂悤�ɂȂ�B���̏ꍇ�g�����i�ފ��w���݂͌������ߍ������Ƃ�����B
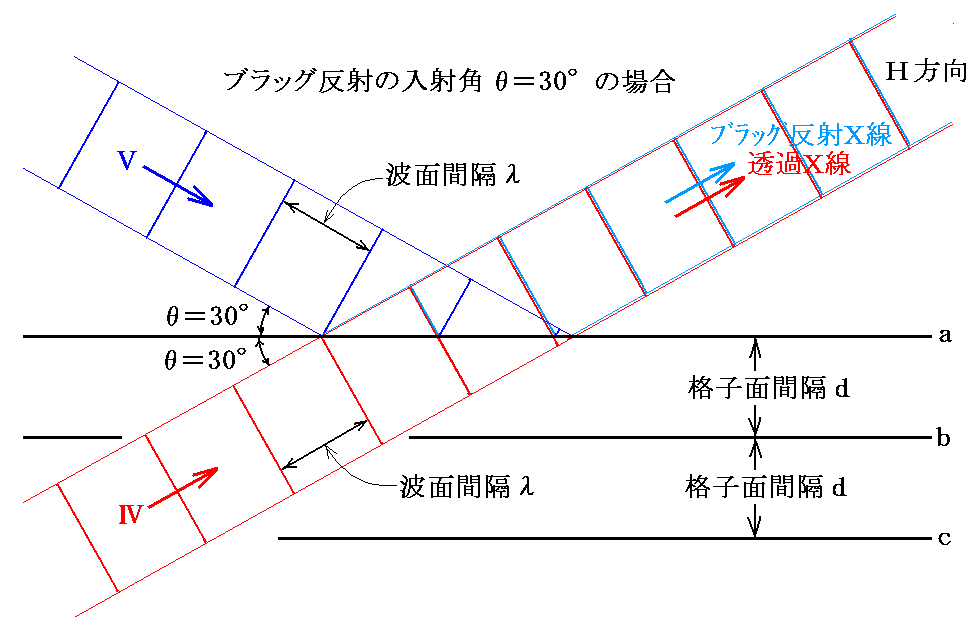
�@���ɁA�������`��Ⴆ���i�q�Ԋu�̔����قǏ���ɂ��炷���m�w���W�̓��߂w���n���m�w���X�̃u���b�O���˂w���n�̈ʑ����͉��}�̂悤�ɂȂ�B���̂��߁A�g�����i�ނQ�̂w���͊����Č݂����ł����������B
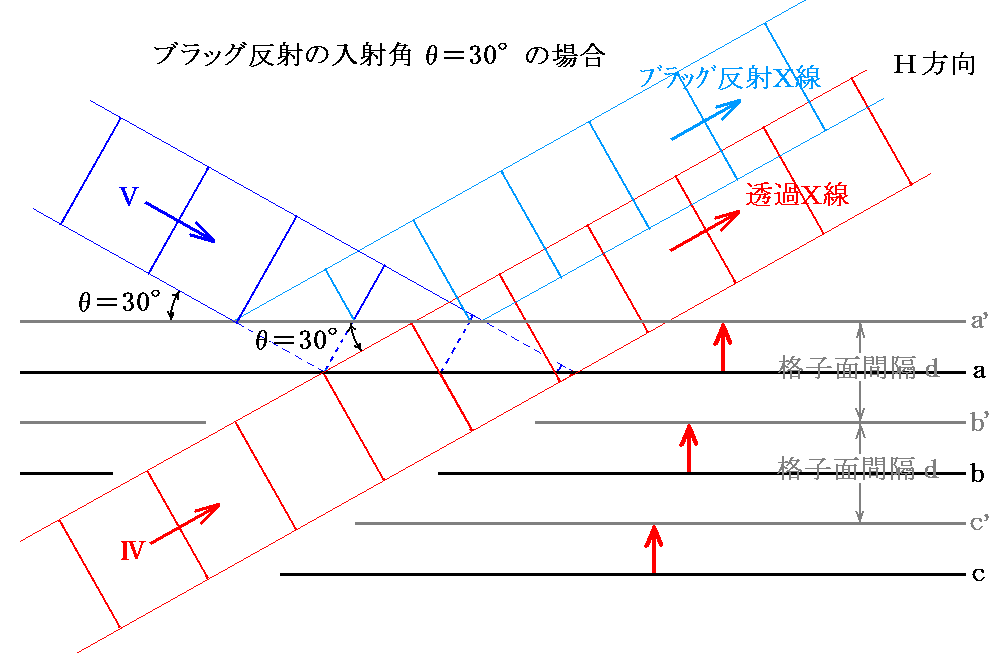
�@���̂Ƃ��A�w���X�̓��˔g�Ŋi�q�ʂ��f�₃�f���甽�˂���Ăg�����i�ޔg�́A���f�ʂ��甽�˂��ꂽ�g�Ɣg���̐����{�̈ʑ����͂��邪�A���f�ʂ��甽�˂��ꂽ�g�Ɗ��S�Ɉʑ���������Ăg�����i�s���邱�Ƃɒ��ӁB���̂��Ƃ��u���b�O�̏������̈Ӗ�����Ƃ���ł����B
�@��}�̊w�I�W���A���ƃɂ̊W������ʂ̏ꍇ�ɂ��čl�@����Β����Ɉȉ��̂��Ƃ�����B
�@��ʂɁA�g�����`�h���g�����r�E�l�h�ɑ����g�i�q�ʊԊu�h���قǕ��s�X���C�h��������m�w���W�̓��߂w���n���m�w���X�̃u���b�O���˂w���n�̍s�H�����g�g���h�������ω������B
�@���̂��߁A�g�����`�h���g�����r�E�l�h�ɑ���ړ��ʂ����[�U�[���v�Ő����ɐ�Α��肵�āA���̈ړ��̊Ԃ��g�����ɐi�ފ��w�������x���ł������𐔂���B�ړ������𖾖ʼnŊ���Ίi�q�ʊԊu���A����ɂw���̔g���ɂ������x�ő���ł����B
�@
�T�D������Ƒ����
�@���ۂ̑���ł́A10p����10-12�����x���̊��炩���ŁA�����Ђ�100�ʂ���0.1������10-4�����x���s�ړ�������B���̊Ԃɂg�����֓��˂��銱�w���͐�������x���ł��邱�ƂɂȂ邪�A�����d�C�M���ɕς��ăJ�E���g����̂ł���B
�@���}�͂��̓d�C�M���̕ω��̗l�q�������B�Ȃ��炩�ȃJ�[�u�͌����Ђ̈ړ������𑪒肷�邽�߂̃��[�U�[���v�̊����̋��x�ω��������Ă���B���[�U�[���i�����j�̂P�g�����x���̈ړ��̊ԂɊ��w�����͉��������ł����l�q���ǂݎ���B
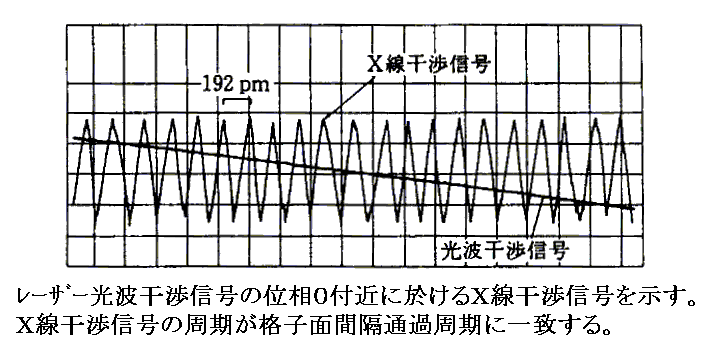
�@�����������ŗp�����Ă���Z�p�̖{���́A�i�q�̎����łw�����M���̋��x���ω�����̂𑪒�ł��邭�炢�Ȃ߂炩�ɂ����ׂɁA�w�����w�v�f���ړ��ł���悤�ɂȂ��������ł��B
�@�����Ђ̈ړ��̓_�C�X�|�̒e���ό`���s�G�]�f�q�̈��͂Ő��������čs���B�܂��A���̍ۂ̊p�x���������������10-9���������x�ł̒������K�v�ł��B
�@�w�����M�����ώ@�����ŁA�U�������炷���ƂƁA���x�����ɕۂ��Ƃ��ł��d�v�ł���B�w�����v�̂Q�̕������ꏏ�ɐU�����郂�[�h�͂�����x�傫���Ă��ǂ����A���ΓI�ψʂ���U���U����10-11���ȉ��Ɍ��炷�K�v������B
�@���̂��߁A���葕�u�͑��i���ϑw�S���̖h�U��Ŏx�����Q�g���̒��S���̒�Ղ̏�ɐݒu����Ă���B�������̉��x�ω��́}0.1���ȉ��ɂ��������Ă���B�܂��A���葕�u�S�̂́}0.01���ȉ��̉��x�ω��ɐ��䂳�ꂽ�f�M�P���e����ɐݒu���Ă���B�����āA���莞�̑S�Ă̑���ׂ͗̕������牓�u���삳���B
�m�⑫�����n
�@���̂Ƃ��A���R�̂��Ƃł����w�����v�̈ړ������𑪒肷�����[�U�[�����v�ɗp������̔g����10-8�ȉ��̑��Ό덷�Ő�������ł��Ă��Ȃ��Ƃ��������B
�@�Ƃ���ŁA�������ʍ��Ő��������悤���^�̌�����299792458���^���Ƃ�����`�l�Ƃ��āA�g�����̒P�ʂP���͌����P�^299792458�b�Ԃɐi�ދ����h�ƒ�`����Ă���B
�@���̌����x�̒�`�l�́A1972�N�ɕč����ۓx�ʍt�ψ���̃G�x���\���B�����߂����l�@����299792456.2�~108�}1.�Pm/s �mK.M.Ebenson, et al., �gSpeed of Light from Direct Frequency and Wavelength
Measurements of the Methane-Stabilized Laser�h, Phys. Rev. Lett., 29(19),
p1346�`1349, 1972�N�n�����ɂȂ����悤�ł��B
�@���̒l�́A���^�����艻He-�me���[�U�[���i�Ɂ�3.39��m�j�����g���������Ԃ̊�ƂȂ��Ă���133�bs���q���v�Ɣ�r���ċ��߂��l �ˁ�88376181627�}50�gz �ƁA���[�U�[�������g����������܂ł̒����̊�ł�����86�jr(2��10-5��5)�̑J�ڂɔ������̔g���i0.6057802105��m�j�Ɣ�r���ċ��߂��l �Ɂ�3392231.376�}0.012pm ���� �����Ɂ~�� �Ōv�Z���ꂽ���̂ł��B���̌�10�N�ɂ킽���Ă��̒l�̐M�������������1983�N�̑�17�ۓx�ʍt����ŏ�L�̒�`���̑����ꂽ�B
�@�G�x���\���B���ǂ̂悤�Ȋ��������g������10-9�̐��x�ŋ��߂邱�Ƃ��ł����̂��ǂ�����܂��A�Ƃɂ��������`�ԊO���̗̈�ł́A���̐��x�̌v�����\�Ȃ悤�ł��B
�@�����x����`�l�Ƃ��Ċm�肵�Ă���̂Ȃ�A�C�ӂ̉������g�����́A���̌����̎��g����10-9�̐��x�ŋ��܂��10-9�̐��x�Ō��܂邱�ƂɂȂ�܂��B���[�U�[�����̎��g���́A���Ԍv���̌��ɂȂ��Ă��錴�q���v�Ɣ�r����A���̐��x�ő���ł������ł��B
�@
�i�Q�j�������ʂ̑���
�@�P�D�i�Q�j�m�⑫�����P�n�Ő��������悤�ɁA�m���������l�n�𐳊m�ɋ��߂�ɂ́A�����ő̒��̓��ʑ̑g���䗦�𐳊m�ɑ��肷��K�v������B���݂���͈ȉ��̗l�Ȏ菇�ōs���Ă���B
�@�܂��A�m�i�q�萔���n���m�������x���n�̑���ɗp����̂������V���R�������C���S�b�g���烂�����ʑ���p�̌������o���B���ɂ��̌����𐅎_���i�g���E���ɗn�����ma2�ri�n3�n�t�Ƃ���B�����s�n���ň�����aa�ri�e6�Ƃ��Ē��a������B��������^�ʼn��M���āA�t�̒��f�����ri�e4�Ƃ���B�����^�C�����ŕs���������������̂��ɃC�I���������ri�e3�{�Ƃ��A���ʕ��͊���p���đ��ݔ�𑪒肷��B
�@���ʕ��͊풆�̎���ɂ��C�I���͋Ȃ����āA�V���R���̎O�̓��ʑ�28�ri�e3�{�A29�ri�e3�{�A30�ri�e3�{�ɑΉ������s�[�N��������B���ꂼ��̃X�y�N�g���s�[�N�̃C�I���d���̔䂩�瑶�ݔ�����肷��B���̐��x�͈��p�����Q�D�i1993�N�j�ł�8�~10-7�̃I�[�_�[�ł��B
�@��L�̕��@�œ���ꂽ���ݔ��ƁA�ri�̍����x���ʑ̌��q���f�[�^��p�������σ����������v�Z����B
�@���̂Ƃ��A�P�D�i�P�j�m�⑫�����R�n�Ő��������悤�ɁA�����x���ʑ̌��q�ʁi���Ύ��ʁj�f�[�^��10-10�̃I�[�_�[�ŋ��߂鎖���ł���Ă���̂ŁA�������ʂ̑��萸�x�����߂�̂͑��ݔ䑪��̐��x�ł��B
�@������ɂ��Ă��A���̂悤�ɂ��ē���ꂽ�������ʂ̑��萸�x�i�L�������j�͈��p�����Q�D�i1993�N�j�ł�8.2�~10-7�I�[�_�[�ł��B
�m�⑫�����P�n
�@���݂̏��A���ʑ́@28�r���A29�r���A30�r�������ݔ䑪�萸�x���A�{�K�h�����̑��萸�x�����߂Ă���̂ł����A28�r����99.99���ȏ�ɔZ�k���ĒP��������葪�萸�x���グ�邽�߂̍��ۃv���W�F�N�g���i�߂��Ă���悤�ł��B
�@���ʑ̂�Z�k����ɂ̓��V�A�̉��S�����Z�p���p������悤�ŁA���̍��ۃv���W�F�N�g����������A�{�K�h���萔�̑��萸�x��2.0�~10-8�܂ʼn��P�ł��邻���ł��B
�@�����Ȃ���S�D���Ő�������A�{�K�h���萔����L���O����������Ē�`����Ă������ł��邩������Ȃ��B
�@
�i�R�j�������x�̑���
�@�m�������x���n��m��ɂ́A��o������������������̐��𑪒肵�Ȃ���Ȃ�Ȃ��B���̂Ƃ����萸�x�̌��E�ɂȂ��Ă���̂͑̐ϑ���ł��B�P�����V���R���̑̐ς������x�Ōv��̂͌��\����̂ł����A���ݍł����x���ǂ��̂̓V���R���P��������ɐ^���ɋ߂����̂ɉ��H���āA���̋��̂̑������̒��a���v�����đ̐ς����߂���@�ł��B
�P�D�V���R�����̂̍�肾��
�@�V���R�������͍d���Ɉٕ��������邽�߁A�]���Z�p�Ő^���x�悭�������邱�Ƃ͍���ł��������A�ŋ߂͉��H�Z�p�̐i���ɂ�苅�̕\�ʂ��ψ�ɁA�܂����H�ώ��w�����Ȃ��������邱�Ƃ��\�ɂȂ�A�V���R���P��������ɐ^���ɋ߂����̂ɉ��H���邱�Ƃ��ł���悤�ɂȂ����B
�@���̂Ƃ��A�L���O��������Ɣ�r���č����x�Ȏ��ʑ��肪�ł���悤�ɁA���ʂ͂قڂPkg�ɋ߂��l�ɂȂ�悤�ȋ��̂ɉ��H�����B���p�����P�D�ŏЉ��Ă��鋅�̂́A���a93.6�����Ő^���x��0.083�ʂ��A���������p�_���Q�D�ŏЉ��Ă�����̂́A���a94�����Ő^���x��0.4�ʂ��ł��B
�@
�Q�D���̑̐ς̑���
�@���̎ʐ^�͒P�����V���R�����̂̒��a�𑪂郌�[�U�[���v�ł��B��93.6�����̒��a���P�i�m���[�g���̕s�m�����ő���ł���B�قڋψ�ɕ��z����70���ʂ��璼�a�𑪂��ċ��̂̑̐ς����߂�B

���}�͂��̏ڍא����ł��B
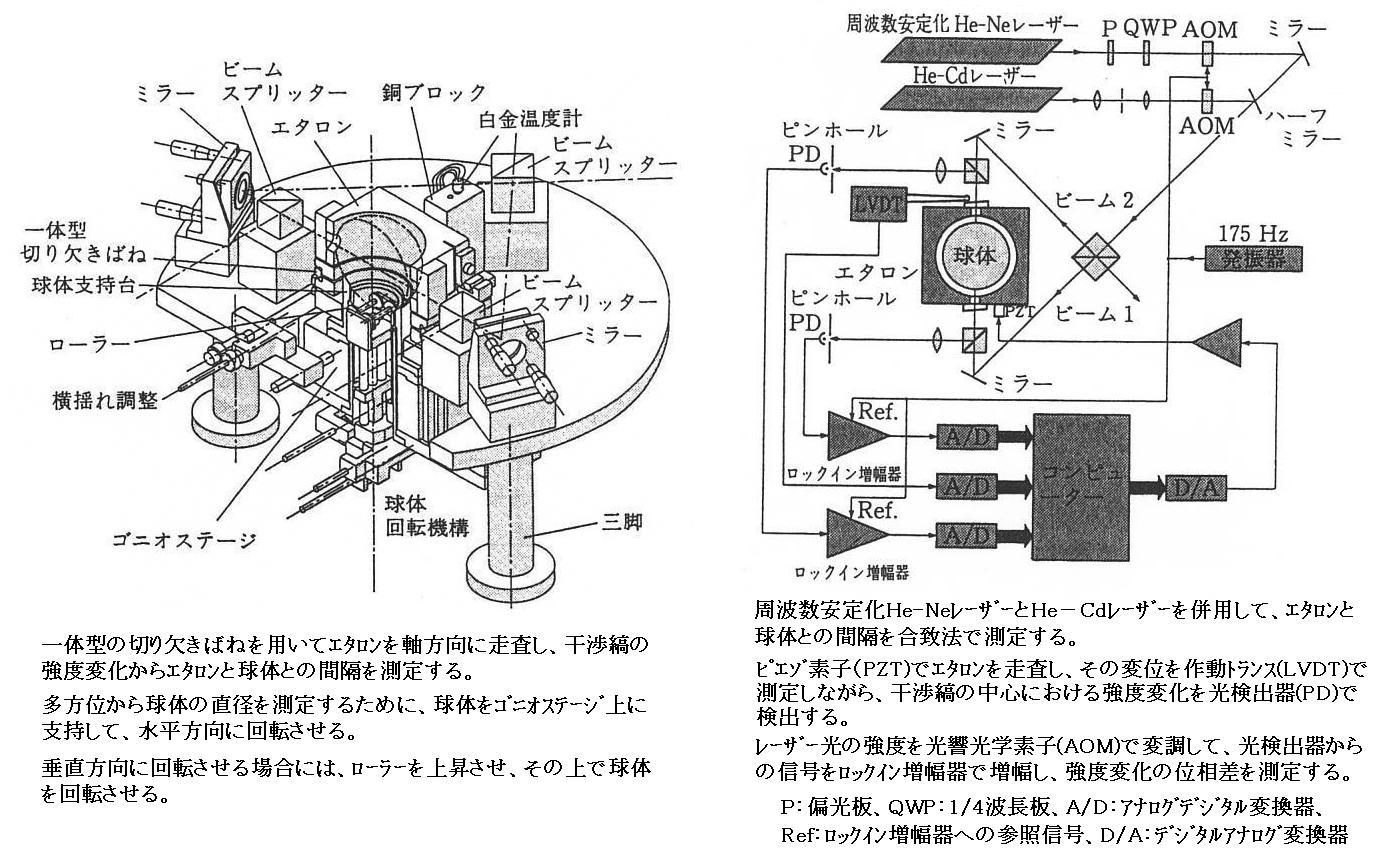
���ۂɂ��̑��u�ő��肳�ꂽ���̑̐ς̑��萸�x�͈��p�����Q�D�i1993�N�j�ł�3.4�~10-7�̃I�[�_�[�Ƃ̂��Ƃł��B
�m�⑫�����P�n
�@���p�����Q�D�ɂ��ƁA�̐ϑ���̌덷�̌����Ƃ��ăV���R���\�ʂ̎_�����̉e����A�����ɕs�����Ƃ��č������Ă���Y�f��_�f�̌��q�������i�q��c�߂���ʂ�����悤�ŁA���̓�����̕�����Ȃ���Ȃ�Ȃ��悤�ł��B
�@�܂���C���ő��肷��ꍇ��C�̋��ܗ��̕s�m�������덷�ɉe������̂ŁA�^�ł̑��肪�]�܂��悤�ł��B
�@
�R�D���̎��ʂ̑���
�@���̂̎��ʂ̓L���O��������Ƃ̔�r����0.1��������0.0000001��10-7�̐��x�ő���\�ł��B���̂Ƃ��p������L���O��������͓��R�����i�Ȃ̂ł����A�ǂ̃��x���̐��x�̕����i���p�����Ă���̂��͗ǂ�����܂���B���̓�����̎���͕ʍe�u�L���O��������̐��E�v���Q�Ƃ��Ă��������B
�@���p�����Q�D�i1993�N�j�ɋL����Ă���V���R�����̂̎��ʑ���덷��40��g�������ł�����A���萸�x��4�~10-8�̃I�[�_�[�ł��B
�m�⑫�����Q�n
�@���ʓV����p��������̍ۂɁA�V���R�������͓��d�������邽�߂ɁA�Ód�C�̉e���͏��Ȃ��悤�ł��B��C���ł̑���̏ꍇ�A���͂̕���ł��d�v�ŁA��C���x�̋ɂ߂Đ��m�ȑ��肪�K�v�Ȃ悤�ł��B
�@
�S�D�������x
�@��L�̌��_�������悤�ɁA�m�������x���n�̑��萸�x�́A���̎��ʂ����A���̑̐ς̑��萸�x�̌���ɂ������Ă���悤�ł��B
�@���p�����Q�D�i1993�N�j�̎��_�́@�m�������x���n�����̎��ʁ^���̑̐��@�̑��萸�x��7.7�~10-7�̃I�[�_�[�ł��B���̗ʂ̐��x�ɂ͂܂����P�̗]�n�����邻���ŁA���̓���10-8�̃I�[�_�[���B���ł������ł��B
�@
�R�D�A�{�K�h�����̌v�Z
�@���p�����Q�D�i1993�N�j�ɋL����Ă���e����l��
�m�i�q�萔���n

�m���������l�n
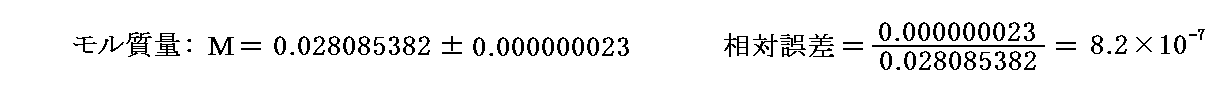
�m�������x���n
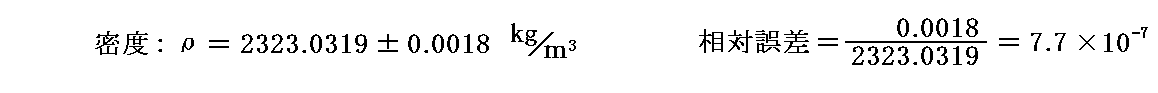
�ł��B
�@�����̒l��p���Č��肳�ꂽ1993�N���_�ł̃A�{�K�h������
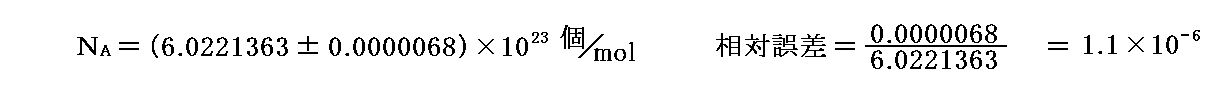
�ƂȂ�B
�@��L�̑��萸�x��1993�N���_�̂��̂ł����A�P�ʊi�q�̐ς��Ɋr�ׂă������ʂl�ƌ������x�ς̑��萸�x���s�����Ă��鎖������B
�@
�S�D�A�{�K�h�����Ǝ��ʒP�ʂ̍Ē�`
�@���݂̎��ʒP�ʂł���L���O��������ɂ�鎿�ʂ̍Č����E���萫�͕ʍe�u�L���O��������̐��E�v�����ǂ݂ɂȂ�Ή���悤��10-8�̃I�[�_�[�ł��B�܂�W���ڂ��s�m���ɕϓ����Ă���B
�@���̂��߁A�����A�{�K�h������10-8�ȉ��̃I�[�_�[�Ő�������ł���悤�ɂȂ����Ȃ�A�A�{�K�h������p���Ď��ʌ�����\���ł���B���Ȃ킿���݂̃L���O��������̗l�Ȑl�H��������Ȃ��āA���R�ɑ��݂��镨����ɂ��ăL���O����������\�����邱�Ƃ��ł���B����͉��L�̗l�Ȃ����Ŏ��������B
�@�L���O��������̒�`�Ƃ���
�@
�g�Pkg�Ƃ́A����Ԃɂ���Î~���Ď��R�ȏ�Ԃɂ���A�Y�f���q12�b��5.018�������~1025�̎��ʂƂ���B�h
�@
�@�����ŁA�g5.018�������~1025�h�Ƃ������l�́A��L�̒�`�ɏ�芷���鎞�_�œ�����ō����x�̃A�{�K�h�����mA���Œ肵�Ē�`�l�Ƃ������l��1000�^12�{���Č��߂�����̂ł��B�@
�@
�@���̐��x�ɂȂ�ƁA�g����Ԃɂ���A�Î~���Ď��R�ȏ�Ԃɂ���h�ƌ����A�������͏d�v�ł��B���Ȃ킿���w������Ԃ̌������̒Y�f���q���ʂ̃A�{�K�h�����{�ł͖����ƌ������Ƃł��B�i���̓�������P�D�i�P�j�m�⑫�����Q�n�̌��ς�����Q�Ɓj
�@��������ɂ́A�����ő̂̊i�q�萔���v���āA�A�{�K�h�������̒Y�f���q12�b�i���邢�͂ri�j���܂ޑ̐ς̉����肾���āA���̎��ʂ����ʌ���Ƃ���킯�ł�����A���w�����G�l���M�[�ɔ������q���ʂ̍����͗ʎq�d�C�͊w���_�ɏ]���ĕ���Ă����K�v������܂��B�@
�@�������̍Ē�`���̗p�����ƁA�A�{�K�h�����mA�͒�`�l�ƂȂ�m�肵���l�������ƂɂȂ��B�������āA�m�V���R�������Ȃǂ̊i�q�ԋ����n��m�������x�n�̑��萸�x�̐i���Ƌ��ɁA�Pkg���\������V���R���������̂̂悤�Ȏ��ʌ��킪��萳�m�ɍX�V����Ă������ƂɂȂ�B
�@����͂��傤�ǁA���j�I�ɂ͎��ԂƋ������킩������x�����肳��Ă����̂��A���̍Č������������x�̑���l���Œ�E�m�肵����`�l�Ƃ��āA���̑��x�Ǝ��Ԃ����萳�m�ȋ���������\�����āA���̌���̍X�V�𑱂��Ă������ƂɂȂ�������Ɏ��Ă��܂��B
�@�܂�A����Z�p�̐i���Ƌ��ɋ����̑��萸�x����萳�m�ɂȂ��Ă������̂Ɠ��l�ɁA���ʂɂ��Ă��V���R���������̂̌����E����Z�p�Ƒ���Z�p�̐i���ɂ��A��萳�m�E�����Ȏ��ʌ��킪�쐬�\�ɂȂ��Ă����ƌ������Ƃł��B
�@
�T�D���Ƃ���
�@���p���������������Â��A�ŐV�̑��萸�x�Ɍ��y���Ă��Ȃ��Đ\����܂���B�ŐV�̎���ɂ��Ă̓C���^�[�l�b�g�ł����������B
�@�Ƃ���ŁA���̍e�ŏЉ�������g���p����,62,1993�N�h�́A1996�N����NIFTY-Serve�̃p�\�R���ʐM��c���ŋ����Ă���������̂ł��B���̍e�����ɓ������ē����̃��O�Ə�L�_����T���o���ēǂݒ����Ă݂��̂ł����A�����̃p�\�R���ʐM�̉�c���͂ƂĂ��ʔ������Ӌ`�[�����̂ł����B�����g�A���܂��܂ȃt�H�[�������瑽���̎��������Ă��炢�܂����B���ǂ��̂g�o�̋L���̒��ɂ��A�����̃p�\�R���ʐM�t�H�[�����ŋ����Ă��������������R�������܂�Ă��܂��B
�@���̂悤�ȋc�_���ł����ԁE�ꂪ���݂������Ǝ��̂��ƂĂ��G�L�T�C�e�B���O�Ȏ���ŁA���O�̉{���E�������݂Ƀ��N���N���������v���o���܂��B�܂��A�C���^�[�l�b�g�̏����A���̑唼���p�\�R���ʐM�����ɓ���Ă��鎞��ł����B���͓�����ɓ��ꂽ�V�F�A�E�F�A�[�\�t�g�i�G�ہA���A�`���[�`���[�}�E�X�j��t���[�\�t�g�i�GCaps�ADDwin�j���A�b�v�f�[�g���Ȃ��炢�܂��Ɏg���Ă��܂��B
�@�C���^�[�l�b�g��html�̐��E���L�������̂͂��ꂵ���̂ł����A������Nifterm�Ȃǂ̉{���\�t�g�����Ă����ƂĂ��g������̗ǂ��������̏�i�{���E�������݁E���Ɋ��p�j�������Ȃ����̂͂ƂĂ��c�O�ł��B�����p�\�R���ʐM������Ă݂悤�Ƃ����l�X�́A�����̃t�H�[�����ŋc�_����Ă���悤�Ȏ����ɂ��ċ����������Ă���l�X���������炱���A�����ł̋c�_������オ�����̂ł��傤�ˁB
�@�C���^�[�l�b�g�����l�ɊJ�����ꂽ�����A����̏������T�C�g�����藧���Ȃ��Ȃ�A�����T�C�g��SNS�������Ɏ���ĕς���Ă��܂����̂ł��傤�ˁB
�m2018�N5���NjL�n
�@�P�ʂ̐V������`��2018�N11���ɍ̑�����A2019�N5��20�����{�s����܂��B�g���ʁh�̓L���O��������ɂ����A�g�v�����N�萔�h���g�A�{�K�h���萔�h���m�肷�邱�Ƃɂ���`�ɕύX����܂��B�܂��A�g�d�C�ʁh���g�d�C�f�ʁh�̒l���m�肷�邱�Ƃɂ��A�g��Ή��x�h���g�{���c�}���萔�h���m�肷�邱�Ƃɂ���`����܂��B
�@�����̈Ӗ���P�ʌn���̂��̂ɂ��Ă͉��L���Ђ≺�L�����N��������������B
�@
�P�c�F���u�V�����P�L���O�����̑�����i�Ȋw���i�߂ΒP�ʂ��ς��j�v�u�k�Ѓu���[�o�b�N�X�i2018�N���j
�Y�ƋZ�p�����������u������Ƃ킩��v�ʕW���v�����Ёi2007�N���j
�v����������w��̊w��u�v���Ɛ���v2014�N��53��1���`8���̃����[��������p
�@�P�D���ےP�ʌn�i�r�h�j�̑̌n�Љ�ƍŐV�����i�T�_�j
�@�Q�D���ʕW���̌���ƃL���O�����ikg�j�̒�`������߂���ŐV����
�@�R�D�d���i�`�j�ɂ��Ă̊�b����ƍŐV����
�@�S�D�����ʁimol�j�ɂ��Ă̊�b����ƍŐV����
�@�T�D���ԁi���j�ɂ��Ă̊�b����ƍŐV����
�@�U�D�����i���j�ɂ��Ă̊�b����ƍŐV����
�@�V�D�����ʁicd�j����ё����E���˕W���ɂ��Ă̊�b����ƍŋ߂̘b��
�@�W�D���x�i�j�j�ɂ��Ă̊�b����ƍŐV����