このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
物理量の数値表現で重要な有効数字(有効桁数)についの説明です。つまり、なぜ 1320000 ではなくて 1.32×106 と表現するか?その理由を説明します。
有効数字とは何か、またどうやって有効桁数を数えるのか、例を用いて説明する。
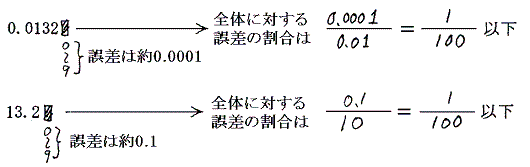
有効桁数3桁とは元になる数字の大きさに対して誤差が100分の1以下になる様な数値表現のことである。以下述べるように数字で表現されている最小桁の次の■の値が0〜9のどれになるか解らないから誤差が生じるのであるから

となる。このとき 0.0132 と 13.2 とでは数値の絶対的な大きさはまったく異なるが、信頼できる数値の桁数はどちらも3桁である。それを有効桁数という。
同様に考えると、以下の二つの数値例の全体に対する誤差の割合はいずれも10000分の1以下だから、有効桁数は5桁となる。
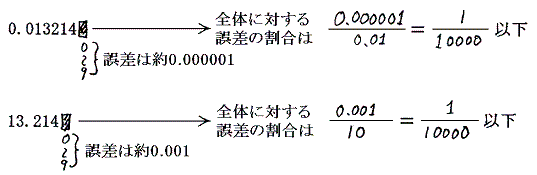
この二つの例の考察から明らかなように、数値表現に於いて数値が存在する最も高い位から最も低い位までの桁数を数えれば良い。その桁数が有効桁数となる。
前項における説明のように、数値に小数点以下の数字があるときは有効桁数はすぐに解る。しかし 1320000 の様な場合 132の次の位の 0 が本当に 0 なのか、位取りの為の 0 なのか区別できない。そのとき 1.3200×106 や 1.320×106 のように表現すれば、本来書く必要のない小数点以下にわざわざ 0 が書かれているので、その 0 は位取りのための 0 ではなくて値としての 0 だと判別できる。前者は有効桁数5桁、後者は有効桁数4桁となる。
一般に小数点より左側に一桁だけ数字が出るようにしてそれ以下の桁の数値を小数点以下に持って行き、絶対的な大きさを 10X の指数表現で表すようにする。そうすると有効桁数は小数点以下の数値の並びの個数から、また絶対的な大きさは指数xの値から直ちに読み取ることができる。
演算に関係する数値の中で、有効数字の末位が最高の位を持つものに、有効な桁の末位が揃ってしまう。以下の例参照。
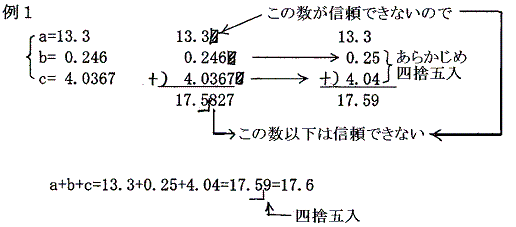
だから加法・減法を行うときに、有効桁の末位の位がバラバラの場合は、末位の位が最も高いものにそろえてから計算しても差し支えない。つまり末位の位が最も高いものの一つ下の位で、あらかじめ四捨五入をしておく。そして加法・減法を実施する。そして最後の結果の末位を四捨五入して信頼できる値にすると良い。
以下の例で、○をつけた数字の次の位が0〜9のどれか解らないので○をつけた数字には1程度の不確かさがある。そのため例2の計算結果は 17.6 となり有効桁数は3桁、例3の結果は 9.4 となり有効桁数は2桁となる。
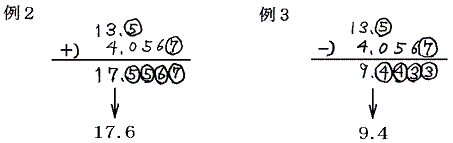
以下の計算で○で囲った数に1程度の誤差がある。そのため○で囲った数値が関わる計算結果の○数字は少し信頼できない。そのとき最終計算結果が何桁信頼できるだろうか。以下の例から明らかなように、掛け算をする二数の内の有効桁数の少ない方の有効桁数に一致する。
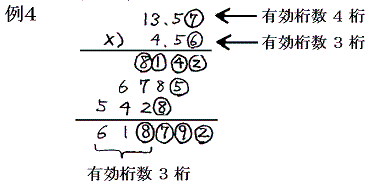
このあたりの事情を明らかにするために 13.57423 と 4.56 を掛け算の順番を入れ替えて計算してみる。例5と例6から明らかなようにどちらも有効桁数は3桁になる。つまり、関係する2数の内の有効桁数の少ない4.56の有効桁数に一致する。
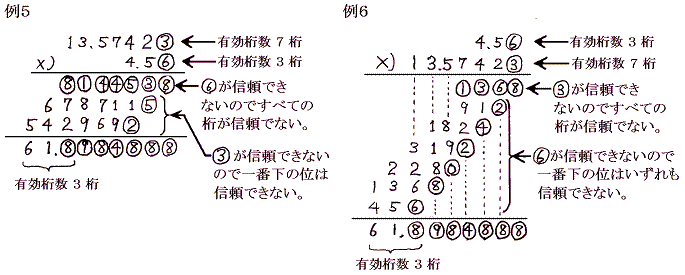
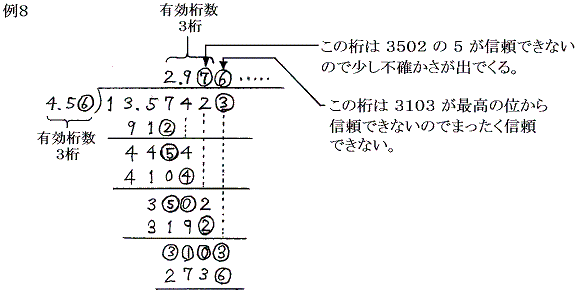
除法についても同様である。○で囲った数値が1程度の誤差で信頼できないので計算結果も○で囲った数値が少し信頼できなくなる。そのため割り算をする二数の内の有効桁数が少ない方の桁数に一致する。
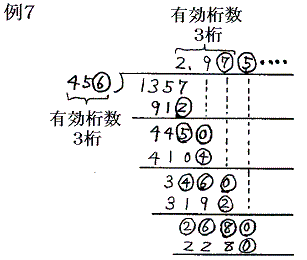
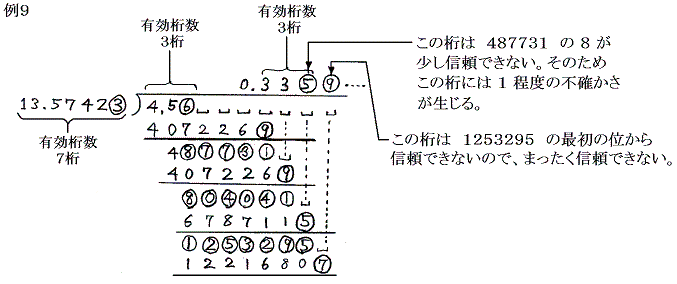
このあたりを確かめるために 13.57423 と 4.56 を割り算の役割を変えて計算してみる。例8、例9のいずれも、最後の計算結果の有効桁数は3桁である。つまり、関係する2数の内の有効桁数の少ない4.56の有効桁数に一致することが解る。