このように定めた1mol当たりの気体定数R’は気体の種類によらずどの気体でも同じ値となる。
中学理科や高校地学で気温は高度とともに低下すると習います。温度がどの様な割合で下がるのか理論的に解りやすく説明します。またその応用として温位と相当温位の定義を説明します。
普通、気体の状態方程式は別稿「絶対温度とは何か(積分因子とは何か)」2.(5)で説明したように、単位モル当たりについて示される。
このように定めた1mol当たりの気体定数R’は気体の種類によらずどの気体でも同じ値となる。
しかし、気象学ではモル当たりではなくて単位質量についての状態方程式を用いる。その場合には上記の値R’をモル質量M[kg/mol]で割った値を気体定数Rとする。
この様に単位質量(1kg)当たりで表した気体定数Rは気体の種類ごとに異なった値となる。気象学では普通空気を取り扱うのでMとしては常に空気の平均モル質量M空気=28.966×10-3kg/molを用いる。そのため気体定数は常にR空気≡Rd=287J/K・kg(添え字dは乾燥“dry”空気の意)となる。
まだここでの温度Tは絶対温度(K)でなければなりません。摂氏温度(℃)を用いると誤ります。「絶対温度とは何か(積分因子とは何か)」2.「絶対温度とは何か(積分因子とは何か)」2.(3)参照。
全ての出発点は、気圧の高さによる変化を理解することです。大気の圧力はその上に積もった空気の重さによって生じる。そのとき、地表に近い部分ではその上に積もった空気の量が多くなるので、より圧縮された状態となり高圧力となる。
大気の圧力の高度による変化は、“静力学平衡”の条件から求まる。この条件は気柱の微少体積部分ΔxΔyΔzに働く重力と、微少体積の上面と下面に働く圧力差が釣り合うことです。
そのとき下記の微分方程式が成り立つ。
これを“静力学平衡”の式というが、ρ>0であるからdp/dz<0となり、気圧は高さと供に減少する事が解る。
気温が対流圏での平均温度T=−18℃=255Kに等しい温度で高空まで堆積していると仮定できる場合を計算してみる。温度がzに依存しない場合、圧力の高度依存性は簡単に求めることがでる。
気圧pと高さzの関係を表す[静力学平衡の式]に[気体(空気)の状態方程式]を連立させて、密度ρ(z)を圧力p(z)で表して解けばよい。つまり、以下の積分を実施する。
全ての高度の温度が同じという荒っぽい近似のもとでの議論ですが、−logep∝zという結論は重要です。
ここで、Hは“大気のスケールハイト”と言われる量で、気圧が地表の1/e培になる高度を表す。
[補足説明]
等温分布の場合の気圧の高度変化については、別稿「二次元・非圧縮性・完全流体の力学(ラグランジュの渦定理とは何か)」3.(5)4.[補足説明1]ですでに説明した。
そこでは流体力学のベルヌーイの定理の応用として説明しましたが、上昇する気塊は、断熱膨張ではなくて、周りの気体と等温的に熱をやり取りしながら移動するというものでした。その点に注意されて理論展開を検討されれば、ここで説明した方法と同じであることが解ります。
[計算例]
大気温度が-18℃=255K=一定であるという仮定のもとで、地表(z0=0)の気圧を観測平均値であるp0=1013hPaとし、上記の式を用いて上空zの気圧pを計算してみる。
全ての高度の温度が同じという荒っぽい近似ですが、後で示す実在大気の観測平均値分布に大体一致します。つまり、圧力−logepがほぼ高度zに比例するということが確かめられる。
実際の大気温度の観測値は、4.(2)2.で示す様に、対流圏では高度と共にほぼ直線的に低下します。
そのことを考慮した計算をしてみます。
大気が、対流圏での気温減率の平均値Γ=0.0065℃/mで、高空まで堆積していると仮定できる場合を計算する。このとき気温変化がzの一次関数になるので積分は容易です。
気圧pと高さzの関係を表す[静力学平衡の式]に[気体(空気)の状態方程式]と[気温の高度変化式]を連立させて解けばよい。
[計算例]
地上(z0=0)の気圧平均値p0=1013hPaと気温平均値T0=15℃=288.2Kを適用して、様々な高度zにおける気圧pを計算すると下表の様になる。
この結果を気圧観測値の平均値分布と比較してみると、対流圏における値が、前節の計算式よりも、観測値に近くなっている。
ただし、ここでの気温分布の仮定から予想されることですが、10km以上の高空については誤差が出て来て観測値と合わなくなります。その当たりを修正するには、高度10km以上を等温分布(観測値平均 -55℃=218.2K)として、(3)で説明した式を用いればよい。それにT=218.2K、p0=p(10000m)=264.54hPa、z0=10000mを代入して計算する。
実際に計算してみると、成層圏以上が観測値に良く一致するようになる。
実際の大気高度における気圧観測の平均値を下表に示す。
実際の大気温度は高度と共に下がっていきます。そのとき、温度が高度と共にどのような割合で低下するかを見積もる拠り所は、地表にあった大気を持ち上げていくと周囲の圧力が減少する為に断熱的に膨張して冷えていくことです。
高度が上がれば周りの大気の温度は下がるのですが、静力学平衡が成り立つということは、大気の温度の高度変化が、上記の様に断熱的に持ち上げた空気塊が示す温度・圧力に周囲の大気もなっているということです。
なぜなら、もしその様な状況が成り立たずに、持ち上げた空気塊の温度が周囲よりも高ければ、その熱は周囲に伝えられて周囲の温度を上げ、もしより低ければ周囲から熱を奪って周囲の温度を下げるので最終的に空気塊の攪拌が終わった状態でのつり合い状態では前記の条件が成り立っているといえるでしょう。
別稿「熱力学関数(状態方程式曲面)の性質」1.(2)2.で説明したように
であり、また同じページの1.(3)2.で説明したように
となる。
d’Qの ’ はdQが全微分ではないことを示している。この意味は別稿「絶対温度とは何か(積分因子とは何か)」を参照されたし。
気象学の議論では、熱量や仕事をやり取りする空気塊は単位質量についてのものであるとします。そのため示量性変数をすべて単位質量当たりについてのものとしている。そのことを強調するために今後それらの量を小文字で表すことにする。また、特にそうする必要は無いのですが、間違いを防ぐために示強性変数も(絶対温度T以外を)小文字で表すことにする。
このとき、気象学の慣例に従って単位質量の気体の体積(“比容積”と呼ばれる)をvではなくて“α”で表す。さらに、空気の単位質量当たりの気体定数R空気を今後は単にRまたはRd(添え字dは乾燥“dry”空気の意)と記すことにする。
上記の方針で表記すると、空気塊に就いての熱力学第一法則は
と書かれる。d’qは単位質量の空気塊に与えられる熱量です。
気塊に対して外から熱の出入りがない変化を断熱変化と言う。断熱変化の場合でも内部で水蒸気の凝結が起きれば潜熱が発生して熱源が存在することになるのですが、今は水蒸気を含んでいても飽和に達していない空気塊で、凝結熱は発生しないとします。このような過程を“乾燥断熱変化”と呼ぶ。
乾燥断熱変化の場合d’q=0だから、熱力学第一法則から以下の微分方程式が得られる。
最初の式は、気塊の体積(比容積)が増加すれば、温度が低下する事を示している。また下の二番目の式は気圧が増加すれば温度が増加する事を示している。
厳密には、ここでのRは混合気体(窒素+酸素+水蒸気)の気体定数ですが、簡単化して乾燥空気(窒素+酸素)の気体定数R≒Rd=287J/K・kgとして議論します。
[計算例]
例えば、1000hPaで気温15℃=288Kの気塊の圧力が10hPaだけ減少したときの気温変化は
となる。cpは空気の定圧比熱ですが、空気が理想気体と見なせる場合は温度、圧力によらずほぼ一定とみなせる。
[補足説明1]
上記の一番目の式をv0からvまで積分すると
となる。
ここで、理想気体に対してマイヤーの関係式 R=cp−cv が成立するので、cp/cv=γと置くと、上式は次のように変形できる。
これは別稿「気体の断熱変化」で説明した断熱変化を表す公式です。
[補足説明2]
全く同様に、上記の二番目の式をp0からpまで積分すると
となる。
ここで、理想気体に対してマイヤーの関係式 R=cp−cv が成立するので、cp/cv=γと置くと、上式は次のように変形できる。
これは別稿「気体の断熱変化」で説明した断熱変化を表す公式です。
気塊が乾燥断熱上昇した場合の温度変化を考える。その温度変化は気塊が上昇して気圧pが変化したときの[断熱温度変化を表す微分方程式]と上昇気塊の周りの気圧pと高さzの関係を表す[静力学平衡の式]を連立させて解けばよい。
ここで、Γdを“乾燥断熱減率”(dry adiabatic lapse rate)と言うが
となり、お馴染みの値が得られる。
[補足説明]
乾燥断熱減率については、別稿「二次元・非圧縮性・完全流体の力学(ラグランジュの渦定理とは何か)」3.(5)4.[補足説明2]ですでに説明した。
そこでは流体力学のベルヌーイの定理の応用として説明しました。そのとき上昇する気塊は、断熱膨張で変化・移動していく。その点に注意されて、ここの理論展開と比較検討されれば、ここで説明した方法と同じであることが解ります。
また、この気温減率にもとずく大気圧の高度変化の様子は、上記リンク先の図をご覧下さい。
2.(2)[補足説明2]で説明した様に、乾燥気塊の断熱変化に対しては次の関係が成り立つ。
気象学では任意の高度(圧力)における気塊を標準気圧(p0=1000hPa)に持って来たときに示す温度T(p0)をその気塊の“温位”(potential temperatrue)といいθで表す。
温位θは気塊を断熱的に標準気圧の高度まで下降させたとき、気塊が持つ温度のことですが、断熱変化をしている気塊では保存される。つまり異なった高度にある気塊でも断熱変化で結ばれている気塊は全て同じ温位を持つ。
任意の高度z(圧力p)と温度Tにおける気塊の温位は当然のことながら、気塊が存在する位置z(圧力p)と温度Tの関数です。
[補足説明1]
気塊の温位θは、気塊が乾燥断熱の条件下で鉛直運動しても不変となり、乾燥断熱過程における保存量となることは以下のようにして証明できる。
はじめの気塊の温度Tと圧力pが断熱変化して微少量ΔTとΔpだけ違ったために温位がΔθだけ変化したとする。θの定義式から
が言える。つまりθは気塊が乾燥断熱変化しても保存される。
上記の微分表示式が何を意味しているか解りにくいので、4.(3)1.で導入するエマグラムの上で説明する。
エマグラムの(p,T)平面に垂直に温位座標θを取り、図中の乾燥断熱線を等高線とするθ(p,T)の三次元曲面を考える。そうすると上記の式は温位θの全微分表示となります。その三次元曲面θ(p,T)のΔT方向の勾配が(θ/T)で、Δp方向の勾配が(θR/cpp)です。
そして気体の乾燥断熱変化とは、その三次元曲面の等圧線に沿ってΔTだけ曲面を下り、次にその点から等温線に沿ってΔpだけ登ると、曲面の高さθが同じ位置に来るような変化だと言うことです。
温位定義式は元々断熱変化の式から導いたもので、乾燥断熱線をθ=一定の等高線としているのですから、乾燥断熱変化はこの等高線(等温位線)に沿ったものとなり、温位が保存されるのは当然です。
[補足説明2]
温位の定義における1000hPaの高度は普通地表高度と考えられます。そのためエマグラム上の(p,T)点に存在する気塊に対して、その気塊が水蒸気を含んで飽和に達していようと、完全に湿度ゼロの乾燥気塊であろうと、その湿度の状況にかかわらず温位は一意に定義できます。なぜなら(p,T)にある気塊が水蒸気を任意に含んでいても1000hPaまで移動させることは圧力が増加して圧縮され気温が高くなる方向への移動となるので、必ず乾燥断熱過程となるからです。
つまり(p,T)平面上の全ての座標点に対して温位θ(p,T)は前記の式に従って一意に定まっている。実際エマグラムのすべての領域に渡って等温位線が引かれていることに注意してください。
このとき注意して欲しいことは、関数
は(p,T)平面上のθの三次元曲面を表しているのですが、前記の全微分
のΔTとΔpは乾燥断熱変化の方向に限る必要は無いことです。
すなわち、(p,T)→(p+Δp,T+ΔT)の変位が任意の方向の変位であっても、その変位に伴う温位θの変化分Δθを与える。この全微分表示は、3.(8)2.で相当温位の数式表現を導くときに用います。
前記の定義式を用いれば、T(p)から温位θが求められる。このとき(p0/p)0.286を“温位関数”と呼び、任意の圧力の下に在る温度T(p)の気塊の温位を求めるために利用される。その具体的な関数値は次表の様になる。
上記の表示では解りにくいので、横軸[気圧pの対数表示]・縦軸[温位θ]にして、気温T=−60℃(213K)、-40℃(233K)、-20℃(253K)、0℃(273K)、20℃(293K)の場合の温位θ(p,T)のグラフを描いてみる。
この線の集まりθ(p,T)は、エマグラムの(p,T)座標平面上に一つの三次元曲面を構成する。つまり、エマグラムの(p,T)平面に垂直に温位座標θを取ると、温位θ(p,T)は低温・高圧側が一番低く、高温・定圧側に向かって次第に傾斜が大きくなる、ほぼ一様に傾斜した平面状の曲面となる。実際エマグラム上の気圧p=500hPa線上の温位θを読み取って、上図500hPaの交点におけるθ値に一致することを確かめてみてください。
その三次元斜面の等高線[θ(p,T)=一定の線]を(p,T)座標平面に射影したものが等温位線であり“乾燥断熱線”です。
ところで、元々の断熱変化を表す式を、温位計算式のようにT(p0)で解くのではなくて、T(p)の関数として見なせば
と表せて、これは乾燥断熱線を表す式そのものになります。
例えばp0=1000hPaにおける気温がT0=-60℃、-40℃、-20℃、0℃、+20℃の気塊の乾燥断熱線を描いてみる。これをグラフ表示するのですが、そのとき縦軸と横軸を入れ替えて表示すると
となり、確かにエマグラムの“乾燥断熱線”が得られるのが解る。
[計算例1]
温度30℃(=303K)で地表(=1000hPa)に存在する気塊の温位はθ=303Kです。また、気圧250hPaの高度にある温度−50℃(=223K)の気塊の温位は、温位関数表を用いるとθ=223×f(250)=223×1.486=331K(=58℃)となります。そのとき、気圧250hPaとなる高度は1.(4)の表で示すように10km程度です。
温度を単純に比較すると高度10km(250hPa)にある-50℃の気塊の方が地表にある30℃の気塊よりも冷たいのですが、高度10km(-50℃)の気塊を地表(p=p0=1000hPa)まで断熱的に引き下ろすと58℃となり、地表にある温度30℃の気塊よりも暖かくなる。そういった意味では、高度10kmにある-50℃の気塊の方が暖かいことになります。温位はその当たりの事情を示す量です。
[計算例2]
グローバルな大気について、温度と温位の関係を比較をしてみる。下図は大気の南北鉛直断面における温度分布図です。温度が最も高いのは熱帯地方の下層であり、温度が最も低いのは同じく熱帯地方の対流圏界面付近であることが解ります。
ところが、同じ大気の南北鉛直断面における温位分布図は下図の様になりまます。温位が最も低いのは極地方の下層です。どの緯度においても温位は高度とともに増加しています。そうなるのは、実際の大気の気温減率が2.(3)で説明する乾燥断熱減率0.98℃/100mよりも小さい値約0.65℃/100mで下がっているからです。そのため温位は高空になるほどどんどん大きくなります。
その変化の度合いが最も大きいのは対流圏界面付近です。温位が圏界面から成層圏下部で急激に上昇していることは、大気がそこで非常に安定な成層を成している事を意味します。下から積乱雲が鉛直上方に発達しても、その層を通過できず雲は水平に広がっていく。つまり鉄床雲(カナトコグモ)になるのはそのことが原因です。
さらに、北緯40度付近では、等温度線・等温位線ともに急激に傾いており、その傾斜方向が逆になっている。これらの事実は地球大気の構造に大きな意味を持つ。すなわち、北緯40より南側では暖かい空気が高く積もり、北側では冷たい空気が低く積もっている事を意味する。
これは別稿「大気大循環」4.の図5あるいは図6の様な関係が生じている事を示している。そのため北緯40度付近の水平面で見れば赤道側が高圧、極側が低圧になる。この気圧傾度が西風のコリオリ力と釣り合い北緯40度付近に強い西風(偏西風)が吹くことになる。これは地衡風の一種で、特に気圧傾度が大きい圏界面付近の風速は大きくなる。これがいわゆるジェット気流です。温度分布図中の西風の風速分布がその当たりの事情を示している。
[計算例3]
気塊の運動が断熱的に起これば、その気塊が上下に運動しても温位は変化しない。つまり気塊は等温位面に沿って移動している。そのため等温位面(下図では305K)の等高度線を引き、その面上にその高度の風速・風向ベクトルを重ねて見れば、その風が上昇しているのが下降しているのかが解る。
下図は寒冷前線が北北西から南南西に走っている時の気象状況を示している。前線の北西部の等温位面の高度が大きくなっていることから前線の北西部に冷たい空気のドームがあることが解る。また等高線が3500m〜4500m付近の風は等高線を横切っている。つまりこの領域で冷たい風が寒冷前線に向かって吹き降りていることが解る。
一般に、上昇気流があるところでは雲が発生して天気が悪く、下降気流があるところでは雲が消えて天気が良い。ところが、空気塊の上下方向の動きは水平方向の動きに比べて観測するのが非常に難しい。4.(2)2.で説明するラジオゾンデでは直接観測できない。
そのような場合でも、等温位面の高度変化を示す図に、その高度での風速・風向ベクトルを重ねてみれば、風の上下方向の動きが読み取れるわけです。
ちなみに、上図で風速・風向が表示されている点は、4.(2)2.で説明する高層気象観測が定常的に行われているアメリカの観測点です。ワイオミング大学気象観測データの地図を参照されたし。
対流圏における気温減率の観測値(地球全体について一年間を平均した値)は−0.65K/100m程度です。
前章で求めた乾燥断熱減率=−0.98K/100mと異なるのは、実際の大気では上昇に伴って水蒸気の凝結が生じ、潜熱の放出(熱源の存在)があるからです。
そのため、実際の大気の気温減率を求めるには、潜熱の解放を考慮した“湿潤断熱変化”に従った考察をしなければなりません。
空気には窒素や酸素と供に水蒸気も含まれている。水蒸気は圧力を持ち、その圧力を“水蒸気圧”(vapour pressure)と呼び気象学では普通“e”で表す。
密閉した真空容器に水を入れて一定温度に保つと、水面から水蒸気が蒸発して水蒸気圧を示す。容器内の温度を一定にして平衡状態が実現されたときの水蒸気圧を“飽和水蒸気圧”(saturation vapour pressure)とよびes(添え字sは“飽和”saturationの意)で表す。
水および氷に対する“飽和水蒸気圧”esは下表の様な値です。
0℃以下では氷に対するものと過冷却水に対するもので、飽和蒸気圧が異なる。このことは雨を降らせるメカニズムにおいて重要な意味を持つ。
より詳細な飽和蒸気圧表はこちらをご覧下さい。
[補足説明1]
エマグラムの下の余白に描かれているスケールは、上記の温度T[℃]と飽和水蒸気圧es(T)[hPa]の対応表を変換スケール表示したものです。これは気塊の湿度R.H.から、その気塊の露点Tdや混合比qを求めるときに用いられる。
ただし、このスケールの0℃以下の部分は、氷に対するものではなくて、過冷却水に対する飽和蒸気圧であることに注意されたし。
[補足説明2]
上記の飽和蒸気圧表は、平らな平面の水(氷)と平衡状態にある場合のものです。水滴のように表面に曲率があると、表面張力が弱くなるので水滴は蒸発しやすくなり、飽和蒸気圧は大きくなります。Kelvinによると[半径rの水滴と平衡状態にあるときの飽和水蒸気圧]esrと[表面が平坦な水と平衡にあるときの飽和水蒸気圧]esとの比は
で与えられる。ここで、aは表面張力a=7.275×10-2N/m、ρwは水滴の密度ρw=1.0×103kg/m3、Rvは水蒸気の気体定数Rv=461J/kg・K、Tは絶対温度、rは水滴の半径で単位はmです。
esr/esの具体的な値を幾つか計算してみると
となる。
水蒸気の温度を下げていって凝結が起きるとき、最初にできる水滴は無限に小さな半径の水滴です。そのため、前記の飽和水蒸気圧よりもかなり過飽和の状態に成らなければ水滴はできないことになります。
ところが、自然界では1%を越える過飽和状態の水蒸気が存在することは希です。それにもかかわらず実際の大気中で水滴は容易にできます。それは大気中に浮遊する微粒子(エアロゾル)が凝結核として働くからです。
実際に水滴ができて雨が降るメカニズムには考慮すべき事情が多々あり、かなり複雑です。それはとても興味深い事柄ですので、参考文献4.の該当部分を引用しておきます。
水(液体)は氷(固体)や水蒸気(気体)などに相変化するが、その様な相変化に伴って吸収・放出される熱エネルギーを“潜熱”latent heatといい、それぞれ下記の様な名称で呼ばれる。
厳密に言うと潜熱は相変化するときの温度に依って変化します。しかし、気象学で対象とする温度範囲ではほぼ一定値と見なすことができる。
液体の水と平衡状態にある水蒸気圧力(飽和水蒸気圧)の温度依存性des/dTは、[潜熱]・[相変化に伴う体積変化]・[転移温度]と以下の様に関係づけられる。
これは“クラウジウス・クラペイロンの式”と言われるもので、これが成り立つメカニズムは別稿「ファン・デル・ワールスの状態方程式(クラウジウス=クラペイロンの式、ジュール=トムソン効果)」4.、あるいは「熱力学関数(状態方程式曲面)の性質」4.(2)で説明しています。
上式を、水蒸気の状態方程式を用いて、変形・積分すると“飽和水蒸気圧”es(添え字sは“飽和”saturationの意)の温度変化を表す式が得られる。
これは後で何度も用いる重要な関係式です。
またこの式を逆に解いた
のesに未飽和状態の水蒸気圧eを代入すれば、3.(3)2.で説明する露点(温度)Tdを求めることができます。
[補足説明1]
氷→水蒸気の相変化(昇華)に対しても同様な計算ができるが、相変化に伴う潜熱が異なるので氷に対する飽和水蒸気圧esは水に対する値と少し異なる。
その当たりの違いは前述の表の0℃以下の部分をご覧下さい。0℃以下でも液体として存在する水を“過冷却水”といいますが、それに対する飽和蒸気圧と、氷に対するものと二通りの飽和蒸気圧があります。
[計算例]
表計算ソフトExcelを用いて、上記の式から様々な温度における飽和水蒸気圧esを計算してみると下表の様になります。ただし、氷に対する飽和水蒸気圧は、昇華熱(L1,3=2.83×106J/kg)を用いて計算しています。
これはおおざっぱな潜熱値を用いた計算ですが、実際の観測値[3.(1)の数表]と良く一致します。
同様な計算、別稿の「ファン・デル・ワールスの状態方程式(クラウジウス=クラペイロンの式、ジュール=トムソン効果)」4.(4)、あるいは「平衡状態の熱力学(気体の化学反応)」3.(3)7.のグラフも参照されたし。
実測値をより正確に再現する計算式については参考文献3.§3.1をご覧ください。
[補足説明2]
現実の空気は乾燥空気(窒素+酸素、圧力pd、平均分子量28.97)と水蒸気(圧力e、分子量18.02)の混合気体です。そのため、現実の空気の圧力は p=pd+e となる。混合気体の状態方程式については別項「ドルトンの分圧の法則と混合気体の状態方程式」3.をご覧下さい。
水蒸気圧eは時間的・空間的に変動しますから、湿潤空気の分子量は定数ではなくて水蒸気の含有量に応じて変化します。だから混合気体の単位質量当たりの気体定数も水蒸気の混合比の変化に伴って変化します。その当たりは3.(4)で説明します。
湿潤空気に含まれる水蒸気量を表すのに様々なやり方がある。それらの定義式と相互の換算式を説明します。
観測された水蒸気圧eを、その温度における飽和水蒸気圧esで割って100倍した値を“相対湿度”R.H.(“相対”relative+“湿度”humidity)と言う。
相対湿度は飽和水蒸気圧に対する比で、水蒸気の絶対量を示す尺度ではない。水蒸気の絶対量を表すには以下の3.で述べる混合比が用いられる。
相対湿度R.H.は乾球・湿球温度計、毛髪湿度計、静電容量湿度センサーなどを用いて直接計測できる。4.(2)2.で説明するように、世界各地の観測点で毎日2回定時に大気の相対湿度の分布が観測されている。
これを各高度の観測温度の飽和水蒸気圧es(既知で数表として与えられている)と組み合わせることで、次式により各高度の気層の水蒸気圧eを求める事ができる。
これは、大気の安定性を論じる上でとても重要な値で気象解析で必須のデータです。
温度T、水蒸気圧eの空気を圧力一定の条件下で冷却すると、水蒸気圧がやがて飽和水蒸気圧に一致する。そのときの温度を“露点”(dewpoint)Td(添え字dは“露”dewの意)と言う。
実際の温度と露点の差を“気温露点差”と呼ぶ。
この差が小さい気塊は飽和に近く湿っており、逆に大きな気塊は乾いていることを意味する。
後で説明するように、この差が小さい気塊は少し上昇するだけで、乾燥断熱過程から湿潤断熱過程に移行します。各高度における露点Tdまたは気温露点差(T−Td)のデータは、大気の安定性を調べるときにとても重要です。地上天気図や高層天気図の解析に使用される。
各高度の気層(気塊)の水蒸気圧が求まってれば
の式によって、各高度における気層(気塊)の気温から、蒸気圧表あるいは換算スケールを用いて、各高度の気層(気塊)の露点Tdを求めることがでます。気層(気塊)の水蒸気圧は前項の方法で、気温と相対湿度の値から求める。
あるいは、3.(2)で説明した数式のesに水蒸気圧eをesとして代入して計算しても良い。
“乾燥空気の質量”md(添え字dは“乾燥”dryの意)に対する“水蒸気の質量”mv(添え字vは“蒸気”vaporの意)の比を“混合比”(mixing ratio)qと言い
で定義する。
混合比qは無次元量ですが、水蒸気量を差し引いた空気1kg中に含まれる水蒸気質量を意味します。そのため普通kg/kgまたはg/kgの単位で表す。
乾燥空気と水蒸気の状態方程式を用いると、混合比qは
であらわされる。つまり、混合比qは気圧pと水蒸気圧eから計算で求めることができる。
さらに、飽和水蒸気に対する混合比を“飽和混合比”qs(添え字sは“飽和”saturationの意)と言います。その定義と、気圧p、飽和水蒸気圧esとの関係は以下の様になる。
この式の飽和蒸気圧esは3.(2)で求めたクラウジウス・クラペイロンの式で与えられるので
が得られる。この式は湿潤断熱減率を求めるとき重要です。
[計算例]
この式に従って、幾つかの気圧、大気温度における飽和混合比を表計算ソフトExcelで計算してみると下表の様になる。ただし、kg/kg表示ではなくてg/kg表示にするために1000倍してある。
後で、正確な表を引用していますが、その表も、ここのやり方を、もう少し精密化して求めたものです。
混合比q、飽和混合比qs、水蒸気圧e、飽和水蒸気圧es、相対湿度R.H.は互いに次の関係にある。
この関係式を用いると、気塊の(p,T)値における飽和混合比の値(下表参照)と相対湿度R.H.のデータから、その気塊の混合比qと露点Tdを求める事ができます。
一定質量(例えば1kg)の湿潤空気を考える。その空気塊に含まれる質量mdは、圧力が高まって体積が減少しても同じです。ところが飽和水蒸気の質量mvはその減少した体積中での飽和水蒸気量で、そのときの温度のみに関係する飽和水蒸気圧と、その気塊の体積によります。そのため、気塊中に含まれる飽和水蒸気質量mvは、もとの圧力時の体積よりも体積が減少した分だけ減少します。
つまり、飽和混合比qs=mv/mdは圧力が増えれば減少する。前述の式の分母にあるpは、その当たりの事情を示しています。その数式表現から明らかなように、飽和混合比は、大気の圧力と温度の両方の関数です。
これは飽和水蒸気圧esが大気の圧力には無関係で、温度のみの関数だったことと大きな違いです。
正確な飽和混合比は次表の様になる。気温が同じでも圧力増大すればqsは小さくなることに注意されたし。
[補足説明1]
上記の表のように大気の圧力と温度が定まれば飽和混合比qsは確定する。そのため(p,T)座標平面に垂直に飽和混合比軸qsを取ると、qs(p,T)関数は一つの三次元曲面を構成する。
後で説明するエマグラムの(p,T)平面に垂直に飽和混合比座標qsを取ったときに構成される三次元曲面qs(p,T)の等高線[qs(p,T)=一定の線]をエマグラムの(p,T)平面に射影したものを“等飽和混合比線”と言う。
これは下図の様に(p,T)平面上で急傾斜・直線状の線の集まりとなります。エマグラム中の(p,T)点における飽和混合比を等飽和混合比線の数値から読み取って、上記の表中のデータと比較して見ると一致していることが解ります。
気温が同じでも圧力pが減少すればqsは大きくなるので、“等飽和混合比線”は圧力の減少とともに低温側に少し傾いています。
[補足説明2]
大気中の気層(気塊)の圧力・温度(p,T)が与えられ、その気塊の相対湿度R.H.が観測できていれば、その気塊のそのときの混合比qと露点Tdをエマグラムから求めることができます。その具体的な方法は4.(3)1.[補足説明]の6.と7.をご覧下さい。
[補足説明3]
エマグラム中の乾燥断熱線に沿って単位質量の気塊が移動するとき、気塊の圧力も温度も変化しますし、気塊中に含まれている水蒸気の圧力も変化します。しかし、元々の単位質量の気塊に含まれている乾燥空気質量mdと水蒸気質量mvは変化しないことに注意してください。
気塊の体積や温度は変化しますが、単位質量を含む境界内のmdやmvの質量は変わらないのですから、乾燥断熱線に沿った変化では混合比q=md/mvは保存されます。しかし、上昇に伴ってやがて凝結が始まり湿潤断熱線に移行すると、保存は成り立たなくなり混合比の変化が始まります。
[補足説明4]
実際の飽和した湿潤大気が断熱的に膨張・冷却してエマグラム上で新しい(p,T)の点に移動したとする。そうすると(p,T)の変化に対応して当然qsの値も異なります。
その変化量dqsが凝結によって(降雨となり)気塊の中から取り除かれた水蒸気質量です。
そして、−[水の単位質量当たりの潜熱]×[dqs]がその移動によって単位質量(1kg)の気塊に生じた発熱量です。dqsは湿潤断熱減率や相当温位を計算するとき重要な量です。
湿潤空気(乾燥空気+水蒸気)の質量に対する水蒸気の質量の比を“比湿”(specific humidity)と呼びsで表す。
比湿sは無次元量ですが、水蒸気量を含めた空気1kg中に含まれる水蒸気質量を意味します。そのため普通kg/kgまたはg/kgの単位で表す。
比湿sは次に示す関係式によって混合比q、あるいは気圧pと水蒸気圧eから求めることができる。
同様に、飽和水蒸気にたいする比湿を“飽和比湿”ss(添え字sは“飽和”saturationの意)と言います。その定義と、気圧p、飽和水蒸気圧esとの関係は下記の様になる。
水蒸気圧e、混合比q、比湿sはいずれも温度Tの増加とともに指数関数的に増大するが、実際の大気の様に30℃以下ではp≫es>eですから、相対湿度をR.H.とすれば、近似的に
が成り立つ。
また
の近似が成り立ちます。
[補足説明]
湿潤空気であっても、未飽和であれば気塊が大気中を上昇あるいは下降して圧力や温度が変わっても“混合比”qおよび“比湿”sは一定に保たれます。それは同じ単位質量(1kg)の気塊の中に含まれる水蒸気の質量は変化しないからです。すなわち未飽和過程において混合比q、比湿sは保存量となる。
これは“温位”θが未飽和過程においては保存量で在ったことと同様にとても重要な性質です。
1.(1)で説明した“乾燥空気の気体定数”はRd=287J/K・kgであり、3.(2)で説明したように“水蒸気の気体定数”はRv=461J/K・kgでした。そのため湿潤空気の気体定数は、水蒸気の含有量に依って変化します。湿潤空気の状態方程式は水蒸気含有量(混合比q)の関数となる気体定数を用いて表現される。
体積vの湿潤空気中の“乾燥空気質量”をmd、“水蒸気質量”をmvとすると、“湿潤空気の密度”ρは
となる。ここでρdは“乾燥空気の密度”、ρvは“水蒸気の密度”です。
ここで、“乾燥空気の分圧”pd、“水蒸気の分圧”eとすれば、それぞれの状態方程式は
と表される。
これらの関係式を使えば“湿潤空気の状態方程式”は
となる。
したがって、混合比qの“湿潤空気の気体定数”Rm(添え字mは“湿った”moistの意)は
となる。実際の大気ではq≪1であるから、Rm≒Rdと置いても差し使えない。そのため以下の議論では、話を簡単にするために、湿潤空気の場合でも乾燥空気の状態方程式をそのまま使うことにする。
[補足説明]
前記の湿潤空気の状態方程式を
の用に書いて、T(1+0.61q)≡Tvを“仮温度”(virtual temperature)と呼ぶ場合もある。
仮温度は混合比qの湿潤空気と同圧・同比容の乾燥空気が持つべき仮想的な温度です。仮温度を導入すれば湿潤大気の状態方程式は見かけ上乾燥大気のそれと同じ形となる。
地球大気では、q<30g/kg=0.03kg/kg程度であるから、TvとTの差は最大でも〜5K程度です。そのため簡単化のために湿潤大気に対しても乾燥大気の状態方程式を用いることにする。
飽和した湿潤空気が上昇すると、水蒸気が凝結して潜熱が放出される。このような過程を“湿潤断熱変化”と言う。上昇に伴って気塊の圧力と温度がpとTからp+ΔpとT+ΔTに変化し、それに応じて飽和混合比も初めのqsからqs+Δqsに変化したとする。この余分の−Δqs(>0)という量の水蒸気が凝結する訳です。このΔqsは
と書くことができる。
この式の意味は解りにくい所ですが、[補足説明2]のエマグラム図において、(p,T)平面に垂直にqs座標を取り、図中の等飽和混合比線を等高線とするqs(p,T)の三次元曲面上での全微分表示と考えればよい。つまり、qs(p,T)曲面のΔT方向の勾配が(qs/es・Δes/ΔT)で、Δp方向の勾配が(−qs/p)です。
厳密に言えば凝結で放出された潜熱は空気のみならず水蒸気および凝結でできた水滴も温めるのですが、その影響は無視する。またここでも湿潤空気の状態方程式を乾燥空気の状態方程式で近似することにする。
凝結熱(潜熱)をL2,3とすれば、3.(3)3.[補足説明4]で説明したように、−L2,3Δqsだけの熱の放出がある。したがって、断熱過程であっても熱源があることになる。
飽和した湿潤気塊が断熱的に上昇した場合の温度変化は気塊が上昇して気圧pが変化したとき、凝結に伴う内部熱源がある[断熱温度変化を表す微分方程式]と上昇気塊の周りの気圧pと高さzの関係を表す[静力学平衡の式]を連立させて解けばよい。
Γsを“湿潤断熱減率”(moist adiabatic lapse rate)と言う。この式の計算値がエマグラム上の湿潤断熱線の勾配に対応します。その図からも解るように、Γsは気塊の温度と圧力によって異なる。温度が高いほど飽和している気塊が含みうる水蒸気量は大きいから、凝結する水蒸気の量は多くて温度の下がり方が少なくなるからです。
大体の目安として、大気下層の暖かい飽和湿潤空気塊が上昇した場合0.4℃/100m程度。対流圏中層の飽和湿潤空気塊が上昇した場合0.6〜0.7℃/100m程度。対流圏上層では温度が低くもともと含みうる水蒸気量も少ないので乾燥断熱減率とほとんど同じくらいになる。
[補足説明1]
上記では飽和混合比qsを気圧p、飽和蒸気圧es、ε=Rd/Rvに置き換えて論じましたが、任意の気圧・温度で飽和気塊が断熱上昇したときのdqs/dTのデータがあれば以下の式で求めることもできます。
ただし、ここで注意して欲しいのですが、温度が下がれば気圧も下がるので単純に 3.(3).3.の表から同じ気圧での温度変化に伴うqsの変化からdqs/dTの値を計算することはできません。温度がdT変化した時のdpの見積もりが必要で、qs(T,p)→qs(T+dT,p+dp)の変化からdqs/dTを計算しなければなりません。つまり∂qs/∂Tではないのです。そのため、dpの変化を考慮すると、結局のところ前記の式を用いなければならない。
[補足説明2]
上記の事柄をエマグラムの上(700hPa,10℃)で確認してみると下右図のようになる。
図から、dT=8℃-10℃=-2K、dqs≒10g/kg−11g/kg=−1g/kg=−0.001kg/kgが読み取れるので
となり、次の[計算例1]と同程度の値が確かに得られる。
[計算例1]
気圧700hPa、気温10℃=283Kで飽和している気塊の湿潤断熱減率を求めてみる。
cpは空気の定圧比熱ですが、空気が理想気体と見なせる場合は温度、圧力によらずほぼ一定とみなせてcp=1004J/K・kgとなる。また凝縮熱L2,3=2.5×106J/kgです。
飽和蒸気圧は 3.(1)の表から温度10℃でes=12.28hPa、温度8℃でes=10.73hPaです。また飽和混合比は 3.(3).3.の表から温度10℃・気圧700hPaでqs=11.13×10-3kg/kgです。これらの値を用いると
となる。
下表のΓs値は同様にして求めたものです。実際そうなることを[計算例2]で確かめる。
[計算例2]
湿潤断熱減率Γsを表す式
のqs(p,T)やdes/dTにその数式表現を代入して計算してみる。
まず、3.(2)で説明したクラウジウス・クラペイロンの式より
が得られる。
次に、3.(3)3.で説明した飽和混合比の近似式から
が得られる。
これらをΓsの式に代入し、定数値としてg=9.8m/s2、cp=1004J/K・kg、Rd=287J/K・kg、ε=Rd/Rv=0.622、L2,3=2.5×106J/kgを用いると
となり、Γsが変数(p,T)の関数として表現できる。
表計算ソフトExcelを用いて計算すると下表の値が得られる。ただし100倍して100m当たりの減率に直している。
近似的な計算ですが、確かに前記の表と一致する。
つまり、このΓsの表には、3.(1)の表で示した飽和蒸気圧esが温度によって変化すること、また、3.(3).3.の表で示した飽和混合比qsが気圧と温度によって変化することが反映されています。
この表から解るように常にΓs≦Γd=0.98K/100mが成り立つ。また、低温になれば Γs は Γd =0.98K/100mに近づいていく。
この表の値を繋いで曲線グラフ表示したものがエマグラム上の“湿潤断熱線”です。表計算ソフトExcelを用いて描く具体的な方法は参考文献5.を参照されたし。
[補足説明3]
1.(4)で説明したように、現実の対流圏での気温減率は0.65K/100m程度です。
一方、現実の対流圏中層での気温・大気圧を1.(4)の表から読み取って上の表に当てはめると、対流圏中層での湿潤断熱減率の理論値は、ほぼ0.65K/100m程度となる。
その両者が良く一致する事は、対流圏(特に中層)における実際の気温減率は湿潤断熱減率Γsのメカニズムで下がっていることを強く示唆する。
[補足説明4]
先に示した湿潤断熱減率は、高度zに対する気温減率を与えるものですが、気圧に対する気温の減率にするには、1.(3)で求めた気圧の高度依存性を表す式を用いて変形すればよい。
底面積が1m2の気柱の中に含まれる水蒸気の総質量を“可降水量”(precipitable water)Pと言う。これは直接に降水量に結びつく量ではないので、本来この用語は適当ではないが、Pが大きいほど実際の降水量も多くなるという意味で、気象用語として慣用されている。
Pの定義から明らかなように、次の関係式が成り立つ。
zに関する積分は地表(z=0)から無限の高度まで行う。圧力に関しては無限高度の圧力(p=0)から地表圧力ps(添え字sは“地表の”surficialの意)表面まで行う。ただし圧力が300(または200)hPa以下の高空になると水蒸気含量は無視できるので、積分は1000hPa(地表圧力)〜300hPaで行えば良い。
高層観測データとして1000、850、700、500、300hPaでsの値が、s1000、s850、s700、s500、s300として与えられていればP値は
の積分近似計算(台形公式)に依って計算できる。
[計算例1]
1000hPa(地表圧力)〜300hPaでのsの平均値が10g/kgのとき可降水量は次のようになる。
これは、水深70mmの量に相当する。このようにPは水深(mm)で表されることもある。
[計算例2]
3.(8)3.[計算例1]の例で与えられている1983年7月22日12時(世界標準時)の福岡上空大気の可降水量Pを計算してみる。そこのワイオミング大のデータから1000、850、700、500、300hPaでのs値
s1000、s850、s700、s500、s300を読み取って上式に代入すると
が得られる。これは、確かにワイオミング大の計算値55.65mmにほぼ一致する。
気塊が上昇して断熱膨張・断熱冷却してゆけば水蒸気はやがて飽和に達して凝結が始まる。凝結した水蒸気は雲粒や氷晶となり、やがて雨滴や雪片が形成されて地上に落下して降水となる。
そのとき、凝結する水蒸気量は“飽和混合比”qsの時間的な変化として評価される。すなわち
と表される。
一方、2.(1)で説明した熱力学第一法則において、凝結熱がある場合の式から
が得られる。
上記(1)、(2)式を連立させてdT/dtを消去すれば
が得られる。
上式は、ω<0(上昇流)の場合には、dqs/dt<0となり、凝結によりqsが減少していくことを示している。つまり大気の凝結は上昇流によって引き起こされる。
ある時間内(単位時間内)の“降水量”は
によって求められる。
“相当温位”(equivalent potential temperature)θeとは、気塊の“温位”(potential temperatrue)θに、潜熱として持っている熱エネルギーを加味した指標です。高温多湿の気塊ほど高い値となる。梅雨前線や、それに伴う集中豪雨などの解析には必須の指標です。
相当温位の概念は解りにくいので、最初にエマグラムの上で温位と比較しながら説明する。
下図の赤二重丸◎A点における圧力p、温度Tの気塊を考える。
2.(4)で説明したように、出発点にある気塊の“温位”(potential temperature)θとは、その気塊を乾燥断熱線(A→E)に沿って1000hPaの高度まで降下させたときの温度の事でした。
一方、赤二重丸◎A点に存在する気塊の“相当温位”(equivalint potentioa temperature)θeとは以下の手順で求められる温度のことです。
出発点での気塊をまず乾燥断熱線(A→B)に沿って飽和に達するまで持ち上げる。B点の位置は、A点での飽和混合比×相対湿度=混合比qで定まる等飽和混合比線(qs=q)と乾燥断熱線(A→B)が交わる点です。そうなることは4.(3)3.を参照されたし。
B点で飽和に達した後は湿潤断熱線(B→C)に沿ってさらに高空まで持ち上げて気塊に含まれる水蒸気を凝結によって全て取り除く。実際に持ち上げる高度は飽和混合比が小さくなって水蒸気含量が無視できる100hPa程度の高度(C点)までで良い。
次に、そこから乾燥断熱線(C→D)に沿って降下させ1000hPaの高度に持ってきたときに気塊が示す温度を求める。その温度が相当温位θeです。
ついでに説明すると、(A→B)に沿って持ち上げ凝結高度(LCL)B点に達した後の気塊を、湿潤断熱線(B→F)に沿って1000hPaの高度まで降下させた時に示す温度を“湿球温位”(wet bulb potential temperature)θwと言う。もちろん降下させると未飽和の状態になりますから湿潤断熱線に沿って降下させることはできないのですが、仮想的にできたとしての話です。つまり1000hPaにある温度θwの飽和気塊を湿潤断熱線に沿って上昇させるとLCLでの値と一致する様な状況を考えているということです。
このとき、降下途中で出発高度(最初の気圧pの高度)を通過するときに示す温度を“湿球温度”(wet bulb temperature)Twと言う。
さらに、B点を通る等飽和混合比線が出発高度の等圧線pと交わるG点の温度が、最初にA点に存在したときの気塊の露点Tdです。そうなることは4.(3)3.を参照されたし。
図から明らかなように以下の関係が成り立つ。
2.(4)1.[補足説明]で説明したように、乾燥した気塊が乾燥断線に沿って変化をするときには“温位”θが保存される。 このとき、3.(3)3.[補足説明3]で説明したように、混合比qも保存されます。
同じように、飽和している気塊が断熱的に上昇する場合には、前記のように定義された“相当温位”θeが保存されます。つまり上記の過程にそって移動している気塊はどの高度に在るときも全て同じ相当温位を持ちます。
A点(p,T)に存在する気塊の、相当温位を数式で表すには、前項の手順を数式でたどればよい。そのとき非常に大切な事柄ですが、(p,T)点の相当温位は2.(4)で説明した温位と違って、座標変数(p,T)のみならず、その点の湿度R.H.(あるいは混合比q、あるいは露点Td)の関数となることです。
つまりA点の相対温位はエマグラム座標(p,T)に依存するだけではなくて、その点での湿度(混合比、露点)に依存します。
そのことを前項で用いたエマグラム上で説明する。例としてA点に存在する湿度100%の気塊、湿度70%の気塊、湿度30%の気塊を考える。前項で説明した方法により、それぞれの気塊の相当温位を求める断熱変化経路図を示すと下図の様になる。
この図の中で、A点の湿度から、それぞれの気塊の凝結高度B1点、B2点、B3点における飽和混合比qs1、qs2、qs3と露点Td1、Td2、Td3を求める方法については、4.(3)1.[補足説明]をご覧ください。
図中のθe1、θe2、θe3はいずれもA点における気塊の相当温位です。ただし、θe1はA点の気塊の露点がTd1(混合比q1=qe1、つまり湿度100%)の相当温位です。θe2はA点の気塊の露点がTd2(混合比q2=qe2=qe1×0.7、つまり湿度70%)の相当温位です。θe3はA点の気塊の露点がTd3(混合比q3=qe3=qe1×0.3、つまり湿度30%)の相当温位です。
この様に、エマグラム上の同じ座標点(p,T)に存在する気塊でも水蒸気の相対湿度が異なれば異なった相当温位を持つ。そのため温位のようにエマグラム上に相当温位線を引いて一意に表示することはできません。
故に、相当温位の数式表現はそのことを考慮して求めなければなりません。ところで乾燥断熱線上の変化では温位θは保存されすべて同じ値を持つのですから、温位が変化するのは湿潤断熱線上の変位だけです。だから図中のBi点→Ci点(i=1,2,3)の変化に伴う温位の変化を見積もればよい。
ところで、湿潤断熱過程での経路の変分(Δp,ΔT)は3.(5)で説明した次の全微分関係式
を満たさねばならない。
一方、2.(4)1.[補足説明2]で述べたように、座標平面(p,T)上の任意の変位(p,T)→(p+Δp,T+ΔT)に伴う温位曲面θ(p,T)の変分Δθは
と表される。そのため湿潤断熱線上の(Δp,ΔT)の変化をここでの(p,T)→(p+Δp,T+ΔT)の変化とすれば、湿潤断熱線に沿った(Δp,ΔT)の変分に伴うdqsの変化分とdθの変化分は以下の関係を満足する事になる。
この式においてL2,3/cpは積分範囲でほぼ一定と見なせるのですが、Tは飽和混合比qsの関数となるので、積分計算は一般に面倒です。
しかしこのとき、3.(5)[計算例1.]で見たように、気圧700hPaで温度が283Kから281Kへ変化したときqsは11.13×10-3から9.70×10-3kg/kgに変化[3.(3).3.の表]する。この場合には
この近似は対流圏内で一般的に成り立つもので、これを利用すると積分が簡単に実施できる。
積分は“持ち上げ凝結高度”Bi点(温度T’、混合比q=qs、θ=θ(p,T))から無限高度Ci点(qs→0、θ→θe)まで行えばよい。このとき積分開始温度T’は持ち上げ凝結高度Bi点での気温ですが、絶対温度で代入するのでA点気塊の露点Tdで代用しても誤差は少ない。等飽和混合比線の傾斜が急なためにその様な近似が許される。
積分を実行すると
となる。ここでqsは積分の出発点である凝結高度での飽和混合比です。絶対温度T’は凝結高度での気温ですが、すでに述べたようにA点での露点温度Tdで近似的に置き換えることができる。
このとき[A点の湿度]が0に近づけば、凝結高度での飽和混合比qs→0と成りますからθe→[A点温位θ]と成ります。また、[A点での湿度]が100%に近づけば、θeは[A点温位θ]のExp[(L2,3/cp)×(A点飽和混合比/A点気温)])培に近づいて行きます。
[補足説明]
厳密には、乾燥空気の分圧(p−e)を用いて定義した乾燥温位
を用いて、浸潤空気の相当温位θeを
で定義する。しかし、多くの場合にはp≫eだから前記の近似式を用いている。
A点気塊の相当温位は、本来A点の座標値(p,T)とそこでの相対湿度R.H.に関係する。ところで(p,T,R.H.)が与えられれば、その気塊のA点における混合比qや露点Tdは求めることができる。A点での混合比qは乾燥断熱過程で保存されるのだから凝結高度での飽和混合比qsと同じです。また凝結高度の温度T’を求めることができる。その温度T’は近似的にA点での気塊の露点Tdで置き換えることもできる。そのため、相対湿度の代わりの変数としてqsと凝結高度でのT’(≒Td)を用いていると考えるべきです。
また、温位θはA点から凝結高度Bi(i=1,2,3)点までの乾燥断熱線上で共通ですから、A点での温位θ(p,T)をそのまま用いればよい。
[計算例1]
下表は[計算例2]で説明する福岡上空の1983年7月22日12時のデータをワイオミング大学のデータサイトから引用したものです。相対湿度のデータが222hPaまでしか得られていないので、それより高空の露点・混合比・相当温位が計算できていないことに注意。
表記の観測時間は世界標準時です。日本の地方時基準点(明石市)の東経は135度ですから日本の地方時は135度÷15度/時=9時間だけ世界標準時よりも先行しています。そのため[計算例2]の図では地方時22日21時の観測値(青ライン上)に相当します。
このデータの気圧、気温、相対湿度を用いて、表計算ソフトExcelで露点と混合比、そして温位と相当温位を計算してみる。その際、気圧は100倍して[hPa]から[Pa]へ、気温と露点は273.2を加えて摂氏温度[℃]から絶対温度[K]へ、混合比は0.001培して[g/kg]から[kg/kg]へ直して、SI単位系に統一してから計算した方が間違いが少ない。
ワイオミング大データサイトの計算値と比較すると良く一致しているのが解る。相当温位に関しては1%程度の差があるが、ワイオミング大では、ここよりもう少し正確な計算式を用いている。いずれにしても、上記の計算式で近似的な計算はできる。
また、この時間帯の福岡上空の対流圏大気は、下層が極めて湿潤(湿度〜100%)で中層−上層は乾燥(湿度〜20%)していることに注目。
相当温位の定義から明らかなように、相当温位θeが高い気塊は温度が高くて湿っている。逆に低い気体は温度が低くて乾いている。そのため低空に相当温位が高い気層(気塊)が侵入し、中・上層に相当温位が低い空気が流れ込むと、対流不安程度が強くなり、集中豪雨の危険が高まる。下図はその一例で、参考文献2より引用した。
[計算例2]
ちなみに、福岡は、4.(2)2.で説明する高層気象観測を定期的に実施している観測点の内の一つです。ワイオミング大学のデータサイトから、該当時刻の福岡上空の相当温位データを読み取ると確かに上図の様に変化していることが解る。
同サイトから該当時刻のエマグラムを引用すると下図になる。図中世界標準時+9時間が上図地方時に相当する。
実際の大気の状態曲線が示す気温と露点曲線が示す露点の差である“気温露点差”が変動する様子に着目してください。この差が小さくなるほど大気が湿潤であることを意味する。
また、右欄の4番目SHOWは4.(3)5.の“シュワルター安定指数”SSI、12番目CAPEは4.(3)4.の“対流有効位置エネルギー”CAPE、14番目CINSは“対流抑制”CIN、最後の行PWATは3.(6)の“可降水量”Pを意味する。
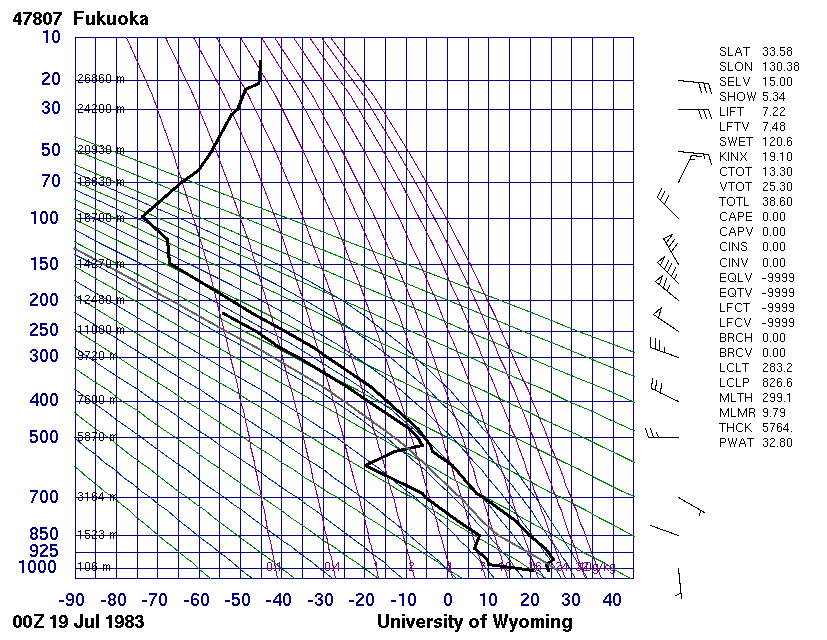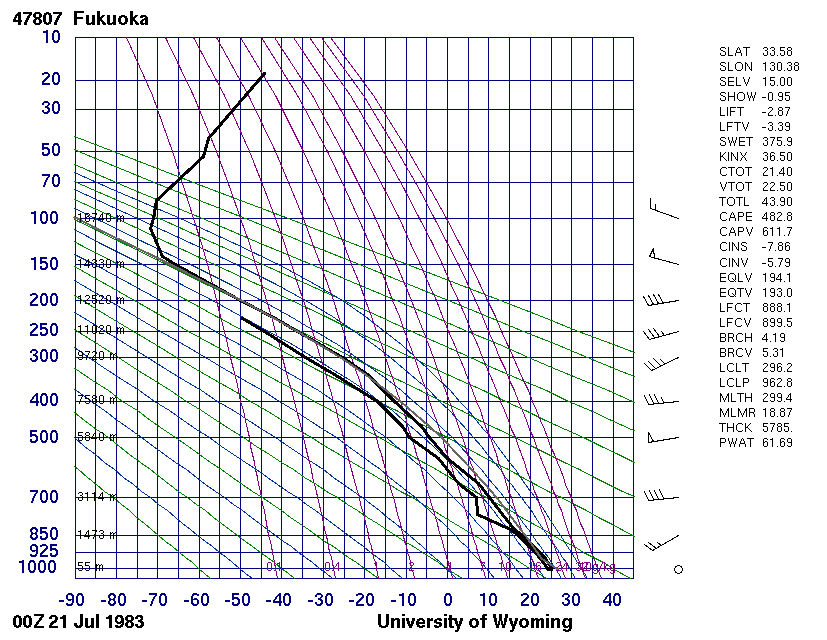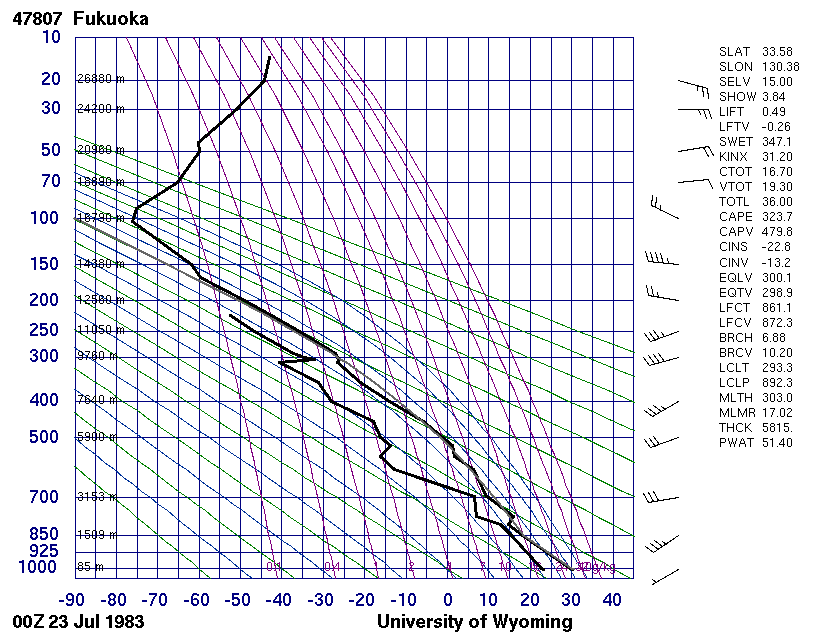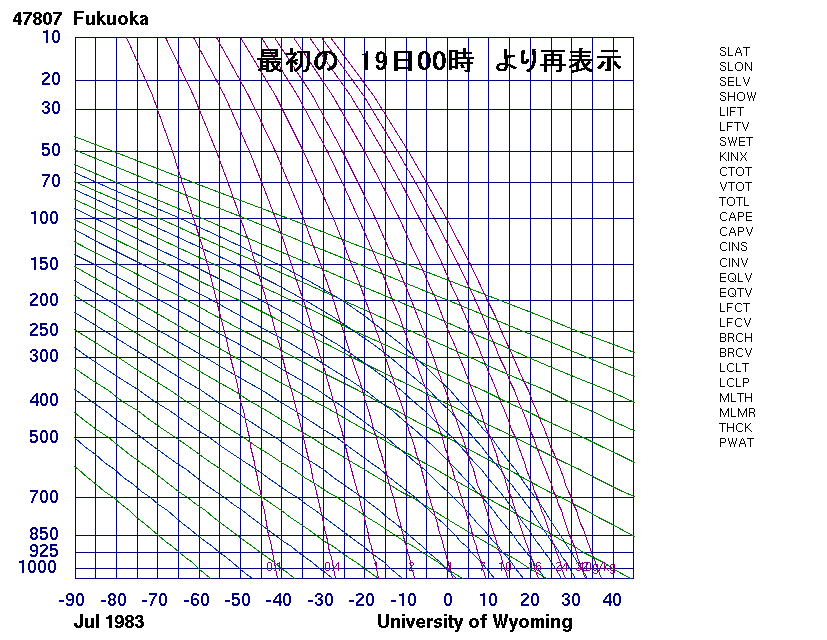
2.(4)2.[計算例2]で引用した温位分布図における“温位”は高空になるほどどんどん大きな値になった。そうなる理由は、そこで説明したように、温位は乾燥断熱減率に関係する量だからです。
ところが、ここで導入した“相当温位”は前掲の図から明らかなように、地上付近にある気塊でも相対湿度が高い気塊の場合その相当温位は対流圏高層の乾燥した気塊とほぼ同じ相当温位となります。つまり湿り具合を考慮することで相当温位は大気圏全体にわたってほぼ同じ値となります。
実際上図において対流圏の全高度に渡ってθe=330〜350程度(圏界面付近の温位にほぼ等しい)に成っていることに注意してください。その様にθe値は対流圏全体でほぼ等しくなるので、それからの±の変位が図の上で明瞭に浮かび上がってきます。上図でも相当温位が低いハッチ部分と相当温位が高い影の部分が明瞭に区別できます。そのためこの例のように相当温位分布の変化を追跡することは、集中豪雨を予測する上でとても大切です。
地球大気は平均的に見れば静力学平衡が成り立ち、鉛直加速度はゼロであるが、特定の状況下では積雲対流が生じて降水をもたらす。
積雲対流は浮力によって駆動されるのだが、どのような条件下で発生するのかは、気塊の安定性をしらべることにより明らかにできる。この安定性の吟味は数式あるいは断熱図を用いてなされる。
乾燥空気の熱力学的保存量として温位が導入された。湿潤空気の熱力学保存量として相当温位が定義される。温位と相当温位の鉛直分布は気層の安定性の解析に使われる。
積雲対流は“浮力”によってひきおこされる気塊の上昇運動です。浮力はアルキメデスの原理“流体中の物体は、物体が排除した流体の重量だけの浮力を受ける。”で説明される。詳細は別稿「アルキメデスの原理(浮力の説明)」を参照。
大気の中の気塊の密度をρ、体積をVとし、その周りの大気密度をρ’、重力加速度をg、気塊の鉛直方向の移動速度をwとすると物体(気塊)の運動方程式は以下のようになる。ここでVρ’gはアルキメデスの原理で説明される気塊に働く“浮力”です。これから上昇速度dw/dtを求めると
となる。このとき、気塊の温度をT、周囲の大気(空気)の温度をT’として気体の状態方程式を用いた。
この式から解るように、気塊の上昇は気塊と周囲の大気の温度差によって決定される。T>T’ならば気塊は上向きに加速されて上昇する。逆なら下降する。
[計算例]
周囲より1K(=1℃)だけ温度が高い気塊が、地上から上昇を始めれば5分後にどれだけの上昇速度に達し、どの高度まで上昇するか求めてみる。なお簡単に見積もるために、周囲の気温は高度によらず一定(283K=10℃)とし気塊と周囲との温度差は保たれるとする。また、摩擦の効果は無視できるとする。
上昇加速度は
となる。
したがって5分(=300s)後の速度は
となる。
また5分間の上昇高度は
となる。
気塊が何らかの原因により僅かに上昇したとき、上昇の結果として温度が降下する。そのとき低下した温度が、周囲の気相(静止しており、しかも高度と共に温度はさがる)の温度よりも高温ならば気塊はさらに上昇するであろう。これは気塊が不安定な状態です。
これに対して、上昇した気塊の温度が周囲に比較して低温になれば下向きに加速されて元の位置にもどる。これは気塊が安定な状態です。
断熱上昇する気塊の温度変化は、気塊が未飽和であるか飽和しているかで異なる。
未飽和気塊の上昇にともなう気温減率は、2.(3)で説明した“乾燥断熱減率”で
となる。ここで、cpは空気の定圧比熱(=1004J/kg・K)です。
飽和気塊の上昇にともなう気温減率は、3.(5)で説明した“湿潤断熱減率”で
で計算される。ここで、Γdは乾燥断熱減率(=0.0098K/m)、L2,3は水→水蒸気の相変化に伴う潜熱(=2.50×106J/kg)、cpは空気の定圧比熱(=1004J/K・kg)、ε=Rd/Rv=0.622、pは気圧、esは温度Tにおける飽和蒸気圧です。
その具体的な値は下表のようになります。
ここの説明は気象庁高層気象台のHP(http://www.jma-net.go.jp/kousou/obs_second_div/index.html)から引用・加工したものです。
高層大気の状態は水素ガスを詰めた気球に気象観測器を吊り下げて空に飛ばして行われる。気象観測器には様々な種類がありますが、これらの観測器を総称して“ラジオゾンデ”(Radiosonde)と言う。
地上から(気球+落下傘+ラジオゾンデ)を空に放つと同時に観測が始まります。ラジオゾンデによって観測されたデータは無線でリアルタイムに地上に送られる。気球は少しずつ膨張しながらかなり高速(5〜7m/s)でどんどん上昇します。気球は気圧低下のために膨張して、やがて破裂します。破裂した高度(約30km)が観測できる最高到達点です。その後ラジオゾンデはパラシュートで降下します。地上に落下する場合もありますが、日本の場合その多くは海上に落下して失われます。観測データは整理してから公開され、世界中で天気予報や気候監視などに利用されます。
放球は毎日2回定時(日本では9時と21時[世界標準時の0時と12時])に行われますが、台風接近時や豪雨が予想される時などには臨時(3時と15時[世界標準時の6時と18時])に観測を行うこともあります。
観測地点は世界各地に約800ヶ所(日本に16ヶ所)あります。
世界中の観測データはワイオミング大学のサイトから常時入手可能です。地域→プロットタイプ→観測日時→観測点(地図上でマウスクリック)の順に指定する。観測日時を期間で指定すると、時系列に沿ったデータを入手可能でエマグラムのアニメーション表示も可能。また、平面的な分布図も入手可能な優れもののサイトです。
日本の高層気象データは気象庁HPからも取得可能。ただし、数値データですので、エマグラムは自分で描かねばなりません。その際、数値データ表の範囲をマウスで選択してコピーすれば、表計算ソフトExcelなどに数表としてそのまま取り込めます。Excel表に3.(2)や3.(3)3.で説明した関数を設定しておけば、水蒸気圧・露点・混合比を自動的に計算できます。ついでに、温位と相当温位の計算式も設定しておくと良い。
ただし、ワイオミング大学のサイトではそれらの計算値も含めて日本の観測点データを全て入手できますからそちらを利用する方が良いかもしれません。
いずれにしても、そうして得たデータを元に、4.(3)2.の手順に従ってエマグラムを描けば良い。
この当たりのExcelを用いた自動計算・自動グラフ描画については参考文献5.のサイトが有益。
下写真はGPSゾンデ放球時の様子。落下傘の下にぶら下がっているのがラジオゾンデです。

万が一飛行機と衝突しても被害が生じないように、またできるだけ環境汚染しないように、気球は天然ゴム製、パラシュートは和紙製でゾンデ容器は発泡スチロール製です。ゾンデは100〜300g程度の軽量で、急速に上昇・下降させて不測の事態を避けます。
気球につり下げたラジオゾンデ(気象観測器)により、大気のデータが高度変化とともに観測されます。以前はラジオゾンデを電波方向探知機で追跡してその位置情報から風向、風速、高度などを得ていましたが、現在はすべて、GPSを内蔵したゾンデで位置情報を得ています。現在用いられているラジオゾンデのタイプには以下のようなものがあります。
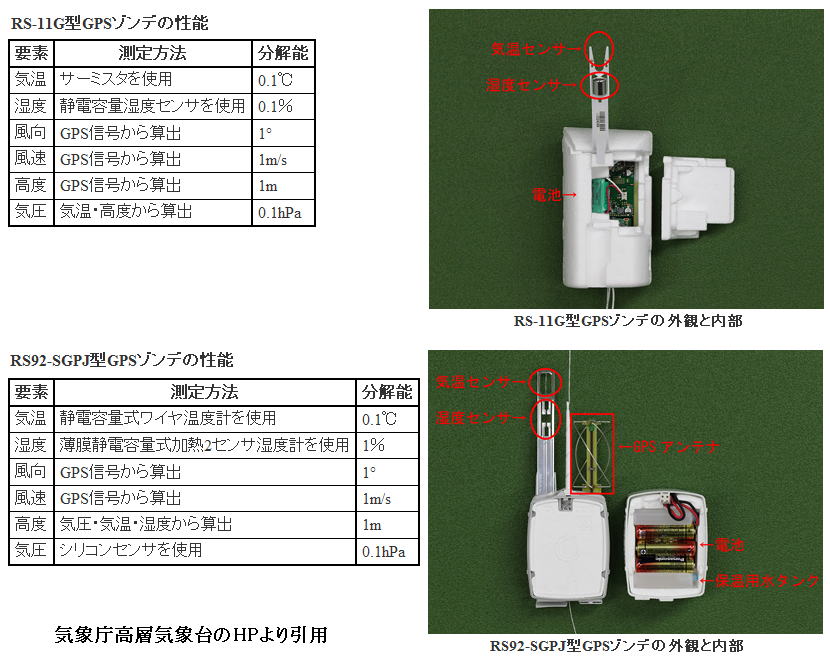
観測方法の歴史的変遷について、上記HPに興味深い説明がありますのでご覧下さい。
GPSによる位置情報と組み合わせて大気中の気圧、気温、湿度、風向、風速、高度が観測されます。次図はその観測データの一例です。
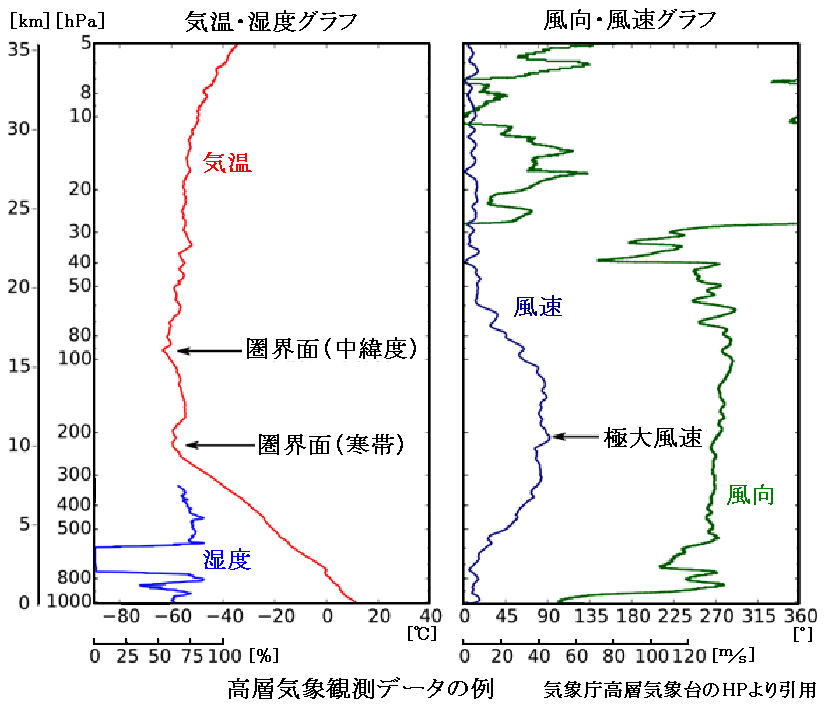
実在大気の気温減率Γは観測地T(z)から
によって計算される。
湿度が解れば、3.(3)1.で説明した式により、各高度(気圧)における水蒸気圧eが計算で求まる。eが求まれば、3.(3)2.で説明した式により、各高度(気圧)における露点(温度)Tdが、また3.(3)3.で説明した式により混合比qが、3.(3)4.で説明した式により比湿sが求まる。
気塊とは気層の任意の一部分が上下に移動する場合の塊を意味する。いま最初の高さz0において、温度T0も圧力p0も周囲の大気と等しい気層中の一部分が、気塊としてΔzだけ上昇した場合を考えると、高さz0に存在したときの元々の気塊が乾燥気塊なのか湿潤気塊なのかによって、z+Δzにおける周辺大気(太線)の状態との関係が下図(a)(b)(c)のいずれかになる。
それぞれの場合の気層を次の様に言う。つまり上記太線で表される気温減率[実際の大気の観測値]を持つ気層に対して(a)の場合を“絶対安定な気層”と言い、(b)の場合を“条件付き不安定な気層”、(c)の場合を“絶対不安定な気層”という。
この中で気層の状態が(c)の場合、気層の一部(気塊)が周囲の気層の中で少しでも持ち上げられれば直ちに浮力の増加が生じてさらなる上昇を続ける事になります。つまり、ごく僅かな攪乱で上下方向の激しい混合が生じて気温減率の修正が行われます。そのため実際の大気では絶対不安定な気層は過渡的・一時的にしか存在しません。
気層の安定性は断熱図(横軸−温度、縦軸−気圧の対数)によって判定できる。
断熱図には幾つかの形式があるが日本の気象庁では、RefsdalとStu¨veが1930年に考案した、エマグラム(emagram)が伝統的に使われている。[印刷用の拡大版]
| 横軸 | 温度 [℃] [気層・気塊の温度] |
| 縦軸 | −logep ∝ z [hPa][気層・気塊の圧力] |
| 急傾斜直線 | 等飽和混合比線 [qs(p,T)=一定となる点を結んだもの] |
| 左上がり直線(傾斜約45度) | 乾燥断熱線 [乾燥断熱減率で(p,T)点を結んだもの] |
| 左上がり太曲線 | 湿潤断熱線 [湿潤断熱減率で(p,T)点を結んだもの] |
[補足説明]
4.(2)2.で説明した方法で、高層の観測値(pi,Ti,R.H.i,zi)が得られると、これから各気層(気塊)の(ei,Tdi,qi)が求まる。添え字のiは様々な高度(圧力)地点のデータ番号を示している。p=気圧、T=気温、R.H.=湿度、z=高度、e=蒸気圧、Td=露点温度、q=混合比を示す。
エマグラム上での気塊の断熱上昇を追跡してみる。気塊の主発点を(pi,Ti)で示す(ここの添え字iは“出発”(initial)点の意)。
初めは未飽和(Ti>Tdi)であるので、乾燥断熱線に沿って変化する。そして、出発点での混合比qiの値を持つ等飽和混合比線[(pi,Ti)の露点Tdiが解っていれば(pi,Tdi)点を通る等飽和混合比線]に交わる点で飽和に達する。この点の高度を“持ち上げ凝結高度”(LCL:lifting condensation level)と呼ぶ。
LCLよりさらに上昇すれば、気塊の温度は湿潤断熱線に沿って変化する。湿潤断熱線が状態曲線に交わる点を“自由対流高度”(LFC:level of free convection)と呼ぶ。そこで、気塊の温度が周りの大気の温度と一致して浮力と重力がつり合う。その点を越えれば気塊の温度が周りの大気温度より高くなるので、気塊の浮力が重力を上回り自動的に上昇していく自由対流となる。
湿潤断熱線にそってさらに気塊を上昇させると、気塊の温度が再び外界(状態曲線)と等しくなる点に到達する。この点を“中立浮力高度”(LNB:level of neutral buoyancy)と呼ぶ。この点で気塊は再び浮力を失う。
気塊の出発点での気圧piとLFCの間の気層では、上昇する気塊の温度は外界より低温で、下向きの浮力を受けるから安定で、本来自然には上昇しない。
LFCとLNBの間では気塊は周囲の大気よりも高温となり、浮力を受けて自然に上昇する[“自由対流”]。このような状況を“レイテント不安定”(latent:隠れた)と言う。
[計算例]
フェーン現象を例にして、気塊の断熱上昇・断熱下降をエマグラフの上で説明する。4.(3)1.[補足説明]の6.で取り上げた地上付近のB点(p,T)=(1000hPa,20℃)に存在する湿度R.H.=60%の気塊を取り上げる。この気塊が風によって流されて高度3000mの山を越えて反対側の地上(1000hPa)に吹き下ろされた時、気塊の温度と湿度がどのように変化するかを調べてみる。
まず、4.(3)1.[補足説明]の6.あるいは7.の方法によりB点(1000hPa,20℃)に存在する気塊の露点Tdが11.9℃であることが求まる。その時の気塊の混合比はq=14.7×0.6=8.82g/kgです。この気塊が風に流されて山肌の斜面を上昇していきます。その時の気塊はまだ未飽和ですから乾燥断熱過程で変化していきます。すなわち図中の乾燥断熱線に沿って上昇していきます。それがqs=8.82g/kgの等飽和混合比線と交わったC点で飽和に達します。このときの気圧は880hPaで気温10℃ですが、このように飽和に達した時の高度(気圧)を持ち上げ凝結高度(LCL)と言う。
C点で飽和に達した後、気塊は雨を降らしながら湿潤断熱減率で変化していきますので、その付近に引かれている湿潤断熱線に平行になるように変位線(桃色太線)を引きます。それが高度3000mの気圧である700hPaと交わるD点で山頂に達します。C→Dの過程で凝結した水滴は全て雨となって気塊から取り除かれると考えています。山頂に達した気塊の飽和混合比はqs=5.45g/kgであることが等飽和混合比線から読み取れます。
その後は未飽和の状況で山肌を降下しますので、乾燥断熱線に沿って移動していきます。そうして地上高度(1000hPa)E点まで吹き降ります。この乾燥断熱過程では気塊の混合比は保存されてq=5.45g/kgのままです。E点での気温は28.6°、飽和混合比はqs=25.0g/kgであることがエマグラムから読み取れます。
つまり、最初気温20°、湿度R.H.=60%であった気塊は山を越えるときに、その中に含まれた水蒸気を雨として降らしながら乾燥していきます。そして再び地上にもどった時には気温28.6°湿度R.H.=5.45÷25.0×100=22%の高温・乾燥した気塊に変化しています。これがフェーン現象といわれるものです。
4.(1)で説明したように、気塊の上昇加速度は
で表される。ただし、wは気塊の上昇速度、T(≡Tp)は気塊の温度、T’(≡Ta)は周囲の大気温度です。
この量を用いると、前項で考察した気塊の安定・不安定性を定量的に表現することができる。それが“対流有効位置エネルギー”CAPE(convective available potential energy)と“対流抑制”CIN(convective inhibition)で、以下の様に定義されている。Tpは上昇する気塊の温度、Taは周囲の大気温度です。
式の意味から明らかな様に、CAPEは下図の桃色領域の面積(>0)に関係する。この面積が大きいほど不安定性が強い事を意味する。またCINは下図の空色領域の面積(<0)に関係する。この面積が大きいほど対流は起きにくい事を意味する。
CINの面積が小さくCAPEの面積が大きい状態では、積乱雲ができやすく、このような状態をレイテント不安定(latent:隠れた)と言う。
CAPE、CINの平面的な分布を時系列で示しているサイトもあります。
成層の安定性を示す尺度として“シュワルター安定指数”SSI(Showalter stability index)がある。これは500hPaと850hPaにおける大気の温度・湿度の相対的な関係によって定義される指数です。(Showalter, A. K., “A stability index
for forecasting thunderstorms.”, Bull. Amer. Meteor. Soc., 34, p250〜252, 1947年)
下図の様に850hPaから仮想的に気塊を上昇させる。未飽和のうちは乾燥断熱線に沿って変化し、LCLで飽和に達した後は湿潤断熱線に沿って上昇する。そして500hPaに達した気塊の温度をT850*(500)と記す。これは850hPaから出発上昇した気塊が断熱変化しながら500hPaに達した時の温度を示す。
最初850hPaにある気塊が湿っていればLCLは低くなりより高温側の湿潤断熱線に沿って上昇し、逆に乾いていればLCLは高くなりより低温側の湿潤断熱線に沿って上昇します。そのため最初の気塊が湿っていればT850*(500)の位置は右に移動、乾いていれば左に移動します。
500hPaにおける周囲の大気温度(観測値)をT500とすると、SSIは次のように定義される。
SSIの値の大小で成層の安定性を見るのですが、実際の判定は850hPaの気塊を500hPaまでエマグラム上で上昇させて、その気塊の位置が状態曲線(実際の大気温度分布曲線)の何℃分左側にあるか、何℃分右側にあるかで判定します。
左側にあるときは、SSIの符号は+であり、比較的安定な大気構造です。右側にあればSSIの符号は−となり、不安定な大気構造です。特にSSI≦−3の場合には雷が生じるような激しい積乱雲が発生します。
エマグラムに大気データが記入してあれば、SSIは図的な解析で簡単に求まります。
もちろん、高層気象データがあれば850hPaにある気塊の(p,T,R.H.)が解るのでそれから湿潤断熱線に移行するLCL点の(p,T)が求まる。任意の(p,T)を通る湿潤断熱線の数値データがあればその湿潤断熱線の500hPaにおける温度を知ることができそうです。そうすればSSIを計算で求めることもできると思います[実際の具体的な手順はどうやるのかは私自身まだ調べていません。ワイオミング大のサイトにもその計算手順の説明はなさそうです。どなたか教えてくださるとうれしいのですが]。
SSIの平面的な分布図を時系列で示しているサイトもあります。このサイトではどうやって計算しているのだろう?
上記では気塊の出発点を850hPaとしたが、900hPaや1000hPaにする場合もあります。その場合には
となりますが、そのときには出発点の気圧piを明示しておく必要があります。
湿潤断熱減率の数式表現を理解する鍵は、飽和混合比とは何か、また飽和混合比が温度と圧力の両方に関係するメカニズムは何かを理解することですね。このたびこのページを作ることで、私自身やっと理解できました。
このページは以下の文献1.〜3.に全面的に依存しています。できるだけ解りやすくすることに努めました。