1820年代にイギリスのヤングやフランスのアラゴ、フレネルの光の性質（偏光現象や干渉の現象）の研究から、光は波動であり、しかも進行方向に対して垂直に振動する横波であろうという考え方が確立してきます。実際のところ、光が粒子なのか波動なのかの論争はその後も永く続くのですが、そのとき光の波動説に取って波動を伝える媒質とは何かが最重要なテーマとなる。
この当たりは別稿「フィゾーが運動媒質中の光速度（随伴係数）を測定した方法（1851年）」１．で説明しておりますのでそこを参照されて下さい。
光の波動説と粒子説(放射説)の優劣を論じるときに、繰り返し取り上げられたのは光行差の問題です。
1727年にブラッドリーは光行差の現象を見つけました。光行差とは、我々が地球上で地球と共に動きながら（地球は太陽のまわりを公転し、さらに自転している）遠い恒星からくる光を観測するとき、光の方向は実際に恒星がある方向とは異なって見える現象です。彼はその現象を光の“粒子説”で説明していた。
下図で光の粒子はＳの方向から速度ｃで来るものとし、観測者はＯＯ’の方向へ速度ｖで走っているとする。観測者はその望遠鏡をＯＡの方向に向けており、Ａで望遠鏡に入った光がＡからＯ’へ達する時間ｔ内に望遠鏡はＯＡからＯ’Ａ’の位置まで移動する。
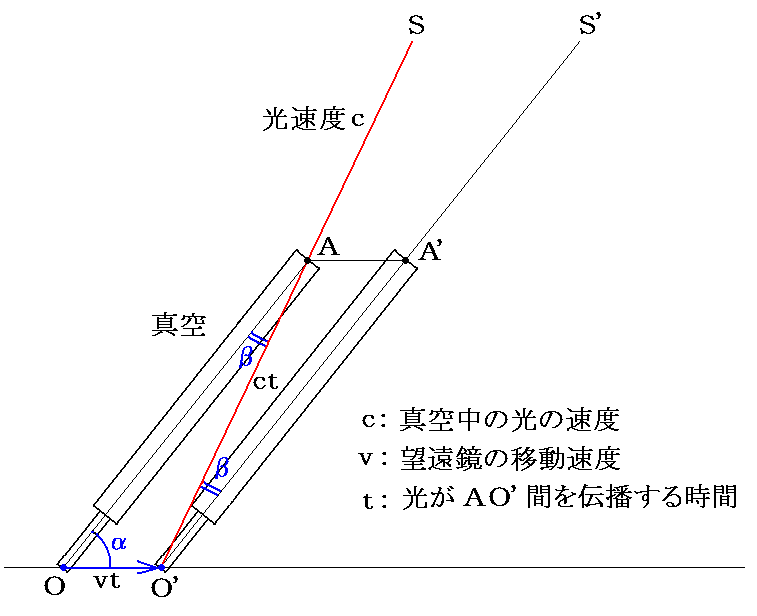
今望遠鏡がＯＯ’となる角をα、Ｏ’Ｓが見かけの方向Ｏ’Ｓ’と成す角をβとすれば、△ＡＯＯ’に“正弦定理”を適用して変形して
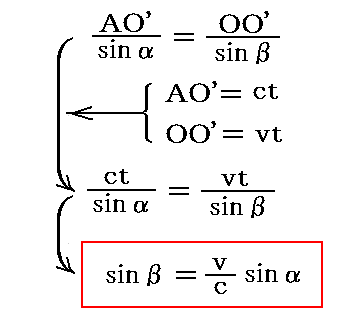
が得られる。ここで、α、βの測定値と、地球の公転速度ｖ＝3.0×104ｍ／ｓを代入して光速度ｃを求めると、レーマーが木星の衛星周期の遅れから求めていた値と良く一致した。
以上がブラッドレーの説明ですが、彼は光が真空中を真っ直ぐに進んで行く粒子であるとして、これらの現象を説明した。もちろん光の粒子がなぜいつも同じ速度で、真っ直ぐに飛んで行くのかは大きな謎ですが、そこさえ認めれば光行差の現象自体は旨く説明できます。［別稿「ブラッドリーが光行差を見つけた方法（1727年）」参照］
［補足説明１］
粒子説では（ａ）光の速さは放射源の運動に対して相対的な速度ｃで動くのか、あるいは（ｂ）放射源の速度に関係なく絶対静止空間に対して速度ｃで動くのかの二通りの考え方があります。仮説（ａ）は動いている列車から発射された弾丸の速さが列車の速さぶん変化することと同じで、仮説（ｂ）は波動説の媒質を伝わる波動の様に放射源の速度によらないことを意味する。
このとき、連星の運動の観察から仮説（ｂ）が正しいことが直ちに判明する。天文学で知られているように星雲ガスが収縮して恒星系となるとき、ガス量とガス雲が持つ角運動量の兼ね合いから太陽系のような惑星系を伴った恒星となったり、連星あるいは単独の恒星となったりする。そのとき恒星の半分程度が連星系になると言われている。
連星を構成する二つの星の距離は地球から連星系までの距離に比べてきわめて小さいが、連星は互いの重心のまわりを比較的大きな速度で公転運動している。一方の星は我々から遠ざかり、他方は我々に近づく。連星系と地球との距離は莫大なために、仮説（ａ）では二つの恒星から同時に射出された光が地球に到着するまでに大きな時間差を生じる。
その時刻差Δｔのおよその値は
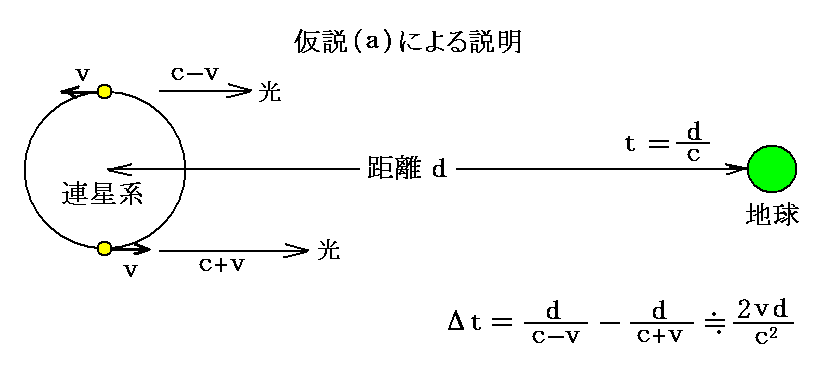
で計算できる。
ところでｃ～3×108m／sですが、連星までの距離ｄが1019ｍ～1000光年を越え、公転速度が104m／ｓを越える連星系は多数ある。そのとき時間差はΔｔ＞106ｓ（～12日）となるので、この効果が観測を逃れることはありえない。つまり仮説（ａ）が正しければ連星系の運動はゆがんで見えるはずだが、観測によるとその様なことは無い。
W de Sitter, “Ein astronomischer Beweis fu¨r die Konstanz der Lichtgeschwindigkeit”, Phys. Z. 14 ( 1913) 429.
de Sitter はｃ’(光の速度)＝ｃ＋ｋ×ｖ(星の速度)としてｋ＜0.002を得た。［Ｐ．Ｇ．ベルグマン著「相対性理論序説」秀潤社 第Ⅲ章、やパウリ著「相対性理論」筑摩学芸文庫
第Ⅰ編§3を参照。］
あらゆる光が同じ速度で地球に到着するというのは極めて不思議なことですが、粒子説でも光は仮説（ｂ）の様に伝わると考えなければならない。この事はその後も様々な方法で検証された。
D.Sadeh, Phys. Rev Letters, 10, p271, 1963年
Sadehは静止した電子にほぼ光速に近い速度を持つ陽電子を追突させた。この衝突実験の電子対消滅により二つのγ線が放射される。元々の光源（陽子と陽電子）の重心系はｃ／2近い速さを持つ。そのときγ線を重心系で見ればそれぞれｃの速さで180度の角度で放出されるのだが、もし光（γ線）の速度が光源の速度に依存するのならば、対消滅が起きた点（電子の位置）から等距離にある2個のカウンターに到着するγ線の検出時間は異なるはずである。しかしその様なことは起こらず常に同時であった。［バークレー物理学コース『力学（下）』丸善1975年刊］
T.Alva¨ger, F.J.M.Farley,J.Kjellman and I.Wallin, Phys. Letters, 12, p260, 1964年
これは光速に近い速度で運動するπ0中間子が二つのγ線（光）に分解するときのその速度を測定するもので、ｃ’＝（0.99997±0.00013）ｃ すなわちｋ＜0.00004以下であることをえた。[平川浩正著『相対論 第2版』共立出版（2011年刊］
K.Brecher, Phys.Rev.Lett. 39, p1051, 1977年
BrecherはＸ線を出す二重星（連星）の観測からｋ＜2×10-9を得て、さらに精度を高めた検証をした。
今日まで行われたあらゆる実験に於いて、光速が光を放射する物体の速度に依存する効果はまったく見つかっていない。
［補足説明２］
これは光が粒子であると考えると非常に奇妙な性質ですが、アインシュタインの相対論的速度の合成則を用いると旨く説明できる。
静止した観測者（地球）に対して速度Ｖで動く［光の放射源（恒星）］を考える。その放射源と共に動く慣性系から観測した粒子（光）の速度をｖ’とする。その粒子（光）の速度を静止系（地球）から観測したときの速度ｖは、相対論的速度合成則によると
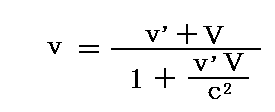
と表される。ただしｃは光速である。
ここでは特別にｖ’＝光速（ｃ）と考えねばならないので、上式は
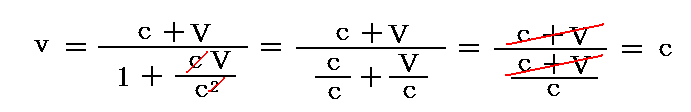
となる。
もともと相対論的速度合成則は「光速不変の原理（光速度は光源の速度に依存せず、どのように動いている観測者から見ても一定値ｃとなる）」が成り立つことから導かれたものですから、こうなることは当たり前です。。
しかし、やがて時代が下ると、光が示す様々な現象（反射、屈折、偏光、干渉、回折、分散、・・・）が発見されてきます。そして、ヤング、マリュス、フレネルなどの人々が、それらの現象を説明するためには、光が波動でありしかも横波であることが必要であると考えるようになりました。
波動説を提唱したヤングは1804年の論文［“Experiment and Calculation Relating to Physical Optics”, Phil. Trans.,
94, p1～16, 1804年］で次の様に書いています。
「星の光行差の現象を考察してすぐに、私は発光エーテルがあらゆる物体の内部に、たぶん風が森をふきぬけるのと同じように自由に、ほとんど、あるいはまったく抵抗を受けずに浸透すると信ずる気になった。」
すなわち、波動説において光を伝える媒質であるエーテルは、絶対静止の宇宙空間に静止していていると考えれば、“波動説”でも光行差の現象を旨く説明できるとしたのです。
波動説で光行差の現象を説明するためには、光を伝える媒質であるエーテルは絶対静止の空間に対して静止しており、光は絶対静止の空間に対して一定の速度で伝播することを仮定しなければならない。決して音波のように、地球と共に動く媒質（空気）に対して一定の速度で伝播するのではありません。例えば地球にまとわりつく空気に対してどの方向にも一様な速度で伝播する音波の場合には、地球の大気圏上層の例えば天頂付近に音源があって、それから発せられた音波が地上に伝わる場合、たとえ大地と大気がその音源に対して動いていても、決して光行差の様には成らないと言うことです。
光行差の現象を光の波動説で説明するためには、波となって伝わる光を伝える媒質である仮想的なエーテルは絶対静止の空間に対して静止しており、それは観測に用いた望遠鏡はもちろんのこと、大気も地球もすり抜けて静止し続けていると考えなければならない。
これは光行差の現象を波動説で説明する場合避けては通れない前提ですが、あらゆる物体を幽霊のようにすり抜けるエーテルの性質は非常に奇妙なものです。
［補足説明］
波動説ではホイヘンスの原理がとても重要になる。このとき素元波の包絡線である波面が伝わる方向（つまり波面に垂直な方向）と波のエネルギーが伝わる方向との違いに注意する必要がある。光線を光のエネルギーの流れであると定義すれば光線の方向を放出した粒子の流れであるかの様に取り扱うことができる。そのあたりの詳細はマックス・ボルン著「アインシュタインの相対性理論」東京書籍第Ⅳ章10を参照。
エーテルが絶対静止の宇宙空間に対して静止していれば、波動説でも、粒子説と同様に光行差の現象を一応説明できるようにみえます。しかし、光が水やガラスの中に進行すると屈折することが知られています。
“波動説”では、屈折の現象をホイヘンスの原理によって説明します。そのとき、波の伝播速度が媒質が異なれば変化するとしています。光の伝播速度が媒質によって変化することが検証されるのはもう少し後［1850年のフーコーの実験］ですが、速度が変化する事は様々な干渉現象からもほぼ確実だと考えられていました。
この事を考慮すると新たに様々な疑問が湧いてきます。
例えば、“星からの光を屈折率が１よりも大きなガラスを通して観測するとします。そのとき、平らな面を持つガラス板が地球の運動によっては運ばれ、有る星からやってくる光線が、このガラス板に入ったとき曲げられないようにガラスの向きを調整したいと望んだとしよう。その時ガラスの表面は光行差とは関係なく星の真の方向に直角に置くべきであろうか、あるいは光行差の影響を受けた見かけの方向に直角におくべきなのだろうか？”
あるいは、ミッチェル（Michell）が提起(1784年)したように、“星からやって来る光線は、地球とともに動いている地上の光源から発する光線と違う屈折を受けるのではないか？”
また、ロビソン（Robison）とウイルソン（Wilson）が主張したように、“色収差の無い望遠鏡を地球の進行方向にある星に向けた場合と、その反対方向にある星に向けた場合では、光の望遠鏡レンズに対する相対速度が変化する。レンズによる屈折率はレンズの内外での光速により決定されるので、屈折率も変化して星の像を結ぶ位置（焦点距離と言っても良い）は変化するはずである？”［下図参照］
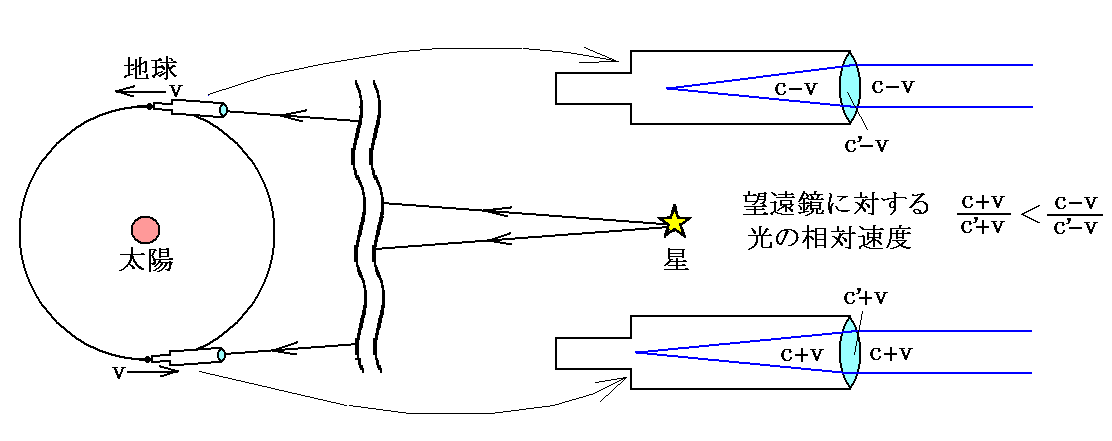
その他様々な問題提起がなされ、様々な実験がなされた。中でも有名なのが、1766年にボスコヴィッチ（Boscovich）が提起した問題と1810年にアラゴ（Arago）が行ったプリズム実験です。他の提案、実験もこの二つと大同小異ですので、この二つを代表例として説明します。
ボスコピッチは、“水を満たした望遠鏡で光行差を観察すれば光行差の大きさが大きくなるはずだ！”と予想した。
水の存在により光の伝播速度はｃ／ｎ（ただしｎは水の屈折率）に遅くなりますが、エーテルが絶対静止の空間に対して静止しているのなら光の伝播する方向は水の移動に影響されることはないのですから、絶対静止のエーテルを仮定する限りこれは避けがたい結論です。
ボスコヴィッチの主張は光行差のメカニズムを考慮すると直ちに了解できます。真空中の光速度ｃはそのままだから望遠鏡の部分のみを拡大して説明する。また、望遠鏡に光が入射するＡ’点では屈折の効果があるのですが、話を簡単にするために、天頂にある星を観測するとし、さらにＡ’における水面は移動方向Ｂ’Ｃ’に平行であるとする。そうすると
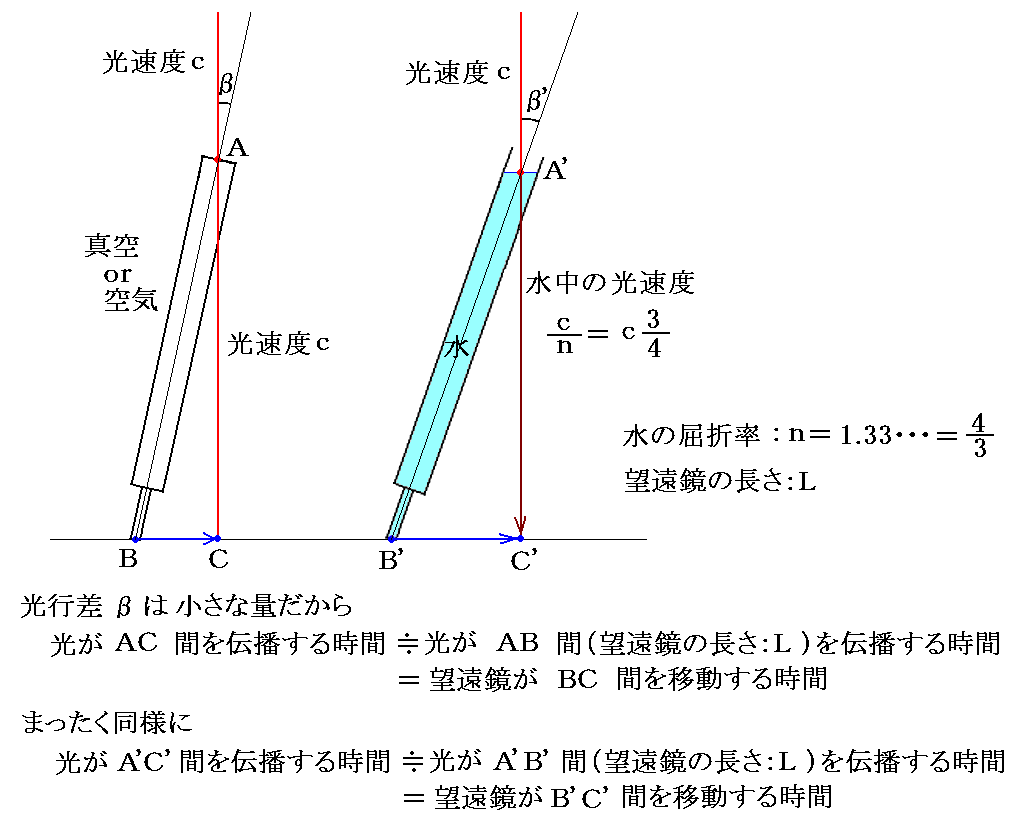
となる。
上図から明らかなように、水中の光速度は真空（空気）中の光速度の3／4倍だから、水で満たした望遠鏡で観測した場合の光行差β’は真の値βの4／3倍になる。波動説に於けるホイヘンスの原理が正しく、仮想的なエーテルが静止しているとする限り、このようになります。
これが文献１．でフレネルが引用している“ボスコピッチが提案した実験”です。ただし、これが実際に行われるのはかなり後（1871年 エアリー）です。
［補足説明１］
エーテルが地球の運動に完全に随伴するという説では光行差の現象をまったく説明できませんから、ここではヤングが掲げた地球の運動の影響をまったく受けないエーテル仮説にもとづいて説明している。媒質中で速度が遅くなるのはなぜなのかは解りませんが、とにかく地球の運動にかかわらず星からの光は絶対静止空間に対して直進すると考えています。
［補足説明２］
地球表面ではエーテルが地球の運動に完全に随伴しており、宇宙空間では静止しているとして光行差の現象を説明しようとした“ストークスの理論”があります。しかし、この理論には内部的な矛盾があり、この理論を改良して光行差現象を説明しようとする多くの努力にもかかわらず結局旨くいきませんでした。その当たりを説明したローレンツの文章を引用しておきます。
エアリー（Airy）は1871年に、りゅう座γ星が天頂を通過するときの赤緯を、春と秋に半年の間隔をおいて、鏡筒を水で満たした子午環儀で観測してボスコピッチの予想を確かめます。りゅう座γ星の位置は別項「ブラッドリーが光行差を見つけた方法」で説明したように下図の様になります。
［拡大図］
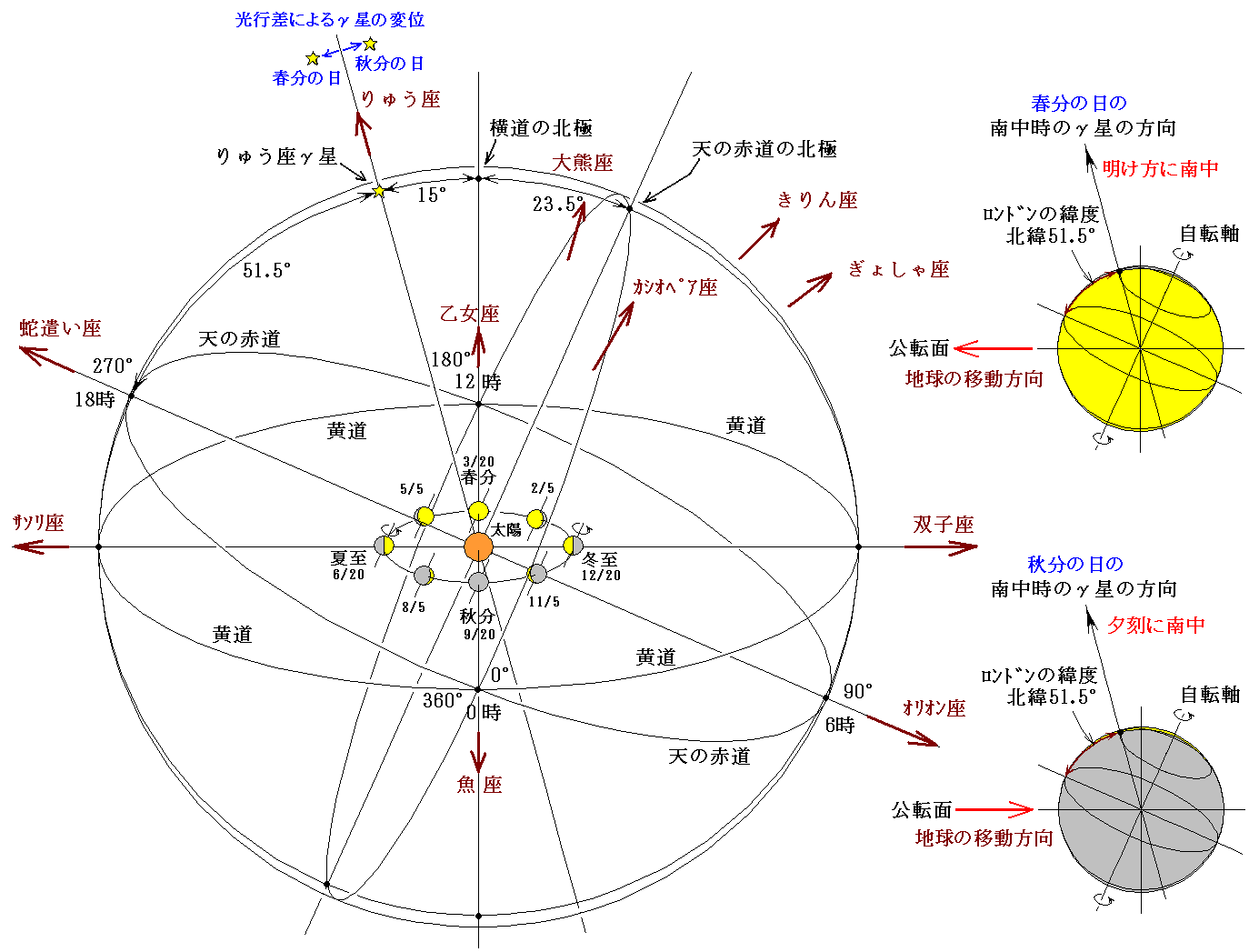
γ星の天頂通過時の赤緯観測値から光行差の量を補正して観測地点の緯度を算出します。春分・秋分の位置でγ星と黄道面の成す角が約75°ですから、補正する光行差の量は20.5”×sin75°＝19.8”程度となります。Ａｉｒｙの論文では春分・秋分における光行差補正量は19.74”となっていますが、当時の公転半径の観測値から求まる地球の公転速度と、光速度の測定値からこのような値になるのでしょう。
そのとき、水を満たすことで光行差の量が変化するのなら春と秋の観測値から得られる(子午環儀の設置場所の）緯度が異なるはずです。水の屈折率から考えてその違いは±15秒程度になると考えられるから充分観測できるはずです。
下図のＡ、Ａ’が春分の日と秋分の日にγ星が南中するときの天頂からの北向き偏角です。Ｂ、Ｂ’は子午環儀設置場所での、光行差補正が施された、γ星の春分と秋分の日の“航海暦赤緯（Nautical Almanac）”です。また、Ｃ、Ｃ’が光行差を考慮してγ星の赤緯から計算される子午環儀のある場所の“地理学的な緯度”です。［詳細は文献４．参照］
［拡大図］
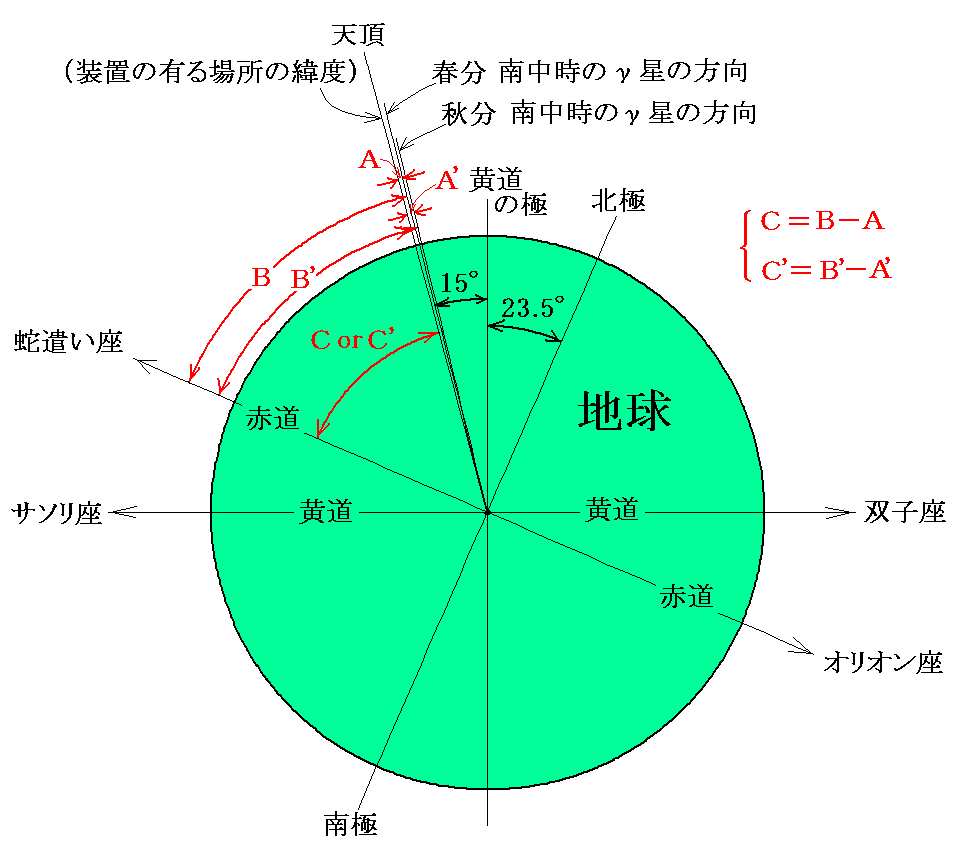
エアリーは1871年と1872年に二度実施しますが、どの観測においても、光行差理論から計算された緯度ＣとＣ’は全て同じ値となり変化は認められなかったのです。すなわち、望遠鏡を水で満たしても満たさなくても、光行差の角度βは変わらなかったのです。これは有る意味、1868年に行われたHoekの実験結果[原論文はこちら]を追認するものだとも言えます。
これらの結果はきわめて不思議なものですが、“フレネルの随伴説”によってすでに1818年の段階で説明［４．（２）２．参照］されていたことです。
［補足説明］
Sir George Biddell Airy(1801～1892年)イギリスの天文学・物理学者。1835～1881年グリニッジ天文台長として観測設備を完備。同天文台で観測した恒星・月・惑星の位置を整理集約し、基礎天文学に貢献。
もう一つ有名な実験が1810年に行われた“アラゴ（Arago）のプリズム実験”［文献３．参照］です。これは元々１．（２）で述べたミッチェル、ロビンソン、ウイルソン等が提起した問題に起源を持つ。
アラゴは、子午環儀の対物レンズの前に、クラウンガラスとフリントガラスを貼り合わせて色消しとした角度24°のプリズムをとりつけた。彼は、幾つかの星の南中時の赤緯を、プリズムを通した場合と、プリズム無しの場合で観測して、その赤緯の差を求めてみた。
もしもエーテルがプリズムを素通りして運動して行くものとすれば、光の方向がプリズムの運動方向と一致している状態と、そうでない状態ではプリズムによる星の方向の振れ角は異なってくることが予想される。様々な南中時刻の星々を同じ日に観測してみれば、光の方向とプリズムの運動方向が異なりますので、赤緯の差に変化が起こることが予想されます。
［補足説明１］
子午儀とは子午線上（南北方向）にのみ向きを移動できるように作られた天体望遠鏡の一種です。子午儀で恒星の子午線通過時刻を計測することで、その恒星の赤経や子午儀の設置地点の経度を正確に求めることができる。また子午儀に目標天体の高度を測定する目盛りを刻んだ環を付加した子午環儀を用いると恒星の赤緯や観測地の緯度も測定できる。
アラゴは1810年の3月19、27日と10月8日に、下図の様々な方向にある星が観測地点（パリ）で南中するときに、それらの星々の天頂からの距離（角度）をプリズムを設置した場合と、プリズム無しの場合で測定した。そして両方の差を取った。その時アラゴは、地球の公転速度の影響が最も大きく現れると考えられる、黄道面付近の星々を選んで観測しています。
図中の時刻は、それぞれの方向の星が子午環儀が設置されている場所（パリ）で南中するおよその時刻（パリ時）を示している。
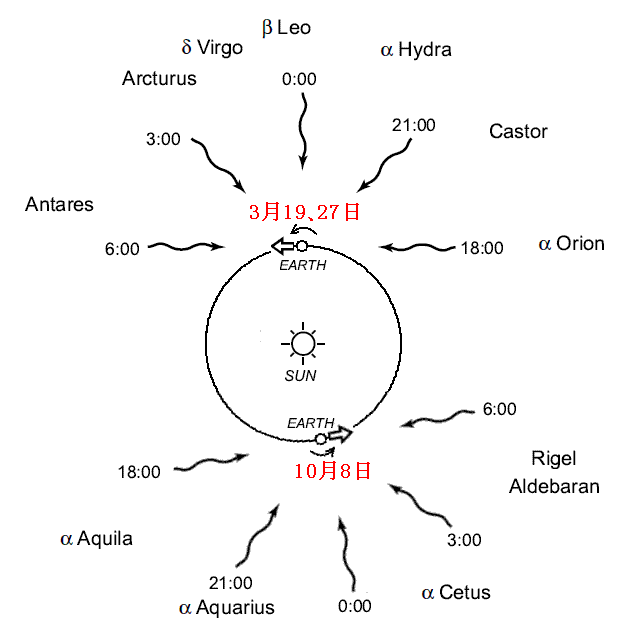
星が見える方向の天頂からの角度のプリズム有りと無しの偏差は下表の様になった。
論文には明記してないが、3月の観測ではプリズムを設置した状態の観測のみ行って、偏差は当時数表として与えられていた光行差補正が施された“航海暦赤緯（Nautical Almanac）”と差し引きすることで求めたのではないだろうか？
下表は3月の観測結果ですが、最初の欄はそれぞれの星の南中時刻（パリ時）です。表から明らかなように、様々な黄径（赤径）の星々について観測されたが、それらの間には偏差の違いはほとんど無かった。
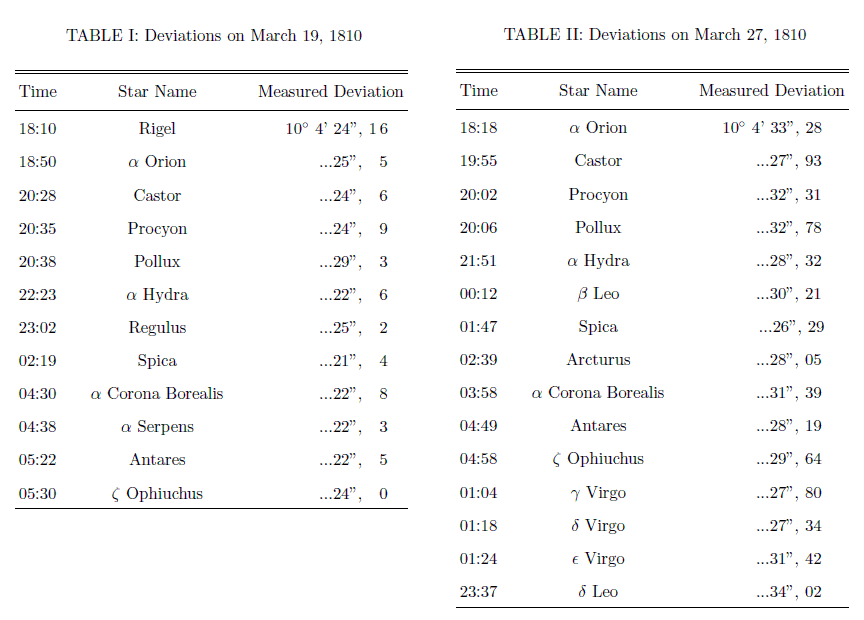
アラゴは半年後の10月8日にも同じような観測を行い同様な結果を得た。その結果が下表です。
3月と10月で偏差の値が大きく異なるのは、10月の観測ではより大きな性能の良い別のプリズムに交換したためです。そのため3月と10月の偏差の違いは関係有りません。同じ日の異なる南中時間の星との間で比較して下さい。
10月の観測では対物レンズの半分のみをプリズムで覆い、プリズム有りとプリズム無しの赤緯観測を両方行い、それから偏差を求めたようです。両方の観測を行う時間的なズレは星の運行を考慮した計算で補正されています。
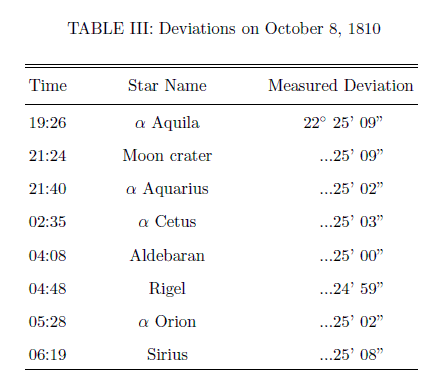
表から解るように、いずれの場合も顕著な偏差角の違いは見いだされなかった。つまり“動いているプリズムの見かけの屈折は静止したプリズムの屈折とまったく等しかった”のです。
地球の公転速度は約30km／sですから、同じ日の午前6.00頃南中する星と午後6.00頃南中する星とでは、プリズム有る無しの赤緯の観測結果の偏差には当然観測可能な変動があるはずです。アラゴは黄道付近にある星の場合、6:00南中の星の編差と18:00南中の星の偏差の違いは、３月の角度24°のプリズムを用いた場合には12”程度、10月のより大きなプリズムを用いた場合には28”程度であろうと見積もっていました。それにもかかわらず、その様な変化はまったく観測されなかったのです。これはきわめて不思議な結果でした。
これが文献１．でフレネルが引用している“アラゴのプリズム実験”（1810年）の内容です。これの結果は、１．（２）で説明したロビソンとウイルソンの主張も同様に否定される事を意味します。
［補足説明２］
この時点のアラゴは、光の放射説(粒子説)の立場から自分の観測結果を説明しています［文献３．のp46の後半］。それはかなり恣意的な論理で、今日の目から見てとうてい納得できるものではありません。フレネルが文献２．の段落1で引用しているのが、そのアラゴの説明です。
［補足説明３］
いずれも黄道面付近にある星を観測するのですが、南中時間が異なれば星を観測するときの仰角は異なります。そのため“大気差”は観測する星毎にかなり変化します。しかし、この“大気差”はプリズム有りと無しの両方の観測に等しく関係してきますので、その差を取った最後のデータには表れてこないことに注意して下さい。［大気差については別稿参照］
1815年～1823年頃にかけてヤング、アラゴ、フレネル等により“光の横波波動説”が確立して行きます。そういった流れの中で、アラゴは“自分が1810年に行ったプリズム実験の結果が光の“波動説”によって旨く説明できるかどうか考えてみて欲しい”と言って1818年にフレネル対して問題提起します。
その要請に応えてフレネルが考え出したのが、“光を伝える媒質としてエーテルは絶対静止の空間に静止しているのだが、物体が移動するとエーテルの一部が引きずられてあたかも動いているように見える［エーテルの随伴説］”というものです。
以下で説明しますが、彼の随伴説は、“アラゴのプリズム実験”や“エアリーの光行差実験（ボスコピッチが提案した）”を含めた諸々の類似の実験や観測を見事に説明するものでした。
弾性体力学理論によれば、弾性体内を伝播する横波の速度は、媒質の剛性率と密度をＮ、ρとすれば
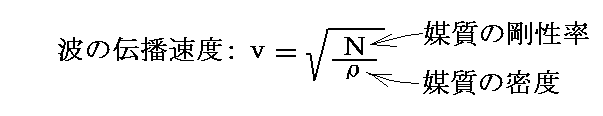
で与えられる。
フレネルは、この関係が光を伝える媒質としてのエーテルに対しても成り立つとした。真空中のエーテルの剛性率と密度をＮ、ρとし、任意媒質のそれをＮ’、ρ’とした。そしてフレネルは真空中と媒質中での光速度の違いはそれぞれの中のエーテルの密度に由来し、剛性率は同じであると仮定した。
この仮定は元々、ヤングの“透明体の屈折能力はその内部のエーテルの濃度による”という示唆を採用したものです。その場合
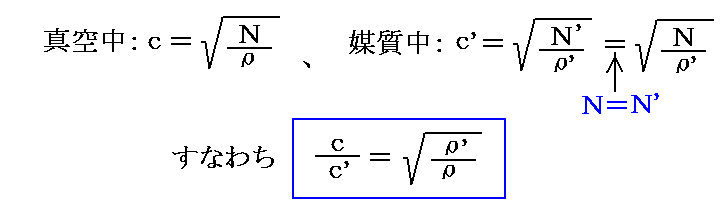
となる。
このときｃ＞ｃ’であるからρ＜ρ’となる。すなわち、種々の媒質中ではエーテルの密度は異なり、屈折率が１より大きい媒質は真空中よりもより多くのエーテルを含んでいるとした。
［補足説明１］
これが、フレネルが文献２．の段落12で“媒質の密度比は、波動の伝播速度の2乗の比の逆数でなければならない、ということが知られているからです”と述べている部分です。
しかし、当時はまだ弾性理論は発展途上で弾性体内を伝わる横波の速度が最初に述べた関係式で表されることが確立していたわけではありません。フレネルなどの研究とともにまさに手探りの状態で少しずつ弾性体の理論が形作られていった時代です。
［補足説明２］
フレネルはここで述べた弾性理論の助けをかりて、次節で説明するように“エーテルが物質の運動に部分的に随伴する”という仮説から随伴係数（1－１／ｎ2）をまず導きます。そしてこれが成り立つとアラゴの実験、エアリーの観測が旨く説明できるとしています。
しかし、ここで注意して欲しいことは、以下で述べるようにアラゴの実験、エアリーの観測、ヘックの実験結果をそのまま素直に解釈することから逆にフレネルの随伴係数が導き出されることです。そこでは、ここに述べたような恣意的な弾性理論による助けを必要とするわけではありません。このようにして得られた実験事実を説明する随伴係数を、弾性理論の助けを借りて次節で述べる説明を逆にたどって解釈すれば、弾性流体としてのエーテルが物質の運動に部分的に随伴するという考え方にたどり着けます。
フレネルはさらに次の仮定を設けた。
屈折率が１より大きな物質は、真空中でこれと同体積に含まれるエーテルよりもより多くのエーテルを含む。そして、この物質が運動すれば、この余分のエーテル（真空のエーテル密度を超える部分）は物質とともに運ばれていくが、残りのエーテル（真空のエーテル密度の分）は物質の運動によって何ら影響を受けずに絶対静止の空間にそのまま残っている。
上記の仮定は次のように解釈することができる。今単位体積の立方体の形をした物質が速度ｖで図の矢印の方向に運動しているとする。そして、物質内のエーテル（密度ρ’）は速度ｖ’でやはり矢印の方向へ運動する。
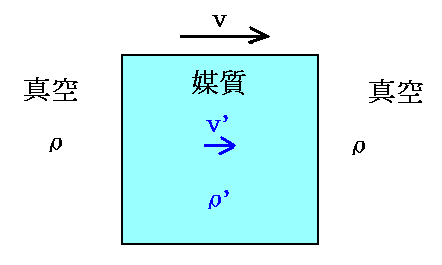
物質内のエーテルの速度は遅くなるのだが、仮定のように常に物質内のエーテル密度ρ’が保たれるためには、単位時間に物質内へ入るエーテルの量と、単位時間内に物質から流れ出るエーテルの量が等しくなければならない。すなわち
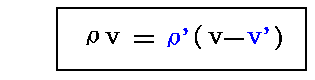
が成り立たねばならない。
この式の意味が解りにくいので図で説明します。
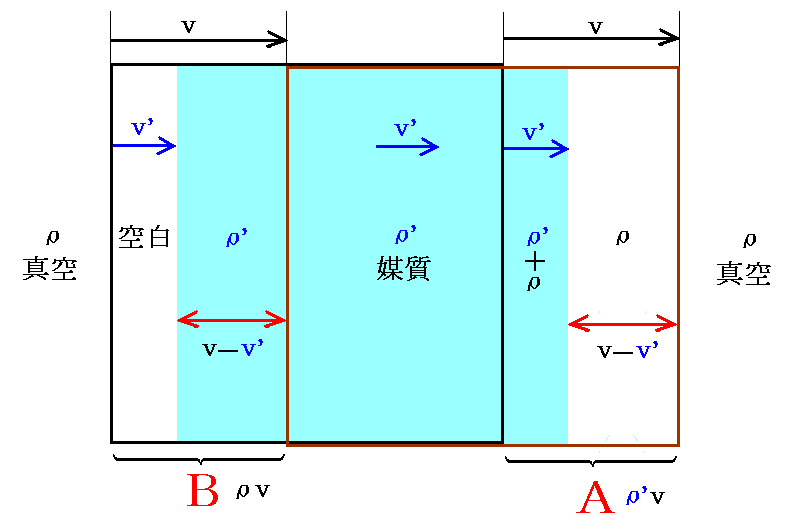
上図の領域Ａでは、元々真空のエーテルの量ρｖが存在する。それに新たにρ’ｖ’が付け加わる。それらをあわせたものが領域Ａ全体でならされたと考えてρ’ｖとならねばならない。つまり
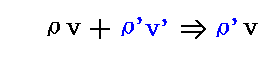
となる。
一方領域Ｂでは媒質が移動したためにエーテルが存在しない空白の領域ができる。そのとき媒質中のエーテルはｖ’の速度でしか移動しないのでρ’（ｖ－ｖ’）のエーテル量が領域Ｂの中に取り残されている。これが領域Ｂ全体に広がったと考えて真空のエーテル量ρｖになればよいので
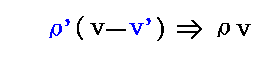
となる。［ここは解りにくいところですので、文献７．p9～11の説明も参照されたし。］
いずれにしても前記の関係式が満たされることになる。つまり、この関係式が成り立てば“物質内部のエーテル密度は常にρ’を保ちながら、真空のエーテル密度からの過剰分だけが物質と共に移動していくように見える”と言えるのだが、これはまた、“物質内部では密度ρ’のエーテルが全体としてあたかもｖ’で動いているように見える”のである。［この当たりは別稿「フィゾーが運動媒質中の光速度（随伴係数）を測定した方法（1851年）」２．（３）３．の説明も参照されて下さい。］
従って
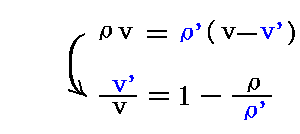
となる。一方前節で述べた弾性理論から得られる関係式から
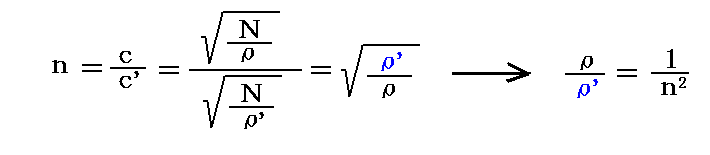
であるから
となる。ｖ’／ｖを随伴係数と呼ぶのはｖ’＝ｆｖの関係があり、物質がｖの速度で移動すれば、それに含まれるエーテルはｆｖの速度で動くことになるからです。
従って屈折率がｎの物質が速度ｖで動いているとき、そのなかにおける光の速度は絶対静止空間から見て物質の進行方向に対しては
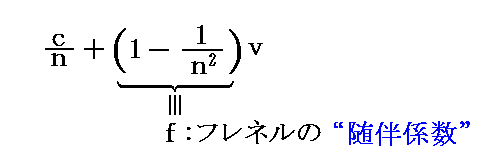
の速度で伝播することになる。
フレネルの随伴説によって、アラゴのプリズム実験の結果を説明します。
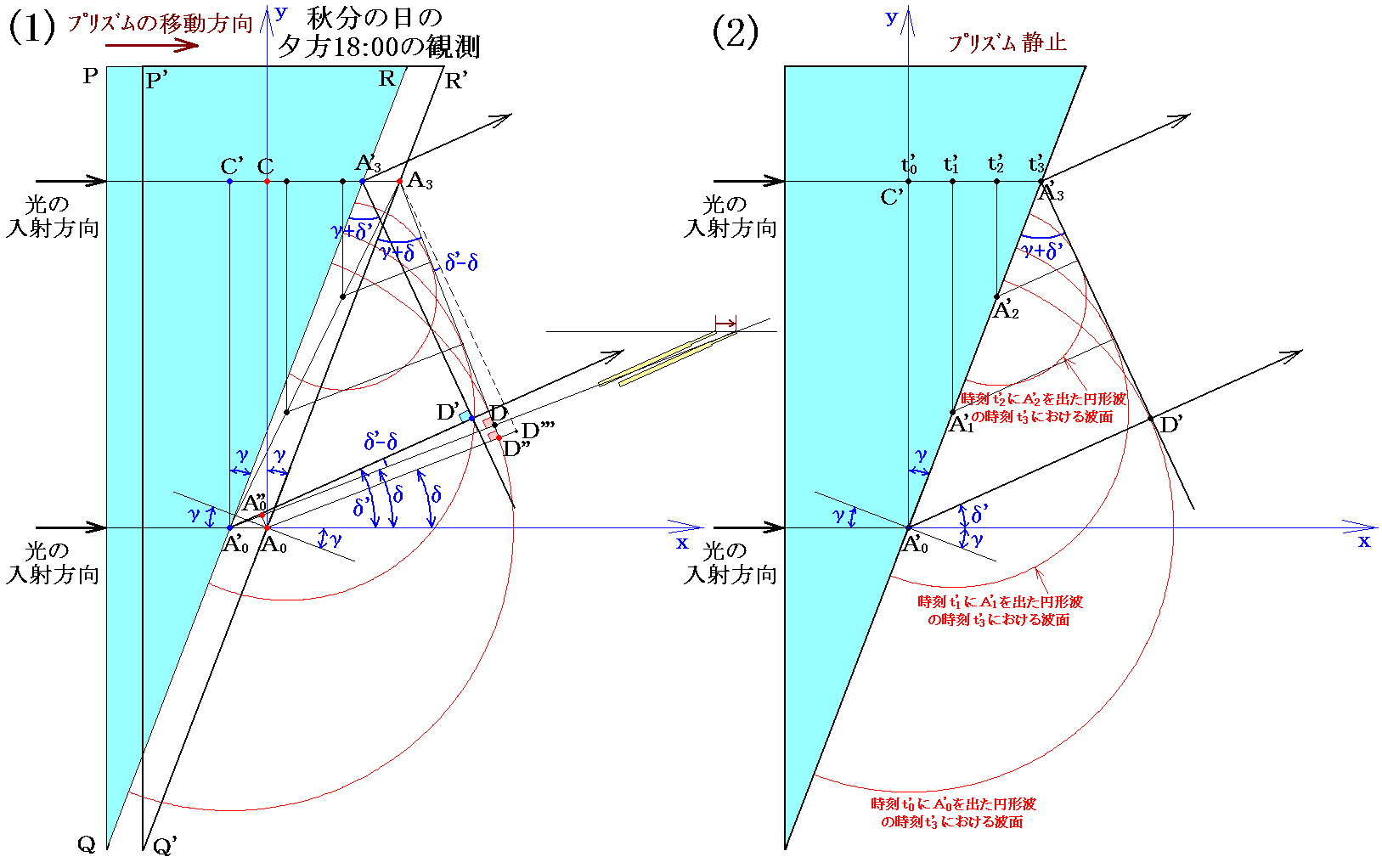
話しを簡単にするために秋分の日のパリ時刻の明方6：00と夕方18：00に南中する黄道方向にある２つの恒星をプリズム有りとプリズム無しの状態で子午環儀で測定する。その時さらに話を簡単にするために、プリズム有りの場合に星の光はプリズム面に垂直入射するように取り付けられているとする。パリの緯度は48.85°だから、6：00と18：00の観測の様子は下図の様になる。
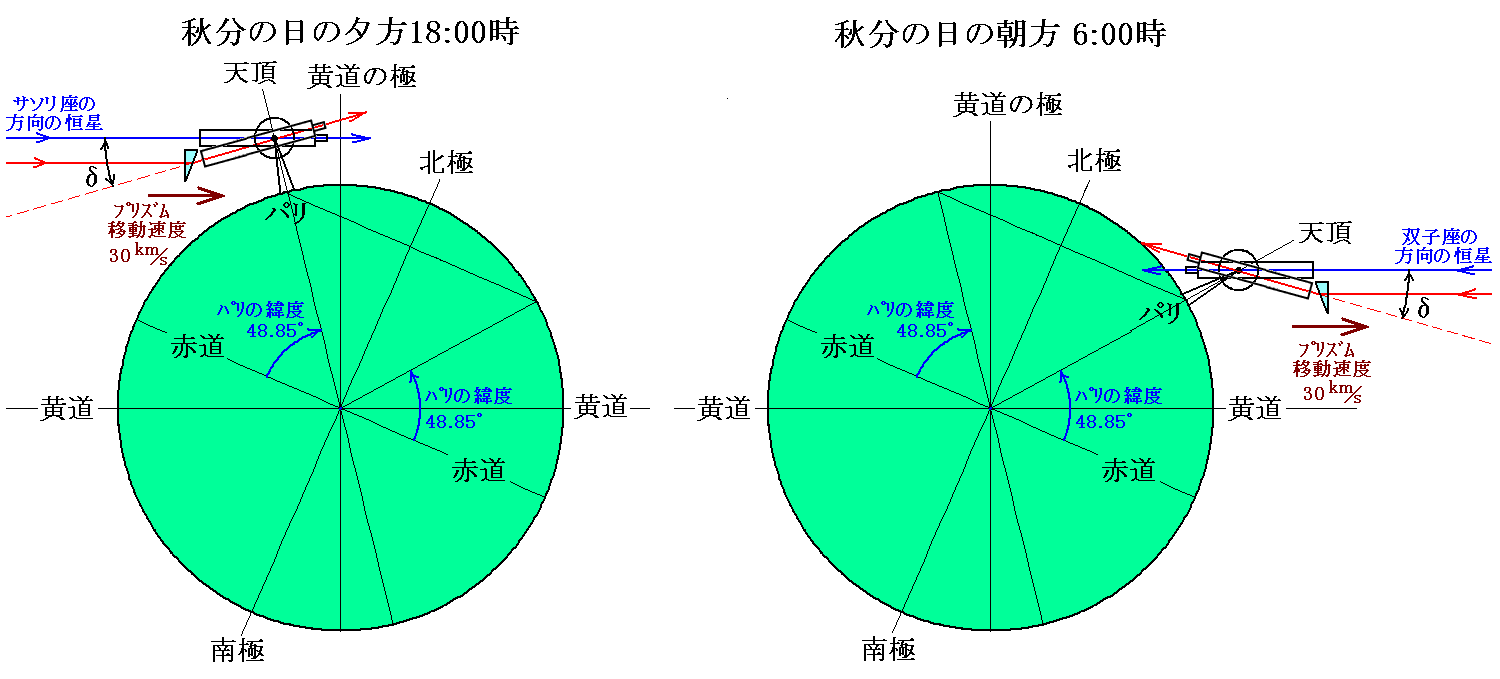
このとき確かめたい事は、“地球の公転運動に伴ってプリズムが絶対静止空間（エーテルが静止している）に対して動いているとき、プリズムの運動速度や運動方向によって図の偏角δが異なるのか？”と言うことです。
その時、別稿「 フィゾーが運動媒質中の光速度（随伴係数）を測定した方法（1851年）」１．（２）で説明した、光を伝える媒質として考えられているエーテルについての三つの仮説に分けて検討してみる。
まず、［仮説２］ エーテルには付着性があり、物体の分子に固定されていて、物体が運動すれば物体と共に動く。
の場合ですが、１．（１）２．で説明したように光行差の現象がまったく説明できないので直ちに否定される。
そのため以下では、［仮説１］と［仮説３（フレネルの随伴説）］の正当性について考察する。
空気の屈折率はほとんど１に近いので、プリズム以外の空間部分は真空空間と同じと考える。また簡単の為に、プリズムを構成するガラスの屈折率はｎ＝2.0と仮定する。つまり、真空中での光速度をｃとするとプリズム中の光の伝播速度はｃ’＝ｃ／2となる。
この場合には、入射光に対するプリズムの動きに対応して、屈折波の波面は下図のようになる。これらは絶対静止の空間に対する素元波の広がりや、波面を表していることに注意して下さい。ガラスの中での光の伝播速度はプリズムが動いているいないにかかわらず、絶対静止空間に対して ｃ’＝ｃ／2 となります。
［拡大図］
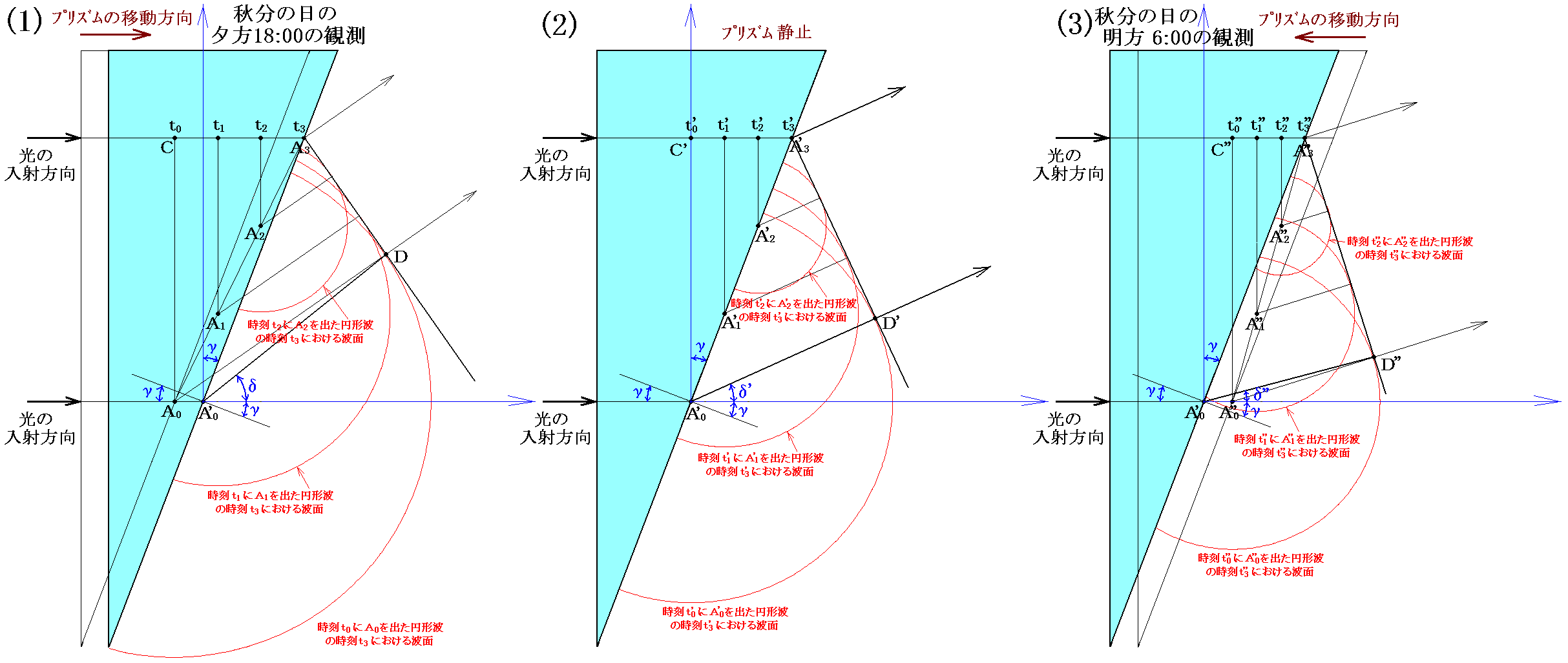
光を伝播する媒質であるエーテルは絶対静止の空間に静止しており、そのエーテルに対してプリズム中では速度ｃ’＝ｃ／2で、真空中(空気中)ではｃで伝わる。
またこのとき、（２）のプリズム静止の場合の屈折波の波面Ａ3’Ｄ’と射線Ａ0’Ｄ’は垂直になるが、（１）の場合に波面Ａ3Ｄと垂直になるのはＡ0’ＤではなくてＡ0Ｄであり、（３）の場合に波面Ａ3”Ｄ”と垂直になるのはＡ0’Ｄ”ではなくてＡ0”Ｄ”であることに注意して下さい。このようになるのは、ちょうど異方性媒質中を光が伝播する場合と同じように、境界面から広がる素元波が見かけ上半円にならないためです。そのとき、“実際にエネルギーが伝播する射線Ａ0ＤやＡ0”Ｄ”の方向”と“波が伝播する波面Ａ3ＤやＡ3”Ｄ”の垂線の方向”とは一致しています。
図から明らかなように、[仮説１]の場合屈折角（γ＋δ）、（γ＋δ’）、（γ＋δ”）はプリズムの絶対静止空間に対する運動状態に応じて変化する。アラゴは、（１）と（３）の差δ－δ”は３月に行ったプリズム実験では12”程度、10月の実験では28”程度と予想しており、この差を観測で確かめようとしました。このとき（１）や（３）の状態で実際に望遠鏡を向ける方向に対しては光行差による変化分も入ることに注意して下さい。
ところが観測結果は、プリズムが運動していても、していなくても屈折角の違いは生じなかったのです。
フレネルは、アラゴの要請に応えて、その様になるためには何が起こればよいかを考えて、文献１．で報告しました。それが［仮説３］“エーテルの随伴説”です。
フレネルは、実際に起こっている事を波動説で説明するために、運動媒質中のエーテルは、その運動媒質の速度ｖの有る割合ｆで引きずられると仮定すれば旨くいくことに気付きます。この割合ｆを“フレネルの随伴係数”と言います。実際のところｆの値を調整すれば、（１）～（３）の全ての場合で屈折角を同じδ’にすることができます。それを前図を用いて説明します。
まず（１）の状況では、プリズム中ではエーテルが右方向に引きずられる為に、光の伝播速度が前記の場合よりも速くなります。そのため距離ＣＡ3を伝播するのに要する時間は前記のｔ3よりも短くなります。そのためＡ0から広がる真空中の二次波の伝達半径Ａ0Ｄも短くなります。そのとき二次波の包絡線ＡＤはより立ち上がってきてδは（２）のδ’に近づいていきます。
一方（３）の状況では、プリズム中ではエーテルが左方向に引きずられる為に、光の伝播速度が前記の場合よりも遅くなります。そのため距離Ｃ”Ａ3”を伝播するのに要する時間は前記のｔ3”よりも長くなります。そのためＡ0”から広がる真空中の二次波の伝達半径Ａ0”Ｄ”も長くなります。そのとき二次波の包絡線Ａ”Ｄ”はより寝てきてδ”は（２）のδ’に近づいていきます。
［拡大図］
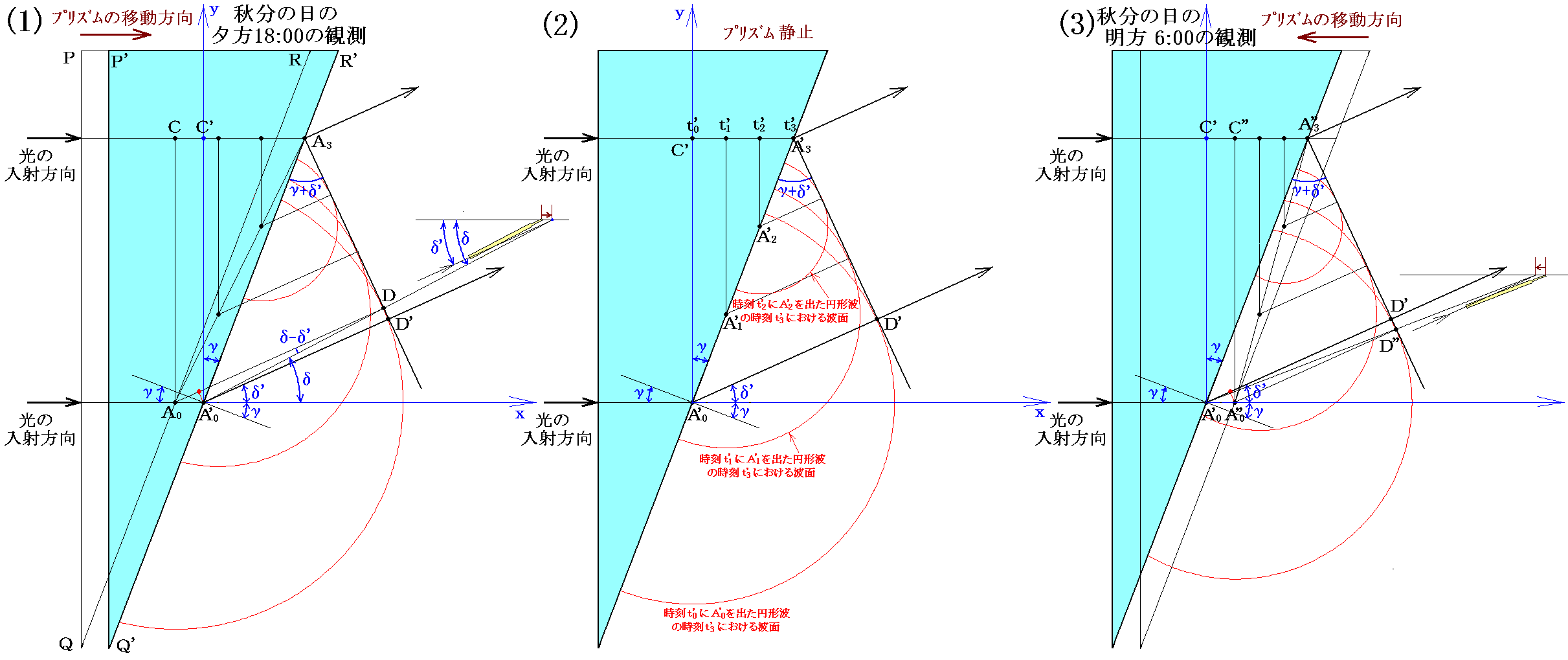
随伴係数ｆを旨く選べば（１）と（３）の状況の屈折角を（２）と同じδ’にできそうです。以下でそのための条件を求めてみる。
実験結果より、（１）の状況でも（３）の状況でも、その屈折角は（２）と同じだったのですから、そうなることを仮定して前図の様な状況が満たされるときの随伴係数ｆを求めてみようと言うことです。
このとき前図（１）に於いて素元円形波の射線Ａ0Ｄは波面Ａ3Ｄに垂直になり、（３）に於いても素元円形波の射線Ａ0”Ｄ”は波面Ａ3”Ｄ”に垂直になることに注意して下さい。
この図で特に注意して欲しいことは、プリズムは絶対静止の空間に対して動いていても上図の真空中（空気中）部分の素元円形波も波面も絶対静止の空間に於ける様子を表していると言うことです。その時（１）や（３）の状況では望遠鏡は動いており、しかも光の絶対静止空間に於ける進行方向に対して有る角δ’で動いています。だから当然のことながら望遠鏡を向ける方向はＤ’Ａ0’の方向ではなくて（１）ではＤＡ0’の方向、（３）ではＤ”Ａ0’の方向です。その様になることは１．（１）１．で導いた光行差の公式sinβ＝（ｖ／ｃ）sinα（ここではα＝δ’）を思い出せば了解できます。つまり光行差分の偏差は（１）と（３）の状況では必ず存在します。この差分が付け加わった上でのさらなる偏差を［仮説１］で検出しようとしたのです。
実際１．（４）で述べたアラゴの実験結果の中には、光行差による変分も含まれているはずです。黄道上の星の場合3月の実験ではδ’＝α＝10°程度ですからβ＝sin-1［（ｖ／ｃ）sin10°］～3.5”程度、10月実験で～7”程度となります。もちろん星は黄道面上に有るとは限りませんので、その値はばらつきます。
もともと［仮説１］で検出しようとしていた（１）～（３）の状況の違いで生じる屈折角の変化分も光行差と同程度のオーダーですから、その当たりを厳密に考察しないといけません。そのためアラゴの実験に合うように随伴係数ｆを決定するのは容易ではありません。以下でまず導出の為の注意事項の説明から始めます。
［補足説明］
上記の説明のように光行差の変化分は３月実験で±3.5”程度、10月実験で±7”程度です。そのため、アラゴの観測データの解釈で、ｖが変わっても偏角の差が無かったと言っても、（Ａ）“光行差の変化分を含めて差がなかった”のか、それとも（Ｂ）“光行差の変化分が存在するのだが、データの測定誤差のバラツキの中に埋もれて良く解らない”のどちらなのかは何とも言えないところです。［仮説１］で予想されるほどの変化は観測できなかったことは言えるのですが、光行差の取り扱いをどちらで解釈するかを判定するのはアラゴの実験の精度では難しい。
その時、エアリーの実験結果は、望遠鏡を水で満たそうと満たすまいと、光行差は望遠鏡の速度に依存して存在し、しかもその量が望遠鏡を水で満たした場合と満たさなかった場合とで同じであったのですから、アラゴのデータも上記の（Ｂ）で解釈すべきかも知れません。（３）節１．項で説明するものは（Ｂ）の立場で証明しています。
さらに付け加えると、（Ａ）の解釈に従って議論を組み立てても随伴係数ｆ＝1－1／ｎ2はまったく同様に導けます。実際、フレネルは（Ａ）を仮定して証明しているようです。
まず、随伴係数ｆを求める手順を、前図（１）の場合について整理しておきます。
プリズムＰＱＲが真空中で地球の運動（速度ｖとする）によって運ばれ、その表面ＰＱは運動方向と直角をなし、星からの光がこの面に垂直に入射すると仮定する。光線は入射の際、屈折しないので、第二の表面ＱＲによって生ずる効果だけを考えればよい。時間ｔの間にプリズムはＰＱＲの位置からＰ’Ｑ’Ｒ’の位置まで移動するとする。
この間にＣに於ける光の攪乱はＡ3に達し、Ａ0における攪乱は（ホイヘンスの原理に従って）一つの球面波を作る。Ａ3からこの球面に引いた接平面Ａ3Ｄが出てゆく波の波面になる。
今ガラスの屈折率をｎ、フレネルが仮定した随伴係数をｆとすると、ガラスの中の絶対速度はｃ／ｎよりもｆｖだけ速くなるので
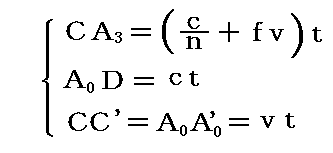
となる。これらの関係式を用いると
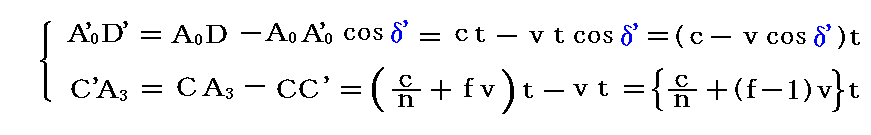
となる。ここで
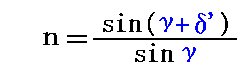
ですから、これを四角形Ｃ’Ａ0’Ｄ’Ａ3に適用すると
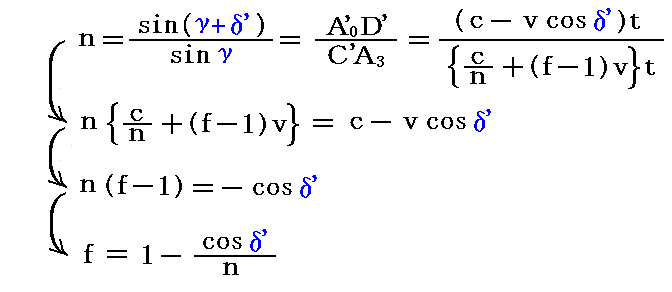
が得られますが、この形の表現では意味がありません。なぜならδ’は屈折率ｎに関係するのはもちろんですがプリズム面の傾斜角γにも依存しますから求めたい答えではありません。実際、図のγ＝21°のプリズムでｎ＝2とするとδ’＝25°となり
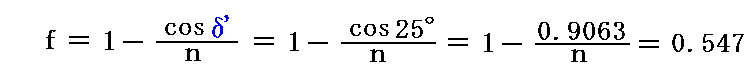
となりますが、これは求めたい
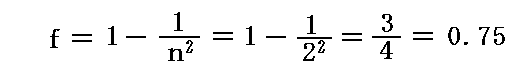
とはまったく違った値となります。
また、（１）の場合、ｖ：ｃ＝0.5：4.22 ですがｃｔ、ｖｔ、ＣＡ3の値を図から求めて
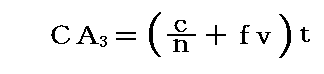
に代入してｆ を求めると ｆ＝0.62 となります。
また、（３）の場合のｖ：ｃ＝0.5：3.75 で、図から同様にして求めてみると ｆ＝0.030 となります。
つまり、ｃ／ｖが大きくなると屈折率ｎが定まっていても同一の随伴係数とはなりません。確かに、（１）～（３）の図から明らかなようにｆの値を調整することで射線の方向δ’が等しくなる様にすることは常に可能ですが、ｖやγが変われば、たとえｎが一定でもｆの値は変化します。だからｃ／ｖが大きくなるとｆ＝一定とした
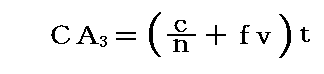
は成り立たなくなるのだと思います。
そのため解決すべき問題は、“（ｃ／ｖ）＜＜１の場合に、ｖやγが変化しても、常にδ’が一定となるような（屈折率のみの関数）ｆがあるか？”ということです。
（ｖ／ｃ）＜＜1の場合、上図の状況を満足する随伴係数は ｆ＝1－1／ｎ2 となることを導きます。
最初に、文献５．でWhittakerが証明しているものを紹介します。ただし解りやすくするために少し変更しています。前節図の（１）と（２）の状態を比較しながら説明しますが、Whittakerの証明は３．（１）［補足説明］の（Ｂ）の立場のようです。
ここでのδは前節の図中のδとは取り方を変えていますので注意して下さい。このようにしてもδ’－δが光行差の角度になる事情は同じです。証明の鍵は、光行差角（δ’－δ）が光行差の関係式δ’－δ＝（ｖ／ｃ）sinδを満足することです。
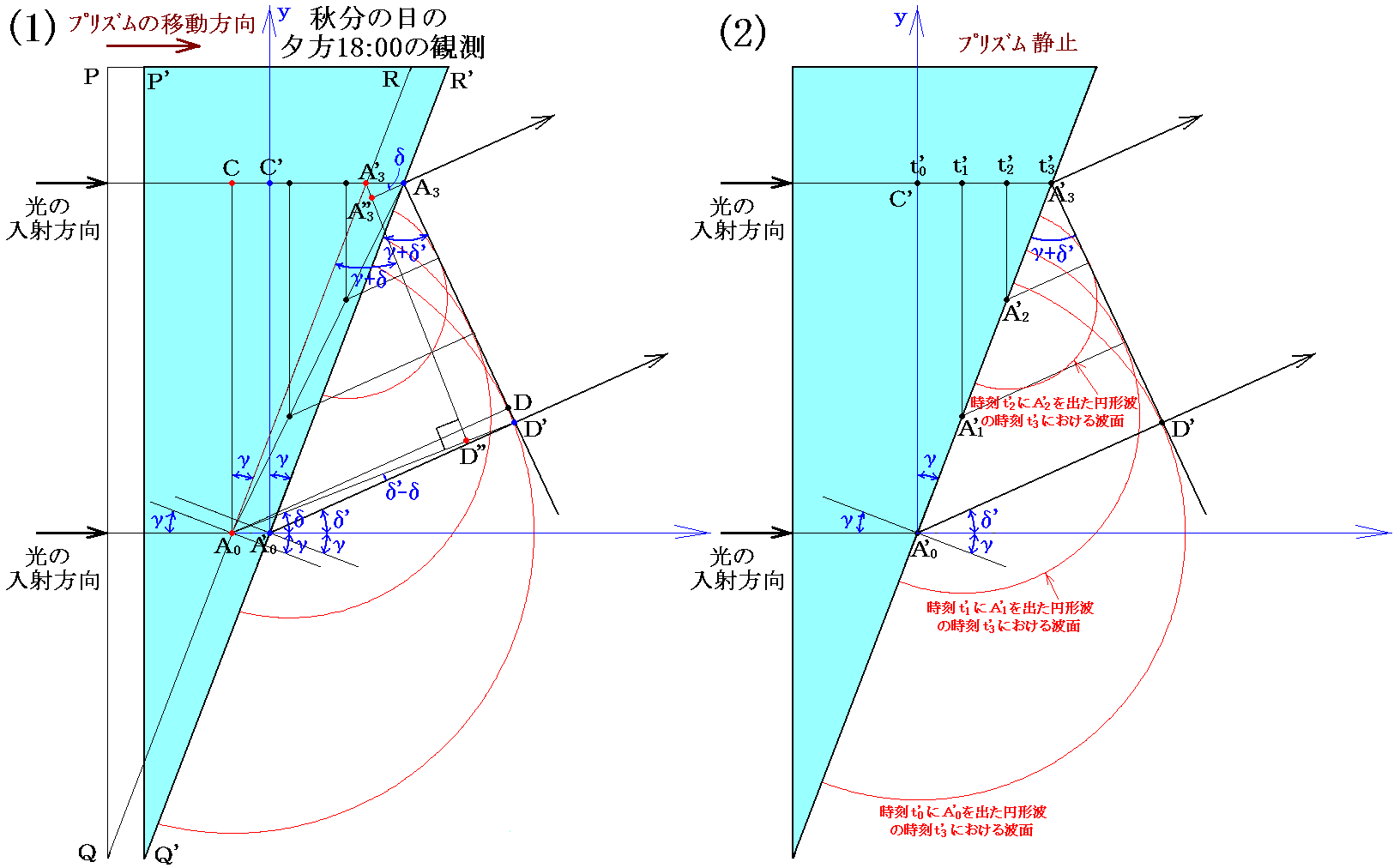
３．（２）で述べたように
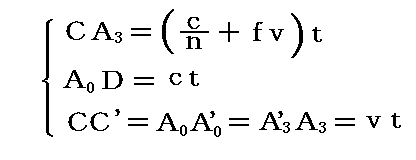
だから、これらの関係式を用いると
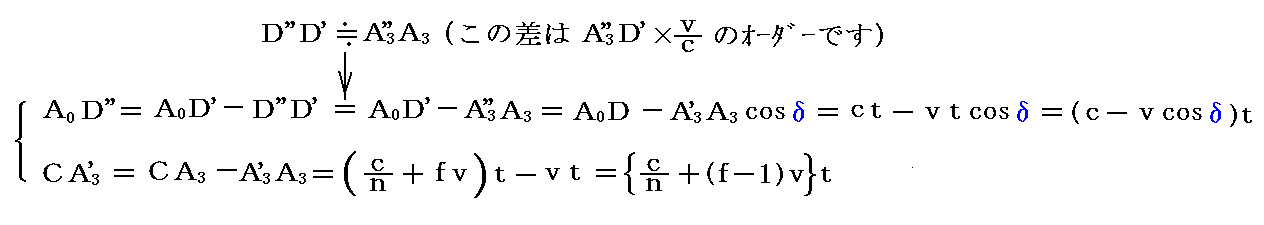
が得られる。
これを四角形ＣＡ0Ｄ”Ａ3’に適用すると
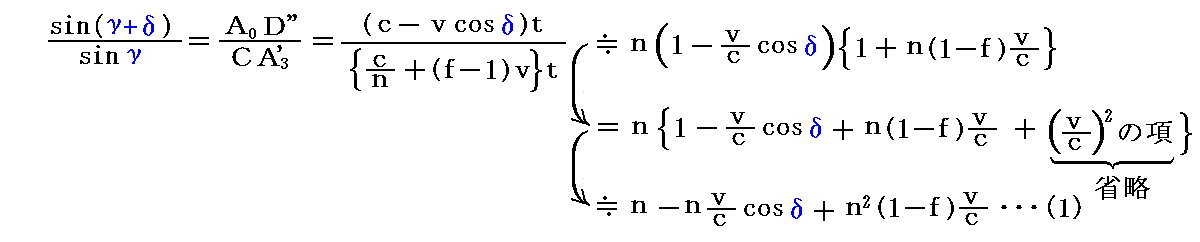
が得られます。
一方四角形Ｃ’Ａ0’Ｄ’Ａ3からはプリズムの移動速度ｖ＝0の時のスネルの法則
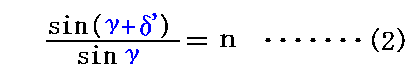
が得られます。
このときδ’＞δですから
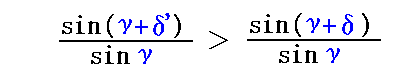
となります。
だから
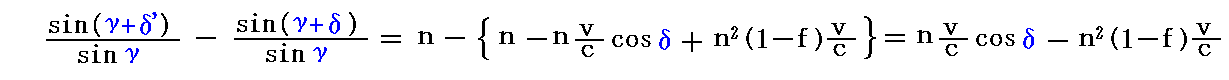
が、その差分を表しています。
この両辺を変形して行きましょう。
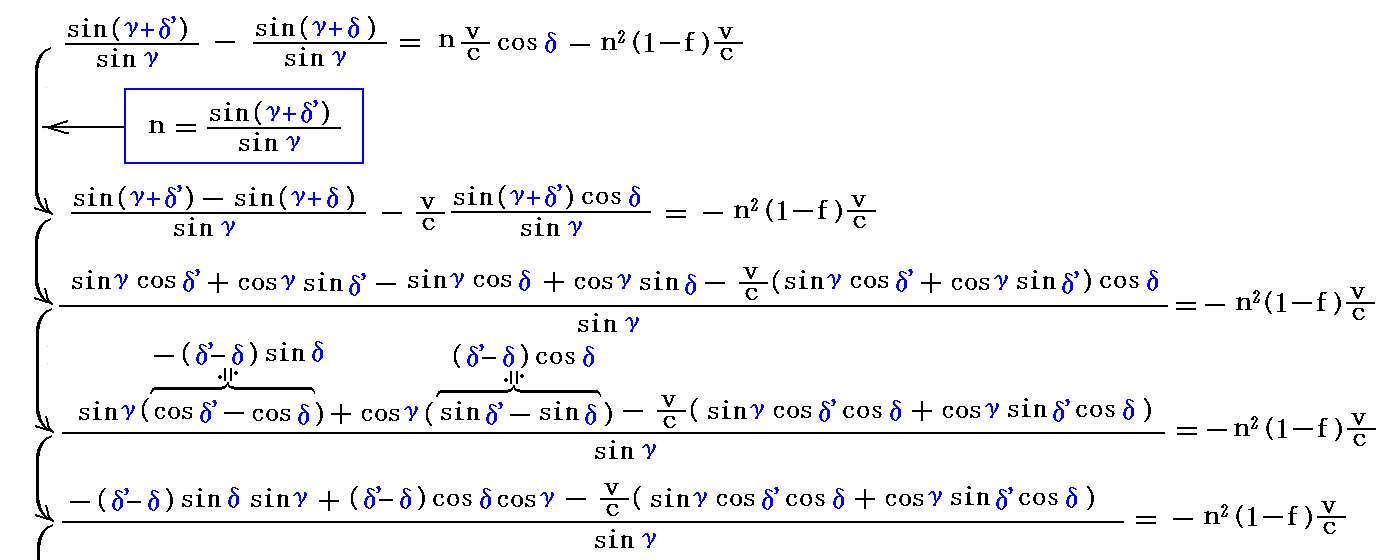
となり、フレネルの随伴係数の表現形が得られる。
ここでフレネルの論文にある証明を紹介します。私自身フレネルの式展開の意味が今ひとつ理解できないのですが、フレネルは３．（１）［補足説明］の（Ａ）の立場で証明しているようです。
フレネルはＡ０’Ｄ’の方向をプリズムが絶対静止空間に静止している時の屈折波の射線の方向とすると、プリズムが運動している場合の屈折波の射線の方向はＡ0’Ｄの方向であり、しかも両直線が成す角（δ’－δ）が望遠鏡がプリズムと同じ速度ｖで動いていることによる光行差に一致しなければならないとした。そうすればプリズムと望遠鏡が静止していようと、運動していようと星の見える方向は同じになると言うものです。
フレネル論文中の記号（下図の黒字）はこの稿の記号（下図の赤字）と下記のように対応します。
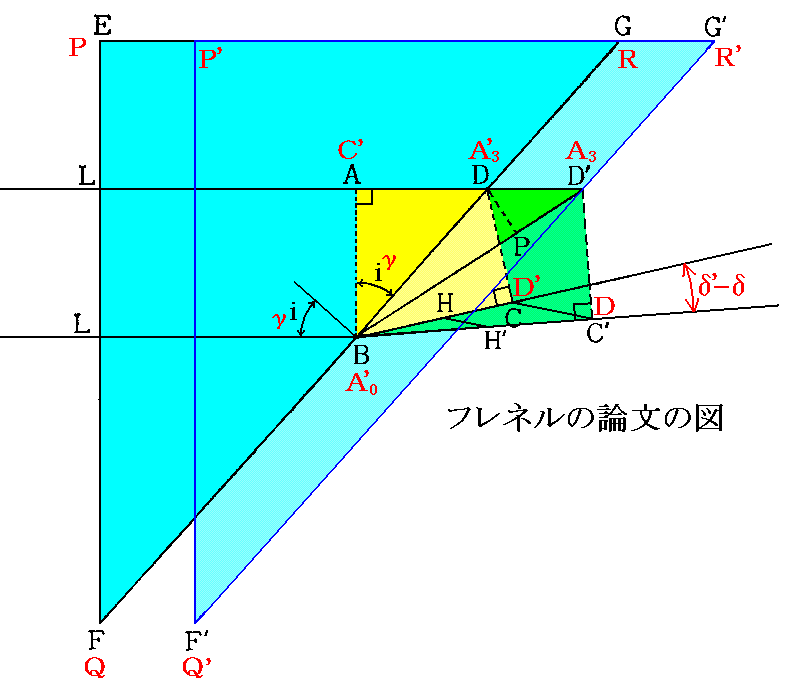
文献２．の段落14でフレネルが、“対象物を観測する望遠鏡の光軸はＢＨに沿って向けられているので、光線が地球の運動によって引きずられている望遠鏡のクロスワイヤーと同時に、Ｈ’に達するためには方向ＢＨ’をたどらねばなりません。”と述べているのは、まさに∠ＣＢＣ’＝∠ＨＢＨ’が光行差角（δ’－δ）であるということを言っています。
ここは非常に解りにくいところですが、前項のWhitatkerの説明と比較されてみて下さい。その時ホィテッカーは３．（１）［補足説明］の（Ｂ）の立場であり、フレネルは（Ａ）の立場であることに注意して下さい。
フレネルの（Ａ）の立場でも図から
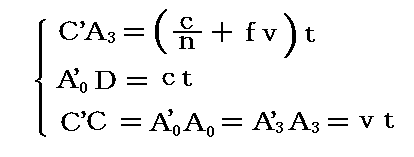
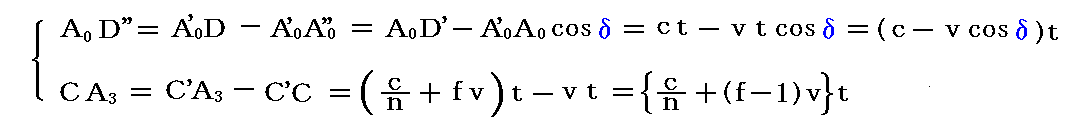
となりますので
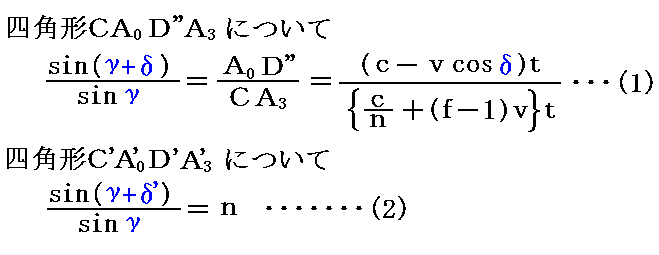
が成り立ちます。この（１）（２）式は前項のWhittaterの場合とまったく同じですので以下の議論もまったく同様に成り立ち、随伴係数ｆ＝1－1／ｎ2が導けます。
［補足説明］
フレネルは文献２．の段落13、14で
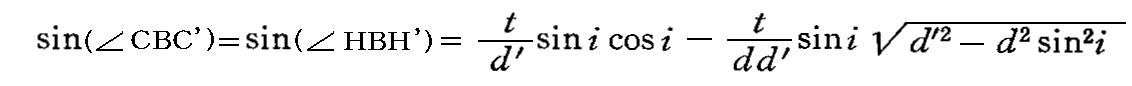
の関係を導いています。彼がこの関係式をどうやって導いたのか良く解らないのですが、この式は（δ’－δ）が光行差角ならば直ちに証明できます。
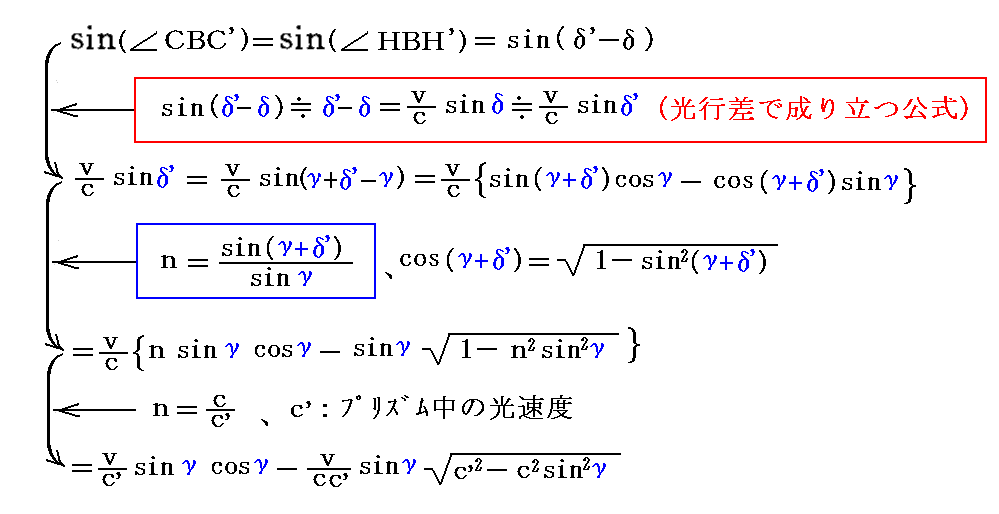
となります。
この稿の記号γ、ｖ、ｃ、ｃ’をフレネルの論文中の記号ｉ、ｕ、ｖ、ｖ’に置き換えると
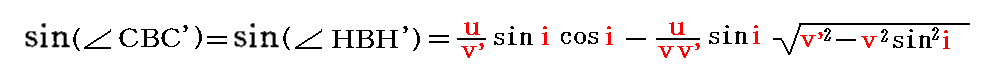
となりますが、このとき光の振動周期をＴとすると
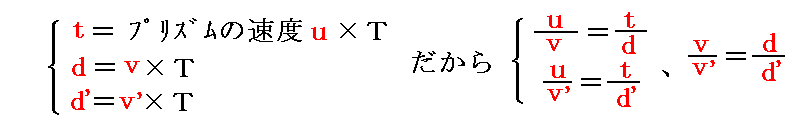
の関係にあるので
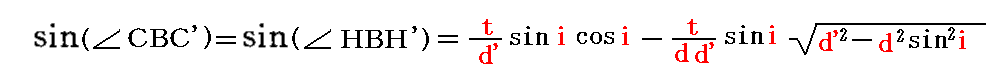
となる。
“アラゴのプリズム実験”の結果が説明できれば、“ボスコピッチが提案した光行差実験”も同じことですから直ちに“望遠鏡を水で満たそうが、満たすまいが光行差の量に変化が無い”ことは直ちに言えます。ボスコピッチの提案した実験が実際に行われるのはかなり後ですが、1818年の時点でそうなることをフレネルは断言しています。1871年にエアリーが行った実験の結果はまさにフレネルが予言した通りでした。
３章の証明と同じですが、Airyが用いた天頂付近の星（竜座のγ星）の光行差観測の状況に即してその様になることを証明します。これはフレネルが文献１．（文献２．）中で説明している内容そのままです。
話を簡単にするために黄道の極付近に有る恒星を観測する。さらに、その恒星を黄道面に沿って公転速度ｖで移動する望遠鏡で見た結果を［真空中で見た場合］、屈折率ｎ（簡単のためにｎ＝2とする）の媒質で望遠鏡を満たして観測して［仮説１］と［仮説３］で説明する場合を考察します。ここでも［仮説２］は光行差の現象をまったく説明できないのではぶきます。
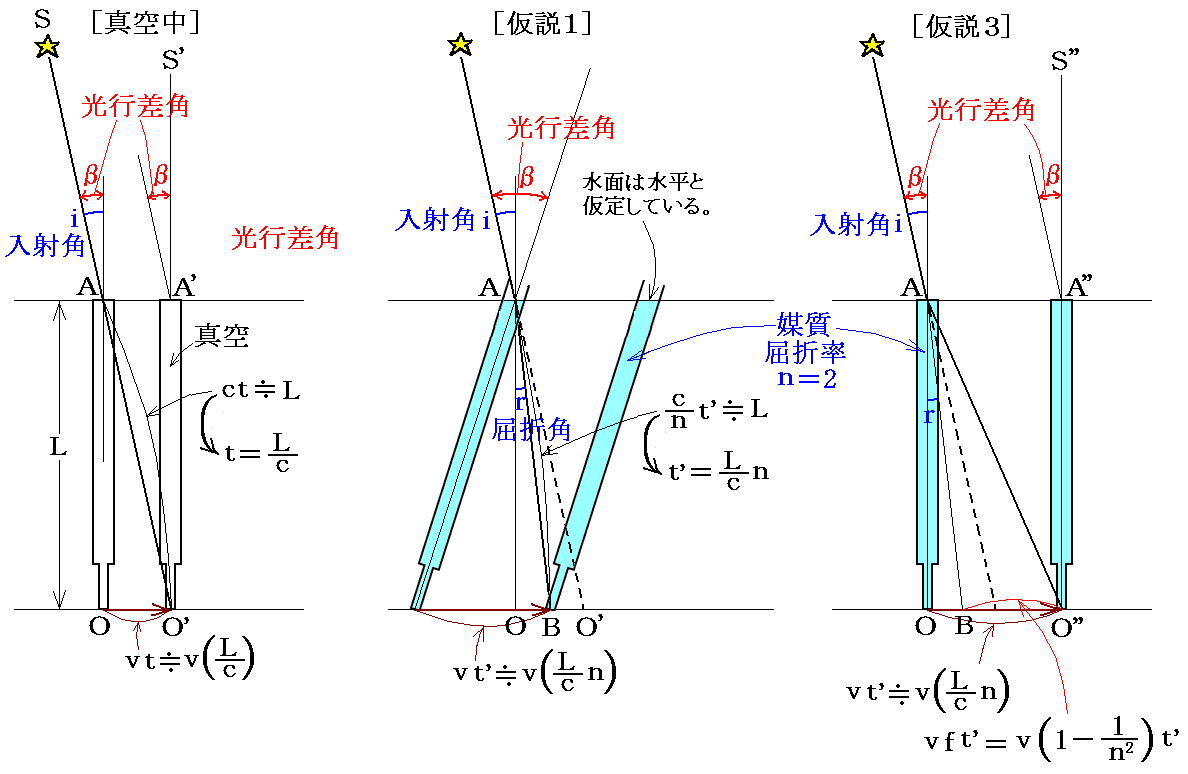
今は、媒質の屈折率をｎ＝2とし入射角 ｉ が微小であると仮定しているので、 ｔ’≒2ｔ となる事を考慮すると、だいたいの様子は上図のようになる。
［仮説１］では、望遠鏡を媒質で満たすと光行差角βは真空中での値の約2倍となります。
一方、［仮説３］のように媒質中を伝播する光が随伴係数（1－1／ｎ2）に従って望遠鏡（媒質）の運動方向に引きずられるとすると光行差角βは変化しないことが解る。つまり、光行差角は望遠鏡を媒質で満たそうが、満たすまいが同じになる。
前節の考察をもう少し厳密にする。
いま、恒星Ｓを、ＯＯ’の方向に地球の公転速度ｖで移動する、望遠鏡で見るとする。下図中の記号は前節の図に対応するようにしてある。ただし、より一般的に論じるために、望遠鏡には水が一杯みたされており、その水面は望遠鏡の筒軸に垂直であるとし、観測する星も黄道の極から外れていても良いとする。［文献７．p11～13］
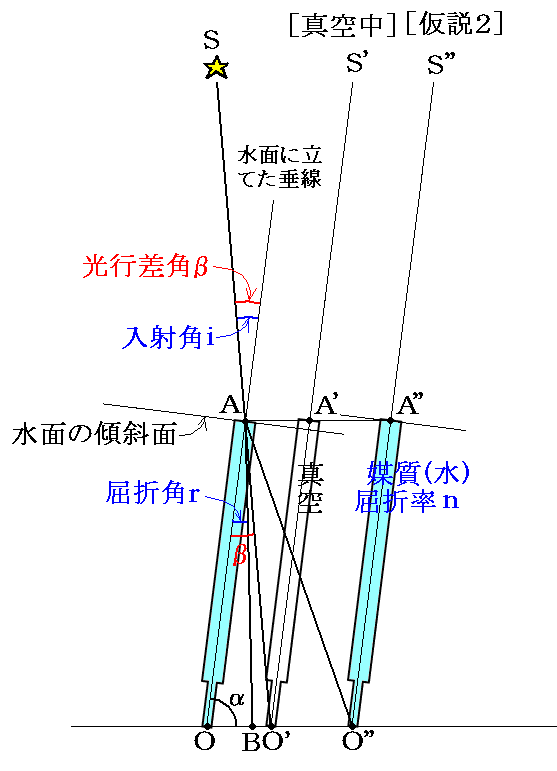
今、望遠鏡の傾きをαとし、望遠鏡に水を入れないときの光行差をβとする。望遠鏡に水を入れない場合には、点Ａで望遠鏡に入った光が点Ｏ’に達するまでに望遠鏡はＯＡの位置からＯ’Ａ’の位置まで動き、したがって光はＯ’Ｓ’の方向に見える。このとき１．（１）１．で説明したように、三角形ＡＯＯ’に正弦定理を適用して変形すれば、真空中での光行差の関係式
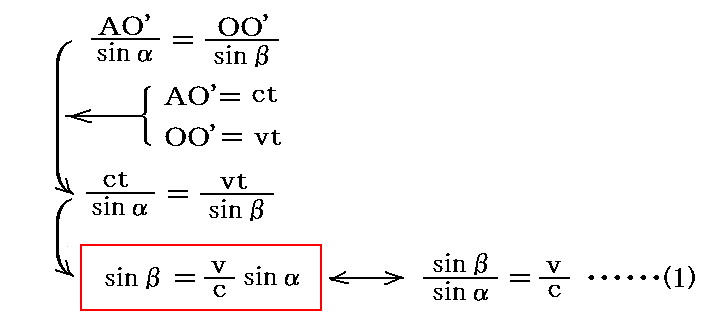
が得られる。
望遠鏡を水で満たすと、［仮説１］が正しい場合には点Ａで望遠鏡に入る光は、屈折角ｒで屈折して図のＡＢの方向に進むはずです。そのとき、光がＡＢを伝わるのに要する時間は真空中のＡＯ’を伝わる時間よりも約ｎ倍ほど長くなるので、前節で見たように［仮説１］の立場では望遠鏡をより寝かさないと星は見えなくなる。ところがAiryの実験結果は望遠鏡を水で満たしても光行差角βは変わらなかった。
ここでは同じ光行差角βとなるためには［仮説２］のフレネルの随伴係数ｆがどのような関係を満たさなければいけないかを求めてみる。
フレネルの随伴説によると光がＡＢを伝わる時間ｔ’の間に光はＯＯ”の方向に距離ＢＯ”＝ｆｖｔ’だけ引きずられる。そのとき望遠鏡は距離ＯＯ”＝ｖｔ’だけ動く。そのため距離ＯＢについて
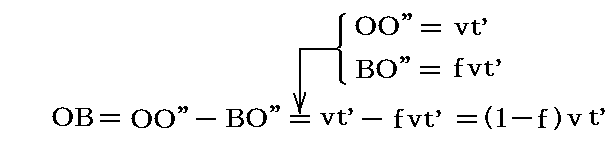
の関係が成り立つ。
このとき、△ＡＯＢに対して正弦定理を適用すると
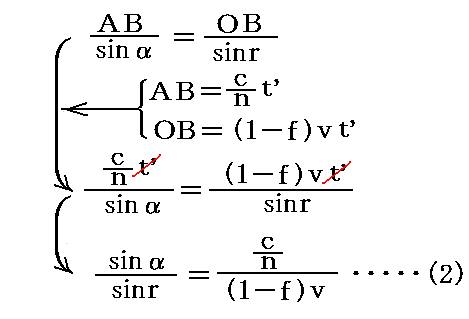
が得られる。
また、水の屈折率ｎは
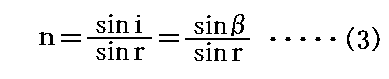
で与えられる。
上で求めた(1)(2)(3)より直ちに
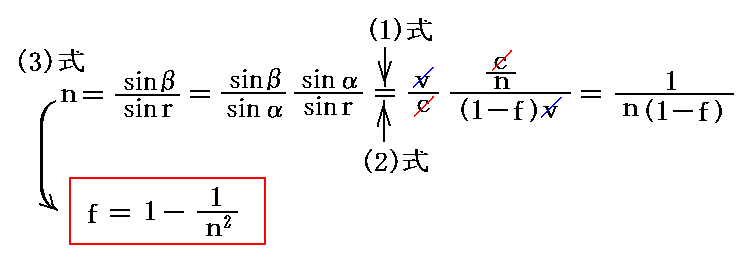
が得られる。
フレネルの論文(文献２．)では、逆に随伴係数の形
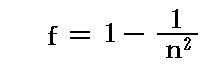
を仮定してから、Airyの観測結果を説明しています。
この稿のｖ／ｃがフレネル論文中のｔ／ｄに相当します。ただし、このｔとｄの定義はアラゴの実験の説明のときの定義と違いますので注意して下さい。フレネルの論文中ではｎ＝ｄ／ｄ’ですから、上記の式は
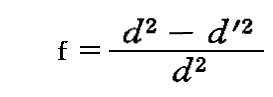
となります。
また、フレネル論文中の図の記号(黒字)はこの稿の記号(赤字)と下図の様に対応します。フレネルの図では、線分Ａ’ｇ（ＡＯ”）があたかも線分ＭＡ’（ＳＡ）の延長線のように見えますが、そうではありませんので注意して下さい。
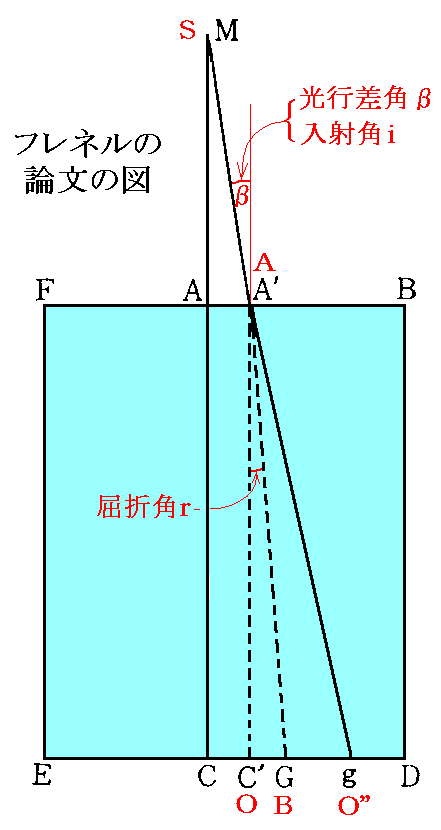
記号の対応関係に注意されてフレネルの論文を読まれると、この稿で説明した内容とまったく同じであることが解ります。
フレネルの文献２．の段落19の内容を上図を利用して説明します。ただし、この稿の記号で置き換えています。
まず、角度βは真空中での光行差の角度だから
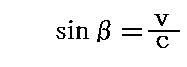
が成り立ちます。
また、屈折に関するスネルの法則より
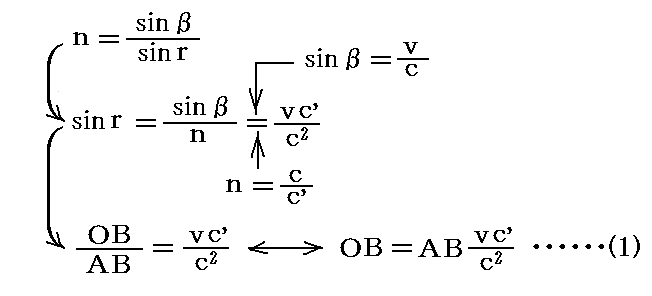
が言えます。
また、フレネルの随伴係数の仮説より
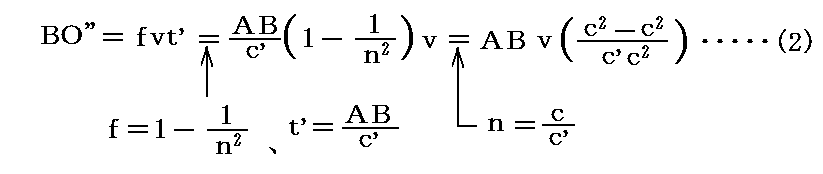
が成り立ちます。
上で求めた(1)(2)より直ちに
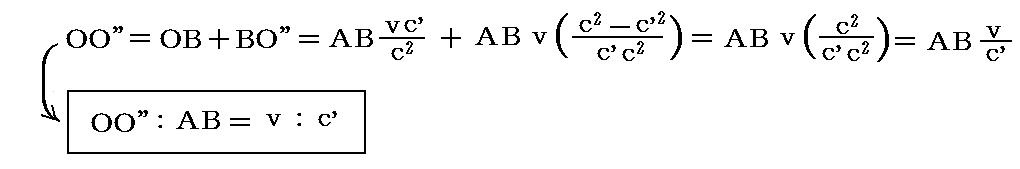
が得られる。その結果、点Ｓの星の像は望遠鏡の接眼部のクロスワイヤーと同時にＯ”に達するでしょう。つまり、望遠鏡を水で満たそうと満たすまいと、光行差の角度βは変化しない事になる。
［補足説明］
フレネルは文献２．の段落18で、光の放射説(粒子説)でもAiryの観測が説明できると言っています。確かに図の方向に屈折する場合には旨くいきます。しかし、望遠鏡の進行方向に対して反対に屈折する場合には旨くいきませんから、放射説ではAiryの観測結果を旨く説明できないと思います。
“フレネルの随伴説”を地上の実験で検証したのが1851年に行われたフィゾーの実験（別稿「フィゾーが運動媒質中の光速度（随伴係数）を測定した方法（1851年）」）です。［残念な事にフレネルは1827年に39歳の若さで夭折しますので、フィゾーの実験の結果を知ることはできませんでした。］
後の1886年にマイケルソンとモーリーが、そして1914年にゼーマンが同様な実験をさらに高い精度で行って随伴説の正しいことを確かめています。
ちなみに、水の屈折率はｎ＝1.333ですから、水の場合の随伴係数は
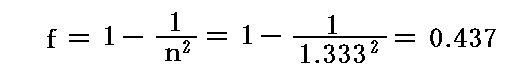
となります。1886年の実験［http://en.wikisource.org/wiki/Influence_of_Motion_of_the_Medium_on_the_Velocity_of_Light］でマイケルソンとモーリーが得た水の随伴係数はｆ＝0.434±0.02でしたからきわめて良い一致が得られたと言えます。
そして、ローレンツは1892年の論文「Maxwellの電磁理論とその運動物体への応用」で、彼が展開する電子論により、静止エーテルを理論の基礎に置いて全ての粒子が並進運動を共有するような系の内部での光の伝播を考察して、フレネルの随伴係数が導き出されることを証明します。この事については別稿で説明予定。
ローレンツはさらに1895年の小冊子で随伴係数の中に光の屈折率が波長に依存するための効果も存在することを導きます。これは、フレネルの随伴説に内在していた屈折率の波長依存性に関する疑問を解決するものです。この部分の簡単な解説は別項の第Ⅴ章§12をご覧下さい。
ちなみに、1914年にゼーマンが行った実験は、ローレンツの波長依存性も含んだより正確な随伴係数を実験的に証明するものでした。［Zeeman, Proc. Amsterdam
Akademie Versel., 17, p445, 1914年, and 18, p398, 1915年］
ローレンツの考察はアインシュタインの特殊相対性理論につながるもので、フレネルの随伴係数は、最終的にアインシュタインの特殊相対性理論によって説明されます。この事については別稿で説明。
結局のところ物体の運動速度ｖと光速度ｃの比（ｖ／ｃ）の一次の項までが効いてくる現象は、全てフレネルの随伴説で旨く説明できます。しかし、やがて（ｖ／ｃ）の二次の項まで考慮した実験を行うとどうしても旨く説明できない事実が出てきます。それが1887年に行われる“マイケルソン・モーリーの実験”です。このことについては別稿で説明。
随伴係数を説明したフレネルの論文は有名ですが、その内容を理解するのはかなり難しい。このページを作るに当たって参考にした文献を挙げておきます。
