マイケルソン・モーリーの実験(1887年)
光を伝える媒質であると仮定されていたエーテルに対する地球の相対運動を検出する目的でなされた実験です。後の“光速不変の原理”と関係する、この有名な実験をできるだけ解りやすく説明します。文献1又は文献2.(日本語訳)を参照されながらお読み下さい。
1.この実験の意義
マイケルソン・モーリーの実験は特殊相対性理論を理解する上で最も基礎になる実験です。それは光の伝播速度が、その光を発した光源の速度に依存するのか?あるいは、音波の伝播速度がそれを伝える媒質(空気)に対して常に一定値であったように、光を伝える媒質(エーテル)が存在して、そのエーテルに対して一定の速度で伝播するのか?という疑問に関係しています。
この疑問には光が有限の速度で伝播することが解って以来の長い歴史がありますが、光が電磁波の一種であるという考え方が確立してからますます重要な問題となりました。
それまでの観察・実験は、絶対静止の空間(その空間に対してエーテルは静止している)に対して、光は一定の速度で伝わる事を仮定するものでした。それは“波動説”によって光行差の現象を説明するためには是非必要な仮定であった。
その時、光の速度が光源の速度に依存するかどうかについての判定は決着がついていなかったが、光がエーテルの波動であるとする“波動説”の立場では当然光源の速度に依存しないことが要請され且つ仮定されていたし、1913年頃になると連星系の観測からそれは確実な事であろうと考えられるようになった。
この当たりの事情を[地球上の光源を用いて光の速度を地上で測定する場合]と、[天文学的な光源を用いて天文学的に測定する場合]に分けて復習してみる。
(1)地球上の光源
光の速度を地上で測定する場合、フィゾーの実験(1849年)やフーコーの実験(1862年)を復習すれば解るように、いずれの場合も光の速度は光源Qを出た光線が離れたところにある鏡Sで反射されて戻ってくるまでの時間を計測することにより行われる。
光は同じ道を往復するので、測定されるのは往復過程全体における平均の速度である。
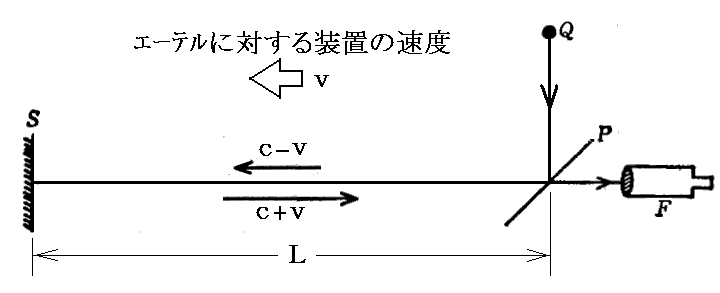
装置が“エーテルに対して静止している場合”の平均速度と、装置が“エーテルに対して速度vで運動している場合”の平均速度を比較してみる。
装置がエーテルに対して静止している場合の平均速度は当然cです。
一方、装置全体がエーテルに対してP→Sの方向に速度vで移動している場合、光が装置の運動方向に沿って往路をLだけ進むのに要する時間はL/(c-v)であり、復路に要する時間はL/(c+v)です。そのため、全所要時間は
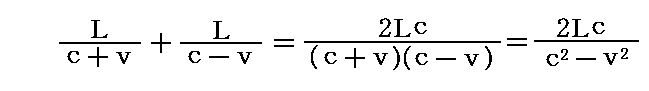
となる。平均速度は2Lをこの時間で割ったものだから
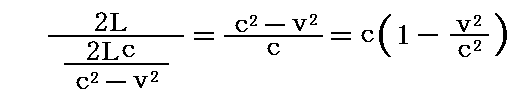
となる。
つまり、装置がエーテルに対して静止している場合と速度vで動いているときの平均速度の違いはc・(v/c)2の微小量となる。vを地球の公転速度3.0×104m/sとしてもc~3.0×108m/sだから(v/c)2~10-8程度となる。地上で行われる通常の実験による光速度の測定値はエーテル理論に従うと常にこれだけの誤差を含んだものであると言うことです。それまでの技術では、地上の実験でその差分を測定するのは不可能でした。
実は相対性理論に依るとその誤差は消滅するのですがそれはまだ後の話です。
だから、随伴係数を確認したフィゾーの実験(1851年)も装置全体はエーテルに対して動いていましたが、その時のエーテルに対する速度の差は無視されています。別稿でも注意しましたが、この実験は光が絶対静止空間(エーテル)に対して速度cで伝播していると仮定した上で、運動している媒質(水)中の光速度の変化(随伴係数)を測定したのです。このとき別稿を復習されると解りますが(v/c)の二次以上の項を省略した上での話しです。
また、別稿で説明したヘックの実験(1868年)も、絶対静止のエーテルに対して光が速度cで伝播するとしたとき、速度vで移動する媒質(水)中の速度が随伴係数に従って変化する事を確認した実験です。そこの議論を復習されると解るように(v/c)の二次以上の項を省略した上での話しでした。つまり、これらの実験結果がエーテル理論で旨く説明できたのもあくまで(v/c)の二次以上の項を省略したからです。
これらの実験では(v/c)の二次以上の効果を測定する精度は有りません。実際のところ“光が絶対静止の空間(エーテル)に対してcで伝播しいている”のか、それともアインシュタインの相対性理論が言うように“地球(測定装置)と共に動く空間に対して速度cで伝播する”のかを判定することはできていないのです。
その時別稿の最後で注意しましたが、ヘックの実験は(v/c)の二次以上の効果を無視する条件でエーテル理論を救うには運動媒質中の光速度は随伴係数に従った速度になれば良いと言うだけですから、見方を変えて(v/c)の一次までの効果では地球に対するエーテルの風は観測できないことを確認する実験だと言ってもヘックの実験結果を旨く説明できます。つまりアインシュタインの相対性理論で解釈すれば、ヘックの観測結果はしごく当然の結果であるわけです。
また、フィゾーが実験的に確かめた随伴係数も、相対性理論に依ってより精密な形で導き出すことができます。これは別稿で説明する予定。
これまでの説明から明らかなように、“可秤量物体”中の光の速度の変化の問題は、相対性理論に少なからず関係しますが、精度が粗いレベルの問題であるためにローレンツの初期段階の近似的な電子論で充分説明できる。すなわち、媒質が速度vで走っていることに起因する現象で、実験的に観測される全ての現象の内(v/c)について1次のものは、エーテルの中に埋もれている電子の運動を考慮することにより、定量的にエーテル理論によって説明できるのです。
しかれども、これらの観測・実験は後に相対性理論で要請される“光速不変の原理”を否定するものでも有りません。つまり(v/c)の二次以上の効果を確かめることができない観察・実験では、絶対静止の空間(エーテル)の存在を明らかにすることも、それを否定する(つまり相対性理論が正しいことを示す)こともできないと言うことです。
[補足説明]
“可秤量物体”という言葉は、エーテルの様にその存在を量的に測定することはできない媒体に対して、水やガラスや空気の様に、質量を持ちその存在を量的に測定できる媒体の事を意味します。
(2)天文学的な光源
天文学的な光源を用いた実験で有名なのはアラゴのプリズム実験(1810年)です。しかし、この実験はあくまで光が絶対静止の空間(エーテル)に対して一定の速度で伝播するとする波動説でこの実験が示す結論を説明できるかという問題で、エーテル理論の中での話しでした。別稿で説明したようにフレネルの随伴説を用いれば光の波動説に基づくエーテル理論で旨く説明できます。
確かに、これは光が絶対静止空間(エーテル)に対して一定の速度で伝播することを仮定しています。しかし、良く考えるとこの実験結果の解釈に於いても(v/c)の二次の項は省略していますので、この実験は地球の運動に対してエーテルの風が有るかどうかを判定してくれる実験ではないことが解ります。前項のヘックの実験と同様に運動する地球に対して一定の速度で光が伝播していると仮定してもこの現象は旨く説明できます。つまりこの実験からも絶対静止の空間の存在を明らかにする事も否定する事もできないのです。
さらに、天文学的な光源を用いた観測として“光行差の現象”がありました。これは光線の方向が観測者(地球)の運動の影響を受けると言うものです。別稿の議論は、波動説に基づく絶対静止空間(エーテル)を仮定した上で説明したものでした。またエアリーの実験(1871年)の結果もエーテル理論に基づいて、フレネルの随伴説を援用すれば旨く説明できます。
光行差の現象は地球の運動速度vに依存して星の見える方向が異なると言うものです。そのため、一見すると光行差の現象を利用すれば星の見える方向の変化から絶対静止空間(エーテル)に対する地球の運動速度vを定めることができそうに思えます。実際、レーナルトは光行差の現象は運動の相対性に矛盾する事実を突きつけると主張(“レーナルトの批判”)しました。【ただし、別稿「Einsteinの特殊相対性理論(1905年)」3.(2)3.[補足説明2]で説明しますように、“レーナルトの批判”は的外れで誤った批判であることが後に判明します。】
ところが今日、地球は太陽のまわりの公転運動のみならず、太陽系の銀河回転運動に伴う速度や、銀河自体の移動に伴う速度ベクトルが重なった運動をしていることが解っています。もちろん、観測する恒星も銀河系内を高速で移動しています。そのため、光行差を観測する1つの星に対して地球は単純な円運動をしているわけではありません。それならば、別稿の説明の様に光行差の観測値が地球の公転運動(つまり問題の恒星と地球の相対的な運動)にのみ関係している様に見えるという方がもっと不思議な事です。
[補足説明1]
光行差の現象はアインシュタインの相対性理論を用いないと旨く説明できません。アインシュタインは1905年の最初の論文の第Ⅱ部で相対性原理から直接光行差の公式をより精密な形で導いています。よく知られている公式は(v/c)が小さい場合にのみ成り立つ近似式です。だから光行差の現象は絶対静止の空間(エーテル)の存在を知る手がかりにはならないのです。
“光行差の現象”を相対性理論に基づいて理解するのは結構難しいのですが、簡単に説明すると
『・・・・・・光行差は地球の空間における絶対運動を示すものではなく、(観測している恒星に対する)年間の運動の相対運動を示すものである。換言すればいろいろな季節における地球の速度の変化によるものである(つまり観測している恒星に対する相対的な回転運動は測定することができる)。・・・・もしも地球の運動方向の変化が無ければ、即ち地球が直線運動をしているならば光行差は観測にかからなかったであろう。・・・・・光行差は相対論による時間単位
t’と t との偏差の直接的な効果である。古典運動学の見地からすると光行差は普遍定数cと調和させることは困難であるが、今日では光行差は光の伝播速度が座標系に依らないことの必然の結果として認められている。・・・・・・』(ゾンマーフェルト著「光学」§10より)
となります。
上記Sommerfeldの説明を理解するのも難しいのですが、このことについ別稿「アインシュタインの特殊相対性理論」3.(2)3.[補足説明2]から[補足説明4]にかけての一連の説明をご覧下さい。
[補足説明2]
また、エアリーの実験(1871年)が示す“望遠鏡の鏡筒を水で満たしても光行差の角度が変化しない”という事実は、相対性理論により以下の様に説明される。
『・・・相対性理論の立場に立ってエアリーの実験を眺めれば、この結論は当然である。いま望遠鏡を恒星の見かけの位置の方向に向ければ、その恒星から発射された光は望遠鏡の方向に平行に鏡筒内に入射してくる。鏡筒を水で満たしていても、光はレンズに垂直(従って水面にも垂直)に入射するのだから、光は鏡筒の内部に水が無かったときと同じ方向に進む。つまりエアリーの実験の観測者(地球)の静止系からながめれば、それは“入射角が0の入射光の屈折角は0である”という周知の事実を表しているにすぎない。・・・』(パウリ著「相対性理論」第Ⅲ編§36より)
パウリの説明は難解ですが、以下の事を言っている。“エーテル理論では、エーテルに対して移動する観測者にとって光線の方向(つまり波のエネルギーが伝播する方向)は波面が伝播する方向(つまり波面に垂直な方向)とは必ずしも一致しないが、相対性理論では、全ての慣性系の観測者にとってエネルギーが移動する方向である光線の方向は波面に垂直となる。” このことに付いても別稿「アインシュタインの特殊相対性理論」3.(2)3.[補足説明5]をご覧下さい。
最後に、天文学的な光源で絶対静止の空間に対する地球(太陽系)の速度を確かめる方法としてマックスウェルが提案した木星の衛星の食現象を用いる方法があります。
これは確かに(v/c)の一次の効果で現れるものですから、もしこの効果による時間差が観測できなければ、以下で説明するマイケルソン・モーリーの実験と同様に、それまでのエーテル理論では解決不可能な難問を突きつける事になります。しかし残念ながら、その当時までの観測精度では、その効果を判定することはできませんでした。
(3)(v/c)の二次の効果
ここで非常に大切な事をもう一度確認しておきます。
前節と前々節の議論を読まれると、そこで行われた観察・実験があたかも、“光が絶対静止空間に静止しているエーテルに対して速度cで伝播することを仮定した上で、フレネルの随伴係数を確かめるために行われた”と勘違いされるかも知れません。
しかし、元々の目的は別稿で述べた[仮説1]、[仮説2]あるいは[仮説3]のどれが正しいかを確かめるためのものでは有りません。
大多数の天文・物理学者は、[仮説1]が正しいと考えていました。それならば、その絶対静止空間(エーテル)に対して動いているであろう地球から見れば、光が示す様々な現象に対して[その動く速度vの関数としての何らかの偏差]が観測されるはすだ。そのvの関数の偏差が観測できれば絶対静止空間(エーテル)に対する地球の動きが解るのだから[絶対的な基準となる一つの座標系を確認することができるであろう]と言うものだったのです。
つまり、“物理現象が起こる様々な慣性系(座標系)が存在するが、その中で唯一つ絶対的な基準となる絶対静止空間(エーテルはそこを満たしている)が存在することが確認できるだろう”と言うものだった。そして“光はその空間に対して一定速度cで伝播する”と考えられていた。
例えば
- ヘックの実験(1868年)では、[仮説1]が正しければ(v/c)の一次の精度において
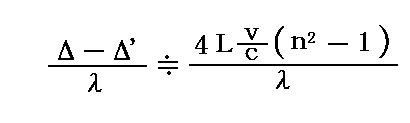
の量の干渉縞の移動が観測されるはずです。
- アラゴのプリズム実験(1810年)では、[仮説1]が正しいとして黄道面上にある星々の観測をすれば、(v/c)の一次の精度において、その星の方向が地球の運動方向からずれるに従ってプリズム有りとプリズム無しの星の見かけ角の違いに変化が生じるはずです。
- エアリーの水望遠鏡による光行差の観測(1871年)では、[仮説1]が正しければ、ボスコピッチが提起したように、(v/c)の一次の精度において、水の屈折率nと地球速度vの関数として光行差の偏角が変化するはずです。
ただし、フィゾーの実験(1851年)やマイケルソン・モーリーの実験(1886年)は、フレネルの随伴係数を確かめることに特化した実験だったので、[仮説1]が正しくても、(v/c)の一次の精度においては、干渉縞の移動は起こりません。
ところが、“全ての観測・実験において、そのような特別な空間(エーテルが占める絶対静止空間)が存在することを示す様な偏差は、(v/c)の一次の精度に於いて、まったく観測できなかった”のです。
結局の所“可秤量物体”の速度をvとしたとき、(v/c)の一次の効果を調べることで、絶対静止の空間(エーテル)が存在するのか、それともそれは単なる仮想的なものなのかを判定することはできなかったのです。
[ローレンツは彼の著書『電子論』の§146~§154で、ホイヘンスの原理(フェルマーの原理)に基づくこれらの現象の説明に於いて、v/cについて1次までの効果に関する限り、エーテル理論と相対性理論が一致することを証明しています。メラー著『相対性理論』§6と§10には同じことがさらに解りやすく説明されています。]
これは極めて不思議な事でした。その時、(v/c)の二次以上の精度を問わなければ、“フレネルの随伴説”を採用すれば絶対静止の空間に存在するエーテル説(ただし絶対静止空間は確認できないのだから単なる仮説でしか有りません)で全ての現象を説明することができます。しかし、これはもっと革命的な解釈が有ることを否定するものではありません。
すなわち、“絶対静止の空間を認識できないのならあらゆる慣性系に対して光速は一定である”という解釈も成り立つと言うアインシュタインの相対性理論です。実際のところ“光速不変の原理”に基礎を置くこの理論でも全てが旨く説明できます。そのとき、時間の同時性の概念や長さの絶対性の概念に変革を迫られますが、より高い精度で、光行差の公式、随伴係数の公式、ドップラー効果の公式、等々・・・が全て導けます。そして、それまでに得られていた公式は(v/c)が小さい場合に成り立つ近似的な式でしかないということが明らかになります。
良く考えてみれば、絶対静止の空間を光が一定速度で伝播するということも非常に不思議なことですが、いずれにしても絶対静止の空間(エーテル)の存在を判定するには、どうしても最初に述べた(v/c)の二次の効果を検証することが必要です。それを実行したのが、1881年のマイケルソンの実験と1887年のマイケルソン・モーリーの実験です。
これらの実験の詳細についてはR. S. Shanklandが解りやすく解説していますので引用しておきます。以下の説明の準備として御覧下さい。また歴史的な詳細は文献5.6.が詳しい。
2.実験装置
(1)1881年のマイケルソンの実験装置
マイケルソンはベルリン大学のヘルムホルツのもとに留学しているときに最初の試みをしています。装置の原理は1887年の装置と同じで下記の様なものでした。bdあるいはbcの腕(真鍮製)の長さは約1.2mです。
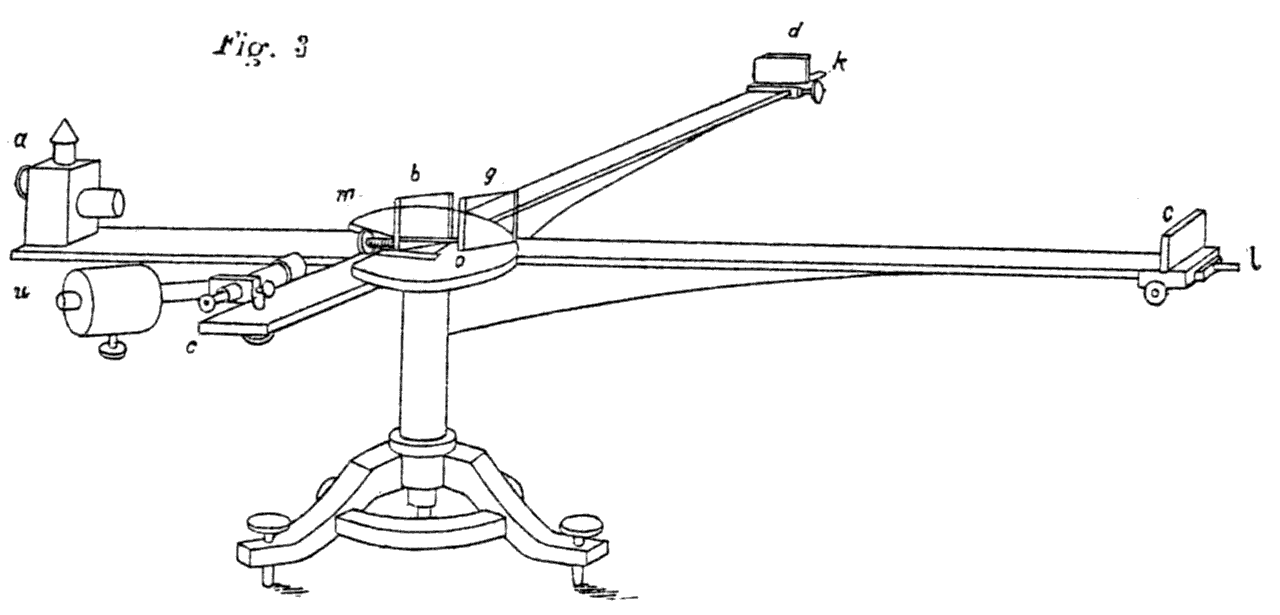
ヘルムホルツの実験室の硬い石の台の上に取り付けられたにもかかわらず、ベルリンの交通による振動が昼といわず夜といわず観測の邪魔をした。また、装置の機械的な緊張やたわみも干渉縞を不安定にした。干渉縞の移動量はエーテルの動きから予想されるより大きくなったりすることもしばしばであった。
そのためマイケルソンは4月に装置を分解してポツダムの天文台に移設して観測することにした。人里離れたこの場所でも、一ブロック先の家の床を人が歩くときのかすかな振動が観測に影響した。それほど微妙な実験だった。
もし静止エーテルの[仮説1]が正しいのなら、この装置を90度回したときの干渉縞の移動量は縞の幅の0.04培になるはずでした。安定した測定をすることは極めて難しかったのですが、得られた結果はそのような干渉縞の移動は観測されないと言うものでした(実際のところ干渉縞の変動は縞の幅の0.02培程度あった)。
装置の精度に疑問があったが、マイケルソンはこの結果を、“地球とエーテルの相対運動”, Am. J. Sci., Series 3, Vol.
22, p120~129, 1881年として発表します。しかし、観測精度に疑問が有るために、この否定的な結果は決定的なものとは見なされなかった。
(2)1887年のマイケルソン・モーリーの実験装置
下図はマイケルソンとモーリーが1887年に用いた装置です。文献1.や文献2.(日本語訳)を参照されながらお読み下さい。

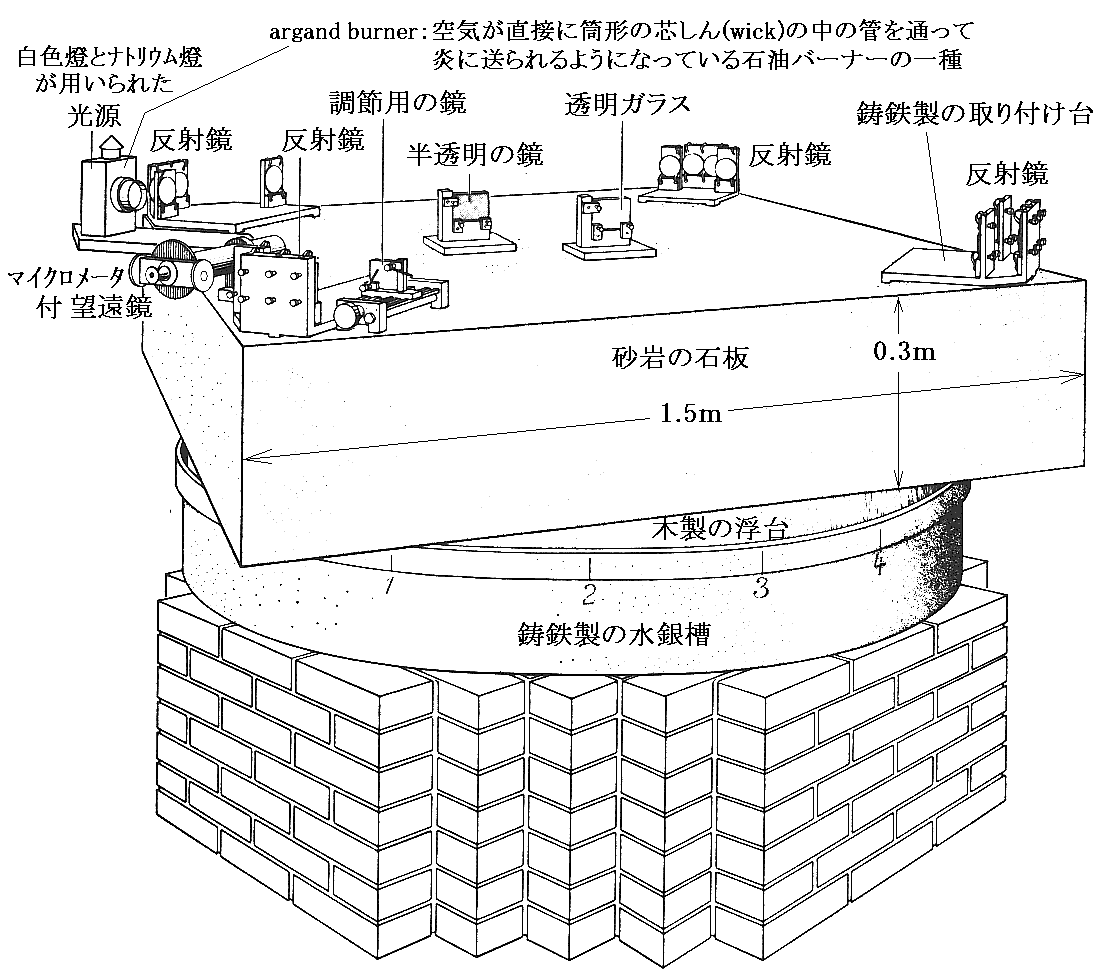
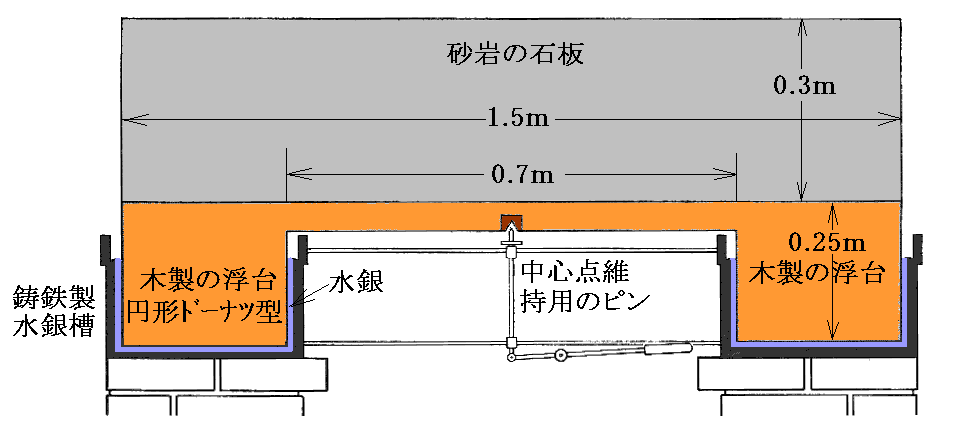
この装置には、精度を高めるための様々な工夫がなされている。
- 干渉計は真鍮棒ではなくて、厚さ30cm、1.5m四方の砂岩の石板の上に設置された。石板は硬く強固なために光路にゆがみやたわみが生じない回転が可能になった。
- 石板は摩擦のない水銀槽に浮かべた木製の円形浮台の上に設置されたので、振動の無い極めて滑らかな回転が可能になった。
- 石板は重く慣性モーメントが大きいので一度回転させると何時までもその回転を保持できた。1回転に6分程度かける極めてゆっくりとした回転も可能で、装置を回転させながら観測することができた。
- 反射鏡で反射を繰り返すことにより、光路長を1881年の装置の約10倍(11m)に増加させた。このことによりエーテル理論から予想される干渉縞の移動量は縞の間隔の0.4培程度に増加した。
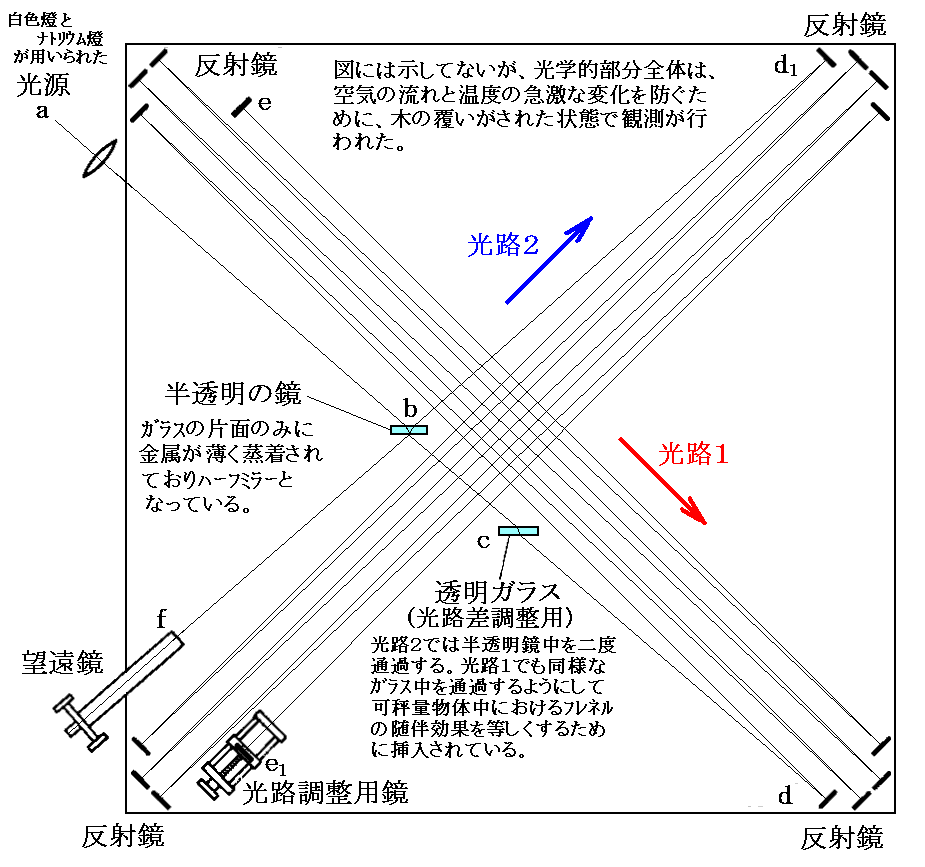
3.測定理論
(1)光が到着する時間差
1.最初の時間差
反射を繰り返したトータルとしての光路長を、光路1についてはac=L1、光路2についてはab=L2とする。acとabを厳密に等しくすることは難しいので、取りあえず異なる値にしていますが、最終的な結論では両者の微小な違いは効いてこなくなります。1887年の装置ではL1あるいはL2は約11mでした。
絶対静止の空間が存在して、それの中に静止しているエーテルに対して光りが一定の速度c=3.0×108m/sで伝わるとする。エーテルの中を移動しながら光の速さを測れば、光を走らせる方向によりその値が異なるはずです。最初の状況に置いて装置全体はエーテルに対して下図の様に動いていると仮定する。
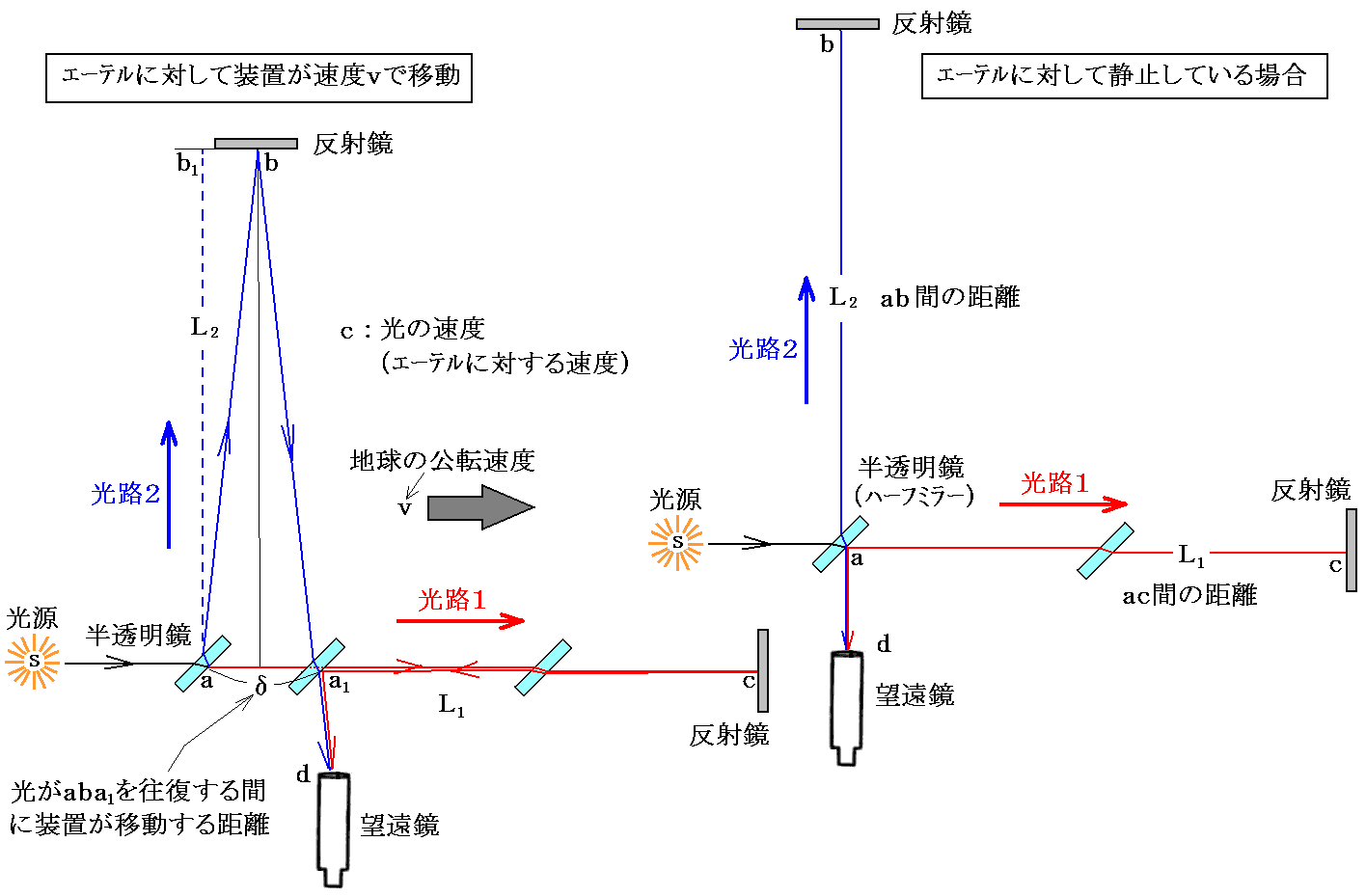
今光がaからcまで進むときには装置に対して光はc-vの速度で進むことになる。またcからa1まで進むときには装置に対する光の速度はc+vとなる。そのため光がaca1を往復する時間t1は
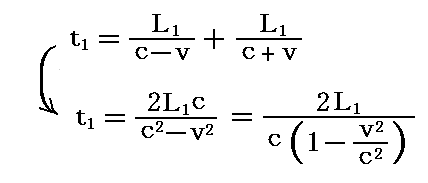
となる。
一方光がbの鏡で反射されてaba1を進む場合の時間をt2とすると、t2は以下のように計算できる。まず距離aba1はピタゴラスの定理を用いると
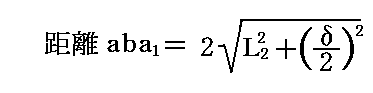
となる。この距離を速度cで光は走るので、光がaba1を伝わる時間t2は
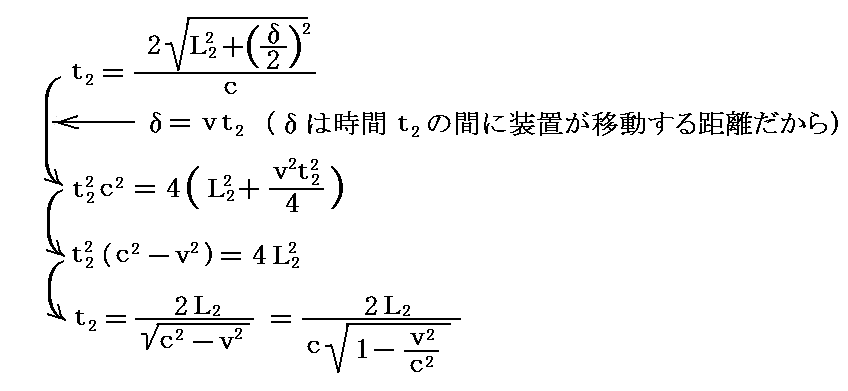
となる。
そのためa→c→a1と進む光とa→b→a1と進む光がa1に到着したときの時間差Δtは
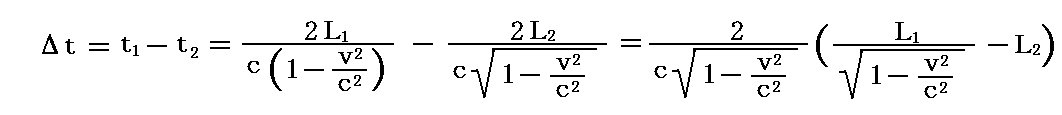
となる。
2.装置全体を90°回転したときの時間差
次に装置全体を反時計回りに90度回転させると、それぞれの光路は下図のようになる。
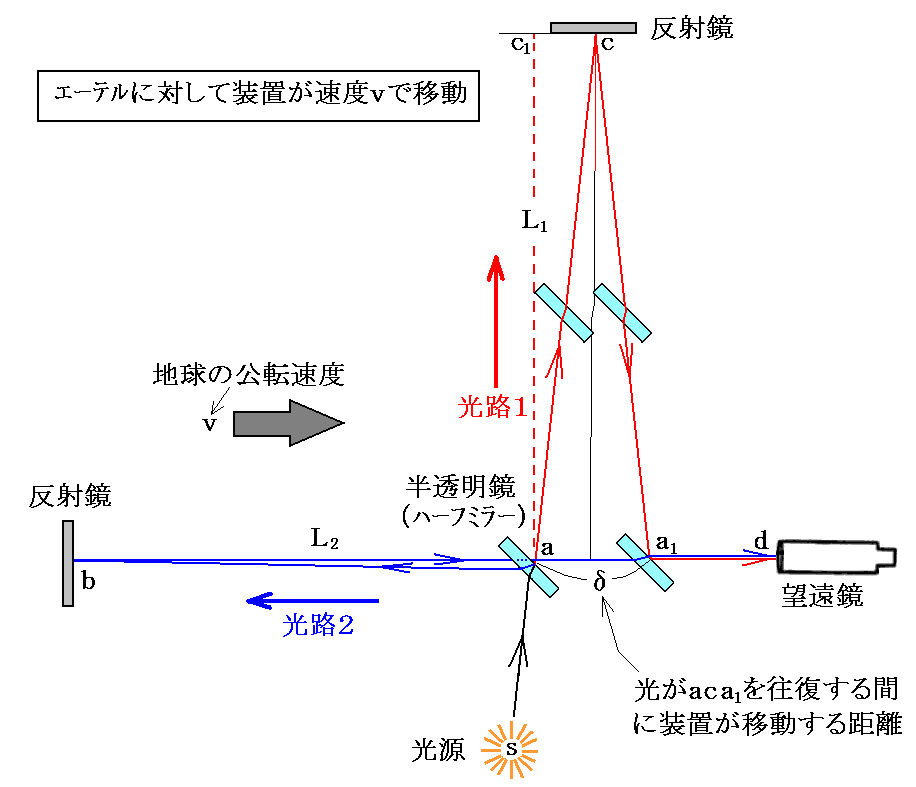
この状況で光がaca1を往復する時間をt1’とすると、前記のa→b→a1の光路で行ったのと同様な手順に従って
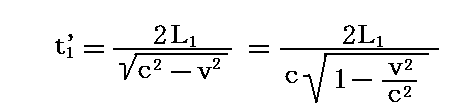
が得られる。
また光がaba1を往復する時間をt2’とすると、前記のa→c→a1の光路で行ったのと同様な手順に従って
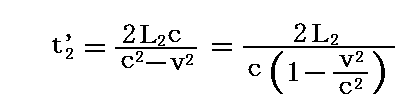
が得られる。
そのためa→c→a1と進む光とa→b→a1と進む光がa1に到着したときの時間差Δt’は
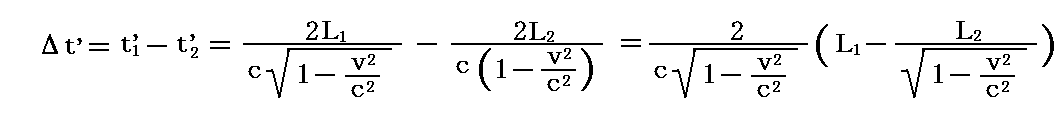
となる。
3.回転に伴う時間差の変動
ここで、以下の事に注意すべきである。
v2/c2は10-8程度の値と予想されるから
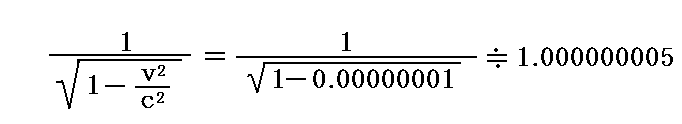
となる。このときL1とL2の距離の差をL1≒L2で割った値が0.000000005以下になるような精度でL1とL2の長さを一致させることは不可能です。そのためΔt、とΔt’のどちらが正でどちらが負になるかは予測できない。さらにその絶対値の大小がどうなるかも解らない。
しかし、装置全体を90°回転することによって光路1と光路2で生じる時間差が変動するが、その変動量Δt’-Δtは
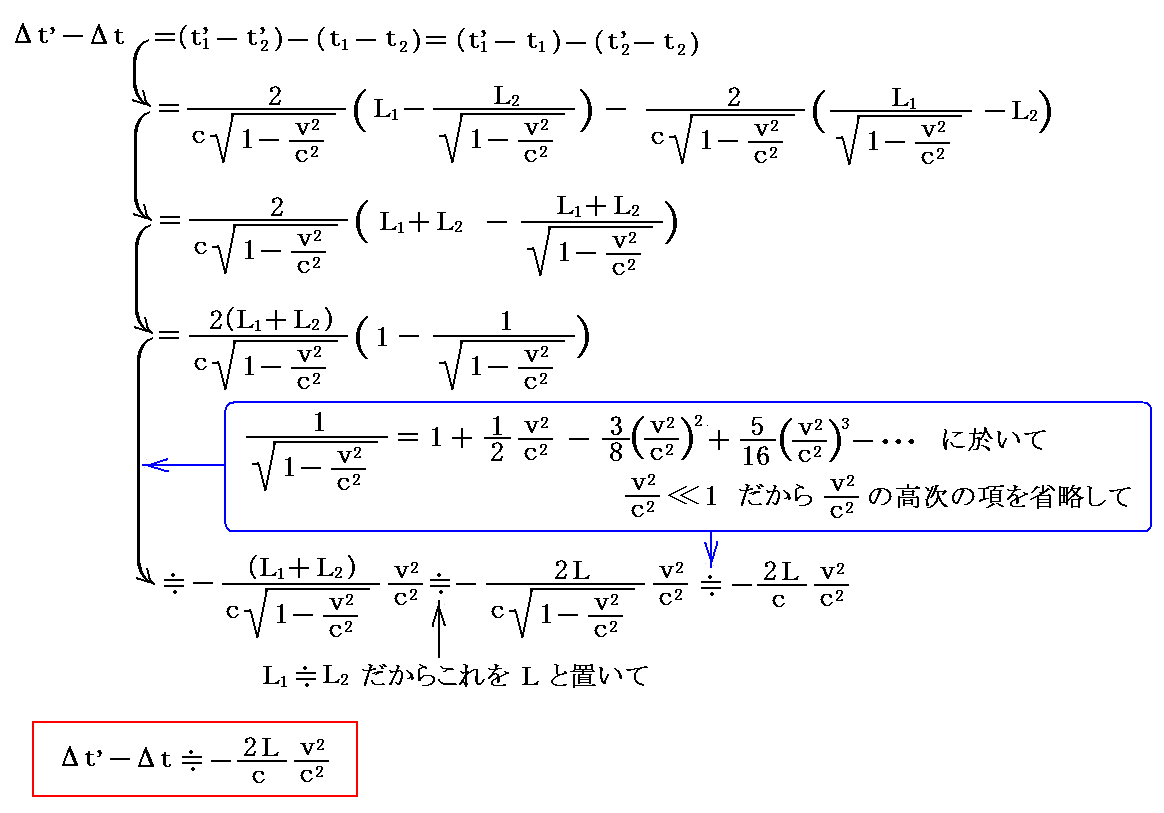
で表され、結局L1とL2の距離の微小な違いには依存しなくなる。
つまり、この時間差の変動量はL1とL2の長さが厳密に等しいLであるとしたときに得られる変動量の最大幅と同じである。
このとき、装置をさらに90°反時計回りに回転させて、最初の位置からトータル180°回転させると再び時間差はΔtに戻る。そしてさらに90°反時計回りに回転させて、最初の位置からトータル270°回転させると時間差はΔt’となる。これらを考慮すると、回転角θを変数としたΔtのグラフは、(Δt’-Δt)の絶対値の半分|Δt’-Δt|/2を振幅とした周期が180°の余弦関数の様なグラフとなる。
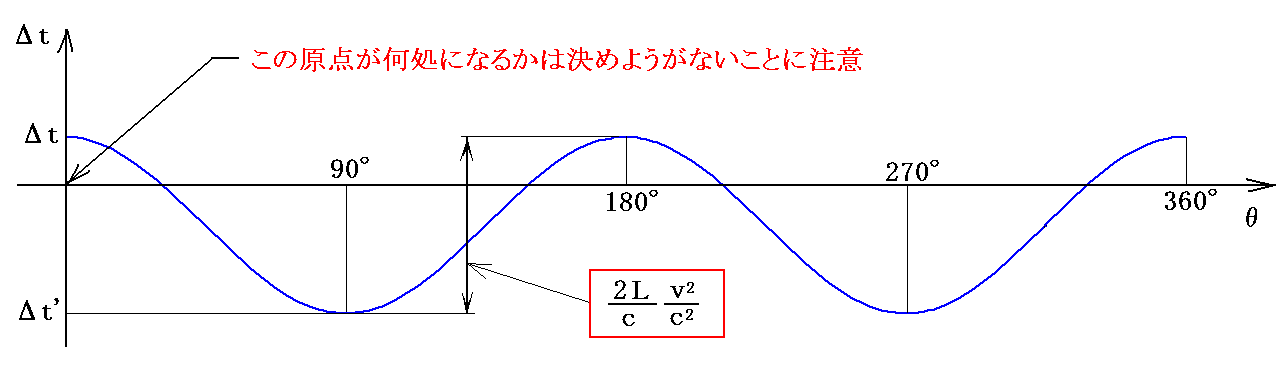
文献1.のグラフ中の理論曲線(点線)は、このグラフの横軸を変動幅の中央に移動して、その1周期分(180°幅)を取り出したものです。凸凹については実験値の変動にできるだけ合うようにしてある。
(2)干渉縞
光路1と光路2を走った光が望遠鏡の位置で完全な平行光線で入射することは無い。そのため望遠鏡の焦点の位置に、光路1から入射する光と光路2から入射する光が互いに干渉して“干渉縞”が見える。
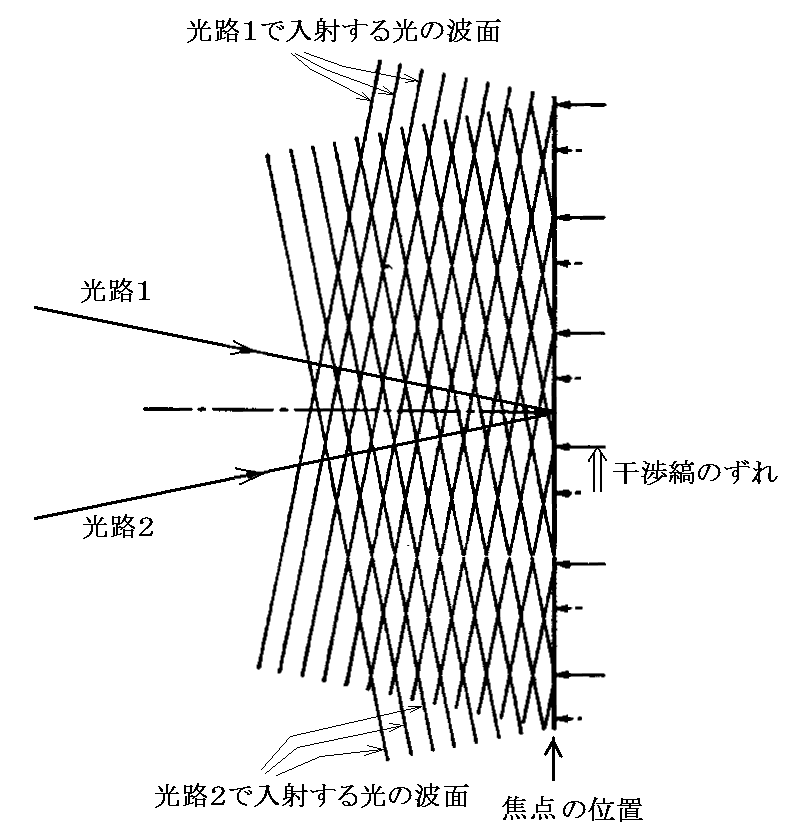
下図は実際にマイケルソン・モーリーの装置の望遠鏡視野内に現れた干渉縞の写真です。

(3)装置の回転に伴う干渉縞の移動量の最大値
前節で述べた時間差の変化のために、装置全体の回転と共に、望遠鏡中に見える干渉縞は変化するはずです。[光路1と光路2によって望遠鏡のところに到達する光の時間差の90°回転に伴う変動量]を、観測する光の[到達位置の差の変動量]で表すと
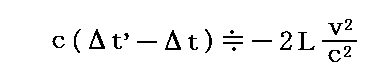
となる。これが文献1.の中でマイケルソンが求めている式 2Dv2/V2 に相当します。(マイケルソンはL→D、c→Vと置いている。)
この光路長の差分を、光の波長λを単位として表す。用いた可視光の波長は5.5×10-7m程度だから

となる。
つまり絶対静止のエーテル仮説が正しければ、a1の位置における光の到達位置の差の変動量が最大で、波長の0.4倍程度になるはずである。そのため、装置全体を最初の位置から90°回転させると、望遠鏡の視野における干渉縞は“縞の間隔”の0.4培程度移動するはずである。
4.観測結果
マイケルソンとモーリーは最初1年間にわたって毎月観測を行い、宇宙空間中の地球の公転方向変化が全て含まれる様にした。こうすれば宇宙空間を動く太陽系の速度がもしも観測に影響したとしても、それによる影響が検出できるからです。[ここは文献4でShanklandが言っていることで、本実験の前にマイケルソンとモーリーが本当に1年を通して同様な予備実験を繰り返していたのか良く解りません。]
彼らの論文に報告されているのは、1887年の7月8、9、11日の正午頃と7月8、9、12日の午後6時頃に行われたものです。6時間へだてた実験を行ったのは、彼らの装置に対して地球公転の影響が最も現れる場合と、そうでない場合を比較するためです。
観測は干渉計を回転させながら、干渉縞のズレを全方位で観測した。測定は1周を16等分した角度を通過するごとに行われた。下表一行目の数字は測定時に通過中の位置番号(水銀槽の側面に書かれている番号)に対応する。
各実験における装置の回転方向は、正午の観測では反時計回り、午後6時の観測では時計回りであった。
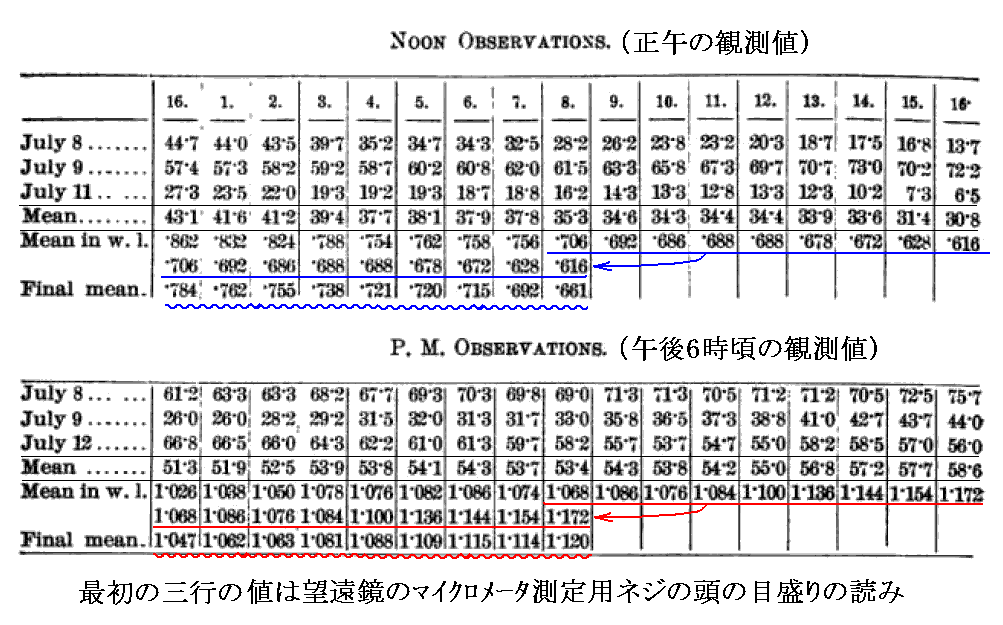
ネジの頭の目盛りで、干渉縞の幅(間隔)は40~60目盛りであり、平均値は50目盛りであった(干渉縞の幅が測定毎に変動するほどこの実験は微妙なものだった)。そのため、ネジの1目盛りは波長の0.02培に相当する光学的距離の変動を意味する事になる。
表中の最初の3行の数値はネジの目盛りの読み取り値そのままです。5行目のMean in w. 1. の値は、その上の4行目の平均値Meanの数値を0.02倍して、波長を単位とした光学的距離の変動量に換算してある。
表のデータの平均を取った最終的な青波線部データと赤波線部データをそのままグラフにすると

のようになる。
いずれの場合も、装置全体の回転と共にだらだらとした干渉縞の遷移が存在する。
遷移の原因としては、最初に光学系の配置の特性が考えられる。例えば装置の中の半透明鏡と透明ガラスに光が入射する角度は装置全体の回転と共に変わってきます。また光源から半透明鏡へ入射する光線の位置も半透明鏡上でずれてきます。そのため最終的に望遠鏡へ入射する位置もレンズ上で左右にずれてきます。だからこのような干渉縞の全体的な移動が生じる可能性はある。
しかしそれが原因ならば一回転してもとに戻れば、干渉縞も最初の位置に戻るはずだがそうなっていない。また、観測の日により回転に伴う遷移の方向やその変化幅が異なっている。そのため遷移の原因は光学系の配置ではないであろう。
論文中に、石板を運動状態から静止状態にすると、少なくとも30秒間は石板の変形の影響が見られ、この時間内に温度の変化の影響も生じたと記されている。このことから、1回転の測定中に室温(石板の温度)が持続的に一方向へ変化したために起こったと考えるのが最も確からしい。一般的に正午頃は気温が上昇していく時間帯であり、夕方は気温が下降していく時間帯だから、各時刻での観測値を平均したものの遷移方向が両者で逆になることも了解できる。
結局、遷移の原因は良く解らないが、いずれにしても180°回転した後には光が到着する時間差の変位値は一致すべきである。そのためマイケルソンは、両端の値を直線で結すんだ平均遷移直線からの差分が求めるべき変化であるとして以下の解析を進めている。
文献1.に載っているグラフがそれです。ただし、理論曲線の凸凹に対応させてグラフの正負は逆にしてある。
観測された変動幅(約±0.01λ)に対してゼロ点の移動が、6分間(装置の1回転時間)程度の間に0.1~0.2λも生じるのでは、このデータは信頼できないと思われる方がおられるかも知れません。しかし、6分も経てば、石板の温度変化により経路1と2の光路差に0.1~0.2λ程度(10-8のオーダ)の変化が起こることは充分予想できることです[光はそれぞれの経路で8回行き来しているので、石板に生じる伸縮の差は前記のさらに1/8、つまり波長の1/50のオーダーです]。
さらに、この変化は極めて滑らかに生じており、エーテル理論の予想最大変化幅0.4λよりも小さな値です。
つまり、この実験はそれほどの精度を初めて達成した実験だったと言うことです。だから、マイケルソンとモーリーの取り扱いは適切だと思います。
実際に表の値から差分を計算して、正負を逆にしたグラフにしてみると
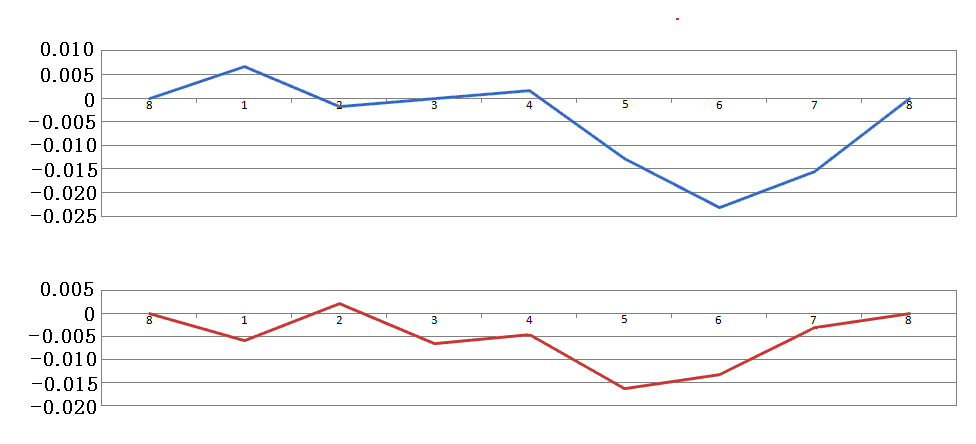
のようになる。
下図は文献1.に載っているものですが、上のグラフに理論曲線を併記したものです。グラフ中NESとSWNの記述は、角度0°→180°の変位と180°→360°の変位を重ね合わせた平均値であることを意味する。
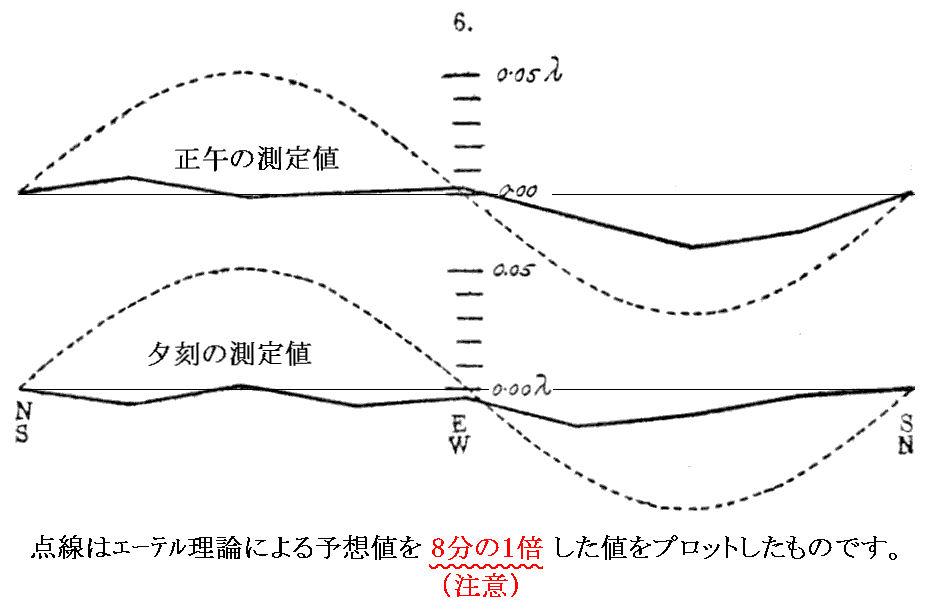
グラフから明らかなように、干渉縞の移動量は予想された値(0.4λ)の40分の1(0.01λ)以下であった。これは地球がエーテルに対して動いているにしていも、その相対速度は地球の公転速度の6分の1以下である事を意味する(公転速度へは平方根で影響する故に)。
マイケルソン・モーリーの実験は(v/c)の二次の精度において、絶対静止の空間に対する地球の運動を検出できるはずのものでした。しかし、観測結果は予想外のもので、エーテルに対する地球の相対的な運動は検出できなかったのです。
つまり、絶対静止の基準系(エーテル)に対する地球の運動は(v/c)の二次の精度においても検出できなかったのです。
すなわち、光の速さがあらゆる方向に向かって等しい速度cで伝播する座標系を見いだそうとする試みは失敗したわけです。
これ以後、様々な研究者によってこの実験の追試が何度も何度も行われます。1930年までに行われた主なものだけでも、10回以上になります。追試の結果と文献リストはこちらを参照。
その後に行われた A. Brillet and J. L. Hall, “Improved Laser Test of the Isotrpy
of Space”, Phys. Rev. Lett. 42, p549~552, 1979年 の実験では、その精度はマイケルソン・モーリーの実験の10万分の1に達しています。おなじ実験の別の説明。
いくら精度を上げても結果は同じで、光の到着時間の差の変動はまったく生じないのです。
5.ローレンツ・フィツジェラルドの収縮説
マイケルソン・モーリーの実験が突きつけた現象を説明するために、フィツジェラルド(1889年)とH.A.ローレンツ(1892年)は、互いに独立に、いわゆる収縮説を提唱した。ローレンツが当初(1892年)求めた収縮率は(1-v2/2c2)と言う近似的な式でしたが後(1895年)に正しい式を導きます。詳細は文献6のp153~156をご覧下さい。
彼らの言うところによると、速度vで運動している物体は、運動方向に
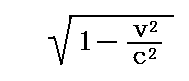
培の割合で収縮すると言うのである。
実際、そのようなことが起こると前述の3.(1)3.の式に於いて
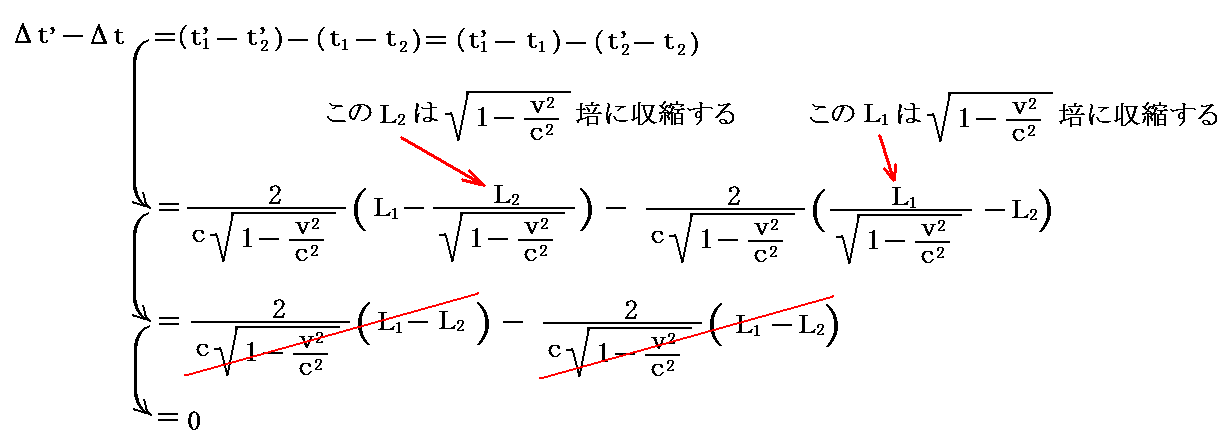
が常に成り立つので、装置を回転させても干渉縞の移動は認められないことになる。これは在る意味で正しい結論ですが、真に正しい解釈はアインシュタインの特殊相対性理論によって与えられます。
[補足説明1]
このような収縮の状況は観測装置と共に動く観測者に取っては決して確認できない。なぜなら、全ての物差しが同じ仕方で収縮するからです。
[補足説明2]
地球の外に在って、エーテル中に静止する観測者なら、この収縮が観測できる。地球は地上の全てのものと一緒に、その進行方向に添って扁平になっているであろう。そのとき、絶対静止のエーテルに静止した観測者が肉眼でその収縮を直接に見ることができるかというと、物体の先端と後端からくる光の到着のずれの効果のために、見かけ上ローレンツ収縮を打ち消してしまう場合が有るので注意深い考察が必要です。
[テレル(J. Terrell 1959年)、ワインスタイン(R. Weinstein 1960年)、等々・・・]。
収縮を確かめるためには特別な考察が必要で、時間の同時性の概念に対するするさらに進んだ理解が必要です。ローレンツの収縮仮説を真に理解するにはアインシュタインの相対性理論が必要で、この当たりは別稿で説明します。
[補足説明3]
ローレンツは彼の電子論による考察から収縮説を導いたのですが、さらに収縮仮説が果たして相対性原理(つまり電磁場の方程式が運動する系と静止エーテル中とで全く同じになる)を導くのに充分であるか否かを研究した。困難な計算の末、彼はそれだけでは不十分であることを確認した。そして、運動する系における電磁現象が静止エーテル中とまったく同じになるためには、どんな仮説を付け加えれば良いかを発見した(1899年)。
彼の結論は収縮仮説と同程度に意表をつくものであった。即ち等速運動をする系では、系ごとに新しい時間尺度を用いなければならない。ローレンツは系ごとに異なるこの時間を局所時と呼んだ。収縮仮説もこれに習ってつぎのように明確に言い表せる。運動する系における長さの尺度はエーテル中におけるそれとは異なる。
二つの仮説は一緒になって次のことを述べている。運動する系とエーテルとでは、時間と空間は異なった尺度ではからねばならない。
ローレンツは、様々な系における測定量について、一方を他方に変換する法則を確立し、この変換を行って電子論の場の方程式は不変であることを証明した。
ラーモア(1900年)とポアンカレ(1905年)もほぼ同じ頃に類似の結果を得た。
[ここは吉田伸夫著『思考の飛躍(アインシュタインの頭脳)』新潮選書(2010年刊)p24~39の説明が解りやすいので引用しておきます。あわせて文献6の第6章と文献7の第Ⅴ章もご覧下さい。]
[補足説明4]
ローレンツは静止エーテルの呪縛からのがれることはできなかったのですが、1905年にアインシュタインはエーテルを廃して、全ての慣性系は等価であるという相対性理論を打ち立てます。
この新しい見方によると、動くものの長さが縮む理由は、実は動くものの時間の進み方が遅くなることに関係しています。そのとき、固有の本当の長さというものはありません。どれも正しい長さであり、数字の違いは、物がとまっているか、動いているかによる相対的な違いにしかすぎず、長さ(空間の二点の間の長さの測り方)は相対的に変化する物だったのです。[佐藤勝彦「相対性理論を楽しむ本」PHP文庫]
[補足説明5]
我々の様な凡人がもっとも理解に苦しむのは、アインシュタインの言う「光速不変の原理」です。これを承認するためには、我々が“光が進む”と言う言葉で表そうとしている現象が何を意味するのかもう一度詳しく検討してみる必要がある。
ボルンやゾンマーフェルトがそのことを的確に説明していますので以下のリンク文章を熟読してください。
M.ボルン著「アインシュタインの相対性理論」東京図書(1972年刊)p198~199
A.ゾンマーフェルト著理論物理学講座Ⅳ「光学」講談社(1969年刊)p89~90、p383~384
この中で、ゾンマーフェルトがドップラー効果や光の圧力は粒子説で説明できると言っている部分を補足しておきます。ドップラー効果の説明はこちら、光の圧力の説明はこちら。
また、ゾンマーフェルトは“ハイゼンベルグの不確定性原理は波としての考え方と粒子としての考え方の二つの記述様式が論理的に相互に矛盾しないようにとの配慮である。”(「原子構造とスペクトル線」§7)と述べているが、これは至言です。
つまり、我々は光が進む様を見ているわけではないのです、我々が知ることができるのは光が物質から放たれた場所と時間、そして光を受け取った場所と時間だけです。その途中でどのようなことが起こっているのかは決して知りようがないのです。
もし、(我々が迷信として思いこんでいる様に)光の波が進んでいる様を直接見ることができれば、動いている観測者と静止している観測者が見る光の速度は違って見えるでしょう。しかしその様な事はできないのです。我々ができるのはそれぞれの観測者がもっている物指し棒でもって、その一端から放射された光の発射された時刻と物指し棒の他端に光が到着した時の時刻を観測者(物指し棒)と共に動く時計によって測り、それぞれの物指し棒の目盛りと、時計の時間経過によって光の速度を決めることができるだけなのです。
そのとき、光が出発した時間と光を受け取った時間の差を絶対的に決める方法が無いことに注意してください。それこそ光の信号などを用いて運動系と静止系のそれぞれの系に設置してある多数の時計の時刻を合わせておいて、それぞれの系の幾つかの時計(具体的にいうと物指し棒の両端に設置してある時計)の計時の差を知るしかないのです。それはそれぞれの系に於いて両方の場所の時計を合わせて知る(観測系ごとで異なる)相対的な時間差でしかないのです。
また光が出発した場所と受け取った場所の距離は、やはり光の信号などを使って計った相対的な距離しか知ることはできません。なぜなら物差しの長さが動く方向によって伸びたり縮んだりするかも知れないのですから。そのとき、物差しとともに動いている者は物差しの伸び縮みを決して見ることはできません。なぜなら全ての物が同じように伸び縮みしているからです。
それならば、あらゆる慣性系で測定した光の速度が一定であるとして何らかの不都合はあるだろうか。実は何の不都合も無いのです。ただ時間と空間の概念(それぞれの系に於ける物質[時計と物指し棒]の性質の違いと言っても良い)に変革を迫られるだけです。すなわち、光(電磁気学的現象)は相対性理論で説明しないと説明できない性質を持っていると言うことです。物質を構成する原子・分子間の結合も究極的には電磁気学的現象ですから、この性質は世界を構成する物質を含めたものだと言ってよい。
6.特殊相対性理論による説明
5.章の収縮仮説は解りにくい所なので、少し先走りますが、ここで特殊相対性理論による説明をします。
3.章ではL1、L2と置いて必ずしも等しくなくて良かった行路長ですが、ここでは簡単化のために、厳密に等しいL1=L2≡Lとして説明します。
(1)絶対静止(エーテル)空間から見た場合
今考えている絶対静止(エーテル)空間[つまり宇宙空間]に静止した観測者から、地球と共に動いている砂岩製の光学台を見ます。その観測者から見ると、マイケルソン・モーリーの実験に於いて光の伝わる有様は
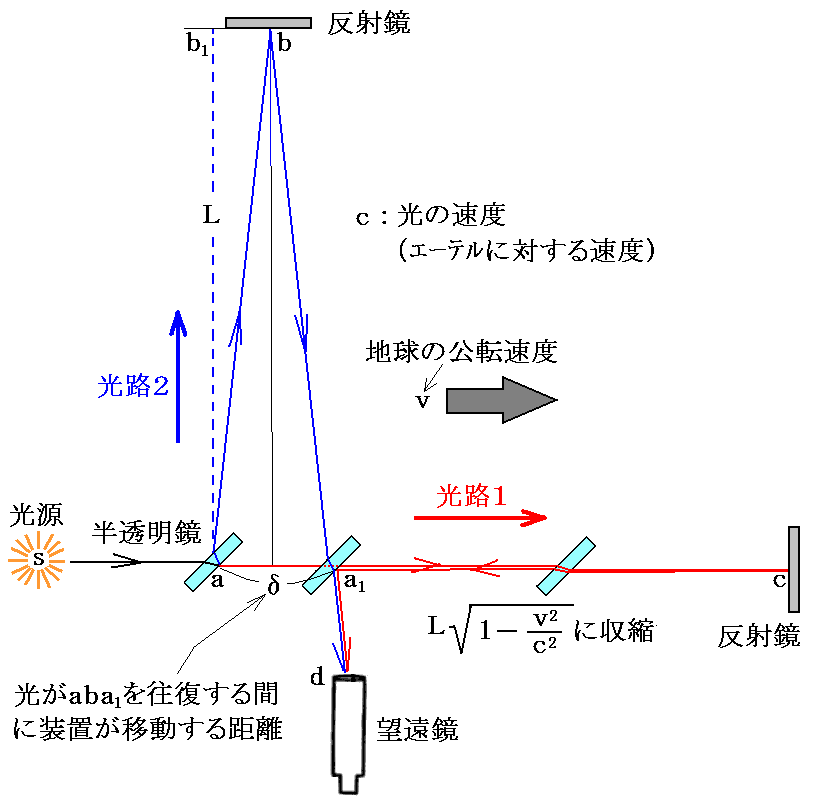
の様に見えます。
装置が90回転した状態では
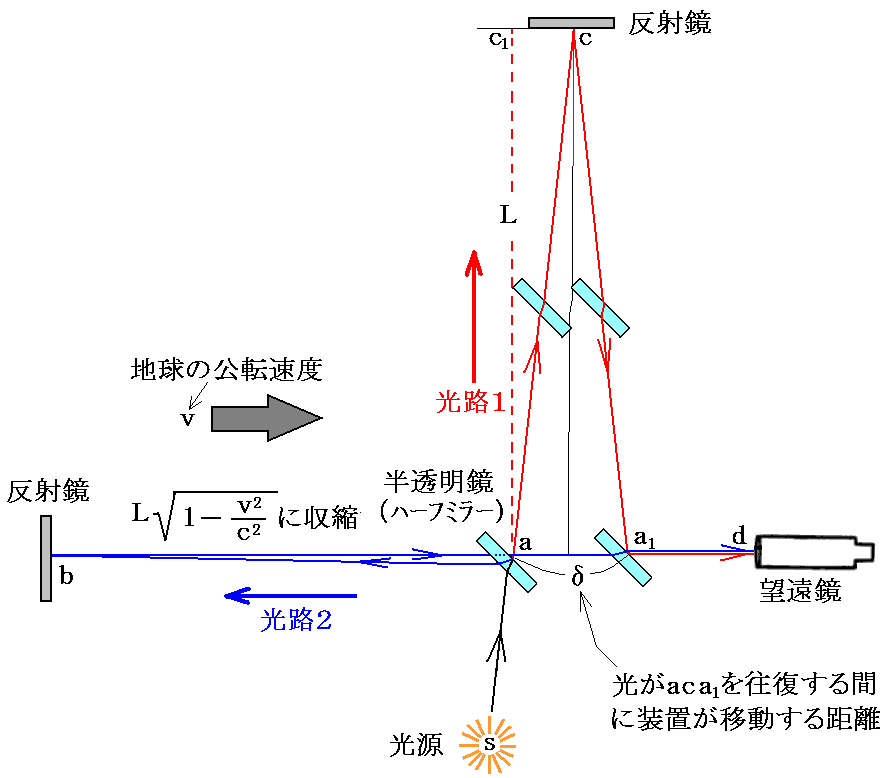
の様に見えます。
このとき光は、あくまで光速不変の原理に基づく一定の速度cで伝播しているように見えます。もちろん5.章[補足説明5]で説明したように波として伝播する光が見えるわけではありませんが、上図で説明したような状況で光は進んだと考えられます。
このとき、ハーフミラーも進行方向に少し縮みますからハーフミラーに対する光の入射角や反射角も少し変わりますが、鏡が動きながら反射するために反射光の進方向は確かに図のようになります。鏡が動くと反射角が変わる様子は、こちらの説明と図を参照されたし。
この場合光学台は、その進行方向に少し縮んだように見えるために、5.章で説明したように、二方向に伝播して反射して返ってきた光の伝播した距離に差が無く、従って到着時間に差が無くなります。
[補足説明]
特殊相対性理論によると、絶対静止(エーテル)空間[つまり宇宙空間]に静止した観測者から見ると、[光学台と共に動く観測者が持っている時計]は少しゆっくり進む様に見えるのですが、二方向の光線の伝播時間は同じ時計を用いて計っていますから、この実験に関しては時計の遅れは到着時間の差に影響しません。
光学台と共に動く観測者が持っている時計が指し示す光の往復に要する時間は、宇宙空間に居る観測者には少なすぎる[つまり時計がゆっくり進む]ように見えるのですが、[宇宙空間に静止している者が持っている時計]では、光が2Lよりも長い距離を不変光速度cで往復するのに要する時間をちゃんと指し示しています。
そのとき、たとえ宇宙空間に静止した観測者から、[光学台と共に動く観測者が持っている時計]がゆっくり進むように見えたとしても、次節(2)で説明する状況下では2Lの距離を不変光速度cで往復するのに要する時間経過をちゃんと指し示しているのです。
これは、等速運動をする系では、系ごとに新しい時間尺度を用いなければならないことの現れです。
このとき以下の事柄に注意してください。
光学台のそばに居る観測者から見たら、宇宙空間にいる観測者は速度-vで動いている様に見えますから、その者が持つ時計は光学台のそばに居る観測者の持つ時計よりもゆっくり進むように見えます。
なぜなら、今用いている光学実験台を宇宙空間にいる観測者に貸し与えて全く同じ実験をしてもらえば、同様な状況が立場を変えて生じるからです。
お互いに相手の時間が遅れる様に見えるのはとても不思議ですが、それはお互いに相手の過去を見ているからです。そのとき、特殊相対性理論が成り立つ前提である“お互いに相手に対して一定速度で真っ直ぐに進む”状況が続く限りに於いて、再び出会ってお互いの時計の進み具合を確かめるすべは無いのですから矛盾は生じない。
もし、一方が途中で向きを変えてもとに戻って再び会い、時計の進み具合を調べたとする。そのときに生じることを知るには、一般相対性理論が必要です。
[佐藤勝彦著「『相対性理論』の世界へようこそ」PHP文庫]
(2)地球と共に動いている光学台のそばで見た場合
地球と共に動いている光学台のそばに立っている観測者が、同じ実験を観察すると
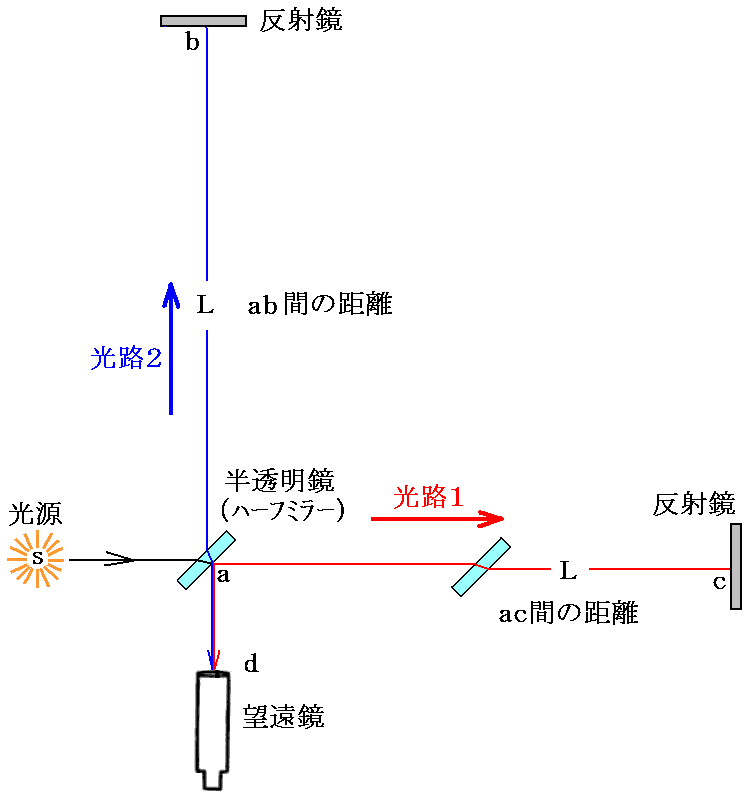
の様に見えます。
装置が90回転した状態では
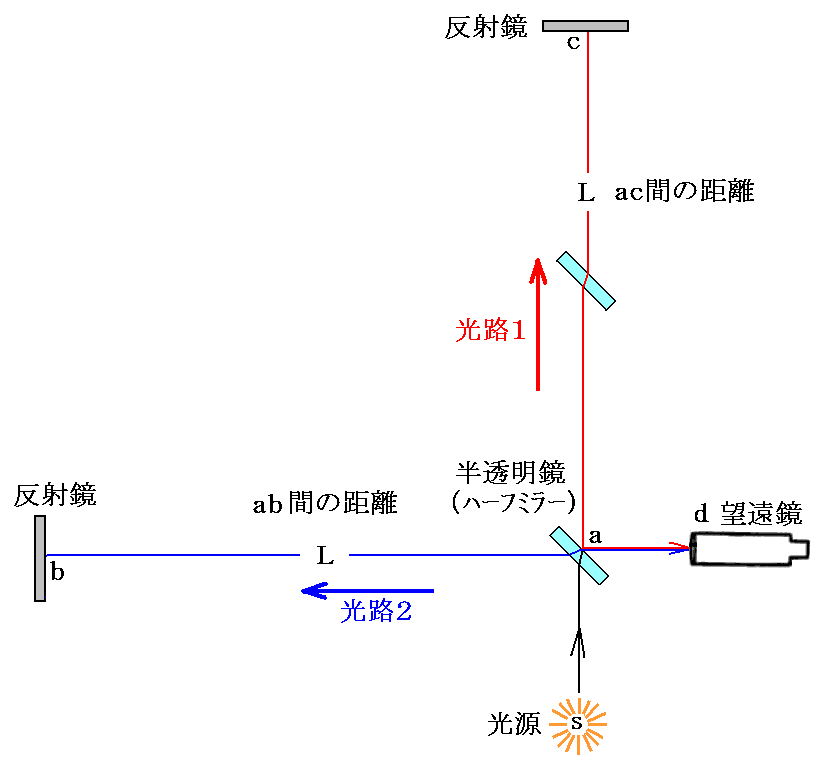
の様に見えます。
光は光速度不変の原理による光速度cで伝播し、二つの経路の行路長は全く同じなのですから、二方向に伝播して反射して返ってきた光の到着時間に差は在りません。
[補足説明]
絶対静止の空間から見ると前項の様に斜めに伝播する光を速度vで移動する光学台のそばで見ると上図の様になるのですが、相対性理論が確立るする前の考え方では、絶対静止の空間を光速度cで斜めに伝播する光を動きながら見たために直線的な動きになっただけですから、光の伝播速度はcよりも少し遅くなるはずです。
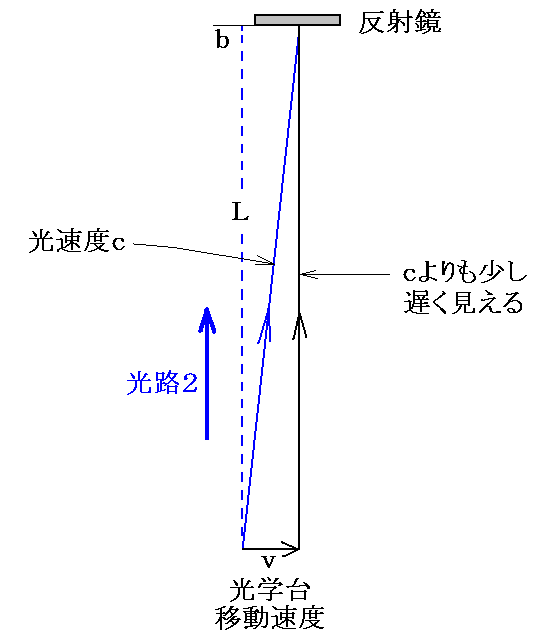
そのため2Lの距離を往復するための時間は、今説明した時間よりも長くなり、前項で説明した宇宙空間に静止している観測者の時計で測った時間と同じになるはずです。
ところが実験結果はそのようなことはなく、光の伝播速度は慣性系に依らず一定であると考える方が理にかなっていたのです。だから、宇宙空間に静止した観測者からみると[光学台と共に動く観測者が持っている時計]はゆっくり進むように見えるのです。また、速度の合成法則も相対性理論で習うような形になるのです。
特殊相対性理論をまだ説明していないので、6章の説明は解りにくいと思います。ぜひ以下の順番で特殊相対性理論を学ばれる事を勧めます。
1.「アインシュタインの特殊相対性理論(1905年)」(これはアインシュタインの有名な1905年論文の説明です)
2.「ローレンツ変換とは何か[Einsteinのローレン変換導出法(1905年)への補足]」
3.「マイケルソン・モーリーの実験(1887年)の特殊相対性理論による説明」
7.参考文献
この稿は有名なマイケルソン・モーリーの実験の説明ですが、[解析に用いる理論式]と[結果を示す数値]の意味を読み解くときに注意が必要です。このページは以下の文献を参考にして作りました。
- Albert Abraham Michelson and Edward Morley, “On the Relative Motion of
the Earth and the Luminiferous Ether”, American Journal of Science, Series
3, Vol. 34 (203): p333~345, 1887年(又はPhilosophical Magazine, Vol. 24, 1887年)
これは特殊相対性理論を学ぶ準備として必須の文献ですが、下記URLからpdfファイルでダウンロードできます。
http://www.aip.org/history/exhibits/gap/Michelson/Michelson.html
- 大野陽朗監修「近代科学の源流-物理学篇Ⅱ」北大図書刊行会(1976年刊)p287~298
これは文献1.の日本語訳です。
- P. G. Bergmann著「相対性理論序説」秀潤社(1978年刊)第1編第Ⅲ章
計算式の詳細はこの本を参考にした。
- R. S. Shankland著「マイケルソン・モーレーの実験」講談社(1972年刊)p134~154
これは“Michelson-Morley Experiment”, American Journal of Physics, 32(1),
p16~35, 1964年 から転載・翻訳したものです。
- バーナード・ヤッフェ著「マイケルソンと光の速度 -相対性理論への道-」河出書房(1969刊)
マイケルソンの伝記です。古い本ですが、この稿を読まれた高校生に薦めます。図書館にはきっと有ると思います。この中のマイケルソンの光速度測定の業績に関して別ページ(1878年の測定、1924年の測定および1935年の測定)にて引用。また、マイケルソンの論文・著書一覧はこちらで引用。
光速度測定一般に関してはこちらも参照されたし。
- Abraham Pais著「神は老獪にして・・・」産業図書、6章
この中に、この稿で説明したマイケルソン・モーリーの実験とアインシュタインの考察との関わりについて興味深い論考(p142~148)が在りますので引用。
- Max Born著「アインシュタインの相対性原理」講談社(1971年刊)
第Ⅴ章“電気力学の基本法則”を引用。第Ⅳ章“光学の基本法則”の内容は私どものページで大体の所は説明しましたので、その一部のみを引用。。
相対性理論への導入としてBornの説明に勝るものは無いと思います。簡単な数学しか用いていませんが含蓄深い文章です。熟読されることを勧めます。
- 吉田伸夫著『思考の飛躍(アインシュタインの頭脳)』新潮選書(2010年刊)
第1章“動くことと動かないこと(特殊相対論)”のp24~39を別稿で引用。