ラーモアの定理によるゼーマン効果と反磁性の古典論
前稿で説明したゼーマン効果の理論はラーモアにより一般化されます。この稿はその事とラーモアの定理による反磁性の古典論を説明します。電磁気学の単位系はMKSA有理化(SI)単位系を用います。
1.ラーモアによる一般化
前稿の議論は電子軌道の回転面が磁場に垂直な特別な場合についてのものでした。ラーモアは1897年の論文
J.Larmor,“On the Theory of the Magnetic Influence on Spectra; and on the
Radiation from moving Ions”, Phil. Mag., (5), 44, P503~512, 1897年
物理学古典論文叢書8「電子」東海大学出版会(1969年刊)の4.“スペクトル線に及ぼす磁気的影響の理論について、そして運動するイオンからの放射について”
で、電子回転の軌道面が磁場に対して任意の方向を向いていても、スペクトル線の偏向状態を含めて全ての現象が正確に再現されることを理論的に示した。その中で今日“ラーモアの定理”として知られている事柄の証明と、運動電荷から放射される“電磁波エネルギー流”の公式を導いた。
(1)一般的な方程式の解
今、正の電荷が座標原点に固定されていて、-eの電荷を持つ電子が原点からの距離に比例する引力を受けて回転している場合を考える。実際にはクーロン引力と考えるべきですが、弾性的な力で考えています。後で説明しますが、この違いは本質的ではなくてどちらの場合でも良いことが解ります。電子の運動を規定するニュートンの運動方程式は磁場が存在しないときは
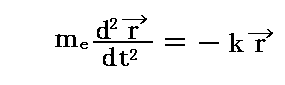
となり、磁場があるときには外力としてローレンツ力=-e[v×B]が付け加わり

となる。ここでは前稿の議論をふまえて最初からk/me=ω02と置いています。これは磁場が存在しないときの回転角速度の二乗を意味する。また、磁場が座標軸のz軸の方向を向いていて(Bx,By,Bz)=(0,0,B)であるとする。
そのとき、ベクトル方程式は三つのスカラー方程式になる。
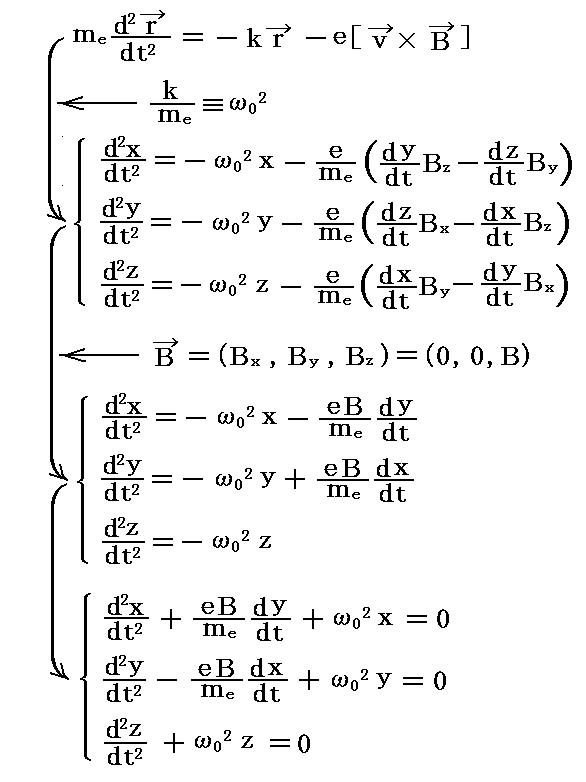
この微分方程式の解として
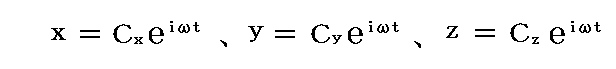
の形のものを求めてみる。これらをスカラー方程式に代入すると
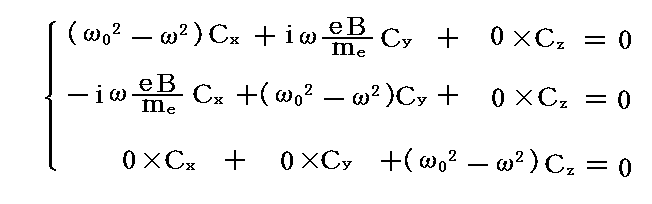
のCx,Cy,Czを未知数とする一次の三元連立方程式が得られる。
線形代数学で習うように、このような連立方程式は係数から作られる行列式が0に等しいときのみ、ゼロでない解(Cx,Cy,Cz)を持つ。つまり軌道回転の角振動数ωは以下の方程式
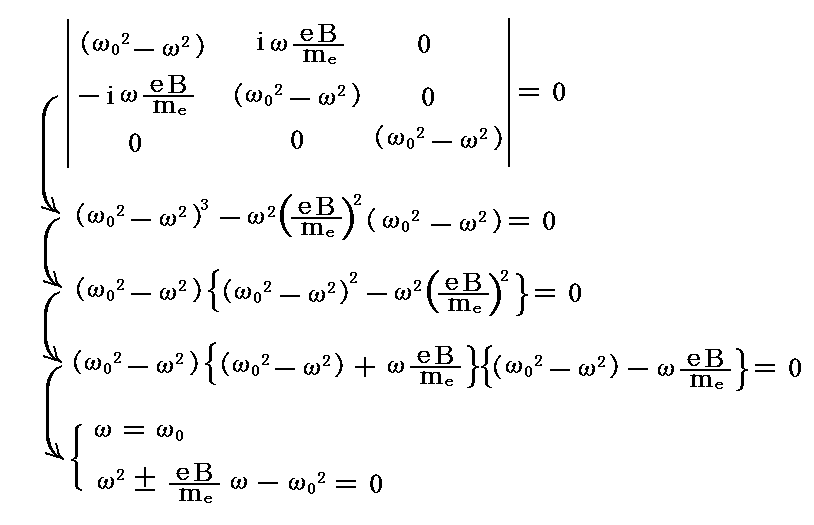
を満足しなければならない。
これらの二次方程式は別稿で説明したものと同じです。二つの二次方程式から得られる4つの解の内ただ二つだけが正となる。すなわち
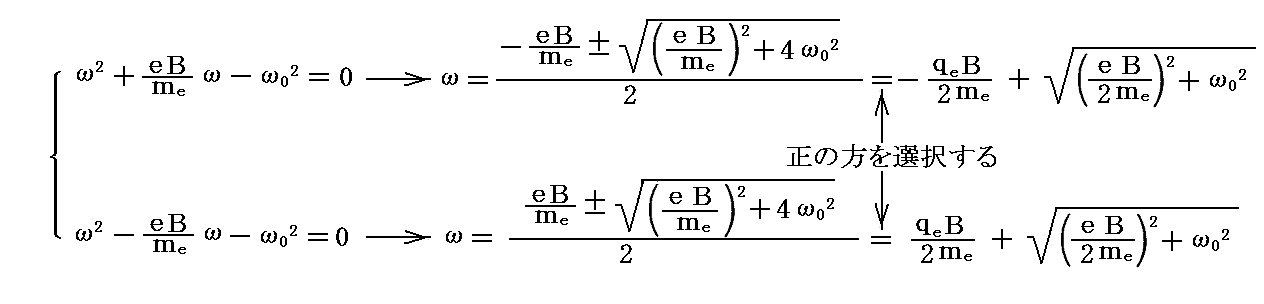
が得られる。
このとき、別稿で説明したように
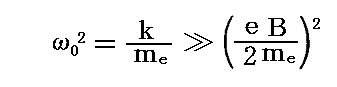
が成り立つので、上記方程式系の解として
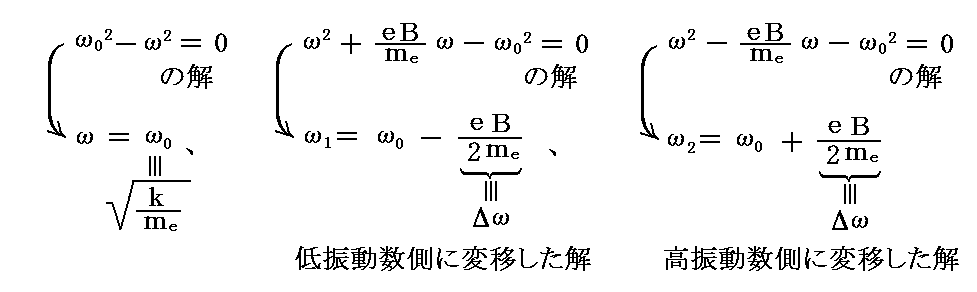
が得られる。
(2)解の意味
前節で示したように、回転の角振動数は磁場が存在しないときのω0に加えて、二つの異なった解が得られた。この解が何を意味するのかを元の方程式
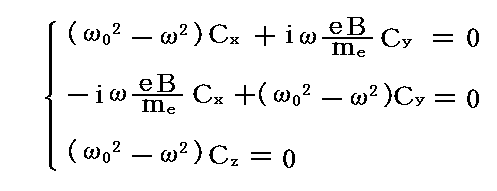
を用いて読み解いてみる。
最初の式あるいは二番目の式のいずれかに、低振動数側に変移した解ω=ω1を代入すると
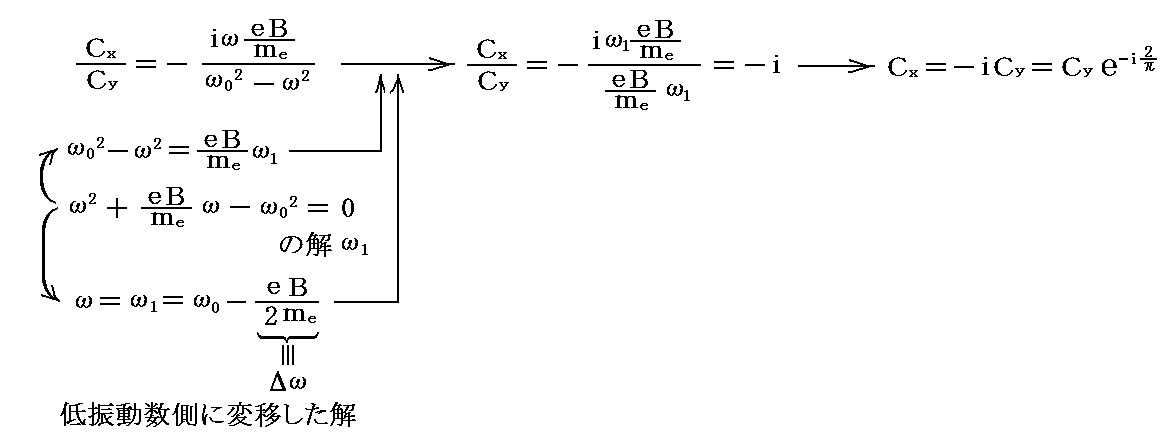
となる。これはx軸にそった振動はy軸にそった振動よりも位相がπ/2だけ遅れる事を意味する。両方の振動を合成したものはxy平面上に射影された楕円回転運動を与える。さらに上記の位相関係を考慮すると、z軸の正の方向から見て時計回りすなわち右円偏光を与える。
同様に最初の式あるいは二番目の式のいずれかに、高振動数側に変移した解ω=ω2を代入すると
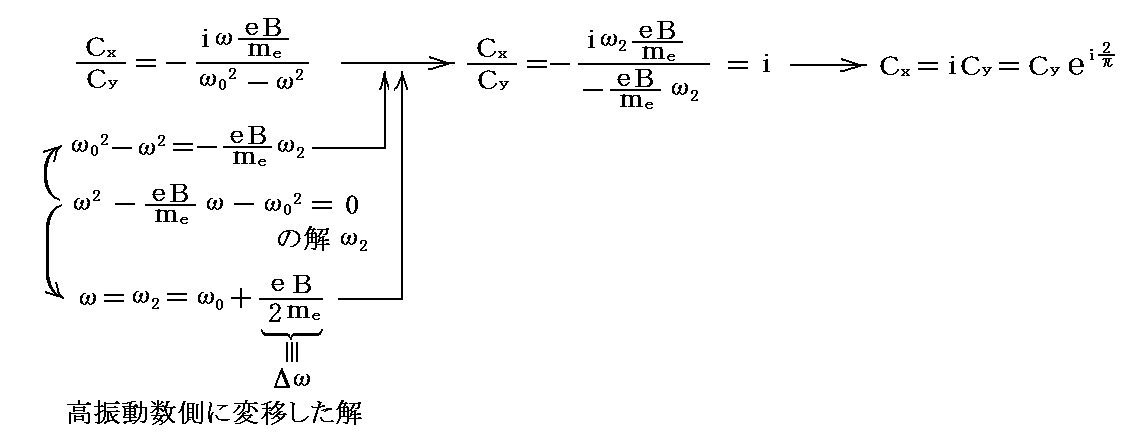
がえられる。これはx軸にそった振動はy軸にそった振動よりも位相がπ/2だけ進んでいる事を意味する。これから解ω2は左円偏向であることが結論される。
最後に連立方程式の第三番目の方程式
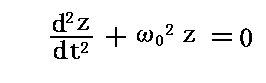
はz軸(磁場の方向)にそった振動は振動数の変化なしに起こることを示している。それは直線的偏りを持っている。ところで振動方向の電磁波の輻射は0であるから、磁場方向(z軸の正の方向)から眺める観測者にはこの第三の成分は見えない。
以上の様にして、電子の回転軌道が磁場に対して任意の方向を向いていても、別稿3.で述べた観測結果が完全に説明される。
2.ラーモアの定理
ラーモアは引き続いて、前記の結論に対して新しい解釈を与えます。それが、今日“ラーモアの定理”として知られているものです。
(1)磁気双極子モーメントと軌道角運動量モーメント
まず、軌道上をまわっている電子は円形電流をなしている。電気力学の法則によれば、このような円形電流は定まった磁気モーメントを持ち、一つの“磁気双極子”と見なすことができる。閉じた電流の磁気モーメントは別稿「電磁気学の単位系が難しい理由」3.(3)で説明したように
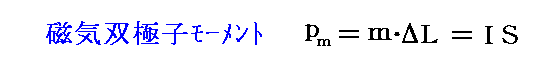
と表される。ただし I は円電流の電流値、Sは電流によって囲まれている円軌道面積です。
円形軌道の電子の回転数がν=1/T (Tは回転周期)ならば、電子は円軌道の一断面を1秒間にν回通過するのでI=eν=e/Tとなり
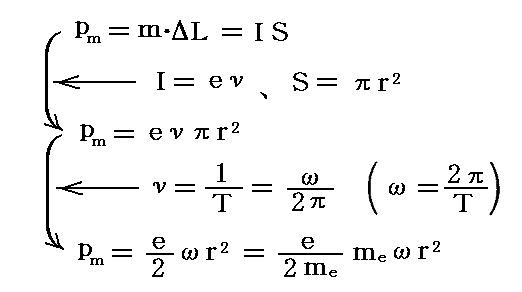
が得られる。
一方、電子は質量を持つので、円形の軌道運動をすれば“角運動量”を持つことになる。すなわち
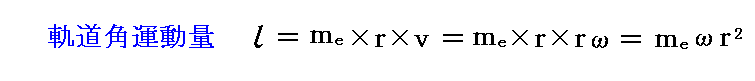
の軌道角運動量モーメントが付随する。
すなわち、回転電子を含む原子は、磁気双極子モーメントと軌道角運動量モーメントの両方を持つ。しかも、両者は二つのモーメントの表現式を比較すれば明らかなように
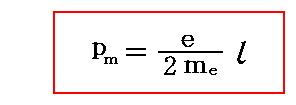
の関係式で結び付けられている。
当時は原子の内部構造に関しては何も解っていない時代ですから、これはとても大胆な仮説です。
(2)電子軌道の歳差運動
いま考えている軌道電子を含む原子が磁場中に置かれたとする。前節で述べた事によって原子は定まった磁気モーメントを持っているから、それは外部磁場の中で磁石として振る舞う。つまり磁気モーメントベクトルが外部磁場に平行に成るような力を受ける事になる。
ところで、電子は質量を持つので軌道運動には角運動量モーメントが付随している。つまり、原子は一つの回転するコマと見なすこともできる。もし軌道角運動量モーメントのベクトルが外部磁場の方向と一致していない場合。つまり電子の円運動軌道面が外部磁場に垂直ではなくて斜めに成っている場合にには、磁気モーメントベクトルと外部磁場ベクトルの相互作用により、両ベクトルが同じ方向を向くような力が磁気モーメントベクトルに働く。これは角運動量モーメントベクトルに関してその力が働くことを意味する。
つまり、電子を含む原子の角運動量モーメントベクトルが磁場ベクトルと同じ方向、あるいは真反対の方向に向くようなトルクを受けることになる。コマの理論から知られているように、その様な原子(電子軌道)の回転軸は外部磁場ベクトルBのまわりに“歳差運動”をする事になる。 これは普通のコマが地球の重力場に於いて、コマの回転軸が鉛直方向から傾いている場合には重力の影響のために歳差運動(味噌すり運動)をするのと同じです。つまり、磁気双極子モーメントが重力場におけるのと同様なトルクを生み出す。
その場合、電子の運動はもともとの軌道運動に歳差運動が重なった運動をする事になる。これを静止系から見ると、あたかも電子の軌道運動の回転速度ω0が1章で説明した角振動数変化分Δωだけ変化したω0±Δωの回転をすることになる。
コマの理論にしたがって[歳差運動の方向]と[電子の回転方向]と[トルクの作用する方向]の間に成り立つ関係を確認すると以下のようになる。
まず、外部磁場ベクトルBの方向が右ねじの関係になる様に電子(e<0)が回転しているとする。
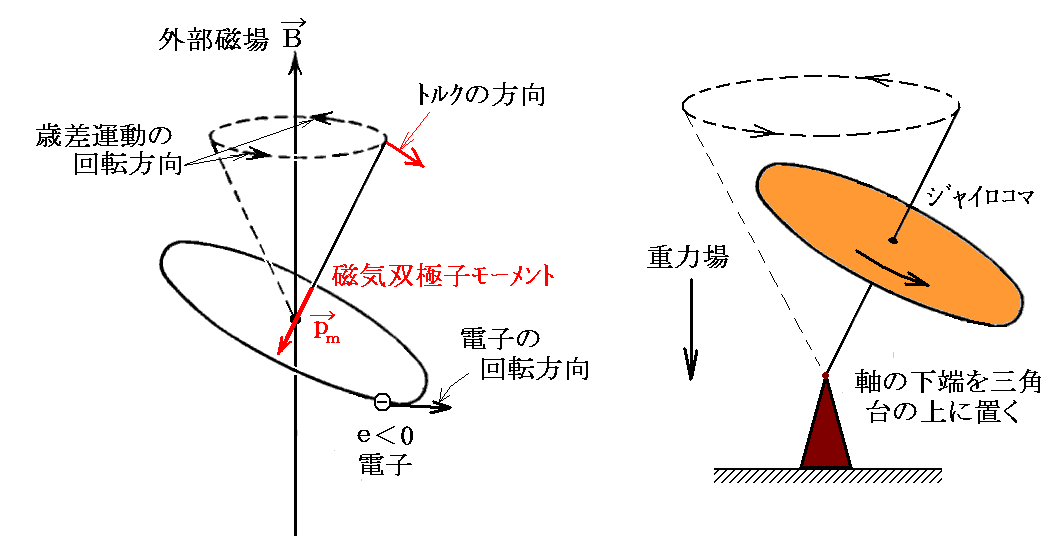
このとき、原子の磁気双極子モーメントベクトルpmの方向は外部磁場ベクトルBとは逆向きだから、電磁気学の理論により回転コマの軸を磁場ベクトルBの方向から離れる方向に倒そうとするトルクが働く。
電子(質量me)の回転方向と回転軸に働くトルクの方向から定まる歳差運動の回転方向は、コマの理論によると図のようになる。そのため、静止系から見た電子の回転角振動数は磁場が無い時のω0に歳差運動の角振動数Δωが加わったω0+Δωとなる。そうなることは電子の回転軌道面を磁場Bの方向を回転軸として歳差運動に従って動かして見れば了解できる。このとき磁場ベクトルの正の方向から放射光を眺めると“左円偏向”に成っている。
次に、外部磁場ベクトルBの方向が左ねじの関係になる様に電子(e<0)が回転しているとする。
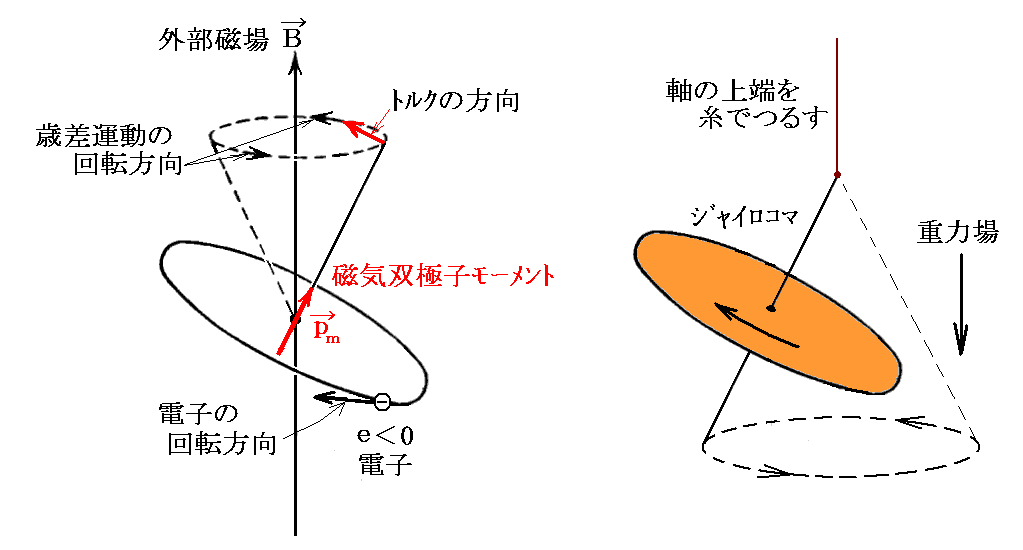
このとき、原子の磁気双極子モーメントベクトルpmの方向は外部磁場ベクトルBと同じ向きだから、電磁気学の理論により回転コマの軸を磁場ベクトルBの方向に傾けるトルクが働く。
電子(質量me)の回転方向とトルクの方向から定まる歳差運動の回転方向は、コマの理論によると図のようになる。この場合には、静止系から見た電子の回転角振動数は磁場が無い時のω0に歳差運動の角振動数Δωを差し引いたω0-Δωとなる。そうなることは、この場合も電子の回転軌道面を磁場Bの方向を回転軸として動かして見れば了解できる。このとき磁場ベクトルの正の方向から眺めた放射光は“右円偏向”となる。
ここで、電子の回転方向が逆転しても電子回転軸の歳差運動方向は同じになることに注意されたし。それは、電子の回転方向が逆になると磁気双極子モーメントの方向が逆になるので外部磁場Bが磁気双極子モーメントに及ぼすトルクの方向が逆転するからです。また、それだからこそ別稿3.で述べた観測結果から回転している電荷は負であることが解る。
これがラーモアが見つけたことですが、それまでに電荷の回転で構成されるコマの事を考えた人はいなかったのですから、まさしく大発見です。
ここでは、コマの理論の詳細に立ち入らないが、上記の事柄は写真に示すようなジャイロコマ

を玩具店で購入して、下図に示す状況の実験をやってみれば直ちに了解できる。
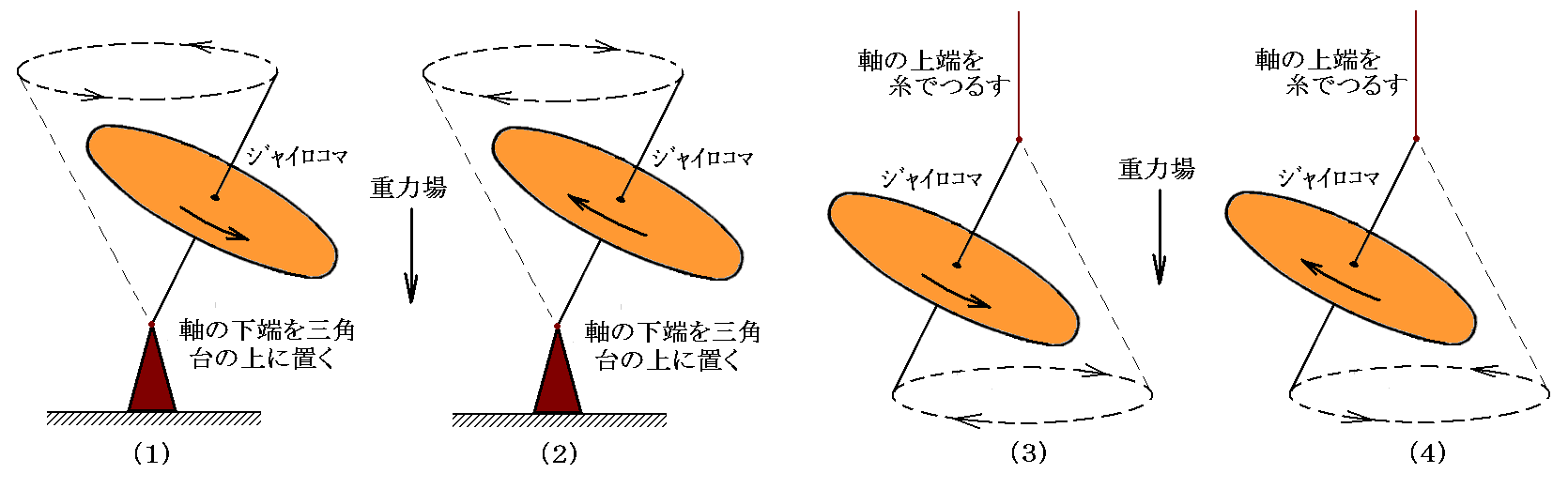
歳差運動が起きるメカニズムの解りやすい説明。[拡大版]
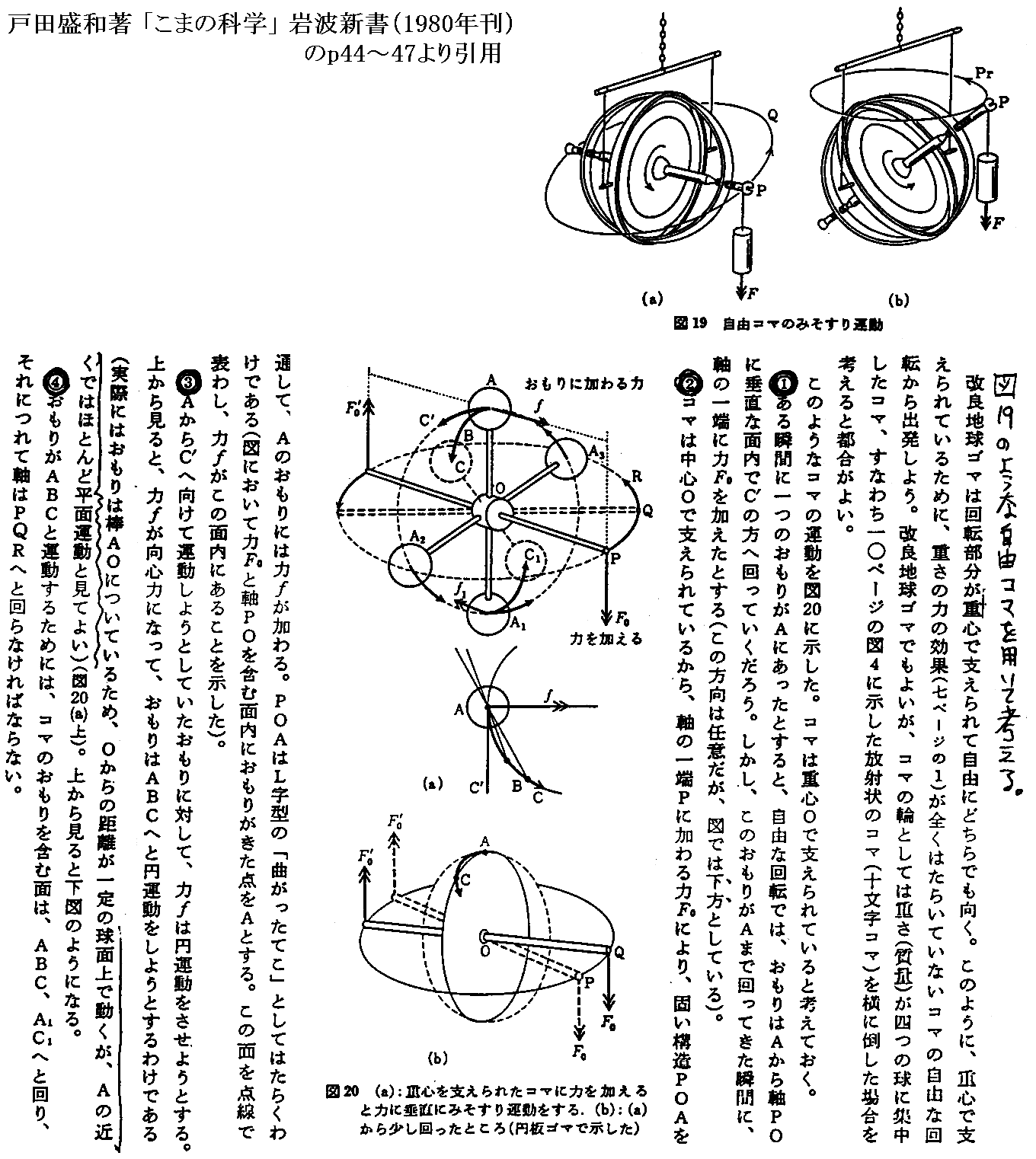
他のおもりについての補足

(3)歳差運動の角振動数Δω
ここで、歳差運動の回転角振動数Δωがいくらになるか求めておこう。いま電子の軌道を静止させ座標系から眺めると円運動に歳差運動が重なった複雑な軌道を描く運動になる。このとき、歳差運動の軸の周りを軌道の回転と供に動く座標系を導入しよう。このような座標系から電子の運動を眺めれば軌道はその形を保つであろう。そのとき残る問題は歳差運動の角速度を求める事になる。
磁場Bの方向をz軸に取った静止座標系(x,y,z)と、z’軸は磁場Bの方向に取るが、x’軸、y’軸はz’軸を回転軸とし、ちょうど歳差運動の角振動数Δωで回転する座標系(x’,y’,z’)を考える。
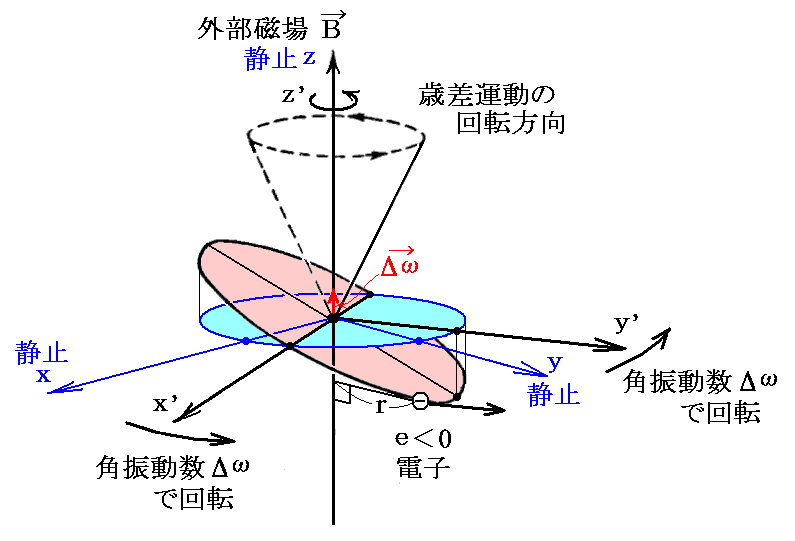
軌道上を運動している電子の速度を静止座標系から見たものをv、回転座標系から見たものをv’とする。歳差運動によって電子に加わる線速度は、歳差運動が無いときの電子の軌道速度に比べて非常に小さいと仮定できる。すなわち
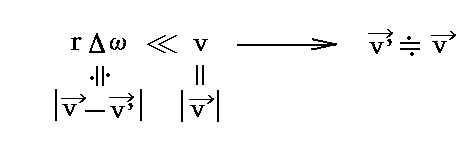
とできる。つまり回転座標系から見た速度ベクトルv’は静止座標系から見た速度ベクトルvとほぼ等しいとおける。ここで r は歳差運動の軸(z or z’軸)から電子までの距離です。この仮定は後で求まるΔωがω0に比較して極めて小さいことから確認できる。
このとき、別稿「慣性力」3.と4.で説明したように、回転座標系(x’,y’,z’)から見ると電子に対して付加的な慣性力である遠心力とコリオリ力が働いている様に見える[数学的な証明はこちらを参照]。
それぞれの力は
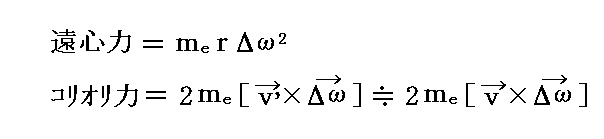
と表されるが、コリオリ力に比べて遠心力は無視することができる。このことは、実際の場合について具体的な数値を当てはめて計算してみると正当化されます。
このとき、磁場Bが働いている状況下での回転座標系に於いて、前記のコリオリ力に加えてローレンツ力
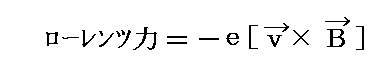
が働いている。負の符号は電子の電荷が負であることによる。磁場ベクトルBの方向は歳差運動の角振動数ベクトルΔωの方向と一致するので、ベクトル積の規則から明らかなように、コリオリ力とローレンツ力は互いに反対方向を向く。
このとき、回転座標系から見たときの電子の回転の様子が磁場が存在しないとき静止座標系から見た回転の様子と同じ(つまり歳差運動が見かけ上なくなる)であるためには、コリオリ力とローレンツ力の大きさは数値的に等しく
なければならない。すなわち

となるはずである。これがラーモアの論文に載っているやり方ですが、実に巧妙ですね。
磁場Bの方向を回転軸とし上記の回転角振動数Δωで回転する座標系に於いて、電子は磁場のないときと同じ軌道を描く。つまり、一様な磁場Bを追加することは、軌道の形、磁力線に対する姿勢、および軌道上の運動を変化させないが、磁力線の方向の周りに軌道の歳差運動を誘起する。その歳差運動の角振動数は
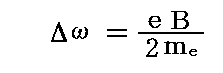
である。これを“ラーモアの定理”という。
この定理が成立するために仮定されていることは、歳差運動で電子に与えられる追加の速度成分が歳差運動なしのときの軌道上の速度より充分に小さい事(rΔω≪v)です。今まで何度も注意したが、この条件は実際の状況では常に満足されている。
また、この定理は、電子に円運動をさせる向心力については、F=-krであろうとF=-k’/r2であろうとそのf(r)の形に依存しないことに注意されたし。
このとき、さらに注意して欲しいことは、2.(1)で求めた磁気双極子モーメントpmと軌道角運動量モーメントlの比例係数e/2meは電子の内部的な運動状態(軌道半径や速度)には依存しないことに注意してください。そのため古典論によれば電子の系は(印加磁場Bが同じなら)全て同じ角振動数Δωの歳差運動をする事になる。つまり、最初の電子軌道運動の回転軸ベクトルが印加磁場ベクトルBに対してどの方向を向いていても全て同じ角振動数Δωの歳差運動をする。
もう一つ注意すると、印加磁場Bの大きさが増大すれば、歳差運動の角振動数Δωは増大します。その当たりに付いて、次章で追加の説明をします。
3.外部磁場の印加
(1)磁場の印加
前稿の説明やこの稿の1.(1)の説明は、磁場が存在しない場合と磁場が存在する場合を比較した議論で、磁場が存在しない状態から磁場が存在する状態へ徐々に変化するとき、ラーモアの磁気モーメントや角運動量モーメントがどのようになるのかは説明されていません。
実際のところ磁場が存在するときに運動電荷に働くローレンツ力は電荷の運動方向に垂直で、電荷の運動方向に関しては加速も減速も行わず電子の回転系に対して何の仕事もしませんので、その当たりの変移過程はマクスウェルの電磁気学方程式に立ち返って論じなければなりません。
ラーモアは1894年と1895年にに発表した論文(Phil. Tran.)で、その当たりの議論を展開しました。それはおよそ以下のようなものです。
電子の回転系に対する磁場の印加は、即座に最終的な状態に成るのではなくて、ある時間をかけてその値に達する。この時間は電子の回転周期に比較すると極めて長く、熱力学における準静的断熱過程の様に無限にゆっくりした過程と見なすことができます。
従って各瞬間において、[中心核から電子に働くクーロン引力]と[運動電荷に働くローレンツ力]の和が[向心力]となり円運動を保持しながら変化していきます。これは電子と共に回転する座標系から見ると [クーロン引力]+[ローレンツ力]が[見かけの力である遠心力]と釣り合いながら変化している事を意味する。
このとき、別項で説明したマックスウェルの電磁気学方程式

中のファラデーの電磁誘導の法則が示す様に、磁場の増大速度に比例する量の電場がサークル状に出現する。
この方程式は別稿ですでに説明したが、
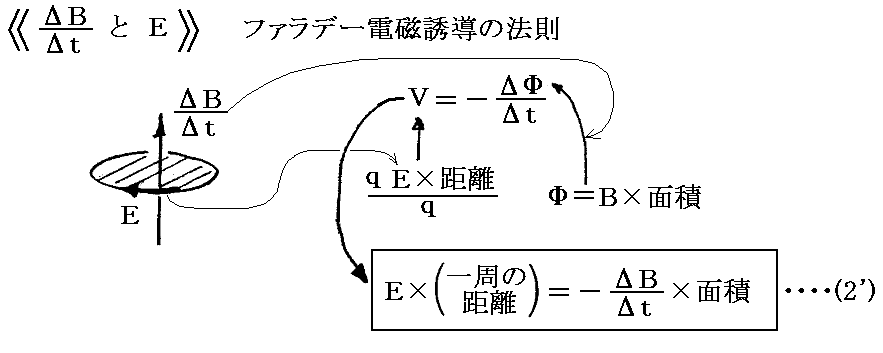
の関係を意味する。このとき、磁場が時間的に変化するとそのまわりに渦状の誘導電場Eができるのだが、その電場の方向はΔB/Δtの変化を打ち消すような電流を生じる方向です。
そこにおかれた回路に沿って電荷が動くと,誘導電場Eがローレンツ力F=qEに従って電荷に力を及ぼして仕事をする。単位電荷が回路を1周する間に誘導電場がする仕事が誘導起電力です。誘導電場 Eの回路に沿った成分を El とすれば,誘導起電力Vは回路を1周する線積分
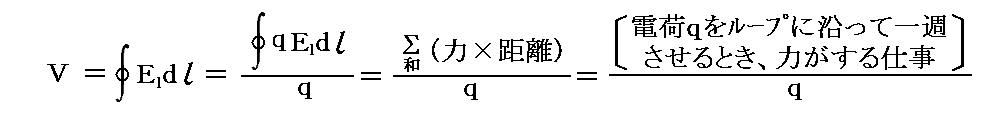
で表され電圧(電位差)と同じ量となる。これが前記(2’)式の左辺に相当するものです。
qをここでの議論の-eに置き換え。さらに磁場が0からBまで増大する時間に電子がn回転すると考え、電子の回転周期をTとする。磁場が0からBに増大するまでに電子に対して成された仕事をΔWとして(2’)式をさらに変形すると
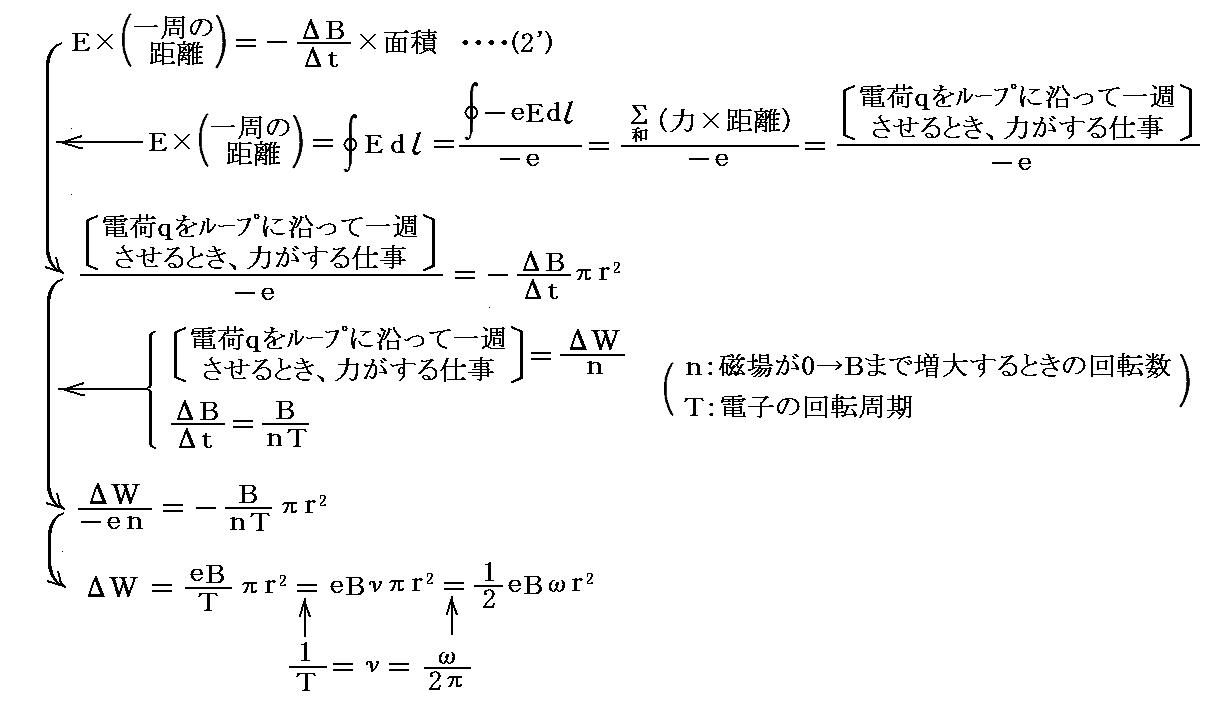
となる。このとき、nの項は両辺で打ち消し合うので、磁場の印加に要する時間の長さには関係なくなることに注意してください。
この仕事は分子の運動エネルギーの増加ΔEkinと、(もし軌道半径が変化するならば)位置エネルギーの増加ΔEpotになる。

となります。
一方、無限にゆっくりと(断熱的に)状態を変える際には、各瞬間に電子に作用するクーロン力とローレンツ力の和が丁度円運動の向心力となっているので、磁場の増加が終わったときの状態においても

が成り立つ。
(A)(B)を未知数Δω、Δrの二元連立代数方程式と見なして解くと、その解として
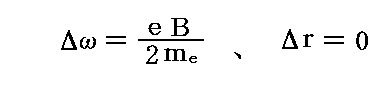
が得られる。
つまり電子軌道の半径は不変で、ただ角振動数だけが変化する。これは、角振動数が増えて軌道速度が増大しても、ローレンツ力による中心を向く力が増大して、同じ半径の回転運動を維持するのに必要な向心力の増大がまかなえるからです。
(2)外部磁場の印加による磁気双極子モーメントの変化
電子軌道の回転角振動数の変化Δωは、角運動量の変化Δlを意味する。そのとき、2.(1)で述べたことから解るように磁気双極子モーメントもΔpmだけ変化する。
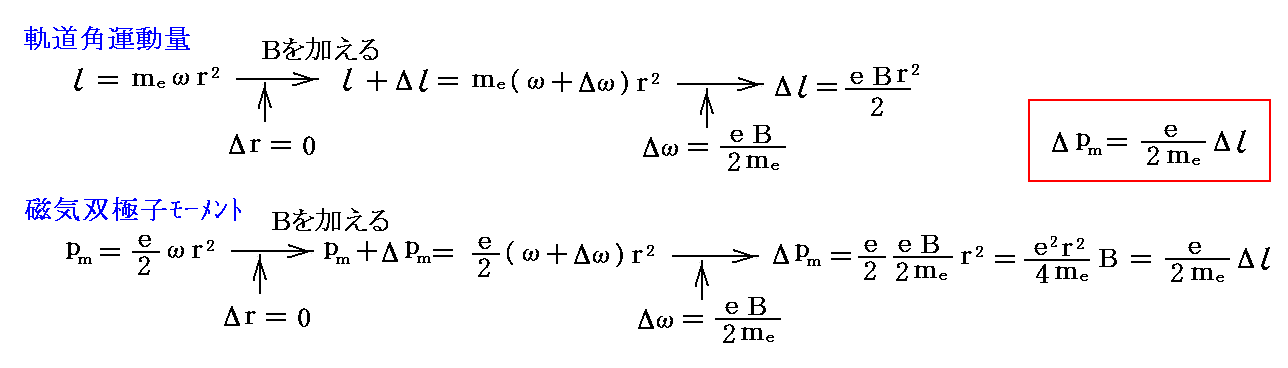
電子の回転方向と磁気モーメントの変化の対応関係は下図の様になる。
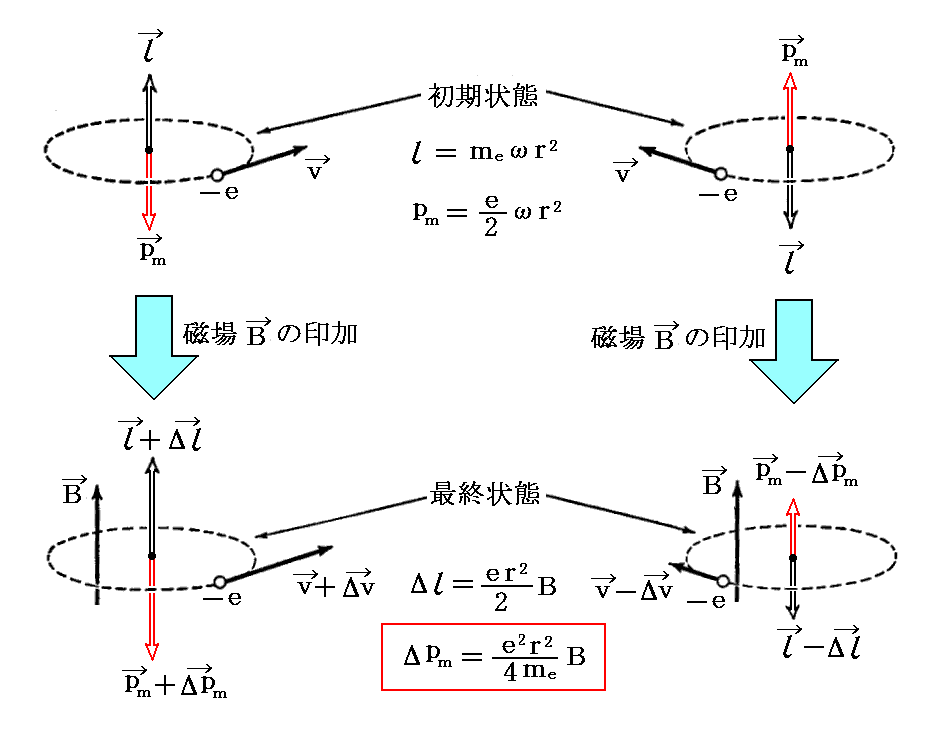
これらの図を2.(2)で示した図と比較してみられたし。結局はそこと同じ事が導けたことになる。
磁場Bの印加は原子(電子系)の磁気モーメントに磁場と逆方向の変化を生じさせる。そのとき回転する電荷の符号が逆でも、また回転方向が逆転しても全く同様な事情が生じることに注意されたし。これが次に説明する“反磁性”の古典的な説明です。
4.ラーモアの定理と反磁性
(1)磁性の分類
1.常磁性と反磁性
反磁性・常磁性・強磁性の言葉の意味の説明から始めます。
基本的には全ての物質は微少な磁石からできていると考えられる。ただし、普通の状態ではその微少な磁石はあらゆる方向にばらばらに向いており、その方向の分布は均等である。微少磁石は原子レベルでアトランダムな方向を向いているので、その中のどんな微少部分でも方向変化の一様性は保たれている。そのためそういった微少磁石の集合体からなる物質は巨視的に見れば磁性を持っていないように見えます。
所が実際の物質を下図の様な“磁場強度が場所的に変化する場所”に置いてから電磁石に電流を流して磁場をかけると、下記赤矢印のいずれかの方向の“力”が生じます。このとき資料物質を置いている所の磁場が場所的に変化していることが重要です。磁場が場所的に一様な場合には力は現れません。実際そうであることは4.(2)で確認します。
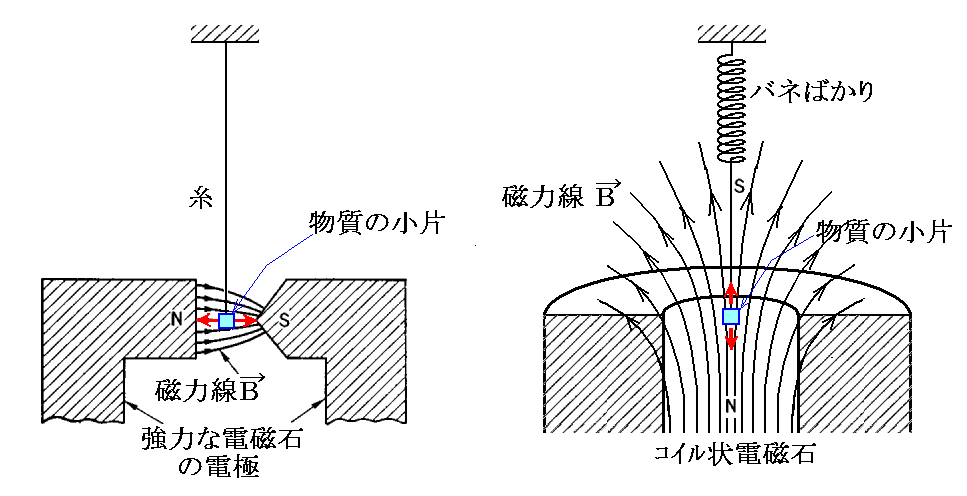
そのとき磁場の強い領域へ引かれるものを“常磁性体”といい、磁場の弱い領域へ引かれるものを“反磁性体”と呼びます。
つまり上記の状況の磁場中に入れると小物体が、巨視的にあたかも一つの小磁石の様に成るのです。実際にどのような磁石が誘起されているかは4.(2)で確認します。
2.強磁性
前項で説明した常磁性体のなかには、誘起される磁石の強度が、普通の常磁性体の場合の数万倍以上の強い磁石となるものがあります。しかも、この磁石は外部磁場を取り除いても磁気をそのまま保持します。常磁性や反磁性は外部磁場を取り除くと資料塊に誘起された巨視的な磁気は消失しますから、これは明らかに特異な性質です。そのためこの場合を特に“強磁性体”といいます。
つまり誘起される磁性は常磁性的ですが、強度において桁違いに大きく、その磁性の性質も特異なものです。特異性については4.(3)で説明します。
(2)分類のメカニズム
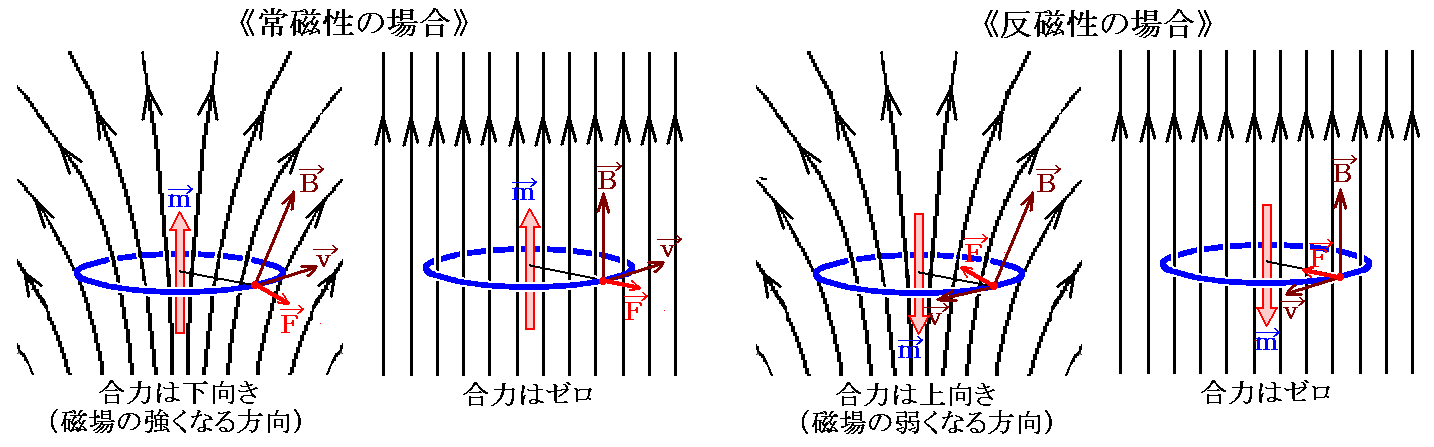
前節で示した図の左側のものは文献4.から、右側のものは文献5.から引用したものですが、左右の図は外部磁場の[磁極の方向]と[磁力線密度の変化の方向]が互いに逆の場合を取り上げていることに注意してください。前節の常磁性・反磁性の定義の元となる“力”の方向は、外部磁場の磁極の方向(つまり磁力線の方向)ではなくて、磁力線の密度が変化する方向に関係しています。ここはなかなか解りにくいところなので詳しく説明します。
1.常磁性
最初に、“常磁性体”の場合を図示すると、下図のような小磁石が物体の中に誘起される。
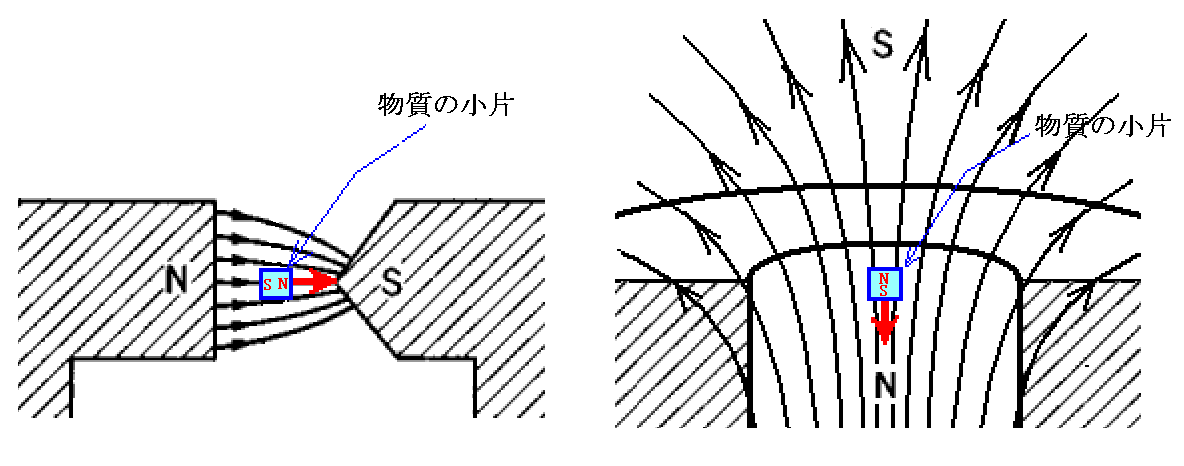
外部磁場によって誘起される小磁石の磁極の向きと、小磁石に生じる力の向きは左右の図で逆転していますが、いずれも誘起小磁石のNS極の向きは外部磁場の方向を向いていることに注意してください。そのためこの場合を“常磁性”という。
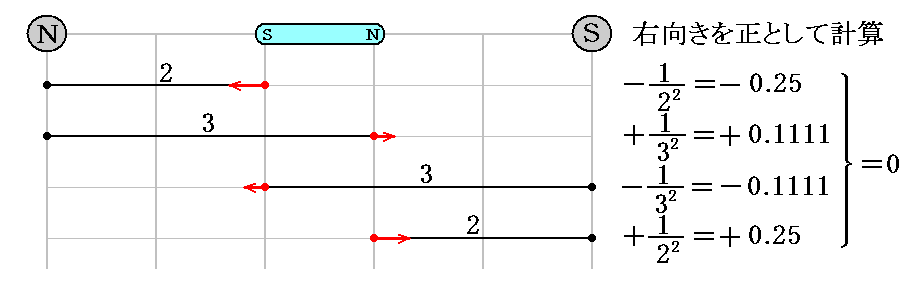
このとき、実際に赤矢印の方向の力が生じる事は次の計算をしてみれば解る。このとき外部磁場の磁力線密度の変化を外部磁極NとSからの距離の違いで表しています。そのあたりは下図の状況から了解していただけると思います。
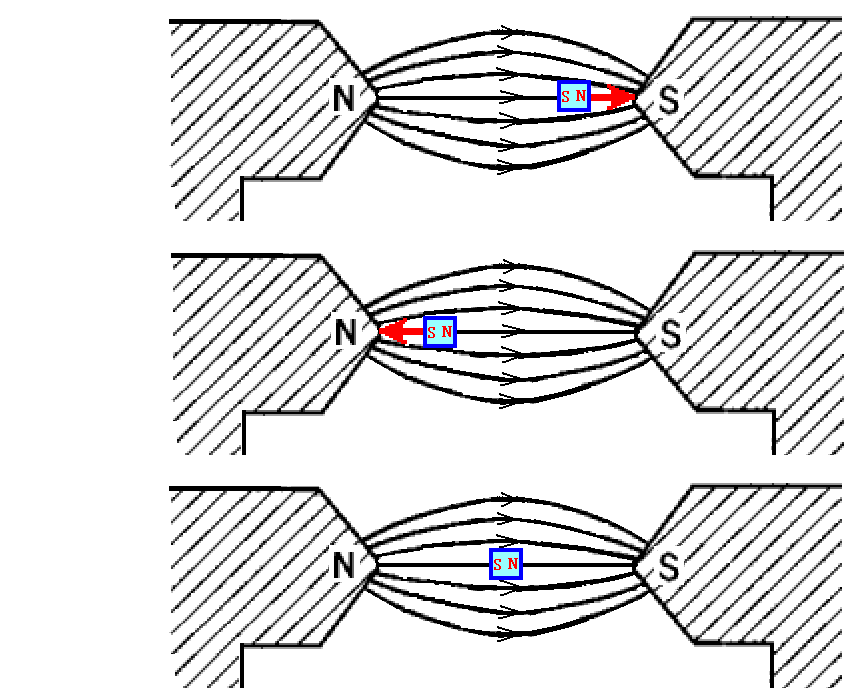
以下の上側の計算が上左図の場合であり、下側の計算が上右図の場合です。それぞれの磁極間の距離は1~4の間で変化するとし、磁極間にクーロンの法則に従った距離の逆二乗則で異種磁極間に引力、同種磁極間には斥力が働くとしています。
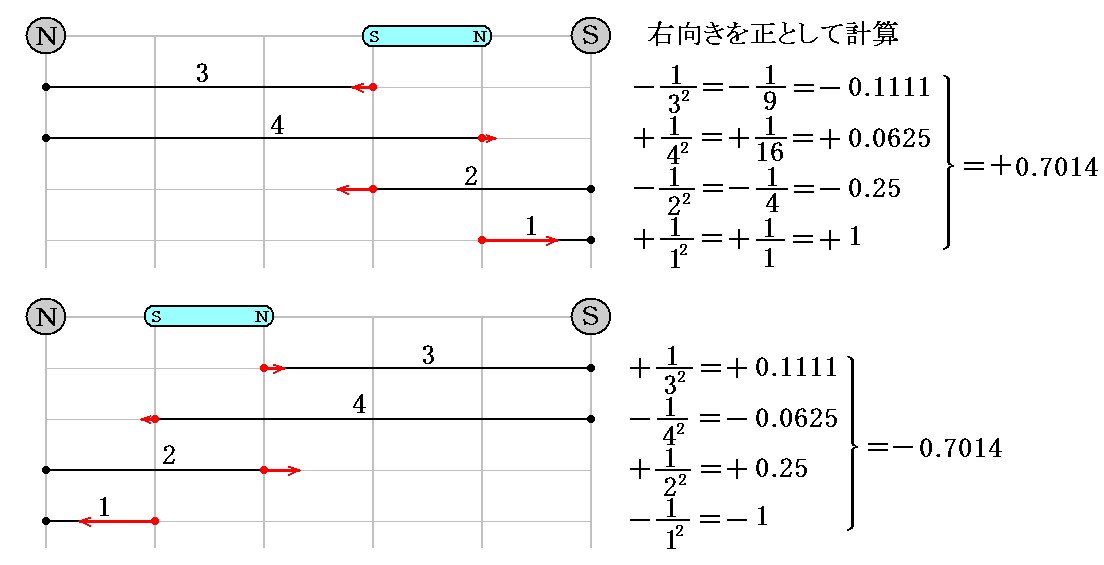
誘起された微少磁石に働く力の合力は、確かに図の赤矢印の方向を向くことが解る。
もし、外部磁場が磁力線密度の変化しない一様な場であったら小磁石に働く力の合力はゼロに成ることを注意してください。それは下図の様に誘起小磁石を外部磁極NとSの中間に置いて同様な計算をしてみれば解る。
2.反磁性
一方、“反磁性体”の場合は下図の様に誘起小磁石が生じます。
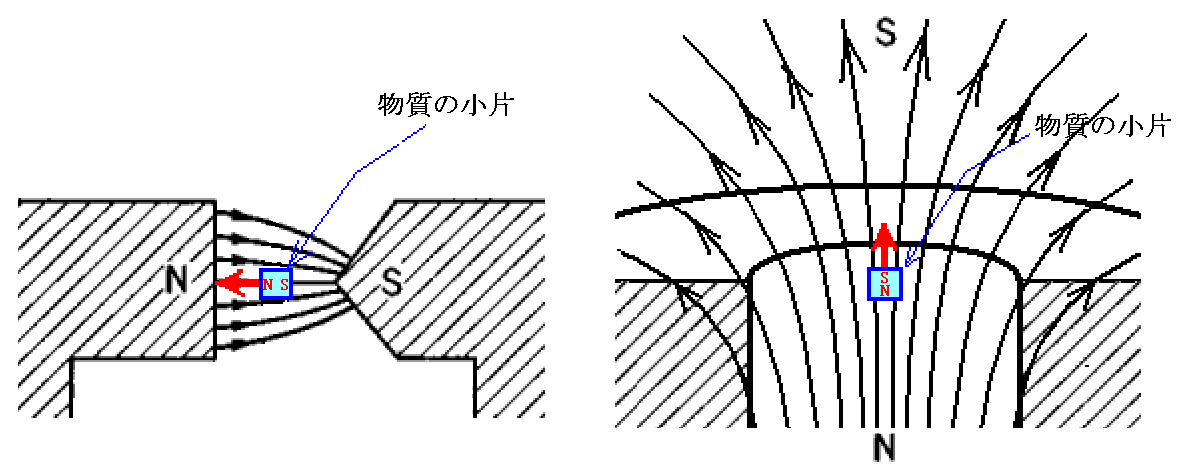
この場合も、誘起される小磁石の磁極の向きと小磁石に生じる力の向きは左右の図で逆転していますが、いずれも誘起小磁石のNS極は外部磁場と反対の方向です。そのためこの場合を“反磁性”という。
このときも前項に習って計算してみると、確かに赤矢印の方向の力が生じる事が解る。上側の計算が上左図の場合であり、下側の計算が上右図の場合です。
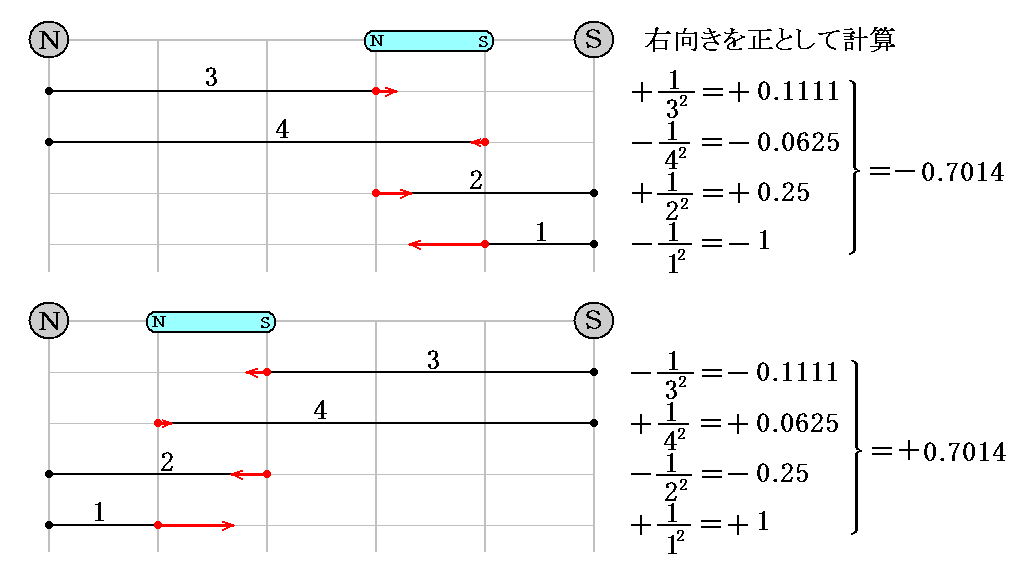
外部磁場が磁力線密度の変化しない一様な場であったら、この場合にも誘起小磁石に働く力の合力はゼロに成る。
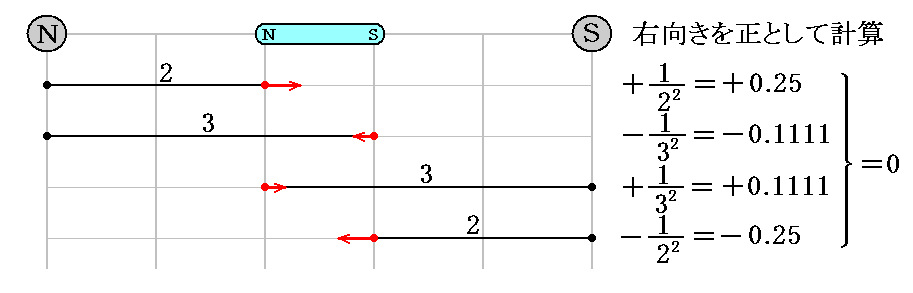
ここまでの説明で注意して欲しいことは、物質に磁気モーメントを誘起するのに外部磁場が不均一である必要は無いことです。均一な外部磁場でも常磁性あるいは反磁性のどちらかの磁気モーメントは生じます。その生じた磁気モーメントの存在を確かめるために不均一な外部磁場が必要だと言うことです。
最初から永久磁石として存在するのなら、均一磁場の中に入れれば磁石の回転の様子から磁石であることが解りますが、外部磁場によって励起される誘起磁石の場合には、その極性は常に印加される外部磁場の方向か、あるいは真反対の方向に生じますから、その回転の様子で磁石に成ったかどうかを調べることはできないのです。
その様に考えると“反磁性”というのはとても不思議な磁性です。外部磁場とは反対の方向に磁石の極性は生じるのに外部磁場に沿った方向に回転することは無いのですから。 と言うよりも資料が回転すると、その状況の外部磁場の方向と反対向きにただちに磁化し直されるのです。だから、上記の様な方法を用いないと磁化されたことを知ることができないのです。
その様に考えると“強磁性”も不思議な磁性です。外部磁場中にいれて一端磁化すると、その磁極の方向は強く固定されてしまうのですから。
3.円電流磁気モーメントによる証明
以上は磁極による説明ですが、この稿で用いている円電流による磁気双極子モーメントについても、磁場が一様ならば力は生じず、磁場が場所的に変化する場合にのみ力が生じることが同様に証明できる。
力の方向の関係を確認するだけなら、下図の様に電流の流れる方向を変えて、その[電荷の速度ベクトルv]と[磁場ベクトルB]の関係に“ローレンツの力の法則”q[v×B]を適用すればよい。下図は正電荷が回転して磁気モーメントを生じる場合で示していますが、負電荷に置き換えても同じです。。
力がdB/dzに比例する事を含めて証明したければ次のようにすればよい。



(3)磁性体の例
強磁性体の例として鉄や磁鉄鉱はよく知られていますが、普通の多くの物質も前項で述べた意味で常磁性あるいは反磁性のいずれかを示します。前節で述べた磁力線密度が場所的に変化する磁場中に置いたとき、実際にどのくらいの力が発生するかを下表に示す(参考文献5.より引用)。
物質を置く場所の磁束密度はB=1.8テスラ、その場所の磁束密度変化量はdB/dz=17テスラ/mです。資料として1gの塊を置いた場合に発生する力を示しています。力の働く方向は磁束密度が増大する方向を正(+)、その逆を負(-)としています。
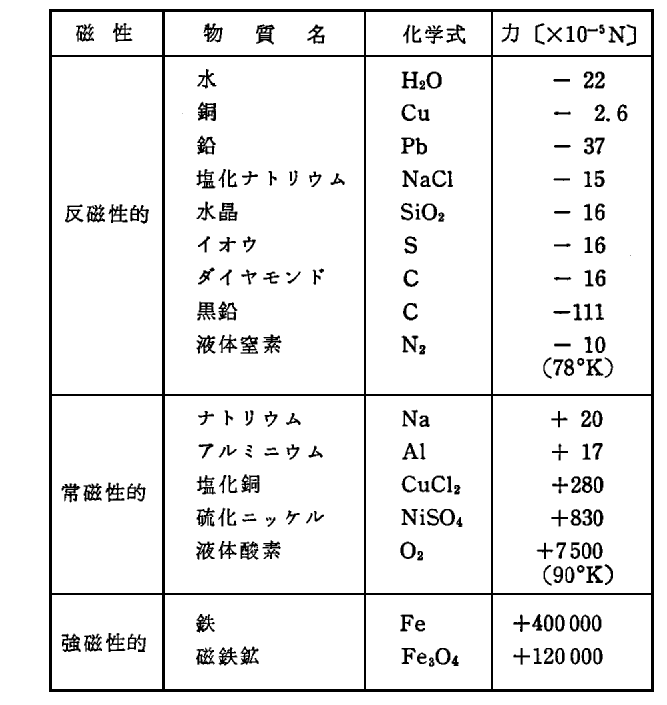
この表に関してもう少し補足すると以下のような特徴がある。
- 力の単位が×10-5Nであることに注意。1Nは高校物理で習うように100gの物質を地表で支えるときに手の平が感じる力の大きさですから、×10-5Nがどんなに小さな力であるか想像してください。1.8テスラと17テスラ/mはかなり強力な磁場であり磁場の変化量です。それでも“反磁性”や“常磁性”は非常に鋭敏な秤を用いないと測定できないくらい小さな値です。それに対して“強磁性”は普通の鉄でできた磁石が示す大きさです。
- 磁場中に置いたときに誘起される磁気モーメントの大きさは、“反磁性”と“常磁性”の場合は印加された磁場の強さに比例して大きくなる。もちろんいくらでも強くなると言うわけではなくて、ある程度大きくなると飽和に達する。
- そのとき生じた誘起磁気モーメントに働く外部磁場による力は、磁場の変化量dB/dzにほぼ比例する。だから実際のところ反磁性・常磁性物質が受ける“力”は、その物質を置いた場所におけるB×dB/dzに比例する。つまり生じる力は大体のところ磁場の二乗に比例する。
- 常磁性の場合、誘起される磁気モーメントは温度に関係するように見える。つまり温度が低いほどより大きな磁気モーメントが誘起され高温になると小さくなる。ところが、反磁性の場合には温度依存性はほとんどない。
- “強磁性”に関しては、誘起される磁気モーメントの大きさは反磁性・常磁性と違って印加する外部磁場の大きさにあまり依存しないように見える。
そのため、強磁性体に生じる“力”は外部磁場のdB/dzのみに比例する。つまり加えた磁場の大きさの一乗に比例する。
- “強磁性”物質(純鉄、純ニッケル、・・・)はある温度以上に加熱されると、その強磁性を突然失って常磁性物質の様にふるまう。純鉄の場合その温度は770℃です。そのとき純鉄は770℃以下に冷やすと再び強磁性の性質を回復する。この転移温度を“キュリー点”という。物質が異なれば転移温度も異なる。純ニッケルの転移温度は358℃です。
- “強磁性”物質の場合温度をキュリー点以上に上げて外部磁場の無い状態で冷却すると、巨視的な磁性は現れませんが、外部磁場を掛けた状態で冷却すると、その外部磁場の方向に強く磁化される。そうして励起される磁気の強さは外部磁場の強度にほとんど関係しない。また、その様にして励起された磁気は外部磁場を無くしてもそのまま保持される。
(4)磁性の古典論
1.常磁性
常磁性は古典的には次のように説明される。物質の内部には微少な磁石が多数存在し、物質の塊はそれらの集合体から構成されている。微少な磁石は本来様々な方向を向いており、その分布は各部分で均等と考えられるので、普段の状況では巨視的な磁気双極子として認識されることはない。
所が、その様な微少磁石の集合体を磁場の中に入れると、微少磁石の磁気モーメントベクトルの方向を磁場ベクトルBと平行にする力が働く。この当たりは別稿「回転運動の運動方程式」2.(3)や「ガウスによる地磁気の絶対測定(1832年)」で説明しました。
ここで説明している円形電流ループが構成する磁気双極子モーメントについても同様な効果が証明できる。
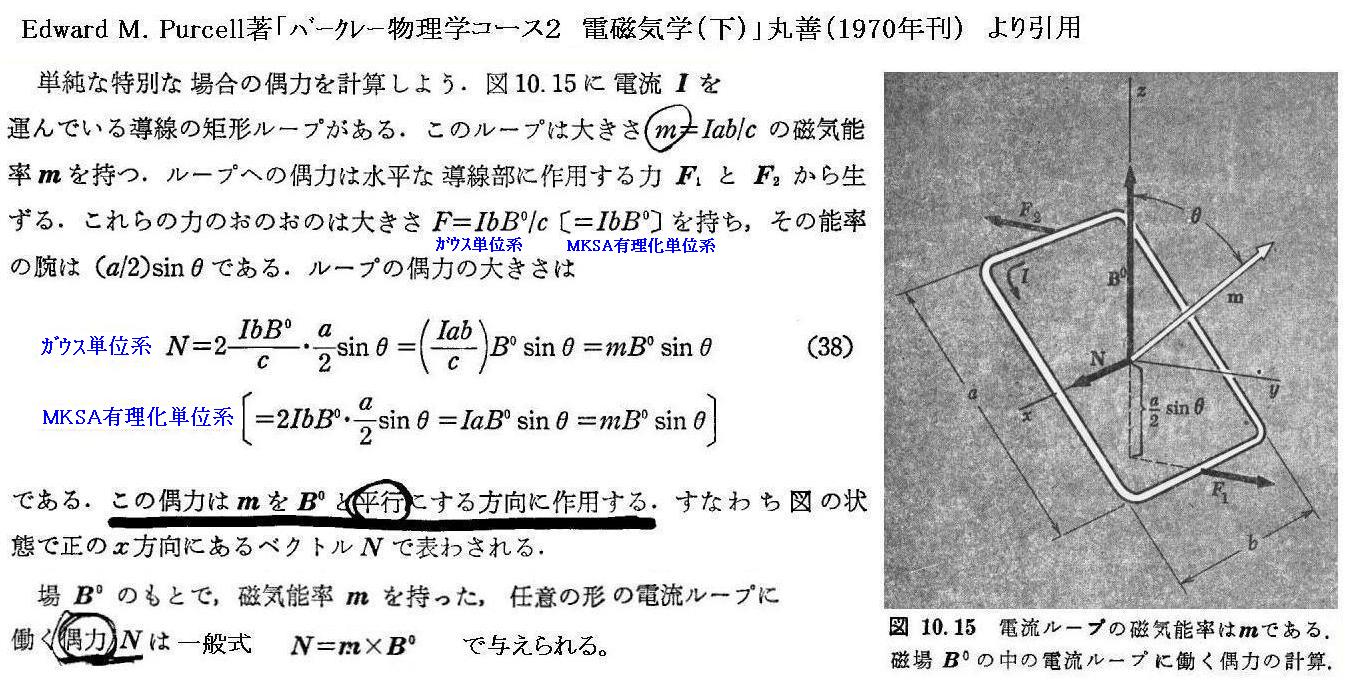
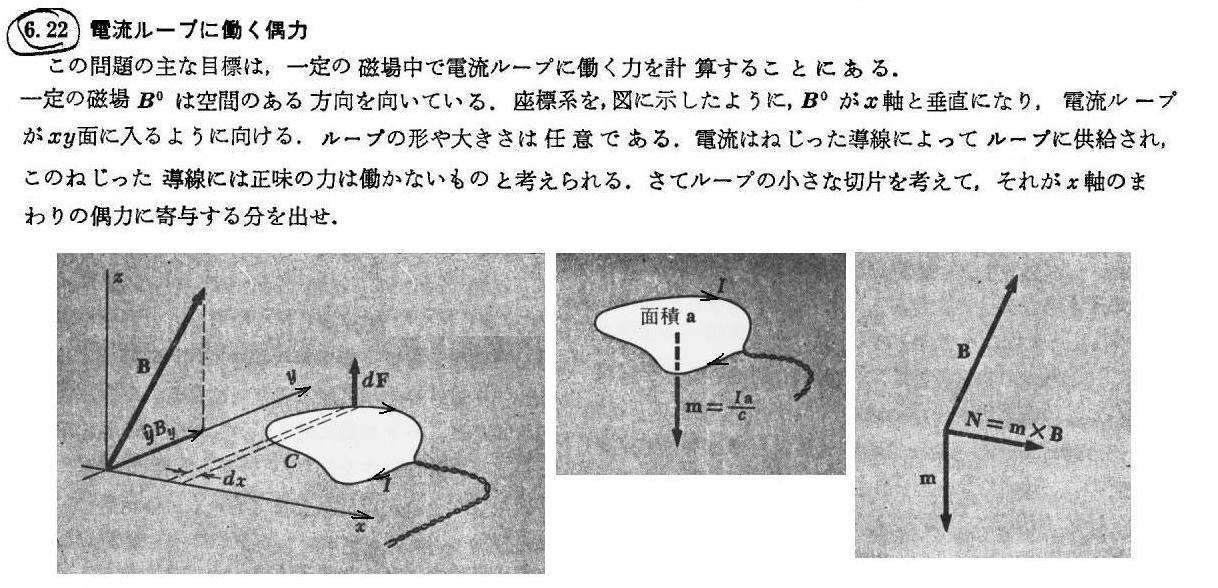

いずれにしても上記のメカニズムのために、全体として巨視的な磁気双曲モーメントが現れ磁気が励起される。この全磁気モーメントは印加磁場Bに比例するであろう。
また、一様でない外部磁場中に資料を置いたときに誘起磁気モーメントに生じる“力”はその誘起磁気モーメントを生じる外部磁場BにさらにdB/dzを乗じたものに比例することになる。
さらにこのとき、微少磁石の方向は熱的な擾乱運動により、常にアトランダムな方向を向こうとしますから、誘起される磁気双極子モーメントの大きさは温度に逆比例することになる。
このように考えれば常磁性の原因は古典的に説明できそうです。
しかし、その微少磁石の実態に関しては何も解っていないことに注意してください。
これは、量子力学によってその存在が解明される電子スピンに関係しており、その挙動に付いても量子力学的な議論をしないと説明できません。
実際、なぜ全ての物質が常磁性とならないのかも量子力学を用いないと説明できません。その理由は、たいていの原子と分子では、電子は対を作り、各対の中では印加磁場のいかんにかかわらず二つの電子のスピンが逆方向に向かうように強制されている。その結果として、一つの電子対の磁気能率は互いに完全に打ち消しあっている。
そのとき、遷移金属や希土類元素は部分的にしか満たされない軌道電子があり、その磁気モーメントが打ち消されずに残っている。これが磁場の方向を向くために常磁性を示す。
2.反磁性
反磁性の古典的説明は常磁性よりも難しいが、この稿で取り上げた“ラーモアの定理”が適用できそうです。反磁性の場合も常磁性の場合と同様に、微少磁気モーメントを生じる電荷の回転方向は本来あらゆる方向をアトランダムに向いている。そのため外部磁場が印加されないときは、それらの微少磁気モーメントは互いに打ち消しあって巨視的な磁気双極子モーメントは現れない。
そこへ外部磁場が印加されると3.(2)で述べたメカニズムにより、反磁性が生じる。
そこで説明したように、外部磁場に対して同じ方向を向く微少磁石と反対方向を向く微少磁石の割合は同じですが、そのどちらについても外部磁場とは逆方向の磁気モーメントの変化を生じます。ここの所に“ラーモアの定理”の真骨頂があります。そのため反磁性が誘起される。
もう一つ重要なことは、磁気モーメントは質量に関係する慣性モーメント(角運動量モーメント)も持っており、その微少磁石の方向が外部磁場の方向とは逆向きでも、コマの理論から明らかなように、歳差運動は生じるが単純に外部磁場の方向に向いてしまう事がない事です。
反磁性についても3.(2)で述べたメカニズムにより誘起される磁気モーメントの大きさは外部磁場Bの強さに比例します。
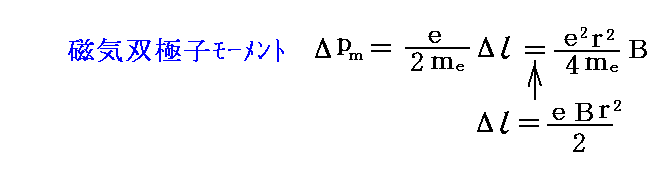
そのため常磁性と同じように誘起磁気モーメントに生じる“力”はその誘起磁気モーメントを生じる外部磁場BにさらにdB/dzを乗じたものに比例することになる。
また、反磁性をしめす磁気双極子モーメントの変化を生じるメカニズムから、誘起反磁性が常磁性と違って温度に依存しないことも納得できる。
このように考えれば、反磁性の原因も古典的に説明できそうに見えます。
ところが、この場合にも反磁性を生じる微少磁石の実態は何も解っていないことに注意してください。
さらに、反磁性で最も解らないところは、コマが外力で単純にその回転軸が回転する事はない(歳差運動をするが印加磁場の方向に向く事はない)と言っても、それらの微少磁石は熱的な擾乱を常に受けているはずですから、やがては外部磁場の方向へそろうはずです。つまり最初は反対方向を向いていた二つの微少磁石もやがては両方とも外部磁場の方向を向いてしまうであろう。なぜそうならずに反磁性が保たれるのか。これはとても不思議なことです。
この疑問も量子力学によらなければ理解できません。それは、多くの場合その二個の微少磁石(2個の電子)は量子力学によって軌道回転の方向を互いに反対方向に保つように要請されている。そのため電子は互いに反対向きのスピンを持つ組が対を作って磁場は相殺されている。だからこそ反磁性が生じる。
以上のように、常磁性も反磁性も量子力学によらないと理解できない現象です。特に電子スピンの発見とその性質の解明が不可欠です。これは異常ゼーマン効果の説明に量子論が必要であることと同様です。
3.強磁性
強誘電体が外部電場におかれると、物体内の微少電気双極子が外部電場の方向を向き、その事が互いの微少電気双極子に相互作用(協同現象)を起こす。そうして、全ての微少電気双極子が同じ方向を向き強い巨視的な強い誘電分極が生じる。
一見、磁気に関しても同じメカニズムが使えそうです。しかし、それは無理です。磁気的な力は電気的な力に比べて非常に小さいので、熱による擾乱に打ち勝つ事はできません。
強磁性が示す不思議な性質は量子的な効果に基づいており、量子力学を学ばないと理解できません。
5.参考文献
この稿を作るに当たって、以下の文献を参照しました。ここで説明したラーモアの考え方は物質の磁性理論や量子論の展開に大きな影響を与えたものです。いつかその当たりの所を含めた量子理論による理解をきちんとしたいところです。
- E.シュポルスキー著「原子物理學Ⅰ」東京図書(1965年刊)第5章§76~78、附録Ⅲ
- A.Sommerfeld著「原子構造とスペクトル線Ⅰ(下)」講談社(1973年刊)第6章§4
- A.Sommerfeld著「理論物理学講座Ⅳ 光学」講談社(1969年刊)第Ⅲ章§21、演習問題Ⅲ.4
- ファインマン、レイトン、サンズ著「ファインマン物理学Ⅳ 電磁波と物性」岩波書店(1971年刊)§13
- Edward M. Purcell著「バークレー物理学コース2 電磁気学(下)」丸善(1970年刊)の第10章