�������_�i���p�ʑ��ƃW���[�R�t�X�L�[�̉���j
�P�D�����_�̉萶��
�@���֔��Ă��邱�Ƃ͐l�ނ̍ő�̖��ł����B���̎����ɂ͗��̎������̗������K�{�ł��B�����ł͗��̒����ړ����闃�����ݏo���g�͂̃��J�j�Y����������܂��B
�@�����i�X�p���j���L���ȗ��i�O�������ƌ����j�̋c�_�͂��Ȃ����Ȃ邽�߁A�����ł͗����������ɒ������̂܂��̗��ꂪ���I�ɉ�͂ł�������Ɍ����ċc�_���܂��B�O�������ɂ��Ă͕ʍe�Ő������܂��B
�@�g�͂Ƃ͉����𗝉����邽�߂ɂ́A���̎�����������ɖ��炩�ɂ���Ă������j�I�ȗ����c�����Ă������Ƃ��K�v�ł�������Ƃ��čŏ��ɕʍe�u�����_�̉萶���i�����G���^�[���A�����O���[�A���C�g�Z��̔�s�j�v���䗗�������B
�@
�Q�D�z���_�̉萶��
�@���������_�ł͏z�Ƃ����T�O�����S�I�Ȗ������ʂ����܂��̂ŁA�܂����̐�������n�߂܂��B�����_�ւ̍ŏ��̍v���͂����炭1852�N�Ƀ}�O�i�X���ώ@���������ł��B
�i�P�j�n�C�����b�q�E�}�O�i�X�i1802�`1870�N�j
�@1878�N�A���C���[�͉~�������s�Ȉ�l�����ɂ������m�܂��́A�~�����Î~���̒�����l�ȑ��x�œ����n�ꍇ�ɁA�������s�Ȉ�l���ɏz���d�˂�ƁA���Ƃ̈�l���̕����m�܂��́A�~���̐i�s�����n�ɐ����ɁA�����܂����͂��������Ƃ𖾂炩�ɂ��܂����B
�@����́A19���I�̏��߂ɂ͖C�p�Ƃ����ɍL���m���Ă����}�O�k�X�������̂��̂ł��B�}�O�k�X��1852�N���ɖC�e�m�����̖C�e�͋��`�������n�̔�s�̌�������m�����̂ł����A�{�[���ɉ�]��^����ƋȂ����Ĕ�ԂƂ������̓e�j�X�v���[���[��S���t�v���[���[�ɂ͗ǂ��m���Ă����B
�@���̌��ۂ́A���̏ꍇ�A�x���k�[�C�̒藝��p����Δ�r�I�ȒP�ɐ����ł��܂��B��]����{�[����~���́A�����͂����݂����C�̔S���ɂ��A���̎������]���闬���U�N���܂��B���̗��ꂪ��l���ɏd�ˍ��킳��̂ŁA��]�������ꍇ�̉����}�̗��ꂪ���E�}�̂悤�ɂȂ�܂��B
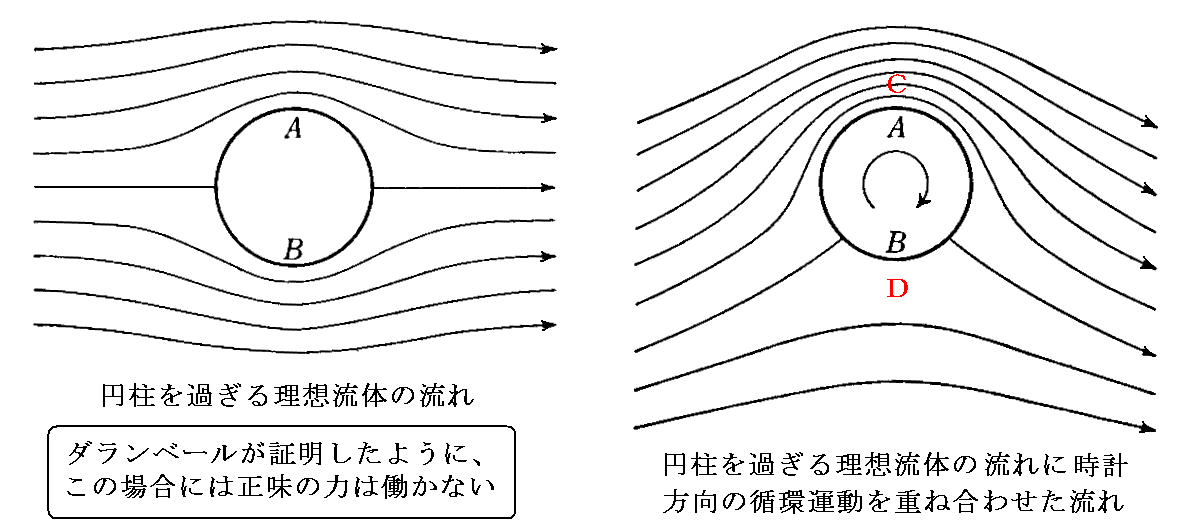
�@�E�}�̂`�̏㑤�b�ł͗����͑傫���A�a�̉����c�ł͗����͏������Ȃ�܂��B�S���������]����~���\�ʂɗ��̂�����t���Ă���ꍇ�ɂ��Q�����̗���ɂ͂Ȃ�܂������A��헬�ƍl���邱�Ƃ��ł���̂ŗ����ɉ������x���k�[�C�̒藝�����藧���܂��B���̂Ƃ�����̏㗬���ł͈�l��헬�����痬���̈Ⴂ�ɂ�����炸�ϕ��萔�������l�ɂȂ�x���k�[�C�̒藝�����藧�ƍl���ėǂ��̂ŁA����
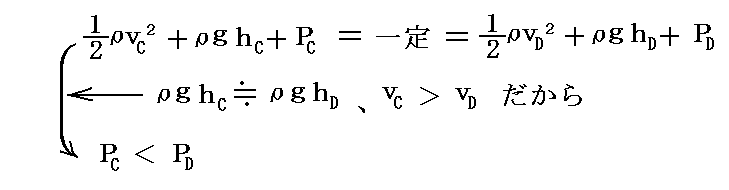
�ƂȂ�B���̂��߉�]���鋅���邢�͉~���͈�l���ɐ����ȕ����̗͂��邱�ƂɂȂ�܂��B���̓�����̓��[���[����1878�N�̘_���Ő������Ă���B���̂Ƃ����}�̗���ł́A�_�����x�[�����ؖ������悤�������̗͓͂����Ȃ��������Ƃɒ��ӂ��Ă��������B
�i�Q�j�t���f���b�N�E�����`�F�X�^�[�i1868�`1946�N�j
�@�O�߂̃}�O�i�X���ʂ𗃂̗g�͂ƌ��т��čl�����ŏ��̐l�͂����炭�t���f���b�N�E�����`�F�X�^�[�m�C�M���X�̍H�ƋZ�p�ҁn�ł��傤�B�ނ�1891�`1892�N���A�L�����p�[���Ɋւ����A�̎��������āA���̗g�͂ɕt���Ă̗L������m�����B�ނ̓t�B���b�v�X����G���^�[���̐�s�����ɂ͋C�t�������̎���m�����悤�ł��B
�@�����`�F�X�^�[�̓L�����o�[���̗g�͂ɂ��Ď��̂悤�ɍl�����B����̗��q���A���ɐڋ߂���Ƃ��ɂ͏�����̉����x���āA�O���ɐڐG����Ƃ��ɂ͏�����̗��������B���̉��������͏��ʉ߂���Ԃɗ���͉������ƂȂ艺���ւ̉^���ɕϊ������B���̗l�ɋȂ����������́A�g�͖ʂƂ͖��W�Ȏ��R���̉^���ɏz�^�����d�ˍ��킳���ƍl����Ǝ����ł����B���̂悤�ɍl����ΑO�߂̂悤�Ƀx���k�[�C�̒藝����g�͂��������邱�ƂɂȂ�B
�@�ނ́A��������̗l�ȏz��1858�N�Ƀw�����z���c����Ă����Q�������������ɕ���ł���m��������������Q�ƌĂԁn���Ƃɂ�萶����ƍl�����B���̂Ƃ��C���������ʂ̍����̈悩�痃��ʂ̒ሳ�̈�Ɍ������ė��̐�[�ŋȂ��藃�[�t�߂ɖ���̉Q�^���m�ނ͂�����Q���ƌĂ��������R�Q�ƌĂ��n�������Ɛ��������B
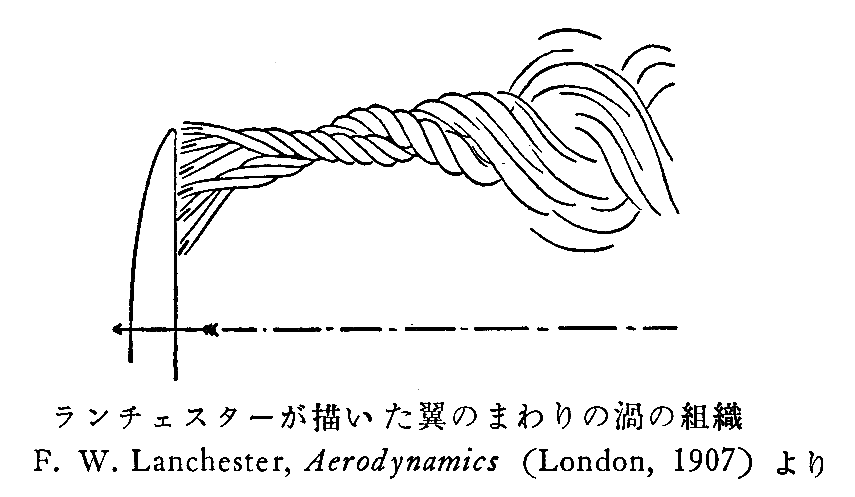
�@�w�����z���c��1858�N���Q�Ɋւ���L���Ș_���ŁA�Q�͋�C���Ŏn�܂鎖���I��邱�Ƃ��ł��Ȃ��B�K���ǂ̂Ƃ���ŏI��邩�A�����Ȃ��Ε����ւɂȂ�Ȃ���Ȃ�Ȃ������ؖ������B����ŁA�����`�F�X�^�[�͌��_�Ƃ��������Q�����[�ŏI���Ȃ�A�������̑������K�v�ł���A����͎��R�Q�ɂȂ�˂Ȃ�Ȃ��ƍl�����̂ł����B
�@�܂�A�����`�F�X�^�[�ɂ��ƗL�����̎���̗���́A�㗬���̈�l���A���������ɕ��Q���Q�ɂ����o�����z���A���[���牺���Ɍ������ĐL�тĂ������R�Q�m�Q���n���������ꂽ���̂ƌ������ƂɂȂ�܂��B�ނ̍l�����͏�}�ɒ[�I�ɕ\����Ă���B
�@���̍l�����ɂ͓�̏d�v�Ȏ������܂܂�Ă��܂��B
�m�U����R�n
�@���̈�Ԗڂ͎��R�Q�̈����N��������͗��̈ʒu�ɉ������̐������낵�̗���ݏo�����Ƃł��B���̂��ߗ��ɑ��鎩�R���̗��ꂪ�����������ɂȂ�A�z�ɔ������ɓ����͂̍��͂̕��������������������ƂɂȂ�܂��B���̂��ߒ�R�̐������������Ă��āA�����g�́^�R�͔����������Ȃ��Ă��܂��܂��B���̂Ƃ��������R�͗g�͂̔����ɔ����ĕK�R�I�ɐ�����i�܂�g�͂���U�������j������������R���U����R�ƌ����܂��B�����ɂ͈��͒�R�̈��Ȃ̂ł������[�Q�����݂��邱�ƂɋN�����Đ����܂��B�U���Ƃ������O��t�����̂̓v�����g���̗D�G�Ȓ�q�ł������}�C�P���E�}�b�N�X�E�����N�ł��B
�m�A�X�y�N�g��n
�@��Ԗڂ́A���������������ɒ�����Ώ�L�̗l�Ȏ��R�Q�m�Q���n�͑��݂��Ȃ��ƌ������Ƃł��B���̏ꍇ��L�̍R�͂̑����͔������܂���B�����ϗ������Ŋ������l���A�X�y�N�g���ƌ����܂����A�X�y�N�g�䂪�傫�����قǗg�́^�R�͔䂪�傫���Ȃ邱�Ƃ��Ӗ����܂��B����͔�s�̎����Ɏ���Ă���߂ďd�v�Ȏ����ł��B
�@�����`�F�X�^�[�����̂��ƂɊւ��Ăǂ��܂Ő��m�ɗ������Ă������͋^��ł����A����͂܂������v�����g�����W�J�����g�͐����_�̓��e���̂��̂ƌ����ėǂ��ł��傤�B���̂��ƂɊւ��Ă͕ʍe�ŏڂ����������܂��B�����`�F�X�^�[��1908�N��1909�N�ɃQ�b�e�B���Q���̃v�����g����K�₵�āA���̂��ƂɊւ��ċc�_���Ă��܂��B�v�����g���������`�F�X�^�[����ǂ̒��x�e�������̂����ƂȂ��Ă͗ǂ�����܂��A���炩�̃q���g���̂����m��܂���B
�@�����`�F�X�^�[�͂܂��Ƃɗǂ����������Ă����̂ł����A1894�N�ɔ��\���ꂽ�ނ̍l���̓C�M���X�ł͗₽����������A���ڂ���邱�Ƃ��Ȃ�������Ă��܂��܂��B�ŏI�I�ɔނ�1907�N�Ɂu��C�͊w�v�A1908�N�u����͊w�v�Ƃ�������̖{���o�ł��܂��B���ɑO�҂̓h�C�c��ƃt�����X��ɖ|��āA��ʂ̉Ȋw�ҒB���ނ̗g�͂Ɋւ���l������m�邱�Ƃ��ł���悤�ɂȂ�܂��B
�@���̂Ƃ��ɂȂ��Ĕނ̒����������ꂽ�͎̂���̗��ꂪ�ς��������ł��B1903�N�̃��C�g�Z��̏���s��1908�N�̃��[���b�p�ɂ�����E�B���o�[�E���C�g�̃f�����X�g���[�V������s�́A�����̐l�X�ɋ���ԋ@�B�ɑ��鋻���E�S���Z���Z�[�V���i���Ɋ��N���܂����B�܂��ɔ�s�@�̎��オ�n�܂�A�����_�̌��������̗͊w�̐��Ƃ̑傫�ȊS���ɂȂ��Ă����̂ł��B
�m�����`�F�X�^�[�ɂ��ẮA����19�D��3-10���Q�Ƃ���Ă��������B�B�n
�i�R�j�E�B���w�����E�N�b�^�i1867�`1944�N�j
�@1902�N�~�����w����w�̃N�b�^�͉~�ʗ��^����̔k�����S���̗̂���ɂ���ėg�͂��������郁�J�j�Y�����������_���u���̉^���ɂ�����g�́v�i�o�ł���邱�Ƃ̖����������m�_���j�\�����B���_������ɓ���Ȃ��̂ŏڍׂ��悭����Ȃ����A�Q�l�����P�D��P�Q�D�̋L�q���琄�@����Ɖ��L�̗l�Ȃ��̂������̂��낤�B�i�ނ�1902�N�̔��m�_���͑���E���ŏĎ����Ă��܂��A���̔��������c���Ă��Ȃ��B�悭�Q�l�����ɏグ���Ă���̂͂��̔����W�̂悤�ł��B�j
�@�ނ́A�~�ʗ��^����̗����\�����̗����������߂��B�������̓������̕����������ł��邪�A�ނ͉~�ʏ�̗��^�̏�ʂƉ��ʂɒ��ڐڐG���Ă��闬���͋ȖʂƓ����`��łȂ���Ȃ�Ȃ����Ɖ����ł͕��s��l���ł���Ƃ��������p���ė������̋�ԕ��z�����߂��̂ł��낤�B�����������܂�A�����������邱�Ƃɂ���ė��^�̏�ʂƉ��ʂ̋Ǐ��I�ȗ��������߂邱�Ƃ��ł���B�N�b�^�͂��̗l�ɂ��ċ��߂������Ƀx���k�[�C�̎���K�p���ė��ɓ������͕��z�����߁A�����ώZ���鎖�ɂ���Ď��Ɏ����g�͂̎����B

����͌}���p���[���̉~�ʗ��̗g�͂�\�����ł��B
�@���ۂ̏��A���̎��̒��ɂ͏z��\���\���͖����B���̂Ƃ��̔ނ͏z�̍l�����ɋC�t���Ă͂��炸�A�����炭�A���̎��ƉQ�����̗���̉��肩�瓾���郉�v���X�̕����������E�����ɏ]���ĉ������̂ł��낤�B���̂Ƃ����f���_�̓��p�ʑ��̕��@��p�����悤�ł��m���̂������V�D�i�R�j�ŏڂ����������܂��n�B��������Ή��}�̗l�ȗ��ꂪ������B���̏ꍇ���R�̂��Ƃł����~�ʗ��̏�ʂ̗������傫���Ȃ�A���ʂ̗����͏������Ȃ�̂ŏ�����̗͂��������܂��B

�@�ŏ��A�ނ͂��̉��̒��ɗ��̕\�ʂɉ����đ��݂���z�̑��݂�ǂݎ�邱�Ƃ͂ł��Ȃ��������A��ɂ��̂��ƂɋC�t���āu��s���̊�b�Ɋւ�������ɂ��āv�i1910�N�j�Ƃ����_����1902�N�̗��_���ĉ��߂��Ă���B���̒��ŁA�ނ́A1902�N�̎���ό`���āA�g�͂𖧓x�ρE�����t�E�z���̐ςƂ��ĕ\�������Ă���B�����1906�N�ɃW���[�R�t�X�L�[���g�͂̏z���_�\������ł��������A�O�L�̎��̒��ɂ��̗��_���܂܂�Ă���A�������_��1902�N�ɂ��łɓ��Ă����ƌ������ƂŁA�N�b�^���g�͂̏z���_�̊J�������ɒS�����ƌ��Ȃ���Ă���B
�i�S�j�j�R���C�E�W���[�R�t�X�L�[�i1847�`1921�N�j
�@���V�A�̃W���[�R�t�X�L�[��1906�N�̘_���ŁA�����̒P�ʕ�������ɓ����g�͂̎��Ƃ���

�����B�����Ń��͗��^���܂ޔC�ӂ̕Ȑ��ɉ����ė�������ϕ����ē�����z���Ӗ�����B����́A�N�b�^��������1902�N�̘_�����ɖ�����Ă����W���Ƃ���1910�N�̘_���œ��������ł�����B���̂��߁A���̎����N�b�^�E�W���[�R�t�X�L�[�̒藝�ƌ����B
�@���̎��̌����ڂ̊ȒP���Ƃ͗����ɁA���闬���t�̒��Ɍ}���p���Œu���ꂽ�C�ӂ̗��^�̏z�����v�Z���邱�Ƃ͊ȒP�ł͂���܂���B�N�b�^��W���[�R�t�X�L�[�͕��f���_�̓��p�ʑ��̃e�N�j�b�N��p���āA�z���Ɨ��^�Ƃ��W�Â���v�Z���@���J�����āA�ᑬ�E�k���E���S���̂ɂ���������v�@���m�������B�ȉ��ł��̕��@���������B
�@
�R�D�z�����~������̗���
�@���E�k���E���S���̂̉Q�����̗���ł͕��f���_�̃e�N�j�b�N���g���܂��B����Ɋ���Ă����Ȃ����́A��Ɂu�J���}���Q��i���I���萫��́j�v�A�u�Q��R�i�J���}���Q��ƍR�́j�v�A�u���f���̐ϕ��i�u���W�E�X�̌����j�v�����ǂ݉������B
�i�P�j��l�����ɐÎ~���Ă���~���̎���̗���
�@�ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�P�D�i�R�j�Q�D�̑�������n�߂܂��B�����̌��_��p����ƁA�����̐��̕��������x�t�ŗ���Ă���m���x�t�̌������A�����Ƃ͋t�ɂ��Ă���n��l�������Î~���Ēu���ꂽ���a���̉~���i���S�����_�Ƃ���j�̂܂��̗����̕��f���x�|�e���V�������f��
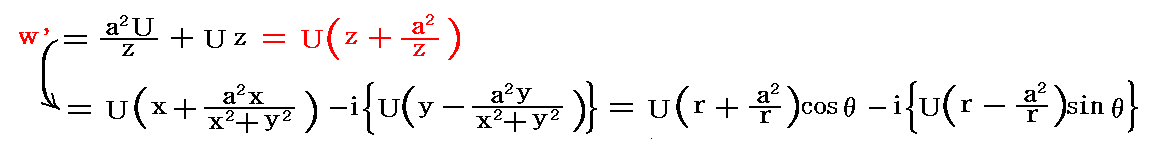
�ƂȂ�B���̉~������̗���̑��x�|�e���V�����Ɨ������̃O���t�A�y�єC�ӓ_�ɂ����鑬�x�x�N�g���ɂ��ẮA�ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�P�D�i�R�j�Q�D���䗗���������B������l����x���̐��̕����ɗ�����Ƃ���B
�@���ɁA��L�̗���ɁA���_���������i��0�j�̎��v������Q���i�|����0�j�����݂���Ƃ��̓�����\�����f���x�|�e���V�������h
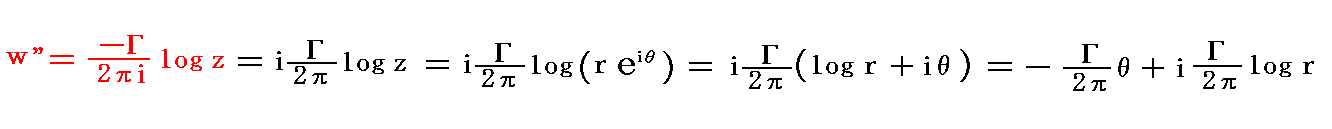
���d�ˍ��킹�Ă݂�B�Q���̋����͔����v���̏ꍇ�𐳂Ƃ���̂ō��́|���Ƃ��Ă����B���̂Ƃ��ʍe�u�J���}���Q��i���I���萫��́j�v�Q�D�i�Q�j�Q�D�Œ��ӂ����悤�ɁA���̗���͓��ٓ_�ł��錴�_���������Q�����̗����ł��邱�Ƃɒ��ӂ��Ă��������B�܂����̗���̗����͓��S�~�ł��邩��A�O�L�̋��E�����𗐂����Ƃ͂Ȃ��A������d�ˍ��킹���������͂�~���̎���𗬂���Q�����̗�����\���B
�@�d�ˍ��킳�ꂽ�����\�����f���x�|�e���V�������Ƒ��x�|�e���V�������A����������
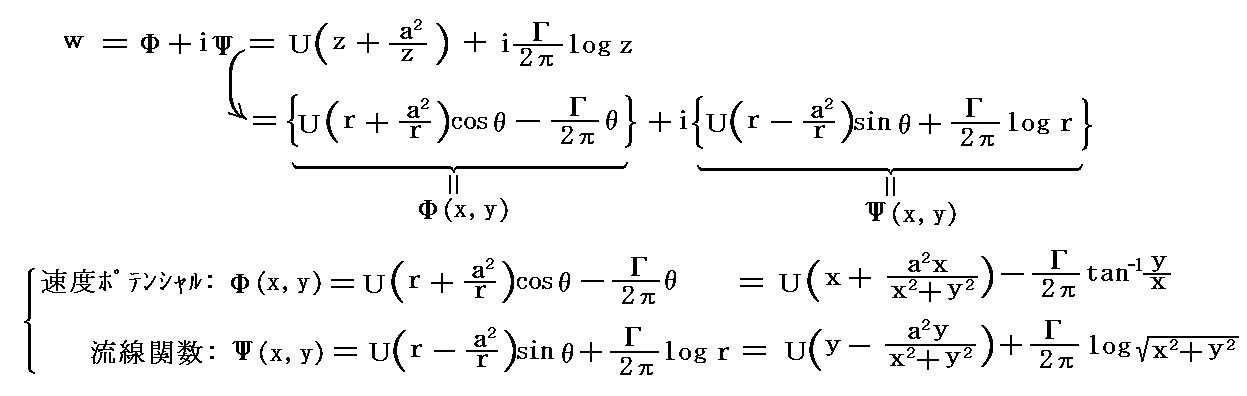
�ƂȂ�B
�@���̂悤�ȉ��́A�������Ƒ��x�|�e���V���������f���_�ɂ������R�[�V�[�E���[�}���̊W��������ƌ������Ƃ���o�Ă����B�܂�����炪�R�[�V�[�E���[�}���̊W�������邱�Ƃ́A�ʍe�u���E�k���E���S���̗̂͊w�i���O�����W���̉Q�藝�Ƃ͉����j�v�S�D�i�Q�j�Ő��������悤�ɓ��E�k���E���S���̂̉Q�����̗���Ő��������A���̕��������^������������o�Ă����B���̂Ƃ��^���������́A�������̏㗬��ʼnQ�����̗���ł��������̂́A�~���̕t�߂ɗ��ꉺ����������͂�Q�����̗��ꂪ���藧���Ă���Ƃ������O�����W���̉Q�藝��K�p����Ƃ���Ɏg���Ă���B
�@
�@���̂Ƃ��z���͂ǂ�����o�Ă����̂��ƌ����ƁA�ŏ����瑶�݂��Ă����̂ł����B�������A���̋c�_�ōł�����ɂ����Ƃ��낾���A�~���̎������]����悤�ȗ���͍ŏ����瑶�݂��Ă���Ƃ��Ă���B�����āA�j���[�g���̊����̖@���������l�ɓ����Ă��镨�̂͂��܂ł�����������B�܂�~���̎���̉�]�^���͎������ꑱ����B
�@���̂Ƃ���]����^����S�����͎̂��X�Ɠ���ւ���Ă���̂ɁA���̂悤�Ȏ����\�Ȃ̂��Ǝv���邩���m��Ȃ����A���̗l�ȗ���l����Δ[�����Ă��炦��Ǝv���B�����C�̂Ȃ����̏�ɑ�R�̕��̂�����ʼnE�����Ɉ�l�ȑ��x�œ����Ă���Ƃ��悤�B���̂Ƃ�����u�Ԃɂ��̒��̈�̕��̂��̓������~�߂��Ƃ���B�m���ꂪ�z��^�������Ƃɑ�������n

�@���ꂩ�班�����Ԃ��o�ƍ����痈��ׂ̕��̂��{�P���A���̂��ɏՓ˂��ĕ��̂��{�P�������Ă����^���ʂ����ɗ^�����̂��{�P�͂��̏�ɐÎ~������B���̂��͍Ăѓ����o���ĉE�����ɗ���Ă䂭�B�����ĐV�����Î~�������̂��{�P�ɁA����ɍ����痈�镨�̂��{�Q���Փ˂��ĕ��̂��{�P���E�����ɓ������A����͂����ɐÎ~����B�ȉ����l�ł���B���̂悤�ɂ��ĕ��̗̂���̒��̂��镔�����Î~�����ƌ����́A���̌���ۑ�����Ă����B
�@��L�̎���́A���ʂ�`�d���Ă����d�͕\�ʔg�̂悤�Ȃ��̂��ƍl���邱�Ƃ��ł���B�g�̂Ƃ���ŏK���悤�ɁA�g�̐���オ�肪�`�d���Ă����̗��q�͌��̈ʒu�ɂƂǂ܂��Ă���B�܂�A�g�����B�����Ƃ��������̗��q�͉�]�^�������Ĕg�̉^���ɎQ������̂ł����āA�i�s����g���\�����闬�̗��q�͂ǂ�ǂ����ւ���Ă���B���̂悤�Ȍ��ۂ��\�Ȃ��Ƃ̓j���[�g���̉^���̎O�@���������Ă���邱�Ƃł��B��L�̂悤�ɗ��̗��q�����X�Ɠ���ւ��Ȃ���z�i�Q�^���j���ۑ�����ē`�d���Ă����̂�����Ɨގ��̌��ۂ��ƍl����悢�B
�@
�i�Q�j�������Ƒ��x�|�e���V����
�@�O���̗������Ƒ��x�|�e���V������}�����Ă݂�B���̂Ƃ�����̗l�q�͉Q���̋������i�z�j�ɂ�莟�̎O�ʂ�ɕ������B���̗l�ɂȂ邱�Ƃ��R�D�i�R�j�R�D�Ő�������B
�P�D����4���t�̏ꍇ
�@����́A�~���̎���̏z����r�I�������ꍇ�ŁA���ݓ_�͉~���\�ʂ̉����̍��E�Ώ̂̈ʒu�ɓ�����B
�m����2���t�̏ꍇ�n
�@�������A�c�����A�����P�A�������Ԋu0.2�t�A���C���������x�|�e���V�������m���i���C���j�����̐��n�A�ԃ��C���������m���i���C���j�����̐��n
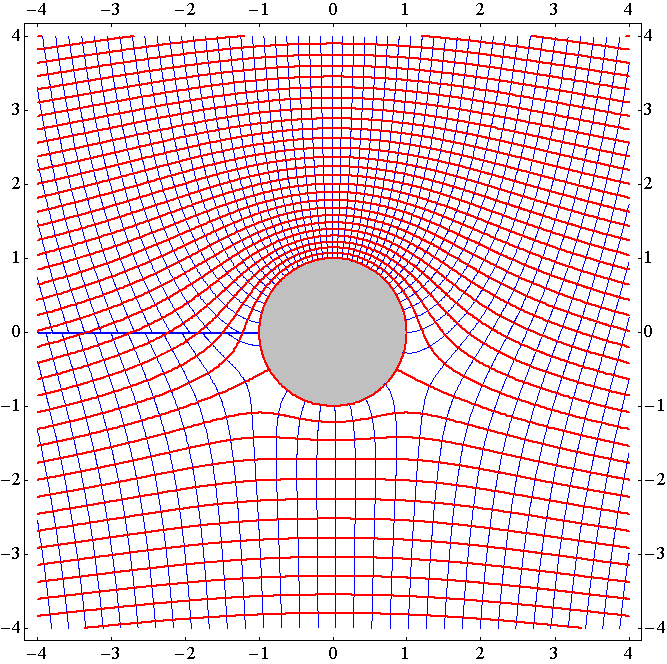
�@���x�|�e���V�����ʂ͑������ƂȂ�̂ŁA���̐}�ł͂����̕��̕����ɒi��������B���̂��ߓ����x�|�e���V�������m���C���n�͂����̕��̕����ł���Ă���B���������x�|�e���V�����ʂ����z�͘A���I�Ɍq�����Ă���̂ŁA�����i����0�j������ő��x�ɒi���������邱�Ƃ͂Ȃ��B
�@���̐}�͂ƂĂ����P�I�ł��B���ꂪ�~���̏㑤�Ɍ������ĉI�Ă���A�~�����߂���ƍ��x�͉����Ɍ������ė����B���̂��߉~���̏㑤��ʂ闬��͉�����ʂ闬�������蒷�������𗬂�Ȃ���Ȃ炸�A�~���̏㑤�̑��x�͉������������Ȃ�B
�@����ɒ��ӂ��Ăق������Ƃ́A�~���̉����ŏ㉺�̗��ꂪ�o��ꏊ�ɂ����āA�ォ��̗���Ɖ�����̗���̗����ɍ�������킯�ł͂Ȃ����ł��B��U�����̓[���ɂȂ�A���ݓ_�Ŋ��炩�ɍ������Ă���B�����炱�̗��ݓ_�ō�������ォ��̗���Ɖ�����̗���Ɉ��͍������݂���킯�ł͂���܂���B����͗��ݓ_�ȍ~�̗����̏㉺�ɕt���Ă����l�ł��B����͗��̒��̈�̖ʂ̕\���̎��ł����瓖�R�̂��Ƃł��B
�@�ʍe�u���E�k���E���S���̗̂͊w�v�R�D�i�S�j�T�D�̍Ō�Œ��ӂ����悤�ɁA�k�܂Ȃ����̂̉����͖�����̑����œ`�d����B���̂��ߗ��̒��ɕ��̂����݂��A���̕��̂̎���ɏz�����݂���Ƃ������́Aꡂ��㗬���̗��̂ɓ`����Ă���B�S�Ă̗̈�̗��̂́A���̒��ɕ��̂����݂��A���̕��̂̎���ɏz�����݂���Ƃ�����m������Ō݂��ɒ����������ė�����`�����Ă���B���̂��ߕ��̂̏㗬�����畨�̂̋߂��ɗ��ꉺ���Ă������̂́A�~���̎���ɑ��݂���z���ɎQ�����ď�����Ɍ�����ς���B�����ĕ��̂�ʂ�߂���Ɖ������ɕ�����ς��ė��ꋎ��B
�@�����̗��̂ɂ͈��k��������܂����A����̑��x�����������x���ꍇ�ɂ͏�L�̎����͐��藧�ƌ�����B�������̑��x�������ɋ߂Â��ƁA���k���̉e�����傫������Ă��܂����痬��̗l�q�͕ς���Ă��܂��B
�Q�D����4���t�̏ꍇ
�@���̏ꍇ�A���ݓ_�͉~���\�ʂ̍ʼn��_�ɂP���������B
�m����4���t�̏ꍇ�n
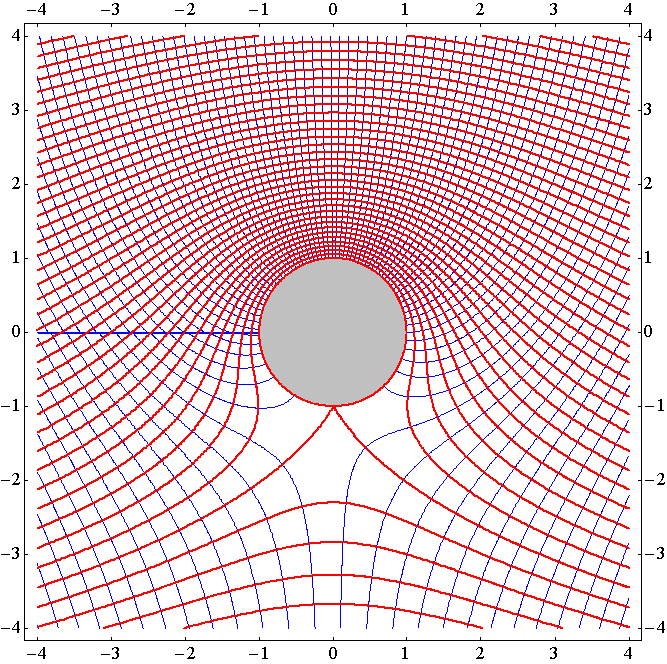
�R�D����4���t�̏ꍇ
�@����́A�~���̎���̏z�����Ȃ�傫�������ŁA���ݓ_�͉~���̐^���̗��ꂽ�ʒu�ɂP���������B�����āA���̗��ݓ_��ʂ闬���ɂ���āA����̏�͉~�������z���ƊO���̗���ɓ����B
�m����6���t�̏ꍇ�n
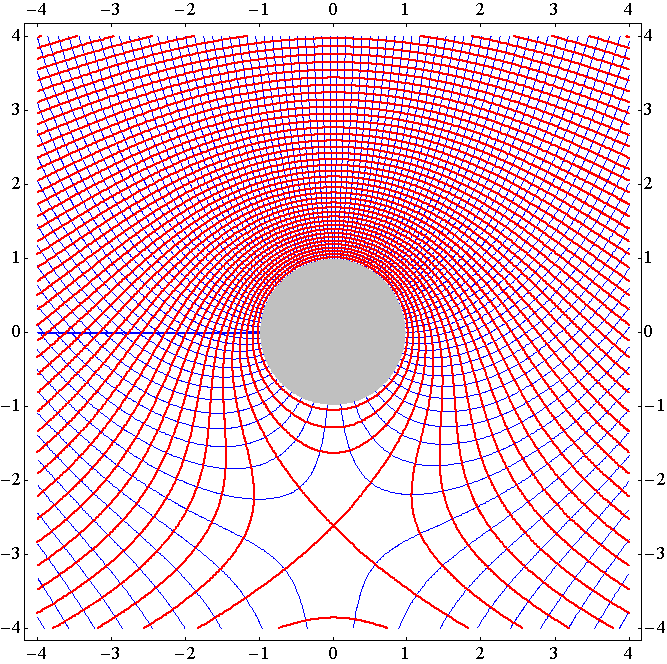
�@���̗�̂悤�ɗ��̂��~���̎���ɂ܂Ƃ����Ă���Ƃ��́A�~���̎���̏z���ۑ������Ƃ����͉̂���₷���B����4���t�̂悤�ɗ��̗v�f�����X�Ɠ���ւ��ꍇ�����l�ɕۑ������̂ł��B
�@
�i�R�j���x�x�N�g����
�P�D���x�x�N�g��
�@�C�ӓ_�i���C���j�ɂ����鑬�x�����i���C���j���ʍe�Ő��������悤�ɕ��f���x���狁�܂�̂�
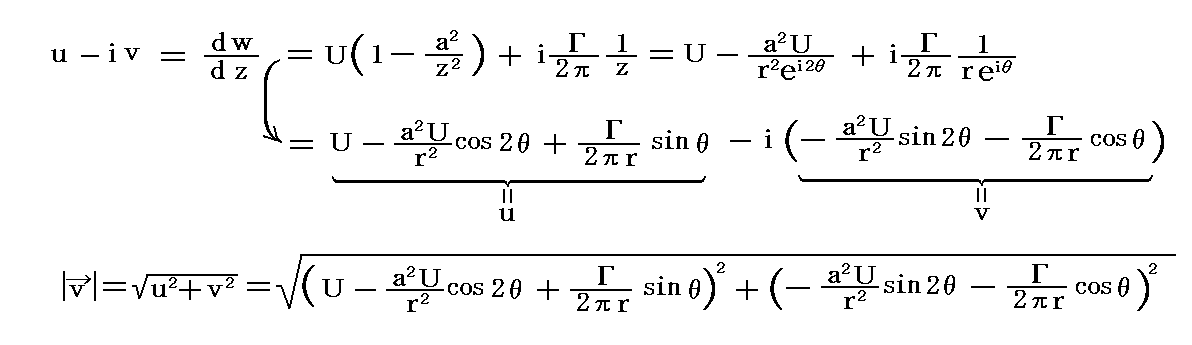
�ƂȂ�B
�@���邢�́A���̒��́i���C�Ɓj�ɂ����铮�a������r�Ɖ~�������̑��x�����͋ɍ��W�ł�grad�����狁�߂邱�Ƃ��ł���B���ꂼ��
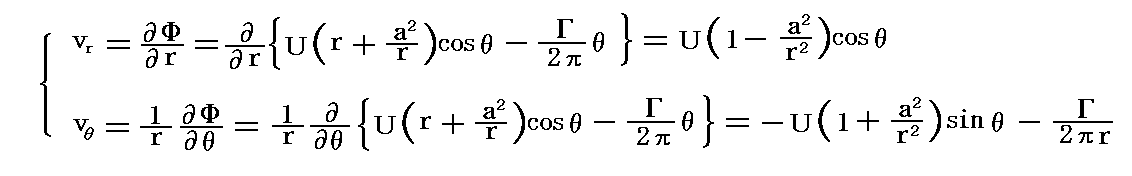
�ƂȂ�B
�@�~���\�ʂɂ����鑬�x���z�͏㎮�ł���������������܂�
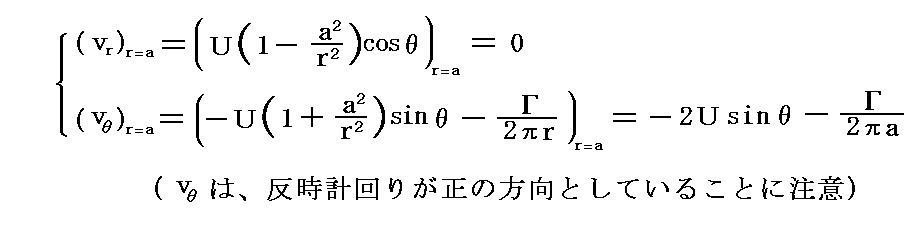
�ƂȂ�B
�@�Ƃ�����R�D�i�R�j�R�D�߂Ő�������悤�ɗ��ݓ_�̂����W�|������������́|���^�i4�t�j�����牺�}�̗l�ȊW��������B����̓���20���Ƃ��ĕ`�����}�ł��B
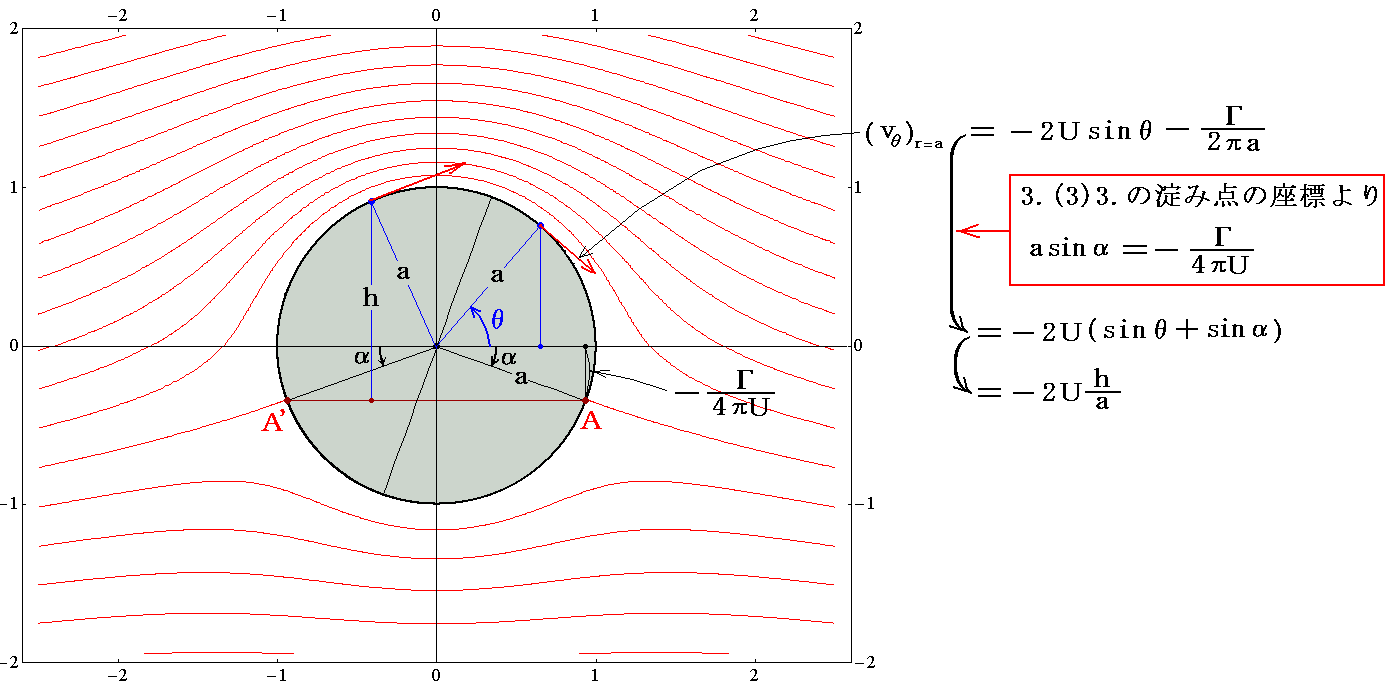
�܂�B�~����̓_�̑��x�̑傫���͓�̗��ݓ_�`�`�f�����Ԓ������炻�̓_�܂ł̍��������~�̔��a�Ŋ�����2�t���|�������̂ɓ������Ƃ������ɊȒP�Ȍ`�ŕ\���ł���B����́A��ɉ~�ʗ���W���[�R�t�X�L�[���Ɏʑ�����錳�~�̎���̗���ɕt���Ă���ʓI�ɐ��藧�֗��ȕ\���ł�����o���Ă������Ɨǂ��B
�@�~���\�ʏ�̑��x�̑傫������}�̃Ƃ������ɂ��ĕ`���Ă݂��
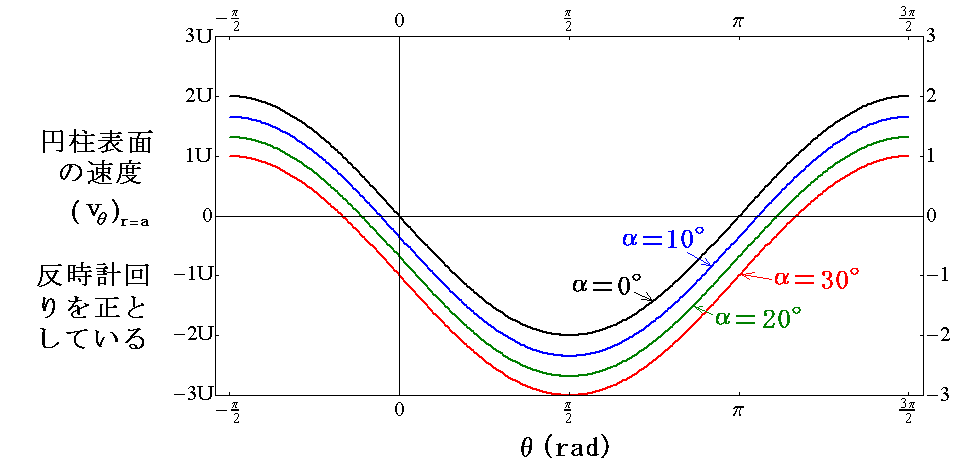
�ƂȂ�B
�Q�D�z��
�@�@���̂����݂���̈�͒P�A���̈�Ƃ͂Ȃ炸��d�A���̈�ƂȂ邪�A���̒��̂�����̕�����div����0�rot����0������B�~���\�ʂ͈�̗����ƂȂ�A���̗����ɉ����Ĕ����v���ɑ��x�����̐��ϕ������{�����z�������߂Ă݂��
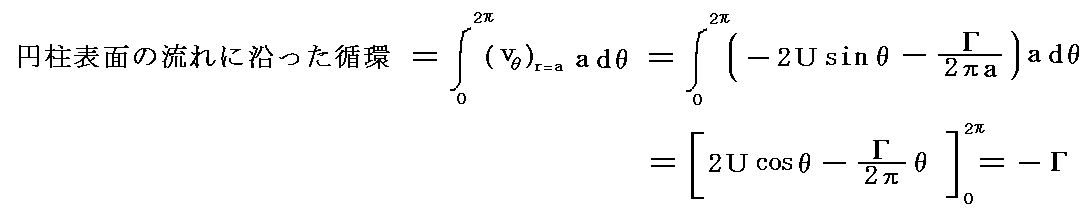
�ƂȂ�B�܂�Q���̋������z�̑傫�����̂��̂ł��邱�Ƃ�����B�z����`�͂������B
�R�D���ݓ_
�@�Q���̋������i�z�j�̒l�ɂ�藬��̗l�q�͈قȂ������A����͗��ݓ_�̌�����ɊW����B���ݓ_�́i���C���j���i0�C0�j�̏������狁�܂�B�܂������
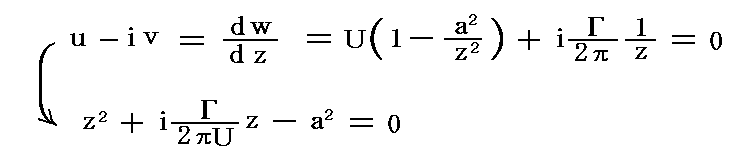
�̉������ݓ_�̈ʒu�ł��B���f�W�����������̉��̌������g���Β����ɋ��܂�܂��B
�@�������Ƃł����A�����ł͓D�L���v�Z���Ă݂܂��B�������̍�����1�A��2�Ƃ���ƍ��ƌW���̊W�����
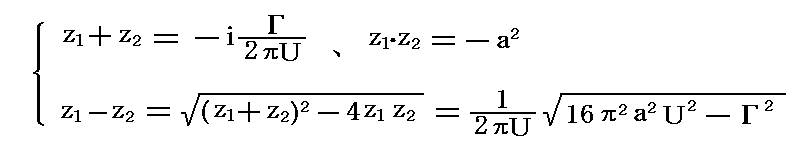
�ƂȂ�B����̗l�q�́A��1�|��2�̍����������A0�A���̈Ⴂ�ŎO�̏ꍇ�ɕ������B
�m����4���t�̏ꍇ�n
�@���̏ꍇ����1�|��2�������ƂȂ�B���̂Ƃ��A��1����1�{����1�A��2����2�{����2�ƒu���A��1�|��2���i��1�|��2�j�{���i��1�|��2�j�͎���������A��1����2�ƂȂ�B����ɂ�1�{��2���i��1�{��2�j�{��2��1���|�����^2�t���A��1����2���|���^2�t�A��2���|��1�ƂȂ�B
�@�܂���1���2���i��1�{����1�j�i�|��1�{����1�j���|�i��12�{��12�j���|��2������|��1|��|��2|�����ƂȂ�B
�@�܂藄�ݓ_�͉~���\�ʂɓ����B
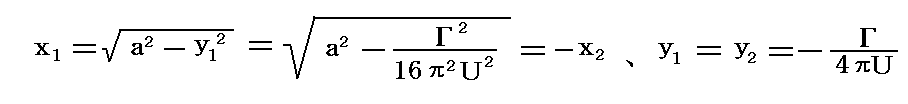
�̓_�ł���B
�m����4���t�̏ꍇ�n
�@���̏ꍇ�ɂ�
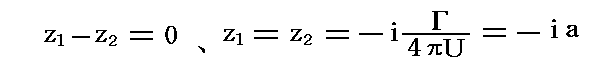
�ƂȂ�A�~����ɂ�����̗��ݓ_�����݂���B
�m����4���t�̏ꍇ�n
�@���̏ꍇ����1�|��2�������ƂȂ�B��1�|��2��\�����̍����������ł��邱�ƂɋC�����āA����4���t�̏ꍇ�Ɠ��l�Ȍv�Z�������
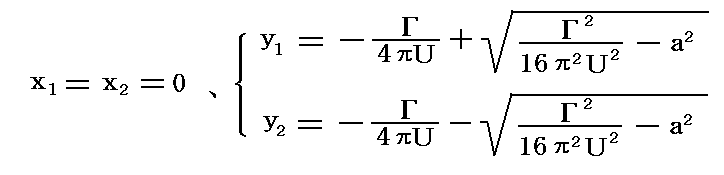
�ƂȂ�B�܂�A���ݓ_�͂�����ň�͉~�̊O�A������͉~�̓��ɂ���B
�@
�i�S�j�~���ɓ�����
�@�����S���̂��l���Ă���̂ʼn~���\�ʂɉ��������C�͓͂��������݂͂̂��\�ʂɐ����ɓ����B���̂Ƃ��~���\�ʂ̗����ɂ����Q�����E��헬�Ő��藧���x���k�[�C�̒藝��K������B���������̈�l���t�̏ꏊ�ɂ����鈳�͂���0�A���x���̈ʒu�̈��͂����A�܂����̖̂��x���ςƂ��A�ʒu�G�l���M�[�̍��������
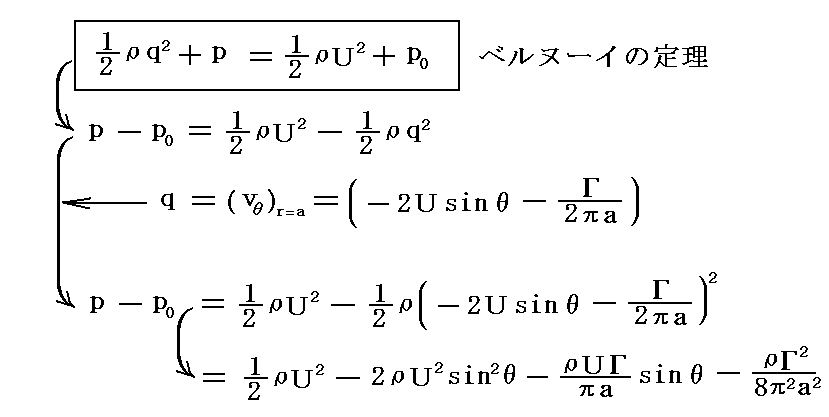
�@�~���\�ʂɓ������͂�ώZ���āA�P�ʂ̍��������~���ɓ����͂̍��́i�ex�C�ey�j�����߂Ă݂�B
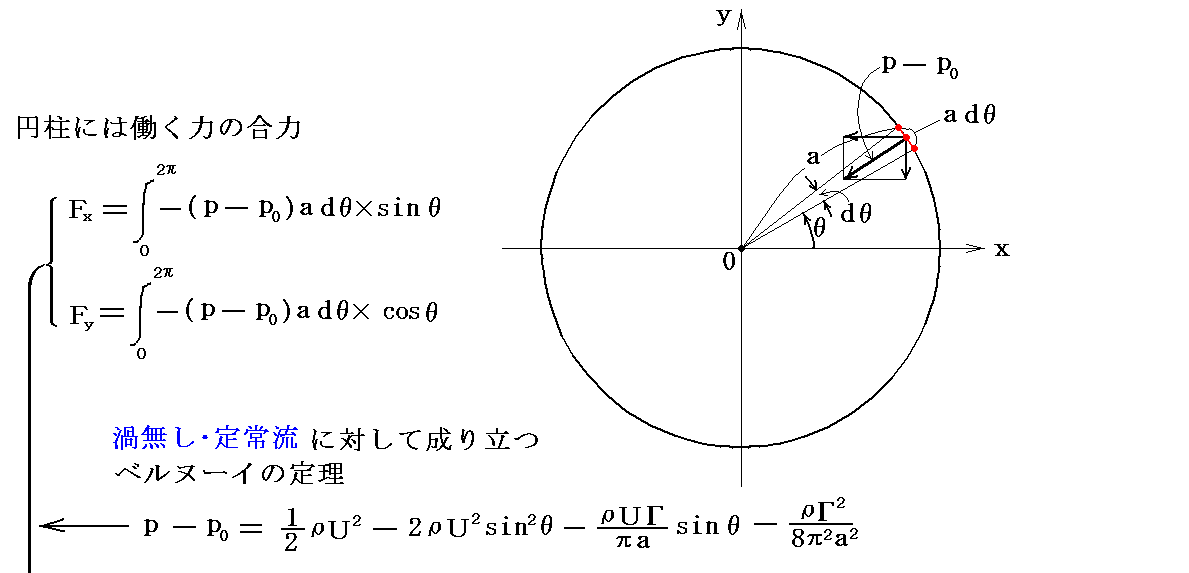

�܂�A���̎���ɏz�������~���́A�������ɂ����闬��̕����ɐ����ɁA�~���̒P�ʂ̒���������ςt���Ȃ�傫���̗͂������ƂɂȂ�B
�@����́A���̕\�ʏエ��т��̊O���̗��̗̈�ɗN���o���_�◬���_�����݂��Ȃ��ꍇ�ɁA�C�ӂ̒f�ʌ`����������̂ɑ��Ĉ�ʓI�ɐ��藧�AKutta�EJoukowski�̒藝�m�ؖ����S�D�i�Q�j�P�D�Q�Ɓn�̓��ʂȏꍇ�ł��B
�@
�i�T�j�Î~���̒����ړ�����~���̎���̗���
�P�D���f���x�|�e���V����
�@���܂ł͑��x�t�̈�l�����ɒu���ꂽ�z���~���ɓ����̘͂b�ł������B��L�̉��ɑ��x�t�̔��Ό����̈�l�����d�ˍ��킹��A�Î~���̒����z���đ��x�t�ňړ�����~���ɓ����͂��������B
�@�܂��A�R�D�i�P�j�̂��ɁA���Ό����̈�l���̕��f���x�|�e���V�������|�t�����������
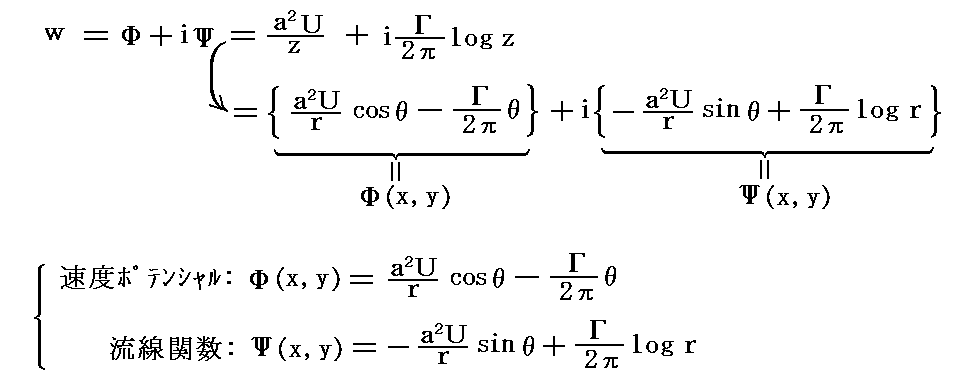
�ƂȂ�B����͐Î~���̒��x�t�ł����̕������i�މ~���̒��S�����_��ʉ߂���u�Ԃ̗��������킷���f���x�|�e���V�����ł��B��l����\�����f���x�|�e���V�������|�t���ɂȂ邱�Ƃ͕ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�P�D�i�R�j�P�D�Ő��������B
�Q�D�����x�|�e���V�������Ɨ���
�@�������A�c�����A�����P�A�������Ԋu0.2�t�A���C���������x�|�e���V�������m���i���C���j�����̐��n�A�ԃ��C���������m���i���C���j�����̐��n�A����͒�헬�ł͂���܂���̂ŁA���̏u�Ԃɂ͉~���͂����̕������ֈړ����Ă���A�����A�����x�|�e���V�������̕��z������ɔ����Ĉړ����Ă���B
�m����0.5���t�̏ꍇ�n
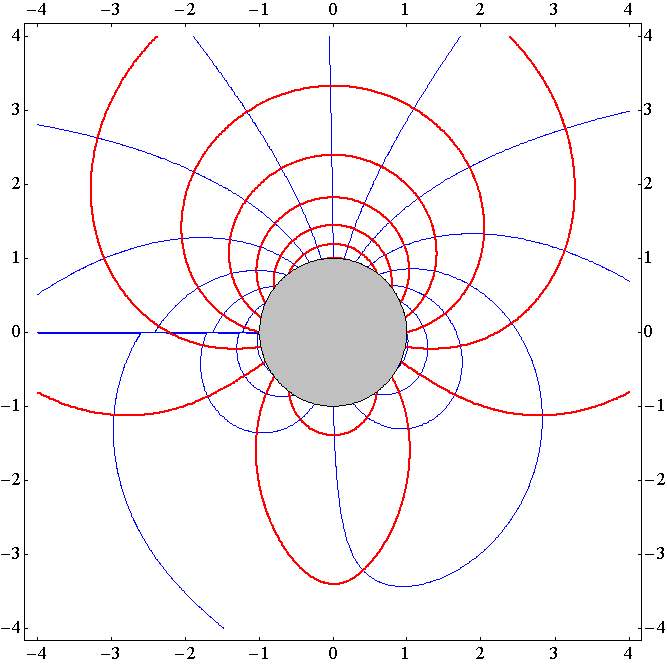
�m����1.0���t�̏ꍇ�n
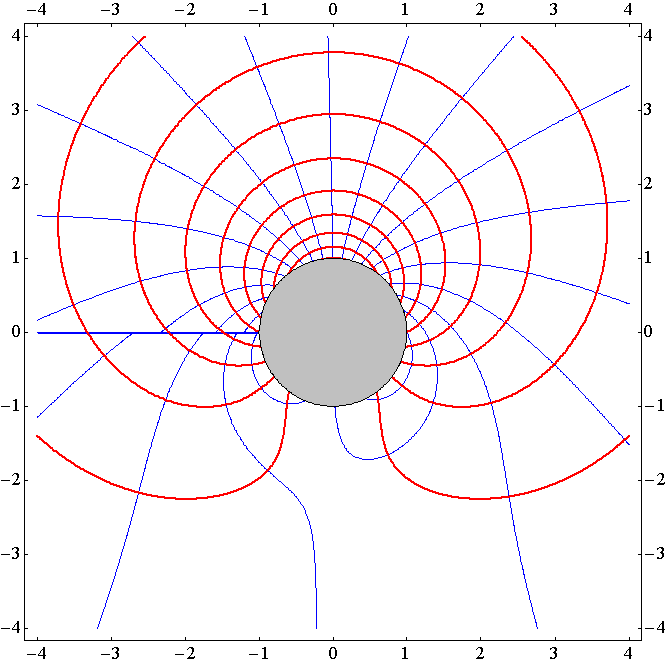
�m����2.0���t�̏ꍇ�n
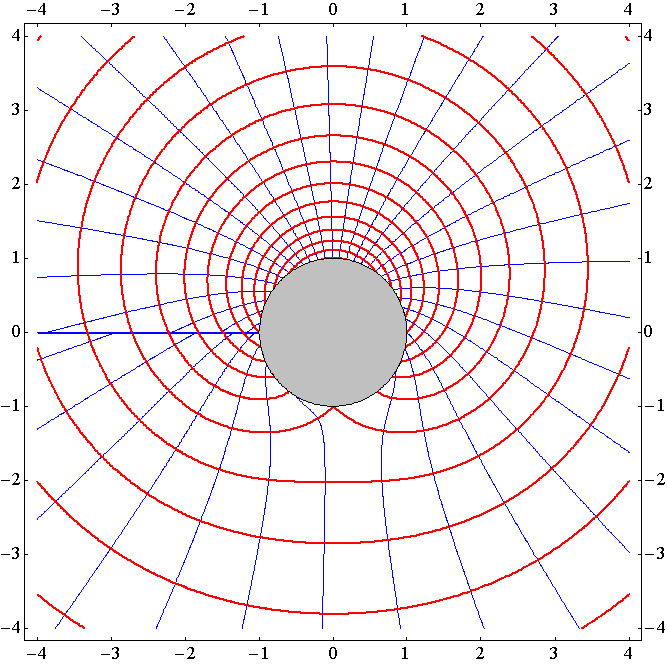
�m����4.0���t�̏ꍇ�n
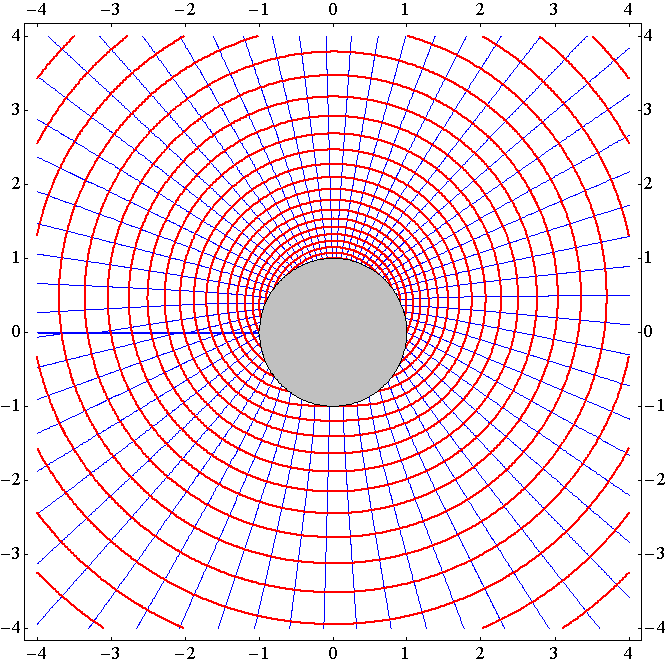
�R�D���f���x
�@���f���x���|�������i�����^�����j��
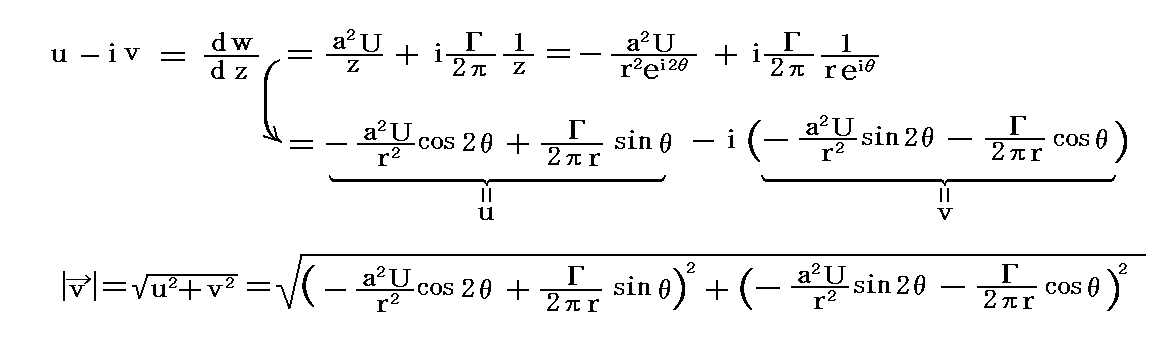
�ƂȂ�B
�@���̏ꍇ��헬�ł͂Ȃ����A�Q�����̗����ł��邱�Ƃ͊ԈႢ�Ȃ��̂ŁA�g�����ꂽ�x���k�[�C�̒藝�����藧�B���̂��ߐϕ��萔�͗��̑S�̂ɓn���ċ��ʂȒl�ƂȂ�B�~���\�ʂ̑��x�͕��s��l���̐����������āA��l�����ɉ~�����Î~���Ă���ꍇ�ƑS�������ɂȂ�̂ŁA�~���ɓ����͂̍��͂͑O�L�̏ꍇ�Ɠ����ɂȂ�A�~���̐i�s�����ɐ����ɂe����U���̗͂��������ƂɂȂ�B
�S�D�g�͂Əd�͂̒ނ荇��
�@���̂悤�ɐi�s�����ɐ����ȗg�͂��Ȃ���A���̒��𐅕��Ɉړ�����͕̂ς��Ǝv���邩���m��܂��A�~���ɓ����̐ϗ͂ł���d�͂��������ɓ����Ă��Ă��̗͂Ƃ荇���Ă���ƍl����悢�B����͂��傤�ǁA���C�̖����ʏ��ʂ���鐂���R�͂Əd�͂��荇������ԂŖʏ���x�Ŋ����Ă������̂Ɠ����悤�Ȏ���ł���ƍl����悢�B
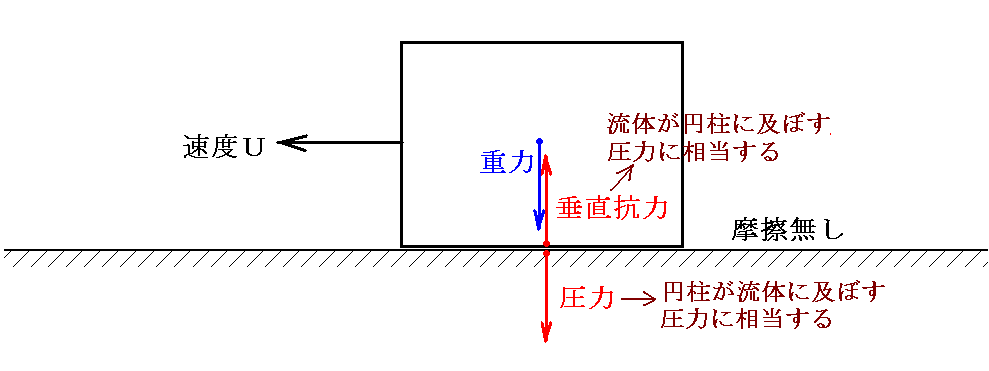
�@�܂��������̗͂�����Ȃ��̂́A�_�����x�[���̔w���̂Ƃ���Ő��������̂Ɠ�������ł��B
�@����ɁA�R�D�i�Q�j�R�D�m����4���t�̏ꍇ�n�̂悤�ɁA�Q�̏z���\����������̗��̗��q���~���Ƌ��Ɉړ����Ă����ꍇ������킯�ł��B
�@���̓�������ʍe�̂S�D�i�Q�j�R�D�̍Ō�Ő�����������Ɠ����ł��B�������A�����ł͉Q���`�����ē�̉Q�����݂��ɉe�����������ƂŒ��i����̂ł����A�Q�̎���̗���͒P�Ƃ̉Q���̏ꍇ�ƈႢ�܂��B�����ł͒P�Ƃ̉Q�����d�͂Ƃ荇�����ƂŒ��i���܂��B�d�͂�������A�����Ă���P�Ƃ̉Q���̋O�Ղ͉~��`�����ƂɂȂ�ł��傤�B
�@���̂Ƃ��A�����ɍL���������̒��ł͂Ȃ��āA�n�ʂ̂�������s����ꍇ�����ɋ�������܂��B���̗l�ȏ̗��̎���̗���̉���������ɂ́A�ʍe�̂S�D�i�Q�j�R�D�Ő������������̕��@��p����悢�B�n�ʂ̉��ɉ��z�I�ȑɂȂ�Q�����l���āA�n�ʂɂ����闬�����n�ʂɉ����Ă���Ƃ������E������������̂ł��B
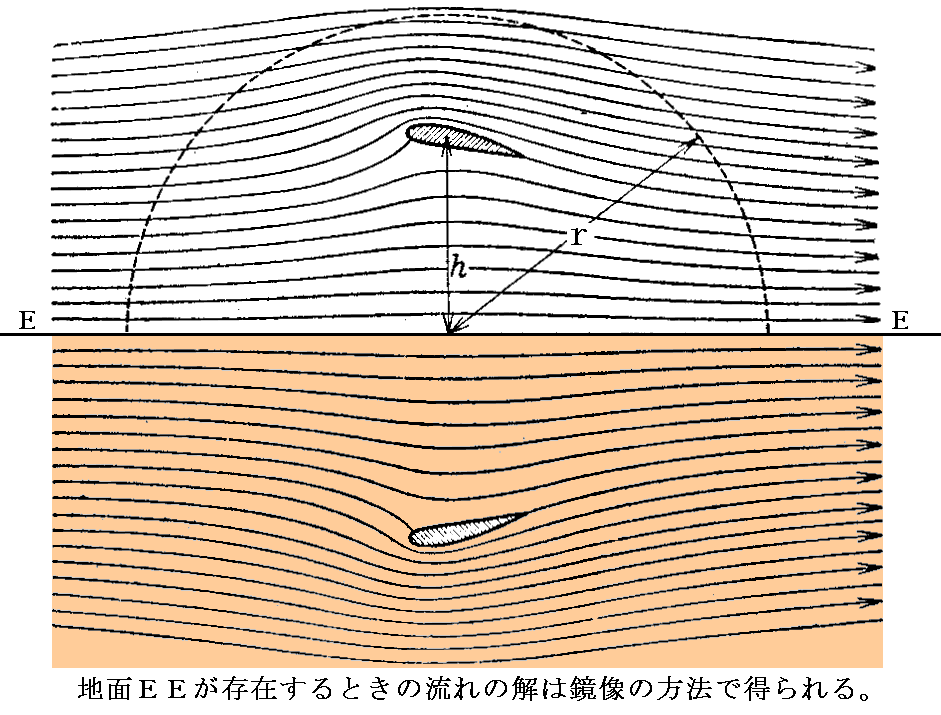
�@���̂Ƃ����ӂ��ė~�������Ƃ͉Q����闬���͒P�Ƃ̉Q�̏ꍇ�ƈقȂ邱�Ƃł��B���ɂ������ɉ����ē�̉Q������鑬�x�����݂͌��ɔ��Ό����őł�������̂ŗ������݂��邱�Ƃɂ�闬��̗���͂������ƂƂ��ɋ}���ɏ������Ȃ�B�܂����̂Ƃ����̉����̒n�ʂ̈��͂������Ȃ��Ă���B���͒n�ʂ�������C�̔���p�Ŏ����グ���Ă���̂ł���B���̓�������S�D�i�Q�j�Q�D�ł��������ڂ�����������B
�@
�S�D�N�b�^�E�W���[�R�t�X�L�[�̒藝
�@�g�͂ɕt���Ă̑O�߂̋c�_�͉~���̂ɂ��Ă̂��̂ł������A�C�ӂ̌`�����������i�܂���́j���̂ɂ��Đ��藧���܂��B�ؖ��͕����u���W�E�X�̌�����p���čs����̂ł��̐�������n�߂܂��B
�i�P�j�u���W�E�X�̌���
�P�D�u���W�E�X�̑�����
�@�u���W�E�X�̑������́A�ʍe�u���f���̐ϕ��v�Q�D�i�P�j�ŏؖ������悤���k�������ɂ��Ă��^���ʂ̒藝�����E�Q�����E��헬�ɓ������̂Ɠ����ł��B
�@���E�k���E���S���̂̉Q�����E��헬�����Î~���Ă��镨�����l����B���̂Ƃ��A���̕\�ʂ̕Ȑ��ƕ��̂����͂ނ悤�ɗ��̒��Ɏ�����C�ӕȐ��b�̊Ԃɓ��ٓ_�����݂��Ȃ����A���邢�͂������ٓ_�����݂����Ƃ��Ă��A���̗����̘a���[���ɂȂ�ꍇ�ɂ́A���̂ɓ������f�������w�|���x�́A���̂����͂ޔC�ӕȐ��b�ɉ����ĉ��L�̐ϕ������s���邱�Ƃŋ��܂�B
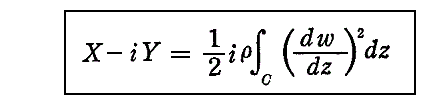
�������A�i�����^�����j�͕��̂����͂ޗl�Ɏ�������̒��̔C�ӕ��Ȗʂb��̓_�������{�����ɂ����镡�f���x���|�����ł��B������u���W�E�X�iBlasius�j�̑������ƌ����B
�@���̒藝��p����Ɖ~���ɂ����R�D�i�S�j�œ������_���ȒP�ɋ��܂�m�ʍe�u���f���̐ϕ��v�Q�D�i�P�j�R�D�Q�Ɓn�B
�Q�D�u���W�E�X�̑�����
�@����ɁA�ʍe�u���f���̐ϕ��v�Q�D�i�Q�j�ŏؖ������悤�Ɏ��̌��������藧�B����͕��̂ɓ����͂̃��[�����g�i�g���N�j�����߂邽�ߎg���B
�@���E�k���E���S���̂̉Q�����E��헬�����Î~���Ă��镨���ɓ������_�̂܂��̗͂̃��[�����g�i�g���N�j�l�́A���̂����͂ޔC�ӕȐ��b�ɉ����ĉ��L�̐ϕ������s������܂�B
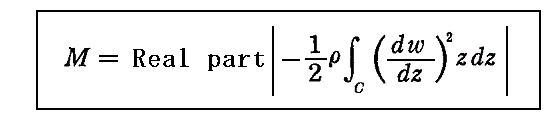
�������A���̕\�ʂ̕Ȑ��ƕ��̂����͂ޔC�ӕȐ��b�̊Ԃɓ��ٓ_�����݂��Ȃ����A���邢�͂������ٓ_�����݂����Ƃ��Ă��A���̗����̘a���[���ɂȂ�ꍇ�Ƃ��Ă���B������u���W�E�X�iBlasius�j�̑������ƌ����B
�@
�i�Q�j�N�b�^�E�W���[�R�t�X�L�[�̒藝
�P�D���̂ɓ�����
�@����̒��̂̂܂����z���̗��ꂪ�t�����Ă����A�������l�ȗ����t�����������Ƃ���B���̂Ƃ����̂���l���t�̕����Ɛ����ȕ����Ƀςt���̗͂����B���������͗��̖̂��x�ł���B�����Kuta-Joukowski�̒藝�Ƃ����B
�@�����ł́A���̕\�ʏエ��т��̊O�����̗̈���ɗN�o�_�A�����_�A�Q���Ȃ̂ǂ̓��ٓ_�͑��݂��Ȃ��Q�����̗���ł��邱�Ƃ����肵�Ă���B���̂Ƃ����̂����E�k���E���S���̂ł���A�㗬�̗��̗̂��ꂪ�����ƉQ�����̗���ł���A���O�����W���̉Q�藝�ɂ��A��ɏ�L�̉��肪��������邱�Ƃ͕ۏႳ��Ă���B�܂��A�����ł����̂̒f�ʌ`��₻�̑傫���͂ǂ̗l�Ȃ��̂ł��ǂ��B
�@���̒藝�́A���̂̂܂��ɔ����z���̑傫�����A���̂̌`���t�Ƃǂ̗l�ɊW����̂��͉��������Ă��Ȃ����ɒ��ӂ��Ă��������B�z�������肷�郁�J�j�Y���͂V�D�͂Ő������܂��B
�m�ؖ��n
�@���A���W���_�̂̓����Ɏ��A��l���t�͂����ɕ��t�ł����̐��̕����������A�z�͎��v���Ƃ���B����̗l�ɕ��̂̕\�ʂ���ъO���̗��̓��ɓ��ٓ_�����݂��Ȃ��̂ŁA���̂����͂ޏ[���傫�ȕȐ��b���Ƃ�ƁA�O�L���u���W�E�X�̑����������藧�B
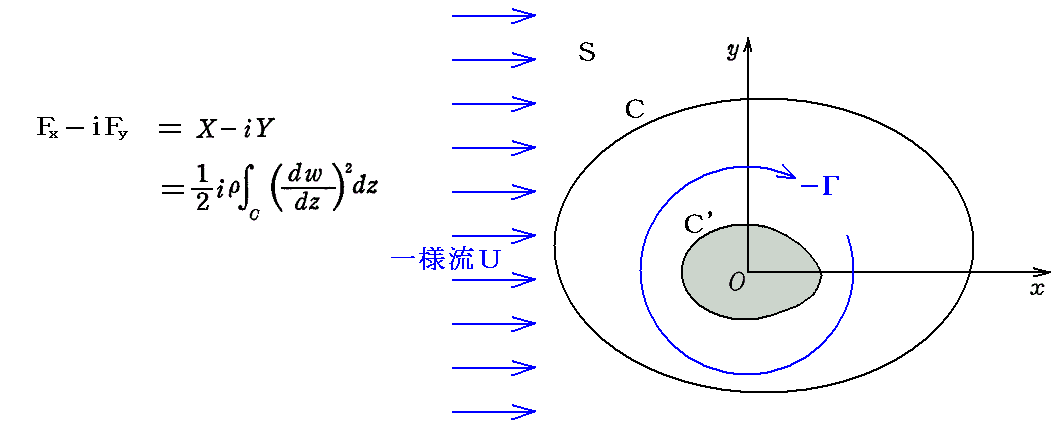
�@�Ȑ��b�̏�ł͂��͑傫������A�����傫���Ƃ��̂��̋ߎ�����m��ΐϕ��l�����߂邱�Ƃ��ł���B
�������ɕ��s�ɂ��̐������Ɉ�葬�x�t�ŗ�����l�ȗ���̕��f���x�|�e���V������
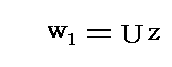
�ƂȂ�B�܂����̂̂܂��̏z���́A���̑傫���Ƃ���ł́A���̗��������_�𒆐S�Ƃ���~�Ƃ݂Ȃ���邩��A���̌��������v���Ƃ��ďz�萔���|���i����0�j�Ƃ����
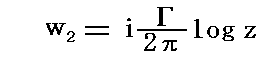
�ŗ^������B���̂ɂ�靘���͕��̂��牓������Ή�������قǏ������Ȃ邩��A�Ȑ��b�̏�ł͂��̕��f���x�|�e���V������
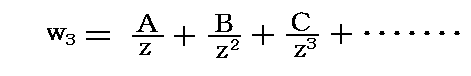
�̗l�ɕ\�����Ƃ��ł���B�������`�C�a�C�����͕��̂̌`��Ƃt�A���ɊW���镡�f�萔�ł���B���Ȃ݂ɕ��̂����a���̉~���̏ꍇ�͂`���t��2�A�a���b�������0 �ł������B
�@�̂ɁA�b�̏�ł͗���̕��f���x�|�e���V��������т��ɂ������͋ߎ��I��
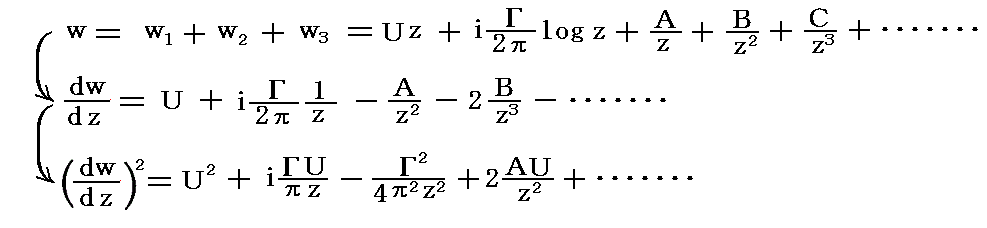
�ƂȂ�B������u���W�E�X�̑������ɑ�����āA�R�[�V�[�̒藝���g����

���Ȃ킿
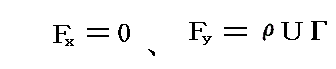
�ƂȂ�B
�m�ؖ��I���n
�܂��ƂɃG���K���g�ȏؖ��Ȃ̂����A���̕����I�ȈӖ��͈ȉ��̂悤�ɍl����悢�B
�Q�D�N�b�^�E�W���[�R�t�X�L�[�̒藝�̕����I�ȈӖ�
�@�O�L�̒萔�`�A�a�A�b�A�E�E�E�͕��f���̒萔�ł��邪�A�����̒萔�ɂ���ďz���������s���͂��̌`��ς���B�܂�����̕ό`�̓x�����͕��́i���j�̌`��ɂ��̂ł`�A�a�A�b�A�E�E�E�͕��̂̌`�Ɉˑ�����B�Ƃ��낪���́i���j���痣�ꂽ�Ƃ���ł͂`�A�a�A�b�A�E�E�E���|���������i�P�^��2�ȏ�̍����̍��j�͋����Ƌ��ɂ��̉e���͏������Ȃ�̂Ŗ����ł��āA���x�̏�͂����������_�ɗB��̉Q���i�z���j���������݂��邩�̗l�Ɍ�����B
�@���̂Ƃ��A��L���ϕ������{����Ȑ���Ⴆ�����̂̑��݂���_�𒆐S�Ƃ��A���́i���j���ޏ\���傫�Ȕ��a�̉~�ɂ���A���̐ϕ��H��̑��x�x�N�g���͈�l���x�N�g���t�ɏz���N�����~���ɉ����������̑��x�x�N�g�����u�m�傫�����^�i2���j�n�������������̂ɂȂ�B
�@���̉~�`�����ʂɕʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�Q�D�i�R�j���u���f���̐ϕ��v�Q�D�i�P�j�Q�D�Ő��������^���ʂ̒藝��K������B����ɂ��ƁA�m�������Ȗʓ��ɂ��镨�́i���j�ɓ����́n�́A�m�����ʂɓ������͂̍��́n���m�����ʂ�ʉ߂��闬�̉^���ʂ̎��ԓI�ω��̘a�̔���p�n�̘a�ɂȂ�B
�@
�m�^���ʐϕ��n
�@�R�D�i�Q�j�P�D�̗����}������Ζ��炩�Ȃ悤�����́i���j�̑O���ł͏�������������x���A���̌���ł͉������ɕς�����̂ł��邩��A���������^���ʕω��͉������ł���B�������ė��̂ɂ�锽��p�͕��́i���j�ɏ�����̗g�͂�^�����B���ۂɌv�Z���Ă݂�Ƃ�������悤�ɗ���̑Ώ̐����炘�����̉^���ʗ��ʂ̕ω��͖����B�������Ɋւ���̐ώZ��
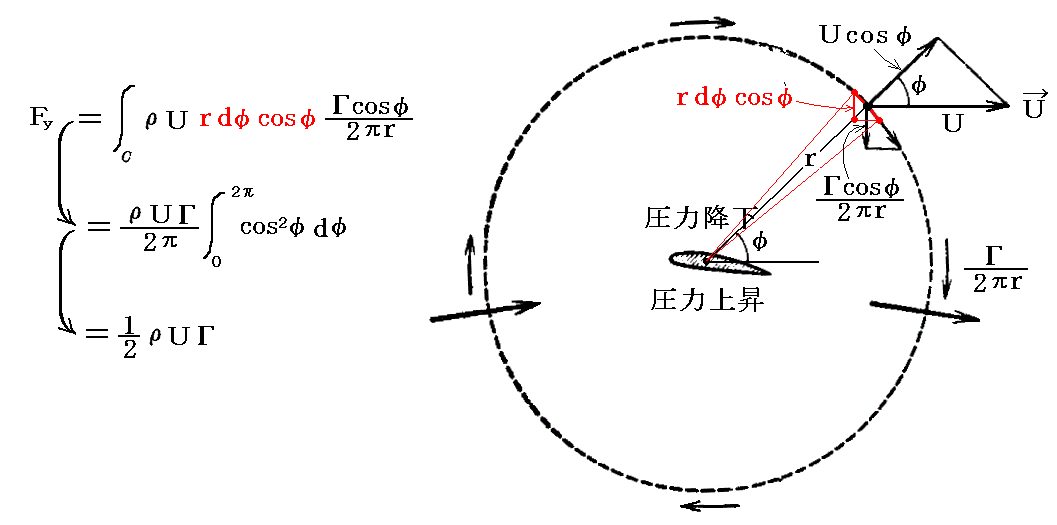
�ƂȂ�B
�@
�m���͐ϕ��n
�@���͐ϕ��́A�����ʂɂ����闬�����x���k�[�C�̒藝��p���Ĉ��͂ɕϊ����Đϕ������{����悢�B�������Ɋւ��Ă͈��͕��z�̑Ώ̐�����[���ɂȂ�B�������Ɋւ��Ă�
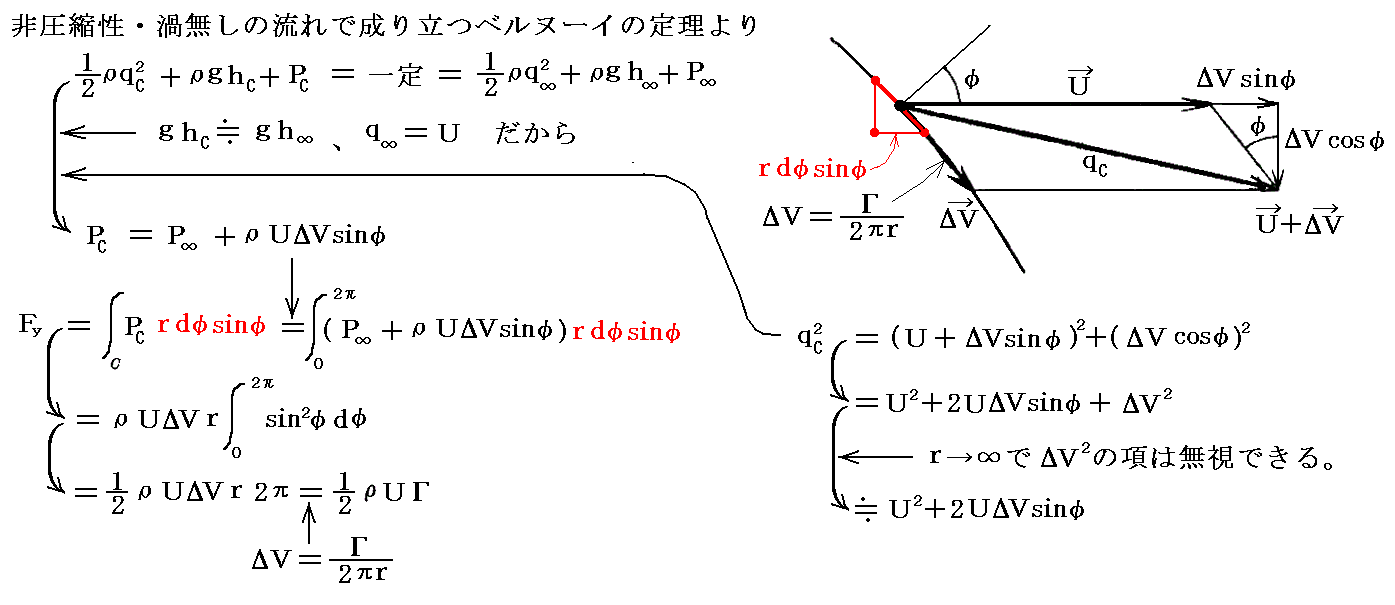
�ƂȂ�B
�@���̉^���ʐϕ��ƈ��͐ϕ������Z����N�b�^�E�W���[�R�t�X�L�[�̒藝�ɂ���ċ��߂��̂Ɠ������_��������B���j�I�ɂ́A�W���[�R�t�X�L�[�͍ŏ������ŏq�ׂ����@�ŃN�b�^�E�W���[�R�t�X�L�[�̒藝���ؖ������悤�ł��B�m�v�����g���u����w�i��j�v�R���i��P94�n
�@�����ŁA���ӂ��ׂ��́A�����ʂ��~�`�̏ꍇ�́A���܂��܉^���ʐ����ƈ��͐����̊�^�����X�ƂȂ������A�����ʂ̌`���ς��Ƃ��̊������ω����邱�Ƃł��B�Ⴆ�Ή������̋�`�����ʂ������}�̗l�ɏ㉺�̌����ӂ��㉺�̖������Ɏ����čs���ƁA���͐ϕ����̓[���ƂȂ�^���ʐϕ������g�͂̌����ƂȂ�B������E�}�̗l�ɍ��E�̌����ӂ����E�̖������Ɏ����čs���ƁA���x�͉^���ʐϕ������[���ƂȂ舳�͐ϕ������O�g�͂Ɠ������Ȃ�B
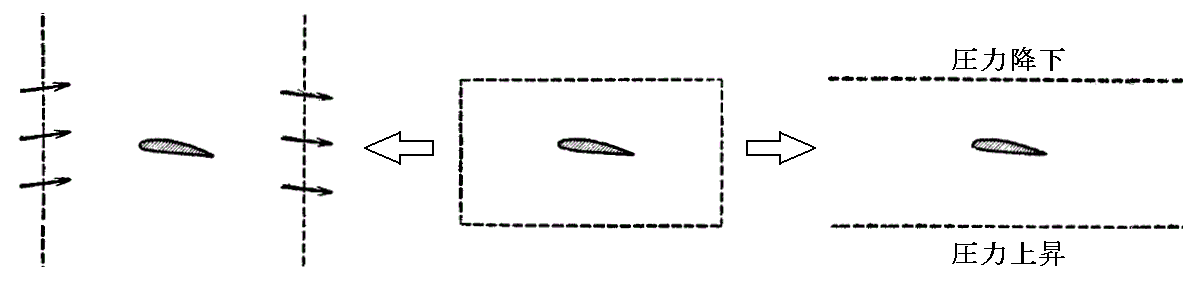
�@���̂悤�ɖ����ɍL�����Ă����C���ł͌����ʂ��K�肵�Ȃ��Ƃ��̊����͌���ł��Ȃ��B
�@���������Ƃ��Ēn�ʂ̏�ɗ������݂���ꍇ������B
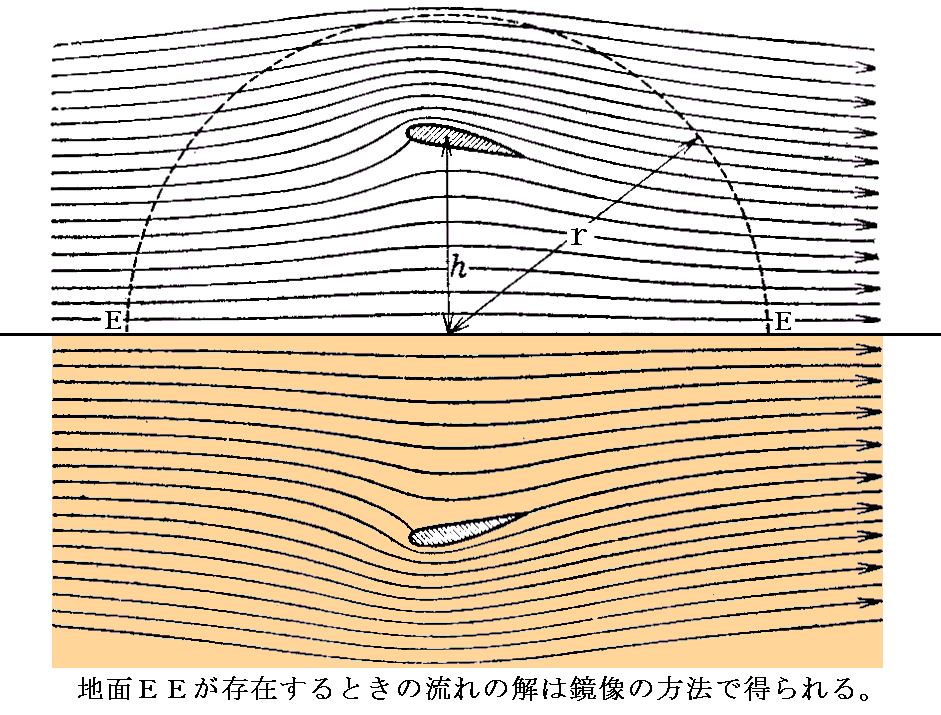
�@���̏̉���������ɂ́A�ʍe�̂S�D�i�Q�j�R�D�Ő������������̕��@��p���Ēn�ʂ̉��ɉ��z�I�ȑɂȂ�Q�����l����悢�B����������n�ʂɂ����闬�����n�ʂɉ����Ă���Ƃ������E�����������邱�Ƃ��ł���B
�@���̂悤�ȉQ�����z�ɔ������x�x�N�g���́A�ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�R�D�i�R�j�P�D�Œ��ӂ����悤�ɁA�����ʂ̔��a�����傫���Ȃ�ɂ�ċ}���Ƀ[���ɋ߂Â��B�P�Ƃ̉Q���̏ꍇ�͑��x�̑傫���͂P�^���Ō������邪�A�ϕ��H�͂��ɔ�Ⴕ�Ē����Ȃ�̂ŁA���̉e���͂������ɂ��Ă������邱�Ƃ͂Ȃ������B�������Q�̏ꍇ�ɂ͕��́i���j�����݂��邱�Ƃɂ���Đ����鑬�x��̕ϕ��̐ϕ��l�͂������ƂƂ��ɖ����ł���悤�ɂȂ�B
�@���̂Ƃ������ʏ�̐ϕ��Ŏc��̂͒n�\�d�d�ɉ��������͐ϕ��������ɂȂ�܂��B�����̗l�q���疾�炩�Ȃ悤�ɁA����͒n�ʂɂ��傫�Ȉ��͂��y�ڂ����Ƃ��Ӗ�����B���̔���p�����������グ��͂ƂȂ�B
�R�D���̂ɓ����g���N
�@���̂ɍ�p���闬�̗͂̌��_�ɑ��郂�[�����g�i�g���N�j���u���W�E�X�̑������ɂ���ċ��܂�B���Ȃ킿

�ƂȂ�B�܂�A���`�̎����́|2�ςt�|�ŗ^�������B�����`�͕��̂̌`��ɊW���镡�f�萔�ł��B
�@���Ȃ݂ɕ��̂����a���̉~���ł��̒��S�����_�Ƃ���ꍇ�ɂ͂`���t��2�������A�a���b�������0 �ł�������A�~���̒��S�̂܂��̃��[�����g�̓[���ƂȂ�B
�@
�T�D���p�ʑ�
�@���f���_�ɂ����鐳�����̓��p�ʑ����͂ǂ̋��ȏ��ł���������Ă��܂������\������ł��B�y�[�W����������̂����Ƃ킸�ł��邾������₷���������܂��B
�i�P�j�ʑ��̈�ʘ_
�@��̕��f�ϐ��������{�����A�ā��́{���ł�
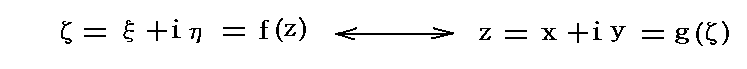
�Ȃ�W�Ō��т����Ă���Ƃ���B���������i���j�͂��́A���i�āj�̓Ă̐������i��͊��j�Ƃ���B���̂悤�ȊW�ɂ���Ă����ʏ�̂o�_��0�̓ĕ��ʏ�̂o�f�_��0�ɑΉ��Â����Ă���B���̂悤�ȑΉ��W���ʑ��Ƃ����B
�@���̂Ƃ������ʏ�̂o�_�ł��i��0�j���L���ŁA���̈ꎟ�̔����W�����ā^���������f�i��0�j���L���ŁA���[���łȂ��Ƃ��ɁA�o�_�����ʓ_�Ƃ����B�܂����ā^���������f�i��0�j���[���܂��͖�����ɂȂ�_�����ٓ_�ƌ����B
�P�D���ʓ_�ɂ�����ʑ�
�@���̂Ƃ��Ⴆ�A�����ʏ�ɂ����Ċ����i���j�̎������́���(x,y)����肪�����Ȑ��́A���E�k���E���S���̂̉Q��������̓����x�|�e���V�������ł���A�������Ł���(x,y)����肪�����Ȑ��͓��������E�k���E���S���̂̉Q��������̗����ƌ��Ȃ����Ƃ��ł���B�ʍe�S�D�i�Q�j�Q�D�ŏؖ������悤�ɓ����x�|�e���V�������m�́����̋Ȑ��n�Ɨ����m�Ł����̋Ȑ��n�݂͌��ɒ��������B
�@���̒��𐫂̓R�[�V�[�E���[�}���̊W������ʂ̐������ɂ��Đ��藧���̂ł�������A�����Ő����������f���x�|�e���V�����ɂ��Ă��A������藧������ł��B�m���}�Q�Ɓn
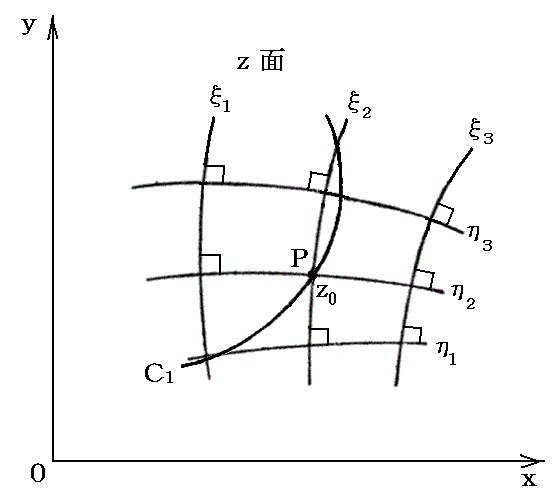
�@�܂�A�ĕ��ʂŌ݂��ɒ�������́����ƃŁ����̒����������ʂɎʑ��������̂͂����ʏ�Ō݂��ɒ�������Ȑ��Q�ƂȂ��Ă���B
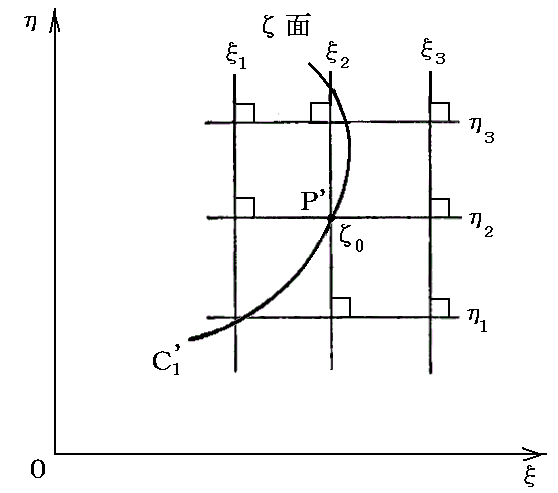
�@���̂Ƃ��A�����ʏ�̔C�ӋȐ��b1���ā����i���j�ɂ���ăĕ��ʏ�ł̋Ȑ��b1�f�Ɏʑ������Ƃ��A�b1�Ƃb1�f�Ɋւ��Ăǂ̗l�Ȏ��������邩���ׂĂ݂�B���܁A���ʏ�̔C�ӋȐ��b1��ɓ_��0���Ƃ�B���̂Ƃ��b1���Ėʏ�֎ˉe�����Ȑ��b1�f��ł̓�0���Ή�����Ƃ���B
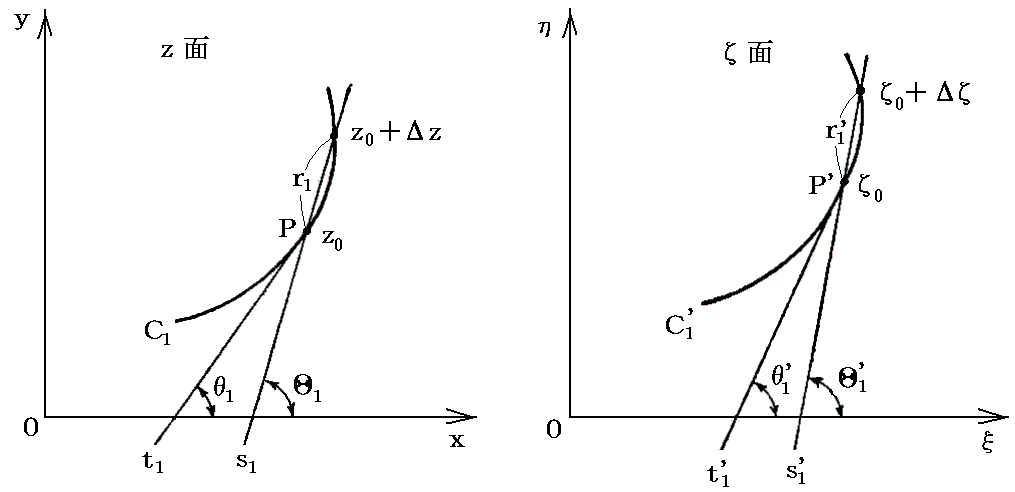
�Ȑ��b1��̂�0�̋߂��̓_��0�{�������Ƃ�A���̂Q�_��ʉ߂��钼����1�������ƃ�1�̊p�𐬂�����Ƃ������������1������1�ƂȂ�B�����Ń�����0�̋Ɍ����l����A������1�͂�0�ɂ�����Ȑ��b1�ւ̐ڐ���1�ƂȂ�B���̐ڐ���1�������ƂȂ��p��
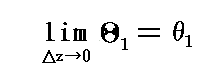
�ŗ^������B���̂Ƃ��ā����i���j�ɂ���Ă�0�Ƃ�0�{�����ɑΉ�����_�̓�0�����i��0�j�A��0�{���ā����i��0�{�����j�ŗ^������B���̂���
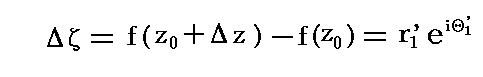
�ƂȂ�B�����ă�����0�ɂ����Ɍ��ł̓�0�����i��0�j�ƃ�0�{���ā����i��0�{�����j��ʂ钼����1�f�̓�0�ɂ�����Ȑ��b1�f�ւ̐ڐ���1�f�ƂȂ�B����̎����ƂȂ��p��
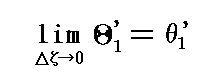
�ŗ^������B���̂Ƃ����i���j�̂��ɂ����������f�i���j�Ƃ����
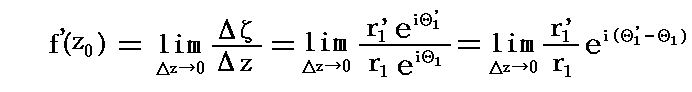
�ł��邩��

�ƂȂ�B
�@���l�ɁA��0��ʂ鑼�̋Ȑ��b2�ƁA������ĖʂɎʑ�������0��ʂ�Ȑ��b2�f�ɑ��Ă�
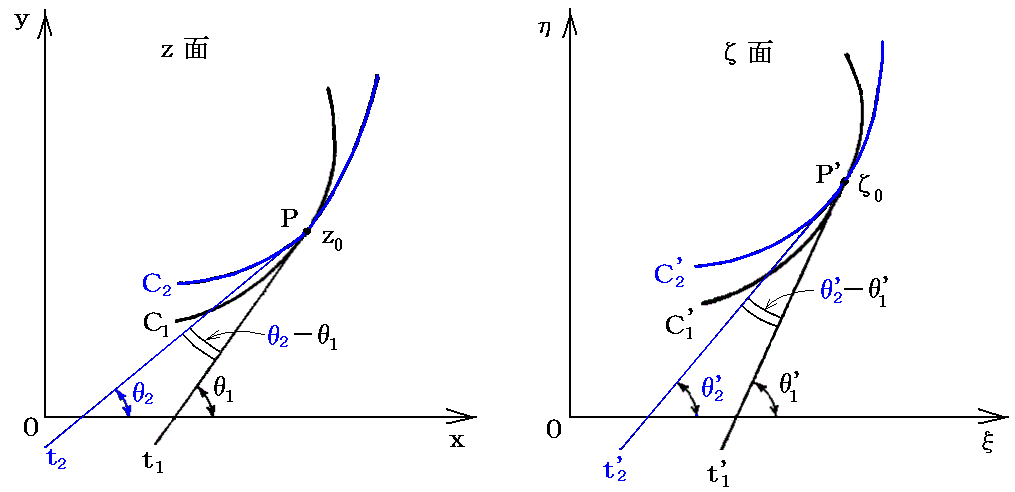
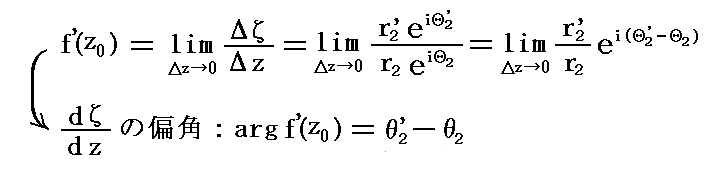
�ƂȂ�B
�@�������ā����i���j�͂��̐������ł��邩��A���ā^�����̓����̕����ɂ�����炸���łȂ���Ȃ�Ȃ��̂�
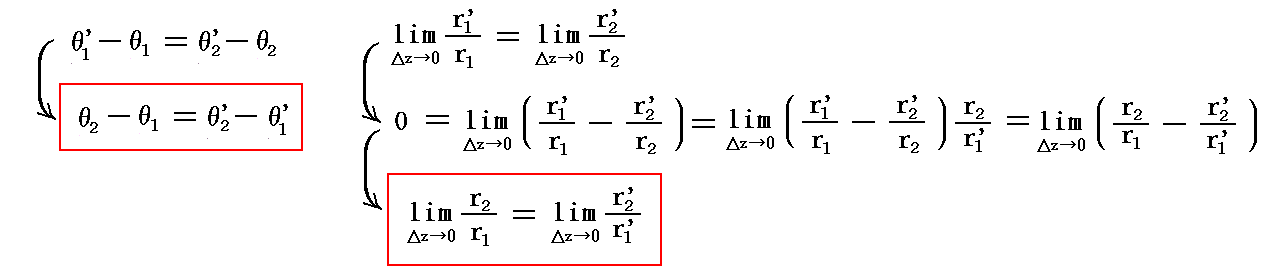
�ƂȂ�B
�@���Ȃ킿�A�ā����i���j�Ȃ�W���́A���ʂɂ������C�ӂ̐}�`���p�̕ω������ɁA���p�I�ɃĖʂ֎ʑ������B���̂悤�ȊW�����p�ʑ��Ƃ����B
�Q�D���ٓ_�ɂ�����ʑ�
�@������0�����ٓ_�̏ꍇ�ɂǂ̗l�Ȏ����N���邩���ׂĂ݂�B���܁A��0�ɂ����Ă��ā^���������f�i���j��0�ƂȂ�T�^�I�ȗ�Ƃ���
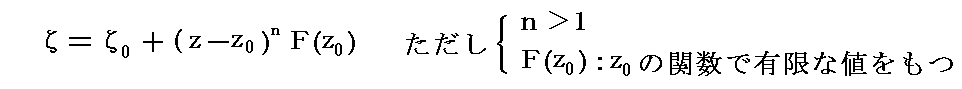
�Ȃ�ʑ����l����B���̂Ƃ�
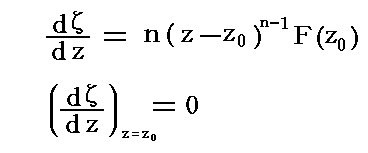
�ƂȂ�B
�@��0�̋߂��̂�����0�{�����������Ƃ�ρA�ā���0�{��n����n���e�i��0�j�ƂȂ�B���̊��ł͂��ʏ�ŕΊp�����Ƃ�����������A����ɑΉ�����Ėʏ�ł͂�����Ƃ�����������B
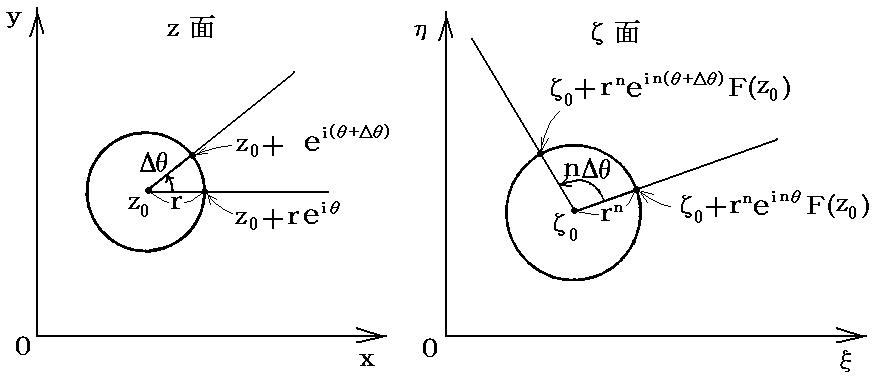
���������đΉ�����}�`�����p�ɂ͂Ȃ�Ȃ��B
�@�N���o���m�ā���log�i���|��0�j�n�A�z�����݁m�ā��|��log�i���|��0�j�n�A�Q���m�ā�����log�i���|��0�j�n�A��d�N���o���m�ā��|�ʁ^�i���|��0�j�n�Ȃǂ�\�����f���x�|�e���V�����͂�0�ɓ��ٓ_������ł��B���ۂ��ā^�������v�Z���Ă݂�ƁA������0�ɂ�����|���ā^����|�����ƂȂ�B���̂悤��|���ā^����|�����ƂȂ�_�����p�ʑ��ɂ͂Ȃ�܂���B�Ȃ��Ȃ�A���܂ł̓Ă����̊��ƍl�������t�ɂ����Ă̊��ƍl����A|���ā^����|�����̓_��|�����^����|��0�ƂȂ�A�O�L�̗�̑Ή��Ƃ��傤�Njt�ɂȂ��Ă��邩��ł��B
�@
�@�ȉ��œ��p�ʑ��̗�������������B
�i�Q�j�����ʂ��ĕ��ʂ̊p�̈�֎ʑ�
�P�D�ʑ���
�@�����ʂ���ĕ��ʂւ̎ʑ���^���鐳�����ā����i���j�Ƃ���
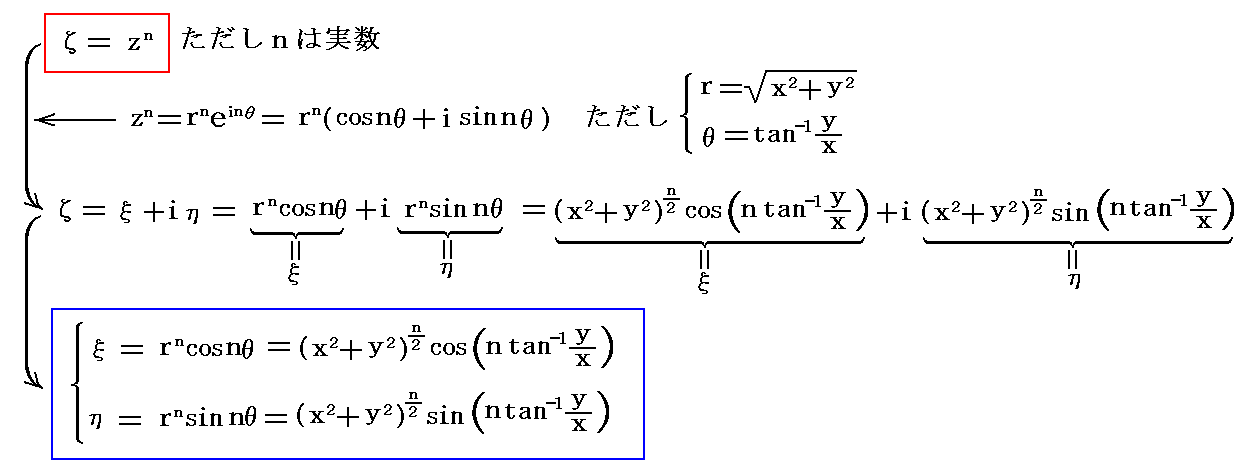
���l����B����������ʂɂ�����_���A�ĕ��ʂ̌��_����̋��������̐�Βl��������{�m�����n�̋����ŁA�Ίp�����̕Ίp�Ƃ����{�m���Ɓn�̈ʒu�Ɏʑ���������̂ł��邱�Ƃ�����B
�@���������͂ݐ����̎��́A�ĕ��ʂ̃́����ƃŁ����̊i�q���������ʂɂ����Ăǂ̗l�ȋȐ��Q�ɂȂ邩��\���Ƃ��֗��Ȍ`�ł����āA�����ʂɂ����邘�����Ƃ������̊i�q�����ĕ��ʏ�ɂ����Ăǂ̗l�ȋȐ��Q�ɂȂ邩��m��ɂ́A��L�̎��̋t���𗘗p���Ȃ���Ȃ�Ȃ��B�܂�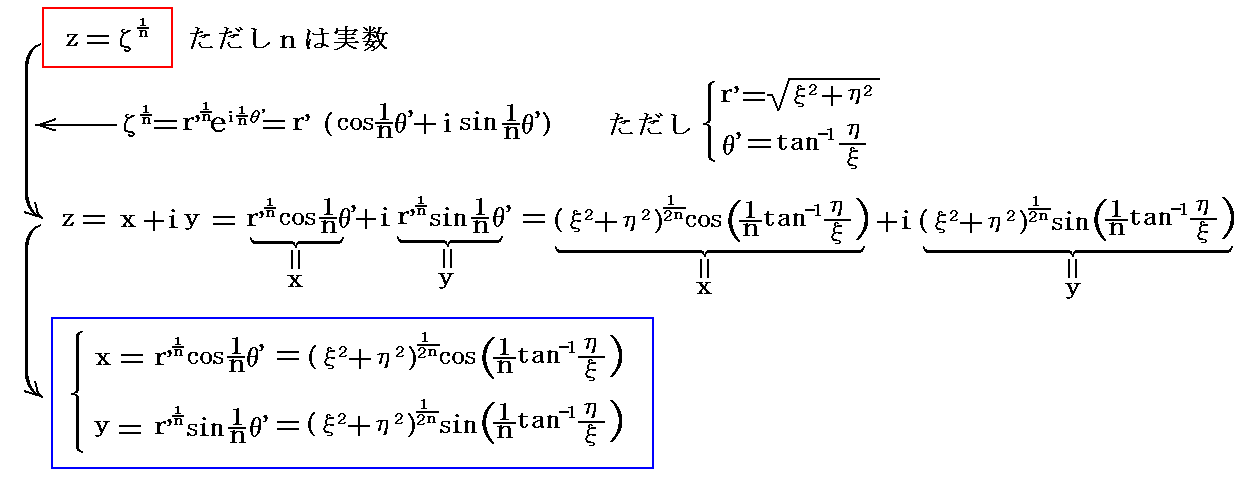
�̎��ł������A�������ƒu�����Ȑ��̃O���t���ĕ��ʏ�ɕ`���悢�B�Q�̗�ł��̓�����̗l�q�������Ă݂�B
�Q�D����0.5�̏ꍇ
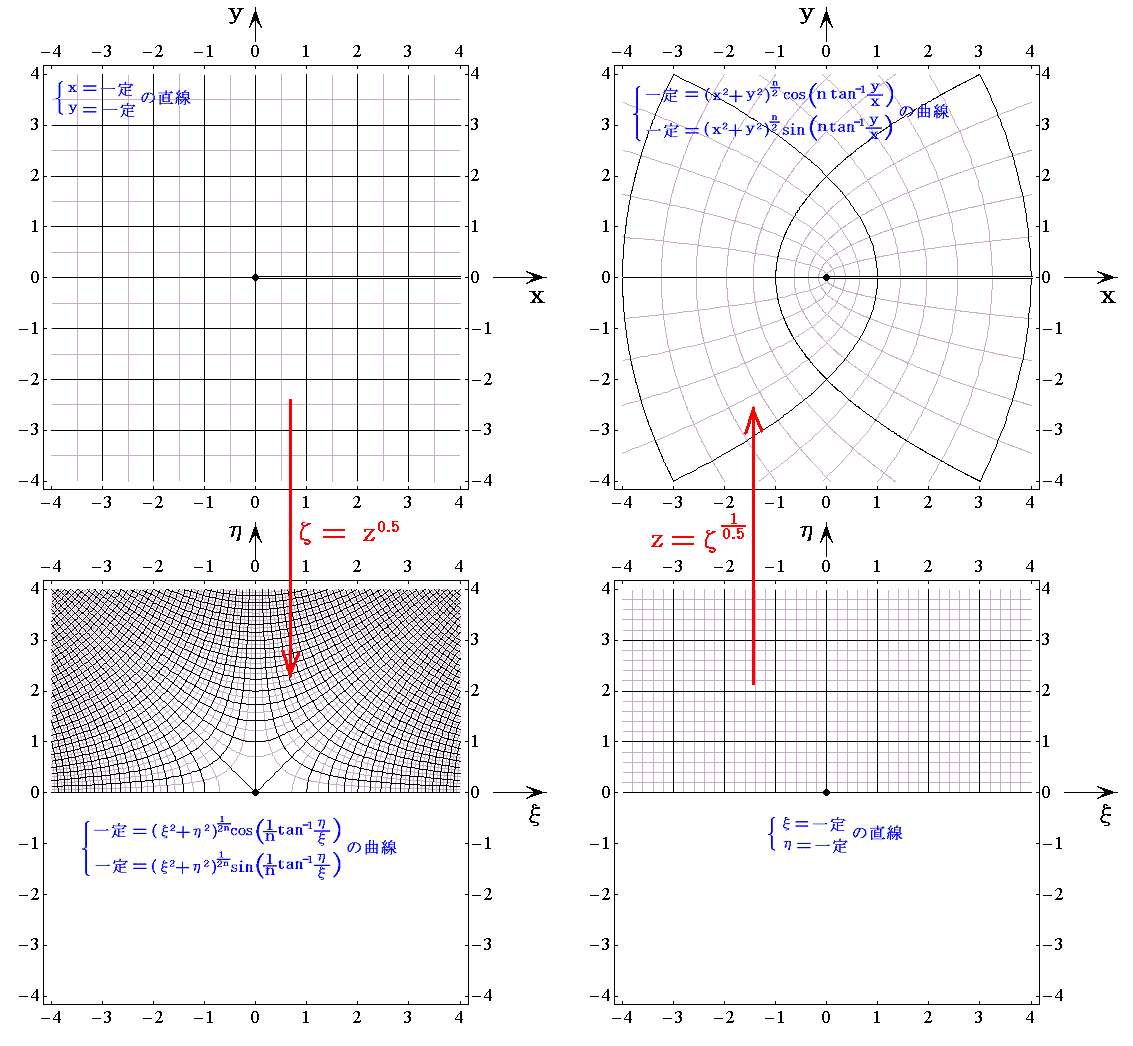
�����������ʂ̊i�q���ĕ��ʂɎʑ������ꍇ���A�E�����ĕ��ʂ̊i�q�������ʂɎʑ������ꍇ�������Ă���B���E�̐}�`�̈Ⴂ���ᖡ���ꂽ���B���p�ʑ�������Ȃ��Ȃ�̂́A���X�ɂ��Ă��̗��҂��������邱�Ƃ��琶�����B
�R�D����1.5�̏ꍇ
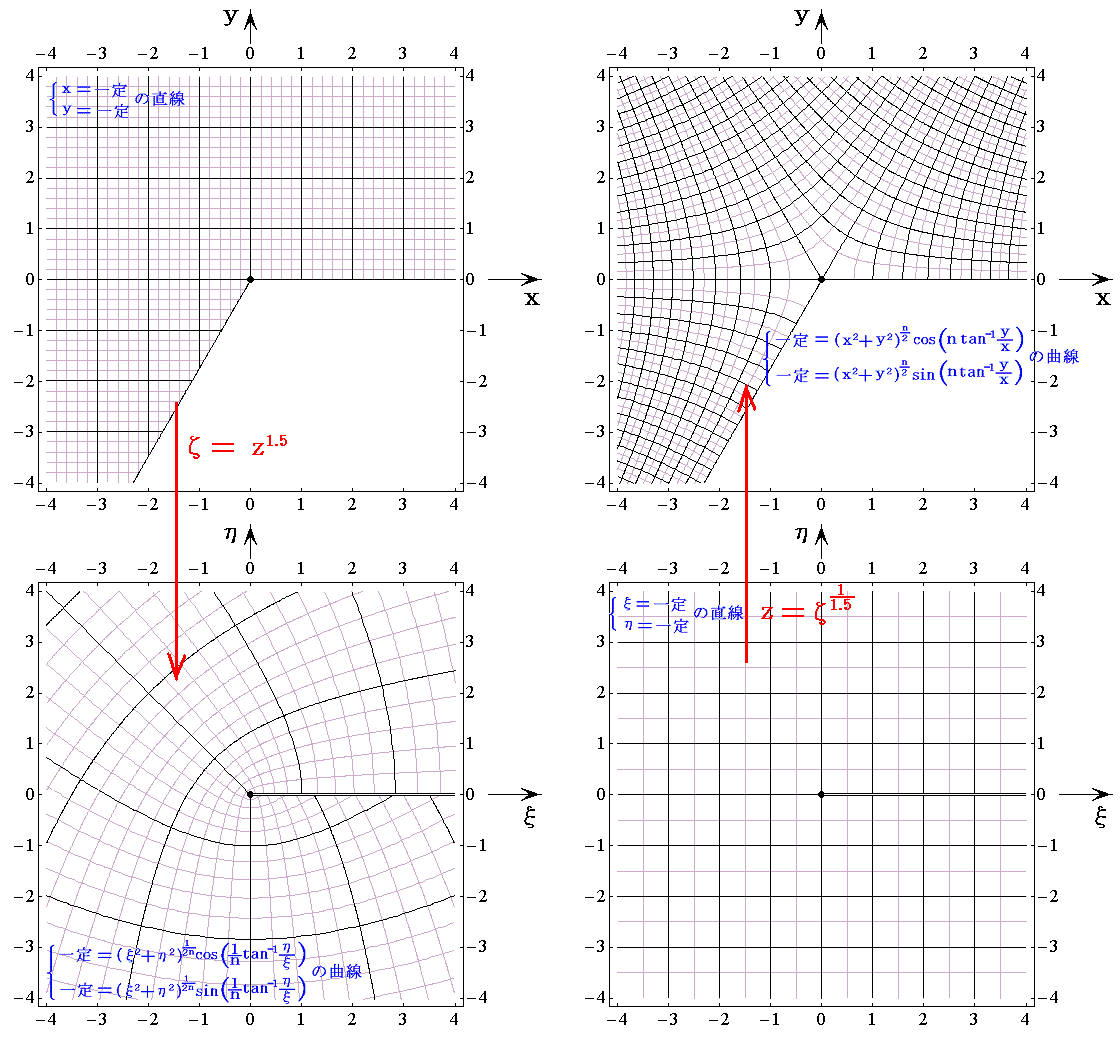
�@
�i�R�j�����ʂ��ĕ��ʂ̉~�̊O���̈�֎ʑ��@�@
�P�D�ʑ���
�@�ʑ����ā����i���j�Ƃ���

���l����B
�@���ꂪ�ǂ̗l�Ȏʑ����Ӗ�����̂��ׂĂ݂�B�O�߂Œ��ӂ����悤�ɁA�����ʂɂ����邘�����Ƃ������̊i�q�����ĕ��ʂ̂ǂ̗l�ȋȐ��Q�Ɏʑ�����邩��m��ɂ́A�㎮�̋t���𗘗p����悢�B�t����
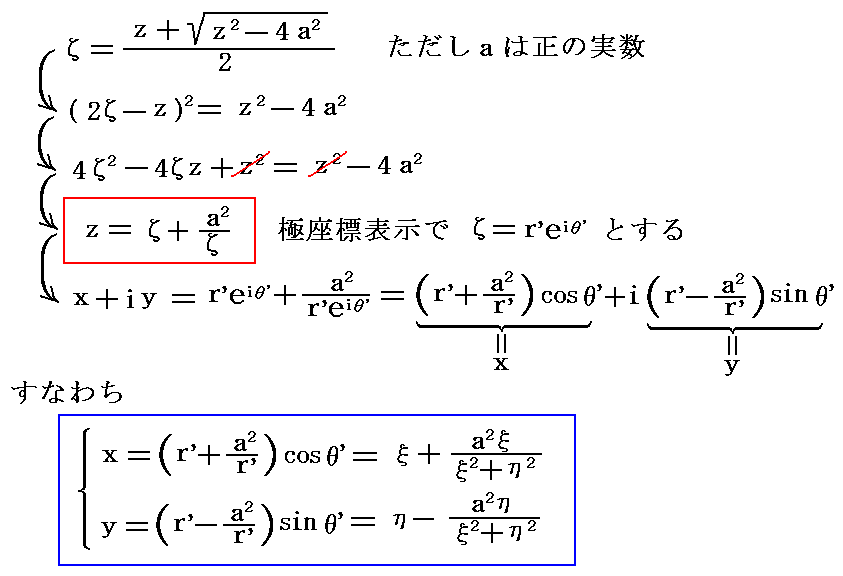
�ƂȂ�B����̓ĕ��ʂ������ʂɎʑ�������ł����A���̎��̂������Ƃ�=���̋Ȑ���`���Ă݂�悢�B
�Q�D�ʑ��̉���
����1�̏ꍇ��}�������
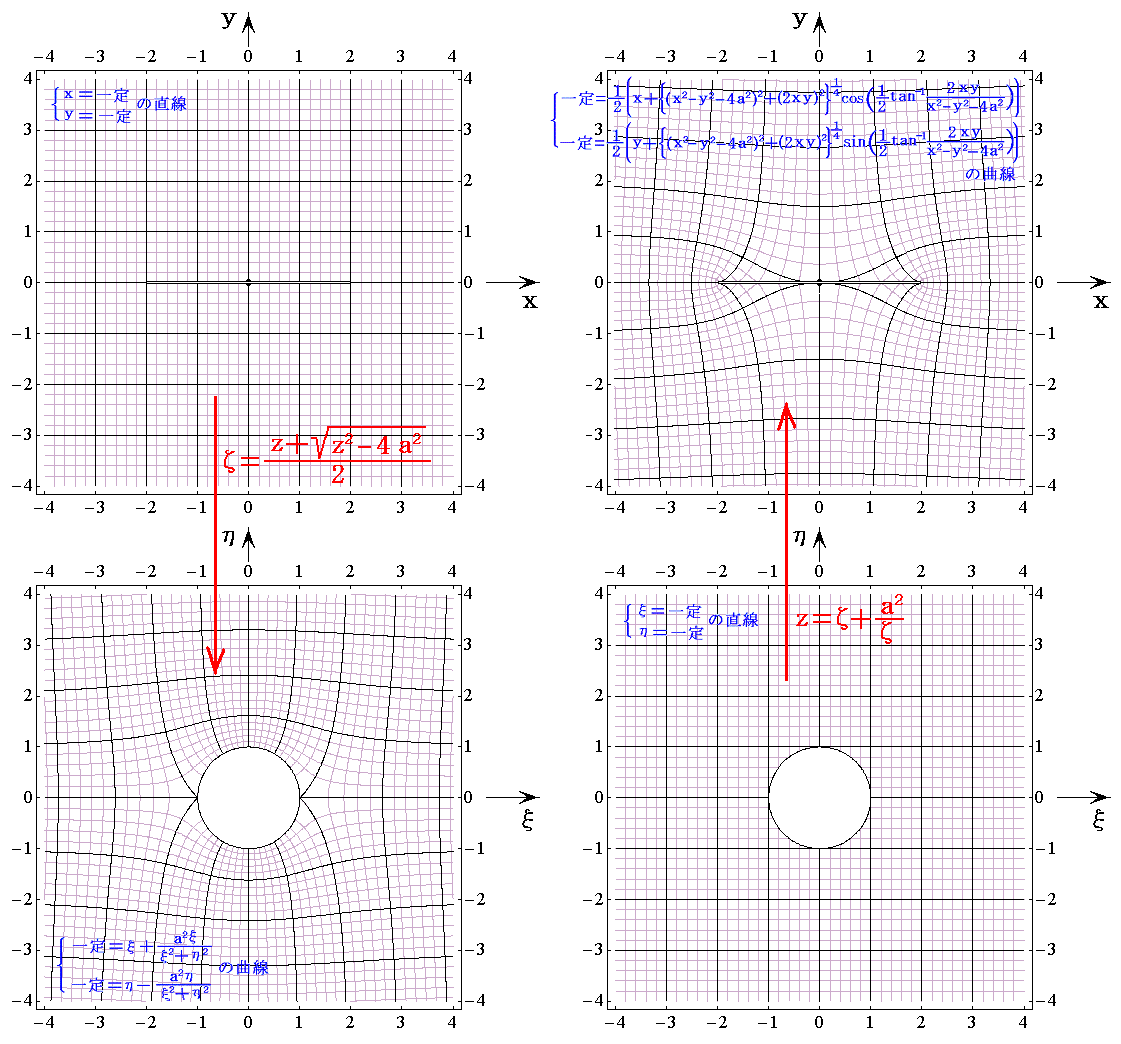
�ƂȂ�B����͂܂������A
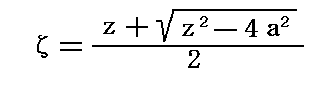
�������ʂ̌��_�ɑ��݂��钷��4���̐����̎���̗̈���A�ĕ��ʂ̌��_�ɒ��S�����锼�a���̉~�̎���Ɏʑ�������ł��邱�Ƃ�����B
�@���̏ꍇ���A�����ʂ̊i�q���ĕ��ʂɎʑ������ꍇ�ƁA�ĕ��ʂ̊i�q�������ʂɎʑ������ꍇ�̐}�`�̈Ⴂ�ɒ��ӂ��Ă��������B
�@
�i�S�j�����ʂ̉~��������ĕ��ʂ̕�����Ɏʑ��i�W���[�R�t�X�L�[�ϊ��j
�P�D�~���Ɏʑ������
�@�����ʂ���ĕ��ʂւ̎ʑ���^���鐳�����ā����i���j�Ƃ���
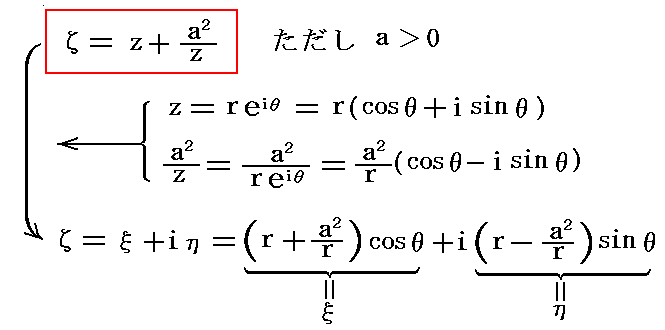
���l����B������W���[�R�t�X�L�[�ϊ��iJoukowski transformation�j�Ƃ����B���̕ϊ��͂��ʏ�̓_�����}�̗l�ȃĖʏ�̓_�֎ʑ�����B
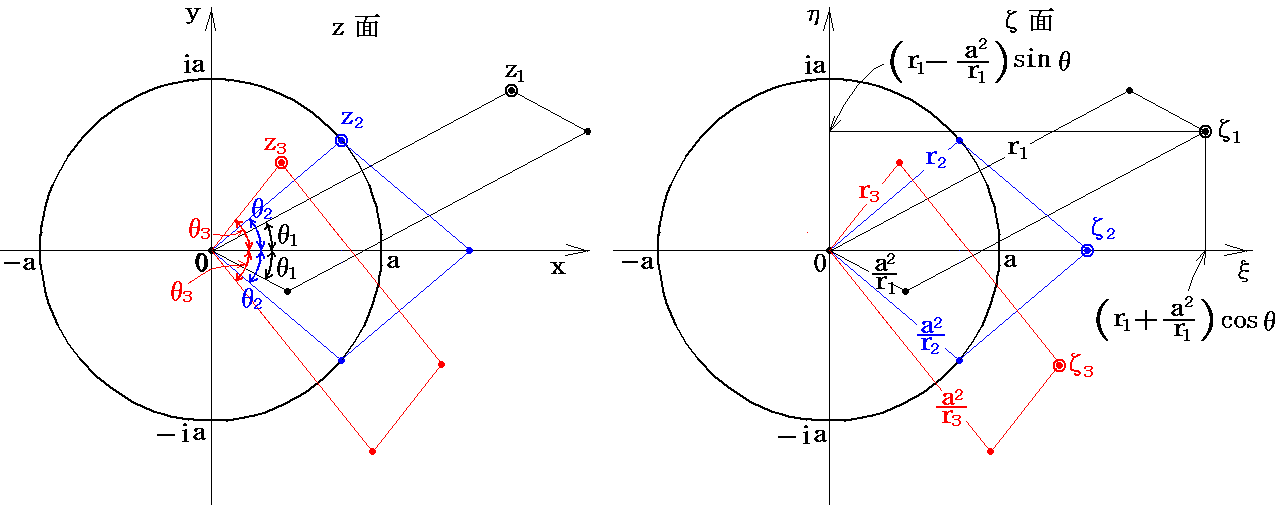
���������⑫�����
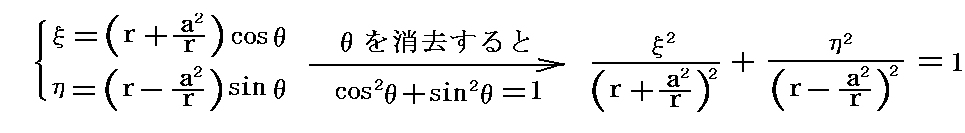
�ƂȂ�ȉ~�̕�������������B�܂肚�ʏ�̂������i�����j�̉~�A�y�т������i�����j�̉~�͌��_��ʂ钷��4���̒����̊O�̑ȉ~�Ɏʑ������B���̑ȉ~�̏œ_�́i-���C0�j�Ɓi���C0�j�ƂȂ�B�܂����ʏ�̔��a���̉~�̓Ėʏ�̎�����́i2a�C0�j�Ɓi-2a�C0�j�𗼒[�Ƃ��钷��4���̐����Ɏʑ������B����͑ȉ~�������܂łԂꂽ���̂ƌ��Ȃ���B
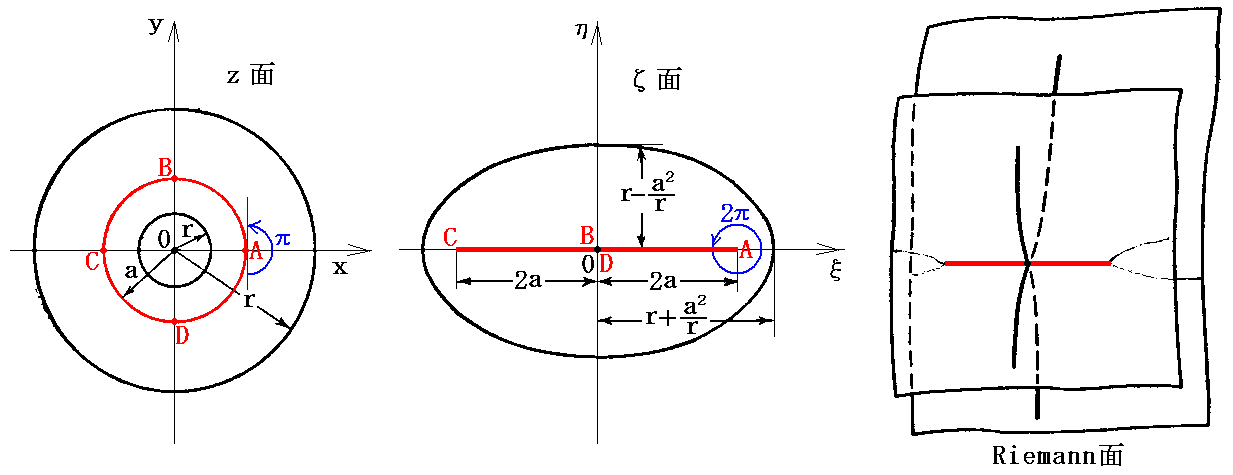
�@�}���疾�炩�Ȃ悤�ɃĖʏ�̂P�_�ɑΉ�����_�����ʏ�ɓ���݂���B���ʂ̓_�ƃĖʂ̓_���P�P�őΉ�������ɂ́A�ĖʂƂ��Ē���4���̐��������L�����̖ʁm��E�}�Q�Ɓn����������悢�B���̂悤�ɉ������d�˂đ�������\���ʂ̂��Ƃ�Riemann���Ƃ����B
�Q�D�����ʂƃĕ��ʂ̑Ή��W
�@������������₷�����邽�߂ɂ��ʂƃĖʂ̑Ή��𐬕��\���ŕ\���Ă݂�B�ā����i���j�𐬕��\�������
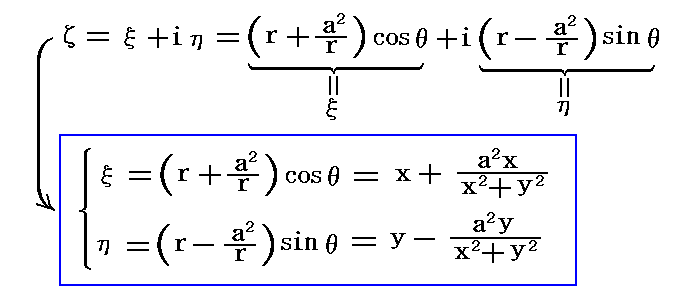
�ƂȂ�B
�@���̋t�ϊ��͏�L�̎��𖢒m�����A���̘A���������ƌ��Ȃ��ĉ����悢�B����͂Ƃ���Ȃ������ā����i���j�����ɕt���ĉ�����
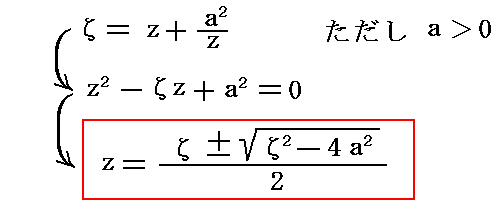
�̂������{�������́A�ł̐����\���������̂ɑ��Ȃ�Ȃ��B�����ŁA���������Z���{�����͋ɍ��W�\���̐�Βl�����{�ɂ��āA�Ίp���ɂ��邱��
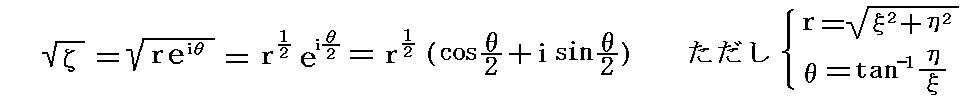
�ɒ��ӂ���ƁA�㎮�͎��̂悤�ɕό`�ł���B
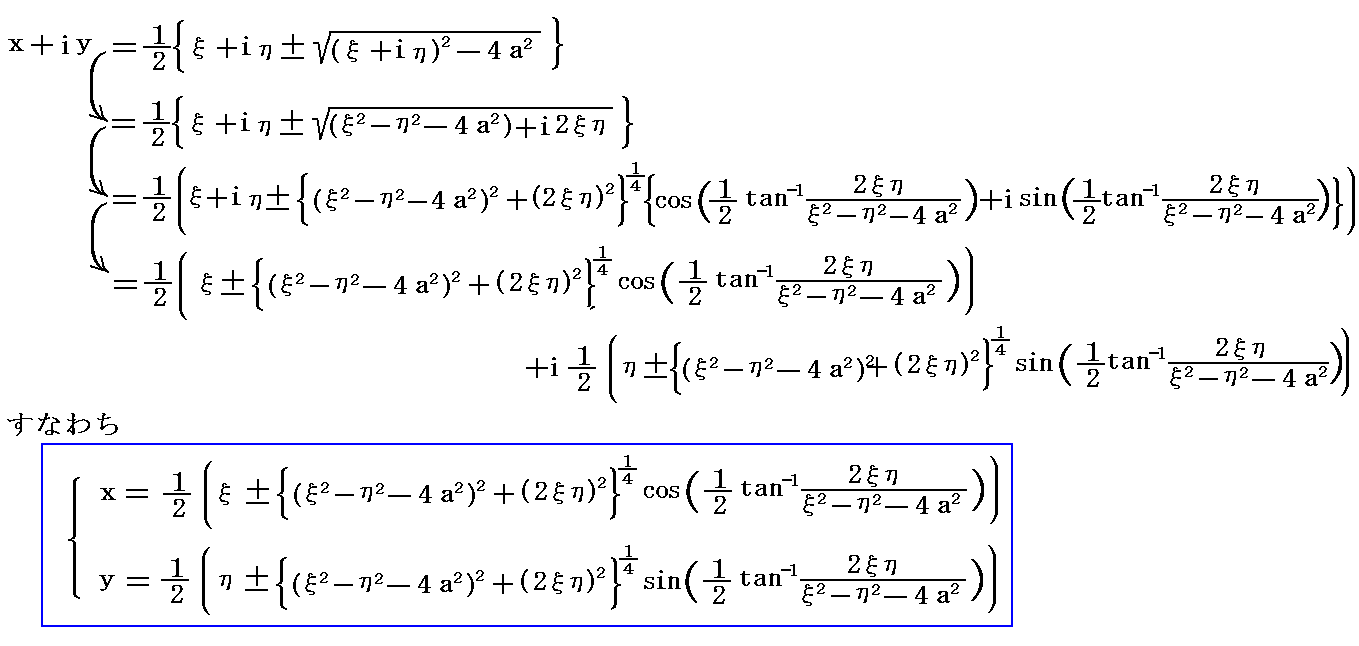
�ƂȂ�B���̏ꍇ�A��̃ē_�i�́C�Łj�ɑ��ē�̂��_�i���C���j���Ή�����B�㎮�Ł{������|��|�����ɑ���|��|�������Ή�����̂ł����ʂ̔��a���̉~�̊O���ĖʑS�̂ɁA�|�����ꍇ�͉~�̓����ĕ��ʑS�̂ɑΉ�����B���̂��Ƃ͎��Ɏ����悤�Ɉ�̂����ʂ���̃ĕ��ʂɑΉ����邱�Ƃ��Ӗ�����B
�R�D�ʑ��̉���
�@�����P�̏ꍇ��}������B
�m|��|�����̗̈�̎ʑ��n
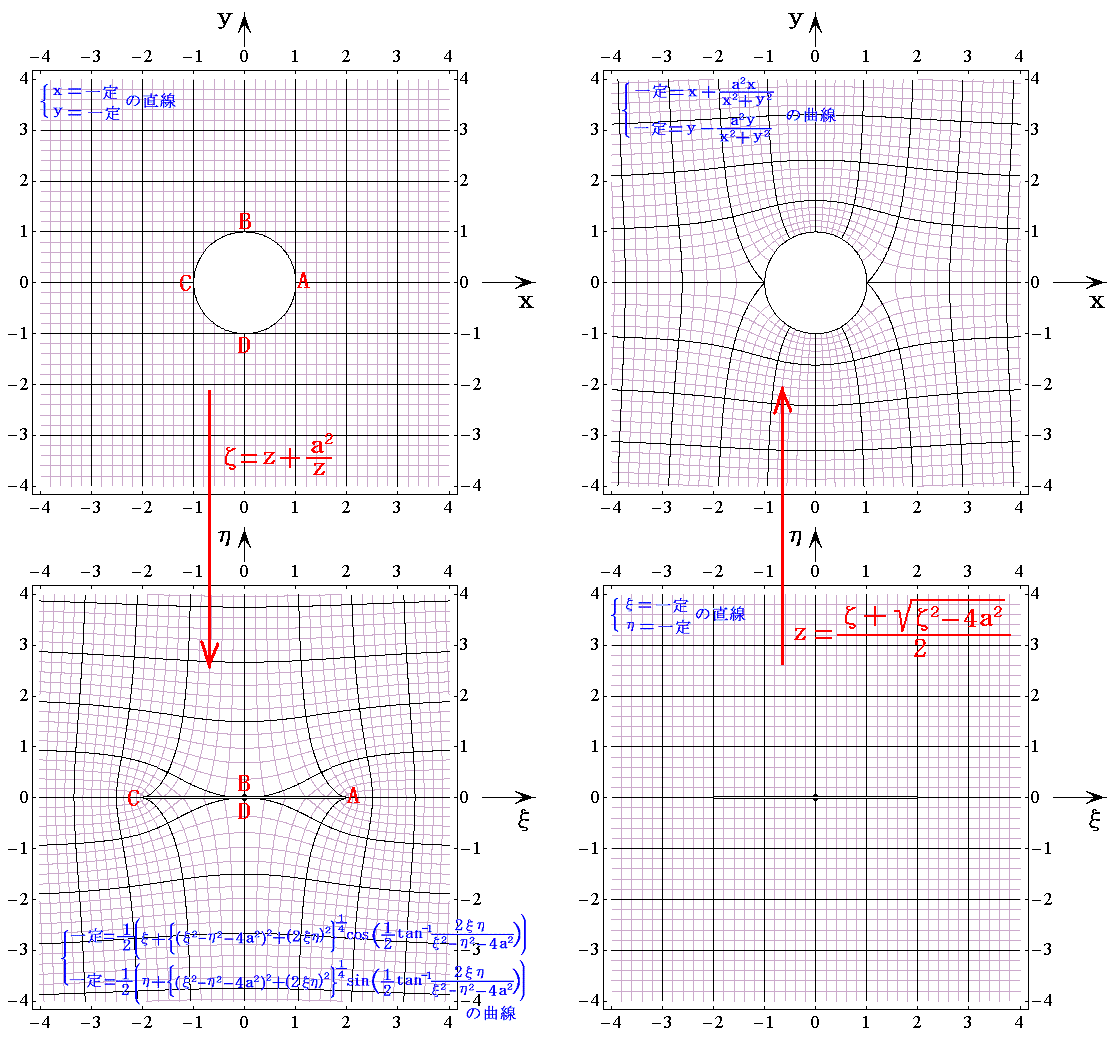
���̐}�͑O���T�D�i�R�j�Q�D�Ő��������ʑ��̋t�ɂȂ��Ă���B
�@�����Œ��ӂ��ׂ��́A�~�̊O���ʼn~���痣�ꂽ�ʒu�̂��_�́A�Ėʂɂ����Ăقړ����ʒu�Ɏʑ�����邱�Ƃł��B�܂��~�̋ߖT����������4���̒����ɋ߂Â��悤�ɘc��Ŏʑ�����邪�A���̘c�݂̒��x�͉~���痣���Ƌ}���ɏ������Ȃ��B���ꂱ���~���̂܂��̗���̂܂��̗���Ɏʑ�����Ƃ��A�����ł̋��E�����������߂ɕK�v�Ȏ��ł��B
�@����ɒ��ӂ��ׂ��́A���ʏ�̂`�_�m�������{��0�n�Ƃb�_�m�����|���{��0�n�œ������ā^���������f�i���j���P�|��2�^��2�̒l���[���ƂȂ邱�Ƃł��B�����̓_�����ٓ_�ƂȂ�A�����ł̎ʑ��͓��p�I�ł͂Ȃ��Ȃ�B
�m|��|�����̗̈�̎ʑ��n
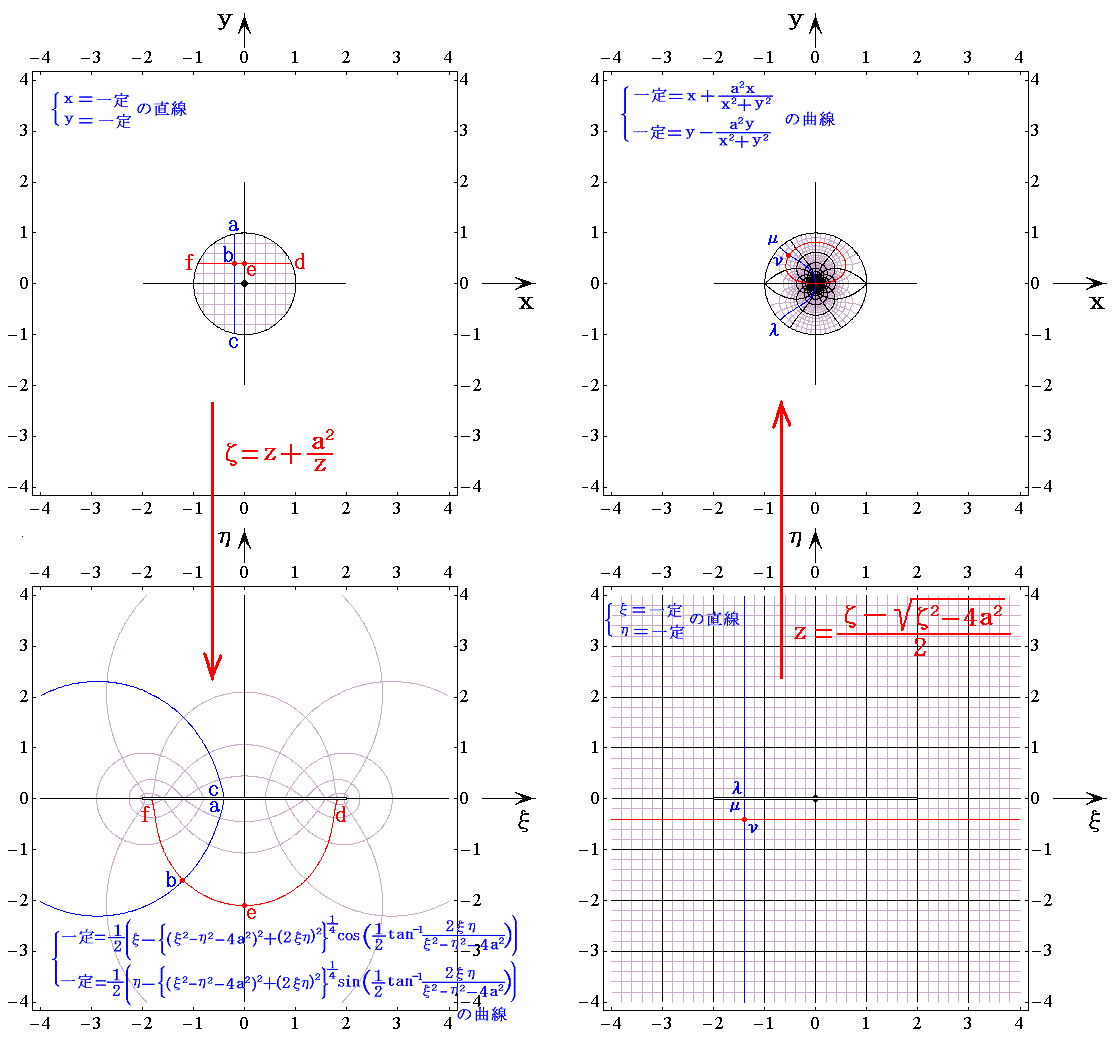
�@�����ʏ�̔��a���̉~�̓ĕ��ʂ̒���4���̐����Ɏʑ�����邪�A�����ʂ̌��_�̓ĕ��ʂ�|��|�����֎ʑ�����邱�Ƃɒ��ӂ��Ă��������B�Ή��W������ɂ������A�T�D�i�S�j�P�D�̎ʑ��Ή��_�}���Q�Ƃ���Ċm�F���Ă��������B
�@����ɒ��ӂ��ׂ��́A���ʏ�̌��_����0��|���f�i0�j|��|�P�|��2�^��2|�����ƂȂ����ٓ_�ł��B�ĕ��ʂɂ�����ʑ��_�͖������ɂȂ邽�ߐ}��Ŋm���߂邱�Ƃ͂ł��܂��A���_�̎ʑ��͓��p�I�ł͂���܂���B
�@
�i�T�j�����ʂ̉~��������ĕ��ʂ̌X����������Ɏʑ��i���ǃW���[�R�t�X�L�[�ϊ��j
�P�D�~���X�������Ɏʑ������
�@���܃W���[�R�t�X�L�[�ϊ��������ς���
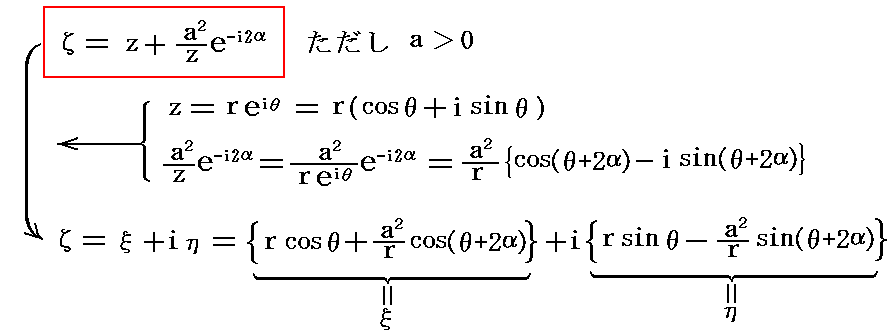
�Ȃ�ʑ����l����B������������ǃW���[�R�t�X�L�[�ϊ��ƌĂԂ��Ƃɂ��܂��B���̂Ƃ���ʂ̊����i���j�ɂ�-i�����悶�����͉̂��}�Ɏ����悤�Ɍ��_�ɑ��ā|�Ƃ�����]�������̂Ɏʑ�����܂��B
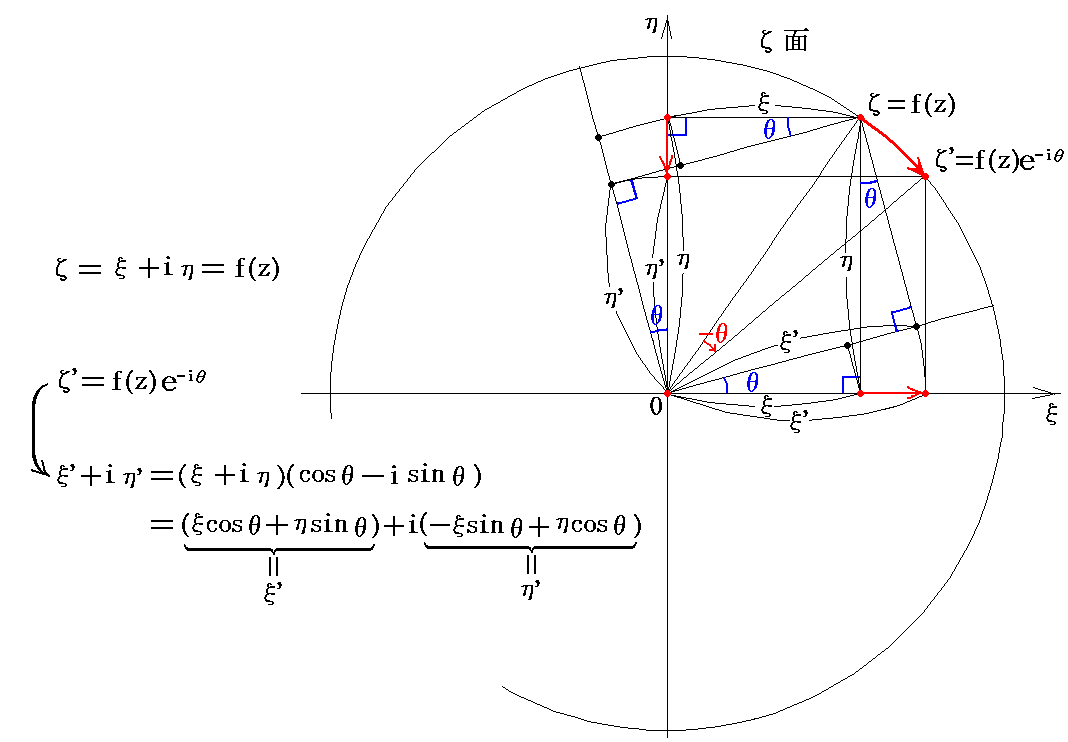
���̂��ߏ�L�̕ϊ��͉��}�̗l�Ȏʑ����Ӗ�����B
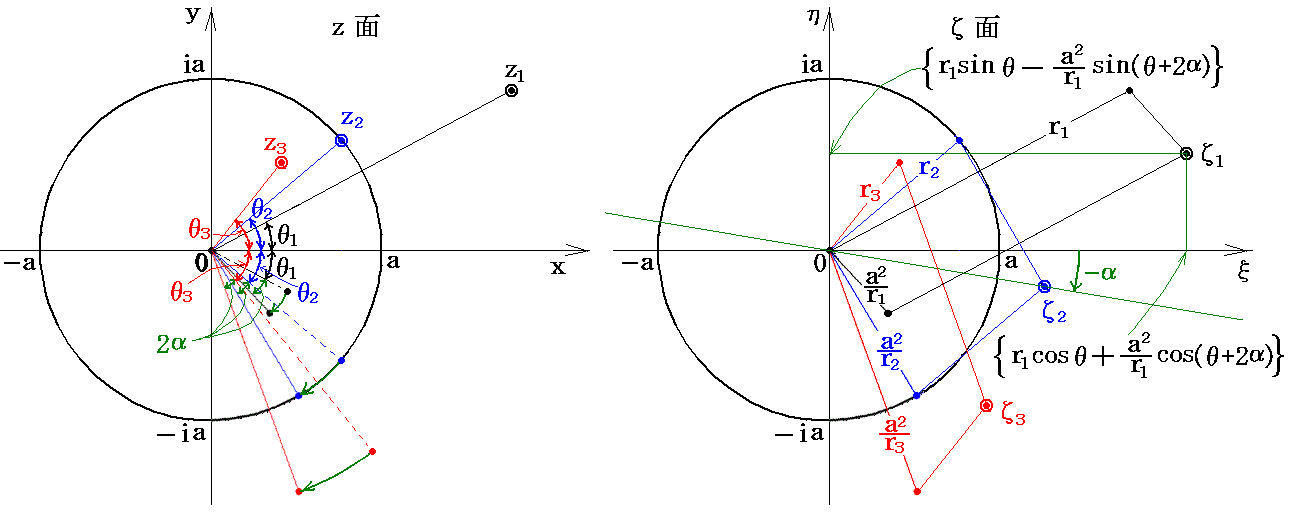
���̂Ƃ��́A�ō��W�����|��������]�����V���ȍ��W�����́f�A�Łf���Ƃ����
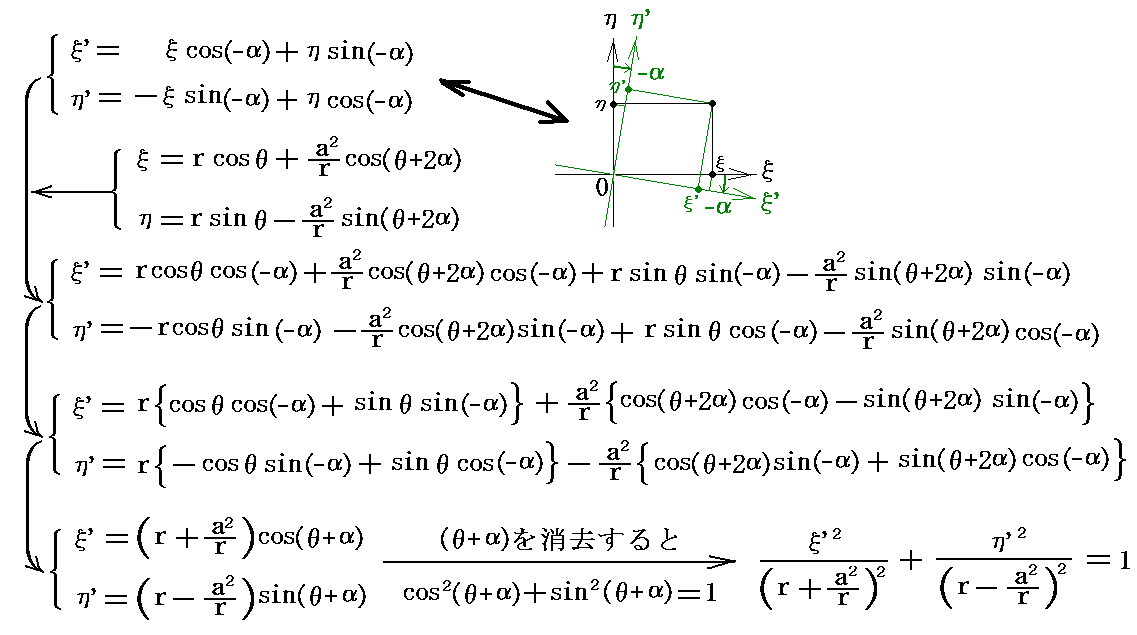
�ƂȂ�ȉ~�̕�������������B�܂肚�ʏ�̂������i�����j�̉~�A�y�т������i�����j�̉~���T�D�i�S�j�P�D�̑ȉ~���|��������]�����ȉ~�Ɏʑ�����Ă���B���̑ȉ~�̏œ_�́i-���C0�j�Ɓi���C0�j���|���x��]�����ʒu�ɂȂ�B�܂������ʏ�̔��a���̉~�̓ĕ��ʏ�̎����Ɗp�x�|���Ō���钷��4���̐����Ɏʑ������B�m���}�Q�Ɓn
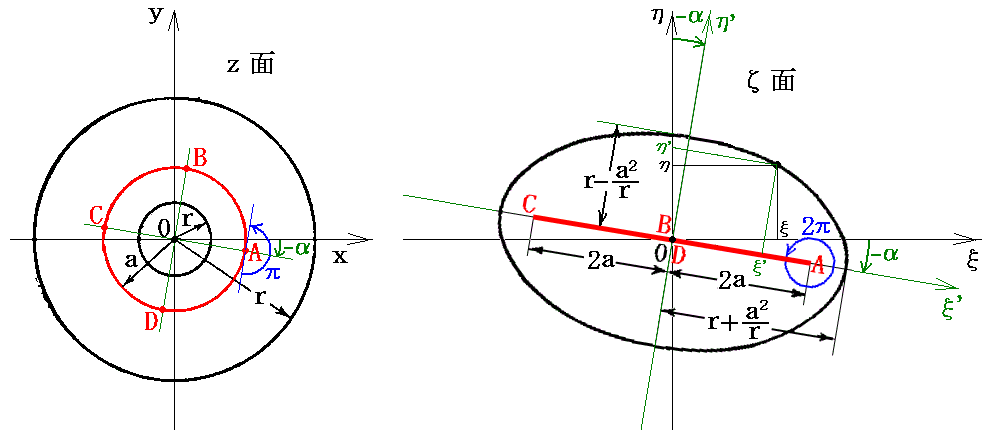
�Q�D�����ʂƃĕ��ʂ̑Ή��W
�@������������₷�����邽�߂ɂ��ʂƃĖʂ̑Ή��𐬕��\���ŕ\���Ă݂�B�ā����i���j�𐬕��\�������
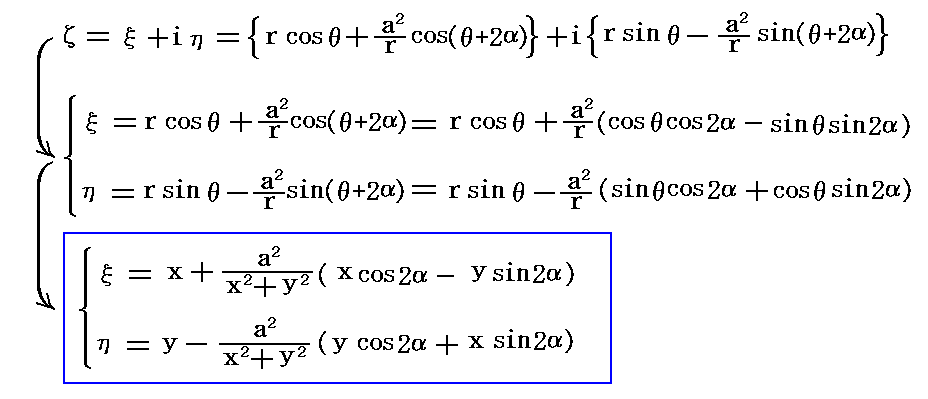
�ƂȂ�B
�@���̋t�ϊ��͏�L�̎��𖢒m�����A���̘A���������ƌ��Ȃ��ĉ����悢�B����͂Ƃ���Ȃ������ā����i���j�����ɕt���ĉ�����
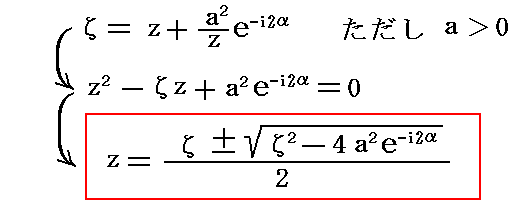
�̂������{�������́A�ł̐����\���������̂ɑ��Ȃ�Ȃ��B�����ŁA���������Z���{�����͋ɍ��W�\���̐�Βl�����{�ɂ��āA�Ίp���ɂ��邱��

�ł��邩��A�㎮�͎��̂悤�ɕό`�ł���B
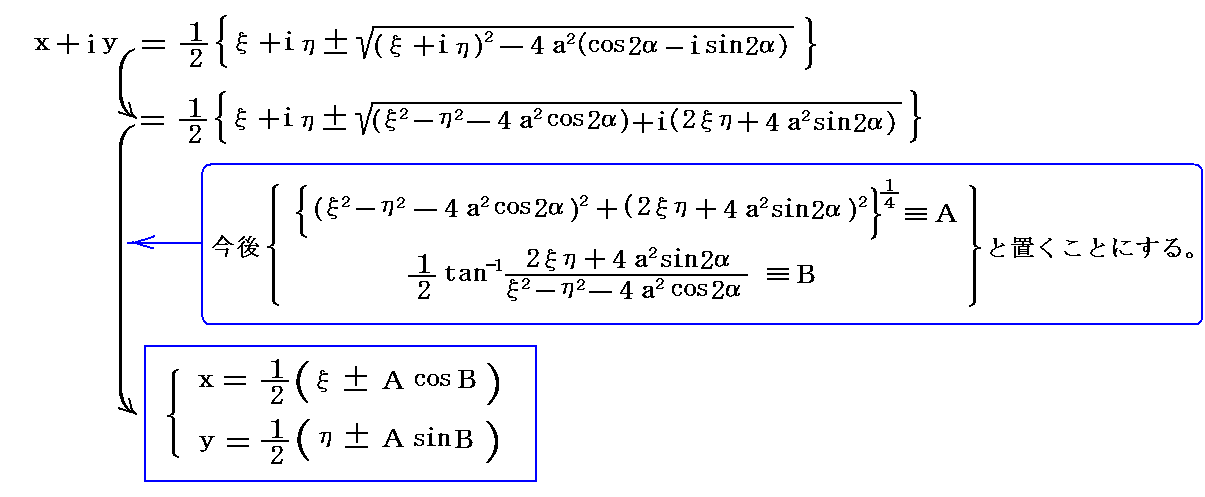
�ƂȂ�B�T�D�i�S�j�R�D�Ɠ��l�ɁA��̓_�i�́C�Łj�ɑ��ē�̓_�i���C���j���Ή�����B�������{�̏ꍇ�́A|��|�����ɑ���|��|�������Ή�����̂Ŕ��a���̉~�O�̓_�ɁA�|�̏ꍇ���~���̓_�ɑΉ�����B���̂��Ƃ͉��}�̗l�Ɉ�̂����ʂ���̃ĕ��ʂɎʑ�����邱�Ƃ��Ӗ�����B
�R�D�ʑ��̉���
�@�����P�A����30�����^6rad�̏ꍇ��}������B
�m|��|�����̗̈�̎ʑ��n
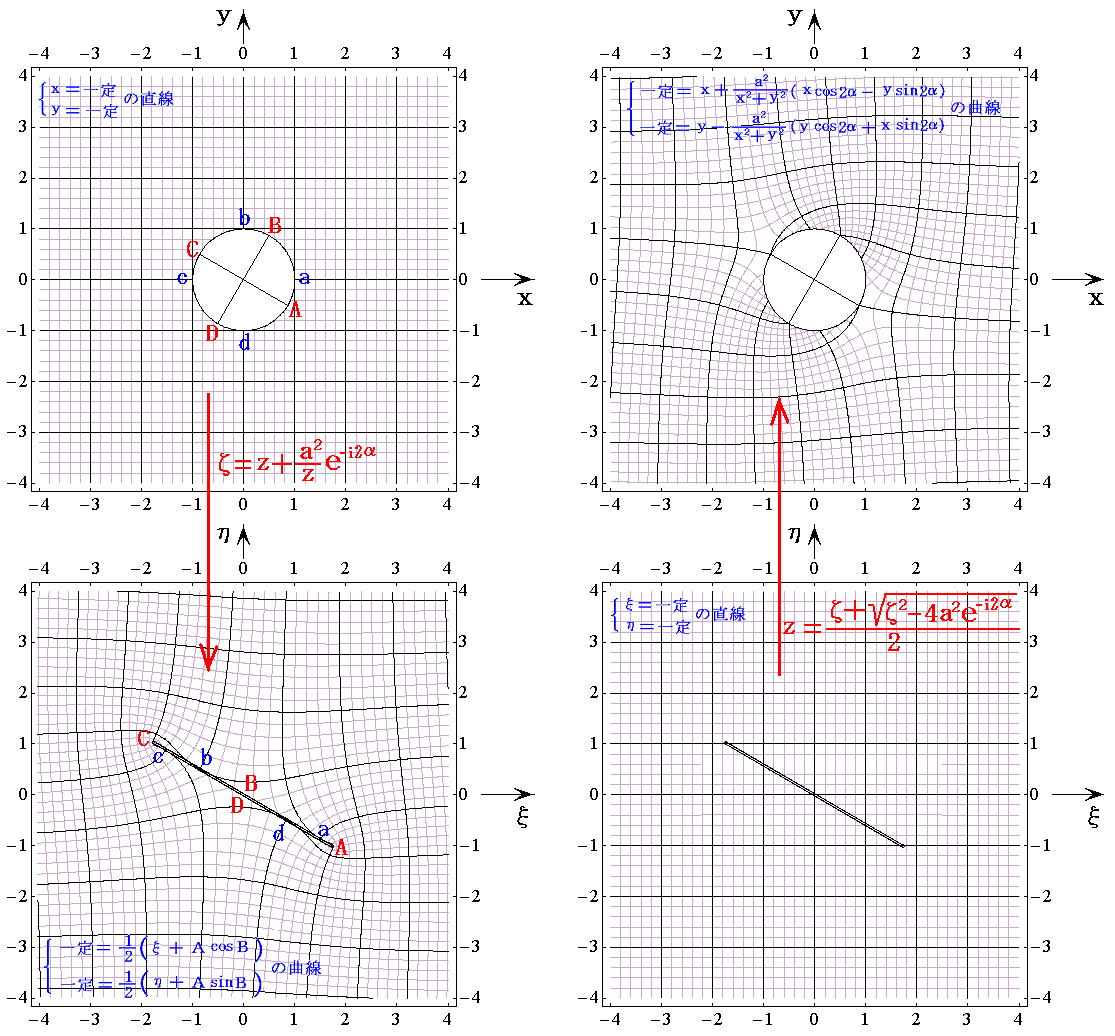
�@���̐}�͑O���T�D�i�S�j�R�D�Ɏ��Ă��邪�ׂ����Ƃ��낪�����Ɉ���Ă���̂Ŏq�ׂɌ������Ă݂Ă��������B���̂Ƃ����̐}���X����������̗����E�����x�|�e���V�������}�ƍ������Ȃ��ł��������B
�@�����ł��T�D�i�S�j�Ɠ��l�ɁA�����ʂ̉~���痣�ꂽ�ʒu�́A�Ėʂɂ����Ăقړ����ʒu�Ɏʑ������B�����ʂ̉~�̋ߖT�������ĕ��ʂ̒���4���̌X���������̎���ɘc��Ŏʑ�����邪�A���̘c�݂̒��x�͉~���痣���Ƌ}���ɏ������Ȃ�B���ꂱ���~���̂܂��̗�����X�������̂܂��̗���Ɏʑ�����Ƃ��K�v�ȏ����ł��B
�@���ʏ�̂`�_�Ƃb�_�́A�����ł̓������ā^���������f�i���j���P�|��2���-i2���^��2���[���ƂȂ����ٓ_�ł��B���̂��߂����̓_�̎ʑ��͓��p�I�ł͂Ȃ��̂͂������ł����}�̏k�ڂ��傫���ω����Ă���B���ɉ��}�̕��[�_�̂܂�肪��}�ő傫���g�傳��Ă��邱�Ƃɒ��ӂ��Ă��������B
�m|��|�����̗̈�̎ʑ��n
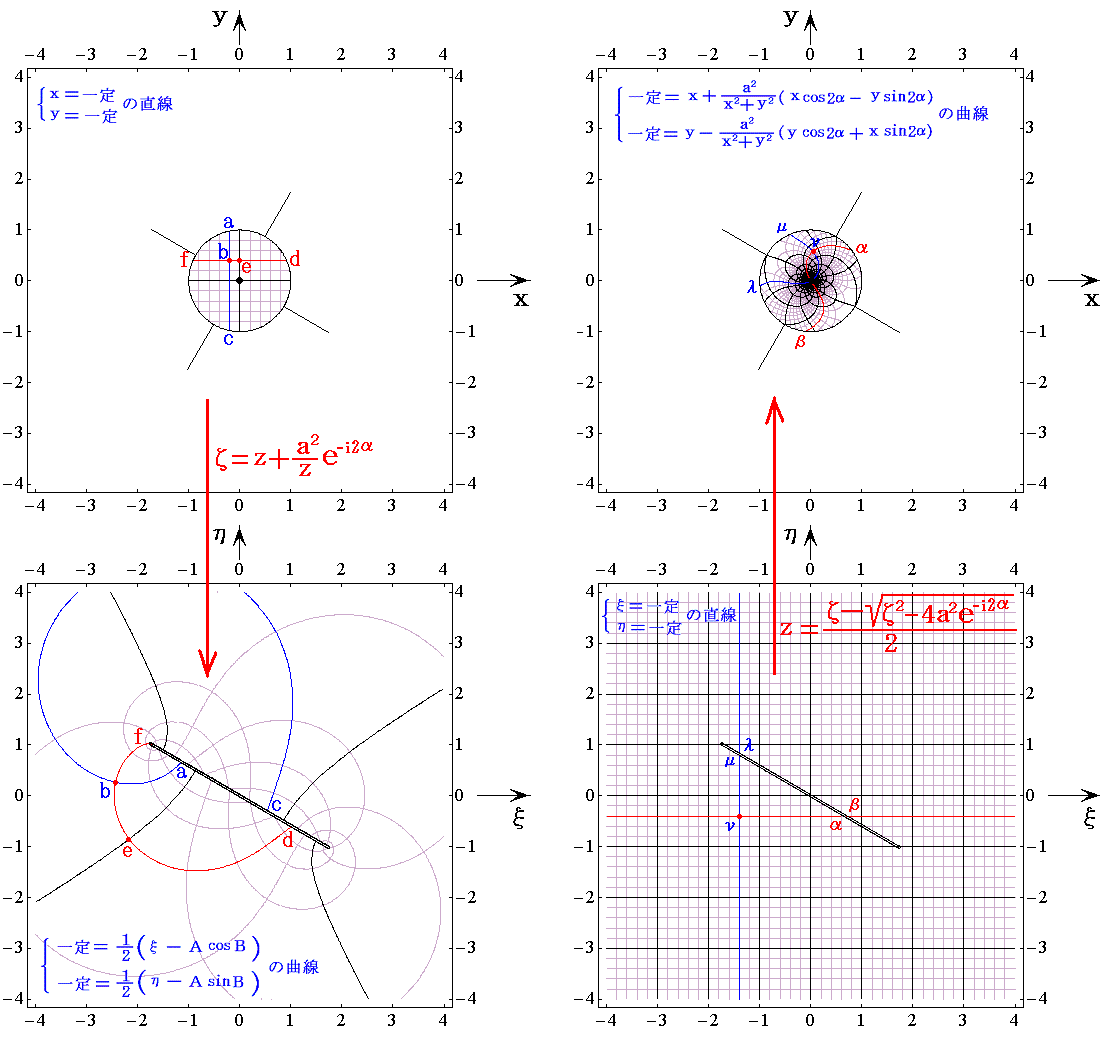
�̂悤�ɂȂ�B�����ʂ̌��_�̓ĕ��ʂ�|��|�����֎ʑ������B�܂��A�����ʏ�̔��a���̉~���ĕ��ʂ̒���4���̐����Ɏʑ������B�Ή��W������ɂ������A�T�D�i�T�j�P�D�̎ʑ��Ή��_�}���Q�Ƃ���Ċm�F���Ă��������B
�@�����ʏ�̔��a���̉~�̓ĕ��ʂ̒���4���̐����Ɏʑ�����邪�A�����ʂ̌��_�̓ĕ��ʂ�|��|�����֎ʑ������B�܂��A���ʏ�̌��_����0��|���f�i0�j|��|�P�|��2���-i2���^��2|�����ƂȂ����ٓ_�ł��B
�@���ۂɂ͉~���̊O���̗����̂܂��̗����Ɏʑ��������̂�����A����͎�ɂ������̗̈����舵�����ƂɂȂ��B
�@
�i�U�j�W���[�R�t�X�L�[�ϊ��̈�ʉ�
�P�D�����ʂ̉~��������ĕ��ʂ̃����Y����Ɏʑ��i�J���}���E�g���t�c�ϊ��j
�@�T�D�i�S�j�P�D�Ő��������W���[�R�t�X�L�[�ϊ������������ό`����
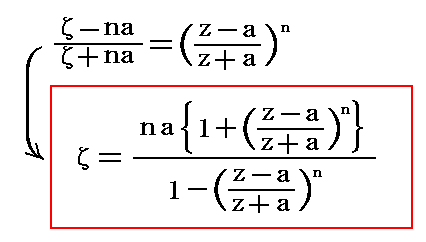
�Ȃ�ϊ����l����B������J���}���E�g���t�c�ϊ��ƌĂ����̂ł��B
�@�����ł���2�Ƃ����
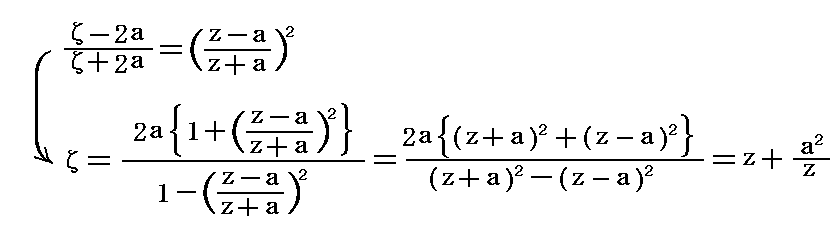
�ƂȂ�̂ŁA���̏ꍇ�̓W���[�R�t�X�L�[�ϊ����̂��̂ł��B
�@�܂�����1�̏ꍇ��

�ƂȂ�B����͂����ʂ̌��_�𒆐S�Ƃ��锼�a���̉~�����̂܂ܕό`���邱�ƂȂ��ĕ��ʂ̉~�Ɏʑ�����ϊ��ł��B
�@�����̓��ʂȏꍇ����\�z�����悤���P�������Q�̏ꍇ�̃J���}���E�g���t�c�ϊ��͂����ʏ�̉~��������ĕ��ʏ�̃����Y�`�̊O���̈�ɕϊ����܂��B
�@���W�i�q�̕ϊ��̗l�q��}�������
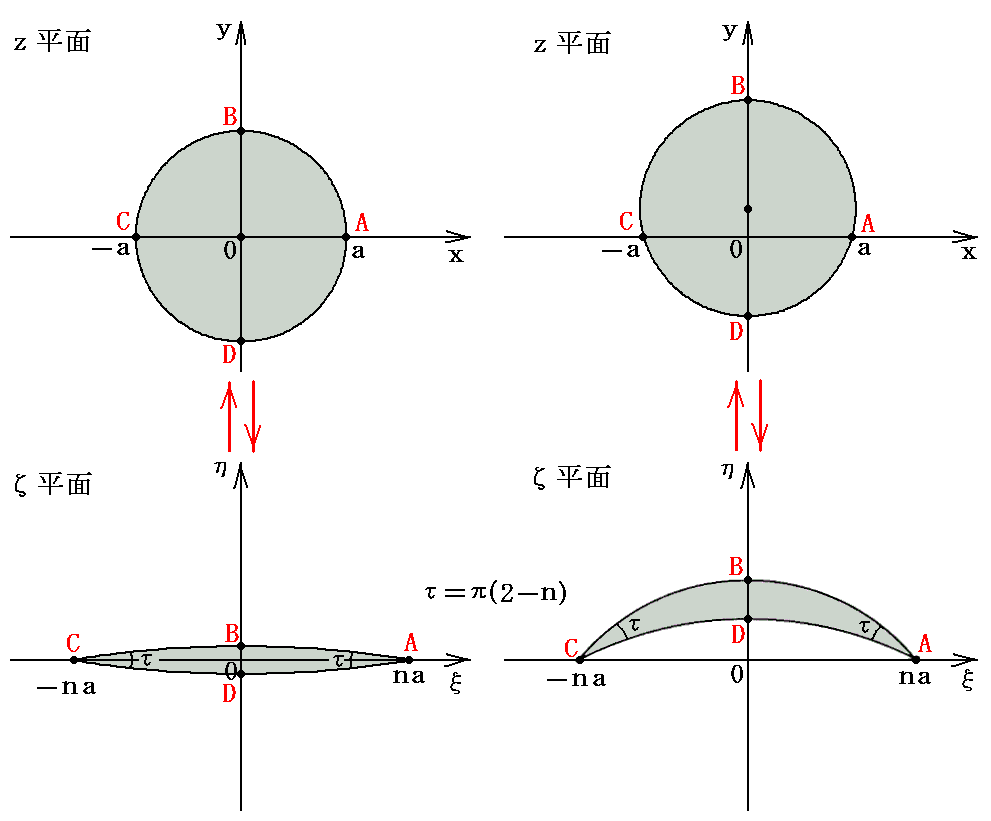
�̂悤�ɂȂ�܂��B�c�O�Ȃ���W���[�R�t�X�L�[�ϊ��̂悤�ɊȒP�ȕϊ��}�`�ŕϊ��̗l�q���������Ƃ͂ł��܂���B
�@���̕ϊ���p������U�D�i�X�j�P�D�Ő�������悤������p�̑傫���т⒆�����̖c��݂����Ȃ莩�R�ɒ����������^����邱�Ƃ��ł����B
�Q�D����Ȃ��ʉ�
�@�W���[�R�t�X�L�[�ʑ���������Ɉ�ʉ������
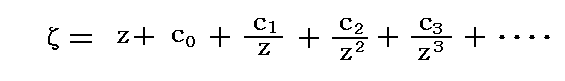
�Ƃ������������ŕ\�����Ƃ��ł���B���̎ʑ����͂������̓��ٓ_�������A���̓��̈�����^�̌㉏�Ɏʑ������悤�ɂ��A���̓��ٓ_���~���ɂ���悤�ɂ���B�W����0�A��1�A��2�A�E�E�E�E�����邱�ƂŔC�ӂ̕ό`�ݏo�����Ƃ��ł���B
�@�ڍׂ͏ȗ����܂��B�Q�l�����Q�D�A�W�D�A�P�R�D�A�P�S�D�A�P�V�D�����Q�Ƃ���Ă��������B
�@
�@�����܂ł̂Ƃ���A����̏�Ƃ͉���W���Ă��Ȃ����Ƃɒ������Ă��������B���p�ʑ��𗬂�̏�ŗ��p����ɂ͂�����H�v�K�v�ł��B���ɂ��鋳�ȏ��͂����̐������B���ʼn���ɂ����̂ň�͂�݂��ďڂ����������܂��B
�@
�U�D����̎ʑ�
�@�����ŗ��̗͊w�ɂ����铙�p�ʑ��̗��p��������܂��B
�i�P�j����̏�̎ʑ��̈�ʘ_
�P�D���f���x�|�e���V�����̎ʑ�
�@�C�ӂ̐��������i���j���������Ő�����Q�����̗���ɑ������f���x�|�e���V�������i���j����(x,y)�{����(x,y)�ƍl���鎖���ł���B���̂Ƃ��Ё����{�����ō\������镡�f���ʂ��Ёi�V�O�}�j���ʂƖ��t���鎖�ɂ����ƁA���f���x�|�e���V���������i���j
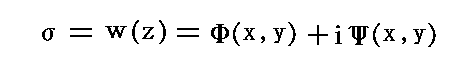
�͂����ʂƃЕ��ʂ̊Ԃ̎ʑ��W��\���܂��B
�@�������Ё����i���j�̋t�����������i�Ёj�Ƃ���m�O�͂Ő������������ʂƃĕ��ʂɂ�����ʑ����������i�āj�ƃā����i���j�̊W�Ɠ����ł��n�B�������ăЕ��ʂ̊i�q���i�������A�������̒����Q�j���������i�Ёj�ɂ���Ă����ʂɎʑ����܂��B
�@�Е��ʂŌ݂��ɒ������郳�����A�������̊i�q���������ʏ�Ɏˉe�����ƌ݂��ɒ������郳(x,y)�����ƃ�(x,y)�����̋Ȑ��Q�ƂȂ�B�ʑ��̓��p���ɂ��A�����̋Ȑ��Q�͋Ǐ��I�ɐ����`�̖Ԗڂ��`�Â���B
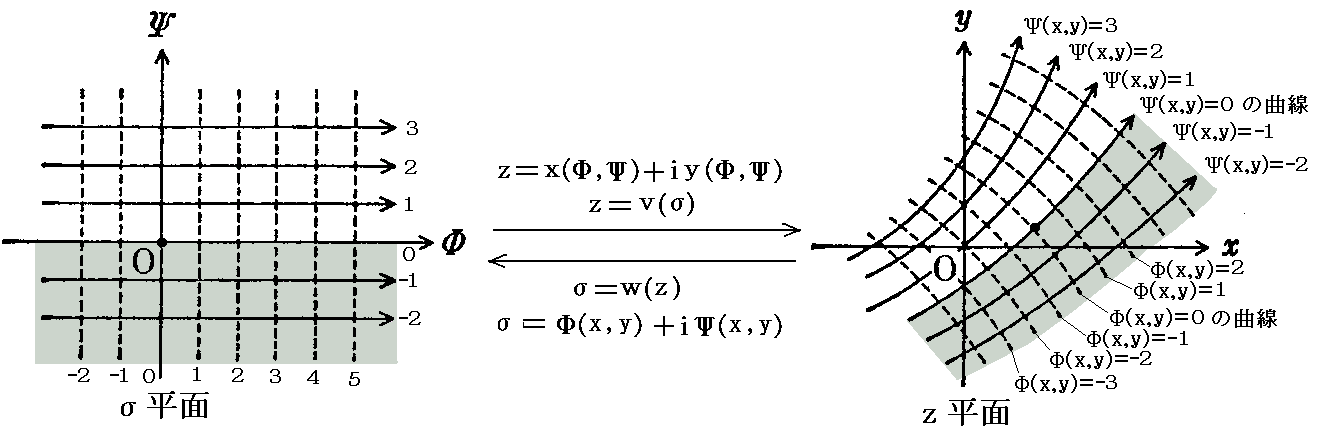
�@���̂Ƃ�������Ȑ��Q���������ʂɂ����������x�|�e���V�������m��(x,y)�����n�������m��(x,y)�����n��\���B���̂��Ƃ͕ʍe�u�J���}���Q��v�R�D�i�Q�j�Q�D�Ő������܂����B����ɂ����Ő��������悤�ɂ��i���j�����Ŕ������������^���������f���x�ƌ�������ł���A���̎������Ƌ����������ꂼ�ꂚ���ʏ�̓_���ɂ����鑬�x�������Ɓ|����^���܂��B
�@�����œ���ꂽ�Ȑ��Q��������ā����i���j�Ȃ�ϊ��ɂ�����ĕ����Ɏʑ����܂��B
�@���̂Ƃ��ā����i���j�̋t�����������i�āj�ƕ\�����Ƃɂ���ƁA�����ʂ̕��f���x�|�e���V�������i���j���������i�āj�̕ϊ��ɂ���āA�ĕ��ʂ̕��f���x�|�e���V�������f�i�āj�ɕϊ�����܂��B
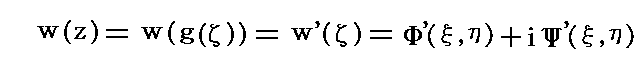
������Ă̐������ł��B�Ȃ��Ȃ��������̋t�����������ł���A�������̐���������͂萳�����ɂȂ邩��ł��m�ؖ��͕��f���_�̋��ȏ����Q�Ƃ��Ă��������n�B
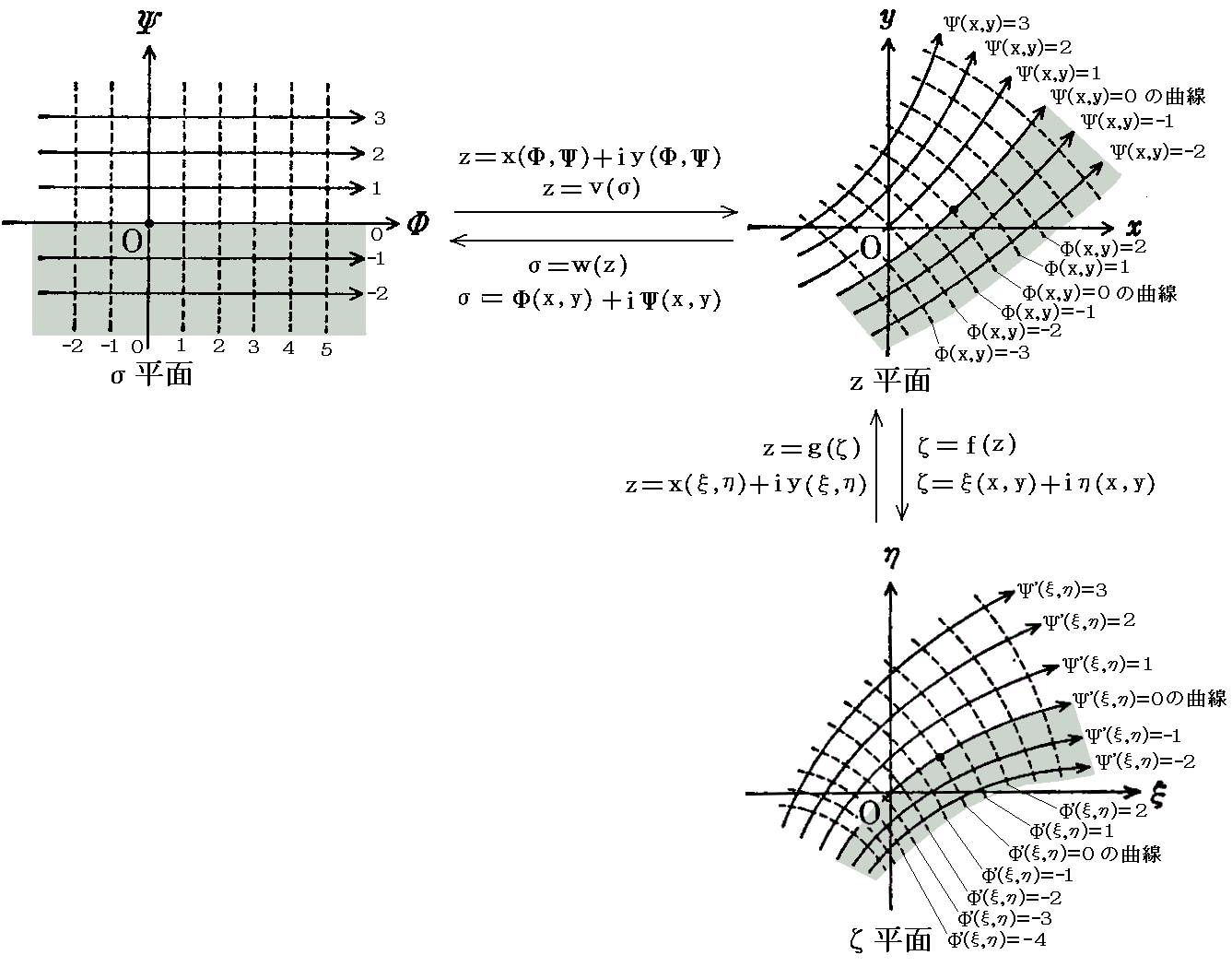
�@���̂Ƃ��T�D�i�P�j�P�D�̓��p�ʑ��Ő��������悤�ɁA�����ʂ̃�(x,y)�����ƃ�(x,y)�����̋Ȑ��Q�̓ā����i���j�ɂ���ăĕ��ʂŌ݂��ɒ�������Ȑ��Q�m���f(x,y)�����ƃ��f(x,y)�����̋Ȑ��Q�n�Ɏʑ�����܂��B���̂��߃ĕ��ʏ�Ɏʑ����ꂽ�����̋Ȑ��Q�̎����Ƌ����̂��ꂼ�ꂪ�����x�|�e���V�������Ɨ����Ƃ��Ă̐�����ێ����Ă���B�Ȃ��Ȃ����f�i�āj�̎����Ƌ����������x�|�e���V�������Ɨ����ƌ��Ȃ���ׂɕK�v�Ȃ��Ƃ́A���f�i�āj�̎������Ƌ��������R�[�V�[�E���[�}���̊W���������Ƃł������A�������ł��邗�f�i�āj�͓��R�̂��ƂƂ��Ă�������Ă�������ł��B
�@���̂Ƃ��ƂĂ��d�v�Ȃ��Ƃł����A���i���C���j�͂������i�́C�Łj�{�����i�́C�Łj�m�܂肘�����i�́C�Łj�Ƃ������i�́C�Łj�n�ɂ���ă��f�i�́C�Łj�ցA���i���C���j�����l�ɂ������i�́C�Łj�Ƃ������i�́C�Łj�ɂ���ă��f�i�́C�Łj�֕ϊ������̂ł����A���i���j�����i���C���j�{�����i���C���j�������Ƌ����͂��ꂼ��ʁX�����f�i���j�̎������f�i�́C�Łj�Ƌ������f�i�́C�Łj�֕ϊ�����܂��B���i���j�̎����Ƌ���������������Ă��f�i�́C�Łj�̎����Ƌ����ɕϊ�����邱�Ƃ͂���܂���B
�@���̂������i���C���j�����i���Ƃ���j�̓��f�i�́C�Łj�����ցA���l�Ƀ��i���C���j�����i���Ƃ���j�̓��f�i�́C�Łj�����֕ϊ������B�܂�E�ӂ̈��l�������܂܂ŕϊ�������̂ł��m�U�D�i�S�j�R�D�Q�Ɓn�B
�@
�@����́A�Ƃ���Ȃ��������f�i�āj�����f�i��,��)�{�����f�i��,��)�Ƃ����Ƃ����f�i��,��)�����̋Ȑ��Q���A��(x,y)�������ĕ��ʏ�Ɏˉe�����Ȑ��ł���A���������f�i��,��)�����̋Ȑ��Q���A��(x,y)�������ĕ��ʏ�Ɏˉe�����Ȑ��ɂȂ��Ă��鎖���Ӗ�����B
�@�܂肗�f�i�āj�̓ĕ��ʏ�ʼnQ�����̗����\�����f���x�|�e���V�����ł���A���f�i��,��)�����̋Ȑ����������l�ɑ��������x�|�e���V���������A���f�i��,��)�����̋Ȑ�����͂��������l�ɑ���������\���Ƃ����Ă悢�B
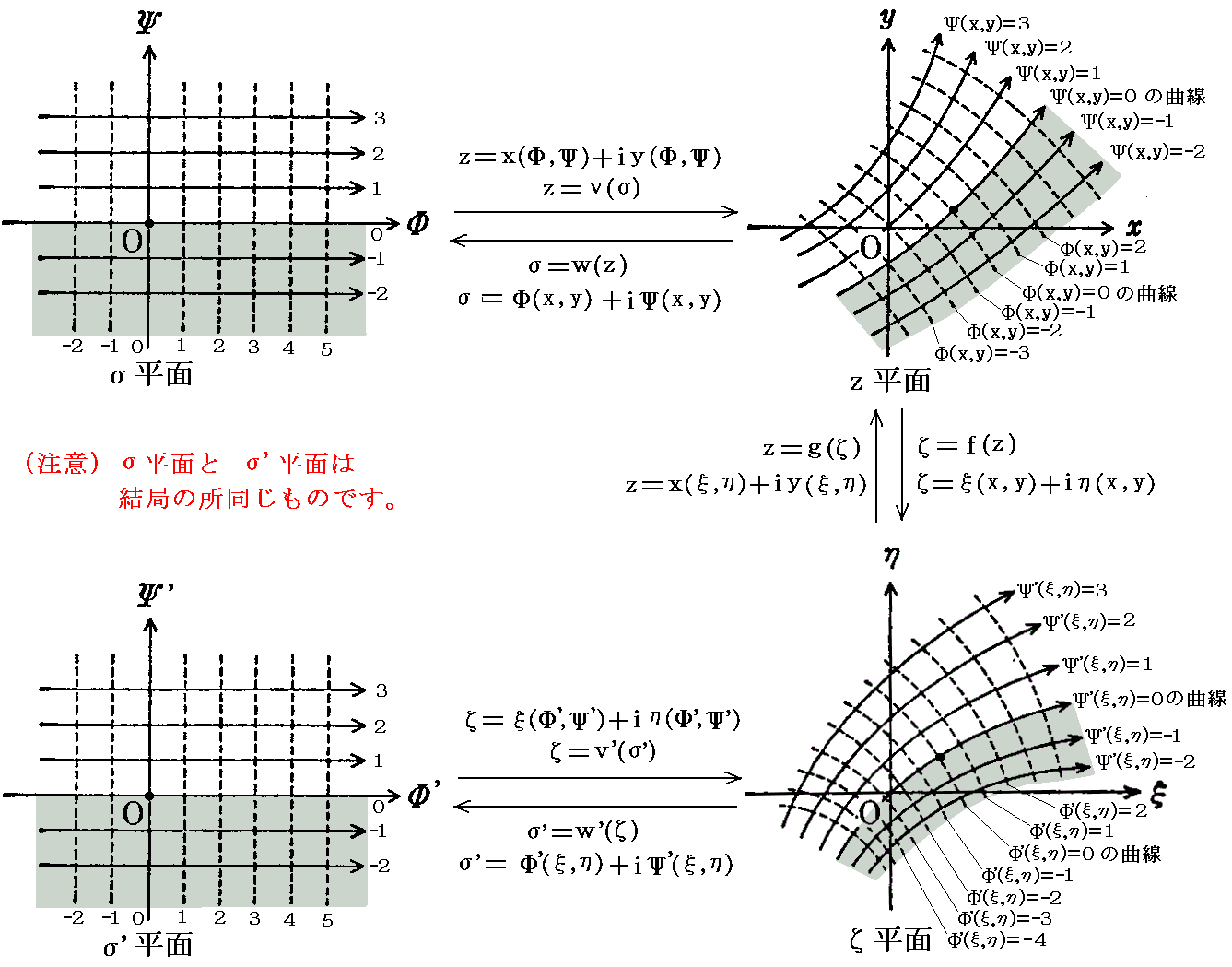
�@��L�̎����́A�V���ȕ��f���ʃЁf�����f�{�����f�����݂��ăЁf���ʂɂ�����i�q���i���f�����ƃ��f�����j�����p�ʑ��ā��́i���f�C���f�j�{���Łi���f�C���f�j�ɂ��ĕ��ʏ�̕��f���x�|�e���V�������f�i���f�C���f�j�Ɏʑ����ꂽ�ƍl���邱�Ƃ��ł���B
�@���̂Ƃ���(x,y)�����f�i��,��)�����ƃ�(x,y)�����f�i��,��)�����̋Ȑ��Q�́A���̈��l�����ʂȂ̂�����Е��ʂƃЁf���ʂ͌��Ǔ������̂ł��B
�@�����͗��̗͊w�ɂ����铙�p�ʑ��̗��p�ōł�����ɂ����Ƃ���ł�����A�U�D�i�Q�j�`�i�X�j�̋�̓I�ȗ�ł���ɐ������܂��B
�Q�D����̏�ɂ�����z�̓��p�ʑ��s�ϐ�
�@�����ʏ�̔C�ӂ̕��̕\�ʂb0�͓��p�ʑ�
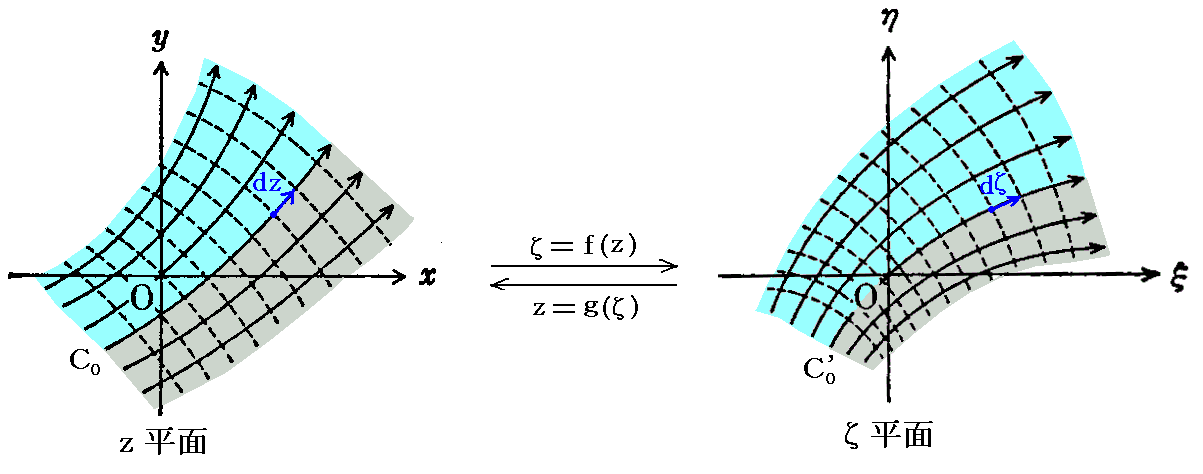
�ɂ���ăĕ��ʏ�̂���Ȑ��b0�f�Ɏʑ������B�܂������ʏ�̔C�Ӑ��������̓ĕ��ʏ�̐������Ă֎ʑ������B����ɂ����ʏ�̂�0�ɂ����邗�i��0�j�̓ĕ��ʏ�̃�0�����i��0�j�̓_�̂��f�i��0�j�ƂȂ�B�����^���������l�ɂ����f�^���ĂƂȂ�B���̂���
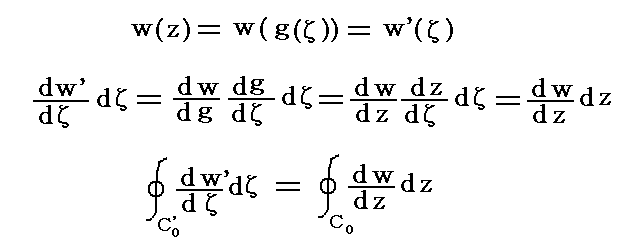
��������B
�@��ʂɕ��̕\�ʂb0�͈�̗����ƂȂ�̂����������� �������|���������O ������m�ʍe�u���E�k���E���S���̗̂͊w�v�Q�D(�Q)�Q�Ɓn�B���������Ă����ʂɂ����镨�̂̎���̏z����

�̂悤�ɋ��f���x�����^�����̐ϕ��ŕ\�����B���f���x�ɂ��Ă͕ʍe�u�J���}���Q��v�R�D�i�Q�j�Q�D�Ő��������B
�@����A�S�����l�ɂ��Ă����ʂ̕��̐}�`���ĕ��ʂɎʑ������Ƃ��̕��̕\�ʂb0�f�̎���̏z���f��
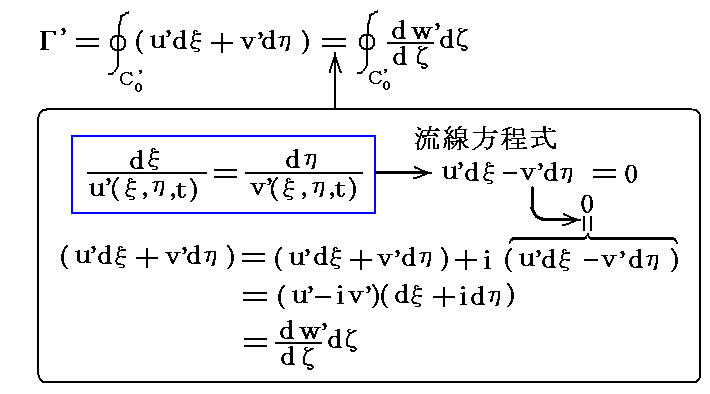
�ƕ\�����B���̂Ƃ�
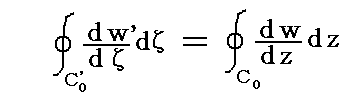
�ł��鎖���l�������
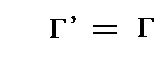
�ƂȂ�B�܂����̕\�ʂ̏z�͓��p�ʑ��ɂ���ĕω����Ȃ��B
�@�Ƃ���ł����^�����͂����ʏ�ł̐������A�����f�^���Ă̓ĕ��ʏ�ł̐�����������A���ꂼ��̕��ʂ̕��̂̎���Ɏ�����C�ӕȐ��b�A�b�f�ƕ��̕\�ʂb0�A�b0�f�̒��ԗ̈�ɓ��ٓ_���Ȃ���A�ʍe�u���f���̐ϕ��v�P�D(�Q)�ŏؖ������R�[�V�[�̒藝�ɂ��A���̕\�ʂɉ��������f�ϕ��͔C�ӕȐ��ɉ��������f�ϕ��Ɠ������Ȃ�B
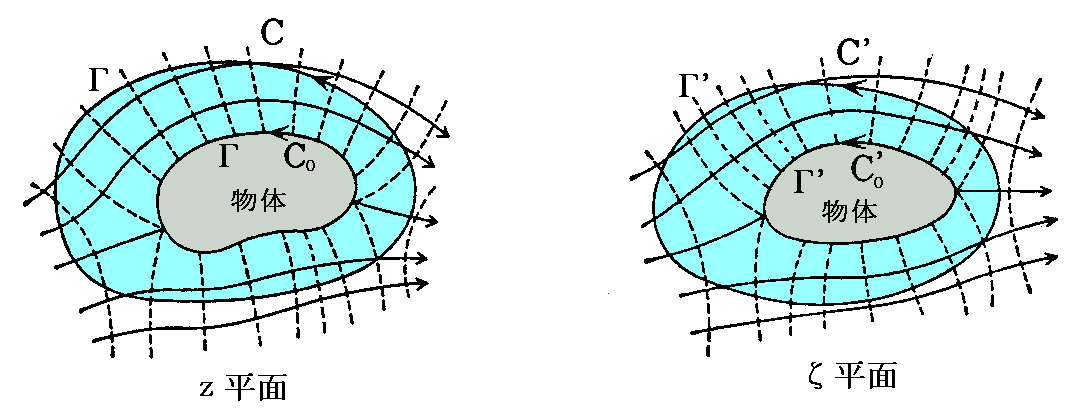
���̂������̂����͂ޔC�ӕȐ��ɉ������z�͓��p�ʑ��ɂ���ĕω����Ȃ��B
�R�D����̏�ɂ�������ٓ_�̎ʑ�
�@�@�N���o���m������log�i���|��0�j�n�A�z�����݁m�����|��log�i���|��0�j�n�A�Q���m��������log�i���|��0�j�n�A��d�N���o���m�����|�ʁ^�i���|��0�j�n�Ȃǂŕ\����镡�f���x�|�e���V�����͂����ʏ�̂�����0�ɂ����ē��ٓ_�����T�^�I�ȗ�ł��B
�@��ʂɗN���o����Q���Ȃǂ̓��ٓ_�́A�������i�āj�����ā����i���j�Ȃ鐳�����ɂ���āA��0�����i��0�j�ɂ��ꂼ�ꓯ�������̗N���o����Q�������݂��镡�f���x�|�e���V�������f�i�āj�Ɏʑ�����܂��B
�@�܂���d�N���o���͗N���o���̋����₻�̕����͕ω����邪��0�����i��0�j�ɓ�d�N���o���_�����݂��镡�f���x�|�e���V�������f�i�āj�Ɏʑ�����܂��B
�@��ʓI�ȂQn�d�N���o���͂Qm�d�N���o��(�������j��g�ݍ��킹�����̂Ɏʑ�����܂��B
�m�ؖ��͎Q�l�����P�U�D�Ȃǂ��Q�Ɓn
�@���̂悤�ȓ��p�ʑ��̕��@���g���ƁA���ʂɂ����邠��ȒP�Ȍ`�̒f�ʂ�L���钌��̂̂܂��̗��ꂪ�m���Ă���ƁA�Ėʂɂ����鑼�̌`�̒f�ʂ�L���钌��̂̂܂��̗����m�邱�Ƃ��ł���B
�@�Ⴆ����}���p���������������E�����Ƃ��闬��̉���������̂͊ȒP�ł͂���܂���B���̗l�ȗ����\�����f���x�|�e���V�����͕��G�Ȋ��Œ��ڋ��߂�̂�����߂č����ł��B
�@�Ƃ��낪�~���̂܂��̗���͗ǂ��m���Ă��܂��B���̋��E�����������f���x�|�e���V�����͊ȒP�Ɍ����邱�Ƃ��ł��āA��������r�I�ȒP�Ȋ��ŕ\���܂��B�܂��~��������}���p�����������Ɏʑ���������ȒP�Ȋ��ł��B���̓�̊ȒP�Ȋ���g�ݍ��킹�邱�Ƃɂ��A�}���p�����������̂܂��̗����\���ƂĂ����G�ȕ��f���x�|�e���V������������ƌ������Ƃł��B���ꂪ�q��H�w�̓������_�ŕ��f���_�����p����闝�R�ł��B
�@�������A���̌`���G�ɂȂ�Ɖ~���痃�^�֕ϊ�����ʑ�����T���͈̂�ʂɓ���Ȃ�܂��B�ʑ��ɂ��Đ��藧�l�X�Ȓ藝���X�̓T�^����Q�l�ɂ��Ȃ���A���s����ʼn~�����̗��^�Ɏʑ���������ߎ��I�Ɍ����Ȃ���Ȃ�܂���B�ʑ����������鍢����l�����Ă��A��ʓI�Ȍ`��̗��^�ɑ��镡�f���x�|�e���V�����ڌ����邱�Ƃɔ�ׂ���ꡂ��ɊȒP�ł��B
�@
�i�Q�j���s��l������p���Ȃ��闬��ւ̎ʑ�
�P�D�����ʂ̕��s��l�����ĕ��ʂ̂X�O�x�̊p���Ȃ��闬��Ɏʑ����邱��
�@����͂����ʂɂ����Ă����̐������ɑ��x�t�ŗ�����l����\�����f���x�|�e���V�������i���j�m�ʍe�u�Q��R(�J���}���Q��ƍR��)�v�P�D(�R)�P�D�Q�Ɓn
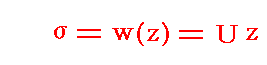
���T�D�i�Q�j�Q�D�ŏq�ׂ��������i����0.5�̏ꍇ�j

�ɂ��ĕ��ʏ�Ɏʑ�����悢�B
�@�������ē����镡�f���x�|�e���V�������f�i�́C�Łj�̎��������f�i�́C�Łj�����̋Ȑ��̓ĕ��ʂ̊p���Ȃ��闬��̓����x�|�e���V�������ƌ��Ȃ���B�܂����f�i�́C�Łj�̋��������f�i�́C�Łj�����̋Ȑ��̓ĕ��ʂ̊p���Ȃ��闬��̗����ƌ��Ȃ����Ƃ��ł���B
�@�����ł��t��2.5���^���Ƃ��āA�O�߂Ő��������m�Е��ʂ̊i�q���n���m�����ʂ̗����i��(x,y)�����j�Ɠ����x�|�e���V�������i��(x,y)�����j�n�̊W��}�������
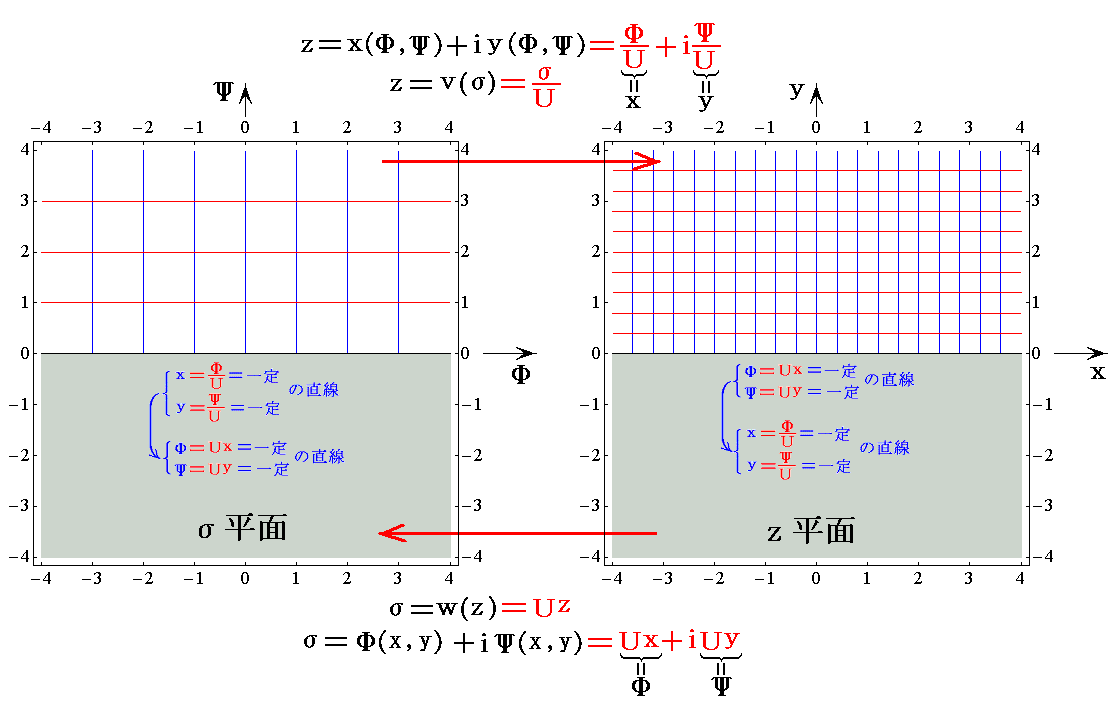
�ƂȂ�B���̂悤�ɂ��ē���ꂽ�����ʂ̓��|�e���V�������Ɨ������ʑ����ā���0.5�ɂ���ăĕ��ʂɎʑ������

�ƂȂ�B����͎ʑ��Ё����i���j�Ƀā����i���j�̋t���������i�āj��g�ݍ��킹�����̂�����
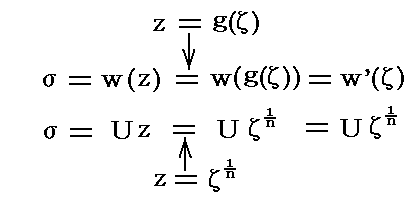
�ƂȂ�B���f�i�āj���ĕ��ʂɂ����Ċp���Ȃ��闬���\�����f���x�|�e���V�����ł���B���f�i�āj�̊��`����̓I�ɕ`�������̂��ŏ��ɏq�ׂ��Е��ʂ̊i�q�����ĕ��ʂ֎ʑ�������ƂȂ�B������A�O�߂ŏq�ׂ��Ёf���ʂƂ̊W�Ƃ��ĕ\����
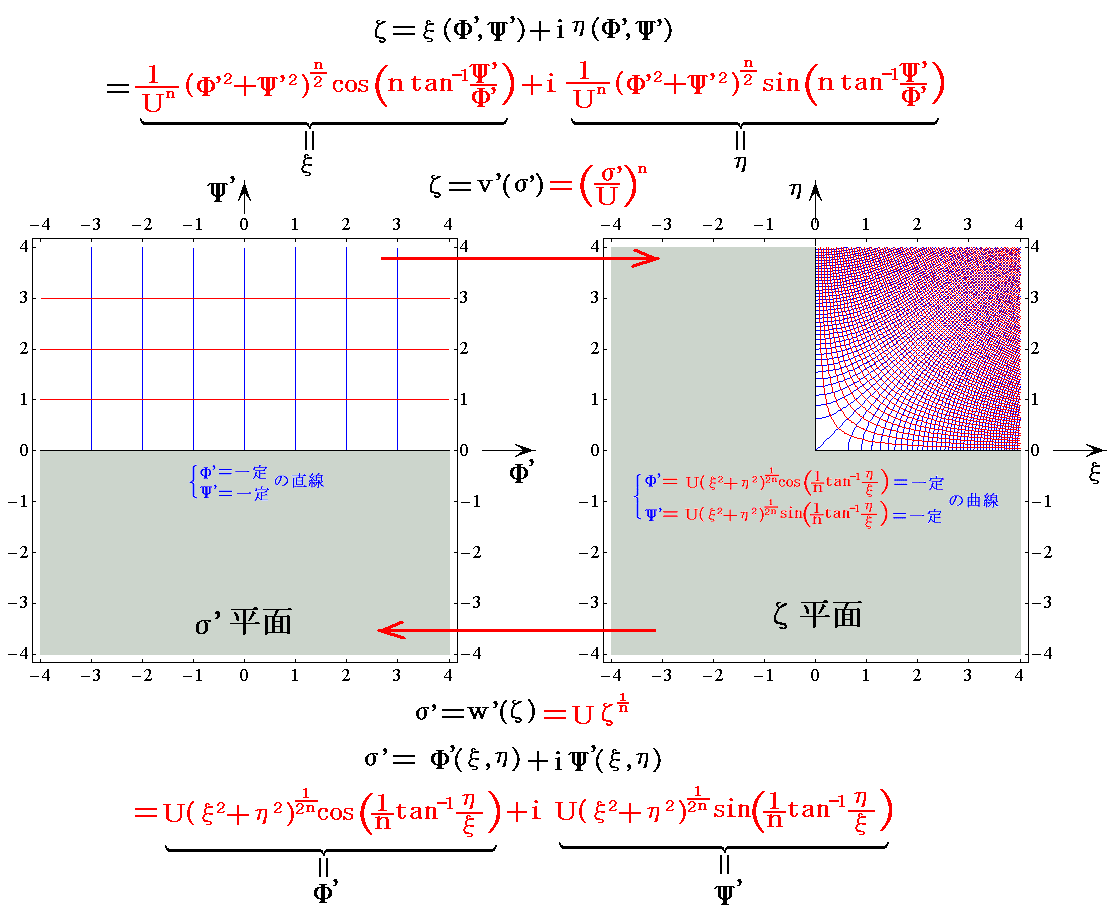
�ƂȂ�B�U�D�i�P�j�P�D�Œ��ӂ����悤�ɃЕ��ʂƃЁf���ʂ͓������̂ł��B
�@���p�ʑ��̗��̗͊w�ւ̉��p�ōł����ӂ��ׂ����m�Е��ʁ������ʁ��ĕ��ʁi�܂�Ёf���ʁ��ĕ��ʁj�ւ̎ʑ��n���m�����ʁ��ĕ��ʂւ̎ʑ��n���������Ȃ����Ƃł��B���̓�̎ʑ��̈Ⴂ�𗝉����Ȃ��Ɨ����_�ŗp��������@���Ȃ��Ȃ������ł��܂���B
�Q�D�����ʂ̕��s��l�����ĕ��ʂ�270�x�̊p���Ȃ��闬��Ɏʑ����邱��
�@����������ʂɂ����ĕ��s����\�����f���x�|�e���V�������T�D�i�Q�j�R�D�ŏq�ׂ��������i����1.5�̏ꍇ�j�ɂ��ĕ��ʏ�Ɏʑ�����悢�B�菇�͑O���Ɠ����Ȃ̂ŁA�t��2.5���^���̏ꍇ�̊W�}�����������B
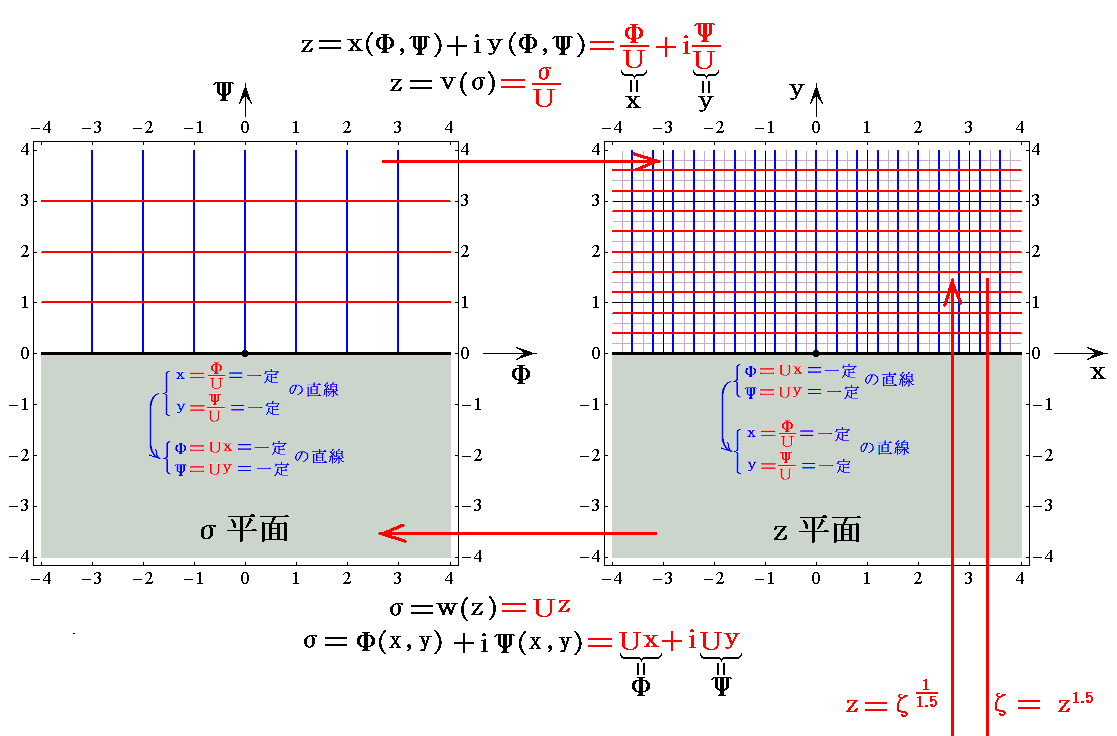
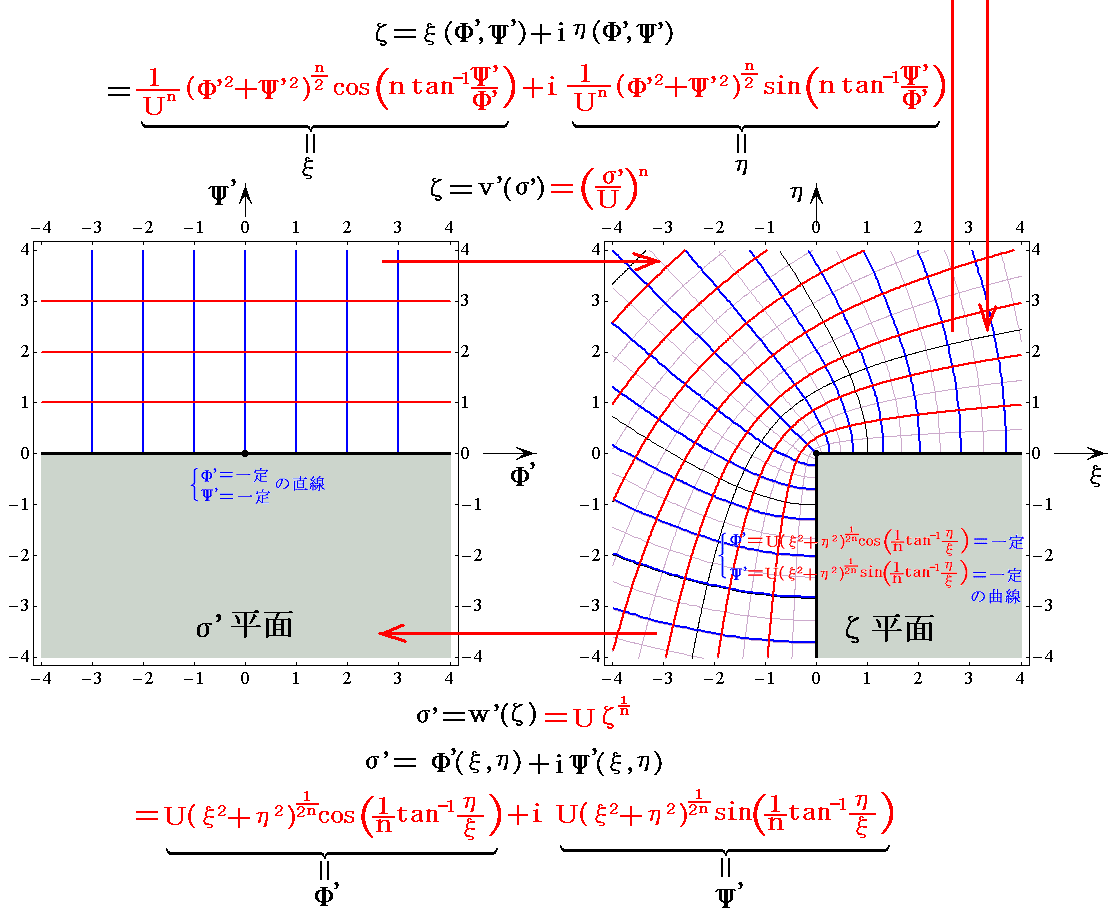
�@���̐}�ł��m���f���x�|�e���V�����̓����x�|�e���V�������Ɨ����̎ʑ��}�n���m���W�i�q�̎ʑ��}�n�����Ă��邽�ߗ��҂̈Ⴂ���ڗ����Ȃ��B���̂��߁A�T�D�i�Q�j�R�D�̍��W�ʑ��}���E���̂��̂ɕς��č���x�`���Ă݂��

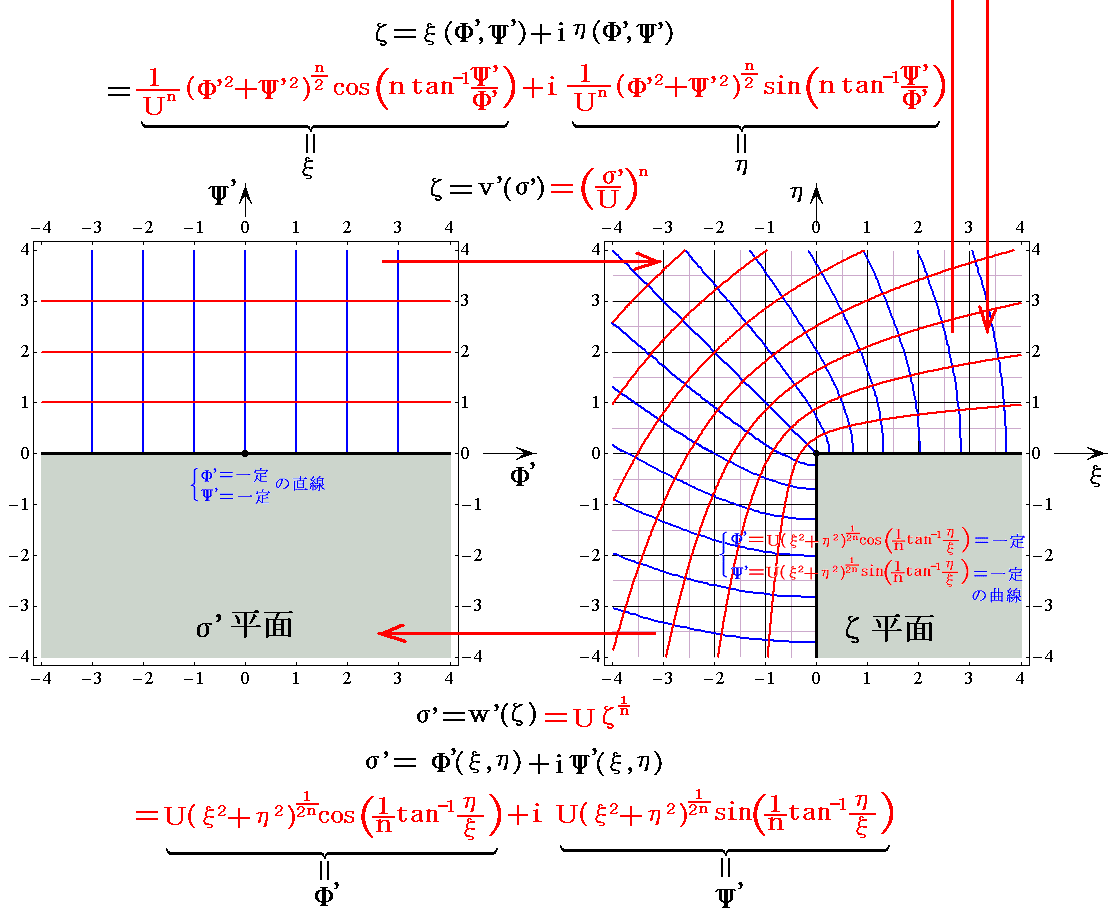
�ƂȂ�B
�@�@�ϊ���̃ĕ��ʂ̍��W���i�q��ɂȂ���������}�̕����A�Ėʍ��W�l�Ɠ����x�|�e���V�������E�����������Ƃ̊W���ǂ�����B���̂��߁A����͍��W�ϊ��}�͉E���̂��̂�p���邱�Ƃɂ����B
�R�D�p�ɂ����闬��
�@�O���̃ĕ��ʂɂ��������f���x�|�e���V����
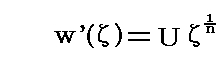
�ɂ����āA����1�̏ꍇ�͊p�̊J���p�����������ȃR�[�i�[����闬��
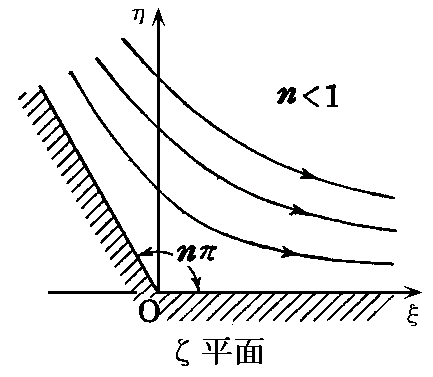
�ƂȂ�A�P�������Q�̏ꍇ�̓ĕ��ʏ�ł̊J���p�������傫�ȃR�[�i�[����闬��
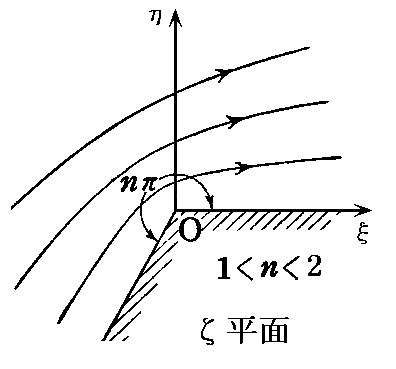
�ƂȂ�B
�@�ʍe�Ő��������悤�ɕ��f���x�|�e���V�������f���ĂŔ����������̂̓ĕ��ʂɂ��������f���x�ƂȂ�B
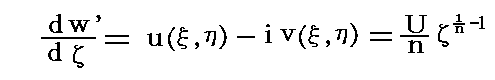
�@���̂Ƃ������P�̏ꍇ�ɂ̓ā�0�ł����f�^���ā�0�ƂȂ藬���͗�ƂȂ�̂ŁA�p�͗��ݓ_�ƂȂ�B����A�P�������Q�̏ꍇ�ɂ̓ā�0�ł̗����́��ƂȂ�B
�@�x���k�[�C�̒藝�ɂ��Ƃ����P�̏ꍇ�ɂ̓ā�0�̓_�̈��͂͗L���Ȓl�ƂȂ���Ȃ��B
�@�������P�������Q�̏ꍇ�ɂ̓ā�0�ɂ����鈳�͂́|���ƂȂ�B�܂����̓_�ł͗����ɉ����Ė�����̈��͌��z�����݂��邱�ƂɂȂ�B�܂�A������p�����R�[�i�[��ǂɉ����ĉ��ɂ͖�����̈��͌��z�ɂ���ė��̗̂��������ς��Ă��˂Ȃ�Ȃ��Ƃ������Ƃł��B�����̗��͕̂K�����k���������Ă���̂ŁA������̈��͌��z�Ō݂��ɉe�����y�ڂ��������Ƃ͂ł��Ȃ��B�܂薳����̑��x�A������̈��͌��z�͌����ɂ͑��݂ł��Ȃ��̂������̗��̂������̖@���ɏ]�����ŏ��̕�����ۂ����܂ܗ��ꋎ�낤�Ƃ����B���̂��߂ɗ���͕ǂ��甍�����A�Q���������悪�`�������B�����̈����`�������ƁA����͊��炩�ȃJ�[�v��`���ėL���ȑ��x�ŗ���邱�Ƃ��ł���B
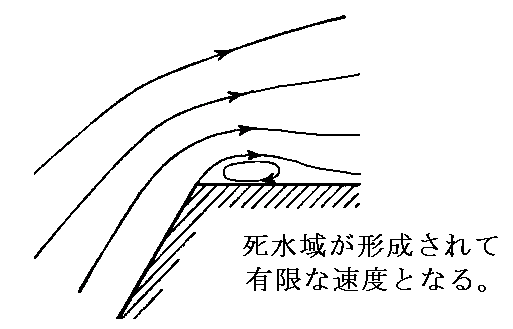
���̎����́A�����_���l�@����Ƃ��d�v�ł��B
�@
�i�R�j���ɕ��s�ȗ�����~������̗���֎ʑ��@�@
�P�D�~�̒��S�����_�̏ꍇ
�@����͂����ʂɂ����ĕ��s����\�����f���x�|�e���V����
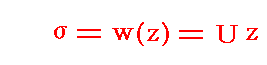
���T�D�i�R�j�P�D�̐�����

�ɂ��ĕ��ʏ�Ɏʑ�����悢�B
�@�������ē����镡�f���x�|�e���V�������f�i�́C�Łj�̎��������瓾���郳�f�i�́C�Łj�����̋Ȑ��̓ĕ��ʏ�̉~������̗���̓����x�|�e���V�������ƌ��Ȃ���B�܂����f�i�́C�Łj�̋��������瓾���郵�f�i�́C�Łj�����̋Ȑ��̓ĕ��ʏ�̉~������̗���̗����ƌ��Ȃ����Ƃ��ł���B
�@�����ł��t��5.0���^���Ƃ��ăЕ��ʂ̊i�q���Ƃ����ʂ̗����m��(x,y)�����n�Ɠ����x�|�e���V�������m��(x,y)�����n�̊W��}�������
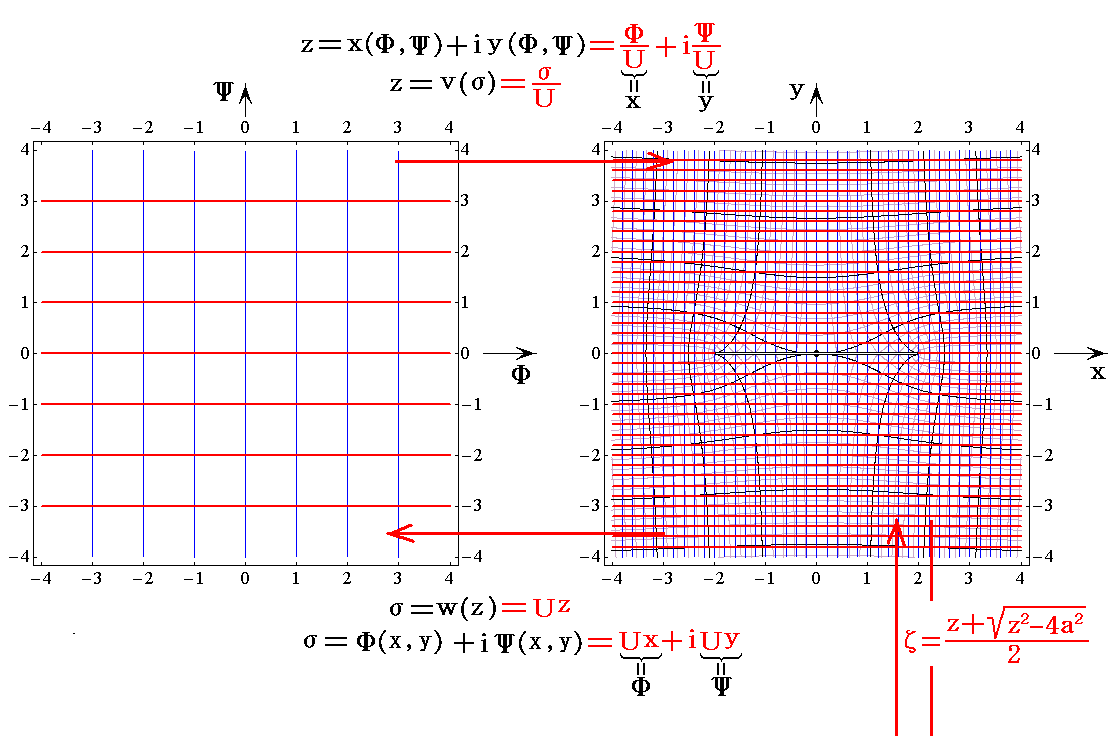
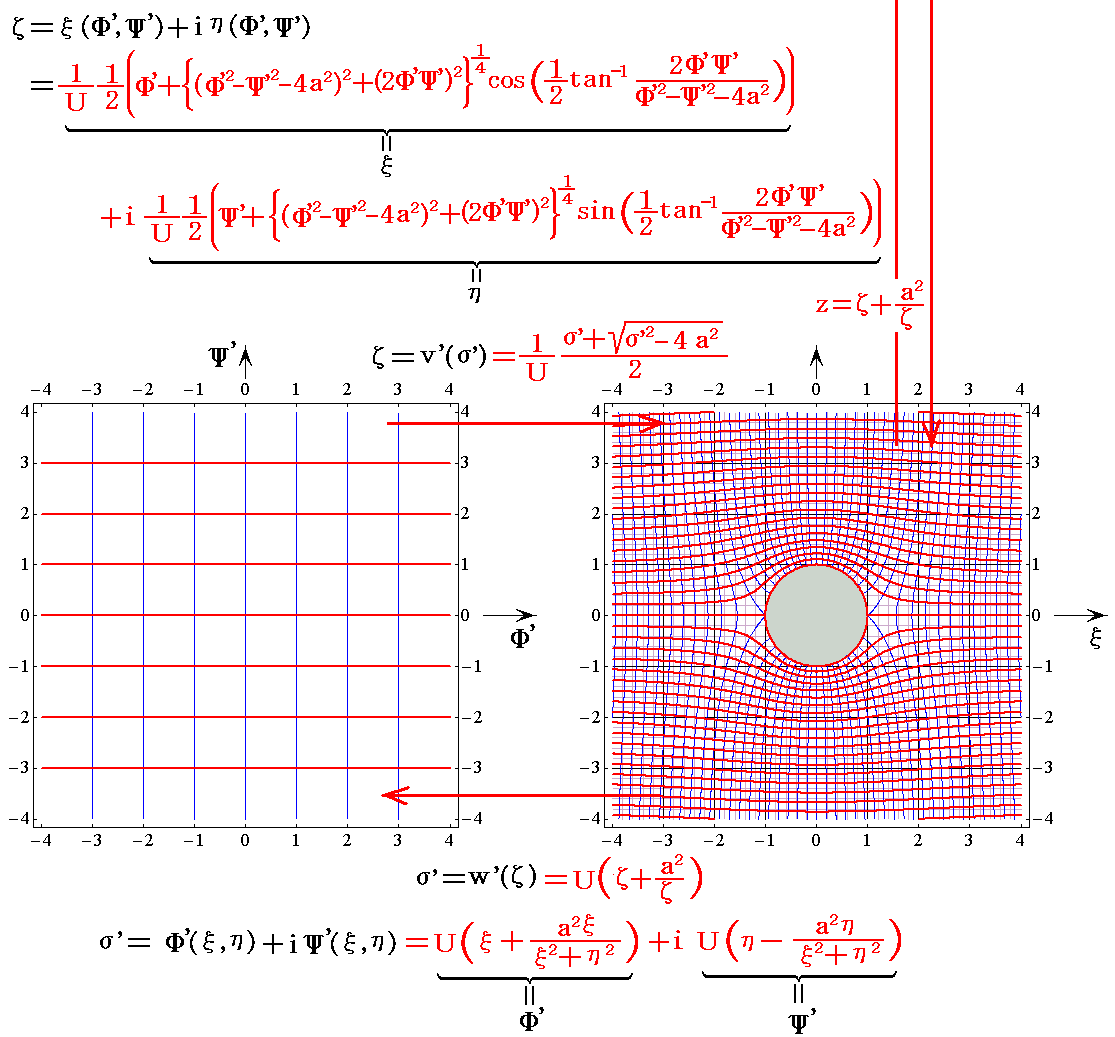
�@����͕ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�P�D�i�Q�j�P�D�Ő��������悤�ɂ��Ƃ��ƕΔ����������ɋ��E������K�p���邱�Ƃœ����܂����B
�@�������Ƃ��A���̎���̗����\���ȒP�ȕ��f���x�|�e���V�����ɁA����܂��ȒP�Ȃ����ʏ�̕����ĕ��ʏ�̉~�Ɏʑ���������d�ˍ��킹�Ă�������ƌ������Ƃł��B
�@�܂��Ɏ菇�ɏ]���ċ@�B�I�ɂł���Ƃ����Ƃ��낪�A���f���_�̓��p�ʑ����З͂���R���ł��B
�Q�D�~�̒��S����0�̏ꍇ
�@����͕ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�P�D�i�S�j�̓��e���A��L�Ɠ����悤�ɂ��ĕ��f���ʂ̎ʑ��W�ʼn��߂����������Ȃ̂Ő����͏ȗ����܂��B
�@
�i�S�j�~������̗������̗���Ɏʑ�
�@���s��l�������Ȍ`��̋��E�ʂ̎���̗���Ɏʑ����邱�Ƃ���ł����A���̗͊w�œ��p�ʑ��̈З͂����������̂́A���s���ł͂Ȃ��������Ȍ`��̋��E�ʎ���̗�����A����ɕʂȌ`��̋��E�ʂ̎���̗���Ɏʑ����邱�Ƃł��B����͂����ʂƂ����ʁA�����ʂƃĕ��ʂƓ�̎ʑ���g�ݍ��킹�ĊW�Â����܂��B
�P�D�z�������i����0�j�ꍇ
�@�����ʂɂ����Ă����̐������ɑ��x�t�ŗ�����l�����̌��_�ɔ��a���̉~�����������Ƃ��A���̎���̗����\�����f���x�|�e���V�������i���j���R�D�i�P�j�ŏq�ׂ��悤��
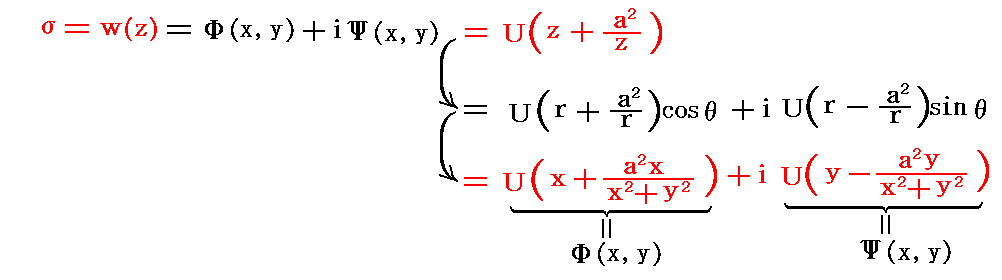
�ƂȂ�B
�@�U�D�i�P�j�P�D�ŏq�ׂ��悤�ɁA���̕��f���x�|�e���V�������i���j���T�D�i�S�j�P�D�̐������������i�āj�ɂ���ăĕ��ʏ�̕��f���x�|�e���V�������f�i�āj�Ɏʑ�����悢�B�܂�
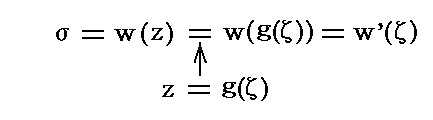
�ł���B
�@����ɋ�̓I�Ȋ��Ă͂߂�B�܂��A���a���̉~���̎���m|��|�����n�̔C�ӂ̓_���̕��ʂ̌��_�ɐ����ɒu���ꂽ����4���̕��̎���Ɏʑ����鐳�������T�D�i�S�j�P�D�ŏq�ׂ��W���[�R�t�X�L�[�ϊ�

�ł������B�Ă̈�̒l�ɑ��Ă��̓�̒l���Ή����Ă��邪�A�����ł͉~�̊O���m|��|�����n�������l���Ă���̂Ł{�����̕��݂̂�I��ł���B
�@���̎ʑ�����O�L�̕��f���x�|�e���V�����ɑ�������
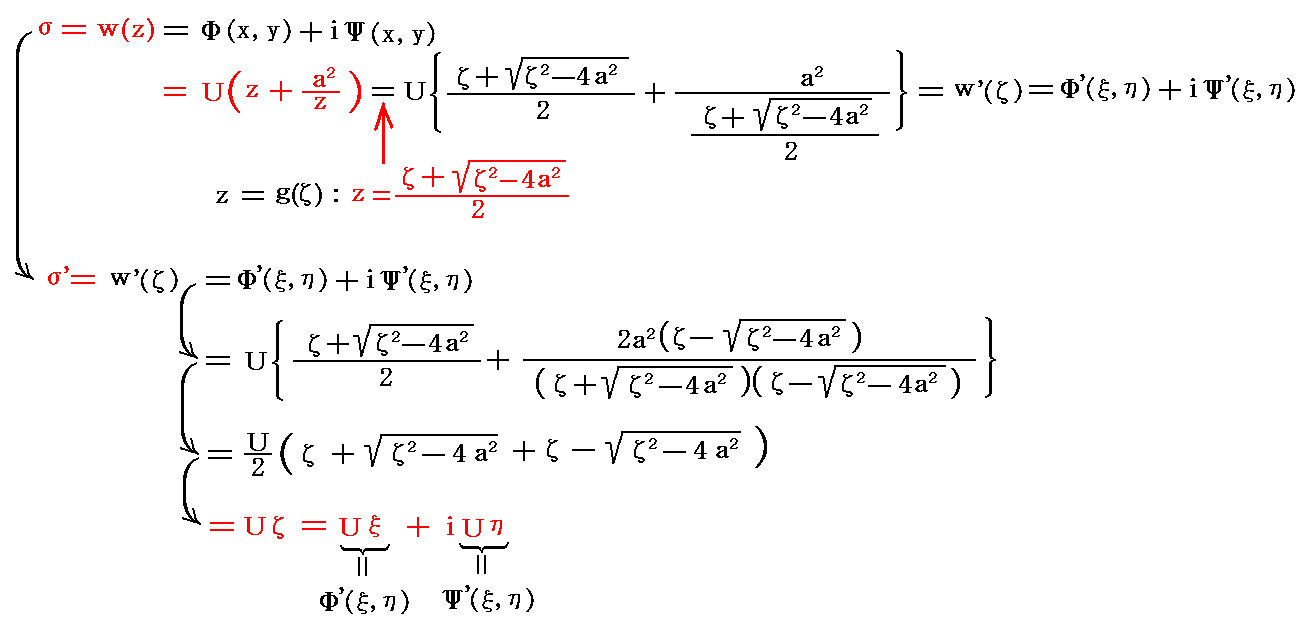
�ƂȂ�A�Ėʏ�ł̕��f���x�|�e���V�������f�i�āj��������B���̕��f���x�|�e���V�������f�i�́C�Łj�̎��������f�i�́C�Łj�����̋Ȑ��̓ĕ��ʂɂ����镽�̎���̗���̓����x�|�e���V���������A���������f�i�́C�Łj�����̋Ȑ��͗�����\���B
�@�t��0.5���^���̏ꍇ���m�Ёf���ʂ̊i�q���n���m�����x�|�e���V�������i���f(x,y)�����j�Ɨ����i���f(x,y)�����j�n�̊W��}�������
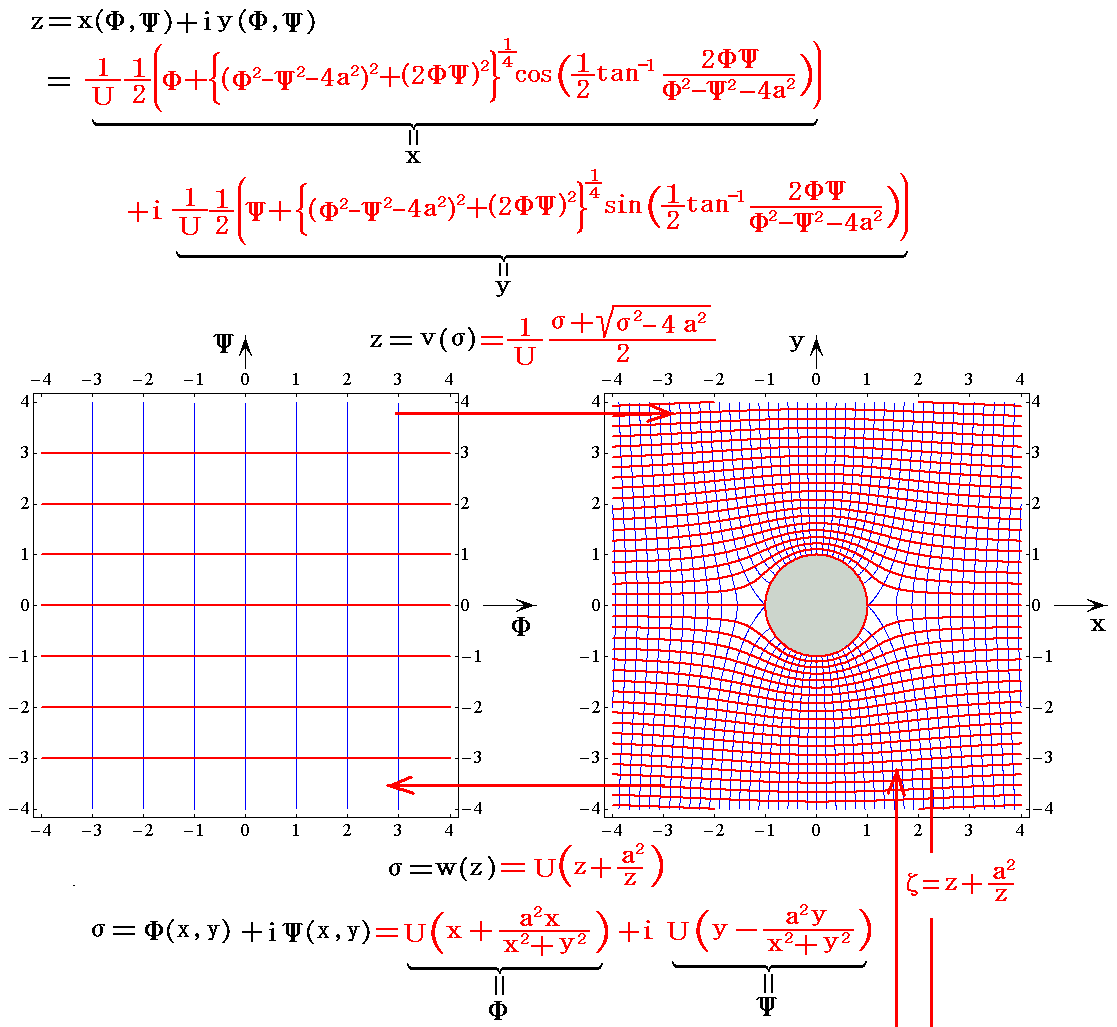
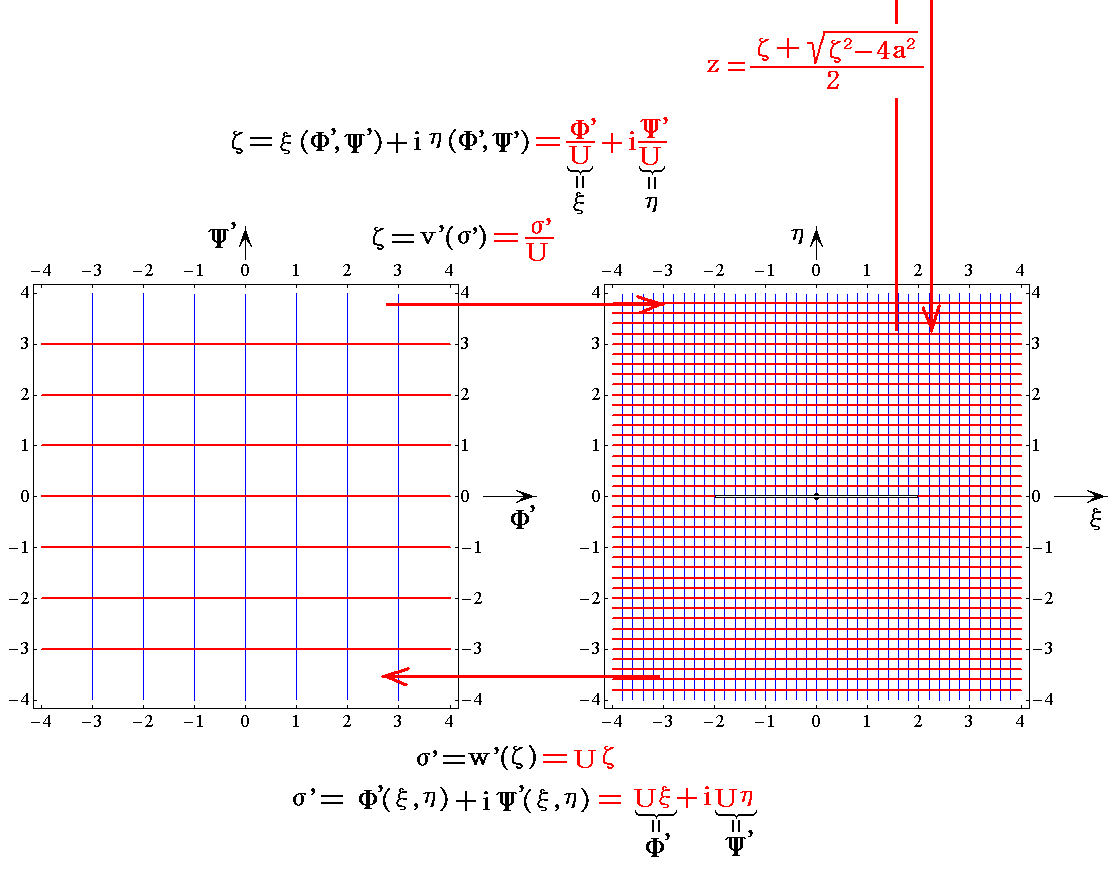
�ƂȂ�B���̏ꍇ�A���W�ϊ��������i�q��������̐}�ɏd�Ȃ��Ă��܂����W�ϊ��̗l�q������ɂ������A������U�D�i�R�j�P�D�̋t���s���������ł��B���҂̈Ⴂ����������ĉ������B
�Q�D�z��������ꍇ
�@���ɏz��������ꍇ���l���Ă݂�B�R�D�i�P�j�ŏq�ׂ��悤�ɏz�������~������̗����\�����f���x�|�e���V������
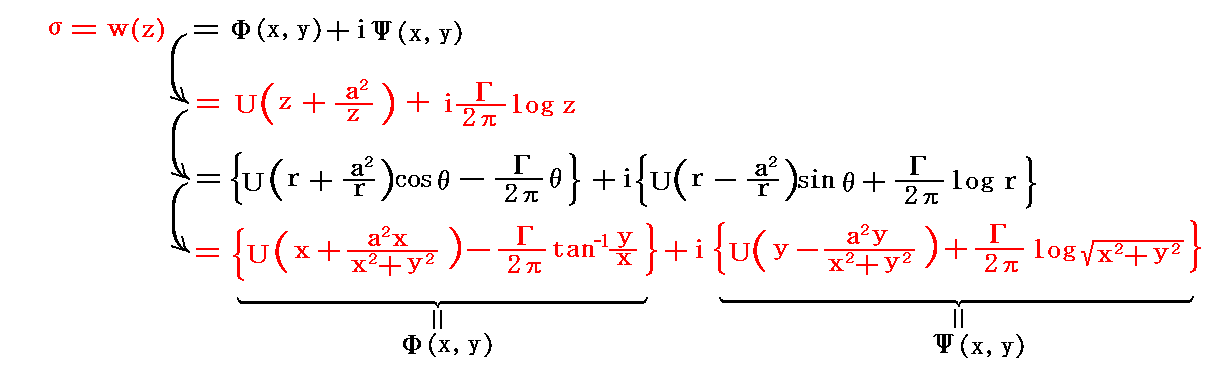
�ƕ\�����B
�@���̎��ɑO�L�̎ʑ������������
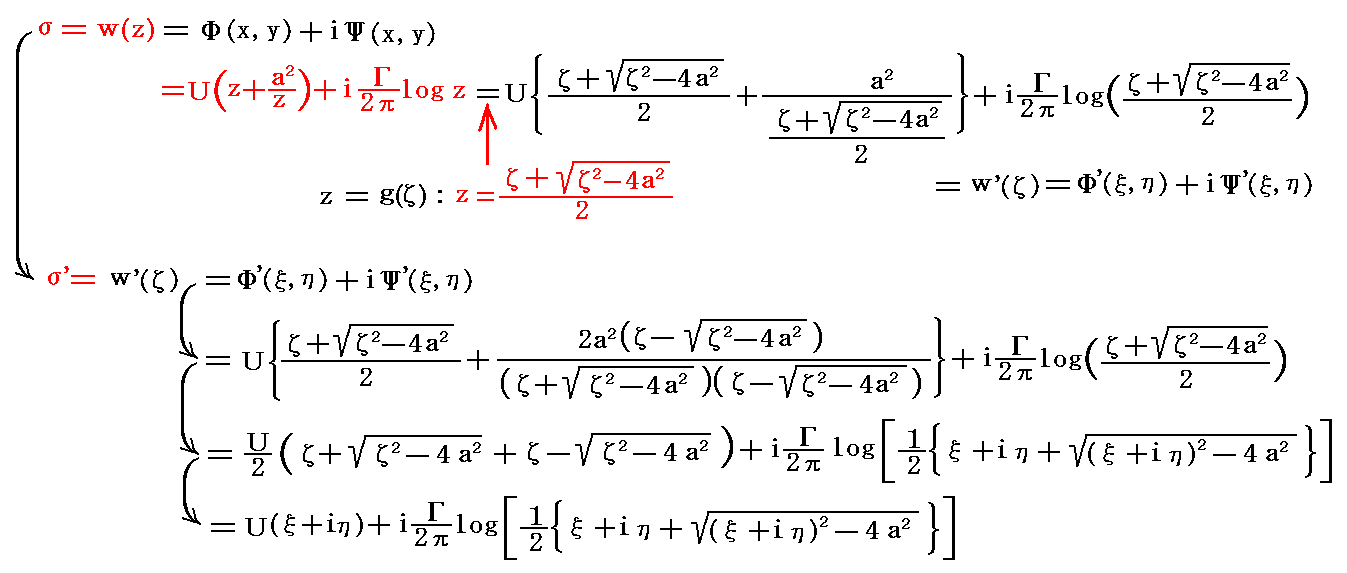
�ƂȂ�A�Ėʏ�ł̕��f���x�|�e���V�������f�i�āj��������B
�@����������Ƌ����ɕ����邽�߂ɂ���ɕό`����Blog���́m�n�����̎��������q���i�́C�Łj�A���������hm�i�́C�Łj�A��Βl�����i�́C�Łj�A�Ίp���Ɓi�́C�Łj�Ƃ��āA�T�D�i�S�j�Q�D�̌v�Z���ʂ𗘗p�����
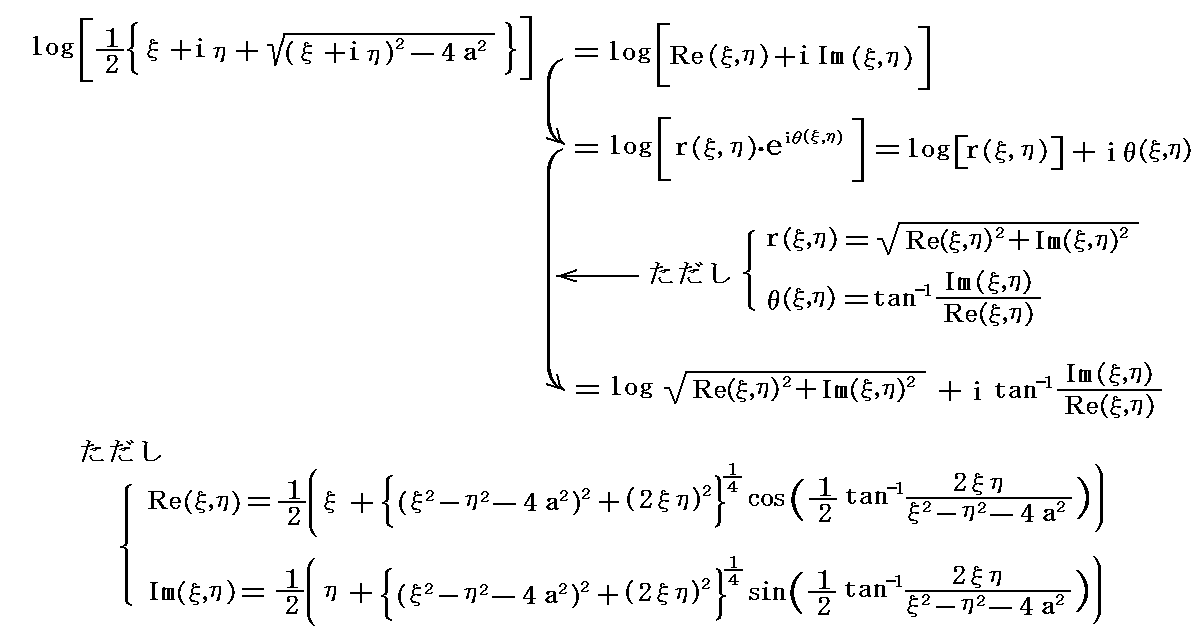
�ł��邩��
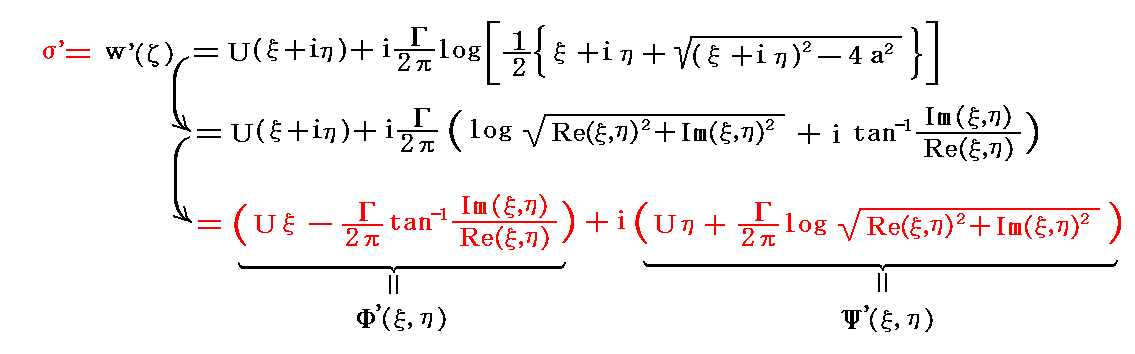
�ƂȂ�B
�@�t��5.0���^���ŁA����4���t�̏ꍇ�ɂ����m�Ёf���ʂ̊i�q���n���m�ĕ��ʏ�̓����x�|�e���V�������i���f(x,y)�����j�Ɨ����i���f(x,y)�����j�n�̊W��}������
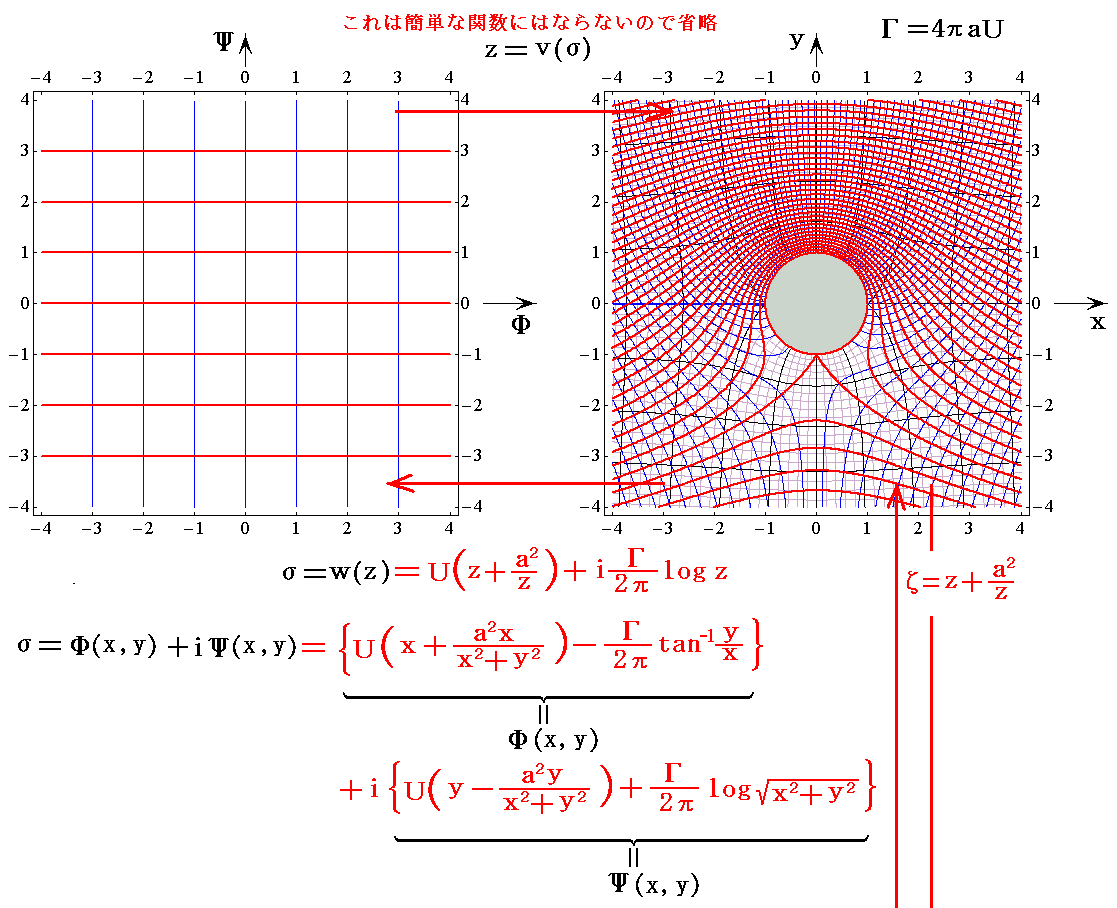
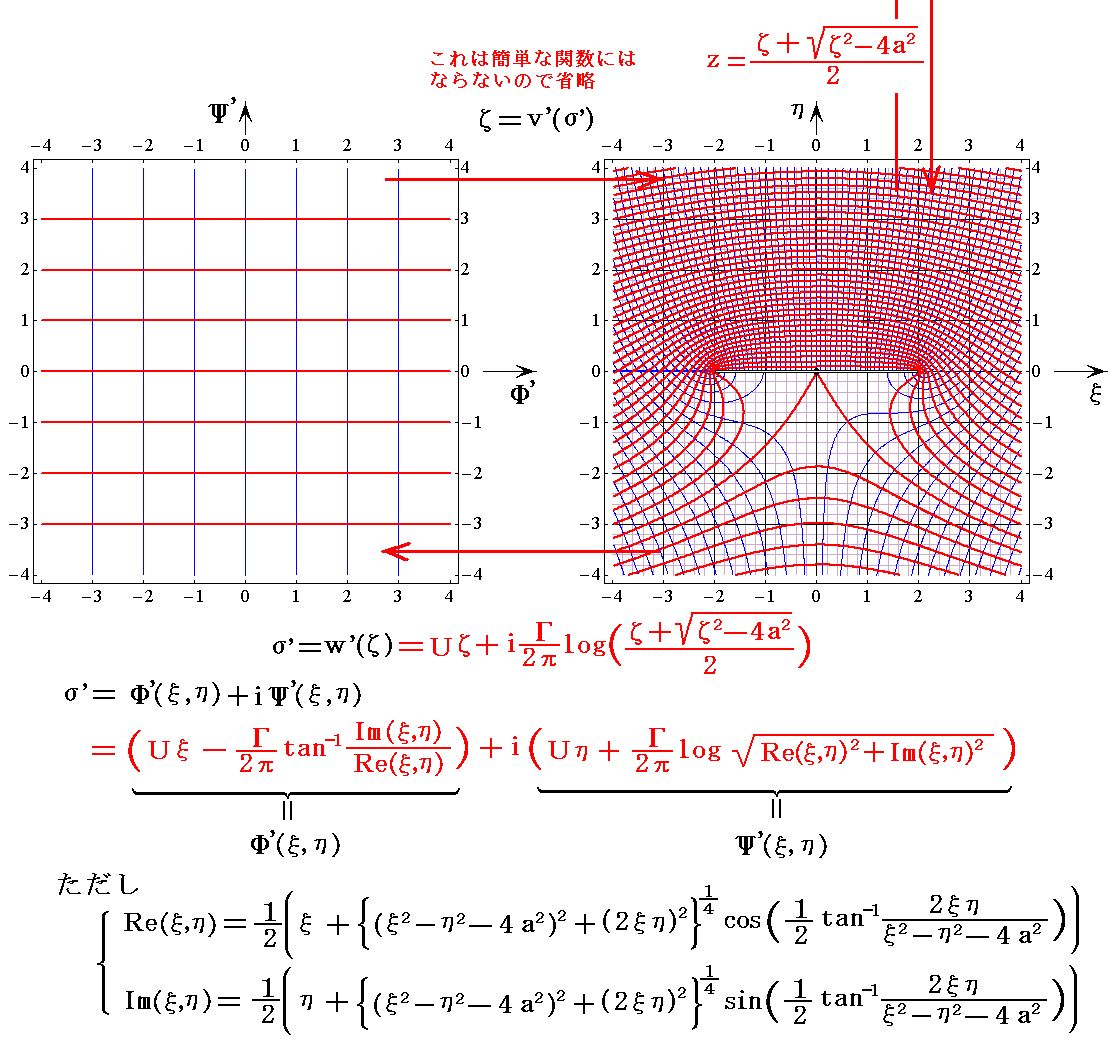
�@��ʂɊȒP�Ȑ}�`���畡�G�Ȑ}�`�ւ̎ʑ��������A���̋t�̊��̕������G�ɂȂ�B�Ё����i���j��Ёf�����f�i�āj�̋t�������߂�̂͗e�ՂłȂ��̂ŏ�}�ł͏ȗ������B
�@���̗�Ɍ�����悤�ɁA�Ō�ɓ����镡�f���x�|�e���V�����͕��G�Ȋ��ŁA����ڋ��߂�̂͂���߂č���ł��B���̂悤�ȕ��G�ȉ��ł��ȒP�Ȏʑ����J��Ԃ����œ�����ƌ������Ƃ��A�ʑ��ϊ��𗘗p����ő�̃����b�g�ł��B
�@�ȉ��ɁA�t��5.0���^���Ƃ�������2���t������6���t�̏ꍇ��}������B�菇�͓����Ȃ̂ŁA�Е��ʂ�Ёf���ʂւ̎ʑ��W���͏ȗ����Ă����ʂƃĕ��ʂɂ��Ă̂ݎ����B
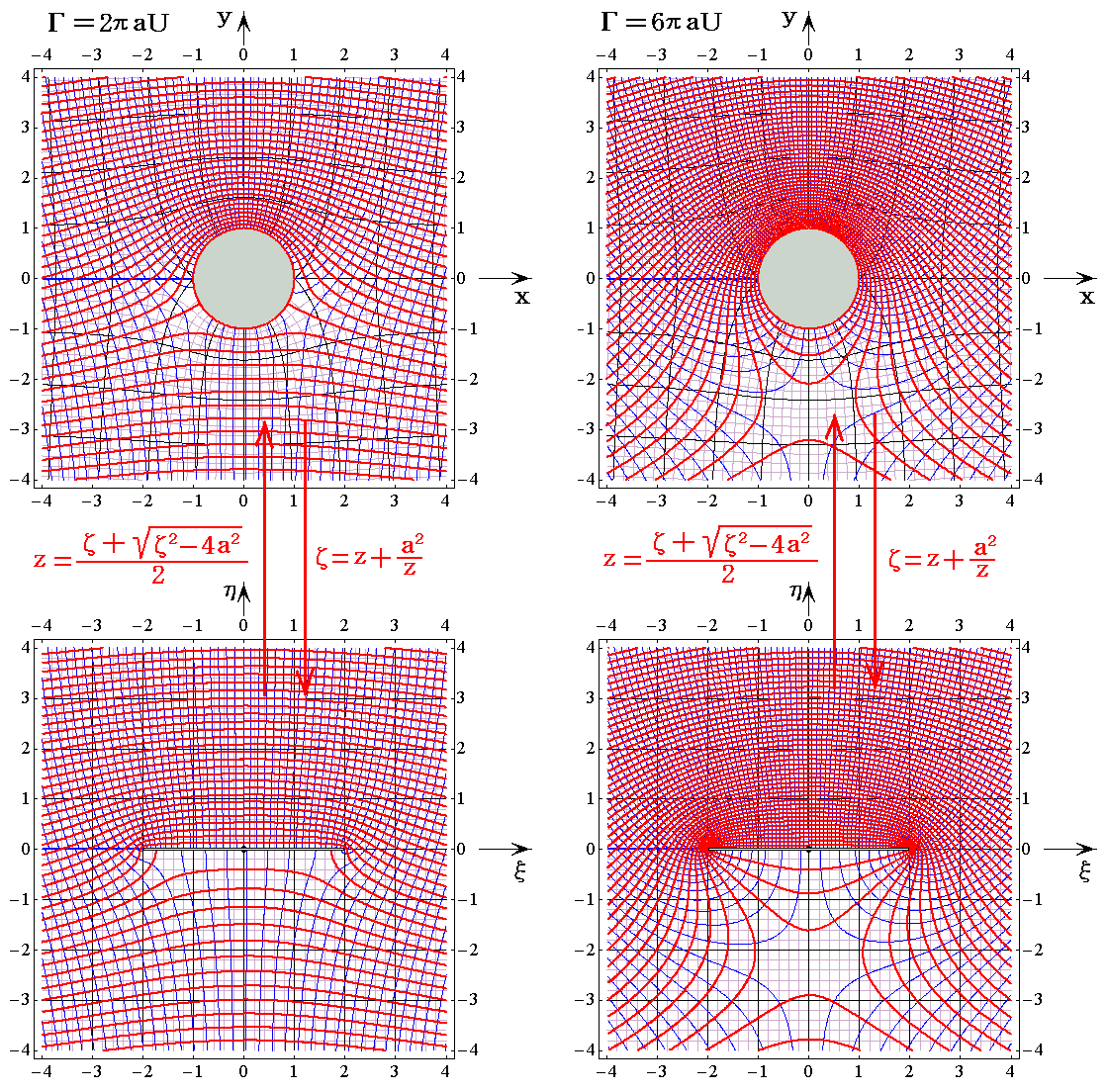
�@�z���̑���Ƌ��ɗ��ݓ_���ǂ̗l�ɕω����邩�ɒ��ӁB����4���t�ł͗��ݓ_�͕����痣��āA���̎���ɉ�]���闬�ꂪ�t������悤�ɂȂ�B
�R�D�d�v�Ȓ���
�@�����łU�D(�P)�P�D�ŋ����������Ƃ��m�F���Ă����܂��B������u���i���j�����i���C���j�{�����i���C���j�������Ƌ����͂��ꂼ��ʁX�����f�i���j�̎������f�i�́C�Łj�Ƌ������f�i�́C�Łj�֕ϊ������B�v�Ƃ������Ƃł��B
�@���܂ł̗�ł͕��f�ϐ��̂܂܂ŁA�ʑ�����K�����ĐV�������W�ɂ����镡�f���x�|�e���V���������߂��B�Ⴆ�ΑO���̗�ł�
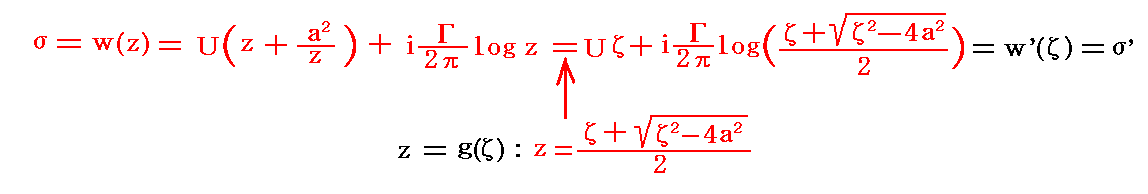
�̗l�ɁB����������ł��u���i���j�̎����Ƌ���������������Ă��f�i�́C�Łj�̎����Ƌ����ɕϊ�����邱�Ɩ����B�v�ƌ������Ƃ����Ăł͂���܂���B
�@��L�̒��ӂ��m���߂邽�߂ɐ����\���ŕ\���������ŕϊ����Ă݂�B
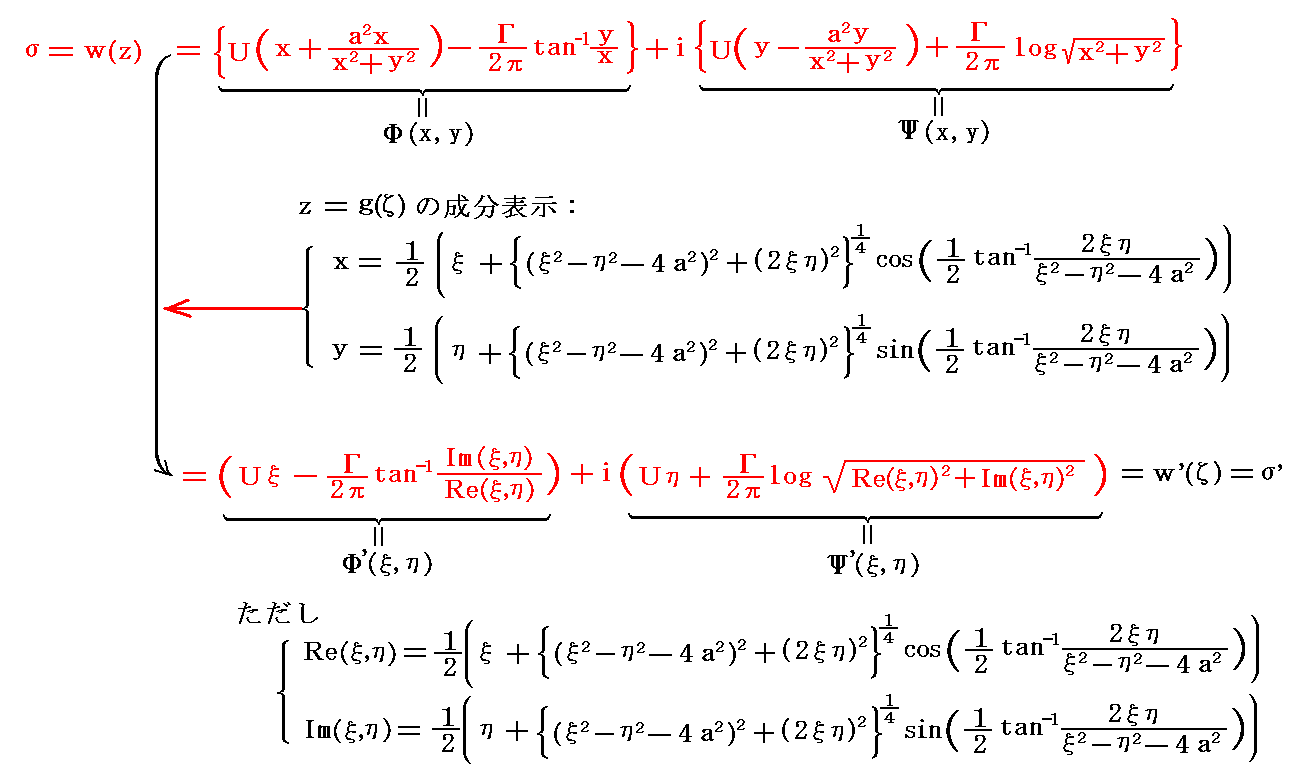
�@���̌v�Z�͖ʓ|�ł���
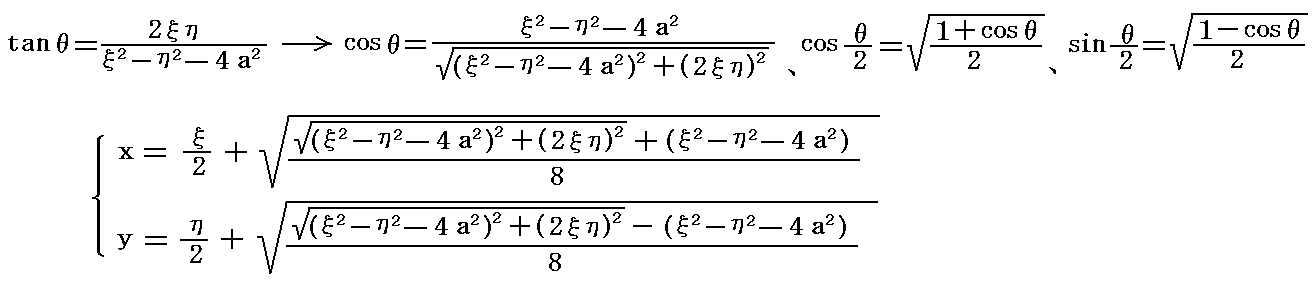
�ł��邱�Ƃɒ��ӂ���ƁA�����w�i�́C�Łj�Ƃ����x�i�́C�Łj�̂�������������ł�����A���i���j�̎��������i���C���j�͂��̂܂܂��f�i�āj�̎��������f�i�́C�Łj�ցA���i���j�̋��������i���C���j�͂��̂܂܂��f�i�āj�̋��������f�i�́C�Łj�֕ϊ�����邱�Ƃ�����܂��B���ꂼ��̕����������ŕϊ����Ă���̂ŋ��������荬���鎖�͂���܂���B
�@
�i�T�j�~������̗�����X����������̗���Ɏʑ�
�P�D�z�������i����0�j�ꍇ
�@�����ʂɂ����Ă����̐������ɑ��x�t�ŗ�����l�����̌��_�ɔ��a���̉~�����������Ƃ��A���̎���̗����\�����f���x�|�e���V�������i���j���R�D�i�P�j�ŏq�ׂ��悤��
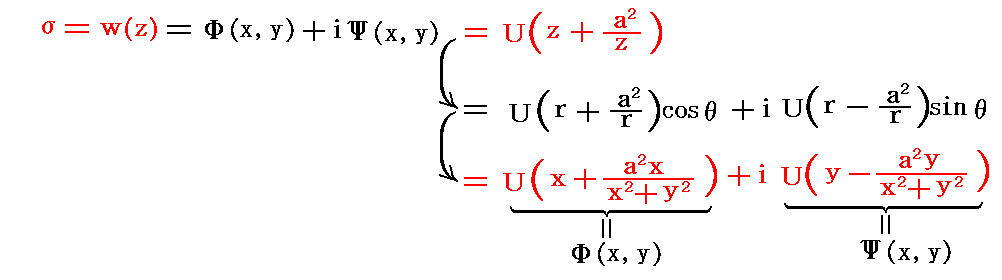
�ł������B
�@�܂��A���a���̉~���̎���m|��|�����n�̔C�ӂ̓_���̕��ʂ̌��_�Ɋp�x���ŌX���Ēu���ꂽ����4���̕��̎���Ɏʑ����鐳�������T�D�i�T�j�P�D�ŏq�ׂ����ǃW���[�R�t�X�L�[�ϊ�

�ł���B�Ă̈�̒l�ɑ��Ă��̓�̒l���Ή����Ă���̂ł��邪�A�����ł͉~�̊O���m|��|�����n�������l���Ă���̂Ł{�����̕��݂̂�I��ł���B
�@���̎���O�L�̕��f���x�|�e���V�����ɑ������Ėʏ�ł̕��f���x�|�e���V�������f�i�āj��������B
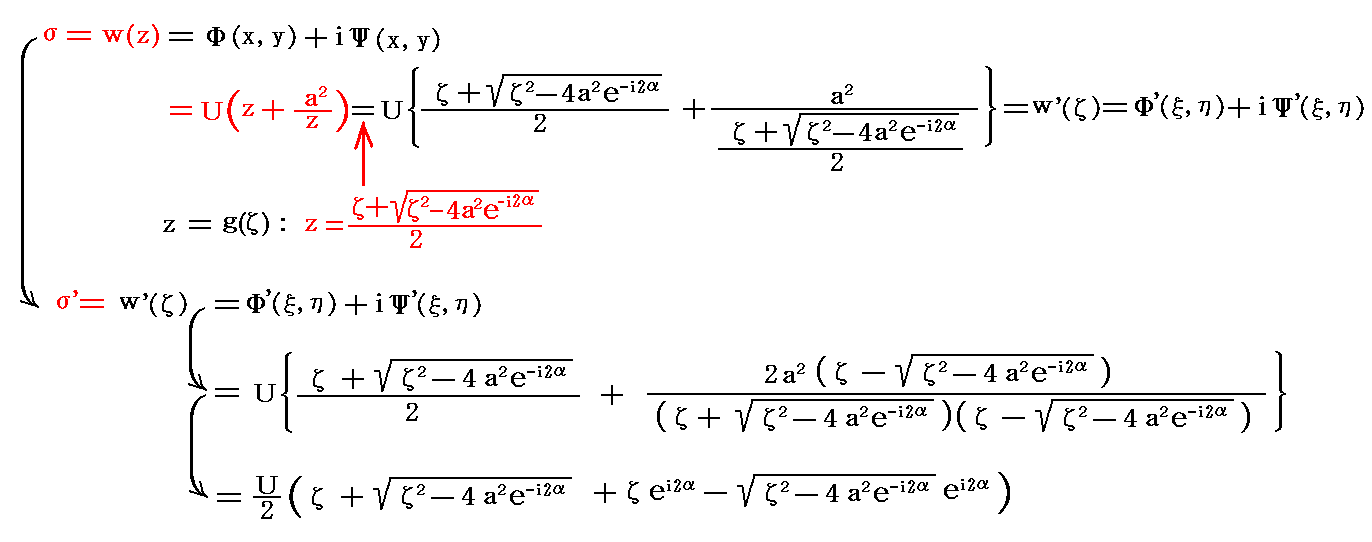
�������A���̎��������Ƌ����ɕ�������͖̂ʓ|�Ȃ̂ŁA�����\���ŕϊ������

�ƂȂ�B
�@�t��5.0���^���̏ꍇ���m�Ёf���ʂ̊i�q���n���m�����x�|�e���V�������i���f(x,y)�����j�Ɨ����i���f(x,y)�����j�n�̊W��}�������
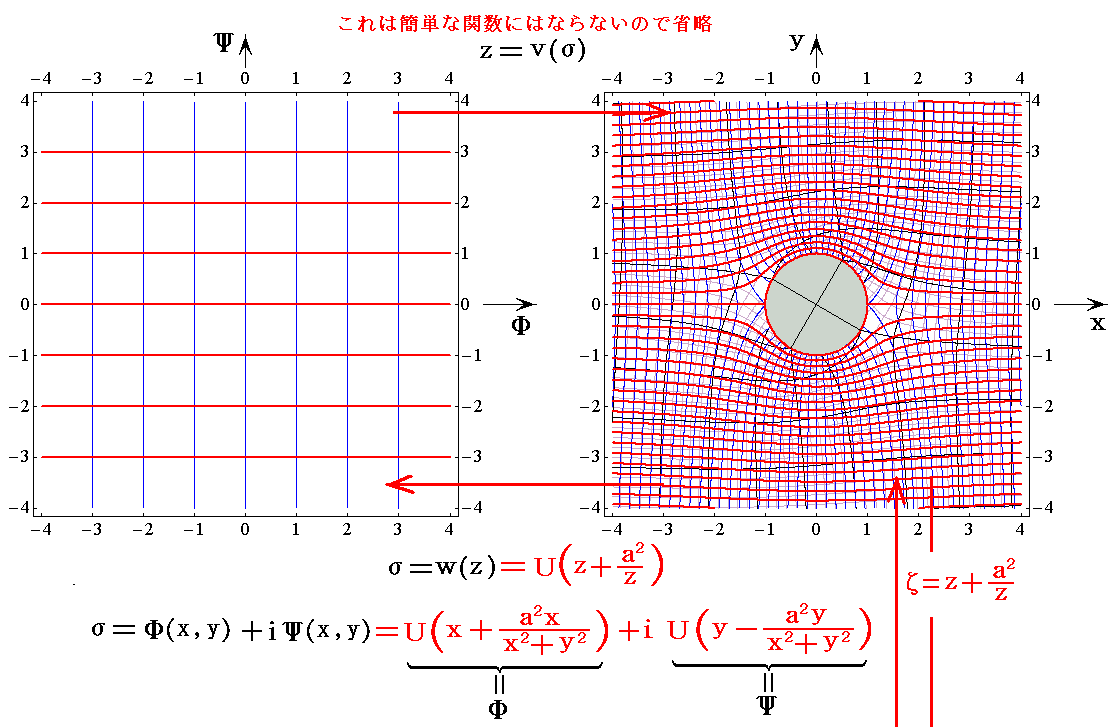
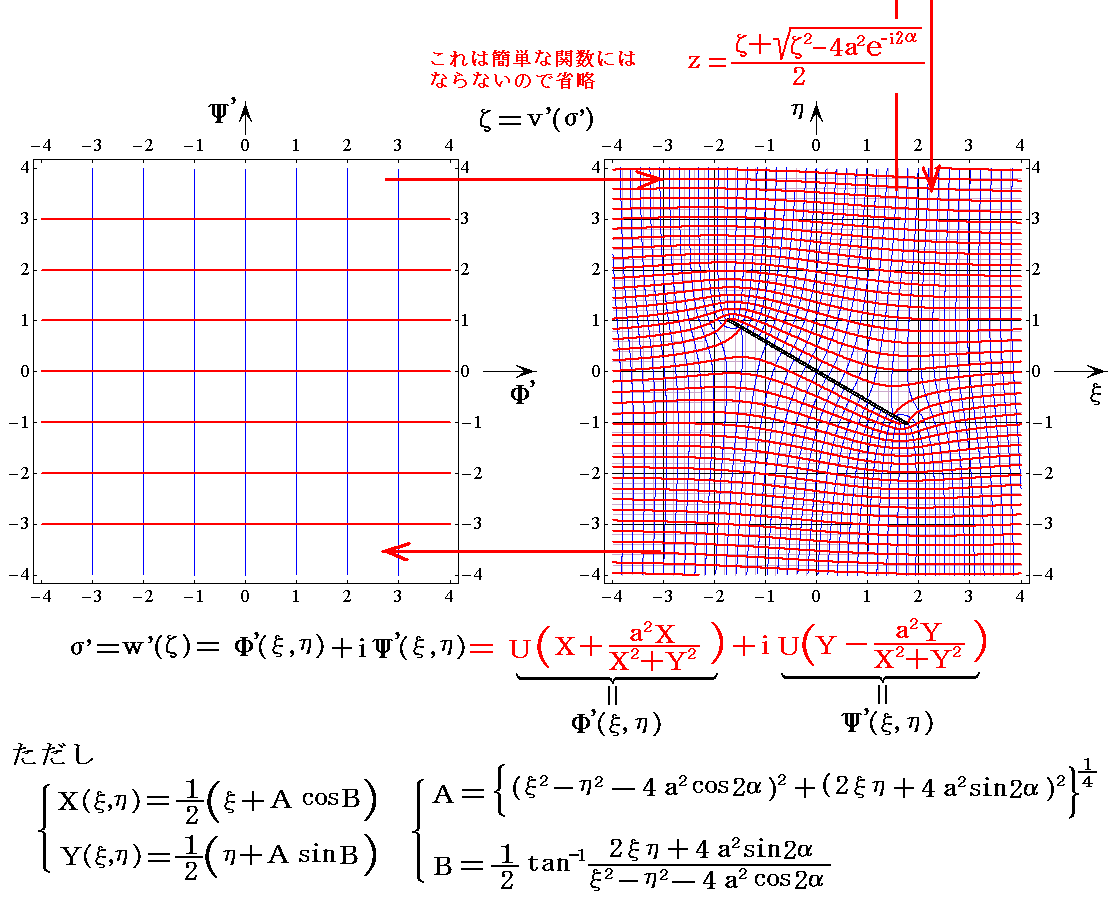
�@���̐}�̔w�i�ɕ`���Ă�����W�i�q���̕ω��Ɨ����̕ω����ǂ̗l�ɑΉ����Ă��邩�ǂ��ᖡ���Ă��������B���̐}�͓��E�k���E���S���̂̈�l�����ɕ����X���Ă������Ƃ��̗���̗����Ɠ����x�|�e���V�������̗l�q��\���Ă���B�@
�Q�D�z��������ꍇ
�@�z�������~������̗����\�����f���x�|�e���V������
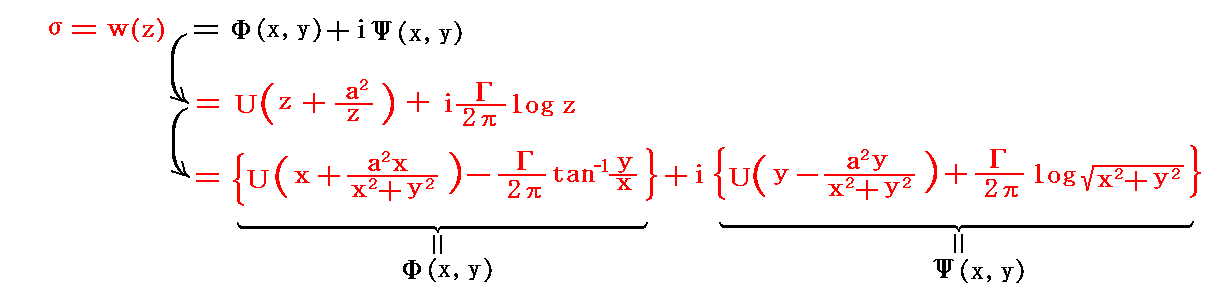
�ł������B���̎��ɑO���̎ʑ������������
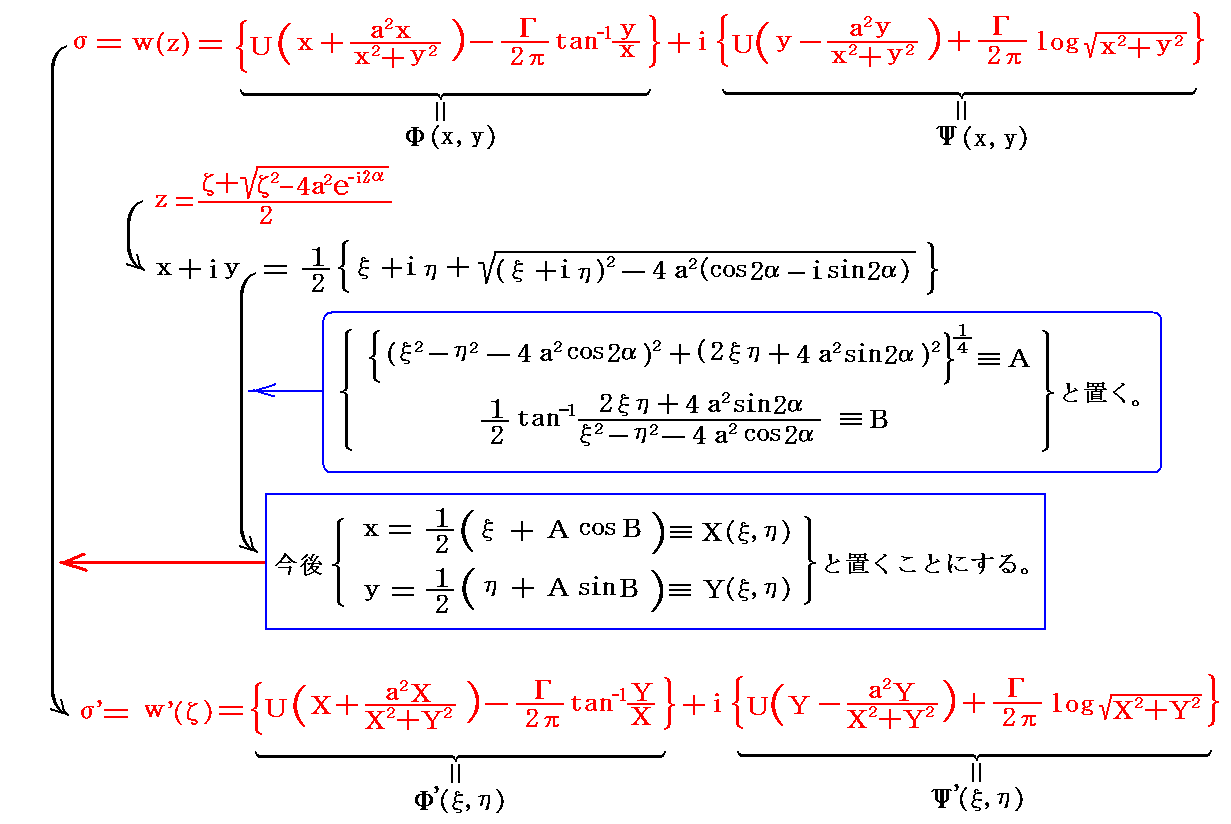
�ƂȂ�B
�@�t��5.0���^���Ƃ�������1���t�A����2���t�A����3���t�A����4���t�A�̏ꍇ��}������B�菇�͓��l�Ȃ̂ŁA�����ʂƃĕ��ʂɂ������m���W�i�q���n���m�����x�|�e���V�������E�����n�̊W�}�̂ݎ����B
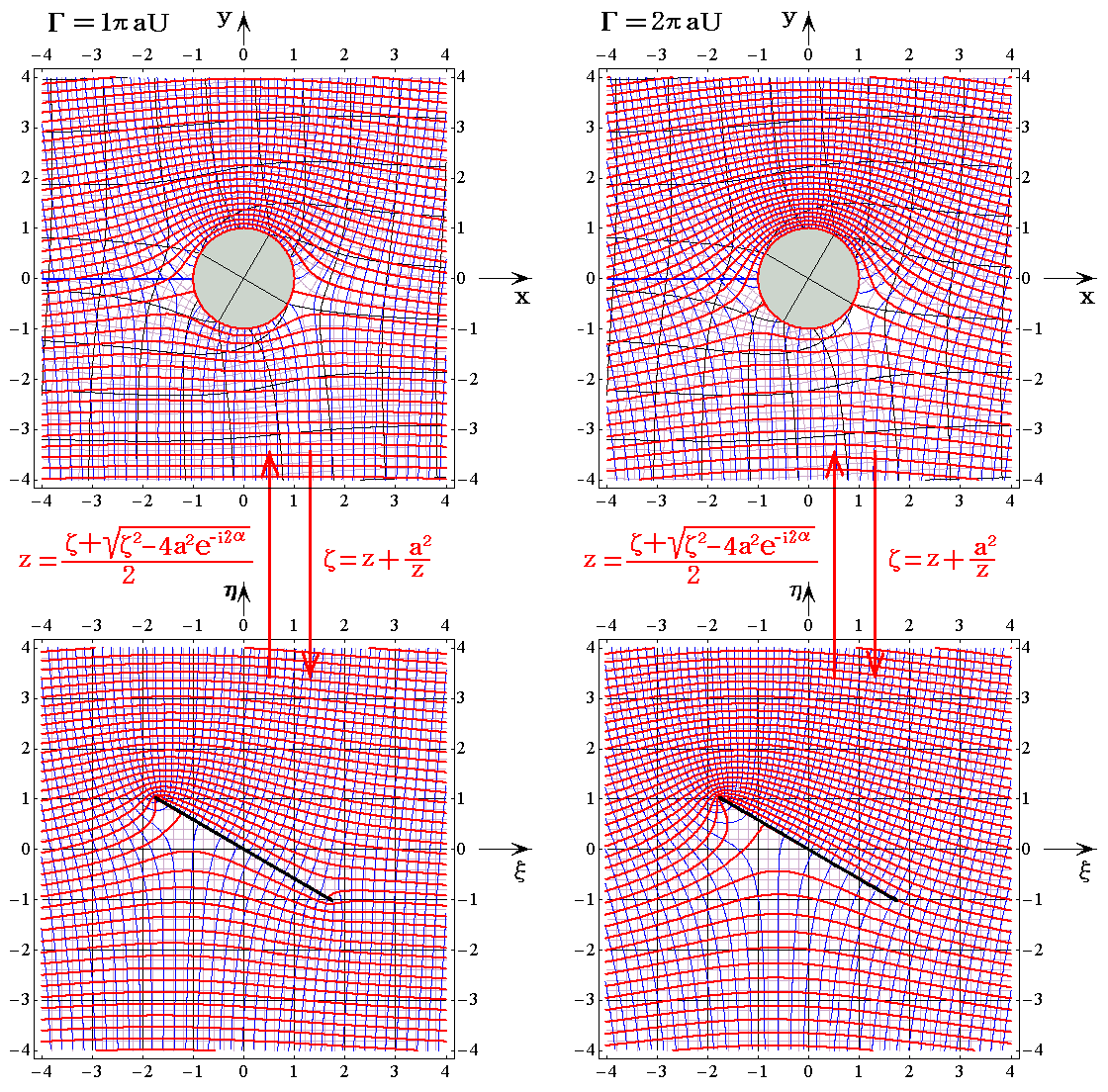
�@��E�}�̕��̌�[�ɒ��ڂ��Ă��������B�~������̏z���̑傫��������ƁA���̌�[�Ɏʑ������~����̓_�ɗ��ݓ_����v�����邱�Ƃ��ł���B���̂Ƃ����̌�[�̗���͕����犊�炩�ɗ��ꋎ�邱�ƂɂȂ�B
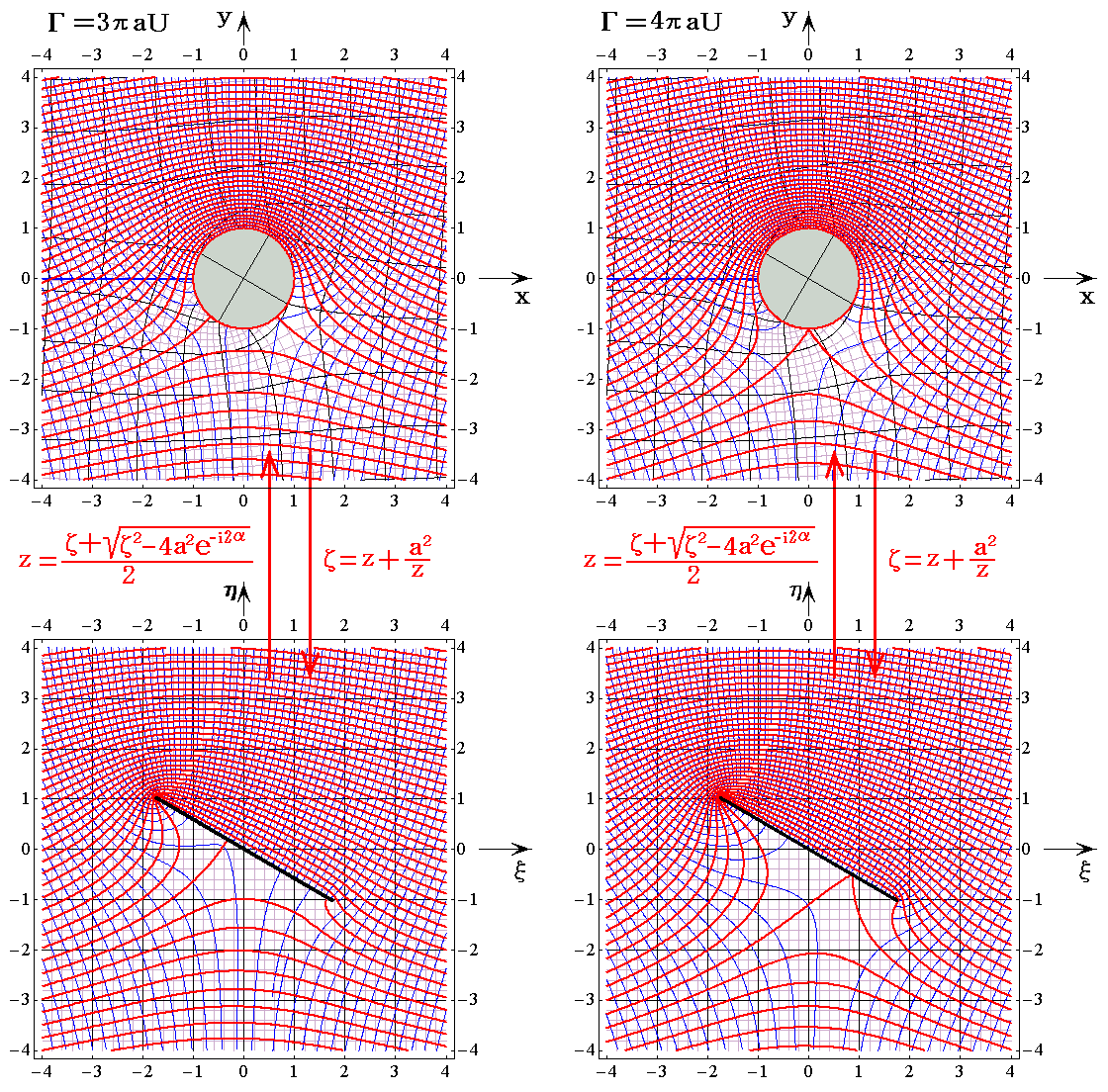
�@�����S�̏z�ɂ��Ă̐}�͋��P�I�ł��B�U�D�i�P�j�Q�D�Œ��ӂ����悤�ɁA�z�̑傫���͓��p�ʑ��ɂ���ĕω����Ȃ��̂ŕ�����ɂ��Ă������z�������B�t������z���傫���Ȃ�ɂ�ĉ~���╽�̏㑤�̗��������ɂȂ艺�����a�ɂȂ�B�܂�㑤�̗��������債�A�����̗�������������B����́A�x���k�[�C�̒藝��p����ƁA��ʂ̈��͂����������ʂ̈��͂����傷�邱�Ƃ��Ӗ�����B���̂��߉~���╽���������̗́i�g�́j�͏z�Ƌ��ɑ��傷���B���ꂪ�S�D�i�Q�j�P�D���N�b�^�E�W���[�R�t�X�L�[�̒藝�������Ă��邱�Ƃł��B
�m�⑫�����n
�@�z�����݂���Ƒ��x�|�e���V�����ʂ͉~�╽�̎�����������ƂȂ�A�����x�|�e���V�������i�F���j�͂ǂ����ŐH���Ⴂ�������܂��B�����������ɂ����Ă������x�|�e���V�����ʂ̌��z�i�������Ԋu�j�͘A���I��������͂���܂���B
�@�}�`�`��\�t�g�̓����̂��߂ɁA��}�̉~������ł͂����̕��̕����ŐH������Ă��܂��B�����̕�����ł͑O���̏㑤�ƌ�[�t�߂̉����ŐH������Ă��܂��B���̂悤�����x�|�e���V�����ʂ̓������͂ǂ����ŐH���Ⴂ��������̂ŁA����͓����x���ݼ�ِ��͏ȗ����ė����݂̂�}�������B
�@
�i�U�j�~������̗�����~�ʗ�����̗���֎ʑ����邱��
�P�D�~�ʗ�����̗���̉�͂̎菇
�@�~�ʗ�����̗������͂���ɂ�
�@�@�i�`�j���̌��}�`�i�����ʁj�Ƃ��ĕϐS�������a�̈قȂ�~��p����B
�@�@�i�a�j�ϐS�����~���̎���̗���i�����ʁj��\���V�������f���x�|�e���V�������߂�B
�@�@�i�b�j�����ʏ�̕��f���x�|�e���V�������ʑ����ɂ���ăĕ��ʏ�̕��f���x�|�e���V�����ɕϊ�����B
�Ƃ����R�̎菇���K�v�ł��B
�@�U�D�i�S�j�̏ꍇ�ƈႤ�̂́i�`�j�Ɓi�a�j�ł����āA�i�b�j�͂U�D�i�S�j�ŗp�����̂Ɠ����W���[�R�t�X�L�[�ϊ���p���܂��B�B�i�`�j�i�a�j�i�b�j�̎菇����������Ɩ킩��Ȃ��Ȃ�܂��̂ŁA�����̈Ⴂ�ɒ��ӂ��ĉ������B�U�D�i�X�j�P�D�Ő�������J���}���E�g���t�c���̏ꍇ�́i�b�j�̎ʑ������ʂȂ��̂��g���܂��̂ŁA�����Ɣ�r�����Ɨǂ�����܂��B
�Q�D�~�ʗ��ɂ��邽�߂̕ϐS�����~
�@�����ł��T�D�i�S�j�ŏq�ׂ��̂Ɠ����W���[�R�t�X�L�[�ϊ���p���܂��B�������A�ʑ����̂����ʂɂ�����~�����}�̗l�ɂ��̒��S����0���i0�C���j�ɂ��炵�����̂ɂ��܂��B���̂Ƃ��~�����_��A���i���C0�j�Ƃ�C���i�|���C0�j��ʂ�l�ɂ��܂��B���̗l�ɂ���̂́A���̓_���ĕ��ʂ̉~�ʗ��̒[�_�Ɏʑ�����邩��ł��B��������Ɖ~�̔��a�� �i��2�{��2�j0.5 �ƂȂ��ď����傫���Ȃ�܂��B
�@�����Œ��ӂ��ė~�������Ƃ́A�ʑ����邚���ʂ̌��~��ς��܂����A�����ʂ��ĕ��ʂ֎ʑ�������͓����W���[�R�t�X�L�[�ϊ���p���邱�Ƃł��B���}����������A���̂悤�ɐݒ肵�������ʏ�̉~���ĕ��ʂ̉~�ʗ��Ɏʑ�����邱�Ƃ�����܂��B���̂��߉~�ʗ��̗�������4����4�ƂȂ�܂��B
�@�ȉ��̐}������1�A����0.4���Ƃ��ĕ`�������̂ł��B
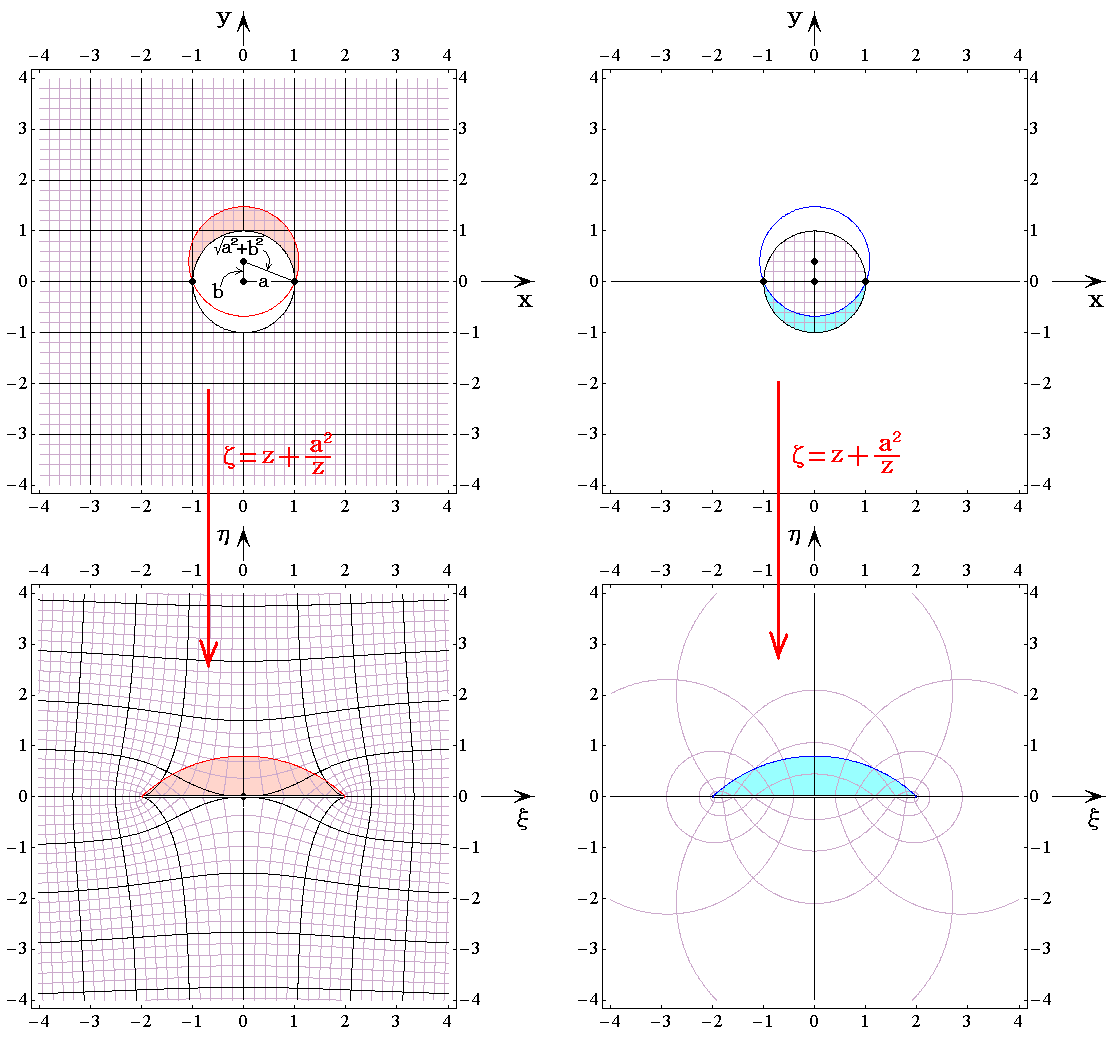
�@��}�͕��G�ł����A�~�ʗ��̉����̕����̃��[�}���ʂ��̎���Ōq���ς���Ă���A���lj��}�̗l�ɂȂ�܂��B
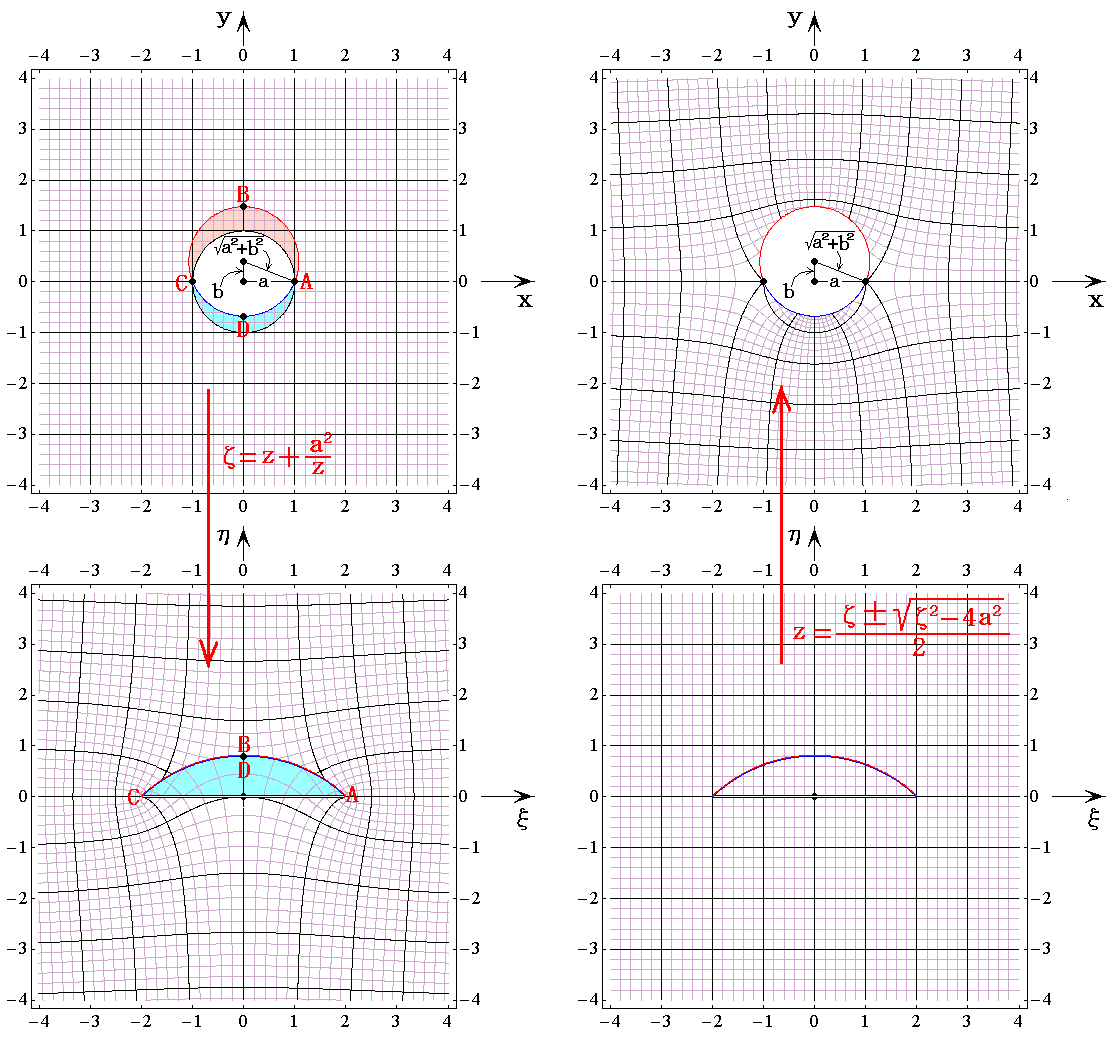
�@���̂Ƃ��A�ʑ����̐����\��
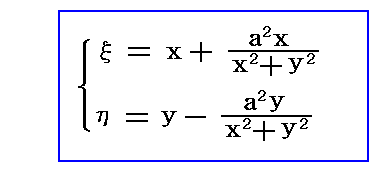
�ɑ�����Ă݂�Β����ɉ���悤�ɁA�}���̓_��A���i���C0�j�͓_��A���i2���C0�j�ցA�_��C���i�|���C0�j�͓_��C���i�|2���C0�j�֎ʑ�����܂��B�܂��~�̍ŏ�_��B���i0�C���{�i��2�{��2�j0.5�j�ƍʼn��_��D���i0�C���|�i��2�{��2�j0.5�j�͂ǂ�����_��B����D���i0�C2���j�֎ʑ�����܂��B
�@���̂Ƃ������i��j�𗃌����Ŋ������l���L�����o�[���ƌ����܂����A�ĕ��ʂ̉~�ʗ��̃L�����o�[���
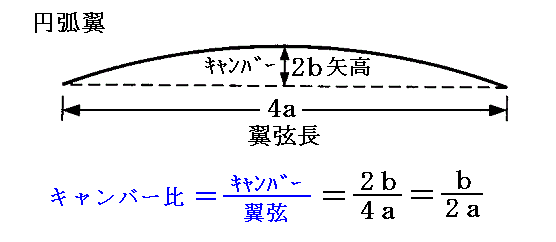
�ƂȂ�܂��B
�R�D�����ʉ~������̗���̕��f���x�|�e���V����
�@�����ʂ̌��~���ς��܂�����A���W�ϊ�����O�̂����ʏ�̉~������̗����\�����f���x�|�e���V�������V�����ʒu�̉~������̗����\�����f���x�|�e���V������p���Ȃ���Ȃ�܂���B
�@�~�̒��S�����_���炚0�ֈړ����A�~�̔��a��������i��2�{��2�j0.5�ɂ����~������l�����ɂ������Ƃ��̕��f���x�|�e���V�����͕ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�P�D�i�S�j�Ő��������悤�ɂ����i���|��0�j�m�܂肘�͂��̂܂܂ŁA�������|���Łn�Œu�������A�����i��2�{��2�j0.5�Œu��������悢�B�R�D�i�P�j���U�D�i�S�j �Q�D���Q�l�ɂ��āA�z�������݂����ʂ̏ꍇ��������
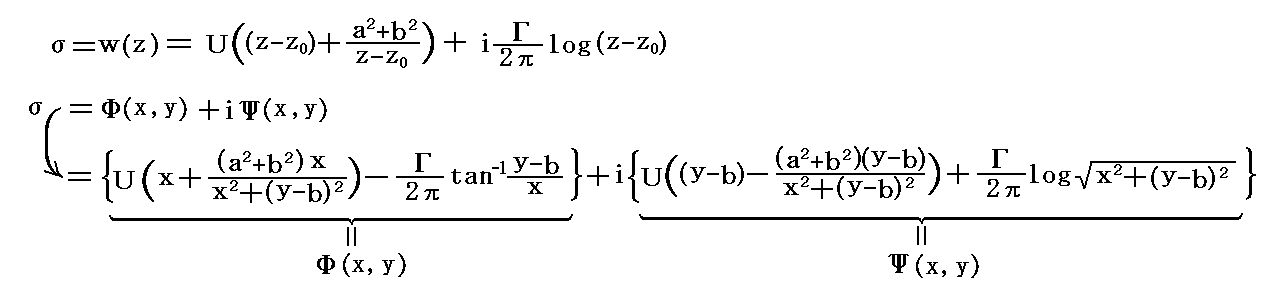
�ƂȂ�B���̕��f���x�|�e���V�������瓱����闬����O���̂����ʏ�̍��W�i�q�ɏd�˂ĕ`�������̂������Ŏ����B
�S�D�ĕ��ʉ~�ʗ�����̗���̕��f���x�|�e���V����
�@�O���ŋ��߂������ʂ̕��f���x�|�e���V�������ĕ��ʂ̕��f���x�|�e���V�����Ёf�����f�i�āj�ɕϊ�����B���̂Ƃ��p������W�ϊ����́A�T�D�i�S�j�Q�D�Ő��������W���[�R�t�X�L�[�ϊ��ł��B�����Ő��������l�ɑO���̎��̂��Ƃ���
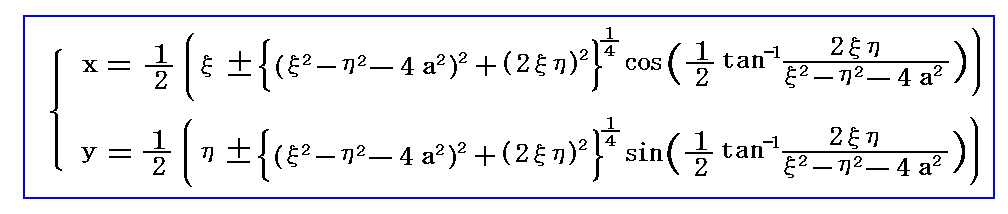
�ɂ���ă̂ƃłɒu��������悢�B�u�����������͒������G�ɂȂ�̂ŏȗ����邪�A�O�����i���j�̂��Ƃ��ɑ�����邾���ł��B�������ē����镡�f���x�|�e���V�������f�i�āj�̎��������f�i�́C�Łj�����̋Ȑ��������x�|�e���V�������A���������f�i�́C�Łj�����̋Ȑ��������ƂȂ�܂��B
�T�D����̗l�q
�@���̗l�ɂ��ē���ꂽ�����ʂƃĕ��ʂ̗����}���ȉ��Ɏ����B�����Ŏ����}�͑S������1���A����0.4���A�t��5.0���^���̏ꍇ�ł��B���̂Ƃ��~�ʗ��̗�������4���A���2���ƂȂ�܂��B
�@�ȉ��̐}�ŁA�����ʂ̗����ƍ��W�i�q�����A���ꂼ��ǂ̗l�Ƀĕ��ʂ̗����ƍ��W�i�q���֕ϊ�����邩���m���߂Ă��������B �U�D�i�S�j�������W���[�R�t�X�L�[�ϊ���p���Ă��܂����A�~���̑傫���ƈʒu���ς�����̂ŗ����̗l�q���ς���Ă��܂��B���̂��߃ĕ��ʂł͉~�ʗ�����̗���ɂȂ����B
�@�ŏ����z����0�̏ꍇ�̗����}�������B�����Ɖ��E�}�̍��W�i�q�����ς��Ă��邪�A�ǂ���������W���[�R�t�X�L�[�ϊ��ł��B
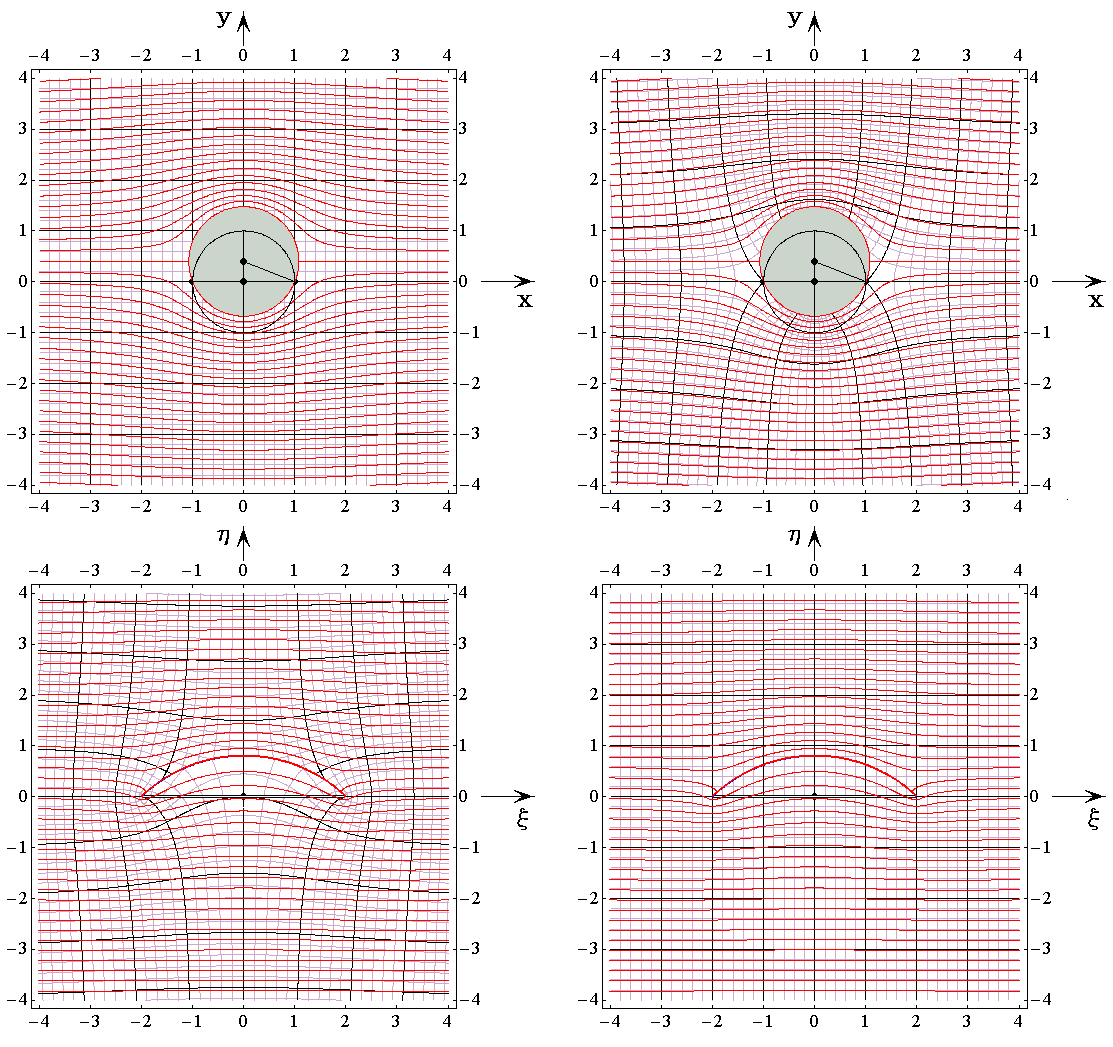
�@�ȉ��̐}������1�A����0.4���A�t��5.0�ŏz�l������0.5�~4�t���A����1�~4�t���A����1.5�~4�t���A����2.0�~4�t���̗����}�ł��B�����̐}�ł͗������̓������̊�_�́A�������K�����ݓ_��ʂ�悤�ɒ�������Ă��܂��B���W�i�q���ʑ������l�q�͓����Ȃ̂ŁA����͍��W�i�q���ȗ����ė����̂L���B
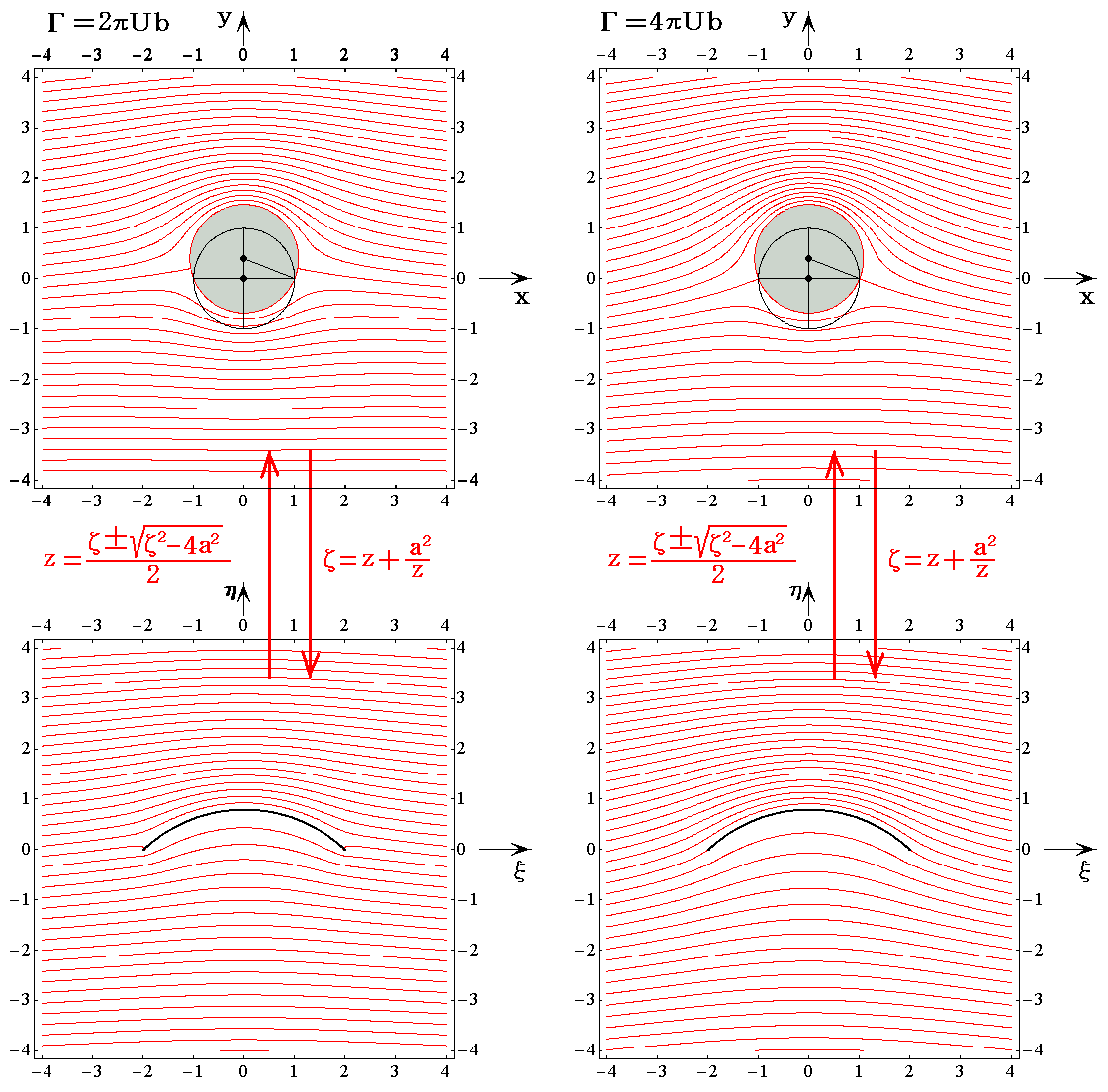
�@��E�}������4�t�����W���[�R�t�X�L�[�̉��������Ă��闬��ł��B
�@�t������z������ɑ傫���Ȃ�Ǝ��}�̂悤�ɂȂ�B
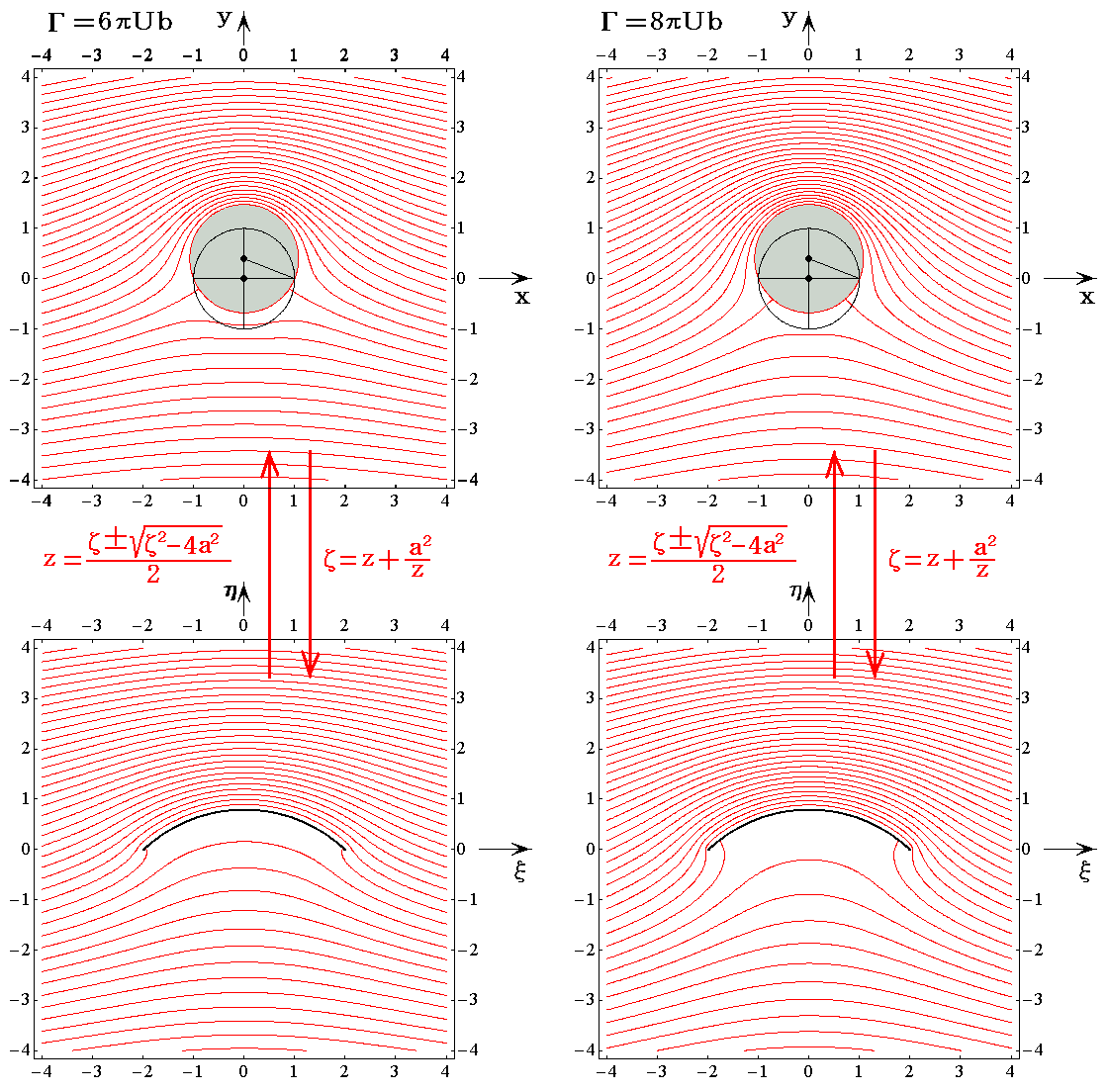
�@
�i�V�j�~������̗�����X�����~�ʗ�����̗���֎ʑ����邱��
�P�D�X�����~�ʗ��ɂȂ邽�߂̕ϐS�����~
�@�����ł͍��W�ϊ����Ƃ����T�D�i�T�j�Ő����������ǃW���[�R�t�X�L�[�ϊ���p���܂��B
�@�U�D�i�U�j�P�D�ŏq�ׂ��菇�i�`�j�̎ʑ����̂����ʂɂ�����~�����}�̗l�Ɏ��܂��B�~�̒��S����0���i���sin���C���cos���j�ɂ��炵�A���܂��~�����_��A���i���cos���C�|���sin���j�Ƃ�C���i�|���cos���C���sin���j��ʂ�l�ɂ��܂��B���̗l�ɂ���̂́A���̓_���ĕ��ʂ̉~�ʗ��̒[�_�Ɏʑ�����邩��ł��B��������Ɖ~�̔��a��
�i��2�{��2�j0.5 �ƂȂ�܂��B
�@���}������1�A����0.2���̏ꍇ�ł��B
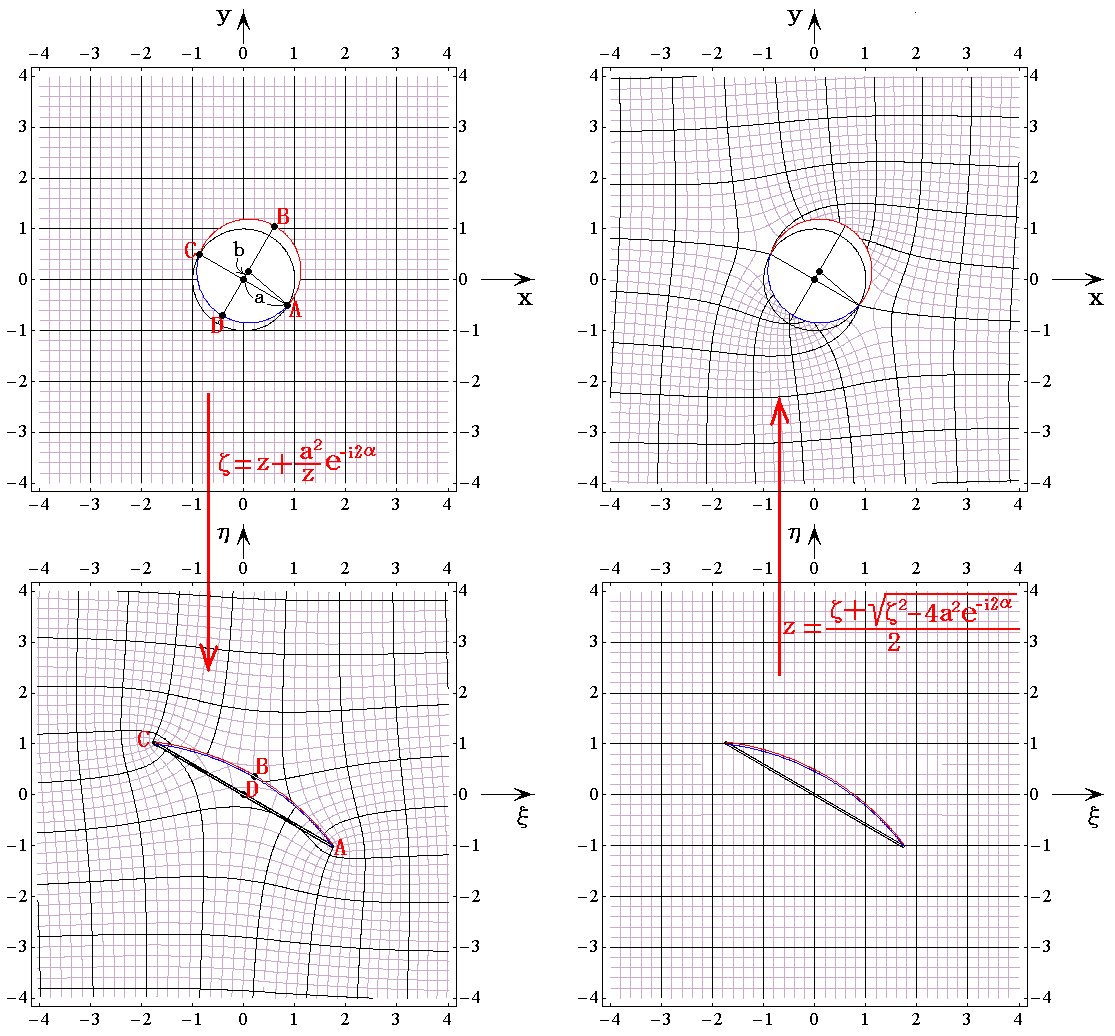
�@�ʑ����̐����\��
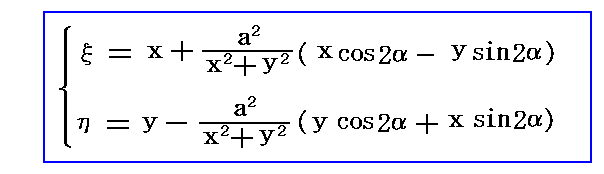
�ɑ�����Ă݂�Β����ɉ���悤�ɁA�}���̓_��A���i���cos���C�|���sin���j�͓_��A���i2���cos���C�|2���sin���j�ցA�_��C���i�|���cos���C���sin���j�͓_��C���i�|2���cos���C2���sin���j�֎ʑ�����܂��B�܂��_��B���i�i�i��2�{��2�j0.5�{���j�sin���C�i�i��2�{��2�j0.5�{���j�cos���j�Ɠ_��D���i�|�i�i��2�{��2�j0.5�|���j�sin���C�|�i�i��2�{��2�j0.5�|���j�cos���j�͂ǂ�����_��B����D���i2���sin���C2���cos���j�֎ʑ�����܂��B
�@���̂��߁A���̏ꍇ���ʑ���̉~�ʗ��̗�������4���A�L�����o�[�i��j��2���ƂȂ�܂��B
�Q�D�����ʉ~������̗���̕��f���x�|�e���V����
�@�����ʂ̌��~���ς��܂�����A���W�ϊ�����O�̂����ʏ�̉~������̗����\�����f���x�|�e���V�������V�����ʒu�̉~������̗����\�����f���x�|�e���V������p���Ȃ���Ȃ�܂���B
�@�~�̒��S�����_���炚0���i���sin���C���cos���j�ֈړ����A�~�̔��a��������i��2�{��2�j0.5�ɂ����~������l�����ɂ������Ƃ��̕��f���x�|�e���V�����͕ʍe�u�Q��R�i�J���}���Q��ƍR�́j�v�P�D�i�S�j�Ő��������悤�ɂ����i���|��0�j�Ɂm�܂肘�����|���sin���ɁA�������|���cos���Ɂn�u�������A�����i��2�{��2�j0.5�ɒu��������悢�B�T�D�i�T�j�Q�D���Q�l�ɂ��āA�z�������݂����ʂ̏ꍇ�������ƈȉ��̂悤�ɂȂ�B
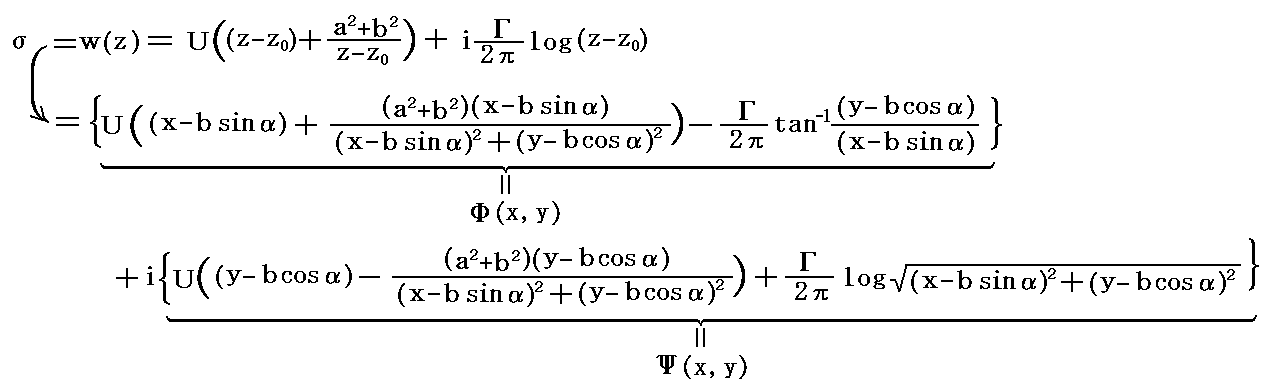
���̕��f���x�|�e���V�������瓱����闬���m���i���C���j�����̋Ȑ��Q�n�͌�Ŏ����܂��B
�R�D�ĕ��ʉ~�ʗ�����̗���̕��f���x�|�e���V����
�@�O���ŋ��߂������ʂ̕��f���x�|�e���V�������ĕ��ʂ̕��f���x�|�e���V�����Ёf�����f�i�āj�ɕϊ�����B���̂Ƃ��p������W�ϊ����́A�T�D�i�T�j�Q�D�Ő����������ǃW���[�R�t�X�L�[�ϊ��ł��B�����Ő��������l�ɑO���̎��̂��Ƃ���
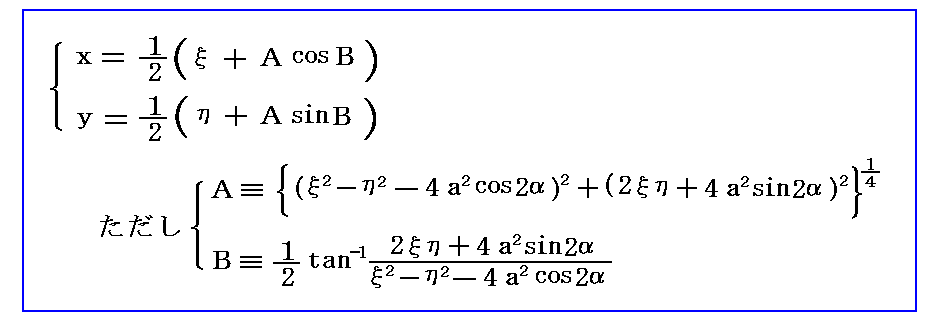
�ɂ���ă̂ƃłɒu��������悢�B�u�����������͒������G�ɂȂ�̂ŏȗ����邪�A�O�����i���j�̂��Ƃ��ɑ�����邾���ł��B�������ē����镡�f���x�|�e���V�������f�i�āj�̎��������f�i�́C�Łj�����̋Ȑ��������x�|�e���V�������A���������f�i�́C�Łj�����̋Ȑ��������ƂȂ�܂��B
�S�D����̗l�q
�@��������1���A����0.2���A�t��5.0���^���̏ꍇ�ɂ��āA�����ʂƃĕ��ʂ̗����}�������B�U�D�i�T�j���������ǃW���[�R�t�X�L�[�ϊ���p���Ă��܂����A�~���̑傫���ƈʒu���ς�����̂Ńĕ��ʏ�ł͗�����4���A�2���̉~�ʗ�����̗���ɂȂ�B
�@�܂��ŏ��ɁA�}���p��20���ɌŒ肵�ėl�X�ȏz�����ꍇ�̗����}��`���Ă݂�B
�@�z�͎��Œ�`������s��P�ʂƂ��Ď����Ă��܂��B
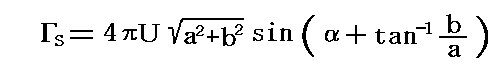
��s���V�D�i�R�j�R�D�Ő����������ݓ_�����[�`�Ɉ�v����Ƃ��̏z�l�ŁA�Y�����̂������ݓ_�istagnation point�j�̂����Ӗ�����B
�@
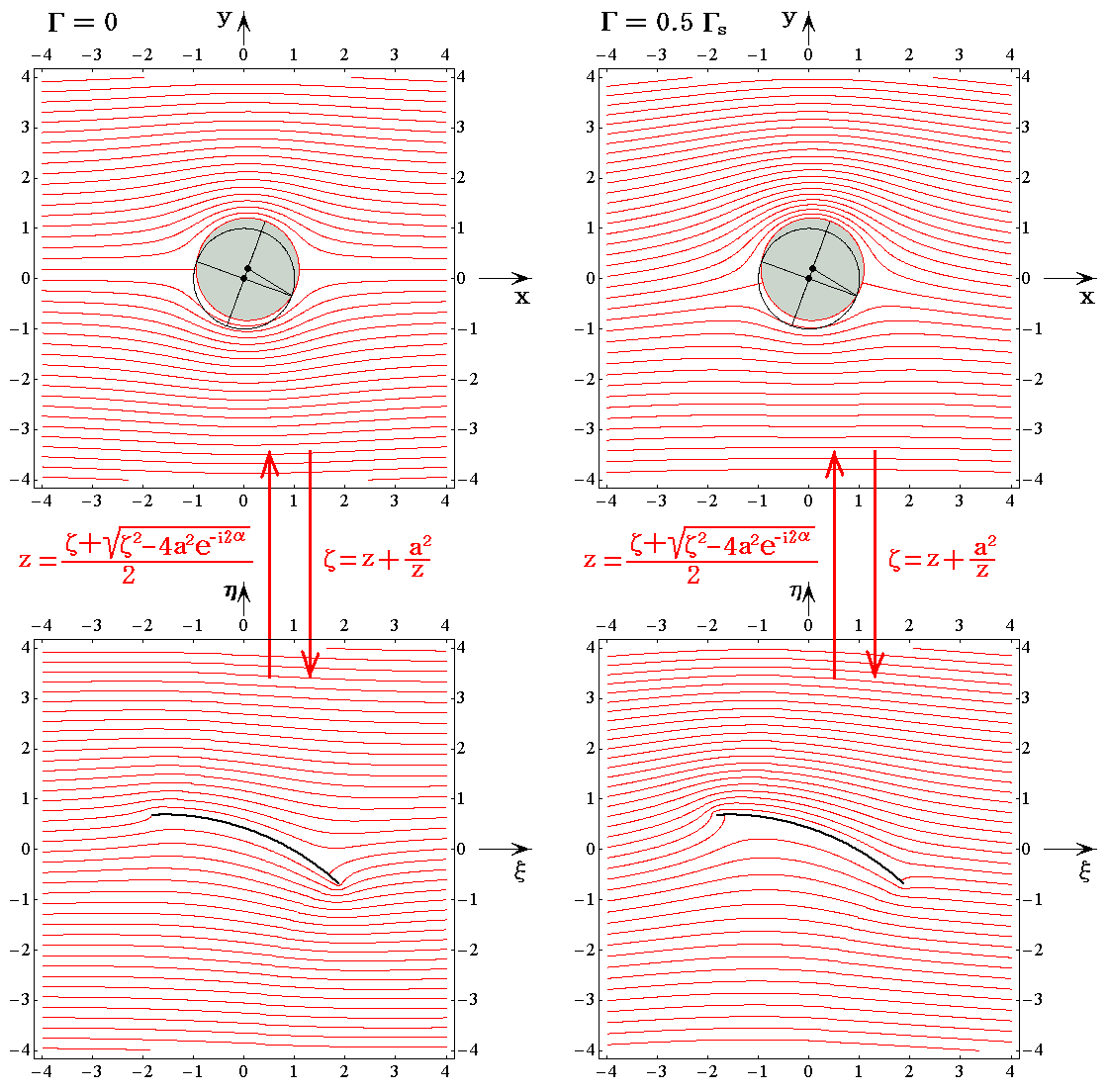
�@�����}���V�D�i�P�j�R�D�Ő��������W���[�R�t�X�L�[�̉��������闬��ł��B����[�̗����������犊�炩�ɗ��ꋎ���Ă��邱�Ƃɒ��ӂ��Ă��������B
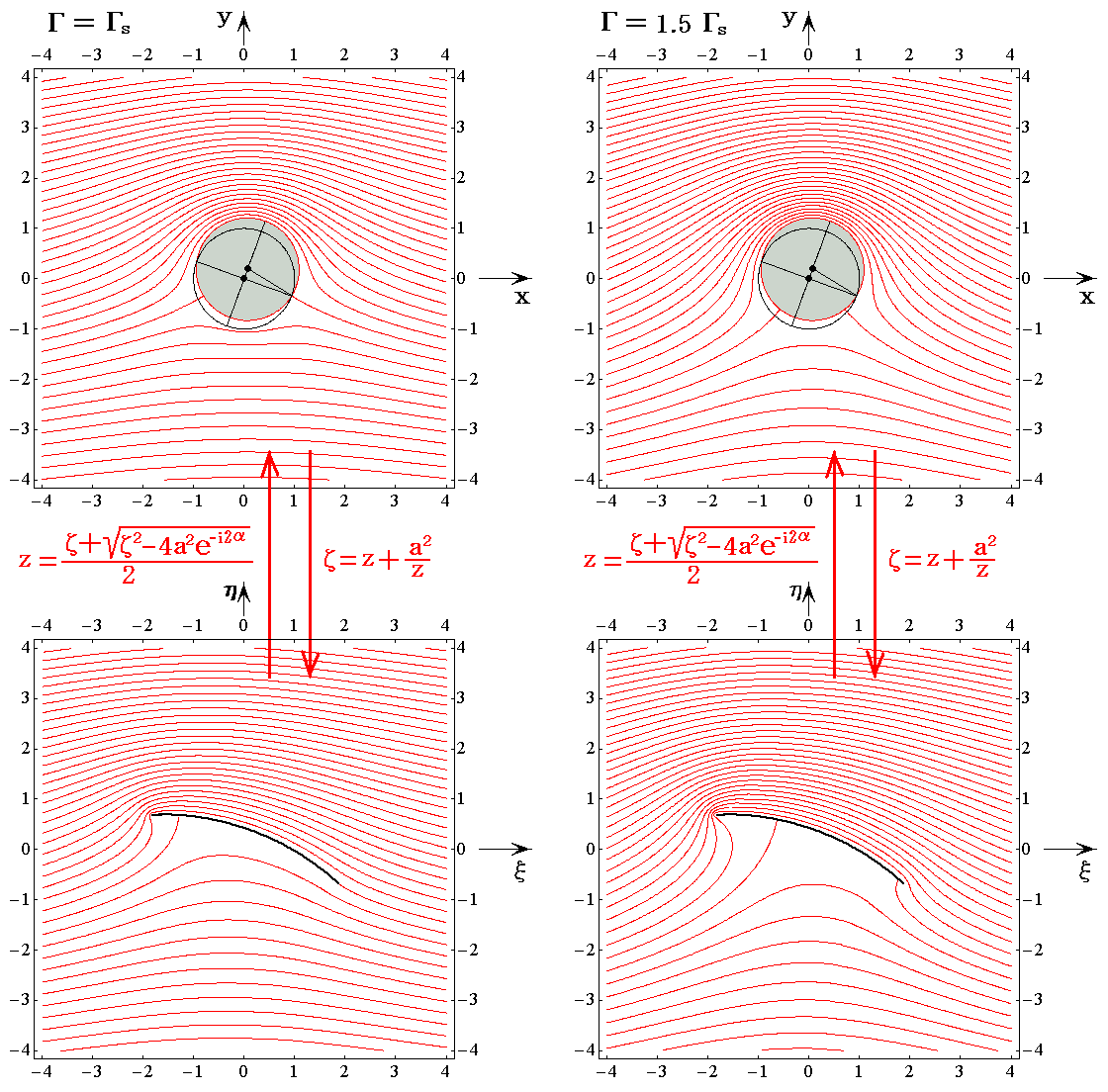
�t������z�̒l���傫���Ȃ�ƁA���}�̗l�ɗ��̎������]���Ȃ��痃�Ƌ��ɓ������̗v�f���o�Ă���B
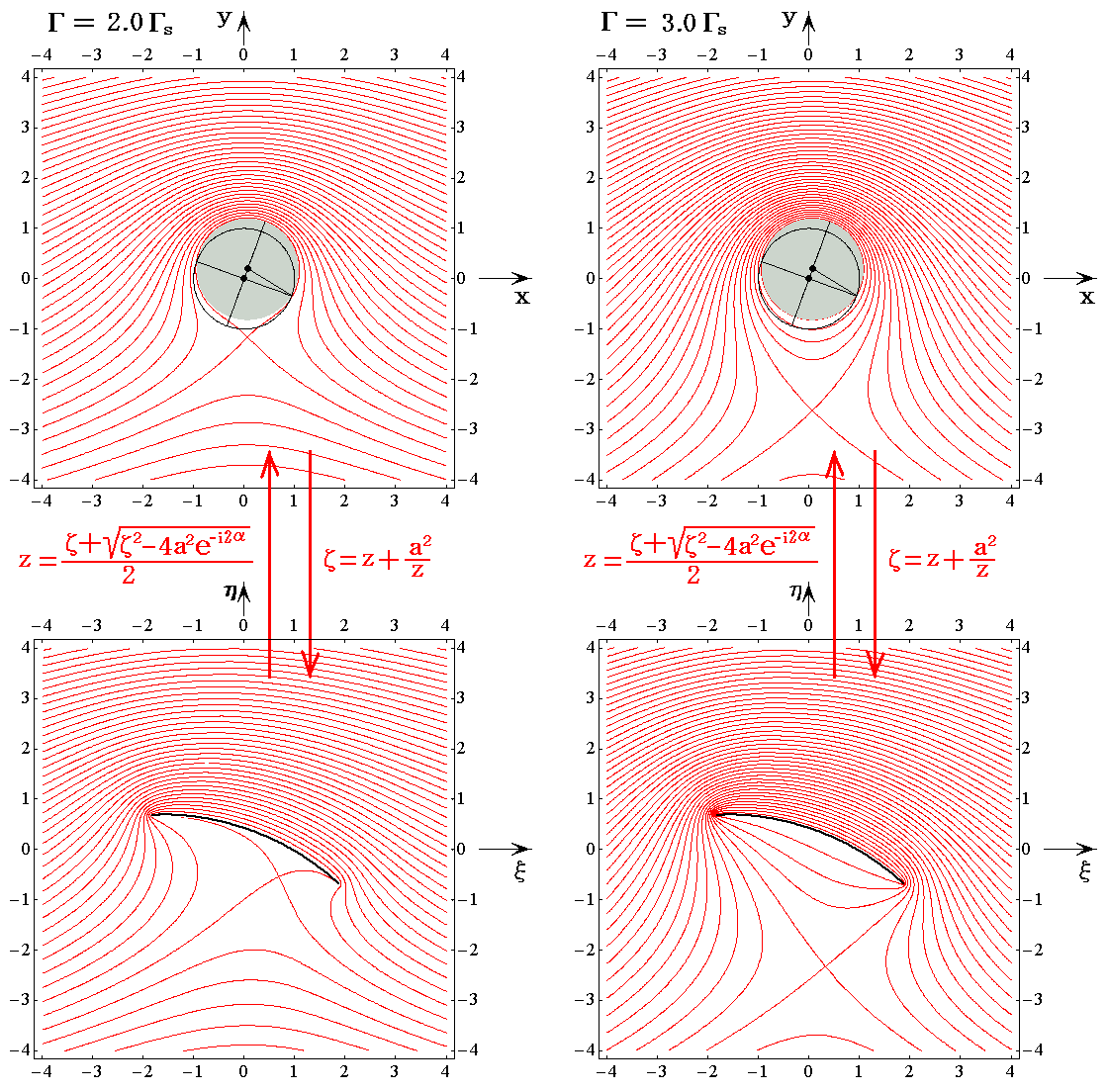
�@���ɁA�}���p����10����30���ƕς��āA������W���[�R�t�X�L�[�̉��������藧�ꍇ��`���Ă݂�B���̏ꍇ�t������z�l�͗��ݓ_�����[�`�Ɉ�v����Ƃ��̏z�l��s�ɂȂ�܂��B
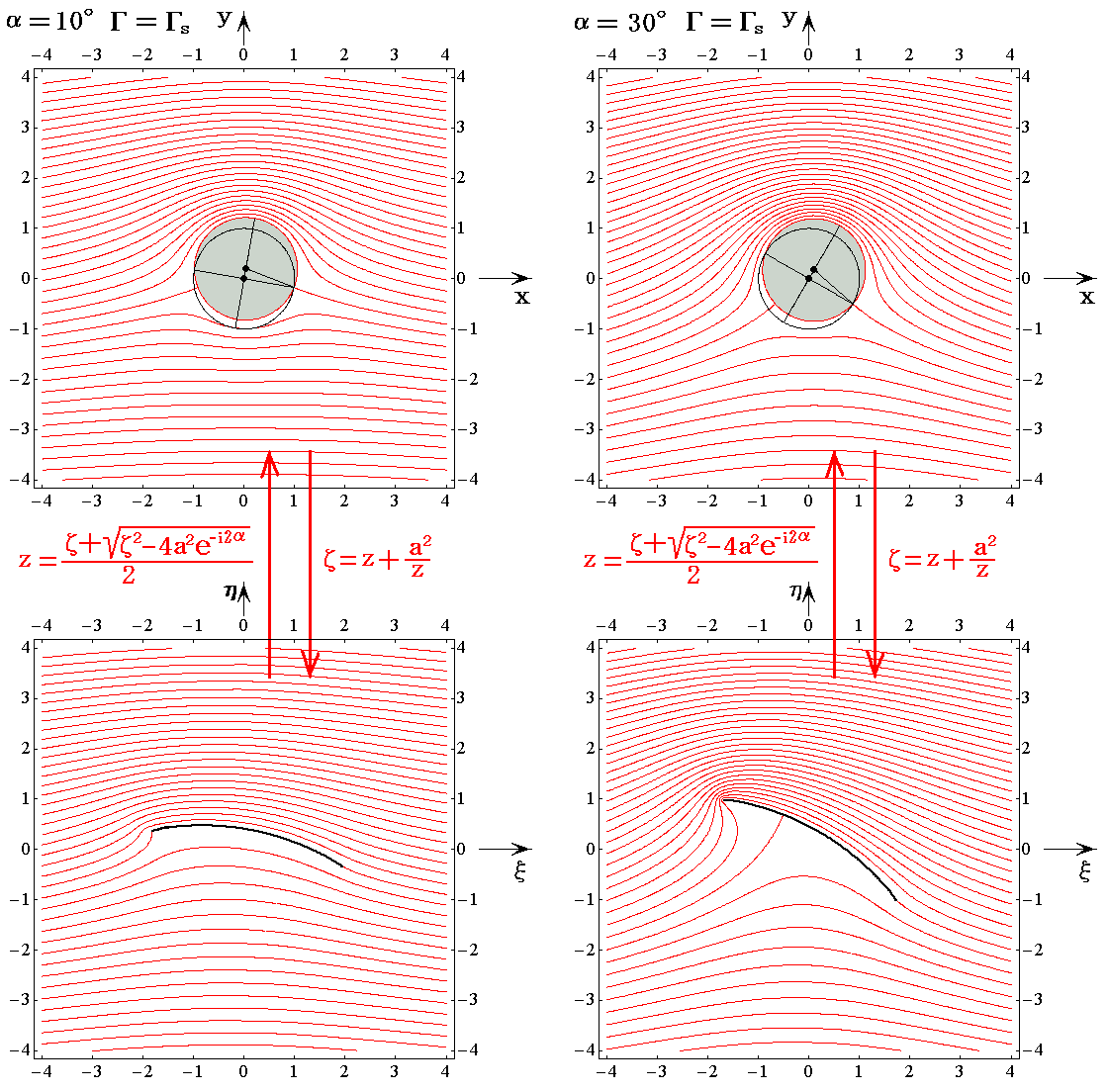
�@
�i�W�j�~������̗���������i�W���[�R�t�X�L�[���j����̗���֎ʑ����邱��
�P�D�}���p�E�L�����o�[�E�����̂��闃�`�i�W���[�R�t�X�L�[���j�֎ʑ�����錳�̉~
�@���W�ϊ������T�D�i�T�j�Ő����������ǃW���[�R�t�X�L�[�ϊ������̂܂ܗp����悢�B
�@�ʑ����̂����ʂɂ�����~�����}�̗l�ɂƂ�܂��B�~�̒��S�����}�̗l�ɂ�0���i���cos���|�o���{�i��2�{��2�j0.5�pcos�i���{���j�C�|���sin���{�o���{�i��2�{��2�j0.5�psin�i���{���j�j�ɂ��炵�A���܂��~�����_��A���i���cos���C�|���sin���j��ʂ�l�ɂ��܂��B���������͌}���p�A����������-1�i���^���j�ł��B��������Ɖ~�̔��a�� ���{�i��2�{��2�j0.5 �ƂȂ�܂��B
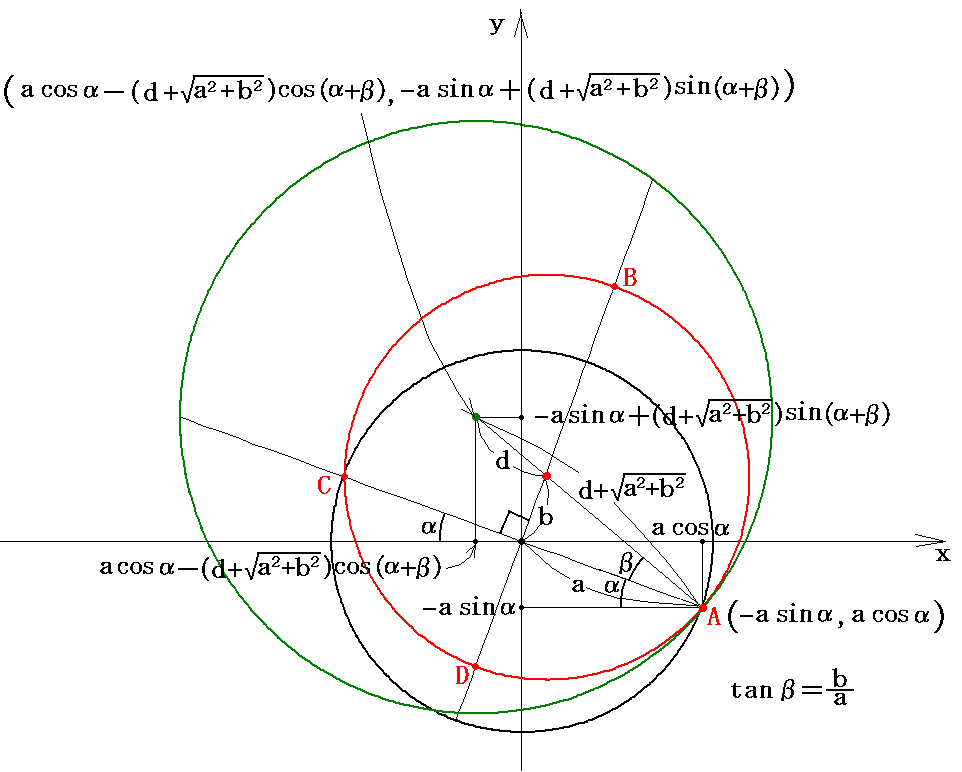
�@���̗l�ɂ���̂́A�`�_���ĕ��ʂ̗��̌㉏�Ɏʑ�����A���̑傫�������邱�ƂŃL�����o�[��ς��A���߂��邱�Ƃŗ��̌��݂�ω������A�������O�����ۂ݂�тт����`�������ł��邩��ł��B���̗��^���W���[�R�t�X�L�[���ƌ����܂��B
�@���}������1�A����0.2���A����0.15���A����30���A����tan-10.2��11.31���̏ꍇ�ł����A���W�i�q�̕ϊ������l�q�����L�̎������[���ł���B
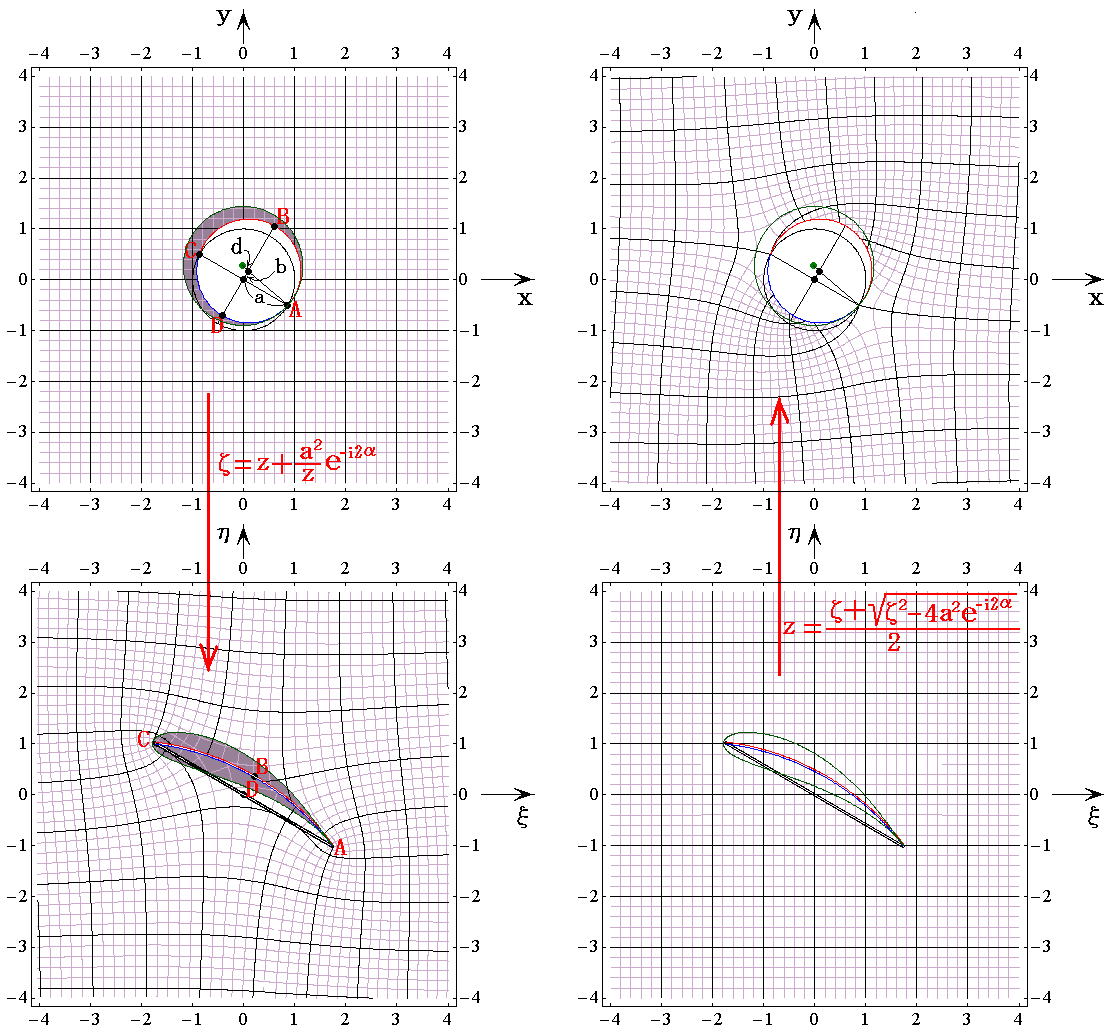
���̂Ƃ��A�ʑ����̐����\�����U�D�i�V�j�P�D�̏ꍇ�Ɠ����ł�����
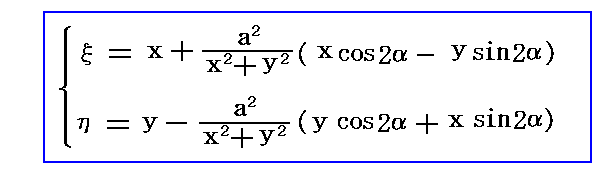
�ɂ���Ă����ʂ̌��~���ĕ��ʂ̂ǂ��Ɏʑ�����邩�v�Z�ł��܂��B
�@�L�����o�[2����0�ł���0�̏ꍇ���Ώ̗��Ƃ����܂����A���̏ꍇ�ŗ����̃p�����[�^����^�����Ƃ��ɗ�������4������ǂꂭ�炢�ω����邩���ׂĂ݂܂��B���}�͂���1�A����0�A����0.15�A����0���Ƃ����Ώ̗��̕ϊ��}�ł��B
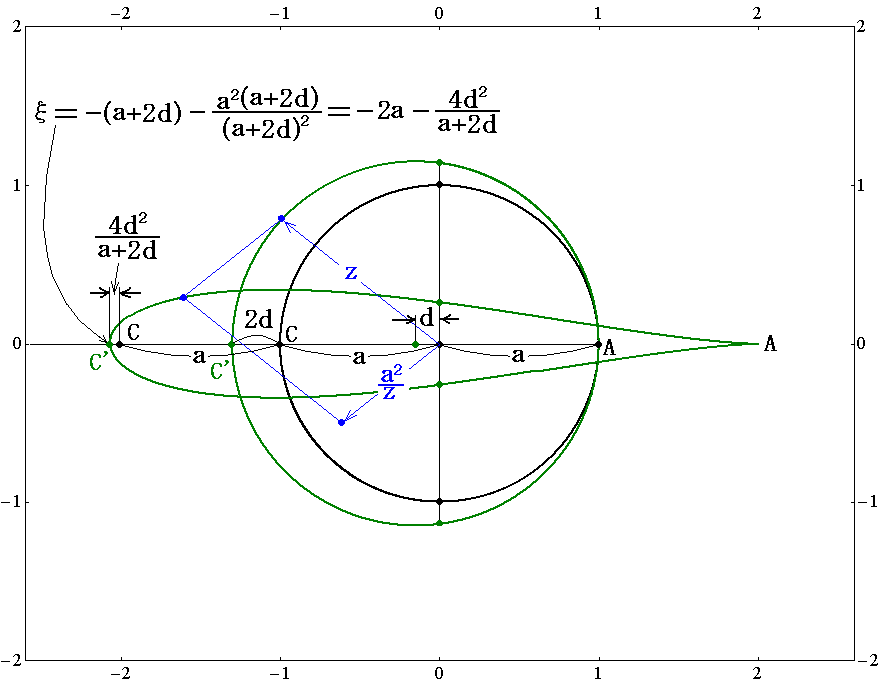
�@���~�̍��[��C'���i�|���|2���C0�j�̓�C'���i�|2���|4��2�^�i���{2���j�A0�j�̓_�Ɏʑ�����A�E�[��A���i���C0�j�̓�A���i2���C0�j�Ɏʑ������B���̂��ߗ�������4������4���{4��2�^�i���{2���j�ƂȂ�B�Ⴆ�A����1�A����0.15���̏ꍇ4����4.069���ɂȂ�B
�@�����Ƃ��̗̈�͂����ʂ���ĕ��ʂւ̎ʑ��ŋ������k�ޏꏊ�Ȃ̂ł��̍��͂��܂�ڗ������A�������͂قڂ��̂܂�4���ɋ߂��l�ɂȂ�A�L�����o�[���ق�2���ɋ߂��l�ɂȂ�܂��B���̌��ʂ͎�ɗ��̌��݂Ɍ�����B���̂��߁A�ʑ���̃W���[�R�t�X�L�[���̗������͂ق�4���A�L�����o�[�i��j���ق�2���ŋߎ��ł��܂��B
�@���Ȃ݂ɂ���1�A����0.2���A����0.15���A����10���Ƃ����ꍇ�̕ϊ��}�͉��}�̗l�ɂȂ�܂��B
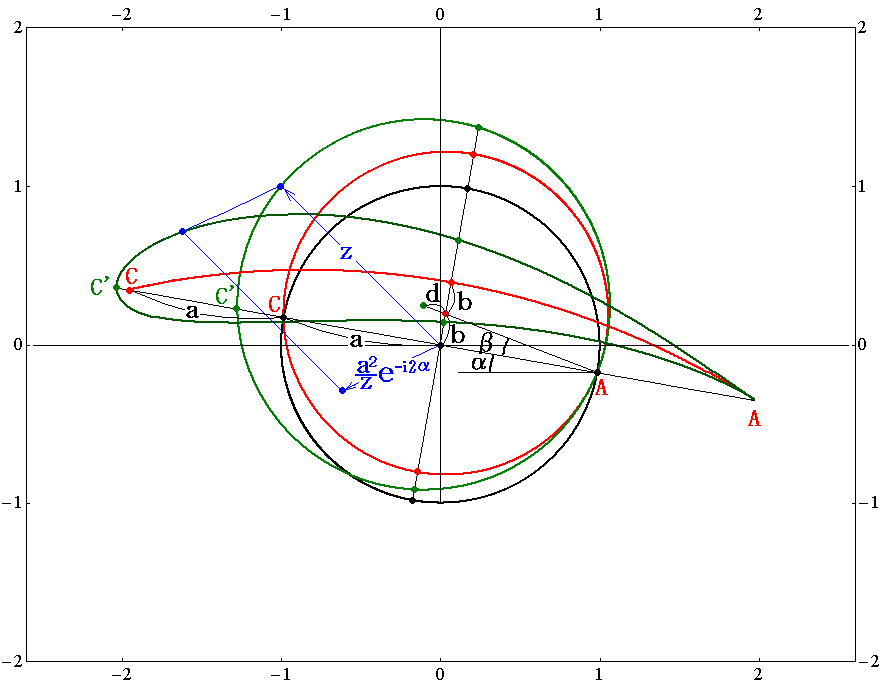
�@
�m�⑫�����n
�@�����̃p�����[�^�̒�`�̎d���ɂ͐F�X�Ȃ��̂�����܂��B���L�̒�`�͂��̈��ł��B
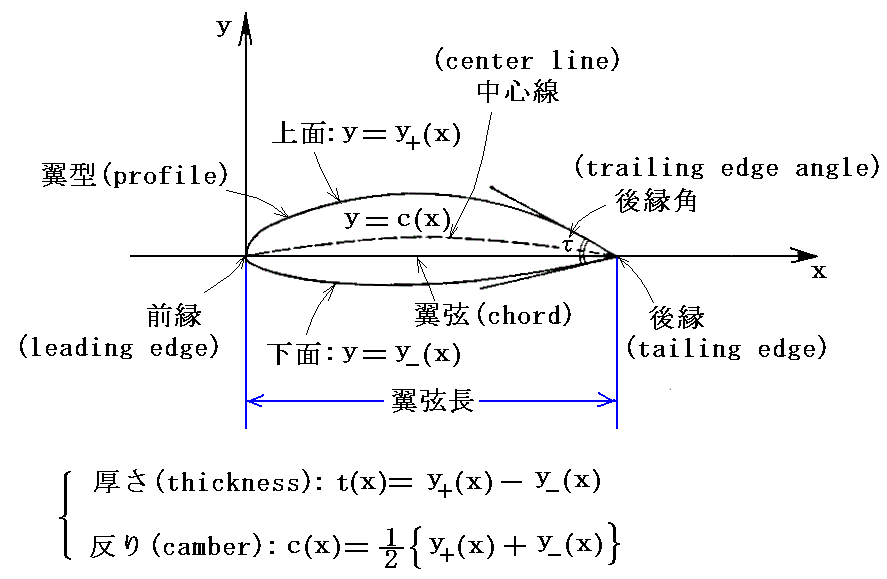
�����āA��l���̗���̕����Ɨ����̐����p���}���p��(angle of attack)�ƌĂԁB
�@��L�W���[�R�t�X�L�[���ł̒�`�́A���̒�`�Ƃ͔����Ɉ���Ă��邱�Ƃɒ��ӂ��Ă��������B
�Q�D�����ʉ~������̗���̕��f���x�|�e���V����
�@�����ʂ̌��~���ς��܂�����A���W�ϊ�����O�̂����ʏ�̉~������̗����\�����f���x�|�e���V�������V�����ʒu�̉~������̗����\�����f���x�|�e���V������p���Ȃ���Ȃ�܂���B
�@�~�̒��S�����_���炚0���i���cos���|�o���{�i��2�{��2�j0.5�pcos�i���{���j�C�|���sin���{�o���{�i��2�{��2�j0.5�psin�i���{���j�j�Ɉړ����A�~�̔��a�� ���{�i��2�{��2�j0.5 �ɂ����~������l�����ɂ������Ƃ��̕��f���x�|�e���V�����ɂȂ�܂��B�ȑO�Ɠ��l�ɒ��S���W�����炵���a��ς���悢�̂ŏz�������݂���ꍇ�̂����ʂɂ����镡�f���x�|�e���V�����͈ȉ��̂悤�ɂȂ�B
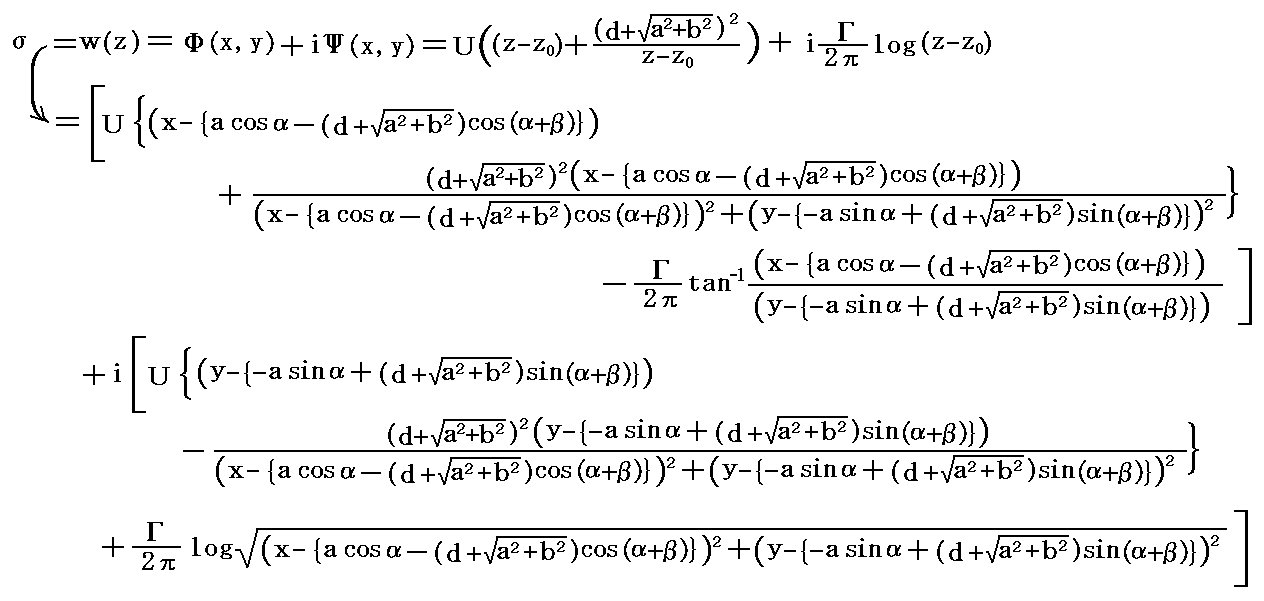
���͕��G�ɂȂ�܂����A�l�������̂͒P���ł��B���̕��f���x�|�e���V�������瓱����闬���m���i���C���j�����̋Ȑ��Q�n�͌�Ŏ����܂��B
�R�D�ĕ��ʉ~�ʗ�����̗���̕��f���x�|�e���V����
�@�O���ŋ��߂������ʂ̕��f���x�|�e���V�������ĕ��ʂ̕��f���x�|�e���V�����Ёf�����f�i�āj�ɕϊ�����B���̂Ƃ��p������W�ϊ����́A�������ǃW���[�R�t�X�L�[�ϊ��ł�����A�O���̎��̂��Ƃ���
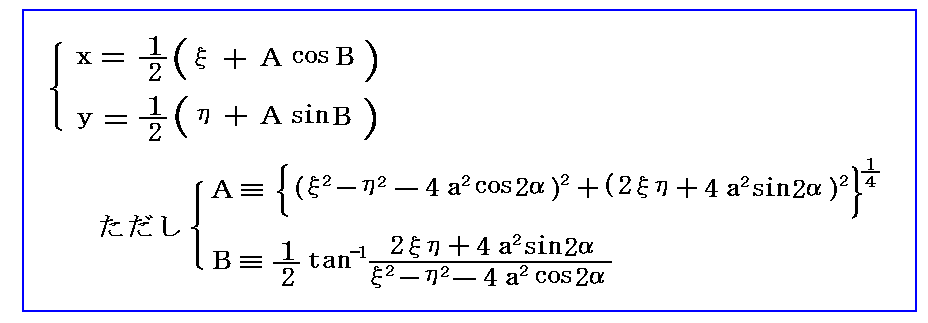
�ɂ���ă̂ƃłɒu��������悢�B�u�����������͒������G�ɂȂ�̂ŏȗ����邪�A�������ē����镡�f���x�|�e���V�������f�i�āj�̎��������f�i�́C�Łj�����̋Ȑ��������x�|�e���V�������A���������f�i�́C�Łj�����̋Ȑ��������ƂȂ�܂��B
�S�D����̗l�q
�@��������1�A����0.2���A����0.15���A����tan-10.2��11.31���A�t��5.0������10���ƃ���30���ꍇ�́A�����ʂƃĕ��ʂ̗����}�������B�������ǃW���[�R�t�X�L�[�ϊ���p���Ă��܂����A�~���̑傫���ƈʒu���ς�����̂Ńĕ��ʏ�ł͗�������4���A���2���̌�������̗���ɂȂ����B
�@���̂Ƃ��A�z�����ݓ_�����[�`�Ɉ�v����Ƃ��̏z�l��s�ɂ��Ă��܂��B
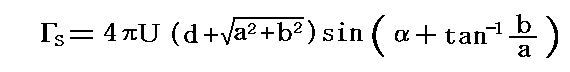
�@
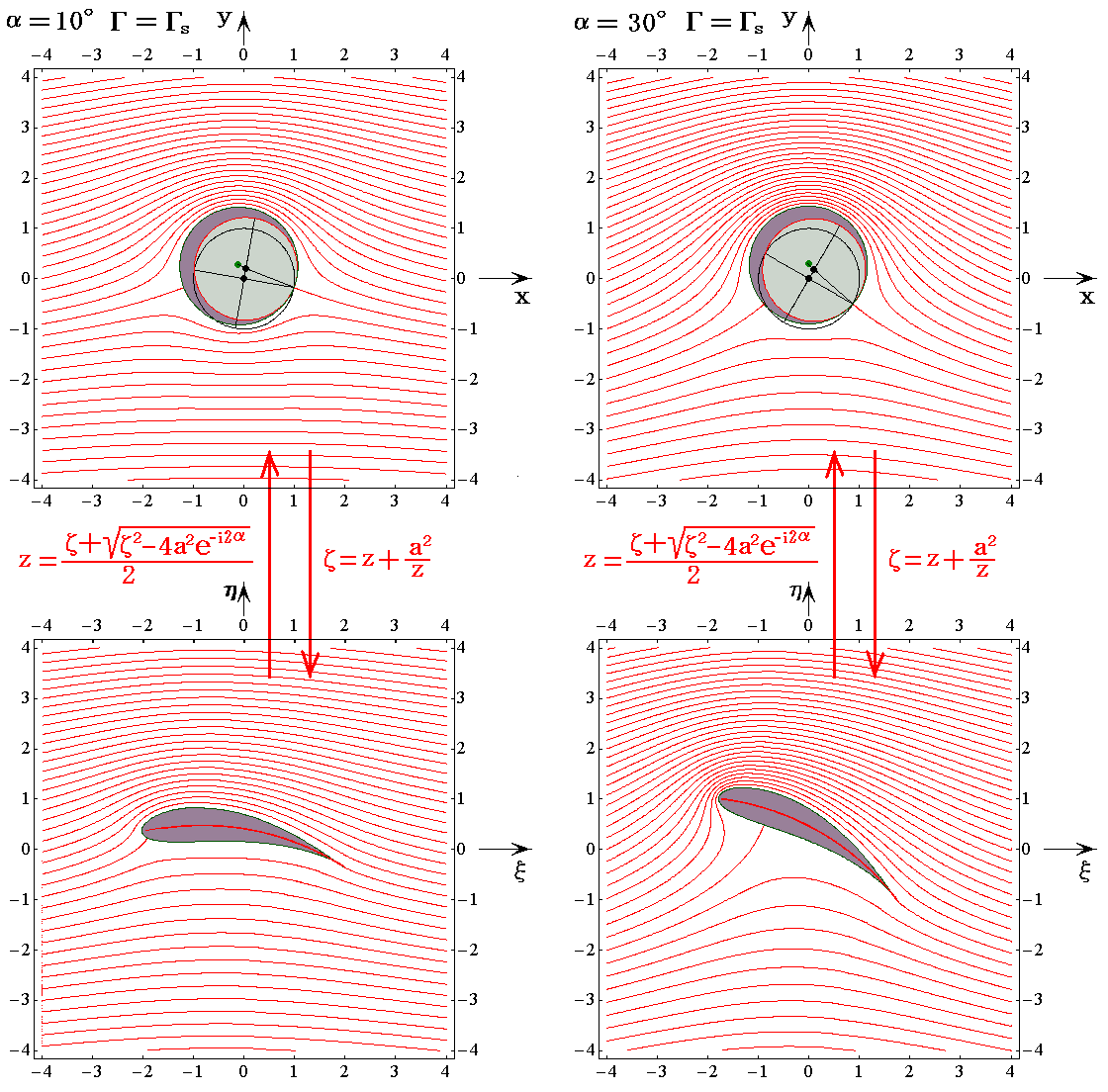
�@���̐}���U�i�V�j�S�D�̍Ō�Ɏ������A�����}���p�A������̉~�ʗ��̂܂��̗����}�Ɣ�r���Ă݂Ă��������B�W���[�R�t�X�L�[���̕����A���̑O�����̑��x���z�����₩�ɂȂ�A��芊�炩�ȗ��ꂪ�����ł���B���ꂪ�����ɂ��邱�Ƃ̍ő�̌��ʂł��B
�@�����̗��̂͊��S���̂ł͂Ȃ��S�������݂��邽�߂ɑO�����̋}���ȑ��x���z�∳�͌��z�͗���̔����ݏo�������\�����ቺ������B���̂Ƃ��A�W���[�R�t�X�L�[���̗l�Ɋ��炩�Ŋۂ݂�тт��O�����̌`��͂��̕����̗���̈��萫�ɑ傫����^����ł��낤����A�S�����̒����s������ۂ̗��ł͂���߂ďd�v�ȈӖ������B���̓�����͂V�D(�T)�ŏڂ����������܂��B
�@
�i�X�j�~������̗����C�ӗ��^�̗�����̗���֎ʑ����邱��
�P�D�J���}���E�g���t�c�ϊ�
�@�O�߂̗l�ɉ~�����ǃW���[�R�t�X�L�[�ϊ��ŕϊ������W���[�R�t�X�L�[���͌㉏�ɂ�����ł̊p�x���[���ɂȂ�̂Ŏ��ۂ̗��̎���Ƃ���Ȃ��B�܂��������O���ɕ�A�������ɂ�����ӂ���݂̒���������B������������邽�߂ɍl����ꂽ�ʑ������T�D�i�U�j�P�D�Ő��������J���}���E�g���t�c�ϊ��ł��B
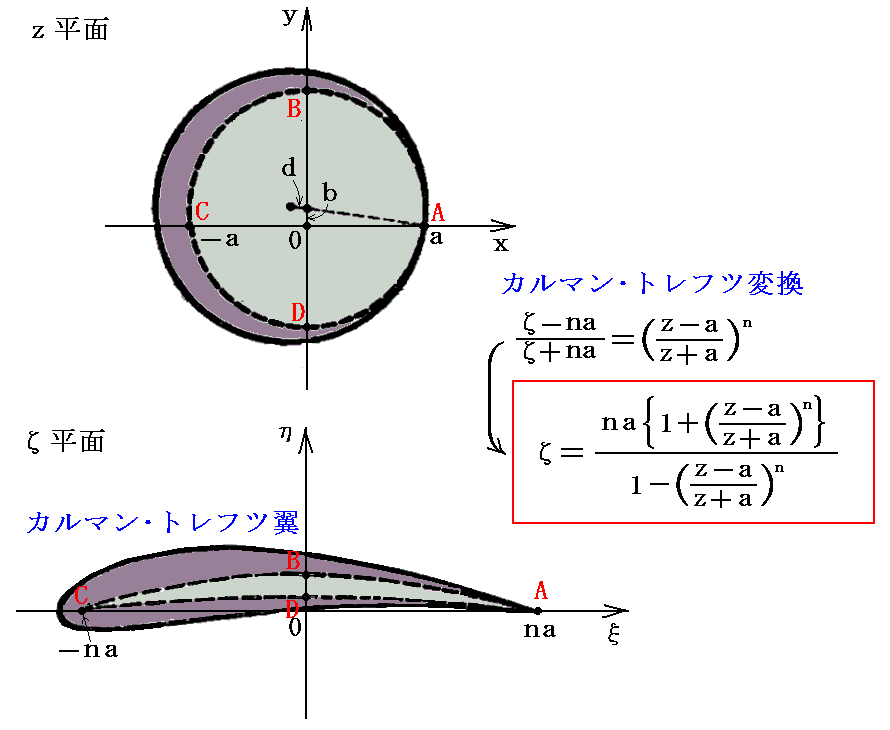
�@�����p����Ή~���~�ʂł͂Ȃ��ă����Y��̈�Ɏʑ��ł���̂��ʑ����̎w�������~�̒��S�̂��A���ƈꏏ�ɒ������邱�Ƃ������̌��݂Ɨ���[�p�߂ł����B���̂悤�ȗ����J���}���E�g���t�c���ƌ����܂��B���̋Z�@�����\���ꂽ�̂�1918�N�ł����A�J����1914�N�ɍs��ꂽ�B
�@�J���}���͎Q�l�����P�P�D�̂�81�A��118�ł��̕��@���J�������A�[�w���H�ȑ�w�ɒ��C�i1913�N�j������������z���Ă���B����͂��Ƃ��ƃq���[�S�[�E�����J�[�X�i�����P���j��������������̌����Ў������̒P�t�@�ׂ̗̈��^��v���鐔�w�I�Z�@�̊J�����˗�����āA�G�[���b�q�E�g���t�c�Ƌ����J���i1914�N�j�������̂̂悤�ł��B�ނ�͓����Ƃ��Ă͗B��̗��p�ł��闝�_�ł������W���[�R�t�X�L�[�̗����_���������ĉ��ǂ��܂��B���̐��ʂ�p���āA1915�N�ɍ��ꂽ�����J�[�X�i�P�͂����炭���E�ŏ����������E�Ў����E�P�t�E�����̔�s�@���낤�B�m�g��ʐ^�n

�i�P�̎O�ʐ}�m�g��O�ʐ}�n
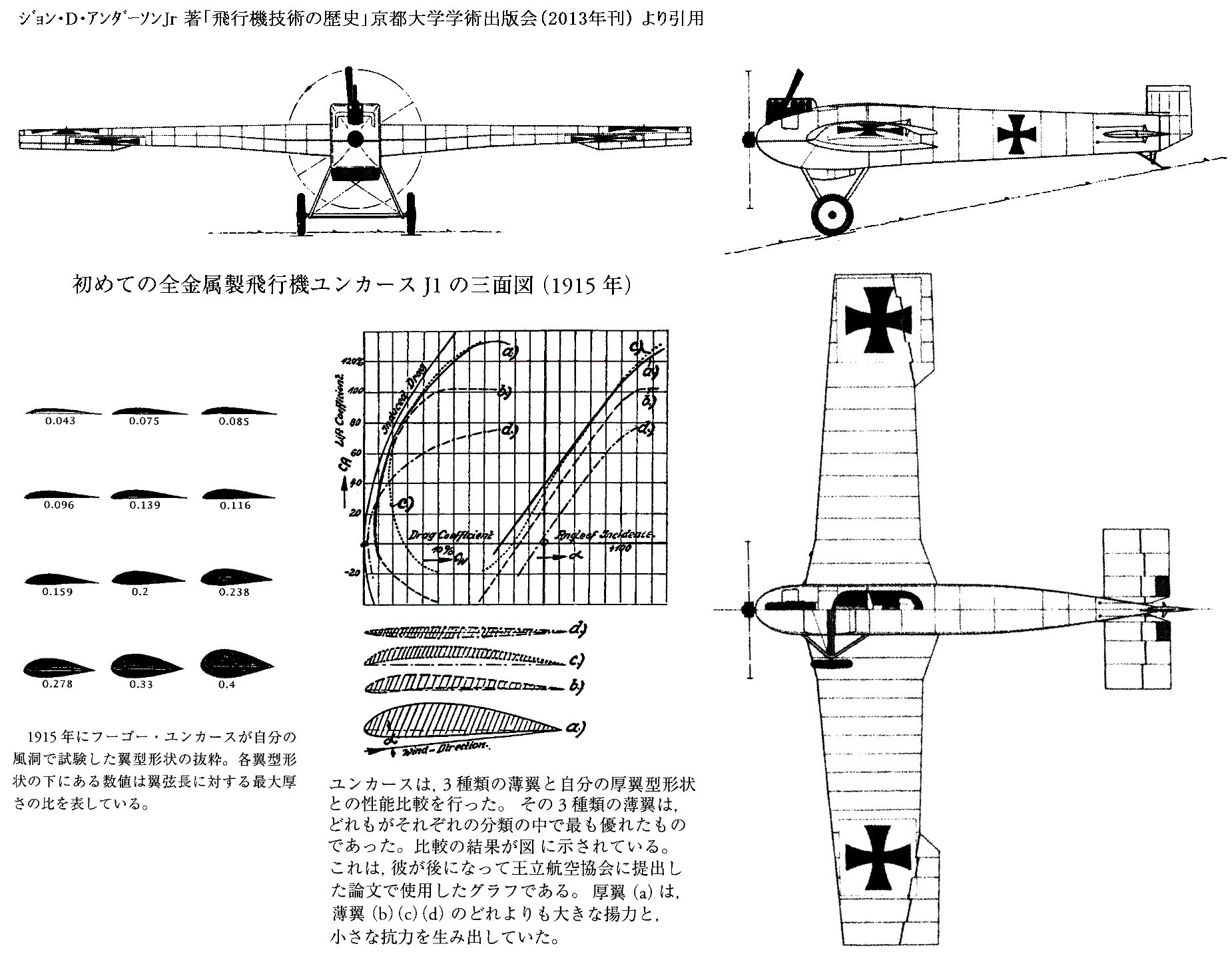
�@�J���}���̓����J�[�X���Ў��������̒P�t���̃A�C�f�B�A�ɋC�t�����ߒ�����79�ŁA�܂����̓����Ɋւ��Ă�118�ŋL�q���Ă��胆���J�[�X�̒��z�������]�����Ă���B�����̎v�z�̓����J�[�X�̋��͎҃A���\�j�[�E�t�H�b�J�[�ɂ������p�����̂ł����A�s�v�c�Ȃ̂̓J���}���͑��̃y�[�W�ŃA���\�j�[�E�t�H�b�J�[�̎����L���Ƃ��A�t�H�b�J�[���J�������@�e�ƃv���y���̓������u�ɂ͂ӂ�Ă���̂ł����A�ނ��ւ���������@�ɂ��Ă͉����L���Ă��Ȃ����Ƃł��B�����̒��z�̓����J�[�X���ŏ������炠���Č��y���Ȃ������̂��낤���H
�@�m���ɁA���̎���@�͍\���I�Ɋv�V�I�Ȃ��̂ł���A��ꎟ����̏��Ɣ�s�@�̑����ɂ��̌`���̗p����邳�������ƂȂ����@�̂��Ǝv���B�������A�v�V�I�ȍ\���ł͂��������d���ēݏd�ȋ@�̂������̂ŁA�����̗D�ꂽ��C�͊w�I�������A�s�[���ł��Ȃ������̂ł͂Ȃ����낤���B
�@�����̋�C�͊w�I�����̗D�G��������ɂ́A�����嗬�̕��t����p���������ƌy���ȋ@�̂̕����K���Ă����̂��낤�B�������̂�����ɏo������t�H�b�J�[�c���D�T��c�D�Z�̃Z���Z�[�V���i���ȋ@�̂ɔ�r����ƁA�����J�[�X�̈�A�̌����@�i�i�X�A�e�P�R�j�́A���̊v�V���ɂ�������炸�A�����ɂ��n���ł���B
�@������ɂ��Ă��A����Ɏ嗬�ƂȂ�������E�P�t�E�����̋@�̍\���́A�����J�[�X�̒Nj������P�t�̍\���I�Ȋv�V���ƁA�t�H�b�J�[�������������̋�C�͊w�I�ȗD�G�����Z���������̂ł��邱�Ƃ͊m���ł��B
�����J�[�X�i�P�ɂ�������20�ɋ����[���L�q���݂��̂Œlj����p�B
�Q�D��ʂ̕ϊ�
�@����Ɉ�ʉ����ꂽ���������ŕ\�����ϊ���p����ƁA�����Ƒ��l�ȗ��^�ɑΉ��ł��܂��B���f���_�ɂ��A�ĕ��ʏ�̔C�ӗ��^�̊O���̈���A�����ʏ�̉~�̊O���̈�Ɏʑ������͊��ā����i���j�͕K�����݂���
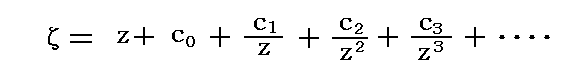
�̌`�ŕ\�����B�mRiemann�̎ʑ��藝�n�B���̂Ƃ����������ŕ\������͊��̌W���͒����ߎ��@�ɂ���Č��߂�̂ł����A���̕��@�̏ڍׂ͎Q�l�����Q�D�A�R�D�A�W�D�A�P�R�D�A�P�S�D�A�P�V�D�Ȃǂ��Q�Ƃ���Ă��������B�����ł̐����͑S�ďȗ����܂��B
�@
�V�D�������_
�@�������_�̐��w�I�{�����T�A�U�͂Ő����������p�ʑ��ł����A�����I�{�������ɏq�ׂ��W���[�R�t�X�L�[�̉����ł��B
�i�P�j��������߂����
�P�D�t������z�̑��l��
�@�R�D�i�P�j�Ő��������悤�ɁA���̂̂܂��ɏz�킹�鎖���ł��܂��B�����Œ��ӂ����悤�ɔC�ӂ̑傫���̏z����^���Ă����S���̗̂l�ɔS���̖�������ł͂��̏z��ێ���������m���O�����W����w�����z���c�̉Q�藝�n�B
�@�S�D�i�Q�j�Ő��������悤�ɁA���̎���ɂ܂Ƃ����Ă���z�������g�͂ݏo�������Ȃ̂ł����A���S���̂ł͂ǂ̗l�ȏz�̑傫���ł����Ƃ��ċ������B���̂Ƃ����ۂ̗���̒��ɂ����ꂽ���ɕt������z�̑傫�������߂郁�J�j�Y��������̂��낤���H
�@�z�̑傫������܂�Η������ݏo���g�͂̑傫�����v�Z�ł���̂ł�����A���^���^����ꂽ�Ƃ��ɂǂ̗l�ȑ傫���̏z���t������̂����肷�邱�Ƃ��ł��邩�H���d�v�ł��B�������������_�̒��S(�v)�ł����A����͎����ŏq�ׂ�l�ɁA������̗���̉��̑��l���̒��ŁA�ǂꂪ�����ɋN���闬��ł��邩�I�Ԃ��ƂƐ[���W���Ă���B
�Q�D���̑��l��
�@���E�k���E���S���̂̃R�[�V�[�E���[�}���̊W�����闬��ɂ͗l�X�Ȃ̂������݂��A�����̂���������^���������ɖ������Ȃ��������Ƃ��v���o���Ă��������B�ʍe�u�Q��R�v�ŏq�ׂ��_�����x�[���w���̗������A�ʍe�u�����_�̉萶���v�ŏq�ׂ��L���q�z�b�t��C���[�̎������_�̗������A�ʍe�u�J���}���Q��v�ŏq�ׂ��Q��������������ׂĉ^�������������Ă���B����������̂̎���ɐ����闬��ł��B�@�����_�̓���́A�^����ꂽ�`����߂��闬��̉�����ӂłȂ����ƂɋN������B
�@�ȉ��ɁA��������̖��C�̂Ȃ�����ɑ������̉\�ȉ��������B
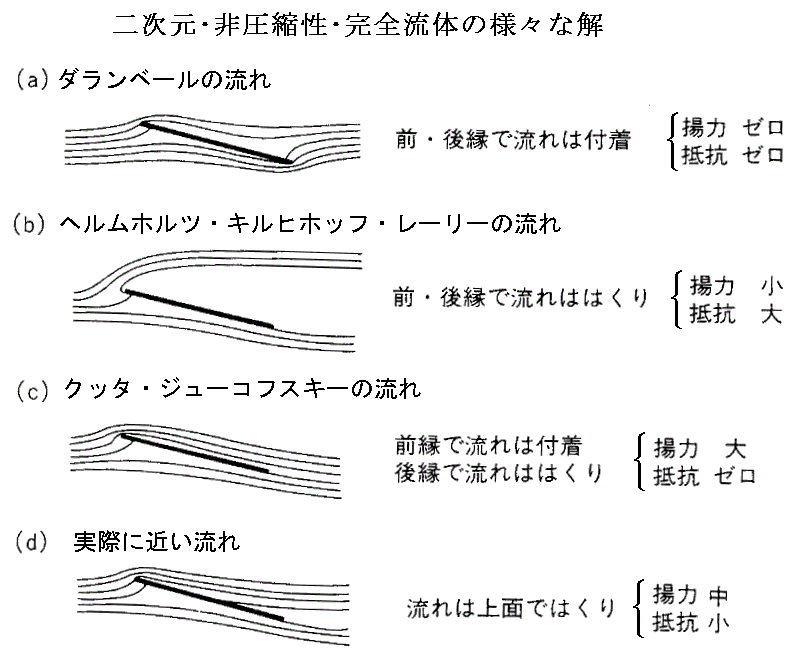
�i���j
�@�_�����x�[����������������Ɠ������̂ł��B���ݓ_�͑O���t�߂̉����ƌ㉏�t�߂̏㕔�ɕt�����Ă���B���ݓ_����̗����͏�ʌ㕔�ŗ��𗣂�Ă���B���̂悤�ȗ���ł͎��v���̗͂̃��[�����g�͐����邪�A�����̗g�͂�R�͂͐����Ȃ��B
�@���[�����g��������̂́A��ʂł͍�����E�Ɍ������ė������傫���Ȃ��Ă���̂ɉ����č������ሳ�āK�E���������ɁA���ʂł͉E���獶�Ɍ������ė������傫���Ȃ�̂ō����������ʼnE�����ሳ�ɂȂ邩��ł��B�g�͂��R�������Ȃ��̂͗��ꂪ���E�E�㉺�ɑ��đΏۓI������ł��B
�i���j
�@�w�����z���c�A�L���q�z�b�t�A���[���[���ɂ�茤�����ꂽ����ł��B�Ƃ��ɗ��ɔ������������ł̗g�͂�R�͂�����Ȃ�ɐ����ł��邪�A�}���p�����������̌����̗���ƍ���Ȃ��B
�i���j�A�i���j
�@�����̗���ɋ߂����A���S�Ȕ��̏ꍇ�ɂ́A�O������鑬�x�͖�����ɂȂ�B
�@�����́A��������k���E���S���̂̉^�������������Ă��܂��B���̂Ƃ��A�����̗���̒��̂ǂꂪ�����̗���ƂȂ邩���肷�郁�J�j�Y��������̂��H
�@���̂�����ɂȂ�̂��́A�����炭���̒��ɂ킸�����݂���S���A���̕\�ʂ̖��C�A�����ɂ͖����嗬���△���刳�͌��z�����݂ł��Ȃ��E�E�E�������߂Ă���͂��ł��B����ł́A���̂悤���킸���ɑ��݂���S���△���刳�͌��z�̕s�\���ɂ���āA�����̗��ꂪ��L�̂ǂ�ɂȂ�̂�������ł���̂��H
�@�^�������������������X�L��͕̂ʂɕs�v�c�ł����ł��L��܂���B�Ⴆ�P���̎�������f���̋O���Ɋ��ʂ���̉����L��̂Ɠ����ł��B���̂Ƃ��ǂ̉��ɂȂ邩�͏���������(�A���̗̂͊w�ł�)���E�����Ō��܂�킯�ł��B�Ƃ��낪�������E�������k�E��S���̂��������̉^���������Ɛ������̂��鋫�E�����ɂȂ��Ă��Ȃ��Ƃ��낪����Ȃ̂��Ǝv���܂��B���Nj��E�ɔ������鋫�E�w�̐��������̈Ⴂ�ݏo���B���������̐���������̈Ⴂ���������͎̂���ł��B
�R�D�W���[�R�t�X�L�[�̉���
�@�����ɐ����Ă���̂͑O���́i���j��i���j�̗���ł��B�������A�Ȃ����̗��ꂪ�I�������̂��A���̗��R�𖾂炩�ɂ��邱�Ƃ͍���ł��B���̂��߁A�W���[�R�t�X�L�[�͂��̗��R�͗ǂ�����Ȃ����A�����̗���͂����Ȃ��Ă���̂�����A�Ƃɂ������̎���̗���͂��̂悤�ɂȂ�Ɖ��肵�܂����B���ꂪ�W���[�R�t�X�L�[�̉����ƌ�������̂ł��B�������Ĕނ́A���̗l�ȗ���ł���Ɖ��肷��ƁA���̗��ꂪ�������邽�߂ɂ́A�ǂ̗l�ȑ傫���̏z�����ɕt�����Ă��Ȃ���Ȃ�Ȃ���������ł��邱�ƂɋC�t�����̂ł��B���̏z�̑傫�������߂邱�Ƃ��ł���Ό���N�b�^�W���[�R�t�X�L�[�̒藝�ɂ��A���ɓ����͂�[�����g���v�Z�ł��܂��B
�i�P�j
�@�U�D�i�T�j�Q�D�Ő��������悤�����i���j�̌�[���痬�ꂪ���炩�ɗ��ꋎ���m�W���[�R�t�X�L�[�̉���n���߂ɂ́A���̗�������o�����ʑ��O�̉~������̗���ɂ����āA����̌�둤�̗��ݓ_�i�~���ɂ�荶�E�ɕ����ꂽ���ꂪ�Ăяo��_)���A���i���j�̌�[�Ɏʑ������_�ɂȂ��Ă���悢�B
�@���̂Ƃ��A�~������̗���̗��ݓ_�̈ʒu�͉~���܂��̗���ɕt��������z���̑傫����ς���Β��߂ł��܂��B���̑傫�����������i���j�̌�[�Ɏʑ������_�����ݓ_�ƈ�v����悤�ɂ����Ƃ��̏z�l�����A���i���j�̎���ɕt������z�l�ł��B�Ȃ��Ȃ�A�U�D�i�P�j�Q�D�ŏؖ������悤�ɁA���̂̂܂��̏z�l�͓��p�ʑ��ɂ���ĕω����Ȃ��̂ʼn~������̏z�l�����̂܂ܕ��i���j����̏z�l�ƂȂ邩��ł��B
�@
�i�Q�j
�@���i���j����̏z����܂�A�N�b�^�E�W���[�R�t�X�L�[�̒藝�ɂ�蕽�i���j�ɓ����g�͂�͂̃��[�����g�͒����Ɍv�Z�ł��܂��B�g�͂͗��ɓ����������̏d�͂ƒނ荇���Ă���A���S�̂Ƃ��Ă͗͂������Ă��܂���A�����̖@���ɂ�藃�͗��̂̒������̂܂ܓ����x�^���𑱂��܂��B�����x�^�����Ă��闃�ɑ��ĐV���Ȏd�������邱�Ƃ�������A������O���ɑ��Ďd�����邱�Ƃ�����܂���B
�@�������L���ȎO�������̏ꍇ�ɂ́A���[������Ɍ������ďz���̑����i�܂�Q���̗��[�̉��������j�����݂��܂��B�Q���̘A�����ɂ��A���[���痬�̒��ɉQ�����c���Ȃ��痃���O�i���邱�ƂɂȂ�܂��B�܂�A���̒��Ɏ��X�Ǝc���Ă����Q�ɉ^���ʂ�^�������Ȃ���Ȃ�Ȃ��ƌ������Ƃ́A�����O�i���邽�߂Ɏd�������������Ȃ���Ȃ�Ȃ��ƌ������Ƃł��B���ꂪ�U����R�ɍR����d���ƂƂȂ�܂��B���̕��̎d�������������Ȃ��Ɨ��͑O�i���邱�Ƃ͂ł��܂���B
�@�������A���͗����������ɒ������̃|�e���V�������ɂ��Ă̋c�_�ł�����A���̂悤�ȗU����R�͐����܂���B�܂��_�����x�[���̔w���ŏq�ׂ��̂Ɠ�������Ō`���R�m���C��R�{���͒�R�n�͐����܂���B
�@
�i�R�j
�@���i���j�̈�l���ɑ���}���p����ς���W���[�R�t�X�L�[�̉��������z�l�͕ς���Ă��܂��B�e�}���p�̂Ƃ��ɕt������z�l���v�Z����A�}���p�̕ω��Ɨg�͂�͂̃��[�����g�̊W���v�Z�ł��܂��B�m�V�D�i�Q�j�`�i�S�j�Q���n
�@
�i�S�j
�@�p����~����ς�����A�����ʂ���ĕ��ʂւ̎ʑ�����ς���Ύʑ���̌`����茻���̗��ɋ߂Â��邱�Ƃ��ł���B�ʑ������ς��̂�����A�W���[�R�t�X�L�[�̉���������߂ɕt������z�l�͗��^���Ƃɕς���Ă��܂��B���̂Ƃ��̏z�l��p����Η��^���Ƃ̗g�͂�[�����g�◃�\�ʂ̈��͕��z���v�Z�ł��܂��B�m�V�D�i�R�j�`�i�S�j�Q���n
�@���ꂪ�������_�ŗp�����Ă���l�����ł��B�Ƃɂ����A���̌㉏�ɉ����ė��̏㉺�ʂ̗��ꂪ���炩�ɗ��ꋎ��Ƃ���������������邽�߂ɂ͗��̎���ɏz�����݂��Ă��Ă��邱�Ƃ��K�v�ɂȂ�A���̏z���d�ˍ��킳�ꂽ����Ƀx���k�[�C�̒藝��K�����ė��ʂ̈��͂𑫂����킹��Ɗm���ɗ��ɂ͗g�͂�[�����g���������Ƃ�������̂ł��B
�@���ǁA���̏z���_�͂��܍��킹�̊���Ƃ�Ȃ��B�Ȃ��Ȃ�A���̗l�ȗ���ɂȂ邱�Ƃ������ŋc�_���Ă���k���E���S���̂̉^�����������瓱������ł͂Ȃ�����ł��B���܍��킹�Ȃ̂ł����A���Ƃ��Ƃ��������������^�������������Ă���킯�ł�����A���̈Ӗ��ɉ����Ė����͗L��܂���B
�S�D�W���[�R�t�X�L�[�̉���̕����I�ȈӖ�
�@�����Œ��ӂ��Ăق������Ƃ��Q�D�i�P�j�ŏq�ׂ�Magnus���ʂ́A���Ƃ��Ɨ��̂��S���������Ƃƕ��̕\�ʂɖ��C�����邱�Ƃɂ�萶�����B���̂��߂ɋ���~������]���Ȃ��痬�̒���i�s����ƁA���̕\�ʂ̉�]�Ɉ��������Ă��̎���ɏz�����������̂ł��B�����S���╨�̕\�ʂ̖��C�����������Ȃ�A���S�ɑΏƓI�Ȍ`������Ă��鋅��~�����������]���Ȃ���i�s���Ă��z���������ĕt�����邱�Ƃ͂���܂���B
�@�Ƃ��낪���̗l�ɏ㉺����Ώ��ł�������A�ΏƓI�ȕ��ł��}���p�������ĉ^�������肷��ƁA���S���̒��ł��A���╽�̎���ɏz�����t������ƌ����Ă���̂ł��B
�@���S���̂̏ꍇ�ɂ͏z�̖���������^�������������Ă��܂����B�m�z�̖�������n�ƁA�m���̌�[�ɉ����ė��ꂪ���炩��ɗ��ꋎ��Ƃ����W���[�R�t�X�L�[�̉��肪���藧����i�z�L��j�n�̂ǂ��炪�����ɑ��݂��闬��ƂȂ邩�́A�����炭�@�m���̒��̔S���n�A�m���\�ʂ̖��C�n�A�m���̒��ɖ����呬�x�△����̈��͌��z�Ȃǂ����݂����Ȃ��n�Ȃǂ��痈��̂��낤�B
�@�Ȃ��ł��A���̌����Ƃ����m�����̋C�̂ɂ͈��k�������邽�߂ɖ�����̈��͌��z�������ł��Ȃ��n���ł��[���W���Ă���悤�Ɏv����B���̌�[�ŗ��̉��ʂ����ʂ։s����荞�ޗ��ꂪ�ł��邽�߂ɂ͂��̓_�ɖ�����̈��͌��z�����݂��Ȃ���Ȃ�Ȃ��B�k���̊��S���̂Ȃ���̗l�Ȏ����\�ł����A�����̗��̂ɂ͈��k�������邽�ߗ���̌������s���ς��鈳�͑���ݏo�����Ƃ͂ł��܂���B������ς���͂������ł��Ȃ��̂Ȃ�A���̂͊����̖@���ɏ]���Đ^�������A���ʂɉ�����������ۂ����܂܉������֗���čs���ł��傤�B
�@�܂��W���[�R�t�X�L�[�̉��肪���藧�̂́A�����̗��̂ł͖�����̈��͌��z�������ł��Ȃ����Ƃ��痈��̂��낤�B
�m�⑫�����P�n
�@�����̖{�m�Ⴆ�Ε����T�D�n�ł́A���݂̋C�̂��S���������߂ɗ��\�ʂɉ����Ĕ������E�w���ł��邪�A���ʂɂł������E�w�͌㉏����肫���ď�ʂɒB���邱�Ƃ��ł����ɁA�����痣��ĉQ�����B���̉Q�̈�ł̒ሳ�Ɉ�����ď�ʂ̗��ݓ_�͂������Ɍ㉏�ɋ߂Â����Ɍ㉏�Ɉ�v���A����͌㉏���犊�炩�ɗ��ꋎ��悤�ɂȂ��Ɛ�������Ă��܂��B�܂�S�����W���[�R�t�X�L�[�̉��肪���藧�������Ɛ������Ă��܂��B
�@���C�̂��߂ɋ��E�ʂł̑��x���[���ɂȂ�Ƃ���ƁA������̗�������ׂɂ́A���E�w���ɂ͖�����̑��x���z���K�v�ɂȂ�܂��B�S����������C�̂ł͂���͕s�\�ł��B�܂����݂̋C�̂ł͈��k�������邽�߂ɖ�����̈��͌��z�������ł��܂���B���ǁA���C�̂̔S���∳�k���ׂ̈ɗ��㉏���}���ɋȂ��闬��͎����ł����A�����̖@���ɏ]���ė��̂����̂܂ܐ^�������ɗ��ꋎ�邱�Ƃ��炭��̂��Ǝv���܂��B
�m�⑫�����Q�n
�@�k���E���S���̗̂���̏ꍇ�ɂ͕��̑O���ɂ����Ă�������̗����A������̈��͌��z���K�v�ł����B����Ȃ�A�W���[�R�t�X�L�[�̉����O�����ɂ��Ă��ݒ肵�Ȃ��ėǂ��̂ł��낤���H
�@�O���ɂ��Ă͕��ʎ��̂悤�ɍl���邱�Ƃɂ���Ė���������邱�Ƃ��ł���Ƃ��āA�O�����ɂ��Ă̓W���[�R�t�X�L�[�̉�����������܂���B��������ł��闝�R������܂����B
�@�U�D�i�Q�j�R�D�ŏq�ׂ����R�ɂ��A�O���ł͉Q�̖X�q�������悤�ȏ�Ԃ������\�ŁA�O���𗄂ݓ_�Ɉ�v�����Ȃ��Ă��O������闬�ꂪ�����呬�x�△���呬�x���z��K�v�Ƃ��Ȃ��������ł���Ƃ���B���R���̉Q�̖X�q�͗g�͂̌v�Z�l��ω�������͂��ł����A�Ȍ�̌v�Z�ł͂��̉e�������Ă��܂��B
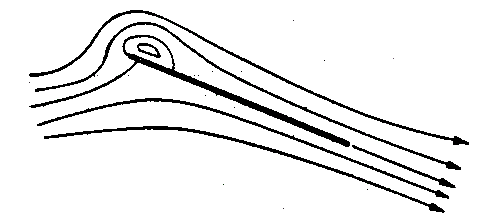
�@�������A�L�����o�[�������������̏ꍇ�A�O�������ɃJ�[�u�����Ă���̂ŁA�O���ɂ����Ă��W���[�R�t�X�L�[�̉�������\��������B���ۃN�b�^�̉~�ʗ��ł͌}���p���[���̎��ɂ��̗l�ɂȂ��Ă���B���̏ꍇ�͕����̂悤�ɉQ�̖X�q���O�����Ɍ`������鎖�����肵�Ȃ��Ă��A�O�����ɂ����閳���嗬���̖����͉���ł����B
�@���邢�́A�����̌����ł͑O���͖c��~�ʏ�����Ă���̂ŁA���ݓ_���O���Ɉ�v���Ȃ��Ă��O�����̗��ꂪ�����呬�x�△���刳�͌��z�ƂȂ鎖�͂Ȃ��B
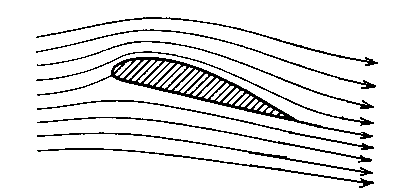
�����V�D�i�U�j�T�D�Ő�������悤�Ɍ����ł͋p�̕ω��ɉ����ė��ݓ_�͑O���̉~�ʂ̏���ړ����܂��B
�@�����̎���ŁA�O���ɂ��Ă͗��ݓ_��O���Ɉ�v������������������Ȃ����A�܂������ł��闝�R���Ȃ��B
�@���̓�����̎���A�����̗L�����ݏo���A�ʍ��u�����_�̉萶���v�T�D�i�P�j�m�⑫�����R�n--�Ȃ��������H--�Ő��������A�����Ɣ����̃��C�m���Y���ɑ��闃���\�ˑ����̈Ⴂ�ݏo���B
�m�⑫�����R�n
�@�ʍe�u���E�k���E���S���̗̂͊w�v�Ő����������O�����W���A�w�����z���c�A�P���r���̉Q�藝�ɂ��ƉQ�i�z�j���ۑ�����˂Ȃ�Ȃ��B�܂�
�m�P���r���̏z�藝�n
�@���̂����S�����m�S���������Ȃ��n�ŁA��������ԕ��������ρ����i���j�ŗ^������m�o���g���s�[���́n�A���������̂��̐ϗv�f�ɓ����͂��ۑ����m�܂�|�e���V�����Ȗʂ̌��z�ŕ\�����n�ł���ꍇ�A���̒��ɂ���A���̂ƂƂ��ɓ����C�ӂ̕Ȑ��ɉ����Ă̏z�͎��Ԃ��o�߂��Ă��s�ςł���B
�ł���B�Ȃ�Ώ�L�̗l�ȃ��J�j�Y���Ő����闃����̏z�͂��̏z�藝�����Ă���̂��낤���H
�@����͎��̂悤�ȃ��J�j�Y���ŗ������̒����n�߂�Ƃ��ɂ��̔w��ɗ�����̏z�Ƃ͔��Ε����̏z���c����邱�Ƃɂ��Q�i�z�j�̕ۑ����͐��藧���Ă���ƍl�����Ă���B�܂����̒��ŗ��������n�߂��ŏ��̒i�K�ł͗����͏������̂ŁA���}�̂悤�Ȕk���E���S���̂��|�e���V����������������Ă��邾�낤�B
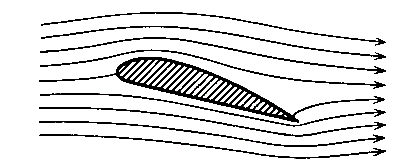
���������̑��x�������Ȃ�ƁA���S���̗̂�����������邽�߂̈��͌��z��B���ł��Ȃ��Ȃ��ĉ��}�̗l�Ɍ㉏���ŗ���͊p���甍�����ĉQ��������B���̕����̈��͂͒Ⴂ���߂ɁA����ʂ̌�[�t�߂ɑ��݂������ݓ_�͌�[�Ɉ������A�₪�Č�[�Ɉʒu����B�����ė���͌㉏���犊�炩�ɗ��ꋎ���B���ۂ��̂悤�ȏʼnQ���������邱�Ƃ̐����͕ʍe�u�J���}���Q��i���I���萫��́j�v�Ő��������w�����z���c�̌����Ɏn�܂�B
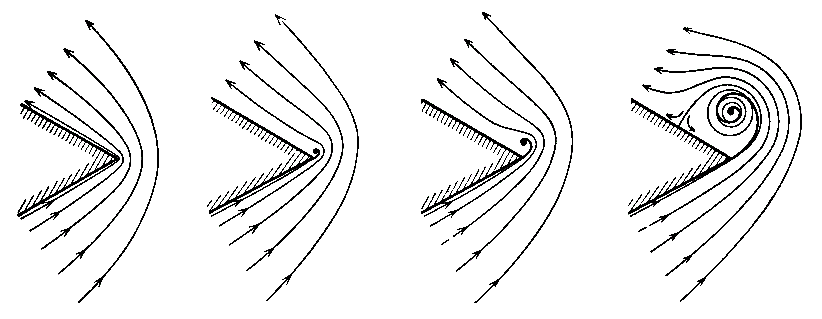
�@���̗l�ɂ��āA��[�ɔ��������Q�͗��̌��̗��̒��Ɏc����A�����g�̓W���[�R�t�X�L�[�̉���������őO�i���Ă����B�w�����z���c�̉Q�藝�ɂ��Q�͗��̗v�f�ɕt�����Ă���̂�����A�����Î~���̒����ꍇ�́A�Q�͏o���ʒu�Ɏc����A���邢�͈�l�����ɗ���������Ă���ꍇ�ɂ͉Q�͗��̗v�f�Ƌ��ɗ��̌���֗��ꋎ���Ă����B
�@���̂Ƃ����̎���ɕt������Q�m�����Q�n�Ɋւ��Ă͉Q���\�����闬�̗��q�͎��X�Ɠ���ւ���Ă���̂ŁA�Q�̗v�f�͏�ɓ������̗v�f����\������Ă���Ƃ������S���̂Ő��藧�w�����z���c�̉Q�藝�����Ă��Ȃ��B������V�D�i�P�j�T�D�m�⑫�����V�n�Ő�������悤�ɗL�������̗��ł͗��̗��[���玟�X�ƐV���ȉQ�m���R�Q�n�����ꗃ�̔w��Ɏc����Ă����̂ʼnQ�̕ۑ����͐��藧���Ȃ��B
�@�������A�����̉Q�͊��S���̂̉�������Ă��Ȃ��S�����̂����E�ʂƂ̍�p�̂��߂ɐ�����̂ł���B�ʍe�u���E�k���E���S���̗̂͊w�v�A�u�J���}���̉Q��v�Ő��������悤�ɁA�S���ɂ�苫�E�ʂ���Q��������̂ł��邪�A��U�����Ă��܂��Ό�͊��S���̂Ƃ��Ď�舵���Ă悢�ł��낤�B���̓�����͉��Ƃ��������肱�Ȃ����ł����A���ꂪ���̗͊w�̂����ł��B
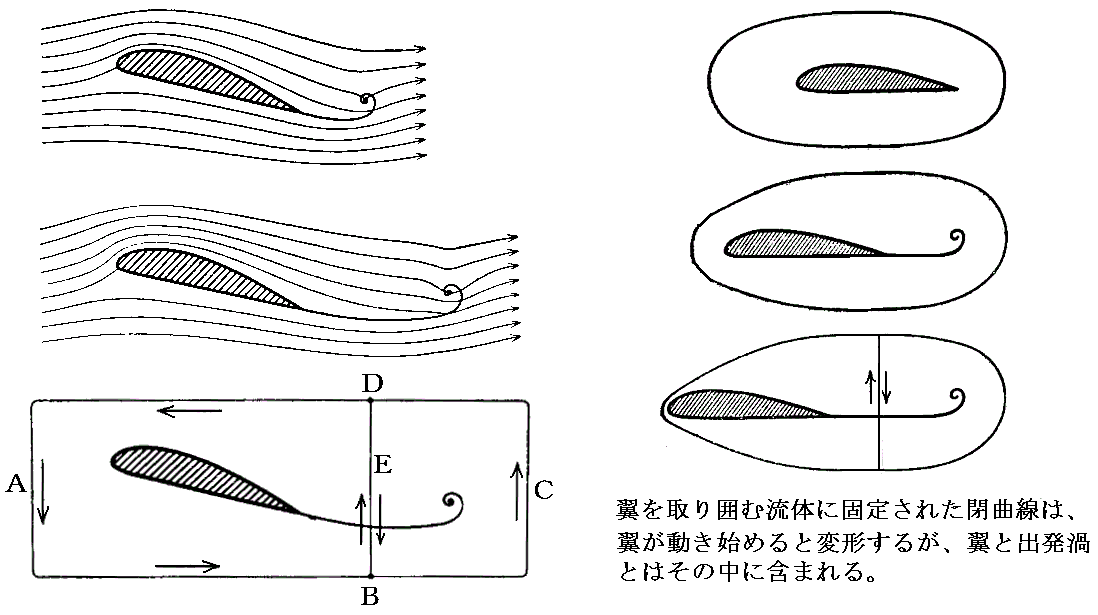
�@�ŏ��ɗ����Î~���Ă���Ƃ��ɁA�������݂͂��������̗v�f�ɕt�����Ă���Ȑ��`�a�b�c���[���傫�������̎���̏z�͗�ł��B���̂Ƃ����������ƕȐ��͑����ό`���邩���m��܂��A�P���r���̏z�藝�ɂ�藬�̗v�f�ɕt�����ē����Ȑ��`�a�b�c�ɂ��Ă̐��ϕ��l�͂ǂ̏u�Ԃł��[���ƂȂ�Q�̕ۑ����͐��藧���Ă���͂��ł��B���̂��߂ɂ͕Ȑ��`�a�d�c�ɕt���Đ��ϕ������z�l���Ȑ��a�b�c�d�ɂ��Đ��ϕ������z�l�Ɣ��Ε����ɂȂ��Ă���ƍl����悢�B���Ȃ킿���̎���ɂ͗��̒��Ɏc���ꂽ�z�Ƃ͔��Ό����̏z���t�����Ă����B
�@�����͎��ۂ̊ώ@�ɂ���ė��t�����Ă���B�ȉ����Q�l�����P�D������p�������̂ł����A��������L���Ȏʐ^�ł��B
�@�ʐ^�P�̓i�C�t�G�b�W���E���獶�����ɓ��������Ƃ����̎���ɐ����闬����i�C�t�G�b�W�Ƌ��ɓ����J�����ŎB�������̂ł��B

�@���̎ʐ^�́A���𗬑̒��œ������n�߂�����i�ʐ^�Q�j���炾�x�𑝂��Ă����i�K�i�ʐ^�R���V�j�ɂ��āA���̎���̗����A���I�ɎB�������̂ł��B�J�����͗��ƂƂ��ɓ����悤�ɂ��Ă���̂ŗ��̗��q�̋O�Ձm�V���b�^�[���ԓ��ɓ��������n���Q���V�Ɨ��̑��x���傫���Ȃ�ɂ�Ē����Ȃ��Ă��邱�Ƃɒ��ӁB
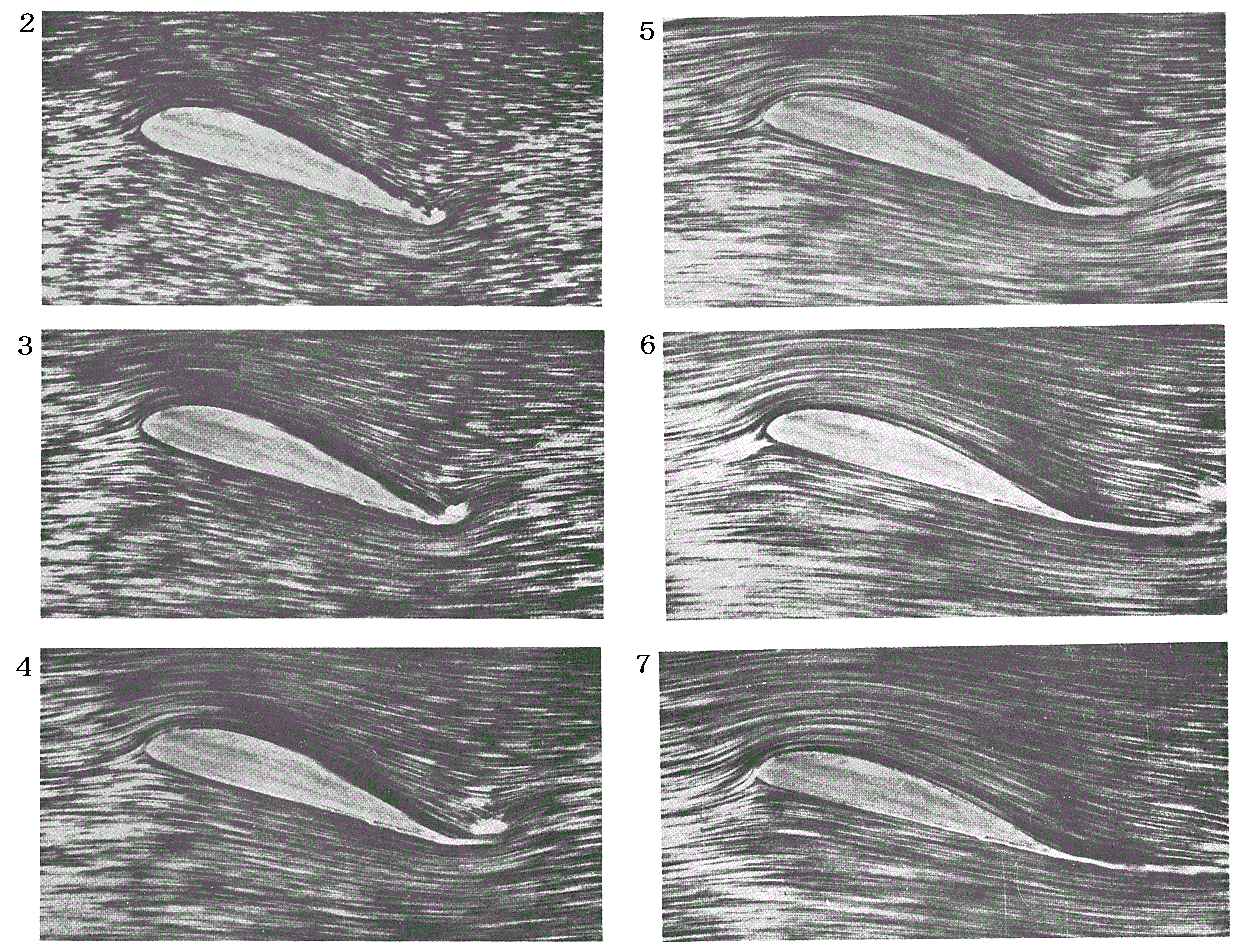
�@���Ƌ��ɓ����Č���ƉQ�̗l�q�͂Ȃ��Ȃ��ǂݎ��Ȃ����A�Q�͉��}�̓_���ŕ`�����ʒu�ɂ���B�ʐ^�W���X�^�[�g����łX��10��11�ɂȂ�ɂ�ė��̑��x�͑傫���Ȃ�B�����Œ��ڂ��ׂ��̓X�^�[�g����i�ʐ^�W�j�ɉ����Ă͏z�̖����|�e���V�������ɂȂ��Ă���l�q���ǂݎ�ꎖ�ł��B

�@���}�����̂ɑ��ĐÎ~���Ă���J�����ŎB�������̂ł��B���̓J�����ɑ��ē����Ă���̂ŗ��̌`���s���ڂ��ɂȂ��Ă��邪�A����̗��̂͐Î~���Č����Ă���B���̒��ɉQ���������Ă���l�q���N���ɓǂݎ���B��̎ʐ^�Ɖ��̎ʐ^�̊W�́A�ʍe�u�J���}���Q��i���I���萫��́j�v�Ɍf�ڂ����T�D�i�R�j�S�D�̎ʐ^�ƁA�T�D�i�R�j�Q�D�̎ʐ^�̊W�ɑΉ����܂��B
�@�ʐ^12�͎ʐ^�T�A�X�̏ɁA�ʐ^13�͎ʐ^�V�A11�̏ɑΉ�����B���̂Ƃ����̗��̂ɑ��鑬�x������������Ɨ�����̏z�Ɣw��Ɏc�����Q�̑傫���͑��債�����邪�A���̑��x�����ɂȂ�Ɨ�����̏z��w��Ɏc���ꂽ�Q�̑傫�������l�ɂȂ��B

�@���̎ʐ^14�͗��̌}���p�𑝂₵���ꍇ�ł����A�ʐ^12�ɔ�ׂ�Ƃ�苭�͂ȉQ�i�z�j���������Ă��邱�Ƃ�����B
�@���̑��x�����炵����A�}���p������������ƁA������̏z�͌��������B�ʐ^15�͎ʐ^�U�A10�̏œ����Ă�������ˑR�~�߂�����̗l�q��Î~�����J�����ŎB�������̂ł����A���̎���ɕt�����Ă����z�����̌�[���痬�̒��ɓf���o����ė�����̏z�͖����Ȃ鎖�������Ă���B

�m�⑫�����S�n
�@�O�����ʐ^�Q�`�P�P���ʐ^�P�Q�`�P�T�̊W������ɂ����̂ŕ⑫���Ă����܂��B�U�D�i�T�j�Q�D�Ő��������悤�Ɉ�l�����Ɍ}���p30���Œu���ꂽ�����̎���̗����}��
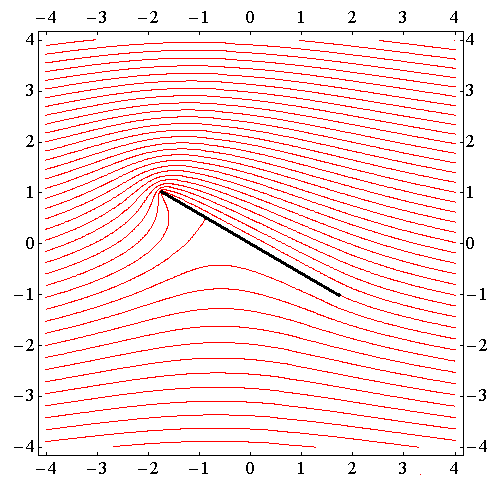
�̗l�ɂȂ����B���̂Ƃ��W���[�R�t�X�L�[�̉���������߂Ƀ���2���t�̏z���t�����Ă��܂��B
�@������E�����֑��x�t�ŗ�����l�����ɐÎ~���Ēu���ꂽ�����̏ꍇ�A���������헬�̗�����\���Ă���B
�@����A�Î~�������̒����������ɑ��x�t�ňړ����镽���̏ꍇ�A�J�����x�t�ō����Ɂm���Ƌ��Ɂn�ړ����Ȃ��痬�̗��q���ʐ^�ɎB�������̏u�Ԃ̗��̗��q���J�����ɑ������ΓI�ȑ��x�x�N�g���̕�����A�˂����̂ɂȂ�܂��B���̏ꍇ�͗��̗��q�̉^�����Ȃ��猩�Ă���̂ŏ�}�̐Ԑ��͗��̗��q�̎��ۂ̉^�������Ƃ͈�v���܂���B���̂��ߗ����ł͂���܂��A�����猩��Η��̗��q�͑��ΓI�ɂ��̗l�ɓ����Č�����̂������������������Ƃ����Ă��悢�����m��܂���B
�@������̏ꍇ�ɂ��Ă���}�̓J�����𗃂ɑ��ČŒ肵���Ƃ��̗�����̗���̗l�q��\���Ă���A�O���̎ʐ^�Q�`�P�T�ɑ������܂��B
�@���ɁA��L�̗��̗��q�̗������l���̐����Əz�����ɕ��������
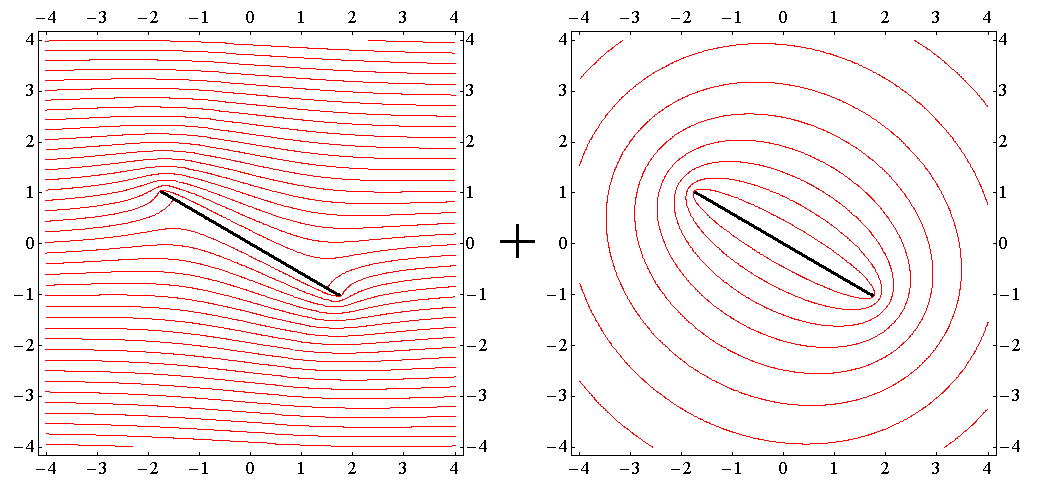
�ƂȂ邪�A���̂悤�ɕ������̂ł͂��߂Ȃ̂ł��B�m���ɏ㍶�}�͏z�̂Ȃ���l�����̗�����̗����m���邢�͐Î~���̒��x�t�œ�����������������������n�ł���A��E�}�͗�����̏z��\�������@�m���邢���������������n�ł��B
�@�������O���̎ʐ^�P�Q�`�P�T�͏�E�}���������̂ł͂���܂���B�����̎ʐ^�͑O�q�̏z������������}�̂悤�ɕ��������Ƃ��̉��E�}�ɑ����������̂ł��B
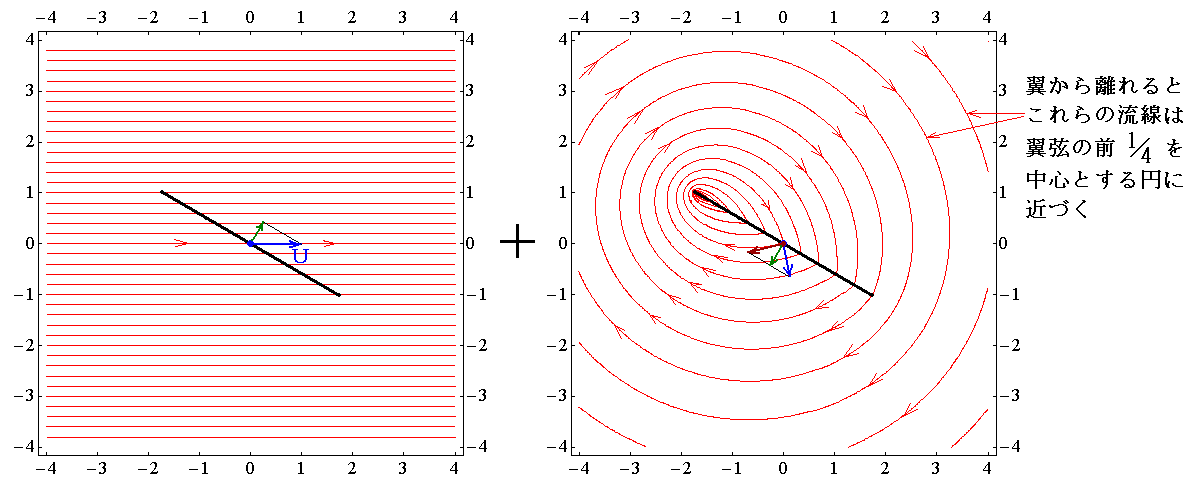
�@���̕����̉E�}�́A�E�����ɑ��x�t�ŗ�����l�����ɐÎ~���Ēu���ꂽ�����̏ꍇ�́A���̂Ƌ��ɉE�����֑��x�t�œ����J�����ŎB�����Ƃ��́A���̗��q�̏z�����̃J�����ɑ��ΓI�ȑ��x�x�N�g����A�˂��Ȑ��m�������������n��\���Ă���B
�@����A�Î~�������̒��x�t�ō��ֈړ����镽���̏ꍇ�́A�Î~�����J�����ŎB�����z�������^��������\���Ă���B���̏ꍇ�͒�헬�ɂ͂Ȃ�܂��A�e�u�Ԃɗ��̂����ۂɓ���������\���Ă��邱�Ƃ͊m���ł��B
�@�ǂ���̏ꍇ�ł��낤�ƁA���͕̂���˂������邱�Ƃ͂ł��Ȃ��̂ł�����A��E�}�̕��ɐ����ȏz�ɂ�闬��̐����m�Ζ��n�͍��}�̂tsin���m�Ζ��n�Ɣ��Ε����������Ă��Ȃ���Ȃ�Ȃ��B���ɉ����������ւ͎��R�ɗ���邱�Ƃ��ł���̂ŁA���ɉ����������ł݂͌��ɔ��������K�v�͂Ȃ��B���̂ɑ��ĐÎ~���Ă���J�����Ō������̗��q�̓����l�q������ɂ͍ŏ��̗��ɑ��ČŒ肵���J�����œ���ꂽ���̗��q�̓������獷�������ׂ������́|�t�̑��x�x�N�g���ł����āA����͗��̎��肾�낤�Ɨ��̒��ł��낤�ƑS�ē��������������Ă��Ȃ���Ȃ�܂���B�ʐ^�P�Q�`�P�T�͌����ׂ̈ɏ�L�̕����̏ꍇ�Ə����Ⴂ�܂��������̗����}�ł��B
�@������ɂ��Ă��A���̓�ʂ�̕���@�����Ⴆ��Ɩ킩��Ȃ��Ȃ�̂ŁA���ꂮ������̗��҂��������Ȃ��ł��������B
�m�⑫�����T�n
�@�@�S���������ꍇ�͗��܂��̏z�͕ۑ�����܂����A���ۂ̗��̂ɂ͔S�������邽�ߗ�����̏z�͎���ɏ��ł���͂��ł��B�������A�����̖@���ɂ��W���[�R�t�X�L�[�̏��������藧�悤�ȗ��ꂪ��������邱�ƂŁA�z��ێ����郁�J�j�Y�����������ł�h���ł���̂��낤�B
�m�⑫�����U�n
�@�W���[�R�t�X�L�[�̉��肪�Ӗ������̂͗��ꂪ���ʂ���͂���鎖���Ȃ��ꍇ�ł��B���ۂ̗��̂ɂ͔S�������藃�\�ʂɂ����C������܂��B���̂��ߗ��\�ʂł͗��̂͗��\�ʂɒ���t���Ă��藃�\�ʂ̋ɔ����͈͂ő傫�ȑ��x���z������������ȗ̈��m���E�w�n���`������܂��B
�@���̌}���p���������ꍇ�́A���ʂ����E�w�͌㉏�܂ł��̂܂ܗ��ɒ���t���Ă��܂����A�}���p���傫���Ȃ�Ƌ��E�w�͌㉏�ɒB����O�ɗ�����͂���Ă��܂��܂��B�����āA���̓����ɉQ���܂����̈悪�`�����ꗬ��̗l�q�͑S���قȂ������̂ɂȂ�܂��m�V�D�i�P�j�Q�D�́i���j�̏�ԁn�B�������������ƌ�������̂ŕK�v�ȗg�͂��ł��Ȃ��Ȃ�܂��B
�@����̔������A�����A�ǂ̏ꏊ�ŁA�ǂ̗l�ȏŐ�����̂��m�邱�Ƃ́A�����̔S���∳�k���̂���C�̒����s���闃�̗��_�ł͂���߂ďd�v�ł��B�������A������c�_����ɂ͋��E�w���_�̏ڍׂɗ�������Ȃ���Ȃ�Ȃ��̂ł����ł͂��܂���B
�T�D�o����R
�@�O���̃��J�j�Y���œ����o�������ɕt������z���|���Ƃ���ƁA����Ɏc���ꂽ�Q�̋����̓��ƂȂ�B���̂Ƃ�����Ɏc���ꂽ�Q�͗��̈ʒu�ɉ������̑��x�����u
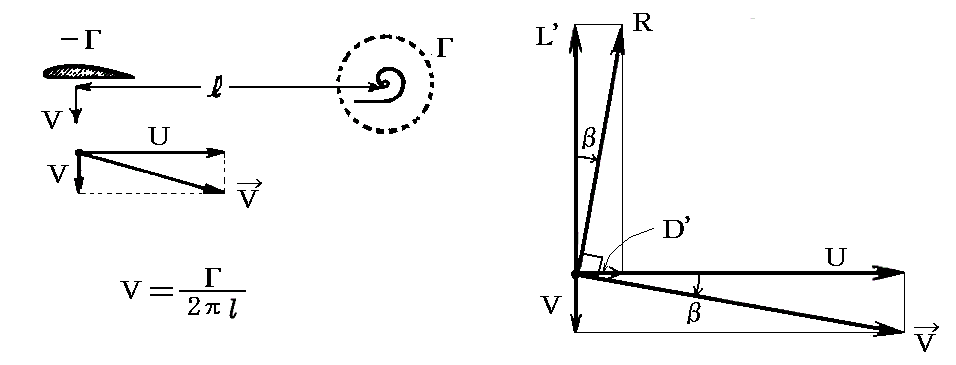
��t��������m�ʍe�u�J���}���Q��v�Q�Ɓn�B�������� �͗��Əo���Q�Ƃ̋����Ƃ���B
�@���̂��ߗ�����̈�l���͂t�Ƃu�̍��킳�������x�x�N�g���u�ƂȂ�B���̂Ƃ���l���ɑ��闃�̌}���p�����ς�邪�A���̌}���p�ł̗g�͂q�������x�x�N�g���u�ɐ����ɂȂ�̂ł���B�g�͂q�͍����x�x�N�g���u�ɐ����Ȃ̂ŁA���̐i�s�����ɐ����ȕ�������p�x�����������������i�u�^�t�j�����������ɉ�]����B���̂��ߗ��̐i�s�����Ƃ͔��Ό����̗͂̐����������B
�@�����������d�͂Ƃ荇���Ă���ƍl���邱�Ƃ��ł���̂ł��ꂪ�V���Ȍ������̗g�͂k�f�ƂȂ�B���̂Ƃ��i�s�����Ƃ͋t�����̐����͍R�͂c�f�ƂȂ�B�����͈�l���ɑ�����̂ł͂Ȃ��������̗g�͂ƍR�͂Ȃ̂Łf(�_�b�V���j��t���ĕ\���Ă���B
�@���ɂ͂��̍R�͂c�f�̔��Ε����̗͂������Ȃ���O�i�����˂Ȃ�Ȃ��B���̂Ƃ����� �O�i������ׂɉ����Ȃ���Ȃ�Ȃ��d�����v��
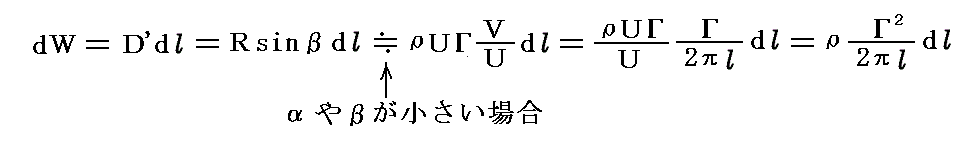
�ƂȂ�B�����o���Q�ɑ�����1�̋���������2�̋����܂œ����ԂɁA���ɑ��Đ�����Ȃ���Ȃ�Ȃ��d���v��
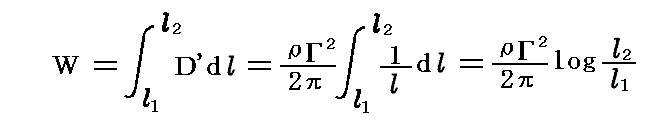
�ƂȂ�B
�@������̎���ɂ͏z�ɔ����^���G�l���M�[���t������B���̎���̔��a��1���炒2�܂ł̊Ԃɂ���^���G�l���M�[�j�D�d�D��
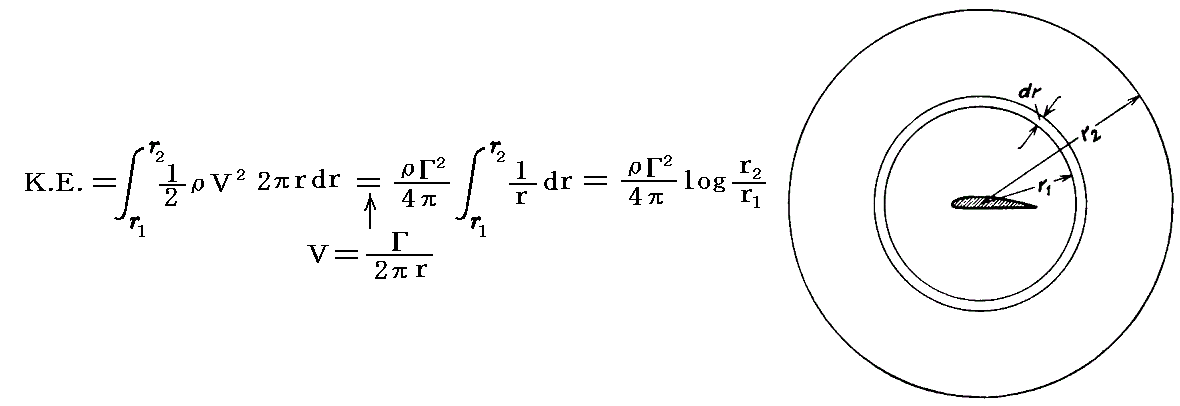
�ƂȂ�B
�@��ŋ��߂���̐ϕ��ɉ�������2�����A��2�����ɂ����Ƃ��ϕ��l�͖�����ƂȂ�A���̏ꍇ�ɂ͎c�O�Ȃ���������Ȃ��B�������A�����悻�̂Ƃ��뗃�ɉ������d���̔��������̎���̗��̂̎��^���G�l���M�[�ɂȂ����ƍl���ėǂ��ł��낤�B���̂Ƃ��c��̔��������Ɏc���Ă����Q�̂��^���G�l���M�[�ƂȂ����ƍl����悢�B
�@���ꂪ����������̑��x�œ����悤�ɂȂ�܂ʼn����Ȃ���Ȃ�Ȃ��d���ƁA���̎d���̌��ʐ����鎖���ł��B���ł͂���ȏ�̍l�@�͓�����A�������L���Œn�ʂ��߂��ɂ���ꍇ�ɂ́A�R�͂ɂ��d����A������̉^���G�l���M�[���тɉQ�̉^���G�l���M�[�͗L���Ȓl�ƂȂ�B
�m�⑫�����V�n
�@�������̗g�͂��������������Ŕ�s���Ă���ꍇ�A���̏�Ԃ�ۂ��߂ɃG�l���M�[��₦����������K�v�͂Ȃ��B���́A�O����������̗���A����͐������낵�̗���ƂȂ邠���̔g�ɏ���āA���̔g�Ƌ��ɑO���i��ł����̂ł���B���̂Ƃ��̗�����������猩��Əz�������P��̉Q���i��ł����l�Ɍ�����B���̂Ƃ����͉Q�̔g�ɏ���Đi��ł����T�[�t�{�[�h�̗l�Ȃ��̂ł��B
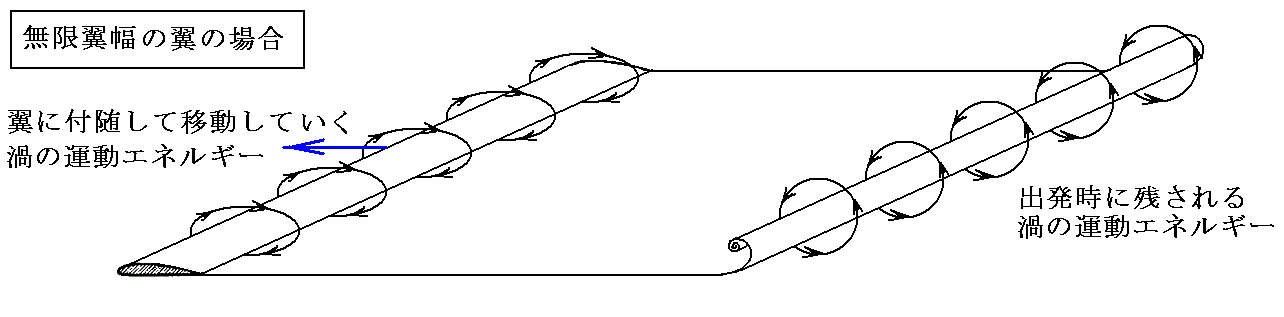
�@���̕\�ʔg���ŏ��G�l���M�[��^�����Đi�s���n�߂�ƁA���̌�͐V���ȃG�l���M�[���������Ȃ��Ă��i��ł������ƂƓ��l�ɁA�����Î~��Ԃ���z���������ē����o���܂ŃG�l���M�[����������A���Ƃ̓G�l���M�[���������Ȃ��Ă��z�����Ƌ��Ɉړ����Ă����B���̂Ƃ��A�Q�^�������闬�̗v�f�͕\�ʔg�̏ꍇ�Ɠ��l�Ɏ��X�Ɠ���ւ���Ă����܂��B
�@�������A����(�X�p��)���L���ȎO�������ł͗��[����㗬�ɘA�Ȃ�Q�̐Ղ��c���Đi�s���邱�ƂɂȂ�܂��B�����O���ɓ������Ƃ��Ɍ㗬�͂ǂ�ǂ�L����̂ŃG�l���M�[�̘A���I�ȋ������K�v�ɂȂ�܂��B���̃G�l���M�[�̋����ɔ�����R���U����R�m�Q��R�n�ł��B
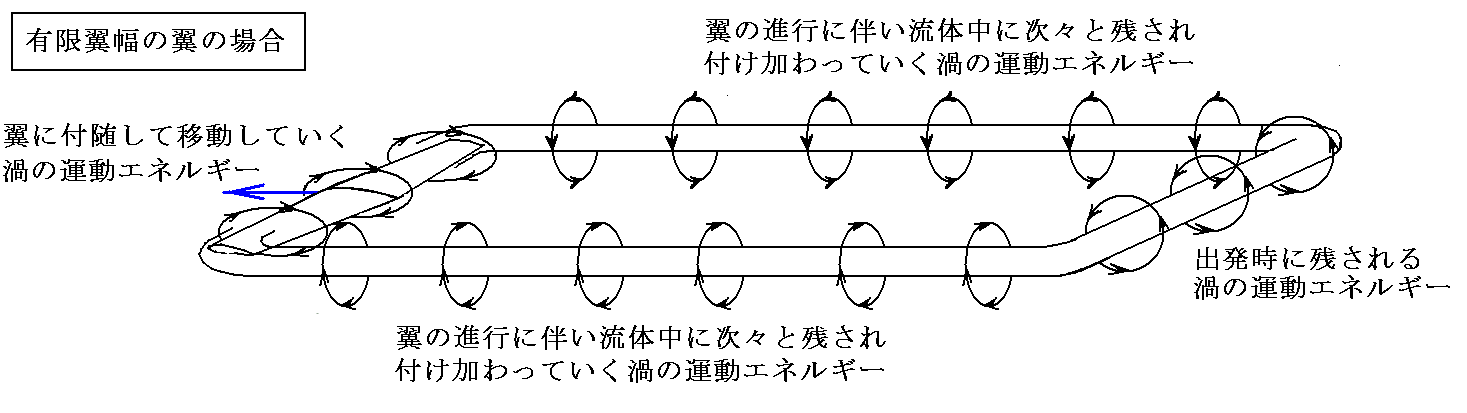
�@
�i�Q�j����
�@�V�D�i�P�j�R�D�Ő��������菇�ɏ]���ĕ����̐��\�ׂĂ݂�B
�P�D�}���p���Əz���̊W�B
�@�U�D�i�T�j�ŗp�����ʑ����̐������A��l���ɑ���}���p�����̕����̌�[�Ɏʑ������~����̈ʒu�������{�����͂�������|���X�����_�ɂ���B�܂肘������������i�|���j�A��������������i�|���j���邢�͂������i�|���j�����^��
�ł���B
�@�Ƃ���ŗ��ݓ_���������ׂ�����������A���ݓ_����
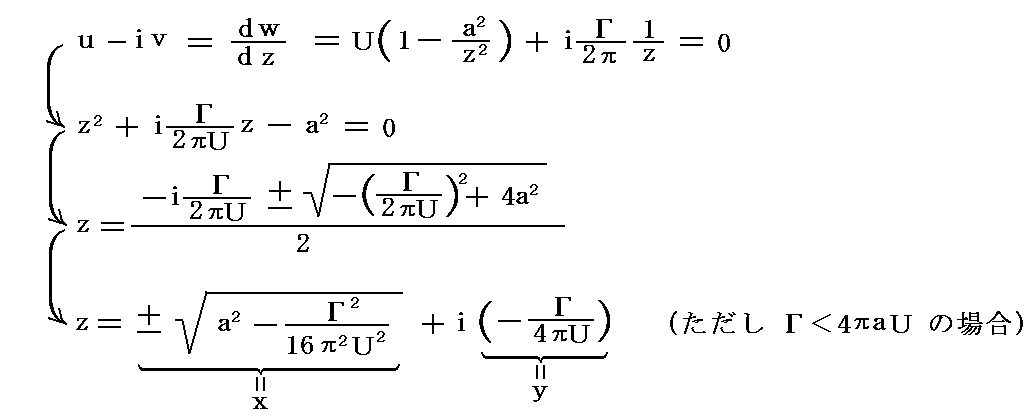
�ŕ\�����̂ŁA���ݓ_���i���C���j���i����������i�|���j�C����������i�|���j�j�Ɉ�v���邽�߂ɂ�
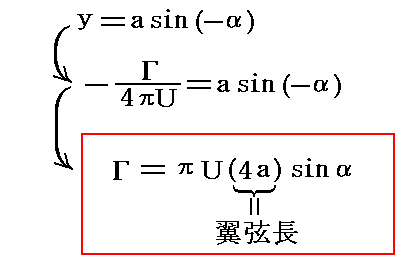
�Ȃ�z���~������̗���ɕt������悢�B�U�D�i�P�j�Q�D�ŏؖ������悤�ɁA�z�͓��p�ʑ��ɂ���Ă��s�ςɕۂ����̂ŁA���ꂪ�ĕ��ʂ̕����̂܂��̏z�l�ƂȂ�悢�B���̂Ƃ��A��������̗���͌�[���犊�炩�ɗ��ꋎ���W���[�R�t�X�L�[�̉��������闬��ƂȂ�B
�Q�D�}���p�Ɨg�͂̊W
�@�S�D�i�Q�j�P�D�ŏؖ������N�b�^�E�W���[�R�t�X�L�[�̒藝�ɂ��ƁA��l�����ɂ����ꂽ���̂ɏz�����t�����Ă���ƁA���̕��̂ɂ͈�l���ɐ����ȕ����m�����̐������n��
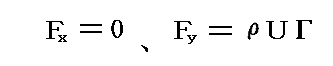
�̗́i�ex���g�́j�������̂ł����B
�@���̂��ߗ��ɓ����g����

�ƂȂ�B�܂������X����A�W���[�t�R�X�L�[�̉��������藧���˂Ȃ�Ȃ����Ƃ��痬�ꂪ��Ώ��ɂȂ�A������ɏz���t��������Ȃ��Ȃ�A���ꂪ�g�͂��������̂ł��B
�@���ꂱ���ʍe�u�����_�̉萶���v�Q�D�i�P�j�̍Ō��Ő��������������ʂƍ������_�ł��B�����ɋL�����悤�ɁA����܂ł̗͊w���_�͌}���p���������̈�ł̋����ׂ��傫���̗g�͑���l������ł��Ȃ������̂ł��B���̗��_�͂����̏��������ɐ������Ă��܂��B
�@�}���p���������Ƃ���Ŕ������邱�̑傫�ȗg�͂����A�����̔�s�@�����Ƃɔ�s�̉\�����m�M���������̂ł������A���̒i�K�i1906�`1910�N���j�Ɏ����Ă���Ɨ��_�͎����E�ϑ����ʂ�����ł����ƌ����܂��B
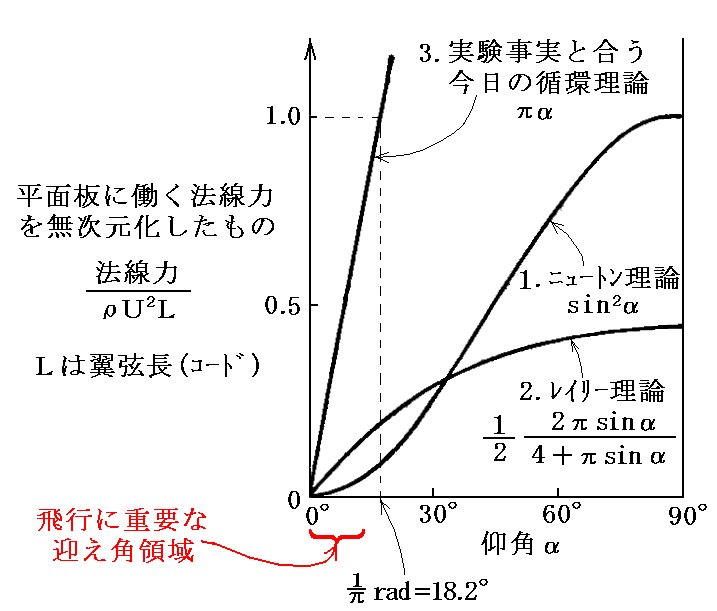
�@���͗����i�X�p���j�͖����̒���������Ƃ��Ă�����E�k���E���S���̂̃|�e���V�������ł��B�@���͂̒l�͒P�ʕ�������̂��̂ŁA�������i�R�[�g�j�k��4���Ƃ��ăςt2�k�Ŋ����ċK�i�����Ă���܂��B�}���p�����������̈�ł͖@���͂͗g�͂��̂��̂��ƌ��Ȃ��܂��B�܂��_�����x�[���̔w���Ő��������̂Ɠ������R�ɂ��R�͂ex��0�ɂȂ�܂��B
�m���Ӂn
�@���ʂ́i1/2�j�ςt2�k�Ŋ����Ė����������܂��̂ŁA�c���̒l�����ʂ̗g�́|�}�p�O���t�̔����ɂȂ��Ă��܂��B
�m�⑫�����n
�@�@�����ɓ������͂̍��͂��u���W�E�X�̑�������p���Ē��ڋ��߂邱�Ƃ��ł���B���̂Ƃ��p���镡�f���x�|�e���V�����͎ʑ���̕������`�����Ă���ĕ��ʂɂ����邗�f�i�āj�ł��B�܂�
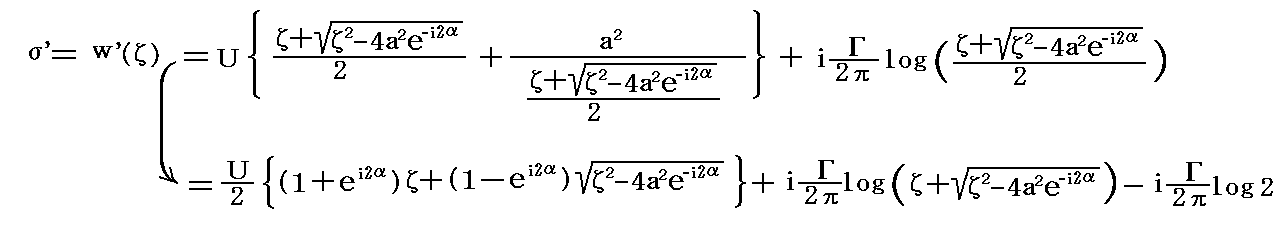
�ł��B������Ăɂ��Ĕ��������
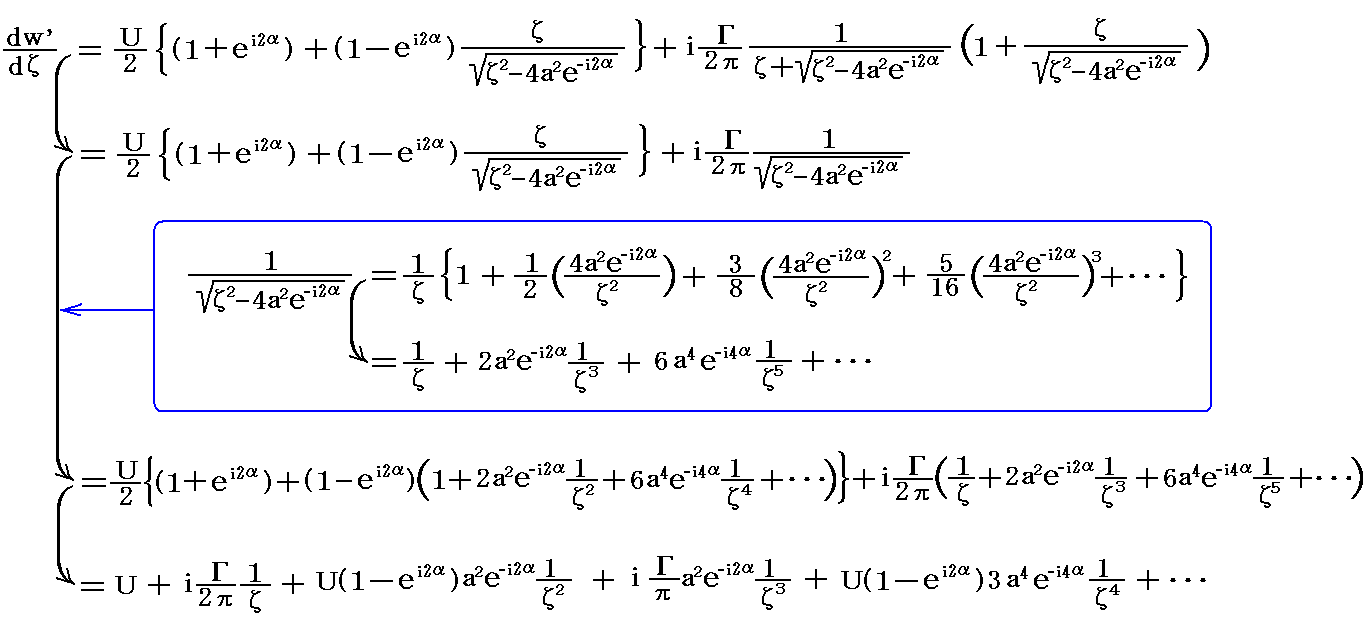
�ƂȂ�B������悷���
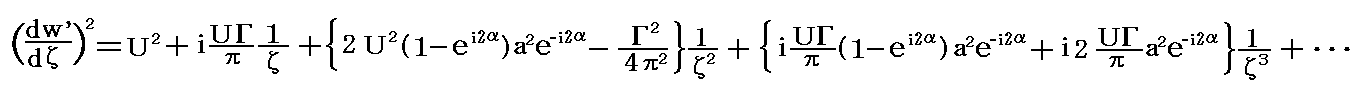
�ƂȂ�B������u���W�E�X�̑������ɑ�����ė��ɓ������͂����߂��

�ƂȂ�A�������_��������B
�R�D�}���p�Ɨ͂̃��[�����g�̊W
�@�����ɓ������_�̎������͂̃��[�����g���v�Z���Ă݂�B����͕��ʂ̖{�̃��[�����g�̒�`�m�O���̎���n�ƈႤ�̂Œ��ӂ��Ă��������B���̂��߂ɂ��S�D�i�Q�j�R�D�ŏq�ׂ��u���W�E�X�̑�������p����悢�B���̂Ƃ��p���镡�f���x�|�e���V�����͎ʑ���̕������`�����Ă���ĕ��ʂɂ����邗�f�i�āj�ł��B�O���m�⑫�����n�ŋ��߂��i�����f�^���āj2���u���W�E�X�̑������ɑ������Ɨ͂̃��[�����g��
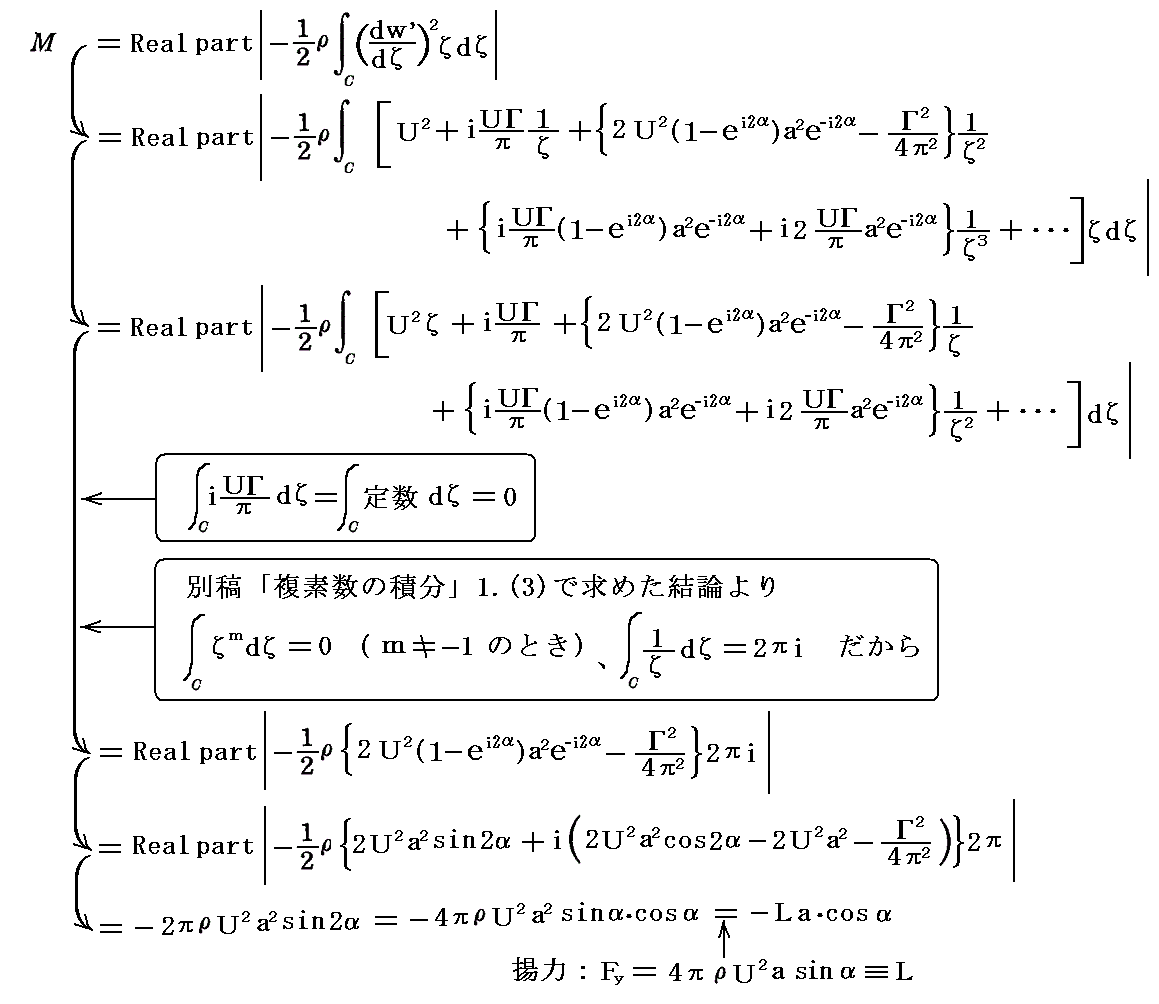
�ƂȂ�B������4�ςt2��������������ey���k�͗g�͂�����g�͂̍��͂������ʒu�m���͒��S�n�͕����̏ꍇ�O�����痃����1/4�̋����̏��ɂ��邱�ƂɂȂ�B
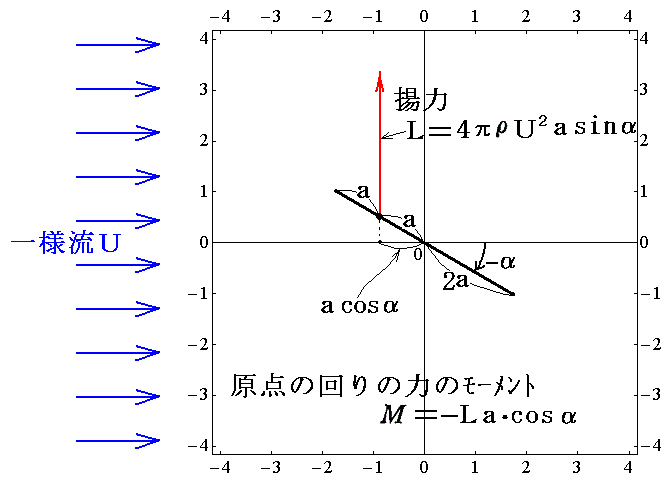
�@���̈Ӗ���}��ʼn��߂���Ζ��炩�Ȃ悤�������̏ꍇ�ɂ͈��͒��S�̈ʒu�͌}���p�ɂ���ĕϓ����������̑O����25���̏��ɂȂ��B���������ۂ̗���ł͌}���p���傫���Ȃ�Ɣ����������Ă��̂��Ƃ͐��藧���Ȃ��Ȃ�B
�S�D��������̈��͕��z
�@�����\�ʂ̈��͕��z��m��ɂ́A���\�ʂ̑��x���z������悢�B�Ȃ��Ȃ��x���k�[�C�̒藝��藬��������Β����ɂ��̓_�̈��͂����邩��ł��B�k���E���S���́E���������̗���Ő��藧�x���k�[�C�̒藝���

�ŕ\�����Ƃ������̂ŁA����͂�������\�ʂ̈�����\���B�����ł́A���x�̂��������ƍ������Ȃ��悤�ɁA�����������x�̑傫���͂��ŕ\���Ă���B�Y�����̂��͗��\�ʂ̒l�ł��邱�Ƃ������āB�܂��Y�������͖������ł̈�l���̗����������B
�@���\�ʂ̑��x���z�͗��Ɏʑ�����錳�̉~���̎���̑��x���z������Ηǂ��B�Ȃ��Ȃ炚���ʏ�̉~������̗���̋��f���x��z�|����z�ƍ��W�ϊ���̃ĕ��ʏ�̗�����̗���̋��f���x�����|�������̊Ԃɂ�
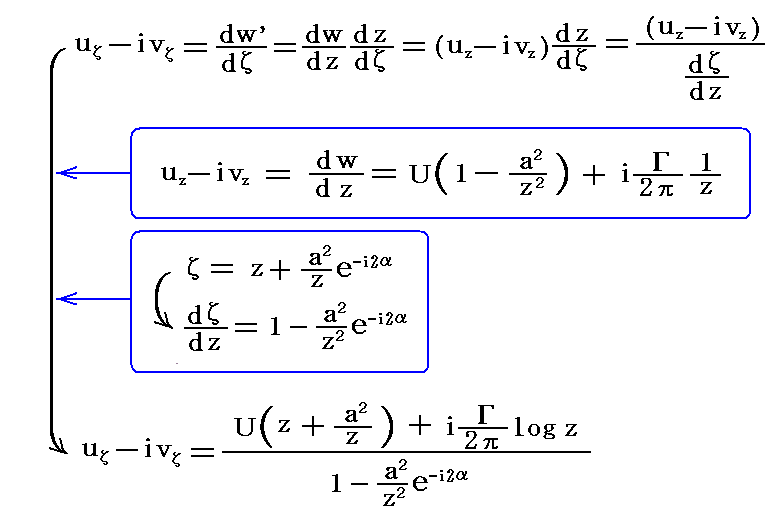
�̊W�����邩��ł��B���ہA���̎��̂��ɗ��㉏�[�Ɏʑ�����邚A����cos���|����sin����������|������O���[�Ɏʑ�����邚C���|��cos���{����sin�����|������|�����������Ă݂�b�����|�������b�����ƂȂ邱�Ƃ�����B
�@��L�̎��͋��f���x�ɕt���Ă̊W�ł������A�T�D�i�P�j�P�D�Ő�������
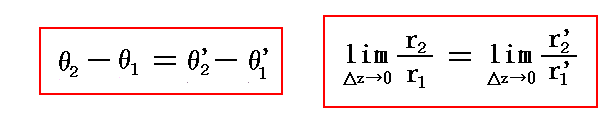
�̊W���疾�炩�Ȃ悤�ɁA���̊W�͌��~�\�ʂ̑��x�̑傫����sz�ƕϊ���̗��\�ʂ̑��x�̑傫����s���ɕt���Ă����藧���܂��B�܂�
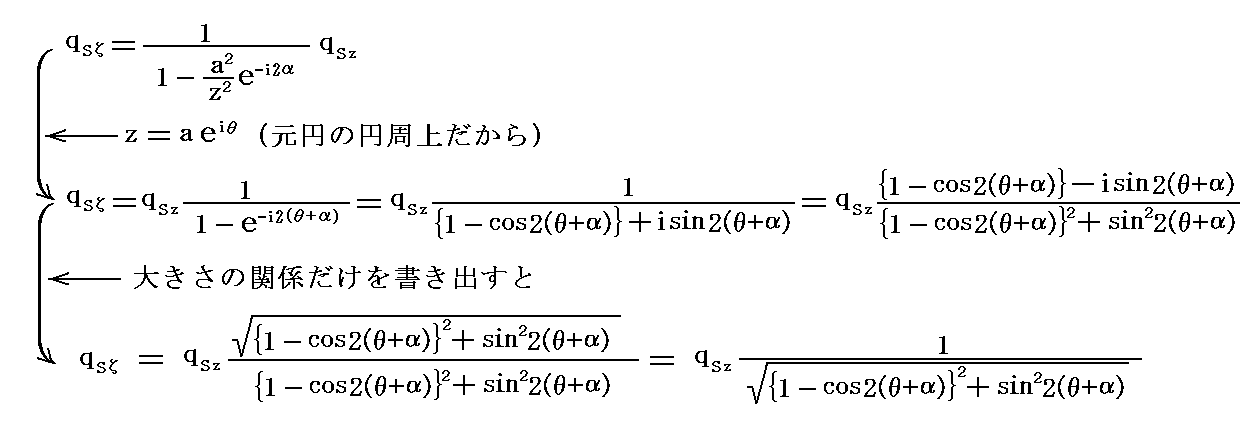
�������܂��B���̎���p���Ă����������߂܂��B
�@��l���ɏz�����t�������ꍇ�̌��~�\�ʂ̑��x���R�D�i�R�j�P�D�ł��łɋ��߂Ă���
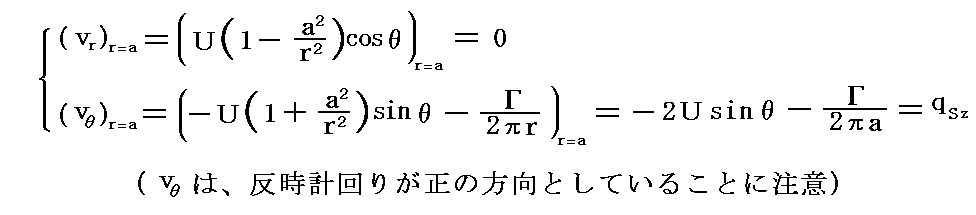
�ł����B�܂��z���Ɨ��ݓ_�Ƃ̊W���R�D�i�R�j�R�D�ŋ��߂Ă���
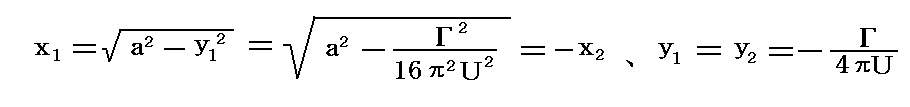
�ł����B
�@���x�x�N�g���͌��~�\�ʂ̗���ƕϊ����ꂽ���\�ʂ̗���̗����ɉ����ĕ\�ʂɉ����Ă������A�~���\�ʂ̑��x�x�N�g���̑傫�����R�D(�R)�P�D�ł��łɐ��������悤�ɉ��L�̎��ŕ\���܂��B�W���[�R�t�X�L�[�̉��������}���p20���̕����Ɏʑ�����錳�~�̎���̗���Ő��������
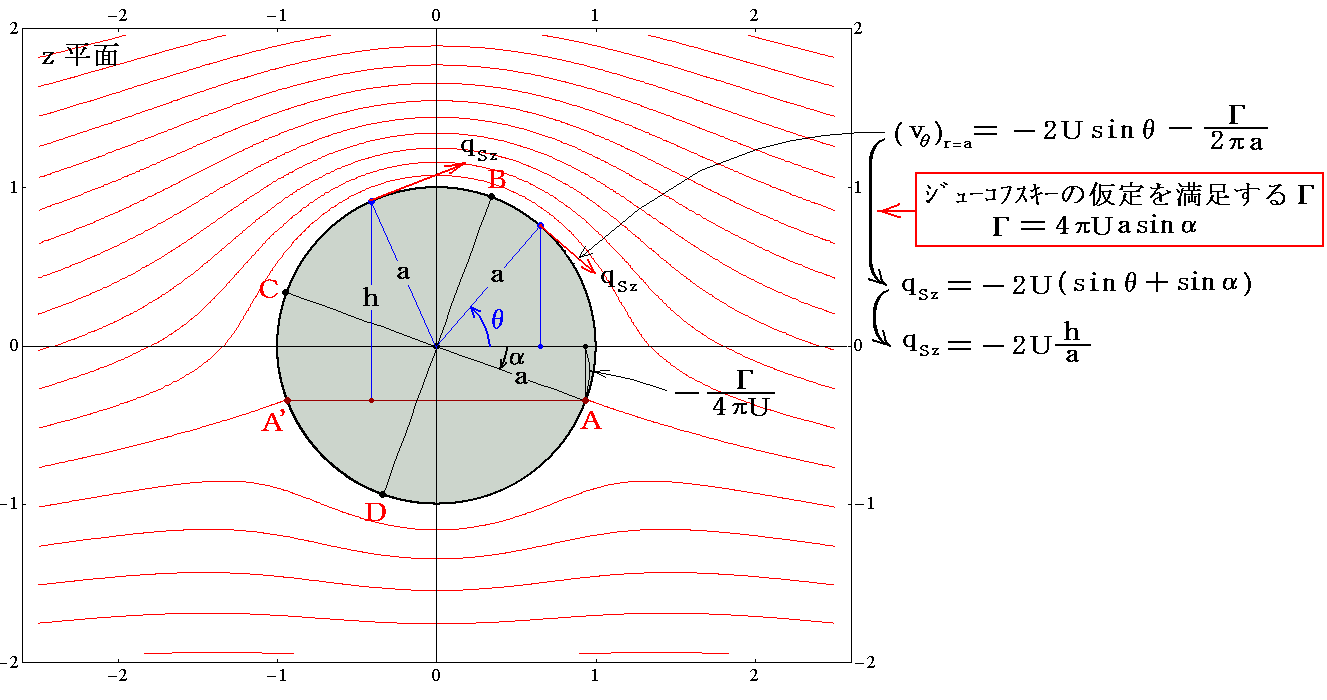
�ƂȂ�܂��B�܂��~����̓_�̑��x�͓�̗��ݓ_�`�`�f�����Ԓ������炻�̓_�܂ł̍��������~�̔��a�Ŋ�����2�t���|�������̂ɓ������B�����ł̓��͎ʑ���̕����̌}���p�ł���A�W���[�R�t�X�L�[�̉����ɂ�����z�����}���p���Ɍ��т����Ă��鎖�ɒ��ӂ��Ă��������B
�@�~���\�ʂ̈ʒu���p�����[�^�Ƃ̊��Ƃ��ĕ\�����Ƃ��A�����ʉ~���̃p�����[�^�Ƃ̈ʒu�����i���C���j���i���cos�ƁC���sin�Ɓj�́A�T�D�i�T�j�Q�D�ŋ��߂����ɂ���āA�ā��i�́C�Łj�Ȃ�_�Ɏʑ������B
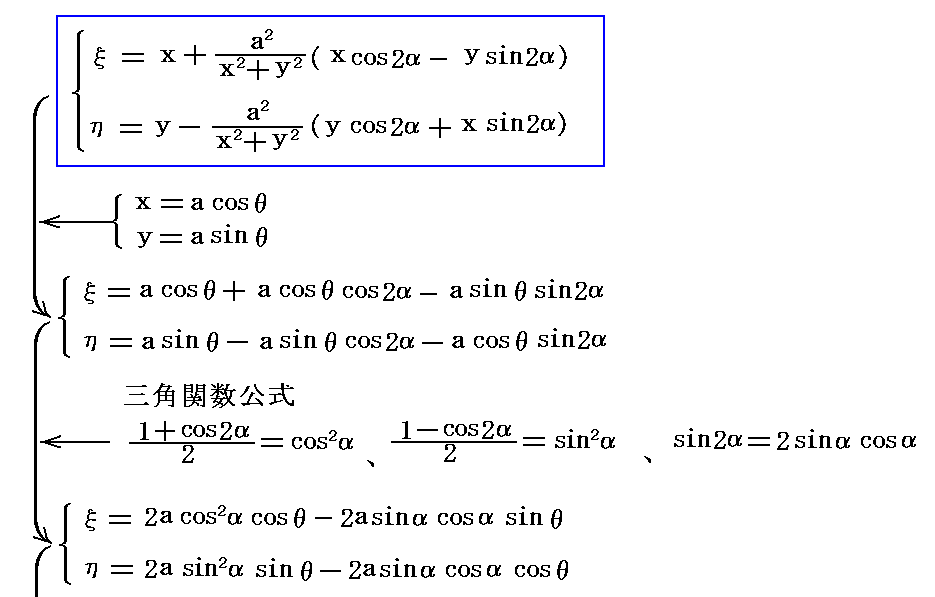

���̎���}������ƁA�C�ӂ̌}���p���ɂ����镽���̃̍��W�ƌ��~��̃Ƃ̑Ή��W�͉����}�ŕ\�����B�܂��A���E�}�͌��~�̊e�Ƃ̈ʒu�̉~���\�ʑ��x�������������O���t�ŁA������R�D�i�R�j�P�D�Ŏ��������̂��c�ɂ��������ł��B
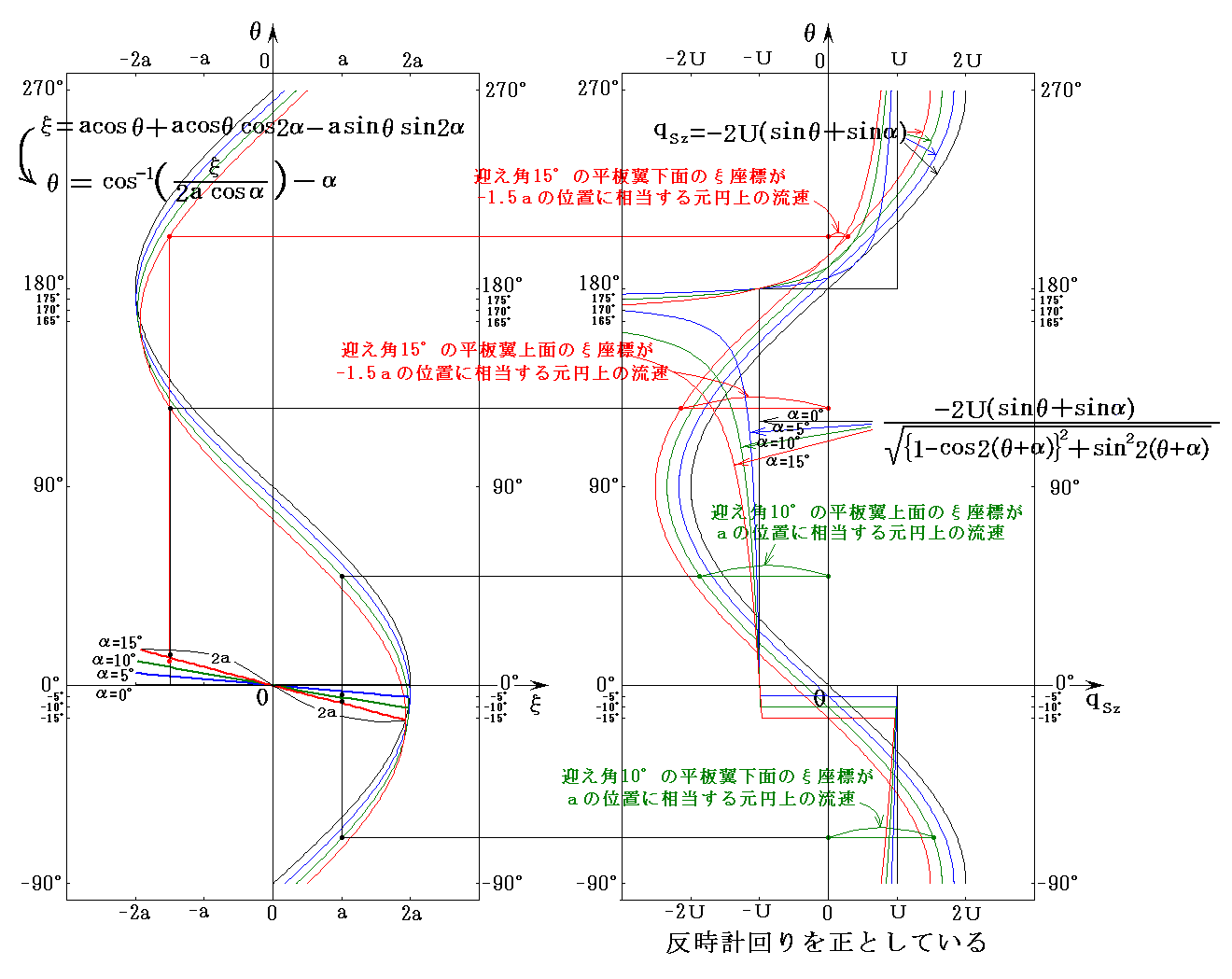
�@��̍��E��̃O���t��Ή�������ƁA�C�ӂ̌}���p���ɂ����镽���̃̍��W�̗���E���ʂɑΉ����錳�~��̑��x��������ǂݎ���邱�Ƃ��ł���B���̑��x�������� �P�^[�o�i�P�|cos2(��+��)�p2�{sin22(��+��)]0.5 �{�������̂��̍��W�̗��\�ʑ��x�������ł��B�܂�

�ł��B���ۂɌv�Z����͖̂ʓ|�ł����A���������\�t�g���g���Čv�Z���ăO���t�������
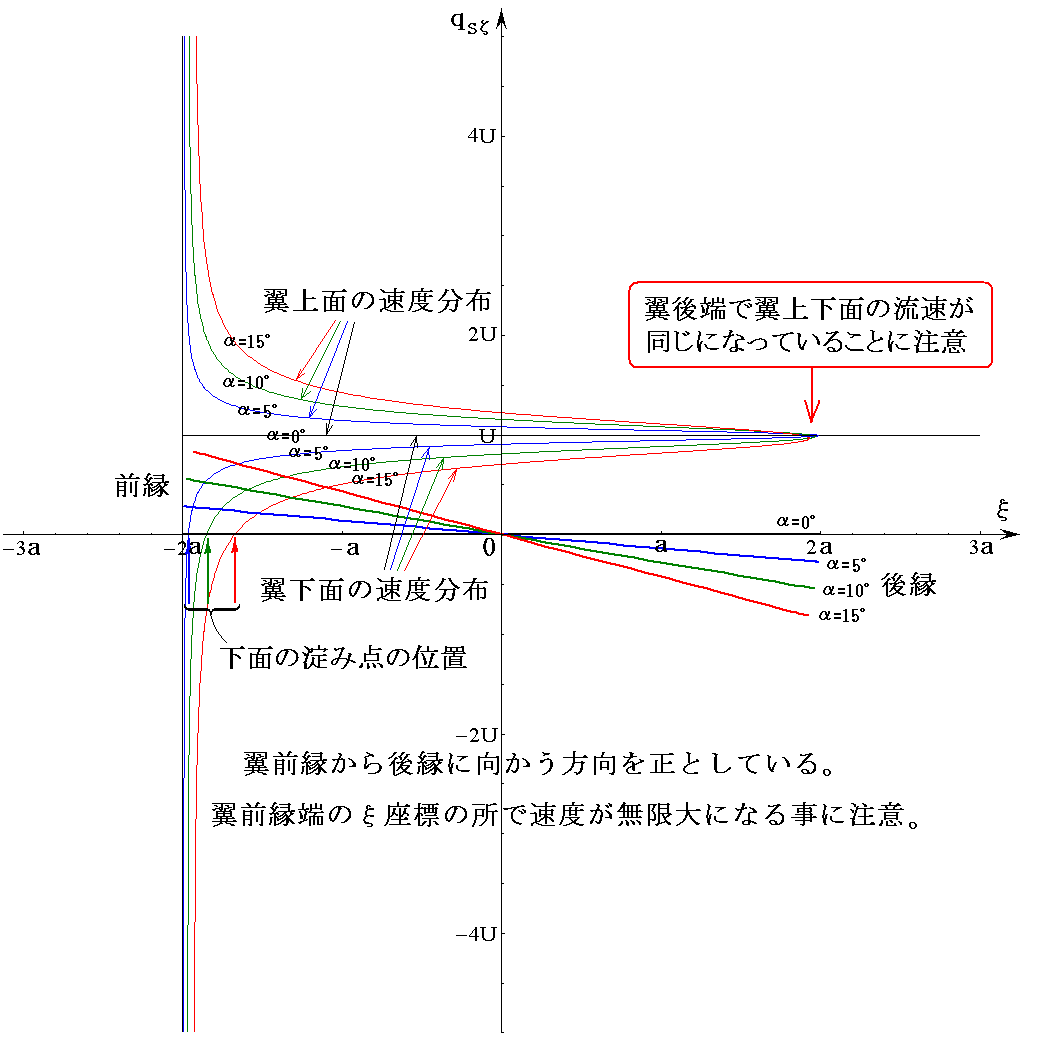
�ƂȂ�܂��B���̂Ƃ������͗��ʂɉ������ʒu���W�ł͂Ȃ��āA�e�}���p�ɂ����闃�ʈʒu�̃̍��W�ł��邱�Ƃɒ��ӂ��Ă��������B����ɁA�x���k�[�C�̒藝��p���Ĉ��͕��z���v�Z���āA�K�i���������͂ŕ\���Ɖ��}�̗l�ɂȂ�B
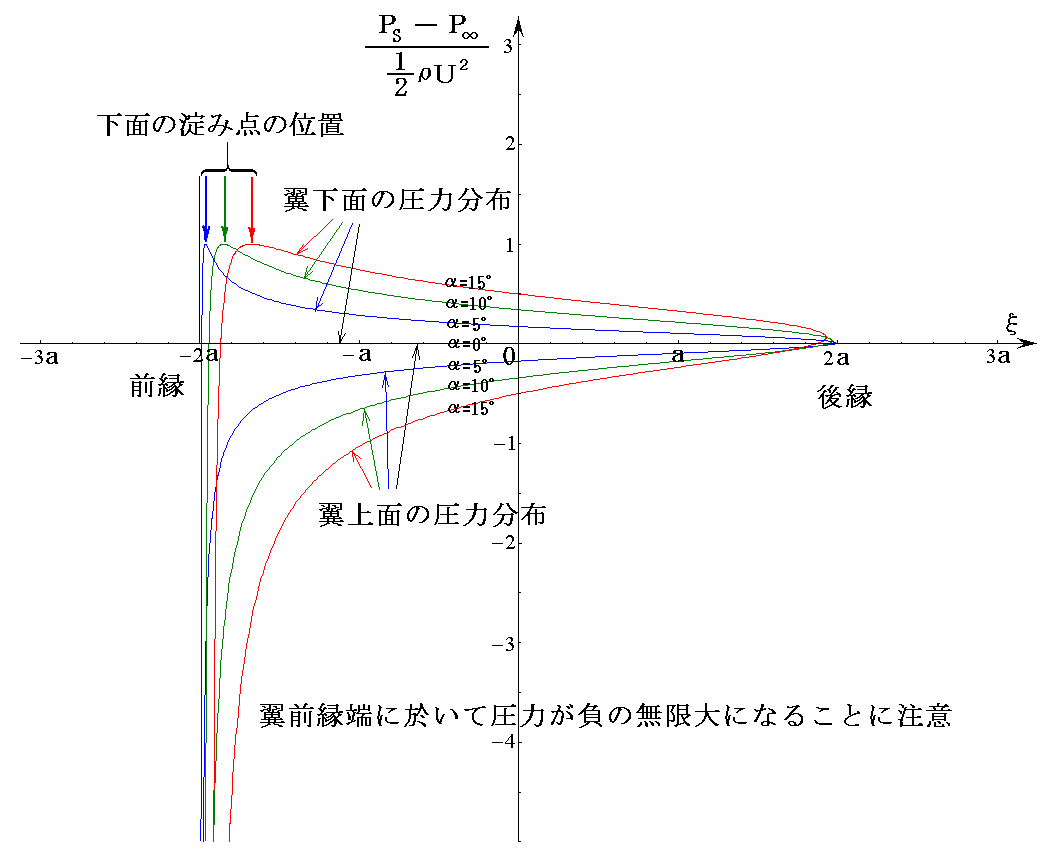
�@�����ʂň��͂�1.0�ɂȂ�̒l�̂Ƃ���ɗ��ݓ_������B�����ł͑O����������̂��߂ɁA�����ŗ�����������ɂȂ�A���͂����̖�����ɂȂ�B���������ۂ̗��͌����Ŋۂ݂������Ă��邽�߂ɗL���ȗ����ɂȂ舳�͂��L���ȕ��̒l�ɂƂǂ܂�B���̓�������V�D�i�U�j�T�D���䗗�������B
�@
�i�R�j�~�ʗ�
�@�U�D�i�U�j�R�D�ŋ��߂������ʂɂ����镡�f���x�|�e���V�������i���j�ƃĕ��ʂɂ����镡�f���x�|�e���V�������f�i�āj��p���ĉ�͂���悢�B
�P�D�2���Əz���̊W
�@���̂Ƃ������i��j�𗃌����Ŋ������l���L�����o�[���ƌ����܂����A�U�D�i�U�j�Q�D�ŋ��߂��l�ɁA�ĕ��ʂ̉~�ʗ��̃L�����o�[���
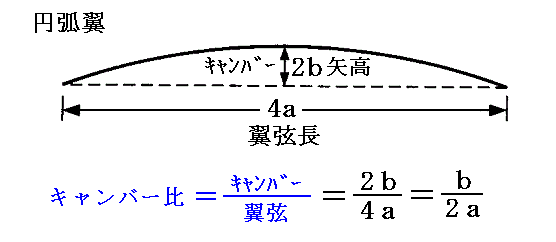
�ƂȂ�܂��B���͂����ʂɂ�����~�̕ϐS�����ł��B
�@�z������ꍇ�A�����ʏ�̉~������̗���̗��ݓ_���ǂ��ɐ����邩���ׂĂ݂�B���ݓ_�͗�������ƂȂ�_�����狤�f���x�������^������0�ƂȂ�_�����߂�悢�B
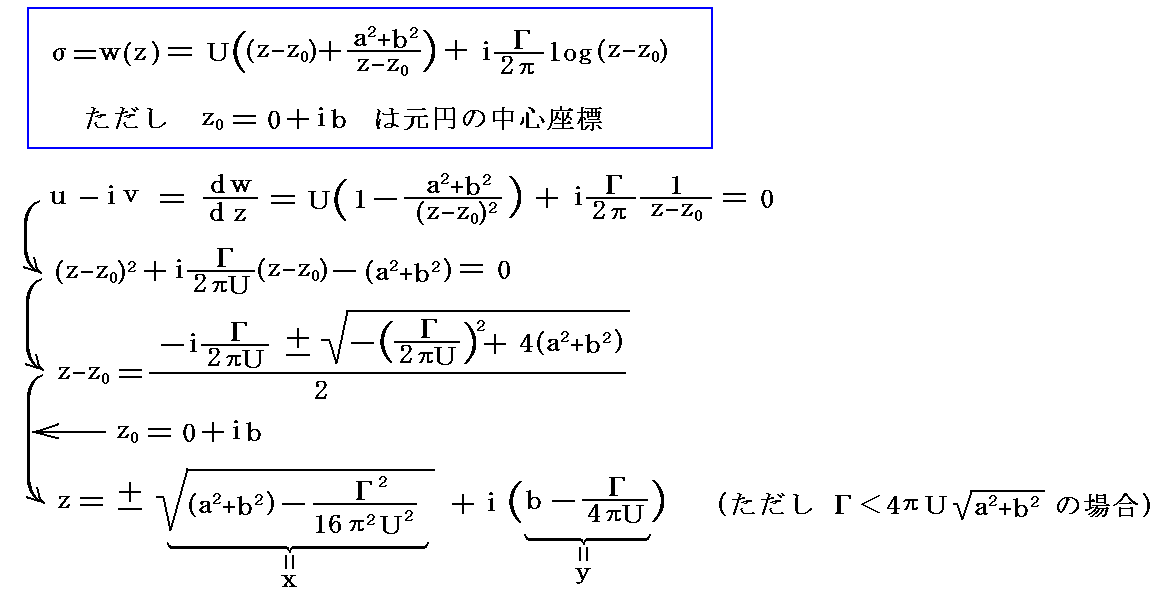
�@�ĕ��ʏ�̉~�ʗ��̌�[�����ݓ_�ƂȂ����W���[�R�t�X�L�[�̉��������邽�߂ɂ́A�����ʂ̌��~�̂����i���C0�j�̓_�����ݓ_�ƂȂ�悢�̂�
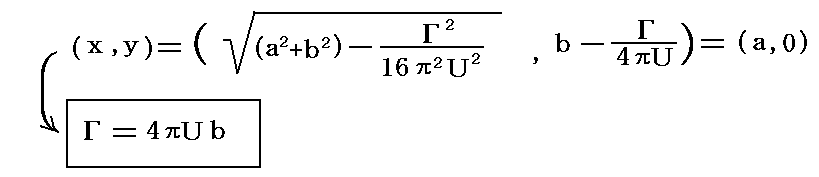
�ƂȂ�B���ꂪ�A�W���[�R�t�X�L�[�̉����������}���p���[���̂Ƃ����~�ʗ�����̗���ɕt������z�̒l�ł��B
�@�~�ʗ��ł́A�}���p���[���̏ꍇ�ɑO���������ݓ_�ƂȂ�W���[�R�t�X�L�[�̉��肪�O�����ɉ����Ă���������邱�Ƃɒ��ӂ��Ă��������B
�Q�D�L�����o�[�Ɨg�͂̊W
�@�O���ŋ��߂��悤�ɁA�~�ʗ��ł��}���p���[���ł��z�����Ƃ��Ȃ��B���̂Ƃ��̗g�͂��N�b�^�E�W���[�R�t�X�L�[�̒藝�ɂ��
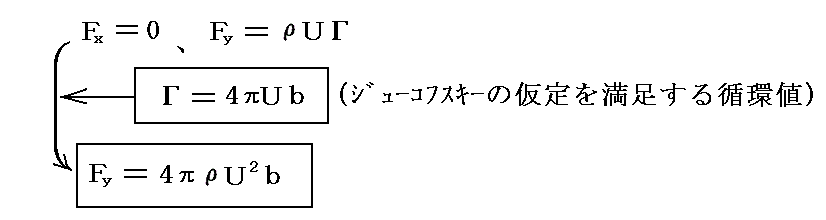
�ƂȂ�B���ꂪ�}���p�[���̉~�ʗ��ɔ�������g�͂ł��B�܂��g�͂̑傫���̓L�����o�[�̖2���ɔ�Ⴕ�đ��傷���B
�@�g�͂̌����ł���z�傳����ɂ́A�}���p�����������Ƃɂ���ĒB������邪�A�L�����o�[��t����������Ώ��ɂ��邱�Ƃɂ���Ă��z��ł����Ƃ������Ƃł��B���ꂱ���������̔�s�@�����Ƃ����ڂ��Ă������Ƃł��B
�@�L�����o�[��t����Ηg�͂����傷�邱�Ƃ́A�t�B���b�v�X�i1884�N�j����G���^�[���i1889�N�j�̎����ɂ�葁�����疾�炩�ɂ���Ă��܂����B�����Ď��ۂ̔�s�@���L�����o�[�����̗p���Ă��܂����B���������̌��ʂ𗝘_�I�ɐ����ł���悤�ɂȂ����̂�20���I�ɓ����Ă���ł��B
�@���̉𖾂ɍŏ��ɐ��������̂��Q�D�i�R�j�ŏq�ׂ��E�B���w�����E�N�b�^�i1902�N�j�ł��B�N�b�^���������}���p�[���̉~�ʗ��̗g�͂�\������

�ł������A�w��p���Ė2���Ƃ��A�Ƃ̊W�����߂Ă݂��
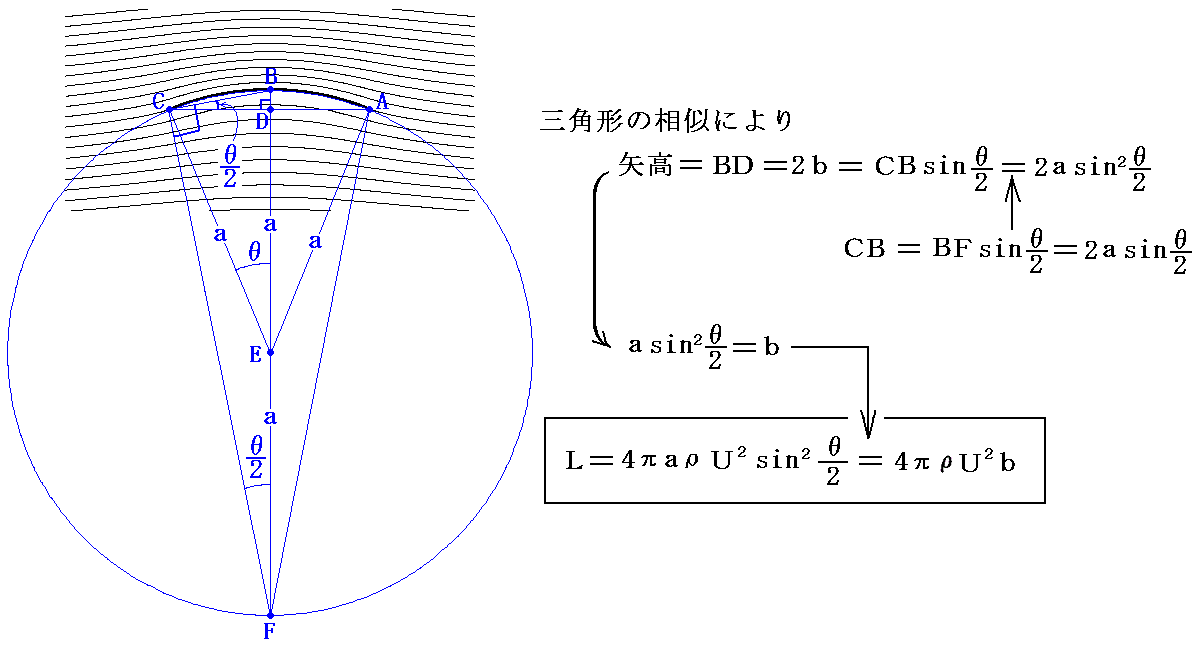
�ƂȂ�B�܂�A�����ŋ��߂����ƑS���������_�Ă������ƂɂȂ�B
�@1902�N�̃N�b�^�ɂ͗�����̗���ɏz���t������Ƃ����l�����͖����A���ꂪ�~�ʗ��ɉ����Ċ��炩�ɗ����Ƃ��������݂̂����L�̎����l�ł��B���̂Ƃ����p�����̂́A�����Ő��������̂Ɠ������p�ʑ���p������@�ł��B
�@�W���[�R�t�X�L�[�ɏ����x��܂����A�N�b�^��1910�N�ɂ͗g�͂Əz�̊W�ɋC�Â��ĕ��f���_�̎�@�ƂƂ��ɉ��߂ďڂ����������Ă��܂��B
�m�⑫�����P�n
�@���傫������Ηg�͂����傷�邩��Ƃ����Ăނ�݂ɑ傫�����邱�Ƃ͂ł��܂���B�����ł��}���p��傫�������痬��̔������������̂Ɠ��l�ɁA�~�ʗ��̖��傫������ƁA�S���̂��߂ɔ������鋫�E�w�̉e���ŗ��̏�ʌ㕔�ŗ���̔����������ėg�͂͌������R�͂����債�܂��B�܂��O�����ɂ����锍���������Ă��܂��B����Ɉ��͒��S�̈ʒu�̕ϓ����傫���Ȃ�s����ɂȂ�܂��B���̂��߃L�����o�[��̌��ʂ͖�������Ȕ͈̗͂��ł̂ݗL���ł��B
�@�܂��A���ۂ̎O�����I�ȗ��ł́A�L�������i�X�p���j�ł��邱�Ƃɂ��A�X�y�N�g����ʂׂ̈ɁA�����œ������g�͂����邱�Ƃ͂ł��܂���B���̗��z�l�������Ȃ菬�����Ȃ�܂��B
�R�D�}���p���������~�ʗ��̎���̏z��
�@�~�ʗ����}���p����������Ԃň�l�����ɑ��݂���Ƃ��A����ɓ����g�͂��}���p�Ƌ��ɂǂ̗l�ɕω����邩�ׂ�B���̂��߂ɂ́A�e�}���p�ɉ����ăW���[�R�t�X�L�[�̉��肪���������z�l�����߂�悢�B����́A�Ƃ���Ȃ��������̉~������̗���̗��ݓ_���U�D�i�V�j�P�D�Ő��������_��A���i���cos���C�|���sin���j�Ɉ�v����悢�B
�@���ݓ_�͗�������ƂȂ�_�����狤�f���x�������^������0�ƂȂ�_�����߂�悢�B
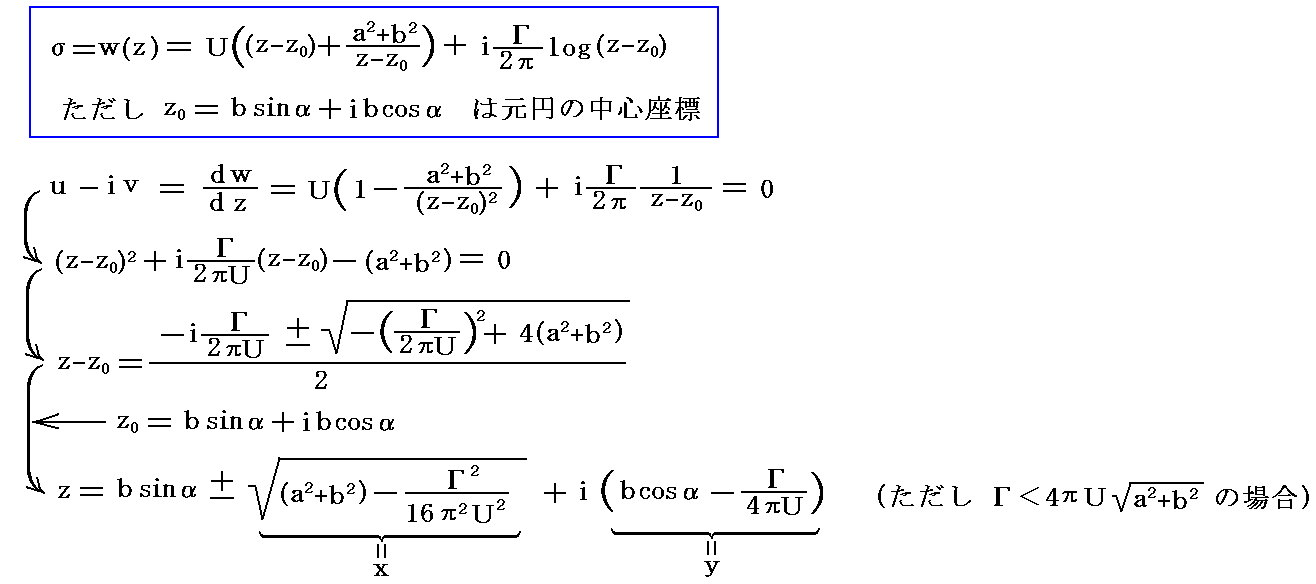
�@�ĕ��ʏ�̉~�ʗ��̌�[�����ݓ_�ƂȂ����W���[�R�t�X�L�[�̉��������邽�߂ɂ́A�����ʂ̌��~�̂�A���i���cos���C�|���sin���j�̓_�����ݓ_�ƂȂ�悢�̂�
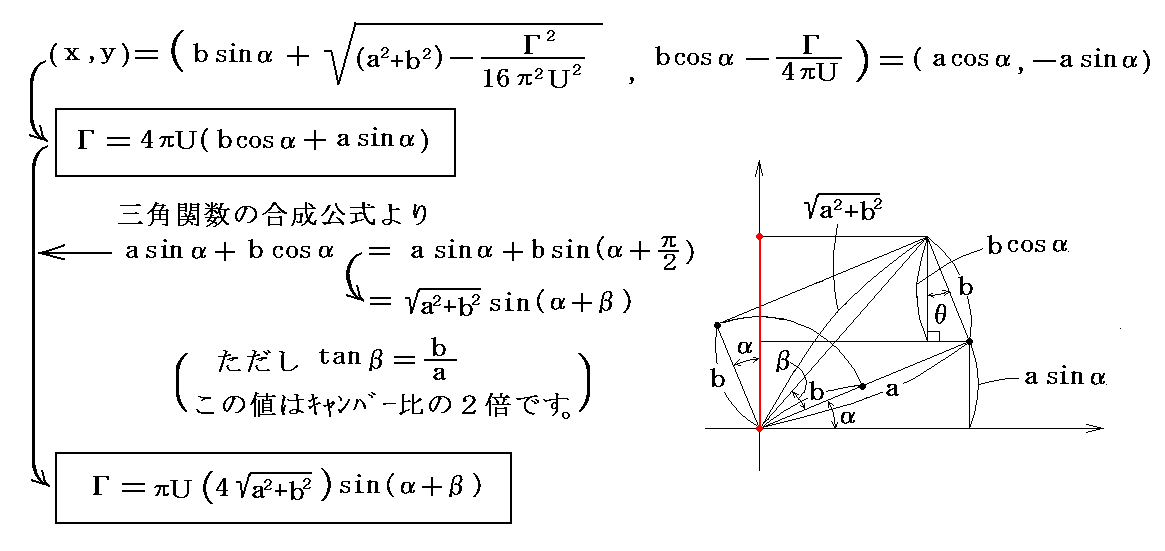
�ƂȂ�B���ꂪ�A�W���[�R�t�X�L�[�̉����������}���p�����̂Ƃ����~�ʗ��m�L�����o�[�䁁���^2���n����̗���ɕt������z�̒l�ł��B
�@�}���p����0�̂Ƃ����V�D�i�R�j�P�D�̎��ƁA�L�����o�[2����0�̂Ƃ����V�D�i�Q�j�P�D�̎��Ɠ����ɂȂ�܂��B
�S�D�}���p���������~�ʗ��ɓ����g��
�@�S�D�i�Q�j�P�D�ŏؖ������N�b�^�E�W���[�R�t�X�L�[�̒藝�ɂ��ƁA��l�����ɂ����ꂽ���̂ɏz�����t�����Ă���ƁA���̕��̂ɂ͈�l���ɐ����ȕ����m�����̐������n��
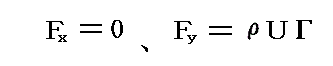
�̗́i�ex���g�́j�������̂ł����B
�@���̂��ߌ}���p�����~�ʗ��m�L�����o�[�䁁���^2���n�ɓ����g����

�ƂȂ�B���炩���L�����o�[�i2���j�����ƁA�}���p���������������傫�ȗg�͂����������B
�@���̂Ƃ��}���p����0�ł�sin����0������g�́�0�ł��邪�A�O�����������ĕ��̌}���p�����|���ɂȂ�Ɨg�͂̓[���ƂȂ�B���̂Ƃ�������̏z�̓���0�ł���Ȃ���A����̓W���[�t�R�X�L�[�̉�������Č㉏���犊�炩�ɗ��ꋎ��B�܂����̂Ƃ��O���̗��ݓ_�͗���ʂɗL��܂��B�m�g�嗬���}�n
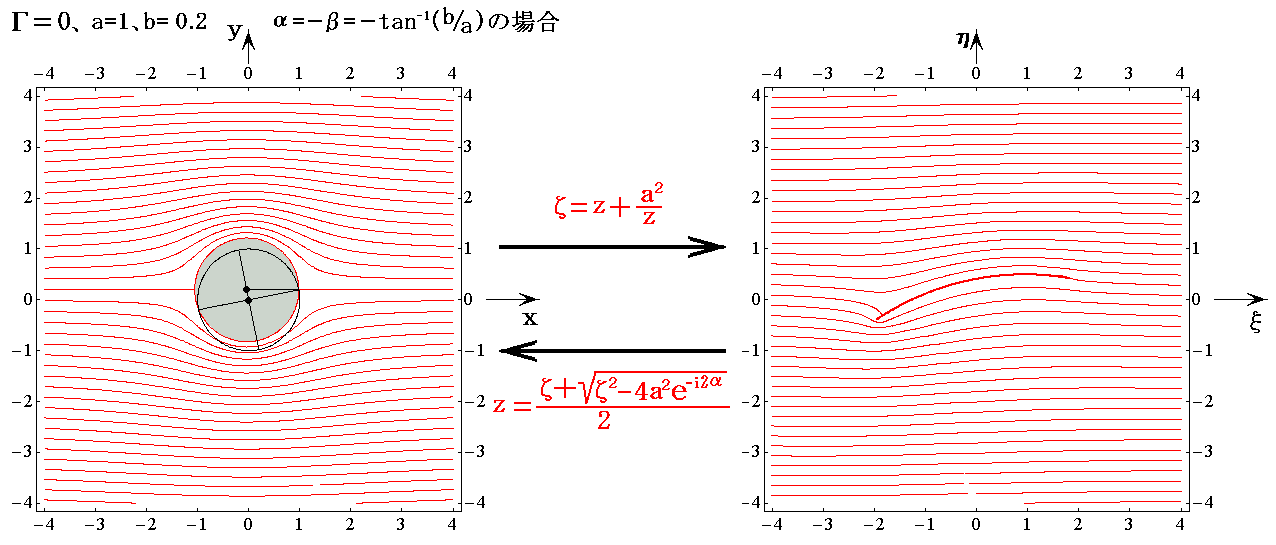
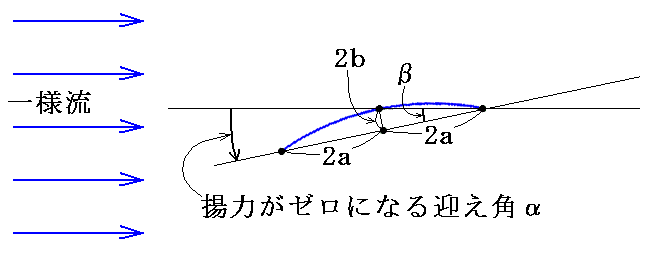
�@���̂Ƃ����̂��Ƃɒ��ӂ��ĉ������B�g�͂͊m���Ƀ[���ł����A�����}�̗����Ԋu���狁�܂闬�����z���瓱���闃�ʂ̈��͕��z���疾�炩�Ȃ悤�ɁA���̏�Ԃ̗��ɂ͋��������v���̃g���N�������܂��B���̂��߁A���̂悤�ȏ�Ԃ͂���߂ĕs����Ȕ�s�ƌ����܂��B����͎��߂̗��_�I��͂�����A�܂��o��������e�Ղɗ\�z����邱�Ƃł��B���̂��߂��̂悤�ȃ��[�����g��ł��������炩�̋@�\�i���������̗l�ȁj���K�{�ɂȂ�܂��B
�@�}���p�Ɩ���������ꍇ�ɂ́A�g�͂ƌ}���p�̊W�́@�g�͂k���萔�P�~���{�萔�Q�@���ꎟ���̃O���t�ŋߎ��ł���B���ɃL�����o�[(����j�����邱�Ƃ́A�V�D�i�Q�j�Q�D�ŏq�ׂ����_��ʂ�ꎟ���̃O���t�@�g�͂k���萔�~���@������萔�Q�������s�ړ����ėg�͂������邱�Ƃɑ�������B
�@���̂Ƃ��g�͂̑�����ʂ��ő�L�����o�[�̈ʒu�ɂ��W���܂��B���̓�������Q�l����1�Q������p�����͎��}�Ŏ�����
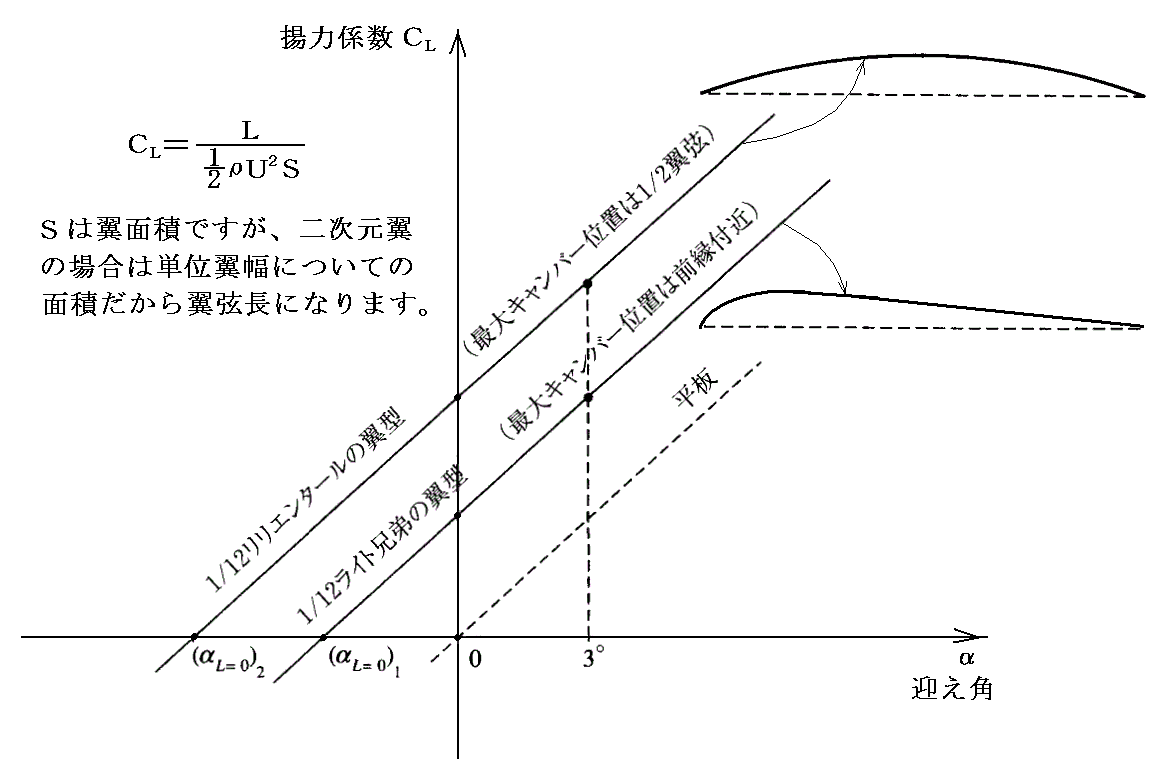
�̗l�ɂȂ�܂��B
�@���̐}�̂悤�ɗg�͂𑝂��ɂ͍ő�L�����o�[�ʒu�͐^�ɂ�������L���Ȃ̂ł����A1901�N�̃O���C�_�[�������I���������_�̃��C�g�Z��́A�ő�L�����o�[�ʒu�̏d�v���ɂ͂܂��C�t���Ă��Ȃ��悤�ł��B�����炭1901�N9���`12���̕���������ɂ͂��̂��Ƃ��c�������͂��ł����A1901�N�̒i�K�̃��C�g�Z��ɂ͍ő�L�����o�[�ʒu�Ɋւ��ėg�͂������͒��S�̈ړ��̕����d�v�ȊS���������悤�ł��B
�@���̓�������q�ׂ����C�g��1901�N�̘_���̋L�q�͓����̔�s�@�����Ƃ̏�������Ă��ĂƂĂ������[���B�Q�l����1�Q������p���Ă����܂��B�������A�����ɕ`����Ă��鈳�͒��S�̈ړ������������Ȍ}���p�Ŕ��]���錻�ۂɂ��āA���C�g�Z�킪���^�����߂��i�K�Ńn�b�L���F�����Ă�����ł͂���܂���B�ʍe�Ő��������悤�ɔނ炪�����m��̂�1901�N�̃O���C�_�[������i�_�����M���_�̏����O�j�ł��B
�@�E�E�E�[���Ȃ������ʂł́A90��(�}���p)�ɂ����鈳�͒��S�͖ʂ̒����t�߂ɂ���A����_�܂ł͊p�x���������Ȃ�ɏ]���đO���ֈړ����邪�A���̓_�͘p�Ȃ̐[���ɂ���ĕω�����B���̓_��ʉ߂�����́A�p�x�̌����ɔ����Ĉ��͒��S�͑O���ֈړ������������ɔ��]���ċ}���Ɍ���������Ĉړ�����B
�@���̌��ۂ́A�����Ȋp�x�ł͕����ʂ̑O�������ɏՓ˂���ۂɉ��ʂł͂Ȃ���ʂɓ����邱�ƂɋN�����Ă���A����䂦�ɂ��̕����͕��̏ꍇ�̂悤�ɍł��L���ȕ����Ƃ��ċ@�\���邱�ƂȂ��g�͂����Ȃ��Ȃ�B�����G���^�[���͂��̏�ʂ̓����̂��߂ɁA1/8���̑傫�Șp�Ȃ����ʂ�p���邱�Ƃ̊댯���ɒ��ӂ��Ă����B�������A�ނ͂��̌��ۂ����S�ɔ������Ȃ��Ȃ�p�x�Ƙp�Ȃ���x���������Ă��Ȃ������悤�Ɏv����B
�@���ƒ�����̖��ɑ��ēƎ��̒������s���Ă��Ȃ��������A�����G���^�[����1/12�̘p�Ȃ���ɕ\���쐬���Ă����̂ŁA���̘p�Ȃɂ͖�肪�Ȃ��Ǝv����B�������A���S����Ƃ��ĉ~�ʂ��g�p�������ɁA�������̈��͂ɂ��炷�ʐς��ŏ��ɂȂ�悤�ɑO���ŋ}���ɕω�����Ȗʂ���X�̋@�̂ɍ̗p�����B�E�E�E
�iWilbur Wright ,�gSome Aeronautical Experiments�h, Journal of the Western Society of Engineers 6 ,1901,p489-510�j
�m2017�N7���@����21�Dp95�`98�ɂ��NjL�n
�@���̘_���̓I�N�^�[���E�V���k�[�g���E�B���o�[�Ɉ˗�����1901�N9��18���̐����Z�p�ҋ���ɉ�����u���̈���łŁA�ŏ��ɋ���̋@�֎��Ɍf�ڂ��ꂽ���̂ł��B
�@��L�_���́A���̌�W�E�G���W�j�A�����O�E�}�K�W���A�T�C�G���e�B�t�B�b�N�E�A�����J���A�t���C���O�Ȃǂ̎G����X�~�\�j�A������̔N�����iSmithonian Report for 1902,p133�`148�j�Ȃǂɂ��S���������͈ꕔ���]�ڂ��ꂽ�B�����Č�ɗl�X�Ȑl�X�ɂ��J��Ԃ����y�E���p���ꂽ�L���Ș_���ł��B
�@�����ǂ߂A�ނ炪��s�@�B���������邽�߂ɂ͂��̋@�B�I�\�������A���̋@�\�ɂ���ĕ��ɏ��\�͂��l���E�������邱�Ƃ��ƂĂ��厖���ƓI�m�ɗ������Ă������Ƃ�����B�ނ�ɂƂ��Ĕ�s�@�́A��s���Ƀo�����X��ۂ��A�@�̂𑀂�A���ɏ�葱���邱�Ƃ��\�ɂ�����̂łȂ���Ȃ�Ȃ������̂ł��B�ނ�͂��̉\����O��I�ɒNj����Ă��܂����B�ނ�́A�����G���^�[���Ɠ��l�ɁA���̔��Ă��@��閈�ɉ����Ԃ��O�����ƂȂ��ώ@���Ă���A���̔��Ă̔閧��O��I�ɉ𖾂���w�͂����Ă��܂��B���̔F���������A�ނ�����Đl�ޏ��̗L�l���͔�s�̐����ɓ������Ƃ����ėǂ��ł��傤�B
�m�⑫�����Q�n
�@�L�����o�[�̕��z��A���̌`���ς������ʂ𗝘_�I�Ɋm���߂�ɂ́A���p�ʑ��̕��@�͌��\�ʓ|�ł��B���̏ꍇ�ɂ�1922�N�Ƀ}�b�N�X�E�����N�ɂ���ĊJ�����ꂽ�������_�̕��@���֗��ł��B���Ƀ��[�����g�����͗����̉e���͏��Ȃ���ɕ��ϖ�Ȑ��ɂ���Č��܂�܂����甖�����_�͗L���ł��B�������_�̎�@�́A���̓r���̐ϕ��菇�Œ��ӂ��ׂ��Ƃ���͂���܂����A����Ӗ������ŏq�ׂĂ��铙�p�ʑ���p������@�����ȒP�ł��B
�@�m�Q�l�����P�Q�A�P�V�ɂ��ƁA�����N�̂����͓��p�ʑ��@�𔖗��ɓK�p������̂������l�ł����A1923�N�Ƀr�����o�E��(��)���L�����o�[�Ȑ����Q�w�Œu����������@�ɂ��đ������W�J�ʼn������B�����1924�N�ɃO���A�[�g���������̉�@�ɁA�������W�J�ł͂Ȃ��āA�t�[���G������p�����@�m1926�N���̕����Q�ŏЉ��Ă�����@�n���J�������悤�ł��B�����l�X�ȋ��ȏ��ŏЉ��Ă�����̂̓O���A�[�g���莮���������̗̂l�ł��B�n
�@�������_�ɂ��Ă͂����ł͐������܂��A�Q�l�����ɗg�����Q�D�A�R�D�A�T�D�A�W�D�A�X�D�A�P�V�D�A�P�W�D���܂߂Ă����Ă��̗����_�̖{�ɍڂ��Ă��܂��̂Ő���䗗�ɂȂ��ĉ������B���ɏq�ׂ鎖���ɂ��W����̂ł����A���㉏������֔���グ��ƌ}���p��ς��Ă����͒��S���ړ����Ȃ��悤�ɂł������ƂȂǂ��̕��@�Ŋ��ƊȒP�ɏؖ��ł��܂��B
�T�D�~�ʗ��ɓ����͂̃��[�����g
�@���[�����g�����߂�ɂ̓ĕ��ʏ�̉~�ʗ�����̗���̕��f���x�|�e���V�����ƃu���W�E�X�̑�������p����悢�̂����A�V�D�i�S�j�R�D�ł����ƈ�ʓI�ȃW���[�R�t�X�L�[���̏ꍇ�����߂Ă���̂ŁA���̌��_��p����B�����̎��ł���0�ƒu���Ή~�ʗ������_�������͂̃��[�����g�ƂȂ�B
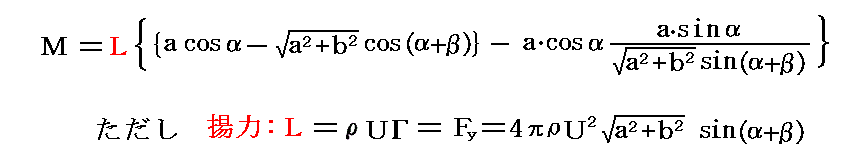
�@�܂��L�����o�[�����������ł͌}���p���ω�����Ɨg�͂̍�p�_�m���͒��S�n���ړ�����B�܂��~�ʗ��ł͌}���p��0�̂Ƃ��ɂ͈��͒��S�̈ʒu�͗��̂قڒ����ɂ��邱�Ƃ������B
�@�����P�A����0.1���Atan�������^����0.1�A����20���̏ꍇ��}������Ɖ��}�̂悤�ɂȂ�B
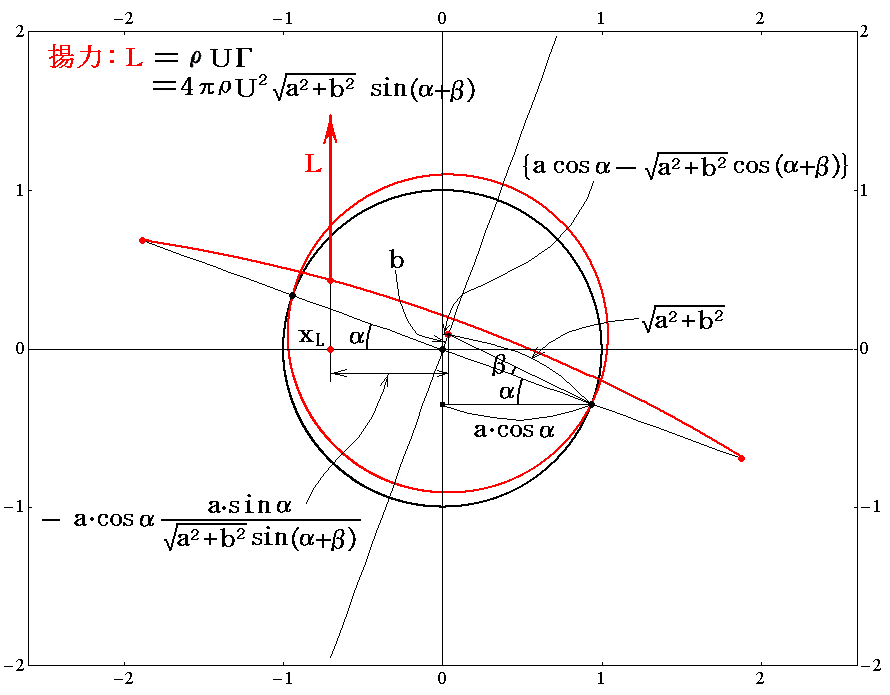
�@���̂Ƃ��A�g�͂̍�p����_�̂����W��L���}���p�Ƌ��ɂǂ̗l�ɕω����邩���O���t�ɂ��Ă݂�ƈȉ��̂悤�ɂȂ�B�}���p���[���̎��ɗ����̒����ɂ��������͒��S�͌}���p�Ƌ��ɑO�i����B�܂����̌}���p�̏ꍇ�ɂ͗����̒����������Ɉړ�����B
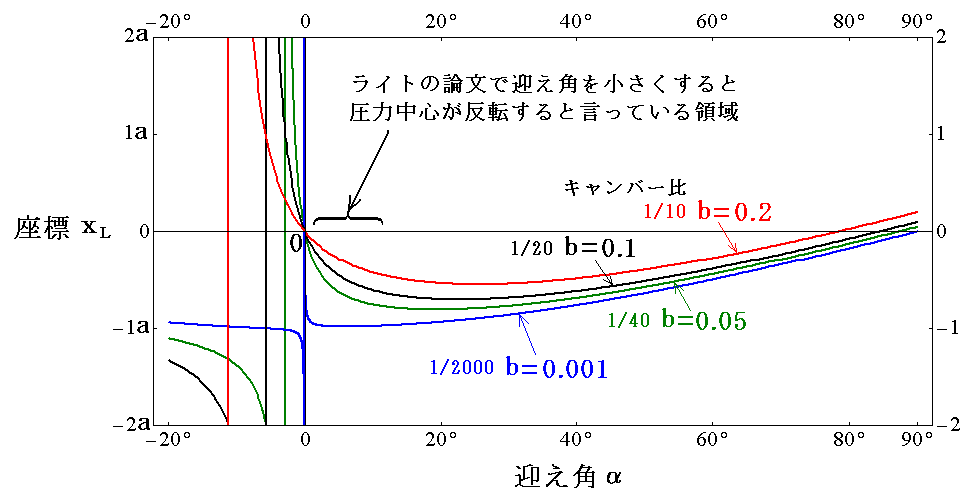
�@�L�����o�[���[���ɋ߂Â��Ɨg�͂̍�p�_�͑O������ق�25���̂Ƃ���ɌŒ肳��Ă��ĕ����ɋ߂Â��B�t�ɃL�����o�[��������ƁA�}���p���������Ƃ��ɂ͗��̒��S�t�߂ɂ�������p�_���A�킸���̌}���p�̕ω��ő傫���O�i���邱�Ƃ�����B���̑O�i�ʂ͂���}���p�ŋɑ���Ƃ�A�������ƍ�p�_�͔��]���čĂь㉏�̕��ֈړ�����B
�@�������A�}���p��20������Ǝ��ۂ̗���ɂ͔����������ăW���[�R�t�X�L�[�̉��肪�S�����藧���Ȃ��Ȃ�̂ŁA�O���t�̃���20���̕����͐M���ł��Ȃ��B
�@�܂��}���p�����ɂȂ�Ɨg�͂̍�p�_�͑傫��������Ɉړ����āA���Ɂi��}�ł́j�����v���̃g���N����������B����̓L�����p�[���������~�ʗ��ł͌o��������e�Ղɗ\�z�ł��邱�Ƃł����A����߂ĕs����ȏ�ԂɊׂ鎖���Ӗ����܂��B
�@������ɂ��Ă��}���p���ω�����ƈ��͒��S���ړ����邽�߂ɁA���ۂ̔�s�@�ł͎嗃�̈��͒��S�̈ړ��Ő�����g���N��ł������@�\�i���������̗l�ȁj���K�v�ł��B
�@�ȏ�ɏq�ׂ��悤�ɗ����L�����o�[�����Ɨ��ɓ������́i�g�́j�̍�p�_�͌}���p�Ƌ��Ɉړ����܂��B����̓����G���^�[������O���[��������������I�ɋC�Â��Ă������Ƃł���A���ۂ̔�s�@�̐v�ɉ����Ă���߂ďd�v�ȈӖ��������܂��B���_���x����Ȃ���A���̎��������܂��������邱�Ƃ��ł��܂����B
�@
�i�S�j�W���[�R�t�X�L�[��
�P�D�W���[�R�t�X�L�[���Əz��
�@�U�D�i�W�j�Ő������������̃W���[�R�t�X�L�[�����W���[�R�t�X�L�[�̉��������Ƃ��̏z�l��s�����߂�B����́A�ȑO�Ɠ��l�Ɍ��̉~������̗���̗��ݓ_���_��A���i���cos���C�|���sin���j�Ɉ�v����������狁�߂�悢�B����͈ȑO�̕������̂�0����0���i���cos���|�o���{�i��2�{��2�j0.5�pcos�i���{���j�C�|���sin���{�o���{�i��2�{��2�j0.5�psin�i���{���j�j�ɒu�������A���i��2�{��2�j���o���{�i��2�{��2�j0.5�p2�ɒu��������Ηǂ��B
���ݓ_�͗�������ƂȂ�_�����狤�f���x�������^������0�ƂȂ�_�����߂�B

�@�ĕ��ʏ�̌����̌�[�����ݓ_�ƂȂ����W���[�R�t�X�L�[�̉��������邽�߂ɂ́A�����ʂ̌��~�̂�A���i���cos���C�|���sin���j�̓_�����ݓ_�ƂȂ�悢�̂�
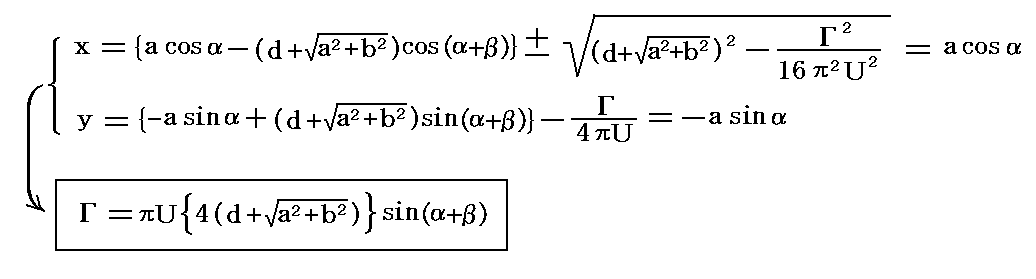
�ƂȂ�B
�@�����Œ��ӂ��ė~�������Ƃ́A��L�̏z�����̂܂܃ĕ��ʂ̗��̎���̏z�ƂȂ�̂ŁA�W���[�R�t�X�L�[�̉���������z�l��\�������~�𗃌^�ɕϊ�������W�ϊ��̎ʑ����̕ω��Ɉˑ����Ȃ����Ƃł��B�@�܂����^���ς���Ă���Ɂm��l���̗����t�n�~�m���~�̔��a�n�~�msin�i���{���j�n�̌`�ɏ������B
�@������^���قȂ�Ύʑ��O�̌��~�̂��₂������قȂ�̂ł�����A�z�l���̒l���̂��̂͗��^�ɂ���ĈقȂ�܂��B
�@��Ƃ��Ă����P�A����0.1���A����0.15���A����10���A����tan-1�i���^���j��5.7���́A���~����̗����i���j�Ɨ�����̗����i�Ԑ��j��}������B
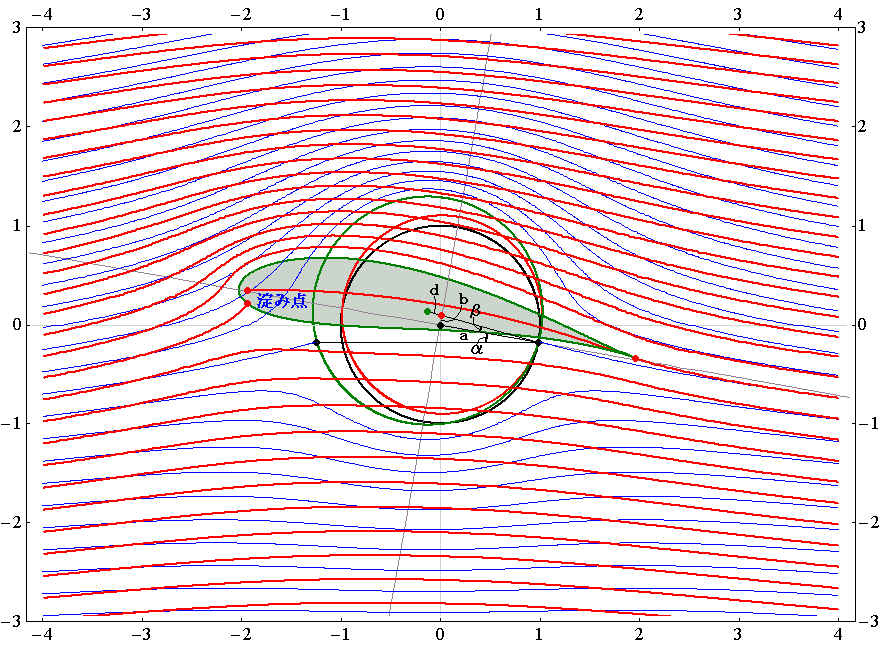
�@���̐}�Ŏ��̂��Ƃɒ��ӂ��ė~�����B���ʂ̎g�p�ŗ������}���p�i�|5���`10���j�ł́A�O���̗��ݓ_�͑O���~�ʂ̏���ړ����邾���ŁA�����Ė�����̑��x�Ƃ������刳�͌��z�������邱�Ƃ͂Ȃ��B���̂����V�D�i�T�j�Q�D�Ő�������悤�Ɏ��ۂ̃��C�m���Y���ł͌����̔����͋N����ɂ����Ȃ�܂��B���ꂱ���������ɂ���ő�̌��ʂł��B
�Q�D�W���[�R�t�X�L�[���ɓ����g��
�@���܂łƓ��l���N�b�^�E�W���[�R�t�X�L�[�̒藝�ɂ��A�}���p���̃W���[�R�t�X�L�[���ɓ����g����

�ƂȂ�B
�@���������Ɋ|����W�����i��2�{��2�j0.5����o���{�i��2�{��2�j0.5�p�ɂȂ�̂Ō����ɂ���Ɨg�͂����������܂��B�����̌W���͂��Ƃ��Ɨ������i�R�[�h�j�ɊW����Ƃ���ŁA�U�D�i�W�j�P�D�Œ��ӂ����悤����0�ɂ���Ɨ�����4���{4��2�^�i���{2���j�ɑ����܂��̂ł��̎����l�����Ȃ���Ȃ�܂��A�����ɂ������Ƃł�͂�A������Ώ̐����������ėg�͂�������̂͊m���ł��B
�@���Ǘg�͂�������v���́m�}���p���n�Ɓm�L�����o�[2���n�Ɓm�����n�����ݏo���������Ώ̐��ł��B�܂��l���ɑ��闃�̔�Ώ̐��̂��߂��W���[�R�t�X�L�[�̉���������ɂ͏z������ɕt����������A���ꂪ�g�͂�����̂ł��B
�@�����������Œ��ӂ��ė~�����̂ł����A4�o���{�i��2�{��2�j0.5�p���قڗ������ɋ߂��l�ł��邱�Ƃ��l������ƃL�����p�[�̌��ʂ͌}���p������tan-1�i���^���j�������₵�����Ƃɉ߂����A�g�g�͂̌��ʂ��V�D�i�Q�j�Q�D�Ő��������������}���p���������Ƃ��ɐ���������ׂ��傫���̗g�͂����郁�J�j�Y���Ős������Ă���h�̂ł��B�L�����p�[����������������ɂ��邱�Ƃ̌��ʂ́A�V�i�T�j�A�i�U�j�Ő�������悤�Ɂg�}���p���������Ƃ����ꂪ�����ɂ��Ĕ������Ȃ��ŃW���[�R�t�X�L�[�̗��������悤�ɂł��邩�h�Ƃ����Ƃ���ɂ���܂��B�g�L�����p�[����������������ɂ���ƁA�����̂Ƃ��낪�傫�����P�ł���h�̂ł��B�����͔S���ɔ������E�w�̐��䂪�傫��������鏊�ŁA�m���̌`�n���m���C�m���Y���n�ɐ[���W���܂��B
�m�⑫�����P�n
�@�@�W���[�R�t�X�L�[���ɓ������͂̍��͂��u���W�E�X�̑�������p���Ē��ڋ��߂邱�Ƃ��ł���B���̂Ƃ��p���镡�f���x�|�e���V�����̓W���[�R�t�X�L�[�����`�����Ă���ϊ���̃ĕ��ʂɂ����邗�f�i�āj�ł��B�܂�
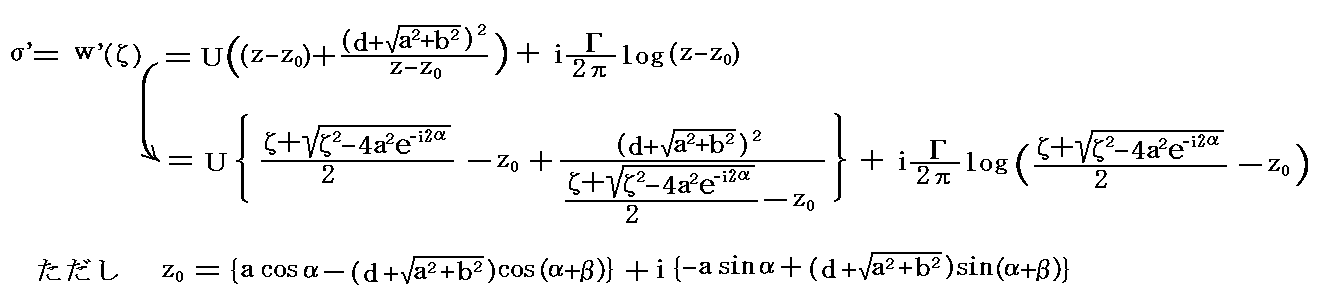
�ł��B���܂܂łƓ��l�ɁA������Ăɂ��Ĕ������ċ��f���x�����߂�悢�̂ł����A���̂܂ܔ��������̂ł͌v�Z���ƂĂ��ʓ|�Ȃ̂�

�ƒu���āA�������̔�������
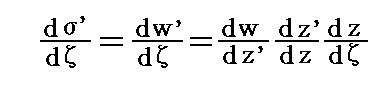
��p���܂��B
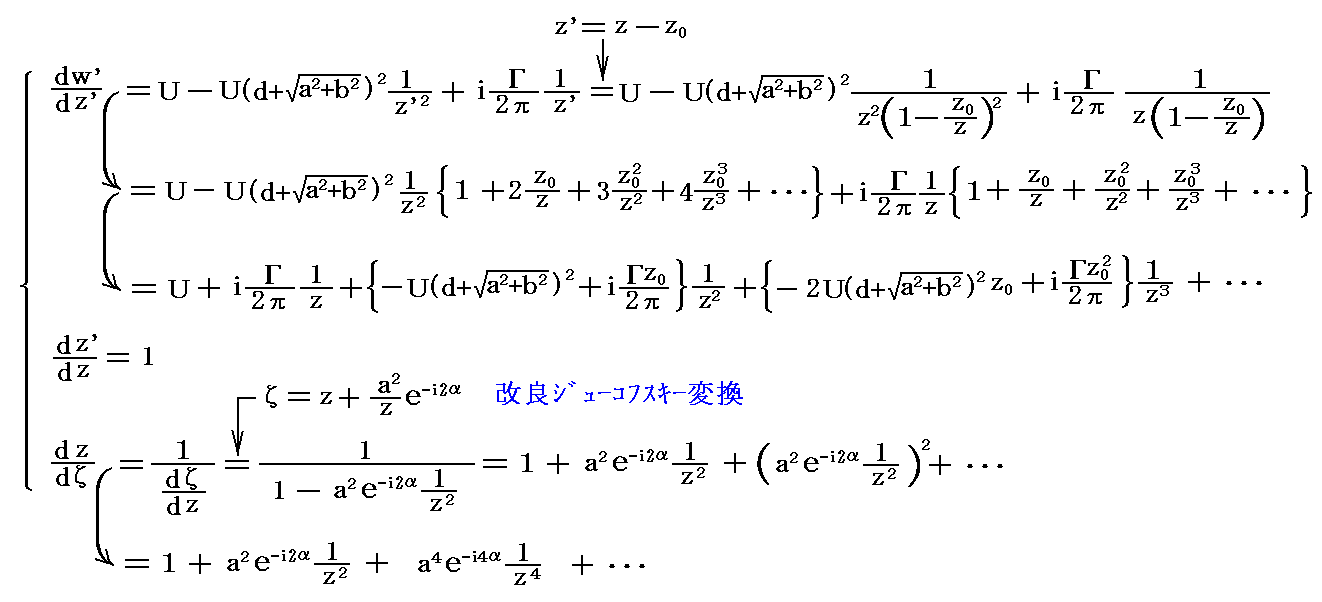
������
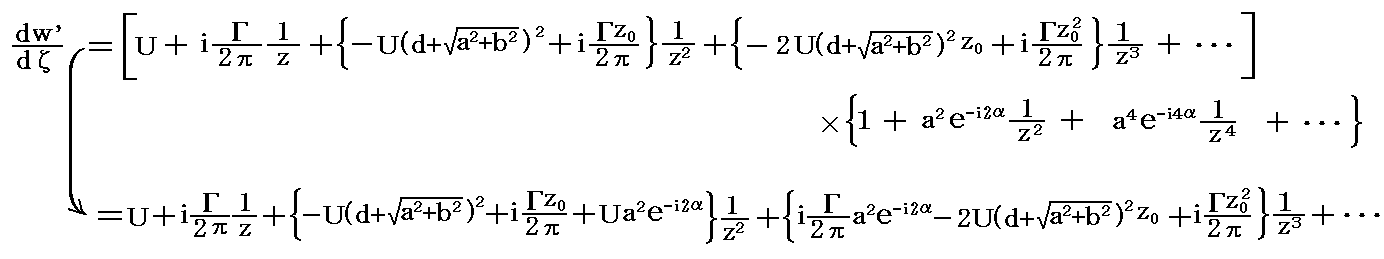
�ƂȂ�B������悷���
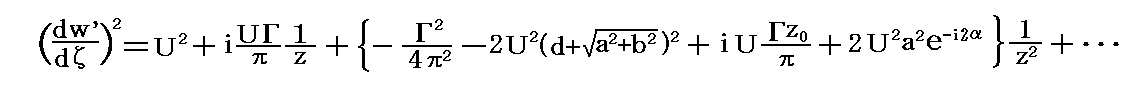
�ƂȂ�B������u���W�E�X�̑������ɑ�����ė��ɓ������͂����߂��

�ƂȂ�A�������_��������B
�R�D�W���[�R�t�X�L�[���ɂ͂��炭�͂̃��[�����g
�@�W���[�R�t�X�L�[���ɓ������_�̎������͂̃��[�����g���S�D�i�Q�j�R�D�ŏq�ׂ��u���W�E�X�̑�������p���Čv�Z���Ă݂�B���̂Ƃ��p���镡�f���x�|�e���V�����̓W���[�R�t�X�L�[�����`����Ă���ϊ���̃ĕ��ʂɂ����邗�f�i�āj�ł��B�O���m�⑫�����P�n�ŋ��߂��i�����f�^���āj2���u���W�E�X�̑������ɑ������ƌ��_�̂܂��̗͂̃��[�����g��
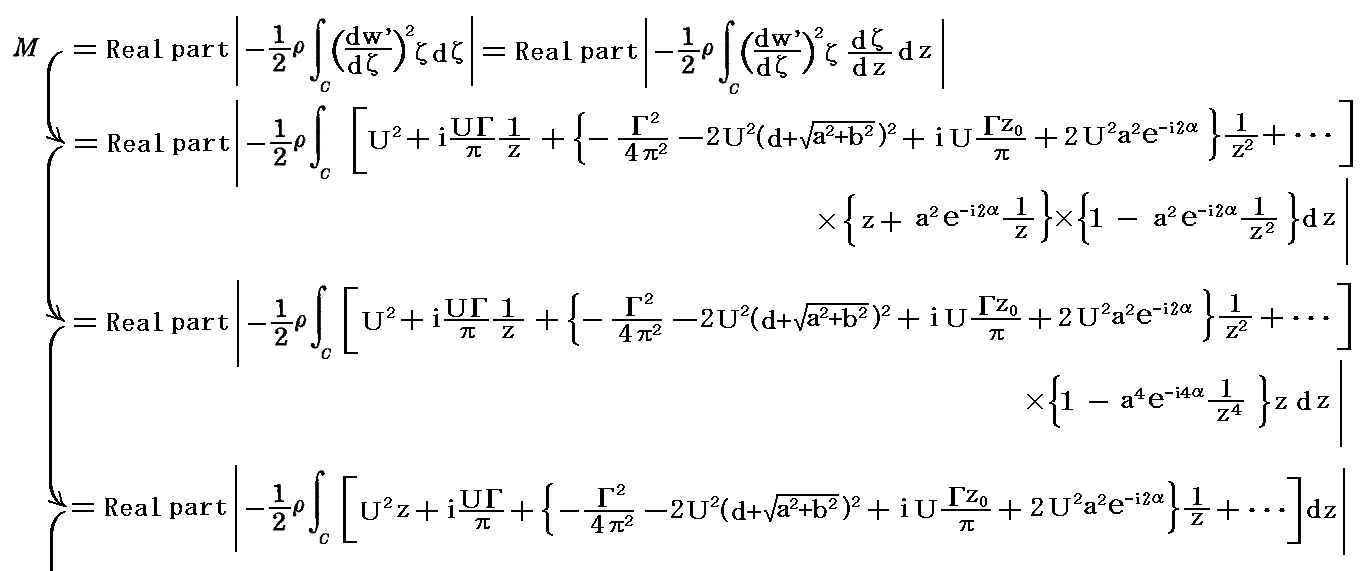

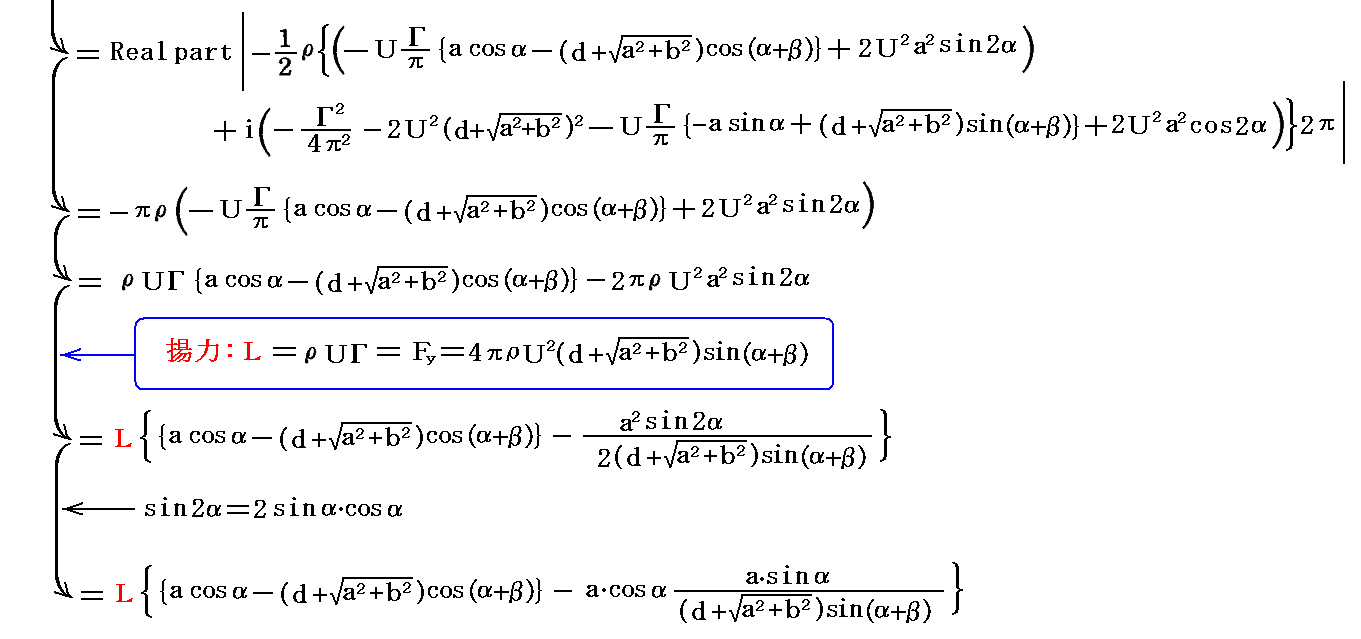
�ƂȂ�B����͌��_�̎���̃��[�����g�ł����āA���ʂ̖{�̃��[�����g�̒�`�m�O���̎���n�ƈႤ�̂Œ��ӂ��Ă��������B
�@���̈Ӗ��́A�����P�A����0.1���A����0.15���Atan�������^����0.1�A����20���̏ꍇ�����������̐}����ǂݎ���Ă��������B
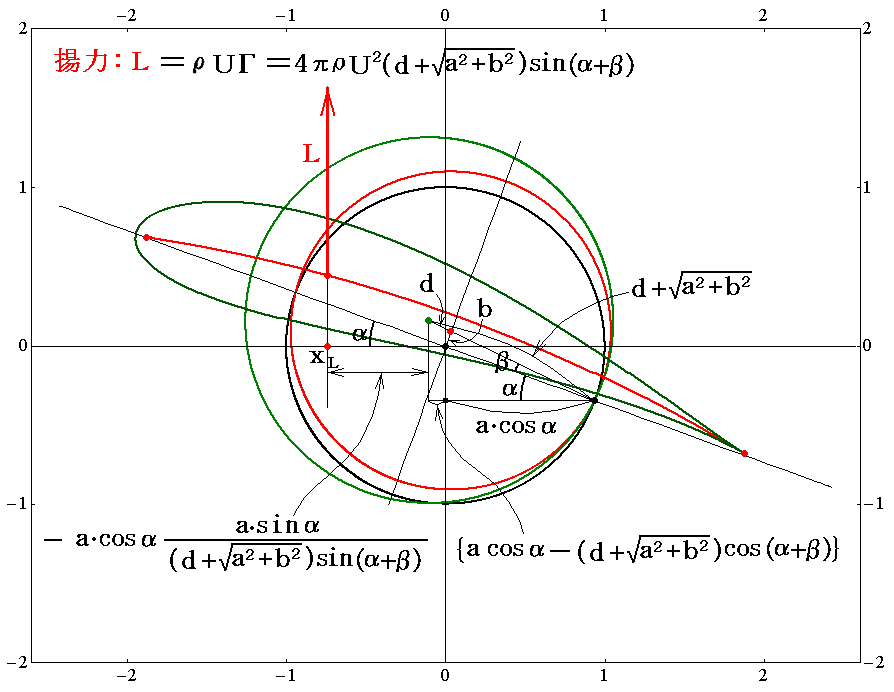
�@���̂Ƃ��A�g�͂̍�p����_�̂����W��L���}���p�Ƌ��ɂǂ̗l�ɕω����邩���O���t�ɂ��Ă݂�B�L�����o�[��ς����Ƃ��̕ω��̗l�q�͕����Ƃقړ����Ȃ̂ŁA�����ł̓L�����o�[�����Œ肵�ė�������ς������̂��d�˂ĕ\���Ă���B
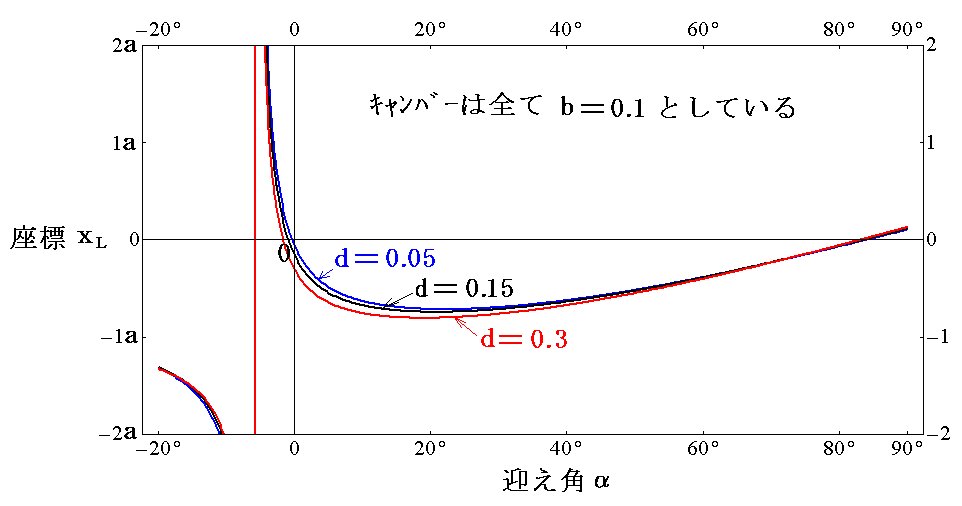
�@�g�͂̍�p�_�m���͒��S�n�̈ړ��Ɋւ��āA�����̕ω��̓L�����o�[�̕ω��قǂ̌����ȈႢ�͐����Ȃ����A�~�ʗ��ƈ���ė��Ɍ������L��ƌ}���p���[���̎����炷�łɐ^���O���Ɉړ����Ă���B�}���p�𑝂₷�ƁA���������قǂ��O���Ɉړ�����B
�@��[�����Ώ̗��ɂ��ď�L�̃��[�����g�̎���
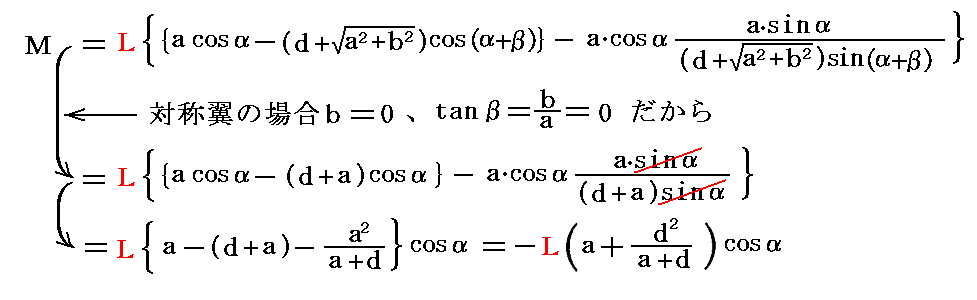
�ƂȂ�B����͌}���p�����ς���Ă����͒��S�͗����̑O����25���̏��ɌŒ肳��邱�Ƃ������Ă���B����͕����̏ꍇ�Ɠ����ł��B�m���}�Q�Ɓn
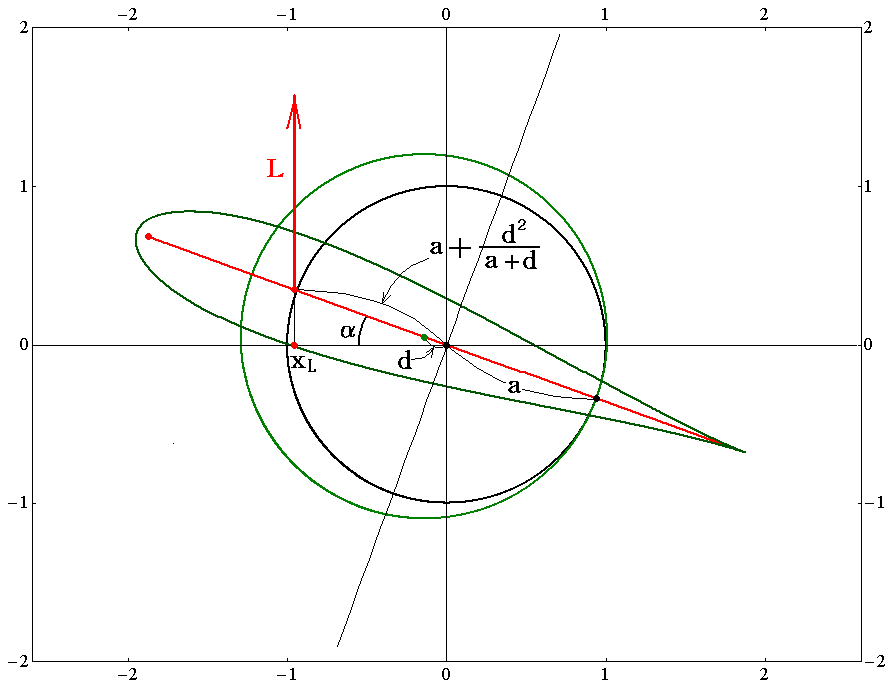
�m�⑫�����Q�n
�@�U�D(�X)�Q�D�Ő��������悤�ɁA�ĕ��ʏ�̔C�ӗ��^�̊O���̈���A�����ʏ�̉~�̊O���̈�Ɏʑ������͊��ā����i���j�͕K�����݂���
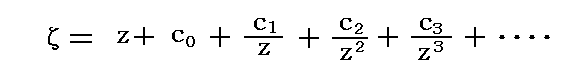
�̌`�ŕ\�����B�mRiemann�̎ʑ��藝�n
�@���̂����V�D(�S)�Q�D�m�⑫�����P�n�̎��W�J�����ǃW���[�R�t�X�L�[�ϊ���p����������L�̖����������ɒu��������A�����ƑS�������菇���C�ӗ��^�ɓ����g�������[�����g�����߂邱�Ƃ��ł���B���̂Ƃ����̓W�J��ǂ��Ă݂�Ζ��炩�Ȃ悤�ɁA���������̕ϊ����̂����ƂP�^�����̌W���̂ݍŏI�I�Ȍ��ʂɊW���Ă���B���̂��ߔC�ӗ��^�̗g�͂ƃ��[�����g�̕\���̓W���[�R�t�X�L�[���̏ꍇ�Ɠ����悤�Ȏ��ɂȂ�B�m�Q�l�����Q�D�A�U�D�A�P�S�D�����Q�Ƃ��ꂽ���n
�S�D���͕��z
�@�V�D(�Q)�S�D�̕����ōs�����c�_����ʉ�����悢�B�����Ő��������悤�ɁA�~����̓_�̑��x�͓�̗��ݓ_�`�`�f�����Ԓ������炻�̓_�܂ł̍��������~�̔��a�Ŋ�����2�t���|�������̂ɓ������B�����藧�B�����ł̎��̂������{�i��2�{��2�j0.5�Œu�������A����(���{��)�Œu��������悢�̂�
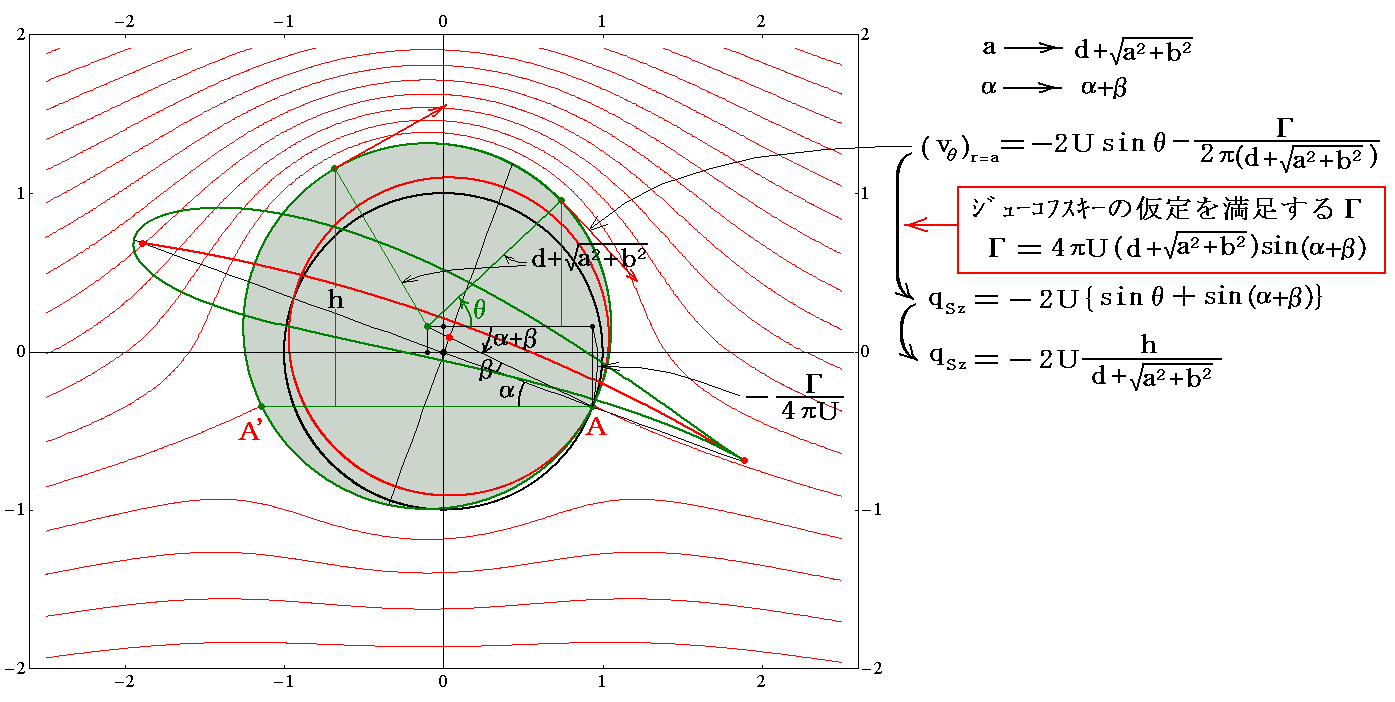
�ƂȂ�B�����ł����͎ʑ���̃W���[�R�t�X�L�[���̌}���p�ł���A�W���[�R�t�X�L�[�̉����ɂ�����z�����p(���{��)�Ɍ��т����Ă���B
�@���~�\�ʂ̑��x�̑傫����sz�ƕϊ���̗��\�ʂ̑��x�̑傫����s���̕ϊ����́A�����ł��������ǃW���[�R�t�X�L�[�ϊ���p����̂ŁA���l�ɂ���悢�B�܂�
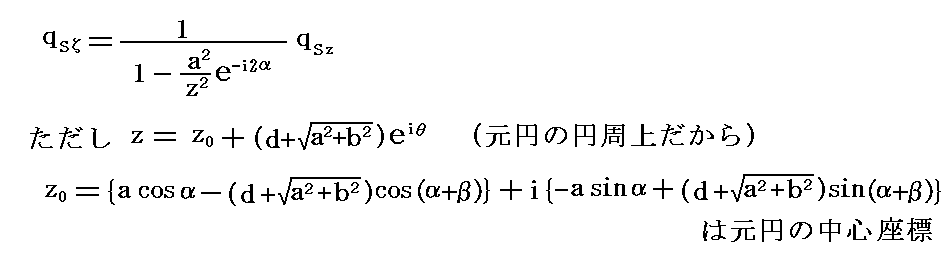
���v�Z����Ηǂ��B�������v�Z�͖ʓ|�����炱���ł͂��Ȃ��B
�@���l�ɁA(���C���j����(�́C�Łj�ւ̍��W�ϊ���
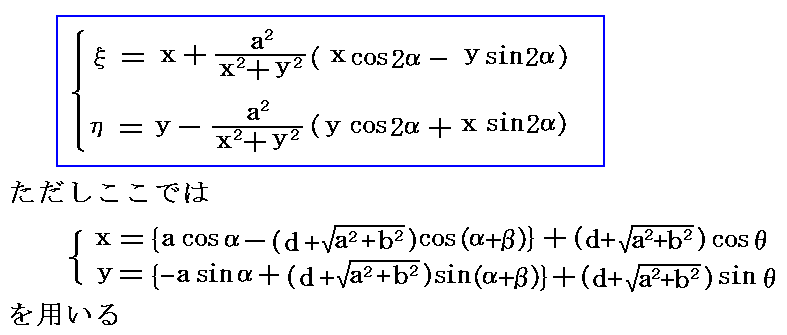
�@�������A���ۂ̌v�Z�͂��Ȃ�ʓ|�Ȃ̂ňȌ�̐����͏ȗ����܂��B�V�D�i�U�j�T�D�Ŏ��ۂ̗��̑���l��������Ă���܂��̂ł�������䗗�������B
�@
�i�T�j�����̌��\
�P�D�����̌`���R
�@�����ŋc�_���Ă���N�b�^�E�W���[�R�t�X�L�[�̗���ł́A���͒�R�������ɗg�͂���������B����́u�_�����x�[���̔w���v�Ƃ��Ēm���Ă���S���i���C�j�̂Ȃ��|�e���V�������̓����ł����A���ۂ̗���ł����炩�ȕ\�ʂ��������`���^�̏ꍇ���̏��قڎ��������̂��m���߂邱�Ƃ��ł���B
�@������ۂ��߂ɕ����̕������ς��ɍL����ꂽ�����������}�̗��ƃ��C���[�̒�R���قړ����Ȃ̂ł��B����͋����ׂ����ł��B���͐�[�Ńςt2�^�Q�̃I�[�_�[�ň��͂����邪�A����͗��̌㕔�őO�����ɓ����Ă��鈳�͂Ƃ荇���āA���̒�R�͂قƂ�ǑS�Ă��\�ʖ��C��R�݂̂ƂȂ�B����݂��`���������C���[�͌���ŗ���̔���������������B���ʂƂ��Ē�R�̓ςt2�^�Q�ƑO�ʂ̖ʐς̐ςɂقړ������Ȃ�B���Ӑ[�����ꂽ���̕��O�ꂽ�����ɂ͋��������B
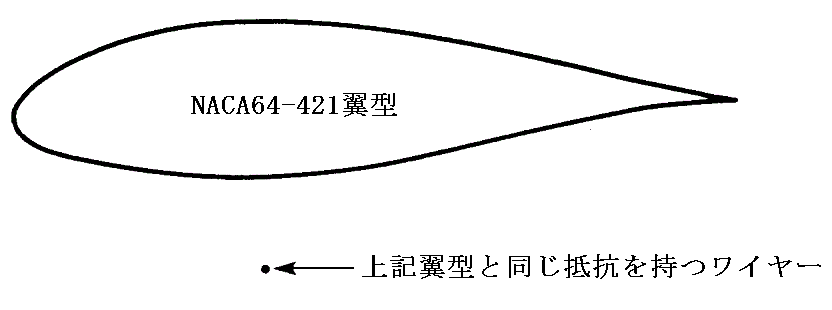
�@���̎�������A�����̔�s�@�����Ƃ��ׂ��Ă������̌��݂𑝂����Ƃ���R�傳����̂ł͂Ȃ����Ƃ������O�͊Ԉ���Ă������ƂɂȂ�B���̎��������炩�ɂȂ�A���̑O�����Ɋۂ݂��������������̗L�����������炩�ɂȂ�̂�1910�N��̌㔼�ł��B���̓�����͕ʍ��u�����_�̉萶���v�T�D�i�P�j�Łm�⑫�����R�n���܂������A�����ł��������ڂ���������܂��B
�Q�D�O�����̔���
�@�����̍ő�̌��\���U�D�i�W�j�S�D�Ő��������悤�ɑO��������闬��̈��萫�ւ̊�^�ł��B�O�����͂��Ƃ��ƃW���[�R�t�X�L�[�̉�������闬������������邱�Ƃ͂ł��Ȃ��̈�ł�����A���̕����̗���̑��x���z�∳�͌��z�����������Ċ��炩�ȗ���ɂ��邱�Ƃ͂���߂ďd�v�ł��B
�@�����̕�����~�ʗ��̗l�������ł͑O�����ɉQ�̖X�q�i7.(1)4.�m�⑫����2�n�j���ł��āA�����呬�x���z�△���刳�͌��z������Ă��܂��B���C�m���Y�����Ⴂ�̈�ł́A���̗l�ɂ��ĕs�s�����������Ă��܂��B�������A���ۂ̔�s�Ɠ����������C�m���Y���ł͏����Ȍ}���p�ł������ł͑O���ŗ���̔����������āA���̐��\���ቺ���܂��i���̂��Ƃɂ���7.�i6�j5.�m�⑫�����P�n���Q�Ɓj�B�����̕����ł͒�C�m���Y���ł̎��������ł��Ȃ������̂ŁA���̔����̐��\�ቺ�͌��m����Ă��܂���ł����B
�@��������̏ꍇ�A��C�m���Y���̗���ł͏����Ȍ}���p�ł����Ă����邱�Ƃő�K�͂Ȕ������������w�������A���O���t�߂ɐ��������B�O�������A������ƒ�R��傫���Ȃ�A�g�͌W�͏������Ȃ�B�w�������A�Ƃ́A�w�����E�w������������ɗ����ɑJ�ڂ��ĕ\�ʂɍĕt�������Ƃ��A���̔����_����ĕt���_�܂ł̔����̈���Ӗ�����B�����������ꂪ�ĕt�����Ȃ��Ȃ錻�ۂ��w�������A�̕���ƌ����錻�ۂł��B�{���͌����̕����L���Ȃ̂ɁA��C�m���Y���Ő����邱�̌��ۂ̂��߂Ɍ����̗L�������Ȃ��Ȃ���������Ȃ������B
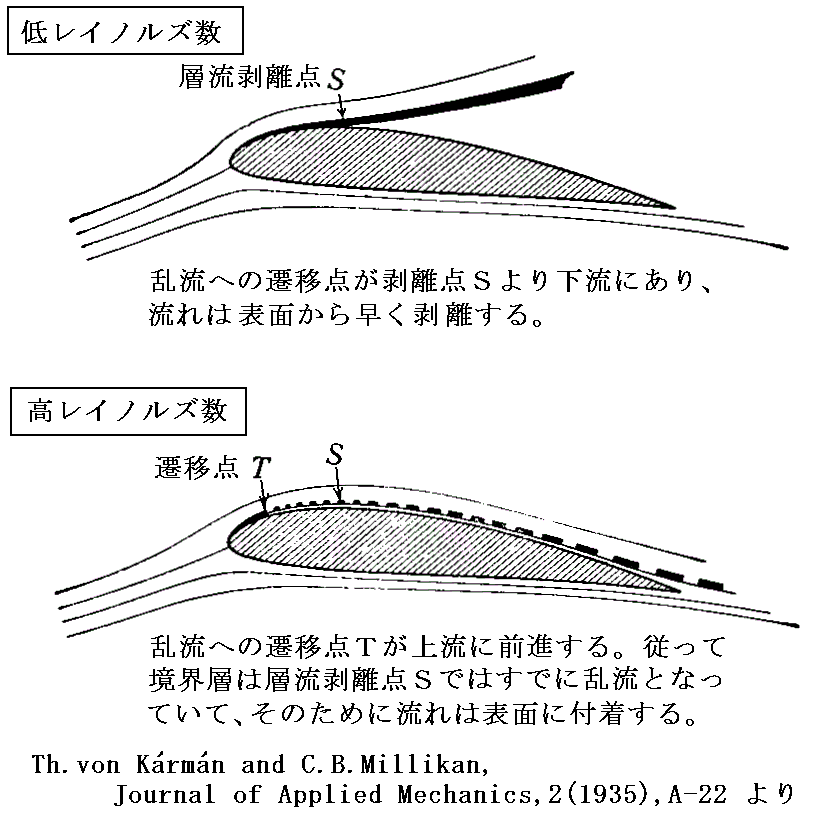
�@���̎����́A�w�����E�w�Ŕ������Ă������̂��A���C�m���Y�����グ�āi�܂藬�����グ�āj�������E�w�ɂ���Ɣ������h����鎖�������Ă���B
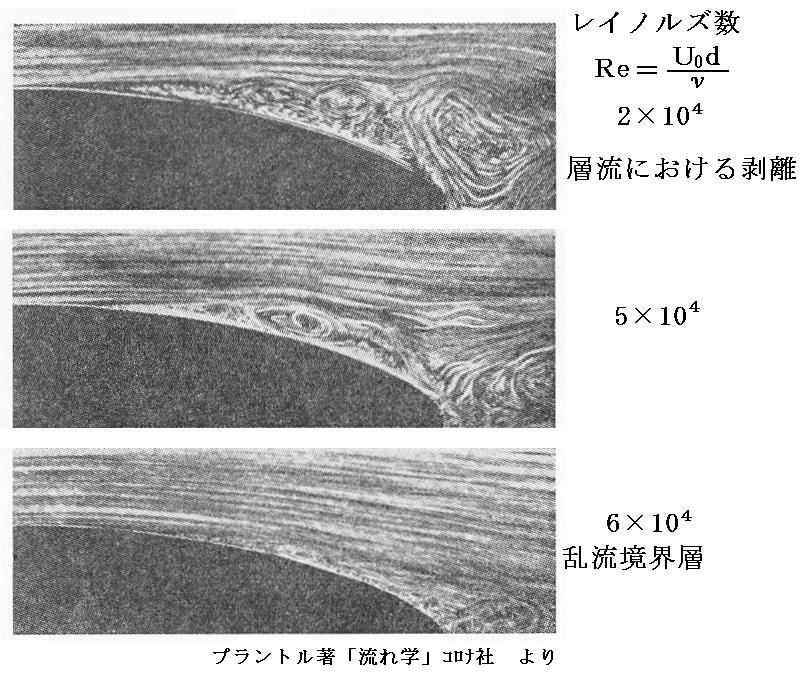
�@���̎ʐ^�͓������C�m���Y���̗���̒��ɒu���ꂽ���̎���̗���������Ă���B��͋��E�w���w���̏ꍇ�ő��߂ɔ������Ă���B���̎ʐ^�͑w�������_�̂킸���O���ɐj���̗ւ������t�������̂ł��B�j���͋��E�w�ɗ����^���ċ��E�w�𗐗��ɑJ�ڂ����܂����A��������Ɣ����_����ނ��鎖�������Ă���B���̌㕔����o���ꂽ���ɂ���Ĕ����͈̔͂����܂�̂����ĂɎ�����Ă���B
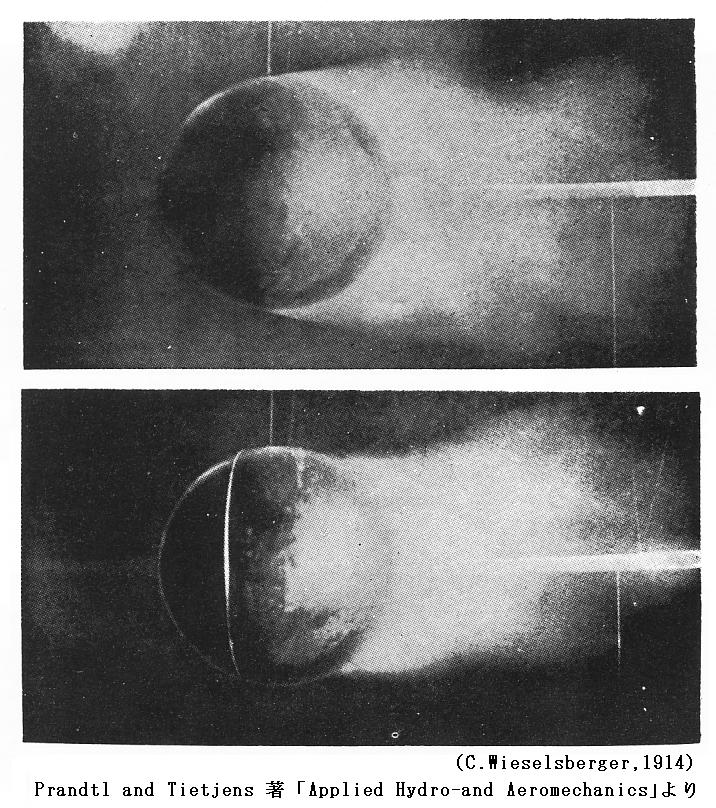
�@�t�����X���G�b�t�F����1912�N�ɁA���̎���𗬂�闬��̃��C�m���Y��������l����ƁA��R�W�����}���Ɍ������邱�Ƃ����܂��m�ʍe�̐}�Q���n�B
�@�m�G�b�t�F���̎����ɕt���Ă�����19�D��3-4�Q�Ɓn
�@�v�����g���͂��̗��R����������L���Ș_����1914�N�ɔ��\���܂��B������g�w���̋��E�w�͉^���G�l���M�[���R�������ߕ\�ʂ��瑁���������邪�A���C�m���Y���������Ɨ������E�w�ɑJ�ڂ��ċ��E�w���̌��������������̂��߂ɔ����_�ɂ����鞶����Ȃ��������悩�痬�̂������ċ��E�w�����̂ɗǂ��t������悤�ɂȂ�B���̂��ߔ����_������Ɉړ����Ĕ����̑傫�����������Ȃ��R�W������������h�Ƃ������̂ł��B��̎ʐ^�̓v�����g���̒�Ăɏ]���ă��B�[�[�X�x���K�[���s���������̘_���i1914�N�j�ɍڂ��Ă���L���Ȏʐ^�ł��B
�@�m���B�[�[�X�x���K�[�̎����ɂ��Ă�����19�D��3-6�Q�Ɓn
�@[�]�k�ł����A���B�[�[�X�x���K�[�͌�ɗ����i1922�N�`1932�N�j���āA���{�̍q��H�w�i���ɕ����Z�p�j�̔��W�ɑ���Ȍ��т��c���Ă��܂��B]
�@������������Ɣw��ɐ�����Q�̈�i������j�̈��͂��Ⴂ���߂ɑ傫�ȍR�͂������܂��B���̂��ߔ�����h�����Ƃ͂���߂ďd�v�ł��B���ۂ̏��A��s���C�m���Y���ŗ����̑啔���ɓn���đw�����ێ����邱�Ƃ͍���ŁA�����i�K�ŋ��E�w�͗����ɑJ�ڂ��܂��B����͏����̌����Ŗ��炩�ɂ��ꂽ�d�v�Ȏ����ł��B
�@
�@��C�m���Y���ł͊m���Ɍ����̕��������������\�͗ǂ��Ȃ��̂ł����A���ۂ̔�s�ł��������C�m���Y���̈��ł͏\���Ɋۂ݂�тт��O�����������̕������炩�ȗ���������ł��A�O���ł̔������N���ɂ����Ȃ�܂��B���̂��ߍ����p�܂ł��̗g�͂�ێ����邱�Ƃ��ł��܂��B���̑傫�ȋp�ł̈��萫�͔�s�@�̏㏸����^�����ɑ��ėL���ɓ����܂��B
�@�����Œ��ӂ��ė~�������Ƃ́A�S���ɔ������E�w�̈�̒��œ�������N�����Ă���̂ł����A���E�w���̂͂ƂĂ��������̂悤�ȗ̈�Ȃ̂ŁA����̔������N����Ȃ�����A���̊O���̗̈�̗���́A�����ŋc�_���Ă��铙�p�ʑ��̐��w�I�e�N�j�b�N���g�����k���E���S���̂̂������������ł���ƍl���ėǂ����Ƃł��B�܂��A���c�_���Ă��锍���̗L���Ő��������͒�R�̈Ⴂ�ƁA�w�����E�w���������E�w���̈Ⴂ�Ő����闃�\�ʂ����C��R�̈Ⴂ�m�V�D�i�U�j�U�D�Ő�������n���������Ȃ��ł��������B
�@���̌����̗L�����́A1910�N��ɃW���[�R�t�X�L�[��v�����g���̈��ɂ�萸�͓I�ɍs��ꂽ�����i�W���[�R�t�X�L�[���j�����_�I�����ƁA���C�m���Y���̏d�v���̗������i���E�w�̑w�����痐���ւ̑J�ڂ̐U�镑���������̗���ɑ傫���e�����邱�Ƃ������Ă�����Ɏ����I�ɓ���ꂽ�����̐��\�f�[�^���疾�炩�ɂȂ������Ƃł��B
�@���ۃG�b�t�F����v�����g�����ɂ���āA���E�w�̑w�����痐���ւ̑J�ڂ�����ɋy�ڂ��e���ɂ��Ă̏d�v�Ȕ��������X�ƍs����̂�1910�N��ł��B�L���ȋ��E�w�̗����J�ڂɂ�蔍�����N����ɂ����Ȃ錻�ۂ̔�����A�J���}���̉Q��̌����͂��̎���̂��̂ł��B
�@��L�̋��E�w�̔����A�w���Ɨ����̈Ⴂ�A�����ɉe�����郌�C�m���Y���̌��ʂȂǂ̉𖾂ɂ́A���̎���̕����Z�p�̐i�����[���ւ���Ă��܂��B�����Ɋ֘A���������[������������19�D��3�́g�V������C�͊w���_�̒a���h�ɗL��܂��̂ł����������B
�@���}��1917�N�Ƀv�����g�����v�������Q�b�e�B���Q��298���^�̋ɋȐ��}�ł����A����̓��C�m���Y��2.1�~106�Ƃ����[�������l�ōs��ꂽ���̂ł��B�����̃h�C�c�̕\�L�@�Ȃ̂Ő��l�͍�����100�{�ɂȂ��Ă���A�L���������̂��̂ƈ���Ă��܂����A�����̗D�ꂽ���\�������Ă���B
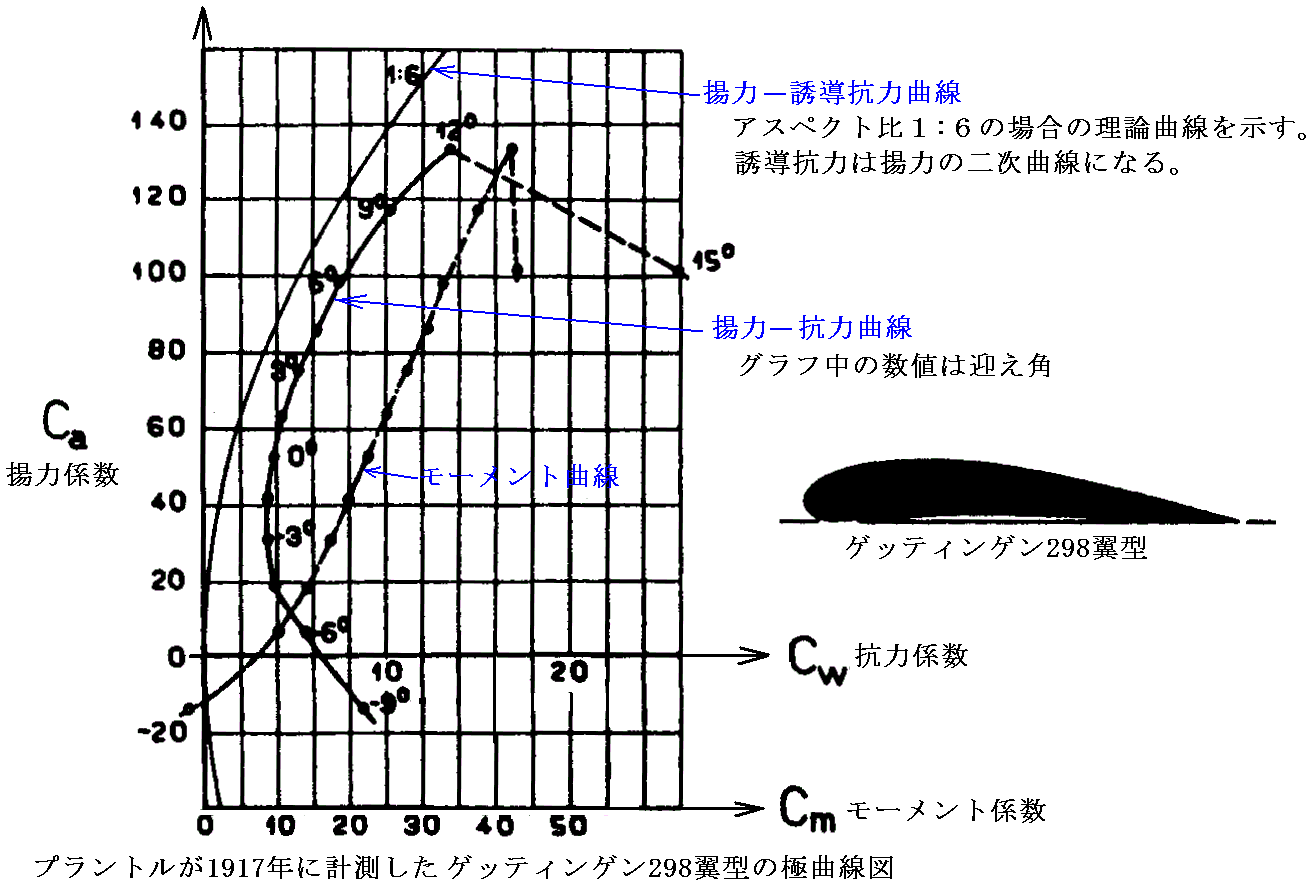
���̃O���t�̈Ӗ��͂��̐ߍŌ���V�D�i�T�j�T�D�g�����\�\�L�@�h���Q�Ƃ��ĉ������B�����̂bL�������̂b���A�bD���bW�A�bM���bm�ɑ������܂��B
�R�D�����@�̓o��
�@�L���Ȑv�҂ł���A���\�j�[�E�t�H�b�J�[�͒����ɏ�L�̊v�V�I�Ȕ����ɒ��ڂ��āA13���̌��������Q�b�e�B���Q��298���^��V�^���t�H�b�J�[�cr�D�T�ɍ̗p���܂��B���ꂪ�u���b�h�E�o�����v���ƃ}���t���[�g�E�t�H���E���q�g�z�[�t�F���̓���@�Ƃ��ėL���ȎO�����@�ł��B�m�g��ʐ^�n[���P�x���j�^�[�p]�A�@�@[�ʎʐ^�P]�A�m�ʎʐ^�Q�n

�t�H�b�J�[�cr�D�T�̎O�ʐ}�m�g��O�ʐ}�n
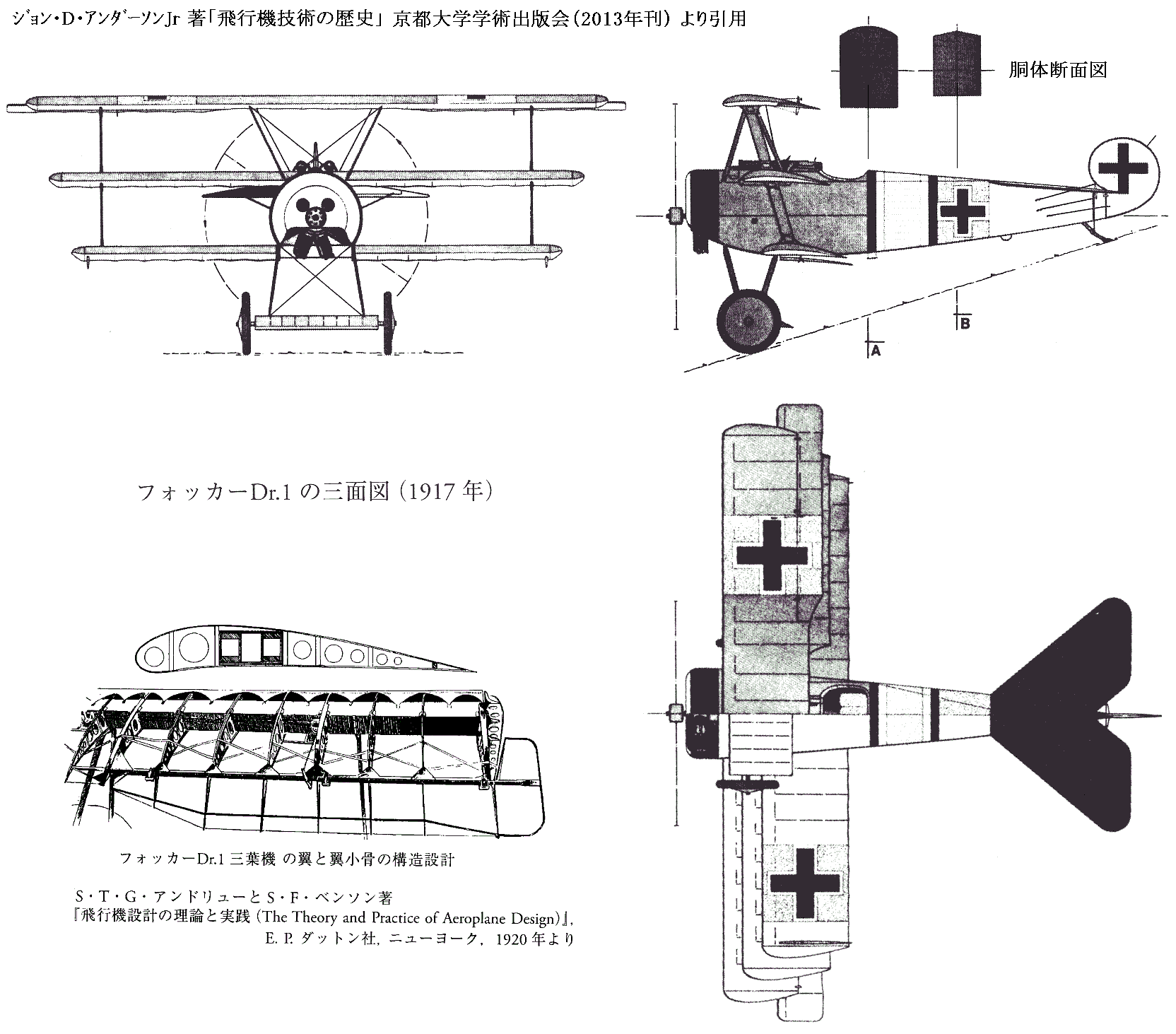
�@���̋@�̂͌������̗p�������ƂŕЎ������̍\���Ń��C���[�⋭���s�v�ɂȂ�A�R�͂�ጸ���邱�Ƃ��ł����B�܂����̑傫�ȍő�g�͌W�����甲�Q�̏㏸���Ɖ^�������������͑傢�Ɋ����B�������A�O�����ɂ͍\���I�Ȗ��������莋�E���������c���萫���ǂ��Ȃ������̂�1918�N�̔��[����͐V�^�@�ɓ���ւ��ޖ����Ă����B
�@���Ȃ݂Ƀt�H�b�J�[�c���D�T�̃G���W���̓v���y���ƃG���W������̂ƂȂ��ĉ�]���ăG���W��(9�C���j���p�������[�^���[�G���W���ł��B�����ł͗p�����邱�Ƃ͂���܂���ꎟ��퓖���ɂ͑����̋@�킪�̗p���Ă����B�ʐ^������J�E�����O�����ɏ��������Ă���V�����_�[����]���Ă���l�q������������B
�@�t�H�b�J�[�͂���Ɍ����̗L������Nj������t�H�b�J�[�c�D�Z�̐v��1917�N�㔼�ɊJ�n����1918�N4���ɏA�q�����܂��B���̋@�̂́A�����̗D�ꂽ��C�͊w�����ɂ��A����E�ᑬ�ł��������ɂ����A�D�ꂽ�㏸�����Ɖ^���������������c�̂��₷���@�̂ł����B��ꎟ���E��풆�ɓo�ꂵ���h�C�c�@�̒��ōł��D�ꂽ�@�̂Ƃ݂Ȃ���Ă���B���̗D�G���͒�틦���S���ɋL���ꂽ�h�C�c����A�������Ɉ����n����v�����ꂽ�푈�@�ނ̃��X�g�ɔ�s�@�ł͗B��t�H�b�J�[�c�D�Z�����邱�Ƃ��������B
�@���}�̓t�H�b�J�[�c�D�Z�̍\���}�m�g��\���}�A�c�D�Z�̎ʐ^�n�ł����A������̒����̒��菄�炳�ꂽ�����Ȕ������t�@�Ɣ�ׂ�ƁA�͂邩�ɐ������ꂽ�������@�̂ł��邱�Ƃ�����B
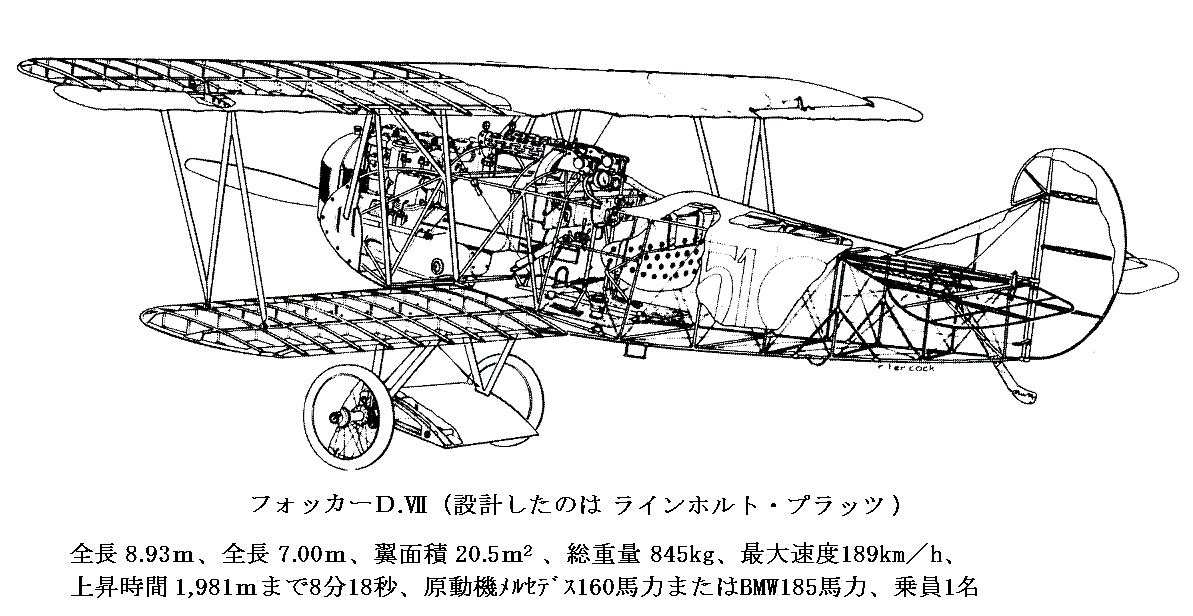
�t�H�b�J�[�c�D�Z�̎O�ʐ}�m�g��O�ʐ}�A�G���W���J�E�����n
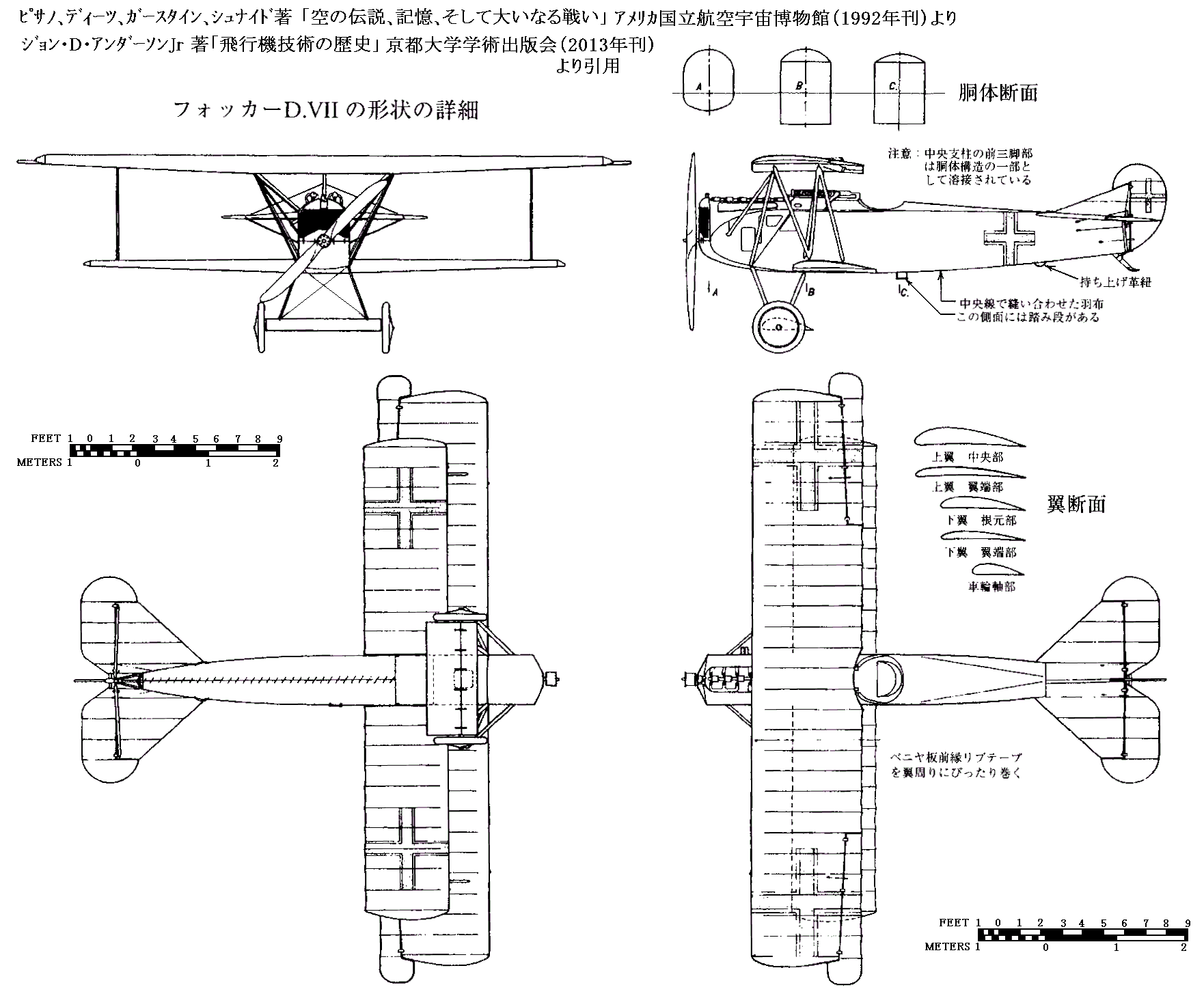
�@�����ɂ���Ό��ƃ��u�Ɨ��ʂł��̌`��Ƌ��x��ۂ��Ƃ��ł��邽�߂Ɏx���⒣�����s�v�ɂȂ�B���̂��ߋ�C��R�����Ȃ��A���E�̗ǂ��P�t���@�ɂł��܂��B����ɁA���̒��ɔR���^���N��A�������p�̎ԗւ����[������A�G���W���ڗ��Ɏ��t���邱�Ƃ��ł��܂��B�P�t�Ō������͔�s�@�̍\���Ɋv���������炵�܂��B
�@��ꎟ���E���܂łɓo�ꂵ����s�@�̂قƂ�ǂ͔����̕��t�@�ł������A���͂قƂ�ǂ������P�t�����̗p���܂��B���̌������̗p����Ƃ����Z�p�v�V�͖��炩�Ƀv�����g�������͂��߂Ƃ��闬�̗͊w���Ƃ̗��_�I�E�����I�����ɗR��������̂ł��B�����ɂ������čq�̗͊w�͊w��I�ɂ����p�I�ɂ��傫�Ȑ��ʂ��グ�n�߂܂��B
�����̎v�z�ɂ�������20�ɋ����[���L�q���݂��̂Œlj����p�B
�S�D���������E�ϖ��x�����E����^����
�@���̗��_�I�E�����I�������i�ނɂ�ă��C�m���Y���̏d�v�����܂��܂����炩�ɂȂ��Ă��܂��B����Ɠ����Ɏ��������̋C���Ɋ܂܂�闐��̉e���������Ă��܂��B
�@���p���̎���Ŏ��ۂɋN���邱�Ƃ𐳊m�ɍČ�����ɂ́A����̏��Ȃ����炩�ȋ�C���𑗂�o���������K�v�ł��B���ۂ̂Ƃ��돉���̕����ł͗���Ɋ܂܂�闐��̑召���A�������ʂɑ傫���e�����Č�������_�����Ƃ������������̂ł�����B
�@����ɑ�Ȏ��͎��ۂ̔�s�ɂ����郌�C�m���Y���Ɠ������Ȃ�悤�ȕ������������邱�Ƃł��B���C�m���Y����

�Œ�`�����ʂŁA�t0�͗����A���͋@�̂̑傫���ɊW���鋗���A�˂͓��S���W���i�S���W���ʂ𗬑̖��x�ςŊ��������́j�ł��B���ۂ̔�s�ɂ����郌�C�m���Y���͉��}�̗l�ȗ̈敪�z�ƂȂ�܂��B

�@���Ȃ݂ɂP�C���̋�C�̓��S���W���ƔS���W���͉��}�̗l�Ȓl�ł����A���x�ɂ�肩�Ȃ�ω����܂��B
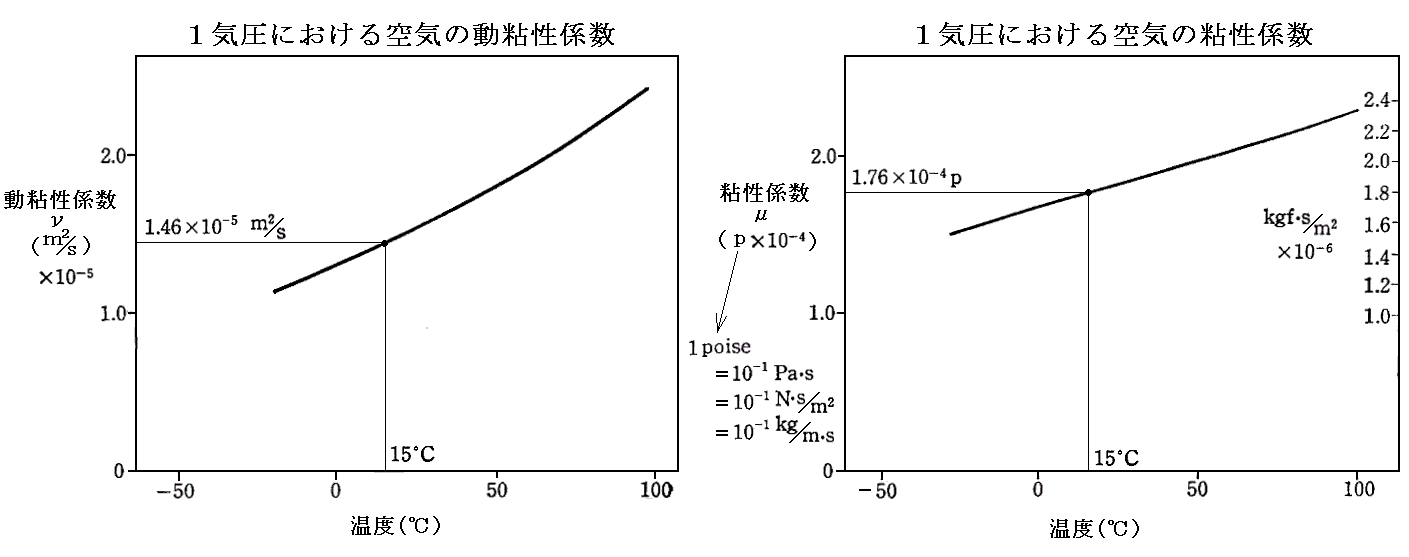
�@�����Ŏ��������͌^�͈�ʂɎ����������Ȃ菬���Ȃ��̂��p�����܂����烌�C�m���Y���͂ǂ����Ă��������Ȃ��Ă��܂��܂��B���ۂ̃��C�m���Y���ł̎������������邽�߂ɂ́A�m�C���̕������グ��n�����m���S���W��������������n�����m�����͌^�̃T�C�Y��傫������n��������܂���B
�m���������n
�@�����̍������ɂ��ẮA�����̑傫�ȕ��������X�i�Q�b�e�B���Q��52���^���A�A�����J72���^���A���X�N��80���^���j�ƍ���܂��B
�@���}��1916�N�ɃQ�b�e�B���Q���̃v�����g���̏��ɍ��ꂽ�����Ƃ��Ă͋��ٓI��52���^���i187km/h�j�̋C�����x���o����{�i�I�ȉ^�����ł��B�m�Y���̑O�Ƀn�j�J���\���̖Ԗڂ�ݒu���āA���������ꂽ����̏��Ȃ��C����������悤�ɂ��Ă���B�m�S�̐}�n
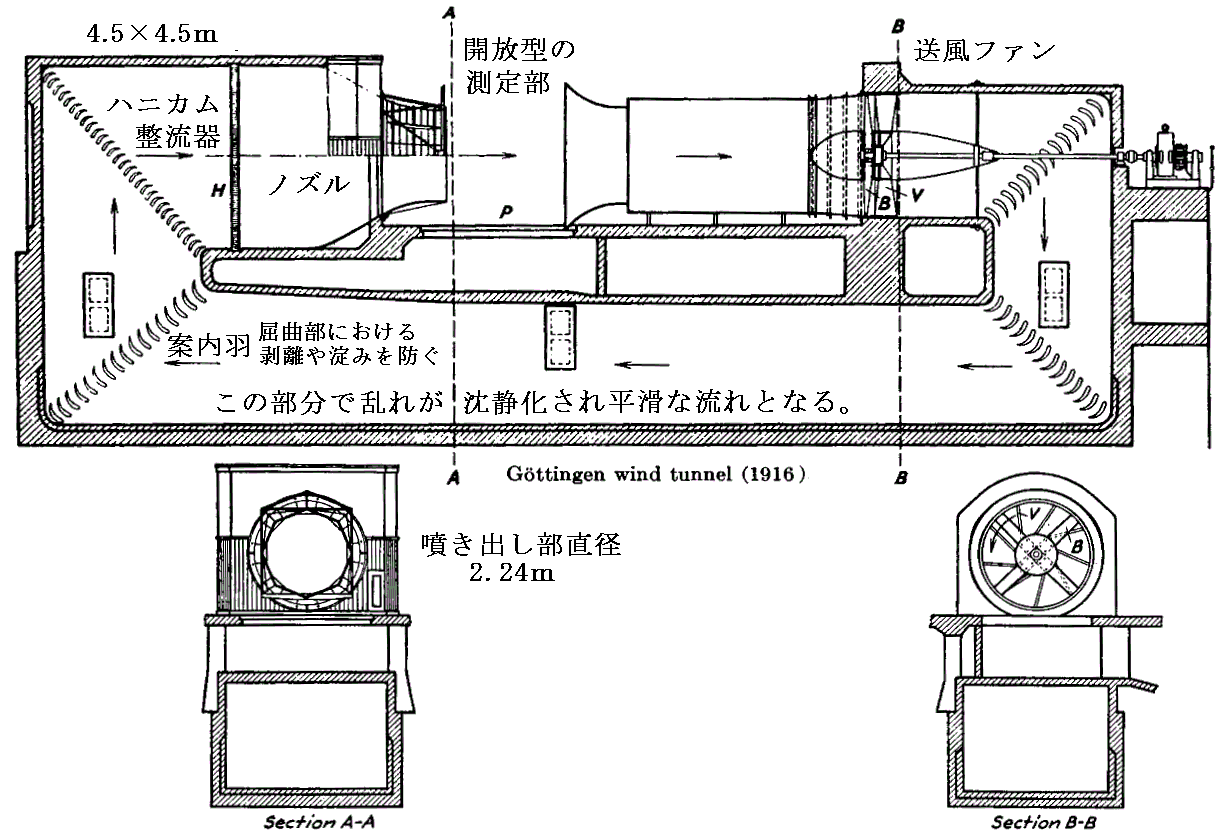
�@����͓����ŐV�s�̕����ő����̐��ʂ��グ���B����͑��蕔���J�������J�������^�̋@�\���̗p���Ă���A�����͌^���Œ�ǂň͂�������܂ł̕��������D��Ă����B
�@�܂������t�@���ɂ�蝘�����ꂽ�C���o�m�Y���Ɏ��鏙�X�ɑ����Ȃ��L�̒���ʂ����Ƃŗ���̏��Ȃ������ȗ���ɂ��邱�Ƃɐ��������B
�@����ɕt��������ƁA�����t�@���̑O�ɐݒu����Ă���g�U�^�~���idefuser�j�̓G�b�t�F���̉��ǒ�Ă����ꂽ���̂��Ǝv���܂��B
�@�����̉��Ǔ_�́A�v�����g����1908�N�ɍ�����ŏ��̕����Ɣ�r���Č�����Ɨǂ��ł��傤�B
�@������ɂ��Ă��A���̌`�͌�̂قƂ�ǂ̕����ɓ��P�E�̗p����āA�����\���̎�{�ƂȂ�܂��B
�m�ϖ��x�����n
�@���S���W���̏������C�̂�p������@�ł����A�S���W���ʂ͖��x�i���́j�ɂ���ĂقƂ�Ǖω����܂���̂ō����̋�C��p���Ė��x��������Γ��S���W���˂����������邱�Ƃ��ł��܂��B
�@���}�̓����N���v���āA1922�N10������^�]���J�n�����A�����J�̃����O���[�������̉������ϖ��x�����ł��B���o�����a1.52���A����20���^���ł��������A�e������͂�20�C���܂ŏグ�邱�Ƃ��ł����̂ŁA�P�^20�k�ږ͌^��p���������ł������僌�C�m���Y����B���ł����B
�@���̕����̋�C�z���t�@���̑O�Ɋg�U�^�̉~���idefuser�j��ݒu���Ă���̂́A���炩���G�b�t�F���̕����Ɏ{���ꂽ�H�v��������邱�ƂŁA�����̑���ƋC���̈��艻��}���Ă���B�����N���ݐЂ��Ă����Q�b�`���Q���̃v�����g���������ł̓G�b�t�F��������defuser�̗L�����͑�������F�����Ă����悤�ł��̂Ń����N������������ꂽ�̂ł��傤�B
�@�܂��A���̕����̑��蕔�������~���ǂň͂܂�Ă������A���ǂ̉e����h�����߂Ɍ�ɊJ���^�ɉ��ǂ���܂��B���E�}�͉��nj�̒f�ʐ}�ł��B

�@���̕����͎��ۂ̃��C�m���Y�������ŗ��^���s�@�`��̎������\�ȍŏ��̕����ł������̂ŁA���̕��������ݏo���f�[�^�Q�͂��̌�15�N�Ԃɓn���ĉ��p��C�͊w�̌�����擱�����B����NACA���^�Ɋւ����A�̑�K�͂������̃f�[�^�Q�͍ł��d�v�Ȍ������ʂł��B
�@�������A�}�������悤�ɂ��̕����͍\���I�ɖ��������Ă���A����ɗ���⓯���쓮���[�^�[�ɂ�鍂���g���ϓ��Ȃǂ����݂����̂ŁA���ɏq�ׂ��^������1931�N�Ɋ������đ�C���������̗���̂Ȃ����肵���C���Ŏ����ł���悤�ɂȂ�Ƥ1940�N�㏉���ɂ��̖�ڂ��I�����B
�m����^�����n
�@���������剻���Ă��傫���͌^�Ŏ�����������ł́A���E�e�n�ŕ����f�ʐς̑傫�ȕ��������X�i�C�M���X9.1��2�A�A�����J��30��2�A120��2�j�ƍ���Ă����B
�@���}��1927�N�ɃA�����J��NACA�����O���[�������ɍ��ꂽ�����f�ʐ�30��2�̋��啗���ł��BNACA��National Advisory Committee for Aeronautics�i�č��q��]�c�ψ���)�̂��ƂŁANASA�iNtional
Aeronuties and Space Administration �č��q��F���ǁj�̑O�i�ł��B
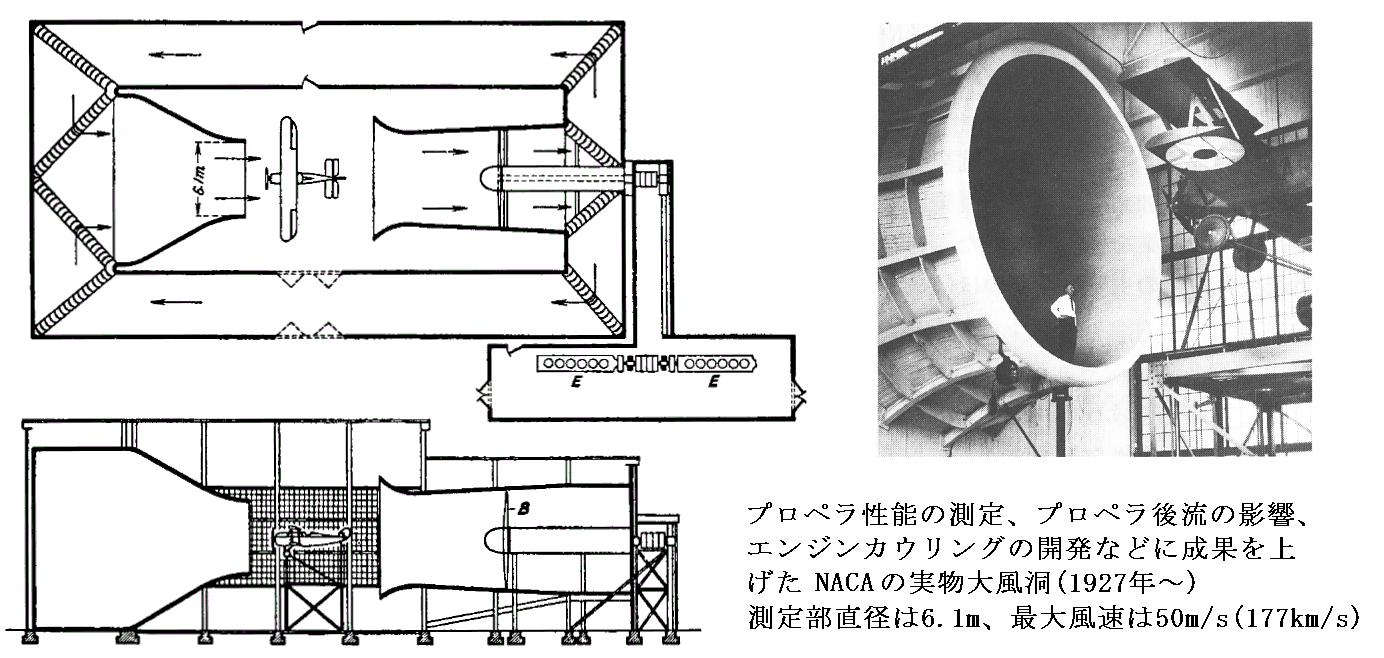
�@
�@���̎ʐ^��1931�N�����O���[�������ɍ��ꂽ�����啗���̑��蕔�ł��B8000�n�͂̓d���@�Q�@�ɂ�蕬���f�ʐ�120��2�A�ő啗��53m�^���̋�C�������o�����Ƃ��ł����B�E���ʐ^�̉��ɓ�@�̓d���t�@����������B

�@�����啗���̌��\�͎��ۂ̃��C�m���Y���̎��������邱�ƂȂ���A����̔��ɏ��Ȃ��C���邱�Ƃ��ł������Ƃł��B���̂���1930�N��̌㔼�ɍs��ꂽ�R�͏����i��C�͊w�I�ȗ����`���j�̌����ł͗��z�I�ȑ��u�ł����B���̕����͗D�ꂽ���\�������Ă����̂ŁA80�N���2010�N�܂Ō����ʼnғ����Ă�����2011�N�ɐɂ��܂�Ȃ����̂��ꂽ�B
�@NASA�����O���[�������̂g�o
�@�@https://history.nasa.gov/SP-440/contents.htm
�@�@http://crgis.ndc.nasa.gov/historic/30_X_60_Full_Scale_Tunnel
�@�@http://crgis.ndc.nasa.gov/historic/643
�@�@http://www.nasa.gov/centers/langley/home/index.html
�ɍs���ƁA���̕����̋M�d�Ȏʐ^�����������܂��B
�@���̎���̕����ɕt���āA�����[��������Q�l�����P�D��P�Q�D�ɂ���܂��B�����̕�����1910�`1930�N��ɑ����̐��ʂ��グ�܂����A���̐��ʂ̐����ɂ͔S�����l��������C�͊w�A����1904�N�Ƀv�����g���ɂ����ꂽ���E�w�̗��_�Ƃ��̉��p���[���ւ���Ă���A���̍e�̖ړI����O��Ă��܂��܂��̂ł����ł͂��܂���B
�m2016�N1���NjL�n
�@���{�̕���������L�������͂��ŋߋ��R�����܂����B�����[�����e�Ȃ̂� �Љ�܂��B
�O��͒��u�����v���o���v���{���̗͊w�w��Avol.4�ANo.4�p307�`314�A1985�N
����� https://www.jstage.jst.go.jp/article/nagare1982/4/4/4_4_307/_pdf
�܂��� https://www.jstage.jst.go.jp/browse/nagare1982/4/4/_contents/-char/ja/
����_�E�����[�h�ł��܂��B
�@���́A������w4�N�̂Ƃ��̑��_�w���������O��搶�������̂ł��B���͂̕��͋C�ɐ搶�̖ʉe���������ĂƂĂ����������v�����܂����B���X�Ȃ���l�b�g���[�N�̐i���ɋ����܂��B
�@�J�搶�́u�䂪���̗��̗͊w�̐�o�����vhttps://www.jstage.jst.go.jp/article/nagare1982/4/1/4_1_3/_pdf
��A����搶�́u�����������ӂ�Ԃ��āvhttps://www.jstage.jst.go.jp/article/nagare1982/4/3/4_3_180/_pdf
�������[�����͂ł��̂ŁA���킹�Ă����������B
�T�D�����\�\�L�@
�@�q�̗͊w�ɉ����ė����\��\�����߂ɗp������O���t�ɂ��Đ������܂��B���ʂ��O�ɘp�Ȃ��Ă��闃�ł͉��}�̗l�ɗ��f�ʑO���̋ȗ����S���g���ċp���߂�m�U�D�i�W�j1�D�m�⑫�����n���Q�Ɓn�B
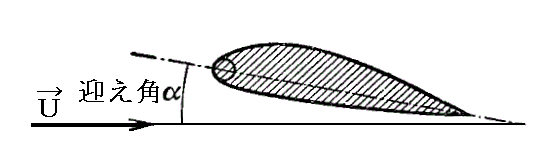
���邢�́A���}�̗l�Ȋȕւȕ��@�ŋp�ƃ��[�����g���S���`����ꍇ������B
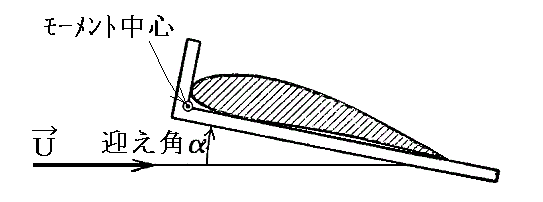
�@���ɓ����͂̃x�N�g�����߂�Ƃ��p��[�����g���S�̒�`���قȂ�Η͂̃x�N�g����[�����g�̈Ӗ��������ɈقȂ�B�ȉ��̐����́A���̒�`�̈Ⴂ�ɉ����ēǂݑւ��Ă��������B
�@�g�͌W���A�R�͌W���A���[�����g�W�������L�̗l�ɒ�`����B��������i1/2�j�ςt2�r�Ŋ����Ė������̋K�i�������ʂɂ��Ă���B�ς͋C�̖��x�A�t�͑C���x�A�r�͗��ʐςł���B��`���̏ꍇ�͂r�������i�X�p�����j�~�����i�R�[�h���j�ƂȂ邪�A�����_�ł͗g�͂��R�͂��P�ʗ���������ōl���Ă���̂ŁA�r�͒P�ʕ�������̗��ʐςƂȂ萔�l�I�ɂ͗����������Ɠ����ɂȂ��B
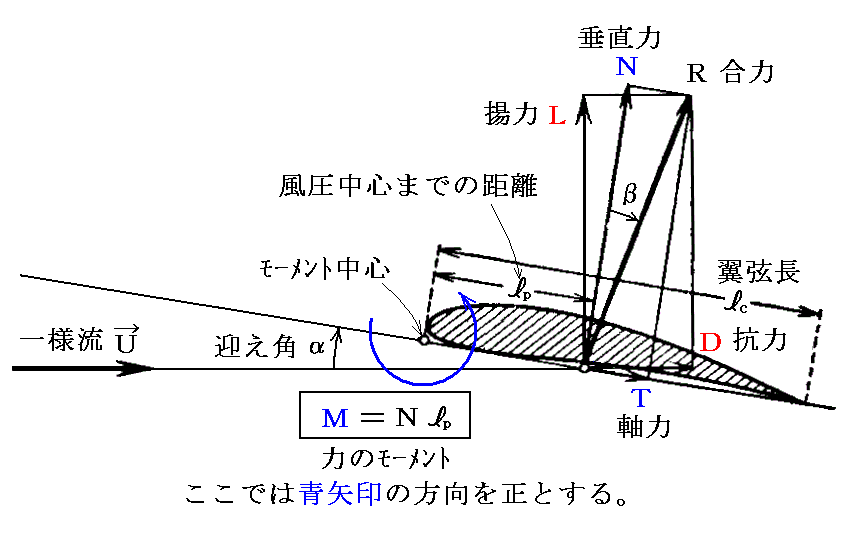
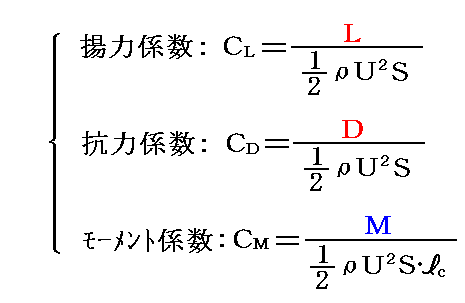
�m�g�͋Ȑ��ƍR�͋Ȑ��n
�@�����Ɍ}���p�A�c���ɗg�͌W���܂��͍R�͌W����������O���t�B���ʗg�͂ƍR�̗͂������ꖇ�̃O���t�ɋL�����Ƃ��������A�R�͌W���͈�ʂɗg�͌W���̂P�^�T���x�ȉ�������c���X�P�[����ς��邩�A�R�͌W�������{���������̂ŋL���B
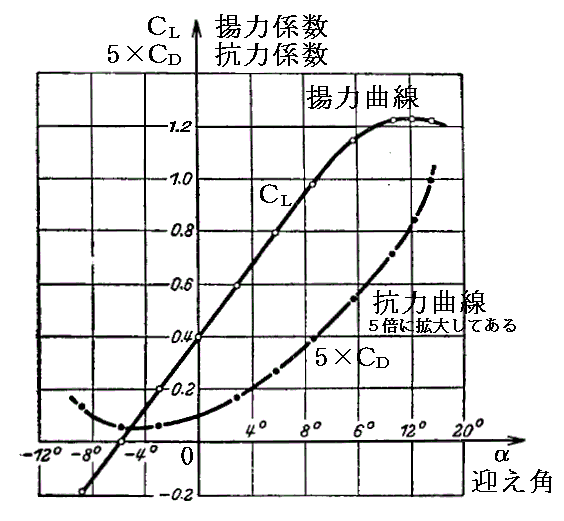
�m�ɋȐ��n
�@�����G���^�[���ɂ��ŏ��ɗp����ꂽ�O���t�ŁA�������R�͌W���A�c�����g�͌W���ɂ��Ă���܂��B�O���t�̋Ȑ����Ɍ}���p���L�����Ă���B
�@���_�Ɗe�}���p�̋ɋȓ_���������̌X���́A���̌}���p�ł̗g�R����Ӗ����܂��B���̌X�����ő�ɂȂ�_�A�܂茴�_��ʂ钼�����ɋȐ��ɐڂ���_�̌}���p���g�R�䂪�ő�ƂȂ�p�ł��B
�@���ۂ̔�s�@�ł͗g�͂ƍR�͂̌��ˍ������d�v�ł�����A���̐��\��ǂݎ��ɂ͂��̌`�̃O���t���ł��K���Ă���B
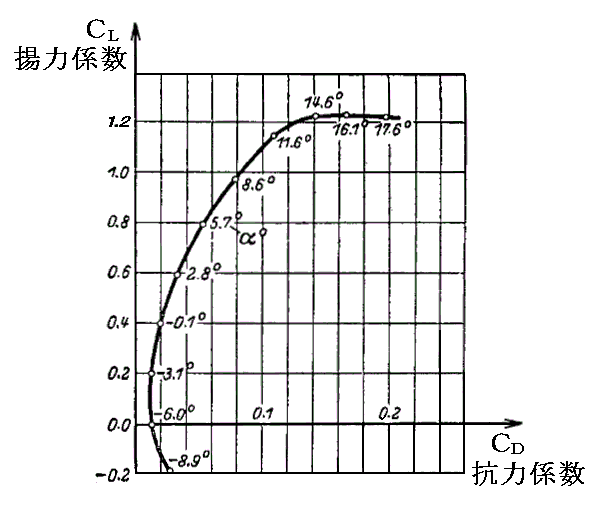
�@���̃O���t�Ɨ��_���瓱�����g�́|�U���R�͂̊W��\���O���t�Ƃ̑Ή��͔��ɏd�v�ł��B���̓�����͕ʍe�u�l�͔�s�@���������錴���m�v�����g���̗g�͐����_�n�v�T�D(�S)�Q�D�Ő������܂��B
�m���[�����g�Ȑ��n
�@���[�����g�̕\���@�͗l�X����܂��B�����̐������Q�l�����P�D�Ńv�����g�����̗p���Ă�����̂ł��B�c���ɗg�͌W���A�����Ƀ��[�����g�W�������A�p�����p�����[�^�[�Ƃ��ċȐ���ɋL���������̂ł��B
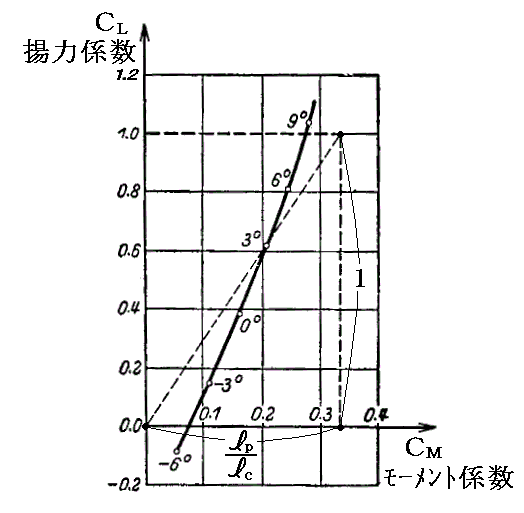
�����Ő����͌W��(�@���͌W���j��
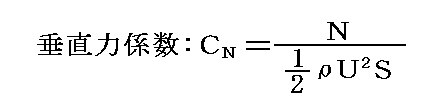
�ƒ�`�����
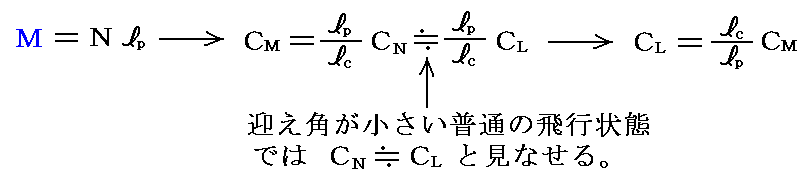
��������B
�@���̂��߁A�Ⴆ�Ό}���p���R���̏ꍇ�A���_�ƌ}���p�R���̓_�����Ԓ�����L���ĂbL��1�̐������ƌ�������_�̂bM�l��ǂݎ��A����͑O�����痃�����̉����̏��Ɉ��͒��S�����邩�������Ă���B
�m�g�R��Ȑ��n
�@����́A�e�}���p�ɂ�����i�g�͌W�����R�͌W���j�̒l���c���ɁA�������}���p�ɂ��ăv���b�g�������̂ł��B����́m�ɋȐ��}�n�ɉ����āA���_�Ɗe�}���p�̋ɋȓ_���������̌X�����c���ɁA�}���p�������ɂ��ăv���b�g�������̂Ɠ����ł��B
�@�g�R��͕��ʌ}���p��0�`���x�͈̔͂ōő�l10�`30���x�����܂��B���̒l���傫���قǏ����ȓ��͂ŕ����яオ�邱�Ƃ��ł��A���\���ǂ����Ƃ��Ӗ����܂��B���̂��߁A���̗g�R�䂪�ő�ɂȂ铖����̌}���p�ʼn^�p�ł���悤�ɐv����ƌo�ϓI�ɗD�ꂽ�@�̂ƂȂ�B
�@
�i�U�j�C�ӌ`�̃f�[�^
�����Â��f�[�^�ł����A�Q�l�����P�D�̑���l�ň�ʓI�X����������܂��B
�P�D��ʓI����
�@���ɓ����R�͂ɂ��m�U���R�́n�Ɓm�`��R�́n������܂��B�m�`��R�́n�ɂ͗��\�ʂɓ����m���C�R�́n�Ɨ�����̉Q�����̈�̔����ɔ����m���͍R�́n������܂��B
�@���̒��ŗ��[�Q�ɂ���m�U���R�́n�͗����A�X�y�N�g���ɑ傫���W���܂��̂ŁA�g�́E�R�͂̃f�[�^�������Ƃ��ɂ͗��̃A�X�y�N�g�������K�v������܂��B�g�͂�������Ɨ��ɕt������z���傫���Ȃ藃�[���痬�̒��Ɏc�����z�i�Q�̉^���G�l���M�[�j�����傫���Ȃ�̂ŁA�g�͂̑���Ƌ��ɗU����R�͑����܂��B�������[�Q�ɂ��m�U���R�́n�͗g�͂̓��ɂȂ�܂��m�ʍe�Ő����n�̂ŁA���̍R�͋Ȑ��͌��_�_�Ƃ���������ɂȂ�܂��B�����g�͂Ŕ�r�������_�U���R�͋Ȑ��Ǝ����R�͋Ȑ��̍��������́m�`���R�n�ƌ��Ȃ��܂��B�ȉ��̃O���t�͂�������A�X�y�N�g��T�̎������̑��茋�ʂł��B
�@�m���C�R�́n�͗��\�ʂ����炩�ȏꍇ�ɂ͂���߂ď������Ȃ�܂��B���\�ʂ��e���ꍇ�́A��ɍR�͂͑������g�͂͌���܂��B���ɗ��̑O�����炻�̒����܂ł��d�v�ŁA���̌㉏�t�߁m�����ł͋��E�w�͗����ɑJ�ڂ��Ă���n�ɂ͑����ȍr���������Ă��債�ĉe�����܂���B
�@�m���͍R�́n�͗���̔����������Ȃ���Ώ������B�������A�p���傫���Ȃ蔍���������Ă���Ƒ傫���Ȃ�܂��B�����͕��ʌ㉏����O���֍L�����Ă䂫�܂����A�O�����甍������ꍇ������܂��B����}���p����Ɨ��̏�ʑS�̂����������ɂȂ��C�ɍR�͂������܂��B���̏�Ԃ������ƌ�����s�ɂƂ��Ċ댯�ȏł��B
�Q�D�L�����o�[�̌���
�@�����A�p���������Ă���i�L�����o�[�j�������Ɨg�͂͑������܂��B�������R�͂���������̂ōő�g�R��͂ނ��돬�����Ȃ�܂��B�O���Œ�`�������[�����g�Ȑ��͖�����炷�قǒ����ɋ߂��Ȃ�A�Ώ̗��ł͌��_��ʂ�悤�ɂȂ�B����͈��͒��S���p��ς��Ă��ړ����Ȃ����Ƃ��Ӗ�����B�ʍ��Ő������܂������A�L�����o�[�������������̏ꍇ�㉏����┽�肠�������`�ɂ���ƈ��͒��S�̈ړ������Ȃ��Ȃ邱�Ƃ������Ă��܂��B���[�����g�����ɑ��ė����̉e���͏��Ȃ��A��ɕ��ϖ(�L�����o�[)�Ȑ��̌`��ɂ���Č��܂�܂��B
�@���̎O�̃O���t���r����Ɩ��炩�Ȃ悤�ɃL�����o�[����������ƌ}���p���傫���Ƃ��̗g�͌W����傫�����P�ł��܂��B����͓��R�\�z����邱�Ƃł����A�L�����o�[�ɂ��O���������ɘp�Ȃ����邱�ƂŌ}���p��傫�����Ă��O�����̔������������邱�Ƃ��ł��邩��ł��B���ꂱ���L�����o�[��t����ő�̌��\�ł��B���E�}�̂悤�ɖ���[���̑Ώ̗��ł͗L��p����ƍR�͂��ˑR�����܂����A����͗���ʂ̗���ɋ}���ɔ������������Ĉ��͒�R�������邱�Ƃɂ��܂��B�B
�@���̂Ƃ����R�\�z����邱�Ƃł����A���p�ɂ���Ɖ����}�̂悤�ɃL�����o�[�̑傫�ȗ��͊K�i��ɋ}�ɍR�͂������鏊������܂��B����͑O�����ʂ̗��ꂪ�������čĕt�����錻�ۂ������ׂł��B
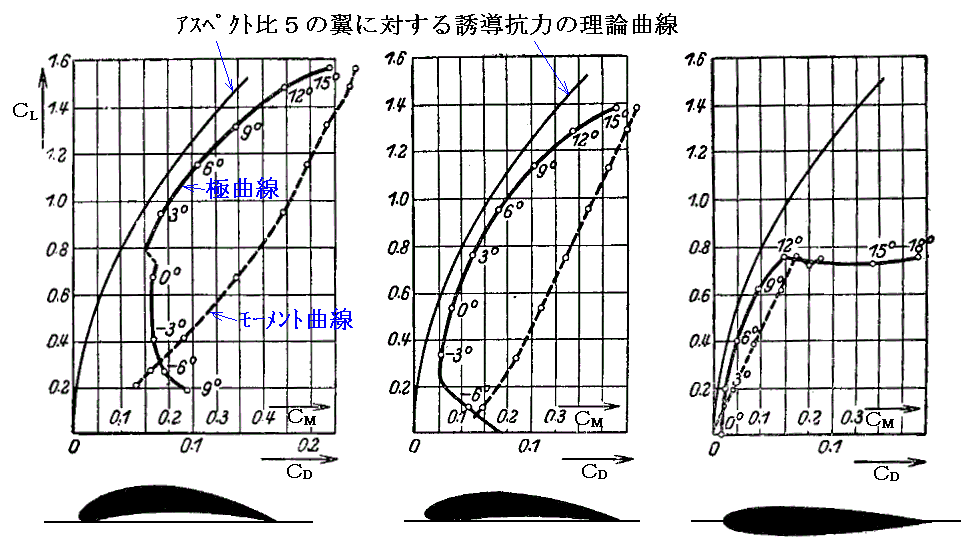
�@�����̔�s�@�́A���������̗l�ɔ�s���x���x���Ȃ��ėg�͂��������鎞�ɂ͌}���p�傳���܂����A����Ɠ����Ɉꎞ�I���O���t���b�v���㉏�t���b�v�������ăL�����o�[�傳���ėg�͌W���傳���Ă��܂��B��}���疾�炩�ȗl�ɁA�L�����o�[�����͐��̌}���p�̈�ł͗g�͌W���̑����Ɍ��ʓI�Ȃ̂ł�����B
�@���̂Ƃ��R�͂��������܂����A���������ɂ͔�s���x��x�����Ȃ��Ƃ����Ȃ��̂ŁA���̂��Ƃ͂ނ���]�܂������ƂŖ��ɂȂ�܂���B�����ɍ����ŏ��q���Ă���Ƃ��ɂ͌��ɖ߂��ăL�����o�[�����������čR�͂̑�����h���܂��B
�R�D�����̌���
�@�(�L�����o�[)���ɂ��ė����𑝂��ƁA�ɋȐ��̃J�[�u���i���ɕ��p�ƍ��p���Łj�U���R�̗͂��_�l�ɋ߂Â��܂��B���̂��ߍő�g�͌W�����傫���Ȃ�ƂƂ������p�ƍ��p�ŗ��̐��\���ǂ��Ȃ�܂��B����͌����ɂ���Ɨ��O���̗��ݓ_���O���~�ʂ̏���ړ����邾���Ȃ̂Ŕ����̏ꍇ�ƈ���ċ}���Ȉ��͕ω�������邱�Ƃ��ł��܂��B���̂��߃��C�m���Y�����������ۂ̔�s�ł́A���p�⍂�p�ŗ���̔������N����ɂ����Ȃ�܂��B����͓��R�\�z����鎖�ł����A�����̍ő�̌��\�Ƃ����ėǂ��ł��傤�B�����𑝂����Ƃ������ɍR�͂傳�����ł͂Ȃ����Ƃɒ��ӂ��Ă��������B���[�����g�Ȑ��ɂ��Ă͗������ω����Ă�����Ȃɑ傫�ȕω��͂Ȃ��B
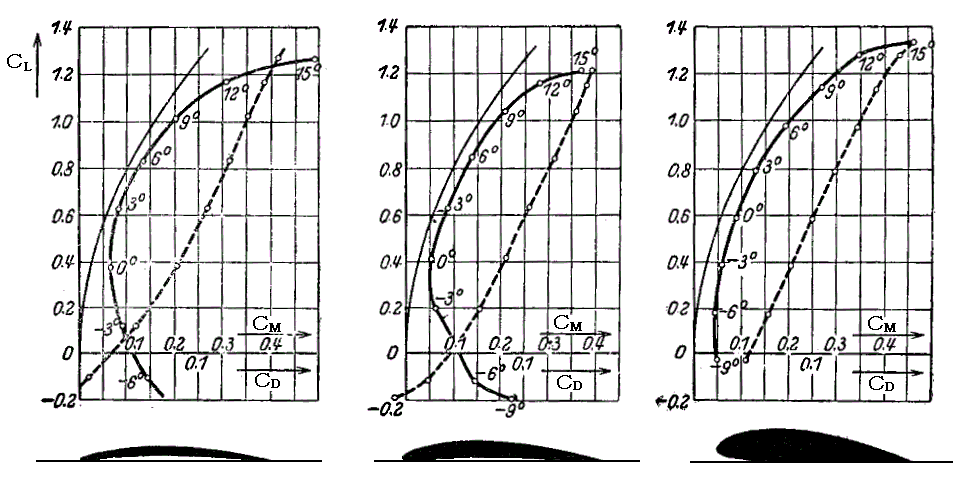
�@���R�ȉ��ʂ������̗����𑝂�(���R���������)�ƍő�g�͂͊m���ɑ��債�܂����A�����g�͂Ŕ�r����ƍR�͂������Ă��܂��B����͗��㉏�t�߂̔����̈悪�����Ĉ��͒�R�������邱�Ƃɂ��܂��B�܂��������S�͌��ɂ����B
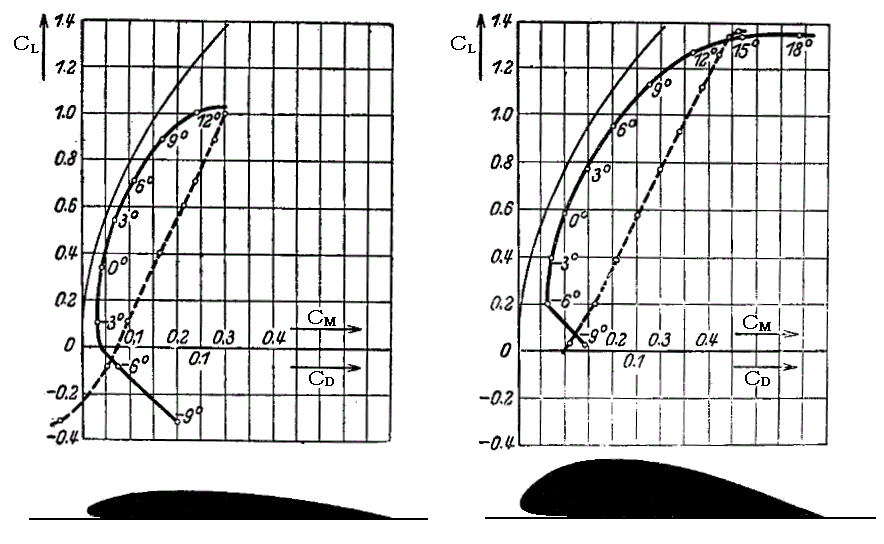
�S�D�O���̌`�����
�m�O���̌`����ʁn
�@���E�}�̗l�ɑO����������ƁA�傫�ȋp�ł̓����͗ǂ��Ȃ邪�A�傫�ȕ��p�ōR�͂������܂��B
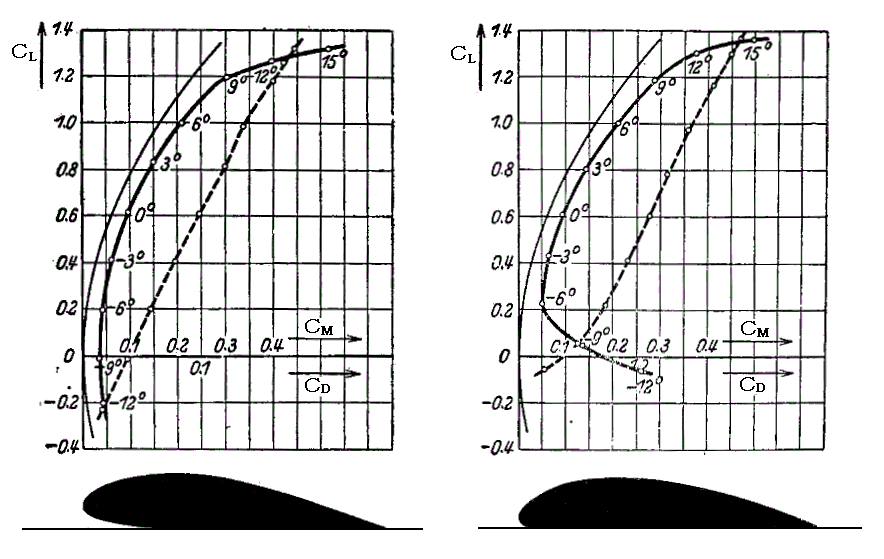
�@��s�@������������Ƃ��ɂ͔�s���x���x���Ȃ�܂��B���x���x���Ȃ�Ɨ��͂͌������܂��B���̗l�ɂ��Č�������g�͂�₤���߂ɔ�s�@�͗��������ɂ͗���傫�Ȍ}���p�ɂ��ĉ^�p���܂��B
�@���̂Ƃ��A�����̔�s�@���O���t���b�v�Ƃ������̂őO�����ꎞ�I�ɉ��Ɍ����đ傫�Ȍ}���p�ł̗����\�����P���܂��B�܂��A�O�����������܂܂��ƁA�}���p���������Ƃ��ɂ͏�}�̗l�ɕs�s�����܂��̂ŁA������s�̏��q���ɂ͌��̌`�ɖ߂��Ă����܂��B
�T�D���ʈ��͕��z
�@�V�D(�S)�S�D�ŃW���[�R�t�X�L�[���\�ʂ̈��͕��z�����߂���@�̊T����������܂������A�C�ӂ̌`�̗��ɑ��鈳�͕��z���v�Z�������1931�N����NACA�����O���[���������e�I�h���Z�����K���b�N�ɂ���ĉ����ꂽ�B����́A�܂��^����ꂽ���^�ɃW���[�R�t�X�L�[�ϊ��̋t�ʑ����قǂ����A���̗��^���~�ɋ߂��`�ɕς���B���̉~����̂�����t�[���G��������ݍ��ݐϕ����܂ޒ����ߎ��@�ŏ������Čv�Z������̂ł����B�m�Q�l�����P�V�̂�100�`104�ɂ��̕��@���Љ��Ă��܂��B�܂��������Ƃ�������@�Ƃ��ē��{�ŕ��y���Ă����牮�̗��_(1942�N)����95�`100�Ő�������Ă��܂��B�n
�@�������ĉ����ꂽ���ʏ�̈��͕��z�������g�͌W���Ŏ����I�ɑ��肳�ꂽ���͕��z�Ɣ��ɗǂ���v�����B�����g�͌W���̎����l�Ɣ�r����͈̂ȉ��̗��R�ɂ��B���_�l���S�����l�����Ȃ����S���̂̂��̂ł���A�����l�͔S���̉e�������������̂ł��邽�߂ɁA���_�l�̗g�͂̕����ǂ����Ă��傫�߂ɂȂ�܂��B���̂��ߗ��̎���̏z�̑傫�����������ʂ̗g�͂�^����悤�Ɍ��������̂Ɣ�r����킯�ł��B���̂悤�ȕ������Ɨ��_�Ǝ����͂���߂ėǂ���v�������܂��B
�@��ʗ��̈��͕��z�̎������ʂ��Q�l�����P�D�����p���Ĉȉ��Ɏ����B
�@�����̐}�́A���\�ʂɒ��a1�������x�̏����Ȍ��������āA���̌��ƃ}�m���[�^�[�𗃓�����ʂ����ǂɂ��q���ŁA�e�_�̈��͂𑪒肵�����̂ł��B���͓͂���(1/2)�ς�2��P�ʂƂ��āA�F�X�ȋp�ɑ��闃�������̈��͕��z��\���Ă��܂��B�����͍ʼn��i�Ɏ������^�m�Q�b�e�B���Q���R�W�X�i�ɋȐ��}�j�n�̗������f�ʂɂ����鑪��l�ł��B
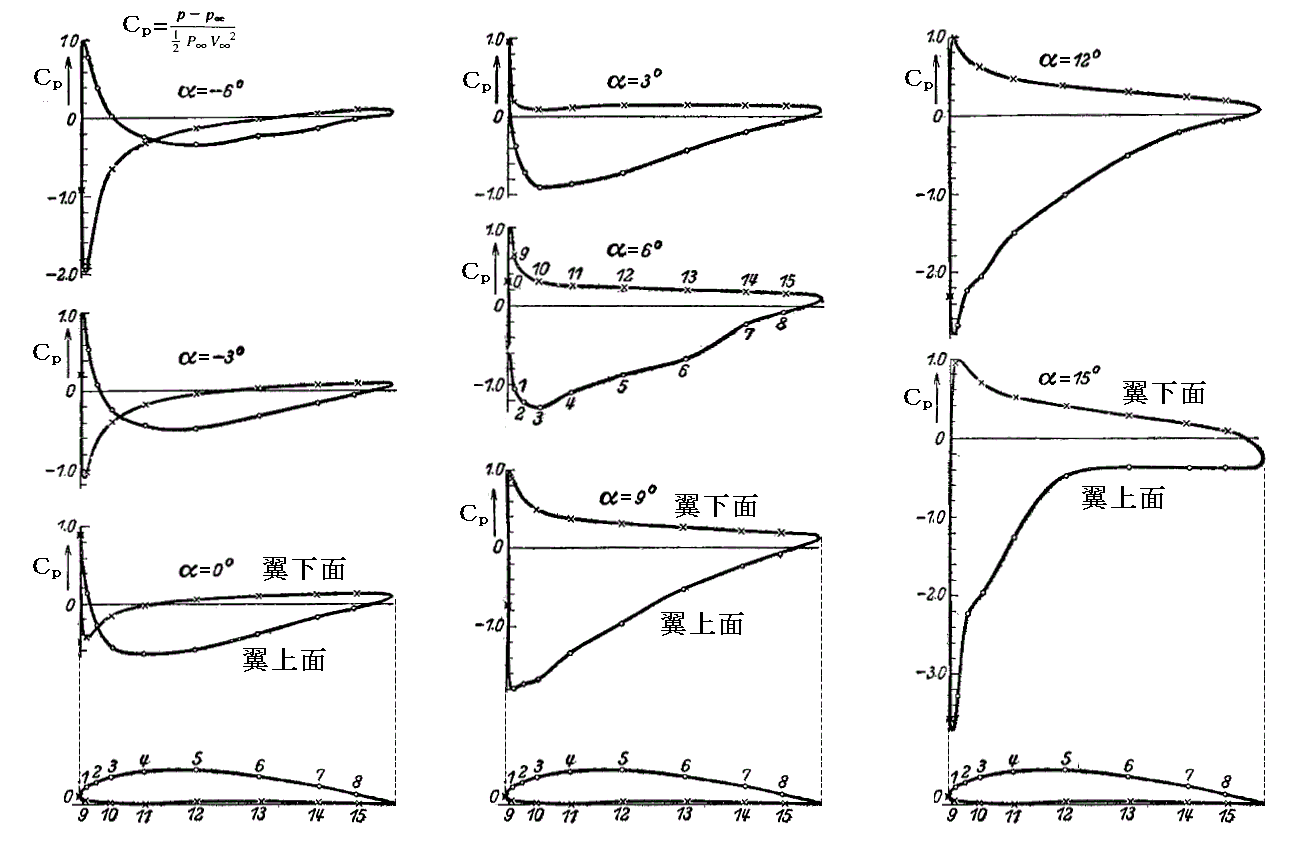
�@��̃O���t�ŁA���O�������͂�1.0�ƂȂ�ʒu���������[���ɂȂ闄�ݓ_�ł��B�}���p��0���ȉ��̕��̏ꍇ�͗��ݓ_�͗���ʂɂ��邪3������Ɖ��ʑ��Ɉړ����Ă���̂�����B
�@����ʂ̈��͕��z�Ȑ��Ɖ����Ƃň͂܂��ʐς͗��̏㑤�ł̋z���グ��p��\���B���͂͌X�������ʂɓ����̂ŁA���S�Ɉ�v�͂��Ȃ�����̂̏��͂��̗l�Ɍ��Ȃ��ėǂ��B���l�ɁA�����ʂ̈��͕��z�Ȑ��Ɖ����ň͂܂��ʐς́A�����ł̉����グ��p��\���B�}�����g�͂̑啔������ʂ̋z���グ��p�ɂ�����Ƃ�����B
�@�}���p15���̃O���t�̗���ʌ㔼�ŕ�������������̂͗���ɔ����������Ď�����̈��͂���������ł��B
�@���}�͑Ώ̗��ɋp��^���ė���̒��ɒu�����Ƃ�������T�^�I�ȗ���̃^�C�v�������Ă���B�_�����|�e���V�������̗��_�l�Ŏ����������l�ł��B
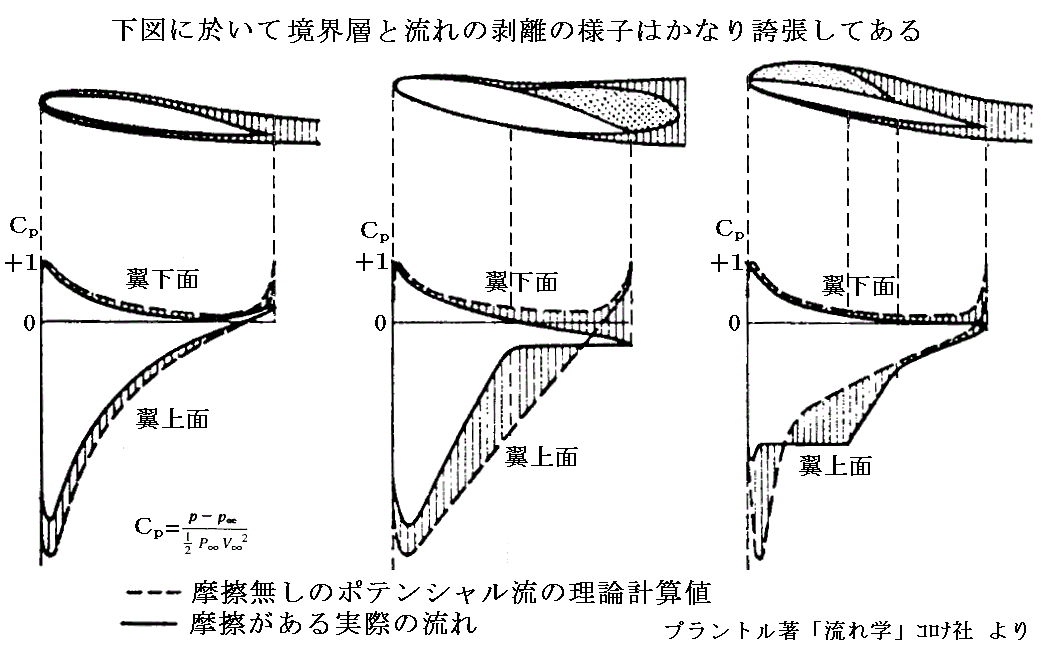
�@�K���ȗ��^�Ō}���p���������ꍇ�́A���}�̗l�ɋ������͏㏸�ɑς��ė��ʂɉ��������ꂪ�قڎ��������B�������A�������ꂽ���̓T�[�N���̖ʐς͗��_�T�[�N���̖ʐς����������B����͗��\�ʂ̖��C�ɂ����̂Ǝv����B�܂��A�㉏�t�߂ɂ͔����������B�����̗��ł́A���̂悤�Ȕ��������㉏�ɐ����邱�Ƃ◃�\�ʂ̖��C�̂��߂ɁA�g�͂̎����l�͗��_�l�����������Ȃ�A�R�́i���͒�R�j������Ă��܂��B�B
�@���������Ȃ�ƒ��}�̗l�ɗ��̌㔼�ɕ��������̈悪�`�������B���̂��ߓ��ɗ���ʌ㔼���̈��͂��㏸���܂��B�O�}�̋p15���̏ꍇ������ɑ������܂��B
�@�E�}�͑O���ł����ɔ������N����A���̌�ĕt������ꍇ�ł��B�O�����s���������̏ꍇ�ɋN����₷���̂ł����A���̂Ƃ�����ʑO���̈��̓J�[�u�ɕ����ւ̖c��݂��ł��܂��B���̃^�C�v�̈��͕��z�Ɋւ��ăt�����X�̃G�b�t�F�����m�⑫�����P�n�Ő�������l�������[������i1910�N�j�����Ă���B�ނ̓G�b�t�F�����ŗL���ł����A�q�̗͊w�ɉ����Ă��t�����X�ɂ�����̑�Ȑ�o�҂ł��B
�@���̂悤�ȗ���̂����̂ǂꂪ���ۂɋN���邩�͗����A�L�����o�[�A�}���p�A���C�m���Y�����Ɉˑ����܂��B�܂��A���͕��z�̌`�͗��^�Ɉˑ����Ă���A������L�����o�[�̗����ɉ��������z�`�ς����Ȃ�ω����܂��B���ꂪ����w�����̍l�����ɔ��W���܂��B
�@���ʂ̌`����l�����ď�L�̈��͕��z��ώZ����Ηg�͂ƍR�͂��v�Z���邱�Ƃ��ł���B���}�͏�̈��͕��z����l����Z�o�������̂ƕ����̗g�́E�R�͑���V���̑���l�Ƃ̔�r�ł��B
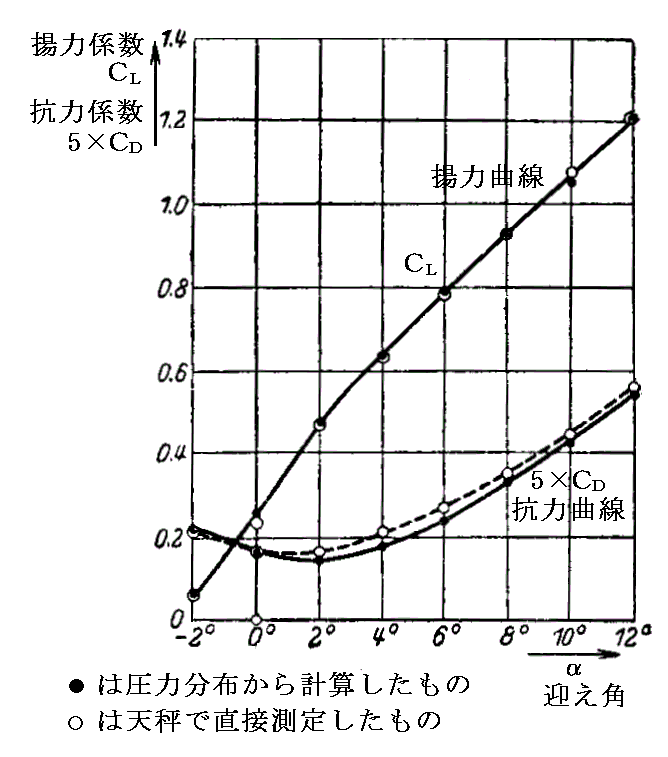
�@�g�͂ɂ��Ă͗��҂͗ǂ���v���邪�A�R�͂ɂ��Ă͈��͕��z���狁�߂����̂��V���̎����l�̕�����ɑ傫���Ȃ�B���̍��͗��\�ʂ��m���C�R�́n�ɂ����̂ł���ƍl������B
�m�⑫�����P�n

�@����͍ő啗����20m/s�܂ŏo����(Champs-de-Mars��)���㕗����p���Čv�����ꂽ���̂�1910�N�ɔ��\���ꂽ�B
�@�G�b�t�F���̕����i����19�D�j�@�@����1�A�@����2�A�@����3�A�@���㕗���A�@��㕗��
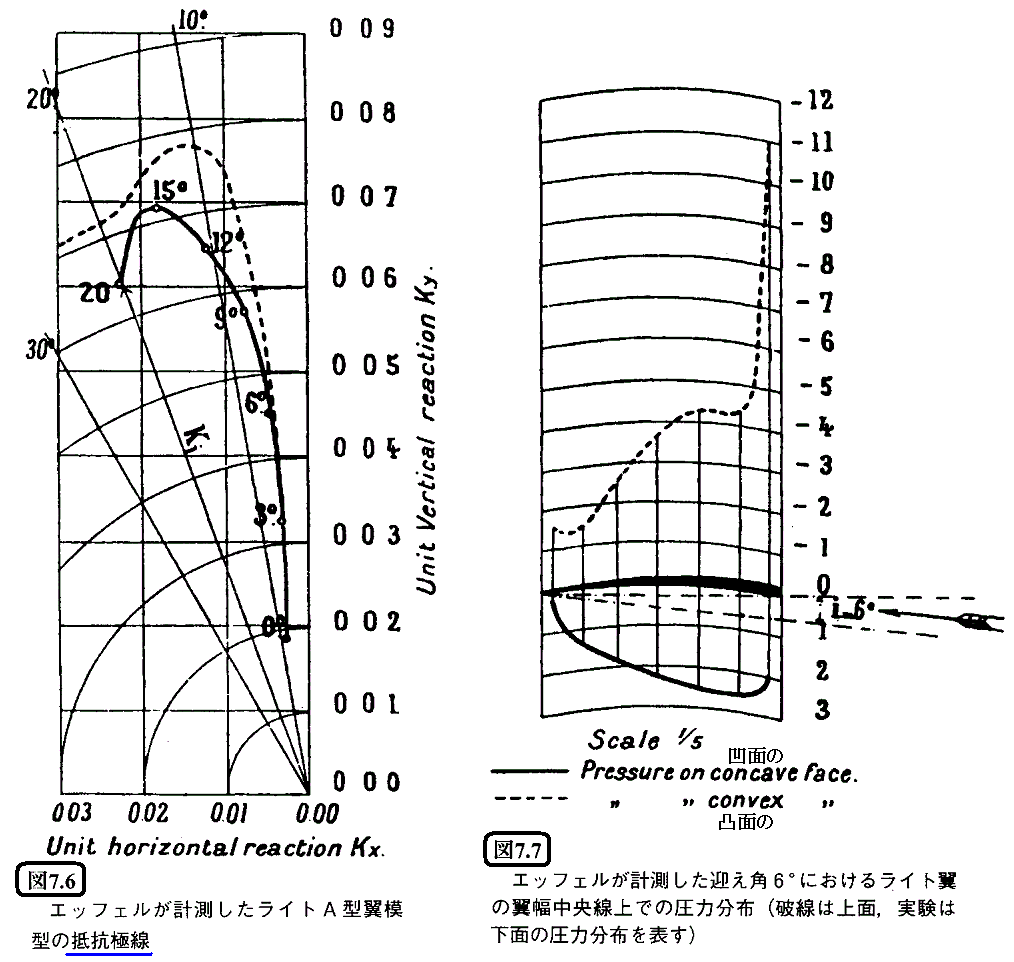



�U�D�w����
�@���܂܂ʼn��x�����ӂ��܂������A���\�ʂɐ����鋫�E�w�ɂ͑w���̗��̂����̂܂ܗ��ɉ������ʂł��ꍇ���l�ɂ��đ��x���z���`�������w�����E�w�ƁA���E�w���̗��̂��������Q�������a����Ȃ��痬��̑��x���z���`�������������E�w������܂��B
�@�����̕����̋C���ɂ͗��ꂪ�܂܂�Ă����̂ŁA���̗��҂̈Ⴂ�������I�Ɋm���߂�͍̂���ł������A�v�����g���̋��E�w�̌����ȗ��A�w���ł̕\�ʖ��C��R�͂͗����ł̕\�ʖ��C��R�͂������Ȃ菬�����Ȃ����Ƃ��ǂ��m����悤�ɂȂ�܂��B���}�͍��������Ă��邻�̓�����̎���������O���t�ł��B
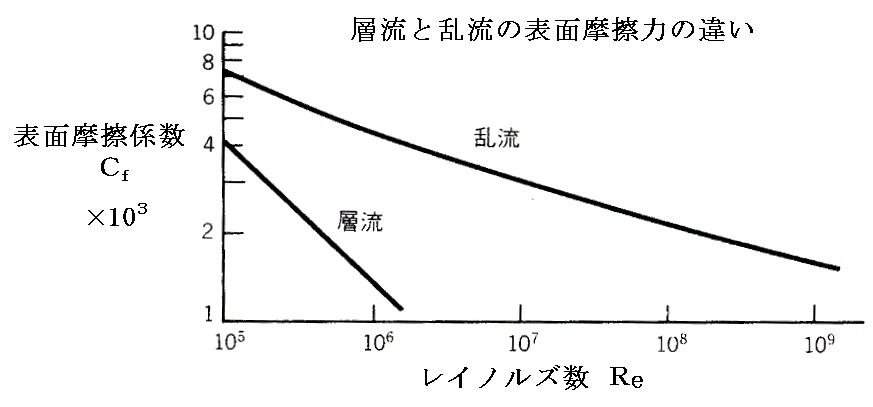
�@���ہA�J��Y�͌��1968�N�ɁA�w�����̌������n�߂�1938�N�����̏����̂悤�ɉ�ڂ��Ă��܂��B
�w�E�E�E1935�N���̔�s�@�́A�x���Ȃǂ��I�o����Ȃ��u�����`�v�ɂȂ��Ă���A������Ԃł̒�R�̑啔���́A�\�ʂ̖��C��R�ɂ����̂ł���܂�������A�\�ʐς̉ߔ����߂�嗃�̖��C��R�̌����ɁA���x�����ڎw���v�҂̊��҂�������ꂽ�͓̂��R�ł��B�E�E�E�x�i����19�D��
p210 ���� p272 or 291 ���j
�@1930�N��ɓ���p�����a�E�����r���E�W���[���Y�iBennett Melvill Jones 1887�`1975�N�j���W�F�t���[�E�h�E�e�C���[�iGeoffrey Ingram Taylor 1886�`1975�N�j�B�͗��̍R�͂����ʂɐ�߂�w�����E�w��Ɨ������E�w��̖ʐς̕ϓ��Ɍ����ɉe������邱�Ƃ����������܂��B����ɑw�����E�w�̈��萫�͗��\�ʂ̗���ɉ����������ł̈��͂̕ω��̎d���ɂ��W���鎖�������܂��B�܂��\�ʈ��͂����������Ɍ������Č����i�����͌��z�j��������Ȃ�Αw�����E�w�͑w����Ԃ��ێ����A����̕����Ɉ��͂������i�t���͌��z�j���n�߂�ʒu�̕t�߂ŗ����ւ̑J�ڂ��N�����������܂��B���ۂ̔�s���������������őw���ɂȂ��Ă���̈�͏������z�̗̈�ł��邱�Ƃ��m���߂��܂��B
�@�A�����J�̃����O���[���������C�[�X�g�}���E�m�E�W�F�B�R�u�Y�́A1935�N�̌㔼�ɏ�L�̎�����m���Ď��̂悤�ɍl���܂����B���\�ʂ̈��͕��z�͗��^�Ɉˑ�����B�Ȃ�Η����̑啔���ɉ����Ĉ��͂���������悤�ȗ��^��v���邱�Ƃ͂ł��Ȃ����낤���B�������̗l�ȗ��^��v�ł���A���̗��ʂ̑啔���ɓn���đw�����ێ��ł��A�\�ʖ��C��R�̑啝�ɏ��Ȃ������ł��邾�낤�B���ꂪ�w�����̒��z�ł��B
�@�ނ́A�e�I�h���Z����ɂ���Ĕ��W������ꂽ���v���_���������Ă�������ǂ��܂��B�����ė����̑啔���ɓn���ď������͌��z���B������闃�^�̐v�ɐ������܂��B�m�����������Ă��Ȃ��̂ŃW�F�B�R�u�Y�̕��@���ǂ̗l�Ȃ��̂Ȃ̂�����܂��A�Q�l�����P�V�̂�118�`126�ɗ^����ꂽ���͕��z�����^�����߂�牮-�Γc�̕��@(1942�N)����������Ă��܂��B�n
�@���}�͂��̗l�ɂ��ē���ꂽ�w�����^�Ə]���^�̗��^�̈��͕��z���r�������̂ł��B
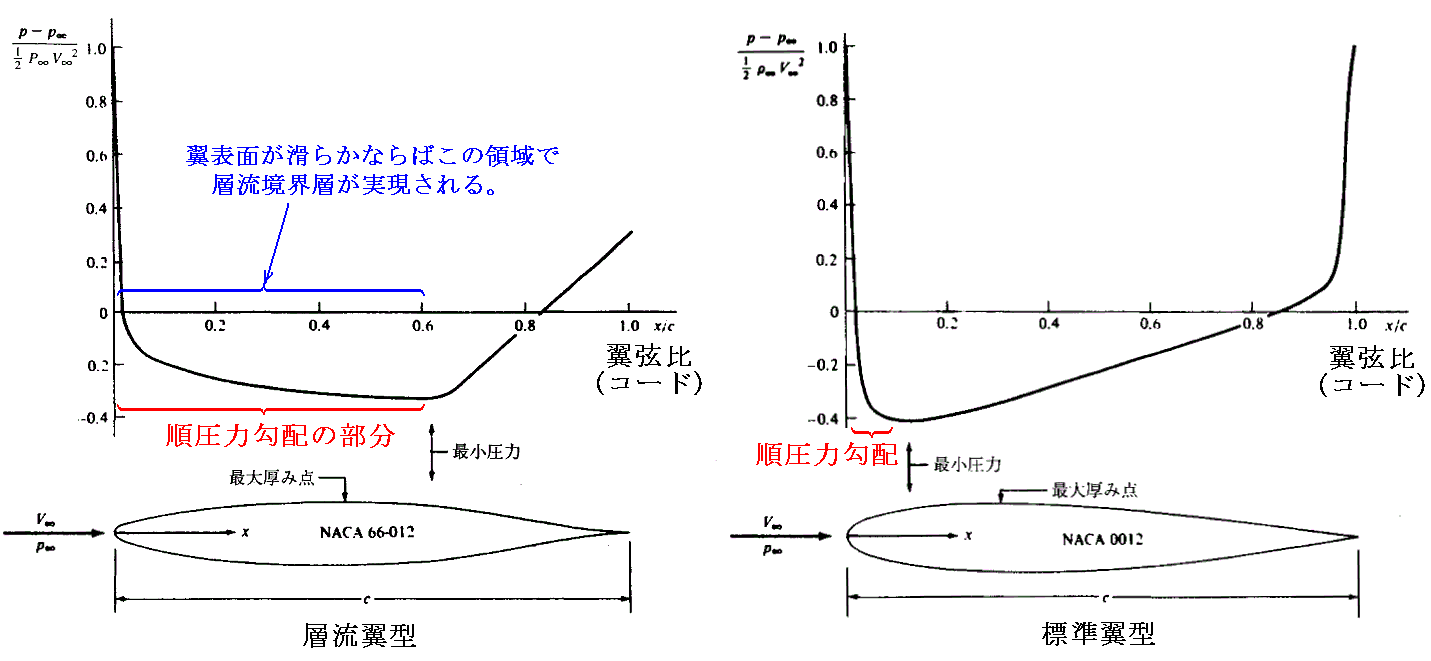
�@���̑w�����^�͒ᗐ�������̎������ʂ�����R�͌W�����]���̗��^��1/3�`1/2�Ɍ������邱�Ƃ��m���߂��܂��B
�@���̌�������������1938�N�Ƃ��������͑���E���̒��O�ŁA���̏d�v�Ȑ��ʂ͈��S�ۏ��̗��R�ŋɔ�ɂ���܂��B�������A����Ɠ��l�Ȍ������A1930�N��̌㔼�ɓ��{�̒J��Y��ɂ���đS���Ɨ��ɍs���Ă������Ƃ͗ǂ��m���Ă��܂��B
�@���̌������ʂ�P-51���X�^���O�퓬�@�i�}�N�_�l���Ё@�O�ʐ}�@�\���}�j�̗��v�ɍ̗p���ꂽ�BP-51�͑w�������ŏ��Ɏ��p�����ꂽ��s�@�Ƃ��ėL���ł����A�g�[�^���Ƃ��Ă̗D�ꂽ�v�ɂ�����E��풆�Ɋ����퓬�@�̒��ł��ŗD�G�ȋ@�̂ƌ��Ȃ���Ă���B
�@���Ȃ݂ɁA���{�ł͋����A���d�A���d���Ȃǂ��w�������̗p���Ă��܂��B���̏ڍׂɕt���Ă͕���19�D��7�͂������������B
�m�⑫�����n
�@���ۂ̔�s�@�̗��ł́A��L�̑w�����̌��ʂ������o����قǂɗ��\�ʂ����炩�Ɏd�グ�邱�Ƃ͓���A�����\�z���ꂽ�قǂ̌��ʂ��グ�邱�Ƃ͂ł��Ȃ����Ƃ������Ă����i���̂��Ƃɕt���āA����19�D��7�́�9�D�ɋ����[���L�q������̂��ʃy�[�W�ň��p�j�B
�@�����ł͖��C��R�����炷�ׂƂ��������A���̗D�ꂽ�������\�ׂ̈ɑw�����͍̗p�����ꍇ�������B
�@
�@������A���̏����̌����̗L�p���͔�s���C�m���Y���ł̗���(�R�[�h�j�̑啔����w���Ɉێ����邱�Ƃ�����ł��鎖�𖾂炩�ɂ������Ƃł���ƌ����������ǂ������m��Ȃ��B���̂��߁A�����ł́A�����̑O��30���`50���܂ł̂�苷���̈��w���ɕۂ悤�ȗ��^�̐v�ɏd�_���u����Ă���B
�@
�@�܂��A�����ł͋��E�w�̌����𑼂̕��@�Ő������ė����ւ̑J�ڂ�x�点����@������Ă��܂��B���̕��@�Ƃ��Ă͗��̕\�ʂɍa�⌊���J���āA���E�w�̋�C���z������ŋ��E�w�������Ȃ�̂�h������A�t�ɋ��E�w�ɗ��ʂ����C���𐁂��o���ċ��E�w�̑��x���z������������Ȃǂ�����B
�@
�W�D�Q�l����
�@�����Ő��������������_�̖{���̈���T�A�U�͂Ő����������p�ʑ��ł��B���p�ʑ��Ɋւ��Ĉȉ��ɋ������{��ǂ�ł݂܂������A�����ɂ͒ʂ��ӂ̐��������Ȃ��ė�������̂��Ȃ��Ȃ�����B�{�������ނɂ́A��͂莩�����g���ʑ��W��\���}���R�`���āA������ڂ������������ȊO�ɗǂ����@�͂���܂���B�}��`���Ă݂ď��߂Ă��̓��e�������ł��܂����B
�@����Ƃ�����̖{����7�́i�P�j�Ő��������W���[�R�t�X�L�[�̉����ł��B������ǂ̗l�ɐ��������邩�ŗ����_�����W���Ă����ƌ����Ă��ǂ��Ǝv���܂��B
�@���ۂɂ͑O�����ɂ����锍���̖��A�S���ɔ������E�w�̌`���Ƃ��̔����̖��ȂǁA�����̗��ł͒P���ł͂���܂���B�������}���p�������������ۂ̔�s�@�̗������ݏo���g�͂̉�͂ɉ����āA�������_���傫�Ȑ��ʂ��グ�����Ƃ͊m���ł��B
�@
�@�������_�ɂ́A�����Ő����������p�ʑ��@�ȊO�����ٓ_�@�Ƃ������̂�����܂��B����̓����N�̔������_�i1922�N�j�Ɏn�܂���̂ł����A�Q���Ɛ����o�����R���ׂāA�������ٓ_���z�����邱�ƂŔC�ӂ̗��^�ƁA���̗��^����̗�������o�����̂ł��B���������̐����͑S�ďȗ����܂��B
- Prandtl and Tietjens ���iJ. P. Den Hartog�@�p��j�uFundamentals of Hydro-and Aeromechanics�v�A�uApplied
Hydro-and Aeromechanics� Dover Publications�v�i���{��1929�N���j
�@����̓v�����g���̍u�`���q�̃e�B�[�`�F���X�iTietjens�j���܂Ƃ߂��{�̉p��łł��B�q�̗͊w�̍ł���{�I�ȌÂ������ł����A���ꂪ��ԉ���₷���B���ɗg�͂̌����Ƃ��ďz�����ڂ����悤�ɂȂ����o�܂��l�X�ȗ�ɂ���Ē��J�ɐ�������Ă��܂��B��̋��ȏ��̑�����������Q�l�ɂ��Ă��܂��B
�@����ɂ͖|��{������܂��B�v�����g���A�e�B�[�`�F���X���i�V����Y�A����p�v�A���쏹���A�O�Q����j�u�q�̗͊w�v���Y�Z�p�Z���^�[�i1975�N���j�B����͐�O�i1940�N�j�ɖ|��o�ł��ꂽ���̂̕����ł��B
- H. Glauert ���uThe elements of aerofoil and airscrew theory (Second Edition)�vCambridge
University Press�i1946�N���j
�@��������ł�1926�N�ɏo�ł��ꂽ�L���ȋ��ȏ��ŁA���̓��e�������̖{�Ɉ��p����Ă��܂��BChapter�W�`�Z���W����Ƃ���ł��B����ɂ��펞���i1943�N�j�ɖ|��o�ł��ꂽ���̂�����܂����A���̖�{�̌Ï��͂ƂĂ������ł��B
- ���o�[�g�E�s�E�W���[���Y���i�ѐA�r��A������ ��j�u�����_�v�����H�ƐV���Ёi1993�N���j
�@�����Robert T. Jones���uWing Theory��i1989�N���j�̖|��{�ł��B�Ȍ��Ȑ����ł����A���x�ȓ��e���ܒ~�[�������ɐ�������Ă��܂��B���҂͗����_�ł͗L���ȕ��ł��B
- �F�ߐW ���u���̗͊w�v�����o�Łi1940�N�j�̕����Ђɂ�镜���Łi1972�N���j��T��
H�DLamb�̖{�̍s�Ԃ����Ē��J�ɐ�������Ă��܂��B���{��œǂ߂闬�̗͊w���ȏ��̑������I���݂ł��B
- ����� ���u���̗͊w�v��g�S���i1970�N���j
����� ���u���̗͊w�i�O�ҁj�v�։ؖ[�i1973�N���j�S�́A�U��
����₷�����J�ɐ�������Ă��܂��B���ɑO���͗��̗͊w�̓��发�Ƃ��Ă�����Ă���Ǝv���܂��B
- �F�F�� ���u���̗͊w�v�|���فi1982�N���j�V��W��
- �A�����Y ���u���̗͊w�i�@�B�H�w�u��15�j�v�����o�Łi1959�N���j
�@�����{�ł�����r�I����₷����������Ă��܂��B��Q�́g���̂��������^���h���W����Ƃ���ł��B
- ���R�N�j ���u���̗͊w�i�T�j�v�����H�ƐV���Ёi1971�N���j�S�`�U��
�@���e�͑����̂ł����ȗ��Ȑ��������Ȃ��̂ŗ�������͓̂���B
- ���{���� ���u���� ���̗͊w��{�����i1969�N���j��Q�́A��U��
�@���e�͑����̂ł����A���̖{�������痝������͓̂���B
�@
�����_�̗��j�I�ȋL�q�ɂ��Ă͈ȉ��̖{���Q�l�ɂ����B�@
- �e�I�h�[���E�t�H���E�J���}�����i�J��Y��j�u��s�̗��_�v��g���X�i1971�N���j
�@���_�I���W�̗��ꂪ�ǂ�����B�ڂ��������\�����Ă���̂����肪�����B���̒���p65�`70�g������R�ƉQ��h�����͕ʃy�[�W�ň��p���Ă��܂��B
- �e�I�h�[���E�t�H���E�J���}�����u���ւ̒���v�X�k�o�Ŋ�����Ёi1995�N���j
�@20���I�O���̃��[���b�p�Ƃ��Ƀh�C�c�𒆐S�Ƃ���Ȋw�E�Z�p�̏ɂ��ĂƂĂ������[���L�q������B�����̎����m���ꋉ�̎j���ł��B�mhttp://www.morikita.co.jp/cgi-bin/9451/oozora.cgi�n
- �W�����E�c�E�A���_�[�\���ir
���u��C�͊w�̗��j�v���s��w�w�p�o�ʼn�i2009�N���j
�@���{��1997�N���́gA History of Aerodynamics and Its Impact on Flying Machines�h�ł��B���ۂ̔�s�@�Ƃ̊W���ڂ�����������Ă��āA�ƂĂ��ʔ����B�����̕������ƂĂ��Q�l�ɂȂ�܂����B
�@
�@���f���_�̎Q�l���ɕt���Ă͎������K�ɗ��p�������̂������Ă����܂��B
- �|���[�O���u�����_�i��j�i���j�v�։ؖ[�i1971�N���̐V�Łj
- ���{�N�j���u���f�����v�_�C�������h�Ёi1968�N���j
- �c�����Y���u���p���w�i�����_�A���v���X�ϊ��A�t�[���G�ϊ��A�s�K���g�j�vꠏ��X�i1968�N���j
- ��������u���̗͊w�ƕ��f��́i���医��̐��w�R�j�v���{�]�_�Ёi1981�N���j�@
�@
�m�Q�l�����̒NjL�n
- �牮�x���Y���u��C�͊w�����v�{����(1959�N��)
�@����͂��̃y�[�W���������(2011.12.3)�Ɏ�ɓ��ꂽ�̂ł����A���w�I�ɂ��Ȃ�ڂ����������W�J����Ă��܂��B���ɂ͌��\����{�ł����A���̃y�[�W��������ゾ�����̂ʼn��Ƃ������ł��܂����B
�@���ɂV�D(�U)�T�D�Ő��������e�I�h���Z���ƃK���b�N�ɂ��C�ӗ��^�̉�͖@�A�������Ƃ������@�Ƃ��ē��{�ŕ��y���Ă����牮�̗��_����95�`104�ɁA�܂��V�D(�U)�U�D�Ŏ��グ���C�ӈ��͕��z��^���āA���̈��͕��z���������闃�^�����߂���@����118�`126�ɏڂ�����������Ă��܂��B
- �q����Y���u�q��͊w�̊�b�i��2�Łj�v�Y�Ɛ}���i2011�N���A���ł�1980�N�j
�@��������̃y�[�W���������Ŏ�ɓ���ēǂ̂ł����A�ƂĂ��ǂ��܂Ƃ߂��Ă���{�ł��B��3.3�Ŕ������_����3.9�ŗg�͐����_������Ղ���������Ă��܂��̂Ō䗗�ɂȂ��ĉ������B����ȊO�̏������J�ɐ�������Ă��܂��̂ŁA�ӗ~���鍂�Z�����܂߂āA�q��͊w�ɋ����������ꂽ���͍ŏ��ɂ��̖{��ǂ܂��̂��ǂ������m��܂���B
- ���{�B�F���u��s�@�̒a���Ƌ�C�͊w�̌`���v������w�o�ʼn�i2012�N9�����j
�@�ŋߏo�ł��ꂽ�{�ł����A���̍e��ǂ܂ꂽ���ɑE�߂܂��B�O�L����10�`12�ƑΔ䂳��Ȃ���ǂ܂��Ɨ��j�I�ȗ��ꂪ�ǂ�����܂��B���ɃC�M���X�ɂ�����q��͊w�̔��W�̓���╶��2�̒��҂ł���w���}���E�O���A�[�g���ʂ����������A�܂����{�ɂ�����w���������̓�����ǂ�����܂��B���̒�����3�́g�V������C�͊w���_�̒a���h�����p�B
- �W�����E�c�E�A���_�[�\���ir ���u��s�@�Z�p�̗��j�v���s��w�w�p�o�ʼn�i2013�N���j
�@���{��2002�N���́gThe Airplane:A History of Its Technology�h�ł��B����12�Əd������Ƃ�����݂�܂����A�V�����������Љ��Ă��܂��B���ꂩ�����̎O�ʐ}�Ɖ����lj����p���܂����B
- �f���B�b�h�E�}�J���[�iDavid MaCullough�j���u���C�g�Z��v�iThe Wright
Brothers�j���v�Ёi2017�N���j
�@�ŋߏo�ł��ꂽ���C�g�Z��̕]�`�ł����A�ꎟ�����Ɋ�Â��Ă���A�ƂĂ������[�����e�ł��B���ǂ݂ɂȂ邱�Ƃ����߂܂��B
�@�ʍe�u�����_�̉萶���v�̍Ō�ɏq�ׂ��O�̉ۑ�
�@�@�i�P�j���̌}���p���������̈�Ŕ�������g�͂̋����ׂ��傫���̐����B
�@�@�i�Q�j���ɃL�����o�[��t���邱�Ƃŗg�͂̑���ݏo���邱�Ƃ̐����B
�@�@�i�R�j�A�X�y�N�g���傫�����邱�Ƃŗg�́^�R�͔�����P�ł��邱�Ƃ̐����B
�̂����i�P�j�Ɓi�Q�j�ɂ��ẮA�����Ő��������������_�ňꉞ�����ł��܂����B
�@�c��́i�R�j�ł��B�l�͔�s�@�̂悤�ɐ��i���͂��ア���A���邢�͎����Ă��Ȃ�����q��@�Ɏ���āA�R�͂͂ł��邾���������A�g�͂͂ł��邾���傫�Ȃ��Ƃ��d�v�ł��B���̂Ƃ��R�͂��m�U����R�n���m�`���R�n���琶���܂��B�U����R�͗g�͂ݏo��������̏z�ɂ���ė��[����f���o�����Q�i���[�Q�j�������N����������������R�Ȃ̂ł����A���̃A�X�y�N�g���傫������Ώ������ł��܂��B
�@�����i�X�p���j������ɂȂ�Η��ʐς�������̂ŁA�m�`���R�n���m�\�ʖ��C��R�n�{�m����̔����ɂ�鈳�͒�R�n�@�������܂����A�l�͔�s�@�̂悤�Ȓᑬ�@�ł͋�C���͂قڊ��S���̂̃|�e���V�������ɋ߂��̂ŁA�`���R�����U����R�̒ጸ�̕����d�v�ɂȂ�܂��B���̂��ߐl�͔�s�@�̐v�ł̓A�X�y�N�g���傫�����ėg�́^�U����R������P���邱�Ƃ��ł��d�v�ł��B
�@�U����R�����̃A�X�y�N�g��ɊW���邱�Ƃ𖾂炩�ɂ����̂̓����`�F�X�^�[��v�����g���ł��B���ꂱ�����O���������_�̒��S�ۑ�ł��B�������A�y�[�W���������������̂ł��̐����͕ʍe�u�l�͔�s�@���������錴���m�v�����g���̗g�͐����_�n(�A�X�y�N�g��Ɨg�́^�U���R�͔�j�v�ɂ܂킵�܂��B