大空へ飛翔することは人類の最大の夢でした。その夢に挑戦した人々の話です。
流体力学の最大の課題は
１．流体中を移動する物体に働く抗力や管や水路の中を流れる流体の抵抗のメカニズムを明らかにすること。
２．翼に揚力が発生するメカニズムを解明すること。
です。
１．の問題は流体が絡むあらゆる現象に関係しており、化学工学、土木工学、機械工学、航空工学、地球物理学、気象学、海洋学、天体物理学･･･等々の多くの分野に絡んできて応用上最も重要です。
２．は飛行機の翼の生み出す効果の解明です。航空工学の最大の課題だと言って良いでしょう。空を飛ぶ機械を作ることは人類の最大の夢だったのですから。また翼の持つ優れた機能はは各種流体機械の広い範囲［プロペラ、スクリュー、風車、蒸気タービン、ガスタービン、ジェットエンジン、タービンポンプ、等々・・・］で利用されておりその性質の究明はきわめて重要です。
しかし、この二つはとても難しい問題でその理解は容易ではありませんでした。
ニュートンはプリンキピア（自然哲学の数学的原理1687年刊）の第２巻“物体の運動について（抵抗のある媒質中における）”の第７章“流体の運動と投射体の抵抗について”の命題３３で、相似な形の物体について成り立つ三つの定理を与えました。そこでニュートンは、流体中を運動する物体に働く力は
１．速度の二乗
２．物体の直径の二乗
３．流体の密度
の積に比例する事を説明しています。
その理由は以下の様に説明されます。物体は動かないで、ある定まった速度の一様な流れの中におかれた場合を考える。ニートン力学の一般法則［運動の法則、力積と運動量］によれば、流体に働く力は流体粒子の運動量変化を生じさせる力の反作用となります。流体中に生ずる運動量の変化は、流体粒子の密度に比例し、運動に預かる個々の流体粒子の速度の二乗に比例する。もちろん衝突する面積に比例するから物体の直径の２乗に比例する。［これは高校物理Ⅱで習う気体分子運動論的な考察をすれば納得できる結論です。完全弾性衝突とすれば、運動量の変化は衝突速度に比例するし、単位時間に衝突する流体粒子はその速度に比例するからです。］
さらにニュートンは次の命題３４で希薄な流体中を動く球と、その中心軸の方向に動く円柱（その直径は球と同じとする。）に働く抗力の違いを考察しています。それは円柱の円盤状の先頭面に働く抗力と球面に働く力を上記の気体分子運動論的な考察で比較したものです。そこで、球に対して働く抗力が円柱に対して働く抗力の半分になることを証明しています。
さらに、第９章“流体の円運動について”において流体中の面に働く剪断応力が、その面に垂直な方向の速度勾配に比例するという仮説を立てて、その正当性を論じています。これは後の粘性流体の運動方程式に通じる重要な考察です。
［補足説明１］
最初の翼理論は、まさにニュートンの考察を傾斜した平面板が一様な気流中に置かれるときに受ける力に適応したものです。これはニュートンが論じたのではなく、後の学者がニュートンの考え方を借用して論じたものですが、以下のような結論が導かれます。
流体の密度をρ、板の面積をＳ、板の速度をＵ、板の傾斜角をαとすると傾斜した平板に働く力は、平板に垂直な方向に Ｆ＝ρＳＵ2sin2α となる。
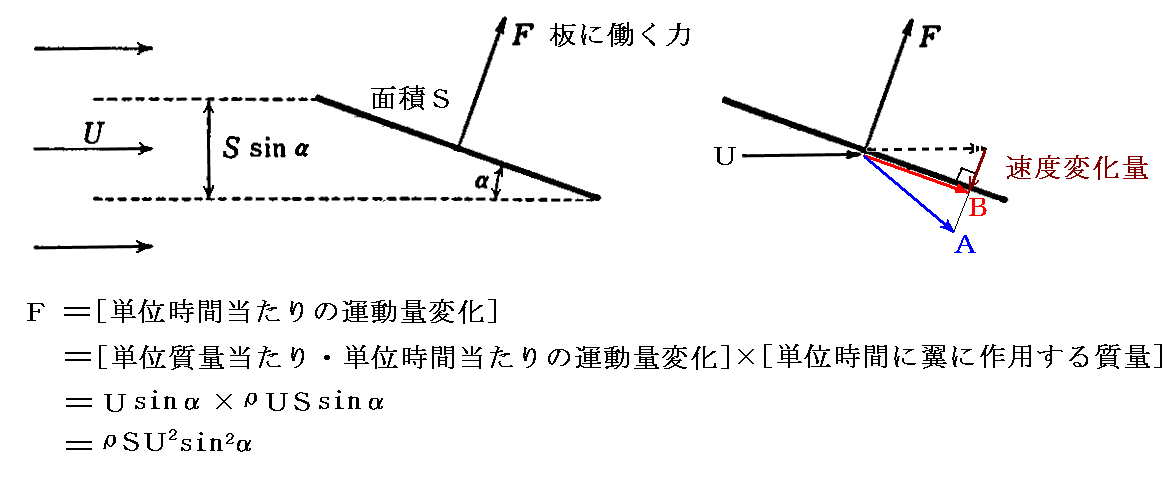
このとき重要なことは板に衝突した流体粒子は図のＡの様に跳ね返されるのではなくて、図のＢの様に平板に沿って動くと考え、しかもその速度はＵcosαとすることです。ここがいかにも流体力学的な少しいい加減な仮定ですが、そのように仮定すると流体粒子の運動量ベクトルの変化量を表すベクトルは平板に垂直な方向を向きその大きさはＵsinαとなります。この結論はニュートンの正弦二乗法則と呼ばれています。
抵抗がＵ2に比例すると言うことは、ニュートン以前にマリオット(1673年)やホイヘンス(1668年)がすでに実験によって見いだしています。ニュートンが証明した
抗力∝ρＳＵ2 という結論も、後に繰り返し実験によって確かめられるのですが、正しい結論です。
しかしながら、この結論を流体中に迎え角αを持った平板に働く力に適用すると旨くいきません。もし上記の考え方が正しいとすると、飛行方向に垂直な力［揚力］はsin2αcosαに比例し、飛行方向に平行な力［抗力］はsin3αに比例するはずです。
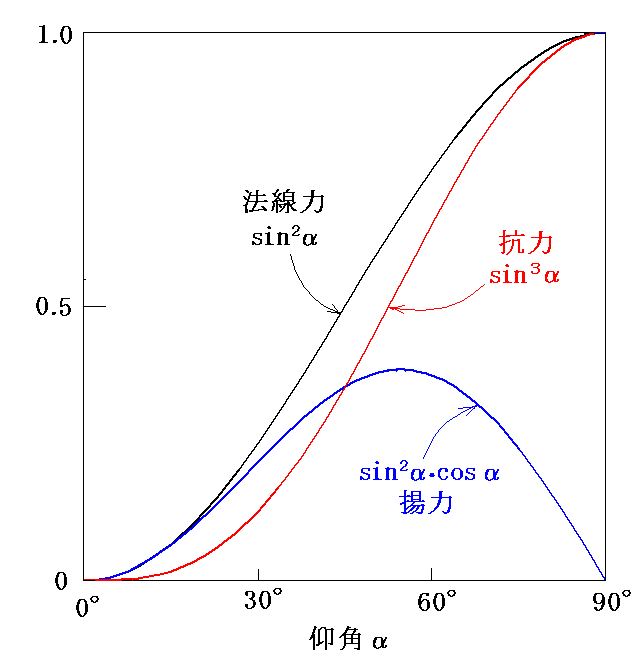
しかし、２．（１）で説明するように、これは実際の状況とは全く合いません。
ダランベールは流体力学の数学的大系化に大いに貢献したのですが、1744年の「動力学論応用のための流体の平衡と運動に関する概論」という論文の中で、“閉じた形状を持つ２次元物体まわりの非圧縮性・非粘性流れの抗力はゼロになる”事を導いています。さらに1752年の「流体抵抗新理論の試み」で今一度解析を行い、最終的に1768年の数学小論文集第5巻、第3編の中でも同じ結果を報告している。
これは別稿「渦抵抗（カルマン渦列と抗力）」１．（４）３．で説明したように、非粘性流体では物体のまわりの流れは物体の左右で対称的(下左図）になり、流速・圧力分布が物体の前後で対称的になります。そのとき完全流体では、物体表面に沿った摩擦力は働かず物体に働く圧力は全て物体表面に垂直に働きます。そのため圧力の合力はゼロとなり物体にはいかなる抗力も作用しないのです。
ダランベールの得た結論は、“流体中を等速度で動いている物体に働く力はゼロである”という、実際とはかけ離れた奇妙なものでダランベールの背理と言われました。
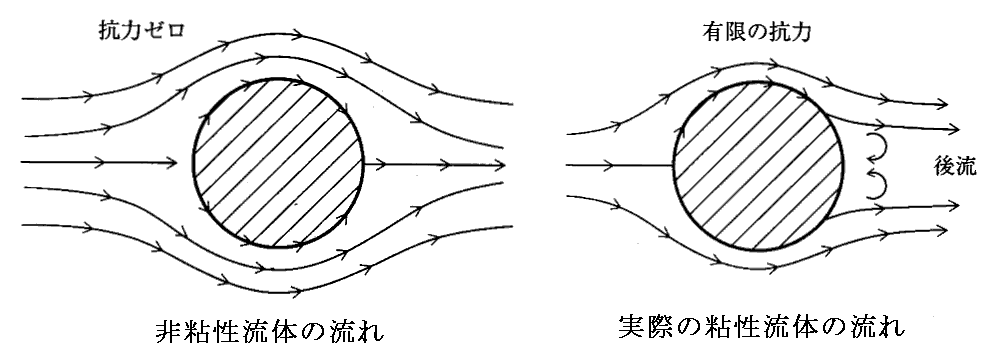
実際の流れでは物体表面の摩擦力は存在するし、また流れの様子も上右図の様になります。当時の数学理論ではその様な流れが存在することや、またそれを仮定したうえでの圧力分布などを導きだすことは出来なかったのです。
［補足説明］
１８世紀後半になると、
○ ダニエル・ベルヌーイ：圧力と流速の関係の記述（1738年「ハイドロダイナミカ」［ベルヌーイの定理］）
○ ダランベール：背理の発表（1744年、1752年、1768年）
○ オイラー：非粘性流体に対する運動方程式（1753年「流体平衡状態の一般原理」［オイラーの方程式］）
○ ラグランジュ：ラグランジュ形式の運動方程式や速度ポテンシャル・流線関数の導入（1788年）
○ ラプラス：非圧縮性・完全流体・渦無し流れについてのラプラスの方程式（1789年）
さらに、１９世紀に入ると
○ ポアソン：ポアソンの方程式（Bulletin de la socie'te' philomatique 1813年）
○ グリーン：グリーンの定理（1828年）
○ ナビエ（1823年）、ストークス（1845年）：粘性流体の運動方程式であるナビエ・ストークスの方程式
等々によって流体力学の数学大系が確立してくる。
前節で述べたように完全流体の数学理論では、物体に働く抵抗を全く説明できませんでした。その矛盾を解決するために考えられたのが死水理論です。これも完全流体に対して適応されるものですが、ヘルムホルツ（1868年）、キルヒホッフ（1869年）、レイリー（1876年）等により研究されました。
この理論の要点は別稿「カルマン渦列（動的安定性解析）」１．（１）で述べた通りです。つまり粘性のない完全流体の非回転運動では板の端で速度が無限大になるような流線が得られるのですが、その様な事を避けるためにヘルムホルツは流線は板から剥離して流れ去ってゆき、物体の背後に死水域が生じるとしたのです。いま粘性がない流体を考えていますから、その境界面(自由流線)で流体は滑り合っていると考えるわけです（1868年）。
このときヘルムホルツによって考え出された渦糸・渦層の概念は、40年後にランチェスター、クッタ、ジューコフスキー、プラントル等によって翼理論の中に取り入れられて、きわめて重要な働きをしますが、そのことについては別稿で詳しく説明します。
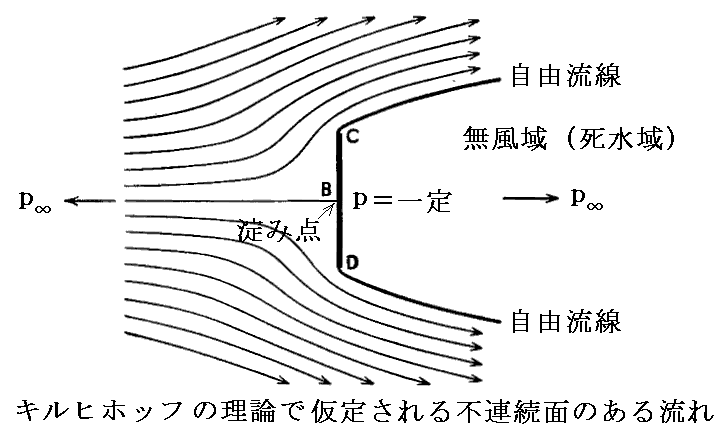
ヘルムホルツの理論が発表されるとキルヒホッフ（1824～1887年）は直ちにこれがダランベールの背理の解決に使えると考えました。キルヒホッフは、板の後ろに無風域が無限下流まで広がり、その無風域とその外部の領域が接する部分（自由流線）に沿って圧力は無限下流の圧力ｐ∞に等しいと仮定しました。このような仮定をすると死水域に接する流体の速度は一様流の流速Ｕと同じになります。一方板の前面ではよどみ点が存在して板面に沿う流速ｑはＵよりも小さくなります。そのためベルヌーイの定理により、板の前面に働く圧力の方が背面に働く圧力よりも大きくなり、流体の粘性による摩擦を省略しても、ゼロでない力が板に働くことを導き出せます（1869年）。
レイリー（1842～1919年）はキルヒホッフとは独立に同様な考察をすすめ、平板が一様流に対して斜めに置かれている場合の揚力と抗力の変化を迎え角αの関数として表す式を導きました（1876年）。
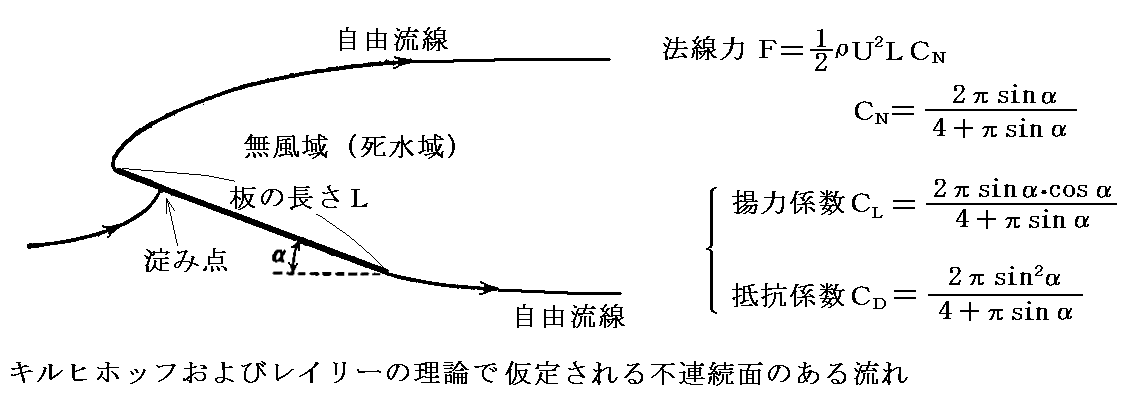
実際の計算は複素関数論を用るかなり面倒なものなので、その説明は省略します［詳細は今井「流体力学（前編）」第７章、あるいは Lord Rayleigh,
“On the Resistance of Fluids”, Phil. Mag., Vol. 2, series 5, 1876, p430～441（これはGoogle
Booksから無料ダウンロードできます）を御覧ください］。
これは完全流体の理論でダランベールの背理を避けることができたということで画期的なものですが、これも実際の揚力と迎え角αの関係式とは全く合わないものでした。
［ここは、文献17．§3-7も参照されてください。］
上に述べた理論的な発展とは全く別に実験による空気力学の研究が進んでいました。その主な人物と成果を列挙すると
1742年 ベンジャミン・ロビンス（1707～1751年）
弾道振り子試験装置と［下図ケイリーの物と同様な］回転アーム試験装置を用いて以下の事実を明らかにした。
○空気抵抗が流速の二乗に比例することを確かめる。
（これはマリオット、ホイヘンス、ニュートン等がすでに明らかにしていたもの）
○45°の迎え角で長方形平板の抵抗を調べて、長辺を前縁にしたときよりも短辺を前縁にした方が抵抗は大きいことを見つける。（アスペクト比効果の最も初期の発見）
○回転している飛翔体が直線軌道からずれる事を観察。（1852年に発見されるマグヌス効果の先がけ）
○音速に近い速度では抗力が著しく増加することに気付く。
1759年 ジョン・スミートン（1724～1792年）
○回転アーム試験器で、同じ迎え角を取ったとき平板よりも湾曲した板の方が揚力は大きくなることを確認。
（翼のキャンバー効果を観察）
○抗力を表す式 D＝ｋＳＵ2 の比例係数ｋを測定。その値はスミートン係数といわれ後に多くの実験結果の解析で使われた。スミートンは抗力Ｄの単位としてポンド重(ｌｂ)、面積Ｓの単位として平方フィート(ｆｔ2)、速度Ｕの単位としてマイル／時(ｍｉｌ／ｈ)を用いてｋ＝0.005と報告している。このとき、この公式は流れに対して垂直に設置された平板が等速度の流れから受ける抵抗に対してのみ適応出来ることは銘記されなければならない。
これは長さの単位としてフィート(ｆｔ)とマイル(ｍｉｌ)が混在しており、力もポンド重なのできわめて分かり難い。当時の標準的な質量単位(スラグ)、時間単位(秒ｓ)、長さ単位(フィートｆｔ)に換算すると下記の様になる。１スラグとは１ポンド重の力で１ｆｔ／ｓ2の加速度を生じる質量の事ですから １ポンド重＝１スラグ・1ｆｔ／ｓ2 となる。つまり １スラグ＝0.4536ｋｇ×9.8ｍ／ｓ2÷0.3048ｍ／ｓ2＝14.5939ｋｇのことです。
右下にメートル単位に換算したものも記しておく。工学では力の単位としてニュートンＮではなくてｋｇｗ(工学ではｋｇｆと書く)を用いるのでそれを使って表してある。
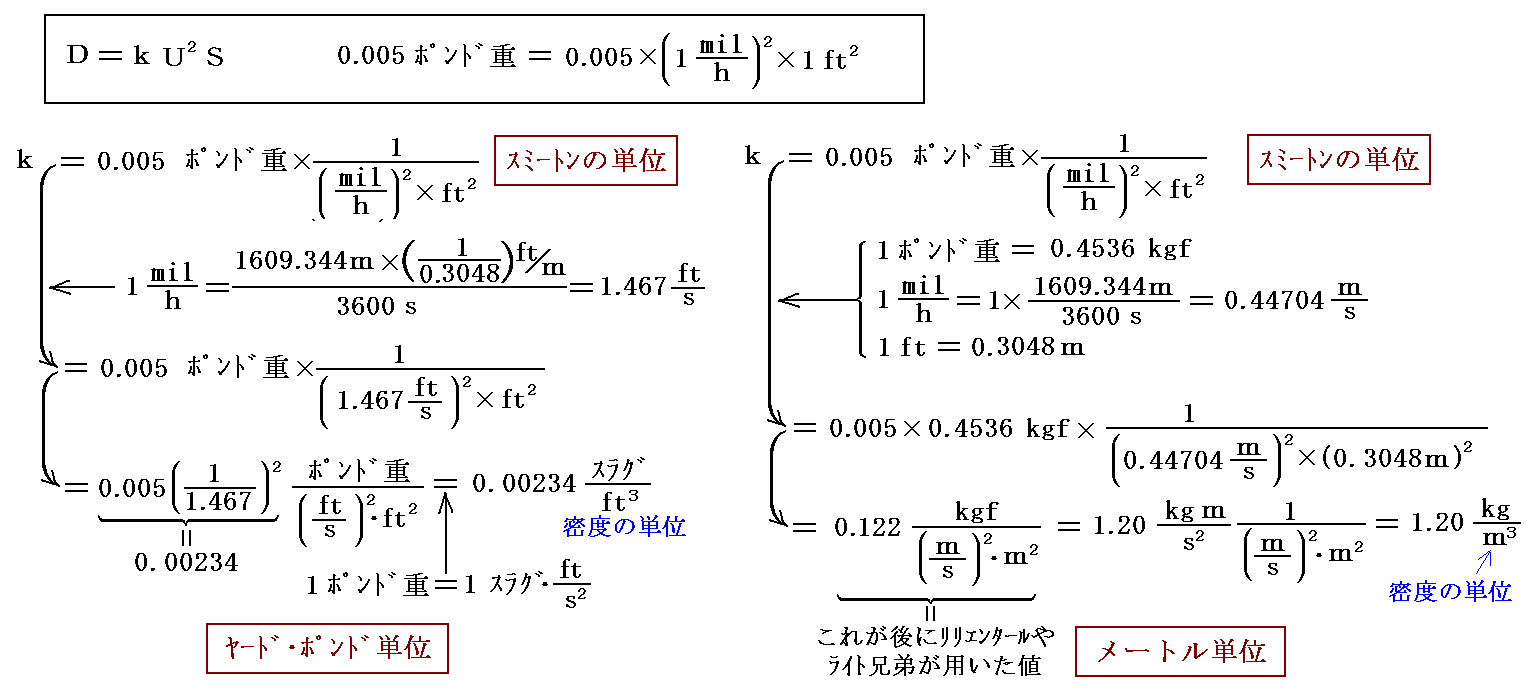
これらがスミートンが得た値なのですが、その後19世紀末までこの値が正しいと思われて用いられる。
［補足説明１］
今日得られている正しい値は［スミートンの単位で0.00289］、［ヤード・ポンド単位で0.00134］、［ｋｇｆを用いたメートル単位で0.0705］となります。つまりスミートン係数の正しい値はスミートンが与えたものの約半分程度しかありません。そのため後にライト兄弟が、リリエンタールのデータにスミートンが与えたスミートン係数値を適用して計算した揚力の大きさが実際よりも大きめに出ることになった。
1763年 ジャン=シャルル・ボルダ（1733～1799年）
○回転アーム試験器で抵抗が流速の二乗に比例することを確かめた。
○迎え角を取った平板に働く法線力が迎え角αの正弦sinαに比例する事を確かめた。
（ニュートン理論のように sin2α に比例するのではない）
○二つの球を接近した状態で移動させたときの抗力が単独の場合の抗力の和にはならない事を発見した。
○ダクト内の流れにおいて、剥離の効果のために流管の面積がダクト断面積とは異なることを見つけた。
1810年 ジョーン・ケイリー（1773～1857年）
○回転アーム試験器［下図］によって、飛行に重要な微小角における揚力と迎え角αの関係を調べた。
その結果、揚力はsinの二乗ではなく一乗に比例することを確かめた。つまり微小迎え角ではニュートン理論よりも遙かに大きな揚力が発生することを確かめている。
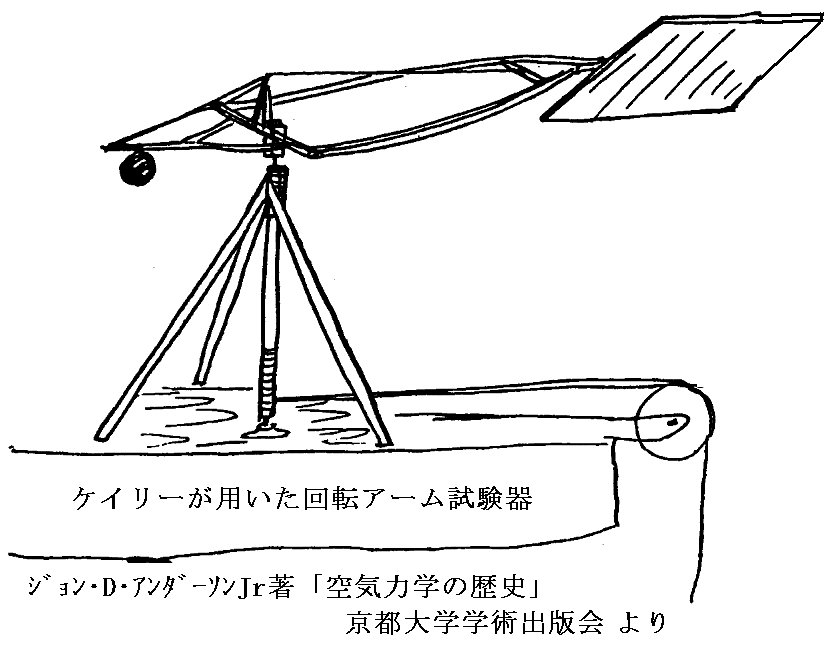
○板に働く力を揚力と抵抗力に分けて、飛行を持続させるために推進装置で補わねばならない抵抗力と重力を支えて機体を浮き上がらせる揚力を明確に区別して理解した。
○キャンパー（平板を湾曲させること）の揚力に対する効果を明確に認めた。
○流れに対して垂直に向けられた平板の受ける抗力に関係するスミトーン係数について、その値は従来言われているよりも小さい事を測定により確かめた。
実際にケイリーが計測した結果によると、流れに垂直に置かれた１平方フィート(0.093ｍ2）の平板に１ポンド重(0.4536ｋｇｆ）の抗力を発生させる速度は23.6フィート／秒(7.19ｍ／ｓ）であった。この値を用いてスミートン係数を計算すると
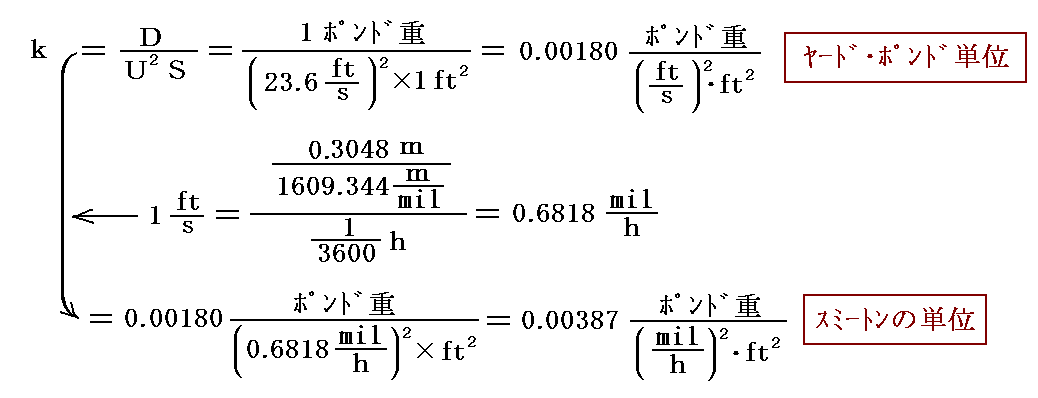
となる。つまり、スミートンが与えた0.005に対して、ケイリーの得た値は0.00387であるからスミートン係数の値は大きすぎるのではないかと指摘している。しかし何故かこの主張は世の中に広まらなかった。
○気流の剥離に伴う抵抗の概念を理解し、流線型の重要性をはっきりと認識した。
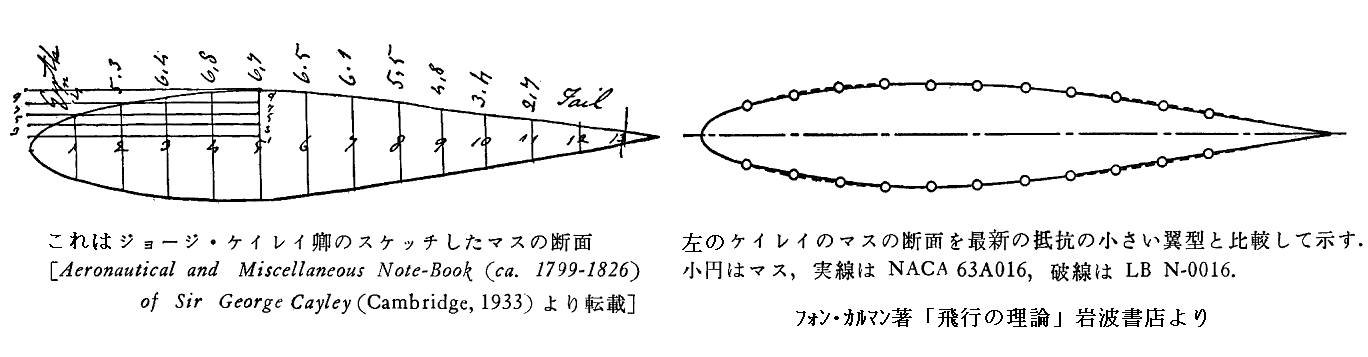
○飛行機の模型を作り飛行機械の可能性を考察した。
ここまでの実験は主に回転アーム試験器によるものでしたが、２．（１）で述べた揚力理論が予測するものは、実際の実験結果とはかけ離れたものでした。次図のグラフから解るようにニュートン理論も死水理論も実験事実を旨く説明できません。グラフの縦軸は平板に働く法線力を無次元化したもの、横軸は平板の一様流に対する迎え角αです。
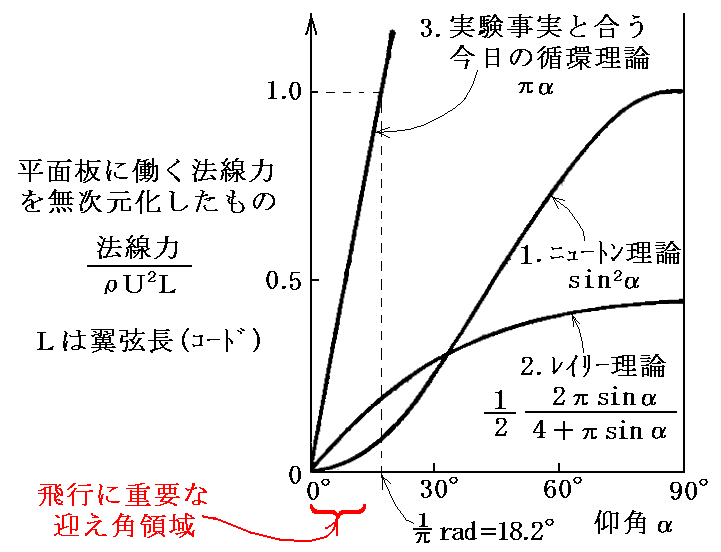
飛行機の設計で大事なのは迎え角が小さい領域での値です。実験結果は迎え角が小さい領域において理論よりも遙かに大きな揚力を発生していたのですから、最も大切なその領域の値を説明できない理論では意味がありません。
また、歴史的には１９世紀の終わりまでには、実験的研究から翼のキャンバーが揚力に取って重要であることが広く知られる様になります。つまり翼を湾曲させると迎え角がゼロでも大きな揚力が発生することが解っていたのです。しかし１９世紀の流体力学理論はこのキャンバーの効果に付いて旨く説明できませんでした。
［補足説明２］
今日の知識で、レイリーの理論値が実測と合わなかったことが説明できます。彼が死水領域の圧力として無限遠の一様流の圧力を用いたからです。今日剥離領域の圧力はそれよりも低いことが解っています。今日の実験から得られる正しい圧力を用いれば、彼の理論でも仰角が大きい失速領域については実測値を旨く説明できます。しかし仰角が小さい領域においてはやはり無力です。
１９世紀に行われた実験的研究の主なものをもう少し取り上げてみましょう。
1839年 ゴットヒルフ・ハインリヒ・ラドウィグ・ハーゲン（1797～1884年）
管内の流れには二つの異なる形態が存在する事を報告。彼は1855年の報告で二つの流れの間の遷移が温度や圧力に依存する事を述べている。（層流と乱流の違いの発見）
1852年 ハインリッヒ・グスタフ・マグヌス（1802～1870年）
マグヌスは回転しながら飛行する砲弾の研究から、回転している物体に回転軸と直角方向に流れが当たるとき、物体は流れに直角な力をうける事を発見した（マグヌス効果）。その力の大きさは流速と回転角速度に比例する。
1870年 フランシス・ウェナム（1824～1908年）
1866年の英国航空協会の創立会員の一人であるウェナムは、史上初めての風洞を制作をした。それは一辺が46ｃｍの正方形断面を持つ長さ３ｍの長方形ダクトからなり、蒸気機関で駆動されたファンにより送風された。ただし、この段階の風洞は後のもののように安定した風が作り出せる訳ではない。
ウェスムは、この風洞を用いて平板翼の実験をして、小さな迎え角では、随伴する抗力よりもかなり大きな揚力を発生できる（つまり迎え角が小さいときに揚力／抗力比がおおきくなる）ことや、高アスペクト比翼に利点があることを明らかにすることが出来た。
1883年 オズボーン・レイノルズ（1842～1912年）
彼は下図の装置で層流と乱流の存在を明らかにして、その遷移の条件を追求した。
彼は最終的に、遷移現象は流速Ｕ、流体密度ρ、流れの大きさｄ（管径）、粘性係数μなどの変数のそれぞれに単独に関係するのではなくて、それらの変数を組み合わせたρＵｄ／μなる無次元量に依存することを明らかにした。そして、流れが乱流になるのはこの値が2300を超えたときに起こることを突き止めた。
今日このパラメータの事をレイノルズ数（命名はゾンマーフェルト1908年）と言う。これは1910年のプラントルの論文で最初に使用された。
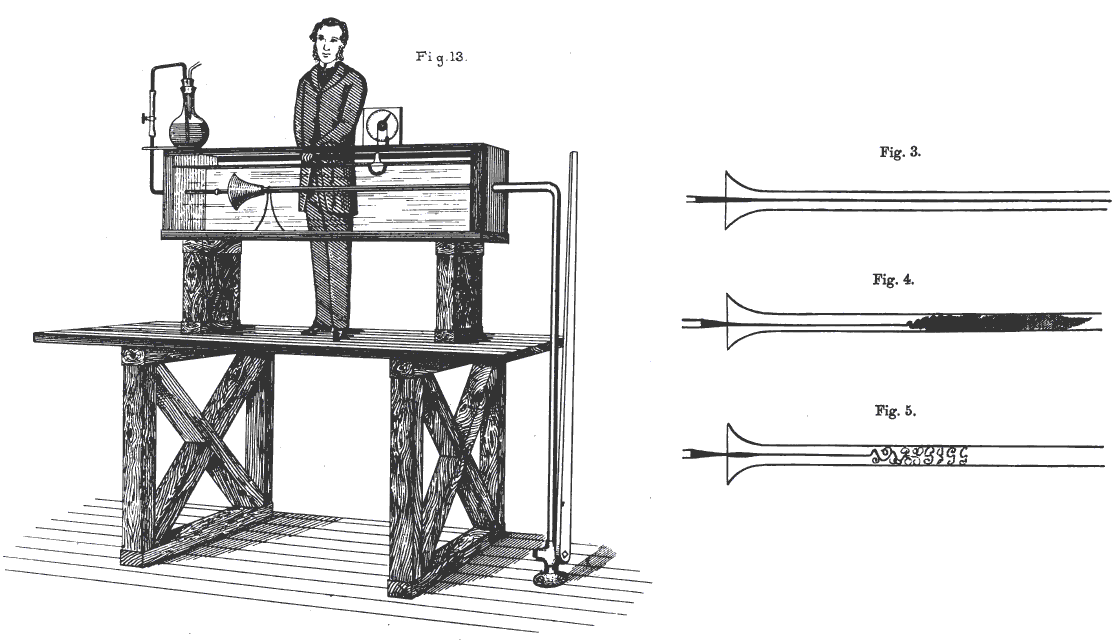
このレイノルズ数の概念は実在流体のあらゆる現象に深く関係します。特に翼の表面において層流から乱流への遷移が生じる位置を正確に求めることは翼理論で最も重要な課題ですから、この発見は航空流体力学においてもきわめて重要な発見です。［Osborne
Reynolds, “An Experimental Investigation of the Circumstances which Determine
whether the Motion of Water Shall be Direct or Sinuous, and of the Law
of Resistance in Parallel Channels”, Phil. Trans., 1883, Vol.174, 3, p935～982,これはGoogle Booksから無料ダウンロードできます］
さらにレイノルズは1894年に乱流をモデル化する時間平均方程式を発表して、その後の乱流理論的解析の中核となる考え方を示した。
［レイノルズの発見の重要性に付いては文献17．第3章などをご覧下さい。］
1884年 ホレイショー・Ｆ・フィリップス（1845～1924年）
彼は史上二番目の風洞を制作します。彼の風洞はボイラーから導かれた高圧水蒸気を蒸気噴射装置（蒸気エゼクタ）で噴射して空気の流れをつくるという特殊な機構を用いていました。彼は、それを用いて下図の様なキャンパー翼型の有利さを初めて定量的に実証した。
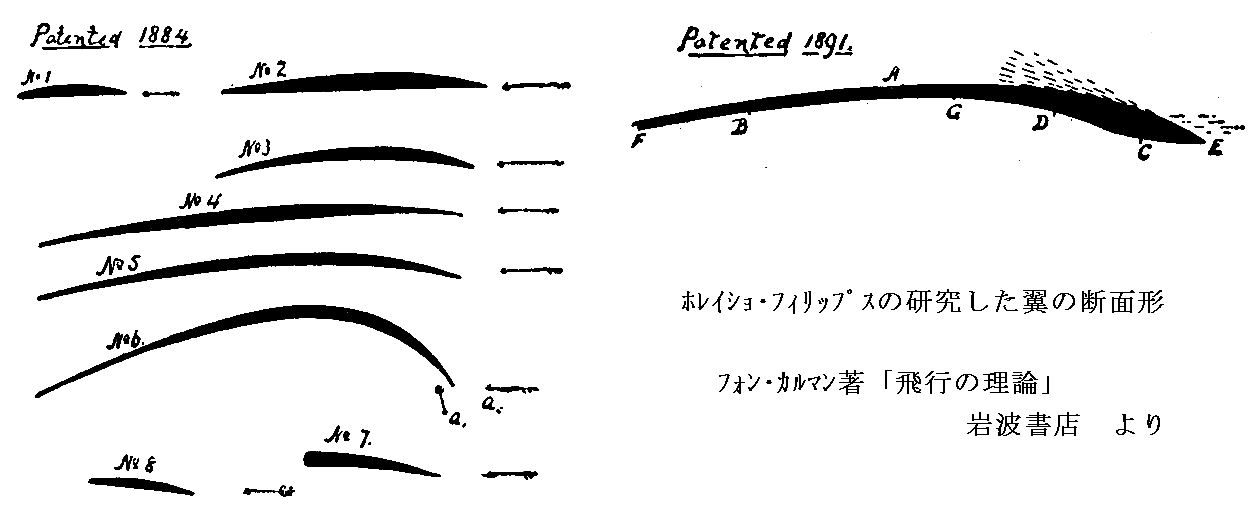
ただし、今日の知識で振り返ると、彼の実験方法は適切なものではなく、また実験データの解釈も誤ったものでした。しかし、キャンパー翼の有利さを示すことはできた。彼の研究成果は公開されて、その後の飛行機制作者にキャンバー翼型の重要性を知らしめることになった。
空を飛ぶ機械を作る試みの、初期の考え方は実際に飛行している鳥の翼を模倣することでした。最初の有人グライダー飛行で有名なリリエンタールも鳥の翼を研究しています。彼は２３年に及ぶコウノトリの飛行術の観察・研究をもとに翼の性能実験を行い、グライダーおよび動力飛行の可能性を論じた「航空技術の基礎としての鳥の飛翔（1889年）」を出版します。これは彼の理論的・実験的研究の集大成と言うべきものです。下図はその付録図です［参考文献３．］。
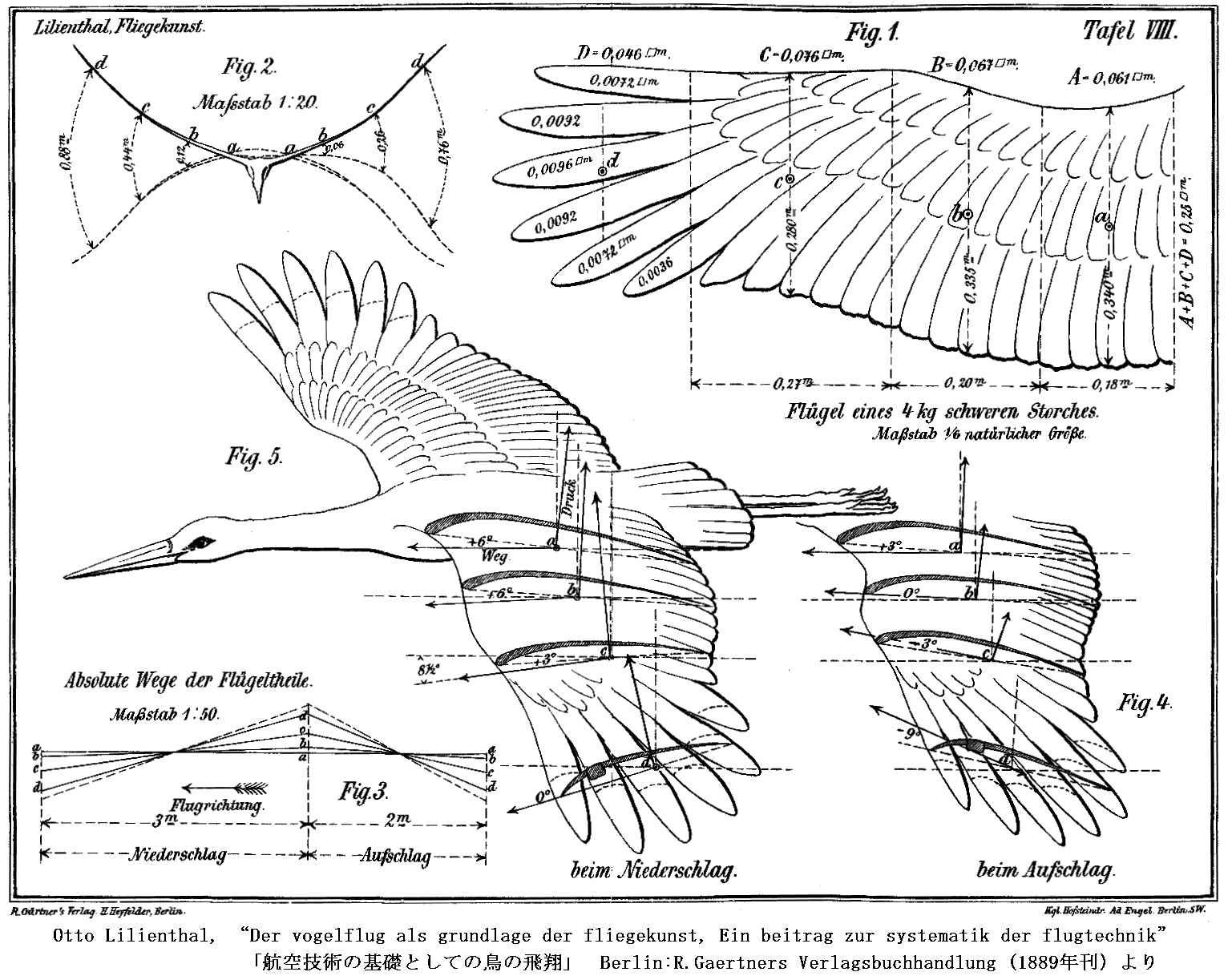
この本の出版後、彼はこの研究をもとにして木と布でグライダーを造り滑空に成功します。次図は兄オットーの死後1911年に弟グスタフが出版した「鳥の飛翔」第2版に載っている兄の飛行写真です。［他の飛行写真１、飛行写真２とグライダー三面図］
オットーは、不幸なことに飛行実験中の墜落事故により落命（1896年）してしまいますが、人類最初の有人飛行可能なグライダーを作り多くの飛行実験をしたことで有名です。しかし、彼の本当の業績は彼が残した翼の性能測定データです。鳥の研究から翼面が上に凸状に湾曲しているキャンバー翼型の優位性をはっきりと認識して、その性能を示すデータ群を後世に残したことで、リリエンタールの功績は偉大です。
オットー・リリエンタール（兄 1848～1896年）は弟のグスタフ・リリエンタールの協力を得ながら1866～1889年に行った実験から、その後の飛行機研究家に大きな影響を与えることになる翼性能データを得る。
彼らは下図の様な回転アーム試験装置で揚力Ｌ（lift）と抗力Ｄ（drag）を測定した。揚力Ｌとは翼に働く力の自由流に垂直な力の成分であり、抗力Ｄとは自由流に平行な力の成分のことです。
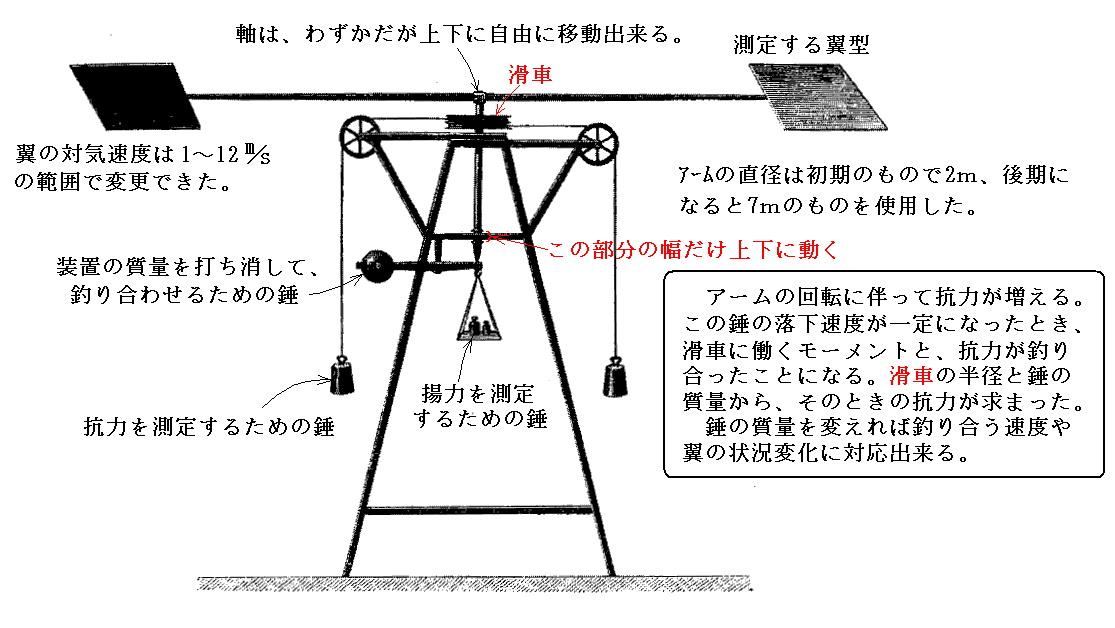
翼の迎え角αが変われば当然抵抗Ｄが変わるので、同じ質量の錘をつり下げても釣り合い時のアームの回転速度は変わる。リリエンタールは明確には書いていないが、落下する錘の力と空気抵抗が釣り合って等速度で回転する状況になったところでの回転速度と錘の質量から、その迎え角での翼の対気速度と水平抗力を測定したようです。そして抗力は速度の二乗に比例するという公式を用いて抵抗値を速度に関係しないように規格化して、迎え角の変化による速度の変化の影響を取り除いたようです。
回転用の錘を落下させアームを回転させるとやがて一定速度で回転するようになる。そのときの抗力Ｄがトルクの釣り合いの式、つまり［抗力Ｄ］×［アームの半径］＝［回転用の錘に働く重力］×［錘釣り下げ索が巻き付けられている滑車の半径］、から求まる。
また、真ん中の回転心棒につり下げられている皿の上の錘を調整して回転心棒が上下可動範囲の途中で止まるようにする。そうして皿上の錘の質量から揚力Ｌが求まる。
もちろん彼は、アーム自身の重さは釣り合い用の錘で取り除き、アームに働く空気抵抗はアームだけを回転させたときの測定値を差し引くことにより取り除いた。
以上の方法で揚力Ｌと抗力Ｄが直接測定できる。ＬとＤが解れば下記の関係式を用いて翼に垂直な方向の力の成分垂直力Ｎ(normal)と翼に平行な成分軸力Ｔ(tangential)が求まる。また翼に働く空気力の合力Ｒも求まる。
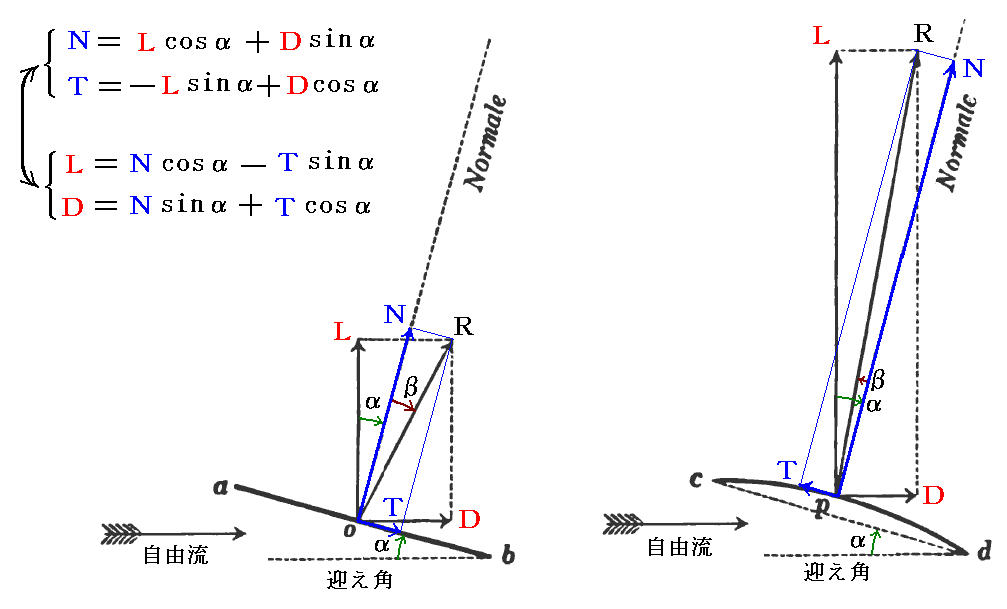
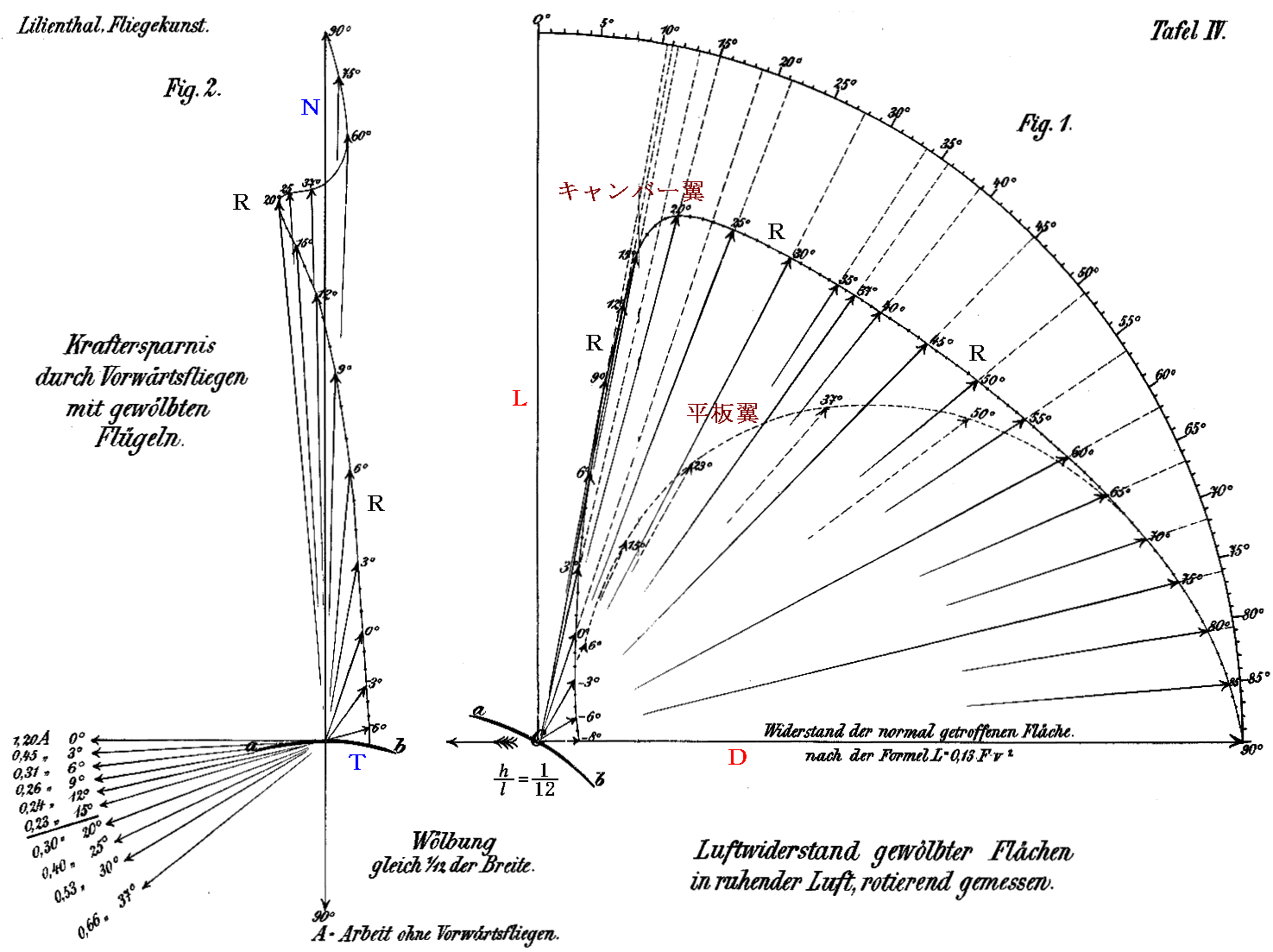
その様にして得られた平板翼に対する測定値が下図です。
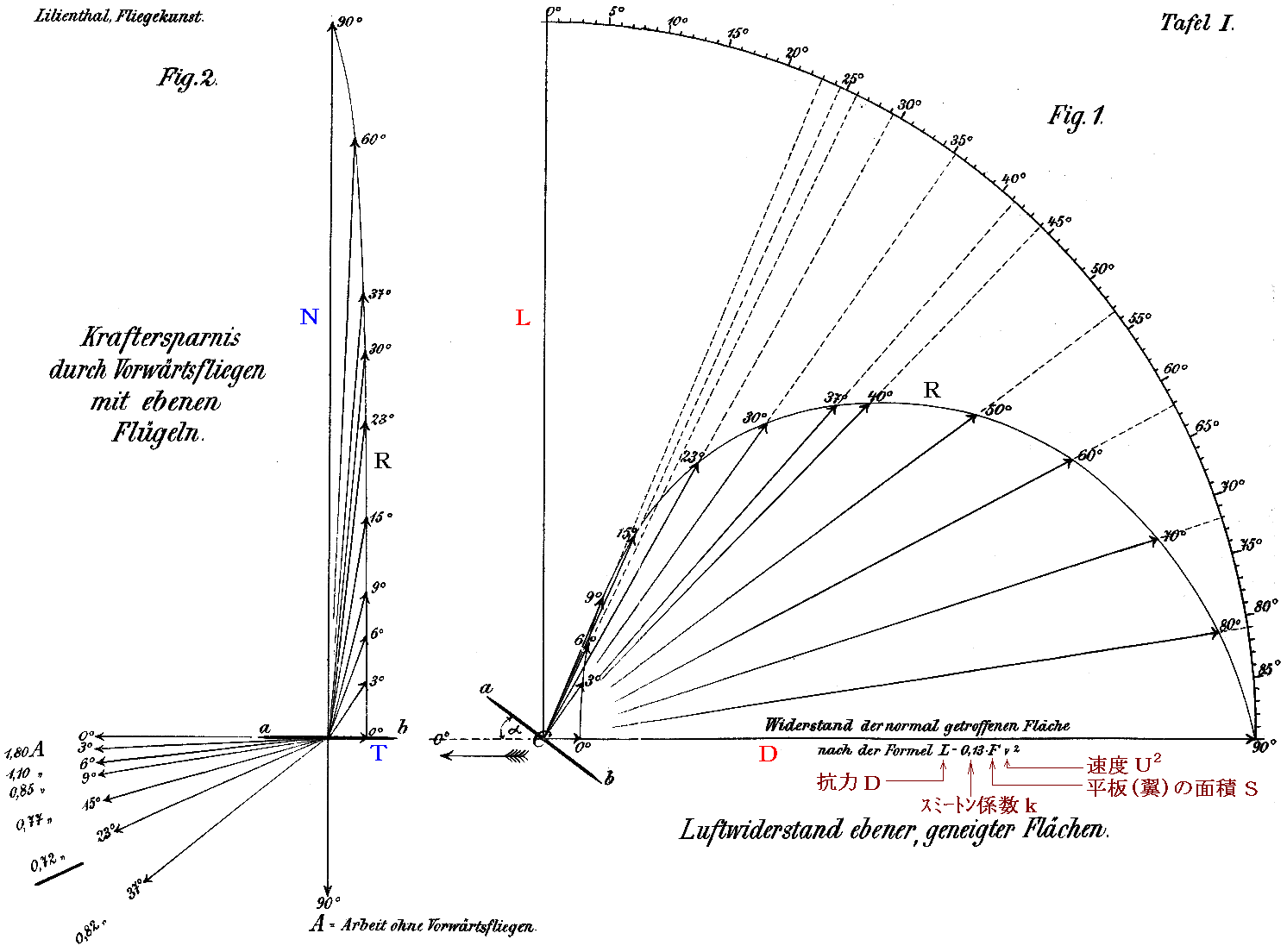
Fig１では自由流の方向は水平軸方向であり、矢印の大きさは迎え角90°の抗力で規格化されている。揚力Ｌ（縦成分)と抗力Ｄ(横成分)の合力である空気力合力Ｒが矢印で表されている。矢印先端の数字が迎え角です。外側の目盛りは合力Ｒの正確な方向を示すための分度器です。
注意して欲しいのは合力先端から伸ばした点線の交わる位置の角度が迎え角αとは異なることです。リリエンタールは合力Ｒが平板に垂直ではないことを正確に示している。当時まで板(翼)に働く力の合力Ｒが板(翼)に垂直であるのか、そうでないのかは論争の的だったのですから、その疑問を完全に解決したリリエンタールの実験は画期的です。
Fig２は平板(翼弦)の方向を水平軸にして、自由流の方向(左下の矢印)と合力Ｒの方向・大きさを表示したものです。
Fig１、Fig２のいずれの合力も迎え角α＝90°の時の抗力Ｄを基準にした相対値で表されていることに注意してください。この表示方法は画期的です。実際の力の大きさは平板(翼弦)を流れに対して垂直に立てた時の抗力Ｄが解りさえすれば任意αにおける値が直ちに計算できるのですから。実際、リリエンタールは彼の著書「鳥の飛翔」の中で、このやり方を繰り返し説明して実際の値を求める時にはその様にするように示唆している。
［補足説明］
α＝90°の時の抗力は平板の面積Ｓに比例し風速Ｕの二乗に比例することが解っていた。それは２．（１）で説明した公式 Ｄ＝ｋＳＵ2 です。この公式は、多くの人々が過去に繰り返し行った実験により、その正しさが確かめられていたものです。その中の比例定数ｋさえ解っていれば任意の風速Ｕにおける抗力Ｄが直ちに計算できる。
このｋこそ２．(１)で説明したスミートン係数で、とても重要な意味を持つ。スミートン係数ｋは流れに対して垂直に設置された平板が等速度の流れから受ける抵抗に対してのものであることに注意してください。図中の0.13kgf･ｓ2／ｍ4は当時流布していたスミートン係数をｍ、ｋｇ、ｓおよび力を ｋｇｆ で表したものです｡ ｋｇｆ は、物理学でｋｇ重＝ｋｇｗ（＝9.8Ｎのこと）と表すもので、工学ではキログラムフォースと言う。リリエンタールは２．(１)で説明した0.122kgf･ｓ2／ｍ4を0.13として用いていました。しかし、そこで説明したようにこの値は正しい値よりも約２倍程度大きな値です。そのため後にリリエンタールのデータを解釈するときに、この値0.13を用いた人々は様々な問題に遭遇することになる。
リリエンタールは平板に続いて主目的であるキャンバー翼型の空気力学特性を調べます。彼が用いた翼型は下図の様なものです。
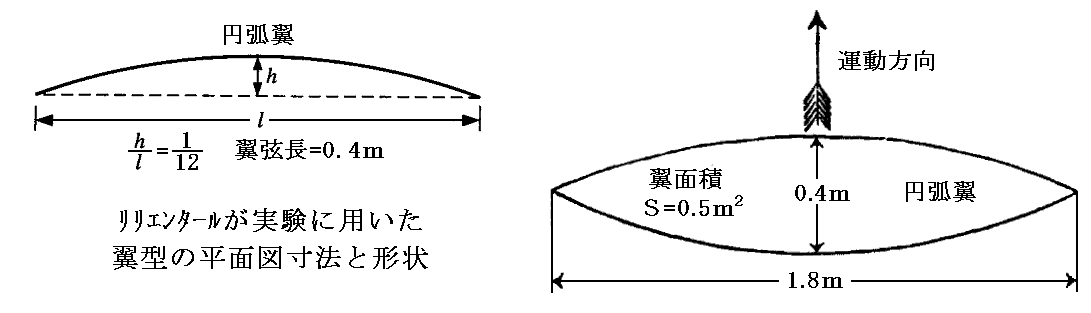
翼の湾曲の度合いは下記のキャンパー比で表される。
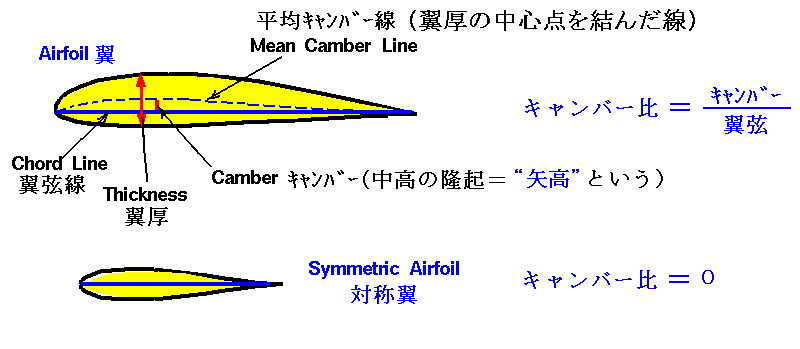
測定値は下図の様になりました。
これはキャンバー比(矢高と翼弦長の比)が1/12のものですが、彼はキャンバー比を1/40、1/25、1/12と変えて実験しています。
上図には比較のために平板のデータが点線で示してありますが、キャンバー翼の有効性は明らかです。キャンバーを付けることが翼の揚力を大きくするためにきわめて重要な要素であることを系統的な精密実験で明らかにしたことはリリエンタールの最も重要な功績です。
さらに、この図から実際の飛行に関係する迎え角が0°～10°の範囲では、ニュートン理論による揚力公式とは異なって、迎え角の増大にほぼ比例して揚力は急速に増大することが解る。抗力が小さいままで揚力が増大するこの事実こそが飛行機の実現可能性を知らしめるものですから、これもきわめて重要な発見です。
彼は回転アームによる実験の限界も熟知していました。回転アームでは遠心力による外向きの流れが生じる事に加えて、回転アームは同じ場所をくるくる回るために、先の通過で乱れ、且つ回転を始めた空気の中で実験をすることになる。［この欠点の為に、20世紀に入ると回転アーム試験器は全く使われなくなり、風洞実験が取って代わる。］
回転アーム実験の誤差を避けるために、彼は1874年から下図の様な装置で平原を吹く自然風の中での測定を開始します。
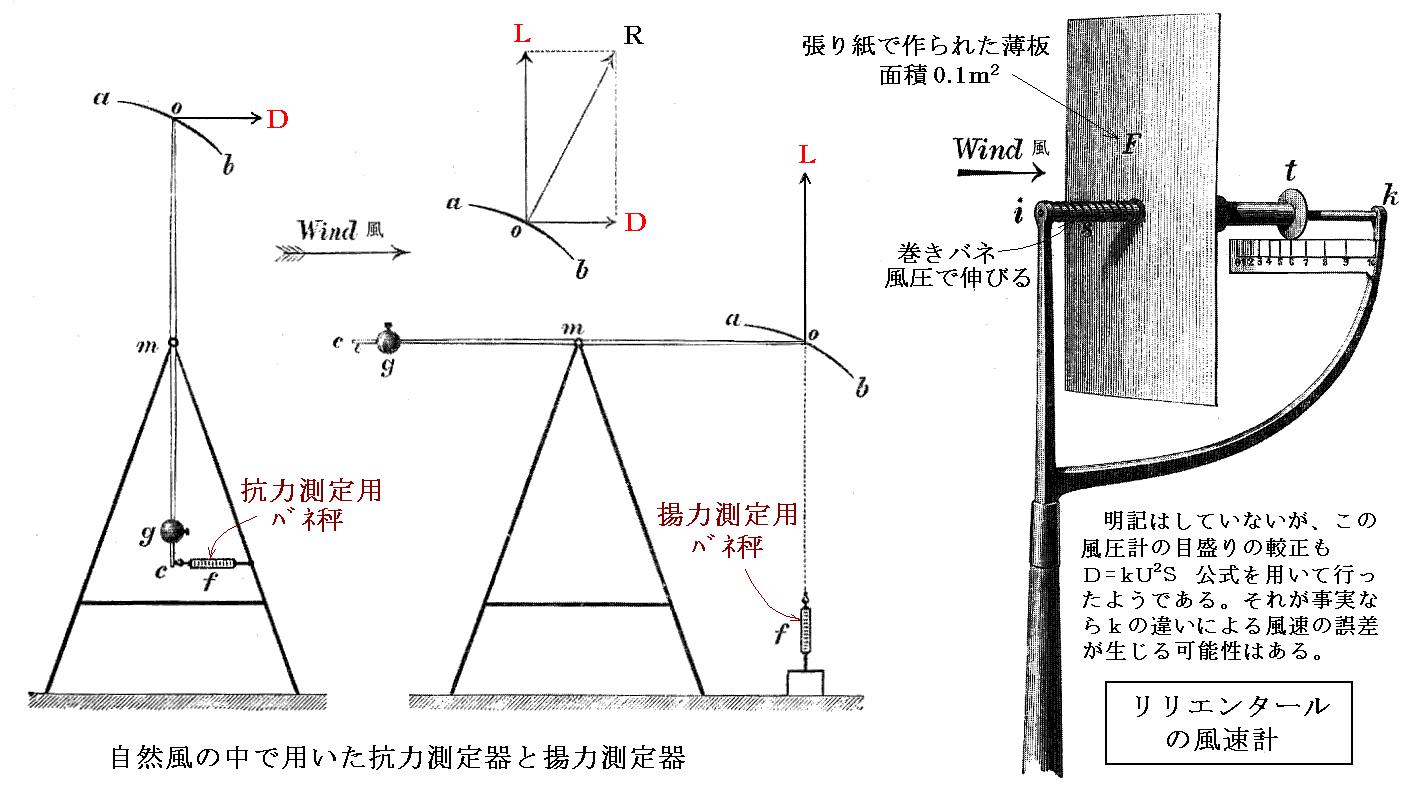
自然風の風向・風速は常に変動しているために測定はきわめて困難でした。そのため三人の観測者をそれぞれの装置に割り当てた。風速計を読み取る者が次々と各瞬間の風速値を読み上げる。それに続いて他の二人がそのときの抗力／揚力測定用バネ秤の値を読み上げる。それらの読み上げ値を次々に記録した。風速を読み上げるときと、抗力／揚力値を読み上げるときの時間的遅れによる風速変動の誤差があるが、リリエンタールは多くの測定値を統計的に処理することで、その誤差を相殺して精度をあげた。つまり風速が増大しているタイミングと、風速が減少しているタイミングが同じ割合で現れて互いにその誤差を相殺すると考えたのです。
その様にして得られたデータ一の一例が下図です。
自然風の下で得られたデータの方が全ての迎え角で揚力、揚力／抵抗比ともに大きくなっている。そして迎え角3°以下の部分では、迎え角の増大と共に揚力はもちろん増えるのですが、抗力はむしろ減少してくることが解る。またキャンバー翼では合力Ｒは翼に垂直な方向Ｎよりもさらに前に傾く有利さがあることも判明した。
リリエンタールは回転アーム実験の限界を知っていたので自然風のデータこそ真の値に近いものであると思っていましたから、上記の結果は飛行機の実現可能性をさらに高めるものでした。
おそらくこれらのデータを得たリリエンタールは飛行機実現の可能性を確信して天にも昇る思いだったでしょうね。1889年に出版された「鳥の飛翔」を読むと彼の胸の高鳴りがひしひと伝わってきます。事実、彼はこの発表の後すぐに人を乗せて飛行するグライダーの制作に取りかかります。
［補足説明］
彼は、キャンバー比を増加させることには限界があり、特に速度が大きい場合にはキャンバー比が小さい方が有利になることや、キャンバー比が大きくなると仰角の変動に伴う空気力合力の作用点の移動が激しくなって、翼の制御が困難になる事を発見している。
リリエンタールのデータは飛行機制作者に取って重要な情報を教えてくれます。ただし、当時の飛行機製作者がそのデータの意味を正しく理解できていたかどうかは疑問が残ります。実際、ライト兄弟なども最初は誤った解釈をしていた。この事については５．（２）［補足説明３］を参照。
彼のデータから得られる合力Ｒを垂直上向きに取ると、図からグライダー滑空時の沈下角(滑空角度）が直ちに求まる。もちろん翼以外の部分に働く抵抗力は無視した上での話ですが、各翼型の滑空性能が直ちに求まる。揚力Ｌも抗力Ｄも対気速度の二乗に比例して増加しますから、重力ｍｇを支えるＲになるまで滑空速度は大きくなります。そのとき沈下角は滑空速度には関係せずに定まります。
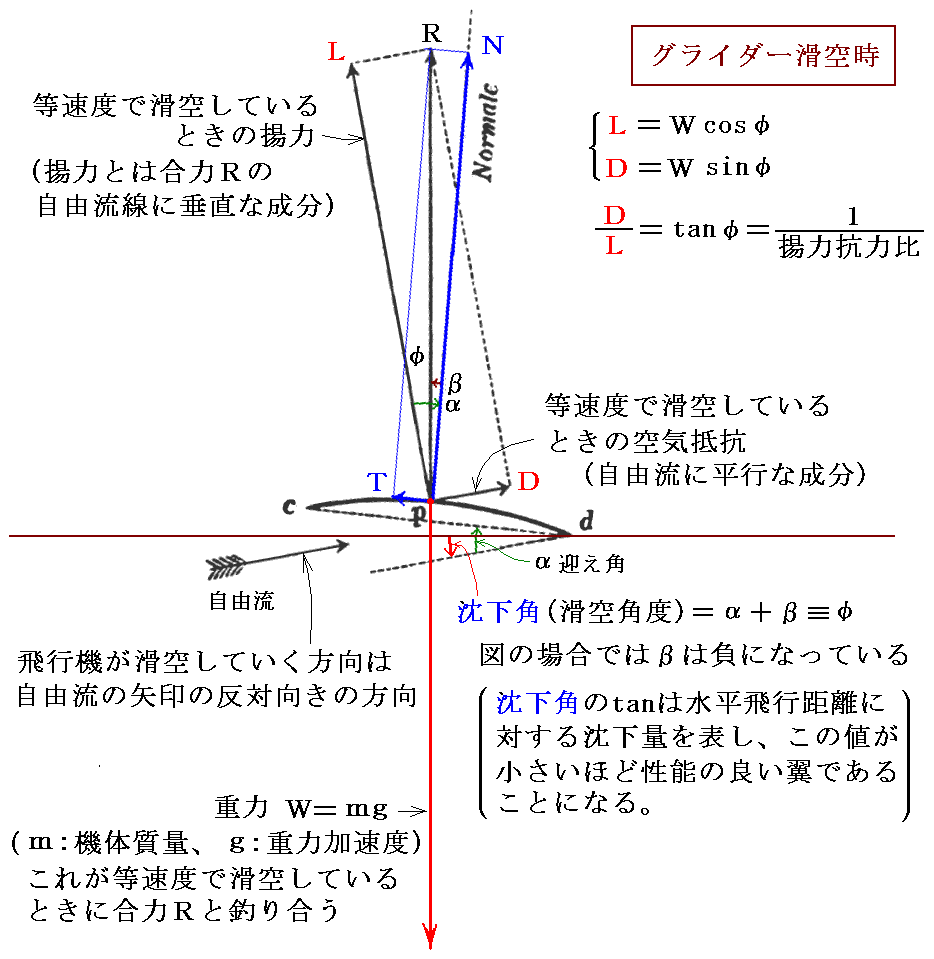
さらに、揚力Ｌが垂直になるようにすると動力飛行時に必要な揚力Ｌと、飛行に必要なエンジン出力が直ちに求まります。すなわち、［相対値ではないＤの実値］×［飛行速度Ｕ］＝［エンジン仕事率（馬力に相当）］×［プロペラ効率］となる。これも動力飛行を目指す者には必須の情報です。
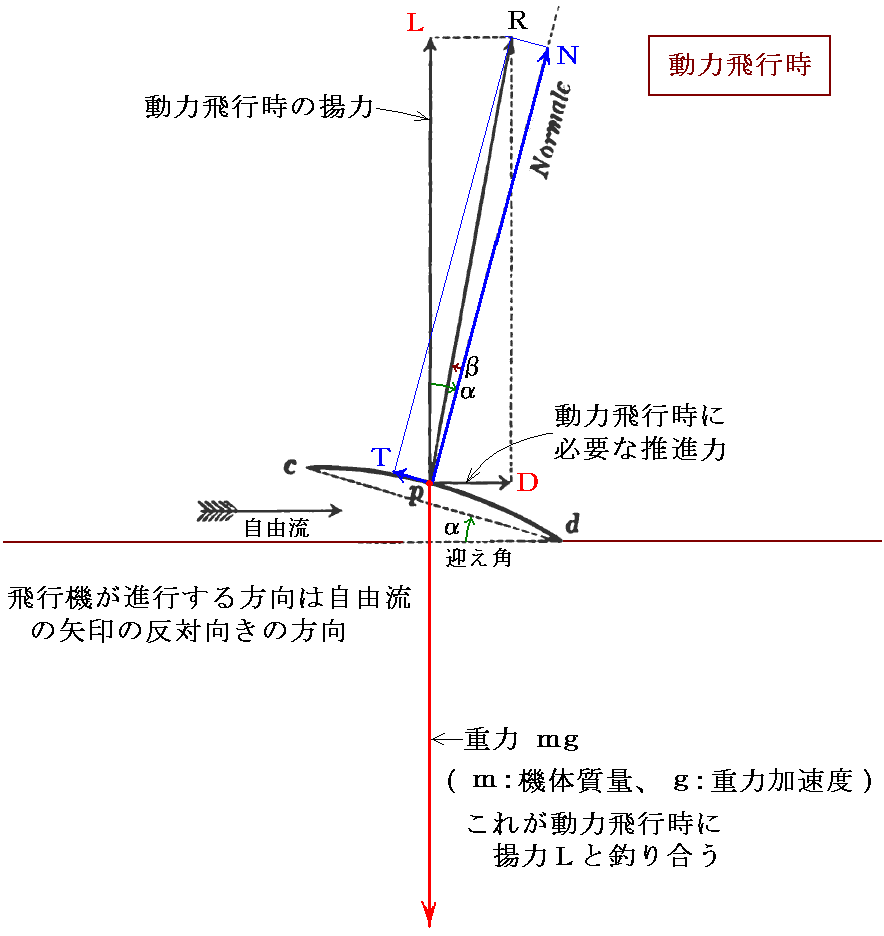
飛行機制作にきわめて重要なデータを手にしたリリエンタールは、次なる段階としてグライダーによる飛行術の習得と、動力による羽ばたき飛行を追求していきます。何故彼が、当時主流になりつつあった固定翼とプロペラ推進の方式ではなくて、羽ばたき飛行機に固執したのかは今となっては解りません。彼は道半端の1896年に、試験飛行の墜落事故で落命してしまうからです。しかしながら、リリエンタールの残したデータはラングレー、シャヌート、ライト兄弟をはじめとして後の飛行機制作者に大きな影響を与えます。
［補足説明］
［揚力］は［迎え角］のみならず、［翼面積］と［対気速度の二乗］に比例します。そのため［揚力］・［抗力］・［重力］の釣り合いには注意すべきことが幾つかあります。
○迎え角とは翼の翼弦線と実際に翼に当たる相対風の方向とがなす角度で、翼弦線と水平線がなす角度ではありません。当然のことですが、飛行機が降下や上昇しているときには両者は一致しません。初期の飛行機研究家にとって、両者の違いを理解することは特に重要なことでした。
○飛行機を浮かばせる揚力が発生できるかどうかは翼の総面積に関係します。そのため、飛行機の重量を翼面積で割った翼面荷重はとても重要なパラメーターです。
例えば、速度の速い飛行機を造るには、翼面積を小さくして翼面荷重を大きくする必要がありすます。飛行機の受ける抵抗は速度の二乗に比例して増加しますからそれに打ち勝つ動力が必要なのはもちろんですが、動力に応じて翼を小さく（翼面荷重を大きく）しないと、揚力が増えすぎて上昇ばかりが生じて速く飛ぶことはできないのです。
○また、翼を小さくして翼面荷重を増やしても滑空の沈下角は大きくはなりません。翼が小さくなると抗力は小さくなり、滑空速度が増大します。速度増大は飛行機に働く重力と釣り合う揚力と抗力が発生するまで続きます。だから、滑空機の沈下角（滑空角）は揚力／抗力比だけで決まり翼面荷重には関係しません。もちろん飛行速度が大きくなりますので同じ高度を降下する時間は短くなります。つまり沈下率［毎秒当たりに降下する高度の割合］は大きくなります。このことは、もし翼を大きくして翼面荷重を小さくできれば同じ沈下角度でゆっくり降下していける事を意味する。
○飛行機を操縦しているときに、高度をさげるつもりで水平尾翼を操作して機首を下げても高度は簡単には下がりません。なぜなら降下角を大きくして翼弦線を前傾させると、揚力・抗力・重力の合力が機体前方を向くベクトルとなり飛行機は増速します。飛行速度が増えると揚力が増えて飛行機は浮き上がってしまうからです。
○高度を下げるには、エンジンの出力を絞ったりスポイラーを出して飛行速度を遅くすることが必要です。速度が遅くなると揚力が減少しますから飛行機は高度を下げてゆきます。ただし着陸時には低速でも重力に打ち勝つ揚力が必要ですからフラップや前縁スロットによって一時的に揚力性能を良くしてやる必要があります。
アレガニー天文台の館長であったラングレーは1887年にリリエンタールと同じような回転アーム試験器（アーム地上高2.4ｍ、直径8ｍ）を造り、平板の空力特性の測定を開始します。そして4年後の1894年に「空気力学実験」という本でその成果を発表します。
1887年に実験を始めたとき、ラングレーはウェナムとフィリップスの研究は知っていましたが、リリエンタールの実験はまだ気づいていません。後にリリエンタールの成果を知り、彼の本を取り寄せて研究しています。
彼の空気力学データは全て平板についてのものですが、特にニュートンの正弦二乗法則の正当性を確かめることに集中しました。
ラングレーは予備的な実験としてまず迎え角90°の場合の抵抗係数［２．（１）で説明したスミートン係数］を求めています。彼が求めた値は、力をkgfを用いるメートル単位でｋ＝0.08kgf･ｓ2／ｍ4［リリエンタールは0.13とした］、スミートンの単位で0.003ポンド重･ｈ2／mil2･ｆｔ2となります。これはスミートンの値0.005の約半分で、今日の正しい値0.00289にきわめて近い値です。
ラングレーは回転アームに取り付けた巧妙な測定装置により揚力Ｌと抗力Ｄを計測してその合力である空気力合力Ｒを求めた。そしてリリエンタールと同じように迎え角90°の抵抗値で規格化した合力係数ＣRでデータを示しています。その規格化されたＣR［３．（２）のリリエンタールの図のＲに相当するもの］の迎え角αに対する変化は下図の様になった。
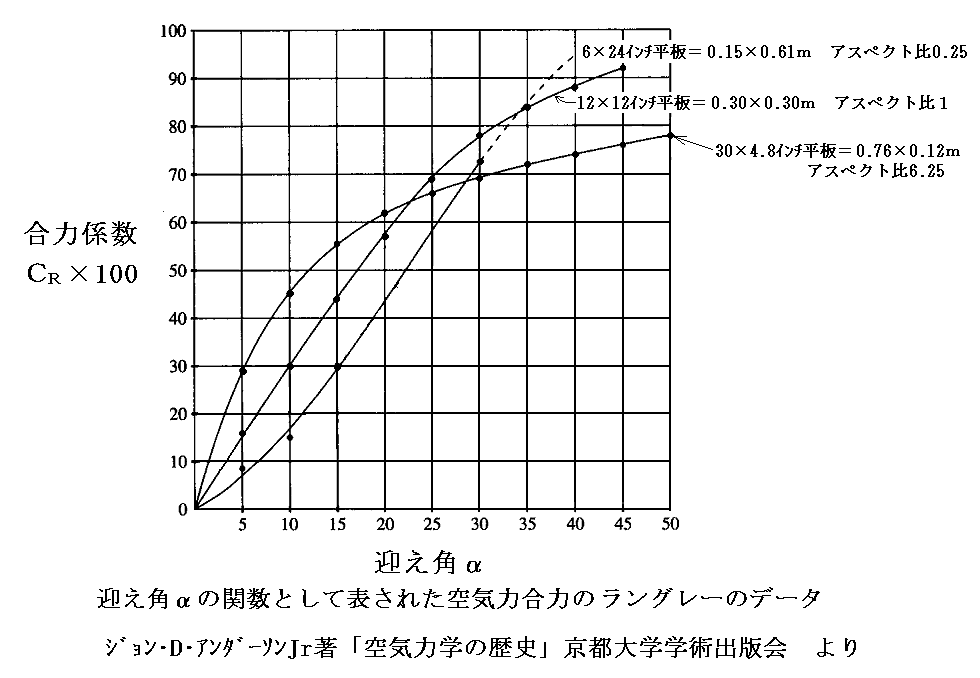
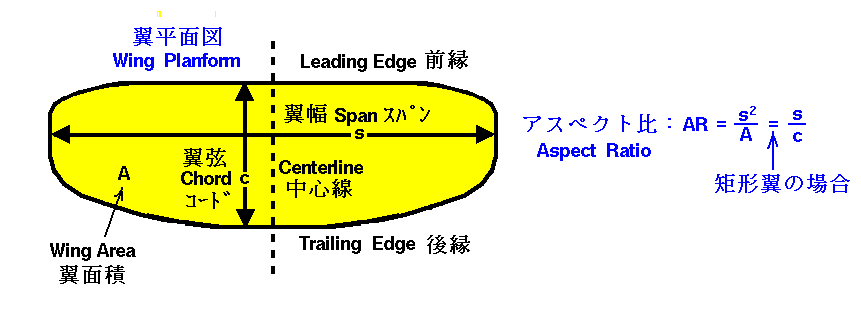
ラングレーは平板の縦横の比率が違う３種類の板で測定している。彼は、平板の種類を変えたとき、どの縁が流れに対して垂直になるようにセットしてあるかを説明するために“アスペクト”（aspect 向き）という言葉を用いたのですが、これが今日アスペクト比(aspect ratio）と呼ばれる言葉の由来の様です。ちなみにアスペクト比の定義は アスペクト比＝翼幅2÷翼面積＝矩形翼の場合には翼幅÷翼弦 です。
迎え角が小さくなると合力Ｒはほぼ揚力Ｌに近いと見なして良いのですが、データは迎え角が小さな領域ではアスペクト比が大きな平板ほど合力Ｒが大きくなることを示している。この傾向は今日の知識でも正しい結論で、三次元翼の性能を論じるときにとても重要です。ラングレーはその重要な事実を実験によって明確に示すことができました。
ラングレーは“平板落下実験”からも高アスペクト比の平板が揚力について有利であることを確かめています。平板落下実験では回転アームの先端に1.2ｍの鉛直ガイドを取り付ける。平板翼がそのガイドを上下に自由にスライドできるようにして様々なアスペクト比の平板翼を水平に取り付ける。アームを一定速度で回転させている状態で、平板翼を自由落下させ1.2ｍのガイドを落下する時間を測定する。その落下時間が長いほど落下距離に対する水平移動距離が長くなり、平板翼の滑空性能が良いことになる。
今日の知識に基づけば、落下中の平板には斜め下から風が当たることになるので、平板は空気流に対して正の迎え角を持つことになる。そのため揚力が発生して落下時間に差が生じる。
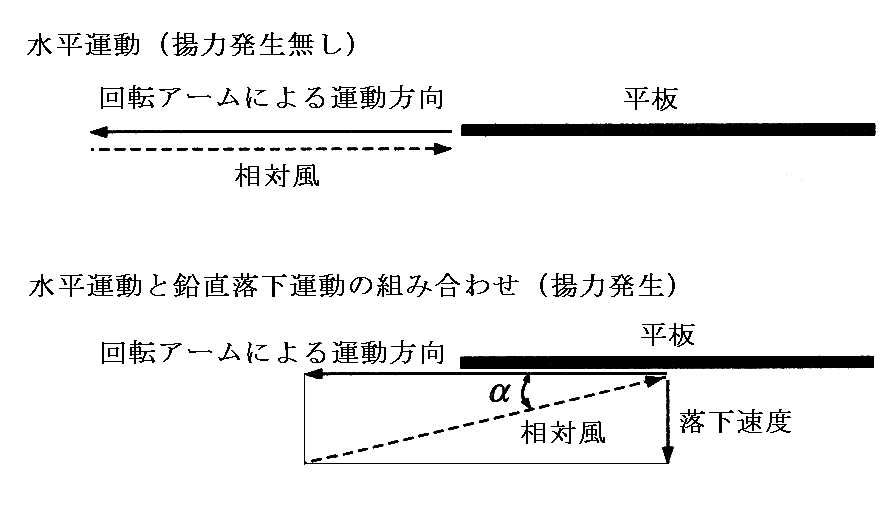
ラングレーが揚力のメカニズムについてそこまではっきり認識していたかどうかは不明ですが、高アスペクト平板翼の滑空性能が良いことを実験で示すことはできた。その実験結果が下図です。
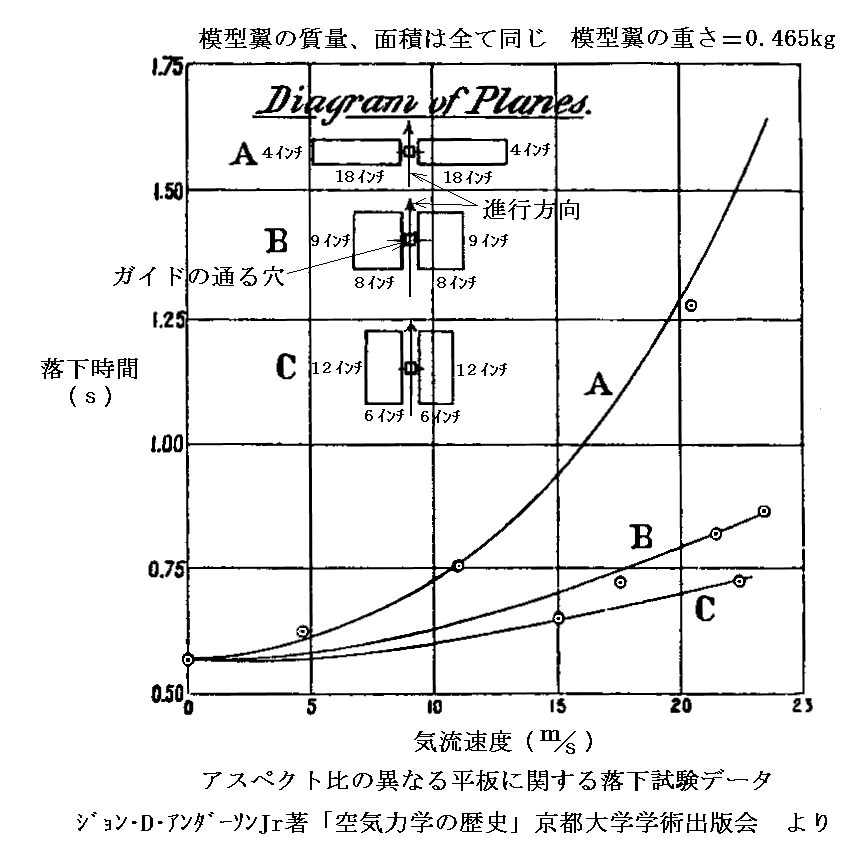
この実験結果からも高アスペクト比が揚力発生にきわめて有利であることが解る。２．（２）で説明したように、1870年頃にフランシス・ウェナムが高アスペクト比翼が揚力発生において効率が良いことをすでに認識していたのですが、高アスペクト翼の優位性を系統だった実験ではっきりと示したのはラングレーが最初です。この効果を理論的に解明したのが、プラントルの揚力線理論（1918頃）です［別稿で説明］。
ラングレーは空気力合力についてもう一つ重要な発見をしています。それは「平行偏心板」による実験で発見された。彼は回転アームに平板を取り付けるとき、その平板が回転アーム軸のまわりに回転できるようにして、しかも取り付け位置を平板の中で前後に移動できるようにした。そのとき平板の前縁から回転軸までの距離を実験ごとに変えて回転アーム試験器を回転させると、回転軸の位置変化に応じて抵抗力合力と釣り合う迎え角が変わったのです。彼は平衡の釣り合い状態における迎え角αの値が変わると回転軸の相対的位置が変わることを発見して、その間の関係を詳しく調べた。
その結果、圧力の働く中心位置が、迎え角90°のときは平板の中心にあったものが、迎え角を小さくするにつれて前方に移動し、迎え角αが減少すると前縁から翼弦の１／４の位置まで前進することを見つけた。
また、後になってキャンバー翼について行った同様な実験から、平板とキャンバー翼ではその移動の仕方が異なる事を発見している。
さらに、彼は助手のハフェイカーと共に迎え角が小さくなると圧力中心は反転して後ろに下がる事も見つけている。これらの知見は実際に飛行機（特に翼の形状）を設計する上で極めて重要です。
ラングレーは実際の飛行に不可欠の小さな迎え角での揚力は、ニュートンの正弦二乗法則から予測される値よりも遙かに大きいことを認識して動力による飛行の実現性に自信を深めた。次に彼が目指したことは実際に飛行できる動力飛行機を作って飛行できる事を実証することです。
彼は抵抗の計測に基づいた動力の計算から、エンジンでプロペラを駆動して飛行する機械の実現性を確信していましたから飛行機の制作に邁進します。彼は飛行機械のことをエアロドロームと呼んでいましたが、ゴム動力模型から始まって蒸気動力、ガソリンエンジンと次第に大型化した沢山の飛行機械を作りました。
中でも最も成功したのは蒸気動力を用いたものの中の５番目のエアロドロームです。それは下図の様なもので、上反角を持った翼幅4ｍ、アスペクト比5、翼面積6.4ｍ2、翼面加重（重さを翼面積で割った値）1.8kg／ｍ2の翼で、キャンバー比1：12、最大キャンバーは翼弦の前から23.8％の位置にありました。
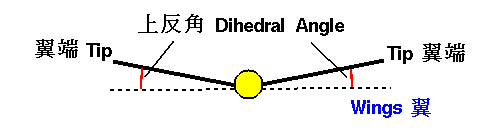
下図の拡大版。５号機の詳細写真はこちらを参照。下右写真はスミソニアン航空宇宙博物館本館に展示されている５号機です。
この５号機は1896年5月6日に1回目は１分30秒間、２回目は90秒間の蒸気動力による飛行に成功しました。これは模型飛行機ながら実際の動力による初めての飛行に成功した画期的な実験でした［拡大写真］。
その後ラングレーは陸軍省からの財政的な支援を受けて1898年から5年の歳月をかけて助手のチャールズ・マンリーとともに5号機の4倍の大きさで、ガソリンエンジンを動力とした人が乗れる大型エアロドローム［全長約17ｍ、全幅約15ｍ、三面図］を完成させます。しかし1903年のライト兄弟の初飛行にわずか先んじた飛行実験は、構造的な強度不足や操縦安定性の欠陥により失敗に終わります。そして彼はそれ以後飛行機の開発をやめてしまい3年後の1906年に失意のうちに亡くなります。
彼の動力飛行機はもう少し改良を続ければおそらく飛行に成功したと思われる段階に達していましたから誠に残念なことです。またマンリーが作った高性能エンジン［ガンストン氏の説明、鈴木孝氏の説明］が生かされなかったのもさらに残念なことです。
［補足説明１］
飛行機の操縦性を論じるときには三次元的な回転を下記のように呼びます。
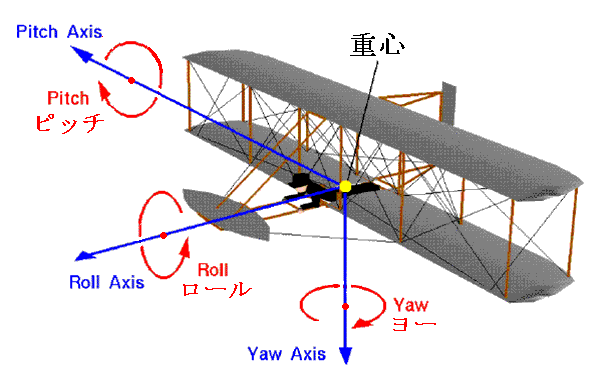
［補足説明２］
ラングレーのエアロドロームは上反角が採用されています。翼に上反角を付けると上図のロール方向の安定性が生じます。この事をハッキリ認識したのもおそらくラングレーが最初だろう。
揚力は翼面に垂直に働きますから、飛行機が何らかの要因で左右に傾くと、重力との釣り合いが崩れて飛行機は傾いた方向に横滑りをします［下左図］。飛行機は前進しつつ横に滑るので実際には斜め前に滑っていきます［下右図］。
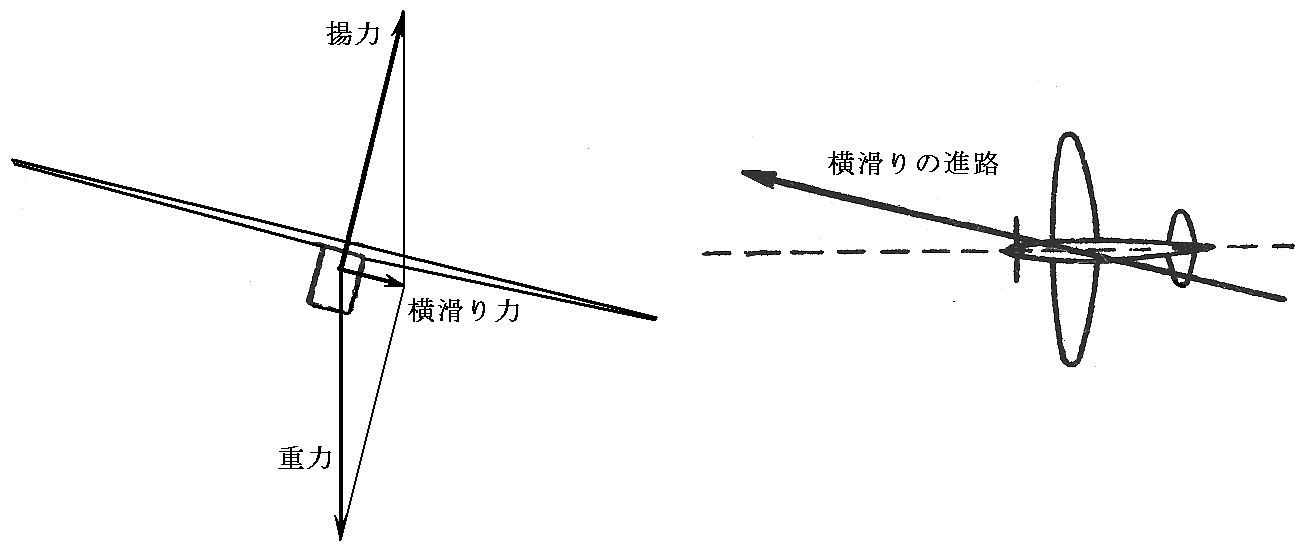
翼が上反角を持っていると横風に対する角度は左右の翼で異なってきます。実際には横風と前方からの風を合成した風が翼に当たります［下左図］。合成した風に対する迎え角は右翼の方が大きくなるために右翼には左翼よりも大きな揚力が生じて飛行機を水平に戻してくれます［下右図］。これがロール方向の安定性を生み出す上反角効果です。
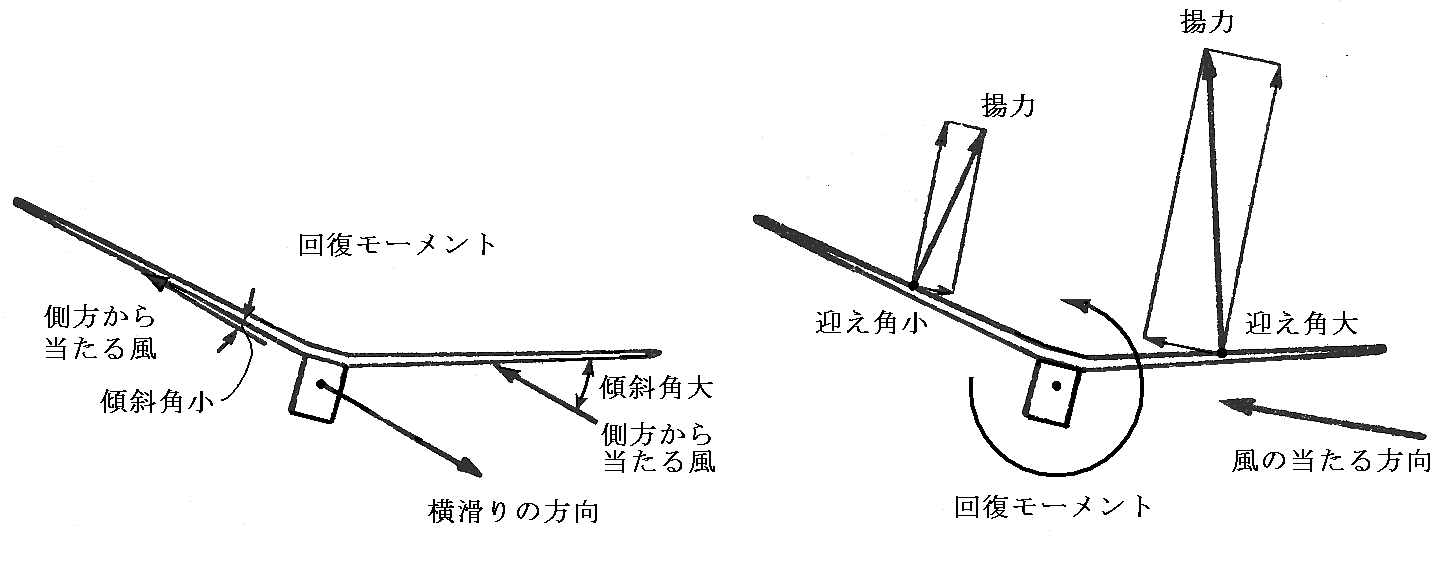
［2013年4月追記］この事について、もう少し解りやすい説明と図を引用。
ここで注意しなければならないのは、この効果は横滑りが起こって初めて働き出すのであって、横滑りがなければ水平に戻すモーメントは生じません［下図］。
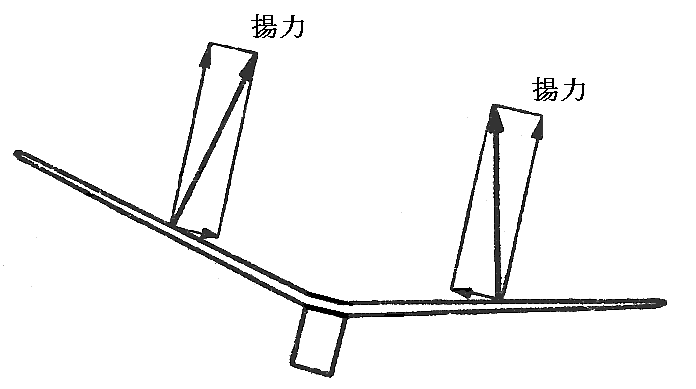
そのため上反角が過大で、垂直尾翼が小さくて風見効果（風見鶏の様に機首を風上に向ける効果）が充分でない場合、お尻を振り子のように左右に振るダッチ・ロール（Dutch roll）不安定性が生じる場合があります。つまり横滑りをしないとロール回復効果が生じないのでバンクするとまず横滑りが生じます。その横滑りが過剰な回復モーメントを生じて逆方向までバンクしてしまいます。そうなると反対側の横滑りが生じて、それがまた過剰な回復モーメントを生じる。以下その過程を繰り返していつまでもロール振動が減衰しないのです。
［補足］ダッチ・ロールという言葉はオランダ人がよくやったスケートの形に似ているところからきたようです。
ライト兄弟は1899年から飛行機と翼に関する資料を精力的に集めて飛行機の研究を始めます。彼らはこの頃ラングレーの本「空気力学実験（1894年刊）」やシャヌートの「飛行機の進歩（1894年刊）」などを手に入れて、揚力と抗力、あるいは揚力／抗力比などの知識を得ていきます。また1900年にはシャヌートが1897年の「航空年鑑」に転載したリリエンタールの自然風に対するキャンバー翼の垂直力係数と軸力係数の表を入手します。これは３．（４）で説明したTufelⅥ図のFig2の垂直力Ｎと軸力Ｔをリリエンタールが表にして公開していたものを転載したものです。［下図参照］
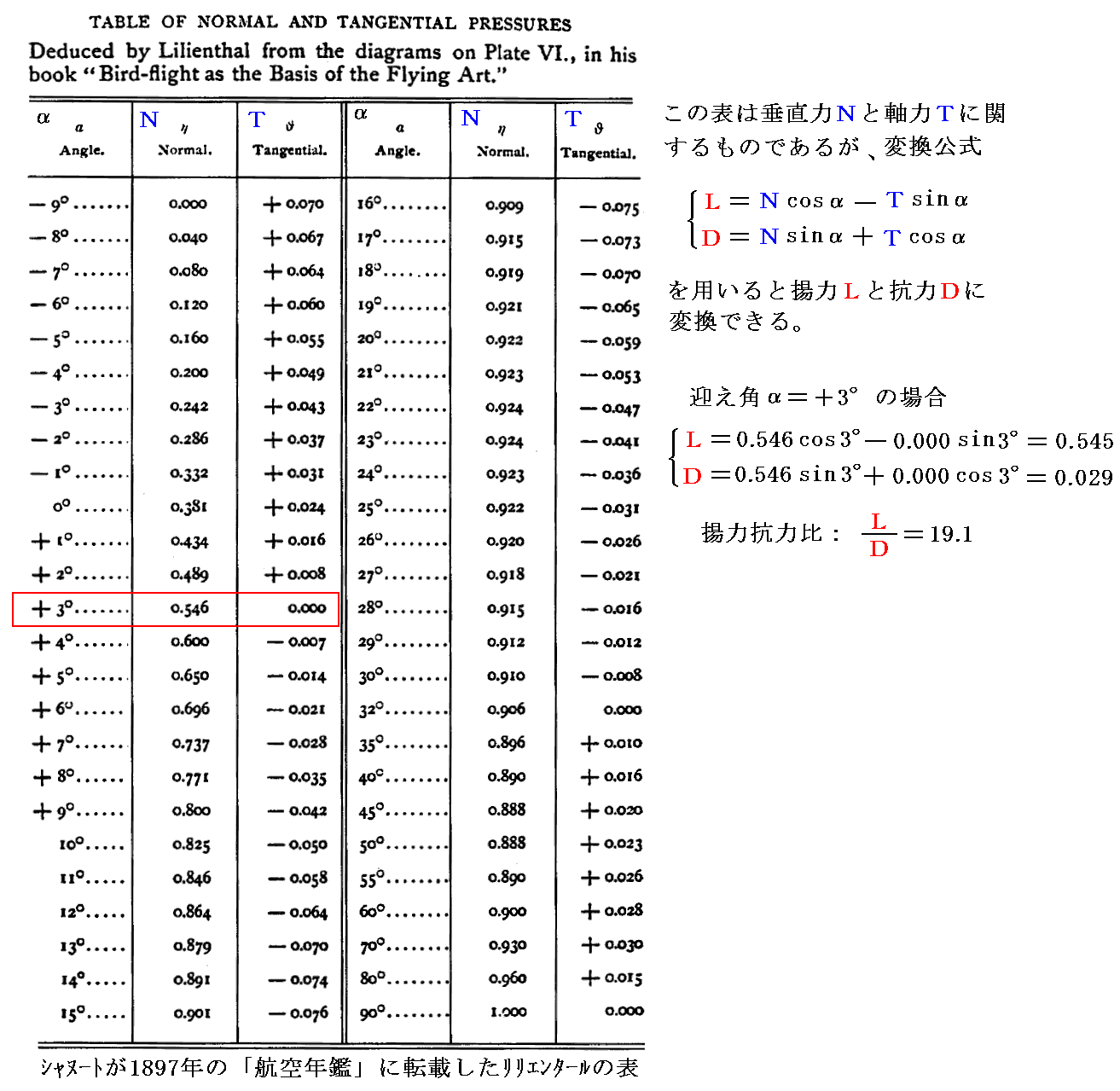
この表こそライト兄弟が1900年と1901年のグライダーの設計に用いたものです。
この表は解りにくいので、翼理論で一般に用いられる、揚力と抗力を迎え角の関数で表したグラフにしてみるとこの様になる。
ライト兄弟は1900年のグライダーを設計する際に前記のリリエンタールの表の値を用いた。ただし、当時の彼らには、表の値が翼の形状、翼のアスペクト比、翼の断面形状［キャンバーの大きさ、や翼弦の中でのキャンバーの最大位置］等に関係するという認識は無かった。彼らが知り得た表にも翼の状況データが記載されていなかったので、彼らは単純に翼面積と飛行速度のみを考慮して計算した。
上記の表で揚力／抗力比が一番大きくなる（＝19.1）迎え角3°における揚力係数Ｌ（＝0.545前表参照）を用いて、彼らが行った計算を再現してみる。1900年のグライダーは翼面積175ｆｔ2（16.3ｍ2）［実際に作られたものは材料の入手の関係で15.3ｍ2であった］で計画された。
ライト兄弟が用いた値をメートル法になおすと
となるので
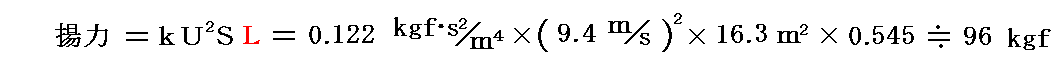
が得られる。これは彼らが予想した荷重
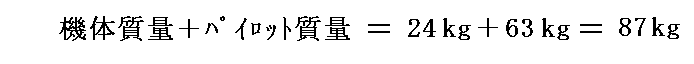
を充分支えることができるはずです。
この計算に基づいて1900年に作ったグライダーが翼幅5.2ｍ（約18ｆｔ）、翼弦1.5ｍ（約5ｆｔ）、一葉当たりの翼面積7.65ｍ2の複葉グライダーです。これから アスペクト比＝翼幅2÷翼面積＝(矩形翼の場合には翼幅÷翼弦となる)＝5.22÷7.65＝3.5 となる。ただし彼らのグライダーは複葉なので総翼面積は15.3ｍ2（150ｆｔ2）となります。キャンバー比は１／22で、キャンバーが最大の位置は前縁近くにしてあった。質量は23.6kgでした。
彼らはこのグライダーをキティーホークに持って行って実験した。前方に付けた水平舵の動作をたしかめ、その働きが良好なことを確認した。また翼をたわませる機構も試したが、機体は翼のたわみにうまく反応して左右に傾斜して横滑りする。また逆にたわませれば傾斜を回復できることが確認できた。
［補足説明１］
１．今日、ピッチ方向の安定性は下図のような水平尾翼によって達成します。主翼の揚力の作用点と重力の作用点が前後で一致していればよいのですが、迎え角の変化、ペイロードの移動、その他の要因でずれが生じます。そのとき下左図のようにずれれば飛行機は下を向きます。また下右図のようにずれれば上を向きます。
このとき左図の状況が生じると水平尾翼の風に対する迎え角は負になるため下向きの揚力が生じて飛行機を水平に戻します。逆に右図の状況が生じると水平尾翼の迎え角は生徒なり上向きの揚力が生じて飛行機をやはり水平に戻します。これがピッチ(縦)方向の安定性を生じる水平尾翼（昇降舵）の働きです。
２．さらに、揚力中心が重心と一致しているとき尾翼の角度を調節すると下図のように主翼の迎え角を変えることができます。下図のいずれの場合も水平尾翼は風の方向に平行になるように調整されています。
迎え角が変われば揚力が変わります。このとき揚力は飛行速度の二乗に比例することを思い出してください。迎え角を大きくして揚力係数を増大するとより遅い速度で飛行できます。また迎え角を小さくして揚力係数は減少すればより高速度で飛行できます。つまり昇降舵は飛行速度を調節する働きもする。
ライト兄弟は縦方向（ピッチ）の安定性を得るために主翼の前に昇降舵を付けました。主翼の前に付けても上記２．の働きは同じようにできますが、１．の働きは期待できません。機首が下に傾くと前方の昇降舵には下向きの揚力が働きます下向きを増長します。逆に上に傾いた場合は上向きをさらに増長します。つまり前方に付けた昇降舵は安定性に欠けます。そのため圧力中心が重心位置からずれると、ライト兄弟は細かく昇降舵の方向を調節して飛行の安定性を保たなければならなかったでしょう。【彼らが、何故今日の常識に反して昇降舵を主翼の前方に付けたのか？】については［補足説明４］で、さらに５．（２）で説明します。
昇降舵を前方に付ける形はその後のライト機に踏襲されていきますが、1910年頃になると、彼らも尾部につけた昇降舵のピッチ安定性効果に気付いたようで、前方の昇降舵に付け加えて尾部にも水平尾翼を取り付けます。そしてモデルＢ(1910年)以降になると前部の昇降舵を廃止して、当時のヨーロッパの飛行機と同じように尾部に垂直な方向舵(rudder）と水平な昇降舵（elevator）を付ける形になります。
しかし揚力は予想した値がでなかった。人が乗った状態で機体を浮かせるには迎え角が20度以上、風速が11ｍ／ｓ（25ｍｉｌ／ｈ）以上が必要であった。その様な迎え角では翼上面の気流は激しく乱れ、空気抵抗も大きくなり、グライダーの制御はきわめて難しいものになった。
実際、彼らは翼に取り付けた係留索に雑貨屋で用いるバネばかりを取り付けて糸の張力Ｒ’を測定した。彼らは索の取り付け位置をかえると、釣り合い時の迎え角が変わることを利用して、様々な迎え角α、風速Ｕの時の揚力Ｌと抗力Ｄ、圧力中心の位置を求めた［下右図］。そして風が充分強いときには実際に翼に乗って翼の揚力を確認した。その結果解ったのですが、揚力が計算値の半分から３分の１程度しか発生しなかったのです。
その年の実験の最後の段階ではグライダーをKill Devil Hillに運んで、実際にグライダーに乗って丘の斜面を利用した自由滑空に挑戦した。それを十数回程度（a
dozen)試して、10月の末にその年の実験を終えます。
［2017年7月 文献13．p81～82による追記］
10月中旬以降に実施されたＫill Devill Hillに於ける飛行回数は正確にわかっていません。飛行回数の記録が残っていないからです。上記のａ
dozenは後にオービルが記憶に基づいて語った回数です。
距離についてはウィルバーは記録を残している。良く飛べた時の距離は300～400ft（91～122m）でした。ただし良く飛べた時の着陸時の速度は30mil／h（48km／h）近い高速でした。それだけ高速でないと浮き上がれなかったのだろう。飛行したのはすべてウィルバーでした。おそらくとても危険な飛行だったので兄のウィルバーが行ったのだろう。
文献13．にはライト兄弟が、実験の合間に、キティホークの砂丘地帯の空を飛ぶ様々な鳥の飛行述の観察を飽くなき探求心を持って行っていたことが、様々な記録に基づいて紹介されています。
1900年グライダー［拡大写真はこちら］の詳細
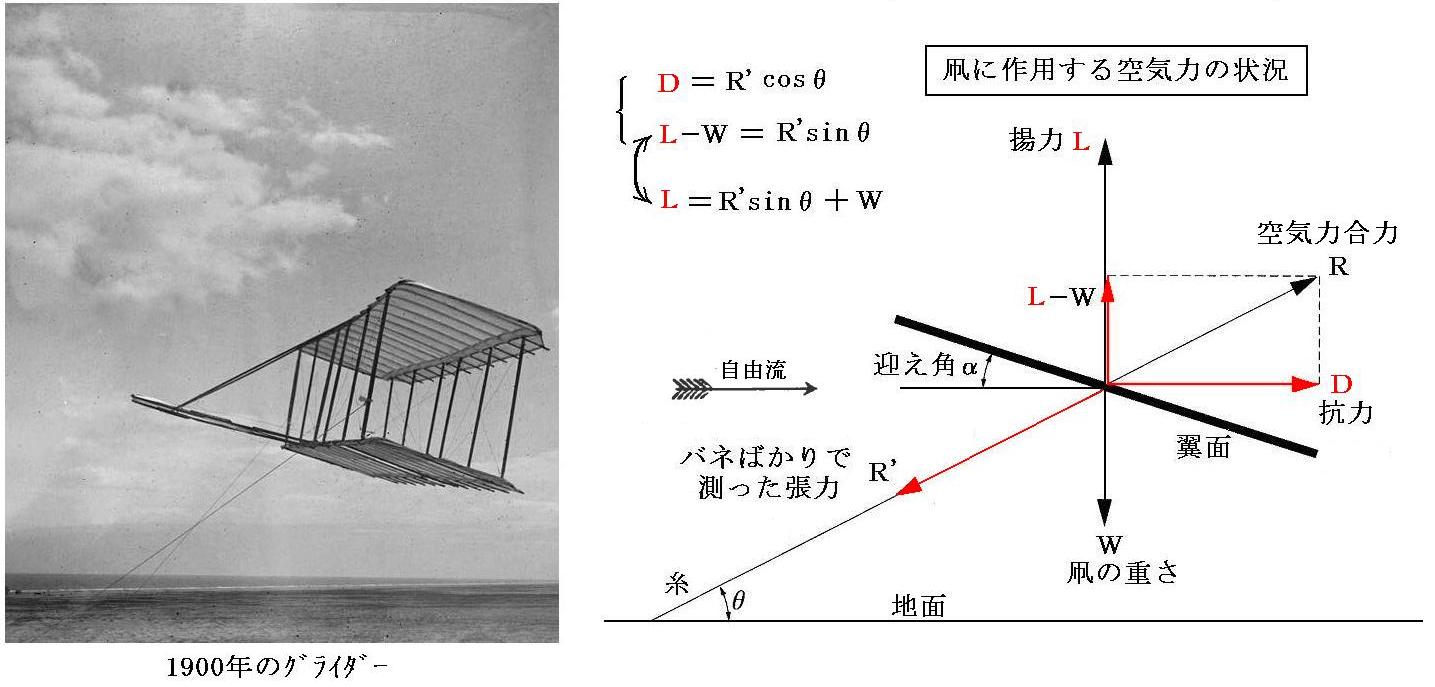
1900年のグライダーのまともな形状の写真はこれしか残っていないようです。参考文献６．でオービル・ライトがその構造の詳細を説明していますので、その部分を引用しておきます。
The machine had two superposed surfaces measuring eighteen feet from tip
to tip and about five feet from front to rear.
The surfaces were spaced five feet apart and were connected at the extreme forward edge by six upright posts, and at about one foot from the rear edge by another row of uprights or struts.
The struts were connected to the surfaces by means of flexible joints.
The ribs were made of thin strips of ash, slightly bent near their forward
extremities.
These ribs were bound to the forward spar on the spar's upper side, so that the spar and curvature given to the ribs produced a wing curvature of about one-eighteenth to one-twentieth of the chord [the straight-line distance from front to rear edge of wing].
The spars were enclosed in a sheath formed by sewing a strip of cloth
over them, resulting in the elimination of all sharp angles or corners.
The ribs were enclosed likewise.
Both the forward and the rear rows of uprights were trussed by wires much
like the Chanute glider.
The machine thus had two systems of rigid trusses laterally; but, unlike the Chanute machine, it was not rigidly trussed from front to rear.
On the contrary, a flexible cable was connected to the upper surface at
the extreme outer upright in the rear, passed diagonally downward through
a pulley on the lower surface at the outermost forward upright, thence
across to a pulley in a corresponding position on the lower plane on the
opposite side of the machine, and then diagonally upward to a connection
to the upper surface at the outermost rear upright.
Another flexible cable was attached to the upper surface at its forward edge at the outermost upright on the one side, passed diagonally downward and backward and crossing the first-mentioned flexible cable to a pulley at the rear of the lower surface, then across to a pulley at the rear of the lower surface at the opposite side, and then up to the connection of the forward upright to the upper surface.
A cradle in which the operator lay was connected to the cable running along the forward edge of the lower surface, so that when the cable was pushed to the right the upper rear corner of the machine was pulled downward and forward and the corresponding part on the opposite side of the machine was allowed to move upward and rearward.
In this manner a helicoidal warp was imparted to the surfaces.
The horizontal rudder, or elevator, was attached to a framework about four feet forward of the lower main plane.
This elevator was pivoted about one-third back from its front edge.
To the forward edge of the elevator were attached two springs which extended horizontally forward to the framework which supported the elevator.
The rear edge of the elevator could be raised or lowered by means of two arms extending from the operator and connecting to the rear edge of the elevator through links.
Thus when the rear edge of the elevator was raised, the springs referred to prevented the front edge from moving downward to a like angle, and as a result a curvature was given to the elevator on its upper side.
When the rear edge of the elevator was moved downward a curvature on the underside was produced.
この中の赤字説明のワイヤーは拡大写真に写っていますが、青字説明のクロスワイヤーは見えません？真ん中付近に写っている上翼前縁と下翼後縁を結ぶ二本のワイヤーがそれかもしれませんが、おそらくオービルは1906年に特許出願したときのＦｉｇ１、Ｆｉｇ２の構造と記憶違いしているのではないでしょうか？この文章は1920年に法律問題に関係して書かれた文章のようで、他の所でも1906年の特許図に言及している部分がありますから、おそらくそうでしょう。
さらにこのグライダーでcradleを用いて翼のねじる機構を採用したと言っています（緑字部分）が、写真を見る限りそれらしい構造は見えません？これも記憶違いでしょう。
参考文献８．の１番目のURL
http://www.wright-brothers.org/Adventure_Wing/Hangar/1900_Glider/1900_Glider.htm
に、翼端に斜めに張られたワイヤーの中程の点とフットバーのアームを結んで翼のたわみを制御する機構が示されています。しかし拡大写真を見る限りその様な連結ワイヤーは見えない。1900年のグライダーが翼をどの様なメカニズムでたわませたのか良く解らない。
昇降舵についての説明は1906年の特許出願図Ｆｉｇ３の昇降舵の変形の様子と同じ事柄を説明しているのでしょう。
ライト兄弟が彼らのグライダーを複葉翼にしたのは、彼らが考案した翼をねじって揚力を変える方法を実現するために複葉の箱形構造がどうしても必要だったからです（青字部分）。実際の所、彼らは紙箱をねじることからその機構を思いついたのです（赤字部分）。参考文献６のオービルによるその部分の説明を引用しておきます。
The first method that occurred to us for maintaining the lateral equilibrium
was that of pivoting the wings on the right and left sides on shafts carrying
gears at the center of the machine, which, being in mesh, would cause one
wing to turn upward in front when the other wing was turned downward.
By this method we thought it would be possible to get a greater lift on
one side than on the other, so that the shifting of weight would not be
necessary for the maintenance of balance.
However, we did not see any method of building this device sufficiently strong and at the same time light enough to enable us to use it.
A short time afterward, one evening when I returned home with my sister
and Miss Harriet Silliman, who was at that time a guest of my sister's
in our home, Wilbur showed me a method of getting the same results as we
had contemplated in our first idea without the structural defects of the
original.
He demonstrated the method by means of a small pasteboard box, which had
. . . the opposite ends removed.
By holding the top forward corner and the rear lower corner of one end
of the box between his thumb and forefinger and the rear upper corner and
the lower forward corner of the other end of the box in the like manner,
and by pressing the corners together, the upper and lower surface of the
box were given a helicoidal [spiral] twist, presenting the top and bottom surfaces of the box at different
angles on the right and left sides.
From this it was apparent that the wings of a machine of the Chanute double-deck
type, with the fore-and-aft trussing removed, could be warped in like manner,
so that, in flying, the wings on the right and left sides could be warped
so as to present their surfaces to the air at different angles of incidence
and thus secure unequal lifts on the two sides.
しかし、複葉翼の効能はそれだけではありません。おそらく下記の理由が最も大きかったのではないでしょうか。
［補足説明２］-----なぜ複葉か？-----
初期のグライダーや動力飛行機が複葉なのは、翼が薄翼であったためです。薄い翼では、その中に設置した桁やリブだけでその形状や翼面に掛かる力を支えることができません。単葉翼の場合にはリリエンタールやラングレーの様に中央に支柱を立て、それから張り巡らせた張線によって、複葉翼、多葉翼の場合には支柱と張線でトラスを組むことによって強度を保っしかなかったのです。
できるだけ空気抵抗を小さくして揚力を大きくし、かつ翼の剛性を保つ方法として複葉翼構造はきわめて合理的で優れたアイディアです。そのため初期の多くの飛行機が複葉翼を採用しました。
実際の所、ウィルバーは、1901年9月18日に西部技術者協会で行った講演で、自分たちはシャヌートの複葉構造をまねてグライダーを作ったのだと話しており、シャヌートが開発していた複葉型のグライダーを「構造上の偉大なる進歩」としてシャヌートの業績を高く賞賛しています。
［補足説明３］-----なぜ薄翼か？-----
初期の飛行機が薄い翼を用いたのには理由があります。
○飛行機の翼を設計するとき、誰でも手本として参考にするのは実際に飛行を実現している鳥の翼です。
鳥の翼はまさにその様な薄い構造をしていました［３．（１）のコウノトリ参照］。
もう一つの理由は、
○翼の性能試験に風洞が用いられる時代になっても、初期の航空工学で用いられた風洞は小規模で低速であったために低いレイノルズ数でしか翼の性能測定ができなかったからです。
レイノルズ数106以上では翼型の特性はレイノルズ数によって余り変化しませんが、低レイノルズ数(105)程度では急激に変化します。下図はドイツのF. W. Schmitzによって得られた翼型のレイノルズ特性です。
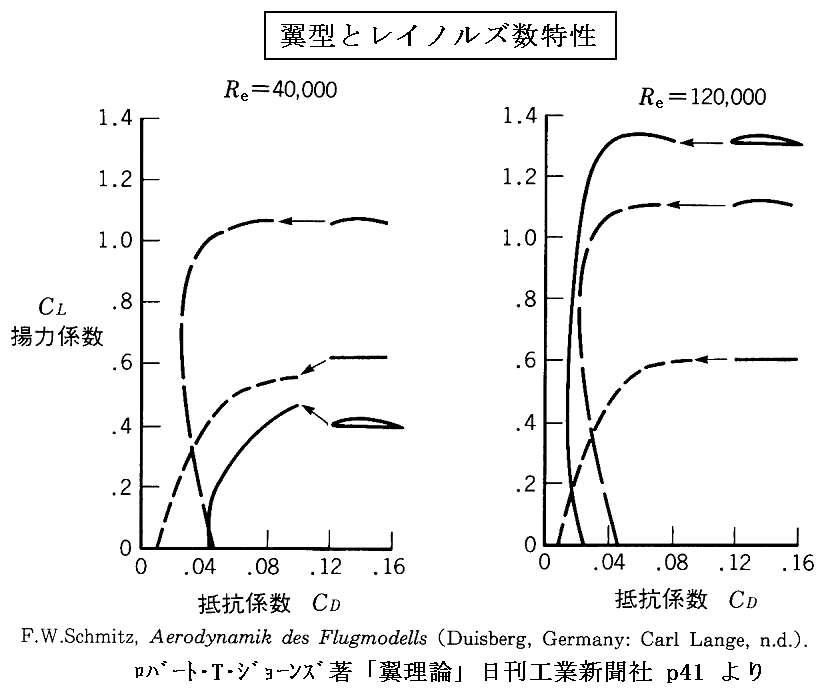
レイノルズ数はＲe＝Ｕ0ｄ／ν［ν：動粘性係数、Ｕ0：風速、ｄ：代表的な長さ］で定義されますが、空気の動粘性係数（＝粘性係数μ÷流体密度ρ）は1気圧、15℃で約1.5×10-5ｍ2／ｓ程度です。ライト兄弟が行ったであろう典型的な風洞実験ではν～1.5×10-5ｍ2／ｓ、ｄ(翼弦)～0.05ｍ、Ｕ0(風速)～12ｍ／ｓ程度ですからＲe～40000となり上左図に相当する。この場合単純な平板の方が厚翼型よりも優れているのです。ところが実際の飛行機の大きさ、飛行速度におけるレイノルズ数はＲe＞106ですから上右図の状態に相当します。
今日の知識によると、上記の二つのレイノルズ数の違いにより厚翼と薄翼の性能が逆転する原因は以下のように説明されています。
厚翼の場合低レイノルズ数において小さな迎え角でも層流剥離泡が前縁付近に生成することにより大規模な剥離が生じやすくなり抵抗係数が大きく揚力係数は小さくなる。しかし、厚翼の場合このような現象は高レイノルズ数では発生しない。
また薄翼では実際の飛行と同じ高レイノルズ数に於いて、（平板翼と同じように）小さな迎え角でも剥離が生じやすくなるのだが低レイノルズ数ではその現象が目立たなくなる。
この二つの傾向のために、低レイノルズ数では薄翼が、高レイノルズ数では厚翼が有利である様にあらわれる。
常識で考えると薄い翼よりも厚い翼の方が空気抵抗は大きいと思いますから、初期の飛行機制作者が誤ったのもうなずけます。実際の飛行機の大きさと飛行速度から定まるレイノルズ数領域では厚翼の方が優れているのに、初期の飛行機制作者はレイノルズ数の効果など知るはずもなく、風洞実験で厚い翼を試してみようなどと考えが及ぶはずも無かった。本当の所、抵抗係数には厚さは関係ないと言うことは、理論的な空気力学が発達して初めて予想できる事柄です。
レイノルズの研究は２．（２）に記したように1883年に報告されていたのですが、“レイノルズ数”の概念の重要性が認識されて風洞実験や飛行機設計に取り入れられるのは1910年代以降です。そのためライト兄弟の風洞実験も実際の飛行機のレイノルズ数よりもかなり低い値でなされた事は確かです。１９世紀の飛行機製作者に取ってレイノルズ数の重要性は予想だにできないものだったのですから。
厚翼にすれば支柱や張線が不要になり、桁とリブでその形状と強度を保つことができます。そのため空気抵抗の少ない単葉翼にできます。さらに、翼の中に燃料タンクや、離着陸用の車輪を収納することもできます。またエンジンを直接翼に取り付けることもできます。
つまり、《単葉》で《厚い翼》は飛行機の構造・形状にその後革命をもたらします。このことについては、別稿「二次元翼理論」７．（５）で詳しく説明します。
［補足説明４］-----なぜ先尾翼（カナード）にしたのか？-----
ライト兄弟が昇降舵を主翼の前に配置するカナード（Canard前尾翼）タイプの機体構造を選んだ理由として、文献12に興味深い記述が在りますので引用しておきます。
本当は、５．(２)［補足説明１］で説明する様に、迎え角の増大が小さい間は迎え角の増加と共に揚力中心(圧力中心)は前方に移動します。揚力中心（圧力中心）が後方に移動するのは失速する迎え角を越えてからです。その為、主翼の迎え角が増大すると揚力中心は後方に移動すると考えていたライト兄弟は（当時の飛行機研究家と同じ様に）間違っていたのです。
この間違った考え方にとらわれている限り、５．(１)［補足説明１］で説明したメカニズムにより、先尾翼の方が飛行を安定させると考える事ができます。これがライト兄弟が先尾翼を採用した理由の一つです。ここは、後の５．（２）でオービルの文章を引用してもう一度説明します。
アンダーソンは、上記の理由に付け加えてもう一つの理由を説明しています。それが以下の部分です。
実際、ウィルバーはグライダー実験を進める過程で何度も墜落しており、上記の効果により、何度も命を救われる事になる。そのように彼らが試みたグライダー飛行は極めて危険なものでした。
初期の飛行実験のパイロットは、ほとんどすべてをウィルバーが努めているのですが、それも弟オービルを危険な目に遭わせたくないという兄としての思いやりからでしょう。
ラングレーがエアロドロームの試験飛行を水上で試みたのも墜落時にパイロットの命を救うためですが、初期の飛行実験は現在の我々が想像するよりも遙かに危険なリスクを伴っていたのでしょう
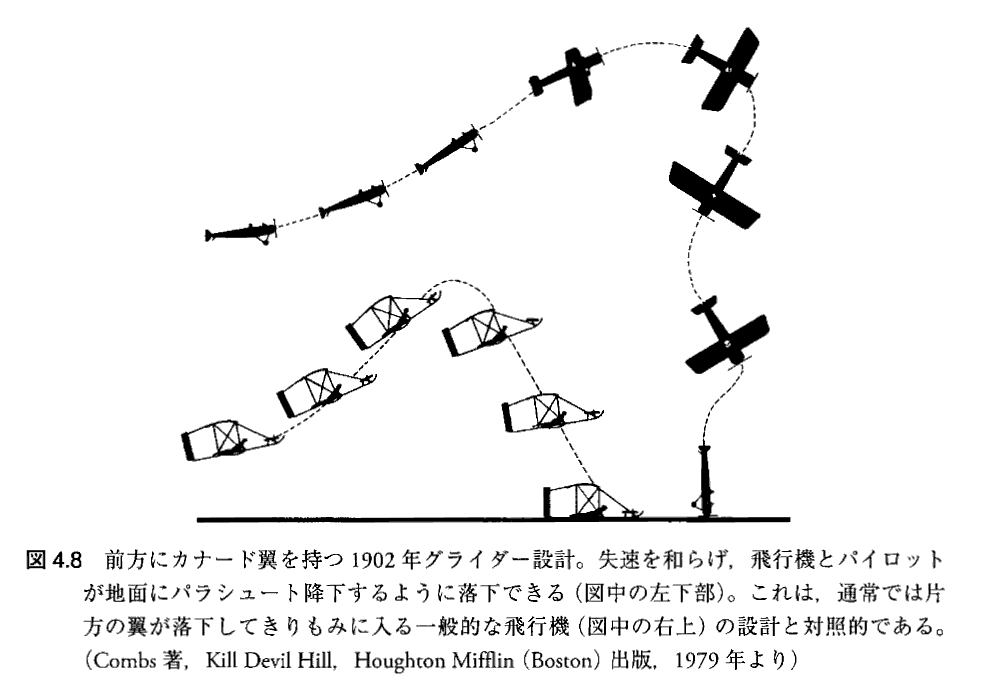
要するに、“失速”とは主翼が揚力を失うことです。当時のライトは主翼が揚力を生むメカニズムを理解していたわけではありませんが、今日【主翼が揚力保持するには空気の流れが翼を横切る方向に、しかも翼表面に密着して流れていなければならない】ことが解っています。だから揚力を失うとは、《翼を横切る方向》でしかも《表面に密着した》空気流が実現できなく成ることです。
正常な空気流が失われるメカニズムには様々あります。最も解りやすいのは、何らかの原因で《主翼の仰角が増大》しすぎて空気の流れが翼面から剥離してしまい揚力を失うことです。（ただし、こちらの揚力喪失のメカニズムは初期の飛行実験家達も十分理解していました。やっかいなのは次に述べるメカニズムによる失速です。）
それ以外には主翼が何らかの原因（例えばアドバース･ヨーやテイル・スピンなど）によって《翼が傾いて》しまい、主翼が横滑りを起こして、空気の流れが主翼を斜めに流れることになって揚力を失うなどが考えられます。
いずれにしても、主翼が揚力を失って落下が始まると、後尾翼機では尾翼が風圧を受けて尾部を持ち上げるので、機首から落下することになりますが、先尾翼機では、主翼が揚力を失うと先尾翼が落下時の風圧を受けて機首を持ち上げますので、先尾翼機はお尻から落下することになる。
ライト兄弟が、1910年のライトＢ型以降、水平尾翼を後部に置くことにしたのは、おそらくその時点までに、失速が起こるメカニズム（アドバース･ヨーやテイル・スピンなど）を見極めて失速自体を防げるようになったことと、５．(２)［補足説明１］で説明する揚力中心（圧力中心）の移動特性を正しく理解して、５．(１)［補足説明１］で説明した後尾翼の飛行安定性への効果を認めることができたからでしょう。
1900年のグライダー試験から得た経験を基に1901年に新しいグライダーを作った。それは揚力不足を改善するために反り（camber）を１／12まで拡大できるようにし、思い切って翼面積を大きくしたものです。キャンバーの最高値は翼弦の33％の位置にあり、翼幅（span）6.7ｍ（22ｆｔ）、翼弦（chord）2.1ｍ（7ｆｔ）、二葉の総翼面積は27ｍ2（290ｆｔ2）、重量44kg（98ｌｂ）でした。しかしアスペクト比3.3で1900年のグライダーのアスペクト比より小さくなった。
このグライダーは1900年のグライダーと同じように、足で操作する翼のたわみ機構採用していたようです。彼らはキャンバーの効果を見極めるために翼のキャンバーが簡単に変更できる機構を取り付けた。また着陸用の小さな橇も取り付けた。［拡大写真、超拡大写真１、超拡大写真２
このように改良したことで、かなり意気込んで1901年の7月からグライダー実験を開始したのですが、彼らは様々なトラブルに遭遇します。
最初に解ったのは、この機体は1900年の機体より、ピッチ方向の安定性や操作性が悪いことです。また1900年のグライダーは斜面を滑空すると連続的にスピードをましたのですが、1901年のグライダーは速度が出ずしかも、その沈下角は1900年グライダーよりも大きくて明らかに滑空性能が悪かったのです。しかし、新しい機体の横方向のコントロールはとても効果的にみえた。
この実験結果から、兄弟はキャンバーの量を減らすことにします。このグライダーはキャンバーを変更できるような仕組みを持たせて組み立てられていました。それは翼の中程に立てられた短い支柱とこれに張られたワイヤーを調節して行われます［写真参照］。
この当たりの説明は参考文献８．に上げた２番目のURL
http://www.wright-brothers.org/Adventure_Wing/Hangar/1901_Glider/1901_Glider.htm
が詳しい。後で小支柱の天辺と上翼を繋いで上翼のキャンバーも変更できるようにしたようです。超拡大写真１と２を見れば、かすかにそのワイヤーが写っている。
この支柱とワイヤーは飛行中に翼が圧力のためにキャンパーが変化するのを防ぐ働きもします。彼らはグライダーテストや凧としての係留テストを繰り返して機体の調整をしていきます。
次に解ったのはピッチ方向の不安定性です［ピッチについては４．（２）［補足説明１］を参照］。
どの様な翼でも迎え角が90度から0度に向かって減少すると、圧力中心は翼面上を前方へ移動します。反り（camber）が大きくなると迎え角の変動に伴う圧力中心の移動が大きくなり操縦が難しくなることはリリエンタールがすでに指摘していました。また４．（１）で説明したようにラングレーも圧力中心の前方への移動は気付いていた。
ライト兄弟も、本や論文を読んでこの圧力中心の移動を知っていました。そのため、1900と1901年のグライダーはそのことを考慮して作られていました。昇降舵を主翼の前方に付けたのは、彼らが迎え角が減少すれば圧力中心が前方に移動し、迎え角が増えれば後方に移動すると信じていたからです。もし圧力中心がそのように移動するのであれば前方にある昇降舵の方が後方にある昇降舵よりも安定性に対してより適切に働くことを、その動きを仮定して５．（１）［補足説明１］と同じような図を描いて確かめてみてください。
このことを、オービルが文献６の中で説明しています。これは、今日の常識に反して、彼らがなぜ昇降舵を主翼の前方につけたのかを述べたきわめて興味深い所（赤字の部分）ですから、その箇所を引用しておきます。
Aｌｌ the books and papers which my brother and I had read in which there
was any reference to the travel of the center of pressure had taught that
the center of pressure was approximately at the center of the surface when
it was exposed at right angles to the wind; and that this center of pressure
moved forward as the angle of incidence was decreased.
We had built both the 1900 and the 1901 machines assuming this to be well verified.
Our elevator was placed in front of the surfaces with the idea of producing
inherent stability fore and aft, which it should have done had the travel
of the center of pressure been forward as we had been led to believe.
We found, however, that these machines were anything but inherently stable
fore and aft.
In our 1900 experiments we had even found the inherent stability much improved when we tested the machine by gliding it down a hill loaded with a small sack of sand with the trailing edge of the main plane forward and the elevator trailing behind [in short, when flying it backward].
Doctor Spratt and Mr. Huffaker [then staying at the Wright camp] both suggested
that there might be a rearward travel of the center of pressure on the
curved surfaces at the small angles of incidence.
We later demonstrated this fact by flying one of the surfaces alone as
a kite.
When the surface was exposed to the wind at large angles of incidence
the pull on the flying cords was upward and when exposed at small angles
of incidence the pull was downward.
In the first case it was apparent that the center of pressure was in front
of the center of gravity, and in the latter case behind the center of gravity.
This clearly demonstrated that the center of pressure moved backward at
small angles of incidence.
さらに興味深いのは、彼らは1900年のグライダー試験の時に、砂袋を主翼の後ろ側に載せて昇降舵が後ろになるように［つまり、後ろ向きに］滑空させるとこのピッチ方向の不安定性が著しく改善される（緑字の部分）ことを見つけている事です。これは、まさしく５．（１）［補足説明１］で述べた水平尾翼のピッチ安定化の効果です。しかし、残念なことに彼らがこの尾翼方式を取り入れるのは1910年以降のことです。
オービルがこの文章を書いた1920年と言えば水平尾翼のピッチ安定性の効果はすでに明らかになった時代です。彼らが尾翼方式を取り入れることはなかったのですから、唐突にこの一文を書き加えた真意がよく解らない。法廷闘争に関係しているのかも知れない？
下記［補足説明１］に記すように、実際の滑空時の小さな迎え角では、彼らが信じ込んでいたのとは反対に迎え角が大きくなると圧力中心は前方へ移動したのですから、彼らの機体が前後方向に関して不安定で昇降蛇が思うように働いてくれなかったのは当然です。
丁度そのころ彼らのキャンプに滞在していたSprattとHuffakerが、キャンバーのある翼では迎え角が小さくなると、圧力中心は再び後方に移動することを教えてくれます（茶字部分）。発表されることは無かったのですが、ラングレーとその助手ハフェイカーは小さな迎え角になると圧力中心の移動方向が反転することをすでに計測していた。
後に、ライト兄弟も単葉にした翼を凧として飛ばして、小さな迎え角では迎え角の減少に伴い圧力中心が後ろへ移動することを確かめます（青字部分）。
そのとき、１／12のように大きなキャンパー翼では小さな迎え角に於いても比較的大きな移動が起こるので、機体のキャンパーをより小さな1／19程度に変更したのは正解でした。キャンパーを小さくすることで圧力中心の移動は小さくなり、昇降舵の調整に対する応答も良くなってグライダーは操作しやすくなった。
［補足説明１］
上に膨らんでいる普通の翼型では、迎え角がゼロのとき圧力中心は翼弦の前から35～40％あたりにある。ところが迎え角を大きくしていくと、圧力中心はすこしずつ前方に移動していく。普通、失速直前の大きな迎え角の時に最も前方の30％当たりまで前進する。
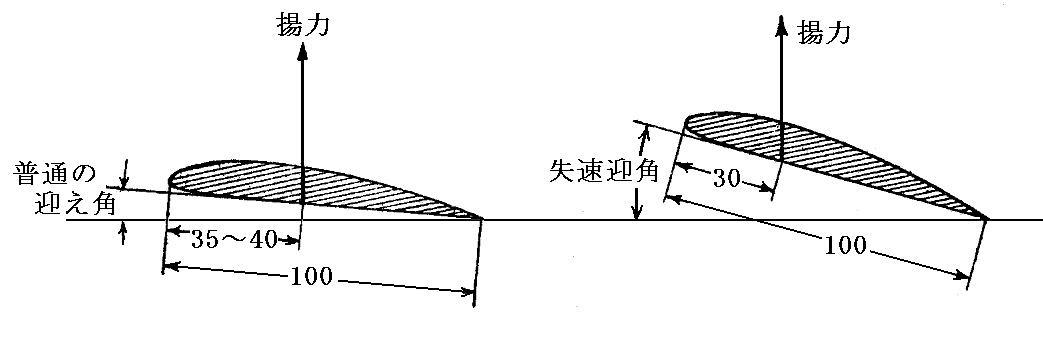
薄いキャンバー翼の場合下図のようになる。
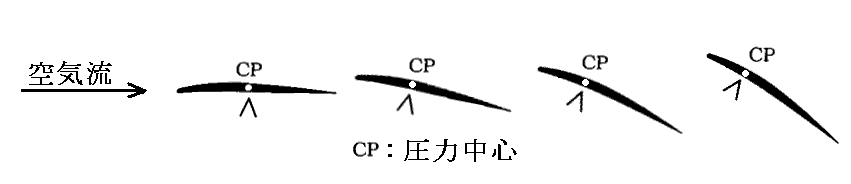
ライト兄弟を含めて初期の飛行機研究家が、この部分の挙動を知るのはかなり後になってからです。
失速する迎え角を超えてさらに迎え角を増やしていくと、翼の背後は完全に剥離した状態になるが、圧力中心は再び後ろに下がり始める。
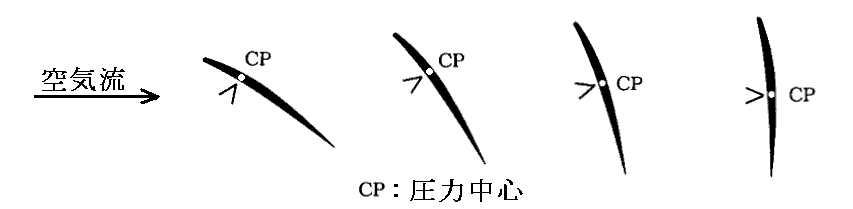
最終的に迎え角90度で翼弦の中央に位置するようになる。初期の飛行機研究家はこの部分のみを観測していた。
このような圧力中心の移動は飛行機のピッチ方向の安定性を損ないます。そのとき、昇降舵を主翼の後ろに付ける（つまり尾翼にする）と５．（１）［補足説明１］のように、その変化をカバーしてくれます。
普通に飛行しているときの迎え角範囲（0～10度）では、迎え角が変わっても圧力中心がなるべく移動しない方が望ましい。
圧力中心の移動の仕方は翼型に依存します。例えば矢高ゼロの対称翼では圧力中心は翼弦の25％当たりにほぼ固定される。
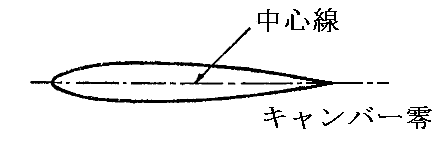
また、下図の様にキャンバー（矢高）を比較的小さくして、後縁をやや反りあがった形にすると、圧力中心が翼弦の25％程度に固定されて移動が少なくなる。［この当たりは二次元翼理論で計算することができます。］
グライダー試験を重ねるうちに、彼らはさらに予期しない現象に遭遇します。1901年のグライダーには垂直尾翼はなく、翼の捻れで機体をバンクさせて旋回しようとするものでしたが、それが不安定性を生じるのです。例えば右に旋回しようとして翼を右に傾ける為に左の翼の後縁を捻り下げると、左の揚力は増えるのですが抗力も増えて左翼の速度が減り、機体は左に旋回したのです。主翼は右に傾きながら機体軸は左を向く［アドバース・ヨー］というまことに不安定な挙動をして墜落した。
参考文献６．のその部分の記述を次に引用する。
As we gained in proficiency in handling the machine in gliding flight,
we began to encounter occasionally a phenomenon which we had not foreseen.
Sometimes in warping the wings to recover lateral balance, it was found
that the wing having the greater angle would at first tend to lift, but
at the same time it would lose speed as compared with the opposite wing
having a smaller angle of incidence.
As a result the machine would begin turning a sharp circle, which generally
resulted in a forced landing with the machine skidding outward on the ground.
From this phenomenon we were led to the discovery that the relative velocities of the right and left wings of the machine bore a very important part in lateral equilibrium, a fact apparently never before considered by any investigators.
I may state that in some of the flights just related, the wing having
the larger angle and the lesser speed had a less lift than the other wing
with the small angle and the greater speed.
今日の知識で説明すると誠にもっともな挙動なのですが、彼らには初めての体験です。彼らは、“風に乗って浮かび上がると言うことがいかに難しいか”身に染みて思い知らされる。
1902年のグライダーに垂直尾翼を付けたのもこの点を改善するためです。彼らは、主翼の左右の翼が異なった角度にねじられたとき、垂直尾翼があれば、左右の翼の速度を同じに保ってくれるだろうと考えたからです。
［補足説明２］
１．垂直尾翼の一番の目的は飛行時のヨー方向の安定性です。何らかの影響で機体の向きが左右にぶれた場合、風に対する尾翼の迎え角が変化します。後方にある垂直尾翼には飛行方向を元の方向に戻す方向の揚力が働きヨー方向の安定性を生み出します。これを“風見安定性”と言います。
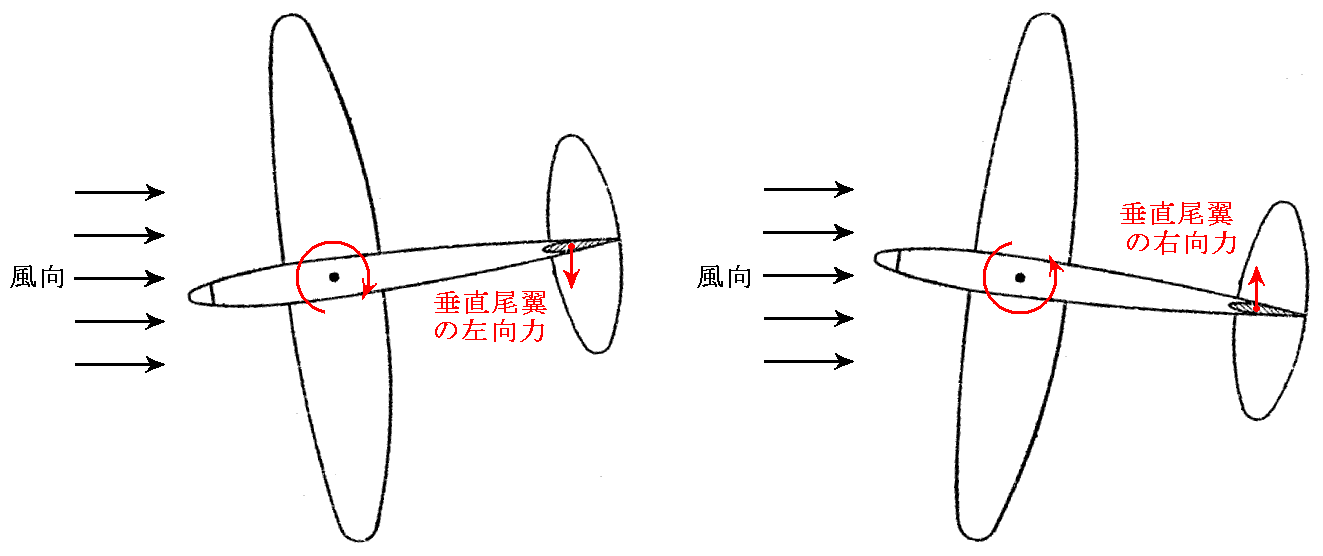
２．垂直尾翼の二番目の働きはいうまでもなく飛行機の方向を変えることです。しかし垂直尾翼を用いただけでは下右図のように機首を右に傾けたまま横滑りをして直進してしまい、決して左図の様な右旋回してくれません。
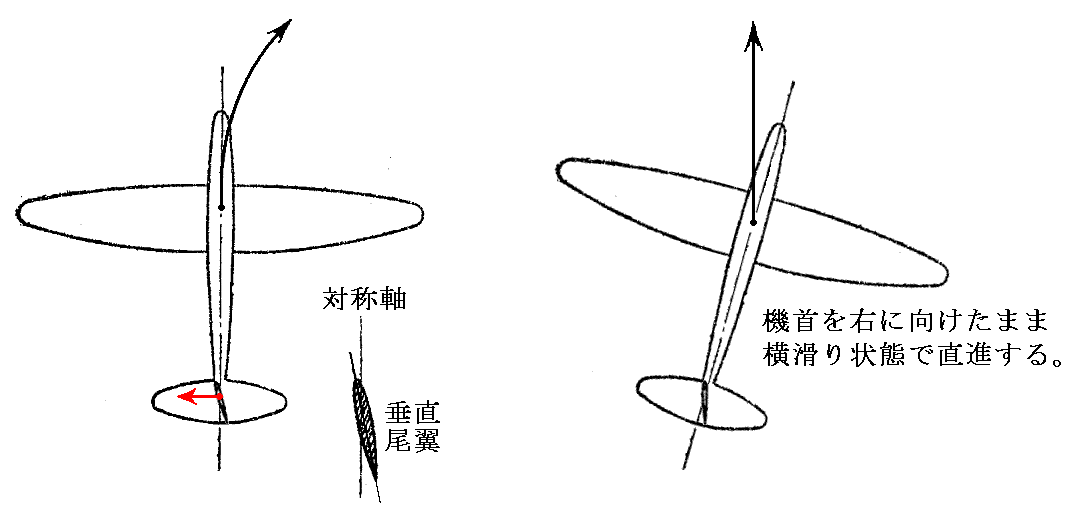
右旋回するためには主翼を右に傾けて主翼に働く［揚力］と［重力］の合力が右回転の［向心力］を生じるようにする必要があります［下右図］。同様に左に回る場合には主翼を左に傾ける必要があります［下左図］。
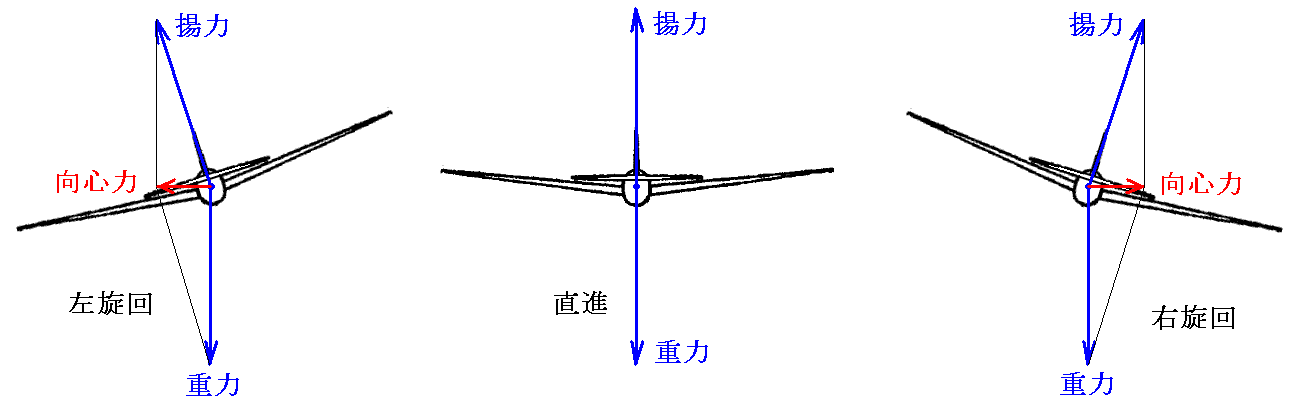
そのとき、主翼を傾けるには主翼を捻るか、翼端に付けた補助翼（エルロン）を操作して左右の翼の揚力を変えて行います。ところがライトのグライダーのように飛行速度が遅く、垂直尾翼が付いていない機体では右に曲がろうとして左翼の揚力を増やすと抗力も増えてしまい機体はむしろ左を向いてしまいます。つまりロールでは右に傾きながらヨーでは左を向くというきわめて不安定な状況に陥ります。これが1901年のグライダーでライト兄弟が体験した事です。このような現象をアドバース・ヨー（adverse yaw）による不安定性と言います。
そのとき、垂直尾翼が有れば風見安定性が生じますから上記の左を向く傾向を押さえることができます。そのためにライト兄弟は1902年のグライダーに垂直尾翼を付けることにした。しかしこれが後で説明するように新たな不安定性（テイル・スピン）を生みます。
彼らは、飛行実験をしながら何度も翼形状を変更していきました。最も重要な変更は、最初の主翼は水平に組み立てられていたのですが、翼の支柱間に張ったクロスケーブルの長さを調節して翼端を中央より3～4インチ下げた（つまり下反角を与えた）ことです。
彼らがその様な改造を加えたのは、自由滑空をしているときに、風が斜め前から当たると、風上側となった翼がより大きな揚力を発生して持ち上がり、横方向（ロール）の平衡が乱される事が解った（赤字部分）からです。
下反角を与えると、風が正面からではなくて斜めから当たる状況になったとき、風上側の翼の迎え角が、風下側の翼の迎え角に比較して小さくなり、上記の不安定性が解消できた（青字部分）のです。
しかし、下反角は横方向の平衡に不安定性をもたらします。確かに側面からの突風に対してはより安定になったのですが、横滑りが生じた場合には横方向の平衡を失う傾向が出てきたのです。しかし彼らが実験していたKill Devil Hillの丘のようにその斜面の表面が凸凹しているような地形では、垂れた翼のほうが地形の変化により柔軟に対応できて、不安定性の不利益を上回る効果を発揮してくれました（緑字部分）。
参考文献６．のその部分の記述は、彼らが、主翼になぜ下反角を持たせたのかを説明した興味深い部分ですから、以下に引用しておきます。
Changes in the arrangement of the spars were made several times during
the series of experiments, the most important of which was produced by
changing the length of the brace wires, so as to produce a curvature in
the spars from wing to wing.
The spars at the center of the machine were raised three or four inches above their extremities at the wing tips.
The spars when the machine was first assembled were straight, the diagonal
brace wires in each section being of equal lengths.
We had found in the free flights that when the wind entered the machine
from one side or the other at an angle to the longitudinal axis of the
machine, the wing on that side from which the wind was blowing received
a greater lift, thus causing a disturbance in the lateral equilibrium of
the machine.
By giving the wings a curvature from side to side this disturbance was
avoided, because the air entering from the side met the surface of the
wing on that side at a smaller angle of incidence than it met the surface
on the opposite wing.
This, however, tends to produce a machine with unstable equilibrium laterally.
While the equilibrium is disturbed less from side gusts, the machine tends
to lose its own equilibrium when it slips sidewise on the air, but under
the peculiar conditions existing on the Kill Devil Hill [partly the hill's
convex surface] we found the advantages of the drooped wings more than
overcame the disadvantages.
しかし、一番大切な揚力が予想していた値に全然達しないことが兄弟を最も落胆させました。骨組みの正面抵抗も彼らが予測した値と違うものでした。例えば、1901年7月30日の測定では18マイル／時（8.0m／s）の風速で迎え角10°の時の揚力は100ポンド（45.36kgf）、抗力は18ポンドでした。少し改良を加えた後の8月1日の測定値は17ｍｉｌ／ｈの風速、迎え角6°で揚力100ポンド、抗力15ポンドでした。
リリエンタールの表を用いた計算では風速18ｍｉｌ／ｈのとき人を乗せても停止した状態で浮き上がり、機体の性能試験ができる予定でしたが、その1／3程度しか揚力は発生しなかったのです。その風速では浮かび上がれず、もっと強風の中か、風に対して滑空して初めて浮き上がれた。
そのため飛行実験をする機会が当初の予定よりも大幅に少なくなって、性能試験がなかなかはかどらなかった。それでも、彼らはその年には数百回のフライトを実行することができた。その飛行距離は50ｆｔ～400ｆｔの間でしたが、主な距離は300ｆｔ前後でした。
以上の様に1901年のグライダー実験が終わったとき、彼らは様々な成果を得ることはできたが、揚力値が予想値を大幅に下回ったことに於いて惨憺たる状況でした。1901年に発表されたウイルバーの論文によると、この時点で彼らは以下の様な疑問を持っていたことが解る。
結局、彼らは自分達自身で一つ一つ確かめて行くしかないと悟り、一連の有名な実験に取りかかります。この実験こそが彼らを成功に導いたと言えるでしょう。
その話しに入る前に、揚力が彼らの予想の1／3しか発生しなかった理由を今日の空気力学の知識に基づいて説明しておきます。これは参考文献５．で説明してあるものですが、その原因として
［原因１］
彼らが用いたスミートン係数が正しい値の2倍近い大きさの0.005を用いて計算したことによる。
［原因２］
リリエンタールと自分たちの翼におけるアスペクト比の相違による差を修正していなかった。リリエンタールが実験した翼（6.48）よりも彼らのグライダーのアスペクト比は小さい（3.5）ため揚係数は小さくなる［別稿「人力飛行機を実現する原理［プラントルの揚力線理論］」５．（４）４．参照］。
［原因３］
リリエンタールの円弧翼型（最大キャンバー位置は1／2翼弦）と前縁近くに最大キャンバー位置を持つ自分たちの翼型における最大キャンバー位置の相違による差を考慮していなかった。今日の航空力学によるとリリエンタール翼の方が揚力は大きくなる。［別稿「二次元翼理論」７．（３）４．参照］
上記の原因２、３よりも影響は小さいが、
［原因４］
リリエンタール実験の翼の平面形は木の葉形だか、ライトグライダーの翼は矩形であることによる違い。
が考えられる。さらに
［原因５］
リリエンタールの実験におけるレイノルズ数とライト・グライダーが飛行しているときのレイノルズ数の違いによる差。［別稿「二次元翼理論」７．（５）２．参照］
等が考えられる。
［補足説明３］
ライト兄弟は、［原因１］のスミートン係数については、後にラングレーの測定値（正しい値に近い）を知り、彼ら自身も正しい値を測定してこのことを理解します。
また［原因２］～［原因４］は、彼らが、リリエンタールの表を誤って解釈したために生じたものです。ライト兄弟はリリエンタールの表が円弧翼で真ん中に最高の反りがある木の葉形の翼についてのデータである事を明確に認識していなくて、この表がキャンバー比さえ同じならどの様なものでも使えると思っていた。彼らは後に行った風洞実験から［原因２］～［原因４］の重要性を明確に認識します。
ただし、［原因５］については彼らの時代には想像もできないことでした。
1901年のグライダー実験を終えた兄弟は、失意のどん底で8月20日にキティホークを発ってデイトンへの帰路につきます。そして９月に自転車に取り付けた車輪リム天秤実験を行います。ちょうどそのころ彼らはラングレーが得たスミートン係数の値0.0032ポンド重･ｈ2／mil2･ｆｔ2（これは本当の値0.0289に近い）を知ったようです。
この時期のライト兄弟の状況については文献13．のp95～98や文献14．を参照されたし。
下図は彼らが自転車に付けて用いたリム天秤装置です。［高輝度モニター用］
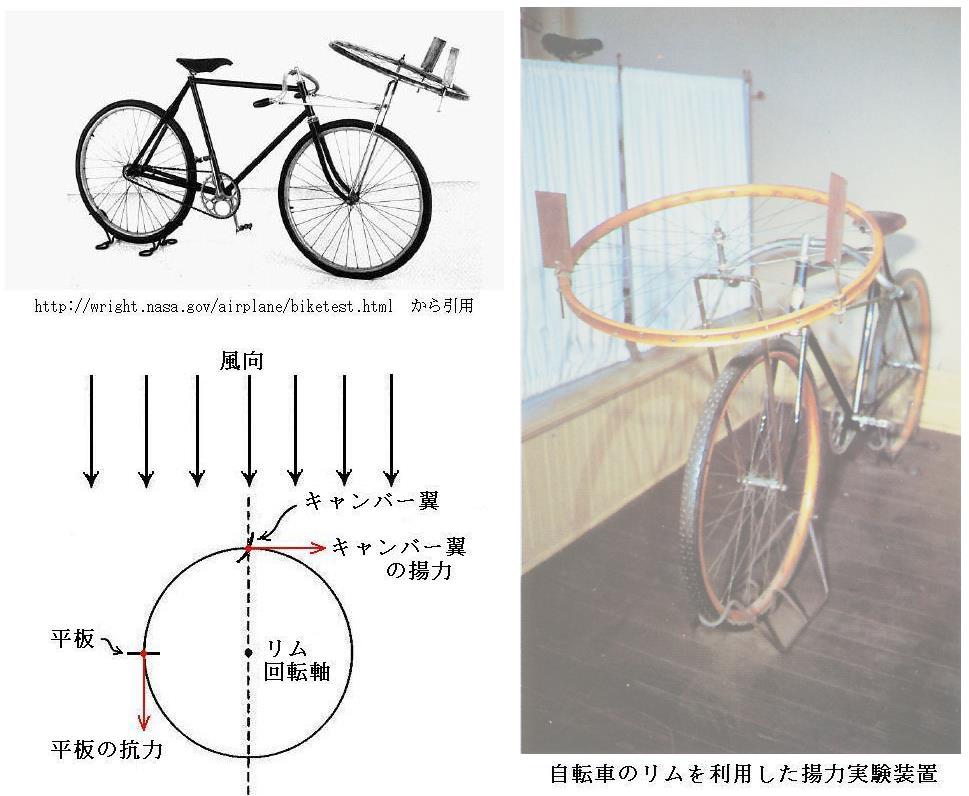
上図のように翼と平板を直角に配置して、リムの回転を手で止めた状態で自転車を走らせる。この状態で走った場合、翼に働く抗力はリムを回転させる力は生じず、平板に働く垂直な抗力と翼に働く揚力が働くことになる。そして走りながら、手を離してどちらに回転するかを確かめる。彼らは手を離してもリムが回転しなくなるキャンバー翼の迎え角を探した。さらに平板の面積を変えて同様な実験を繰り返した。そのようにして、リリエンタールの表を確かめてみたのですが、５．(２)に述べたうちの［原因２］～［原因４］の理由により、当然異なった値になりました。
このような実験を受けて、キティホークでのグライダー試験の生じた可能性のある誤差要因を注意深く探すようになります。この考察を通じて、スミートン係数の値も疑うようになります。スミートン係数は彼らが用いた0.005（メートル法では0.13）ではなくて、ラングレーが測定していた0.0033が真実に近いと確信します。そして、それ以後のグライダーの設計にはラングレーが計測した値を採用することに決めました。
それと同時に、彼らは翼の性能試験を自分達でやってみる決心をします。
彼らは、自転車リム天秤の方法では充分な翼データを得るのは難しかったので、風洞を造ることにしました。彼らの風洞試験は1901年9月～12月に行われます。最初に簡単な風洞を試作して予備的な実験をした。その有効性を確かめてから下写真の様な風洞を造ります。［拡大写真］
この風洞は適切に設計されていて、揚力と抗力を系統的にかつ広範囲に収集するために使用された初めての風洞となった。測定装置はダクトの出口付近に設置されて、上面のガラス窓から角度測定用の分度器目盛りを読み取りながら実施された。
彼らは、沢山の翼型の揚力係数を簡単に、しかも手早く測定できるように極めて巧妙な装置を考案した［下図］。
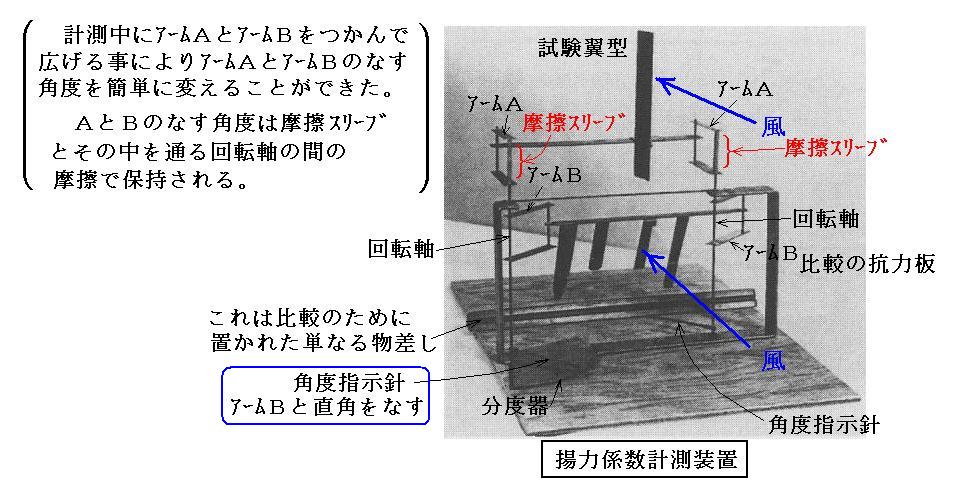
測定装置は、風が図の方向から当たる様にして、ダクト下流の出口付近に設置される。二つのアームＡに渡した横棒は風に垂直を保ったまま左右にスイングする。この横棒にさみ金具が付属している試験翼を取りつける。試験翼の風に対する迎え角αは摩擦で挟み込んでいるはさみ金具を捻って簡単に変えることができる。二つのアームＢに渡されている横棒も同様に風に垂直を保ったままで左右にスイングする。これに比較用の抵抗板が取り付けられている。この抵抗板は全ての実験に共通して用いられる。
測定は下図の様にしてなされる。気流の中でアームＡとアームＢがなす角度を広げてアームＡが丁度風に平行になる状況を探す。その状態の釣り合いが達成されたときに角度指示針により角度ａを読み取る。
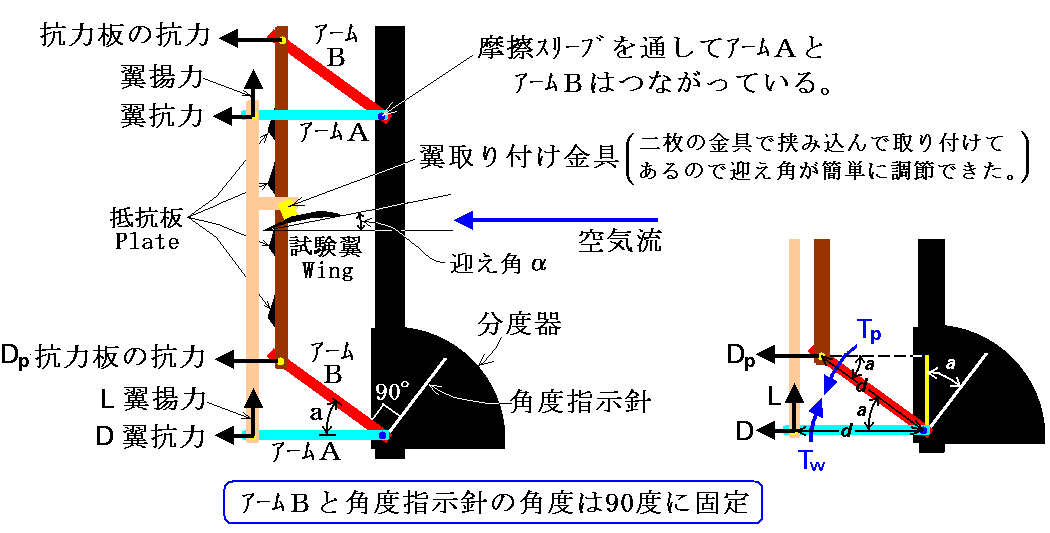
アームＢと角度指示針の間の角度は90度に固定されている。アームＡが気流に平行になったときにはアームＡとＢは気流の中で静止している。そのときアームＡに働く時計回りのトルクとアームＢに働く反時計回りのトルクは等しくなるので
となる。ここで翼の揚力係数と抵抗板の抗力係数を
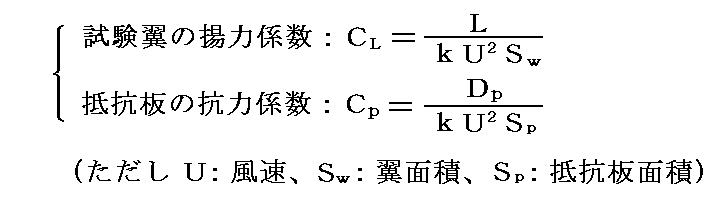
で定義する。ｋはスミートン係数だから抵抗板が平板の場合には抵抗板の抗力係数は1.0となる。
そのため、試験翼の迎え角αのときの揚力係数ＣLは
で表されることになる。
ライト兄弟は迎え角αを少しずつ変えながら揚力係数：ＣLを測定していった。そして一つの翼型のデータが得られると、別の翼型について同様な測定を行った。
彼らは、翼形の揚力／抗力比を測定するために下図の様な装置も作りました。この装置はSprattによって示唆されたアイディアを利用したものです。
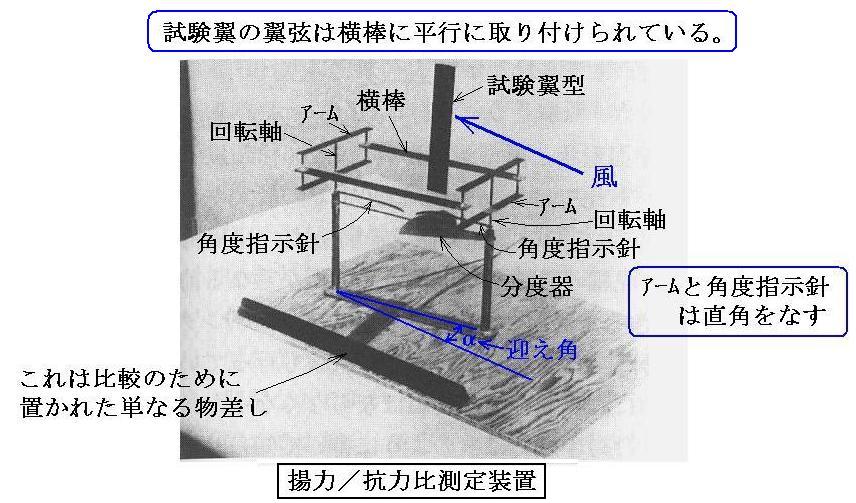
揚力／抗力比の測定は下図の様になされる。翼弦が横棒に平行になる様に試験翼を取り付ける。アームと横棒が形作る平行四辺形は回転軸の周りの回転で平行四辺形を保ったまま自由に変形する。風洞の気流に対して翼が測定したい迎え角αを持っように装置全体を下図のように設置する。気流の中では、試験翼型に発生する揚力と抗力の合力の方向がアームに平行な状態で釣り合う。
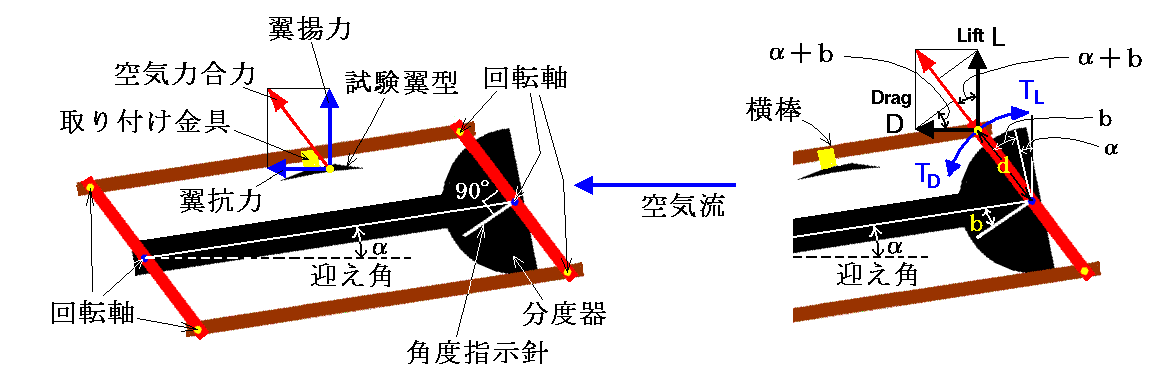
釣り合った状態でアームに働くトルクの合力は零となるので
となる。ここで翼の揚力係数と抗力係数を
で定義すると、迎え角αのときの揚力／抗力比は
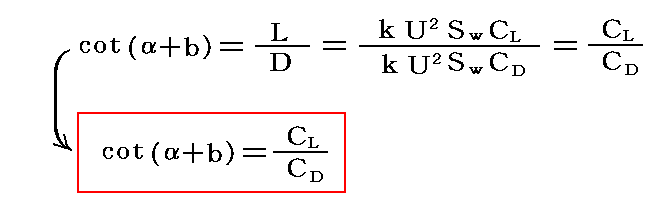
となる。迎え角αを少しずつ変えながら角度ｂを読み取って揚力／抗力比を求める。一つの翼型が終わると別な翼型について同様な測定を行う。
前節の実験から揚力係数：ＣLがすでに求まっているので、ここでの実験から揚力／抗力比：ＣL／ＣDが求まれば両式を連立させて解くことにより各翼の任意の迎え角αにおける抗力係数：ＣDは直ちに求まる。
兄弟は、実物の1／20程度の大きさの試験翼を鉄板で200種類以上作り、各種のパラメーターを系統的に変化させた。アスペクト比に関しては1～10まで、キャンパー比については1／6～1／20まで変化させ、反りの最大位置も翼中央から前縁近くまで変化させた。翼の平面形状に関しては、正方形、長方形、楕円形、先細り翼端を持つ翼面、円弧からなる前縁と後縁が翼端で鋭く尖った形で合わさった翼面が試験された。彼らはさらに前後に二枚並べたタンデム翼構成、上下に並べた複葉翼構成、三葉翼構成の試験も行った。[拡大写真]
彼らは1901年10月から数ヶ月にわたって数千種に及ぶ一連の実験を行い、翼性能に関する膨大なデータベースを獲得することができた。そのデータから翼の性能にはアスペクト比、キャンバー比、キャンバーの最大位置、翼の平面形状が重要な意味を持つことを知った。この時点で彼らは、翼の空気力学的な特性に関して世界で最も詳細なデータ群を持っていたと言える。
下図は彼らのノートに残されている揚力係数と迎え角の関係図の例です。これは３．で説明したリリエンタールの揚力係数と抗力係数の関係図とは違いますが、この形のデータも翼の性能を論じるときには重要です。
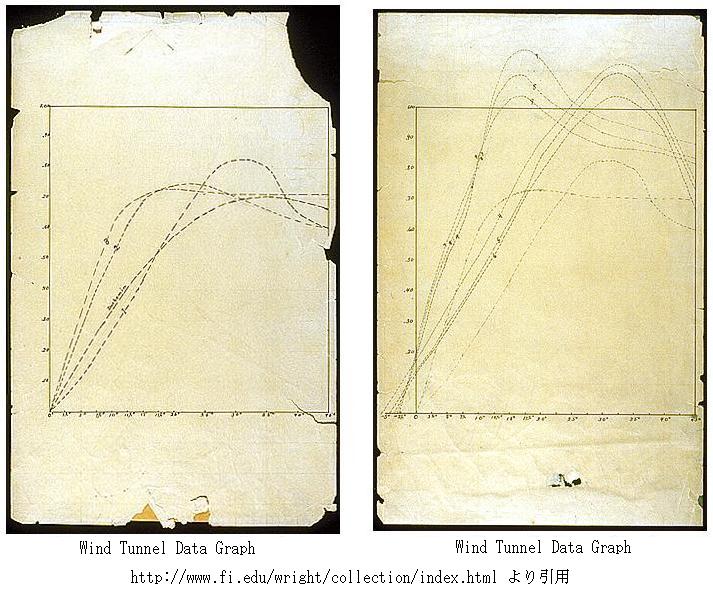
左は平板翼、右はキャンバー翼の場合のデータ例です。
［補足説明］
ライト兄弟は1901年10月24日にシャヌートからリリエンタールの本「鳥の飛翔」を手に入れます。シャヌートはこの本の一部を英訳したものもライト兄弟に送っていた。これは風洞実験がだいぶ進んだ時期でしたが、彼らはこの本を夢中になって読みます。そしてリリエンタールの実験の内容を知り、また自分達が行った実験と比較することでリリエンタールのデータは間違っていなかった事を知ります。さらに、何故自分達が間違ってしまったのか本当の原因を理解します。
ライト兄弟は、風洞実験から得られた詳細なデータから、より小さいキャンバー比とより大きなアスペクト比を持った翼が有利だということを理解します。彼らは自分達のデータを最大限利用して1902年のグライダーを設計します。
その機体は翼幅(スパン）が9.8ｍ（32ｆｔ）、翼弦（コード）1.5ｍ（5ｆｔ）、アスペクト比6.7、総翼面積28.3ｍ2（305ｆｔ2）、質量は53kgでした。キャンバー比は翼弦の1／24～1／26の範囲としました。主翼の上下間隔は5ｆｔです。前方の昇降舵の面積は15ｆｔ2、後部の二枚の垂直尾翼の総面積は112/3ｆｔ2でした。
また彼らは、うまく操作できなかった足で操作する翼のたわみ機構を廃止し、下の翼に腰を乗せる木製の鞍を取り付けてそれが左右に動くようにした。その鞍と翼をワイヤーでつないで、鞍の動きと翼のたわみが連動するようにした。つまり翼が左（右）に傾けば、腰を右（左)に移動させて翼の傾きが水平に回復するように翼をたわませるのです。
このグライダーの一番の特徴は以前のグライダーのアスペクト比（1900年は3.5、1901年は3.3）よりも遙かに大きなアスペクト比6.7を採用したことです。このため誘導抵抗が50％減少しきわめて高性能なグライダーとなった。［誘導抵抗やアスペクト比効果については別稿「人力飛行機を実現する原理」を御覧下さい］
ライト兄弟は新しいグライダーと共に1902年8月28日にキティホークに到着します。そして9月19日に組み立てが完了します。下の二枚の写真は組み立て完了直後に撮られた写真です。係留索がほぼ垂直に立ち上がっていることから、揚力／抗力比が大きな高性能な機体に仕上がっていることが解る。これは彼らが得た翼実験データに基づいて計算した通りの性能でした。この機体は最初固定された二枚の垂直尾翼を持っていた。また右の写真から解るように、この機体は最初左右の主翼が完全に水平に作られており下反角は付いていなかったことが判る。［拡大写真］
最初の滑空試験で解ったことは、1902年のグライダーは1900、1901年のものに比較してきわめて小さな沈下角で滑空できることです。そして横方向のコントロールが、固定した垂直尾翼を付けたことで改善されたように思われました。
この機体の翼は最初下反角の無い水平な構造に組まれていたのですが、初期の試験飛行で、1901年の機体が水平翼だった時に生じたのと同じ不安定性を示すことが解りました。この機体についても、上反角の無い水平な翼でも横風にあおられると上反角効果がみとめられ不安定になったのです［５．（２）参照］。そのため、9月22日に、彼らは翼のトラスを構成しているクロスワイヤーの長さを調節して、翼の先端を中心に対して4インチ下げる下反角を与えることにした。それと同時に翼端の迎え角を中央より少し大きくした。この改良の結果、状況は良くなって10月2日の飛行では152ｍを超える滑空を記録した。下の写真は下反角を与えた10月最初の段階の写真です。この段階ではまだ尾翼の改造は行われていない。［拡大写真］
これでうまくいくように思えたのですが、実験を続けていると1901年に体験したアドバース・ヨー不安定性とは異なる別のタイプの不安定性が生じることが解ってくる。それは飛行速度が小さい時の旋回時に発生した。
例えば、右へ旋回しようとして左翼を上げて右に横滑りが始まったとき、翼の捻りを元に戻してその横滑りを止めようとしても、左の翼はさらに上昇し右翼はさらに下がって右下に突っ込む様にして落下してしまうのです。その部分の記述を参考文献６．より引用しておきます。
Later, when we began to make free flights with the machine, we found that
when the wings were warped, first with the larger angle on one side and
then on the other, the machine descended the hill rolling from side to
side.
But later in some of the flights , when the machine was allowed to slide
a little to one side or the other as the result of one wing being at an
almost imperceptibly lower height than the other ,we found that the fixed
vertical vane, instead of maintaining an equal speed at the two opposite
wing tips, as we had expected, as a matter of fact did just the reverse,
and caused one wing to be checked and the other one to be speeded up.
This was due to the fact that when the machine began sliding laterally
a pressure was created on the fixed vanes on that side which was toward
the lower side of the machine and the side toward which the machine was
sliding.
The increased speed of the high wing gave it a still greater lift, and the decreased speed of the lower wing produced a lesser lift upon it, with the result that the lower wing dropped and the higher wing went still higher.
When the wings were warped in an attempt to recover balance, with the low wing having a greater angle of incidence than the upper wing, a still greater drag was produced upon the low wing, with a result that its speed was further decreased and the speed of the higher wing was increased.
These flights ended usually with disaster to the machine in what is called
today a "tail spin"
［補足説明］
今日これはスパイラル・ダイブ spiral dive（別名 テイル・スピン tail spin）と言われる不安定性です。それは下図のメカニズムで生じます。
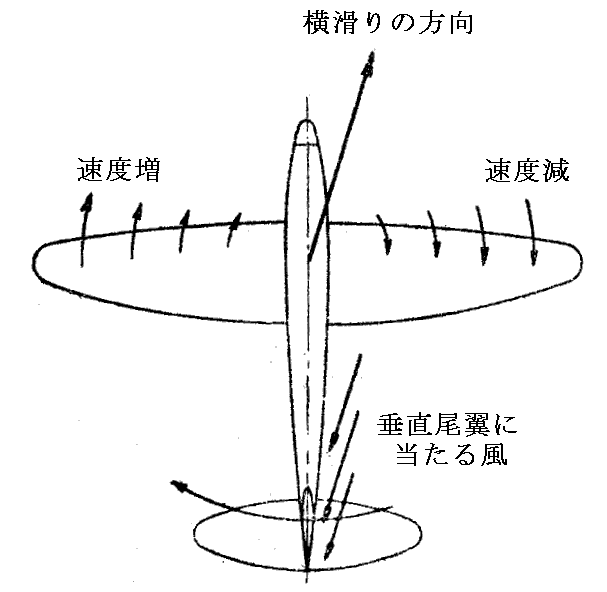
右に旋回しようとして左翼を上げ、右翼を下げたときに、もし右方向への横滑りが生じると垂直尾翼に当たる風は主翼を図のように回転させようとします。そうすると左翼は速度が増すので揚力が増加してさらに上昇し、右翼は速度が減少するで揚力が減りさらに下降します。そのため横滑りがますます大きくなって、上記の効果がさらに強まります。
また、これを回復しようとして右翼の後縁をねじり下げ左翼の後縁を捻り上げると、右翼の抗力は増え左翼の抗力は減って、ますます上記の翼端の速度変化を助長する結果となる。そのため飛行機は螺旋を描いて錐もみ状態になり、最後は墜落します。これがスパイラル・ダイブです。
本来、主翼と垂直尾翼取り付け位置の距離が十分長ければ、風見安定性によって横滑りを正してくれるのですが、垂直尾翼までの距離が短いと横風にあおられることで不安定性が生じるのです。
この不安定性は上反角が小さくて上反角効果があまり期待できず、垂直尾翼が大きすぎて横滑りによるあおりを受けやすい機体に起こります。４．（２）［補足説明２］で説明したダッチ・ロール不安定性のちょうど逆です。
ライトのグライダーのように上反角が無くて、主翼と垂直尾翼の距離が短い機体では起こりやすかったと思われます。
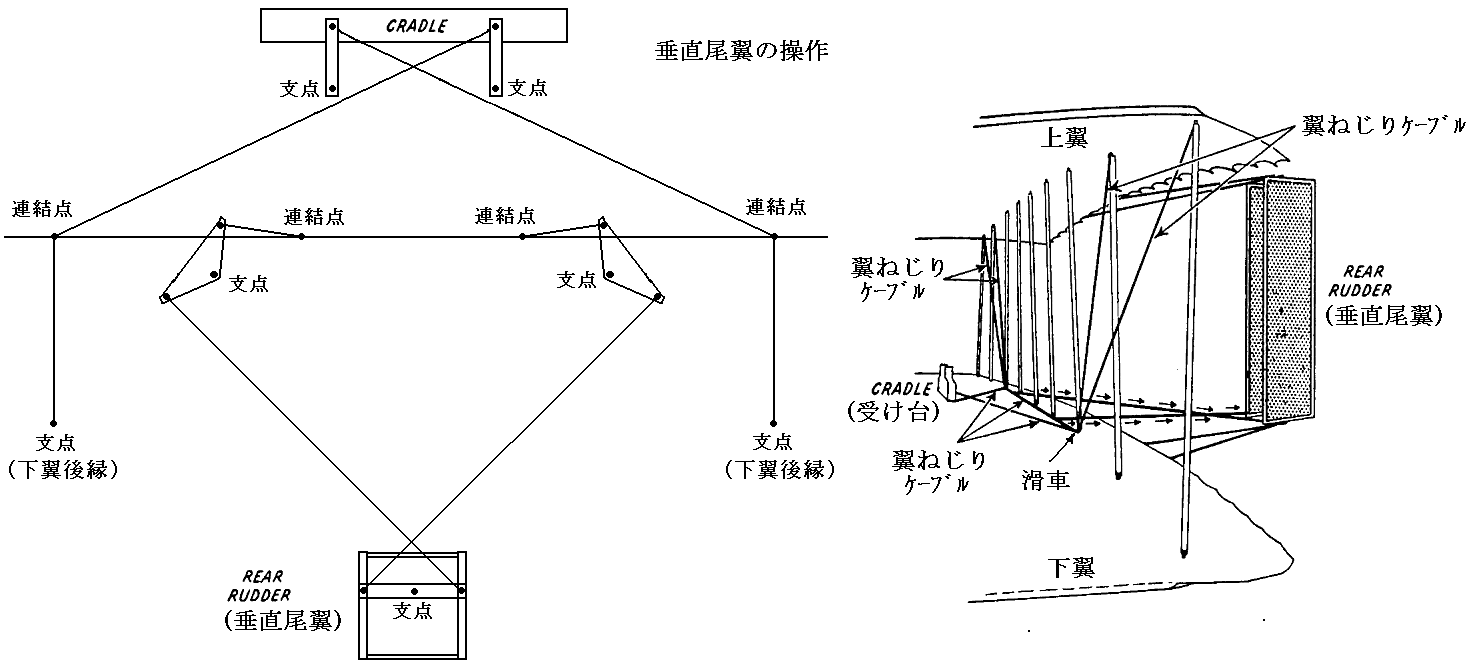
上記の不安定性を解決するために、２枚あった垂直尾翼を１枚に減らし、垂直尾翼を可動式に改良します。そのとき、ただでさえ厄介な水平舵と翼のねじりに加えて、垂直尾翼を操作するのは大変だった。そこで主翼をねじるワイヤーを垂直尾翼にも繋いで、体を左右に移動させ、主翼のねじりと垂直尾翼の操作を同時に行うことにした。つまり左（右）翼の後縁をねじり下（上）げて右にバンクした場合には、垂直尾翼の後縁は右にふれる様にした。左にバンクした場合はこの逆になる。このようにして旋回動作と向心力とうまくつり合うようにした。
この操縦様式はこの後のライト機に踏襲されていく。以下は参考文献６．のその説明部分です。
Our first change in the machine, as the result of our experiences in these flights just mentioned, was to remove one of the vertical vanes in the rear of the machine.
By doing this we hoped to remove at least a part of the disturbing effect
of the vanes when the machine was sliding slightly sidewise.
We found that this only slightly mitigated the evil influence of vanes.
After a good deal of thought the idea occurred to us that by making the
vane in the rear adjustable, so that it could be turned, . . . to entirely
relieve the pressure on that side toward the low side of the machine, and
to create a pressure on the side toward the high wing equal to or greater
than the differences in the resistances of the high and low wings, due
to their different angles of incidence, all of the good properties of a
vane in the rear would be secured without any of its bad properties.
But this was going to add one more burden to the operator.
He would now not only have to think, and think quickly, in operating the
front elevator for maintaining the longitudinal equilibrium, but he would
also have to think so as to operate this rudder . . . to present its surface
to the wind on that side which is toward the high wing, or the wing having
the smaller angle of incidence.
While this change to make the vane adjustable was being made, the idea
came to us of connecting the wires which operated the rudder to the cables
which operated the wing warping, so that whenever the wings were warped
the rudder was simultaneously adjusted, . . . to produce a pressure on
that side of the rudder which was toward the wing having the smaller angle
of incidence.
この改造の効果はすばらしいものでした。このことでバンクしたとき機首をうまく旋回する方向に向ける事ができて、［揚力］・［重力］・［向心力］がつり合った横滑りの無い滑らかな旋回ができるようになった。新しい機体は完全に制御されて、楽々と飛行することができた。兄弟は何度も何度も飛行を繰り返し、ウィルバーの最長飛行時間は26秒（190ｍ）を超えた。また、この年初めて飛行したオービル（5.(1)［補足説明4］参照）も21秒（188ｍ）の飛行を記録した。［拡大写真］
最後の写真の主翼のねじれと垂直尾翼の方向が予想されるものと反対だと思われるかも知れませんが、これはすでに右旋回が始まっていて、右に横滑りして右の主翼が過剰に下がろうとする動作を回復するために行われている操作です。そのため右翼の後縁が捻り下げられており、それに連動して垂直尾翼の後縁は左に向けられている。その瞬間をとらえたものです。
彼らは、この年の飛行によほど感激したのであろう。この時期の写真を数多く残している［飛行写真１、写真２］。
兄弟は多くの成果を得て、1902年10月28日にキティホークのキャンプ地を去り31日にデイトンに帰着します。
1902年10月末の段階で、ライト兄弟は、1899～1902年の４年間にわたって行ってきた空気力学実験とグライダー飛行実験から、後は動力の問題さえ解決できれば空に飛び立てることを確信していた。そのためすぐにエンジンとプロペラの開発に取りかかります。エンジンについてはオービルと当時ライト自転車店のために雇用していた機械工のチャーリー・テイラーが主に、プロペラについてはウィルバーが主に担当した。
兄弟は互いに議論しながらプロペラの本質について理解を深めていった。彼らは、プロペラとは揚力がおおむね飛行方向を向くように方向がねじってある翼以外の何者でもないと認識します。そのときプロペラの中心からの距離に応じて、また飛行機の前進する速度に応じて、空気に対する迎え角と対気速度は変化します。兄弟は今日「翼素理論」と呼ばれる理論と同じ方法でプロベラを回転軸からの距離に応じて細かく分割して、それぞれに風洞実験から得た翼性能のデータを適用して、最適な捻り角と形状を導き出します。
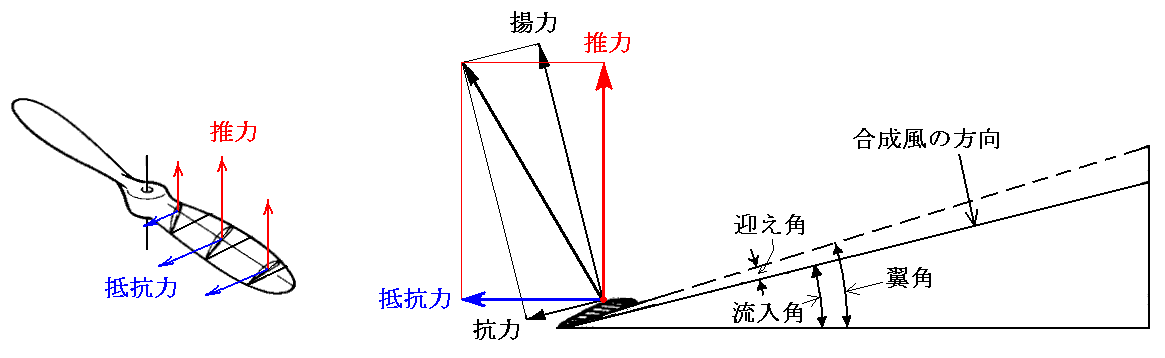
プロペラの捻れている度合いを表す角度を翼角といいます。その翼角で単純に一回転したときプロペラが進む距離をピッチといいます。しかし実際にはプロペラが一回転する間に進む距離は下図の様にピッチとは異なります。この距離は実際に静止している空気に対して、プロペラが１回転する時間に飛行機が進む距離だと言っても良いでしょう。
そのためプロペラを翼と見なした場合、実際の気流の方向に対する迎え角は下図の様になります。
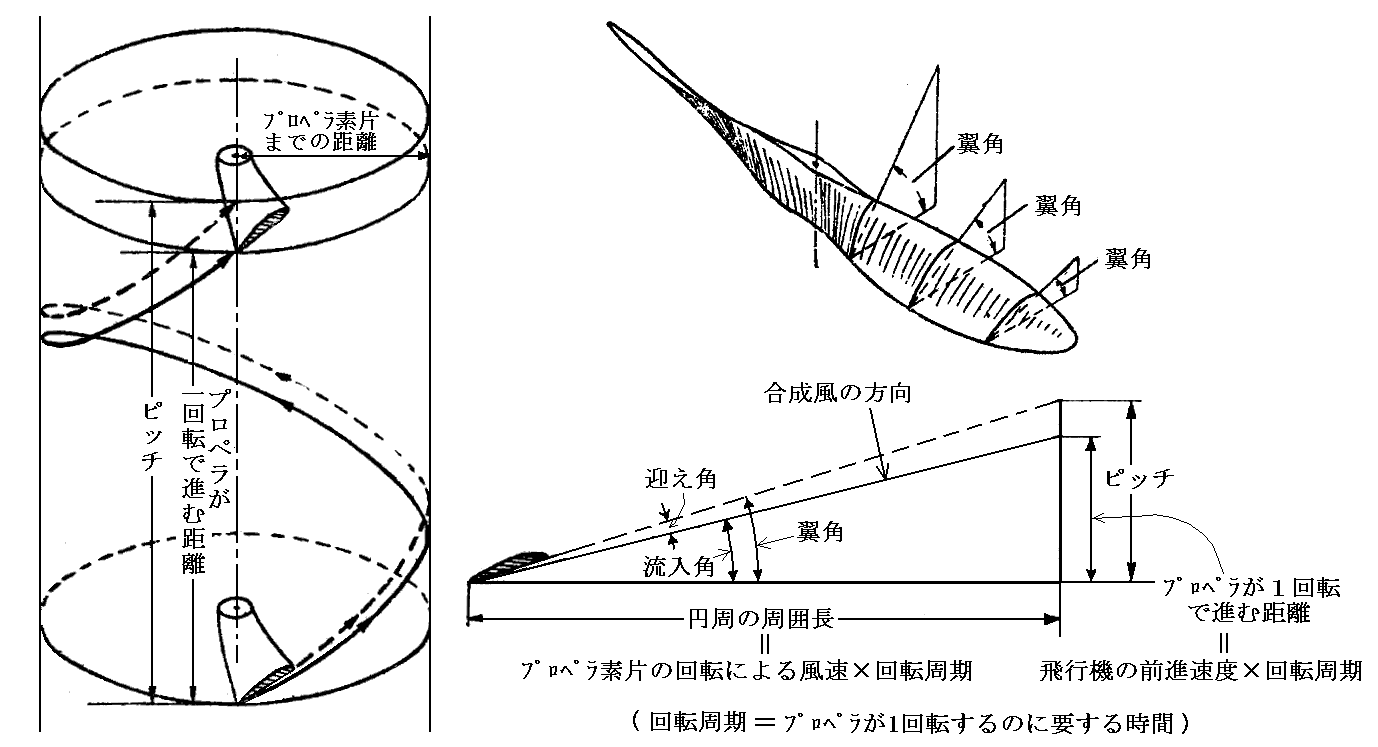
このときプロペラも翼の一種ですから、すでに述べた翼の性能データを用いて最も抵抗が少なくて前方に引っ張ってくれる力［推力］が大きくなる迎え角になるように捻りの角度(翼角)を決めればよいのです。揚力とは自由流（合成風の方向）に垂直な成分であり、抗力とは自由流に平行な成分のことですから、翼データの揚力と抗力から進行方向の引っ張り力（推力）とそれに垂直な方向の抵抗力に変換した上での最も効率の良い迎え角を求めなければなりません。
ただし、ここで注意しなければならいなのは、プロペラは中心の周りを回転しているのでプロペラ要素の中心からの距離が変われば１回転で進む回転方向の距離が異なることです［下図参照］。
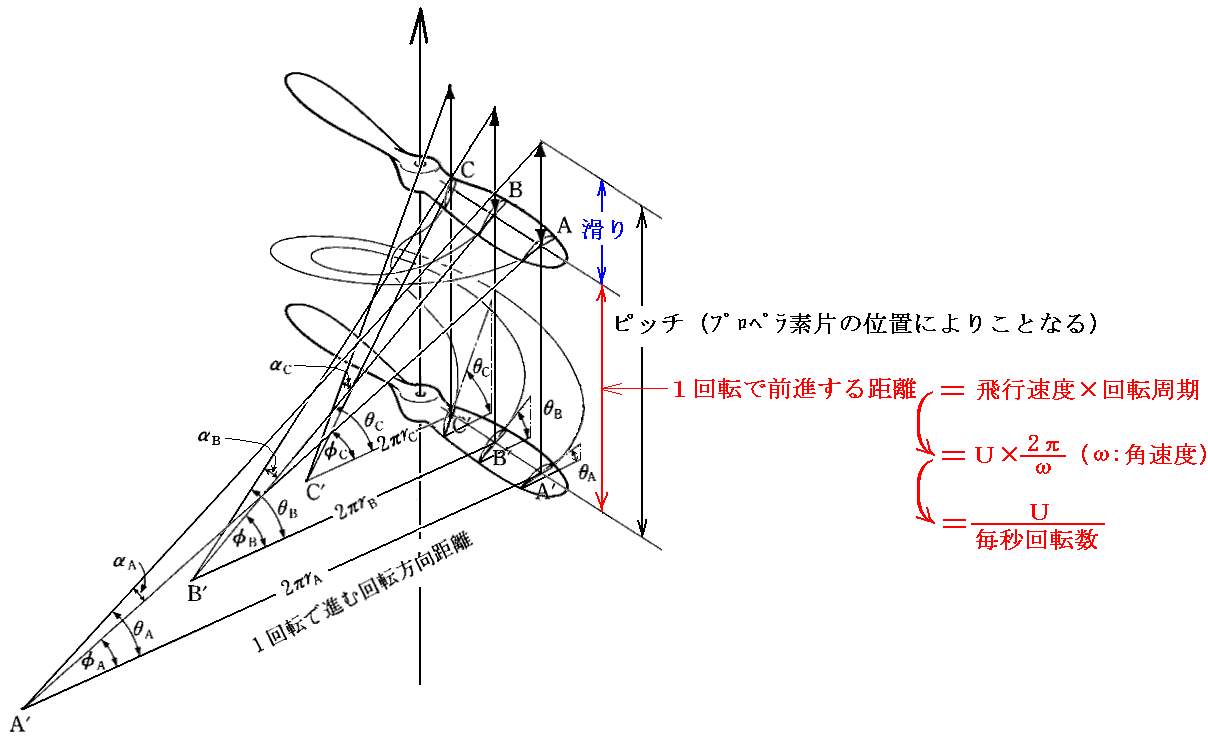
その様な諸々の事情を考慮してプロペラの素片ごとに最適な迎え角を見極めてピッチ（翼角）を決めてゆく必要があります。
プロペラ素片ごとに翼データを適応してプロペラを設計すれば、各素片に働く抗力の大きさも翼データから計算できます。各部分に働く抵抗力に中心からの距離をかけたものをプロペラ全体に渡って加え合わせればプロペラに加えるべきトルクの大きさが計算できます。トルクが解ればエンジンに必要な馬力も計算できます。
ライト兄弟はお互いに議論しながら、上記のプロペラ理論を自分たちで見つけ出して、当時の水準を遙かに超えた高性能のプロペラを作り上げることができました。
［補足説明］
１回転で進む回転方向の距離はプロペラ要素までの回転半径が決まれば一義的に決まります。このとき、飛行機の進行方向に一回転で進む距離はプロペラ素片が全て同一のプロペラに付属しているので全て同じになるように見えますが、実は異なる可能性があります。例えば、中心付近に近い部分では胴体の影響のために前進によって生ずる風力が他よりも低下するような事が起こるからです。そのため、普通は中心付近のピッチは少し少なめにします。
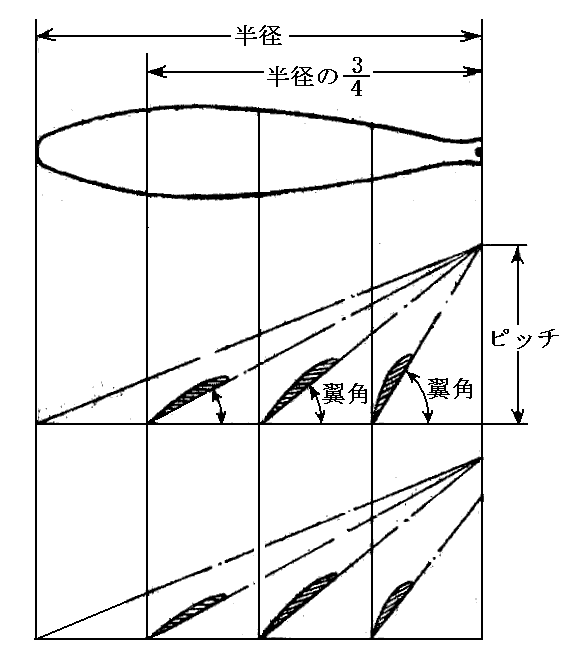
最適な迎え角を各素片ごとに割り当てていくのですが、たとえ同じ迎え角を割り当てても流入角が素片ごとに異なりますから、その意味に於いても、ピッチはプロペラ素片ごとに少し変化します。
彼らが作ったエンジンの詳細については別稿「ライト・フライヤー号（1903年）のエンジン」で説明しましたのでここでは省略します。
彼らがうつ伏せ状態で搭乗する形式にしたのは、操縦者の空気抵抗を最小にしたかったからだろう。これが彼らの機体特有の腰を置いた鞍(cradle）による操縦様式を生み出した。腰を置くＵ字型の鞍が、それに付けた支柱の支点を中心に左右に動くようになっていた。それから伸ばされたワイヤーによって主翼の後縁をねじる。ほんの１～２インチ動かせば、十分な効果が生み出せたようです。主翼の後縁がたわみやすいように外側後ろ側の３本の支柱間にはトラスを作るための交差ワイヤーは張られていません。ワイヤーの張られている状況はこちらの写真１と写真２で確認してください。
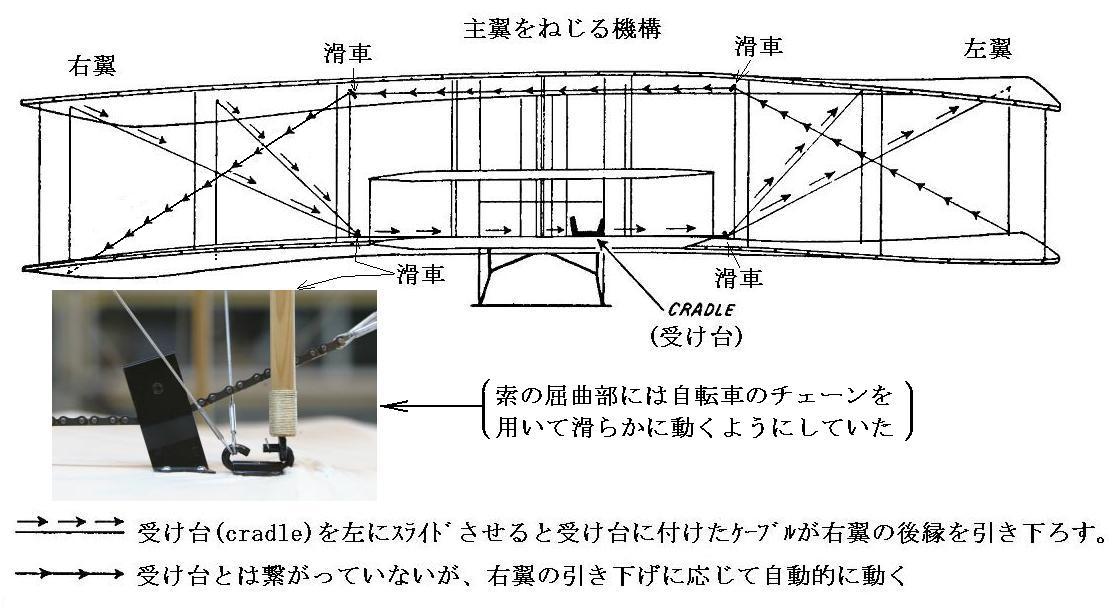
下図は本物のフライヤー号のコックピットです。操縦索やプロペラ（直径2.6ｍ）の様子が良く解る。［拡大写真］
主翼を捻るワイヤーは途中の三角板を介して後ろの垂直尾翼にも連結されていて、両方が連動して動く様になっている。
オリジナルなライト・フライヤー号を下から見た写真。［拡大写真１］、［高輝度モニター用］
前方の昇降蛇は左手のレバーにより操作された。詳細は上記写真の拡大版で確認されたし。
フライヤー号の三面図。［拡大三面図1］［拡大三面図2］［ライトが描いた設計図］
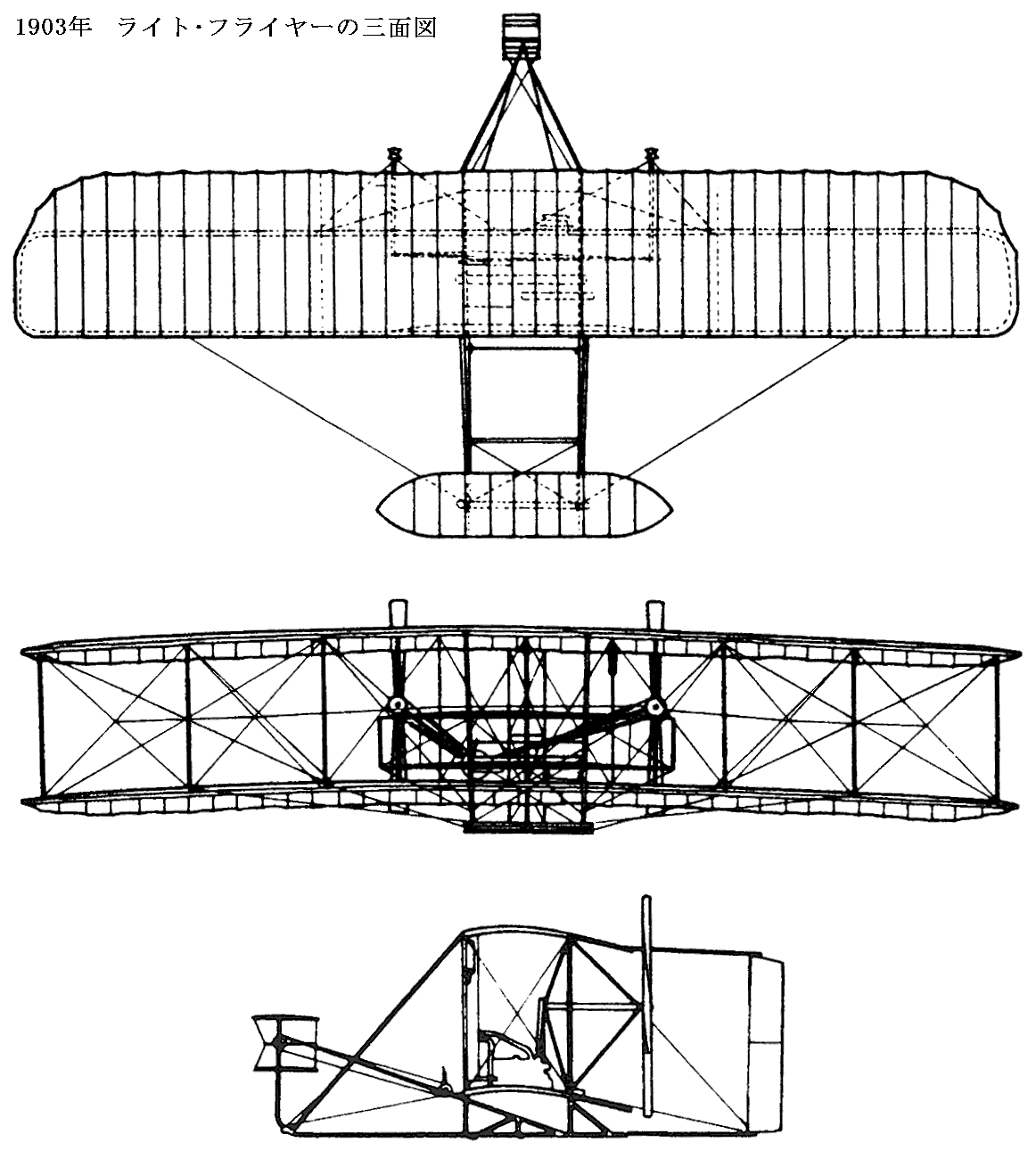
この機体の主翼は翼幅40feet6inches、翼弦6feeｔ6inches、総翼面積は500ｆｔ2を少し超えるくらいでした。
1903年のフライヤー号は下反角を付けた主翼や前方に取り付けた昇降舵など、今日の常識に反する構造をしています。４．（２）［補足説明２］や５．（１）［補足説明１］に記したように、確かにそういった構造は飛行に不安定性をもたらします。
しかし、そこで説明したように、彼らかその様にしたのには理由があります。彼らは膨大な回数の飛行実験を実施して何度も何度も調整を繰り返した結果そうしたのです。彼らが発明した主翼の捻りと方向舵の向きを連動させた操縦方法により、上記の不安定要素を克服して、当時のあまたの飛行機研究家の水準を遙かに超えた操縦性と飛行の安定性を達成していたのです。
彼らはエンジンとプロペラの開発に時間がかかったために遅くなってしまったが、1903年9月23日にキティーホークの試験場に出発します。それから初飛行成功の12月17日までに様々なトラブルに見舞われますが、彼らはついに人類初の有人動力飛行に成功します。［拡大詳細写真］
1903年12月17日午前10時35分のフライヤー号の飛行はあまりにも有名ですから説明は省略します。また、これ以後の飛行機の発展・進歩についても省略します。詳しくは参考文献１．２．４．や適当なＨＰを御覧ください。［初期の飛行機研究の歴史］
［補足説明１］
昇降舵を前方に付ける形はその後のライト機にしばらく踏襲されますが、1910年頃になると、前方の昇降舵につけ加えて尾部にも水平尾翼を取り付けます［モデルＡとＢの過渡期の機体］。
そしてライト・フライヤー・モデルＢ(1910年)以降になると前部の昇降舵を廃止して、当時のヨーロッパの飛行機と同じように尾部に垂直な方向舵(rudder）と水平な昇降舵（elevator）を付ける形になります。
さらに1916年には主翼の捻りの代わりに補助翼(aileron エルロン)を採用します。
［補足説明２］
操作方法も、1905年のフライヤー３号機では方向舵と主翼の捻り操作を分離した。腰を載せた鞍で主翼の捻りを、そして右手で方向舵、左手で昇降舵と、それぞれ別々に操作できるように改良した。
その後1907年のライト・フライヤー・モデルＡ（改良型フライヤー３号機の商用標準機）になると、初期のうつ伏せ状態で手のレバーと腰を納めた鞍(cradle）で操作する方法から、座って左右のレバーで昇降蛇、方向舵、主翼の捻りを操作する方法になります。それは左手レバーで昇降舵を、右手レバーの前後の動きで方向舵、左右の動きで主翼の捻りを操作する方法でした。
さらに、1912年頃になると当時の主流（今日と同じ）であった操縦棹(輪）とフットバーで操作する方式にします。
［補足説明３］
参考文献16．より、ライト・フライヤー号の興味深い写真を別ページにて引用していますのでご覧下さい。
空を飛ぶ事は人類の夢だったのですね。このＨＰを作っていて改めてそのことを強く感じました。またライト兄弟がなぜ有人動力飛行の成功者としてたたえられるのかも良く解りました。確かに彼らの業績は抜群です。
［参考文献の追記］
ここに記述した段階までは流体力学の理論的研究からの寄与はほとんど有りませんでした。１．（２）［補足説明］に記したように流体力学の数学的体系化について１８世紀後半から１９世紀にかけて大きな進歩があったのですが、翼の働きで最も重要な迎え角が小さい時の驚くべく揚力／抗力比の大きさを説明することはできませんでした。これこそが多くの飛行機研究家に飛行の可能性を確信させた事柄なのですが、流体力学理論はその説明に全く寄与していません。
さらにキャンバー効果、アスペクト比効果も飛行機の翼性能にきわめて重要な影響を与えるのですが、その説明にも理論はまだ関与していません。それらの効果の謎が理論的に解明されるのは２０世紀に入ってからです。そのことに関しては別稿
「二次元翼理論（等角写像とジューコフスキーの仮定）」 と
「人力飛行機を実現する原理［プラントルの揚力線理論］(アスペクト比と揚力／誘導抗力比）」
を御覧下さい。
