このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
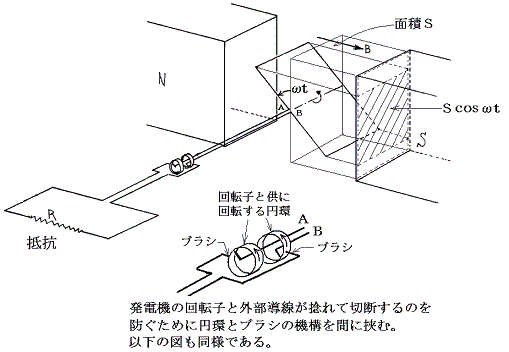
高等学校では交流発電機の回転子を外力によって回すとき発生する交流電圧は、ファラデーの電磁誘導の法則を用いて説明する。

回転子コイルの面積をSとすると、回転子コイルをつらぬく磁束Φは磁束密度をBとするとΦ=BScosωt となる。「コイルに生じる誘導起電力の大きさはコイルを貫く磁束の単位時間あたりの変化に比例する」というのがのファラデーの電磁誘導の法則である。
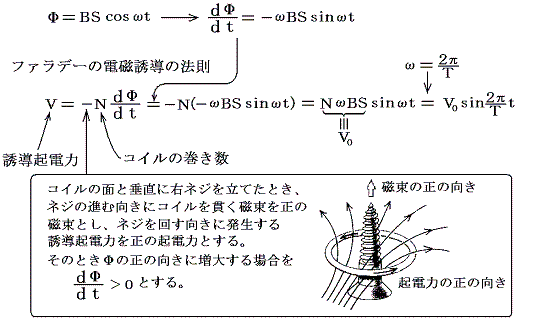

ただしこの誘導起電力という言葉は高校生に取って非常にわかりにくい。正確に述べると、
磁場が時間的に変化するとそのまわりに渦状の誘導電場Eができる。そこにおかれた回路に沿って電荷が動くと,誘導電場Eがローレンツ力F=qEに従って電荷に力を及ぼして仕事をする。単位電荷が回路を1周する間に誘導電場がする仕事が誘導起電力である。誘導電場 Eの回路に沿った成分を El とすれば,誘導起電力Vは回路を1周する線積分
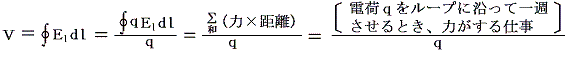
で表される。
[補足説明]
これはコイルは静止していて磁場が変化する場合に成り立つ式である。だから上記の説明も各瞬間瞬間ではコイルは静止していて磁束密度が変化していると考えなければならない。そのときv=0と考えているからローレンツ力の中のqv×Bの項目は無い。ただし回路を流れる電流に伴う速度は存在する。この電流を生じる速度によるローレンツ力qv×Bは回路導線に垂直に働くからここでは考えなくて良い。
しかし実際は、磁場は変化せずコイルが運動しているのだから、次に述べるように静磁場中を回路が動くときに回路を動かす外力がローレンツ力を媒介として電荷に仕事をして誘導起電力が発生すると考える方がよい。この様に見ると回路に沿った誘導電場Eは存在しない。磁束密度Bの中を運動する電荷にローレンツ力F=qE+qv×B が働く。ここのEについて、誘導電場による成分は零だか(3)で説明する電荷の偏りにより生じる静電場成分は存在する。この静電場による電気力とqv×Bによるローレンツ力がつり合っている。
観測系の立場により電場や磁場の現れ方が異なるのは電磁気学の本質に関わるところで、この事実の深い考察からアインシュタインは“特殊相対性理論”を導いた。
上記の説明はここらあたりを適当にごまかしており、高校生には非常に解りにくい。しかし、そのあたりを説明すると長くなり、高校レベルを越えるので省略する。
[2019年11月追記]
興味のある方は別稿「アインシュタインの特殊相対性理論」2.(1)[補足説明1]をご覧下さい。このことのさらに詳しい説明は別稿「電磁場の相対性と特殊相対性理論」および「電磁場の相対性と特殊相対性理論(補足説明)」にあります。
[補足説明2]2020年4月追記
前記の補足説明を更に補います。どうぞ下記別稿の説明を御覧下さい。
江沢洋著「動く電気力線は磁場を生む」、「電磁誘導の法則、言い表し方に意義あり」、「動く磁束線は電場を生むか?」
別稿「二次元・非圧縮性・完全流体の力学」5.(4)2.[補足説明1]
静磁場中を回転子が動くと導線中の電荷にローレンツ力が働く。以後話を簡単にするために電流の担い手は正電荷とし、その動きで説明する。下図のようにコイルB→Aに沿った力が正電荷に働き、この力が電荷を外部抵抗に向かって動かす。電荷がコイル導線に沿って動く(電流)とこれが新たにローレンツ力を生じてコイルの回転を制止する力を発生する。これが外力とつり合う。
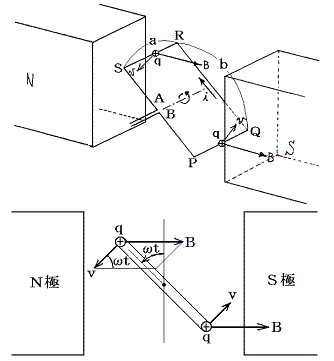
回転速度vにより生じるローレンツ力は、辺PQ、RS上でF=qvBsinωtが導線方向に、辺BP、QR、SA上で導線に垂直な方向(導線に平行な成分は零)に働く。ここで方形コイルの縦横の長さをa、bとすると、コイルB→P→Q→R→S→Aに沿った方向に生じる起電力の総和は定義により次の様になる。
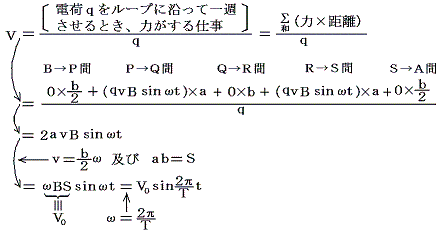
この結論は前記「(1)高校教科書の説明」の結論と同じである。同じであるから、高校では(1)で代用しているのだが、本来真に正しい「(2)ローレンツ力による説明」でなされるべきである。
ファラデーの電磁誘導の法則だろうと、ローレンツ力による説明だろうと、同じ式で表される誘導起電力が生じる。この誘導起電力により電荷が外部抵抗Rの方へ押し込まれる。そのとき抵抗Rが流れ込む電荷の移動を妨げるために抵抗Rの前に電荷が溜まり抵抗Rの前側電位が上がり逆側電位が下がる。これは電荷の偏りによる電位の上昇で、この電位変化による電界が発電機コイル中にA→S→R→Q→P→Bの向きに発生する。その電界による力が、誘導起電力による電荷を抵抗側へ流そうとする力を打ち消す。そのとき電荷に働く力がつり合うまで電位が上がり、その電荷の偏りを実現するまで抵抗Rの前側の電荷はたまってくる。下図参照
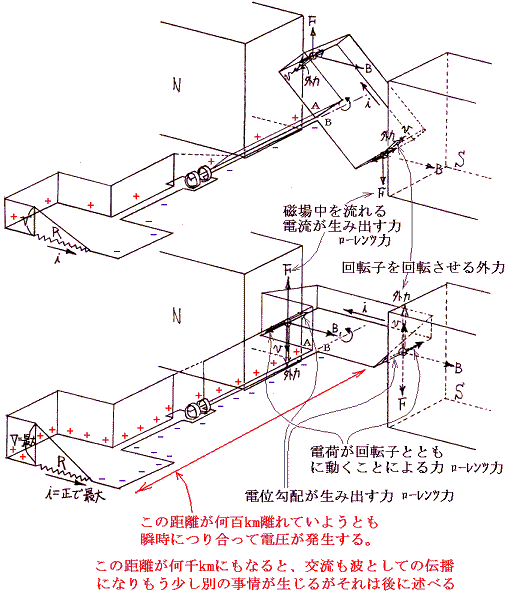
結局交流回路のすべての場所で、各瞬間瞬間において、電荷に働く力はつり合っており定常状態が実現されている。発電機と外部抵抗Rがいかに離れていようと、その間をほぼ光速に近い速さで情報のやり取りがおこなわれ、上記の電圧上昇と回転子コイル内の電位勾配が実現されて、定常状態が瞬時に実現される。実際には電流も電圧も変動しているので厳密には定常状態と言えないが、それら回転子の運動速度や交流の電圧変動、電流変動は、上記の状態が実現される速度に比べると遙かに遅く、各瞬間瞬間に定常状態が実現していると見なせる。
3.項以下の議論は別稿「発電機とモーターの理論」で用いた図(直流)と比較すると解りやすい。

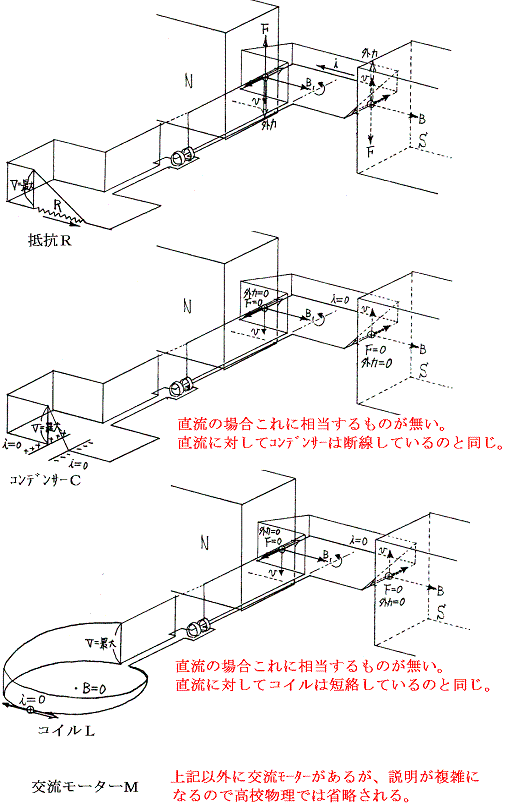
抵抗のレジスタンスをR、その両端にかかる交流電圧の瞬時値はv=V0sinωt で表わす。このとき交流電圧の変化は、電荷が平衡状態を実現するための時間に比較すると遙かにゆっくりした変化である。だから各瞬間瞬間において、いつも定常状態が実現されながら電流が流れているとして良い。故に瞬時値について定常状態に於けるオームの法則がそのまま成立する。別稿「オームの法則」参照。
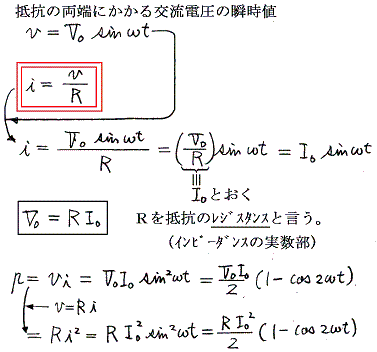
ここで大切なことは、回路素子抵抗を流れる電流iは、その両端にかかる電圧vと同位相であることと、電圧の振幅は電流の振幅のR倍になることである。sinやcosなどの関数形は時間軸の原点の取り方でどのようにでも表現できる。
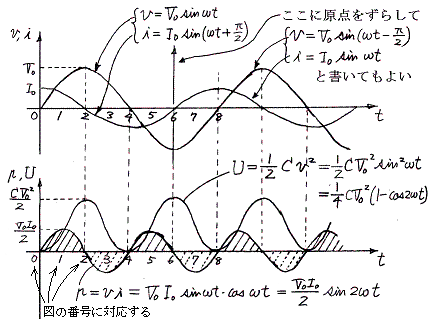
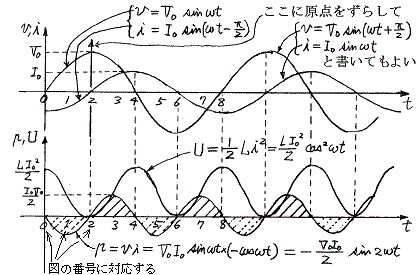
発電機は抵抗に対して周期的な変動はあるが、連続的に正の仕事をする。その仕事は結局抵抗で発生する熱エネルギーとなって周囲に発散する。下記グラフ参照。
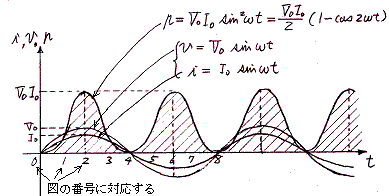
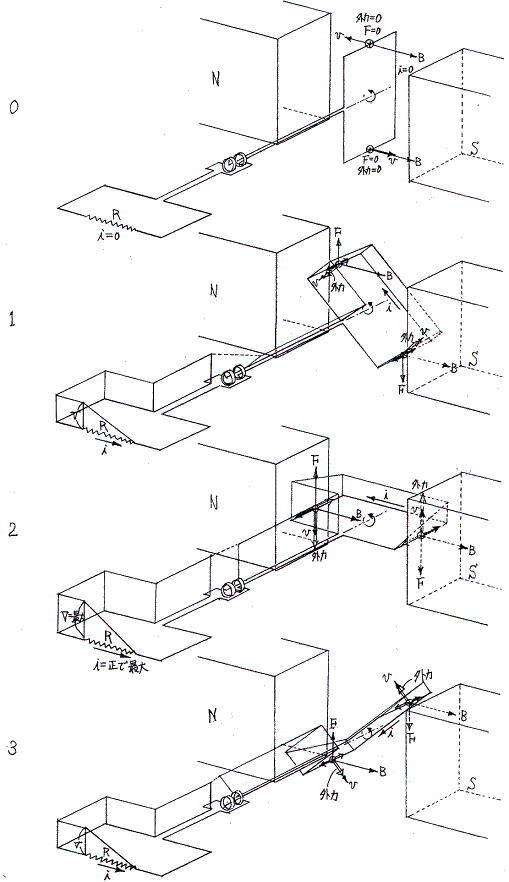
以上の変化を図示すると次のようになる。上記グラフ横軸の番号が下図の番号に対応する。1、2、3と5、6、7図の外力が常に回転方向を向いていることに注意。そのため外力は常に発電機に対して仕事をし、その仕事は送電線を通じて抵抗に伝達される。
ここでの本質はコンデンサーの公式である。コンデンサーのキャパシタンスをC、コンデンサーの両端にかかる電圧の瞬時値をv、コンデンサーにたまっている電荷の瞬時値をqとすると
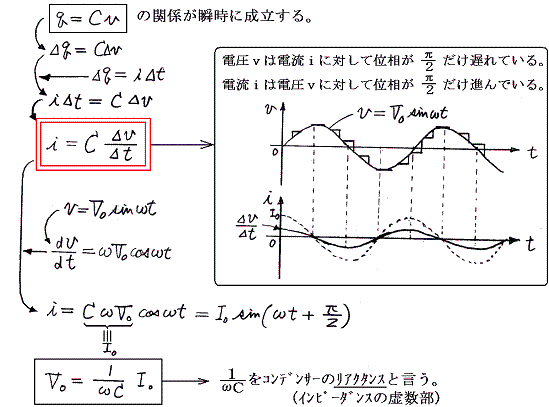
ここで大切なことは、回路素子コンデンサーを流れる電流iは、その両端にかかる電圧vより位相がπ/2だけ進むことと、電圧の振幅は電流の振幅の(1/ωC)倍になることである。sinやcosなどの関数形は時間軸の原点の取り方でどのようにでも表現できる。
電圧と電流の位相がずれているため、最初の1/4回転で発電機がコンデンサーに注入した仕事は、次の1/4回転でコンデンサーから発電機に返される。そのため時間的に平均化すると発電機はコンデンサーに対して仕事をしない。コンデンサーに注入された仕事は電場のエネルギーUとしてコンデンサー中に蓄えられるが、その値は下記グラフの様に周期的に変動する。このとき、振動する電場は電磁波となってコンデンサーから周囲に漏れ出てしまうので実際には少しずつエネルギーは消費される
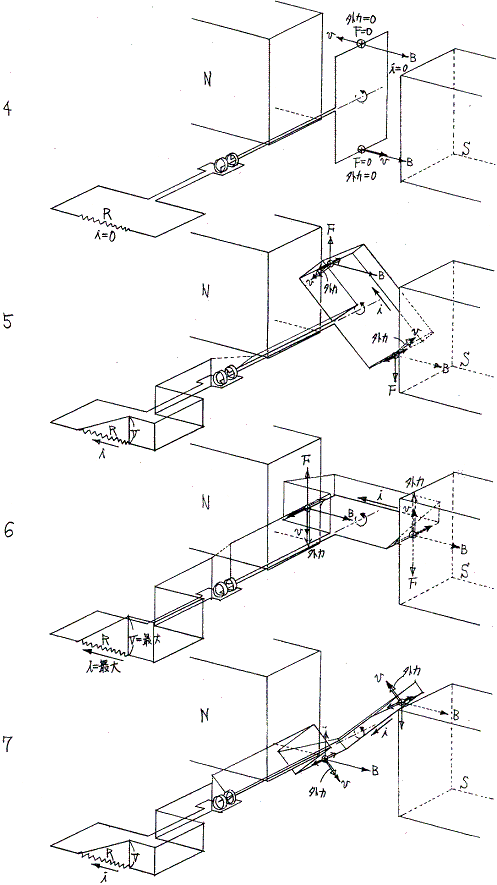
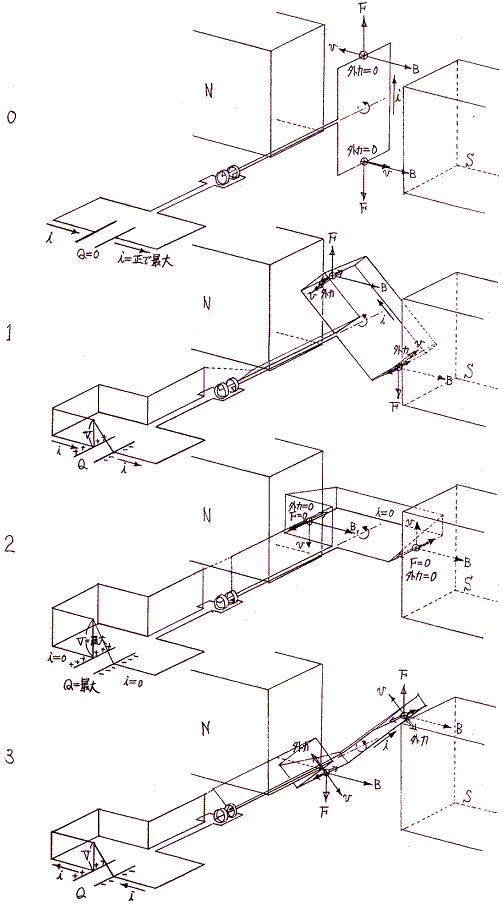
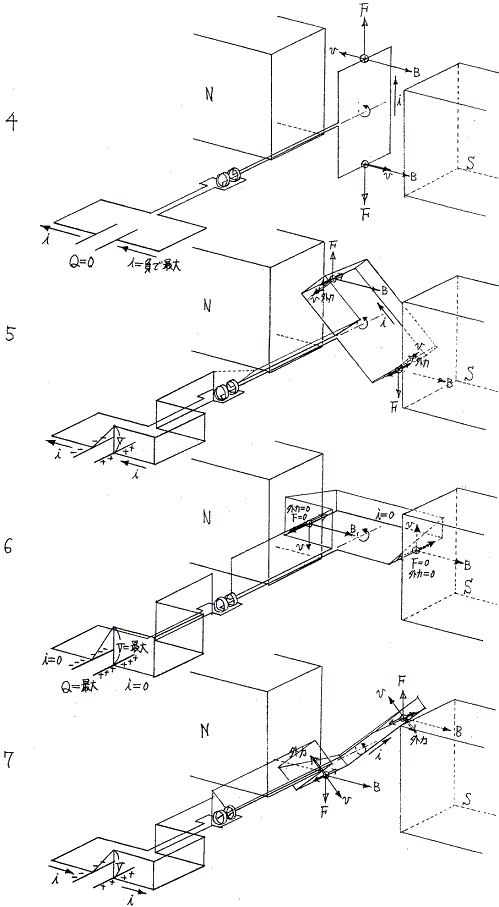
以上の変化を図示すると次のようになる。上記グラフ横軸の番号が下図の番号に対応する。1、5図では外力が回転方向を向き、3、7図ではその逆になっていることに注意。つまり1、5図の状態では外力は発電機に対して仕事をし、その仕事がコンデンサーの中に蓄えられる。そして3、7図の状態では発電機は外力を及ぼすものに仕事を返しており、その仕事のもとはコンデンサーが発電機に返した仕事である。
それは、0〜7図に於いて回転子中の電圧の分布は負荷が抵抗の場合(項目3.)とまったく同じなのに、電流が流れる方向が異なっている事による。そうなったのは根本の式がオームの法則からコンデンサーの式に変わったからである。
図0→図1→図2にかけてコンデンサーに電荷が貯まり、コンデンサーのプラス側電位が上がっていくのは、電荷をコンデンサーに押し込もうとする力(発電機コイルの中に発生する)がどんどん増大していくからである。
図2→図3→図4にかけてコンデンサーの電荷が減少し、コイルにそれまでとは逆向きの電流が流れるのは、コンデンサーに電荷を押し込もうとする力(発電機コイルの中に発生する)が減少するため、コンデンサーの中に電荷を閉じこめておくことができなくなるからである。コンデンサーの中に閉じこめられている電荷は同種電荷間に働く反発力の為にコンデンサーから流れ出るのである。
この様な事が起こっても良いのは、再三強調するが、交流を担う電荷に働く力はいつもつり合っており常に合力が零であると考えて良いところにある。つまりローレンツ力による力と電圧分布に伴う静電気力(これもローレンツ力の一種)が瞬時につり合うように電圧分布が決まり、その動きに比較したら電荷の動く速さは止まっていると考えても良いくらいにゆっくりした動きなのだ。だから電流の方向など外部負荷の事情に合わせていかようにでも調節できる。そのとき電圧の分布は極微量の電荷の極微量の移動でいかようにでも調節できる。
エネルギーはコンデンサーの極板間に電場のエネルギーとして蓄えられる。
ここでの本質は自己誘導の公式である。コイルのインダクタンスをL、コイルの両端にかかる電圧の瞬時値をv、コイルを流れる電流の瞬時値をiとすると
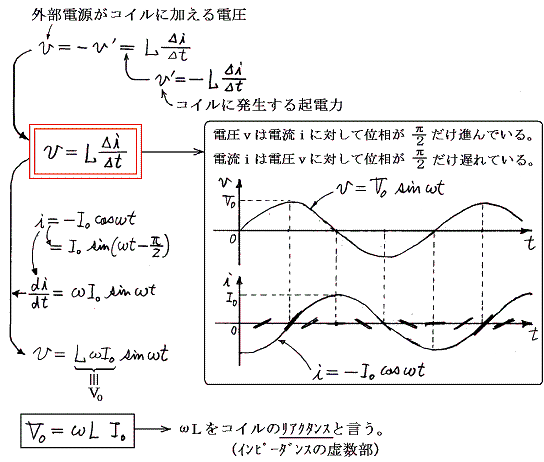
ここで大切なことは、回路素子コイルを流れる電流iは、その両端にかかる電圧vより位相がπ/2だけ遅れることと、電圧の振幅は電流の振幅のωL倍になることである。sinやcosなどの関数形は時間軸の原点の取り方でどのようにでも表現できる。
電圧と電流の位相がずれているため、1/4回転で発電機がコイル注入した仕事は、次の1/4回転でコイルから発電機に返される。そのため時間的に平均化すると発電機はコイルに対して仕事をしない。コイルに注入された仕事は磁場のエネルギーUとしてコイル中に蓄えられるが、その値は下記グラフの様に周期的に変動する。このとき、振動する磁場は電磁波となってコイルから周囲に漏れ出てしまうので実際にはすこしづつエネルギーは消費される。
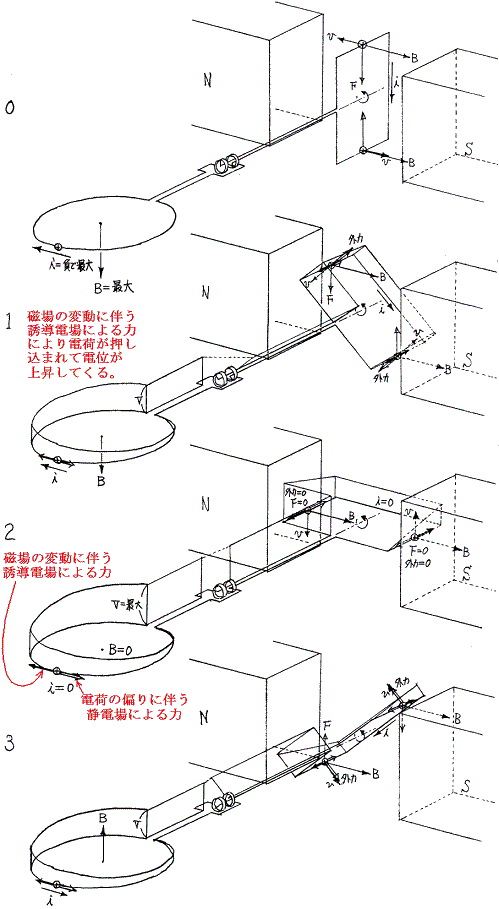
以上の変化を図示すると次のようになる。上記グラフ横軸の番号が下図の番号に対応する。3、7図では外力が回転方向を向き、1、5図ではその逆になっていることに注意。つまり3、7図の状態では外力は発電機に対して仕事をし、その仕事がコイルの中に蓄えられる。そして1、5図の状態では発電機は外力を及ぼすものに仕事を返しており、その仕事のもとはコイルが発電機に返した仕事である。
それは、0〜7図に於いて回転子中の電圧の分布は負荷が抵抗の場合(項目3.)とまったく同じなのに、電流が流れる方向が異なっている事による。そうなったのは根本の式がオームの法則から自己誘導の式に変わったからである。
図0→図1→図2にかけて負荷コイルに流れる電流が減少していくのは、電荷を負荷コイルに押し込もうとする力(発電機コイルの中に発生する)がどんどん増大していくからである。つまりそのとき流れている電流を押しとどめようとする力が増えていく。
そのとき負荷コイル中の電流が減少すると負荷コイル内の磁場が減少する。そのため自己誘導により、電荷を流し続けようとする力が発生する。これが発電機コイル中に発生する力と釣り合う。
電流の方向から解るように、この間はコイル内の磁場のエネルギーが減少して、発電機にエネルギーが返されている。つまり発電機は負の仕事をしている。仕事が負になったのは発電機にかかっている電圧(これは負荷コイルに発生する電圧と同じ)を生み出しているのが負荷コイル内に発生する自己誘導に伴う誘導起電力だからである。この力が電流を発電機の方へ押し流し続けようとしているのである。(自己誘導現象そのものについては別稿「自己誘導とRL回路」参照)
図2→図3→図4にかけて負荷コイル内の磁場が増大していくのは、負荷コイルに電荷を押し込もうとする力(発電機コイルの中に発生する)が減少するため、負荷コイル内に働く電流の流れを押しとどめようとする力が減少して、電荷の偏りに伴う静電場による力により負荷コイル内に図で示した方向の電流が増大するからである。負荷コイル内に発生する磁場はエネルギーとして蓄えられ、この間は発電機が負荷コイルに対して正の仕事を行う。仕事が正になったのは電荷の偏りに伴う静電場による力(これが電流を負荷コイルの方へ押し流している)を生み出しているのが、発電機に加えられている外力だからである。
この様な事が起こっても良いのは、再三強調するが、交流を担う電荷に働く力はいつもつり合っており常に合力が零であると考えて良いところにある。つまりローレンツ力による力と電圧分布に伴う静電気力(これもローレンツ力の一種)が瞬時につり合うように電圧分布が決まり、その動きに比較したら電荷の動く速さは止まっていると考えても良いくらいにゆっくりした動きなのだ。だから電流の方向など外部負荷の事情に合わせていかようにでも調節できる。そのとき電圧の分布は極微量の電荷の極微量の移動でいかようにでも調節できる。
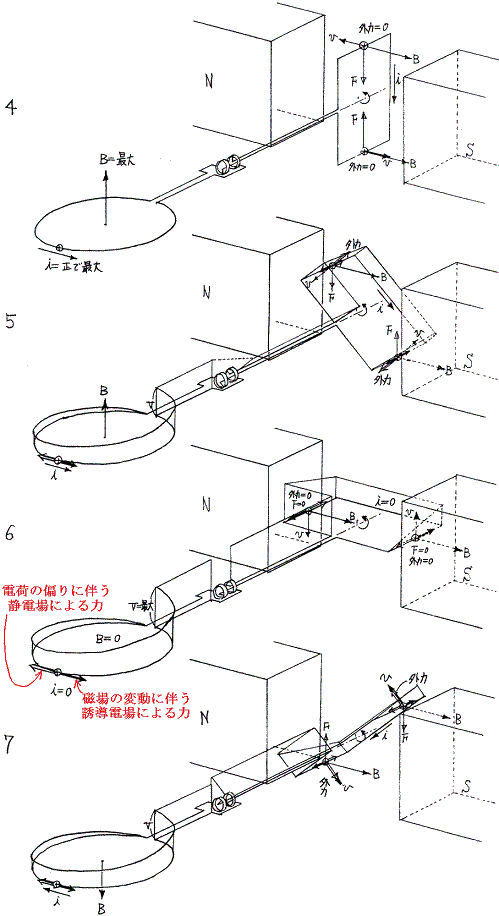
エネルギーはコイル内に磁場のエネルギーとして蓄えられる。
抵抗の場合は[回路素子を特徴づける法則]と[インピーダンス定義のもとになった法則]がたまたま共通だが、コンデンサーとコイルの場合に異なるから、言葉の意味に混乱が起こり、人を惑わせる。
幾つかの回路素子が直列に結合されているときには合成インピーダンスは各インピーダンスの和になり、並列結合のときには合成アドミタンスが各アドミタンスの和になる。
そのため場合により両者を使い分けると計算が簡単になる。このあたりの事情は「直列と並列」4.補足を参照。
交流は波として送電線を伝播していく。そのあたりを説明するために電圧の書き方を下記A図からB図へ変換する。つまり回転子コイルの中点を電圧の零点とする。
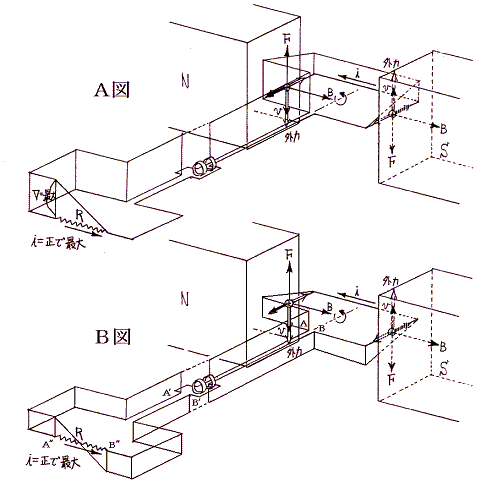
このように描いても状況はまったく同じであるが、伝播する交流を表すには適している。3.、4.、5.項目の図をこの様に書き直して見れば、AからA→A’→A”の方向へ、BからB→B’→B”の方向へ、それぞれ交流が波として送り出されているのが理解できる。
60Hzの交流では、、交流波の波長は波の公式v=λfを用いてλ=約5000kmになる。ゆえに送電線A’A”の長さは少なくとも数千km以上なければならない。送電線がその程度以上になれば1.(3)で述べた電圧の発生する理由は負荷抵抗により電流がせき止められて滞ることによるのではなくて、電気の情報が光速よりも早く伝わることができないために電子の動きが滞り送電線の中に密度の高い部分ができてしまうことによる。つまり遙か彼方の負荷(抵抗やコンデンサーやコイル)によって電圧が生じるのではなくて、送電線中を信号が光速以上で伝わることができないために生じる。
その結果生じる電荷の偏りによって電圧上昇が起こる。その電圧上昇には当然電流が付随する。その電圧上昇値を電流値で割ったものが、まさに送電線のインピーダンスである。単に抵抗(レジスタンス)と言わず、インピーダンスと言ったのは平行に走る送電線にはコンデンサーとしての働きやコイルとしての働きもあり、リアクタンス成分もあるからである。実際、抵抗R=0の理想的な送電線は下図の様な等価回路で近似できる。
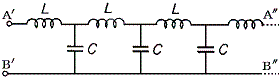
L、Cを単位長さあたりの値とすると、面白いことに、この様な回路のインピーダンスはZ=(L/C)1/2の実数値になり純粋の抵抗と同じになる。そしてその値は送電線の長さに関係しない。(「波動方程式と一般解」3.(4)電線を伝わる波の補足で証明)そため、電圧と電流の位相は一致する。いずれにしても発電機につながる送電線の性質により、発電機の回転子コイル内に発生する電圧と電流の関係は決まってくる。
上記の様に発電機のA端子、B端子で発生した電圧の波は二本の送電線内をどちらも遙か彼方の末端に向かって、ほぼ光速度で伝播していく。その様子を下図は表している。そのとき注意すべき点を以下に記す。
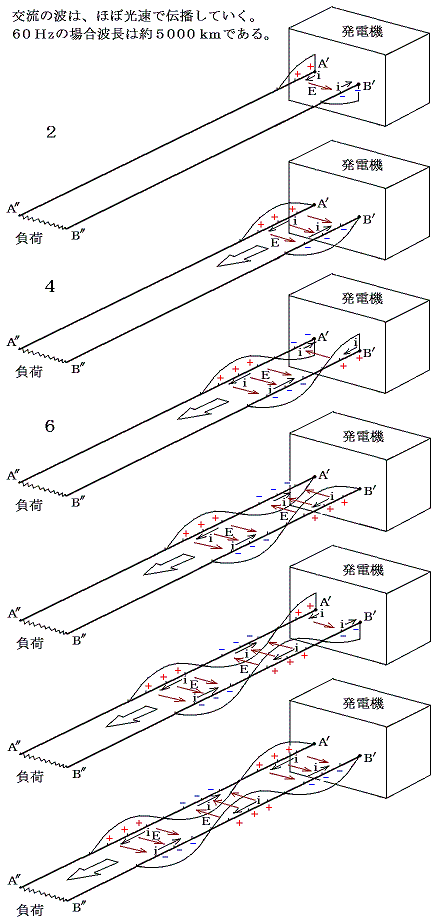
上記の図で注意しなければいけないのは、発電機から負荷に向かって送り出される電圧波形の波長についてです。図中の波の進行する速度は別稿「オームの法則」1.で注意した3種類の速度の3番目に相当します。
つまり、ほぼ光速度に近い速度です。その上図中に例示したように60Hzの交流の場合の波長は
30万km/s÷60/s≒約5000km程度
となります。
所で、発電所からの伸びる送電線の長さは、精々数百km程度以内の場合が大半ですから、送電線中の波の位相はほとんど同じと見なせて、本稿で図示してきた様な状況が実現されます。
波としてA→A’→A”、B→B’→B”の方向に伝播してきた交流波がその末端の負荷(抵抗、コンデンサー、コイル、モーター)の所にやってきたらどの様な事が起こるであろうか。当然一般の波と同じ事が起こる。入射波の一部は末端部を透過して負荷の中に侵入し、エネルギーが消費される。一部は末端部で反射され、元来た道を反射波として帰っていく。その様子は別稿「波の反射」で述べた通りである。そのとき反射波と透過波の割合は送電線と負荷のインピーダンス値による。そこではインピーダンスマッチングが重要な意味を持つ。
負荷との接合部で反射した波は再び発電機の所に舞い戻るが、そこでも送電線と発電機のインピーダンスの関係によりエネルギーが発電機内に返されたり、また接続部で再度反射されたりする。そして反射が繰り返され、次々と送り出される新たな交流波とともに送電線内部に一種の定常状態が実現される。
(注意)
電線のインピーダンスは ( L0/C0)1/2 だから、2本の導線の端をR=( L0/C0)1/2 のオーム抵抗で結合すれば(電流−電圧関係に不連続が表れず)反射が起こらない。完全なインピーダンスマッチングが取れて、波はすべて抵抗に吸収され熱エネルギーとなって消費される。