線形振動子と電磁波の平衡(「プランクの熱輻射法則」の付録1)
ここの説明は別稿「プランクの熱輻射法則」1章~3章(1)の内容をより解りやすくしたものです。
プランク自身も上記別稿の説明はかなり込み入っていて解りにくいと感じていたようです。そのため後の論文
「正常輻射場における線形共鳴子の振動法則の簡単化された導出」, Physikalische Zeitschrift 2, p530~534, 1901年
でもっと簡単な導出法を報告しています。それが彼の著書「熱輻射論」の§116~123で説明されているものです。
また、この内容が ゾンマーフェルト「熱力学及び統計力学」の§20.D.、 ファインマン「ファインマン物理学Ⅱ」の§16-2、16-3、 太田浩一「電磁気学の基礎Ⅱ」の§14.7、等々・・・ で説明されているものです。これらはすべてPlanckの上記論文からの引用だと思います。
ここではゾンマーフェルトの文献の§20.D.[MKSA有理化単位系]に記載されているものをさらに解りやすくして説明します。
ここでのρが別稿のσ・νに相当することに注意されて別稿の説明と比較してみて下さい。“黒い輻射”に関して思い切った仮定をすることで論理展開は見通しが良くなって理解しやすくなっています。ただし、その中で設定されている等方性と独立性の仮定自体が解りやすくなっているわけではありません。別稿「プランクの熱輻射法則」1章~3章(1)を参考にされながらお読み下さい。
(1)線形振動子の運動方程式
熱輻射論の重要な問題は、黒体輻射のエネルギースペクトル分布を導き出すことです。これはウィーンの変位則で未知のままに残されていた関数F(ν/T)を見いだすことです。
そのときの出発点はキルヒホッフの法則です。それによると、「鏡のように反射する壁によって囲まれた真空は、その中に任意の放出吸収物質が任意の配置でおかれているとき、時間を経ると黒体輻射の定常状態になる。それは一つのパラメーター温度によって完全に決められ、物体の配置や性質には依存しない。つまり、黒体輻射の性質を調べるためには、真空中に存在すると仮定される物体がどんな種類かということはどうでもよく、任意に選ばれた特定の放出・吸収系に対して、完全な安定性によって他と区別される輻射状態を示すこに成功しさえすれば、その状態こそ黒体輻射といえる。」
この法則によって保証される無拘束性を利用して、すべての放出・吸収系の中で最も簡単な系、すなわち静止したある一つの振動子を選ぶ。それは反対符号の当量の電気を帯びた二つの極から成り、それらは固定した直線上を互いに振動運動する。
運動は本来三次元的なものであるが、空間的な運動を互いに垂直な直線成分に分解すれば一成分の運動に限って扱うことができるであろう。そのため以下の状況を考察する。
任意の電磁波に満たされた真空中に線形(z軸方向にのみ振動する)の電気的共鳴子が存在しており、その固有振動数は共鳴子の一次元の大きさに比べて十分大きい波長の光の振動数に対応しているとする。また、その振動の振幅は定常電流の抵抗とか、共鳴子内部で作用する摩擦のようなものではなくて、ただ周囲の空間に輻射としてエネルギーを放出することによってのみ減衰するものとする。
つまり、プランクは輻射場の中へ、これといくらか作用し合う一次の振動子を入れた。それは決まった固有角振動数ω0を持つヘルツ双極子で、その大きさは問題とする波長よりも十分小さいものである。
そのとき振動子が満たすべき運動方程式は別稿「調和振動子」5.(1)で説明したように以下の形で表される。そこのxをzで置き換えると

となる。eとmは運動する電子の電荷と質量である。この中でeEzは振動を励起する外力を表し、輻射場の電場Eの運動方向zの成分です。
この式の中で振動を減衰させる“減衰力”は
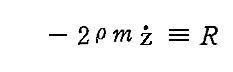
の部分ですが、これこそ別稿「線形振動子(電気双極子)による電磁波の放出」4.(1)で説明した“輻射の反作用力”
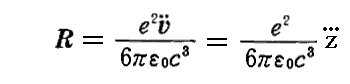
に他ならない。
そのとき別稿「調和振動子」5.(2)で説明したように、減衰力が小さい場合には、振動子は固有角振動数ω0に近い角振動数ωの入射電磁波に対して強く反応し、励起される振動は
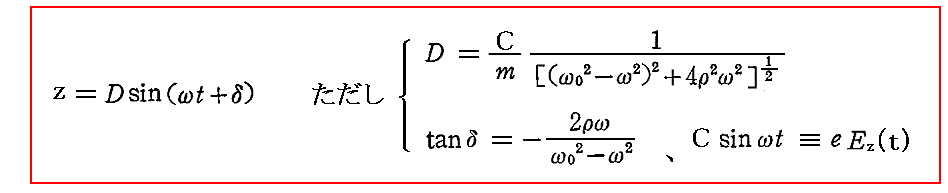
の形で表される。
これを用いると“輻射の反作用力”は
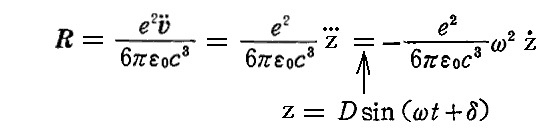
と表されるので、上記の“減衰力”と比較すればρとして
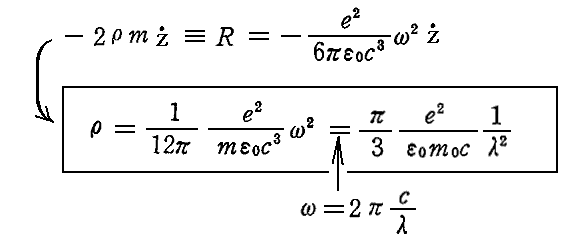
とすればよいことが解る。これは別稿「線形振動子(電気双極子)による電磁波の放出」の3.(2)や4.(3)で何度か説明した関係式です。
(2)振動子の持つエネルギー
振動子のエネルギーUは運動エネルギーと位置エネルギーの和で表される。
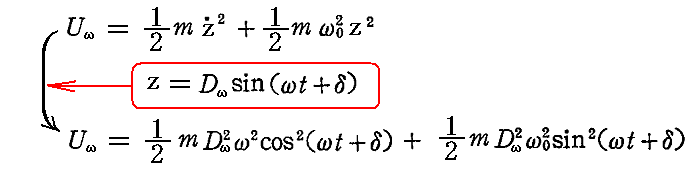
この時間平均を取ると、別稿「調和振動子」5.(2)で求めた解を利用して
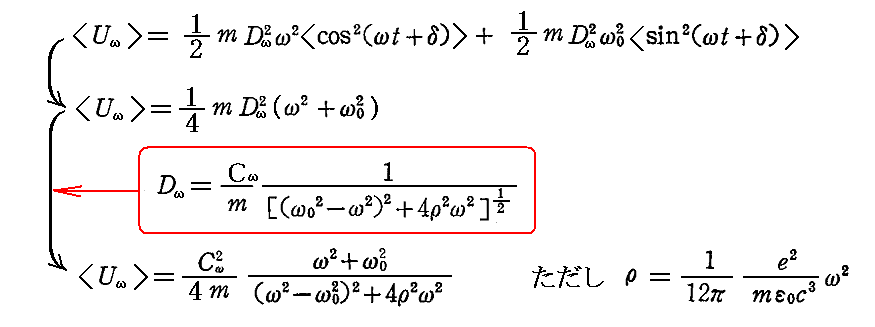
となる。ここでエネルギーUや振幅C、Dに添え字ωをつけたのは、ここまでは単一の単色振動を考えてきたことを示すためです。
ここで、振動子は輻射場の中で全く互いに干渉し合わない振動Cωの連続スペクトルによって励起されると考えて良いであろう。これは全く互いに干渉し合わない振動子の振動を起こすことに対応する。
この干渉し合わないという性質は“白い自然光”について必要なことですが、それと同様に“黒い輻射”にも必要なものです。
ここで考えている様な輻射場が互いに干渉し合わないと考えて良いことの理由はなかなか解りにくいところですが、例えば§「ファインマン物理Ⅱ 光、熱、波動」岩波書店(1968年刊)7-4の記述や別稿「線型振動子(電気双極子)による電磁波の放出」4.(2)(3)などを参照されて下さい。
このことから、干渉性の光のように振幅が加えられるのではなくて、その自乗(強度)が加え合わされることになる。従って振動子の持つ平均的エネルギーは輻射場のすべての角振動数の光によって励起された振動エネルギーの和(つまりdωについての積分)となる。すなわち
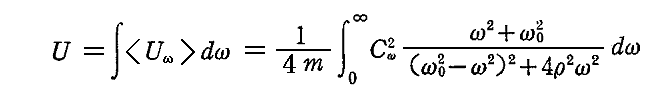
と表される。
右辺の被積分関数の分数関数の部分はωと共に急激に変わる関数で、ω=ω0の近傍で極大を持つ。そのときρが小さいためにその形は極めて鋭く立ち上がったものになる[別稿「調和振動子」5.(3)参照]。それに対して、Cω2はωが変わってもゆっくりと変わるのでCω2をω=ω0での値C02でおきかえても良いであろう。
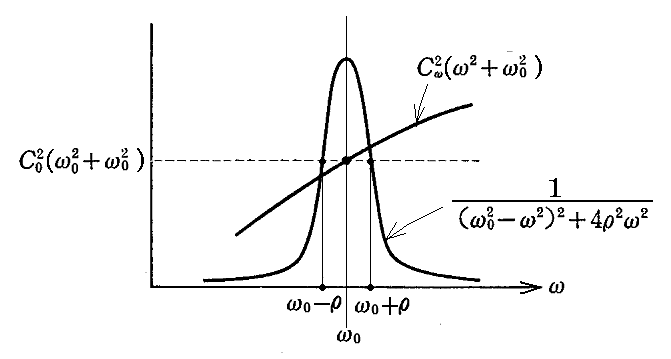
そのため上式は
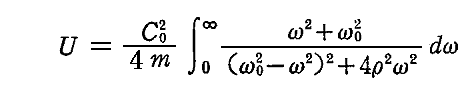
となる。
この積分の被積分関数の分子と4ρ2ω2はゆるやかに変化するので更に簡単になる。すなわち、この二項はそれぞれ
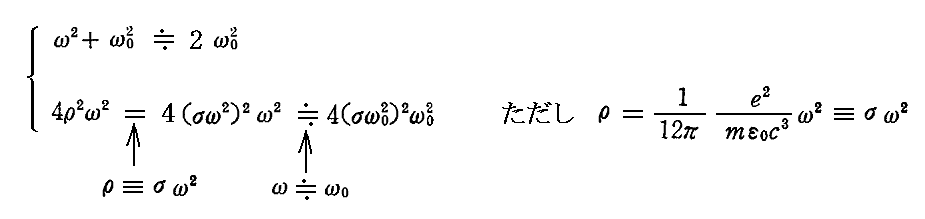
で置き換えられる。さらに
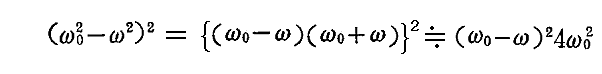
と書けるから、今考えている積分は
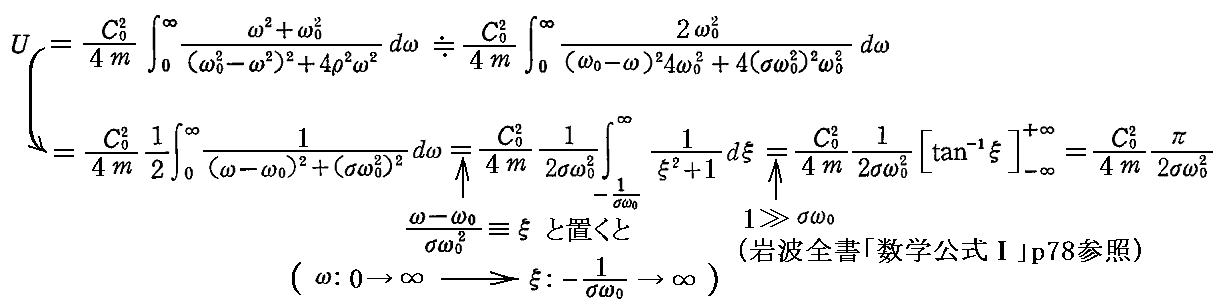
となる。
そのため任意のスペクトル分布をする輻射場の中で、輻射場と平衡状態にある固有角振動数がω0の振動子が持つエネルギーは

と書ける。
(3)振動子のエネルギーと空洞輻射のエネルギー密度の関係
ここでC0は輻射場中の角振動数ω0の電磁波の電場の振幅にeを乗じたものであるが、これは輻射のエネルギー密度uωに関係づけることができる。
輻射のエネルギー密度は、別稿「光の圧力(輻射圧」2.(5)1.で説明した式を別稿「電磁波の伝播」2.(2)や「線型振動子(電気双極子)による電磁波の放出」2.(3)で述べたEとBの関係に注意して変形すると、電場によるエネルギー密度の2倍に等しいことが解る。すなわち
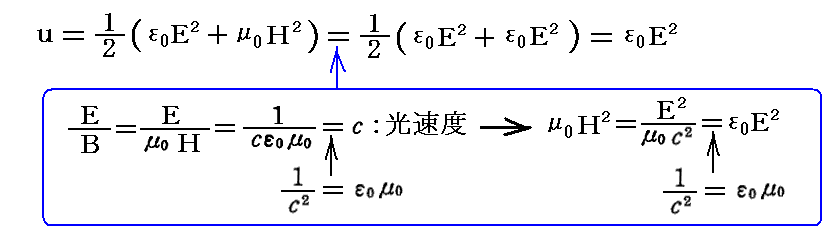
となる。
等方的な輻射について時間平均を取れば
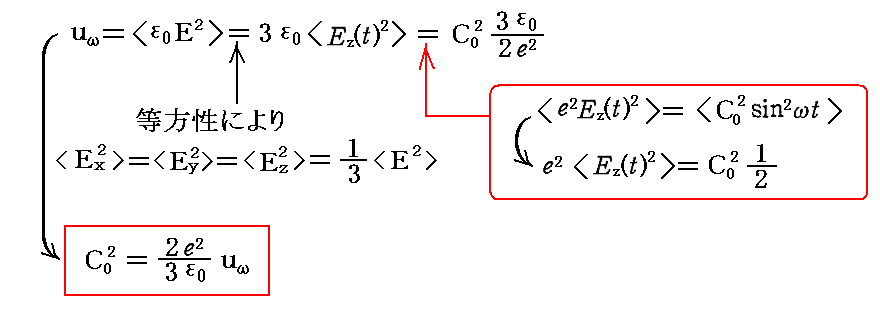
となる。ここではωの尺度を用いてエネルギー密度を考えている。uωはω=ω0のところでのdωの角振動数範囲にあるエネルギー密度である。
ところで
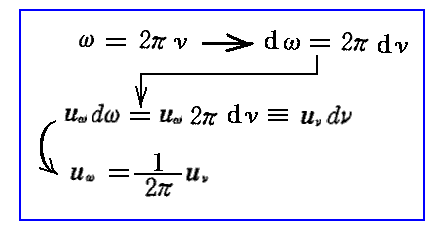
であるからωの代わりにdνの振動数範囲にあるエネルギー密度uνで表すと前記の式は
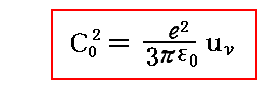
となる。これを前項の最後の式に代入すると
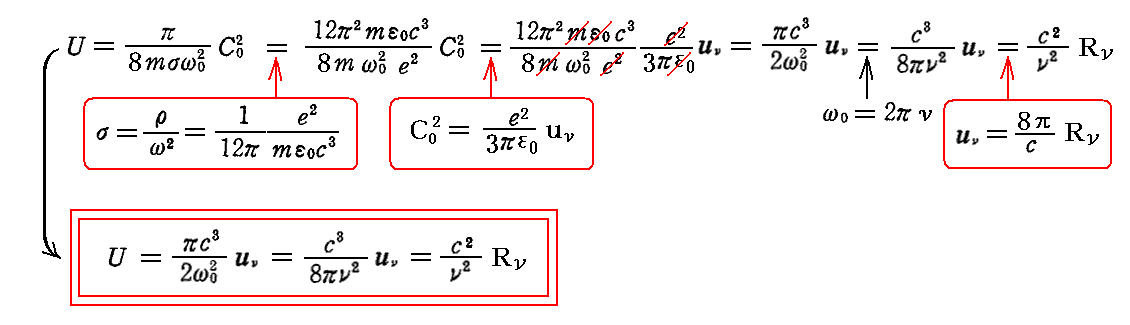
が得られる。
最後の式変形に用いたuνとRνの関係式については別稿「キルヒホッフの法則(熱的放射平衡における 1859~1860年)」3.(2)を参照されたし。Rνはそこで説明したように単色(振動数νを中心とした単位の振動数幅に含まれる)で直線偏光した単位立体角の方向へ進行する輻射強度(輝度)を表す。
最後の式では、振動子に対して用いた特殊なモデルに固有な量eやmは消去されており、また定数ε0も落ちていることに注意されたし。つまり、熱平衡状態にあるときには振動体に固有な性質には関係せずこの関係は一般的に成り立つのである。
これによって等方的な輻射場と平衡にある振動子に対して、[1個の振動子のエネルギーU]と[空洞輻射のエネルギー密度uν(あるいは単色光の偏光した輻射強度[輝度]Rν)]の満たすべき関係式が示された。
これは極めて普遍的な関係で、プランクは熱輻射論の議論を進めるに当たって[前者U]を[後者uν(あるいはRν)]の代わりに用いることができたのです。ここで注意して欲しいことはUはただ一つの振動子(共鳴子)のエネルギーの平均値でありuνは輻射場の中の振動数νの輻射のエネルギー密度であることです。
[補足説明1]
ここで得られた事柄が、プランクが「ノーベル賞講演」に於いて
“・・・その際、明らかになったのば、この関係が共振子の性質にまったく依存せず、とりわけ、その減衰定数にも依存しないという、まことに注目すべき結果であるが、これは私にとって非常に喜ばしい、好都合な事情であった。
なぜなら、そのことによって、輻射のエネルギーの代りに共振子のエネルギーをとることができ、こうしてまた多くの自由度からなる錯綜した系の代りに、唯一の自由度をもつ単純な系を当てうるということで、問題全体が簡単になったからである。・・・”
と言っているものです。プランクは最初もっと一般的な議論で導いたのですが、考え方の本質はここで説明したのと同じです。
[補足説明2]
量子理論が確立した後の立場で見れば、ここで説明した様な共鳴子と電磁波の相互作用が正しいのか心配になるところです。
事実、振動子の平均エネルギーは、測定データとの比較が行われている領域では、hνより小さくなる。そのため振動子のエネルギーも量子化されるべきで、ここでの議論の様に振動子が任意のエネルギーを持ちえると仮定したことに抵触します。実際の所プランクも1906年の著書「熱輻射論」の§154の脚注や§166に記載しているように、そのことは承知していました。その事に関して“hの直接的な電気力学的な意味付けは未解決の問題である”と認めています。
アインシュタインも“振動子の平均エネルギーは、測定データとの比較が行われている領域では、hνより小さくなる”として批判(1906年)していたそうです。しかし「ファインマン物理学Ⅱ 光、熱、波動」の§16-3の末文によると、光と振動子との相互作用についての量子論はここで説明した古典論によるものとまったく同じ結果を与えるそうです。だからアインシュタインの批判は杞憂だったことになる。